Загадочная красота математики – Красота математики — математика, мероприятия
Красота математики — математика, мероприятия
12
Содержание
1. Введение ………………………………………………………………….2
2. Математика и числы ……………………………………………………. 2
3. Поверхности второго порядка. Загадочная красота…………………….4
4. Симметрия в природе …………………………………………………….6
5. Дерево Пифагора…………………………………………………………. 8
6.Математическая музыка……………………………………………………9
7. Золотое сечение……………………………………………………………10
8. Заключение ……………………………………………………………… 11
9. Список литературы …………………………………………………….. 12
«Математика владеет не только
истиной, но и высшей красотой»
Бертран Рассел.
Математика – царица всех наук, символ мудрости. Красота математики среди наук недосягаема, а красота является одним из связующих звеньев науки и искусства.
Математика – это не только стройная система законов, теорем, задач, но и уникальное средство познания красоты. А красота многогранна и многолика. Она выражает высшую целесообразность устройства мира, подтверждает универсальность математических закономерностей, которые действуют одинаково эффективно в кристаллах и в живых организмах, в атомах и во Вселенной, в произведениях искусства и научных открытиях. Целью данной работы
показать применение математики в других науках, в окружающей действительности.
Люди придумали цифры и действия с ними, а потом в них же открыли множество законов, правил и теорем.
В жизни цифр, линий, углов и бесконечно малых величин можно увидеть много красивого – изящные теоремы, тела, поверхности, даже условия задач.
Числа живут своей жизнью, и мы, соприкоснувшись с ней, удивляемся, а иногда и любуемся ею.
Математическая пирамида №1
1 x 8 + 1 = 9
12 x 8 + 2 = 98
123 x 8 + 3 = 987
1234 x 8 + 4 = 9876
12345 x 8 + 5 = 987 65
Какие вычисления будут выполнены в следующей строке и в последующих?

Математическая пирамида №2
1x 9 + 2 = 11
12 x 9 + 3 = 111
123 x 9 + 4 = 1111
1234 x 9 + 5 = 11111
Какие вычисления будут выполнены в следующей строке и в последующих?

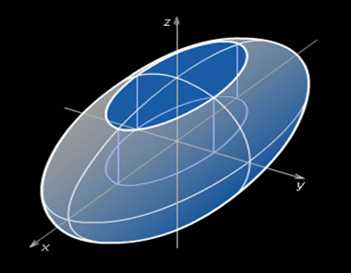
Поверхности второго порядка. Загадочная красота.
Поверхность второго порядка — геометрическое место точек трёхмерного пространства, прямоугольные координаты которых удовлетворяют уравнению вида
Симметрия — закономерное расположение элементов формы относительно плоскости, оси или точки. Человек давно осмыслил симметрию в творениях природы и стал использовать се как средство организации искусственных форм. В Древней Греции слово «симметрия» было синонимом красоты, гармонии формы.
« …быть прекрасным значит быть симметричным и соразмерным» (Платон)
…быть прекрасным значит быть симметричным и соразмерным» (Платон)
Тадж-Махал — мавзолей-мечеть, находящийся в Агре, Индия, на берегу реки Ямуна. Усыпальница имеет центральную симметрию относительно гробницы Мумтаз-Махал. Единственным нарушением этой симметрии является гробница Шах-Джахана, которую там соорудили после его смерти.
О
Если преобразование симметрии относительно плоскости переводит фигуру в себя, то фигура называется симметричной относительно плоскости, а данная плоскость – плоскостью симметрии этой фигуры. В некоторых источниках такую симметрию называют зеркальной. А зеркало не просто копирует объект, но и меняет местами передние и задние по отношению к зеркалу части объекта.
Симметрия широко распространена в природе. Ее можно наблюдать в форме листьев и цветов растений, в расположении различных органов животных. Красота растений привлекла внимание математиков веками. Активнее всего изучались интересные геометрические свойства растений , такие как симметрия листьев относительно центральной оси, радиальная симметрия цветов, и спиральное расположение семечек в шишках. Красота связана с симметрией.
Р ассматривая расположение листьев на ветке дерева, видим, что один лист не только отстоит от другого, но и повёрнут вокруг оси ствола. Листья располагаются на стволе по винтовой линии (принцип винтовой симметрии). Семена подсолнечника располагаются по спиралям, опять же по принципу симметрии.
ассматривая расположение листьев на ветке дерева, видим, что один лист не только отстоит от другого, но и повёрнут вокруг оси ствола. Листья располагаются на стволе по винтовой линии (принцип винтовой симметрии). Семена подсолнечника располагаются по спиралям, опять же по принципу симметрии.
Симметрия в неживой природе
В мир неживой природы очарование симметрии вносят кристаллы. Каждая снежинка- это маленький кристалл замерзшей воды. Форма снежинок может быть очень разнообразной, но все они обладают симметрией — поворотной симметрией 6-го порядка и, кроме того, зеркальной симметрией.
мир неживой природы очарование симметрии вносят кристаллы. Каждая снежинка- это маленький кристалл замерзшей воды. Форма снежинок может быть очень разнообразной, но все они обладают симметрией — поворотной симметрией 6-го порядка и, кроме того, зеркальной симметрией.
О, симметрия! Гимн тебе пою!
Тебя повсюду в мире узнаю.
Ты в Эйфелевой башне, в малой мошке,
Ты в елочке, что у лесной дорожки.
С тобою в дружбе и тюльпан, и роза,
И снежный рой – творение мороза!
Симметрия является фундаментальным свойством природы, представление о котором слагалось в течение десятков, сотен, тысяч поколений.
В 1968г. Венгерский биолог и ботаник Аристид Линденмайер (Aristid Lindenmayer) предложил математическую модель для изучения развития простых многоклеточных организмов, которая позже была расширена и используется для моделирования сложных ветвящихся структур — разнообразных деревьев и цветов.
1968г. Венгерский биолог и ботаник Аристид Линденмайер (Aristid Lindenmayer) предложил математическую модель для изучения развития простых многоклеточных организмов, которая позже была расширена и используется для моделирования сложных ветвящихся структур — разнообразных деревьев и цветов.
Rewriting — это способ получения сложных объектов путем замены частей простого начального объекта по некоторым правилам. Классическим примером является снежинка. На рисунке initiator — это начальный объект, грани которого заменяются на generator. Далее с новым объектом проделывается то же самое.
Дерево Пифагора
Пифагор, доказывая свою знаменитую теорему, построил фигуру, где на сторонах прямоугольного треугольника расположены квадраты. В наш век эта фигура Пифагора выросла в целое дерево. Впервые дерево Пифагора построил А. Е. Босман (1891—1961) во время второй мировой войны, используя обычную чертёжную линейку.
О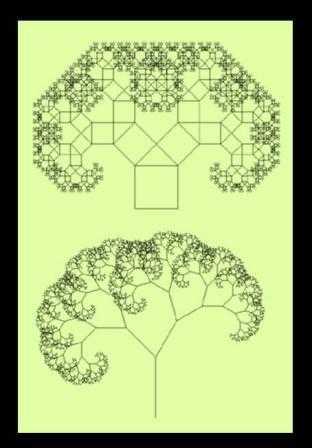 дним из свойств дерева Пифагора является то, что, если площадь первого квадрата равна единице, то на каждом уровне сумма площадей квадратов тоже будет равна единице.
дним из свойств дерева Пифагора является то, что, если площадь первого квадрата равна единице, то на каждом уровне сумма площадей квадратов тоже будет равна единице.
Красота есть истина, а истина — красота.
Джон Китс
Первые примеры самоподобных множеств с необычными свойствами появились в XIX веке (например, множество Кантора). Термин «фрактал» был введён Бенуа Мандельбротом в 1975 году и получил широкую популярность с выходом в 1977 году его книги «Фрактальная геометрия природы». Определение фрактала, данное Мандельбротом, звучит так: «Фракталом называется структура, состоящая из частей, которые в каком-то смысле подобны целому»

Галерея изображений фракталов Они кажутся более живыми и красивыми, чем многие рисунки, несмотря на то, что являются результатом работы программы.
Математическая музыка
Пифагор создал свою школу мудрости, положив в ее основу два искусства — музыку и математику. Он считал, что гармония чисел сродни гармонии звуков и что оба этих занятия упорядочивают хаотичность мышления и дополн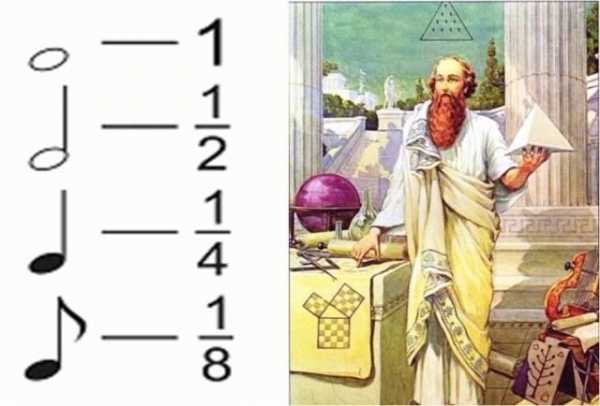
Математика и музыка — два полюса человеческой культуры. Слушая музыку, мы попадаем в волшебный мир звуков. Решая задачи, погружаемся в строгое пространство чисел. И не задумываемся о том, что мир звуков и пространство чисел издавна соседствуют друг с другом.
Золотое сечение
З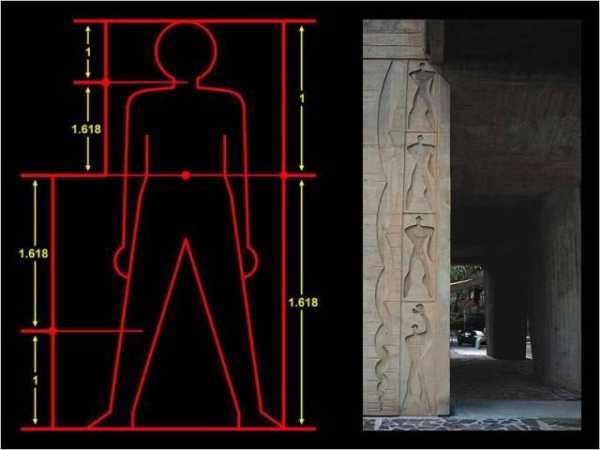 олотое сечение (золотая пропорция, деление в крайнем и среднем отношении) — деление непрерывной величины на две части в таком отношении, при котором меньшая часть так относится к большей, как большая ко всей величине. В биологических исследованиях 70-90 гг. показано, что, начиная с вирусов и растений и кончая организмом человека, всюду выявляется золотая пропорция, характеризующая соразмерность и гармоничность их строения. Золотое сечение признано универсальным законом живых систем. Закономерности золотой симметрии проявляются в энергетических переходах элементарных частиц, в строении некоторых химических соединений, в планетарных и космических системах, в генных структурах живых организмов. Эти закономерности есть в строении отдельных органов человека и тела в целом.
олотое сечение (золотая пропорция, деление в крайнем и среднем отношении) — деление непрерывной величины на две части в таком отношении, при котором меньшая часть так относится к большей, как большая ко всей величине. В биологических исследованиях 70-90 гг. показано, что, начиная с вирусов и растений и кончая организмом человека, всюду выявляется золотая пропорция, характеризующая соразмерность и гармоничность их строения. Золотое сечение признано универсальным законом живых систем. Закономерности золотой симметрии проявляются в энергетических переходах элементарных частиц, в строении некоторых химических соединений, в планетарных и космических системах, в генных структурах живых организмов. Эти закономерности есть в строении отдельных органов человека и тела в целом.
Математик так же, как художник или поэт, создаёт узоры…
В математике есть тоже своя красота, как в живописи и поэзии. Эта красота проявляется иногда в отчетливых, ярко очертанных идеях, где на виду всякая деталь умозаключения, а иногда поражает она нас в широких замыслах, скрывающих в себе кое-что недосказанное, но многообещающее. (Н.Е. Жуковский )
Мы поняли, что без математики невозможна красота и гармония в нашем мире. Что бы видеть и чувствовать красоту нам достаточно знать математические законы и факты. В ходе нашей исследовательской работы мы проследили связь математики с наукой, архитектурой, литературой, музыкой и искусством.
«Математика есть прообраз красоты мира»
(В.Гейзенберг)
Использованная литература
1. А. В. Волошинов, «Математика и искусство», “Просвещение”, 2000г.
2. Е.С.Смирнова, Н.А. Леонидова; «Математическое путешествие в мир гармонии»,издательство — Мир, 1972.
3.Мартин Гарднер, Математические чудеса и тайны, 1982.
4. Мартин Гарднер, Математические досуги, издательство ―Мир, 1972.
5.Журнал «Математика в школе» № 3, 1993г.
kopilkaurokov.ru
Фракталы — потрясающая красота математики в природе — МЕСТО СИЛЫ
Фракталы — потрясающая красота математики в природе
Природа так загадочна, что чем больше изучаешь ее, тем больше вопросов появляется… Ночные молнии – синие «струи» ветвящихся разрядов, морозные узоры на окне, снежинки, горы, облака, кора дерева – все это выходит за рамки привычной евклидовой геометрии. Мы не можем описать камень или границы острова с помощью прямых, кружков и треугольников. И здесь нам приходят на помощь фракталы.
Фрактал – это сложная геометрическая фигура, обладающая свойством самоподобия. То есть она составлена из нескольких частей, каждая из которых повторяет всю фигуру целиком. По определению Википедии фрактал — это бесконечно самоподобная геометрическая фигура, каждый фрагмент которой повторяется при уменьшении масштаба.
Это свойство объектов американский (правда, выросший во Франции) математик Бенуа Мандельброт назвал фрактальностью, а сами такие объекты — фракталами (от латинского fractus — изломанный).
Фракталы находят все большее и большее применение в науке и технике. Основная причина этого заключается в том, что они описывают реальный мир иногда даже лучше, чем традиционная физика или математика. Можно до бесконечности приводить примеры фрактальных объектов в природе, – это и облака, и хлопья снега, и горы, и вспышка молнии, и наконец, цветная капуста.
Фрактал как природный объект – это вечное непрерывное движение, новое становление и развитие.
Фракталы встречаются всюду: в продуктах питания, в бактериях,в растениях, в животных, в горах, в небе и в воде.






















Фракталы — потрясающая красота математики в природе
4.8 (95%) 4 vote[s]mesto-sily.club
Творческая работа по математике » Красота и математика»(8 класс)
Содержание
1. Введение ………………………………………………………………….2
2. Математика и числы ……………………………………………………. 2
3. Поверхности второго порядка. Загадочная красота…………………….4
4. Симметрия в природе …………………………………………………….6
5. Дерево Пифагора…………………………………………………………. 8
6.Математическая музыка……………………………………………………9
7. Золотое сечение……………………………………………………………10
8. Заключение ……………………………………………………………… 11
9. Список литературы …………………………………………………….. 12
«Математика владеет не только
истиной, но и высшей красотой»
Бертран Рассел.
Математика – царица всех наук, символ мудрости. Красота математики среди наук недосягаема, а красота является одним из связующих звеньев науки и искусства.
Математика – это не только стройная система законов, теорем, задач, но и уникальное средство познания красоты. А красота многогранна и многолика. Она выражает высшую целесообразность устройства мира, подтверждает универсальность математических закономерностей, которые действуют одинаково эффективно в кристаллах и в живых организмах, в атомах и во Вселенной, в произведениях искусства и научных открытиях. Целью данной работы
показать применение математики в других науках, в окружающей действительности.
Люди придумали цифры и действия с ними, а потом в них же открыли множество законов, правил и теорем.
В жизни цифр, линий, углов и бесконечно малых величин можно увидеть много красивого – изящные теоремы, тела, поверхности, даже условия задач.
Числа живут своей жизнью, и мы, соприкоснувшись с ней, удивляемся, а иногда и любуемся ею.
Математическая пирамида №1
1 x 8 + 1 = 9
12 x 8 + 2 = 98
123 x 8 + 3 = 987
1234 x 8 + 4 = 9876
12345 x 8 + 5 = 987 65
Какие вычисления будут выполнены в следующей строке и в последующих?

Математическая пирамида №2
1x 9 + 2 = 11
12 x 9 + 3 = 111
123 x 9 + 4 = 1111
1234 x 9 + 5 = 11111
Какие вычисления будут выполнены в следующей строке и в последующих?

Поверхности второго порядка. Загадочная красота.
Поверхность второго порядка — геометрическое место точек трёхмерного пространства, прямоугольные координаты которых удовлетворяют уравнению вида
Симметрия — закономерное расположение элементов формы относительно плоскости, оси или точки. Человек давно осмыслил симметрию в творениях природы и стал использовать се как средство организации искусственных форм. В Древней Греции слово «симметрия» было синонимом красоты, гармонии формы.
« …быть прекрасным значит быть симметричным и соразмерным» (Платон)
…быть прекрасным значит быть симметричным и соразмерным» (Платон)
Тадж-Махал — мавзолей-мечеть, находящийся в Агре, Индия, на берегу реки Ямуна. Усыпальница имеет центральную симметрию относительно гробницы Мумтаз-Махал. Единственным нарушением этой симметрии является гробница Шах-Джахана, которую там соорудили после его смерти.
О собенно блистательно использовали симметрию в архитектурных сооружениях древние зодчие. Древнегреческие архитекторы были убеждены, что в своих произведениях они руководствуются законами, которые управляют природой. Выбирая симметричные формы, художник тем самым выражал свое понимание природной гармонии как устойчивости, спокойствия и равновесия.
собенно блистательно использовали симметрию в архитектурных сооружениях древние зодчие. Древнегреческие архитекторы были убеждены, что в своих произведениях они руководствуются законами, которые управляют природой. Выбирая симметричные формы, художник тем самым выражал свое понимание природной гармонии как устойчивости, спокойствия и равновесия.
Если преобразование симметрии относительно плоскости переводит фигуру в себя, то фигура называется симметричной относительно плоскости, а данная плоскость – плоскостью симметрии этой фигуры. В некоторых источниках такую симметрию называют зеркальной. А зеркало не просто копирует объект, но и меняет местами передние и задние по отношению к зеркалу части объекта.
Симметрия широко распространена в природе. Ее можно наблюдать в форме листьев и цветов растений, в расположении различных органов животных. Красота растений привлекла внимание математиков веками. Активнее всего изучались интересные геометрические свойства растений , такие как симметрия листьев относительно центральной оси, радиальная симметрия цветов, и спиральное расположение семечек в шишках. Красота связана с симметрией.
Р ассматривая расположение листьев на ветке дерева, видим, что один лист не только отстоит от другого, но и повёрнут вокруг оси ствола. Листья располагаются на стволе по винтовой линии (принцип винтовой симметрии). Семена подсолнечника располагаются по спиралям, опять же по принципу симметрии.
ассматривая расположение листьев на ветке дерева, видим, что один лист не только отстоит от другого, но и повёрнут вокруг оси ствола. Листья располагаются на стволе по винтовой линии (принцип винтовой симметрии). Семена подсолнечника располагаются по спиралям, опять же по принципу симметрии.
Симметрия в неживой природе
В мир неживой природы очарование симметрии вносят кристаллы. Каждая снежинка- это маленький кристалл замерзшей воды. Форма снежинок может быть очень разнообразной, но все они обладают симметрией — поворотной симметрией 6-го порядка и, кроме того, зеркальной симметрией.
мир неживой природы очарование симметрии вносят кристаллы. Каждая снежинка- это маленький кристалл замерзшей воды. Форма снежинок может быть очень разнообразной, но все они обладают симметрией — поворотной симметрией 6-го порядка и, кроме того, зеркальной симметрией.
О, симметрия! Гимн тебе пою!
Тебя повсюду в мире узнаю.
Ты в Эйфелевой башне, в малой мошке,
Ты в елочке, что у лесной дорожки.
С тобою в дружбе и тюльпан, и роза,
И снежный рой – творение мороза!
Симметрия является фундаментальным свойством природы, представление о котором слагалось в течение десятков, сотен, тысяч поколений.
В 1968г. Венгерский биолог и ботаник Аристид Линденмайер (Aristid Lindenmayer) предложил математическую модель для изучения развития простых многоклеточных организмов, которая позже была расширена и используется для моделирования сложных ветвящихся структур — разнообразных деревьев и цветов.
1968г. Венгерский биолог и ботаник Аристид Линденмайер (Aristid Lindenmayer) предложил математическую модель для изучения развития простых многоклеточных организмов, которая позже была расширена и используется для моделирования сложных ветвящихся структур — разнообразных деревьев и цветов.
Rewriting — это способ получения сложных объектов путем замены частей простого начального объекта по некоторым правилам. Классическим примером является снежинка. На рисунке initiator — это начальный объект, грани которого заменяются на generator. Далее с новым объектом проделывается то же самое.
Дерево Пифагора
Пифагор, доказывая свою знаменитую теорему, построил фигуру, где на сторонах прямоугольного треугольника расположены квадраты. В наш век эта фигура Пифагора выросла в целое дерево. Впервые дерево Пифагора построил А. Е. Босман (1891—1961) во время второй мировой войны, используя обычную чертёжную линейку.
О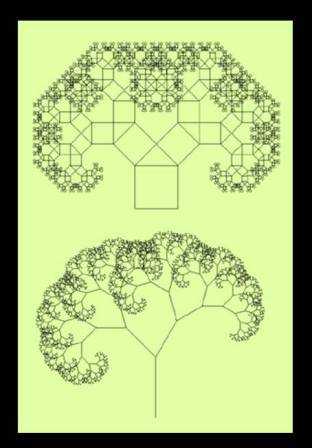 дним из свойств дерева Пифагора является то, что, если площадь первого квадрата равна единице, то на каждом уровне сумма площадей квадратов тоже будет равна единице.
дним из свойств дерева Пифагора является то, что, если площадь первого квадрата равна единице, то на каждом уровне сумма площадей квадратов тоже будет равна единице.
Красота есть истина, а истина — красота.
Джон Китс
Первые примеры самоподобных множеств с необычными свойствами появились в XIX веке (например, множество Кантора). Термин «фрактал» был введён Бенуа Мандельбротом в 1975 году и получил широкую популярность с выходом в 1977 году его книги «Фрактальная геометрия природы». Определение фрактала, данное Мандельбротом, звучит так: «Фракталом называется структура, состоящая из частей, которые в каком-то смысле подобны целому»

Галерея изображений фракталов Они кажутся более живыми и красивыми, чем многие рисунки, несмотря на то, что являются результатом работы программы.
Математическая музыка
Пифагор создал свою школу мудрости, положив в ее основу два искусства — музыку и математику. Он считал, что гармония чисел сродни гармонии звуков и что оба этих занятия упорядочивают хаотичность мышления и дополн яют друг друга. Пифагор говорил своим ученикам, что числа правят миром. Дроби широко используются в музыке для обозначения длительностей нот.
яют друг друга. Пифагор говорил своим ученикам, что числа правят миром. Дроби широко используются в музыке для обозначения длительностей нот.
Математика и музыка — два полюса человеческой культуры. Слушая музыку, мы попадаем в волшебный мир звуков. Решая задачи, погружаемся в строгое пространство чисел. И не задумываемся о том, что мир звуков и пространство чисел издавна соседствуют друг с другом.
Золотое сечение
З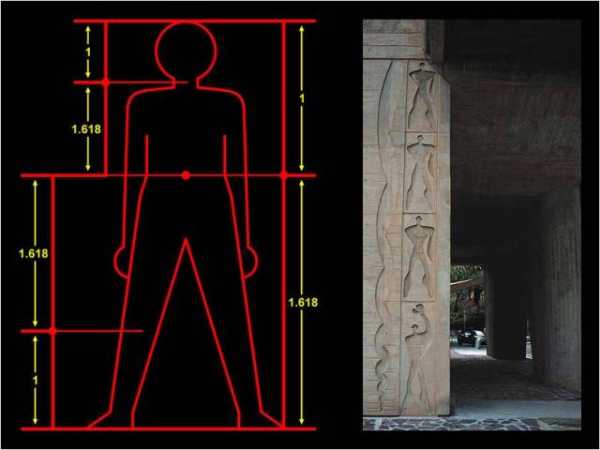 олотое сечение (золотая пропорция, деление в крайнем и среднем отношении) — деление непрерывной величины на две части в таком отношении, при котором меньшая часть так относится к большей, как большая ко всей величине. В биологических исследованиях 70-90 гг. показано, что, начиная с вирусов и растений и кончая организмом человека, всюду выявляется золотая пропорция, характеризующая соразмерность и гармоничность их строения. Золотое сечение признано универсальным законом живых систем. Закономерности золотой симметрии проявляются в энергетических переходах элементарных частиц, в строении некоторых химических соединений, в планетарных и космических системах, в генных структурах живых организмов. Эти закономерности есть в строении отдельных органов человека и тела в целом.
олотое сечение (золотая пропорция, деление в крайнем и среднем отношении) — деление непрерывной величины на две части в таком отношении, при котором меньшая часть так относится к большей, как большая ко всей величине. В биологических исследованиях 70-90 гг. показано, что, начиная с вирусов и растений и кончая организмом человека, всюду выявляется золотая пропорция, характеризующая соразмерность и гармоничность их строения. Золотое сечение признано универсальным законом живых систем. Закономерности золотой симметрии проявляются в энергетических переходах элементарных частиц, в строении некоторых химических соединений, в планетарных и космических системах, в генных структурах живых организмов. Эти закономерности есть в строении отдельных органов человека и тела в целом.
Математик так же, как художник или поэт, создаёт узоры…
В математике есть тоже своя красота, как в живописи и поэзии. Эта красота проявляется иногда в отчетливых, ярко очертанных идеях, где на виду всякая деталь умозаключения, а иногда поражает она нас в широких замыслах, скрывающих в себе кое-что недосказанное, но многообещающее. (Н.Е. Жуковский )
Мы поняли, что без математики невозможна красота и гармония в нашем мире. Что бы видеть и чувствовать красоту нам достаточно знать математические законы и факты. В ходе нашей исследовательской работы мы проследили связь математики с наукой, архитектурой, литературой, музыкой и искусством.
«Математика есть прообраз красоты мира»
(В.Гейзенберг)
Использованная литература
1. А. В. Волошинов, «Математика и искусство», “Просвещение”, 2000г.
2. Е.С.Смирнова, Н.А. Леонидова; «Математическое путешествие в мир гармонии»,издательство — Мир, 1972.
3.Мартин Гарднер, Математические чудеса и тайны, 1982.
4. Мартин Гарднер, Математические досуги, издательство ―Мир, 1972.
5.Журнал «Математика в школе» № 3, 1993г.
infourok.ru
Проектная работа «Математика — это красота»
Муниципальное бюджетное общеобразовательное учреждение
Шиковская средняя школа Павловского района Ульяновской области
Научный проект
Тема: «Математика — это красота»

Авторы:
Палей Анастасия,
Мальцев Кирилл,
ученики 6 класса
Секция: математика
Руководитель:
КрестининаВ.П.
2017-2018 учебный год
Оглавление
1. Введение (цель, задачи, гипотеза, методы исследования)
2. Теоретическая часть:
Вступление.
Глава I. Из истории возникновения математики и её взаимосвязи с категорией «красота».
§ 1. Красота в древней арифметике и теории чисел.
§ 2. Античная математика и красота.
§ 3. Страны ислама.
§ 4. Математика средневековья: IV-XV века.
§ 5. Математика на Руси.
§ 6. Искусство счета.
Глава II. Применение законов математики как законов красоты в окружающей нас жизни.
§ 1. Математика в мире растений.
§ 2. Математика в жизни животных.
§ 3. Математика геометрических тел и фигур.
§ 4. Математика и культура.
§ 5. Математика в живой и неживой природе.
3. Практическая часть
4. Заключение
5. Список использованных источников информации
Введение
Данная работа относится к разделу проблемно – исследовательских работ.
Цель работы: выяснить, как соотносятся два понятия: «математика» и «красота». Применима ли математика в жизни людей как наука о красоте или математика и красота это абсолютно различные категории.
Задачи работы:
1) рассмотреть взаимосвязь между математикой, жизнью и категорией «красота».
2) проанализировать, как жизнь зависит от математической основы понятия «красота».
Гипотеза: если понятия «математика» и «красота» абсолютно не взаимосвязаны, то математические законы не влияют на каноны красоты и не востребованы в жизни: в искусстве, в строительстве, дизайне, архитектуре и многих других областях жизнедеятельности человека.
Практическая значимость: если гипотеза подтверждается, то можно утверждать, что без математических законов красоты можно обойтись; если же нет, то без знания математики вся современная жизнь невозможна.
Методы исследования:
изучение и анализ литературы по данной теме;
подбор примеров, подтверждающих связь математики с жизнью и категорией «красота»;
сбор и анализ общественного мнения.
Теоретическая часть
Вступление.
На факультативах, готовясь к олимпиаде по математике, мы встретили задачи на золотое сечение. И нам стало интересно узнать про взаимосвязь математики и красоты; есть ли другие примеры зависимости категории «красота» от математических законов; узнать историю применения математики в искусстве и архитектуре и других областях жизни человека.
Чтобы ответить на эти вопросы, мы обратились к книгам и к более современному помощнику по имени «Интернет». В них мы нашли много интересного материала и поняли, что человека окружает громадное количество фактов и явлений, которые в силу своей огромности кажутся хаотичными, далекими и недоступными пониманию, но при глубоком изучении становятся близкими, интересными, загадочными.
Все в мире и в жизни тесно связано с математикой и всё стремится соответствовать понятию «красота»! Вот и нашлась интересная тема для проекта: «Математика – это красота».
В своей работе мы попытаемся выяснить, как же математика связана с красотой? Может быть, математические законы красоты это законы жизни, а может быть, это просто наука, которая является для нас второстепенной и заниматься ею нужно только ученым?
Своё исследование мы решили начать с изучения истории математики.
Глава I. Из истории возникновения математики и её взаимосвязи с категорией «красота».
§ 1. Возникновение арифметики и теории чисел.
Учёные — археологи при раскопках в Египте обнаружили математические записи на папирусах. Много тысячелетий прошло с тех пор.
Одна из древнейших нумераций, дошедших до нас в древних папирусах и рисунках, была – египетская.

Для записи чисел египтяне использовали картинки-иероглифы, означавшие буквально следующее:
— собственно 1.
— 10.
— 100.
— 1 000.
— 10 000.
— 100 000.
— 1 000 000.
— 10 000 000.
К примеру, число 2253 на этой картинке было изображено так:
— две тысячи, две сотни, пять десятков и три единицы.
Можно отметить, что знаки, обозначающие числа, расположены не хаотично, а упорядоченно, в стройной системе, подчиняясь законам симметрии, стройности, а значит, и красоты.
Как писать, так и считать тогда умели только специально обученные люди, для простых людей счет был так же недоступен, как и письменность. Эта система применялась в Древнем Египте при торговле и сборе податей, особенно распространившись при постройке Великих Пирамид, и постепенно угасла вместе с кастой строителей и счетоводов, при упадке Египта и подчинении его власти Александра Македонского.
Но прошло много тысячелетий, прежде чем люди научились пересчитывать предметы. Для этого им пришлось придумать названия для чисел. Недаром ведь говорят: «Без названия нет знания».
О том, как появились имена у чисел, учёные узнают, изучая языки разных народов и племён. Ведь, как известно, учёные считают, что сначала названия получили числа 1 и 2.
Когда римляне (в древности они говорили на латыни) придумывали имя числу 1(солюс), они исходили из того, что Солнце на небе одно. А название для числа 2 во многих языках связано с предметами, встречающимися попарно, — крыльями, ушами, руками и т.д.То есть, римляне исходили из соображений целесообразности, опираясь на природные явления и объекты. Вольно или невольно, но получалось точно и красиво.
§ 2. Античная математика.
Третий век до нашей эры был золотым веком античной математики.
В 389 году до н. э. Платон основывает в Афинах свою школу — знаменитую Академию.
В III веке до н. э. в городе Александрия Птолемей I основал Дом Муз и пригласил туда виднейших учёных. Это была первая академии, с богатейшей библиотекой, которая к I веку до н. э. насчитывала 70000 книг.
Но самая громкая слава выпала на долю трёх великих геометров античной математики – это, конечно же, Евклид, Архимед и Апполоний Пергский. Евклид (написал книгу «Начала», авторитет которой был и остается огромным более 2000 лет), Архимед (развил метод вычисления площадей и объёмов геометрических фигур и тел), Аполлоний Пергский (автор исследования сечений геометрических тел).
А такие два достижения греческой математики далеко пережили своих творцов.
1) греки построили и представили миру математику как целостную науку;
2) греки провозгласили, что законы природы, в том числе законы математики, постижимы для человеческого разума и могут быть использованы в искусстве, а значит, в творении прекрасного.
§3. Страны ислама
Математика Востока, в отличие от греческой, всегда носила более практический характер. Основными областями применения математики были торговля, ремесло, строительство, география, астрономия, механика, оптика. Преследование греческих учёных-нехристиан в Римской империи V—VI веков вызвало их массовое бегство на восток, в Персию и Индию. При дворе Хосрова I они переводили античных классиков на сирийский язык, а два века спустя появились арабские переводы этих трудов. Так было положено начало ближневосточной математической школе. Большое влияние на неё оказала и индийская математика, также испытавшая сильное древнегреческое влияние. В начале IX века научным центром халифата становится Багдад, где халифы создают «Дом мудрости», в который приглашаются виднейшие учёные всего исламского мира —сабии (потомки вавилонских жрецов-звездопоклонников), тюрки и другие. На западе халифата, в испанской Кордове, сформировался другой научный центр, благодаря которому античные знания стали понемногу возвращаться в Европу. Ряд интересных математических задач, стимулировавших развитие сферической геометрии и астрономии, были задачи о расчёте лунного календаря, об определении киблы — точного направления на Мекку.
В целом, эпоха исламской цивилизации в математических науках может быть охарактеризована не как эпоха поиска новых знаний, но — как эпоха передачи и улучшения знаний, полученных от греческих математиков, а, значит, знаний. Включающих в себя законы золотого сечения (диктует идеально красивые пропорции) .
§4. Средневековье, IV — XV века
В это время мы можем отметить расцвет математики как науки.
В конце XII века на базе нескольких монастырских школ был создан Парижский университет. Возникают Оксфорд и Кембридж в Британии.
Первым крупным математиком средневековья стал Леонардо Пизанский, известный под прозвищем Фибоначчи. Множество красивейших замков, башен, фонтанов, храмов построено именно в то время, не без использования математических законов.
§5. Математика у русского народа
Интерес к науке на Руси появился рано. Сохранились сведения о школах при Владимире Святославовиче и Ярославе Мудром (XI век).
Русский народ создал свою собственную систему мер:
1 миля = 7 верстам ( 7,47 км)
7,47 км)
1 верста = 500 саженям ( 1,07 км)
1,07 км)
1 сажень = 3 аршинам = 7 футам ( 2,13 м)
2,13 м)
1 аршин = 16 вершкам = 28 дюймам ( 71,12 см)
71,12 см)
1 фут = 12 дюймам ( 30,48 см)
30,48 см)
1 дюйм = 10 линиям ( 2,54 см)
2,54 см)
1 линия = 10 точкам ( 2,54 мм).
2,54 мм).
Интересно, что на Руси когда говорили о росте человека, то указывали лишь, на сколько вершков он превышает 2 аршина. Поэтому слова «человек 12 вершков роста» означали, что его рост равен 2 аршинам 12 вершкам, то есть 196 см, или о богатырях говорили «Богатырь, косая сажень в плечах», т.е. у такого человека по диагонали от мизинца левой руки до пятки правой ноги почти 2 метра 13 сантиметров. Меткие выражения математического характера, применяемые в речи русичей, делали русский язык звучным и красивым.
§ 6. Искусство счета.
Изучив этот материал, мы поняли, что искусство счета развивалось с развитием человечества. На ранних ступенях развития общества люди почти не умели считать. В те времена, когда человек лишь собирал в лесу плоды и охотился, ему для счета хватало четырех слов: один, два, три и много. Это был еще не счет, а лишь его зародыш. Именно так считают и сейчас некоторые племена, живущие в джунглях Южной Америки.
Впоследствии способность различать друг от друга небольшие совокупности развивалась; появились слова обозначающие числа «четыре», «пять», «шесть», «семь». Последнее слово длительное время обозначало также неопределенно большое количество. Народные пословицы сохранили память о появлении названий числа 7. К примеру, такие как: «семь раз отмерь – один раз отрежь», «у семи нянек дитя без глазу», «семь бед – один ответ», «семеро одного не ждут» и другие.
Однако когда люди начали заниматься животноводством и земледелием, то им уже стало необходимо пересчитывать коз в стаде или количество корзин с выращенными плодами (которых было больше семи), заготовленными на зиму. Поэтому счет получил свое дальнейшее развитие.
Способов счета было придумано немало: делались зарубки на палке по числу предметов, завязывались узлы на веревке, складывались в кучу камешки. Такой вид счета носит название унарной системы счисления, т.е. система счисления, в которой для записи числа применяется только один вид знаков.
Но палку с зарубками с собой не возьмешь, да и камни таскать не очень приятно, а пастуху нужно знать, не отбилась ли какая коза от стада. И тут на помощь приходят пальцы рук — отличный счетный материал, кстати.
Таким образом, можно сделать первый вывод: древний человек хотел учитывать вещи, которыми он владел. Сколько у него инструментов? Сколько оружия? Сколько животных?
Жизнь наших предков была намного проще, но даже они вынуждены были прибегать к использованию числа.
Продолжая изучать литературу по данной теме, мы заметили, что математика — это не только стройная система законов, но и уникальное средство познания красоты. А красота многогранна и многолика.
Рассмотрим применение математики в окружающей нас жизни.
Глава II. Применение законов математики как законов красоты в окружающей нас жизни
§ 1. Математика в мире растений.
Мир растений — величайшее чудо природы, царство красоты и наше целительное богатство. Изучением лекарственных растений занимается наука фитотерапия. Конечно, в этой науке математика играет не последнюю роль. О том, что и здесь применяется математика, мы можем найти сколь угодно много подтверждений. Симметрия листьев, красота цветов, палитра природных окрасов, пропорции стройных деревьев – всё подчинено закону симметричности, пропорциональности и целесообразности.
§ 2. Математика в жизни животных и насекомых.
Мир животных и насекомых — богатый и разнообразный мир живых существ. Этот мир, скажете вы, изучает раздел биологии — зоология. Но позвольте Вам всем возразить! Ведь и здесь не обойтись без математики. Вы когда-нибудь обращали внимание на симметрию крыльев бабочки, на причудливые узоры змеиной кожи, а какие есть красивые по цвету морские и аквариумные рыбки, ведь мы смотрим на них как завороженные. Да таких примеров можно приводить и приводить.


Вот, к примеру, пчёлы — удивительное творение природы. Они маленькие экономисты. Пчелиные соты представляют собой пространственный паркет (шестигранные призмы), поскольку заполняют пространство так, что не остаётся просвета.
Это математический шедевр из воска. А пауки умудряются плести свои паутины, соблюдая строгие пропорции. Как это возможно, ведь пчёлы и пауки не знают высшей математики?




§ 3. Математика геометрических тел и фигур.
Тела и фигуры изучает раздел математики, который называется геометрией. Эта наука возникла в Древней Греции исключительно из практических целей, для измерения участков земли. В том, что с фигурами и телами мы имеем дело в жизни, убеждать, думаем, никого не придётся, а вот понять роль математики в этом можно на примере формул архитектуры, использующей в основе геометрические тела.
§ 4. Математика и культура.
Нам стало интересно, а какое отношение имеет математика к культуре: ведь это и памятники архитектуры, прекрасные скульптуры и, в конце концов, это и живопись. Неужели и здесь мы можем наблюдать «незримое» влияние математики на культуру?! А начать решили с удивительных архитектурных памятников.
Даже сейчас, когда он стоит на развалинах, Парфенон в Афинах — это одно из самых знаменитых сооружений в мире. Он был построен в эпоху расцвета древнегреческой математики.
Фасад Парфенона вписывается в прямоугольник, стороны которого образуют так называемое золотое сечение. Длина прямоугольника больше его ширины примерно в 1,6 раза. А это соотношение в математике принято считать «золотой пропорцией».
Золотое соотношение мы можем увидеть и в пирамиде Хеопса, и в здании собора Парижской Богоматери, и в храме Василия Блаженного на Красной площади.
Золотая пропорция применялась многими античными скульпторами. Известна золотая пропорция статуи Аполлона Бельведерского: рост изображённого человека делится пупочной линией в золотом сечении (талия делит совершенное человеческое тело в отношении золотого сечения примерно )
Скульпторы утверждают, что пропорции мужчин ближе к золотому сечению, нежели пропорции женщин (однако, женщина в обуви на каблуках может оказаться ближе к золотым пропорциям).
Ещё в эпоху Возрождения художники открыли, что любая картина имеет определённые точки, невольно приковывающие внимание, так называемые зрительные центры. Таких точек всего 4, они делят величину изображения по горизонтали и вертикали в золотом сечении. Данное открытие у художников того времени получило название «Золотое сечение» картины.
Переходя к примерам в живописи, нельзя не остановить своего внимания на творчестве Леонардо да Винчи.
Портрет Моны Лизы привлекает нас тем, что композиция рисунка построена на «золотых треугольниках».
На этой замечательной картине И. И. Шишкина («Сосновая роща») так же просматриваются мотивы золотого сечения.
Наличие в картине вертикалей и горизонталей, делящих её в отношении золотого сечения, придаёт ей характер уравновешенности и спокойствия.
Золотое сечение можно встретить в бытовых предметах и шрифтах.
§ 5. Математика в живой и неживой природе.
Ещё Гете подчёркивал тенденцию природы к спиральности. Паук плетёт паутину спиралеобразно. Спирально закручивается смерч. Испуганные стада животных разбегается по спирали, а косяки рыб как бы мелькают мимо сети тоже по спирали. Молекула ДНК закручена двойной спиралью. Спираль мы можем увидеть в расположении семян подсолнечника, в шишках сосны, кедра ананасах, кактусах и т.д. Спираль создает не только красоту и порядок, но и модель бытия.
Снежинки: ярче примера очаровательной красоты и порядка в природе вы не найдете. Изучением снежинок занимался знаменитый Рене Декарт. А вообще-то, снежинки — это звёздчатые многоугольники. Они очаровательны ещё и потому, что они симметричны. А симметрия, как сказал Г. Вейль «Симметрия – это идея, с помощью которой человек веками пытался объяснить и создать порядок, красоту, совершенство».
Проанализировав приложение математики в окружающей нас жизни, хочется заметить, что красота помогает с радостью воспринимать окружающий мир, а математика даёт возможность открывать всё новые и новые слагаемые красоты. Так и хочется сказать словами поэта
Все в мире связано в единое начало:
В движенье волн – шекспировский сонет,
В симметрии цветка – основы мирозданья,
А в пенье птиц — симфония планет.
У. Блейк
Изучив весь представленный вам материал, мы поняли, что о математике можно говорить вечно. Наверное, поэтому и символ вечности «∞» (бесконечность) мог появиться только с развитием этой науки «Математика». Мы решили перейти к практической части исследования и для начала провели небольшой социологический опрос, который должен нам помочь подтвердить или опровергнуть выдвинутую ранее гипотезу: если математика второстепенная наука, то можно утверждать, что без математических законов красоты можно обойтись; если же нет, то без знания математики вся современная жизнь невозможна.
Практическая часть
Прежде чем сделать окончательный вывод, что для нас математика, мы предлагаем изучить результаты социологического опроса.
Цель опроса — изучение общественного мнения по данной теме.
Опрос вёлся по следующим направлениям:
1) математика — это красота,
2) нужны ли математические законы красоты в жизни людей,
3) где находят свое применение математические законы красоты.
Опрос проводился среди следующих категорий:
1) учащиеся 7. 8, 9, 11 классов МБОУ Шиковской СШ,
2) учителя МБОУ Шиковской СШ (выборочно),
3) родители учащихся 7. 8, 9, 11 классов МБОУ Шиковской СШ (выборочно)
В опросе приняли участие 27 человек.
Вот что у нас получилось:
I направление. Математика — это красота
Результаты данного направления говорят о том, что математика является красотой для 17 человек из числа всех опрошенных, для 8 человек математика — это просто наука, 2 человека затруднялись ответить, что для них математика.
II направление. Нужны ли математические законы красоты в жизни людей?
Нужны ли математические законы красоты в жизни людей?
Данная диаграмма показывает, что математические законы красоты нужны 74% (20 человек из 27) и не нужны 26% (7 человек из 27).
III направление. Где находят свое применение математические законы красоты?
Ответы на этот вопрос приведены в следующей таблице.
5 | |
2 | |
2 | |
7 | |
1 | |
2 | |
8 |
всего: 27 человек
Так отвечали не только дети, но и взрослые.
Заключение
Результаты исследования
Итак, гипотеза, которую мы выдвинули в начале нашего исследования, на практике не подтвердилась. Следовательно, предположение о том, что математические законы красоты не важны — неверно.
Таким образом, на основании изученной литературы и анализа результатов общественного мнения, мы можем сделать вывод о том, что без знания математических законов красоты вся современная жизнь невозможна. Например, у нас не было бы хороших домов с красивыми изящными линиями, т. к. строители должны уметь измерять, считать, сооружать. Наша одежда была бы грубой, т. к. её нужно хорошо, красиво скроить. Не было бы ни прекрасно спланированных парковых зон, никакой лёгкой промышленности и тысячи других вещей, составляющих часть нашей цивилизации.
В данной работе мы выяснили, математика — часть мира, напрямую связанная с категорией красоты, которая создаётся по математическим формулам; часть мира, в котором мы живём.
Поэтому мы может с полной и абсолютной уверенностью воскликнуть:
Математика — это красота.!
Список использованных источников информации
1. За страницами учебника математики. — И. Я. Депман, Н. Я. Виленкин
2. С математикой в путь. — Н. Лэнгдон, Ч. Снейп
3. www.abc-people.com/data/leonardov/zolot_sech-txt.htm — Золотое сечение.
4. http://tmn.fio.ru/works/04x/304/p4_21k.htm — Биология.
5. http://festival.1september.ru/2004_2005/index.php?numb_artic=213063-
История математики.
6. http://bse.sci-lib.com/article048077.html — Золотое сечение.
7. http://www.mjagkov.de/ser/archives/42-,.html
8. http://namangan34.connect.uz/lifemath/links.php — Живая математика
9. Учебник «Математика – 6». – Алдамуратова Т.А., Байшоланов Т.С.,
издательство «Атамұра», 2011 год.
multiurok.ru
В ЧЕМ КРАСОТА МАТЕМАТИКИ?
В ЧЕМ КРАСОТА МАТЕМАТИКИ?
Дудникова Е.Н. 11МБОУ СОШ №16 г. Краснодара
Снытко Е.В. 11МБОУ «СОШ №16 г. Краснодара»
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
«..А если это так, то что есть красота
И почему её обожествляют люди?
Сосуд она, в котором пустота,
Или огонь, мерцающий в сосуде?»
Н. Заболоцкий, 1955г.
Введение
Принято считать, что математика – основа рационального знания, точная наука, оперирующая лишь сухими цифрами и символами, совершенно далекая от красоты музыки, идеалов гармонии и мира искусства в целом. Между тем, многие выдающиеся математики видят в ней красоту. Наиболее полно охарактеризовал это британский математик Бертран Рассел: «Правильный взгляд на математику открывает не только истину, но и безупречную красоту — холодную и суровую, как скульптура, отстранённую от человеческих слабостей, лишённую вычурных уловок живописи и музыки — горную кристальность и строгое совершенство великого искусства. Подлинный вкус наслаждения, восторг, освобождение от бренной человеческой оболочки — всё это критерии высшего совершенства, которыми математика обладает наравне с поэзией» [1]. Обращаясь к истории, мы можем узнать, что в древней Греции «математикой занимались ради её красоты», то же самое о математике пишут А.Н. Колмогоров и Г. Харди, называя «красивыми» и «изящными» некоторые теоремы, гипотезы и их решения. [2,3,4] Бесспорно, совершенно очевидна полезность математики для точных и естественных наук, таких как физика, химия, экономика, медицина и многие другие. Математику смело можно назвать языком современной науки. Но в чем же ее эстетическая привлекательность? Может ли обычный человек, не являющийся ученым-математиком постичь эту красоту?
Целью нашей работы стало изучение эстетического потенциала математики.
Исследования математической красоты
Орбитофронтальная кора
Рис.1
Как уже было сказано, многие из математиков — Бертран Рассел, Герман Вейль, физик Пол Дирак и искусствовед Клайв Белл, писали о важности красоты в математической формулировке и сравнивали ощущение математической красоты с ощущением, полученным от произведений искусства [1,4,5]. Их описания показывают, что ощущение математической красоты имеет много общего с ощущением, полученным из других источников, хотя математическая красота обладает гораздо большей интеллектуальной глубиной, чем визуальная или музыкальная красота, которые более «разумны» и основаны на восприятии. Неоднократно проводились исследования, в которых изучалась нейробиология красоты — исследования изображений отдельных областей мозга, реагирующих на визуальные, музыкальные и психологические воздействия [6,7]. Как выяснилось, все они взаимосвязаны с деятельностью одной и той же области мозга – орбитофронтальной коры (рис. 1) [8].
Действительно ли ощущение красоты, полученное из такого высокоинтеллектуального и абстрактного источника, как математика, взаимосвязано с деятельностью той же части мозга, что и впечатления от источников, основанных на зрительном и слуховом восприятии? Ответ на этот вопрос был недавно получен. В феврале 2014 года в журнале Frontiers in Humann Neuroscience было опубликовано совместное исследование нейробиологов и математиков, посвященное изучению феномена красоты математики [9]. Чтобы определить это, была использована функциональная магнитно-резонансная томография для изображения активности мозга 16-ти математиков, когда они рассматривали математические формулы, которые они оценивали индивидуально как красивые, нейтральные или уродливые. Результаты показали, что восприятие математической красоты тесно взаимосвязано с активностью в той же части эмоционального мозга, что и восприятие музыки, поэзии, живописи, а именно орбитофронтальной борозды [9].
Какие же математические формулы красивы?
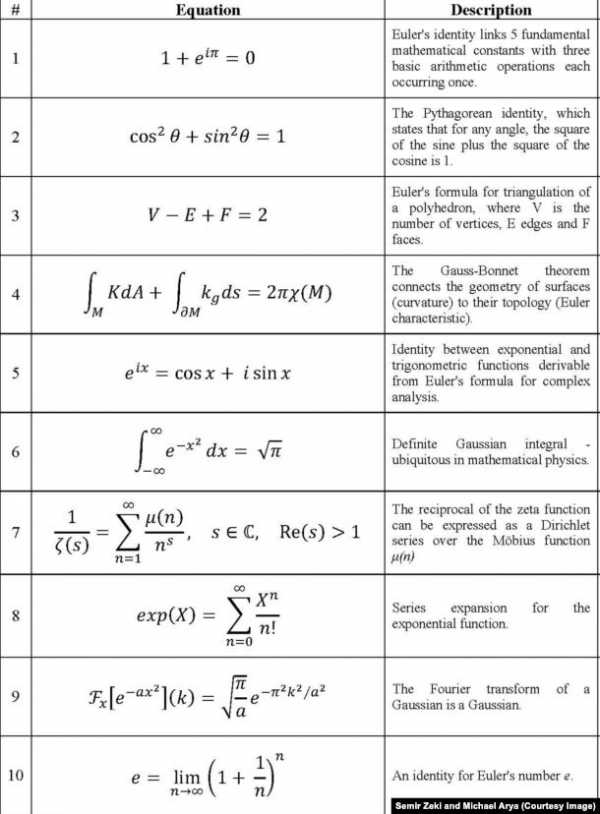
Формулой, наиболее часто оцениваемой как красивая, в вышеприведенном исследовании, оказалось тождество Эйлера, которое связывает 5 фундаментальных математических констант с тремя основными арифметическими операциями:
eiπ+1=0;
где е — число Эйлера, основание натурального логарифма, предел последовательности (1+1/n)n,
i— «мнимая единица», квадрат которой равен минус единице, «основание» комплексных чисел,
π — число «пи».
Формула Эйлера, из которой сразу следует данное тождество, была опубликована Эйлером в 1740 году. Тождество уже тогда произвело глубокое впечатление на научный мир. Были даже попытки мистически истолковать его как символ единства математики: числа 0 и 1 относятся к арифметике, i — к алгебре, число π — к геометрии, а число e — к математическому анализу [10].
Сама формула Эйлера, утверждающая, что для любого комплексного числа (действительного в частности) x выполнено следующее равенство: eix= isinx + cosx, тожерасценивалась участниками как красивая (рис 2) [10].
Другой, высоко оцененной формулой стала теорема Пифагора:
Рис. 2
a 2 + b 2 = c 2;
«В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах» (рис.3) [11].
Рис.3
Это одна из основополагающих теорем евклидовой геометрии, которая устанавливает соотношение между сторонами прямоугольного треугольника. В этой теореме верно и обратное утверждение: треугольник, сумма квадратов длин двух сторон которого равна квадрату длины третьей стороны, является прямоугольным [11]. В научной литературе имеется около четырехсот доказательств теоремы Пифагора [11], что объясняется как фундаментальным значением для геометрии, так и элементарностью результата. Основные направления доказательств: алгебраическое использование соотношений элементов треугольника (таков, например, популярный метод подобия), метод площадей, существуют также различные экзотические доказательства (например, с помощью дифференциальных уравнений) [12].
К красивым формулам были отнесены и уравнения Коши-Римана:
— дифференциальные уравнения, которым удовлетворяют вещественная и мнимая части аналитической функции [13].
Формулы, считающиеся нейтральными, включали формулу Эйлера для многогранников: В-Р+Г=2, где В – число вершин, Р- число ребер, Г – число граней. Данная теорема устанавливает взаимосвязь между числом ребер, граней и вершин для многогранников, топологически эквивалентных сфере (например: тетраэдр, куб, октаэдр) [15].
Теорема Гаусса Бонне также была отнесена к нейтральным:
Данная теорема относится к области дифференциальной геометрии и топологии [16].
К числу нейтральных отнесена также спектральная теорема — наименование утверждений из класса теорем о линейных операторах или о матрицах в линейной алгебре и функциональном анализе.
Наиболее негативные эмоции у испытуемых вызывала формула, которая выражает обратную π в виде бесконечной суммы, предложенная индийским математиком Сринивасом Рамануджаном в 1910 году [13]:
Обсуждение
Искусство и математика, по большей части совершенно противоположны друг другу: искусство имеет более «разумный» источник и является доступным для многих, в то время как математика обладает высоким познавательным, интеллектуальным началом и доступна не для всех. Тем не менее, и то и другое может спровоцировать эстетические эмоции, вызывая ощущение красоты, хотя не все великие произведения искусства и не все великие математические формулы и теоремы способны на это.
Математическая красота, описанная Платоном, является высшей формой красоты, поскольку происходит от одного только интеллекта и связана с вечными и неизменными истинами, также является одним из самых абстрактных эмоциональных переживаний [17]. Несмотря на свою абстрактную природу, для Клайва Белла, сильна связь между математической и художественной красотой, потому что математик чувствует эмоцию для своих размышлений, которые «возникают … из сердца абстрактной науки»[5]. В то время как для Бертрана Рассела «Истинный дух восторга, блаженства, чувства что ты больше, чем Человек, каковое есть критерий высшего совершенства, присутствует в математике так же несомненно, как и в поэзии» [1]. Платоновская традиция подчеркивала бы, что математические формулировки воспринимаются как прекрасные, потому что они дают представление о фундаментальной структуре вселенной [17]. Для Иммануила Канта, напротив, эстетический опыт так же обоснован в нашей собственной природе, потому что для него «эстетические суждения могут поэтому рассматриваться как выражение нашего чувства, что что-то имеет для нас смысл» [17].
Очевидно, что математическая и художественная красота были написаны с одним и тем же вдохновением математиками и гуманистами, и именно поэтому вызывают похожие физиологические и эстетические эмоции. Это означает, что существует и общий абстрактный характер ощущения красоты, полученного из самых разных источников. В свете этого деятельность в области эмоционального мозга, которая взаимосвязана с чувством красоты, полученным из разных источников, просто отражает нейробиологически тот же мощный и эмоциональный опыт красоты, о котором говорили и математики и художники.
Отношения взаимосвязи красоты с удовольствием и вознаграждением обычно обсуждались в философии эстетики без четкого вывода [17]. С точки зрения физиологии это, наверное, не удивительно, потому что все три сливаются друг с другом, без четких границ между ними, вызывая активность орбитофронтальной коры, что отражает, возможно, субъективную трудность разделения этих переживаний. Ученые, исследуя красоту математики, давали различные формулы эстетической привлекательности математического объекта. Например, Г. Биркгоф дал следующую формулу: M = O/C,
где M — мера красоты объекта, O — мера порядка, а C — мера усилий, затрачиваемых для понимания сущности объекта [18].
Другой подход к оценке красоты математического объекта предложил российский советский математик В. Г. Болтянский [19]. Предложенная им формула включает изоморфизм между математическим объектом и его наглядной моделью, простоту модели, а также неожиданность появления модели:
КРАСОТА = НАГЛЯДНОСТЬ + НЕОЖИДАННОСТЬ = ИЗОМОРФИЗМ + ПРОСТОТА + НЕОЖИДАННОСТЬ [19].
И та, и другая формулы созвучны: в них красота математического объекта обусловлена взаимодействием его обобщенного образа, созданного нашей психикой, и оригинальности, выделяющей этот объект из множества других.
Заключение
В ходе нашего исследования мы сделали вывод, что ощущение красоты, полученное от математических формулировок, представляет собой наверное самый уникальный случай ощущения красоты, который зависит от уровня обучения и культуры. О красоте математики написано немало. Многие авторы видят её в гармонии чисел и форм, геометрической выразительности, стройности математических формул, решении задач различными способами, изяществе математических доказательств, порядке, универсальности математических методов.
Таким образом, красота математики, как правило, не лежит на поверхности, для ее постижения нужны некоторые — иногда значительные интеллектуальные и волевые усилия. Математик находится посередине между наукой и искусством, и это подтверждает неизбежную связь между самой абстрактной из наук и человеческими эмоциями.
Нельзя не вспомнить слова Анри Пуанкаре: «Думать, что математика затрагивает лишь интеллект, означало бы забыть о красоте математики, элегантности геометрии, которые прекрасны в самом полном смысле этого слова».
Перспективы дальнейшей разработки темы
В ходе нашей работы я узнала очень много нового и интересного. Большая часть формул и теорем до этого была мне не известна, однако первое знакомство состоялось и со многими из них я еще встречусь в своей школьной и студенческой жизни! В дальнейшей перспективе, я хотела бы провести исследование на восприятие школьниками формул из физики и математики курса средней общеобразовательной школы на предмет их «красоты». Таким образом, я надеюсь не только узнать: какие же формулы из школьных учебников самые красивые, но и привлечь внимание учеников к изучению точных наук.
Список литературы
Russell Bertrand. The Study of Mathematics. Mysticism and Logic: And Other Essays. — Longman, 1919. — P. 60.
Лурье Л. И.. Математическое образование в пространстве эстетического опыта. Образование и наука (Известия уральского отделения Российской академии образования). — 2006. — № 6 (42). — С 120.
Колмогоров А. Н. О профессии математика. Квант. — 1973. — № 4. (выдержки из брошюры «О профессии математика»).
Панов В. Ф. Математика древняя и юная. — Изд. 2-е, исправленное. — М.: МГТУ им. Баумана, 2006. — С. 330—332. — 648 с.
Клайв Белл [Электронный ресурс]. – Режим доступа: http://en.wikipedia.org/wiki/Clive_Bell (дата обращения 27.11.2017)
Kawabata, H., and Zeki, S. Neural correlates of beauty. J. Neurophysiol. 91, 1699–2004. doi: 10.1152/jn.00696.2003
Kringelbach, M. H., O’Doherty, J., Rolls, E. T., and Andrews, C. Activation of the human orbitofrontal cortex to a liquid food stimulus is correlated with its subjective pleasantness. Cereb. Cortex 13. 2003: 1064–1071. doi: 10.1093/cercor/13.10.1064
[Электронный ресурс]. – Режим доступа: https://ru.wikipedia.org/wiki/ Орбитофронтальная_кора (дата обращения 28.11.2017)
Semir Zeki, John Paul Romaya, Dionigi M. T. Benincasa, Michael F. Atiyah. The experience of mathematical beauty and its neural correlates. Front. Hum. Neurosci.2014;13 | https://doi.org/10.3389/fnhum.2014.00068
Данциг Тобиас. Числа — язык науки. — М.: Техносфера. 2008. — С. 111.
Глейзер Г. И. История математики в школе. — М., 1982
Сайт о теореме Пифагора с большим числом доказательств, материал взят из книги В. Литцмана, большое число чертежей представлено в виде отдельных графических файлов. [Электронный ресурс]. – Режим доступа: http://th-pif.narod.ru/other.htm (дата обращения 30.11.2017)
Уравнения Коши-Римана. [Электронный ресурс]. – Режим доступа: https://slovar.wikireading.ru/98619 (дата обращения 29.11.2017)
Харди Г. Двенадцать лекций о Рамануджане. — М.: Институт компьютерных исследований, 2002. — 336 с.
Курант Р., Роббинс Г.Что такое математика? Перевод с английского под редакцией А. Н. Колмогорова Издательство: М.: МЦНМО. Год издания: 2015. 564 С.
[Электронный ресурс]. – Режим доступа: https://ru.wikipedia.org/wiki/ Формула_Гаусса_—_Бонне (дата обращения 28.11.2017)
Современная философия: Словарь и хрестоматия. Ростов-на-Дону. Феникс, 1996 г. 511 с.
Биркгоф Г. Математика и психология. — М.: Советское радио, 1997.
Болтянский Б. Г. Математическая культура и эстетика. Математика в школе. 1982. N 2.
Просмотров работы: 675
school-science.ru
Красота математики — Математика — СУЗ

М
А
А
Т
И
К
А
Математика владеет не только истиной, но и высшей красотой.
В математике есть своя красота, как в живописи и поэзии.
(Н.Е. Жуковский)
Т
М
Е

Цели мероприятия
- Познание математических закономерностей в мире;
- определение значения математики в мировой культуре ;
- «Золотое Сечение» как гармония окружающего мира;
- Математика в астрономии, метеорологии, геологии, химии

Математика – царица всех наук, символ мудрости. Красота математики среди наук недосягаема, а красота является одним из связующих звеньев науки и искусства.
Это не только стройная система законов, но и уникальное средство познания красоты.
«Математика есть прообраз красоты мира»
(В.Гейзенберг)

Люди придумали цифры и действия с ними, а потом в них же открыли множество законов, правил и теорем
В жизни цифр, линий, углов и бесконечно малых величин можно увидеть много красивого – изящные теоремы, тела, поверхности, даже условия задач
Числа живут своей жизнью, и мы, соприкоснувшись с ней, удивляемся, а иногда и любуемся ею

С древних времён человечеству известны «фокусы» с числами, из которых по некоторому фиксированному правилу строят числовые пирамиды.

Математическая пирамида №1
1 x 8 + 1 = 9 12 x 8 + 2 = 9 8 123 x 8 + 3 = 9 8 7 1234 x 8 + 4 = 9 8 7 6 12345 x 8 + 5 = 9 8 7 65 5 123456 x 8 + 6 = 9 8 7 65 4 1234567 x 8 + 7 = 9 8 7 65 4 3 12345678 x 8 + 8 = 9 8 7 65 4 32 2 123456789 x 8 + 9 = 9 8 7 65 4 32 1
Какие вычисления будут выполнены в следующей строке и в последующих?
Математика — это красота и чудо в чистом виде.

Пирамида Хеопса
1*8+1=9
12*8+2=98
123*8+3=987
1234*8+4=9876
12345*8+5=98765
123456*8+6=987654
1234567*8+7=9876543
12345678*8+8=98765432
123456789*8+9=987654321

Математическая пирамида №2
1 x 9 + 2 = 11 12 x 9 + 3 = 111 123 x 9 + 4 = 1111 1234 x 9 + 5 = 11111 12345 x 9 + 6 = 111111 123456 x 9 + 7 = 1111111 1234567 x 9 + 8 = 11111111 12345678 x 9 + 9 = 111111111 123456789 x 9 +10= 1111111111
Какие вычисления будут выполнены в следующей строке и в последующих?
Математика — это единственная наука, которая имеет дело с абсолютным идеалом.

Пирамида Хефрена
1*9+2=11
12*9+3=111
123*9+4=1111
1234*9+5=11111
12345*9+6=111111
123456*9+7=1111111
1234567*9+8=11111111
12345678*9+9=111111111

Математическая пирамида №3
9 x 9 + 7 = 88 98 x 9 + 6 = 888 987 x 9 + 5 = 8888 9876 x 9 + 4 = 88888 98765 x 9 + 3 = 888888 987654 x 9 + 2 = 8888888 9876543 x 9 + 1 = 88888888 98765432 x 9 + 0 = 888888888
Какие вычисления будут выполнены в следующей строке и в последующих?
Замечательно! Не правда ли?

Пирамида Хуфу
9*9+7=88
98*9+6=888
987*9+5=8888
9876*9+4=88888
98765*9+3=888888
987654*9+2=8888888
9876543*9+1=88888888
98765432*9+0=888888888

Математическая пирамида №4
1 x 1 = 1 11 x 11 = 121 111 x 111 = 1 2 3 2 1 1111 x 1111 = 1 23 4 32 1 11111 x 11111 = 1 234 5 432 1 111111 x 111111 = 1 2345 6 5432 1 1111111 x 1111111 = 1 23456 7 65432 1 11111111 x 11111111 = 1 234567 8 765432 1 111111111 x 111111111 = 1 2345678 9 8765432 1
Какие вычисления будут выполнены в следующей строке и в последующих?
Математика в своей сущности достаточно таинственна и романтична.

Это интересно
- Возьмем число 142857 .
- Удвоим его.
- Удвоим его.
- Удвоим его.
- Удвоим его.
- Удвоим его.
Получилось 285714 .
Внимательно вглядываемся —
числа те же, только в другом порядке!
б) Интересно, а если утроить? Учетверить?
Получаем последовательно:
428571, 571428, 714285, 857142.
Наша закономерность продолжает выполняться .
Цифры просто переставляются местами.
Красиво.!
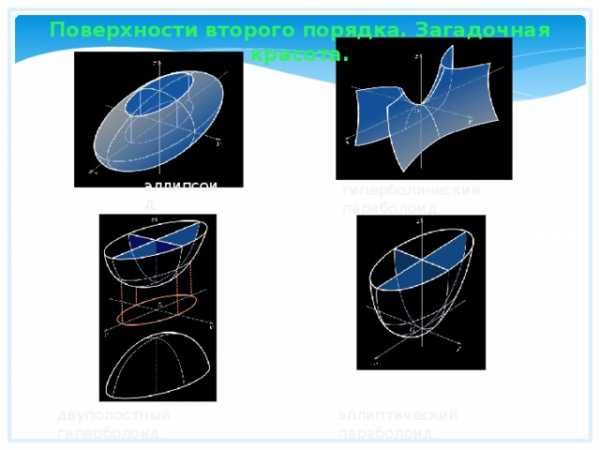
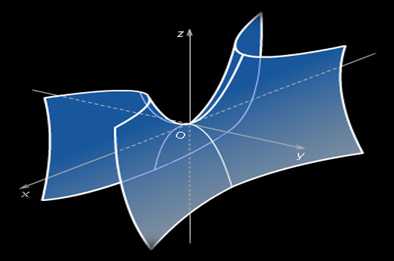
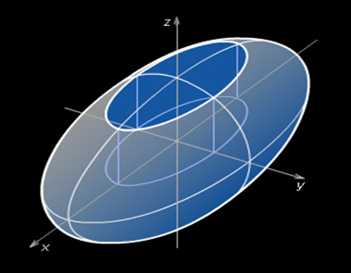
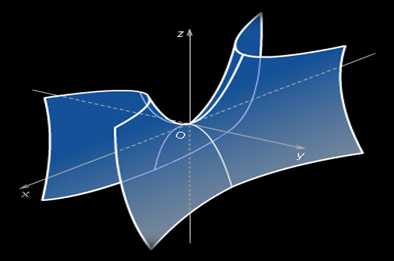
Поверхности второго порядка. Загадочная красота.
эллипсоид
гиперболический параболоид
эллиптический параболоид
двуполостный гиперболоид

МАТЕМАТИКА В АСТРОНОМИИ

МАТЕМАТИКА В МЕТЕОРОЛОГИИ

МАТЕМАТИКА В ГЕОЛОГИИ

МАТЕМАТИКА В ХИМИИ

МАТЕМАТИКА В БИОЛОГИИ

Симметрия — закономерное расположение элементов формы относительно плоскости, оси или точки.
Человек давно осмыслил симметрию в творениях природы и стал использовать се как средство организации искусственных форм.
В Древней Греции слово «симметрия» было синонимом красоты, гармонии формы.
«…быть прекрасным значит быть симметричным и соразмерным» (Платон )

Тадж-Махал — мавзолей-мечеть, находящийся в Агре, Индия, на берегу реки Ямуна. Усыпальница имеет центральную симметрию относительно гробницы Мумтаз-Махал. Единственным нарушением этой симметрии является гробница Шах-Джахана, которую там соорудили после его смерти.

Особенно блистательно использовали симметрию в архитектурных сооружениях древние зодчие. Древнегреческие архитекторы были убеждены, что в своих произведениях они руководствуются законами, которые управляют природой. Выбирая симметричные формы, художник тем самым выражал свое понимание природной гармонии как устойчивости, спокойствия и равновесия.

Зеркальная симметрия
Если преобразование симметрии относительно плоскости переводит фигуру в себя, то фигура называется симметричной относительно плоскости, а данная плоскость – плоскостью симметрии этой фигуры. В некоторых источниках такую симметрию называют зеркальной. А зеркало не просто копирует объект, но и меняет местами передние и задние по отношению к зеркалу части объекта.

Симметрия в природе
Симметрия широко распространена в природе. Ее можно наблюдать в форме листьев и цветов растений, в расположении различных органов животных.

Симметрия в природе
Рассматривая расположение листьев на ветке дерева, видим, что один лист не только отстоит от другого , но и повёрнут вокруг оси ствола. Листья располагаются на стволе по винтовой линии (принцип винтовой симметрии). Семена подсолнечника располагаются по спиралям, опять же по принципу симметрии.
Красота растений привлекала внимание математиков веками. Активнее всего изучались интересные геометрические свойства растений, такие как симметрия листьев относительно центральной оси, радиальная симметрия цветов, и спиральное расположение семечек в шишках. Красота связана с симметрией.

Симметрия в неживой природе
В мир неживой природы очарование симметрии вносят кристаллы. Каждая снежинка- это маленький кристалл замерзшей воды. Форма снежинок может быть очень разнообразной, но все они обладают симметрией — поворотной симметрией 6-го порядка и, кроме того, зеркальной симметрией.

О, симметрия! Гимн тебе пою!
Тебя повсюду в мире узнаю.
Ты в Эйфелевой башне, в малой мошке,
Ты в елочке, что у лесной дорожки.
С тобою в дружбе и тюльпан, и роза,
И снежный рой – творение мороза!
Симметрия является фундаментальным свойством природы, представление о котором слагалось в течение десятков, сотен, тысяч поколений.

Аристид Линденмайер
В 1968г. Венгерский биолог и ботаник Аристид Линденмайер (Aristid Lindenmayer) предложил математическую модель для изучения развития простых многоклеточных организмов, которая позже была расширена и используется для моделирования сложных ветвящихся структур — разнообразных деревьев и цветов.

Rewriting
Rewriting — это способ получения сложных объектов путем замены частей простого начального объекта по некоторым правилам. Классическим примером является снежинка. На рисунке initiator — это начальный объект, грани которого заменяются на generator. Далее с новым объектом проделывается то же самое.
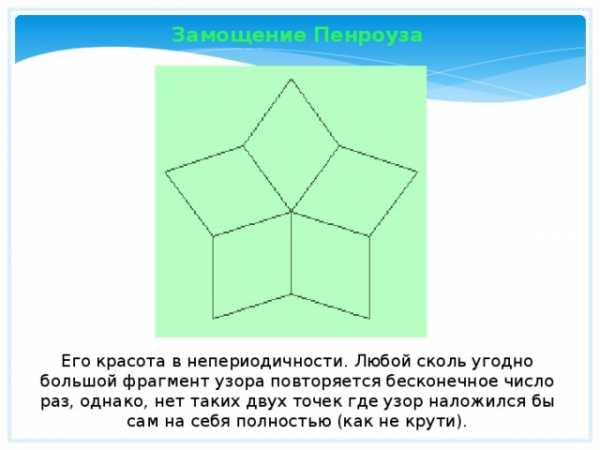
Замощение Пенроуза
Его красота в непериодичности. Любой сколь угодно большой фрагмент узора повторяется бесконечное число раз, однако, нет таких двух точек где узор наложился бы сам на себя полностью (как не крути).

Дерево Пифагора
Пифагор, доказывая свою знаменитую теорему, построил фигуру, где на сторонах прямоугольного треугольника расположены квадраты. В наш век эта фигура Пифагора выросла в целое дерево.
Впервые дерево Пифагора построил А. Е. Босман (1891—1961) во время второй мировой войны, используя обычную чертёжную линейку.
Одним из свойств дерева Пифагора является то, что, если площадь первого квадрата равна единице, то на каждом уровне сумма площадей квадратов тоже будет равна единице.
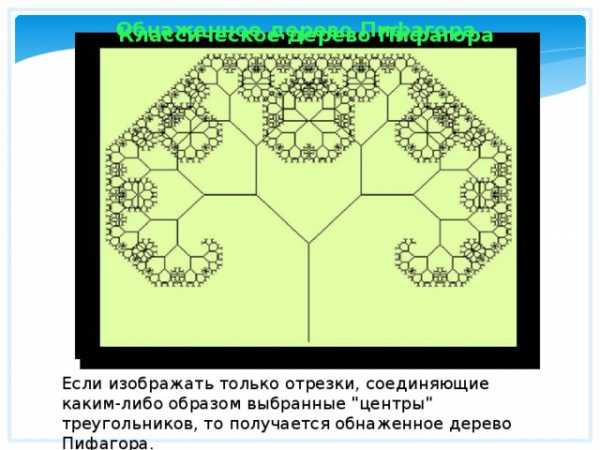
Обнаженное дерево Пифагора
Классическое дерево Пифагора
Если изображать только отрезки, соединяющие каким-либо образом выбранные «центры» треугольников, то получается обнаженное дерево Пифагора.
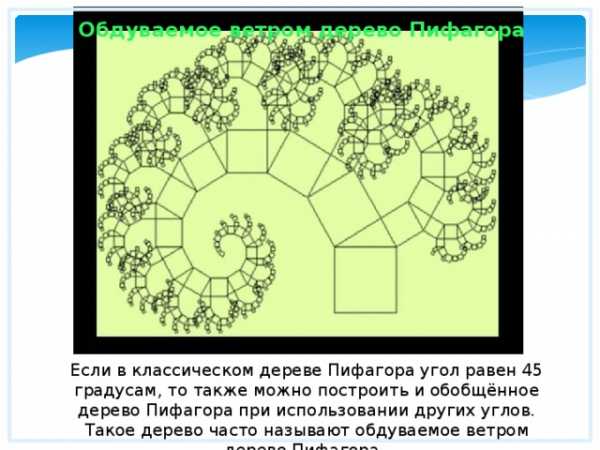
Обдуваемое ветром дерево Пифагора
Если в классическом дереве Пифагора угол равен 45 градусам, то также можно построить и обобщённое дерево Пифагора при использовании других углов. Такое дерево часто называют обдуваемое ветром дерево Пифагора.

Красота есть истина, а истина — красота.
Джон Китс
Первые примеры самоподобных множеств с необычными свойствами появились в XIX веке.
Термин «фрактал» был введён Бенуа Мандельбротом в 1975 году и получил широкую популярность с выходом в 1977 году его книги «Фрактальная геометрия природы».
«Фракталом называется структура, состоящая из частей, которые в каком-то смысле подобны целому»

Галерея изображений фракталов
Они кажутся более живыми и красивыми, чем многие рисунки, несмотря на то, что являются результатом работы программы.

Математическая музыка
Пифагор создал свою школу мудрости, положив в ее основу два искусства — музыку и математику. Он считал, что гармония чисел сродни гармонии звуков и что оба этих занятия упорядочивают хаотичность мышления и дополняют друг друга. Пифагор говорил своим ученикам, что числа правят миром.
Математика и музыка — два полюса человеческой культуры. Слушая музыку, мы попадаем в волшебный мир звуков. Решая задачи, погружаемся в строгое пространство чисел. И не задумываемся о том, что мир звуков и пространство чисел издавна соседствуют друг с другом.
Дроби широко используются в музыке для обозначения длительностей нот.

Золотое сечение
Средневековая математика подарила нам понятие о «золотом сечении» и последовательности Фибоначчи.
Золотое сечение — это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему a : b = b : c или с : b = b : а.
Эта последовательность имеет следующий вид: 1,1,2,3,5,8,13,21,…
То есть каждое последующее число равно сумме двух предыдущих. При этом в пределе деление каждого числа на предыдущее даёт приблизительно 1,618 — это число и определяет «золотое сечение».

Золотое сечение
» Золотое сечение» в конструкции Парфенона, Афины, Греция
Собор «Нотредам де Пари» в Париже, Франция
Золотое сечение (золотая пропорция, деление в крайнем и среднем отношении) — деление непрерывной величины на две части в таком отношении, при котором меньшая часть так относится к большей, как большая ко всей величине.
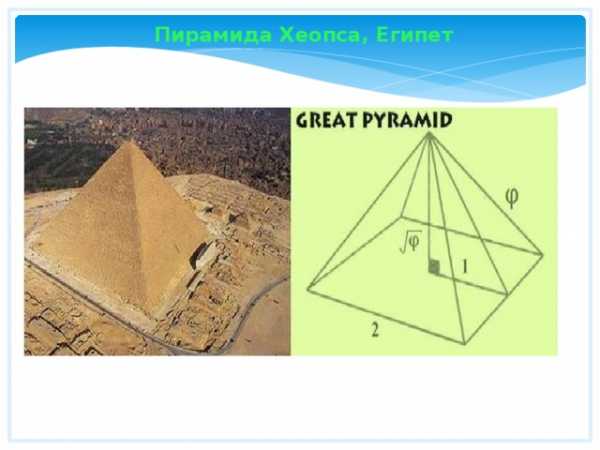
Пирамида Хеопса, Египет

Золотая пропорция в архитектуре
Голицынская (1-я городская) больница в Москве. 1796—1801. Архитектор М. Ф. Казаков.
Василия Блаженного Храм в Москве.

Пропорции Фибоначчи в природе
Еще Гете подчеркивал тенденцию природы к спиральности. Выяснилось, что в расположении листьев на ветке семян подсолнечника, шишек сосны проявляет себя ряд Фибоначчи, а стало быть, проявляет себя закон золотого сечения. Паук плетет паутину спиралеобразно. Спиралью закручивается ураган. Испуганное стадо северных оленей разбегается по спирали. Молекула ДНK закручена двойной спиралью. Гете называл спираль «кривой жизни».

Синусоида
Кардиоида
Логарифмическая спираль

Прямые углы и треугольники в лесу и на лугу

Величины отростков и лепестков цикория подчинены правилу золотой пропорции.
Золотое сечение лист розы

Золотая пропорция в теле ящерицы – длина хвоста так относится к длине остального тела, как 62 к 38.

- У многих бабочек узоры на крыльях, соотношение размеров грудной и брюшной части тела соответствуют золотой пропорции

- Отношение длин хвоста и корпуса равно отношению общей длины к длине хвоста.
- Прозрачные крылья стрекоз — это шедевр «инженерного» мастерства природы.

Можно заметить золотые пропорции, если внимательно посмотреть на яйцо птицы.

Золотое сечение в природе
Все, что приобретало какую-то форму, образовывалось, росло, стремилось занять место в пространстве и сохранить себя.
Это стремление находит осуществление в основном в двух вариантах – рост вверх или расстилание по поверхности земли и закручивание по спирали.
Гете называл спираль «кривой жизни». Спираль увидели в расположении семян подсолнечника, в шишках сосны, ананасах, кактусах и т.д. Паук плетет паутину спиралеобразно.



- Цветки и семена подсолнуха, ромашки, чешуйки в плодах ананаса, хвойных шишках «упакованы» по логарифмическим («золотым») спиралям , завивающимся навстречу друг другу , причем числа «правых «и «левых» спиралей всегда относятся друг к другу, как соседние числа Фибоначчи.


Рога и бивни животных развиваются в форме спирали. Бивни слонов и вымерших мамонтов, когти львов и клювы попугаев являют собой логарифмические формы и напоминают форму оси, склонной обратиться в спираль.
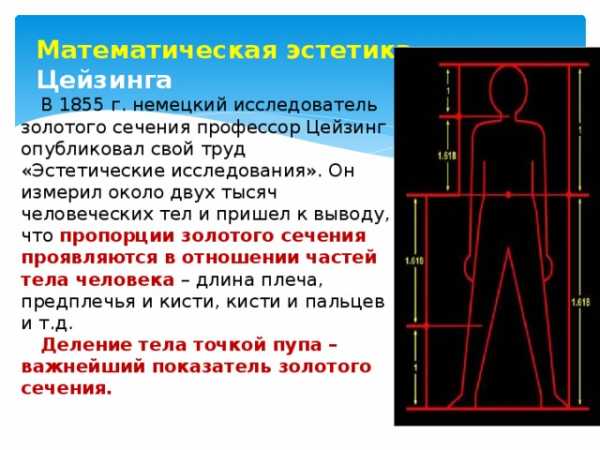
Математическая эстетика Цейзинга
В 1855 г. немецкий исследователь золотого сечения профессор Цейзинг опубликовал свой труд «Эстетические исследования». Он измерил около двух тысяч человеческих тел и пришел к выводу, что пропорции золотого сечения проявляются в отношении частей тела человека – длина плеча, предплечья и кисти, кисти и пальцев и т.д.
Деление тела точкой пупа – важнейший показатель золотого сечения.
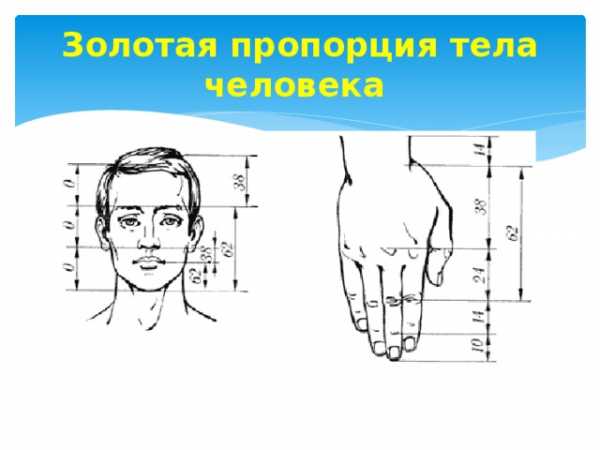
Золотая пропорция тела человека
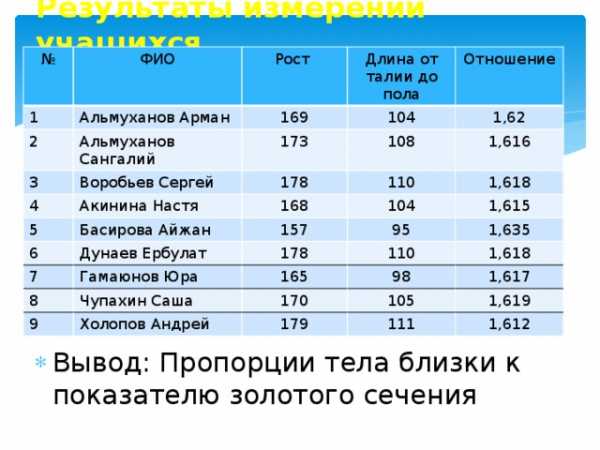
Результаты измерений учащихся
№
ФИО
1
Рост
2
Альмуханов Арман
Альмуханов Сангалий
169
Длина от талии до пола
3
104
Воробьев Сергей
Отношение
173
4
Акинина Настя
5
178
108
1,62
1,616
168
Басирова Айжан
110
6
Дунаев Ербулат
1,618
104
157
7
Гамаюнов Юра
8
178
95
1,615
110
Чупахин Саша
165
9
1,635
Холопов Андрей
1,618
170
98
105
1,617
179
1,619
111
1,612
- Вывод: Пропорции тела близки к показателю золотого сечения

- Соотношение воды и суши на планете Земля составляет 62% и 38%.
- У Земли отношение радиусов равно числу золотого сечения в первой степени

Золотое сечение
В биологических исследованиях 70-90 гг. показано, что, начиная с вирусов и растений и кончая организмом человека, всюду выявляется золотая пропорция, характеризующая соразмерность и гармоничность их строения. Золотое сечение признано универсальным законом живых систем.

Золотое сечение в живописи

Золотое сечение
Закономерности золотой симметрии проявляются в энергетических переходах элементарных частиц, в строении некоторых химических соединений, в планетарных и космических системах, в генных структурах живых организмов. Эти закономерности есть в строении отдельных органов человека и тела в целом.

Математик так же, как художник или поэт, создаёт узоры…
В математике есть тоже своя красота, как в живописи и поэзии. Эта красота проявляется иногда в отчетливых, ярко очертанных идеях, где на виду всякая деталь умозаключения, а иногда поражает она нас в широких замыслах, скрывающих в себе кое-что недосказанное, но многообещающее. (Н.Е. Жуковский )

.
Спасибо за внимание!
Использованные ресурсы:
http://mcs.open.ac.uk/ugg2/jpg/med_RS_0065.jpg
http://en.wikipedia.org/wiki/Penrose_tiling
http://habrahabr.ru/blogs/biotech/69989
http://ru.wikipedia.org/wiki/ Фрактал
http://fractals.narod.ru/intro.htm
http://www.wack.ch/frac/gallery.html
http://www.ug.ru/issue/?action=topic&toid=8652
http://www.mathematics.ru/
«Математика и искусство», А. В. Волошинов, Москва, “Просвещение”, 2000г.
«Математическое путешествие в мир гармонии», Е.С.Смирнова, Н.А. Леонидова, журнал «Математика в школе» № 3, 1993г.
Презентация учителя физики и информатики Александрова З.В.,
МОУ СОШ №5 п.Печенга, Мурманская обл., 2010 г
multiurok.ru
Аркадий Красильщиков: КРАСОТА МАТЕМАТИКИ
Совместное исследование нейробиологов и математиков показало, что восприятие красивых математических формул затрагивает тот же отдел мозга, что и восприятие живописи и музыки. Эта работа стала одной из первых попыток разобраться с понятием математической красоты с помощью строгого научного метода. Однако, знаменитый американский специалист в области алгебраической геометрии Дэвид Мамфорд считает, что красота математических рассуждений слишком сложна и многогранна, чтобы точно указать в мозгу центр, отвечающий за ее восприятие.
Красота и подброшенная монетка
Однажды у петербургского математика, известного специалиста в области динамических систем Анатолия Вершика брали интервью для телевидения. Корреспондент попросил написать на доске какую-нибудь красивую формулу – для фона. Вершик написал формулировку Большой эргодической теоремы – широкого обобщения закона больших чисел.
Основная часть формулировки Большой эргодической теоремы (она же теорема Биркгофа – Хинчина)
Этот закон объясняет, что суммарный эффект большого числа случайных событий мало зависит от исхода каждого отдельного из них. Молекулы воздуха движутся хаотично, но они вдруг не разлетятся вокруг вас в разные стороны, и вы не задохнетесь. Единожды подброшенная монета может выпасть орлом или решкой – это случайность, но если подбросить монету сто, тысячу, миллион раз, число выпадений орла и решки окажутся почти равными – случайность пасует перед количеством. Вообще говоря, именно благодаря закону больших чисел мы можем изучать явления нашего мира, не отвлекаясь на его хаотическую сущность, благодаря ему мы можем с уверенностью делать вывод о большом на основе малого. Это удивительный случай, когда математика явно обнажает фундаментальное устройства природы – красота эргодической теоремы определяется, конечно, этим, а не симпатичными греческими буквами “фи”, “мю” и “сигма” в ее формулировке.
Красота и мозг
Первая часть формул из эксперимента Атьи и Зеки
“Математика, если правильно на нее посмотреть, несет не только правду, но и высшую красоту”, – писал философ Бертран Рассел в работе “Мистицизм и логика” в 1918 году. О красоте математического рассуждения, теоремы и даже определения, наверное, хотя бы раз в жизни задумывался любой исследователь, использующий математику в своей работе. Но насколько эта категория универсальна, даже среди самих математиков? Можно ли сравнить понятие о прекрасном в этой точной науке с красотой в поэзии, музыке, изобразительном искусстве? В начале 2014 года в журнале Frontiers in Humann Neuroscience была опубликована статья группы авторов, ключевыми из которых были британский нейробиолог Семир Зеки и британский математик Майкл Атья. Зеки прославился работами, связывающими чувственное восприятие с конкретными областями в мозгу, на протяжении своей карьеры он поставил множество экспериментов над приматами и людьми, в которых искал корреляции между опытом любви, красоты и ненависти с работой тех или иных отделов мозга. Майкл Атья – лауреат обеих крупнейших в математике Филдсовской и Абелевской премий, известен в первую очередь работами в области алгебраической топологии, в частности, созданием K-теории.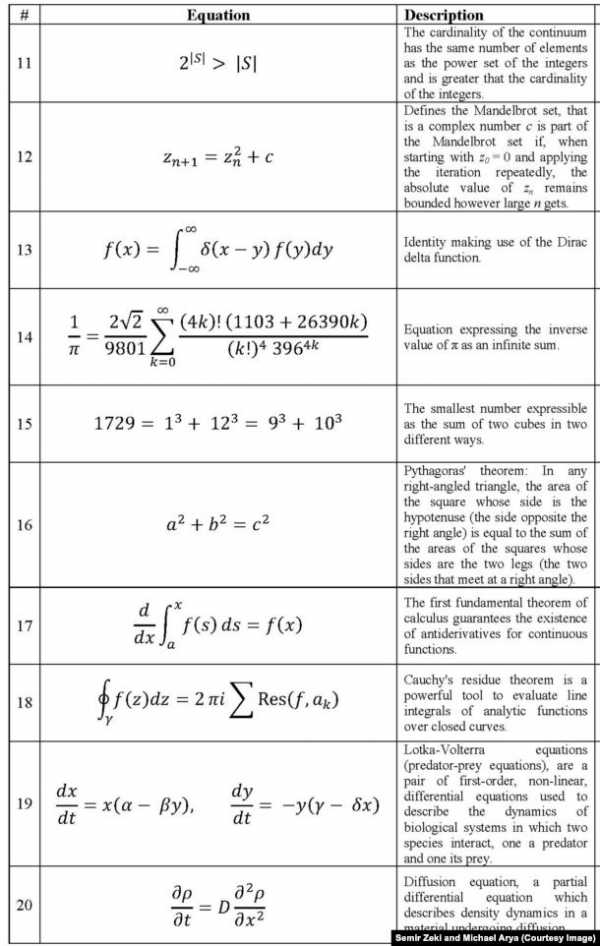
Вторая часть формул из эксперимента Атьи и Зеки
Эти заслуженные специалисты в очень далеких друг от друга научных направлениях встретились, чтобы попробовать подступиться к математической красоте с помощью строгого научного подхода. В 2004 году Зеки опубликовал работу, в которой обсуждалась физиологическая подоплека опыта восприятия изобразительного искусства. В том опыте группе испытуемых было предложено оценить 300 картин по шкале “прекрасная – нейтральная – уродливая”. Затем участникам опыта демонстрировали те же полотна, а происходящие в их мозгу процессы параллельно отслеживали с помощью магнитно-резонансной томографии. Оказалось, разница в реакции на красивые и отвратительные изображения особенно заметна в отделе мозга, называющемся медиальная орбитофронтальная кора – мОФК (это часть коры головного мозга, находящаяся примерно за глазами и завернутая “внутрь”). Научные данные о конкретных функциях тех или иных участков мозга далеко не полны, но другие исследования связывают орбитофронтальную кору с контролем импульсов (ее повреждения могут привести, например, к агрессии и сексуальной распущенности), а также за представление ценности вознаграждения на основе сенсорной информации. Можно ли сказать, что Зеки открыл в мозге “центр красоты”? Вряд ли, да и сам нейробиолог этого совсем не утверждает: он лишь говорит, что между восприятием прекрасного изобразительного искусства и работой мОФК наблюдается определенная корреляция.Через девять лет после этого эксперимента, в 2011 году, Семир Зеки опубликовал еще одну работу – на этот раз он изучал восприятие музыки. И тут важнейшую роль, как показал опыт, играет отдел оМФК. К концу 2013 года Зеки и Майкл Атья задались вопросом: не связано ли и восприятие математической красоты с тем же отделом мозга? Новый опыт во многом повторял эксперименты 2004 и 2011 годов: 15 молодым математикам показали 60 формул – в списке были и знаменитые теоремы, и фундаментальные тождества и определения. Сначала испытуемые поставили каждой из них оценку по шкале от –5 (уродливая) до +5 (прекрасная). Спустя 2-3 недели им снова продемонстрировали все 60 формул одну за другой, но в другом порядке, параллельно наблюдая за функциональной магнитно-резонансной томограммой. Исследователи также попросили участников опыта оценить понятность каждой формулы – чтобы затем статистически разобраться с ловушкой “красиво – то, что понятно”.
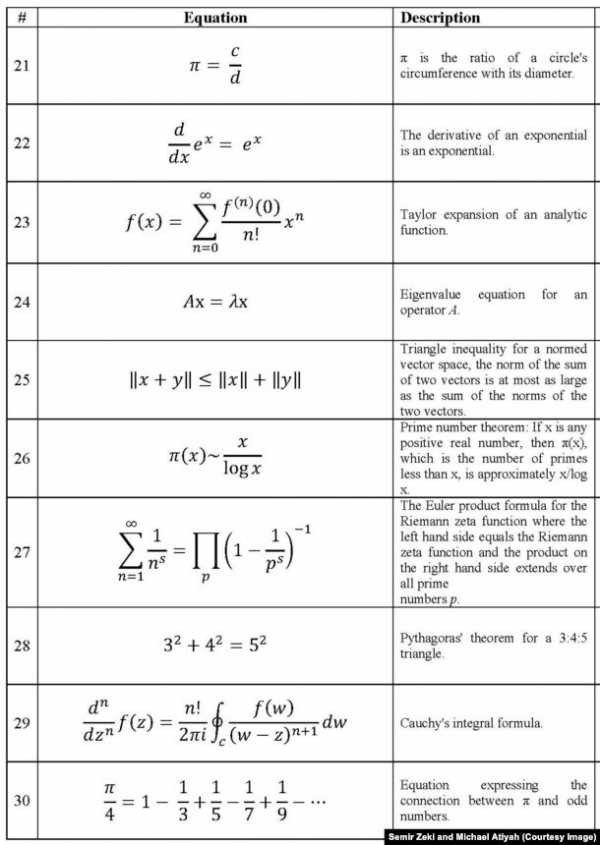
Третья часть формул из эксперимента Атьи и Зеки
Скорее любопытными, чем существенными с научной точки зрения оказались результаты субъективной оценки красоты формул из списка. Лучшую среднюю оценку (3,375) с заметным отрывом от других получила формула Эйлера, номер 1 в списке, связывающая самые важные математические константы: 0, 1, e, Pi, корень из минус единицы и три действия – сложение, умножение и возведение в степень, причем каждая константа и каждое действие участвуют в формуле только один раз. Действительно, это выражение в элементарном виде связывает чрезвычайно далекие на первый взгляд области математики; легко предположить, что формула Эйлера была бы названа самым красивым математическим тождеством и при глобальном опросе. Самой уродливой, опять же, с большим отрывом от остальных (средний балл –1,687), оказалась формула Рамануджана (номер 14 в списке) для разложения в ряд 1/Pi – в списке не было более громоздкого и несимметричного выражения. В то же время, эта внешне уродливая формула чрезвычайно полезна для инженеров – с ее помощью можно быстро получать приближенные значения числа Pi. Даже первый член ряда (для k=1) дает значение Pi с точностью до шестого знака после запятой. Можно найти в тождестве Рамануджана и абстрактную красоту – она связывает фундаментальную константу, описывающую свойства правильной окружности, с чрезвычайно прихотливо выбранными числами – 9801, 1103, 396 и 26390. Почему именно они дают возможность вычислить Pi? Чем хуже какие-нибудь другие числа, например, условные 1110, 47569, 7890 и 515? В несимметричности устройства природы тоже легко обнаружить прекрасное.
А вот значимым результатом опыта оказалось подтверждение гипотезы – различие в восприятии красивых формул по сравнению с уродливыми и нейтральными отражалось в первую очередь (хотя и не исключительно) в работе той же зоны мозга, медиальной орбитофронтальной коры, что и восприятие художественной красоты в эксперименте десятилетней давности. Значит ли это, что математическая и художественная красота влияют на нас схожим образом, что у этого чувственного опыта одинаковая физиологическая подоплека? Видимо, отчасти это верно. С другой стороны, низкий балл формулы Рамануджана говорит о том, что как минимум отчасти при оценке учитывались внешние характеристики записи выражения – его краткость и симметричность. Естественно, что такое восприятие красоты очень похоже на восприятие художественного полотна и задействует те же участки мозга.
Красота и математические племена
А как быть с той стороной математической красоты, которая определила выбор Анатолия Вершика, – с изяществом, глубиной и проникновением в подлинную суть природы? В середине октября американский математик Дэвид Мамфорд, как и Майкл Атья, лауреат «математического Нобеля», Филдсовской медали, ответил на статью Зеки и Атьи пространным эссе “Математика, красота и отделы мозга”. Мамфорд подчеркивает, что его рассуждения основаны не на строгом научном методе, а на собственном богатом опыте и общении с крупнейшими математическими мыслителями 20-го и 21-го века. Мамфорд предлагает разделить математиков на четыре группы (или “племени”) по тому, что движет ими в исследовательской работе – “в путешествии по эзотерическому миру”, как формулирует автор. Эти группы – Первооткрыватели, Алхимики, Борцы и Детективы.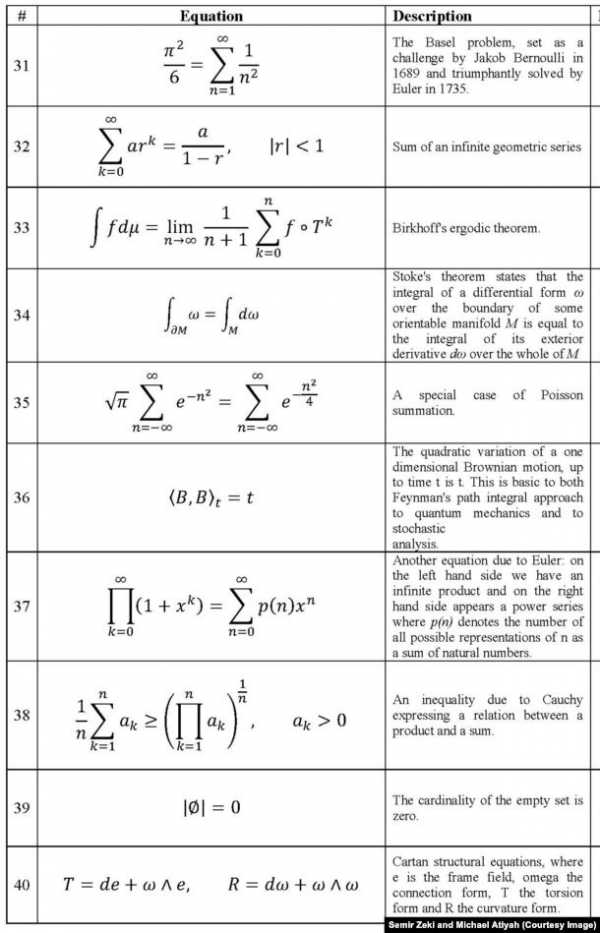
Четвертая часть формул из эксперимента Атьи и Зеки
К Первооткрывателям американский ученый относит исследователей, которые, подобно путешественникам прошлого, исследуют малоизведанные математические континенты и открывают новые материки. Среди Первооткрывателей Мамфорд выделяет Собирателей драгоценных камней, для которых важнее всего найти новый математический объект, и Картографов, которые прокладывают на новых землях маршруты, по которым вслед за Первооткрывателями пройдут другие ученые.
К числу первооткрывателей относятся, например, античные математики, когда-то нашедшие все правильные многогранники – трехмерные многогранники, каждая грань которых – правильный многоугольник, а в каждой вершине сходится одинаковое число ребер. Таких многогранников существует только пять – тетраэдр, октаэдр, икосаэдр, куб и додекаэдр. По всей видимости, три из них были известны еще Пифагору, но еще два, октаэдр и икосаэдр, были открыты Таэтетом Афинским только 100 лет спустя. Как могло быть сделано такое открытие? Наитие, фантазия, пространственное воображение, озарение – вот главные инструменты Первооткрывателей, которых среди математиков много и сегодня. Конечно же, не все из них геометры, так, Дэвид Мамфорт упоминает американского математика Майка Артина, построившего теорию так называемых некоммутативных колец – абстрактных математических структур, в которых объекты можно складывать и перемножать, но x умножить на y не обязательно равно y умножить на x. Вряд ли сам Артин мог бы рассказать, как ему удалось наткнуться на этот богатейший математический материк, но воображение, способность представлять себе геометрические фигуры, свойственная многим Первооткрывателям, вряд ли сыграла здесь роль. Согласно апокрифу, когда алгебраиста Ирвина Каплански спросили, что он видит, когда думает о кольце (ring), он ответил: “Я вижу букву R”, то есть стандартное обозначение кольца в математической записи.
Мамфорд отмечает, что из 60 формул исследования Зеки и Атьи только три (с номерами 12, 15 и 28), так или иначе, имели отношение к открытиям Первооткрывателей. Но разве мало красоты в способности человека к озарению – и имеет ли эта красота отношение к визуальному восприятию прекрасного?
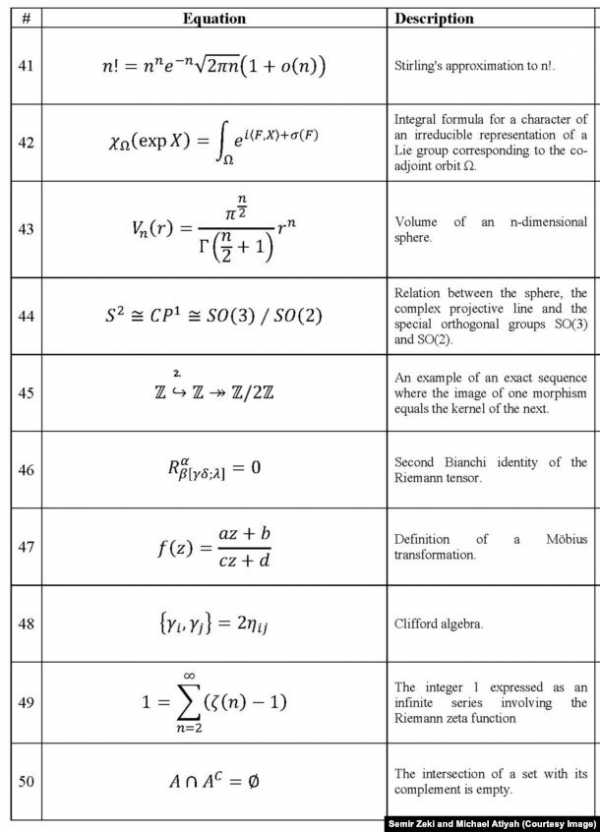
Пятая часть формул из эксперимента Атьи и Зеки
Второе математическое племя – Алхимики. Источник их вдохновения – скрытые связи между различными математическими областями. Обнаружение таких связей, похоже, по словам Мамфорда, “как если бы мы налили содержимое одной мензурки в другую и получили бы что-то удивительное, подобное взрыву”. Алхимической можно назвать связь между трисекцией угла и поиском корней многочлена третьей степени, найденную в эпоху Возрождения. Связывающая e, Pi и корень из минус единицы формула Эйлера – тоже, безусловно, алхимическая. Но и формула Рамануджана, в которой Pi выражено через несколько чисел, могла быть придумана только Алхимиком. Красота математической алхимии – в обнажении общности законов природы, она как раз того рода, что заставила сделать свой выбор Анатолия Вершика.
Третья группа – Борцы. Хотя математика точная наука, в ней слишком много объектов и величин, которые мы можем оценить, только сравнивая друг с другом. Хлеб Борцов – сравнения, асимптотические приближения, приближенные оценки. Характерным плодом Борца в списке Зеки – Атьи является формула Стирлинга для факториала (номер 41 в списке). Факториал натурального числа N – это произведение всех чисел от 1 до N. Такая функция повсеместно встречается в математике – от комбинаторики и теории вероятностей, где факториалы позволяют подсчитывать число событий определенного рода, до анализа, где они возникают, например, при разложении в ряд. Но факториалы неудобны, математикам куда проще обращаться с показательными функциями и экспонентами и перейти от одного к другому позволяет – пусть и асимптотически – как раз формула Стирлинга. “Важно осознавать, что за пределами чистой математики именно неравенства играют центральную роль в экономике, компьютерных науках, статистике, теории игр и исследовании операций. Возможно, обсессия тождествами – аберрация, уникальная для специалистов в чистой математике, – тогда как реальный мир управляется неравенствами”, – пишет Мамфорд. Математическая красота, которой добиваются Борцы, – не в последнюю очередь красота способности математики сложить людям на практике, в которой этой точной науке так часто наивно отказывают.
Обычное состояние математика – находиться в тупике
Наконец, последние – Детективы. Это люди, цель которых – раскрыть большое дело, найти решение какой-то особенно важной и глубокой задачи. Они повсюду ищут улики, они могут вскрыть в комнате паркет, надеясь найти под ним другой уровень объяснения. Они пользуются плодами Первооткрывателей, Алхимиков и Борцов, но ради своей собственной цели. И продвижение дается дорого: “Обычное состояние математика – находиться в тупике”, – говорил американский математик Питер Сарнак. Типичный детектив – Эндрю Уайлз, доказавший не поддававшуюся никому три с половиной века Большую теорему Ферма (номер 58 в списке). Еще один Детектив – Григорий Перельман, за несколько лет аскетического затворничества разобравшийся с гипотезой Пуанкаре. Именно такие люди становятся образцами для массового архетипа математика – гении, посвятившие себя решению абстрактной головоломки. И даже если путь к доказательству не обязательно окажется изящным, подвиг их разума, нашедшего выход из вечного тупика, красив особой красотой, не похожей на красоту открытий остальных математических племен.
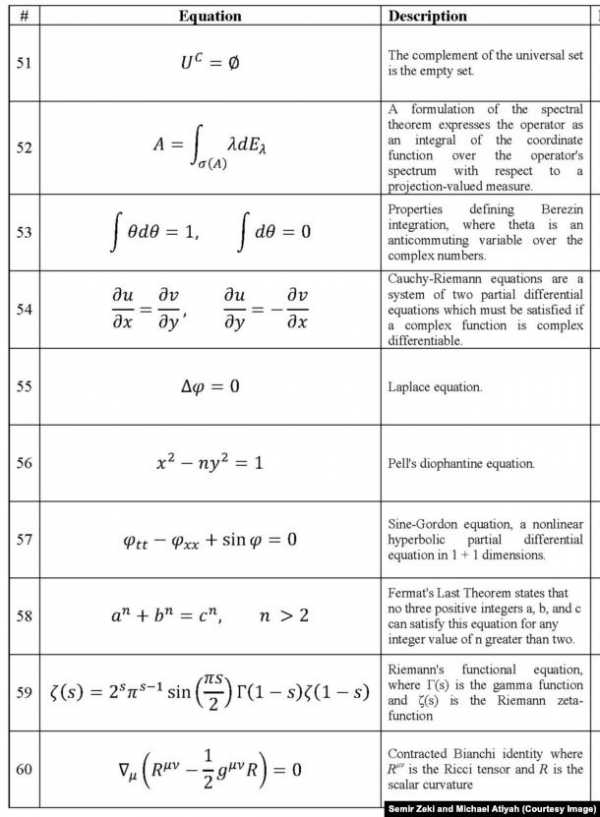
Шестая часть формул из эксперимента Атьи и Зеки
Мамфорд отмечает, что для каждой из четырех групп – Первооткрывателей, Алхимиков, Борцов и Детективов можно подобрать отдел мозга, наиболее соответствующий их методам, и это будут разные участки мозга, а не одна только медиальная орбитофронтальная кора. Но даже такая попытка описать физиологическую основу математической красоты – спекуляция. “Предвидение нового абстрактного мира, раскрытие новых тайн, построение глобальных иерархий и решение сложнейших головоломок – вот четыре аспекта математики, которые ученые находят наиболее красивыми, – заключает Дэвид Мамфорд. – Но каждый из этих характерных видов красоты связан с различными видами ментальной деятельности. Можно ли надеяться связать каждую из них с конкретной зоной мозга?” Действительно, исследование Зеки и Атьи, основанное на достаточно ограниченном эксперименте, доказывает лишь то, что восприятие математической красоты в одном из ее аспектов в чем-то похоже на восприятие каких-то граней художественной или музыкальной красоты.
***
Но есть ли что-то в математической красоте, объединяющее все ее ипостаси, описанные Мамфордом, и фундаментально отличающее ее от других видов прекрасного (а может, наоборот – связывающее с ними)? “Платон считал математическую красоту высшей формой прекрасного, – пишут Семир Зеки и Майкл Атья, – ведь она происходит из чистого разума и связана с вечной и неизменной истиной”.
Именно те правила, которые кажутся интересными математику, и выбрала природа
Анатолий Вершик написал на доске формулировку Большой эргодической теоремы, потому что она, плод чистого разума, описывает глубинное устройство природы. “Математик играет в игру, правила для которой он выдумывает сам, физик играет игру по правилам, которые даны природой, – писал один из создателей квантовой механики, Нобелевский лауреат Поль Дирак в 1939 году. – Но со временем становится все более очевидно, что именно те правила, которые кажутся интересными математику, и выбрала природа”. Красота математики – в способности увидеть истинную суть вещей. Пожалуй, это относится к любой красоте.
a.kras.cc

