Таблица деления (математика для детей, 2, 3 класс)

На 1
1 ÷ 1 = 1
2 ÷ 1 = 2
3 ÷ 1 = 3
4 ÷ 1 = 4
5 ÷ 1 = 5
6 ÷ 1 = 6
7 ÷ 1 = 7
8 ÷ 1 = 8
9 ÷ 1 = 9
10 ÷ 1 = 10

На 2
2 ÷ 2 = 1
4 ÷ 2 = 2
6 ÷ 2 = 3
8 ÷ 2 = 4
10 ÷ 2 = 5
12 ÷ 2 = 6
14 ÷ 2 = 7
16 ÷ 2 = 8
18 ÷ 2 = 9
20 ÷ 2 = 10

На 3
3 ÷ 3 = 1
6 ÷ 3 = 2
9 ÷ 3 = 3
12 ÷ 3 = 4
15 ÷ 3 = 5
18 ÷ 3 = 6
21 ÷ 3 = 7
24 ÷ 3 = 8
27 ÷ 3 = 9
30 ÷ 3 = 10

На 4
4 ÷ 4 = 1
8 ÷ 4 = 2
12 ÷ 4 = 3
16 ÷ 4 = 4
20 ÷ 4 = 5
24 ÷ 4 = 6
28 ÷ 4 = 7
32 ÷ 4 = 8
36 ÷ 4 = 9
40 ÷ 4 = 10

На 5
5 ÷ 5 = 1
10 ÷ 5 = 2
15 ÷ 5 = 3
20 ÷ 5 = 4
25 ÷ 5 = 5
30 ÷ 5 = 6
35 ÷ 5 = 7
40 ÷ 5 = 8
45 ÷ 5 = 9
50 ÷ 5 = 10

На 6
6 ÷ 6 = 1
12 ÷ 6 = 2
18 ÷ 6 = 3
24 ÷ 6 = 4
30 ÷ 6 = 5
36 ÷ 6 = 6
42 ÷ 6 = 7
48 ÷ 6 = 8
54 ÷ 6 = 9
60 ÷ 6 = 10

На 7
7 ÷ 7 = 1
14 ÷ 7 = 2
21 ÷ 7 = 3
28 ÷ 7 = 4
35 ÷ 7 = 5
42 ÷ 7 = 6
49 ÷ 7 = 7
56 ÷ 7 = 8
63 ÷ 7 = 9
70 ÷ 7 = 10

На 8
8 ÷ 8 = 1
16 ÷ 8 = 2
24 ÷ 8 = 3
32 ÷ 8 = 4
40 ÷ 8 = 5
48 ÷ 8 = 6
56 ÷ 8 = 7
64 ÷ 8 = 8
72 ÷ 8 = 9
80 ÷ 8 = 10

На 9
9 ÷ 9 = 1
18 ÷ 9 = 2
27 ÷ 9 = 3
36 ÷ 9 = 4
45 ÷ 9 = 5
54 ÷ 9 = 6
63 ÷ 9 = 7
72 ÷ 9 = 8
81 ÷ 9 = 9
90 ÷ 9 = 10

На 10
10 ÷ 10 = 1
20 ÷ 10 = 2
30 ÷ 10 = 3
40 ÷ 10 = 4
50 ÷ 10 = 5
60 ÷ 10 = 6
70 ÷ 10 = 7
80 ÷ 10 = 8
90 ÷ 10 = 9
100 ÷ 10 = 10

(на 0 делить нельзя)

Учить таблицу деления — игра

Математическим действием, которое противоположно умножению, называется деление. Деление обозначается дробной чертой или знаком «:». Число, которое делится, называется «делимым». Делимое всегда находится в числителе дроби – над дробной чертой. Число, на которое делят, называется «делителем». Делитель всегда находится в знаменателе дроби – под дробной чертой. Результат деления называется «частным». Частное всегда положительно, если делятся положительные числа. Если одно из двух чисел, делимое или делитель, отрицательно, результат получается отрицательным – плюс на минус дает минус, минус на плюс дает минус. При делении отрицательного числа на отрицательное получается положительное число – минус на минус дает плюс. Из результатов деления получается таблица деления. Её можно представить правильными или десятичными дробями.

Таблица деления в виде картинки

Чтобы распечатать, скопируйте картинку в любой редактор. Обычно таблицу деления дети проходят на математике в третьем классе.

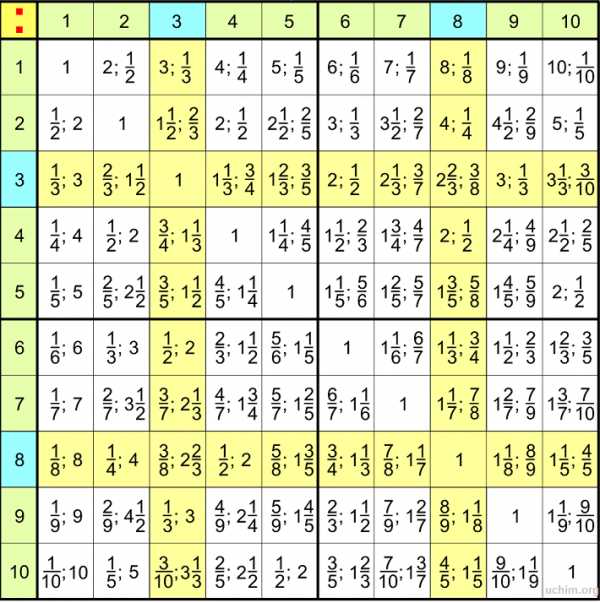
Открыть в отдельном окне в полном размере

Деление онлайн

/

Посмотрите также видео о делении в столбик.

Таблица деления для этого может пригодиться.

Всё для учебы » Математика в школе » Таблица деления (математика для детей, 2, 3 класс)

Группа с кучей полезной информации (подпишитесь, если предстоит ЕГЭ или ОГЭ):

uchim.org

Деление на 2 и с ответом 2

- Здравствуйте, ребята! Знаете, вчера наши любимые знаки Плюс и Минус ходили на рынок и принесли много разных фруктов. А потом они чуть не поссорились из-за того, что никак не могли разобраться, по сколько фруктов должен взять каждый из них так, чтобы получилось поровну. Каждый из них должен был взять половину купленных фруктов. А что для этого надо было сделать? Конечно, разделить каждый вид фруктов на две равные части.

Хорошо, что Плюс и Минус настоящие друзья. Поэтому они не стали ссориться, а пришли ко мне, и я объяснила им, как нужно делить на два, то есть находить половину. А сейчас я расскажу это и вам, чтобы и вам не приходилось ссориться по пустякам.

Итак, начнём. Я уверена, что вы уже выучили таблицу умножения на два. А кто до сих пор это не сделал, обязательно доучит её. Ведь именно таблица умножения поможет вам справиться с делением. Давайте вспомним её. А поможет нам песенка-считалка Плюса:

А теперь я расскажу, как мы со знаками делили фрукты. Кстати, вы помните, что при умножении на 2 в ответах получаются чётные числа? И делить на 2 можно тоже только чётные числа. Вот, например, манго у друзей было 3, число нечётное, и пополам его разделить невозможно. Друзья, нет-нет, не подрались, а взяли каждый по одному, а третье принесли мне.

Стали делить персики. Их 6. 6 разделить на 2. Можно, конечно, раскладывать по одному Но лучше, конечно, воспользоваться знанием таблицы умножения. Ведь вы уже знаете, как связаны между собой действия умножение и деление. Если произведение двух множителей разделить на один из них, то получится другой множитель. 6 получается в результате умножения чисел 2 и 3. Значит, получится:

А как на двоих поровну разделить 8 апельсинов? Восемь мы получаем в результате умножения 4 на 2. Значит получим:

Делим на две половины 18 яблок. 18 — это произведение чисел 9 и 2. Поэтому получаем:

Кстати, хочу вам заметить. Представляете, иногда можно услышать от людей такие фразы: «большая половина» или «меньшая половина». Такие слова меня просто в ужас приводят! Как половина может быть большей или меньшей? Половина всегда равна другой половине. А большей или меньшей может быть только часть чего-либо.

Но вернёмся к нашему делению на 2. Ну что, друзья мои, вы поняли, как находить результат деления на 2? На основе умножения на 2. А сейчас мы с вами составим таблицу деления на два. Сначала запишем таблицу умножения, и напротив каждого примера запишем пример на деление на 2:

Но это ещё не всё. Вы знаете такое правило: Если произведение двух множителей разделить на один из них, то получится другой множитель.

Мы с вами делили пока только на один множитель — 2. А теперь давайте попробуем составить таблицу, в которой делителем будет выступать не число 2, а второй множитель:

Эти примеры тоже составляются на основе умножения. Видите, как важно уверенно знать наизусть таблицу умножения. Она поможет вам быстро и безошибочно выполнять не только действие умножения, но и деление на два и с ответом два. Но и эти таблицы деления, которые мы сегодня составили, постарайтесь тоже выучить. Во-первых, вы решать будете значительно быстрее, и конечно, отметки получать отличные. А во-вторых, скажу вам по секрету, чем больше мы заучиваем наизусть, тем лучше становится наша память.

И ещё хочу поделиться маленьким секретом. Когда будете учить таблицу, не просто проговаривайте её, а ещё и записывайте эти примеры. Тогда вы запомните её гораздо быстрее. Ну что же, пришло время нам попрощаться. Я удаляюсь — меня ждут дела нашего государства. А вам я предлагаю ещё раз внимательно посмотреть на таблицы и постараться запомнить их. Успехов вам, друзья мои!

videouroki.net

Математика во 2 классе. Тема. Деление на 2.

Математика во 2 классе

Тема. Деление на 2. (Уч. с. 83)

Цели: закреплять знание учащимися таблицы умножения на 2, продолжать формировать умения учеников находить значение частного, опираясь на соответствующий пример на умножение, решать задачи действием деления; развивать навыки счёта, умение выполнять чертежи.

Планируемые результаты

Предметные. Составят таблицу деления на 2 на основе связи между компонентами действия умножения; научатся решать задачи на деление; отработают вычислительные навыки; выполнят задания на развитие математическою смекалки.

УУД. Регулятивные : применять установленные правила в планировании способа решения; активизировать свои силы и энергию к волевому усилию в ситуации мотивационного конфликта

Познавательные : владеть общими приемами решения задач. Коммуникативные : осуществлять взаимный контроль; проявлять активность во взаимодействии для решения коммуникативных и познавательных задач.

Личностные результаты. Проявляют познавательную инициативу в оказании помощи соученикам; адекватно понимают причины успешности / неуспешности учебной деятельности.

Ход урока

I. Мотивирование к учебной деятельности.

II. Каллиграфическая минутка.

18 18 18 18 18

20 20 20 20 20

III. Устный счет.

1. Какое число больше на 9, чем 25? 36? 47?

Какое число меньше на 8, чем 51? 62? 73?

2. Найдите значение произведения:

k · 10, если:

k = 1

k = 3

k = 5

k = 8

k = 10

Найдите значение частного k : 10, если:

k = 70

k = 90

k =100

IV. Умножение и деление на 2.

1. – Рассмотрите рисунки в задании 1 (с. 83 учебника, часть 2).

– Соотнесите рисунки с произведениями, записанными ниже.

– Как получены частные в каждом столбике?

– Опираясь на произведения, найдите значения частных.

Работа выполняется фронтально.

2. С комментированием выполняется задание 2 (с. 83 учебника, часть 2).

V. Работа над задачами.

1. Учащиеся читают задачу 3 (с. 83 учебника, часть 2).

– Что в задаче известно?

– Что требуется узнать?

– Каким действием будете решать задачу?

– Почему?

– Запишите решение. (18 : 2)

– Какая строчка таблицы умножения поможет найти ответ? (2· 9 = 18.)

– Чему будет равно значение частного? (Девяти.)

2. Аналогично разбирается задача 4 (с. 83 учебника, часть 2).

3. Прочитать текст в задании 5 (с. 83 учебника, часть 2).

– Вы прочитали задачу?

– Почему так считаете?

– Задайте вопрос так, чтобы получилась составная задача. (Сколько денег было у Саши?)

– Рассмотрите выражения:

8 – 5 8 + 5 8 + 5 + 2

– Скажите: какое из них является решением задачи? (8 + 5 + 2.)

– Что узнаете, решив оставшиеся выражения?

8 – 5

– На сколько ручка дороже ластика? На сколько ластик дешевле ручки?

8 + 5

– Сколько Саша заплатил за ластик и ручку вместе?

VI. Работа с геометрическим материалом (задание 6)

– Рассмотрите чертёж на полях с. 83 (учебник, часть 2).

– Как называется изображённая линия?

– Сколько звеньев в данной линии? (4)

– Узнайте длину каждого звена.

– Что заметили? (Все звенья имеют одинаковую длину – 2 см.)

– Как можно найти длину этой ломаной? (Умножением.)

– Запишите решение. (2 · 4.)

– Начертите квадрат, периметр, которого будет равен длине этой ломаной.

– Как найдёте длину стороны квадрата?

(Делением, 8: 4 = 2 (см).)

VII. Итог урока. Рефлексия.

– Чему научил вас урок?

– Что было особенно интересно?

– Всё ли было понятно?

– Как вы сегодня работали?

infourok.ru

Деление / Справочник по математике для начальной школы

1. Главная
2. Справочники
3. Справочник по математике для начальной школы
4. Деление

В этом разделе познакомимся с делением и узнаем, что деление – это математическая операция, обратная умножению.

Умножение – это последовательное сложение чисел, а деление – это последовательное вычитание чисел.

В математике существует знак для умножения — это точка ( • ) посередине строки между числами, которые нужно перемножить, а для деления существует особый знак — это две точки ( : ) между числами, которые нужно поделить между собой.

Как ёжикам поделить между собой яблоки поровну?

Нужно воспользоваться действием деления и узнать, сколько раз по 3 содержится в 6.

1) 6 : 3 = 2 (яб.) — мы узнали, сколько яблок получит каждый ёжик.

2) 6 : 2 = 3 (ёж.) — мы узнали, сколько ёжиков получат по 2 яблока.

3) 2 • 3 = 6 (яб.) — мы узнали, сколько яблок нужно, чтобы у каждого из трёх ёжиков было по 2 яблока.

---

Любой пример на умножение можно представить двумя примерами на деление.

Например, для выражения 6 • 4 = 24 есть два обратных выражения:

24 : 4 = 6 — нужно из 24 вычесть число 4 ровно 6 раз.

24 : 6 = 4 — нужно из 24 вычесть число 6 ровно 4 раз.

---

Числа при делении

При делении, как и при другом математическом действии, каждое число имеет свое название.

Число, которое делят, называется делимое.

Число, на которое делят, называется делитель.

Результат деления называется частное.

---

Чтение числовых выражений

24 : 6 = 4

Этот пример можно прочитать по-разному.

• 24 разделить на 6 равняется 4.
• 24 уменьшить в 6 раз – получится 4.
• Делимое – 24, делитель – 6, частное – 4.
• Частное от деления числа 24 на 6 равно 4.

---

Деление на 1

4 : 1 = 4

23 : 1 = 23

---

Деление на 0

---

Деление числа само на себя

---

Связь деления и умножения

---

Чётные и нечётные числа

Числа, которые делятся на 2 без остатка, назы­ваются чётными, а числа, которые не делятся на 2 без остатка, называются нечётными.

Чётные: 6, 22 44, 60, 74, 82, 96

Нечётные: 7, 13, 21, 37, 45, 97

---

В несколько раз меньше

Для примера решим задачу:

В магазине было 8 котят, а лисичек в 4 раза меньше. Сколько было лисичек?

составим схему:

Значит, чтобы узнать, сколько было лисичек, нужно 8 : 4 = 2 (л.)

Вывод: Если в задаче есть слова «в … раз меньше», то задача решается делением.

---

Во сколько раз больше? Во сколько раз меньше?

Например, решим задачу: В магазине было 8 котят и 2 лисички. Во сколько раз котят было больше, чем лисичек? Во сколько раз лисичек было меньше, чем котят?

Чтобы ответить на эти вопросы, нужно узнать, сколько раз по 2 содержится в 8?

8 : 2 = 4 (раза)

Значит, котят в 4 раза больше, чем лисичек, а лисичек в 4 раза меньше, чем котят.

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Табличное деление

Внетабличное деление

Деление с остатком

Деление суммы на число

Деление на однозначное число

Деление чисел, оканчивающихся нулями

Деление на двузначное и трёхзначное число

Правило встречается в следующих упражнениях:

2 класс

Страница 57. Вариант 2. № 3, Моро, Волкова, Проверочные работы

Страница 58. Вариант 1. № 1, Моро, Волкова, Проверочные работы

Страница 58, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 59, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 64, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 66, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 74, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 83, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 103, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 71, Моро, Волкова, Рабочая тетрадь, 2 часть

3 класс

Страница 58, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 87, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 108, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 111, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 55, Моро, Волкова, Рабочая тетрадь, 1 часть

Страница 56, Моро, Волкова, Рабочая тетрадь, 1 часть

Страница 72, Моро, Волкова, Рабочая тетрадь, 1 часть

Страница 11, Моро, Волкова, Рабочая тетрадь, 2 часть

Страница 25, Моро, Волкова, Рабочая тетрадь, 2 часть

Страница 32, Моро, Волкова, Рабочая тетрадь, 2 часть

5 класс

Упражнение 36, Мерзляк, Полонский, Якир, Учебник

Упражнение 1, Мерзляк, Полонский, Якир, Учебник

---

© 2019 — budu5.com, Буду отличником!

budu5.com

Деление столбиком на двузначное число

Деление столбиком или, правильнее сказать, письменный прием деления уголком, школьники проходят уже в третьем классе начальной школы, но зачастую этой теме уделяется так мало внимания, что к 9-11 классу не все ученики могут им свободно пользоваться. Деление столбиком на двузначное число проходят в 4 классе, как и деление на трехзначное число, а далее этот прием используется только как вспомогательный при решении каких-либо уравнений или нахождении значения выражения.

Очевидно, что уделив делению столбиком больше внимания, чем заложено в школьной программе, ребенок облегчит себе выполнение заданий по математике вплоть до 11 класса. А для этого нужно немногое — понять тему и позаниматься, порешать, держа алгоритм в голове, довести навык вычисления до автоматизма.

Алгоритм деления столбиком на двузначное число

Как и при делении на однозначное число, будем последовательно переходить от деления более крупных счетных единиц к делению более мелких единиц.

1. Находим первое неполное делимое. Это число, которое делится на делитель с получением числа больше или равного 1. Это значит, что первое неполное делимое всегда больше делителя. При делении на двузначное число в первом неполном делимом минимум 2 знака. 

           Примеры        768:24. Первое неполное делимое 76
                                265:53  26 меньше 53, значит не подходит. Нужно добавить следующую цифру (5). Первое неполное делимое 265.

2. Определяем количество цифр в частном. Для определения числа цифр в частном следует помнить, что неполному делимому соответствует одна цифра частного, а всем остальным цифрам делимого — еще по одной цифре частного.

           Примеры       768:24. Первое неполное делимое 76. Ему соответствует 1 цифра частного. После первого неполного делителя есть еще одна цифра. Значит в частном будет всего 2 цифры.
                                265:53. Первое неполное делимое 265. Оно даст 1 цифру частного. Больше в делимом цифр нет. Значит в частном будет всего 1 цифра.
                               15344:56. Первое неполное делимое 153, а после него еще 2 цифры. Значит в частном будет всего 3 цифры.

3. Находим цифры в каждом разряде частного. Сначала найдем первую цифру частного. Подбираем такое целое число, чтобы при умножении его на наш делитель получилось число, максимально приближенное к первому неполному делимому. Цифру частного записываем под уголок, а значение произведения вычитаем столбиком из неполного делителя. Записываем остаток. Проверяем, что он меньше делителя.

Затем находим вторую цифру частного. Переписываем в строку с остатком цифру, следующую за первым неполным делителем в делимом. Полученное неполное делимое снова делим на делитель и так находим каждое последующее число частного, пока не закончатся цифры делителя.

4. Находим остаток (если есть).

Если цифры частного закончились и получился остаток 0, то деление выполнено без остатка. В ином случае значение частного записывается с остатком.

Так же выполняется деление на любое многозначное число (трехзначное, четырехзначное и т. д.)

Разбор примеров на деление столбиком на двузначное число

Сначала рассмотрим простые случаи деления, когда в частном получается однозначное число.

— Найдем значение частного чисел 265 и 53.

Первое неполное делимое 265. Больше в делимом цифр нет. Значит в частном будет однозначное число.

  

Чтобы было легче подобрать цифру частного, разделим 265 не на 53, а на близкое круглое число 50. Для этого 265 разделим на 10, будет 26 (остаток 5). И 26 разделим на 5, будет 5 (остаток 1). Цифру 5 нельзя сразу записывать в частном, поскольку это пробная цифра. Сначала нужно проверить, подойдет ли она. Умножим 53*5=265. Мы видим, что цифра 5 подошла. И теперь можем ее записать в частном под уголок. 265-265=0. Деление выполнено без остатка.

Значение частного чисел 265 и 53 равно 5.

Иногда при делении пробная цифра частного не подходит, и тогда ее нужно менять.

— Найдем значение частного чисел 184 и 23.

В частном будет однозначное число. 

Чтобы было легче подобрать цифру частного, разделим 184 не на 23, а на 20. Для этого разделим 184 на 10, будет 18 (остаток 4). И 18 разделим на 2, будет 9. 9 – это пробная цифра, мы ее сразу писать в частном не будем, а проверим, подойдет ли она. Умножим 23*9=207. 207 больше, чем 184. Мы видим, что цифра 9 не подходит. В частном будет меньше 9. Попробуем, подойдет ли цифра 8. Умножим 23*8=184. Мы видим, что цифра 8 подходит. Можем ее записать в частном. 184-184=0. Деление выполнено без остатка.

Значение частного чисел 184 и 23 равно 8.

Рассмотрим более сложные случаи деления.

— Найдем значение частного чисел 768 и 24.

Первое неполное делимое – 76 десятков. Значит, в частном будут 2 цифры.

Определим первую цифру частного. Разделим 76 на 24. Чтобы легче было подобрать цифру частного, разделим 76 не на 24, а на 20. То есть нужно 76 разделить на 10, будет 7 (остаток 6). И 7 разделим на 2, получится 3 (остаток 1). 3 – это пробная цифра частного. Сначала проверим, подойдет ли она. Умножим 24*3=72 . 76-72=4. Остаток меньше делителя. Значит, цифра 3 подошла и теперь мы ее можем записать на месте десятков частного. 72 пишем под первым неполным делимым, между ними ставим знак минус, под чертой записываем остаток.

Продолжим деление. Перепишем в строку с остатком цифру 8, следующую за первым неполным делимым. Получим следующее неполное делимое – 48 единиц. Разделим 48 на 24. Чтобы было легче подобрать цифру частного, разделим 48 не на 24, а на 20. То есть разделим 48 на 10, будет 4 (остаток 8). И 4 разделим на 2, будет 2. Это пробная цифра частного. Мы должны сначала проверить, подойдет ли она. Умножим 24*2=48. Мы видим, что цифра 2 подошла и, значит, можем ее записать на месте единиц частного. 48-48=0, деление выполнено без остатка.

 Значение частного чисел 768 и 24 равно 32.

— Найдем значение частного чисел 15344 и 56.

Первое неполное делимое – 153 сотни, значит, в частном будут три цифры.

Определим первую цифру частного. Разделим 153 на 56. Чтобы легче было подобрать цифру частного, разделим 153 не на 56, а на 50. Для этого разделим 153 на 10, будет 15 (остаток 3). И 15 разделим на 5, будет 3. 3 – это пробная цифра частного. Помните: ее нельзя сразу записывать в частном, а нужно сначала проверить, подойдет ли она. Умножим 56*3=168. 168 больше, чем 153. Значит, в частном будет меньше, чем 3. Проверим, подойдет ли цифра 2. Умножим 56*2=112. 153-112=41. Остаток меньше делителя, значит, цифра 2 подходит, ее можно записать на месте сотен в частном.

Образуем следующее неполное делимое. 153-112=41. Переписываем в ту же строку цифру 4, следующую за первым неполным делимым. Получаем второе неполное делимое  414 десятков. Разделим 414 на 56. Чтобы удобнее было подобрать цифру частного, разделим 414 не на 56, а на 50. 414:10=41(ост.4). 41:5=8(ост.1). Помните: 8 – это пробная цифра. Проверим ее. 56*8=448. 448 больше, чем 414, значит, в частном будет меньше, чем 8. Проверим, подойдет ли цифра 7. Умножим 56 на 7, получится 392. 414-392=22. Остаток меньше делителя. Значит, цифра подошла и в частном на месте десятков можем записать 7.

Пишем в строку с новым остатком 4 единицы. Значит следующее неполное делимое – 224 единицы. Продолжим деление. Разделим 224 на 56. Чтобы легче было подобрать цифру частного, разделим 224 на 50. То есть сначала на 10, будет 22 (остаток 4). И 22 разделим на 5, будет 4 (остаток 2). 4 – это пробная цифра, проверим ее, подойдет ли она. 56*4=224. И мы видим, что цифра подошла. Запишем 4 на месте единиц в частном. 224-224=0, деление выполнено без остатка.

Значение частного чисел 15344 и 56 равно 274.

Пример на деление с остатком

Чтобы провести аналогию, возьмем пример, похожий на пример выше, и отличающийся лишь последней цифрой

— Найдем значение частного чисел 15345:56

Делим сначала точно так же, как в примере 15344:56, пока не дойдем до последнего неполного делимого 225. Разделим 225 на 56. Чтобы легче было подобрать цифру частного, разделим 225 на 50. То есть сначала на 10, будет 22 (остаток 5). И 22 разделим на 5, будет 4 (остаток 2). 4 – это пробная цифра, проверим ее, подойдет ли она. 56*4=224. И мы видим, что цифра подошла. Запишем 4 на месте единиц в частном. 225-224=1, деление выполнено с остатком.

Значение частного чисел 15345 и 56 равно 274 (остаток 1).

Деление с нулем в частном

Иногда в частном одним из чисел получается 0, и дети зачастую пропускают его, отсюда неправильное решение. Разберем, откуда может взяться 0 и как его не забыть.

— Найдем значение частного чисел 2870:14

Первое неполное делимое — 28 сотен. Значит в частном будет 3 цифры. Ставим под уголок три точки. Это важный момент. Если ребенок потеряет ноль, останется лишняя точка, которая заставит задуматься, что где-то упущена цифра.

Определим первую цифру частного. Разделим 28 на 14. Подбором получается 2. Проверим, подойдет ли цифра 2. Умножим 14*2=28. Цифра 2 подходит, ее можно записать на месте сотен в частном. 28-28=0.

Получился нулевой остаток. Мы обозначили его розовым для наглядности, но записывать его не нужно. Переписываем в строку с остатком цифру 7 из делимого. Но 7 не делится на 14 с получением целого числа, поэтому записываем на месте десятков в частном 0.

Теперь переписываем в ту же строку последнюю цифру делимого (количество единиц).

70:14=5 Записываем вместо последней точки в частном цифру 5. 70-70=0. Остатка нет.

Значение частного чисел 2870 и 14 равно 205.

Деление нужно непременно проверить умножением.

Примеры на деление для самопроверки

Найдите первое неполное делимое и определите количество цифр в частном.

3432:66          2450:98         15145:65      18354:42     17323:17

Усвоили тему, а теперь потренируйтесь решить несколько примеров столбиком самостоятельно.

1428 : 42           30296 : 56           254415 : 35        16514 : 718

2924 : 68          136576 : 64          710278 : 91        15830 : 293

 

7gy.ru

3000 примеров по математике для 2 класса. Табличное умножение и деление

Три тысячи примеров от практикующего педагога Узоровой О. помогут второклассникам выучить математику «на отлично». Всевозможные случаи деления и умножения, дух соревновательности, насыщенность  и простота заданий делают сборник привлекательным для маленьких учеников.

“Примеры по математике для 2 класса. Умножение и деление” – тема элементарная и одновременно трудная. Дети сразу усваивают суть умножения, как суммы равнозначных слагаемых, но не в силах запомнить всю таблицу сразу. Можно механически зазубривать ответы вразброс. Но насколько увлекательнее решать примеры по математике 2 класс на умножение и деление в задачниках, в которых можно записывать ответы и даже свой результат! Таким образом, второклассники будут вынуждены вспоминать таблицу в произвольном порядке, тратя на это все меньше времени.

Примеры на умножение и деление по математике во 2 классе разделены на два блока: упражнения и коррекции недочетов. В конце работы второклассник сам оценивает, как быстро он решал примеры по математике 2 класс на умножение, и лучшее время отмечает в отдельной графе. А смайлики в нижней части листа подскажут второкласснику, хорошо ли он поработал.

Авторы пособия рекомендуют решать по 7 столбцов ежедневно. Но если ребенок отказывается решать все примеры, не настаивайте, ведь гораздо важнее, если второклассник считает примеры по математике с охотой. Так Вы сохраните в своем ребенке увлеченное отношение к предмету, а это большой плюс при изучении нового материала.

Скачивайте сборник примеров Узоровой О. в библиотеке нашего сайта, и Ваш второклассник научится умножать запросто!

Издательство: АСТ
Год издания: 2011
Автор: Узорова О.В.
Формат: PDF
Количество страниц: 16
Язык: Русский

 

Скачать бесплатно primeri_po_matematike_2_klass_umnogenie_i_delenie_uchebnik.pdf

www.vse-dlya-detey.ru

Приёмы деления для случаев вида 87:29 и 66:22. Видеоурок. Математика 3 Класс

На этом уроке мы научимся делить двузначные на двузначные числа. Познакомимся с методом подбора. Решим много интересных примеров и заданий. Отточим мастерство деления. Выучим новый материал и закрепим его путём решения заданий. Данный урок очень полезен, если вам надо научиться решать примеры, такие как, например, 81 ÷ 27 или 66 ÷ 22. Вы узнаете, что такое метод подбора, как он работает, как ним пользоваться для правильного решения задач.

Если необходимо решать примеры с делением двузначных чисел, то лучше всего использовать метод подбора. Но как он работает? Рассмотрим, например, такое выражение: . Будем решать его, рассуждая так. Умножим делитель на 2, получим 58 и сравним его с делимым.

;

Если полученное число меньше делимого, необходимо увеличивать число, на которое умножаем делитель, до тех пор, пока не получим нужное произведение, которое совпадает с делимым.

.

Таким образом:

.

Рассмотрим следующий пример: .

Следовательно:

.

Решите примеры методом подбора.

а)                   б)                   в)

Решение: 1. Для первого примера подберём необходимое частное:

.

2. Решим второй пример:

;

.

3. Решим последний пример:

.

Условие: сколько масла получится из 75 л молока (рис. 1), если из 50 л молока получается 2 кг масла?

Рис. 1. Молоко (Источник)

Решение: 1. Узнаем, сколько л молока идёт на 1 кг масла.

 (л)

2. Теперь, узнаем, сколько кг масла можно получить из 75 л молока.

 (кг)

3. Проверим результат.

 

.

На какие две группы можно разделить эти примеры?

а)                   в)                     д)                     е)

б)                     г)                     э)                   ё)

Решение: 1. Если мы внимательно посмотрим на выражения, то увидим, что их можно распределить на две группы. В одной группе будут те, у которых делитель – двузначное число, а во второй те, у которых делитель – однозначное число.

а)                   б)

э)                   в)

е)                   г)

ё)                   д)

2. Дальше применим наши знания для того, чтобы выполнить деление и заполнить таблицу 1.

Таблица 1. Деление чисел

	12	36	48	72
	1	3	4	6
	3	9	12	18

Решите самостоятельно задание № 2. Дайте ответы на вопросы. Полученные ответы сверьте с правильными.

1. На какое число нужно умножить 16, чтобы получить 64?

2. Во сколько раз число 54 больше, чем 3?

3. Чему равно частное чисел 96 и 32?

4. Какую цифру нужно приписать к 8 справа, чтобы полученное двузначное число можно было разделить на 7 и на 14?

Ответы: 1. 4; 2. 18; 3. 3; 4. 4.

 

Список литературы

1. Математика. 3 класс. Учеб. для общеобразоват. учреждений с прил. на электрон. носителе. В 2 ч. Ч. 1 / [М.И. Моро, М.А. Бантова, Г.В. Бельтюкова и др.] – 2-е изд. – М.: Просвещение, 2012. – 112 с.: ил. – (Школа России). 
2. Рудницкая В.Н., Юдачёва Т.В. Математика, 3 класс. – М.: ВЕНТАНА-ГРАФ.
3. Петерсон Л.Г. Математика, 3 класс. – М.: Ювента.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Kakprosto.ru (Источник).
2. Samouchka.com.ua (Источник).
3. 5fan.ru (Источник).

 

Домашнее задание

1. Математика. 3 класс. Учеб. для общеобразоват. учреждений с прил. на электрон. носителе. В 2 ч. Ч. 2 / [М.И. Моро, М.А. Бантова, Г.В. Бельтюкова и др.] – 2-е изд. – М.: Просвещение, 2012., ст. 18 № 1–3.
2. Раздели.
   а)                     б)                    
   в)                     г)
3. Выполни деление методом подбора.
   а)                   б)                  
   в)                   г)      

^*Заполни таблицу (табл. 2)

Таблица 2. Определение частного чисел

	36	84	96

 

interneturok.ru