Параметры в математике это – Примеры с параметрами и методы их решения
Примеры с параметрами и методы их решения
Разделы: Математика
В последние годы на вступительных экзаменах, на итоговом тестировании в форме ЕГЭ предлагаются задачи с параметрами. Эти задачи позволяют диагностировать уровень математического и, главное, логического мышления абитуриентов, способность осуществлять исследовательскую деятельность, а также просто знание основных разделов школьного курса математики.
Взгляд на параметр как на равноправную переменную находит своё отражение в графических методах. В самом деле, поскольку параметр “равен в правах” с переменной, то ему, естественно, можно “выделить” и свою координатную ось. Таким образом, возникает координатная плоскость . Отказ от традиционного выбора букв и для обозначения осей, определяет один из эффективнейших методов решения задач с параметрами – “метод областей”. Наряду с другими методами, применяемыми при решении задач с параметрами, я знакомлю своих учеников и с графическими приёмами, обращая внимание на то, как распознать “такие” задачи и как выглядит процесс решения задачи.
Самые общие признаки, которые помогут узнавать задачи, подходящие под рассматриваемый метод:
Задача 1. “При каких значениях параметра неравенство выполняется при всех ?”
Решение. 1). Раскроем модули с учётом знака подмодульного выражения:
2). Запишем все системы получившихся неравенств:
а)
б) в)
г)
3). Покажем множество точек, удовлетворяющих каждой системе неравенств (рис.1а).
4). Объединяя все области, показанные на рисунке штриховкой, можно заметить, что неравенству не удовлетворяют точки , лежащие внутри парабол.
На рисунке видно, что при любом значении параметра можно найти область, где лежат точки, координаты которых удовлетворяют исходному неравенству. Неравенство выполняется при всех , если . Ответ: при .
Рассмотренный пример представляет собой “открытую задачу” — можно рассмотреть решение целого класса задач, не изменяя рассмотренное в примере выражение, в которых технические трудности построения графиков уже преодолены.
Задача. При каких значениях параметра уравнение не имеет решений? Ответ: при .
Задача. При каких значениях параметра уравнение имеет два решения? Запишите оба найденных решения.
Ответ: , тогда , ;
, тогда ;
, тогда ; , тогда , .
Задача. При каких значениях параметра уравнение имеет один корень? Найдите этот корень. Ответ: при при .
Задача. Решите неравенство .
(“Работают” точки, лежащие внутри парабол).
Ответ: , ;
, ; , решений нет;
, ; , .
Задача 2.Найдите все значения параметра а, при каждом из которых система неравенств образует на числовой прямой отрезок длины 1.
Решение. Перепишем исходную систему в таком виде
Все решения этой системы (пары вида ) образуют некоторую область, ограниченную параболами и (рис 1).
Очевидно, решением системы неравенств будет отрезок длины 1 при и при . Ответ: ; .
Задача 3.Найдите все значения параметра , при которых множество решений неравенства содержит число , а так же содержит два отрезка длиной , не имеющие общих точек.
Решение. По смыслу неравенства ; перепишем неравенство, умножив обе его части на (), получаем неравенство:
, ,
, ,
(1)
Неравенство (1) равносильно совокупности двух систем:
1) 2)
Покажем области, которые соответствуют этим системам (рис. 2).
Очевидно, интервал не может содержать отрезка длины . Значит, два непересекающихся отрезка длины содержатся в интервале Это возможно при , т.е. при . Ответ: .
Задача 4.Найдите все значения параметра , при каждом из которых множество решений неравенства содержит отрезок длиной 4 и при этом содержи
ПАРАМЕТР (в математике) — это… Что такое ПАРАМЕТР (в математике)?
- ПАРАМЕТР (в математике)
- ПАРАМЕТР (в математике)
ПАРА́МЕТР (от греч. parametron — отмеривающий) в математике, величина, числовые значения которой позволяют выделить определенный элемент (напр., кривую) из множества элементов (кривых) того же рода. Напр., в уравнении x2 + y2 = r2 величина r является параметром окружности.
Энциклопедический словарь. 2009.
- ПАРАЛЛЕЛЬНЫЕ РЕАКЦИИ
- ПАРАМЕТР (в технике)
Смотреть что такое «ПАРАМЕТР (в математике)» в других словарях:
ПАРАМЕТР — (от греч. parametron отмеривающий) в математике величина, числовые значения которой позволяют выделить определенный элемент (напр., кривую) из множества элементов (кривых) того же рода. Напр., в уравнении x2 + y2 = r2 величина r является… … Большой Энциклопедический словарь
ПАРАМЕТР — (от греч. parametnm отмеривать) англ. parameter; нем. Parameter. 1. В математике величина, значение к рой является постоянным в пределах рассматриваемой задачи. 2. Величина, характеризующая к. л. свойство устройства, процесса, вещества; то же,… … Энциклопедия социологии
параметр — 1. В математике величина, входящая в формулы и выражения, значение коей в рамках рассматриваемой задачи является постоянным. 2. Величина, характеризующая некое свойство процесса, устройства, вещества, то же, что и показатель. Словарь… … Большая психологическая энциклопедия
Параметр — У этого термина существуют и другие значения, см. Параметр (значения). В Викисловаре есть статья «параметр» Параметр (от др. греч. παραμετρέω … Википедия
параметр
ПАРАМЕТР — (от греч. parametron отмеривающий) в математике, величина, числовые значения к рой позволяют выделить определ. элемент (напр., кривую) из множества элементов (кривых) того же рода. Напр., в ур нии х2 + у2 = r2 величина r является П. окружности … Естествознание. Энциклопедический словарь
параметр — сущ., м., употр. сравн. часто Морфология: (нет) чего? параметра, чему? параметру, (вижу) что? параметр, чем? параметром, о чём? о параметре; мн. что? параметры, (нет) чего? параметров, чему? параметрам, (вижу) что? параметры, чем? параметрами, о… … Толковый словарь Дмитриева
Параметр — (от греч. parametron отмеривающий) 1) (в математике) величина, входящая в формулы и выражения, значение которой является постоянной в пределах рассматриваемой задачи, но изменяется при переходе к другой задаче; 2) (в технике) величина,… … Начала современного естествознания
Параметр — (греч. parametron – отмеривающий) – 1. признак, критерий, характеризующий какое то явление и определяющий его оценку; 2. в математике – некая константа в формуле или выражении; 3. в статистике – значение, которое вводится в математическую функцию … Энциклопедический словарь по психологии и педагогике
ПАРАМЕТР — (от греч. parametnm отмеривать) англ. parameter; нем. Parameter. 1. В математике величина, значение к рой является постоянным в пределах рассматриваемой задачи. 2. Величина, характеризующая к. л. свойство устройства, процесса, вещества; то же,… … Толковый словарь по социологии
Параметры в школьном курсе математики
Разделы: Математика
Пояснительная записка
Основной задачей модернизации российского образования является обеспечение нового качества школьного образования, соответствующего требованиям изменившейся системы общественных отношений и ценностей. В свете профилизации и модернизации школьного образования возникла необходимость создания элективного курса «Параметры в школьном курсе математики» для развития целостной математической составляющей картины мира и для расширения возможностей учащихся по свободному выбору своего образовательного пути. Предлагаемый элективный курс предназначен для реализации в старших классах профильного обучения с физико-математическим направлением. Курс систематизирует и упорядочивает, закрепляет и углубляет математические знания, умения и навыки учащихся. В процессе изучения данного элективного курса учащиеся познакомится с различными методами решения задач с параметрами.
Элективный курс предусматривает не только овладение различными умениями, навыками, приемами для решения задач, но и создает условия для формирования мировоззрения ученика, логической и эвристической составляющих мышления. Задачи с параметрами, как правило, относятся к наиболее трудным задачам, носят исследовательский характер. В школьных учебниках по математике таких задач недостаточно. Практика итоговых экзаменов в школе и приемных экзаменов в высшие учебные заведения показывает, что задачи с параметрами представляют для учащихся наибольшую сложность, как в логическом, так и в техническом плане, и поэтому умение их решать во многом предопределяет успешную сдачу экзамена в любое высшее учебное заведение. Старшеклассники, изучившие данный материал, смогут более успешно реализовать полученные знания и умения на итоговой аттестации в форме ЕГЭ.
Ценность задач данного элективного курса - демонстрация их общности с точки зрения исследования и анализа реальных процессов средствами математики. Значительное место в курсе уделено практической направленности материала, его приложений, мотивации процесса познания. Данная программа позволяет школьнику решать задачи интегративного характера, в частности задачи физического содержания и задачи на объемные доли и концентрацию вещества.
Многообразие задач с параметрами охватывает весь курс школьной математики. Владение приемами решения задач с параметрами можно считать критерием знаний основных разделов школьной математики, уровня математического и логического мышления. Приемы и методы, которые получат учащиеся в ходе изучения данного курса, применимы и в других предметных областях. В, частности, приемы обобщения, анализа, классификации, систематизации и другие надпредметные компетентности. Не секрет, что уровень развития надпредметных умений и навыков, в настоящее время, не высок. Поэтому возникла необходимость создания этого элективного курса, который не только напрямую углубляет и расширят математические способности детей, но и развивает их творческий и интеллектуальный потенциал.
Основными целями изучения курса является:
- Систематизация и углубление знаний, закрепление и упрочение умений, необходимых для продолжения образования в ВУЗах с повышенными требованиями к математическому образованию выпускников средней школы.
- Получение общего представления об элементарной алгебре и применяемых в ней методах как о составляющей всей математике как науки.
- Овладение общими приемами организации действий: планированием, осуществлением плана, анализом и выражением результатов действий.
- Развитие внутренней мотивации к поисковой активности в предметной деятельности, формирование устойчивого и осознанного интереса к ней.
При изучении данного курса перед учащимися ставятся следующие задачи:
- Приобретение знаний и овладение различными умениями, навыками, приемами для решения параметрических заданий.
- Освоение методов решения и исследование вычислительных и логических задач с параметрами.
- Создание условий для формирования математического мировоззрения учащихся, развитие логической и эвристической составляющей части мышления.
- Создание условий для развития исследовательской и познавательной деятельности учащихся.
Образовательные результаты
Предметные знания, которыми должны овладеть учащиеся в результате данного курса:
- Овладение учащимися основными приемами и методами решения уравнений, неравенств систем уравнений с параметрами.
- Овладение учащимися методами исследовательской и поисковой деятельности.
Предметные умения, которыми должны овладеть учащиеся по изучении данного курса:
- Умение применять алгоритм решения уравнений, неравенств, содержащих параметр,
- Умение проводить полное обоснование при решении задач с параметрами;
- Умение понимать и правильно интерпретировать задачи с параметрами, логические и кванторные задачи; умение применять изученные методы исследования и решения задач с параметрами: аналитический и координатный.
Общеинтеллектуальные умения:
- умение анализировать различные задачи и ситуации, выделять главное, достоверное в той или иной информации;
- владеть логическим, доказательным стилем мышления, умение логически обосновывать свои суждения;
- умение конструктивно подходить к предлагаемым задачам;
- умение планировать и проектировать свою деятельность, проверять и оценивать свои результаты.
Программа курса
Содержание курса
Предлагаемый элективный курс рассчитан на 34 часа и предлагается его организовать во втором полугодии 10 класса и в первом полугодии 11 класса следующим образом:
| 10 класс | ||||
| № занятия | Тема занятия | Содержание деятельности | Количество часов | |
| 1 | 1 | Введение | Обзорная лекция | 1 |
| 2-7 | 2 | Решение уравнений различного типа | 7 | |
| 2,3 | 2.1 | Линейные уравнения и уравнения, сводящиеся к линейным | Семинар, практикум | 2 |
| 4,5 | 2.2 | Квадратные уравнения и уравнения, сводящиеся к квадратным | Семинар, практикум, исследовательская работа | 2 |
| 6-8 | 2.3 | Тригонометрические уравнения | Семинар, практикум, исследовательская работа | 3 |
| 9-16 | 3 | Решение неравенств различного вида | 8 | |
| 9,10 | 3.1 | Линейные неравенства и неравенства, сводящиеся к линейным. | Семинар, практикум | 2 |
| 11-13 | 3.2 | Квадратные неравенства и неравенства, сводящиеся к квадратным | Семинар, практикум, исследовательская работа, проектная деятельность | 3 |
| 14-16 | 3.3 | Тригонометрические неравенства | Семинар, практикум, проектная деятельность | 3 |
| 17 | Защита проектов | Представление результатов деятельности | 1 | |
| Итого | 17 | |||
| 11 класс | ||||
| 18 | 4 | Введение | Обзорная лекция | 1 |
| 19-25 | 5 | Логарифмические, показательные уравнения и неравенства | 7 | |
| 19-21 | 5.1 | Логарифмические и показательные уравнения | Семинар, практик | |
xn--i1abbnckbmcl9fb.xn--p1ai
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
egeprof.ru
Статья о задачах с параметрами в школьном курсе математики
Задачи с параметром в школьном курсе математики 8-го класса
Задачи с параметрами играют важную роль в формировании логического мышления и математической культуры учащихся. Они имеют принципиально исследовательский характер, и с этим связаны как методическое значение таких задач, так и трудности выработки навыков их решения. Важность понятия параметра связана с тем, что, как правило, именно в терминах параметров происходит описание свойств математических объектов: функций, уравнений, неравенств. Под параметрами мы понимаем входящие в алгебраические выражения величины, численные значения которых явно не заданы, однако считаются принадлежащими определенным числовым множествам. Учащимся 8 класса известны линейная функция и ее частный случай – прямая пропорциональность:
(параметры и определяют расположение графика функции на плоскости и точки пересечения с осями), а также линейное и квадратное уравнение и соответствующие неравенства:
(параметры , и определяют, вообще говоря, не только существование и количество корней, но и степень уравнения).
Решение задач с параметрами требует исследования, даже если это слово не упомянуто в формулировке задачи. Недостаточно механического применения формул, необходимо понимание закономерностей, навыки анализа конкретного случая на основе известных общих свойств объекта, системность и последовательность в решении, умение объединить рассматриваемые частные случаи в единый результат. Этим обусловлены трудности, возникающие у учащихся при решении таких задач, и этим же объясняется справедливое включение задач с параметрами в экзаменационные работы в школе и на вступительных экзаменах в вузы.
Таким образом, очевидна необходимость отработки приемов решения различных задач с параметрами. Ниже приводится система упражнений по решению и исследованию квадратных уравнений и неравенств с одним параметром в курсе 8 класса.
Квадратные уравнения с параметром
1. При каких значениях уравнение имеет единственное решение?
Решение.
Ошибочно считать данное уравнение квадратным. На самом деле это уравнение степени не выше второй. Исходя из этого соображения, рассмотрим следующие случаи:
а) . При этом уравнение принимает вид , откуда , т.е. решение единственно.
б) , тогда – квадратное уравнение, дискриминант . Для того, чтобы уравнение имело единственное решение, нужно, чтобы , откуда .
Ответ: или .
2. При каких значениях уравнение имеет единственное решение?
Решение.
1) При исходное уравнение не имеет решения.
2) , тогда данное уравнение является квадратным и принимает вид . Искомые значения параметра – это корни дискриминанта, который обращается в нуль при .
Ответ: .
3. При каких значениях уравнение имеет более одного корня?
Решение.
1) При уравнение имеет единственный корень .
2) При исходное уравнение, будучи квадратным, имеет два корня, если его дискриминант положителен, т.е. . Решая неравенство, получаем . Из этого промежутка следует исключить число нуль.
Ответ: или .
4. При каких значениях уравнения и равносильны?
Решение.
1) При : имеет два различных корня, имеет один корень. Равносильности нет.
2) При решения уравнений совпадают.
3) При ни первое, ни второе уравнения решений не имеют. Как известно, такие уравнения считаются равносильными.
Ответ: .
5. При каких значениях уравнения и равносильны?
6. При каких значениях параметра уравнение имеет одно решение?
7. При каких значениях ровно один из корней уравнения равен нулю?
8. При каких значениях корни уравнения равны по модулю, но противоположны по знаку: 9. При каких значениях оба корня уравнения равны нулю?а) ; б)
10. Решите уравнения:
I.
II. III. IV. V. 11. При каких значениях произведение корней квадратного уравнения равно нулю?12. При каких значениях сумма корней квадратного уравнения равна нулю?
13. В уравнении сумма квадратов корней равна 16. Найти .
14. В уравнении квадрат разности корней равен 16. Найти .
15. При каких значениях сумма корней уравнения равна сумме квадратов корней?
16. При каком значении параметра сумма квадратов корней уравнения наименьшая?
17. При каком значении параметра сумма квадратов корней уравнения наибольшая?
18. При каких значениях параметра один из корней квадратного уравнения в два раза больше другого?
19. Известно, что корни уравнения на 1 меньше корней уравнения . Найдите и корни каждого из уравнений.
20. Найдите наименьшее целое значение , при котором уравнение имеет два различных действительных корня.
21. При каких значениях уравнение имеет более двух корней?
22. При каких значениях уравнение имеет хотя бы один общий корень с уравнением ?
23. При каком соотношении между , , уравнение имеет один корень? Может ли данное уравнение иметь два действительных различных корня?
24. При каком значении параметра уравнение имеет три корня?
Неравенства с параметром
1. Решите неравенство, где – параметр:
2. Найдите все значения , при которых квадратное уравнение имеет два действительных различных корня: 3. Найдите все значения , при которых квадратное уравнение не имеет действительных корней: 4. При каких значениях уравнение имеет положительное решение?5. При каких значениях уравнение имеет отрицательное решение?
6. При каких значениях уравнение имеет одно положительное решение?
7. При каких значениях уравнение имеет решения, удовлетворяющее условию ?
8. При каких значениях система неравенств имеет хотя бы одно решение:
а)б)
в)
г)
9. При каких значениях система неравенств не имеет решений:
а)б)
в)
г)
10. При каких значениях система неравенств имеет хотя бы одно решение?
11. При каких значениях уравнение имеет корни разных знаков?
12. При каких значениях уравнение имеет корни и такие, что ?
13. Найдите все значения , при которых корни уравнения меньше, чем 1.
14. Найдите все значения , при которых один из корней уравнения меньше 1, а другой больше 1.
15. При каких значениях система уравнений
имеет решение ?
16. При каких значениях система уравнений
имеет решение ?
17. Для каждого решите неравенство:
I.
II. III. IV.infourok.ru
уравнения и неравенства с параметром
Существует ровно три генеральных метода решения задач 18:
- Метод перебора — классический перебор вариантов. Например, когда выражение под модулем больше нуля и когда меньше;
- Графический метод — привлечение чертежа. Во многих задачах 18 достаточно начертить графики функций — и решение становится очевидным;
- Метод следствий — нестандартный и, как правило, самый изощренный. Если в исходном условии удастся подметить что-нибудь полезное, в дальнейшем можно значительно упростить решение всей задачи.
Конечно, одну и ту же задачу зачастую можно решить разными способами. Но далеко не все они оптимальны: выбрав неправильный «путь», можно увязнуть в вычислениях, так и не дойдя до ответа.
Поэтому в данном разделе я рассмотрю все способы, а ваша задача — практиковаться и учиться правильно выбирать.:)
- Глава 1.
- Графический подход
- § 1.
- Вебинар по задачам 18: модуль и окружности
- § 2.
- Как решать задачу 18: графический подход
- § 3.
- Задача 18: две окружности и модуль
- § 4.
- Задача 18: пересечение графиков окружности и модуля
- § 5.
- Новая задача 18 из пробного ЕГЭ — наглядный пример того, как эффективно работает графическое решение задач с параметром.
- Глава 2.
- Аналитический подход
- § 1.
- Задачи 18: Аналитическое решение
- § 2.
- Окружность и модуль: задачи 18 с двумя параметрами
- § 3.
- Аналитическое решение задачи 18 с перебором различных вариантов
- Глава 3.
- Нестандартные приемы
- § 1.
- Задача 18: метод симметричных корней
- § 2.
- Как увидеть симметрию корней в задаче 18?
- § 3.
- Метод мажорант в задаче 18
- § 4.
- Графическое решение сложных задач 18 с модулем
- § 5.
- Задание 18: Симметрия корней в системе уравнений
- § 6.
- Анализ знаков квадратного трёхчлена в сложных задачах 18
- § 7.
- Применение производной для отыскания точек пересечения графиков
- § 8.
- Продвинутый метод симметричных корней
- § 9.
- Новая задача 18 с графическим решением
- Функции с параметром
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- Уравнения с параметром
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- Неравенства с параметром
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- Системы с параметром
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
- 160
- 161
- 162
- 163
- 164
- 165
- 166
- 167
- 168
- 169
- 170
- 171
- 172
- 173
- 174
- 175
- 176
- 177
- 178
- 179
- 180
- 181
- 182
- 183
- 184
- 185
- 186
- 187
- 188
- 189
- 190
- 191
- 192
- 193
- 194
- 195
- 196
- 197
www.berdov.com
Что такое параметры? Значение слова
С этим существительным все мы сталкиваемся практически каждый день. Причем совершенно в разных сферах. Речь идет о слове «параметр» (или «параметры»). Какое же оно значение имеет? Откуда пришло? В каких отраслях чаще всего используется? Давайте найдем ответы на эти вопросы.
Происхождение изучаемого существительного
Прежде чем узнать, что означает слово «параметры», стоит узнать о его этимологии.
Как и большинство специфических терминов, этот был заимствован из древнегреческого языка. В давние времена в нем принялся глагол παραμετρέω («соизмеряю»). Именно от него и было образовано существительное «параметр».
В российский, украинский и другие славянские языки это название могло попасть через посредничество либо немецкого (Parameter), либо английского (parameter). Менее вероятно, но все же возможно, что оно пришло из французского (paramètre) или польского (parametr). В любом случае данный термин можно считать интернациональным, поскольку в большинстве языков мира он пишется и произносится почти идентично.
Общее определение слова «параметр»
Разобравшись с этимологией, стоит перейти к трактовке лексического значения рассматриваемого существительного.
Итак, что такое «параметры» (или «параметр»)? Так называется величина, с помощью которой характеризуются какие-то свойства, способности, состояние, размер или форма объекта, процесса, явления системы и т. п.
Стоит отметить, что в большинстве случаев, параметры можно измерить. Результатом этого является величина или число.
К примеру, покупая компьютер, всегда стоит узнавать у продавца о его параметрах. В данном случае речь идет об объеме жесткого диска и его разбивке (от этого зависит, сколько данных можно сохранить в памяти прибора и как быстро он будет работать), мощности процессора, типе материнской платы, версии операционной системы, установленной на компьютере («Виндовс», «Линукс») и т. п. Все это называется «параметрами компьютера». Они есть и у планшетов, ноутбуков, смартфонов и прочей современной «интеллектуальной» техники.
Стоит отметить, что у других электроприборов тоже есть подобные характеристики, однако они отличаются в зависимости от типа аппарата и его назначения.
Рассматриваемый термин используется не толь
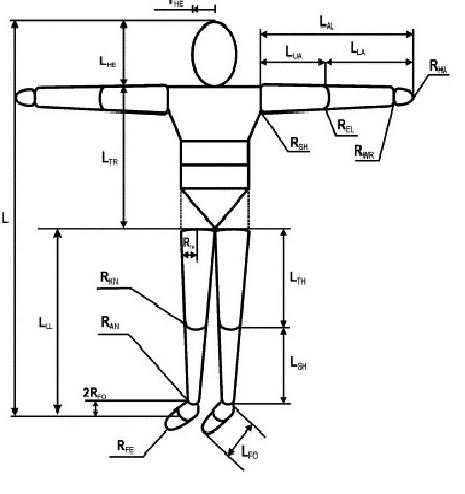ко для характеристики различных приборов, но и для описания уникальных особенностей человеческого тела. К так называемым параметрам фигуры, относятся не только размеры грудной клетки, талии и бедер, но плеч, икр, запястий и шеи.Математические параметры
Узнав ответ на вопрос о том, что такое параметры, стоит подробнее рассмотреть значение данного термина в различных отраслях.
Довольно активно он используется в царице всех наук – математике. В ней изучаемый термин означает величину, числовые значения которой, предоставляют возможность выделить определенный элемент среди ему подобных.
Например, в уравнении параболы у = ах² + bx + с, величины, зашифрованные в литерах а, b и с – это и есть параметры. В зависимости от того, какие значения им соответствуют, отличаются и параболы.
Кроме указанного выше, в математике есть еще один способ трактовки изучаемого термина. Так именуется дополнительная переменная величина, используемая для параметрического представления функции.
Технический параметр
Разобравшись с тем, что такое параметры в математике, стоит обратить внимание на значение данного термина в технике. В данной области так именуют характеристику определенного свойства процесса или объекта, допускающую количественную оценку.
Например, это может быть масса, скорость, размер или мощность.
Технические параметры по типу отношения к объекту или процессу делятся на: внешние и внутренние
В зависимости от вида процессов или объектов в технике, выделяются: механические (натяжение, масса, коэффициент трения), теплотехнические (удельная теплоемкость, плотность, коэффициент теплопроводности) и электрические параметры (индуктивность, сопротивление и т. д.).
Характеристики системы (термодинамика)
В данной сфере такое название носят физические величины, с помощью которых описывается состояние термодинамической системы. К ним относится: давление, объем, температура, концентрация вещества и подобные.
Как и в случае с техническими, системные параметры также делятся на виды.
- Интенсивные — являются независимыми от массы всей системы. Это давление, температура, концентрация вещества, магнитная индукция и другие.
- Экстенсивные параметры системы – пропорциональны ее массе. К ним относится объем, внутренняя энергия, энтропия, энтальпия, свободная энергия и энергия Гиббса.
Использования в других сферах
Узнав, что такое параметры в математике, механике и термодинамике, стоит изучить, в каких еще областях применяется данный термин.
В сфере создания компьютерных программ, изучаемым существительным именуется переменная, которой присваивается значение константы, переменной и т.д.
- Весьма активно применяется данный термин в социологии. Ученые этой отрасли используют систему структурных параметров, которые позволяют им изучать структуру и характер современного общества.
Чтобы определить место конкретной личности в социуме, ее характеризуют по номинальным (пол, раса, национальность, язык, вероисповедание, страна и регион проживания и т. д.) и ранговым параметрам (происхождение, образование, сфера деятельности, должность, количество денег и подобные).- Широко используется это слово и в горной промышленности. В зависимости от способа извлечения полезных ископаемых, применяются разные их характеристики.
Например, для взрывных скважин это такие параметры, как диаметр, глубина или угол наклона, а для карьеров – конечная глубина, запасы ископаемых и подобные. При системе открытой разработки месторождения также учитывают ее уникальные характеристики (ширина рабочей площадки, темпы углубления работ и подобные).
- Диетология является еще одной сферой, в которой существует целый ряд параметров. Так при составлении правильного рациона учитываются свойства тела конкретного человека (рост, вес, соотношение количества жира и мышц, индивидуальный метаболизм).
Кстати, многие из этих характеристик также берутся во внимание при составлении графика тренировок для спортсменов, а также при подборе различных снарядов.
Данный список далеко не полный, поскольку практически в каждой отрасли приходится учитывать параметры. Также данный термин применяется в логике, логистике, медицине, биологии, химии и т. п.
Какие можно подобрать к слову «параметры» синонимы?
Разобравшись со значение и сферой применения изучаемого существительного, стоит обратить внимание на то, можно ли подобрать к нему синонимы.
Стопроцентного аналога для этого термина нет, однако, в зависимости от сферы применения, его можно заменять следующими словами: характеристики, величины, меры, размеры, габариты, формат, норма.
fb.ru