Метод координат в пространстве контрольная работа – Контрольная работа по теме «Метод координат в пространстве»
Контрольная работа по геометрии для 11 класса по теме: «Метод координат в пространстве»
Просмотр содержимого документа
«Контрольная работа по геометрии для 11 класса по теме: «Метод координат в пространстве»»
Контрольная работа №2 по теме
«Метод координат в пространстве»
Вариант 1
Даны точки А (1;2;3), В (3;2;-1), С (5;8;-1).
а) найдите координаты векторов АВ, ВС.
б) найдите абсолютную величину вектора АС.
2. Даны векторы а{3;-4;-3}, b{-5;2;-4}. Найдите координаты вектора с=4а -2b.
3. При каком значении n данные векторы перпендикулярны:
а{-7;-n;3}, b{1;5;n}
4. При каких значениях m и k векторы c{14; m;-3} и d{-6;3;k} коллинеарные.
5. Точки А(2; 1; 5), B(0;-1;1) , С(2;1;3) – вершины параллелограмма АВСD. Найдите координаты вершины D и длины сторон параллелограмма.
6. Найдите градусную меру угла М треугольника MNT, если M(1;-1;3),
N(3;-1;1), T(-1;1;3).
Контрольная работа №2 по теме
«Метод координат в пространстве»
Вариант 2
1. Даны точки А (1;-2;1), В (0;-2;4), С (3;-2;1).
а) найдите координаты векторов абсолютную величину векторов АВ и BС.
б) найдите абсолютную величину вектора АC.
2. Даны векторы а{3;-4;-3}, b{-5;2;-4}. Найдите координаты вектора d=2а-3b
3. При каком значении n данные векторы перпендикулярны:
а{n;-2; 5}, b {-4;-n;1}.
4. При каких значениях m и k векторы c{14; m;-3} и d{-6;3;k} коллинеарные.
5. Точки A(2;-1;3), С(1;-3;4), D(0;-1;3) — вершины параллелограмма АВСD. Найдите координаты вершины B и длины сторон параллелограмма.
6. Найдите градусную меру угла В треугольника ABC, если A(-1;-2;4), B(-4;-2;0), C(3;-2;1).
multiurok.ru
Контрольная работа №2 по теме «Метод координат в пространстве»
КОНТРОЛЬНАЯ РАБОТА № 2
по теме «Метод координат в пространстве».
ВАРИАНТ 1.
Даны координаты точек С(3; -2; 1), D(-1; 2; 1), M(2; -3; 3), N(-1; 1; -2). Найдите косинус угла между векторами и .
При каком значении (значениях) а векторы (6 — k; k; 2) и (-3; 5 + 5k; -9) перпендикулярны?
При каком значении а векторы

Известно, что || = 4, || = 1,
 = 600. найдите соs
,
где
— угол между векторами
= 600. найдите соs
,
где
— угол между векторами  и
.
и
.Найдите длину вектора
 ,
если ||
= 1, ||
= 2, ||
=3,
= 900,
= 1200,
= 600.
,
если ||
= 1, ||
= 2, ||
=3,
= 900,
= 1200,
= 600.В кубе АВСDА1В1С1D 1 точка М лежит на ребре АА1, причем АМ : АМ1 = 3 : 1, а точка N – середина ребра ВС. Вычислите косинус угла между прямыми а) MN и DD1; б) MN и А1С.
КОНТРОЛЬНАЯ РАБОТА № 2
по теме «Метод координат в пространстве».
ВАРИАНТ 2.
Даны координаты точек А(1; -1; -4), D(2; -3; 1), С(-1; 2; 5), В(-3; -1; 0). Найдите косинус угла между векторами и .
При каком значении (значениях) m векторы (4; m — 1; m) и (-2; 4; 3 — m) перпендикулярны?
При каком значении а
Известно, что || = 2, || =3, = 1200. найдите соs , где — угол между векторами и .
Найдите длину вектора , если || = 2, || = 3, || =4, = 600, = 1200, = 900.
В прямоугольном параллелепипеде АВСDА1В1С1D1 АВ = ВС = АА1. Вычислите косинус угла между прямыми а) В
D и CD1; б) AC и АС1.
КОНТРОЛЬНАЯ РАБОТА № 2
по теме «Метод координат в пространстве».
ВАРИАНТ 2.
Даны координаты точек А(1; -1; -4), D(2; -3; 1), С(-1; 2; 5), В(-3; -1; 0). Найдите косинус угла между векторами и .
При каком значении (значениях) m векторы (4; m — 1; m) и (-2; 4; 3 — m) перпендикулярны?
При каком значении а векторы и коллинеарны, если M(1; -2; a), В(-1; a + 3; -1), С(-3; 2; 4), D(1; -4; 2)?
Известно, что |
Найдите длину вектора , если || = 2, || = 3, || =4, = 600, = 1200, = 900.
В прямоугольном параллелепипеде АВСDА1В1С1D1 АВ = ВС = АА1. Вычислите косинус угла между прямыми а) ВD и CD1; б) AC и АС1.
Г– 11 К — 2
КОНТРОЛЬНАЯ РАБОТА № 2
по теме«Метод координат в пространстве».
(Атанасян)
gigabaza.ru
Контрольная работа по геометрии «Метод координат в пространстве» Вариант 1
B(0; 0; ), C (0; 2; 0) и D (; 1; ).
В(-1,2,3), С(8,-4,9). Найдите координаты вектора , если ВМ – медиана треугольника АВС. | Контрольная работа по геометрии «Метод координат в пространстве» Вариант 2
B(8; -2; 4), C (12; -6; 4) и D (; -6; ).
А(-1,2,3), В(1,0,4), С(3,-2,1). Найдите координаты вектора если АМ – медиана треугольника АВС. | Контрольная работа по геометрии «Метод координат в пространстве» Вариант 1
B(0; 0; ), C (0; 2; 0) и D (; 1; ).
В(-1,2,3), С(8,-4,9). Найдите координаты вектора , если ВМ – медиана треугольника АВС. | Контрольная работа по геометрии «Метод координат в пространстве» Вариант 2
B(8; -2; 4), C (12; -6; 4) и D (; -6; ).
А(-1,2,3), В(1,0,4), С(3,-2,1). Найдите координаты вектора если АМ – медиана треугольника АВС. |
infourok.ru
1 вариант. 1). Найдите координаты вектора , если А(5; -1; 3), В(2; -2; 4). 2). Даны векторы {3; 1; -2} и {1; 4; -3}. Найдите . 3). Изобразите систему координат Охуz и постройте точку А( 1; -2; -4). Найдите расстояние от этой точки до координатных плоскостей. 4). Вершины ∆АВС имеют координаты: А( -2; 0; 1 ), В( -1; 2; 3 ), С( 8; -4; 9 ). Найдите координаты вектора , если ВМ – медиана ∆АВС. | 2 вариант. 1). Найдите координаты вектора , если А(6; 3; -2), В(2; 4; -5). 2). Даны векторы {5; -1; 2} и {3; 2; -4}. Найдите . 3). Изобразите систему координат Охуz и постройте точку В( -2; -3; 4). Найдите расстояние от этой точки до координатных плоскостей. 4). Вершины ∆АВС имеют координаты: А ( -1; 2; 3 ), В ( 1; 0; 4 ), С ( 3; -2; 1 ). Найдите координаты вектора , если АМ – медиана ∆АВС. |
multiurok.ru
Контрольная работа по теме: » Метод координат «
Контрольная работа по теме
«Векторы в пространстве. Метод координат»
I вариант
Найти длины векторов a =

Найти
 если
если  { 3; -2; 1},
{ 3; -2; 1},  { -2; 3; 1}
{ -2; 3; 1}Построить точку М( — 4; 7; 0). Найти расстояние от точки M до начала координат.
Определить вид треугольника, если
А( 5; -5; -1), В(5; -3; -1), С( 4; -3; 0)
Найти скалярное произведение векторов
 {
{ ;
;  ; 2),
; 2),  { -3; -3; 0)
{ -3; -3; 0)
Вычислить угол между прямыми АВ и СD, если А(
 ; 1; 0), В( 0; 0; 2
; 1; 0), В( 0; 0; 2 ),
),
С( 0; 2; 0), D( ; 1 2
; 1 2
Контрольная работа по теме
«Векторы в пространстве. Метод координат»
II вариант
Найти длины векторов b =

Найти
 если
если  { 3; -2; 1},
{ 3; -2; 1},  { -2; 3; 1}
{ -2; 3; 1}Построить точку N ( 0; -1; 2). Найти расстояние от точки N до начала координат.
Определить вид треугольника, если
А( — 5; 2; 0), В(- 4; 3; 0), С( -5; 2; — 2)
Найти скалярное произведение векторов
 {- 2.5;2.5; 0),
{- 2.5;2.5; 0), 
 )
)Вычислить угол между прямыми АВ и СD, если А(6; -4; 8), В( 8; -2; 4),
С( 12; — 6; 4), D(14; -6; 2)
Контрольная работа по теме
«Векторы в пространстве. Метод координат»
I вариант
Найти длины векторов a =

Найти
 если
если  { 3; -2; 1},
{ 3; -2; 1},  { -2; 3; 1}
{ -2; 3; 1}Построить точку М( — 4; 7; 0). Найти расстояние от точки M до начала координат.
Определить вид треугольника, если
А( 5; -5; -1), В(5; -3; -1), С( 4; -3; 0)
Найти скалярное произведение векторов
 {
{ ;
;  ; 2),
; 2),  { -3; -3; 0)
{ -3; -3; 0)
Вычислить угол между прямыми АВ и СD, если А(
 ; 1; 0), В( 0; 0; 2
; 1; 0), В( 0; 0; 2 ),
),
С( 0; 2; 0), D( ; 1 2
; 1 2 )
)
Контрольная работа по теме
«Векторы в пространстве. Метод координат»
II вариант
Найти длины векторов b =

Найти
 если
если  { 3; -2; 1},
{ 3; -2; 1},  { -2; 3; 1}
{ -2; 3; 1}Построить точку N ( 0; -1; 2). Найти расстояние от точки N до начала координат.
Определить вид треугольника, если
А( — 5; 2; 0), В(- 4; 3; 0), С( -5; 2; — 2)
Найти скалярное произведение векторов
 {- 2.5;2.5; 0),
{- 2.5;2.5; 0),  { -5; 5; 5
{ -5; 5; 5 )
)
Вычислить угол между прямыми АВ и СD, если А(6; -4; 8), В( 8; -2; 4),
С( 12; — 6; 4), D(14; -6; 2)
Контрольная работа по теме
«Векторы в пространстве. Метод координат»
I вариант
Найти длины векторов a =

Найти
 если
если  { 3; -2; 1},
{ 3; -2; 1},  { -2; 3; 1}
{ -2; 3; 1}Построить точку М( — 4; 7; 0). Найти расстояние от точки M до начала координат.
Определить вид треугольника, если
А( 5; -5; -1), В(5; -3; -1), С( 4; -3; 0)
Найти скалярное произведение векторов
 {
{ ;
;  ; 2),
; 2),  { -3; -3; 0)
{ -3; -3; 0)
Вычислить угол между прямыми АВ и СD, если А(
 ; 1; 0), В( 0; 0; 2
; 1; 0), В( 0; 0; 2 ),
),
С( 0; 2; 0), D( ; 1 2
; 1 2 )
)
Контрольная работа по теме
«Векторы в пространстве. Метод координат»
II вариант
Найти длины векторов b =

Найти
 если
если  { 3; -2; 1},
{ 3; -2; 1},  { -2; 3; 1}
{ -2; 3; 1}Построить точку N ( 0; -1; 2). Найти расстояние от точки N до начала координат.
Определить вид треугольника, если
А( — 5; 2; 0), В(- 4; 3; 0), С( -5; 2; — 2)
Найти скалярное произведение векторов
 {- 2.5;2.5; 0),
{- 2.5;2.5; 0),  { -5; 5; 5
{ -5; 5; 5 )
)
Вычислить угол между прямыми АВ и СD, если А(6; -4; 8), В( 8; -2; 4),
С( 12; — 6; 4), D(14; -6; 2)
infourok.ru
Контрольная работа по теме «Метод координат в пространстве»
Контрольная работа №3
по теме «Метод координат в пространстве»
Вариант 1
Даны векторы , причём Найти: а)
б) значение m, при котором векторы и перпендикулярны.
Найти угол между прямыми АВ и CD, если А(3; -1; 3), В(3; -2; 2), С(2; 2; 3), D(1; 2; 2).
Дан куб с ребром a. При симметрии относительно прямой точка D перешла в точку D2. Найдите ВD2.
———————————————————————————————————
Контрольная работа №3
по теме «Метод координат в пространстве»
Вариант 2
Даны векторы , причём Найти: а)
б) значение m, при котором векторы и перпендикулярны.
Найти угол между прямыми АВ и CD, если А(1; 1; 2), В(0; 1; 1), С(2; -2; 2), D(2; -3; 1).
Дан куб с ребром a. При симметрии относительно плоскости точка B1 перешла в точку B2. Найдите АВ2.
multiurok.ru
Контрольная работа по геометрии в 11 классе «Метод координат в пространстве»
Контрольная работа
по теме: «Метод координат в пространстве»
Вариант 1.
Вычислите скалярное произведение векторов и , если =, , 60o,
Дан куб ABCDA1B1C1D1. Найдите угол между прямыми А D1 и ВМ, где М – середина ребра D D1.
Контрольная работа
по теме: «Метод координат в пространстве»
Вариант 2.
Вычислите скалярное произведение векторов и , если =, , 60o,
Дан куб ABCDA1B1C1D1. Найдите угол между прямыми АС и D C1..
Контрольная работа
по теме: «Метод координат в пространстве»
Вариант 1.
Вычислите скалярное произведение векторов и , если =, , 60o,
Дан куб ABCDA1B1C1D1. Найдите угол между прямыми А D1 и ВМ, где М – середина ребра D D1.
Контрольная работа
по теме: «Метод координат в пространстве»
Вариант 2.
Вычислите скалярное произведение векторов и , если =, , 60o,
Дан куб ABCDA1B1C1D1. Найдите угол между прямыми АС и D C1..
Контрольная работа
по теме: «Метод координат в пространстве»
Вариант 1.
Вычислите скалярное произведение векторов и , если =, , 60o,
Дан куб ABCDA1B1C1D1. Найдите угол между прямыми А D1 и ВМ, где М – середина ребра D D1.
Контрольная работа
по теме: «Метод координат в пространстве»
Вариант 2.
Вычислите скалярное произведение векторов и , если =, , 60o,
Дан куб ABCDA1B1C1D1. Найдите угол между прямыми АС и D C1..
multiurok.ru



 = 600. найдите соs
,
где
— угол между векторами
= 600. найдите соs
,
где
— угол между векторами  и
.
и
. ,
если ||
= 1, ||
= 2, ||
=3,
= 900,
= 1200,
= 600.
,
если ||
= 1, ||
= 2, ||
=3,
= 900,
= 1200,
= 600.
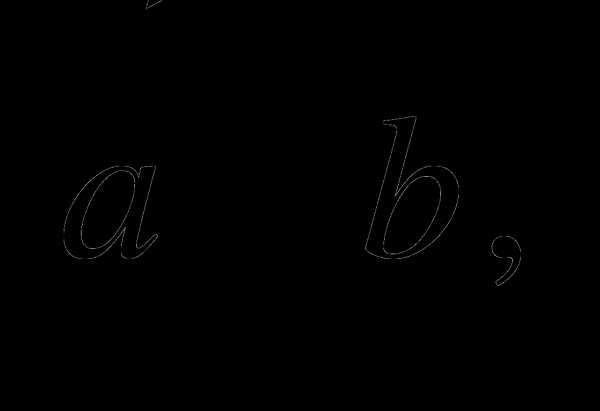 если
если  { 3; -2; 1},
{ 3; -2; 1}, 
 если
если