Логарифм презентация – Презентация по математике на тему «Определение логарифма. Основное логарифмическое тождество»
Презентация на тему «Логарифмы вокруг нас» (11 класс)
МБОУ Федосеевская СОШ.
Исследовательская работа:
Выполнили уч-цы 10-го класса
Соитова Милана и Ахматова Яхита.
Цель: показать, что логарифмы нужны не только на уроках математики но, могут быть использованы и в других областях.
Проблема: показать практическую значимость логарифмов для окружения.
Задача: применение логарифмов в различных областях науки и повседневной жизни.
Логарифмы были изобретены шотландским математиком Джоном Непером (1550–1617) в 1614 г. Его «Канон о логарифмах» начинался так: «Осознав, что в математике нет ничего более, скучного и утомительного, чем умножение, деление, извлечение квадратных и кубических корней, и что названные операции являются бесполезной тратой времени и неиссякаемым источником неуловимых ошибок, я решил найти простое и надежное средство, чтобы избавиться от них».
С точки зрения вычислительной практики, изобретение логарифмов по возможности можно смело поставить рядом с другими, более древним великим изобретением индусов – нашей десятичной системы нумерации.
Через десяток лет после появления логарифмов Непера английский ученый Гунтер изобрел очень популярный прежде счетный прибор – логарифмическую линейку. Она помогала астрономам и инженерам при вычислениях, она позволяла быстро получать ответ с достаточной точностью в три значащие цифры.
Таким образом, потребность в сложных расчётах быстро росла. Теория логарифмов связана с именами целого ряда математиков: Генри Бригс, Эдмунд Уингейт, Уильям Отред, Н. Меркатор, Джон Спейдел, К. Бремикер, Ф. Клейн.
Термин «логарифм» (logarithmus) принадлежит Неперу. Он возник из сочетания греческих слов: logos – «отношение» и ariqmo – «число», которое означало «число отношений». Первоначально Непер пользовался другим термином: numeri artificiales — «искусственные числа», в противоположность numeri naturalts – «числам естественным».
В ходе тригонометрических расчётов, Неперу пришла в голову идея: заменить трудоёмкое умножение на простое, сложение, сопоставив с помощью специальных таблиц геометрическую и арифметическую прогрессии, при этом геометрическая будет исходной.
В 1614 году Непер опубликовал в Эдинбурге сочинение под названием «Описание удивительной таблицы логарифмов», на латинском языке. Там было краткое описание логарифмов и их свойств, а также 8-значные таблицы логарифмов синусов, косинусов и тангенсов, с шагом 1′.
Сочинение было разделено на 2 книги, из которых первая посвящена логарифмам, а вторая — плоской и сферической тригонометрии, причём вторая часть одновременно служит практическим пособием по первой. Более развёрнутое, описание содержалось в другом труде, изданном посмертно его сыном; там же Непер пояснил, как он составлял свои таблицы.
Понятия функции тогда ещё не было, и Непер определил логарифм кинематически, сопоставив равномерное и логарифмически-замедленное движение. В современной записи модель Непера можно изобразить дифференциальным уравнением:
Строго говоря, Непер табулировал не ту функцию, которая сейчас называется логарифмом.
К сожалению, все значения таблицы Непера содержали вычислительную ошибку после шестого знака. Однако это не помешало новой методике вычислений получить широчайшую популярность, и составлением логарифмических таблиц занялись многие европейские математики, включая Кеплера.
В 1615 году в беседе с профессором математики Грешем Колледжа в Лондоне Генри Бригсом (1561-1631) Непер предложил принять за логарифм единицы нуль, а за логарифм десяти — 100, или, что сводится к тому же, просто 1. Так появились десятичные логарифмы и были напечатаны первые логарифмические таблицы. Непер уже был болен, поэтому не смог усовершенствовать свои таблицы, однако дал Бригсу рекомендации видоизменить определение логарифма, приблизив его к современному. Бригс опубликовал свои таблицы в год смерти Непера (1617).
Но и в таблицах Бригса обнаружились ошибки. Первое безошибочное издание на основе таблиц Вега́ появилось только в 1857 году в Берлине (таблицы Бремивера).
В 1620-е годы Эдмунд Уингейт и Уильям Отред изобрели первую логарифмическую линейку, до появления карманных калькуляторов — незаменимый инструмент инженера.
Знаки log и Log были введены в 1624 году И. Кеплером.
Термин «натуральный логарифм» ввели Менголи в 1659 г. и вслед за ним Н. Меркатор в 1668 г., а издал таблицы натуральных логарифмов чисел от 1 до 1000 под названием «Новые логарифмы» лондонский учитель Джон Спейдел.
На русском языке первые логарифмические таблицы были изданы в 1703 году. Но во всех логарифмических таблицах были допущены ошибки при вычислении. Первые безошибочные таблицы вышли в 1857 году в Берлине в обработке немецкого математика К. Бремикера (1804-1877).
Дальнейшее развитие теории логарифмов связано с более широким применением аналитической геометрии и исчисления бесконечно малых. К тому времени относится установление связи между квадратурой равносторонней гиперболы и натуральным логарифмом.
С открытием логарифмического ряда изменилась техника вычисления логарифмов: они стали определяться с помощью бесконечных рядов.
В своих лекциях «Элементарная математика с высшей точки зрения», прочитанных в 1907-1908 годах, Ф. Клейн предложил использовать формулу в качестве исходного пункта построения теории логарифмов.
Таким образом, прошло 394 года с тех пор, как логарифмы впервые были введены (считая с 1614 г.), прежде чем математики пришли к определению понятия логарифма, которое положено теперь в основу школьного курса.
Радиоактивный распад. Изменение массы радиоактивного вещества происходит по формуле 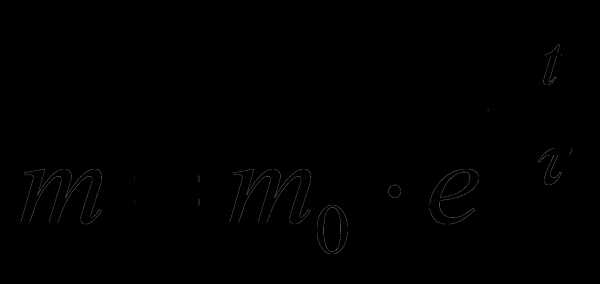 , где m0 – где масса вещества в начальный период времени t=0, m – масса вещества в момент времени t,
, где m0 – где масса вещества в начальный период времени t=0, m – масса вещества в момент времени t,
 .
.
T — период полураспада.
Это означает, что через время Т после начального момента времени, масса радиоактивного вещества уменьшается вдвое.
Народонаселение. Изменение количества людей в стране на небольшом отрезке времени с хорошей точностью описывается формулой 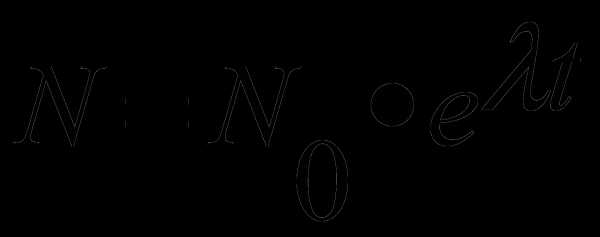 , где N
, где N
Формула Циолковского. Эта формула, связывающая скорость ракеты V с ее массой m:  , где Vr – скорость вылетающих газов, m0 – стартовая масса ракеты.
, где Vr – скорость вылетающих газов, m0 – стартовая масса ракеты.
Скорость истечения газа при сгорании топлива Vr невелика (в настоящее время она меньше или равна 2 км/с). Логарифм растет очень медленно, и для того чтобы достичь космической скорости, необходимо сделать большим отношение  , т.е. почти всю стартовую массу отдать под топливо.
, т.е. почти всю стартовую массу отдать под топливо.
Звукоизоляция стен. Коэффициент звукоизоляции стен измеряется по формуле
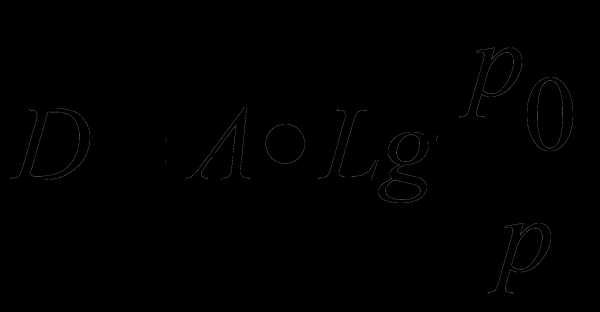 , где p0 – давление звука до поглощения, p – давление звука, прошедшего через стену, А – некоторая константа, которая в расчетах принимается равной 20 децибелам.
, где p0 – давление звука до поглощения, p – давление звука, прошедшего через стену, А – некоторая константа, которая в расчетах принимается равной 20 децибелам.
Если коэффициент звукоизоляции D равен, например 20 децибел, то это означает, что
 и p0 =10p, т.е. стена снижает давление звука в 10 раз. Такую изоляцию имеет деревянная дверь.
и p0 =10p, т.е. стена снижает давление звука в 10 раз. Такую изоляцию имеет деревянная дверь.
Логарифмическая спираль.
Логарифмическая спираль- плоская трансцендентная кривая, уравнение которой в полярных координатах имеет вид p=a φ, a>0.

Рога козлов, раковина улитки и семечки в подсолнухе закручены по логарифмической спирали


Если вычислительные потребности практической жизни и технического обихода вполне обеспечиваются трех и четырехзначными таблицами то с другой стороны, к услугам теоретического исследователя имеются таблицы и с гораздо большим числом знаков, чем даже 14- значные логарифмы. Вообще говоря, логарифм в большинстве случаев есть число иррациональное и не может быть точно выражен никаким числом цифр; логарифмы большинства чисел, сколько бы знаков ни брать, выражаются лишь приближенно, тем точней, чем больше цифр в их мантиссе. Для научных работ оказывается иногда недостаточной точность 14- значных логарифмов, но среди пятисот всевозможных образов логарифмических таблиц вышедших в свет, со времени их изобретения, исследователь всегда найдет такие, которые его удовлетворяют.
Например, 20- значные логарифмы чисел от 2 до1200, изданные во Франции Кале.
Для еще более ограниченной группы чисел имеются таблицы логарифмов с огромным числом десятичных знаков — настоящие логарифмические диковинки о существование которых не подозревают многие математики.
Вот эти логарифмы – исполины все они — не десятичные, а натуральные: (натуральными называются логарифмы, вычисленные не при основании 10, а при основании 2,718…, о котором у вас еще будет речь впереди. 48–значные таблицы Вольфрама для чисел до 10000; 61-значные таблицы Шарпа; 102-значные таблицы Паркхерста.
Счетная линейка.
К логарифмическим диковинкам можно было бы с полным основанием отнести и счетную линейку – «деревянные логарифмы», — если бы этот остроумный прибор не сделался благодаря своему удобству столь же обычным, счетным орудием для техников, как десятикосточковые счеты для конторских работников. Привычка угашает чувство изумления перед прибором, работающим по принципу логарифмов и, тем не менее, не требующим от пользующихся им даже знания того, что такое логарифм.
Молекула ДНК.
Её молекулы имеют огромную по молекулярным масштабам длину и состоят из 2-х нитей, сплетённых между собой в двойную спираль. Каждую из нитей можно сравнить с длинной нитки бус. С нитями бус мы сравниваем и белки. У белков «бусинами» являются аминокислоты 20 различных типов. У ДНК-всего 4 типа «бусин» и зовутся они нуклеотидами. «Бусины» двух нитей двойной спирали ДНК связаны между собой и строго друг другу соответствуют. Мы часто встречаем изготовление предметов по шаблону, называемому матрицей. Отливка монет или медалей, типографского шрифта. По аналогии происходящее в живой клетке восстановление двойной спирали по одной её цепи, как по матрице, так же называют матричным синтезом.
Вывод:
Многие природные явления не могли быть изучены без понятия логарифма;
Логарифмы используются для описания природных явлений астрономами, физиками, биологами.
Понятие логарифма широко применяется человеком во многих науках.
infourok.ru
Презентация: «Логарифмы»

ГБПОУ КК «Славянский сельскохозяйственный техникум»
Логарифмы
г. Славянск –на- Кубани.
2016г.
 0,а ≠ 1 ,называется показатель степени, в которую надо возвести число а, чтобы получить b / Что такое логарифм? Логарифмы – это рифмы, Словно в музыке слова. С ними проще вычисленья – Не сложней, чем дважды два. «
0,а ≠ 1 ,называется показатель степени, в которую надо возвести число а, чтобы получить b / Что такое логарифм? Логарифмы – это рифмы, Словно в музыке слова. С ними проще вычисленья – Не сложней, чем дважды два. «
Логарифм положительного числа b по основанию а , где а 0,а ≠ 1 ,называется показатель степени, в которую надо возвести число а, чтобы получить b /
Что такое логарифм?
Логарифмы – это рифмы,
Словно в музыке слова.
С ними проще вычисленья –
Не сложней, чем дважды два.

Слово ЛОГАРИФМ происходит от греческих слов — число и — отношение. переводится как отношение чисел, одно из которых является членом арифметической прогрессии, а другое геометрической.

ЛОГАРИФМ число, применение которого позволяет упростить многие сложные операции арифметики. Использование в вычислениях вместо чисел их логарифмов позволяет заменить умножение более простой операцией сложения, деление — вычитанием, возведение в степень — умножением и извлечение корней – делением.

Впервые понятие логарифмов ввел английский математик Джон Непер. Потомок старинного воинственного шотландского рода. Изучал логику, теологию, право, физику, математику, этику. Увлекался алхимией и астрологией. Изобрел несколько полезных сельскохозяйственных орудий.
Джон Непер 1550-1617

Первые таблицы десятичных логарифмов были составлены в 1617 г. английским математиком Бриггсом. Многие из них были выведены с помощью выведенной Бриггсом формулы.
Изобретатели логарифмов не ограничились созданием логарифмических таблиц, уже через 9 лет после их разработки в 1623 г. Английским математиком Гантером была создана первая логарифмическая линейка. Она стала рабочим инструментом для многих поколений. В настоящее время мы можем находить значения логарифмов, используя компьютер. Так, в языке программирования BASIC с помощью встроенной функции можно находить натуральные логарифмы чисел.

Логарифмическая линейка

«Логарифмы бывают разные…»
Бригсов логарифм — то же, что десятичный логарифм. Назван по имени Г. Бригса.
Десятичный логарифм — логарифм по основанию 10. Десятичный логарифм числа а обозначают lgа.
Неперов логарифм — (по имени Дж. Непера), то же, что натуральный логарифм.
Натуральный логарифм — логарифм, основание которого — неперово число е = 2,718 28… Натуральный логарифм числа а обозначают ln а.
Джон Непер ( 1550-1617)

Наибольшее влияние оказали логарифмы на развитие астрономии. Успехи мореплавания в средние века обусловливали большой спрос на астрономические таблицы, составление которых требовало весьма сложных вычислений. Использование логарифмических таблиц значительно облегчало и ускоряло эти вычисления. По образному выражению французского математика Лапласа (1749—1827), изобретение логарифмов, сократив работу астронома, продлило ему жизнь.

Общее определение логарифмической функции и ее широкое обобщение дал Леонард Эйлер .

В математике логарифмическая спираль
впервые упоминается в 1638 году
Рене Декартом.

Логарифмическая спираль в природе
Хищные птицы кружат над добычей по логарифмической спирали. Дело в том, что они лучше видят, если смотрят не прямо на добычу, а чуть в сторону.

Логарифмическая спираль в природе
Один из наиболее распространенных пауков, сплетая паутину, закручивает нити вокруг центра по логарифмической спирали.

Применение логарифмов
Музыка
Так называемые ступени темперированной хроматической гаммы (12- звуковой) частот звуковых колебаний представляют собой логарифмы. Только основание этих логарифмов равно 2 (а не 10, как принято в других случаях). Номера клавишей рояля представляют собой логарифмы чисел колебаний соответствующих звуков

Звезды, шум и логарифмы
Громкость шума и яркость звезд оцениваются одинаковым образом – по логарифмической шкале.

Психология
Изучая логарифмы, ученые пришли к выводу о том, что величина ощущения пропорциональна логарифму величины раздражения.

Зачем мы изучаем логарифмы?
Во-первых , логарифмы и сегодня позволяют упрощать вычисления.
Во-вторых , испокон веков целью математической науки было помочь людям узнать больше об окружающем мире, познать его закономерности и тайны.
Вывод : логарифмы – важные составляющие не только математики, но и всего окружающего мира, поэтому интерес к ним не ослабевает с годами и их необходимо продолжать изучать.
videouroki.net
Урок- презентация » Определение логарифма.Основное логарифмическое тождество.Виды логарифмов»

Определение логарифма. Основное логарифмическое тождество. Десятичные и натуральные логарифмы.
ПРЕПОДАВАТЕЛЬ МАТЕМАТИКИ:
Александрина Людмила Владимировна
ГБПОУ «Муравленковский колледж»
ЯНАО, г. Муравленко

Цель урока:
— Дать определение логарифма и его свойств, основного логарифмического тождества
— Показать полезность применения логарифмов;
— Научить видеть знакомое в незнакомом, развить интерес к истории математики и её приложениям.

« Возьми столько, сколько ты можешь и хочешь, но не меньше обязательного.»

Задача 1
Найдите положительный корень уравнения
х 2 = 9 ответ : х=3
х 3 = 8 ответ х=2
х 4 = 81 ответ : х=3

Задача 2
Решите уравнение
2 х =8 ответ: х=3
3 х =27 ответ: х=3
5 х =7 ответ: ?
 0 и а 1 называется показатель степени, в которую нужно возвести число а, чтобы получить число b . = х Логарифм с произвольным основанием.»
0 и а 1 называется показатель степени, в которую нужно возвести число а, чтобы получить число b . = х Логарифм с произвольным основанием.»
Определение логарифма
Логарифмом положительного числа b по основанию а0 и а 1 называется показатель степени, в которую нужно возвести число а, чтобы получить число b .
= х
Логарифм с произвольным основанием.

Примеры:

Логарифмы с основанием 10, называются десятичными.
Обозначение:Lg
Например: Lg100=2
Lg 1\10 =-1
Логарифмы с основанием е = 2.718 … называются натуральными.
Обозначение: Ln

Основное логарифмическое тождество
Действие нахождения логарифма числа называется логарифмированием

Свойства логарифмов

Примеры:

Вычислите
loq 3 27=
loq 5 125=
loq 2 2=
loq 8 1=
loq 2 16=
loq 3 9=
3 loq 3 18 =
loq 0,5 0,25=
loq 2 х= 3
7 loq 7 3 =

Вычислите
loq 4 1=
loq 13 13=
loq 3 х=2
6 loq 6 12 =
loq 4 х=2
loq 2 х=5
loq 13 13=
loq 3 х=2
5 loq 5 12 =
loq 9 1=

Тест
1
А -6
2
3
Б 8
И 30
Е 57
4
Б 11
М 49
В 14
П 54
5
Х 40
Г 6
У — 3
М — 4
Р — 2
Г 1
6
Ф 3
Л -12
Е 2
В — 1
Т 33
П 6
Л 1
Е 0,5
П 16
Е 5

Вычислите самостоятельно
loq 3 3=
loq 2 16=
loq 2 х=3
3 loq 3 18 =
loq 2 2=
loq 2 64=
loq 15 15=
loq 3 х=2
4 loq 4 12 =
loq 9 1=

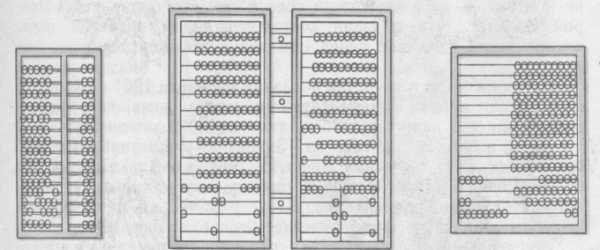
Логарифмическая разминка «Немного истории».
Логари́фм — от греч. λόγος — «слово», «отношение» и ἀριθμός — «число», «показатель»
Поистине безграничны приложения показательной и логарифмической функций в самых различных областях науки и техники, а ведь придумывали логарифмы для облегчения вычислений. Уже прошло четыре столетия с того дня, как в 1614 году были опубликованы первые логарифмические таблицы, составленные Джоном Непером. Они помогли астрономам и инженерам, сокращая время на вычисления, и тем самым, как сказал знаменитый французский ученый Лаплас, «удлиняли жизнь вычислителям».
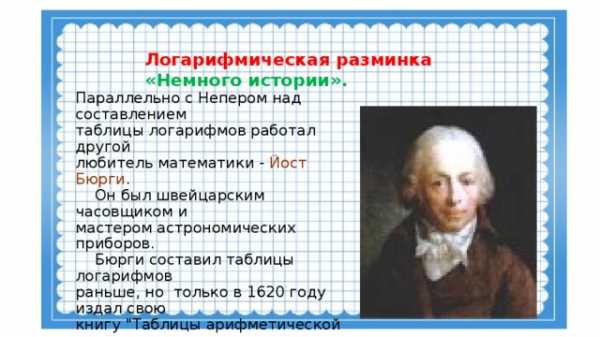
Логарифмическая разминка «Немного истории».
Параллельно с Непером над составлением
таблицы логарифмов работал другой
любитель математики — Йост Бюрги .
Он был швейцарским часовщиком и
мастером астрономических приборов.
Бюрги составил таблицы логарифмов
раньше, но только в 1620 году издал свою
книгу «Таблицы арифметической и
геометрической прогрессии с обстоятельным
наставлением, как пользоваться ими при
всякого рода вычислениях».

Логарифмическая разминка «Немного истории».
В 1623 г., т. е. всего через 9 лет после издания
первых таблиц, английским математиком Эдмундом
Гантером была изобретена первая логарифмическая
линейка, ставшая рабочим инструментом для многих
поколений вплоть до появления ЭВМ.


Логарифмическая спираль «Удивительное рядом »
Спираль – это плоская кривая линия, многократно обходящая одну из точек на плоскости, которая называется полюсом спирали.

Логарифмическая спираль «Удивительное рядом»
По логарифмическим спиралям выстраиваются
цветки в соцветиях подсолнечника

Логарифмическая спираль «Удивительное рядом»
По логарифмическим спиралям выстраиваются
рога многих животных

Логарифмическая спираль «Удивительное рядом»
Живые существа обычно растут, сохраняя общее очертание своей формы. При этом они растут чаще всего во всех направлениях — взрослое существо и выше и толще детеныша. Но раковины морских животных могут расти лишь в одном направлении.

Логарифмическая спираль «Удивительное рядом»
По логарифмической спирали свёрнуты раковины
многих улиток и моллюсков.

Логарифмическая спираль «Удивительное рядом»
По логарифмической спирали формируется тело циклона
По логарифмической спирали формируется тело циклона

Логарифмическая спираль «Удивительное рядом»
Даже пауки, сплетая паутину, закручивают нити вокруг центра по логарифмической спирали .

Логарифмическая спираль «Удивительное рядом»
Улитка является органом, воспринимающим звук, в котором самой природой заложена
ЛОГАРИФМИЧЕСКАЯ СПИРАЛЬ!
Человеческое ухо – это маленькое чудо !
!

Логарифмическая спираль «Удивительное рядом»
Траектории насекомых
летящих на свет также описывают логарифмическую спираль.
Логарифмическая спираль единственная из спиралей не меняет своей формы при увеличении размеров. Видимо, это свойство и послужило причиной того, что в живой природе логарифмическая спираль встречается чаще других.

Логарифмическая спираль «Удивительное рядом»
По логарифмическим спиралям закручены многие галактики, в частности Галактика, которой принадлежит Солнечная система.

Логарифмическая спираль «Удивительное рядом»
Очертания, выраженные логарифмической спиралью, имеют не только раковины. Спираль увидели в расположении семян подсолнечника, в шишках сосны, ананасах, кактусах и т.д.

Испуганное стадо северных оленей разбегается по спирали.

Спиралью закручиваются ураганы и смерчи

Молекула ДНК закручена двойной спиралью.

Звезды, шум и логарифмы
Этот заголовок связывает столь, казалось бы, несоединимые вещи. Шум и звезды объединяются здесь потому, что громкость шума и яркость звезд оцениваются одинаковым образом — по логарифмической шкале.

kopilkaurokov.ru
Презентация по теме «Практическое применение логарифмов»
Слайд 1
Практическое применение логарифмовСлайд 2
Логарифмические функции распространены чрезвычайно широко как в математике, так и в естественных науках. Ряд явлений природы помогает описать логарифмическая зависимость. Иначе говоря, математики, пытаясь составить математическую модель того или иного явления, достаточно часто обращаются именно к логарифмической функции.
Слайд 3
Одним из наиболее наглядных примеров является логарифмическая спираль. Спираль в одну сторону развертывается до бесконечности, а вокруг полюса, напротив, закручивается, стремясь к нему, но не достигая.
Слайд 4
Раковины морских животных могут расти лишь в одном направлении. Чтобы не слишком вытягиваться в длину, им приходится скручиваться, причем рост совершается так, что сохраняется подобие раковины с её первоначальной формой. А такой рост может совершаться лишь по логарифмической спирали. Биология
Слайд 5
Один из наиболее распространенных пауков, эпейра , сплетая паутину, закручивает нити вокруг центра по логарифмическим спиралям. Биология
Слайд 6
Рога таких млекопитающих, как горные козлы, закручены по логарифмической спирали В подсолнухе семечки расположены по дугам, близким к логарифмической спирали. Биология
Слайд 7
Механика и физика Принцип Больцмана в статистической термодинамике — одна из важнейших функций состояния термодинамической системы, характеризующая степень её хаотичности . Формула Циолковского применяется для расчёта скорости ракеты.
Слайд 8
Единицей громкости звука служит «бел», практически — его десятая доля, «децибел». Разности громкостей в 1 бел отвечает отношение силы шумов 10. Значит, громкость шума, выраженная в белах, равна десятичному логарифму его физической силы.
Слайд 9
Химия Водородный показатель, » pH «, — это мера активности ионов водорода в растворе, количественно выражающая его кислотность, вычисляется как отрицательный десятичный логарифм концентрации водородных ионов, выраженной в молях на литр
Слайд 10
Астрономия По логарифмическим спиралям закручены и многие Галактики, в частности Галактика, которой принадлежит Солнечная система.
Слайд 11
Астрономы распределяют звезды по степеням видимой яркости на светила первой величины, второй величины, третьей и т. д. Легко понять, что «величина» звезды представляет собой не что иное, как логарифм ее физической яркости. Оценивая видимую яркость звезд, астроном оперирует с таблицей логарифмов, составленной при основании 2,5.
Слайд 12
Музыка «Ступени » темперированной хроматической гаммы не расставлены на равных расстояниях ни по отношению к числам колебаний, ни по отношению к длинам волн соответствующих звуков, а представляют собой логарифмы этих величин. Отсюда видим, что номера клавишей рояля представляют собой логарифмы чисел колебаний соответствующих звуков.
Слайд 13
География Рихтер предложил для оценки силы землетрясения (в его эпицентре) десятичный логарифм перемещения (в микрометрах) иглы стандартного сейсмографа Вуда-Андерсона , расположенного на расстоянии не более 600 км от эпицентра.
Слайд 14
Психология Закон Вебера — Фехнера — эмпирический психофизиологический закон, заключающийся в том, что интенсивность ощущения пропорциональна логарифму интенсивности раздражителя.
Слайд 15
Психология Закон Фи́ттса — общий закон , связывающий время движения с точностью движения и с расстоянием перемещения: чем дальше или точнее выполняется движение, тем больше коррекции необходимо для его выполнения, и соответственно, больше времени требуется для внесения этой коррекции
Слайд 16
Психология Время на принятие решения при наличии выбора можно оценить по закону Хикса.
Слайд 17
Информатика Применяется для вычисления основной единицы – бита. Бит — это двоичный логарифм вероятности равновероятных событий или сумма произведений вероятности на двоичный логарифм вероятности при равновероятных событиях
Слайд 18
Источники информации: http://ru.wikipedia.org/wiki/ http://s_2_petrop.ven.edu54.ru/p89aa1.html http://images.yandex.ru/?uinfo=ww-1341-wh-591-fw-1274-fh-448-pd-1
nsportal.ru
Презентация на тему «Логарифмы. Свойства логарифмов».
презентация к уроку изучения новой темы «Логарифмы. Совйства логарифмов».
Просмотр содержимого документа
«Презентация на тему «Логарифмы. Свойства логарифмов».»

А. Дистервег
РАЗВИТИЕ И ОБРАЗОВАНИЕ НИ ОДНОМУ ЧЕЛОВЕКУ НЕ МОГУТ БЫТЬ ДАНЫ ИЛИ СООБЩЕНЫ. ВСЯКИЙ, КТО ЖЕЛАЕТ К НИМ ПРИОБЩИТЬСЯ, ДОЛЖЕН ДОСТИГНУТЬ ЭТОГО СОБСТВЕННОЙ ДЕЯТЕЛЬНОСТЬЮ, СОБСТВЕННЫМИ СИЛАМИ, СОБСТВЕННЫМ НАПРЯЖЕНИЕМ .

Определите тему урока, решив уравнения
- 2 х = ; 3 х = ; 5 х = 1/125; 2 х = 1/4; 2 х = 4; 3 х = 81; 7 х = 1/7; 3 х = 1/81
З
5
М
Л
– 4
Г
2 / 3
Е
– 3
– 2 / 7
Р
2
Ф
– 1
О
1 / 2
И
4
А
– 2

Логарифм и его свойства
11 класс

Джон Непер, изобретатель логарифмов
В 1590 году пришел к идее логарифмических вычислений и составил первые таблицы логарифмов, опубликовал труд «Описание удивительных таблиц логарифмов». В этом труде содержались определение логарифмов, объяснение их свойств. Изобрел логарифмическую линейку, счетный инструмент, использующий таблицы Непера для упрощения вычислений.

Логарифмическая линейка
В настоящее время, с появлением компактных калькуляторов и компьютеров, необходимость в использовании таблиц
логарифмов и логарифмических линеек отпала.

Определение логарифма
- Логарифмом числа в 0 по основанию а 0 и а 1 называется показатель степени, в которую нужно возвести число а, чтобы получить число в.
- — логарифм с произвольным основанием.
- Например: а) log 3 81 = 4, так как 3 4 = 81; б) log 5 125 = 3, так как 5 3 = 125; в) log 0,5 16 = -4, так как (0,5) -4 = 16;

Применение логарифма: Банковские расчёты, география, расчёты в производстве, биология, химия, физика, астрономия, психология, социология, музыка.

Логарифмическая спираль в природе
Раковина наутилуса
Расположение семян на подсолнечнике
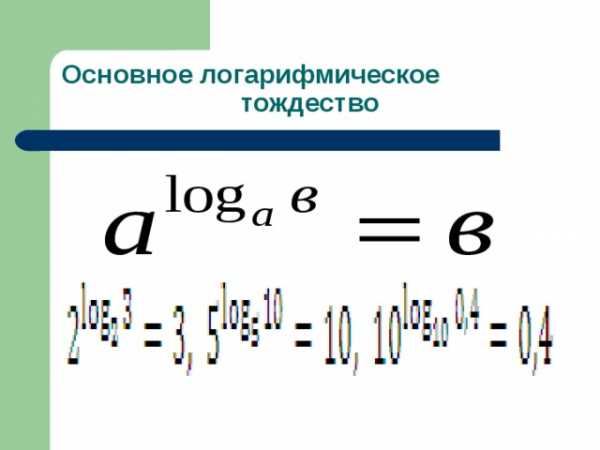
Основное логарифмическое тождество

Свойства логарифмов
- log a 1 = 0.
- log a a = 1.
- log a xy = log a x + log a y.
- log a х ∕ у = log a x — log a y.
- log a x p = p log a x
- log a р x = 1 ∕ р log a x

Формула перехода от логарифмов по одному основанию к логарифмам по другому основанию

Десятичные логарифмы
- Если основание логарифма равно 10, то логарифм называется десятичным:

Натуральные логарифмы
- Если основание логарифма е 2,7, то логарифм называется натуральным:

- 1. Найдите логарифм числа 64 по основанию 4.
Решение : log 4 64 = 3, так как 4 3 = 64.
Ответ: 3
- 2. Найдите число x , если log 5 x = 2
Решение: log 5 x = 2, x = 5 2 (по определению логарифма), x = 25.
Ответ : 25.
- 3. Вычислить: log 3 1/ 81 = x ,
Решение: log 3 1/ 81 = x , 3 x = 1/ 81, x = – 4.
Ответ: – 4.

- 1. Вычислить: log 6 12 + log 6 3
Решение:
log 6 12 +log 6 3 = log 6 (12*3) = log 6 36 = log 6 6 2 = 2
Ответ : 2.
- 2. Вычислить: log 5 250 – log 5 2.
Решение:
log 5 250 – log 5 2 = log 5 (250/2) = log 5 125 = 3
Ответ : 3.
Решение :
=
Ответ: 8.

Вычислите

Спасибо за урок!
kopilkaurokov.ru
презентация на тему Логарифмы | Социальная сеть работников образования
Слайд 1
«Изобретение логарифмов, сократив работу астронома, продлило ему жизнь» П.С.Лаплас Логарифмы Подготовил Антонов.Б 10 «А»Слайд 2
Джон Непер, изобретатель логарифмов Определение логарифмов и таблицу их значений впервые опубликовал в 1614 году шотландский математик Джон Непер. Логарифмические таблицы, расширенные и уточнённые другими математиками, повсеместно использовались для научных и инженерных расчётов более трёх веков.
Слайд 3
В кодификаторе элементов содержания ЕГЭ по математике в 2012 году по теме « Логарифмы» указаны элементы : 1.3.1 Логарифм числа 1.3.2 Логарифм произведения, частного, степени 1.3.3 Десятичный и натуральный логарифмы, число е 1. 4.5 Преобразование выражений, включающих операцию логарифмирования 2.1.6 Логарифмические уравнения 2.1.10 Использование свойств и графиков функций при решении уравнений 2.2.4 Логарифмические неравенства 3.3.7 Логарифмическая функция, ее график
Слайд 4
Алгоритм решения логарифмических уравнений Найти ОДЗ или сделать проверку Выбрать ответ Решить по определению или потенцируя
Слайд 5
+ 3+5 : 32 2+3 Работа на месте (задания части В) 1)Вычислить 2) Решить уравнения ,если b = -2 = 2 = 2 2 = 3
Слайд 6
Правильные ответы Вычислить Решить уравнения 4 -46 125 0,2 8 7 9 270
Слайд 7
Леонард Эйлер нем. Leonhard Euler Дата рождения: 4 (15) апреля 1707 Место рождения: Базель, Швейцария Дата смерти: 7 (18) сентября 1783 (76 лет) Место смерти: Санкт-Петербург, Российская империя Научная сфера: Математика, механика, физика, астрономия Современное определение показательной, логарифмической функции — заслуга Леонарда Эйлера, так же как и их символика. 7
Слайд 8
Алгоритм решения логарифмических неравенств I Найти ОДЗ III Выбор ответа с учётом ОДЗ II Решить неравенство
Слайд 10
В России первые таблицы логарифмов были изданы в 1703 году при участии Л. Ф. Магницкого. Таблицы Брадиса (1921) использовались в учебных заведениях и в инженерных расчётах, не требующих большой точности. Они содержали мантиссы десятичных логарифмов чисел и тригонометрических функций, натуральные логарифмы и некоторые другие полезные расчётные инструменты. Профессиональный сборник для точных вычислений
Слайд 11
Примеры использования неравномерности логарифмической зависимости Акустика — интенсивность звука (децибелы). Отношение сигнал/шум в радиотехнике и электросвязи. Астрономия — шкала яркости звёзд. Химия — активность водородных ионов (pH). Сейсмология — шкала Рихтера. Теория музыки — нотная шкала, по отношению к частотам нотных звуков. История — логарифмическая шкала времени.
Слайд 12
Логарифмическая линейка В настоящее время, с появлением компактных калькуляторов и компьютеров, необходимость в использовании таблиц логарифмов и логарифмических линеек отпала.
Слайд 13
Логарифмическая спираль в природе Расположение семян на подсолнечнике Раковина наутилуса
Слайд 14
Развитие и образование ни одному человеку не могут быть даны или сообщены. Всякий, кто желает к ним приобщиться, должен достигнуть этого собственной деятельностью, собственными силами, собственным напряжением. А. Дистервег Спасибо за внимание!
nsportal.ru
Презентация на тему Логарифмы. Применение логарифмов
Слайд 1Логарифмы. Применение логарифмов.
Слайд 2повторить определение логарифма; закрепить основные свойства логарифмов; — способствовать формированию умения применять свойства логарифмов при упрощении выражений; — развивать математическое мышление; технику вычисления; умение логически мыслить и рационально работать; — воспитание познавательной активности, чувства ответственности, уважения друг к другу.
Цели урока:
Слайд 3ДЖОН НЕПЕР (1550-1617)
Шотландский математик – изобретатель логарифмов. В 1590-х годах пришел к идее логарифмических вычислений и составил первые таблицы логарифмов, однако свой знаменитый “Описание удивительных таблиц логарифмов” опубликовал лишь в 1614 году. Ему принадлежит определение логарифмов, объяснение их свойств, таблицы логарифмов синусов, косинусов, тангенсов и приложения логарифмов в сферической тригонометрии.
Слайд 4Разминка
Слайд 51. Логарифмом числа b по …………… а называется …………….. степени, в которую нужно……………. основание а, чтобы получить число b. 2. Основание и число, стоящее под знаком логарифма, должны быть…………. 3. Если основание а =….., то такой логарифм называется десятичным и обозначается lg b.
основанию показатель возвести положительными 10
Продолжи предложение…..
Слайд 6Установите соответствие
Слайд 71 9 8 2 Обгонялки
Слайд 8Вычислить: Тест
Слайд 9Музыканты редко увлекаются математикой. Большинство из них питают к этой науке чувство уважения. Между тем, музыканты – даже те, которые не проверяют подобно Сальери у Пушкина “алгеброй гармонию”, встречаются с математикой гораздо чаще, чем сами подозревают, и притом с такими “странными” вещами, как логарифмы.
Применение логарифмов
Слайд 10Понятия логарифмической спирали
Логарифмическая спираль – это плоские линии в геометрии, отличные от прямых и окружностей, которые могут скользить по себе.
Слайд 11Поэтому раковины многих моллюсков, улиток, а так же рога таких млекопитающих как архары (горные козлы), закручены по логарифмической спирали.
Семечки в подсолнухе расположены по дугам, так же близким к логарифмической спирали.
Слайд 12Раковины морских животных могут расти лишь в одном направлении. Чтобы не слишком вытягиваться им приходиться скручиваться, причём каждый следующий виток подобен предыдущему. А такой рост может совершаться лишь по логарифмической спирали, можно сказать что эта спираль является математическим символом соотношения форм роста.
Слайд 13Логарифмическая спираль в природе
Один из наиболее распространенных пауков ЭПЕЙРА, сплетая паутину, закручивает нити вокруг центра по логарифмической спирали.
По логарифмическим спиралям закручены и многие галактики, в частности, галактика которой принадлежит Солнечная Система.
Слайд 14Молекула ДНК
Её молекулы имеют огромную по молекулярным масштабам длину и состоят из 2-х нитей, сплетённых между собой в двойную спираль. Каждую из нитей можно сравнить с длинной нитки бус. С нитями бус мы сравниваем и белки.
Слайд 15Логарифмы в космосе
Слайд 16Яркость звезд составляет геометрическую прогрессию со знаменателем 2,5 легко понять, что «величина» звезды представляют собой логарифм её физической яркости. Оценивая яркость звезд, астроном оценивает таблицей логарифмов составленной при основании 2,5. Аналогично оценивается и громкость шума. Вредное влияние промышленных шумов на здоровье рабочих и производстве труда.
Слайд 17н о ь ч а с т н о о с у м е о с н в а н и е п о к з а т е л ь н е п е д е с я т ч н ы й
л о г а р и м и р о в а н и е
Кроссворд
Слайд 18Спасибо за урок!
prezentacii.org

