исследовательская работа по математике на тему «Золотое сечение»

МОУ «Парфеньевская средняя общеобразовательная школа»

Автор проекта Смирнова Полина, ученица 11 класса

Руководитель Смирнова Л.А., учитель математики

2010-2011 учебный год

Вступление

Есть вещи, которые нельзя объяснить. Вот вы подходите к пустой скамейке и садитесь на нее. Где вы сядете — посередине? Или, может быть, с самого края? Нет, скорее всего, не то и не другое. Вы сядете так, что отношение одной части скамейки к другой, относительно вашего тела, будет равно примерно 1,62. Простая вещь, абсолютно инстинктивная… Садясь на скамейку, вы произвели «золотое сечение». О золотом сечении знали еще в древнем Египте и Вавилоне, в Индии и Китае. Великий Пифагор создал тайную школу, где изучалась мистическая суть «золотого сечения». Евклид применил его, создавая свою геометрию, а Фидий — свои бессмертные скульптуры. Платон рассказывал, что Вселенная устроена согласно «золотому сечению». А Аристотель нашел соответствие «золотого сечения» этическому закону. Высшую гармонию «золотого сечения» будут проповедовать Леонардо да Винчи и Микеланджело, ведь красота и «золотое сечение» — это одно и то же. А христианские мистики будут рисовать на стенах своих монастырей пентаграммы «золотого сечения», спасаясь от Дьявола. При этом ученые — от Пачоли до Эйнштейна — будут искать, но так и не найдут его точного значения. Бесконечный ряд после запятой — 1,6180339887… Странная, загадочная, необъяснимая вещь: эта божественная пропорция мистическим образом сопутствует всему живому. Неживая природа не знает, что такое «золотое сечение». Но вы непременно увидите эту пропорцию и в изгибах морских раковин, и в форме цветов, и в облике жуков, и в красивом человеческом теле. Все живое и все красивое — все подчиняется божественному закону, имя которому — «золотое сечение». Так что же такое «золотое сечение»?.. Что это за идеальное, божественное сочетание? Может быть, это закон красоты? Или все-таки он — мистическая тайна? Научный феномен или этический принцип? Ответ неизвестен до сих пор. Точнее — нет, известен. «Золотое сечение» — это и то, и другое, и третье. Только не по отдельности, а одновременно… И в этом его подлинная загадка, его великая тайна.

Понятие «золотое сечение».

Золотое сечение – это такое пропорциональное деление отрезка на неравные части, при котором меньший отрезок так относится к большему, как больший ко всему.

a : b = b : c или с : b = b : а.

Эта пропорция равна:

Свойства золотого сечения создали вокруг этого числа романтический ореол таинственности и чуть ли не мистического поклонения.

К примеру, в правильной пятиконечной звезде, каждый сегмент делится пересекающим его сегментом в золотом сечении (т. е. отношение синего отрезка к зелёному, красного к синему, зелёного к фиолетовому, равны

1.618 Принято считать, что понятие о золотом сечении ввел в научный обиход Пифагор. Есть предположение, что Пифагор свое знание позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании.

Примеры применения золотого сечения

Золотое сечение в математике

Практическое знакомство с золотым сечением начинают с деления отрезка прямой в золотой пропорции с помощью циркуля и линейки. Из точки В восставляется перпендикуляр, равный половине АВ. Полученная точка С соединяется линией с точкой А. На полученной линии откладывается отрезок ВС

, заканчивающийся точкой D. Отрезок AD переносится на прямую АВ. Полученная при этом точка Е делит отрезок АВ в соотношении золотой пропорции. Отрезки золотой пропорции выражаются бесконечной иррациональной дробью AE = 0,618…, если АВ принять за единицу, ВЕ = 0,382… Для практических целей часто используют приближенные значения 0,62 и 0,38. Если отрезок АВ принять за 100 частей, то большая часть отрезка равна 62, а меньшая – 38 частям.

Свойства золотого сечения описываются уравнением: x² – x – 1 = 0. Решение этого уравнения:

Золотое сечение в искусстве

в музыке

Наиболее обширное исследование проявлений золотого сечения в музыке было предпринято в 1925 году искусствоведом Л.Сабанеевым . Им было изучено две тысячи произведений различных композиторов. По его мнению, временное протяжение музыкального произведения делится «некоторыми вехами», которые выделяются при восприятии музыки и облегчают созерцание формы целого. Все эти музыкальные вехи делят целое на части, как правило, по закону золотого сечения.

По наблюдениям Л.Сабанеева, в музыкальных произведениях различных композиторов обычно констатируется не одно золотое сечение, а целая серия подобных сечений. Каждое такое сечение отражает свое музыкальное событие, качественный скачок в развитии музыкальной темы. В изученных им 1770 сочинениях 42 композиторов наблюдалось 3275 золотых сечений. Количество произведений, в которых наблюдалось хотя бы одно золотое сечение, составило 1338. Наибольшее количество музыкальных произведений, в которых имеется золотое сечение, у Аренского (95%), Бетховена (97%), Гайдна (97%), Моцарта (91%), Скрябина (90%), Шопена (92%), Шуберта (91%).
Наиболее детально были изучены все 27 этюдов Шопена. В них обнаружено 154 золотых сечения; всего в трех этюдах золотое сечение отсутствовало. В некоторых случаях строение музыкального произведения сочетало в себе симметричность и золотое сечение одновременно; в этих случаях оно делилось на несколько симметричных частей, в каждой из которых проявляется золотое сечение. У Бетховена также сочинения делятся на две симметричные части, а внутри каждой из них наблюдаются проявления золотой пропорции.

Причем, чем талантливее композитор, тем в большем количестве его произведений найдено золотых сечений. У Аренского, Бетховена, Бородина, Гайдна, Моцарта, Скрябина, Шопена и Шуберта золотые сечения найдены в 90% всех произведений. По мнению Сабанеева, золотое сечение приводит к впечатлению особой стройности музыкального сочинения. Можно признать, что золотая пропорция является критерием гармонии композиции музыкального произведения.

в кино

В кино С. Эйзенштейн искусственно построил фильм Броненосец Потёмкин по правилам «золотого сечения». Он разбил ленту на пять частей. В первых трёх действие разворачивается на корабле. В двух последних — в Одессе, где разворачивается восстание. Этот переход в город происходит точно в точке золотого сечения. Да и в каждой части есть свой перелом, происходящий по закону золотого сечения.

Золотое сечение в живописи

Переходя к примерам “золотого сечения” в живописи, нельзя не остановить своего внимания на творчестве Леонардо да Винчи. Его личность – одна из загадок истории. Сам Леонардо да Винчи говорил: «Пусть никто, не будучи математиком, не дерзнет читать мои труды». Посмотрим внимательно на картину «Джоконда». Портрет Моны Лизы (Джоконды) долгие годы привлекает внимание исследователей, которые обнаружили, что композиция рисунка основана на золотых треугольниках, являющихся частями правильного звездчатого пятиугольника.

Также пропорция золотого сечения проявляется в картине Шишкина. На этой знаменитой картине И. И. Шишкина с очевидностью просматриваются мотивы золотого сечения. Ярко освещенная солнцем сосна (стоящая на первом плане) делит длину картины по золотому сечению. Справа от сосны — освещенный солнцем пригорок. Он делит по золотому сечению правую часть картины по горизонтали.  

В картине Рафаэля «Избиение младенцев» просматривается другой элемент золотой пропорции — золотая спираль. На подготовительном эскизе Рафаэля проведены красные линии, идущие от смыслового центра композиции — точки, где пальцы воина сомкнулись вокруг лодыжки ребенка — вдоль фигур ребенка, женщины, прижимающей его к себе, воина с занесенным мечом и затем вдоль фигур такой же группы в правой части эскиза. Неизвестно, строил ли Рафаэль золотую спираль или чувствовал её.

Т.Кук использовал при анализе картины Сандро Боттичелли «рождение Венеры» золотое сечение.

Золотое сечение в архитектуре

Одним из красивейших произведений древнегреческой архитектуры является Парфенон (V в. до н. э.).

На рисунках виден целый ряд закономерностей, связанных с золотым сечением. Пропорции здания можно выразить через различные степени числа Ф=0,618…

На плане пола Парфенона также можно заметить «золотые прямоугольники»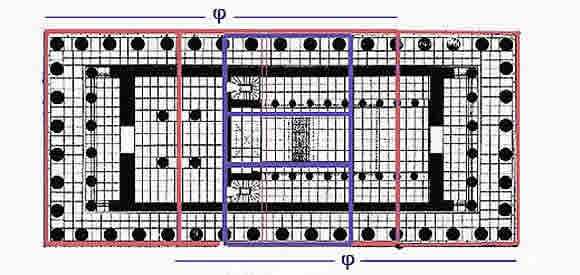

Золотое соотношение мы можем увидеть и в здании собора Парижской Богоматери (Нотр-дам де Пари) и в пирамиде Хеопса:

Не только египетские пиpамиды постpоены в соответствии с совеpшенными пpопоpциями золотого сечения, то же самое явление обнаpужено и у мексиканских пиpамид.

Я решила рассмотреть планы церквей Парфеньева и посмотреть, нет ли там золотого отношения. Результат — приложение (мультимедийная презентация).

Золотое сечение в скульптуре

Золотая пропорция применялась многими античными скульпторами. Известна золотая пропорция статуи Аполлона Бельведерского: рост изображенного человека делится пупочной линией в золотом сечении.

Афина Парфенос Зевс Олимпийский

Еще в эпоху Возрождения художники открыли, что любая картина имеет определенные точки, невольно приковывающие наше внимание, так называемые зрительные центры. При этом абсолютно неважно, какой формат имеет картина — горизонтальный или вертикальный. Таких точек всего четыре, они делят величину изображения по горизонтали и вертикали в золотом сечении, т.е. расположены они на расстоянии примерно 3/8 и 5/8 от соответствующих краев плоскости.

Золотое сечение в шрифтах и бытовых предметах

Золотые пропорции в частях тела человека

В 1855 г. немецкий исследователь золотого сечения профессор Цейзинг опубликовал свой труд «Эстетические исследования». Цейзинг измерил около двух тысяч человеческих тел и пришел к выводу, что золотое сечение выражает средний статистический закон. Деление тела точкой пупа – важнейший показатель золотого сечения. Пропорции мужского тела колеблются в пределах среднего отношения 13 : 8 = 1,625 и несколько ближе подходят к золотому сечению, чем пропорции женского тела, в отношении которого среднее значение пропорции выражается в соотношении 8 : 5 = 1,6. У новорожденного пропорция составляет отношение 1 : 1, к 13 годам она равна 1,6, а к 21 году равняется мужской.
Пропорции золотого сечения проявляются и в отношении других частей тела – длина плеча, предплечья и кисти, кисти и пальцев и т.д.
Справедливость своей теории Цейзинг проверял на греческих статуях. Наиболее подробно он разработал пропорции Аполлона Бельведерского. Подверглись исследованию греческие вазы, архитектурные сооружения различных эпох, растения, животные, птичьи яйца, музыкальные тона, стихотворные размеры.

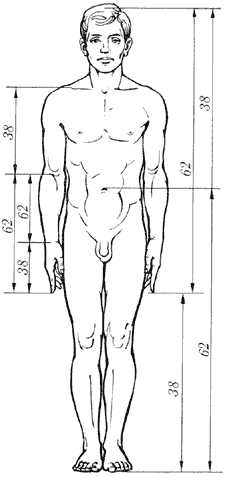
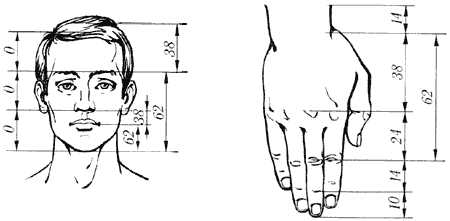
Я провела подобное исследование в 11 классе. Результаты измерений приведены в таблице. Приложение (мультимедийная презентация).

Золотое сечение в биологии и живой природе

В биологических исследованиях было показано, что, начиная с вирусов и растений и кончая организмом человека, всюду выявляется золотая пропорция, характеризующая соразмерность и гармоничность их строения. Золотое сечение признано универсальным законом живых систем.

Рассмотрим побег цикория. От основного стебля образовался отросток. Тут же расположился первый листок. Отросток делает сильный выброс в пространство, останавливается, выпускает листок, но уже короче первого, снова делает выброс в пространство, но уже меньшей силы, выпускает листок еще меньшего размера и снова выброс.

Если первый выброс принять за 100 единиц, то второй равен 62 единицам, третий – 38, четвертый – 24 и т.д. Длина лепестков тоже подчинена золотой пропорции. В росте, завоевании пространства растение сохраняло определенные пропорции. Импульсы его роста постепенно уменьшались в пропорции золотого сечения. Было установлено, что числовой ряд чисел Фибоначчи характеризует структурную организацию многих живых систем. Например, винтовое листорасположение на ветке составляет дробь (число оборотов на стебле/число листьев в цикле, напр. 2/5; 3/8; 5/13), соответствующую рядам Фибоначчи. Хорошо известна «золотая» пропорция пятилепестковых цветков яблони, груши и многих других растений. Носители генетического кода — молекулы ДНК и РНК — имеют структуру двойной спирали; ее размеры почти полностью соответствуют числам ряда Фибоначчи. Гете подчеркивал тенденцию природы к спиральности.

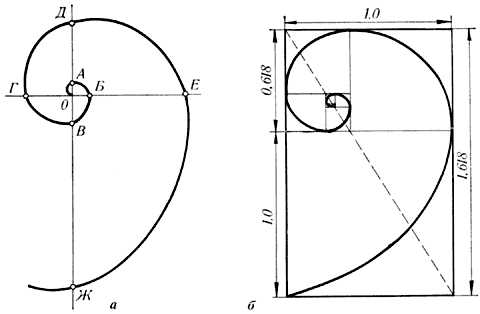
Паук плетет паутину спиралеобразно. Спиралью закручивается ураган. Испуганное стадо северных оленей разбегается по спирали. Гете называл спираль «кривой жизни». Спираль увидели в расположении семян подсолнечника, в шишках сосны, ананасах, кактусах и т.д. У многих бабочек соотношение размеров грудной и брюшной части тела отвечает золотой пропорции. Сложив крылья, ночная бабочка образует правильный равносторонний треугольник. Но стоит развести крылья, и вы увидите тот же принцип членения тела на 2,3,5,8. Стрекоза также создана по законам золотой пропорции: отношение длин хвоста и корпуса равно отношению общей длины к длине хвоста

В ящерице длина ее хвоста так относится к длине остального тела, как 62 к 38. Можно заметить золотые пропорции, если внимательно посмотреть на яйцо птицы.

Все живое создано в соответствии с пропорцией Золотого Сечения

Некоторые открытия и теории современной науки,
связанные с «золотым сечением»

1.Плитки Пенроуза

В античной науке была широко известна «проблема паркета», которая сводится к плотному заполнению плоскости геометрическими фигурами одного вида. Как известно, такое заполнение может быть осуществлено с помощью треугольников, квадратов и шестиугольников. С помощью пятиугольников (пентагонов) такое заполнение невозможно.

Проблема паркета

Рассмотрим еще раз внимательно правильный пятиугольник, называемый также пентагоном или пентаграммой, плоскую геометрическую фигуру, основанную на «золотом сечении».

Правильный пятиугольник или пентагон

Как известно, после проведения в пентагоне диагоналей исходный пентагон может быть представлен как совокупность трех типов геометрических фигур. В центре находится новый пентагон, образуемый точками пересечения диагоналей. Остальная часть пентагона включает в себя пять равнобедренных треугольников, окрашенных в желтый цвет, и пять равнобедренных треугольников, окрашенных в красный цвет. Желтые треугольники являются «золотыми», так как отношение бедра к основанию равно золотой пропорции; они имеют острые углы в 36 при вершине и острые углы в 72 при основании. Красные треугольники также являются «золотыми», так как отношение бедра к основанию равно золотой пропорции; они имеют тупой угол в 108 при вершине и острые углы в 36 при основании. А теперь соединим два желтых треугольника и два красных треугольника их основаниями. В результате мы получим два «золотых» ромба. Первый из них (желтый) имеет острый угол в 36 и тупой угол в 144. Левый ромб будем называть тонким ромбом, а правый ромб – толстым ромбом.

«Золотые» ромбы

Английский математик и физик Роджерс Пенроуз использовал «золотые» ромбы для конструирования «золотого» паркета, который был назван плитками Пенроуза. Плитки Пенроуза представляют собой комбинацию толстых и тонких ромбов.

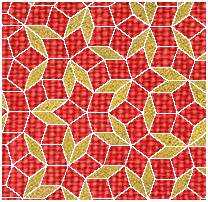Плитки Пенроуза

Важно подчеркнуть, что плитки Пенроуза имеют «пентагональную» симметрию или симметрию 5-го порядка, а отношение числа толстых ромбов к тонким стремится к золотой пропорции!

2.Квазикристаллы

12 ноября 1984 г. в небольшой статье, опубликованной в авторитетном журнале «Physical Review Letters» израильским физиком Даном Шехтманом, было предъявлено экспериментальное доказательство существования металлического сплава с исключительными свойствами. При исследовании методами электронной дифракции этот сплав проявил все признаки кристалла. Его дифракционная картина составлена из ярких и регулярно расположенных точек, совсем как у кристалла. Однако эта картина характеризуется наличием «икосаэдрической» или «пентангональной» симметрии, строго запрещенной в кристалле из геометрических соображений. Такие необычные сплавы были названы квазикристаллами. Менее чем за год были открыты многие другие сплавы подобного типа. Их было так много, что квазикристаллическое состояние оказалось намного более распространенным, чем это можно было бы представить. Открытие квазикристаллов является еще одним научным подтверждением, что, возможно, именно «золотая пропорция», проявляющая себя как в мире живой природы, так и в мире минералов, является главной пропорцией Мироздания.

3.Фуллерены

Термином «фуллерены» называют замкнутые молекулы типа С₆₀, С₇₀, С₇₆, С₈₄, в которых все атомы углерода находятся на сферической или сфероидальной поверхности. В этих молекулах атомы углерода расположены в вершинах правильных шестиугольников или пятиугольников, которые покрывают поверхность сферы или сфероида. Центральное место среди фуллеренов занимает молекула С₆₀, которая характеризуется наибольшей симметрией и как следствие наибольшей стабильностью. В этой молекуле, напоминающей покрышку футбольного мяча и имеющую структуру правильного усеченного икосаэдра, атомы углерода располагаются на сферической поверхности в вершинах 20 правильных шестиугольников и 12 правильных пятиугольников, так что каждый шестиугольник граничит с тремя шестиугольниками и тремя пятиугольниками, а каждый пятиугольник граничит с шестиугольниками. «Фуллерены» по существу представляют собой «рукотворные» структуры, вытекающие из фундаментальных физических исследований. Впервые они были синтезированы в 1985 учеными Г. Крото и Р. Смолли (получившими в 1996 г. Нобелевскую премию за это открытие). Но в 1992 их неожиданно обнаружили в породах докембрийского периода, то есть фуллерены оказались не только «рукотворными», но и природными образованиями. Сейчас фуллерены интенсивно изучают в лабораториях разных стран, пытаясь установить условия их образования, структуру, свойства и возможные сферы применения.

4.Резонансная теория Солнечной системы

Частоты обращения планет и разности частот обращений образуют спектр с интервалом, равным золотой пропорции.

5. Фибоначчиевые резонансы генетического кода

Установление наукой ныне широко известного факта поразительной простоты основных принципов кодирования наследственной информации в живых организмах относится к числу важнейших открытий человечества. Эта простота заключается в том, что наследственная информация кодируется текстами из трехбуквенных слов – триплетов или кодонов, составленных на базе алфавита из четырех букв – азотистых оснований А (аденин), С (цитозин), G (гуанин), T (тимин). Данная система записи по существу едина для всего необозримого множества разнообразных живых организмов и называется генетическим кодом. В 1990 г. французский исследователь Jean-Claude Perez, работавший в тот период научным сотрудником фирмы IBM, сделал весьма неожиданное открытие в области генетического кодирования. Он открыл математический закон, управляющий самоорганизацией оснований Т, С, А, G внутри ДНК. Он обнаружил, что последовательные множества нуклеотидов ДНК организованы в структуры дальнего порядка, называемые РЕЗОНАНСАМИ. Резонанс представляет собой особую пропорцию, обеспечивающую разделение ДНК в соответствии с числами Фибоначчи (1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …). Например, генетический код  -цепи инсулина имеет следующий вид:

ATG-TTG-GTC-AAT-CAG-CAC-CTT—TGT-GGT—TCT-CAC-CTC-GTT-GAA-GCT
—TTG-TAC-CTT-GTT—TGC-GGT-GAA-CGT-GGT—TTC-TTC-TAC-ACT-CCT-AAG-
ACT

6. Золотая пропорция в теории трансфинитных множеств Кантора и квантовой физике (E-infinity theory)

В последние годы наблюдается повышенный интерес теоретической физики к «золотому сечению». В работах английского физика египетского происхождения Мохаммеда Эль Нашие показана связь «золотого сечения» с квантовой физикой.

Заключение

Длившаяся несколько тысячелетий драматическая история Золотого Сечения в начале 21-го века — «Века Гармонии» — может закончиться большим триумфом для Золотого Сечения. Плитки Пенроуза, резонансная теория Солнечной системы (Молчанов, Бутусов), квазикристаллы (Шехтман), фуллерены (Крото и Смолли, Нобелевская Премия 1996 г.) стали только предвестниками этого триумфа. «Математика гармонии» (Стахов), гиперболические функции Фибоначчи и Люка (Стахов, Ткаченко, Розин), «геометрия Боднара», «Закон структурной гармонии систем» (Сороко), «теория E-infinity» (Эль Нашие), матрицы Фибоначчи и «золотые» квадратные матрицы (Стахов) и, наконец, «золотые» геноматрицы (Петухов) – вот далеко не полный перечень современных научных открытий, основанных на Золотом Сечении. Эти открытия дают основание высказать предположение, что Золотое Сечение является некоторым «метафизическим» знанием, «проточислом», «универсальным кодом Природы», который может стать основой для дальнейшего развития науки, в частности, математики, теоретической физики, генетики, компьютерной науки.

infourok.ru

Исследовательская работа по математике «Золотое сечение»

Слайд 1 Здравствуйте Уважаемые члены жюри, мы представляем вашему вниманию исследовательскую работу на тему : «Золотое сечение». И хотим мы начать с замечательной фразы Святого Фомы Аквинского: «Чувствам человека приятны объекты, обладающие правильными пропорциями.»

Слайд 2 Цель нашей работа: Выявить что же такое «Золотое сечение», исследовать принцип «золотого сечения – красоты и гармонии» в окружающем мире. Основная задача стоящая перед нами: Изучить красоту окружающих предметов с математической точки зрения

Слайд 3 Теперь более чем когда-либо все в нашем мире основано на числах. Некоторые из них имеют даже свои имена (число π). Среди всех замечательных чисел есть одно особенно интересное: 1,6180339887…

С особым благоговением относились к этому числу: золотое число, божественное число, божественное сечение… Мы назовем его золотым сечением. Оно обозначается греческой буквой Ф (фи) и играет в математике выдающуюся роль, обладая удивительными свойствами и неожиданными связями с творениями природы и человека.

Слайд 4 Золотое сечение – это иррациональное число. Оно было открыто древними греками, и его документированная история начинается с одной из самых известных книг всех времен и народов «Начал» Евклида, написанной около 300 г. до н.э. «Начала» состоят из 13 книг, а именно 6 книга содержит текст, с которого началась история золотого сечения:

«Разделить прямую линию в крайнем и среднем отношении значит разделить ее на два таких отрезка, чтобы отношение всей линии к большему отрезку равнялось отношению большего отрезка к меньшему». Иными словами «Целое относится к большей части, как большая часть к меньшей»

Слайд 5 Для записи золотого сечения используют математическую формулу:

(1+√5)/2=1,6180339887

Как мы видим это число чуть больше единицы, состоит из бесконечного ряда цифр, которые никогда не образуют повторяющуюся группу.

Чтобы подойти к золотому сечению геометрически, можно построить прямоугольник, у которого одна сторона в 1,618 раз длиннее другой

Слайд 6 На слайде представлено более точное значение числа Фи

Слайд 7 Мы решили провести эксперимент: Взяли две кредитные карты. Одну разместили горизонтально, а другую вертикально так, чтобы нижние стороны находились на одной линии.

Если в горизонтальной карте мы проведем диагональную линию и продолжим ее, то увидим, что она пройдет в точности через правый верхний угол вертикальной карты – приятная неожиданность.

Слайд 8 Еще мы провели небольшое исследование по методу немецкого экспериментального психолога Густава Теодора Фехнера. В 1876 году он провел исследование с людьми не имеющими отношение к искусству. Им было необходимо из прямоугольников, включая квадрат, выбрать один, который наиболее приятен глазу. Подавляющее большинство выбрали прямоугольник с «золотым » соотношением сторон. Мы предлагаем вам тоже выбрать прямоугольник который наиболее вам приятен.

Слайд 9 А теперь мы посмотрим что-же представляет собой каждый прямоугольник. ( показать прямоугольники на слайде и прочитать что они обозначают)

Слайд 10 Мы повторили этот эксперимент в 6-7 классах. И отметили одну особенность, дети которые выбрали «золотой прямоугольник», либо хорошо рисуют, либо занимаются в художественной школе, т.е. все же имеют отношение к искусству.

Слайд 11 Далее мы приступаем к изучению красоты окружающих предметов с математической точки зрения. Начнем мы с идеальных пропорций. На слайде представлена статуя Апполона, который являлся примером тех самых идеальных пропорций. Рост человека= размаху рук (расстоянию между кончиками пальцев разведенных в стороны рук) = 8 ладоням = 6 ступням = 8 лицам = 1,618, умноженному на высоту пупка ( расстоянию от пупка до земли. Мы добрались до соотношения 1,618, что является приблизительным значением числа Фи. При проверке этих пропорций в наших телах мы, несомненно, расстроимся. Ведь идеалу соответствовать трудно.

Слайд 12 Золотое сечение встречается и в живописи. Композиционные элементы картины Леонардо «Тайная вечеря» содержат золотые пропорции. Хотя прямых доказательств этого нет. Но «золотые прямоугольники» определяют как размеры картины, так и положение Христа и его учеников. Стены и окна на заднем плане следуют правилу золотого сечения.

Слайд 13 Даже портрет Моны Лизы построен на золотом сечении. Ее лицо и в целом, и в деталях обрамлено элегантной последовательностью «золотых» прямоугольников разных размеров.

Слайд 14 Символ пентаграммы, который по утверждению Пифагора скрывает в себе золотое сечение, помогал в определении пространства картины, в расположении человеческих фигур. «Святое семейство» Микеланджело служит тому примером.

Слайд 15 Золотое сечение в архитектуре. В других цивилизациях, далеких от классической културы, тоже ценили золотое сечение. Рядом с озером Титикака, недалеко от столицы Боливии, находятся Врата Солнца – каменная арка доинковской эпохи с пропорциями, которые полностью диктуются золотым сечением. Врата разрушены, время постройки датируется примерно 1500 г до н.э.

Слайд 16 Врата Солнца в виде «золотых прямоугольников»

Слайд 17 Фасад Университета Саламанки содержит большой «золотой прямоугольник». Испания 1218 г.

Слайд 18 Музей Гуггенхайма в Нью-Йорке. Вид снаружи похож на золотую спираль. А золотая спираль – это в геометрии логарифмическая спираль, скорость роста которой равна Фи, золотой пропорции. И опять мы пришли к золотому числу.

Слайд 19 На слайде представлен вид сверху на школу им. Хайнца Галински. Идея навеяна расположением лепестков. В то время как архитектор подражает природе, расположение лепестков тесно связано с числом Фи.

Слайд 20 Золотое сечение в дизайне. Логотип Toyota использует соотношение a и b, формируя сетку, в которой образуются три кольца. Обратите внимание, как этот логотип использует прямоугольники вместо кругов для создания золотого сечения. Компания Apple видимо использовала золотую спираль, ведь она так отлично вписывается в логотип компании.

Слайд 21 Золотое сечение в природе. Рассмотрим листья шершавого вяза и фигового дерева. Они имеют форму в соответствии с золотой пропорцией.

Слайд 22 Рассмотрим обычное куриное яйцо. В его изображение отлично вписывается золотая (логарифмическая спираль)

Слайд 23 А задумывались ли вы о пропорциях ящерицы? В ящерице с первого взглядя улавливается приятная для нашего глаза пропорция. Длина ее хвоста так относится к длине остального тела как 62:38. Разделим 62 на 38 получим 1,631… что близко к числу Фи.

Слайд 24 Мир золотого сечения глубок и сложен, мы лишь едва коснулись его. Роль Фи вовсе не ограничивается тем, что мы видели. Но самое интересное заключается в том, что это древнее и прославленное число, появившееся в математике более 20 веков назад, до сих пор встречается в новых областях современной науки. «Божественное» число вовсе не является отслужившей своей игрушкой, оно и сегодня продолжает играть важную роль.

Слайд 25 На слайде список использованной литературы и источников в сети Интернет. Спасибо за внимание.

infourok.ru

Золотое сечение. Исследовательская работа по математике

Золотое сечение. Исследовательская работа по математике

Скачать исследовательскую работу «Золотое сечение» в формате doc.

Скачать презентацию «Золотое сечение» в формате ppt.

Автор исследования: ученица 11 класса МОУ «СОРМШ № 7» г. Дубоссары − Чередниченко Наталья Васильевна. Руководитель: Тараканова Мария Фёдоровна, учитель математики высшей квалификационной категории.

Автор исследовательской работы «Золотое сечение», представленной на Школьном портале, искал ответ на вопрос: «Что такое золотое сечение, золотая пропорция?», знакомился с доказательной базой научного обоснования золотой пропорции и связанных с золотым сечением отношений. В работе рассмотрено, как повлияло «золотое сечение» на историю человечества и планет, на исторический ход развития, на живую и неживую природу в целом.

Анализируя результаты исследования можно еще раз подивиться грандиозностью процесса познания мира, открытиям все новых и новых его закономерностей, а также сделать соответствующий вывод: принцип золотого сечения − это высочайшее проявление функционального и структурного совершенства отдельных частей и целого в природе, технике, науке и искусстве.

 

Золотое сечение. Актуальность

Данная тема не только интересна, но и по-прежнему актуальна. Золотая пропорция не потерялась во времени, а скорее наполнилась современными обстоятельными примерами. Золотое сечение, безусловно, можно назвать «Божественной пропорцией». Автор считает, что золотая пропорция окружает нас, приводит научные доказательства распространенности его в солнечной системе. Кроме того, события, происходящие с нами, по мнению автора, тоже происходят согласно золотой пропорции, золотому сечению.

 

Важным результатом и выводом исследования данной темы является вездесущее применение принципа золотого сечения, который обнаруживается практически повсюду: в науке, природе, человеке, музыке, искусстве, фотографии и во многом другом, объединяя весь мир в единое гармоничное целое.

Золотое сечение. Анкетирование

Автором данного исследования, в рамках социологического опроса проводилось анкетирование, где были заданы учащимся старших классов два вопроса:

1. Знаете ли вы, что называется «Золотым сечением»?

2. Напишите, что Вы знаете о ней, и в каких еще науках кроме математики используется?

По результатам опроса, Чередниченко Наталья в своей работе приводит выявленные данные по процентному соотношению владеющих информацией о золотом сечении. В итоге, более 70% опрошенных школьников не знают о золотой пропорции. Что еще раз подтверждает актуальность выбранной темы.

Золотое сечение. Заключение

Кроме того, автор провел исследование на выявление соответствия тела человека идеальному сложению согласно золотой пропорции на примере учеников 11 класса МОУ «СОРМШ №7» г. Дубоссары.

В работе представлено большое количество иллюстраций, подробно описаны цели, задачи, методы, средства, приложения, а также грамотно выполненная презентация к данному исследованию, которые вы можете скачать по ссылкам в начале статьи. Работу можно дополнить новыми материалами, а также представить ее в форме реферата по математике на тему «Золотое сечение» или «Золотая пропорция вокруг нас».

nashashcola.ru

Научно-исследовательская работа по математике «Золотое сечение» (с приложением)

Введение.

Феномен золотого сечения известен человечеству очень давно. Его тайну пытались осмыслить многие крупнейшие мыслители человечества. Они неразрывно связывали золотое сечение с понятием всеобщей гармонии, пронизывающей вселенную от микромира до макрокосмоса. Классическими проявлениями золотого сечения являются предметы обихода, скульптура и архитектура, математика, музыка и эстетика. Мы довольно часто в повседневной жизни встречаемся с такими понятиями, как красота природы, красота человека, красота архитектурного сооружения.

И часто с этими понятиями совмещаем пропорциональность, то есть употребляем такие термины: «пропорционально сложенный человек», «у ее фигуры правильные пропорции», «в архитектуре этого здания не выдержаны пропорции».  Красота скульптуры, красота храма, красота человеческого тела, окружающей природы… Что между ними общего? Разве можно сравнивать красоту храма с красотой растения? Оказывается можно, если будут найдены единые критерии, объединяющие прекрасное, если будут открыты общие формулы красоты, понятие прекрасного самых различных объектов — от цветка ромашки до красоты человеческого тела.

Актуальность исследования обусловлена стремлением углублять математические знания через выявление связи между   многими точными и естественными науками, представления о красоте, порядке и гармонии, бытовые и производственные сферы жизни В школьном курсе математики теме «Золотого сечения» отводится несправедливо мало учебного времени. Начиная с шестого класса, только в общих чертах говорится о золотом сечении, о решении задачи: деление отрезка в среднем и крайнем отношении.

А между тем тема «Золотого сечения» является универсальной в том смысле, что она. Перед тем как начать работу по теме «Золотое сечение», я провела опрос среди  школьников ОСОШ №2. Нужно было ответить на вопрос «Знаете ли вы, что такое « золотая пропорция» или «золотое сечение»? Оказывается, большая часть школьников не имеют представления, что это такое. Если вернуться к эпиграфу работы: теорему Пифагора знает каждый, а вот что такое “золотое сечение” – далеко не все. (Приложение 9) Поэтому я решила рассказать об этом “драгоценном камне”

Гипотеза: золотое сечение является отображением окружающего мира.

Объект исследования: золотое сечение.

Предметы исследования: предметы скульптуры, архитектуры, живописи.

Цель:

исследование золотого сечения в различных областях знаний.

Задачи:

Изучить понятие и историю возникновения золотого сечения

Рассмотреть применение золотого сечения в скульптуре, архитектуре, живописи, природе, музыке

Исследовать обучающихся школы на соответствие идеальным пропорциям золотого сечения

Проанализировать полученные результаты и сделать вывод.

Методы исследования: 

Анализ теоретической литературы;

Математические расчеты пропорциональных отношений;

Сопоставление полученных данных

Глава I. Золотое сечение и гармония форм.

1.1. История золотого сечения.

Принято считать, что понятие о золотом делении ввел в научный обиход Пифагор, древнегреческий философ и математик (VI в. до н.э.). Есть предположение, что Пифагор (Приложение 1) свое знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании.

В фасаде древнегреческого храма Парфенона (Приложение 3) присутствуют золотые пропорции. При его раскопках обнаружены циркули (Приложение 2), которыми пользовались архитекторы и скульпторы античного мира. В Помпейском циркуле (музей в Неаполе) также заложены пропорции золотого деления.

В дошедшей до нас античной литературе золотое деление впервые упоминается в “Началах” Евклида. Во 2-й книге “Начал” дается геометрическое построение золотого деления.  После Евклида исследованием золотого деления занимались Гипсикл (II в. до н.э.), Папп (III в. н.э.) и др. В средневековой Европе с золотым делением познакомились по арабским переводам “Начал” Евклида. Секреты золотого деления ревностно оберегались, хранились в строгой тайне. Они были известны только посвященным. В эпоху Возрождения усиливается интерес к золотому делению среди ученых и художников в связи с его применением как в геометрии, так и в искусстве, особенно в архитектуре Леонардо да Винчи.

В то же время на севере Европы, в Германии, над теми же проблемами трудился Альбрехт Дюрер. Он делает наброски введения к первому варианту трактата о пропорциях. Дюрер пишет.  “Необходимо, чтобы тот, кто что-либо умеет, обучил этому других, которые в этом нуждаются. Это я и вознамерился сделать”. Альбрехт Дюрер подробно разработал теорию пропорций человеческого тела.  Важное место в своей системе соотношений Дюрер отводил золотому сечению. Рост человека делится в золотых пропорциях линией пояса, а также линией, проведенной через кончики средних пальцев опущенных рук, нижняя часть лица – ртом и т.д. Известен пропорциональный циркуль Дюрера.

Великий астроном XVI в. Иоганн Кеплер назвал золотое сечение одним из сокровищ геометрии. Он первый обращает внимание на значение золотой пропорции для ботаники (рост растений и их строение). Кеплер называл золотую пропорцию продолжающей саму себя “Устроена она так, – писал он, – что два младших члена этой нескончаемой пропорции в сумме дают третий член, а любые два последних члена, если их сложить, дают следующий член, причем та же пропорция сохраняется до бесконечности”. [2]

Таким образом, изучением понятия золотого сечения с древних времен занимались великие ученые.  Золотое сечение нашло отображение в различных областях науки. В дальнейшем мы попытаемся подтвердить нашу гипотезу, что  золотое сечение является отображением окружающего мира в скульптуре, архитектуре, живописи и т.д.

1.2. Алгебраический и геометрический подходы к определению понятия золотого сечения.

В математике пропорцией (лат. proportio) называют равенство двух отношений: a:b=c:d. [3]

Золотое сечение (золотая пропорция) — пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему a : b = b : c или с : b = b : а.

Весь материал — в архиве.

videouroki.net

Исследовательская работа по математике «Золотое сечение»

СМОЛЕНСКОЕ ОБЛАСТНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ

ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

«ВЕРХНЕДНЕПРОВСКИЙ ТЕХНОЛОГИЧЕСКИЙ ТЕХНИКУМ»

ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА ПО МАТЕМАТИКЕ

«Золотое сечение»

Работу выполнил: студент гр. №23 «Автомеханик»

Черногузов Р.А.

Руководитель: преподаватель Журавлёва Л.В.

2016 .
Содержание

1.Введение

2. Наши знания о «Золотом сечении»

3. Что такое «Золотое сечение» или «Золотая пропорция»

4. Исследования в области живописи.

5. Исследования в области архитектуры.

6. Золотая пропорция и тело человека

7.Заключение и выводы

8. Список литературы

1.Введение

«Геометрия обладает двумя великими сокровищами.

Первое — это теорема Пифагора, второе — деления отрезка в крайнем и среднем отношении.

Первое можно сравнить с мерой золота,

второе же больше напоминает драгоценный камень».

Иоганн Кеплер
Человек различает окружающие его предметы по форме. Интерес к форме какого-либо предмета может быть продиктован жизненной необходимостью, а может быть вызван красотой формы. Форма, в основе построения которой лежат сочетание симметрии и золотого сечения, способствует наилучшему зрительному восприятию и появлению ощущения красоты и гармонии. Целое всегда состоит из частей, части разной величины находятся в определенном отношении друг к другу и к целому. Принцип золотого сечения – высшее проявление структурного и функционального совершенства целого и его частей в искусстве, науке, технике и природе.

Цели исследовательской работы:
-Узнать что такое «Золотое сечение»

-Узнать историю золотого сечения

-Рассмотреть « золотое сечение» в математике, архитектуре, искусстве, биологии

-Научиться находить предметы золотого сечения в окружающем нас мире

Задачи исследовательской работы:

1. Изучить научно-популярную литературу по данной теме;

2. Исследовать известные картины, скульптуры и архитектурные сооружения;

3. Выявить и изучить проявления «золотого сечения» и ее производных в моем окружении и привести свои примеры исследований.

Актуальность исследования

«золотого сечения» или «золотой пропорции» как универсальной мировой константы я вижу в том, чтобы убедиться в достоверности высказывания Иоганна Кеплера о «двух сокровищах» и развить это представление дальше, за пределы геометрии. Если «золотая пропорция» универсальная мировая константа, то она встречается в окружающем нас мире.

Новизна исследования:

раскрытие «золотого сечения» в окружающей нас действительности. Красота скульптуры, красота храма, красота человеческого тела, окружающей природы…Что между ними общего? Разве можно сравнивать красоту храма с красотой человеческого тела? Оказывается можно, если будут найдены единые критерии прекрасного, если будут открыты общие формулы красоты, объединяющие понятие прекрасного самых различных объектов.

Данная работа представляет собой теоретическое и практическое исследования, где в качестве объекта рассматривается всестороннее применение «золотого сечения», и доказывается его универсальность.

Теоретическая значимость работы заключается в том, что в процессе работы была изучена научно-популярная литература по данной теме, выяснено, что во многих гениальных творениях можно найти элементы золотого сечения.

Практическая значимость работы заключается в применении «золотой пропорции» на уроках математики, биологии, физики. Инновационность своей работы я вижу в том, чтобы заинтересовать студентов занятием научно-исследовательской деятельностью, потому что она повышает интеллектуальный уровень, расширяет кругозор, формирует потребности к целенаправленному самообразованию

2.Наши знания о «Золотом сечении».

Перед тем как начать работу по теме « Золотое сечение», я провел опрос среди студентов и преподавателей нашеготехникума. Нужно было ответить на вопрос «Знаете ли вы, что такое « золотая пропорция» или «золотое сечение»? Результаты опроса изображены на диаграмме.

Студенты преподаватели

40% преподавателей знают что такое « Золотая пропорция» или

« Золотое сечение», а студенты не имеют представления, что это такое.

Как вы думаете, что общего между египетскими пирамидами, полотнами Леонардо да Винчи, подсолнухом, улиткой, сосновой шишкой?

Есть вещи, которые нельзя объяснить. Вот вы подходите к пустой скамейке и садитесь на нее. Где вы сядете — посередине? Или, может быть, с самого края? Нет, скорее всего, не то и не другое. Вы сядете так, что отношение одной части скамейки к другой, относительно вашего тела, будет равно примерно 1,62. Простая вещь, абсолютно инстинктивная… Садясь на скамейку, вы произвели «золотое сечение». А ЧТО ЖЕ ЭТО ТАКОЕ? Давайте разберемся!….

3.Золотое сечение в математике

Деление отрезка в среднем и крайнем отношении называют золотым сечением. В истории утвердилось ещё одно название – «золотая пропорция».

Пусть С АВ и производит, как говорят, «золотое сечение» отрезка АВ, так что АС: АВ =СВ: АС

Золотым сечением — называется такое деление отрезка, при котором большая часть так относится к целому, как меньшая часть к большей

Если отрезок АВ принять за 100 частей, то большая часть отрезка равна 62, а меньшая – 38 частям.

Коэффициент «золотого сечения» обозначается буквой Ф=1,618034…

Ф — прописная форма греческой буквы «фи». Такое обозначение принято в честь древнегреческого скульптора Фидия (V век до н. э.), в творениях которого «золотая пропорция» встречается многократно.

Ряд Фибоначчи

С историей золотого сечения косвенным образом связано имя итальянского математика монаха Леонардо известного под именем Фибоначчи (сын Боначчи). Он много путешествовал по Востоку, познакомил Европу с индийскими (арабскими) цифрами. В 1202 г вышел в свет его математический труд «Книга об абаке» (счетной доске), в котором были собраны все известные на то время задачи. Одна из задач гласила «Сколько пар кроликов в один год от одной пары родится». Размышляя на эту тему, Фибоначчи выстроил такой ряд цифр:

Месяцы 0 1 2 3 4 5 6 7 8 9 10

Пары кроликов 0 1 1 2 3 5 8 13 21 34 55

Ряд чисел 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т.д. известен как ряд Фибоначчи.

Особенность последовательности чисел состоит в том, что каждый ее член, начиная с третьего, равен сумме двух предыдущих 2 + 3 = 5; 3 + 5 = 8; 5 + 8 = 13, 8 + 13 = 21; 13 + 21 = 34 и т.д., а отношение смежных чисел ряда приближается к отношению золотого деления. Так, 21 : 34 = 0,617, а 34 : 55 = 0,618

Работая по теме «Золотое сечение», я познакомился с «золотыми фигурами» и научился их строить с помощью циркуля и линейки:

1. 
   Могу разделить любой отрезок в золотом соотношении
   

Построение.

Построим прямоугольный треугольник, у которого один катет в два раза больше другого. Для этого восстановим в точке В перпендикуляр к прямой АВ и на нем отложим отрезок ВС= ½ АВ .

Далее, соединим точки А и С, отложим отрезок CD=CB,

и наконец AE=AD.

Точка Е является искомой, она производит золотое сечение отрезка АВ.

2. 
   Могу построить правильный пятиугольник – пентаграмму.
   

Если в пентаграмме провести все диагонали, то в результате получим пятиугольную звезду.

Точки пересечения диагоналей в пентаграмме являются точками золотого сечения диагоналей. При этом эти точки образуют новую пентаграмму и пять правильных треугольников.

Здание военного ведомства США имеет форму пентаграммы и получило название «Пентагон», что значит правильный пятиугольник.

Пятиконечная звезда – пентаграмма – очень красива, недаром ее помещают на свои флаги и гербы многие страны.

3. 
   Могу построить Золотой треугольник
   

Золотым называется такой равнобедренный треугольник, основание и боковая сторона которого находятся в золотом отношении:

, ϕ=1,62

4. 
   Могу построить Золотой прямоугольник
   

Прямоугольник, стороны которого находятся в золотом отношении, т.е. отношение длины к ширине даёт число φ, называется золотым прямоугольником.

5. 
   Могу построить Золотую спираль
   

Последовательно отрезая от золотого прямоугольника квадраты и вписывая в каждый по четверти окружности, получаем золотую логарифмическую спираль.

Форма спирально завитой раковины привлекла внимание Архимеда. Он изучал ее и вывел уравнение спирали. Спираль, вычерченная по этому уравнению, называется спираль Архимеда.

Очень многие явления в природе описываются именно золотой спиралью.

Выяснилось, что в расположении листьев на ветке (филлотаксис), семян подсолнечника, шишек сосны проявляет себя ряд Фибоначчи, а стало быть, проявляет себя закон золотого сечения.

Паук плетет паутину спиралеобразно. Спиралью закручивается ураган. Испуганное стадо северных оленей разбегается по спирали. Молекула ДНК закручена двойной спиралью. Гете называл спираль «кривой жизни».

Не так давно спиральные структуры обнаружены и в неживой природе.

Из истории золотого сечения

Принято считать, что понятие о золотом делении ввел в научный обиход Пифагор. Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании.

4. Исследования в области живописи.
Еще в эпоху Возрождения художники открыли, что любая картина имеет определенные точки, невольно приковывающие наше внимание, так называемые зрительные центры. При этом абсолютно неважно, какой формат имеет картина — горизонтальный или вертикальный. Таких точек всего четыре, и расположены они на расстоянии 3/8 и 5/8 от соответствующих краев плоскости.

Данное открытие у художников того времени получило название «золотое сечение» картины. Поэтому, для того чтобы привлечь внимание к главному элементу картины, необходимо совместить этот элемент с одним из зрительных центров, как это видим в знаменитой«Тайной вечери» и «Джаконде» Леонардо да Винчи. Портрет Монны Лизы (Джоконды) долгие годы привлекает внимание исследователей, которые обнаружили, что композиция рисунка основана на золотых треугольниках, являющихся частями правильного звездчатого пятиугольника.

Мною была проведена исследовательская работа с репродукциями картин: Васильева «У окна», Иванова «Явление Христа народу», «Поющий один» (8 век), Айвазовского «Солнечный день», Карамзина Н. «Незнакомая». Измерения показали, что создатели этих картин все объекты, несущие смысловую нагрузку в соответствии с художественным замыслом разместили по правилу золотого сечения.

5. Исследования в области архитектуры.

В книгах о «золотом сечении» можно найти замечание о том, что в архитектуре, как и в живописи, все зависит от положения наблюдателя, и что, если некоторые пропорции в здании с одной стороны кажутся образующими «золотое сечение», то с других точек зрения они будут выглядеть иначе. «Золотое сечение» дает наиболее спокойное соотношение размеров тех или иных длин.

Как была построена Большая Пирамида Хеопса — это вопрос, на который нельзя ответить, но в основе постройки этой пирамиды лежит все то же золотое сечение, и этот факт лишний раз доказывает, что эта пропорция была известна еще в Древнем Египте.

Одним из красивейших произведений древнегреческой архитектуры является Парфенон (V в. до н. э.).

Парфенон имеет 8 колонн по коротким сторонам и 17 по длинным. Выступы сделаны целиком из квадратов пентилейского мрамора. Благородство материала, из которого построен храм, позволило ограничить применение обычной в греческой архитектуре раскраски, она только подчеркивает детали и образует цветной фон (синий и красный) для скульптуры. Отношение высоты здания к его длине равно 0,618. Если произвести деление Парфенона по «золотому сечению», то получим те или иные выступы фасада.Принцип золотого сечения положен в основу и знаменитого Собора Парижской Богоматери.

Долгое время считали, что зодчие Древней Руси строили все «на глазок», без особых математических расчетов. Однако новейшие исследования показали, что русские архитекторы хорошо знали математические пропорции, о чем свидетельствует анализ геометрии древних храмов.Трудно найти человека, который бы не знал и не видел собора Василия Блаженного на Красной площади. Храм этот особенный; он отличается удивительным разнообразием форм и деталей, красочных покрытий; ему нет равных в нашей стране. Исследуя его, пришли к выводу о преобладании в нем ряда золотого сечения. Если принять высоту собора за единицу, то основные пропорции, определяющие членение целого на части, образуют ряд золотого сечения.

В этом членении и заключена основная архитектурная идея создания собора, единая для всех восьми куполов, объединяющая их в одну композицию.

В качестве примера «золотого сечения» в России можно полюбоваться фасадом знаменитого Большого театра в Москве и архитектурным шедевром Москвы – домом Пашкова (1786 г.), который является одним из наиболее совершенных произведений архитектуры Василия Ивановича Баженова.

Свое исследование в архитектуре я провел на примере фотографий памятников архитектуры Дорогобужского района: храма в д.Болдино и усадьбы Барышникова д.Алексино и оказалось, что при делении основных масс конструкций использовалось золотое сечение.
6. Золотая пропорция и тело человека
Леонардо да Винчи говорил о пропорции человеческого тела: “Если мы человеческую фигуру – самое совершенное творение Вселенной – перевяжем поясом и отмерим потом расстояние от пояса до ступней, то эта величина будет относиться к расстоянию от того же пояса до макушки, как весь рост человека к длине от пояса до ступней”.Я решил проверить, как проявляются закономерности «золотого сечения» в пропорциях тела современного человека на студентах 2 курса. Для этого я провел измерения пяти юношей и пяти девушек. Мы выполнили измерения длины тела до талии и ниже талии, вычислили отношения этих длин. Результаты отношений я отразил в виде таблиц.

студенты		1	2			3	4		5			Среднее значение
девушки		1,596		1,583		1,627		1,606		1,624		1,607
юноши		1,604		1,628		1,608		1,626		1,632		1,619

Рука человека

Достаточно лишь приблизить сейчас вашу ладонь к себе и внимательно посмотреть на указательный палец, и вы сразу же найдете в нем формулу золотого сечения. Каждый палец нашей руки состоит из трех фаланг.

Сумма двух первых фаланг пальца в соотношении со всей длиной пальца и дает число золотого сечения (за исключением большого пальца).

Кроме того, соотношение между средним пальцем и мизинцем также равно числу золотого сечения.

У человека 2 руки, пальцы на каждой руке состоят из 3 фаланг (за исключением большого пальца). На каждой руке имеется по 5 пальцев, то есть всего 10, но за исключением двух двухфаланговых больших пальцев только 8 пальцев создано по принципу золотого сечения. Тогда как все эти цифры 2, 3, 5 и 8 есть числа последовательности Фибоначчи
Золотое сечение в чертах лица человека как критерий совершенной красоты
В строении черт лица человека также есть множество примеров, приближающихся по значению к формуле золотого сечения. Однако не бросайтесь тотчас же за линейкой, чтобы обмерять лица всех людей. Потому что точные соответствия золотому сечению, по мнению ученых и людей искусства, художников и скульпторов, существуют только у людей с совершенной красотой. Собственно точное наличие золотой пропорции в лице человека и есть идеал красоты для человеческого взора.

К примеру, если мы суммируем ширину двух передних верхних зубов и разделим эту сумму на высоту зубов, то, получив при этом число золотого сечения, можно утверждать, что строение этих зубов идеально.

На человеческом лице существуют и иные воплощения правила золотого сечения. Приведем несколько таких соотношений:

-Высота лица / ширина лица,

-Центральная точка соединения губ до основания носа / длина носа.

-Высота лица / расстояние от кончика подбородка до центральной точки соединения губ

-Ширина рта / ширина носа,

-Ширина носа / расстояние между ноздрями,

-Расстояние между зрачками / расстояние между бровями.

Золотое сечение и счастье
Исследования социологов подтверждают, что численность удовлетворённых и неудовлетворённых своими обстоятельствами людей подчиняется пропорциям знаменитого «золотого сечения».

По результатам опроса отечественных и зарубежных психологов оказалось, что счастливыми считают себя 63% опрошенных. Поразительная цифра, ибо золотое сечение приходится на 62%.

7.Заключение

В результате исследовательской работы я познакомился с историей золотого сечения, применением золотого сечения в архитектуре, живописи, искусстве. Приобрел навыки исследовательской работы, опыт работы в поисковой системе Интернет.

Выводы:

1. Закономерности золотого сечения были известны с древних времён и использовались в науке и искусстве.

2. Проведенные опыты показывают, что окружающие нас предметы и явления, в которых есть элементы, связанные друг с другом золотой пропорцией, большинству людей кажутся красивыми, такая пропорция создает зрительное ощущение гармонии, красоты и равновесия.

3. Принцип «золотого сечения» – высшее проявление структурного и функционального совершенства целого и его частей в искусстве, науке, природе.

8. Список литературы
1. Н. Васютинский “Золотая пропорция” –М.,”Молодая гвардия”, 1990
2. А. Азевич “Двадцать уроков гармонии” –М., “Школа-Пресс”, 1998
3. М. Гарднер “Математические головоломки и развлечения” –М., “Мир”, 1971
4. Д. Пидоу “Геометрия и искусство” – М., “Мир”, 1989
5. Энциклопедический словарь юного математика –М.,1989
6. Журнал “Квант”, 1973, № 8
7. Журнал “Математика в школе”, 1994, № 2, № 3
8. Для подготовки данной работы были использованы материалы с сайта http://www.ed.vseved.ru/

9. http://www.km.ru/referats/93E692B0594D4BB68486A53C943DC155#

10. http://yandex.by/yandsearch?text=%D1%82.%D0%BA%D1%83

11.http://ogog2.goroo-оrsha.by/index.php?option=com_content&view=

Поделитесь с Вашими друзьями:

zodorov.ru

Исследовательская работа по математике «Золотое сечение и гармония форм»

Автор: 

Должикова Алина

Новизна и практическое применение данной работы заключается в создании интерактивного плаката алгоритма построения «золотых фигур» с помощью циркуля и линейки.

Цель: изучение истории возникновения золотого сечения, нахождение практического применения золотого сечения в различных сферах жизнедеятельности человека, создание интерактивного плаката алгоритма построения «золотых» фигур.

Задачи:

1. Узнать о происхождении «золотого сечения».

2. Проанализировать литературу по данному вопросу из различных источников.

3. Провести локальный эксперимент.

4. Создать интерактивный плакат алгоритма построения «золотых фигур» с помощью циркуля и линейки.

Скачать:

Предварительный просмотр:

Чтобы пользоваться предварительным просмотром создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com

Предварительный просмотр:

Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com

Подписи к слайдам:

Слайд 1

А В А К = К В = В С С Д С Д = С В Е А Е = А Д К Алгоритм деления отрезка прямой в золотой пропорции с помощью циркуля и линейки ЗОЛОТАЯ ПРОПОРЦИЯ т. Е –ЗОЛОТОЕ СЕЧЕНИЕ

Предварительный просмотр:

Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com

Подписи к слайдам:

Слайд 1

Алгоритм построения «золотого» треугольника 1. Проводим луч АВ А 2. От точки А откладываем на нем три раза отрезок O произвольной величины 3. Через полученную точку Р проводим перпендикуляр к линии АВ P o o o 4 . На перпендикуляре вправо и влево от точки Р откладываем отрезки о o o d d1 5 . Полученные точки d и d1 соединяем прямыми с точкой А 6. Отрезок dd1 откладываем на линию Ad1, получая точку С С Точка С разделила линию Ad1 в пропорции золотого сечения Золотым называется такой равнобедренный треугольник, основание и боковая сторона которого находятся в золотом отношении В

nsportal.ru

Исследовательская работа по математике «Золотое сечение в архитектуре»(8 класс)

Природа осуществила деление на симметричные части и золотые пропорции. В частях проявляется повторение строения целого.

Большой интерес представляет исследование форм птичьих яиц. Такие формы птичьих яиц не являются случайными, поскольку в настоящее время установлено, что форме яиц, описываемых отношением золотого сечения, отвечают более высокие прочностные характеристики оболочки яйца.

Бивни слонов и вымерших мамонтов, когти львов и клювы попугаев являют собой логарифмические формы и напоминают форму оси, склонной обратиться в спираль.

В живой природе широко распространены формы, основанные на «пентагональной» симметрии (морские звезды, морские ежи, цветы).

Золотое сечение присутствует в строении всех кристаллов, но большинство кристаллов микроскопически малы, так что мы не можем разглядеть их невооруженным глазом. Рис. 21
Однако снежинки, также представляющие собой водные кристаллы, вполне доступны нашему взору.

Все изысканной красоты фигуры, которые образуют снежинки, все оси, окружности и геометрические фигуры в снежинках также всегда без исключений построены по совершенной четкой формуле золотого сечения.

Особенность бронхов, составляющих легкие человека, заключена в их асимметричности. Бронхи состоят из двух основных дыхательных путей, один из которых (левый) длиннее, а другой (правый) короче.

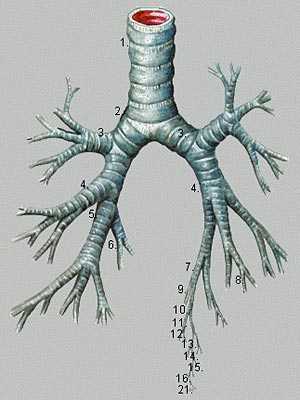
Рис. 22

Было установлено, что эта асимметричность продолжается и в ответвлениях бронхов, во всех более мелких дыхательных путях. Причем соотношение длины коротких и длинных бронхов также составляет золотое сечение и равно 1:1,618.

Давление крови изменяется в процессе работы сердца. Наибольшей величины оно достигает в левом желудочке сердца в момент его сжатия (систолы). В артериях во время систолы желудочков сердца кровяное давление достигает максимальной величины, равной 115-125 мм ртутного столбца у молодого, здорового человека. В момент расслабления сердечной мышцы (диастола) давление уменьшается до 70-80 мм рт.ст. Отношение максимального (систолического) к минимальному (диастолическому) давлению равно в среднем 1,6, то есть близко к золотой пропорции.

Если взять за единицу среднее давление крови в аорте, то систолическое давление крови в аорте составляет 0,382, а диастолическое — 0,618, то есть их отношение соответствует золотой пропорции. Это означает, что работа сердца в отношении временных циклов и изменения давления крови оптимизированы по одному и тому же принципу — закону золотой пропорции.

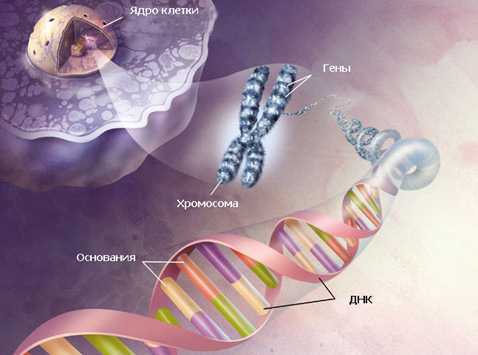Молекула ДНК состоит из двух вертикально переплетенных между собой спиралей. Длина каждой из этих спиралей составляет 34 ангстрема, ширина 21 ангстрема. (1 ангстрем — одна стомиллионная доля сантиметра).

Так вот 21 и 34 — это цифры, следующие друг за другом в последовательности чисел Фибоначчи, то есть соотношение длины и ширины логарифмической спирали молекулы ДНК несет в себе формулу золотого сечения 1:1,618

Рис.23

Любое музыкальное произведение имеет временное протяжение и делится некоторыми «эстетическими вехами» на отдельные части, которые обращают на себя внимание и облегчают восприятие в целом. Этими вехами могут быть динамические и интонационные кульминационные пункты музыкального произведения. Отдельные временные интервалы музыкального произведения, соединяемые «кульминационным событием», как правило, находятся в соотношении Золотого сечения.

Еще в 1925 году искусствовед Л.Л.Сабанеев, проанализировав 1770 музыкальных произведений 42 авторов, показал, что подавляющее большинство выдающихся сочинений можно легко разделить на части или по теме, или по интонационному строю, или по ладовому строю, которые находятся между собой в отношении золотого сечения. Причем, чем талантливее композитор, тем в большем количестве его произведений найдено золотых сечений. По мнению Сабанеева, золотое сечение приводит к впечатлению особой стройности музыкального сочинения. Этот результат Сабанеев проверил на всех 27 этюдах Шопена. Он обнаружил в них 178 золотых сечений. При этом оказалось, что не только большие части этюдов делятся по длительности в отношении золотого сечения, но и части этюдов внутри зачастую делятся в таком же отношении.

Композитор и ученый М.А.Марутаев подсчитал количество тактов в знаменитой сонате «Аппассионата» и нашел ряд интересных числовых соотношений. В частности, в разработке – центральной структурной единице сонаты, где интенсивно развиваются темы и сменяют друг друга тональности, — два основных раздела. В первом 43,25 такта, во втором – 26,75. Отношение 43,25:26,75=0,618:0,382=1,618 дает золотое сечение.

Наибольшее количество произведений, в которых имеется Золоте сечение, у Аренского (95%), Бетховена (97%), Гайдна (97%), Моцарта (91%), Шопена (92%), Шуберта (91%)

Страдивари писал, что с помощью золотого сечения он определял места для f-образных вырезов на корпусах своих знаменитых скрипок.

Особый вид изобразительного искусства Древней Греции следует выделить изготовление и роспись всевозможных сосудов. В изящной форме легко угадываются пропорции золотого сечения .

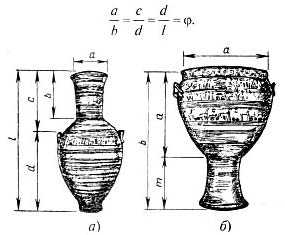
Рис. 24

В живописи и скульптуре храмов, на предметах домашнего обихода древние египтяне чаще всего изображали богов и фараонов. Были установлены каноны изображения стоящего человека идущего, сидящего и т.д. Художники обязаны были заучивать отдельные формы и схемы изображения по таблицам и образцам. Художники Древней Греции совершали специальные путешествия в Египет, чтобы поучиться умению пользоваться каноном.

Еще в эпоху Возрождения художники открыли, что любая картина имеет определенные точки, невольно приковывающие наше внимание, так называемые зрительные центры. При этом абсолютно неважно, какой формат имеет картина — горизонтальный или вертикальный. Таких точек всего четыре, и расположены они на расстоянии 3/8 и 5/8 от соответствующих краев плоскости.

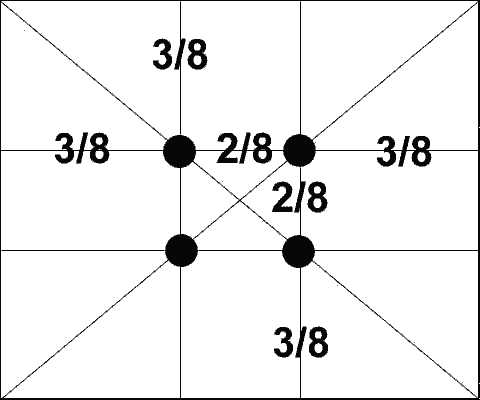
Рис. 25

Данное открытие у художников того времени получило название «золотое сечение» картин.

Золотое сечение в картине И. И. Шишкина «Сосновая роща»
На этой знаменитой картине И. И. Шишкина с очевидностью просматриваются мотивы золотого сечения. Ярко освещенная солнцем сосна (стоящая на первом плане) делит длину картины по золотому сечению. Справа от сосны — освещенный солнцем пригорок. Он делит по золотому сечению правую часть картины по горизонтали. Слева от главной сосны находится множество сосен — при желании можно с успехом продолжить деление картины по золотому сечению и дальше. Наличие в картине ярких вертикалей и горизонталей, делящих ее в отношении золотого сечения, придает ей характер уравновешенности и спокойствия, в соответствии с замыслом художника. Когда же замысел художника иной, если, скажем, он создает картину с бурно развивающимся действием, подобная геометрическая схема композиции (с преобладанием вертикалей и горизонталей) становится неприемлемой.

Рис. 26

Рис. 27

В.И.Суриков.«Боярыня Морозова».
Роли ее отведена средняя часть картины. Она окована точкой высшего взлёта и точкой низшего спадания сюжета картины.

1) Это — взлёт руки Морозовой с двуперстным крестным знамением как высшая точка.

2) Это — беспомощно протянутая к той же боярыне рука, но на этот раз — рука старухи — нищей странницы, рука, из-под которой вместе с последней надеждой на спасение выскальзывает конец розвальней.

А как обстоит дело с «высшей точкой»? На первый взгляд имеем кажущееся противоречие: ведь сечение А1В1, отстоящее на 0,618… от правого края картины, проходит не через руку, не даже через голову или глаз боярыни, а оказывается где-то перед ртом боярыни!

Золотое сечение режет здесь действительно по самому главному.
В нём, и именно в нём, — величайшая сила Морозовой.

Золотое сечение в картине Леонардо да Винчи «Джоконда»

Портрет Моны Лизы привлекает тем, что композиция рисунка построена на»золотых треугольниках» (точнее на треугольниках, являющихся кусками правильного звездчатого пятиугольника).

Нет живописи более поэтичней, чем живопись Боттичелли Сандро, и нет у великого Сандро картины более знаменитой, чем его “Венера”. Для Боттичелли его Венера – это воплощение идеи универсальной гармонии “золотого сечения”, господствующего в природе.

Рис. 28 Рис. 29

Из истории астрономии известно, что И.Тициус, немецкий астроном XVIII в., с помощью этого ряда нашел закономерность и порядок в расстояниях между планетами солнечной системы.
Однако один случай, который, казалось бы, противоречил закону: между Марсом и Юпитером не было планеты.Cосредоточенное наблюдение за этим участком неба привело к открытию пояса астероидов. Произошло это после смерти Тициуса в начале XIX в. Pяд Фибоначчи используют широко: с его помощью представляют архитектонику и живых существ, и рукотворных сооружений, и строение Галактик. Эти факты — свидетельства независимости числового ряда от условий его проявления, что является одним из признаков его универсальности.

Во Вселенной все известные человечеству галактики и все тела в них существуют в форме спирали, соответствующей формуле золотого сечения. В спирали нашей галактики лежит коэффициент золотого сечения

Рис.30

5) «Золотое сечение» в архитектуре

Одним из красивейших произведений древнегреческой архитектуры является Парфенон (V в. до н. э.).

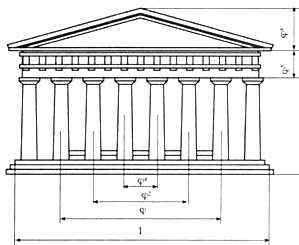
Рис. 31

На рисунках виден целый ряд закономерностей, связанных с золотым сечением. Пропорции здания можно выразить через различные степени числа Ф=0,618…

Парфенон имеет 8 колонн по коротким сторонам и 17 по длинным. выступы сделаны целиком из квадратов пентилейского мрамора. Благородство материала, из которого построен храм, позволило ограничить применение обычной в греческой архитектуре раскраски, она только подчеркивает детали и образует цветной фон (синий и красный) для скульптуры. Отношение высоты здания к его длине равно 0,618. Если произвести деление Парфенона по “золотому сечению”, то получим те или иные выступы фасада.

На плане пола Парфенона также можно заметить «золотые прямоугольники»:

Рис. 32

Золотое соотношение мы можем увидеть и в здании собора Парижской Богоматери (Нотр-дам де Пари), и в пирамиде Хеопса:

Рис. 33

В книгах о “золотом сечении” можно найти замечание о том, что в архитектуре, как и в живописи, все зависит от положения наблюдателя, и что, если некоторые пропорции в здании с одной стороны кажутся образующими “золотое сечение”, то с других точек зрения они будут выглядеть иначе. “Золотое сечение” дает наиболее спокойное соотношение размеров тех или иных длин.

Не только египетские пиpамиды постpоены в соответствии с совеpшенными пpопоpциями золотого сечения; то же самое явление обнаpужено и у мексиканских пиpамид.

Долгое время считали, что зодчие Древней Руси строили все «на глазок», без особых математических расчетов. Однако новейшие исследования показали, что русские архитекторы хорошо знали математические пропорции, о чем свидетельствует анализ геометрии древних храмов.

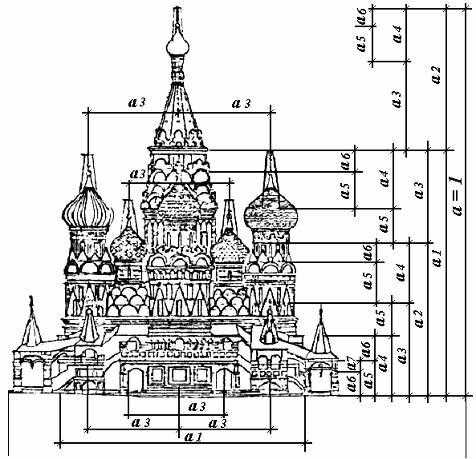
Рис. 34

Известный русский архитектор М. Казаков в своем творчестве широко использовал “золотое сечение”.

Его талант был многогранным, но в большей степени он раскрылся в многочисленных осуществленных проектах жилых домов и усадеб. Например, “золотое сечение” можно обнаружить в архитектуре здания сената в Кремле. По проекту М. Казакова в Москве была построена Голицынская больница, которая в настоящее время называется Первой клинической больницей имени Н.И. Пирогова (Ленинский проспект, д. Петровский дворец в Москве. Построен по проекту М.Ф. Казакова)

Рис. 35

Рис. 36

Еще один архитектурный шедевр Москвы – дом Пашкова – является одним из наиболее совершенных произведений архитектуры В. Баженова.

Рис. 37

Прекрасное творение В. Баженова прочно вошло в ансамбль центра современной Москвы, обогатило его. Наружный вид дома сохранился почти без изменений до наших дней, несмотря на то, что он сильно обгорел в 1812 г.

При восстановлении здание приобрело более массивные формы. Не сохранилась и внутренняя планировка здания, о которой дают представления только чертеж нижнего этажа.

Многие высказывания зодчего заслуживают внимание и в наши дни. О своем любимом искусстве В. Баженов говорил: “Архитектура – главнейшие имеет три предмета: красоту, спокойность и прочность здания… К достижению сего служит руководством знание пропорции, перспектива, механика или вообще физика, а всем им общим вождем является рассудок”.

6)Практическая часть работы

Я изучила архитектуру нашего села. Она представлена, в основном, зданиями в деревянном исполнении. Большую часть всех зданий занимают частные одноэтажные и двухэтажные многоквартирные деревянные дома. В селе только четыре трехэтажных здания, выполненных в капитальном исполнении.

Я провела исследование по выявлению « Золотого сечения» в архитектуре Саранпауля. Для этого я сделала фотографии многих зданий. Так как реальные здания и их модели на фотографии можно считать подобными фигурами, то отношение длин нужных мне отрезков на них будут являться равными.

Измерив длину и ширину зданий, найдя их отношение, я определила, относятся ли их фасады к числу «Золотых прямоугольников». Кроме этого, я определила отношение высоты зданий до уровня крыши к высоте самой крыши. Результаты измерений и вычислений представлены в таблице.

п/п

 

длина

ширина

отношение длин

длина большей части

длина меньшей части

отношение длин

1

Магазин «Лесной»

31,5

12

2,625

8

4

2

2

Магазин» Смешанные товары»

35

10,5

3,333333

5

5

1

3

Магазин «Рябинушка»

34

11,5

2,956522

7

4,5

1,555556

4

Трехэтажка

37,5

8,5

4,411765

6

1,5

4

5

Новый ДК

36,5

10,5

3,47619

7

2,5

2,8

6

Старый ДК

35,5

15

2,366667

10

3,5

2,857143

7

«Элаль»

37,5

8

4,6875

5

2

2,5

Магазин «Перекресток»

33,5

8

4,1875

3,5

4

0,875

8

9

Школа

18,5

3,5

5,285714

2

1

2

10

Детский сад «Олененок»

11,5

2

5,75

1,5

0,5

3

11

Частный дом 1

8

7,5

1,066667

3,5

4

0,875

12

Частный дом 2

9,5

5,5

1,727273

2,5

3

0,833333

13

Частный дом 3

8,5

7

1,214286

4

3

1,333333

14

Жилой дом

12,5

4

3,125

1,5

2,5

0,6

Таблица 3

Рассмотрев 14 зданий села, я установила, что фасад только одного из них является «Золотым прямоугольником» (частный дом). Только одно здание построено по принципу «Золотой пропорции» (магазин «Рябинушка»). Это говорит о том, что, к сожалению, в современной архитектуре «золотым сечением» чаще пренебрегают. Даже беглый взгляд на здания показал, что его вряд ли можно обнаружить в современных зданиях села.

4,5

7

Рис. 38 Магазин «Рябинушка»,

отношение длин отрезков 1,6

9,5

5,5

Рис. 39.Частный дом,

фасад здания является «Золотым прямоугольником»

1. 7. Заключение.

Иоганн Кеплер говорил:“Геометрия владеет двумя сокровищами: одно из них — это теорема Пифагора, а другое — деление отрезка в среднем и крайнем отношении … Первое можно сравнить с мерой золота ; второе же больше напоминает драгоценный камень.” «Другое» в этом высказывании- это «Золотое сечение». Я в своей работе попыталась разобраться, что это такое. В ходе работы я убедилась в грандиозности процесса познания мира, открытием все новых его закономерностей и сделала вывод: принцип золотого сечения – высшее проявление структурного и функционального совершенства целого и его частей в искусстве, науке, технике и природе. Можно ожидать, что законы развития различных систем природы, законы роста не очень разнообразны и прослеживаются в самых различных образованьях. В этом и проявляется единство природы. Идея такого единства, основанная на проявлении одних и тех же закономерностей в разнородных явлениях природы, сохранила свою актуальность от Пифагора до наших дней.

Познакомившись с феноменом « Золотого сечения» и его влиянием на архитектуру, я попыталась ответить на вопрос: являются ли здания нашего села красивыми и гармоничными? Я предположила, что архитектура села не соответствует общепринятым канонам красоты, так как в строительстве многих зданий не использовалось «Золотое сечение».

Проведя исследование, целью которого было применения «Золотого сечения» в архитектуре села Саранпауль, я подтвердила свою гипотезу. Только одно здание в селе построено по принципу « Золотого сечения», а значит, по общепринятым канонам красоты его можно считать гармоничным.

Выполняя исследовательскую работу, я еще раз убедилась в том, что математика, геометрия являются «оформлением» строительной деятельности, без которых она просто невозможна. Недаром геометрия оказалась впереди других наук и вооружила человека в его созидательной деятельности. Благодаря математическим знаниям и навыкам мы решаем не только арифметические задачи. Это наука позволяет развивать гибкость ума, что нужно для принятия объективного решения любой задачи. Эта не только задачи математического характера, но и различные жизненные ситуации, требующие рассмотрения «под разными углами». Эта наука просто необходима в жизни современного человечества.

В моей исследовательской работе я рассмотрела применение «Золотого сечения» только на нескольких зданиях села, но считаю, что их гораздо больше.

1. 8. Список использованной литературы

1. Азевич А.И. «От золотой пропорции к ее производным» // — «Квант», 1995. — № 3.

2. Азевич А. «Двадцать уроков гармонии» // –М., «Школа-Пресс», 1998.

3. Васютинский Н.А. «Золотая пропорция» // – М., «Молодая гвардия», 1990.

4. Бендукидзе А.Д. «Золотое сечение» // «Квант», 1973. — № 8.

5. «Энциклопедический словарь юного математика» // –М.,1989.

6. Воробьев Н.Н. «Числа Фибоначчи» // – М., «Наука», 1992.

7. Гарднер М. «Математические головоломки и развлечения» // – М., «Мир», 1971.

8. «Еще раз о золотом сечении» // — «Квант», 1989. — № 8.

9. Ковалев Ф.В. «Золотое сечение в живописи» // — К., «Выща школа», 1989.
10. Кеплер И. «О шестиугольных снежинках» // — М., 1982.

11. Кокстер Г.С.М. «Введение в геометрию» // – М., «Наука», 1966.

12. Стахов А. «Коды золотой пропорции»

13. Пидоу Д. «Геометрия и искусство» // – М., «Мир», 1979.

14. Прохоров А.И. «Золотая спираль» // — «Квант», 1984 — № 9.

15. Смирнова И.М. «В мире многогранников» // – М., «Просвещение», 1995.

16. Журнал «Математика в школе» // — 1994,- № 2; № 3.

17. Шевелев И.Ш., Марутаев М.А., Шмелев И.П. «Золотое сечение» // – М., Стройиздат», 1990.

18. «Математика. Я познаю мир»// – М. «Аванта +», 1998
19. Цеков-Карандаш Ц. «О втором золотом сечении» // — София, 1983.

20. Информация из интернета.

Конец формы

infourok.ru