Решение задач на движение тел по наклонной плоскости. Видеоурок. Физика 11 Класс

Мы ежедневно сталкиваемся с движением по наклонной плоскости, когда транспорт едет с горы или в гору, при проведении лабораторных работ, и сегодня мы рассмотрим, как решаются задачи на движение тел по наклонной плоскости.

Брусок находится на наклонной плоскости и может скользить вниз при наличии трения, на него будут действовать сила притяжения к земле, сила реакции опоры и сила трения (Рис. 1).

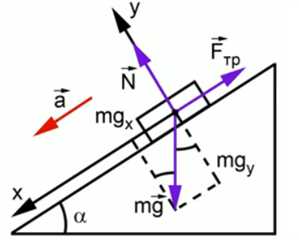
Рис. 1. Получение стандартного уравнения движения тел по наклонной плоскости

 =>

Векторная сумма этих трех сил будет равна произведению массы на ускорение. Координатная ось  будет направлена в сторону ускорения вдоль наклонной плоскости – вниз, ось  будет перпендикулярна оси х, соответственно, она совпадает по направлению с силой реакции опоры.

Тогда в проекциях на ось  мы имеем: составляющая  противолежащая углу , как мы помним, углы со взаимно перпендикулярными сторонами равны,  – вертикальная линия, основание плоскости – горизонтальная линия. Линия проецирования перпендикулярна поверхности плоскости, поэтому эти два угла будут равны. Сила трения проецируется со знаком «минус», а сила реакции опоры проекции не имеет.

По оси  проецируются две силы:  проецируется через  со знаком «минус», так как проекция направлена против оси , и сила реакции опоры.

Находим силу трения через произведение коэффициента трения и силы реакции опоры, которую находим из второго уравнения.

Подставляя это выражение силы трения в уравнение по оси , получаем стандартное уравнение движения тела по наклонной плоскости.

Тело скользит равномерно по наклонной плоскости с углом наклона . Чему равен коэффициент трения?

1.      2.  3.  4.

Составляем краткую запись условия задачи и решаем:

Записываем стандартное уравнение движения тела по наклонной плоскости, ускорение в данном случае будет равно нулю, так как тело движется равномерно по наклонной плоскости. Так как  у нас не может быть равно нулю, значит, нулю будет равна разность в скобочках, отсюда мы и находим коэффициент трения, который будет равен , по выборке это ответ 3.

Троллейбус массой 12 т движется равномерно под гору с уклоном 0,05 рад при силе тяги 4 кН. Определить силу сопротивления движению.

Записываем краткое условие задачи и выполняем поясняющий чертеж (рис. 2):

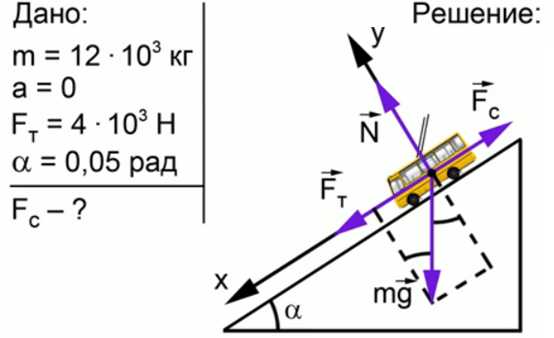
Рис. 2. Решение задачи 2

 при

Ответ: .

Запишем общее уравнение динамики по второму закону Ньютона и в проекции ох, необходимо помнить, что если угол α меньше или равен 0,1 рад, то в задачах по физике можно применять равенство, где угол  численно равен  и равен , а  равен единице. В таком случае мы можем выразить силу сопротивления через уравнение и, подставив значения, получим, что

На наклонной плоскости с углом 30⁰ находится брусок массой m, на который воздействует горизонтальная сила, равная mg/2, прижимающая брусок к поверхности плоскости. С каким ускорением будет двигаться брусок при коэффициенте трения, равном 0,065?

Запишем краткое условие задачи и поясняющий чертеж (рис. 3):

Рис. 3. Решение задачи 3

 ; ;

Ответ : .

К бруску приложено несколько сил. Горизонтальная сила, прижимающая брусок к плоскости, направлена в одну сторону, сила тяжести действует так, что брусок должен двигаться в другую сторону, поэтому необходимо вычислить силы, которые могут подействовать на брусок, сдвинув его с места. Сила  имеет проекцию , которая будет равна , так как  равен . Сила  пытается сдвинуть брусок вверх по наклонной плоскости, но она имеет проекцию , которая, в свою очередь, равна произведению  на , который меньше единицы. В таком случае  будет больше силы, действующей на тело, это означает, что брусок будет двигаться вниз и сила трения будет направлена вверх. Применив уравнение динамики по второму закону Ньютона и спроецировав его на координатные оси, мы выразим силу реакции опоры и подставим в уравнение по оси , откуда и получим выражение для ускорения.

Подставляя числовые значения, определим, что ускорение будет отрицательным. Это значит, что тело не может двигаться вниз по наклонной плоскости, но и при наличии силы притяжения и силы, прижимающей брусок, тело не может двигаться вверх по наклонной плоскости. Это говорит о том, что ускорение равно нулю, то есть тело могло бы двигаться вниз, но силе тяжести не удается преодолеть возникающую при этом силу трения. Сила трения не будет достигать своего максимального значения, будет принимать несколько меньшее значение, а ускорение тела будет равно нулю.

Мы разобрали основные типы задач на движение тел по наклонной плоскости, использование основных законов механики для различных способов решения задач не только на уроках физики, но даже в практической и повседневной жизни.

 

Список литературы

1. Тихомирова С.А., Яворский Б.М. Физика (базовый уровень) – М.: Мнемозина, 2012.
2. Генденштейн Л.Э., Дик Ю.И. Физика 10 класс. – М.: Мнемозина, 2014.
3. Кикоин И.К., Кикоин А.К. Физика-9. – М.: Просвещение, 1990.

 

Домашнее задание

1. Каким законом мы пользуемся при составлении уравнений?
2. Какое равенство используется при решении задач, когда угол меньше или равен 0,1 рад?

  

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-портал Dist-tutor.info (Источник).
2. Интернет-портал Repetitors.info (Источник).
3. Интернет-портал Bambookes.ru (Источник).

interneturok.ru

Движение тел по наклонной плоскости

«Требуются очень глубокие знания,

чтобы заметить простейшие, но

подлинные отношения вещей между собой».

Георг Кристоф Лихтенберг

Данная тема будет посвящена изучению движения тел по наклонной плоскости.

Задача 1. Тело массой 20 кг перемещается вверх по наклонной плоскости с углом наклона 45^о и коэффициентом трения 0,03. Определите ускорение, с которым движется тело, если к нему параллельно основанию плоскости приложена сила 650 Н.

ДАНО:	РЕШЕНИЕ: На основании второго закона Ньютона, составим уравнение движения тела В проекциях на ось Оx: В проекциях на ось Оy: Тогда сила трения равна Следовательно Преобразуем последнюю формулу Тогда ускорение, с которым движется тело равно

Ответ: 14,8 м/с².

Задача 2. Тело массой 4 кг перемещается вверх по наклонной плоскости под действием связанного с ним невесомой и нерастяжимой нитью грузом массой 12 кг. Начальные скорости тела и груза равны нулю, коэффициент трения тела о плоскость равен 0,05, угол наклона плоскости равен 30^о. Определите ускорение, с которым движется тело, и силу натяжения нити. Считать, что блок невесом и трение в блоке отсутствует.

ДАНО:

РЕШЕНИЕ: Запишем второй закон Ньютона для тела и груза В проекциях на ось Ох: В проекциях на ось Оy: В проекциях на ось О’y’: Получаем систему уравнений Так как нить невесома и нерастяжима, а в блоке отсутствует трение, то: С учётом последних выражений преобразуем систему уравнений Для того, чтобы решить эту систему уравнений сложим первое и второе уравнение. Тогда получим Преобразуем данное уравнение и выразим искомое ускорение Теперь определим силу натяжения нити

Ответ: 6,4 м/с²; 43,2 Н.

Задача 3. Два груза массами

т₁ = 5 кг и т₂ = 2 кг связаны невесомой нерастяжимой нитью, переброшенной через невесомый блок, который прикреплен к вершине призмы, и могут скользить по граням этой призмы. Определите ускорение грузов, если начальные скорости грузов равны нулю, α = 60^о, β = 30^о, а коэффициент трения — 0,3.

ДАНО:

РЕШЕНИЕ: Запишем второй закон Ньютона для обоих грузов В проекциях на ось Оx и O’x’: В проекциях на ось Оy и О’у’: С учётом последних выражений преобразуем систему уравнений в проекциях на ось Оx и O’x’: Так как нить и блок невесомы: Так как нить нерастяжима и в блоке нет сил трения: С учётом последних равенств сложим первое и второе уравнение системы в проекциях на ось Оx и O’x’: Тогда искомое ускорение равно

Ответ: 2,6 м/с².

videouroki.net

Проецирование сил. Движение по наклонной плоскости

Проецирование сил. Движение по наклонной плоскости

Задачи по динамике.

I и II закон Ньютона.

Ввод и направление осей.

Неколлинеарные силы.

Проецирование сил на оси.

Решение систем уравнений.

Самые типовые задачи по динамике

---

Начнем с I и II законов Ньютона.

Откроем учебник физики и прочтем. I закон Ньютона: существуют такие инерциальные системы отсчета в которых… Закроем такой учебник, я тоже не понимаю. Ладно шучу, понимаю, но объясню проще.

I закон Ньютона: если тело стоит на месте либо движется равномерно (без ускорения), сумма действующих на него сил равна нулю.

Вывод: Если тело движется с постоянной скоростью или стоит на месте векторная сумма сил будет ноль.

II закон Ньютона: если тело движется равноускоренно или равнозамедленно (с ускорением), сумма сил, действующих на него, равна произведению массы на ускорение.

Вывод: Если тело двигается с изменяющейся скоростью, то векторная сумма сил, которые как-то влияют на это тело ( сила тяги, сила трения, сила сопротивления воздуха), равна массе этого тело умножить на ускорение.

При этом одно и то же тело чаще всего движется по-разному (равномерно или с ускорением) в разных осях. Рассмотрим именно такой пример.

Задача 1. Определите коэффициент трения шин автомобиля массой 600 кг, если сила тяги двигателя 4500 Н вызывает ускорение 5 м/с².

Сделаем рисунок, покажем силы, которые дествуют на машину.

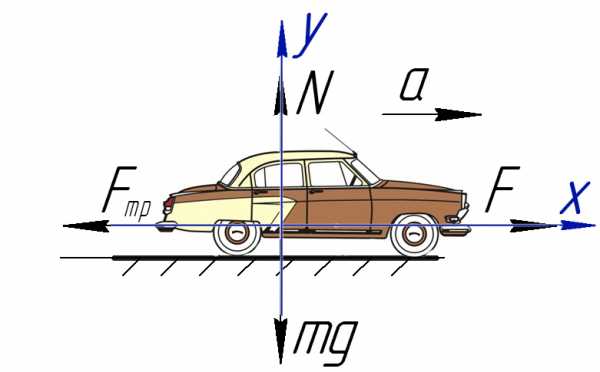
На Ось Х: движение с ускорением 

На Ось Y: нет движения (здесь координата, как была ноль так и останется, перемещение будет тольков вдоль оси Х)

Те силы, направление которых совпадает с направлением осей, будут с плюсом, в противоположном случае — с минусом.

Fтр = μN, где N — сила реакции опоры. На оси Y:  N = mg, тогда в данной задаче Fтр = μmg.

Получаем, что: 

Коэффициент трения — безразмерная величина. Следовательно, единиц измерения нет.

Задача 2. Груз массой 5кг, привязанный к невесомой нерастяжимой нити, поднимают вверх с ускорением 3м/с². Определите силу натяжения нити.

Сделаем рисунок, покажем силы, которые дествуют на груз

T — сила натяжения нити

Разберемся с направлением сил на ось Y:

Выразим T и подставим числительные значения:

Самое главное не запутаться с направлением сил (по оси или против), все остальное сделает калькулятор или всеми любимый столбик.

Далеко не всегда все силы, действующие на тело, направлены вдоль осей.

Простой пример: мальчик тянет санки

Если мы так же построим оси X и Y, то сила натяжения (тяги) не будет лежать ни на одной из осей. 

Чтобы спроецировать силу тяги на оси, вспомним прямоугольный треугольник.

Отношение противолежащего катета к гипотенузе — это синус.

Отношение прилежащего катета к гипотенузе — это косинус.

Сила тяги на ось Y — отрезок (вектор) BC.

Сила тяги на ось X — отрезок (вектор) AC.

Если это непонятно, посмотрите задачу №4.

Чем длинее будет верека и, соответсвенно, меньше угол α, тем проще будет тянуть санки. Идеальный вариант, когда веревка параллельна земле, ведь сила, которая действуют на ось X— это Fнcosα. Чем больше будет этот катет, тем сильнее горизонтальная сила.

Задача 3. Брусок подвешен на двух нитях. Сила натяжения первой составляет 34Н, второй — 21Н, θ1 = 45°, θ2 = 60°. Найдите массу бруска.

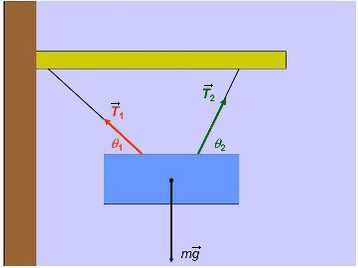
Введем оси и спроецируем силы:

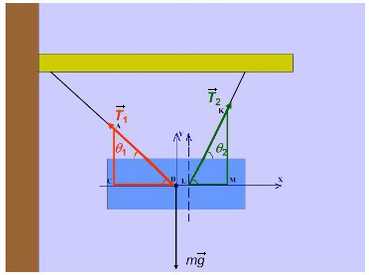
Получаем два прямоугольных треугольника. Гипотенузы AB и KL — силы натяжения. LM и BC — силы натяжения, спроецированные на ось X, AC и KM — на ось Y.

Задача 4. Брусок массой 5 кг (масса в этой задаче не нужна, но, чтобы в уравнениях все было известно, возьмем конкретное значение) соскальзывает с плоскости, которая наклонена под углом 45°, с коэффициентом трения μ = 0,1. Найдите ускорение движения бруска? 

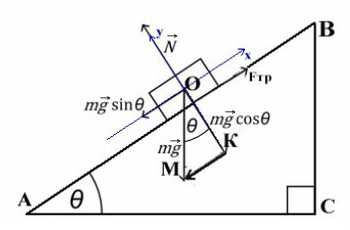
Когда же есть наклонная плоскость, оси (X и Y) лучше всего направить по направлению движения тела. Некоторые силы в данном случае ( здесь это mg) не будут лежать ни на одной из осей. Эту силу нужно спроецировать, чтобы она имела такое же направление, как и взятые оси.
Всегда ΔABC подобен ΔKOM в таких задачах (по прямому углу и углу наклона плоскости).

Рассмотрим поподробнее ΔKOM: 

Получим, что KO лежит на оси Y, и проекция mg на ось Y будет с косинусом. А вектор MK коллинеарен (отрезок МК параллелен) оси X, проекция mg на ось X будет с синусом, и вектор МК направлен против оси X (то есть будет с минусом).

Не забываем, что, если направления оси и силы не совпадают, ее нужно взять с минусом!

Из оси Y выражаем N и подставляем в уравнение оси X, находим ускорение:

Как видно, массу в числителе можно вынести за скобки и сократить со знаменаталем. Тогда знать ее не обязательно, получить ответ реально и без нее.
Да-да, в идеальных условиях (когда нет силы сопротивления воздуха и т.п.), что перо, что гиря скатятся (упадут) за одно и тоже время. 

Задача 5. Автобус съезжает с горки под уклоном 60° с ускорением 8 м/с²  и с силой тяги 8 кН. Коэффициент трения шин об асфальт равен 0,4. Найдите массу автобуса.

Сделаем рисунок с силами:

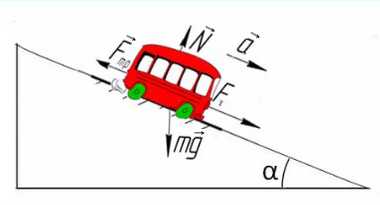
Введем оси X и Y. Спроецируем mg на оси:

Запишем второй закон Ньютона на X и Y:

Задача 6. Поезд движется по закруглению радиуса 800 м со скоростью 72 км/ч. Определить, на сколько внешний рельс должен быть выше внутреннего. Расстояние между рельсами 1,5 м.

Самое сложное — понять, какие силы куда действуют, и как угол влияет на них.

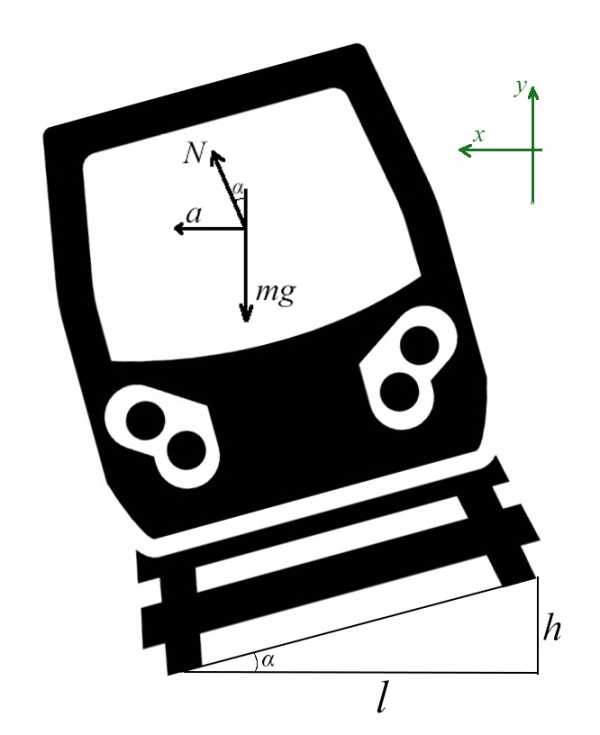Вспомни, когда едешь по кругу на машине или в автобусе, куда тебя выталкивает? Для этого и нужен наклон, чтобы поезд не упал набок!

Угол α задает отношение разницы высоты рельсов к расстоянию между ними (если бы рельсы находились горизонтально)

Запишем какие силы действуют на оси:

Ускорение в данной задачи центростремительное!

Поделим одно уравнение на другое:

Тангенс — это отношение противолежащего катета к прилежащему:

Как мы выяснили, решение подобных задач сводится к расстановке направлений сил, проецированию их на оси и к решению систем уравнений, почти сущий пустяк.

В качестве закрепления материала решите несколько похожих задач с подсказками и ответами. 

Будь в курсе новых статеек, видео и легкого технического юмора.

ik-study.ru

Задачи на тему Движение по наклонной плоскости

Нашли ошибку? Сообщите в комментариях (внизу страницы)

На наклонной плоскости длиной 13 м и высотой 5 м лежит груз массой 26 кг. Коэффициент трения равен 0,5. Какую силу надо приложить к грузу вдоль плоскости, чтобы втащить груз? чтобы стащить груз
РЕШЕНИЕ

Какую силу надо приложить для подъема вагонетки массой 600 кг по эстакаде с углом наклона 20°, если коэффициент сопротивления движению равен 0,05
РЕШЕНИЕ

При проведении лабораторной работы были получены следующие данные: длина наклонной плоскости 1 м, высота 20 см, масса деревянного бруска 200 г, сила тяги при движении бруска вверх 1 Н. Найти коэффициент трения
РЕШЕНИЕ

На наклонной плоскости длиной 50 см и высотой 10 см покоится брусок массой 2 кг. При помощи динамометра, расположенного параллельно плоскости, брусок сначала втащили вверх по наклонной плоскости, а затем стащили вниз. Найти разность показаний динамометра
РЕШЕНИЕ

Чтобы удерживать тележку на наклонной плоскости с углом наклона α, надо приложить силу F1 направленную вверх вдоль наклонной плоскости, а чтобы поднимать вверх, надо приложить силу F2. Найти коэффициент сопротивления
РЕШЕНИЕ

Наклонная плоскость расположена под углом α = 30° к горизонту. При каких значениях коэффициента трения μ тянуть по ней груз труднее, чем поднимать его вертикально
РЕШЕНИЕ

На наклонной плоскости длиной 5 м и высотой 3 м находится груз массой 50 кг. Какую силу, направленную вдоль плоскости, надо приложить, чтобы удержать этот груз? тянуть равномерно вверх? тянуть с ускорением 1 м/с2? Коэффициент трения 0,2
РЕШЕНИЕ

Автомобиль массой 4 т движется в гору с ускорением 0,2 м/с2. Найти силу тяги, если уклон равен 0,02 и коэффициент сопротивления 0,04
РЕШЕНИЕ

Поезд массой 3000 т движется вниз под уклон, равный 0,003. Коэффициент сопротивления движению равен 0,008. С каким ускорением движется поезд, если сила тяги локомотива равна: а) 300 кН; б) 150 кН; в) 90 кН
РЕШЕНИЕ

Мотоцикл массой 300 кг начал движение из состояния покоя на горизонтальном участке дороги. Затем дорога пошла под уклон, равный 0,02. Какую скорость приобрел мотоцикл через 10 с после начала движения, если горизонтальный участок дороги он проехал за половину этого времени? Сила тяги и коэффициент сопротивления движению на всем пути постоянны и соответственно равны 180 Н и 0,04
РЕШЕНИЕ

Брусок массой 2 кг находится на наклонной плоскости с углом наклона 30°. Какую силу, направленную горизонтально (рис. 39), надо приложить к бруску, чтобы он двигался равномерно по наклонной плоскости? Коэффициент трения бруска о наклонную плоскость равен 0,3
РЕШЕНИЕ

Поместите на линейке небольшой предмет (резинку, монету и т. д.). Постепенно поднимайте конец линейки, пока предмет не начнет скользить. Измерьте высоту h и основание b полученной наклонной плоскости и вычислите коэффициент трения
РЕШЕНИЕ

С каким ускорением а скользит брусок по наклонной плоскости с углом наклона α = 30° при коэффициенте трения μ = 0,2
РЕШЕНИЕ

В момент начала свободного падения первого тела с некоторой высоты h второе тело стало скользить без трения с наклонной плоскости, имеющей ту же высоту h и длину l = nh. Сравнить конечные скорости тел у основания наклонной плоскости и время их движения.
РЕШЕНИЕ

bambookes.ru

Решение задач по динамике. Движение по горизонтали и вдоль наклонной плоскости

Мы продолжаем изучать динамику. Это раздел физики, который изучает причины механического движения.

Сегодня мы займемся решением задач на движение по горизонтали и вдоль наклонной плоскости. Как решать такие задачи?

У нас есть тело, которое находится на горизонтальной или наклонной плоскости. На него в любом случае действует сила тяжести и сила реакции опоры. Если поверхность не гладкая, на тело действует сила трения, направленная против направления движения. Тело могут тащить за нить, в таком случае на него будет действовать сила натяжения нити. Наличие той или иной силы зависит от условия задачи, но равнодействующая всех сил, действующих на тело, в общем случае вызывает ускорение тела, . Это следствие из второго закона Ньютона – главного инструмента решения задач по динамике.

Итак, мы разобрали, что происходит при движении тела вдоль плоскости, определили действующие на тело силы и описали процесс математически, применив второй закон Ньютона. На этом физика заканчивается, и остается математика.

Решать уравнения в векторной форме математически сложно, поэтому нужно переписать следствие из второго закона Ньютона в проекциях на оси координат.

Если плоскость наклонная, она ориентирована под определенным углом к горизонту, а значит, сила тяжести будет направлена под углом к плоскости, знаем мы этот угол или нет. Это делает важным выбор системы координат.

Мы свободны в выборе, результат не будет зависеть от выбора системы координат, но нужно выбрать такую, при которой математические преобразования будут максимально простыми. Мы увидим это на примере одной из задач.

И только теперь, когда получена система уравнений, описывающая физический процесс, мы решаем задачу математически: решаем уравнения и находим неизвестное.

Приступим к решению задач.

Камень, скользивший по горизонтальной поверхности льда, остановился, пройдя расстояние S =48 м. Найдите начальную скорость  камня, если сила трения скольжения камня о лед составляет 0,06 силы нормального давления камня на лед.

Анализ условия:

— в задаче описано тело, которое движется под действием сил, значит, будем применять второй закон Ньютона;

— на камень действует сила тяжести, сила реакции опоры и сила трения. Отметим их (см. рис. 1).

Рис. 1. Действующие на камень силы

— сила трения равна ;

— камень останавливается, движется с ускорением, которое по второму закону Ньютона вызвано равнодействующей силой;

-при равноускоренном движении тело проходит путь  и приобретает скорость .

 

Решение

Выберем систему координат. Удобно направить ось х в направлении движения камня, а ось у перпендикулярно оси х (см. рис. 2).

Рис. 2. Выбор системы координат

Применим второй закон Ньютона:

 

 

Учитывая, что сила трения равна , запишем в проекциях на выбранные оси координат. Сила трения направлена против движения камня, туда же направлено и ускорение (камень замедляется) (см. рис. 3):

 

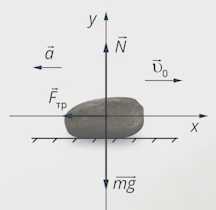
Рис. 3. Направление ускорения

За время остановки  камень по условию задачи пройдет расстояние . Начальная скорость направлена в направлении оси х, ее проекция будет иметь знак «+», ускорение – против оси х, ставим знак «-»:

 

 

Тело остановится, то есть его скорость через время  будет равна нулю:

 

 

Получили систему уравнений, которую остается решить и получить начальную скорость камня, равную 7,6 м/с:

 

Математическая часть решения задачи

Выразим из второго уравнения силу реакции опоры:     Подставим ее в первое уравнение:     Выразим из четвертого уравнения время Т:     Подставим его в третье уравнение:     Выразим скорость и подставим найденное выше ускорение:

Теперь решим задачу на движение вдоль наклонной плоскости.

Тело массы m без начальной скорости соскальзывает с наклонной плоскости с углом  с высоты h (см. рис. 4).

Рис. 4. Рисунок к условию задачи 2

Коэффициент трения тела о поверхность равен . За какое время тело достигнет подножья?

 

Анализ условия

— Задан прямоугольный треугольник, в котором известна одна сторона и угол. Значит, известны все стороны, и определен путь, который проходит тело.

— На тело действуют сила тяжести, сила реакции опоры и сила трения (см. рис. 5).

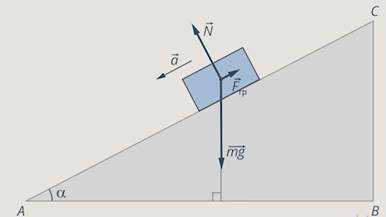
Рис. 5. Силы, которые действуют на тело

Равнодействующая этих сил создает ускорение – будем применять второй закон Ньютона.

— В задаче нужно найти время движения тела, которое движется с ускорением, равноускоренное движение описывается уравнениями кинематики.

 

Решение

Выберем систему координат. Здесь есть своя особенность: движение бруска происходит вдоль наклонной плоскости, сила трения направлена противоположно направлению движения, сила реакции опоры перпендикулярна плоскости, а сила тяжести направлена под углом к плоскости. Нам особенно важно выбрать удобную систему координат. Для математических расчетов удобно направить оси координат, как показано на рисунке: ось х вдоль в направлении движения бруска, ось у перпендикулярно поверхности (см. рис. 6).

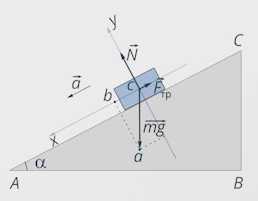
Рис. 6. Выбор системы координат

Применим второй закон Ньютона:

 

 

Учитывая, что сила трения равна , запишем в проекциях на выбранные оси координат.

Сила тяжести направлена под углом к обеим осям координат. Треугольники АВС и авс подобны, и угол  равен углу cab. Следовательно, проекция силы тяжести на ось х равна , на ось у –  (см. рис. 7).

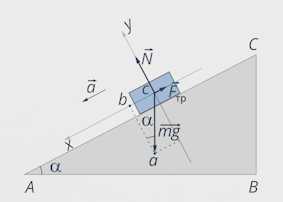
Рис. 7. Проекции сил на оси координат

Тогда:

 

 

Нахождение проекций силы тяжести

interneturok.ru

Презентация «Решение задач на движение по наклонной плоскости»

Слайды и текст этой презентации

Слайд 1

Решение задач на движение по наклонной плоскости.

Слайд 2

План решения задач по динамике
1. Сделать рисунок, на котором обозначить направление координатных осей, ускорения и всех сил, приложенных к телу .
2. Для каждого тела записать в векторном виде уравнение второго закона Ньютона, перечислив в его правой части в любом порядке все силы, приложенные к телу
3. Записать полученные в п. 2 уравнения в проекции на оси координат.
5. Найти численное значение неизвестной величины, если этого требует условие задачи.
4. Из полученного уравнения (системы уравнений) выразить неизвестную величину.

Слайд 3

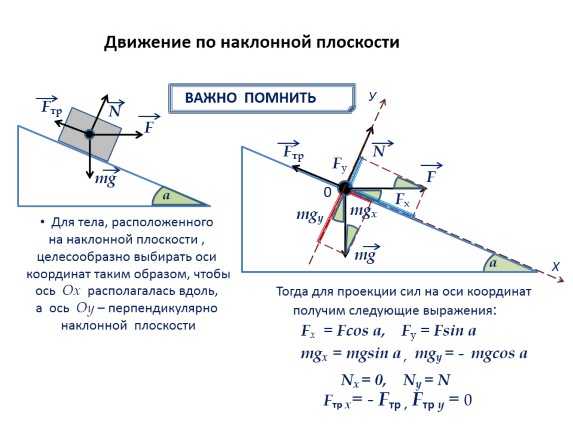
Движение по наклонной плоскости
ВАЖНО ПОМНИТЬ
mg
N
F
Fтр.
Для тела, расположенного на наклонной плоскости , целесообразно выбирать оси координат таким образом, чтобы ось Ох располагалась вдоль, а ось Оу – перпендикулярно наклонной плоскости
а
Тогда для проекции сил на оси координат получим следующие выражения:
Fх. = Fcos а, Fу = Fsin а
mgх. = mgsin а , mgу = — mgcos а
Nx = 0,
Ny = N
Fтр x= — Fтр., Fтр у = 0 .

Слайд 4

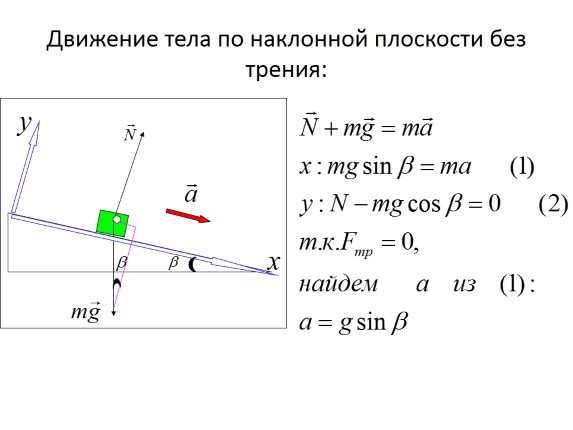Движение тела по наклонной плоскости без трения:

Слайд 5

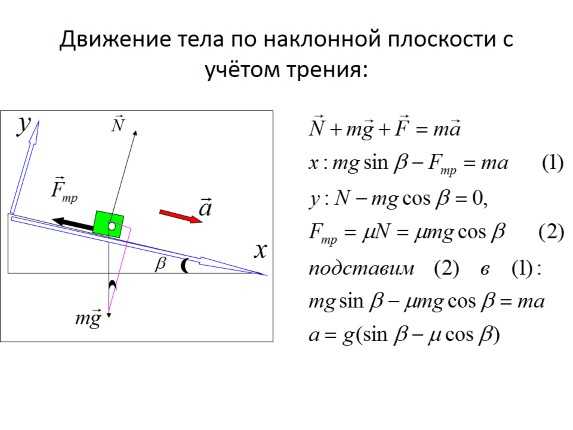
Движение тела по наклонной плоскости с учётом трения:

Слайд 6

а
β
m1g
m2g
N1
N2
T
T
У
У
Х
Х
а
а
Задача 1.С каким ускорением будут двигаться грузы массами 2 кг и 4 кг, если а =300, β =600. Найти натяжение нити. Блоки и нить невесомы, трением пренебречь.
m1= 2 кг
m2= 4 кг
Дано:
а =300
β =600
а — ?
Решение:
1
2
Удобно выбрать для каждого тела свою систему координат (как на рисунке)
m1a = m1g + Т+ N1
m2a = m2g + Т + N2
3
Оx: m1a = – m1gsin а + Т (1)
Оy: 0 = – m1gcos а +N1 (2)
Оx: m2a = m2gsin β – Т (3)
Оy: 0 = – m1gcos β + N2 (4)
4
Складывая (1) и (3), и выражая ускорение, получим:
g (m2sin β — m1sin

a =
m2+ m1
Т = 17,8 H
T = m1a + m1gsin а
5
a = 4 м/с2
Ответ: а = 4 м/с2 , T = 17,8 H

Слайд 7

Задача2.Человек массой m1 , упираясь ногами в ящик массой m2 подтягивает его с помощью каната, перекинутого через блок, по наклонной плоскости с углом наклона а. С какой минимальной силой нужно тянуть канат, чтобы подтянуть ящик к блоку? Коэффициент трения между яиом и наклонной плоскостью μ

Слайд 8

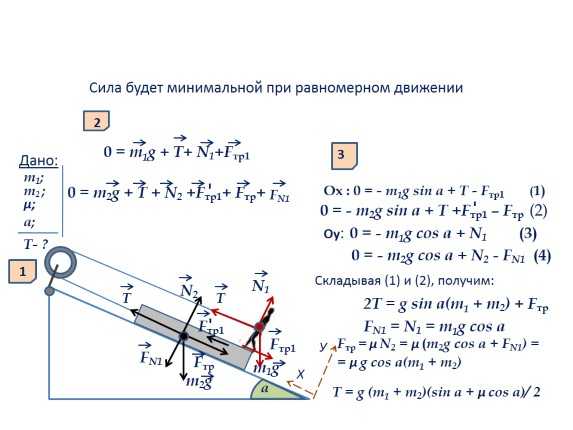
а
У
Х
FN1
N2
m1g
m2g
T
T
Fтр.
Fтр1.1
1
Дано:
m1;
m2 ;
μ;
а;
T- ?
Сила будет минимальной при равномерном движении
2
0 = m1g + Т+ N1+Fтр1
0 = m2g + Т + N2 +Fтр1+ Fтр+
3
Ох : 0 = — m1g sin а + Т — Fтр1 (1)
0 = — m2g sin а + Т +Fтр1 – Fтр (2)
Оу: 0 = — m1g cos а + N1 (3)
0 = — m2g cos а + N2 — FN1 (4)
N1
FN1 = N1 = m1g cos а
Складывая (1) и (2), получим:
2Т = g sin а(m1 + m2) + Fтр
Fтр = μ N2 = μ (m2g cos а + FN1) = = μ g cos а(m1 + m2)
Т = g (m1 + m2)(sin а + μ cos а)/ 2
FN1

Слайд 9

а
Х
FN1
N2
m1g
m2g
T
1
У
T
Fтр.1
N1
Задача 3. К концам троса, перекинутого через блок, привязаны бруски с массами m1= m и m2 = 4m, находящиеся на гладкой наклонной плоскости с углом наклона 300. При каком минимальном значении коэффициента трения между брусками они будут покоиться?
m1= m
m2 = 4m
а = 300
μ — ?
Дано:
Решение:
m1a = m1g + Т+ N1+Fтр
m2a = m2g + Т + N2 +Fтр+ FN1
Ох : 0 = — m1g sin а + Т- Fтр (1)
0 = — m2g sin а + Т +Fтр (2)
Оу: 0 = — m1g cos а + N1 (3)
0 = — m2g cos а + N2 — FN1 (4)
Из (3): N1 = m1g cos а
Из (4): N2 = m2g cos а + FN1
N1 = FN1 , поэтому N2 = m2g cos а — m1g cos а
Вычтем из (1) (2) и учитывая, что
Fтр = Fтр
получим:
2
2 Fтр = m2g sin а — m1g sin а
Fтр = μ N1 = μ m1g cos а
μ =
m2g sin а — m1g sin а
2m1g cos а
3 tgа
=
2
3
4
5

Слайд 10

Задача 4.Д/з На наклонную плоскость с углом наклона 300 положили кирпич массой2кг. Коэффициент трения скольжения между поверхностями равен 0,8. Чему равна сила трения, действующая на кирпич?

Слайд 11

lusana.ru

Движение по наклонной плоскости

Автор Сергей Валерьевич

Четверг, Декабрь 31, 2015

В данной статье рассказывается о том, как решать задачи про движение по наклонной плоскости. Рассмотрено подробное решение задачи о движении связанных тел по наклонной плоскости из ЕГЭ по физике.

Определите ускорение грузов, связанных невесомой и нерастяжимой нитью, перекинутой через невесомый блок, как показано на рисунке, если массы левого и правого груза равны 0.4 и 0.3 кг, соответственно, коэффициент трения левого груза о поверхность наклонной плоскости равен 0.1, а угол наклона наклонной плоскости равен . Трением в блоке пренебречь.

Решение задачи о движении по наклонной плоскости

Прежде чем перейти непосредственно к решению задачи, как репетитор по математике и физике, рекомендую тщательно проанализировать ее условие. Начать нужно с изображения сил, которые действуют на связанные тела:

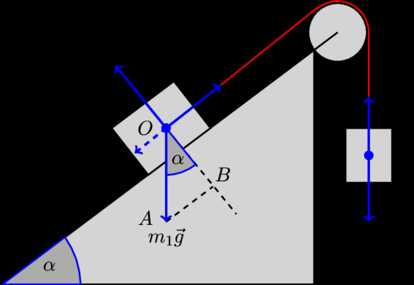
Здесь и — силы натяжения нити, действующие на левое и правое тело, соответственно, — сила реакции опоры, действующая на левое тело, и — силы тяжести, действующие на левое и правое тело, соответственно. С направлением этих сил все понятно. Сила натяжения направлена вдоль нити, сила тяжести вертикально вниз, а сила реакции опоры перпендикулярно наклонной плоскости.

А вот с направлением силы трения придется разбираться отдельно. Поэтому на рисунке она изображена пунктирной линией и подписана со знаком вопроса. Интуитивно понятно, что если правый груз будет «перевешивать» левый, то сила трения будет направлена противоположно вектору . Наоборот, если левый груз будет «перевешивать» правый, то сила трения будет сонаправлена с вектором .

Правый груз тянет вниз сила Н. Здесь мы взяли ускорение свободного падения м/с². Левый груз вниз тоже тянет сила тяжести, но не вся целиком, а только ее «часть», поскольку груз лежит на наклонной плоскости. Эта «часть» равна проекции силы тяжести на наклонную плоскости, то есть катету в прямоугольном треугольнике

yourtutor.info