Числовая окружность в координатной плоскости — урок. Алгебра, 10 класс.

Расположим числовую окружность в координатной плоскости так, чтобы центр окружности совместился с началом координат, а её радиус принимаем за единичный отрезок.

Начальная точка числовой окружности \(A\) совмещена с точкой \((1;0)\).

 

 

Каждая точка числовой окружности имеет в координатной плоскости свои координаты.

 

Найдём сначала координаты тех точек координатной плоскости, которые получены на макетах числовой окружности.

Точка Mπ4 — середина \(I\) четверти. Опустим перпендикуляр \(MP\) на прямую \(OA\) и рассмотрим треугольник \(OMP\). Так как дуга \(AM\) составляет половину дуги \(AB\), то ∡MOP=45°.   Значит, треугольник \( OMP \) — равнобедренный прямоугольный треугольник и \(OP = MP\), т. е. у точки \(M\) абсцисса и ордината равны: \(x = y\).   Так как координаты точки \(M(x;y)\) удовлетворяют уравнению числовой окружности x2+y2=1, то для их нахождения нужно решить систему уравнений: x2+y2=1x=y

 

Подставив \(x\) вместо \(y\) в первое уравнение системы, получим следующее решение:

 

x2+x2=1;2×2=1;x2=12;x=12=22;y=x=22.

 

При решении учитываем, что абсцисса точки \(M\) положительна.

Получили, что координаты точки \(M\), соответствующей числу π4, будут   Mπ4=M22;22.

Аналогично можно получить координаты и других точек первого макета числовой окружности, учитывая только знаки координат в каждой четверти.

Полученные результаты запишем в таблицу.

Точка окружности

	\(0\)	π4	π2	3π4	π	5π4	3π2	7π4	2π
Абсцисса \(x\)	\(1\)	22	\(0\)	−22	\(-1\)	−22	\(0\)	22	\(1\)
Ордината \(y\)	\(0\)	22	\(1\)	22	\(0\)	−22	\(-1\)	−22	\(0\)

 

Рассуждаем аналогично для точки \(M\), если теперь она соответствует числу π6.

 

Треугольник \(MOP\) прямоугольный. Так как дуга \(AM\) составляет третью часть дуги \(AB\), то ∡MOP=30°.   Катет \(MP\) лежит против угла \(30\) градусов в прямоугольном треугольнике, значит, равен половине гипотенузы, т. е. ордината точки \(M\) равна  MP=12;y=12

 

Абсциссу \(x\) точки \(M\) найдём, решив уравнение:

 

x2+y2=1;

x2=1−122=1−14=34;x=32.

 

При решении учитываем, что абсцисса точки \(M\) положительна.

Получили, что координаты точки \(M\), соответствующей числу π6, будут  Mπ6=M32;12.

Аналогично можно получить координаты и других точек второго макета числовой окружности, учитывая только знаки координат в каждой четверти.

Полученные результаты запишем в таблицу.

Точка окружности

	π6	π3	2π3	5π6	7π6	4π3	5π3	11π6
Абсцисса \(x\)	32	12	−12	−32	−32	−12	12	32
Ордината \(y\)	12	32	32	12	−12	−32	−32	−12

www.yaklass.ru

10 класс. Алгебра. Тригонометрические функции. Числовая окружность. — Числовая окружность. Числовая окружность на координатной плоскости.

Комментарии преподавателя

Для  любой функ­ции неза­ви­си­мый ар­гу­мент от­кла­ды­ва­ет­ся либо на чис­ло­вой пря­мой, либо на окруж­но­сти. Оха­рак­те­ри­зу­ем и чис­ло­вую пря­мую, и чис­ло­вую окруж­ность.

Пря­мая ста­но­вит­ся чис­ло­вой (ко­ор­ди­нат­ной) пря­мой, если от­ме­че­но на­ча­ло ко­ор­ди­нат, вы­бра­ны на­прав­ле­ние и мас­штаб (рис. 1).

Чис­ло­вая пря­мая уста­нав­ли­ва­ет вза­им­но-од­но­знач­ное со­от­вет­ствие между всеми точ­ка­ми пря­мой и всеми дей­стви­тель­ны­ми чис­ла­ми.

На­при­мер, берем число  от­кла­ды­ва­ем на ко­ор­ди­нат­ной оси, по­лу­ча­ем точку  Возь­мем число  от­кла­ды­ва­ем на оси, по­лу­ча­ем точку  (рис. 2).

И на­о­бо­рот, если мы взяли любую точку  на ко­ор­ди­нат­ной пря­мой, то най­дет­ся един­ствен­ное со­от­вет­ству­ю­щее ей дей­стви­тель­ное число (рис. 2).

К та­ко­му со­от­вет­ствию люди при­шли не сразу. Чтобы по­нять это, вспом­ним ос­нов­ные чис­ло­вые мно­же­ства.

Сна­ча­ла ввели мно­же­ство на­ту­раль­ных чисел 

Затем мно­же­ство целых чисел 

Мно­же­ство ра­ци­о­наль­ных чисел 

Пред­по­ла­га­лось, что этих мно­жеств будет до­ста­точ­но, и су­ще­ству­ет вза­им­но-од­но­знач­ное со­от­вет­ствие между всеми ра­ци­о­наль­ны­ми чис­ла­ми и точ­ка­ми пря­мой. Но ока­за­лось, что на чис­ло­вой пря­мой есть бес­чис­лен­ное мно­же­ство точек, ко­то­рые нель­зя опи­сать чис­ла­ми вида 

При­мер – ги­по­те­ну­за пря­мо­уголь­но­го тре­уголь­ни­ка с ка­

www.kursoteka.ru

Конспект уроков «Числовая окружность на координатной плоскости»

Название предмета Алгебра и начала математического анализа

Класс 10

УМК Алгебра и начала математического анализа, 10-11 классы. В 2 . Ч.1. Учебник для общеобразовательных учреждений(базовый уровень) /А.Г. Мордкович. – 10-еизд., стер.- М.: Мнемозина,2012. Ч.2. Задачник для общеобразовательных учреждений(базовый уровень) /[А.Г. Мордкович и др.]; под ред. А.Г. Мордковича. – 10-еизд., стер.- М.: Мнемозина,2012.

Уровень обучения. Базовый

Тема урока Числовая окружность на координатной плоскости (3 часа)

Урок №1

Цели: ввести понятие модели числовой окружности в декартовой и криволинейной системе координат.

Задачи: формировать умение находить декартовы координаты точек числовой окружности и выполнять обратное действие: зная декартовы координаты точки, определять её числовое значение на числовой окружности.

Развивать вычислительные навыки, правильную математическую речь, логическое мышление учащихся.

Прививать самостоятельность, внимание и аккуратность. Воспитывать ответственное отношение к обучению.

Планируемые результаты:

Знать, понимать: — числовая окружность.

Уметь: — находить на окружности точки по заданным координатам; — находить координаты точки, расположенной на числовой окружности.

Уметь применять изученный теоретический материал при выполнении письменной работы.

Техническое обеспечение урока Компьютер, экран, проектор, учебник, задачник.

Дополнительное методическое и дидактическое обеспечение урока: Мордкович А. Г. М79 Алгебра и начала математического анализа. 10— 11 классы (базовый уровень) : методическое пособие для учителя / А. Г. Мордкович, П. В. Семенов. — М. : Мнемози- на, 2010. — 202 с. : ил

Ход урока

1. Организационный момент.

Психологический настрой учащихся.

Проверка домашнего задания 1. № 4.17 (в; г), № 4.18 (в; г), № 4.19 (в; г), № 4.20 (в; г).

Разобрать решение заданий вызвавших затруднение.

II. Устная работа.

(На слайде)

1. Назовите координаты точек плоскости:

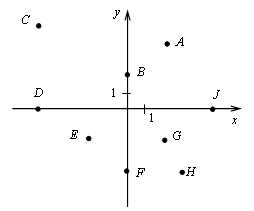
2. Назовите число, соответствующее заданной точке на числовой окружности.

III. Объяснение нового материала.

1. Объяснение проводить согласно пункту учебника. Разместив числовую окружность в декартовой системе координат, следует подробно разобрать свойства точек числовой окружности, находящихся в различных координатных четвертях. Дело в том, что, изучая данную модель, учащиеся сталкиваются с определенными трудностями. Им необходимо учиться работать одновременно в двух системах координат – криволинейной и декартовой.

Для преодоления этой трудности авторы учебника применяют следующий методический прием: для точки М числовой окружности используют запись М(t), если речь идет о криволинейной координате точки М, или запись М (х; у), если речь идет о декартовых координатах точки.

(Мордкович А. Г. М79 Алгебра и начала математического анализа. 10— 11 классы (базовый уровень) : методическое пособие для учителя / А. Г. Мордкович, П. В. Семенов. — М. : Мнемози- на, 2010. — 202 с. : ил.)

2. Проводим 7-ю методическую «игру» – отыскание декартовых координат «хороших» точек числовой окружности. Речь идет о переходе от записи М(t) к М (х; у).

Можно организовать работу в парах с последующей самопроверкой (верные ответы в таблице 1 со с. 38 учебника).

3. Проводим 8-ю методическую «игру» – отыскание знаков координат «плохих» точек числовой окружности. Если, например,

М(2) = М (х; у), то х 0; у  0. В процессе этой «игры» школьники фактически учатся определять знаки тригонометрических функций по четвертям числовой окружности.

Динамическая пауза

IV. Формирование умений и навыков.

1. № 5.1 (а; б), № 5.2 (а; б), № 5.3 (а; б).

Данная группа заданий направлена на формирование умения отыскивать декартовы координаты «хороших» точек на числовой окружности.

Решение:

№ 5.1 (а).

2. № 5.4 (а; б), № 5.5 (а; б).

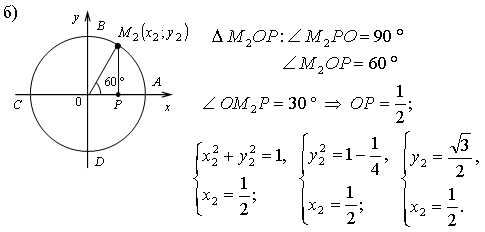
Эта группа заданий направлена на формирование умений находить криволинейные координаты точки по её декартовым координатам.

Решение:

№ 5.5 (б).

3. № 5.10 (а; б).

Данное упражнение направлено на формирование умения находить декартовы координаты «плохих» точек.

V. Итоги урока.

Вопросы учащимся:

– Что собой представляет модель – числовая окружность на координатной плоскости?

– Как, зная криволинейные координаты точки на числовой окружности, найти её декартовы координаты и наоборот?

Домашнее задание: , стр. 36. № 5.1 (в; г) – 5.5 (в; г), № 5.10 (в; г).

Урок №2

Цель: закрепить понятие модели числовой окружности в декартовой и криволинейной системе координат

Задачи: продолжить формирование умения переходить от криволинейных координат точки на числовой окружности к декартовым координатам; формировать умение отыскивать на числовой окружности точки, координаты которых удовлетворяют заданному уравнению или неравенству.

Развивать вычислительные навыки, правильную математическую речь, логическое мышление учащихся.

Прививать самостоятельность, внимание и аккуратность. Воспитывать ответственное отношение к обучению.

Планируемые результаты:

Знать, понимать: — числовая окружность.

Уметь: — находить на окружности точки по заданным координатам; — находить координаты точки, расположенной на числовой окружности.

Уметь применять изученный теоретический материал при выполнении письменной работы.

Техническое обеспечение урока Компьютер, экран, проектор, учебник, задачник.

Дополнительное методическое и дидактическое обеспечение урока: Мордкович А. Г. М79 Алгебра и начала математического анализа. 10— 11 классы (базовый уровень) : методическое пособие для учителя / А. Г. Мордкович, П. В. Семенов. — М. : Мнемози- на, 2010. — 202 с. : ил

Ход урока

1. Организационный момент.

1. Психологический настрой учащихся.

2. Проверка домашнего задания № 5.1 (в; г) – 5.5 (в; г), № 5.10 (в; г).

Разобрать решение заданий вызвавших затруднение.

2. Устная работа.

(на слайде)

1. Назовите криволинейные и декартовы координаты точек на числовой окружности.

2. Сопоставьте дугу на окружности и её аналитическую запись.

а

б

в

г

III. Объяснение нового материала.

1. На этом уроке учащиеся, по замыслу авторов учебника, отрабатывают две последние дидактические «игры», связанные с изучаемой моделью.

(Мордкович А. Г. М79 Алгебра и начала математического анализа. 10— 11 классы (базовый уровень) : методическое пособие для учителя / А. Г. Мордкович, П. В. Семенов. — М. : Мнемози- на, 2010. — 202 с. : ил.)

2. 9-я «игра» – отыскание на числовой окружности точек, координаты которых удовлетворяют заданному уравнению.

Рассматриваем примеры 2 и 3 со с. 41–42 учебника.

Важность этой «игры» очевидна: учащиеся готовятся к решению простейших тригонометрических уравнений вида Для понимания сути дела следует прежде всего научить школьников решать эти уравнения с помощью числовой окружности, не переходя к готовым формулам.

При рассмотрении примера на нахождение точки с абсциссой обращаем внимание учащихся на возможность объединения ддвух серий ответов в одну формулу:

3. 10-я «игра» – отыскание на числовой окружности точек, координаты которых удовлетворяют заданному неравенству.

Рассматриваем примеры 4–7 со с. 43–44 учебника. Решая подобные задачи, мы готовим учащихся к решению тригонометрических неравенств вида

После рассмотрения примеров учащиеся могут самостоятельно сформулировать алгоритм решения неравенств указанного типа:

1) от аналитической модели переходим к геометрической модели – дуга МР числовой окружности;

2) составляем ядро аналитической записи МР; для дуги получаем

3) составляем общую запись:

Динамическая пауза

IV. Формирование умений и навыков.

Работа в группах

1-я группа. Нахождение точки на числовой окружности с координатой, удовлетворяющей заданному уравнению.

№ 5.6 (а; б) – № 5.9 (а; б).

В процессе работы над этими упражнениями отрабатываем пошаговость выполнения: запись ядра точки, аналитической записи.

2-я группа. Нахождение точек на числовой окружности с координатой, удовлетворяющей заданному неравенству.

№ 5.11 (а; б) – 5.14 (а;б).

Главное умение, которое должны приобрести школьники при выполнении данных упражнений, – это составление ядра аналитической записи дуги.

V. Самостоятельная работа.

Вариант 1

1. Обозначьте на числовой окружности точку, которая соответствует заданному числу, и найдите её декартовы координаты:

2. Найдите на числовой окружности точки с данной абсциссой и запишите, каким числам t они соответствуют.

3. Обозначьте на числовой окружности точки с ординатой, удовлетворяющей неравенству и запишите при помощи двойного неравенства, каким числам t они соответствуют.

Вариант 2

1. Обозначьте на числовой окружности точку, которая соответствует данному числу, и найдите её декартовы координаты:

2. Найдите на числовой окружности точки с данной ординатой у = 0,5 и запишите, каким числам t они соответствуют.

3. Обозначьте на числовой окружности точки с абсциссой, удовлетворяющей неравенству и запишите при помощи двойного неравенства, каким числам t они соответствуют.

VI. Итоги урока.

Вопросы учащимся:

– Как найти на окружности точку, абсцисса которой удовлетворяет заданному уравнению?

– Как найти на окружности точку, ордината которой удовлетворяет заданному уравнению?

– Назовите алгоритм решения неравенств с помощью числовой окружности.

Домашнее задание: , стр. 36. № 5.6 (в; г) – № 5.9 (в; г),

№ 5.11 (в; г) – № 5.14 (в; г).

Урок №3

Цели: ввести понятие модели числовой окружности в декартовой и криволинейной системе координат.

Задачи: проверить степень усвоения ранее изученного материала,

актуализировать знания учащихся, необходимые при изучении новой темы.

Развивать вычислительные навыки, правильную математическую речь, логическое мышление учащихся.

Прививать самостоятельность, внимание и аккуратность. Воспитывать ответственное отношение к обучению.

Планируемые результаты:

Знать, понимать: — числовая окружность.

Уметь: — находить на окружности точки по заданным координатам; — находить координаты точки, расположенной на числовой окружности.

Уметь применять изученный теоретический материал при выполнении письменной работы.

Техническое обеспечение урока Компьютер, экран, проектор, учебник, задачник.

Дополнительное методическое и дидактическое обеспечение урока: Мордкович А. Г. М79 Алгебра и начала математического анализа. 10— 11 классы (базовый уровень) : методическое пособие для учителя / А. Г. Мордкович, П. В. Семенов. — М. : Мнемози- на, 2010. — 202 с. : ил

Ход урока

1. Организационный момент.

1. Приветствие учеников, поверка отсутствующих Психологический настрой учащихся.

2. Проверка домашнего задания № 5.6 (в; г) – № 5.9 (в; г), № 5.11 (в; г) – № 5.14 (в; г).

Разобрать решение заданий вызвавших затруднение.

II. Фронтальный опрос по теме:

1. 1. 1. Дайте определение числовой окружности

      2. Сколько четвертей имеем в единичной окружности?
         Как они называются?

      3. Определите знаки в каждой из четверти.

3. Проверочная работа

После выполнения заданий, учащиеся сдают листочки, а затем вместе с учителем проверяют правильные ответы.

2

Постройте геометрическую модель дуги числовой окружности, все точки которой удовлетворяют неравенству .

3

Найдите множество чисел, которым соответствуют отмеченные на числовой окружности точки

Вариант №2

1

Найдите на числовой окружности точки, которые соответствуют данным числам: .

2

Постройте геометрическую модель дуги числовой окружности, все точки которой удовлетворяют неравенству .

3

Найдите множество чисел, которым соответствуют отмеченные на числовой окружности точки

Вариант №3

1

Найдите на числовой окружности точки, которые соответствуют данным числам: .

2

Постройте геометрическую модель дуги числовой окружности, все точки которой удовлетворяют неравенству .

3

Найдите множество чисел, которым соответствуют отмеченные на числовой окружности точки

Вариант №4

1

Найдите на числовой окружности точки, которые соответствуют данным числам: .

2

Постройте геометрическую модель дуги числовой окружности, все точки которой удовлетворяют неравенству .

3

Найдите множество чисел, которым соответствуют отмеченные на числовой окружности точки

Динамическая пауза

IV. Обобщение материала

1. Рассмотреть числовую окружность в декартовой системе координат.

2. Составить таблицу координат чисел числовой окружности для первого макета.

3. Составить таблицу координат чисел числовой окружности для второго макета.

У каждого из вас в тетради есть три макета числовой окружности. Каждая точка числовой окружности имеет в координатной плоскости свои координаты. Найдём сначала координаты тех точек координатной плоскости, которые получены на макетах числовой окружности.

На первом макете возьмем точку M(π/4) середина I четверти. Опустим перпендикуляр MP на прямую OA и рассмотрим треугольник OMP. Так как дуга AM составляет половину дуги AB, то ∡MOP=45°. Значит, треугольник OMP — равнобедренный прямоугольный треугольник и OP=MP, т.е. у точки M абсцисса и ордината равны: x=y. Так как координаты точки M(x;y) удовлетворяют уравнению числовой окружности x²+y²=1, то для их нахождения нужно решить систему уравнений:

 

Подставив x вместо y в первое уравнение системы, получим следующее решение:

 

 

При решении учитываем, что абсцисса точки M положительна.

Получили, что координаты точки M, соответствующей числу π/4 будут   M(π/4)=M(2√2;2√2)

Аналогично можно получить координаты и других точек первого макета числовой окружности, учитывая только знаки координат в каждой четверти.

Полученные результаты запишем в таблицу:

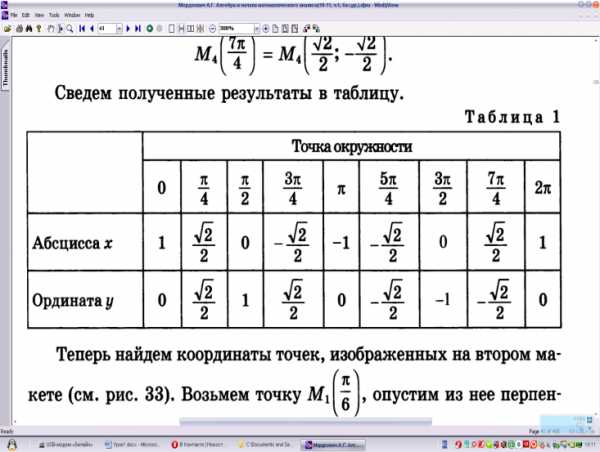
Перейдем на второй макет. Рассуждаем аналогично для точки M, если теперь она соответствует числу π/6

Треугольник MOP прямоугольный. Так как дуга AM составляет третью часть дуги AB, то ∡MOP=30°.

Катет MP лежит против угла 30 градусов в прямоугольном треугольнике, значит, равен половине гипотенузы, т.е. ордината точки M равна

 MP=1/2 y=1/2

Абсциссу x точки M найдём, решив уравнение:

 

 

При решении учитываем, что абсцисса точки M положительна.

Получили, что координаты точки M, соответствующей числу π/6 будут  M(π/6)=M(3√2;1/2)  

Аналогично можно получить координаты и других точек второго макета числовой окружности, учитывая только знаки координат в каждой четверти.

На третьем макете возьмем угол в 60⁰ или π/3. Треугольник OKF прямоугольный. Так как дуга AK составляет третью часть дуги AB, то ∡KOF=60°, а ∡OKF=30°,

Катет OF лежит против угла 30 градусов в прямоугольном треугольнике, значит, равен половине гипотенузы, т.е. абсцисса точки F равна

 OF=1/2 x=1/2

Ординату y точки K найдём, решив уравнение:

 

 

При решении учитываем, что ордината точки K положительна.

Получили, что координаты точки K, соответствующей числу π/3 будут  K(π/3)=F(1/2, 3√2) . Полученные данные занесем в таблицу:

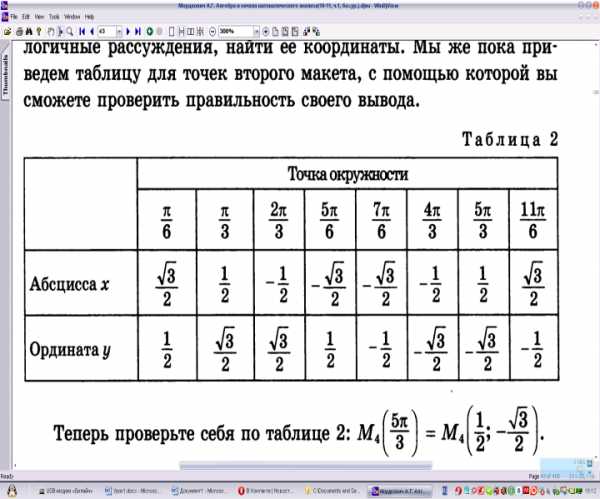
V. Подведение итогов урока, постановка домашнего задания, рефлексия.

Понятие числовой окружности вы изучали для того чтобы перейти к изучению таких важных с точки зрения математики и геометрии понятий как синус, косинус, тангенс и котангенс.

Вопросы учащимся:

Итак, что мы сегодня узнали на уроке нового?

Домашнее задание: , стр. 36. № 5.8, № 5.13 (в,г)

infourok.ru

10 класс. Алгебра. Тригонометрические функции. Числовая окружность. — Числовая окружность. Числовая окружность на координатной плоскости.

Комментарии преподавателя

Для  любой функ­ции неза­ви­си­мый ар­гу­мент от­кла­ды­ва­ет­ся либо на чис­ло­вой пря­мой, либо на окруж­но­сти. Оха­рак­те­ри­зу­ем и чис­ло­вую пря­мую, и чис­ло­вую окруж­ность.

Пря­мая ста­но­вит­ся чис­ло­вой (ко­ор­ди­нат­ной) пря­мой, если от­ме­че­но на­ча­ло ко­ор­ди­нат, вы­бра­ны на­прав­ле­ние и мас­штаб (рис. 1).

Чис­ло­вая пря­мая уста­нав­ли­ва­ет вза­им­но-од­но­знач­ное со­от­вет­ствие между всеми точ­ка­ми пря­мой и всеми дей­стви­тель­ны­ми чис­ла­ми.

На­при­мер, берем число  от­кла­ды­ва­ем на ко­ор­ди­нат­ной оси, по­лу­ча­ем точку  Возь­мем число  от­кла­ды­ва­ем на оси, по­лу­ча­ем точку  (рис. 2).

И на­о­бо­рот, если мы взяли любую точку  на ко­ор­ди­нат­ной пря­мой, то най­дет­ся един­ствен­ное со­от­вет­ству­ю­щее ей дей­стви­тель­ное число (рис. 2).

К та­ко­му со­от­вет­ствию люди при­шли не сразу. Чтобы по­нять это, вспом­ним ос­нов­ные чис­ло­вые мно­же­ства.

Сна­ча­ла ввели мно­же­ство на­ту­раль­ных чисел 

Затем мно­же­ство целых чисел 

Мно­же­ство ра­ци­о­наль­ных чисел 

Пред­по­ла­га­лось, что этих мно­жеств будет до­ста­точ­но, и су­ще­ству­ет вза­им­но-од­но­знач­ное со­от­вет­ствие между всеми ра­ци­о­наль­ны­ми чис­ла­ми и точ­ка­ми пря­мой. Но ока­за­лось, что на чис­ло­вой пря­мой есть бес­чис­лен­ное мно­же­ство точек, ко­то­рые нель­зя опи­сать чис­ла­ми вида 

При­мер – ги­по­те­ну­за пря­мо­уголь­но­го тре­уголь­ни­ка с ка­те­та­ми 1 и 1. Она равна  (рис. 3).

Най­дет­ся ли среди мно­же­ства ра­ци­о­наль­ных чисел число, в точ­но­сти рав­ное  Нет, не най­дет­ся. До­ка­жем этот факт.

До­ка­жем ме­то­дом от про­тив­но­го. Пред­по­ло­жим, что су­ще­ству­ет дробь, рав­ная т.е. 

Тогда  Воз­ве­дем обе части в квад­рат,   Оче­вид­но, что пра­вая часть ра­вен­ства де­лит­ся на 2, . Зна­чит и  Тогда  Но тогда и  А зна­чит,  Тогда по­лу­ча­ет­ся, что дробь  со­кра­ти­мая. Это про­ти­во­ре­чит усло­вию, зна­чит 

Число  ир­ра­ци­о­наль­ное. Мно­же­ство ра­ци­о­наль­ных и ир­ра­ци­о­наль­ных чисел об­ра­зу­ют мно­же­ство дей­стви­тель­ных чисел  Если мы возь­мем любую точку на пря­мой, ей будет со­от­вет­ство­вать ка­кое-ли­бо дей­стви­тель­ное число. И если мы возь­мем любое дей­стви­тель­ное число, ему будет со­от­вет­ство­вать един­ствен­ная точка на ко­ор­ди­нат­ной пря­мой.

Уточ­ним, что такое чис­ло­вая окруж­ность и ка­ко­вы вза­и­мо­от­но­ше­ния между мно­же­ством точек окруж­но­сти и мно­же­ством дей­стви­тель­ных чисел.

На­ча­ло от­сче­та – точка A. На­прав­ле­ние от­сче­та – про­тив ча­со­вой стрел­ки – по­ло­жи­тель­ное, по ча­со­вой стрел­ке – от­ри­ца­тель­ное.  Мас­штаб – длина окруж­но­сти  (рис. 4).

Вводя эти три по­ло­же­ния, мы имеем чис­ло­вую окруж­ность. Ука­жем, каким об­ра­зом каж­до­му числу  по­ста­вить в со­от­вет­ствие точку на окруж­но­сти и на­о­бо­рот.

Задав число  по­лу­ча­ем точку на окруж­но­сти  

 (рис. 4).

Каж­до­му дей­стви­тель­но­му числу со­от­вет­ству­ет точка на окруж­но­сти. А на­о­бо­рот?

Точка  со­от­вет­ству­ет числу 

www.kursoteka.ru

Внеклассный урок — Числовая окружность

Числовая окружность

Числовая окружность – это единичная окружность, точки которой соответствуют определенным действительным числам.

Единичной окружностью называют окружность радиуса 1.

 

Общий вид числовой окружности.

1) Ее радиус принимается за единицу измерения.

2) Горизонтальный и вертикальный диаметры делят числовую окружность на четыре четверти (см.рисунок). Их соответственно называют первой, второй, третьей и четвертой четвертью.

3) Горизонтальный диаметр обозначают AC, причем А – это крайняя правая точка.
Вертикальный диаметр обозначают BD, причем B – это крайняя верхняя точка.
Соответственно:

первая четверть – это дуга AB

вторая четверть – дуга BC

третья четверть – дуга CD

четвертая четверть – дуга DA

4) Начальная точка числовой окружности – точка А.

Отсчет по числовой окружности может вестись как по часовой стрелке, так и против часовой стрелки.
Отсчет от точки А против часовой стрелки называется положительным направлением.
Отсчет от точки А по часовой стрелке называется отрицательным направлением.

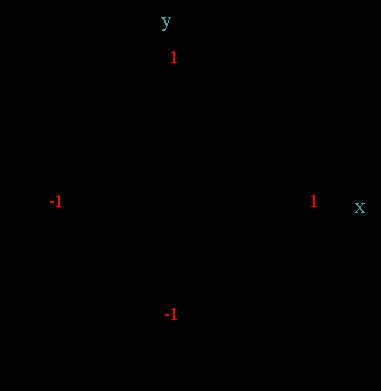 Числовая окружность на координатной плоскости.

Центр радиуса числовой окружности соответствует началу координат (числу 0).

Горизонтальный диаметр соответствует оси x, вертикальный – оси y.

Начальная точка А числовой окружности находится на оси x и имеет координаты (1; 0).

 

Значения x и y в четвертях числовой окружности:

1-я четверть	2-я четверть	3-я четверть	4-я четверть
x > 0, y > 0	x < 0, y > 0	x < 0, y < 0	x > 0, y < 0

 

Значение любой точки числовой окружности:

Любая точка числовой окружности с координатами (x; y) не может быть меньше -1, но не может быть больше 1: –1 ≤ x ≤ 1;   –1 ≤ y ≤ 1

 

Основные величины числовой окружности:

	Величина в радианах	Величина в радиусах
Окружность	2π	360º
Полуокружность	π	180º
Четверть окружности	π — 2	90º

 

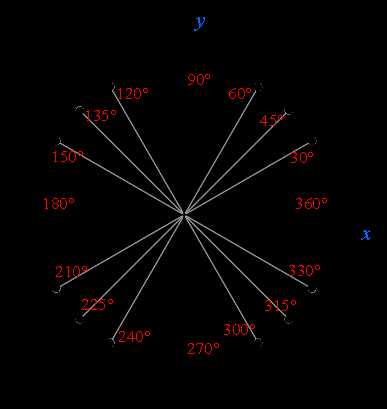
Имена и местонахождение основных точек числовой окружности:

  
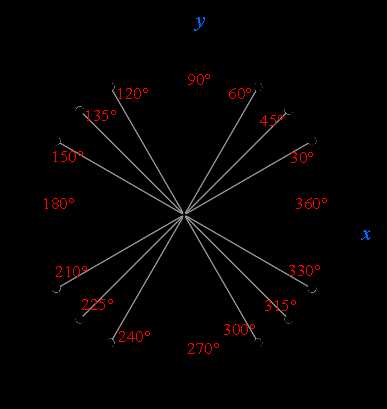
Как запомнить имена числовой окружности.

Есть несколько простых закономерностей, которые помогут вам легко запомнить основные имена числовой окружности.

Перед тем как начать, напомним: отсчет ведется в положительном направлении, то есть от точки А (2π) против часовой стрелки.

1) Начнем с крайних точек на осях координат.

Начальная точка – это 2π (крайняя правая точка на оси х, равная 1).

Как вы знаете, 2π – это длина окружности. Значит, половина окружности – это 1π или π. Ось х делит окружность как раз пополам. Соответственно, крайняя левая точка на оси х, равная -1, называется π.

Крайняя верхняя точка на оси у, равная 1, делит верхнюю полуокружность пополам. Значит, если полуокружность – это π, то половина полуокружности – это π/2.

Одновременно π/2 – это и четверть окружности. Отсчитаем три таких четверти от первой до третьей – и мы придем в крайнюю нижнюю точку на оси у, равной -1. Но если она включает три четверти – значит имя ей 3π/2.

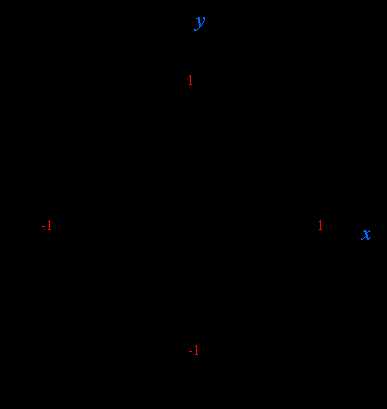
2) Теперь перейдем к остальным точкам. Обратите внимание: все противоположные точки имеют одинаковый числитель – причем это противоположные точки и относительно оси у, и относительно центра осей, и относительно оси х. Это нам и поможет знать их значения точек без зубрежки.

Надо запомнить лишь значение точек первой четверти: π/6, π/4 и π/3. И тогда мы «увидим» некоторые закономерности:

— Относительно оси у в точках второй четверти, противоположных точкам первой четверти, числа в числителях на 1 меньше величины знаменателей. К примеру, возьмем точку π/6. Противоположная ей точка относительно оси у тоже в знаменателе имеет 6, а в числителе 5 (на 1 меньше). То есть имя этой точки: 5π/6. Точка, противоположная π/4, тоже имеет в знаменателе 4, а в числителе 3 (на 1 меньше, чем 4) – то есть это точка 3π/4.
Точка, противоположная π/3, тоже имеет в знаменателе 3, а в числителе на 1 меньше: 2π/3.

  — Относительно центра осей координат все наоборот: числа в числителях противоположных точек (в третьей четверти) на 1 больше значения знаменателей. Возьмем опять точку π/6. Противоположная ей относительно центра точка тоже имеет в знаменателе 6, а в числителе число на 1 больше – то есть это 7π/6.

Точка, противоположная точке π/4, тоже имеет в знаменателе 4, а в числителе число на 1 больше: 5π/4.
Точка, противоположная точке π/3, тоже имеет в знаменателе 3, а в числителе число на 1 больше: 4π/3.

— Относительно оси х (четвертая четверть) дело посложнее. Здесь надо к величине знаменателя прибавить число, которое на 1 меньше – эта сумма и будет равна числовой части числителя противоположной точки. Начнем опять с π/6. Прибавим к величине знаменателя, равной 6, число, которое на 1 меньше этого числа – то есть 5. Получаем: 6 + 5 = 11. Значит, противоположная ей относительно оси х точка будет иметь в знаменателе 6, а в числителе 11 – то есть 11π/6.

Точка π/4. Прибавляем к величине знаменателя число на 1 меньше: 4 + 3 = 7. Значит, противоположная ей относительно оси х точка имеет в знаменателе 4, а в числителе 7 – то есть 7π/4.
Точка π/3. Знаменатель равен 3. Прибавляем к 3 на единицу меньшее число – то есть 2. Получаем 5. Значит, противоположная ей точка имеет в числителе 5 – и это точка 5π/3.

3) Еще одна закономерность для точек середин четвертей. Понятно, что их знаменатель равен 4. Обратим внимание на числители. Числитель середины первой четверти – это 1π (но 1 не принято писать). Числитель середины второй четверти – это 3π. Числитель середины третьей четверти – это 5π. Числитель середины четвертой четверти – это 7π. Получается, что в числителях середин четвертей – четыре первых нечетных числа в порядке их возрастания:
(1)π, 3π, 5π, 7π.
Это тоже очень просто. Поскольку середины всех четвертей имеют в знаменателе 4, то мы уже знаем их полные имена: π/4, 3π/4, 5π/4, 7π/4.

 

Особенности числовой окружности. Сравнение с числовой прямой.

Как вы знаете, на числовой прямой каждая точка соответствует единственному числу. К примеру, если точка А на прямой равна 3, то она уже не может равняться никакому другому числу.

На числовой окружности все иначе, поскольку это окружность. К примеру, чтобы из точки А окружности прийти к точке M, можно сделать это, как на прямой (только пройдя дугу), а можно и обогнуть целый круг, а потом уже прийти к точке M. Вывод:

Пусть точка M равна какому-то числу t. Как мы знаем, длина окружности равна 2π. Значит, точку окружности t мы можем записать двояко: t или t + 2π. Это равнозначные величины.
То есть t = t + 2π. Разница лишь в том, что в первом случае вы пришли к точке M сразу, не делая круга, а во втором случае вы совершили круг, но в итоге оказались в той же точке M. Таких кругов можно сделать и два, и три, и двести. Если обозначить количество кругов буквой k, то получим новое выражение:
t = t + 2πk.

Отсюда формула:

Если точка M числовой окружности равна числу t, то она равна и числу вида t + 2πk, где k – любое целое число: M(t) = M(t + 2πk), где k ∈ Z. Число k называется параметром.

 

Уравнение числовой окружности
(второе уравнение – в разделе «Синус, косинус, тангенс, котангенс»):

 

raal100.narod.ru

Числовая окружность на координатной плоскости

.

Дата: Урок 1
тема: Числовая окружность на координатной прямой

Цели: ввести понятие модели числовой окружности в декартовой и криволинейной системе координат; формировать умение находить декартовы координаты точек числовой окружности и выполнять обратное действие: зная декартовы координаты точки, определять её числовое значение на числовой окружности.

Ход урока

I. Организационный момент.

II. Объяснение нового материала.

1. Разместив числовую окружность в декартовой системе координат, подробно разбираем свойства точек числовой окружности, находящихся в различных координатных четвертях.

Для точки М числовой окружности используют запись М(t), если речь идет о криволинейной координате точки М, или запись М (х; у), если речь идет о декартовых координатах точки.

2. Отыскание декартовых координат «хороших» точек числовой окружности. Речь идет о переходе от записи М(t) к М (х; у).

3. Отыскание знаков координат «плохих» точек числовой окружности. Если, например, М(2) = М (х; у), то х 0; у 0. ( школьники учатся определять знаки тригонометрических функций по четвертям числовой окружности.)

IV. Формирование умений и навыков.

1. № 5.1 (а; б), № 5.2 (а; б), № 5.3 (а; б).

Данная группа заданий направлена на формирование умения отыскивать декартовы координаты «хороших» точек на числовой окружности.

Решение:

№ 5.1 (а).

2. № 5.4 (а; б), № 5.5 (а; б).

Эта группа заданий направлена на формирование умений находить криволинейные координаты точки по её декартовым координатам.

Решение:

№ 5.5 (б).

3. № 5.10 (а; б).

Данное упражнение направлено на формирование умения находить декартовы координаты «плохих» точек.

V. Итоги урока.

Вопросы учащимся:

– Что собой представляет модель – числовая окружность на координатной плоскости?

– Как, зная криволинейные координаты точки на числовой окружности, найти её декартовы координаты и наоборот?

Домашнее задание: № 5.1 (в; г) – 5.5 (в; г), № 5.10 (в; г).

Дата: Урок 2
ТЕМА: Решение задач на модели «числовая окружность на координатной плоскости»

Цели: продолжить формирование умения переходить от криволинейных координат точки на числовой окружности к декартовым координатам; формировать умение отыскивать на числовой окружности точки, координаты которых удовлетворяют заданному уравнению или неравенству.

Ход урока

I. Организационный момент.

II. Устная работа.

1. Назовите криволинейные и декартовы координаты точек на числовой окружности.

2. Сопоставьте дугу на окружности и её аналитическую запись.

III. Объяснение нового материала.

1. На этом уроке учащиеся, по замыслу авторов учебника, отрабатывают две последние дидактические «игры», связанные с изучаемой моделью.

2. Отыскание на числовой окружности точек, координаты которых удовлетворяют заданному уравнению.

Рассматриваем примеры 2 и 3 со с. 41–42 учебника.

Важность этой «игры» очевидна: учащиеся готовятся к решению простейших тригонометрических уравнений вида Для понимания сути дела следует прежде всего научить школьников решать эти уравнения с помощью числовой окружности, не переходя к готовым формулам.

При рассмотрении примера на нахождение точки с абсциссой обращаем внимание учащихся на возможность объединения ддвух серий ответов в одну формулу:

3. Отыскание на числовой окружности точек, координаты которых удовлетворяют заданному неравенству.

Рассматриваем примеры 4–7 со с. 43–44 учебника. Решая подобные задачи, мы готовим учащихся к решению тригонометрических неравенств вида

После рассмотрения примеров учащиеся могут самостоятельно сформулировать алгоритм решения неравенств указанного типа:

1) от аналитической модели переходим к геометрической модели – дуга МР числовой окружности;

2) составляем ядро аналитической записи МР; для дуги получаем

3) составляем общую запись:

IV. Формирование умений и навыков.

1-я группа. Нахождение точки на числовой окружности с координатой, удовлетворяющей заданному уравнению.

№ 5.6 (а; б) – № 5.9 (а; б).

В процессе работы над этими упражнениями отрабатываем пошаговость выполнения: запись ядра точки, аналитической записи.

2-я группа. Нахождение точек на числовой окружности с координатой, удовлетворяющей заданному неравенству.

№ 5.11 (а; б) – 5.14 (а;б).

Главное умение, которое должны приобрести школьники при выполнении данных упражнений, – это составление ядра аналитической записи дуги.

V. Самостоятельная работа.

Вариант 1

1. Обозначьте на числовой окружности точку, которая соответствует заданному числу, и найдите её декартовы координаты:

2. Найдите на числовой окружности точки с данной абсциссой и запишите, каким числам t они соответствуют.

3. Обозначьте на числовой окружности точки с ординатой, удовлетворяющей неравенству и запишите при помощи двойного неравенства, каким числам t они соответствуют.

Вариант 2

1. Обозначьте на числовой окружности точку, которая соответствует данному числу, и найдите её декартовы координаты:

2. Найдите на числовой окружности точки с данной ординатой у = 0,5 и запишите, каким числам t они соответствуют.

3. Обозначьте на числовой окружности точки с абсциссой, удовлетворяющей неравенству и запишите при помощи двойного неравенства, каким числам t они соответствуют.

VI. Итоги урока.

Вопросы учащимся:

– Как найти на окружности точку, абсцисса которой удовлетворяет заданному уравнению?

– Как найти на окружности точку, ордината которой удовлетворяет заданному уравнению?

– Назовите алгоритм решения неравенств с помощью числовой окружности.

Домашнее задание: № 5.6 (в; г) – № 5.9 (в; г),

№ 5.11 (в; г) – № 5.14 (в; г).

multiurok.ru

Конспект урока по алгебре 10 класс на тему Числовая окружность на координатной прямой

МБОУ Калининская СОШ

Цимлянский район

Алгебра

и начала

математического

анализа 10 класс

Конспект урока

на тему

«Числовая окружность на координатной плоскости»

Подготовил учитель

Математики

Поцелуева Е.В.

Тема Числовая окружность на координатной плоскости

Что будем изучать: 
1. Определение.
2. Важные координаты числовой окружности.
3. Как искать координату числовой окружности?
4. Таблица основных координат числовой окружности.
5. Примеры решения задач. 
Определение числовой окружности на координатной плоскости

Расположим числовую окружность в координатной плоскости так, чтобы центр окружности совместился с началом координат, а её радиус принимаем за единичный отрезок. Начальная точка числовой окружности A совмещена с точкой (1;0). 
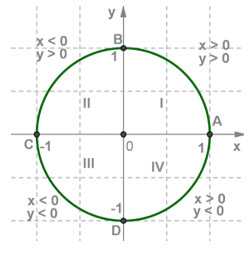
Каждая точка числовой окружности имеет в координатной плоскости свои координаты х и у, причем:
1) при x>0x>0, у>0у>0 – в первой четверти;
2) при х<0х<0, у>0у>0 – во второй четверти;
3) при х<0х<0, у<0у<0 – в третьей четверти;
4) при х>0х>0, у<0у<0 – в четвертой четверти.
Для любой точки М(х;у)М(х;у) числовой окружности выполняются неравенства: −1Запомните уравнение числовой окружности: x2+y2=1×2+y2=1.

Нам важно научиться находить координаты точек числовой окружности, представленных на рисунке.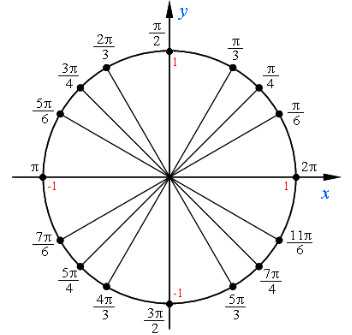

Найдем координату точки π4π4

Точка М(π4)М(π4) – середина первой четверти. Опустим из точки М перпендикуляр МР на прямую ОА и рассмотрим треугольник OMP.Так как дуга АМ составляет половину дуги АВ, то ∠MOP=45°∠MOP=45°.
Значит, треугольник OMP – равнобедренный прямоугольный треугольник и OP=MPOP=MP, т.е. у точки M абсцисса и ордината равны: x=yx=y.
Так как координаты точки M(х;y)M(х;y) удовлетворяют уравнению числовой окружности, то для их нахождения нужно решить систему уравнений:
{x2+y2=1,x=y.{x2+y2=1,x=y.
Решив данную систему, получаем: y=x=√22y=x=22.
Значит, координаты точки M, соответствующей числу π4π4, будут M(π4)=M(√22;√22)M(π4)=M(22;22).
Аналогичным образом рассчитываются координаты точек, представленных на предыдущем рисунке.
Координаты точек числовой окружности

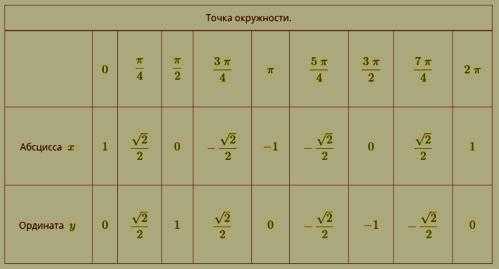
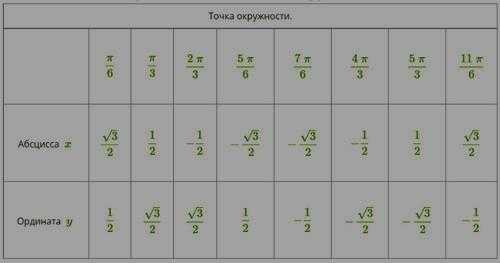
Рассмотрим примеры

Пример 1.
Найти координату точки числовой окружности: Р(45π4)Р(45π4). 
Решение: 
Т.к. числам tt и t+2π∗kt+2π∗k, где k-целое число, соответствует одна и та же точка числовой окружности то: 
45π4=(10+54)∗π=10π+5π4=5π4+2π∗545π4=(10+54)∗π=10π+5π4=5π4+2π∗5.
Значит, числу 45π445π4 соответствует та же точка числовой окружности, что и числу 5π45π4. Посмотрев значение точки 5π45π4 в таблице, получаем: P(45π4)=P(−√22;−√22)P(45π4)=P(−22;−22).
Пример 2.
Найти координату точки числовой окружности: Р(−37π3)Р(−37π3). 
Решение: 
Т.к. числам tt и t+2π∗kt+2π∗k, где k-целое число, соответствует одна и та же точка числовой окружности то: 
−37π3=−(12+13)∗π=−12π–π3=−π3+2π∗(−6)−37π3=−(12+13)∗π=−12π–π3=−π3+2π∗(−6).
Значит, числу −37π3−37π3 соответствует та же точка числовой окружности, что и числу –π3–π3, а числу –π3π3 соответствует та же точка, что и 5π35π3. Посмотрев значение точки 5π35π3 в таблице, получаем:
P(−37π3)=P(12;−√32)P(−37π3)=P(12;−32). 
Пример 3.
Найти на числовой окружности точки с ординатой у=12у=12 и записать, каким числам tt они соответствуют?
Решение: 
Прямая у=12у=12 пересекает числовую окружность в точках М и Р. Точка М соответствует числу π6π6 (из данных таблицы). Значит, и любому числу вида: π6+2π∗kπ6+2π∗k. Точка Р соответствует числу 5π65π6, а значит, и любому числу вида 5π6+2π∗k5π6+2π∗k.
Получили, как часто говорят в таких случаях, две серии значений: 
π6+2π∗kπ6+2π∗k и 5π6+2π∗k5π6+2π∗k.
Ответ : t=π6+2π∗kt=π6+2π∗k и t=5π6+2π∗kt=5π6+2π∗k.

Пример 4.
Найти на числовой окружности точки с абсциссой x≥−√22x≥−22 и записать, каким числам ttони соответствуют.

Решение: 

Прямая x=−√22x=−22 пересекает числовую окружность в точках М и Р. Неравенству x≥−√22x≥−22соответствуют точки дуги РМ. Точка М соответствует числу 3π43π4 (из данных таблицы). Значит, и любому числу вида −3π4+2π∗k−3π4+2π∗k. Точка Р соответствует числу −3π4−3π4, а значит, и любому числу вида −3π4+2π∗k−3π4+2π∗k.

Тогда получим −3π4+2π∗k≤t≤3π4+2πk−3π4+2π∗k≤t≤3π4+2πk.

Ответ : −3π4+2π∗k≤t≤3π4+2πk−3π4+2π∗k≤t≤3π4+2πk.
Задачи для самостоятельного решения

1. Найти координату точки числовой окружности: Р(61π6)Р(61π6).
   2) Найти координату точки числовой окружности: Р(−52π3)Р(−52π3).
   3) Найти на числовой окружности точки с ординатой у=−12у=−12 и записать, каким числам ttони соответствуют.
   4) Найти на числовой окружности точки с ординатой у≥−12у≥−12 и записать, каким числам ttони соответствуют.
   5) Найти на числовой окружности точки с абсциссой x≥−√32x≥−32 и записать, каким числам tt

Домашние задание: красн. учебник § 5, №5.5
№ 5.7-5.8(в,г), №5.10, №5.12-5.13(в,г)

Раздаточный материал

infourok.ru