Задачи с диаграммами и таблицами: Простая физика — EASY-PHYSIC
Простая физика — EASY-PHYSIC
1. В городе имеются следующие учебные заведения: школы, колледжи, училища и институты. Данные об их количестве представлены на диаграмме. Какое из утверждений неверно, если всего в городе 120 учебных заведений?
1) В городе более 60 школ.
2) В городе школ, колледжей и училищ более 5/6 всех учебных заведений.
3) В городе примерно восьмая часть всех учебных заведений — институты.
4) В городе больше половины учебных заведений — училища.
Если всего в городе 120 учреждений, то этому количеству соответствует вся площадь круга. Разберем высказывания. Первое: площадь рыжего сектора занимает более половины, значит, это соответствует высказыванию, что школ в городе более 60, ведь более 60 — это больше половины от 120:высказывание верно. Второе: вместе сектора, соответствующие школам, колледжам и училищам, занимают очень большую площадь — весь круг, кроме синего сектора. Прикинем площадь синего сектора. Мысленно поделим круг на две половины. Поскольку синий — это менее трети от полкруга, то площадь синего сектора — это менее 1/6 круга, значит, оставшаяся площадь — более 5/6. Высказывание верно. Третье: синий сектор, обозначающий институты, составляет около четверти от половины круга, то есть, 1/8 — верно. Четвертое: училища на диаграмме обозначены фиолетовым цветом. Этот цвет не занимает более половины круга, значит, высказывание неверно.
Мысленно поделим круг на две половины. Поскольку синий — это менее трети от полкруга, то площадь синего сектора — это менее 1/6 круга, значит, оставшаяся площадь — более 5/6. Высказывание верно. Третье: синий сектор, обозначающий институты, составляет около четверти от половины круга, то есть, 1/8 — верно. Четвертое: училища на диаграмме обозначены фиолетовым цветом. Этот цвет не занимает более половины круга, значит, высказывание неверно.
Ответ: 4.
2. Участников конференции разместили в гостинице в одноместных номерах, расположенных на этажах со второго по пятый. Количество номеров на этажах представлено на круговой диаграмме. Какое утверждение относительно расселения верно, если в гостинице разместились 150 участников?
1) Менее четверти всех участников разместились на втором этаже.
2) На третьем этаже разместилось более чем в 2 раза больше участников, чем на втором.
3) Около 25% всех участников конференции разместились на пятом этаже.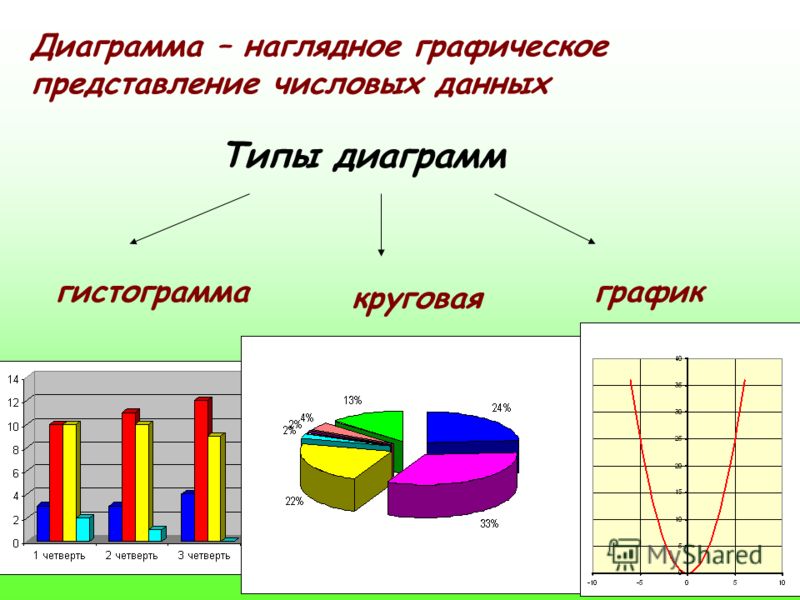
4) Меньше 25 человек разместились на четвертом этаже.
Проанализируем высказывания, первое: второй этаж и соответствующее количество участников обозначены на диаграмме желтым цветом.
То, что этот сектор занимает менее четверти площади круга, вызывает сомнения, так как угол этого сектора близок к прямому. Рассмотрим другие высказывания, второе:площадь зеленого сектора, соответствующего третьему этажу, действительно, составляет более половины круга. Верно. Третье: 25% — это 1/4. У сектора, площадь которого 1/4 круга, угол должен составлять 90 градусов, быть прямым. А угол бежевого сектора, который обозначает пятый этаж — острый. Высказывание неверно. Четвертое высказывание: если всего участников 150, то какую часть из их составят 25 человек? Определим это. . Тогда площадь голубого сектора должна быть равной 1/6 круга, это было бы так, если бы угол голубого сектора был равен 60 градусам, а это явно не так: угол меньше. Высказывание неверно. Значит, верно единственное высказывание — 2.
Ответ: 2.
3. На диаграмме показано распределение питательных веществ в молочном шоколаде. Определите по диаграмме, в каких пределах находится содержание углеводов.
1) 5-15%
2) 15-25%
3) 25-50%
4) 50-70%
Углеводам соответствует желтый цвет и желтый сектор на диаграмме. Он занимает по площади чуть более половины круга, а половина — это 50%. Выбираем 4 вариант ответа, более 50%.
Ответ: 4.
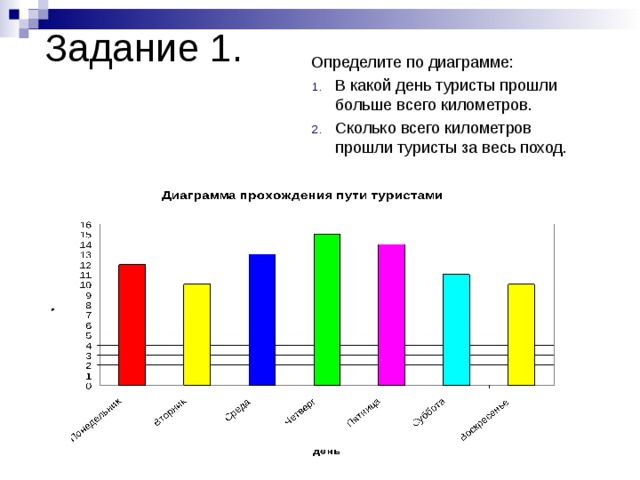
4. Завуч школы подвел итоги по выбору предметов для сдачи ЕГЭ учащимися 11-х классов. Результаты представлены на диаграмме. Сколько примерно учащихся выбрали для сдачи ЕГЭ обществознание?
1) 24
2) 26
3) 22
4) 20
Столбик, соответствующий обществознанию — второй по счету. Он выше отметки «24», но ниже отметки «28». Этому соответствует число 26, указанное во втором варианте. Его и выберем.
Ответ: 2.
5. На рисунке изображена зависимость температуры (в градусах Цельсия) от высоты (в метрах) над уровнем моря. Определите по графику, на сколько градусов температура на высоте 200 метров выше, чем на высоте 750 метров.
На рисунке изображена зависимость температуры (в градусах Цельсия) от высоты (в метрах) над уровнем моря. Определите по графику, на сколько градусов температура на высоте 200 метров выше, чем на высоте 750 метров.
Для того, чтобы узнать разность, необходимо сначала определить по графику температуры на данных высотах. Находим на горизонтальной оси высоту «200» и двигаемся вверх от этой отметки до пересечения с графиком. Потом от точки пересечения с графиком двигаемся влево к вертикальной оси, на которой и определяем температуру — 22 градуса. Так же действуем и для того, чтобы определить температуру на высоте 750 метров — только нужно внимательно определять, где точка, соответствующая такой высоте: находим отметку 700, и рассотяние между этой отметкой и отметкой 800 делим пополам, как это показано на рисунке:
Видим, что на высоте 750 температура более 16 градусов и менее 18 — это 17 градусов. Тогда найдем требуемую разность: .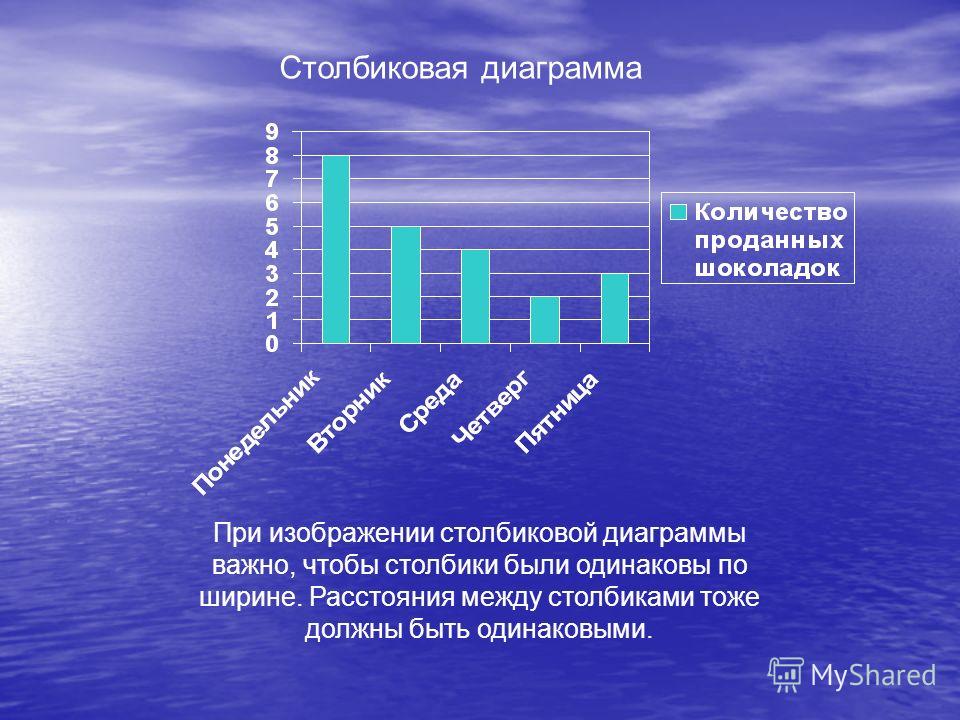
Ответ: 5.
6. Учёный Потапов выезжает из Москвы на деловую встречу в Санкт-Петербургский университет.Встреча назначена на 9:30. В таблице дано расписание ночных поездов Москва — Санкт-Петербург.
| Номер поезда | Отправление из Москвы | Прибытие в Санкт-Петербург |
| Экспресс | 23:00 | 06:30 |
| Две столицы | 23:55 | 07:55 |
| Красная стрела | 00:44 | 08:48 |
| Смена | 01:00 | 08:38 |
Путь от вокзала до университета занимает 50 минут. Укажите номер самого позднего (по времени отправления) из московских поездов, которые подходят учёному Иванову.
1) Экспресс
2) Две столицы
3) Красная стрела
4) Смена
Чтобы успеть на встречу, ученый должен прибыть на вокзал не позднее 8.40, так как еще пятьдесят минут он потратит на дорогу в университет: 9. 30-0.50=8.40. Таким образом, ему подойдет любой поезд, кроме «Красной стрелы», которая прибывает позже 8.40. Но нас интересует самый поздний поезд (действительно, чего болтаться на вокзале). «Смена» прибывает на вокзал за две минуты до «контрольного времени» — она-то нам и подойдет наилучшим образом.
30-0.50=8.40. Таким образом, ему подойдет любой поезд, кроме «Красной стрелы», которая прибывает позже 8.40. Но нас интересует самый поздний поезд (действительно, чего болтаться на вокзале). «Смена» прибывает на вокзал за две минуты до «контрольного времени» — она-то нам и подойдет наилучшим образом.
Ответ: 4.
7.
| Вещество | Дети от 1 года до 14 лет | Мужчины | Женщины |
| Жиры | 40−97 | 70−154 | 60−102 |
| Белки | 36−87 | 65−117 | 58−87 |
| Углеводы | 170−420 | 257−586 | |
Какой вывод о суточном потреблении жиров 12-летней девочкой можно сделать, если по подсчётам диетолога в среднем за сутки она потребляет 90 г жиров?
1) Потребление в норме.
2) Потребление выше рекомендуемой нормы.
3) Потребление ниже рекомендуемой нормы.
4) В таблице недостаточно данных.
Находим в таблице строку «жиры», так ка речь о них. Теперь находим столбец, соответствующий возрасту девочки: это, естественно, дети. Находим ячейку таблицы на пересечении нужных столбца и строки. В этой ячейке указано, что норма потребления от 40 до 97 граммов. Наша девочка потребляет 90 г, это как раз в указанном промежутке: больше 40, но меньше 97- то есть соответствует норме.
Ответ: 1.
ЕГЭ по информатике — Задание 7 (Таблицы, Диаграммы)
Это задание в 2021 году изменилось, поэтому здесь можете посмотреть статью в новом формате!
Добрый день! Разбираемся с 7 (седьмым) заданием из ЕГЭ по информатике.
Седьмое задание обычно связано с диаграммами и таблицами. Некоторые задачи данной категории из ЕГЭ по информатике удобно решать или проверять в программе Excel.
Задача (классика)
Дан фрагмент электронной таблицы. Из ячейки B2 в ячейку C3 была скопирована формула. При копировании адреса ячеек в формуле автоматически изменились. Какое числовое значение находится в ячейке C3 ?
Примечание: знак $ обозначает абсолютную адресацию.
Решение:
Первый шаг при решении данной задачи из ЕГЭ по информатике — не обращать внимание на значки доллара($).
Посмотрим, какие ячейки участвуют в формуле до её копирования, записывая себе на черновик их положение относительно первоначальной ячейки B2
- A2, находится от начальной ячейки B2: 1 шаг влево.
- D4, находится от начальной ячейки B2: 2 шага вправо, 2 вниз.
Следующий шаг. Переносим мысленно формулу из B2 в ячейку C3. Отсчитываем от С3 те координаты, которые мы записали в предыдущем пункте.
Для A2: отсчитываем от нового положения формулы (ячейки C3) 1 шаг влево. Попадаем на ячейку B3
Для D4: отсчитываем от нового положения формулы (ячейки C3) 2 шага вправо, 2 вниз. Попадаем на ячейку E5
Мы бы использовали значения ячеек B3 и E5 в формуле, если бы не было значков доллара($).
Знак «$» «цементирует» либо столбец (если $ стоит перед названием столбца), либо строчку (если $ стоит перед названием строки).
Например, в первом выражении нашей формулы $ стоит перед столбцом A, значит, вычисленная после копирования ячейка B3 превратится в $A3. Столбец A должен обязательно остаться!
Во втором выражении $ стоит перед четвёртой строчкой. Значит, в данном выражении обязательно должна остаться четвёртая строчка! Ячейка E5 превращается в ячейку E$4.
Таким образом, численный результат формулы после копирования можно записать следующим образом

Ответ: 23.
Ещё один тип задач задания номер 7 из ЕГЭ по информатике.
Задача (встречается в тренировочных вариантах ЕГЭ по информатике)
В электронной таблице значение формулы =CPЗHAЧ(C2:D5) равно 4. Чему равно значение формулы =CУMM(C5:D5), если значение формулы =CPЗHAЧ(C2:D4) равно 5? Пустых ячеек в таблице нет.
Решение:
Для начала нам нужно в черновике нарисовать ячейки таблицы, как в программе Excel, чтобы там были С2 и D5.
Теперь отметим разными цветами то, что нам дано в условии задачи.
- =CPЗHAЧ(C2:D5) — Отметим красным цветом (Равно 4)
- =CPЗHAЧ(C2:D4) — Отметим оранжевым цветом (Равно 5)
- =CУMM(C5:D5) — Отметим зелёным цветом (Нужно найти)
Важно, что действие формулы =CPЗHAЧ(C2:D5) именно прямоугольная область. В левом верхнем углу ячейка С2, в правом нижнем углу ячейка D5. Аналогично и для других формул.
В левом верхнем углу ячейка С2, в правом нижнем углу ячейка D5. Аналогично и для других формул.
Распишем формулы подробно.
CPЗHAЧ — это среднее значение! (Сумма всех ячеек, делённое на их количество)
Нужно найти сумму двух ячеек C5 + D5.
Из второго (2) уравнения выразим сумму всех ячеек и подставим в первое (1) уравнение.
Тогда
Ответ: 2.
Задание на диаграммы из тренировочного варианта ЕГЭ по информатике.
Задача (диаграммы)
Дан фрагмент электронной таблицы.
Какое целое число должно быть записано в ячейке A1, чтобы диаграмма, построенная по значениям ячеек A2:C2, соответствовала рисунку ? Известно, что все значения ячеек из рассматриваемого диапазона неотрицательны.
Решение:
Подставим в каждую формулу из второй строчки таблицы те значения, которые мы уже знаем.
Ячейка A2 : 2 * 4 / (A1 + 1) = 8 / (A1 + 1)
Ячейка B2 : (A1 + 1) / (5 — 4) = A1 + 1
Ячейка C2 : A1 / (5 — 4) + 1 = A1 + 1
В формулах осталась только ячейка A1, которую и нужно найти.
Посмотрим на диаграмму справа, которая соответствует второй строчке (три ячейки A2, B2, C2). Видим, что на диаграмме 2 части имеют одинаковое значение, а третья часть в два раз больше, чем остальные.
При упрощении выражений, у нас тоже получились две ячейки одинаковые: B2 и C2, и каждая равна A1 + 1. Значит, ячейка A2 будет больше, чем C2 и B2 в 2 раза.
Значит, ячейка A2 будет больше, чем C2 и B2 в 2 раза.
Составим уравнение:
В условии задачи сказано, что все ячейки неотрицательные. Значит, ответ будет 1.
Ответ: 1.
В последнее время всё чаще встречается в тренировочных вариантах ЕГЭ по информатике такой вид задания 7.
Задача (редкая, не сложная)
На предприятии работают 100 человек. Каждый из них владеет как минимум одним иностранным языком (английским, немецким или французским), На следующей диаграмме отражено количество человек, владеющих каждым из языков.
Вторая диаграмма отражает количество человек, знающих только один язык, только два языка или все три иностранных языка.
Определите количество человек, владеющих одновременно английским и немецким, но не говорящих по-французски.
Решение:
Десять человек знают только французский язык (это видно из первой диаграммы), но из второй диаграммы видно, что 10 человек знают все три языка! Значит, на второй диаграмме 10 человек, которые будут французский и ещё два.
На второй диаграмме показано, что 20 человек знают 2 языка, но те кто знаю французский язык уже вошли в предыдущий сектор. Следовательно, 20 человек знают два языка: английский и немецкий, но не знают французский.
Ответ: 20.
Ещё один тип задач задания 7 ЕГЭ по информатике, похожий на 1-ю из разобранных нами в этой статье. Отличается данная задача вопросом.
Задача (редкая)
Дан фрагмент электронной таблицы. Из ячейки D2 в одну из ячеек диапазона E1:E4 была скопирована формула. При копировании адреса ячеек в формуле автоматически изменились, и значение формулы стало равным 8. В какую ячейку была скопирована формула? В ответе укажите только одно число – номер строки, в которой расположена ячейка.
В какую ячейку была скопирована формула? В ответе укажите только одно число – номер строки, в которой расположена ячейка.
Примечание. Знак $ обозначает абсолютную адресацию.
Решение:
Нам сказано, что формулу скопировали в одну из четырёх ячеек E1, E2, E3, E4. Значит, нам нужно проверить каждую из них, и посмотреть, где будет формула иметь значение 8.
Запишем координаты для двух ячеек, участвующих в формуле.
- B3, находится от начальной ячейки D2: 2 шага влево, 1 шаг вниз.
- C2, находится от начальной ячейки D2: 1 шаг влево.
Проверяем ячейку E4
Отсчитываем от E4 записанные координаты. На рисунке отмечены красным цветом отсчитанные ячейки относительно E4:
Т.к. в формуле в первом выражении (B$3) перед 3 (тройкой) стоит знак $, то мы должны обязательно брать значение из третьей строчки. Поднимаемся на третью строчку, и теперь будем брать значение для этого выражения из ячейки C$3. На рисунке отмечено зелёным цветом.
Поднимаемся на третью строчку, и теперь будем брать значение для этого выражения из ячейки C$3. На рисунке отмечено зелёным цветом.
Тоже самое будет и для второго выражения ($C2), но теперь «цементируется» столбец С. Тогда численное значение берём из ячейки $С4.
Получается, что численное значение формулы в ячейке E4 будет С$3+$С4 = 11. А нам нужно 8. Значит, данная ячейка не подходит.
Проверяем ячейку E3
Аналогичным образом проверяем и остальные ячейки.
В этом случае, при попадании формулы в ячейку E3 два выражения в формуле будут ссылаться на численное значение из ячейки C3.
Получается, что численное значение формулы в ячейке E3 будет С$3+$С3 = 5 + 5 = 10. А нам нужно 8. Значит, данная ячейка не подходит.
Проверяем ячейку E2
Как всегда, красным цветом отмечены ячейки, на которые бы ссылалась формула, если бы не было знака $. При использовании формулы со знаком $, ячейки, отмеченные красным цветом, «превращаются» в ячейки, отмеченные зелёным цветом.
Получается, что численное значение формулы в ячейке E2 будет С$3 + $C2 = 4 + 5 = 9. А нам нужно 8. Значит, данная ячейка не подходит.
Проверяем ячейку E1
Получается, что численное значение формулы в ячейке E1 будет С$3 + $C1 = 3 + 5 = 8. Нам и нужно 8. Значит, данная ячейка подходит!
В ответе нужно записать только строчку нужной ячейки.
Ответ: 1.
Забористая задача седьмого задания ЕГЭ по информатике, но встречается не часто.
Задача (редкая)
В ячейке F10 электронной таблицы записана формула. Эту формулу скопировали в ячейку Е11. В соответствии с формулой, полученной в ячейке Е11, значение в этой ячейке равно сумме значений в ячейках В16 и А17.
Напишите, сколько из следующих четырёх утверждений не противоречат этим данным.
A)Значение в ячейке F10 равно х+у, где х — значение в ячейке В16, а у — значение в ячейке А17.
Б)Значение в ячейке F10 равно х+у, где х — значение в ячейке С15, а у — значение в ячейке А17.
В)Значение в ячейке F10 вычисляется по формуле х+у, где х — значение в ячейке С16, а у — значение в ячейке A16.
Г)Значение в ячейке F10 равно 2 · х, где х — значение в ячейке В16.
Решение:
Нарисуем примерную сетку, чтобы были ячейки, которые описаны в условии задачи.
Синим цветом овальным знаком показано начальное положение формулы, а овал бордового цвета — копия этой формулы.
В условии сказано, что численное значение для новой копии равно сумме В16 и А17. Эти ячейки обозначены так же бордовым цветом. Тогда мы можем вычислить местоположение ячеек, которые были бы задействованы в первоначальной формуле, если бы совсем не использовалась абсолютная адресация (т.е. без использования знака $).
Т.к. первоначальная формула расположена от новой копии на расстоянии: одного шага вправо и одного шага вверх, то и от каждой бордовой ячейки тоже нужно отступить один шаг вправо и один вверх. Получим ячейки, которые обозначим синим цваетом!
Получим ячейки, которые обозначим синим цваетом!
Ещё раз подчеркну, данный рисунок сделан исходя из того, что в формуле не было знаков $ для более ясного представления ситуации.
Теперь нужно разобрать каждое из 4-х утверждений (А-Г) на противоречние!
1. A)Значение в ячейке F10 равно х+у, где х — значение в ячейке В16, а у — значение в ячейке А17
В этом утверждении говорится, что в первоначальной ячейке F10 были использованы значения B16 и A17. Но мы знаем, что эти ячейки используются в новой копии формулы. Т.е получается копирование формулы не изменило значения её аргументов ? Да, такое возможно, если мы «зацементируем» в наших ячейках и столбцы, и строчки. Т.е. если прописать в первоначальной формуле =$A$17 + $B$16. Значит, данное утверждение не противоречит условию задаче!
2. Б)Значение в ячейке F10 равно х+у, где х — значение в ячейке С15, а у — значение в ячейке А17.
Теперь утверждается, что в первоначальной ячейке F10 суммировались значения из С15 и A17. Но С15, у нас отмечена синим квадратом! Значит, эта ячейка нами предполагалась, как участник данной формулы, только без использования абсолютной адресации $.
Воторой компонент (Ячейка A17) остался в неизменном виде, что до копирования, что после! Такое может быть, если строка и столбец этой ячейки «зацементированы».
Получается, что утверждение обосновано, если в первоначальной формуле будет формула =С15 + $A$17.
3. В)Значение в ячейке F10 вычисляется по формуле х+у, где х — значение в ячейке С16, а у — значение в ячейке A16
Синим цветом отмечены те ячейки, которые в утверждении участвуют в сумме для первоначальной формулы в F10 (рисунок ниже). Если бы в них не было бы абсолютной адресации ($), то они бы перешли при копировании в те ячейки, которые отмечены оранжевым цветом. (Одна ячейка ушла за пределы таблицы, такое не допускается!). Но по условию задачи, при копировании у нас получились те ячейки, которые отмечены бордовым цветом. Как такое могло произойти ? Дело в том, что у нас присутствовала абсолютная адресация!
(Одна ячейка ушла за пределы таблицы, такое не допускается!). Но по условию задачи, при копировании у нас получились те ячейки, которые отмечены бордовым цветом. Как такое могло произойти ? Дело в том, что у нас присутствовала абсолютная адресация!
Получается, чтобы всё было нормально, в ячейке C16 «зацементируем» 16 строчку, а в ячейке A16, столбец A.
Тогда, в первоначальной формуле будет значение =С$16 + $A16. И это утверждение не противоречит условию задачи!
4. Г) Значение в ячейке F10 равно 2 · х, где х — значение в ячейке В16
Последнюю формулу можно составить для F10 следующим образом = B16 + $B$16. Тогда после копирования ячейка B16 превратится в A17, а $B$16 полностью «зацементирована», так и останется на значении B16. Таким образом, утверждение так же не противоречит условию задачи.
Все четыре утверждения подходят под условия задачи.
Ответ: 4.
Дистанционный репетитор — онлайн-репетиторы России и зарубежья
КАК ПРОХОДЯТ
ОНЛАЙН-ЗАНЯТИЯ?
Ученик и учитель видят и слышат
друг друга, совместно пишут на
виртуальной доске, не выходя из
дома!
КАК ВЫБРАТЬ репетитора
Выбрать репетитора самостоятельно
ИЛИ
Позвонить и Вам поможет специалист
8 (800) 333 58 91
* Звонок является бесплатным на территории РФ
** Время приема звонков с 10 до 22 по МСК
ПОДАТЬ ЗАЯВКУ
Россия +7Украина +380Австралия +61Белоруссия +375Великобритания +44Израиль +972Канада, США +1Китай +86Швейцария +41
Выбранные репетиторы
Заполните форму, и мы быстро и бесплатно подберем Вам дистанционного репетитора по Вашим пожеланиям.
Менеджер свяжется с Вами в течение 15 минут и порекомендует специалиста.
Отправляя форму, Вы принимаете Условия использования и даёте Согласие на обработку персональных данных
Вы также можете воспользоваться
расширенной формой подачи заявки
Как оплачивать и СКОЛЬКО ЭТО СТОИТ
от
800 до 5000 ₽
за 60 мин.
и зависит
ОТ ОПЫТА и
квалификации
репетитора
ОТ ПОСТАВЛЕННЫХ ЦЕЛЕЙ ОБУЧЕНИЯ
(например, подготовка к олимпиадам, ДВИ стоит дороже, чем подготовка к ЕГЭ)
ОТ ПРЕДМЕТА (например, услуги репетиторовиностранных языков дороже)
Оплата непосредственно репетитору, удобным для Вас способом
Почему я выбираю DisTTutor
БЫСТРЫЙ ПОДБОР
РЕПЕТИТОРА И
ИНДИВИДУАЛЬНЫЙ ПОДХОД
ОПТИМАЛЬНОЕ
СООТНОШЕНИЕ ЦЕНЫ И
КАЧЕСТВА
ПРОВЕРЕНЫ ДОКУМЕНТЫ ОБ ОБРАЗОВАНИИ У ВСЕХ РЕПЕТИТОРОВ
НАДЕЖНОСТЬ И ОПЫТ.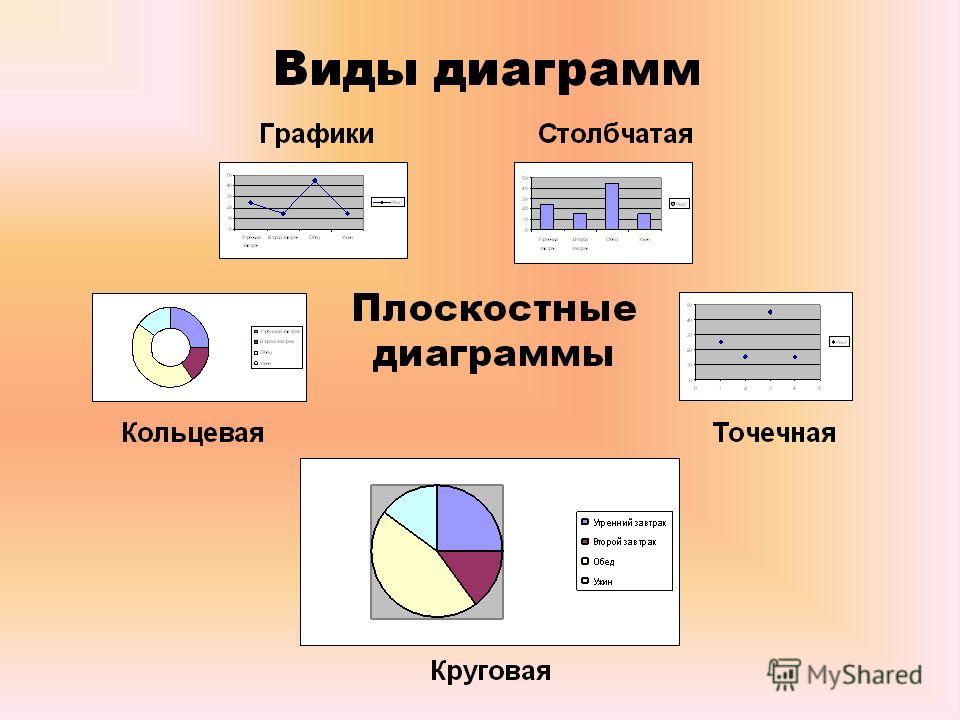
DisTTutor на рынке с 2008 года.
ПРОВЕДЕНИЕ БЕСПЛАТНОГО, ПРОБНОГО УРОКА
ЗАМЕНА РЕПЕТИТОРА, ЕСЛИ ЭТО НЕОБХОДИМО
375458 УЧЕНИКОВ ИЗ РАЗНЫХ СТРАН МИРА
уже сделали свой выбор
И вот, что УЧЕНИКИ ГОВОРЯТ
о наших репетиторах
Владимир Александрович Кузьмин
«
Тренинг у Кузьмина В. А. проходил в экстремальных условиях. Мой модем совершенно не держал соединение. За время часового тренинга связь прерывалась практически постоянно. Ясно, что в таких условиях чрезвычайно непросто чему-то учить.
Однако Владимир Александрович проявил удивительную выдержку и терпение. Неоднократно он перезванивал мне на сотовый телефон, чтобы дать пояснения или комментарии.
Ценой больших усилий нам удалось рассмотреть три программы: ConceptDraw MINDMAP Professional Ru, GeoGebra и Ultra Flash Video FLV Converter. Владимир Александрович открыл мне курс на платформе dist-tutor.info и научил подключать и настраивать Виртуальный кабинет, порекомендовав изучать возможности этого ресурса, чтобы постепенно уходить от использования Skype. В итоге, занятие мне очень понравилось! Спокойное объяснение материала, дружелюбный настрой, подбадривание дистанционного ученика даже в самых непростых ситуациях — вот далеко не полный перечень качеств Владимира Александровича как дистанционного педагога. Мне следует учиться у такого замечательного репетитора!
В итоге, занятие мне очень понравилось! Спокойное объяснение материала, дружелюбный настрой, подбадривание дистанционного ученика даже в самых непростых ситуациях — вот далеко не полный перечень качеств Владимира Александровича как дистанционного педагога. Мне следует учиться у такого замечательного репетитора!
«
Вячеслав Юрьевич Матыкин
Чулпан Равилевна Насырова
«
Я очень довольна репетитором по химии. Очень хороший подход к ученику,внятно объясняет. У меня появились сдвиги, стала получать хорошие оценки по химии. Очень хороший преподаватель. Всем , кто хочет изучать химию, советую только её !!!
«
Алина Крякина
Надежда Васильевна Токарева
«
Мы занимались с Надеждой Васильевной по математике 5 класса. Занятия проходили в удобное для обоих сторон время. Если необходимо было дополнительно позаниматься во внеурочное время, Надежда Васильевна всегда шла навстречу. Ей можно было позванить, чтобы просто задать вопрос по непонятной задачке из домашнего задания.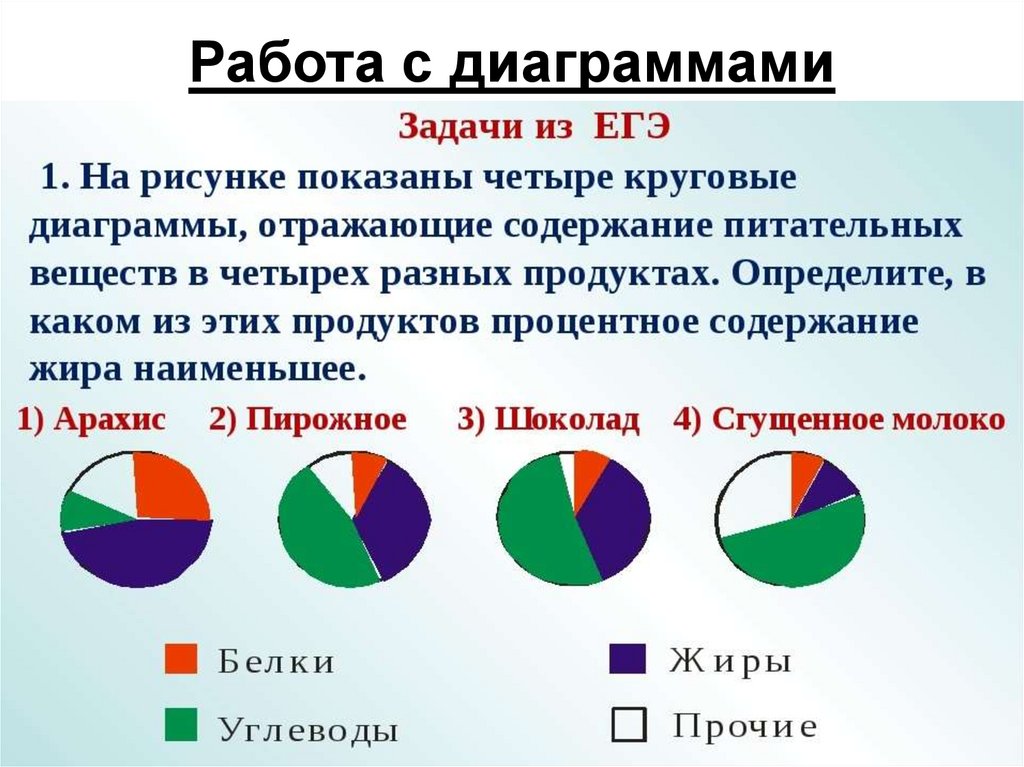 Моя дочь существенно подняла свой уровень знаний по математике и начала демонстрировать хорошие оценки. Мы очень благодарны Надежде Васильевне за помощь в этом учебном году, надеемся на продолжение отношений осенью.
Моя дочь существенно подняла свой уровень знаний по математике и начала демонстрировать хорошие оценки. Мы очень благодарны Надежде Васильевне за помощь в этом учебном году, надеемся на продолжение отношений осенью.
«
Эльмира Есеноманова
Ольга Александровна Мухаметзянова
«
Подготовку к ЕГЭ по русскому языку мой сын начал с 10 класса. Ольга Александровна грамотный педагог, пунктуальный, ответственный человек. Она всегда старается построить занятие так, чтобы оно прошло максимально плодотворно и интересно. Нас абсолютно все устраивает в работе педагога. Сотрудничество приносит отличные результаты, и мы его продолжаем. Спасибо.
«
Оксана Александровна
Клиентам
- Репетиторы по математике
- Репетиторы по русскому языку
- Репетиторы по химии
- Репетиторы по биологии
- Репетиторы английского языка
- Репетиторы немецкого языка
Репетиторам
- Регистрация
- Публичная оферта
- Библиотека
- Бан-лист репетиторов
Партнеры
- ChemSchool
-
PREPY.
 RU
RU
- Class
Дистанционный репетитор — онлайн-репетиторы России и зарубежья
КАК ПРОХОДЯТ
ОНЛАЙН-ЗАНЯТИЯ?
Ученик и учитель видят и слышат
друг друга, совместно пишут на
виртуальной доске, не выходя из
дома!
КАК ВЫБРАТЬ репетитора
Выбрать репетитора самостоятельно
ИЛИ
Позвонить и Вам поможет специалист
8 (800) 333 58 91
* Звонок является бесплатным на территории РФ
** Время приема звонков с 10 до 22 по МСК
ПОДАТЬ ЗАЯВКУ
Россия +7Украина +380Австралия +61Белоруссия +375Великобритания +44Израиль +972Канада, США +1Китай +86Швейцария +41
Выбранные репетиторы
Заполните форму, и мы быстро и бесплатно подберем Вам дистанционного репетитора по Вашим пожеланиям.
Менеджер свяжется с Вами в течение 15 минут и порекомендует специалиста.
Отправляя форму, Вы принимаете Условия использования и даёте Согласие на обработку персональных данных
Вы также можете воспользоваться
расширенной формой подачи заявки
Как оплачивать и СКОЛЬКО ЭТО СТОИТ
от
800 до 5000 ₽
за 60 мин.
и зависит
ОТ ОПЫТА и
квалификации
репетитора
ОТ ПОСТАВЛЕННЫХ ЦЕЛЕЙ ОБУЧЕНИЯ
(например, подготовка к олимпиадам, ДВИ стоит дороже, чем подготовка к ЕГЭ)
ОТ ПРЕДМЕТА (например, услуги репетиторовиностранных языков дороже)
Оплата непосредственно репетитору, удобным для Вас способом
Почему я выбираю DisTTutor
БЫСТРЫЙ ПОДБОР
РЕПЕТИТОРА И
ИНДИВИДУАЛЬНЫЙ ПОДХОД
ОПТИМАЛЬНОЕ
СООТНОШЕНИЕ ЦЕНЫ И
КАЧЕСТВА
ПРОВЕРЕНЫ ДОКУМЕНТЫ ОБ ОБРАЗОВАНИИ У ВСЕХ РЕПЕТИТОРОВ
НАДЕЖНОСТЬ И ОПЫТ.
DisTTutor на рынке с 2008 года.
ПРОВЕДЕНИЕ БЕСПЛАТНОГО, ПРОБНОГО УРОКА
ЗАМЕНА РЕПЕТИТОРА, ЕСЛИ ЭТО НЕОБХОДИМО
375458 УЧЕНИКОВ ИЗ РАЗНЫХ СТРАН МИРА
уже сделали свой выбор
И вот, что УЧЕНИКИ ГОВОРЯТ
о наших репетиторах
Владимир Александрович Кузьмин
«
Тренинг у Кузьмина В. А. проходил в экстремальных условиях. Мой модем совершенно не держал соединение. За время часового тренинга связь прерывалась практически постоянно. Ясно, что в таких условиях чрезвычайно непросто чему-то учить.
Однако Владимир Александрович проявил удивительную выдержку и терпение. Неоднократно он перезванивал мне на сотовый телефон, чтобы дать пояснения или комментарии.
Ценой больших усилий нам удалось рассмотреть три программы: ConceptDraw MINDMAP Professional Ru, GeoGebra и Ultra Flash Video FLV Converter. Владимир Александрович открыл мне курс на платформе dist-tutor.info и научил подключать и настраивать Виртуальный кабинет, порекомендовав изучать возможности этого ресурса, чтобы постепенно уходить от использования Skype. В итоге, занятие мне очень понравилось! Спокойное объяснение материала, дружелюбный настрой, подбадривание дистанционного ученика даже в самых непростых ситуациях — вот далеко не полный перечень качеств Владимира Александровича как дистанционного педагога. Мне следует учиться у такого замечательного репетитора!
В итоге, занятие мне очень понравилось! Спокойное объяснение материала, дружелюбный настрой, подбадривание дистанционного ученика даже в самых непростых ситуациях — вот далеко не полный перечень качеств Владимира Александровича как дистанционного педагога. Мне следует учиться у такого замечательного репетитора!
«
Вячеслав Юрьевич Матыкин
Чулпан Равилевна Насырова
«
Я очень довольна репетитором по химии. Очень хороший подход к ученику,внятно объясняет. У меня появились сдвиги, стала получать хорошие оценки по химии. Очень хороший преподаватель. Всем , кто хочет изучать химию, советую только её !!!
«
Алина Крякина
Надежда Васильевна Токарева
«
Мы занимались с Надеждой Васильевной по математике 5 класса. Занятия проходили в удобное для обоих сторон время. Если необходимо было дополнительно позаниматься во внеурочное время, Надежда Васильевна всегда шла навстречу. Ей можно было позванить, чтобы просто задать вопрос по непонятной задачке из домашнего задания. Моя дочь существенно подняла свой уровень знаний по математике и начала демонстрировать хорошие оценки. Мы очень благодарны Надежде Васильевне за помощь в этом учебном году, надеемся на продолжение отношений осенью.
Моя дочь существенно подняла свой уровень знаний по математике и начала демонстрировать хорошие оценки. Мы очень благодарны Надежде Васильевне за помощь в этом учебном году, надеемся на продолжение отношений осенью.
«
Эльмира Есеноманова
Ольга Александровна Мухаметзянова
«
Подготовку к ЕГЭ по русскому языку мой сын начал с 10 класса. Ольга Александровна грамотный педагог, пунктуальный, ответственный человек. Она всегда старается построить занятие так, чтобы оно прошло максимально плодотворно и интересно. Нас абсолютно все устраивает в работе педагога. Сотрудничество приносит отличные результаты, и мы его продолжаем. Спасибо.
«
Оксана Александровна
Клиентам
- Репетиторы по математике
- Репетиторы по русскому языку
- Репетиторы по химии
- Репетиторы по биологии
- Репетиторы английского языка
- Репетиторы немецкого языка
Репетиторам
- Регистрация
- Публичная оферта
- Библиотека
- Бан-лист репетиторов
Партнеры
- ChemSchool
-
PREPY.
 RU
RU
- Class
«Круговые и столбчатые диаграммы». 5-й класс
Цель: Закрепить навыки построения диаграмм; чтения диаграмм.
Задачи:
Общеобразовательные:
- определять тип диаграммы в зависимости от ее назначения;
- выделять и группировать данные, которые должны быть отражены на диаграмме;
- интерпретировать количественную информацию, представленную в форме диаграмм.
Воспитательные:
- обучить эстетическому оформлению работ;
- развивать коммуникативные навыки, учить работать в группе;
- воспитывать стремление к здоровому образу жизни;
- расширить словарный запас;
- совершенствовать навыки работы с компьютерной
техникой и повышать интерес к современным
компьютерным технологиям.

Развивающие:
- развивать внимание;
- учить сравнивать данные, анализировать их, обобщать и делать выводы.
Оборудование: компьютеры персональные — 12 шт., мобильный класс – 13 ноутбуков Macintosh, принтер струйный, карточки с диаграммой “Незнайка торгует газетами”, карточки с вопросами по этой диаграмме, карточки с данными для составления диаграмм “Нормы питания для подростков”, “Таблица занятости ученика 5 класса”, учебная таблица и карточки для групп: “Незнайка, Торопыжка и Пончик торгуют газетами”, фишки для поощрения за правильный ответ или правильно выполненное задание.
Ход урока
I. Повторение изученного материала о видах диаграмм, их преимуществах и недостатках.
Фронтальный опрос:
- Какие виды диаграмм мы изучили? (Столбчатые и
круговые.
 )
) - Когда и какую диаграмму лучше использовать? (Круговая диаграмма для сравнения нескольких величин в одной точке, особенно если величины в сумме составляют 100%. Столбчатая – для сравнения нескольких величин в нескольких точках.)
- Для чего используются диаграммы? (Для наглядного представления информации.)
- Каковы преимущества диаграмм по сравнению с таблицами? (Наглядность, возможность сравнивать разные величины друг с другом, возможность представить большой объем информации.)
- Каковы недостатки диаграмм? (Приближенное значение величин.)
II. Сообщение темы и цели урока.
III. Работа над чтением диаграммы и решение задачи по ней.
Фронтальная работа.
Учащиеся обдумывают вопросы, совещаются с
товарищами по группе. Отвечают те, кто первый
подготовил ответ.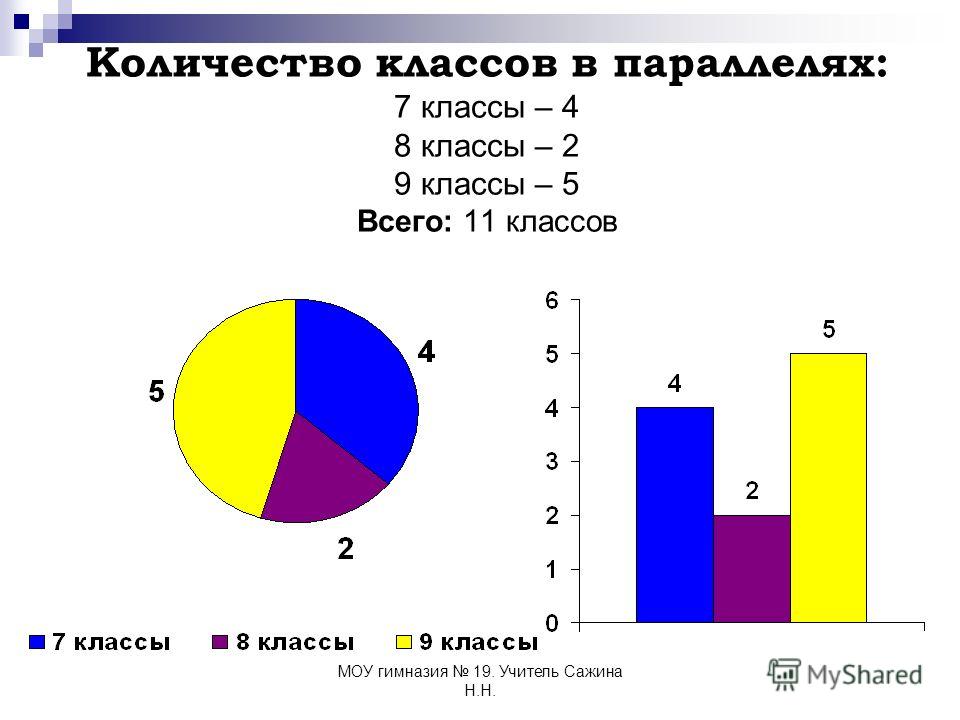
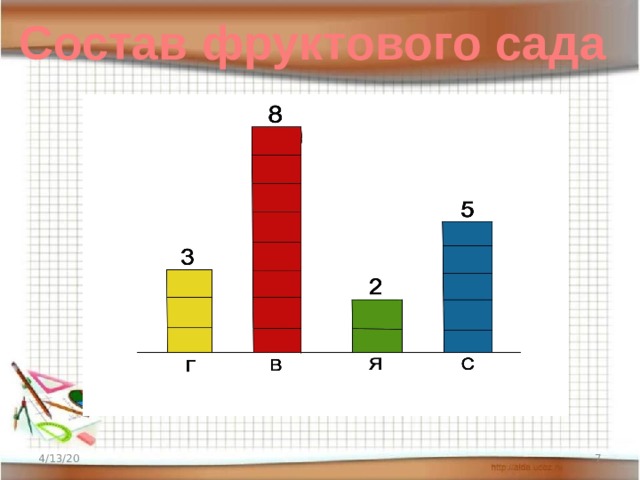
Задание 1. Незнайка торгует газетами.
- Каково название диаграммы? Какую информацию дает диаграмма?
(Пн-20 Вт-25 Ср-32 Чт-30 Пт-23 Сб-30 Вс-20)
- Найдем, сколько газет в среднем продавал Незнайка ежедневно?
(20+25+32+30+23+30+20):7= 180:7=25,71…?26 г.
- Почему в ответе мы применили округление? (Ответ выражает количество предметов.)
IV. Чтение диаграммы, анализ и сравнение данных.
Работа по группам.
Чтение вопросов по карточкам и обсуждение ответов на них. Ответы представителей групп на вопросы по учебной таблице “Незнайка, Торопыжка и Пончик торгуют газетами” у доски.
Задание 2. Торговля газетами. (Приложение)
1 группа: На сколько меньше газет продал Незнайка в понедельник, чем в субботу?
(На 10 газет)
2 группа: Кто продал наименьшее и наибольшее количество газет и в какой день? (Наибольшее Пончик в субботу, наименьшее Пончик в понедельник)
3 группа: В какой день Незнайка и Торопыжка
продали одинаковое количество газет? (В
воскресенье по 20 г. )
)
4 группа: На сколько газет больше продал Незнайка, чем Пончик во вторник?
(25-20=5)
5 группа: Сколько всего газет продали наши герои в субботу? (30+25+35=90)
6 группа: В какой день количество проданных газет записано в порядке убывания? (Среда: 32,25,22)
7 группа: Когда Незнайка продал больше газет, чем Торопыжка и Пончик? (Среда, четверг)
V. Построение круговой диаграммы “Нормы питания для подростков”.
Работа по группам.
Доля белков, жиров и углеводов. Беседа о
сбалансированном питании. Повторение нахождения
доли белков для девочек в диаграмме. Если строить
круговую диаграмму в тетради нужно узнать
сколько градусов приходится на 1 грамм и
полученное число умножить на количество грамм
питательных веществ: 360° :(85*2+340)*85 » 60° . Такой угол
нужно построить для представления доли белков и
жиров в рационе девочек 11-13 лет.
Введение данных и построение диаграммы на ноутбуках Macintosh. Учитель информатики напоминает, что для построения диаграмм на этих компьютерах используются электронные таблицы из офисного пакета “AppleWorks”, дает указания, как настроить беспроводную локальную сеть, чтоб подключиться к общей папке на учительском компьютере, на котором подключен принтер, и сохранить в нее свой файл. Учащиеся в группе обсуждают задание и строят диаграмму, с помощью электронных таблиц. Сравнение машинного способа построения диаграммы и ручного. Проверять помогают учителям ученики, быстрее выполнившие свою работу.
Задание 3. Нормы питания.
Вариант 1. Построить круговую диаграмму “Нормы питания девочек 11-13 лет”. Девочки 11-13 лет должны получать в день 85г белков, 85г жиров, 340г углеводов.
Решение:
| Белки | Жиры | Углеводы |
| 85 | 85 | 340 |
Вариант 2. Построить круговую диаграмму
“Нормы питания мальчиков 11-13 лет”. Мальчики 11-13
лет должны получать в день 85г белков, 85г жиров, 340г
углеводов.
Построить круговую диаграмму
“Нормы питания мальчиков 11-13 лет”. Мальчики 11-13
лет должны получать в день 85г белков, 85г жиров, 340г
углеводов.
Решение:
| Белки | Жиры | Углеводы |
| 93 | 93 | 370 |
VI. Построение круговой диаграммы “Распределение времени учеником 5 класса”
Работа по парам на ноутбуках.
Задание 4.
Таблица занятости ученика 5 Б класса
- Сон — 9 час.
- Учеба в школе – 6 час
- Домашняя работа – 2 часа
- Отдых – 3 часа
- Работа с ПК – 0,5 час
- Просмотр телевизионных передач – 1,5 часа
Обсуждение: Можно ли строить диаграмму? (Нет,
занято 22 часа, не все сутки). Уточнение таблицы
данных: Что нужно добавить, чтобы распределение
времени было рациональным и разумным? (Занятия
спортом – 2 часа). Беседа о распределении времени,
о чередовании умственных и физических занятий).
Учащиеся выполняют на Макинтошах задание,
сохраняют файл в общую папку. Учителя математики
и информатики проверяют работу.
Уточнение таблицы
данных: Что нужно добавить, чтобы распределение
времени было рациональным и разумным? (Занятия
спортом – 2 часа). Беседа о распределении времени,
о чередовании умственных и физических занятий).
Учащиеся выполняют на Макинтошах задание,
сохраняют файл в общую папку. Учителя математики
и информатики проверяют работу.
VII. Построение столбчатой диаграммы по подготовленным данным.
(Домашняя работа к уроку включала сбор информации). Индивидуальная работа учащихся на компьютерах. Пятиклассники рассаживаются за персональные компьютеры и за ноутбуки по одному и строят диаграммы с применением домашних заготовок. Учителя проверяют работы.
- Итоги спортивной игры (5-9 класс).
- Количество слов, прочитанных за минуту (5 класс).
- Количество учащихся по классам (5-8 класс).
- Численность населения столиц мира.
- Численность населения стран мира.

- Продолжительность жизни в разных странах.
- Число мигрантов в 2005 г.
- Количество уроков по предметам (5 класс за год).
- Площади стран мира.
- Итоги Зимней Олимпиады.
- Количество букв в словах в двух первых строках стихотворения А.С. Пушкина “Я памятник…”
- Сдача макулатуры (5-8 класс).
Примеры построенных диаграмм
Количество слов, прочитанных за 1 минуту (скорость чтения)
| Кочкин Сергей | Матвеев Андрей | Гусев Миша | Чечерин Антон | Котельникова Алена | Потапочкин Дима | Шуляковский Дима |
| 189 | 180 | 172 | 171 | 173 | 130 | 129 |
Площади стран мира (км2)
| Россия | Монако | Франция | Мексика | США | Чили | Перу | Китай | Турция | Египет | Сейшелы |
| 17075400 | 2 | 547026 | 1972547 | 9363123 | 765945 | 1285216 | 9596961 | 780576 | 1001449 | 280 |
Количество букв в словах двух первых строк
стихотворения А. С. Пушкина “Я памятник себе
воздвиг нерукотворный, к нему не зарастет
народная тропа…”
С. Пушкина “Я памятник себе
воздвиг нерукотворный, к нему не зарастет
народная тропа…”
| Номер слова | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| Кол-во букв | 1 | 8 | 4 | 7 | 13 | 1 | 4 | 2 | 8 | 8 | 5 |
VIII. Проверка работ. Просмотр диаграмм
учениками, обсуждение. Подведение итогов
Проверка работ. Просмотр диаграмм
учениками, обсуждение. Подведение итогов
Проводится “экскурсия”: ученики ходят по классу и рассматривают диаграммы. Выставляются оценки. Обсуждение преимуществ интегрированного урока. Подсчитывается количество фишек, заработанных каждой группой. Вручаются грамоты самым активным. Гостям раздаются диаграммы, распечатанные на принтере.
Создание сводной диаграммы
Сводные таблицы
Сводные таблицы
Сводные таблицы
Создание сводной диаграммы
-
Создание сводной таблицы для анализа данных листа
Статья -
Упорядочение полей сводной таблицы с помощью списка полей
Статья -
Группировка и отмена группировки данных в сводной таблице
Статья -
Фильтрация данных в сводной таблице
Статья -
Создание сводной диаграммы
Статья
Далее: Общий доступ и совместное редактирование
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 for Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Еще. ..Меньше
..Меньше
Иногда трудно увидеть общую картину, когда необработанные данные не суммированы. Вашим первым желанием может быть создание сводной таблицы, но не каждый может посмотреть на числа в таблице и быстро понять, что происходит. Сводные диаграммы — отличный способ наглядного предоставления данных.
Создание сводной диаграммы
-
Выделите ячейку в таблице.
-
Выберите элементы Вставка > Сводная диаграмма .
-
Выберите, где вы хотите, чтобы сводная диаграмма отображалась.

-
Нажмите кнопку ОК.
-
Выберите поля для отображения в меню.
|
Данные о расходах семьи |
Соответствующая сводная диаграмма |
|
|
|
Создание диаграммы на основе сводной таблицы
Выделите ячейку в таблице.
Выберите элементы Работа со сводными таблицами > Анализ > Сводная диаграмма.
Выберите диаграмму.
Нажмите кнопку ОК.
Чтобы создать сводную диаграмму на Mac, необходимо сначала создать сводную таблицу, а затем вставить диаграмму. После этого диаграмма будет вести себя как сводная диаграмма при изменении полей в списке полей сводной таблицы.
После этого диаграмма будет вести себя как сводная диаграмма при изменении полей в списке полей сводной таблицы.
-
Создайте сводную таблицу.
-
Выберите любую ячейку в сводной таблице.
-
На вкладке Вставка нажмите кнопку для вставки гистограммы, графика, круговой или лепестковой диаграммы. Обратите внимание на то, что другие типы диаграмм в настоящее время не поддерживают сводные таблицы. Например, диаграммы «дерево», а также статистические и комбинированные диаграммы использовать нельзя.

-
После вставки гистограммы, графика, круговой или лепестковой диаграммы вы сможете сводить данные в ней путем изменения или перемещения полей в списке полей сводной таблицы.
-
Вы также можете фильтровать данные в сводной таблице и использовать срезы. При этом также фильтруются данные в диаграмме.
Чтобы создать сводную диаграмму в Excel в Интернете, вам сначала нужно создать сводную таблицу. Для этого см. раздел «Создание сводной таблицы для анализа данных листа».
-
Выделите ячейку в сводной таблице.

-
На вкладке Вставка выберите Вставить диаграмму из раскрывающегося менюи затем выберите любой вариант диаграммы.
Теперь диаграмма появится на рабочем листе. Если щелкнуть в любом месте диаграммы, на ленте появится вкладка Диаграмма. Вы можете использовать любой из параметров на вкладке Диаграмма, чтобы изменить диаграмму.
См. также
Добавление названий осей на диаграмму
Изменение подписей осей на диаграмме
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
См. также
Создание сводной таблицы
Упорядочение полей сводной таблицы с помощью списка полей
Использование срезов для фильтрации данных
Создание временной шкалы сводной таблицы для фильтрации дат
Вводящие в заблуждение графики: примеры из реальной жизни
Вводящие в заблуждение графики в реальной жизни: обзор
Вводящие в заблуждение графики иногда преднамеренно вводят в заблуждение, а иногда это просто случай, когда люди не понимают данные, лежащие в основе построенного ими графика. К «классическим» типам вводящих в заблуждение графиков относятся случаи, когда:
- Вертикальный масштаб слишком велик или слишком мал, или пропускает числа, или не начинается с нуля.

- Граф не помечен должным образом.
- Данные пропущены.
Но некоторые вводящие в заблуждение графики из реальной жизни выходят за рамки классических типов. Одни призваны ввести в заблуждение, другие – шокировать. А в некоторых случаях люди из лучших побуждений просто ошибались. Это одни из моих любимых графиков из реальной жизни, вводящих в заблуждение в недавней истории.
Посмотрите видео с несколькими примерами:
Вводящие в заблуждение графики Примеры из реальной жизни
Посмотрите это видео на YouTube.
Видео не видно? Кликните сюда.
Вводящие в заблуждение графики: отсутствует базовая линия.
«Таймс» оставляет позади остальных… или нет?
Изображение: Университет Кентукки.
Вы можете подумать, что график справа показывает, что продажи The Times вдвое превышают продажи The Daily Telegraph. Но присмотритесь повнимательнее к шкале, и вы увидите, что, хотя The Times действительно продает больше, она превосходит конкурентов лишь примерно на 10%.
USA Today
США сегодня печально известны суетливыми графиками, которые содержат слишком много информации и вводят в заблуждение. На этом графике наша проблема благосостояния выглядит так, будто она выходит из-под контроля. Но обратите внимание, где начинается ось Y … в 94 миллиона!
У этого есть правильные цифры, но этот БОЛЬШОЙ ЗАГОЛОВОК заставляет вас думать, что 5,3% детей получают травмы спинного мозга… довольно страшная статистика для родителей:
Для справки, реальная цифра составляет около 0,0000003% ( на основе 2000 травм в год при населении около 74 000 000 человек).
Fox News вводящие в заблуждение графики.
Fox News показала этот график того, что произойдет, если истечет срок действия налоговых льгот Буша. Катастрофически, правда? Снова проверьте масштаб (он начинается с 34). Все не то, чем кажется.
Рисунок 1. Источник: https://twitter.com/DanaDanger/status/230851016344600576/photo/1/large
Не для того, чтобы продолжать критиковать Fox News, но их имя снова и снова всплывало при поиске вводящих в заблуждение графиков.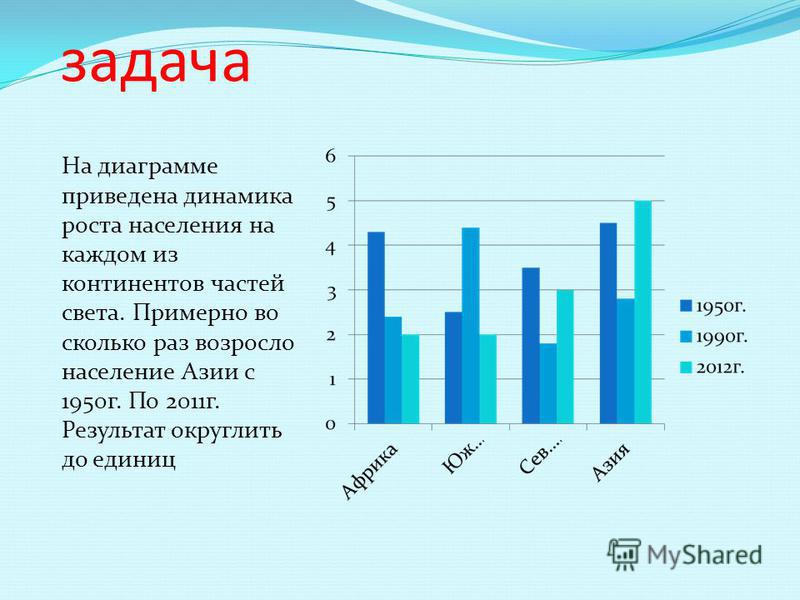 из реальной жизни. Вот еще один, призванный показать, что после небольшого падения безработицы она росла и росла в администрации Обамы.
из реальной жизни. Вот еще один, призванный показать, что после небольшого падения безработицы она росла и росла в администрации Обамы.
Источник изображения: http://cloudfront.mediamatters.org
Обратите внимание, что значение для ноября (8,6) нанесено неправильно. Он находится на 9 месте.0 позиция. Это не единственная проблема с этим графиком. Было задумано, что это экспоненциальный рост, хотя на самом деле общая тенденция занятости довольно стабильна и составляет около 9%.
Вот как должен был бы выглядеть график , если бы он был построен правильно. Увидеть разницу?
Источник: http://freethoughtblogs.com/lousycanuck/2011/12/14/im-better-at-graphs-than-fox-news/
Эти проклятые либералы!
Последний пример вводящего в заблуждение графика. Терри Скьяво был отключен от аппарата жизнеобеспечения после многолетнего судебного разбирательства. CNN использовала график, аналогичный приведенному ниже, чтобы показать, кто согласен с решением удалить питательную трубку.
Изображение: Western Reserve Public Media.
При первом взгляде на этот график кажется, что это решение поддержало в три раза больше демократов. Но при ближайшем рассмотрении обратите внимание на шкалу по вертикальной оси. Лишь немного больше демократов поддержали, чем республиканцев (62% против 54%).
В чем проблема с этими вводящими в заблуждение графиками из реальной жизни? Как правило, графики должны показывать базовый уровень. Базовая линия равна нулю на вертикальной шкале. Графики, у которых отсутствует базовая линия и которые начинаются с произвольного числа (34 на изображении Fox News), как правило, вводят в заблуждение. Когда вы смотрите на график и пытаетесь выяснить, является ли он истинным представлением того, что происходит на самом деле, проверьте этот базовый уровень.
Вводящие в заблуждение графики: неполные данные.
Если вы действительно хотите сделать шокирующее заявление, убедитесь, что вы включили только часть данных. Возьмите этот первый пример вводящего в заблуждение графика, который доказывает реальность глобального потепления.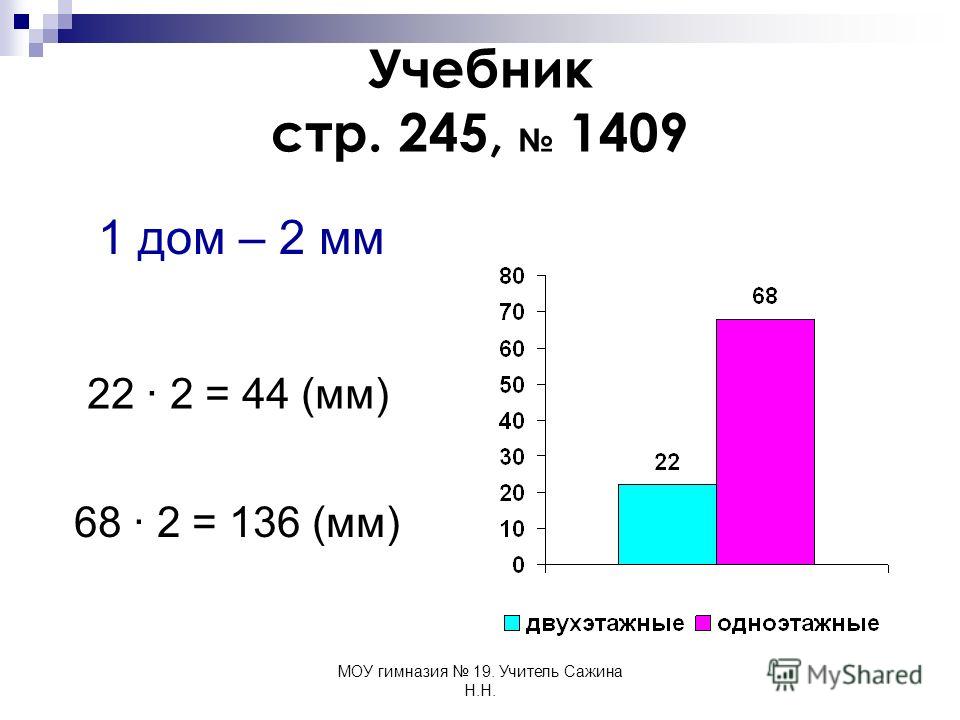
Глобальное потепление выходит из-под контроля!
Среднемесячная температура в Нью-Хейвене, Коннектикут. Изображение: Йельский университет
Что не так с этой картинкой? Он показывает только первую половину года , так что, конечно, температура резко повышается.
Дефицит — постоянная проблема!
Вот еще один пример неполных данных. На этом графике создается впечатление, что дефицит всегда был высоким, потому что график начинается в 2009 году. Это может натолкнуть вас на мысль, что дефицит был постоянной проблемой. Это не так: дефицит составлял всего 1,2 процента ВВП в 2007 году, когда рынок жилья рухнул.
Наш крем устраняет зуд!
Не знаю, что сказать об этом графике крема против зуда Lanacane.
Похоже, ланакан работает лучше, чем обычный крем от зуда, верно? Обратите внимание на отсутствие этикеток. Что на самом деле говорит нам этот график? Практически ничего, кроме того, что их статистики очень хороши в построении не очень хороших графиков.
Вводящие в заблуждение графики: просто читается неправильно
Глобальное потепление остановлено!
Вот еще одно изображение глобального потепления, опубликованное британским таблоидом The Mail on Sunday. Газета использовала его, чтобы заявить, что глобальное потепление остановилось .
Изображение предоставлено: Почта в воскресенье.
Когда мы читаем газеты, мы часто думаем, что люди, пишущие статьи, являются экспертами. На самом деле, журналист, написавший статью к этой картинке (Дэвид Роуз), просто не понял, о чем ему говорит график. Он сделал две ошибки:
- График показывает температуры воздуха . Это очень плохой показатель глобального потепления, так как большая часть тепла попадает в океаны.
- Это очень краткосрочный график. Вы не можете делать хорошие прогнозы на основе небольшого количества данных. Если вы выиграете первый купленный лотерейный билет, это не значит, что ваши шансы на выигрыш равны 100%.
 Вам придется купить (и стереть) десятки или даже сотни билетов, чтобы действительно увидеть тенденцию. Более совершенный график глобального потепления показал бы тенденцию со времен промышленной революции.
Вам придется купить (и стереть) десятки или даже сотни билетов, чтобы действительно увидеть тенденцию. Более совершенный график глобального потепления показал бы тенденцию со времен промышленной революции.
Колледж не стоит вашего времени и денег!
Как насчет этой диаграммы, которая «доказывает», что высшее образование больше не стоит денег?
Масштаб на этой диаграмме в порядке. То, что Business Insider вывел из графика, не соответствует действительности. Неужели мы «…потеряли повсеместную положительную финансовую отдачу от образования»? Нет. Дэвид Блейк читал диаграмму, не принимая во внимание ключевой факт, что не было на диаграмме: стоимость обучения в колледже , а не уменьшилась тем более . Это означает, что ваши перспективы как выпускника средней школы намного хуже, чем ваши перспективы как выпускника колледжа.
Еще одна ключевая информация находится на самой диаграмме. Обратите внимание, что средний годовой доход, на который может рассчитывать выпускник колледжа, составляет около 45 000 долларов в 2010 году. Это 90 103 в год. За среднюю продолжительность трудовой жизни (скажем, 43 года при условии выхода на пенсию в возрасте 65 лет) это дает вам доход в размере 45 000 * 43 = 1 935 000 долларов. Вычтите это дорогое образование в колледже (95 000 долларов), и ваш чистый заработок составит 1 840 000 долларов. Сравните это со своим средним выпускником средней школы. Они могут рассчитывать заработать 1 300 000 долларов за всю свою жизнь (Источник: Министерство образования США). Это большая разница!
Это 90 103 в год. За среднюю продолжительность трудовой жизни (скажем, 43 года при условии выхода на пенсию в возрасте 65 лет) это дает вам доход в размере 45 000 * 43 = 1 935 000 долларов. Вычтите это дорогое образование в колледже (95 000 долларов), и ваш чистый заработок составит 1 840 000 долларов. Сравните это со своим средним выпускником средней школы. Они могут рассчитывать заработать 1 300 000 долларов за всю свою жизнь (Источник: Министерство образования США). Это большая разница!
Мораль сказки? Будьте осторожны, пытаясь прочитать диаграмму по теме, в которой вы не являетесь экспертом!
Wii барахтается!
Каждый может быть экспертом в игровых системах, верно? Ведь что тут знать? Как вставить диск в консоль? Как держать контроллер? Как стрелять из оружия? Этот график за 2009 год показывает, что 6% владельцев Wii на самом деле использовали свою Wii:
Изображение: Kotaku.com.Ли Эванс в своей статье, посвященной нисходящей совместимости, «Приключения в вводящих в заблуждение графиках» выразился лучше всего:
Взгляните на верхнюю цифру на графике.
Только 11% владельцев 360 активно используют свои 360 и только 10% владельцев PS3 активно используют свои PS3. Теперь давайте немного посчитаем.
50 миллионов владельцев Wii. 6% от этого числа составляет 3 миллиона.
Есть 30 миллионов 360 владельцев. 11% от этого числа составляет 3,3 миллиона человек.
20 миллионов владельцев PS3. 10% от этого числа составляют 2 миллиона.
Другими словами, почти одинаковое количество пользователей регулярно используют их систему. Разрыв в процентах не так уж велик, но график (и то, как люди его читают) заставляет его выглядеть так: «О боже, ОГРОМНЫЙ РАЗРЫВ!»
Вводящие в заблуждение графики: цифры, которые не складываются
Пэйлин для Прес!
По-видимому, 70% людей поддержали Пэйлин на президентских выборах 2012 года. Но ждать! Статистики Fox News снова взялись за дело. На круговой диаграмме сумма должна составлять 100%. Не этот:
Изображение: http://flowingdata.com/2009/11/26/fox-news-makes-the-best-pie-chart-ever/Вводящие в заблуждение графики: две оси Y
Работа и здоровье страховые потери ускоряются!
Изображение: Комната Вонк.
На первый взгляд кажется, что это утверждение верно. Но взгляните на график, и вы увидите две оси Y . Этот особый тип манипулирования данными выходит за рамки классических методов обмана. Что на самом деле здесь происходит (пропуская математическую часть), так это то, что если вы извлечете данные из этого запутанного графика, вы получите:
- Отсутствие страховки увеличивается очень незначительно (с ~ 15 процентов до ~ 16 процентов).
- Безработица растет быстрее (с ~ 4,5% до 7,5%).
И победителем в категории «Вводящие в заблуждение графики» стал…
Награда в категории «Вводящие в заблуждение графики в реальной жизни» достается (барабанная дробь, пожалуйста…) Fox News за эту жемчужину:
Изображение: Media Matters
Каковы настоящие данные за этим шокирующим графиком? Действительно ли людей, получающих пособие, больше, чем тех, кто работает полный рабочий день? Как указывает Media Matters:
«Цифра Fox в 108,6 млн человек, получающих пособие, взята из отчета Бюро переписи населения… об участии в программах проверки нуждаемости, в которые входят «любые лица, проживающие в домашнем хозяйстве, в котором один или больше людей получили пособия» в четвертом квартале 2011 года, таким образом, включая лиц, которые сами не получали государственных пособий .
С другой стороны, цифра «люди с полной занятостью», которую использовал Фокс, включала только работающих, а не лиц, проживающих в домашнем хозяйстве, где работает хотя бы один человек».
Другими словами, если вы живете с мамой, папой, братом Джо и двоюродным братом Сэмом, и Сэм (на короткое время) участвовал в какой-либо программе социального обеспечения, это засчитывалось против вас и всех членов вашей семьи.
Ссылки
Хафф, Д. (1993). Как лгать со статистикой. WW Norton & Company
Гоник, Л. (1993). Мультяшный путеводитель по статистике. HarperPerennial.
УКАЗЫВАЙТЕ ЭТО КАК:
Стефани Глен . «Вводящие в заблуждение графики: примеры из реальной жизни» от StatisticsHowTo.com : Элементарная статистика для всех нас! https://www.statisticshowto.com/probability-and-statistics/descriptive-statistics/misleading-graphs/
————————————————— ————————-
Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на ваши вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!
Ваши первые 30 минут с репетитором Chegg бесплатны!
Комментарии? Нужно опубликовать исправление? Пожалуйста, Свяжитесь с нами .
Диаграммы и таблицы или когда лучше использовать одну вместо другой
Опубликовано Обновлено автором WPDT Staff
Мы живем в мире, управляемом данными, поэтому способность понимать, обрабатывать и передавать данные является важным навыком. Крайне важно знать, как лучше отображать данные для максимального воздействия. В этой статье, созданной нашей командой в wpDataTables, объясняется, как эффективно использовать диаграммы и таблицы.
Что такое диаграмма? Диаграмма, созданная с помощью wpDataTables, лучшего плагина WordPress для таблиц и диаграмм Диаграммы и графики отображают данные в визуальном формате, показывая отношения между различными наборами данных. Легко увидеть закономерности, а в некоторых случаях можно определить будущие тенденции.
Легко увидеть закономерности, а в некоторых случаях можно определить будущие тенденции.
Диаграммы могут принимать разные формы, и одна из их ключевых функций — отображать большие объемы данных простым и понятным способом.
Диаграмма используется, когда вам нужно передать сложную информацию, чтобы показать закономерности и тенденции. Круговые диаграммы могут быстро объяснить относительные пропорции использования времени или ресурсов. Гистограммы показывают распределение результатов. Диаграмму X-Y можно использовать для расчета уравнения взаимосвязи между двумя наборами данных.
Диаграмма позволяет зрителю быстро понять данные и дает возможность углубиться в данные, чтобы полностью понять их. Диаграммы помогают легко ответить на такие вопросы, как: Проблема увеличивается со временем? Кто тратит больше всего на этот тип отдыха? Как легирующие элементы влияют на прочность моего стального стержня?
Диаграммы и таблицы. Когда использовать диаграммы? Диаграмма, созданная с помощью wpDataTables, лучшего плагина WordPress для таблиц и диаграмм Если у вас есть сложные данные, которые необходимо упростить и представить таким образом, чтобы показать закономерность или тенденцию, всегда следует использовать диаграмму. Их можно использовать для отображения следующего:
Их можно использовать для отображения следующего:
- Тенденции с течением времени. Сколько новых случаев Covid-19 регистрируется каждый день?
- Шаблоны или формы данных. Наблюдается ли прямолинейный рост спроса на мороженое или на этот рост накладываются сезонные колебания?
- Объяснение связи между двумя или более наборами данных. Влияет ли ИМТ (индекс массы тела) человека на его кровяное давление?
- Иллюстрация размера значений по сравнению друг с другом. Пузырьковая диаграмма, например, может отображать цену и общий объем продаж для группы продуктовых линеек.
- Отображение изменчивости либо с помощью кривой распределения с использованием гистограммы, либо с помощью линии наилучшего соответствия на диаграмме X-Y, чтобы проиллюстрировать отклонение от «нормы».
- Выделение «странных» результатов и помощь в их объяснении.

- Сбор больших объемов данных. Глобальные демографические тенденции можно обобщить средними значениями по континентам или отдельным странам.
- Визуализация аспектов ваших данных. Появляются ли географические закономерности? В каком штате США самый высокий средний IQ?
Если есть сомнения, всегда пользуйтесь диаграммой, а не таблицей. Наш разум, как правило, получает информацию быстрее с диаграммой.
Диаграммы можно использовать слишком часто. Выберите ключевую информацию и используйте наиболее подходящую диаграмму. Существует тенденция заполнять наши презентации слишком большим количеством круговых диаграмм, которые могут отвлекать от важной информации в вашей презентации.
Диаграммы и таблицы. Когда использовать таблицы? Таблица, созданная с помощью wpDataTables, лучшего плагина WordPress для таблиц и диаграмм Таблица — это данные, расположенные в столбцах и строках. Он также может включать линии сетки для разделения данных. Каждое пересечение столбца и строки представляет одну часть данных. Это называется «клетка».
Он также может включать линии сетки для разделения данных. Каждое пересечение столбца и строки представляет одну часть данных. Это называется «клетка».
Таблицы также могут отображать текст, цвет, символы или любую другую важную информацию. Таблицы могут быть любыми: от нескольких столбцов и строк до многомерных наборов данных, таких как таблицы умножения.
Таблица, созданная с помощью wpDataTables, лучшего плагина WordPress для таблиц и диаграммТаблицы следует использовать вместо диаграмм, когда точность является ключевой, например, в отчете о научном или медицинском исследовании. Эти читатели должны иметь возможность глубже изучить результаты, а не получать общую картину из диаграммы или графика.
Таблицы также полезны для просмотра многомерной информации, которую невозможно отобразить на диаграмме.
Таблица Дилемма диаграммы – когда использовать таблицу? Таблица, созданная с помощью wpDataTables, лучший плагин WordPress для таблиц и диаграмм Таблица — лучший вариант, если у вас есть данные, которые необходимо подробно проанализировать, поскольку они менее абстрактны и позволяют тщательно изучить конкретные результаты. Важно помнить об использовании таблиц при использовании данных научных исследований или медицинских испытаний.
Важно помнить об использовании таблиц при использовании данных научных исследований или медицинских испытаний.
Иногда данные просто не отображаются на графике. Если у вас есть четырнадцать переменных, связанных с конечной прочностью образца стали, это трудно показать визуально.
Используйте таблицу в следующих ситуациях:
- Если читателю необходимо просмотреть определенные значения в наборе данных.
- Если точное значение является ключевым, а не трендом или общей закономерностью.
- Если необходимо проанализировать несколько выходов или входов.
- Если в данные включена конкретная информация и усредненные результаты.
Это зависит от аудитории и от того, как вы хотите использовать данные. Люди по-разному реагируют на то, как представлена информация, и очень важно, чтобы вы сосредоточились на эффективности своего сообщения. Нет смысла просто развлекать зрителя гламурной диаграммой, когда конкретные данные не понятны.
Все начинается с вашей аудитории. Если они склонны к аналитике и хотят изучить необработанные данные, лучшим выбором будет таблица. Если они предпочитают краткое изложение информации, достаточно диаграммы.
Необработанные и обработанные данные Данные Диаграмма, созданная с помощью wpDataTables, лучшего плагина WordPress для таблиц и диаграммТаблицы показывают необработанные данные. Диаграммы суммируют и сглаживают данные для визуального эффекта. Если вам нужны точные значения, используйте таблицы. Если вам нужны обобщения, используйте диаграммы.
Формат публикации Диаграмма, построенная с помощью wpDataTables и Highcharts То, как вы представляете данные зрителю, имеет большое значение. Если вы отправляете распечатанный отчет своим коллегам, то таблицу можно просмотреть на досуге. Если ваши данные будут представлены по телевидению или в социальных сетях, то следует использовать диаграммы.
Если ваши данные будут представлены по телевидению или в социальных сетях, то следует использовать диаграммы.
Помимо форматирования данных, необходимо учитывать способ взаимодействия аудитории с ними. Такие вопросы, как; будет ли у аудитории время сидеть сложа руки и читать информацию? Будете ли вы иметь возможность прояснить моменты, или документ должен выдержать проверку сам по себе?
Insights Диаграмма, созданная с помощью wpDataTables, лучшего плагина WordPress для таблиц и диаграмм Диаграммы отлично подходят для сводных данных. Они показывают формы и закономерности, которые быстро и эффективно дают информацию. Таблицы дают необработанные данные и оставляют читателю возможность понять, что они показывают. Сочетание этих двух может быть полезным. Отобразите данные на одной или двух диаграммах. Затем покажите необработанные данные в виде таблицы либо в тексте отчета, либо в приложении.
Использование как диаграмм, так и таблиц имеет свои преимущества:
- В таблицах и диаграммах данные будут представлены по-разному.
- Метки данных на диаграмме могут выделять фактические результаты.
- Сводная диаграмма может содержать дополнительную информацию из таблицы, содержащей дополнительные сведения и контекст.
- Для одной и той же презентации разным аудиториям нужны разные способы коммуникации.
На панели инструментов WordPress как таблицы, так и диаграммы могут быть полезны при отображении данных. Ваша панель инструментов WordPress должна иллюстрировать ваш анализ. Это должно усилить ваши утверждения, используя правильное представление данных. В этой статье объясняется, что следует учитывать при принятии решения об использовании диаграмм или таблиц, например о вашей аудитории и вашем конкретном типе необработанных данных. Чего вы пытаетесь достичь, отображая данные? Или какой реакции вы хотите от публики?
В этой статье объясняется, что следует учитывать при принятии решения об использовании диаграмм или таблиц, например о вашей аудитории и вашем конкретном типе необработанных данных. Чего вы пытаетесь достичь, отображая данные? Или какой реакции вы хотите от публики?
wpDataTables — это плагин для WordPress, который помогает управлять всеми вашими данными с помощью таблиц и диаграмм. Используя wpDataTables, вы:
- Возможность создавать настраиваемые диаграммы и таблицы для ваших сообщений или страниц WordPress.
- Редактировать таблицы на серверной и внешней стороне и разрешить утвержденным пользователям просматривать и редактировать таблицы.
- Настройка таблиц с использованием сложных функций, форматирования, фильтрации и т. д.
Выделите цены, статистику производительности или любой другой указанный вами набор данных. Ваша цель — создавать красивые страницы. Выбрав правильную диаграмму и таблицу, ваш веб-сайт WordPress может стать визуально приятным и информативным.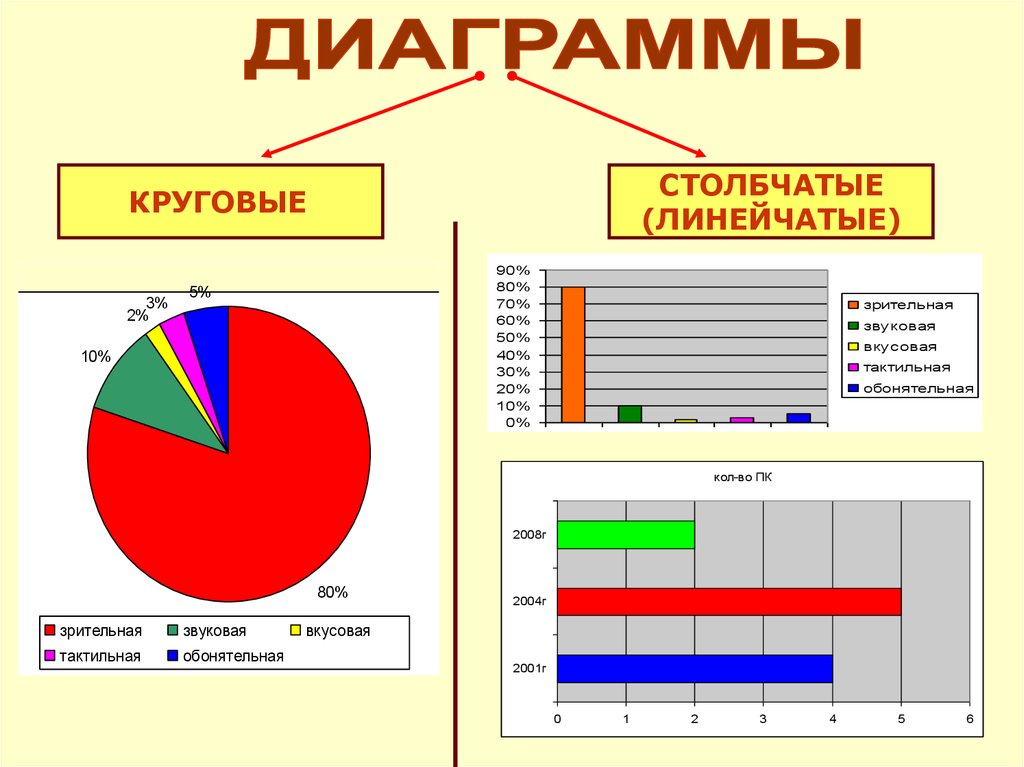
Если вам понравилось читать эту статью о диаграммах и таблицах, вы должны прочитать эту о том, как импортировать данные с помощью плагина электронных таблиц WordPress Excel.
Мы также писали о нескольких связанных темах, таких как цвет фона таблицы, таблицы Bootstrap, статистические таблицы, как центрировать таблицу с помощью CSS, таблицы HTML, плагины диаграмм WordPress, адаптивные таблицы с CSS, таблицы CSS и плагины таблиц jQuery.
решений: данные и графики | Математические вкусности
Форма поиска
Поиск
Данные и линейные графики
| Упражнение | Проблема | Ответить |
| 1 | В каком месяце вандалов было больше всего? | июнь |
| 2 | В каком месяце вандалов было меньше всего? | января |
| 3 | Сколько вандалов было в марте? | 19 |
| 4 | В каком месяце было 24 вандала? | апрель |
| 5 | Сколько вандалов было в феврале? | 15 |
Построение линейных графиков
| Упражнение 1: | В 2000 году был принят закон, запрещающий использование сотовых телефонов за рулем в Anytown, штат Нью-Йорк. С тех пор количество людей, использующих сотовые телефоны за рулем в Anytown, менялось каждый год, как показано в таблице ниже. Постройте линейный график, чтобы визуально отобразить эти данные. С тех пор количество людей, использующих сотовые телефоны за рулем в Anytown, менялось каждый год, как показано в таблице ниже. Постройте линейный график, чтобы визуально отобразить эти данные. | ||||||||||||||||||||
| |||||||||||||||||||||
| Решение: | Ответы будут различаться в зависимости от используемых шкал. Образец линейного графика показан ниже. Образец линейного графика показан ниже. | ||||||||||||||||||||
| Упражнение 2: | Всего в школе было проведено 7 соревнований по бегу на 50 метров. Время выигрыша было записано в секундах, как показано в таблице ниже. Постройте линейный график, чтобы визуально отобразить эти данные. | ||||||||||||||||||
| |||||||||||||||||||
| Решение: | Ответы будут различаться в зависимости от используемых шкал.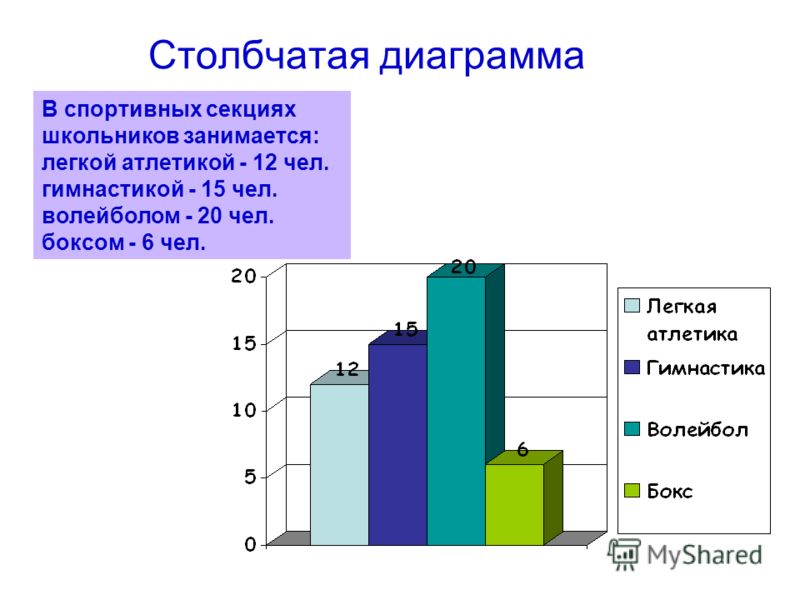 Образец линейного графика показан ниже. Образец линейного графика показан ниже. | ||||||||||||||||||
Данные и гистограммы
Учащихся класса миссис Глоссер опрашивали о закусках и просили выбрать из списка закуску, которая им больше всего нравится. Гистограмма ниже обобщает данные, собранные в ходе этого опроса.
| Упражнение | Задача | Ответить |
| 1 | Какая закуска понравилась больше всего? | Печенье |
| 2 | Какую закуску предпочли 2 ученика? | Крекеры |
| 3 | Сколько студентов предпочли крендельки? | 5 |
| 4 | Какую закуску предпочли 3 ученика? | Чипсы |
| 5 | Какому значению согласно графику соответствует количество учащихся, одинаково предпочитающих фрукты и овощи? | 1 |
Построение гистограмм
| Упражнение 1: | Средняя высота различных деревьев в США была записана в метрах, как показано в таблице ниже.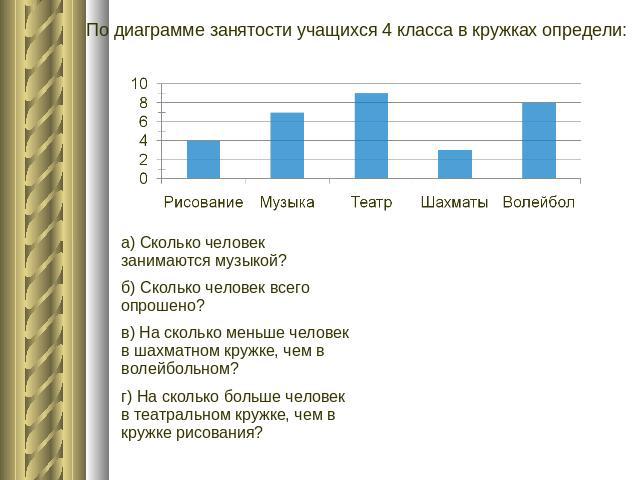 Постройте гистограмму, чтобы визуально отобразить эти данные. Постройте гистограмму, чтобы визуально отобразить эти данные. | ||||||||||||||||||
| |||||||||||||||||||
| Решение: | Ответы будут различаться в зависимости от используемого масштаба и от того, расположены ли полосы горизонтально или вертикально. Примеры графиков показаны ниже. Примеры графиков показаны ниже. | ||||||||||||||||||
| Упражнение 2: | Шесть детей были опрошены, чтобы выяснить, на какой процент прибавки получает каждый из них в своем пособии, как показано в таблице ниже. Постройте гистограмму, чтобы визуально отобразить эти данные. | ||||||||||||||||
| |||||||||||||||||
| Решение: | Ответы будут различаться в зависимости от используемого масштаба и от того, расположены ли полосы горизонтально или вертикально.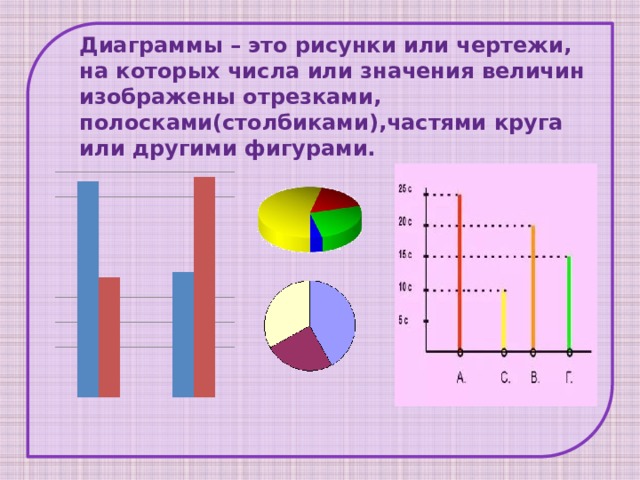 Примеры графиков показаны ниже. Примеры графиков показаны ниже. | ||||||||||||||||
Данные и круговые диаграммы
| Упражнение | Проблема | Ответить |
| 1 | Сколько секторов в графе? | 6 |
| 2 | Какой тип домашних животных покупают чаще всего? | Собаки |
| 3 | Какое домашнее животное покупают меньше всего? | Другое |
| 4 | Какой процент покупателей покупает песчанок? | 9 |
| 5 | Какой процент клиентов покупает птиц? | 18 |
Построение круговых графов
| Упражнение 1: | Источники доходов федерального правительства были зарегистрированы, как показано в таблице ниже. Постройте круговую диаграмму, чтобы визуально отобразить эти данные. Постройте круговую диаграмму, чтобы визуально отобразить эти данные. | ||||||||||||
| |||||||||||||
| Решение: | Пример круговой диаграммы показан ниже.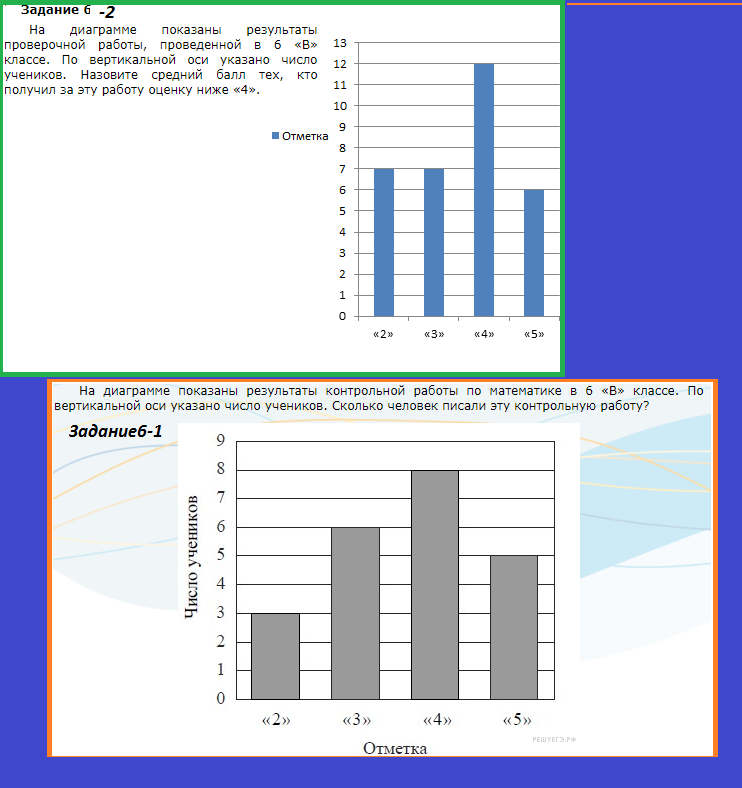 | ||||||||||||
| Упражнение 2: | Учащиеся небольшой школы были опрошены, чтобы определить, какой вид транспорта используется, чтобы добраться до школы и обратно, как показано в таблице ниже. Постройте круговую диаграмму, чтобы визуально отобразить эти данные. | ||||||||||||||
| |||||||||||||||
| Решение: | Пример круговой диаграммы показан ниже. | ||||||||||||||
Сравнение графиков
| Упражнение | Проблема | Ответить |
| 1 | Возраст 7 трубачей в оркестре: 13, 12, 11, 12, 11, 10 и 12 лет. Какой тип графика подходит для сравнения возраста этих трубачей? | бар |
| 2 | Федеральная почасовая минимальная заработная плата регистрировалась каждый год с 1990 по 2007 год. Какой тип графика лучше всего покажет изменения минимальной заработной платы за этот период времени? | строка |
| 3 | На вопрос, состоит ли слово «антидезистеблишментарианство» из 28 букв, 50 человек ответили да , 35 человек ответили нет и 15 человек ответили Не знаю. График какого типа лучше всего подходит для сравнения этих ответов друг с другом и с итоговым значением? График какого типа лучше всего подходит для сравнения этих ответов друг с другом и с итоговым значением? | круг |
| 4 | Рост 7 различных растений был записан в сантиметрах. Какой тип графика лучше всего подходит для сравнения роста каждого растения? | бар |
| 5 | В городе каждый месяц в течение 12 месяцев регистрировалось количество осадков в дюймах. Какой тип графика лучше всего отображает изменение количества осадков? | строка |
Практические упражнения
См. линейный график ниже для упражнений 1–3.
| Упражнение | Проблема | Ответить |
| 1 | Какое самое большое число на вертикальной шкале? | 140 |
| 2 | Какая частота пульса была зарегистрирована через 2 минуты? | 95 |
| 3 | На скольких минутах была зарегистрирована частота пульса 121 удар в минуту? | 3 |
См.
 гистограмму ниже для упражнений 4–6.
гистограмму ниже для упражнений 4–6.
См. круговую диаграмму ниже для упражнений 7–10.
Упражнения с вызовом
1. | Класс миссис Глоссер проголосовал за свою любимую игрушку. Каждый студент проголосовал один раз. Вот голосование: кукла 4, фигурка 4, обучающая игрушка 3, видеоигра 6, электроника 5, строительные блоки 1. Какая из следующих гистограмм правильно отображает все эти факты? (Обратите внимание, что заголовок каждого графика опущен.) |
Вариант 1 неверен, поскольку он показывает 6 для куклы, а не 4; и потому что он показывает 4 для видеоигры, а не 6.
Вариант 2 неверен, потому что он показывает 2 для электроники, а не 5.
Вариант 3 правильный, потому что он правильно показывает все факты.
| 2. | Вес младенца регистрировали в фунтах в течение каждой из 7 недель. Вот данные: Неделя 1 : 7,5 фунтов; Неделя 2 : 7,1 фунта; Неделя 3 : 7,4 фунта; Неделя 4 : 7,7 фунта; Неделя 5 : 8,2 фунта; Неделя 6 : 8,6 фунта; Неделя 7 : 9,0 фунтов. Какой из следующих линейных графиков правильно отображает все эти факты? (Обратите внимание, что заголовок каждого графика опущен. Кроме того, значения для каждой точки не обозначены.) Какой из следующих линейных графиков правильно отображает все эти факты? (Обратите внимание, что заголовок каждого графика опущен. Кроме того, значения для каждой точки не обозначены.) |
Вариант 1 неверен, так как значение, которое он показывает для недели 1, составляет около 9 фунтов, а не 7,5 фунтов.
Вариант 3 неверен, так как значение, которое он показывает для недели 4, составляет около 9 фунтов, а не 7,7 фунтов.
Вариант 2 правильный, потому что он правильно показывает все факты.
| 3. | Количество времени, потраченного на повседневную деятельность, указано в часах следующим образом: школа 8, сон 6, развлечения 5, домашняя работа 3, приемы пищи 2. На каком из следующих круговых графиков правильно показаны все эти факты? (Обратите внимание, что все заголовки опущены.) |
Вариант 1 неверен, поскольку: [1] Проценты для каждого сектора не соответствуют заданным данным. [2] Секторы , а не , нарисованы от большего к меньшему по часовой стрелке.
[2] Секторы , а не , нарисованы от большего к меньшему по часовой стрелке.
Вариант 2 неверен, потому что: [1] Проценты для каждого сектора не соответствуют заданным данным. [2] Секторы , а не , нарисованы от большего к меньшему по часовой стрелке.
Вариант 3 правильный, потому что он правильно показывает все факты.
| Упражнение | Проблема | Ответить |
| 4 | Какой график вы бы использовали для представления скорости в км в час 20 самых быстрых животных в мире? | бар |
| 5 | Какой график вы бы использовали для представления годового количества ДТП со смертельным исходом в вашем штате за последние 10 лет? | строка |
| 6 | Какой график вы бы использовали для представления количества пользователей Интернета в 10 разных странах? | бар |
| 7 | Какой график вы бы использовали для представления процентной доли учащихся в вашей школе по классам? | круг |
Обратитесь к линейному графику ниже, чтобы ответить на упражнение 8.
Шкала начинается с 60 вместо 0,
Обратитесь к гистограмме ниже, чтобы ответить на упражнение 9.
На вертикальной шкале нет меток.
Обратитесь к круговой диаграмме ниже, чтобы ответить на упражнение 10.
Эта круговая диаграмма состоит из 7 секторов. Он загроможден и его трудно читать. На этом графике представлено слишком много данных.
| Уроки по данным и графикам |
| Данные и графики |
| Построение линейных графиков |
| Данные и гистограммы |
| Построение гистограмм |
| Данные и круговые диаграммы |
| Построение круговых диаграмм |
| Сравнение графиков |
| Практические упражнения |
| Упражнения с вызовом |
| Решения |
Подпишитесь на нашу БЕСПЛАТНУЮ рассылку новостей!
Подпишитесь на нашу БЕСПЛАТНУЮ рассылку новостей!
Адрес электронной почты *
Интерпретация соответствующей информации из таблиц, диаграмм и графиков: TEAS
Штатные авторы RegisteredNursing.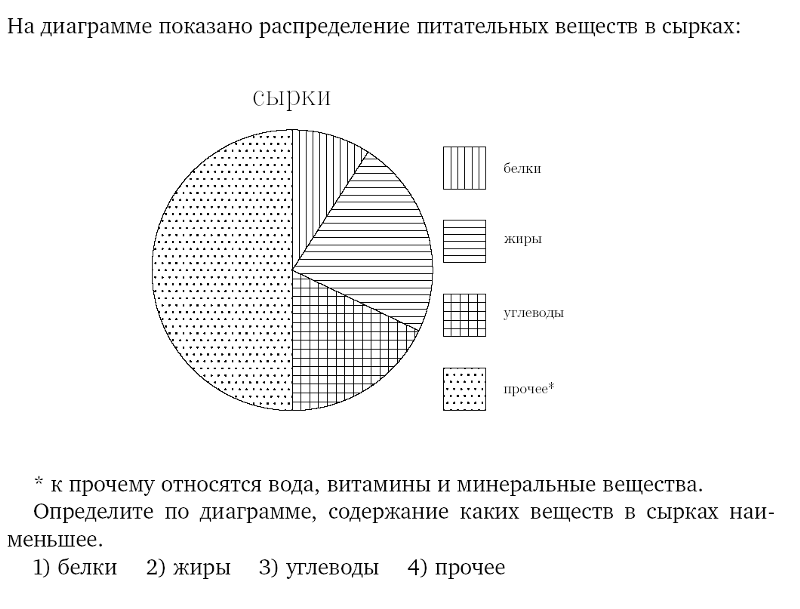 org | Обновлено/проверено: 24 августа 2022 г.
org | Обновлено/проверено: 24 августа 2022 г.
Основные термины и терминология, относящиеся к интерпретации соответствующей информации из таблиц, диаграмм и графиков
- Причинно-следственная диаграмма. Также называемая диаграммой «рыбья кость», диаграммой Исикавы, причинно-следственной диаграммой и диаграммой «елочка». причины проблем и опасений при уходе за пациентами
- Блок-схема: эта диаграмма отображает этапы процессов и очень полезна для выявления ошибочных и проблемных процессов и этапов процесса.
- Контрольный лист: используется как для сбора, так и для визуализации данных. Они могут сигнализировать о некоторой частоте событий без выполнения сложной статистики.
- Линейный график: одна из самых простых диаграмм и графиков, имеющая две оси; вертикальная ось называется осью у, а горизонтальная ось — осью х.
- Гистограмма: график, аналогичный линейному графику, за исключением того, что гистограмма отображает данные в виде полос вдоль осей x и y, а не линий, как линейный график.

- Контрольная диаграмма: Также называемая диаграммой Шухарта, эта диаграмма основана на статистических данных, в отличие от многих других часто используемых диаграмм и графиков.
- Диаграмма Парето: комбинация гистограммы и контрольной диаграммы, которая отображает данные в порядке убывания.
- Гистограмма: Эти графики отображают данные о частоте в контексте ее распределения.
- Диаграмма рассеяния: Также называемая диаграммой рассеяния и диаграммой рассеяния, показывает корреляции двух переменных.
- Легенда: краткое изложение того, что изображено в таблице, диаграмме или графике
- Метки: Метки включают имя графика, которое сообщает вам, что изображено на графике, и имена осей x и y с точки зрения переменных, которые они представляют.
- Интервалы: Интервалы — это регулярно расположенные сегменты графика, которые помечены, чтобы мы могли определить точное или приблизительное значение для каждой точки данных.
- Оси: стандарт построения графиков указывает, что горизонтальная линия — это ось x, а вертикальная линия графика — это ось y.

- Исходная точка: исходная точка в таблице, диаграмме и графике иногда отображается как ноль, а иногда остается без метки, но понимается как ноль и обозначается как 0,0 в соответствии с декартовой системой координат.
- Декартова система координат: стандартизированная терминология для идентификации координат, которые представляют собой точки, в которых точка данных на оси x и точка данных на оси y идентичны. Эти координаты идентифицируются и помечаются двумя числами, разделенными запятой.
- Квадрант I: один из четырех квадрантов на графике, который имеет положительные числа по горизонтальной оси X и положительные числа по вертикальной оси Y. Квадрант I — это верхний правый угол графика с четырьмя квадрантами.
- Квадрант II: один из четырех квадрантов на графике, который имеет отрицательные числа по горизонтальной оси x и положительные числа по вертикальной оси y. Квадрант II — это верхний левый угол графика с четырьмя квадрантами.
- Квадрант III: один из четырех квадрантов на графике с отрицательными числами по горизонтальной оси x и отрицательными числами по вертикальной оси y.
 Квадрант III — нижний левый угол графика с четырьмя квадрантами.
Квадрант III — нижний левый угол графика с четырьмя квадрантами. - Квадрант IV: один из четырех квадрантов на графике, который имеет положительные числа по горизонтальной оси x и отрицательные числа по вертикальной оси y. Квадрант IV — нижний правый угол графика с четырьмя квадрантами.
Таблицы, диаграммы и графики
Таблицы, диаграммы и графики — прекрасный способ отображения данных и информации.
Некоторые из наиболее часто используемых таблиц, графиков и диаграмм:
- Диаграммы причинно-следственных связей, также называемые «рыбьей костью» или диаграммой Исикавы
- Блок-схема
- Контрольные листы
- Линейный график
- Гистограмма
- КРУГОВАЯ диаграмма
- Контрольные карты
- Гистограммы
- Диаграммы Парето
- Диаграммы рассеяния
Причинно-следственная диаграмма
Причинно-следственные диаграммы также называются диаграммой Исикавы для разработчика этой диаграммы, причинно-следственной диаграммой, диаграммой «рыбья кость» и диаграммой «елочка».
Диаграммы причинно-следственных связей очень полезны в деловом мире и в сфере здравоохранения, так как они могут определять причины дефектов продукции, а также причины проблем и проблем, связанных с уходом за пациентами. Выявление различных причин проблем облегчает исправление проблем и улучшение процессов для предотвращения проблем и дефектов в будущем.
На центральной продольной линии рыбьей кости обозначена проблема или дефект. Каждая из линий, отходящих от этой продольной линии «рыбьей кости», помечена для каждой из категорий возможных причин, а меньшие линии, являющиеся частью «рыбьей кости», помечены всеми возможными причинами дефекта или проблемы, которая исследуется.
Блок-схема
Простая блок-схема, представляющая процесс работы с неработающей лампой.
Блок-схемы отображают этапы процессов. Например, больница может захотеть увидеть процесс и рабочий поток для обработки лабораторного образца или визуализировать процессы заказа и обработки лекарств.
Блок-схемы часто используются для выявления ошибочных и проблемных процессов.
Контрольные листы
Контрольный лист используется для сбора и визуализации данных.
Данные контрольного списка могут использоваться для различных целей, включая, помимо прочего, построение графика с данными, которые были собраны в контрольном списке, и для получения представления о частоте события или проблемы. без использования сложной статистики.
Линейный график
Линейный график, пожалуй, самый простой из всех графиков и диаграмм, и они имеют некоторые общие черты с другими графиками и графиками. Например, линейные графики и другие диаграммы и графики имеют две оси. Вертикальная ось называется осью y, а горизонтальная ось — осью x, как показано на рисунке выше. Эти оси используются в других типах диаграмм и графиков, таких как контрольная диаграмма и гистограмма, например, как подробно описано ниже.
Линейные графики также имеют:
- Интервалы по осям x и y.
 Миллиметровая бумага используется, чтобы избежать необходимости рисовать эти интервалы вручную, как показано на графике выше.
Миллиметровая бумага используется, чтобы избежать необходимости рисовать эти интервалы вручную, как показано на графике выше. - Координаты точек пересечения линий интервалов по осям x и y.
- Точки, являющиеся точным расположением координат, представляющих данные. Точки обозначены точкой (.) на графике, как показано на графике ниже.
Когда координаты определены, они обозначаются двумя числами; одно из этих чисел — это точка, в которой проходит горизонтальная линия от исходной точки, а другое число — точка, в которой проходит вертикальная линия от исходной точки.
Координаты
Примеры координат:
- 4,3
- 5,9
- 6, 2
- 0,0
- -3, 8
- 8, -3
- -3, -5
Эти координаты в определенном порядке. Первый номер координаты — это точка на горизонтальной оси или оси x, а второй номер координаты — это точка на вертикальной оси или оси y.
Например, координата 6,8 находится в точке, где 6 появляется на оси x, а 8 находится на оси y, а координата 8,6 находится в точке, где 8 появляется на оси x и 6 находится на оси y.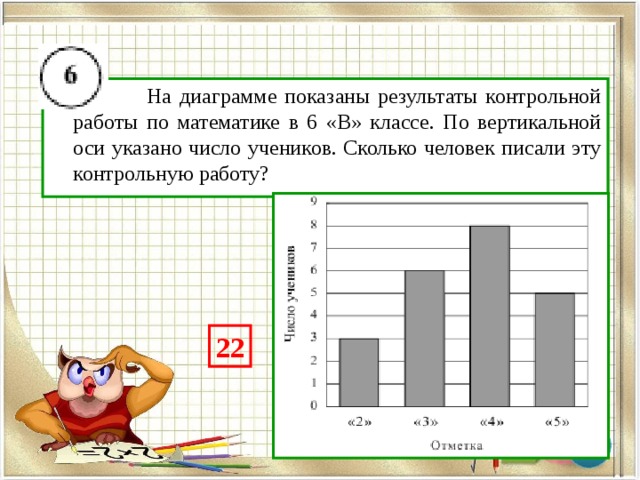 Вы должны знать, что, основываясь на этих двух примерах, порядок координат очень важен. Вы всегда должны размещать первое число координат по горизонтальной оси или оси x, а второе число координат по вертикальной оси или оси y. Если вы этого не сделаете, вы окажетесь не в том месте. Помните, сначала поместите первый номер координаты на горизонтальную ось или ось Y, а второй номер координаты на вертикальную ось или ось x.
Вы должны знать, что, основываясь на этих двух примерах, порядок координат очень важен. Вы всегда должны размещать первое число координат по горизонтальной оси или оси x, а второе число координат по вертикальной оси или оси y. Если вы этого не сделаете, вы окажетесь не в том месте. Помните, сначала поместите первый номер координаты на горизонтальную ось или ось Y, а второй номер координаты на вертикальную ось или ось x.
Некоторые линейные графики имеют начальную точку или ноль в центре графика, отрицательные значения слева от этой начальной точки по оси x и ниже исходной точки по оси y.
Другие, такие как приведенный ниже, не имеют центральной точки происхождения. Начальная точка этого графика, равная нулю, видна в левом нижнем углу этого графика и помечена как ноль (0).
Как вы можете видеть ниже, линейные графики могут включать несколько переменных, чтобы можно было увидеть визуальное сравнение данных.
Гистограмма
В некоторых отношениях гистограмма похожа на линейную диаграмму. Гистограмма отображает данные с полосами вдоль осей x и y. Гистограмма выше имеет:
Гистограмма отображает данные с полосами вдоль осей x и y. Гистограмма выше имеет:
- Интервалы вдоль осей x и y
- Координаты точек пересечения полос по осям x и y.
- Точки, являющиеся точным расположением координат, представляющих данные. Точки на гистограмме указаны вверху каждого столбца
Приведенная выше гистограмма представляет собой сравнение трех точек данных (восток, север и запад) и некоторых числовых значений во времени для 1 st , 2 nd 3 rd и 4 th кварталов год.
Хотя на приведенной выше гистограмме показаны вертикальные столбцы, гистограммы также можно построить с помощью продольных столбцов.
Круговая диаграмма
Круговая диаграмма, как следует из названия, представляет собой круговую диаграмму для отображения относительно простых и несложных данных. Круговые диаграммы, в отличие от линейных и гистограмм, не имеют интервалов, точек данных, координат, оси x или оси y.
Круговые диаграммы обычно используются для отображения частей целого, подобных правильным дробям. Например, можно использовать проценты или действительные числа. В приведенных выше примерах CDC и другие круговые диаграммы показывают проценты. Если вы сложите все проценты для обоих графиков, они дадут в сумме 100%, что является целым.
Контрольная диаграмма
Контрольные диаграммы, которые также называются диаграммами Шухарта по имени разработчика этой диаграммы или графика, процесс – поведенческая диаграмма или график, основаны на статистических данных, в отличие от многих других диаграмм и часто используемые графики.
Контрольные диаграммы могут содержать, например, среднее значение, диапазон, верхний и нижний пределы, стандартное отклонение и пропорции.
Гистограммы
На первый взгляд гистограмма выглядит как гистограмма, однако она отличается от гистограммы.
Гистограммы отображают данные частоты в контексте ее распределения. Они строятся с использованием частотных данных и размещения частотных данных так, чтобы они максимально приближались к колоколообразной кривой, как показано ниже.
Они строятся с использованием частотных данных и размещения частотных данных так, чтобы они максимально приближались к колоколообразной кривой, как показано ниже.
Диаграмма Парето
Диаграмма Парето, названная в честь разработчика, представляет собой комбинацию гистограммы и контрольной диаграммы. Диаграммы Парето отображают данные в порядке убывания. Как видно на диаграмме выше, данные по вертикальной оси представляют собой наибольшее значение, а остальные данные отображаются в порядке убывания или убывания.
Диаграмма рассеяния
Диаграмма рассеяния, также называемая диаграммой рассеяния и графиком рассеяния, показывает корреляции двух переменных. Как обсуждалось ранее, корреляция представляет собой отрицательную или положительную связь между двумя переменными. Положительная корреляция возникает, когда отношения между двумя переменными увеличиваются ИЛИ обе переменные уменьшаются. Отрицательная корреляция возникает, когда связь между двумя переменными заключается в том, что одна из переменных увеличивается, а другая уменьшается. Существует два типа корреляции. Корреляции могут быть положительными или отрицательными. Положительная корреляция возникает, когда как независимые, так и зависимые переменные увеличиваются или уменьшаются. Отрицательная корреляция возникает, когда одна из переменных увеличивается, а другая уменьшается.
Существует два типа корреляции. Корреляции могут быть положительными или отрицательными. Положительная корреляция возникает, когда как независимые, так и зависимые переменные увеличиваются или уменьшаются. Отрицательная корреляция возникает, когда одна из переменных увеличивается, а другая уменьшается.
Приведенная выше диаграмма рассеяния показывает положительную корреляцию, поскольку обе переменные по осям x и y увеличиваются вместе.
Структурные части таблиц, диаграмм и графиков
Таблицы, диаграммы и графики, как обсуждалось выше, могут дать нам много данных, которые затем можно интерпретировать для получения достоверной информации. Большинство таблиц, диаграмм и графиков показывают и отображают две переменные; эти таблицы, диаграммы и графики называются двумерными таблицами, диаграммами и графиками. Примеры двумерных таблиц, диаграмм и графиков включают диаграмму рассеяния и линейный график с двумя осями и двумя переменными. Точно так же некоторые таблицы, диаграммы и графики являются трехмерными с тремя переменными. Однако несколько редких таблиц, диаграмм и графиков показывают и отображают только одну переменную; эти таблицы, диаграммы и графики называются одномерными таблицами, диаграммами и графиками.
Однако несколько редких таблиц, диаграмм и графиков показывают и отображают только одну переменную; эти таблицы, диаграммы и графики называются одномерными таблицами, диаграммами и графиками.
Некоторые из структурных частей графика включают его:
- Легенда
- Этикетки
- Интервалы
- Оси
- Пункт отправления
Легенда
Легенда к таблице, диаграмме или графику дает вам краткую информацию о том, что изображено в таблице, диаграмме или графике. Обычно он размещается рядом с графиком в правом или левом верхнем углу или в правом или левом нижнем углу отображения графика и СНАРУЖИ точек данных, чтобы эти данные не были стерты.
Некоторые легенды относительно просты и понятны, например, приведенная ниже, которая дает вам информацию о полосах и их цветах, а также значениях каждой из них с точки зрения расположения внутри здания, такого как северное крыло, восточное крыло и западное крыло. крыло.
Метки
Метки являются неотъемлемой частью графика. Без меток вы не будете знать, что показывают данные и что они представляют. Метки включают имя графика и имена осей x и y.
Без меток вы не будете знать, что показывают данные и что они представляют. Метки включают имя графика и имена осей x и y.
Как показано на графике ниже, заголовок графика — «Высота черешневых деревьев»; ось X помечена как «Высота в футах», а ось Y помечена как «Частота».
Интервалы
Во всех таблицах, диаграммах и графиках должны быть четко обозначены интервалы. Эти помеченные интервалы позволяют нам определить точное или приблизительное значение для каждой точки данных. Без интервалов и меток интервалов мы бы не знали, например, сколько черешневых деревьев имеют определенную высоту, и не знали, какой высоты эти черешневые деревья.
На приведенной выше диаграмме интервалы высоты черешневых деревьев колеблются от 60 до 90 футов, и каждый интервал представляет собой интервал равный пяти футам, потому что слева направо по горизонтальной оси x высоты расположены в порядке возрастания. равны 60, 65, 70, 75, 80, 85 и 90.
Другой пример интервалов и маркировки интервалов показан ниже. Интервалы не обозначены на графике ниже так четко, как на графике выше. Поэтому вам необходимо определить вертикальный и горизонтальный интервалы на основе имеющейся у вас информации, чтобы вы могли получить более точные значения для каждой из точек данных.
Интервалы не обозначены на графике ниже так четко, как на графике выше. Поэтому вам необходимо определить вертикальный и горизонтальный интервалы на основе имеющейся у вас информации, чтобы вы могли получить более точные значения для каждой из точек данных.
Например, интервалы по оси Y указаны с шагом 1000, но отдельные горизонтальные линии интервалов не помечены. Вы можете определить и пометить эти точки следующим образом:
- Подсчитав немаркированные линии между помеченными линиями из 1000, чтобы найти 9 линий
- Определение того, что каждая немаркированная строка между помеченными строками из 1000 является приращением 100, поскольку между помеченными строками из 1000 есть 9 немаркированных строк
Затем вы можете пометить каждую из немаркированных горизонтальных линий интервала, например:
- 1100, 1200, 1300, 1400, 1500, 1600, 1700, 1800 и 1900 и как
- 100, 200, 300, 400, 500, 600, 700, 800, 900
Оси
Подавляющее большинство таблиц, диаграмм и графиков имеют оси. Исключением, например, является круговая диаграмма без оси.
Исключением, например, является круговая диаграмма без оси.
Стандарт построения графиков указывает, что горизонтальная линия представляет собой ось x, а вертикальная линия графика представляет собой ось y.
Место отправления
Исходная точка в таблице, диаграмме и графике иногда отображается как ноль, а иногда остается без метки, но понимается как ноль.
Некоторые графики, такие как приведенный выше, имеют точку начала отсчета или ноль в центре графика с отрицательными значениями слева от этой точки отсчета по оси X и ниже от точки отсчета по оси X. оси y и положительные значения справа от этой точки начала координат по оси x и выше точки начала координат по оси y. Другие, такие как показанное ниже только с положительными значениями, имеют исходную точку, поскольку ноль виден в левом нижнем углу этого графика и помечен как ноль (0).
Декартовы координаты
Как указано выше, некоторые графики имеют все положительные числа; тот, что ниже, имеет как положительные, так и отрицательные числа. Графики с положительными и отрицательными числами имеют четыре квадранта, как показано на графике ниже.
Графики с положительными и отрицательными числами имеют четыре квадранта, как показано на графике ниже.
Четыре квадранта на приведенном выше графике обозначены как I, II, III и IV.
- Квадрант I имеет положительные числа по горизонтальной оси x и положительные числа по вертикальной оси y.
- Квадрант II имеет отрицательные числа по горизонтальной оси x и положительные числа по вертикальной оси y.
- Квадрант III имеет отрицательные числа по горизонтальной оси x и отрицательные числа по вертикальной оси y.
- Квадрант IV имеет положительные числа по горизонтальной оси x и отрицательные числа по вертикальной оси y.
Стандартизированная терминология для идентификации координат, представляющих собой точки, в которых точка данных на оси X и точка данных на оси Y идентичны. Эти координаты идентифицируются и помечаются двумя числами, разделенными запятой. Одно из этих чисел — это точка, в которой проходит горизонтальная линия или ось x от исходной точки, а другое число — точка, в которой проходит вертикальная линия от исходной точки.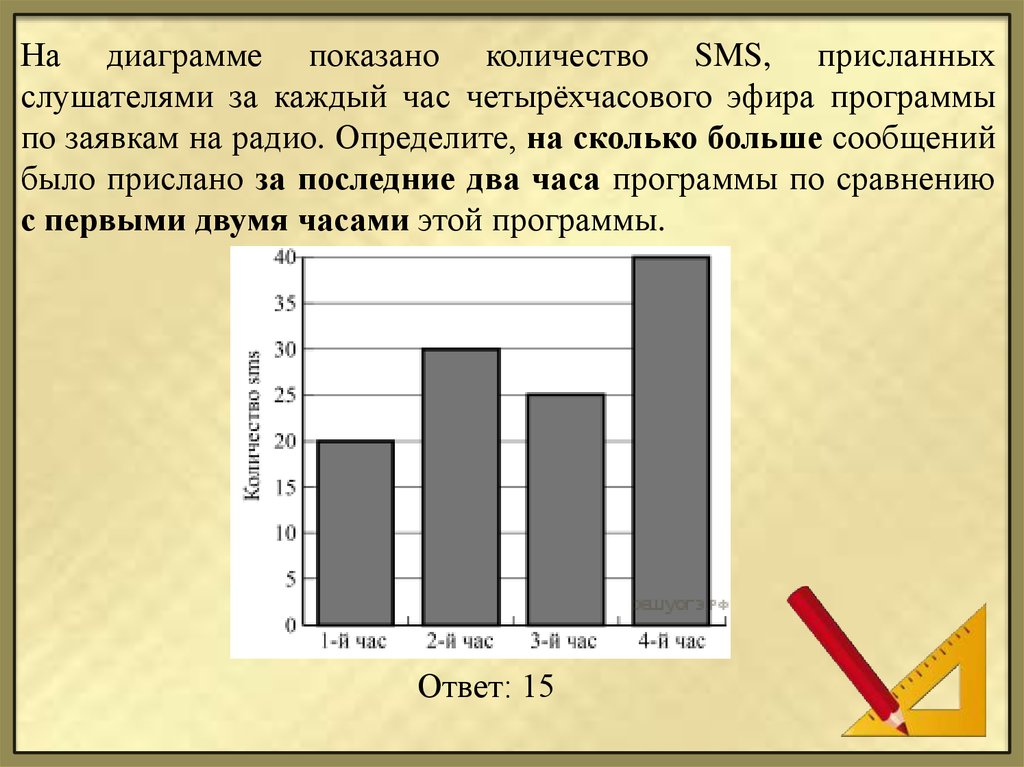 Он отображается как x, y.
Он отображается как x, y.
Исходная точка 0,0
Эта декартова система координат используется для интерпретации данных на графике, а также для построения графика путем нанесения точек на график.
Примеры координат:
- 4,3 где 4 по оси x и 3 по оси y
- 5,9, где 5 — по оси x, 9 — по оси y
- 6, 2, где 6 — по оси x, а 2 — по оси y
- 0,0, где 0 на оси x и 0 на оси y, и это исходная точка на четырехквадрантном графике
- -3, 8, где – 3 по оси x и 8 по оси y
- 8, -3, где 8 по оси X и -3 по оси Y
- -3, -5, где -3 по оси x и -5 по оси y
Глядя на координаты, перечисленные выше, вы можете не только нанести эти координаты на график, но и определить, в каком квадранте из четырех квадрантов находятся координаты.
Например, следующие координаты находятся в этих квадрантах. .
- 4,3 — это точка, где 4 находится на оси x, а 3 — на оси y, и она находится в квадранте I, потому что квадрант I имеет положительные числа по горизонтальной оси x и положительные числа по вертикальной оси y.
 . Квадрант I — единственный квадрант, в котором есть два положительных числа: одно по оси х, а другое — по оси у.
. Квадрант I — единственный квадрант, в котором есть два положительных числа: одно по оси х, а другое — по оси у. - 5,9 — это где 5 на оси x и 9 на оси y, и это также находится в квадранте I, потому что квадрант I имеет положительные числа по горизонтальной оси x и положительные числа по вертикальной оси y; квадрант I — единственный квадрант, в котором есть два положительных числа: одно по оси x, а другое по оси y.
- 6, 2 — это 6 по оси x и 2 по оси y. Опять же, обе эти координаты являются положительными числами и, следовательно, находятся в квадранте I.
- -3, 8 — это где — 3 по оси x и 8 по оси y, и это находится в квадранте II, потому что квадрант II имеет отрицательные числа по горизонтальной оси x и положительные числа по вертикальной оси y. Квадрант II — единственный квадрант, который имеет отрицательные числа по горизонтальной оси x и положительные числа по вертикальной оси y.
- В отличие от координат непосредственно выше, 8, -3, где – 3 находится на оси x и 8 на оси y, и эта точка находится в квадранте III.
 Квадрант III — единственный из четырех квадрантов, который имеет положительные числа по горизонтальной оси x и отрицательные числа по вертикальной оси y.
Квадрант III — единственный из четырех квадрантов, который имеет положительные числа по горизонтальной оси x и отрицательные числа по вертикальной оси y. - -3, -5, где -3 находится на оси x и -5 на оси y, и эта точка находится в квадранте III. Квадрант III — единственный из четырех квадрантов, который имеет отрицательные числа по горизонтальной оси x и отрицательные числа по вертикальной оси y.
СООТВЕТСТВУЮЩИЕ ИЗМЕРЕНИЯ И СОДЕРЖАНИЕ ДАННЫХ :
- Интерпретация соответствующей информации из таблиц, диаграмм и графиков (в настоящее время здесь)
- Оценка информации в таблицах, диаграммах и графиках с использованием статистики
- Объяснение связи между двумя переменными
- Расчет геометрических величин
- Преобразование внутри и между стандартной и метрической системами
- Автор
- Recent Posts
Alene Burke, RN, MSN
Alene Burke RN, MSN — признанный на национальном уровне преподаватель медсестер. Она начала свою трудовую деятельность учителем начальной школы в Нью-Йорке, а затем поступила в муниципальный колледж Квинсборо, чтобы получить степень младшего специалиста по сестринскому делу. Она работала дипломированной медсестрой в отделении интенсивной терапии местной больницы, и в это время она решила стать преподавателем медсестер. Она получила степень бакалавра наук в области сестринского дела в колледже Эксельсиор, входящем в состав Университета штата Нью-Йорк, и сразу после окончания учебы поступила в аспирантуру Университета Адельфи на Лонг-Айленде, штат Нью-Йорк. Она получила диплом с отличием в Адельфи, получив двойную степень магистра в области сестринского образования и управления сестринским делом, и сразу же начала работу над докторской диссертацией по сестринскому делу в том же университете. Она является автором сотен курсов для медицинских работников, включая медсестер, она работает консультантом по медсестрам в медицинских учреждениях и частных корпорациях, она также является утвержденным поставщиком непрерывного образования для медсестер и других дисциплин, а также является членом Американской ассоциации медсестер.
Она начала свою трудовую деятельность учителем начальной школы в Нью-Йорке, а затем поступила в муниципальный колледж Квинсборо, чтобы получить степень младшего специалиста по сестринскому делу. Она работала дипломированной медсестрой в отделении интенсивной терапии местной больницы, и в это время она решила стать преподавателем медсестер. Она получила степень бакалавра наук в области сестринского дела в колледже Эксельсиор, входящем в состав Университета штата Нью-Йорк, и сразу после окончания учебы поступила в аспирантуру Университета Адельфи на Лонг-Айленде, штат Нью-Йорк. Она получила диплом с отличием в Адельфи, получив двойную степень магистра в области сестринского образования и управления сестринским делом, и сразу же начала работу над докторской диссертацией по сестринскому делу в том же университете. Она является автором сотен курсов для медицинских работников, включая медсестер, она работает консультантом по медсестрам в медицинских учреждениях и частных корпорациях, она также является утвержденным поставщиком непрерывного образования для медсестер и других дисциплин, а также является членом Американской ассоциации медсестер.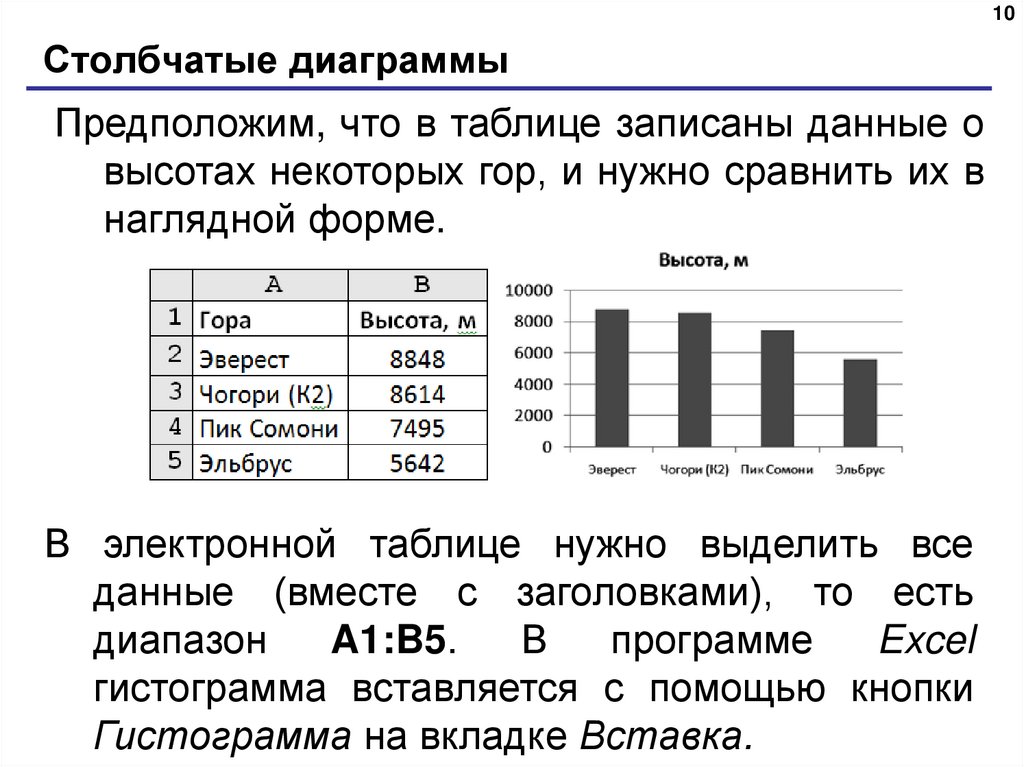 Целевая группа ассоциации по компетентности и обучению членов медсестер.
Целевая группа ассоциации по компетентности и обучению членов медсестер.
Последние сообщения Alene Burke, RN, MSN (см. все)
Таблицы и графики | Банки ресурсов для оценки
Крис Джойс, Алекс Нил, Верена Уотсон, Джонатан Фишер (2008)
- Что такое таблицы и графики?
- Почему мы хотим, чтобы учащиеся знали о таблицах и графиках?
- Учебная программа
- Ключевые компетенции
- Каковы проблемные области для студентов?
- Язык – Таблицы – Графики,
- Переменные – что это такое?
- Изготовление столов
- Цели – Структура – О чем может рассказать таблица – Ограничения
- Построение графиков
- Цели – Структура (гистограммы – линейные графики – круговые графики – гистограммы) – о чем может рассказать график – ограничения .

- Интерпретация таблиц и графиков
- Ключевые вопросы, которые нужно задать
- Значение для обучения
- Строительство — интерпретация
- Возможные успехи в обучении графам
- Ссылки
| Этот ресурс предназначен для использования учителями в целях их профессионального развития |
Что такое таблицы и графики?
Таблицы и графики являются визуальными представлениями. Они используются для организации информации, чтобы показать закономерности и отношения. График показывает эту информацию, представляя ее в виде фигуры. Исследователи и ученые часто используют таблицы и графики, чтобы сообщить о результатах своих исследований. В газетах, журналах и на телевидении они часто используются для поддержки аргумента или точки зрения.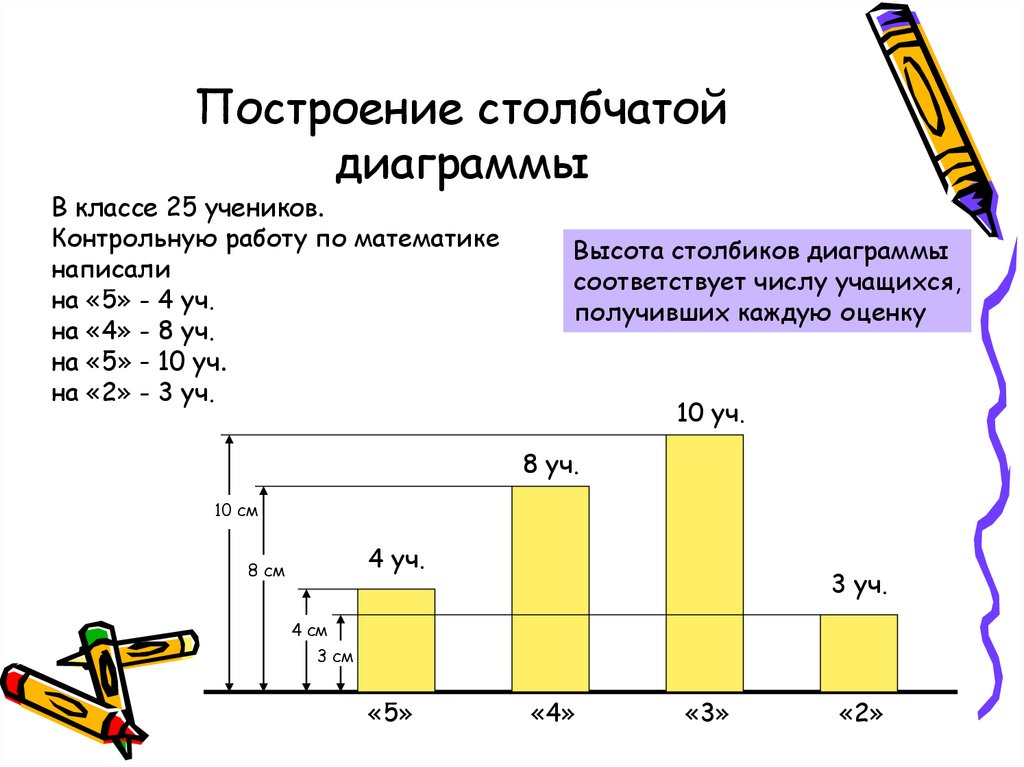
Почему мы хотим, чтобы учащиеся знали о таблицах и графиках?
Таблицы и графики могут быть полезными инструментами, помогающими людям принимать решения. Однако они представляют собой лишь часть истории. Часто приходится делать выводы из показанных данных. Помимо возможности четко определить, о чем говорит нам график или таблица, важно определить, каких частей истории не хватает. Это может помочь читателю решить, какая еще информация ему нужна, или следует ли отклонить аргумент, поскольку подтверждающие доказательства вызывают подозрения. Студенты должны знать, как критически анализировать данные и способ их представления. Таблица или график могут исказить информацию на
- упущение важной информации. Отсутствие учащихся – это пример графика с отсутствующими функциями.
- построение его таким образом, что оно искажает отношения. Это может быть из-за плохих навыков, или это может быть сделано преднамеренно, чтобы поддержать конкретный аргумент, например, с использованием 2-мерных форм для увеличения видимого роста.
 Примеры вводящих в заблуждение графиков см. в газетных статьях.
Примеры вводящих в заблуждение графиков см. в газетных статьях.
Легко, если учащиеся не умеют читать графики и таблицы, неправильно интерпретировать их. Они могут принимать неправильные решения, потому что основывают их на ложных выводах. При построении графиков и таблиц также возможно искажение данных. Исследования показывают, что учащиеся часто рассматривают таблицы и графики как самоцель. Немногие ссылаются на них как на источник доказательств или как на способ изучения закономерностей и взаимосвязей в данных или информации.
Учебная программа
Таблицы и графики относятся практически ко всем разделам учебной программы. Условные обозначения таблиц и графиков одинаковы для всех учебных программ. Именно контекст, в котором они используются, идентифицирует их как научные, социальные науки, географию и т. д. В таблице ниже приведены примеры ресурсов ARB по английскому языку, математике и естественным наукам, которые включают таблицы или графики.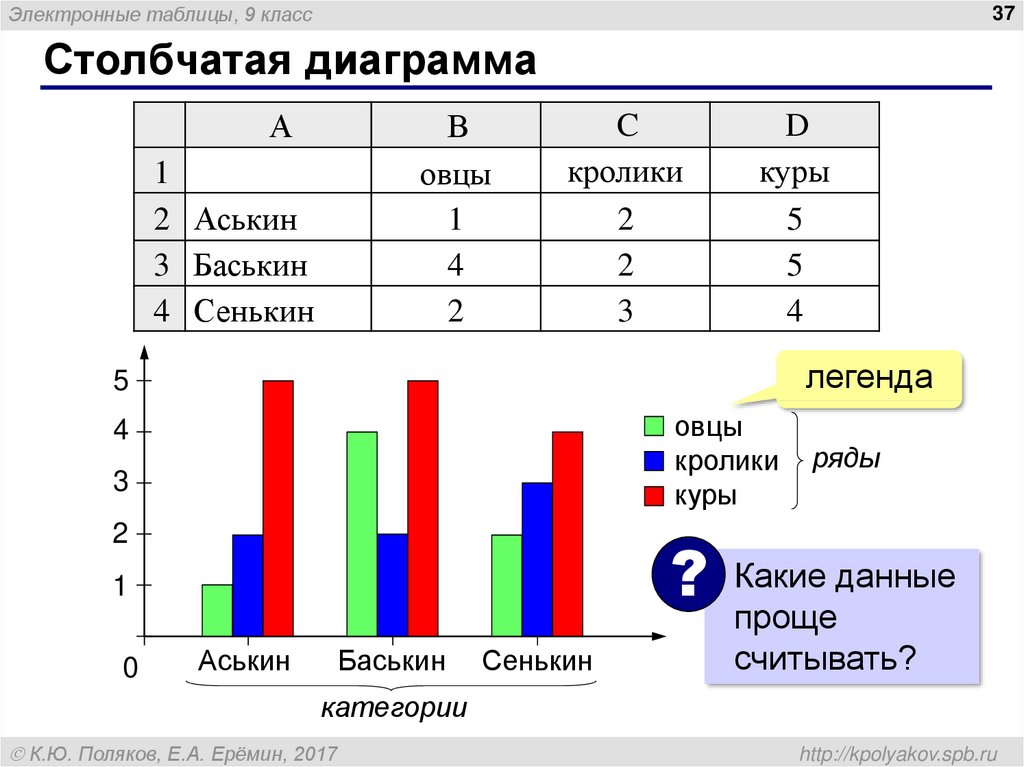
Примеры из банков ресурсов для оценки
| Столы | Графики |
| English Постройте график, чтобы показать тенденции в эмоциях персонажа, связанные с конкретным событием: Младенцы Катберта. | |
| Математика Заполните таблицу, чтобы показать сумму рождественской премии сотрудников, а затем используйте ее, чтобы подсчитать, сколько денег осталось: премия в размере 200 долларов. | Математика Заполните и с помощью таблицы начертите стоимость часа ремонта автомобиля: Техническое обслуживание автомобиля. |
| Наука Заполните таблицу о свойствах бумажных полотенец: лучший верх для протирки шваброй. | Естествознание Интерпретируйте график движения автомобиля и добавьте к графику дополнительное описание путешествия: Автомобильное путешествие. |
Ключевые компетенции
Изучение таблиц и графиков потенциально укрепляет несколько ключевых компетенций.
- Использование языка, символов и текстов: знание графиков и таблиц укрепляет способность учащихся получать доступ к идеям других и критиковать их. Это также помогает им эффективно общаться самостоятельно. Заявление о том, что учащиеся «уверенно используют ИКТ» (стр. 12), усиливает роль вспомогательных технологий в таблицах и графиках. Это должно включать организацию, анализ и осмысление информации, а также способность «получать доступ к информации и предоставлять ее, а также общаться с другими» (Министерство образования, 2007 г., стр. 12).
- Участие и вклад: интерпретация и критика иногда противоречивых данных является необходимым навыком для принятия решений. Таблицы и графики являются полезным инструментом для организации имеющихся данных для принятия решений. Они также являются полезным способом предоставления доказательств, чтобы убедить других в пользу определенного аргумента.
- Мышление: анализ и синтез данных из различных источников является важной частью аргументации и принятия решений.

Каковы проблемные области для студентов?
Национальный проект мониторинга образования (NEMP) определил два соответствующих набора навыков
- извлечение и интерпретация информации
- построение или заполнение графиков и таблиц.
NEMP (2003) сообщил, что многие новозеландские студенты
- не дали своим графикам и таблицам соответствующее название
- не правильно пометил оси
- испытывали трудности с работой более чем с одной переменной одновременно, т. е. со сравнением, расчетом и работой с несколькими источниками.
Испытания ресурсов ARB выявили дополнительные трудности для учащихся.
Язык
Некоторая техническая лексика может вызвать проблемы у некоторых учащихся.
- Таблицу иногда называют диаграммой. Это правильное использование, но может запутать учащихся.
Некоторые студенты знакомы только с бытовым значением таблицы. Эти учащиеся рисуют кухонный стол, когда их просят «нарисовать стол». Перейти к Языковые барьеры.
Эти учащиеся рисуют кухонный стол, когда их просят «нарисовать стол». Перейти к Языковые барьеры.
- В математике и естественных науках термин «диапазон» часто используется для обозначения одного числа, тогда как в повседневных ситуациях мы склонны использовать слово «диапазон» для обозначения набора чисел между нижним и верхним пределом. Например, в вопросе «Какой диапазон колебаний температуры показан в этом месте?» правильный ответ будет 14 °C, если диапазон интерпретируется в математическом смысле, и от 35°C до 49°C, если диапазон интерпретируется в повседневном контексте. Математика также называет ось Y графика диапазоном (ось X называется доменом).
Таблицы
В наших испытаниях ARB мы обнаружили, что большинство учащихся могут выполнять простые задания по чтению таблиц. У учащихся возникли трудности с:
- построение более сложных таблиц, например. двусторонние столы
- преобразование данных из текстов
- интерполяция и экстраполяция информации
- ответы на вопросы, связанные с вычислениями.

Другие области, которые вызывают затруднения у студентов:
Тем не менее, многие учащиеся также плохо справляются с подобными заданиями в контексте, отличном от таблиц. Организация информации в виде таблицы является полезной стратегией, помогающей учащимся развить эти навыки. |
Графики
В наших испытаниях ARB мы обнаружили, что учащиеся могут испытывать трудности с
- выбор подходящего графика для сообщения своих выводов
- предоставление названия для графика
- наименование осей
- чтение шкалы осей и сопоставление их с формой или тенденциями на графике
- выбор подходящего масштаба для использования при построении графиков
- маркировка узлов на осях через равные промежутки (хотя иногда допустима маркировка через неравные промежутки)
- включая единицы измерения (плюс любые множители) по каждой оси графика
- ответы на вопросы, связанные с вычислениями
- нанесение информации из статьи/письменного текста
- выявление тенденций, объяснение или синтез взаимосвязей между двумя графиками или двумя или более переменными
- чтение общей формы или тренда графика
- интерпретация графиков время/расстояние.
 Они читают или строят их как картину того, что произошло, например,
Они читают или строят их как картину того, что произошло, например,
интерпретируют, когда линия идет вверх, как движение в гору
, возвращаясь к исходной точке, чтобы добраться до «дома».
В 4 классе большинство учащихся могут прочитать информацию на простом графике. Круговые диаграммы могут быть более сложными, чем гистограммы или линейные диаграммы. В 8 классе многие учащиеся могут экстраполировать информацию из простого линейного графика. В 10-м классе большинство учащихся достаточно успешно преобразовывают простую таблицу в график.
| При принятии решений об интерпретации учащимися графиков важно также учитывать их знакомство с контекстом. Отсутствие знаний о контексте может повлиять на их способность интерпретировать график. |
Переменные – что это такое?
В графиках и таблицах компоненты, которые сравниваются или измеряются, называются переменными. Например, если вопрос: как меняется длина тени в течение дня? Длина тени — это одна переменная, а время суток — другая. Часто полезно описывать переменные как зависимые или независимые. Зависимые переменные — это то, что может изменяться по отношению к конкретным уровням независимых переменных. В приведенном выше примере
Например, если вопрос: как меняется длина тени в течение дня? Длина тени — это одна переменная, а время суток — другая. Часто полезно описывать переменные как зависимые или независимые. Зависимые переменные — это то, что может изменяться по отношению к конкретным уровням независимых переменных. В приведенном выше примере
- независимая переменная — время суток
- длина тени является зависимой переменной, так как зависит от времени суток.
Однако во многих случаях очевидной связи такого типа между переменными нет. В других ситуациях нас интересует, как многие переменные взаимодействуют друг с другом. Существует 4 основных типа переменных:
- категориальная переменная – описывается словом label, а не числом, например, разные марки бумажных полотенец
- упорядоченная переменная — категориальные переменные, которые можно упорядочить, например, прохладно, тепло, горячо
- дискретная переменная – описывается только целыми числами, например, 1, 2, 3 чайные ложки
- непрерывная переменная — описывается любым числом или номером детали, например, 35,5 °.

Исследование может иметь любую комбинацию переменных. Это определяется вопросом. Переменные, которые подвержены некоторым случайным статистическим ошибкам, известны как случайные переменные. Большинство переменных в реальных исследованиях относятся к этому типу (и обычно их просто называют переменными).
Составление таблиц
Столы
- организатор расследования
- способ представления данных в отчете
- органайзер для помощи пониманию и мышлению.
Цели
Для исследований без числовых данных обычно лучше использовать таблицу для представления данных. Таблицу с многочисленными переменными можно разбить на более мелкие таблицы, в которых каждая переменная рассматривается отдельно. Затем можно исследовать взаимодействие между различными переменными.
Структура
- Независимые переменные (если они были идентифицированы) помещаются в левые столбцы, а зависимые переменные — в правые.

| Независимая переменная → | Тип бумажного полотенца | Количество абсорбированной воды (мл) | ← Зависимая переменная |
- Любой заголовок столбца должен содержать всю информацию, необходимую для определения значения таблицы. Категориальная переменная должна включать описание класса. Дискретная или непрерывная переменная должна идентифицировать единицы и любые множители (например, сотни людей, миллионы долларов, километры).
- Заголовок резюмирует то, что показывает таблица.
- При расследовании порядок записей произвольный. При представлении результатов их следует сортировать по порядку.
- Иногда лучше поместить данные в диапазоны, например, < 10 лет, 10-15 лет, 16-20 лет… это делает их более управляемыми и позволяет легче увидеть тенденции и закономерности.
О чем может рассказать таблица
- Таблица помогает организовать информацию, чтобы было легче увидеть закономерности и взаимосвязи.

- Если переменная является непрерывной, таблица показывает намного больше информации. Он может показывать диапазон, интервал и количество показаний.
- Таблицы с несколькими переменными могут предоставить много информации. Их можно прочитать, выбрав и контролируя факторы для поиска закономерностей в данных.
Ограничения
- Может быть трудно увидеть числовые отношения и закономерности. График может сделать их более ясными.
- При объединении информации в группы не указывается, сколько их в каждой категории.
Построение графиков
Цели
Графики
- способ изучения отношений в данных
- способ отображения и представления данных, упрощающий отчет о шаблонах и отношениях, формах распределений и тенденциях.
Структура
Любой график, используемый для отчета о результатах, должен показывать
- существенные особенности и результаты расследования в честной и легко читаемой форме
- базовая структура исследования с точки зрения взаимосвязей между переменными и внутри них
- единицы измерения
- количество чтений (хотя иногда они будут в сопроводительном тексте)
- диапазон и интервал показаний, где это необходимо.

Хорошей практикой (но только соглашением) является размещение зависимой переменной по горизонтальной оси (x), а независимой по вертикальной оси (y).
Гистограммы
Гистограммы следует использовать для категориальных, упорядоченных и дискретных переменных. Если количество единиц в дискретной переменной велико, она может отображаться как непрерывная переменная.
Линейные графики
Линейные графики следует использовать для непрерывных переменных.
Круговые диаграммы
Круговые диаграммы (иногда называемые круговыми или круговыми диаграммами) используются для отображения частей, составляющих единое целое. Они могут быть полезны для сравнения размеров относительных частей. Поскольку трудно сравнивать разные круговые диаграммы и часто трудно сравнивать углы разных секторов круговой диаграммы, иногда лучше выбирать другие виды диаграмм.
| Гистограммы Используйте гистограммы, когда по оси Y указана частота или появление непрерывных данных, отсортированных по группам, например, 20–24 метра.  Все полосы обычно имеют одинаковую ширину. Их можно превратить в линейные графики, соединив середину верхней части каждой вертикальной полосы. Гистограммы не являются объединенными столбчатыми диаграммами и не должны использоваться для категорийных данных (если количество единиц в каждой группе не велико). Все полосы обычно имеют одинаковую ширину. Их можно превратить в линейные графики, соединив середину верхней части каждой вертикальной полосы. Гистограммы не являются объединенными столбчатыми диаграммами и не должны использоваться для категорийных данных (если количество единиц в каждой группе не велико). |
О чем может рассказать график
На графике вы видите общую форму переменной или отношения между переменными. Линейный график представляет собой числовое или математическое соотношение, поэтому в нем «спрятано» больше информации, чем в других графиках. Линейные графики иногда можно использовать для прогнозирования значений, которые не были измерены, путем интерполяции или экстраполяции тренда или анализа формы.
Ограничения:
- Графики могут многое рассказать о ходе расследования, но не все. Например, они обычно не сообщают вам, какие переменные контролировались, размер выборки или метод измерения.
 Таким образом, есть много вопросов, которые нужно задать, чтобы узнать о достоверности и надежности, а также о фактическом контексте расследования.
Таким образом, есть много вопросов, которые нужно задать, чтобы узнать о достоверности и надежности, а также о фактическом контексте расследования. - Шкалы на осях можно растягивать или сужать, чтобы подчеркнуть одну сторону взаимосвязи или подчеркнуть точку зрения, которая может не подтверждаться данными.
- График подразумевает отношение, но не обязательно причину. Например, график может показать, что в марте дома стоили меньше, чем в феврале, но он не показывает, почему это произошло. Мы можем сделать вывод, что это потому, что процентные ставки выросли.
Интерпретация таблиц и графиков
Готт и Дагган определили уровни сложности чтения, интерпретации и анализа данных, представленных в таблицах и графиках. К ним относятся
- считывание определенных данных с точек в таблице или на графике (просто)
- выбор разделов релевантных данных из сложных наборов данных (более сложных)
- выявление и интерпретация закономерностей в различных типах данных (наиболее сложных).

Исследование 12- и 14-летних детей показало, что отдельные учащиеся по-разному замечали закономерности линейных графиков. Их ответы были сгруппированы в пять категорий.
Как учащиеся интерпретировали линейные графики:
| Категория | Описание | Пример ответа учащегося |
| Без шаблона | — | — |
| Числовые образцы | Идентифицированные числовые закономерности, сгенерированные по одной или обеим осям. Они не имели отношения к «сообщениям» графиков. Некоторых студентов отвлекли от обобщения взаимосвязей очевидные числовые закономерности. | Числа, если расставить их по порядку, становятся четными, нечетными, нечетными, четными и так далее. |
| Графические узоры | Описал форму или направление линии. Эти студенты не связывали эту форму с тем, что представляли оси. | Он опускается, а затем снова поднимается. |
| Несвязанные тенденции в переменной | Описал общую тенденцию в отдельных переменных, но не связал их друг с другом, или описал тенденцию в одной переменной, но не в другой. | Длина тени уменьшилась. |
| Обобщенные отношения между переменными | Удалось обобщить взаимосвязь между зависимыми и независимыми переменными. Предыдущий опыт контекста, по-видимому, был фактором, позволяющим делать обобщения. | Чем выше был брошен мяч, тем выше он отскочил. |
Основные вопросы, которые необходимо задать
Вопросы ниже
- помочь учащимся критически анализировать свои собственные и чужие таблицы и графики
- предоставить учителям полезные учебные моменты, когда они планируют следующее обучение
Учителя должны учитывать возраст своих учеников и переформулировать на соответствующем уровне.
Вопросы
По материалам Gott and Duggan (2003) |
Значение для обучения
Строительство
- Учите не только согласованным условностям, но и их причинам.

- Студенты с большей вероятностью будут включать заголовки и называть оси, если они понимают их цель.
- Помогите учащимся подумать о наиболее подходящем типе таблицы или графика для представления их данных.
- Помогите учащимся выбрать подходящий масштаб для своих данных.
- Младшим ученикам может быть полезно физически представлять данные с помощью реквизита, включая самих себя.
- Интерактивные доски, электронные таблицы Excel, графические калькуляторы и другие формы ИКТ успешно используются некоторыми учителями для развития навыков построения графиков. Некоторые компьютерные программы могут быть использованы для построения графиков. Обсуждение является важной частью использования этих реквизитов и инструментов.
- Развитие словарного запаса для описания частей таблиц и графиков.
Интерпретация
- Помогите учащимся исследовать историю, рассказанную таблицей или диаграммой.
- Предложите учащимся попрактиковаться в изучении взаимосвязей, представленных в таблицах и графиках, и в выводах из них.

- Научите учащихся разбивать график на части, читать отдельно, а затем реконструировать, чтобы рассказать историю.
- Предложите учащимся решить, какую еще информацию им нужно знать, прежде чем они смогут принимать решения на основе представленных данных.
- Развивайте словарный запас, который описывает и сравнивает.
Возможные успехи в обучении графам
Прогрессии в построении и интерпретации графиков следует использовать с осторожностью. Уровень навыков учащихся, вероятно, зависит от
- их знакомство с контекстом, в котором они работают в
- сложность контекста они работают в
- сложность данных
- сложность построения графика.
Тем не менее, следующая таблица дает некоторые полезные рекомендации.
| Строительство | Интерпретация | |
1. | При поддержке:
| Считать данные с отмеченных точек Описать закономерность, показанную на графике |
| 2. | Независимо:
| Считать данные из любых точек Описать взаимосвязь, представленную на графике Распознать и дать простое объяснение несоответствия данных, показанных на графике |
| 3. | При поддержке выберите соответствующий график и масштаб Нанесите два (или более) набора данных на одну и ту же ось. | Описывать взаимосвязи между переменными, включая зависимые и независимые, если это уместно Выявлять и объяснять аномальные результаты Интерпретировать информацию из графика Делать выводы о неизвестных значениях, используя форму графика для прогнозирования повторяющейся модели При поддержке использовать закономерности на графике как доказательство.  |
| 4. | Выберите подходящий график и масштаб Знайте, когда и как провести линию наилучшего соответствия. Самостоятельно построить ряд более сложных графиков | Делайте выводы и прогнозы на основе графиков и обосновывайте Делайте выводы, согласующиеся с графическими данными. Использовать закономерности и взаимосвязи, представленные на графиках, для вынесения суждений Критиковать интерпретации графиков другими, оценивая информацию, показанную на графике, и то, как она представлена. |
Ссылки
- Остин, Р., Холдинг, Б., Белл, Дж. и Дэниэлс, С. (nd). Оценка имеет значение: No.7. Модели и отношения в школьной науке. Лондон: СЕАК.
- Флоктон Л., Крукс Т. и Гилмор А. (2004). Графики, таблицы и карты: результаты оценки 2003 г. Данидин: отдел исследований в области образования, Университет Отаго.
- Голдсуорси, А. (2004). Приобретение научных навыков (см.
 особенно страницы 40-49). В Sharp, J. (ред.) (2004). Развитие первичной науки. Эксетер: Обучение имеет значение. Получено 10 мая 2008 г. с http://www.learningmatters.co.uk/sampleChapters/pdfs/DPS03.pdf .
особенно страницы 40-49). В Sharp, J. (ред.) (2004). Развитие первичной науки. Эксетер: Обучение имеет значение. Получено 10 мая 2008 г. с http://www.learningmatters.co.uk/sampleChapters/pdfs/DPS03.pdf . - Готт, Р. и Дагган, С. (2003). Понимание и использование научных данных: как критически оценивать данные. Лондон: публикации SAGE.
- Министерство образования (2007 г.). Учебная программа Новой Зеландии. Веллингтон: обучающие СМИ.
Math Scene — Графики неравенств и таблицы знаков
Math Scene — Графики неравенств и таблицы знаков 2008 Расмус Эхф | Печать |
Как
можем ли мы решить квадратное неравенство, такое как x 2 − 1 0 ?
Если
решаем соответствующее квадратное уравнение, получаем два решения.
х 2 — 1 = 0
(х + 1)(х — 1) = 0
Решения: x = 1 и х = −1.
Мы нашли точки, где выражение равно 0, теперь нам нужно найти, где меньше 0. Другими словами, мы должны выяснить, когда выражение отрицательный. Для этого рассмотрим признаки множители (x + 1) и (x − 1) . Другими словами, мы ищем интервалы, в которых они положительны или отрицательны. Для этого делаем таблицу знаков
Начнем с того, что подставим 0 в значения, где каждый из
факторы равны нулю. (x+1) = 0, когда x = −1, и (x − 1) = 0
когда x = 1. Затем мы ставим + или — в зависимости от того, являются ли факторы
положительный или отрицательный. Теперь мы можем использовать
эту информацию для решения неравенства.
Мы знаем, что (x + 1)(x — 1) = x 2 — 1.
Мы также знаем, что −∙− = + и +∙+
= +. Это означает, что выражение (x + 1)(x − 1)
положительна, когда обе скобки имеют одинаковый знак, и отрицательна, когда они
имеют противоположные знаки. Теперь мы можем заполнить таблицу. Мы ищем
интервал, на котором x 2 − 1 < 0, то есть отрицательно.
Теперь мы можем заполнить таблицу. Мы ищем
интервал, на котором x 2 − 1 < 0, то есть отрицательно.
Этот интервал удовлетворяет неравенству.
−1 х 1
Теперь давайте решим неравенство без факторизации первый.
Мы просто находим корни, решая соответствующие уравнение, а затем подставьте любое значение x между этими корнями. .
Если мы выберем, например, x = 0, мы получим следующее
Если f(x) = x 2 − 1, тогда f(0) = 0 2 — 1 = -1.
Это показывает нам, что f(x) = x 2 − 1 отрицательно на интервале
−1 х 1 .
Если мы попробуем любое значение x, которое меньше -1 og больше 1 мы получаем положительные значения для функции. Итак, линия реального числа будет выглядеть так:
Решение
Мы также можем найти решение, посмотрев на график
f(x) = x 2 — 1 . Решение x 2 − 1 0
это интервал, в котором график лежит на оси x или ниже нее.
Решение x 2 − 1 0
это интервал, в котором график лежит на оси x или ниже нее.
Посмотрите на график ниже.
График лежит на оси x или вокруг нее на интервале −1 х 1 (заштрихованная область графика).
Если мы перевернем знак неравенства, какое решение из
х 2 − 1 0?
Глядя на график, площадь над осью x удовлетворяет этому условию. Если мы посмотрим на таблицу знаков, то там, где выражение положительное.
Решение: x −1 Решение: х 1
Решение неравенства х 2 − 1 0 состоит из двух частей.
х −1 или х 1.
Пример 1
Решить неравенство x 2 − 2x − 3 < x + 1,
Первый решаем соответствующее уравнение х 2 — 2х — 3 = х + 1
х 2 — 2х — 3 = х + 1
х 2 — 3х — 4 = 0
(х + 1)(х — 4) = 0
Решение: х = -1 и х = 4
Следующий
делаем таблицу признаков.
Решение: −1 < x < 4
Если мы нарисуем два графика в одной координате
система
f (х) = х 2 — 2х
− 3 и g(x) = x + 1, то мы ищем область, в которой f(x) (
левая часть выражения ) меньше, чем g(x) (правая часть).
Это заштрихованная область графика, где x принимает значения от -1 до
4.
Пример 2
| Решить неравенство |
Начнем с рассмотрения знаков числителя (x + 1) и знаменатель (x − 1). Те же правила применяются для деления что касается умножения. (-/- = + и -/+ = -). Итак, если числитель и знаменатель совпадают знак, что результат положительный. Если они имеют противоположные знаки, то результат равен отрицательный
Решение
Теперь нам нужно позаботиться о том, чтобы x не мог быть равен
на 1, потому что тогда мы будем делить на 0.
Таким образом, решение равно −1 . х < 1.
х < 1.
Рисуем график, предварительно составив таблицу значений.
Х | f(x) = (x + 1) / (x — 1) | |
| -2 | ≈ 0,3 | |
| -1 | 0 | |
| 0 | -1 | |
| -3 | ||
| 1 | асимптота | |
1 | 5 | |
| 2 | 3 | |
| 3 | 2 |
График имеет вертикальную асимптоту, когда x = 1 и
лежит под осью x на интервале между −1 и 1 (заштрихованная
область).
Решить
Мы начинаем с перемещения 1 к другому часть уравнения, оставив там 0. Мы можем пользоваться таблицей знаков только в том случае, если правая часть равна нулю.
| Мы Найдите общий знаменатель и упростите дробь. |
Далее делаем таблицу знаков.
Решение х < 1
Теперь рисуем графики левой части и правая часть неравенства. Левая сторона такая же, как в пример 2. Правая часть g(x) = 1 (горизонтальная линия, на единицу выше x оси).
Мы видим, что график f(x) находится под графиком g(x) для всех значений x слева от вертикальная асимптота x = 1 (см. заштрихованную область). х = 1 не включены в решение, так как это означало бы, что мы делим на ноль.
Пример 4 Решить неравенство x 2 < х.
Уравнение x 2 = х имеет решения х = 0 и х = 1.
x 2 < х
х 2 − х < 0 | Упорядочить оба члена в левой части |
Выберите значение x между 0 и 1, например, и введите значение в функцию.
f(x) = x 2 − х
Результат отрицательный, поэтому знак f(x) такой, как показано ниже.
не существует
Решение: 0 < x < 1
Теперь посмотрите на график левой и правой руки. стороны.
График f(x) = x 2 находится ниже графика g(x) = х включено интервал от 0 до 1. (см. заштрихованную область).
Пример 5Решить неравенство ln x л 1 / х .
Максимально упрощаем и переносим оба термина в
левую часть уравнения.


 RU
RU
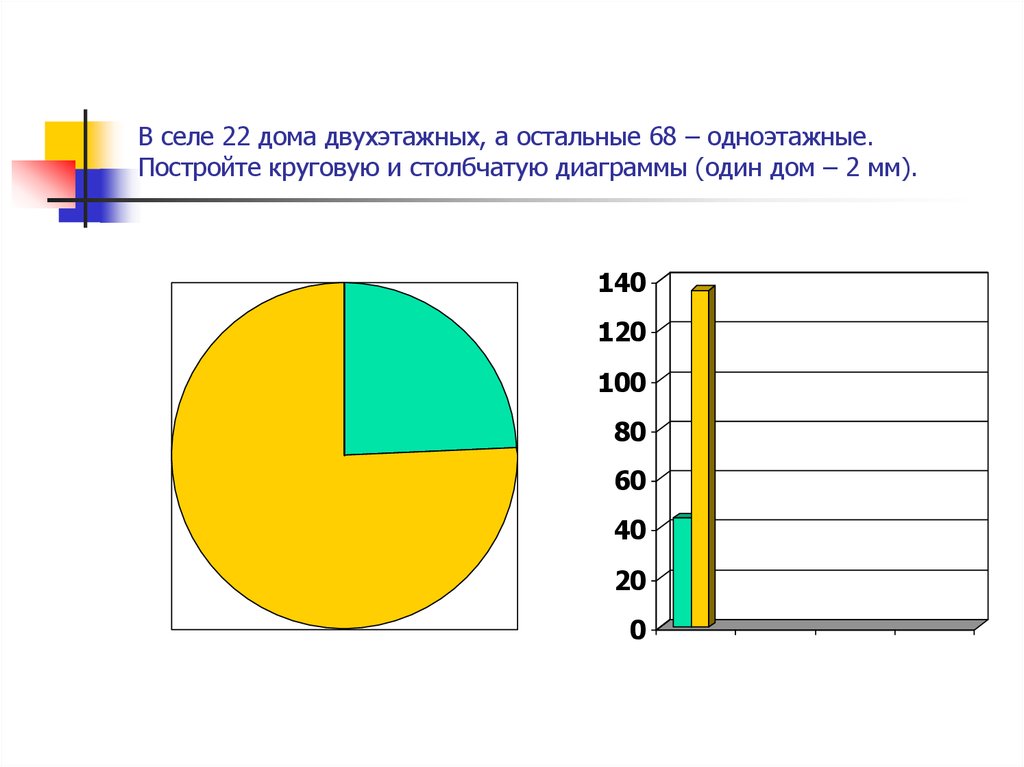 RU
RU
 )
)
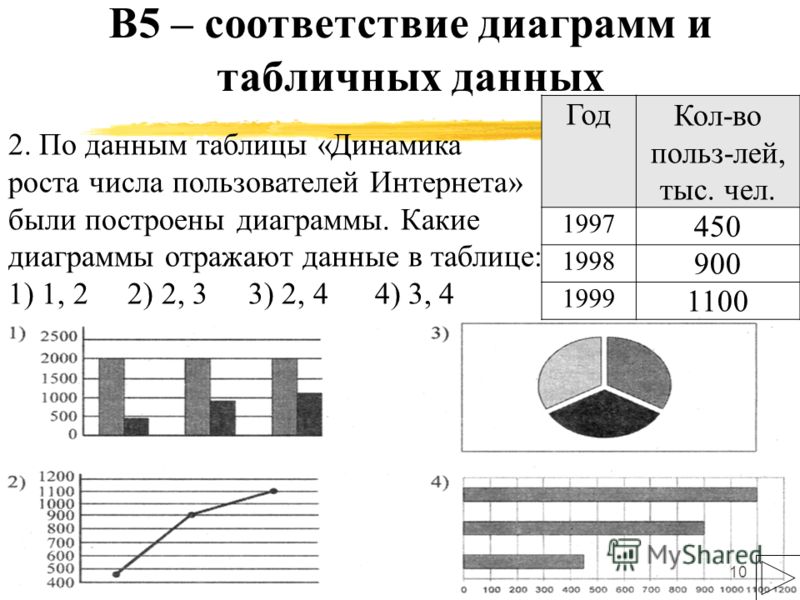

 Вам придется купить (и стереть) десятки или даже сотни билетов, чтобы действительно увидеть тенденцию. Более совершенный график глобального потепления показал бы тенденцию со времен промышленной революции.
Вам придется купить (и стереть) десятки или даже сотни билетов, чтобы действительно увидеть тенденцию. Более совершенный график глобального потепления показал бы тенденцию со времен промышленной революции. Только 11% владельцев 360 активно используют свои 360 и только 10% владельцев PS3 активно используют свои PS3. Теперь давайте немного посчитаем.
Только 11% владельцев 360 активно используют свои 360 и только 10% владельцев PS3 активно используют свои PS3. Теперь давайте немного посчитаем. С другой стороны, цифра «люди с полной занятостью», которую использовал Фокс, включала только работающих, а не лиц, проживающих в домашнем хозяйстве, где работает хотя бы один человек».
С другой стороны, цифра «люди с полной занятостью», которую использовал Фокс, включала только работающих, а не лиц, проживающих в домашнем хозяйстве, где работает хотя бы один человек».
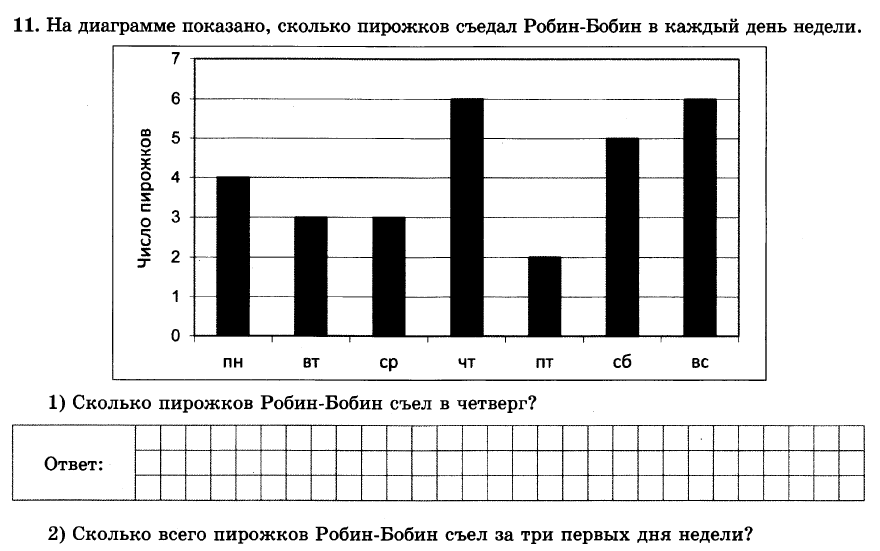
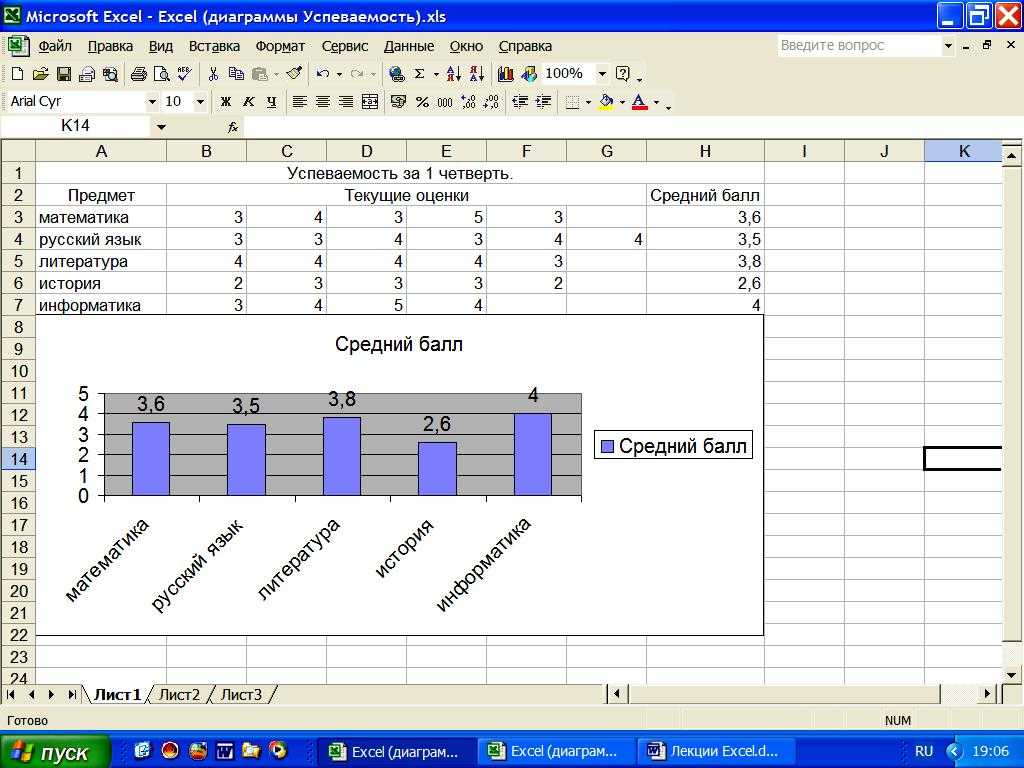
 Квадрант III — нижний левый угол графика с четырьмя квадрантами.
Квадрант III — нижний левый угол графика с четырьмя квадрантами.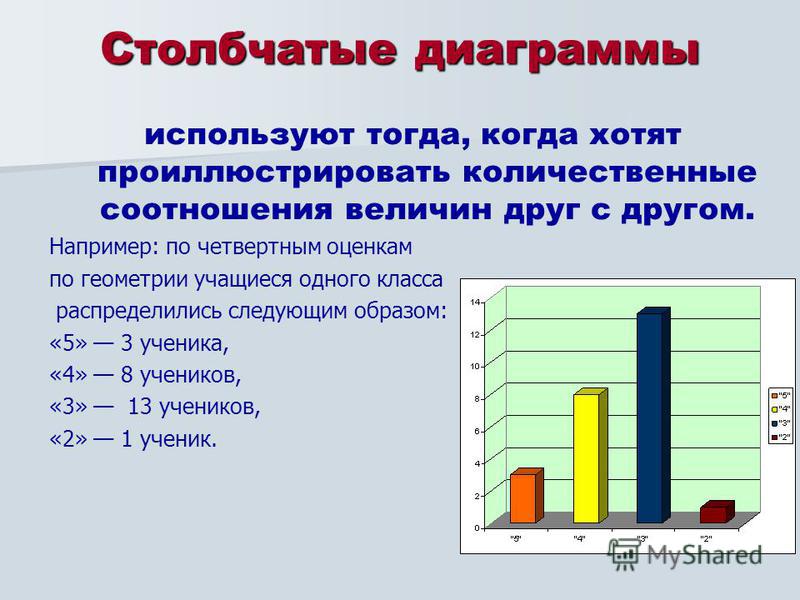 Миллиметровая бумага используется, чтобы избежать необходимости рисовать эти интервалы вручную, как показано на графике выше.
Миллиметровая бумага используется, чтобы избежать необходимости рисовать эти интервалы вручную, как показано на графике выше.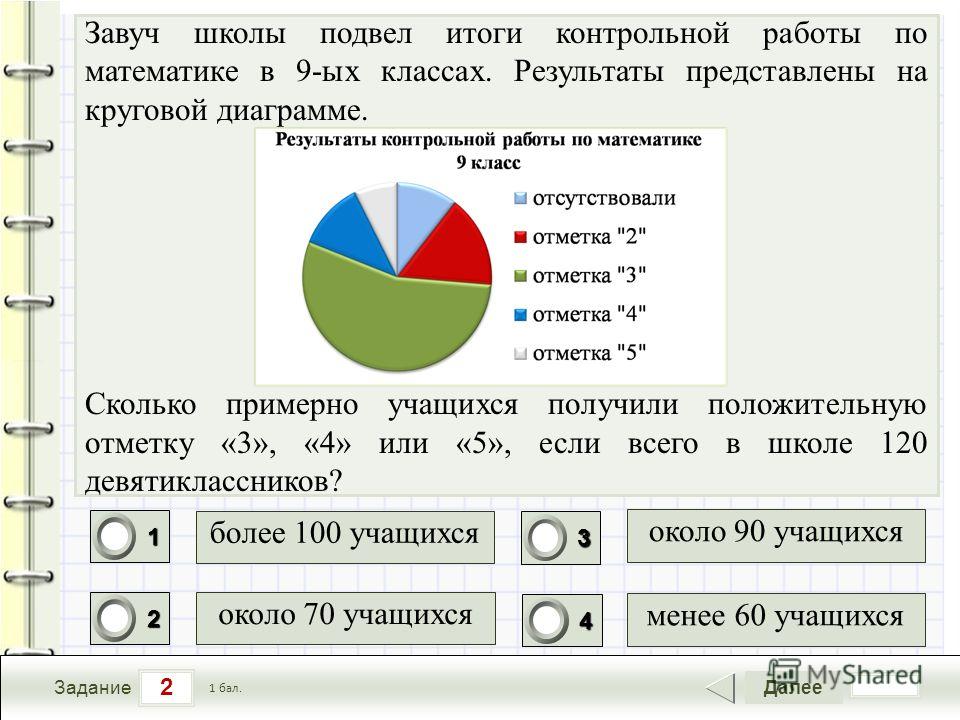 . Квадрант I — единственный квадрант, в котором есть два положительных числа: одно по оси х, а другое — по оси у.
. Квадрант I — единственный квадрант, в котором есть два положительных числа: одно по оси х, а другое — по оси у.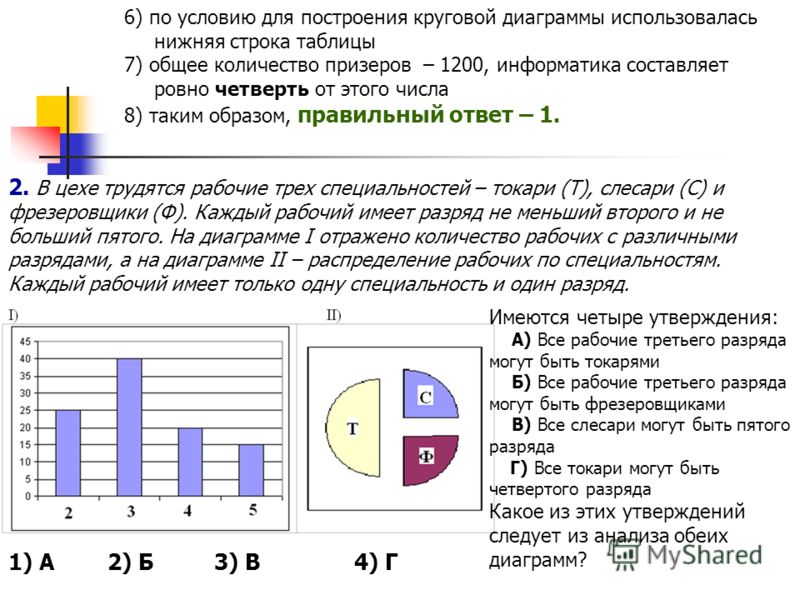 Квадрант III — единственный из четырех квадрантов, который имеет положительные числа по горизонтальной оси x и отрицательные числа по вертикальной оси y.
Квадрант III — единственный из четырех квадрантов, который имеет положительные числа по горизонтальной оси x и отрицательные числа по вертикальной оси y.
 Примеры вводящих в заблуждение графиков см. в газетных статьях.
Примеры вводящих в заблуждение графиков см. в газетных статьях.