Взаимное расположение прямых в пространстве видеоурок: Взаимное расположение прямых в пространстве. Угол между двумя прямыми — урок. Геометрия, 10 класс.
Геометрия Скрещивающиеся прямые
Материалы к уроку
Конспект урока
Скрещивающиеся прямые
|
Вам уже известны два случая взаимного расположения прямых в пространстве:
Вспомним их определения. Определение. Прямые в пространстве называются пересекающимися, если они лежат в одной плоскости и имеют одну общую точку Определение. Прямые в пространстве называются параллельными, если они лежат в одной плоскости и не имеют общих точек.
Общим для этих определений является то, что прямые лежат в одной плоскости.
|
Прямые а и b – пересекаются.
Прямые a и b параллельны
|
|
В пространстве так бывает не всегда. Мы можем иметь дело с несколькими плоскостями, и не всякие две прямые будут лежать в одной плоскости. Например, ребра куба ABCDA1B1C1D1 AB и A1D1 лежатв разных плоскостях.
|
AB и A1D1 лежат в разных плоскостях. |
|
Определение. Две прямые называются скрещивающимися, если не существует такой плоскости, которая б проходила через эти прямые. Из определения понятно, что данные прямые не пересекаются и не параллельны.
|
Определение . Две прямые называются скрещивающимися, если не существует такой плоскости, которая б проходила через эти прямые. Две прямые называются скрещивающимися, если не существует такой плоскости, которая б проходила через эти прямые.
|
|
Докажем теорему, которая выражает признак скрещивающихся прямых. Теорема (признак скрещивающихся прямых). Если одна из прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке не принадлежащей этой прямой, то эти прямые скрещивающиеся.
|
Теорема (признак скрещивающихся прямых). Если одна из прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке не принадлежащей этой прямой, то эти прямые скрещивающиеся.
|
|
Дано. Прямая AB лежит в плоскости α. Прямая CD пересекает плоскость α в точке С, не принадлежащей прямой АВ. Доказать, что прямые AB и DC – скрещиваются. Доказательство Доказательство будем вести методом от противного.
Допустим, АВ и CD лежат в одной плоскости, обозначим ее β. Тогда плоскость β проходит через прямую AB и точку C.
По следствию из аксиом, через прямую AB и не лежащую на ней точку C можно провести плоскость, и притом только одну. Но у нас уже есть такая плоскость — плоскость α. Следовательно, плоскости β и α совпадают.
Но это невозможно, т.к. прямая CD пересекает α, а не лежит в ней. Мы пришли к противоречию, следовательно, наше предположение неверно. AB и CD лежат в разных плоскостях и являются скрещивающимися. Теорема доказана.
|
Дано: AB⊂α CD ∩ α=C, C ∉ AB Доказать: AB скрещивается с DC
Доказательство Допустим, АВ и CD лежат в некоторой плоскости β. Тогда плоскость β проходит через прямую AB и точку C. Через прямую AB и не лежащую на ней точку C можно провести плоскость, и притом только одну (следствие из аксиом). Следовательно, β≡α. Но это невозможно, т.к. прямая CD пересекает α. Пришли к противоречию, ⇒ AB и CD лежат в разных плоскостях (скрещиваются). Теорема доказана.
|
|
Итак, возможны три способа взаимного расположения прямых в пространстве: А) Прямые пересекаются, т.е имеют только одну общую точку. Б) Прямые параллельны, т.е. лежат в одной плоскости и не имеют общих точек. В) Прямые скрещиваются, т.е. не лежат в одной плоскости. |
Взаимное расположение прямых в пространстве |
|
Рассмотрим еще одну теорему о скрещивающихся прямых Теорема.
Дано: АВ и CD – скрещивающиеся прямые Доказать, что существует плоскость α такая, что прямая AB лежит в плоскости α, а прямая CD параллельна плоскости α.
Доказательство Докажем существование такой плоскости.
Плоскость α — искомая плоскость.
Докажем, что плоскость α – единственная, удовлетворяющая условию.
Любая другая плоскость, проходящая через прямую АВ, будет пересекать AE, а значит и параллельную ей прямую CD. Т.е., любая другая плоскость, проходящая через AB пересекается с прямой CD, поэтому не является ей параллельной. Следовательно, плоскость α – единственная. Теорема доказана.
|
Теорема. Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна. Дано: АВ и CD – скрещивающиеся прямые Доказать: ∃ α: AB ⊂α, CD∥α
Доказательство Докажем существование.
Плоскость α — искомая плоскость.
Докажем единственность.
Любая другая плоскость будет пересекать AB, а значит и параллельную ей прямую CD. Поэтому α – единственная. Теорема доказана
|
|
Перейдем к задачам. Точка D не лежит в плоскости треугольника ABC, точки M, N, и P – середины отрезков DA, DB, и DC соответственно, точка K лежит на отрезке BN. Выясните взаимное расположение прямых: а) ND и AB; б) PK и BC; в) MN и AB; г) MP и AC; д) NK и AC; е) MD и BC.
Решение а) ND пересекается с AB в точке B, поскольку N лежит между B и D; б) PK пересекается с BC, поскольку PK не является средней линией BCD и поэтому не параллельна BC. в) MN параллельна AB, т.к. MN – средняя линия ABD. Средняя линия треугольника параллельна основанию. г) MP параллельна AC, т.к. MP – средняя линия ACD; д) NK и AC скрещивающиеся, т.к. они не принадлежат одной плоскости; е) MD и BC – скрещивающиеся, т.к.
|
Дано: ΔABC D ∉ ΔABC M — середина AD P -середина CD K ∈BN Выяснить взаимное расположение прямых: а) ND и AB; б) PK и BC; в) MN и AB; г) MPи AC; д) NK и AC; е) MD и BC. Решение а) ND ∩ AB = B ; б) PK ∩ BC = P1; в) MN ∥ AB; г) MP ∥ AC; д) NK и AC скрещивающиеся; е) MD и BC — скрещивающиеся. |
|
Задача. Прямая с пересекает прямую а, параллельную прямой b. Доказательство Мы с вами знаем признак скрещивающихся прямых. Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещиваются.
Что и требовалось доказать.
|
Остались вопросы по теме? Наши педагоги готовы помочь!
Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ
Выбрать педагогаОставить заявку на подбор
Урок по теме «Взаимное расположение прямых в пространстве»
Тема урока: Взаимное расположение прямых в пространстве
Цель: организовать деятельность учащихся по установлению способов взаимного расположения прямых в пространстве, их признакам и взаимосвязям. Вывести признак скрещивающихся прямых и умение его применять при доказательстве задач. Развитие пространственного мышления. Формировать умение логического умозаключения и формулирования выводов. Воспитывать умение работать в коллективе, поддержки друг друга, взаимопомощи.
Задачи: достигнуть поставленной цели через организацию работы в группах, создания диалога и полилога.
СО: карточки, макеты фигур, проектор, учебник.
Тип урока: частично – поисковый
Ход урока:
1. Организационный момент
2. Собрать домашнюю работу. В домашней работе есть задание на взаимное расположение прямых. Так как по 2 следствию из аксиом, им известно о пересекающихся прямых, которые лежат в одной плоскости, а из курса планиметрии – о параллельных прямых, то трудность в определении прямых возникает только при скрещивающихся прямых, которые они еще не изучили. На что им было указано, если встретятся такие прямые, о которых вы не можете сказать, параллельны они или пересекаются, то поставить между такими прямыми кружок.
3. Напомнить учащимся о таких прямых в пространстве, и в результате вывести учащихся на цель урока (выяснить все случаи взаимного расположения прямых в пространстве и установить их признаки).
4. Далее работа в группах (четыре группы).
Первая группа, из предложенных чертежей, указывает только те, где прямые не имеют точек. Вторая – где прямые имеют одну общую точку. Третья – где прямые лежат в одной плоскости. Четвертая – где прямые не лежат в одной плоскости. ( На экране так же проецируются чертежи).
По одному учащемуся от группы выходят к доске и вписывают номера рисунков, соответствующих им условий.
Заполняется следующая таблица.
Номера рисунков, где прямые не имеют общих точек | Номера рисунков, где прямые имеют одну общую точку | Номера рисунков, где прямые лежат в одной плоскости | Номера рисунков, где прямые не лежат в одной плоскости |
2 4 5 6 7 8 11 12 13 14 15 17 | 1 3 9 10 16 | 1 2 3 7 9 10 12 13 14 15 16 | 4 5 6 8 11 17 |
5. Далее идет анализ таблицы, и дети выясняют, что каждый случай располагается в двух колонках. Делается выборка этих рисунков (запись выводится на доску).
Далее идет анализ таблицы, и дети выясняют, что каждый случай располагается в двух колонках. Делается выборка этих рисунков (запись выводится на доску).
Вследствие анализа дети устанавливают, что одни прямые пересекающиеся, другие параллельные. Третьи в учебнике они находят – скрещивающиеся.
Анализ:
1, 3, 9, 10, 16 — ___________________________________________ (это пересекающиеся прямые)
Имеют общую точку и лежат в одной плоскости
2, 7, 12, 13, 14, 15 — _______________________________________ (это параллельные прямые)
Не имеют общих точек и лежат в одной плоскости
4, 5, 6, 8, 11, 17 — _________________________________________ (это скрещивающиеся прямые)
Не имеют общих точек и не лежат в одной плоскости.
6. Исходя из этих условий, детям предлагается расставить стрелки между условиями и согласно условиям выполнить чертеж.
Эту табличку они вклеивают в тетрадь (обязательно вызываются учащиеся, для заполнения схемы, потом на экране показывается в готовом виде схема, учащиеся делают поправки).
7. Далее учащимся предлагается ответить о взаимном расположении прямых в пространстве по макетам фигур. Сначала учитель указывает на прямые – дети отвечают, потом преподаватель называет расположение, а кто-нибудь из детей – показывает на макете.
8. В ходе ответов по макетам фигур, устанавливается (так как постоянно делается акцент), что одна прямая лежит в некоторой плоскости, а другая прямая обязательно ее пересекает в точке, не лежащей на первой прямой. Следовательно, это и есть тот признак, по которому определяют скрещивающиеся прямые.
9. И теперь по учебнику, дети заполняют в тетрадях таблицу на теорему: признак скрещивающихся прямых.
Название теоремы (леммы, следствия, свойства). | Формулировка теоремы (леммы, следствия, свойства). | Чертеж к теореме (лемме, следствию, свойству). | Буквенная запись |
Эталон:
Название теоремы (леммы, следствия, свойства). | Формулировка теоремы (леммы, следствия, свойства). | Чертеж к теореме (лемме, следствию, свойству). | Буквенная запись |
Признак скрещивающихся прямых | Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся |
10. Отработка навыка применения теоремы (решение задач):
Можно воспользоваться задачами из учебника геометрии 10 – 11 класса Л.С. Атанасяна — №36, 38, 39, потом: №35, 37, 40, 41, 42.
А можно и из другой литературы:
11. Желательно на дом дать из учебника №34, или такое задание: начертить пирамиду, ввести обозначения вершин и назвать пары параллельных, пересекающихся, скрещивающихся прямых. И для самостоятельного разбора дома следующей темы: Угол между прямыми и предложит такие задания:
5
Объяснение урока: Точки, линии и плоскости в пространстве
В этом объяснении мы научимся идентифицировать и моделировать геометрические понятия, такие как точки, линии и плоскости в пространстве, а также их свойства.
Возможно, вы слышали о человеке по имени Евклид, которого иногда называют отцом геометрии. Слово геометрия происходит от греческого префикса «гео-», что означает «земля», и суффикса «-метрия», что означает процесс измерения. Мы понимаем мир вокруг нас из его работ по объемной геометрии, которая имеет дело с трехмерными объектами, такими как кубы и сферы, и плоской геометрии, которая имеет дело с объектами в двухмерном пространстве. В частности, точки, линии и плоскости являются геометрическими понятиями, которые относятся к положениям в пространстве и служат отправной точкой для определения всех других геометрических понятий.
По сути, мы начинаем с точки. Точка — это место в пространстве, не имеющее ни формы, ни размера. Однако, чтобы иметь возможность смоделировать эту концепцию, мы используем маленькую точку для представления идеи точки. Точка обычно обозначается заглавной буквой.
Определение: Точка
Точка — это место в пространстве. У него нет ни формы, ни размера.
У него нет ни формы, ни размера.
Имея любые две точки в пространстве, мы можем провести ровно одну прямую линию между этими точками. Особенно важно помнить, что когда мы работаем с линиями в пространстве, мы всегда работаем с прямыми линиями, бесконечно простирающимися в обоих направлениях. Мы рисуем их как прямые линии со стрелками на обоих концах. Линия обычно называется с использованием двух точек на этой линии.
Три или более точек, лежащих на одной прямой, называются коллинеарными точками. Если точка не лежит на той же прямой, что и другие точки, говорят, что это множество точек неколлинеарно.
Здесь также следует отметить, что расстояние между любыми двумя точками на прямой называется отрезком. Мы говорим, что линия, соединяющая точки 𝐴 и 𝐵 и заканчивающаяся на каждом конце, является отрезком 𝐴𝐵 или 𝐴𝐵.
Определение: Прямая линия
Линия — это связанный набор точек, бесконечно простирающийся в двух направлениях. Прямую, проходящую через точки 𝐴 и 𝐵, можно назвать по-разному. Например, линия, проходящая через 𝐴𝐵, может быть определена как ⃖⃗𝐴𝐵, ⃖⃗𝐵𝐴, линия 𝐴𝐵, линия 𝐵𝐴 или линия 𝑙.
Например, линия, проходящая через 𝐴𝐵, может быть определена как ⃖⃗𝐴𝐵, ⃖⃗𝐵𝐴, линия 𝐴𝐵, линия 𝐵𝐴 или линия 𝑙.
Третье понятие, которое мы рассмотрим, — это самолет . Плоскость — это двумерная поверхность, состоящая из точек, бесконечно простирающихся во всех направлениях. Через любые три неколлинеарные точки существует ровно одна плоскость. Три и более точки, лежащие на плоскости, называются компланарными. Если точка не лежит в одной плоскости с тремя другими точками, такое множество точек называется некомпланарным. Мы также можем определить плоскость в терминах двух параллельных прямых, двух пересекающихся прямых или прямой и внешней точки. Это связано с тем, что две параллельные прямые, две пересекающиеся прямые, а также прямая и точка будут иметь как минимум три неколлинеарных точки.
Плоскость обычно определяется одной заглавной буквой или, реже, тремя или более неколлинеарными точками этой плоскости. Обычно вы видите самолеты, смоделированные как четырехугольник. Показанная плоскость может быть определена как плоскость 𝐾, плоскость 𝐴𝐵𝐶, плоскость 𝐵𝐴𝐶 или плоскость 𝐶𝐵𝐴.
Показанная плоскость может быть определена как плоскость 𝐾, плоскость 𝐴𝐵𝐶, плоскость 𝐵𝐴𝐶 или плоскость 𝐶𝐵𝐴.
Определение: Плоскости
Плоскость — это двумерная поверхность, состоящая из точек, бесконечно простирающихся во всех направлениях. Через любые три неколлинеарные точки существует ровно одна плоскость.
При работе с точками, линиями и плоскостями нас особенно интересует то, как они взаимодействуют друг с другом.
Вспомним, что для любой точки пространства существует бесконечное количество прямых, проходящих через эту точку. Тот же принцип справедлив и для самолетов. Через любую точку пространства проходит бесконечное количество плоскостей.
В наших первых двух примерах мы покажем, как идентифицировать количество линий или плоскостей, проходящих через точку.
Пример 1. Нахождение количества прямых, проходящих через определенную точку в пространстве
Найдите прямые, проходящие через точку 𝐵.
Ответ
На этом рисунке мы видим несколько различных отрезков, которые включают точку 𝐵.
𝐴𝐵, 𝐶𝐵 и 𝑀𝐵 — это отрезки, конечная точка которых находится в 𝐵. Мы знаем, что через любые две точки в пространстве проходят прямые, а это значит, что через точку 𝐵 будет проходить три прямые, которые мы можем обозначить: ⃖⃗𝐴𝐵,⃖⃗𝐶𝐵,⃖⃗𝑀𝐵.и
Прямые, проходящие через точку 𝐵, равны ⃖ ⃗𝐴𝐵, ⃖⃗𝐶𝐵 и ⃖ ⃗𝑀𝐵.
Пример 2. Определение плоскостей, проходящих через определенные точки
Найдите три плоскости, проходящие через обе точки 𝐴 и 𝐵.
Ответ
Плоскости, проходящие через обе точки 𝐴 и 𝐵, будут плоскостями, проходящими через прямую ⃖⃗𝐴𝐵. Мы знаем, что плоскость может существовать через любые три неколлинеарные точки. В этой прямоугольной призме мы можем визуализировать эти плоскости как пространство, которое будет содержать определенные грани призмы. Одной из граней будет грань, содержащая две параллельные линии ⃖⃗𝐴′𝐵′ и ⃖⃗𝐴𝐵. Мы можем назвать этот самолет 𝐴𝐵𝐵′.
Существует еще одна плоскость, содержащая две параллельные линии ⃖⃗𝐴𝐵 и ⃖⃗𝐶𝐷. Назовем этот самолет 𝐴𝐵𝐶.
Назовем этот самолет 𝐴𝐵𝐶.
Третий самолет сразу не бросается в глаза. Напомним, что любые три неколлинеарные точки образуют плоскость. Следовательно, существует некоторая плоскость, которая будет содержать точки 𝐶′, 𝐴 и 𝐵. Эта третья плоскость — 𝐴𝐵𝐶′.
Через точки 𝐴 и 𝐵 проходят три плоскости 𝐴𝐵𝐶, 𝐴𝐵𝐵′ и 𝐴𝐵𝐶′.
Связь между двумя линиями в пространстве:
Две линии могут иметь три возможных отношения. Во-первых, рассмотрим пару копланарных линий. Эти линии могут пересекаться под любым углом, как показано на следующей диаграмме, или они могут быть перпендикулярны (т. Е. Они пересекаются ортогонально).
Если копланарные прямые не пересекаются, то они параллельны. Они никогда не встретятся.
Пара прямых, которые не пересекаются и не параллельны друг другу, называется косой. Наклонные линии могут существовать только в трех измерениях.
Связь между линией и плоскостью в пространстве:
Линия и плоскость могут иметь три отношения.
Линия может лежать на плоскости. В этом случае каждая точка прямой будет лежать на плоскости.
Если прямая пересекает плоскость, пересечение означает наличие общей точки, лежащей на обеих плоскостях.
Прямая также может пересекать плоскость ортогонально, и в этом случае говорят, что прямая перпендикулярна плоскости. Тогда эта прямая перпендикулярна всем прямым на этой плоскости, пересекающим эту прямую.
Если прямая не пересекает плоскость, то прямая параллельна плоскости.
Связь между двумя плоскостями в космосе:
Наконец, есть три возможных связи, которые могут существовать между двумя плоскостями в космосе. Если две плоскости делят все точки, говорят, что их 9.0009 совпадает с .
Если пересекаются две плоскости, пересечение всегда является линией. Эти две плоскости могут пересекаться ортогонально, поэтому говорят, что они перпендикулярны.
Эти две плоскости не пересекаются. Это параллельные плоскости.
Примечание
Пока мы рассматривали пару плоскостей в пространстве, три пересекающиеся плоскости могут иметь общую точку.
В следующем примере мы продемонстрируем, как определить отношения между отрезками прямоугольной призмы.
Пример 3. Определение отношения между отрезками в пространстве
Рассмотрим прямоугольную призму 𝐴𝐵𝐶𝐷𝐸𝐹𝐺𝐻, где 𝐴𝐵≠𝐵𝐶≠𝐴𝐸.
- Что можно сказать о 𝐸𝐹 и 𝐹𝐺?
- Они параллельны.
- Они перпендикулярны.
- Они не параллельны и не перпендикулярны.
- Они перекошены.
- Что можно сказать о 𝐴𝐸 и 𝐶𝐺?
- Они перекошены.
- Они перпендикулярны.
- Они параллельны.
- Они не параллельны и не перпендикулярны.
- Что можно сказать о 𝐵𝐷 и 𝐷𝐻?
- Они перпендикулярны.
- Они не параллельны и не перпендикулярны.
- Они перекошены.
- Они параллельны.
- Что можно сказать о 𝐵𝐷 и 𝐴𝐶?
- Они параллельны.
- Они перпендикулярны.
- Они не параллельны и не перпендикулярны.

- Они перекошены.
Ответ
Часть 1
В прямоугольной призме мы хотим определить взаимосвязь между различными парами отрезков, а именно 𝐸𝐹 и 𝐹𝐺.
Прямоугольные призмы состоят из 6 прямоугольных граней, а в прямоугольнике смежные стороны перпендикулярны. Поскольку 𝐸𝐹𝐺𝐻 — прямоугольник, мы можем сказать, что 𝐸𝐹 и 𝐹𝐺 пересекаются под углом 90∘. Итак, ответ — вариант Б; 𝐸𝐹 и 𝐹𝐺 перпендикулярны.
Часть 2
𝐴𝐸 и 𝐶𝐺 — отрезки, лежащие на противоположных гранях прямоугольной призмы.
Они не пересекаются. Поскольку эти две грани являются противоположными гранями прямоугольной призмы, мы можем сказать, что 𝐴𝐸 и 𝐶𝐺 параллельны. Ответ — вариант C.
Часть 3
𝐵𝐷 и 𝐷𝐻 — отрезки прямых, лежащие на перпендикулярных гранях призмы и пересекающиеся в точке 𝐷.
Это означает, что в точке пересечения 𝐵𝐷 и 𝐷𝐻 перпендикулярны. Это вариант А.
Часть 4
𝐵𝐷 и 𝐴𝐶 — отрезки, лежащие в одной плоскости, 𝐴𝐵𝐶. Поскольку отрезки не параллельны, они должны пересекаться.
Поскольку отрезки не параллельны, они должны пересекаться.
Мы знаем, что диагонали прямоугольника не перпендикулярны, поэтому 𝐵𝐷 и 𝐴𝐶 не параллельны и не перпендикулярны. Ответ – вариант C.
Примечание
Хотя ⃖⃗𝐵𝐷 и ⃖⃗𝐴𝐶 не параллельны и не перпендикулярны, это не означает, что они косые линии. ⃖⃗𝐵𝐷 и ⃖⃗𝐴𝐶 не скрещиваются, так как пересекаются и лежат в одной плоскости.
Теперь мы продемонстрируем, как мы можем идентифицировать наклонные линии на изображении.
Пример 4. Определение наклонных линий
Используя приведенную ниже прямоугольную призму, решите, какая из следующих линий наклонена к ⃖⃗𝐶𝐺.
𝐻Ответить
Отзыв что косые линии — это прямые, которые не пересекаются, но не параллельны. Наклонные линии некомпланарны и поэтому могут существовать только в трех измерениях. Прямая, наклоненная к ⃖⃗𝐶𝐺, не может быть параллельна ⃖⃗𝐶𝐺 и не может пересекать эту прямую. Это означает, что ⃖⃗𝐶𝐺 можно преобразовать только в линии ⃖⃗𝐸𝐻, ⃖⃗𝐴𝐷,
⃖⃗𝐴𝐵 и ⃖⃗𝐸𝐹.
Это означает, что ⃖⃗𝐶𝐺 можно преобразовать только в линии ⃖⃗𝐸𝐻, ⃖⃗𝐴𝐷,
⃖⃗𝐴𝐵 и ⃖⃗𝐸𝐹.
Из списка вариантов правильный ответ C.
Рисунок в следующем примере покажет нам возможную конфигурацию линии и плоскости.
Пример 5. Определение пересечения плоскости и прямой
Рассмотрите данный рисунок и выберите правильное утверждение.
- Прямая параллельна плоскости.
- Прямая содержится внутри плоскости.
- Прямая пересекает плоскость.
Ответ
На рисунке показана плоскость, обозначенная как 𝑋, бесконечно простирающаяся во всех направлениях. Из диаграммы видно, что точка 𝐴 лежит на плоскости 𝑋.
Мы также видим, что точка 𝐴 лежит на прямой 𝐿. Поскольку плоскость 𝑋 и прямая 𝐿 имеют общую точку, то есть точку 𝐴, можно сказать, что прямая пересекает плоскость. Следовательно, вариант С правильный. Прямая пересекает плоскость.
Следующий пример — возможная конфигурация двух самолетов в космосе.
Пример 6. Определение пересечения двух плоскостей
Что такое пересечение плоскости, проходящей через 𝐴𝐵𝐵′𝐴′, и плоскости, проходящей через 𝐵𝐶𝐶′𝐵′?
Ответ
В этой прямоугольной призме плоскость, содержащая точки 𝐴, 𝐵, 𝐵′ и 𝐴′, является плоскостью, содержащей вертикальную грань справа на диаграмме. Плоскость, содержащая точки 𝐵, 𝐶, 𝐶′ и 𝐵′, — это плоскость, содержащая вертикальную грань перед этой призмой. Пересечение этих двух граней представляет собой линию. Мы знаем, что это правда, потому что обе эти грани содержат точки 𝐵 и 𝐵′. Линия между 𝐵 и 𝐵′ будет линией пересечения этих двух плоскостей.
Здесь выделено, что общая линия и, следовательно, пересечение плоскости 𝐴𝐵𝐵′ и плоскости 𝐵𝐶𝐵′ равно ⃖⃗𝐵𝐵′.
Последний пример показывает нам конфигурацию трех самолетов в пространстве.
Пример 7. Определение пересечения трех плоскостей
Что такое пересечение плоскостей 𝑀𝐴𝐵, 𝑀𝐵𝐶 и 𝑀𝐴𝐶?
Ответ
Эта пирамида состоит из четырех треугольных граней. Поскольку через любые три неколлинеарные точки существует ровно одна плоскость, каждая из треугольных граней лежит на единственной плоскости. Нас интересуют плоскости 𝑀𝐴𝐵, 𝑀𝐵𝐶 и 𝑀𝐴𝐶, каждая из которых содержит точку 𝑀. Это означает, что точка 𝑀 лежит во всех трех этих плоскостях. Поскольку точка 𝑀 является общей точкой каждой из этих плоскостей, пересечение этих плоскостей будет {𝑀}.
Поскольку через любые три неколлинеарные точки существует ровно одна плоскость, каждая из треугольных граней лежит на единственной плоскости. Нас интересуют плоскости 𝑀𝐴𝐵, 𝑀𝐵𝐶 и 𝑀𝐴𝐶, каждая из которых содержит точку 𝑀. Это означает, что точка 𝑀 лежит во всех трех этих плоскостях. Поскольку точка 𝑀 является общей точкой каждой из этих плоскостей, пересечение этих плоскостей будет {𝑀}.
Давайте закончим повторением ключевых моментов.
Ключевые точки
- Точка — это место в пространстве. У него нет ни формы, ни размера.
- Линия — это связанный набор точек, бесконечно простирающийся в двух направлениях.
- Плоскость может быть определена тремя не лежащими на одной прямой точками, двумя параллельными прямыми или двумя пересекающимися прямыми.
- Набор точек называется коллинеарным, если они лежат на одной прямой. В противном случае они называются неколлинеарными.
- Набор точек называется компланарным, если они лежат в одной плоскости.
 В противном случае они называются некомпланарными.
В противном случае они называются некомпланарными. - Для любых двух копланарных линий возможные отношения параллельны, пересекаются под углом или перпендикулярны.
- Для любых двух прямых в пространстве возможные отношения будут параллельными, пересекающимися под углом, перпендикулярными или косыми.
- Для линии и плоскости в пространстве возможными конфигурациями будут пересечение в точке (под любым углом), перпендикулярность, вхождение в плоскость или параллельность плоскости.
- Для любых двух плоскостей возможные конфигурации будут совпадающими, параллельными, пересекающимися по прямой (под любым углом) или перпендикулярными. Три плоскости могут пересекаться в одной точке или по прямой.
Относительное положение прямой и плоскости : урок математики в 10 классе
Уроки математики в 10 классе Сообщить об ошибке / Примечание?
Sommaire de cette fiche
- 1 I.
 Обычные твердые вещества
Обычные твердые вещества - 2 II. Линии и плоскости
- 2.1 1. Что такое план?
- 2.2 2. Взаимные положения двух прямых
- 2.3 3. Взаимные положения двух плоскостей в геометрии пространства
- 2.4 4. Взаимные положения прямой и плоскости
- 3 Поняли ли вы этот урок по взаимному положению между плоскостью и линией в космосе в 10 классе?
- 3.0.1 Итоги викторины
- 3.0.2 Информация
- 3.0.3 Результаты
- 3.0.4 Категории
Курс геометрии в пространстве по 10 класс по обычным телам (прямоугольный параллелепипед, пирамида, конус вращения, цилиндр вращения, сфера и шар). В этом уроке десятого класса мы будем изучать взаимное расположение линий и плоскостей в пространстве.
Знания колледжа, необходимые для этой главы
- Знать формулы площади для обычных чисел;
- Знать формулы объема обычных твердых тел;
- Найдите свой путь вокруг фигуры в кавалерийской перспективе;
- Построить массив обычного твердого тела.

I. Обычные твердые тела
Определение:
Тело представляет собой рельефный объект.
Его нельзя отследить в полном размере на плоском листе бумаги.
Примечания:
- Шаблон используется для изготовления твердого тела путем складывания;
- Кавалерийская перспектива позволяет представить твердое тело на листе бумаги с помощью 3D-печати
.
II. Линии и плоскости
1. Что такое план?
Определение:
Пусть A, B, C — три различные и несоосные точки в пространстве.
- Для определения плоскости достаточно задать 3 не совпадающие точки или 2 пересекающиеся прямые или 2 параллельные прямые (не слитые).
- Отмеченная плоскость (ABC) образована точками прямых, проходящих через A и параллельных или секущих линии (BC).
Примечание:
В каждой плоскости пространства мы можем применить все теоремы геометрии
плоскости.
Пример:
ABCDEFGH – прямоугольный параллелепипед такой, что:
– AB = 7 см – I – середина [AB]
– AD = 6 см – J – середина [AD]
1) Название цветной самолет.
2) Рассчитайте длину BD.
Исправление:
1) Цветная плоскость пересекает края блока в точках I, J, K и L, поэтому (I JK) является возможным именем.
2) Грань блока ABCD является прямоугольником, поэтому треугольник ABD прямоугольен в A.
Согласно теореме Пифагора:
BD² = BA²+ AD² = 72 + 62 = 49 + 36 = 85.
Длина всегда равна положительный, поэтому BD = см.
2. Взаимное расположение двух прямых
Определение:
Две прямые, лежащие в одной плоскости, называются компланарными.
Право собственности:
Две линии в пространстве либо компланарны, либо некомпланарны:
3. Относительное положение двух плоскостей в геометрии пространства
Право собственности:
- Плоскость разрезает две параллельные плоскости по двум параллельным линиям.

- Две плоскости параллельны тогда и только тогда, когда две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.
Примечание:
Две плоскости считаются параллельными.
4. Относительное положение прямой и плоскости
Право собственности:
Прямая параллельна плоскости тогда и только тогда, когда она параллельна прямой плоскости.
Вы поняли этот урок об относительном положении между плоскостью и линией в пространстве в 10-м классе?
Сдайте этот ВСК по космической геометрии в десятом классе .
La géométrie dans l’espace
Un QCM sur la geométrie dans l’espace
Эта публикация доступна на следующих языках: Français (французский) Español (испанский) العربية (арабский)
Загрузите и распечатайте этот документ в формате PDF бесплатно
У вас есть возможность скачать и распечатать этот документ бесплатно « Взаимное положение прямой и плоскости в пространстве : урок математики 10 класс » в формате PDF.
Другие документы в категории Уроки математики в 10 классе
- Уравнения, неравенства и графическое решение: урок математики в 10 классе
- Статистика: урок математики в 10 классе – бесплатный PDF для печати
- Векторы и перевод : урок математики в 10 классе. PDF
- Числовые функции: урок математики в 10 классе
- Наборы чисел и расчеты: урок математики в 10 классе
- Вспомнить из колледжа о множествах чисел: урок математики в 10 классе
- Относительное положение прямой и плоскости в пространстве: урок математики в 10 классе
- Общие положения о функциях и обычных функциях: урок математики в 10 классе
- Общие положения о числовых функции : Урок математики 10 класса
- Полиномиальные функции второй степени : Урок математики 10 класса
Другие формы, подобные взаимному положению прямой и плоскости в пространстве : Урок математики 10 класса.
4 действия со сложением, вычитанием, умножением и делением: Урок математики для 6-го класса
94
Урок математики по непрерывности десятичных чисел по четырем операциям, которые необходимо освоить.
 Сложение и его биномиальное вычитание и другое биномиальное: умножение и деление, которые являются основой для выполнения более трудоемких и сложных вычислений позже. I. Сложение и сумма…
Сложение и его биномиальное вычитание и другое биномиальное: умножение и деление, которые являются основой для выполнения более трудоемких и сложных вычислений позже. I. Сложение и сумма…Геометрия в пространстве: Рабочие листы по математике для 11 класса с ответами в формате PDF
93
Рабочие листы по математике в 11 классе по геометрии в пространстве. Упражнение 1. Расположение окружностей и точек Настоятельно рекомендуется использовать геометрическую программу… 1. Предварительная часть: мы рассматриваем треугольник ABC, G его центр тяжести, Ω центр описанной окружности и H его ортоцентр. Показать…
Вероятность : рабочие листы по математике для 10-го класса с ответами в формате PDF
93
рабочие листы по математике для 10-го класса с ответами в формате на вероятность. Упражнение №1: 1. а. Выполните 50 бросков двух монет. Для каждого броска отметьте выполняемое событие: A: «Выпадение двух решек»; B: получить две стороны; C: Получите один орел и одну решку».






 Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна.
Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна.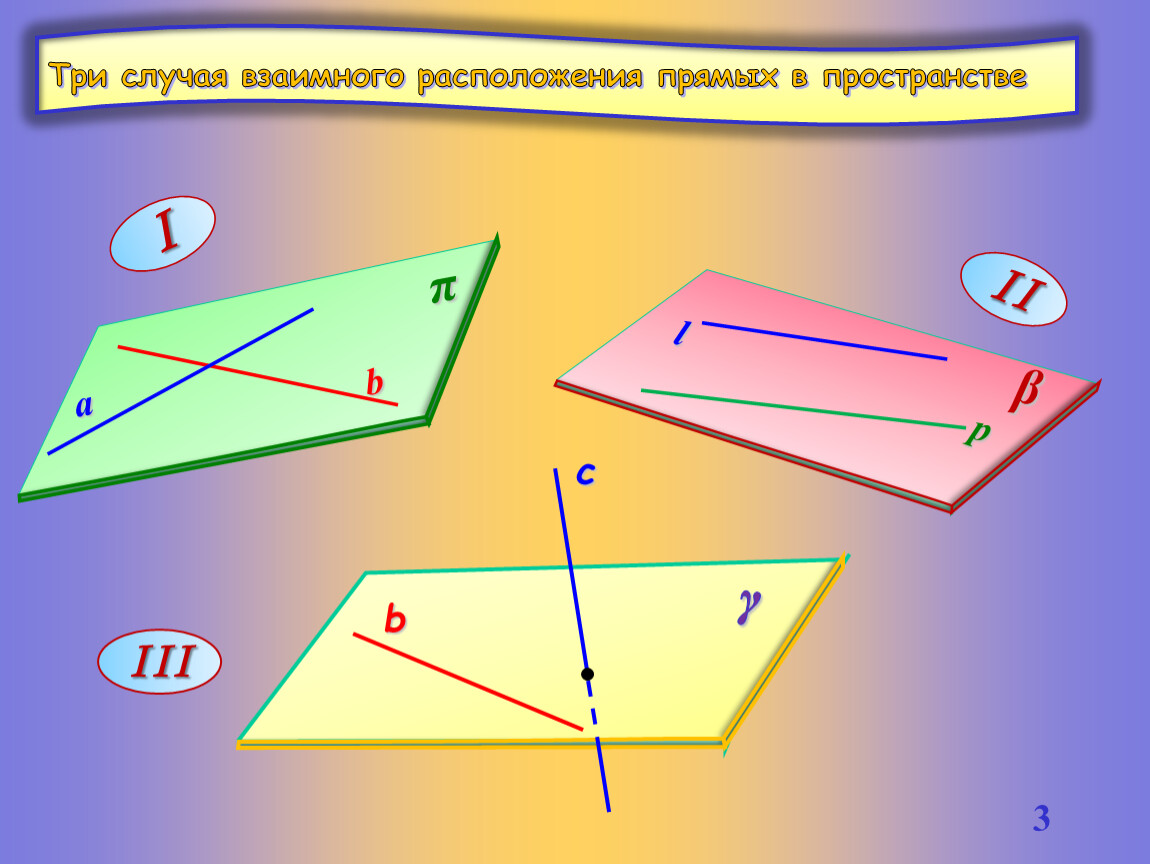


 не принадлежат одной плоскости.
не принадлежат одной плоскости. Докажите, что b и c – скрещивающиеся прямые.
Докажите, что b и c – скрещивающиеся прямые.


 В противном случае они называются некомпланарными.
В противном случае они называются некомпланарными. Обычные твердые вещества
Обычные твердые вещества

 Сложение и его биномиальное вычитание и другое биномиальное: умножение и деление, которые являются основой для выполнения более трудоемких и сложных вычислений позже. I. Сложение и сумма…
Сложение и его биномиальное вычитание и другое биномиальное: умножение и деление, которые являются основой для выполнения более трудоемких и сложных вычислений позже. I. Сложение и сумма…