Тест 1 рациональные дроби и их свойства вариант 1: 8.1. Рациональные дроби и их свойства. — математика в тестах
Тест по теме рациональные дроби. – УчМет
Тест 1
Рациональные дроби
Вариант 1
ЧАСТЬ А
А1.
Найдите значение алгебраической дроби 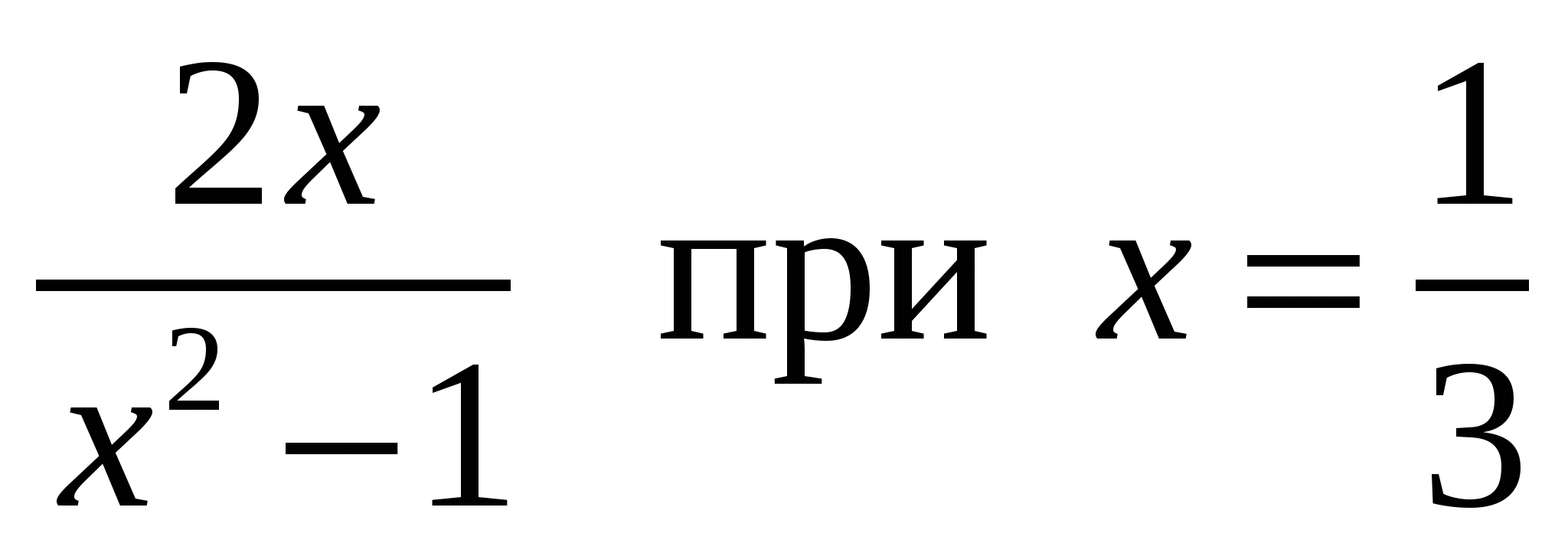 .
.
1)  2)
2) 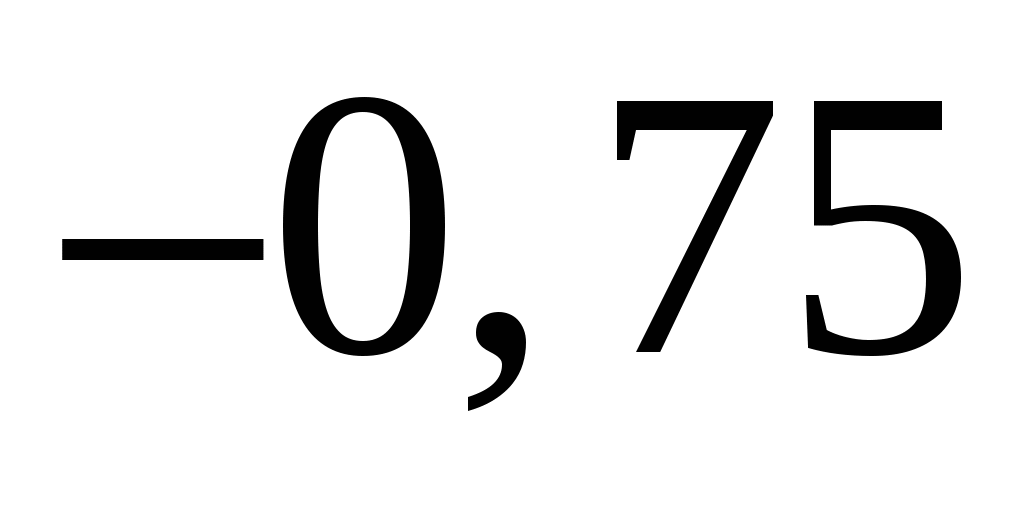 3)
3) 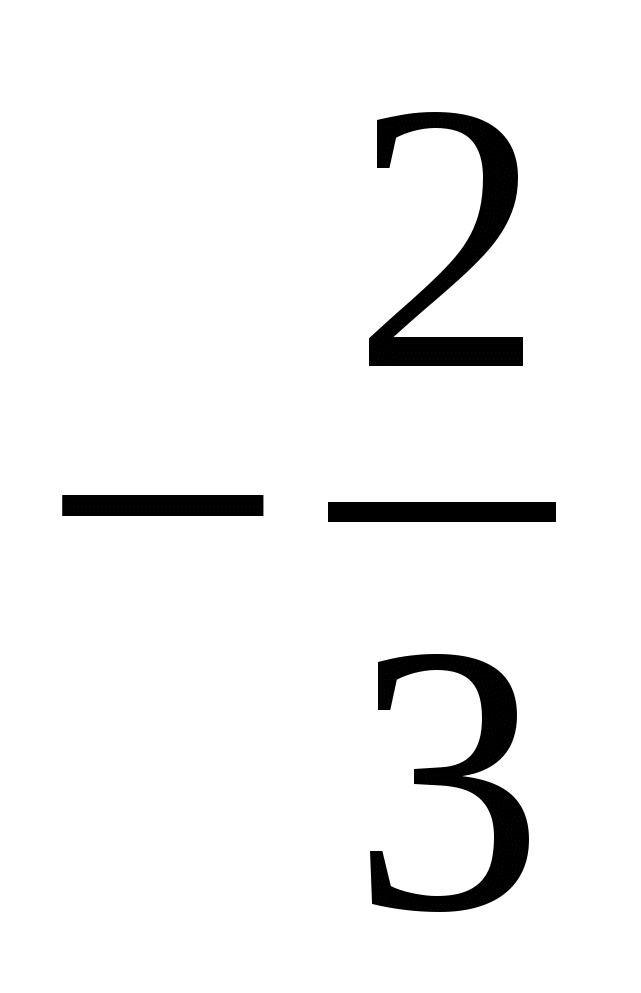 4)
4) 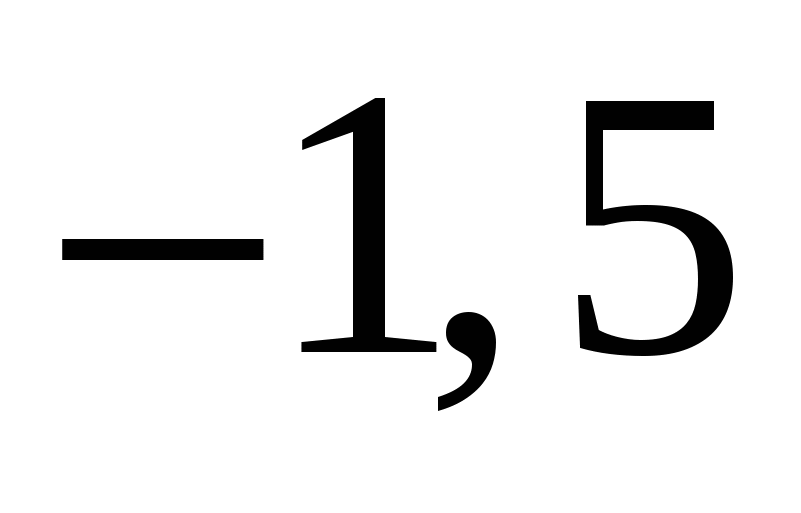
А2.
Сократите дробь 
 2)
2) 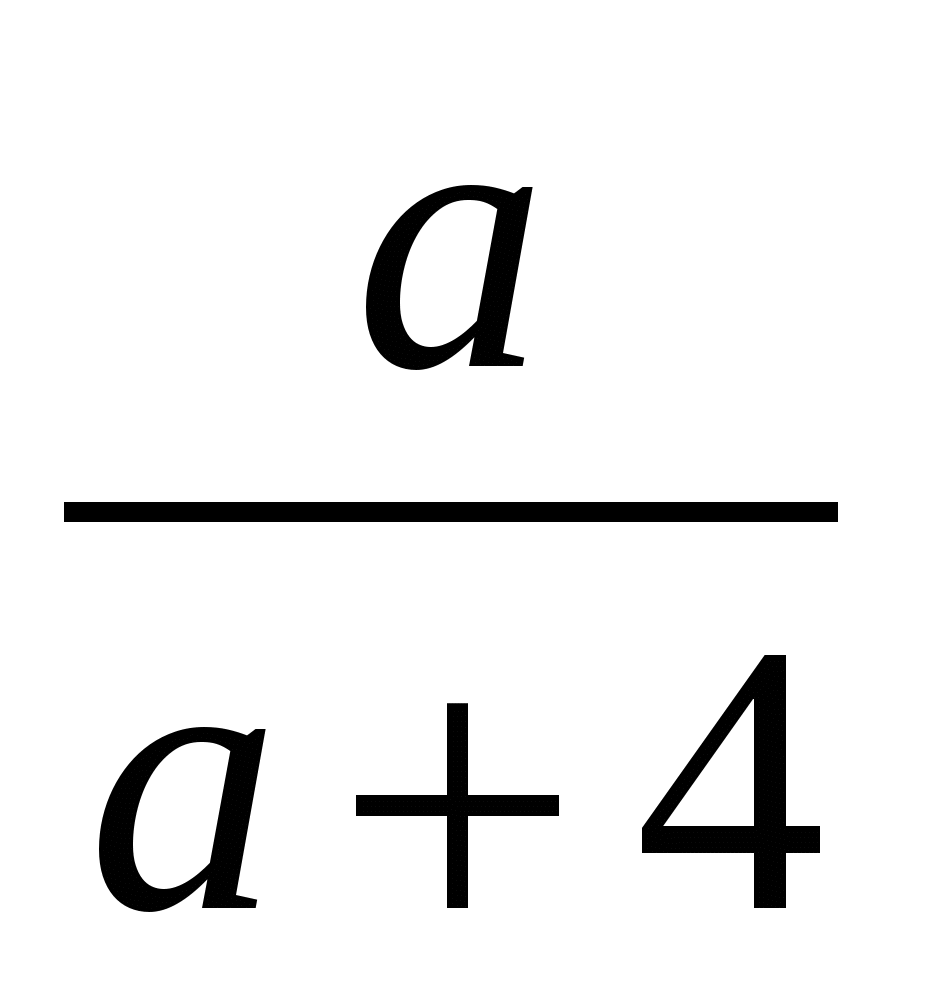 3)
3)  4)
4) 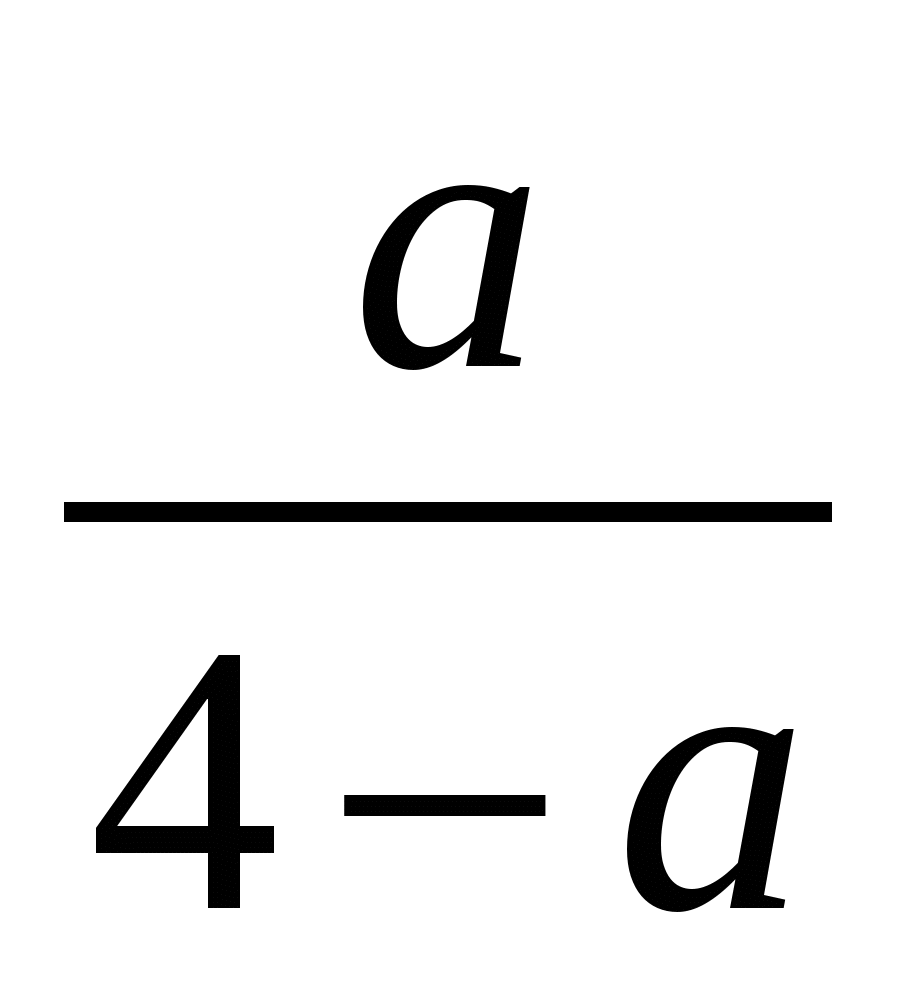
А3.
Найдите значение 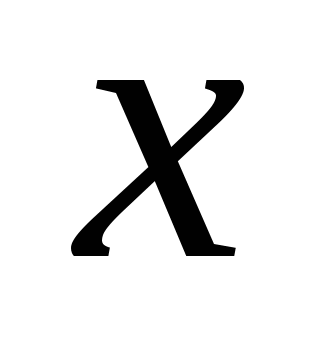 ,
при котором дробь
,
при котором дробь 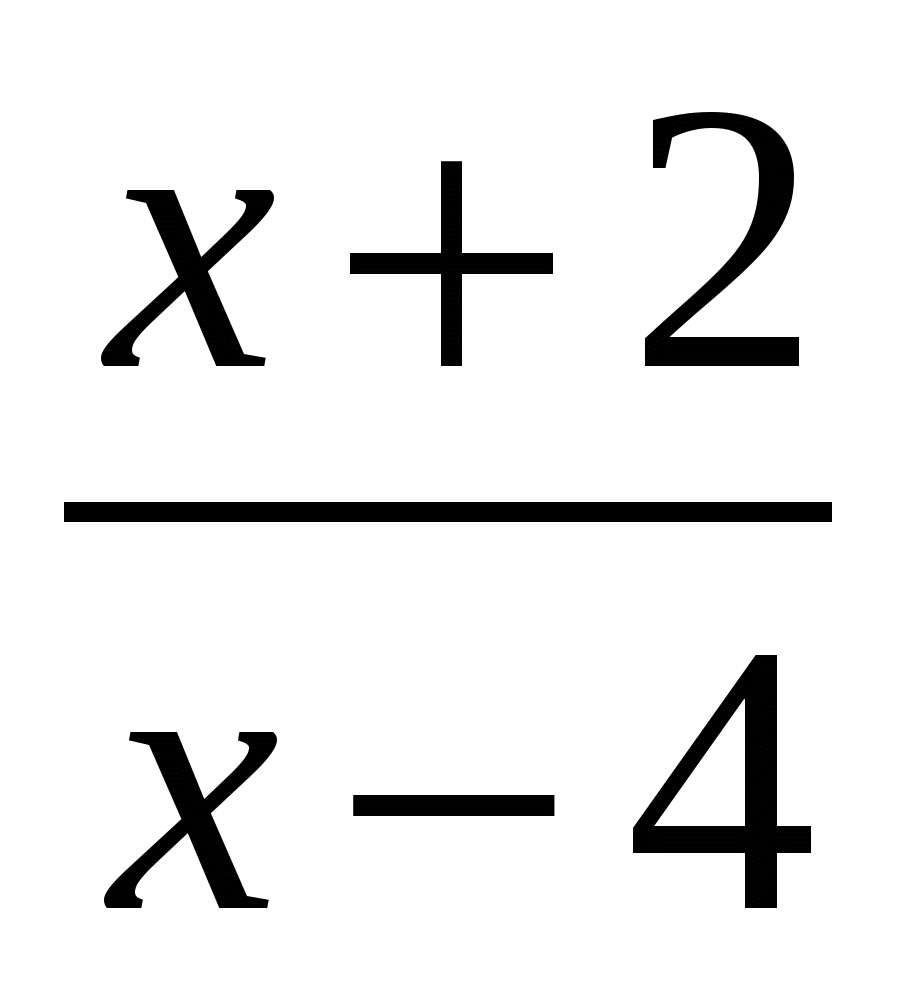
1) 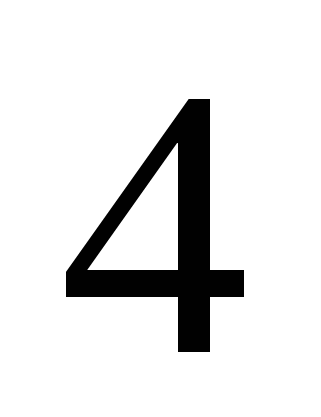 2)
2) 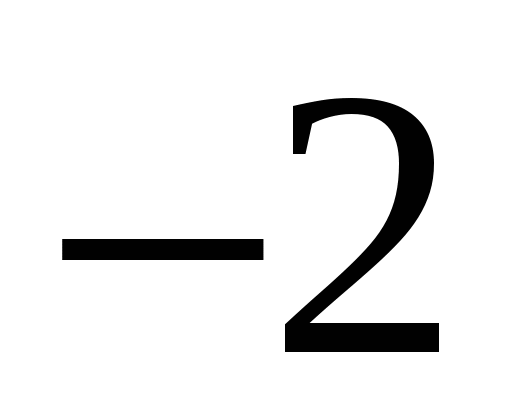 3)
3) 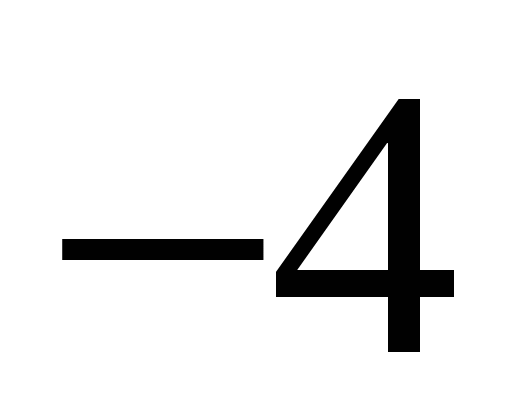 4) нет таких
значений
4) нет таких
значений
А4.
Выполните сложение 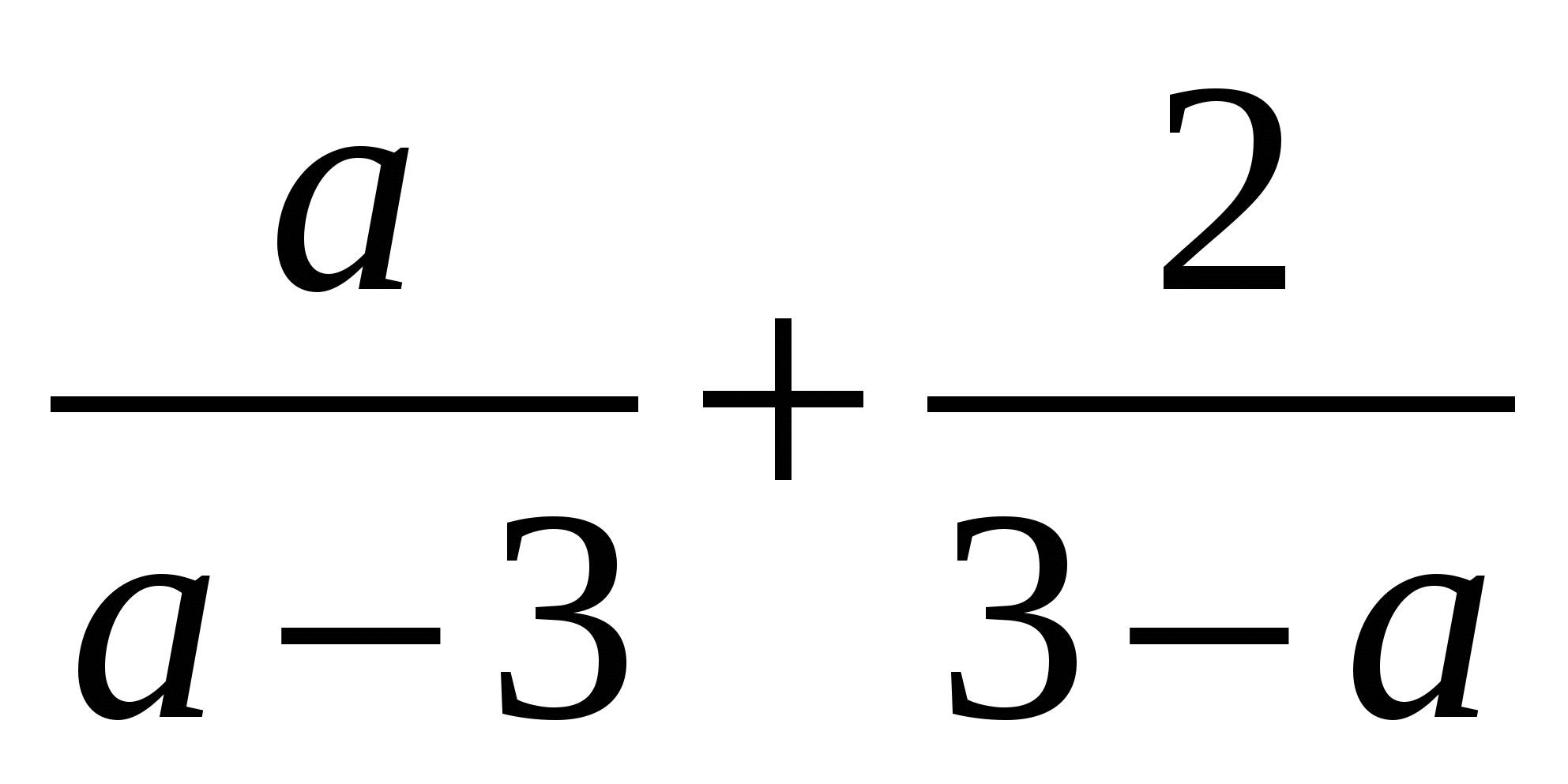 .
.
1)  2)
2) 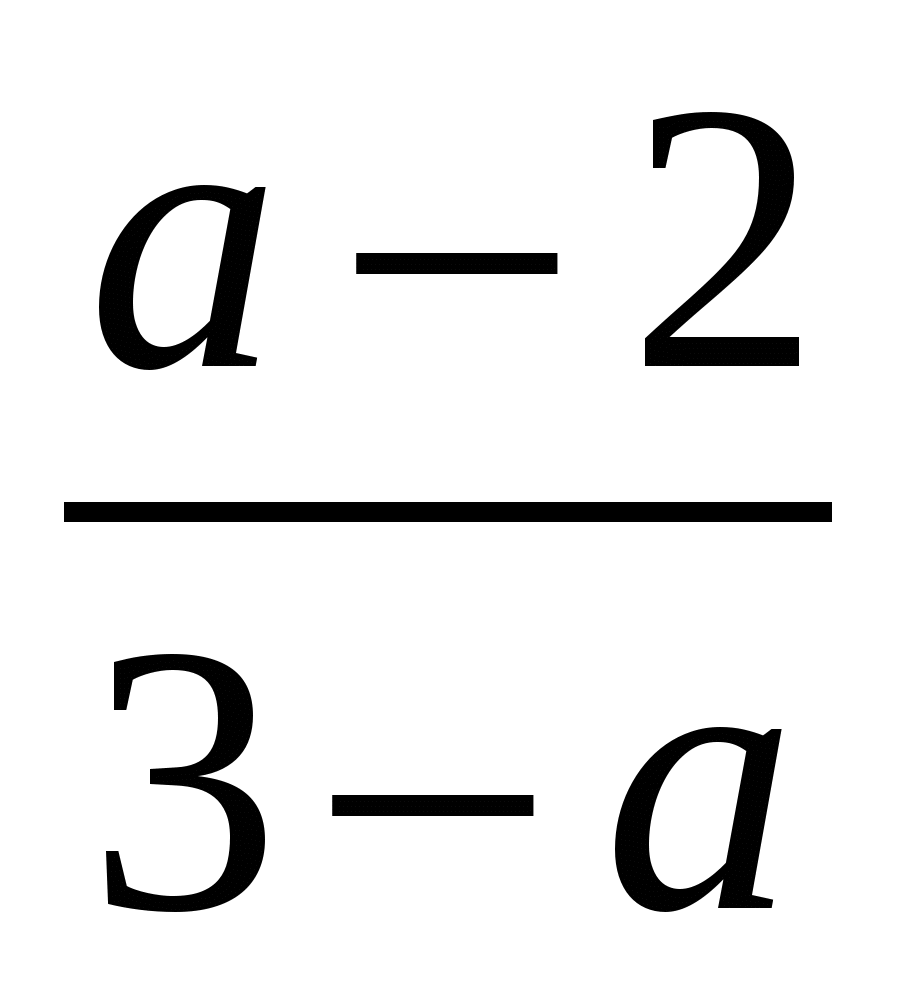 3)
3) 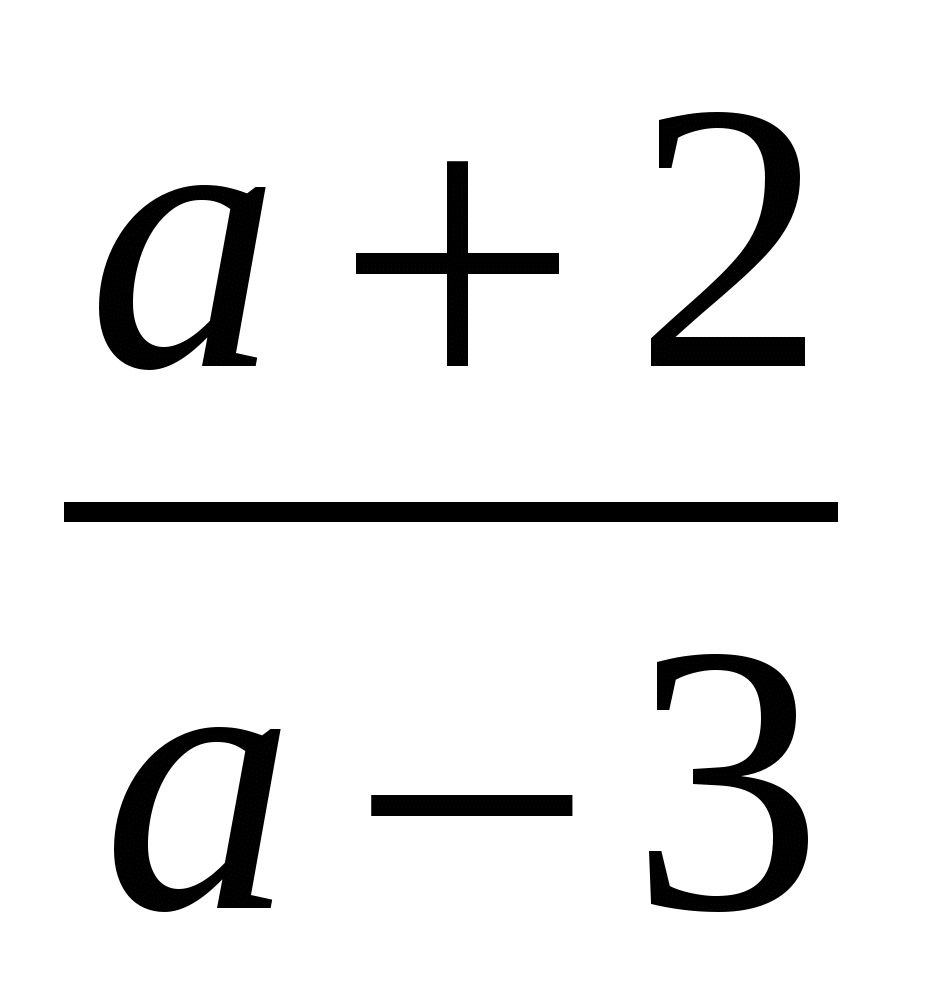
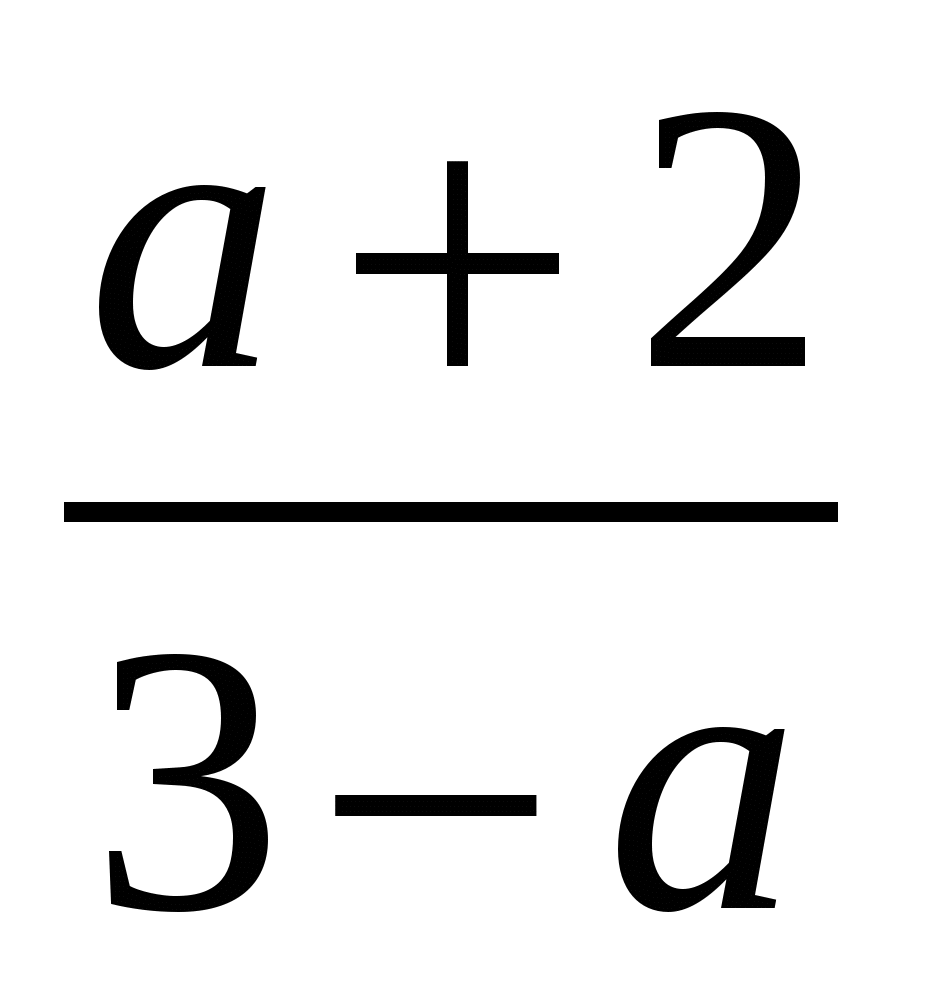
А5.
Выполните действия 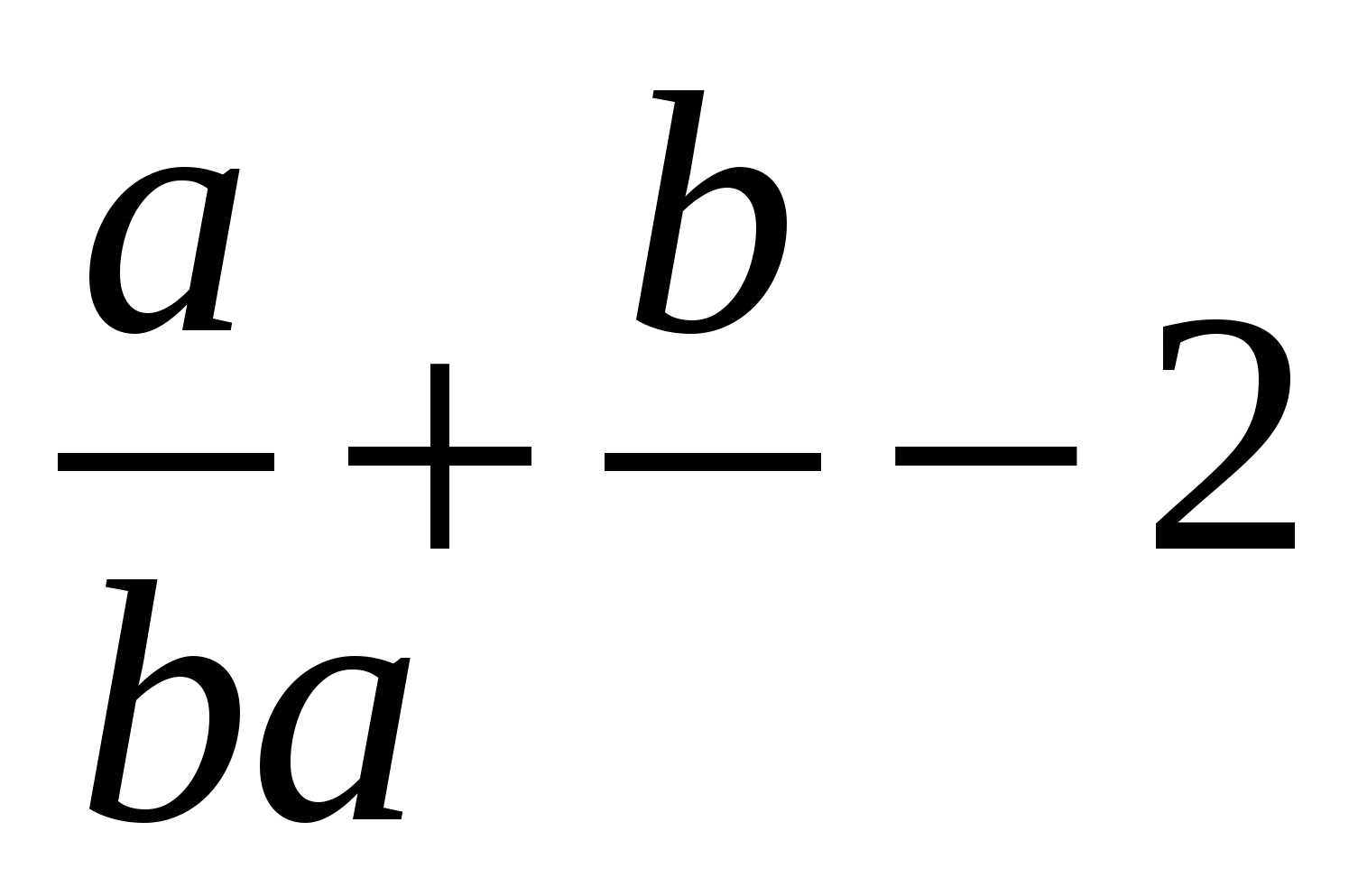 .
.
1) 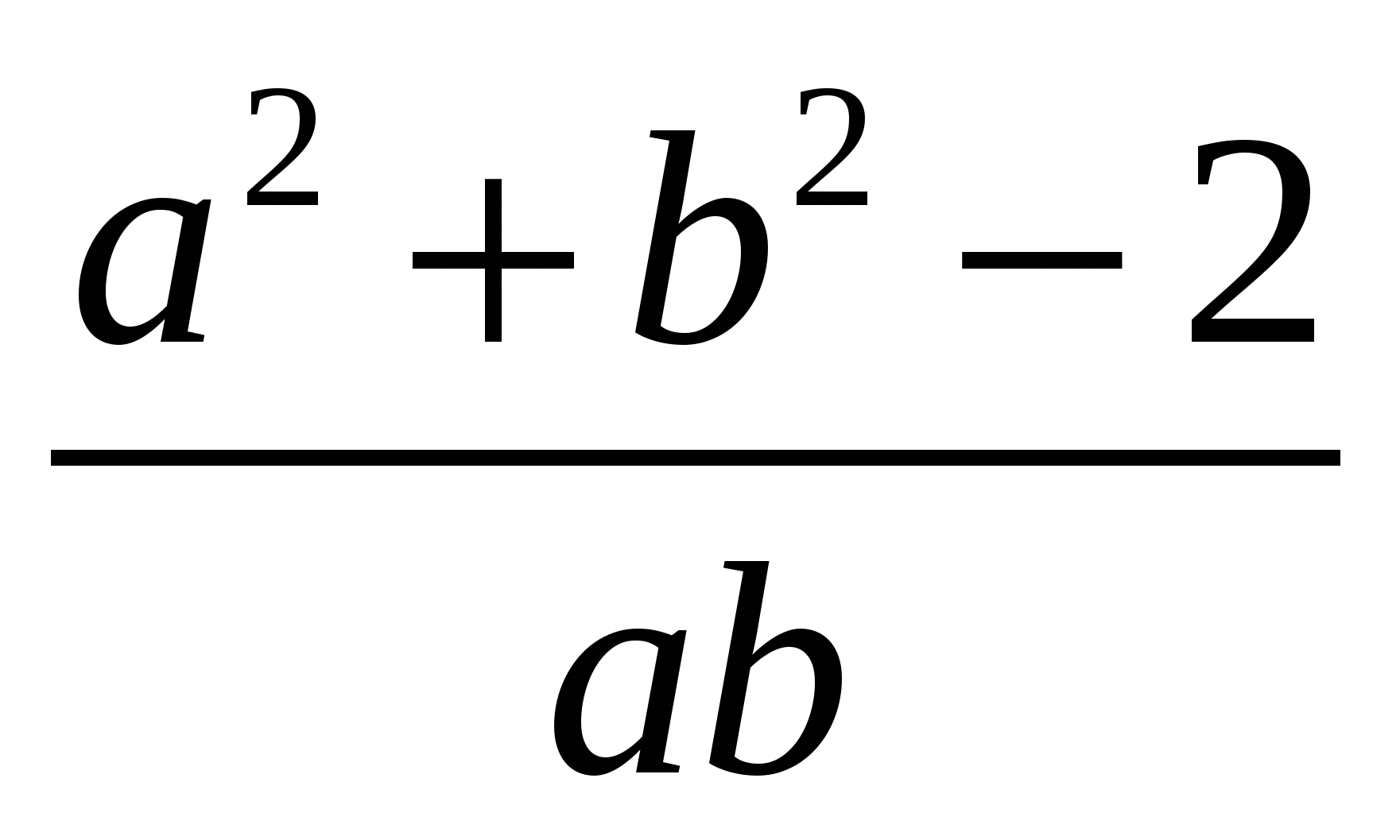 2)
2) 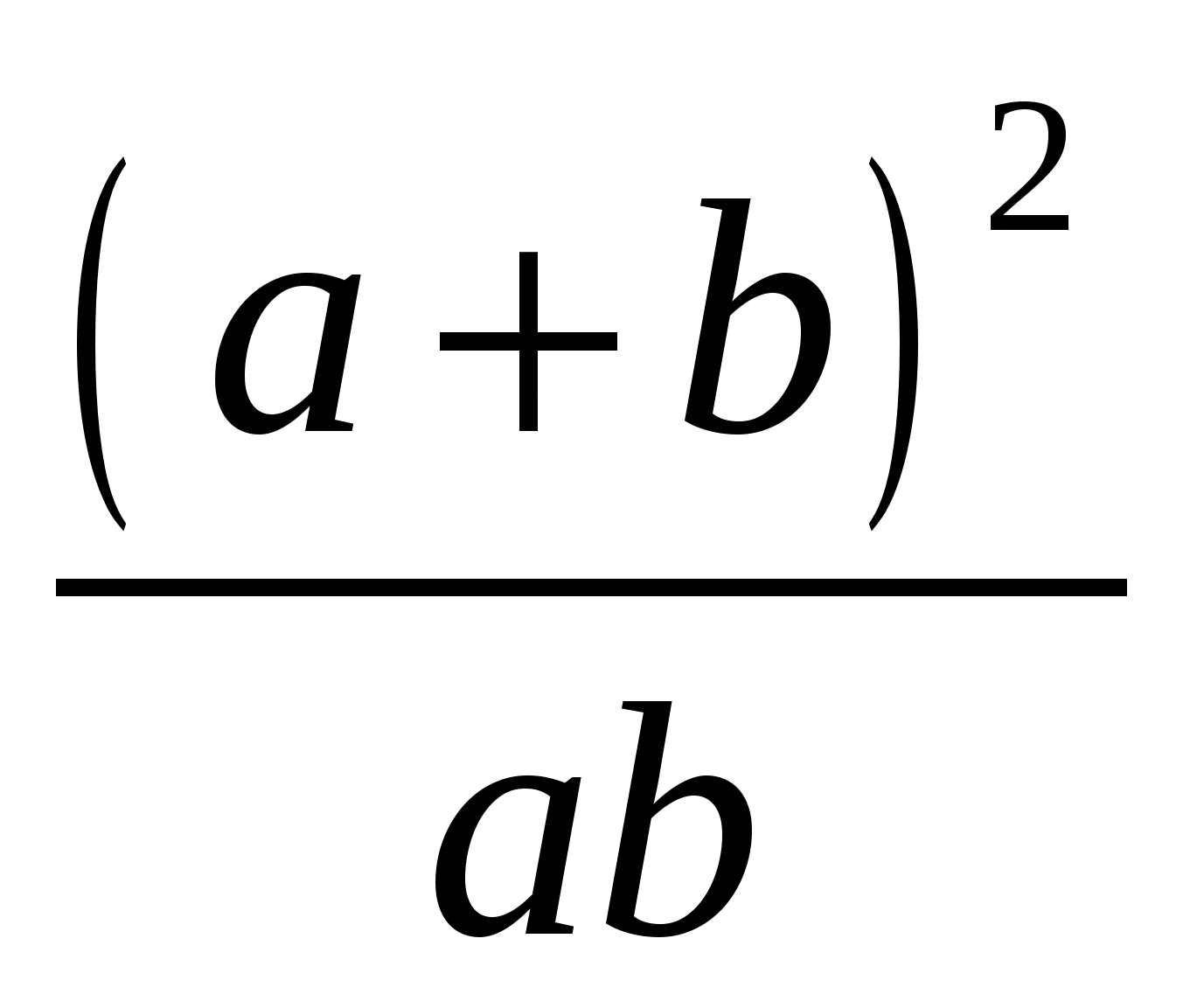 3)
3) 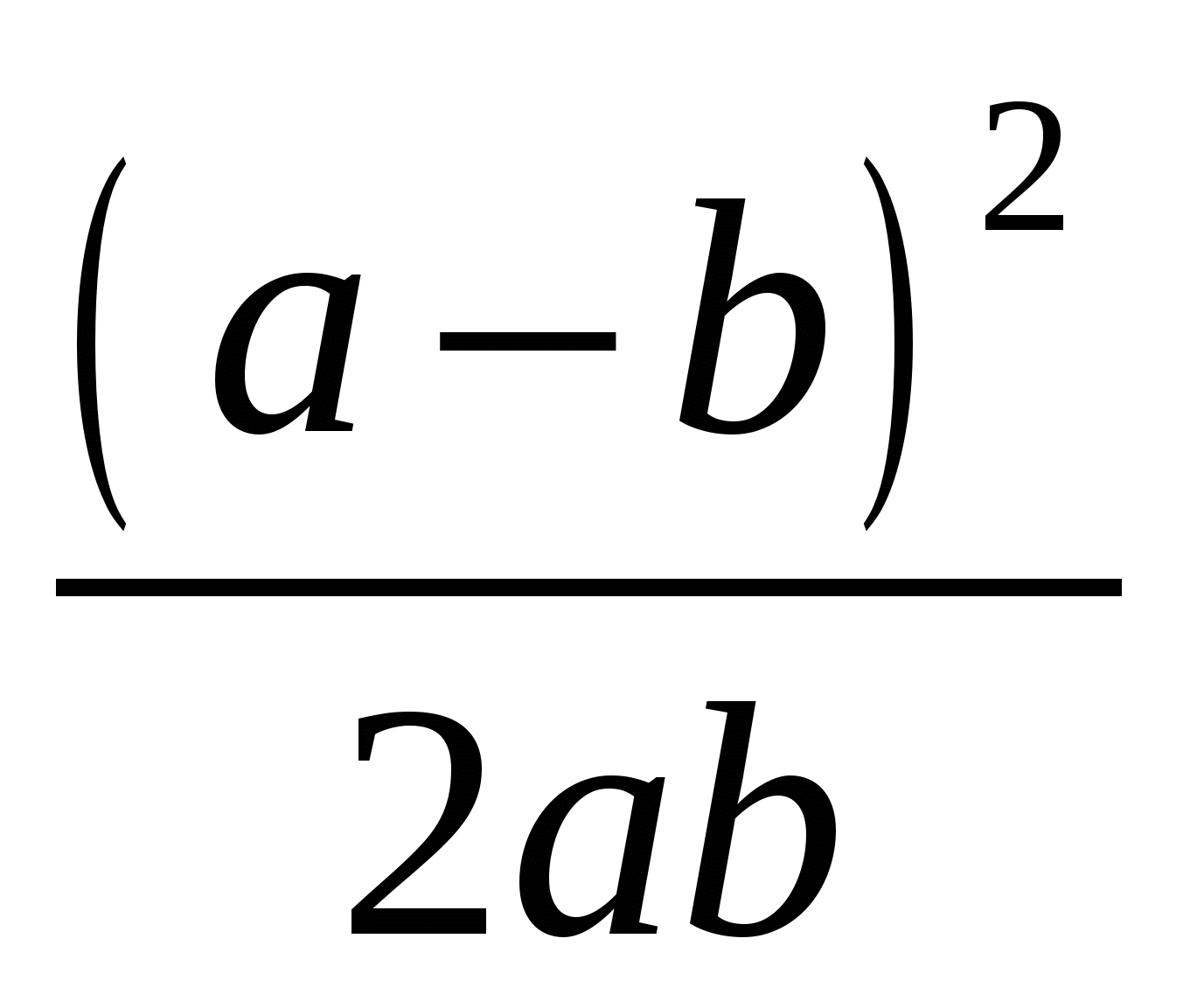 4)
4) 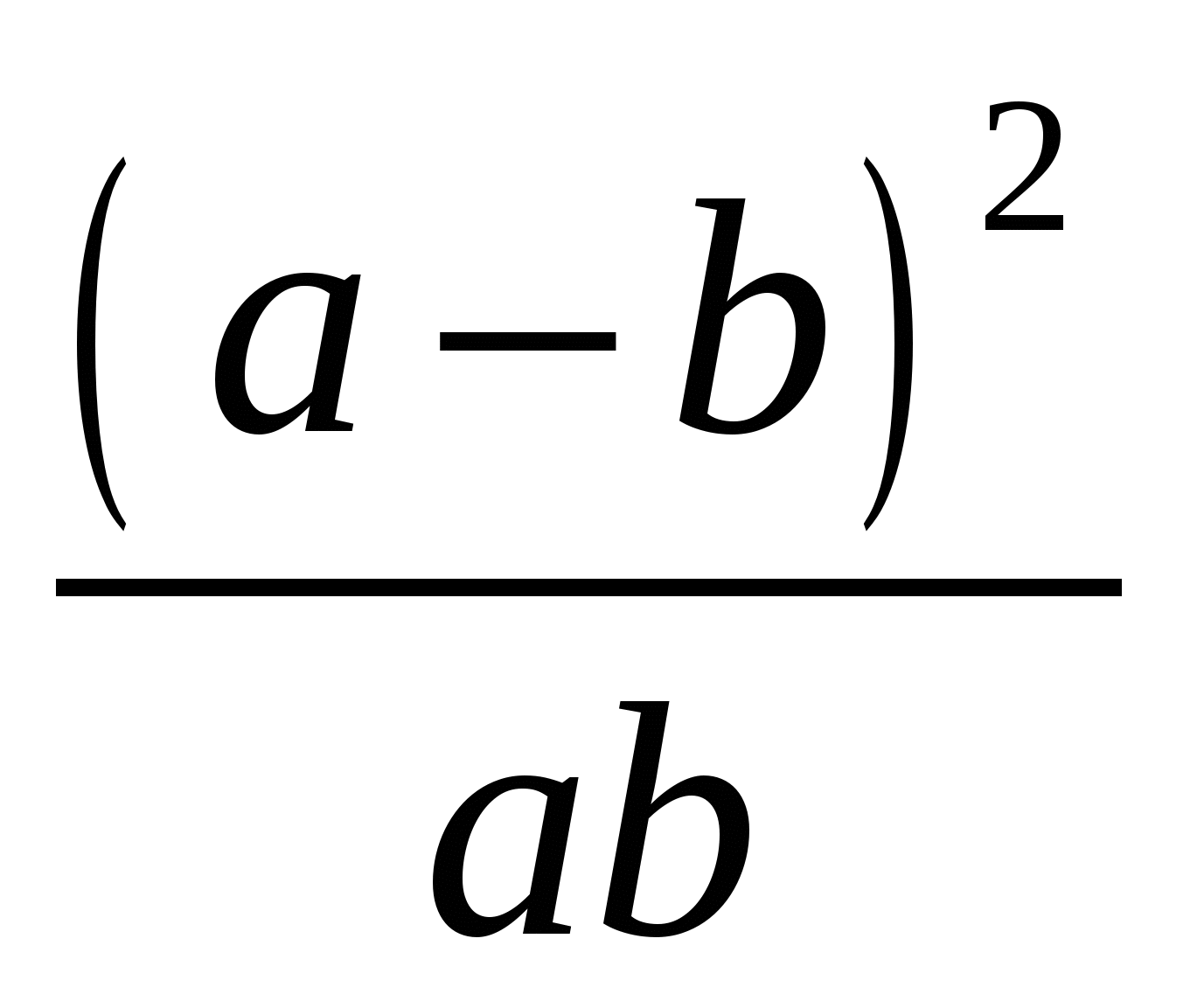
А6.
Выполните действия 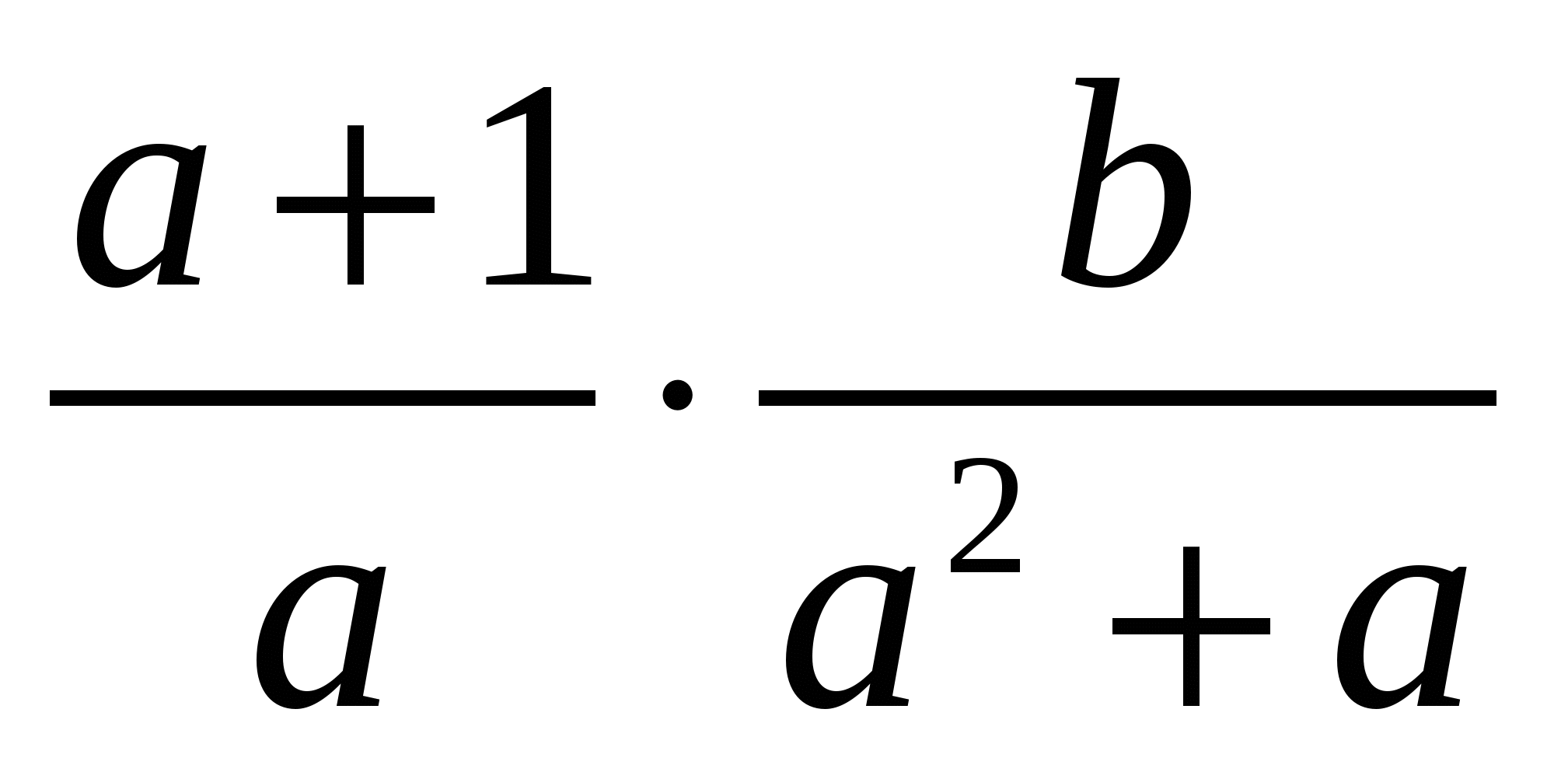 .
1)
.
1) 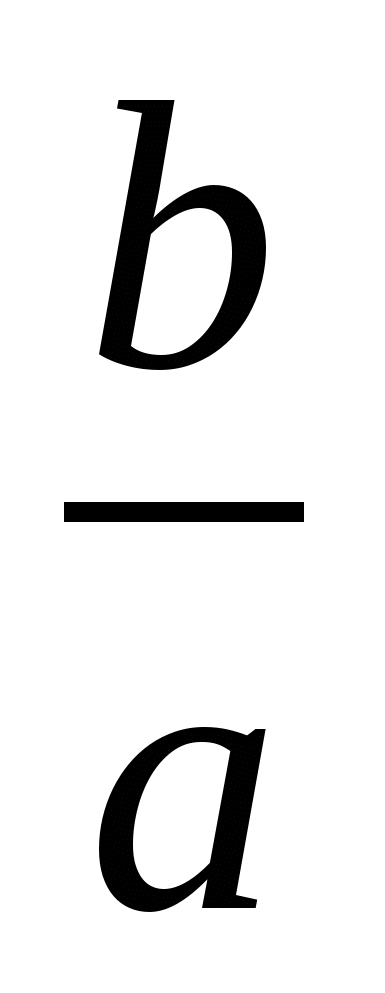 2)
2) 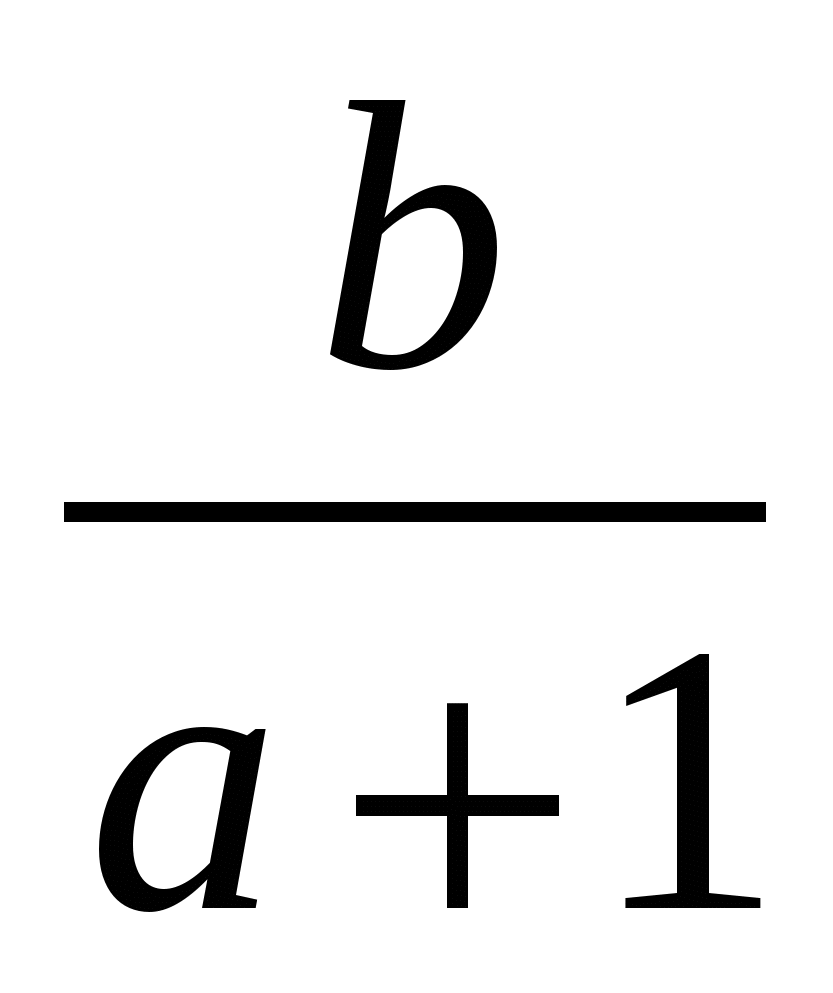 3)
3) 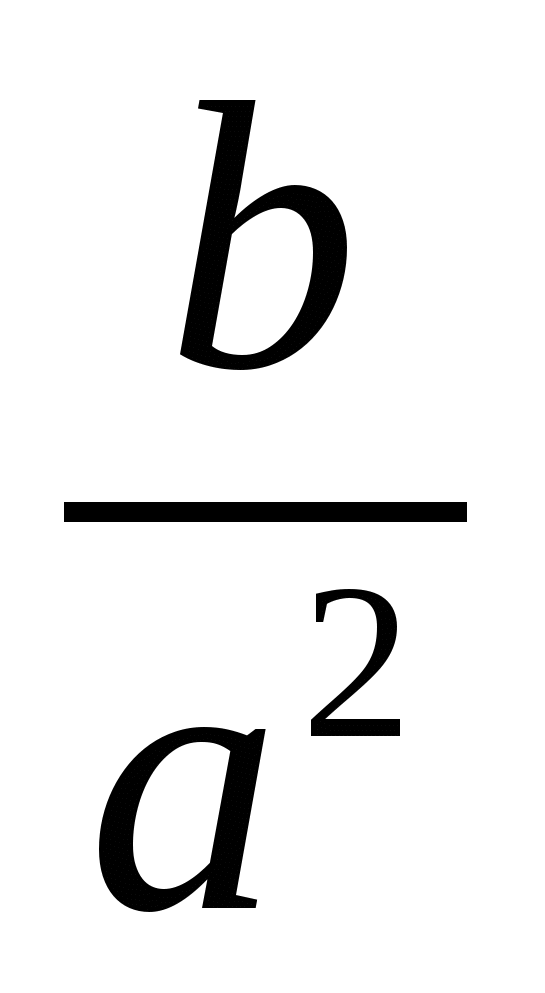 4)
4) 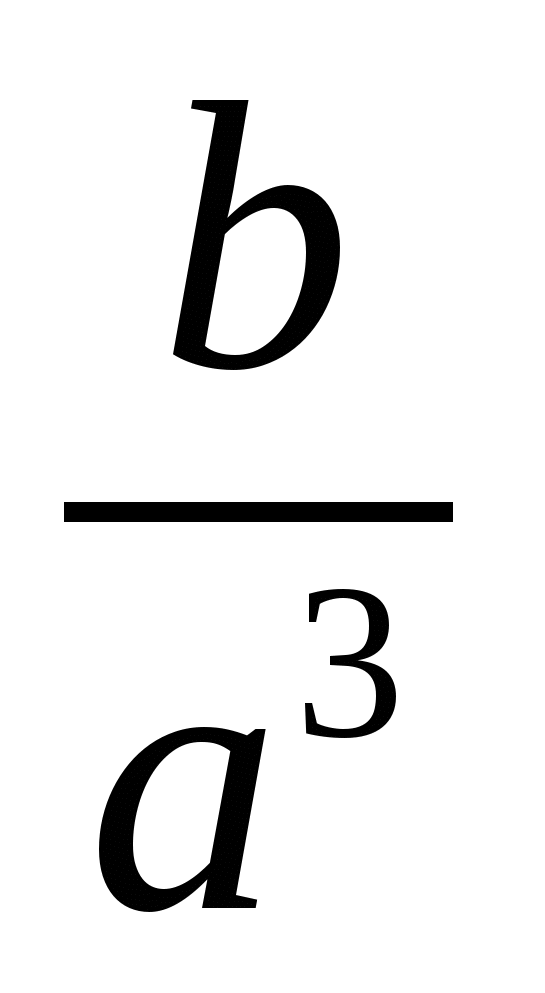
А7.
Выполните действия 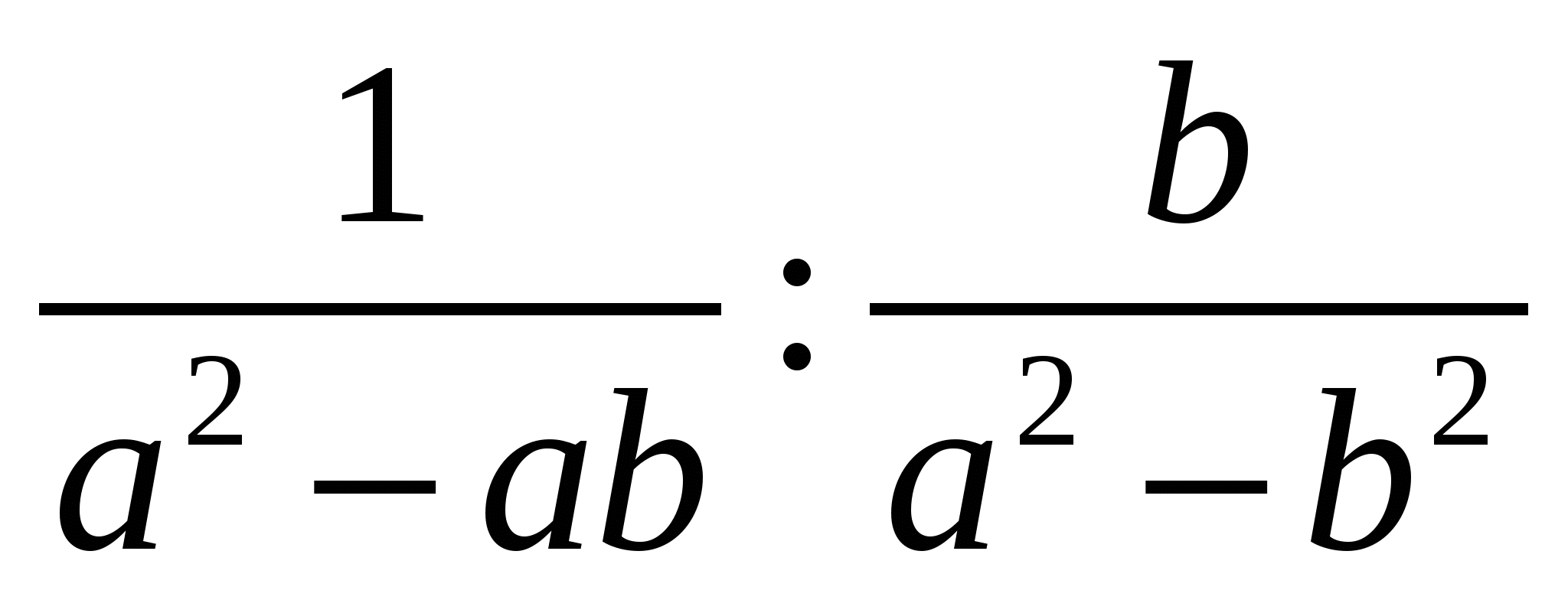 .
.
1) 
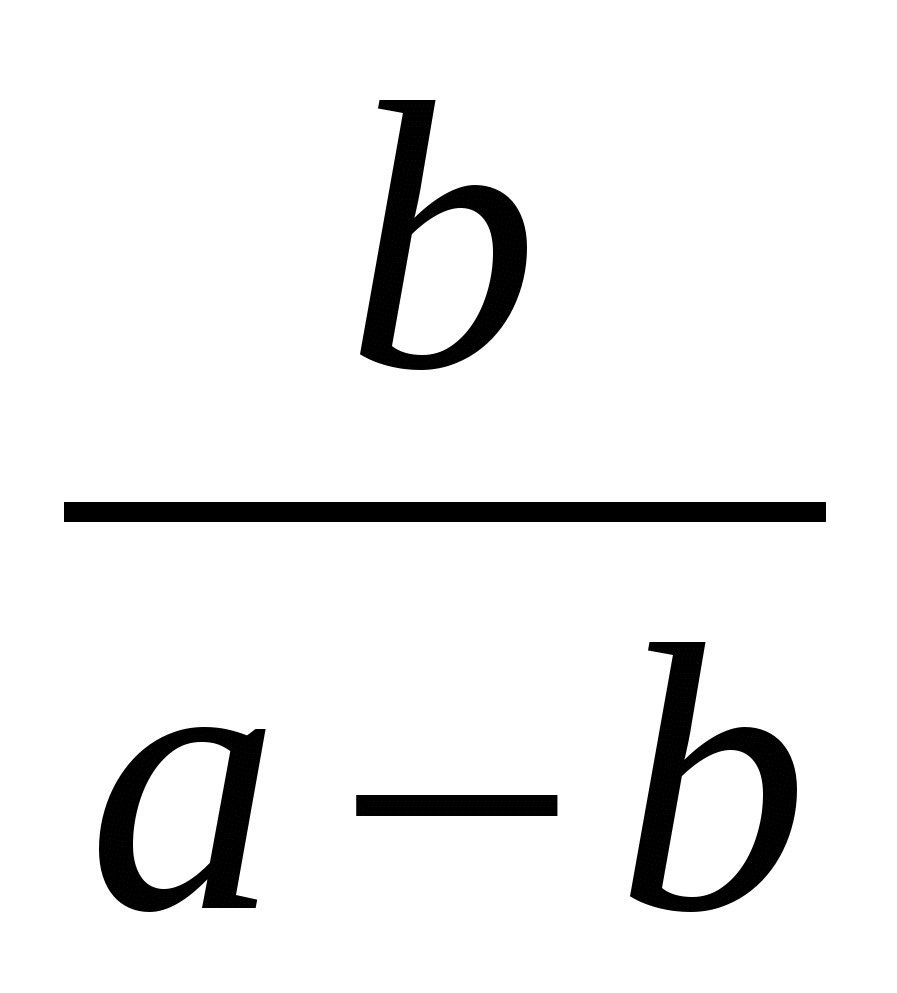 3)
3) 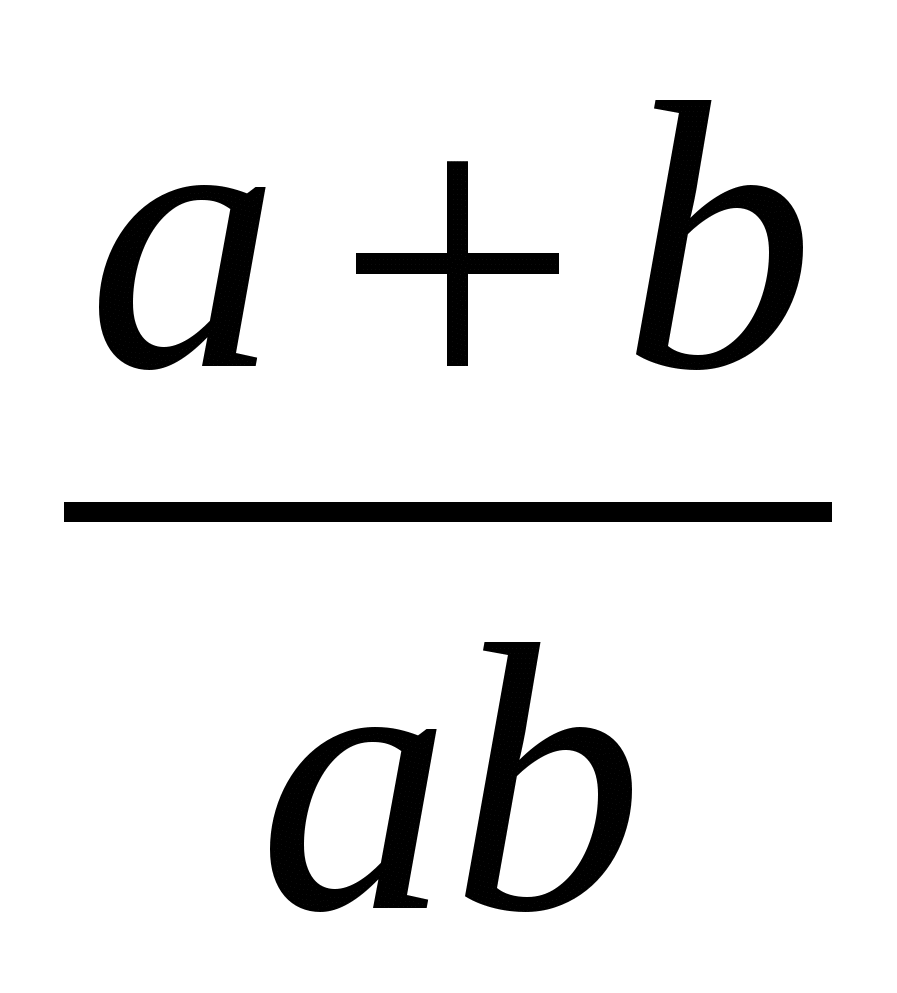 4)
4) 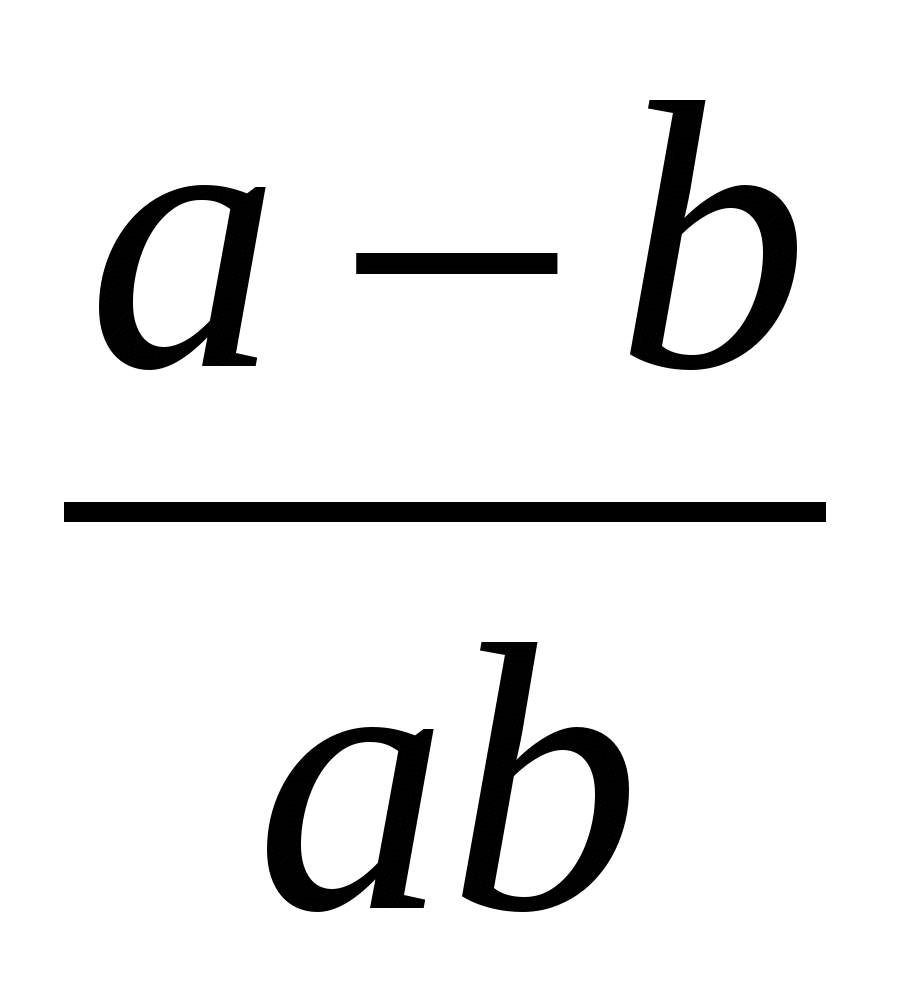
А8.
Выполните действия 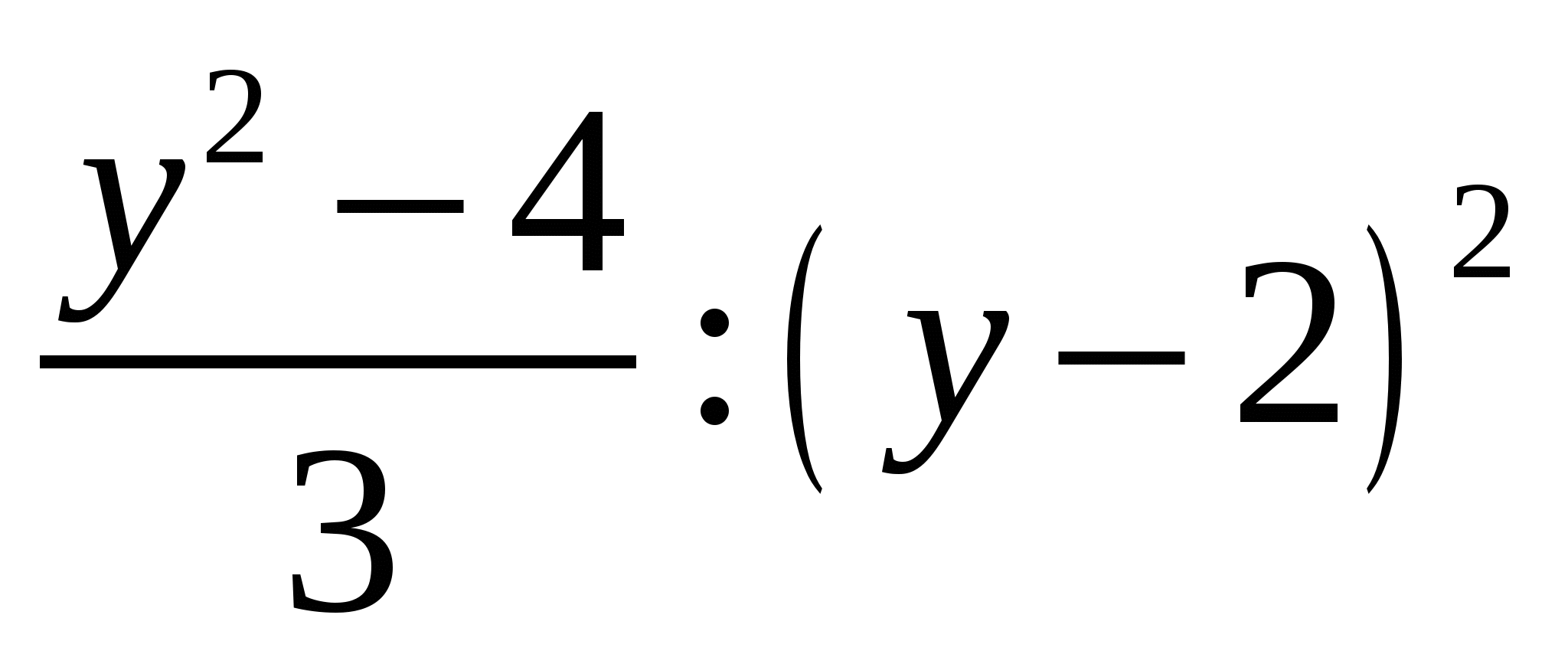 .
.
1) 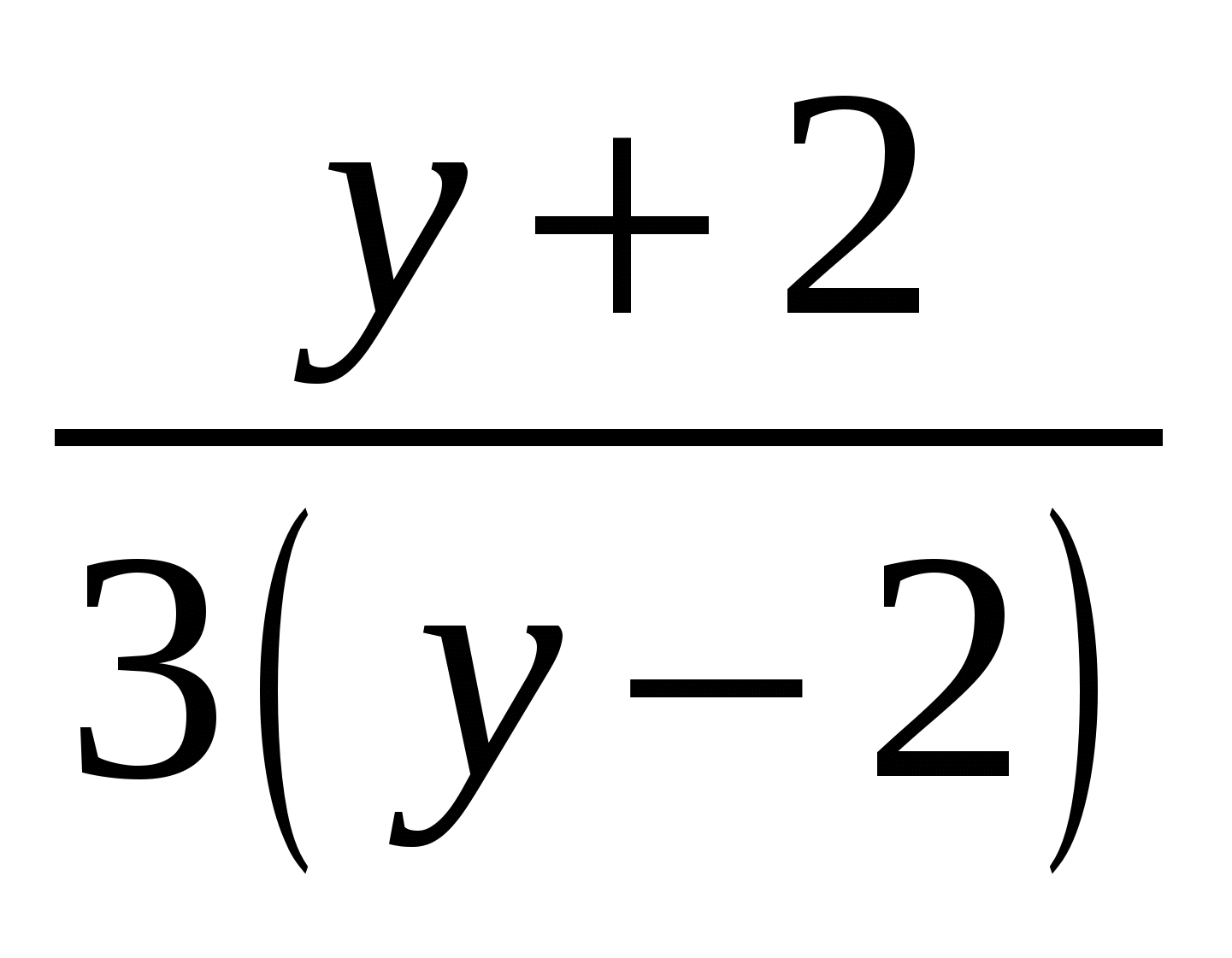 2)
2) 
 4)
4) 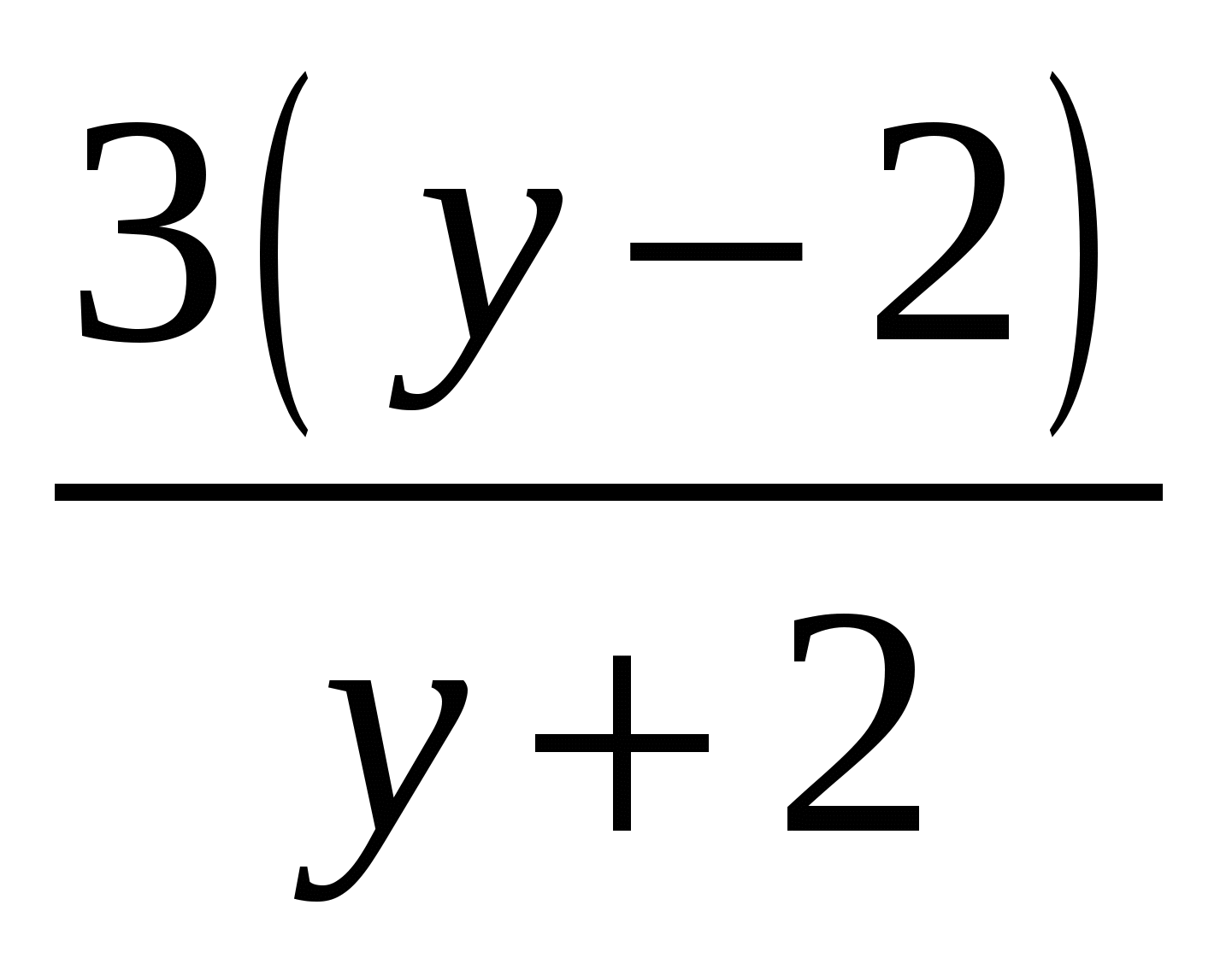
А9.
Выполните действия 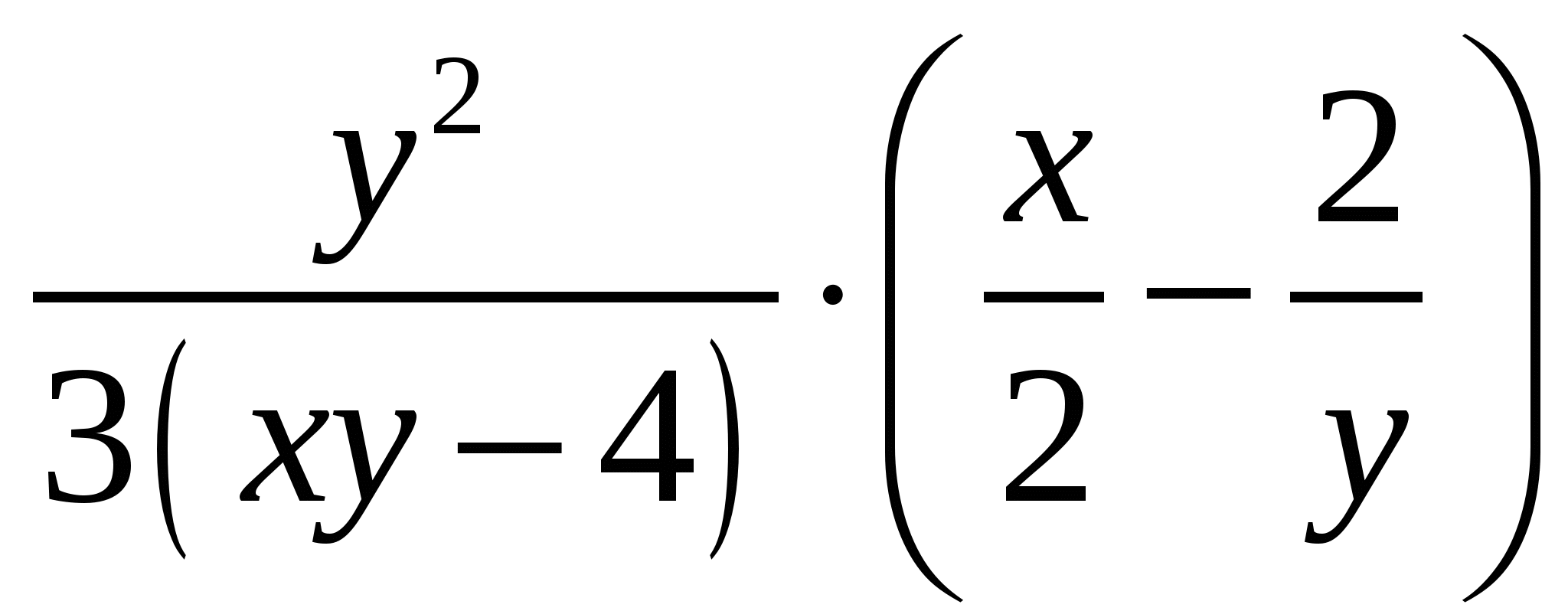 .
.
1) 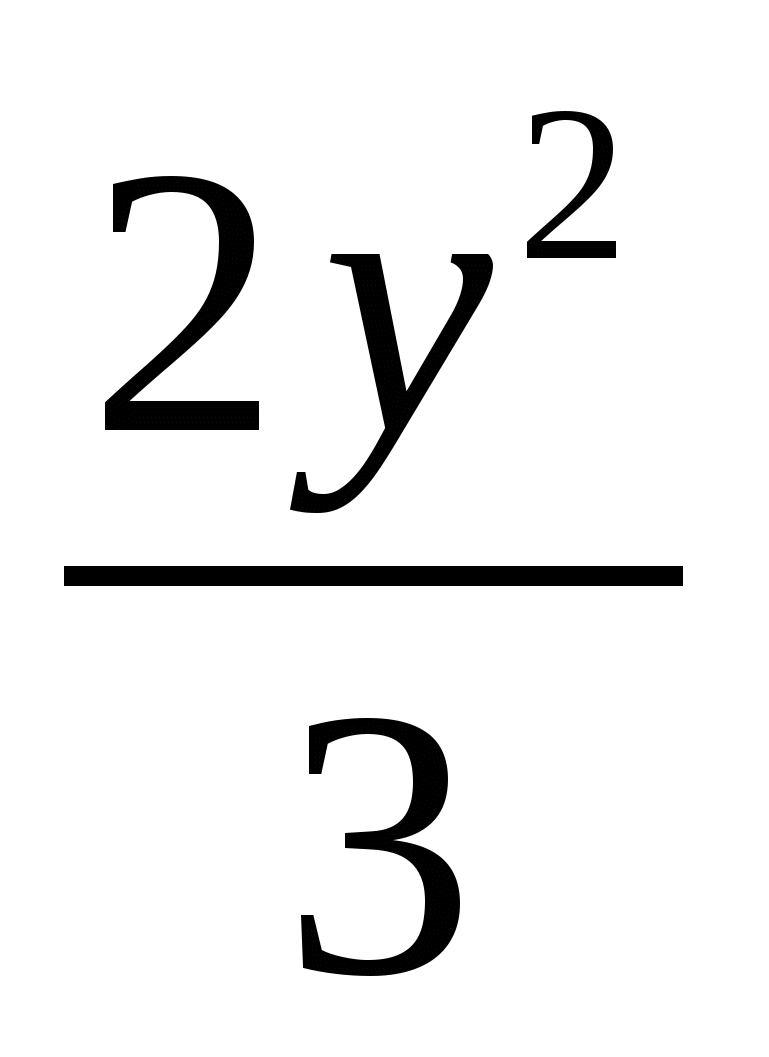 2)
2) 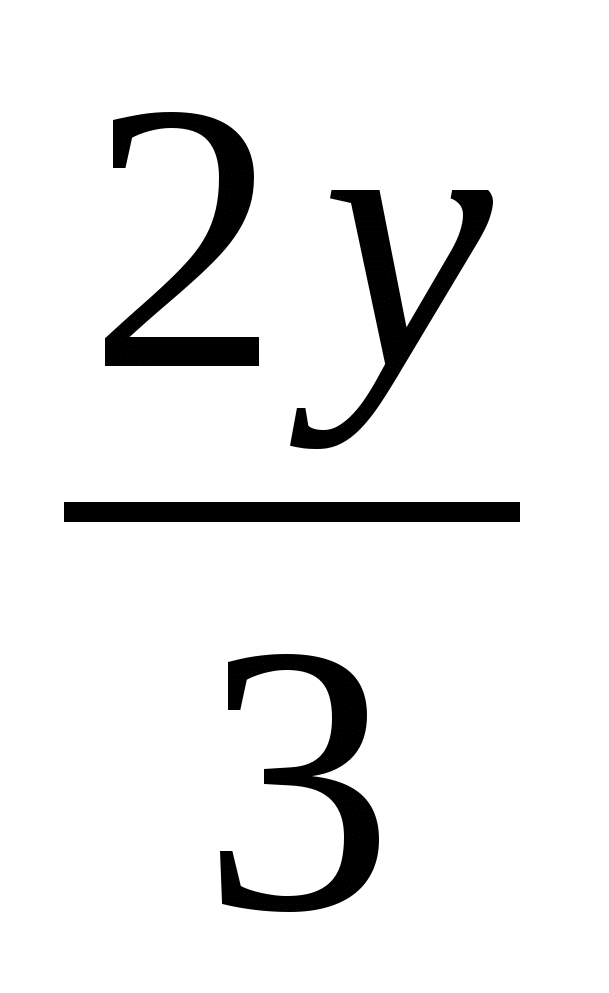 3)
3)  4)
4) 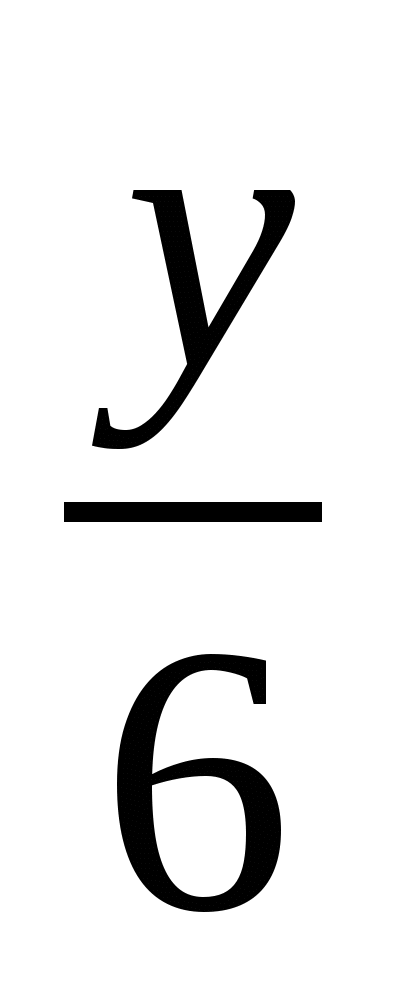
А10.
Найдите значение выражения  .
.
1) 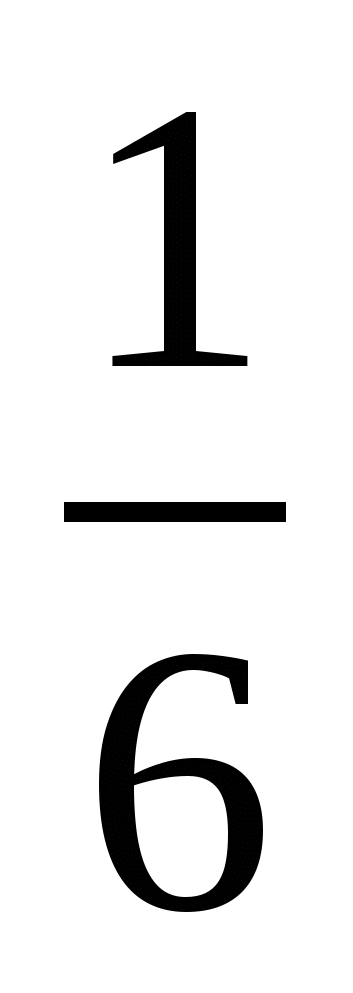 2)
2) 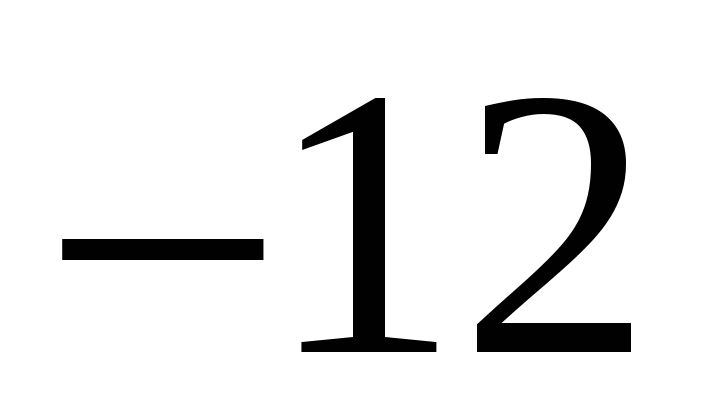 3)
3) 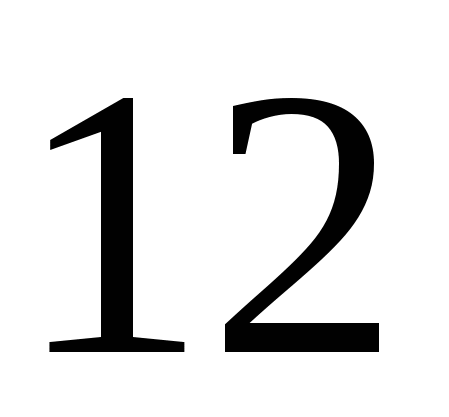 4)
4) 
Тест 1
Рациональные дроби
Вариант 2
ЧАСТЬ А
А1.
Найдите значение алгебраической дроби  .
.
1) 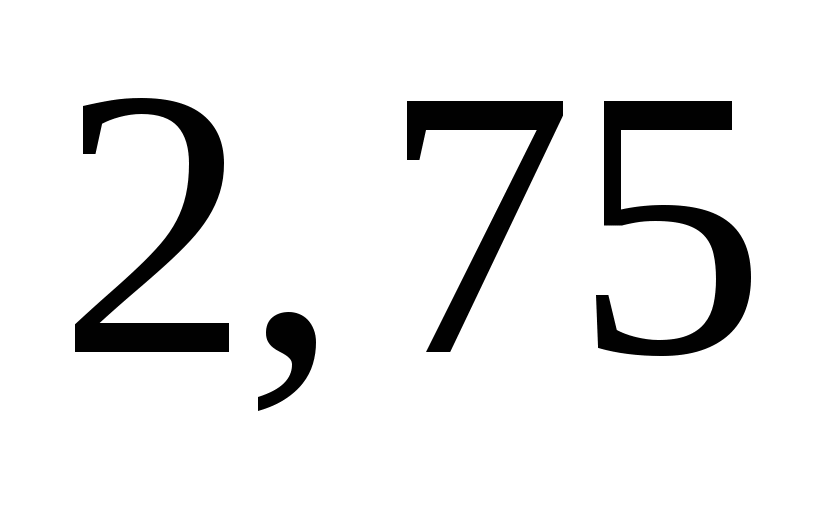 2)
2) 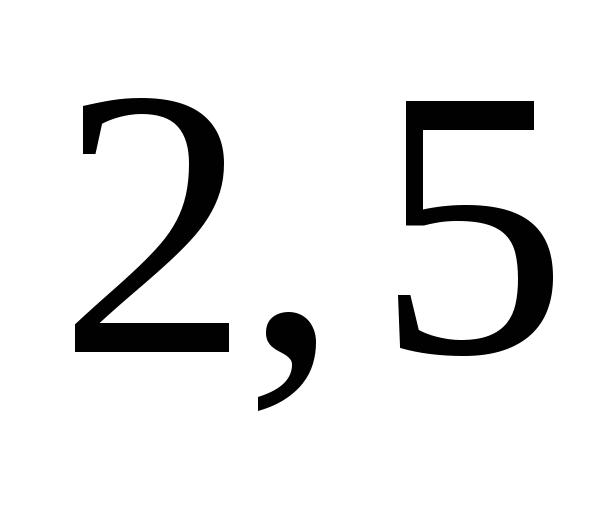 3)
3) 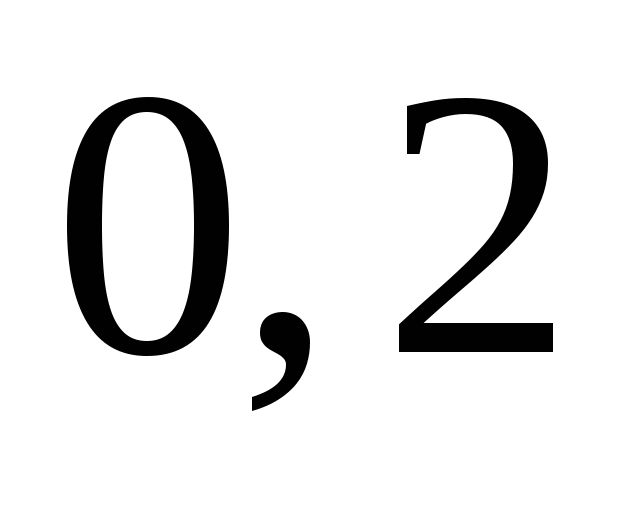 4)
4) 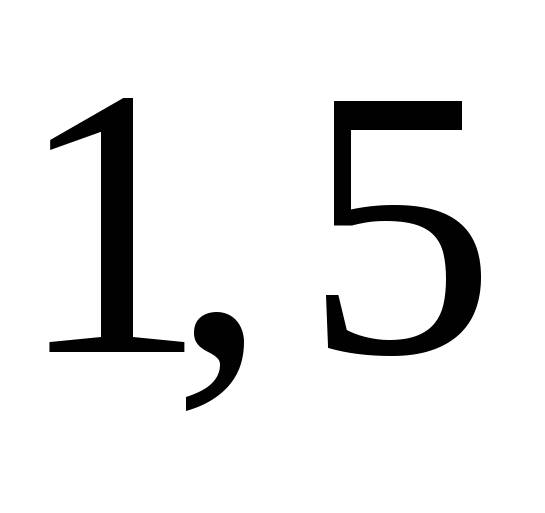
А2.
Сократите дробь 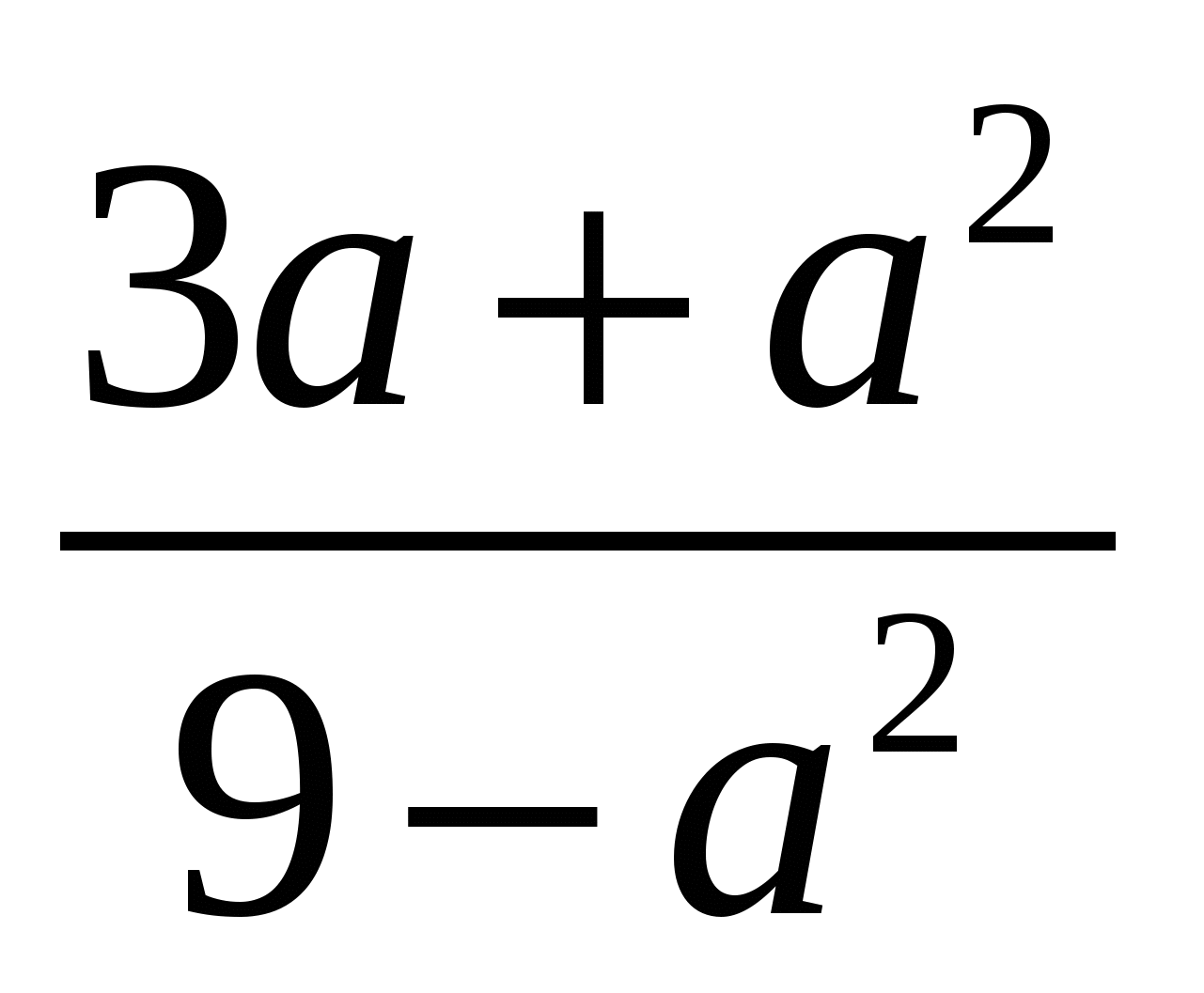
 2)
2) 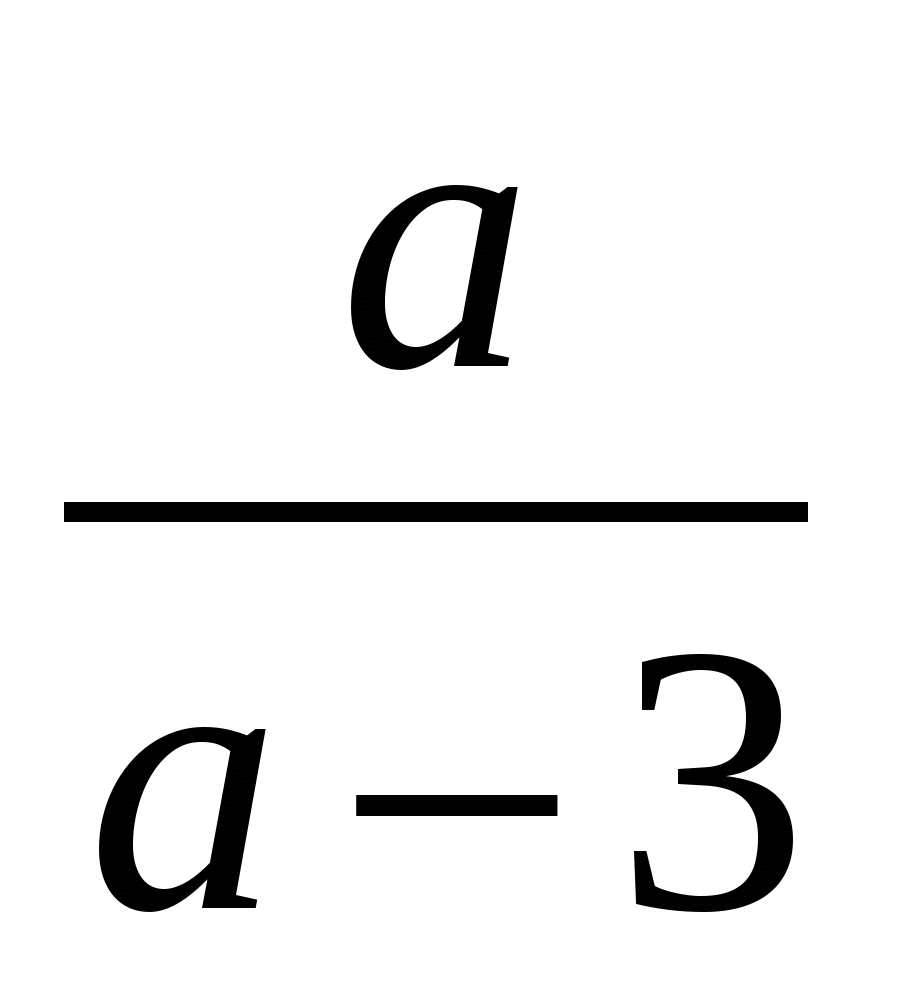 3)
3) 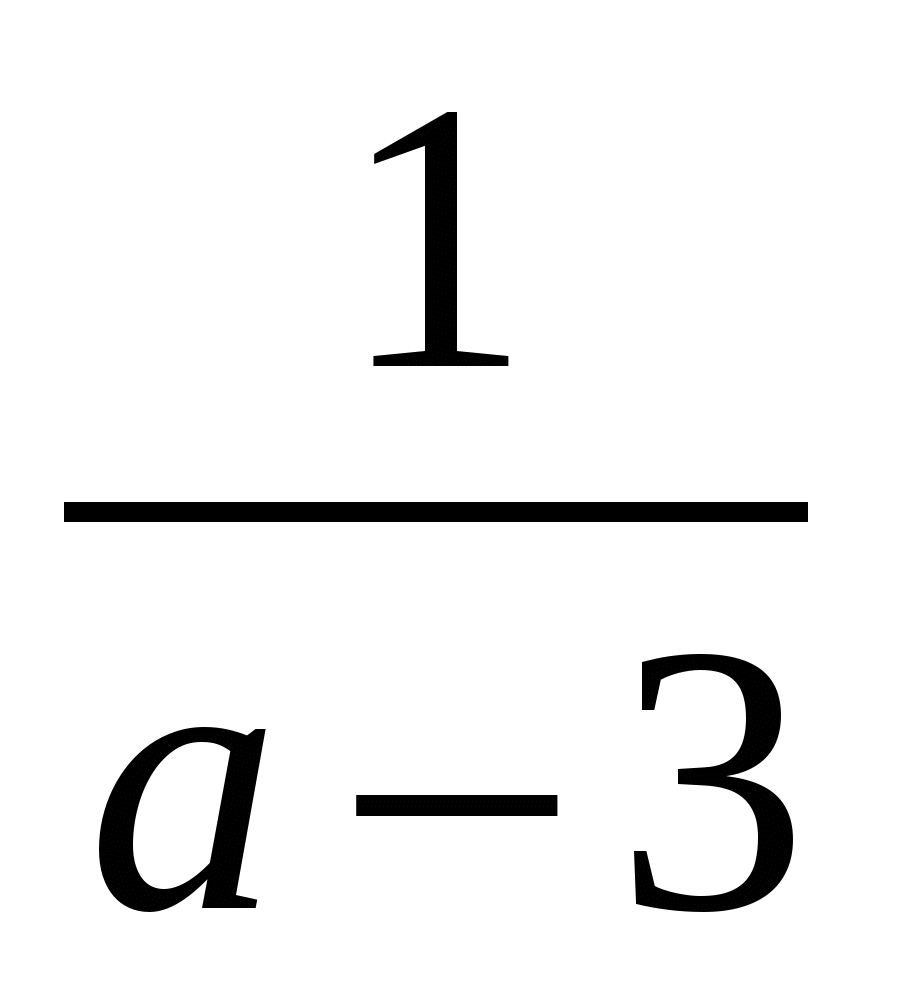 4)
4)
А3.
Найдите значение 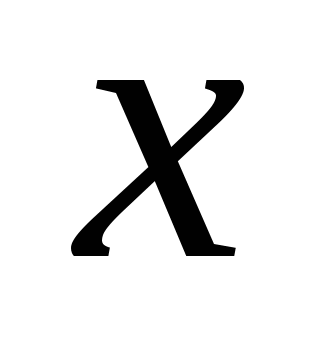 ,
при котором дробь
,
при котором дробь 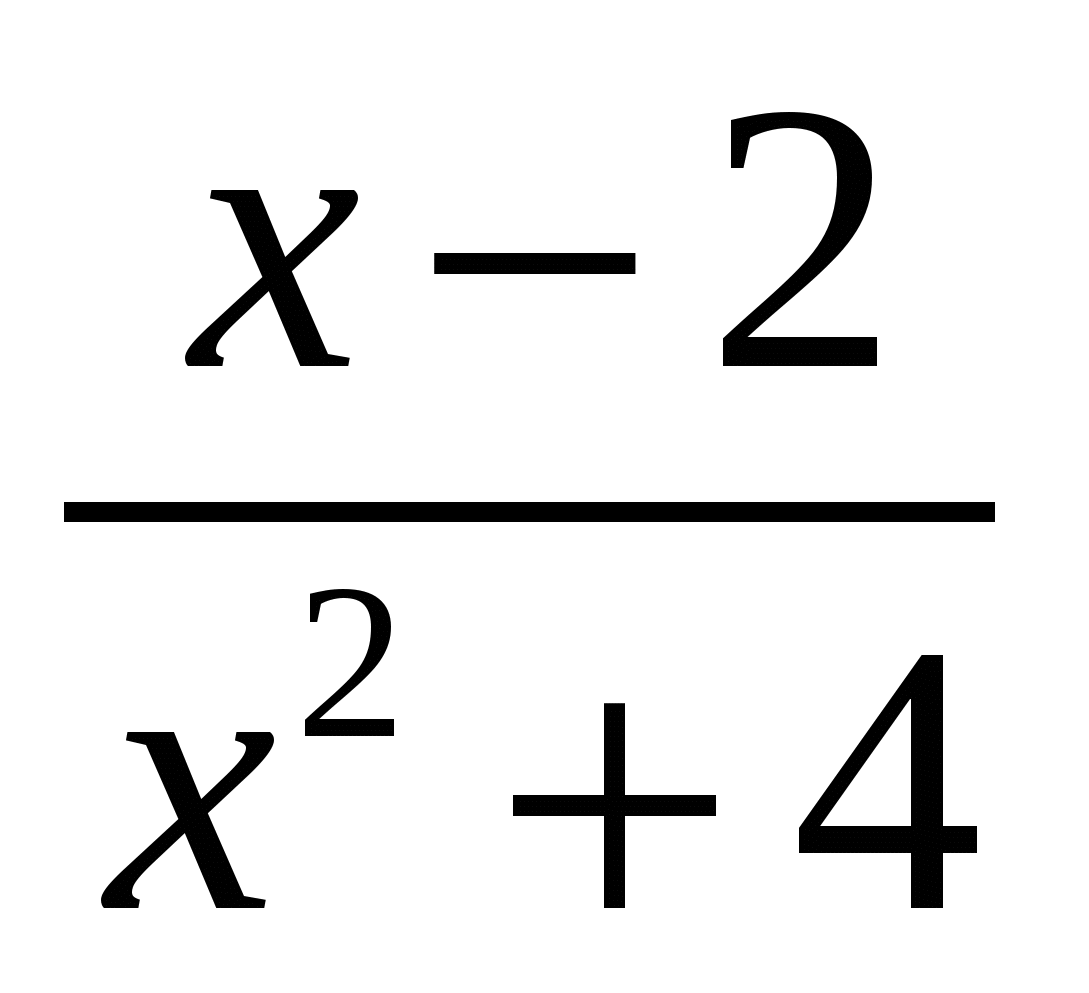 не имеет смысла
не имеет смысла
1) 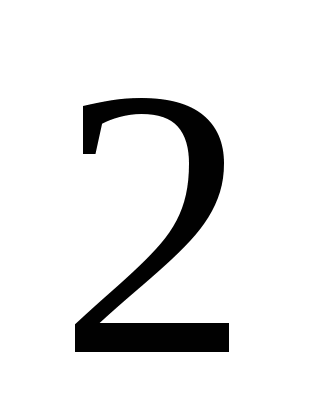
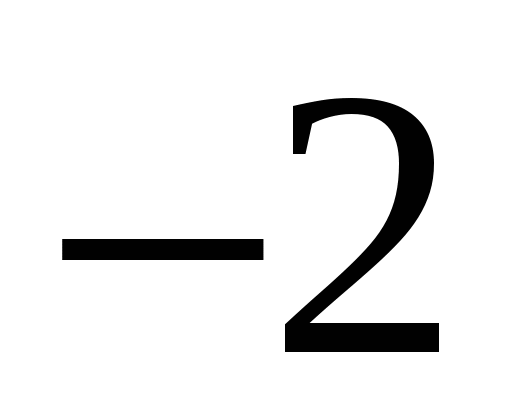 3)
3) 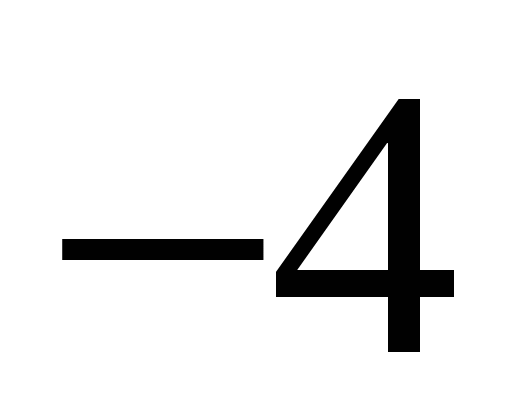 4) нет таких
значений
4) нет таких
значенийА4.
Выполните вычитание 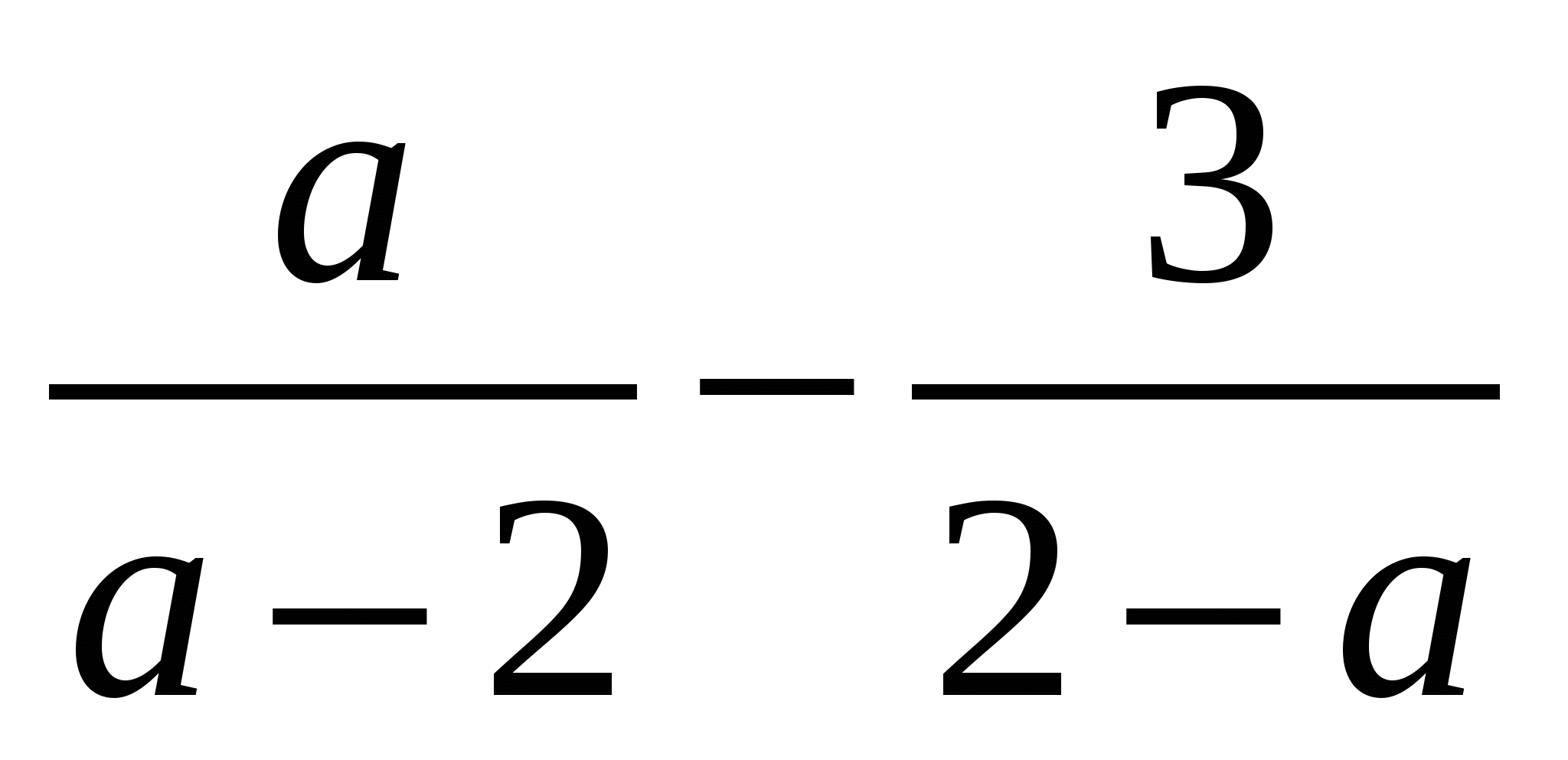 .
.
1) 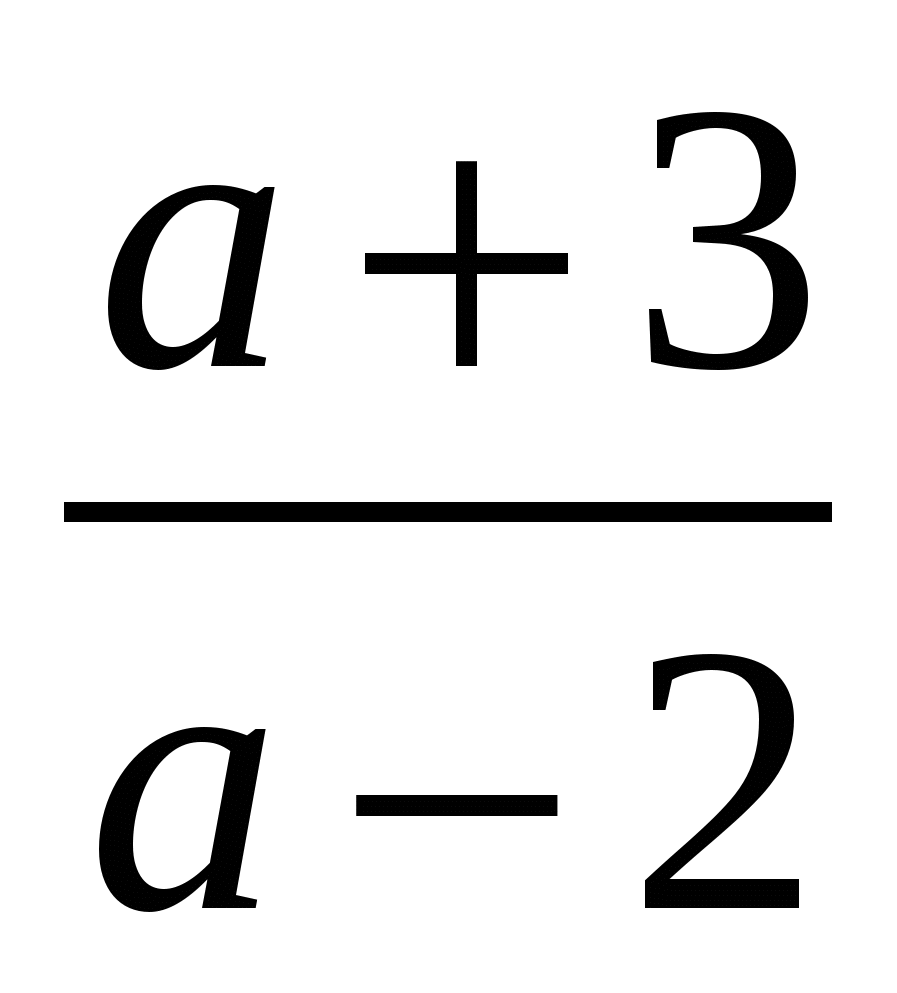 2)
2) 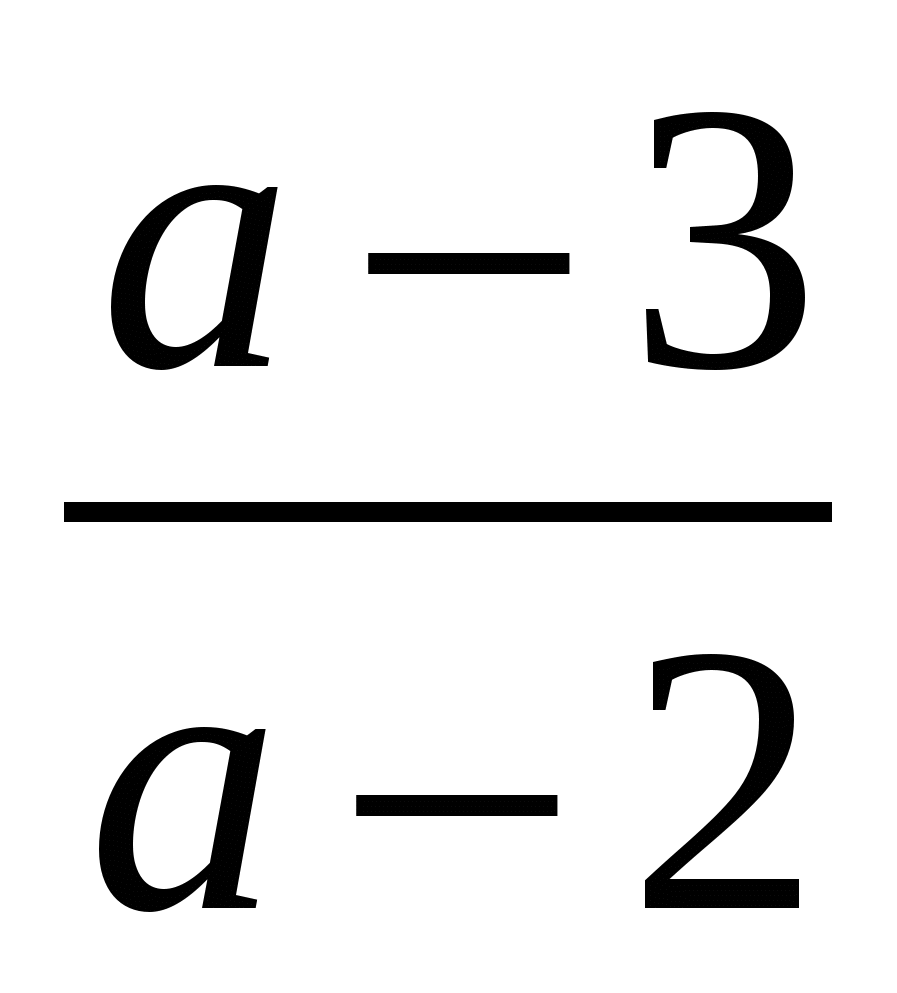 3)
3) 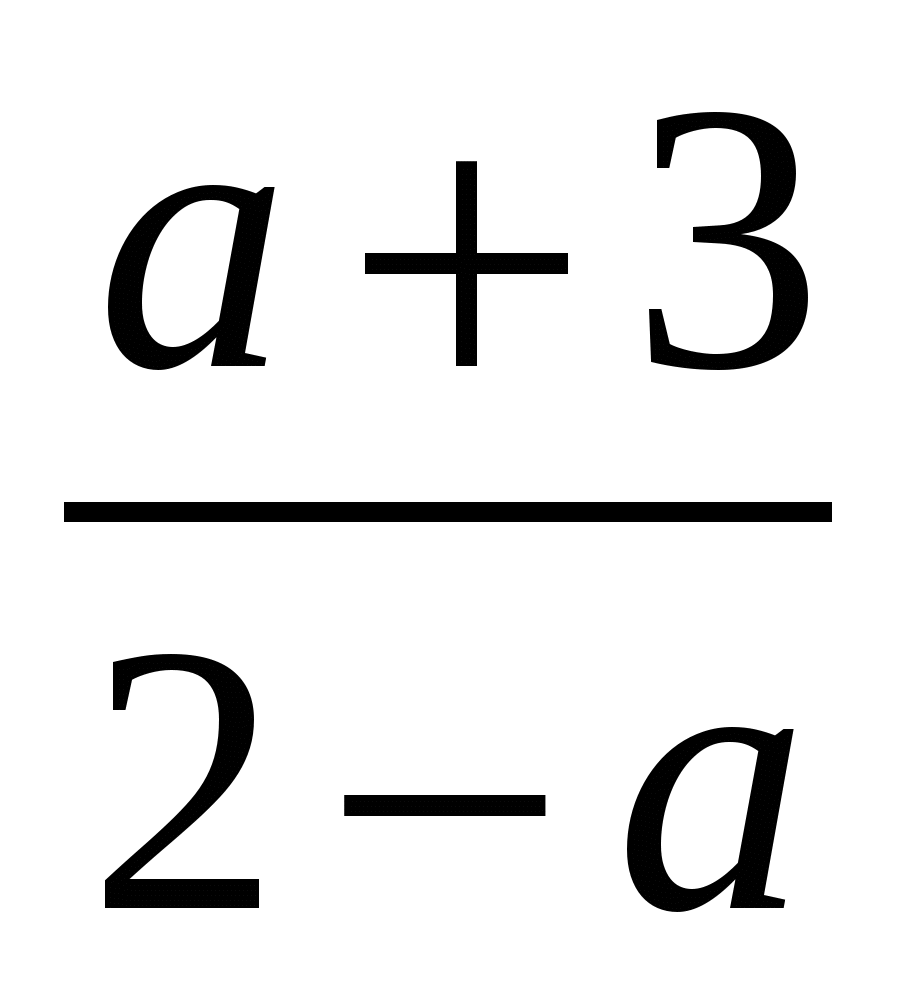
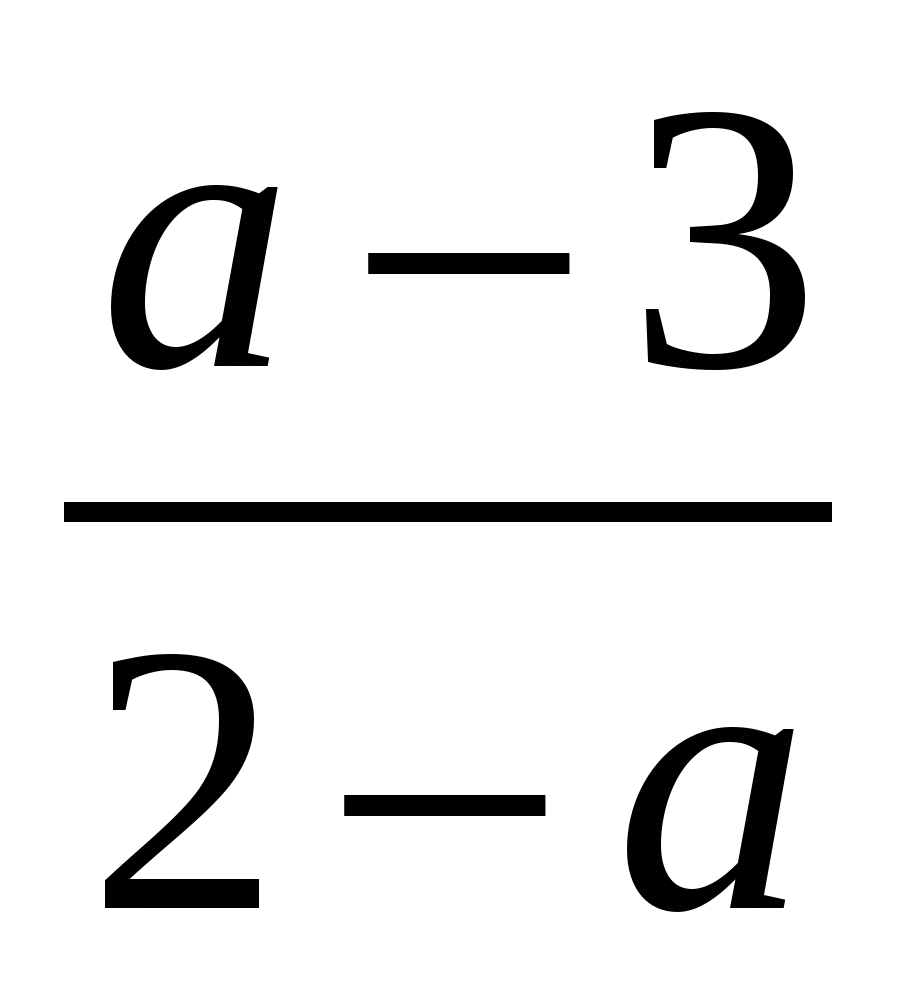
А5.
Выполните действия 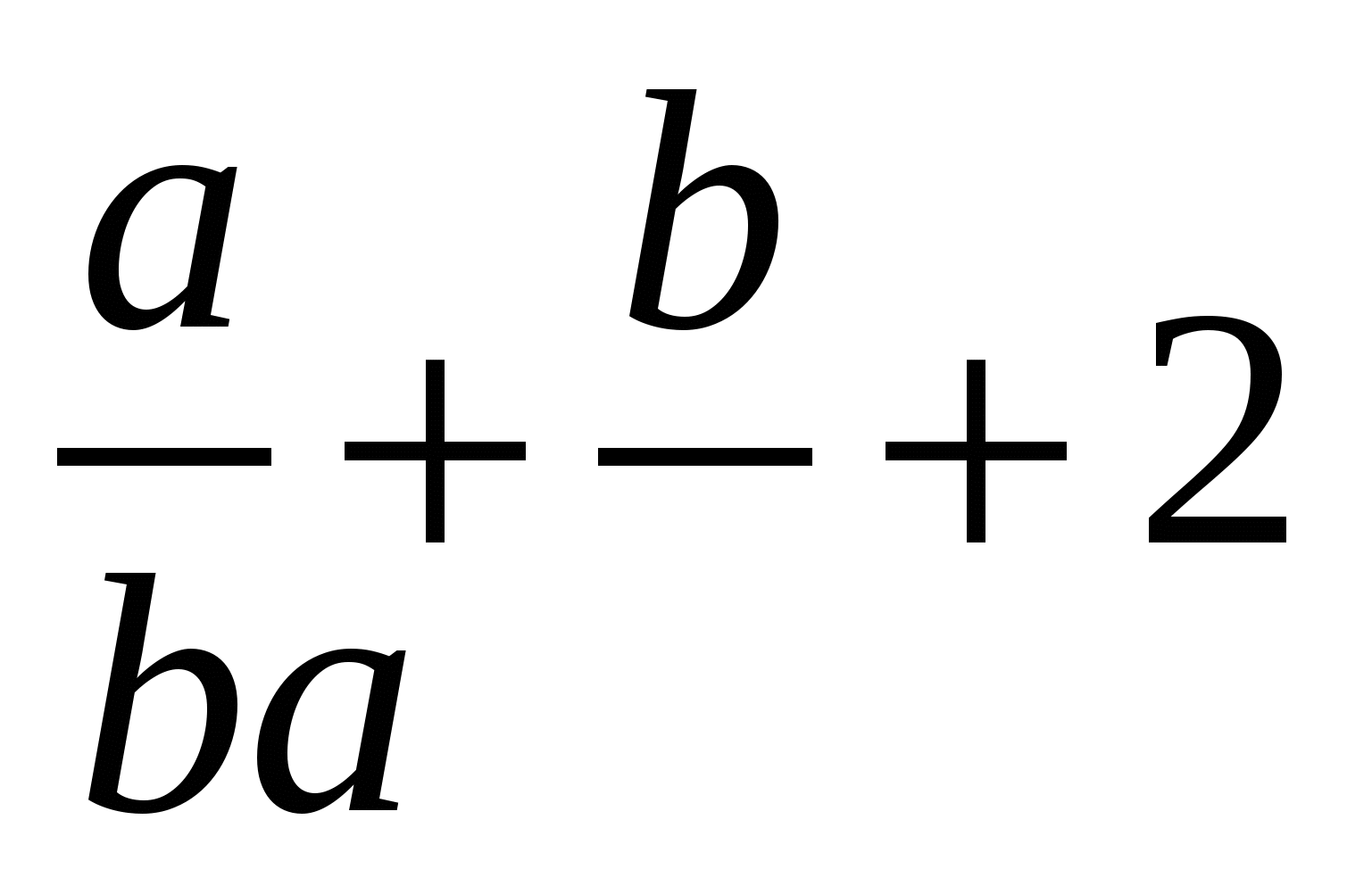 .
.
1) 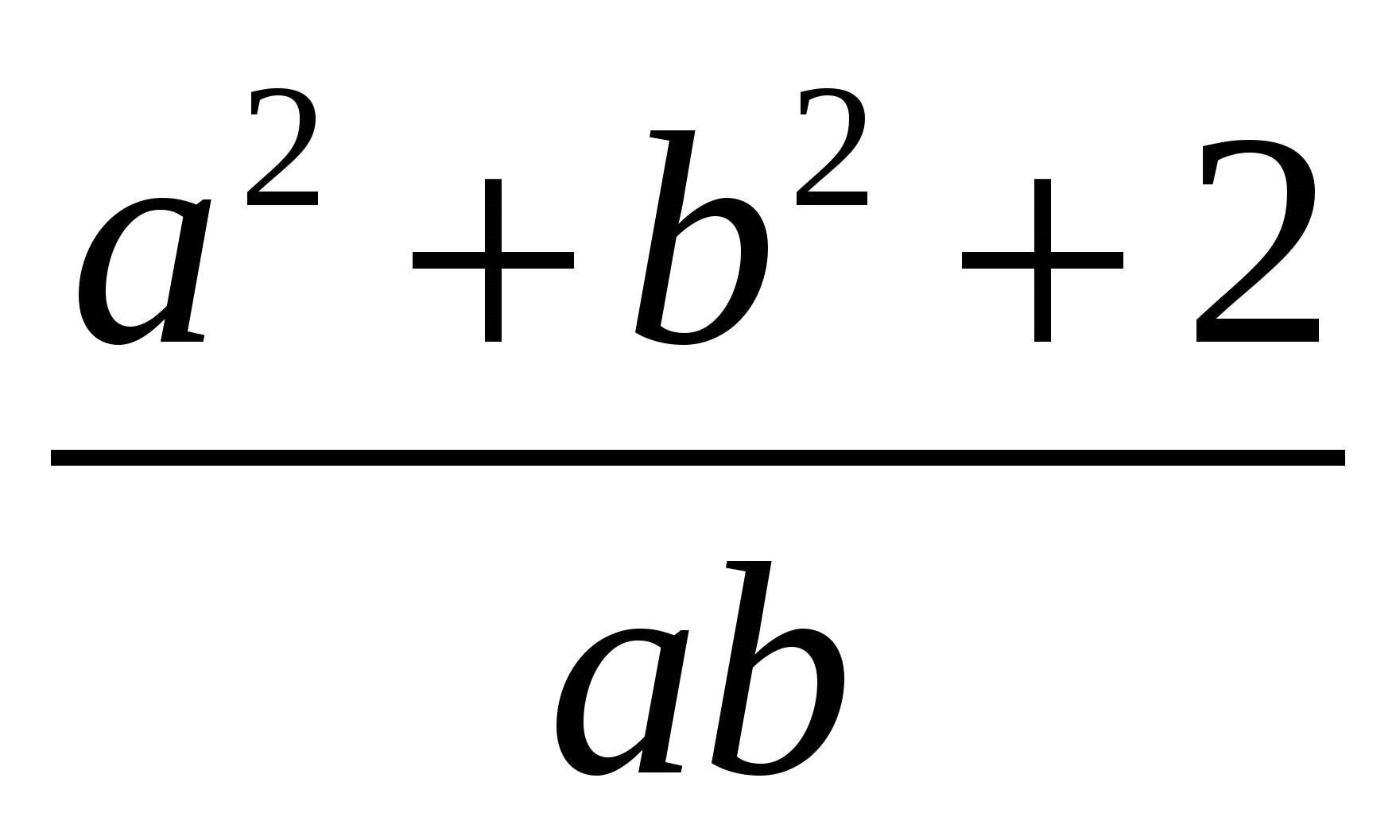 2)
2) 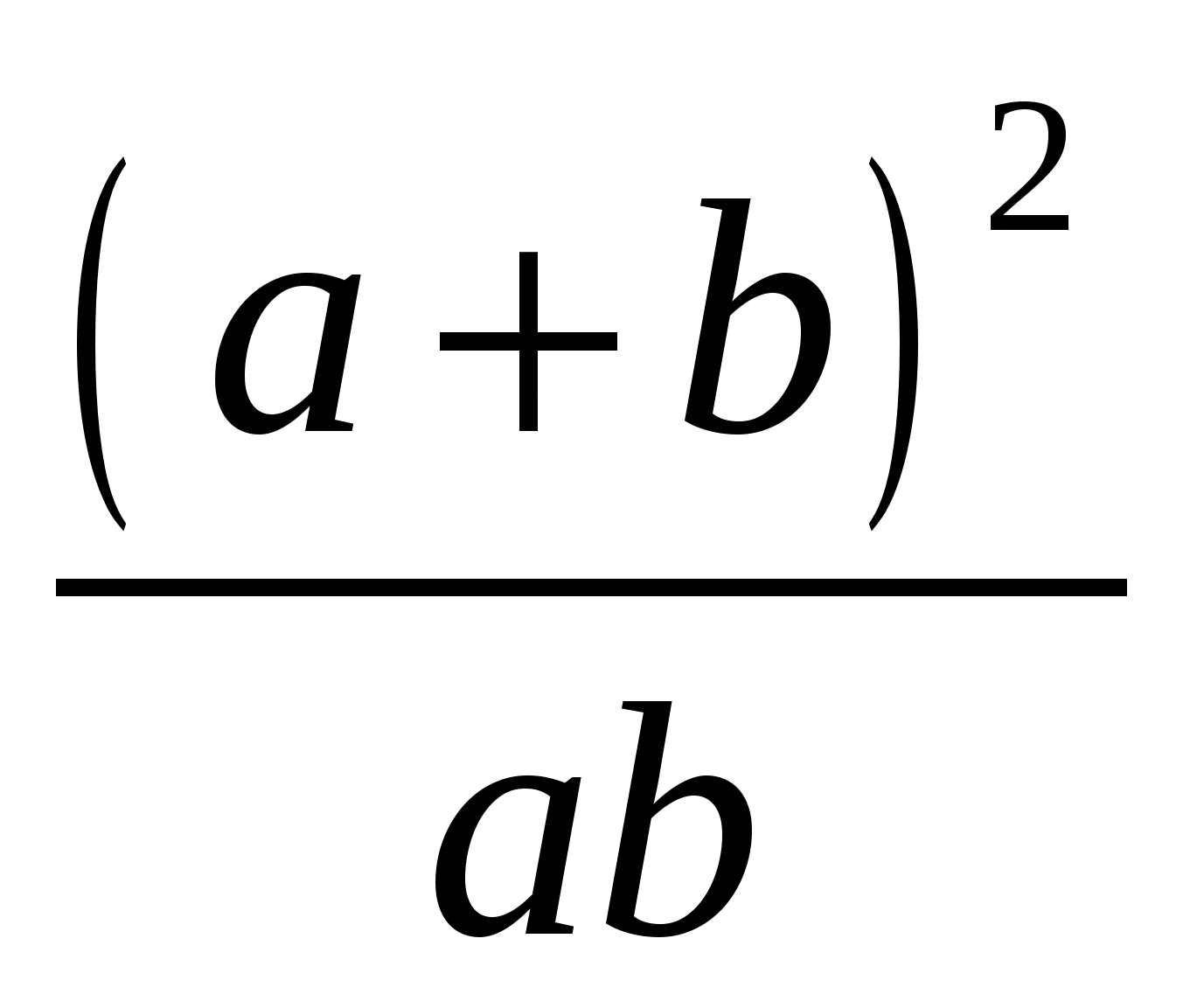 3)
3) 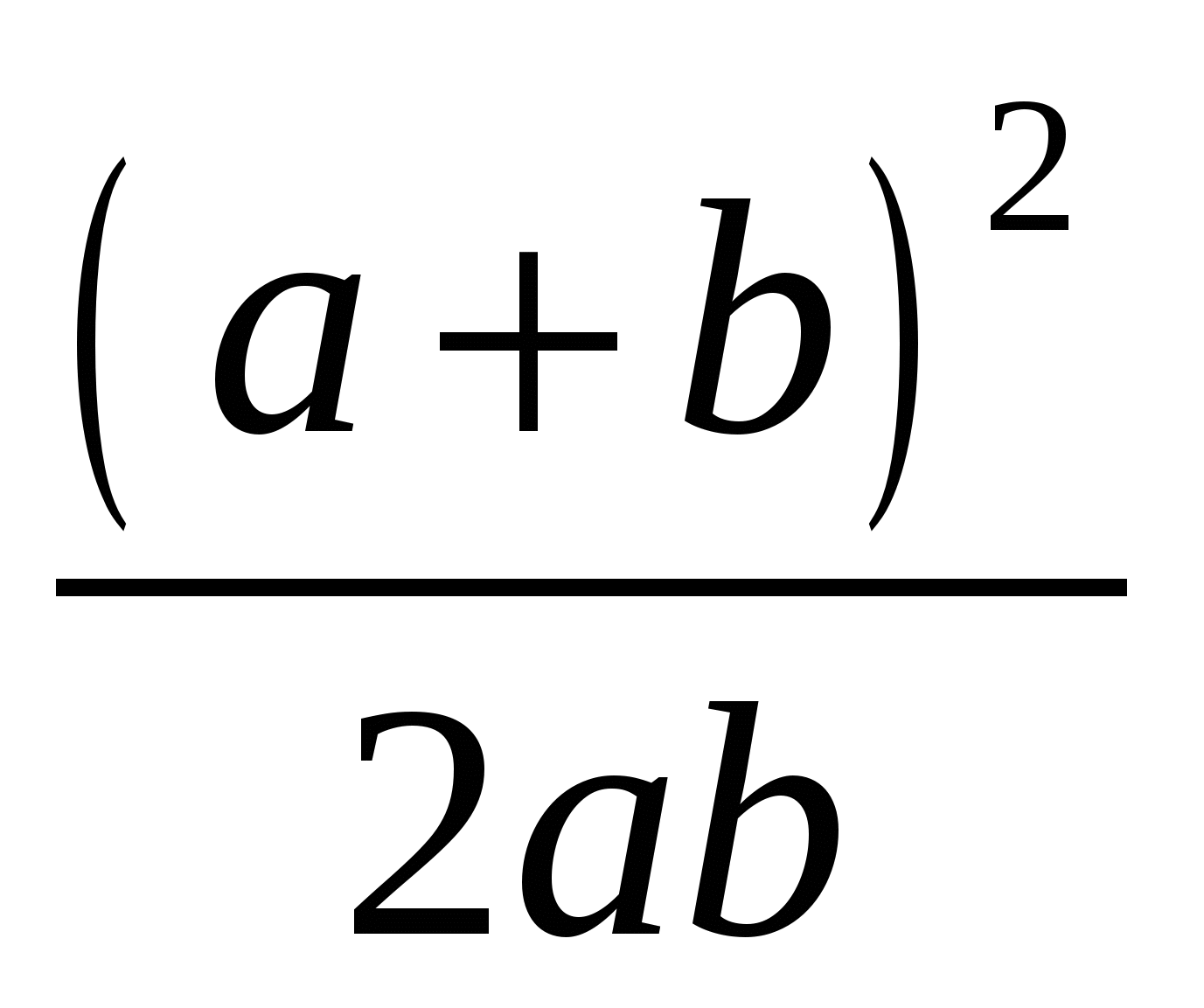 4)
4) 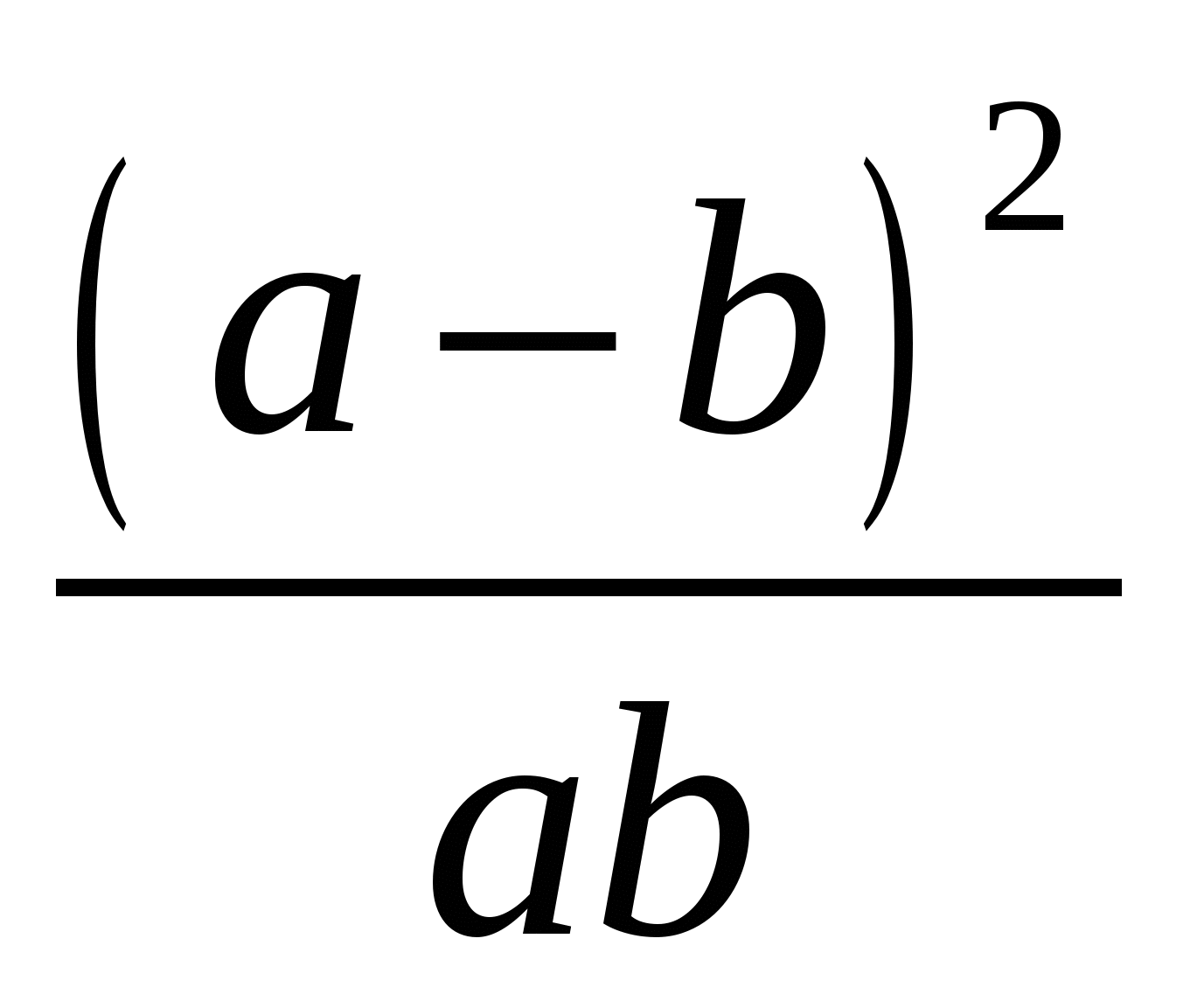
А6.
Выполните действия 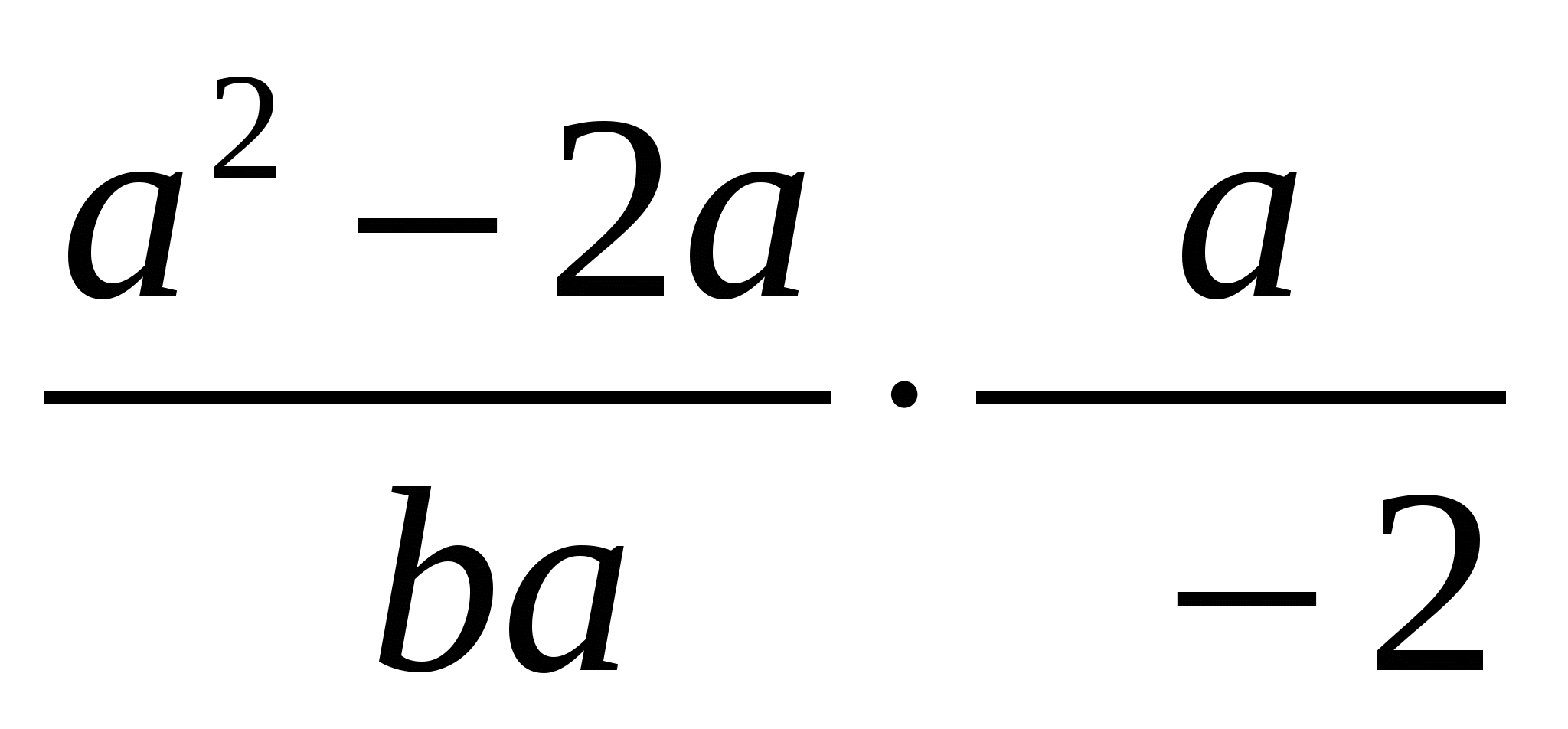 .
1)
.
1) 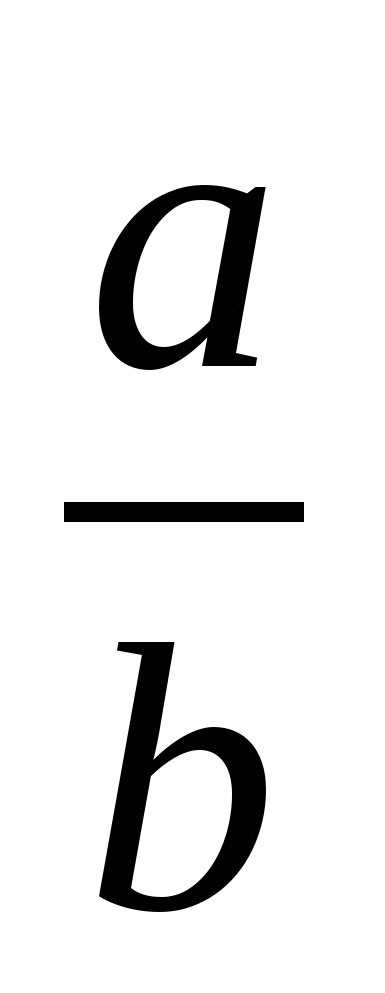 2)
2) 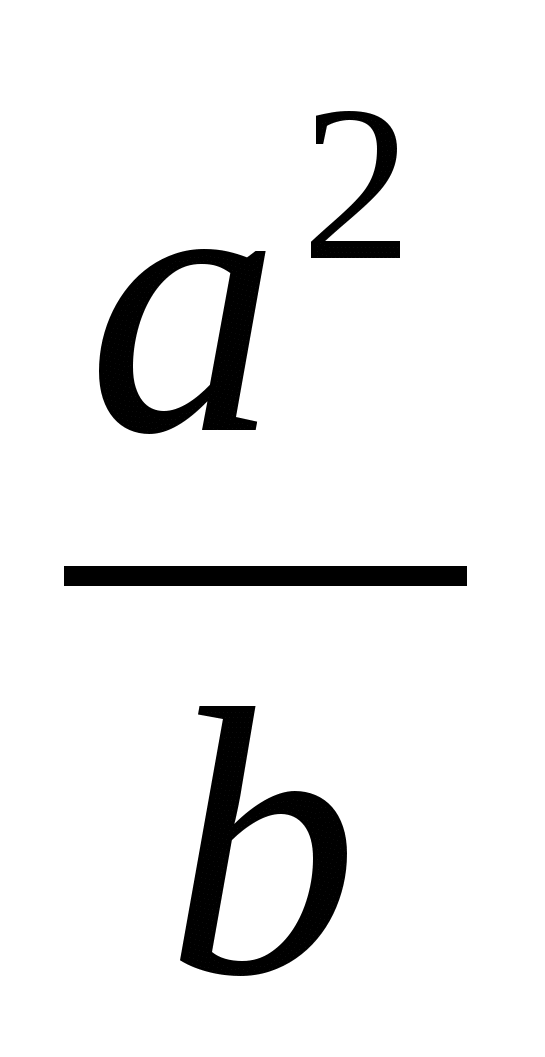 3)
3) 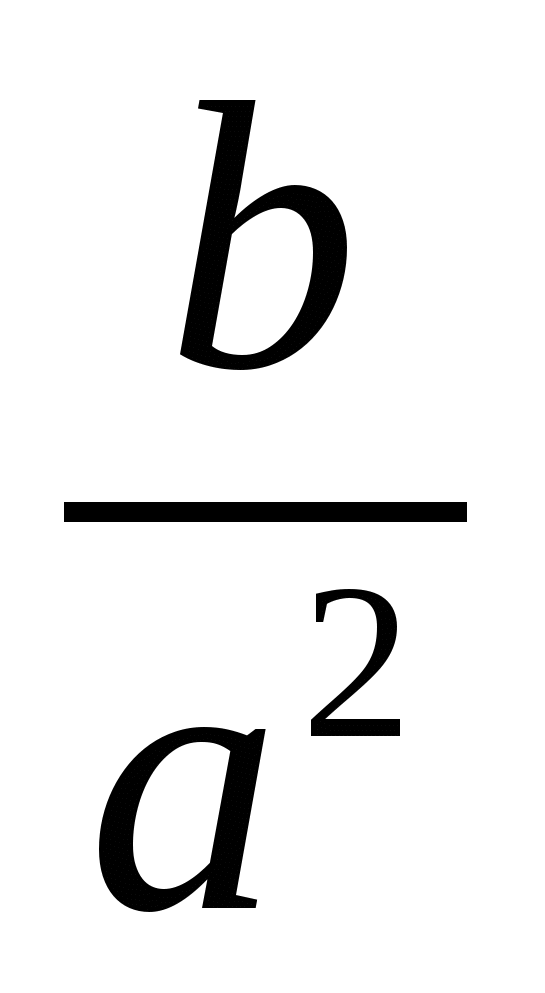 4)
4) 
А7.
Выполните действия 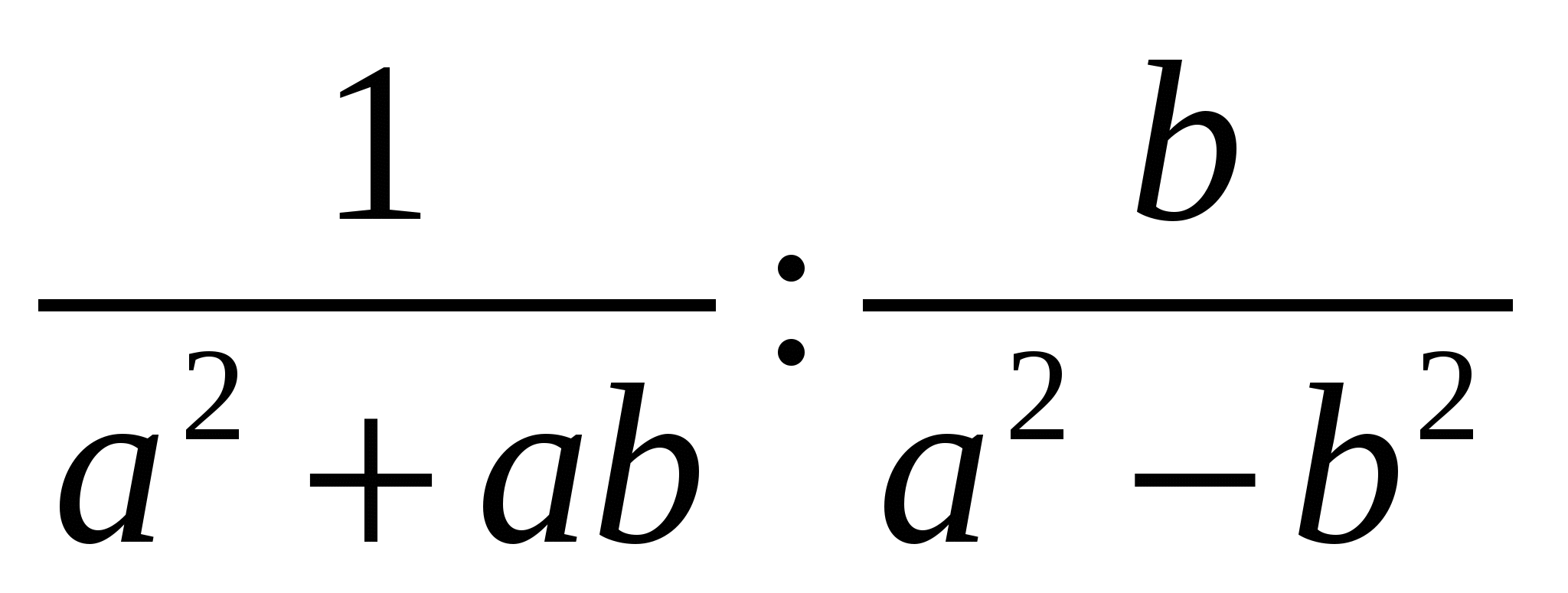 .
.
1)  2)
2) 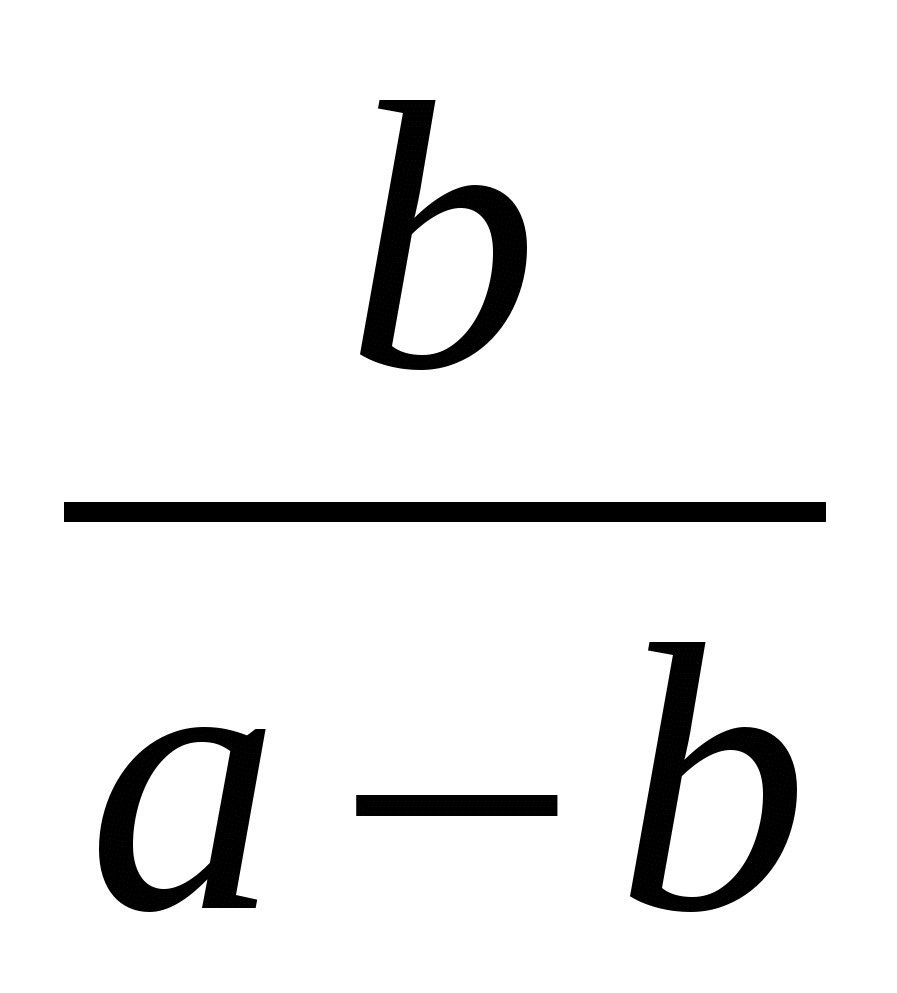 3)
3) 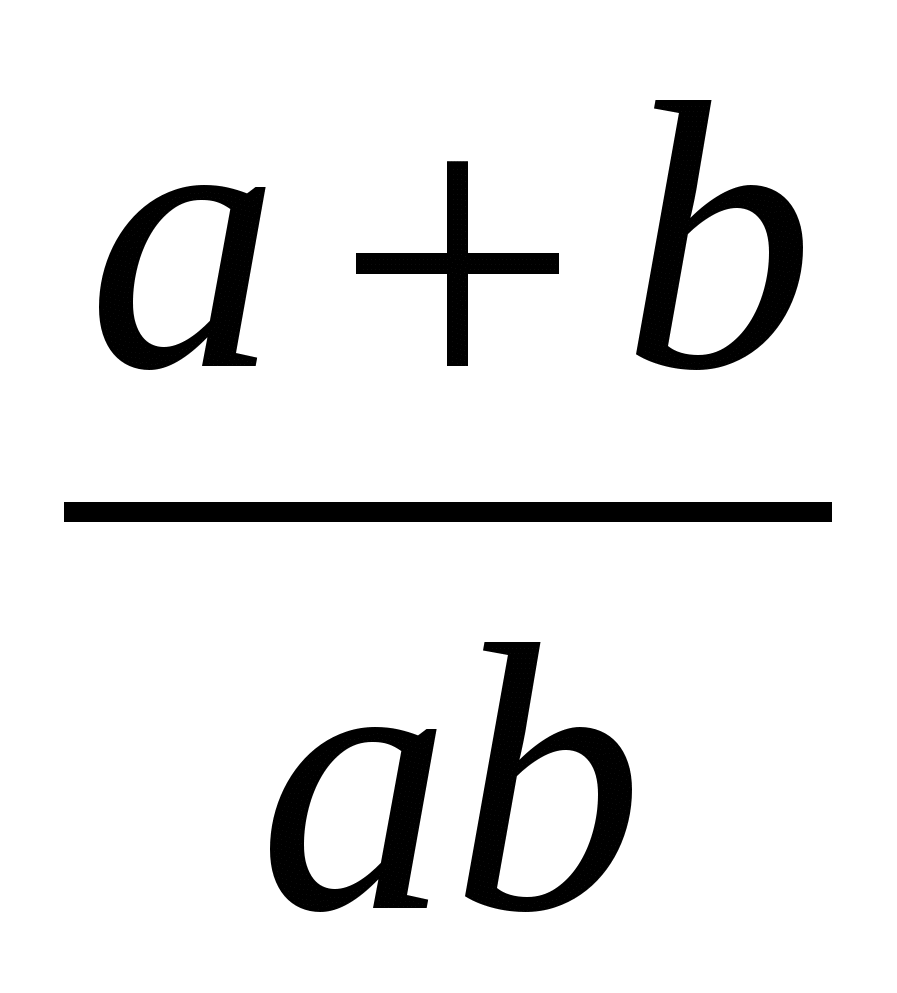 4)
4) 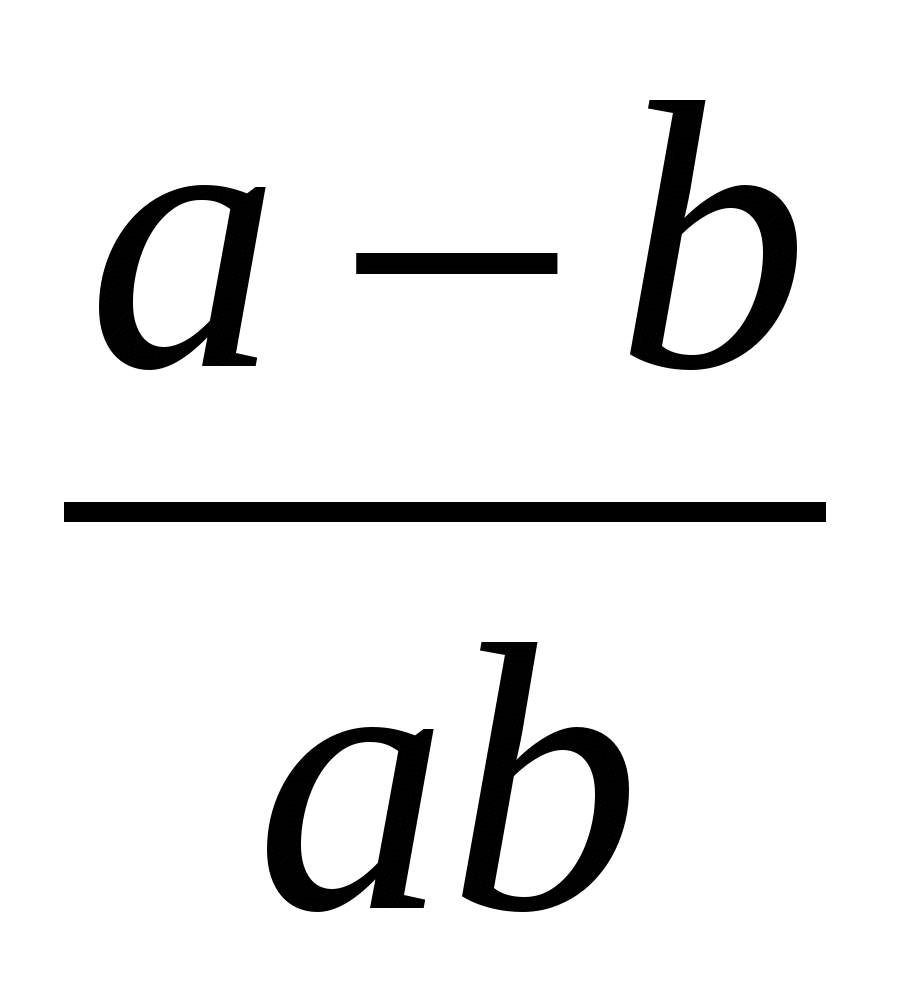
А8.
Выполните действия  .
.
1) 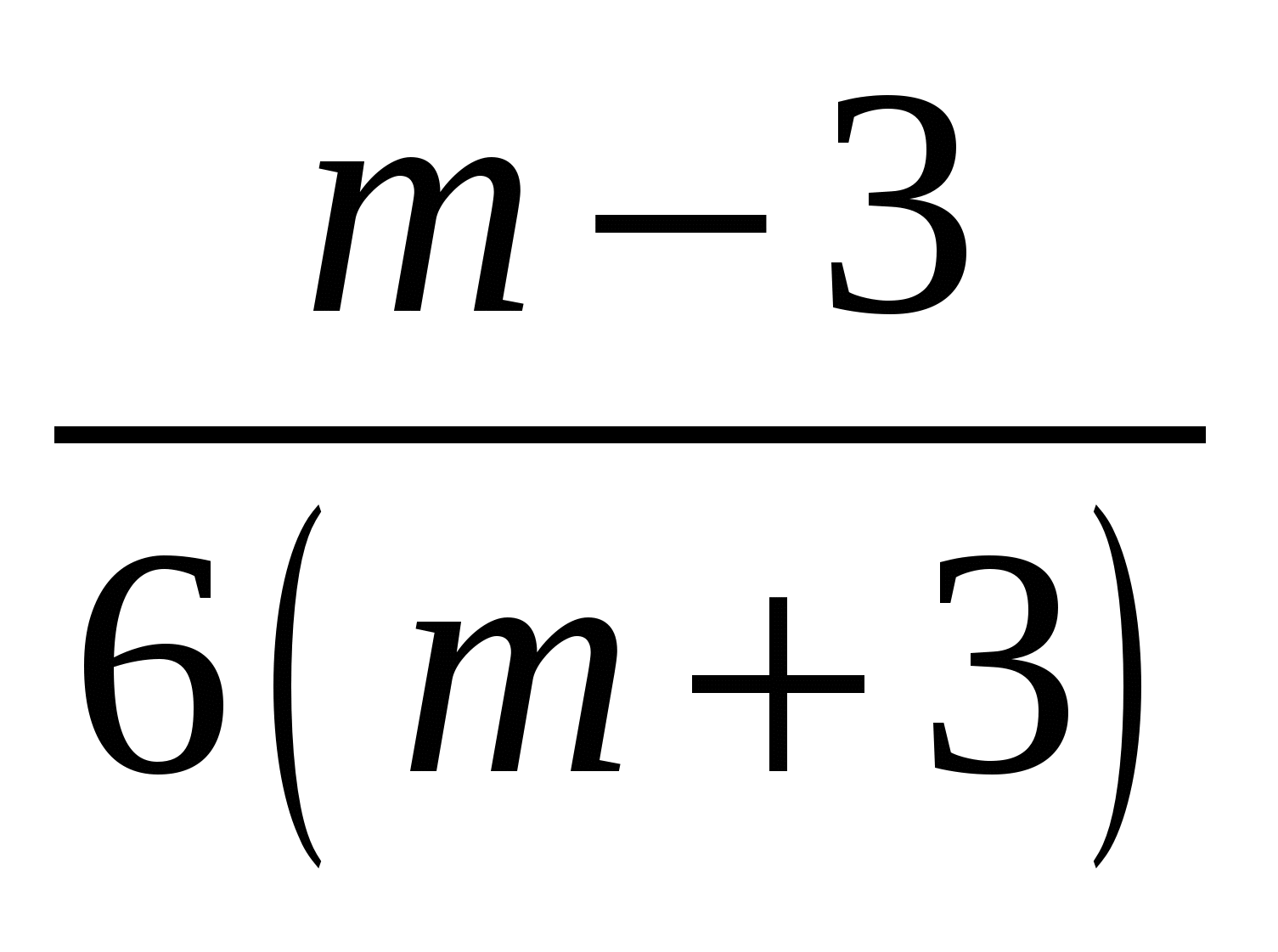 2)
2) 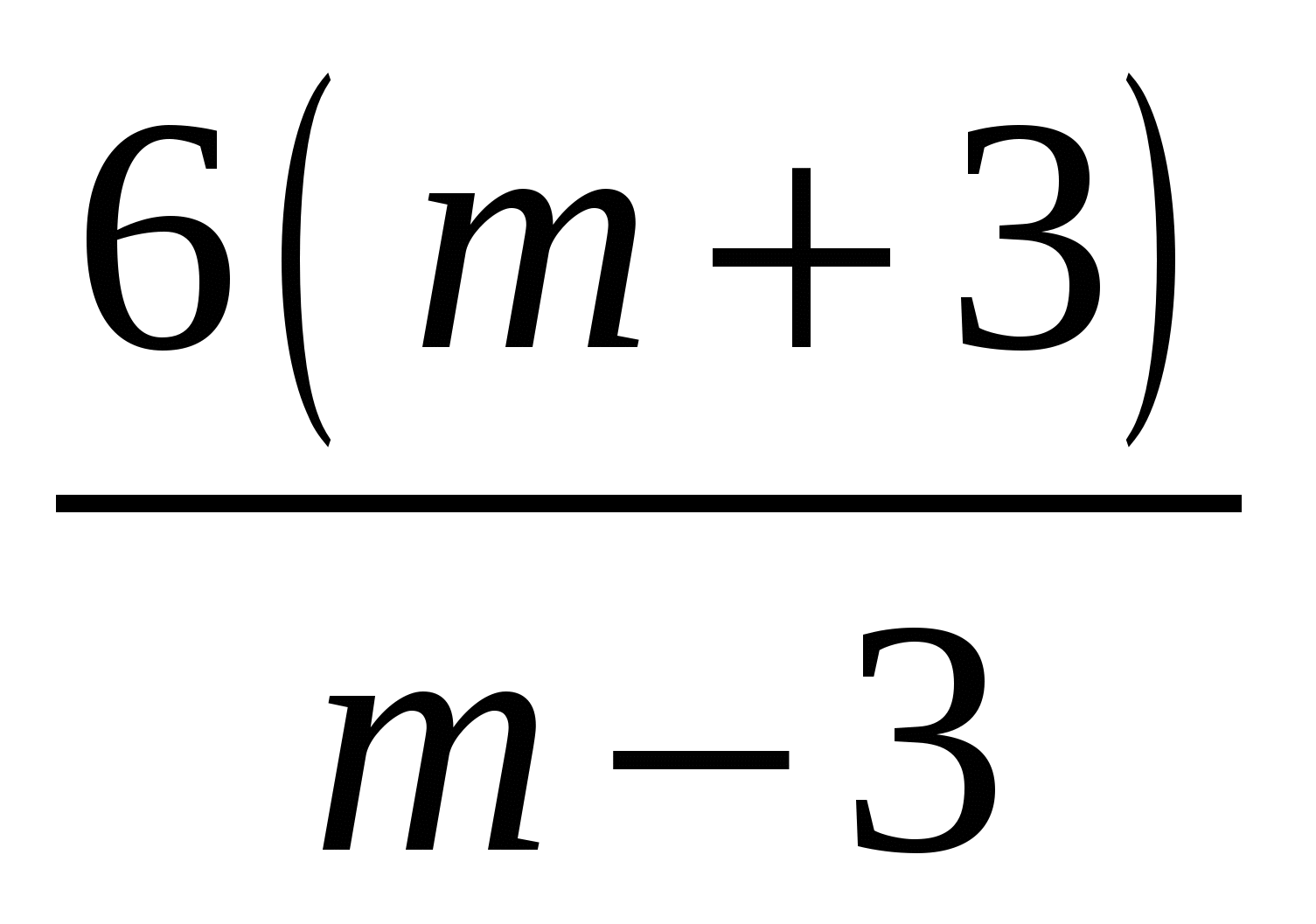 3)
3) 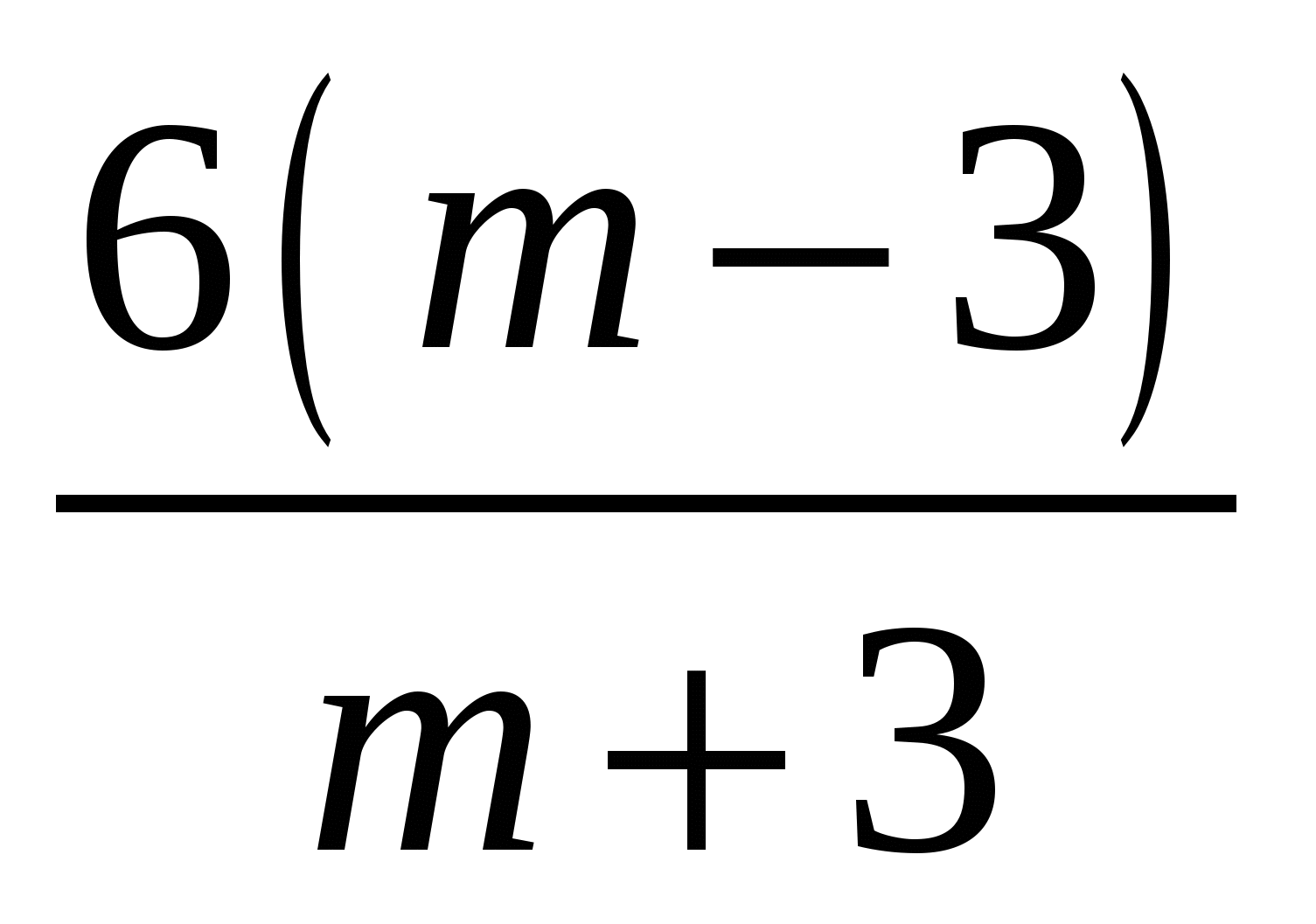 4)
4) 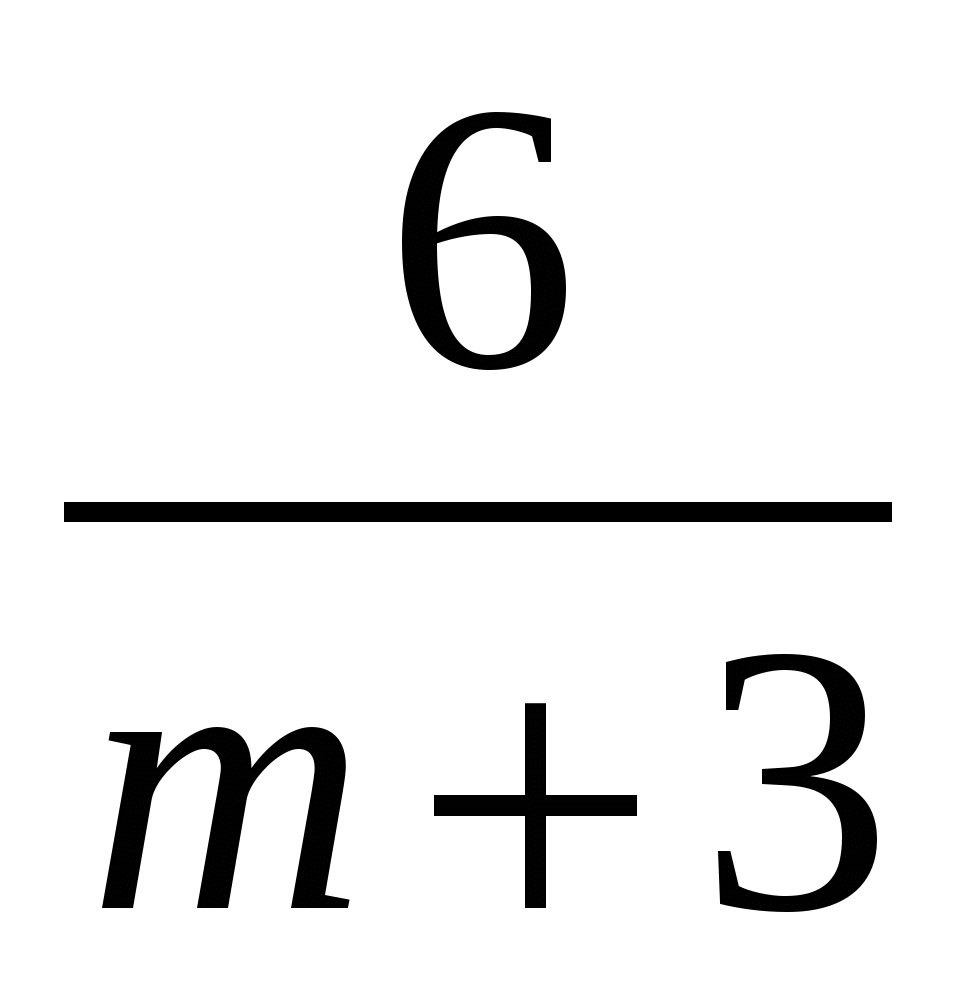
А9.
Выполните действия 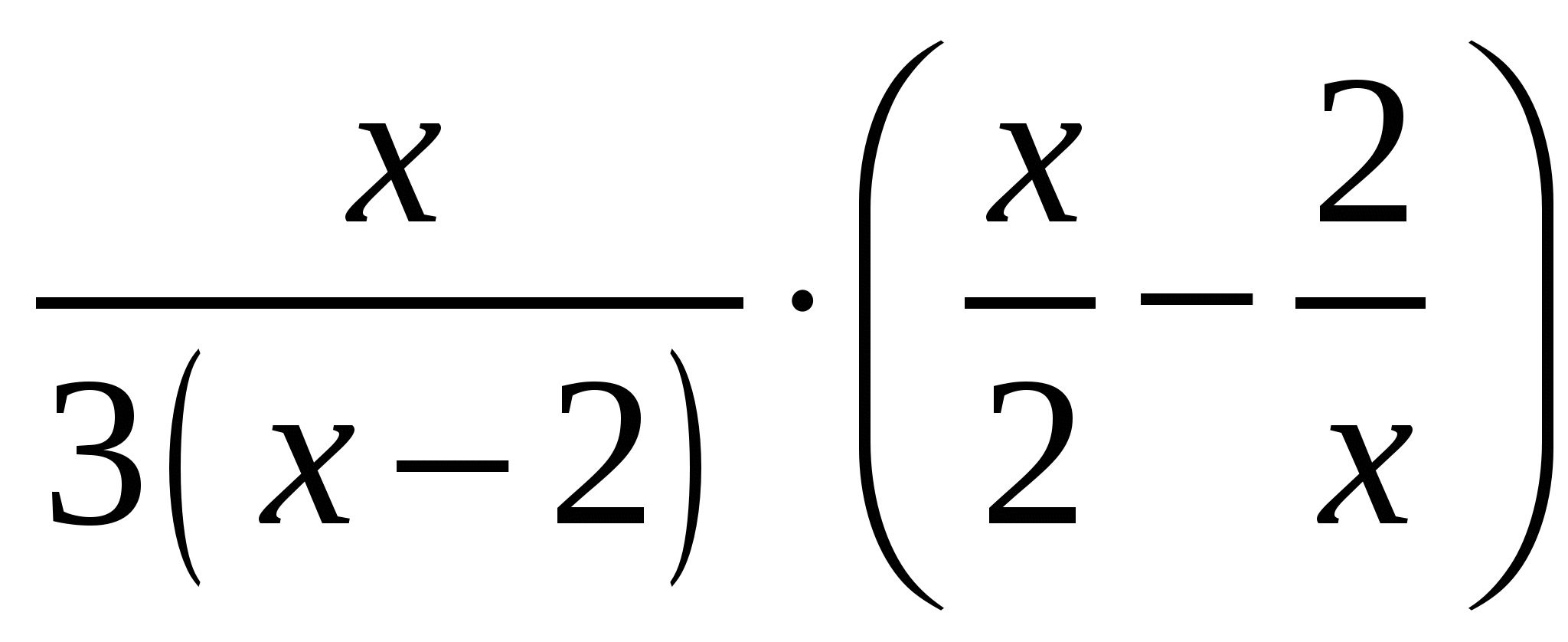 .
.
1) 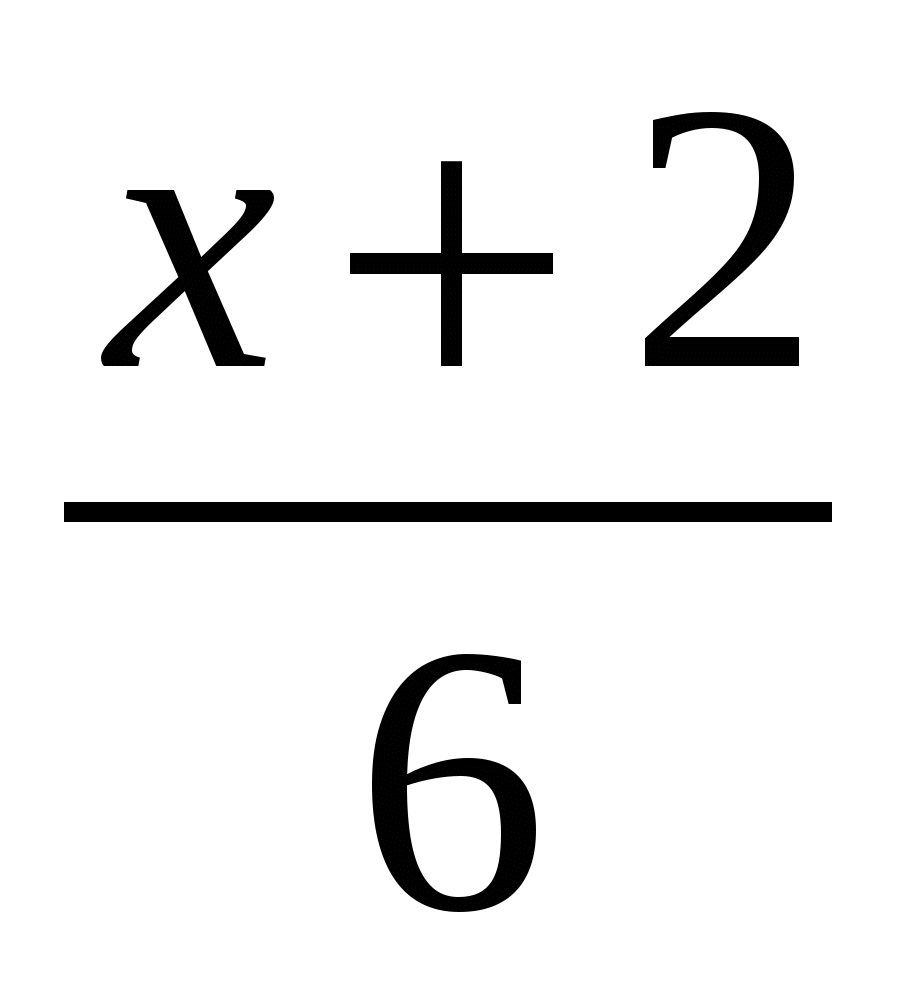 2)
2) 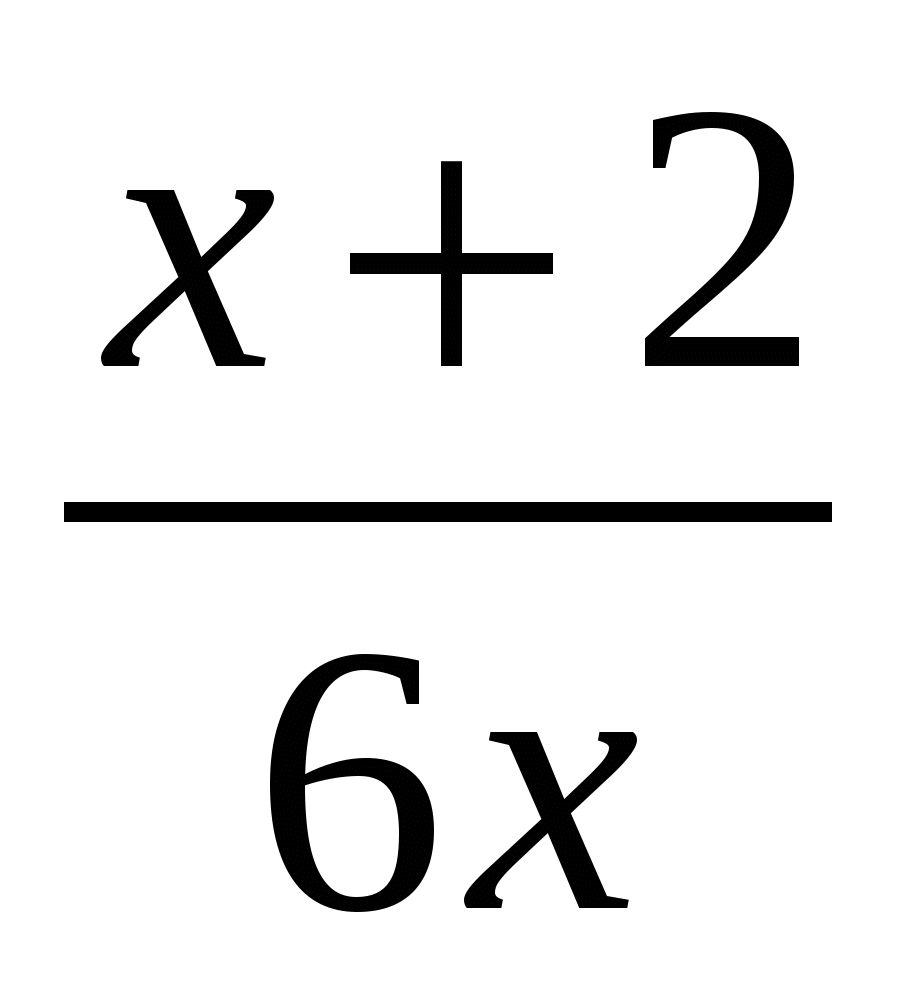 3)
3) 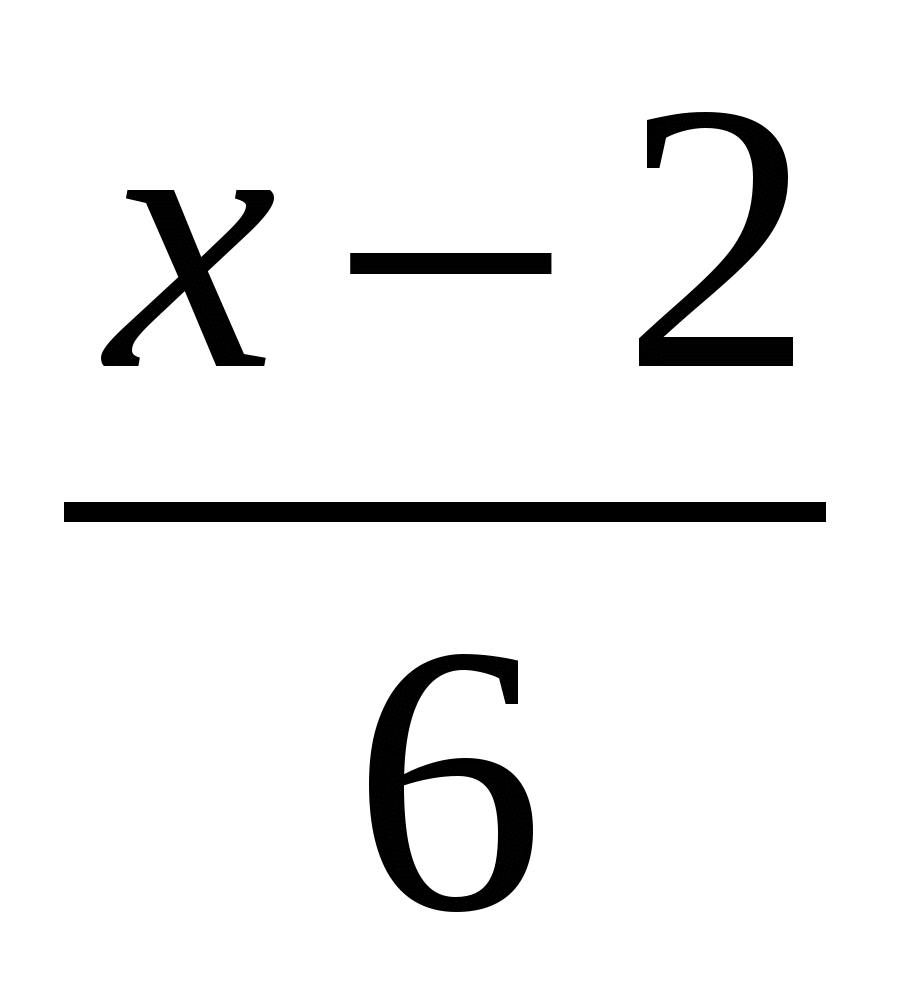 4)
4) 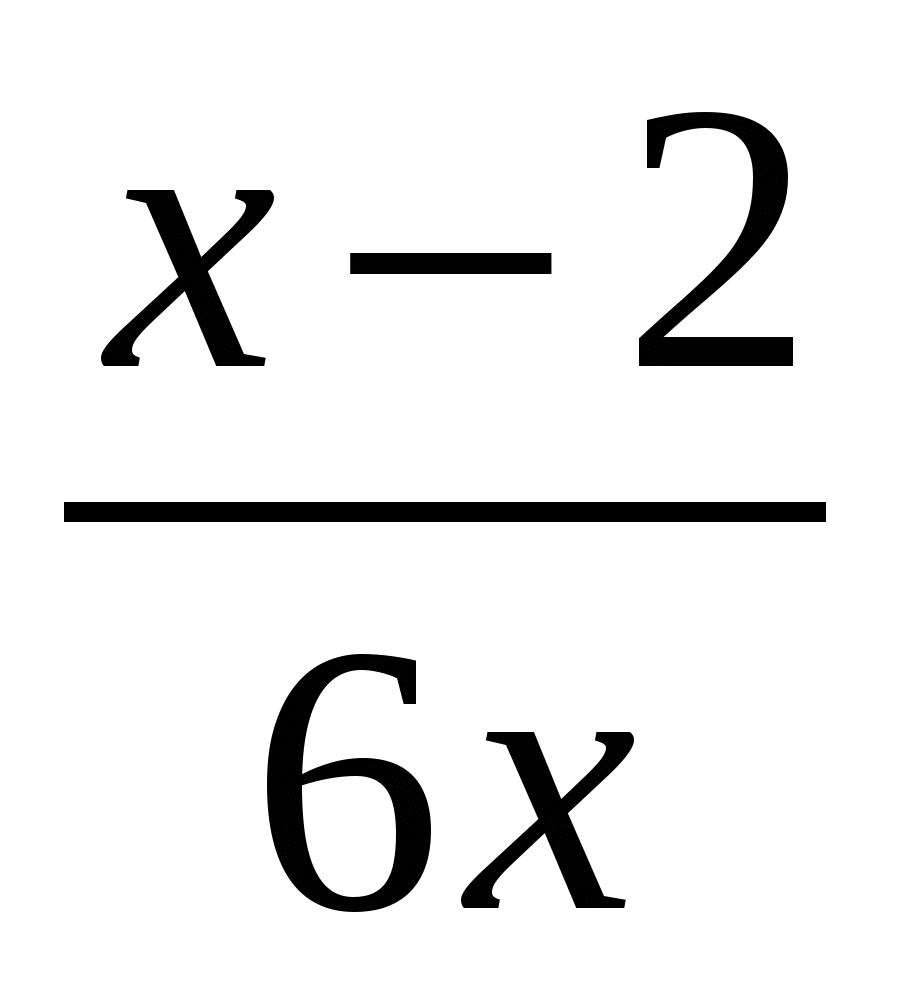
А10.
Найдите значение выражения 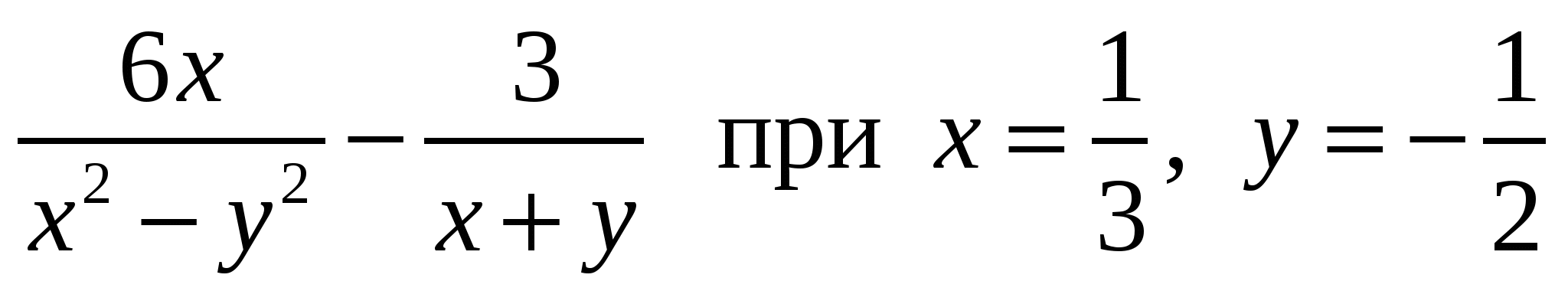 .
.
1) 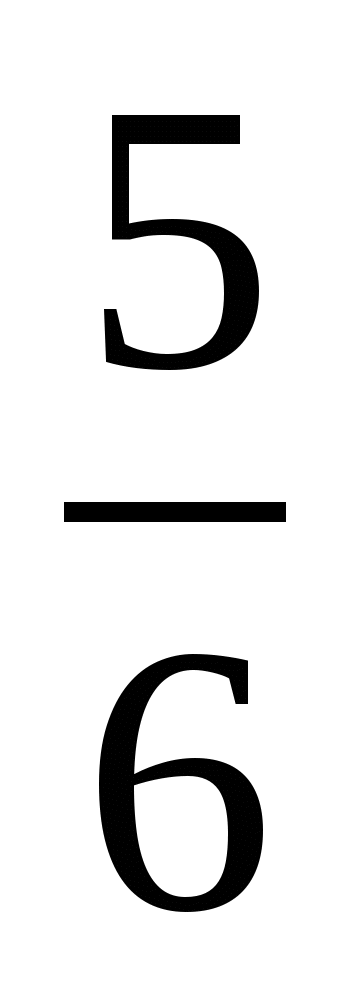 2)
2) 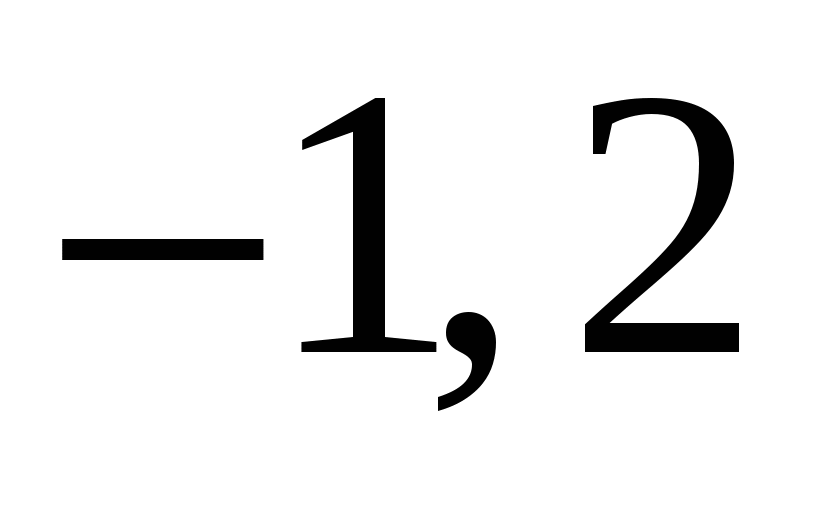 3)
3) 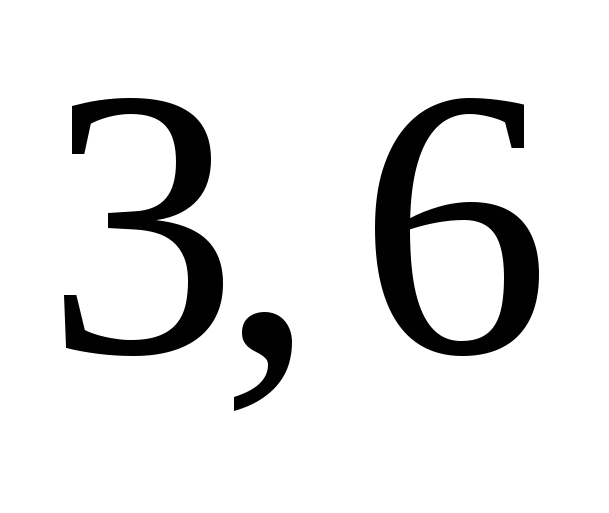 4)
4) 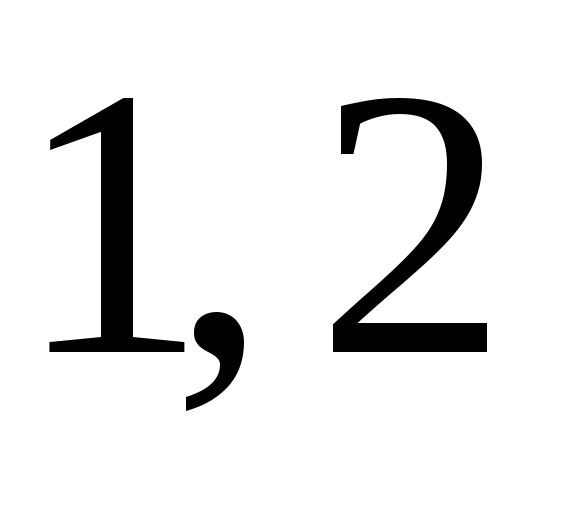
Ответы:
Вариант | А1 | А2 | А3 | А4 | А5 | А6 | А7 | А8 | А9 | А10 |
1 | 2 | 2 | 1 | 1 | 4 | 3 | 3 | 1 | 4 | 3 |
2 | 2 | 4 | 4 | 1 | 2 | 2 | 4 | 3 | 1 | 3 |
Тест 2
Квадратные корни
Вариант 1
ЧАСТЬ 1
А1. Вычислить .
1) 4 2) 3 3) 5 4) 15
А2. Вычислить .
1) 0,4 2) 0,04 3) 0,02 4) 0,16
А3. Выберите число, которое может принимать а в выражении .
1) 4; 2) 3,1; 3) -5; 4) 15.
А4. Вычислить .
1) 2) 3) 4)
А5. Упростите выражение
1) 2) 3) 4)
А6. Вычислите .
1) 9,1; 2) 2,9; 3) 89,9; 4) 8,9.
А7. Вычислить .
1) 225 2) 15 3) 25 4) 30
А8. Вычислить .
1) 2) 3) 4)
А9. Упростите выражение .
1) 1 2) 2 3) 4) 0
А10. Вычислить .
1) 7 2) 3) 1 4) 49
ЧАСТЬ 2
В1. Выполните действия: .
В2. Найдите значение выражения: .
Тест 2
Квадратные корни
Вариант 2
ЧАСТЬ 1
А1. Вычислить .
1) 19 2) 1 3) 0,5 4) 1,5
А2. Вычислить .
1) 1 2) 0,02 3) 0,01 4) 0,1
А3. Выберите число, которое может принимать а в выражении .
1) 8; 2) 8,1; 3) 9; 4) 15.
А4. Вычислить .
1) 2) 3) 4)
А5. Упростите выражение
1) 2) 3) 4)
А6. Вычислите .
1) 12,2 2) 6,2 3) 60,2 4) 71,8
А7. Вычислить .
1) 49 2) 7 3) 4)
А8. Вычислить .
1) 2) 3) 7 4) 49
А9. Упростите выражение .
1) 2) 3) 4) 0
А10. Вычислить .
1) 9 2)81 3) 27 4) 3
ЧАСТЬ 2
В1. Выполните действия: .
В2. Найдите значение выражения: .
Ответы:
Вариант | А1 | А2 | А3 | А4 | А5 | А6 | А7 | А8 | А9 | А10 | В1 | В2 |
1 | 2 | 1 | 3 | 2 | 4 | 1 | 2 | 3 | 1 | 4 | 4 | 1 |
2 | 3 | 4 | 1 | 4 | 1 | 2 | 2 | 3 | 2 | 3 | 4 | 2 |
Макарычев Тест 1. Рациональные дроби
Алгебра 8 класс. Тест 1 по учебнику Макарычева с ответами. Тема теста: Рациональные дроби. Сложение и вычитание дробей с одинаковыми знаменателями. Цитаты из пособия «Алгебра. Тематические тесты. 8 класс / Ю. П. Дудницын, В. Л. Кронгауз. — М. : Просвещение» использованы в учебных целях.
Тест 1. Рациональные дроби
Ответы на тест № 1
смотреть ОТВЕТЫ на Вариант 1
Вариант 1.
№1) 4. №2) 3. №3) 2. №4) 2. №5) 1. №6) 3. №7) 2,5.
№8)
смотреть ОТВЕТЫ на Вариант 2
Вариант 2.
№1) 2. №2) 3. №3) 1. №4) 4. №5) 1. №6) 4. №7) -4.
№8)
смотреть ОТВЕТЫ на Вариант 3
Вариант 3.
№1) 2. №2) 4. №3) 1. №4) 3. №5) 4. №6) 5. №7) 3,6.
№8)
смотреть ОТВЕТЫ на Вариант 4
Вариант 4.
№1) 3. №2) 3. №3) 2. №4) 4. №5) 1. №6) 2. №7) 1,9.
№8)
Алгебра 8 класс. Тест 1 по учебнику Макарычева с ответами. Тема теста: Рациональные дроби. Сложение и вычитание дробей с одинаковыми знаменателями. Авторы теста: Дудницын, Кронгауз. Ответы на тесты адресованы родителям.
Вернуться к Списку тематических тестов по алгебре (УМК Макарычев)
Просмотров: 1 609
Итоговый тест по теме: «Рациональные дроби»
1 вариант
ЧАСТЬ 1
А1. Найдите значение выражения при х=
А) В)
А2. Упростите выражение (а-4)-2а(3а-4)
А) -5а+16
Б) -5а+8а-16
В) -5а+8
Г) -5а+8с-4
А3. Из формулы =- выразите переменную а.
А) а= Б) а= В) а= Г) а=
А4. Сравните аи а, если известно, что 0а1
А) аа
Б) аа
В) аа
Г) для сравнения не хватает данных.
А5. Укажите наименьшее из следующих чисел:
0,8; ; ;
А) 0,8 Б) В) Г)
А6. Сократите дробь
.
ЧАСТЬ 2.
В1. Разложите на множители
а-ав-ав+а
В2. Сократите дробь
В3. Найдите значение выражения
1- при а=0,9.
Итоговый тест по теме: «Рациональные дроби»
2 вариант
ЧАСТЬ 1
А1. Найдите значение выражения при х= -0,17
А) 0,07 Б) 0,7 В) 1,24 Г) при х= -0,17 выражение не имеет смысла
А2. Упростите выражение (с+5) -с(10-3с)
А) -2с+25 Б) 4с-10с+25 В) 4с-5с+25 Г) 4с+25
А3. Из формулы =+ выразите переменную в.
А) а= Б) а= В) а= Г) а=
А4. Сравните а и а, если известно, что 0а1
А) аа
Б) аа
В) аа
Г) для сравнения не хватает данных.
А5. Укажите наименьшее из следующих чисел:
0,7; ; ;
А) 0,7 Б) В) Г)
А6. Сократите дробь
ЧАСТЬ 2.
В1. Разложите на множители
ху-х-ху+х
В2. Сократите дробь
В3. Найдите значение выражения
при а=0,4.
Итоговый тест по теме: «Рациональные дроби»
1 вариант
ЧАСТЬ 1
А1. Найдите значение выражения при х=
А) В)
А2. Упростите выражение (а-4)-2а(3а-4)
А) -5а+16
Б) -5а+8а-16
В) -5а+8
Г) -5а+8с-4
А3. Из формулы =- выразите переменную а.
А) а= Б) а= В) а= Г) а=
А4. Сравните аи а, если известно, что 0а1
А) аа
Б) аа
В) аа
Г) для сравнения не хватает данных.
А5. Укажите наименьшее из следующих чисел:
0,8; ; ;
А) 0,8 Б) В) Г)
А6. Сократите дробь
.
ЧАСТЬ 2.
В1. Разложите на множители
а-ав-ав+а
В2. Сократите дробь
В3. Найдите значение выражения
1- при а=0,9.
Итоговый тест по теме: «Рациональные дроби»
2 вариант
ЧАСТЬ 1
А1. Найдите значение выражения при х= -0,17
А) 0,07 Б) 0,7 В) 1,24 Г) при х= -0,17 выражение не имеет смысла
А2. Упростите выражение (с+5) -с(10-3с)
А) -2с+25 Б) 4с-10с+25 В) 4с-5с+25 Г) 4с+25
А3. Из формулы =+ выразите переменную в.
А) а= Б) а= В) а= Г) а=
А4. Сравните а и а, если известно, что 0а1
А) аа
Б) аа
В) аа
Г) для сравнения не хватает данных.
А5. Укажите наименьшее из следующих чисел:
0,7; ; ;
А) 0,7 Б) В) Г)
А6. Сократите дробь
ЧАСТЬ 2.
В1. Разложите на множители
ху-х-ху+х
В2. Сократите дробь
В3. Найдите значение выражения
при а=0,4.
Тесты п алгебре для 8 класса
Тест 4
Неравенства
Вариант 1
A1. Найдите наибольшее целое число x , удовлетворяющее неравенству х < 4.
1) 4; 2) 3; 3) 5; 4) 0.
А2. Найдите наименьшее целое число у , удовлетворяющее неравенству у > -2.
1) -3; 2) 0; 3) -2; 4) -1.
А3. Найдите наибольшее целое число m , удовлетворяющее неравенству 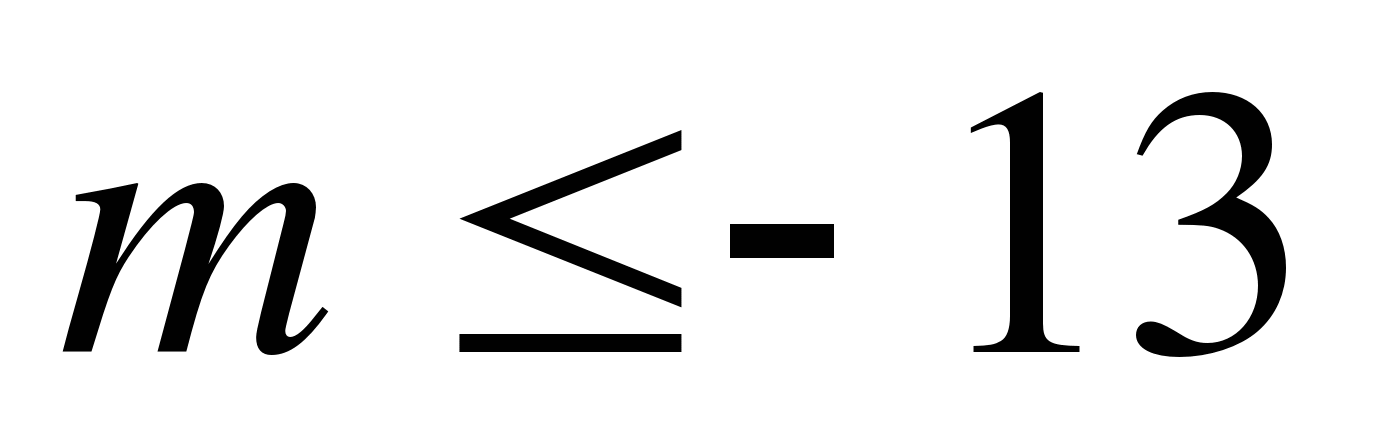 .
.
1) -13; 2) -14; 3) -12; 4) 0.
А4. Найдите наименьшее целое число у , удовлетворяющее неравенству 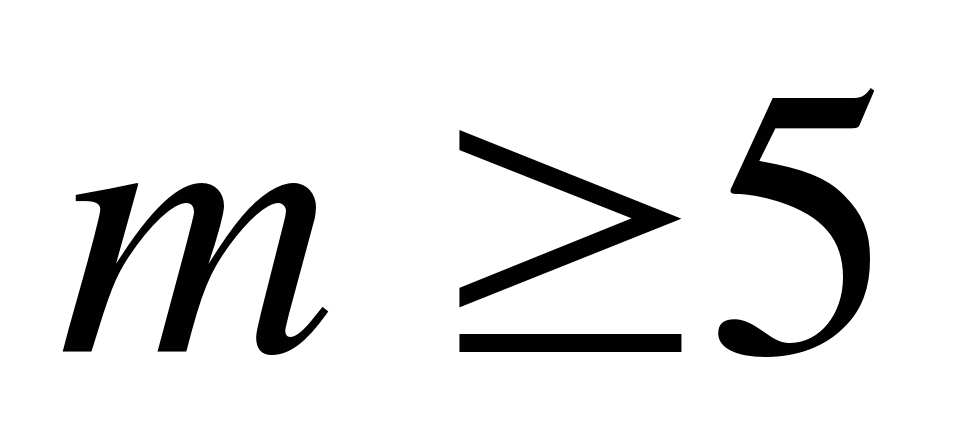 .
.
1) 6; 2) 4; 3) 5; 4) 10.
А5. Найдите наибольшее целое число x , удовлетворяющее неравенству 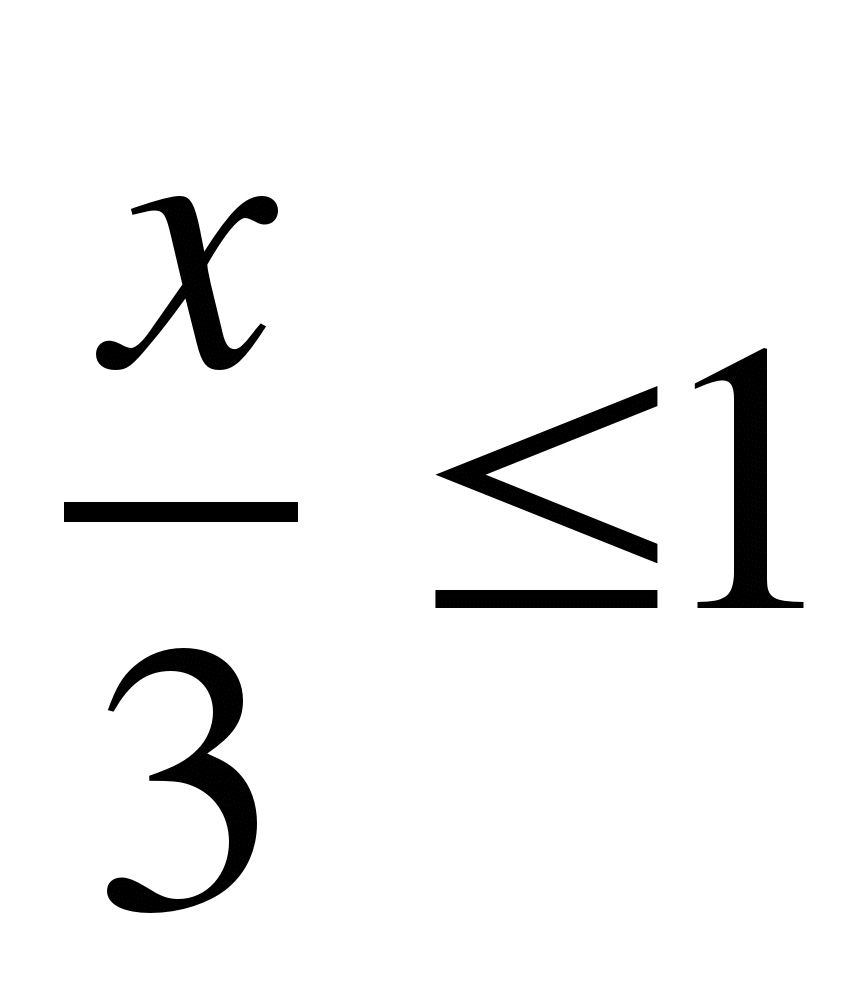 .
.
1) 3; 2) 2; 3) 1; 4) 4.
А6. Найдите наименьшее целое число x , удовлетворяющее неравенству 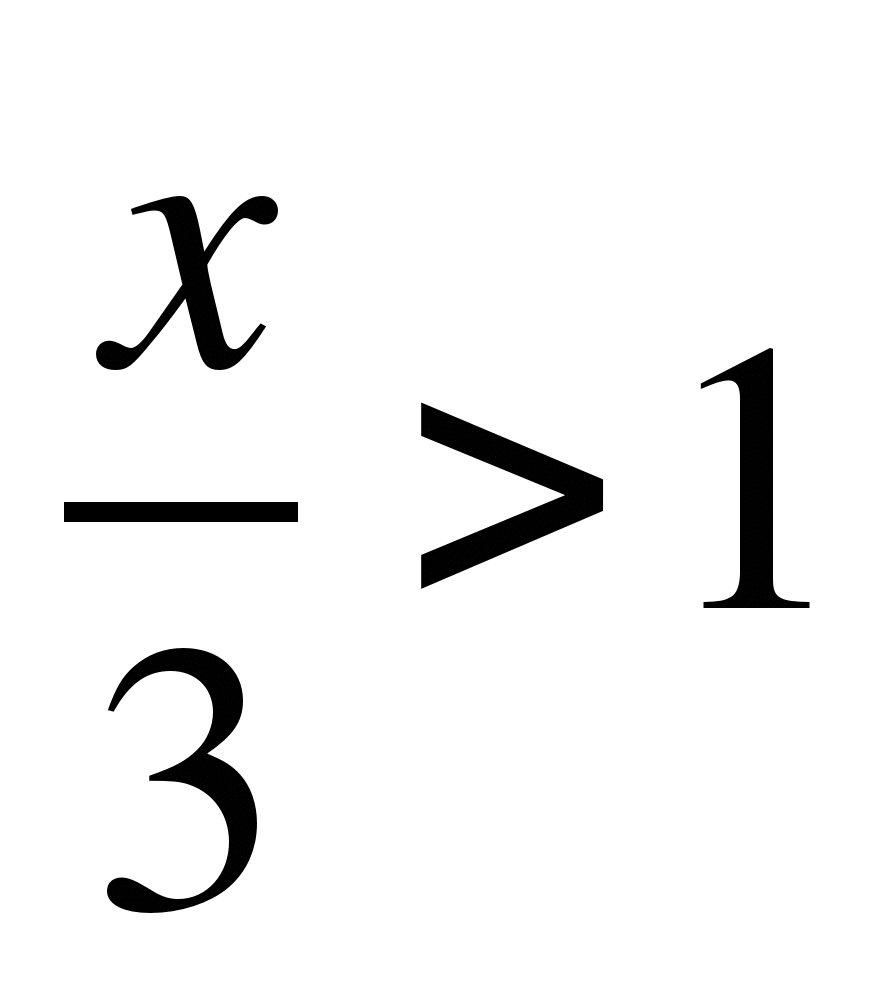 .
.
1) 3; 2) 2; 3) 1; 4) 4.
А7. Решите неравенство 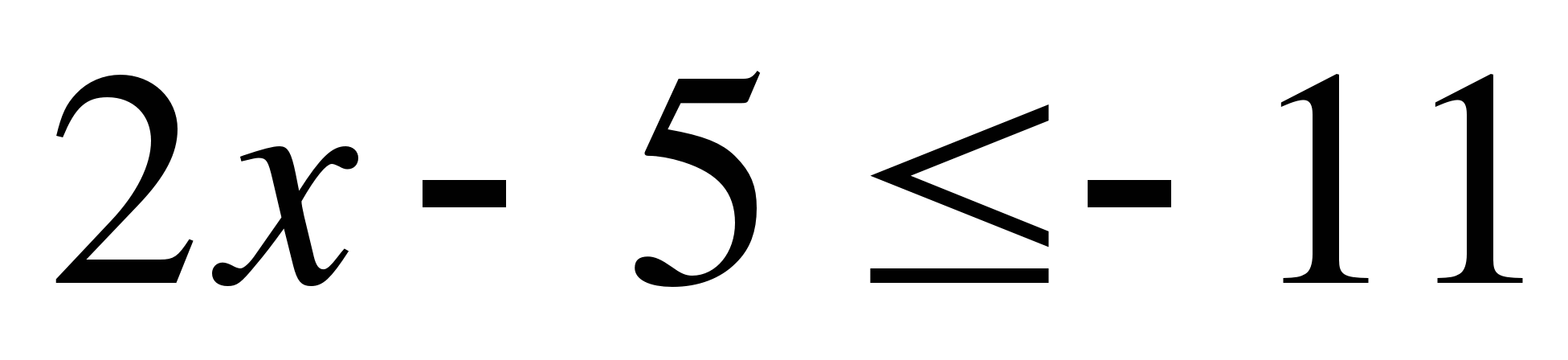 .
.
1) 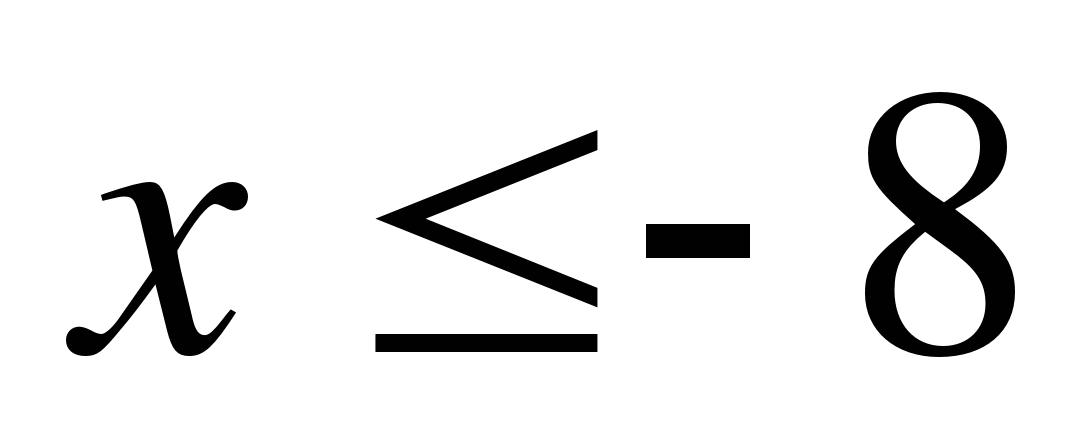 ; 2)
; 2) 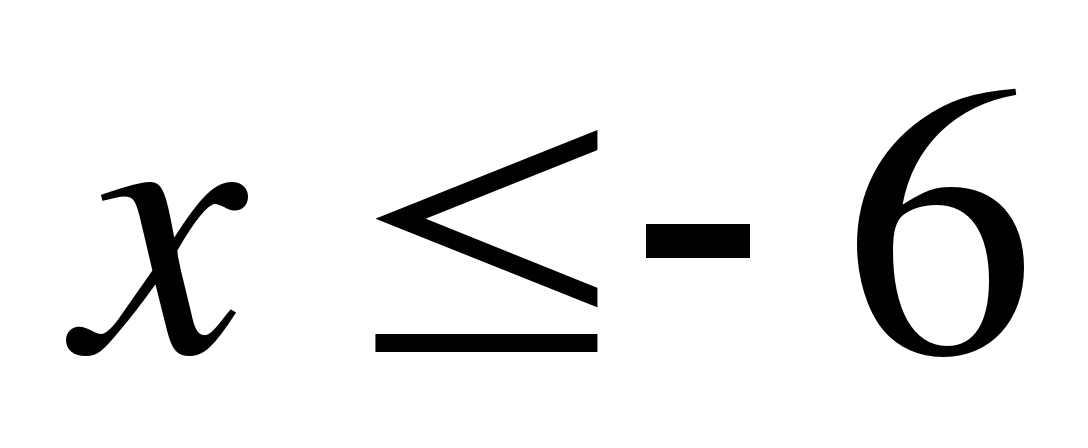 ; 3)
; 3) 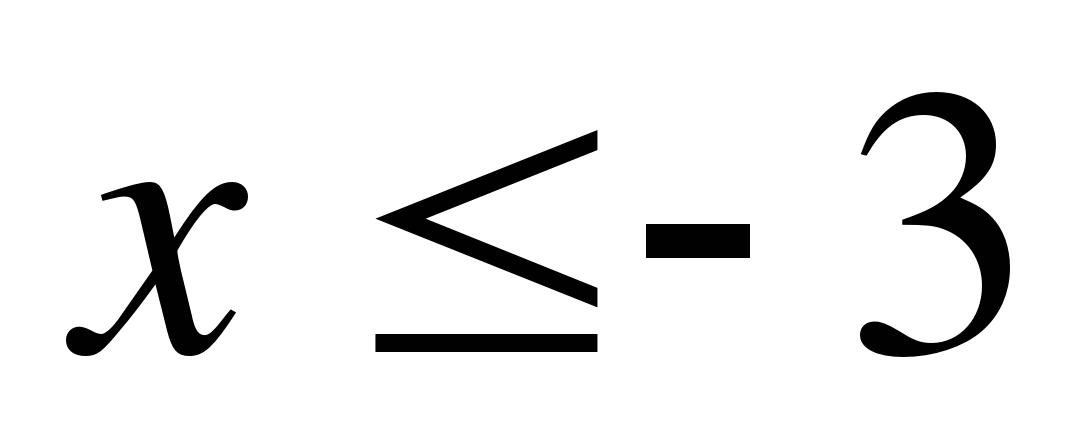 ; 4)
; 4) 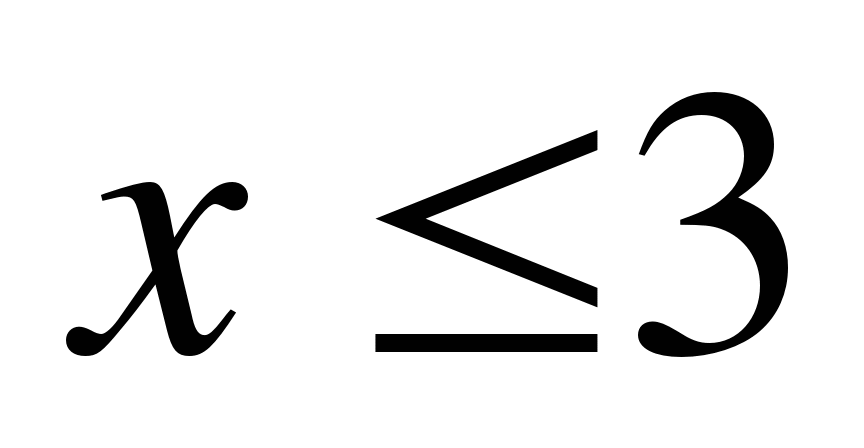 .
.
А8. Решите неравенство 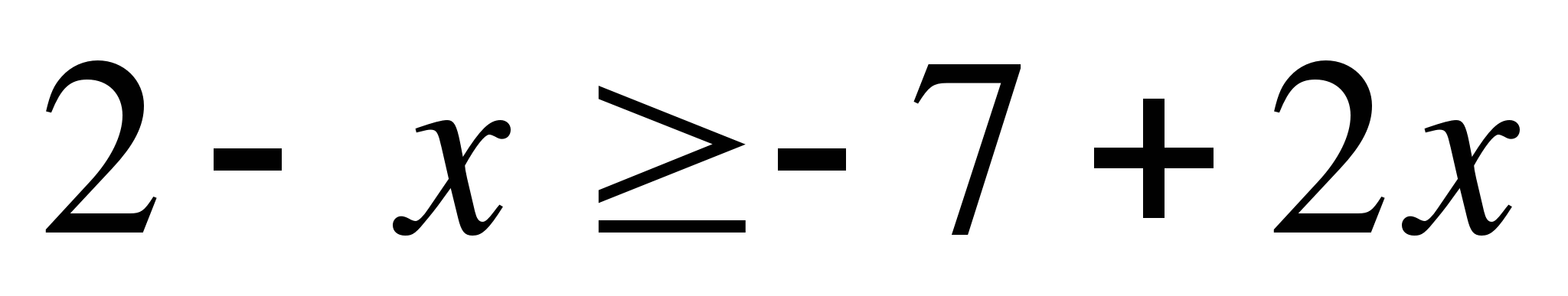 .
.
1) 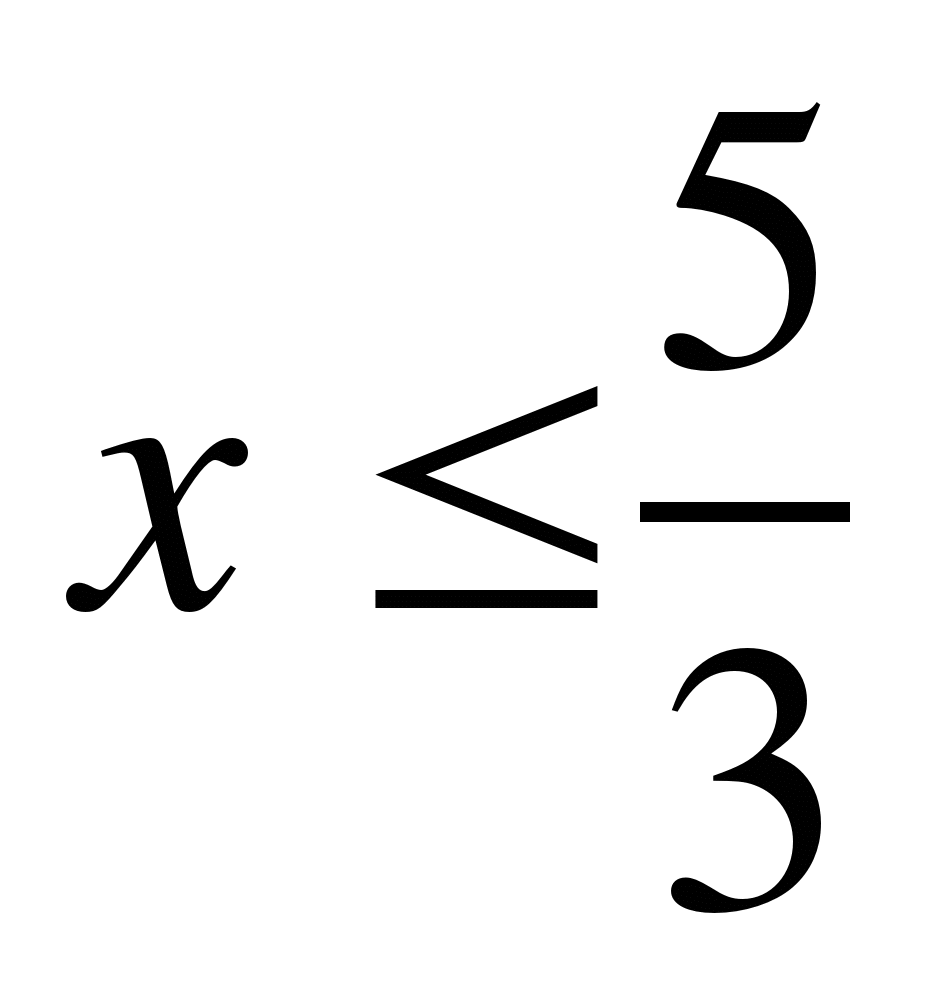 ; 2)
; 2) 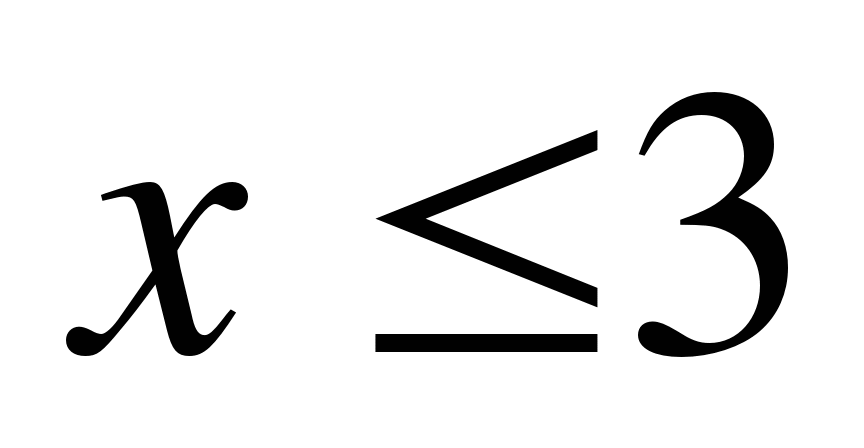 ; 3)
; 3) 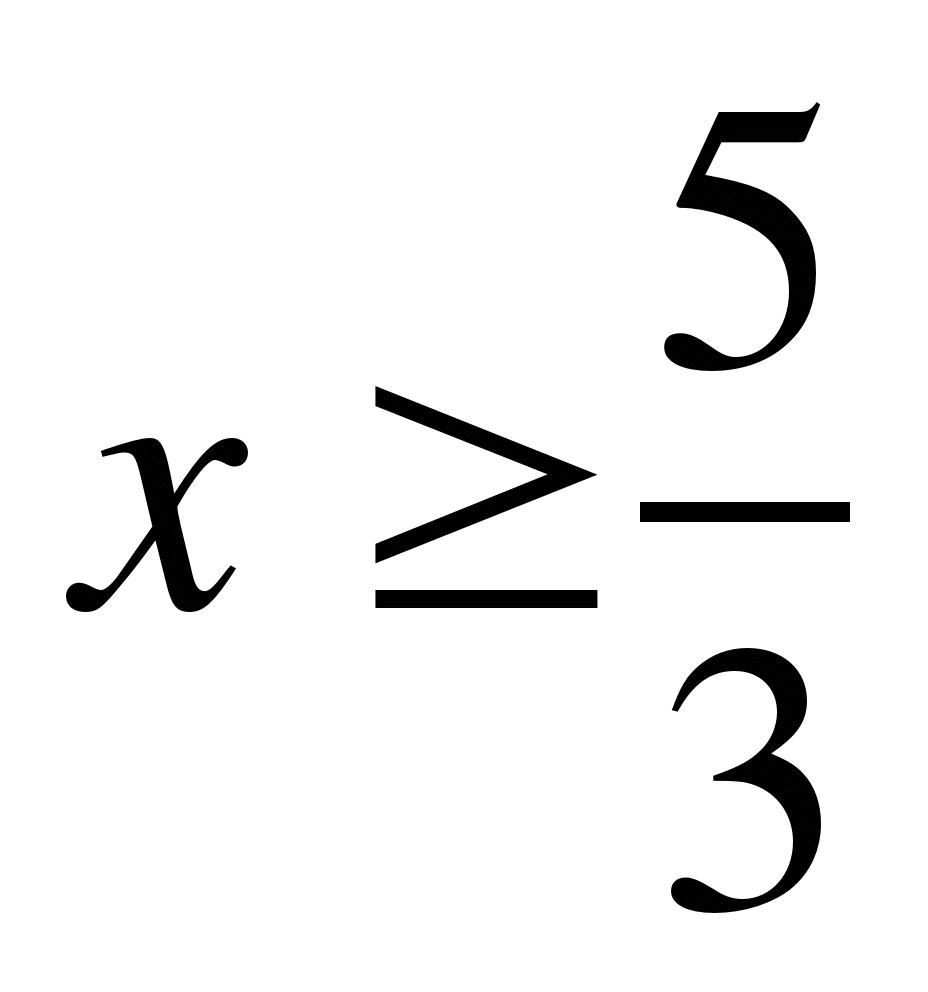 ; 4)
; 4) 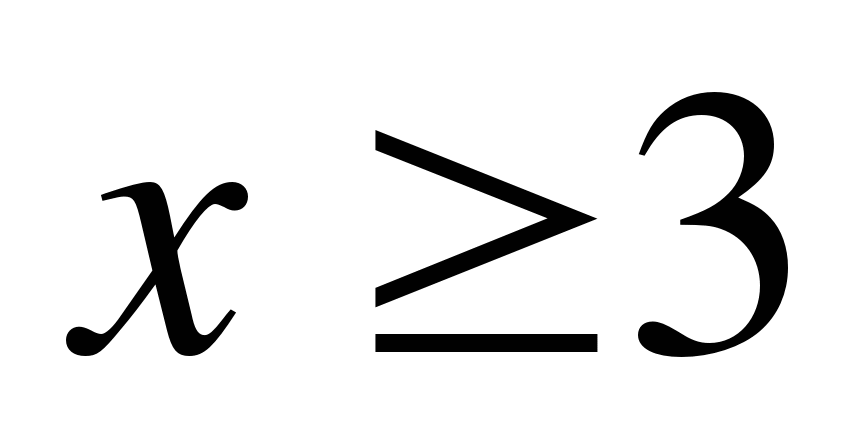 .
.
А9. Решите неравенство 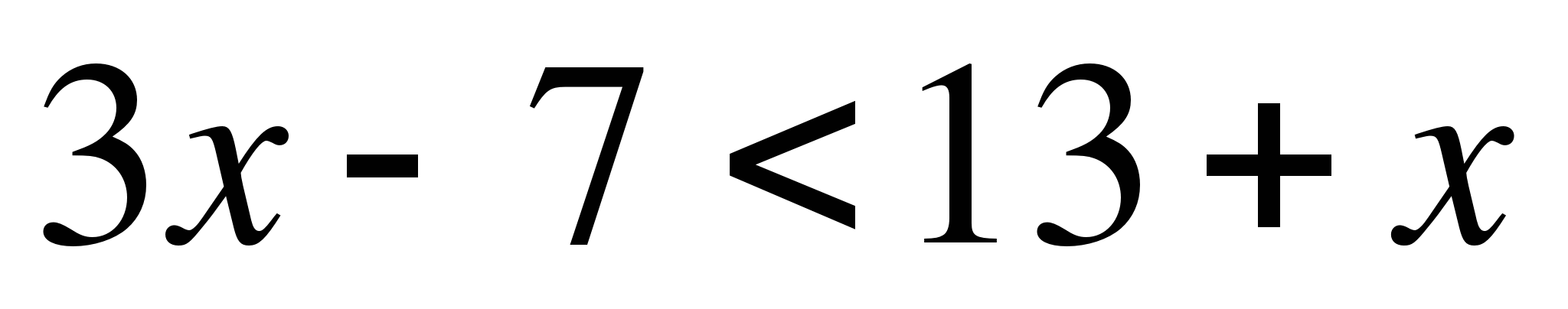 . В ответе укажите наибольшее целое число.
. В ответе укажите наибольшее целое число.
1) 4; 2) 5; 3) 10; 4) 9.
А10. Решите неравенство 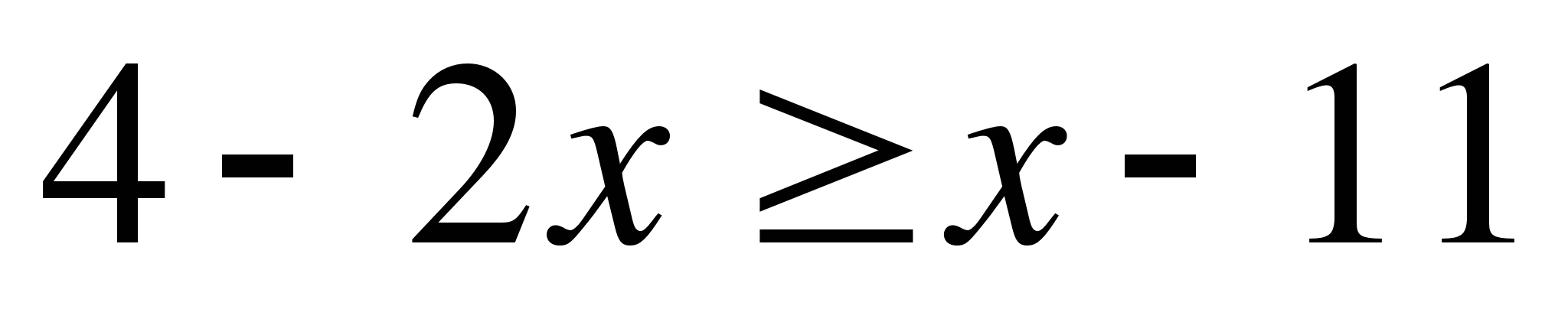 . В ответе укажите наибольшее целое число.
. В ответе укажите наибольшее целое число.
1) 4; 2) 5; 3) 6; 4) -5.
А11. Решите систему неравенств 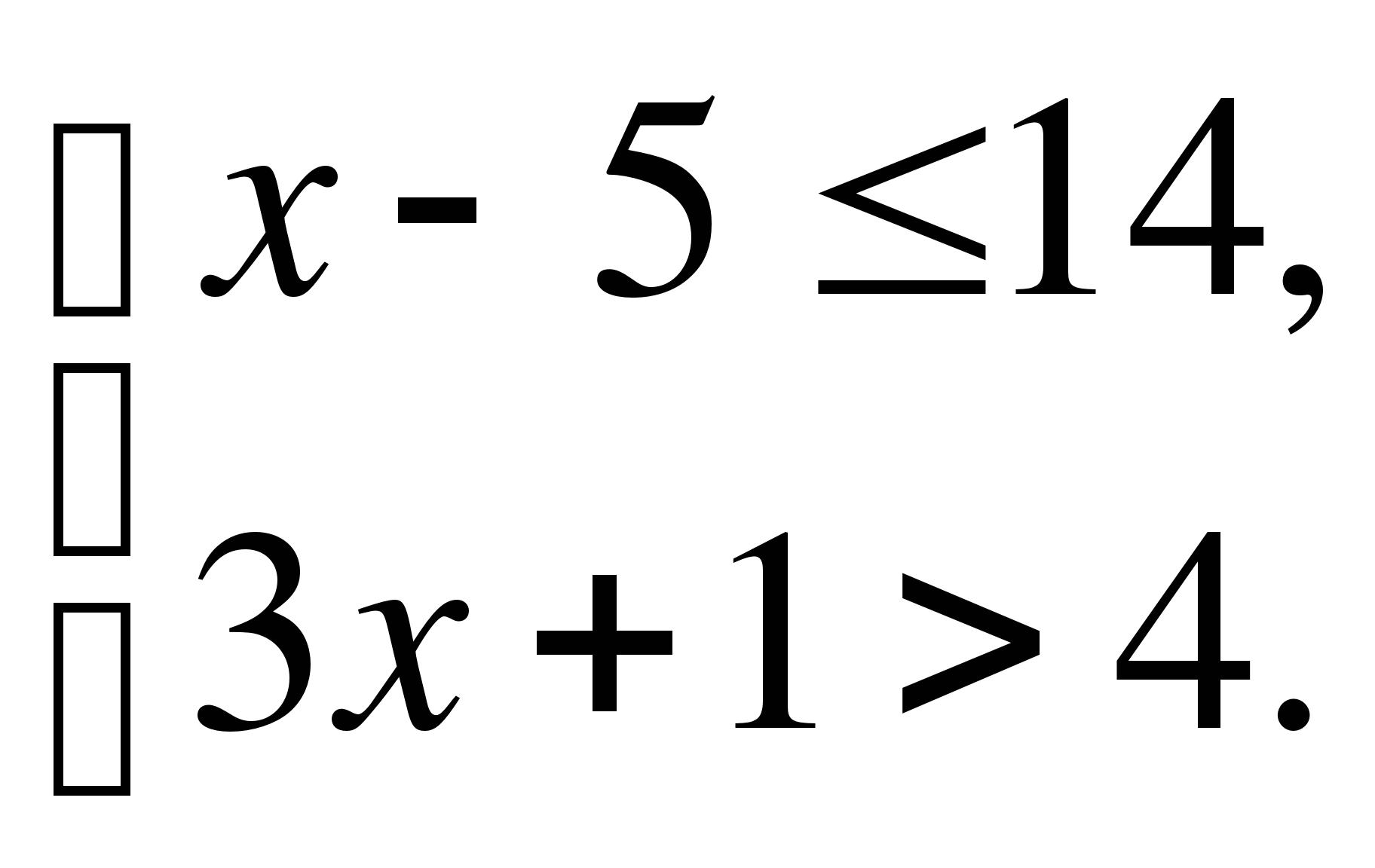
1) 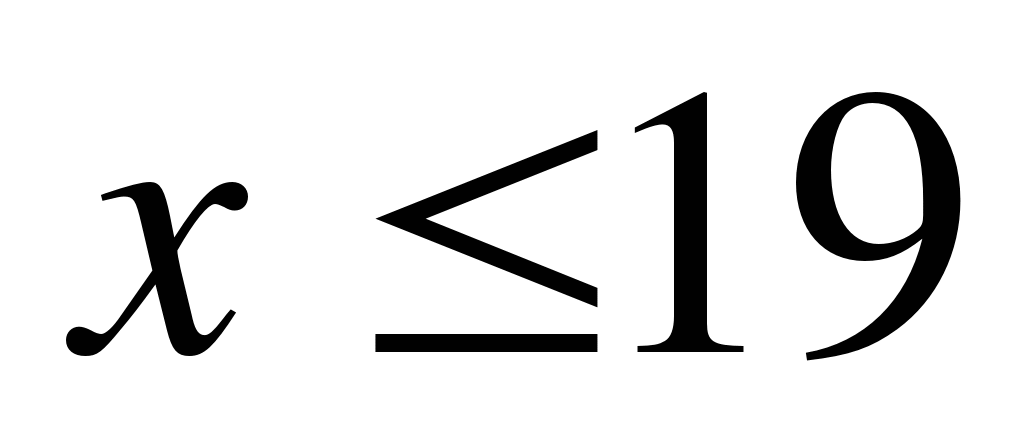 ; 2)
; 2) 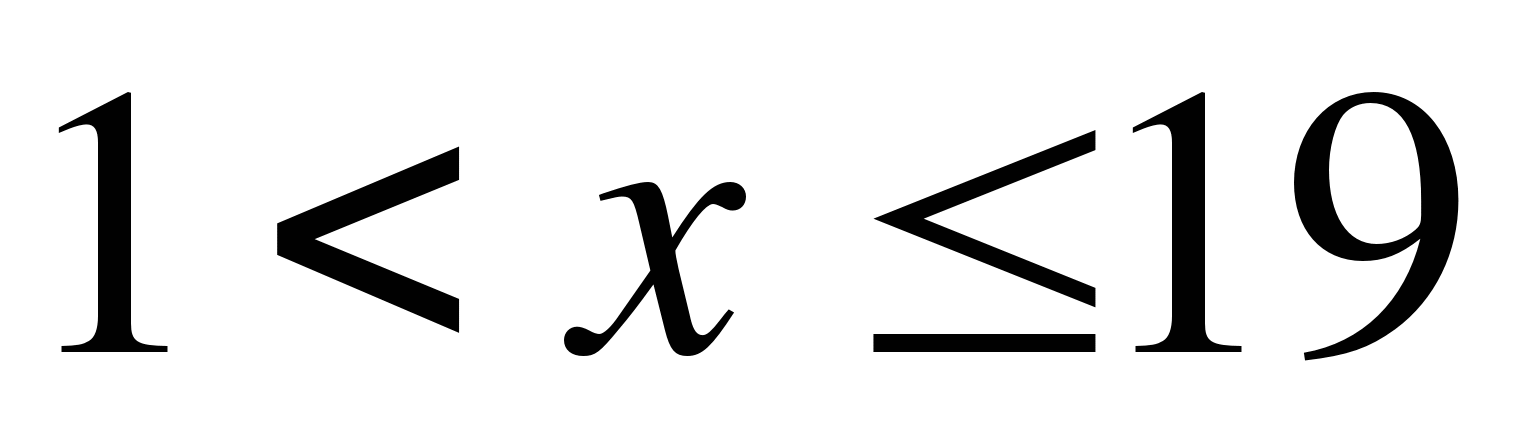 ; 3)
; 3) 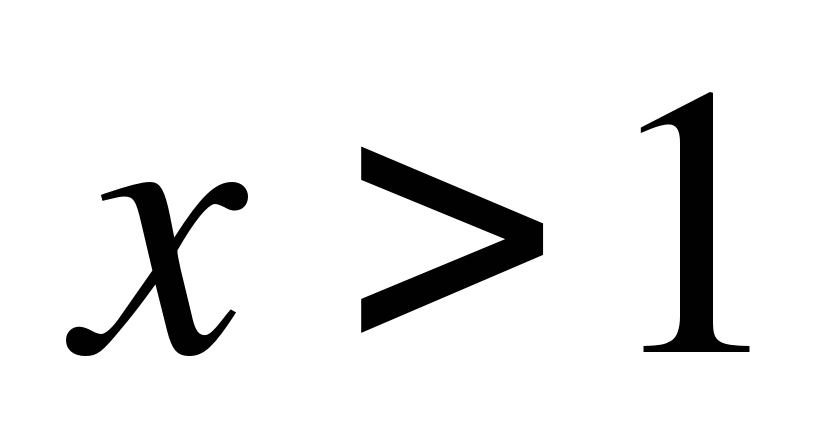 ; 4)
; 4) 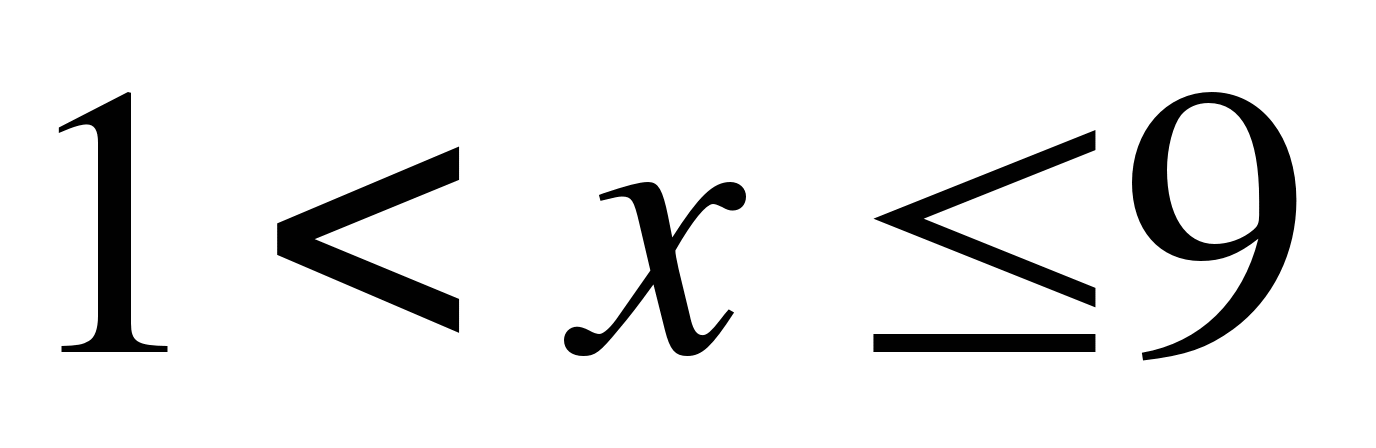 .
.
А12. Множество чисел, изображенных на рисунке запишите в виде неравенства
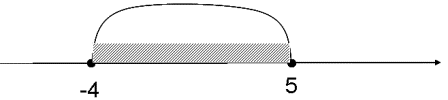
1) 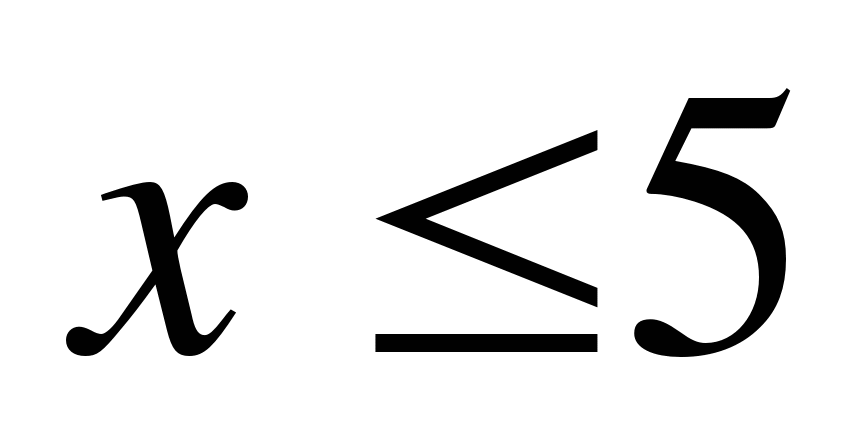 ; 2)
; 2) 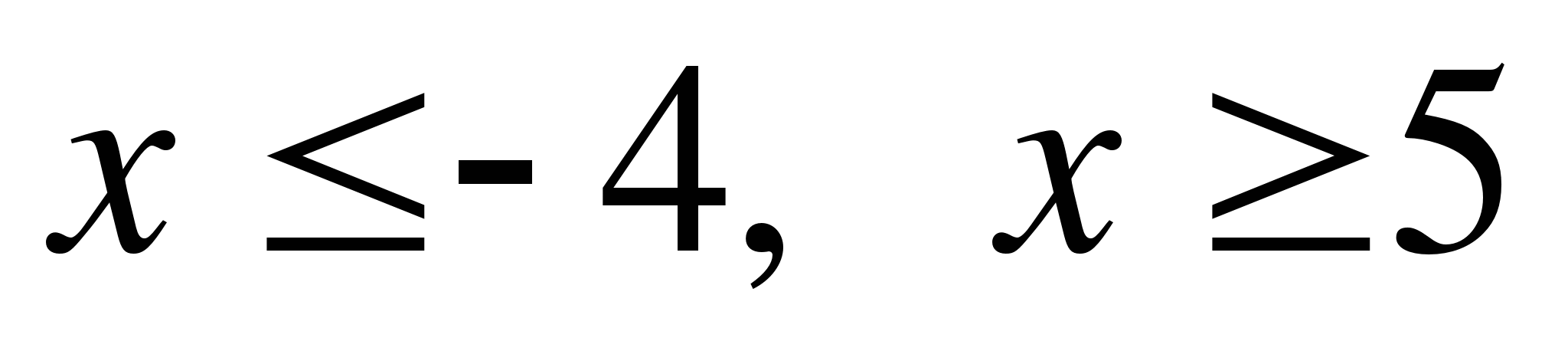 ;
;
3) 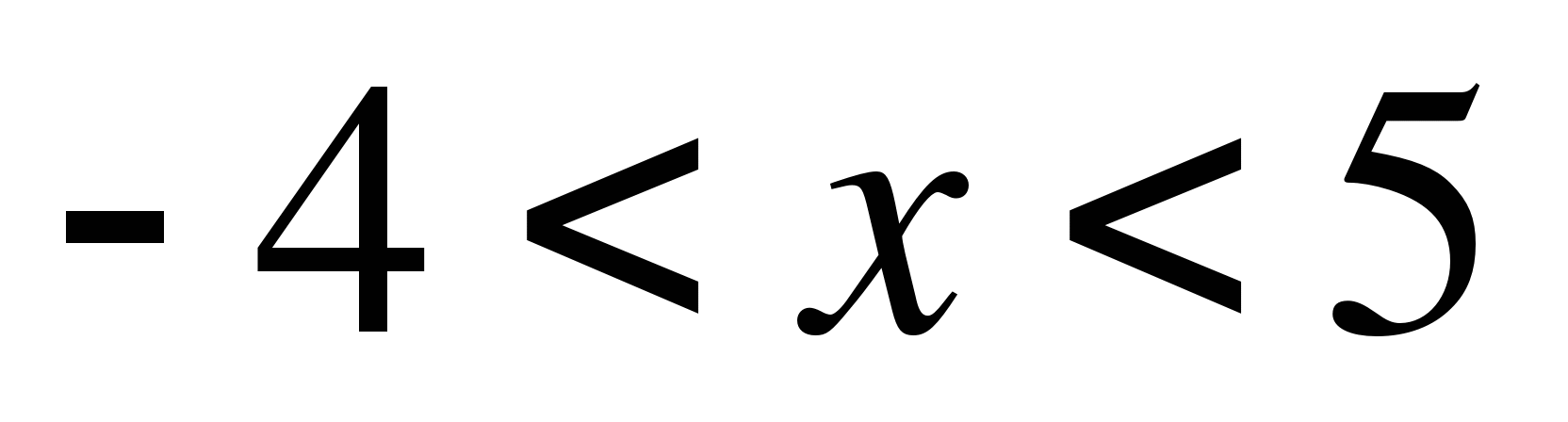 ; 4)
; 4) 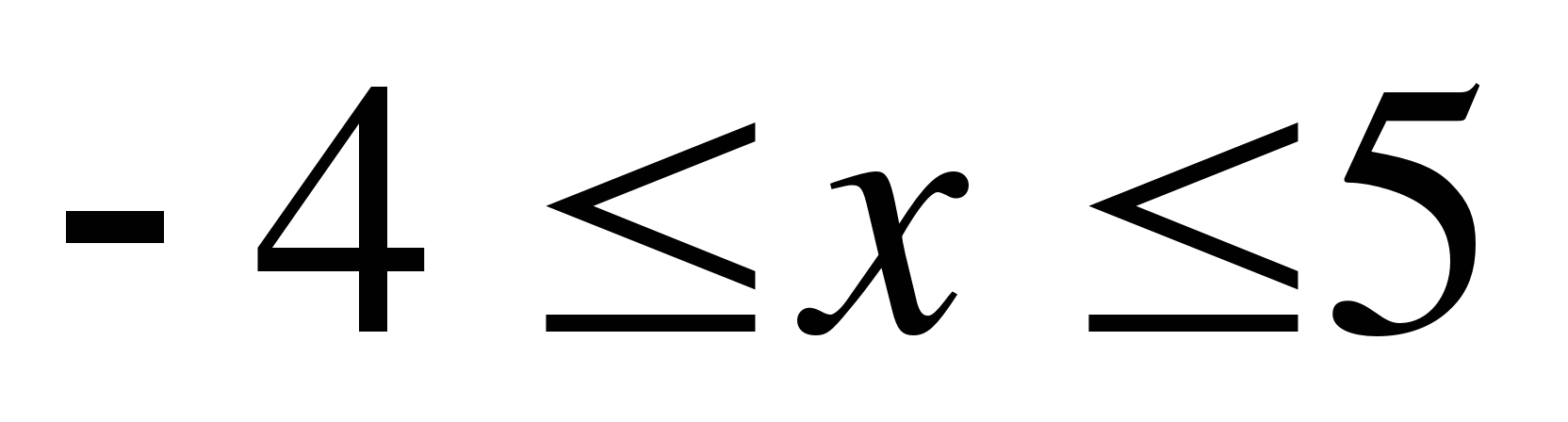 .
.
Тест 4
Неравенства
Вариант 2
А1. Найдите наибольшее целое число x , удовлетворяющее неравенству х < -5.
1) -4; 2) -3; 3) -5; 4) 0.
А2. Найдите наименьшее целое число у , удовлетворяющее неравенству у > 2.
1) 3; 2) 0; 3) 2; 4) 1.
А3. Найдите наибольшее целое число m , удовлетворяющее неравенству 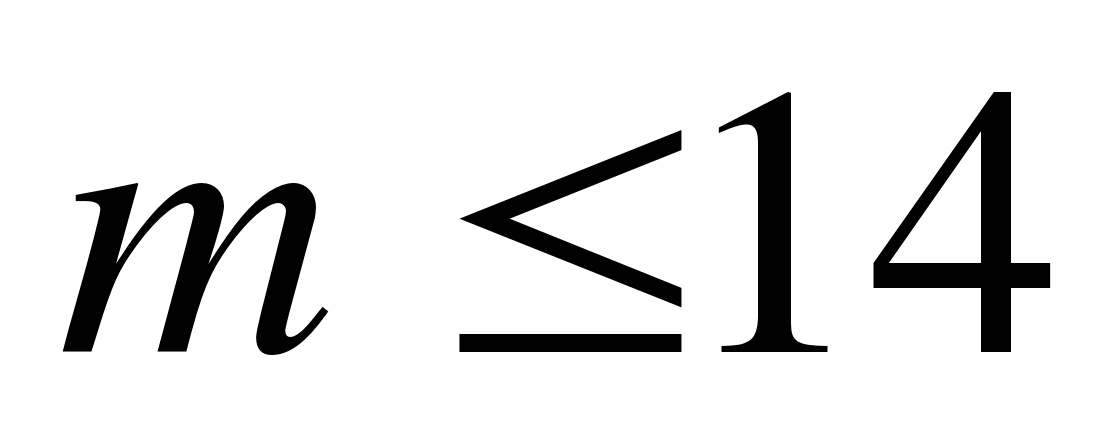 .
.
1) 13; 2) 14; 3) 15; 4) 0.
А4. Найдите наименьшее целое число у , удовлетворяющее неравенству 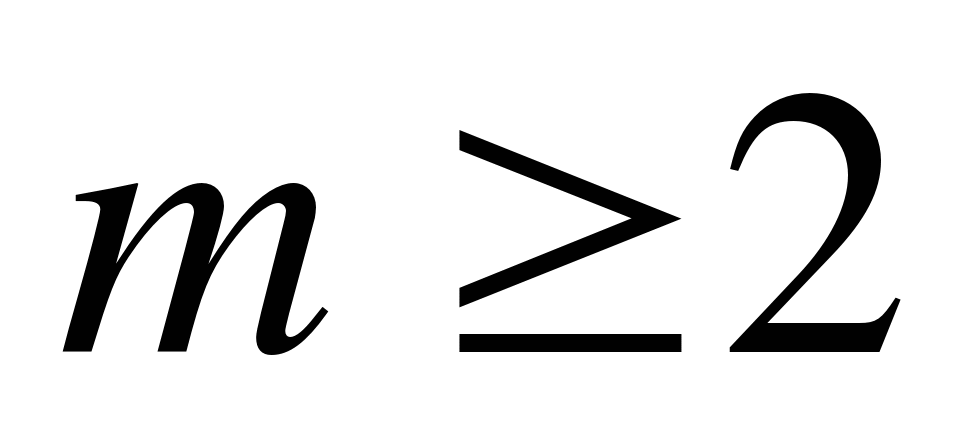 .
.
1) 1; 2) 2; 3) 0; 4) 3.
А5. Найдите наибольшее целое число x , удовлетворяющее неравенству 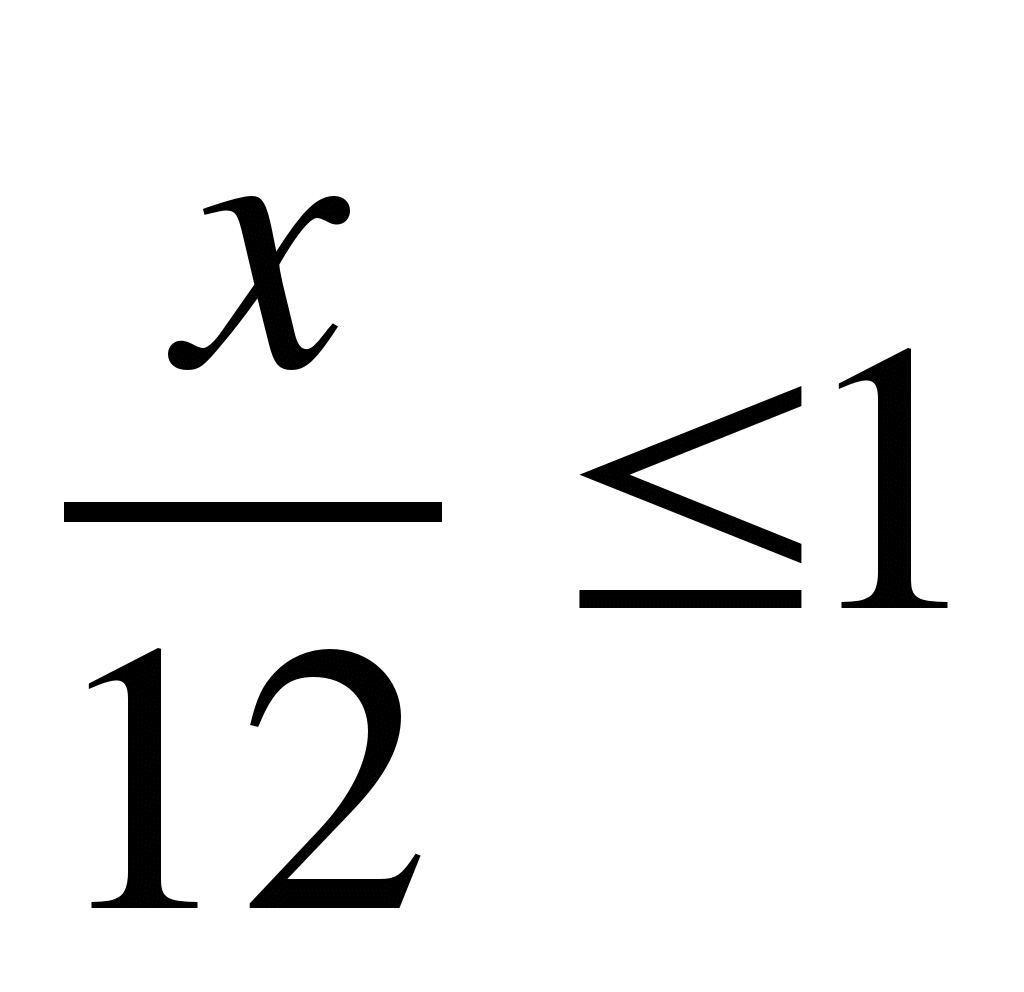 .
.
1) 12; 2) 11; 3) 1; 4) 13.
А6. Найдите наибольшее целое число x , удовлетворяющее неравенству 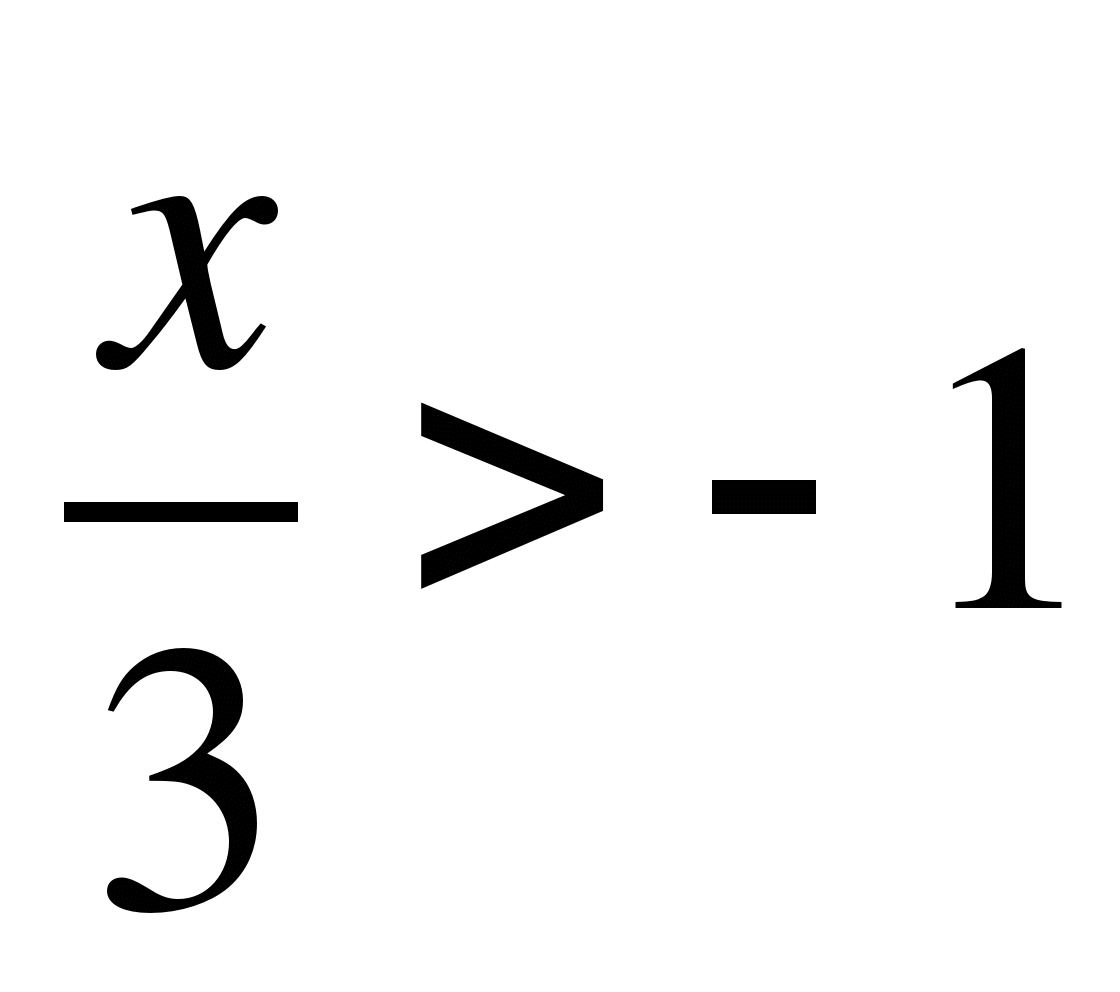 .
.
1) -3; 2) -2; 3) -1; 4) -4.
А7. Решите неравенство 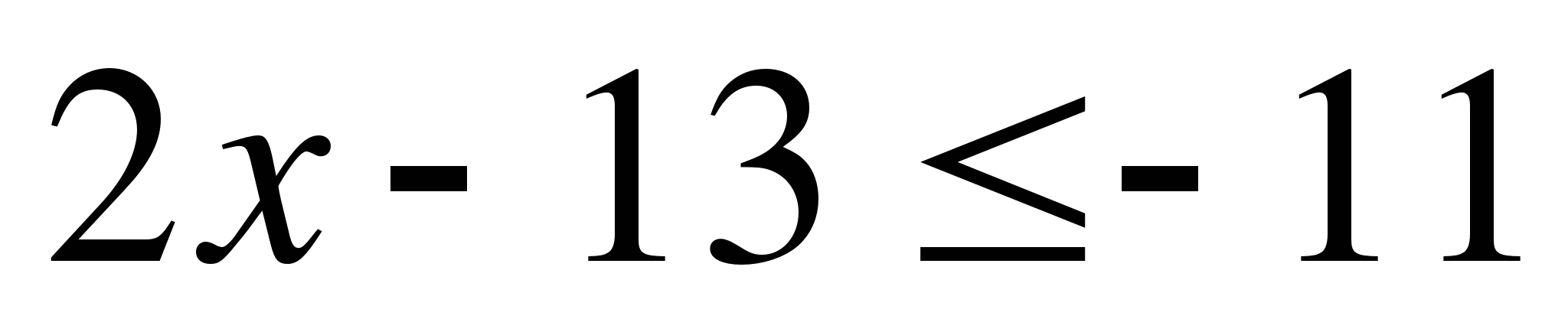 .
.
1) 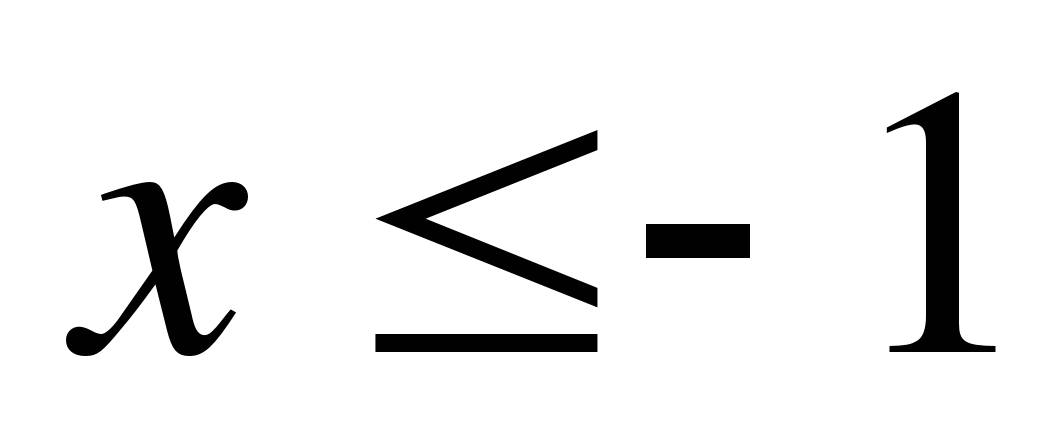 ; 2)
; 2) 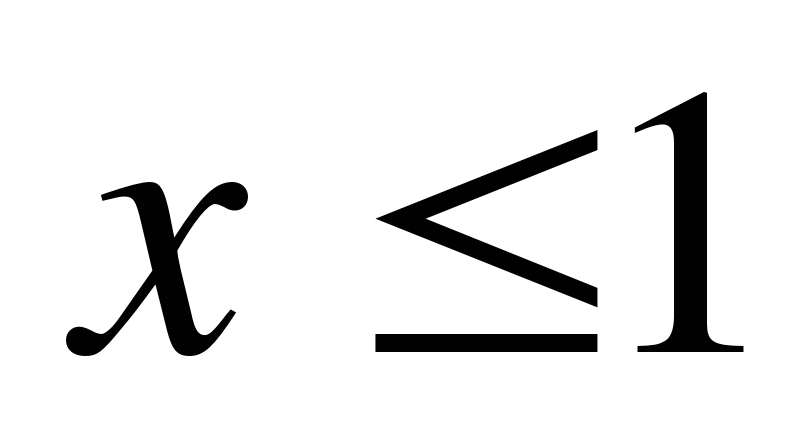 ; 3)
; 3) 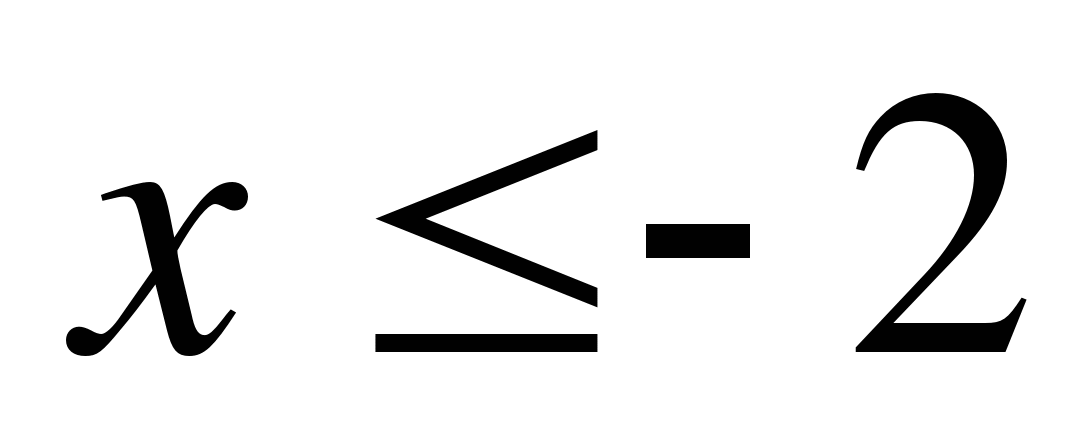 ; 4)
; 4) 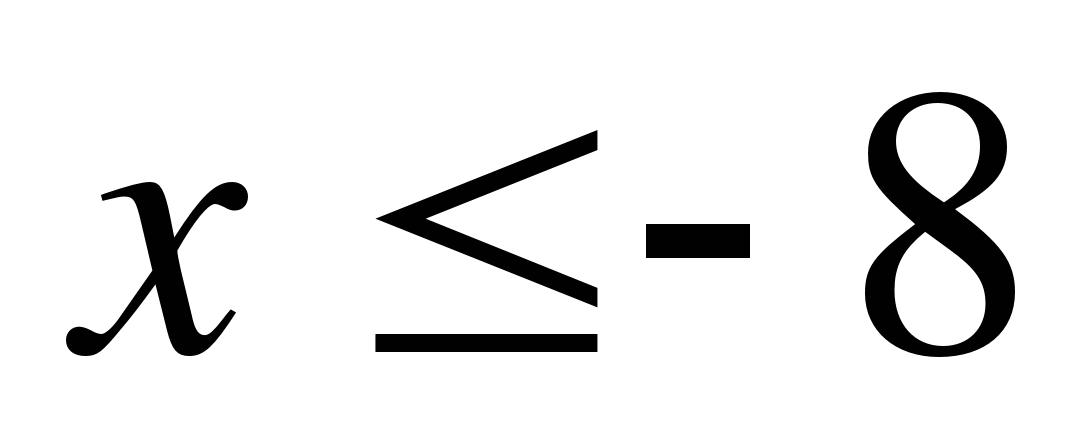 .
.
А8. Решите неравенство 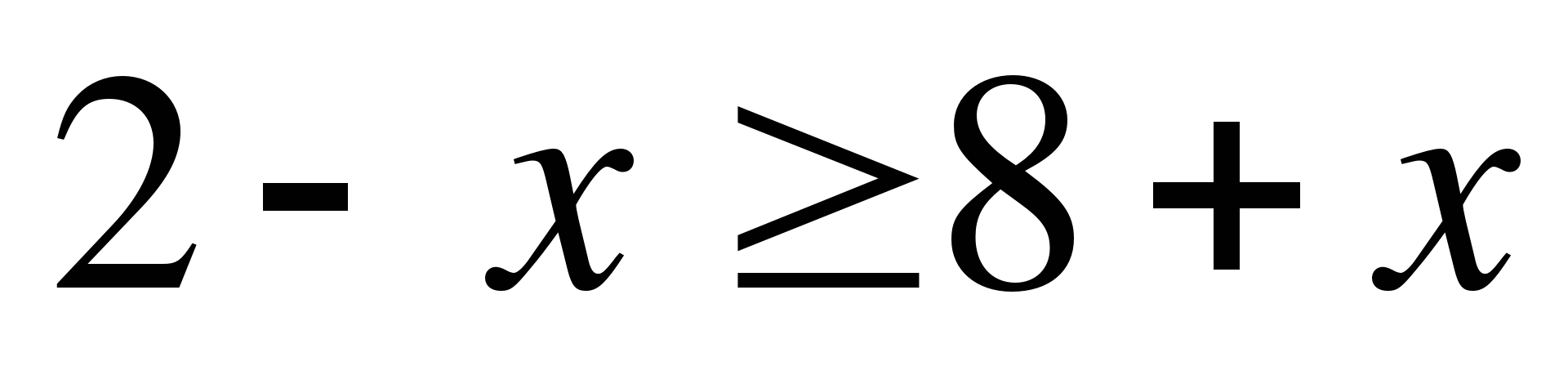 .
.
1) 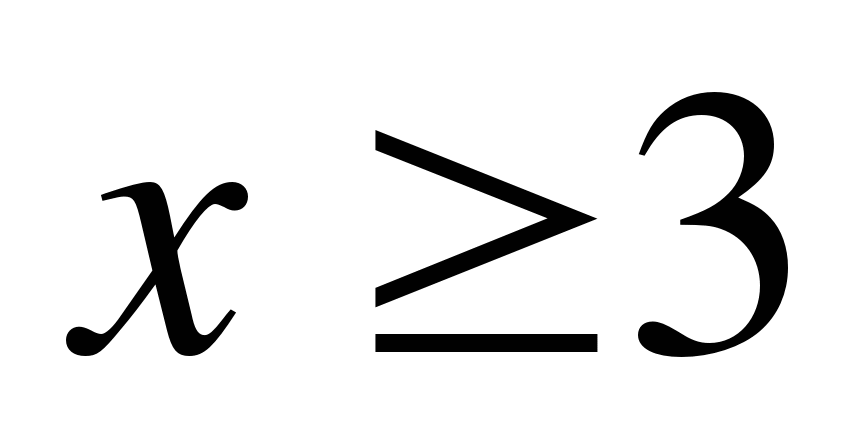 ; 2)
; 2) 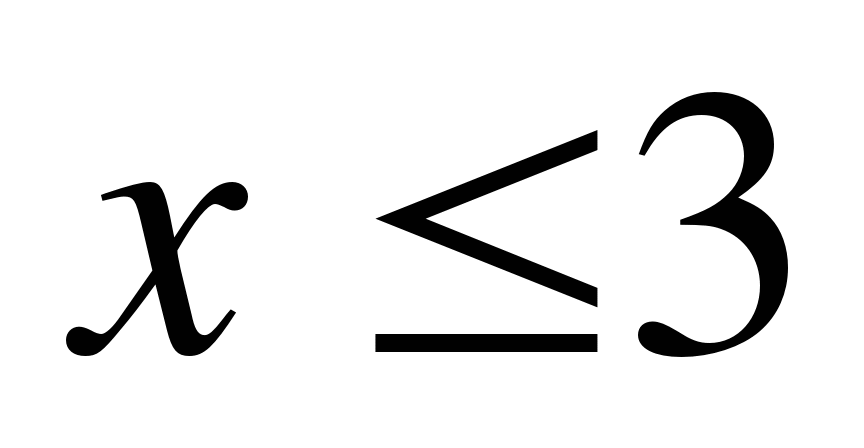 ; 3)
; 3) 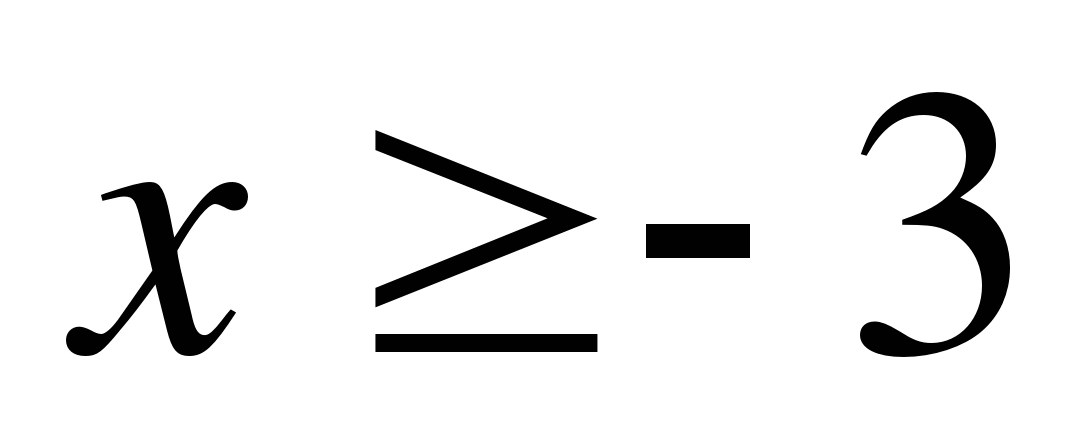 ; 4)
; 4) 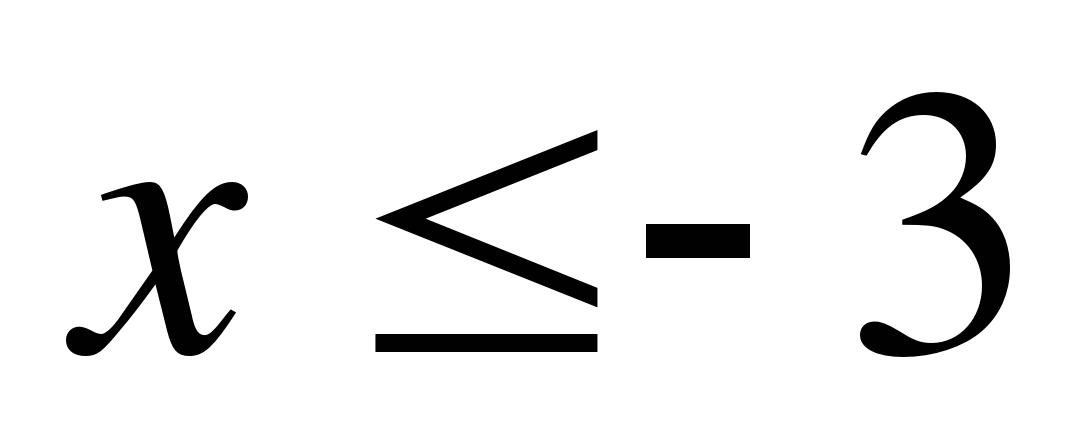 .
.
А9. Решите неравенство 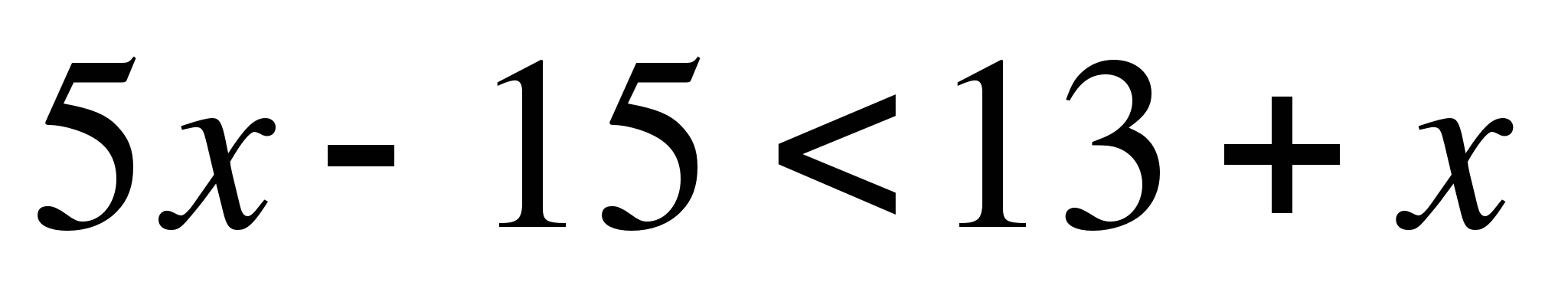 . В ответе укажите наибольшее целое число.
. В ответе укажите наибольшее целое число.
1) 6; 2) 7; 3) 10; 4) 8.
А10. Решите неравенство 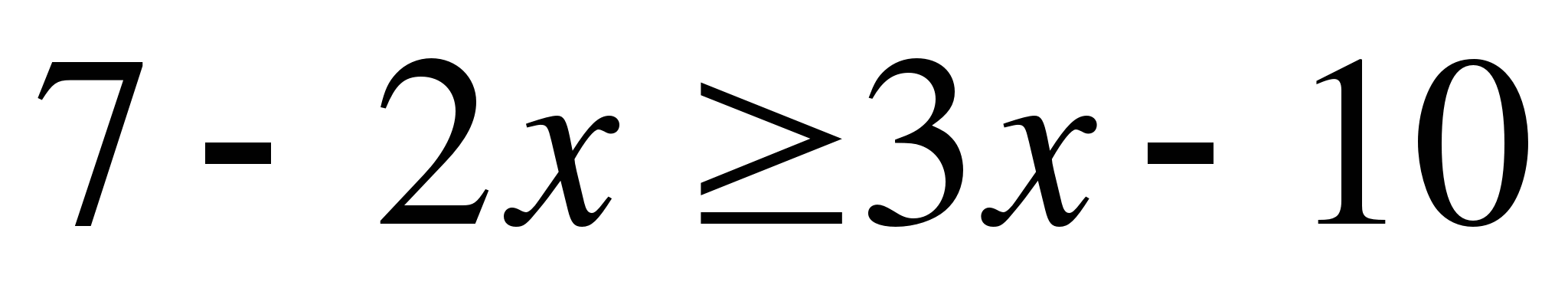 . В ответе укажите наибольшее целое число.
. В ответе укажите наибольшее целое число.
1) 2; 2) 3; 3) 4; 4) 5.
А11. Решите систему неравенств 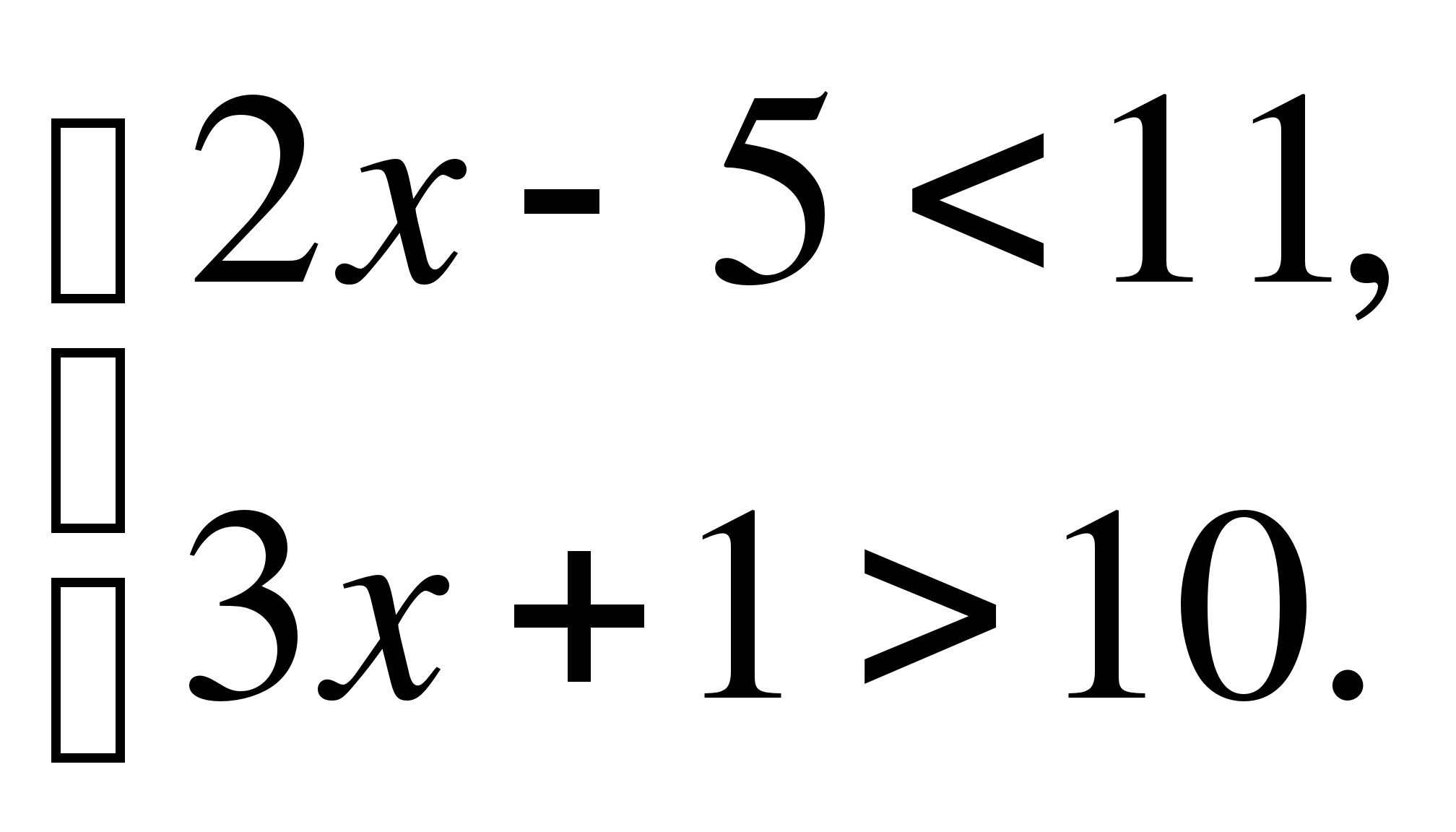
1) 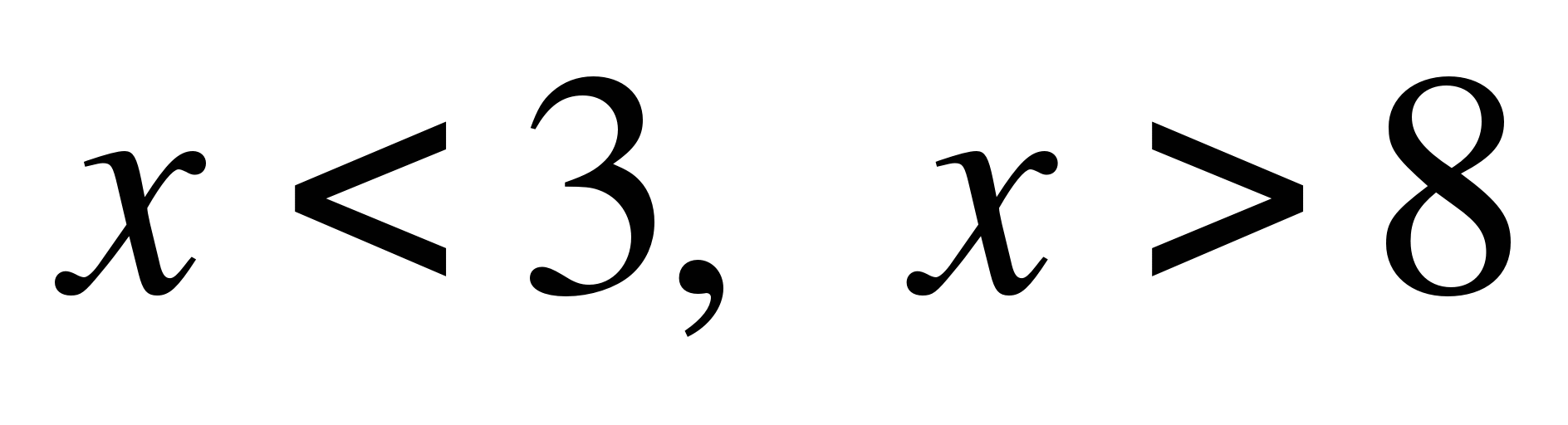 ; 2)
; 2)  ; 3)
; 3) 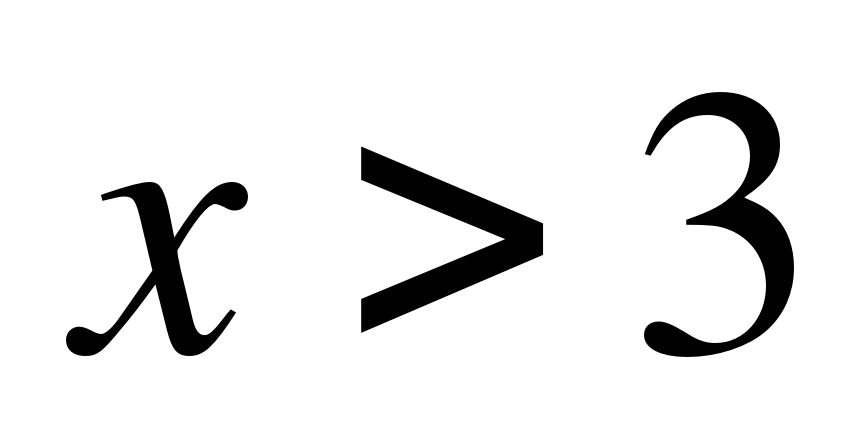 ; 4)
; 4) 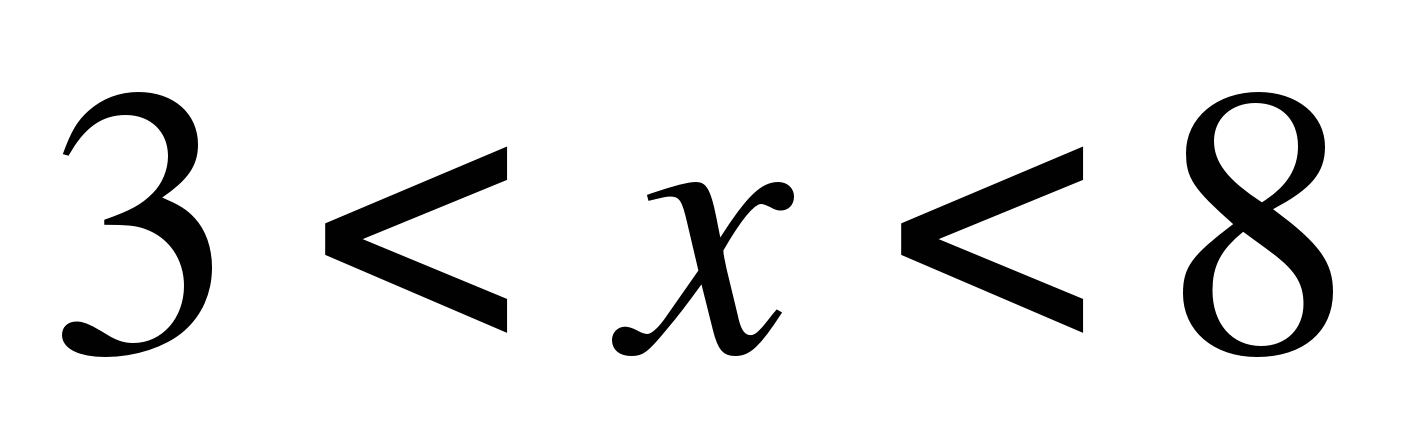 .
.
А12. Множество чисел, изображенных на рисунке запишите в виде неравенства
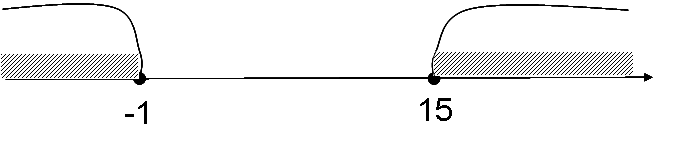 1)
1) 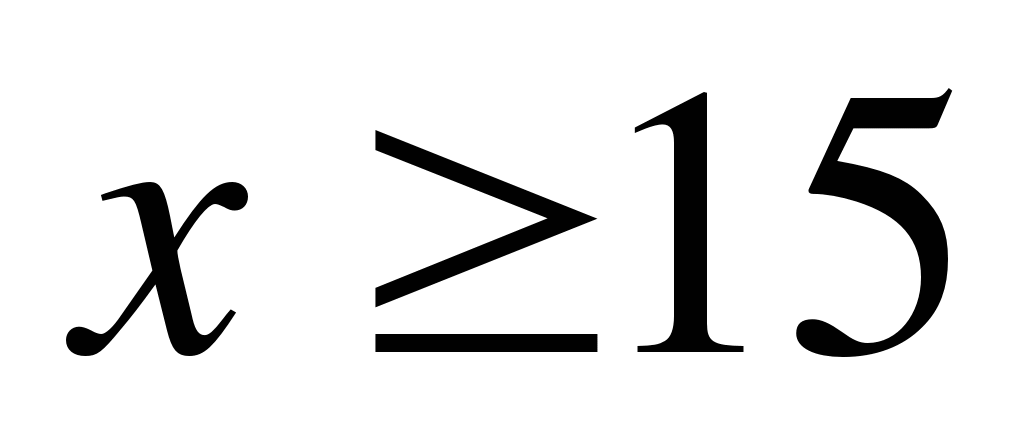 ; 2)
; 2) 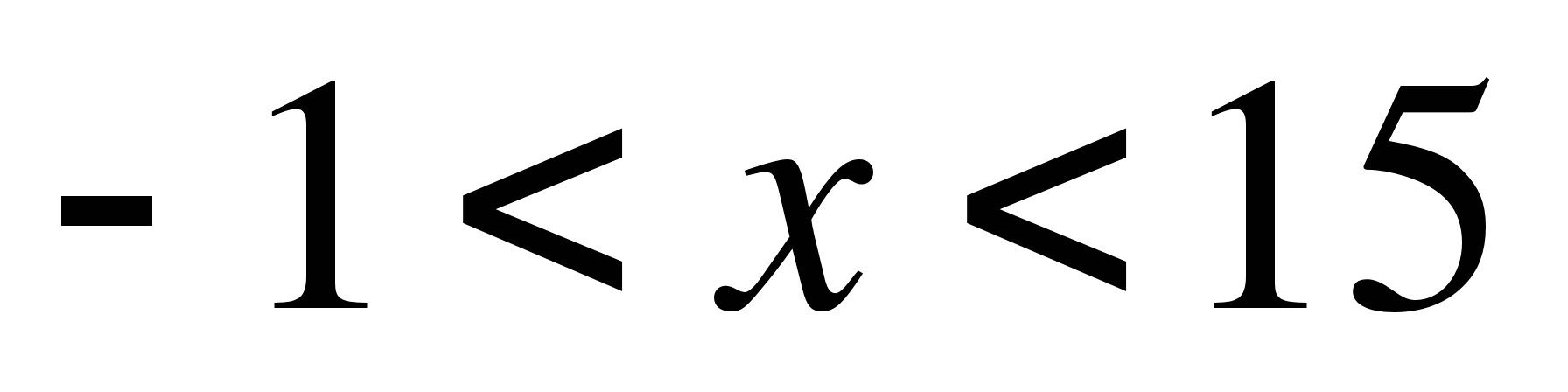 ;
;
3) 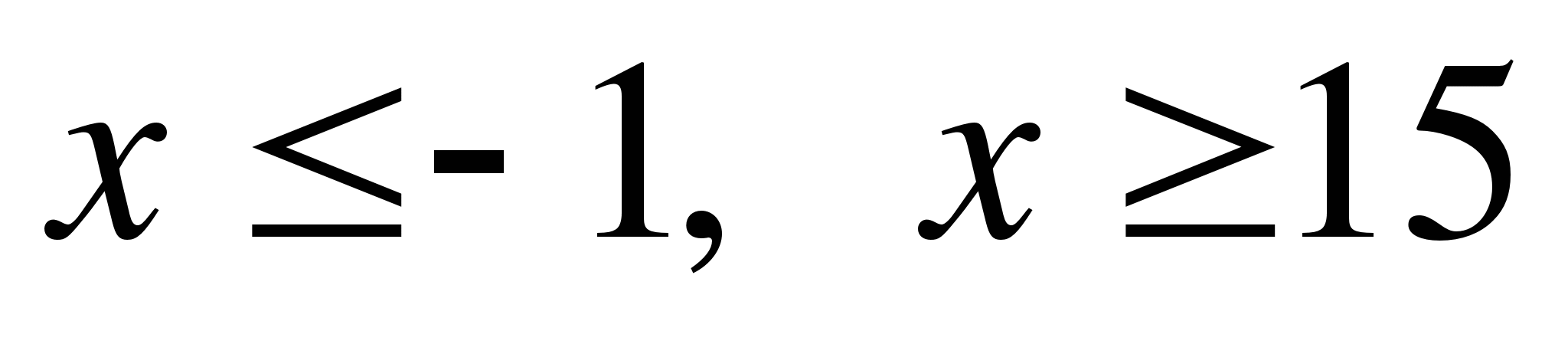 ; 4)
; 4) 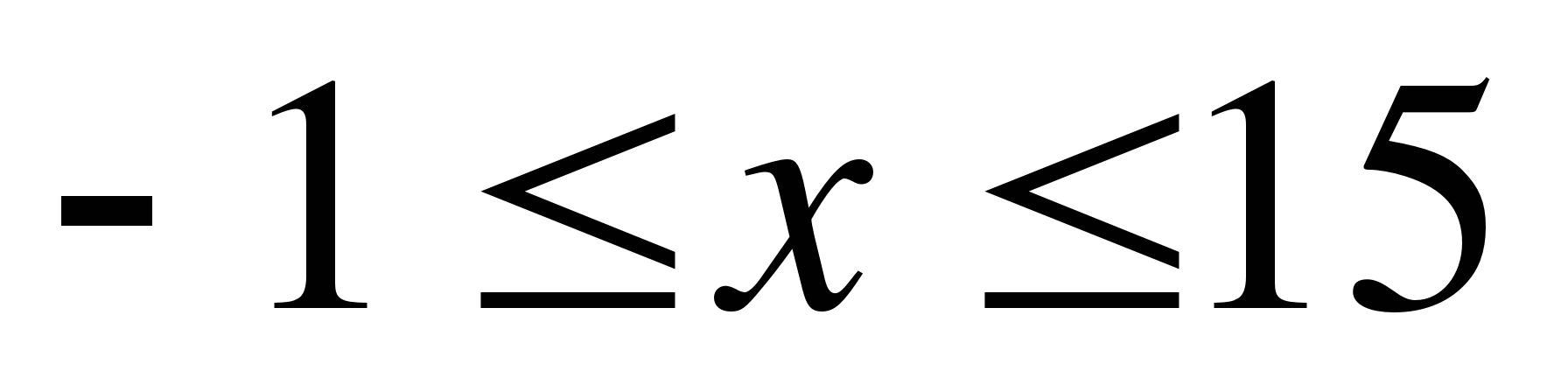 .
.
Ответы:
Тест по теме
«Действия с рациональными дробями
В заданиях 1 – 9 выберите правильный ответ
1. Найдите значение алгебраической дроби .
1) 2) 3) 4)
2. Сократите дробь . 1) 2) 3) 4)
3. Найдите значение , при котором дробь не имеет смысла
1) 2) 3) 4) нет таких значений
4. Выполните сложение .
1) 2) 3) 4)
5. Выполните действия .
1) 2) 3) 4)
6. Выполните действия . 1) 2) 3) 4)
7. Выполните действия .
1) 2) 3) 4)
8. Выполните действия .
1) 2) 3) 4)
В заданиях 9 – 10 запишите ответ
9. Выполните действия .
Ответ._________________________________
10. Найдите значение выражения .
Ответ .___________________________________________________
рациональных выражений: поиск домена
Рациональный Выражения: в поисках домена (страница 1 из 3)
Разделы: Поиск область, упрощающая рациональные выражения

«Рациональное выражение» является полиномиальной дробью, и все, что вы могли бы сделать с регулярными дробями Вы можете сделать с рациональными выражениями.Тем не менее, так как есть переменные в рациональных выражениях есть некоторые дополнительные соображения.
Когда вы имели дело с дробями, вы знали, что дробь может иметь любые целые числа для числителя и знаменатель, пока вы не попытались разделить на ноль. При общении с рациональными выражениями, вам часто нужно будет оценить выражение, и это может быть полезно знать, какие значения вызовут деление на ноль, так что вы можете избежать этих значений x .Так вероятно, первое, что вы сделаете с рациональными выражениями, это найдите их домены.
- Найти домен 3 / x .
Домен всех ценностей что х разрешено быть. Поскольку я не могу делить на ноль (деление на ноль не разрешено), мне нужно найти все значения x , которые могли бы вызвать деление на ноль.Домен тогда будет иметь все , другие , x -значения. Когда этот знаменатель равен нулю? Когда x = 0.
Тогда домен «все x не равно нулю» .
- Определить домен из x / 3 . авторское право © Elizabeth Stapel 2003-2011 Все права защищены.
Домен не волнует что находится в числителе рационального выражения.Домен только под влиянием нулей знаменателя. Будет «3» всегда равен нулю? Конечно нет. Так как знаменатель никогда не будет равным ноль, независимо от значения x , тогда для этого рационального выражения нет запрещенных значений, а х может быть чем угодно. Таким образом, домен «все x » .
- Даешь домен следующее выражение:
Чтобы найти домен я игнорировать « x + 2» в числитель (так как числитель не вызывает деление на ноль) и вместо этого я посмотрю на знаменатель.Я установлю знаменатель равным в ноль, и решить. Значения x в решении будут значения x что приведет к делению на ноль. В этом случае домен будет иметь все остальные значения x .
x 2 + 2 x — 15 = 0
( x + 5) ( x -3) = 0
x = –5, x = 3
Факторинг
квадратичный,
Я нашел нули знаменателя.Домен будет все остальные x -значения:
- Найти домен следующее выражение:
Чтобы найти домен я решить для нулей знаменателя:
Это не имеет решения, поэтому знаменатель никогда не равен нулю.Тогда домен «все х » .
Топ | 1 | 2 | 3 | Вернуться к оглавлению Следующая >>
| Цитировать эту статью как: | Stapel, Elizabeth.
Рациональные выражения: поиск домена.» Purplemath . Доступен с |
Рациональных Чисел
Рациональное число может быть получено путем деления двух целых чисел.
(Целое число — число без дробной части.)
Пример:
1,5 — рациональное число , потому что 1,5 = 3/2 (3 и 2 — целые числа)
Большинство чисел, которые мы используем в повседневной жизни, — это рациональные числа.
Вот еще несколько примеров:
| номер | как фракция | Рациональный? |
|---|---|---|
| 5 | 5/1 | да |
| 1.75 | 7/4 | да |
| ,001 | 1/1000 | да |
| −0,1 | -1/10 | да |
| 0,111 … | 1/9 | да |
| √2 (квадратный корень из 2) | ? | НЕТ! |
Ой! Квадратный корень из 2 не может быть записан как простая дробь! И есть еще много таких чисел, и потому что они , а не рационально , их называют Иррациональными.
Другой известный иррациональный номер — это Pi (π):
Формальное определение рационального числа
Более формально мы говорим:
Рациональное число — это число, которое может иметь вид p / q
, где p и q являются целыми числами, а q не равно нулю.
Итак, рациональное число может быть:
Где q не ноль
Примеры:
| р | кв | п / к | = |
|---|---|---|---|
| 1 | 1 | 1/1 | 1 |
| 1 | 2 | 1/2 | 0.5 |
| 55 | 100 | 55/100 | 0,55 |
| 1 | 1000 | 1/1000 | 0,001 |
| 253 | 10 | 253/10 | 25.3 |
| 7 | 0 | 7/0 | Нет! «д» не может быть нулем! |
Просто помните: д не может быть нулем
Использование рациональных чисел
интересных фактов ….
Древнегреческий математик Пифагор считал, что все числа рациональны, но один из его учеников Гиппас доказал (используя геометрию, как полагают), что вы могли бы , а не написать квадратный корень из 2 как дробь, и так было , нерационально .
Но последователи Пифагора не могли принять существование иррациональных чисел, и говорят, что Гиппас был потоплен в море как наказание от богов!
,Транскрипция
1 Лекция 1 (Обзор математики средней школы: функции и модели) Введение: числа и их свойства
2 Дополнение: (1) (Ассоциативный закон) Если a, b и c являются любыми числами, то () () ( 2) (Существование аддитивного тождества) Если a — любое число, то (3) (Существование аддитивных инверсий) Для каждого числа a существует такое число a, что () () (4) (Коммутативный закон) Если a и b — любые числа, то
3 Умножение: (5) (Ассоциативный закон) Если a, b и c — любые числа, то () () (6) (Существование мультипликативного тождества) Если a — любое число , тогда (7) (Существование мультипликативных инверсий) Для каждого числа существует такое число, что (Примечание: деление на 0 всегда неопределенно!) (8) (Коммутативный закон) Если a и b — любые числа, то (9 ) (Закон распределения) Если a, b и c являются любыми числами, то ()
4 Определение: числа a удовлетворяющие называются положительными, а числа удовлетворяющие — отрицательными.Для любого числа a мы определяем абсолютное значение a a следующим образом: {Примечание: a всегда положительно, за исключением случаев, когда Пример:
5 Теорема (неравенство треугольника): Для всех чисел a и b мы имеем Доказательство: Примечание:
6 1. Докажите следующее: (a) () () Упражнения (b) () (c) () ()
7 2. Что не так со следующим «доказательством»? Пусть тогда () () ()
8 Какие типы чисел существуют ?… Простейшими числами являются «счетные числа»: 1, 2, 3, … Мы называем их натуральными числами и обозначаем через. Самым основным свойством является принцип «математической индукции».

9 Математическая индукция. Предположим, что P (n) означает, что свойство P верно для числа n. Тогда P (n) истинно для всех натуральных чисел n при условии, что (1) P (1) истинно (2) Всякий раз, когда P (k) истинно, P (k + 1) истинно.Стандартная аналогия — это цепочка домино, которые организованы таким образом, что если любое конкретное домино опрокидывается, то оно, в свою очередь, опрокидывает следующее. Эта аналогия хороша, но это всего лишь аналогия, и мы должны помнить, что в ситуации с домино существует только конечное число домино.
10 Пример: Show that () Решение:
11 Упражнение Докажите по индукции по n, что если (обратите внимание, что если, вы можете легко вычислить сумму)
12 Другие числа: Целые числа :…, -2, -1, 0, 1, 2, … Этот набор обозначается. Рациональное число:. Этот набор обозначается. Действительные числа: обозначены. Вещественные числа включают рациональные и иррациональные числа (например, числа, которые могут быть представлены бесконечными десятичными знаками). или, т. е.
13 Обозначение множества и операции над множествами Определение: множество A — это совокупность объектов, которые называются элементами или элементами. Пример: символы, которые мы будем использовать: (x принадлежит A) (x не принадлежит A)
14 Подмножество: Диаграмма Венна: Дополнение:
15 Объединение: Пересечение: Пустое множество:
16 Интервалы: ()) (
17 Пример: () () () () (
18 Устранение неравенств Пример: решение.Выразите ответ как интервал и графически.
19 Пример:
20 Пример: решение
21 Функции Что такое функция? — Функция — это правило, которое присваивает каждому из определенных действительных чисел некоторое другое действительное число. Обозначения: ().
22 Пример: Правило, которое присваивает каждому числу куб этого числа: ()
23 Использование обозначений: Функция f — это правило, которое присваивает каждому элементу x из некоторого набора D ровно один элемент, (), в набор Е.D — это набор действительных чисел, называемый областью функции. E — это набор действительных чисел, называемый диапазоном функции, это набор всех возможных значений (), определенных для каждого x в домене. Мы называем x независимой переменной, а () зависимой переменной. Примеры: Найти домен и диапазон в интервальной записи. (1) () (2) ()
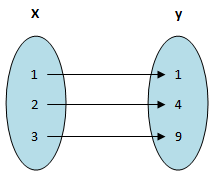
24 Визуализация функции Существуют разные способы изображения функции.Одна из них представляет собой диаграмму со стрелкой: каждая стрелка соединяет элемент D с элементом E.
25 Наиболее распространенный способ изобразить функцию — нарисовать график. Определение: граф — это множество упорядоченных пар (()). Пример: Given (), find ().
26 Пример: Graph () Пример: Graph ()

27 function? Когда вы смотрите на график, как вы узнаете, что смотрите на тест вертикальной линии: Кривая в плоскости xy — это график функции x тогда и только тогда, когда вертикальная линия не пересекает кривую более одного раза.
28 Пример:
29 Математические модели: какие существуют функции? Математическая модель — это математическое описание (функция или уравнение) реального явления. Пример. Между мужем и женой существует сильная положительная линейная связь. Мы можем использовать линейную модель для описания этих отношений!
30 Определение: Мы говорим, что у — линейная функция х, если () уравнение линии, где — наклон линии, величина, на которую у изменяется, когда х увеличивается на одну единицу.b — точка пересечения y, значение y когда. Пример:
31 Определение: Функция f является полиномиальной функцией, если существуют действительные числа, такие что () (), для всех x, n является неотрицательным целым числом. Числа называются коэффициентами полинома. Наивысшая степень x с ненулевым коэффициентом называется степенью полинома. Примеры: 1) Полином степени 0 является постоянной функцией (), например, 2) Полином степени 1 является линейной функцией ().
32 3) Многочлен степени 2 является квадратичной функцией (), например, Граф называется параболой. 4) Полином степени 3 является кубической функцией (), например,
33 Определение: если () () для каждого, то f называется четной функцией. Если () () для каждого, то f называется нечетной функцией. Пример: () является четной полиномиальной функцией. График четной функции симметричен относительно оси y.() является нечетной полиномиальной функцией. График нечетной функции симметричен относительно начала координат.
34 Как насчет ()?
35 Определение: функция f называется возрастающей на интервале I if () () всякий раз в I Это называется убывающей на I if () () всякий раз в I
36 Пример: Given (), найти интервалы где () увеличивается / уменьшается.
37 Определение: Функция вида (), где a является константой, называется степенной функцией.Рассмотрим следующие случаи: если a = n, где n — положительное целое число, то () — полиномиальная функция. Если a = 1 / n, где n — положительное целое число, то () — корневая функция. Пример:
38 Если a =, то () является обратной функцией. Граф называется гиперболой с осями координат в качестве асимптот.
39 Определение: Функция f называется рациональной функцией, если ее можно записать в виде отношения двух полиномов: () () () Пример: ()
40 Определение: Функция f называется алгебраической функцией, если он строится путем применения алгебраических операций (таких как сложение, вычитание, умножение, деление и получение корней) к полиномам.Примеры: () () ()
41 Тригонометрические функции (обзор): () ()
42 () Остальные функции: cosecant, secant и cotangent — обратные функции, указанные выше.
43 Таблица неполных значений для тригонометрических функций:
44 Идентичности
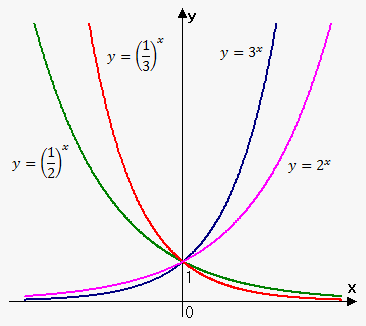
45 Экспоненциальные функции Определение: Функция константы form () называется экспоненциальной функцией.Давайте вспомним, что это значит., Где основание a является положительным
46 законов экспонент: если a и b положительные числа, а x и y любые действительные числа, то () 4. () Пример: Упростить
47 Число е
48 Как мы можем получить новые функции от тех, которые мы знаем? Преобразования функций вертикальных и горизонтальных сдвигов: предположим. Чтобы получить график (), сдвиньте график () расстояния c единиц вверх / вниз (), сдвиньте график () расстояния c единиц влево / вправо Пример: () ()
49 Вертикально и Горизонтальное растяжение: предположим.Чтобы получить график (), растяните график () по вертикали с коэффициентом c (), уменьшите график () по вертикали с коэффициентом c (), сузьте график () по горизонтали с коэффициентом c (), растяните график () по горизонтали на коэффициент c Пример:
50 Отражение: Чтобы получить график (), отразите график () относительно оси x (), отразите график () о оси Y Пример:
51 Комбинации функций () () () () (сумма / отклонение) () () () () (product) () () () () () (частное) () () (()) (составная функция) Пример: If () и (), find ,, и.Что о?
52 Обратные функции Определение: Функция f называется функцией «один к одному», если она никогда не принимает одно и то же значение дважды, т. Е. () () Всякий раз, когда Example :. Это один к одному?

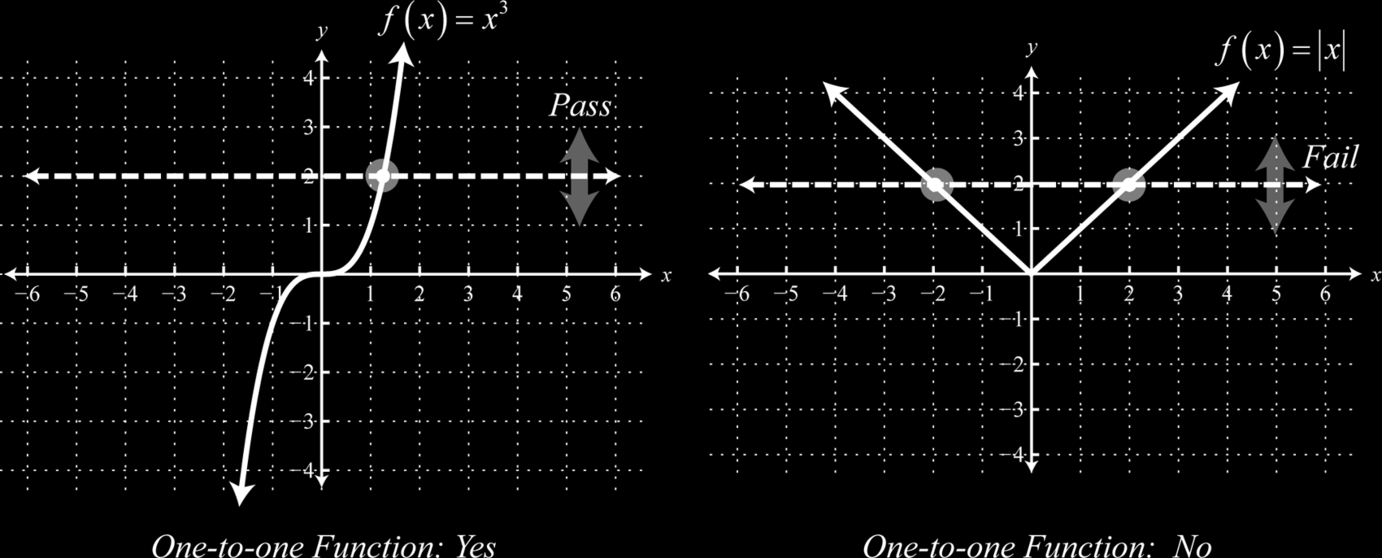
53 Как проверить? Проверка горизонтальной линии: функция является взаимно-однозначной в том и только в том случае, если горизонтальная линия не пересекает свой график более одного раза.

54 Определение: пусть обратная функция будет взаимно-однозначной функцией с областью A и диапазоном B. Затем она имеет область B и диапазон A и определяется () () для любого примечания: () () Пример: задано что () является взаимно-однозначным, и () () () Find () () и (()).
55 Примечание: Инверсные функции обладают уникальным свойством, которое, будучи составлено из их исходных функций, отменяет обе функции.Математически это означает, что (()) (()) Поскольку функции и обратные функции содержат одинаковые числа в своей упорядоченной паре, только в обратном порядке, их графики будут отражать друг друга на линии y = x:
56 Пример: ()
57 Как найти обратную функцию? Чтобы найти обратную функцию для функции «один к одному», выполните следующие действия: 1. Перепишите функцию, используя y вместо f (x).2. Решите уравнение для x через y. 3. Переключите переменные x и y. 4. Получив уравнение (). 5. Убедитесь, что полученная обратная функция равна 1: 1. Если это не так, ограничьте домен для прохождения теста горизонтальной линии.
58 Пример: Given (), найти f 1 (x). Примечание: x 0 для f 1 (x). Без этого ограничения f 1 (x) не прошла бы тест горизонтальной линии. Очевидно, что он должен быть один к одному, поскольку он должен обладать обратным к f (x).Вы должны использовать эту часть графика, потому что она отражает f (x) по линии y = x, в отличие от части на x <0.
59 Примеры обратных функций Вам нужно знать логарифмические функции Если и, Экспоненциальная функция () является взаимно-однозначной, поэтому она имеет обратную функцию, называемую логарифмической функцией с основанием a. Обозначения: Таким образом, свойство отмены: () () (()) () (())
60 Законы логарифмов: дано (положительные целые числа) 1.() Примечание: Пример: оценка
61 Определение: Логарифм с основанием e называется натуральным логарифмом. Обозначения: Итак, Пример: Решить
62 Изменение базовой формулы: Пример: Оценить
63 Обратные тригонометрические функции Обратные функции синуса или функции акрсина: Область: [-1,1] Диапазон: не один-к-одному, но ибо это так.
64 Итак, мы имеем и () () Пример: Evaluate (a) (b)
65 Аналогично мы можем определить обратные функции для других тригонометрических функций: f (x) = cos -1 (x) f (x) = arccos (x) f (x) = загар -1 (x) f (x) = arctan (x) домен: [-1,1] диапазон: домен: диапазон:
66 ())) ((
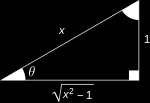
) 67 Диаграмма
68 Общие решения Примечание. Тригонометрические функции являются периодическими.Эта периодичность отражается в общих инверсиях: или, или
69 Пример: Решите уравнение
.Транскрипция

1 Рациональное получение чисел: акцент на дроби и десятичные дроби Брэдли Витцель, к.т.н. Профессор Уинтроп Университет Обоснование для достижения рационального низкого уровня в математике является серьезной проблемой, особенно в области рациональных чисел.Знание дробей и десятичных дробей влияет на будущую успеваемость студента по математике. На этом занятии д-р Витцель предоставит 5 рекомендаций для эффективного обучения студентов понятиям, связанным с рациональными числами, в том числе тем, кто нуждается в дополнительной помощи. Витцель, Витцель, Рациональные числа — это общие трудности (Сандерс, Риккомини и Витцель, 2005). Все начинается с инструкции! Категория кода Ввод Math Tech 1 Ввод алгебры 1 Фракции FRAC и их приложения 3 (3,6%) 43 (44.8%) десятичные дроби DECM, их операции и применение: проценты 11 (13,1%) 64 (66,7%) EXPS Exponents и Square Roots; Научная нотация 27 (21,1%) 62 (64,6%) GRPH Графическое представление 13 (15,5%) 59 (61,5%) INTG Целочисленные, их операции и приложения 27 (32,1%) 83 (86,5%) Общее количество студентов на курс Witzel, Witzel, Назовите наиболее распространенный ответ (Ryan & McCrae, 2005) I) 0,3 x 0,24 a) b) 0,08 c) 0,72 d) 0,8 e) 7,2 I) 0,3 x 0,24 Частота ошибочного восприятия ответа a) ПРАВИЛЬНО 36.1% б) 0,08 в) 0,72 г) составляет одну треть, или десятичная дробь подразумевает деление 3х24 и корректируется до 2 десятичных знаков 0,3 — одна треть или десятичная дробь подразумевает деление и корректируется до 1 десятичного знака 3,5% 41,1% 2,8% е) x 0,24 = 3 x% Пропущено 1,4% Witzel,


2 Практическое руководство по десятичным дробям 1) Построить на студентах неформальное понимание разделения и пропорциональности.2) Научите, что дроби — это числа. Используйте числовые линии в качестве центрального инструмента представления. 3) Научитесь понимать, почему процедуры для вычислений с дробями имеют смысл. 4) Разработать концептуальное понимание стратегий для решения проблем отношения, скорости и пропорции до или вместо коротких путей. 5) Программы профессионального развития должны отдавать приоритет пониманию фракций. Назовите наиболее распространенный ответ (Ryan & McCrae, 2005) II) / 100 в десятичной форме a) b) c) d) e) Witzel, II) / 100 в десятичной форме Частота ошибочных представлений ответа a) Сотые доли — первое десятичное место 3 ,5% б) ПРАВИЛЬНО 76,3% в) Десятые; Десятые, сотые 12,2% d) / 100 — это ¼ или = 1/25 =% e) = 25, а одни десятые, десятые и сотые 1,6% опущены 0,7% Назовите наиболее распространенный ответ (Ryan & McCrae, 2005) III) a) б) в) г) д) Витцель, III) Внимание! Частота неверного представления ответа Ответ а) Переместите десятичную точку на 2 позиции вправо 0% b) Переместите десятичную точку на 1 позицию влево 6,4%. Эти ошибки не были допущены учащимися класса P-12. Они были сделаны кандидатами в учителя. в) Отменить ноль 2,6% г) ПРАВИЛЬНО 68.8% e) 3,62 Целочисленное десятичное разделение или отмена 2 нулей 22,0% Пропущено 0% Witzel, Witzel,
3 Общие проблемы с дробями (Риккомини, Хьюз, Морано, Хванг и Витцель, в прессе) Пески Остается! Дробная ошибка анализа элементов групп с низким, средним и высоким уровнем достижения Категории элементов M Группы достижений SD Rak Низкий Средний Высокий M SD-рейтинг M SD Ранговое деление Порядок умножения Проблемы со словами сложение D (1) Вычитание D (1) Преобразование L (2) ) Преобразование E (3) Вычитание S (4) Сложение S (4) Примечание.(1) Другой знаменатель, (2) Наименьшая форма, (3) Эквивалентная форма, (4) Тот же знаменатель. Ранговые числа от 1 до 10 означают наибольшую частоту ошибок от 1 до наименьшей частоты ошибок 10. «Джон берет с собой 10 друзей в поездку. Каждая машина вмещает 3 человека. Сколько машин понадобится Джону для поездки? Обоснуйте свой ответ». Объясните значение количества автомобилей. Почему не дробный ответ? Разберитесь в математике Witzel, Witzel, Picture This! Фракции как дивизия «Мария была очень взволнована тем, что получила целую пачку конфет Starburst, как и все ее друзья.Она хотела показать, какая она хорошая подруга, и решила поделиться пакетом поровну между своими шестью друзьями. Всего в упаковке насчитывалось 49 конфет. Сколько конфет каждый должен получить? Как бы вы смоделировали эту ситуацию? »Избегайте хитростей: конвертирование дробей Преобразуйте эту смешанную дробь в неподходящую дробь. 4 2/5 Как вы узнали, как это сделать? Вы a. 4×5 b. + 2 = 22 c. 5 скользит по д. 22/5 Почему? Скажем, четыре и две пятых 4 / / 5 или 20 / / 5 = 22/5 Витцель, Витцель, Избегай трюков: деление дробей Почему понимаешь дроби? Почему это когда делишь дроби ответ может быть больше? Кроме того, почему вы инвертировать и умножить? Просто переверните его! 2/3 1/4 = 2/3 (4/1) = 8/3 2/3 (4/1) 8/3 8/3 8/3 1/4 (4/1) 4/4 1/1 Witzel, Witzel,
4 Зачем учить основам правильно (2/5) (2/4) Добавление с разными знаменателями Деление дробей по Витцелю , Witzel, Что мы должны сделать, чтобы помочь? Десятичное вычитание (Boerst, 2015) Узнайте, как студенты решают проблемы рациональных чисел.Помогите учителям овладеть навыками пропуска в рамках рационального именования чисел, величины и вычислений. Преподавайте учебные и интервенционные стратегии, которые помогают учащимся выучить десятичные дроби и дроби. S Сделайте проблему вычитания самостоятельно. Think-Pair-Share Какие стратегии могут использовать пятиклассники для решения этой проблемы? Witzel, Witzel, Использование представлений для поддержки обучения и изучения десятичных дробей A. Понимание дробей и десятичных дробей A. Понимание десятичных дробей a) Проблемы с использованием обобщений из работы с целыми числами b) Распространенные заблуждения учащихся c) Создание связей с дробями B.Представление десятичных чисел a) Выбор и использование представлений C. Сравнение десятичных дробей a) Моделирование сравнения b) Выбор числовых примеров D. Представление и осмысление вычислений a) Анализ распространенных ошибок учащихся b) Моделирование вычислений с помощью десятичных дробей E. Бонус за вмешательство Witzel, Witzel,

5 Что математически сложно в десятичных числах? Пример ошибки. 34>. 5,75> в десять раз больше, чем.2 Сотни, десятки, единицы, десятые, десятые, сотые … По материалам Boerst & Shaughnessy, 2015; Ирвин, 2001 Основополагающее заблуждение Более длинные десятичные дроби больше (чрезмерное обобщение из целых чисел) Более длинные десятичные дроби меньше (чрезмерное обобщение новых представлений в десятичные дроби) Добавление нуля вправо увеличивает число в десять раз (чрезмерное обобщение из целых чисел) Отсутствие понимания специфики одного из них в системе значений места Распространенные недоразумения о соединении дробей и десятичных дробей Как ученик может дать этот ответ? Запись числителя в виде десятичной дроби Распространенные недоразумения о соединении дробей и десятичных дробей Как ученики могут дать эти ответы? Разделение знаменателя на числитель (и не зная, как выразить остаток) Распространенные недоразумения о соединении дробей и знаменателей Разделение числителя и знаменателя с десятичной точкой Запись числителя в виде десятичной дроби Разделение знаменателя на числитель Игнорирование целых чисел Как мы можем помочь студенту понять десятичные числа как числа? 27 Witzel, Place Value Skills 27 = 2 десятка и 7 единиц 45 = 4 десятка и 5 единиц Должны быть представлены физически и устно. Продвинутые учащиеся должны использовать значение места в упражнении по вычислению.Сотни Десяток Гонка к одной партнерской работе — Повторите каждое новое число в виде общей суммы и приращений стоимости. Десятки. Десятки. Сот. Десят.,. Сот.
. это помогает детям отображать численно выраженные дроби (N 1 / N 2) в числовые линии, прямоугольники и (особенно) круги, например, вездесущее круговое представление пиццы (Bailey et al., 2015, с. 80) Обычные / типичные десятичные представления, используемые в обучении Какие представления используют учителя, чтобы помочь учащимся понять дроби и дробно-десятичные дроби? Какие контексты используют учителя, чтобы помочь учащимся понять десятичные дроби? Зачем? Witzel, Witzel, Как учителя представляют десятичные дроби студентам? Преимущества числовой линии Представляет десятичные дроби в виде чисел. Адреса этих (неправильных) понятий и других. Более длинные десятичные дроби. Более длинные десятичные дроби меньше. Добавление нуля вправо увеличивает число в десять раз. Плотность рациональных чисел. Бесконечно много имен для любой точки. на линии (Глазго и др.al, 2000) Witzel, Соединить десятичные дроби и дроби Используя числовую строку Соединить десятичные дроби и дроби Используя числовую строку Записать в виде десятичной дроби создавать основанные на длине модели дробных линий. Полоски составлены для сравнения. Задайте такие вопросы, как: Какая полоса составляет одну четвертую часть целого? и какая полоса составляет половину четверти? 1/2 1 целое 1/2 Целостное мышление: создание и исследование десятичных полос Студенты обрезают, складывают и раскрашивают полоски бумаги для создания основанных на длине моделей десятичных дробей.Полоски сложены для сравнения. Задайте такие вопросы, как: Какие полоски показывают четыре десятых целого? а какая полоса половина? Что составляет половину двух десятых? 1 целое 0,5 1/5 1/5 1/5 1/5 1 / / 10 1/10 1/10 1/10 1/10 1/10 1/10 1/10 1/10 1 / Witzel, Witzel, Whole Разделяя мышление: дробные и десятичные полоски Используйте термин целое, а не единицу, чтобы учащиеся поняли пропорциональность дробей на единое целое. В парах попросите учеников общаться. Перечислите все отношения на диаграмме и попросите студентов подтвердить или опровергнуть эти отношения.Дробная бельевая веревка 0 1 Вариации включают в себя: бельевую веревку и клейкую ленту. Использование ключевых показателей дробной части, чтобы помочь студентам перейти от целого класса к небольшой группе или к индивидуальному Витцелю, дробная бельевая веревка (продолжение) Протянуть бельевую веревку по комнате. Закрепите карточки, чтобы указать расположение в числовой строке. Измените карточки между дробями, десятичными числами, процентами и комбинацией. Измените цель от упорядочения до сравнения. Попросите учащихся объяснить свои рассуждения. Десятичная веревка для белья: расширение Следующие шаги: a) дроби до десятичных долей до процентов b) комбинации карт в) изменить представление целого Witzel,8 Проблемы использования числовой линии 0 1 Следующие шаги: а) дроби до десятичных знаков в процент б) комбинации карт в) изменить представление целого Это студентам сложно генерировать представления числовых линий с частями, меньшими, чем десятые. Предварительно разделенные числовые строки могут показывать части, меньшие десятых, но часто требуют дополнительной работы, чтобы сделать разделение значимым для учащихся. Количество десятичных разрядов, которое вы хотите представить, может ограничить диапазон чисел, которые вы можете использовать Из Рекомендации № 2 Руководства IES: помогите учащимся понять, что дроби — это числа, и они расширяют систему счисления за пределы целых чисел.C. Сравнение десятичных чисел Попробовать: использовать представления для поддержки значимого соединения дробей и десятичных чисел. Анализировать возможности различных представлений / контекстов в свете математических целей. Упорядочивание десятичных дробей с помощью числовых линий. Расставьте первую строку десятичных знаков по порядку, используя числовую строку. а) Если вы закончите, попробуйте вторую строку: б) Что вы заметили, приведя десятичные числа в порядок, используя числовую строку? Что показывают числовые линии и как они помогают с типичными трудностями, которые мы обсуждали? Возможные наблюдения Величины десятичных дробей видны Эквивалентность нескольких десятичных представлений видна (это одна и та же точка, даже если разделение выглядит по-разному) Десятичные дроби необходимо выбирать стратегически. Числовая строка не дает ответов, которые учащиеся должны узнать о ее особенностях и свойства, а также разработать способы их использования для выполнения математической работы.

9 Разработка задач, которые освещают большие идеи десятичных чисел. Разработайте набор из пяти чисел, которые потребуют, чтобы учащиеся боролись с десятичными вызовами и неправильными представлениями посредством использования числовых линий. больше (или более длинные десятичные дроби меньше). Из Рекомендации № 2 Руководства по практике IES: Помогите учащимся распознать, что дроби — это числа и что они расширяют систему счисления за пределы целых чисел. Добавление нуля вправо увеличивает число в десять раз. Вы можете игнорировать все Z эрос справа от десятичной запятой Вещи, которые нужно попробовать: создать числовые примеры, чтобы поддержать продуктивную борьбу с ключевыми десятичными идеями и вероятными заблуждениями. Проанализируйте возможности различных представлений / контекстов для конкретных числовых примеров D.Представление и осмысление вычислений Результаты метаанализа для алгебраических вмешательств (Хьюз, Витцель и др., 2014) Когнитивное и основанное на модели решение задач ES = Конкретное представление-аннотация ES = 0,431 Обучение с равными равными ES = 0,102 Только для графических организаторов ES = 0,106 Технология ES = 0,890 Однополая инструкция ES = CRA как эффективная инструкция / вмешательство (Gersten et al, 2009; NMP, 2008; Riccomini & Witzel, 2010; Witzel, 2005) Используйте значение Place Place для добавления к конкретному или репрезентативному к абстрактному Последовательность инструкций (CRA) Конкретные (быстрое использование манипуляций) Представления (изобразительные) Абстрактные методики Отлично подходят для обучения точности и понимания Примеры: Адаптировано из (Witzel, et al, 2013) 54 9
10 Один раз — одни.Есть 8 из них. (4.3) (2.4) Использование CRA Десятые — десятые. Есть 6 десятых. (4.3) (2.4), используя CRA. Есть 8 из них. Х Х Х Х Х Х Х Х Х Х Х Х Х Х Х Х Х Х Х Х Х Х Х Х Х Х Х Х Х Х Х Х Х Х Х Х Х Х Х Х Х Х Х Х Х Х Х Х Х Х Х Х Х Х Х Х Х Десятые, десятые — десятые. Есть 6 десятых. Один раз десятые десятые. Есть 16 десятых. Всего = 8 единиц; 22 десятых; 12 сотых 8,0_ 2,2_ _ Десятые, десятые — это сотые. Есть 12 сотых. Один раз десятые десятые.Есть 16 десятых. Всего = 8 единиц; 22 десятых; 12 сотых 8,0_ 2,2_ _ Десятые, десятые — это сотые. Есть 12 сотых (4,3) (2,4) с использованием CRA multi Total = 8 единиц; 22 десятых; 12 сотых 8.0_ 2.2_ _ Пересмотр Практического руководства IES Рекомендация № 3: Помогите студентам понять, почему процедуры для вычислений с дробями имеют смысл. Вещи, которые нужно попробовать: Используйте представления для поддержки осмысления вычислительных процедур и решений. Не гонитесь за коммутативностью, в то время как ответы будут одинаковыми, представления процесса будут выглядеть по-разному. Разрабатывайте / отбирайте проблемы, которые выявляют и работают через общие заблуждения. Инструкция по поддержке понимания десятичных чисел Чтобы помочь учащимся понять, что дроби (и десятичные дроби) являются числами и что они расширяют систему счисления за пределы целых чисел, попробуйте: Использовать представления для поддержки содержательного соединения дробей и десятичных дробей. Анализ возможностей различных представлений / контекстов. в свете математических целей. Сгенерируйте числовые примеры для поддержки продуктивной борьбы с ключевыми десятичными идеями и вероятными заблуждениями. Проанализируйте возможности различных представлений / контекстов для конкретных числовых примеров. Улучшение инструкций для поддержки понимания десятичных чисел. Чтобы помочь студентам понять, почему процедуры вычислений w i-ые дроби (и десятичные дроби) имеют смысл.Используйте представления для поддержки осмысления вычислительных процедур и решений. Не гонитесь за коммутативностью, в то время как ответы будут в итоге одинаковыми, представления процесса будут выглядеть по-разному. E. Фракции и десятичные дроби — Вмешательства Вмешательство с процедурами дробей (Witzel & Riccomini, 2009) 2 / / = (2 + 2) () 7 + = (3 + 3) () Цель Вмешательства в процедурных процессах (Witzel & Riccomini, 2009) ) 1/3 2 / = — Соединение с десятичными знаками (Witzel & Little, 2016) Дроби показывают знаменатель, в то время как для десятичных знаков это устно интерпретируется Соединение с десятичными дробями Дроби показывают знаменатель, в то время как для десятичных знаков это устно интерпретируется Заключение Понимание баланса с представлениями десятичных знаков Соедините область и линию модели для понимания дробей Использование языка и представлений для помощи в вычислении десятичных дробей
12 Список литературы Бэйли Д.H., Zhou X., Zhang Y., Cui J., Fuchs L., Jordan N.C., Gersten R., Siegler R. S. (2015). Разработка концепций и процедур дроби у детей США и Китая. Журнал экспериментальной психологии, 129, National Math Advisory Panel (2008). Основы успеха: итоговый отчет Национальной математической консультативной группы. Департамент образования США. Вашингтон, округ Колумбия: Автор. Сандерс С., Риккомини П. и Витцель Б. С. (2005). Готовность к алгебре у старшеклассников в Южной Каролине: последствия для учителей математики средней школы.Журнал средней школы Южной Каролины, 13, Зиглер Р., Карпентер Т., Феннелл Ф., Гири Д., Льюис Дж., Окамото Ю., Томпсон Л. и Рэй Дж. (2010) ). Разработка эффективного обучения фракциям для детского сада до 8-го класса: практическое руководство (NCEE #). Вашингтон, округ Колумбия: Национальный центр оценки образования и региональной помощи, Институт педагогических наук, Департамент образования США, Зиглер, Р.С., Дункан, Дж. Дж., Дэвис-Кин, ЧП, Дакворт, К., Клаессенс, А., Энгель, М. , Суспергуй, М.I. & Chen, M. (2012). Ранние предикторы школьной математики. Psychological Science, 23, Witzel, B.S. & Little, M. (2016). Элементарная математика для трудных учеников. Нью-Йорк: Гилфорд
.
