Прямоугольная система координат в пространстве презентация савченко: Презентация по математике на тему «Прямоугольная система координат в пространстве»
Описание презентации по отдельным слайдам:
1 слайд
Описание слайда:Прямоугольная система координат в пространстве
Описание слайда:Вы уже знакомы с прямоугольной (Декартовой) системой координат на плоскости, которую в XIX в. ввёл французский математик Рене Декарт
3 слайд
Описание слайда:А, вот, прямоугольную систему координат в пространстве ввёл швейцарский, немецкий, российский математик Леонард Эйлер в XVIIIв.
4 слайд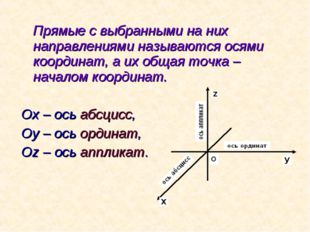
Описание слайда:Прямые с выбранными на них направлениями называются осями координат, а их общая точка – началом координат. Ох – ось абсцисс, Оу – ось ординат, Оz – ось аппликат.
5 слайд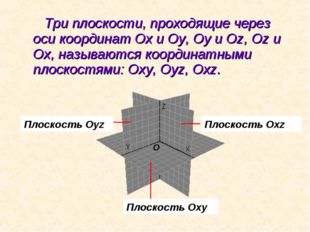
Три плоскости, проходящие через оси координат Ох и Оу, Оу и Оz, Оz и Ох, называются координатными плоскостями: Оху, Оуz, Оxz. Плоскость Oxz Плоскость Oxy Плоскость Oyz O
6 слайд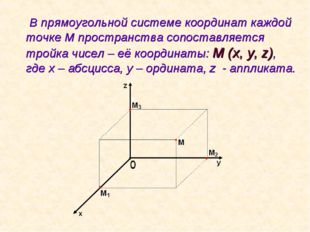
Описание слайда:В прямоугольной системе координат каждой точке М пространства сопоставляется тройка чисел – её координаты: М (х, у, z), где х – абсцисса, у – ордината, z — аппликата.
7 слайд
Описание слайда:Нахождение точки на координатной плоскости. Если, например, точка M лежит на координатной плоскости или на оси координат, то некоторые её координаты равны нулю. Так, если M принадлежит Oxy, то аппликата точка M равна нулю: z=0. Аналогично если M принадлежит Oхz, то y=0, а если M принадлежит Oyz, то x=0. Если M принадлежит Ox, то ордината и аппликата точки M равна нулю: y=0 и z=0. Если M принадлежит Oy, то x=0 и z=0; если M принадлежит Oz, то x=0 и y=0. Все три координаты начала координат равны нулю: О (0;0;0).
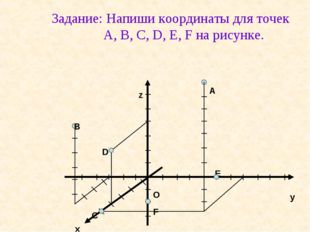
Описание слайда:Задание: Напиши координаты для точек A, B, C, D, E, F на рисунке. B C O E F D z y x A
9 слайд
Описание слайда:Ответы. A(5; 4; 10), B(4; -3; 6), C(5; 0; 0), D(4; 0; 4), E(0; 5; 0), F(0; 0; -2). Сравни свои ответы.
10 слайд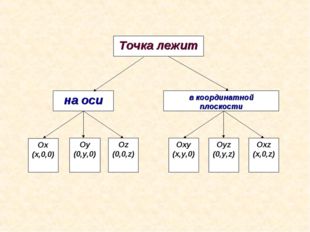
Описание слайда:Оу (0,у,0)
11 слайд
Описание слайда:Если М ОХУ, то z=0 Если М OXZ, то у=0 Если М OУZ, то X=0 Если М ОХ, то У=0 и Z=0 Если М OУ, то Х=0 и Z=0 Если М OZ, то Х=0 и У=0 Нахождение точки на координатной плоскости.
Описание слайда:Координаты вектора в пространстве
13 слайд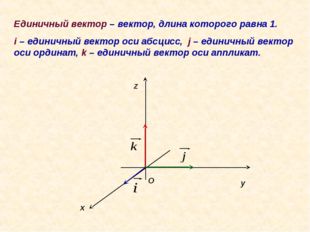
Описание слайда:Единичный вектор – вектор, длина которого равна 1. i – единичный вектор оси абсцисс, j – единичный вектор оси ординат, k – единичный вектор оси аппликат. x z y O
14 слайд
Описание слайда:Любой вектор ā можно разложить по координатным векторам, т.е. представить в виде: Нулевой вектор можно представить в виде: Координаты равных векторов соответственно равны, т.е., если ā { x1; y1; z1 } = b { x2; y2; z2 }, то x1 = x2, y1 = y2, z1 = z2.
15 слайд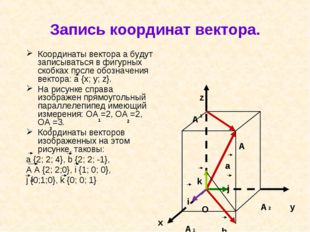
Запись координат вектора. Координаты вектора а будут записываться в фигурных скобках после обозначения вектора: а {x; y; z}. На рисунке справа изображен прямоугольный параллелепипед имеющий измерения: OA =2, OA =2, OA =3. Координаты векторов изображенных на этом рисунке, таковы: a {2; 2; 4}, b {2; 2; -1}, A A {2; 2;0}, i {1; 0; 0}, j {0;1;0}, k {0; 0; 1} A A A A O y x z a j i k b 3 2 1 1 2 3 3
16 слайд
Описание слайда:Сложение векторов Правило треугольника. Правило параллелограмма. Правило многоугольника. Правило параллелепипеда.
17 слайд
Описание слайда:Правило треугольника А B C
18 слайд
Правило треугольника А B C Для любых трех точек А, В и С справедливо равенство:
19 слайд
Описание слайда:Правило параллелограмма А B C
20 слайд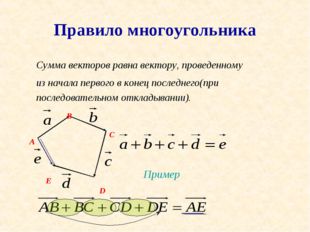
Описание слайда:Правило многоугольника Сумма векторов равна вектору, проведенному из начала первого в конец последнего(при последовательном откладывании). B A C D E Пример
21 слайд
Описание слайда:Правило параллелепипеда B А C D A1 B1 C1 D1 Вектор, лежащий на диагонали параллелепипеда, равен сумме векторов, проведенных из той же точки и лежащих на трех измерениях параллелепипеда.
22 слайд
Описание слайда:Угол между векторами
23 слайд
Описание слайда:Угол между двумя ненулевыми векторами называется угол между направлениями этих векторов. ) a b a b
24 слайд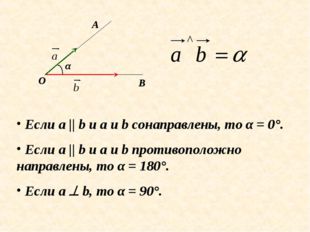
Описание слайда:О А В α Если а || b и а и b сонаправлены, то α = 0°. Если a || b и a и b противоположно направлены, то α = 180°. Если а b, то α = 90°.
25 слайд
Описание слайда:Перпендикулярные векторы (или ортогональные) Коллинеарные векторы Сонаправленные Противоположно направленные a b a b a b 90° 0° 180°
26 слайд
Описание слайда:Скалярное произведение векторов
27 слайд
Описание слайда:Скалярное произведение Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними.
28 слайд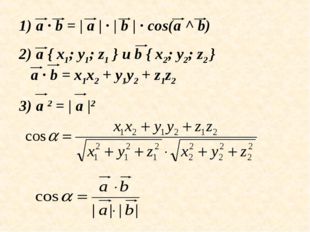
Описание слайда:a · b = | a | · | b | · cos(a ^ b) 2) a { x1; y1; z1 } и b { x2; y2; z2 } a · b = x1x2 + y1y2 + z1z2 3) a 2 = | a |2
29 слайд
Описание слайда: 
Курс повышения квалификации
Курс повышения квалификации
Курс профессиональной переподготовки
Учитель математики и информатики
Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:
Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВнеурочная деятельностьВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое
Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс
Выберите учебник: Все учебники
Выберите тему: Все темы
также Вы можете выбрать тип материала:
Общая информация
Номер материала: ДВ-462167
Похожие материалы
Вам будут интересны эти курсы:
Оставьте свой комментарий
Слайд 1
Работу выполнила учитель математики МБОУ «Острожская СОШ» Нохрина Т.А.Слайд 2
Вы уже знакомы с прямоугольной (Декартовой) системой координат на плоскости , которую в XIX в. ввёл французский математик Рене Декарт
Слайд 3
А, вот, прямоугольную систему координат в пространстве ввёл швейцарский, немецкий, российский математик Леонард Эйлер в XVIII в.
Слайд 5
Работа с учебником — Прочитайте первый абзац стр. 102
Слайд 6
И так: Выбрать точку пространства Провести через неё 3 попарно перпендикулярные прямые Указать стрелкой направление На каждой оси выбрать единицу измерения (строим на доске и в тетради)
Слайд 7
у X z o k i j Ось абсцисс Ось ординат Ось аппликат
Слайд 8
Запишем в тетради: ОХ – ось абсцисс ОУ – ось ординат OZ – ось аппликат i , j , k – единицы измерения (координатные векторы) О – начало координат
Слайд 10
— Вспомните, что определяло положение точки на плоскости ? Пример: М(3;7)
Слайд 11
— По аналогии ответим на вопрос: «Что определяет положение точки в пространстве ?» Пример: М(3;7;5)
Слайд 12
Работа по учебнику стр.102 Прочитаем 3 абзац Рассмотрим рис. 122
Слайд 13
Координаты точки пространства М (М 1 ,М 2 ,М 3 )
Слайд 14
И так: — Чтобы определить координаты токи в пространстве, надо через точку провести плоскости параллельно осям.
Слайд 15
Если М ОХУ, то z=0 Если М OXZ , то у=0 Если М O У Z , то X=0 Если М ОХ, то У=0 и Z=0 Если М O У, то Х=0 и Z=0 Если М OZ , то Х=0 и У=0
Слайд 16
Закрепление (учебник «Геометрия 10-11» Л.С. Атанасян и др. 2011г.) № 400 № 401 а № 402
Слайд 17
№ 400 Ответ: а) С(2;0;0) б) Е(0;-1;0) В) В(0;0;-7) г) А(3;-1;0) д) G(0 ;5;-7) е) D (-4 ;0;3)
Слайд 18
№ 401 (a) Ответ: а) A 1 (2;0;5), B 1 (3;0;1/2), C 1 (- ;0; — ) A 2 (2;-3;0), B 2 (3-5;0),C 2 (- ;- /2;0) A 3 (0;-3;5),B 3( 0;-5;1/2), C 3 (- ; — /2;0)
Слайд 19
№ 402 Дано: А(0;0;0) В(0;0;1) D(0;1;0) A 1 (1;0;0) Найти: В 1 , D 1 , С, С 1 Ответ: В 1 (1;0;1), D 1 (1 ;1;0), С(0;1;1), С 1 (1;1;1)
Слайд 20
Домашнее задание: п. 46, №401 (б)
Слайд 21
Источники: Учебник «Геометрия 10-11» Л.С.Атанасян, 2011г http://ru.wikipedia.org
Презентация по теме «Прямоугольная сиситема координат в пространстве» по геометрии для 11 класса. Предназначена для изучения новой темы, ознакомления учащихся с прямоугольной системой координат в пространстве, координатами вектора, правилами вычисления координат векторов, содержит примеры простых действий с координатами векторов. Материал соответствует программе и учебнику Л.C.Атанасяна.
Просмотр содержимого документа
«Презентация по теме «Прямоугольная система координат в пространстве» »
Прямоугольная система координат в пространстве
Геометрия – 11 класс
Белоброва Татьяна Валерьевна
учитель математики высшей категории
МКОУ СОШ №1 г.Сим
Челябинской области
z
1
A
y
1
О
1
x
Задание прямоугольной системы координат в пространстве
z
О z – ось аппликат
1
A
Оу – ось ординат
1
y
О
1
Ох – ось абсцисс
О y О z
A (1; 1; 1)
О z О x
Определите координаты точек
на рис. 116 учебника.
О y О x
x
Нахождение координат точек (Работа с учебником по рис 116)
Точка лежит
в координатной плоскости
на оси
Ох (х; 0; 0)
Оху (х; у; 0)
Оу z ( 0 ; у; z )
Ох z (х; 0 ; z )
Оу (0; у; 0)
№ 400 – устно.
О z (0; 0; z)
Даны точки:
Назовите точки, лежащие
в плоскости Оу z
А (2; -1; 0)
В (0; 0; -7)
С (2; 0; 0)
Назовите точки, лежащие
в плоскости Ох z
D ( -4 ; -1; 0)
Е (0; -3; 0)
Назовите точки, лежащие
в плоскости Оху
F ( 1 ; 2 ; 3 )
Р (0; 5; -7)
К (2; 0; -4)
Определите координаты точек
z
А ( 3 ; 5 ; 6 )
А
В (0; -2; -1)
D
С (0; 5; 0)
D (-3; -1; 0)
1
С
1
1
y
В
x
Координаты вектора
z
j
k
а =x + y + z
i { 1 ;0;0}
i
j { 0 ; 1 ;0}
k { 0 ;0; 1 }
а
y
k
zk
a { x ; y ; z }
i
j
x i
x
y j
Координаты вектора
z
1
О
y
1
1
x
Правила действий над векторами с заданными координатами
1. Равные векторы имеют равные координаты
, тогда
Пусть
х 1 = х 2 ; у 1 = у 2 ; z 1 = z 2
2 . Каждая координата суммы двух (и более) векторов равна сумме соответствующих координат этих векторов
Дано:
Следовательно
3. Каждая координата произведения вектора на число равна произведению соответствующей координаты на это число.
4. Каждая координата разности двух векторов равна разности соответствующих координат на этих векторов.
Дано:
Выполнить задание устно:
- Найти вектор равный:
Слайд 1
Прямоугольная система координат в пространстве. Геометрия – 11 классСлайд 2
Цели урока: Ввести понятие системы координат в пространстве. Выработать умение строить точку по заданным координатам и находить координаты точки, изображенной в заданной системе координат.
Слайд 3
Повторение: 1. Даны точки А ( — 1; 7 ) и В ( 7; 1). а) Найдите координаты середины отрезка АВ. С ( 3; 4) б) Найдите длину отрезка АВ. | АВ | = 10
Слайд 4
Повторение: 2. Запишите координаты вектора Ненулевые векторы наз. коллинеарными , если они лежат либо на одной прямой, либо на параллельных прямых 3. Среди векторов укажите пару коллинеарных векторов. ? k 0
Слайд 5
Повторение: 4. Найдите координаты вектора , если Е ( -2; 3), F ( 1; 2). 5. Найдите расстояние между точками А (а; 0) и В ( b; 0).
Слайд 6
Вопросы: 1. Сколькими координатами может быть задана точка на прямой? Одной . 2. Сколькими координатами может быть задана точка в координатной плоскости? Двумя . 3. Сколькими координатами может быть задана точка в пространстве? Вопрос урока.
Слайд 7
Задание прямоугольной системы координат в пространстве: О y О y О z О z О x О y О x x z 1 1 1 A A (1; 1; 1) Ох – ось абсцисс Оу – ось ординат О z – ось аппликат Определите координаты точек на рис. 116 учебника.
Слайд 8
Нахождение координат точек. (Работа с учебником по рис 116) Точка лежит на оси Оу (0; у; 0) Ох (х; 0; 0) О z (0; 0; z) в координатной плоскости Оху (х; у; 0) Ох z (х; 0 ; z ) Оу z ( 0 ; у; z ) № 400 – устно.
Слайд 9
Решение задач. № 401 (а) Рассмотрим точку А (2; -3; 5) х у z 0 2 5 -3 A 1) A 1 : Oxy A 1 A 1 (2; -3; 0) A 2 2) A 2 : Oxz A 2 (2; 0; 5) 3) A 3 : Oyz A 3 A 3 (0; -3; 5) Точки В и С рассмотреть самостоятельно.
Слайд 10
Решение задач. № 401 (б) Рассмотрим точку А (2; -3; 5) х у z 0 2 5 -3 A 1) A 4 : Ox A 4 A 4 (2; 0 ; 0) A 5 2) A 5 : O у A 5 ( 0 ; -3 ; 0 ) 3) A 6 : Oz A 6 A 6 (0; 0 ; 5) Точки В и С рассмотреть самостоятельно.
Слайд 11
Решение задач. № 402 х у z C 1 — ? C — ? A 1 (1;0;0) B 1 — ? D 1 — ? A (0;0;0) B (0;0;1) D (0;1;0) В 1 (1; 0; 1) С (0; 1; 0) С 1 (1; 1; 0) D 1 (1; 1; 1 )
Слайд 12
Домашнее задание: П.42 Задачи на повторение: №№ 376; 387; 393.
Описание презентации по отдельным слайдам:
1 слайд
Описание слайда:Прямоугольная система координат в пространстве
2 слайд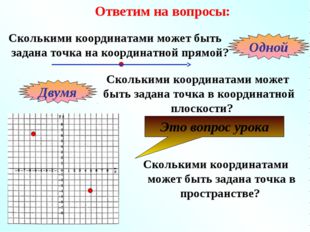
Описание слайда:Ответим на вопросы: Сколькими координатами может быть задана точка на координатной прямой? Одной Сколькими координатами может быть задана точка в координатной плоскости? Двумя Сколькими координатами может быть задана точка в пространстве? Это вопрос урока
3 слайд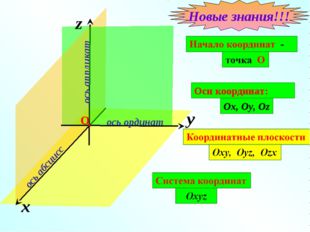
Описание слайда:Новые знания!!!
4 слайд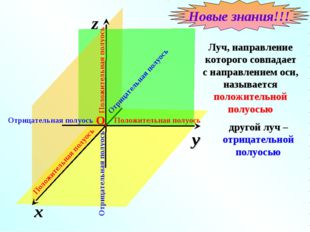
Описание слайда:x z y Луч, направление которого совпадает с направлением оси, называется положительной полуосью Новые знания!!! другой луч – отрицательной полуосью
5 слайд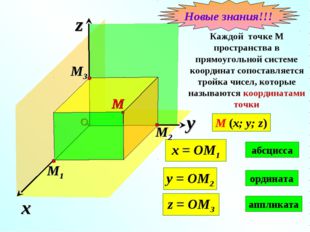
Описание слайда:x z Каждой точке М пространства в прямоугольной системе координат сопоставляется тройка чисел, которые называются координатами точки y M (x; y; z) M Новые знания!!!
6 слайд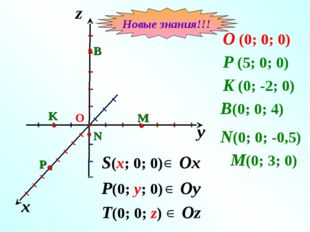
Описание слайда:y x z O (0; 0; 0) P (5; 0; 0) I I I I I I I I I I I I I I I I I I I K (0; -2; 0) B(0; 0; 4) N(0; 0; -0,5) M(0; 3; 0) S(x; 0; 0) P(0; y; 0) T(0; 0; z) Новые знания!!!
7 слайд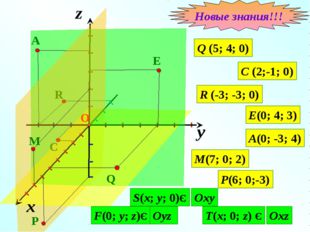
Описание слайда:z Q (5; 4; 0) C (2;-1; 0) I I I I I I I I I I I R (-3; -3; 0) E(0; 4; 3) A(0; -3; 4) M(7; 0; 2) S(x; y; 0)Є F(0; y; z)Є T(x; 0; z) Є Oxy Oyz Oxz y I I I I I I I I x P(6; 0;-3) Новые знания!!!
8 слайд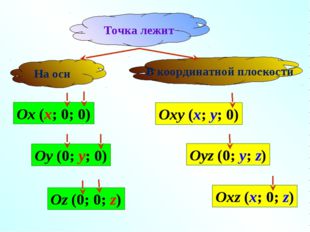
Описание слайда:В координатной плоскости Oxy (x; y; 0) Oyz (0; y; z) Oxz (x; 0; z) Ox (x; 0; 0) Oy (0; y; 0) Oz (0; 0; z) На оси Точка лежит
9 слайд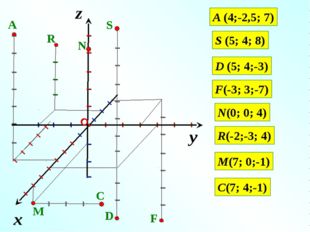
Описание слайда:z A (4;-2,5; 7) S (5; 4; 8) I I I I I I I I I I I D (5; 4;-3) F(-3; 3;-7) N(0; 0; 4) R(-2;-3; 4) y I I I I I I I I I I I I I I I I I x M(7; 0;-1) C(7; 4;-1)
10 слайд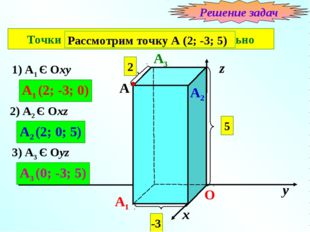
Описание слайда:№ 401 (а) х у z О 2 5 -3 A 1) A1 Є Oxy A1 A1 (2; -3; 0) A2 2) A2 Є Oxz A2 (2; 0; 5) 3) A3 Є Oyz A3 A3 (0; -3; 5) Точки В и С рассмотреть самостоятельно Решение задач Рассмотрим точку А (2; -3; 5)
11 слайд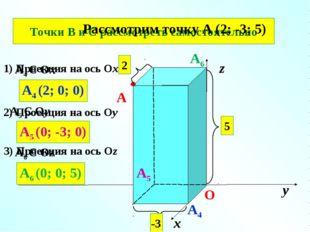
Описание слайда:№ 401 (б) х у z О 2 5 -3 A A4 Є Ox A4 A4 (2; 0; 0) A5 A5 Є Oу A5 (0; -3; 0) A6 Є Oz A6 A6 (0; 0; 5) Точки В и С рассмотреть самостоятельно Рассмотрим точку А (2; -3; 5) 1) Проекция на ось Ox 2) Проекция на ось Oу 3) Проекция на ось Oz
Курс повышения квалификации
Курс повышения квалификации
Курс профессиональной переподготовки
Учитель математики и информатики
Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:
Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВнеурочная деятельностьВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое
Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс
Выберите учебник: Все учебники
Выберите тему: Все темы
также Вы можете выбрать тип материала:
Общая информация
Номер материала: ДВ-052099
Похожие материалы
Вам будут интересны эти курсы:
Оставьте свой комментарий
Слайды и текст этой презентации
Слайд 1
Преподаватель ГАПОУ РО «РКТМ»
Колыхалина К.А.
Прямоугольная система координат в пространстве. Координаты вектора
Слайд 2
Прямоугольная система координат
Если через точку пространства проведены три попарно перпендикулярные прямые, на каждой из них выбрано направление и выбрана единица измерения отрезков, то говорят, что задана прямоугольная система координат в пространстве
Слайд 3
Прямые, с выбранными на них направлениями, называются осями координат, а их общая точка — началом координат. Она обозначается обычно буквой О. Оси координат обозначаются так: Ох, Оу, Оz — и имеют названия: ось абсцисс, ось ординат, ось аппликат.
Прямоугольная система координат
Слайд 4
Прямоугольная система координат
Вся система координат обозначается Охуz.
Плоскости, проходящие соответственно через оси координат Ох и Оу, Оу и Оz, Оz и Ох, называются координатными плоскостями и обозначаются Оху, Оуz, Оzх.
Слайд 5
Точка О разделяет каждую из осей координат на два луча. Луч, направление которого совпадает с направлением оси, называется положительной полуосью, а другой луч отрицательной полуосью.
Прямоугольная система координат
Слайд 6
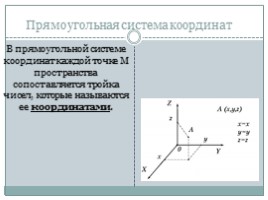
В прямоугольной системе координат каждой точке М пространства сопоставляется тройка чисел, которые называются ее координатами.
Прямоугольная система координат
Слайд 7
Алгоритм определения координаты точки в пространстве
Слайд 8
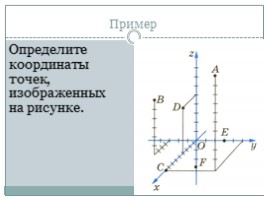
Определите координаты точек, изображенных на рисунке.
Пример
Слайд 9
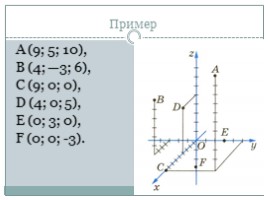
А (9; 5; 10),
В (4; —3; 6),
С (9; 0; 0),
D (4; 0; 5),
Е (0; 3; 0),
F (0; 0; -3).
Пример
Слайд 10
Координаты вектора
Слайд 11
Что такое вектор?
Вектором называется направленный отрезок, для которого указано его начало и конец.
В данном случае началом отрезка является точка A, концом отрезка – точка B. Сам вектор обозначен через . Направление имеет существенное значение, если переставить стрелку в другой конец отрезка, то получится вектор , и это уже совершенно другой вектор.
Понятие вектора удобно отождествлять с движением физического тела: согласитесь, зайти в двери колледжа или выйти из дверей колледжа – это совершенно разные вещи.
Отдельные точки плоскости, пространства удобно считать так называемым нулевым вектором . У такого вектора конец и начало совпадают.
Слайд 12
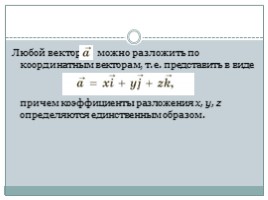
Любой вектор можно разложить по координатным векторам, т. е. представить в виде
причем коэффициенты разложения х, у, z определяются единственным образом.
Слайд 13
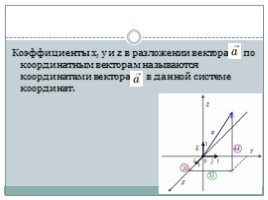
Коэффициенты х, у и z в разложении вектора по координатным векторам называются координатами вектора в данной системе координат.
Слайд 14
Правила
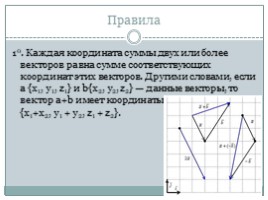
10. Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов. Другими словами, если a {х1, у1, z1} и b{х2, у2, z2} — данные векторы, то вектор a+b имеет координаты {х1+х2, у1 + у2, z1 + z2}.
Слайд 15
Правила
20. Каждая координата разности двух векторов равна разности соответствующих координат этих векторов. Другими словами, если r1 {х1, y1, z1} и r2{х2 у2; z2} — данные векторы, то вектор a — b имеет координаты {х1- х2, y1 — y2, z1 — z2}.
Слайд 16
Правила
30. Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число. Другими словами, если а {х; у; х} — данный вектор, α — данное число, то вектор αa имеет координаты {αх; αу; αz).
Слайд 1
Прямоугольная система координат в пространстве. Координаты вектора.Слайд 2
Прямоугольная система координат
Слайд 3
Если через точку пространства проведены три попарно перпендикулярные прямые, на каждой из них выбрано направление и выбрана единица измерения отрезков, то говорят, что задана прямоугольная система координат в пространстве
Слайд 4
Прямые, с выбранными на них направлениями, называются осями координат , а их общая точка — началом координат . Она обозначается обычно буквой О. Оси координат обозначаются так: Ох, Оу , О z — и имеют названия: ось абсцисс, ось ординат, ось аппликат.
Слайд 5
Вся система координат обозначается Оху z . Плоскости, проходящие соответственно через оси координат Ох и Оу, Оу и О z , О z и Ох, называются координатными плоскостями и обозначаются Оху, Оу z , О z х.
Слайд 6
Точка О разделяет каждую из осей координат на два луча. Луч, направление которого совпадает с направлением оси, называется положительной полуосью , а другой луч отрицательной полуосью .
Слайд 7
В прямоугольной системе координат каждой точке М пространства сопоставляется тройка чисел, которые называются ее координатами .
Слайд 8
На рисунке изображены шесть точек А (9; 5; 10), В (4; —3; 6), С (9; 0; 0), D (4; 0; 5), Е (0; 3; 0), F (0; 0; -3).
Слайд 9
Координаты вектора
Слайд 10
Любой вектор можно разложить по координатным векторам, т. е. представить в виде причем коэффициенты разложения х , у, z определяются единственным образом.
Слайд 11
Коэффициенты х , у и z в разложении вектора по координатным векторам называются координатами вектора в данной системе координат.
Слайд 12
Рассмотрим правила, которые позволяют по координатам данных векторов найти координаты их суммы и разности, а также координаты произведения данного вектора на данное число.
Слайд 13
1 0 . Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов. Другими словами, если a {х 1 , у 1 , z 1 } и b {х 2 , у 2 , z 2 } — данные векторы, то вектор a + b имеет координаты {х 1 +х 2 , у 1 + у 2 , z 1 + z 2 }.
Слайд 14
2 0 . Каждая координата разности двух векторов равна разности соответствующих координат этих векторов. Другими словами, если a {х 1 , y 1 , z 1 } и b {х 2 у 2 ; z 2 } — данные векторы, то вектор a — b имеет координаты {х 1 — х 2 , y 1 — y 2 , z 1 — z 2 }.
Слайд 15
3 0 . Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число. Другими словами, если а {х; у; х} — данный вектор, α — данное число, то вектор α a имеет координаты {αх; αу; α z ).
Прямоугольная система координат— скачать ppt
Презентация на тему: «Прямоугольная система координат» — Стенограмма презентации:
1 Прямоугольная система координат 
2 Определения Ось X — горизонтальная ось Y — ось — вертикальная ось
Прямоугольная система координат: где пересекаются ось X и ось Y Упорядоченная пара: определяет местоположение точки в прямоугольной системе координат (координата X , координата y) Начало координат: (0,0) — пересечение оси x и y. Квадрант: участок прямоугольной системы координат.
3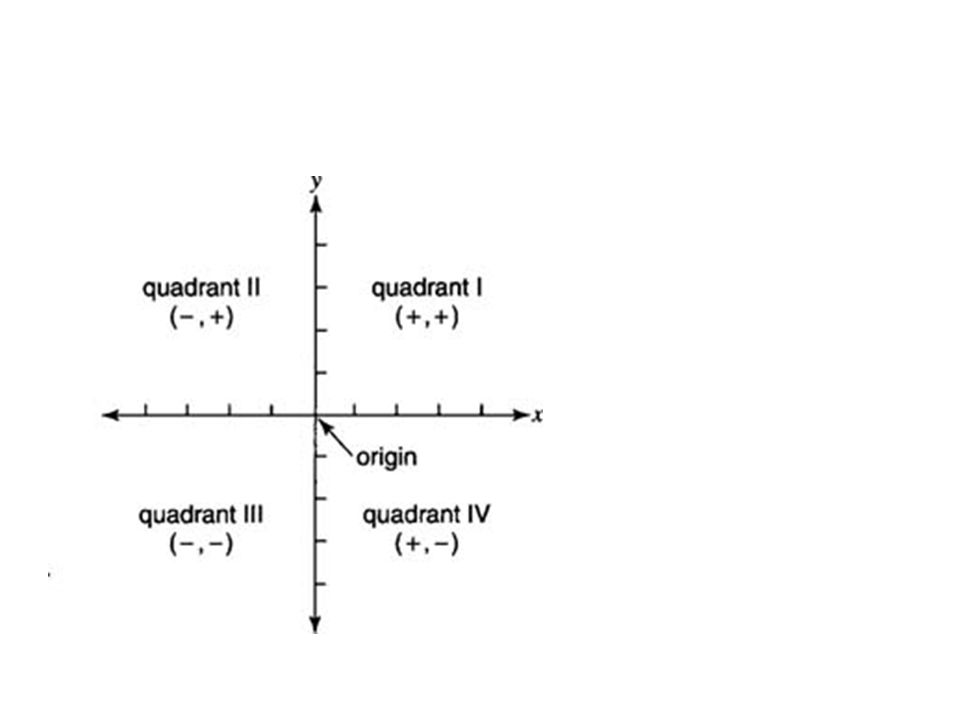 
4 Как определить точку? Сначала найдите источник
Во-вторых, определите, идете ли вы влево или вправо от начала координат. Если вы идете налево, ваша координата x отрицательна. Если вы идете направо, ваша координата x положительна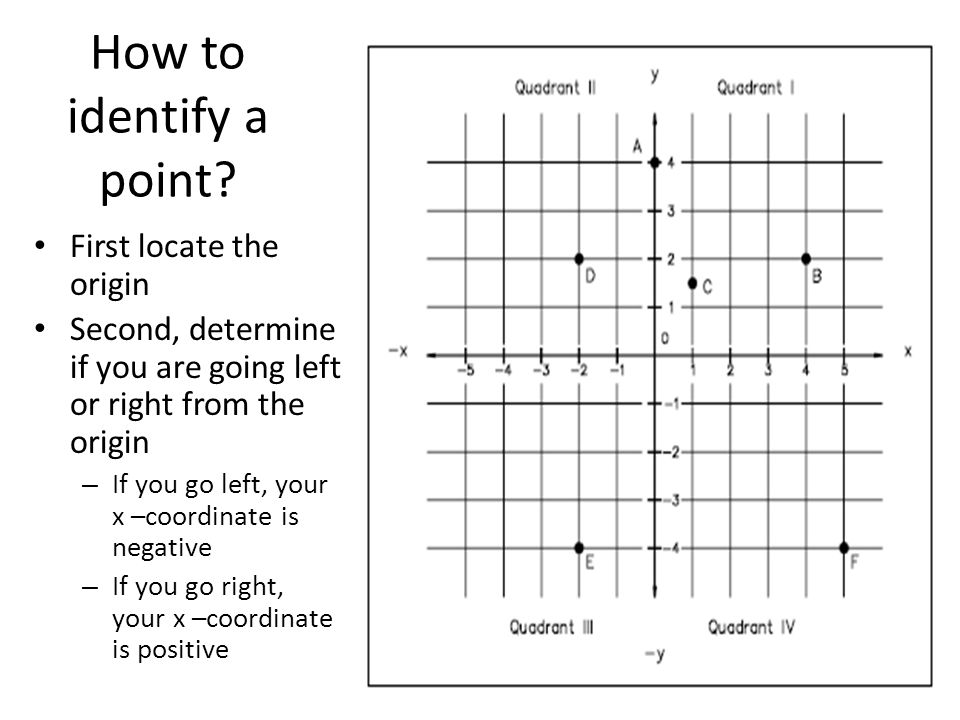 
5 В-третьих, определите, будете ли вы подниматься или опускаться от начала координат
Если вы опускаетесь, ваша координата y отрицательна Если вы поднимаетесь, ваша координата y положительна
6 Как изобразить точку? Сначала найдите начало координат.
. Во-вторых, нанесите на график вашу координату x: ЕСЛИ значение вашей координаты x положительное, то сдвиньте вправо, если отрицательное — влево. В-третьих, нарисуйте вашу координату y: ЕСЛИ значение вашей координаты y положительное движение вверх, если отрицательное движение вниз 
7 Как идентифицировать квадрант?
Первый — определите, где ваша точка. Второй — проверьте график, в каком квадранте он находится.
8 Определите, является ли упорядоченная пара решением
Подставьте упорядоченную пару в уравнение: проверьте, верно ли утверждение. Пример: 3x — y = 12 Является ли (0, 12) решением? 3 (0) — (12) = 12 0 — 12 = 12 Нет, поэтому (0,12) не является решением Пример: 3x — y = 12 Является ли (1, -9) решением? Пример: y = -2x Является ли (-3, 8) решением? Пример: x = 9 (4, 9) — решение? 
9 Найдите отсутствующую координату.
Сначала подставьте заданную координату в уравнение.Пример: X + 2y = 8 (____, 9) X + 2 (9) = 8 Упростить и решить для отсутствующей координаты X + 18 = 8 X = -10 
10 Практика X — 4y = 4 (____, -2) 3x + y = 9 (4, ____) -2x + 7y = 14
(3, _____) (_____, 5) Y = 9 (5, ___) ( ____, 9)
Презентация на тему: «Сферическая система координат прямоугольной системы координат» — Стенограмма презентации:
1 Определите систему координат, которая лучше всего описывает симметрию относительно начала координат.
прямоугольная система координат сферическая система координат цилиндрическая система координат 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 
2 Построить точку с цилиндрическими координатами {image}
Построить точку с цилиндрическими координатами {image}. Затем найдите прямоугольные координаты точки.(0, 0, 2) (0, 2, 8) (0, 8, 2) (8, 8, 2) (a, 0, 2) 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
3 Запишите уравнение в цилиндрических координатах: {изображение}.
1. 2. 3. 4. 5. 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
4 Твердое тело лежит над конусом {изображение} и ниже сферы {изображение}
Твердое тело лежит над конусом {изображение} и ниже сферы {изображение}.Напишите описание тела в терминах неравенств со сферическими координатами. {image} ни один из этих 1. 2. 3. 4. 5. 6. 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
Прямоугольные координаты
Прямоугольная система координат также известна как декартова система координат по Рене Декарту, который популяризировал его использование в аналитической геометрии. Прямоугольная система координат основанный на сетке, и каждая точка на плоскости может быть идентифицирована уникальным x и и координат, так же как любая точка на Земле может быть идентифицирована давая свою широту и долготу.
Оси
Местоположения в сетке измеряются относительно фиксированной точки, называемой , начало , и измеряются в соответствии с расстоянием вдоль пары осей. x и оси и аналогичны числовой линии с положительным расстоянием до вправо и отрицательно влево в случае оси x и положительных расстояний измерено вверх и отрицательно для оси и . Любое смещение прочь от начала координат может быть построен путем перемещения на определенное расстояние в х направление, а затем еще одно расстояние в направлении и . Думайте об этом как если вы давали указания кому-то, говоря что-то вроде идти три блокирует Восток и затем 2 блока Север.
координаты, Графические точки
Мы указываем местоположение точки, сначала давая ее x координату (смещение влево или вправо от начала координат), а затем и координата (смещение вверх или вниз от начала координат). Таким образом, каждая точка на плоскость может быть идентифицирована парой чисел ( x , и ), назвал его координат .
Примеры:
квадрантов
Иногда мы просто хотим знать, какую общую часть графика мы говорим около.Оси естественно делят плоскость на четверти. Мы называем эти квадрантов , и пронумеруйте их от одного до четырех. Обратите внимание, что нумерация начинается в верхнем правый квадрант и продолжается в направлении против часовой стрелки. уведомление также, что каждый квадрант может быть идентифицирован уникальным сочетанием положительного и отрицательные знаки для координат точки в этом квадранте.
,CARTESIAN COORDINATE SYSTEMS — PPT видео онлайн скачать
Презентация на тему: «СИСТЕМЫ КАРТИНСКИХ КАРТИНОВ» — Стенограмма презентации:
1 CARTESIAN COORDINATE SYSTEMS
ОБЗОР МАТА 
2 Что такое система координат?
Системы координат — это системы отсчета, используемые для уникального определения местоположения точки в пространстве.Есть несколько систем координат в использовании; у каждого есть приложения в разных ситуациях. Примерами систем координат являются сферическая, цилиндрическая и декартова. Этот урок исследует декартову систему координат. 
3 CARTESIAN COORDINATE SYSTEM
Эта система состоит из двух осей, перпендикулярных друг другу. Точка в пространстве представляется точкой y с парой ординат (x, y) в координатах x и измерениях y 2 (2D).В 3D было бы 3 оси и точки (x, y, z) x 
4 Чтобы представить точки в этой системе…
… просто найдите значение координаты «x» (при необходимости перемещаясь вдоль горизонтальной линии). Затем переместите руку вверх вдоль вертикальной линии столько, сколько необходимо, чтобы найти координату «у». Пометьте свою точку «точкой».
5
ЗАМЕЧАНИЯ О СИСТЕМЕ. Точка, где встречаются две оси, является координатой (0,0), также называемой началом координат.В общем, ось «х» рисуется горизонтально, а ось «у» вертикально. Однако важно то, что они встречаются под углами 90 °. Каждая пара ординат (x, y) представляет одну точку в системе осей.