Теоремы Чевы и Менелая — презентация онлайн

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. Презентация к уроку

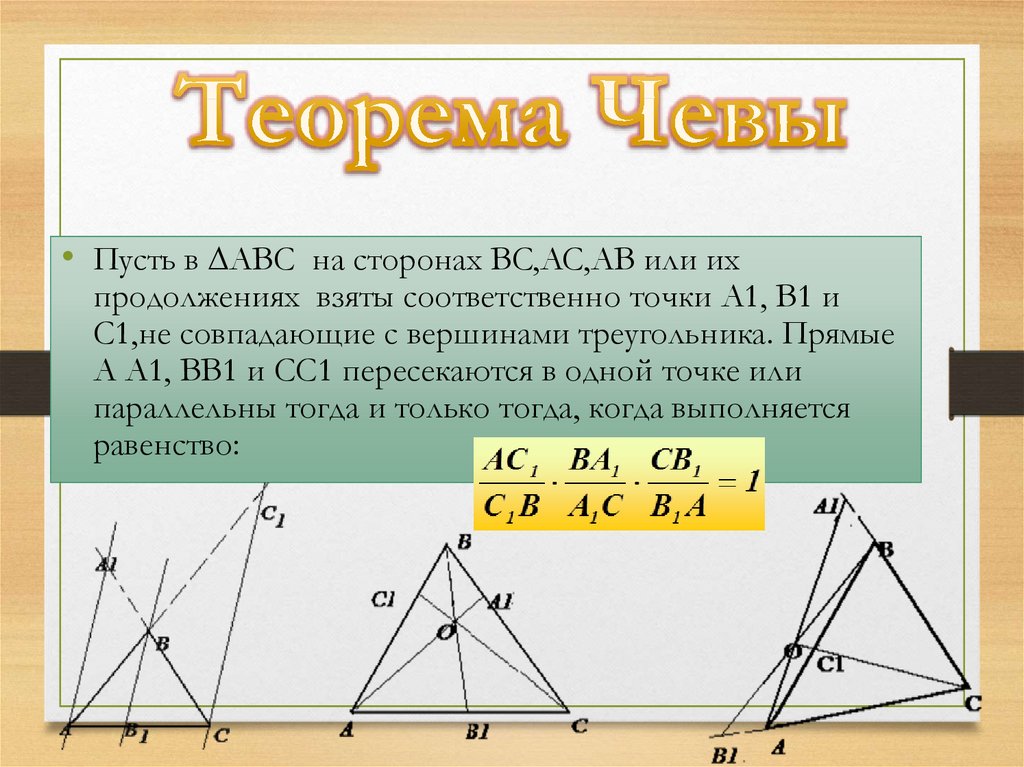
Геометрия 10 класс
Теоремы Чевы и Менелая

2. Теоремы Чевы и Менелая

«Обладая литературой более обширной, чем
алгебра и арифметика вместе взятые, и по
крайней мере столь же обширной, как анализ,
геометрия в большей степени чем любой
другой раздел математики, является
богатейшей сокровищницей интереснейших,
но полузабытых вещей, которыми спешащее
поколение не имеет времени насладиться».
Е. Т. Белл.

3. ЧЕВИАНА

Отрезок, соединяющий
вершину треугольника с
некоторой точкой на
противоположной стороне,
называется чевианой.
• Таким образом, если в
треугольнике АВС X, Y и Zточки, лежащие на сторонах
ВС, СА, АВ соответственно,
то отрезки АX, ВY, СZ
являются чевианами.
• Этот термин происходит от
имени итальянского
математика Джованни Чевы,
который в 1687 году
опубликовал следующую
очень полезную теорему
Теорема названа в честь
итальянского математика
Джованни Чевы, который
доказал её в 1678 году.
День рождения: 07.12.1647 года
Дата смерти: 15.06.1734 года
Гражданство: Италия
Джованни Чева родился в 1647 году в
Италии. Он окончил иезуитский
колледж в Милане, после чего стал
студентом Университета в Пизе, где
позже и стал работать профессором
математики.
С 1686 года Чева работал в
Университете в Мантуе, оставаясь на
этом посту до самого конца своей
жизни.
Университет Пизы .Университетом учебное заведение было признано в
1343 году декретом Папы Климента VI.

6. Теорема Чевы

• Если три чевианы
АX, ВY, СZ ( по
одной из каждой
вершины )
треугольнка АВС
конкурентны, то
BX
XC
CY
YA
AZ
ZB
1
Когда мы говорим,
что три прямые (
или отрезка )
конкурентны, то
мы имеем в виду,
что все они
проходят через одну
точку, которую
обозначим через Р.

8. ДОКАЗАТЕЛЬСТВО

• Для доказательства теоремы Чевы
вспомним, что площади треугольников с
равными высотами пропорциональны
основаниям треугольников.
• Ссылаясь на рисунок, мы имеем
BX
XC
BX
XC
AZ
ZB
S ABX S BPX S ABX S BPX S ABP
S AXC S XPC S AXC S PXC SCPA
S ABX S BPX S ABX S BPX S ABP
S AXC S XPC S AXC S PXC S CPA
S ACZ S APZ S ACZ S APZ S ACP
S BCZ
S ZPB S BCZ S ZPB S BCP
• Теперь, если мы перемножим их, то
получим
.
BX
CY
AZ
S ABP S CPB S ACP
х
х
1
XC YA ZB S CPA S ABP S BCP
Рассмотрим доказательство некоторых
следствий теоремы Чевы.
Задача 1: Доказать, что биссектрисы углов
треугольника пересекаются в одной точке.
Доказательство:
Пусть АА1, ВВ1, СС1 – биссектрисы
треугольника АВС.
Так как биссектриса угла треугольника делит
противолежащую сторону на отрезки,
длины которых пропорциональны
противолежащим сторонам, то
Перемножив полученные равенства,
получим:
Следовательно, по теореме Чевы,
биссектрисы пересекаются в одной точке.
Задача 2: Докажите, что медианы
треугольника пересекаются в одной
точке.
Доказательство.
Так как точки А1, С1, В1 лежат на сторонах
треугольника, достаточно доказать, что
выполняется равенство :
Так как ВВ1, СС1, АА1 медианы, то:
Тогда в силу теоремы Чевы прямые ВВ1,
СС1, АА1 пересекаются в одной точке. Ч.т.д.

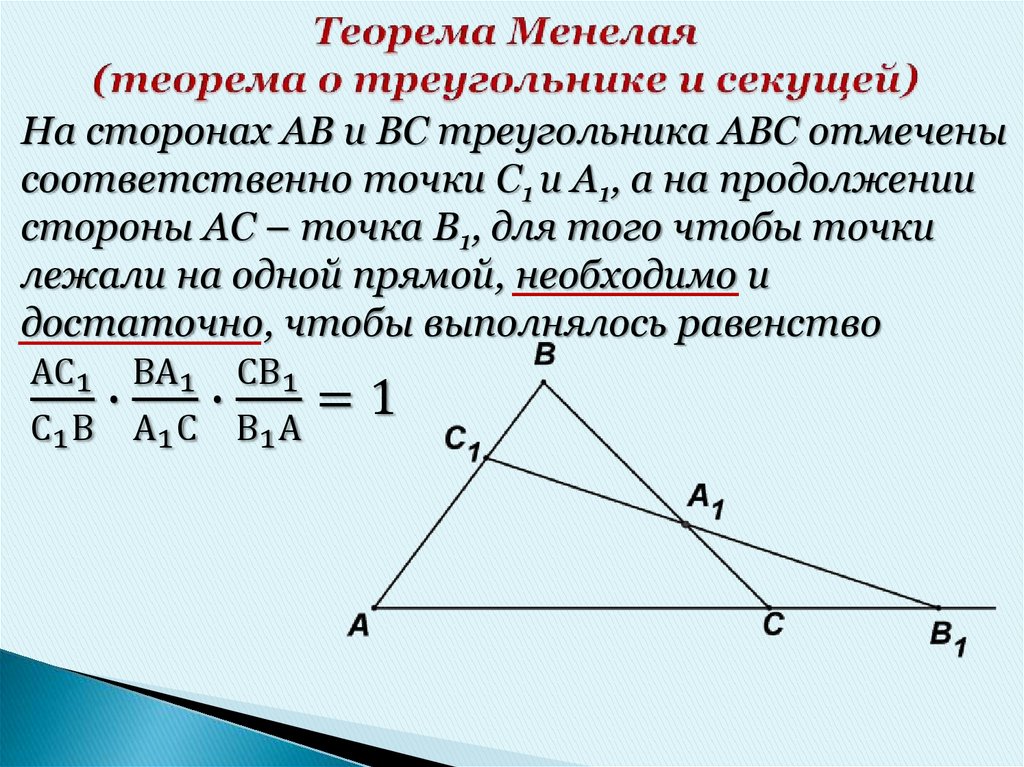
13. Теорема Менелая:

• Пусть точка А1 лежит на стороне ВС
треугольника АВС, точка С1 – на
стороне АВ, точка В1 – на продолжении
стороны АС за точку С. Точки А1,В1 иС1
лежат на одной прямой тогда и только
тогда, когда выполняется равенство
AC 1 BA1 CB1
1.
C 1B A1 C B1 A
В
BA1 CB1 AC 1
1
A1 C B1 A C 1B
С1
А1
А
С
В1
CA1 BC 1 AB1
1.
A1 B C 1 A B 1 C
Эта теорема Входит в золотой фонд древнегреческой математики. Она дошла
до нас в арабском переводе книги «Сферика» Менелая Александрийского.
Равенство Менелая можно записывать, начиная с любой вершины треугольника,
в любом направлении ( по часовой стрелке, против часовой стрелки ).

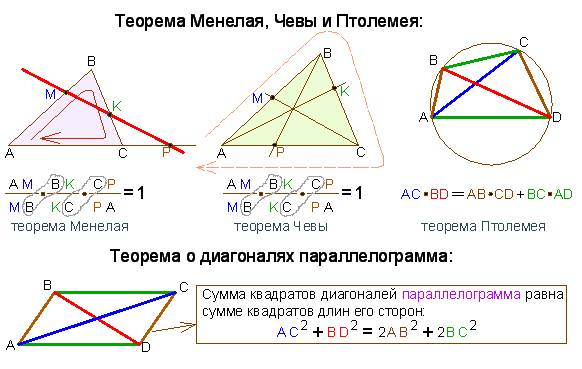
15. Задача 1. В треугольнике АВС на стороне ВС взята точка N так, что NC = 3BN; на продолжении стороны АС за точку А взята точка М

так, что МА=АС. Прямая
MN пересекает сторону АВ в точке F.
Найдите: отношение BF
FA

16. Решение

В
k
N
F
M
b
А
3k
b
C
• По условию задачи
МА = АС, NC = 3BN.
Пусть МА = АС = b,
• BN = k, NC = 3k.
Прямая MN
пересекает две
стороны треугольника
АВС и продолжение
третьей. По теореме
Менелая
3 BF b
CN BF AM
BF 3
BF 2
1, k
1,
1,
NB FA MC
k FA 2 b
FA 2
FA 3.
Ответ:2:3.

English     Русский Правила

Теоремы Чевы и Менелая. Геометрия 10 класс (профильный уровень)

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. Теоремы Чевы и Менелая

Геометрия 10 класс
(профильный уровень)

2. Изучение нового материала

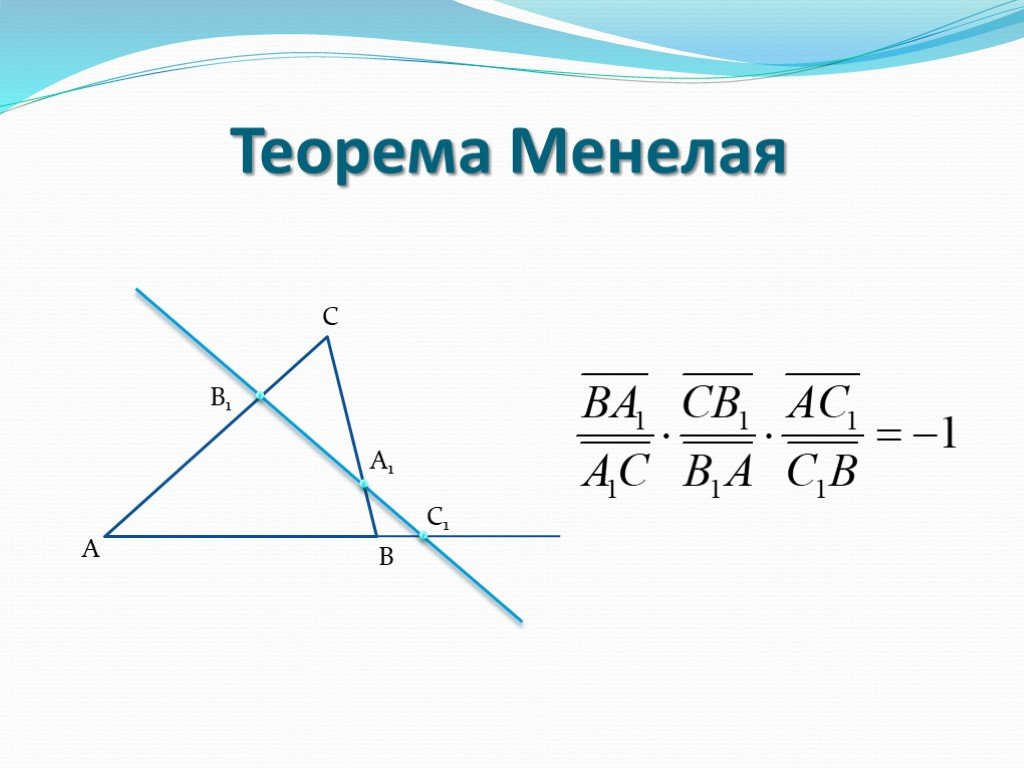
Теорема Менелая
Менелай Александрийский – древнегреческий
математик (Iв.н.э.)
Пусть на сторонах или продолжениях сторон АВ,
ВС и СА треугольника АВС отмечены точки С1,
А1, В1, не совпадающие с его вершинами, причем
.
С1
Тогда если точки С1, А1, В1 лежат на одной
прямой, то рqr=-1; обратно: если рqr=-1, то точки
С1, А1, В1 лежат на одной прямой.
А
В
А1
АС1 рС1 В, ВА1 q A1C, CB1 r B1 A
С
В1
Пусть точка А1 лежит на стороне ВС треугольника АВС, точка С1 – на стороне
АВ, точка В1 – на продолжении стороны АС за точку С. Тогда точки А1, В1 и С1
лежат на одной прямой тогда и только тогда, когда выполняется равенство
АС1 ВА1 СВ1
1
С1 В А1С В1 А

3. Изучение нового материала

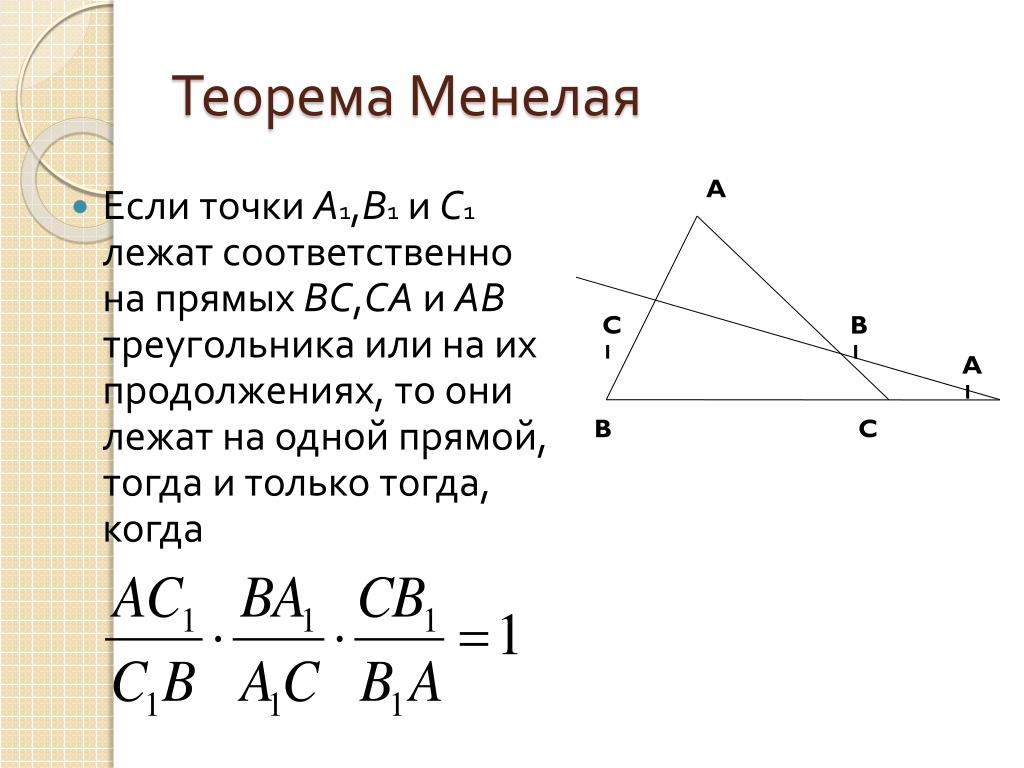
В
Теорема Чевы
(Джованни Чева — итальянский математик 1678г)
Пусть на сторонах или продолжениях сторон АВ, ВС и
СА треугольника АВС отмечены точки С1, А1, В1, не
совпадающие с его вершинами, причем
А1
С1
АС1 рС1 В, ВА1 q A1C, CB1 r B1 A
Тогда если прямые АА1, ВВ1, СС1 пересекаются в одной
точке или попарно параллельны, то
рqr=1; обратно: если рqr=1, то прямые АА1, ВВ1, СС1
пересекаются в одной точке или попарно
параллельны.
А
С
В1
Пусть точка в треугольнике АВС точка А1 лежит на стороне ВС, точка В1 – на
стороне АС, точка С1 – на стороне АВ. Отрезки АА1, ВВ1, СС1 пересекаются в
одной точке тогда и только тогда, когда выполняется равенство
АВ1 СА1 ВС1
1
В1С А1 В С1 А

4. Решение задач

№1. В треугольнике АВС на стороне ВС взята точка N так, что NC=3BN; на
продолжении стороны АС за точку А взята точка М так, что МА=АС. Прямая
MN пересекает сторону АВ в точке F. Найдите отношение BF .
FA

5. Решение задач

№2. В треугольнике АВС, описанном около окружности, АВ = 8, ВС = 5, АС = 4. А1 и С1 –
точки касания, принадлежащие соответственно сторонам ВС и ВА. Р – точка
пересечения отрезков АА1 и СС1. Точка Р лежит на биссектрисе ВВ1. Найдите АР : РА1.
Решение:
Точка касания окружности со стороной АС не
совпадает с В1, так как треугольник АВС –
разносторонний.
2. Пусть С1В = х, тогда, используя свойство
касательных, проведенных к окружности из одной
точки, введем обозначения 8 – х + 5 – х = 4, х =4,5.
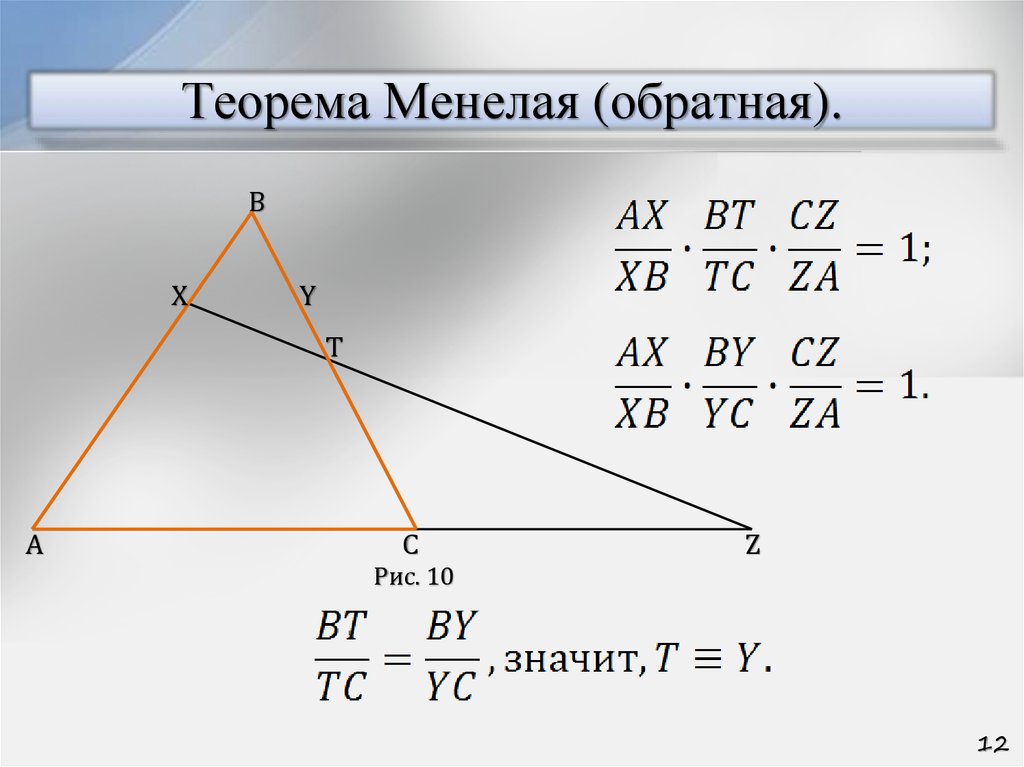
Значит, С1В = ВА1 = 4,5, А1С = 5 – 4,5= 0,5 АС1 = 8 – 4,5=3,5 .
В треугольнике АВА1 прямая С1С пересекает две его стороны и продолжение
третьей стороны. По теореме Менелая …
1.
3.
4.
Ответ: 70 : 9.

6. Решение задач

№2. В треугольнике АВС, описанном около окружности, АВ=13, ВС=12, АС=9,
А1 и С1 – точки касания, лежащие соответственно на сторонах ВС и АВ.
N – точка пересечения отрезков АА1 и ВВ1. Точка N лежит на высоте ВВ1.
Найдите отношение BN:NB1.
.

7. Домашнее задание

пп.95,96
Задачи.
1. В треугольнике АВС АD – медиана, точка О– середина медианы. Прямая ВО
пересекает сторону АС в точке К. В каком отношении точка К делит АС,
считая от точки А? (Примечание. Рассмотрите треугольник АDC)
2. Стороны треугольника 5, 6 и 7. Найдите отношение отрезков, на которые
биссектриса большего угла треугольника разделена центром окружности,
вписанной в треугольник.

English     Русский Правила

Изучение теоремы Менелая в геометрии Гильберта — математика в действии

Юмна Хабиб

Биография:

На последнем курсе я изучаю математику.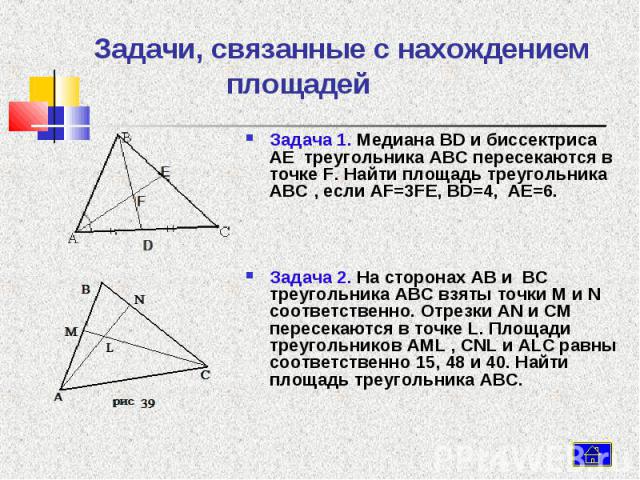 Я также участвую в программе параллельного обучения учителей и в следующем году буду поступать в Институт исследований в области образования Онтарио, чтобы получить степень бакалавра образования. В будущем планирую преподавать математику в средней школе.

Введение:

Менелай был греческим математиком, родившимся около 70 г. н.э. в Александрии. Он глубоко исследовал геометрию, а его самая известная работа под названием Sphaerica подробно описала сферические треугольники и их приложения к астрономии [3]. Возможно, один из его самых известных вкладов в математику. Теорема Менелая утверждает, что точки, лежащие на трех сторонах треугольника, коллинеарны тогда и только тогда, когда отношение произведений несмежных сторон равно 1. Как видно, теорема Менелая такова. тесно связан с теоремой Чевы. В то время как первый демонстрирует, когда определенные точки треугольника лежат на одной прямой, второй исследует, когда определенные сегменты прямой треугольника совпадают. Это свойство сходства между теоремами называется двойственностью [3].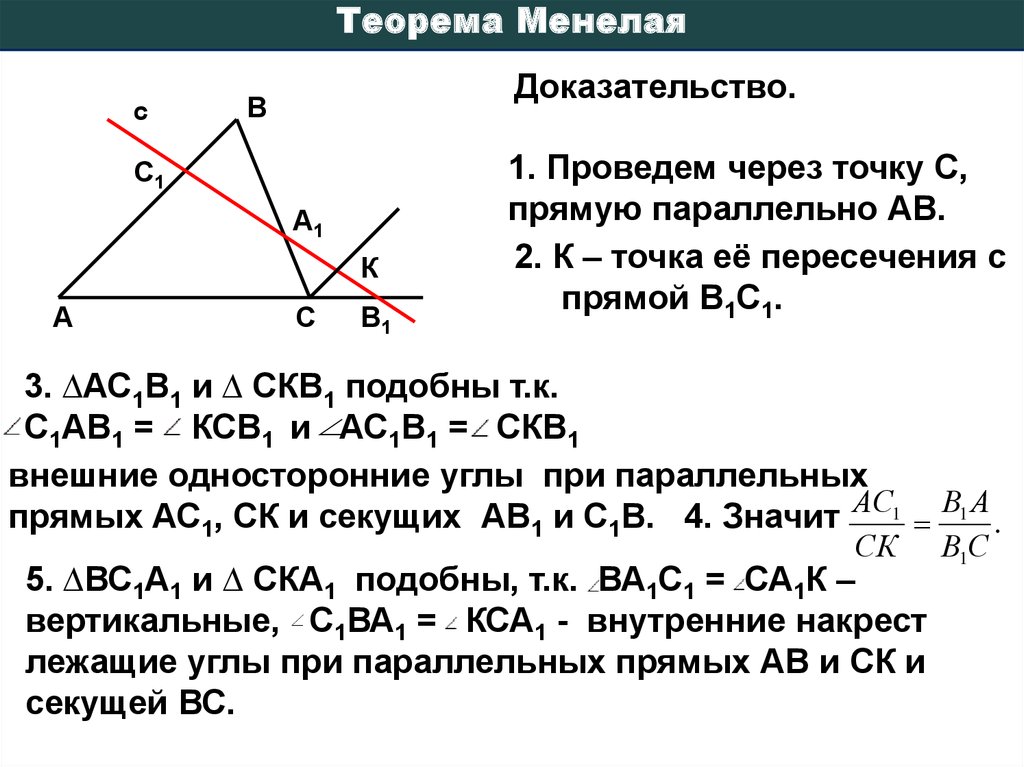

Более того, для обеих теорем верны и обратные.

Теорема Менелая в гиперболической геометрии:

Учитывая различные виды геометрии, с которыми мы сталкиваемся в математике, используется несколько версий теорем Менелая. Когда мы работаем с этой теоремой в евклидовой геометрии, мы используем отношения со знаком. Хотя мы можем определить аналогичные отношения в гиперболической геометрии, они не будут очень полезными величинами. Следовательно, мы используем другое отношение, а именно гиперболическое отношение:

Определение 1 (гиперболическое отношение):

Пусть A, B и X — три различные точки на гиперболической прямой. Их гиперболическое отношение равно

, где 𝑠𝑖𝑛 h(𝑑(𝐴,𝑋)) — функция гиперболического синуса.

Как показано выше, важно отметить, что значение h(A,X,B) определяет положение точки X относительно положений точек A и B. Теперь мы определим теорему Менелая в гиперболической геометрии, используя гиперболическое отношение:

Теорема 1 (Менелай в гиперболической геометрии):

Пусть треугольник ABC гиперболический. Пусть L — гиперболическая прямая, которая не проходит через вершины Δ ABC, но пересекает BC в Q, AC в R и AB в P. Тогда модуль их гиперболических отношений равен 1. То есть

Доказательство:

Поскольку мы хотим показать, что абсолютное значение произведения гиперболических отношений равно 1, мы можем пометить вершины Δ ABC в любом порядке, и это не повлияет на наш результат. Мы применяем гиперболическое правило синусов к Δ APR и получаем следующее:

Аналогично, из Δ BPQ и Δ CRQ получаем следующее:

Из рисунка 1 мы видим следующие соотношения:

Приведенные выше уравнения приводят нас к требуемому продукту:

Обратите внимание, что приведенное выше доказательство справедливо только для одного случая.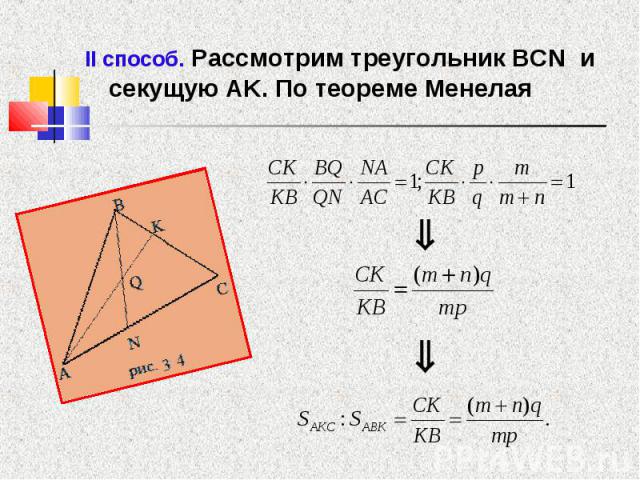

Возможны и другие случаи, все из которых можно доказать с помощью аналогичного метода Q.E.D. 9n и проходящую через них прямую обозначим через AB, а открытый отрезок с концами A и B через AB [2]. Теперь определим перекрестное отношение в гильбертовой геометрии:

Определение 2 (поперечное отношение): Пусть A и B — различные точки в Rn с точками X,Y ∈ AB, такие, что они могут быть выражены с помощью линейных комбинаций X = λ1A + µ1B и Y = λ2A + µ2B, где λ1, λ2, µ1, µ2 — действительные числа. Тогда перекрестное соотношение A, B, X и Y равно

. 9n, n ≥ 2, с границей ∂H. Метрика Гильберта на H — это функция dH : H × H → R такая, что

Пара (H, dH) называется гильбертовой геометрией в H.

Показано, что гильбертова геометрия, в которой справедлива теорема Менелая, является гиперболической. Причина этого в том, что такая геометрия оказывается телом, все сечения которого являются эллипсами, т.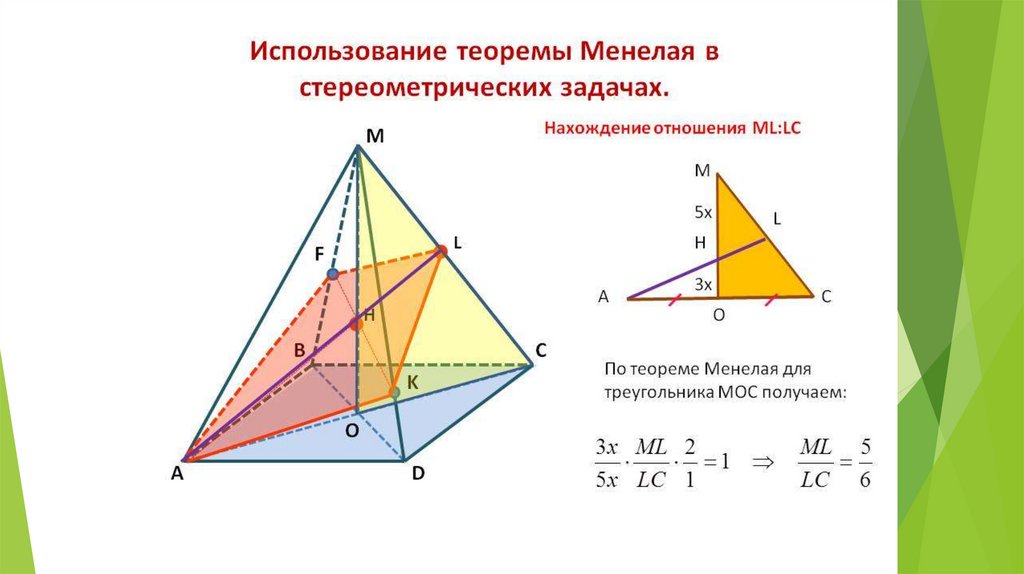

е. эллипсоидом. Однако мы находим, что H является эллипсоидом тогда и только тогда, когда он гиперболичен [2].

Ссылки:

[1] H. Busemann, PJ Kelly, Projective Geometry and Projective Metrics, New York: Academic Press, 1957.

[2] J. Kozma, Á. Теоремы Куруса, Чевы и Менелая характеризуют гиперболическую геометрию среди гильбертовых геометрий, Journal of Geometry, 106, 465-470 (2015)

[3] J.J. О’Коннор, Э. Ф. Робертсон. Менелай Александрийский http://www-history.mcs.st-and.ac.uk/Biographies/Menelaus.html (обновлено в апреле 1999 г.)

[4] Доказательство теоремы Менелая http://www.maths.gla .ac.uk/wws/cabripages/hyperbolic/pmenelaus.html

 

Нажмите здесь, чтобы просмотреть/загрузить расширенный реферат в формате PDF

Нажмите здесь, чтобы вернуться к видео 2017 года

Теорема Чевы

Теорема Чевы — это теорема о треугольниках, лежащих в евклидовой плоской геометрии. Он считает отношение длин сторон треугольника, которые делятся чевианами.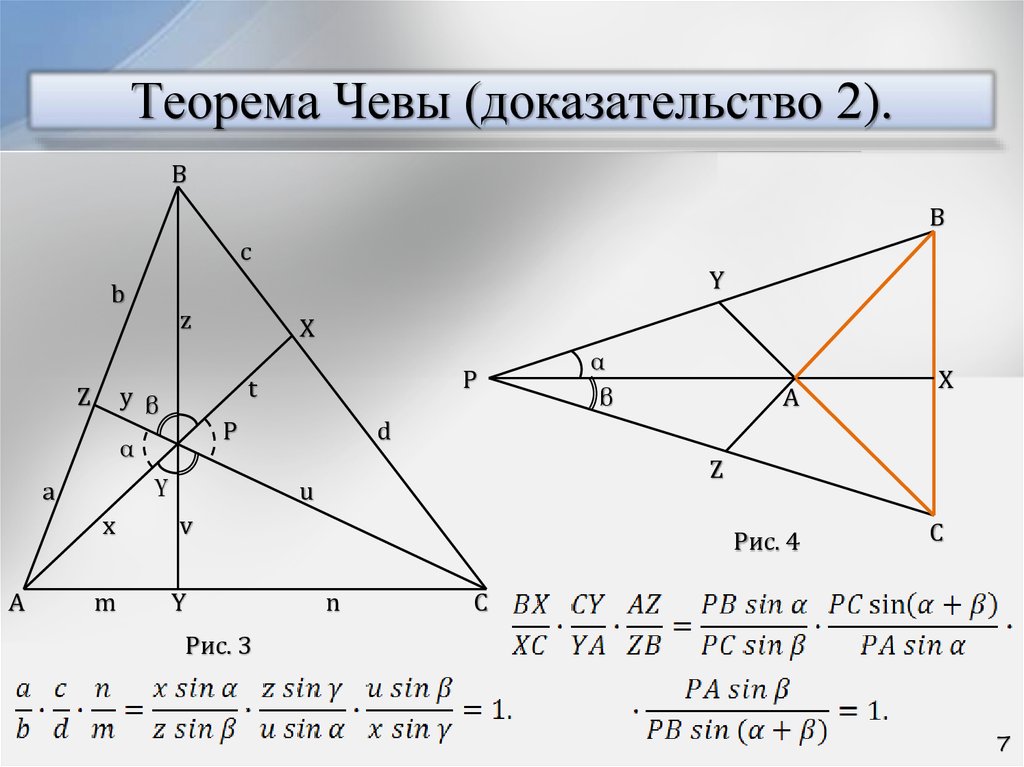

 

Возьмем в качестве примера треугольник DEF, линии DO, EO и FO начертим над его вершинами к общей точке O так, чтобы его противоположные стороны пересекались в точках G, H и I.

 

Теорема Чевы является теоремой аффинной геометрии в том контексте, что она может быть сформулирована и доказана без использования понятий углов, площадей и длин (за исключением отношения длин двух данных отрезков, которые коллинеарны). Следовательно, это верно для треугольников в любой аффинной плоскости над любым полем. Теорема Чевы помогает доказать совпадение чевиан в треугольниках и обычно используется в олимпийской геометрии. В этой статье мы подробно узнаем о теореме Чевы и обратной теореме Чевы.

Формулировка теоремы Чевы

Рассмотрим треугольник ABC с точкой P, лежащей внутри треугольника. Рассмотрите линии AP, BP и CP, чтобы попасть в BC, CA и AB в точках D, E, F, D, E и F соответственно.

Согласно теореме Чевы,

AF/FB . БД/ДК. CE/EA = 1

Обратное утверждение теоремы Чевы также верно. если точки D, E и F лежат на сторонах BC, CA и AB соответственно так, что

AF/FB . БД/ДК. СЕ/ЕА = 1

, то прямые AD, BE и CF пересекаются в точке P.

Доказательство теоремы Чевы

Рассмотрим тот же треугольник.

Поскольку треугольники △AFP и △FBP имеют одинаковые высоты, вы можете написать

AF/FB = [AFB]/[FBP] = [AFC]/[FBC]

Если вычесть площадь треугольника из второго качества из области первого равенства получаем

AF/FB = [APC]/[BPC]

Аналогично,

BD/DC = [APB]/[APC] и CE/EA = [BPC ]/[APB]

Если вы перемножите три предыдущих уравнения вместе, вы получите

AF/FB . БД/ДК. CE/EA = APC/BPC. АПБ/АПК. BPC/APB

Обратная теорема Чевы

Было сделано несколько доказательств теоремы.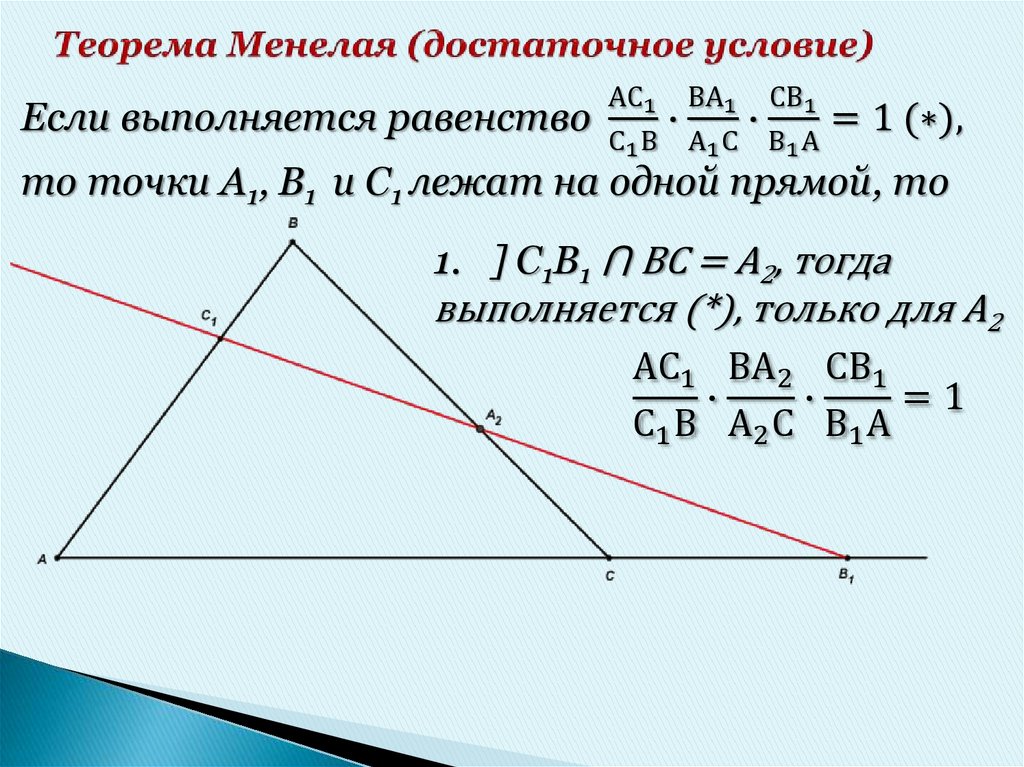 Два из них обсуждаются ниже: 

Первый показан с использованием основных свойств площадей треугольника. Однако это не так просто, потому что необходимо рассмотреть множество случаев, которые зависят от положения точки O.

Другое доказательство показано с использованием векторов и барицентрических координат и кажется более естественным и зависящим от случая. Он работает на любом поле в любой аффинной плоскости.

Первый подход

Знак слева положительный по двум причинам. Когда O находится внутри треугольника, в этом случае все три отношения кажутся положительными. Когда O находится вне треугольника, в этом случае один положительный, а остальные два кажутся отрицательными.

Если вы хотите проверить величину, площадь треугольника с заданной высотой пропорциональна основанию треугольника.

Рассмотрим следующий треугольник.

Как вы знаете, согласно теореме Чевы,

AF/FB .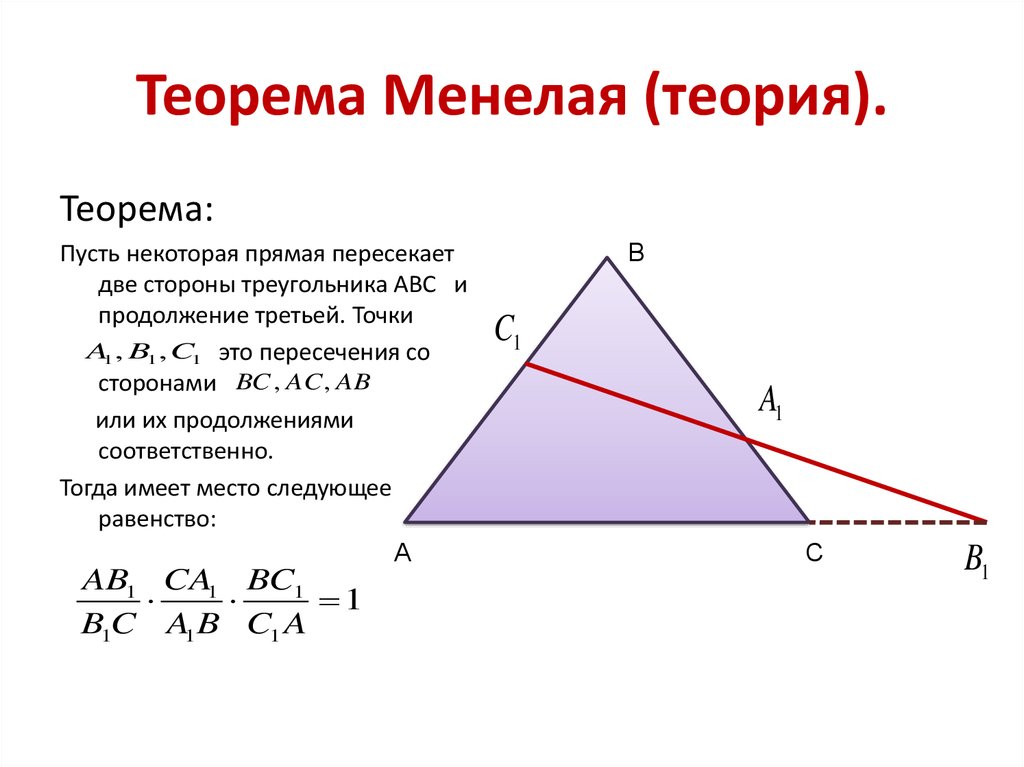 БД/ДК. CE/EA = 1

Вам нужно доказать, что чевианские числа AD, BE и CF совпадают в одной точке.

Пусть AD и BE пересекаются в произвольной точке P. Пусть третий чевиан, проходящий через точку P, равен CK. Согласно предыдущему доказательству у вас есть

(BD/CD) . (СЕ/АЭ) . (AK/BK) = 1

Но вы предположили, что

(BD/CD) . (СЕ/АЭ) . (AF/BF) = 1

Следовательно, вы можете сказать, что

(AK/BK) = (AF/BF)

Следовательно, очевидно, что K = F, и вы можете заключить, что AD, BE и CF параллельны.

Джованни Чева опубликовал эту теорему в своей работе De lineis rectis в 1678 году. Но есть свидетельства того, что она была доказана намного раньше королем Сарагосы XI века по имени Юсуф Аль-Му’таман ибн Худ.

Второй подход

Три точки D, E, F, которые не лежат на одной прямой с точкой O и находятся в одной плоскости, Получают три уникальных числа относительно барицентрических координат точки O. Эти уникальные числа при суммировании равны 1.

В теореме Чевы точка O не должна принадлежать никакой прямой, проходящей через две вершины треугольника. Это показывает, что эти три уникальных числа не равны 0. 

После преобразования последнего уравнения путем замены X на F новое уравнение будет иметь вектор в левой части с тем же направлением, что и линия EF. С правой стороны она будет иметь то же направление, что и линия DE.

 

Поскольку D, E и F не лежат на одной прямой, направления этих линий будут разными. Он показывает, что два члена уравнения равны нулевому вектору, а также показывает, что отношение со знаком длин коллинеарных отрезков находится в левой части дроби.

Решенные примеры

1. Докажите, что если X, Y и Z — середины сторон, то три чевианы совпадают.

Решение: Если рассмотреть тот же треугольник

, то можно сказать, что D, E и F являются серединами соответствующих сторон BC, AC и AB.