Метод треугольника: Определитель матрицы методом треугольника | Мозган калькулятор онлайн
теоремы и примеры нахождения определителей
Содержание:
- Вычисления определителей второго порядка
- Методы вычисления определителей третьего порядка
- Приведение определителя к треугольному виду
- Правило треугольника
- Правило Саррюса
- Разложение определителя по строке или столбцу
- Разложение определителя по элементам строки или столбца
- Теорема Лапласа
В общем случае правило вычисления определителей $n$-го порядка является довольно громоздким. Для определителей второго и третьего порядка существуют рациональные способы их вычислений.
Вычисления определителей второго порядка
Чтобы вычислить определитель матрицы второго порядка, надо от произведения элементов главной диагонали отнять произведение элементов побочной диагонали:
$$\left| \begin{array}{ll}{a_{11}} & {a_{12}} \\ {a_{21}} & {a_{22}}\end{array}\right|=a_{11} \cdot a_{22}-a_{12} \cdot a_{21}$$
Пример
Задание. Вычислить определитель второго порядка
$\left| \begin{array}{rr}{11} & {-2} \\ {7} & {5}\end{array}\right|$
Вычислить определитель второго порядка
$\left| \begin{array}{rr}{11} & {-2} \\ {7} & {5}\end{array}\right|$
Решение. $\left| \begin{array}{rr}{11} & {-2} \\ {7} & {5}\end{array}\right|=11 \cdot 5-(-2) \cdot 7=55+14=69$
Ответ. $\left| \begin{array}{rr}{11} & {-2} \\ {7} & {5}\end{array}\right|=69$
Методы вычисления определителей третьего порядка
Для вычисления определителей третьего порядка существует такие правила.
Правило треугольника
Схематически это правило можно изобразить следующим образом:
Произведение элементов в первом определителе, которые соединены прямыми, берется со знаком «плюс»; аналогично, для второго определителя — соответствующие произведения берутся со знаком «минус», т.е.
$$\left| \begin{array}{ccc}{a_{11}} & {a_{12}} & {a_{13}} \\ {a_{21}} & {a_{22}} & {a_{23}} \\ {a_{31}} & {a_{32}} & {a_{33}}\end{array}\right|=a_{11} a_{22} a_{33}+a_{12} a_{23} a_{31}+a_{13} a_{21} a_{32}-$$
$$-a_{11} a_{23} a_{32}-a_{12} a_{21} a_{33}-a_{13} a_{22} a_{31}$$
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание.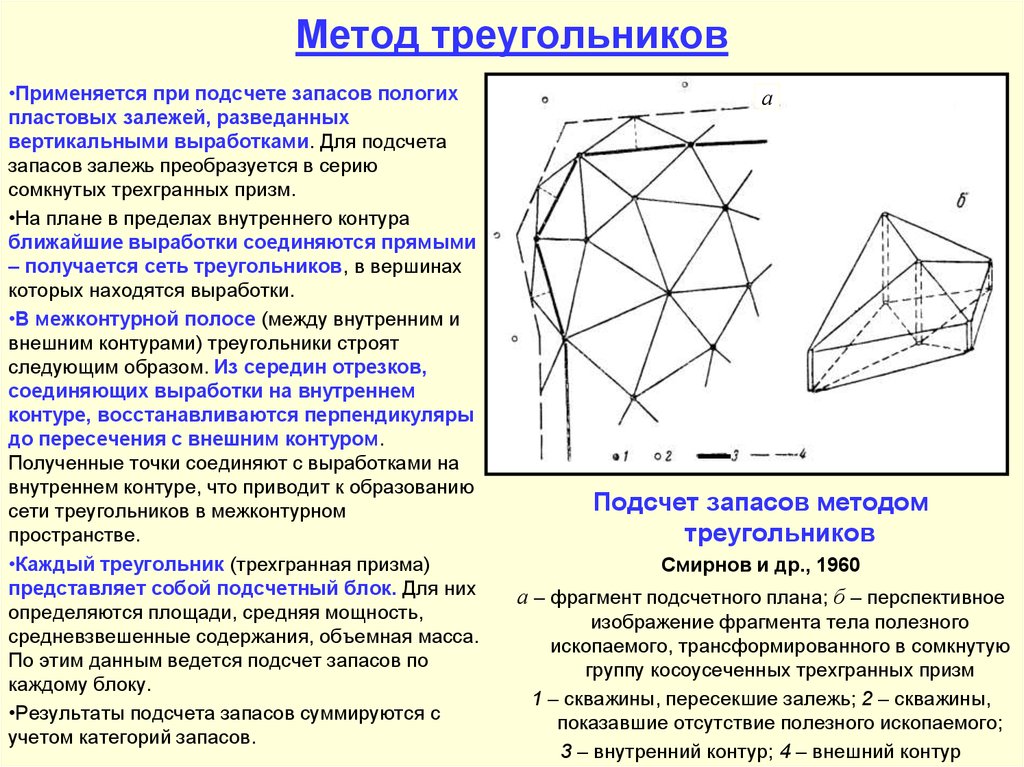 Вычислить определитель $\left| \begin{array}{rrr}{3} & {3} & {-1} \\ {4} & {1} & {3} \\ {1} & {-2} & {-2}\end{array}\right|$ методом треугольников.
Вычислить определитель $\left| \begin{array}{rrr}{3} & {3} & {-1} \\ {4} & {1} & {3} \\ {1} & {-2} & {-2}\end{array}\right|$ методом треугольников.
Решение. $\left| \begin{array}{rrr}{3} & {3} & {-1} \\ {4} & {1} & {3} \\ {1} & {-2} & {-2}\end{array}\right|=3 \cdot 1 \cdot(-2)+4 \cdot(-2) \cdot(-1)+$
$$+3 \cdot 3 \cdot 1-(-1) \cdot 1 \cdot 1-3 \cdot(-2) \cdot 3-4 \cdot 3 \cdot(-2)=54$$
Ответ. $\left| \begin{array}{rrr}{3} & {3} & {-1} \\ {4} & {1} & {3} \\ {1} & {-2} & {-2}\end{array}\right|=54$
Правило Саррюса
Справа от определителя дописывают первых два столбца и произведения элементов на главной диагонали и на диагоналях, ей параллельных, берут со знаком «плюс»; а произведения элементов побочной диагонали и диагоналей, ей параллельных, со знаком «минус»:
$$-a_{13} a_{22} a_{31}-a_{11} a_{23} a_{32}-a_{12} a_{21} a_{33}$$
Пример
Задание. Вычислить определитель $\left| \begin{array}{rrr}{3} & {3} & {-1} \\ {4} & {1} & {3} \\ {1} & {-2} & {-2}\end{array}\right|$ с помощью правила Саррюса.
Вычислить определитель $\left| \begin{array}{rrr}{3} & {3} & {-1} \\ {4} & {1} & {3} \\ {1} & {-2} & {-2}\end{array}\right|$ с помощью правила Саррюса.
Решение.
$$+(-1) \cdot 4 \cdot(-2)-(-1) \cdot 1 \cdot 1-3 \cdot 3 \cdot(-2)-3 \cdot 4 \cdot(-2)=54$$
Ответ. $\left| \begin{array}{rrr}{3} & {3} & {-1} \\ {4} & {1} & {3} \\ {1} & {-2} & {-2}\end{array}\right|=54$
Разложение определителя по строке или столбцу
Определитель равен сумме произведений элементов строки определителя на их алгебраические дополнения. Обычно выбирают ту строку/столбец, в которой/ом есть нули. Строку или столбец, по которой/ому ведется разложение, будет обозначать стрелкой.
Пример
Задание. Разложив по первой строке, вычислить определитель $\left| \begin{array}{lll}{1} & {2} & {3} \\ {4} & {5} & {6} \\ {7} & {8} & {9}\end{array}\right|$
Решение. Ответ. $\left| \begin{array}{lll}{1} & {2} & {3} \\ {4} & {5} & {6} \\ {7} & {8} & {9}\end{array}\right|=0$ Этот метод позволяет вычисление определителя свести к вычислению определителя более низкого порядка.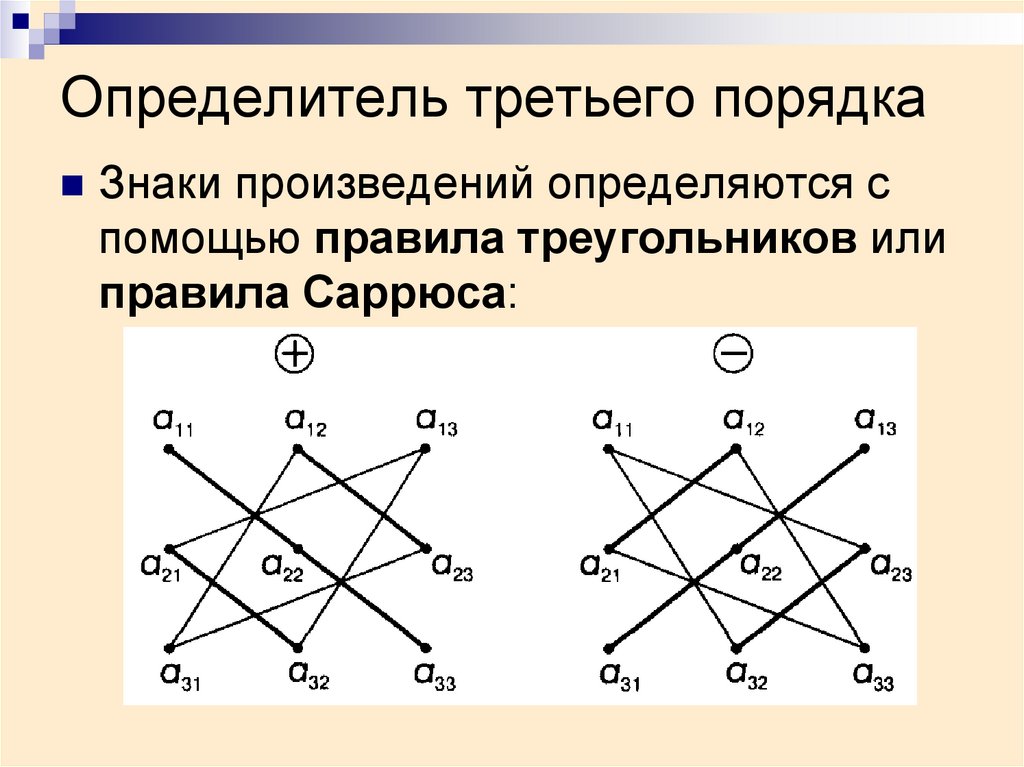 {1+3} \cdot \left| \begin{array}{cc}{4} & {5} \\ {7} & {8}\end{array}\right|=-3+12-9=0$
{1+3} \cdot \left| \begin{array}{cc}{4} & {5} \\ {7} & {8}\end{array}\right|=-3+12-9=0$
Задание. Вычислить определитель $\left| \begin{array}{lll}{1} & {2} & {3} \\ {4} & {5} & {6} \\ {7} & {8} & {9}\end{array}\right|$
Решение. Выполним следующие преобразования над строками определителя: из второй строки отнимем четыре первых, а из третьей первую строку, умноженную на семь, в результате, согласно свойствам определителя, получим определитель, равный данному.
$$\left| \begin{array}{ccc}{1} & {2} & {3} \\ {4} & {5} & {6} \\ {7} & {8} & {9}\end{array}\right|=\left| \begin{array}{ccc}{1} & {2} & {3} \\ {4-4 \cdot 1} & {5-4 \cdot 2} & {6-4 \cdot 3} \\ {7-7 \cdot 1} & {8-7 \cdot 2} & {9-7 \cdot 3}\end{array}\right|=$$
$$=\left| \begin{array}{rrr}{1} & {2} & {3} \\ {0} & {-3} & {-6} \\ {0} & {-6} & {-12}\end{array}\right|=\left| \begin{array}{ccc}{1} & {2} & {3} \\ {0} & {-3} & {-6} \\ {0} & {2 \cdot(-3)} & {2 \cdot(-6)}\end{array}\right|=0$$
Определитель равен нулю, так как вторая и третья строки являются пропорциональными.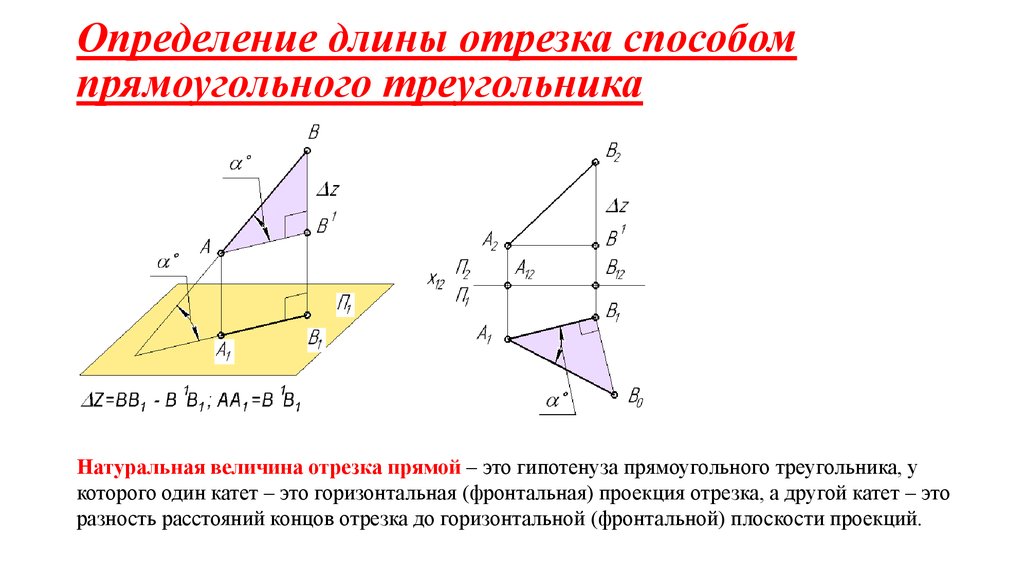
Ответ. $\left| \begin{array}{lll}{1} & {2} & {3} \\ {4} & {5} & {6} \\ {7} & {8} & {9}\end{array}\right|=0$
Для вычисления определителей четвертого порядка и выше применяется либо разложение по строке/столбцу, либо приведение к треугольному виду, либо с помощью теоремы Лапласа.
Разложение определителя по элементам строки или столбца
Пример
Задание. Вычислить определитель $\left| \begin{array}{llll}{9} & {8} & {7} & {6} \\ {5} & {4} & {3} & {2} \\ {1} & {0} & {1} & {2} \\ {3} & {4} & {5} & {6}\end{array}\right|$ , разложив его по элементам какой-то строки или какого-то столбца.
Решение. Предварительно выполним элементарные преобразования над строками определителя, сделав как можно больше нулей либо в строке, либо в столбце. Для этого вначале от первой строки отнимем девять третьих, от второй — пять третьих и от четвертой — три третьих строки, получаем:
$$\left| \begin{array}{cccc}{9} & {8} & {7} & {6} \\ {5} & {4} & {3} & {2} \\ {1} & {0} & {1} & {2} \\ {3} & {4} & {5} & {6}\end{array}\right|=\left| \begin{array}{cccc}{9-1} & {8-0} & {7-9} & {6-18} \\ {5-5} & {4-0} & {3-5} & {2-10} \\ {1} & {0} & {1} & {2} \\ {0} & {4} & {2} & {0}\end{array}\right|=\left| \begin{array}{rrrr}{0} & {8} & {-2} & {-12} \\ {0} & {4} & {-2} & {-8} \\ {1} & {0} & {1} & {2} \\ {0} & {4} & {2} & {0}\end{array}\right|$$
Полученный определитель разложим по элементам первого столбца:
$$\left| \begin{array}{rrrr}{0} & {8} & {-2} & {-12} \\ {0} & {4} & {-2} & {-8} \\ {1} & {0} & {1} & {2} \\ {0} & {4} & {2} & {0}\end{array}\right|=0+0+1 \cdot(-1)^{3+1} \cdot \left| \begin{array}{rrr}{8} & {-2} & {-12} \\ {4} & {-2} & {-8} \\ {4} & {2} & {0}\end{array}\right|+0$$
Полученный определитель третьего порядка также разложим по элементам строки и столбца, предварительно получив нули,
например, в первом столбце.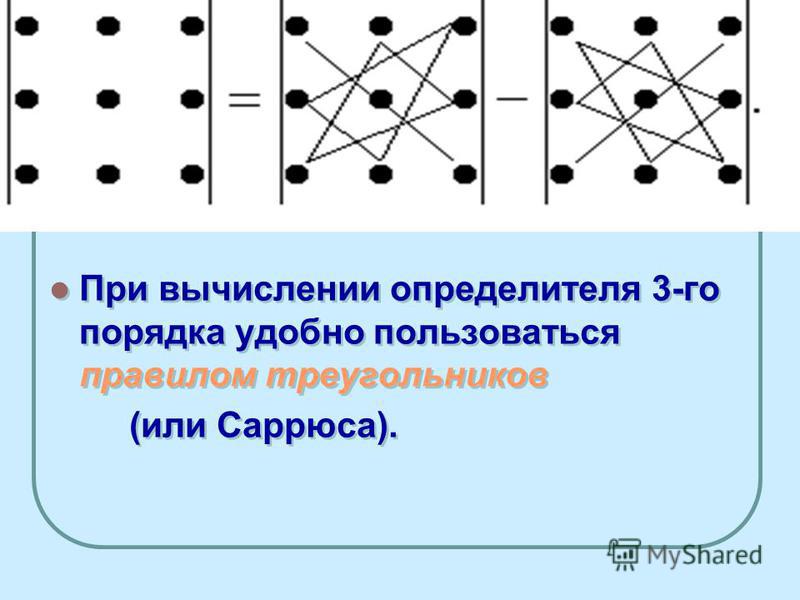 {2+2} \cdot \left| \begin{array}{ll}{2} & {4} \\ {4} & {8}\end{array}\right|=$$
{2+2} \cdot \left| \begin{array}{ll}{2} & {4} \\ {4} & {8}\end{array}\right|=$$
$$=4 \cdot(2 \cdot 8-4 \cdot 4)=0$$
Ответ. $\left| \begin{array}{cccc}{9} & {8} & {7} & {6} \\ {5} & {4} & {3} & {2} \\ {1} & {0} & {1} & {2} \\ {3} & {4} & {5} & {6}\end{array}\right|=0$
Замечание
Последний и предпоследний определители можно было бы и не вычислять, а сразу сделать вывод о том, что они равны нулю, так как содержат пропорциональные строки.
Приведение определителя к треугольному виду
С помощью элементарных преобразований над строками или столбцами определитель приводится к треугольному виду и тогда его значение, согласно свойствам определителя, равно произведению элементов стоящих на главной диагонали.
Пример
Задание. Вычислить определитель
$\Delta=\left| \begin{array}{rrrr}{-2} & {1} & {3} & {2} \\ {3} & {0} & {-1} & {2} \\ {-5} & {2} & {3} & {0} \\ {4} & {-1} & {2} & {-3}\end{array}\right|$ приведением его к треугольному виду.
Решение. Сначала делаем нули в первом столбце под главной диагональю. Все преобразования будет выполнять проще, если элемент $a_{11}$ будет равен 1. Для этого мы поменяем местами первый и второй столбцы определителя, что, согласно свойствам определителя, приведет к тому, что он сменит знак на противоположный:
$$\Delta=\left| \begin{array}{rrrr}{-2} & {1} & {3} & {2} \\ {3} & {0} & {-1} & {2} \\ {-5} & {2} & {3} & {0} \\ {4} & {-1} & {2} & {-3}\end{array}\right|=-\left| \begin{array}{rrrr}{1} & {-2} & {3} & {2} \\ {0} & {3} & {-1} & {2} \\ {2} & {-5} & {3} & {0} \\ {-1} & {4} & {2} & {-3}\end{array}\right|$$
Далее получим нули в первом столбце, кроме элемента $a_{11}$ , для этого из третьей строки вычтем две первых, а к четвертой строке прибавим первую, будем иметь:
$$\Delta=-\left| \begin{array}{rrrr}{1} & {-2} & {3} & {2} \\ {0} & {3} & {-1} & {2} \\ {0} & {-1} & {-3} & {-4} \\ {0} & {2} & {5} & {-1}\end{array}\right|$$
Далее получаем нули во втором столбце на месте элементов, стоящих под главной диагональю.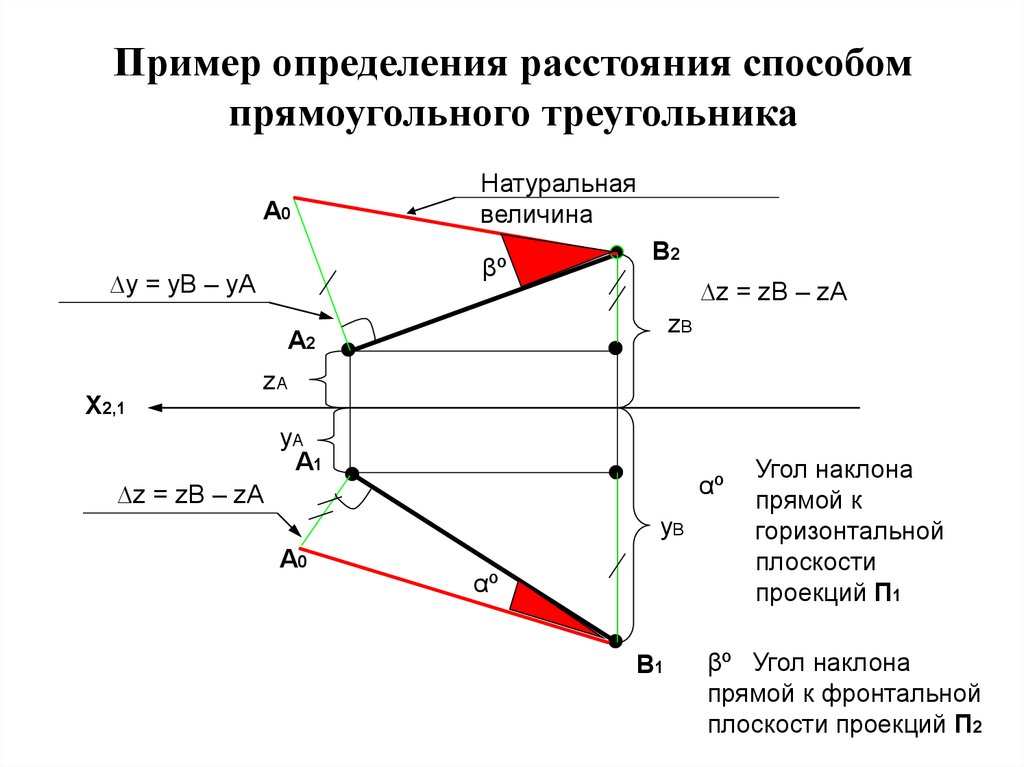 И снова, если
диагональный элемент будет равен $\pm 1$ , то
вычисления будут более простыми. Для этого меняем местами вторую и третью строки (и при этом меняется на
противоположный знак определителя):
И снова, если
диагональный элемент будет равен $\pm 1$ , то
вычисления будут более простыми. Для этого меняем местами вторую и третью строки (и при этом меняется на
противоположный знак определителя):
$$\Delta=\left| \begin{array}{rrrr}{1} & {-2} & {3} & {2} \\ {0} & {-1} & {-3} & {-4} \\ {0} & {3} & {-1} & {2} \\ {0} & {2} & {5} & {-1}\end{array}\right|$$
Далее делаем нули во втором столбце под главной диагональю, для этого поступаем следующим образом: к третьей строке прибавляем три вторых, а к четвертой — две вторых строки, получаем:
$$\Delta=\left| \begin{array}{rrrr}{1} & {-2} & {3} & {2} \\ {0} & {-1} & {-3} & {-4} \\ {0} & {0} & {-10} & {-10} \\ {0} & {0} & {-1} & {-9}\end{array}\right|$$
Далее из третьей строки выносим (-10) за определитель и делаем нули в третьем столбце под главной диагональю, а для этого к последней строке прибавляем третью:
$$\Delta=-10 \left| \begin{array}{rrrr}{1} & {-2} & {3} & {2} \\ {0} & {-1} & {-3} & {-4} \\ {0} & {0} & {1} & {1} \\ {0} & {0} & {-1} & {-9}\end{array}\right|=$$
$$=-10 \cdot \left| \begin{array}{cccc}{1} & {-2} & {3} & {2} \\ {0} & {-1} & {-3} & {-4} \\ {0} & {0} & {1} & {1} \\ {0} & {0} & {0} & {-8}\end{array}\right|=(-10) \cdot 1 \cdot(-1) \cdot 1 \cdot(-8)=-80$$
Ответ. $\Delta=-80$
$\Delta=-80$
Теорема Лапласа
Теорема
Пусть $\Delta$ — определитель $n$-го порядка. Выберем в нем произвольные $k$ строк (или столбцов), причем $k \leq n-1$ . Тогда сумма произведений всех миноров $k$-го порядка, которые содержатся в выбранных $k$ строках (столбцах), на их алгебраические дополнения равна определителю.
Пример
Задание. Используя теорему Лапласа, вычислить определитель $\left| \begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \\ {0} & {1} & {0} & {-1} & {2} \\ {3} & {2} & {1} & {0} & {1} \\ {0} & {4} & {0} & {-5} & {0} \\ {1} & {1} & {2} & {-2} & {1}\end{array}\right|$
Решение. Выберем в данном определителе пятого порядка две строки — вторую и третью, тогда получаем (слагаемые, которые равны нулю, опускаем):
$$\left| \begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \\ {0} & {1} & {0} & {-1} & {2} \\ {3} & {2} & {1} & {0} & {1} \\ {0} & {4} & {0} & {-5} & {0} \\ {1} & {1} & {2} & {-2} & {1}\end{array}\right|=\left| \begin{array}{cc}{1} & {-1} \\ {4} & {-5}\end{array}\right| \cdot(-1)^{2+4+2+4} \cdot \left| \begin{array}{ccc}{2} & {0} & {5} \\ {3} & {1} & {1} \\ {1} & {2} & {1}\end{array}\right|+$$
$$+\left| \begin{array}{ll}{1} & {2} \\ {4} & {0}\end{array}\right| \cdot(-1)^{2+4+2+5} \cdot \left| \begin{array}{rrr}{2} & {0} & {4} \\ {3} & {1} & {0} \\ {1} & {2} & {-2}\end{array}\right|+\left| \begin{array}{cc}{-1} & {2} \\ {-5} & {0}\end{array}\right| \cdot(-1)^{2+4+5} \cdot \left| \begin{array}{ccc}{2} & {3} & {0} \\ {3} & {2} & {1} \\ {1} & {1} & {2}\end{array}\right|=$$
$$=-23+128+90=195$$
Ответ.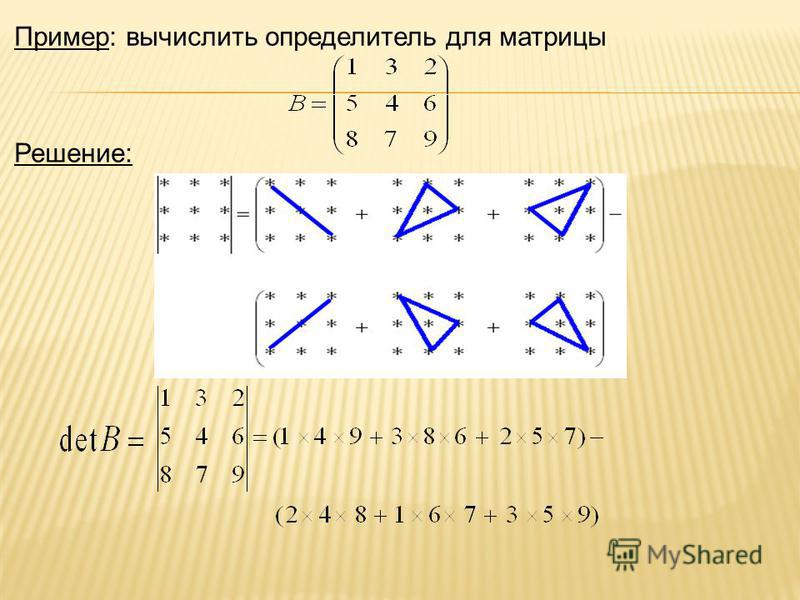 $\left| \begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \\ {0} & {1} & {0} & {-1} & {2} \\ {3} & {2} & {1} & {0} & {1} \\ {0} & {4} & {0} & {-5} & {0} \\ {1} & {1} & {2} & {-2} & {1}\end{array}\right|=195$
$\left| \begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \\ {0} & {1} & {0} & {-1} & {2} \\ {3} & {2} & {1} & {0} & {1} \\ {0} & {4} & {0} & {-5} & {0} \\ {1} & {1} & {2} & {-2} & {1}\end{array}\right|=195$
Читать дальше: обратная матрица.
Треугольник в шахматах: его суть и содержание
Автор: Дядя Валера
День добрый, дорогой друг!
Благополучно изучив квадрат, не забудем еще одно базовое понятие из области окончаний. А именно — треугольник в шахматах. Это технический прием, являющийся фундаментальным.
Его суть — маневр короля в форме треугольника, позволяющий кардинально изменить ситуацию на доске. Конкретнее — чуть ниже.
Правило треугольника чаще всего применимо в пешечном эндшпиле.
Для того, чтобы его лучше понять, — вначале разберемся с еще одним понятием — минированных полей.
Коль скоро вы оказались на этой странице, — сохраните себе в закладках наши Программы подготовки шахматистов — отличное подспорье для усиления игры. А также программы подготовки для игры в блиц и рапид.
Минированные поля в пешечном окончании
Смотрим на диаграмму. Ход белых.
Итак, белый король может подойти к пешке с угрозой взятия. То же самое «грозится»сделать его черный оппонент.
Позиция симметричная и может показаться простой, — кто первый нападет на пешку и побьет ее, тот и выиграет. Что называется: «Кто успел, тот и съел».
Однако все получается с точностью до наоборот.
Напрашивается 1.Кре6. Однако это прямолинейное нападение – серьезная ошибка, типичная для начинающего игрока.
Поле е6 — «минированное». После 1.Кре6?? Крс5 – белый король вынужден отступить. После чего черный король забирает белую пешку и выигрывает партию.
Поэтому белые должны действовать иначе, хитрее.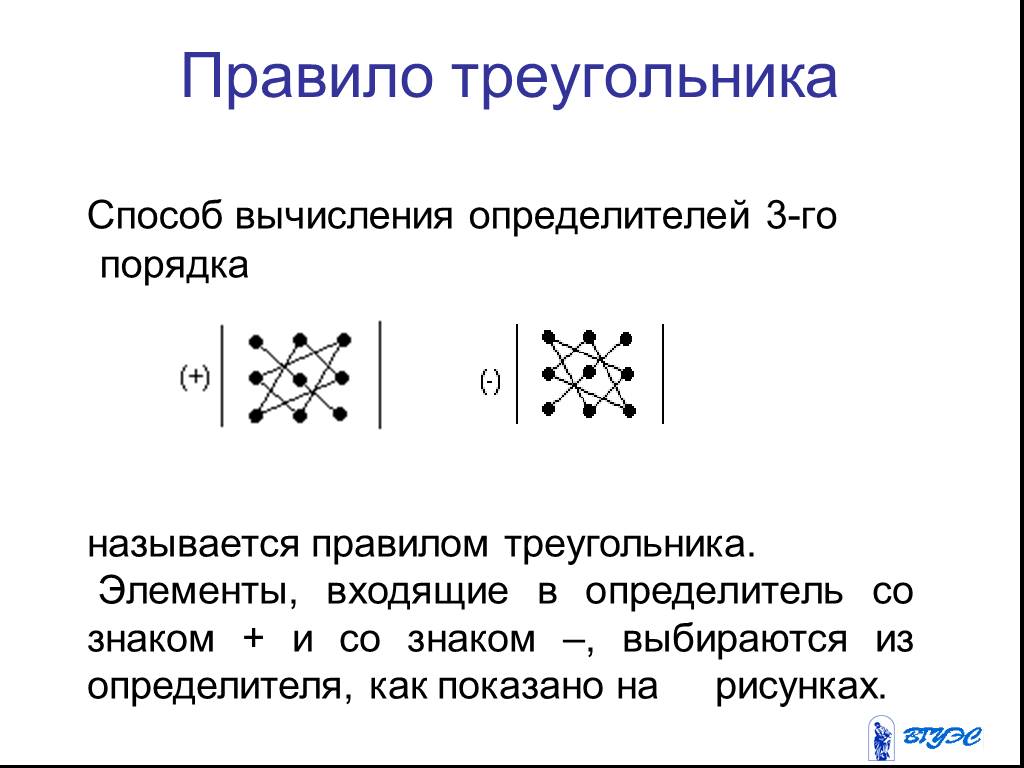
Правильно 1.Кре7!
После 1.Кре7! Крс5 2.Кре6
Выигрывают уже белые. Ибо черный король первым ступил на «минированное» поле с5 и сейчас, при своем ходе, — должен отступить, отдавая свою пешку.
Если же ход черных, выигрывают уже они. 1…Крс4!
Белый король вынужден первым зайти на минированное поле, — поле е6.
После 2.Кре6 Крс5 – выигрывают черные.
Позиция с положением королей на е6 и с5 — типичный пример взаимного цугцванга.
Ситуации, когда право хода — не благо, а проблема. В данном случае очередь хода ведет к проигрышу. При ходе белых они проигрывают. При ходе черных — проигрывают черные.
Для того, чтобы выиграть, белый король при своем ходе использует траекторию движения, похожую на треугольник.
Метод треугольника
Это маневр короля с целью передать очередь хода противнику.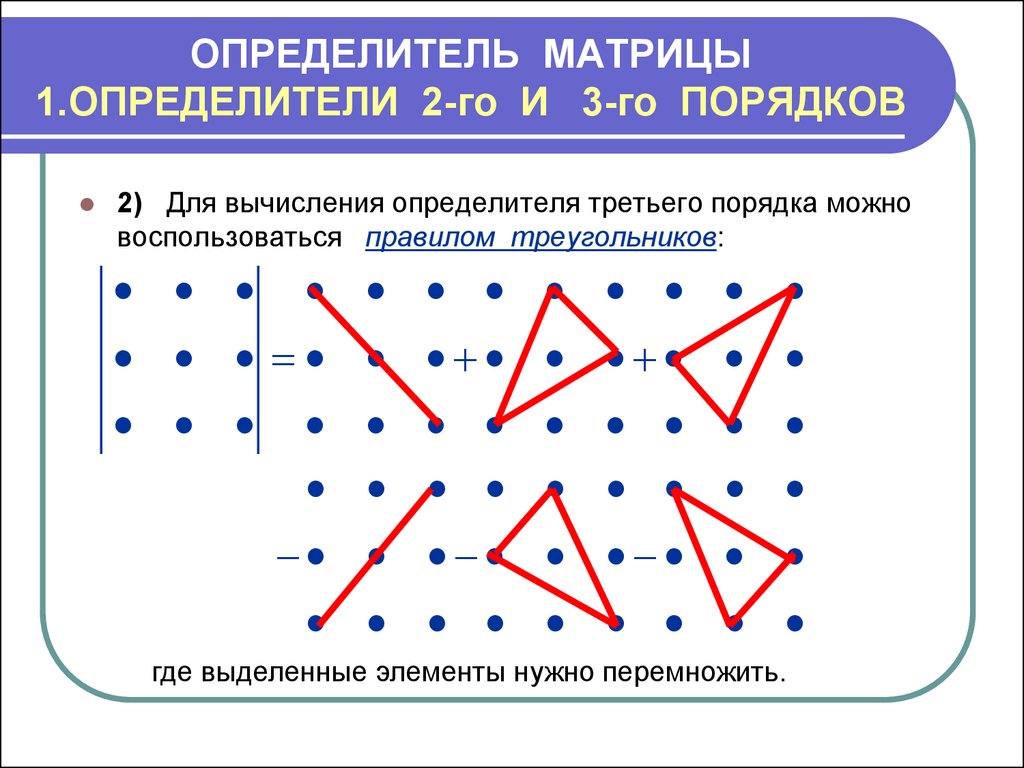 После чего соперник оказывается в цугцванге и любой его ход ведет к проигрышу.
После чего соперник оказывается в цугцванге и любой его ход ведет к проигрышу.
Рассмотрим на другом примере:
В позиции на диаграмме белые хотят победить. Для этого необходимо провесим в ферзи свою пешку. Чтобы это сделать, — король белых должен занять одно из ключевых полей: d7 или b7.
Полагаю, вы уже догадались, что прямолинейный путь «напролом» успеха не принесет:
На напрашивающееся 1.Крс5? следует 1…Крс7!,
а на 1.Крd6 – 1…Крd8.
Черный король препятствует проникновению белого оппонента на ключевые поля d7 или b7.
Что же делать? Использовать «военную хитрость» !
К победе белых ведет маневр короля по треугольнику d5-c4-d4. Маневр, похожий на «пляску».
1.Крd4!
1…Крd8! 2.Крс4! Крс8 3.Крd5! Крd8 4.Крd6
Позиция аналогична той, что отражена на диаграмме чуть выше. Однако есть «две большие разницы».
Однако есть «две большие разницы».
В данном случае белые с помощью треугольника передали ход черным. И это меняет все!
4…Крс8 5.с7 Крb7 6.Крd7
и пешка проходить в ферзи.
А на 3…Крс7 выигрыш достигается путем 4.Крс5
И снова позиция та же, но ход черных. И они проигрывают. При ходе белых была бы ничья.
4…Крс8 5.Крb6 Крb8 6. Кр:а6 Крс7 7.Крb5
И белые выигрывают.
Обратите внимание: Черные проигрывают потому, что их король не может также, как и белый «сплясать» в форме треугольника – доска не резиновая и девятой горизонтали на ней нет )
Надеюсь, суть правила треугольника понятна. Остались вопросы — милости просим в комментарии.
И в заключение упражнение.
Упражнение
Белые начинают и выигрывают:
Благодарю за интерес к статье.
Если вы нашли ее полезной, сделайте следующее:
- Поделитесь с друзьями, нажав на кнопки социальных сетей.

- Напишите комментарий (внизу страницы)
- Подпишитесь на обновления блога (форма под кнопками соцсетей) и получайте статьи к себе на почту.
Рейтинг статьи:
Отправить ссылку на статью друзьям
Твитнуть
Поделиться
Плюсануть
Поделиться
Класснуть
Отправить
Получай свежие статьи блога на e-mail
Техника TikTok «Метод треугольника» — ключ к лучшему флирту
Отношения
Все дело в зрительном контакте.
by Кэролайн Стебер
Getty Images/Willie B. Thomas
9000 2 Удивительное свидание нередко заканчивается неловким моментом, когда вы стоите и смеетесь нервничайте, говорите о погоде и пытайтесь уловить флюиды перед первым поцелуем. Если вы любите упиваться милой застенчивостью, продолжайте и посмотрите, что произойдет. Если вы боитесь этого момента или хотите перейти к делу, метод треугольника для вас.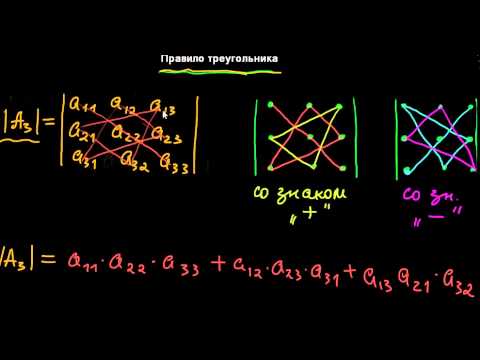
Метод треугольника — это кокетливая техника языка тела, которая предположительно посылает сообщение о том, что вы в кого-то влюблены, не говоря об этом вслух. На TikTok у него более 24 миллионов просмотров и видео бесчисленного количества людей, которые говорят, что это надежный способ влюбить в себя любимого человека. Все, что для этого требуется, — это преднамеренный зрительный контакт.
Чтобы успешно освоить метод треугольника, просто обведите глазами форму перевернутого треугольника. Когда вы смотрите на своего партнера, взгляните на один из его глаз, быстро посмотрите вниз на его рот, затем вернитесь к другому глазу, чтобы сформировать треугольник. Вот и все.
Этот прием не только показывает, что вы наслаждаетесь моментом и, вероятно, заинтересованы в поцелуях, но также может вызвать у вашего свидания определенные чувства. Здесь эксперт по языку тела опровергает легитимность техники зрительного контакта методом треугольника.
По словам Патти Вуд, магистра искусств, эксперта по языку тела и автора книги SNAP: максимальное использование первых впечатлений, языка тела и харизмы , люди постоянно обмениваются невербальными сигналами, чтобы показать либо интерес, либо незаинтересованность, особенно на свидание. Если вы кому-то нравитесь, она говорит, что они могут наклоняться вперед во время разговора, мягко касаться вас или даже наклонять ноги в вашу сторону.
Если вы кому-то нравитесь, она говорит, что они могут наклоняться вперед во время разговора, мягко касаться вас или даже наклонять ноги в вашу сторону.
Когда вы кому-то нравитесь, они также могут краснеть, когда вы говорите и флиртуете. Это одна из причин, почему люди носят красную помаду и розовые румяна, говорит Вуд. Цвет посылает биологический сигнал о том, что ваша кровь кипит, вы в настроении и, возможно, даже влюбляетесь. Обратите внимание на один или два из этих сигналов — или все вышеперечисленные — и, скорее всего, поцелуй уже не за горами.
Метод треугольника — это просто еще один сигнал языка тела, который посылает тонкое сообщение об интересе и связи. Хотя поцелуй может произойти и без него, этот сигнал ускоряет процесс, показывая, что вы заперты и заинтересованы в сближении.
Ваши рот и глаза являются частью того, что Вуд называет «золотым треугольником» вашего лица. Это ваши глаза, лоб и рот, и это та область, на которую вы больше всего смотрите во время взаимодействия. Если вы и ваше свидание не ладите, вы, вероятно, не будете так сильно сосредотачиваться на лицах друг друга. Вместо этого вы отводите взгляд в знак незаинтересованности или говорите закрытым языком тела, например, скрестив руки.
Если вы и ваше свидание не ладите, вы, вероятно, не будете так сильно сосредотачиваться на лицах друг друга. Вместо этого вы отводите взгляд в знак незаинтересованности или говорите закрытым языком тела, например, скрестив руки.
Если вы оба увлечены этим, тогда начинается много зрительного контакта. В конце концов, затяжной зрительный контакт воспринимается как очень возбуждающий. По данным 2019 г.исследование, опубликованное в Frontiers in Psychology , это также улица с двусторонним движением: люди создают и получают это как форму общения.
Взгляд на рот собеседника также разрушает стены, поэтому метод треугольника может вызвать у кого-то возбуждение и беспокойство. Другой человек почувствует интенсивность вашего зрительного контакта и заметит, что вы постоянно смотрите ему в рот — и, если у вас обоих есть химия, в этот момент имеет смысл наклониться и поцеловаться.
Как только вы узнаете, что метод треугольника существует, вы можете заметить, что кто-то пытается применить его на вас.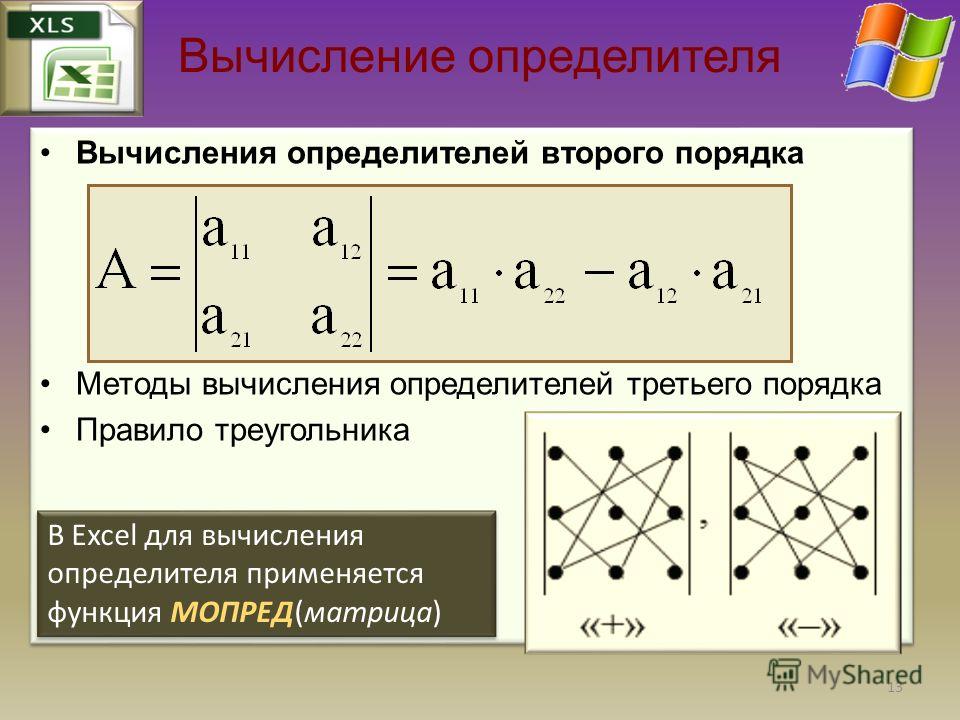 Хотя это не всегда происходит сознательно, скорее всего, они хотя бы немного заинтересованы в поцелуе, если их взгляд продолжает перемещаться вниз к вашим губам. Либо так, либо они собираются предложить вам немного бальзама для губ.
Хотя это не всегда происходит сознательно, скорее всего, они хотя бы немного заинтересованы в поцелуе, если их взгляд продолжает перемещаться вниз к вашим губам. Либо так, либо они собираются предложить вам немного бальзама для губ.
Ссылки на исследования:
Де Стефани, Э. (2019). Язык, жесты и эмоциональное общение: воплощенный взгляд на социальное взаимодействие. Фронт Псих. doi: 10.3389/fpsyg.2019.02063.
Джарик, М. (2019). Зрительный контакт — это улица с двусторонним движением: возбуждение вызывается отправкой и получением информации о взгляде. Фронт Псих. doi: 10.3389/fpsyg.2019.01262.
Kennair, LEO (2022). Воспринимаемая эффективность тактики флирта: влияние контекста спаривания и индивидуальных различий в выборках США и Норвегии. Эволюционная психология. https://doi.org/10.1177/14747049221088011.
Уэйд, Дж.А. (2018). (Я думаю) Ты красивая: поведенческая аналитическая концептуализация флирта.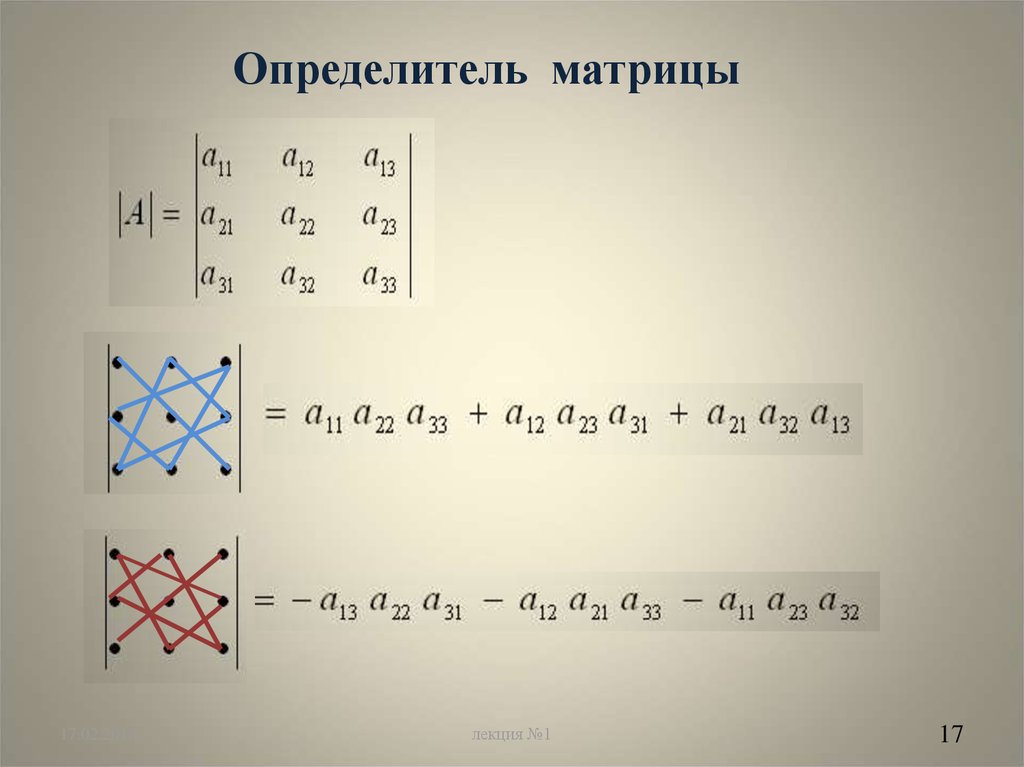 Перспектива Behav Sci. doi: 10.1007/s40614-018-0136-y.
Перспектива Behav Sci. doi: 10.1007/s40614-018-0136-y.
Источник:
Патти Вуд, Массачусетс, эксперт по языку тела, автор книги SNAP: максимальное использование первых впечатлений, языка тела и харизмы
Что такое метод треугольника? Взгляд на последнюю тенденцию TikTok
Когда вы совершаете покупку по ссылкам на нашем сайте, мы можем получать партнерскую комиссию. Вот как это работает.
(Изображение предоставлено Getty)
Что такое метод треугольника? TikTok спешит помочь в любовном отделе.
В последнее время платформа для обмена видео была особенно настроена на сердечные дела, как раз к самому романтичному дню в году. Тенденция к белому лаку для ногтей — это скромный способ сообщить о своем статусе отношений во время публикации видео, в то время как синдром счастливой девушки — это метод проявления, к которому женщины обращаются в надежде найти свою вторую половинку.
В данный момент кажется, что все в вашем FYP сфокусированы на лазере, и метод треугольника тому доказательство. Готовы узнать больше?
Что такое метод треугольника в TikTok?
Метод треугольника — это способ установить зрительный контакт, чтобы показать собеседнику, что вы хорошо проводите время вместе и, возможно, готовы к поцелуям. Рассмотрим тенденцию быть виртуальным напарником или женщиной.
Хотя, да, нервы могут помешать сентиментальному моменту — и, возможно, некоторые из нас даже оценят неловкие паузы и тому подобное во время свидания — ваши глаза позволяют вам сказать многое, не говоря вообще ничего. Чтобы показать свой интерес и эффективно освоить Метод Треугольника, вам нужно обвести учениками форму перевернутого треугольника. Вуаля! Вы на один шаг ближе к замку губ.
Извлекая фигуры из уравнения, наведите лазер на глаз собеседника, переместитесь к его губам, а затем вернитесь к другому глазу. Это все, что вам нужно сделать! И в конце концов, если вы приближаете чьи-то губы, пусть и ненадолго, есть большая вероятность, что ваш партнер это заметит.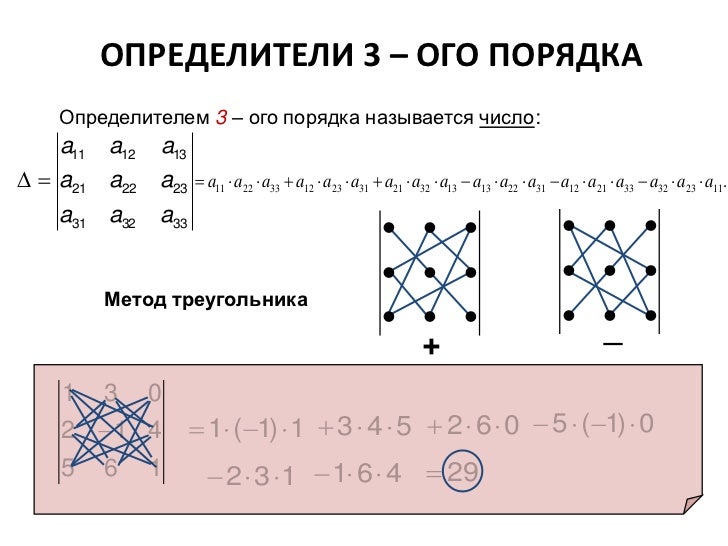
@_gracey21 (откроется в новой вкладке) ♬ Originalton — darkvideoz (открывается в новой вкладке)
Метод Треугольника действительно работает?
Для скептиков зрительный контакт на самом деле имеет большую силу в наших взаимодействиях, так что не сомневайтесь в них! Зрительный контакт указывает на то, что вы обращаете внимание и заинтересованы в связи, которую вы пытаетесь установить с кем-то, и профессионалы соглашаются.
По словам Майкла Эллсберга, автора книги Сила зрительного контакта: ваш секрет успеха в бизнесе, любви и жизни , зрительный контакт настаивает на том, что кто-то «слушает, присутствует и принимает нас. » Это показывает, что они заботятся о нас.
Он пишет: «Глаза открывают целый мир информации, находящийся за пределами нашего внимания. Подумайте обо всех эмоциях — счастье, гневе, печали, удивлении, страхе, — которые можно громко и отчетливо обнаружить, просто взглянув на чью-то голову. глаза (точнее, мимические мышцы вокруг глаз, создающие различные выражения)».
глаза (точнее, мимические мышцы вокруг глаз, создающие различные выражения)».
Если вы сомневаетесь, может ли трюк с быстрым треугольником быть эффективным, Эллсберг дает немного больше уверенности: «Когда мы устанавливаем зрительный контакт с другим человеком, мы в каком-то смысле даем этому человеку ключи к нашему эмоциональному миру. мы чувствуем, другой человек, скорее всего, уловит, по крайней мере, внутреннее состояние нашего ума».
Если вы чувствуете себя особенно кокетливо в преддверии Дня святого Валентина, почему бы не попробовать? Только не делайте это слишком очевидным, иначе ваши результаты могут иметь неприятные последствия (см. ниже). Мы малыш! Но взгляните на тенденции знакомств 2023 года, которые могут помочь вам найти любовь в этом году!
@tyler_banksss (откроется в новой вкладке)«о, ты видел этот тик-ток»
♬ оригинальный звук — sissy (открывается в новой вкладке)
Даниэлла пишет для Woman&Home и My Imperfect Life, освещая все новости, образ жизни и развлечения.


