Какая цифра записана в разряде десятков: Какая цифра записана в разряде десятков класса тысяч числа 243 786? А)2 Б)4 В)3 Г)8
Вопрос: Какая цифра записана в разряде десятков миллионов в числе 410 253 006? Ответ на вопрос – iq2u
Точные науки Математика
Ответ:
1
Проверь себя, пройди тесты онлайн
Математика. Тест 24. Для поступающих.
Статистика теста
0–25% 108 человек | |
26–50% 68 человек | |
51–75% 35 человек | |
76–100% 31 человек |
0% Пройти тест
ЕГЭ 2017. Математика. Вариант 43
Математика. Вариант 43Статистика теста
0–25% 21 человек | |
26–50% 17 человек | |
51–75% 3 человека | |
76–100% 7 человек |
0% Пройти тест
ОГЭ 2018.
Статистика теста
0–25% 1 человек | |
26–50% 2 человека | |
51–75% 0 человек | |
76–100% 0 человек |
0% Пройти тест
Выражения. 7 класс.
7 класс.
Статистика теста
0–25% 4153 человека | |
26–50% 3632 человека | |
51–75% 3753 человека | |
76–100% 8304 человека |
0% Пройти тест
все тесты
Что? Где? Когда? Эрудит онлайн: ответы на вопросы:
- Сколько целочисленных решений имеет неравенство |х – 3| < 4?
- Какая страна находится на Пиренейском полуострове?
- Какая из функций является нечётной?
- Сколько трехзначных чисел (без повторения цифр в числе) можно составить из цифр 1, 2, 3, 4, 5, 6?
- Какая единица лишняя?
- Что из перечисленного является физической величиной?
- Сколько целочисленных решений имеет неравенство |lоg<sub>0,25</sub> x| ≤ 2? А. Есенина?»> Какая тема является основной в лирике С.А. Есенина?
- Сколько целочисленных решений неравенства (х – 3)(х + 4)<sup>2</sup> > 0 принадлежит отрезку [1; 7]?
- Что отсутствует в числе 345 000 465 592?
- Расстояние от Нептуна до его спутника Тритона равно 0,3548 млн км. В каком случае записана эта же величина?
- Какая из единиц не является единицей объёма? В каком случае записана эта же величина?»> Расстояние от Юпитера до Солнца равно 778,1 млн км. В каком случае записана эта же величина?
Дано число 1234567890. Какая цифра записана в разряде : 1… -reshimne.ru
Новые вопросы
Ответы
Похожие вопросы
С противоположных берегов одновременно навстречу друг другу начили заплывать два спортсмена первый спортсмен плыл со скоростью 5 метров в секунду а второй 7 метров в секунду какого расстояние между берегами если спортсмен встретились через 3 минуты…
В забеге на дистанцию 120 метров,когда Арсений приходит к финишу,Богдану остаётся пробежать ещё 20 метров.А когда Богдан приходит к финишу,Владимиру остаётся пробежать ещё 18 метров. Сколько метров останется пробежать до финиша Владимиру,когда финиширует Арсений?…
Сколько метров останется пробежать до финиша Владимиру,когда финиширует Арсений?…
В первый день полина прочитала 1/2 часть книги.во второй день 3/4 остатка.какую часть книги осталось прочитать ей?…
Территория школы имеет прямоугольную форму.Территория огорожена забором,одна сторона которого равна 64м,а другая на 19м короче.Какова площадь огороженной территории?Здание школы занимает пятую часть школьной территории.А фруктовый сад-треть оставшегося участка.Какую площадьзанимает фруктовый сад?…
Cлаве было 19 лет, Юре 15 л.Сколько лет было Славе, когда Юре было 10лет?…
Отцу столько лет сколько сыну и дочери вместе, а сын в полтора раза старше сестры и на 22 года моложе отца. Сколько лет отцу?…
Сколько лет отцу?…
Математика
Литература
Алгебра
Русский язык
Геометрия
Английский язык
Химия
Физика
Биология
Другие предметы
История
Обществознание
Окружающий мир
География
Українська мова
Українська література
Қазақ тiлi
Беларуская мова
Информатика
Экономика
Музыка
Право
Французский язык
Немецкий язык
МХК
ОБЖ
Психология
Разряды для начинающих
Наш первый урок назывался числа. Мы рассмотрели лишь малую часть этой темы. На самом деле тема чисел достаточно обширна. В ней много тонкостей и нюансов, много хитростей и интересных фишек.
Мы рассмотрели лишь малую часть этой темы. На самом деле тема чисел достаточно обширна. В ней много тонкостей и нюансов, много хитростей и интересных фишек.
Сегодня мы продолжим тему чисел, но опять же не будем рассматривать её всю, чтобы не затруднять обучение лишней информацией, которая на первых порах не особо то и нужна. Мы поговорим о разрядах.
Что такое разряд?
Если говорить простым языком, то разряд это позиция цифры в числе или место, где располагается цифра. Возьмём для примера число 635. Это число состоит из трёх цифр: 6, 3 и 5.
Разряды надо читать справа налево. В числе 635 на первой позиции располагается цифра 5, на второй позиции – цифра 3, на третьей позиции – цифра 6.
Позиция, где располагается цифра 5, называется разрядом единиц
Позиция, где располагается цифра 3, называется разрядом десятков
Позиция, где располагается цифра 6, называется разрядом сотен
Каждый из нас слышал со школы такие вещи как «единицы», «десятки», «сотни». Разряды помимо того, что играют роль позиции цифры в числе, сообщают нам некоторую информацию о самом числе. В частности, разряды сообщают нам вес числа. Они сообщают сколько в числе единиц, сколько десятков и сколько сотен.
Разряды помимо того, что играют роль позиции цифры в числе, сообщают нам некоторую информацию о самом числе. В частности, разряды сообщают нам вес числа. Они сообщают сколько в числе единиц, сколько десятков и сколько сотен.
Вернёмся к нашему числу 635. В разряде единиц располагается пятёрка. О чём это говорит? А говорит это о том, что разряд единиц содержит пять единичек. Выглядит это так:
В разряде десятков располагается тройка. Это говорит о том, что разряд десятков содержит три десятка. Выглядит это так:
В разряде сотен располагается шестёрка. Это говорит о том, что в разряде сотен располагаются шесть сотен. Выглядит это так:
Если сложить число получившихся единиц, число десятков и число сотен, то получим наше изначальное число 635
Существуют и более старшие разряды такие как разряд тысяч, разряд десятков тысяч, разряд сотен тысяч, разряд миллионов и так далее. Такие большие числа мы будем рассматривать редко, но тем не менее о них тоже желательно знать.
Например, в числе 1 645 832 разряд единиц содержит 2 единицы, разряд десятков — 3 десятка, разряд сотен — 8 сотен, разряд тысяч — 5 тысяч, разряд десятков тысяч — 4 десятка тысяч, разряд сотен тысяч — 6 сотен тысяч, разряд миллионов — 1 миллион.
На первых этапах изучения разрядов желательно разбираться сколько единиц, десятков, сотен содержит то или иное число. К примеру, число 9 содержит 9 единиц. Число 12 содержит две единицы и один десяток. Число 123 содержит три единицы, два десятка и одну сотню.
Группировка предметов
После подсчета каких-нибудь предметов, разряды можно использовать для группировки этих предметов. К примеру, если мы насчитали во дворе 35 кирпичей, то можно использовать разряды для группировки этих кирпичей. В случае группировки предметов, разряды можно читать слева направо. Так, цифра 3 в числе 35 будет говорить о том, что в числе 35 содержатся три десятка. А это значит, что 35 кирпичей можно сгруппировать три раза по десять штук.
Итак, сгруппируем кирпичи три раза по десять штук:
Получилось тридцать кирпичей. Но осталось еще пять единиц кирпичей. Их мы назовем как «пять единиц»
Получилось три десятка и пять единиц кирпичей.
А если бы мы не стали группировать кирпичи на десятки и единицы, то можно было бы сказать, что число 35 содержит тридцать пять единиц. Такая группировка тоже была бы допустимой:
Аналогично можно рассуждать и про другие числа. К примеру, о числе 123. Ранее мы сказали, что это число содержит три единицы, два десятка и одну сотню. Но можно ещё сказать, что это число содержит 123 единицы. Более того, можно сгруппировать это число и другим образом, сказав что оно содержит 12 десятков и 3 единицы.
Слова единицы, десятки, сотни, заменяют собой множимые 1, 10 и 100. К примеру, в разряде единиц числа 123 располагается цифра 3. С помощью множимого 1 можно записать, что эта единица содержится в разряде единиц три раза:
1 × 3 = 3
Далее в разряде десятков числа 123 располагается цифра 2. С помощью множимого 10 можно записать, что эта десятка содержится в разряде десятков два раза:
С помощью множимого 10 можно записать, что эта десятка содержится в разряде десятков два раза:
10 × 2 = 20
Далее в разряде сотен числа 123 располагается цифра 1. С помощью множимого 100 можно записать, что эта сотня содержится в разряде сотен один раз:
100 × 1 = 100
Если сложить полученные результаты 3, 20 и 100, то получим число 123
3 + 20 + 100 = 123
То же самое будет происходить если мы скажем, что число 123 содержит 12 десятков и 3 единицы. Другими словами, десятки будут сгруппированы 12 раз:
10 × 12 = 120
А единицы три раза:
1 × 3 = 3
Это можно понять на следующем примере. Если имеется 123 яблока, то можно сгруппировать первые 120 яблок 12 раз по 10 штук:
Получилось сто двадцать яблок. Но осталось еще три яблока. Их мы назовем как «три единицы»
Если сложить полученные результаты 120 и 3, снова получим число 123
120 + 3 = 123
Ещё можно сгруппировать 123 яблока на одну сотню, два десятка и три единицы.
Сгруппируем сотню:
Сгруппируем два десятка:
Сгруппируем три единицы:
Если сложить полученные результаты 100, 20 и 3, снова получим число 123
100 + 20 + 3 = 123
Ну и наконец, рассмотрим последнюю возможную группировку, где яблоки не будут распределяться на десятки и сотни, а будут собраны вместе. В таком случае число 123 будет читаться как «сто двадцать три единицы». Такая группировка тоже будет допустимой:
1 × 123 = 123
Пример 3. Прочитать число 523 всеми возможными способами.
Число 523 можно прочесть, как 3 единицы, 2 десятка и 5 сотен:
1 × 3 = 3 (три единицы)
10 × 2 = 20 (два десятка)
100 × 5 = 500 (пять сотен)
3 + 20 + 500 = 523
Ещё можно прочесть, как 3 единицы 52 десятка:
1 × 3 = 3 (три единицы)
10 × 52 = 520 (пятьдесят два десятка)
3 + 520 = 523
Ещё число 523 можно прочесть, как 523 единицы:
1 × 523 = 523 (пятьсот двадцать три единицы)
Где применить разряды?
Разряды существенно облегчают некоторые вычисления. Представьте, что вы у доски и решаете задачу. Вы почти закончили задачу, осталось только вычислить последнее выражение и получить ответ. Выражение, которое надо вычислить, выглядит следующим образом:
Представьте, что вы у доски и решаете задачу. Вы почти закончили задачу, осталось только вычислить последнее выражение и получить ответ. Выражение, которое надо вычислить, выглядит следующим образом:
Калькулятора под рукой нет, а хочется быстро записать ответ и удивить всех скоростью своих вычислений. Всё просто, если отдельно сложить единицы, отдельно десятки и отдельно сотни. Начинать нужно с разряда единиц. В первую очередь после знака равно (=) необходимо мысленно поставить три точки. Вместо этих точек будет располагаться новое число (наш ответ):
Теперь начинаем складывать. В разряде единиц числа 632 располагается цифра 2, а в разряде единиц числа 264 — цифра 4. Это означает, разряд единиц числа 632 содержит две единицы, а разряд единиц числа 264 содержит четыре единицы. Складываем 2 и 4 единицы — получаем 6 единиц. Записываем цифру 6 в разряде единиц нового числа (нашего ответа):
Далее складываем десятки. В разряде десятков числа 632 располагается цифра 3, а в разряде десятков числа 264 — цифра 6. Это означает, что разряд десятков числа 632 содержит три десятка, а разряд десятков числа 264 содержит шесть десятков. Складываем 3 и 6 десятков — получаем 9 десятков. Записываем цифру 9 в разряде десятков нового числа (нашего ответа):
Это означает, что разряд десятков числа 632 содержит три десятка, а разряд десятков числа 264 содержит шесть десятков. Складываем 3 и 6 десятков — получаем 9 десятков. Записываем цифру 9 в разряде десятков нового числа (нашего ответа):
Ну и в завершении складываем отдельно сотни. В разряде сотен числа 632 располагается цифра 6, а в разряде сотен числа 264 — цифра 2. Это означает, что разряд сотен числа 632 содержит шесть сотен, а разряд сотен числа 264 содержит две сотни. Складываем 6 и 2 сотни, получаем 8 сотен. Записываем цифру 8 в разряде сотен нового числа (нашего ответа):
Таким образом, если к числу 632 прибавить 264, получается 896. Конечно, вы вычислите подобное выражение быстрее и окружающие начнут удивляться вашим способностям. Они будут думать, что вы быстро вычисляете большие числа, а на самом деле вы вычисляли маленькие. Согласитесь, что маленькие числа вычислять легче, чем большие.
Переполнение разряда
Разряд характеризуется одной цифрой от 0 до 9.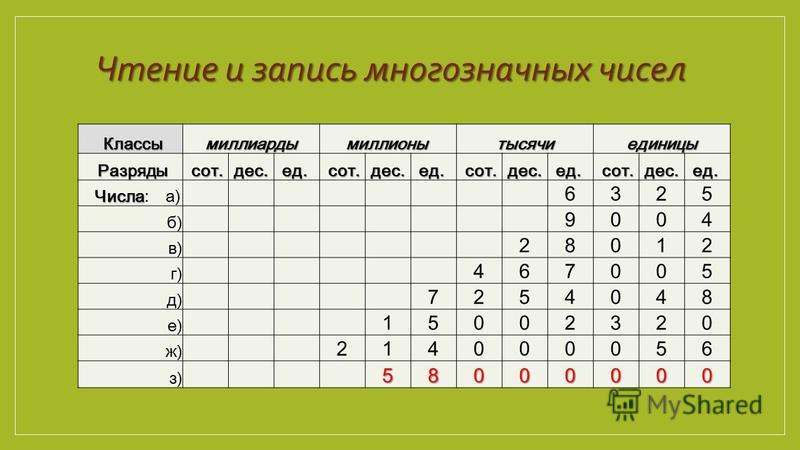 Но иногда при вычислении числового выражения в середине решения может произойти переполнение разряда.
Но иногда при вычислении числового выражения в середине решения может произойти переполнение разряда.
Например, при сложении чисел 32 и 14 переполнения не происходит. Сложение единиц этих чисел даст 6 единиц в новом числе. А сложение десятков этих чисел даст 4 десятка в новом числе. Получится ответ 46 или шесть единиц и четыре десятка.
А вот при сложении чисел 29 и 13 произойдёт переполнение. Сложение единиц этих чисел даёт 12 единиц, а сложение десятков 3 десятка. Если в новом числе в разряде единиц записать полученные 12 единиц, а в разряде десятков записать полученные 3 десятка, то получится ошибка:
Значение выражения 29 + 13 равно 42, а не 312. Как же следует поступать при переполнении? В нашем случае переполнение случилось в разряде единиц нового числа. При сложении девяти и трёх единиц у нас получилось 12 единиц. А в разряд единиц можно записывать только цифры в диапазоне от 0 до 9.
Дело в том, что 12 единиц это не просто «двенадцать единиц». По другому это число можно прочитать как «две единицы и один десяток». Разряд единиц предназначен только для единиц. Десяткам там не место. Здесь и заключается наша ошибка. Сложив 9 единиц и 3 единицы мы получили 12 единиц, которые по-другому можно назвать двумя единицами и одним десятком. Записав две единицы и один десяток в одном разряде, мы допустили ошибку, которая в итоге привела к неправильному ответу.
По другому это число можно прочитать как «две единицы и один десяток». Разряд единиц предназначен только для единиц. Десяткам там не место. Здесь и заключается наша ошибка. Сложив 9 единиц и 3 единицы мы получили 12 единиц, которые по-другому можно назвать двумя единицами и одним десятком. Записав две единицы и один десяток в одном разряде, мы допустили ошибку, которая в итоге привела к неправильному ответу.
Чтобы исправить ситуацию, две единицы нужно записать в разряде единиц нового числа, а оставшийся десяток перенести на следующий разряд десятков. После сложения десятков в примере 29 + 13, мы прибавим к полученному результату тот десяток, который остался при сложении единиц.
Итак, из 12 единиц две единицы запишем в разряде единиц нового числа, а один десяток перенесем на следующий разряд
Как видно на рисунке, 12 единиц мы представили как 1 десяток и 2 единицы. Две единицы мы записали в разряде единиц нового числа. А один десяток перенесли к разрядам десятков. Этот десяток мы прибавим к результату сложения десятков чисел 29 и 13. Чтобы не забыть о нем, мы надписали его над десятками числа 29.
Этот десяток мы прибавим к результату сложения десятков чисел 29 и 13. Чтобы не забыть о нем, мы надписали его над десятками числа 29.
Теперь складываем десятки. Два десятка плюс один десяток будет три десятка, плюс один десяток, который остался от предыдущего сложения. В результате в разряде десятков получаем четыре десятка:
Пример 2. Сложить по разрядам числа 862 и 372.
Начинаем с разряда единиц. В разряде единиц числа 862 располагается цифра 2, в разряде единиц числа 372 — также цифра 2. Это означает, что разряд единиц числа 862 содержит две единицы, и разряд единиц числа 372 также содержит две единицы. Складываем 2 единицы плюс 2 единицы — получаем 4 единицы. Записываем цифру 4 в разряде единиц нового числа:
Далее складываем десятки. В разряде десятков числа 862 располагается цифра 6, а в разряде десятков числа 372 — число 7. Это означает, что разряд десятков числа 862 содержит шесть десятков, а разряд десятков числа 372 содержит семь десятков. Складываем 6 десятков и 7 десятков — получаем 13 десятков. Произошло переполнение разряда. 13 десятков это десятка повторенная 13 раз. А если повторить десятку 13 раз, то получится число 130
Складываем 6 десятков и 7 десятков — получаем 13 десятков. Произошло переполнение разряда. 13 десятков это десятка повторенная 13 раз. А если повторить десятку 13 раз, то получится число 130
10 × 13 = 130
Число 130 состоит из трех десятков и одной сотни. Три десятка мы запишем в разряде десятков нового числа, а одну сотню отправим на следующий разряд:
Как видно на рисунке, 13 десятков (число 130) мы представили как 1 сотню и 3 десятка. Три десятка мы записали в разряде десятков нового числа. А одну сотню перенесли к разрядам сотен. Эту сотню мы прибавим к результату сложения сотен чисел 862 и 372. Чтобы не забыть о ней, мы надписали её над сотнями числа 862.
Теперь складываем сотни. Восемь сотен плюс три сотни будет одиннадцать сотен плюс одна сотня, которая осталась от предыдущего сложения. В результате в разряде сотен получаем двенадцать сотен:
Здесь также происходит переполнение разряда сотен, но это не приводит к ошибке, поскольку решение завершено.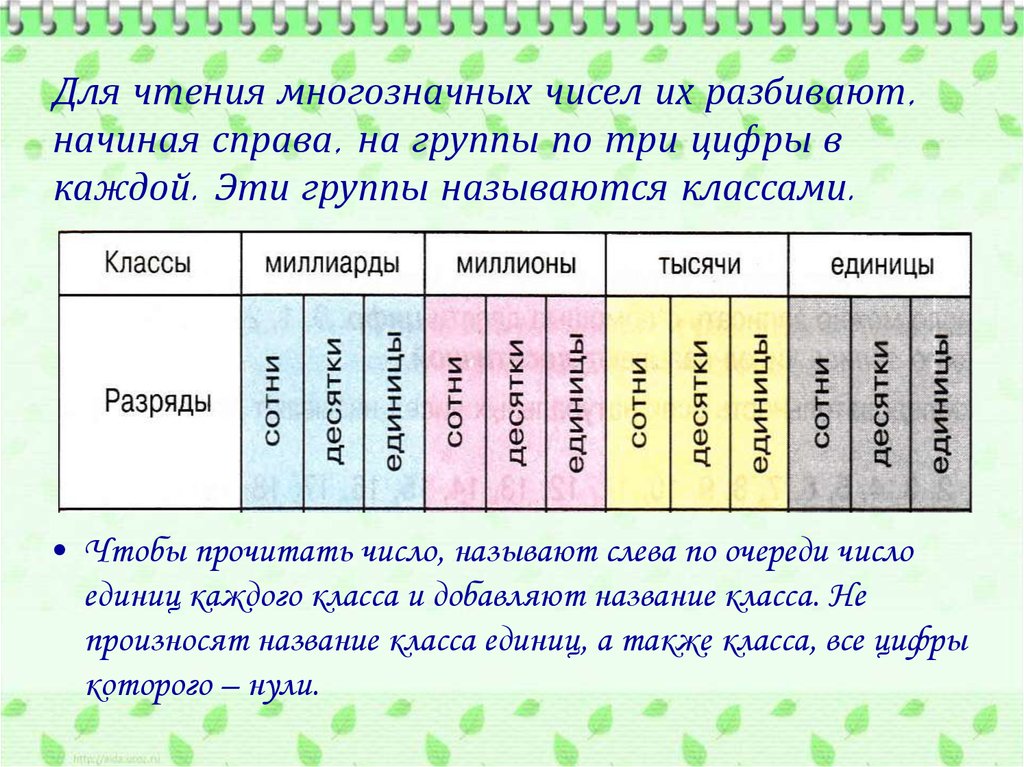 При желании с 12 сотнями можно провести те же действия, что мы провели с 13 десятками.
При желании с 12 сотнями можно провести те же действия, что мы провели с 13 десятками.
12 сотен это сотня, повторенная 12 раз. А если повторить сотню 12 раз, то получится 1200
100 × 12 = 1200
В числе 1200 две сотни и одна тысяча. Две сотни записываются в разряд сотен нового числа, а одна тысяча перенеслась к разряду тысяч.
Теперь рассмотрим примеры на вычитание. Для начала вспомним, что такое вычитание. Это операция, которая позволяет от одного числа вычесть другое. Вычитание состоит из трёх параметров: уменьшаемого, вычитаемого и разности. Вычитать тоже нужно по разрядам.
Пример 3. Вычесть из числа 65 число 12.
Начинаем с разряда единиц. В разряде единиц числа 65 располагается цифра 5, а в разряде единиц числа 12 — цифра 2. Это означает, что разряд единиц числа 65 содержит пять единиц, а разряд единиц числа 12 содержит две единицы. Вычтем из пяти единиц две единицы, получим три единицы. Записываем цифру 3 в разряде единиц нового числа:
Теперь вычитаем десятки. В разряде десятков числа 65 располагается цифра 6, а в разряде десятков числа 12 — цифра 1. Это означает, что разряд десятков числа 65 содержит шесть десятков, а разряд десятков числа 12 содержит один десяток. Вычтем из шести десятков один десяток, получим пять десятков. Записываем цифру 5 в разряде десятков нового числа:
В разряде десятков числа 65 располагается цифра 6, а в разряде десятков числа 12 — цифра 1. Это означает, что разряд десятков числа 65 содержит шесть десятков, а разряд десятков числа 12 содержит один десяток. Вычтем из шести десятков один десяток, получим пять десятков. Записываем цифру 5 в разряде десятков нового числа:
Пример 4. Вычесть из числа 32 число 15
В разряде единиц числа 32 содержится две единицы, а в разряде единиц числа 15 — пять единиц. От двух единиц не вычесть пять единиц, поскольку две единицы меньше, чем пять единиц.
Сгруппируем 32 яблока так, чтобы в первой группе было три десятка яблок, а во второй — оставшиеся две единицы яблок:
Итак, нам нужно из этих 32 яблок вычесть 15 яблок, то есть вычесть пять единиц и один десяток яблок. Причем вычесть по разрядам.
От двух единиц яблок нельзя вычесть пять единиц яблок. Чтобы выполнить вычитание, две единицы должны взять несколько яблок у соседней группы (разряда десятков). Но нельзя брать сколько хочется, поскольку десятки строго упорядочены по десять штук. Разряд десятков может дать двум единицам только один целый десяток.
Но нельзя брать сколько хочется, поскольку десятки строго упорядочены по десять штук. Разряд десятков может дать двум единицам только один целый десяток.
Итак, берём один десяток из разряда десятков и отдаём его двум единицам:
К двум единицам яблок теперь присоединился один десяток яблок. Получается 12 единиц яблок. А от двенадцати можно вычесть пять, получится семь. Записываем цифру 7 в разряде единиц нового числа:
Теперь вычитаем десятки. Поскольку разряд десятков отдал единицам один десяток, сейчас он имеет не три, а два десятка. Поэтому вычитаем из двух десятков один десяток. Останется один десяток. Записываем цифру 1 в разряде десятков нового числа:
Чтобы не забывать, что в каком-то разряде был взят один десяток (либо сотня либо тысяча), над этим разрядом принято ставить точку.
Пример 5. Вычесть из числа 653 число 286
В разряде единиц числа 653 содержится три единицы, а в разряде единиц числа 286 — шесть единиц.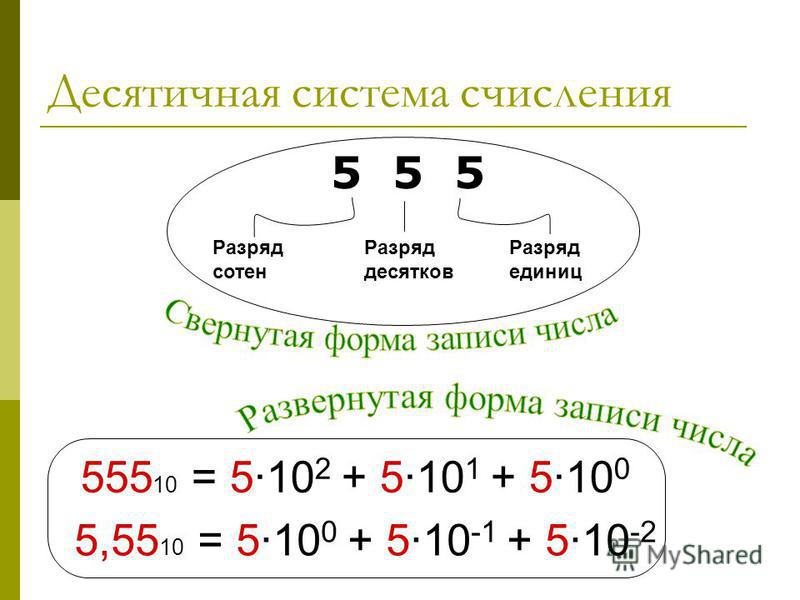 От трёх единиц не вычесть шесть единиц, поэтому берем один десяток у разряда десятков. Ставим точку над разрядом десятков, чтобы помнить о том, что мы взяли оттуда один десяток:
От трёх единиц не вычесть шесть единиц, поэтому берем один десяток у разряда десятков. Ставим точку над разрядом десятков, чтобы помнить о том, что мы взяли оттуда один десяток:
Взятый один десяток и три единицы вместе образуют тринадцать единиц. От тринадцати единиц можно вычесть шесть единиц, получится семь единиц. Записываем цифру 7 в разряде единиц нового числа:
Теперь вычитаем десятки. Раньше разряд десятков числа 653 содержал пять десятков, но мы взяли с него один десяток, и теперь в разряде десятков содержатся четыре десятка. Из четырех десятков не вычесть восемь десятков, поэтому берем одну сотню у разряда сотен. Ставим точку над разрядом сотен, чтобы помнить о том, что мы взяли оттуда одну сотню:
Взятая одна сотня и четыре десятка вместе образуют четырнадцать десятков. От четырнадцати десятков можно вычесть восемь десятков, получится шесть десятков. Записываем цифру 6 в разряде десятков нового числа:
Теперь вычитаем сотни. Раньше разряд сотен числа 653 содержал шесть сотен, но мы взяли с него одну сотню, и теперь в разряде сотен содержатся пять сотен. Из пяти сотен можно вычесть две сотни, получается три сотни. Записываем цифру 3 в разряде сотен нового числа:
Из пяти сотен можно вычесть две сотни, получается три сотни. Записываем цифру 3 в разряде сотен нового числа:
Намного сложнее вычитать из чисел вида 100, 200, 300, 1000, 10000. То есть числа, у которых на конце нули. Чтобы выполнить вычитание, каждому разряду приходится занимать десятки/сотни/ тысячи у следующего разряда. Давайте посмотрим, как это происходит.
Пример 6. Вычесть из числа 200 число 84
В разряде единиц числа 200 содержится ноль единиц, а в разряде единиц числа 84 — четыре единицы. От нуля не вычесть четыре единицы, поэтому берем один десяток у разряда десятков. Ставим точку над разрядом десятков, чтобы помнить о том, что мы взяли оттуда один десяток:
Но в разряде десятков нет десятков, которые мы могли бы взять, поскольку там тоже ноль. Чтобы разряд десятков смог дать нам один десяток, мы должны взять для него одну сотню у разряда сотен. Ставим точку над разрядом сотен, чтобы помнить о том, что мы взяли оттуда одну сотню для разряда десятков:
Взятая одна сотня это десять десятков.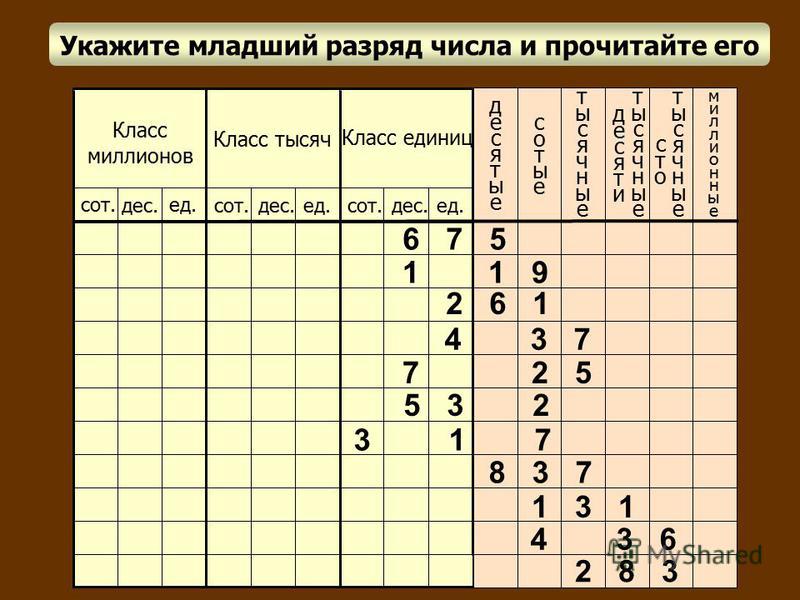 От этих десяти десятков мы берём один десяток и отдаём его единицам. Этот взятый один десяток и прежние ноль единиц вместе образуют десять единиц. От десяти единиц можно вычесть четыре единицы, получится шесть единиц. Записываем цифру 6 в разряде единиц нового числа:
От этих десяти десятков мы берём один десяток и отдаём его единицам. Этот взятый один десяток и прежние ноль единиц вместе образуют десять единиц. От десяти единиц можно вычесть четыре единицы, получится шесть единиц. Записываем цифру 6 в разряде единиц нового числа:
Теперь вычитаем десятки. Чтобы вычесть единицы мы обратились к разряду десятков за одним десятком, но на тот момент этот разряд был пуст. Чтобы разряд десятков смог дать нам один десяток, мы взяли одну сотню у разряда сотен. Эту одну сотню мы назвали «десять десятков». Один десяток мы отдали единицам. Значит на данный момент в разряде десятков содержатся не десять, а девять десятков. От девяти десятков можно вычесть восемь десятков, получится один десяток. Записываем цифру 1 в разряде десятков нового числа:
Теперь вычитаем сотни. Для разряда десятков мы брали у разряда сотен одну сотню. Значит сейчас в разряде сотен содержатся не две сотни, а одна. Поскольку в вычитаемом разряд сотен отсутствует, мы переносим эту одну сотню в разряд сотен нового числа:
Получили окончательный ответ 116.
Естественно, выполнять вычитание таким традиционным методом довольно сложно, особенно на первых порах. Поняв сам принцип вычитания, можно воспользоваться нестандартными способами.
Первый способ заключается в том, чтобы уменьшить число, у которого на конце нули на одну единицу. Далее из полученного результата вычесть вычитаемое и к полученной разности прибавить единицу, которую изначально вычли из уменьшаемого. Давайте решим предыдущий пример этим способом:
Уменьшаемое здесь это число 200. Уменьшим это число на единицу. Если от 200 вычесть 1 получится 199. Теперь в примере 200 − 84 вместо числа 200 записываем число 199 и решаем пример 199 − 84. А решение этого примера не составляет особого труда. Единицы вычтем из единиц, десятки из десятков, а сотню просто перенесем к новому числу, поскольку в числе 84 нет сотен:
Получили ответ 115. Теперь к этому ответу прибавляем единицу, которую мы изначально вычли из числа 200
Получили окончательный ответ 116.
Пример 7. Вычесть из числа 100000 число 91899
Вычтем из 100000 единицу, получим 99999
Теперь из 99999 вычитаем 91899
К полученному результату 8100 прибавим единицу, которую мы вычли из 100000
Получили окончательный ответ 8101.
Второй способ вычитания заключается в том, чтобы рассматривать цифру, находящуюся в разряде, как самостоятельное число. Решим несколько примеров этим способом.
Пример 8. Вычесть из числа 75 число 36
Будем считать, что каждая цифра в разряде это самостоятельное число.
Итак, в разряде единиц числа 75 располагается число 5, а в разряде единиц числа 36 располагается число 6. Из пяти не вычесть шести, поэтому берем одну единицу у следующего числа, находящегося в разряде десятков.
В разряде десятков располагается число 7. Берем от этого числа одну единицу и мысленно дописываем её слева от числа 5
А поскольку от числа 7 взята одна единица, это число уменьшится на одну единицу и обратится в число 6
Теперь в разряде единиц числа 75 располагается число 15, а в разряде единиц числа 36 число 6. Из 15 можно вычесть 6, получится 9. Записываем число 9 в разряде единиц нового числа:
Из 15 можно вычесть 6, получится 9. Записываем число 9 в разряде единиц нового числа:
Переходим к следующему числу, находящемуся в разряде десятков. Раньше там располагалось число 7, но мы взяли с этого числа одну единицу, поэтому сейчас там располагается число 6. А в разряде десятков числа 36 располагается число 3. Из 6 можно вычесть 3, получится 3. Записываем число 3 в разряде десятков нового числа:
Пример 9. Вычесть из числа 200 число 84
Будем считать, что каждая цифра в разряде это самостоятельно число.
Итак, в разряде единиц числа 200 располагается ноль, а в разряде единиц числа 84 — располагается четыре. От нуля не вычесть четыре, поэтому берем одну единицу у следующего числа, находящегося в разряде десятков. Но в разряде десятков тоже ноль. Ноль не сможет дать нам единицу. В таком случае за следующее принимаем число 20.
Берём одну единицу от числа 20 и мысленно дописываем её слева от нуля, располагающегося в разряде единиц. А поскольку от числа 20 взята одна единица, это число обратится в число 19
А поскольку от числа 20 взята одна единица, это число обратится в число 19
Теперь в разряде единиц располагается число 10. Десять минус четыре равно шесть. Записываем число 6 в разряде единиц нового числа:
Переходим к следующему числу, находящемуся в разряде десятков. Раньше там располагался ноль, но этот ноль вместе со следующей цифрой 2 образовал число 20, от которого мы брали одну единицу. В результате число 20 обратилось в число 19. Получается, что теперь в разряде десятков числа 200 располагается число 9, а в разряде десятков числа 84 располагается число 8. Девять минус восемь равно одному. Записываем число 1 в разряде десятков нашего ответа:
Переходим к следующему числу, находящемуся к разряду сотен. Раньше там располагалось число 2, но это число вместе с цифрой 0 мы приняли за число 20, от которого взяли одну единицу. В результате число 20 обратилось в число 19. Получается, что теперь в разряде сотен числа 200 располагается число 1, а в числе 84 разряд сотен пустой, поэтому мы переносим эту единицу к новому числу:
Этот метод поначалу кажется сложным и лишенным всякого смысла, но на деле он самый лёгкий. В основном мы будем им пользоваться при сложении и вычитании чисел в столбик.
В основном мы будем им пользоваться при сложении и вычитании чисел в столбик.
Сложение в столбик
Сложение в столбик это школьная операция, которую помнят многие, но не мешает вспомнить её ещё раз. Сложение в столбик происходит по разрядам — единицы складываются с единицами, десятки с десятками, сотни с сотнями, тысячи с тысячами.
Рассмотрим несколько примеров.
Пример 1. Сложить 61 и 23.
Сначала записываем первое число, а под ним второе число так, чтобы единицы и десятки второго числа оказались под единицами и десятками первого числа. Всё это соединяем знаком сложения (+) по вертикали:
Теперь единицы первого числа складываем с единицами второго числа, а десятки первого числа складываем с десятками второго числа:
Получили 61 + 23 = 84.
Пример 2. Сложить 108 и 60
Записываем числа в столбик. Единицы под единицами, десятки под десятками:
Теперь складываем единицы первого числа с единицами второго числа, десятки первого числа с десятками второго числа, сотни первого числа с сотнями второго числа. Но сотня есть только у первого числа 108. В этом случае цифра 1 из разряда сотен добавляется к новому числу (нашему ответу). Как говорили в школе «сносится»:
Но сотня есть только у первого числа 108. В этом случае цифра 1 из разряда сотен добавляется к новому числу (нашему ответу). Как говорили в школе «сносится»:
Видно, что мы снесли цифру 1 к нашему ответу.
Когда речь идёт о сложении, нет разницы в каком порядке записывать числа. Наш пример вполне можно было записать и так:
Первая запись, где число 108 было наверху, более удобнее для вычисления. Человек вправе выбирать любую запись, но обязательно нужно помнить, что единицы надо записывать строго под единицами, десятки под десятками, сотни под сотнями. Другими словами, следующие записи будут неправильными:
Если вдруг при сложении соответствующих разрядов получится число, которое не помещается в разряд нового числа, то необходимо записать одну цифру из младшего разряда, а оставшуюся перенести на следующий разряд.
Речь в данном случае идет о переполнении разряда, о котором мы говорили ранее. Например, при сложении 26 и 98 получается 124. Давайте посмотрим, как это получилось.
Записываем числа в столбик. Единицы под единицами, десятки под десятками:
Складываем единицы первого числа с единицами второго числа: 6+8=14. Получили число 14, которое не вместится в разряд единиц нашего ответа. В таких случаях мы сначала вытаскиваем из 14 цифру, находящуюся в разряде единиц и записываем её в разряде единиц нашего ответа. В разряде единиц числа 14 располагается цифра 4. Записываем эту цифру в разряде единиц нашего ответа:
А куда девать цифру 1 из числа 14? Здесь начинается самое интересное. Эту единицу мы переносим на следующий разряд. Она будет добавлена к разряду десятков нашего ответа.
Складываем десятки с десятками. 2 плюс 9 равно 11, плюс добавляем единицу, которая досталась нам от числа 14. Добавив к 11 нашу единицу, мы получим число 12, которое и запишем в разряде десятков нашего ответа. Поскольку это конец решения, здесь уже не стоит вопрос о том, вместится ли полученный ответ в разряд десятков. 12 мы записываем целиком, образуя окончательный ответ.
Получили ответ 124.
Говоря традиционным методом сложения, при сложении 6 и 8 единиц получилось 14 единиц. 14 единиц это 4 единицы и 1 десяток. Четыре единицы мы записали в разряде единиц, а один десяток отправили на следующий разряд (к разрядам десятков). Затем сложив 2 десятка и 9 десятков, мы получили 11 десятков, плюс добавили 1 десяток, который остался при сложении единиц. В результате получили 12 десятков. Эти двенадцать десятков мы записали целиком, образуя окончательный ответ 124.
Этот простенький пример демонстрирует школьную ситуацию, в которой говорят «четыре пишем, один в уме». Если вы будете решать примеры и у вас после сложения разрядов останется цифра, которую надо держать в уме, запишите её над тем разрядом, куда она будет потом добавлена. Это позволит вам не забыть о ней:
Пример 2. Сложить числа 784 и 548
Записываем числа в столбик. Единицы под единицами, десятки под десятками, сотни под сотнями:
Складываем единицы первого числа с единицами второго числа: 4+8=12. Число 12 не вмещается в разряд единиц нашего ответа, поэтому мы из 12 вынимаем цифру 2 из разряда единиц и записываем её в разряд единиц нашего ответа. А цифру 1 переносим на следующий разряд:
Число 12 не вмещается в разряд единиц нашего ответа, поэтому мы из 12 вынимаем цифру 2 из разряда единиц и записываем её в разряд единиц нашего ответа. А цифру 1 переносим на следующий разряд:
Теперь складываем десятки. Складываем 8 и 4 плюс единица, которая осталась от предыдущей операции (единица осталась от 12, на рисунке она выделена синим цветом). Складываем 8+4+1=13. Число 13 не вместится в разряд десятков нашего ответа, поэтому мы запишем цифру 3 в разряде десятков, а единицу перенесём на следующий разряд:
Теперь складываем сотни. Складываем 7 и 5 плюс единица, которая осталась от предыдущей операции: 7+5+1=13. Записываем число 13 в разряд сотен:
Вычитание в столбик
Пример 1. Вычтем из числа 69 число 53.
Запишем числа в столбик. Единицы под единицами, десятки под десятками. Затем вычитаем по разрядам. Из единиц первого числа вычитаем единицы второго числа. Из десятков первого числа вычитаем десятки второго числа:
Получили ответ 16.
Пример 2. Найти значение выражения 95 − 26
Записываем в столбик данное выражение:
Разряд единиц числа 95 содержит 5 единиц, а разряд единиц числа 26 содержит 6 единиц. От пяти единиц нельзя вычесть шесть единиц, поэтому берем один десяток у разряда десятков. Этот десяток и имеющиеся пять единиц вместе составляют 15 единиц. Из 15 единиц можно вычесть 6 единиц, получится 9 единиц. Записываем цифру 9 в разряде единиц нашего ответа:
Теперь вычитаем десятки. Разряд десятков числа 95 раньше содержал 9 десятков, но мы взяли с этого разряда один десяток, и сейчас он содержит 8 десятков. А разряд десятков числа 26 содержит 2 десятка. Из восьми десятков можно вычесть два десятка, получится шесть десятков. Записываем цифру 6 в разряде десятков нашего ответа:
Воспользуемся нестандартным способом вычитания при котором каждая цифра, входящая в число, рассматривается как отдельное число. При вычитании больших чисел в столбик этот способ очень удобен.
В разряде единиц уменьшаемого располагается число 5. А в разряде единиц вычитаемого число 6. Из пятёрки не вычесть шестёрку. Поэтому берем одну единицу у числа 9. Взятая единица мысленно дописывается слева от пятёрки. А поскольку у числа 9 мы взяли одну единицу, это число уменьшится на одну единицу:
В результате пятёрка обращается в число 15. Теперь можно из 15 вычесть 6. Получается 9. Записываем число 9 в разряде единиц нашего ответа:
Переходим к разряду десятков. Раньше там располагалось число 9, но поскольку мы взяли у него одну единицу оно обратилось в число 8. В разряде десятков второго числа располагается число 2. Восемь минус два будет шесть. Записываем число 6 в разряде десятков нашего ответа:
Пример 3. Найдем значение выражения 2412 − 2317
Записываем в столбик данное выражение:
В разряде единиц числа 2412 располагается число 2, а в разряде единиц числа 2317 располагается число 7. Из двойки не вычесть семёрку, поэтому берем единицу у следующего числа 1. Взятую единицу мысленно дописываем слева от двойки:
Взятую единицу мысленно дописываем слева от двойки:
В результате двойка обращается в число 12. Теперь можно из 12 вычесть 7. Получается 5. Записываем цифру 5 в разряде единиц нашего ответа:
Переходим к десяткам. В разряде десятков числа 2412 раньше располагалось число 1, но поскольку мы взяли у него одну единицу, оно обратилось в 0. А в разряде десятков числа 2317 располагается число 1. Из нуля не вычесть единицу. Поэтому берем одну единицу у следующего числа 4. Взятую единицу мысленно дописываем слева от нуля. А поскольку у числа 4 мы взяли одну единицу, это число уменьшится на одну единицу:
В результате ноль обращается в число 10. Теперь можно из 10 вычесть 1. Получается 9. Записываем цифру 9 в разряде десятков нашего ответа:
В разряде сотен числа 2412 раньше располагалось число 4, но сейчас там располагается число 3. В разряде сотен числа 2317 также располагается число 3. Три минус три равно нулю. То же самое и с разрядами тысяч в обоих числах. Два минус два равно нулю. А если разность старших разрядов равна нулю, то этот ноль не записывают. Поэтому окончательным ответом будет число 95.
Два минус два равно нулю. А если разность старших разрядов равна нулю, то этот ноль не записывают. Поэтому окончательным ответом будет число 95.
Пример 4. Найти значение выражения 600 − 8
Запишем в столбик данное выражение:
В разряде единиц числа 600 располагается ноль, а в разряде единиц числа 8 само это число. Из нуля не вычесть восьмерку, поэтому берем единицу у следующего числа. Но следующее число это тоже ноль. Тогда за следующее число принимаем число 60. Берем одну единицу у этого числа и мысленно дописываем её слева от нуля. А поскольку у числа 60 мы взяли одну единицу, это число уменьшится на одну единицу:
Теперь в разряде единиц располагается число 10. Из 10 можно вычесть 8, получится 2. Записываем число 2 в разряде единиц нового числа:
Переходим к следующему числу, находящемуся в разряде десятков. В разряде десятков раньше располагался ноль, но сейчас там располагается число 9, а во втором числе разряд десятков отсутствует. Поэтому число 9 переносится к новому числу:
Поэтому число 9 переносится к новому числу:
Переходим к следующему числу, находящемуся в разряде сотен. В разряде сотен раньше располагалось число 6, но сейчас там располагается число 5, а во втором числе разряд сотен отсутствует. Поэтому число 5 переносится к новому числу:
Пример 5. Найти значение выражения 10000 − 999
Запишем в столбик данное выражение:
В разряде единиц числа 10000 располагается 0, а в разряде единиц числа 999 располагается число 9. Из нуля не вычесть девятку, поэтому берем одну единицу у следующего числа, находящегося в разряде десятков. Но в следующем разряде тоже ноль. Тогда за следующее число принимаем 1000 и берем от этого числа единицу:
Следующее число в данном случае было 1000. Взяв у него единицу, мы обратили его в число 999. А взятую единицу дописали слева от нуля.
Дальнейшее вычисление не составило особого труда. Десять минус девять равно одному. Вычитание чисел, находящихся в разряде десятков обоих чисел дало ноль. Вычитание чисел, находящихся в разряде сотен обоих чисел тоже дало ноль. А девятка из разряда тысяч была перенесена к новому числу:
Вычитание чисел, находящихся в разряде сотен обоих чисел тоже дало ноль. А девятка из разряда тысяч была перенесена к новому числу:
Пример 6. Найти значение выражения 12301 − 9046
Запишем в столбик данное выражение:
В разряде единиц числа 12301 располагается число 1, а в разряде единиц числа 9046 располагается число 6. Из единицы не вычесть шесть, поэтому берем одну единицу у следующего числа, находящегося в разряде десятков. Но в следующем разряде располагается ноль. Ноль ничего нам дать не сможет. Тогда за следующее число принимаем 1230 и берем от этого числа единицу:
Следующее число в данном случае было 1230. Взяв у него единицу, мы обратили его в число 1229. А взятую единицу мысленно дописали слева от единицы, находящейся в разряде единиц.
Дальнейшее вычисление не составило особого труда. Одиннадцать минус шесть равно пять. Вычитание чисел, находящихся в разряде десятков обоих чисел дало число 5. Вычитание чисел, находящихся в разряде сотен обоих чисел дало число 2. Вычитание чисел, находящихся в разряде тысяч обоих чисел дало число 3.
Вычитание чисел, находящихся в разряде тысяч обоих чисел дало число 3.
Задания для самостоятельного решения
Задание 1. Выполните сложение:
Решение:
Показать решение
Задание 2. Выполните сложение:
Решение:
Показать решение
Задание 3. Выполните сложение:
Решение:
Показать решение
Задание 4. Выполните сложение:
Решение:
Показать решение
Задание 5. Выполните сложение:
Решение:
Показать решение
Задание 6. Выполните сложение:
Решение:
Показать решение
Задание 7. Выполните сложение:
Решение:
Показать решение
Задание 8. Выполните вычитание:
Решение:
Показать решение
Задание 9. Выполните вычитание:
Решение:
Показать решение
Задание 10. Выполните вычитание:
Решение:
Показать решение
Задание 11. Выполните вычитание:
Решение:
Показать решение
Задание 12. Выполните вычитание:
Решение:
Показать решение
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Презентация по математике 6 класс на тему Понятие положительной десятичной дроби доклад, проект
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация на тему Презентация по математике 6 класс на тему Понятие положительной десятичной дроби, предмет презентации: Математика.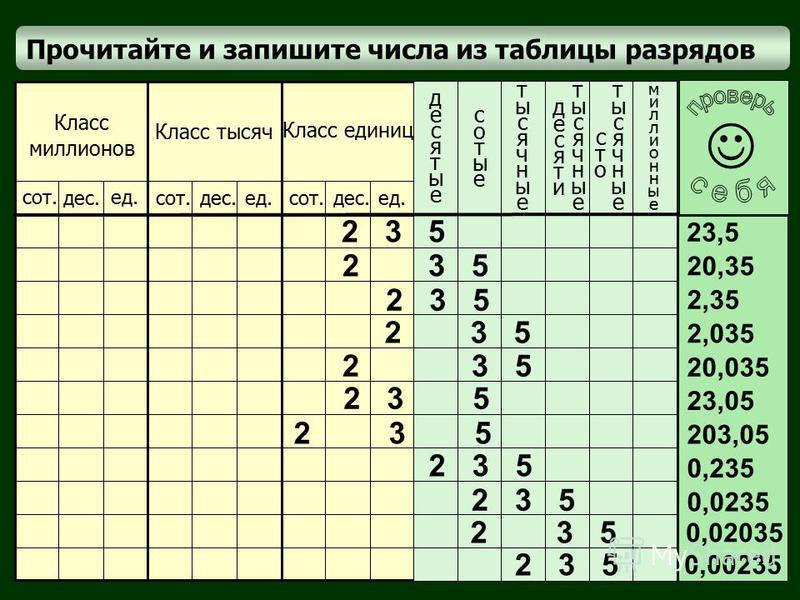 Этот материал в формате pptx (PowerPoint) содержит 21 слайдов, для просмотра воспользуйтесь проигрывателем. Презентацию на заданную тему можно скачать внизу страницы, поделившись ссылкой в социальных сетях! Презентации взяты из открытого доступа или загружены их авторами, администрация сайта не отвечает за достоверность информации в них, все права принадлежат авторам презентаций и могут быть удалены по их требованию.
Этот материал в формате pptx (PowerPoint) содержит 21 слайдов, для просмотра воспользуйтесь проигрывателем. Презентацию на заданную тему можно скачать внизу страницы, поделившись ссылкой в социальных сетях! Презентации взяты из открытого доступа или загружены их авторами, администрация сайта не отвечает за достоверность информации в них, все права принадлежат авторам презентаций и могут быть удалены по их требованию.
Дано число 719524.
Какая цифра записана в разряде:
а) тысяч; г) единиц;
б) десятков; д) десятков тысяч;
в) сотен тысяч; е) сотен?
5
2
7
4
1
9
Дано число 2532843.
В каких разрядах записана цифра 2; 3; 4; 5; 8?
2 : разряд тысяч, разряд миллионов
3 : разряд единиц, разряд десятков тысяч
4 : разряд десятков
5 : разряд сотен тысяч
8 : разряд сотен
Вставить пропущенные числа
А) 5см 7мм = см
Б) 52см= м
В) 4км 82м = км
Г) 1см 3мм = см
Д) 8кг 1г = кг
Е) 34кг = ц
Понятие положительной десятичной дроби
6 класс
3
4
5
5
3
4
5
5
Смотри! Думай! Делай вывод!
Алгоритм десятичной записи
1. Уравнять, если необходимо, число цифр в числителе с числом нулей в знаменателе.
Уравнять, если необходимо, число цифр в числителе с числом нулей в знаменателе.
2. Записать целую часть (она может быть равной нулю).
3. Поставить запятую, определяющую целую часть от дробной.
4. Записать числитель дробной части.
Как быть в случае, если в числителе дроби цифр меньше чем нулей в знаменателе?
Запишите в виде десятичной
дроби:
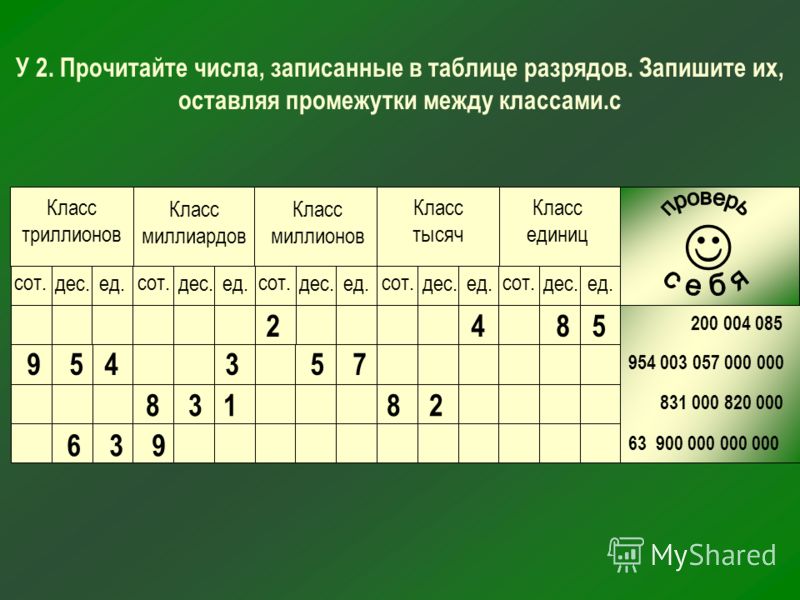
Прочитайте числа, записанные в таблице разрядов. Запишите их.
27,805
3,29
230,09
0,004
Таблица разрядов десятичных дробей
Знаки, стоящие в десятичной дроби после запятой, называют десятичными знаками. Любую десятичную дробь легко записать в виде обыкновенной дроби (простой или смешанной):
Запиши в виде десятичной дроби
№2. Замени десятичную дробь обыкновенной или смешанным числом.
Замени десятичную дробь обыкновенной или смешанным числом.
0,2 = 5,6 =
0,04 = 25,18 =
1,049 = 0,0005 =
Прочитайте и запишите в виде обыкновенной дроби
3,2=
7,12=
12,333=
9,02=
16,023=
ИГРА «ОТГАДАЙ слово»
Иоганн Кеплер
(1571-1630)
предложил современную запись десятичных дробей
ИЗ ИСТОРИИ
Метрическая система мер
Расстояние; Масса; площадь; объем.
Деци — ; санти — ; милли – эти приставки возникли от латинских слов decima, centima, millesima (одна десятая, одна сотая и одна тысячная)
1 дм = 0,1 м; 1 см = 0,01 м; 1 мм = 0,001 м.
1 копейка = 0,01 рубля; 1 цент = 0,01 доллара и т.п.
Задание
№724 (а,б)
№ 725 (а,в)
Домашнее задание:
П 4.1 стр 142
№726(а,б)
№727 (а-ж)
Спасибо за внимание!
Скачать презентацию
Это сайт презентаций, где можно хранить и обмениваться своими презентациями, докладами, проектами, шаблонами в формате PowerPoint с другими пользователями. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами.
Для правообладателей
Обратная связь
Email: Нажмите что бы посмотреть
§ Разряды и классы. Класс единиц, тысяч и миллионов
Разряды и классы Разрядные слагаемые
Для записи чисел люди придумали десять знаков, которые называются цифрами. Это:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Это:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
С помощью десяти цифр можно записать любое натуральное число.
От количества знаков (цифр) в числе зависит его название.
Число, состоящее из одного знака (цифры), называется однозначным. Наименьшее однозначное натуральное число — «1» , наибольшее — «9».
Число, состоящее из двух знаков (цифр), называется двузначным. Наименьшее двузначное число — «10», наибольшее — «99» .
Числа, записанные с помощью двух, трёх, четырёх и более цифр, называются двузначными, трёхзначными, четырёхзначными или многозначными. Наименьшее трёхзначное число — «100», наибольшее — «999».
Каждая цифра в записи многозначного числа занимает определённое место — позицию.
Запомните!
Разряд — это место (позиция), на котором в записи числа стоит цифра.
Одна и та же цифра в записи числа может иметь разные значения в зависимости от того,
в каком разряде она стоит.
Разряды отсчитываются с конца числа.
Разряд единиц — это самый младший разряд, которым заканчивается любое число.
Цифра «5» — означает «5» единиц, если пятёрка стоит на последнем месте в записи числа (в разряде единиц).
Разряд десятков — это разряд, который стоит перед разрядом единиц.
Цифра «5» — означает «5» десятков, если она стоит на предпоследнем месте (в разряде десятков).
Разряд сотен — это разряд, который стоит перед разрядом десятков. Цифра «5» означает «5» сотен, если она стоит на третьем месте от конца числа (в разряде сотен).
Запомните!
Если в числе отсутствует какой-либо разряд, то в записи числа на его месте будет стоять цифра «0» (ноль).
Пример. В числе «807» содержится
8 сотен,
0 десятков и
7 единиц —
такая запись называется разрядным составом числа.
807 = 8 сотен 0 десятков 7 единиц
Каждые 10 единиц любого разряда образуют новую единицу более высокого разряда. Например, 10 единиц образуют 1 десяток, а 10 десятков образуют 1 сотню.
Таким образом, значение цифры от разряда к разряду (от единиц к десяткам, от десятков к сотням) увеличивается в 10 раз. Поэтому система счёта (счисления), которую мы используем, называется десятичной системой счисления.
В записи числа разряды, начиная справа, группируются в классы по три разряда в каждом.
Класс единиц или первый класс — это класс, который образуют первые три разряда (справа от конца числа): разряд единиц, разряд десятков и разряд сотен.
Пример.
| Числа | Класс единиц (первый класс) | ||
|---|---|---|---|
| сотни | десятки | единицы | |
| 6 | — | — | 6 |
| 34 | — | 3 | 4 |
| 148 | 1 | 4 | 8 |
| Числа | Класс единиц (первый класс) | ||
|---|---|---|---|
| сотни | десятки | единицы | |
| 6 | — | — | 6 |
| 34 | — | 3 | 4 |
| 148 | 1 | 4 | 8 |
Класс тысяч или второй класс — это класс, который образуют следующие
три разряда: единицы тысяч, десятки тысяч и сотни тысяч.
Пример.
| Числа | Класс тысяч (второй класс) | Класс единиц (первый класс) | ||||
|---|---|---|---|---|---|---|
| сотни тысяч | десятки тысяч | единицы тысяч | сотни | десятки | единицы | |
| 5 234 | — | — | 5 | 2 | 3 | 4 |
| 12 803 | — | 1 | 2 | 8 | 0 | 3 |
| 356 149 | 3 | 5 | 6 | 1 | 4 | 9 |
| Числа | Класс тысяч (второй класс) | Класс единиц (первый класс) | ||||
|---|---|---|---|---|---|---|
| сотни тысяч | десятки тысяч | единицы тысяч | сотни | десятки | единицы | |
| 12 803 | — | 1 | 2 | 8 | 0 | 3 |
| 356 149 | 3 | 5 | 6 | 1 | 4 | 9 |
Напоминаем, что 10 единиц разряда сотен (из класса единиц) образуют одну тысячу
(единицу следующего разряда: единицу тысяч в классе тысяч).
10 сотен = 1 тысяча
Класс миллионов или третий класс — это класс, который образуют следующие три разряда: единицы миллионов, десятки миллионов и сотни миллионов.
Единица разряда миллионов — это один миллион или тысяча тысяч (1 000 тысяч). Один миллион можно записать в виде числа «1 000 000».
Десять таких единиц образуют новую разрядную единицу — десять миллионов «10 000 000»
Десять десятков миллионов образуют новую разрядную единицу — сто миллионов или в записи цифрами «100 000 000».
Пример.
| Числа | Класс миллионов (третий класс) | Класс тысяч (второй класс) | Класс единиц (первый класс) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| сотни миллионов | десятки миллионов | единицы миллионов | сотни тысяч | десятки тысяч | единицы тысяч | сотни | десятки | единицы | |
| 8 345 216 | — | — | 8 | 3 | 4 | 5 | 2 | 1 | 6 |
| 93 785 342 | — | 9 | 3 | 7 | 8 | 5 | 3 | 4 | 2 |
| 134 590 720 | 1 | 3 | 4 | 5 | 9 | 0 | 7 | 2 | 0 |
| Числа | Класс миллионов (третий класс) | Класс тысяч (второй класс) | Класс единиц (первый класс) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| сотни миллионов | десятки миллионов | единицы миллионов | сотни тысяч | десятки тысяч | единицы тысяч | сотни | десятки | единицы | |
| 8 345 216 | — | — | 8 | 3 | 4 | 5 | 2 | 1 | 6 |
| 93 785 342 | — | 9 | 3 | 7 | 8 | 5 | 3 | 4 | 2 |
| 134 590 720 | 1 | 3 | 4 | 5 | 9 | 0 | 7 | 2 | 0 |
Как прочитать многозначное число
Запомните!
Чтобы прочитать многозначное число, надо назвать по очереди слева направо число единиц каждого класса и
добавить название класса.
Не произносят название класса единиц, а также название класса, все три цифры которого нули.
Например, число «134 590 720» читаем: сто тридцать четыре миллиона пятьсот девяносто тысяч семьсот двадцать.
Число «418 000 547» читаем: четыреста восемнадцать миллионов пятьсот сорок семь.
На нашем сайте для проверки своих результатов вы можете воспользоваться калькулятором разложения числа на разряды онлайн.
Важно!
Чтобы легче запомнить, как читать и записывать многозначные числа, советуем использовать выше приведённую «Таблицу классов и разрядов».
Разряды и классы Разрядные слагаемые
В зависимости от давления газа, конфигурации электродов и параметров внешней цепи существует четыре типа самостоятельных разрядов:
1. Тлеющий разряд возникает при низких давлениях. Его можно наблюдать в стеклянной трубке с впаянными у концов плоскими металлическими электродами (рис. 8.5). Вблизи катода располагается тонкий светящийся слой, называемый катодной светящейся пленкой 2. Между катодом и пленкой находится астоново темное пространство 1. Справа от светящейся пленки помещается слабо светящийся слой, называемый катодным темным пространством 3. Этот слой переходит в светящуюся область, которую называют тлеющим свечением 4, с тлеющим пространством граничит тёмный промежуток – фарадеево тёмное пространство 5. Все перечисленные слои образуют катодную часть тлеющего разряда. Вся остальная часть трубки заполнена святящимся газом. Эту часть называют положительным столбом 6. При понижении давления катодная часть разряда и фарадеево тёмное пространство увеличивается, а положительный столб укорачивается. Измерения показали, что почти все падения потенциала
приходятся на первые три участка разряда (астоново темное пространство,
катодная святящаяся плёнка и катодное тёмное пятно). В области тлеющего свечения потенциал не изменяется – здесь напряженность поля равна нулю. Наконец, в фарадеевом тёмном пространстве и положительном столбе потенциал медленно растёт. Такое распределение потенциала вызвано образованием в катодном темном пространстве положительного пространственного заряда, обусловленного повышенной концентрацией положительных ионов. Положительные ионы, ускоренные катодным падением
потенциала, бомбардируют катод и выбивают из него электроны. В астоновом темном
пространстве эти электроны, пролетевшие без столкновений в область катодного
тёмного пространства, имеют большую энергию, вследствие чего они чаще
ионизируют молекулы, чем возбуждают. Т.е. интенсивность свечения газа
уменьшается, но зато образуется много электронов и положительных ионов.
Образовавшиеся ионы в начале имеют очень малую скорость и потому в катодном
тёмном пространстве создаётся положительный пространственный заряд, что и приводит
к перераспределению потенциала вдоль трубки и к возникновению катодного падения
потенциала. Электроны, возникшие в катодном тёмном пространстве, проникают в область тлеющего свечения, которая характеризуется высокой концентрацией электронов и положительных ионов коленарным пространственным зарядом, близким к нулю (плазма). Поэтому напряженность поля здесь очень мала. В области тлеющего свечения идёт интенсивный процесс рекомбинации, сопровождающийся излучением выделяющейся при этом энергии. Таким образом, тлеющее свечение есть, в основном, свечение рекомбинации. Из области тлеющего свечения в фарадеево тёмное
пространство электроны и ионы проникают за счёт диффузии. Вероятность рекомбинации
здесь сильно падает, т.к. концентрация заряженных частиц невелика. Поэтому в
фарадеевом тёмном пространстве имеется поле. Увлекаемые этим полем электроны
накапливают энергию и часто в конце концов возникают условия, необходимые для
существования плазмы. Положительный столб представляет собой газоразрядную
плазму. Он выполняет роль проводника, соединяющего анод с катодными частями
разряда. 2. Искровой разряд возникает в газе обычно при давлениях порядка атмосферного. Он характеризуется прерывистой формой. По внешнему виду искровой разряд представляет собой пучок ярких зигзагообразных разветвляющихся тонких полос, мгновенно пронизывающих разрядный промежуток, быстро гаснущих и постоянно сменяющих друг друга (рис. 8.6). Эти полоски называют искровыми каналами .
После того, как разрядный
промежуток «пробит» искровым каналом, сопротивление его становится малым, через
канал проходит кратковременный импульс тока большой силы, в течение которого на
разрядный промежуток приходится лишь незначительное напряжение. В естественных природных условиях искровой разряд наблюдается в виде молнии. На рисунке 8.7 изображен пример искрового разряда – молния, продолжительностью 0,2 ÷ 0,3 с силой тока 10 4 – 10 5 А, длиной 20 км (рис. 8.7). 3. Дуговой разряд . Если после получения искрового разряда от мощного источника постепенно уменьшать расстояние между электродами, то разряд из прерывистого становится непрерывным, возникает новая форма газового разряда, называемая дуговым разрядом (рис. 8.8).
При этом ток резко увеличивается, достигая десятков и
сотен ампер, а напряжение на разрядном промежутке падает до нескольких десятков
вольт. 4. Коронный разряд (рис. 8.9).возникает в сильном неоднородном электрическом поле при сравнительно высоких давлениях газа (порядка атмосферного). Такое поле можно получить между двумя электродами, поверхность одного из которых обладает большой кривизной (тонкая проволочка, острие). Наличие второго электрода необязательна, но его роль могут играть ближайшие, окружающие заземленные металлические предметы. Когда электрическое поле вблизи электрода с большой кривизной достигает примерно 3∙10 6 В/м, вокруг него возникает свечение, имеющее вид оболочки или короны, откуда и произошло название заряда. | ||
Что такое разрядное значение? — [Факты и примеры определения]
Что такое разрядное значение?
В математике каждая цифра в числе имеет разрядное значение.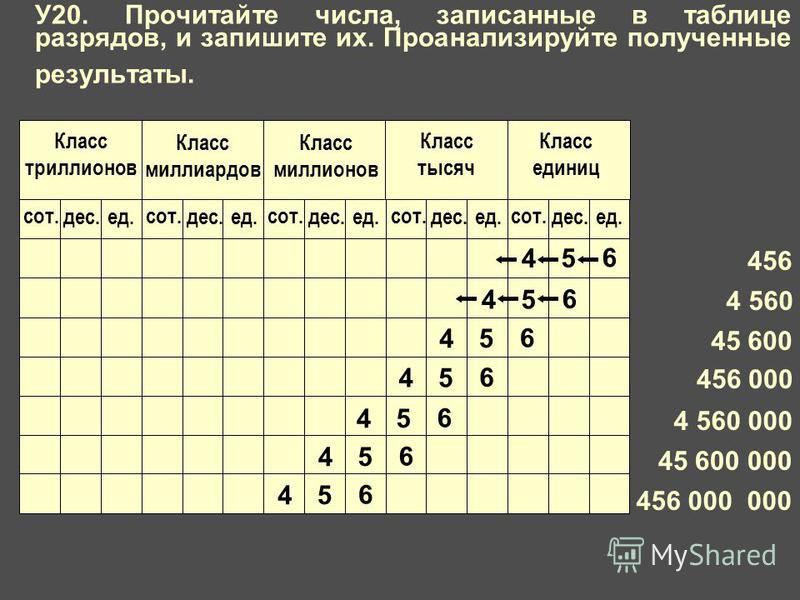 Значение места может быть определено как значение, представленное цифрой в числе на основе ее положения в числе.
Значение места может быть определено как значение, представленное цифрой в числе на основе ее положения в числе.
Например, разряд 7 из 3743 равен 7 сотням или 700. Однако разряд 7 из 7432 равен 7 тысячам или 7000. Здесь мы видим, что, несмотря на то, что цифры в обоих числах одинаковы, его разрядное значение меняется с изменением его положения.
Таблица разрядных значений
Таблица разрядных значений — это очень полезный формат таблицы, который помогает нам найти разрядное значение каждой цифры на основе ее положения в числе.
Разрядное значение цифры увеличивается в десять раз по мере того, как мы двигаемся влево по таблице разрядных значений, и уменьшается в десять раз по мере того, как мы двигаемся вправо.
Вот пример того, как рисование диаграммы разряда может помочь в определении разряда числа.
В числе 13 548
1 стоит в разряде десятков тысяч и имеет разрядное значение 10 000.
3 находится в разряде тысяч и имеет разрядное значение 3000.
5 находится в сотнях и имеет разрядное значение 500.
4 находится в разряде десятков и имеет разрядное значение 40.
8 находится в разряде единиц и имеет разрядное значение 8.
Понимание разрядное значение цифр в числах помогает сравнивать числа. Это также помогает в написании чисел в их расширенной форме. Например, расширенная форма приведенного выше числа 13 548 равна 10 000 + 3 000 + 500 + 40 + 8.
Разрядное значение с использованием десятичных блоков
Разрядное значение цифр в числах также может быть представлено с использованием десятичных блоков, что может помочь нам записывать числа в их расширенной форме.
Прежде чем использовать блоки десятичной системы счисления для нахождения разрядного значения каждой цифры в числе, давайте сначала поймем, что представляют собой эти блоки.
Вот как число 13 548 может быть представлено с помощью десятичных блоков.
Десятичное разрядное значение
Десятичные числа — это дроби или смешанные числа со знаменателем в степени десятки. В десятичном числе цифры слева от запятой представляют собой целое число. Цифры справа от десятичной дроби обозначают части. По мере продвижения сразу после запятой разрядное значение цифр становится в 10 раз меньше.
В десятичном числе цифры слева от запятой представляют собой целое число. Цифры справа от десятичной дроби обозначают части. По мере продвижения сразу после запятой разрядное значение цифр становится в 10 раз меньше.
Первая цифра справа от запятой означает десятые доли, т.е. 110. Следующее место становится в десять раз меньше и называется сотыми, т.е. 1100 и так далее.
В 27.356 27 — это целая часть числа, 2 — это разряд десятков, 20, 7 — это разряд единиц, а его разрядность — 7.
Три цифры справа от десятичной точки ,
3 стоит на десятом месте, и его разрядное значение равно 0,3 или 3 10
5 находится на сотом, и его стоимость места составляет 0,05 или 5 100
6 находится в турнирной площадке, а его стоимость места — 0,006 или 6 1000
. Номинальная стоимость
Местная стоимость и номинальная стоимость не совпадают. Номинальное значение цифры — это значение цифры, а разрядное значение цифры — это ее место в числе. Проще говоря, номинальное значение сообщает фактическое значение цифры, тогда как значение разряда сообщает значение цифры на основе ее положения.
Номинальное значение цифры — это значение цифры, а разрядное значение цифры — это ее место в числе. Проще говоря, номинальное значение сообщает фактическое значение цифры, тогда как значение разряда сообщает значение цифры на основе ее положения.
Следовательно, номинал цифры никогда не меняется независимо от ее положения в числе. Принимая во внимание, что значение разряда цифры изменяется с изменением позиции.
Например, номинальная стоимость 2 в числах 283 и 823 равна 2. В то время как разрядная стоимость 2 равна 200 в 283 и 20 в 823. из 4 в числе 84 527?
Решение:
Число 4 из 84 527 равно 4000 (четыре тысячи).
- Запишите 412 397 словами, используя разрядную систему.
Решение:
Четыреста двенадцать тысяч триста девяносто семь.
- Запишите числа цифрами и в развернутом виде:
- Десять тысяч двести тридцать шесть
- Семь тысяч четыреста восемьдесят пять
Решение:
- Десять тысяч двести тридцать- шесть = 10 236
= 10 000 + 200 + 30 + 6
- Seven thousand four hundred and eighty-five = 7,485
= 7,000 + 400 + 80 + 5
Practice Problems
7 4 8 5 Correct answer is: 8 44 221 40,421 44 211 44,201 Правильный ответ: 44,211 800 80 9 + 1 = 44211 $ 9000 80080 +0005 0,08 0,8 Правильный ответ: 0,8 |
Часто задаваемые вопросы
Почему важно понимать значение места?
Разрядное значение применяется во многих математических понятиях. Он закладывает основу для перегруппировки, умножения и т. д.
Какие манипуляции используются для обучения разрядному значению?
Манипуляторы, такие как блоки с основанием 10, снэп-кубы, unifix-кубы, bean-компоненты и т. д., используются для развития понимания разрядного значения.
Увеличивается ли разрядность цифры при ее перемещении слева направо?
Нет. Разрядность цифры уменьшается в 10 раз при ее перемещении слева направо.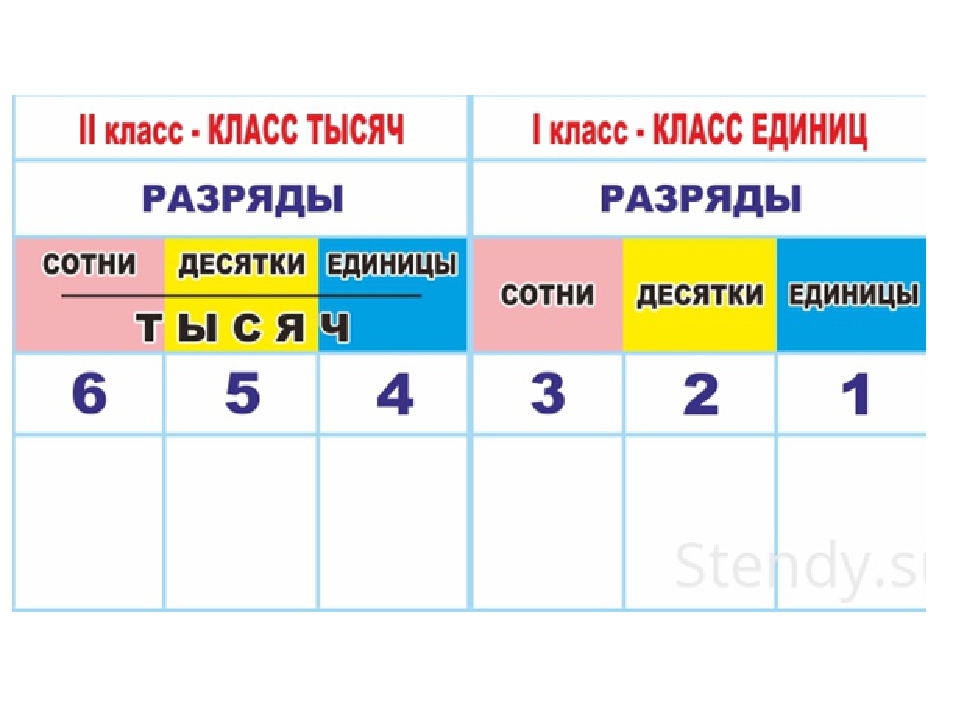
В чем разница между номиналом и разрядом цифры?
Номинальная стоимость цифры — это величина, которой она обладает естественным образом. Не зависит от положения цифры в числе. Позиция цифры зависит от ее положения в числе. Например, цифра 5 в числе 253 имеет номинальную стоимость 5, а разрядную стоимость — 50.
Разрядное значение — диаграммы с десятичными знаками
Разрядное значение в математике описывает значение каждой цифры в числе в зависимости от ее положения. Эти позиции начинаются с разряда единиц (единиц). Порядок разряда цифр в числе справа налево выражается единицами/единицами, десятками, сотнями, тысячами, десятками тысяч и так далее.
| 1. | Что такое разрядное значение? |
| 2. | Таблица стоимости мест |
| 3. | Таблица разрядов с десятичными знаками |
| 4. | Разрядная стоимость и номинальная стоимость |
5. | Часто задаваемые вопросы о стоимости места |
Что такое разрядное значение?
Разрядное значение — это значение каждой цифры в числе. Значение каждой цифры в числе зависит от ее положения. Число может иметь две одинаковые цифры, но разные значения, что определяется позицией, которую занимает цифра в числе.
Разрядное значение Значение
Разрядное значение — это значение цифры в соответствии с ее положением в числе, например единицы, десятки, сотни и т. д. Например, разрядное значение 5 в 3458 равно 5 десяткам или 50. Однако разрядное значение 5 в 5781 выражается как 5 тысяч или 5000. Важно понимать, что цифра может быть одной и той же, но ее значение зависит от ее положения в числе.
Пример: Запишите разрядность каждой цифры в числе 543.
Решение: Правильное значение разряда каждой цифры в числе может быть выражено следующим образом:
- 5 × 100 = 500 или 5 сотен
- 4 × 10 = 40 или 4 десятка
- 3 × 1 = 3 или 3 единицы
Таблица стоимости места
Таблицы разрядов помогают нам убедиться, что цифры выровнены в правильных местах.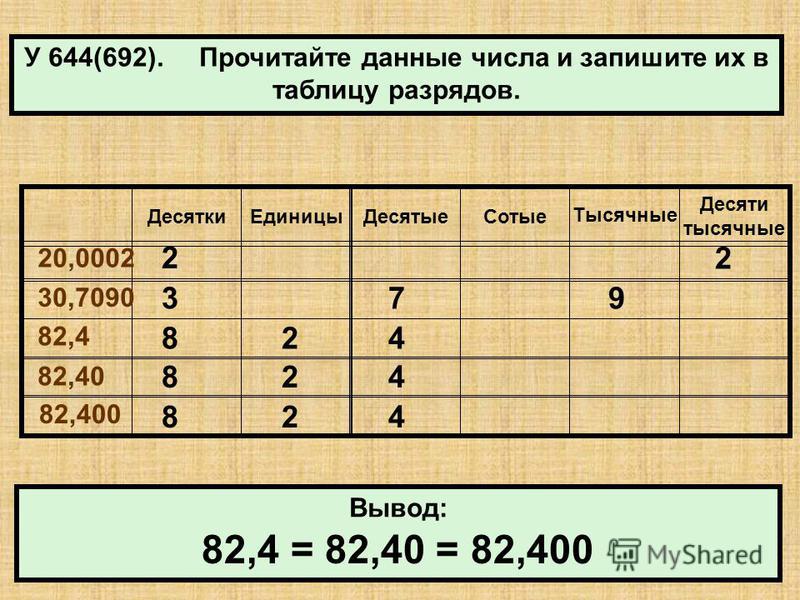 Диаграмма разряда показывает правильное положение или место цифры в числе. Чтобы точно определить позиционные значения или ценность различных цифр в числе, мы сначала записываем данные цифры в диаграмму разрядности, чтобы проверить их положение. Чтобы упростить процесс, большие числа разбиты на точки, разделенные запятыми. Наиболее часто используются два типа диаграмм стоимости мест:
Диаграмма разряда показывает правильное положение или место цифры в числе. Чтобы точно определить позиционные значения или ценность различных цифр в числе, мы сначала записываем данные цифры в диаграмму разрядности, чтобы проверить их положение. Чтобы упростить процесс, большие числа разбиты на точки, разделенные запятыми. Наиболее часто используются два типа диаграмм стоимости мест:
- Индийская таблица разрядности
- Таблица международных разрядов
Мы можем обратиться к международной или индийской диаграмме стоимости мест, основанной на системе счисления, которой следуют обе диаграммы. Индийская диаграмма стоимости места основана на индийской системе счисления, в то время как международная диаграмма стоимости места основана на международно принятой системе счисления. Основное различие между индийской и международной системами счисления заключается в размещении разделителей (запятых) и номенклатуре различных разрядных значений.
Индийская диаграмма разрядности
Индийская диаграмма разрядности представляет собой таблицу, которая используется для определения значения каждой цифры в числе на основе ее положения в соответствии с индийской системой счисления.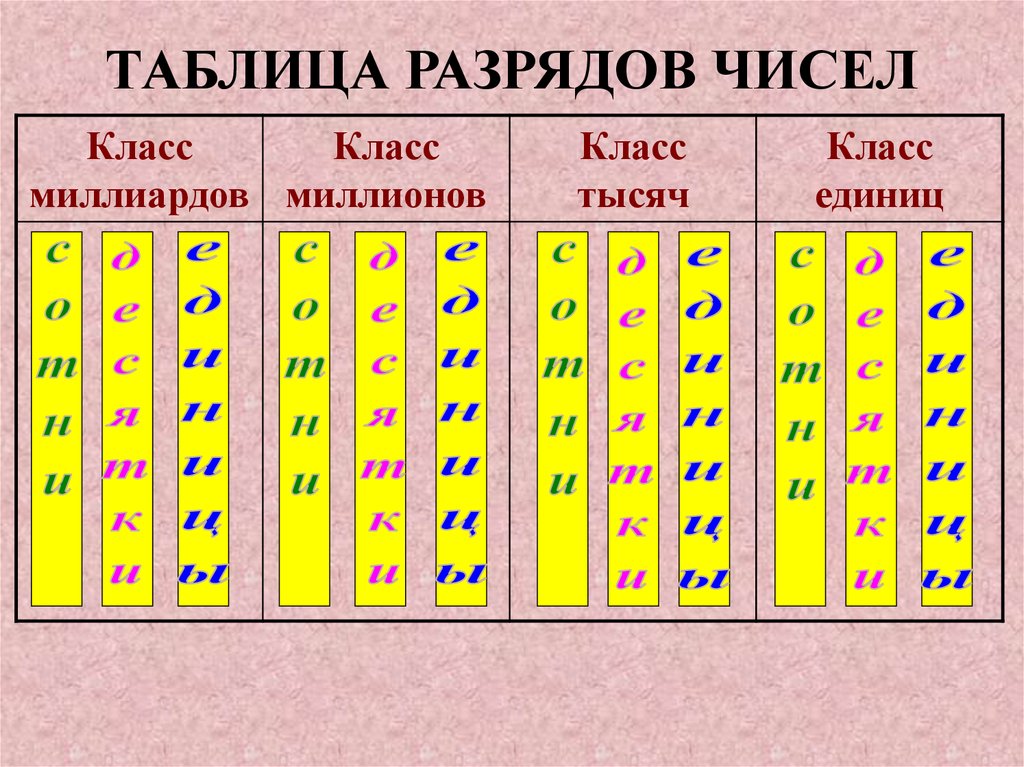 На этой диаграмме стоимости места 10-значное число сгруппировано в периоды единиц, тысяч, лакхов, крор и так далее. Эти числа разделяются запятыми по правилу 3:2:2. Это означает, что начиная справа первая запятая ставится после 3 цифр, затем следующие запятые ставятся после каждых 2 цифр. Например, обратите внимание на запятые в следующем числе: 5,43,13,62,283
На этой диаграмме стоимости места 10-значное число сгруппировано в периоды единиц, тысяч, лакхов, крор и так далее. Эти числа разделяются запятыми по правилу 3:2:2. Это означает, что начиная справа первая запятая ставится после 3 цифр, затем следующие запятые ставятся после каждых 2 цифр. Например, обратите внимание на запятые в следующем числе: 5,43,13,62,283
Обратите внимание на приведенную ниже таблицу индийских разрядов, которая показывает разрядность цифр до десяти крор.
Международная таблица стоимостей мест
Международная система счисления используется во всем мире, в которой мы считаем в порядке единиц, десятков, сотен, тысяч, десятков тысяч, сотен тысяч, миллионов и так далее. В этой диаграмме разрядности числа сгруппированы в периоды единиц, тысяч, миллионов и т. д. и разделены запятой после каждых трех цифр, начиная справа. Например, обратите внимание на запятые в следующем числе: 135,912 332. Обратите внимание на приведенную ниже международную диаграмму разрядности, которая показывает разрядность цифр до сотен миллионов.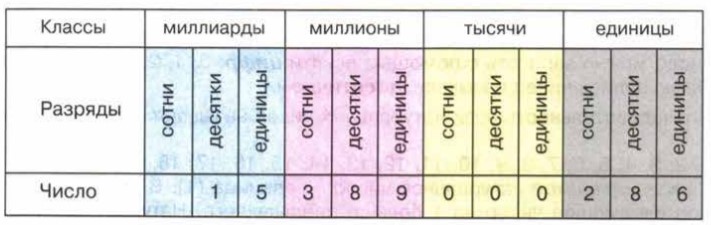
Пригодные для печати таблицы разрядной стоимости
Запоминание и решение задач по системам разрядной стоимости упрощается с помощью печатаемой таблицы разрядной стоимости. На этих диаграммах значения мест напечатаны в табличной форме через пробелы для каждой цифры в числе. Обращаясь к этим таблицам для решения задачи, мы можем напрямую размещать цифры в соответствующих позициях в соответствии с цифрами в числе и соответственно оценивать их позиционные значения.
Таблица разрядов с десятичными знаками
Таблица значений десятичных разрядов показывает разрядность цифр в десятичном числе. Десятичная система счисления используется для выражения целых чисел и дробей вместе с помощью десятичной точки. Эта десятичная точка находится между целой частью числа и дробной частью. В то время как целая числовая часть соответствует обычной таблице разрядов единиц, десятков, сотен и т. д., есть небольшая разница в разрядах чисел справа от десятичной точки.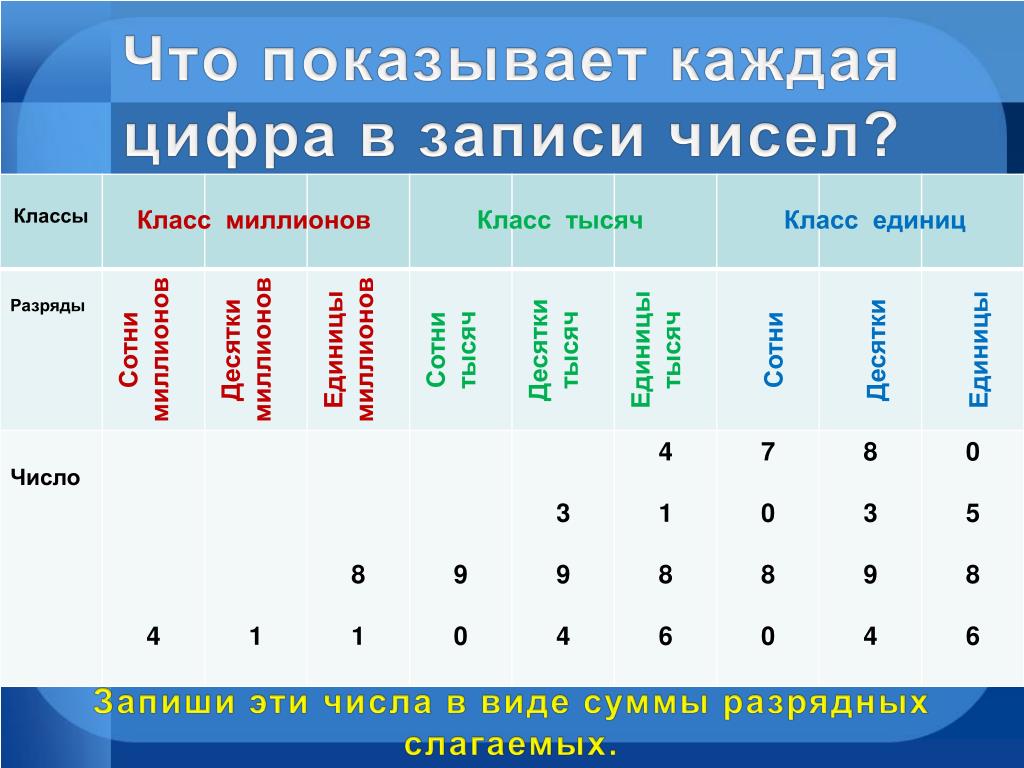 Если мы пойдем вправо после запятой, значения разрядов начнутся с десятых и продолжатся как сотые, тысячные и так далее. Первое место справа от запятой стоит на одной десятой (1/10 -й ), следующая 1/100 и так далее. Обратите внимание на следующую таблицу значений разрядов для десятичных чисел.
Если мы пойдем вправо после запятой, значения разрядов начнутся с десятых и продолжатся как сотые, тысячные и так далее. Первое место справа от запятой стоит на одной десятой (1/10 -й ), следующая 1/100 и так далее. Обратите внимание на следующую таблицу значений разрядов для десятичных чисел.
Разрядная стоимость и номинальная стоимость
Номинальная стоимость цифры в любом числе — это сама цифра. Независимо от того, является ли число однозначным, двузначным или любым числом, каждая цифра имеет свое номинальное значение. Давайте разберемся в этом на следующих примерах.
- Если задано число 4, то номинальная стоимость 4 равна 4, а разрядная стоимость 4 также равна 4 (4 единицы = 4 × 1 = 4).
- Для заданного числа 78 номинальная стоимость 7 равна 7, а разрядность равна 70 (7 десятков = 7 × 10 = 70).
- Для 52369 номинальная стоимость 3 равна 3, а разрядная стоимость равна 300 (3 сотни = 3 × 100 = 300).
Разница между разрядным значением и номиналом
Местное значение описывает положение цифры в заданном числе. С другой стороны, номинал представляет собой само число. Возьмем в качестве примера число, скажем, 1437. Таблица, приведенная ниже, объясняет разницу между разрядным значением и номиналом цифр в этом числе.
С другой стороны, номинал представляет собой само число. Возьмем в качестве примера число, скажем, 1437. Таблица, приведенная ниже, объясняет разницу между разрядным значением и номиналом цифр в этом числе.
Цифры в номере 1437 | Место Значение | Номинальная стоимость |
|---|---|---|
1 | 1 тысяча (1 × 1000 = 1000) | 1 |
4 | 4 Сотни (4 × 100 = 400) | 4 |
3 | 3 Десятки (3 × 10 = 30) | 3 |
| 7 | 7 Единицы или единицы ( 7 × 1 = 7) | 7 |
Разрядное значение в числах
Разрядное значение в числах может быть выражено двумя различными способами. Например, разрядное значение 4 в числе 2458 может быть выражено как 4 сотни или 400.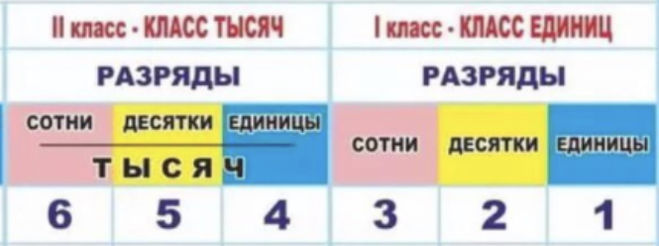 В другом примере разрядное значение 4 в числе 4681 выражается как 4 тысячи или 4000.
В другом примере разрядное значение 4 в числе 4681 выражается как 4 тысячи или 4000.
Проще говоря, если нам нужно выразить значение разряда в числовой форме, мы просто умножаем число на имя столбца, к которому оно относится. Например, если нам нужно найти значение разряда 5 в 67538, мы сначала поместим данное число под таблицу значений разряда так, чтобы каждая цифра была правильно размещена в соответствующем столбце. В этом случае мы видим, что 5 находится в столбце сотен. Итак, мы можем сказать, что разрядное значение числа 5 равно 5 × 100 = 500. Следовательно, разрядное значение числа 5 равно 500 в данном числе.
☛ Статьи по теме
- Калькулятор стоимости места
- Разница между разрядной стоимостью и номинальной стоимостью
Часто задаваемые вопросы о стоимости места
Что такое разрядное значение в математике?
Разрядное значение — это значение каждой цифры в числе.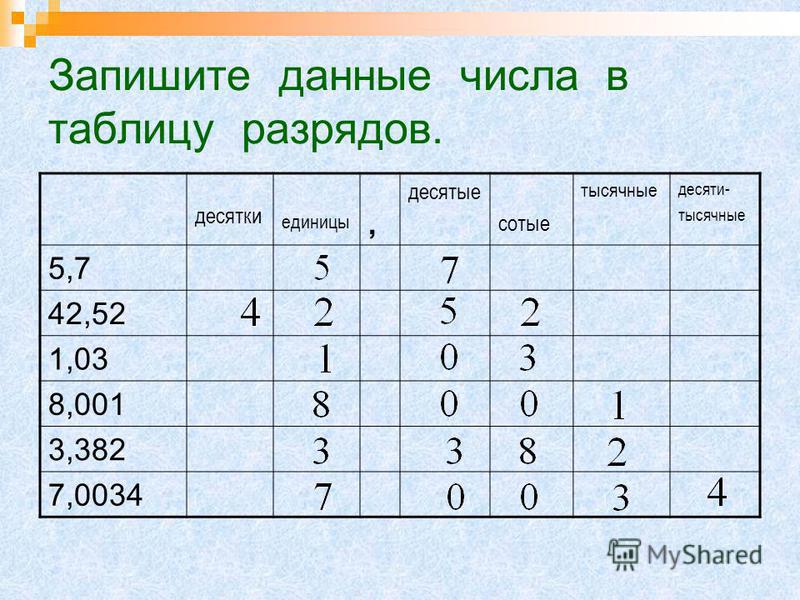 Значение каждой цифры в числе зависит от ее положения. Число может иметь две одинаковые цифры, но разные значения, что определяется позицией, которую занимает цифра в числе. Например, разрядное значение ‘9’ в числе 8934 будет 9 сотен или 900, потому что 9 стоит на разряде сотен.
Значение каждой цифры в числе зависит от ее положения. Число может иметь две одинаковые цифры, но разные значения, что определяется позицией, которую занимает цифра в числе. Например, разрядное значение ‘9’ в числе 8934 будет 9 сотен или 900, потому что 9 стоит на разряде сотен.
Какое место занимает число 6 в числе 64?
Поскольку 6 стоит в разряде десятков, разрядное значение числа 6 в 64 равно 6 десяткам, т. е. 6 × 10 = 60.
Каков пример разрядного значения в числах?
Разрядное значение представляет ценность цифры в числе. Ниже приведены несколько примеров разрядных значений:
Каково разрядное значение числа 5 из 50?
Разрядное значение — это значение каждой цифры в числе. Порядковый номер цифры 5 в числе 50 равен 5 десяткам, т. е. 5 × 10 = 50,
Что такое разрядная стоимость и номинальная стоимость с примером?
Номинал цифры в любом числе — это сама цифра, а разрядность — это ее позиция в числе. Например, номинальная стоимость 7 в числе 2769 равна 7, а разрядная стоимость равна 7 сотням или 700.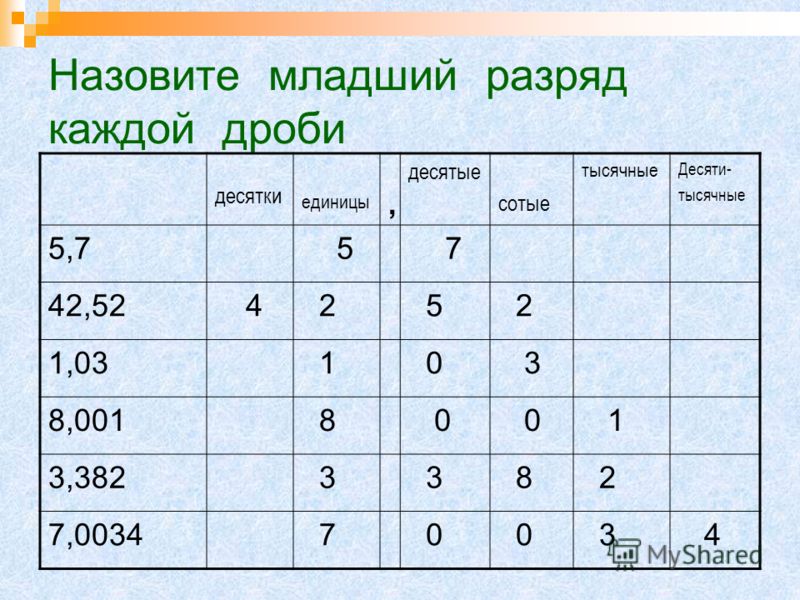
Что такое таблица разрядов?
Таблица разряда — это таблица, которая используется для определения значения каждой цифры в числе на основе ее положения в системе счисления. Чтобы точно определить ценность различных цифр в числе, мы помещаем данное число в таблицу разрядности так, чтобы было видно разрядность каждой цифры. Чтобы упростить процесс, большие числа разбиты на точки, разделенные запятыми. Наиболее часто используются два типа диаграмм места: индийская диаграмма места и международная диаграмма места.
Как составить таблицу стоимости мест?
Чтобы составить диаграмму стоимости мест, мы можем использовать следующие шаги:
- Шаг 1: Нарисуйте столбцы, показывающие разные периоды в соответствии с типом системы счисления: единицы, десятки, сотни, тысячи и т. д.
- Шаг 2: Под каждым периодом нарисуйте подстолбцы, чтобы показать различные значения мест.
Вы можете обратиться к индийской диаграмме разрядности и международной диаграмме разрядности в приведенных выше разделах для различных периодов и разрядности цифр в числе в соответствии с типом системы счисления.
Почему значение разряда в числах важно?
Концепция разряда в числах важна, поскольку она дает значение каждой цифры в числе в соответствии с ее положением. Сущность чисел в целом можно понять только через знание разрядных значений.
Каково разрядное значение нуля?
Нулевой разряд всегда равен нулю. Например, в данном числе 4078 ноль стоит под разрядом сотен. Итак, это выражается как 0 сотен, то есть 0 × 100 = 0,9.0005
Как найти разрядное значение в десятичных числах?
В десятичных числах порядковый номер цифр после запятой выражается немного по-другому. Мы знаем, что десятичное число состоит из целого числа и дробной части, которая пишется после запятой. Целая числовая часть следует обычной таблице разрядов единиц, десятков, сотен. Теперь, если мы пойдем вправо после запятой, разрядные значения начинаются с десятых и продолжаются как сотые, тысячные и так далее. Например, запишем разрядное значение всех цифр в следующем десятичном числе: 578,43
- 5 находится в столбце сотен, поэтому разрядное значение числа 5 равно 5 сотням, или 5 × 100 = 500 .
- 7 находится в столбце десятков, поэтому разрядное значение 7 равно 7 десяткам, или 7 × 10 = 70
- 8 находится в столбце единиц, следовательно, разрядное значение 8 равно 8 единицам, или 8 × 1 = 8
- 4 находится под столбцом десятых, следовательно, разрядное значение 4 равно 4 десятым, или 4/10 = 0,4
- 3 находится под столбцом сотых, поэтому разрядное значение 3 равно 3 сотым, или 3/100 = 0,03

Разрядное значение числа (Видео и практические вопросы)
Иногда на уроках математики и естественных наук можно увидеть очень большие числа, например… :
\(0,015\)
В этом видео мы поговорим о том, как писать и понимать числа, подобные этим, и как определить, насколько они большие или маленькие на самом деле!
Для начала давайте посмотрим на число 125. Это число состоит из трех чисел, сложенных вместе: 1, 2 и 5. Поскольку существует три числа, мы говорим, что 125 имеет три 9.0049 цифр .
Точно так же число 79 состоит из двух цифр, потому что оно состоит из двух чисел, 7 и 9.
3,044 состоит из четырех цифр, потому что оно состоит из четырех цифр: 3, 0 и двух 4.
Давайте немного уменьшим масштаб и подумаем, как строятся большие числа. Взгляните на число 2175. Каждая цифра в этом числе имеет название. Самая дальняя справа цифра называется разрядом единиц, потому что первое число в математике с одной цифрой — это 1. В этом примере 5 находится в разряде 9.0049 разряд единиц .
Слева от единицы находится разряд десятков . Десятки — это то место, где идет вторая цифра, и мы можем это запомнить, потому что первое число с двумя цифрами — 10. Здесь 7 стоит в разряде десятков.
Третья цифра справа называется разрядом сотен , и именно здесь мы пишем цифру, когда говорим о числах 100 или больше! В нашем примере цифра 1 стоит в разряде сотен.
Четвертая цифра справа называется тысяч место , и именно здесь мы пишем цифру всякий раз, когда говорим о числах 1000 или больше. В этом примере цифра 2 стоит в разряде тысяч. Для чисел от 1000 и больше цифры могут стать немного сложнее для чтения. Чтобы упростить организацию цифр, мы используем запятые после каждой третьей цифры справа. Для чисел в тысячах мы ставим запятую после разряда тысяч!
В этом примере цифра 2 стоит в разряде тысяч. Для чисел от 1000 и больше цифры могут стать немного сложнее для чтения. Чтобы упростить организацию цифр, мы используем запятые после каждой третьей цифры справа. Для чисел в тысячах мы ставим запятую после разряда тысяч!
Давайте на минутку обозначим разряды цифр в числах 125, 79.и 3044.
В числе 125 на каком месте стоит цифра 5? Поскольку 5 — число, расположенное дальше всего справа, оно стоит на разряде единиц, поэтому можно сказать, что разрядное значение числа 5 в числе 125 равно пяти единицам, или 5.
На каком месте стоит число 2? Поскольку 2 — второе число справа, мы видим, что оно стоит в разряде десятков. Таким образом, разрядное значение числа 2 из 125 равно двум десяткам, или 20.
Каково разрядное значение числа 1 из 125? Поскольку 1 — это третья цифра справа, она находится в разряде сотен и имеет разрядное значение 100.
А число 79? Какое число стоит в разряде десятков? 7 есть, потому что это вторая цифра справа. На каком месте 9? 9 стоит на месте единиц.
На каком месте 9? 9 стоит на месте единиц.
Теперь проверим число 3044. Каково место числа 3? Поскольку 3 — это четвертая цифра справа, и поскольку она стоит перед запятой, она находится в тысячном разряде, и ее разрядное значение равно 3 тысячам. Какое число стоит в разряде сотен? Ноль есть, так как это третья цифра справа. А как же четверки? Первые 4 стоят в разряде десятков, а вторые 4 — в разряде единиц.
Как я уже упоминал в начале этого видео, есть также имена для цифр, намного превышающих разряд тысяч! Давайте посмотрим на число из семи цифр.
\(1 350 942\)
Мы уже знаем, как обозначать первые четыре цифры справа как разряд единиц, разряд десятков, разряд сотен и разряд тысяч. Но как мы называем цифру, на которой стоит 5? Эта цифра называется разрядом десяти тысяч , потому что первое пятизначное число равно 10000. Угадайте, как называется шестая цифра? Шестая цифра называется 9.0049 сто тысяч место. И, наконец, 1 в этом числе — это седьмая цифра справа, за которой следует еще одна запятая. Это сигнализирует нам, что он находится в -м разряде миллионов!
Это сигнализирует нам, что он находится в -м разряде миллионов!
Давайте сделаем еще один пример маркировки разрядов цифр в большом числе.
Какое число в числе 3 571 068 стоит в разряде десятков тысяч? Разряд десятков тысяч находится слева от разряда тысяч, поэтому 7 находится в разряде десятков тысяч.
Каково разрядное значение числа 0? Поскольку 0 — это третья цифра справа, она стоит в разряде сотен.
Какое число стоит в разряде миллионов? Мы знаем, что разряд миллионов стоит сразу слева от запятой и является седьмой цифрой справа, так что это означает, что 3 стоит в разряде миллионов.
Каково разрядное значение числа 5? Пятерка стоит справа от запятой, поэтому мы знаем, что это либо разряд сотен, либо разряд сотен тысяч. Поскольку он находится в шестой цифре справа, он находится в разряде сотен тысяч и имеет разрядное значение 500 000.
Какое число стоит в разряде десятков? Десятки — это вторая цифра справа, поэтому мы видим, что 6 стоит на десятках.
Какое место занимает 1? Поскольку 1 — это четвертая цифра справа и слева от запятой, мы можем сказать, что она находится в разряде тысяч и имеет разрядное значение 1 тысяча.
И, наконец, какое число стоит в разряде единиц? 8, потому что это самая дальняя цифра справа.
Иногда бывает полезно переписать число в расширенная форма , где мы записываем число как сумму разрядов каждой цифры. Например, число 125 можно записать в развернутом виде как \(100+20+5\). Точно так же наше трехмиллионное число можно записать в расширенной форме как \(3 000 000+500 000+70 000+1 000+0+60+8\).
Теперь, когда мы рассмотрели названия цифр для очень больших чисел, нам также нужно поговорить о названиях цифр для очень маленьких чисел. Эти очень маленькие числа записываются в виде цифр после точки или десятичной точки после разряда единиц. Например, число 1,5 — это то же самое, что и \(1\frac{1}{2}\), но записанное в десятичной форме. Единица, конечно, стоит на месте единиц, но пятерка находится в позиции, называемой десятым местом. Это называется десятым местом, потому что 0,1 — это одна десятая от 1!
Это называется десятым местом, потому что 0,1 — это одна десятая от 1!
Однако числа в десятичной форме могут иметь более одной цифры после запятой. На самом деле после запятой могут быть десятки цифр! Однако обычно нас интересуют только первые несколько. Как мы только что видели, первая цифра справа от запятой называется десятых долей . Вторая цифра после запятой называется сотой, потому что 0,01 равно одной сотой от 1. А третья цифра после запятой называется тысячной. Очень важно включать «th», когда речь идет о названиях цифр после запятой, потому что «th» отличает их от имени цифры слева от десятичной дроби!
Давайте сделаем еще один пример. Обозначьте цифры числа 18.725.
Мы знаем, что первое число, 1, стоит в разряде десятков, а 8 — в разряде единиц, потому что эти два числа стоят перед десятичной запятой. 7, 2 и 5 идут после запятой, поэтому они будут занимать позиции в десятых, сотых и тысячных долях.
Надеюсь, этот урок был вам полезен!
Спасибо за просмотр и удачной учебы!
Часто задаваемые вопросы
Q
Что является примером разряда?
A
Разрядное значение — это удобный способ разделения значения каждой цифры в числе. Пример стоимости места можно увидеть при работе с деньгами. Например, \($45,86\) состоит из цифр в разряде десятков, единиц, десятых и сотых. Когда это значение делится на части в соответствии с его значением места, сумма становится \($40+$5+$\frac{8}{10}+$\frac{6}{100}\). Значение места основано на системе счисления с основанием десять, поэтому цифры увеличиваются или уменьшаются в десять раз.
Пример стоимости места можно увидеть при работе с деньгами. Например, \($45,86\) состоит из цифр в разряде десятков, единиц, десятых и сотых. Когда это значение делится на части в соответствии с его значением места, сумма становится \($40+$5+$\frac{8}{10}+$\frac{6}{100}\). Значение места основано на системе счисления с основанием десять, поэтому цифры увеличиваются или уменьшаются в десять раз.
Q
Что такое десятки и единицы?
A
Десятки и единицы представлены двумя первыми цифрами слева от десятичной точки. Например, в значении \(94,0\) \(4\) представляет \(4\) группы одного \((4)\), а \(9\) представляет \(9\) группы \(10\) \((90)\). Когда \(4\) единиц и \(9\) десятков объединяются, общее значение становится \(90+4=94\).
Q
Сколько единиц в десятичной дроби?
А
Единица — это цифра, стоящая непосредственно слева от запятой. Например, в значении \(3.4\) цифра \(3\) стоит на месте единиц. В числе без десятичной запятой единицей считается крайняя справа цифра. Например, в значении \(459\) \(9\) стоит на месте единиц, потому что \(459\) по сути равно \(459,0\).
Например, в значении \(459\) \(9\) стоит на месте единиц, потому что \(459\) по сути равно \(459,0\).
Q
Почему нет единого места?
A
Единиц нет, потому что цифры справа от запятой уменьшаются в десять раз. Это означает, что переход от разряда единиц к разряду десятых является результатом деления \(1\) на \(10\), что составляет одну десятую, а не одну одну.
Q
Какое место занимает десятое место?
A
В десятичном значении первая цифра справа от запятой находится в десятых долях. Например, в значении \(34,592\) цифра \(5\) стоит на десятом месте. Это \(5\) представляет собой пять десятых, или \(\frac{5}{10}\).
Q
Что такое десятая часть?
A
Десятая представляет долю «из десяти». В десятичном значении, таком как \(3.4\), это означает три единицы и \(4\) десятые доли. Другой способ взглянуть на \(3.4\) — это \(\frac{3}{1}+\frac{4}{10}\). Десятым разрядом всегда является цифра непосредственно справа от десятичной точки.
Q
Где в числе стоят десятки?
A
Разряд десятков всегда располагается на две цифры левее запятой. Помните, что даже целые числа можно записывать с десятичной точкой. Например, \(34\) можно записать как \(34,0\), что означает, что \(3\) стоит в разряде десятков. Это \(3\) представляет \(3\) группы по десять. В десятичном значении \(198,478\) вторая цифра слева от десятичной дроби равна \(9\). Это означает, что \(9\) представляет \(9\) группы \(10\) или \(90\).
Q
Сколько десятков составляет тысяча?
A
Десятичная система счисления удобна тем, что все цифры, смещающиеся влево, становятся в \(10\) раз больше, а все цифры, смещающиеся вправо, становятся в \(10\) раз меньше. Это означает, что все значения мест можно сравнивать с десятикратным коэффициентом. Например, десятки в \(10\) раз больше единиц. Сотни в \(10\) раз больше десятков. Тысячи в 10 раз больше сотен. При переходе от десятков к тысячам нам нужно дважды умножить на \(10\). Таким образом, чтобы получить тысячу, потребуется \(100\) десятков. Например, \(1{,}000\) в \(100\) раз больше, чем \(10\).
Таким образом, чтобы получить тысячу, потребуется \(100\) десятков. Например, \(1{,}000\) в \(100\) раз больше, чем \(10\).
Практические вопросы
Вопрос №1:
Что такое 7645 в расширенной форме?
\(7+6+4+5\)
\(76+45\)
\(7,000+600+40+5\)
\(700+64+5\)
Показать ответ
Ответ:
Правильный ответ: \(7000+600+40+5\). Чтобы записать число в развернутой форме, напишите задачу на сложение, которая складывает значение каждого числа. 7 стоит в разряде тысяч, значит, это 7000. 6 стоит в разряде сотен, значит это 600. 4 стоит в разряде десятков, значит это 40. А 5 стоит в разряде единиц, значит это 5. В сумме это выглядит так: \(7,000+600+40 +5\).
Скрыть ответ
Вопрос № 2:
Какое место занимает число 9 в числе 293,76?
Сотни
Десятки
Десятки
Сотни
Показать Ответ
Ответ:
Правильный ответ — Десятки. Местоимения можно определить по их положению относительно десятичной точки. Позиция слева от десятичной точки — это единица. Слева от него — разряд десятков, а слева — разряд сотен. Положение справа от запятой соответствует десятому разряду, а справа от него — сотому разряду. Следовательно, 9находится в разряде десятков.
Местоимения можно определить по их положению относительно десятичной точки. Позиция слева от десятичной точки — это единица. Слева от него — разряд десятков, а слева — разряд сотен. Положение справа от запятой соответствует десятому разряду, а справа от него — сотому разряду. Следовательно, 9находится в разряде десятков.
Скрыть ответ
Вопрос № 3:
Что такое 12 643,57 в развернутом виде?
\(10 000+2 000+600+40+3+\frac{5}{10}+\frac{7}{100}\)
\(12 000+643+\frac{57}{100}\ )
\(12,000+600+43+\frac{57}{100}\)
\(12,643+\frac{57}{100}\)
Показать ответ
Ответ:
правильный ответ: \(10 000+2 000+600+40+3+\frac{5}{10}+\frac{7}{100}\). Чтобы записать число в развернутой форме, напишите задачу на сложение, которая складывает значение каждого числа. 1 находится в разряде десятков тысяч, значит, это 10 000. 2 стоит в тысячном разряде, значит, это 2000. 6 стоит в разряде сотен, значит, это 600. 4 стоит в разряде десятков, значит, это 40. 3 стоит в разряде единиц, значит, это 3. 5 стоит в разряде десятых, значит, это \(\frac {5}{10}\). И 7 стоит на сотом месте, поэтому представляет \(\frac{7}{100}\). В сумме это выглядит так: \(10 000+2 000+600+40+3+\frac{5}{10}+\frac{7}{100}\)
2 стоит в тысячном разряде, значит, это 2000. 6 стоит в разряде сотен, значит, это 600. 4 стоит в разряде десятков, значит, это 40. 3 стоит в разряде единиц, значит, это 3. 5 стоит в разряде десятых, значит, это \(\frac {5}{10}\). И 7 стоит на сотом месте, поэтому представляет \(\frac{7}{100}\). В сумме это выглядит так: \(10 000+2 000+600+40+3+\frac{5}{10}+\frac{7}{100}\)
Скрыть ответ
Вопрос № 4:
Какое место занимает 3 в 192,36?
Десятки
Единицы
Десятки
Сотни
Показать Ответ
Ответ:
Правильный ответ Десятки. Местоимения можно определить по их положению относительно десятичной точки. Позиция слева от десятичной точки — это единица. Слева от него — разряд десятков, а слева — разряд сотен. Положение справа от запятой соответствует десятому разряду, а справа от него — сотому разряду. Следовательно, 3 находится на десятом месте.
Следовательно, 3 находится на десятом месте.
Скрыть ответ
Вопрос № 5:
Какое место занимает 6 в 162 497 132,498?
Десять миллионов
Миллионов
Сотни тысяч
Десятитысячных
Показать ответ
Ответ:
Десять миллионов. Порядок разрядов, начиная с позиции слева от десятичной дроби и продолжая двигаться влево, следующий: единицы, десятки, сотни, тысячи, десятки тысяч, сто тысяч, миллионы, десять миллионов и сто миллионов. Следовательно, 6 находится в разряде десяти миллионов.
Скрыть ответ
Содержание | Главная | Введение Урок 2 Раздел 2 Назад к разделу 1 ОРГАНИЗАЦИОННЫМ ПРИНЦИПОМ в нашей системе наименования и записи чисел являются силы
10. 2 тысячи + 3 сотни + 6 десятков + 4 единицы. Это показывает, что, начиная с единиц справа, мы выбрали степени числа 10 в качестве единиц. Есть 2 этой единицы (тысячи), плюс 3 этой единицы (сотни), плюс 6 той единицы (десятки), плюс 4 тех (единицы). Однако, когда мы пишем число, мы опускаем наименований единиц и знаки + и пишем просто .2364. После единиц справа каждое место имеет в качестве значения следующую степень числа 10. Мы называем такую системную разрядность или позиционную нумерацию. | ||||||||||||||||||||||
| ||||||||||||||||||||||
Пример 1. В этом номере 139 072 658 0 в каком месте? Ответить . Сотни тысяч. В каждом классе из трех цифр имеется единиц , десятков и сотен . 0 находится в классе тысяч и на месте сотен . Степень 10 в этой позиции – Сотни тысяч . Пример 2. В этом номере 386 214 035 сколько десять миллионов есть? То есть, какая цифра стоит в разряде десятков миллионов? Ответить . 8. Ибо при счете справа миллионы представляют собой третью группу из трех цифр, 386. Десятки место является средним ( Единицы, Десятки, Сотни ). Есть 8 Десять миллионов. Разрядное значение против абсолютного значения цифры Помимо того, что мы говорим о том, что цифра находится «в» месте, мы также говорим о разрядном значении самой цифры. 6 666 каждая цифра имеет одно и то же абсолютное или неизменное значение 6, но разные значение места. 6 в крайнем левом углу имеет разрядное значение 6000; следующие 6 имеют значение 600; следующий, 60; и последний, 6. Расширенная форма Цифра для каждого целого числа означает сумму . 364 = 3 сотни + 6 десятков + 4 единицы. (Даже одна цифра обозначает сумму: 5 = 1 + 1 + 1 + 1 + 1.) То, что написано выше, называется расширенной формой числа 364. | ||||||||||||||||||||||
| ||||||||||||||||||||||
Пример 3. Ответить . Напишите 6 325 = 6 тысяч + 3 сотни + 2 десятка + 5 единиц. Однако на практике часто бывает полезнее расширить число следующим образом: 6 325 = 6 000 + 300 + 20 + 5. Пример 4. Напишите развернутую форму числа 10 000. Ответить . 10 000 = 1 десять тысяч + 0 тысяч + 0 сотен + 0 десятков + 0 единиц. Пример 5. Независимо от единицы измерения:
И так далее. Ибо нет «42», кроме 42 единиц, хотя мы и не говорим слова «единицы». Единицы стоимости смежного разряда Следующий вопрос для подготовки к стандартным письменным методам сложения и вычитания. Ответ следует из того, что каждая цифра 6 325 имеет разрядное значение , которое десять раз умножается на цифру справа от него. Поскольку каждая степень числа 10 равна десятикратно единице справа от нее: 1000 100 10 1 1000 состоит из десяти сотен. 100 состоит из десяти десятков. 10 состоит из десяти единиц. И так далее. | ||||||||||||||||||||||
| ||||||||||||||||||||||
Десять единиц могут быть составлены из в одну 10. Десять десятков можно составить в одну сотню. Десять сотен могут быть объединены в одну 1000. И так далее. Обратно: 1000 100 10 1 Одна 1000 может быть разложена на на десять сотен. Одна 100 может быть разложена на десять десятков. Одна десятка может быть разложена на десять единиц. 1000 100 10 1 Мы увидим это, когда перейдем к перегруппировке сложения и вычитания. Округление | ||||||||||||||||||||||
| ||||||||||||||||||||||
Пример 6. Округлите 6 528 до ближайших десяти. Ответить . 6 5286 530 (Волнистый знак равенства означает «приблизительно равно «) 2 стоит в разряде десятков. Чтобы округлить до ближайших десяти, посмотрите на цифру справа: 8 (больше 5). Пример 7. Округлите 6 528 до ближайшей сотни. Ответ . 6 5286 500 5 находится в разряде сотен. Чтобы округлить до ближайшей сотни, посмотрите на цифру справа: 2 (меньше 5). Поэтому разряд сотен оставьте без изменений. Замените 28 на 00. Пример 8. Округлите 6 528 до ближайшей тысячи. Ответить . 6 5287 000 6 находится в разряде тысяч. Чтобы округлить до ближайшей тысячи, посмотрите на цифру справа: 5. Поэтому прибавьте 1 к разряду тысяч. Замените 528 на 000. Пример 9. Округлите 79 521 до ближайшей тысячи. Ответить . 79,52180,000 9 находится в разряде тысяч. Чтобы округлить до ближайшей тысячи, посмотрите на цифру справа: 5. Следовательно, прибавьте 1 к 79 – получится 80. Замените 521 на 000. Чтобы округлить десятичные дроби, см. В этот момент, пожалуйста, «переверните» страницу и сделайте Проблемы. или Перейдите к следующему разделу. Раздел 1 этого урока Введение | Главная | Содержание Copyright © 2021 Лоуренс Спектор Вопросы или комментарии? Электронная почта: [email protected] | ||||||||||||||||||||||
Разрядное значение – объяснение и примеры
В математике каждое целое число имеет разрядное значение. Таким образом, разрядное значение числа — это значение, представленное цифрой в числе в зависимости от ее положения в числе.
В то время как разрядное значение — это значение, которое цифра занимает на месте в числе, с другой стороны, номинальная стоимость цифры для любого места в заданном числе — это значение самого целого числа.
Таблица разрядных значений — это диаграмма, которая помогает нам находить и сравнивать разрядные значения цифр в числах до миллионов. Позиционное значение цифры в таблице разрядных значений увеличивается в десять раз при смещении влево и уменьшается в десять раз при смещении вправо.
Позиционное значение цифры в таблице разрядных значений увеличивается в десять раз при смещении влево и уменьшается в десять раз при смещении вправо.
| PLACE VALUE CHART |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||
1 0 0 0 0 | 1 9000 9000 9000 9000 9000 9000 | 1 0 0 0 | 1 0 0 | 1 0 | 1 | Десятичная точка | 0 . 1 | 0 . 0 1 | 0 . 0 0 1 | 0 . 0 0 0 1 | 0 . 0 0 0 0 1 | 0 . 0 0 0 0 0 1 | ||
| 9 | 9 | 9 | ||||||||||||
| 3 | 1 | 8 | 5 |
Example 1
Consider a number: 24.3185
- The digit 2 is in the tens place, and имеет значение 2 × 10 = 20
- Цифра 4 стоит на месте единицы и имеет значение 4 × 1 = 4
- Цифра 3 стоит на десятом месте и имеет значение 3 × 1/10 = 3/10 = 0,3
- Цифра 1 стоит в сотых долях и имеет значение 1 × 1/100 = 1/100 = 0,01
- Цифра 8 стоит в разряде тысячных и имеет значение 8 × 1000 = 8/1000 = 0,008
- Цифра 5 находится в разряде десятитысячных и имеет значение 5 × 10000 = 5 /10000 = 0,0005
Следовательно, разрядность числа находится путем умножения номинала на значение самого числа
Разрядность однозначного числа эквивалентна его номиналу. Например, разрядное значение и номинальная стоимость 1, 2, 3, 4, 5, 6, 7, 8 и 9равны 1, 2, 3, 4, 5, 6, 7, 8 и 9 соответственно.
Например, разрядное значение и номинальная стоимость 1, 2, 3, 4, 5, 6, 7, 8 и 9равны 1, 2, 3, 4, 5, 6, 7, 8 и 9 соответственно.
Место нуля в любом числе всегда равно нулю. Ноль может занимать любое место в числе, но его значение останется равным нулю.
Пример 2
В числах, содержащих нули, таких как 105, 350, 42017,
Для двузначного числа разряд десятков равен 10-кратное число. Например, разрядное значение 5 в числе 57 равно 5 x 10 = 50, а разрядное значение однозначного числа равно 7 x 1 = 7.
Аналогично, разрядное значение сотен цифр в трехзначном числе равно 100-кратному номинальному значению цифры. Например, разрядное значение 4 в числе 475 равно 4 x 100 = 400. 90 135 Таким образом, для разрядного значения цифры цифра умножается на разрядное значение 1; это должно быть то место. Способы нахождения и записи разряда любой цифры в числе проиллюстрированы ниже на различных примерах.
Пример 3
Запишите разрядность каждой цифры в числе: 768;
- Разрядное значение 8 = 8 × 1 = 8
- Разрядное значение 6 = 6 × 10 = 60
- Разрядное значение 7 равно 7 × 100 = 700.
Подытожим, что число сохраняет свое разрядное значение как произведение числа и разрядного значения единицы, находящейся в этой позиции. Пример 4
Пример 5
Запишите значение цифров в 2965.
- На разряде тысяч стоит цифра 2; следовательно, его место 1000 x 2 = 2000
- Цифра 9 — это разряд сотен, и поэтому разрядное значение равно 9 x 100 = 900
- Число 6 стоит на десятом месте, значит, разрядное значение 6 = 6 х 10 = 60
- Число 5 занимает место единицы в числе 2965; следовательно, разрядное значение числа 5 равно 5 x 1 = 5
Пример 6
Запишите места цифр в следующем числе: 9721. 9721. Таким образом, разряд 9 равен 9 x 1000 = 9000.
9721. Таким образом, разряд 9 равен 9 x 1000 = 9000.
Разрядное значение
fshyCNqHIbw
Мы записываем числа, используя только десять символов (называемых цифрами).
Важно, где мы их размещаем.
Десять цифр
Цифры, которые мы используем сегодня, называются «индийско-арабскими цифрами»:
0 1 2 3 4 5 6 7 8 9
Мы можем использовать их сами по себе, чтобы считать до 9:
| 0 | |
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| ?? |
Но что происходит после 9?
Десять и более .
 ..
..Когда у нас больше 9 элементов, мы начинаем другой столбец — столбец «десятки» — и записываем сколько у нас «десятков», а затем сколько «единиц» (также называемых «единицами»).
Итак, мы пишем:
Пример: так мы записываем
двенадцать :Десятки | Единицы |
| 1 | 2 |
Число «12»
Здесь сказано, что у нас есть 1 Десять и 2 Единицы , что составляет 12.
Это также может быть записано как 1 × 10 + 2 × 1.
Пример: «35» означает 3 десятка и 5 единиц, что также равно 3 × 10 + 5 × 1
Десятки | Единицы |
| 3 | 5 |
Номер «35»
Ноль
Что, если у нас есть 1 Десятка, но нет Единиц? Мы показываем «Нет» к поставив ноль там:
Десятки | Единицы |
| 1 | 0 |
Цифра «10»
Мы должны поставить ноль вместо единиц, иначе «10» выглядит как «1».
Сотня или больше…
Когда у нас больше 99 пунктов, начинаем еще один столбец — столбец «сотни». Теперь нам нужно чтобы показать, сколько сотен, десятков и единиц:
Сотни | Десятки | Единицы |
| 1 | 4 | 3 |
Номер 143
Это показывает, что у нас есть 1 сотня, 4 десятка и 3 единицы:
Это также может быть записано как 1 × 100 + 4 × 10 + 3 × 1.
Пример: «369» означает 3 сотни, 6 десятков и 9 единиц
Что также равно 3 × 100 + 6 × 10 + 9 × 1
Мы также используем ноль, когда нет десятков:
Пример: «104» означает 1 сотню,
ноль десятков и 4 единицы.Сотни | Десятки | Единицы |
| 1 | 0 | 4 |
Номер 104
И так далее.



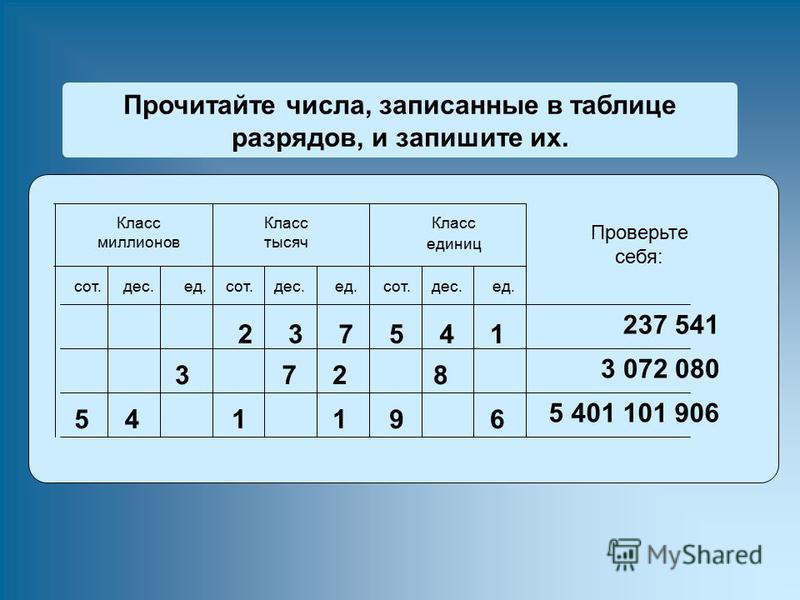
 О числе можно сказать, что оно: однозначное (одноразрядное), например 5; двузначное (двухразрядное), например 15; трехзначное (трехразрядное), например 551, и т. д.
О числе можно сказать, что оно: однозначное (одноразрядное), например 5; двузначное (двухразрядное), например 15; трехзначное (трехразрядное), например 551, и т. д. Три разряда каждого класса читаются как трехзначные числа: сто двадцать семь, четыреста тридцать два, семьсот шесть, четыреста восемь. К каждому классу трехзначного числа добавляется наименование класса: «миллиардов», «миллионов», «тысяч».
Три разряда каждого класса читаются как трехзначные числа: сто двадцать семь, четыреста тридцать два, семьсот шесть, четыреста восемь. К каждому классу трехзначного числа добавляется наименование класса: «миллиардов», «миллионов», «тысяч».
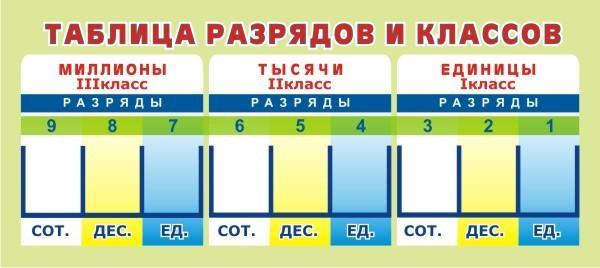 п. При склонении этого местоимения используются простые предлоги, которые ставятся в интерпозицию между компонентами местоимения друг друга (друг для друга, друг с другом). Производные предлоги могут стоять как в интерпозиции, так и в препозиции перед целым местоимением (друг напротив друга, друг относительно друга и напротив друг друга, относительно друг друга).
п. При склонении этого местоимения используются простые предлоги, которые ставятся в интерпозицию между компонентами местоимения друг друга (друг для друга, друг с другом). Производные предлоги могут стоять как в интерпозиции, так и в препозиции перед целым местоимением (друг напротив друга, друг относительно друга и напротив друг друга, относительно друг друга). Местоимение таков выступает в предложении в роли сказуемого (Задание таково, что потребуется много времени для его выполнения
Местоимение таков выступает в предложении в роли сказуемого (Задание таково, что потребуется много времени для его выполнения Например: Я увидел избушку, что стояла на опушке леса. Я никогда не видел её такою, какою Дом, в котором я вырос, был построен ещё моим дедом.
Например: Я увидел избушку, что стояла на опушке леса. Я никогда не видел её такою, какою Дом, в котором я вырос, был построен ещё моим дедом. Он услышал чьи-то шаги. Ты уже потерял несколько книг
Он услышал чьи-то шаги. Ты уже потерял несколько книг
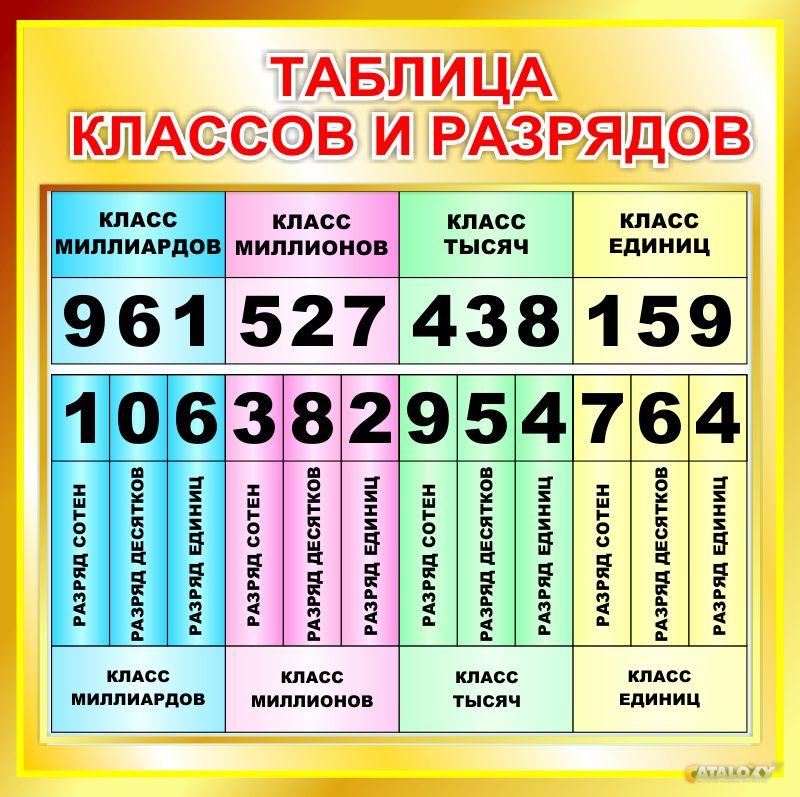 Его сочинение лучше моего. Они согласуются с существительными, выступая при них в роли определений.
Его сочинение лучше моего. Они согласуются с существительными, выступая при них в роли определений.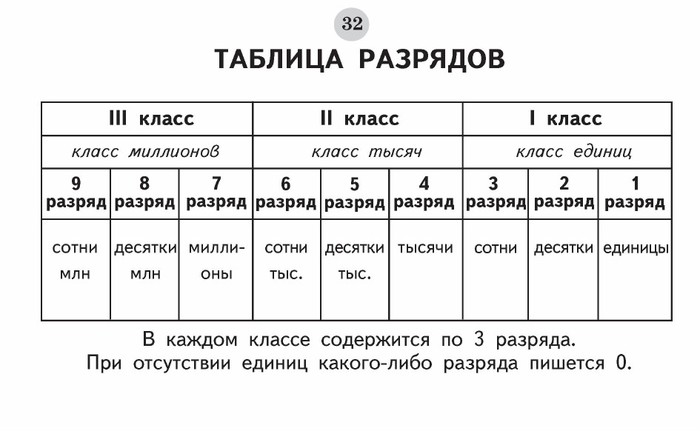 Глагол-сказуемое при нём ставится в мужском роде, даже если вопрос относится к лицу женского пола (Кто из студенток выполнил задание?). Местоимение что указывает на неодушевлённый предмет или абстрактное понятие. Глагол-сказуемое при нём ставится в среднем роде (Что случилось?).
Глагол-сказуемое при нём ставится в мужском роде, даже если вопрос относится к лицу женского пола (Кто из студенток выполнил задание?). Местоимение что указывает на неодушевлённый предмет или абстрактное понятие. Глагол-сказуемое при нём ставится в среднем роде (Что случилось?).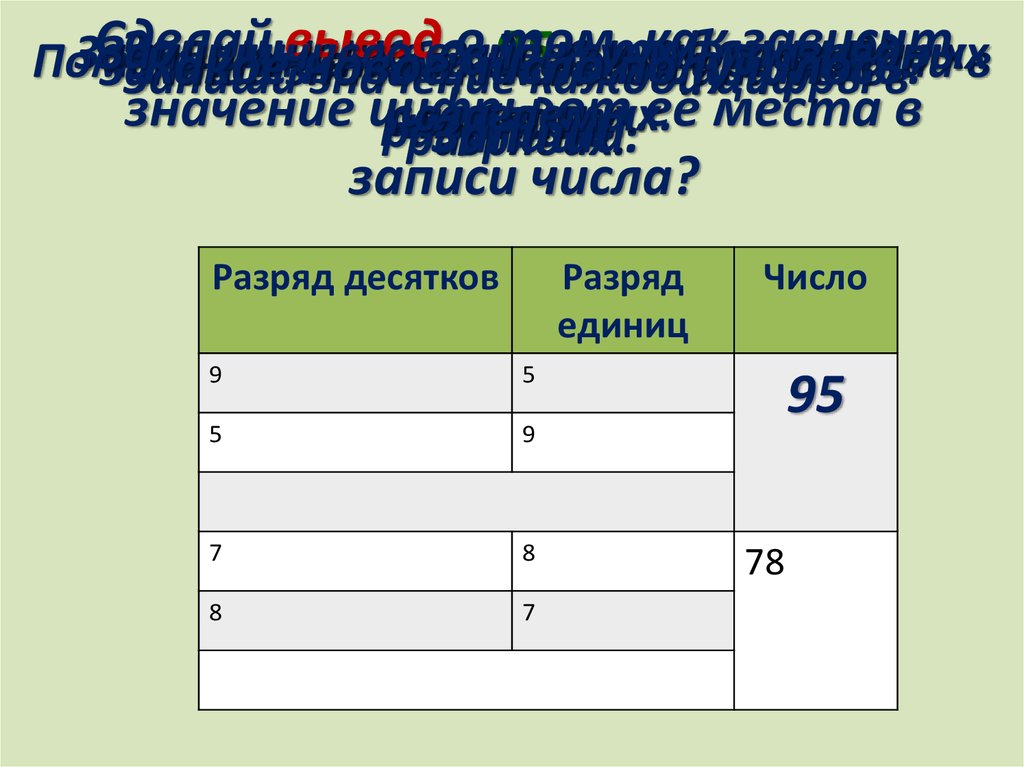 Я никогда не видел кенгуру. Он никуда сегодня не пойдёт. Отрицательные местоимения образуются префиксальным способом от вопросительных местоимений. Местоимения никто, ничто, никакой, ничей видно, никого не узнал
Я никогда не видел кенгуру. Он никуда сегодня не пойдёт. Отрицательные местоимения образуются префиксальным способом от вопросительных местоимений. Местоимения никто, ничто, никакой, ничей видно, никого не узнал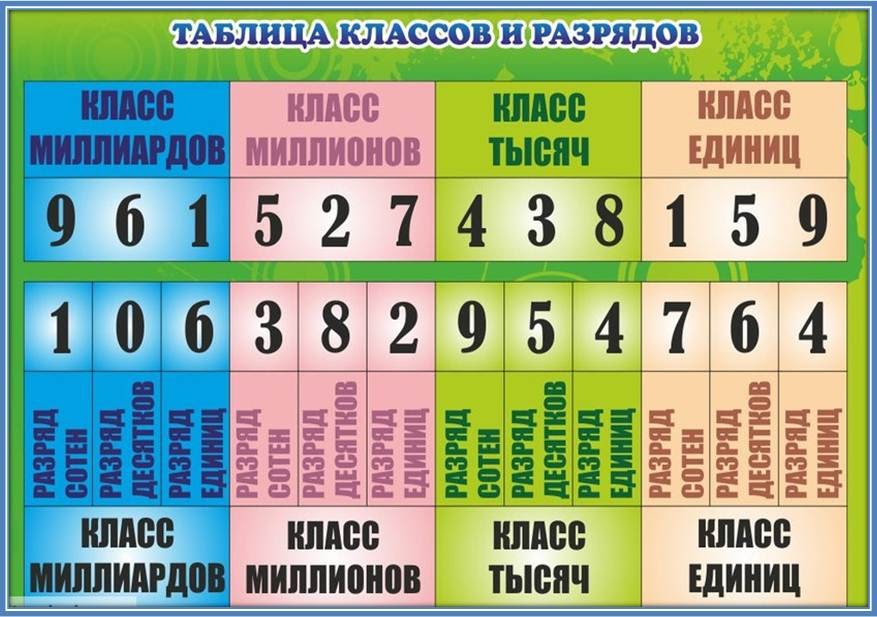 Мы рассмотрели лишь малую часть этой темы. На самом деле тема чисел достаточно обширна. В ней много тонкостей и нюансов, много хитростей и интересных фишек.
Мы рассмотрели лишь малую часть этой темы. На самом деле тема чисел достаточно обширна. В ней много тонкостей и нюансов, много хитростей и интересных фишек. В частности, разряды сообщают нам вес числа. Они сообщают сколько в числе единиц, сколько десятков и сколько сотен.
В частности, разряды сообщают нам вес числа. Они сообщают сколько в числе единиц, сколько десятков и сколько сотен.
 Такая группировка тоже была бы допустимой:
Такая группировка тоже была бы допустимой: Если имеется 123 яблока, то можно сгруппировать первые 120 яблок 12 раз по 10 штук:
Если имеется 123 яблока, то можно сгруппировать первые 120 яблок 12 раз по 10 штук: Представьте, что вы у доски и решаете задачу. Вы почти закончили задачу, осталось только вычислить последнее выражение и получить ответ. Выражение, которое надо вычислить, выглядит следующим образом:
Представьте, что вы у доски и решаете задачу. Вы почти закончили задачу, осталось только вычислить последнее выражение и получить ответ. Выражение, которое надо вычислить, выглядит следующим образом: Это означает, что разряд десятков числа 632 содержит три десятка, а разряд десятков числа 264 содержит шесть десятков. Складываем 3 и 6 десятков — получаем 9 десятков. Записываем цифру 9 в разряде десятков нового числа (нашего ответа):
Это означает, что разряд десятков числа 632 содержит три десятка, а разряд десятков числа 264 содержит шесть десятков. Складываем 3 и 6 десятков — получаем 9 десятков. Записываем цифру 9 в разряде десятков нового числа (нашего ответа): Но иногда при вычислении числового выражения в середине решения может произойти переполнение разряда.
Но иногда при вычислении числового выражения в середине решения может произойти переполнение разряда. По другому это число можно прочитать как «две единицы и один десяток» . Разряд единиц предназначен только для единиц. Десяткам там не место. Здесь и заключается наша ошибка. Сложив 9 единиц и 3 единицы мы получили 12 единиц, которые по-другому можно назвать двумя единицами и одним десятком. Записав две единицы и один десяток в одном разряде, мы допустили ошибку, которая в итоге привела к неправильному ответу.
По другому это число можно прочитать как «две единицы и один десяток» . Разряд единиц предназначен только для единиц. Десяткам там не место. Здесь и заключается наша ошибка. Сложив 9 единиц и 3 единицы мы получили 12 единиц, которые по-другому можно назвать двумя единицами и одним десятком. Записав две единицы и один десяток в одном разряде, мы допустили ошибку, которая в итоге привела к неправильному ответу. Этот десяток мы прибавим к результату сложения десятков чисел 29 и 13. Чтобы не забыть о нем, мы надписали его над десятками числа 29.
Этот десяток мы прибавим к результату сложения десятков чисел 29 и 13. Чтобы не забыть о нем, мы надписали его над десятками числа 29. Произошло переполнение разряда. 13 десятков это десятка повторенная 13 раз. А если повторить десятку 13 раз, то получится число 130
Произошло переполнение разряда. 13 десятков это десятка повторенная 13 раз. А если повторить десятку 13 раз, то получится число 130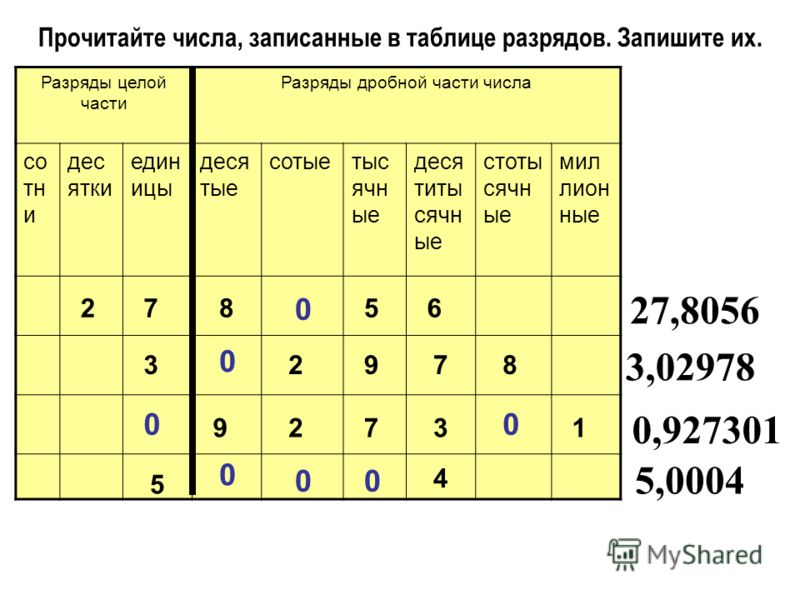
 Это означает, что разряд десятков числа 65 содержит шесть десятков, а разряд десятков числа 12 содержит один десяток. Вычтем из шести десятков один десяток, получим пять десятков. Записываем цифру 5 в разряде десятков нового числа:
Это означает, что разряд десятков числа 65 содержит шесть десятков, а разряд десятков числа 12 содержит один десяток. Вычтем из шести десятков один десяток, получим пять десятков. Записываем цифру 5 в разряде десятков нового числа:
 От тринадцати единиц можно вычесть шесть единиц, получится семь единиц. Записываем цифру 7 в разряде единиц нового числа:
От тринадцати единиц можно вычесть шесть единиц, получится семь единиц. Записываем цифру 7 в разряде единиц нового числа: То есть, числа у которых на конце нули. Чтобы выполнить вычитание, каждому разряду приходится занимать десятки/сотни/ тысячи у следующего разряда. Давайте посмотрим, как это происходит.
То есть, числа у которых на конце нули. Чтобы выполнить вычитание, каждому разряду приходится занимать десятки/сотни/ тысячи у следующего разряда. Давайте посмотрим, как это происходит. Записываем цифру 6 в разряде единиц нового числа:
Записываем цифру 6 в разряде единиц нового числа: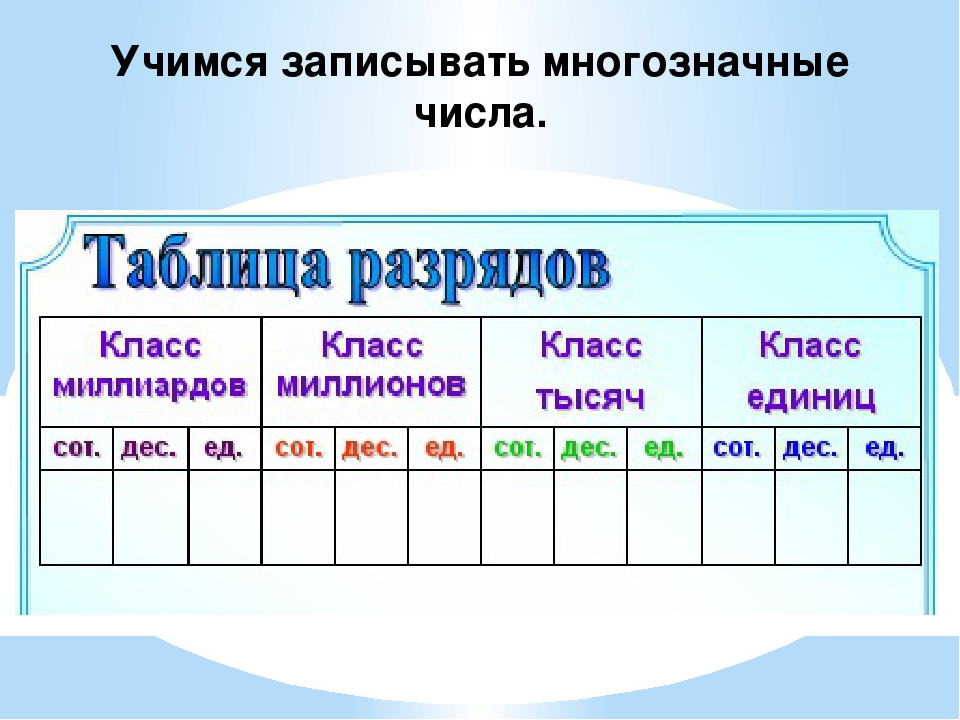
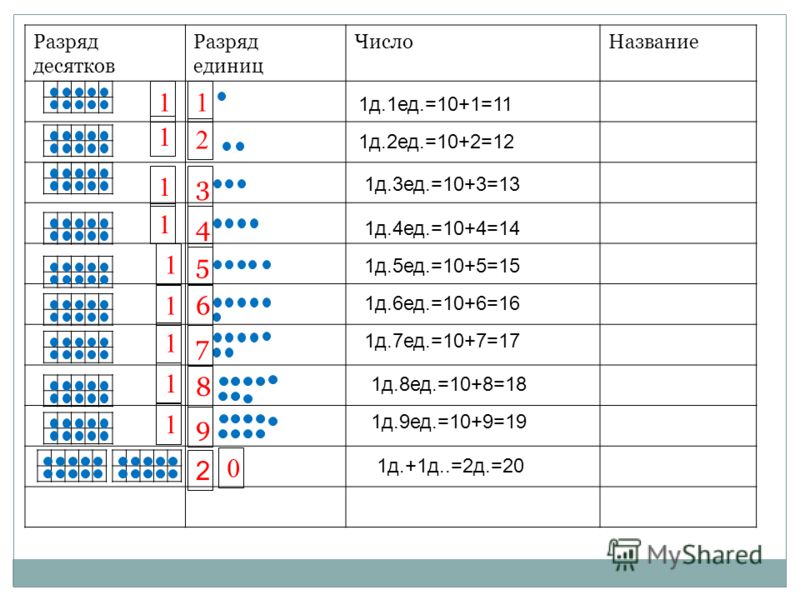
 А в разряде десятков числа 36 располагается число 3. Из 6 можно вычесть 3, получится 3. Записываем число 3 в разряде десятков нового числа:
А в разряде десятков числа 36 располагается число 3. Из 6 можно вычесть 3, получится 3. Записываем число 3 в разряде десятков нового числа: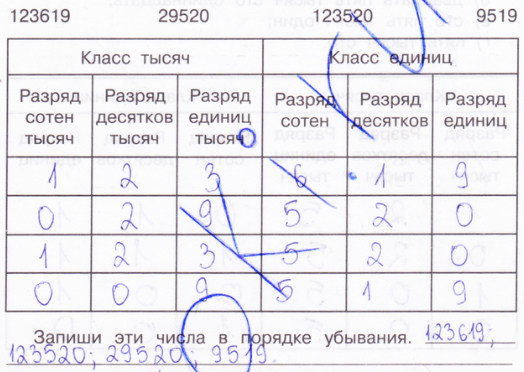 В результате число 20 обратилось в число 19. Получается, что теперь в разряде десятков числа 200 располагается число 9, а в разряде десятков числа 84 располагается число 8. Девять минус восемь равно одному. Записываем число 1 в разряде десятков нашего ответа:
В результате число 20 обратилось в число 19. Получается, что теперь в разряде десятков числа 200 располагается число 9, а в разряде десятков числа 84 располагается число 8. Девять минус восемь равно одному. Записываем число 1 в разряде десятков нашего ответа:
 Человек вправе выбирать любую запись, но обязательно нужно помнить, что единицы надо записывать строго под единицами, десятки под десятками, сотни под сотнями. Другими словами, следующие записи будут неправильными:
Человек вправе выбирать любую запись, но обязательно нужно помнить, что единицы надо записывать строго под единицами, десятки под десятками, сотни под сотнями. Другими словами, следующие записи будут неправильными: Записываем эту цифру в разряде единиц нашего ответа:
Записываем эту цифру в разряде единиц нашего ответа: В результате получили 12 десятков. Эти двенадцать десятков мы записали целиком, образуя окончательный ответ 124.
В результате получили 12 десятков. Эти двенадцать десятков мы записали целиком, образуя окончательный ответ 124. Складываем 8+4+1=13. Число 13 не вместится в разряд десятков нашего ответа, поэтому мы запишем цифру 3 в разряде десятков, а единицу перенесём на следующий разряд:
Складываем 8+4+1=13. Число 13 не вместится в разряд десятков нашего ответа, поэтому мы запишем цифру 3 в разряде десятков, а единицу перенесём на следующий разряд: Записываем цифру 9 в разряде единиц нашего ответа:
Записываем цифру 9 в разряде единиц нашего ответа: Раньше там располагалось число 9, но поскольку мы взяли у него одну единицу оно обратилось в число 8. В разряде десятков второго числа располагается число 2. Восемь минус два будет шесть. Записываем число 6 в разряде десятков нашего ответа:
Раньше там располагалось число 9, но поскольку мы взяли у него одну единицу оно обратилось в число 8. В разряде десятков второго числа располагается число 2. Восемь минус два будет шесть. Записываем число 6 в разряде десятков нашего ответа: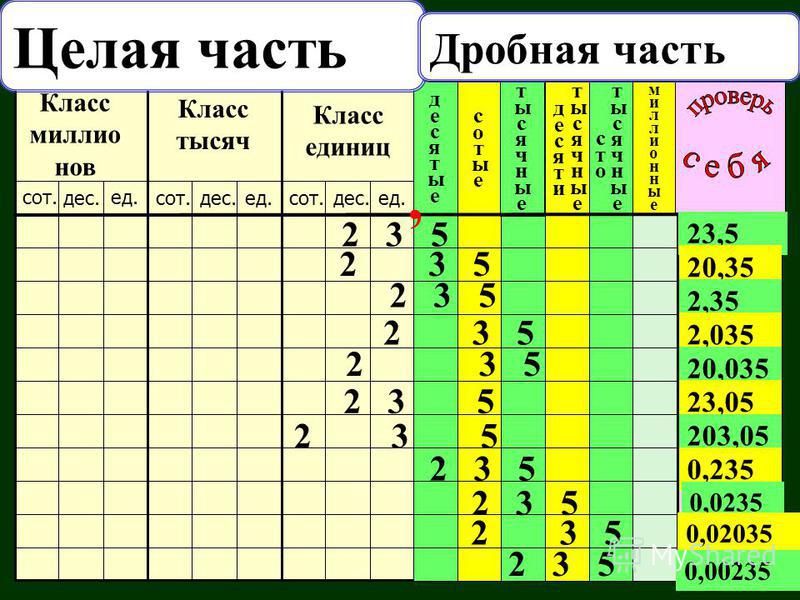 Взятую единицу мысленно дописываем слева от нуля. А поскольку у числа 4 мы взяли одну единицу, это число уменьшится на одну единицу:
Взятую единицу мысленно дописываем слева от нуля. А поскольку у числа 4 мы взяли одну единицу, это число уменьшится на одну единицу: А поскольку у числа 60 мы взяли одну единицу, это число уменьшится на одну единицу:
А поскольку у числа 60 мы взяли одну единицу, это число уменьшится на одну единицу: Но в следующем разряде тоже ноль. Тогда за следующее число принимаем 1000 и берем от этого числа единицу:
Но в следующем разряде тоже ноль. Тогда за следующее число принимаем 1000 и берем от этого числа единицу:
 Эту часть напряжения, приложенного
к трубке, называют катодным падением потенциала .
Эту часть напряжения, приложенного
к трубке, называют катодным падением потенциала .
 Свечение положительного столба вызвано, в основном, переходами
возбужденных молекул в основное состояние.
Свечение положительного столба вызвано, в основном, переходами
возбужденных молекул в основное состояние.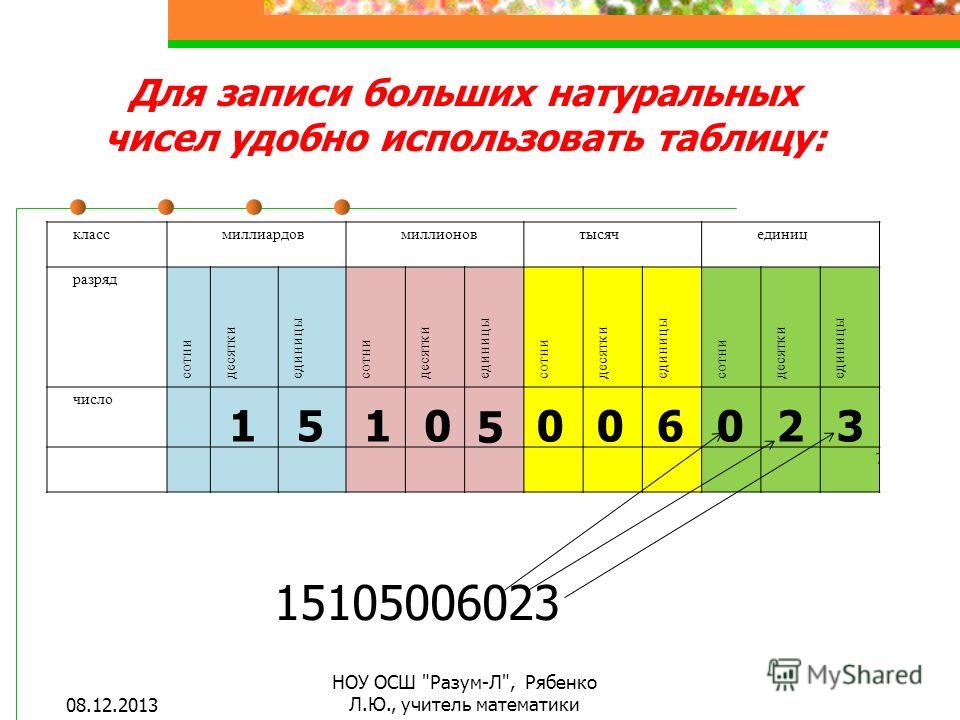 Если мощность
источника не очень велика, то после этого импульса тока разряд прекращается.
Напряжение между электродами начинает повышаться до прежнего значения, и пробой
газа повторяется с образованием нового искрового канала.
Если мощность
источника не очень велика, то после этого импульса тока разряд прекращается.
Напряжение между электродами начинает повышаться до прежнего значения, и пробой
газа повторяется с образованием нового искрового канала. Согласно В.Ф. Литкевичу (1872 –
1951), дуговой разряд поддерживается, главным образом, за счет
термоэлектронной эмиссии с поверхности катода. На практике – это сварка, мощные
дуговые печи.
Согласно В.Ф. Литкевичу (1872 –
1951), дуговой разряд поддерживается, главным образом, за счет
термоэлектронной эмиссии с поверхности катода. На практике – это сварка, мощные
дуговые печи.