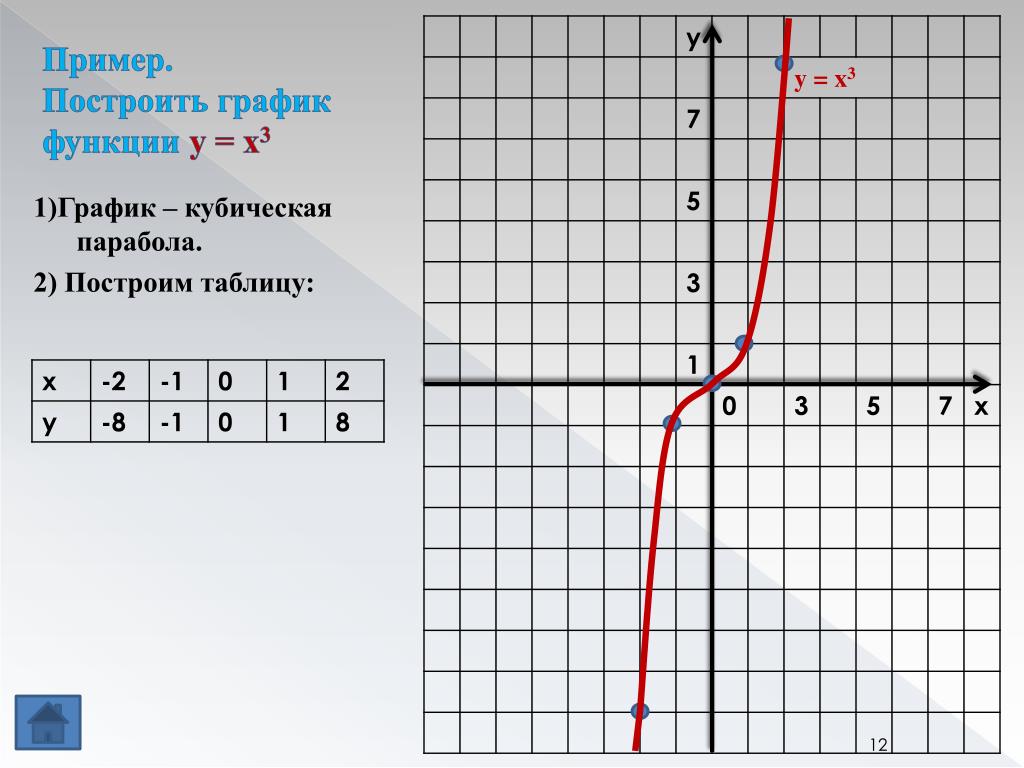
Как построить кубическую параболу: График кубической функции. Построить кубическую функцию. Кубическая парабола график.

3 + k\).

Если \(k > 0\), то график сдвигается на \(k\) единиц вверх; если \(k < 0\), то график сдвигается на \(k\) единиц вниз.
Если \(h > 0\),то график сдвигается на \(h\) единиц вправо; если \(h < 0\), то график смещается на \(h\) единиц влево.
Если \(a < 0\), график переворачивается.

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Наши преподаватели

Татьяна Валентиновна Лукьянчик

Репетитор по математике

Стаж (лет)

Образование:

Гродненский государственный университет им. Янки Купалы

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Танрыкули Азатович Сейткулиев

Репетитор по математике

Стаж (лет)

Образование:

Международный туркмено-турецкий университет

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Алла Александровна Коледа

Репетитор по математике

Стаж (лет)

Образование:

Барановичский высший педагогический колледж

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Предметы

Математика

Репетитор по физике
Репетитор по химии
Репетитор по русскому языку
Репетитор по английскому языку
Репетитор по обществознанию
Репетитор по истории России
Репетитор по биологии
Репетитор по географии
Репетитор по информатике

Специализации

Подготовка к ЕГЭ по математике (базовый уровень)

Подготовка к олимпиадам по химии
Подготовка к ОГЭ по русскому языку
Репетитор грамматики английского языка
Репетитор для подготовки к ЕГЭ по истории
Репетитор по истории для подготовки к ОГЭ
ВПР по обществознанию
Репетитор по обществознанию для подготовки к ОГЭ
Подготовка к ЕГЭ по географии
Подготовка к ЕГЭ по информатике

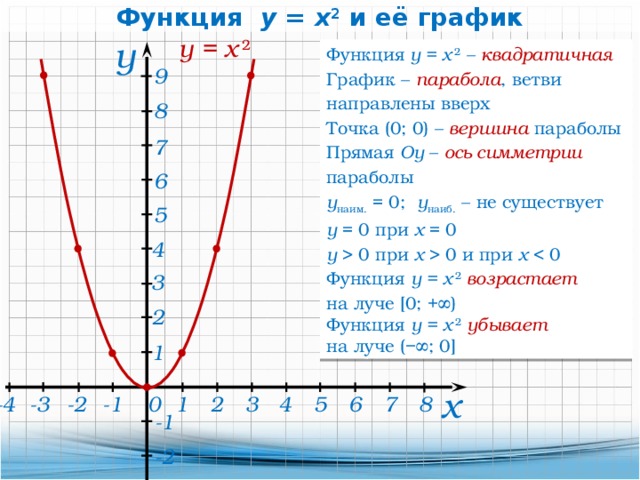
Кубическая парабола

Кубическая парабола задается функцией .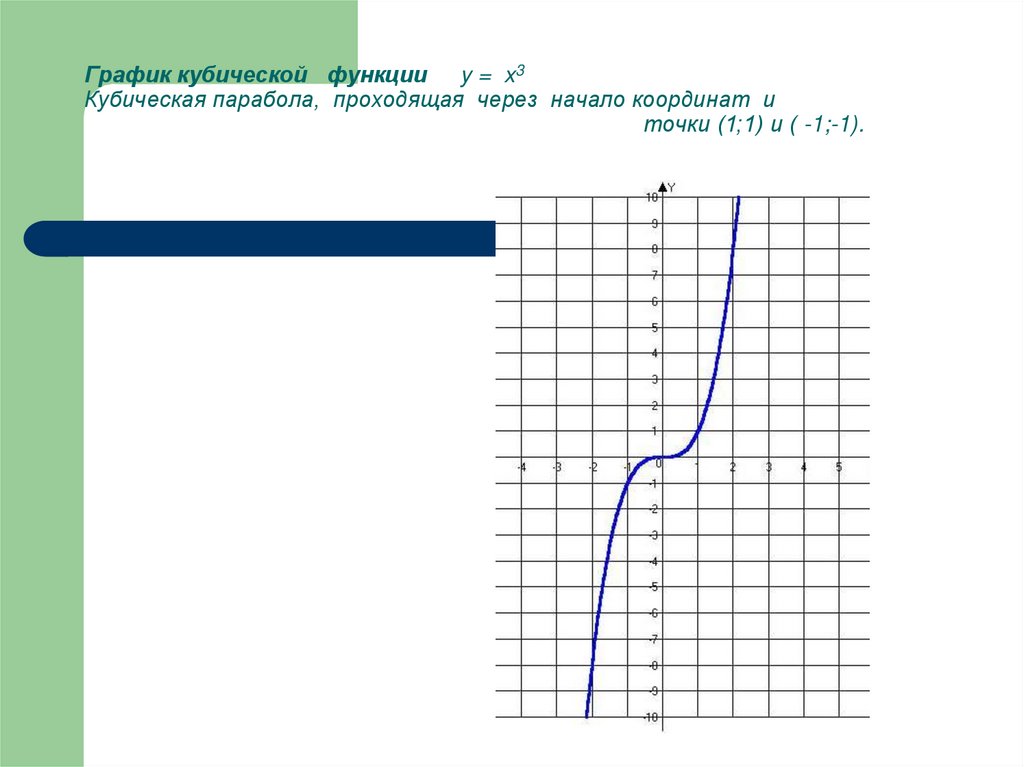 Вот знакомый со школы чертеж:

Перечислим основные свойства функции

Область определения – любое действительное число: .

Область значений – любое действительное число: .

Функция является нечётной. Если функция является нечётной, то ее график симметричен относительно начала координат. Аналитически нечётность функции выражается условием . Выполним проверку для кубической функции, для этого вместо «икс» подставим «минус икс»: , значит, функция является нечетной.

Функция не ограничена. На языке пределов функции это можно записать так: , Кубическую параболу тоже эффективнее строить с помощью Анфисы Чеховой алгоритма «челнока»:

Наверняка, вы заметили, в чем ещё проявляется нечетность функции. Если мы нашли, что , то при вычислении уже не нужно ничего считать, автоматом записываем, что . Эта особенность справедлива для любой нечетной функции.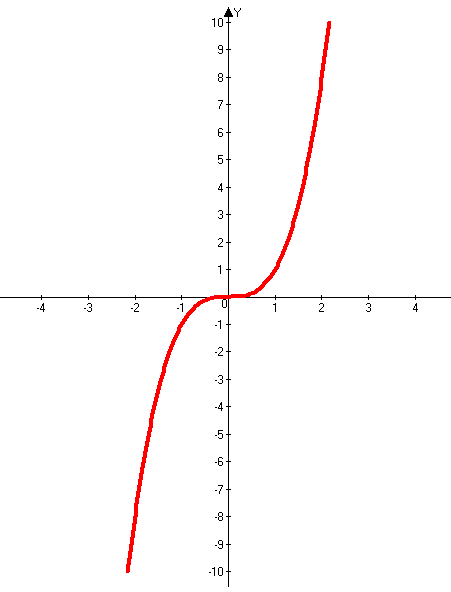

Теперь немного поговорим о графиках многочленов.

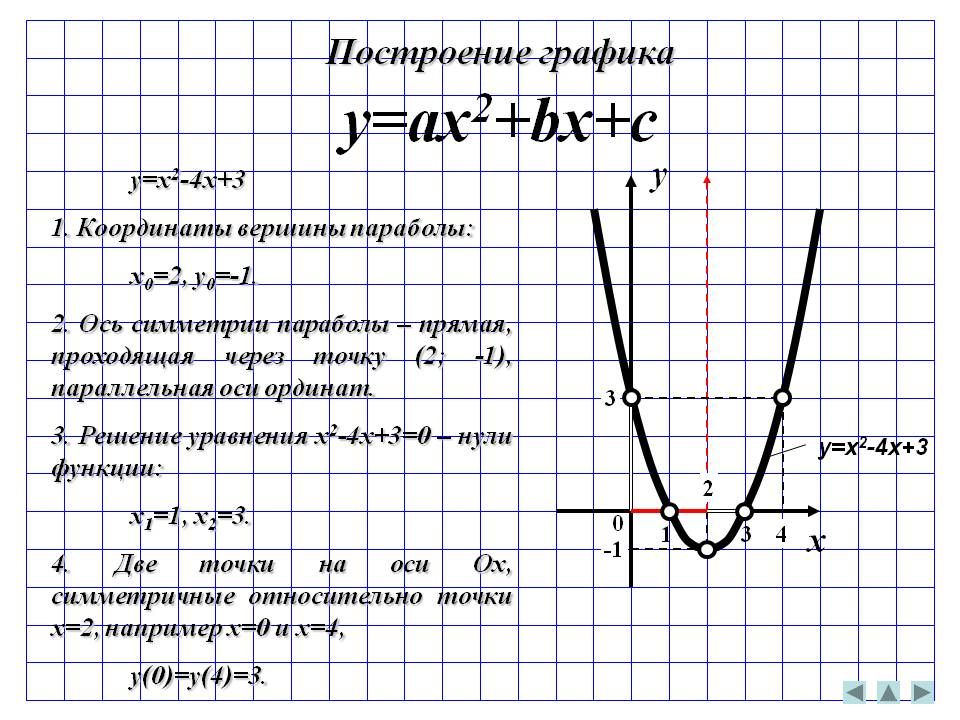
График любого многочлена третьей степени ( ) принципиально имеет следующий вид:

В этом примере коэффициент при старшей степени , поэтому график развёрнут «наоборот». Принципиально такой же вид имеют графики многочленов 5-ой, 7-ой, 9-ой и других нечетных степеней. Чем выше степень, тем больше промежуточных «загибулин».

Многочлены 4-ой, 6-ой и других четных степеней имеют график принципиально следующего вида:

Эти знания полезны при исследовании графиков функций.

График функции

Выполним чертеж:

Основные свойства функции :

Область определения: .

Область значений: .

То есть, график функции полностью находится в первой координатной четверти.

Функция не ограничена сверху. Или с помощью предела:

При построении простейших графиков с корнями также уместен поточечный способ построения, при этом выгодно подбирать такие значения «икс», чтобы корень извлекался нацело:

На самом деле хочется разобрать еще примеры с корнями, например, , но они встречаются значительно реже.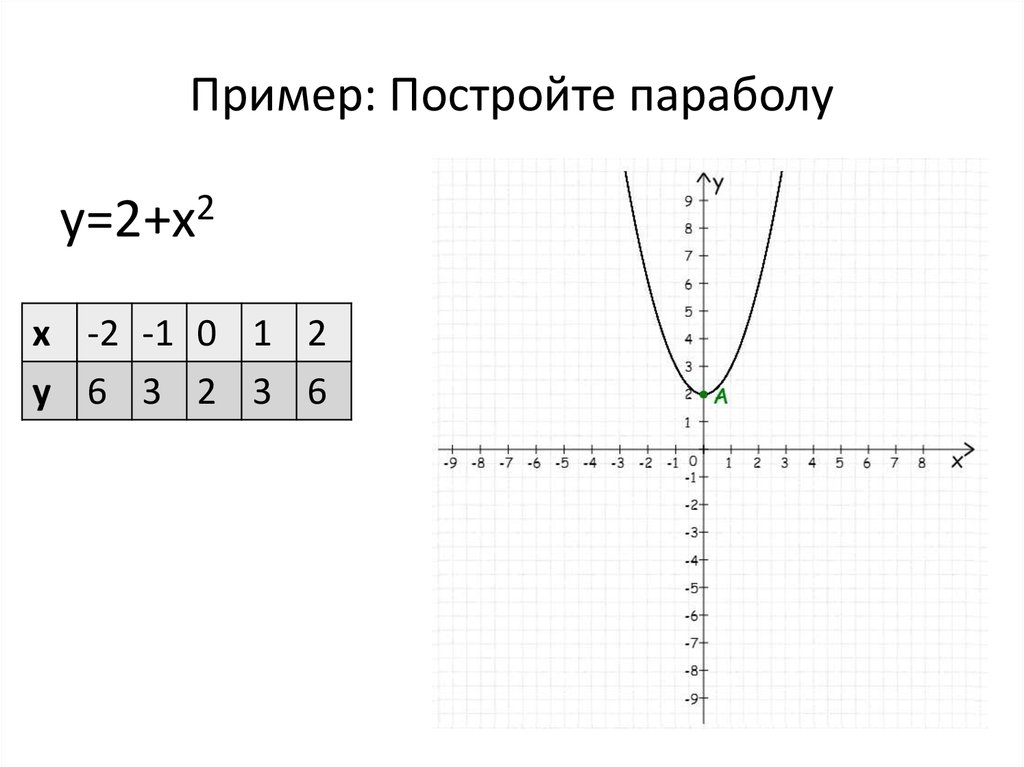 Я ориентируюсь на более распространенные случаи, и, как показывает практика, что-нибудь вроде приходиться строить значительно чаще. Если возникнет необходимость выяснить, как выглядят графики с другими корнями, то, рекомендую заглянуть в школьный учебник или математический справочник.

График гиперболы

Опять же вспоминаем тривиальную «школьную» гиперболу .

Выполним чертеж: Основные свойства функции :

Область определения: .

Область значений: .

Запись обозначает: «любое действительное число, исключая ноль»

В точке функция терпит бесконечный разрыв. Или с помощью одностороннихпределов: , . Немного поговорим об односторонних пределах. Запись обозначает, что мы бесконечно близко приближаемся по оси к нулю слева. Как при этом ведёт себя график? Он уходит вниз на минус бесконечность, бесконечно близко приближаясь к оси . Именно этот факт и записывается пределом . Аналогично, запись обозначает, что мы

бесконечно близко приближаемся по оси к нулю справа. При этом ветвь гиперболы уходит вверх на плюс бесконечность,бесконечно близко приближаясь к оси . Или коротко: .

Такая прямая (к которой бесконечно близко приближается график какой-либо функции) называется асимптотой.

В данном случае ось является вертикальной асимптотой для графика гиперболы при .

Будет ГРУБОЙ ошибкой, если при оформлении чертежа по небрежности допустить пересечение графика с асимптотой.

Также односторонние пределы , говорят нам о том, что гипербола не ограничена сверху и не ограничена снизу.

Исследуем функцию на бесконечности: , то есть, если мы начнем уходить по оси влево (или вправо) на бесконечность, то «игреки» стройным шагом будут бесконечно близко

приближаться к нулю, и, соответственно, ветви гиперболы бесконечно близкоприближаться к оси .

Таким образом, ось является горизонтальной асимптотой для графика функции , если «икс» стремится к плюс или минус бесконечности.

Функция является нечётной, а, значит, гипербола симметрична относительно начала координат. Данный факт очевиден из чертежа, кроме того, легко проверяется аналитически: .

График функции вида ( ) представляют собой две ветви гиперболы.

Если , то гипербола расположена в первой и третьей координатных четвертях(см. рисунок выше).

Если , то гипербола расположена во второй и четвертой координатных четвертях.

Пример 3

Построить правую ветвь гиперболы

Используем поточечный метод построения, при этом, значения выгодно подбирать так, чтобы делилось нацело:

Выполним чертеж:

Не составит труда построить и левую ветвь гиперболы, здесь как раз поможет нечетность функции.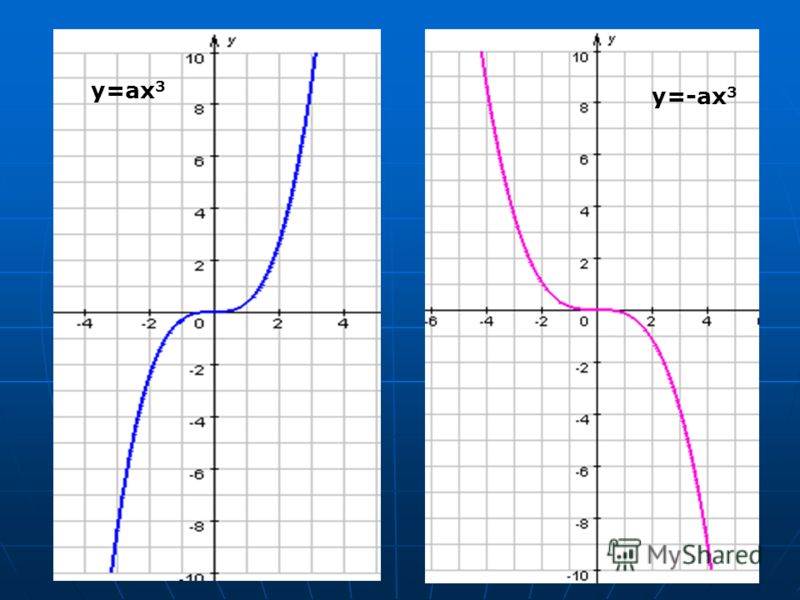 Грубо говоря, в таблице поточечного построения мысленно добавляем к каждому числу минус, ставим соответствующие точки и прочерчиваем вторую ветвь.

Параболы и кубики

Параболы и кубики

На этом уроке мы познакомимся с графиками уравнений вида y = x ² и y = ax ³ . Мы видели ранее, что график y = m x + b — это график линии. Что произойдет, если там является членом x ² в этом выражении? Давайте сначала посмотрим на простейшее уравнение, которое имеет х ² срок.

Пример 1

Что такое график

y = x ²

Раствор

Чтобы нарисовать это, мы можем придумать несколько точек. Давайте сделаем T-таблицу с значения -3,-2,-1,0,1,2 для х .

У нас есть

(-3) ² = 9 (-2) ² = 4 (-1) ² = 1

(0) ² = 0 (1) ² = 1 (2) ² = 4 (3) ² = 9

Мы можем поместить их в Т-таблицу.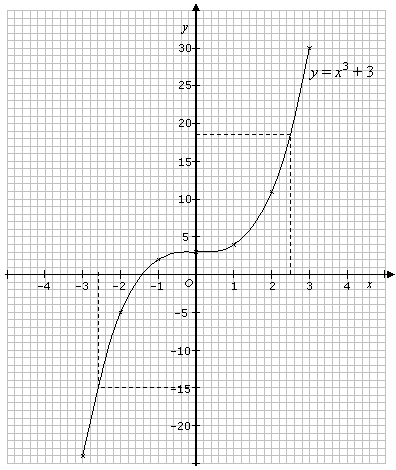

х	г
-3	9
-2	4
-1	1
0	0
1	1
2	4
3	9

Эта таблица дает нам баллы (-3,9), (-2,4), (-1,1), (0,0), (1,1), (2,4) и (3,9). Затем мы нанесем эти точки на плоскость xy . Обратите внимание, что все эти точки имеют неотрицательное и -координата.

Наконец, на графике мы можем соединить точки плавной кривой. график показан ниже.

Обратите внимание, что график остается над осью x .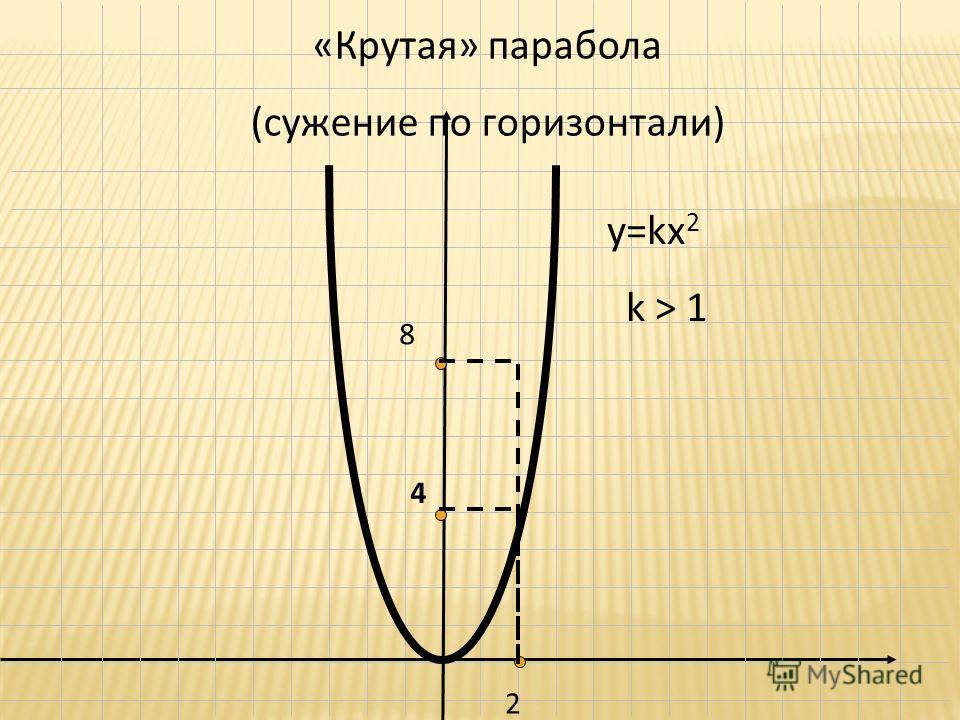 Если вы думаете о ось y как зеркало, то правая часть графика такая же, как левая часть графика отражена через y -ось. Мы видим что форма немного похожа на улыбку. Он круче вдали от истока и менее крутой вблизи начала координат. Мы называем этот тип графа парабола.

Теперь давайте рассмотрим другой пример построения графика уравнения, содержащего х ² .

Пример 2

Нарисуйте график

у = — x ²

Раствор

Мы следуем тому же процессу, что и в примере 1.

Создадим Т-таблицу со значениями -3,-2,-1,0,1,2 для х .

У нас есть

-(-3) ² = -9 -(-2) ² = -4 -(-1) ² = -1

-(0) ² = -0 -(1) ² = -1 -(2) ² = -4 -(3) ² = -9

Мы можем поместить их в Т-таблицу.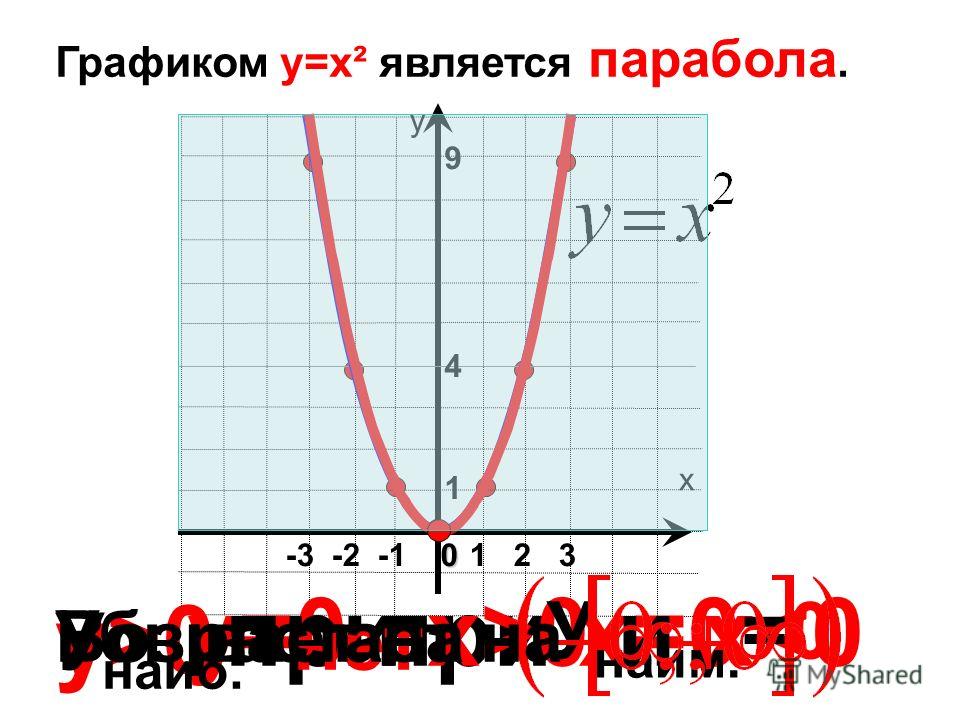

х	г
-3	-9
-2	-4
-1	-1
0	-0
1	-1
2	-4
3	-9

Эта таблица дает нам баллы (-3,-9), (-2,-4), (-1,-1), (0,-0), (1,-1), (2,-4) и (3,-9). Затем мы наносим эти точки на плоскость xy . и соедините точки плавной кривой. Обратите внимание, что все эти точки имеют неположительную координату y .

Мы видим, что эта кривая имеет ту же форму, но перевернута, как хмурый взгляд.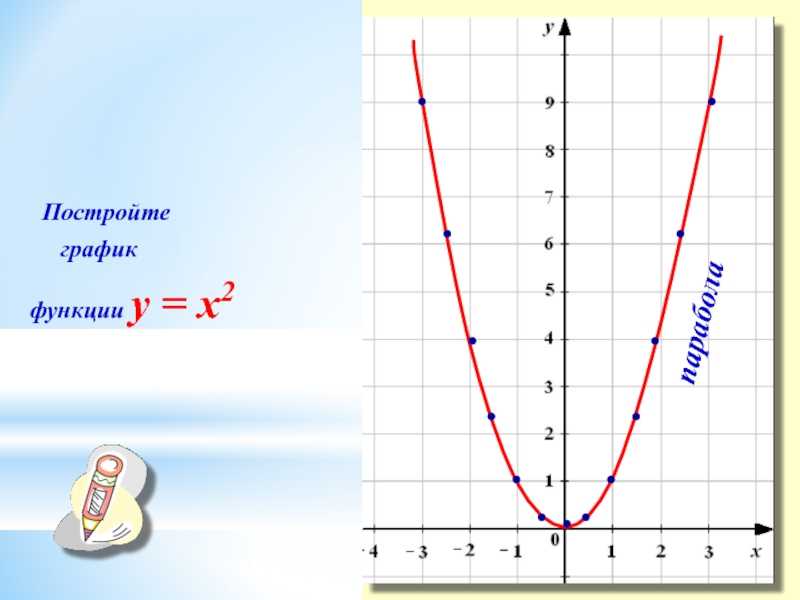 Небрежно мы называем это «параболой хмурого взгляда».

Получается, что все графики уравнений вида

у = ах ²

, где a — ненулевое число, имеют форму парабола. Чтобы определить, похоже ли это на улыбку или хмурый взгляд, следуйте принцип:

Если a > 0, то парабола выглядит как улыбка
Если a < 0, то парабола выглядит как хмурый взгляд

Пример 3

Графики, показанные ниже, представляют собой графики парабол. Обратите внимание, что уравнения, которые включают отрицательный знак, имеют графики, которые «хмурятся», в то время как те без «смайлов»

Теперь попробуйте сами. Если хотите увидеть ответ, наведите мышку на желтом прямоугольнике и появится ответ.

Упражнение 1

Что из следующего может быть графиком y = -0,4 x ² для положительных значений х ?

Ответ

Теперь, когда мы понимаем, как распознавать графики y = ax ² , посмотрим когда будем иметь мощность 3 вместо мощности 2. Эти графики называются кубические кривые и имеют уравнение

у = ах ³

Пример 4

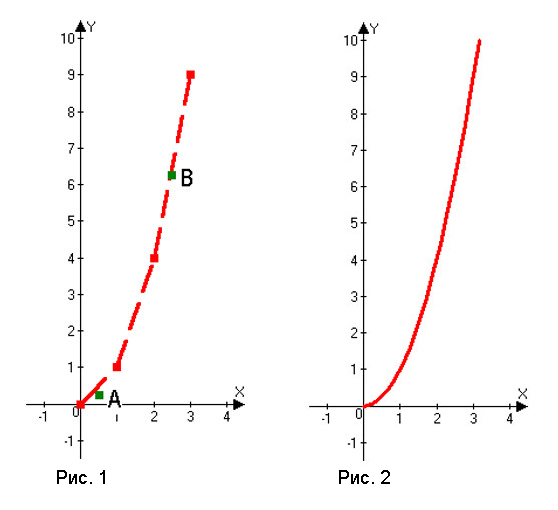
График y = x ³ показан ниже.

Обратите внимание, что этот график начинается снизу слева, резко движется вверх, становится плоским. в начале координат, а затем снова резко поднимается вверх. Это описание будет применяться ко всем графикам уравнений г = ax ³ с положительными значениями a .

Пример 5

График y = -x ³ показан ниже.

Обратите внимание, что этот график совпадает с графиком и . = x ³, но в перевернутом виде. В частности, слева начинается высоко. Затем она резко падает, пока не выравнивается в начале координат. Затем он возобновляет крутой спуск вправо от начала координат. Этот описание будет применяться ко всем графикам уравнений г = x ³ с отрицательными значениями и .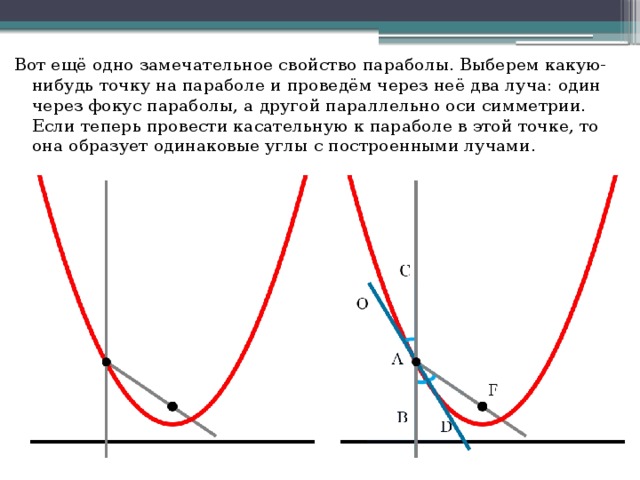

Пример 6

Ниже приведены еще несколько кубических графиков.

Обратите внимание, что при появлении отрицательного знака график идет сверху слева к Нижний правый. В противном случае он идет снизу слева вверх справа.

Теперь попробуйте сами. Если хотите увидеть ответ, наведите мышку на желтом прямоугольнике и появится ответ.

Упражнение 2

Сопоставьте уравнение с его графиком.

A. y = 1/3 x ² Б. y = 1/3 х ³

C. y = -1/3 x ² Д. г = -1/3 x ³

Ответ

Графики кубических функций – объяснение и примеры

Графики кубических функций дают двумерную модель функций, где x возведен в третью степень.

Графики кубических функций в некоторых отношениях аналогичны графикам квадратичных функций. В частности, мы можем использовать базовую форму кубического графика для создания моделей более сложных кубических функций.

Прежде чем научиться строить графики кубических функций, полезно ознакомиться с преобразованиями графиков, геометрией координат и построением графиков квадратичных функций. Графики кубических функций также потребуют приличного знакомства с алгеброй и алгебраическими манипуляциями с уравнениями.

В этом разделе мы рассмотрим:

Как построить график кубической функции

Как построить график кубической функции

Перед построением графика кубической функции важно ознакомиться с исходной функцией , у=х ³ .

Существуют методы исчисления, позволяющие легко находить локальные экстремумы. В частности, мы можем найти производную кубической функции, которая будет квадратичной функцией. Затем мы можем использовать ключевые точки этой функции, чтобы выяснить, где находятся ключевые точки кубической функции. Однако это будет рассмотрено более подробно в разделах исчисления об использовании производной.

Здесь мы сосредоточимся на том, как мы можем использовать преобразования графа, чтобы найти форму и ключевые точки кубической функции.

Ключевые точки родительской функции

Родительская функция x ³ проходит через начало координат. Он имеет форму, похожую на две половинки параболы, направленные в противоположные стороны, склеенные вместе.

Вершина

Вершина кубической функции — это точка, в которой функция меняет направление. В родительской функции эта точка является исходной.

Чтобы сдвинуть эту вершину влево или вправо, мы можем добавлять или вычитать числа из куба функции. Например, функция (x-1) ³ — это кубическая функция, сдвинутая на одну единицу вправо. В этом случае вершина находится в (1, 0).

Чтобы сдвинуть эту функцию вверх или вниз, мы можем добавлять или вычитать числа после кубической части функции.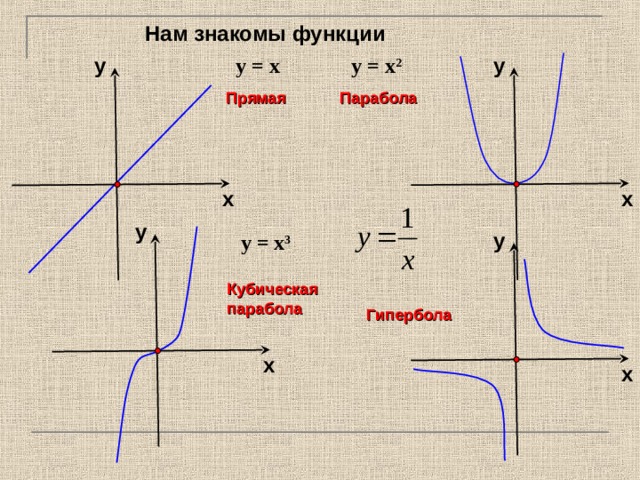 Например, функция x ³ +1 — это кубическая функция, сдвинутая на единицу вверх. Его вершина (0, 1).

Отражение

Как и прежде, если мы умножим возведённую в куб функцию на число а, мы сможем изменить растяжку графика. Например, 0,5x ³ сжимает функцию, а 2x ³ расширяет его.

Если это число a отрицательное, оно переворачивает график вверх дном, как показано на рисунке.

Точка пересечения с осью y

Как и в случае с квадратичными и линейными функциями, точка пересечения с осью y — это точка, в которой x=0. Чтобы найти его, вы просто находите точку f(0).

В родительской функции точка пересечения по оси Y и вершина совпадают. В функции (x-1) ³ точка пересечения с осью y равна (0-1) ³ =-(-1) ³ =-1.

Х-пересечения.

В отличие от квадратичных функций кубические функции всегда имеют хотя бы одно действительное решение. Их может быть до трех. Например, функция x(x-1)(x+1) упрощается до x ³ -x.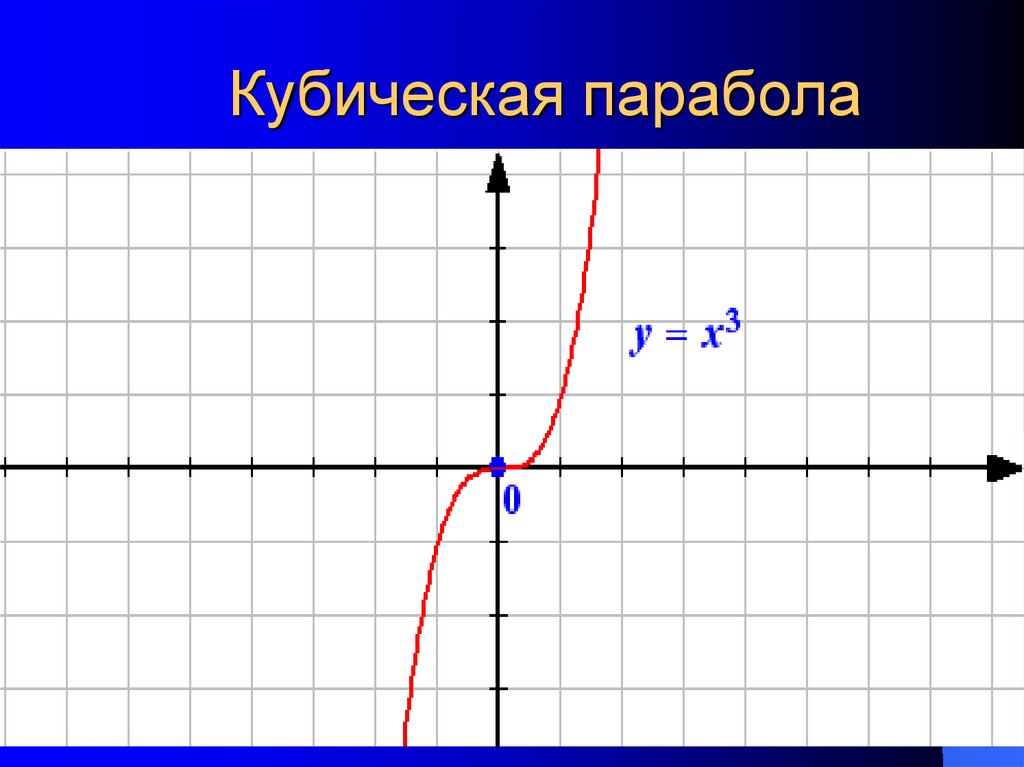 Однако из исходной формы функции видно, что эта функция будет равна 0, когда x=0, x=1 или x=-1.

Для решения кубического уравнения есть формула, но она намного сложнее соответствующей формулы для квадратного уравнения:

^³ √ _{((^-B= /_27A³ + ^{до н.э.} /_6A² —^D /_2A²) + √ _{(^{-B= _{/_{/_{95559555555555559555955955595595559559559559111 гг.} —^D /_{5 2A²}) ² + (^C /_3A —^B² /_9A²) ³)}} + ^{^{3 9001)}}}}} + ^{^{3 9001 2 959595955955955955955955955955955955955955955955955955955955959595959595959595959595959595959595959595959595959595959559)) 27a³ + ^bc / _6a² – ^d / _2a² )+√ _{(( ^-b³ / _27a³ + ^bc / _6a² – ^d / _2a² )²-( ^c / _3a – ^b² / _9a² )³))} – ^b / _3а .}}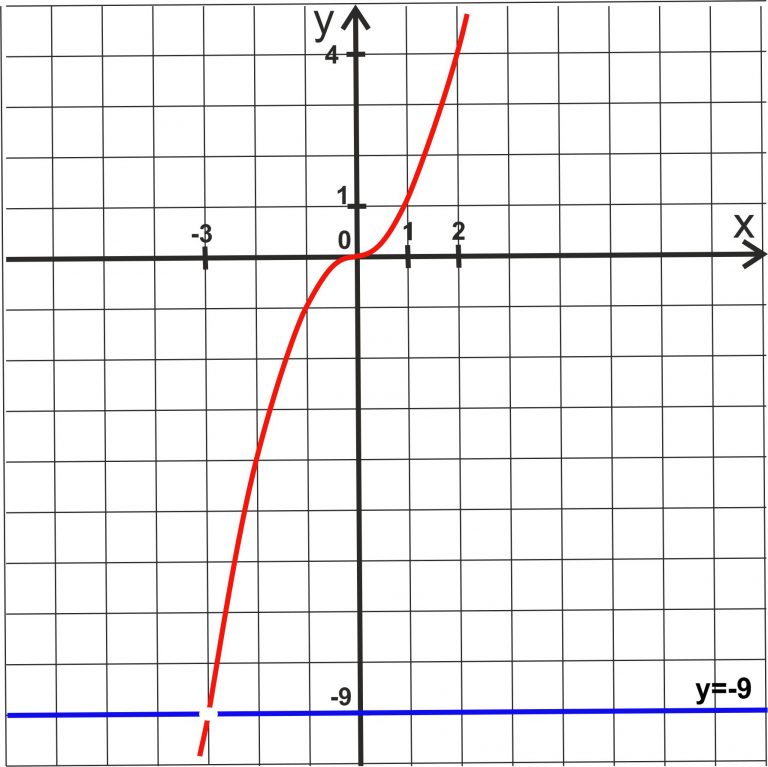

Это довольно длинная формула, поэтому многие люди полагаются на калькуляторы, чтобы найти нули кубических функций, которые нелегко разложить на множители.

Примеры

В этом разделе рассказывается, как строить графики простых примеров кубических функций без использования производных.

Пример 1

График функции -x ³ .

Пример 1 Решение

Единственным отличием данной функции от родительской функции является наличие отрицательного знака. Если мы умножаем кубическую функцию на отрицательное число, она отражает функцию по оси X.

Таким образом, функция -x ³ — это просто функция x ³, отраженная по оси x. Его вершина по-прежнему (0, 0). Эта точка также является единственной точкой пересечения x или y в функции.

Пример 2

График функции (x-2) ³ -4.

Пример 2 Решение

Опять же, мы будем использовать родительскую функцию x ³, чтобы найти график заданной функции.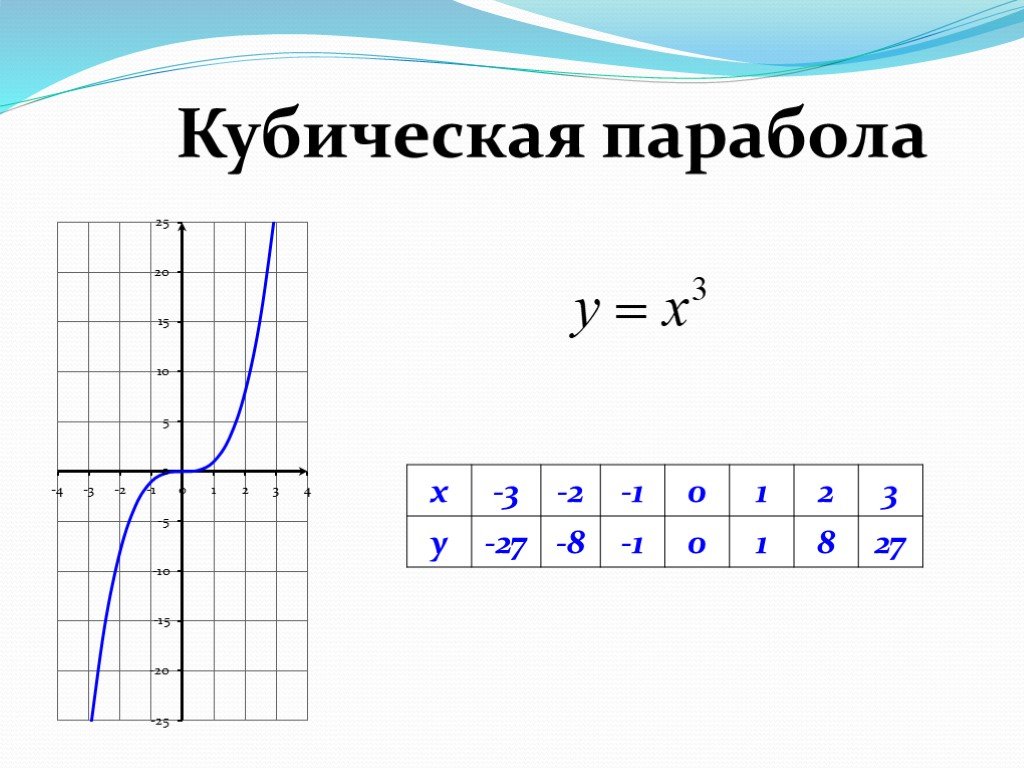

В этом случае нам нужно помнить, что все числа, добавленные к x-члену функции, представляют сдвиг по горизонтали, а все числа, добавленные к функции в целом, представляют сдвиг по вертикали.

В данной функции мы вычитаем 2 из x, что представляет собой сдвиг вершины на две единицы вправо. Это может показаться нелогичным, потому что, как правило, отрицательные числа представляют движение влево, а положительные числа представляют движение вправо. Однако при преобразованиях графа все преобразования, выполняемые непосредственно с x, имеют противоположное ожидаемому направление.

Мы также вычитаем 4 из функции в целом. Это означает, что мы сдвинем вершину на четыре единицы вниз.

За исключением этих двух сдвигов, функция очень похожа на родительскую функцию. Вершина будет в точке (2, -4).

Новый y-отрезок будет:

(0-2) ³ -4

-8-4

Таким образом, точка (0, -12).

Мы можем решить это уравнение для x, чтобы найти точку пересечения x:

0=(x-2) ³ -4

4=(x-2) ³ .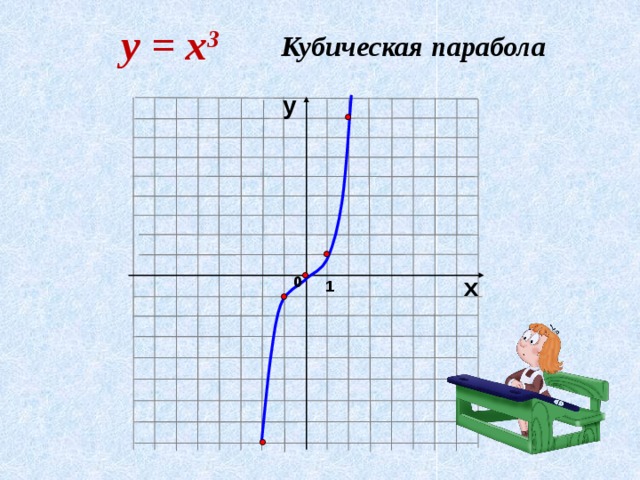

На данный момент мы должны взять кубический корень с обеих сторон. Это дает нам:

∛(4)=x-2

∛(4)+2=x.

Десятичное приближение этого числа равно 3,59, поэтому точка пересечения по оси x приблизительно равна (3,59, 0).

Таким образом, мы построили график функции, как показано ниже.

Пример 3

Упростите функцию x(x-2)(x+2). Затем найдите ключевые точки этой функции.

Пример 3 Решение

В текущей форме легко найти точки пересечения x и y этой функции.

Установка x=0 дает нам 0(-2)(2)=0. Таким образом, точка пересечения по оси y равна (0, 0). Следовательно, это также будет x-intercept.

В этом случае, однако, у нас фактически есть больше чем один x-перехват. Если x=2, средний член (x-2) будет равен 0, а функция будет равна 0. Аналогично, если x=-2, последний член будет равен 0, и, следовательно, функция будет равна 0.

Таким образом, у нас есть три x-отрезка: (0, 0), (-2, 0) и (2, 0).

Расширение функции дает нам x ³ -4x.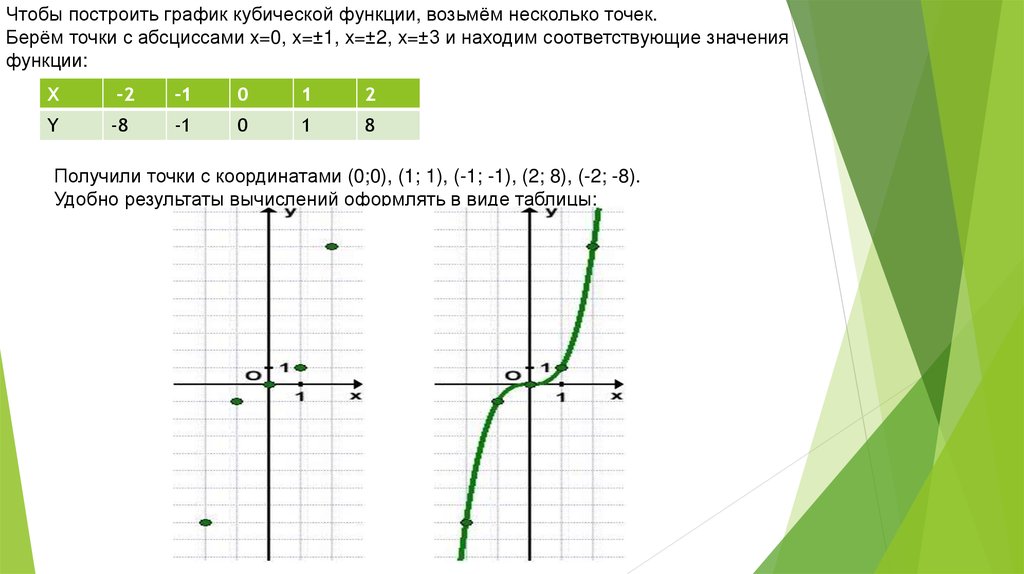 Поскольку мы ничего не добавляем непосредственно к кубу x или к самой функции, вершиной является точка (0, 0).

Следовательно, функция соответствует графику ниже.

Пример 4

Упростите и нарисуйте график функции x(x-1)(x+3)+2. Затем найдите ключевые точки этой функции.

Пример 4 Решение

Предположим на мгновение, что эта функция не содержит двойки в конце. Пересечения по оси x функции x(x-1)(x+3) равны 0, 1 и -3, поскольку, если x равно любому из этих чисел, вся функция будет равна 0. Пересечение по оси y такой функции равен 0, потому что, когда x=0, y=0.

Расширение функции x(x-1)(x+3) дает нам x ³ +2x ² -3x. Опять же, поскольку непосредственно к x ничего не добавляется и в конце функции ничего нет, вершина этой функции равна (0, 0).

Теперь давайте добавим 2 в конце и подумаем, что это делает.

По сути, мы просто сдвигаем функцию x(x-1)(x+3) вверх на две единицы. Мы можем добавить 2 ко всем значениям y в наших перехватах.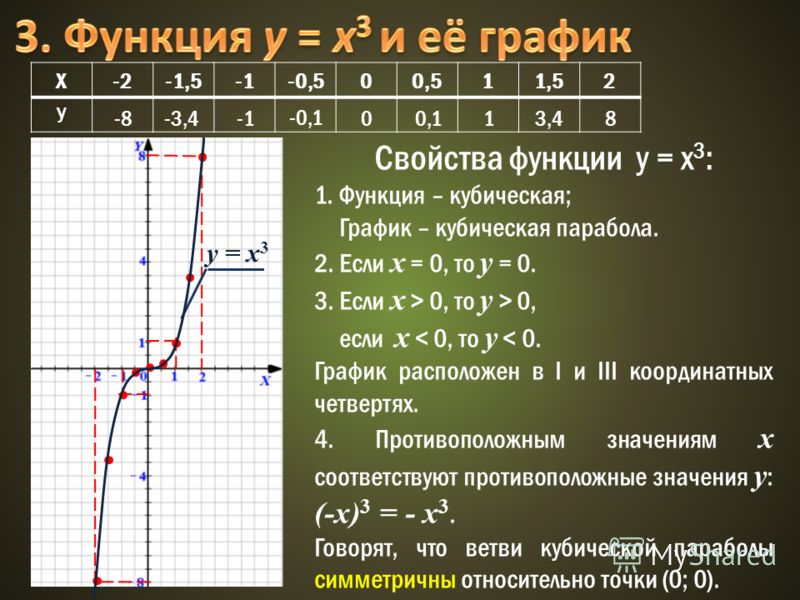

То есть мы теперь знаем точки (0, 2), (1, 2) и (-3, 2). Первая точка (0, 2) является точкой пересечения с осью y.

Х-пересечение этой функции более сложное. Для построения графика мы можем просто аппроксимировать его, сдвинув график функции x(x-1)(x+3) вверх на две единицы, как показано.

Пример 5

Определите алгебраическое выражение для показанной кубической функции. Не забудьте также определить любые ключевые моменты.

Пример 5 Решение

Форма этой функции очень похожа на функцию and x ³. Мы можем увидеть, является ли это просто функцией в кубе x со смещенной вершиной, определив вершину и проверив некоторые точки.

Похоже, вершина находится в точке (1, 5). Мы также можем видеть точки (0, 4), которые являются точкой пересечения с осью y, и (2, 6).

Если функция действительно является просто сдвигом функции x ³ , расположение вершины означает, что ее алгебраическое представление равно (x-1) ³ +5.