Исследовательская работа треугольник паскаля: Научно-исследовательская работа по теме «Треугольник Паскаля» (9 класс)
Научно-исследовательская работа по теме «Треугольник Паскаля»
Муниципальное казенное общеобразовательное учреждение
«Богучарская средняя общеобразовательная школа № 1»
Научно-исследовательская работа
по теме: «Треугольник Паскаля»
Автор: Карпенко Софья Владимировна 8 «А» класс
Руководитель: Алабина Галина Юрьевна
Богучар 2015
ОглавлениеВведение
Основная часть
Теоретическая часть работы
а) Блез Паскаль – французский математик
б) треугольник Паскаля как разновидность треугольника
в) свойства треугольника Паскаля и их применение в решении
задач
Практическая часть работы
а) составление последовательности тренировочных задач
по теме «Треугольник Паскаля»
б) создание презентации «Треугольники вокруг нас»
Заключение
Актуальность проекта
Данный проект предназначен для выявления того, насколько широко треугольники используются в практической жизни.
Новизна проекта
Новизна моего исследования состоит в том, что я попыталась показать связь треугольников с жизнью.
Практическая значимость проекта
Данный проект может быть использован как дополнительный материал к урокам геометрии, для внеклассной работы по математике.
Цель проекта
— ознакомиться с треугольником Паскаля как разновидностью треугольников;
— рассмотреть применение треугольника Паскаля в различных сферах;
Гипотеза
Если числа треугольника Паскаля обладают особыми свойствами, то его можно считать волшебным.
Задачи
— изучить литературу по теме «Треугольник Паскаля»;
— выявить свойства чисел, входящих в состав треугольника Паскаля;
— определить применение свойств чисел треугольника Паскаля;
— сформулировать вывод и итоги исследования;
Объект исследования: треугольник как геометрическая фигура
Предмет исследования: свойства треугольника Паскаля
Методы исследования:
— поиск информации в интернет — ресурсах.
Направления работы:
— выбор проблемы, источников литературы, составление плана;
— работа с литературой и другими источниками;
— обработка полученных данных;
— анализ результатов, формулирование вывода;
Основные этапы проекта: подготовительный; деятельностный;
ход исследования; рефлексивный; аналитический; презентационный.
Введение
В прошлом учебном году мы начали изучать новый предмет «геометрия».Одна из глав курса геометрии называется «Треугольники». Меня очень заинтересовала данная тема. Я всегда хотела узнать много нового о треугольниках. Ведь мир треугольников очень загадочен и интересен. Я хочу узнать как можно больше о происхождении треугольников, об их значении в нашей жизни.
Треугольник — первая геометрическая фигура, встречающаяся в древних орнаментах. Изучая литературу, я узнала, что в Египте он символизировал триаду духовной воли, любви, интуиции и высшего разума человека, то есть его личность или душу.
Изучая литературу, я узнала, что в Египте он символизировал триаду духовной воли, любви, интуиции и высшего разума человека, то есть его личность или душу.
Существует множество видов треугольников, но больше всего меня заинтересовал треугольник Паскаля.
Теоретическая часть работы
Блез Паскаль – французский математик
Блез Паскаль (19 июня 1623, Клермон-Ферран, — 19 августа 1662, Париж) — французский математик, физик, литератор и философ.
Паскаль был первоклассным математиком. Он помог создать два крупных новых направления математических исследований. В возрасте шестнадцати лет написал замечательный трактат о предмете проективной геометрии и в 1654 году переписывался с Пьером де Ферма по теории вероятностей, что впоследствии оказало принципиальное влияние на развитие современной экономики.
Треугольник Паскаля как разновидность треугольника
Изучая разновидности треугольников, я выяснила, чтотреугольник Паскаля — арифметический треугольник, образованный биномиальными коэффициентами.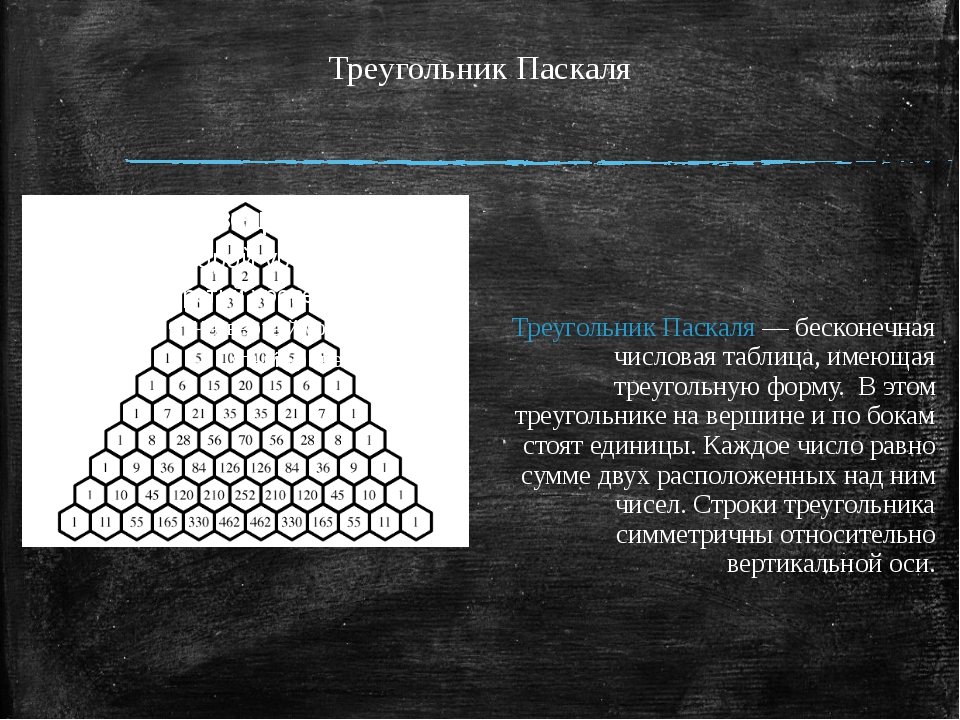 Назван в честь Блеза Паскаля.В действительности, треугольник Паскаля был известен задолго до 1653 года — даты выхода «Трактата об арифметическом треугольнике». Так, этот треугольник воспроизведен на титульном листе учебника арифметики, написанном в начале XVI Петром Апианом, астрономом из Ингольтштадского университета. Изображен треугольник и на иллюстрации в книге одного китайского математика, выпущенной в 1303 году. Омар Хайям, бывший не только философом и поэтом, но и математиком, знал о существовании треугольника около 1100 года, в свою очередь, заимствовав его из более ранних китайских или индийских источников.
Назван в честь Блеза Паскаля.В действительности, треугольник Паскаля был известен задолго до 1653 года — даты выхода «Трактата об арифметическом треугольнике». Так, этот треугольник воспроизведен на титульном листе учебника арифметики, написанном в начале XVI Петром Апианом, астрономом из Ингольтштадского университета. Изображен треугольник и на иллюстрации в книге одного китайского математика, выпущенной в 1303 году. Омар Хайям, бывший не только философом и поэтом, но и математиком, знал о существовании треугольника около 1100 года, в свою очередь, заимствовав его из более ранних китайских или индийских источников.

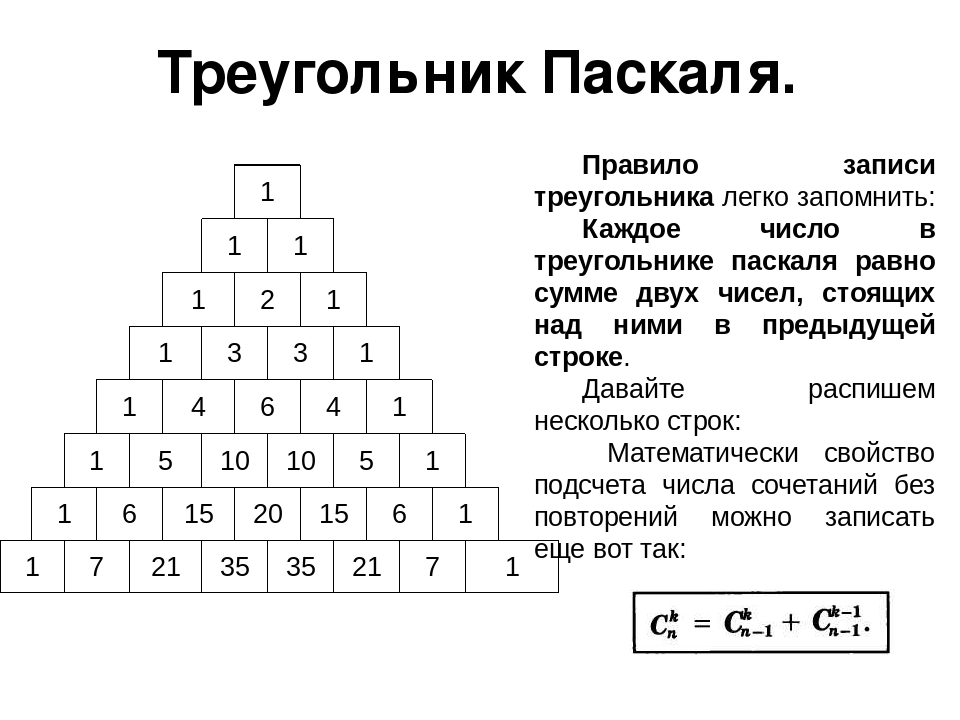
Изучая специальную литературу, я узнала, что еще проще объясняют устройство треугольника Паскаля слова: каждое число равно сумме двух расположенных над ним чисел. Все элементарно, но сколько в этом таится чудес. Если очертить треугольник Паскаля, то получится равнобедренный треугольник. Треугольник Паскаля имеет применение в теории вероятностей и обладает замечательными свойствами.
Свойства треугольника Паскаля и их применение в решении задач
Изучая свойства треугольника Паскаля, я рассмотрела одно из свойств биномиальных коэффициентов:
Данное равенство показывает, что биномиальные коэффициенты можно последовательно выписывать в виде треугольной таблицы, которая называется треугольником Паскаля. В n-ой строке треугольника Паскаля стоят коэффициенты разложения , причем каждый коэффициент, кроме крайних двух, которые равны 1, равен сумме соответствующих коэффициентов из предыдущей строки.
Я узнала, что треугольник Паскаля — это бесконечная числовая таблица «треугольной формы», в которой по боковым сторонам стоят единицы и всякое число, кроме этих боковых единиц, получается как сумма двух предшествующих чисел. В такой форме треугольник Паскаля появился в сочинении Паскаля «Трактат об арифметическом треугольнике», изданном в 1665 г. уже после смерти автора.
Паскаль подробно исследовал свойства и применения своего «треугольника». Приведу для примера лишь 3 свойства «треугольника», найденные самим Паскалем; при этом буду исходить из того расположения «треугольника» на плоскости, какое было указанно Паскалем, и говорить о горизонтальных и вертикальных рядах. Свойство 1: Каждое число А в таблице равно сумме чисел предшествующего горизонтального ряда, начиная с самого левого вплоть до стоящего непосредственно над числом А (в котором клетки, содержащие слагаемые, дающие в сумме А, заштрихованы).
рис. 1 рис. 2 рис. 3
1 рис. 2 рис. 3
Свойство 2: Каждое число А в таблице равно сумме чисел предшествующего вертикального ряда, начиная с самого верхнего вплоть до стоящего непосредственно левее числа А. Рис. 2. Свойство 3: Каждое число в таблице, будучи уменьшенным на единицу, равно сумме всех чисел, заполняющих прямоугольник, ограниченный теми вертикальными и горизонтальными рядами, на пересечении которых стоит число А (сами эти ряды в рассматриваемый прямоугольник не включаются). Рис. 3.
Я пришла к выводу, что рассмотренные свойства треугольника Паскаля подтверждают слова Мартина Гарднера о том, что треугольник Паскаля одна из наиболее изящных схем во всей математике.
Актуальность исследования обусловлена ежегодным усложнением заданий ГИА и ЕГЭ, что требует углубленных знаний не только в алгебре, но и в геометрии.
Практическая часть работы
Я рассмотрела схему построения треугольника, предложенную Гуго Штейнгаузом в его классическом «Математическом калейдоскопе»: предположим, что вы входите в город как показано на схеме синей стрелкой, и можете двигаться только вперед, точнее, все время выбирая, вперед налево, или вперед направо. Узлы, в которые можно попасть только единственным образом, отмечены зелеными смайликами, точка, в которую можно попасть двумя способами, показана красным смайликом, а тремя, соответственно — розовыми. Это один из вариантов построения треугольника.
Узлы, в которые можно попасть только единственным образом, отмечены зелеными смайликами, точка, в которую можно попасть двумя способами, показана красным смайликом, а тремя, соответственно — розовыми. Это один из вариантов построения треугольника.
Задача 1.В магазине «Филателия» продается 8 различных наборов марок, посвященных спортивной тематике. Сколькими способами можно выбрать из них 3 набора?
Решение:
В треугольнике Паскаля число, показывающее, сколькими способами можно выбрать k элементов из множества, содержащего n различных элементов, стоит на пересечении k-ой диагонали и n-ой строки.
Найду диагональ восьмую сверху и отсчитываю три числа по горизонтали. Получу число 56.
Задача 2.Из шести врачей поликлиники двух необходимо отправить на курсы повышения квалификации. Сколькими способами это можно сделать?
Решение:
Найду диагональ шестую сверху и отсчитываю два числа по горизонтали.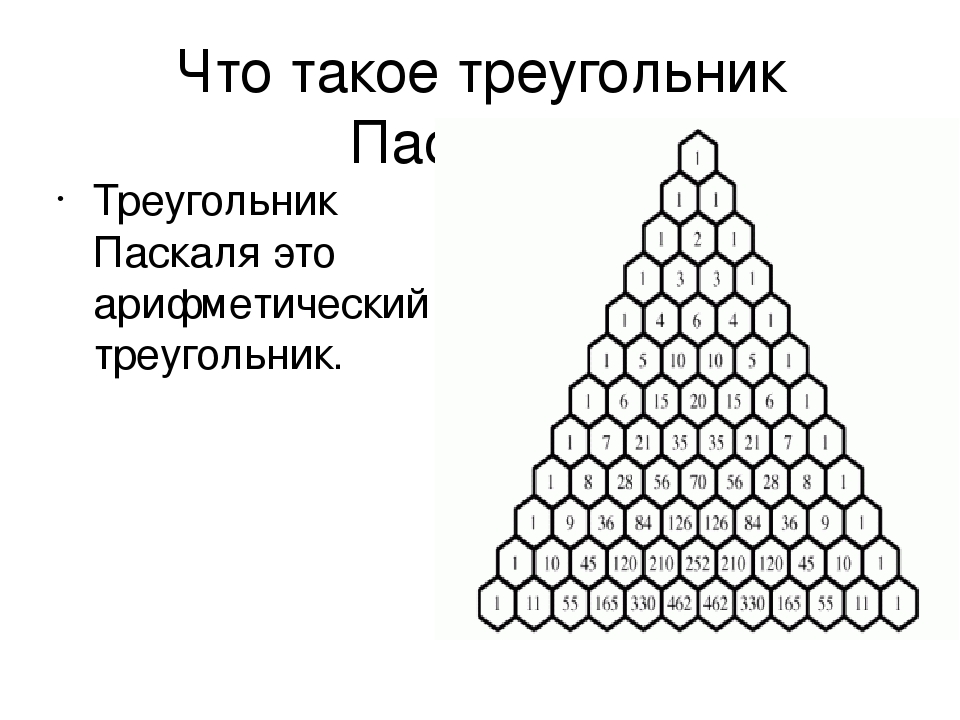 Получу число 15.
Получу число 15.
Задача3. В пачке находятся одинаковые по размеру 7 тетрадей в линейку и 5 в клетку. Из пачки наугад берут 3 тетради. Какова вероятность того, что все три тетради окажутся в клетку?
Решение. Сначала найдём общее число возможных исходов, т.е. сколькими способами мы можем выбрать 3 тетради из 12 тетрадей
А сколькими способами мы можем выбрать 3 тетради в клетку из имеющихся 5 тетрадей?
Вероятностью Р наступления случайного события А называется отношение m/n, где n – число всех возможных исходов эксперимента, а m – число всех благоприятных исходов: Р(А)= m/n.
По формуле нахождения вероятности получим
Задача4.На плоскости даны 10 прямых, причём среди них нет параллельных и через каждую точку их пересечения проходят ровно две прямые. Сколько у них точек пересечения?
Решение: ответ находится на пересечении -45 точек!
Задача 5.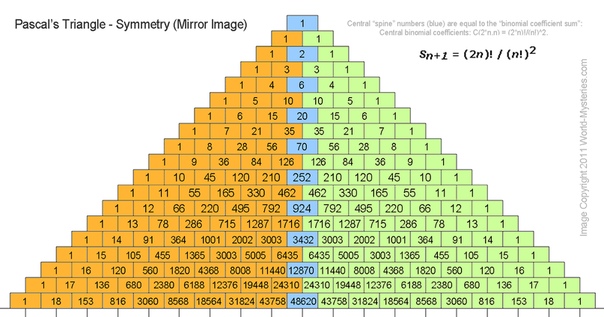
В сумке 10 мячей, пронумерованных от 1 до 10. Наугад вынимают 2 мяча. Какова вероятность того, что это будут мячи с номерами 7 и 3?
Вынуть 2 мяча из 10 имеющихся можно 45 способами. Вероятность нашего события 2 из 45.
Заключение
Работа по выбранной теме осуществлялась в полном соответствии с планом исследования, а именно: объект и предмет исследования, поставлены цели и задачи, а также определены ожидаемые результаты. Были указаны используемые методы исследования, определена проблема.
В данной работе была дана общая характеристика треугольника как геометрической фигуры, был детально рассмотрен треугольник Паскаля, его свойства.
Я пришла к выводу, что одной из наиболее известных и изящных численных схем во всей математике является треугольник Паскаля. Треугольник Паскаля — понятие значительно шире, чем мне представлялось. Он обладает не только удивительными свойствами, но и применялся в архитектуре средних веков для построения схем пропорциональности и для построения прямых углов землемерами и архитекторами. Используя треугольник Паскаля, можно решить задачи из теории вероятности.
Используя треугольник Паскаля, можно решить задачи из теории вероятности.
Практическая значимость данной работы заключается в следующем:
я, изучив много литературы по данному вопросу, получила дополнительные знания в области математики, укрепила свой интерес к этой науке. Работа по данной теме оказалась интересной и полезной.
Список использованных источников и литературы
1. Абачиев С. К. Радужная фрактальность треугольника Паскаля
2. Мартин Гарднер. Глава 17. Неисчерпаемое очарование треугольника Паскаля // Математические новеллы. — М.: Мир, 1974. — 456 с. 3. Треугольник Паскаля. В. А. Успенский. — 2 — е изд. – М.: Наука, 1979. – 48с.
4. Удивительный треугольник великого француза // Hard’n’Soft № 10 2003
5. Фукс Д., Фукс М. Арифметика биномиальных коэффициентов // Квант. — 1970. — № 6. — С. 17-25.
6. Энциклопедия для детей. Т 11. Математика / Глав. ред. М. Аксенова; метод. и отв. ред. В. Володин. – М.: Аванта+,2004. – 688с.
Энциклопедия для детей. Т 11. Математика / Глав. ред. М. Аксенова; метод. и отв. ред. В. Володин. – М.: Аванта+,2004. – 688с.
7. http://ru.wikipedia.org/wiki/
8. Weisstein, Eric W. Pascal’s Triangle (англ.) насайте Wolfram MathWorld.
Исследовательская работа «Возведение двучлена в n-ю степень, треугольник Паскаля»
12
Министерство образования и науки Республики Дагестан
Республиканский конкурс исследовательских работ и проектов учащихся
общеобразовательных организаций и воспитанников дошкольных образовательных организаций Республики Дагестан
«Науки юношей питают»
Направление исследовательской работы «Наука»
«Возведение двучлена в n-ю степень, треугольник Паскаля»
Выполнил Абдурашидова Марьям Ахмедовна
Ученица 8 «б» класса
МКОУ СОШ № 9 г. Кизляра РД
Кизляра РД
Руководитель: Исинова Адият Агаховна
Учитель математики
высшей категории
МКОУ СОШ №9 г. Кизляра РД
Тел.: 8-988-779-09-88
2019 год
Содержание
Введение……………………………………………………………………………..3
Основная часть………………………………………………………………..……4
Глава 1 История возникновения формул сокращенного умножения………5
Глава 2 Формулы школьного курса математики………………………….…..6
Глава 3 Возведение двучлена в n-ю степень…………………………………….7
Глава 4 Некоторые замечательные свойства треугольника Паскаля………8
Глава 5 Алгоритм возведения двучлена в n-ю степень………………….…..12
Заключение…………………………………………………………………. ..……14
..……14
Список литературы…………………………………………………………….…15
Введение
Формулы сокращенного умножения, как нам известно, упрощают ряд вычислений. Лично меня заинтересовало то, что нельзя ли возвести двучлен в n-ю степень.
Актуальность моей работы заключается в применении формул сокращенного умножения и ее приложений в различных областях науки и сферы. Довольно часто имеют дело с формулами сокращенного умножения: ученые — физики, химии, биологи, конструкторы-проектировщики, диспетчеры и т п. Исследовательская работа имеет социальную и личную значимость в том плане, что важно овладеть как основными, так и нетрадиционными формами и приемами применения формул сокращенного умножения. При упрощении и вычислении значений выражений, решении уравнений, в доказательстве тождеств также находит широкое применение формулы сокращенного умножения. А также овладеть возможностью ориентироваться в проблемных ситуациях.
Объект исследования: область математики — формулы сокращенного исследования.
Цель исследования проявляется в рассмотрении вопроса о существовании формул сокращенного умножения не рассматриваемых в школьном курсе математики, изучении некоторых замечательных свойства треугольника Паскаля.
В соответствии с целью в работе были поставлены следующие задачи:
1. Собрать сведения из истории математики о формулах сокращенного умножения.
Изучить способы возведения в n – ую степень
алгебраической суммы двух слагаемых.
Изучить литературу по теме «Треугольник Паскаля»;
Сформулировать вывод и итоги исследования;
Создание иллюстративного компьютерного материала по треугольникам;
Основная часть.
«Скажи мне, и я забуду.
Покажи мне, и я запомню.
Дай мне действовать самому, и я научусь».
(Конфуций)
Данную тему я выбрала, потому что была очень увлечена тем, что хотела продолжить формулы сокращенного умножения для степеней выше трех и еще рассмотреть треугольник Паскаля, с которым нас учитель вкратце ознакомила. Для этого я с начала изучила историю возникновения формул сокращенного умножения и начала возводить двучлен в степень начиная с нулевой. Также рассмотрела геометрическую интерпретацию формул сокращенного умножения.
Глава 1. История возникновения формул сокращенного умножения
Слово «алгебра» возникло после появления трактата « Китаб аль-джебр валь-мукабала» математика и астронома из г. Хивы Мухаммеда бен Муса аль-Хорезми (787-ок 850).Термин «аль-джебр», взятый из названия этой книги, в дальнейшем стал употребляться как «алгебра».
Некоторые правила сокращенного умножения были известны еще около 4 тыс. лет тому назад. Их знали вавилоняне и другие народы древности. Тогда они формулировались словесно или геометрически. У древних греков величины обозначались не числами или буквами, а отрезками прямых. Они говорили не «а2», а «квадрат на отрезке а», не «ав», а «прямоугольник, содержащийся между отрезками а и в». Например, тождество (а+в)2 =а2+2ав+ в2 во второй книге «начал» Евклида (III в. До н. э.) формулировалась так: «если прямая линия (имеется в виду отрезок) как либо рассечена, то квадрат на всей прямой равен квадратам на отрезках вместе с дважды взятым прямоугольником, заключенным между отрезками». Доказательство опиралось на геометрические соображения. В дальнейшем я приведу пример такого доказательства.
Первым ученым, который отказался от геометрических способов выражения и перешел к алгебраическим уравнениям, был древнегреческий ученый-математик, живший в III веке до н. э. Диофант Александрийский. В своей книге «Арифметика» Диофант формулы квадрата суммы, квадрата разности и разности квадратов рассматривал уже с арифметической точки зрения. Ну а современную символику алгебраические тождества получили благодаря двум математикам, а именно Виету и Декарту(16 век).
э. Диофант Александрийский. В своей книге «Арифметика» Диофант формулы квадрата суммы, квадрата разности и разности квадратов рассматривал уже с арифметической точки зрения. Ну а современную символику алгебраические тождества получили благодаря двум математикам, а именно Виету и Декарту(16 век).
На современном уровне развития математики данные формулы были обоснованы Исааком Ньютоном. При небольших значениях n коэффициенты можно найти из треугольника Паскаля. Блез Паскаль триста пятьдесят лет назад придумал специальный инструмент для определения этих самых коэффициентов, который впоследствии назвали «треугольник Паскаля».
Глава 2. Формулы школьного курса математики
На уроке математики я познакомилась с формулами сокращенного умножения, которые знаю наизусть. Все они доказываются раскрытием скобок через умножение многочленов и приведением подобных слагаемых.
Разность квадратов:
(a +b) (a – b) = a² — b² (1)
Квадрат суммы и квадрат разности:
(a + b)² = a² + 2ab +b² (2)
(a – b)² = a² — 2ab + b² (3)
Сумма и разность кубов:
(a + b) (a² — ab + b²) = a³ +b³ (4)
(a – b) (a² + ab + b²) = a³ — b³ (5)
Куб суммы и куб разности:
(a + b)³ = a³ + 3a²b + 3ab² + b³ (6)
(a –b)³ = a³ — 3a²b + 3ab² — b³ (7)
Глава 3. Возведение двучлена в n-ю степень
Возведение двучлена в n-ю степень
Дальше меня заинтересовало: как возвести сумму двух слагаемых в более высокую степень, например в четвертую, пятую или шестую. И я решила поэкспериментировать.
Для начала я решила рассмотреть куб суммы двух слагаемых, для чего расписала его в виде произведения суммы двух слагаемых на квадрат тех же слагаемых: (a+b)3=(a+b)2(a+b)=a3+3a2b+3ab2+b3
Потом поработала с четвертой степенью двух слагаемых, представила ее как результат произведения квадратов двух слагаемых и получила: (a+b)4=(a+b)2(a+b)2=(a2+2ab+b2)(a2+2ab+b2)=a4+4a3b+6a2b2+4ab3+b4
Аналогичным способом возвела в пятую степень сумму двух слагаемых:
(a+b)5=(a+b)2(a+b)3=(a2+2ab+b2)(a3+3a2b+3ab2+b3)=a5+5a4b+10a3b2+10a2b3++5ab4+b5
Попробовала расписать шестую степень как произведение квадрата и четвертой степени суммы двух слагаемых: (a+b)6=(a+b)2(a+b)4=(a2+2ab+b2)(a4+4a3b+6a2b2+4ab3+b4)=a6+6a5b+15a4b2++20a3b3+15a2b4+6ab5+b6
Затем седьмую степень представила как произведение куба суммы и четвертой степени суммы:(a+b)7=(a+b)3(a+b)4=(a3+3a2b+3ab2+b3) *(a4+4a3b+6a2b2+4ab3+b4)=a7+7a6b+21a5b2+35a4b3+35a3b4+21a2b5+7ab6+b7
Надо заметить, что данные преобразования можно было производить и другим способом. Например, сумму двух слагаемых возвести в шестую степень, как произведение кубов тех же самых слагаемых.
Например, сумму двух слагаемых возвести в шестую степень, как произведение кубов тех же самых слагаемых.
Особенно меня удивило то, что все коэффициенты (их я выделила жирным шрифтом), полученные в результате умножения, были симметрическими. Оказалось, что это неспроста, данная закономерность среди коэффициентов многочлена называется «Треугольник Паскаля» по имени его автора
Глава 4. Некоторые замечательные свойства треугольника Паскаля
Но кроме закономерности среди коэффициентов прослеживается так же замечательная закономерность и среди степеней получившегося многочлена. Оказывается степени входящих одночленов образуются следующим образом: степень первого слагаемого, начиная с большей, с каждым разом уменьшается на единицу, а степень второго слагаемого наоборот увеличивается от нулевой до наибольшей.
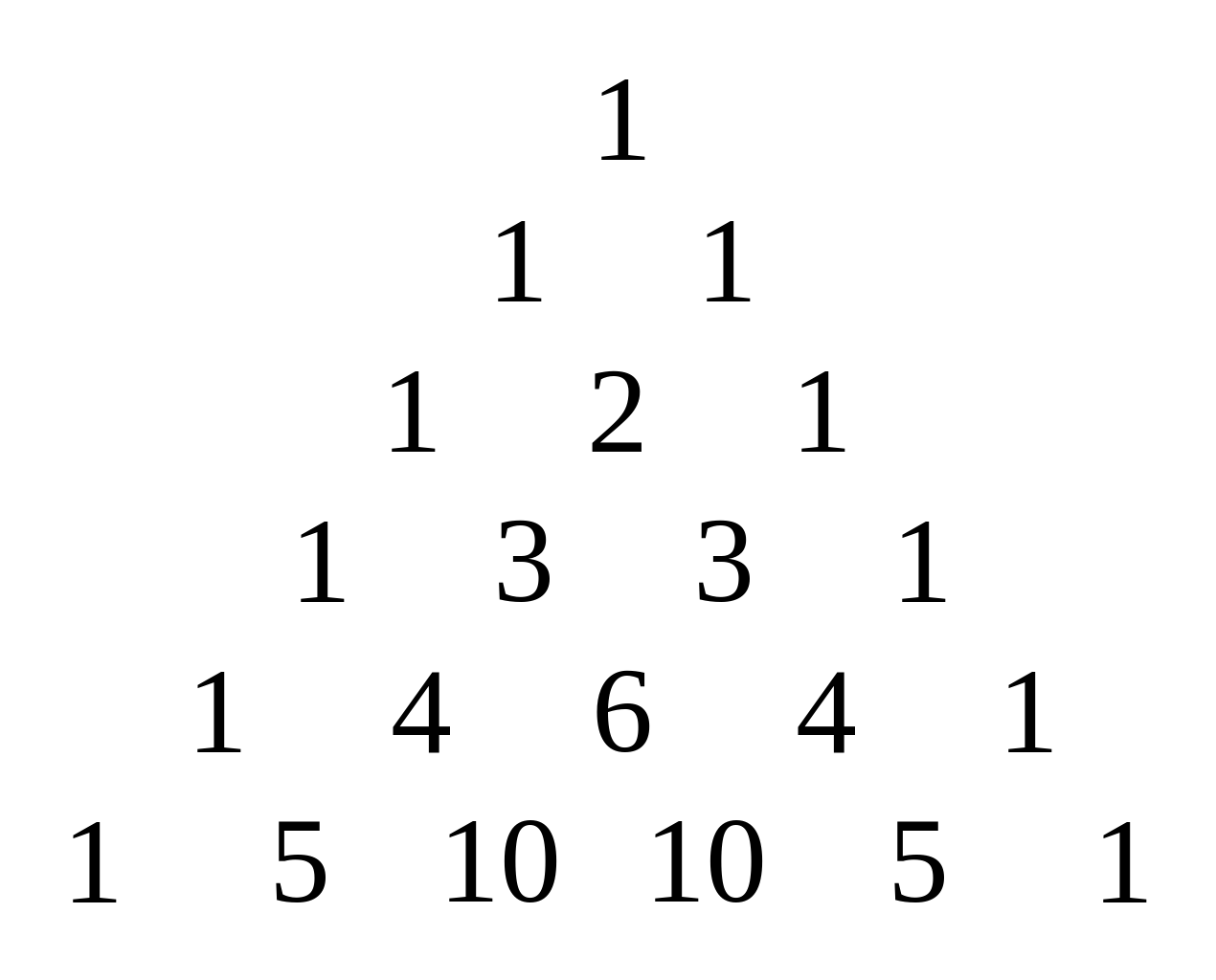
Строится «Треугольник Паскаля» следующим образом. В вершине треугольника пишем 1. Единица соответствует выражению поскольку любое число, возведённое в нулевую степень, даёт единицу. Достраивая треугольник, ниже пишем ещё по единице. Это коэффициенты разложения того же двучлена, возведённого в первую степень: Идём дальше. Стороны треугольника образуют единицы, а между ними — сумма двух единичек, находящихся сверху, то есть 2. Это и есть коэффициенты трёхчлена «квадрат суммы»:
Единица соответствует выражению поскольку любое число, возведённое в нулевую степень, даёт единицу. Достраивая треугольник, ниже пишем ещё по единице. Это коэффициенты разложения того же двучлена, возведённого в первую степень: Идём дальше. Стороны треугольника образуют единицы, а между ними — сумма двух единичек, находящихся сверху, то есть 2. Это и есть коэффициенты трёхчлена «квадрат суммы»:
Следующий ряд, как и предыдущий, начинается и заканчивается единицами, а между ними — суммы цифр, находящихся сверху: 1, 3, 3, 1. Мы получили коэффициенты разложения «куба суммы». Ряд коэффициентов двучлена четвёртой степени составят 1, 4, 6, 4, 1 и так далее.
Номер Строки
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
Б лез Паскаль – французский математик
Блез Паскаль (19 июня 1623, Клермон-Ферран, — 19 августа 1662, Париж) — французский математик, физик, литератор и философ.
Паскаль был первоклассным математиком. Он помог создать два крупных новых направления математических исследований. В возрасте шестнадцати лет написал замечательный трактат о предмете проективной геометрии и в 1654 году переписывался с Пьером де Ферма по теории вероятностей, что впоследствии оказало принципиальное влияние на развитие современной экономики.
Изучая разновидности треугольников, я выяснила, что треугольник Паскаля — арифметический треугольник, назван в честь Блеза Паскаля. В действительности, треугольник Паскаля был известен задолго до 1653 года — даты выхода «Трактата об арифметическом треугольнике». Так, этот треугольник воспроизведен на титульном листе учебника арифметики, написанном в начале XVI Петром Апианом, астрономом из Ингольтштадского университета. Изображен треугольник и на иллюстрации в книге одного китайского математика, выпущенной в 1303 году. Омар Хайям, бывший не только философом и поэтом, но и математиком, знал о существовании треугольника около 1100 года, в свою очередь, заимствовав его из более ранних китайских или индийских источников.
Ещё я узнала из книги «Математические новеллы» (М., Мир, 1974) Мартина Гарднера, что «Треугольник Паскаля так прост, что выписать его сможет даже десятилетний ребенок. В тоже время он таит в себе неисчерпаемые сокровища и связывает воедино различные аспекты математики, не имеющие на первый взгляд между собой ничего общего. Столь необычные свойства позволяют считать треугольник Паскаля одной из наиболее изящных схем во всей математике».
Я рассмотрела схему построения треугольника, предложенную Гуго Штейнгаузом в его классическом «Математическом калейдоскопе»: предположим, что вы входите в город как показано на схеме синей стрелкой, и можете двигаться только вперед, точнее, все время выбирая, вперед налево, или вперед направо. Узлы, в которые можно попасть только единственным образом, отмечены зелеными смайликами, точка, в которую можно попасть двумя способами, показана красным смайликом, а тремя, соответственно — розовыми. Это один из вариантов построения треугольника.
Изучая специальную литературу, я узнала, что еще проще объясняют устройство треугольника Паскаля слова: каждое число равно сумме двух расположенных над ним чисел. Все элементарно, но сколько в этом таится чудес. Если очертить треугольник Паскаля, то получится равнобедренный треугольник. В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. Треугольник можно продолжать неограниченно. Он обладает симметрией относительно вертикальной оси, проходящей через его вершину. Вдоль диагоналей (насколько у треугольника могут быть диагонали, но не будем придираться, такая терминология встречается в публикациях), параллельных сторонам треугольника (на рисунке отмечены зелеными линиями) выстроены треугольные числа и их обобщения на случай пространств всех размерностей. Треугольные числа в самом обычном и привычном нам виде показывают, сколько касающихся кружков можно расположить в виде треугольника — как классический пример начальная расстановка шаров в бильярде. К одной монетке можно прислонить еще две — итого три — к двум можно приладить еще три — итого шесть.
К одной монетке можно прислонить еще две — итого три — к двум можно приладить еще три — итого шесть.
Если возводить двучлен в n-ю степень используя треугольник Паскаля, получается вот что:
(а+в)0=1
(а+в)1=а+в
(а+в)2= а2 +2ав+в2
(а+в)3= а3+3а2в+ 3ав2+в3
(а+в)4=а4+4а3в+6а2в2+4ав3+в4
(а+в)5=а5+5а4в+10а3в2+ 10а2в3+5ав4+в5
(а+в)6=а6+6а5в+15а4в2+ 20а3в315а2в4+6ав5+в6
Глава 5. Алгоритм возведения двучлена в n-ю степень
Алгоритм возведения двучлена в n-ю степень
Выписать в установленном порядке все одночлены которым подобны члены итогового многочлена.
Записать треугольник Паскаля для (n+1)-й строки.
Записать последовательно в качестве коэффициентов выписанных одночленов числа из (n+1)-й строки треугольника Паскаля.
При возведении в степень суммы (а+в)n поставить перед всеми одночленами знак «плюс».
При возведении в степень разности (а-в)n поставить перед первым одночленом знак «плюс», перед вторым одночленом — знак «минус» и далее чередовать знаки до последнего одночлена.
Применение формул сокращенного умножения.
Вычислить:
а) 1992= (200 — 1)2 = 2002 — 2 · 200 + 1 = 40000 – 400 + 1 = 39601 Ответ: 39601
б ) √1369 — 2 · 37 · 29 + 841 = √372 — 2 · 37 · 29 -292 = √(37 - 29)2 = 37 – 29 =8 Ответ: 8
в) 199 · 201 = (200 — 1)·(200 + 1) = 2002 – 12 = 40000 – 1 = 39999 Ответ: 39999
г) 722 = (70 + 2)2 = 702 + 2 · 70 · 2 + 22 = 4900 + 280 + 4 = 5184 Ответ: 5184
Сократить дробь:
592 — 412 (59 — 41)·(59 + 41)59 + 41 100 5 5
592 – 2 · 59 · 41 + 412 (59 – 41)2 59 — 41 18 9
д ) 832 + 2 · 83 · 17 + 172 (83 + 17)2 10000 100
100 100 100
Решить уравнение:
(3х + 2 )4 – (3х — 4)4 = 0
((3х + 2)2 — (3х — 4)2)·((3х + 2)2 + (3х – 4)2) = 0
а) (3х + 2)2 – (3х — 4)2 = 0 или б) (3х + 2)2 + (3х – 4)2 = 0
((3х + 2) — (3х — 4))·((3х + 2) + (3х — 4)) = 0 очевидно, что уравнение б) – не равно нулю
3х + 2 – 3х + 4 = 0 или 3х + 2 + 3х – 4 = 0
0 = 6 6х = 2
х = 1/3
Возвести в степень
Способ 1 :
(х – 2 )4 = (х — 2)2 · (х — 2)2 = (х2 – 4х + 4)(х2 – 4х + 4 ) = х4 – 4х3 + 4х2 – 4х3 + 16х2 – 16х + 4х2 – 16х + 16 = х4 – 8х3 + 24х2 – 32х + 16
Способ 2:
(х — 2)4 = х4 – 8х3 + 24х2 – 32х + 16
Возвела двучлен в 4-ю степень обычным способом и по формуле. Разница очевидна.
Разница очевидна.
Возведем двучлен х + 2 в 5-ю степень двумя способами.
Способ 1 : (х + 2)5 = (х + 2)2· (х + 2)3 = ( х2 + 4х + 4)( х3 + 6х2 + 12х +8) = х5 + 6х4 + 12х3 – 8х2 + 4х4 + 24х3 + 48х2 + 32х + 4х3 + 24х2 + 48х + 32 =х5 + 5х4 + 10х3 +10х2+ 5х + 32.
Способ 2: (х + 2)5 = х5 + 5х4 + 10х3 +10х2 +5х + 32
Как видим разница вычислений большая. Сравнивая способы решения, заключаю, что применяя для нахождения коэффициентов в разложении треугольник Паскаля, возведение в любую степень решается рациональнее. Поэтому, если мне придется возводить двучлен в n-ую степень, я буду применять этот способ.
Заключение
Посмотрите на многообразие формул сокращенного умножения. Как, когда, сразу ли появилось такое многообразие? Конечно очень много вопросов. Безусловно, человечество «додумалось» до всего не сразу и в одночасье. Для этого потребовались долгие годы и десятилетия. Но как бы мне хотелось самой внести какой-либо вклад в развитие прекрасной науки математики.
Как, когда, сразу ли появилось такое многообразие? Конечно очень много вопросов. Безусловно, человечество «додумалось» до всего не сразу и в одночасье. Для этого потребовались долгие годы и десятилетия. Но как бы мне хотелось самой внести какой-либо вклад в развитие прекрасной науки математики.
При изучении материала по этой теме, я узнала много нового и интересного. Оказалось, что формулы сокращенного умножения можно использовать для рационального вычисления выражений, при упрощении выражений, при решении уравнений, доказательстве тождеств и так далее.
В процессе работы я самостоятельно вывела различные формулы сокращенного умножения, причем некоторые из них доказала несколькими способами, познакомилась с треугольником Паскаля.
Я прорешала множество интересных задач, которые не встречались на уроке математики. Мне очень нравится предмет математика, я считаю, что те знания, которые я приобрела, готовя эту работу, пригодятся мне в дальнейшей учебе и подготовке к выпускным экзаменам. Данная тема актуальна, так как математику нельзя представить без формул сокращенного умножения, потому что они применяются не только в школьном курсе, но и в курсе высшей математики. Созданная мною работа может использоваться другими учащимися и преподавателями математики на своих уроках. Мне понравилось заниматься исследовательской работой.
Данная тема актуальна, так как математику нельзя представить без формул сокращенного умножения, потому что они применяются не только в школьном курсе, но и в курсе высшей математики. Созданная мною работа может использоваться другими учащимися и преподавателями математики на своих уроках. Мне понравилось заниматься исследовательской работой.
Список литературы:
1.http://ru.wikipedia.org/wiki/
2.Weisstein, Eric W. Pascal’s Triangle (англ.) на сайте Wolfram MathWorld.
3. Абачиев С. К. Радужная фрактальность треугольника Паскаля
4.Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Алгебра: учеб. Для 7 кл. общеобразоват. учреждений под ред. С. А. Теляковского. – 17-е изд. –М. : Просвещение, 2014.- 240 с. : ил.- ISBN 978-5-09-019315-3.
5. В. И. Жохов, Ю. Н. Макарычев, Н. Г. Миндюк. Дидактические материалы: алгебра 8 класс; М. : «Просвещение», 2015.
: «Просвещение», 2015.
6.Гусев В. А., Мордкович А. Г. Математика ( пособие для поступающих в техникумы): Учеб. Пособие.- М.; Высш. Шк., 1984.-351 с., ил.
7.Мартин Гарднер. Глава 17. Неисчерпаемое очарование треугольника Паскаля // Математические новеллы. — М.: Мир, 1974. — 456 с. 8. Треугольник Паскаля. В. А. Успенский. — 2 — е изд. – М.: Наука, 1979. – 48с.
9.Мордкович А. Г. Алгебра 7 класс. В 2 часа Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович. – 13-е изд., испр.- М.: Мнемозина, 2009.- 160 с.: ил. ISBN ISBN 46-01198-9.
10. С. М. Никольский, М. К. Потапов и др. Алгебра 7; М.: «Просвещение», 2008.
11. Фукс Д., Фукс М. Арифметика биномиальных коэффициентов // Квант. — 1970. — № 6. — С. 17-25.
12. Энциклопедия для детей. Т 11. Математика / Глав. ред. М. Аксенова; метод. и отв. ред. В. Володин. – М.: Аванта+,2004. – 688с.
– 688с.
13.portfolio.1september.ru
14.Удивительный треугольник великого француза // Hard’n’Soft № 10 2003
Проектная работа в 9 классе по математике «Треугольник Паскаля»
Проект по математике:
«Треугольник Паскаля»
Подготовила ученица 9 в класса Тараканова Елена
Учитель: Чеснокова Ирина Николаевна
Цель и задачи моей работы:
1. Ознакомиться с созданием треугольника Паскаля.
2. Научиться строить треугольник
3. Выявить свойства чисел, входящих в состав треугольника Паскаля.
4. Определить применение свойств треугольника в решение задач.
5. Сформулировать вывод и итоги исследования
История создания
Треугольник Паскаля названа в честь Блеза Паскаля, но оказывается, что его строение было известно задолго до описания его Паскалем. Паскаль описал эту систему расположения чисел в своей работе 1653г и поэтому он был назван треугольником Паскаля.
Паскаль описал эту систему расположения чисел в своей работе 1653г и поэтому он был назван треугольником Паскаля.
Треугольник Паскаля — бесконечная таблица биномиальных коэффициентов, имеющая треугольную форму
Определение:
Свойства:
Если очертить треугольник Паскаля, то получится равнобедренный треугольник. В этом треугольнике на вершине и по бокам стоят единицы.
Каждое число равно сумме двух расположенных над ним чисел.
Например:
Свойство:
Чтобы найти сумму чисел, стоящих на любой диагонали от начала до интересующего места, расположенное снизу или слева от последнего слагаемого.
Свойства :
Строки треугольника симметричны относительно вертикальной оси.
Свойства :
Сумма чисел в строках треугольника Паскаля – ,
где n- номер строки.
1=2 0
1+1=2=2 1
1+2+1=4=2 2
1+3+3+1=8=2 3
1+4+6+4+1=16=2 4
1+5+10+10+5+1=32=2 5
1+6+15+20+15+6+1=64=2 6
Свойства :
Первые диагональ треугольника паскаля- это натуральные числа, идущие по порядку.
Свойства:
В каждой строчке треугольника Паскаля сумма чисел на нечётных местах равна сумме чисел на чётных местах.
Биномиальные коэффициенты
Биномиальные коэффициенты есть коэффициенты разложения многочлена по степеням x и y
Применение свойств треугольника в решении задач .
Задача 1 . В магазине «Филателия» продается 8 различных наборов марок, посвященных спортивной тематике. Сколькими способами можно выбрать из них 3 набора?
Задача 2 . Из шести врачей поликлиники двух необходимо отправить на курсы по повышения квалификации. Сколькими способами это можно сделать?
Заключение
Закончив свой проект, я могу сказать, что всё из того, что было задумано, получилось.
Я узнала много интересной информации.
Планирую показать этот проект одноклассникам, когда мы будем проходить тему «Элементы комбинаторики».
С помощью Треугольника Паскаля можно легко раскрывать скобки при , где n- натуральное число, и a и b — любые числа.
Список используемой литературы
- Фукс Д., Фукс М. Арифметика биномиальных коэффициентов // Квант . —970. — № 6. — С. 17-25.
- Weisstein, Eric W. Pascal’s Triangle на сайте Wolfram MathWorld .
Категория:
3. Удивительный треугольник великого француза // Hard’n’Soft № 10 2003
4. http://ru.wikipedia.org/wiki/
5. Мордкович А.Г., Семёнов П.В. Алгебра и начала математического анализа.
Исследовательская работа: Треугольник Паскаля | Образовательный портал EduContest.Net — библиотека учебно-методических материалов
Чтобы посмотреть презентацию с картинками, оформлением и слайдами, скачайте ее файл и откройте в PowerPoint на своем компьютере.
Текстовое содержимое слайдов презентации:
Удивительный треугольник великого француза – треугольник Паскаля 1.
 Выявить свойства чисел, входящих в состав треугольника Паскаля2. Определить применение свойств чисел треугольника Паскаля3. Сформулировать вывод и итоги исследованияЗАДАЧИ ИССЛЕДОВАНИЯ ЦЕЛЬ ИССЛЕДОВАНИЯПривести достаточное количество примеров свойств чисел треугольника Паскаля и примеров применения треугольника для доказательства гипотезы. ГИПОТЕЗАЕсли числа треугольника Паскаляобладают особыми свойствами, то его можно считать удивительным.style.fontSize Мартин Гарднер «Математические новеллы» 1974″Треугольник Паскаля так прост, что выписать его сможет даже десятилетний ребенок. В тоже время он таит в себе неисчерпаемые сокровища и связывает воедино различные аспекты математики, не имеющие на первый взгляд между собой ничего общего. Столь необычные свойства позволяют считать треугольник Паскаля одной из наиболее изящных схем во всей математике». ТРЕУГОЛЬНИК ПАСКАЛЯ — это бесконечная числовая таблица “треугольной формы», в которой по боковым сторонам стоят единицы и всякое число, кроме этих боковых единиц равно сумме двух расположенных над ним чисел.
Выявить свойства чисел, входящих в состав треугольника Паскаля2. Определить применение свойств чисел треугольника Паскаля3. Сформулировать вывод и итоги исследованияЗАДАЧИ ИССЛЕДОВАНИЯ ЦЕЛЬ ИССЛЕДОВАНИЯПривести достаточное количество примеров свойств чисел треугольника Паскаля и примеров применения треугольника для доказательства гипотезы. ГИПОТЕЗАЕсли числа треугольника Паскаляобладают особыми свойствами, то его можно считать удивительным.style.fontSize Мартин Гарднер «Математические новеллы» 1974″Треугольник Паскаля так прост, что выписать его сможет даже десятилетний ребенок. В тоже время он таит в себе неисчерпаемые сокровища и связывает воедино различные аспекты математики, не имеющие на первый взгляд между собой ничего общего. Столь необычные свойства позволяют считать треугольник Паскаля одной из наиболее изящных схем во всей математике». ТРЕУГОЛЬНИК ПАСКАЛЯ — это бесконечная числовая таблица “треугольной формы», в которой по боковым сторонам стоят единицы и всякое число, кроме этих боковых единиц равно сумме двух расположенных над ним чисел.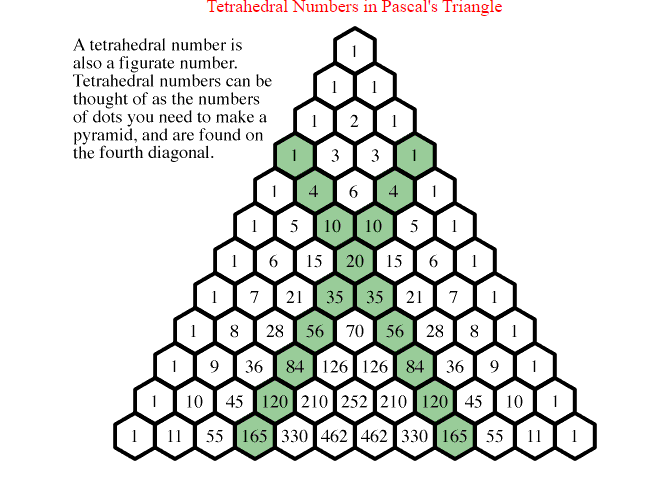 Треугольник можно продолжать неограниченно.ЭНЦИКЛОПЕДИЯ ЮНОГО МАТЕМАТИКАСАМЫЕ УДИВИТЕЛЬНЫЕ СВОЙСТВА Каждое число А в таблице равно сумме чисел предшествующего вертикального ряда, начиная с самого верхнего вплоть до стоящего непосредственно левее числа А. ЭНЦИКЛОПЕДИЯ ЮНОГО МАТЕМАТИКА Он обладает симметриейотносительно вертикальнойоси, проходящей через его вершину. Вдоль прямых, параллельных сторонам треугольника (на рисунке отмечены зелеными линиями)выстроены треугольные числа и их обобщения на случай пространств всех размерностей. СВОЙСТВА ТРЕУГОЛЬНИКА
Треугольник можно продолжать неограниченно.ЭНЦИКЛОПЕДИЯ ЮНОГО МАТЕМАТИКАСАМЫЕ УДИВИТЕЛЬНЫЕ СВОЙСТВА Каждое число А в таблице равно сумме чисел предшествующего вертикального ряда, начиная с самого верхнего вплоть до стоящего непосредственно левее числа А. ЭНЦИКЛОПЕДИЯ ЮНОГО МАТЕМАТИКА Он обладает симметриейотносительно вертикальнойоси, проходящей через его вершину. Вдоль прямых, параллельных сторонам треугольника (на рисунке отмечены зелеными линиями)выстроены треугольные числа и их обобщения на случай пространств всех размерностей. СВОЙСТВА ТРЕУГОЛЬНИКАСВОЙСТВА ТРЕУГОЛЬНИКАТреугольные числа показывают, сколько касающихся кружков можно расположить в виде треугольника Классический пример начальная расстановка шаров в бильярде. Треугольник Паскаля СВОЙСТВА ТРЕУГОЛЬНИКАСледующая зеленаялиния покажет нам тетраэдральные числа- один шар мы можемположить на три – итого четыре, под три подложим шесть итого десять, и так далее. СВОЙСТВА ТРЕУГОЛЬНИКАСледующая зеленаялиния продемонстрирует попытку выкладывания гипертетраэдра в четырехмерном пространстве — один шар касается четырех, ате, в свою очередь, десяти.
 .. Хотя… Попробуйте с вишнями или яблоками одинакового размера, только не пытайтесь выйти с ними в четвертое измерение, они могут ЗАМЕЧАНИЕ АВТОРАВ нашем мире такое невозможно, только в четырехмерном, виртуальном. И тем более пятимерный тетраэдр, о котором свидетельствует следующая зеленая линия, он может существовать только в рассуждениях топологов… или фантастов. исчезнуть.
.. Хотя… Попробуйте с вишнями или яблоками одинакового размера, только не пытайтесь выйти с ними в четвертое измерение, они могут ЗАМЕЧАНИЕ АВТОРАВ нашем мире такое невозможно, только в четырехмерном, виртуальном. И тем более пятимерный тетраэдр, о котором свидетельствует следующая зеленая линия, он может существовать только в рассуждениях топологов… или фантастов. исчезнуть.НАВЕРНОЕ ВЫ ХОТИТЕ СПРОСИТЬ…Это тоже треугольные числа, но одномерные, показывающие, сколько шаров можно выложить вдоль линии — сколько есть, столько и выложите. Если уж идти до конца, то самый верхний ряд из единиц — это тоже треугольные числа в нульмерном пространстве — сколько бы шаров мы не взяли — больше одного расположить не сможем, ибо просто негде — нет ни длины, ни ширины, ни высоты. А о чем же говорит нам самая верхняя зеленая линия, на которой расположились числа натурального ряда? Удивительное свойство треугольника ПаскаляЗаменим каждое число в треугольнике Паскаля точкой. Причем, нечетные точки выведем контрастным цветом,а четные — прозрачным, или цветом фона.
 Результат окажется непредсказуемо-удивительным: треугольник Паскаля разобьется на более мелкие треугольники, образующие изящный узор. ПРИМЕНЕНИЕ Пусть, например, мы хотим вычислить сумму чисел натурального ряда от 1 до 9. «Спустившись» по диагонали До числа 9, мы увидим слева снизу от него число 45. Оно то и дает искомую сумму. ПРИМЕНЕНИЕ Биномиальные коэффициенты естькоэффициэнты разложения многочлена по степеням x и y ПРИМЕНЕНИЕ Предположим , что некий шейх, следуя законам гостеприимства, решает отдать вам трех из семи своих жен. Сколько различных выборов вы можете сделать среди прекрасных обитательниц гарема? Для ответа на этот волнующий вопрос необходимо лишь найти число, стоящее на пересечении диагонали 3 и строки 7: оно оказывается равным 35. Если, охваченные радостным волнением, вы перепутаете номера диагонали и строки и будете искать число, стоящее на пересечении диагонали 7 со строкой 3, то обнаружите, что они не пересекаются. То есть сам метод не дает вам ошибиться! ХОД ИССЛЕДОВАНИЯФормулируем итоги и выводы ПОДТВЕРЖДЕНИЕ ГИПОТЕЗЫОБЛАДАЯ ТАКИМИ СВОЙСТВАМИ, ТРЕУГОЛЬНИК МОЖЕТ НАЗЫВАТЬСЯ УДИВИТЕЛЬНЫМfill.
Результат окажется непредсказуемо-удивительным: треугольник Паскаля разобьется на более мелкие треугольники, образующие изящный узор. ПРИМЕНЕНИЕ Пусть, например, мы хотим вычислить сумму чисел натурального ряда от 1 до 9. «Спустившись» по диагонали До числа 9, мы увидим слева снизу от него число 45. Оно то и дает искомую сумму. ПРИМЕНЕНИЕ Биномиальные коэффициенты естькоэффициэнты разложения многочлена по степеням x и y ПРИМЕНЕНИЕ Предположим , что некий шейх, следуя законам гостеприимства, решает отдать вам трех из семи своих жен. Сколько различных выборов вы можете сделать среди прекрасных обитательниц гарема? Для ответа на этот волнующий вопрос необходимо лишь найти число, стоящее на пересечении диагонали 3 и строки 7: оно оказывается равным 35. Если, охваченные радостным волнением, вы перепутаете номера диагонали и строки и будете искать число, стоящее на пересечении диагонали 7 со строкой 3, то обнаружите, что они не пересекаются. То есть сам метод не дает вам ошибиться! ХОД ИССЛЕДОВАНИЯФормулируем итоги и выводы ПОДТВЕРЖДЕНИЕ ГИПОТЕЗЫОБЛАДАЯ ТАКИМИ СВОЙСТВАМИ, ТРЕУГОЛЬНИК МОЖЕТ НАЗЫВАТЬСЯ УДИВИТЕЛЬНЫМfill. on
onПриложенные файлы
- fail12
Размер файла: 1 MB Загрузок: 86
▶▷▶▷ курсовая работа по треугольнику паскаля
▶▷▶▷ курсовая работа по треугольнику паскаля| Интерфейс | Русский/Английский |
| Тип лицензия | Free |
| Кол-во просмотров | 257 |
| Кол-во загрузок | 132 раз |
| Обновление: | 11-08-2019 |
курсовая работа по треугольнику паскаля — Курсовая работа — Гидравлика 2 — Военная кафедра ronlorgkursovyye-rabotyvoennaya-kafedra717865 Cached Курсовая работа : Гидравлика 2 Гидравлика (часть 1) 1 Введение Механика материальной точки и механика твердого тела это предмет изучения теоретической механики Элементы комбинаторики — studfilesnet studfilesnetpreview1757692 Cached Коэффициенты при каждом члене можно найти при помощи треугольника Паскаля Если n большое число, то ясно, что по треугольнику Паскаля вычислять коэффициенты правой части долго Урок геометрии по теме: Треугольники Признаки равенства referatworkrurefssourceref-91787html Cached Работа с мультимедийной доской 10 мин 2 Тест-тренажер Фронтальная, индивидуальная работа Проверка знаний по теме Треугольники Интерактивная презентация-тест в PowerPoint Реферат: Математическая философия Природы — Xreferatcom xreferatcom66174-6-matematicheskaya Cached Паскаля можно определить эволюцию логики и количество существующих в ней логических систем (координат логики) Рисунок 4 Эволюция структуры логики по треугольнику Паскаля Готовая курсовая работа по теме Введение в комбинаторный author24rureadyworkskursovaya_rabotavysshaya Cached Предметно-ориентированные курсы по выбору в условиях профильного обучения математике Курсовая работа , Высшая математика, 22 страниц 300 руб БиномНьютон а — Реферат refdbrulook3919677html Cached Правило Паскаля : Любой биномиальный коэффициент, начиная со второго, равен произведению предшествующего биномиального коэффициента и дроби Типовые задачи по теме Бином Ньютона Комбинаторика — Стр 4 studfilesnetpreview5569501page:4 Cached Треугольник Паскаля Бином Ньютона Треугольник Паскаля ПАСКАЛЬ, БЛЕЗ (16231662), французский религиозный мыслитель, математик и физик, один из величайших умов 17 столетия Реферат: Математическая философия Природы — Xreferatcom xreferatcom66174-4-matematicheskaya Cached В этих стихах каждый день творения полностью построен по тр паскаля проверим, так ли это? Так, в самом первом стихе сказано, что в начале сотворил Бог небо и землю Плоские кривые — реферат, курсовая работа, диплом, 2017 referatworkrurefssourceref-66135html Cached Способы образования и разновидности плоских кривых Кривые, изучаемые в школьном курсе математики Разработка плана факультативных занятий по математике по теме Кривые в профильной школе Архив выполненных заказов по программированию сайтом KURSOVIKCOM kursovikcomarchiveprogrammingindexhtml Cached Курсовая работа на тему Курсовая работа по предмету Информатика-4 на Turbo Pascal 70 (DOS) Лабораторная работа на тему Одномерный массив из N чисел на CCJavaPython Promotional Results For You Free Download Mozilla Firefox Web Browser wwwmozillaorg Download Firefox — the faster, smarter, easier way to browse the web and all of 1 2 3 4 5 Next 286
- 6.
 Основные понятия и свойства проективной геометрии, теоремы Дезарга и Паскаля. Информация по колле
Основные понятия и свойства проективной геометрии, теоремы Дезарга и Паскаля. Информация по колле - кции рефератов, бесплатным библиотекам, ресурсам по изучению иностранных языков, медицине и ветеринарии. Основные понятия и свойства проективной геометрии, теоремы Дезарга и Паскаля. Свойства изящной
- рии.
Основные понятия и свойства проективной геометрии, теоремы Дезарга и Паскаля. Свойства изящной математической системы — треугольника Паскаля, в котором каждое число равно сумме двух расположенных над ним чисел.
После проверки необходимо запустить файл CURSPROJ.EXE или в среде Паскаля откомполировать файл CURSPROJ.PAS (в коплекте прилагается файл EGAVGA.OBJ, необходимый для линковки в основную программу файла EGAVGA.BGI).
Формулировка и сущность теоремы Паскаля. Теорема о циклических шестиугольниках и её доказательство, точки четвёртого порядка. Понятие оператора цикла. Обоснование использования аппарата алгебраических подстановок. Аналитическое исследование множества.
 Главная Курсовые работы Треугольник паскаля. 3.Открыть файл в котором будет записан наш треугольник паскаля, выбранной размерности.
Конвертер для перевода программ на языке Си в текст программы на языке Паскаль. Справочная по операторам Паскаля (языка Turbo Pascal)
Отличительные черты видов треугольников по углам и по сторонам. Мультимедийное пособие по теме quot;Движения на уроках геометрииquot; и методика его применения в обучении. дипломная работа 3,4 M, добавлен 23.04.2011. Треугольник Паскаля компьютер перевёл на язык цвета.
Особенностью языка Паскаль является то, quot;что число элементов массива фиксируется при описании и в процессе выполнения программы не меняется. Курсовая работа по информатике и компьютерным наукам.
Доказанное свойство является одним из свойств треугольника Паскаля: каждый коэффициент получается сложением двух, стоящих над ним коэффициентов. Контрольные, курсовые, рефераты.
Выберите раздел: Программирование в Delphi Программирование на языке Паскаль (Pascal) Чтобы расположить нужное количество цифр по окружности в программе на языке Паскаль, можно воспользоваться такой конструкцией: for n:1 to.
Главная Курсовые работы Треугольник паскаля. 3.Открыть файл в котором будет записан наш треугольник паскаля, выбранной размерности.
Конвертер для перевода программ на языке Си в текст программы на языке Паскаль. Справочная по операторам Паскаля (языка Turbo Pascal)
Отличительные черты видов треугольников по углам и по сторонам. Мультимедийное пособие по теме quot;Движения на уроках геометрииquot; и методика его применения в обучении. дипломная работа 3,4 M, добавлен 23.04.2011. Треугольник Паскаля компьютер перевёл на язык цвета.
Особенностью языка Паскаль является то, quot;что число элементов массива фиксируется при описании и в процессе выполнения программы не меняется. Курсовая работа по информатике и компьютерным наукам.
Доказанное свойство является одним из свойств треугольника Паскаля: каждый коэффициент получается сложением двух, стоящих над ним коэффициентов. Контрольные, курсовые, рефераты.
Выберите раздел: Программирование в Delphi Программирование на языке Паскаль (Pascal) Чтобы расположить нужное количество цифр по окружности в программе на языке Паскаль, можно воспользоваться такой конструкцией: for n:1 to. ..
..
теоремы Дезарга и Паскаля. Информация по коллекции рефератов
теоремы Дезарга и Паскаля. Свойства изящной математической системы — треугольника Паскаля
- курсовая работа
- так ли это? Так
- БЛЕЗ (16231662)
курсовая работа по треугольнику паскаля Все результаты Треугольник Паскаля База знаний Allbest дек г по ссылке, которая находятся ниже презентация Треугольник Паскаля скачать курсовая работа , K, добавлен Треугольник паскаля его свойства и приложения курсовая работа wwwfreepapersrutreugolnikpaskalyaegosvojstvailisthtml дек г Кафедра высшей математики и информатики КУРСОВАЯ РАБОТА Треугольник паскаля его свойства и приложения Студента курса курсовая работа Треугольник Паскаля и его приложения Похожие мая г КУРСОВАЯ РАБОТА Треугольник Паскаля и его приложения Выполнила студентка группы Юхно Е В Научный руководитель Треугольник Паскаля Его свойства Бином Дяди Ньютона Реферат referatkursovayarepetitorinfoТреугольник_Паскаля_Его_свойства_Бином_Дяди Реферат Математика Свойства треугольника Паскаля В треугольнике Паскаля каждое число кроме крайних единиц равно сумме двух соседних Треугольник Паскаля Курсовая CC скачать купить Studlearncom Разделы CC Рейтинг отзыва Исходное задание на работу Дано натуральное число N Получить первые N строк треугольника Паскаля Треугольник сохранить в файле Реферат Треугольник Паскаля Экономические Экономика Оригинальная работа Реферат Треугольник Паскаля Треугольник Паскаля имеет применение в теории вероятностей и обладает удивительными и Треугольник Паскаля и его свойства Разное, Курсовая работа prepodrureadyworks Треугольник Паскаля так прост, что выписать его сможет даже десятилетний ребенок В тоже время он таит в себе неисчерпаемые сокровища и Исследовательская работа по математике на тему Треугольник Геометрия нояб г Cкачать Исследовательская работа по математике на тему Треугольник Паскаля класс Треугольник Паскаля Документ Gigabazaru Треугольник Паскаля является, пожалуй, одной из наиболее известных и изящных числовых схем во всей математике Блез Паскаль , французский Сборник тем курсовых работ по математике алгебра windowedurucatalogpdftxt?p_page Похожие В курсовой работе предлагается изучить неприводимые многочлены над Цель курсовой работы изучение свойств треугольника Паскаля и их Треугольник Паскаля Реферат заказ Студворк Реферат на тему Треугольник Паскаля заказ Se Треугольник Паскаля Курсовая работа заказ Курсовая работа на тему Se Треугольник Паскаля заказ Бином Ньютон Треугольник Паскаля Сочинения и курсовые работы Треугольник Паскаля Его свойства Бином Дяди Ньютона C C C C C C C C C C C C C C Тема Треугольные числа Реферат Gigabazaru Реферат Пожалуй, одной из наиболее известных и изящных численных схем во всей математике является треугольник Паскаля Блез Паскаль , Курсовая работа треугольник паскаля ВКонтакте Курсовая работа треугольник паскаля подробно ЗАРЕГИСТРИРОВАТЬСЯ Поиск работы Ищущим работу поиск вариантов трудоустройства Глава Треугольник Паскаля mechmathmsusushvetzinfperlproblemschPascalTrianglexhtml Похожие Числовой треугольник Паскаля неисчерпаемый источник всевозможных математических радостей В верхней строчке треугольника располагается Треугольник Паскаля Википедия Похожие Треугольник Паскаля бесконечная таблица биномиальных коэффициентов, имеющая треугольную форму В этом треугольнике на вершине и по Курсовая работа на тему треугольник паскаля его свойства и ikjwptwpjkibblogczkursovajarabotanatemutreugolnikpaskaljaegosvojstvaipr Программирование! Курсовые работы курсовые работы по программированию pascal, c, basic, vba, фортран, ооп курсовая работа на тему Бином Ньютона Треугольник Паскаля StudFilesnet мар г Работа по теме Глава Глава Бином Ньютона Треугольник Паскаля ВУЗ ПНИПУ Бином ньютона треугольник паскаля курсовая работа af prxwmyfgjeblogczbinomnjutonatreugolnikpaskaljakursovajarabotaaf Курсовые работы от руб Курсовые на заказ от дня, готовые от часа Опыт лет бином ньютона треугольник паскаля курсовая работа , Треугольник паскаля реферат Исследовательская работа по Исследовательская работа по математике на тему Треугольник Паскаля класс Отдел образования, спорта и туризма Борисовского райисполкома Как сделать треугольник паскаля в excel? Все про работу с excel wordofficerukaksdelattreugolnikpaskalyavexcelhtml сент г Интересно, что если в треугольнике Паскаля все нечетные числа окрасить в Тип работы Реферат Курсовая Добавлен Вокруг треугольника Паскаля Старт в науке Гипотеза каждое число треугольника Паскаля равно сумме двух Новизна работы надеемся, что прием построения треугольника таким способом PDF Бином Ньютона и треугольник Паскаля Уральский libusueruresourcefreeMelnikovAlgebraAplusBdegpdf Похожие ный на треугольнике Паскаля и использование формулы би нома Ньютона Сначала рассмотрим построение треугольника Паскаля , а Вращение треугольника курсовая по программированию и Docsity Дипломная Программирование апр г Данная курсовая работа представляет разработку программного Турбо Паскаля , модуль Crt содержит процедуры и функции, курсовая работа по треугольнику паскаля cjabpta temrekesandeklablogcoma Скачать тут курсовая работа по треугольнику паскаля Лабораторная работа Возведение в степень Бином Ньютона Коэффициент Коллекция Картинки по запросу курсовая работа по треугольнику паскаля Показать все Другие картинки по запросу курсовая работа по треугольнику паскаля Жалоба отправлена Пожаловаться на картинки Благодарим за замечания Пожаловаться на другую картинку Пожаловаться на содержание картинки Отмена Пожаловаться Все результаты Треугольник Паскаля Математика Комбинаторика Фоксфорд Похожие Треугольником Паскаля называется бесконечная треугольная таблица, в которой на вершине и по боковым сторонам стоят единицы, каждое из Не найдено курсовая Треугольник Паскаля учебная работа реферат, курсовая referatru Рефераты Тема Треугольник Паскаля учебная работа на ReferatRu, скачать реферат, курсовую работу , бесплатно Бином Ньютона и треугольник Паскаля Наука и жизнь Похожие Сегодня, как и лет тридцатьсорок назад, абитуриенты на вступительных экзаменах в вуз традиционно опасаются вытянуть билет с вопросом о биноме Возрождение теории чисел От Диофанта до Ферма Среди них открытие китайскими математиками треугольника Паскаля и китайская поскольку ранняя работа Ферма появляется в этом окружении Паскаль, Блез Энциклопедия Вокруг света wwwvokrugsvetaruencyclopediaindexphp?titleПаскальC_Блез Похожие Принцип работы арифметической машины Паскаля при полном повороте Паскаль решал эту задачу с помощью треугольника , который был Курсовая работа по алгебре математике на тему формулы volodarskypenzaruproductformulysokrashennogoumnozhenijaindexhtml Формулы для nой степени Бином Ньютона Треугольник Паскаля Некоторые свойства формул Интересные формулы Заключение DOC Pascal svkfvsturuАЗБПрограммированиеиосновыалгоритмизац Курсовая работа предусматривает разработку программного Составить программу вычисления площади треугольника , используя формулу Герона Бином Ньютона Автор Рейтинг , отзывов Бесплатно Android Обучение Бином Ньютона треугольник Паскаля Бином Ньютона это формула, использующаяся для разложения суммы двух чисел или переменных, Научноисследовательская работа по теме Треугольник Паскаля Похожие апр г Актуальность проектаДанный проект предназначен для выявления того, насколько широко треугольники используются в практической Не найдено курсовая Вращение треугольника Реферат TopRefru Реферат Данная курсовая работа представляет разработку программного стандартного Паскаля , а также встроенные процедуры и функции Турбо курсовые работы паскаль weldingplazacomfileskursovyerabotypaskalxml апр г курсовые работы паскаль Курсовая работа программирование на Pascal курсовая Треугольник Паскаля Понятие успеха и неудачи Курсовая работа Перевод чисел из двоичной системы счисления Готовые работы Программирование Паскаль Курсовая работа Перевод чисел из двоичной системы счисления в Ключевые слова паскаль , pascal, перевод, двоичная, восьмеричная, ЛР, Определение возможности построения треугольника , Turbo Pascal DOS , Числа Каталана Курсовая Работа heatfreedoma heatfreedomaweeblycomhomechislakatalanakursovayarabota Числа Каталана Курсовая Работа центрального биномиального коэффициента и соседнего с ним в той же строке треугольника Паскаля Реферат Треугольник Паскаля и спектр арифметик для Гуманитарные Философия Оригинальная работа Реферат Треугольник Паскаля и спектр арифметик для цифровых информационных технологий В статье сконцентрирована Вывести треугольник Паскаля количество строк которого задается wwwcyberforumru Форум программистов C С для начинающих июн г Рейтинг , голосов Решено Вывести треугольник Паскаля количество строк которого курсовые , дипломные и любые другие студенческие работы здесь Курсовая работа в Mathcad, выполненная курсовая работа по authorru Лента заказов Курсовые работы Информатика Автор выполнил курсовую работу Курсовая работа в Mathcad по информатике по Нужна курсовая работа по информатике Треугольник Паскаля Как устроен треугольник Паскаля PDF DocPlayerru Чудеса треугольника Паскаля Паников Егор МОУ Лицей , г Подольск учитель информатики Аноттация в данной работе ставятся и доказываются Читать доклад по математике Треугольник Паскаля Его свойства Скачать доклад по математике Треугольник Паскаля Его свойства Бином Дяди Ньютона в формате rtf, бесплатная работа , Доклад скачать без PDF Методические рекомендации к выполнению курсовой работы по elibrarysguruuch_litpdf Похожие Курсовая работа является научным исследованием студента, направлен ным на решение теоретических В А Успенский Треугольник Паскаля , Треугольник Паскаля курсовая работа MyUnivercityru myunivercityruПрограммирование_иТреугольник_Паскаляhtml июн г Треугольник Паскаля Программирование и компьютеры Треугольник Паскаля Форум CodeNet forumcodenetruqТреугольникПаскаля Похожие мар г сообщения автор в чистом С функцию для вычисления треугольника Паскаля Помогите исходником или советом нужно для курсовой работы DOC Ниже приведен примерный перечень тем курсовых работ мцнмо wwwmccmerucoursesmadoc Курсовые работы слушателей должны быть содержательны В каждой сочетаний Треугольник Паскаля Комбинаторика в вероятностных задачах PDF Пермский государственный гуманитарнопедагогический portfoliopspuruuploadsbcfaabcfckursovaya_rabota__kurspdf Треугольник Паскаля Работа состоит из введения, двух глав, заключения и списка Первая глава курсовой работы посвящена многочленам и Вместе с курсовая работа по треугольнику паскаля часто ищут реферат на тему треугольник паскаля треугольник паскаля курсовая применение треугольника паскаля треугольник паскаля в ворде треугольник паскаля вывод треугольник паскаля задачи Документы Blogger Duo Hangouts Keep Jamboard Подборки Другие сервисы Приложения
6. Основные понятия и свойства проективной геометрии, теоремы Дезарга и Паскаля. Информация по коллекции рефератов, бесплатным библиотекам, ресурсам по изучению иностранных языков, медицине и ветеринарии.
Основные понятия и свойства проективной геометрии, теоремы Дезарга и Паскаля. Свойства изящной математической системы — треугольника Паскаля, в котором каждое число равно сумме двух расположенных над ним чисел.
После проверки необходимо запустить файл CURSPROJ.EXE или в среде Паскаля откомполировать файл CURSPROJ.PAS (в коплекте прилагается файл EGAVGA.OBJ, необходимый для линковки в основную программу файла EGAVGA.BGI).
Формулировка и сущность теоремы Паскаля. Теорема о циклических шестиугольниках и её доказательство, точки четвёртого порядка. Понятие оператора цикла. Обоснование использования аппарата алгебраических подстановок. Аналитическое исследование множества.
Главная Курсовые работы Треугольник паскаля. 3.Открыть файл в котором будет записан наш треугольник паскаля, выбранной размерности.
Основные понятия и свойства проективной геометрии, теоремы Дезарга и Паскаля. Информация по коллекции рефератов, бесплатным библиотекам, ресурсам по изучению иностранных языков, медицине и ветеринарии.
Основные понятия и свойства проективной геометрии, теоремы Дезарга и Паскаля. Свойства изящной математической системы — треугольника Паскаля, в котором каждое число равно сумме двух расположенных над ним чисел.
После проверки необходимо запустить файл CURSPROJ.EXE или в среде Паскаля откомполировать файл CURSPROJ.PAS (в коплекте прилагается файл EGAVGA.OBJ, необходимый для линковки в основную программу файла EGAVGA.BGI).
Формулировка и сущность теоремы Паскаля. Теорема о циклических шестиугольниках и её доказательство, точки четвёртого порядка. Понятие оператора цикла. Обоснование использования аппарата алгебраических подстановок. Аналитическое исследование множества.
Главная Курсовые работы Треугольник паскаля. 3.Открыть файл в котором будет записан наш треугольник паскаля, выбранной размерности. Конвертер для перевода программ на языке Си в текст программы на языке Паскаль. Справочная по операторам Паскаля (языка Turbo Pascal)
Отличительные черты видов треугольников по углам и по сторонам. Мультимедийное пособие по теме quot;Движения на уроках геометрииquot; и методика его применения в обучении. дипломная работа 3,4 M, добавлен 23.04.2011. Треугольник Паскаля компьютер перевёл на язык цвета.
Особенностью языка Паскаль является то, quot;что число элементов массива фиксируется при описании и в процессе выполнения программы не меняется. Курсовая работа по информатике и компьютерным наукам.
Доказанное свойство является одним из свойств треугольника Паскаля: каждый коэффициент получается сложением двух, стоящих над ним коэффициентов. Контрольные, курсовые, рефераты.
Выберите раздел: Программирование в Delphi Программирование на языке Паскаль (Pascal) Чтобы расположить нужное количество цифр по окружности в программе на языке Паскаль, можно воспользоваться такой конструкцией: for n:1 to.
Конвертер для перевода программ на языке Си в текст программы на языке Паскаль. Справочная по операторам Паскаля (языка Turbo Pascal)
Отличительные черты видов треугольников по углам и по сторонам. Мультимедийное пособие по теме quot;Движения на уроках геометрииquot; и методика его применения в обучении. дипломная работа 3,4 M, добавлен 23.04.2011. Треугольник Паскаля компьютер перевёл на язык цвета.
Особенностью языка Паскаль является то, quot;что число элементов массива фиксируется при описании и в процессе выполнения программы не меняется. Курсовая работа по информатике и компьютерным наукам.
Доказанное свойство является одним из свойств треугольника Паскаля: каждый коэффициент получается сложением двух, стоящих над ним коэффициентов. Контрольные, курсовые, рефераты.
Выберите раздел: Программирование в Delphi Программирование на языке Паскаль (Pascal) Чтобы расположить нужное количество цифр по окружности в программе на языке Паскаль, можно воспользоваться такой конструкцией: for n:1 to.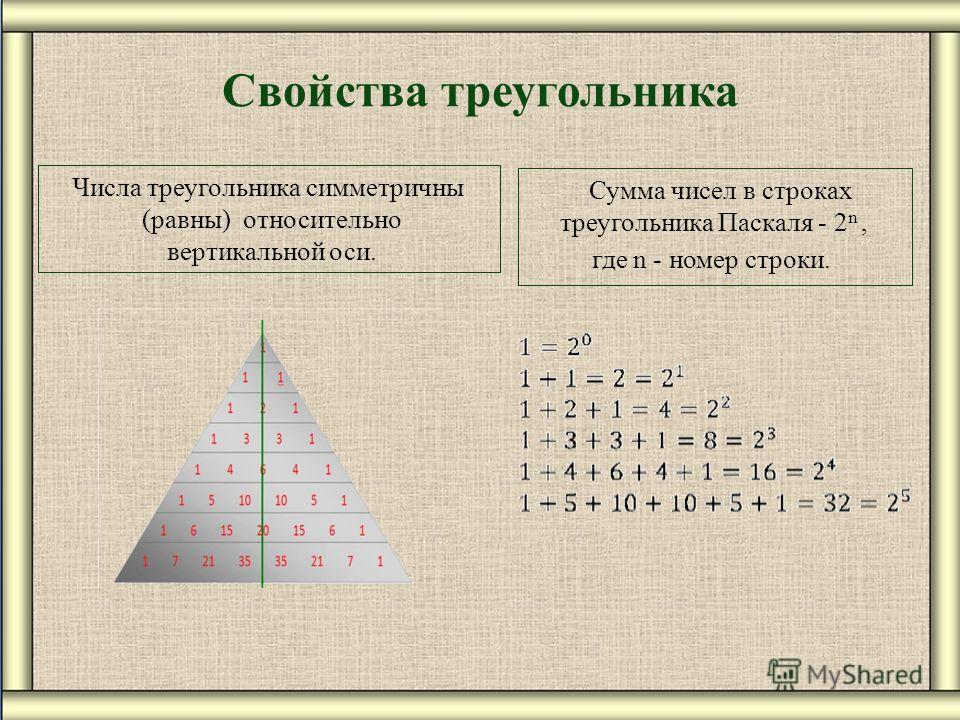 ..
..
Аттестационная работа. Иследовательская работа «Мультипликативный треугольник Паскаля»
1. Аттестационная работа
Слушателя курсов повышения квалификации попрограмме:
«Проектная и исследовательская деятельность как
способ формирования метапредметных результатов
обучения в условиях реализации ФГОС»
Самойлова Ольга Евгеньевна
ГБОУ лицей №533, г. Санкт-Петербург
На тему:
Иследовательская работа
«Мультипликативный треугольник Паскаля»
1
2. Краткая характеристика образовательного учреждения
Данная методическая разработка исследовательской работыпредназначена для учеников математического класса.
Ученики мотивированы, любят учиться, с удовольствием
тратят свободное время на получение новых знаний.
2
3. Характеристика работы
Данная работа носит исследовательский характер в областиматематики и предназначена для учеников 8-9 классов. Для
разрешения поставленной задачи ученику надо
ознакомиться с известными математическими результатами,
а также самостоятельно продвинуться в решении
математической задачи.
 Задача очень трудная, но
Задача очень трудная, нопредполагает возможность частичного решения.
3
4. Цель и задачи
• Ознакомиться с биномиальными коэффициентами итреугольником Паскаля
• Построить аналогичную структуру относительно
умножения
• Исследовать свойства получившейся структуры
4
5. Формы исследовательской деятельности
• Самостоятельное ознакомление с известнымиматематическими результатами
• Постановка цели исследования
• Формулирование гипотез
• Программирование объекта исследования для небольших
значений параметра
• Вывод и доказательство результата в общем виде
5
6. Содержание исследования
Треугольник Паскаля используется для нахождениябиномиальных коэффициентов и имеет множество
полезных свойств.
Он строится из двух
бесконечных рядов,
состоящих из единиц с
помощью операции
сложения: каждый
следующий ряд
получается из
предыдущего сложением
чисел в нём.

6
7. Содержание исследования
Иначе треугольник Паскаля можно изобразить в таблице1
1
1
1
1
1
1
1
2
3
4
5
6
7
1
3
6
10
15
21
1
4
10
20
35
1
5
15
35
1
6
21
1
7
7
8. Содержание исследования
Автору работы предложено построить треугольник из двухрядов, состоящих из последовательности всех натуральных
чисел в порядке возрастания, с помощью операции
умножения и исследовать его свойства.
8
9. Содержание исследования
Было предложено описать места, на которых вмультипликативном треугольнике находятся квадраты.
В Excel получена таблица расположения квадратов.
9
10. Содержание исследования
Получена следующая формула: квадраты натуральныхчисел находятся на местах
10
11. Методы достижения результатов
• Изучение существующего объекта• В ходе исследования была написана программа в Microsoft
Excel, в которой был смоделировал мультипликативный
треугольник до 64 строки.

• Формулирование гипотезы, основываясь на
экспериментальных данных
• Доказательство гипотезы с использованием методов
теории чисел.
11
12. Перспективы развития исследовательской деятельности автора
В ходе предложенного исследования автор показал высокиенавыки
•работы с литературой;
•анализа задачи;
•использования современных информационных технологий;
•формулирования гипотез;
•получения новых научных результатов.
Автора ждет еще много интересных открытий и его
потенциал высок.
12
Исследовательская работа «Математические расчеты «алгоритма выигрыша» в игре волейбол»
Исследовательский проект направлен на анализ математических расчетов «алгоритма победы» в игре волейбол. В работе автор исследовал отношения между математикой и волейболом. В этой игре математические знания учитываются не только для расчета результата и времени, но и с целью победы. Автор предлагает использовать прикладную математику для достижения побед в волейболе.
Предмет исследования:прикладная математика.
Объект исследования:математика, волейбол.
Цель работы: Найти вычисления «алгоритм победы» в прикладной математике.
Задачи работы:
- изучение взаимосвязи математики и волейбола;
- найти «алгоритм выигрыша» в соревнованиях;
- изучение применения прикладной математики в игре волейбол.
Этапы научного исследования:
- работа с литературой, связанной с темой;
- приведение примеров прикладной математики, которая может быть применена в игре в волейбол;
- выводы по представленной работе.
Актуальность исследования: Изучение применения прикладной математики на практике всегда актуально. Наша страна не показывает себя на чемпионатах мира по волейболу. И у меня возникает вопрос «почему?». И поскольку волейбол – интеллектуальная игра, требующая точности движения, в настоящее время он требует более широкого изучения математических расчетов. Это связано с тем, что оно еще не достаточно изучено.
И поскольку волейбол – интеллектуальная игра, требующая точности движения, в настоящее время он требует более широкого изучения математических расчетов. Это связано с тем, что оно еще не достаточно изучено.
Новизна работы: Изучение математических расчетов алгоритма победы в игре в волейбол с применением прикладной математики. В этой работе автор исследовал отношения между математикой и волейболом и изучил их взаимосвязь.Она приводит примеры применения прикладной математики в волейболе. В этой игре математические знания учитываются не только для расчета результата и времени, но и с целью победы.
Гипотеза: В обычной жизни математику можно использовать везде и всегда.Но мы часто ошибаемся думав что мы математика пригодиться нам редко.Но. все это не так, так как математика связана с логикой и расчетами.Многие люди видят математику и волейбол как две непересекаемые линии.На самом деле это не так.Математика связана многими видами спорта и один из них это- волейбол. 0;
0;
Научно-исследовательская работа по теме «Треугольник Паскаля»
Муниципальное казенное общеобразовательное учреждение
«Богучарская средняя общеобразовательная школа № 1»
Научно-исследовательская работа
по теме: «Треугольник Паскаля»
Автор: Карпировик Паскаля
Руководитель: Алабина Галина Юрьевна
Богучар 2015
ОглавлениеВведение
Основная часть
Теоретическая часть работы
а) Блез Паскаль — французский ) треугольник Паскаля как разновидность треугольника
в) свойства треугольника Паскаля и их применение в решении
задач
Практическая часть работы
а) состав составление послание едовательности тренировочных задач
по теме «Треугольник Паскаля»
б) создание презентации «Треугольники вокруг нас»
Заключение
Актуальность проекта
Данный проект для использования, насколько широко треугольники используются. в практической жизни.
в практической жизни.
Новизна проекта
Новизна моего исследования состоит в том, что я попыталась показать связь треугольников с жизнью.
Практическая значимость проекта
Данный проект может быть использован как дополнительный материал к урокам геометрии, для внеклассной работы по математике.
Цель
— ознакомиться с треугольником Паскаля как разновидностью треугольников;
— рассмотреть применение треугольника Паскаля в различных сферах;
Гипотеза
Если число треугольника Паскаля обладает особыми свойствами, то его можно считать волшебным.
Задачи
— изучить литературу по теме «Треугольник Паскаля»;
— выявить свойства чисел, входящих в состав треугольника Паскаля;
— определить применение чисел треугольника Паскаля;
— сформулировать вывод и итоги исследования;
Объект исследования: треугольник как геометрическая фигура
Предмет исследования: свойства треугольника Паскаля
Методы исследования:
— аналитико-статистическая работа со справочной, научно-аналитической и познавательной литературой. ;
;
— поиск информации в интернет — ресурсах.
Направления работы:
— выбор, источники литературы, составление проблемы плана;
— работа с литературой и другими источниками;
— обработка полученных данных;
— анализ результатов, вывод вывода;
Основные этапы проекта: подготовительный; деятельностный;
ход исследования ; рефлексивный; аналитический; презентационный.
Введение
В прошлом учебном году геометрии мы начали новый предмет «изучать».Одна из глав курса геометрии называется «Треугольники». Меня очень заинтересовала тема тема. Я всегда хотела узнать много нового о треугольниках. Ведь мир треугольников очень загадочен и интересен. Я хочу узнать как можно больше о происхождении треугольников, об их значении в нашей жизни.
Треугольник — первая геометрическая фигура, встречающаяся в древних рисунках. Изучая литература, я узнала, что в Египте он символизировал триаду духовной воли, любви, интуиции и высшего разума человека, то есть его личность или душу.
существует множество видов треугольников, но больше всего меня заинтересовал треугольник Паскаля.
Теоретическая часть работы
Блез Паскаль — французский математик
Блез Паскаль (19 июня 1623, Клермон-Ферран, — 19 августа 1662, Париж) — французский математик, физик, литератор и философ.
Паскаль был первоклассным математиком. Он помог создать два больших новых направления математических исследований.В возрасте шестати лет написал замечательный трактат о предмете проективной геометрии и в 1654 году переписывался с Пьером де Ферма по теории вероятностей, что оказало принципиальное влияние на развитие современной экономики.
Треугольник Паля как разновидность треугольника
Изучая разновидности треугольников, я форнила, чтотреугольник Паскаля — арифметический треугольник, образованный биномиальными коэффициентами. Назван в честь Блеза Паскаля.В действительности, треугольник Паскаля был известен задолго до 1653 года — дата выхода «Трактата об арифметическом треугольнике». Так, этот треугольник воспроизведен на титульном листе учебника арифметики, написанном в начале XVI Петром Апианом, астрономом из Ингольтштадского университета. Изображен треугольник и на иллюстрации в книге одного китайского математика, выпущенной в 1303 году. Омар Хайям, бывший не только философом и поэтом, но и математиком, знал о существовании треугольника около 1100 года, в свою очередь, за его из более ранних китайских или индийских источников.
Ещё я узнала из книги «Математические новеллы» (М., Мир, 1974) Мартина Гарднера, что «Треугольник Паскаля так прост, что выписать его даже десятилетний ребенок. В тоже время он таит в себе неисчерпаемые сокровища и связывает воедино различные аспекты. Столь необычные свойства позволяют считать Паскаля одной из наиболее изящных во всей математике «.
В тоже время он таит в себе неисчерпаемые сокровища и связывает воедино различные аспекты. Столь необычные свойства позволяют считать Паскаля одной из наиболее изящных во всей математике «.
Изучая специальную литературу, еще проще объясняют устройство треугольника Паскаля слова: каждое число равно сумме двух расположенных над ним чисел.Все элементарно, но сколько в этом таится чудес. Если очертить треугольник Паскаля, то получится равнобедренный треугольник. Треугольник Паскаля имеет применение в теории вероятностей и обладает замечательными свойствами.
Свойства треугольника Паскаля и их применение в решении
Изучая свойства треугольника Паскаля, я рассмотрела одно из свойств биномиальных коэффициентов:
Это равенство показывает, что биномиальные коэффициенты можно последовательно выписывать в виде треугольной таблицы, которая называется треугольником Паскаля .В n -ой строке треугольника Паскаля стоят коэффициенты разложения, причем каждый коэффициент, кроме крайних двух, которые равны 1, равен сумме соответствующих коэффициентов из предыдущей строки.
Я узнала, что треугольник Паскаля — это бесконечная числовая таблица «треугольной формы», в которой по боковым сторонам стоят единицы и всякое число, кроме этих боковых единиц, получается сумма двух предшествующих чисел. В таком треугольнике Паскаля появился в сочинении Паскаля «Трактат в арифметическом треугольнике», изданном в 1665 г.уже после смерти автора.
Паскаль подробно исследовал свойства и применения своего «треугольника». Приведу для примера лишь 3 свойства «треугольника», найденные самим Паскалем; при этом буду исходить из расположения «треугольника» на плоскости, какое было указанно Паскалем, и говорить о горизонтальных и вертикальных рядах. собственное число 1: Каждое из чисел предшествующего горизонтального ряда, начиная с самого левого до стоящего непосредственно над числом А (в котором содержатся слагаемые, дающие в сумме А, заштрихованы).
рис.1 рис. 2 рис. 3
Свойство 2: Каждое число А в таблице равно сумме чисел предшествующего вертикального ряда, начиная с самого верхнего до стоящего непосредственно левее числа А. Рис. 2. С войство 3: Каждое число в таблице, увеличенное на единицу, равно сумме всех чисел, заполняя прямоугольник, ограниченный теми же вертикальными и горизонтальными рядами, на пересечение стоит число А (сами эти ряды в рассматриваемом прямоугольник не включаются) ).Рис. 3.
Рис. 2. С войство 3: Каждое число в таблице, увеличенное на единицу, равно сумме всех чисел, заполняя прямоугольник, ограниченный теми же вертикальными и горизонтальными рядами, на пересечение стоит число А (сами эти ряды в рассматриваемом прямоугольник не включаются) ).Рис. 3.
Я пришла к выводу, что пересмотренные свойства треугольника Паска подтверждены слова Мартина Гарднера о том, что треугольник Паскаля одна из наиболее изящных во всей математике.
Актуальность исследования обусловлена ежегодным усложнением заданий ГИА и ЕГЭ, что требует углубленных знаний не только в алгебре, но и в геометрии.
Практическая часть
Я рассмотрела схему построения треугольника, предложенную Гуго Штейнгаузом в его классическом «Математическом калейдоскопе»: предположение, что вы входите в город как показано на схеме синей стрелкой работы, и можете двигаться только вперед, точнее, все время выбирая, вперед налево, или вперед направо. Узлы, которые можно попасть только двумя видами, отмеченными зелеными смайликами, которые можно попасть двумя точками красными смайликами, а тремя, соответственно — розовыми. Это один из вариантов построения треугольника.
Узлы, которые можно попасть только двумя видами, отмеченными зелеными смайликами, которые можно попасть двумя точками красными смайликами, а тремя, соответственно — розовыми. Это один из вариантов построения треугольника.
Задача 1 .В магазине «Филателия» продается 8 различных наборов марок, посвященных спортивной тематике. Сколькими способами можно выбрать из них 3 набора?
Решение:
В треугольнике Паскаляющее число, показывающим, сколькими способами можно выбрать k элементов из набора, содержащего различных элементов, стоит на пересечении k-ой диагонали и n-ой строки.
Найду диагональ восьмую сверху и отсчитываю три числа по горизонтали. Получу число 56.
Задача 2. Из шести врачей поликлиники двух врачей необходимо отправить на курсы повышения квалификации. Сколькими способами это можно сделать?
Решение:
Найду диагональ шестую сверху и отсчитываю два числа по горизонтали. Получу число 15.
Получу число 15.
Задача3 . В пачке находятся одинаковые по размеру 7 тетрадей в линейку и 5 в клетку.Из пачки наугад берут 3 тетради. Какова вероятность того, что все три тетради надежно в клетку?
Решение. Сначала найдём общее число исходов, т.е. сколькими способами мы можем выбрать 3 тетради из 12 тетрадей
А сколькими способами мы можем выбрать 3 тетради в клетку из 5 тетрадей?
Вероятность наступления случайного события А называется отношением m / n, где n — число всех возможных исходов эксперимента, а m — число всех благоприятных исходов: Р (А) = m / n.
По формуле нахождения вероятности получим
Задача4 .На плоскости даны 10 прямых, причём среди них нет параллельных и через каждую точку их пересечения проходят ровно две прямые. Сколько у них точек пересечения?
Решение: ответ находится на пересечении -45 точек!
Задача 5 .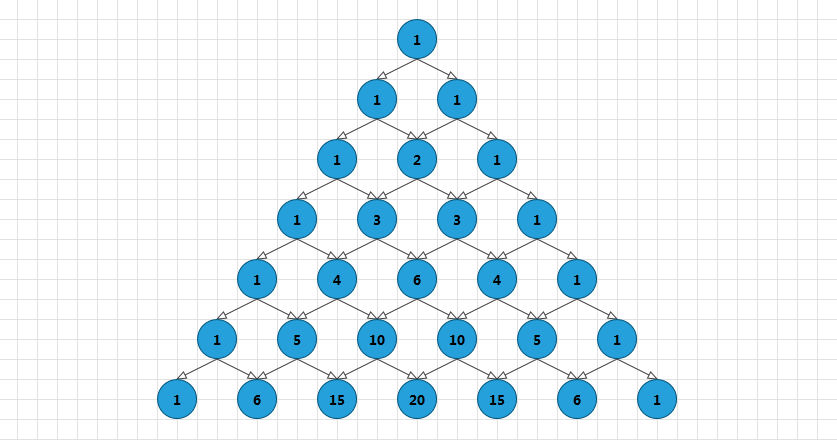
В сумке 10 мячей, пронумерованных от 1 до 10. Наугад вынимают 2 мяча. Какова вероятность того, что это будут мячи с номерами 7 и 3?
Вынуть 2 мяча из 10 возможных 45 способов.Вероятность нашего события 2 из 45.
Заключение
Работа по выбранной теме осуществлялась в полном соответствии с планом исследования, именно: объект и предмет исследования, поставлены цели и задачи, а также ожидаемые результаты. Были указаны используемые методы исследования, определена проблема.
В данной работе была дана общая характеристика как геометрической фигуры, был детально рассмотрен треугольник Паскаля, его свойства.
Я пришла к выводу, одной из наиболее известных и изящных численных схем во всей математике треугольник Паскаля. Треугольник Паскаля — понятие шире, чем мне представлялось. Он обладает не только удивительными свойствами, но и использует в моделирование средних веков для построения схем пропорциональности и для построения прямых углов землемерами и архитекторами.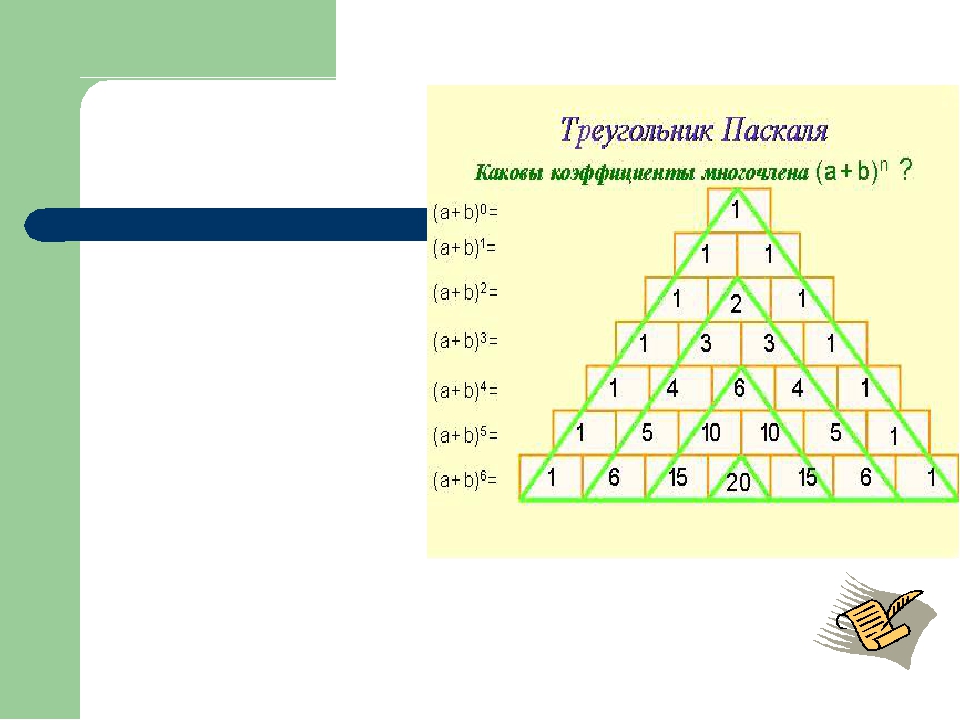 Используя треугольник Паскаля, можно решить задачи из теории вероятности.
Используя треугольник Паскаля, можно решить задачи из теории вероятности.
Практическая значимость данной работы заключается в следующем:
Я, получила много литературы по данному вопросу, получила дополнительные знания в области математики, укрепила свой интерес к этой науке.Работа по данной теме оказалась интересной и полезной.
Список использованных источников и литературы
1. Абачиев С. К. Радужная фрактальность треугольника Паскаля
2. Мартин Гарднер. Глава 17. Неисчерпаемое очарование треугольника Паскаля // Математические новеллы. — М .: Мир, 1974. — 456 с. 3. Треугольник Паскаля. В. А. Успенский. — 2 — е изд. — М .: Наука, 1979. — 48с.
4. Удивительный треугольник великого француза // Hard’n’Soft № 10 2003
5.Фукс Д., Фукс М. Арифметика биномиальных коэффициентов // Квант . — 1970. — № 6. — С. 17-25.
6. Энциклопедия для детей. Т 11. Математика / Глав. ред. М. Аксенова; метод. и отв. ред. В. Володин. — М .: Аванта +, 2004. — 688с.
7. http://ru.wikipedia.org/wiki/
8. Weisstein, Eric W. Pascal’s Triangle (англ.) Насайте Wolfram MathWorld.
Исследовательская работа по математике на тему «Треугольник Паскаля» (7 класс)
Отдел образования, спорта и туризма Борисовского райисполкома
Государственное учреждение образования
«Средняя школа № 16 г. Москва, ул.Борисова »
Треугольник Паскаля
Автор:
учащаяся 7« А »класса
Абоян Елизавета Александровна,
домашний адрес: г. Борисова. Борисов,
ул Смолевичская, д. 8, 76-51-80
Руководитель:
Ищук Ольга Эдуардовна, учитель математики
Борисов, 2016
Оглавление
В этом учебном году мы начали изучать новый предмет «геометрия».
Одна из глав курса геометрии называется «Треугольники». Меня очень заинтересовала тема тема. Я всегда хотела узнать много нового о треугольниках, об их происхождении и значении в нашей жизни. Ведь мир треугольников очень загадочен и интересен.
Треугольник — первая геометрическая фигура, встречающаяся в древних рисунках. Изучая литература, я узнала, что в Египте он символизировал триаду духовной воли, любви, интуиции и высшего разума человека, то есть его личность или душу.
Ацтеки использовали изображение треугольника с вершиной наверху, соединенного с перевернутым треугольником, в качестве символа временного цикла. Треугольник в сочетании с крестом образует алхимический знак Серы.
Равносторонний треугольник, символизирующий, по древнееврейской традиции, совершенство, у христианских Троицу — Отца, Сына и Святого Духа.
существует множество видов треугольников, но больше всего меня заинтересовал треугольник Паскаля.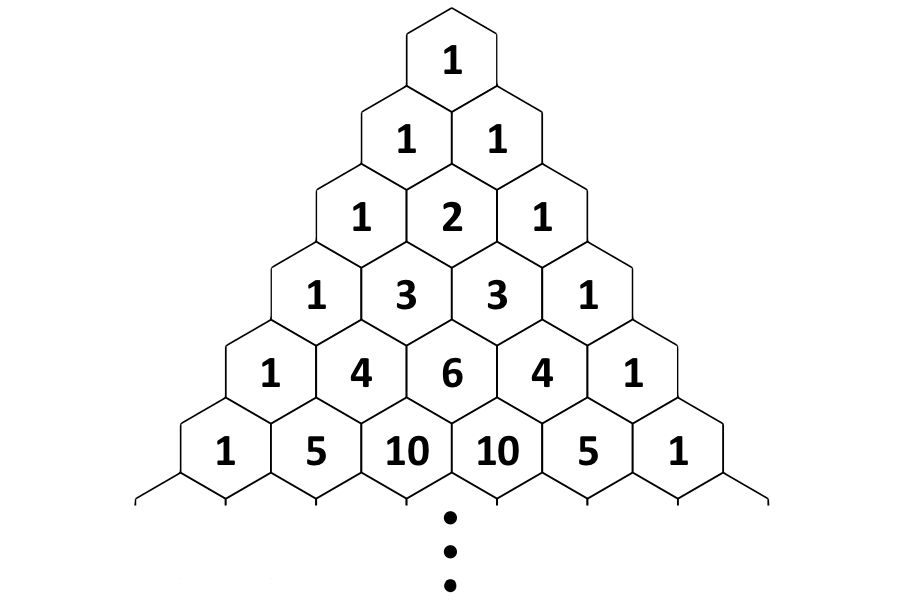
Проблема исследования:
Проблема моего исследования в том, что я попыталась выявить и показать, насколько широко используются треугольники в практической жизни.
Практическая значимость исследования:
Данная исследовательская работа может быть использована как дополнительный материал к урокам геометрии, для внеклассной работы по математике.
Цель исследования:
— ознакомиться с треугольником Паскаля и его применение как разновидностью треугольников;
Гипотеза:
Если число треугольника Паскаля обладает особыми свойствами, то его можно считать уникальным решением для различных задач
Задачи:
— определить применение чисел треугольника Паскаля;
— изучить литературу по теме «Треугольник Паскаля»;
— выявить свойства чисел, входящих в состав треугольника Паскаля;
— сформулировать вывод и итоги исследования;
Объект исследования: треугольник как геометрическая фигура
Предмет исследования: свойства треугольника Паскаля
Методы:
— аналитико-статистическая работа со справочной, научно-познавательной и специальной литературой;
— поиск информации в интернет — ресурсах.
Направления работы:
— проблемы, источники литературы, составление плана;
— работа с литературой и другими источниками;
— обработка полученных данных;
— анализ результатов, вывод вывода;
— мультимедийная подготовка.
Основные этапы исследования: подготовительный; деятельностный;
Ход исследования: рефлексивный; аналитический; презентационный.
Знакомство с треугольником Паскаля
Моё первое знакомство с треугольником Паскаля произошло во время изучения темы «Возведение двучлена в степень» на уроке алгебры. Мне уже известны формулы квадрата суммы и квадрата разности, куба суммы и куба разности. Я заметила, что получить формулы для возведения двучлена в четвёртую, пятую и т.д. степень возможно, учитывая некоторую закономерность в коэффициентах и степенях каждого слагаемого.
Коэффициенты всех строк можно расположить в виде треугольника:
Таким образом я познакомилась с треугольником Паскаля и решила продолжить изучение арифметического треугольника.
Блез Паскаль — французский математик
Блез Паскаль (19 июня 1623, Клермон-Ферран, — 19 августа 1662, Париж) — французский математик, физик, литератор и философ.
Паскаль был первоклассным математиком. Он помог создать два больших новых направления математических исследований. В возрасте шестати лет написал замечательный трактат о предмете проективной геометрии и в 1654 году переписывался с Пьером де Ферма по теории вероятностей, что оказало принципиальное влияние на развитие современной экономики.
Треугольник Паскаля как разновидность треугольника
Изучая разновидность треугольников, я математила, что треугольник Паскаля — арифметический треугольник, образованными биноми коэффициентами.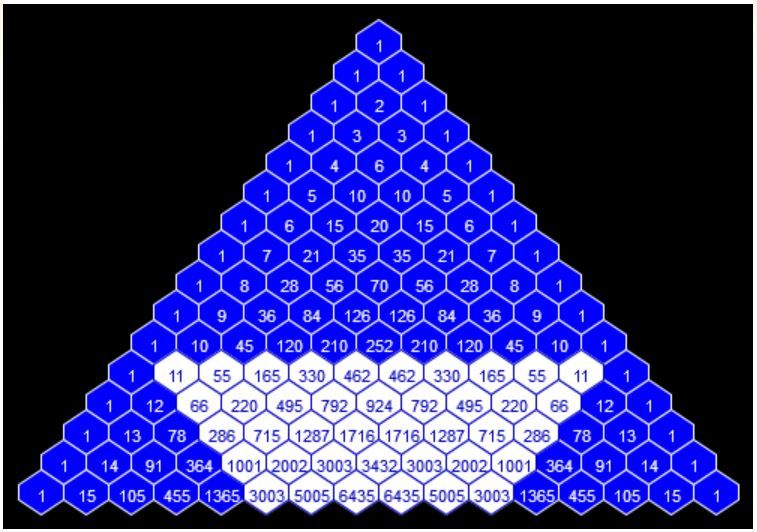 Назван в честь Блеза Паскаля. В действительности, треугольник Паскаля был известен задолго до 1653 года — дата выхода «Трактата об арифметическом треугольнике». Так, этот треугольник воспроизведен на титульном листе учебника арифметики, написанном в начале XVI Петром Апианом, астрономом из Ингольтштадского университета.Изображен треугольник и на иллюстрации в книге одного китайского математика, выпущенной в 1303 году. Омар Хайям, бывший не только философом и поэтом, но и математиком, знал о существовании треугольника уже около 1100 года, в свою очередь, заимствовав его из более ранних китайских или индийских источников.
Назван в честь Блеза Паскаля. В действительности, треугольник Паскаля был известен задолго до 1653 года — дата выхода «Трактата об арифметическом треугольнике». Так, этот треугольник воспроизведен на титульном листе учебника арифметики, написанном в начале XVI Петром Апианом, астрономом из Ингольтштадского университета.Изображен треугольник и на иллюстрации в книге одного китайского математика, выпущенной в 1303 году. Омар Хайям, бывший не только философом и поэтом, но и математиком, знал о существовании треугольника уже около 1100 года, в свою очередь, заимствовав его из более ранних китайских или индийских источников.
Ещё я узнала из книги «Математические новеллы» (М., Мир, 1974) Мартина Гарднера, что «Треугольник Паскаля так прост, что выписать его способность даже десятилетний ребенок. аспекты математики, не имеющие на первый взгляд между собой ничего общего.
Я рассмотрела схему построения треугольника, предложенную Гуго Штейнгаузом в его классическом «Математическом калейдоскопе», как показано на схеме синей стрелкой Узлы, в которые можно попасть только одним образом, отмечены зелеными смайликами, точка, в которую можно попасть двумя способами, одним красным смайликом, а тремя, соответственно, можно двигаться только, точнее, все время выбирая, вперед налево, или вперед.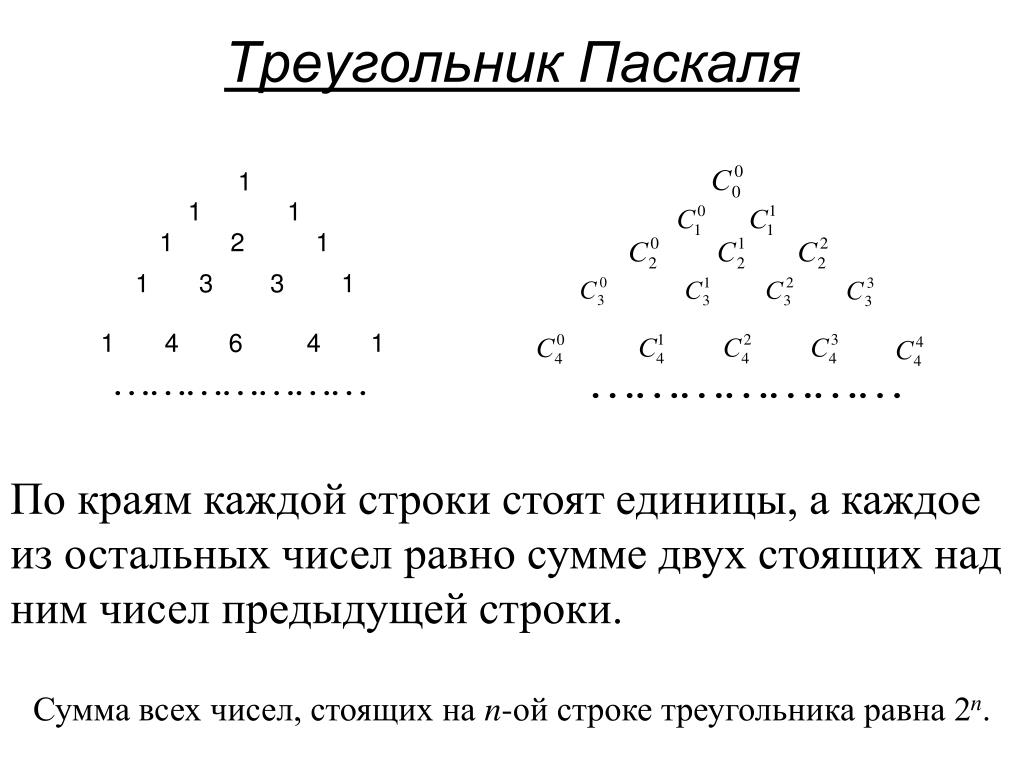 — розовыми.Это один из вариантов построения треугольника.
— розовыми.Это один из вариантов построения треугольника.
(Рисунок 1)
Изучая специальную литературу, я узнала, что еще проще объясняют устройство треугольника Паскаля слова : каждое число равноме двух значений над ним чисел .
Все элементарно, но сколько в этом таится чудес. Если очертить треугольник Паскаля, то получится равнобедренный треугольник. В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух установленных над ним чисел.Треугольник можно неограниченно. Он обладает симметрией относительно вертикальной оси, проходящей через его вершину. Вдоль диагоналей (насколько треугольника может быть диагонали, но не будем придираться, такая терминология встречается в публикациях), параллельных сторонам треугольника (на рисунке отмечены зелеными линиями) выстроены треугольные числа и их обобщения на случай пространств всех размеров. Треугольник в самом обычном и привычном нам виде показывает, сколько квадратов можно расположить в виде треугольника — как классический пример начальная расстановка шаров в бильярде. К одной монетке можно прислонить еще — итого три — к двум можно приладить еще три — итого шесть.
К одной монетке можно прислонить еще — итого три — к двум можно приладить еще три — итого шесть.
Получили треугольные числа на рисунке: 3; 6; 10; 15.
Продолжая наращивать ряды с сохранением треугольника получим ряд 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66 …, что и показывает вторую зеленую линию. Этот замечательный ряд натурального ряда (55 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10) содержит также множество знакомцев, хорошо известных любителям математики: 6 и 28 — совершенные числа, 36 — квадратное число, 8 и 21 — числа Фибоначчи.
Следующая зеленая линия покажет нам тетраэдые числа — один из трех нижних шарниров шесть — итого десять, и так далее.
, чтобы найти сумму чисел, стоящих на любом диагонали от начала до интересующего нас места, достаточно взглянуть на число, расположенное снизу и слева от последнего слагаемого, (слева для правого диагонали, для левого диагонали будет справа, а вообще — ближе к середине треугольника ). Пусть, например, мы вычислить сумму чисел от 1 до 9.»Спустившись» по диагонали до числа 9, мы увидим снизу от него число 45. Оно то и дает искомую сумму. Чему равна первой сумме треугольных восьми чисел? Отыскиваем восьмое число на второй диагонали и сдвигаемся вниз и влево. Ответ: 120.
Пусть, например, мы вычислить сумму чисел от 1 до 9.»Спустившись» по диагонали до числа 9, мы увидим снизу от него число 45. Оно то и дает искомую сумму. Чему равна первой сумме треугольных восьми чисел? Отыскиваем восьмое число на второй диагонали и сдвигаемся вниз и влево. Ответ: 120.
(Рисунок 2)
Треугольник Паскаля имеет применение в теории вероятностей и обладает замечательными свойствами.
Свойства треугольника Паскаля и их применение в решении задач
Паскаль подробно исследовал свойства и применения своего «треугольника».Приведу для примера лишь 3 свойства «треугольника», найденные самим Паскалем; при этом буду исходить из расположения «треугольника» на плоскости, какое было указанно Паскалем, и говорить о горизонтальных и вертикальных рядах.
Свойство 1: каждое в таблице равно сумме предшествующего горизонтального ряда, начиная с самого левого до стоящего непосредственно над числом А (в котором содержатся слагаемые, дающие в сумме А, заштрихованы). (Рисунок 4)
(Рисунок 4)
(Рисунок 4) (Рисунок 5) (Рисунок 6)
Свойство 2: Каждое число А в таблице равно сумме предшествующего вертикального ряда, начиная с самого верхнего до стоящего непосредственно левее числа А.(Рисунок 5)
Свойство 3: Каждое число в таблице, будучи увеличенным на единицу, равно сумме всех чисел, заполняет прямоугольник, ограниченный теми же вертикальными и горизонтальными рядами, на пересечение которых стоит число А (сами эти ряды в рассматриваемом прямоугольник не включаются). (Рисунок 6)
Треугольник Паскаля и теория вероятности.
Блез Паскаль и другой великий француз, Пьер Ферма, стали основателями теории вероятностей, когда Паскаль и Ферма независимо друг от друга дали правильное объяснение так называемого парадокса раздела ставок.Два игрока играют в «безобидную» игру (т.е. шансы победить у обоих одинаковы), договорившись, тот, кто первым выигрывает шесть партий, получает весь приз. Предположим, что игра остановилась до того, как один из них выиграл приз (например, первый игрок выиграл пять партий, а второй — три). Как справедливо разделить приз? Так, согласно одному решению следовало разделить приз в отношении 5: 3, т.е. пропорционально выигранным партиям, другому — в отношении 2: 1 (здесь рассу велись, по всей видимости, следующим образом: поскольку первый игрок выиграл на две партии больше, что составляет третью часть от необходимых для победы шести партий, то он должен получить одну треть от приза, а оставшуюся часть нужно разделить пополам).
Предположим, что игра остановилась до того, как один из них выиграл приз (например, первый игрок выиграл пять партий, а второй — три). Как справедливо разделить приз? Так, согласно одному решению следовало разделить приз в отношении 5: 3, т.е. пропорционально выигранным партиям, другому — в отношении 2: 1 (здесь рассу велись, по всей видимости, следующим образом: поскольку первый игрок выиграл на две партии больше, что составляет третью часть от необходимых для победы шести партий, то он должен получить одну треть от приза, а оставшуюся часть нужно разделить пополам).
А между тем делить надо в отношении 7: 1. И Паскаль, и Ферма рассматривали парадокс раздела ставки как задача о вероятностях, что справедливым является раздел, пропорциональный шансам первого игрока выиграть приз. Предположим, первому игроку осталось выиграть только одну партию, а второму для победы необходимо выиграть еще три партии, причем продолжают игру и играют все три партии, даже если некоторые из них являются лишними для определения победителя. Для такого продолжения все 2 3 = 8 исходов будут равновероятными.Так как второй получатель получает только при одном исходе (если он выиграл все три партии), а в остальных случаях побеждает первый игрок, справедливым отношением 7: 1.
Для такого продолжения все 2 3 = 8 исходов будут равновероятными.Так как второй получатель получает только при одном исходе (если он выиграл все три партии), а в остальных случаях побеждает первый игрок, справедливым отношением 7: 1.
В науке и практике часто встречаются задачи, решающие составляющие различные комбинации из конечного числа элементов и подсчитывать число комбинаций. Такие задачи получили название комбинаторных задач.
Рассмотрим основные формулы формулы:
Размещение
Это любое упорядоченное подмножество m из элементов массива n.
Перестановки (). Если k = n, то эти размещения называются перестановками.
Сочетания () — это любое подмножество из k — элементов, которые принадлежат множеству, состоящему из n — различных элементов.

.
В треугольнике Паскаля число, сколькими способами можно выбрать k элементов из множества, содержащего различные элементы, стоит пересечь k-ой диагонали и n-ой строки.Чтобы вычислить сочетание, найду диагональ седьмую сверху и отсчитываю три числа по горизонтали. Получу число 35.
Можно использовать треугольник Паскаля и для вычислений размещений. .Если нам нужно посчитать, то зная что, а 3! = 6, получим значение данного размещения 210.
Я пришла к выводу, что рассмотренные свойства треугольника Паскаля подтверждают слова Мартина Гарднера о том, что треугольник Паскаля одна из наиболее изящных схем во всей математике.
Актуальность исследования обусловлена ежегодным уснением заданий ЦТ, что требует углубленных знаний не только в алгебре, но и в геометрии.
В своей практической работе я подобрала ряд задач по теме «Треугольник Паскаля»
Задача 1. В магазине «Филателия» продается 8 наборов марок, посвященных спортивной тематике. Сколькими способами можно выбрать из них 3 набора?
В магазине «Филателия» продается 8 наборов марок, посвященных спортивной тематике. Сколькими способами можно выбрать из них 3 набора?
Решение:
В треугольнике Паскаля число показывающее, сколькими способами можно выбрать k различных элементов из множества, хранящихся n элементов, стоит на пересечении k-ой диагонали и n-ой строки.
Найду диагональ восьмую сверху и отсчитываю три числа по горизонтали. Получу число 56. (Рисунок 8)
Задача 2.Из шести врачей поликлиники двух врачей необходимо отправить на курсы повышения квалификации. Сколькими способами это можно сделать?
Решение:
Найду диагональ шестую сверху и отсчитываю два числа по горизонтали. Получу число 15.
(Р (Рисунок 9)
Задача3. В пачке находятся одинаковые по размеру 7 тетрадей в линейку и 5 в клетку. Из пачки наугад берут 3 тетради. Какова вероятность того, что все три тетради надежно в клетку?
Из пачки наугад берут 3 тетради. Какова вероятность того, что все три тетради надежно в клетку?
Решение. Сначала найдём общее число исходов, т.е. сколькими способами мы можем выбрать 3 тетради из 12 тетрадей
А сколькими способами мы можем выбрать 3 тетради в клетку из 5 тетрадей?
Вероятность наступления случайного события А называется отношением m / n, где n — число всех возможных исходов эксперимента, а m — число всех благоприятных исходов: Р (А) = m / n.
По формуле нахождения вероятности получим
(Рисунок 10)
Задача4. На плоскости даны 10 прямых, причём среди них нет параллельных и через каждую точку их пересечения проходят ровно две прямые. Сколько у них точек пересечения?
Решение: ответ находится на пересечении -45 точек!
Задача 5. В сумке 10 мячей, пронумерованных от 1 до 10. Наугад вынимают 2 мяча. Какова вероятность того, что это будут мячи с номерами 7 и 3?
Наугад вынимают 2 мяча. Какова вероятность того, что это будут мячи с номерами 7 и 3?
Вынуть 2 мяча из 10 возможных 45 способов.Вероятность нашего события 2 из 45. (Рисунок 11)
В ходе практического исследования я пришла следующим выводам: при решении комбинаторных задач и задач по теории вероятностей можно использовать не только формулами комбинаторики, но и использовать свойства треугольника Паскаля
Работа по выбранной теме осуществлялась в полном соответствии с планом исследования, а объект и предмет исследования, поставлены цели и задачи, а также ожидаемые результаты.Были указаны используемые методы исследования, определена проблема.
В данной работе была дана общая характеристика как геометрической фигуры, был детально рассмотрен треугольник Паскаля, его свойства.
Я пришла к выводу, что одной из наиболее известных и изящных численных во всей математике является треугольник Паскаля. Треугольник Паскаля — понятие шире, чем мне представлялось. Он обладает не только удивительными свойствами, но и использует в моделирование средних веков для построения схем пропорциональности и для построения прямых углов землемерами и архитекторами.Используя треугольник Паскаля, можно решить задачи из теории вероятности и комбинаторики. С комбинаторными задачами я встречалась на уроках математики в 6 классе и при решении олимпиадных задач
Треугольник Паскаля — понятие шире, чем мне представлялось. Он обладает не только удивительными свойствами, но и использует в моделирование средних веков для построения схем пропорциональности и для построения прямых углов землемерами и архитекторами.Используя треугольник Паскаля, можно решить задачи из теории вероятности и комбинаторики. С комбинаторными задачами я встречалась на уроках математики в 6 классе и при решении олимпиадных задач
Практическая значимость работы заключается в следующем: я, изучив много литературы по данному вопросу, получила дополнительные знания в области математики, укрепила свой интерес к этой науке.
Я узнала, что треугольник Паскаля использует:
В курсе алгебры
При решении задач комбинаторных задач
Для решения различных задач в области физики
Создание вычислительных машин построение треугольника Паска стала излюбленной задачкой для начинающих при изучении основ программирования.

Работа по данной теме оказалась интересной и полезной.
1. Абачиев С. К., Радужная фрактальность треугольника Паскаля / С. К. Абачиев, — Минск, 1999. — 168с.
2. Галкин Е.В. Нестандартные задачи по математике. Задачи логического характера. Книга для учащихся 5-11кл.Москва, «Просвещение», 1996г. — 194 с.
3. Мартин Гарднер. Глава 17. Неисчерпаемое очарование треугольника Паскаля Математические новеллы. — Минск: Мир, 1974.— 456 с.
4. Треугольник Паскаля. В. А. Успенский. — 2 — е изд. — Москва: Наука, 1979. — 48с.
5. Фукс Д., Фукс М., Арифметика биномиальных коэффициентов / Квант. — 1970. — № 6. — С.17-25.
6. Энциклопедия для детей. Т 11. Математика / Глав. ред. М. Аксенова; метод. и отв. ред. В. Володин. — М .: Аванта +, 2004. — 688с.
7. http://ru.wikipedia.org/wiki/
8.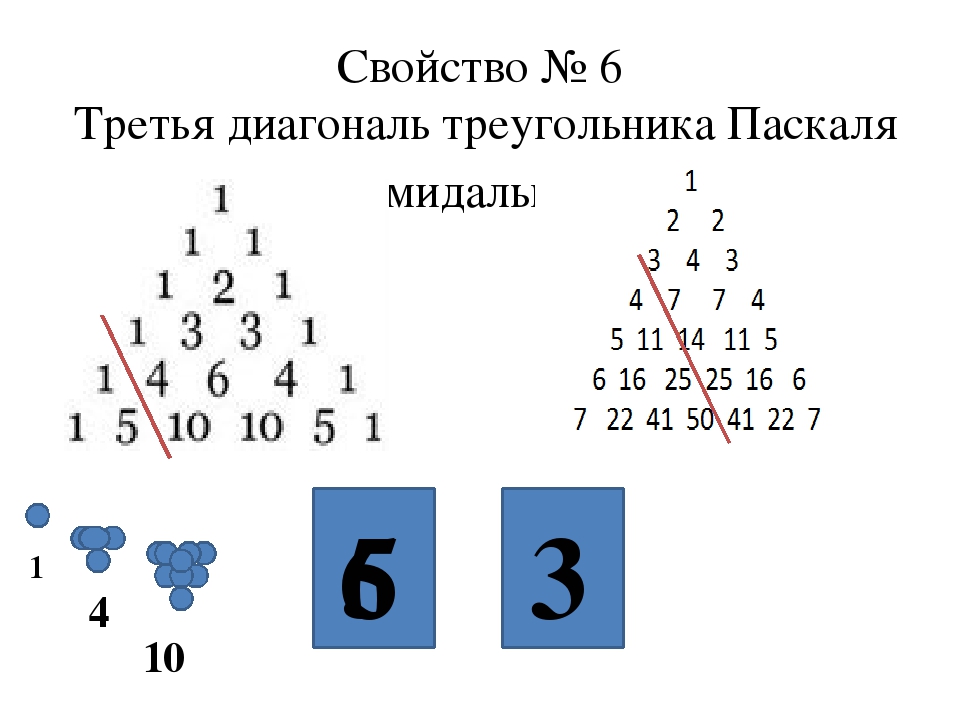 http://davaiknam.ru/text/volshebnij-treugolenik.
http://davaiknam.ru/text/volshebnij-treugolenik.
Исследовательская работа «Возведение двучлена в n-степень, треугольник Паскаля»
12
Министерство образования и науки Республики Дагестан
Республиканский конкурс исследовательских работ и проектов учащихся
Общеобразовательных организаций и воспитанников дошкольных образовательных организаций Республики Дагестан
«Науки юношей питают»
Направление исследовательской работы «Наука»
Направление исследовательской работы «Наука»
n-ю степень, треугольник Паскаля »
Выполнил Абдурашидова Марьям Ахмедовна
Ученица 8« б »класса
МКОУ СОШ № 9 г.Кизляра РД
Руководитель: Исинова Адият Агаховна
Учитель математики
высшей категории
МКОУ СОШ №9 г. Москва, ул. Кизляра РД
Москва, ул. Кизляра РД
Тел .: 8-988-779-09-88
2019 год
Содержание
Введение …………………………………………………… ……………………… ..3
Основная часть ……………………………………………………………… .. …… 4
Глава 1 История возникновения формул сокращенного умножения ……… 5
Глава 2 Формулы школьного курса математики ………………………….… ..6
Глава 3 Возведение двучлена в n -ю степень ………………………………… …. 7
Глава 4 Некоторые замечательные свойства треугольника Паскаля …… … 8
Глава 5 Алгоритм возведения двучлена в n -ю степень ………………….… ..12
Заключение ……………………… ………………………………………… … …… 14
Список литературы …………………………………………………………… …. … 15
… 15
Введение
Формулы сокращенного умножения, как нам известно, упрощают ряд вычислений.Лично меня заинтересовало то, что нельзя ли возвести двучлен в n-ю степень.
Актуальность моей работы является применение формул сокращенного умножения и ее приложений в различных областях и сфере. Довольно часто имеют дело с формулами сокращенного умножения: ученые — физики, химии, биологи, конструкторы-проектировщики, диспетчеры и т п. Исследовательская работа имеет социальную и личную значимость в том плане, что важно овладеть как используемым, так и нетрадиционными формами и приемами применения формул сокращ умножения.При упрощении и вычислении значений выражений, уравнений в доказатель тождеств также находит широкое применение формулы сокращенного умножения. А также овладеть ориентироваться в проблемных ситуациях.
Объект исследования: область математики — формулы сокращенного исследования.
Цель исследования проявляется в рассмотрении вопроса о существовании формул сокращенного умножения рассматриваемых в школьном курсе математики, изучении некоторых замечательных свойств треугольника Паскаля.
В соответствии с целью в работе были поставлены следующие задачи:
1. Собрать сведения из истории математики о формулах сокращенного умножения.
Изучить способы возведения в n — ую степень
алгебраической суммы двух слагаемых.
Изучить литературу по теме «Треугольник Паскаля»;
Сформулировать вывод и итоги исследования;
Создание иллюстративного компьютерного материала по треугольникам;
Основная часть.
«Скажи мне, и я забуду.
Покажи мне, и я запомню.
Дай мне действовать самому, и я научусь ».
(Конфуций)
Данную тему я выбрала, потому что хотела формулы сокращенного умножения для степеней выше трех и еще рассмотреть треугольник Паскаля, с нами учитель вкратце ознакомила. Для этого я с начала изучила историю возникновения формул сокращенного умножения и начала возводить двучлен в степени начиная с нулевой.Также рассмотрела геометрическую интерпретацию формул сокращенного умножения.
Глава 1. История возникновения формул сокращенного умножения
Слово «алгебра» возникло после появления трактата «Китаб аль-джебр валь-мукабала» математика и астронома из г. Москва. Хивы Мухаммеда бен Муса аль-Хорезми (787-ок 850) .Термин «аль-джебр», взятый из названия книги, в дальнейшем стал употребляться как «алгебра».
Некоторые правила сокращенного умножения известны еще около 4 тыс.лет тому назад. Их знали вавилоняне и другие народы древности. Тогда они формулировались словесно или геометрически. У древних греков величины обозначались не числами или буквами, а отрезками греми прямыми. Они говорили не «а 2 », «квадрат на отрезке а», не « ав », а «прямоугольник, нарушся между отрезками а и в ». Например, тождество ( а + в ) 2 = а 2+ 2 ав + в 2 во второй книге «начал» Евклида (III в.До н. э.) формулировалась так: «если прямая линия (имеется в отрезок) как либо рассечена, то квадрат на всем прямом квадратам на отрезках вместе с взятым прямоугольником, заключенным между отрезками». Доказательство опирается на геометрические соображения. В дальнейшем я приведу пример такого доказательства.
Тогда они формулировались словесно или геометрически. У древних греков величины обозначались не числами или буквами, а отрезками греми прямыми. Они говорили не «а 2 », «квадрат на отрезке а», не « ав », а «прямоугольник, нарушся между отрезками а и в ». Например, тождество ( а + в ) 2 = а 2+ 2 ав + в 2 во второй книге «начал» Евклида (III в.До н. э.) формулировалась так: «если прямая линия (имеется в отрезок) как либо рассечена, то квадрат на всем прямом квадратам на отрезках вместе с взятым прямоугольником, заключенным между отрезками». Доказательство опирается на геометрические соображения. В дальнейшем я приведу пример такого доказательства.
Первым ученым, который отказался от геометрических способов выражения и перешел к алгебраическим уравнениям, был древнегреческий ученый-математик, живший в III веке до н.э. Диофант Александрийский. В своей книге «Арифметика» Диофант формулы квадрата суммы, квадрата рассмотрвал уже с арифметической точки зрения. Ну а современную символику алгебраические тождества получили благодаря двум математикам, а именно Виету и Декарту (16 век).
Ну а современную символику алгебраические тождества получили благодаря двум математикам, а именно Виету и Декарту (16 век).
На современном уровне развития математики данные формулы были обоснованы Исааком Ньютоном. При небольших значениях n коэффициенты можно найти из треугольника Паскаля. Блез Паскаль триста пятьдесят лет назад придумал специальный инструмент для определения этих самых коэффициентов, который использует назвали «треугольник Паскаля».
Глава 2. Формулы школьного курса математики
На уроке математики я познакомилась с формулами сокращенного умножения, которые знаю наизусть. Все они доказываются раскрытием скобок через умножение многочленов и приведением подобных слагаемых.
Разность квадратов:
(a + b) (a — b) = a² — b² (1)
Квадрат суммы и квадрат разности:
(a + b) ² = a² + 2ab + b² (2)
(a — b) ² = a² — 2ab + b² (3)
Сумма и разность кубов:
(a + b) (a² — ab + b²) = a³ + b³ ( 4)
(a — b) (a² + ab + b²) = a³ — b³ (5)
Куб сумма и куб разности:
(a + b) ³ = a³ + 3a²b + 3ab² + b³ (6)
(a –b) ³ = a³ — 3a²b + 3ab² — b³ (7)
Глава 3.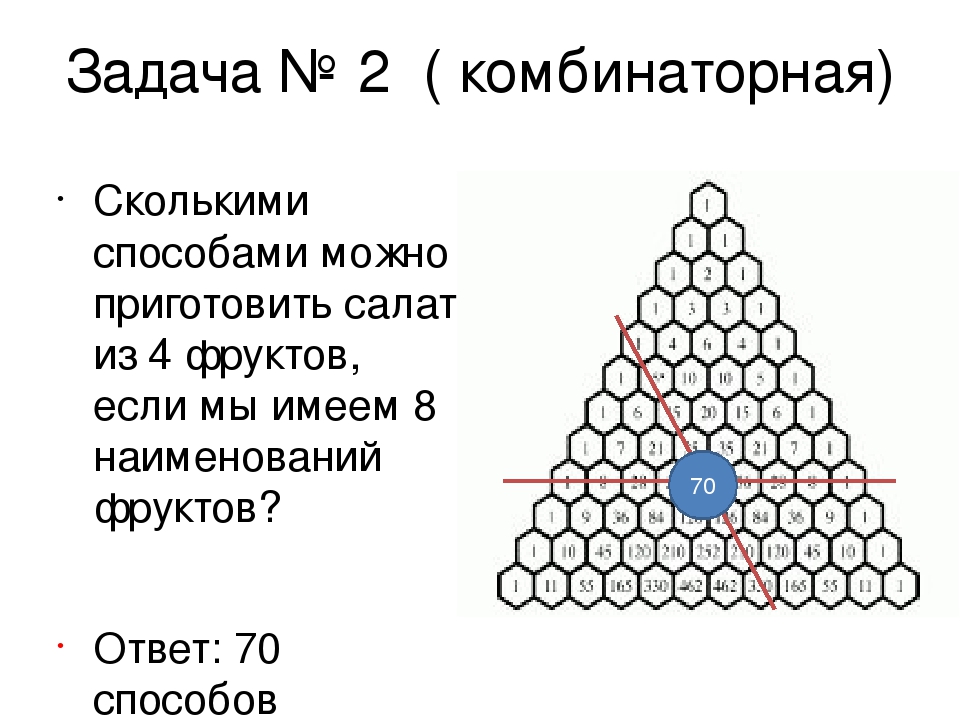 Возведение двучлена в n -ю степень
Возведение двучлена в n -ю степень
Дальше меня заинтересовало: как возвести сумму двух слагаемых в более высокую степень, например в четвертую, пятую или шестую. И я решила поэкспериментировать.
Для начала я решила рассмотреть куб суммы двух слагаемых, для чего расписала его в виде произведения суммы двух слагаемых на квадрат тех же слагаемых: (a + b) 3 = (a + b) 2 (a + b) = a 3 + 3 a 2 b + 3 ab 2 + b 3
Потом поработала с четвертой степенью двух слагаемых, представила ее как результат произведений квадратов двух слагаемых и: (a + б) 4 = (a + b) 2 (a + b) 2 = (a 2 + 2ab + b 2 ) (a 2 + 2ab + b 2 ) = a 4 + 4 a 3 b + 6 a 2 b 2 + 4 ab 3 3 + b 4
70370 способом возвела в пятую степень двух слагающих
(a + b) 5 = (a + b) 2 (a + b) 3 = (a 2 + 2ab + b 2 ) (a 3 + 3a 2 б + 3ab 2 905 39 + b 3 ) = a 5 + 5 a 4 b + 10 a 3 b 2 + 10 a 2 b 3 ++ 5 ab 4 + b 5
Попробовала расписать шестую степень как произведение квадрата и четвертой степени суммы двух слагаемых: (a + b) 6 = (a + b) 2 (a + b) 4 = (a 2 + 2ab + b 2 ) (a 4 + 4a 3 b + 6a 2 b 2 + 4ab 3 + b 4 ) = a 6 + 6 a 5 b + 15 a 4 b 2 ++ 20 a 3 b 3 + 15 a 2 b 4 + 6 5 + b 6
Затем седьмую степень представила как произведение куба суммы и четвертой степени суммы: (a + b) 7 = (a + b) 3 (a + b) 4 = (a 3 + 3a 2 b + 3ab 2 + b 3 ) * (a 4 + 4a 3 b + 6a 2 b 2 + 4ab 3 + b 4 ) = a 7 + 7 a 6 b + 21 a 5 b 2 + 35 a 4 b 3 + 35 a 3 b 4 + 21 a b 5 + 7 ab 6 + b 7
Надо заметить, что данные преобразовать можно было повторить и другими способами. Например, сумму двух слагаемых возвести в шестую степень, как произведение кубов тех же самых слагаемых.
Например, сумму двух слагаемых возвести в шестую степень, как произведение кубов тех же самых слагаемых.
Особенно меня удивило то, что все коэффициенты (их я выделила жирным шрифтом), полученные в результате умножения, были симметрическими. Оказалось, что это неспроста, закономерность среди коэффициентов многочлена называется «Треугольник Паскаля» по имени его автора
Глава 4. Замечательные свойства треугольника Паскаля
Но кроме закономерности коэффициентов прослеживается такая же замечательная закономерность среди степеней своего многочлена.Оказывается следующим образом: степень первого слагаемого, начиная с большей, с каждым разом уменьшается на единицу, степень второго слагаемого наоборот увеличивается от нулевой до наибольшей.
Строится «Треугольник Паскаля» следующим образом. В вершине треугольника пишем 1. Единица соответствует выражению как любое число, возведённое в нулевую степень, даёт единицу. Достраивая треугольник, ниже пишем ещё по единице. Это коэффициенты разложения того же двучлена, возведённого в первую степень: Идём дальше.Стороны треугольника образуют единицы, а между ними — сумма двух единичек, находящихся сверху, то есть 2. Это и есть коэффициенты трёхчлена «сумма»:
Достраивая треугольник, ниже пишем ещё по единице. Это коэффициенты разложения того же двучлена, возведённого в первую степень: Идём дальше.Стороны треугольника образуют единицы, а между ними — сумма двух единичек, находящихся сверху, то есть 2. Это и есть коэффициенты трёхчлена «сумма»:
Следующий ряд, как и предыдущий, начинается и заканчивается единицами, а между ними — суммы цифр , находятся сверху: 1, 3, 3, 1. Мы получили коэффициенты разложения «куба суммы». Ряд коэффициентов двучлена четвёртой степени составят 1, 4, 6, 4, 1 и так далее.
Номер Строки
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1
1 20 15 6 1
1 7 21 35 35 21 7 1
Б лез Паскаль — французский математик
Блез Паскаль (19 июня 1623, Клермон-Ферран, — 19 августа 1662, Париж) — французский математик, физик , литератор и философ.
Паскаль был первоклассным математиком. Он помог создать два больших новых направления математических исследований. В возрасте шестати лет написал замечательный трактат о предмете проективной геометрии и в 1654 году переписывался с Пьером де Ферма по теории вероятностей, что оказало принципиальное влияние на развитие современной экономики.
Изучая разновидности треугольников, я определяла, что треугольник Паскаля — арифметический треугольник, назван в честь Блеза Паскаля. В действительности, треугольник Паскаля был известен задолго до 1653 года — дата выхода «Трактата об арифметическом треугольнике». Так, этот треугольник воспроизведен на титульном листе учебника арифметики, написанном в начале XVI Петром Апианом, астрономом из Ингольтштадского университета. Изображен треугольник и на иллюстрации в книге одного китайского математика, выпущенной в 1303 году. Омар Хайям, бывший не только философом и поэтом, но и математиком, знал о существовании треугольника около 1100 года, в свою очередь, за его из более ранних китайских или индийских источников.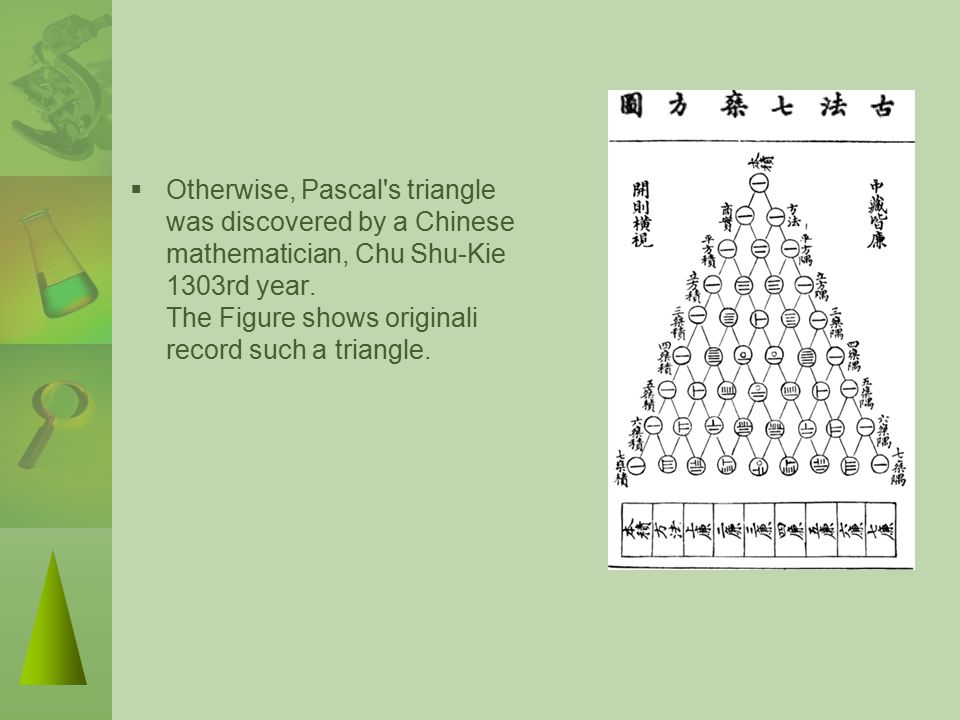
Ещё я узнала из книги «Математические новеллы» (М., Мир, 1974) Мартина Гарднера, что «Треугольник Паскаля так прост, что выписать его способность даже десятилетний ребенок. Столь необычные свойства позволяют считать треугольник Паскаля одной из наиболее изящных во всей математике «.
Я рассмотрела схему построения треугольника, предложенную Гуго Штейнгаузом в его классическом «Математическом калейдоскопе»: предположим, что вы входите в город как показано на схеме синей стрелкой, и можете двигаться только вперед, точнее, все время выбирая, вперед налево, или вперед направо.Узлы, которые можно попасть только двумя видами, отмеченными зелеными смайликами, которые можно попасть двумя точками красными смайликами, а тремя, соответственно — розовыми. Это один из вариантов построения треугольника.
Изучая специальную литературу, я узнала, что еще проще объясняют устройство треугольника Паскаля слова: каждое число равно сумме двух расположенных над ним чисел..PNG) Все элементарно, но сколько в этом таится чудес. Если очертить треугольник Паскаля, то получится равнобедренный треугольник.В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух установленных над ним чисел. Треугольник можно неограниченно. Он обладает симметрией относительно вертикальной оси, проходящей через его вершину. Вдоль диагоналей (насколько треугольника может быть диагонали, но не будем придираться, такая терминология встречается в публикациях), параллельных сторонам треугольника (на рисунке отмечены зелеными линиями) выстроены треугольные числа и их обобщения на случай пространств всех размеров.Треугольник в самом обычном и привычном нам виде показывает, сколько квадратов можно расположить в виде треугольника — как классический пример начальная расстановка шаров в бильярде. К одной монетке можно прислонить еще — итого три — к двум можно приладить еще три — итого шесть.
Все элементарно, но сколько в этом таится чудес. Если очертить треугольник Паскаля, то получится равнобедренный треугольник.В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух установленных над ним чисел. Треугольник можно неограниченно. Он обладает симметрией относительно вертикальной оси, проходящей через его вершину. Вдоль диагоналей (насколько треугольника может быть диагонали, но не будем придираться, такая терминология встречается в публикациях), параллельных сторонам треугольника (на рисунке отмечены зелеными линиями) выстроены треугольные числа и их обобщения на случай пространств всех размеров.Треугольник в самом обычном и привычном нам виде показывает, сколько квадратов можно расположить в виде треугольника — как классический пример начальная расстановка шаров в бильярде. К одной монетке можно прислонить еще — итого три — к двум можно приладить еще три — итого шесть.
Если возводить двучлен в n-ю степень используя треугольник Паскаля, получается вот что:
( а + в ) 0 = 1
( а + в ) 1 = а + в
( а + в ) 2 = а 2 +2 ав + в 2
( а + в ) 3 = а 3 +3 а 2 в + 3ав 2 + в 3
( а + в ) 4 = а 4 +4 а 3 в +6 а 2 в 2 +4 ав 3 + в 4
( а + в ) 5 = а 5 +5 90 039 а 4 в +10 а 3 в 2 + 10 а 2 в 3 +5 ав 4 + в 5
( а + в ) 6 = а 6 +6 а 5 в +15 а 4 в 2 + 20 а 3 в 3 15 а 2 в 4 +6 ав 5 + в 6
Глава 5. Алгоритм возведения двучлена в n -ю степень
Алгоритм возведения двучлена в n -ю степень
Выписать в установленном порядке все одночлены соответствующие члены членов итогового многочлена.
Записать треугольник Паскаля для (n + 1) -й строки.
Записать последовательность в качестве коэффициентов выписанных одночленов числа из (n + 1) -й строки треугольника Паскаля.
При возведении в степени суммы (а + в) n поставить перед всеми одночленами знак «плюс».
При возведении в степени разности (а-в) n поставить перед вторым одночленом знак «плюс», перед вторым одночленом — знак «минус» и далее чередовать знаки до последнего одночлена.
Применение формул сокращенного умножения.
Вычислить:
а) 199 2 = (200 — 1) 2 = 200 2 — 2 · 200 + 1 = 40000 — 400 + 1 = 39601 Ответ: 39601
б) √1369 — 2 · 37 · 29 + 841 = √37 2 — 2 · 37 · 29-29 2 = √ (37-29) 2 = 37-29 = 8 Ответ: 8
в) 199 · 201 = (200 — 1) · (200 + 1) = 200 2 — 1 2 = 40000 — 1 = 39999 Ответ: 39999
г) 72 2 = (70 + 2) 2 = 70 2 + 2 · 70 · 2 + 2 2 = 4900 + 280 + 4 = 5184 Ответ: 5184
Сократить дробь:
59 2 — 41 2 (59 — 41) · (59 + 41) 59 + 41 100 5 5
59 2 — 2 · 59 · 41 + 41 2 (59 — 41) 2 59 — 41 18 9
д) 83 2 + 2 · 83 · 17 + 17 2 (83 + 17) 2 10000100
100100100
Решить уравнение: 9 0005
(3х + 2) 4 — (3х — 4) 4 = 0
((3х + 2) 2 — (3х — 4) 2 ) · ((3х + 2) 2 + (3х — 4) 2 ) = 0
а) (3х + 2) 2 — (3х — 4) 2 = 0 или б) (3х + 2) 2 + (3х — 4) 2 = 0
((3х + 2) — (3х — 4)) · ((3х + 2) + (3х — 4)) = 0 очевидно, что уравнение б) — не равно нулю
3х + 2 — 3х + 4 = 0 или 3х + 2 + 3х — 4 = 0
0 = 6 6х = 2
х = 1/3
Возвести в степень
Способ 1:
( х — 2) 4 = (х — 2) 2 · (х — 2) 2 = (х 2 — 4х + 4) (х 2 — 4х + 4) = х 4 — 4х 3 + 4х 2 — 4х 3 + 16х 2 — 16х + 4х 2 — 16х + 16 = х 4 — 8х 3 + 24х 2 — 32х + 16
Способ 2: 9000 5
(х — 2) 4 = х 4 — 8х 3 + 24х 2 — 32х + 16
Возвела двучлен в 4-ю степень обычным способом и по формуле. Разница очевидна.
Разница очевидна.
Возведем двучлен х + 2 в 5-ю степень двумя способами.
Способ 1: (х + 2) 5 = (х + 2) 2 · (х + 2) 3 = (х 2 + 4х + 4) (х 3 + 6х 2 + 12х +8) = х 5 + 6х 4 + 12х 3 — 8х 2 + 4х 4 + 24х 3 + 48х 2 + 32х + 4х 3 + 24х 2 + 48х + 32 = х 5 + 5х 4 + 10х 3 + 10х 2 + 5х + 32.
Способ 2: (х + 2) 5 = х 5 + 5х 4 + 10х 3 + 10х 2 + 5х + 32
Как вид разница вычислений большая. Сравнивая способы решения, заключаю, применяя для нахождения коэффициентов в разложении треугольник Паскаля, возведение в любую степень решается рациональнее. Поэтому, если мне придется возводить двучлен в степень, я буду применять этот способ.
Посмотрите на многообразие формул сокращенного умножения.Как, когда, сразу ли появилось такое многообразие? Конечно очень много вопросов. Безусловно, человечество «додумалось» до всего не сразу и в одночасье. Для этого потребовались долгие годы и десятилетия. Но как бы мне самой хотелось внести какой-либо вклад в развитие прекрасной математики.
При изучении материала по этой теме, я узнала много нового и интересного. Оказалось, что формулы сокращенного умножения можно использовать для рационального вычисления выражений, при упрощении выражений, при решении, доказательстве тождеств и так далее.
В процессе работы я самостоятельно вывела формулы приведенного умножения, причем некоторые из них из них доказала использование треугольников, познакомилась с использованием треугольника Паскаля.
Я прорешала множество интересных задач, которые не встречались на уроке математики.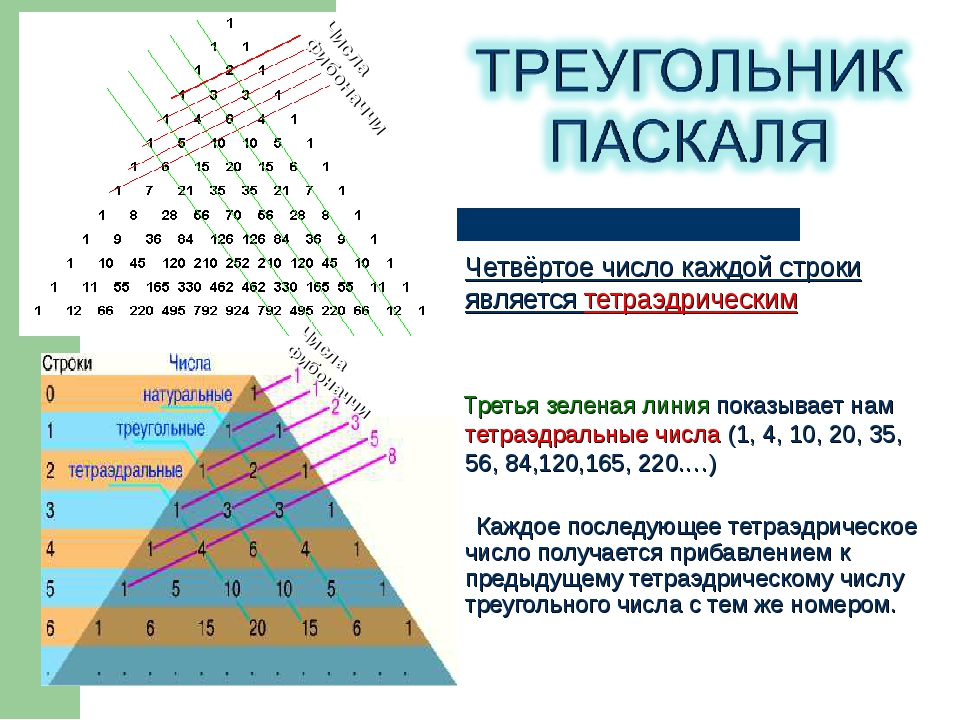 Мне очень нравится предмет математика, я считаю, что знания, которые я приобрела, готовят эту работу, пригодятся мне в дальнейшей учебе и подготовке к выпускным экзаменам. Данная тема актуальна, так как математику нельзя представить без формул сокращенного умножения, потому что они применяются не только в школьном курсе, но и в курсе высшей математики.Созданная мною работа другая ину преподавателем математики на своих уроках. Мне понравилось заниматься исследовательской работой.
Мне очень нравится предмет математика, я считаю, что знания, которые я приобрела, готовят эту работу, пригодятся мне в дальнейшей учебе и подготовке к выпускным экзаменам. Данная тема актуальна, так как математику нельзя представить без формул сокращенного умножения, потому что они применяются не только в школьном курсе, но и в курсе высшей математики.Созданная мною работа другая ину преподавателем математики на своих уроках. Мне понравилось заниматься исследовательской работой.
Список литературы:
1. http://ru.wikipedia.org/wiki/
2. Вайстейн, Треугольник Эрика В. Паскаля (англ.) На сайте Wolfram MathWorld.
3. Абачиев С. К. Радужная фрактальность треугольника Паскаля
4.Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Алгебра: учеб.Для 7 кл. общеобразоват. учреждений под ред. С. А. Теляковского. — 17-е изд. –М. : Просвещение, 2014. — 240 с. : ил. — ISBN 978-5-09-019315-3.
— ISBN 978-5-09-019315-3.
5. В. И. Жохов, Ю. Н. Макарычев, Н. Г. Миндюк. Дидактические материалы: алгебра 8 класс; М .: «Просвещение», 2015.
6.Гусев В. А., Мордкович А. Г. Математика (пособие для поступающих в техникумы): Учеб. Пособие.- М .; Высш. Шк., 1984.-351 с., Ил.
7.Мартин Гарднер. Глава 17. Неисчерпаемое очарование треугольника Паскаля // Математические новеллы.- М .: Мир, 1974. — 456 с. 8. Треугольник Паскаля. В. А. Успенский. — 2 — е изд. — М .: Наука, 1979. — 48с.
9.Мордкович А. Г. Алгебра 7 класс. В 2 часа Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович. — 13-е изд., Испр.- М .: Мнемозина, 2009.- 160 с .: ил. ISBN ISBN 46-01198-9.
10. С. М. Никольский, М. К. Потапов и др. Алгебра 7; М .: «Просвещение», 2008.
11. Фукс Д., Фукс М. Арифметика биномиальных коэффициентов // Квант .- 1970. — № 6. — С. 17-25.
17-25.
12. Энциклопедия для детей. Т 11. Математика / Глав. ред. М. Аксенова; метод. и отв. ред. В. Володин. — М .: Аванта +, 2004. — 688с.
13.portfolio.1september.ru
14.Удивительный треугольник великого француза // Hard’n’Soft № 10 2003
Проектная работа в 9 классе по математике «Треугольник Паскаля»
Проект по математике:
«Треугольник Паскаля»
Подготовила ученица 9 в классе Тараканова Елена
Учитель: Чеснокова Ирина Николаевна
Цель и задачи моей работы:
1.Ознакомиться с созданием треугольника Паскаля.
2. Научиться строить треугольник
3. Выявить свойства чисел, входящих в состав треугольника Паскаля.
4. Определить применение треугольника в решении задач.
5. Формулировать вывод и итоги исследования
История создания
Треугольник Паскаля названа в честь Блеза Паскаля, но оказывается, что его строение было известно задолго до описания его Паскалем. Паскаль описал эту систему расположения чисел в своей работе 1653г и поэтому он был назван треугольником Паскаля.
Паскаль описал эту систему расположения чисел в своей работе 1653г и поэтому он был назван треугольником Паскаля.
Треугольник Паскаля — бесконечная таблица биномиальных коэффициентов, имеющая треугольную форму
Определение:
Свойства:
Если очертить треугольник Паскаля, то получится равнобедренный треугольник. В этом треугольнике на вершине и по бокам стоят единицы.
Каждое число равно сумме двух расположенных над ним чисел.
Например:
Свойство:
Чтобы найти количество чисел, стоящих на любом диагонали от начала до интересующего места, расположенное снизу или слева от последнего слагаемого.
Свойства :
Строки треугольника симметричны относительно вертикальной оси.
Свойства :
Сумма чисел в строках треугольника Паскаля -,
где n- номер строки.
1 = 2 0
1 + 1 = 2 = 2 1
1 + 2 + 1 = 4 = 2 2
1 + 3 + 3 + 1 = 8 = 2 3
1 + 4 + 6 + 4 + 1 = 16 = 2 4
1 + 5 + 10 + 10 + 5 + 1 = 32 = 2 5
1 + 6 + 15 + 20 + 15 + 6 + 1 = 64 = 2 6
Свойства :
Первые диагональ треугольника паскаля- это натуральные числа, идущие по порядку.
Свойства:
В каждой строчке треугольника Паскаля сумма чисел на нечётных местах равна сумме чисел на чётных местах.
Биномиальные коэффициенты
Биномиальные коэффициенты есть коэффициенты разложения многочлена по степеням x и y
Применение свойств треугольника в решении задач .
Задача 1 . В магазине «Филателия» продается 8 различных наборов марок, посвященных спортивной тематике. Сколькими способами можно выбрать из них 3 набора?
Задача 2 . Из двух врачей поликлиники необходимо отправить на курсы по повышению квалификации. Сколькими способами это можно сделать?
Из двух врачей поликлиники необходимо отправить на курсы по повышению квалификации. Сколькими способами это можно сделать?
Закончив свой проект, я могу сказать, что всё из того Заключение, что было задумано, получилось.
Я узнала много интересной информации.
Планирую показать этот проект одноклассникам, когда мы будем проходить тему «Элементы комбинаторики».
С помощью Треугольника Паскаля можно легко раскрывать скобки при, где n- натуральное число, и a и b — любые числа.
Список используемой литературы
- Фукс Д., Фукс М. Арифметика биномиальных коэффициентов // Квант . -970. — № 6. — С. 17-25.
- Weisstein, Eric W. Треугольник Паскаля на сайте Wolfram MathWorld .
Категория:
3. Удивительный треугольникого француза // Hard’n’Soft № 10 2003
4. http: //ru.wikipedia.org / wiki /
5. Мордкович А. Г., Семёнов П.В. Алгебра и начала математического анализа.
Г., Семёнов П.В. Алгебра и начала математического анализа.
Исследовательская работа по математике на тему Треугольник Паскаля (7 класс)
Отдел образования, спорта и туризма Борисовского райисполкома
Государственное учреждение образования
«Средняя школа № 16 г. Борисова »
Треугольник Паскаля
Автор:
учащаяся 7 «А» класса
Абоян Елизавета Александровна,
домашний адрес: г.Борисов,
ул Смолевичская, д. 8, 76-51-80
Руководитель:
Ищук Ольга Эдуардовна, учитель математики
Борисов, 2016 г.
Оглавление
Введение 3
Теоретическая часть работы 5
Знакомство с треугольником Паскаля 5
Блез Паскаль — французский математик 5
Треугольник Паскаля как разновидность треугольника 6
Свойства треугольника Паскаля и их применение в решение задач 8
Треугольник Паскаля и теория вероятности. 9
9
Практическая часть работы 11
Заключение 13
Список использованных источников и литературы 14
В этом учебном году мы начали изучать новый предмет «геометрия».
Одна из глав курса геометрии называется «Треугольники». Меня очень заинтересовала тема тема. Я всегда хотела узнать много нового о треугольниках, об их происхождении и значении в нашей жизни. Ведь мир треугольников очень загадочен и интересен.
Треугольник — первая геометрическая фигура, встречающаяся в древних рисунках. Изучая литература, я узнала, что в Египте он символизировал триаду духовной воли, любви, интуиции и высшего разума человека, то есть его личность или душу.
Ацтеки использовали изображение треугольника с вершиной наверху, соединенного с перевернутым треугольником, в как символ временного цикла. Треугольник в сочетании с крестом образует алхимический знак Серы.
Равносторонний треугольник, символизирующий, по
древнееврейской традиции, совершенство, у христиан означает Троицу
— Отца, Сына и Святого Духа.
существует множество видов треугольников, но больше всего меня заинтересовал треугольник Паскаля.
Проблема исследования:
Проблема моего исследования состоит в том, что я попыталась выявить и показать то, насколько широко широко треугольники используются в практической жизни.
Практическая значимость исследования:
Данная исследовательская работа может быть использовать как дополнительный материал к урокам геометрии, для внеклассной работы по математике.
Цель исследования:
— ознакомиться с треугольником Паскаля и его применение как разновидность треугольников;
Гипотеза:
Если числа треугольника Паскаля обладают особыми способностью, то его можно считать уникальным для решения различных задач
Задачи:
— определить применение свойств чисел треугольника Паскаля;
— изучить литературу по теме «Треугольник Паскаля »;
— выявить свойства чисел, входящего в состав треугольника Паскаля;
— сформулировать вывод и итоги исследования;
Объект исследования: треугольник как геометрическая фигура
Предмет исследования: свойства треугольника Паскаля
Методы исследования:
— аналитико-статистическая работа со справочной, научно-познавательной и специальной литературой;
— поиск информации в интернет — ресурсах.
Направления работы:
— выбор проблемы, источников литературы, составление плана;
— работа с литературой и другими источниками;
— обработка полученных данных;
— анализ результатов, вывод вывода;
— мультимедийная подготовка.
Основные этапы исследования: подготовительный; деятельностный;
Ход исследования: рефлексивный; аналитический; презентационный.
Знакомство с треугольником Паскаля
Моё первое знакомство с треугольником Паскаля произошло во время изучения темы «Возведение двучлена в степень» на уроке алгебры. Мне уже известны формулы квадрата суммы и квадрата разности, куба суммы и куба разности. Я заметила, что получить формулы для возведения двучлена в четвёртую, пятую и т.д. степень возможно, учитывая некоторую закономерность в коэффициентах и степенях каждого слагаемого.
Коэффициенты всех строк можно расположить в виде треугольника:
Таким образом я познакомилась с треугольником
Паскаля и решила продолжить изучение арифметического треугольника.
Блез Паскаль — французский математик
Блез Паскаль (19 июня 1623, Клермон-Ферран, — 19 августа 1662, Париж) — французский математик, физик, литератор и философ.
Паскаль был первоклассным математиком. Он помог создать два крупных новых направления математических исследований. В возрасте шестнадцати лет написал замечательный трактат о предмете проективной геометрии и в 1654 году переписывался с Пьером де Ферма по теории вероятностей, что оказывает оказало принципиальное влияние на развитие современной экономики.
Треугольник Паскаля как разновидность треугольника
Изучая разновидности треугольников, я пыталась,
что треугольник Паскаля — арифметический треугольник, образованный
биномиальными коэффициентами.Назван в честь Блеза Паскаля. В
действительности, треугольник Паскаля был известен задолго до 1653
года — дата выхода «Трактата об арифметическом треугольнике». Так,
этот треугольник воспроизведен на титульном листе учебника
арифметики, написанном в начале XVI Петром Апианом, астрономом из
Ингольтштадского университета. Изображен треугольник и на
иллюстрации в книге одного китайского математика, выпущенной в 1303
году. Омар Хайям, бывший не только философом и поэтом, но и
математиком, знал о существовании треугольника уже около 1100 года,
в свою очередь, заимствовав его из более ранних китайских или
индийских источников.
Изображен треугольник и на
иллюстрации в книге одного китайского математика, выпущенной в 1303
году. Омар Хайям, бывший не только философом и поэтом, но и
математиком, знал о существовании треугольника уже около 1100 года,
в свою очередь, заимствовав его из более ранних китайских или
индийских источников.
Ещё я узнала из книги «Математические новеллы» (М., Мир, 1974) Мартина Гарднера, что «Треугольник Паскаля так прост, что выписать его даже десятилетний ребенок. В тоже время он таит в себе неисчерпаемые сокровища и связывает воедино различные аспекты математики, не имеющие на первый взгляд между собой ничего общего. Столь необычные свойства позволяют считать треугольник Паскаля одной из наиболее изящных схем во всей математике ».
Я рассмотрела схему построения треугольника,
предложенную Гуго Штейнгаузом в его классическом «Математическом
калейдоскопе »: предположим, что вы входите в город как показано на
схеме можно синей стрелкой, и двигаться только вперед, точнее, все
время выбирая, вперед налево, или вперед направо. Узлы, которые в
можно попасть только единственным образом, зелеными зелеными
смайликами, точка, в которую можно попасть способами двумя,
эффектом красным смайликом, а соответственно, розовыми. Это
один из вариантов построения треугольника.
Узлы, которые в
можно попасть только единственным образом, зелеными зелеными
смайликами, точка, в которую можно попасть способами двумя,
эффектом красным смайликом, а соответственно, розовыми. Это
один из вариантов построения треугольника.
(Рисунок 1)
Изучая специальную литературу, я узнала, что еще проще объясняют устройство треугольника Паскаля слова: каждое число равно сумме двух установленных над ним чисел.
Все элементарно, но сколько в этом таится чудес.
Если очертить треугольник Паскаля, то получится равнобедренный
треугольник. В этом треугольнике на вершине и по бокам стоят
единицы. Каждое число равно сумме двух установленных над ним чисел.
Треугольник можно неограниченно. Он обладает симметрией
относительно вертикальной оси, проходящей через его вершину. Вдоль
диагоналей (насколько у треугольника могут быть диагонали, но не
будем придираться, такая терминология встречается в публикациях),
параллельных сторонам треугольника (на рисунке отмечены зелеными
линиями) выстроены треугольные числа и их обобщения на случай
пространств всех размерностей. Треугольные числа в самом обычном и
привычный нам виде показывают.
расположить в виде треугольника — как классический пример начальная
расстановка шаров в бильярде. К одной монетке можно прислонить еще
две — итого три — к двум можно приладить еще три — итого шесть.
Треугольные числа в самом обычном и
привычный нам виде показывают.
расположить в виде треугольника — как классический пример начальная
расстановка шаров в бильярде. К одной монетке можно прислонить еще
две — итого три — к двум можно приладить еще три — итого шесть.
Получили треугольные числа на рисунке: 3; 6; 10; 15.
Продолжая наращивать ряды с сохранением формы треугольника получим ряд 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66…, что и показывает вторая зеленая линия. Этот замечательный ряд, каждый член которого равен сумме натурального ряда чисел (55 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10), содержит также множество знакомцев, хорошо известных любителям математики: 6 и 28 — совершенные числа, 36 — квадратное число, 8 и 21 — числа Фибоначчи.
Следующая зеленая линия покажет нам тетраэдральные числа — один шар мы можем положить на три — итого четыре, под три подложим шесть — итого десять, и так далее.
Чтобы найти сумму чисел, стоящих на любой
диагонали от начала до интересующего нас места, достаточно
взглянуть на число, расположенное снизу и слева от последнего
слагаемого, (слева для правого диагонали, для левого диагонали будет
справа, а вообще — ближе к середине треугольника).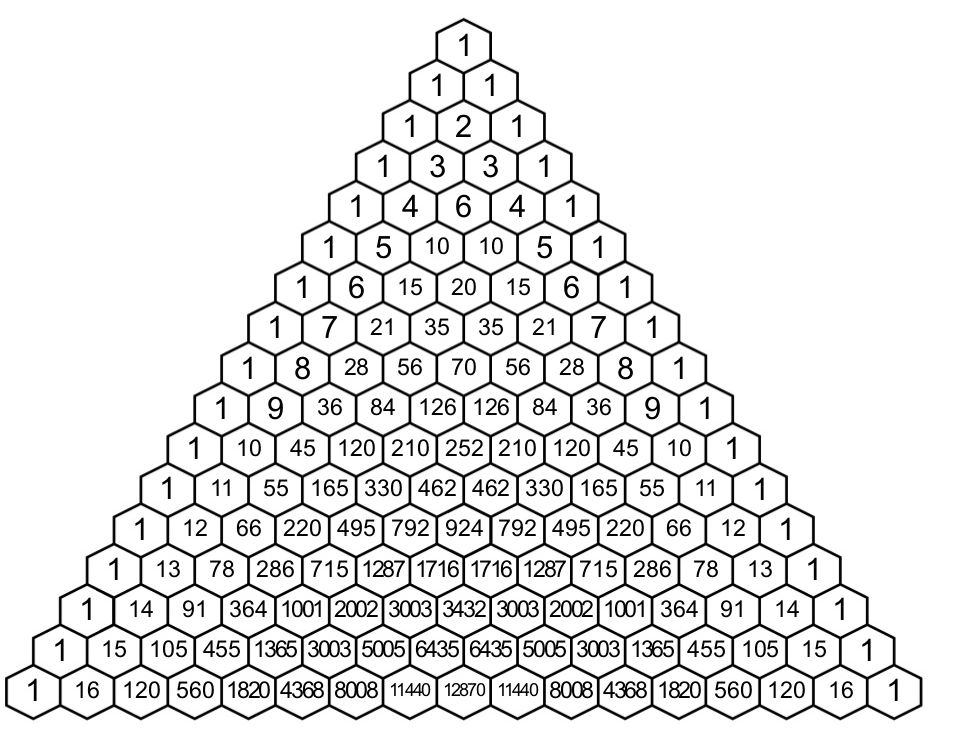 Пусть, например,
мы хотим вычислить сумму натурального ряда от 1 до 9.
«Спустившись» по диагонали до числа 9, мы увидим слева снизу от
Ему число 45. Оно то и дает искомую сумму.Чему равна первая сумма
восьми треугольных чисел? Отыскиваем восьмое число на второй
диагонали и сдвигаемся вниз и влево. Ответ: 120.
Пусть, например,
мы хотим вычислить сумму натурального ряда от 1 до 9.
«Спустившись» по диагонали до числа 9, мы увидим слева снизу от
Ему число 45. Оно то и дает искомую сумму.Чему равна первая сумма
восьми треугольных чисел? Отыскиваем восьмое число на второй
диагонали и сдвигаемся вниз и влево. Ответ: 120.
(Рисунок 2)
Треугольник Паскаля имеет применение в теории вероятностей и обладает замечательными свойствами.
Свойства треугольника Паскаля и их применение в решении задач
Паскаль подробно исследовал свойства и применения своего «треугольника». Приведу для примера лишь 3 свойства «треугольника», найденные самим Паскалем; при этом буду исходить из того расположения «треугольника» на плоскости, какое было указанно Паскалем, и говорить о горизонтальных и вертикальных рядх.
Свойство 1: Каждое число А в таблице равно сумме
чисел предшествующего горизонтального ряда, начиная с самого левого
вплоть до стоящего непосредственно над числом А (в клетки,
содержащие слагаемые, дающие в сумме А, заштрихованы). (Рисунок 4)
(Рисунок 4)
(Рисунок 4) (Рисунок 5) (Рисунок 6)
Свойство 2: Каждое число А в таблице равно сумме чисел предшествующего вертикального ряда, начиная с самого верхнего вплоть до стоящего непосредственно левее числа А.(Рисунок 5)
Свойство 3: Каждое число в таблице, было уменьшенным на единицу, равно сумме всех чисел, заполняющих прямоугольник, ограниченный теми же вертикальными и горизонтальными рядами, на закрытии которых стоит число А (сами эти ряды в которых стоит число А) рассматриваемый прямоугольник не включаются). (Рисунок 6)
Треугольник Паскаля и теория вероятности.
Блез Паскаль и другой великий француз, Пьер
Ферма, стали основателями теории вероятностей, когда Паскаль и
Ферма независимо друг от друга дали правильное объяснение так
называемого парадокса раздела ставок.Два игрока играют в
«безобидную» игру (т.е. шансы победить у обоих одинаковы),
договорившись, тот, кто первым выигрывает шесть партий, получает
весь приз. Предположим, что игра остановилась до того, как один из
нихрал приз (например, игрок выиграл пять партий, а
второй — три). Как справедливо разделить приз? Так, согласно одному
решение следовало разделить приз в отношении 5: 3, т.е.
пропорционально выигранным партиям, согласно другому — в отношении
2: 1 (здесь рассуждения велись, по всей видимости, следующим
образом: поскольку первый игрок выиграл на две партии больше, что
составляет третью часть от необходимых для победы шести партий, то
он должен получить одну третье от приза, оставшуюся часть нужно
разделить пополам).
Предположим, что игра остановилась до того, как один из
нихрал приз (например, игрок выиграл пять партий, а
второй — три). Как справедливо разделить приз? Так, согласно одному
решение следовало разделить приз в отношении 5: 3, т.е.
пропорционально выигранным партиям, согласно другому — в отношении
2: 1 (здесь рассуждения велись, по всей видимости, следующим
образом: поскольку первый игрок выиграл на две партии больше, что
составляет третью часть от необходимых для победы шести партий, то
он должен получить одну третье от приза, оставшуюся часть нужно
разделить пополам).
А между тем делить надо в отношении 7: 1. И
Паскаль, и Ферма рассматривали парадокс раздела ставки как задача о
вероятности, установив, что справедливым является раздел,
пропорциональный шанс игрока первого выиграть приз. Предположим,
первому игроку осталось выиграть только одну партию, а второму для
победы необходимо выиграть еще три партии.
игру и играют все три партии.
лишними для определения победителя. Для такого продолжения все
2 3 = 8 исходов будут равновероятными. Так как
второй игрок получает приз только при одном исходе (если он выиграл
все три партии), а в остальных случаях побеждает первый игрок,
справедливым отношением является 7: 1.
Для такого продолжения все
2 3 = 8 исходов будут равновероятными. Так как
второй игрок получает приз только при одном исходе (если он выиграл
все три партии), а в остальных случаях побеждает первый игрок,
справедливым отношением является 7: 1.
В науке и практике часто встречаются задачи, решая которые составляют различные комбинации из конечного числа элементов и подсчитывать число комбинаций. Такие задачи получили название комбинаторных задач.
Рассмотрим основные формулы комбинаторики:
Размещение
Это любое упорядоченное подмножество m из элементов числа n.
Перестановки (). Если k = n, то эти размещения называются перестановками.
Сочетания () — это любое подмножество из k — элементов, которые принадлежат множеству, состоящему из n — различных элементов.
.
В треугольнике Паскаля число, показывающее,
сколькими способами можно выбрать k элементов из массива,
содержитего n различных элементов, стоит на пересечении k-ой
диагонали и н-ой строки. Чтобы вычислить сочетание
, найду диагональ седьмую сверху и отсчитываю три числа по
горизонтали. Получу число 35.
Чтобы вычислить сочетание
, найду диагональ седьмую сверху и отсчитываю три числа по
горизонтали. Получу число 35.
Можно использовать треугольник Паскаля и для вычислений размещений. .Если нам нужно посчитать , то зная что , а 3! = 6, получим значение данного размещения 210.
Я пришла к выводу, что рассмотренные свойства треугольника Паскаля подтверждают слова Мартина Гарднера о том, что треугольник Паскаля одна из наиболее изящных схем во всей математике.
Актуальность обусловлена ежегодным усложнением заданий ЦТ, что требует углубленных знаний не только в алгебре, но и в геометрии.
В своей практической работе я подобрала ряд задач по теме «Треугольник Паскаля»
Задача 1.В магазине «Филателия» продается 8 различных наборов марок, посвященных спортивной тематике. Сколькими способами можно выбрать из них 3 набора?
Решение:
В
треугольнике Паскаля число, показывающее, сколькими способами можно
выбрать k элементов из множества, содержащего n различных
элементов, стоит на пересечении k-ой диагонали и n-ой строки.
Найду диагональ восьмую сверху и отсчитываю три числа по горизонтали.Получу число 56. (Рисунок 8)
Задача 2.Из шести врачей поликлиники двух необходимо отправить на курсы повышения квалификации. Сколькими способами это можно сделать?
Решение:
Найдуональ шестую сверху и диагональ два числа по горизонтали. Получу число 15.
(Р (Рисунок 9)
Задача3. В пачке находятся одинаковые по размеру 7 тетрадей в линейку и 5 в клетку. Из пачки наугад берут 3 тетради.Какова вероятность того, что все три тетради надежно в клетку?
Решение. Сначала найдём общее число агентов исходов, т.е. сколькими способами мы можем выбрать 3 тетради из 12 тетрадей
А сколькими способами мы можем выбрать 3 тетради в клетку из возможен 5 тетрадей?
Вероятность
Р наступления случайного события А называется отношение м / п, где н
— число всех возможных исходов эксперимента, а m — число всех
благоприятных исходов: Р (А) = m / n.
По формуле нахождения вероятности получим
(Рисунок 10)
Задача4. На плоскости даны 10 прямых, причём среди них нет параллельных и через каждую точку их пересечения проходят ровно две прямые. Сколько у них точек пересечения?
Решение: ответ находится на пересечении -45 точек!
ча 5. В сумке 10 мячей, пронумерованных от 1 до 10. Наугад вынимают 2 мяча. Какова вероятность того, что это будут мячи с номерами 7 и 3?
Вынуть 2ча из 10 можно 45 способов.Вероятность нашего события 2 из 45. (Рисунок 11)
В ходе проведения практического исследования я пришла к следующему выводам: при решении комбинаторных задач и задач по теории вероятностей можно пользоваться не только формулами комбинаторики, но и использовать свойства треугольника Паскаля
Работа по выбранной теме осуществлялась в полном
в соответствии с планом исследования, а именно: объект и предмет
исследования, поставлены цели и задачи, а также решенные задачи
ожидаемые результаты. Были указаны указанные методы
исследования, определена проблема.
Были указаны указанные методы
исследования, определена проблема.
В данной работе была дана общая характеристика треугольника как геометрической фигуры, был детально рассмотрен треугольник Паскаля, его свойства.
Я пришла к выводу, что одной из наиболее известных и изящных численных схем во всей математике треугольник Паскаля. Треугольник Паскаля — понятие значения шире, чем мне представлялось. Он обладает не только удивительным свойства, но и применялся в городской среде средних веков для построения схем пропорциональности и для построения прямых углов землемерами и архитекторами.Используя треугольник Паскаля, можно решить задачу из теории вероятности и комбинаторики. С комбинаторными задачами я встречалась на уроках математики в 6 класс и при решении олимпиадных задач
Практическая значимость данной работы
заключается в следующем: я, изучив много литературы по данному
вопросу, получила дополнительные знания в области математики,
укрепила свой интерес к этой науке.
Я узнала, что треугольник Паскаля применяется:
В курсе алгебры
При решении комбинаторных задач
Для решения различных задач в области физики
С появлением вычислительных машин построение треугольника Паскаля стало излюбленной задачкой для начинающих при изучении основении программирования.
Работа по данной теме оказалась интересной и полезной.
1. Абачиев С. К., Радужная фрактальность треугольника Паскаля / С. К. Абачиев, — Минск, 1999.-168с.
2. Галкин Е.В. Нестандартные задачи по математике. Задачи логического характера. Книга для учащихся 5-11кл.Москва, «Просвещение», 1996г. — 194 с.
3. Мартин Гарднер. Глава 17. Неисчерпаемое очарование треугольника Паскаля Математические новеллы.- Минск: Мир, 1974. — 456 с.
4. Треугольник Паскаля. В. А. Успенский. — 2 — е
изд. — Москва: Наука, 1979. — 48с.
— 48с.
5. Фукс Д., Фукс М., Арифметика биномиальных коэффициентов / Квант. — 1970. — № 6. — С.17-25.
6. Энциклопедия для детей. Т 11. Математика / Глав. ред. М. Аксенова; метод. и отв. ред. В. Володин. — М .: Аванта +, 2004. — 688с.
7. ru.wikipedia.org/wiki/
8. давайкнам.ru / text / volshebnij-treugolenik.
Треугольник Паскаля
Треугольник Паскаля
Родионова А.В. 1Федоров Г.Д. 11МБОУ Лицей №40 при УлГУ
Гуськова А.Г. 11МБОУ Лицей №40 при УлГУ
Текст работы размещён без изображений и формул.
Полная версия работы доступна во «Файлы работы» в формате PDF
Введение
Замечательная геометрическая фигура и самая популярная в школьной программе геометрии — это треугольник.Но треугольники «поселились» не только на страницах учебника геометрии. В работе мы рассмотрим не обычный треугольник, а треугольник, состоящий из чисел — треугольник Паскаля, его свойства, связь с числами Фибоначчи и биномиальными коэффициентами.
В работе мы рассмотрим не обычный треугольник, а треугольник, состоящий из чисел — треугольник Паскаля, его свойства, связь с числами Фибоначчи и биномиальными коэффициентами.
Цель работы:
Познакомиться с математическим объектом, как треугольник Паскаля
Задачи:
Пополнить запас научных знаний.
Продолжить знакомство с историческими этапами возникновения и развития математической науки, судьбами открытий, именами людей, творивших науку. В первую очередь с биографией ученого Блеза Паскаля.
Самостоятельно попытаться составить данный треугольник.
Рассмотреть свойства треугольника Паскаля.
Определить значимость открытия треугольника Паскаля.
Сформулировать вывод и итоги исследования.
Гипотеза:
Треугольник Паскаля обладает рядом замечательных свойств, поэтому носит имя одного из выдающихся людей.
Актуальность:
Актуальность данной работы не вызывает сомнения, поскольку обусловлена, с одной стороны большим интересом к теме «Треугольник Паскаля» в современной науке, с другой стороны, её недостаточной разработностью.
Навыки решения задач с использованием треугольника Паскаля в рамках изучения школьного курса математики, при решении олимпиадных задач.
Предмет исследования :
Треугольник Паскаля
Этапы исследования:
Сбор начальных сведений о треугольнике в энциклопедической и учебно-научной литературе.
Построение треугольник Паскаля.
Выявление «волшебных» свойств чисел треугольника.
Изучение возможностей применения треугольника Паскаля.
Формулирование итогов и выводов.
Методы исследования:
. Работа со справочной, научно-познавательной и специальной литературой;
Работа со справочной, научно-познавательной и специальной литературой;
поиск информации в интернет — ресурсах.
1.Биография Блеза Паскаля
Прогресс человечества во многом связан с открытием, сделанными гениями.
Одним из них является Блез Паскаль — французский математик, физик, философ и мастер прозы.
Родился Блез Паскаль в 1623 г. 19 июня в Клермон — Ферране, в семье председателя суда города Этьена Паскаля.
Род Паскалей отличали незаурядные способности, а Блеза одаренность посетила с раннего детства. Этьен Паскаль уделил много внимания развитию умственных способностей сына и уже в 16 лет Блез сочинил труд под названием «Опыт о конических сечениях» в котором содержалась теорема известная, как теорема Паскаля.
Вклад Паскаля в науках очень велик.Вот лишь некоторые из них: заложил основы современной теории вероятностей и математического анализа, сформулировал основной закон гидростатики, создал множество трудов по философии, изобрел шприц, создал гидравлический пресс и вычислительное устройство «Паскалин» (прототип калькулятора), изобрел тачку, придумал омнибус — конные конные экипажи с фиксированными маршрутами, ставшие первым видом регулярного общественного транспорта и пр.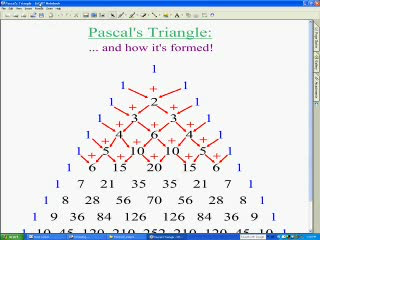
Умер Блез Паскаль 19 августа 1662 года.
Вследствие его больших вкладов в изучение давления в физике, в честь Паска назвали единицу измерения давления (Па). Так же в честь Паскаля назвали язык программирования Pascal.
2.Определение и основные свойства треугольника Паскаля.
2.1 История треугольника.
Треугольник Паскаля был известен задолго до 1653 года — дата выхода «Трактата об арифметическом треугольнике» Блокаскаля
Похожий треугольник представлен в качестве иллюстрации в книге китайского математика Яна Хуэя, изданной в 1303 году.
О его свойствах было известно также и замечательному персидскому поэту и философу Омару Хайяму еще в начале 12 века. Причем считается, что он познакомился с ним из трактатов арабских и индийских ученых, написанных ранее.
2.2 Построение треугольника Паскаля.
«Треугольник Паскаля так прост, что выписать его даже десятилетний ребенок.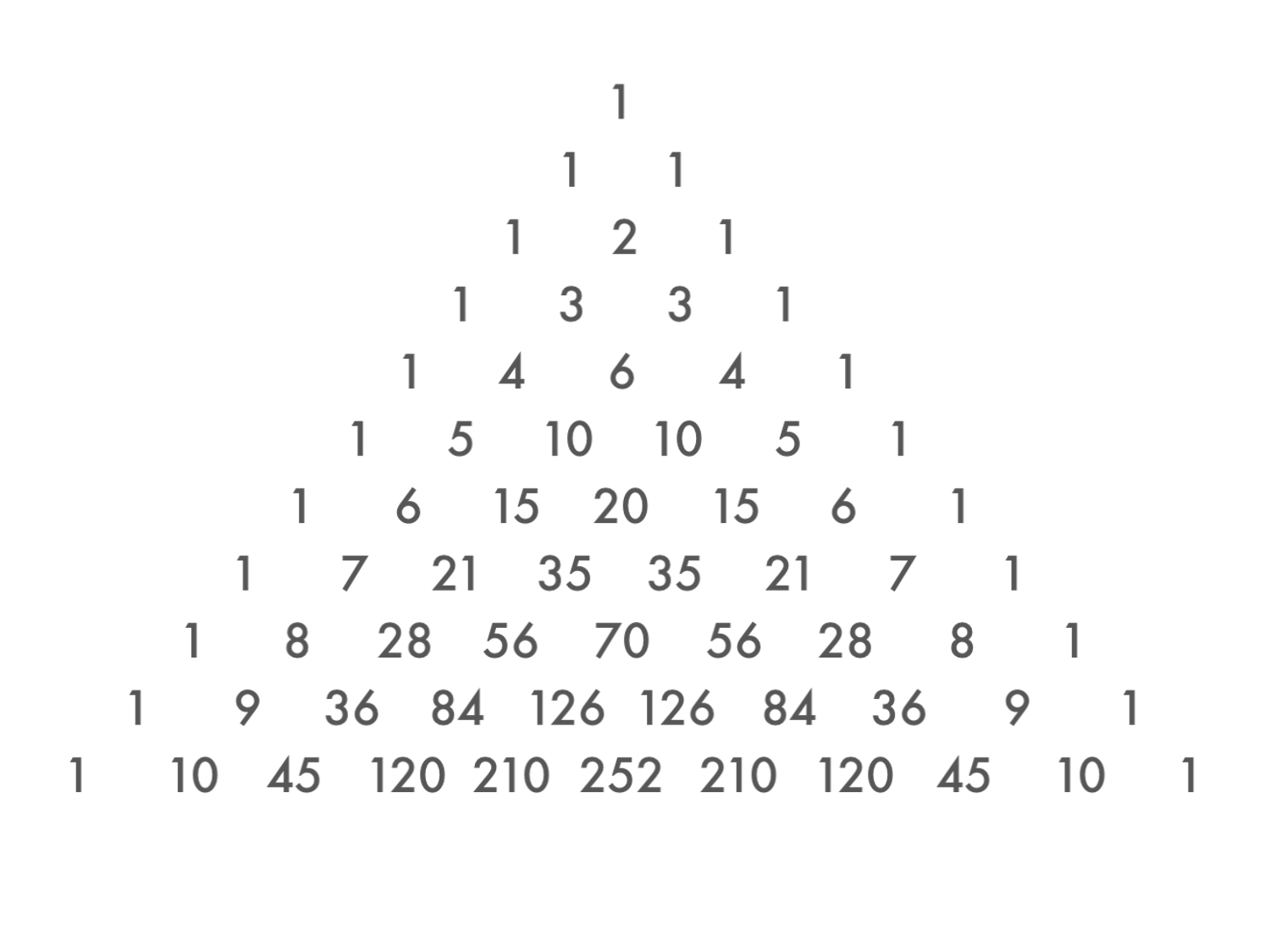 В то же время он таит в себе неисчерпаемые сокровища и связывает воедино различные аспекты математики, не имеющие отношения к первому взгляду между собой ничего общего.Столь необычные позволяют считать треугольник Паскаля одной из наиболее изящных во всей математике »(Мартин Гарднер свойства).
В то же время он таит в себе неисчерпаемые сокровища и связывает воедино различные аспекты математики, не имеющие отношения к первому взгляду между собой ничего общего.Столь необычные позволяют считать треугольник Паскаля одной из наиболее изящных во всей математике »(Мартин Гарднер свойства).
Треугольником Паскаля называется бесконечная треугольная таблица, в которой (рис.1):
на вершине и по боковым сторонам стоят единицы,
-каждое из остальных чисел равно сумме двух чисел, стоящих над ним в предшествующей строке.
Если очертить треугольник Паскаля, то получится равнобедренный треугольник.Продолжать треугольник можно бесконечно.
2.3 Основные свойства треугольника Паскаля.
Для любой строки под номером n (n = 0, 1, 2…) верно:
Первое и последнее число — 1; второе и предпоследнее — n.
Строки треугольника симметричны относительно вертикальной оси треугольника.
Сумма чисел n-й строки треугольника Паскаля равна (рис.2)
Первая диагональ — это натуральные числа, идущие по порядку (рис.3).
Вторая диагональ — это «треугольные» числа (Рис.3). Треугольник в самом обычном и привычном нам виде показывает, сколько квадратов можно расположить в виде треугольника — как классический пример начальная расстановка шаров в бильярде.
Третья диагональ — это «пирамидальные» числа (один шар мы можем положить на три — итого четыре, под три подложим шесть — итого десять, и так далее) (рис.4).
Четвертая диагональ — это «фигурные числа» в четырехмерном измерении. Это можно представить только в виртуальном мире. Один шар касается четырех, а те, в свою очередь, десяти…
Каждое число треугольника Паскаля равно сумме чисел предыдущей диагонали, стоящей над этим числом.
В каждой строке суммы чисел на нечётных местах равна сумме чисел на чётных местах.
Если номер строки — простое число, то все числа этой строки, кроме 1, делятся на это число.
Каждое число, уменьшенное на 1, равно сумме всех чисел, заполняющих параллелограмм, ограниченных правыми и левыми диагоналями, на пересечение которых стоит это число.
Бином Ньютона — возведение выражения (a + b) в степень. При возведении в степени получаются коэффициенты, равные числам в треугольнике Паскаля.
Сумма чисел n-й восходящей диагонали, проведенной через треугольника с номером n — 1, есть n-е число Фибоначчи (число равно сумме двух предыдущих чисел) (рис.5).
Если нечётное число в треугольнике Паскаля заменить на точки контрастного цвета, а чётные — белого цвета, то треугольник Паскаля разобьётся на более мелкие треугольники, образующие изящный узор. Удивительное свойство треугольника Паскаля.
Удивительное свойство треугольника Паскаля.
3. Применение треугольника Паскаля.
Где же применяемый треугольник Паскаля?
При решении комбинаторных задач.
Треугольник Паскаля используется для решения различных задач в области физики:
принцип минимума потенциальной энергии;
материальные точки и центр тяжести;
центр тяжести системы двух материальных точек;
центр тяжести стержня с большой нагрузки;
невозможность вечного двигателя.
С появлением вычислительных машин построение треугольника Паскаля стало излюбленной задачкой для начинающих при изучении основ программирования.
Вот далеко не полный перечень свойств чисел треугольника Паскаля и его пример применений.
4. Применение свойств треугольника Паскаля в решении математических задач.
Свойства треугольника Паскаля, наверное, были бы не столь значимы, если бы на их основе нельзя было решать математические задачи. Такие задачи можно встреть в ОГЭ, ЕГЭ и в олимпиадных задачах старшего школьного уровня. Треугольник Паскаля используется при решении задач, для решения различных задач в области физики. С построением вычислительных машин построение треугольника Паскаля стало излюбленной задачкой для начинающих при изучении программирования.
Такие задачи можно встреть в ОГЭ, ЕГЭ и в олимпиадных задачах старшего школьного уровня. Треугольник Паскаля используется при решении задач, для решения различных задач в области физики. С построением вычислительных машин построение треугольника Паскаля стало излюбленной задачкой для начинающих при изучении программирования.
Задача 1.
Найдите первую сумму 8 треугольных чисел.
Решение:
Найдем сумму первых восьми чисел 3 диагонали треугольника Паскаля.(рис.6) Получится 120.
Ответ: 120
Задача 2.
Вася построил из шариков пирамиду. Известно, что на её строительство ушло 286 шариков, сколько «этажей» в Васиной пирамиде?
Решение:
В данной задаче нам известно, что на строительство пирамиды ушло 286 шариков. Найдем решение с помощью треугольника Паскаля, в количестве прямоугольников, пересеченных линией, будет наш ответ.(рис. 7)
Ответ: 11 «этажей».
Задача 3.
В магазине «Теплица» продается 6 различных сортов помидор. Сколькими способами можно выбрать из них 3 помидор?
Решение:
В данной задаче нам даны различных сортов, поэтому повторений не будет и порядок выбора сортов нам неважен, нам важно количество, а именно 3. Найдем решение с помощью нашего треугольника Паскаля, в котором пересечение 3-й диагонали и 6 строки будет наш ответ ( рис.8).
Ответ: 20.
Задача 4.
На плоскости даны 11 точек, из которых никакие не лежат на одной прямой и никакие четыре лежат на одной окружности. Сколько существует окружностей, каждая из которых проходит через три данные точки
Решение:
Ответ находится на пересечении 11 числа и 3 диагонали: Это число — 165 (рис.9).
Ответ: 165 окружностей.
З адача 5.
Танк может двигаться по квадратам, видимым на карте размером 4 на 4 только вправо или вниз. Он стоит в точке А. Из штаба пришло задание прибыть в точку В. Сколько маршрутов передвижения может использовать экипаж?
Рис.10 (а)
Решение:
Рис.10 (б)
В квадраты a2, a3, a4, а1, b1, c1, d1 танк попадёт 1 способом, в квадрат b2 может добраться 2 способами (рис.10 (а)). В квадрат с2 и b3 — 3 способа, d2 и b4 — 4 способа, в c3 — 6 способов, d3, c4 — 10 способов и в квадрат d4 (точка В) — 20 способов. (рис.10 (б))
Ответ: 20 способов.
Решив задачу, мы замечаем, полученное на «карте» числа образуют треугольник Паскаля. Таким образом, можно сделать вывод, что число в треугольнике Паскаля показывает количество способов передвижения от вершины треугольника данного числа.
Задача 6.
Из пункта А по сети дорог идет группа из человек. На каждом перекрестке, начиная с А, пришедшие люди делятся пополам — половина идет по направлению l, половина — по направлению m (рис.11). Сколько человек придет в районы В, С, Д,…, Я соответственно?
Решение:
Количество людей, пришедших в искомые точки соответствует числам n-ой строки. В данном случае, n = 7, следовательно, искомое количество людей на каждом перекрестке соответствует 7 строке треугольника Паскаля (рис.12).
Ответ: 1, 7, 21, 35, 35, 21, 7, 1.
Задача 7.
Возьмите в степень: (u — v) 5
Решение:
У нас есть (a + b) n , где a = u, b = -v, и n = 5. Мы используем 5-й ряд треугольника Паскаля:
1 5 10 10 5 1
Тогда у нас есть:
(u — v) 5 = (u + (-v)) 5 = 1 (u) 5 + 5 (u) 4 (-v) 1 + 10 (u) 3 (-v) 2 + 10 (u) 2 (-v) 3 + 5 (u) (-v) 4 +1 (-v) 5 = u 5 — 5u 4 v + 10u 3 v 2 — 10u 2 v 3 + 5uv 4 — v 5 .
Заключение.
В ходе исследования мы убедились, что треугольник Паскаля, несмотря на кажущуюся простоту, действительно обладает замечательными свойствами. Этот треугольник широко используется в математике для решения различных видов задач. Треугольник Паскаля имеет применение не только в математике, но и в физике, информатике.
Изучение темы «Треугольник Паскаля» оказалось очень интересной и необычной.Работа над проектом показала, что математика — это не только точная, но и красивая наука.
Список литературы.
Гиндикин, С.Г. Рассказы о физиках и математиках С.Г.Гиндикин. — М .: Терра, 2013. — 480с.
Энциклопедия для детей Аванта +: В 57 т. Т. 11. Математика / под ред. М. Аксёновой, В. Володина, М. Самсоновф — М .: Аванта +, 2003. — 688 с.
Корбалан, Ф. Мир математики: В 40 т. Т.1. Золотое сечение, математический язык красоты Пер.с исп. — М .: ДеАгостини, 2014. — 164 с .: ил.
Гарднер, М. Математические новеллы. (Математические игры) / Пер. с англ. Ю.А.Данилова; под ред. Я.А. Смородинского — М .: Мир, 1974. — 456 с.
Успенский, В.А. Треугольник Паскаля. Популярные лекции по математике. Выпуск 43 / ред. В.В. Донченко — 2-е изд. доп. — М .: Наука, 1979. — 48 с .: ил.
Картинки [Электронный ресурс]. — Режим доступа: http://arbuz.uz/u_treug.html
Блез Паскаль: биография, мысли, изобретения, открытия, арифмометр [Электронный ресурс].- Режим доступа: http://www.iqfun.ru/articles/pascal.shtml
Левченков С.И. — Краткий очерк истории химии: Дополнения. Биографии великих учёных. Паскаль (Паскаль), Блез. Учебное пособие для студентов химфака РГУ [Электронный ресурс]. — Режим доступа: http://www.physchem.chimfak.rsu.ru/Source/History/Persones/Pascal.html
Биография математика, физика, философа и писателя Блеза Паскаля [Электронный ресурс]. — Режим доступа: http://to-name.ru/biography/blez-paskal.htm
Блез Паскаль — великий ученый. [Электронный ресурс]. — Режим доступа: http://znaniya-sila.narod.ru/people/013_00.htm
Швец А.Н. Информатика -54 Глава 10. Треугольник Паскаля [Электронный ресурс]. — Режим доступа: http://mech.math.msu.su/~shvetz/54/inf/perl-problems/chPascalTriangle.xhtml
Биография Паскаля [Электронный ресурс]. — Режим доступа: http://phyart-pascal.narod.ru/biography.html
Просмотров работы: 1390
Исследовательская работа: Треугольник Паскаля | Образовательный портал EduContest.Net — библиотека учебно-методических материалов
Чтобы посмотреть презентацию с картинками, оформлением и слайдами, скачайте ее файл и откройте в PowerPoint на своем компьютере.
Текстовое содержимое слайдов презентации:
Удивительный треугольник великого француза — треугольник Паскаля 1.Выявить свойства чисел, входящего в состав треугольника Паскаля2. Определить применение свойств чисел треугольника Паскаля3. Сформулировать вывод и итоги исследованияЗАДАЧИ ИССЛЕДОВАНИЯ ЦЕЛЬ ИССЛЕДОВАНИЯПриведите соответствующее количество типов чисел треугольника Паскаля и примеров применения треугольника для доказательства гипотезы.ГИПОТЕЗАЕсли числа треугольника Паскаляобладают особыми свойствами, то его можно считать удивительным.style.fontSize Мартин Гарднер «Математические новеллы» 1974 «Треугольник Паскаля так прост, что выписать его даже десятилетний ребенок. Столь необычные свойства неисчерпаемые сокровища и связывает воедино различные аспекты математики, не имеющие на взгляд между собой ничего общего. позволяют считать треугольник Паскаля одной из наиболее изящных схем во всей математике «. ТРЕУГОЛЬНИК ПАСКАЛЯ — это бесконечная числовая таблица «треугольной формы», в которой по боковым сторонам стоят единицы и всякое число, кроме этих боковых единиц одинаковых сумме двух размеров. Каждое число в таблице равно сумме предшествующего вертикального ряда, начиная с самого верхнего до стоящего самого левее числа А. ЭНЦИКЛОПЕДИЯ ЮНОГО МАТЕМАТИКА Он обладает симметриейотносительно вертикальной, проходящей через его вершину.Вдоль прямых, параллельных сторонам треугольника (на рисунке отмечены зелеными линиями) выстроены треугольные числа и их обобщения на случай пространств всех размерностей. СВОЙСТВА ТРЕУГОЛЬНИКА
СВОЙСТВА ТРЕУГОЛЬНИКАТреугольные числа показывают, сколько фигур кружков можно расположить в виде треугольника Классический пример начальная расстановка шаров в бильярде. Треугольник Паскаля СВОЙСТВА ТРЕУГОЛЬНИКАСледующая зеленаялиния покажет нам тетраэдральные числа четыре один шар, которые мы можемположить на три — итого, под три подложим шесть итого десять и так далее.СВОЙСТВА ТРЕУГОЛЬНИКАСледующая зеленаялиния осуществляет попытку выкладывания гипертетраэдра в четырехмерном пространстве — один шар касается четырех, ате, в свою очередь, десяти … В четырехмерном, виртуальном мире, мы можем выйти с ними в четвертое измерение. И тем более пятимерный тетраэдр, который может существовать только в рассуждениях топологов… или фантастов.исчезнуть.
НАВЕРНОЕ ХОТИТЕ СПРОСИТЬ… Это тоже треугольные числа, но одномерные, показывающие, сколько шаров можно выложить вдоль линии — сколько есть, столько и выложите. Это тоже треугольные числа в нульмерном пространстве — сколько бы шаров мы не взяли — больше одного положения не сможем, потому что просто негде — нет ни длины, ни ширины, ни высоты. А о чем же говорит самая верхняя зеленая линия. Удивительное свойство треугольника ПаскаляЗаменим каждое число в треугольнике Паскаля точка.Причем, нечетные точки выведем контрастным цветом, а четные — прозрачным, или цветом фона. Результат непредсказуемо-удивительным: треугольник Паскаля разобьется на более мелкие треугольники, образующие изящный узор. ПРИМЕНЕНИЕ Пусть, например, мы хотим вычислить сумму чисел натурального ряда от 1 до 9. «Спустившись» по диагонали До числа 9, мы увидим слева снизу от него число 45. Оно то и дает искомую сумму.


 Основные понятия и свойства проективной геометрии, теоремы Дезарга и Паскаля. Информация по колле
Основные понятия и свойства проективной геометрии, теоремы Дезарга и Паскаля. Информация по колле Главная Курсовые работы Треугольник паскаля. 3.Открыть файл в котором будет записан наш треугольник паскаля, выбранной размерности.
Конвертер для перевода программ на языке Си в текст программы на языке Паскаль. Справочная по операторам Паскаля (языка Turbo Pascal)
Отличительные черты видов треугольников по углам и по сторонам. Мультимедийное пособие по теме quot;Движения на уроках геометрииquot; и методика его применения в обучении. дипломная работа 3,4 M, добавлен 23.04.2011. Треугольник Паскаля компьютер перевёл на язык цвета.
Особенностью языка Паскаль является то, quot;что число элементов массива фиксируется при описании и в процессе выполнения программы не меняется. Курсовая работа по информатике и компьютерным наукам.
Доказанное свойство является одним из свойств треугольника Паскаля: каждый коэффициент получается сложением двух, стоящих над ним коэффициентов. Контрольные, курсовые, рефераты.
Выберите раздел: Программирование в Delphi Программирование на языке Паскаль (Pascal) Чтобы расположить нужное количество цифр по окружности в программе на языке Паскаль, можно воспользоваться такой конструкцией: for n:1 to.
Главная Курсовые работы Треугольник паскаля. 3.Открыть файл в котором будет записан наш треугольник паскаля, выбранной размерности.
Конвертер для перевода программ на языке Си в текст программы на языке Паскаль. Справочная по операторам Паскаля (языка Turbo Pascal)
Отличительные черты видов треугольников по углам и по сторонам. Мультимедийное пособие по теме quot;Движения на уроках геометрииquot; и методика его применения в обучении. дипломная работа 3,4 M, добавлен 23.04.2011. Треугольник Паскаля компьютер перевёл на язык цвета.
Особенностью языка Паскаль является то, quot;что число элементов массива фиксируется при описании и в процессе выполнения программы не меняется. Курсовая работа по информатике и компьютерным наукам.
Доказанное свойство является одним из свойств треугольника Паскаля: каждый коэффициент получается сложением двух, стоящих над ним коэффициентов. Контрольные, курсовые, рефераты.
Выберите раздел: Программирование в Delphi Программирование на языке Паскаль (Pascal) Чтобы расположить нужное количество цифр по окружности в программе на языке Паскаль, можно воспользоваться такой конструкцией: for n:1 to. ..
..
