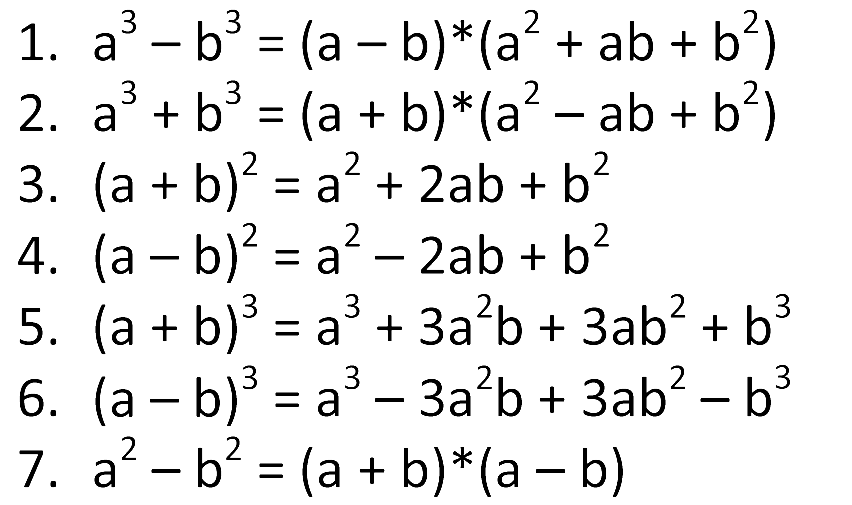Фсу по алгебре: Недопустимое название — Викиверситет

Содержание

Формулы сокращенного умножения 💣

Формулы сокращенного умножения

Вместо букв a, b могут быть любые числа, переменные или даже целые выражения. Для быстрого решения задач лучше выучить основные 7 формул сокращенного умножения (ФСУ) наизусть. Да, алгебра такая, нужно быть готовым много запоминать.

Ниже удобная табличка, которую можно распечатать и использовать, как закладку для быстрого запоминания формул.

Как читать формулы сокращенного умножения

Учимся проговаривать формулы сокращенного выражения:

Разность квадратов двух выражений равна произведению их разности и их суммы.

Квадрат суммы двух выражений равен квадрату первого плюс удвоенное произведение первого на второе плюс квадрат второго.

Квадрат разности двух выражений равен квадрату первого минус удвоенное произведение первого на второе плюс квадрат второго.

Сумма кубов двух выражений равна произведению суммы первого и второго на неполный квадрат их разности.

Разность кубов двух выражений равна произведению разности первого и второго на неполный квадрат их суммы.

Куб суммы двух выражений равен кубу первого плюс утроенное произведение квадрата первого на второе плюс утроенное произведение первого на квадрат второго плюс куб второго.

Куб разности двух выражений равен кубу первого минус утроенное произведение квадрата первого на второе плюс утроенное произведение первого на квадрат второго минус куб второго.

Доказательство формул сокращенного умножения

Напомним, что разность квадратов двух чисел a и b равна произведению их разности и их суммы: a² — b² = (a — b) * (a + b).

Иначе говоря, произведение суммы a и b на их разность равна разности их квадратов: (a — b) * (a + b) = a² — b².

Важно знать, что разность квадратов не равна квадрату разности: a

2 — b² ≠ (a — b)².

Докажем, что a² — b² = (a — b) * (a + b).

Поехали:

Используя искусственный метод, прибавим и отнимем одно и тоже a * b.
+ a * b — a * b = 0
a² — b² = a² — b² + ab — ab

Сгруппируем иначе: a² — b² + a * b — a * b = a² — a * b + a * b — b²

Продолжим группировать: a² — a * b — b² +a * b = (a² — a * b) + (a * b — b²)

Вынесем общие множители за скобки:
(a² — a * b) + (a * b — b²) = a *(a — b) + b *(a — b)

Вынесем за скобки (a — b). a * (a — b) + b * (a — b) = (a — b) * (a + b)

Результат доказательства: a² — b² = (a — b) * (a + b)

Для того, чтобы доказать в обратную сторону: (a — b) * (a + b) = a² — b², нужно раскрыть скобки: (a — b) * (a + b) = a * a + a * b — b * a — b * b = a² — b².

Остальные ФСУ можно доказать аналогичным методом.

Дополнительные формулы сокращенного умножения

К таблице основных ФСУ следует добавить еще несколько важных тождеств, которые пригодятся для решения задач.

Бином Ньютона

Формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных. Записывается вот так:

Пример вычисления биномиальных коэффициентов, которые стоят в строке под номером n в треугольнике Паскаля:

ФСУ для квадрата и куба суммы и разности — являются частными случаями формулы бинома Ньютона при n = 2 и n = 3.

Формула возведения в квадрат суммы трех, четырех и более слагаемых

Пригодится, если слагаемых в сумме, которую нужно возвести в степень, больше, чем два.

(a₁+a₂+…+a_n)² = a₁² + a₂² + … + a_n-1² + a_n² + 2 * a₁ * a₂ + 2 * a₁ * a₃ + 2 * a₁ * a₄ + … +

+ 2 * a₁ * a_n-1 + 2 * a₁ * a_n + 2 * a₂ * a₃ + 2 * a₂ * a₄ + … + 2 * a₂ * a_n-1 + 2 * a₂ * a_n +…+

+ 2 * a_n-1 * a_n

Читается так: квадрат суммы n слагаемых равен сумме квадратов всех этих слагаемых и удвоенных произведений всех возможных пар этих слагаемых.

Формула разности n-ых степеней двух слагаемых

aⁿ − bⁿ = (a − b) * (a^n-1 + a^n-2 * b + a^n-3

* b² + … + a * b^n-2 + b^n-1).

Для четных показателей можно записать так:

a^2*m − b^2*m = (a² − b²) *(a^2*m−2 + a^2*m−4 * b² + a^2*m−6 * b⁴ + … + b^2*m−2).

Для нечетных показателей:

a^2*m+1 − b^2*·m+1 = (a − b) * (a^2*m + a^2*m−1 * b + a^2*m−2 * b² + … + b^2*m).

Частными случаями являются формулы разности квадратов и кубов при n = 2 и n = 3. Для разности кубов b можно также заменить на −b.

Решение задач

Давайте потренируемся и рассмотрим примеры с дробями.

Задание 1

Что сделать: вычислить квадрат произведения (55 + 10)².

Как решаем:

воспользуемся формулой квадрата суммы: (55 + 10)² = 55² + 2 * 55 * 10 + 10² = 3025 + 1100 + 100 = 4225.

Задание 2

Что сделать: упростить выражение 64 * с³ – 8.

Как решаем: применим разность кубов: 64 * с³ – 8 = (4 * с)³ – 2³ = (4 * с – 2)((4 * с)² + 4 * с * 2 + 2²) = (4 * с – 2)(16 * с² + 8 * с + 4).

Задание 3

Что сделать: раскрыть скобки (7 * y — x) * (7 * y + x).

Как решаем:

Произведем умножение: (7 * y — x) * (7 * y + x) = 7 * y * 7 * y + 7 * y * x — x * 7 * y — x * x = 49 * y² + 7 * y * x — 7 * y * x — x² = 49 * y² — x².
Используем формулу сокращенного умножения: (7 * y — x) * (7 * y + x) = (7 * y)² — x² = 49 * y² — x².

Многочленов бояться не стоит, просто совершайте последовательно каждое действие. С формулами решать задачки быстрее и удобнее — сохраняйте шпаргалку, запоминайте и радуйте своих учителей 🙂

Запишите вашего ребенка на увлекательные уроки математики в детскую школу Skysmart. Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой и онлайн-доска, где можно рисовать и чертить вместе с преподавателем.

Формулы сокращенного умножения: таблица, примеры использования

Формулы сокращенного умножения (ФСУ) применяются для возведения в степень и умножения чисел и выражений. Часто эти формулы позволяют произвести вычисления более компактно и быстро.

В данной статье мы перечислим основные формулы сокращенного умножения, сгруппируем их в таблицу, рассмотрим примеры использования этих формул, а также остановимся на принципах доказательств формул сокращенного умножения.

Формулы сокращенного умножения. Таблица

Впервые тема ФСУ рассматривается в рамках курса «Алгебра» за 7 класс. Приведем ниже 7 основных формул.

Формулы сокращенного умножения

формула квадрата суммы: a+b2=a2+2ab+b2
формула квадрата разности: a-b2=a2-2ab+b2
формула куба суммы: a+b3=a3+3a2b+3ab2+b3
формула куба разности: a-b3=a3-3a2b+3ab2-b3
формула разности квадратов: a2-b2=a-ba+b
формула суммы кубов: a3+b3=a+ba2-ab+b2
формула разности кубов: a3-b3=a-ba2+ab+b2

Буквами a, b, c в данных выражениях могут быть любые числа, переменные или выражения. Для удобства использования лучше выучить семь основных формул наизусть. Сведем их в таблицу и приведем ниже, обведя рамкой.

Первые четыре формулы позволяют вычислять соответственно квадрат или куб суммы или разности двух выражений.

Пятая формула вычисляет разность квадратов выражений путем произведения их суммы и разности.

Шестая и седьмая формулы — соответственно умножение суммы и разности выражений на неполный квадрат разности и неполный квадрат суммы.

Формула сокращенного умножения иногда еще называют тождествами сокращенного умножения. В этом нет ничего удивительного, так как каждое равенство представляет собой тождество.

При решении практических примеров часто используют формулы сокращенного умножения с переставленными местами левыми и правыми частями. Это особенно удобно, когда имеет место разложение многочлена на множители.

Дополнительные формулы сокращенного умножения

Не будем ограничиваться курсом 7 класса по алгебре и добавим в нашу таблицу ФСУ еще несколько формул.

Во-первых, рассмотрим формулу бинома Ньютона.

a+bn=Cn0·an+Cn1·an-1·b+Cn2·an-2·b2+..+Cnn-1·a·bn-1+Cnn·bn

Здесь Cnk — биномиальные коэффициенты, которые стоят в строке под номером n в треугольнике паскаля. Биномиальные коэффициенты вычисляются по формуле:

Cnk=n!k!·(n-k)!=n(n-1)(n-2)..(n-(k-1))k!

Как видим, ФСУ для квадрата и куба разности и суммы — это частный случай формулы бинома Ньютона при n=2 и n=3соответственно.

Но что, если слагаемых в сумме, которую нужно возвести в степень, больше, чем два? Полезной будет формула квадрата суммы трех, четырех и более слагаемых.

a1+a2+..+an2=a12+a22+..+an2+2a1a2+2a1a3+..+2a1an+2a2a3+2a2a4+..+2a2an+2an-1an

Как читать эту формулу? Квадрат суммы n слагаемых равен сумме квадратов всех слагаемых и удвоенных произведений всех возможных пар этих слагаемых.

Еще одна формула, которая может пригодится — формула формула разности n-ых степеней двух слагаемых.

an-bn=a-ban-1+an-2b+an-3b2+..+a2bn-2+bn-1

Эту формулу обычно разделяют на две формулы — соответственно для четных и нечетных степеней.

Для четных показателей 2m:

a2m-b2m=a2-b2a2m-2+a2m-4b2+a2m-6b4+..+b2m-2

Для нечетных показателей 2m+1:

a2m+1-b2m+1=a2-b2a2m+a2m-1b+a2m-2b2+. .+b2m

Формулы разности квадратов и разности кубов, как вы догадались, являются частными случаями этой формулы при n=2 и n=3 соответственно. Для разности кубов b также заменяется на -b.

Как читать формулы сокращенного умножения?

Дадим соответствующие формулировки для каждой формулы, но сначала разберемся с принципом чтения формул. Удобнее всего делать это на примере. Возьмем самую первую формулу квадрата суммы двух чисел.

a+b2=a2+2ab+b2.

Говорят: квадрат суммы двух выражений a и b равен сумме квадрата первого выражения, удвоенного произведения выражений и квадрата второго выражения.

Все остальные формулы читаются аналогично. Для квадрата разности a-b2=a2-2ab+b2 запишем:

квадрат разности двух выражений a и b равен сумме квадратов этих выражений минус удвоенное произведение первого и второго выражения.

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание

Прочитаем формулу a+b3=a3+3a2b+3ab2+b3. Куб суммы двух выражений a и b равен сумме кубов этих выражений, утроенного произведения квадрата первого выражения на второе и утроенного произведения квадрата второго выражения на первое выражение.

Переходим к чтению формулы для разности кубов a-b3=a3-3a2b+3ab2-b3. Куб разности двух выражений a и b равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе, плюс утроенное произведение квадрата второго выражения на первое выражение, минус куб второго выражения.

Пятая формула a2-b2=a-ba+b (разность квадратов) читается так: разность квадратов двух выражений равна произведению разности и суммы двух выражений.

Выражения типа a2+ab+b2 и a2-ab+b2 для удобства называют соответственно неполным квадратом суммы и неполным квадратом разности.

С учетом этого, формулы суммы и разности кубов прочитаются так:

Сумма кубов двух выражений равна произведению суммы этих выражений на неполный квадрат их разности.

Разность кубов двух выражений равна произведению разности этих выражений на неполный квадрат их суммы.

Доказательство ФСУ

Доказать ФСУ довольно просто. Основываясь на свойствах умножения, проведем умножение частей формул в скобках.

Для примера рассмотрим формулу квадрата разности.

a-b2=a2-2ab+b2.

Чтобы возвести выражение во вторую степень нужно это выражение умножить само на себя.

a-b2=a-ba-b.

Раскроем скобки:

a-ba-b=a2-ab-ba+b2=a2-2ab+b2.

Формула доказана. Остальные ФСУ доказываются аналогично.

Примеры применения ФСУ

Цель использования формул сокращенного умножения — быстрое и краткое умножение и возведение выражений в степень. Однако, это не вся сфера применения ФСУ. Они широко используются при сокращении выражений, сокращении дробей, разложении многочленов на множители. Приведем примеры.

Пример 1. ФСУ

Упростим выражение 9y-(1+3y)2.

Применим формулу суммы квадратов и получим:

9y-(1+3y)2=9y-(1+6y+9y2)=9y-1-6y-9y2=3y-1-9y2

Пример 2. ФСУ

Сократим дробь 8×3-z64x2-z4.

Замечаем, что выражение в числителе — разность кубов, а в знаменателе — разность квадратов.

8×3-z64x2-z4=2x-z(4×2+2xz+z4)2x-z2x+z.

Сокращаем и получаем:

8×3-z64x2-z4=(4×2+2xz+z4)2x+z

Также ФСУ помогают вычислять значения выражений. Главное — уметь заметить, где применить формулу. Покажем это на примере.

Возведем в квадрат число 79. Вместо громоздких вычислений, запишем:

79=80-1;792=80-12=6400-160+1=6241.

Казалось бы, сложное вычисление проведено быстро всего лишь с использованием формул сокращенного умножения и таблицы умножения.

Еще один важный момент — выделение квадрата двучлена. Выражение 4×2+4x-3 можно преобразовать в вид 2×2+2·2·x·1+12-4=2x+12-4. Такие преобразования широко используются в интегрировании.

Формулы сокращенного умножения. 7 класс. Разработка урока

Слайд 1.

Тема урока:

Слайд 2. Цели урока:

1. Образовательная цель: формирование у учащихся навыков применения формул сокращенного умножения

2. Развивающая цель урока : развивать грамотную устную математическую речь, мыслительную активность, навыки логического мышления, развивать умение наблюдать, сравнивать, обобщать и анализировать математические ситуации

3. Воспитательная цель урока: воспитание внимательности, активности, уважения и терпимости друг к другу, умения слушать и общаться друг с другом.

Краткая характеристика контингента обучающихся

Состав учащихся класса представляет собой обучающихся-осуждённых переводного контингента и учащихся нового набора. Новички, за редким исключением, имеют значительный перерыв в учёбе, большие пробелы в знаниях, часто негативный опыт детской школы, низкую мотивацию учебного труда, неоднократные судимости. Всё это требует от учителя определённых усилий для вовлечения осуждённых в активную познавательную деятельность. Неразвитые психофизические процессы обучающихся, такие, как память, внимание, мышление требуют от учителя внедрения отлаженной системы повторения, закрепления опорных знаний и выстраивания личностной траектории развития каждого учащегося по предмету. Кроме того, учебные планы, учебные программы и весь учебно-методический комплекс не учитывают специфику обучения взрослых, тем более специфику обучения взрослых осуждённых. Решение проблем адаптации учебно-методических комплексов детской школы к условиям обучения взрослых возложили на себя педагоги открытых вечерних школ и педагоги школ пенитенциарной системы

Оборудование: опорные таблицы, дидактический материал, компьютер, проектор, слайдовая презентация.

Слайд 3. Задачи урока:

— формирование умения применять формулы сокращенного умножения для выполнения практических заданий стандартного уровня с переходом на более высокий уровень;

— развитие познавательных процессов, памяти, мышления, наблюдательности, сообразительности;

— выработка самооценки, критериев оценки своей работы;

— формирование у учащихся положительного мотива учения.

Структура урока:

I. Мотивационная беседа с последующей постановкой цели.

II. Актуализация опорных знаний – устная работа, с помощью которой ведется повторение формул сокращенного умножения на основе систематизации знаний.

III. Диагностика усвоения системы знаний и умений и ее применение для выполнения практических заданий стандартного уровня с переходом на более высокий уровень.

IV. Подведение итогов урока, рефлексия.

V. Творческое домашнее задание.

Содержание урока.

I. Мотивационная беседа с последующей постановкой цели.

Казалось бы алгебра сухая наука. Но как любая наука, она дает нам новые знания, умения, новые возможности для их применения на других уроках, в практической жизни. Чтобы знания можно было эффективно применить, нужно, чтобы они были прочно усвоены. Древняя китайская мудрость гласит: «Я слышу – я забываю, я вижу – я запоминаю, я делаю – я понимаю». Для того, чтобы наш урок был плодотворным, давайте последуем совету китайских мудрецов и будем работать по принципу: я слышу – я вижу – я делаю…

Слайд 4. 1.Устная работа.

а) прочитайте выражения: 0,01а²-b²; (m –n)².

б) представьте в виде квадрата одночлена: 25а²; 36с²; 0,64b².

в) представьте в виде удвоенного произведения: 50х; 4ху; 6аb.

г) представьте в виде произведения: а²-2аb+b²; х²+6х+9; а²-25.

д) вычислите: 12²-10²; 13²+5².

Слайд 5. Демонстрируются правила:

1. (а-b)(а+b)=а²-b²

2. (а+b)²=а²+2аb+b²

3. (а-b)²=а²-2аb+b². Правила проговариваются учениками.

Слайд 6. 2.Самостоятельная работа.

1. Представьте в виде многочлена:

а) (а-5)²

б) (х+4)²

в) (-5+х)²

г) (3+0,1х)(0,1х-3)

д) (0,1у-0,5)²

е) (-а-5)²

2. Вычислите:

а) 14²-13²

б) 15²+11²

3. Сократите дробь: 11

————

17² — 16²

Слайд 7. IV. Самопроверка самостоятельной работы по готовому образцу и локализация места затруднения.

№ задания

Выполнено + или — ?

№ правила

1(а)

1(б)

1(в)

1(г)

1(д)

1(е)

2(а)

2(б)

Ребята, вы выяснили, какие сделаны задания правильно, а какие нет. Определите правила, которые неверно использовали. Заполните в таблице номера формул.

Слайд 8. 4. Заполните пропущенные строки в таблице (знаю ли я названия формул, умею ли я подставлять в формулу различные значения букв?)

Пример: х = р + 3 ; у = r³, тогда х² + у²= (р+3)² + (r³)²

Названия формул сокращенного

умножения

Выражения, полученные из формулы при а=-2m, b=n²+1

1) полный квадрат суммы

2) …

3) разность квадратов

4) квадрат суммы

5) …

1) …

2) (-2m-n²-1)²

3) …

4) …

5) 4m²+4m(n²+1)+(n²+1)²

Слайд 9. 5. Найти формулы сокращенного умножения, которые «спрятались» в различных алгебраических выражениях.

Перед вами список различных алгебраических выражений. Впишите рядом с каждым выражением номера формул сокращенного умножения, которые можно применить для преобразования данного выражения.

а) (9р⁴ -1)² ___________

б) (р-3)²(р+3)² ___________

в) (4а²+4а+1)² ___________

г) (b-2)(b²+4)(b+2) ___________

д) (а+8)²- (а-4)(а+4) ___________

Слайд 10. 6. Долгое время одну из известных в древности планет в периоды утренней и вечерней видимости греки считали двумя разными светилами.

Упростите заданные алгебраические выражения. Зачеркните в таблице названия планет, связанные с найденными ответами. Оставшееся название позволит вам узнать, с какой планетой это заблуждение было связано.

(2а-1)² — 4а² = ___________________________________

4а(а-2) – (а-2)² + 4 = _____________________________

(а+2)(а+4) – (а+1)² = _____________________________

(а-1)² — (а+1)(а+2) = ______________________________

4а + 7	— 5а — 1	3а² + 4а	1 – 4а	3а² — 4а
Юпитер	Сатурн	Венера	Марс	Меркурий

Слайд 11. 7. Преобразуйте числовое выражение и определите, какие из высказываний истинные, а какие – ложные:

143² — 67² = ___________________________________________

Значение заданного выражения:

А) четное; О

Б) кратно 5; О

В) кратно 3; О

Г) делится нацело на 38; О

Д) при делении на 210 дает результат 75. О

Слайд 12. 8. Для художественного оформления банкнот используются изображения достопримечательностей городов России.

Узнайте, какие это города и с банкнотами какого достоинства они связаны. Для этого выполните преобразования выражений и запишите результаты в стандартном виде. Используя найденные ответы как алгебраические коды, заполните таблицу названиями городов.

Санкт-Петербург: (х-2)(х² +2х + 4) = ____________________

Красноярск: (1 + х)(х² — х + 1) = ___________________

Архангельск: (х-1)²(х² +2х +1) = ____________________

Ярославль: (х+3)(х² +9) – (х+3)3х = _______________

Достоинство банкноты	Алгебраический код города	Название города
10 руб	х³ + 1
50 руб	х³ — 8
500 руб	(х²)² — 2х² + 1
1 000 руб	х³ + 27

Слайд 13. 9. Заполнить пропуски в решениях (умею ли я комплексно применять формулы сокращенного умножения?)

преобразовать выражение в многочлен несколькими способами:

(а+2+b)²=а²+…+(2+b)²=а²+4а+2аb+…+b²

(а+2+b)²=(…)²+4(а+b)+4=…+4а+4b+4

(а+2+b)²=(…)²⁺2b(а+2)+b²=…+2аb+4b+b²

V. Подведение итогов, рефлексия

1). Чем сегодня занимались на уроке?

2). Достигнута ли цель урока?

3). Какие затруднения еще остаются?

4). Вам было на уроке : легко, обычно, трудно?

5). Довольны ли вы своей работой на уроке?

6). Интересно ли было на уроке?

7). Как оценивают учащиеся свою работу на уроке?

8). Оценивание учителем.

Слайд 14. VI. Творческое домашнее задание.

— составить рекламу формулам сокращенного умножения;

— найти в справочном материале историческую справку по теме;

— составить (подобрать) задания для соседа на применение формул сокращенного умножения.

Желаю удачи!

Тест Формулы сокращенного умножения (7 класс) онлайн по алгебре

Сложность: новичок.Последний раз тест пройден 4 часа назад.

Материал подготовлен совместно с учителем высшей категории

Опыт работы учителем математики — более 33 лет.

Вопрос 1 из 10
Допишите равенство: (3a + 2b)² = 9a² + 12ab + …
- Правильный ответ
- Неправильный ответ
- Вы и еще 94% ответили правильно
- 94% ответили правильно на этот вопрос
В вопросе ошибка?
Следующий вопросОтветить
Вопрос 2 из 10
Раскройте скобки: (2a + 5)²
- Правильный ответ
- Неправильный ответ
- Вы и еще 87% ответили правильно
- 87% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Вопрос 3 из 10
Возведите в куб двучлен 3х + 2:
- Правильный ответ
- Неправильный ответ
- Вы и еще 63% ответили правильно
- 63% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Вопрос 4 из 10
Замените звездочку (*) одночленом так, чтобы получилось верное равенство. (7x + 1)² = (*) + 14x + 1
- Правильный ответ
- Неправильный ответ
- Вы и еще 81% ответили правильно
- 81% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Вопрос 5 из 10
Разложите на множители: 100 — k⁶:
- Правильный ответ
- Неправильный ответ
- Вы и еще 93% ответили правильно
- 93% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Вопрос 6 из 10
Представьте в виде степени: 25x² + 40xy + 16y²
- Правильный ответ
- Неправильный ответ
- Вы и еще 87% ответили правильно
- 87% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Вопрос 7 из 10
Выполните возведение в квадрат: (7b + b⁵)²:
- Правильный ответ
- Неправильный ответ
- Вы и еще 90% ответили правильно
- 90% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Вопрос 8 из 10
Замените знак * таким одночленом, чтобы полученное выражение можно было представить в виде квадрата двучлена: * — 28pq + 49q²:
- Правильный ответ
- Неправильный ответ
- Вы и еще 51% ответили правильно
- 51% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Вопрос 9 из 10
Упростите выражение: (1 — 3х)(1 — 4х + х²) + (3х — 1)(1 — 5х + х²) + 3х²:
- Правильный ответ
- Неправильный ответ
- Вы и еще 67% ответили правильно
- 67% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Вопрос 10 из 10
Раскройте скобки: (2x³ + 3y²)²
- Правильный ответ
- Неправильный ответ
- Вы и еще 81% ответили правильно
- 81% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить

Доска почёта

Чтобы попасть сюда — пройдите тест.

Юра Беляев
10/10
Роза Балгабаевна
10/10
Анна Поплавская
10/10
Ира Шавкунова
8/10
Дима Голдобин
6/10
Дима Титов
9/10
Линар Салимов
8/10
Миляуша Гайсина
7/10
София Денисова
10/10
Сьюзан Корингейл
9/10

ТОП-3 тестакоторые проходят вместе с этим

Тест «Формулы сокращенного умножения» (7 класс) с ответами составлен в соответствии с действующей программой, утвержденной министерством. Данная подборка тестов поможет качественно подготовиться к контрольной работе. Задания удобно просматривать в онлайн режиме с любого доступного устройства. Вопросы проверяют знание формул и умение проверять их на практике. С помощью вопросов теста можно быстро проверить свои знания по теме.

Тест по теме «Формулы сокращенного умножения» поможет быстро и качественно оценить знания данной темы, станут отличным помощником для тех, кто хочет подтянуть алгебру.

Рейтинг теста

Средняя оценка: 4. Всего получено оценок: 1988.

А какую оценку получите вы? Чтобы узнать — пройдите тест.

ГДЗ самостоятельные работы по алгебре 7 класс Александрова Углубленный уровень Мнемозина

Математическая серия углубленного уровня изучения дисциплины для семиклассников включает в себя, в том числе, сборник для проведения самостоятельной проверки полученных знаний, результатов изучения дисциплины. Работать с пособием можно как с привлечением дополнительной репетиторской помощи, так и самостоятельно, например, по гдз самостоятельные работы по алгебре для 7 класса Александрова углубленный уровень

Для того, чтобы получить качественные и эффективные результаты, необходимо организовать занятия с онлайн ответами, опираясь на принципы:

системной работы, то есть регулярно проводя занятия, не допуская возникновения длительных пропусков. Последнее чревато необходимостью впоследствии «наверстывать упущенное», восполняя пробелы. Да и запоминается материал большими блоками значительно хуже;
выделения достаточного количества времени на такую работу. В идеале, занятия следует проводить ежедневно, расходуя не менее часа в день. Если такой режим организовать не получается, можно в качестве альтернативного выбрать еженедельную работу, по полтора-два часа дважды или трижды в неделю;
проведения постоянных самопроверок и самоконтроля достижений.

Кем будет востребован сборник готовых ответов для самостоятельных работ по алгебре 7 класс Александрова углубленный уровень?

Чаще всего этот сборник с решебником используют для подготовки к математическим олимпиадам и конкурсам, а также перед поступлением в физико-математические школы и лицеи. Немало девяти- и одиннадцатиклассников применяют такие сервисы для повторения материала за седьмой класс перед сдачей выпускных итоговых испытаний или внутренних экзаменов, тестирований в колледжи и ВУЗы.

Среди пользователей – не только сами школьники, но и:

их педагоги, которым сервис позволяет быстро и качественно проверить большой объем ученических тетрадей;
репетиторы, отслеживающие по ресурсу технологию грамотного преподавания предмета ученикам в соответствии со Стандартами образования и оформления работ;
родители семиклассников, с помощью ресурса проверяющие степень усвоение своим ребенком материала по программе.

Зачет по теме «Формулы сокращенного умножения» | Методическая разработка по алгебре (7 класс):

№	Запишите формулу и её словесную формулировку.	+/-
	________________________________________(формула) Куб суммы двух выражений ______________________________________________ _____________________________________________________________________________ ______________________________________________________________________________________________________________________________________________________________ ___________________________________________________________________________________
	________________________________________(формула) Квадрат разности двух выражений ______________________________________________ _____________________________________________________________________________ ______________________________________________________________________________________________________________________________________________________________
	________________________________________(формула) Сумма кубов двух выражений ______________________________________________ _____________________________________________________________________________ ______________________________________________________________________________________________________________________________________________________________
	________________________________________(формула) Разность кубов двух выражений ______________________________________________ _____________________________________________________________________________ ______________________________________________________________________________________________________________________________________________________________
	________________________________________(формула) Разность квадратов двух выражений ______________________________________________ _____________________________________________________________________________ ___________________________________________________________________________________
	________________________________________(формула) Квадрат суммы двух выражений ______________________________________________ _____________________________________________________________________________ ______________________________________________________________________________________________________________________________________________________________
	________________________________________(формула) Куб разности двух выражений ______________________________________________ _____________________________________________________________________________ ______________________________________________________________________________________________________________________________________________________________ ___________________________________________________________________________________
Отметка за блок «Теория». Теория изложена без ошибок – ЗАЧЕТ (5), наличие ошибки – НЕЗАЧЕТ (2).

Формулы сокращенного умножения 9 класс онлайн-подготовка на Ростелеком Лицей

ФСУ

ФСУ (формулы сокращенного умножения) – готовые формулы, по которым можно представить некоторые выражения в виде произведения и наоборот.

Важно: вместо букв a и b может стоять любое выражение, любое число.

Задача №1

Разложим выражение 5+с2

Решение:

5+с2=25+2⋅5⋅с+с2=25+10с+с2

Квадрат суммы
a+b2=a2+2ab+b2
Квадрат разности
a−b2=a2−2ab+b2
Разность квадратов.
a2−b2=a−ba+b

Задача №2

145²−45²

Решение:

145−45⋅145+45=100⋅190=19000
1. Выражение похоже на квадрат суммы: 4m2=2m2 , тогда 2m=a , n=b
2. Преобразуем отдельные слагаемые: 4m2+4mn+n2=(2m)2+2⋅2m⋅n+n2
3. Воспользуемся формулой квадрата суммы: (2m)2+2⋅2m⋅n+n2=2m+n2

Алгоритм разложения на множители с помощью ФСУ.

Определяем наиболее похожую на выражение формулу.
С помощью свойств степеней преобразуем отдельные слагаемые так, чтобы выражение приняло вид формулы.
Используем соответствующую формулу.

Задача №3

Преобразовать выражение: 4m2+4mn+n2

Решение:

Сумма кубов
a3+b3=a+ba2−ab+b2
Разность кубов
a3−b3=a−ba2+ab+b2
Куб суммы
a+b3=a3+3a2b+3ab2+b3
Куб разности
a−b3=a3−3a2b+3ab2−b3

Бюллетень бакалавриата стран СНГ

Бакалавриат кафедры

Математика

Колледж искусств и наук

Веб-сайт: https://www.math.fsu.edu/

Председатель: Вашингтон Мио; Ассоциированный председатель по академическим вопросам: Беллено; Заместитель кафедры аспирантуры: Ökten; Заместитель кафедры бакалавриата: Керчеваль; Директор по чистой математике: Альдрованди; Директор по прикладной и вычислительной математике: Галливан; Временный Директор по финансовой математике: Ökten; Директор по биоматематике: Бертрам; Координатор помощников преподавателей: Кирби; Координатор актуарной науки: Париж; Профессора: Альдрованди, Алуффи, Белленот, Бертрам, Бауэрс, Коган, С. Фенли, Галливан, Хейл, Хукаба, Хурдал, Хуссайни, Керчеваль, Классен, Мио, Мусслимани, Нолдер, Октен, Сассман, Там, ван Хойдж; Доценты: Агаше, Фахим, Ким, Маньян, Р. Оберлин, Петерсен; доцентов: Баллас, Бао, Бауэр, Экрен, Фархат, Фостер, Джайн, Ли, Мур, Нидхэм, Резников, Чжу; Научный сотрудник по математике: Бойд; Преподавательский факультет III : Блэквелдер, Григорян, Кирби, Ленуар, Пэрис, Вуланд; Преподавательский факультет II: Эвальд, Харрис; Преподавательский факультет I: Холлингсворт, Малтби, Вальдес; Заслуженные профессора: Блумсак, Брайант, Кейс, Гилмер, Хиронака, Коприва, Креймер, Местертон-Гиббонс, Мотт, Николс, Д.Оберлин Куайн, Самнерс, Райт; Профессора вежливости: Absil, Beaumont, Chen, Croicu, le Dimet, Erlebacher, M. Fenley, Fusaro, Gan, Garreau, Gunzburger, Marcolli, Mascagni, Mathelin, Moorer, Navon, Peterson, Tabak, Tang, van Dooren , Сяоцян, Ван

Департамент математики (https://www. math.fsu.edu) предлагает программы обучения, ведущие к получению степеней бакалавра наук (BS) и бакалавра искусств (BA), магистра наук (MS) и магистра наук. Степень магистра гуманитарных наук и степень доктора философии.(Подробную информацию о степенях магистра и доктора см. В бюллетене для выпускников ). Для сильного студента, особенно для поступающих с повышенным кредитом, может быть разработана комбинированная программа бакалавриата / магистратуры. Это позволяет студенту примерно за пять лет получить как степень бакалавра, так и степень магистра. Диплом по математике можно рассматривать как центральный компонент гуманитарного образования или как подготовку к профессиональному обучению в другой области или как аспирантуру по математике. Студенты также могут рассчитывать на работу в промышленной или финансовой фирме, правительственном учреждении или преподавание в средней школе, колледже или университете.Программа актуарных наук профессионально ориентирована на страховой и финансовый секторы.

На кафедре работает широко признанный исследовательский факультет, каждый из которых обучает студентов бакалавриата. Под руководством преподавателя выбранные студенты могут выбрать индивидуальный исследовательский проект в рамках Major. Для всех студентов университет предоставляет доступ в Интернет, веб-страницы курсов и средства связи, а также доступ к ряду ведущих баз данных, включая Mathematical Review.Кафедра управляет собственной сетью компьютеров и компьютерных классов. Преподаватели и студенты кафедры имеют доступ к разнообразному математическому программному обеспечению, которое используется на курсах и в исследованиях. Для получения дополнительной информации посетите веб-сайт департамента.

Кафедра предлагает возможность своим специалистам участвовать в учебной деятельности вне аудитории. Общество студентов-математиков предоставляет место, где студенты бакалавриата встречаются ежемесячно, чтобы поделиться интересами и сотрудничать с другими единомышленниками. Будущие актуарии семинолов извлекает выгоду из первоклассных профессиональных отношений с актуарными работодателями; актуарии из государственных, страховых и консалтинговых фирм часто посещают отдел, чтобы описать сферу деятельности и провести собеседование со студентами для летней стажировки и трудоустройства. Студенты делятся опытом летних стажировок и готовятся к актуарным экзаменам, а успешные выпускники программы помогают нынешним студентам. Департамент выставляет команду на Экзамен Уильяма Лоуэлла Патнэма , общенациональное соревнование среди студентов-математиков, ежегодно проводимое Математической ассоциацией Америки.Осенний семинар проводится для студентов, чтобы они познакомились с проблемами в стиле Патнэм и отточили свои навыки их решения.

Ведомственные программы

Существует пять специальностей, ведущих к получению степени бакалавра: прикладная и вычислительная математика, чистая математика, биоматематика, математика / FSU-Teach и актуарная наука (см. Раздел «Программа актуарных наук» этого общего бюллетеня ). По любой из этих специальностей студентам, которые намереваются продолжить работу в аспирантуре по высшей математике, рекомендуется включать соответствующие математические последовательности.Под руководством преподавателя студент может выполнять гибкую основную программу, соответствующую конкретным интересам, или индивидуальный исследовательский проект с отличием по основной специальности.

Комбинированные пути BS / MS

Существует два утвержденных курса BS / MS по математике, которые позволяют студенту получить как BS, так и MS путем двойного подсчета до двенадцати кредитных часов для выпускников. Два пути — это курс чистой математики и путь по прикладной и вычислительной математике.

Кандидаты имеют право подать заявление о приеме, если у них есть не менее 60 часов обучения в бакалавриате, из которых не менее 24 в странах бывшего СССР.Минимальный средний балл составляет 3,0, по крайней мере 3,2 балла по математике выше MAC 2311. Обратите внимание, что выполнение этих требований не гарантирует зачисление. Рекомендуется раннее планирование. Если интересно, проконсультируйтесь с консультантом по математике или ассоциированным кафедрой аспирантуры по математике.

Компетентность в области компьютерных навыков

Все студенты Университета штата Флорида должны продемонстрировать базовые навыки работы с компьютером до окончания учебы. Поскольку необходимые навыки владения компьютером варьируются от дисциплины к дисциплине, каждая специальность определяет курсы, необходимые для удовлетворения этого требования.Бакалавриат по специальностям актуар, прикладная математика, биоматематика, математика и математика / FSU-Teach удовлетворяет этому требованию, получая оценку «C–» или выше в COP 3014 или ISC 3313.

Заявление о допуске

Все предварительные условия Общей программы штата, перечисленные как этапы 1–4 семестров, должны быть выполнены с оценкой «C» (C–, C, C +) или выше. Студенты, получившие меньше, чем необходимая оценка на любом из этих курсов, должны будут повторно пройти эти курсы до тех пор, пока стандарт не будет соблюден. Примечание: повторное прохождение курса может задержать его окончание и повлечь за собой повышенные обязательства по оплате (т. Е. Доплата за повторный курс и дополнительная плата за кредит).

Требования к общей программе штата Флорида

Штат Флорида определил общие предварительные требования к этой университетской программе. Для поступления на программу старших классов требуются определенные предварительные условия, и должен пройти студентом муниципального колледжа или государственного университета до поступления на эту программу. Студенты могут быть приняты в Университет без выполнения предварительных требований, но не могут быть приняты на программу.

На момент публикации этого документа некоторые общие программные требования рассматривались штатом Флорида и, возможно, были пересмотрены. Посетите https://dlss.flvc.org/admin-tools/common-prerequisites-manuals, чтобы просмотреть текущий список утвержденных государством предварительных условий.

Ниже перечислены общие предварительные условия программы или их замены, необходимые для приема на эти программы высшего образования:

Математика

COP XXXX: один курс научного программирования на три кредитных часа, предназначенный для специальностей информатики
MAC X311
MAC X312
MAC X313
BSC XXXX / XXXXL или CHM XXXX / XXXXL или GLY XXXX / XXXXL или PHY XXXX / XXXXL: один лабораторный научный курс на четыре кредитных часа, предназначенный для научных специальностей
КАРТА X302

Примечание: Для зачисления требуется оценка «C» или выше по всем курсам.

Актуарная наука

COP XXXX: один курс научного программирования на три кредитных часа, предназначенный для специальностей информатики
ЭКО Х013
ЭКО Х023
MAC X311
MAC X312
MAC X313

Примечание: Для зачисления требуется оценка «C» или выше по всем курсам.

ФГУ — Преподавание математики

COP XXXX: один курс научного программирования на три кредитных часа, предназначенный для специальностей информатики
MAC X311
MAC X312
MAC X313
BSC XXXX / XXXXL или CHM XXXX / XXXXL или PHY XXXX / XXXXL или GLY XXXX / XXXXL: один лабораторный научный курс из четырех кредитных часов, предназначенный для научных специальностей
КАРТА X302
SMT X043
SMT X053

Примечание: Для зачисления требуется оценка «C» или выше по всем курсам.Студенты-переводчики смогут сдавать SMT X043 и SMT X053 при зачислении в старшие классы.

ДЛЯ ВСЕХ ОСНОВНЫХ ПРОГРАММ : Студентам настоятельно рекомендуется выбирать необходимые факультативы для младших классов, которые улучшат их общеобразовательную работу и поддержат их предполагаемую программу получения степени бакалавра. Студенты должны проконсультироваться с научным руководителем в области их основной степени.

Академическая успеваемость

Для засчета этих степеней по всем курсам требуется оценка «C–» или выше.При формальном приеме на специальность студент не должен набирать более 2 неудовлетворительных оценок (оценки ниже «C–» или оценки «U») по предметам, необходимым для основной специальности, за исключением обязательных условий государственной общей программы, указанных в семестрах 1–4. Основные вехи, сделанные после поступления в БСС. Кроме того, по специальностям «Актуарная наука» также необходимо поддерживать средний балл 2,5 по всем основным и дополнительным курсам, а также по предварительным требованиям государственной общей программы, перечисленным как этапы 5–8 семестров. Дополнительные курсы для всех математических специальностей включают COP 3014 или ISC 3313, PHY 2048C, STA 4321.Для биоматематики он включает дополнительные курсы биологии, химии и физики. Для актуарной науки он включает дополнительные курсы с префиксами ACG, ECO, FIN, RMI или STA. Для FSU-Teach он включает дополнительные курсовые работы с префиксами BSC, HIS, MAT, RED, SMT или TSL. Исключения из этой политики требуют подачи петиции в департамент.

Требования

Пожалуйста, ознакомьтесь со всеми общеобразовательными требованиями к получению степени, изложенными в главе «Колледж искусств и наук» настоящего общего бюллетеня .Студент также должен получить в офисе факультета и на веб-сайте исправления к руководящим принципам для получения степени, внесенным после этой публикации.

Степень бакалавра гуманитарных наук (BA) в области математики или актуарных наук может быть получена после выполнения требований к степени бакалавра наук (BS) плюс дополнительные курсы, требуемые Университетом, как указано в главе «Требования к получению степени бакалавра» данного Общий бюллетень .

Студенты должны выполнить предварительные требования к общей программе штата Флорида, включая требования по физике (все специальности математика) или экономике (специальности актуарные науки) в течение первых двух лет обучения в колледже.Специалисты по актуарной науке также должны пройти курс бухгалтерского учета в течение первых двух лет обучения в колледже. Обратите внимание, что у всех специальностей есть требования к вычислениям, которые можно использовать в качестве обязательного курса, но не наоборот.

Студенту, который планирует продолжить работу в докторантуре по математике, рекомендуется выполнить требование по иностранному языку на французском, немецком или русском языках.

Курсы математики на уровне 4000, применяемые к любой предметной специальности, должны быть пройдены в Университете штата Флорида, если кафедра не освобождает от этого требования по письменному запросу.

Все специальности должны заполнить анкету на выход.

С отличием

Кафедра математики присуждает дипломы с отличием по специальности, призванной познакомить студентов с процессом самостоятельных и оригинальных исследований. Требования и другую информацию см. В главе «Управление почестей университетов и общества чести» настоящего общего бюллетеня .

Программа обучения математике ФГУП

Для тех, кто интересуется преподаванием математики, FSU-Teach — это инновационный подход к педагогическому образованию, который предполагает сотрудничество между учеными, математиками и преподавателями педагогического факультета Университета штата Флорида.В программе FSU-Teach учащиеся будут развивать глубокие знания в области естественных наук или математики, а также знания, навыки и опыт, необходимые для того, чтобы стать эффективным учителем естественных наук или математики. Программа будет оплачивать обучение на первых двух курсах, также доступны рабочие места с учеными, математиками и местными школами. Для получения дополнительной информации посетите наш веб-сайт: https://fsu-teach.fsu.edu/.

Требования для несовершеннолетних по математике

Незначительный курс математики состоит из двенадцати семестровых часов по курсам с префиксами MAA, MAC, MAD, MAP, MAS, MAT, MGF, MHF и MTG, но не включает курсы с номерами 1XXX или MAC 2233.Оценка «C–» или выше должна быть получена по каждому предмету, засчитываемому в счет несовершеннолетнего.

Предварительные курсы

Перед посещением любого курса математики студент должен получить оценку «C–» или выше по каждому предмету, необходимому для этого курса. Более того, студент, получивший оценку «C–» или выше по курсу с одним или несколькими заявленными или подразумеваемыми предварительными условиями, может впоследствии не получить зачетные баллы по предварительному (-ым) курсу (-ам). Например, студент, получивший оценку «C–» или выше в MAC 2312, может впоследствии не поступить в MAC 1105, 1114, 1140 или 2311.

Кредитная нота 1. За исключением предыдущего абзаца, переведенный студент может взять MAC 1105 в качестве кредита, даже если студент имеет «C–» или выше в переводном курсе, который приравнивается к курсу, для которого MAC 1105 является обязательным условием при условии, что учащийся прошел тест AMP (Advanced Mathematics Placement) и еще не выполнил требования по математике в области гуманитарных наук.

Кредитная нота 2. В случаях, когда студент получил «D +», «D» или «D–» по курсу и впоследствии проходит аналогичный курс того же уровня, количество часов до окончания учебы для первого курс будет запрещен, как только студент перейдет на второй курс.Это следующие случаи: MAC 2233 после MAC 2311; MAC 2311 после MAC 2233.

Кредит-нота 3. Кредит не может быть получен как для MAD 2104, так и для MGF 3301, если не получено разрешение от департамента.

Бакалавриат по математике

Курсы, необходимые для каждого из вариантов степени по математике: MAP 2302 и MAS 3105. Студент должен продемонстрировать уровень владения языком научного компьютерного программирования, а также должен соответствовать требованиям университета к компьютерным навыкам.Студенты обычно проходят COP 3014 или ISC 3313, чтобы удовлетворить оба этих требования, хотя первое может быть показано курсами на C, C ++, FORTRAN, Java или другом утвержденном языке более высокого уровня. Требуется STA 4321. Ниже приведены репрезентативные требования для четырех основных вариантов математики. Студенты должны обращаться на веб-сайт факультета (https://www.math.fsu.edu) или в офис департамента ( 208 LOV ) для получения самой последней информации.

Специальность — математика. В дополнение к предварительным требованиям к общей программе штата Флорида и указанным выше курсам, студент завершит PHY 2048C и завершит курсы MGF 3301; MAS 4302; MAA 4224 или 4226; и три из следующих, из которых как минимум два должны быть на уровне 4000: MAA 4227, 4402; MAD 3105, 3703, 4704; КАРТА 4103, 4153, 4180, 4202, 4216, 4341, 4342; МАС 4106, 4203, 4303; MAT 4934; MHF 4302; MTG 4302. Должна быть включена по крайней мере одна из следующих последовательностей или утвержденная замена: MAA 4226–4227, MAA 4402 и MTG 4302, MAD 3703–4704, MAP 4341–4342 или MAS 4302–4303.Рекомендуются дополнительные компьютерные языки. Обязательные дополнительные курсы PHY 2048C, COP 3014, STA 4321 и общий предварительный научный курс штата, выбранный из BSC 2010, CHM 1045, GLY 2010 или PHY 2049C, являются приемлемым междисциплинарным дополнительным второстепенным для студентов, изучающих эту специальность.

Студент, намеревающийся выполнять дипломную работу по чистой математике, должен сдать MAA 4226–4227 и MAS 4302–4303, а также MAA 4402 и MTG 4302.

Специальность «Прикладная математика». В дополнение к предварительным требованиям к общей программе штата Флорида и вышеуказанным курсам, студент должен пройти PHY 2048C (настоятельно рекомендуется PHY 2049C) и курсы MAD 3703; MAP 4103; MAP 4341; и MGF 3301; и два из следующих: MAA 4224 или 4226, 4227, 4402; MAD 4704; КАРТА 4153, 4180, 4202, 4216, 4342; MAS 4106; MAT 4934. Необходимые дополнительные курсы PHY 2048C, COP 3014, STA4321 и общий предварительный научный курс штата, выбранный из BSC 2010, CHM 1045, GLY 2010 или PHY 2049C, являются приемлемым междисциплинарным второстепенным второстепенным для студентов, обучающихся по этой специальности. .

Специальность «Биоматематика». Эта современная специальность может привести к работе в области биологических приложений, поступлению в медицинскую школу или аспирантуру по математической биологии или естественным наукам. В дополнение к предварительным требованиям к общей программе штата Флорида, студент должен пройти дополнительные курсы естествознания, включая BSC 2010, 2010L, 2011, 2011L; CHM 1045, 1045L, 1046, 1046L; PHY 2048C; и PCB 3063. Никаких дополнительных второстепенных не требуется. Требуются MGF 3301 и MAP 4481, а также дополнительные выборные требования; Студенты должны проконсультироваться в офисе факультета или на веб-сайте для уточнения требований по выбору.

Специальность математика / ФГУ-преп. В дополнение к тому, что было упомянуто выше (т.е. предварительные требования к общей программе штата Флорида, COP 3014, MAP 2302, MAS 3105 и STA 4321), студент завершит PHY 2048C, MGF 3301 (введение в курс проверки) и курс по каждой из четырех математических областей анализа, алгебры, геометрии и моделирования и один дополнительный факультатив (на уровне 3000 и выше). Курсы, приемлемые для каждой математической области: по алгебре: MAS 3301, MAS 4203 или MAS 4302; для анализа: MAA 4402, MAA 4224 или MAA 4226; для геометрии: MTG 4212; для моделирования: MAP 4103, MAP 4175, MAP 4180 или MAP 4481; и для факультативов: MAA 4227, MAD 3105, MAP 4170, MAP 4153, MAP 4202, MAP 4216, MAP 4341, MAS 4106, MAS 4303, MHF 4302, MTG 4302 или дополнительные курсы по алгебре, анализу, геометрии и / или Группы моделирования.Образовательные курсы FSU-Teach являются второстепенными и могут считаться второстепенными для варианта «Математика / FSU-Teach».

Примечание: Все специальности должны заполнить анкету на выход.

Степень бакалавра актуарных наук

Помимо общих требований к программе штата Флорида, существуют междисциплинарные требования к получению степени. Типичные требования включают: MAP 4170, 4175, COP 3014 или аналогичные; и четыре повторения актуарного учебного пособия MAT 4930r.Требуется STA 4321.

Студент также должен пройти следующие курсы по бизнесу и экономике: ACG 2021; ECO 2013 или 3203 и ECO 2023 или 3101; FIN 3403 и 4504; RMI 3011. Эти курсы удовлетворяют требованиям для несовершеннолетних в бизнесе, и дополнительных несовершеннолетних не требуется.

Примечание: Самую свежую информацию о требованиях к курсу для этой программы см. На https://www.math.fsu.edu.

Дополнительные требования включают в себя шесть курсов из трех групп курсов.Студенты должны заполнить:

Два курса, выбранные из MAP 2302, MAP 4176 и MAS 3105.
По крайней мере, один курс выбран из MAA 4224, 4226, 4227; MAD 3703; MAP 4341; MAS 4106; STA 4203, 4322, 4853.
Минимум один из следующих курсов: ECO 3101, 3203, 4401, 4421; FIN 4514; RMI 4115, 4135, 4224, 4292.

Несовершеннолетние и вторые мажоры

Студенты могут удвоить специализацию по актуарной науке и любой из четырех специальностей математики (чистая, прикладная / вычислительная, биоматематика или математика / преподавание из бывшего СССР), выполнив все предварительные условия и требования к ученой степени для каждой выбранной программы.Студент также может закончить вторую специальность на другом факультете. Специальность с гибким планом особенно подходит для студентов других специальностей, которые стремятся более глубоко изучить математику, или студентов-математиков, которые имеют междисциплинарные интересы. Математика не имеет ограничений на количество часов, которые могут совпадать с другой специальностью.

Информацию о допустимых несовершеннолетних и второстепенных для студентов, обучающихся по программе факультета, можно получить в офисе департамента.Необходимые дополнительные курсы по актуарной науке, прикладной вычислительной математике, биоматематике и математике и математике / специальностям FSU-Teach являются приемлемым междисциплинарным дополнительным второстепенным.

Определение префиксов

MAA — Математика: анализ

MAC — Математика: исчисления и предварительные вычисления

MAD — Математика: Дискретный

MAE — математическое образование

MAP — Прикладная математика

MAS  — Математика: алгебраические структуры

MAT — Математика

MGF — Математика: общая и конечная

MHF — Математика: история и основы

MTG — Математика: топология и геометрия

OCP — Физическая океанография

Бакалавриат

MAA 4224. Введение в анализ I (3) . Предпосылки: MAC 2313, MAS 3105 и предыдущий опыт математических доказательств (MGF 3301, MAD 2104 или другой опыт доказывания). Не открыт для студентов с кредитным баллом MAA 4226. Этот курс представляет собой строгий подход к элементарному исчислению. Темы включают полноту действительных чисел, последовательностей и рядов, пределов и непрерывности, производных, интегралов, фундаментальной теоремы исчисления, а также последовательностей и рядов функций. Студенты, намеревающиеся поступить в аспирантуру по математике, должны сдать MAA 4226.

MAA 4226. Advanced Calculus I (3) . Предварительные требования: MAC 2313 (C- или выше) и MAS 3105 (C- или выше) и MGF 3301 (C- или выше). Этот курс охватывает функции, последовательности, ограничения; преемственность, равномерная преемственность; дифференциация; интеграция; сходимость, равномерная сходимость. Только для сильных студентов с одобрения консультанта.

MAA 4227. Advanced Calculus II (3) . Предпосылка: MAA 4226.Этот курс является продолжением MAA 4226.

MAA 4402. Комплексные переменные (3) . Предпосылка: MAC 2313 (C- или выше). Этот курс охватывает аналитические функции; Условия Коши-Римана; сложная интеграция; Теорема Коши и интегральная формула; степенной ряд; аналитическое продолжение; Римановы поверхности; остатки и аппликации; и конформное отображение.

MAA 4934р. Темы анализа (1–3) .Предварительное условие: разрешение инструктора. Курс специальных тем. Может повторяться максимум двенадцать часов в семестр. Может быть повторено в том же семестре.

MAC 1105. Алгебра колледжа (3) . Предварительные условия: MAT 1033 с оценкой «C–» или выше или подходящая оценка за сдачу экзамена по математике. Рекомендуемый фон: два года обучения алгебре в средней школе. Этот курс представляет собой обзор алгебраических операций, уравнений и неравенств; функции и функциональные обозначения; графики; обратные функции; линейная, квадратичная, рациональная функция; абсолютная величина; радикалы; экспоненциальные и логарифмические функции; система уравнений и неравенств; Приложения.На основании результатов тестов от студента могут потребовать пройти курс общественного колледжа до MAC 1105.

MAC 1114. Аналитическая тригонометрия (3) . Пререквизиты: MAC 1105. Этот курс охватывает тригонометрические функции, обратные тригонометрические функции и их графики; тождества и условные уравнения; решение треугольников; тригонометрическая форма комплексных чисел; Теорема ДеМуавра и корни n-й степени; введение в плоские векторы.

MAC 1140. Алгебра предвычисления (3) . Предварительные требования: MAC 1105 (C- или выше) или MAC 1114 (C- или выше) или MAC 2233 (C- или выше). Этот курс охватывает функции и графики, особенно полиномиальные, рациональные, экспоненциальные и логарифмические функции более высокой степени; системы уравнений; решение линейных систем, матричные методы; детерминанты; последовательности и серии, индукция; и биномиальная теорема. В курсе также исследуются приложения, приближения и методы доказательства. Можно принимать одновременно с MAC 1114.

MAC 1147. Precalculus Algebra / Trigonometry (5) . Предварительные условия: MAC 1105 или соответствующий результат за сдачу экзамена по математике. Этот курс рассчитан на один семестр и охватывает темы MAC 1140 (Precalculus Algebra) и MAC 1114 (аналитическая тригонометрия). См. Темы для MAC 1140 и MAC 1114.

MAC 2233. Расчет для бизнеса (3) . Предварительное условие: MAC 1105 (C– или лучше), MAC 1114 (C– или лучше), MAC 1140 (C– или лучше) или MAC 1147 (C– или лучше).Этот курс охватывает пределы, непрерывность, первую и более высокие производные и дифференциал, с приложениями к построению графиков, скорости изменения и методы оптимизации; методы интеграции и приложения; введение в многомерное исчисление. Не доступен для студентов, которые имеют кредит в MAC 2311 с оценкой «C–» или выше.

MAC 2311. Исчисление с аналитической геометрией I (4) . Предварительные требования: MAC 1147; или MAC 1140 и MAC 1114; или подходящий результат за экзамен по математике.Этот курс охватывает полиномиальные, тригонометрические, экспоненциальные и логарифмические функции; первые и вторые производные и их интерпретации; определение и интерпретация интеграла; правила дифференциации; неявная дифференциация; приложения производной; антипроизводные; основная теорема исчисления. Этот курс должен быть пройден для получения пониженного кредита студентами, которые ранее получили кредит за часть содержания.

MAC 2312. Исчисление с аналитической геометрией II (4) .Предварительные условия: MAC 2311 или соответствующий результат за сдачу экзамена по математике. Этот курс охватывает методы интеграции; приложения интеграции; сериал и сериал Тейлора; дифференциальные уравнения. Этот курс должен быть пройден для получения пониженного кредита студентами, которые ранее получили кредит за часть содержания.

MAC 2313. Исчисление с аналитической геометрией III (5) . Предварительные требования: MAC 2312. Этот курс охватывает функции нескольких переменных и их графические представления; векторы; частные производные и градиенты; оптимизация; множественная интеграция; полярная, сферическая и цилиндрическая системы координат; кривые; векторные поля; линейные интегралы; интегралы потока; Теорема расходимости и теорема Стокса.Этот курс должен быть пройден для получения пониженного кредита студентами, которые ранее получили кредит за часть содержания.

MAD 2104. Дискретная математика I (3) . Предварительное условие: MAC 2311 или COP 3014 и MAC 1140. Рекомендуемое предварительное условие: MAC 2311. Этот курс охватывает методы определения и логического аргумента, множеств и функций, логику высказываний, введение в графы и отношения, а также приложения. Математические специальности должны сдавать MGF 3301 вместо MAD 2104.

MAD 3105. Дискретная математика II (3) . Предварительное условие: MAD 2104 или MGF 3301. Рекомендуемое предварительное условие: MAC 2311. Этот курс охватывает методы определения и логического аргумента, графики и диаграммы, отношения, булеву алгебру и приложения.

MAD 3703. Численный анализ I (3) . Предварительные требования: MAC 2312 с оценкой «B–» или выше или MAC 2313 с оценкой «C–» или выше, MAS 3105 и знание языка программирования, подходящего для числовых вычислений, такого как C, C ++, Fortran, Java или Python.Этот курс охватывает поиск корней, интерполяцию и полиномиальную аппроксимацию, численное дифференцирование и интегрирование, прямые и итерационные методы для систем линейных уравнений.

MAD 4300. Теория графов и сети (3) . Пререквизиты: MAS 3105. Этот курс предоставляет математические инструменты, необходимые для анализа абстрактных и реальных сетей. Темы включают математическое представление сети, различные формы централизации сети, структуру реальных сетей и случайные сети.

MAD 4704. Численный анализ II (3) . Пререквизиты: MAD 3703 и MAP 2302. Этот курс охватывает теорию приближений, численное решение нелинейных систем, краевые задачи и начальные задачи для обыкновенных дифференциальных уравнений.

MAD 4934р. Разделы дискретной или вычислительной математики (1–3) . Предварительное условие: разрешение инструктора. Курс специальных тем. Может повторяться максимум двенадцать часов в семестр.Может быть повторено в том же семестре.

MAE 4816. Элементы геометрии (3) . Этот курс изучает различные традиционные и новаторские геометрические темы с помощью практического подхода. Темы включают конгруэнтность, подобие, тройки Пифагора и области криволинейных фигур. Не открыт для студентов, специализирующихся на математике.

MAP 2302. Обыкновенные дифференциальные уравнения (3) . Предпосылка: MAC 2312 с оценкой «B–» или выше или MAC 2313 с оценкой «C–» или выше.Этот курс охватывает дифференциальные уравнения первого порядка, линейные уравнения второго порядка, системы уравнений первого порядка, решения в виде степенных рядов, преобразования Лапласа, численные методы. Не доступен для студентов, имеющих кредит в MAP 3305.

MAP 2480. Компьютерная лаборатория Biocalculus (1) . Пререквизиты: MAC 2311. Эта компьютерная лаборатория применяет методы расчетов и программное обеспечение математического программирования, чтобы помочь студентам в решении задач из биологии, медицины и психологии.

MAP 3305. Инженерная математика I (3) . Предпосылка: MAC 2313 или MAC 2312 с оценкой «B–» или выше. Этот курс охватывает обыкновенные дифференциальные уравнения, преобразование Лапласа и линейную алгебру: определители, матрицы, собственные значения и собственные векторы. Не доступно для студентов, имеющих кредит в MAP 2302.

MAP 3306. Инженерная математика II (3) . Предварительные требования: MAC 2313 и MAP 2302 или MAP 3305.Этот курс предлагает ряды Фурье и преобразования Фурье, введение в уравнения в частных производных. Не открыт для студентов, имеющих кредит в MAP 4341.

КАРТА 4103. Математическое моделирование (3) . (Только S / U). Предварительные требования: MAC 2313 (C- или выше) и MAP 2302 (C- или выше) и MAS 3105 (C- или выше) и PHY 2048C (C- или выше). Этот курс охватывает применение математики в реальных жизненных ситуациях, построение математических моделей, использование элементарных и продвинутых математических методов, а также тематические исследования.

MAP 4153. Векторное исчисление с введением в тензоры (3) . Предпосылка: MAC 2313 (C- или выше). Этот курс охватывает векторное исчисление: градиент, дивергенцию, завиток; дифференциальные операторы в ортогональных криволинейных координатах; линейные, поверхностные и объемные интегралы; Теоремы Стокса и Грина; индексные обозначения, декартовы тензоры; и приложения.

MAP 4170. Введение в актуарную математику (4) .Предпосылки: MAC 2312. Этот курс охватывает функцию суммы, взвешенные по доллару и времени ставки, силу процента; специальные виды аннуитета, облигации, капитализация и приложения. Кривые доходности, спотовые ставки, форвардные ставки, продолжительность, выпуклость, иммунизация и дополнительные финансовые концепции.

MAP 4175. Актуарные модели (4) . Предварительные требования: MAP 4170 и STA 4321. Этот курс охватывает анализ выживаемости при однократной и многократной жизни; законы о смертности, детерминированные методы и условные выплаты и аннуитеты; принципы и резервы премий для непрерывных, дискретных и полунепрерывных страховых продуктов; теория множественного декремента (конкурирующие риски) и приложения.

MAP 4176. Расширенные актуарные модели, достоверность и моделирование (4) . Предварительные требования: MAP 4175. Этот курс охватывает модели частоты претензий, модели индивидуальных потерь, модели совокупных потерь, модели выживаемости с декрементом нескольких жизней и нескольких смертей, модели переходного периода с несколькими состояниями, теорию достоверности и моделирование.

MAP 4180. Теория игр и приложения (3) . Предварительные требования: MAC 2313, MAS 3105, MAP 2302 и STA 4321.В этом курсе рассматриваются концепции решений для некооперативных игр. Равновесие по Нэшу. Критерий выбора. Эволюционно устойчивые стратегии. Кооперативные игры в стратегической форме. Характерная функция игры. Дилемма заключенных. Приложения.

MAP 4202. Оптимизация (3) . Предварительные требования: MAC 2313, MAD 3703 и MAS 3105. Этот курс охватывает линейное программирование, оптимизацию без ограничений, стратегии поиска, проблемы с ограничениями на равенство и неравенство.

MAP 4216. Вариационное исчисление (3) . Пререквизиты: MAP 2302 и MAA 4226 или MAA 4224 или MAP 4341. Этот курс охватывает фундаментальные проблемы, слабые и сильные экстремумы, необходимые и достаточные условия, теорию Гамильтона-Якоби, динамическое программирование, теорию управления и принцип максимума Понтрягина.

MAP 4341. Элементарные дифференциальные уравнения с частными производными I (3) . Предварительные требования: MAC 2313 и MAP 2302 или MAP 3305.Этот курс охватывает разделение переменных, ряды Фурье, задачи Штурма-Лиувилля, многомерные начально-краевые задачи, неоднородные задачи, функции Бесселя и полиномы Лежандра.

MAP 4342. Элементарные дифференциальные уравнения с частными производными II (3) . Пререквизиты: MAP 4341. Этот курс охватывает решение квазилинейных уравнений в частных производных первого порядка, классификацию и приведение к нормальной форме линейных уравнений второго порядка, функцию Грина, задачи с бесконечной областью, волновое уравнение, условие излучения, сферические гармоники.

MAP 4481. Математическое моделирование в биологии (3) . Пререквизит: MAC 2312. Рекомендуемый пререквизит: MAP 2480. Этот курс представляет собой введение в использование математических моделей в биологии. Линейные и нелинейные разностные и обыкновенные дифференциальные уравнения, линейный анализ устойчивости, анализ фазовой плоскости. Приложения могут включать популяционную биологию, инфекционные заболевания, химическую кинетику и физиологию.

КАРТА 4934р. Темы прикладной математики (1–3) . Предварительное условие: разрешение инструктора. Курс специальных тем. Может повторяться максимум двенадцать часов в семестр. Может быть повторено в том же семестре.

MAS  3105. Прикладная линейная алгебра I (4) . Пререквизиты: MAC 2312. Этот курс охватывает метод исключения Гаусса, векторные пространства, задачи наименьших квадратов, детерминанты, собственные значения и собственные векторы, линейные преобразования, приложения.

МАС 3301. Введение в современную алгебру (3) . Пререквизиты: MAC 2312 и MAS 3105. Этот курс охватывает группы, перестановки и симметрии, кольца, области целостности, свойства целых чисел, поля и рациональные числа. Математические специальности, отличные от FSU-Teach, должны вместо этого сдавать MAS 4302.

MAS  4106. Прикладная линейная алгебра II (3) . Предварительные требования: MAC 2313 (C- или выше) и MAS 3105 (C- или выше). Этот курс охватывает положительно определенные матрицы, вычисление матриц, линейное программирование и теорию игр.Приложения.

MAS  4203. Теория чисел (3) . Предпосылки: MAS 3105 и предыдущий опыт математических доказательств (MGF 3301, MAD 2104 или другой опыт доказывания). Этот курс охватывает алгоритм Евклида; сравнения, квадратичные вычеты, закон квадратичной взаимности и элементарное обсуждение арифметических функций и распределения простых чисел.

MAS  4302. Введение в абстрактную алгебру I (3) .Предпосылки: MAS 3105 и предыдущий опыт математических доказательств (MGF 3301, MAD 2104 или другой опыт доказывания). Этот курс охватывает группы, группы перестановок, подгруппы, гомоморфизмы групп, структуру групп, кольца, идеалы, гомоморфизмы колец, кольца частных, многочлены, факторизацию, поля, расширения полей.

MAS  4303. Введение в абстрактную алгебру II (3) . Пререквизит: MAS 4302. Этот курс является продолжением MAS 4302.

МАС 4934р. Вопросы по алгебре (1–3) . Предварительное условие: разрешение инструктора. Курс специальных тем. Может повторяться максимум двенадцать часов в семестр. Может быть повторено в том же семестре.

MAT 3503. Функции и моделирование (3) . Пререквизиты: MAC 2312. Этот курс включает групповые и индивидуальные занятия, направленные на укрепление знаний и связей между темами средней математики и математики колледжа.Решение проблем; сбор и анализ данных; и моделирование с использованием линейных, полиномиальных и тригонометрических функций, а также параметрических и полярных уравнений. Студенты обсуждают и представляют работу в классе, а также используют различные технологии.

MAT 3930р. Специальные разделы математики (1–3) . Может повторяться в течение одного семестра максимум до двенадцати часов семестра.

MAT 4906р. Управляемое индивидуальное исследование (1–4) .Может повторяться в течение того же семестра максимум до тридцати семестровых часов.

MAT 4930р. Специальные разделы математики (1–3) . (Только оценка S / U.) Может повторяться максимум до двенадцати часов в семестр.

MAT 4934р. Работа с отличием (3) . Может повторяться максимум девять часов в семестр.

MAT 4945р. Бакалавриат, профессиональная практика (1–3) .(Только оценка S / U.) Предварительное условие: разрешение инструктора. Этот курс представляет собой стажировку под руководством, индивидуально назначаемую для обеспечения профессионального развития студента в области приложения (например, актуарных наук; промышленных приложений). Может повторяться не более трех часов в семестр.

MGF 1106. Математика для гуманитарных наук I (3) . Предварительные условия: MAT 1033 с оценкой «C–» или выше или подходящая оценка за сдачу экзамена по математике.Этот курс охватывает теорию множеств; символическая логика; принципы подсчета; перестановки и комбинации; вероятность; статистика; геометрия; приложения и история математики. Рекомендуемый фон: два года обучения алгебре в средней школе. Курс не предназначен для студентов, чьи программы требуют курсов предварительного или математического анализа.

MGF 1107. Темы практической конечной математики (3) . Предварительные требования: MAT 1033 с оценкой «C–» или выше или подходящая оценка за сдачу экзамена по математике.Рекомендуемый уровень подготовки: два года обучения алгебре в средней школе. Этот курс охватывает финансовую математику; линейный и экспоненциальный рост; числа и системы счисления; история математики; элементарная теория чисел; методы голосования; теория графов; теория игры; геометрия; и компьютерные приложения.

MGF 1214. Экологическая математика (3) . Этот курс представляет собой элементарное введение в математические модели, полезные для понимания и решения экологических проблем.Дом H.T. Энергетические диаграммы Odum для потоков энергии предоставляют визуальные модели, которые переводятся в уравнения потока, которые затем могут быть решены с помощью обычных калькуляторов. Рекомендуемый фон: два года обучения алгебре в средней школе.

MGF 3301. Введение в высшую математику (3) . Пререквизиты: MAC 2312. Этот курс представляет собой введение в методы математики по таким разнообразным классическим и современным темам, как теория множеств, алгебра, топология действительных чисел и теория графов.Аксиомы и доказательства подчеркнуты повсюду. Не доступно для студентов, получивших кредит на сумму 2104 дирхамов.

MHF 3111. Исчисление и его история (3) . Необходимые условия: MAC 2311. Этот курс исследует ключевые вехи в развитии математического анализа, начиная с его корней в древности, через средневековье и эпоху Возрождения, и заканчивая работами Ньютона и Лейбница. Курс уделяет особое внимание изучению, анализу и практике методов и приемов важных идей современного исчисления, включая методы касательных, площадей, общих решений, печально известные «вычислительные войны» и быстрое и яростное развитие в течение восемнадцатого и девятнадцатого веков.

MHF 4302. Математическая логика I (3) . Предварительное условие: MGF 3301 или разрешение инструктора. Этот курс охватывает логику высказываний и предикатов, модели, а также теорему Гёделя о полноте и связанные с ней теоремы.

MTG 4212. Геометрия колледжа (3) . Пререквизиты: MAC 2312 и MAS 3105. Этот курс исследует фундаментальные темы геометрии с углубленной точки зрения, в первую очередь предназначен для учителей и будущих учителей математики.

MTG 4302. Элементарная топология I (3) . Предпосылка: MAC 2313 и предыдущий опыт математических доказательств (MGF 3301, MAD 2104 или другой опыт доказывания). В этом курсе изучаются топологические пространства, метрические пространства, связность, компактность, свойства разделения, топология плоскости и пространства произведений.

MTG 4303. Элементарная топология II (3) . Пререквизиты: MTG 4302. Этот курс изучает функциональные пространства, гильбертово пространство, фактор-пространства, континуумы, паракомпактность и метризуемость, сети и фильтры, а также фундаментальную группу.

MTG 4934р. Темы по топологии и геометрии (1–3) . Предварительное условие: разрешение инструктора. Курс специальных тем. Может повторяться максимум двенадцать часов в семестр. Может быть повторено в том же семестре.

Аспирантура

MAA 5306. Advanced Calculus I (3).

MAA 5307. Advanced Calculus II (3).

MAA 5406. Теория функций комплексной переменной I (3).

MAA 5407. Теория функций комплексной переменной II (3).

MAA 5616. Измерение и интегрирование I (3).

MAA 5617. Измерение и интеграция II (3).

MAA 5932р. Темы анализа (1–3).

MAD 5305. Теория графов (3).

МАД 5306. Теория графов и сети (3).

MAD 5403. Основы вычислительной математики I (3).

MAD 5404. Основы вычислительной математики II (3).

MAD 5420. Численная оптимизация (3).

MAD 5427. Численное оптимальное управление дифференциальными уравнениями с частными производными (3).

MAD 5738. Численное решение дифференциальных уравнений с частными производными I (3).

MAD 5739. Численное решение дифференциальных уравнений с частными производными II (3).

MAD 5745. Спектральные методы для уравнений с частными производными (3).

MAD 5932р. Темы по вычислительной математике (1–3).

MAP 5107. Математическое моделирование (3).

MAP 5165. Методы прикладной математики I (3).

MAP 5177. Актуарные модели (3).

MAP 5178. Расширенные актуарные модели, достоверность и моделирование (3).

КАРТА 5207. Оптимизация (3).

MAP 5217. Вариационное исчисление (3).

MAP 5345. Элементарные дифференциальные уравнения с частными производными I (3).

MAP 5346. Элементарные дифференциальные уравнения с частными производными II (3).

MAP 5395. Методы конечных элементов (3).

MAP 5423. Комплексные переменные, асимптотические разложения и интегральные преобразования (3).

MAP 5431. Введение в гидродинамику (3).

MAP 5441. Теория возмущений (3).

MAP 5486. Вычислительные методы в биологии (3).

КАРТА 5513. Теория распространения волн (3).

MAP 5601. Введение в финансовую математику (3).

MAP 5611. Введение в вычислительные финансы (3).

MAP 5615. Методы Монте-Карло в финансовой математике (3).

КАРТА 5932р. Темы прикладной математики (1–3).

MAS  5307. Группы, кольца и векторные пространства I (3).

MAS  5308. Группы, кольца и векторные пространства II (3).

MAS  5311. Абстрактная алгебра I (3).

MAS  5312. Абстрактная алгебра II (3).

MAS  5731. Компьютерная алгебра (3).

МАС 5932р. Темы по алгебре (1–3).

MAT 5907р. Управляемое индивидуальное исследование (1–4).(Только комплектация S / U.)

MAT 5911р. Исследования под руководством (1–5). (Только комплектация S / U.)

MAT 5921р. Коллоквиум по математике для аспирантов (1). (Только комплектация S / U.)

MAT 5932р. Избранные продвинутые темы (1–3).

MAT 5933р. Специальные разделы математики (1–3). (Только комплектация S / U.)

MAT 5939. Семинар для выпускников (1).

MAT 5941. Стажировка в педагогическом колледже (1–3). (Только комплектация S / U.)

MAT 5945р. Graduate Professional Internship (1–3). (Только комплектация S / U.)

MAT 5946р. Обучение под руководством (1–5). (Только комплектация S / U.)

MHF 5206. Основы математики (3).

MHF 5306. Математическая логика I (3).

MTG 5326. Топология I (3).

MTG 5327. Топология II (3).

MTG 5346. Алгебраическая топология I (3).

MTG 5347. Алгебраическая топология II (3).

MTG 5376р. Топологические структуры I (3).

MTG 5932р. Темы по геометрии (1–3).

OCP 5256. Гидродинамика: геофизические приложения (3).

MAA 6416р. Расширенные темы анализа (3).

MAA 6939р. Расширенный семинар по анализу (1). (Только комплектация S / U.)

MAD 6408р. Расширенные темы численного анализа (3).

MAD 6939р. Расширенный семинар по научным вычислениям (1). (Только комплектация S / U.)

КАРТА 6437р. Продвинутые темы прикладной математики (3).

MAP 6621. Финансовый инжиниринг I (3).

КАРТА 6939р. Расширенный семинар по прикладной математике (1). (Только комплектация S / U.)

МАС 6939р. Расширенный семинар по алгебре (1). (Только комплектация S / U.)

MAT 6908р. Управляемое индивидуальное исследование (1–4). (Только комплектация S / U.)

MAT 6932р. Дополнительные темы по математике (1–3).

MAT 6933р. Избранные продвинутые темы (1–3). (Только комплектация S / U.)

MAT 6939р. Advanced Graduate Seminar (1). (Только комплектация S / U.)

MTG 6396р. Продвинутые темы по топологии (3).

MTG 6939р. Расширенный семинар по топологии (1). (Только комплектация S / U.)

Списки, касающиеся дипломных работ для диссертаций, диссертаций, а также магистерских и докторских экзаменов и защиты, см. В бюллетене Graduate Bulletin .

Университет штата Флорида (БСС) Репетиторы по алгебре 1

Найдено 14 репетиторов, показано 1-14

Позвоните сейчас, чтобы записаться на репетиторство: (800) 416-5954

Таллахасси, Флорида

50 долларов в час

Я был учителем математики в средней школе в течение 4 лет и математики в средней школе в течение 6 лет.В 2010 году 78 процентов моих учеников показали успехи в учебе. Я специализируюсь на том, чтобы сделать математику значимой для моих учеников. С обучением также приходит способность эффективно выступать на публике, и я участвовал в …

Лично + онлайн Посмотреть профиль Timothy P.

Таллахасси, Флорида

55 $ / час

Я преподавал предалгебру и алгебру в качестве сертифицированного учителя более 6 лет, но с 2014 года занимаюсь обучением учеников начального возраста через алгебру колледжа.Я недавно оставил профессиональное преподавание в январе 2017 года, чтобы помочь с семейными медицинскими потребностями, поэтому моя доступность стала более гибкой, поскольку я сейчас …

Лично + онлайн Посмотреть профиль Marie E.

Таллахасси, Флорида

Я выпускник Университета Вандербильта в 2014 году с педагогической квалификацией.Я получил степень бакалавра гуманитарных наук по двум специальностям: социология и наука о Земле / окружающей среде. Благодаря учебе я осознал любовь к данным и исследованиям — и, что самое важное, …

Лично + онлайн Просмотреть профиль Sara B.

Таллахасси, Флорида

50 долларов в час

Летом 2019 года я окончила Университет штата Флорида со степенью бакалавра наук в области биохимии, Magna Cum Laude, а также со степенью бакалавра биологии, психологии и математики.У меня есть формальный опыт индивидуального и группового репетиторства за те три года, что я проработал профессиональным репетитором в кампусе …

Лично + онлайн Посмотреть профиль Cameron H.

Таллахасси, Флорида

45 долларов в час

Я люблю репетиторство, потому что оно дает мне возможность демистифицировать мир математики для людей, независимо от того, постоянно ли они пытаются понять концепции, преподаваемые в классе, или просто нуждаются в некотором освежении.Я стараюсь работать со студентами, чтобы убедиться, что они видят значительные улучшения в …

Лично + онлайн Просмотреть профиль Anisha S.

Таллахасси, Флорида

40 долларов в час

Я подхожу к обучению, исходя из подхода, ориентированного на ученика; да, я понимаю, что это клише, однако многие преподаватели преподают в соответствии с тестом, вместо того, чтобы тратить время на подтверждение того, что ученик усвоил основные концепции.Это основная философия моих методов обучения. Моя роль — обеспечить …

Лично + онлайн Посмотреть профиль Thomas L.

Таллахасси, Флорида

50 долларов в час

Моя сила в репетиторстве — это любовь к учебе и терпеливый характер.Я опытный наставник, который более года работает со студентами любого уровня подготовки и любого стиля обучения. Я изучаю историю и заканчиваю институт в мае. Хотя я признаю важность формального образования …

Лично Просмотреть профиль Daniel C.

Таллахасси, Флорида

40 долларов в час

Лэнс получил степень магистра в Университете штата Флорида в области систем обучения и технологий обучения и степень бакалавра образования в Университете Томаса.Он также является автором серии детских книг, первая книга которых вышла в 2018 году. Проведя семнадцать лет вне …

Лично + онлайн Посмотреть профиль Lance D.

Таллахасси, Флорида

$ 35 / час

Я сертифицированный учитель математики с 6 по 12 классы, а также имею степень магистра в области специального образования.У меня был опыт работы в государственной школе и чартерной школе, а также частным репетиторством. Мои области знаний связаны с математикой на уровне колледжа. Я также занимался английским, социальным …

Лично Посмотреть профиль Candace W.

Таллахасси, Флорида

40 долларов в час

Привет! Я Эмма, и я студентка бывшего СССР.Я специализируюсь на криминологии и химии. Я из Камминга, штат Джорджия, маленького городка к северу от Атланты. У меня есть младшие сестры, и я выросла, помогая им в школе, так что теперь это в основном в моей природе. Я также обучал всех своих сверстников …

Лично + онлайн Посмотреть профиль Emma H.

Таллахасси, Флорида

50 долларов в час

Здравствуйте родители и ученики, Меня зовут Гвиан, и я ищу прекрасную возможность обучить ученика математике или чтению.Информация обо мне: Я родом из Северной Каролины, и в декабре 2008 года я получил степень бакалавра экономики и менеджмента и общества в …

Лично + онлайн Посмотреть профиль Guiane B.

Кроуфордвилл, Флорида

65 $ / час

Математика — это предмет, основанный на правилах.Эти правила никогда не меняются, и как только вы усвоите эти правила, вы овладеете математикой! Кроме того, когда вы изучаете новый аспект математики, вы снова и снова практикуетесь в применении. Это повторение — метод обучения, который вы навязываете себе, и он работает …

Лично Просмотреть профиль Charles S.

Таллахасси, Флорида

33 $ / час

Привет! Меня зовут Дилан, и я хотел бы научить вас! Я обучал людей всю свою жизнь, и мне нравится чувство, когда мои ученики понимают то, что они пытаются понять.Я обучаю навыкам решения проблем, и вместо того, чтобы помочь вам понять одну проблему, я считаю, что это наиболее …

Лично + онлайн Посмотреть профиль Dylan R.

Таллахасси, Флорида

30 долларов в час

Я два года работаю учителем математики в средней школе.В настоящее время я замещающий учитель. Мне нравится возможность быть тем, кто помогает людям (студентам) достигать академических высот, которые раньше казались им немыслимыми. Я бы назвал себя учеником на всю жизнь, так как это мой …

Лично Посмотреть профиль Robert C.

Репетиторы по алгебре 1 рядом с ФГУ

ФГУ по алгебре 1 Репетиторы

С Uloop легко связаться с репетиторами по алгебре 1 в бывшем Советском Союзе.com. Поиск репетиторов по алгебре 1 из бывшего СССР и многое другое в Таллахасси, Флорида и его окрестностях. Вы можете проверить списки репетиторов по алгебре 1 от студентов Университета штата Флорида и профилей местных жителей Таллахасси. Чтобы упростить задачу, вы можете сузить поиск репетиторов по алгебре 1 из бывшего Советского Союза, используя фильтры, чтобы уточняйте результаты и расширяйте возможности поиска репетиторов. Поделитесь соответствующими репетиторами по алгебре 1 из бывшего СССР с однокурсниками из Университета штата Флорида, чтобы ускорить для них процесс поиска репетиторов.Воспользуйтесь Uloop.com, чтобы найти репетиторов по алгебре 1 из бывшего СССР!

Университет штата Флорида Подготовка к тесту ALEKS по математике

Какой тест по математике используется в Университете штата Флорида?

Государственный университет Флориды использует тест по математике ALEKS. Чтобы подготовиться к экзамену, вам понадобится учебное пособие, включающее подробные инструкции, практические занятия и интерактивные тесты. Для большинства студентов учебников для подготовки к экзаменам и практических вопросов недостаточно, а уроки и репетиторы слишком дороги.К счастью, онлайн-курсы теперь предлагают баланс доступности и эффективности.

Нужно ли мне сдавать тест по математике ALEKS в Университете штата Флорида?

Большинству студентов Университета штата Флорида необходимо будет сдать тест по математике ALEKS. Однако, если вы считаете, что у вас достаточно высокий балл по SAT или ACT, чтобы вас освободили от прохождения тестового теста, проверьте это онлайн или обратитесь в свой центр тестирования.

Какой тип математики входит в контрольный тест по математике Университета штата Флорида?

Математика на тестовом экзамене ALEKS Университета штата Флорида охватывает предалгебру, алгебру и геометрию.Убедитесь, что ваша подготовка включает только темы теста — ни больше, ни меньше. Лучшие курсы подготовки к экзаменам подчеркивают эффективность.

Сложна ли математика на вступительном экзамене Университета штата Флорида?

Установочный тест по математике ALEKS в Университете штата Флорида не составит труда, если вы получите необходимые индивидуальные инструкции при подготовке к тесту. С учебным пособием, в которое встроен репетитор математики, вы получите всю необходимую помощь.

Чем известен Государственный университет Флориды?

В дополнение к своему основному кампусу в Таллахасси, Университет штата Флорида имеет дополнительный кампус, расположенный в Панама-Сити, Флорида; Художественный музей Джона и Мейбл Ринглинг в Сарасоте; и различные вспомогательные и сельские кампусы, связанные с Медицинским колледжем.Кроме того, он предлагает международные программы через ряд кампусов в Европе, Латинской Америке и Азии. Результирующее разнообразие отражается в студенческом контингенте в 41 900 человек, который состоит из представителей 132 стран. Аккредитация университета была подтверждена в 2014 году Комиссией по колледжам Южной ассоциации колледжей и школ (SACSCOC).

Осенью 2018 года средний балл зачисленных первокурсников составил 4,3, средний общий балл ACT составил 30, а средний балл SAT — 1340.Независимо от результатов SAT, ACT, AP, IB, AICE и / или CLEP, поступающие первокурсники, желающие поступить в колледж алгебры или на более продвинутый курс математики, должны пройти тест на определение уровня ALEKS. Экзамены на современный язык также требуются от студентов, продолжающих изучение языка, начатых на вторичной работе. Для иностранных студентов, желающих продемонстрировать уровень владения английским языком, принимаются следующие тесты: IBTOEFL, TOEFL, Academic IELTS, MELAB и PTE.

Студенты, желающие поступить в Педагогический колледж, должны сдать все четыре раздела экзамена FTCE-General Knowledge (GK), в то время как для программ магистратуры могут потребоваться приемлемые баллы по GRE.Кандидаты, поступающие на программу DNP Колледжа медсестер, должны представить результаты либо по GRE, либо по MAT (тест аналогий Миллера).

лучших репетиторов из Университета штата Флорида

Если вы студент Университета штата Флорида и вам нужна дополнительная помощь с уроками, репетиторы университета помогут вам подключиться. Мы можем связать вас с высококвалифицированными частными репетиторами, прошедшими тщательную проверку, чтобы убедиться, что у них есть знания, опыт и коммуникативные навыки, которые помогут вам в вашем академическом путешествии, независимо от того, с каким предметом или уровнем строгости вы сталкиваетесь.Неважно, ломаете ли вы голову над продвинутой физикой или пытаетесь осмыслить Толстого, наши консультанты по образованию могут подобрать вам пару с репетитором, который ответит на все ваши вопросы. Чтобы узнать больше о том, как все это работает и каковы преимущества репетиторства в штате Флорида, читайте дальше.

Как может ближайший ко мне преподаватель из Университета штата Флорида помочь мне с моей курсовой работой?

Ваш репетитор из Университета штата Флорида может помочь вам в обучении в классе. Каждый раз, когда ваш профессор представляет новую идею, ваш наставник может помочь продолжить этот урок во время вашей сессии, анализируя идею во время вашего совместного времяпрепровождения и выдавая пояснения там, где это необходимо.Если объяснение идеи вашим профессором сбило вас с толку, ваш репетитор из штата Флорида может попытаться подойти к этому по-другому, пока вы не найдете объяснение, которое имеет для вас смысл. Такой вид индивидуального обучения может быть чрезвычайно полезным и часто недоступен в классе колледжа.

Репетиторство в штате Флорида — это все о вас, ваших целях и ваших успехах. В классе у вашего профессора есть программа, расписание, а все остальное зависит от вас. Ожидается, что вы будете учиться в свободное время и не отставать.Репетиторство в Университете штата Флорида — один из способов добиться этого, и ваш репетитор может проявить гибкость, когда вы будете стремиться к достижению своих целей. Если окажется, что вам нужно больше времени, чем ожидалось, чтобы по-настоящему осмыслить электроотрицательность, они могут изменить план игры. Это так просто.

Ваш репетитор из Университета штата Флорида также может помочь вам с домашними заданиями. На самом базовом уровне это может помочь снять часть стресса, связанного с обучением в колледже, но, что более важно, это может помочь углубить ваше понимание материала, который вы изучаете в классе.Например, если вы работаете над заданием по алгебре, ваш репетитор может сначала рассмотреть затронутые темы, прежде чем решать проблему вместе с вами. Затем они могут попросить вас попробовать решить проблему самостоятельно. Если вы допустили ошибку, они могут исправить вас в данный момент. Преимущество поверхностного уровня может заключаться в улучшении работы над заданием, но более важным преимуществом является то, что он дает возможность улучшить ваше понимание задействованных концепций и предотвратить превращение ошибок в привычку.

Репетиторство в Университете штата Флорида

можно настроить в соответствии с вашими предпочтениями в обучении. Эти занятия всегда проходят на индивидуальной основе, что означает, что ваш инструктор получает возможность узнать вас и может использовать эти идеи для адаптации того, как они взаимодействуют с вами. Например, если у вас тяжелые времена в истории Европы и вы в большей степени учитесь наглядно, они могут использовать виртуальную доску на платформе Live Learning Platform, чтобы наметить развитие Первой мировой войны. Ученик на слух, ваш репетитор из штата Флорида может вместо этого использовать мнемонические устройства, чтобы помочь вам запомнить порядок вторжения.Именно такие индивидуальные инструкции могут сделать ваше совместное времяпровождение таким эффективным.

Как репетиторство в Университете штата Флорида может помочь мне подготовиться к экзаменам?

Как только вы узнаете, что вам предстоит тест, ваш репетитор из Университета штата Флорида поможет вам составить план обучения. Они могут разбить материал, который вам нужно просмотреть, и прикрепить его к удобному расписанию. Это может уменьшить беспокойство, помочь вам убедиться, что у вас есть все необходимое, а также научит ценным организационным и учебным навыкам.

Они могут начать процесс обучения с обзора, который поможет выявить слабые места и позволит вам сосредоточить свое время там, где оно вам нужно больше всего. Это поможет вам работать умнее, а не усерднее. Они также могут научить вас ценным навыкам прохождения тестов, таким как эффективные стратегии тайм-менеджмента или тактика сокращения массивов множественного выбора, чтобы помочь вам выбрать наиболее вероятный правильный ответ. Все это может укрепить вашу уверенность перед экзаменом.

Как я могу работать с преподавателем из ближайшего ко мне колледжа в Университете штата Флорида?

Наши консультанты по образованию могут подобрать вам репетитора, который вписывается в ваше расписание, поэтому вам не придется менять уроки или смены на работе, чтобы получить академическую поддержку.Хотя вы всегда можете выбрать личного репетитора, доступность онлайн-обучения на платформе Live Learning Platform предлагает еще больше удобства, поскольку вы можете работать из любого места. Нет причин ждать! Свяжитесь с Varsity Tutors сегодня, и вы сможете получить доступ к репетитору в Университете штата Флорида всего за 24 часа.

Пилотный проект бывшего Советского Союза вдвое сокращает оценки по младшей алгебре

КОНТАКТ: Уил Стайлз, (850) 644-3737, или Аннетт Блэквелдер, (850) 644-1787

ЭКСПЛУАТАЦИОННЫЙ ПРОЕКТ БСС ВЫРЕЗЫВАЕТ НИЗКИЕ СТЕПЕНИ АЛГЕБРЫ НА ПОЛОВИНУ- В «старые времена» математического образования студенты колледжей посещали занятия, где математические задачи решались на классных досках, что слишком часто делало студентов пассивными наблюдателями за тем, чему их учили. Но двухлетняя пилотная программа в Университете штата Флорида изменила способ обучения студентов и подготовки к тестам, а также улучшила результаты тестов.

Фактически, использование компьютерного обучения (CAI) в отделении математики бывшего СССР в своих классах декламации по алгебре сократило вдвое количество заданий D и F.

Студенты курсов алгебры в колледжах бывшего СССР по-прежнему посещают лекции под руководством профессора вместе с 250 другими студентами три раза в неделю. И они по-прежнему посещают небольшие классы декламации из 30 человек раз в неделю. Но вместо того, чтобы пассивно наблюдать, как помощники учителя решают задачи на классной доске, студенты теперь активно работают над задачами на компьютерах для себя.

«Результаты тестов, по-видимому, указывают на то, что это лучший способ научить их, — сказал руководитель проекта Уил Стайлз, доцент математики из бывшего СССР.«До того, как мы начали проект, количество отказов было слишком высоким. Их оценки значительно улучшились».

По словам Стайлза, последствия имеют далеко идущие последствия из-за большого количества студентов, которые должны изучать алгебру в колледже, что является фундаментальной частью карьеры в колледже.

«К сожалению, студенты колледжей могут не иметь мотивации к работе вне уроков», — сказала младший специалист по математике Аннет Блэквелдер, которая реализовывала проект в качестве координатора курсов алгебры в колледжах бывшего СССР.«Но теперь, когда у нас есть студенты-алгебры, которые решают задачи и активно работают над задачами на компьютерах, все изменилось. Студенты также в восторге от усвоения материала».

С помощью программного обеспечения CAI студенты могут проходить тесты — как практические, так и настоящие — через Интернет. Практические тесты и другие учебные пособия, которые можно проходить сколько угодно часто с любого подключенного к Интернету компьютера в мире, позволяют студентам полностью ознакомиться с темами, которые будут рассмотрены в данном тесте.

Настоящие тесты, размещенные на том же Интернет-сайте, что и практические версии, могут быть выполнены только на 120 специально оборудованных компьютерах в четырех классных комнатах Учебной лаборатории Хоффмана в присутствии наблюдателя. Программное обеспечение для тестирования не только случайным образом выбирает вопросы из пула от 20 до 30, написанных преподавателями математики бывшего СССР, но также смешивает порядок возможных ответов по каждому тесту, что делает обман практически невозможным.

Стайлз и Blackwelder знали, что независимо от того, насколько функциональным было программное обеспечение для тестирования, именно вопросы теста будут способствовать или сломать пилотную программу.Поэтому они приняли решение писать вопросы сами вместе с младшим математиком Ишем Григоряном, а не использовать вопросы, которые поставлялись с программным обеспечением. Стайлз говорит, что создание хороших тестов отнимает много времени и сложно, но результат стоит затраченных усилий.

«На основании более высоких результатов тестов, которые были основным аргументом в пользу администрации университета, математическому факультету были предоставлены эти четыре класса», — сказал Стайлз. «Теперь нам нужно больше комнат.Мы хотели бы иметь возможность проводить все наши базовые математические классы для первокурсников и второкурсников в одном и том же режиме CAI ».

После того, как ученик прошел практику или настоящий тест, программное обеспечение для сдачи теста также может сразу же поставить оценку теста Таким образом, учащимся не нужно ждать результатов, но они могут сразу увидеть, что они сделали правильно, а что нет.

Программа также облегчает работу ассистентов преподавателей, которым больше не нужно часами оценивать стопки тестов и затем запишите оценки в журнале успеваемости.Журнал успеваемости программного обеспечения записывает оценки автоматически.

Пилотный проект начался осенью 1998 года, когда 300 студентов использовали тестовое программное обеспечение от Wiley Publishing Company, написанное профессором математики Университета Небраски Джоном Орром.

«Мы считаем, что бывший Советский Союз является национальным лидером в этом виде обучения, и что это лучший проект из подобных в стране», — сказал Стайлз. «У нас было много запросов о проекте, так что слухи о нашем успехе распространяются.Существует также интерес к использованию метода CAI в средних и даже начальных школах. Фактически, мы говорим с должностными лицами школ округа Леон о возможности запуска пилотного проекта в следующем учебном году ».

# # #

Добро пожаловать!

Публикации и препринты

∎ с Максом Халли Тропические деформации 2-го ранга . (В разработке)

∎ с Сэмом Пейном Адические тропики и совместимость с моделями Gubler .(препринт)

∎ в Efrat Bank. Корреляции между простыми числами на коротких интервалах на кривых над конечными полями . arXiv: 1708.07491, август 2017 г. (отправлено для публикации)

∎ с Джозефом Рабиноффом, Фарбодом Шокрие и Алехандро Сото. Неархимедовы и тропические тета-функции . arXiv: 1705.08212, май 2017 г. (отправлено для публикации)

∎ Действия Галуа по аналитике и тропикации . arXiv: 1703.07593, март 2017 г.(представлен для публикации)

∎ в Efrat Bank. Штрихует через короткие интервалы на кривых над конечными полями. arXiv: 1701.06822, январь 2017 г. (отправлено для публикации)

∎ с Дхрувом Ранганатаном, Маттиа Талпо и Мартином Улиршем. Логарифмические группы Пикара, запуск чипа и комбинаторный ранг . arXiv: 1611.10233, ноябрь 2016 г. (представлен для публикации)

∎ с Дхрувом Ранганатаном. Вырождения торических многообразий над оценочными кольцами .Бык. Лондон. Математика. Soc. 48 (2016), нет. 5, 835–847.

∎ Введение в адическую тропикацию . Неархимедова и тропическая геометрия (Мэтью Бейкер и Сэм Пейн, ред.). Simons Symposia, Springer New York, 2016, стр. 337-364

∎ с По Ху и Игорем Кризом. D-структуры и производная двойственность Кошуля для алгебр операд с единицей . J. Pure Appl. Алгебра 220 (2016), вып. 3, 1133–1156.

∎ с Дхрувом Ранганатаном. Анализ Хана и возможность установления связи тропических сортов более высокого ранга .Manuscripta Math. 151 (2016), нет. 3-4, 353–374.

∎ с Morgan Brown. Рациональные возможности подключения и аналитическая сократимость . Journal fu ̈r die reine und angewandte Mathematik (в печати)

∎ Операды высшей конфигурации в алгебраической геометрии: через колчанные грассманианы . ProQuest LLC, Анн-Арбор, Мичиган, 2013. Диссертация (докторская) ⎯ Йельского университета.

∎ Операды высшей конфигурации посредством грассманианов колчана . arXiv: 1211.4525, ноябрь 2012 г.

∎ с Филиппом Гроссом и Сэмом Пейном. Пределы тропикализации . Israel J. Math., 201 (2): 835-846, 2014.

∎ Некоммутативная версия натуральных чисел . arXiv: 1003.2081, март 2010 г.

Как выжить MAC 1105 в Университете штата Флорида

Для студентов, которые предпочли бы вообще исключить математику из своего расписания, но не могут, Университет штата Флорида предлагает MAC 1105 в качестве курса математики более низкого уровня. Многие студенты добавляют его в свое расписание, с нетерпением ожидая выполнения одного из своих общеобразовательных требований.Они входят в курс с мышлением «просто покончим с этим». В конце концов, вы изучали алгебру в восьмом классе. Как трудно это может быть? Что ж, если вы впервые берете курс математики на уровне колледжа, сядьте и пристегнитесь. Алгебра в колледже остается одним из самых неудачных предметов в бывшем Советском Союзе. К счастью для вас, мы вас прикрыли.

Ознакомьтесь с этими 10 советами по плавному плаванию через MAC 1105.

1. Получить материалы класса

giphy.com

Вам понадобится только один обязательный текст: пакет с классными заметками, который вы можете получить только в местном магазине Target Print & Mail на West Tennessee Street.Да, вам придется совершить долгую прогулку за пределы кампуса. Но вы не добьетесь успеха в колледже алгебры без . «Пакет для заметок был настоящей палочкой-выручалочкой для всего класса. Во время лекции преподается так много содержания, что студентам не хватает времени, чтобы записывать вопросы и обращать внимание на то, что она говорит. Сначала я пыталась делать заметки от руки, но к тому времени, когда я закончила писать задачу, мой профессор перешел к следующей, — сказала первокурсница Сара Себальос.Кроме того, возьмите свой верный калькулятор, толстую стопку блокнотов и свой любимый карандаш, чтобы пройти этот курс.

2. Не пропускайте урок

giphy.com

Если вы хотите приходить на занятия, когда вам это нравится, вы можете вообще пропустить регистрацию для MAC 1105. Быстрое посещение страниц «Оцените моих профессоров» для учителей MAC 1105 показывает, что хэштег «пропустить урок, не пройду» как один из самых популярных, выбранных учащимися. «Ходить на занятия так важно. Это математический класс, поэтому пропускать нельзя. Вы просто настроите себя на тяжелые времена, — сказал Себальос. Настройтесь на успех на будущих курсах, включив снаряжение прямо сейчас.

3. Магистр E-Grade

giphy.com

К концу семестра вы возненавидите E-Grade. Все домашние задания, викторины и тесты проводятся на этой устаревшей математической онлайн-платформе. Каждая проблема имеет очень специфический способ включения каждого ответа, и если вы потеряете запятую, точку с запятой или отрицательный знак, вы поймете всю проблему неправильно. «Нет хорошего совета, чтобы справиться с разочарованием из-за E-Grade.Сам сайт не работает. Это слишком разборчиво. Лучше всего много практиковаться на сайте, чтобы привыкнуть к нему », — сказал первокурсник Рен Флеминг. Практика делает безупречные функции как лучший совет для начинающих пользователей E-Grade. «Выполните массу практических задач и поймите, как E-Grade хочет, чтобы каждый ответ вводился для этой конкретной викторины или теста», — сказал первокурсник Кайл Алуф. Не стесняйтесь заходить в рабочее время профессора за дополнительной помощью по E-Grade. Профессора любят, когда студенты приходят и задают вопросы.Это показывает вовлеченность и помогает их офисному времени пролетать незаметно (им тоже становится скучно).

4. Не отставайте от домашнего задания

giphy.com

Хотя оценка, влияющая на силу домашнего задания, оказывается незначительной по сравнению с экзаменами, небольшой процентный вес может иметь значение между положительной и отрицательной оценкой. «Домашнее задание определенно помогло мне сдать урок во второй раз. Я заставлял себя просто выполнять практические задачи, пока не получал три проходящих практических теста подряд.Когда я заставлял себя задавать вопросы, я практиковался и фактически получал работу », — сказал Себальос. Имейте в виду, домашнее задание накапливается быстро. После выполнения каждой задачи в классе в E-Grade появляется новое домашнее задание. Не забывайте часто проверять обновления домашних заданий, так как они могут легко уйти от вас.

5. Дайте ему все

giphy.com

Если вы не считаете, что от природы разбираетесь в математике, этот урок покажется вам ошеломляющим. Дни математики в старших классах, когда можно было просмотреть заметки за час до урока и сдать экзамен, прошли.В MAC 1105, вы будете решать до четырех задач в день различной сложности. «Бывали недели, когда мне было невозможно работать. Это просто зависит от того, насколько вы готовы работать, чтобы понять, чего вы не получаете », — сказал Себальос. Даже если все ваши усилия не увенчаются успехом, продолжайте делать это и не бойтесь просить о помощи. Не переживайте из-за разделительных радикалов и интервальных обозначений. «Прохождение — это не просто вопрос времени. Я лично потратил много-много часов на этот курс, но все же сталкивался с проблемами на тестах и викторинах, которые меня озадачили.Тебе просто нужно держать голову высоко и продвигаться вперед, — сказал Отстраненный.

6. Получите помощь вне класса

giphy.com

Обращение за помощью может только повысить ваши результаты на экзамене MAC 1105. Лаборатории ACE на территории кампуса, расположенные прямо у Лэндиса, служат отличным ресурсом для обучения. Репетиторы студентов, сдавшие курс на оценку «А» или выше, доступны в течение всего дня и готовы помочь вам с любыми вопросами, которые могут у вас возникнуть. У профессоров MAC 1105 всегда есть рабочие часы, и они не могут дождаться, чтобы помочь вам. « Офисные часы станут вашим лучшим другом .Сходите к своему профессору и наладьте с ним отношения, потому что это очень поможет вам, когда дело доходит до экзаменов и выпускной оценки в классе », — сказал Себальос.

7. Примите строгость учебной программы колледжа

giphy.com

Вы с легкостью освоили математику в старших классах? Тогда вас удивит гора испытания, известная как MAC 1105. MAC 1105 дает представление о том, насколько на самом деле строгая учебная программа колледжа, независимо от того, насколько хорошо вы учились в старшей школе. «Это помогло мне развить мое мышление о том, как добиться успеха в учебе в колледже.Стандарт высок, а преданность превыше всего. Если вы преуспеете в MAC 1105, вы научитесь трудовой этике и, вероятно, преуспеете и в других классах », — сказал Флеминг. College Algebra проверяет вас не только на подробных теоремах и сложных задачах. Ваша рабочая этика, мотивация к успеху и психологическая стойкость — все это подвергнется испытанию. С энтузиазмом возьмитесь за каждый сложный аспект MAC 1105, и благодаря этому вы закончите курс более сильным учеником.

8. Не сдавайся

гиф.com

Придет время, когда вы посмотрите на сотни оставшихся без ответа домашних задач, и сильное желание бросить курить захлестнет вас. Не сдавайтесь. Отказ — худшее для вашей оценки. Продолжение и продвижение развивает вашу умственную выносливость и, в конце концов, окупится. «Я определенно был одним из тех студентов, которые бросили обучение в середине семестра, но я напомнил себе, что если я сделаю слабую работу и получу плохую оценку, это войдет в мой отчет. А поскольку это обязательное условие почти для каждой специальности, с таким же успехом можно покончить с этим с первого раза, — сказал Флеминг.

9. Учеба с одноклассниками

giphy.com

Когда дело доходит до математики, групповое обучение приносит вам пользу. У ваших друзей может быть лучший способ описать проблемы, чтобы помочь вам найти решение. Их разные взгляды на понимание различных целей могут помочь вам в чем-то нужном. Пообщайтесь со Строзье или Дираком со своими одноклассниками по алгебре из колледжа и сделайте это домашнее задание. «Групповое обучение очень важно. Если я не понимал вопроса, я мог попросить друга в моей группе помочь мне, и наоборот.Для меня групповое обучение было особенно полезным прямо перед экзаменом, когда я мог задавать друзьям вопросы в последнюю минуту и получать помощь по целям, которых я не достиг, обучаясь в одиночку », — сказал Затворник.

10. Празднуйте свои победы и учитесь на своих ошибках

giphy.com

Попытайтесь понять, почему вы получили плохую оценку. Спросите себя, с какими проблемами вы боретесь больше всего. Вы действительно пытались понять корень своих неудач? «Что касается меня, я всегда записывал проблемы, которые я сделал не так во время практики, и повторял их снова и снова, пока не исправлял их, вместо того, чтобы просматривать их и признавать, что я ошибся.Вот как вы действительно становитесь лучше », — сказал Флеминг. Точно так же не забудьте отпраздновать свои победы в MAC 1105. Это поможет вам мотивировать, а не даст вам упасть в кроличью нору математического отчаяния. Так что, если вы не получаете 100 баллов за каждый тест или викторину? Не ругай себя. «Как человек, который дважды посещал этот курс, я бы рекомендовал просто усердно работать и не упускать из виду конечную цель: учебу. Девиз, который вы научитесь любить, — «C получает степень», поэтому ничего страшного, если вы получите C в классе, если вы его сдадите », — сказал Себальос.