Физические величины таблица: Таблица единиц измерения в физике
1. Физические величины в химии, их обозначение и единицы измерения. Постоянные
В химии используются международные обозначения физических величин и единицы их измерения.
Для использования в химических расчётах некоторые международные единицы оказываются не совсем удобными (слишком большими или слишком маленькими), поэтому чаще применяют кратные единицы — г, мг, дм³, см³.
Иногда в задачах встречаются также несистемные единицы — л, мл.
Физические величины, их обозначения и единицы измерения
Величина | Обозначение | Единицы измерения |
| Число частиц | \(\)N\(\) | частиц |
| Количество вещества | \(\)n\(\) | |
| Масса | \(\)m\(\) | г, кг, мг, а. е. м., u |
| Относительная атомная масса | Ar | — |
| Относительная молекулярная масса | Mr | — |
| Молярная масса | \(\)M\(\) | |
| Объём | \(\)V\(\) | дм³, м³, см³, л, мл |
| Молярный объём | Vm | дм³/моль, л/моль
|
| Плотность | ρ | |
| Массовая доля | \(\)w\(\) | — |
В химических расчётах часто используются постоянные величины, значения которых надо запомнить.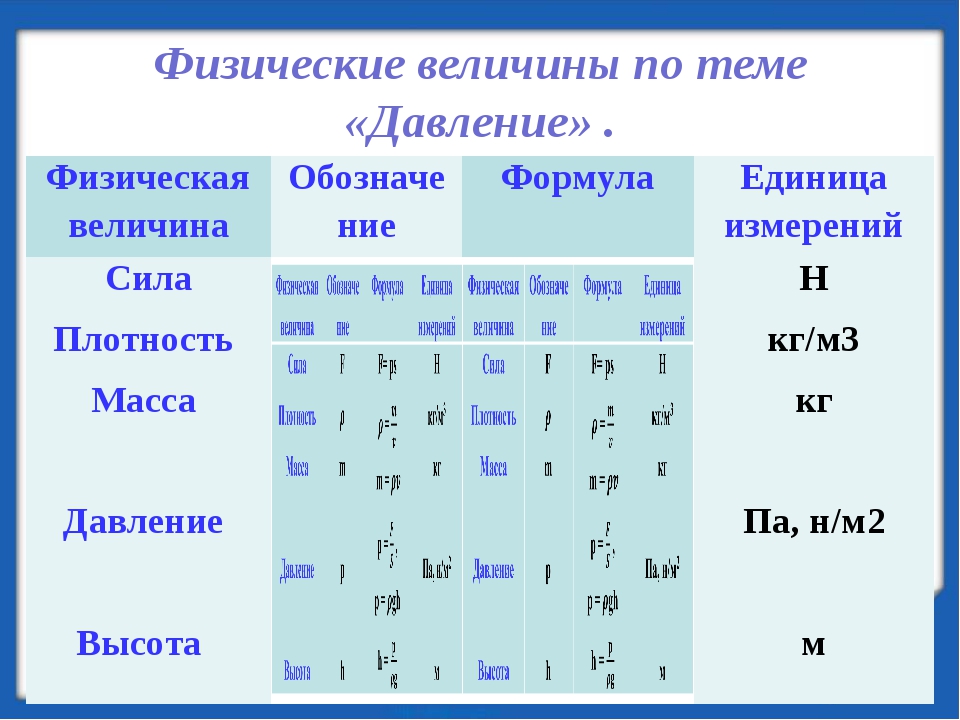
Некоторые постоянные, применяемые в химических расчётах
| Постоянная Авогадро | 6,02⋅1023 моль-1, 6,02⋅1023 1/моль |
| Молярный объём газов при н. у. | \(22,4\) дм³/моль |
| Атомная единица массы | 1,66⋅10−24 г, 1,66⋅10−27 кг |
| Плотность воды при \(4\) °С | \(1\) г/см³, \(1\) г/мл, \(1000\) г/дм³ |
Перевод физических величин: таблицы перевода единиц измерения
Основные и производные (механические и тепловые) единицы СИ: Длина, масса, время, термодинамическая температура, количество вещества, сила электрического тока, сила света, площадь, объем, вместимость, скорость линейная, ускорение линейное, частота вращения, плотность, сила, вес, момент силы, момент пары сил, давление, механическое напряжение, модуль упругости, поверхностное напряжение, динамическая вязкость, кинематическая вязкость, работа, энергия, мощность, поток энергии, количество теплоты, термодинамический потенциал (внутренняя энергия), теплоемкость системы, удельная теплоемкость, удельная энтропия, теплопроводность.
Ниже представлены таблицы перевода величин в другие единицы измерения для основных и производных единиц, для британской системы единиц измерения, даны таблицы соотношения мер вместимости, перевода единиц давления, скорости, объемного расхода и теплопроводности.
Перевод физических величин в другие единицы измерения
Представлены соотношения между единицами измерения для следующих величин: сила, давление, работа, энергия, количество теплоты, тепловой поток, плотность теплового потока, энтальпия, теплота фазового перехода, теплоемкость, динамический коэффициент вязкости (динамическая вязкость), коэффициент теплопроводности (теплопроводность), коэффициент теплопередачи (теплоотдачи), коэффициент излучения.
Перевод физических величин из британской системы единиц измерения в другие
Приведены соотношения между единицами измерения в британской системе для таких величин, как длина, площадь, объем, масса, удельный объем, плотность, давление, коэффициент вязкости, кинематический коэффициент вязкости (кинематическая вязкость), температура, количество теплоты, плотность теплового потока, теплоемкость, коэффициент теплопроводности (теплопроводность), коэффициент теплопередачи (теплоотдачи).
Перевод единиц измерения (основных и производных)
В таблице представлены: основные единицы СИ (системы интернациональной), производные единицы СИ (механические и тепловые единицы измерения).Соотношение мер вместимости
Соотношение между объемами в миллилитрах, литрах, декалитрах, миллиметрах, сантиметрах, дециметрах и метрах кубических.
Перевод единиц измерения давления кгс/см² и м вод. ст. в единицы СИ
В таблице представлены коэффициенты перевода единиц давления кгс/см² (атм.) и м вод. ст. в паскали, килопаскали и мегапаскали.
Перевод единиц измерения давления мм рт. ст. в единицы СИ
Перевод единиц давления мм рт. ст. в паскали, килопаскали и мегапаскали.
Перевод единиц измерения скорости км/ч в м/с
Перевод единиц скорости в диапазоне от 1 до 1000 км/час.
Перевод единиц измерения объемного расхода м³/ч в л/мин и л/с
Перевод единиц измерения объемного расхода в интервале от 1 до 100 м³/ч.
Часто применяемые постоянные величины (константы)
В таблице приведены значения следующих констант: абсолютный нуль температуры, атмосфера нормальная, коэффициент теплового расширения идеальных газов, скорость звука в сухом воздухе при 0°С, скорость света в пустоте, ускорение свободного падения, механический эквивалент теплоты, отношение длины окружности к ее диаметру (число π), объем грамм-молекулы газа.
Коэффициенты перевода единиц измерения теплопроводности
В таблице представлены основные единицы измерения теплопроводности и их переводные коэффициенты.
Источники:
- Михеев М.А., Михеева И.М. Основы теплопередачи.
- Рудин М.Г., Сомов В.Е., Фомин А.С. Карманный справочник нефтепереработчика. 2004. — 333 с.
| ВЕЛИЧИНА | ОБОЗНАЧЕНИЕ | ОПРЕДЕЛЕНИЕ |
| Ампер | А | Сила тока |
| Ватт | W | Мощность, при которой работа в 1 джоуль совершается за 1 секунду |
| Вебер | Wb | Магнитный поток, при убывании которого до нуля в сцепленном с ним контуре сопротивлением 1 ом протекает количество электричества в 1 кулон |
| Вольт | V | Электрическое напряжение, вызывающее в электрической цепи постоянный ток силой 1 ампер при мощности 1 ватт |
| Время | t | непрерывная величина, априорная характеристика мира, ничем не определяемая.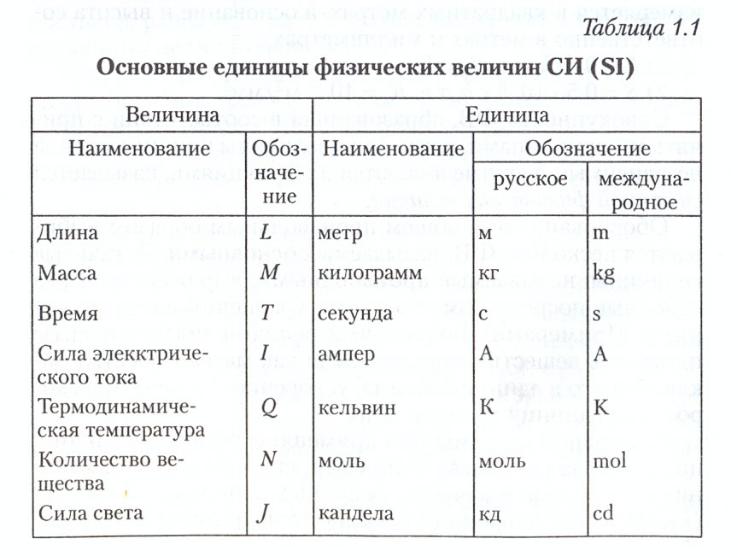 В качестве основы измерения просто берётся некая последовательность событий, про которую считается несомненно верным, что она происходит через равные промежутки времени В качестве основы измерения просто берётся некая последовательность событий, про которую считается несомненно верным, что она происходит через равные промежутки времени |
| Генри | Н | Генри можно определить также как индуктивность электрической цепи, в которой возникает ЭДС в 1 вольт при изменении силы тока в цепи со скоростью 1 ампер в секунду |
| Герц | Нz | Частота периодического процесса, период которого равен 1 секунде |
| Давление | Р | физическая величина, характеризующая состояние сплошной среды и численно равная силе , действующей на единицу площади поверхности перпендикулярно этой поверхности |
| Джоуль | J | Работа, произведенная силой в 1 ньютон при перемещении ею тела на расстояние 1 метр в направлении действия силы |
| Диаметр | d | отрезок, соединяющий две точки) на окружности (сфере, поверхности шара), и проходящий через центр этой окружности (сферы, шара). Также диаметром называют длину этого отрезка. Диаметр окружности является хордой, проходящей через её центр; такая хорда имеет максимальную длину. По величине диаметр равен двум радиусам Также диаметром называют длину этого отрезка. Диаметр окружности является хордой, проходящей через её центр; такая хорда имеет максимальную длину. По величине диаметр равен двум радиусам |
| Диоптрия | δ | Единица для измерения оптической силы сферически-вогнутого стекла, равная оптической силе линзы с фокусным расстоянием 1 метр |
| Длина | L | физическая величина, числовая характеристика протяжённости линий. В узком смысле под длиной понимают размер предмета в продольном направлении (обычно это направление наибольшего размера), т. е. расстояние между его двумя наиболее удалёнными точками, измеренное горизонтально |
| Импульс | Р | мера механического движения; представляет собой векторную величину, в классической механике равную для материальной точки произведению массы m этой точки на её скорость v и направленную так же, как вектор скорости: |
| Индуктивность | L | коэффициент пропорциональности между магнитным потоком (создаваемым током какого-либо витка при отсутствии намагничивающих сред, например, в воздухе) и величиной этого тока |
| Килограмм | kg | Масса платино-иридиевого прототипа, утвержденного международной конференцией в Париже в 1889 г |
| Кулон | с | Количество электричества, проходящее в 1 секунду при силе тока 1 ампер через поперечное сечение проводника |
| Люмен | lm | |
| Люкс | lx | Освещенность поверхности, которая равномерно получает световой поток в 1 люмен на 1 квадратный метр площади |
| Масса | М | одна из важнейших физических величин.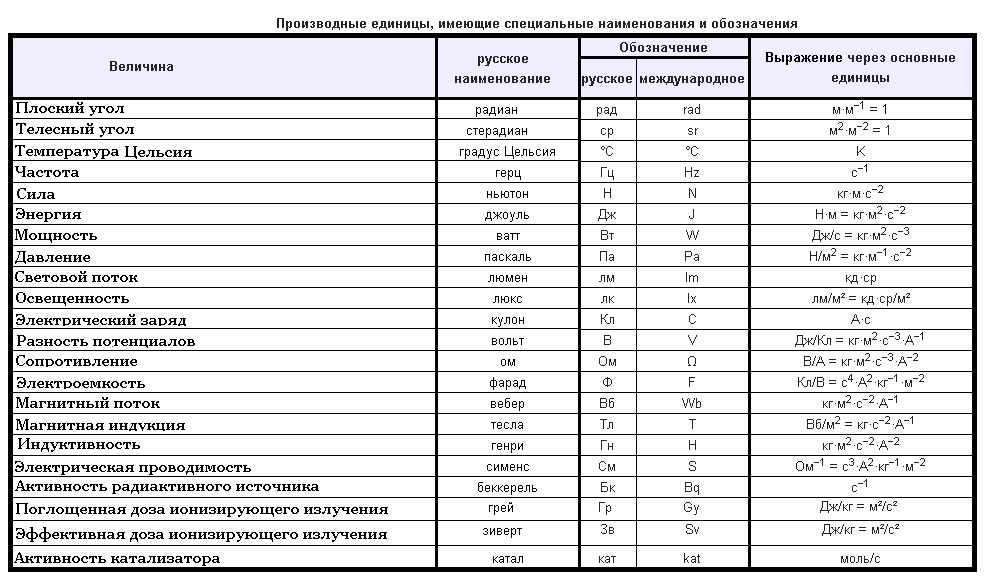 Первоначально (XVII—XIX века) она характеризовала «количество вещества» в физическом объекте, от которого, по представлениям того времени, зависели как способность объекта сопротивляться приложенной силе, так и гравитационные свойства — вес Первоначально (XVII—XIX века) она характеризовала «количество вещества» в физическом объекте, от которого, по представлениям того времени, зависели как способность объекта сопротивляться приложенной силе, так и гравитационные свойства — вес |
| Метр | m | Старый платино-иридиевый эталон метра (международный прототип) хранится в подвалах Севра |
| Метр квадратный | m² | Площадь квадрата, сторона которого равна 1 метру |
| Метр кубический | m³ | Объем куба с длиной ребра, равной 1 метру |
| Метр в секунду | m/s | Скорость движущегося тела, проходящего расстояние в 1 метр за секунду |
| Мощность | Р | физическая величина, равная отношению работы, выполняемой за некоторый промежуток времени, к этому промежутку времени. |
| Ньютон | N | Сила, сообщающая телу массой в 1 килограмм ускорение в 1метр в секунду в направлении действия силы |
| Обьём | m³, cm³, L³ | количественная характеристика пространства, занимаемого телом или веществом.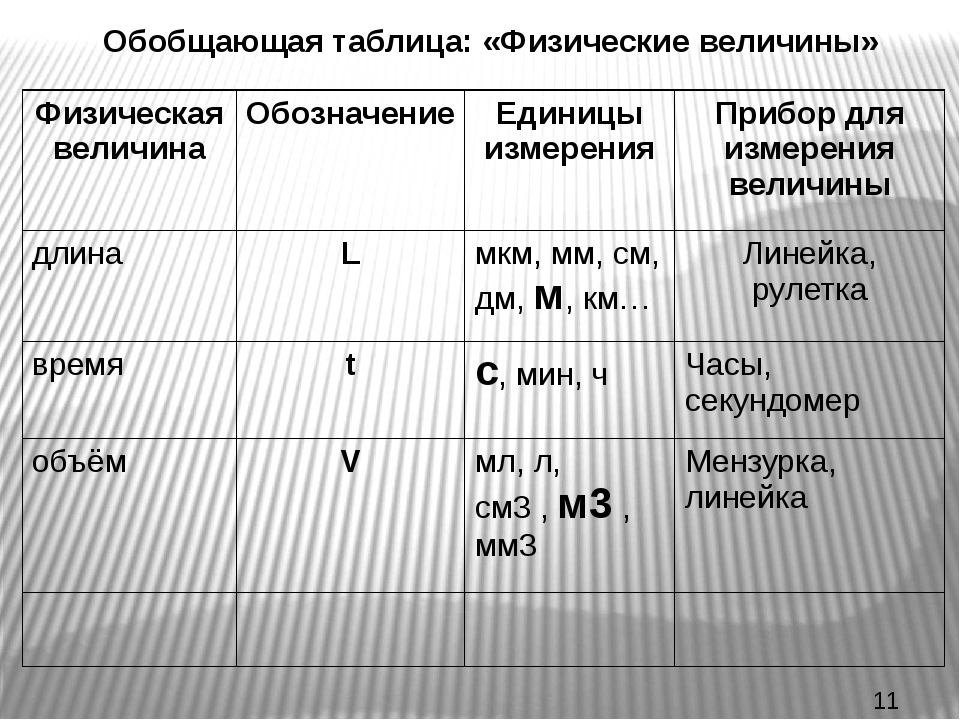 Объём тела или вместимость сосуда определяется его формой и линейными размерами. С понятием объём тесно связано понятие вместимость. Под вместимостью понимают объём внутреннего пространства сосуда или аппарата, укладочных ящиков и т. д Объём тела или вместимость сосуда определяется его формой и линейными размерами. С понятием объём тесно связано понятие вместимость. Под вместимостью понимают объём внутреннего пространства сосуда или аппарата, укладочных ящиков и т. д |
| Ом | Ω | Сопротивление проводника, между концами которого при силе тока 1 ампер возникает напряжение 1 вольт |
| Паскаль | Pa | Давление на 1 квадратный метр с силой в 1 ньютон |
| Площадь | S | Одна из количественных характеристик плоских геометрических фигур и поверхностей |
| Плотность | Р | физическая величина, определяемая для однородного вещества массой его единичного объёма. Для неоднородного вещества плотность в определённой точке вычисляется как предел отношения массы тела (m) к его объёму (V), когда объём стягивается к этой точке |
| Радиус | r | отрезок, соединяющий центр окружности (или сферы) с любой точкой, лежащей на окружности (или поверхности сферы), а также длина этого отрезка |
| Свеча | cd | Свеча — единица силы света, значение которой принимается таким, чтобы яркость полного излучателя при температуре затвердевания платины была равна 60 свечам на один квадратный сантиметр |
| Свеча на м² | cd/м² | Яркость светящейся поверхности площадью в 1 квадратный метр при силе света в 1 свечу |
| Секунда | s | Минута равна 60 секундам, час – 3600 секундам, день — 86400 секундам |
| Сила | F | векторная физическая величина, являющаяся мерой интенсивности взаимодействия тел. Приложенная к массивному телу сила является причиной изменения его скорости или возникновения в нем деформаций Приложенная к массивному телу сила является причиной изменения его скорости или возникновения в нем деформаций |
| Сила света | J | поток излучения, приходящийся на единицу телесного угла, в пределах которого он распространяется |
| Скорость | ύ, u | физическая величина, характеризующая быстроту перемещения и направление движения материальной точки в пространстве относительно выбранной системы отсчёта |
| Сопротивление (электрическое) | R | |
| Температура | °С | физическая величина, примерно характеризующая приходящуюся на одну степень свободы среднюю кинетическую энергию частиц макроскопической системы, находящейся в состоянии термодинамического равновесия. |
| Теплота | Q | мера энергии, переходящей от одного тела к другому в процессе теплопередачи.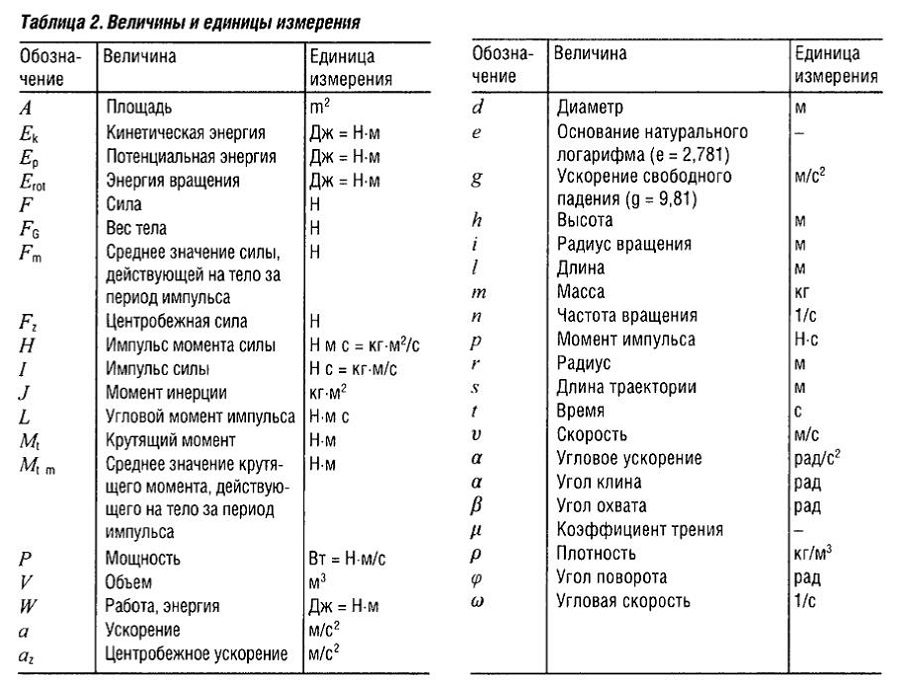 В системе СИ единицей измерения теплоты является джоуль В системе СИ единицей измерения теплоты является джоуль |
| Теплоёмкость | С, Дж/кг | теплоемкостью называется количество теплоты, которое необходимо для нагревания единичного количества вещества |
| Тесла | т | Магнитная индукция, при которой магнитный поток сквозь поперечное сечение площадью 1 квадратный метр равен 1 веберу |
| Ток | I | в проводнике — скалярная величина, численно равная заряду , протекающему в единицу времени через сечение проводника. |
| Частота | F, f, ω | физическая величина, характеристика периодического процесса, равная числу полных циклов, совершённых за единицу времени |
| Фарада | F | Емкость конденсатора, между обкладками которого появляется напряжение в 1 вольт при заряде 1 кулон |
| Энергия | Е | физическая величина, являющаяся единой мерой различных форм движения материи и мерой перехода движения материи из одних форм в другие |
Физические величины, таблицы — Справочник химика 21
Коэффициент теплопроводности.
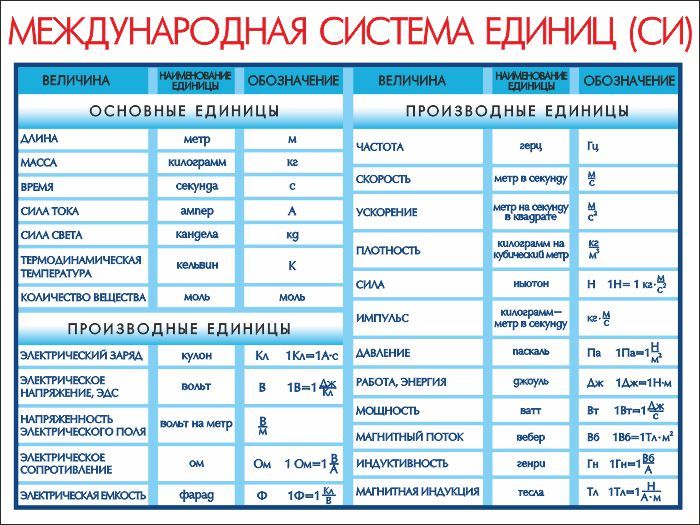 Коэффициент теплопроводности рабочего тела берут из таблиц физических величин при температуре газа 1=1 и). [c.111]
Коэффициент теплопроводности рабочего тела берут из таблиц физических величин при температуре газа 1=1 и). [c.111]Значения коэффициента Я для газов и жидкостей указаны в приложении к книге в таблицах физических величин [c.23]
Соотношения, приведенные в табл. П1-1, позволяют проанализировать влияние выбора граничных условий на результаты определения физической- величины. Если эта величина определяется из решения дифференциального уравнения, то, как видно из таблицы, вид решения может существенно измениться при изменении [c.115]
Соотношения, приведенные в табл. 1У-1, позволяют проанализировать влияние выбора граничных условий на результаты определения физической величины. Если эта величина определяется из решения дифференциального уравнения, то, как видно из таблицы, вид решения может существенно измениться при изменении граничных условий. Однако определяемый из уравнения параметр, как правило, при этом не меняется существенно, если аналитическая запись граничного условия отражает общую физическую картину. Это значит, что для обработки экспериментальных данных можно использовать различные, близкие к физической картине граничные условия. [c.126]
Это значит, что для обработки экспериментальных данных можно использовать различные, близкие к физической картине граничные условия. [c.126]
Для выбора комплексов служит таблица (рис. 6.3), в которую сведены безразмерные комплексы физических величин как для турбин, так и для динамических насосов. Можно использовать также некоторые степени указанных в таблице комплексов или их обратные величины. Их также можно умножить на любое число. Не все комплексы, указанные в таблице, независимые. [c.73]
При математическом моделировании расчеты, как правило, проводятся на вычислительной машине (откуда даже возник термин машинный эксперимент ). В этом случае пользоваться таблицами случайных чисел неудобно, так как они заняли бы много места в памяти ЭВМ, поэтому при расчетах на ЭВМ случайные числа генерируют с помощью специальных датчиков. Датчики бывают двух видов — физические и программные. Физические датчики используют в качестве сигнала какую-нибудь случайно изменяющуюся физическую величину (например, уровень шума в электронной лампе). [c.277]
[c.277]
Единицы измерения всех физических величин выражены в Международной системе единиц (СИ). Таблица перевода единиц измерений приведена ниже. [c.6]
Физические величины, входящие в формулы (УП-38) — (УП-44), берутся из справочных таблиц при так называемой определяющей температуре, которая указывается для каждого частного случая теплообмена, причем различаются средняя температура стенки 4т средняя температура жидкости (газа) — см. формулы (УП-24)—-( 11-28) температура пограничного слоя (пленки) 4 л =0,5 ( ж -1-4, т) [c.557]
Таблица соотношений между некоторыми единицами физических величин, подлежащими изъятию, и единицами СИ [c.311]
С 1 января 1980 г. в СССР в качестве государственного стандарта введен СТ СЭВ 1052—78 Метрология. Единицы физических величин , базирующийся на Международной системе единиц (СИ). В табл. П.1 представлены основные и производные механические и тепловые единицы СИ и соответствующие им единицы других систем. В единицы других систем включены единицы, ранее употреблявшиеся в СССР и неметрические, которые до сих пор применяются в некоторых зарубежных странах. В таблицах даются также соотношения с единицами СИ. В табл. 0.2 представлены электрические, магнитные, световые единицы СИ. [c.433]
В единицы других систем включены единицы, ранее употреблявшиеся в СССР и неметрические, которые до сих пор применяются в некоторых зарубежных странах. В таблицах даются также соотношения с единицами СИ. В табл. 0.2 представлены электрические, магнитные, световые единицы СИ. [c.433]
Пересчет значения физических величин из одних единиц измерения в другие значительно упрощается при наличии специальных таблиц соотношений между единицами измерения [153]. [c.29]
Единицы. Очень важно, чтобы для всех физических величин были приведены единицы, в которых они выражены. ] рафы н таблицах и оси на графиках должны быть выражены в безразмерной форме, например, /г/л моль -с , для величин, приведенных в аналитической форме, должны быть приведены единицы измерения. [c.339]
Составьте сводную таблицу названий и обозначений всех имеющихся в этой главе формульных и эквивалентных физических величин, их математических определений и единиц по следующей форме. [c.48]
[c.48]
Для перевода значений физических величин, встречающихся в книге, в Международную систему (систему СИ) в конце ее помещена таблица с переводными коэффициентами. [c.3]
Некоторые понятия, реакции, методы исследования, индивидуальные соединения описываются ие в самостоятельных, а в более общих статьях. Сведения о них легко найти, пользуясь предметным указателем. В последнем томе читатель найдет также аннотированный именной указатель, содержащий краткие данные об упомянутых в статьях ученых. В начале первого тома приведены справочные материалы по Международной системе единиц (СИ) и таблицы соотношений между этими и внесистемными единицами физических величин. [c.5]
В основе Международной системы единиц (СМ) лежат девять физических величин, приведенных в табл. 40.1. В этой таблице указаны также коэффициенты, используя которые легко переходить из системы СИ в СГС и обратно.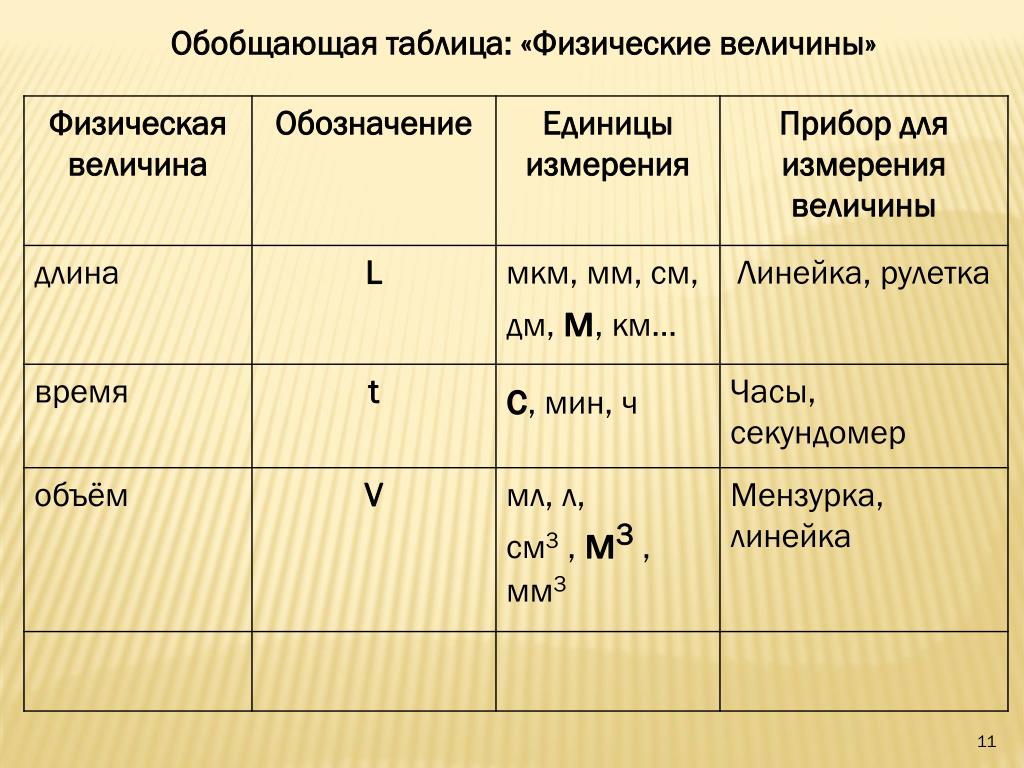 Из этих девяти основных [c.254]
Из этих девяти основных [c.254]
В дальнейшем при ссылке на таблицы физических величин см. приложения. [c.22]
В этом издании сделан важный шаг к использованию единиц СИ (Международной системы единиц). СИ — это тщательно разработанная система единиц, пригодная для выражения всех физических величин и применяемая во всех странах. Но, как ни желательно полностью заменить термохимическую калорию джоулем (единицей СИ для энергии), все же осуществление такой замены в учебнике по физической химии приходится отложить до появления стандартных справочных таблиц в джоулях. В остальном я старался следовать системе СИ по основным единицам, обозначениям и сокращениям. Кроме калории, используются три другие единицы, не входящие в СИ атмосфера (101325 паскалей, т. е. ньютонов на квадратный метр), торр, или миллиметр ртутного столба (1/760 атм), и ангстрем (10 ° м). Международная организация стандартов рекомендовала сохранить еще некоторые внесистемные единицы, имеющие практическое значение или применяемые в специальных областях./177f2936fcd4422.s.siteapi.org/img/2bcde73b465faf7ba4445376e37cae79cd53b88c.jpg) К ним относятся литр (10- м ) и электронвольт (эВ). Дина, эрг и электростатическая единица, входящие в систему СГС (сантиметр — грамм — секунда), в этом издании не используются. [c.6]
К ним относятся литр (10- м ) и электронвольт (эВ). Дина, эрг и электростатическая единица, входящие в систему СГС (сантиметр — грамм — секунда), в этом издании не используются. [c.6]
В настоящем справочном обзоре собраны сведения о физических свойствах водорода в жидком и твердом состояниях. Приведенные в таблицах и на графиках данные представляют собой наиболее достоверные результаты отече-ствениых и зарубежных исследований. Мотивирован выбор и по возможности оценена точность рекомендуемых значений физических величин. Таблиц 58. Иллюстраций 61. Библиография 69 назв. [c.2]
Не.1оп> ст11,мо отделять единит физической величины от числового значения (переносить их на разные строки или страницы), кроме единиц физических величин, П0мешаеуПз1х в- таблицах, выполненных машинописным способом. [c.10]
Физические свойства. Для оценки немеханических колонн таблица содержит две физические величины разность плотностей Ар (в г см или в кг м ), межфазное натяжение а (в дин 1см или в мдж1м ). [c.374]
[c.374]
В табл. 1 — 67 приведены сведения о свойствах некоторых веществ. Во всех таблицах физические величины нри-[ едены в следующих единицах температуры Гь, Т с Tsat в К плотности в кг/м давление Рс, Pg в кПа энтальпии h , /i в кДж/кг теплоемкости p , p g в [c.234]
Результаты расчетов на основе (111.3.23) помещены в той же табл. 111.3.2 (более широкая таблица в /80/ и /81/), среднее квадратичное отклоншие составляет 0,8%. Большие возможности, открываемые приведенными соотношениями, делают скорость звука рекорд-смшом по информативности среди других физических величин. Это утверждение справедливо не только для углеводородов, но и для всего класса нормальных веществ и отчасти для ассоциированных соединений, [c.47]
Программы больших задач математической физики часто используют для своей работы большие поля начальных данных, многие программы нснользуются один и те же таблицы некоторых физических величин или обрабатывают данные физических экспериментов, проводят сравнения физических и вычислительных экс- [c. 268]
268]
Перельман В. И. Краткий справочник химика. — М. Госхимн -дат, 19( )2 (очень iio.iuio обобщены в таблицах данные о химических реактивах, а также приведе1гы таблицы физических величин н другие сведения). [c.181]
В тех случаях, когда новые работы или работы, не учтенные в шести выпусках справочника Физико-химические свойства индивидуальных углеводородов , потребовали исправлепия значений той или другой физической величины для каких-либо углеводородов, такое исправление было сделано. В соответствующих таблицах приводятся ссылки на работы, послужившие основанием для такого пересмотра, исправления или дополнения. Для общей характеристики качества данных (степени их точности) следует отметить, что в Справочнике помещены только те экспериментальные (отобранные) значения, которые получены в работах с достаточно чистыми углеводородами и достаточно точной методикой измерений. Данные экспериментальных работ, проведенных на углеводородах недостаточной (или неизвестной) чистоты, не учитывались, так же как и данные работ, в которых применялись недостаточно точные методы измерений или не была достаточно подробно описана методика измерений. [c.5]
[c.5]
В Международных таблицах физических констант (International riti al Tables), представляющих собой подробную сводку всякого рода химических и физических величин, есть таблица пороговых концентраций запахов разных веществ. Все приведенные в таблице значения этих пороговых концентраций оказались заниженными в 100 раз. Почти наверняка эта ошибка чисто случайно проскользнула мимо внимания человека, хорошо знающего предмет, но странно то, что, хотя таблицы были опубликованы в 1926 г., до 1953 г. этого никто не заметил. [c.125]
Таблица Физические величины и фундаментальные константы (винил)
Цена
Артикул:
Текст:
Выберите категорию:
Все
ДОСКИ АУДИТОРНЫЕ, МОЛЬБЕРТЫ И ПРИНАДЛЕЖНОСТИ
» Доски аудиторные
»» Одноэлементные
»» Трехэлементные
»» Пятиэлементные
»» Напольно — поворотные доски
»» Мольберты
»»» Односторонние
»»» Двухсторонние
»» Доски для объявлений (пробковые)
» Классные инструменты
УЧЕНИЧЕСКАЯ МЕБЕЛЬ
» Мебель для учебных классов и аудиторий
»» Столы ученические
»»» Столы двухместные нерегулируемые
»»» Столы двухместные регулируемые
»»» Столы одноместные нерегулируемые
»»» Столы одноместные регулируемые
»» Столы преподавателей, руководителей
»»» Столы преподователя
»»» Столы руководителя
»» Стулья
»»» Стулья нерегулируемые
»»» Стулья регулируемые
»» Шкафы
»»» Шкаф для журналов
»»» Шкаф с выдвижными полками
»»» Шкаф стеллаж
»»» Шкаф тумба
»»» Шкафы для одежды
»»» Шкафы для учебных пособий
» Мебель для специализиованных классов
»» Мебель для кабинета трудового обучения
»»» Верстаки слесарные
»»» Верстаки столярные
»»» Верстаки комбинированные
»»» Табуреты
»»» Защитные перегородки
»» Мебель для кабинета физики
»»» Столы демонстрационные
»»» Столы лабораторные
»»» Зоны демонстрационные
»» Мебель для кабинета химии
»»» Вытяжные шкафы
»»» Зоны демонстрационные
»»» Столы демонстрационные
»»» Столы лабораторные
»»» Столы лаборантские
»»» Тумбы-мойки
»» Мебель для кабинета черчения и рисования
»»» Столы для черчения
»» Мебель для компьютерного класса
»»» Столы компьютерные
»» Мебель для лингафонного кабинета
»»» Столы для лингафонного кабинета
»» Мебель для логопеда
»»» Столы для логопеда
»» Мебель для спортивного зала
»»» Теннисные столы
» Мебель для столовой
»» Столы обеденные для столовой
»» Табуреты для столовой
» Мебель для библиотеки
»» Стол аудиторный
»» Стол-барьер
»» Шкафы
» Мебель для актового зала
»» Блоки стульев
»»» Неоткидные
»»» Откидные
»»» С пюпитрами
»» Подставка-кафедра для актовых залов
» Мебель для гардеробов и холлов
»» Банкетки для гардеробных
»» Вешалки напольные для гардеробных
»» Настенные вешалки для гардеробных
» Кровати и прикроватные тумбы
»» Кровати
»» Тумбы прикроватные
ДЕТСКАЯ МЕБЕЛЬ
» Столы
» Стульчики
» Дидактические столы и стеллажи
» Детские стенки
» Игровая мебель
» В кабинет естествознания
» Для приема пищи
» Для спален
» Для ИЗО, мольберты
» Для туалетной комнаты
ЕСТЕСТВЕННЫЕ НАУКИ
» ФИЗИКА
»» Электричество. Электродинамика и оптика
»» Механика
»» Механические колебания и волны
»» Модели
»» Молекулярная физика и термодинамика
»» Приборы и принадлежности общего назначения
»» Приборы лабораторные
»» Технические средства обучения
»» Комплекты ГИА по физике
»» ГИА лаборатории по физике
» ХИМИЯ
»» Демонстрационные приборы
»» Коллекции
»» Модели
»» Приборы для лабораторных и практических работ
»» Приборы общего назначения
»» Специализированные приборы
»» Технические средства обучения
» БИОЛОГИЯ
»» Гербарии
»» Коллекции
»» Микропрепараты
»» Модели объемные
»» Модели остеологические (скелеты)
»» Муляжи
»» Приборы лабораторные
Электродинамика и оптика
»» Механика
»» Механические колебания и волны
»» Модели
»» Молекулярная физика и термодинамика
»» Приборы и принадлежности общего назначения
»» Приборы лабораторные
»» Технические средства обучения
»» Комплекты ГИА по физике
»» ГИА лаборатории по физике
» ХИМИЯ
»» Демонстрационные приборы
»» Коллекции
»» Модели
»» Приборы для лабораторных и практических работ
»» Приборы общего назначения
»» Специализированные приборы
»» Технические средства обучения
» БИОЛОГИЯ
»» Гербарии
»» Коллекции
»» Микропрепараты
»» Модели объемные
»» Модели остеологические (скелеты)
»» Муляжи
»» Приборы лабораторные
Производитель: ВсеСветочтестовый произодительШкольный мир
Новинка: Вседанет
Спецпредложение: Вседанет
Результатов на странице: 5203550658095
Найти
| | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Алфавиты, номиналы, единицы / / Перевод единиц измерения величин. Перевод единиц измерения физических величин. Таблицы перевода единиц величин. Перевод химических и технических единиц измерения величин. Величины измерения. Таблицы соответствия величин. Поделиться:
| ||
| Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. Вложите в письмо ссылку на страницу с ошибкой, пожалуйста. | |||
Коды баннеров проекта DPVA. ru ruНачинка: KJR Publisiers Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator | ||
| ЗАДАЧНИК ОНЛ@ЙН БИБЛИОТЕКА 1 БИБЛИОТЕКА 2 Античные учёные, за редким исключением, считали скорость света бесконечной. В Новое время этот вопрос стал предметом дискуссий. Галилей и Гук допускали, что она конечна, хотя и очень велика, в то время как Кеплер, Декарт и Ферма по-прежнему отстаивали бесконечность скорости света. Спустя полвека открытие аберрации позволило подтвердить конечность скорости света и уточнить её оценку.
Наиболее точное измерение скорости света 299 792 458 ± 1,2 м/с на основе эталонного метра было проведено в 1975 году. На данный момент считают, что скорость света в вакууме — фундаментальная физическая постоянная, по определению, точно равная 299 792 458 м/с, или 1 079 252 848,8 км/ч. Точность значения связана с тем, что с 1983 года метр в Международной системе единиц (СИ) определён, как расстояние, которое проходит свет в вакууме за промежуток времени, равный 1 / 299 792 458 секунды[3]. Для решения школьных задач и разного рода оценок, не требующих большой точности, обычно используют значение 300 000 000 м/с (3×108 м/с). | Таблица физических постоянных
.  .. .. |
физических величин и единиц | Физика
Предположим, вы проезжаете 10,0 км от университета до дома за 20,0 мин. Вычислите свою среднюю скорость (a) в километрах в час (км / ч) и (b) в метрах в секунду (м / с). (Примечание: средняя скорость — это расстояние, разделенное на время в пути.)
СтратегияСначала мы вычисляем среднюю скорость с использованием данных единиц. Затем мы можем получить среднюю скорость в желаемых единицах, выбрав правильный коэффициент преобразования и умножив на него.Правильный коэффициент преобразования — это тот, который отменяет ненужную единицу и оставляет желаемую единицу на своем месте.
Решение для (а) (1) Рассчитайте среднюю скорость. Средняя скорость — это расстояние, разделенное на время в пути. (Пока принимайте это определение как данность — средняя скорость и другие концепции движения будут рассмотрены в следующем модуле. ) В форме уравнения,
) В форме уравнения,
[латекс] \ text {средняя скорость =} \ frac {\ text {расстояние}} {\ text {time}} [/ latex].
(2) Подставьте указанные значения для расстояния и времени.
[латекс] \ text {средняя скорость =} \ frac {\ text {10} \ text {.} 0 \ text {km}} {\ text {20} \ text {.} 0 \ text {min}} = 0 \ text {.} \ Text {500} \ frac {\ text {km}} {\ text {min}} [/ latex].
(3) Преобразование км / мин в км / ч: умножьте на коэффициент преобразования, который отменит минуты и оставит часы. Этот коэффициент преобразования составляет 60 мин / час. Таким образом,
[латекс] \ text {средняя скорость =} 0 \ text {.} \ Text {500} \ frac {\ text {km}} {\ text {min}} \ times \ frac {\ text {60} \ text {min}} {1 \ text {h}} = \ text {30} \ text {.} 0 \ frac {\ text {km}} {\ text {h}} [/ latex].
Обсуждение для (а)Чтобы проверить свой ответ, примите во внимание следующее:
(1) Убедитесь, что вы правильно отменили единицы при преобразовании единиц. {2}} [/ latex],
{2}} [/ latex],
, что явно не является желаемой единицей измерения км / ч.
(2) Убедитесь, что единицы окончательного ответа — это желаемые единицы. Задача попросила нас решить для средней скорости в единицах км / ч, и мы действительно получили эти единицы.
(3) Проверьте значащие цифры. Поскольку каждое из значений, приведенных в задаче, состоит из трех значащих цифр, ответ также должен состоять из трех значащих цифр. Ответ 30,0 км / ч действительно состоит из трех значащих цифр, так что это уместно. Обратите внимание, что значащие цифры в коэффициенте преобразования не имеют значения, потому что час равен , а — 60 минутам, поэтому точность коэффициента преобразования идеальна.
(4) Затем проверьте, обоснован ли ответ. Давайте рассмотрим некоторую информацию из проблемы: если вы проехали 10 км за треть часа (20 минут), вы бы проехали в три раза больше за час. Ответ кажется разумным.
Решение для (b) Есть несколько способов перевести среднюю скорость в метры в секунду.
(1) Начните с ответа на вопрос (а) и преобразуйте км / ч в м / с. Требуются два коэффициента преобразования: один для преобразования часов в секунды, а другой для преобразования километров в метры.
(2) Умножение на эти дает
[латекс] \ text {Средняя скорость} = \ text {30} \ text {.} 0 \ frac {\ text {km}} {\ text {h}} \ times \ frac {1 \ text {h}} {\ text {3,600 с}} \ times \ frac {1, \ text {000} \ text {m}} {\ text {1 км}} [/ latex],
[латекс] \ text {Средняя скорость} = 8 \ text {.} \ Text {33} \ frac {\ text {m}} {\ text {s}} [/ latex].
Обсуждение для (б)Если бы мы начали с 0,500 км / мин, нам потребовались бы другие коэффициенты пересчета, но ответ был бы тот же: 8.33 м / с.
Для
простота понимания и удобство, даны 22 производные единицы СИ
специальные имена и символы, как показано в таблице 3.
Примечание о градусах Цельсия. Производная единица в таблице 3 со специальным названием градус Цельсия и
специальный символ ° C заслуживает комментария. Из-за температуры
шкалы, которые раньше определялись, остается обычной практикой выражать термодинамические
температура, условное обозначение T , в части отличия от эталонной
температура Т 0 = 273,15 К, ледяная точка. т = т — т 0 . Единицей измерения температуры по Цельсию является градус Цельсия, символ ° C. В числовое значение температуры Цельсия t , выраженное в градусах Цельсия — t / ° C = T / K — 273,15. Из определения t следует, что градус Цельсия равен
по величине до кельвина, что, в свою очередь, означает, что числовой
значение заданной разницы температур или температурного интервала,
значение выражается в единицах градуса Цельсия (° C) равно
числовое значение той же разницы или интервала, когда его значение равно
выражается в единицах кельвина (К).Таким образом, перепады температур или температура
интервалы могут быть выражены либо в градусах Цельсия, либо в кельвинах. Специальные названия и символы 22 производных единиц СИ со специальными названиями и символами приведенные в таблице 3, сами могут быть включены в названия и символы другие производные единицы СИ, как показано в таблице 4.
Продолжить до префиксов SI | ||||
Физические величины и единицы СИ
Обзор
Международная система единиц (сокращенно единиц СИ от французского названия Système International d’unités) — это международно согласованная метрическая система единиц измерения, которая существует с 1960 года. История метра и килограмма, двух основных единиц, на которых основана система, уходит корнями во времена Французской революции. Сама система основана на концепции семи основных базовых единиц количества, из которых могут быть выведены все остальные единицы количества. После окончания Второй мировой войны становилось все более очевидным, что всемирная система измерения необходима, чтобы заменить многочисленные и разнообразные системы измерений, которые использовались в то время. В 1954 году 10 -я Генеральная конференция по мерам и весам , руководствуясь результатами более раннего исследования, предложила систему, основанную на шести основных величинах.Рекомендованные количества были: метров , килограммов , секунд , ампер , кельвинов и кандел .
История метра и килограмма, двух основных единиц, на которых основана система, уходит корнями во времена Французской революции. Сама система основана на концепции семи основных базовых единиц количества, из которых могут быть выведены все остальные единицы количества. После окончания Второй мировой войны становилось все более очевидным, что всемирная система измерения необходима, чтобы заменить многочисленные и разнообразные системы измерений, которые использовались в то время. В 1954 году 10 -я Генеральная конференция по мерам и весам , руководствуясь результатами более раннего исследования, предложила систему, основанную на шести основных величинах.Рекомендованные количества были: метров , килограммов , секунд , ампер , кельвинов и кандел .
Генеральная конференция по мерам и весам (сокращенно CGPM от французского названия Conférence Générale des Poids et Mesures ), первая из которых состоялась в 1889 году, проводится каждые несколько лет с 1897 года в Севре, недалеко от Парижа. .Следуя предложениям 1954 года, конференция 1960 года (11 -й CGPM) представила миру новую систему.
.Следуя предложениям 1954 года, конференция 1960 года (11 -й CGPM) представила миру новую систему.
Седьмой базовый блок, моль , был добавлен после 14 -го CGPM, который состоялся в 1971 году. Официальное описание системы под названием SI Brochure впервые опубликовано в 1970 году и в настоящее время (по состоянию на 2019 год) его девятое издание можно бесплатно загрузить с веб-сайта Bureau International des Poids et Mesures (BIPM).Брошюра написана и поддерживается подкомитетом Международного комитета мер и весов (сокращенно CIPM от французского названия — Comité International des Poids et Mesures ). Соответствующий международный стандарт — ISO / IEC 80000 .
Роль BIPM включает установление стандартов для основных физических величин и поддержание международных прототипов.Его работа включает в себя метрологических исследований (метрология — это наука об измерениях), проведение сравнений международных прототипов для целей проверки и калибровку эталонов. Работа BIPM контролируется CIPM, который, в свою очередь, подотчетен CGPM. В настоящее время Генеральная конференция собирается каждые четыре года для утверждения новых стандартов и резолюций, а также для согласования финансовых, организационных вопросов и вопросов развития.
Работа BIPM контролируется CIPM, который, в свою очередь, подотчетен CGPM. В настоящее время Генеральная конференция собирается каждые четыре года для утверждения новых стандартов и резолюций, а также для согласования финансовых, организационных вопросов и вопросов развития.
Основные величины и единицы СИ
Значение физической величины обычно выражается как произведение числа и единицы .В прошлом (а в некоторых случаях вплоть до самого недавнего времени) устройство представляло конкретный пример или прототип соответствующей величины, которая использовалась в качестве ориентира. Число представляет отношение значения количества к единице.
По состоянию на 2019 год все базовые единицы теперь определены со ссылкой на семь «определяющих» физических констант, которые включают фундаментальные константы природы, такие как постоянная Планка и скорость света. Самые последние изменения произошли с публикацией девятого издания брошюры СИ в 2019 году. Четыре базовых единицы — килограмм , ампер , кельвин и моль — были переопределены с использованием физических констант. секунд , метров и кандела , уже определенные с использованием физических констант, были исправлены.
Самые последние изменения произошли с публикацией девятого издания брошюры СИ в 2019 году. Четыре базовых единицы — килограмм , ампер , кельвин и моль — были переопределены с использованием физических констант. секунд , метров и кандела , уже определенные с использованием физических констант, были исправлены.
Например, килограмм был ранее определен со ссылкой на прототип.Рассматриваемый прототип представлял собой платино-иридиевый цилиндр, который в строго контролируемых условиях содержался в хранилище BIPM, идентичные копии которого хранятся в идентичных условиях по всему миру. Количество два килограмма (2 кг) было бы определено как ровно вдвое больше массы прототипа или одного из его экземпляров. Однако теперь, согласно версии SI Brochure 2019 года:
«Килограмм (символ кг) — это единица массы в системе СИ.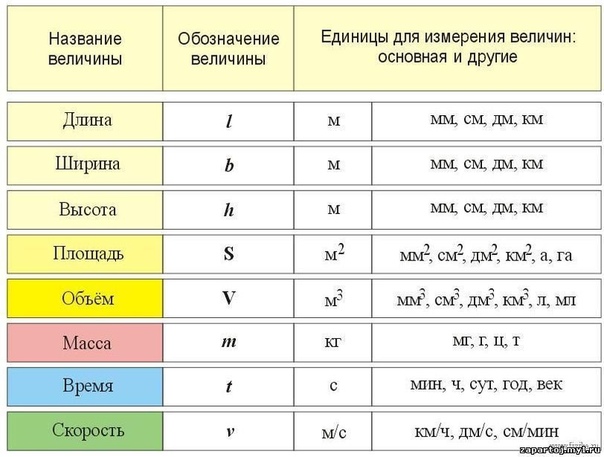 Он определяется путем принятия фиксированного числового значения постоянной Планка h равным 6,626070 15 × 10 −34 при выражении в единицах Дж с, что равно кг · м 2 с −1 , где метр и второй определены в терминах c и Δν Cs «.
Он определяется путем принятия фиксированного числового значения постоянной Планка h равным 6,626070 15 × 10 −34 при выражении в единицах Дж с, что равно кг · м 2 с −1 , где метр и второй определены в терминах c и Δν Cs «.
Также в соответствии с изданием SI Brochure 2019 года семь определяющих физических констант, используемых для определения единиц СИ:
«.. . выбираются таким образом, что любая единица СИ может быть записана либо через саму определяющую константу, либо через произведения или частные определяющих констант ».
Семь определяющих констант, используемых для определения единиц СИ:
- Частота невозмущенного сверхтонкого перехода в основное состояние атома цезия 133 , Δ ν Cs , составляет 9 192 631 770 Гц
- Скорость света в вакууме, c , составляет 299 792 458 м / с
- Постоянная Планка ч равна 6.
 626070 15 × 10 −34 Дж с
626070 15 × 10 −34 Дж с - Элементарный заряд e равен 1,602 176 634 × 10 −19 C
- Постоянная Больцмана k составляет 1,380 649 × 10 −23 Дж / К
- Константа Авогадро N A равна 6.022 140 76 × 10 23 моль -1
- Световая отдача монохроматического излучения частотой 540 × 10 12 Гц, К кд , составляет 683 лм / Вт
где, согласно брошюре SI, герц , джоулей , кулонов , люмен и ватт , с символами единиц измерения Гц, Дж, С, лм и Вт, соответственно, относятся к единицы секунда , метр , килограмм , ампер , кельвин , моль и кандела , с символами единиц измерения s, m, kg, A, K, mol и cd, соответственно, согласно Hz = s –1 , J = кг м 2 s –2 , C = A s, lm = cd m 2 m –2 = cd sr, и W = кг м 2 с –3 .
В Международной системе единиц используются семь базовых величин. Семь базовых величин и соответствующие им единицы:
- время (секунды)
- длина (метр)
- Масса (килограмм)
- электрический ток (ампер)
- термодинамическая температура (кельвин)
- количество вещества (моль)
- сила света (кандела)
Предполагается, что эти базовые количества равны независимым единицам.Другими словами, базовое количество не нужно определять в терминах какого-либо другого базового количества (или количеств). Однако обратите внимание, что хотя сами базовые величины считаются независимыми, их соответствующие базовые единицы в некоторых случаях зависят друг от друга. Например, метр определяется как длина пути, пройденного светом в вакууме за промежуток времени 1/299 792 458 из секунд .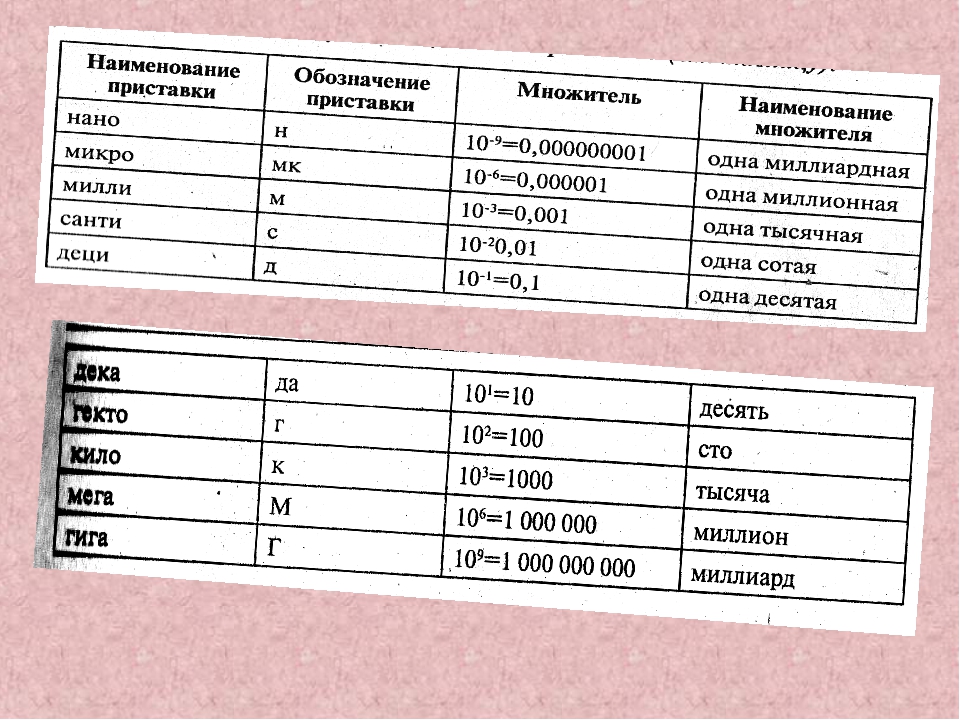
В таблице ниже приведены базовые количества и их единицы.Вы могли заметить, что аномалия возникает в отношении килограмма (единица массы ). Килограмм — единственная базовая единица СИ, название и символ которой включают префикс. Вы должны знать, что кратные и подмножественные единицы этой единицы образуются путем присоединения соответствующего имени префикса к названию единицы грамм и соответствующего символа префикса к символу единицы g . Например, одна миллионная килограмма — это один миллиграмм (1 мг), а не один микрокилограмм (1 мкг).
| Кол-во | Сим. | Блок | Блок Сим. | Определение единицы | |
|---|---|---|---|---|---|
| время | t | секунда | с | Продолжительность 9 192 631 770 периодов излучения, соответствующих переходу между двумя сверхтонкими уровнями основного состояния атом цезия 133 | |
| длина | л | метр | м | Длина пути, пройденного светом в вакууме за промежуток времени длительностью 1/299 792 458 секунды | |
| масса | м | килограмм | кг | Килограмм определяется путем принятия фиксированного числового значения постоянной Планка h равным 6. 626070 15 × 10 −34 при выражении в единицах Дж с, что равно кг м2 с −1 , где счетчик и секунда определены в терминах c и Δ ν Cs . 626070 15 × 10 −34 при выражении в единицах Дж с, что равно кг м2 с −1 , где счетчик и секунда определены в терминах c и Δ ν Cs .Ранее предложенное определение, эквивалентное приведенному выше, описывает килограмм как массу тела в состоянии покоя, эквивалентная энергия которого равна энергии набора фотонов, чьи частоты в сумме составляют [1,3563 | 652 × 10 50 ] герц. |
| электрический ток | I | ампер | A | Электрический ток, соответствующий потоку 1 / (1.602 176 634 × 10 −19 ) элементарных зарядов в секунду | |
| термодинамическая температура | T | кельвин | K | Изменение термодинамической температуры, которое приводит к изменению тепловой энергии кТ на 1,380 649 × 10 −23 J | |
| количество из вещества | n | моль | моль | Количество вещества в системе, содержащей 6. 022 140 76 × 10 23 заданных элементарных объектов (элементарные объекты могут быть атомами, молекулами, ионами, электронами, другими частицами или заданными группами таких частиц) 022 140 76 × 10 23 заданных элементарных объектов (элементарные объекты могут быть атомами, молекулами, ионами, электронами, другими частицами или заданными группами таких частиц) | |
| яркость интенсивность | I v | candela | cd | Сила света в заданном направлении источника, который испускает монохроматическое излучение с частотой 540 × 10 12 Гц и имеет силу излучения в этом направлении 1/683 Вт на стеридиан |
Размеры количеств
Как указывалось ранее, каждая из производных единиц количества, определенных Международной системой единиц, определяется как произведение степеней основных единиц.Считается, что каждая базовая величина имеет свой собственный размер , который представлен с использованием символа верхнего регистра, напечатанного римским шрифтом без засечек. Считается, что производные величины имеют размерности, которые могут быть выражены как произведение степеней размерностей базовых величин, из которых они получены. Таким образом, размер любой величины Q записывается как:
Считается, что производные величины имеют размерности, которые могут быть выражены как произведение степеней размерностей базовых величин, из которых они получены. Таким образом, размер любой величины Q записывается как:
dim Q = L α M β T λ I δ Θ ε N ζ J η
Символы верхнего регистра L, M, T, I, Θ, N и J (Θ — греческий символ верхнего регистра Theta ) представляют размеры основных величин длина , масса , время , электрический ток , термодинамическая температура , количество вещества и сила света соответственно.Надстрочные символы — это первые семь строчных букв греческого алфавита ( альфа , бета , лямбда , дельта , эпсилон , дзета и эта ) и представляют собой целые числа, называемые размерный показатель . Значения размерных показателей могут быть положительными, отрицательными или нулевыми. Размерность производной величины по существу передает ту же информацию о взаимосвязи между производными величинами и базовыми величинами, из которых они получены, как символ единицы СИ для производной величины.
Значения размерных показателей могут быть положительными, отрицательными или нулевыми. Размерность производной величины по существу передает ту же информацию о взаимосвязи между производными величинами и базовыми величинами, из которых они получены, как символ единицы СИ для производной величины.
В некоторых случаях все показатели размерности равны нулю (как, например, в случае, когда величина определяется как отношение двух величин одного вида). Такие количества называются безразмерными или размерностью один . Связной производной единицей для такой величины (как отношения двух идентичных единиц) является число и . Тот же принцип применяется к количествам, которые не могут быть выражены в основных единицах, например, число молекул , что по сути является просто результатом подсчета.Эти величины также считаются безразмерными или имеющими размерность один. Большинство безразмерных величин просто выражаются числами. Исключения включают радиан и стерадиан , используемые для выражения значений плоских углов и телесных углов соответственно. Еще одно заметное исключение — это децибел , описанное выше.
Исключения включают радиан и стерадиан , используемые для выражения значений плоских углов и телесных углов соответственно. Еще одно заметное исключение — это децибел , описанное выше.
Производные единицы
Все производных единиц количества, идентифицированные Международной системой единиц, определяются как произведений мощности основных единиц.Таким образом, производная величина может быть выражена через одну или несколько основных величин в форме алгебраического выражения. Производные единицы, которые являются производными мощностей основных единиц, которые не включают числовой коэффициент, отличный от на , называются когерентными производными единицами . Это означает, что они выводятся исключительно с использованием произведений или частных целых степеней основных величин, и что никакой другой числовой коэффициент, кроме единицы, не используется.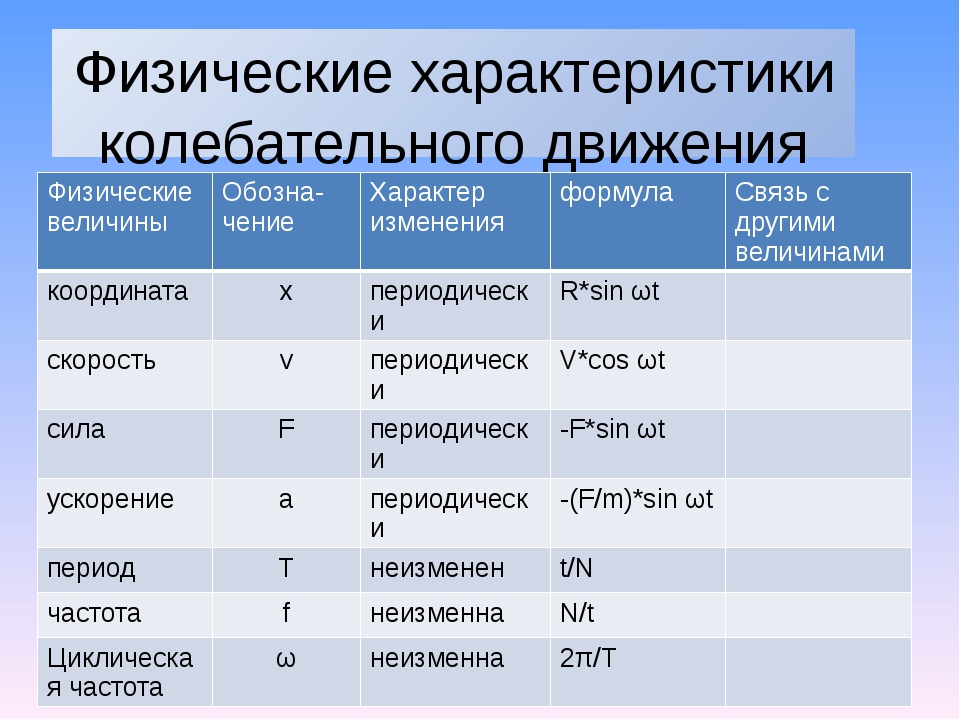
Семь базовых единиц и двадцать две когерентных производных единицы СИ образуют когерентный набор из двадцати девяти единиц, который называется набором когерентных единиц СИ .Все другие единицы СИ являются комбинациями некоторых из этих двадцати девяти единиц. Слово «когерентный» в этом контексте означает, что уравнения между числовыми значениями величин находятся в точно такой же форме, как и соответствующие уравнения между самими величинами.
У двадцати двух связанных производных единиц есть специальные имена и символы. Часто выбранное имя отражает вклад конкретного ученого. Единица силы ( ньютон ) названа в честь сэра Исаака Ньютона , одного из крупнейших авторов в области классической механики.Устройство давления ( паскаль ) названо в честь Блеза Паскаля за его работу в области гидродинамики и гидростатики. В таблице ниже перечислены когерентные производные единицы. Обратите внимание, что каждая единица, названная в таблице ниже, имеет свой собственный символ, но может быть определена в терминах других производных единиц или в терминах основных единиц СИ, как показано в последних двух столбцах.
Обратите внимание, что каждая единица, названная в таблице ниже, имеет свой собственный символ, но может быть определена в терминах других производных единиц или в терминах основных единиц СИ, как показано в последних двух столбцах.
| Кол-во | Единица | Обозначение единицы | Базовая единица | Прочие единицы | |
|---|---|---|---|---|---|
| плоский угол | радиан | рад | м / м | — | |
| телесный угол | телесный угол | sr | m 2 / m 2 | — | |
| частота | Гц | Гц | s -1 | — | |
| ton force | new | кг мс -2 | — | ||
| давление, напряжение | паскаль | Па | кг м -1 с -2 | — | |
| энергия, работа, количество тепла | джоуль | Дж | кг · м 2 с -2 | Н · м | |
| мощность, лучистый поток | 90 109 ВтВт | кг м 2 с -3 | Дж / с | ||
| электрический заряд, количество электричества | кулон | C | A s | — | |
| разность электрических потенциалов, ЭДС | В | В | кг м 2 с -3 A -1 | Вт / А | |
| емкость | фарад | F | кг -1 м -2 с 4 A 2 | C / V | |
| электрическое сопротивление | Ом | Ом | кг м 2 с -3 A -2 | В / А | |
| Электропроводность | siemens | S | кг -1 м -2 с 3 А 2 | А / В | |
| магнитный поток | weber | Wb | кг м 2 с -2 A -1 | В с | |
| плотность магнитного потока | тесла | T | кг с -2 A -1 | Вб / м 2 | |
| индуктивность | Генри | H | кг м 2 с -2 A -2 | Wb / A | |
| Температура | градусов Цельсия | ° C | K | — | |
| световой поток | люмен | лм | cd sr | cd sr | |
| освещенность | lx | lx | -2лм / м 2 | ||
| активность радионуклида | беккерель | Бк | с -1 | — | |
| поглощенная доза, удельная энергия (переданная), керма | серый | Гр | м 2 с -2 | Дж / кг | |
| эквивалент дозы, амбиентный эквивалент дозы, направленный эквивалент дозы , эквивалент индивидуальной дозы | зиверт | Зв | м 2 с -2 | Дж / кг | |
| каталитическая активность | катал | кат | моль с -1 |
Обратите внимание, что единицы для плоского угла и телесного угла ( радиан и стерадиан соответственно) получаются как частное от двух идентичных базовых единиц СИ. Таким образом, говорят, что у них есть единицы и (1). Они описываются как безразмерных единиц или единиц размерности один (концепция размера была описана выше).
Таким образом, говорят, что у них есть единицы и (1). Они описываются как безразмерных единиц или единиц размерности один (концепция размера была описана выше).
Обратите внимание, что разница температур в один градус Цельсия имеет точно такое же значение, что и разница температур в один градус Цельсия . Температурная шкала Цельсия обычно используется для повседневных ненаучных целей, таких как прогноз погоды или для определения температуры, при которой следует хранить продукты питания и лекарства.В таком контексте она имеет большее значение для представителя общественности, чем шкала температуры Кельвина.
Единицы согласованного набора можно комбинировать, чтобы выразить единицы других производных величин. Поскольку это позволяет потенциально неограниченное количество комбинаций, перечислить их все здесь невозможно. В таблице ниже приведены некоторые примеры производных величин вместе с соответствующими согласованными производными единицами, выраженными в базовых единицах.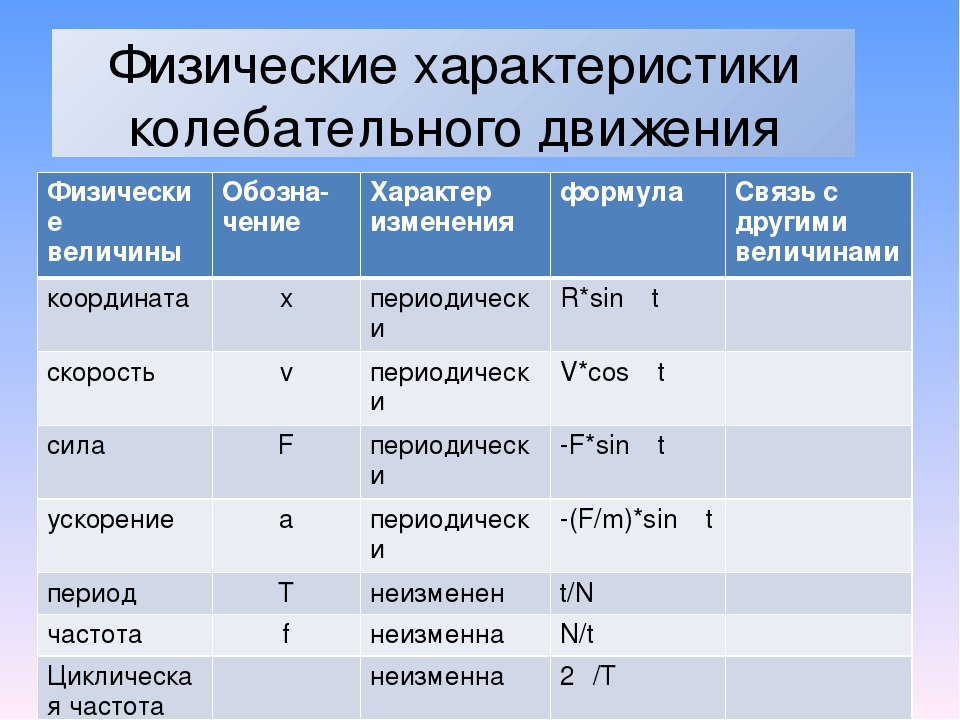
| Кол-во | Сим. | Блок | Блок Сим. | |||
|---|---|---|---|---|---|---|
| площадь | A | квадратный метр | м 2 | |||
| объем | V | кубический метр | м 3 | скоростьv | метр в секунду | мс -1 |
| ускорение | a | метр в секунду в квадрате | мс -2 | |||
| волновое число | 907 | 907 | обратный метр | м -1 | ||
| плотность, массовая плотность | ρ | килограмм на кубический метр | кг м -3 | |||
| поверхностная плотность | ρ A | килограмм на квадратный метр | кг м -2 | |||
| удельный v olume | v | кубических метров на килограмм | м 3 кг -1 | |||
| плотность тока | j | ампер на квадратный метр | A м -2 | |||
| Напряженность магнитного поля | H | ампер на метр | А м -1 | |||
| количество концентрации вещества | c | моль на кубический метр | моль м -3 | |||
| массовая концентрация | ρ , γ | килограмм на кубический метр | кг м -3 | |||
| яркость | L v | кандела109 cd70 -2 |
Примеры когерентных производных единиц СИ, показанные в таблице ниже, основаны на комбинации производных единиц со специальными названиями и базовых единиц СИ.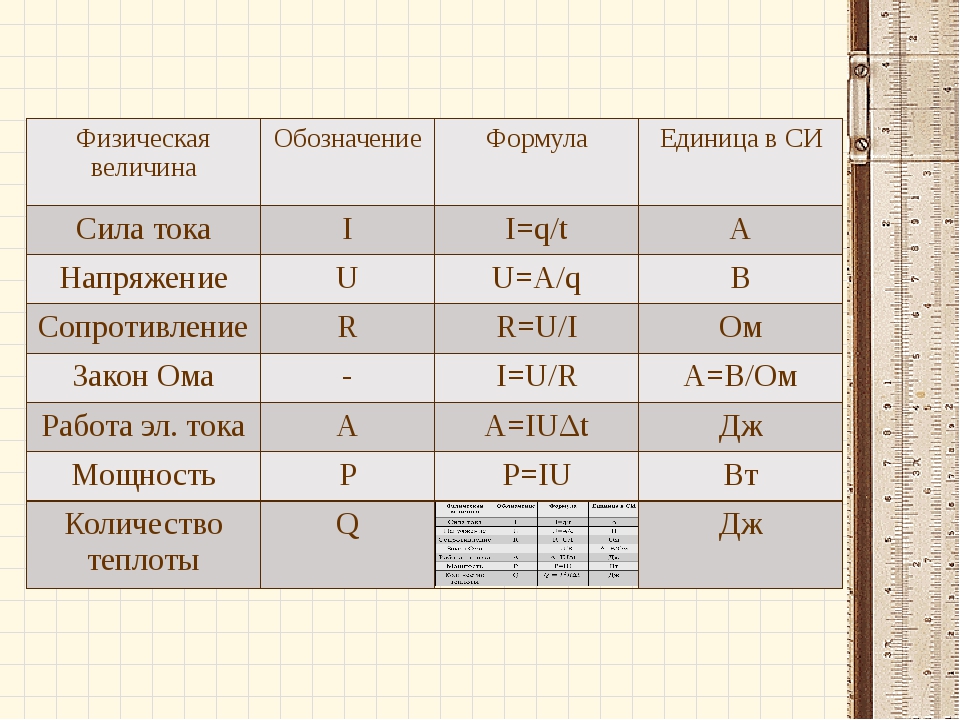 Названия и символы этих единиц отражают гибридную природу этих единиц. Как и в случае с единицами измерения в предыдущей таблице, каждая единица имеет свой собственный символ, но может быть определена в терминах основных единиц СИ, как показано в последнем столбце. Ценность возможности использовать в уравнениях как специальные, так и гибридные символы можно оценить, если посмотреть на длину некоторых выражений базовых единиц.
Названия и символы этих единиц отражают гибридную природу этих единиц. Как и в случае с единицами измерения в предыдущей таблице, каждая единица имеет свой собственный символ, но может быть определена в терминах основных единиц СИ, как показано в последнем столбце. Ценность возможности использовать в уравнениях как специальные, так и гибридные символы можно оценить, если посмотреть на длину некоторых выражений базовых единиц.
| Кол-во | Единица | Единица Символ | Базовая Единица |
|---|---|---|---|
| динамическая вязкость | паскаль-секунда | Па с | кг м -1 с -1 | 9
| ньютон-метр | Н · м | кг · м 2 с -2 | |
| поверхностное натяжение | ньютон на метр | Н · м -1 | кг с -2 |
| угловая скорость, угловая частота | рад в секунду | рад с -1 | с -1 |
| угловое ускорение | радиан в секунду в квадрате | рад / с 2 | с -2 |
| плотность теплового потока, освещенность | ватт на квадратный метр | Вт / м 2 | кг с 9011 2-3 |
| теплоемкость, энтропия | джоуль на кельвин | JK -1 | кг · м 2 с -2 K -1 |
| Удельная теплоемкость, удельная энтропия | джоуль на килограмм кельвин | JK -1 кг -1 | м 2 с -2 K -1 |
| удельная энергия | джоуль на килограмм Дж кг -1 | м 2 с -2 | |
| теплопроводность | ватт на метр кельвин | Вт м -1 K -1 | кг мс -3 K -1 |
| Плотность энергии | Дж на кубический метр | Дж · м -3 | кг · м -1 с -2 |
| Напряженность электрического поля | 9010 9 В на метрВ · м -1 | кг · мс -3 A -1 | |
| Плотность электрического заряда | кулонов на кубический метр | C · м -3 | A см -3 |
| Плотность поверхностного заряда | кулонов на квадратный метр | Кл м -2 | А см -2 |
| Плотность электрического потока, электрическое смещение | кулонов на квадратный метр | C м -2 | A sm -2 |
| диэлектрическая проницаемость | фарад на метр | F м -1 | кг -1 м -3 с 4 A 2 |
| проницаемость | генри на метр | H м -1 | кг мс -2 A -2 |
| молярная энергия | джоуль на моль | Дж моль -1 | кг м 2 с -2 моль -1 |
| молярная энтропия, молярная теплоемкость | джоуль на моль кельвин | JK -1 моль -1 | кг м 2 с -2 моль -1 K -1 |
| экспозиция (рентгеновские и γ-лучи) | кулонов на килограмм | C кг -1 | A с кг -1 |
| Мощность поглощенной дозы | серого в секунду | Гр с -1 | м 2 с -3 |
| Интенсивность излучения | Вт на стерадиан | Вт sr -1 | кг м 2 с -3 |
| сияние | Вт на квадратный метр стерадиан | Вт sr -1 м -2 | кг с -3 9011 3 |
| Концентрация каталитической активности | катал на кубический метр | кат м -3 | моль с -1 м -3 |
Единицы, не относящиеся к системе СИ, принятые для использования с системой СИ
Единицы, указанные в итоговой таблице, принимаются для использования с Международной системой единиц по разным причинам. Многие из них все еще используются, некоторые требуются для интерпретации научных текстов, имеющих историческое значение, а некоторые используются в специализированных областях, таких как медицина. Например, га до сих пор обычно используется для обозначения земельной площади. Для современных научных текстов предпочтительно использовать эквивалентные единицы СИ. Везде, где делается ссылка на единицы, не входящие в систему СИ, они должны иметь перекрестную ссылку с их эквивалентными единицами СИ. Для единиц, показанных в следующей таблице, также показано эквивалентное определение в единицах СИ.Большинство перечисленных устройств широко используются ежедневно и, вероятно, будут таковыми в обозримом будущем.
Многие из них все еще используются, некоторые требуются для интерпретации научных текстов, имеющих историческое значение, а некоторые используются в специализированных областях, таких как медицина. Например, га до сих пор обычно используется для обозначения земельной площади. Для современных научных текстов предпочтительно использовать эквивалентные единицы СИ. Везде, где делается ссылка на единицы, не входящие в систему СИ, они должны иметь перекрестную ссылку с их эквивалентными единицами СИ. Для единиц, показанных в следующей таблице, также показано эквивалентное определение в единицах СИ.Большинство перечисленных устройств широко используются ежедневно и, вероятно, будут таковыми в обозримом будущем.
Обратите внимание, что для большинства целей рекомендуется, чтобы дробные значения плоских углов, выраженные в градусах, выражались десятичными дробями, а не минутами и секундами. Исключения составляют навигация и геодезия (в связи с тем, что одна минута широты на поверхности Земли соответствует приблизительно одной морской миле) и астрономия. В области астрономии очень маленькие углы важны из-за огромных расстояний. Поэтому астрономам удобно использовать единицу измерения, которая может значимым образом отображать очень небольшие различия в углах. Очень маленькие углы могут быть представлены в единицах угловых секунд , микросекунд и пикосекунд .
В области астрономии очень маленькие углы важны из-за огромных расстояний. Поэтому астрономам удобно использовать единицу измерения, которая может значимым образом отображать очень небольшие различия в углах. Очень маленькие углы могут быть представлены в единицах угловых секунд , микросекунд и пикосекунд .
| Кол-во | Единица | Единица Обозначение | SI Единицы |
|---|---|---|---|
| время | минут | мин | 1 мин = 60 с |
| время | час | 10час | 1 ч = 60 мин = 3600 с |
| время | день | д | 1 д = 24 ч = 86400 с |
| длина | астрономическая единица | у.е.495 978 706 91 (6) × 10 11 м | |
| плоскость и фазовый угол | градусов | ° | 1 ° = (π / 180) рад |
| плоскость и фазовый угол | минут | ′ | 1 ′ = (1/60) ° = (π / 10 800) rad |
| плоскость и фазовый угол | секунда | ″ | 1 ″ = (1/60) ′ = (π / 648000) рад |
| площадь | га | га | 1 га = 1 га 2 = 10 4 м 2 |
| объем | литр | л или л | 1 л = 1 дм 3 = 10 3 см 3 = 10 -3 м 3 |
| масса | тонна | т | 1 т = 10 3 кг | 9
| дальтон | Да | 1 Да = 1. 660 539040 (20) × 10 -27 кг 660 539040 (20) × 10 -27 кг | |
| энергия | электронвольт | эВ | 1 эВ = 1,602 176 634 × 10 -19 Дж |
| логарифмическое отношение | непер | непер Np | — |
| логарифмическое отношение | bel | B | — |
| логарифмическое отношение | децибел | дБ | — |
Презентационные соглашения
Существует ряд общепринятых правил выражения величин в рукописных или печатных документах и текстах.Эти соглашения были приняты с относительно небольшими изменениями с тех пор, как Генеральная конференция по мерам и весам впервые представила Систему международных единиц в 1960 году. Они в первую очередь предназначены для обеспечения единообразного подхода к представлению рукописной или печатной информации и обеспечения удобочитаемость научных журналов, учебников, научных статей, таблиц данных, отчетов и других сопутствующих документов. Требования к оформлению будут в некоторой степени варьироваться в зависимости от норм языка, на котором написано произведение.Здесь нас интересуют только условные обозначения, применимые к английскому языку. В следующем списке представлены некоторые из наиболее важных требований.
Требования к оформлению будут в некоторой степени варьироваться в зависимости от норм языка, на котором написано произведение.Здесь нас интересуют только условные обозначения, применимые к английскому языку. В следующем списке представлены некоторые из наиболее важных требований.
- Обозначения единиц — они отображаются римским (вертикальным) шрифтом. Они печатаются строчными буквами, если они не являются производными от имени собственного, и в этом случае первая буква пишется с заглавной буквы (например, «Па» для паскаль). Исключением из правил является символ литра, который может быть записан как «l» или «L».Последнее допускается, чтобы отличить символ, используемый для литра, от числа один (1). Любой префикс кратного или кратного кратного считается частью символа единицы, к которому он добавляется без промежуточного пробела (например, «км» для километра, «мм» для миллиметра или «мкм» для микрометра).
- Имена единиц — пишутся римским шрифтом.
 Все названия единиц измерения печатаются строчными буквами, включая первую букву, независимо от того, названы ли они в честь человека или начинается ли символ единицы с символа верхнего регистра (т.е. «Ньютон», а не «Ньютон»). Если с именем устройства используется префикс, он становится частью имени устройства и формируется как одно слово (например, «микропаскаль», а не «микропаскаль» или «микропаскаль»). Если производная единица является произведением двух или более отдельных единиц, для разделения названий можно использовать пробел или дефис (например, «ньютон-метр» или «ньютон-метр»). Для единиц, возведенных в степень, соответствующий модификатор может предшествовать названию единицы или следовать за ним (например, «квадратный метр» или «метр в кубе»).
Все названия единиц измерения печатаются строчными буквами, включая первую букву, независимо от того, названы ли они в честь человека или начинается ли символ единицы с символа верхнего регистра (т.е. «Ньютон», а не «Ньютон»). Если с именем устройства используется префикс, он становится частью имени устройства и формируется как одно слово (например, «микропаскаль», а не «микропаскаль» или «микропаскаль»). Если производная единица является произведением двух или более отдельных единиц, для разделения названий можно использовать пробел или дефис (например, «ньютон-метр» или «ньютон-метр»). Для единиц, возведенных в степень, соответствующий модификатор может предшествовать названию единицы или следовать за ним (например, «квадратный метр» или «метр в кубе»). - Составные единицы — единицы, выраженные как произведение или частное других единиц, записываются так же, как стандартные алгебраические выражения.Умножение представлено либо пробелом, либо использованием оператора точки (также называемой средней точкой ).
 Например, символ «ньютон-метр» записывается как «Н · м» или «Н · м». Деление представлено с помощью солидуса (прямой ход) или с использованием отрицательных степеней. Обозначение «ньютон на метр» записывается либо как «Н / м», либо как «Н · м -1 »).
Например, символ «ньютон-метр» записывается как «Н · м» или «Н · м». Деление представлено с помощью солидуса (прямой ход) или с использованием отрицательных степеней. Обозначение «ньютон на метр» записывается либо как «Н / м», либо как «Н · м -1 »). - Переменные — неизвестные величины в уравнениях обычно представляются с помощью одного символа курсивным шрифтом, например.грамм. « м » для массы или « I » для электрического тока. Символ количества может быть дополнительно уточнен, как правило, с использованием номера или метки с нижним индексом, например « R НАГРУЗКА » для неизвестного сопротивления нагрузки или « I 1 » для неизвестного тока в определенной ветви электрической цепи (кстати, обратите внимание, что, хотя шрифты с засечками часто используются для уравнений, BIPM конкретно не требует этого).
- Количество — количество известного значения выражается числом, за которым следует пробел, а затем символ единицы.
 Пробел представляет собой оператор умножения. Исключением из правила является угол плоскости, выраженный в градусах, минутах и секундах. Символы градуса, минуты и секунды всегда следуют за соответствующими числами без пробела. Например, значение в тридцать пять градусов записывается как «35 °». Цифры всегда отображаются как римский (вертикальный) текст.
Пробел представляет собой оператор умножения. Исключением из правила является угол плоскости, выраженный в градусах, минутах и секундах. Символы градуса, минуты и секунды всегда следуют за соответствующими числами без пробела. Например, значение в тридцать пять градусов записывается как «35 °». Цифры всегда отображаются как римский (вертикальный) текст. - Объединение единиц — разные единицы следует комбинировать только при выражении количества с использованием единиц, не относящихся к системе СИ, то есть времени или угла.Например, время обычно выражается в часах, минутах и секундах. В таких областях, как навигация или астрономия, по-прежнему принято выражать плоские углы в градусах, минутах и секундах. Обратите внимание, однако, что для других целей углы, указанные в градусах, могут быть альтернативно записаны как десятичные дроби, например «21,255 °», а не «21 ° 15 ′ 18 ″».
- Десятичные маркеры — для любого числа, имеющего дробную часть, десятичный маркер (иногда называемый десятичной точкой ) является символом, отделяющим целую часть числа от его дробной части.
 Обычно это точка или запятая. Для значений от минус один до один десятичному маркеру предшествует ноль, например «0,123».
Обычно это точка или запятая. Для значений от минус один до один десятичному маркеру предшествует ноль, например «0,123». - Разделитель тысяч — числа, состоящие из длинных последовательностей цифр, часто разделяются на группы по три цифры, чтобы их было легче читать. Предпочтительный метод разделения этих групп — использовать пробел, поскольку использование точек или запятых может интерпретироваться по-разному в разных частях мира.Например, скорость света выражается как «299 792 458 м / с». Обратите внимание, что если до или после десятичного маркера есть только четыре цифры, разделитель обычно не считается необходимым.
- Умножение и деление — для обозначения умножения могут использоваться различные методы. Имена перемножаемых переменных могут быть и (размещены рядом друг с другом), например « xy ». Их можно заключить в квадратные скобки, например.
 грамм. «( x ) ( y )». Знак умножения можно использовать для обозначения умножения, помещая его между переменными, которые нужно умножить, например « x × y ». Обратите внимание, что знак умножения всегда следует использовать там, где только числа умножаются вместе, но его лучше избегать, если используются имена переменных (во избежание путаницы с общим именем переменной x ). Использование средней точки («·») не рекомендуется. Дивизия указывается с помощью солида , e.грамм. « x / y » или отрицательный индекс, например « x y -1 «.
грамм. «( x ) ( y )». Знак умножения можно использовать для обозначения умножения, помещая его между переменными, которые нужно умножить, например « x × y ». Обратите внимание, что знак умножения всегда следует использовать там, где только числа умножаются вместе, но его лучше избегать, если используются имена переменных (во избежание путаницы с общим именем переменной x ). Использование средней точки («·») не рекомендуется. Дивизия указывается с помощью солида , e.грамм. « x / y » или отрицательный индекс, например « x y -1 «.
Кратные и подкратные единицы единиц СИ
Кратные и подмножественные единицы единиц СИ обозначаются путем добавления соответствующего префикса к символу единицы. Префиксы печатаются в виде римских (вертикальных) символов, добавляемых к символу единицы без промежуточного пробела. Большинство префиксов единиц представляют собой символы верхнего регистра (за исключением дека (da), гектометров (h) и килограммов (k)). Все префиксы подмножественных единиц являются символами нижнего регистра. Имена префиксов всегда печатаются строчными буквами, за исключением тех случаев, когда они появляются в начале предложения, а единицы с префиксом отображаются как отдельные слова (например, миллиметр , микропаскаль и т. д.). Все кратные и частные кратные — это целые степени десяти .За пределами сто (или сотых ) кратные и подкратные являются целыми степенями одной тысячи , хотя они по-прежнему выражаются в виде степеней десяти. В следующей таблице перечислены наиболее часто встречающиеся множественные и подмножественные префиксы.
Большинство префиксов единиц представляют собой символы верхнего регистра (за исключением дека (da), гектометров (h) и килограммов (k)). Все префиксы подмножественных единиц являются символами нижнего регистра. Имена префиксов всегда печатаются строчными буквами, за исключением тех случаев, когда они появляются в начале предложения, а единицы с префиксом отображаются как отдельные слова (например, миллиметр , микропаскаль и т. д.). Все кратные и частные кратные — это целые степени десяти .За пределами сто (или сотых ) кратные и подкратные являются целыми степенями одной тысячи , хотя они по-прежнему выражаются в виде степеней десяти. В следующей таблице перечислены наиболее часто встречающиеся множественные и подмножественные префиксы.
| Фактор | Название | Символ | Фактор | Название | Символ | ||
|---|---|---|---|---|---|---|---|
| 10 1 | дека | da | 10 -1 | deci | |||
| 10 2 | га | h | 10 -2 | сенти | c | ||
| 10 3 | килограмм | k | 10 709 | k | 10 -3 900| м | | |
| 10 6 | мега | M | 10 -6 | микро | μ | ||
| 10 9 | гига | 10 | G | 1nano | n | ||
| 10 12 | tera | T | 10 -12 | pico | p | ||
| 10 15 | пета | P | 10 -15 | фемто | f | ||
| 10 18 | exa | E0 | 0 | атто | a | ||
| 10 21 | zetta | Z | 10 -21 | zepto | z | ||
| 10 24 | 24 | -24 | yocto | y |
Физические величины — Chemistry LibreTexts
- Последнее обновление
- Сохранить как PDF
- Чтение чисел
- Авторы и авторство
Химия — количественная наука. Количества веществ и энергии всегда должны выражаться в числах и единицах (чтобы иметь некоторое представление о том, о чем вы говорите). Вам также следует создавать ощущение количества каждый раз, когда вы с ними сталкиваетесь; вы должны быть знакомы с названием, префиксом и символом, используемыми для различных величин.
Количества веществ и энергии всегда должны выражаться в числах и единицах (чтобы иметь некоторое представление о том, о чем вы говорите). Вам также следует создавать ощущение количества каждый раз, когда вы с ними сталкиваетесь; вы должны быть знакомы с названием, префиксом и символом, используемыми для различных величин.
Однако из-за того, что мы используем множество различных единиц, выражение количеств довольно сложно. Мы будем иметь дело с числовой частью количеств на этой странице, используя единицы СИ.
выражаются как eXXX или EXXX.
Число слов Префикс Символ Экспонента ----- --------------------- ------ ------ -из 10-- Квиндриллион 1,000,000,000,000,000 e15 Триллион 1 000 000 000 000 Тера-Т е12 Миллиард 1,000,000,000 гига-G e9 Миллион 1,000,000 Mega- M e6 Тысяча 1000 килокилок e3 Сто 100 Десять 10 Один 1 Десятый 0.1 Решение Сотые 0,01 с Тысячная 0,001 Миллим э-3 Миллионная 0,000001 Micro- u (mu) e-6 Миллионная 0.000000001 Nano-n e-9 Триллионная 0,000000000001 Пикоп е-12 ----- --------------------- ------ ------ -------
К настоящему времени вы, вероятно, поняли, что каждый раз, когда число увеличивается в тысячу раз, мы даем новое имя, новый префикс и новый символ в его выражении.
Чтение чисел
После того, как вы познакомитесь со словами, связанными с этими числами, вы сможете легко передавать числа. Рассмотрим следующее число:
123,456,789,101,234,567
На словах это 18-значное число занимает несколько строк:
Сто двадцать три киндриллиона, четыреста пятьдесят шесть триллионов, семьсот восемьдесят девять миллиардов, сто один миллион, двести тридцать четыре тысячи пятьсот шестьдесят семь.
Если количество использует это число, это означает, что количество было измерено точно. Большинство количеств не имеют точного измерения, чтобы оправдать столь много значительных цифр. Вышеупомянутое число часто может быть выражено как 123e15 или прочитано как сто двадцать три киндрильона.
В науке существует семь основных величин, и эти величины, их символы, названия единиц и символы единиц перечислены ниже:
== Базовое количество == ==== Единица =====
Название Обозначение Обозначение Название
============= ====== ====== ========
Длина л м метр
Масса м кг Килограмм
Время т с Секунда
Электрический ток I А Ампер (Кл / с)
Температура T K Кельвин
Количество вещества n моль Моль
Сила света I v кд Кандела
============= ====== ====== ========
* Единица измерения ампер, A, равна кулонам в секунду (A = C / s).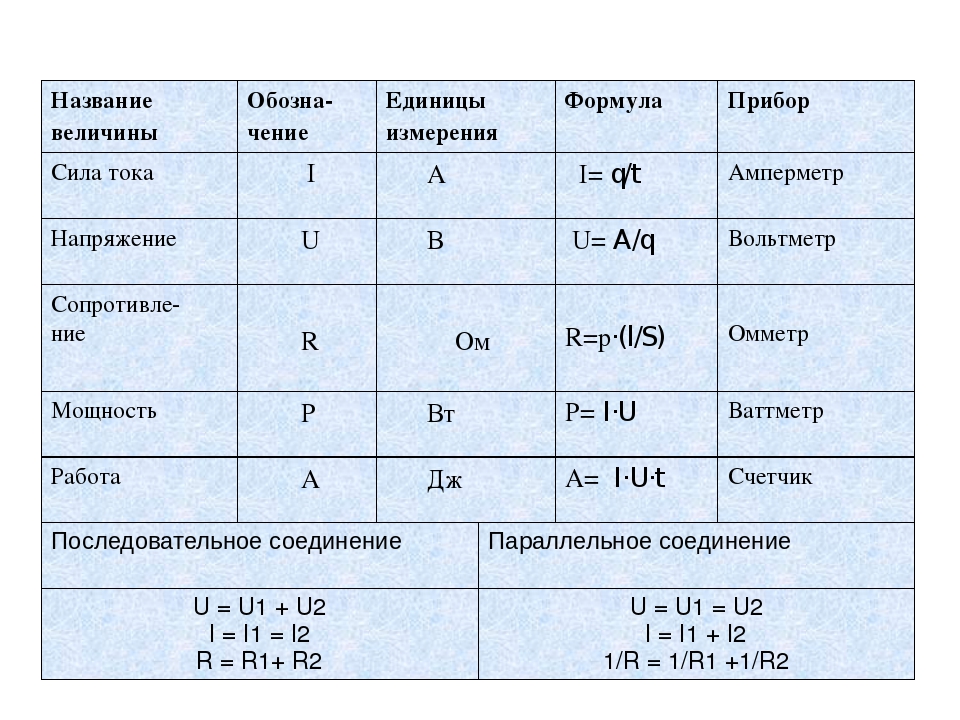
Авторы и авторство
Размеры и единицы
Механическая система, испытывающая одномерные демпфированные колебания, может быть моделируется уравнением
, где \ (m \) — масса системы, \ (b \) — некоторый коэффициент демпфирования, \ (k \) — жесткость пружины, а \ (u (t) \) — смещение система. Это уравнение, выражающее баланс трех физических эффекты: \ (mu » \) (масса, умноженная на ускорение), \ (bu ‘\) (демпфирующая сила) и \ (ку \) (сила пружины).Различные физические величины, такие как \ (m \), \ (u (t) \), \ (b \) и \ (k \), все имеют разные размеры , измеренные в разные единиц , но \ (mu » \), \ (bu ‘\) и \ (ku \) должны иметь одинаковые размерность, иначе добавлять их не было бы смысла.
Основные концепции
Базовые блоки и размеры
Базовые единицы обладают важным свойством, которое получают все остальные единицы.
от них. В системе СИ
таких базовых единиц семь и соответствующих
физические величины:
метр (м) на длину,
килограмм (кг) для массы,
секунды на время,
кельвин (K) для температуры,
ампер (А) для электрического тока,
кандела (кд) для силы света, и
моль (моль) для количества вещества.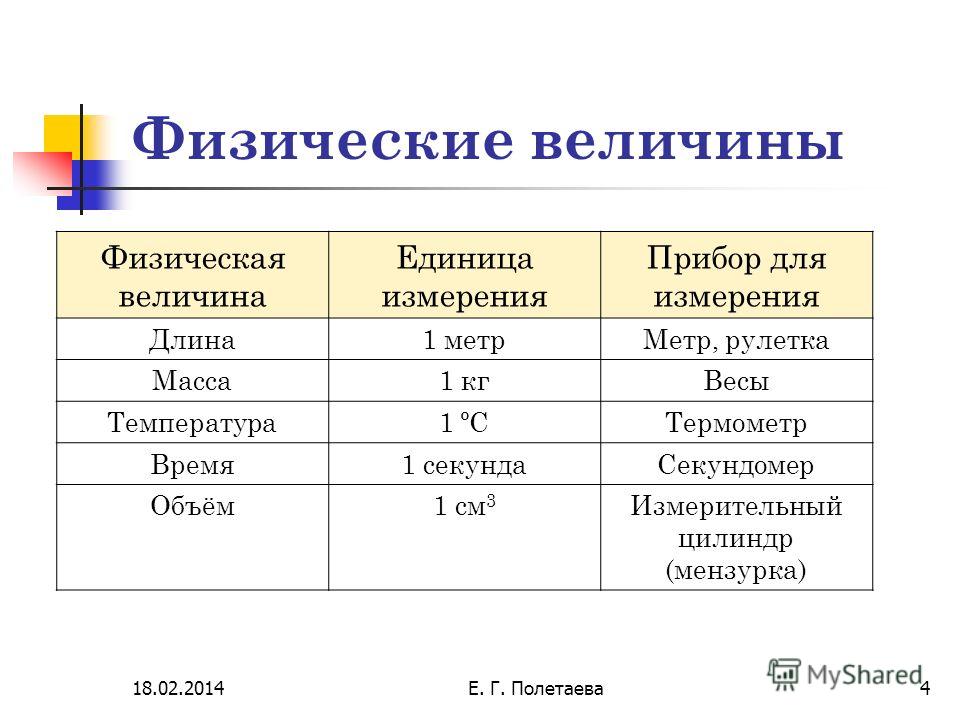 {- 2}] \)
{- 2}] \)
Префиксы для единиц
Единицы часто имеют префиксы.9 \) Па.
Теорема Букингема Пи
Почти все тексты по масштабированию имеют трактовку знаменитого Букингема. Теорема Пи, которую можно использовать для вывода физических законов на основе единицы измерения совместимость, а не лежащие в основе физические механизмы. Этот буклет сосредоточен на моделях, в которых физические механизмы уже выражены через дифференциальные уравнения. Тем не менее, Pi Теорема занимает заметное место в литературе по масштабированию, и поскольку мы время от времени будем на него ссылаться, теорема такова: кратко обсуждается ниже.
Сама теорема просто состоит из двух частей. Во-первых, если проблема
включает \ (n \) физические параметры, в которых \ (m \) независимые типы единиц
(например, длина, масса и т. д.), тогда параметры могут быть
в сочетании с ровно \ (n-m \) независимыми безразмерными числами, отнесенными
как Пи. Во-вторых, любое безразмерное отношение между исходным \ (n \)
параметры могут быть преобразованы в отношение между \ (n-m \)
безразмерные числа.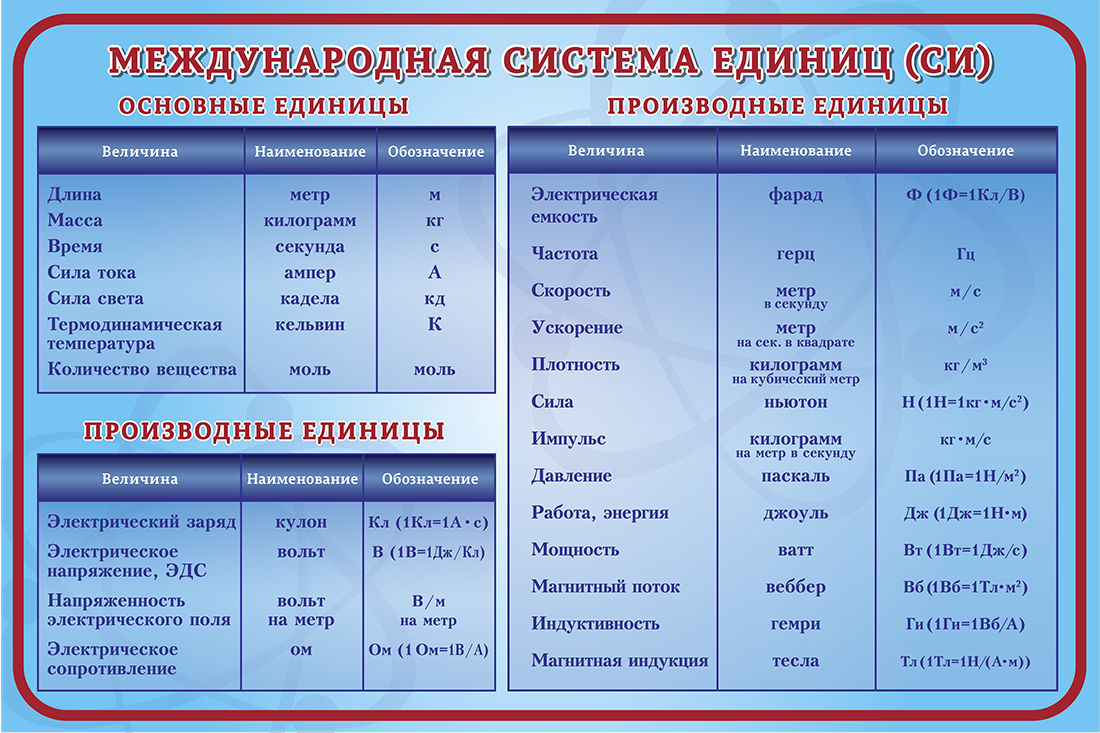 Такие отношения могут быть идентичностями или
неравенства, указывающие, например, на то, является ли данный эффект
незначительный.Более того, преобразование системы уравнений в
безразмерная форма соответствует выражающим коэффициентам, а также
как свободные и зависимые переменные в единицах числа Пи.
Такие отношения могут быть идентичностями или
неравенства, указывающие, например, на то, является ли данный эффект
незначительный.Более того, преобразование системы уравнений в
безразмерная форма соответствует выражающим коэффициентам, а также
как свободные и зависимые переменные в единицах числа Пи.
В качестве примера представьте тело, движущееся с постоянной скоростью \ (v \). Какие расстояние \ (s \), пройденное за время \ (t \)? Теорема Пи приводит к одна безразмерная переменная \ (\ pi = vt / s \) и приводит к формуле \ (s = Cvt \), где \ (C \) — неопределенная константа. Результат очень близко к известной формуле \ (s = vt \), возникающей из дифференциала уравнение \ (s ‘= v \) в физике, но с дополнительной константой.
На первый взгляд теорема Пи может показаться граничащей с
тривиально. Тем не менее, это может привести к значительному прогрессу для избранных
проблемы, такие как турбулентные струи, ядерные взрывы или сходство
решения, без детальных знаний математических или физических
модели. Следовательно, новичку в масштабировании это может показаться чем-то особенным.
очень глубокий, если не волшебный. Во всяком случае, если перейти к более сложным
задач со многими параметрами, использование теоремы дает
сравнительно меньший выигрыш по мере увеличения числа Пи.Многие Пи также могут быть
рекомбинированы разными способами. Итак, хорошо
физическое понимание и / или информация, передаваемая через набор уравнений,
требуется для
выбрать полезные безразмерные числа или соответствующее масштабирование
упомянутый набор уравнений. Иногда изучение уравнений также
показывает, что некоторые числа Пи, полученные в результате применения теоремы, на самом деле
может быть удалено из проблемы. Как следствие, когда
моделирование сложной физической задачи, реальная оценка масштабирования
и безразмерные числа так или иначе будут включены в
анализ основных уравнений вместо того, чтобы быть отдельной проблемой
с теоремой Пи.И в учебниках, и в статьях обсуждение
масштабирование в контексте уравнений слишком часто отсутствует или
представлены в нерешительности.
Следовательно, новичку в масштабировании это может показаться чем-то особенным.
очень глубокий, если не волшебный. Во всяком случае, если перейти к более сложным
задач со многими параметрами, использование теоремы дает
сравнительно меньший выигрыш по мере увеличения числа Пи.Многие Пи также могут быть
рекомбинированы разными способами. Итак, хорошо
физическое понимание и / или информация, передаваемая через набор уравнений,
требуется для
выбрать полезные безразмерные числа или соответствующее масштабирование
упомянутый набор уравнений. Иногда изучение уравнений также
показывает, что некоторые числа Пи, полученные в результате применения теоремы, на самом деле
может быть удалено из проблемы. Как следствие, когда
моделирование сложной физической задачи, реальная оценка масштабирования
и безразмерные числа так или иначе будут включены в
анализ основных уравнений вместо того, чтобы быть отдельной проблемой
с теоремой Пи.И в учебниках, и в статьях обсуждение
масштабирование в контексте уравнений слишком часто отсутствует или
представлены в нерешительности. Следовательно, внимание авторов будет
об этом процессе, хотя мы не приводим много примеров
по теореме Пи. Мы не говорим, что теорема Пи мало
значение. В ряде случаев, например, в экспериментах, он может
предоставить ценные и даже важные рекомендации, но в частности
В учебнике мы стремимся рассказать дополнительную историю о масштабировании.Кроме того, как будет показано в этом буклете, безразмерные числа в
проблема также возникает очень естественным образом из-за масштабирования
дифференциальные уравнения. Если есть модель, основанная на
дифференциальных уравнений, классические
размерный анализ.
Следовательно, внимание авторов будет
об этом процессе, хотя мы не приводим много примеров
по теореме Пи. Мы не говорим, что теорема Пи мало
значение. В ряде случаев, например, в экспериментах, он может
предоставить ценные и даже важные рекомендации, но в частности
В учебнике мы стремимся рассказать дополнительную историю о масштабировании.Кроме того, как будет показано в этом буклете, безразмерные числа в
проблема также возникает очень естественным образом из-за масштабирования
дифференциальные уравнения. Если есть модель, основанная на
дифференциальных уравнений, классические
размерный анализ.
Абсолютные ошибки, относительные ошибки и единицы
Математически не имеет значения, какие единицы мы используем для физического количество. Однако когда мы имеем дело с приближениями и ошибками, единицы важны.{-3} \) независимо от того, измеряется ли длина в км или мм.
Тем не менее, вместо того, чтобы полагаться исключительно на относительные ошибки,
лучше масштабировать проблему так, чтобы количества, входящие в
вычисления имеют размер единицы (или, по крайней мере, умеренные), а не очень
большой или очень маленький. Техника этих заметок показывает, как это
осуществимо.
Техника этих заметок показывает, как это
осуществимо.
Агрегаты и ЭВМ
Традиционные числовые вычисления включают только числа и, следовательно, требует безразмерных математических выражений.Обычно неявный используется тривиальное масштабирование. Можно, например, просто масштабировать по всей длине величин на 1 м, всех временных величин на 1 с и всех массовых величин на 1 кг, чтобы получить необходимые для расчетов безразмерные числа. Это наиболее распространенный подход, хотя он очень редко используется в явном виде. заявил.
Пакеты символьных вычислений, такие как Mathematica и Maple, позволяют
вычисления с величинами, имеющими размерность. Это тоже возможно
в популярных компьютерных языках, используемых для численных вычислений (раздел PhysicalQuantity: инструмент для вычислений с помощью единиц предоставляет конкретный пример на Python).{-3} \)).
Хотя таблицы преобразования единиц измерения
часто встречаются в школе, ошибки при пересчете единиц измерения, вероятно, значат
самый высокий среди всех ошибок, совершаемых учеными и инженерами (и
когда из-за ошибки преобразования единиц в самолете заканчивается топливо,
это серьезно!). Наличие хороших программных инструментов для помощи в подразделении
поэтому конверсия имеет первостепенное значение, что мотивирует лечение этого
тема в разделах PhysicalQuantity: инструмент для вычислений с единицами измерения и Parampool: пользовательские интерфейсы с автоматическим преобразованием единиц.Читатели, которые
в первую очередь заинтересованы в методе математического масштабирования.
смело пропустите этот материал и сразу перейдите к разделу Задачи экспоненциального распада.
Наличие хороших программных инструментов для помощи в подразделении
поэтому конверсия имеет первостепенное значение, что мотивирует лечение этого
тема в разделах PhysicalQuantity: инструмент для вычислений с единицами измерения и Parampool: пользовательские интерфейсы с автоматическим преобразованием единиц.Читатели, которые
в первую очередь заинтересованы в методе математического масштабирования.
смело пропустите этот материал и сразу перейдите к разделу Задачи экспоненциального распада.
Пример проблем, возникающих в системе единиц
Немного проработанный пример масштабирования в реальном
научный / инженерный проект может стимулировать читателя
мотивация. В полном объеме исследование цунами пролетов г.
геофизика, геология, история, гидродинамика, статистика, геодезия,
инженерия и гражданская защита.Эта сложность отражается в
разнообразие практик использования единиц, весов и
концепции. Если сузить рамки до моделирования цунами
распространение, аспект масштабирования, по крайней мере, может показаться простым, поскольку мы
в основном касается продолжительности и времени.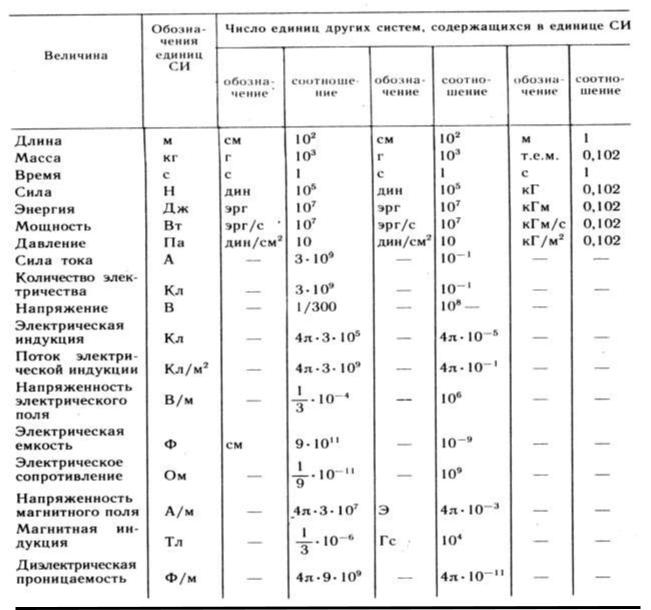 Тем не менее, даже здесь
неоднородность физических единиц является помехой.
Тем не менее, даже здесь
неоднородность физических единиц является помехой.
Незначительной проблемой является случайное использование единиц, не относящихся к системе СИ, таких как дюймы или
в старых диаграммах, даже саженях. Более важна неоднородность
величина различных переменных и различия в
присущие горизонтальные и вертикальные масштабы, в частности.Обычно
отметки поверхности указаны в метрах или меньше. Для дальнего поля в глубокой воде
распространения, а также небольшие цунами (которые до сих пор остаются научными
интереса) отметки поверхности часто указываются в см или даже
мм. В глубоком океане характерная глубина порядка
величина больше этой, обычно \ (5000 \, \ hbox {m} \). Распространение
расстояния, с другой стороны, составляют сотни или тысячи
километров. Часто лучше всего описываются местоположения и вычислительные сети.
в географических координатах (долгота / широта), которые связаны с
Единицы СИ на 1 минуту широты составляют примерно одну морскую милю.
(\ (1852 \, \ hbox {m} \)), и 1 минута долготы составляет это количество раз
косинус широты. Периоды волн цунами в основном колеблются от
от минут до часа, надеюсь, достаточно коротких, чтобы их можно было хорошо разделить
из полусуточного периода приливов. Время распространения
обычно часы или, может быть, лучшая часть дня, когда Тихий океан
Океан пройден.
Периоды волн цунами в основном колеблются от
от минут до часа, надеюсь, достаточно коротких, чтобы их можно было хорошо разделить
из полусуточного периода приливов. Время распространения
обычно часы или, может быть, лучшая часть дня, когда Тихий океан
Океан пройден.
Ученые, инженеры и бюрократы в сообществе цунами
имеют тенденцию быть конкретными и не соответствовать форматам и единицам измерения, поскольку
а также тип требуемых данных. Чтобы удовлетворить эти требования,
Разработчик модели цунами должен производить разнообразные данные, которые представлены в единицах измерения.
и форматы, которые нельзя использовать внутри ее моделей.На
с другой стороны, она также должна быть готова принять входные данные в
разнообразные формы. Некоторые наборы данных могут быть большими, что означает, что
ненужное дублирование с другими единицами измерения или масштабированием должно быть
избегали. Кроме того, модели цунами часто маркируются по
сравнение с экспериментальными данными. Лабораторный масштаб обычно
\ (\ hbox {cm} \) или \ (\ hbox {m} \), самое большее, что подразумевает, что измеренные данные
представлены в единицах, отличных от используемых в реальных событиях земного масштаба,
или даже в вольтах,
с информацией о преобразовании, полученной от измерительных приборов.
Все подробности устройства в различных форматах файлов явно мешают и порождают ряд заблуждений и ошибок, которые могут вызвать потеря драгоценного времени или усилий. Чтобы уменьшить такие проблемы, разработчики вычислительных инструментов должны сочетать разумную гибкость относительно единиц ввода и вывода с четким и последовательным соглашение о масштабировании в инструментах. Фактически, это также относится к академические инструменты для внутреннего использования.
Приведенное выше обсуждение указывает на некоторые передовые методы, которые
продвигает.Во-первых, всегда выполняйте вычисления с помощью масштабированного дифференциального уравнения.
модели. В этом буклете рассказывается, как это сделать. Во-вторых, пользователи программного обеспечения
часто хотят указать входные данные с измерением и получить выходные данные
с размером. Затем программное обеспечение должно применить такие инструменты, как PhysicalQuantity (раздел PhysicalQuantity: инструмент для вычислений с единицами)
или более сложный пакет Parampool (раздел Parampool: пользовательские интерфейсы с автоматическим преобразованием единиц измерения), чтобы разрешить ввод с явными размерами и
при необходимости преобразуйте размеры в нужные типы. Эти инструменты тривиально применять, если вычислительное программное обеспечение
написан на Python, но это просто, если программное обеспечение
написаны на скомпилированных языках, таких как Fortran, C или C ++. В последнем
случай, когда вы просто создаете модуль чтения ввода в Python, который захватывает данные из
пользовательский интерфейс и передает их в вычислительное программное обеспечение, либо
через файлы или вызовы функций (вызываемые соответствующие функции
должны быть обернуты в Python с такими инструментами, как
f2py,
Cython,
Ткать
SWIG,
Мгновенное,
или аналогичный, см. [Ref03] (Приложение C) для основных
примеры обертывания кода C и Fortran в f2py и Cython).
Эти инструменты тривиально применять, если вычислительное программное обеспечение
написан на Python, но это просто, если программное обеспечение
написаны на скомпилированных языках, таких как Fortran, C или C ++. В последнем
случай, когда вы просто создаете модуль чтения ввода в Python, который захватывает данные из
пользовательский интерфейс и передает их в вычислительное программное обеспечение, либо
через файлы или вызовы функций (вызываемые соответствующие функции
должны быть обернуты в Python с такими инструментами, как
f2py,
Cython,
Ткать
SWIG,
Мгновенное,
или аналогичный, см. [Ref03] (Приложение C) для основных
примеры обертывания кода C и Fortran в f2py и Cython).
PhysicalQuantity: инструмент для вычислений с единицами
Эти заметки содержат довольно много компьютерного кода, чтобы проиллюстрировать, как теория
подробно отображает работающее программное обеспечение. Python — это язык программирования
используется, прежде всего потому, что это легко читаемый, мощный,
полноценный язык, позволяющий использовать MATLAB-подобный код
а также код на основе классов, обычно используемый в Java, C # и C ++. Экосистема Python для научных вычислений за последние годы выросла.
быстро набирает популярность и заменяет более специализированные инструменты
как MATLAB, R и IDL.Примеры кодирования в этом буклете требуют только знания основных
процедурное программирование на Python.
Экосистема Python для научных вычислений за последние годы выросла.
быстро набирает популярность и заменяет более специализированные инструменты
как MATLAB, R и IDL.Примеры кодирования в этом буклете требуют только знания основных
процедурное программирование на Python.
Читатели без знания переменных Python, функций, тестов if, и при импорте модулей следует обращаться, например, к краткому руководству по научным Python, конспекты научных лекций Python, или полный учебник [Ref04] параллельно с чтением о Код Python в настоящих заметках.
Эти примечания относятся к Python 2.7
Python существует в двух несовместимых версиях, пронумерованных 2 и 3.Различия можно сделать небольшими, и есть инструменты для написания код, работающий под обеими версиями.
Поскольку Python версии 2 все еще доминирует
в научных вычислениях мы придерживаемся этой версии, но
написать код версии 2.7, максимально приближенный к версии 3.4
и позже. В большинстве наших программ отличается только оператор print . между версиями 2 и 3.
между версиями 2 и 3.
Вычисления с модулями в Python хорошо поддерживаются
очень полезный инструмент PhysicalQuantity из пакета ScientificPython от Конрада
Хинсен.К сожалению, ScientificPython не поддерживает
писать, работать с NumPy версии 1.9 или новее, поэтому мы изолировали PhysicalQuantity объект в модуле PhysicalQuantities и сделал его общедоступным
доступно на GitHub. Также существует альтернативный пакет Unum для вычислений с числами с
единиц, но здесь мы будем придерживаться первого модуля.
Продемонстрируем использование объекта PhysicalQuantity вычисление \ (s = vt \), где \ (v \) — скорость, заданная в единицах измерения ярдов на
минута , а \ (t \) — время в часах.Сначала нам нужно знать, что
единицы называются PhysicalQuantities . Для этого запустите pydoc
Физические количества или
Терминал> pydoc Scientific.Physics.PhysicalQuantities
, если у вас установлен весь пакет ScientificPython. В
итоговая документация показывает имена
единицы. В частности,
ярды задаются ярдов , минуты мин , а часы
по ч . Теперь мы можем вычислить \ (s = vt \) следующим образом:
>>> # С ScientificPython:
>>> от Науч.Physics.PhysicalQuantities import \
... PhysicalQuantity как PQ
>>> # С PhysicalQuantities как отдельным / автономным модулем:
>>> из PhysicalQuantities импортировать PhysicalQuantity как PQ
>>>
>>> v = PQ ('120 ярдов / мин') # скорость
>>> t = PQ ('1 h') # время
>>> s = v * t # расстояние
>>> print s # s - строка
120,0 ч * ярд / мин
Нечетная единица ч * ярд / мин лучше преобразована в стандартную единицу СИ, например
как метр:
>>> с.convertToUnit ('м')
>>> print s
6583,68 м
Обратите внимание, что s — это объект PhysicalQuantity со значением и
Блок. Для математических вычислений нам нужно извлечь
value как объект с плавающей запятой . Мы также можем извлечь единицу в виде строки:
>>> print s.getValue () # float 6583,68 >>> print s.getUnitName () # строка м
Вот пример того, как преобразовать единицы нечетной скорости ярды на минута на что-то более стандартное:
>>> v.{-1} \)
где джоуль заменяет калорийность?
>>> c = PQ ('1 кал / (г * К)')
>>> c.convertToUnit ('Дж / (г * К)')
>>> печать c
4,184 Дж / К / г
Parampool: пользовательские интерфейсы с автоматическим преобразованием единиц измерения
Пакет Parampool позволяет
создание пользовательских интерфейсов с поддержкой юнитов и юнитов
конверсия. Значения параметров можно задать в виде числа с
Блок. Параметры могут быть зарегистрированы заранее с предпочтительным
единица измерения, и все, что предписывает пользователь, значение и единица измерения
преобразован таким образом, чтобы устройство стало зарегистрированным.2 \), \ (t \) быть
время измеряется в с, и, следовательно, \ (с \) будет расстоянием, измеренным в м.
Пул параметров
Во-первых, Parampool требует от нас определения пула всех входных данных.
параметры, которые здесь просто представлены списком словарей, где каждый
словарь содержит информацию об одном параметре. Возможно
организовать входные параметры в древовидной структуре с подпулами, которые
сами могут иметь
субпулы,
но для нашего простого приложения нам просто нужна плоская структура с
три входных параметра:
\ (v_0 \), \ (a \) и \ (t \).Эти параметры помещаются в подпул под названием
"Основной". Пул создается по коду
def define_input ():
бассейн = [
'Основной', [
dict (name = 'начальная скорость', по умолчанию = 1.0, unit = 'm / s'),
dict (name = 'acceleration', по умолчанию = 1.0, unit = 'm / s ** 2'),
dict (name = 'time', по умолчанию = 10.0, unit = 's')
]
]
из parampool.pool.UI import listtree2Pool
pool = listtree2Pool (pool) # преобразовать список в объект Pool
возвратный бассейн
Для каждого параметра мы можем определить логическое имя, например, начальная скорость ,
значение по умолчанию и единица измерения.Дополнительные свойства
также разрешены, см. документацию Parampool.
Совет: укажите значения чисел по умолчанию как объекты с плавающей запятой
Обратите внимание, что мы пишем не просто 1, а 1.0 по умолчанию.
Если бы использовалось 1, Parampool интерпретировал бы наш параметр как
целое число и поэтому преобразует ввод вроде 2,5 м / с в 2 м / с .
Чтобы гарантировать, что параметр с действительным знаком становится объектом float внутри
пула, мы должны указать значение по умолчанию как действительное число: 1. или 1.0 .
(Тип входного параметра также может быть установлен явно с помощью
свойство str2type , например, str2type = float .)
Получение данных пула для вычислений
Мы можем сделать небольшую функцию для получения значений из пула
и вычисление \ (s \):
дистанция def (бассейн):
v_0 = pool.get_value ('начальная скорость')
a = pool.get_value ('ускорение')
t = pool.get_value ('время')
s = v_0 * t + 0.5 * а * т ** 2
вернуть s
Функция pool.get_value возвращает числовое значение
названный параметр, после того, как единица была преобразована из того, что
Пользователь указал, что было зарегистрировано в пуле.
Например, если пользователь предоставляет аргумент командной строки - время '2 ч' , Parampool преобразует это количество в секунды и pool.get_value ('time') вернет 7200.
Чтение параметров командной строки
Для выполнения вычислений мы определяем пул, загружаем значения из
командная строка и вызов , расстояние :
пул = define_input ()
из Parampool.menu.UI import set_values_from_command_line
pool = set_values_from_command_line (пул)
s = расстояние (бассейн)
print 's =% g'% s
В именах параметров с пробелами должен использоваться символ подчеркивания вместо пробела.
в параметре командной строки, например, --Initial_velocity .
Теперь мы можем запустить
Терминал> python distance.py --initial_velocity '10 km / h '\
- ускорение 0 - время '1 ч
s = 10000
Обратите внимание на ответ ( s ), что 10 км / ч преобразуется в м / с, а 1 ч - в с.
Также можно получить значения параметров как PhysicalQuantity объекты из пула по телефону
v_0 = pool.get_value_unit ('Начальная скорость')
Следующий вариант функции расстояние вычисляет с
значений и единиц:
def distance_unit (пул):
# Вычислить с помощью единиц
из parampool.PhysicalQuantities импортировать PhysicalQuantity как PQ
v_0 = pool.get_value_unit ('начальная скорость')
a = pool.get_value_unit ('ускорение')
t = бассейн.get_value_unit ('время')
s = v_0 * t + 0,5 * a * t ** 2
вернуть s.getValue (), s.getUnitName ()
Тогда мы можем сделать
с, s_unit = Distance_unit (пул)
print 's =% g'% s, s_unit
и получите результат с правильным блоком.
Установка значений по умолчанию в файле
В больших приложениях с большим количеством входных параметров часто нравится
для определения (огромного) набора значений по умолчанию для конкретного случая, а затем
переопределите некоторые из них в командной строке.Такие наборы значений по умолчанию
может быть установлен в файле с использованием синтаксиса типа
подпул Главный
начальная скорость = 100! ярд / мин
ускорение = 0! м / с ** 2 # ускорение падения
конец
Аппарат можно отдать после ! (и перед символом комментария # ).
Для чтения таких файлов мы должны добавить строки
из parampool.pool.UI import set_defaults_from_file
pool = set_defaults_from_file (пул)
перед звонком на номер set_defaults_from_command_line .
Если приведенные выше команды сохранены в файле distance.dat , мы даем
информация об этом файле в программу через
option --poolfile distance.dat . Запуск всего
Терминал> python distance.py --poolfile distance.dat
s = 15,25 м
сначала загружает скорость
100 ярдов / мин преобразовано в 1,524 м / с и нулевое ускорение
в систему пула и затем мы вызываем distance_unit , что
загружает эти значения из пула вместе со значением по умолчанию для
время, установленное на 10 с.Тогда расчет будет \ (s = 1,524 \ cdot 10 + 0 = 15,24 \)
с блоком м. Мы можем изменить время и / или два других
параметры в командной строке:
Терминал> python distance.py --poolfile distance.dat --time '2 h'
s = 10972,8 м
Результат вычисления: \ (s = 1,524 \ cdot 7200 + 0 = 10972,8 \).
Предлагаем вам поиграть с программой distance.py.
Указание нескольких значений входных параметров
Parampool имеет интересную особенность: можно назначить несколько значений.
к входному параметру, тем самым облегчая приложению
пройти через все комбинации всех параметров.Мы можем продемонстрировать эту особенность, составив таблицу из \ (v_0 \), \ (a \), \ (t \) и
\ (s \) значения. В функции вычисления нам нужно вызвать pool.get_values вместо pool.get_value , чтобы получить список всех значений, которые
были указаны для рассматриваемого параметра. Вложением петель поверх
все параметры, мы посещаем все комбинации всех параметров как
указано пользователем:
def Distance_table (бассейн):
"" "Получение нескольких значений параметров из пула." ""
таблица = []
для v_0 в пуле.get_values ('начальная скорость'):
для a в pool.get_values ('ускорение'):
для t в pool.get_values ('time'):
s = v_0 * t + 0,5 * a * t ** 2
table.append ((v_0, a, t, s))
таблица возврата
Если для параметра было указано только одно значение, pool.get_values возвращает только это значение, и будет только один проход в связанном
петля.
После загрузки аргументов командной строки в наш объект pool , мы можем вызвать distance_table вместо distance or distance_unit and
напишите красиво оформленную таблицу результатов:
table = distance_table (бассейн)
print '| ----------------------------------------------- ------ | '
печать '| v_0 | а | т | с | '
print '| ----------------------------------------------- ------ | '
для v_0, a, t, s в таблице:
печать '|% 11.3f | % 10.3f | % 10.3f | % 12.3f | ' % (v_0, a, t, s)
print '| ----------------------------------------------- ------ | '
Вот пример выполнения,
Терминал> python distance.py --time '1 ч и 2 ч и 3 ч' \
- ускорение '0 м / с ** 2 и 1 м / с ** 2 и 1 ярд / с ** 2' \
--initial_velocity '1 и 5'
| ------------------------------------------------- ---- |
| v_0 | а | т | s |
| ------------------------------------------------- ---- |
| 1.000 | 0,000 | 3600.000 | 3600.000 |
| 1.000 | 0,000 | 7200.000 | 7200.000 |
| 1.000 | 0,000 | 10800.000 | 10800.000 |
| 1.000 | 1.000 | 3600.000 | 6483600.000 |
| 1.000 | 1.000 | 7200.000 | 250.000 |
| 1.000 | 1.000 | 10800.000 | 58330800.000 |
| 1.000 | 0,914 | 3600.000 | 52.000 |
| 1.000 | 0,914 | 7200.000 | 23708448.000 |
| 1.000 | 0,914 | 10800.000 | 53338608.000 |
| 5.000 | 0,000 | 3600.000 | 18000.000 |
| 5.000 | 0,000 | 7200.000 | 36000.000 |
| 5.000 | 0,000 | 10800.000 | 54000.000 |
| 5.000 | 1.000 | 3600.000 | 6498000.000 |
| 5.000 | 1.000 | 7200.000 | 25956000.000 |
| 5.000 | 1.000 | 10800.000 | 58374000.000 |
| 5.000 | 0,914 | 3600.000 | 5943312.000 |
| 5.000 | 0,914 | 7200.000 | 23737248.000 |
| 5.000 | 0,914 | 10800.000 | 53381808.000 |
| ------------------------------------------------- ---- |
Обратите внимание, что некоторые из нескольких значений имеют разные размеры
из зарегистрированного измерения для этого параметра, а таблица
показывает, что преобразование в правильное измерение имело место.
Создание графического пользовательского интерфейса
Для удовольствия мы можем легко создать графический пользовательский интерфейс.
через Parampool. Мы оборачиваем функцию distance_unit в функцию, которая
возвращает результат в красивом HTML-коде:
def distance_unit2 (пул):
# Перенести результат из distance_unit в HTML
s, s_unit = Distance_unit (пул)
return ' Distance: % .2f% s'% (s, s_unit)
Кроме того, мы должны сделать файл generate_distance_GUI.py с
простое содержание
из импорта parampool.generator.flask сгенерировать
с расстояния импорт distance_unit2, define_input
генерировать (distance_unit2, pool_function = define_input, MathJax = True)
Запуск generate_distance_GUI.py создает веб-сайт на основе Flask.
интерфейс
для нашей функции distance_unit , см. Рисунок Web GUI, где параметры могут быть указаны в единицах измерения.
Текстовые поля в этом графическом интерфейсе позволяют указывать параметры с
числа и единицы, e.g., ускорение с единицей измерения ярдов в минуту в квадрате,
как показано на рисунке. Слегка наведя указатель мыши слева от
текстовое поле вызывает появление маленького черного окошка с зарегистрированным устройством
этого параметра.
Веб-интерфейс, в котором параметры могут быть указаны в единицах измерения
С примерами, показанными выше, читатель должен уметь использовать PhysicalQuantity объект и пакет Parampool в программах
и тем самым безопасно работать с юнитами. В следующем тексте, где мы обсуждаем
умение масштабировать подробно, мы просто будем работать в стандартных единицах СИ
и избегайте преобразования единиц измерения, чтобы больше не использовать PhysicalQuantity и Parampool.
Единицы и размеры - обзор
Проверьте размеры и единицы измерения, указанные в таблице 1.1.
Постоянная гравитации G определяется как
F = GmMr2F = Gm1m2r2
, где F - сила тяжести между двумя массами m1 и m2, центры масс которых находятся на расстоянии r друг от друга. Найдите размеры G и его единиц в системе СИ и британской системе мер.( Ответ : MT 2 L −3 , кгм −3 с 2 , снаряд −3 с 2 )
Предполагая, что период колебаний простого маятника τ зависит от массы объекта, длины маятника l и ускорения свободного падения g , используйте теорию размерного анализа чтобы показать, что масса объекта на самом деле не имеет значения. Затем найдите подходящее выражение для периода колебаний через другие переменные.
( Ответ : τ = cl ∕ g, где c - постоянная)
Тонкий плоский диск диаметром D вращается вокруг шпинделя через его центр со скоростью ω радиан в секунду в жидкости с плотностью ρ и кинематической вязкостью ν . Покажите, что мощность P , необходимая для вращения диска, может быть выражена как
- (a)
P = ρω3D5fvωD2
- (b)
P = ρv3DhωD2v
69 a) решить через индекс ν , а для (b) решить через индекс ω .
Далее, покажите, что ωD2 / ν , PD / ρν3 и P / ρω3D5 - все безразмерные величины.
Сферы различного диаметра D и плотности σ могут свободно падать под действием силы тяжести через различные жидкости (представленные их плотностями ρ и кинематической вязкостью ν ) и их конечными скоростями V измерены. Найдите рациональное выражение, связывающее V с другими переменными, и, следовательно, предложите подходящий график, в котором могут быть представлены результаты.
Примечание: Будет пять неизвестных индексов, поэтому два должны остаться неопределенными, что даст две неизвестные функции в правой части. Сделайте неизвестные индексы равными σ и ν .
( Ответ : V = DgfσρhDvDg; поэтому построите кривые зависимости VDg от DVDg для различных значений σ / ρ .)
Самолет весит 60 000 Н и имеет размах крыльев 17 м. Модель в масштабе 1/10 с опущенными створками испытывается в туннеле со сжатым воздухом при давлении 15 атмосфер и температуре 15 ° C на различных скоростях.Максимальный подъем модели измеряется на различных скоростях с приведенными результатами:
| Скорость (мс -1 ) | 20 | 21 | 22 | 23 | 24 |
| Максимальная подъемная сила (Н) | 2960 | 3460 | 4000 | 4580 | 5200 |
Оцените минимальную скорость полета самолета на уровне моря (т. Е. Скорость, при которой достигается максимальная подъемная сила самолета. равен его весу).
(ответ : 33 мс −1 )
Распределение давления по сечению двумерного крыла при 4 градусах падения можно аппроксимировать следующим образом: –0,8 от передней кромки до 60% хорды, затем линейно увеличивается до + 0,1 на задней кромке. Нижняя поверхность: постоянная Cp при –0,4 от передней кромки до 60% хорды, затем линейно увеличивается до + 0,1 на задней кромке. Оцените коэффициент подъемной силы и коэффициент момента тангажа относительно передней кромки за счет подъемной силы.
(ответ : 0,3192; –0,13)
Статическое давление измеряется в ряде точек на поверхности длинного круглого цилиндра диаметром 150 мм с осью, перпендикулярной потоку эталона. плотность при 30 мс -1 . Точки давления определяются углом θ , который представляет собой угол, образованный в центре дугой между точкой давления и передней точкой торможения. В следующей таблице приведены значения для p –p0, где p - давление на поверхности цилиндра, а p0 - невозмущенное давление набегающего потока, для различных углов θ , все давления даны в Нм. -2 .Показания для верхней и нижней половин цилиндра идентичны. Оцените сопротивление опалубки давлением на метр пробега и соответствующий коэффициент сопротивления.
| θ p - p 0 | (градусы) (Н · м −2 ) | 0 | 10 | 20 | 30 | 40 | 50 | 60 |
| +569 | +502 | +301 | –57 | –392 | –597 | –721 | ||
| θ p - p 0 (градусы) (Н · м −2 ) | 70 | 80 | 90 | 100 | 110 | 120 | ||
| –726 | –707 | –660 | –626 | –588 | –569 |
Для значений θ между 120 и 180 градусами p –p0 является постоянным при –569 Нм –2 .
(ответ : CD = 0,875, D = 7,25 Нм −1 )
Планер имеет размах крыла 18 м и удлинение 16. Ширина фюзеляжа составляет 0,6 м при корневой части крыла, а коэффициент конусности крыла составляет 0,3 с квадратными законцовками крыла. При истинной воздушной скорости 115 км / ч −1 на высоте с относительной плотностью 0,7 подъемная сила и лобовое сопротивление составляют 3500 Н и 145 Н соответственно. Коэффициент тангажа крыла относительно точки четверти хорды равен –0.03 на основе полной площади крыла и средней аэродинамической хорды. Рассчитайте коэффициенты подъемной силы и сопротивления на основе общей площади крыла и момента тангажа относительно точки четверти хорды.
( Ответ : CL = 0,396, CD = 0,0169, M = -322 Нм, поскольку c¯A≈1,245 м)
Опишите качественно результаты, ожидаемые от построения графика давления обычного симметричного тихоходный двумерный профиль. Укажите изменения, ожидаемые при возникновении ситуации, и обсудите процессы определения результирующих сил.Требуются ли какие-либо дополнительные испытания для определения общих сил подъемной силы и сопротивления? Включите в обсуждение ожидаемый порядок величины для различных описанных распределений и сил.
Покажите, что для геометрически подобных аэродинамических систем безразмерные силовые коэффициенты подъемной силы и сопротивления зависят только от числа Рейнольдса и числа Маха. Кратко обсудите важность этой теоремы для испытаний в аэродинамической трубе и простой теории характеристик.
«Пинта - фунт для всего мира» - старая рифма, описывающая вес воды. Учитывая, что пинта составляет одну восьмую галлона, что составляет 231,8 кубических дюйма, а плотность пресной воды (не морской воды) составляет 1,93 пули на кубический фут, решите процентную ошибку в старой рифме.
В физике средней школы W = mg показывает, что 1 пуля весит 32,174 фунта. Однако 1 пуля = 1 фунт2 фут. Точно так же 1 кг весит 9,8 Н. Чему равен 1 кг? Обратите внимание на разницу между «весит» и «равно», которую мы часто упускаем из виду во время домашних заданий и экзаменов.Также обратите внимание, что рабочая система slug-ft-sec идентична единицам mks. Необычной является система фунт-фут-сек.
График в верхней части следующей страницы показывает данные по общедоступным значениям максимальной тяги в сравнении с максимальной взлетной массой для широкого спектра двухмоторных самолетов бизнес-класса. Самолеты из рынка «очень легких реактивных самолетов» находятся внизу слева, а бизнес-джет 737 - вверху справа. Покажите, что максимальное отношение подъемной силы к лобовому сопротивлению для всех этих самолетов составляет примерно 6, если предположить, что они могут взлетать с одним выключенным двигателем.Вы должны предположить, что крен на взлете горизонтальный и что создается достаточная подъемная сила, чтобы начать ускорение по вертикали. Точно так же предположим, что разбег при взлете имеет незначительное ускорение, то есть почти постоянную скорость.
Одним из важных показателей эффективности коммерческого авиалайнера является «долларов за кресло-милю» или стоимость полета одного пассажира на одну милю. Чем меньше это число, тем лучше летные характеристики самолета. Это число не просто функция формы крыла и двигателя; это зависит от того, насколько сильно загружен самолет.Если вы можете управлять маленьким парапланом из бальзового дерева или пенопласта с повторяемой высоты (лестница, балкон, вершина холма и т. Д.), Вы можете оптимизировать для него «долларов на сиденье-милю». Увеличение количества долларов на одно сиденье-милю для планера - это задача минимизировать знаменатель: количество мест, умноженное на мили, или произведение полезной нагрузки и расстояния. Загрузите свой планер различными полезными грузами и запишите расстояние, которое он проходит (вы должны сохранять хорошую дифферентность, поэтому закрепите грузы в центре масс планера). Какая полезная нагрузка обеспечивает продукт с максимальной полезной нагрузкой? Минимум?
Справочник физических величин - 1-е издание - Игорь С.Григорьев
Содержание
Единицы физических величин, А.Г. Чертов
Периодическая таблица элементов, К.А. Кикоин
Механические свойства материалов, Н.В. Кадобнова, А.М. Братковский
Сжимаемость, Б.В. Виноградов
Плотность веществ, А.П. Бабичев
Трение, И.И. Карасик
Акустика, Л.К. Zarembo
Термометрия, А.В. Инюшкин
Теплоемкость, М.Н. Хлопкин
Температурные коэффициенты расширения, Е.Б. Гельман
Давление насыщенных паров, В.Игнатьев В. Криворучко, А.И. Мигачев
Плавка и кипячение, Э. Гельман
Уравнение состояния и критических параметров веществ, Э. Гельман
Surface Tension, B.D. Сумм
Теплопроводность, А.В. Инюшкин
Вязкость, А.В. Елецкий
Распространение, А.В. Елецкий
Элементарные процессы в газах и плазме, А.В. Елецкий
Ионизация атомов и молекул, А.А. Радзиг, В. Шустряков
Явления переноса в слабоионизованной плазме, А.В. Елецкий
Электрические характеристики металлов и сплавов, В.Егоров, И. Хлюстиков
Электрофизические свойства полупроводников, Е.З. Мейлихов, С. Лазарев, Б.А. Изоляторы Aronzon
, А.П. Геппе,
Термоэлектрические явления, Бабушкина Н.А.,
Эмиссия электронов и ионов, Т. Лифшиц, А.Л.Мусатов
Магнитные свойства ДИА- и парамагнетиков, В.Ю. Иванов, Л.И. Винокурова
Магнитные свойства ферромагнитных металлов и сплавов, К.Г. Гуртовой
Антиферромагнетики, В.И. Ожогин, В. Шапиро
Ферриты и другие магнитные диэлектрики, М.В. Быстров, В. Ивашинцева, С.А.Миронов, Р.В. Писарев
Гальваномагнитные и термомагнитные явления, Н.А.Бабушкина, В.С. Егоров
Оптические свойства веществ, Новицкий Л.А.
Атомные и молекулярные спектры, А.А. Radzig
Электро-, магнито-, пьезооптические и нелинейные оптические эффекты, А.А. Малютин, М.Е.Бродов, В.П. Яновский
Лазеры, А.А. Малютин, Э. Бродов, В. Яновский
Рентгеновское излучение, Р. Имамов
Фундаментальные частицы, В.А.П. Никитин
Ядерные свойства нуклидов, В.М. Кулаков,
Мёссбауэровские ядра, С.С.Якимов, В.М. Черепанов
Ядерные реакции, В.П. Рудаков
Ядерное деление, А.И. Обухов, И. Григорьев
Проникновение нейтронов сквозь вещество, С.В. Марин
Прохождение ионизирующего излучения через вещество, В.П. Рудаков
Космические лучи, В.С. Птускин
Геофизика, И.А. Маслов
Астрономия и астрофизика, Ю. Любарский, Р.А. Сюняев


 Перевод единиц измерения физических величин. Таблицы перевода единиц величин. Перевод химических и технических единиц измерения величин. Величины измерения. Таблицы соответствия величин.
Перевод единиц измерения физических величин. Таблицы перевода единиц величин. Перевод химических и технических единиц измерения величин. Величины измерения. Таблицы соответствия величин.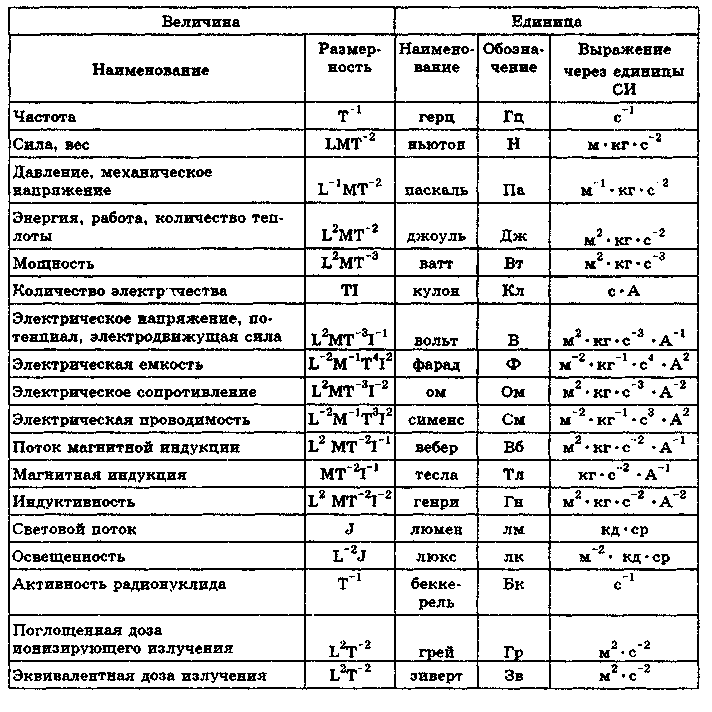 Десятичные приставкиПеревод единиц измерения Осадков (атмосферных), масса и интенсивность, сила осадков — дождя и снега — мм, дюймов, л, фунтов, мм/час, (л/час)/м2, (л/мин)/м2, дюймов/час, gph/ft2, gpm/ft2
Поиск в инженерном справочнике DPVA. Введите свой запрос:
Десятичные приставкиПеревод единиц измерения Осадков (атмосферных), масса и интенсивность, сила осадков — дождя и снега — мм, дюймов, л, фунтов, мм/час, (л/час)/м2, (л/мин)/м2, дюймов/час, gph/ft2, gpm/ft2
Поиск в инженерном справочнике DPVA. Введите свой запрос:
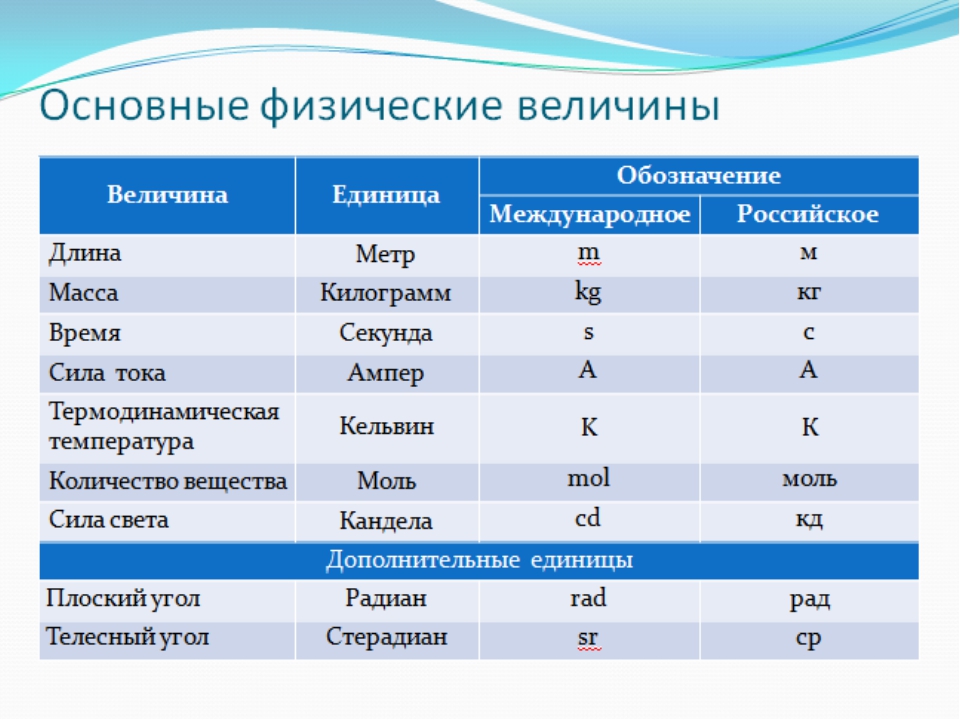 Числа и цифры: действительные, комплексные, мнимые… Римские, арабские, современные, древне — еврейские, египетские, вавилонские, греческие, майя, китайские, индийские цифры (числа).
Числа и цифры: действительные, комплексные, мнимые… Римские, арабские, современные, древне — еврейские, египетские, вавилонские, греческие, майя, китайские, индийские цифры (числа). Первую оценку скорости света дал Олаф Рёмер (1676). Он заметил, что когда Земля и Юпитер находятся по разные стороны от Солнца, затмения спутника Юпитера Ио запаздывают по сравнению с расчётами на 22 минуты. Отсюда он получил значение для скорости света около 220 000 км/с — неточное, но близкое к истинному.
Первую оценку скорости света дал Олаф Рёмер (1676). Он заметил, что когда Земля и Юпитер находятся по разные стороны от Солнца, затмения спутника Юпитера Ио запаздывают по сравнению с расчётами на 22 минуты. Отсюда он получил значение для скорости света около 220 000 км/с — неточное, но близкое к истинному.
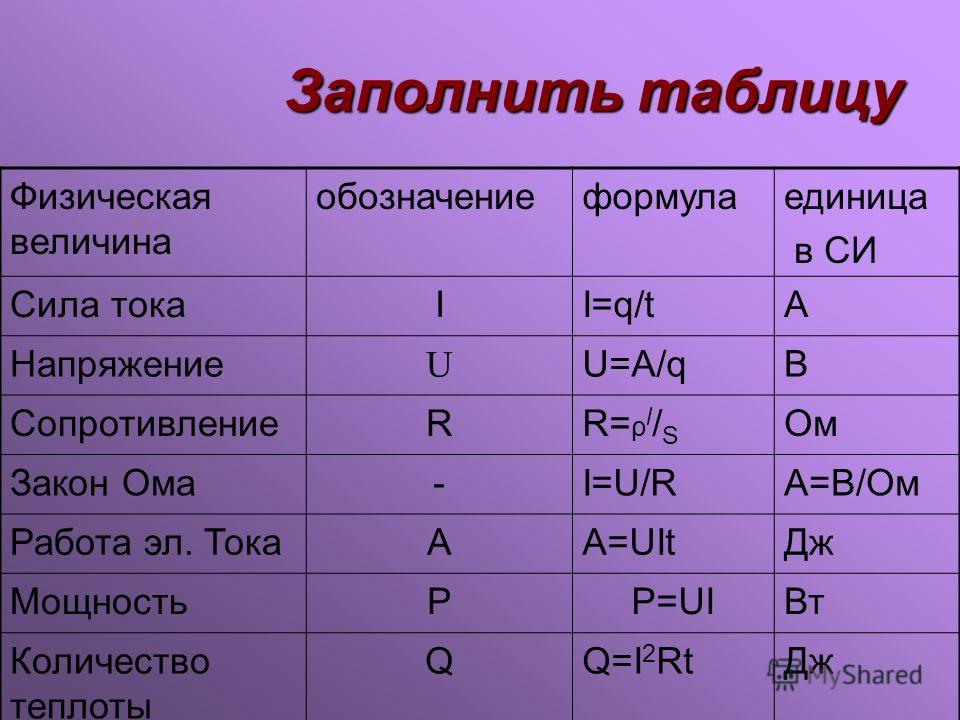
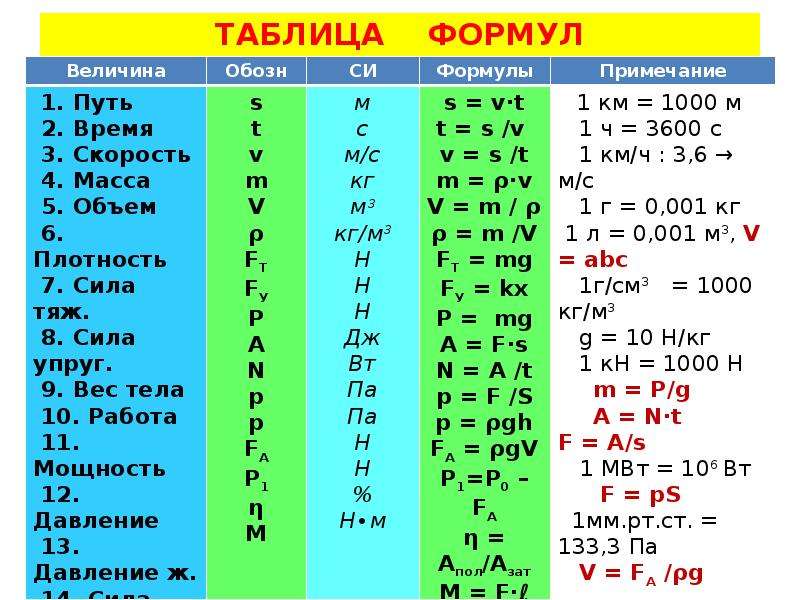 Эта температура
разница называется температурой по Цельсию, символом t , и составляет
определяется количественным уравнением
Эта температура
разница называется температурой по Цельсию, символом t , и составляет
определяется количественным уравнением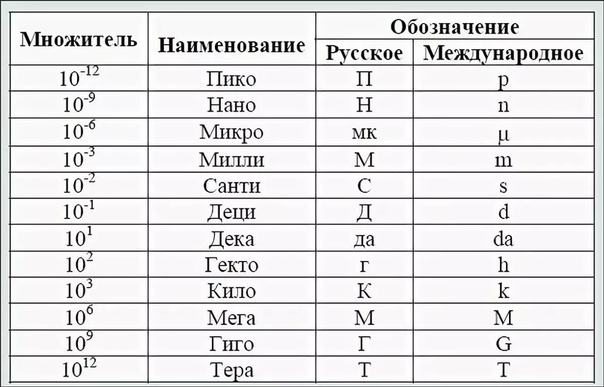 используя то же числовое значение. Например, температура по Цельсию
разница т и термодинамический перепад температур T между точкой плавления галлия и тройной точкой воды может
можно записать как t = 29,7546 ° C = T = 29,7546 К.
используя то же числовое значение. Например, температура по Цельсию
разница т и термодинамический перепад температур T между точкой плавления галлия и тройной точкой воды может
можно записать как t = 29,7546 ° C = T = 29,7546 К. 626070 15 × 10 −34 Дж с
626070 15 × 10 −34 Дж с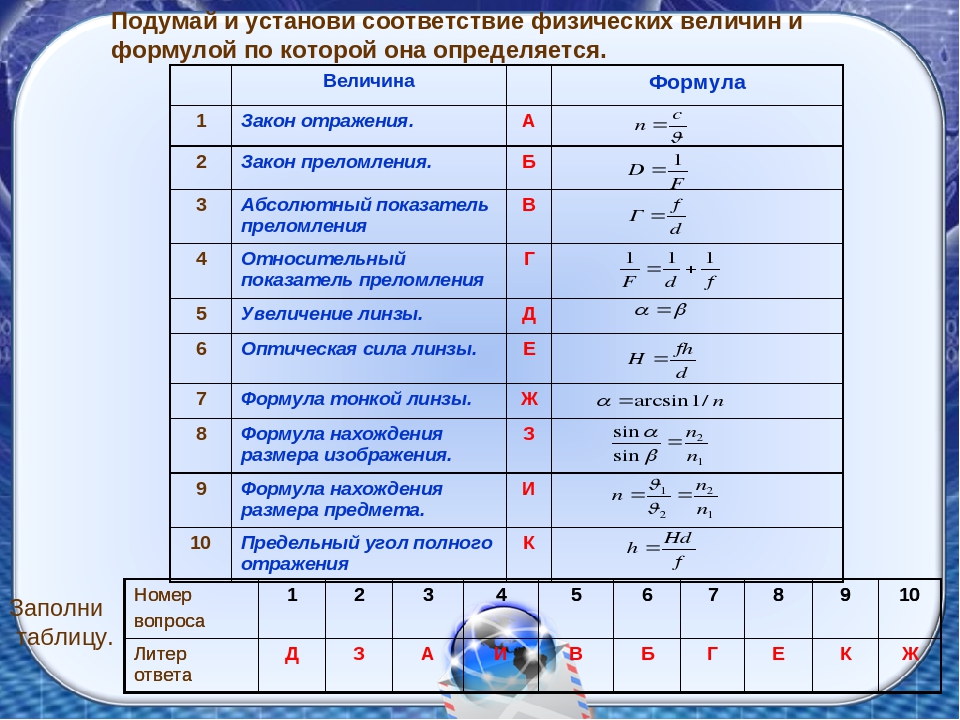 Все названия единиц измерения печатаются строчными буквами, включая первую букву, независимо от того, названы ли они в честь человека или начинается ли символ единицы с символа верхнего регистра (т.е. «Ньютон», а не «Ньютон»). Если с именем устройства используется префикс, он становится частью имени устройства и формируется как одно слово (например, «микропаскаль», а не «микропаскаль» или «микропаскаль»). Если производная единица является произведением двух или более отдельных единиц, для разделения названий можно использовать пробел или дефис (например, «ньютон-метр» или «ньютон-метр»). Для единиц, возведенных в степень, соответствующий модификатор может предшествовать названию единицы или следовать за ним (например, «квадратный метр» или «метр в кубе»).
Все названия единиц измерения печатаются строчными буквами, включая первую букву, независимо от того, названы ли они в честь человека или начинается ли символ единицы с символа верхнего регистра (т.е. «Ньютон», а не «Ньютон»). Если с именем устройства используется префикс, он становится частью имени устройства и формируется как одно слово (например, «микропаскаль», а не «микропаскаль» или «микропаскаль»). Если производная единица является произведением двух или более отдельных единиц, для разделения названий можно использовать пробел или дефис (например, «ньютон-метр» или «ньютон-метр»). Для единиц, возведенных в степень, соответствующий модификатор может предшествовать названию единицы или следовать за ним (например, «квадратный метр» или «метр в кубе»).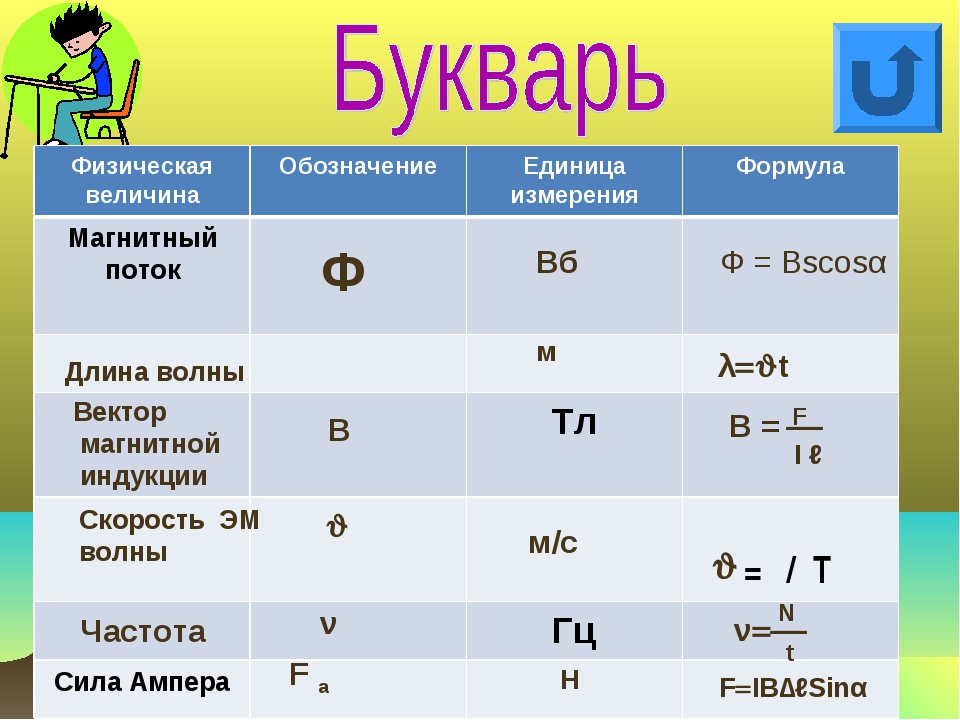 Например, символ «ньютон-метр» записывается как «Н · м» или «Н · м». Деление представлено с помощью солидуса (прямой ход) или с использованием отрицательных степеней. Обозначение «ньютон на метр» записывается либо как «Н / м», либо как «Н · м -1 »).
Например, символ «ньютон-метр» записывается как «Н · м» или «Н · м». Деление представлено с помощью солидуса (прямой ход) или с использованием отрицательных степеней. Обозначение «ньютон на метр» записывается либо как «Н / м», либо как «Н · м -1 »). Пробел представляет собой оператор умножения. Исключением из правила является угол плоскости, выраженный в градусах, минутах и секундах. Символы градуса, минуты и секунды всегда следуют за соответствующими числами без пробела. Например, значение в тридцать пять градусов записывается как «35 °». Цифры всегда отображаются как римский (вертикальный) текст.
Пробел представляет собой оператор умножения. Исключением из правила является угол плоскости, выраженный в градусах, минутах и секундах. Символы градуса, минуты и секунды всегда следуют за соответствующими числами без пробела. Например, значение в тридцать пять градусов записывается как «35 °». Цифры всегда отображаются как римский (вертикальный) текст. Обычно это точка или запятая. Для значений от минус один до один десятичному маркеру предшествует ноль, например «0,123».
Обычно это точка или запятая. Для значений от минус один до один десятичному маркеру предшествует ноль, например «0,123».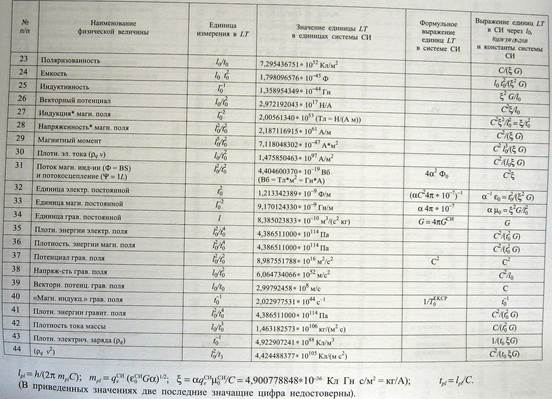 грамм. «( x ) ( y )». Знак умножения можно использовать для обозначения умножения, помещая его между переменными, которые нужно умножить, например « x × y ». Обратите внимание, что знак умножения всегда следует использовать там, где только числа умножаются вместе, но его лучше избегать, если используются имена переменных (во избежание путаницы с общим именем переменной x ). Использование средней точки («·») не рекомендуется. Дивизия указывается с помощью солида , e.грамм. « x / y » или отрицательный индекс, например « x y -1 «.
грамм. «( x ) ( y )». Знак умножения можно использовать для обозначения умножения, помещая его между переменными, которые нужно умножить, например « x × y ». Обратите внимание, что знак умножения всегда следует использовать там, где только числа умножаются вместе, но его лучше избегать, если используются имена переменных (во избежание путаницы с общим именем переменной x ). Использование средней точки («·») не рекомендуется. Дивизия указывается с помощью солида , e.грамм. « x / y » или отрицательный индекс, например « x y -1 «.