Действия над положительными и отрицательными числами – Действия с отрицательными и положительными числами | Учеба-Легко.РФ
Действия с отрицательными и положительными числами | Учеба-Легко.РФ
Абсолютная величина ( модуль ). Для отрицательного числа – это положительное число, получаемое от перемены его знака с « – » на « + »; дляположительного числа и нуля – само это число. Для обозначения абсолютной величины (модуля) числа используются две прямые черты, внутри которых записывается это число.
П р и м е р ы : | – 5 | = 5, | 7 | = 7, | 0 | = 0.
| Сложение: | 1) при сложении двух чисел с одинаковыми знаками складываются их абсолютные величины и перед суммой ставится общий знак. П р и м е р ы : ( + 6 ) + ( + 5 ) = 11 ;
( – 6 ) + ( – 5 ) = – 11
2) при сложении двух чисел с разными знаками их абсолютные величины вычитаются ( из большей меньшая ) и ставится знак числа с большей абсолютной величиной. П р и м е р ы : ( – 6 ) + ( + 9 ) = 3 ;
( – 6 ) + ( + 3 ) = – 3 . |
Вычитание. Можно заменить вычитание двух чисел сложением, при этом уменьшаемое сохраняет свой знак, а вычитаемое берётся с обратным знаком.
П р и м е р ы :
( + 8 ) – ( + 5 ) = ( + 8 ) + ( – 5 ) = 3;
( + 8 ) – ( – 5 ) = ( + 8 ) + ( + 5 ) = 13;
( – 8 ) – ( – 5 ) = ( – 8 ) + ( + 5 ) = – 3;
( – 8 ) – ( + 5 ) = ( – 8 ) + ( – 5 ) = – 13;
Умножение. При умножении двух чисел их абсолютные величины умножаются, а произведение принимает знак « + » , если знаки сомножителей одинаковы, и знак « – » , если знаки сомножителей разные.
Полезна следующая схема (правила знаков при умножении):
+ · + = +
+ · – = –
– · + = –
– · – = +
При умножении нескольких чисел ( двух и более ) произведение имеет знак « + » , если число отрицательных сомножителей чётно, и знак « – » , если их число нечётно.
П р и м е р :
Деление. При делении двух чисел абсолютная величина делимого делится на абсолютную величину делителя, а частное принимает знак « + » , если знаки делимого и делителя одинаковы, и знак « – » , если знаки делимого и делителя разные.
Здесь действуют те же правила знаков, что и при умножении:
+ : + = +
+ : – = –
– : + = –
– : – = +
П р и м е р : ( – 12 ) : ( + 4 ) = – 3 .
uclg.ru
План-конспект урока по алгебре (6 класс) на тему: Действия с положительными и отрицательными числами.
Дата: 17.03.2016
Тема урока: Действия с положительными и отрицательными числами.
Тип урока: обобщение и систематизация знаний
Класс: 6
Цели:
Образовательные: обобщить знания учащихся о правилах действий над положительными и отрицательными числами; закрепить полученные навыки;
Воспитательные: воспитание познавательного интереса к предмету; воспитывать культуру труда, математической речи, активность, самостоятельность, культуру общения.
Оборудование: компьютер; проектор; мультимедийная презентация; оценочные листы; бланки для ответов.
Ход урока:
Ребята, мы с вами долго и упорно изучали арифметику положительных и отрицательных чисел, и вот, пришло время подвести итоги. Так чему же вы научились?
Ученики отвечают: «Мы научились выполнять сложение и вычитание, умножение и деление положительных и отрицательных чисел и т.п.»
А к какой группе чисел можно отнести все положительные и отрицательные числа?
Ученики отвечают: «К рациональным числам!»
Совершенно верно! Ну, тогда начнем наш урок! Сегодня вы узнаете много интересного и закрепите ранее изученный материал. Каждому из вас выдан бланк ответов, который вы будете заполнять в ходе урока. В последующем, вы сможете использоваться его как подсказку. А для начала пройдите блиц-опрос.
Блиц-опрос
- Сумма противоположных чисел равна…
- Какое из чисел больше: отрицательное или 0?
- Какое число больше: -15 или -9?
- Чему равна сумма чисел от -18 до 17?
- Если перемножить 5 положительных и 8 отрицательных чисел, то с каким знаком мы получим результат?
- При каких значениях x и y верно соотношение: ?
Вы можете сравнить свои ответы с ответами на экране. (Приложение 1)
Теперь вам нужно заполнить бланки-подсказки, затем сравнить свои ответы с ответами на экране (обучающиеся заполняют бланки):
Бланк-подсказка
1. Число, отличающееся от данного только знаком, называется
2. Сумма противоположных чисел равна
3. Сумма положительных чисел
4. Сумма отрицательных чисел
5. Сумма чисел с разными знаками имеет знак числа
6. Вычитание можно заменить действием сложения с числом
7. Произведение положительных чисел
8. Произведение четного числа отрицательных множителей
9. Произведение нечетного числа отрицательных множителей
10. a(bc) =
11. a : (bc) =
12. (a ± b)с = или ас ± bc =
13. (a ± b) : с = или а : с ± b : c =
В оценочном листе отметьте, какие знания вы приобрели в ходе изучения действий над рациональными числами и оцените их по пятибалльной шкале:
Оценочный лист
1. Я знаю правила сложения и вычитания рациональных чисел |
|
2. Я знаю правила умножения и деления рациональных чисел |
|
3. Я знаю свойства рациональных чисел |
|
4. Я умею складывать рациональные числа |
|
5. Я умею вычитать рациональные числа |
|
6. Я умею умножать и делить рациональные числа |
|
7. Я умею находить рациональные способы решения, используя свойства рациональных чисел |
А теперь давайте обратимся к истории. Первые понятия об отрицательных величинах сложились примерно к I веку до нашей эры.
Примерно во II веке до н.э. с ними столкнулись китайские ученые, но император Ши Хуан Ди, разгневанный на ученых, повелел сжечь все научные книги, а их авторов казнить. Поэтому, до нас дошли лишь обрывки, откуда известно, что китайцы не знали правила знаков при умножении положительных и отрицательных чисел.
Одними из первых дали весьма естественное истолкование этим числам индийские ученые. Они истолковывали их как «имущество» и «долг». Например, математик и астроном Брахмагупта в книге «Брама- спутта –сидданта», состоящей из 20 книг, написанных в 628 году сформулировал математические действия так:
Правила сложения:
Правила вычитания:
- Долг, вычтенный из нуля, становится имуществом:
- Имущество, вычтенное из нуля – долгом:
- Чтобы вычесть долг из имущества или имущество из долга, нужно составить их сумму: .
Попробуйте сами сформулировать правила умножения и деления положительных и отрицательных чисел на «языке Брахмагупты».
А сейчас давайте познакомимся еще с одним приемом действий с рациональными числами.
Таблица умножения положительных и отрицательных чисел:
Друг это «+», враг это «», моего это «=», мне — это знак «*»
А теперь решите примеры, использовав полученные приемы.
Вариант 1 | Вариант 2 |
И на последок, решите следующую задачу:
Бережливый хозяин должен хорошо знать как размер своего имущества, так и свои долги. И вот однажды ростовщик решил посчитать, с прибылью для себя или с убытком он прожил этот месяц? Если:
- Первый человек отдал ему 32,4 лиры своего долга;
- второму он дал в долг 50% этих денег;
- На строительство башни он пожертвовал 30,8;
- Третий вернул 17,6 лиры;
- И последняя сделка принесла ему доход 10 лир.
Ребята, вот наш урок подошел к концу. Что мы с вами повторили? Что вы узнали нового? Как вы думаете, вы справитесь с контрольной работой?
Сдайте, пожалуйста, ваши оценочные листы и запишите домашнее задание. Спасибо за урок! До завтра!
Домашнее задание: №1257(а,г), №1222.
nsportal.ru
Арифметические действия с положительными и отрицательными числами
Конспект урока в 6 классе.
Автор: Малютин Андрей Анатольевич, учитель математики МБОУ «Спасско-Лутовиновская СОШ им. И.С. Тургенева».
Тема урока: «Арифметические действия с положительными и отрицательными числами».
Продолжительность урока: 45 минут.
Учебник: «Математика. 6 класс», Виленкин Н. Я., Жохов В. И., Чесноков А. С., Шварцбурд С. И.
На уроке применяются элементы следующих современных образовательных технологий: обучение в сотрудничестве, деятельностные технологии, игровые технологии, здоровьесберегающие технологии, информационные компьютерные технологии.
Тип урока: обобщающий урок (интегрированный), форма урока: урок-соревнование.
Место темы по планированию:
при 5 ч. в неделю на изучение математики по учебному плану на тему «Деление положительных и отрицательных чисел» программой предусмотрено 3 часа, данный урок – 3-й.
Цели урока:
Обобщение и систематизация изученного материала.
Закрепление теоретических и практических умений и навыков, полученных при изучении темы.
Развитие логического мышления, мотивации в обучении, любознательности, активности и познавательного интереса обучающихся.
Задачи урока:
Образовательные
совершенствование знаний, умений и навыков по теме урока и пройденному материалу,
отработка вычислительных навыков.
Воспитательные
воспитание у детей трудолюбия, усидчивости и сознательной дисциплины на уроке,
повышение интереса к изучению математики, воспитание любви к родному краю.
Развивающие
развитие логического мышления, памяти и внимания,
развитие умения анализировать, сравнивать, делать выводы.
Оборудование:
Компьютер (или ноутбук), проекционный экран, проектор.
Мультимедиафайлы (презентация, видеоролик, музыкальные треки).
Файл-конверты (по одному на группу), содержащие задания, таблички, оценочные цветные кружки, критерии оценок, карты часовых поясов России, русский алфавит, итоговые листы.
Георгиевские ленточки. Призы (открытки и гирлянды к 70-летию Победы).
Оформление доски: задания для устного счёта.
План урока.
Организация класса. /3 мин/
Разминка (устный счёт). Д/з. /5 мин/
Повторение: видеовопрос, задача из учебника. /10 мин/
Физминутка. /2 мин/
Решение уравнений. /8 мин/
Мозговой штурм. /5 мин/
Закрепление. /7 мин/
Итог урока. /5 мин/
Содержание урока.
Организационный момент.
Здравствуйте. Меня зовут Андрей Анатольевич. Я – учитель математики, и ближайшие 45 минут мы с вами проведём вместе. А приехал я из Спасского-Лутовинова. Знаете такое село? /Ответы детей/
Слайд № 1 – пейзаж села, фото И.С. Тургенева, фото школы.
Проверьте, пожалуйста, наличие необходимых на уроке принадлежностей (тетради, учебники, дневники, ручки…), рассаживайтесь поудобнее (дети рассаживаются за 4 стола – сдвоенные парты – по 5-6 чел.), подарите друг другу улыбки, не забывайте об осанке и начнём урок.
У нас 4 команды, поэтому иногда в ходе урока вы будете соревноваться. Та команда, которая первой даст верный ответ, кладёт себе в копилку красный кружок, остальные команды (если если их ответ тоже правильный) – жёлтый кружок. Если ответа нет или он ошибочный, то ничего не кладёт.
Разминка.
Начнём с разминки. Посмотрите на доску. Здесь 4 столбика по 4 примера. Для каждой команды свой столбик. Посчитайте устно, сверьте ответы в своих группах и направьте кого-нибудь записать их на доске.
/считают и представитель от каждой группы записывает на доске ответы/
Получается следующее:
–11+13=2 –7+8=1 0–(–1)=1 5+(–4)=1
1–(–1)=2 5–(–4)=9 20,2+(–11,2)=9 5/2–(–3/2)=4
–1,5•(–3,2+3,2)=0 –0,4•(7,3–17,3)=4 2•(–5,5+7,5)=4 –0,01•(–100)=1
4/7:2/21=6 –1:(1/3–4/3)=1 –(–1:1/5)=5 –1:(5/16–7/16)=8
Учитель спрашивает, почему в каждом столбике именно 4 примера? /ответы детей – ведь мы изучили 4 арифметических действия: сложение, вычитание, умножение и деление положительных и отрицательных чисел/
Учитель – А как вы думаете, судя по разминке, чем мы сегодня будем заниматься? Попробуйте сформулировать тему урока. /ответы детей/
Да, на этом уроке мы с вами порешаем примеры, уравнения и задачи, содержащие числа с разными знаками. А какие же тогда цели мы поставим перед собой? /ответы детей/. Наша главная цель – закрепить навыки и умения выполнять арифметические действия с числами с разными знаками.
Далее в тетрадях дети записывают дату, «классная работа», тему «Арифметические действия с положительными и отрицательными числами». /слайды № 2-3/
Учитель – А вам ни о чём не говорят полученные в примерах числа? /ответы детей, наводящие реплики учителя/
1941, 1945 – годы начала и окончания ВОВ, 2206 – число и месяц начала войны, 1418 – столько дней и ночей длилась война. И эти числа у нас получились не случайно. На уроке сегодня мы немного коснёмся и темы Великой Отечественной войны.
Историческая справка (сообщает учитель).
22 июня 1941 года началась Великая Отечественная война. Никто не догадывался, что советскому народу предстоит пройти через нечеловеческие испытания, пройти и победить, избавив мир от фашизма. Никто и предположить не мог, что названия городов-героев станут известны всему миру, что Сталинград станет символом стойкости наших людей, Ленинград — символом мужества, Брест — символом отваги. 1418 дней и ночей войны. Свыше 26 миллионов человеческих жизней…
C первых же дней Великой Отечественной Войны огромное число математиков были мобилизованы или ушли на фронт добровольцами. Они храбро воевали и честно исполняли свой гражданский долг, совершенствовали военную технику, разрабатывали теорию стрельбы, вели статистический контроль в военном производстве и т.д.
А теперь запишите в дневник домашнее задание. /слайд № 4/
Повторение:
Видеовопрос. /слайд № 5/
«Здравствуйте, коллеги. Меня зовут… Я учусь в 6 классе в Спасско-Лутовиновской средней школе имени Тургенева Мценского района. Я приготовил(а) для вас несколько вопросов и буду рад(а), если вы ответите на них». Далее из видеофрагмента звучат вопросы:
Запишите в тетрадях число 50 843.
Запишите противоположное ему число.
Назовите модуль каждого из полученных чисел.
Назовите соседние с ними числа.
Сколько целых чисел расположено между данным числом и ему противоположным?
А теперь внимательно посмотрите на первоначально записное число. Не напоминает ли оно вам какую важную дату? Что это за дата?
Спасибо большое. Я очень рад(а), что вы ответили на все мои вопросы. До свидания.
Историческая справка.
5 августа 1943 г. был освобождён г. Орёл войсками 3-й и 63-й армий, которыми командовали генералы Горбатов Александр Васильевич и Колпакчи Владимир Яковлевич. В полночь в Москве был дан салют в честь освобождения Орла и Белгорода. /слайд № 6/
Решение задачи из учебника.
№ 1167 (а). По карте России с часовыми поясами определить поясное время в Екатеринбурге и Владивостоке, если в Москве полночь. Какое время будет в Калининграде? /дети отвечают/
А какая важная дата связана с Москвой в годы ВОВ? Эта дата отмечается как День воинской славы России. /ответы детей/. Конечно же, битва за Москву.
Историческая справка.
5 декабря 1941 года началась Московская наступательная операция, продолжающаяся до 7 января 1942 г. В результате советского контрнаступления противник оказался отброшен от Москвы на 100 – 250 км. Были полностью освобождены Московская, Тульская и Рязанская области, а также ряд районов Калининской, Смоленской и Орловской областей. /слайд № 7/
Физминутка.
А сейчас немного отдохнём от работы. Учитель просит все группы встать и взяться за руки (каждая группа вокруг своего стола). Какую фигуру Вы изобразили? (Круг, окружность). Похлопайте в ладоши, повернитесь направо и немножко помаршируем. (Звучит марш «Прощание славянки», /слайд № 8/). Спасибо, присаживайтесь на свои места. Какая мелодия играла сейчас? /дети предположительно отвечают/.
Решение уравнений.
-0,3х=-21 2) х:(-140)=-0,5 3) -28+х=42 4) х-(-2,5)=72,5
Ответ: 70 Ответ: 70 Ответ: 70 Ответ: 70
Интересный момент: уравнения у всех были разные, но корень получился одинаковый. Вам ни о чём не говорит это число? /ответы детей/. Действительно, в этом году мы отмечаем 70-летие Победы в Великой Отечественной войне. А какого числа празднуется День Победы? Правильно, 9 мая. А какая песня звучит в этот день? А кто может напеть мотив? /звучит отрывок из песни «День Победы», слайд № 9/.
Учитель раздаёт на столы георгиевские ленточки и спрашивает, что означает этот символ и что означают цвета ленты. /ответы детей и корректировка учителя/.
Георгиевская лента — двухцветная лента к ордену Святого Георгия, Георгиевскому кресту или медали. Также их на бескозырке носили матросы гвардейского экипажа корабля, награждённого Георгиевским флагом. Цвета ленты — чёрный и жёлто-оранжевый — означают «дым и пламя» и являются знаком личной доблести солдата на поле боя.
Мозговой штурм.
В войну многие (секретные) сведения шифровали. Для чего? /чтобы в случае перехвата врагом нельзя было понять, о чём говорится в донесении/. Представьте, что к Вам попало такое донесение. Достаньте из конвертов русский алфавит и попробуйте расшифровать слово, записанное так: -1+3-14-16-13-16. Вряд ли Вы это сможете сделать быстро. Поэтому даю вам ключ к шифру. За начало отсчёта принята средняя буква алфавита, а остальным буквам соответствуют числа так, как на координатной прямой. А теперь дело у вас должно пойти быстрее. Получают слово – отвага.
Закрепление.
Учитель просит детей взять из файл-конвертов и заполнить листок с таблицей:
Задание или вопрос: | Ваш ответ: | |
1 | Какое число нужно записать вместо ☼, чтобы равенство ☼ — 2=-7 было верным? | -5 |
2 | Какой знак нужно поставить вместо ☼, чтобы было верным равенство -3,6☼(-1,8)=2? | : |
3 | Какие целые числа удовлетворяют неравенству: -2<х<0,25? | -2,-1,0 |
4 | Вычислите: (-1/2)2, (-3)3 | ¼; -27 |
5 | Упростите выражение: –х–а+12+а–12 | -х |
На экран выводится слайд для контроля правильности ответов /слайд № 10/.
Подведение итогов.
Сегодня на уроке мы повторили пройденный материал, закрепили правила действий с положительными и отрицательными числами, вспомнили некоторые важные события в годы ВОВ. Какие вопросы есть? (дети, по одному от группы, высказываются по итогам урока, используя итоговые листы).
Оценим теперь Вашу работу. Учитель даёт общую характеристику работы класса, обращает внимание на количество заработанных кружков и просит коллективы групп объективно оценить работу каждого члена группы, предлагая после мини-совещания поднять каждому ученику табличку с оценкой.
Команды получают призы с символикой 70-летия Великой Победы.
Если останется время, предлагается заполнить листы по итогам урока.
Заключительное слово учителя. Дорогие ребята! Спасибо за вашу работу сегодня на уроке. Я желаю, чтобы вы росли счастливыми и здоровыми, хорошо учились и любили свою Родину, дороже неё у нас ничего нет. Удачи вам. /слайд № 11/
xn--j1ahfl.xn--p1ai
Действие над положительными и отрицательными числами
Технологическая карта урока
Ф.И.О. учителя Исаева Фарида Болотбековна
Класс: 6 «В»
Дата: 27.04.2018
Предмет: математика
УМК: математика, 6 класс (базовый учебник –Н.Я.Виленкин, В.И. Жохов, и др.- 24-е изд., — М.: Мнемозина , 2009)
Тема урока: Действие над положительными и отрицательными числами
Ключевые компетентности
1.
Информационная: умеют устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение.
2.
Самоорганизации и разрешения проблем : умеют адекватно оценивать правильность или ошибочность выполнения учебной задачи.
3.
Социально — коммуникативная: умение слушать и вступать в диалог; воспитывать чувство взаимопомощи, уважительное отношение к чужому мнению, культуру учебного труда, требовательное отношение к себе и своей работе.
Предметные компетентности
1.
Вычислительная: уметь в процессе реальной ситуации умения выполнить действие над положительными и отрицательными числами
2.
Аналитико – функциональная: уметь сложить, вычесть, разделить , умножить чисел с разными знаками
3.
Наглядно-образная:
4.
Статистико-вероятностная:
Цели: цель урока: Создать условие для закрепления и повторения правило сложение, вычитание , умножение и деление положительных и отрицательных чисел
Обучающая
Закрепить и систематизировать умения и навыки выполнения действий с положительными и отрицательными числами;
Развивающая
развивает интеллектуальные и познавательные способности;
развивает умение анализировать и быстроты работы мысли и памяти;
развивает логическое мышление;
развивает творческие способности.
Воспитывающая
воспитывать чувство коллективизма, ответственности, самоконтроля; формировать интерес к изучению математики
воспитывает детей сотрудничать, оказывать помощь друг другу в процессе решения задачи;
воспитывает умение работать в группе, самостоятельно.
Тип, структура урока: Урокобобщения и закрепления знаний
Форма урока: Урок практической самостоятельной работы группового типа
Общие методы: Наглядно- практический метод.
Приемы работы учеников: Индивидуальная, групповая и самостоятельная работа.
Средства наглядности: Компьютер, проектор, электронная презентация; цветочки с заданиями, лист самооценки учеников и др.наглядные пособии.
Ход урока:
Этап урока
Время
в мин.
Деятельность учителя
(что делает учитель)
Деятельность учеников
(что делают ученики)
Оценивание
I. Организационный момент.
1
Здравствуйте, ребята!
Проверка отсутствующих в классе, создание позитив для совместной деятельности на уроке.
Я надеюсь, что сегодняшний урок будет познавательным, полезным и интересным. Для этого от вас требуется внимание, активность и желание работать.
Слушают учителя, настраиваются на работу. Создание благоприятного психологического климата.
II. Мотивационно- ориентационный этап
2.1 Актуализация знаний
2.2 Постановка проблемной ситуации
2.3 Формулировка темы урока и его целей
2
Сегодня на уроке мы будем работать в группах, участвовать математических турнирах, а также познакомимся с новыми интересными людьми проехавшись из Китая.
“ давным-давно в точечном царстве, в координатном государстве, на берегу нулевой реки жили числа-близнецы. Их домики стояли на одинаковом расстоянии от реки. Только одни из них поселились на правом, а другие – на левом, противоположном берегу. Поэтому числа 1 и -1, 2 и -2, 3 и -3… стали называть противоположными. Но случилась беда, стали пропадать пары противоположных чисел. Сыщики выяснили, что они исчезают в нулевой реке. Тогда правитель координатного государства издал указ, запрещающий противоположным числам одновременно подходить к нулевой реке и участвовать в различных числовых турнирах
Попробуйте сформулировать тему сегодняшнего урока (турнира).
Какой вы цель поставите перед собой?
Что вы ждете от сегодняшнего урока
Давайте сформулируем цель урока:
Закрепить и систематизировать умения и навыки выполнения действий с положительными и отрицательными числами;
развивать творчество, сообразительность, познавательную активность учащихся;
воспитывать чувство коллективизма, ответственности, самоконтроля; формировать интерес к изучению математики. (Слайд 4)
А девиз?
Пусть эти слова послужат девизом сегодняшнего урока
Чтобы участвовать турнир нам необходимо разделится на две команды.
Для того, чтобы узнать название команды я вам предлагаю собрать ПАЗЛы
Возникает вопрос а какой турнире речь идет?
А название турнира?
Учащиеся сформулируют темуурока: «Положительные и отрицательные числа»
Ответы детей
ДЕВИЗ
Французский писатель XIX столетия Анатоль Франс однажды заметил: «Учиться можно весело…. Чтобы переваривать знания, надо поглощать их с аппетитом» .
да
ученики делится на две команды
собирают Пазлы и узнают название команды:
«отрицательные числа»
«положительные числа»
III.
Операционально- исполнительский этап
3.1.Организация исследовательской деятельности учащихся по приобретению новых знаний
3.2 Исследовательская, групповая работа
Физкультминутка
3.3. Первичное закрепление новых знаний
а) практическое задание ( работа с командой)
б) работа по готовым чертежам
в) самостоятельная работа с самопроверкой по эталону
г) работа с учебником
Задание 1 «Сосчитай»
Задание 2 «путешествие»
Щенок путешествует по координатной прямой, на которой отмечены точки A(-5), B(4), C(6), D(-8). Какой из маршрутов самый короткий?
ABCDACBDADCBADBC
Задание 3 «Кросс-опрос»
Какие числа называется противоположными?
Как сложим числа с разными знаками?
Как мы умножаем числа с разными знаками?
Возникновение отрицательных чисел. В какой стране впервые использовались отрицательные числа?
Но я тоже не знаю поэтому пригласила математика из Китая ЧжанЦань
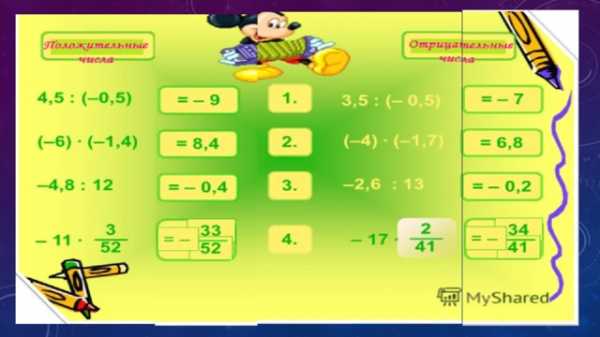
Задание 4
Устный счет «Проверь себя»
Задание 5
« Кто более внимательней »
А теперь, ребята встали. Улыбнитесь. Делаем зарядку.
Подводим итоги нашего урока. Мы с вами плодотворно поработали, я рада такому сотрудничеству. Я хочу, чтобы вы оценили свою работу и работу группы на уроке. Приглашаю капитанов команды к доске.
Давайте считаем заработанные балы на сегодняшнем турнире?
Ребята выходят на доскус каждой команды по одному человекуиначинают решать примеры.
Ответы команды
ADBCACBD
Ответы детей
Говорят, в Китае. Но точно не знаем.
Среди учеников рассказывает возникновение отрицательных чисел
Выполняют построение в тетрадях, делают соответствующие записи.
Ребята выходят на доску с каждой команды по одному человеку и начинают решать примеры.
Ребята делают физкультминутку
Ребята выполняют исследовательскую работу.
.
Капитаны команды оценивает учеников. команды посчитают набранные баллы и объявляют, какая команда победила.
Правильно
Положительные числа получает за правильное решение получают 5 баллов
Хорошо угадали
2 балла
Молодцы
Хорошо
Молодцы
Правильно
IV. Рефлексия урока
А теперь я хочу у вас спросить : «Вам понравился ли урок?» Кому понравился наш сегоднешний урок берем бабочки и приклеиваем к нашему цветку.
Кому непонравился наш урок берем картинку с пауками и приклеиваем на ватман.
Все ученики приклеивают бабочек на цветку.
Взаимнооценивание
V. Домашнее
задание
Учитель раздает карточки с заданиями
Учащиеся записывают в дневники домашнее задание.
До свидание!
Просмотр содержимого документа
«Действие над положительными и отрицательными числами»


“ давным-давно в точечном царстве, в координатном государстве, на берегу нулевой реки жили числа-близнецы. Их домики стояли на одинаковом расстоянии от реки. Только одни из них поселились на правом, а другие – на левом, противоположном берегу. Поэтому числа 1 и -1, 2 и -2, 3 и -3… стали называть противоположными. Но случилась беда, стали пропадать пары противоположных чисел. Сыщики выяснили, что они исчезают в нулевой реке. Тогда правитель координатного государства издал указ, запрещающий противоположным числам одновременно подходить к нулевой реке и участвовать в различных числовых турнирах


Цели урока:
- Закрепить и систематизировать умения и навыки выполнения действий с положительными и отрицательными числами;
- развивать творчество, сообразительность, познавательную активность учащихся;
- воспитывать чувство коллективизма, ответственности, самоконтроля; формировать интерес к изучению математики.

ДЕВИЗ
Французский писатель XIX столетия Анатоль Франс однажды заметил: «Учиться можно весело…. Чтобы переваривать знания, надо поглощать их с аппетитом» .
Пусть эти слова послужат девизом сегодняшнего урока
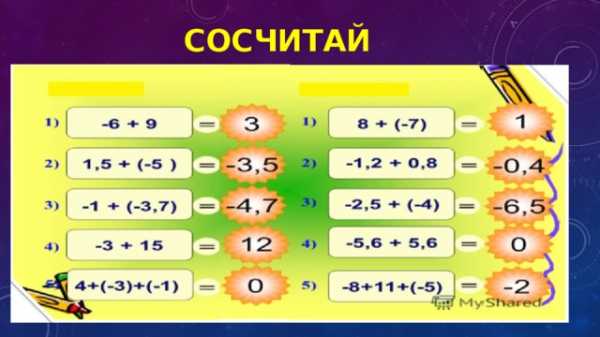
Сосчитай

путешествие
Щенок путешествует по координатной прямой, на которой отмечены точки A(-5), B(4), C(6), D(-8). Какой из маршрутов самый короткий?
ADCB
ABCD
ACBD
ADBC

КРОСС — ОПРОС

- Сформулируйте правило деления отрицательного числа на отрицательное
Чтобы разделить отрицательное число на отрицательное, надо разделить модуль делимого на модуль делителя
- Как перемножаются два отрицательных числа ?
Чтобы перемножить два отрицательных числа, надо перемножить их модули
- Какие числа называют противоположным ?


- Как найти длину отрезка на координатной прямой ?
Чтобы найти длину отрезка на координатной прямой , надо из координаты его правого конца вычесть координату его левого конца
Возникновение отрицательных чисел. В какой стране впервые использовались отрицательные числа?


Устный счет Проверьте себя
15*(-1) =
-24 +32 =
0*(-1,1) =
-2,8-(-0,2) =
-222: 11 =
-(-10)+90 =
-1*(-8):4 =

« Кто более
Внимательней »

Положительные числа
Отрицательные числа

Физкультминутка

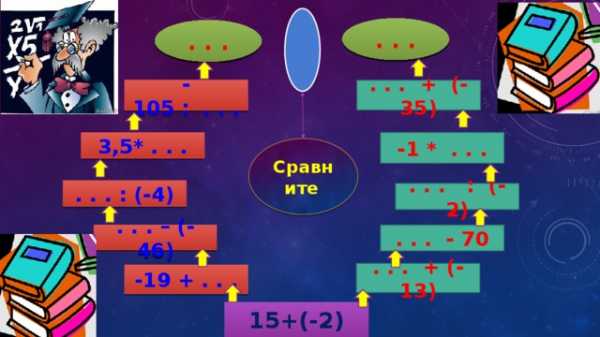
. . .
. . .
-105 : . . .
. . . + (-35)
3,5* . . .
-1 * . . .
Сравните
. . . : (-4)
. . . : (-2)
. . . – (- 46)
. . . — 70
. . . + (-13)
-19 + . . .
15+(-2)
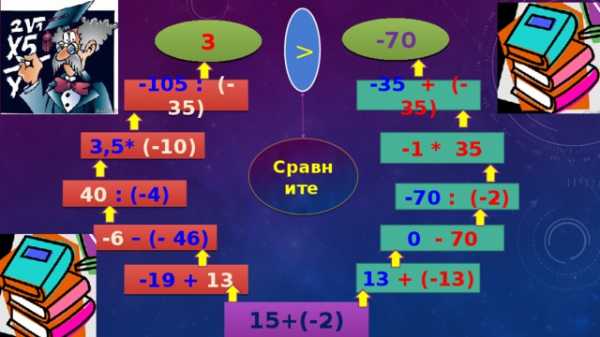 -70 3 -105 : (-35) -35 + (-35) 3,5* (-10) -1 * 35 Сравните 40 : (-4) -70 : (-2) -6 – (- 46) 0 — 70 13 + (-13) -19 + 13 15+(-2) «
-70 3 -105 : (-35) -35 + (-35) 3,5* (-10) -1 * 35 Сравните 40 : (-4) -70 : (-2) -6 – (- 46) 0 — 70 13 + (-13) -19 + 13 15+(-2) «
-70
3
-105 : (-35)
-35 + (-35)
3,5* (-10)
-1 * 35
Сравните
40 : (-4)
-70 : (-2)
-6 – (- 46)
0 — 70
13 + (-13)
-19 + 13
15+(-2)

ОЦЕНКА
После математического турнира собрались все числа на берегу нулевой реки.
На аккуратно начертанной числовой прямой собрались на совещание разные числа: положительные, отрицательные и нуль. Председателем единогласно был избран нуль. Он стал первым держать речь: “Уважаемые числа, мы собрались здесь для того, чтобы произвести оценку нашим действиям. Я должен отметить, хотя, может, это и нескромно, но от меня ведется отсчет всех чисел, поэтому я и буду давать вам оценку. Справа от меня расположены числа положительные, ничего отрицательного о них не скажешь. Слева – числа отрицательные, в жизни очень плохо быть отрицательным, но нам в математике и в других предметах часто без них не получить положительный ответ. Всяческого одобрения заслуживает модуль, который всегда неотрицательный”.
Сидят числа и раздумывают: “Что стоит оценка нуля?”
multiurok.ru
Действия с отрицательными и положительными числами
Действия с отрицательными и положительными числами
Абсолютная величина (модуль). Сложение.
Вычитание. Умножение. Деление.
Абсолютная величина ( модуль ). Для отрицательного числа – это положительное число, получаемое от перемены его знака с « – » на « + »; для положительного числа и нуля – само это число. Для обозначения абсолютной величины (модуля) числа используются две прямые черты, внутри которых записывается это число.
П р и м е р ы : | – 5 | = 5, | 7 | = 7, | 0 | = 0.
| Сложение: | 1) при сложении двух чисел с одинаковыми знаками складываются их абсолютные величины и перед суммой ставится общий знак. П р и м е р ы : ( + 6 ) + ( + 5 ) = 11 ; ( – 6 ) + ( – 5 ) = – 11 . 2) при сложении двух чисел с разными знаками их абсолютные величины вычитаются ( из большей меньшая ) и ставится знак числа с большей абсолютной величиной. П р и м е р ы : ( – 6 ) + ( + 9 ) = 3 ; ( – 6 ) + ( + 3 ) = – 3 . |
Вычитание. Можно заменить вычитание двух чисел сложением, при этом уменьшаемое сохраняет свой знак, а вычитаемое берётся с обратным знаком.
П р и м е р ы :
( + 8 ) – ( + 5 ) = ( + 8 ) + ( – 5 ) = 3;
( + 8 ) – ( – 5 ) = ( + 8 ) + ( + 5 ) = 13;
( – 8 ) – ( – 5 ) = ( – 8 ) + ( + 5 ) = – 3;
( – 8 ) – ( + 5 ) = ( – 8 ) + ( – 5 ) = – 13;
Умножение. При умножении двух чисел их абсолютные величины умножаются, а произведение принимает знак « + » , если знаки сомножителей одинаковы, и знак « – » , если знаки сомножителей разные.
Полезна следующая схема (правила знаков при умножении):
+ · + = +
+ · – = –
– · + = –
– · – = +
При умножении нескольких чисел ( двух и более ) произведение имеет знак « + » , если число отрицательных сомножителей чётно, и знак « – » , если их число нечётно.
П р и м е р :
Деление. При делении двух чисел абсолютная величина делимого делится на абсолютную величину делителя, а частное принимает знак « + » , если знаки делимого и делителя одинаковы, и знак « – » , если знаки делимого и делителя разные.
Здесь действуют те же правила знаков, что и при умножении:
+ : + = +
+ : – = –
– : + = –
– : – = +
П р и м е р : ( – 12 ) : ( + 4 ) = – 3 .
Переместительное свойство
Для любых чисел a и bверны равенства:
a + b = b + a
и
ab = ba
Сочетательное свойство
Для любых чисел a, b и cверны равенства:
(a + b) + c = a + (b + c)
и
(ab)c = a(bc)
Распределительное свойство
Для любых чисел a, b и cверны равенства:
(a + b) + c = a + (b + c)
и
(ab)c = a(bc)
Из переместительного и сочетательного свойств сложения следует, что в любой сумме можно как угодно переставлять слагаемые и произвольным образом объединять их в группы.
Точно также из переместительного и сочетательного свойств умножения следует, что в любом произведении можно как угодно переставлять множители и произвольным образом объединять их в группы.
Распределительное свойство справедливо и в том случае, когда число умножается на сумму трех и более слагаемых.
Для любых чисел a, b, c и d, верно равенство:a(b + c + d) = ab + ac + ad
Так как вычитание можно представить как сложение с отрицательным числом:
a — b = a + (-b), то распределительный и сочетательный законы можно распространить на операцию вычитания.
Так выглядит переместительное свойство для вычитания:
a — b = -b + a
Так выглядит сочетательное свойство для вычитания:
(a — b) + c = a + (- b + c)
Так выглядит распределительное свойство для вычитания:
a(b — c) = ab – ac
Законы сложения и умножения
Переместительный (коммутативный) закон сложения: m + n = n + m . Сумма не меняется от перестановки её слагаемых.
Переместительный (коммутативный) закон умножения: m · n = n · m . Произведение не меняется от перестановки его сомножителей.
Сочетательный (ассоциативный) закон сложения: ( m + n ) + k = m + ( n + k ) = m + n + k . Сумма не зависит от группировки её слагаемых.
Сочетательный (ассоциативный) закон умножения: ( m · n ) · k = m · ( n · k ) = m · n · k . Произведение не зависит от группировки его сомножителей.
Распределительный (дистрибутивный) закон умножения относительно сложения: ( m + n ) · k = m · k + n · k .
Формулы сокращённого умножения
Из правил умножения сумм и многочленов легко получить следующие семь формул сокращённого умножения.
Их следует знать наизусть, так как они применяются практически во всех задачах по математике.
[1] ( a + b )² = a² + 2ab + b² ,
[2] ( a – b )² = a² – 2ab + b² ,
[3] ( a + b ) ( a – b ) = a² – b²,
[4] ( a + b )³ = a³ + 3a² b + 3ab² + b³ ,
[5] ( a – b )³ = a ³ – 3a² b + 3ab² – b³ ,
[6] ( a + b )( a² – ab + b² ) = a³ + b³ ,
[7] ( a – b )( a ² + ab + b² ) = a³ – b³ .
Степени и корни
Операции со степенями и корнями. Степень с отрицательным,
нулевым и дробным показателем. О выражениях, не имеющих смысла.
Операции со степенями.
1. При умножении степеней с одинаковым основанием их показатели складываются:
a m · a n = a m + n .
2. При делении степеней с одинаковым основанием их показатели вычитаются.
3. Степень произведения двух или нескольких сомножителей равна произведению степеней этих сомножителей.
( abc… ) n = a n · b n · c n …
4. Степень отношения (дроби) равна отношению степеней делимого (числителя) и делителя (знаменателя):
( a / b ) n = a n / b n .
5. При возведении степени в степень их показатели перемножаются:
( a m ) n = a m n .
Все вышеприведенные формулы читаются и выполняются в обоих направлениях слева направо и наоборот.
П р и м е р . ( 2 · 3 · 5 / 15 ) ² = 2 ² · 3 ² · 5 ² / 15 ² = 900 / 225 = 4 .
Операции с корнями. Во всех нижеприведенных формулах символ означает арифметический корень (подкоренное выражение положительно).
1. Корень из произведения нескольких сомножителей равен произведению корней из этих сомножителей:
2. Корень из отношения равен отношению корней делимого и делителя:
3. При возведении корня в степень достаточно возвести в эту степень подкоренное число:
4. Если увеличить степень корня в n раз и одновременно возвести в n-ую степень подкоренное число, то значение корня не изменится:
5. Если уменьшить степень корня в n раз и одновременно извлечь корень n-ой степени из подкоренного числа, то значение корня не изменится:
Расширение понятия степени. До сих пор мы рассматривали степени только с натуральным показателем; но действия со степенями и корнями могут приводить также к отрицательным, нулевым и дробным показателям. Все эти показатели степеней требуют дополнительного определения.
Степень с отрицательным показателем. Степень некоторого числа с отрицательным (целым) показателем определяется как единица, делённая на степень того же числа с показателем, равным абсолютной велечине отрицательного показателя:
Теперь формула a m : a n = a m n может быть использована не только при m , большем, чем n , но и при m , меньшем, чем n .
П р и м е р . a4 : a7 = a 47 = a 3 .
Если мы хотим, чтобы формула a m : a n = a m n была справедлива при m = n , нам необходимо определение нулевой степени.
Степень с нулевым показателем. Степень любого ненулевого числа с нулевым показателем равна 1.
П р и м е р ы . 2 0 = 1, ( – 5 ) 0 = 1, ( – 3 / 5 ) 0 = 1.
Степень с дробным показателем. Для того, чтобы возвести действительное число а в степень m / n , нужно извлечь корень n–ой степени из m-ой степени этого числа а :
О выражениях, не имеющих смысла. Есть несколько таких выражений.
Случай 1.
где a ≠ 0 не существует.
В самом деле, если предположить, что x – некоторое число, то в соответствии с определением операции деления имеем: a = 0· x, т.e. a = 0, что противоречит условию: a ≠ 0
Случай 2.
— любое число.
В самом деле, если предположить, что это выражение равно некоторому числу x, то согласно определению операции деления имеем: 0 = 0 · x . Но это равенство имеет место при любом числе x, что и требовалось доказать.
Случай 3.
Если считать, что правила действий со степенями распространяются и на степени с нулевым основанием, то
0 0 — любое число.
Действительно,
Р е ш е н и е . Рассмотрим три основных случая:
1) x = 0 – это значение не удовлетворяет данному уравнению
( Почему? ).
2) при x > 0 получаем: x / x = 1, т.e. 1 = 1, откуда следует,
что x – любое число; но принимая во внимание, что в
нашем случае x > 0 , ответом является x > 0 ;
3) при x
в этом случае нет решения.
Таким образом, x > 0.
p.120-bal.ru
Урок обобщения и систематизации знаний по теме «Действия с положительными и отрицательными числами»
Разделы: Математика
Цели:
Образовательные: обобщить и систематизировать знания учащихся о правилах действий над положительными и отрицательными числами; закрепить умение применять правила в процессе выполнения упражнений;
Развивающие: формировать навыки самостоятельной работы; развивать логическое мышление, вычислительные навыки; расширение кругозора.
Воспитательные: воспитание познавательного интереса к предмету; воспитывать культуру труда, математической речи, активность, самостоятельность, культуру общения.
Оборудование: мультимедийная презентация; компьютер; листы с текстами задач; карточки – подсказки.
I. Учитель: Ребята, все предыдущие уроки мы работали над темой “Арифметика положительных и отрицательных чисел”.Чему вы уже научились?
Ученики: Выполнять действия сложения, вычитания, умножения и деления положительных и отрицательных чисел.
Учитель: И сегодня на уроке мы должны еще раз вспомнить, какими правилами мы пользуемся при выполнении действий с рациональными числами. А как вы думаете, зачем нам это надо? Ученик: Чтобы можно было изучать следующую тему, и хорошо написать контрольную работу. Учитель: А на других предметах это вам понадобится? Ученик: Да, например на уроках ….
II. Учитель: Хорошо. Давайте тогда начнем работу. У вас на партах лежат листочки, с заданиями на урок. На них напечатан план работы. Давайте прочитаем его. Ученик: читает… Учитель: Домашняя работа на карточках, с которой вы легко сможете справиться, если будете очень внимательны на уроке. Найдите листочки с карточками – подсказками, пока пустые, но к концу урока они действительно станут подсказкой.
Урок сегодня будет необычным. Мы с вами отправимся в путешествие, узнаем историю развития отрицательных чисел. А где же они впервые появились, и как звали математика предложившего в то время более удобное обозначение отрицательных чисел? Это вы узнаете, если ответите на вопросы и впишите в кружки соответствующие буквы (карточки у каждого учащегося). Приложение 1.
- Представьте число — 6,9 в виде суммы трех равных слагаемых. Чему равно одно из этих слагаемых? Ответ: — 2,3
- Сумма противоположных чисел равна… Ответ: 0
- Сумма целых чисел от — 50 до 52 равна… Ответ: 103
- Произведение 12 отрицательных чисел и 7 положительных чисел есть число … Ответ: >0
- Найдите сумму целых чисел удовлетворяющих неравенству -8,3 < x < 6 ,2 Ответ: — 15
- Произведение 15 отрицательных и 60 положительных чисел есть число … Ответ: <0
- Произведение целых чисел от — 20 до 21 равно …Ответ: 0
- (-1) : (-1)2: (-1)3 : (-1)4: … :(-1)50 =… Ответ: -1
| — 15 | 2,3 | 0 | 103 | 50 | — 2,3 | >0 | <0 | — 420 | — 1 |
| й | в | и | т | я | к | а | л | н | е |
Ответ: Китай, Ли Е. Приложение 2.Слайды № 3 – 6
Учитель: Теперь заполним карточки – подсказки (учащиеся заполняют п. 1 – 9 карточек, корректируя свои вычисления) слайды № 7 – 9
Карточка – подсказка
1. Число, которое отличается от данного только знаком, называется ____________
2. Сумма противоположных чисел равна
_____
а + ( — а ) = …
3. Сумма положительных чисел ____________
Если а > 0, b > 0, то a + b … 0
4. Сумма отрицательных чисел _____________
Если а < 0, b < 0, то a + b … 0
5. Сумма чисел с разными знаками имеет
знак числа ________________
Если а > 0, b < 0, то a + b > 0, если ¦а¦…¦b¦
a + b < 0, если ¦а¦…¦b¦
6. Вычитание можно заменить действием
сложения с числом ________________
а – b = a +
7. Произведение положительных чисел -
__________________
Если а > 0, b > 0, то ab …0
8. Произведение четного числа
отрицательных множителей — __________________
Если а < 0, то
… 0
9. Произведение нечетного числа
отрицательных множителей — __________________
Если а < 0, то
… 0
10. a(bc) = ________
11. a : (bc) = ________
12. (a ± b)с = ________ или ас ± bc = __________
13. (a ± b) : с = ________ или а : с ± b : c = __________
14. + (+) = … ; — ( — ) = … ; + ( — ) = … ; — ( + ) = … .
| 1. Я знаю правила сложения и вычитания рациональных чисел | |
| 2. Я знаю правила умножения и деления рациональных чисел | |
| 3. Я знаю свойства рациональных чисел | |
| 4. Я умею складывать рациональные числа | |
| 5. Я умею вычитать рациональные числа | |
| 6. Я умею умножать и делить рациональные числа | |
| 7. Я умею находить рациональные способы решения, используя свойства рациональных чисел |
Учитель: Какое слово у вас получилось?
Ученик: Китай, Ли Е. слайды № 10,11
Учитель: Верно. Когда это произошло, нам расскажет …(выступает ученик с исторической справкой).
Историческая справка: “ К созданию понятия отрицательного числа китайские ученые подошли раньше математиков других народов, во II в. до н. э. Положительные количества в китайской математике называли “чжен”, отрицательные – “фу”. Их изображали разными цветами: “ чжен” - красным, “ фу” — черным. Такой способ изображения использовался в Китае до середины ХII столетия, пока Ли Е не предложил более удобное обозначение отрицательных чисел — цифры, которые изображали отрицательные числа перечеркивали черточкой справа налево. Введение отрицательных чисел и правил их сложения и вычитания можно считать одним из самых крупных открытий китайских ученых”
Учитель: Для выполнения следующего задания повторим сначала свойства рациональных чисел. Для этого заполним п. 10 – 13 карточек. слайд № 12
В древнегреческой математике к выполнению действий с отрицательными числами близко подошли в III в. Вы узнаете, кто это был, если решите примеры по вариантам и вместе заполните таблицу, вписав в нее буквы соответствующие полученным ответам. Свободный столбец заполните, учитывая данные: (1 вариант – ф,д,т,а; 2 вариант – н,и,т,о)
Ф ;
Н — 7,089 : (- 2,5 • 7,089)
Д ;
И ;
Т ( 1 – 2 – 3 + 4 + 5 – 6 – 7 + 8) • ( — 1087)
О Определите знак выражения
А Определите знак выражения
| — 10 | — 3,2 | > 0 | — 0,2 | < 0 | 0,4 | |
Ответ:
| — 10 | — 3,2 | > 0 | -0, 2 | < 0 | 0,4 | 0 |
| Д | И | О | Ф | А | Н | Т |
Учитель: Какое слово получилось у вас? Проверка с помощью слайдов № 13 — 19
Ученики: Диофант.
Учитель: Да, это Диофант Александрийский, живший в III в. (слайд с портретом математика) слайд №20
Учитель: Решите уравнения и зачеркните в таблице буквы, соответствующие найденным ответам и вы узнаете, где положительные и отрицательные числа толковали как имущества и долги.
а) 1,2 – ( 0,3 – х ) = — 3,8; слайд № 21
Учитель: заполните п. 14 карточки — подсказки. Каким правилом пользовались, решая это уравнение? слайд № 22
Ученик: Правилом раскрытия скобок.
Учитель: Следующее уравнение решим на доске (ученик решает уравнение на доске, комментируя).
в) . слайд № 23
| 0 | 4,7 | 4,04 | 3 | 4,4 | — 4,7 | 0,5 | — 3,4 | — 5,75 |
| ф | и | л | н | д | о | и | м | я |
Ответ:
а) х = — 4,7;
б) х = — 3;
в) х = 0, х = — 3,4, х = 4,04.
| 0 | 4,7 | 4,04 | 3 | 4,4 | — 4,7 | 0,5 | — 3,4 | — 5,75 |
| и | н | д | и | я |
Индия
Учитель: Какое слово у вас получилось?
Ученики: Индия.
Учитель: Правильно. Об этом нам расскажет …(выступает ученик с исторической справкой) слайды №24 — 26
Историческая справка: “В индийской математике отрицательные числа впервые встречаются у Брахмагупты в VII веке. Ученый пользуется толкованием положительных и отрицательных чисел как имущества, а отрицательных как долга.
Правила умножения и деления положительных и отрицательных чисел впервые появляются у индийского математика в XII в. Бхаскары. В индии отрицательные числа систематически использовали в основном так, как это мы делаем сейчас. Вместе с отрицательными числами ввели понятие ноль, что позволило им создать десятеричную систему исчисления”
Учитель: В Европе понятие отрицательного числа появилось значительно позже. Об этом расскажет ……(выступает ученик с исторической справкой)
Историческая справка: “ В Европе к введению отрицательных чисел довольно близко подошел итальянский математик Леонардо Пизанский. В Италии ростовщики, давая денег в долг, ставили перед именем должника сумму долга и черточку, вроде нашего минуса, а когда должник возвращал деньги, зачеркивали ее, получалось что-то вроде нашего плюса” слайды №27 - 29
Решите задачу, составив выражение, и вы узнаете, в каком веке это было.
Бережливый хозяин должен хорошо знать как размер своего имущества, так и свои долги. И вот однажды ростовщик решил посчитать, с прибылью для себя или с убытком он прожил этот месяц? Если:
1) первый человек отдал ему 32,4 лиры своего долга;
2) второму он отдал в долг 50% этих денег;
3) на строительство башни он пожертвовал 30,8 лиры;
4) третий вернул 17,6 лиры;
5) и последняя сделка принесла ему доход в 10 лир.
Решение: 32,4 — 32,4 • 0,5 – 30,8 + 17,6 + 10 = 13.
Ответ: в XIII веке. слайд № 30
Учитель: И вот отрицательные числа появились во Франции и Германии. Об этом нам расскажет …( выступает ученик с исторической справкой)
Историческая справка: “ В Европе с сознанием уверенности в справедливости своих вычислений начал оперировать с отрицательными числами французский математик Никола Шюке. В своих трудах в 1484 г. Он рассматривает задачи, приводящие к уравнениям с отрицательными корнями. Шюке заявляет, что “это вычисление, которое иные считают невозможным, правильно”.
Чех Ян Видман уже писал “+” и “ — ” для сложения и вычитания. А чуть позднее немецкий ученый Михель Штофель написал “Полную Арифметику”, которая была напечатана в 1544 году. В ней встречаются такие записи для чисел: 0 – 2; 0 + 2; 0 – 5; 0 + 7. Всеобщее признание отрицательные числа получили в первой половине XIX в., когда была развита строгая теория положительных и отрицательных чисел.
Вот почему с большим трудом завоевали себе место в математике отрицательные числа”. слайды № 31 — 39
III. Учитель: Давайте поработаем еще с нашими карточками – подсказками. В таблице поставьте “+”, если утвердительно можете ответить на вопрос, “±” — если сомневаетесь и “ — ” — если над этим вам еще надо поработать (в это время учитель проходит и смотрит как учащиеся заполняют таблицу).
Что мы с вами повторили? Что вы узнали нового? Как вы думаете, вы готовы справиться с контрольной работой?
Ученик: …
Учитель: Спасибо за урок. слайд № 40
Учащимся, выполнившим все задания, предлагается выполнить дополнительные задания.
Дополнительно.
- Для чисел - 0,8; 1,25; найдите модуль суммы и сумму модулей. Сравните полученные результаты. Определите, при каких условиях для нескольких чисел модуль суммы и сумма модулей равны.
- Решите уравнения: а) |х – 1,3|• (5х +2,5) = 0; б) | 0,5х – 4 | + (8 – х)4 = 0.
7.03.2008
urok.1sept.ru
Все действия с положительными и отрицательными числами
Разделы: Математика
Цели:
- систематизация и обобщение знаний учащихся;
- приобщение учащихся к разнообразным формам методам изучения материала;
- воспитание любви к предмету.
Ход урока
1. Устные упражнения:
2. Решите уравнение: а) -х=3,5; б)-8-(-х) = 7; в) -14 : (-с) =2; г)=5.
II. Открыть замок.
Сегодня мы обобщим и повторим тему “Все действия с положительными и отрицательными числами”. Чтобы попасть в страну этих чисел надо открыть замок на двери, получив ключ от замка. Ключей много. Должны выбирать один из них, который подойдет. На ключе есть код и мы должны найти его, решив примеры. Один ученик решает на доске:
.
Остальные решают по вариантам:
.
Код замка -1.
III. Неизвестный остров.
После того, как открывается замок, мы окажемся на неизвестном острове.
Это остров уравнений.
У доски решают два ученика, один решает с комментированием.
1) (х — 8) ;
2) ;
IV. Решение текстовой задачи.
Один ученик решает у доски, остальные на местах.
Задача. Скипидар замерзает при температуре -100, что составляет температуры, при которой замерзает азот, а кислород замерзает при температуре на 8,60 ниже, чем азот. Определите температуру замерзания.
V. Физкультминутка.
Так стало холодно, придется затопить печь.
Три лестницы ведут к одному домику. На каждой ступеньке записаны задания. Выполнять задания надо начинать с нижней ступеньки и постепенно подниматься вверх. Кто быстрее окажется на верху. Задания выполняем по одному представителя от каждого ряда. Выигравшая команда получает право затопить печь, то есть нарисовать дым, идущий из трубы затопленной печи (приложение 1)
VI. Игра “Поле чудес”. Работа по карточкам (приложение 2)
Если правильно решить все примеры должна получиться пословица:
“Что посеешь в юности, то пожнешь в зрелости”
В таблице записаны буквы, которые встречаются в высказывании, под ними ответы, которые соответствуют этим буквам.
Объяснение пословицы: Какой ребенок в детстве, таким же он будет в зрелости, старости. Если хотите быть честным, смелым, трудолюбивым надо стараться быть такими уже сейчас. Как их вырабатывать? Помогать слабым, маленьким и пожилым людям.
VII. Программированный контроль.
I – вариант
1. Вычислите: — 8,7 – (3,6 – 8,7)
1) -3,6;
2) -13,8;
3) 3,6;
4) 13,8.
2. Выполните действия:
1)
2)
3)
4)
3. Выполните действия: -6 . (-5 + 21) : 32 + 8
1) 3 2) -5; 3) 11; 4) 5.
4. Решите уравнение: х : (-16) =
1) 10;
2) 9;
3) 15;
4) 0,8
II – вариант
Вычислите: — 7,8 – (9,1 – 7,8)
1) 9,1;
2) -6,5;
3) -9,1;
4) 6,5.
Выполните действия:
1)
2) —
3)
4) .
3. Выполните действия: -8. (-7 + 23) : 64 + 3
1) 5;
2) 10,5;
3) -4,5;
4) 1.
4. Решите уравнение:
1) 2,5; 2) 10; 3) 14,4; 4) 15.
В результате выполнения работы учащиеся должны получить ответы: I – вариант – 1142,
II – вариант — 3242.
VIII. Итог урока. Повторить правила сложения, вычитания, умножения и деления положительных и отрицательных чисел.
VIII. Домашнее задание.
27.03.2008
Поделиться страницей:urok.1sept.ru

