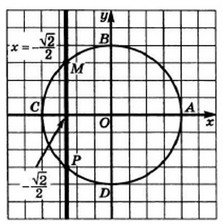
Числовая окружность на координатной: Числовая окружность в координатной плоскости — урок. Алгебра, 10 класс.
Расположим числовую окружность в координатной плоскости так, чтобы центр окружности совместился с началом координат, а её радиус принимаем за единичный отрезок.
Начальная точка числовой окружности \(A\) совмещена с точкой \((1;0)\).
Каждая точка числовой окружности имеет в координатной плоскости свои координаты.
Найдём сначала координаты тех точек координатной плоскости, которые получены на макетах числовой окружности.
Точка Mπ4 — середина \(I\) четверти. Опустим перпендикуляр \(MP\) на прямую \(OA\) и рассмотрим треугольник \(OMP\). Так как дуга \(AM\) составляет половину дуги \(AB\), то ∡MOP=45°.
Значит, треугольник \( OMP \) — равнобедренный прямоугольный треугольник и \(OP = MP\), т. е. у точки \(M\) абсцисса и ордината равны: \(x = y\).
Так как координаты точки \(M(x;y)\) удовлетворяют уравнению числовой окружности x2+y2=1, то для их нахождения нужно решить систему уравнений: x2+y2=1x=y |
Подставив \(x\) вместо \(y\) в первое уравнение системы, получим следующее решение:
x2+x2=1;2×2=1;x2=12;x=12=22;y=x=22.
При решении учитываем, что абсцисса точки \(M\) положительна.
Получили, что координаты точки \(M\), соответствующей числу π4, будут Mπ4=M22;22.
Аналогично можно получить координаты и других точек первого макета числовой окружности, учитывая только знаки координат в каждой четверти.
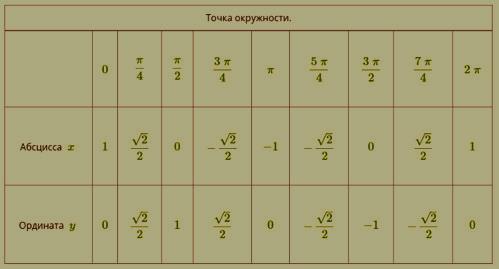
Полученные результаты запишем в таблицу.
Точка окружности |
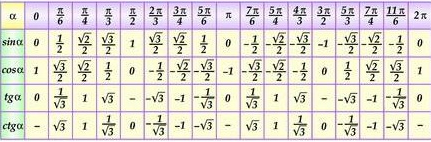
| \(0\) | π4 | π2 | 3π4 | π | 5π4 | 3π2 | 7π4 | 2π |
Абсцисса \(x\) | \(1\) | 22 | \(0\) | −22 | \(-1\) | −22 | \(0\) | 22 | \(1\) |
Ордината \(y\) | \(0\) | 22 | \(1\) | 22 | \(0\) | −22 | \(-1\) | −22 | \(0\) |
Рассуждаем аналогично для точки \(M\), если теперь она соответствует числу π6.
Треугольник \(MOP\) прямоугольный. Так как дуга \(AM\) составляет третью часть дуги \(AB\), то ∡MOP=30°.
Катет \(MP\) лежит против угла \(30\) градусов в прямоугольном треугольнике, значит, равен половине гипотенузы, т. е. ордината точки \(M\) равна MP=12;y=12 |
Абсциссу \(x\) точки \(M\) найдём, решив уравнение:
x2+y2=1;
x2=1−122=1−14=34;x=32.
При решении учитываем, что абсцисса точки \(M\) положительна.
Получили, что координаты точки \(M\), соответствующей числу π6, будут Mπ6=M32;12.
Аналогично можно получить координаты и других точек второго макета числовой окружности, учитывая только знаки координат в каждой четверти.
Полученные результаты запишем в таблицу.
Точка окружности |
π6 | π3 | 2π3 | 5π6 | 7π6 | 4π3 | 5π3 | 11π6 | |
Абсцисса \(x\) | 32 | 12 | −12 | −32 | −32 | −12 | 12 | 32 |
Ордината \(y\) | 12 | 32 | 32 | 12 | −12 | −32 | −32 | −12 |
Внеклассный урок — Числовая окружность
Числовая окружность
Числовая окружность – это единичная окружность, точки которой соответствуют определенным действительным числам.
Единичной окружностью называют окружность радиуса 1.
Общий вид числовой окружности.
1) Ее радиус принимается за единицу измерения.
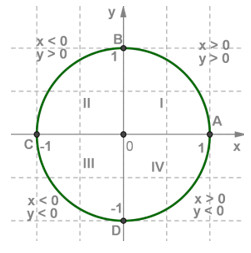
2) Горизонтальный и вертикальный диаметры делят числовую окружность на четыре четверти (см.рисунок). Их соответственно называют первой, второй, третьей и четвертой четвертью.
3) Горизонтальный диаметр обозначают AC, причем А – это крайняя правая точка.
Вертикальный диаметр обозначают BD, причем B – это крайняя верхняя точка.
Соответственно:
первая четверть – это дуга AB
вторая четверть – дуга BC
третья четверть – дуга CD
четвертая четверть – дуга DA
4) Начальная точка числовой окружности – точка А.
Отсчет по числовой окружности может вестись как по часовой стрелке, так и против часовой стрелки.
Отсчет от точки А против часовой стрелки называется положительным направлением.
Отсчет от точки А по часовой стрелке называется отрицательным направлением.
Числовая окружность на координатной плоскости.
Центр радиуса числовой окружности соответствует началу координат (числу 0).
Горизонтальный диаметр соответствует оси x, вертикальный – оси y.
Начальная точка А числовой окружности находится на оси x и имеет координаты (1; 0).
Значения x и y в четвертях числовой окружности:
1-я четверть | 2-я четверть | 3-я четверть | 4-я четверть |
x > 0, y > 0 | x < 0, y > 0 | x < 0, y < 0 | x > 0, y < 0 |
Значение любой точки числовой окружности:
Любая точка числовой окружности с координатами (x; y) не может быть меньше -1, но не может быть больше 1: –1 ≤ x ≤ 1; –1 ≤ y ≤ 1 |
Основные величины числовой окружности:
| | |
|
|
|
|
|
|
| π |
|
Имена и местонахождение основных точек числовой окружности:
Как запомнить имена числовой окружности.
Есть несколько простых закономерностей, которые помогут вам легко запомнить основные имена числовой окружности.
Перед тем как начать, напомним: отсчет ведется в положительном направлении, то есть от точки А (2π) против часовой стрелки.
1) Начнем с крайних точек на осях координат.
Начальная точка – это 2π (крайняя правая точка на оси х, равная 1).
Как вы знаете, 2π – это длина окружности. Значит, половина окружности – это 1π или π. Ось х делит окружность как раз пополам. Соответственно, крайняя левая точка на оси х, равная -1, называется π.
Крайняя верхняя точка на оси у, равная 1, делит верхнюю полуокружность пополам. Значит, если полуокружность – это π, то половина полуокружности – это π/2.
Одновременно π/2 – это и четверть окружности. Отсчитаем три таких четверти от первой до третьей – и мы придем в крайнюю нижнюю точку на оси у, равной -1. Но если она включает три четверти – значит имя ей 3π/2.
2) Теперь перейдем к остальным точкам. Обратите внимание: все противоположные точки имеют одинаковый числитель – причем это противоположные точки и относительно оси у, и относительно центра осей, и относительно оси х. Это нам и поможет знать их значения точек без зубрежки.
Надо запомнить лишь значение точек первой четверти: π/6, π/4 и π/3. И тогда мы «увидим» некоторые закономерности:
— Относительно оси у в точках второй четверти, противоположных точкам первой четверти, числа в числителях на 1 меньше величины знаменателей. К примеру, возьмем точку π/6. Противоположная ей точка относительно оси у тоже в знаменателе имеет 6, а в числителе 5 (на 1 меньше). То есть имя этой точки: 5π/6. Точка, противоположная π/4, тоже имеет в знаменателе 4, а в числителе 3 (на 1 меньше, чем 4) – то есть это точка 3π/4.
Точка, противоположная π/3, тоже имеет в знаменателе 3, а в числителе на 1 меньше: 2π/3.
— Относительно центра осей координат все наоборот: числа в числителях противоположных точек (в третьей четверти) на 1 больше значения знаменателей. Возьмем опять точку π/6. Противоположная ей относительно центра точка тоже имеет в знаменателе 6, а в числителе число на 1 больше – то есть это 7π/6.
Точка, противоположная точке π/4, тоже имеет в знаменателе 4, а в числителе число на 1 больше: 5π/4.
Точка, противоположная точке π/3, тоже имеет в знаменателе 3, а в числителе число на 1 больше: 4π/3.
— Относительно оси х (четвертая четверть) дело посложнее. Здесь надо к величине знаменателя прибавить число, которое на 1 меньше – эта сумма и будет равна числовой части числителя противоположной точки. Начнем опять с π/6. Прибавим к величине знаменателя, равной 6, число, которое на 1 меньше этого числа – то есть 5. Получаем: 6 + 5 = 11. Значит, противоположная ей относительно оси х точка будет иметь в знаменателе 6, а в числителе 11 – то есть 11π/6.
Точка π/4. Прибавляем к величине знаменателя число на 1 меньше: 4 + 3 = 7. Значит, противоположная ей относительно оси х точка имеет в знаменателе 4, а в числителе 7 – то есть 7π/4.
Точка π/3. Знаменатель равен 3. Прибавляем к 3 на единицу меньшее число – то есть 2. Получаем 5. Значит, противоположная ей точка имеет в числителе 5 – и это точка 5π/3.
3) Еще одна закономерность для точек середин четвертей. Понятно, что их знаменатель равен 4. Обратим внимание на числители. Числитель середины первой четверти – это 1π (но 1 не принято писать). Числитель середины второй четверти – это 3π. Числитель середины третьей четверти – это 5π. Числитель середины четвертой четверти – это 7π. Получается, что в числителях середин четвертей – четыре первых нечетных числа в порядке их возрастания:
(1)π, 3π, 5π, 7π.
Это тоже очень просто. Поскольку середины всех четвертей имеют в знаменателе 4, то мы уже знаем их полные имена: π/4, 3π/4, 5π/4, 7π/4.
Особенности числовой окружности. Сравнение с числовой прямой.
Как вы знаете, на числовой прямой каждая точка соответствует единственному числу. К примеру, если точка А на прямой равна 3, то она уже не может равняться никакому другому числу.
На числовой окружности все иначе, поскольку это окружность. К примеру, чтобы из точки А окружности прийти к точке M, можно сделать это, как на прямой (только пройдя дугу), а можно и обогнуть целый круг, а потом уже прийти к точке M. Вывод:
Пусть точка M равна какому-то числу t. Как мы знаем, длина окружности равна 2π. Значит, точку окружности t мы можем записать двояко: t или t + 2π. Это равнозначные величины.
То есть t = t + 2π. Разница лишь в том, что в первом случае вы пришли к точке M сразу, не делая круга, а во втором случае вы совершили круг, но в итоге оказались в той же точке M. Таких кругов можно сделать и два, и три, и двести. Если обозначить количество кругов буквой k, то получим новое выражение:
t = t + 2πk.
Отсюда формула:
Если точка M числовой окружности равна числу t, то она равна и числу вида t + 2πk, где k – любое целое число: M(t) = M(t + 2πk), где k ∈ Z. Число k называется параметром. |
Уравнение числовой окружности
(второе уравнение – в разделе «Синус, косинус, тангенс, котангенс»):
Описание презентации по отдельным слайдам:
1 слайд Описание слайда:
Описание слайда:Алгебра и начала математического анализа, 10 класс. Урок на тему: Числовая окружность на координатной плоскости.
 Описание слайда:
Описание слайда:Определение. Числовая окружность на координатной плоскости. Расположим числовую окружность в координатной плоскости так, чтобы центр окружности совместился с началом координат, а её радиус принимаем за единичный отрезок. Начальная точка числовой окружности A совмещена с точкой (1;0). Каждая точка числовой окружности имеет в координатной плоскости свои координаты х и у, причем: x > 0, у > 0 в первой четверти; х < 0, у > 0 во второй четверти; х < 0, у < 0 в третьей четверти; х > 0, у < 0 в четвертой четверти. Для любой точки М(х; у) числовой окружности выполняются неравенства -1 < x < 1; -1 < у < 1. Запомните! уравнение числовой окружности:
3 слайд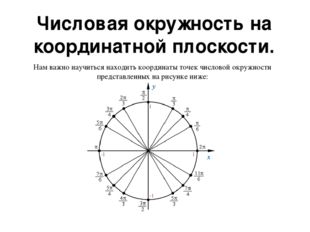 Описание слайда:
Описание слайда:Числовая окружность на координатной плоскости. Нам важно научиться находить координаты точек числовой окружности представленных на рисунке ниже:
4 слайд
Числовая окружность на координатной плоскости. Найдем координату точки π/4: Точка М(π/4) — середина первой четверти. Опустим из точки М перпендикуляр МР на прямую ОА и рассмотрим треугольник OMP.Так как дуга АМ составляет половину дуги АВ, то ∡MOP=45° Значит, треугольник OMP — равнобедренный прямоугольный треугольник и OP=MP, т.е. у точки M абсцисса и ордината равны: x = y Так как координаты точки M(х;y) удовлетворяют уравнению числовой окружности, то для их нахождения нужно решить систему уравнений: Решив данную систему получаем: Получили, что координаты точки M, соответствующей числу π/4 будут Аналогичным образом рассчитываются координаты точек представленных на предыдущем слайде.
5 слайд Описание слайда:
Описание слайда:Координаты точек числовой окружности. Числовая окружность на координатной плоскости.
6 слайд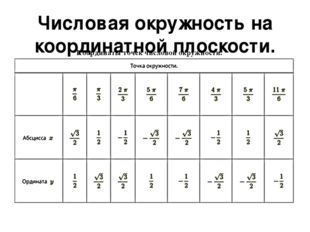 Описание слайда:
Описание слайда:Координаты точек числовой окружности. Числовая окружность на координатной плоскости.

Курс повышения квалификации
Курс повышения квалификации

Курс профессиональной переподготовки
Учитель математики и информатики
Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:
Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВнеурочная деятельностьВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое
Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс
Выберите учебник: Все учебники
Выберите тему: Все темы
также Вы можете выбрать тип материала:

Общая информация
Номер материала: ДБ-194694
Похожие материалы
Вам будут интересны эти курсы:
Оставьте свой комментарий
Тема урока: Числовая окружность на координатной плоскости
Цель урока:
Образовательные:
- на основе повторения и обобщения ранее изученного материала ввести понятие числовой окружности на координатной плоскости;
- изучить основные свойства числовой окружности;
- в ходе изучения нового материала сформировать умения и навыки нахождения значений выражений.
Развивающие:
- развитие памяти, логического мышления, умения анализировать, сравнивать, обобщать, самостоятельно делать выводы;
- развитие грамотной математической речи.
Воспитательные:
- воспитывать аккуратность и точность при выполнении заданий;
- формирование культуры учебного труда;
- продолжить формирование познавательного интереса к предмету.
Тема предыдущего урока: Числовая окружность.
Тема следующего урока: Синус и косинус (комбинированный).
Структура урока
- Актуализация знаний 7 мин
- Объяснение нового материала 20 мин
- Закрепление изученного материала 10 мин
- Подведение итогов урока, постановка домашнего задания, рефлексия (3 мин).
Ход урока:
- Актуализация
- Организационный момент: Приветствие учеников, поверка отсутствующих
- Фронтальный опрос с целью АЗ по теме:
- Дайте определение числовой окружности
- Сколько четвертей имеем в единичной окружности?Как они называются?
- Определите знаки в каждой из четверти.
- Объяснение нового материала 20 мин
Открываем тетради, подписываем число, тему урока: «Числовая окружность на координатной плоскости»
У каждого из вас в тетради есть три макета числовой окружности. Каждая точка числовой окружности имеет в координатной плоскости свои координаты. Найдём сначала координаты тех точек координатной плоскости, которые получены на макетах числовой окружности.
На первом макете возьмем точку M(π/4) середина I четверти. Опустим перпендикуляр MP на прямую OA и рассмотрим треугольник OMP. Так как дуга AM составляет половину дуги AB, то ∡MOP=45°. Значит, треугольник OMP — равнобедренный прямоугольный треугольник и OP=MP, т.е. у точки M абсцисса и ордината равны: x=y. Так как координаты точки M(x;y) удовлетворяют уравнению числовой окружности x2+y2=1, то для их нахождения нужно решить систему уравнений:
Подставив x вместо y в первое уравнение системы, получим следующее решение:
При решении учитываем, что абсцисса точки M положительна.
Получили, что координаты точки M, соответствующей числу π/4 будут M(π/4)=M(2√2;2√2)
Аналогично можно получить координаты и других точек первого макета числовой окружности, учитывая только знаки координат в каждой четверти.
Полученные результаты запишем в таблицу:
Перейдем на второй макет. Рассуждаем аналогично для точки M, если теперь она соответствует числу π/6
Треугольник MOP прямоугольный. Так как дуга AM составляет третью часть дуги AB, то ∡MOP=30°.
Катет MP лежит против угла 30 градусов в прямоугольном треугольнике, значит, равен половине гипотенузы, т.е. ордината точки M равна
MP=1/2 y=1/2
Абсциссу x точки M найдём, решив уравнение:
При решении учитываем, что абсцисса точки M положительна.
Получили, что координаты точки M, соответствующей числу π/6 будут M(π/6)=M(3√2;1/2)
Аналогично можно получить координаты и других точек второго макета числовой окружности, учитывая только знаки координат в каждой четверти.
На третьем макете возьмем угол в 600 или π/3. Треугольник OKF прямоугольный. Так как дуга AK составляет третью часть дуги AB, то ∡KOF=60°, а ∡OKF=30°,
Катет OF лежит против угла 30 градусов в прямоугольном треугольнике, значит, равен половине гипотенузы, т.е. абцисса точки F равна
OF=1/2 x=1/2
Ординату y точки K найдём, решив уравнение:
При решении учитываем, что ордината точки K положительна.
Получили, что координаты точки K, соответствующей числу π/3 будут K(π/3)=F(1/2, 3√2) . Полученные данные занесем в таблицу:
III. Закрепление изученного материала 10 мин
А сейчас выполним несколько заданий с целью закрепления изученного нами материала. №5.1а,б ; № 5.4а
IV. Подведение итогов урока, постановка домашнего задания, рефлексия (3 мин).
Понятие числовой окружности вы изучали для того чтобы перейти к изучению таких важных с точки зрения математики и геометрии понятий как синус, косинус, тангенс и котангенс. Итак, что мы сегодня узнали на уроке нового?
Домашнее задание № 5.2а, № 5.7
МБОУ Калининская СОШ
Цимлянский район
Алгебра
и начала
математического
анализа 10 класс
Конспект урока
на тему
«Числовая окружность на координатной плоскости»
Подготовил учитель
Математики
Поцелуева Е.В.
Тема Числовая окружность на координатной плоскости
Что будем изучать:
1. Определение.
2. Важные координаты числовой окружности.
3. Как искать координату числовой окружности?
4. Таблица основных координат числовой окружности.
5. Примеры решения задач.
Определение числовой окружности на координатной плоскости
Расположим числовую окружность в координатной плоскости так, чтобы центр окружности совместился с началом координат, а её радиус принимаем за единичный отрезок. Начальная точка числовой окружности A совмещена с точкой (1;0).
Каждая точка числовой окружности имеет в координатной плоскости свои координаты х и у, причем:
1) при x>0x>0, у>0у>0 – в первой четверти;
2) при х<0х<0, у>0у>0 – во второй четверти;
3) при х<0х<0, у<0у<0 – в третьей четверти;
4) при х>0х>0, у<0у<0 – в четвертой четверти.
Для любой точки М(х;у)М(х;у) числовой окружности выполняются неравенства: −1Запомните уравнение числовой окружности: x2+y2=1×2+y2=1.
Нам важно научиться находить координаты точек числовой окружности, представленных на рисунке.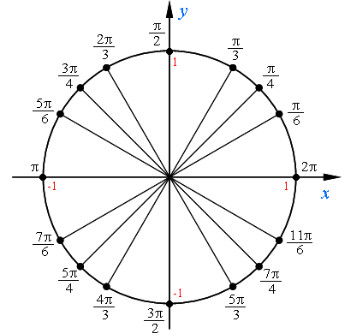
Найдем координату точки π4π4
Точка М(π4)М(π4) – середина первой четверти. Опустим из точки М перпендикуляр МР на прямую ОА и рассмотрим треугольник OMP.Так как дуга АМ составляет половину дуги АВ, то ∠MOP=45°∠MOP=45°.
Значит, треугольник OMP – равнобедренный прямоугольный треугольник и OP=MPOP=MP, т.е. у точки M абсцисса и ордината равны: x=yx=y.
Так как координаты точки M(х;y)M(х;y) удовлетворяют уравнению числовой окружности, то для их нахождения нужно решить систему уравнений:
{x2+y2=1,x=y.{x2+y2=1,x=y.
Решив данную систему, получаем: y=x=√22y=x=22.
Значит, координаты точки M, соответствующей числу π4π4, будут M(π4)=M(√22;√22)M(π4)=M(22;22).
Аналогичным образом рассчитываются координаты точек, представленных на предыдущем рисунке.
Координаты точек числовой окружности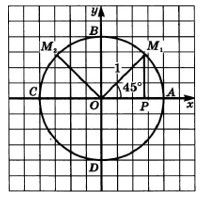

Рассмотрим примеры
Пример 1.
Найти координату точки числовой окружности: Р(45π4)Р(45π4).
Решение:
Т.к. числам tt и t+2π∗kt+2π∗k, где k-целое число, соответствует одна и та же точка числовой окружности то:
45π4=(10+54)∗π=10π+5π4=5π4+2π∗545π4=(10+54)∗π=10π+5π4=5π4+2π∗5.
Значит, числу 45π445π4 соответствует та же точка числовой окружности, что и числу 5π45π4. Посмотрев значение точки 5π45π4 в таблице, получаем: P(45π4)=P(−√22;−√22)P(45π4)=P(−22;−22).
Пример 2.
Найти координату точки числовой окружности: Р(−37π3)Р(−37π3).
Решение:
Т.к. числам tt и t+2π∗kt+2π∗k, где k-целое число, соответствует одна и та же точка числовой окружности то:
−37π3=−(12+13)∗π=−12π–π3=−π3+2π∗(−6)−37π3=−(12+13)∗π=−12π–π3=−π3+2π∗(−6).
Значит, числу −37π3−37π3 соответствует та же точка числовой окружности, что и числу –π3–π3, а числу –π3π3 соответствует та же точка, что и 5π35π3. Посмотрев значение точки 5π35π3 в таблице, получаем:
P(−37π3)=P(12;−√32)P(−37π3)=P(12;−32).
Пример 3.
Найти на числовой окружности точки с ординатой у=12у=12 и записать, каким числам tt они соответствуют?
Решение:
Прямая у=12у=12 пересекает числовую окружность в точках М и Р. Точка М соответствует числу π6π6 (из данных таблицы). Значит, и любому числу вида: π6+2π∗kπ6+2π∗k. Точка Р соответствует числу 5π65π6, а значит, и любому числу вида 5π6+2π∗k5π6+2π∗k.
Получили, как часто говорят в таких случаях, две серии значений:
π6+2π∗kπ6+2π∗k и 5π6+2π∗k5π6+2π∗k.
Ответ : t=π6+2π∗kt=π6+2π∗k и t=5π6+2π∗kt=5π6+2π∗k.
Пример 4.
Найти на числовой окружности точки с абсциссой x≥−√22x≥−22 и записать, каким числам ttони соответствуют.
Решение:
Прямая x=−√22x=−22 пересекает числовую окружность в точках М и Р. Неравенству x≥−√22x≥−22соответствуют точки дуги РМ. Точка М соответствует числу 3π43π4 (из данных таблицы). Значит, и любому числу вида −3π4+2π∗k−3π4+2π∗k. Точка Р соответствует числу −3π4−3π4, а значит, и любому числу вида −3π4+2π∗k−3π4+2π∗k.
Тогда получим −3π4+2π∗k≤t≤3π4+2πk−3π4+2π∗k≤t≤3π4+2πk.
Ответ : −3π4+2π∗k≤t≤3π4+2πk−3π4+2π∗k≤t≤3π4+2πk.
Задачи для самостоятельного решения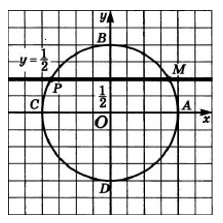
Найти координату точки числовой окружности: Р(61π6)Р(61π6).
2) Найти координату точки числовой окружности: Р(−52π3)Р(−52π3).
3) Найти на числовой окружности точки с ординатой у=−12у=−12 и записать, каким числам ttони соответствуют.
4) Найти на числовой окружности точки с ординатой у≥−12у≥−12 и записать, каким числам ttони соответствуют.
5) Найти на числовой окружности точки с абсциссой x≥−√32x≥−32 и записать, каким числам tt
Домашние задание: красн. учебник § 5, №5.5
№ 5.7-5.8(в,г), №5.10, №5.12-5.13(в,г)
Раздаточный материал



Числовая окружность на координатной плоскости
Инфоурок › Алгебра ›Презентации›Числовая окружность на координатной плоскостиОписание презентации по отдельным слайдам:
1 слайд Описание слайда:
Описание слайда:Числовая окружность на координатной плоскости Выполнил: учитель математики Шубина Т.В.
2 слайд Описание слайда:
Описание слайда:Цель урока: Закрепить умение находить на числовой окружности точки с конкретным значением абсциссы и ординаты, а также умение определить каким числам они соответствуют; Развивать внимание, логическое мышление; Воспитывать внимательность
3 слайд Описание слайда:
Описание слайда:Не будем спорить – будем вычислять. Г. Лейбниц
4 слайд Описание слайда:
Описание слайда:План работы на уроке: Устная работа Самостоятельная работа с индивидуальными картами Работа с учебником
5 слайд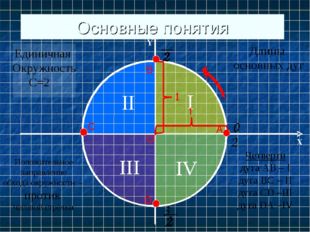 Описание слайда:
Описание слайда:Основные понятия А В С D О Единичная Окружность С=2Π Положительное направление обхода окружности — против часовой стрелки Длины основных дуг 2π Четверти дуга АВ – I дуга ВС – II дуга CD –III дуга DА –IV
6 слайд Описание слайда:
Описание слайда:Найдите на числовой окружности точку, которая соответствует заданному числу
7 слайд Описание слайда:
Описание слайда:Вторая четверть единичной окружности разделена пополам точкой М, а четвертая четверть разделена на 3 равных части точками К и Р. Чему равны длины дуг АМ, РВ, МК, КМ? АМ
8 слайд Описание слайда:
Описание слайда:Ключ
9 слайд Описание слайда:
Описание слайда:№44 (а,б) № 47 (а,б) № 43 Задания для работы с учебником:
10 слайд Описание слайда:
Описание слайда:Оцените на урок по шкале: урок понравился, остались хорошие впечатления ничего не изменилось по сравнению с другими уроками
11 слайд Описание слайда:
Описание слайда:Домашнее задание 1. Повторить §1, 2, 3 2. № 48(а, б), 49 (а, б)

Курс повышения квалификации
Курс повышения квалификации

Курс профессиональной переподготовки
Учитель математики и информатики
Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:
Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВнеурочная деятельностьВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое
Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс
Выберите учебник: Все учебники
Выберите тему: Все темы
также Вы можете выбрать тип материала:

Общая информация
Номер материала: ДБ-324291
Похожие материалы
Вам будут интересны эти курсы:
Оставьте свой комментарий
Единичная окружность — это окружность, радиус которой принимается за единицу измерения.
Длина единичной окружности \(l\) равна l=2π⋅R=2π⋅1=2π.Считаем, что R=1.
Если взять π≈3,14, то длина окружности \(l\) может быть выражена числом 2π≈2⋅3,14=6,28.
Будем пользоваться единичной окружностью, в которой проведены горизонтальный и вертикальный диаметры \(CA\) и \(DB\) (см. рис.)
Принято называть дугу \(AB\) — первой четвертью, дугу \(BC\) — второй четвертью, дугу \(CD\) — третьей четвертью, дугу \(DA\) — четвёртой четвертью, причём это открытые дуги, т. е. дуги без их концов.
Длина каждой четверти единичной окружности равна 14⋅2π=π2.
Принято в обозначении дуги на первом месте писать букву, обозначающую начало дуги, а на втором месте писать букву, обозначающую конец дуги.
Для работы с числовой окружностью часто используются два макета числовой окружности.
Каждая из четырёх четвертей числовой окружности разделена на две равные части, и около каждой из полученных восьми точек записано число, которому она соответствует.
Каждая из четырёх четвертей числовой окружности разделена на три равные части, и около каждой из полученных двенадцати точек записано число, которому она соответствует.
Для числовой окружности верно следующее утверждение:
если точка \(M\) числовой окружности соответствует числу \(t\), то она соответствует и числу вида t+2πk,k∈ℤ.
На указанных двух макетах написаны числа, соответствующие точкам при первом обходе числовой окружности в положительном направлении, т. е. на промежутке 0;2π.
Таким образом,единичная окружность с установленным соответствием между действительными числами и точками окружности называется числовой окружностью.
- Образование
- Математика
- Геометрия
- Как использовать круговые уравнения в координатной геометрии
Марк Раян
Вы можете применять уравнения и алгебру (то есть использовать аналитические методы) к окружностям, расположенным в системе координат x-y . Например, существует хорошая аналитическая связь между уравнением окружности и формулой расстояния, потому что каждая точка на окружности находится на одинаковом расстоянии от его центра.
Вот уравнения круга:
- Круг с центром в начале координат, (0, 0),
x 2 + y 2 = r 2
где r — радиус круга.
- Круг с центром в любой точке ( h , k ),
( x — h ) 2 + ( y — k ) 2 = r 2
где ( h , k ) — центр круга, а r — его радиус.
(Как вы помните из курса алгебры, он кажется задом наперед, но вычитая любое положительное число h из x , фактически перемещает круг вправо на , и вычитая любое положительное число k из y движений круг вверх; , добавив число к x , перемещает круг на влево, и добавив положительное число к , перемещает круг на вниз. )
Теперь попробуйте проблему круга:
Вот схема доказательства.
- Найти уравнение круга.
Все, что вам нужно для уравнения круга, это его центр (вы это знаете) и его радиус. Радиус круга — это просто расстояние от его центра до любой точки круга. Так как точка касания дана, это точка для использования. Для остроумия —Теперь вы закончите, включив координаты центра и радиус в общее уравнение окружности:
- Найти точки круга x и y .
Чтобы найти x -приятия для любого уравнения, вы просто подключаете 0 для y и решаете для x :Нельзя что-то возвести в квадрат и получить негат
Основное уравнение круга
Основное уравнение круга — математическая открытая ссылка Окружность может быть определена как местоположение всех точек, которые удовлетворяют уравнениюx 2 + y 2 = r 2
где x, y — координаты каждой точки, а r — радиус окружности.В простейшем виде уравнение круг Это означает, что для любой точки на круге приведенное выше уравнение будет верным, а для всех остальных точек — нет.Это просто результат Теорема Пифагора. На рисунке выше вы увидите прямоугольный треугольник. гипотенуза радиус окружности, а две другие стороны — это координаты x и y точки P. Применение теоремы Пифагора к этому прямоугольному треугольнику приводит к уравнению окружности.
Перетаскивая точку P по кругу, вы увидите, что отношения между x, y и r всегда сохраняются. Радиус r никогда не меняется, в этом апплете установлено значение 20.Таким образом, x и y изменяются в соответствии с теоремой Пифагора дать координаты P при движении по кругу.
Таким образом, идея заключается в том, что круг является годограф из (форма, образованная) всех точек, которые удовлетворяют уравнению.
Пример
Круг с уравнением Это круг с центром в начале координат и радиусом 8. (8 в квадрате — это 64).
Решение уравнения для радиуса r
Уравнение имеет три переменные (x, y и r).Если мы знаем любые два, то мы можем найти третий. Так что, если нам дают
Точка с известными координатами x и y, мы можем переставить уравнение для решения для r:  Отрицательный корень здесь не имеет смысла.
Обратите внимание, что это работает только тогда, когда центр круга находится в начале координат (0,0), потому что тогда
есть только один круг, который пройдет через заданную точку P. Это находит радиус r этого круга.
Отрицательный корень здесь не имеет смысла.
Обратите внимание, что это работает только тогда, когда центр круга находится в начале координат (0,0), потому что тогда
есть только один круг, который пройдет через заданную точку P. Это находит радиус r этого круга.
Решение по координате
Уравнение имеет три переменные (x, y и r).Если мы знаем любые два, то мы можем найти третий. Так что, если нам дают
радиус r и координата x мы можем найти y, переставив уравнение: 
Обратите внимание, что у этого есть два ответа, из-за плюс / минус. Это ожидается, поскольку на окружности есть две точки с одинаковыми координатами x.
Справа показано, что для данной x-координаты мы видим две точки p1 и p2, которые разделяют эту x-координату.
Что, если центр круга не находится в начале координат?
Затем мы просто добавляем или вычитаем фиксированные суммы к координатам x и y, чтобы вернуть их в начало координат.Подробнее об этом смотрите Общее уравнение круга.
Параметрическая форма
Вместо использования теоремы Пифагора Чтобы решить прямоугольный треугольник в круге выше, мы также можем решить его с помощью тригонометрии. Это приводит к так называемой параметрической форме уравнения окружности, как описано в Параметрическое уравнение круга. Эта параметрическая форма особенно полезна в компьютерных алгоритмах, которые рисуют круги и эллипсы. Это описано в Алгоритм рисования кругов.
Что попробовать
- В вышеприведенном апплете нажмите «сбросить» и «скрыть детали».
- Установите флажок «Показать координаты» и снимите флажок «Радиус замораживания».
- Перетащите точку P, чтобы создать круг по вашему выбору.
- Рассчитайте радиус круга и напишите уравнение круга.
- Нажмите «показать подробности», чтобы проверить свой результат.
Похожие темы
(C) 2011 Copyright Math Открытая ссылка.
Все права защищены
- Товары
- Клиенты
- Случаи использования
- Переполнение стека Публичные вопросы и ответы
- Команды Частные вопросы и ответы для вашей команды
- предприятие Частные вопросы и ответы для вашего предприятия
- работы Программирование и связанные с ним технические возможности карьерного роста
- Талант Нанимать технический талант
- реклама Связаться с разработчиками по всему миру
Загрузка…
- Авторизоваться
Расчет координат в единичном круге — Концепция
Единичный круг — это круг, радиус которого равен единице, и центр которого находится в начале координатной плоскости. Это понятие часто встречается во многих математических предметах, особенно в тех, где используется тригонометрия. Вопросы о единичных круговых координатах часто дают неизвестную координату и требуют, чтобы мы использовали свойства единичного круга для вычисления этих координат.
Единичный круг — это то, о чем мы собираемся начать говорить в геометрии, мы также поговорим об этом в алгебре, и вы поговорите об этом в предварительном исчислении и, возможно, немного в исчислении. также. Так что вы можете также ознакомиться с ним прямо сейчас, давайте начнем с того, что такое круг юнитов? Под единицей измерения в математике обычно подразумевается число 1, поэтому единичная окружность — это круг с радиусом 1 с центром в начале координат.Итак, прямо здесь я нарисовал круг с центром в начале координат, и если радиус равен 1, мы можем нарисовать пару ключевых точек. Я знаю, что эта точка прямо здесь, где мой круг пересекает ось х, будет равна 1,0. Я знаю, что эта точка прямо здесь, где она пересекает ось у, будет в 0 и 1. Так, обычно, на вашей домашней работе или тест, когда у вас есть круг юнитов, они сообщат вам, что это круг юнитов, указав эти 2 точки.
Мы также знаем, что в данный момент здесь просто ради информации, будет отрицательным 1, 0, и эта точка здесь будет в 0, отрицательным 1.Так как это связано с теоремой Пифагора? Ну, у вас, вероятно, будет проблема, когда они рисуют в радиусе, поэтому я думаю, что мы могли бы сказать, что рисовать в радиусе r, так что вы собираетесь сказать хорошо r, так как радиус из этого круга 1 будет 1, и чтобы найти значение r на основе некоторой точки x и y, вы собираетесь сбросить высоту. Итак, я собираюсь взять другой цветной маркер здесь, и вы будете сбрасывать высоту вплоть до оси X, создавая прямоугольный треугольник.Так что, если бы я перерисовал этот треугольник здесь, ваша гипотенуза, которая будет противоположна вашему прямому углу, будет иметь значение r, равное 1. 1 нога будет вашей координатой x, а другая нога будет ваша координата у.
Теперь, когда вы попадете во второй, третий и четвертый квадранты здесь, где x отрицателен, здесь, где x и y отрицательны, а четвертый, где y отрицателен, вы будете использовать абсолютное значение x и y, потому что вы хотите иметь положительные числа. Таким образом, ключ к использованию окружности юнитов состоит в том, чтобы помнить, что ваш радиус будет и что вы всегда можете сбросить высоту или, если вы находитесь здесь, поднять высоту, чтобы создать правильный треугольник.

