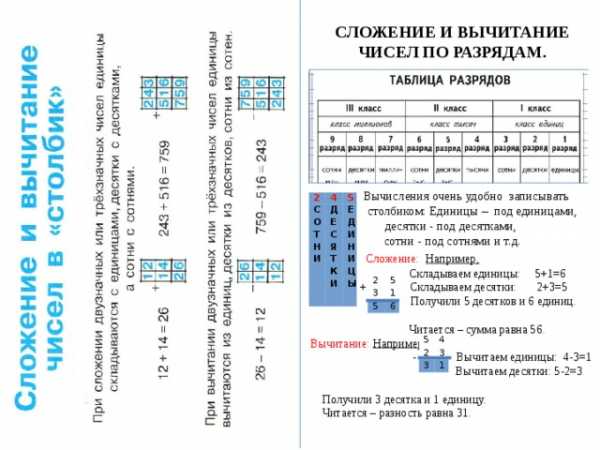
СЛОЖЕНИЕ И ВЫЧИТАНИЕ ЧИСЕЛ ПО РАЗРЯДАМ.

Вычисления очень удобно записывать

столбиком: Единицы – под единицами,

десятки — под десятками,

сотни — под сотнями и т.д.

Сложение: Например,

Складываем единицы: 5+1=6

+ Складываем десятки: 2+3=5

Получили 5 десятков и 6 единиц.

Читается – сумма равна 56.

Вычитание: Например,

— Вычитаем единицы: 4-3=1

Вычитаем десятки: 5-2=3

Получили 3 десятка и 1 единицу.

Читается – разность равна 31.

2

С

4

Д

О

5

Е

Т

Е

Н

С

Д

И

И

Я

Н

Т

И

К

И

Ц

Ы

2

3

5

5

1

6

5

2

4

3

3

1

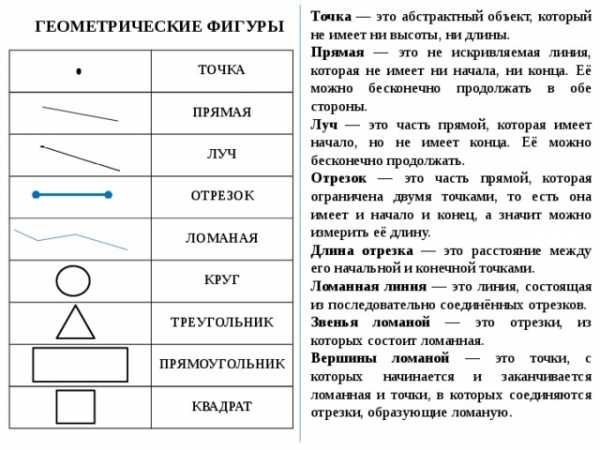
Точка — это абстрактный объект, который не имеет ни высоты, ни длины.

Прямая — это не искривляемая линия, которая не имеет ни начала, ни конца. Её можно бесконечно продолжать в обе стороны.

Луч — это часть прямой, которая имеет начало, но не имеет конца. Её можно бесконечно продолжать.

Отрезок — это часть прямой, которая ограничена двумя точками, то есть она имеет и начало и конец, а значит можно измерить её длину.

Длина отрезка — это расстояние между его начальной и конечной точками.

Ломанная линия — это линия, состоящая из последовательно соединённых отрезков.

Звенья ломаной — это отрезки, из которых состоит ломанная.

Вершины ломаной — это точки, с которых начинается и заканчивается ломанная и точки, в которых соединяются отрезки, образующие ломаную.

ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ

ТОЧКА

ПРЯМАЯ

ЛУЧ

ОТРЕЗОК

ЛОМАНАЯ

КРУГ

ТРЕУГОЛЬНИК

ПРЯМОУГОЛЬНИК

КВАДРАТ

Чтобы определить прямой угол или нет, нужно взять особый инструмент – угольник.

Если, приложив угольник к углу, вершиной к вершине, стороны совпадут, то угол — прямой . Не совпадут – непрямой.

Непрямые углы делятся на тупые и острые .

Угол, величина которого меньше величины прямого – острый,

Угол, величина которого больше величины прямого – тупой.

Прямоугольник – это четырёхугольник, у которого все углы прямые. Противополож-ные стороны прямоугольника равны.

Одним цветом показаны

противоположные стороны

прямоугольника.

Квадрат – это прямоугольник, у которого все стороны равны.

УГОЛ. ВИДЫ УГЛОВ.

Угол – это геометрическая фигура, состоящая из двух лучей, исходящих из одной точки.

Лучи, образующие угол, называются сторонами угла, общее начало называется вершиной.

Углы могут быть прямыми и непрямыми.

Как решить задачу?

1. Внимательно и выразительно прочитать задачу.

2. Представить себе то, о чём в ней говорится.

3. Выделить устно, что известно и что неизвестно.

4. Определить главный вопрос задачи.

5. Записать кратко условие задачи (краткую запись).

6. Составить и записать решение задачи.

7. Записать ответ.

Как оформит краткую запись?

Примеры:

• У Вани 3 яблока, а у Кати – 5 груш. Сколько всего фруктов у ребят?

Ваня – 3 яб.

Катя – 5 гр.

• Коля нашел 4 гриба, а Витя – 7 грибов. Кто нашел грибов больше и на сколько?

Коля – 4 г.

Катя – 5 г.

3. Дима купил 10 тетрадей, а Света на 6 меньше. Сколько тетрадей купила Света?

Дима – 10 т.

Света — ? т., на 6 т. меньше

4. Вера купила 9 карандашей, а Маша на 4 больше. Сколько карандашей купила Маша?

Вера – 9 к.

Маша — ? к., на 4 к. больше

УРАВНЕНИЕ.

ЭТО РАВЕНСТВО, СОДЕРЖАЩЕЕ НЕИЗВЕСТНОЕ ЧИСЛО, КОТОРОЕ НАДО НАЙТИ.

Неизвестное число обозначают маленькими латинскими буквами, например х (икс) или y (игрик).

Х+4=16 – это уравнение.

Х= 16-4 — это решение уравнения.

Х=12. — это решение уравнения.

12+4=16 — это проверка правильнос-

16=16 ти решения уравнения.

В первоначальное уравнение вместо неизвестного, т.е. Х ставим полученное значение. В данном примере – это число 12. Все остальное переписываем из первоначального уравнения. Решаем и проверяем равенство полученных значений с правой и левой стороны.

? Ф.

? г.

— скобка. Ставится в краткой записи задачи тогда, когда в вопросе звучит, что надо найти … всего…

УМНОЖЕНИЕ.

ДЕЛЕНИЕ.

Знак деления — :

Знаки умножения : или х

6 : 2 = 3

2 3 = 6

ДЕЛИМОЕ ЧАСТНОЕ

ДЕЛИТЕЛЬ

ПРАВИЛА ДЕЛЕНИЯ.

• Самое большое число в частном — делимое.
• На нуль делить нельзя!
• Если делимое равно делителю, то частное равно 1.

2 : 2 = 1

• Частное равно делимому, если делитель равен 1.

2 : 1 = 2

• Частное равно 0, если делимое равно 0.

0 : 2 = 0

1 МНОЖИТЕЛЬ ПРОИЗВЕДЕНИЕ

2 МНОЖИТЕЛЬ

ПРАВИЛА УМНОЖЕНИЯ.

• Если один из множителей равен 0 , то и произведение равно 0 .

2 х 0 = 0 или 0 3 = 0

• Если один из множителей равен 1, то произведение равно другому множителю.

3 х 1 = 3 или 1 3 = 3

• От перестановки множителей значение произведения не меняется.

3 х 5 = 5 х 3 или 3 5 = 5 3

Вертикальный крайний левый столбец и горизонтальная верхняя строка пред- ставляют собой слагаемые. Для того что бы сложить два числа, нужно найти их в вертикальном столбце и в горизонтальной строке. Пересечение образует сумму этих двух слагаемых.

multiurok.ru

ПРАВИЛА ПО МАТЕМАТИКЕ для начальной школы

Транскрипт

1 ПРАВИЛА ПО МАТЕМАТИКЕ для начальной школы

2 Справочное пособие предназначено для учащихся начальных классов и подготовлено в соответствии с требованиями школьной программы. СОДЕРЖАНИЕ 1. Числа и цифры. 2. Натуральные числа. 3. Сравнение чисел. 4. Сложение. 5. Вычитание. 6. Законы сложения. 7. Умножение. 8. Деление. 9. Нахождение компонентов деления. 10. Таблица умножения Пифагора. 11. Особые случаи умножения. 12. Особые случаи деления. 13. Признаки делимости. 14. Именованные числа. 15. Преобразование именованных чисел. 16. Сложение и вычитание именованных чисел. 17. Умножение и деление именованных чисел. 18. Выражения. 19. Порядок действий в выражениях. 20. Уравнения. 21. Решение простейших уравнений. 22. Учимся решать задачи. 23. Задачи на нахождение суммы двух чисел. 24. Задачи на нахождение остатка. 25. Задачи на увеличение числа на несколько единиц. 26. Задачи на уменьшение числа на несколько единиц. 27. Задачи на разностное сравнение двух чисел. 28. Задачи на нахождение неизвестного слагаемого. 29. Задачи на нахождение неизвестного уменьшаемого. 30. Задачи на нахождение неизвестного вычитаемого. 31. Задачи на нахождение произведения двух чисел. 32. Задачи на нахождение частного двух чисел. 33. Задачи на увеличение числа в несколько раз. 34. Задачи на уменьшение числа в несколько раз. 35. Задачи на кратное сравнение двух чисел. 36. Задачи на нахождение неизвестного множителя. 37. Задачи в косвенной форме. 38. Цена, количество, стоимость.

3 39. Составные задачи. 40. Задачи на пропорциональное деление. 41. Задачи на нахождение слагаемого и вычитаемого. 42. Составные задачи на совместную работу. 43. Задачи на движение. 44. Задачи на встречное движение. 45. Задачи на движение в противоположных направлениях. 46. Задачи на движение в одном направлении. 47. Основы геометрии. 48. Площадь. ЧИСЛА И ЦИФРЫ. Числа это единицы счёта. С помощью чисел можно сосчитать количество предметов и определить различные величины (длину, ширину, высоту и т.д.). Для записи чисел используются специальные знаки цифры. Цифр десять: НАТУРАЛЬНЫЕ ЧИСЛА. Числа, которые используются при счёте, называются натуральными. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20,, 1 самое маленькое число. самого большого числа не существует. Число 0 (нуль) обозначает отсутствие предмета. Нуль не является натуральным число. СРАВНЕНИЕ ЧИСЕЛ. Правило 1. Из двух натуральных чисел больше то, которое в натуральном ряду расположено правее, а меньше то, которое расположено левее:, 10, 11, 12, 13, 14, 15, 14 > 11 Правило 2. Из двух натуральных чисел с разным количеством разрядов больше то число, в котором разрядов больше. Правило < < 1263

4 Из двух натуральных чисел с одинаковым количеством разрядов больше то, у которого больше цифра старшего разряда и < > СЛОЖЕНИЕ. Сложение это математическое действие. Числа, которые складываются, называются слагаемыми. Результат сложение называется суммой. сумма a + b = c первое слагаемое второе слагаемое сумма = 5 сумма Правило 1. Если одно из слагаемых равно 0, сумма равна второму слагаемому: a + 0 = a 0 + a = a = = 5 Правило 2. Если оба слагаемых равны 0, то и сумма равна 0: = 0 Таблица сложение натуральных чисел в пределах = 7. Научись пользоваться таблицей:

5 ВЫЧИТАНИЕ. Вычитание действие, обратное сложению. разность a — b = c уменьшаемое вычитаемое разность 5-3 = 2 разность Правило 1. Если к разности прибавить вычитаемое, то получится уменьшаемое. Правило 2. Если из уменьшаемого вычесть разность, то получится вычитаемое. ЗАКОНЫ СЛОЖЕНИЯ. Закон 1. Переместительный закон сложения. От перемены мест слагаемых значение суммы не меняется: a + b = b + a = Закон 2. Сочетательный закон сложения. Чтобы к сумме двух чисел прибавить третье число, можно к первому числу прибавить сумму второго и третьего чисел или ко второму числу прибавить сумму первого и третьего чисел: (a + b) + c = a + (b + c) = (a + c) + b (2 + 4) + 8 = 2 + (4 + 8) = (2 + 8) + 4 УМНОЖЕНИЕ. Умножение это сложение одинаковых слагаемых = 2 3 = 6

6 2 слагаемое 3 число, которое показывает, сколько раз повторяется слагаемое 2 (по два три раза), — знаки умножения. a b = a + a + a + + a b раз произведение a b = c первый множитель второй множитель произведение 2 3 = 5 произведение ДЕЛЕНИЕ. Деление это действие, обратное умножению. 6 : 2 = 3 6 : 3 = 2 частное a : b = c делимое делитель частное 6 : 3 = 2 частное ЗАКОНЫ УМНОЖЕНИЯ. Закон 1. Переместительный закон умножения. От перестановки множителей произведение не меняется: a b = b a 4 2 = = 8 Закон 2. Сочетательный закон умножения. Чтобы произведение двух чисел умножить на третье число, можно первое число умножить на произведение второго и третьего чисел или второе число умножить на произведении первого и третьего чисел: (a b) c = a (b c) = (a c) b (2 4) 8 = 2 (4 8) = (2 8) 4

7 Закон 3. Распределительный закон умножения. Относительно сложения Произведение суммы на число равно сумме произведений каждого слагаемого на это число. (a + b + c) d = a d + b d + c d ( ) 2 = = 20 Относительно вычитания Чтобы умножить разность на число, достаточно умножить на это число отдельно уменьшаемое и вычитаемое, а затем из первого произведения вычесть второе произведение. (a — b) d = a d — b d (15-5) 4 = = = 40 Правило 1. СВОЙСТВА ДЕЛЕНИЯ. Чтобы разделить сумму на число, достаточно разделить каждое слагаемое на это число, а полученные результаты сложить. Правило 2. (a + b) : c = a : c + b : c Чтобы разделить разность на число, достаточно разделить на это число уменьшаемое и вычитаемое, а затем из первого частного вычесть второе частное. Правило 3. (a — b) : c = a : c — b : c Частное от деления произведений двух множителей на число равно произведению одного из множителей на частное от деления второго множителя на это число. Правило 4. (a b) : c = (a : c) b = a (b : c) Чтобы разделить число на частное, достаточно разделить это число на делимое и полученный результат умножить на делитель. Правило 5. a (b : c) = (a : b) c Чтобы разделить частное на число, достаточно умножить делитель на это число и разделить делимое на полученный результат Можно так же разделить делимое на это число, а полученный результат разделить на делитель. (a : b) : c = a : (b c) или

8 (a : b) : c = (a : c) : b НАХОЖДЕНИЕ КОМПОНЕНТОВ ДЕЛЕНИЯ. Правило. Чтобы найти неизвестный делитель, нужно делимое разделить на частное. a 😕 = c? = a : c Чтобы найти неизвестное делимое, нужно частное умножить на делитель.? : b = c? = c b ТАБЛИЦА УМНОЖЕНИЯ ПИФАГОРА ОСОБЫЕ СЛУЧАИ УМНОЖЕНИЯ. a 1 = a 4 1 = 4 0 a = = 0 1 a = a 1 4 = 4 a 0 = = 0

9 ОСОБЫЕ СЛУЧАИ ДЕЛЕНИЯ. a : 1 = a 8 : 1 = 8 0 : a = 0 0 : 6 = 0 На нуль делить НЕЛЬЗЯ! a : 0 a : a = 1 8 : 8 = 1 Нуль можно делить на любое число, получится 0. ПРИЗНАКИ ДЕЛИМОСТИ. На 2 делятся все чётные числа, то есть числа, которые оканчиваются цифрами 0, 2, 4, 6, 8. На 3 делятся все числа, сумма цифр которых делится на 3. На 5 делятся все числа, которые оканчиваются на 0 или 5. На 6 делятся числа, которые делятся одновременно и на 2, и на 3. На 9 делятся числа, сумма цифр которых делится на 9. ИМЕНОВАННЫЕ ЧИСЛА. Именованные числа это числа, полученные при измерении величин и сопровождающиеся названием единиц измерения. Например: 2 кг, 4 см, 8 л. Именованные числа бывают простые и составные. Простые именованные числа: 7 м, 18 т, 21 кг в них входит только одна единица измерения. Составные именованные числа: 2 м 4 см, 24 кг 45 г, 8 км 520 м в них входят несколько единиц измерения. ПРЕОБРАЗОВАНИЕ ИМЕНОВАННЫХ ЧИСЕЛ. Чтобы перейти от одних единиц измерения к другим, пользуйся таблицей величин. Таблица величин. Единицы измерения длины 1 см = 10 мм

10 1 дм = 10 см 1 м = 10 дм = 100 см = 1000 мм 1 км = 1000 м = дм = см Единицы измерения массы 1 кг = 1000 г 1 ц = 100 кг 1 т = 10 ц = 1000 кг Единицы измерения времени 1 мин = 60 с 1 ч = 60 мин = 3600 с 1 сутки = 24 часа 1 неделя = 7 дней 1 месяц = 30 или 31 день (в феврале 28 или 29 дней) 1 год = 12 месяцев = 52 недели = 365 или 366 дней 1 век (столетие) = 100 лет Единицы измерения площади 1 мм 2 1 см 2 = 100 мм 2 1 дм 2 = 100 см 2 1 м 2 = 100 дм 2 = см 2 1 км 2 = м 2 1 ар (1 а) = 1 сотка = 100 м 2 1 гектар (1 га) = м 2 СЛОЖЕНИЕ И ВЫЧИТАНИЕ ИМЕНОВАННЫХ ЧИСЕЛ. Правило. Складывать и вычитать можно именованные числа, выраженные в одинаковых единицах измерения. УМНОЖЕНИЕ И ДЕЛЕНИЕ ИМЕНОВАННЫХ ЧИСЕЛ. Запомни! При умножении и делении составные именованные числа сначала заменяют простыми, а затем выполняют вычисления. В ответе простое именованное число заменяют составным. ВЫРАЖЕНИЯ. Математическое выражение это фраза, записанная с помощью чисел, знаков и букв.

11 Выражение, записанное только с помощью чисел и знаков, называется числовым. Выражение, в котором кроме чисел и знаков есть буквы, называется буквенным. Любое числовое выражение имеет значение. Найти значение числового выражения значит найти его ответ. Правило 1. ПОРЯДОК ДЕЙСТВИЙ В ВЫРАЖЕНИЯХ. В выражениях без скобок, где выполняются только сложение и вычитание, действия выполняются в том порядке, в котором они записаны (то есть слева направо) = = = 41 Правило 2. В выражениях без скобок, где выполняются только умножение деление, действия выполняются в том порядке, в котором они записаны : 5 = 8 и Правило : 10 3 = : 9 3 = 12 В выражениях со скобками первым выполняется действие в скобках, затем умножение или деление и только потом сложение или вычитание (46-14) = (30-20) = : (2 5) = 9

12 Правило 4. В выражениях, где есть действия первой и второй ступеней (то есть +, -,, :), сначала выполняются умножение и деление, а затем по порядку сложение и вычитание : 2 = : = 70 УРАВНЕНИЯ. Уравнение это равенство, которое содержит в себе неизвестное (переменную), значение которого нужно найти, чтобы равенство было верным. x + 3 = 5 5 x = 20 y — 2 = 7 8 : a = 2 Решить уравнение значит найти все значения переменной, при которых уравнение превращается в верное равенство. x + 3 = 5 x = 5-3 x = = 5 5 = 5 Значение переменной, при котором уравнение превращается в верное равенство, называется корнем уравнения: y — 2 = 7 y = 9 — корень уравнения, так как 9-2 = 7 Правило 1. РЕШЕНИЕ ПРОСТЕЙШИХ УРАВНЕНИЙ. Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое. x + 3 = 5 x = 5-3 Правило 2. Чтобы найти неизвестное уменьшаемое, нужно к вычитаемому прибавить разность. x — 3 = 5 x = 5 + 3

13 Правило 3. Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность. 8 — x = 5 x = 8-5 Правило 4. Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель. x 3 = 15 x = 15 : 3 Правило 5. Чтобы найти неизвестное делимое, нужно к вычитаемому прибавить разность. x : 3 = 5 x = 5 3 Правило 6. Чтобы найти неизвестный делитель, нужно делимое разделить на частное. 8 : x = 2 x = 8 : 2 Как работать над задачей. УЧИМСЯ РЕШАТЬ ЗАДАЧИ. 1. Прочитай внимательно условие задачи и представь то, о чём идёт речь. 2. Запиши кратко задачу или сделай к ней рисунок, схему, чертёж. 3. Объясни, что означает каждое число. 4. Устно составь план решения задачи. 5. Реши задачу и найди ответ. 6. Проверь решение, составив обратную задачу. 7. Запиши ответ. Знак Действие Знак Действие + Увеличить на — Найти разность — Уменьшить на (х) Увеличить в несколько раз — На сколько больше? : Уменьшить в несколько раз — На сколько меньше? : Во сколько раз больше? + Найти сумму : Во сколько раз меньше? ЗАДАЧИ НА НАХОЖДЕНИЕ СУММЫ ДВУХ ЧИСЕЛ.

14 Запомни! Задачи этого вида решаются сложением, потому что находим сумму. Белочка припасла для маленьких друзей 4 гриба и 5 орехов. Сколько всего гостинцев приготовила белочка? Грибов — Орехов -? = 9 (гост.) Ответ: 9 гостинцев. ЗАДАЧИ НА НАХОЖДЕНИЕ ОСТАТКА. Запомни! Задачи этого вида решаются вычитанием, потому что находим остаток. На ветке было 7 ягод рябины. Снегирь склевал 3 ягоды. Сколько ягод осталось? Было 7 яг. Склевал 3 яг. Осталось -? яг. 7-3 = 4 (яг.) Ответ: 4 ягоды. ЗАДАЧИ НА УВЕЛИЧЕНИЕ ЧИСЛА НА НЕСКОЛЬКО ЕДИНИЦ. Во дворе гуляло 6 утят, а гусят на 2 больше. Сколько гуляло гусят? Утят 6 пт. Гусят? пт., на 2 больше (>) = 8 (гус.) Ответ: 8 гусят. ЗАДАЧИ НА УМЕНЬШЕНИЕ ЧИСЛА

15 НА НЕСКОЛЬКО ЕДИНИЦ. На столе лежало 9 столовых ложек, а чайных на 3 меньше. Сколько чайных ложек лежало на столе? Стол. 9 лож. Чайн.? лож., на 3 меньше (<) 9-3 = 6 (лож.) Ответ: 6 чайных ложек. Правило. ЗАДАЧИ НА РАЗНОСТНОЕ СРАВНЕНИЕ ДВУХ ЧИСЕЛ. Чтобы узнать, на сколько одно число больше (меньше) другого, нужно из большего числа вычесть меньшее. В одной корзине 7 яблок, а в другой 10 груш. На сколько груш больше, чем яблок? Яб. 7 шт. Гр. 10 шт., на? шт. больше (>) 10-7 = 3 (гр.) Ответ: на 3 груши. ЗАДАЧИ НА НАХОЖДЕНИЕ НЕИЗВЕСТНОГО СЛАГАЕМОГО. Два петушка нашли 8 червячков. Первый нашёл 5. Сколько червячков нашёл второй петушок? 1 пет. 5 чер. 8 чер. 2 пет. -? чер. 8-5 = 3 (чер.) Ответ: 3 червячка. ЗАДАЧИ НА НАХОЖДЕНИЕ

16 НЕИЗВЕСТНОГО УМЕНЬШАЕМОГО. На тарелке лежали пряники. Когда дети взяли 4 пряника, на тарелке осталось 8. Сколько пряников было на тарелке? Было? пр. Взяли 4 пр. Осталось 8 пр = 12 (пр.) Ответ: 12 пряников. ЗАДАЧИ НА НАХОЖДЕНИЕ НЕИЗВЕСТНОГО ВЫЧИТАЕМОГО. В вазе стояло 7 гвоздик. Когда несколько гвоздик отдали, в вазе осталось 5 гвоздик. Сколько гвоздик отдали? Было 7 гв. Отдали? гв. Осталось 5 гв. 7-5 = 2 (гв.) Ответ: 2 гвоздики. ЗАДАЧИ НА НАХОЖДЕНИЕ ПРОИЗВЕДЕНИЯ ДВУХ ЧИСЕЛ. В одной коробке 6 карандашей. Сколько карандашей в 4 коробках? 1 кор. 6 кар. 4 кор. -? кар. 6 4 = 24 (кар.) Ответ: 24 карандаша. ЗАДАЧИ НА НАХОЖДЕНИЕ ЧАСТНОГО ДВУХ ЧИСЕЛ.

17 Задача 1. ДЕЛЕНИЕ НА РАВНЫЕ ЧАСТИ. 15 шариков раздали 5 ученикам поровну. Сколько шариков получил каждый ученик? 15 шар. 5 уч. Поровну шар. 1 уч. 15 : 5 = 3 (шар.) Ответ: 3 шарика. Задача 2. ДЕЛЕНИЕ ПО СОДЕРЖАНИЮ. 12 лимонов разложили в пакеты по 4 лимона в каждый. Сколько получилось пакетов с лимонами? 12 лим.? пак. 4 лим. 1 пак. 12 : 4 = 3 (пак.) Ответ: 3 пакета. ЗАДАЧИ НА УВЕЛИЧЕНИЕ ЧИСЛА В НЕСКОЛЬКО РАЗ. У Тани было 4 ириски, а карамелек в 2 раза больше. Сколько карамелек было у Тани? Ириски 4 шт. Карамельки? шт., в 2 раза больше (>) 4 2 = 8 (кар.) Ответ: 8 карамелек. ЗАДАЧИ НА УМЕНЬШЕНИЕ ЧИСЛА В НЕСКОЛЬКО РАЗ.

18 На одной полке стоит 12 книг, а на второй в 3 раза меньше. Сколько книг на второй полке? I 12 кн. II? кн., в 3 раза меньше (<) 12 : 3 = 4 (кн.) Ответ: 4 книг. Правило. ЗАДАЧИ НА КРАТНОЕ СРАВНЕНИЕ ДВУХ ЧИСЕЛ. Чтобы узнать, во сколько раз одно число больше (меньше) другого, нужно большее число разделить на меньшее. Петя почистил 27 картофелин, а Коля 9. Во сколько раз больше картофелин почистил Петя, чем Коля? Петя 27 кар. во? раз больше (>) Коля 9 кар., 27 : 9 = 3 (гр.) Ответ: в 3 раза больше. ЗАДАЧИ НА НАХОЖДЕНИЕ НЕИЗВЕСТНОГО МНОЖИТЕЛЯ. 20 яблок разложили в сетки по 5 яблок в каждую. Сколько потребовалось сеток? 1 сет. 5 яб.? сет. 20 яб. 1-ый способ: 20 : 5 = 4 (сет.) 2-ой способ: запишем решение задачи, составив уравнение.

19 х 5 = 20 х = 20 : 5 х = 4 (сет.) Ответ: 4 сетки. Правило. ЗАДАЧИ В КОСВЕННОЙ ФОРМЕ. При решении задач в косвенной форме помни: если одна величина на несколько единиц (в несколько раз) больше, то другая на столько же единиц (во столько же раз) меньше. Брату 5 лет, он на 2 года старше сестры. Сколько лет сестре? Брат 5 лет, на 2 года больше (>) Сестра? лет Если брат старше на 2 года, значит, сестра на 2 года младше. Чтобы стало меньше, нужно вычитать. 5-2 = 3 (г.) Ответ: 3 года. У Нины 7 марок. Это на 4 марки меньше, чес у Тани. Сколько марок у Тани? Нина 7 мар., на 4 мар. меньше (<) Таня? мар. Если у Нины на 4 марки меньше, значит, у Тани на 4 марки больше. Чтобы стало больше, нужно прибавлять = 11 (мар.) Ответ: 11 марок. ЦЕНА, КОЛИЧЕСТВО, СТОИМОСТЬ. Цена (Ц) это количество денег, которое нужно заплатить за 1 предмет (1 кг), то есть за единицу товара.

20 Количество (К) это число, которое показывает, сколько куплено единиц товара. Стоимость (С) это количество денег, затраченных на всю покупку. Правило 1. Чтобы найти стоимость, нужно цену умножить на количество. С = Ц К Правило 2. Чтобы найти количество, нужно стоимость разделить на цену. К = С : Ц Правило 3. Чтобы найти цену, нужно стоимость разделить на количество. Вид записи задачи: Ц = С : К Цена Количество Стоимость СОСТАВНЫЕ ЗАДАЧИ. Запомни! Составные задачи состоят из нескольких простых и решаются в два и больше действия. Рыбак поймал 10 щук, а лещей на 8 больше. Сколько всего рыб поймал рыбак? Щуки 10 рыб Лещи? рыб, на 8 рыб больше (>)? рыб Схема анализа задачи: — Можем ли мы сразу ответь на главный вопрос задачи? — Нет. — Почему? — Мы не знаем количество лещей. — А мы можем сразу это узнать? — Да. Из условия нам известно, что лещей было на 8 больше, чем щук. — Каким действием и почему? — Сложением. Чтобы стало больше, нужно прибавить. — Теперь можно ответить на главный вопрос задачи? — Да. 1) = 18 (рыб) лещей. 2) = 28 (рыб) 10 + ( ) = 28

21 Ответ: 28 рыб всего. ЗАДАЧИ НА ПРОПОРЦИОНАЛЬНОЕ ДЕЛЕНИЕ. В 6 коробках 72 кг печенья. Сколько потребуется коробок, чтобы разложить 48 кг печенья? 6 кор. 72 кг? кор. 48 кг 1 кор. -? кг Сначала надо узнать, сколько кг печенья в одной коробке. 1) 72 : 6 = 12 (кг) печенья в одной коробке 2) 48 : 12 = 4 (кор.) 48 : (72 : 6) = 4 Ответ: 4 коробки потребуется. ЗАДАЧИ НА НАХОЖДЕНИЕ СЛАГАЕМОГО И ВЫЧИТАЕМОГО. Папа съел 16 пельменей, мама 10, а сын на 20 пельменей меньше, чем папа и мама вместе. Сколько пельменей съел сын? Папа 16 п.? п. Мама 10 п. Сын -? п., на 20 п. меньше (<) Сразу ответить на главный вопрос задачи нельзя, потому что неизвестно, сколько пельменей съели папа и мама вместе. 1) = 26 (п.) съели мама и папа вместе 2) = 6 (п.) ( ) — 20 = 6 Ответ: 6 пельменей съел сын. СОСТАВНЫЕ ЗАДАЧИ НА СОВМЕСТНУЮ РАБОТУ.

22 Первый насос выкачивает 960 вёдер воды за 32 минуты, а второй за 48 минут. За сколько минут оба насоса выкачают 1000 вёдер воды, если будут работать одновременно?? I 960 в. 32 мин 1000 в. II 960 в. 48 мин.? мин 1) 960 : 32 = 30 (в.) выкачивает за 1 минуту 1 насос 2) 960 : 48 = 20 (в.) выкачивает за 1 минуту 2 насос 3) = 50 (в.) 4) 1000 : 50 = 20 (мин) 1000 : (960 : : 48) = 20 Ответ: за 20 минут. ЗАДАЧИ НА ДВИЖЕНИЕ. Задачи на движение содержат пропорциональные величины: скорость (V), время (t), расстояние (S). Правило 1. Чтобы найти расстояние, нужно скорость умножить на время. S = V t Электропоезд двигается со скоростью 65 км/ч. Какое расстояние он пройдёт за 7 часов? 65 7 = 455 (км) V t S 65 км/ч 7 ч.? км Ответ: 455 км пройдёт электропоезд. Правило 2. Чтобы найти скорость, нужно расстояние разделить на время. V = S : t За 3 часа автобус проехал 195 км. С какой скоростью двигался автобус? V t S? км/ч 3 ч. 195 км

23 195 : 3 = 65 (км/ч) Ответ: 65 км/ч скорость автобуса. Правило 3. Чтобы найти время, нужно расстояние разделить на скорость. t = S : V Пешеход двигался со скоростью 5 км/ч и прошёл 15 км. Сколько часов пешеход был в пути? 15 : 5 = 3 (ч) Ответ: 3 часа пешеход был в пути. V t S 5 км/ч? ч. 15 км ЗАДАЧИ НА ВСТРЕЧНОЕ ДВИЖЕНИЕ. Если два тела одновременно движутся навстречу друг другу, то расстояние между ними постоянно изменяется на одно и то же число, равное сумме расстояний, которые проходят тела за единицу времени. Два лыжника одновременно вышли навстречу друг другу из двух посёлков и встретились через 3 часа. Первый лыжник шёл со скоростью 12 км/ч, а второй 14 км/ч. На каком расстоянии находятся посёлки? V = 12 км/ч t = 3 ч V = 14 км/ч S =? км

24 Схема анализа задачи: 1 способ: — О чём говорится в задаче? — О движении двух лыжников. Поэтому краткое условие оформляем в виде чертежа. — Что известно о начале движения? — Лыжники начали двигаться одновременно. Покажем это стрелочками «навстречу». Выводы: 1. Расстояние между лыжниками всё время уменьшается. 2. Всё расстояние складывается из расстояния, которое прошёл первый лыжник, и расстояния, которое прошёл второй лыжник. 3. Лыжники начали и закончили движение одновременно, поэтому они провели в пути одинаковое количество времени. Решим задачу, опираясь на схему:? — расстояние между посёлками S -? — первый лыжник S -? — второй лыжник 1) 12 3 = 36 (км) прошёл первый лыжник 2) 14 3 = 42 (км) прошёл второй лыжник 3) = 78 (км) = 78 Ответ: 78 км расстояние между посёлками. 2 способ: Решим эту задачу, используя понятие «скорость сближения». Если первый лыжник пройдёт за 1 час 12 км, а второй 14 км, то расстояние между ними за 1 час уменьшится (это и есть скорость сближения) на: = 26 км. За второй час расстояние уменьшится ещё на 26 км ) = 26 (км) скорость сближения 2) 26 3 = 78 (км) прошёл второй лыжник ( ) 3 = 78 Ответ: 78 км расстояние между посёлками.

25 ЗАДАЧИ НА ДВИЖЕНИЕ В ПРОТИВОПОЛОЖНЫХ НАПРАВЛЕНИЯХ. Два лыжника одновременно вышли из пункта А в противоположных направлениях. Первый лыжник шёл со скоростью 12 км/ч, а второй 14 км/ч. На каком расстоянии друг от друга они будут через 3 часа? V = 12 км/ч А V = 14 км/ч 1 способ: S =? км 1) 12 3 = 36 (км) прошёл первый лыжник за 3 часа 2) 14 3 = 42 (км) прошёл второй лыжник за 3 часа 3) = 78 (км) = 78 Ответ: 78 км расстояние между лыжниками через 3 часа. 2 способ: Обрати внимание, что расстояние, которое проходят лыжники за 1 час при движении в противоположных направлениях, называется скоростью удаления. 3) = 26 (км) скорость удаления 4) 26 3 = 78 (км) прошёл второй лыжник

26 ( ) 3 = 78 Ответ: 78 км расстояние между лыжниками через 3 часа. Правило. Решая задачи на нахождение расстояния при одновременном движении навстречу или в противоположных направлениях, пользуйся планом: 1. Находим скорость сближения (удаления). 2. Находим расстояние, которое прошли объекты. ЗАДАЧИ НА ДВИЖЕНИЕ В ОДНОМ НАПРАВЛЕНИИ. А Автомобиль за 2 часа проехал 192 км. Следующие 3 часа он двигался со скоростью на 6 км/ч меньше. Сколько всего километров проехал автомобиль? V =? км/ч V =? км/ч, на 6 км/ч меньше (<) t = 2 ч. t = 3 ч. 192 км? км S =? км 1) 192 : 2 = 96 (км/ч) первая скорость 2) 96-6 = 90 (км/ч) вторая скорость 3) 90 3 = 270 (км) второе расстояние 4) = 462 (км) (192 : 2-6) 3 = 462 Ответ: 462 км проехал автомобиль. ОСНОВЫ ГЕОМЕТРИИ. ТОЧКА.

27 Точку обозначают заглавной буквой латинского алфавита: A, D, E, K, M, O, B, C, N и т.д. Буква пишется рядом с точкой. M N K C ПРЯМАЯ И КРИВАЯ ЛИНИИ. У прямой линии нет ни начала, ни конца она бесконечна. прямая линия кривая линия Правило 1. Через одну точку можно провести сколько угодно прямых или кривых линий. А А Правило 2. Через две точки можно провести только одну прямую линию, а кривых — сколько угодно. О С ОТРЕЗОК. Отрезок это часть прямой линии, ограниченная двумя точками началом и концом. Начало и конец отрезка обозначают точками или штрихами. А В ЛУЧ. Луч имеет начало (точку), но не имеет конца. А

28 луч ЛОМАНАЯ ЛИНИЯ. Ломаная линия состоит из отрезков, последовательно соединённых друг с другом. незамкнутая ломаная линия ABCDE замкнутая ломаная линия ABCDEF А B D E А B C D C F E ОКРУЖНОСТЬ, КРУГ. Окружность это замкнутая кривая, все точки которой одинаково удалены от центра (точки О). Круг это геометрическая фигура, которая ограничена окружностью. центр окружности диаметр C радиус Окружность Круг УГОЛ. Угол образуют два луча, выходящие из одной точки (1 вершина, 2 стороны).

29 Виды углов острый прямой тупой меньше прямого равен 90 больше прямого ТРЕУГОЛЬНИК. Треугольник это геометрическая фигура, у которой три угла (вершины) и три стороны. Точки A, B, C вершины. AB, BC, AC стороны. A, B, C углы. Виды треугольников прямоугольный равнобедренный

30 равносторонний разносторонний ЧЕТЫРЁХУГОЛЬНИКИ. Четырёхугольник это геометрическая фигура, у которой четыре угла, четыре вершины и четыре стороны. Прямоугольник это четырёхугольник, у которого все углы прямые. Противоположные стороны прямоугольника равны между собой. AB = CD; BC = AD BC длина AB — ширина B A C D Квадрат это прямоугольник, у которого все стороны равны. MK = NO = MN = KO M K N O ПЕРИМЕТР. Периметр (Р) — это сумма длин всех сторон многоугольника. Периметр треугольника b c P тр. = a + b + c a

31 Периметр прямоугольника b a b a P пр. = (a + b) 2 a = P : 2 — b Периметр квадрата a a a a P кв. = a 4 a = P : 4 ПЛОЩАДЬ. Площадь (S) это внутренняя часть любой плоской геометрической фигуры. Периметр прямоугольника a b b a S. = a b Зная площадь и одну из сторон, можно найти другую сторону: a = S : b b = S : a Периметр квадрата a a a a S. = a a