+ — + — + — +

-1,5 -1 -8 2 3

1. Из перечисленных методов какой метод не всегда рационален и почему?

Графический, не всегда можно по графику определить координаты точки.

1. Вспомним схему решения нелинейных неравенств: ( ученики у доски)

ПГК 5а21(1) 5а21 (2) 5в37(2) 5в36(1) 5а28(1)

4х² -360 3х²+27²-10х²+3х-40 (х+11)(х+3)(х-8)0

4×2=36 3×2=-27 x(5x-10)=0 d=9+16=25 x=-11 x=-3 x=8

x²=9 x²= -9 x=0 x=2 x=1 x=-4

x=±3 нет точек

+ — + + + — + + — + — + — +

-3 3 0 2 -4 1 -11 -3 8

(-∞;-3)(3;+∞) 0 (0;2) (-∞;-4)(1;+∞) (-11;-3)(8;+∞)

1. Тема урока связана с несколькими неравенствами. Сформулируйте определение системы неравенств.

Совокупность неравенств верных на одном промежутке, называется системой неравенств.

1. Как решается система неравенств?

Решаем каждое неравенство отдельно; на числовой прямой находим пересечение промежутков.

1. Решим несколько линейных систем

ПГК 5а31(1) 5а12(2) 5а30(1)

2х+4 5х-8 3х-2 ≥ х+1 5х+83х+15

3х+2 ≤ 4-2х 7х-14

2х-5х-4-8 3x-x2+1 5x-3×15-8

3x-x

-3x-12 2×3 2×7

2x

x1,5 x3,5

x

//////////__________ /////////////________ /////////_________

/////////1//////4 1,5////2/////////// 2 3,5////////

(-∞;1) [1,5;2] 0

1. При решении каких задач используется тема «неравенства»

при нахождении области определения функции.

1. Изучение нового материала.

Рассмотрим несколькосистем

3х+60 3х²-5х+20

5х²-200 х²-5х+60 (х-5)(х+6)(4х-1)0

Из каких неравенств состоит система?

Линейное квадратное линейное

квадратное квадртное нелинейное

Можно ли системы назвать нелинейными? Да

Попробуем сформулировать определение нелинейной системы-

Система содержащая хотябы одно нелинейное неравенство, называется нелинейной.

Применим знания решения систем линейных неравенств к данным системам.

Решаются системы:

3х+60 3х²-5х+20

5х²-200 х²-5х+60 (х-5)(х+6)(4х-1)0

4. Закрепление материала.

ПГК 5с60

х²— 6х+8 0 2х²-7х+5 ≤ 0

5 – 2х ≤ 0 2 — х 0

Резерв — номер из учебника № 80,83

5. Рефлексия

Оцените работу класса и каждого в отдельности ответив на вопросы.

а) приступая к работе достаточно ли знаний для изучения нового материала?

б) были ли трудности при рассмотрении заданий и вопросов на уроке?

в) для изучения материала требовалась помощь учителя?

г) оцените работу класса и свою на уроке.

6. Постановка домашнего задания.

№ 79, 81 (запись самостоятельно в начале урока.)

Спасибо за урок.

kopilkaurokov.ru

Конспект урока «Система нелинейных неравенств с одной переменной»

План-конспект

Предмет: Алгебра

Класс: 9

Тема: «Система нелинейных неравенств с одной переменной»

Цель урока:

• Повторить и закрепить понятия системы нелинейных неравенств с одной переменной, алгоритм решения системы нелинейных неравенств с одной переменной.

• Обобщить и повторить умения решать систему нелинейных дробных неравенств с одной переменной; закрепить умения находить область допустимых значений функции;развивать познавательные навыки, навыки учебного труда;

• воспитывать положительные мотивы к учебе, добросовестное отношение к труду, культуру общения в группе; формирование умения работать в группе, формированию умения четко и ясно излагать свои мысли; взаимно оценивать друг друга.

Цель (для учеников):

Знать: определение системы нелинейных неравенств с одной переменной, определение области допустимых значений;

Уметь: составлять систему нелинейных неравенств и решать по алгоритму;

решать системы нелинейных дробных неравенств с одной переменной; находить область допустимых значений функций; работать в группе, анализировать материал, умение делать выводы.

тип урока:комбинированный урок.

форма работы: групповая работа, индивидуальная работа.

Оборудование: компьютер, интерактивная доска, проектор, учебник, раздаточный материал.

Ход урока.

1. Организационный момент.

Здравствуйте, ребята.Сегодня мы с вами продолжим закрепление темы прошлого урока. А сейчас выслушаем оценки за прошлый урок. ( комментирую оценки за прошлый урок) Работать мы будем в группах (На группы сегодня делит один из учащихся, которому розданы карточки для раздачи одноклассникам, для деления на группы) Вот образовались новые микро группы. Работу группы на каждом этапе урока оценивает командир группы. В каждой группе выберем: тайм спикера (следит за временем) и командира, который будет заполнять лист, с критериальным оцениваем каждого члена группы.

(оценивание проводиться по пятибалльной системе и в итоге выводиться средняя оценка)

№

Ф.И. учащегося

Критерии оценивания в работы в группе каждого ученика

Средний балл.

Задавал вопросы

Отвечал на вопросы

Участвовал в решении задач.

Записывал все (вес записи урока имеются в тетради)

Участвовал во всех этапах урока.

1

2

3

4

5

У вас на столах лежат цветные листочки, на которых вы сейчас напишите свои фамилии, и я вас прошу, поставить цифру 1 написать один словом ваше настроение. Все? Спасибо. Отложите пока эти листочки. Откройте тетради и запишите сегодняшние число, и мы продолжаем тему.

2. Опрос д/з.

На доске записано решение № 84 (1,2). Каждый учащийся отдает свою тетрадь для проверки домашнего задания соседу справа, он проверяет и оценку ставит в тетради в форме одного предложения об работы.

3. Подготовка к восприятию

4. Обобщения и систематизация материала.(использование метода «Карусель»)

1) Для дальнейшей работы каждая группа получает задание( решить систему нелинейных дробных неравенств с одной переменной, решение выполнять на листочке сообща всей группой)

Задание группам:

1 группа — № 86 (а)

2группа -№ (б)

3 группа — № 86 (в)

4 группа _ № 86 (г)

( подготовка 5 минут, работа в каждой группе по 2мин, работает таймер)

Выступление в каждой группы, обсуждение решений, самооценка группы.

— А сейчас я вас попрошу вернуться к цветным листочкам, поставить цифру 2 – и снова одним словом отразить ваше настроение на данный момент.

Спасибо большое за вашу работу в группах.

2) А сейчас я вас рассчитаю в командах на 1,2,3,4 после полного моего расчеты вы только с ручкой и листом А4 в руках проходить за тот столик номер, которого я вам сказала.

В новые образованные группы дается задание. В ходе обсуждения всей новой группы решить данное задание, на время. ( Таймер включен)

Задание:

Проверить правильность решения неравенства

Каждой новой группе дается на выполнение задания 2 минуты, после выполнения 1 учащейся новой группы оглашает ответ.

После выполнения данного задания. Учащиеся возвращаются на свои места, а листочки с

выполненным заданием оставляют в той группе на столе, где работали.

5. Проверка полученных навыков.

А теперь проверим ваши умения и знания, при решении неравенств. Сейчас я укажу вариант каждого и вы получите задание по своему варианту.

Задание: Найти область допустимых значений

1вариант

2 вариант

3 вариант

4 вариант

(На выполнение 2 минуты , включен таймер.)

Листочки с выполненным заданием командир складывает на край стола. Я соберу после окончания урока и оценки за эту работу я оглашу на следующем уроке.

6. Подведение итогов урока.

АНАЛИЗ работы за урок.

А сейчас у меня вопросы к командирам команд:

1. Что у вас удалось при выполнении задания?

2. Была ли работа группы слаженной?

3. Что не получилось, на ваш взгляд?

4. Назовите сильные и слабые стороны команды?

5. Прокомментируйте лист оценивания вашей группы.

ОБСУЖДЕНИЕ.

— Я вас прошу вернуться к цветным листочкам, поставить цифру 3, и отобразить одним словом ваше настроения на данный момент. Все? Спасибо.

— А сейчас я вам предлагаю заполнить листы по рефлексии

Утверждения

Поставьте знаки «+» или «-», «?».

1. Я понял как выполнить…

2. У меня сегодня всё получилось.

3. Работая в парах, я допустил ошибки (перечисли какие).

4. В самостоятельной работе я допустил ошибки (перечисли какие).

6. Домашнее задание.

www.metod-kopilka.ru

Урок алгебры «Системы нелинейных неравенств»

г.Уральск, сош№14

Учитель: Марьянова С.Б.

Урок алгебры

Тема: «Системы нелинейных неравенств с одной переменной», 9 класс

Цели урока:

— образовательные:

систематизировать понятия линейного и нелинейного неравенства с одной переменной; научить решать системы нелинейных неравенств с одной переменной; совершенствовать умения и навыки учащихся решать квадратные неравенства методом интервалов.

— развивающие:

развивать логическое мышление, математическую речь, вычислительные навыки;

развивать умение сравнивать, анализировать, делать выводы.

— воспитывающие:

воспитывать положительные мотивы к учебе, добросовестное отношение к труду, культуру общения в группе; формирование умения работать в группе, формированию умения четко и ясно излагать свои мысли; взаимно оценивать друг друга.

Результат обучения: Учащиеся должны знать понятие системы нелинейных неравенств с одной переменной, уметь решать системы нелинейных неравенств с одной переменной по составленному алгоритму. Создание условий для изучения материала через групповую работу. Обучение проведению рефлексии.

Ход урока.

1.Организационный момент. 2мин

Приветствие учащихся учителем, организация внимания учащихся.

Наш урок сегодня пройдет под девизом «Математику нельзя изучать, наблюдая как это делает сосед». Наша с вами задача — повторить, обобщить и систематизировать теоретические знания по теме и отработать практические навыки.

В течение урока учащиеся заполняют «лист успеха», оценивая свою деятельность на разных его этапах.

Лист успеха (Оценочный лист) Ф.И.__________________

2. Актуализация знаний. Повторение. Мозговая атака. 3мин

Цель этапа: обеспечить деятельность учащихся при повторении линейных и квадратных неравенств, создания проблемной ситуации и умения сообщить тему урока, сформулировать цели урока.

Деятельность учителя – с помощью заданий повторяет знания по данной теме, изученные ранее; 

деятельность учащихся – отвечают на вопросы, называют тему урока, формулируют цели урока.

Приемы: самопроверка, взаимопроверка, самооценка.

«Незаконченное предложение» (Слайд 3)

1. Неравенства вида aхb где а и b некоторые числа, х — переменная, называются…(…линейными неравенствами с одной переменной).

2. Неравенство содержащие знак = или

3. Неравенство со знаками или

4. Если обе части неравенства умножить или разделить на одно и тоже положительное число, то знак неравенства…(…не изменится (сохраниться).

5. Если обе части неравенства умножить на одно и тоже отрицательное число, то знак у неравенства…(…изменится на противоположный).

6. Решение неравенства с одной переменной называется значение переменной, которое обращает его…(…в верное числовое неравенство).

7. Любое слагаемое можно перенести из одной части неравенства в другую,…(…изменив знак этого слагаемого на противоположный).

Установить соответствие: (Слайд 4-5)

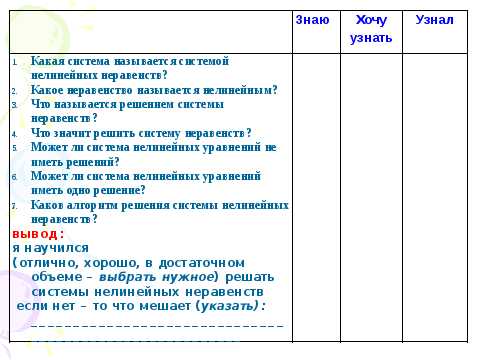
Таблица «Знаем – Хотим узнать – Узнаем» (З – Х – У) (Слайд 6)

З – знаем Х – хотим узнать У – узнал

Урок начинается с активизации того, что дети уже знают по данной теме. Для начала спрашиваем, что они знают. В колонку «Хочу узнать» предлагается внести свои спорные мысли и вопросы, возникшие в ходе обсуждения темы урока. После изучения темы и решения тренировочных упражнений учащиеся заполняют колонку «Узнал». В конце урока учащиеся сравнивают, что они знали раньше, с информацией, полученной на уроке. При этом желательно излагать сведения, понятия или факты только своими словами, не цитируя учебник.

3. Творческое домашнее задание 5 мин

1 группа презентует алгоритм решения линейных неравенств,

2 группа – нелинейных неравенств.

4.Устный счет. (Презентация). 2 мин.

Техника ВОУД подразумевает жёсткий временной контроль.

Поэтому важна скорость решения заданий там, где это возможно.

1). х² – 225 = 0 — 15 ; 15

2). х² – 6х = 0 0; 6

3). х² – 10х +25 = 0 5

4). 3х² – 5х +2 = 0 1; 2/3

5). х² + 9 = 0 нет корней

6). 7х² + 4х – 3 = 0 — 1 ; 3/7

7). х² + 16х + 64 = 0 — 8

8). 8х — х² = 0 0; 8

5. Найти ошибку. 2 мин При решении тестовых заданий, в частности, при выборе ответа важно вырабатывать такое качество, как внимание. В следующих примерах найти и исправить ошибку.

(приложение)

6.Карта обмена. 5 мин Учащиеся решают задания, взаимоконтроль

Карта по обмену 1 вариант

1.Решить неравенство: (х -5)(х + 4) 0

А) (- — 4)) В) (- 4; 5) С) (- — 5)) Д) (- — 4])

2.Решить неравенство: х (х -3) ≤ 0

А) (- — 3)) В) (- -0)) С) [0; 3] Д) (- 0])

3.Решить неравенство: (х +2)²(8 — х)

А) (- — 2)) В) () С) (- 2; 8) Д) (- 2])

Карта по обмену 2 вариант

1.Решить неравенство: (х -7)(х + 9) ≥ 0

А) ) В) [- 9; 7] С) (- — 9)) Д) (- — 9])

2.Решить неравенство: (1 –х) (х + 3) ≥ 0

А) [- 3;1] В) (1; 3) С) (- — 1)) Д) (- -1])

3.Решить неравенство: х ²(х — 6) 0

А) (- 0)) В) (6) С) (0; 6) Д) (- 0])

Ключ

1 вариант 1.А 2.С 3.В

2 вариант 1.Д 2.А 3.В

7. Релаксация (под музыку гимнастика для глаз). 1 мин

8.Решение задач по уровням 10- 15 мин

Алгоритм решения систем неравенств

Чтобы решить систему неравенств, надо:

— решить каждое неравенство системы;

— изобразить решение каждого неравенства данной системы на одной числовой прямой.

— записать решение системы

1.Решить систему неравенств и указать наибольшее целое решение

2.Решить систему неравенств и найти сумму целых решений

3.Найти область определения функции: у = +

4.Решить систему неравенств. Сколько целых решений?

5.Сборник экзаменационных заданий 5С.57 (б)

9.Практическое применение неравенств (Мироненко). Презентация.2мин

Задача1.

Для лагеря нужно огородить делянку прямоугольной формы, одна сторона которой прилегает к речке. Какие размеры должна иметь делянка, если её площадь должна быть не меньше чем 0,5 га, а длина ограды равна 205м?

Решение:

Пусть одна сторона равна х м, тогда смежная сторона будет равна (205-2х) м. Отсюда площадь делянки: S = х ( 205-2х)=-2х²+ 205х (м²).
По условию S ≥ 0,5га=5000 м², поэтому -2х² + 205х — 5000 ≥ 0. Решив неравенство, имеем :
40 ≤ x ≤ 62,5 , величина смежной стороны 80≤205-2х≤125 (м)

Задача2.

Катер с экскурсантами должен совершить рейс между двумя пристанями туда и назад, приодолев расстояние не больше, чем за 3 часа. Какой должна быть скорость катера, если скорость течения реки равна 3км/ч, расстояние между пристанями 28 км и остановка на пристане длилась 40 мин?

Учитывая, что остановка длилась 40мин = 2/3 ч, имеем неравенство

Ответ : скорость катера должна быть не меньше 25 км/ч.

10. Итог урока. 2мин

В течение урока учащимися заполняется оценочный лист.

Считается итоговый балл.

Домашнее задание: Сборник 5А26 (б), 5В. 47(б), 5С59 (а)

На следующем уроке – контрольный тест.

Рефлексия (нужное подчеркнуть)

Усвоил новый материал отлично, хорошо, удовлетворительно, не усвоил Мне на уроке было интересно, трудно, скучно, я устал Своей работой на уроке я доволен, не доволен Завтра я планирую быть активнее, больше самостоятельности, задавать вопросы

Пригодится ли вам математика в вашей профессии?

Какую оценку вы планируете по математике на экзамене ?

5

compedu.ru

План-конспект урока по алгебре (9 класс) на тему: Урок в 9 классе «Неравенства с одной переменной»

I группа
IIгруппа
III группа
Решить неравенство с помощью графика квадратичной функции 3хІ — 5х +2>0
Решить методом интервалов: хІ – 12Найти область определения функции: у =
Ответ: (- ∞; ) (1; + ∞)
Ответ:(-2 ; 2 )
Ответ: [ ; 1]
Найти область определения функции:у =
Доказать, что при любом значении переменной верно неравенство: -5хІ + 8х – 5 Решить неравенство: хІ + 7х + 1

I группа
IIгруппа
III группа
Решить неравенство с помощью графика квадратичной функции 3хІ — 5х +2>0
Решить методом интервалов: хІ – 12Найти область определения функции: у =
Ответ: (- ∞; ) (1; + ∞)
Ответ:(-2 ; 2 )
Ответ: [ ; 1]
Найти область определения функции:у =
Доказать, что при любом значении переменной верно неравенство: -5хІ + 8х – 5 Решить неравенство: хІ + 7х + 1 Ответ:[-4; 7]
Ответ: х є R
Ответ: Ш
Фонтан смотрится лучше, если капли воды достигают высоты, большей, чем высота статуи. При высоте статуи Евы 3м и угле наклона 60є, получим неравенство:

Механика устанавливает следующее соотношениедля высоты подъема тела над землей (h)

Если мотоциклист совершает прыжок через 10 установленных в ряд автобусов длиной ряда 40 м, то для определения скорости разгона при прыжке под углом в 45є надо решить задачу:

Решить неравенство:хІ +

Решить неравенство:хІ +
х + 4 — 5хІ хІ +

х
Решение
4
4
[-4; 0]
(-4; 0)
Выбрать верное решение неравенства:
I группа
II группа
III группа
х2 + 4х — х2 + 4х – 6 ≥ 0
— х2 + 6х – 9 1.
1. х = 2
1. х = 3
2.
2.
2.
3.
3.
3.
4.
4.
4.

1 2 3 4 5 6 7
-7 -6 -5 -4 -3 -2 -1
7 6 5 4 3 2 1
-1 -2 -3 -4 -5 -6 -7
[-4; 0]
(-4; 0)
2
1
3
4
ПОДУМАЙ!
ВЕРНО!
ПОДУМАЙ!
Тренировочный тест
Решите неравенство х2 + 4х ПОДУМАЙ!
1 2 3 4 5 6 7
-7 -6 -5 -4 -3 -2 -1
7 6 5 4 3 2 1
-1 -2 -3 -4 -5 -6 -7
x=2
3
1
2
ПОДУМАЙ!
ВЕРНО!
ПОДУМАЙ!
Тренировочный тест
Решите неравенство – х2 + 4х–6 0
4
ПОДУМАЙ!
1 2 3 4 5 6 7
-7 -6 -5 -4 -3 -2 -1
7 6 5 4 3 2 1
-1 -2 -3 -4 -5 -6 -7
x = 3
3
1
2
ПОДУМАЙ!
ВЕРНО!
ПОДУМАЙ!
Тренировочный тест
Решите неравенство – х2 + 6х–9 4
ВЕРНО!
1.
2.
3.
4.
а
в
с
d
e
f

4
3
2). Выберите из таблицы графическую интерпретацию для каждого из неравенств
1). Укажите верное решение неравенства хІ — 3х — 4 ≤ 0
А (-1; 4) В (- ∞; -1] [ 4; + ∞) С [-1; 4] Д ( — ∞; -1) (4; + ∞)
Учебник: п. 14-15, Повт. п.12-13, № 376(е), 389(д)2. Пособие под редакцией Ф.Ф.Лысенко «Подготовка к ГИА»:с. 46 № 13 – базовый уровеньс. 155 № 186 – повышенный уровень
На уроке я работал активно / пассивноСвоей работой на уроке я доволен / не доволенУрок для меня показался коротким / длиннымЗа урок я не устал / усталМатериал урока мне был понятен / не понятен полезен / бесполезен интересен / скученДомашнее задание для меня не вызовет затруднений / будет трудным

nsportal.ru

Урок по алгебре в 9 классе

Урок алгебры в 9 классе по теме » Система нелинейных неравенств с одной переменной «

Предмет: алгебра

Тема: «Система нелинейных неравенств с одной переменной»

Цель урока:

• Сформировать у учащихся понятия системы нелинейных неравенств с одной переменной, алгоритм решения системы нелинейных неравенств с одной переменной, повторить понятие нелинейного неравенства с одной переменной; повторить алгоритм решения нелинейного неравенства с одной переменной;

• Развить умения отличать систему линейных неравенств с одной переменной от системы с нелинейными неравенствами с одной переменной; развивать познавательные навыки, навыки учебного труда, техники вычисления, умение работать с имеющейся информацией в необычной ситуации

• воспитывать положительные мотивы к учебе, добросовестное отношение к труду, культуру общения в группе; формирование умения работать в группе, формированию умения четко и ясно излагать свои мысли;

тип урока: урок закрепления

форма работы: работа в группе.

Оборудование: учебник, раздаточный материал.

Ход урока.

1. Организационный момент.

1. Работа в группах (группы разделены заранее и рассажены) Вашу работу на каждом этапе урока оценивает командир группы. У вас на столах лежат лист-опросники, пожалуйста напишите свое имя и фамилию

2. Так как мы разделены на группы, то нам с вами нужно правила работы в группе. Самостоятельно разработайте правила работы в группе.

Повторение пройденного материала

Тест

(самостоятельная работа, с последующей взаимопроверкой).

Заполнить таблицу: Критерии оценок : 6-«5», 4,5-«4» 3-«3»

1. 1. 1. 1. На каком рисунке изображено множество решений системы

А. Б. В.

2 — 3 — 3 2 — 3 2

2. Запишите обозначение промежутка :

— 10 5

А. (-10; — 5) Б. В.

3. Решите неравенство 2 – 5х < 0.

А. (0,4; + ∞) Б. [0,4; + ∞) В. (- ∞; 0,4)

4. При каких значениях у дробь меньше дроби ?

А. (- ∞; 4,4) Б. (- ∞; — 4,4) В. (4,4; + ∞)

5. Промежутку [- 2,5; 2,4] принадлежит число …

А. – 2,6 Б. 0 В. 3

6. Для любых значений х верно неравенство:

А. (х – 2)² < 0 Б. (х + 3)² > 0

В. (х + 3)² > 0 Г. х² – 10х + 25 ≥ 0

Коды правильных ответов:

2 Закрепление изученного нового материала. Метод «Карусель»

1)Итак, каждая группа получит свое задание, который я вам раздам. Ваша задача в течение 8 минут раскрыть свою тему в виде схемы, кластера. Для этого я вам предлагаю использовать бумагу и фломастеры. После того, как все команды будут готовы, мы выслушаем выступление каждой группы (2мин).

Критерии оценивания выступления:

1. Доступность изложения

2. Оформление

3. Регламент

Задание группам:

1. Понятие определения «Системы нелинейных неравенств с одной переменной».

2. Алгоритм решения неравенства второй степени с одной переменной.

3. Решение системы нелинейных неравенств с одной переменной.

Раздатка для групп:

1 группа — «Понятие определения «Системы нелинейных неравенств с одной переменной»

Задание:

1) дать определение системы нелинейных неравенств с одной переменной,

2) указать отличия от других систем неравенств,

3) что значить решить систему нелинейных неравенств

4) что является решением системы нелинейных неравенств с одной переменной.

5) данные системы систематизировать по типу линейные и нелинейные.

Системы неравенств:

1. 2) 3) 4) 5)

Стр.23 в учебнике

2 группа — Алгоритм решения неравенства второй степени с одной переменной.

Задание: учащимся выдается алгоритм в неправильном расположении, их цель сформировать правильный алгоритм решения.

Алгоритм решения квадратного неравенства ax ²+ bx + c>0 , (ax ² + bx + c<0)

1. Рассмотрим функцию

2. Находим точки пересечения параболы с осью OX, для чего решаем уравнение

3. Определяем направление ветвей параболы.

4. Схематично изображаем параболу, не обозначая координат ее вершины.

5. С помощью графика находим промежутки, в которых функция принимает положительные (отрицательные) значения.

6. Записываем ответ.

(готовый алгоритм учащиеся крепят на плакат и при выступлении показывают всем ребятам)

3 группа— Решение системы нелинейных неравенств с одной переменной.

Рассмотреть решение примера 1 ( стр23-24) по данному решению составить алгоритм решения системы нелинейных неравенств с одной переменной.

1. Физминутка

2. Выступление групп

После выступления групп.

Взаимооценивание методом «Две звезды одно пожелание»

5. Систематизация и закрепление

Самостоятельная работа

1Вариант

2вариант

6. Домашнее задание

• параграф 5, №82 (в,г,д)

infourok.ru

Решение систем нелинейных неравенств | Уроки по Математике

Решение систем нелинейных неравенств