Траектория путь перемещение 9 класс презентация: Презентация по физике на тему » Перемещение» (9 класс)
Урок 2 в 9 классе
Фоминова Елена Владимировна,
учитель физики МБОУ СОШ № 23
МО Усть-Лабинский район
Перемещение тела – это вектор, проведенный из начального положения тела в его конечное положение.
Перемещение тела
Траектория – непрерывная линия, вдоль которой движется тело. Траектория – непрерывная линия, вдоль которой движется тело. Путь- длина траектории, пройденной за время наблюдения.L- путь (скалярная величина)
-перемещение
Виды движения Траектория – линия, которая показывает как движется тело.криволинейное
прямолинейное
Различие между путём и перемещением- Путь – скаляр, а перемещение вектор.
- Путь зависит от траектории, а перемещение нет.
- Перемещение может быть положительным и отрицательным, а путь всегда строго положителен.
- При движении тела путь может только увеличиваться, а модуль перемещения может как увеличиваться, так и уменьшаться.
- Если тело вернулось в начальную точку, его перемещение равно нулю, а путь нулю не равен.
0 х0 х1 х
Проекция положительная (Sx>0), если направление вектора совпадает с направлением оси.
В противном случае проекция вектора отрицательна (Sx<0).
Если вектор перпендикулярен оси, то при любом направлении вектора его проекция на ось равна нулю (Sx=0).
0
X
X0
X
Задача. Автомобиль переместился из точки с координатой Х0=200м в точку с координатой Х=-200м. Определите проекцию перемещения автомобиля.
Дано:
Х0=200 м
Х=-200 м
Sх-?
Решение:
Sх =-200 м-200 м= -400 м
Ответ: Sх=-400 м
Домашнее задание- Выучить материал § 2,3 записи в тетради.
- Упражнение 3 (учебник, стр. 15)
Слайд 1 http://physik.ucoz.ru/_ph/3/820049735.gif
Слайд 2
https://thumbs.dreamstime.com/z/3d-man-going-upstairs-15519950.jpg
Слайд 3 http://ok-t.ru/img/baza8/Mehanika—lekciya-1383668626.files/image013.jpg
Самолет http://fizikaklass.ru/images/10_klass/illustration-ch-1/11/Picture.png
Слайд 4 мячик http://www.gagolf.is/static/news/screenshot-17.jpg
Самолет https://ds03.infourok.ru/uploads/ex/0b6b/00006d12-25a80892/img13.jpg
Слайд 5 http://www.azbukafasada.ru/sites/default/files/chelovechek_galochka.jpg
Слайд 8 https://vinozemtseva.ru/wp-content/uploads/2016/12/80d18da457cdacc454f7b5b02edadf2f.jpg
Слайд 9 http://avtomobilist-sbor.ru/wp-content/uploads/2014/07/чел21.jpg
Описание презентации по отдельным слайдам:
1 слайд Описание слайда:
Описание слайда:Путь. Перемещение. Определение координаты движущегося тела. 9 класс
2 слайд Описание слайда:
Описание слайда:Какую систему координат следует выбрать для определения положения тел: А) трактор в поле Б) вертолет Г) поезд Д) шахматная фигура
3 слайд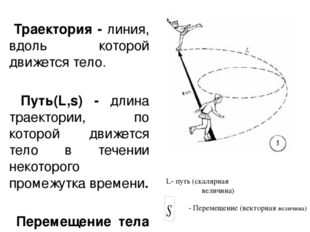
Траектория — линия, вдоль которой движется тело. Путь(L,s) — длина траектории, по которой движется тело в течении некоторого промежутка времени. Перемещение тела – это вектор, проведенный из начального положения тела в его конечное положение. L- путь (скалярная величина) — Перемещение (векторная величина)
4 слайд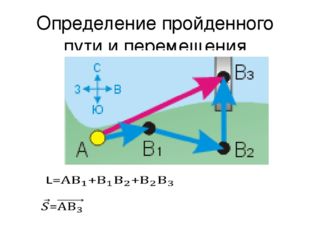 Описание слайда:
Описание слайда:Определение пройденного пути и перемещения
5 слайд Описание слайда:
Описание слайда:Вычислить положение тела, т.е определить его координаты. Проекции векторов- величины, представляющие собой положительные или отрицательные числа, но не имеющие направления.
6 слайд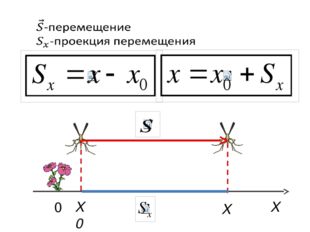 Описание слайда:
Описание слайда:0 X X0 X
7 слайд
Проекция вектора на ось считается положительной, если вектор сонаправлен с этой осью, и отрицательной, если вектор направлен противоположно оси. Sx>0, Sx<0
8 слайд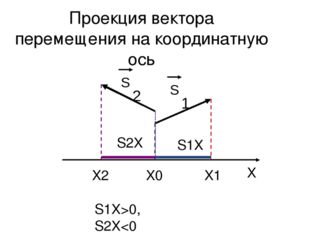 Описание слайда:
Описание слайда:Проекция вектора перемещения на координатную ось S 1 S 2 X X0 X1 X2 S1X>0, S2X<0 S1X S2X
9 слайд Описание слайда:
Описание слайда:Проекция перемещения на ось ОX Проекция перемещения на ось ОУ
10 слайд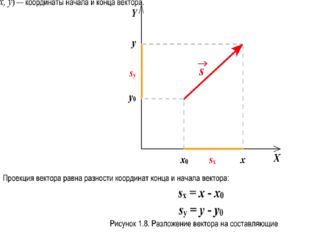 Описание слайда: 11 слайд
Описание слайда: 11 слайд 
Модуль вектора перемещения
12 слайд Описание слайда:
Описание слайда:АЛГОРИТМ РЕШЕНИЯ ЗАДАЧ ПО КИНЕМАТИКЕ : 1.Выбрать удобную систему координат. 2.Схематично показать тела или материальные точки. 3.Показать векторы, начальные координаты, проекции векторов. 4.Записать основные уравнения ( в векторной форме или в проекциях). 5.Найти проекции всех известных величин и подставить в уравнения. 6.Решить уравнения.
13 слайд Описание слайда:
Описание слайда:Задача Два катера идут по реке в противоположных направлениях и встречаются в 100 км к востоку от пристани П. Продолжая движение, за некоторый промежуток времени t первый катер переместился от места встречи на 60 км к востоку, а второй на 50 км к западу. Определите координаты каждого катера по отношению к пристани и расстояние между катерами через промежуток времени t после их встречи.
14 слайд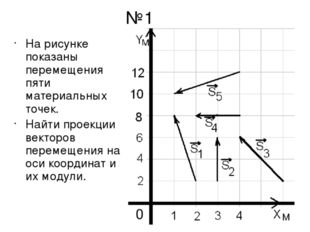
№1 На рисунке показаны перемещения пяти материальных точек. Найти проекции векторов перемещения на оси координат и их модули.
15 слайд Описание слайда:
Описание слайда:№2 Мяч упал с высоты 3 м, отскочил от пола и был пойман на высоте 1 м. Найти путь и перемещение мяча.
16 слайд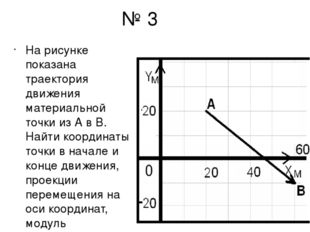 Описание слайда:
Описание слайда:№ 3 На рисунке показана траектория движения материальной точки из А в В. Найти координаты точки в начале и конце движения, проекции перемещения на оси координат, модуль перемещения.
17 слайд Описание слайда:
Описание слайда:№ 4 Тело переместилось из точки с координатами х1=0, y1=2 м в точку с координатами x2=4м, y2=-1м. Сделать чертеж, найти перемещение и его проекции на оси координат.
18 слайд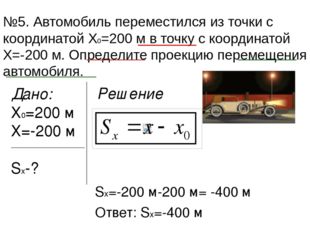 Описание слайда:
Описание слайда:№5. Автомобиль переместился из точки с координатой Х0=200 м в точку с координатой Х=-200 м. Определите проекцию перемещения автомобиля. Дано: Х0=200 м Х=-200 м Sх-? Решение Sх=-200 м-200 м= -400 м Ответ: Sх=-400 м
19 слайд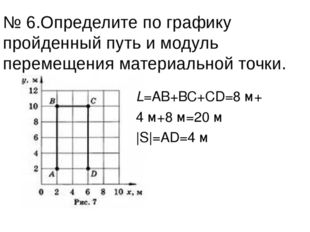 Описание слайда:
Описание слайда:№ 6.Определите по графику пройденный путь и модуль перемещения материальной точки. L=АВ+ВС+СD=8 м+ 4 м+8 м=20 м |S|=АD=4 м
20 слайд Описание слайда:
Описание слайда:Электронные ресурсы http://physics.kgsu.ru/school/sprav_mat/pic/0035r3.jpg http://spr-formula.narod.ru/kn_bibl.htm http://andrey2.taba.ru/fid/aW1hZ2U6MTU0NDA5NC8v/original.jpg http://www.fizika.ru/kniga/index.php?mode=paragraf&theme=12&id=12030 http://5terka.com/classes/10?page=70 http://animo2.ucoz.ru/photo/specialnye_kategorii/2_deo/animacija_komar/108-0-10752 http://animo2.ucoz.ru/photo/specialnye_kategorii/2_deo/animacija_cvety/108-0-9975

Курс повышения квалификации

Курс повышения квалификации

Курс повышения квалификации
Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:
Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВнеурочная деятельностьВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое
Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс
Выберите учебник: Все учебники
Выберите тему: Все темы
также Вы можете выбрать тип материала:

Общая информация
Номер материала: ДБ-215887
Похожие материалы
Вам будут интересны эти курсы:
Оставьте свой комментарий
- повторение основных понятий кинематики, видов движения, графиков и формул кинематики в соответствии с кодификатором ГИА и планом демонстрационного варианта экзаменационной работы
- Механическим движением тела называют изменение его положения в пространстве относительно других тел с течением времени;
- Механическое движение тел изучает механика.
- Раздел механики, описывающий геометрические свойства движения без учета масс тел и действующих сил, называется кинематикой.
- Тело, относительно которого рассматривается движение, называется началом отсчета.
- Для определения положения тела в пространстве через начало отсчета проводятся три взаимно перпендикулярные координатные оси с одинаковыми масштабами по осям. Совокупность начала отсчета и координатных осей называется системой координат.
- Система координат и часы, измеряющие время, составляют систему отсчета.
- Покой и движение – понятия относительные
- Тело, размерами которого в данных условиях можно пренебречь, называется материальной точкой;
- Траектория — некоторая линия, которую описывает тело (материальная точка) с течением времени, перемещаясь из одной точки в другую, называют движения тела;
- Движение тела, при котором все его точки в данный момент времени движутся одинаково, называется поступательным движением.
- Для описания поступательного движения тела достаточно выбрать одну точку и описать ее движение
- Движение, при котором траектории всех точек тела являются окружностями с центрами на одной прямой и все плоскости окружностей перпендикулярны этой прямой, называется вращательным движением
- Перемещением тела называют направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением.
- Перемещение есть векторная величина. Пройденный путь l равен длине дуги траектории, пройденной телом за некоторое время t.
- Путь – скалярная величина.
- Пройденный путь l и вектор перемещения при криволинейном движении тела.
- a и b – начальная и конечная точки пути
- может, если движется в ту же сторону со скоростью 1 м/с
- может, если движется в противоположную сторону со скоростью 1 м/с
- может, если стоит на эскалаторе
- не может ни при каких условиях
- движется равномерно по прямолинейному участку шоссе
- разгоняется по прямолинейному участку шоссе
- движется равномерно по извилистой дороге
- по инерции вкатывается на гору
- Только 1
- Только 2
- Только 3.
- 2 и 3.
- Только 1
- Только 2
- Только 3.
- 2 и 3.
- Только в первом случае.
- Только во втором случае.
- В обоих случаях.
- Ни в первом, ни во втором случаях.
- Только в первом случае.
- Только во втором случае.
- В обоих случаях.
- Ни в первом, ни во втором случаях.
- Точка
- Прямая
- Окружность
- Винтовая линия
- Точка
- Прямая
- Окружность
- Винтовая линия
- l = 109 км, S = 0 км
- l = 218 км, S = 0 км.
- l = S = 218 км
- l = S =0 км.
- l = S = 0 м
- l = S = 400 м.
- l = 800 м, S = 0 м
- l = 0 м, S = 400 м.
- L = 2 R; S = π R
- L = π R; S = 2 R
- L = 0; S = 2π R
- L = 2π R; S = 0
4 м
3 м
s
S2 = 42 + 32
ГИА-2010-1. Камень брошен из окна второго этажа с высоты 4 м и падает на Землю на расстоянии 3 м от стены дома. Чему равен модуль перемещения камня?4 м
3 м
s
S2 = 42 + 32
ГИА-2010-1. На графике изображена зависимость проекции скорости тела, движущегося вдоль оси ОХ от времени. Чему равен модуль перемещения тела к моменту времени t = 10 с?2 м/с ∙3 с = 6 м
-1 м/с ∙7 с = -7 м
Литература- Гутник, Е. М., Физика. 7 класс. Учебник для общеобразовательных школ / Е. М. Гутник, А. В. Перышкин. — М.: Дрофа, 2009. – 302 с.
- Зорин, Н.И. ГИА 2010. Физика. Тренировочные задания: 9 класс / Н.И. Зорин. – М.: Эксмо, 2010. – 112 с. – (Государственная (итоговая) аттестация (в новой форме).
- Кабардин, О.Ф. Физика. 9 кл.: сборник тестовых заданий для подготовки к итоговой аттестации за курс основной школы / О.Ф. Кабардин. – М.: Дрофа, 2008. – 219 с;
- МЕХАНИЧЕСКОЕ ДВИЖЕНИЕ. ФИЗИКА. Образовательный портал Курганской области //[Электронный ресурс]// http://www.hde.kurganobl.ru/dist/disk/Shcool/Book/Sprav_material/Mech/p1.htm
- Основные понятия кинематики //[Электронный ресурс]// http://files.school-collection.edu.ru/dlrstore/f3591263-ecae-d464-caf0-9105f5d9cda5/00119626139675510.htm
- Перышкин, А. В., Физика. 7 класс. Учебник для общеобразовательных школ / А. В. Перышкин. — М.: Дрофа, 2009. – 198 с.
- Перышкин, А. В., Физика. 8 класс. Учебник для общеобразовательных школ / А. В. Перышкин. — М.: Дрофа, 2009. – 196 с.
- Урок 5/17. Материальная точка. Траектория движения. Координаты точки. Перемещение и путь (§§ 2.6, 2.7). Единая коллекция цифровых образовательных ресурсов //[Электронный ресурс]// http://school-collection.edu.ru/catalog/rubr/ffb3b711-8f44-408c-aea4-a29842431067/110204/
- Федеральный институт педагогических измерений. Контрольные измерительные материалы (КИМ) Физика ГИА-9 2010 г. / /[Электронный ресурс]// http://fipi.ru/view/sections/214/docs/
- Федеральный институт педагогических измерений. Контрольные измерительные материалы (КИМ) Физика ЕГЭ 2001-2010//[Электронный ресурс]// http://fipi.ru/view/sections/92/docs/
Учебный предмет: физика
Класс: 9
Тема: Законы взаимодействия и движения тел.
Урок №2: «Перемещение. Путь. Траектория».
Тип урока: комбинированный
Цели: 1) обучающая: учащиеся должны знать понятия перемещение, путь, траектория, уметь определять координаты движущегося тела;
2) развивающая: развитие познавательных интересов, умения анализировать, делать выводы;
3) воспитательная: воспитание аккуратности, трудолюбия, общечеловеческой культуры.
Ход урока.
Орг. момент.
Проверка д/з:
Что такое механическое движение?
Обладает ли материальная точка массой? Имеет ли она размеры?
Материальная точка- это реальный объект или абстрактное понятие?
С какой целью используется понятие «материальная точка»?
В каких случаях движущееся тело обычно рассматривают как материальную точку?
Приведите пример, показывающий, что одно и то же тело в одной ситуации можно считать материальной точкой, а в другой- нет.
При каком движении тела его можно рассматривать как материальную точку даже в том случае, если проходимые им расстояния сравнимы с его размерами?
Что такое материальная точка?
Виды систем координат.
В каком случае положение движущегося тела можно задать с помощью одной координатной оси?
Что такое система отсчёта?
Упражнение № 1.
Из формулы v=at выразите a через v и t; t через a и v.
Из формулы v= v0 + at выразите v0 , a, t.
Изучение нового материала.
Тема сегодняшнего урока «Перемещение. Путь. Траектория».
Сегодня мы вспомним, что такое путь, траектория, узнаем, что называется перемещением тела, а также научимся определять координаты движущегося тела.
В различных задачах необходимо определить положение тела в данный момент времени. Но во многих случаях мы этого сделать не сможем, даже если будем знать, какой путь тело пройдёт за данный промежуток времени.
Например, тело движется из точки О и за один час проходит 20 километров.
Где будет находиться тело? (Ответы учащихся)
Действительно, тело может находиться в разных точках. Рассмотрим некоторые возможные положения тела.
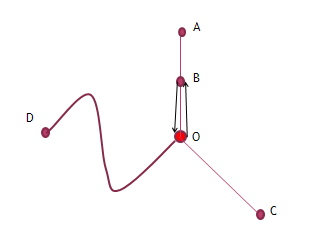
Так как же определить, где действительно будет находиться тело?
Чтобы не было такой неопределённости, ввели физическую величину, называемую перемещением.
Перемещением тела (материальной точки) называется вектор, соединяющий начальное положение тела с его последующим положением.
Обозначение:
Единицы измерения в СИ: метр
Давайте рассмотрим , какое будет перемещение в рассмотренных случаях.
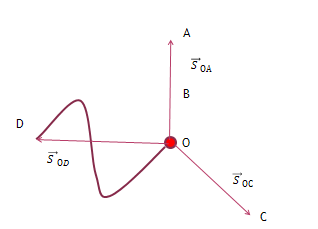
Знать вектор перемещения-это значит знать его направление и модуль.
Непрерывную линию, которую описывает движущееся тело (рассматриваемое как материальная точка) по отношению к выбранной системе отсчёта, называют траекторией.
Длина траектории — это путь.
Путь — скалярная величина. Обозначение: S.
Решим задачу.
Два катера идут по реке в противоположных направлениях и встречаются в 100 км от пристани П. Продолжая движение, за некоторый промежуток времени t первый катер переместился от места встречи на 60 км к востоку, а второй- на 50 км к западу. Определите координаты каждого катера по отношению к пристани и расстояние между катерами через промежуток времени t после их встречи.
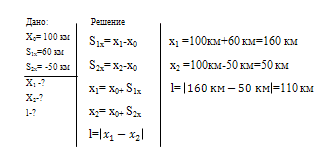
Закрепление.
Что такое перемещение?
Как обозначается, в каких единицах измеряется?
Что такое траектория?
Что такое путь?
Путь или перемещение мы оплачиваем при поездке на такси?
Мяч упал с высоты 3 м, отскочил от пола и был пойман на высоте 1 м. Найдите путь и перемещение мяча
Велосипедист движется по окружности с радиусом 30 м. Чему равен путь и перемещение за половину оборота? За полный оборот?
Подведение итогов, постановка д/з:
§ 2,3, упр. 2,3, Р№ 15.
Цели урока: введение понятий «перемещение», «путь», «траектория».
Задачи урока:
образовательная: научить определять координаты движущегося тела.
развивающая: развивать логическое мышление, правильную физическую речь, использовать соответствующую терминологию.
воспитательная: достигать высокой активности класса, внимания, сосредоточенности учащихся.
Ресурс содержит конспект урока, презентацию к уроку, самостоятельную работу из 4-х вариантов.


Понравилось? Сохраните и поделитесь:
По кнопке ниже вы можете скачать Разработка урока 2 по теме «Траектория, путь и перемещение. Определение координаты движущегося тела» категории Физика 9 класс бесплатно. Будем благодарны, если вы оставите отзыв или посмотрите еще другие материалы на нашем сайте. Документ является презентация, конспект.

Скачать материал 1.1Mb
Загрузка началась… Понравился сайт? Получайте ссылки
на лучшие материалы еженедельно!
 Подарок каждому подписчику!
Подарок каждому подписчику! Перемещение. Путь. Траектория 9 класс
Обратная связь
Если не удалось найти и скачать доклад-презентацию, Вы можете заказать её на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:
Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:
Email: [email protected]
Мы в социальных сетях
Социальные сети давно стали неотъемлемой частью нашей жизни. Мы узнаем из них новости, общаемся с друзьями, участвуем в интерактивных клубах по интересам
ВКонтакте >
Что такое Myslide.ru?
Myslide.ru — это сайт презентаций, докладов, проектов в формате PowerPoint. Мы помогаем учителям, школьникам, студентам, преподавателям хранить и обмениваться своими учебными материалами с другими пользователями.
Для правообладателей >
«Система отсчёта. Траектория, путь и перемещение».
Инфоурок › Физика ›Презентации›Презентация по физике по теме: «Система отсчёта. Траектория, путь и перемещение».Описание презентации по отдельным слайдам:
1 слайд Описание слайда:
Описание слайда:Система отсчёта. Траектория, путь и перемещение.
2 слайд Описание слайда:
Описание слайда:Определение механического движения. Механическое движение – изменение положения тела в пространстве относительно других тел с течением времени.
3 слайд Описание слайда:
Описание слайда:Виды движения Поступательное движение – это такое движение, при котором все точки тела движутся одинаково.
4 слайд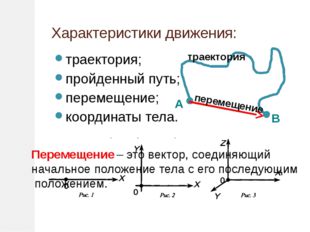 Описание слайда:
Описание слайда:Характеристики движения: траектория; пройденный путь; перемещение; координаты тела. А В траектория Перемещение – это вектор, соединяющий начальное положение тела с его последующим положением. перемещение
5 слайд Описание слайда:
Описание слайда:р Решите задачу.
6 слайд Описание слайда:
Описание слайда:Материальная точка – это тело, размерами которого можно пренебречь в условиях данной задачи. Определение материальной точки.
7 слайд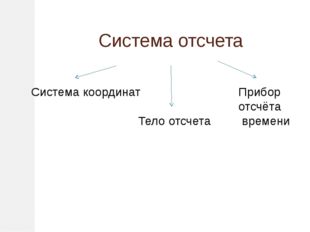 Описание слайда:
Описание слайда:Система отсчета Система координат Тело отсчета Прибор отсчёта времени

Курс повышения квалификации

Курс повышения квалификации

Курс повышения квалификации
Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:
Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВнеурочная деятельностьВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое
Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс
Выберите учебник: Все учебники
Выберите тему: Все темы
также Вы можете выбрать тип материала:

Общая информация
Номер материала: ДA-042713
Похожие материалы
Вам будут интересны эти курсы:
Оставьте свой комментарий
Презентация на тему: «Глава 5 Планирование траекторий 5.1 ВВЕДЕНИЕ В этих главах ……. Планирование траекторий и траекторий означает способ перемещения робота из одного места». — Стенограмма презентации:
1 
2
Глава 5 Планирование траектории 5.1 ВВЕДЕНИЕ В этой главе ……. Планирование траектории и траектории означает, что робот перемещается из одного места в другое контролируемым образом. Последовательность движений для контролируемого движения между сегментами движения, в прямолинейном движении или в последовательных движениях. Это требует использования как кинематики, так и динамики роботов. 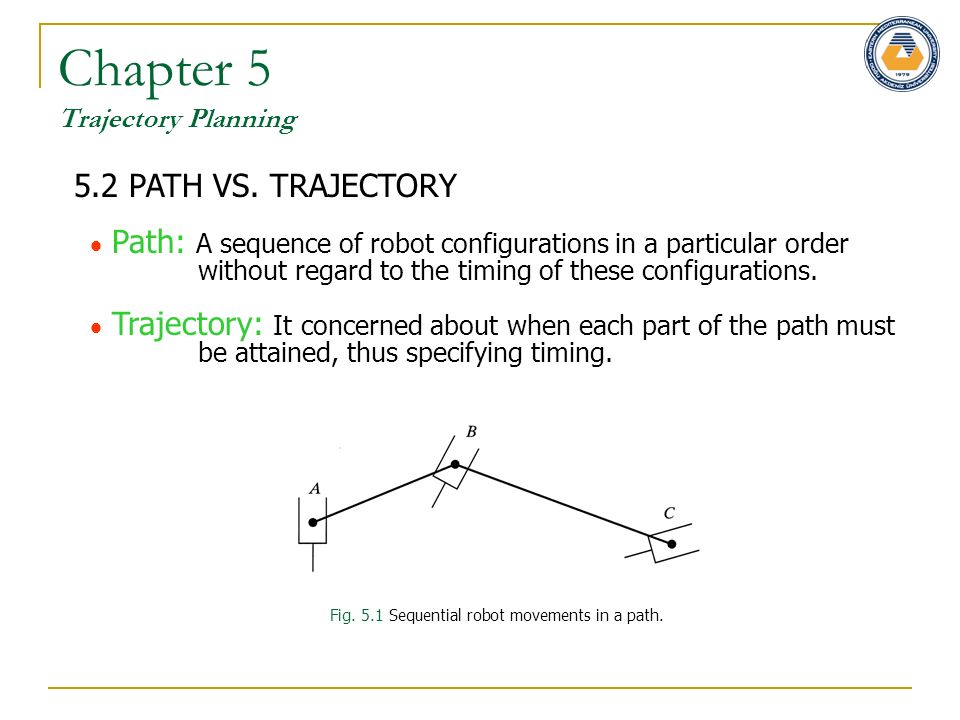
3
Глава 5 Планирование траектории 5.2 ПУТИ VS. TRAJECTORY Путь: последовательность конфигураций робота в определенном порядке, независимо от времени этих конфигураций. Траектория: она касается того, когда каждая часть пути должна быть достигнута, таким образом, определяя время. Рис. 5.1 Последовательные движения робота на пути. 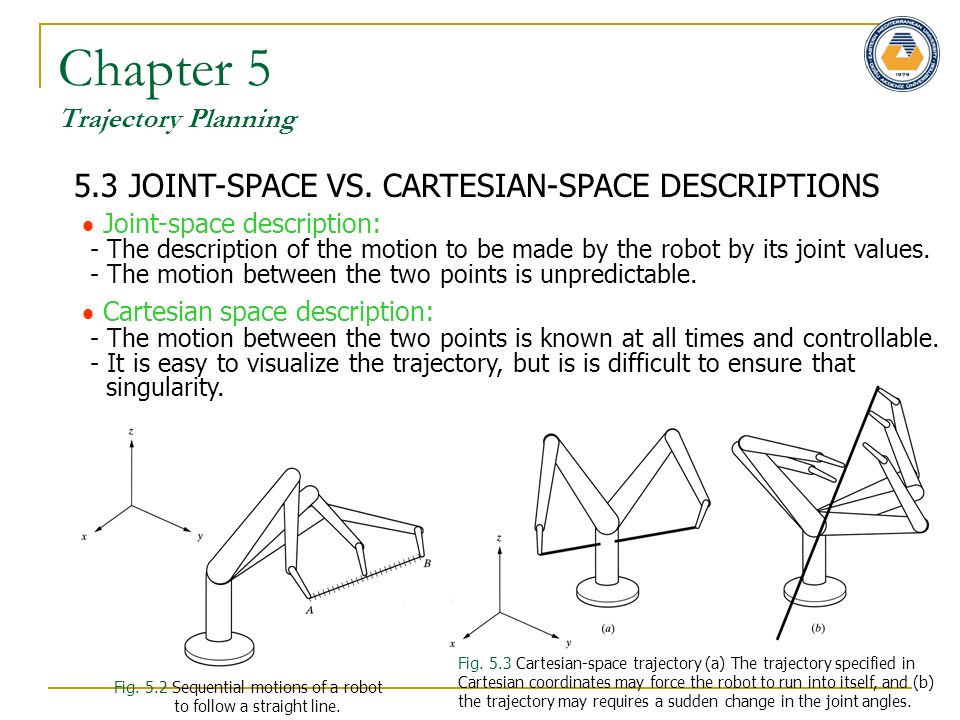
4
Глава 5 Планирование траектории 5.3 СОВМЕСТНОЕ ПРОСТРАНСТВО VS. ОПИСАНИЕ КАРТЕСНО-ПРОСТРАНСТВЕННОГО ПРОСТРАНСТВА Описание пространства в суставах: — Описание движения, которое должен делать робот по его совместным значениям.- Движение между двумя точками непредсказуемо. Описание декартового пространства: — Движение между двумя точками всегда известно и управляемо. — Легко визуализировать траекторию, но трудно обеспечить эту особенность. Рис. 5.2 Последовательные движения робота по прямой. Рис. 5.3. Дорожная декартова траектория (а) Траектория, указанная в декартовых координатах, может заставить робота столкнуться с самим собой, и (б) траектория может потребовать внезапного изменения углов сустава.
5
Глава 5 Планирование траектории 5.4 ОСНОВЫ ТРАЕКТОРНОГО ПЛАНИРОВАНИЯ Давайте рассмотрим простого робота с 2 степенями свободы. Мы хотим переместить робота из точки A в точку B. Предположим, что оба сустава робота могут двигаться с максимальной скоростью 10 градусов / сек. Предположим, что оба сустава робота могут двигаться с максимальной скоростью 10 градусов в секунду. Рис. 5.4. Ненормализованные движения в пространстве сустава робота с двумя степенями свободы. Переместите робот из А в В, чтобы запустить оба сустава с их максимальными угловыми скоростями. Через 2 [секунды] нижняя ссылка закончит движение, а верхняя ссылка будет продолжаться еще 3 [секунды]. Траектория нерегулярна, а расстояния, пройденные концом робота, неодинаковы. ![ We desire to move the robot from Point A to Point B. Let ’ s assume that both joints of the robot can move at the maximum rate of 10 degree/sec. Let ’ s assume that both joints of the robot can move at the maximum rate of 10 degree/sec. Fig. 5.4 Joint-space nonnormalized movements of a robot with two degrees of freedom. Move the robot from A to B, to run both joints at their maximum angular velocities. After 2 [sec], the lower link will have finished its motion, while the upper link continues for another 3 [sec]. The path is irregular and the distances traveled by the robot’s end are not uniform.. Chapter 5 Trajectory Planning 5.4 BASICS OF TRAJECTORY PLANNING Let ’ s consider a simple 2 degree of freedom robot.](/800/600/https/images.slideplayer.com/25/7600070/slides/slide_5.jpg)
6
Глава 5 Планирование траектории 5.4 ОСНОВЫ ТРАЕКТОРНОГО ПЛАНИРОВАНИЯ Рис. 5.5 Совместное пространство, нормализованные движения робота с двумя степенями свободы. Оба сустава движутся с разными скоростями, но движутся непрерывно вместе. Полученная траектория будет отличаться. Предположим, что движения обоих суставов нормализованы общим фактором, так что сустав с меньшим движением будет двигаться пропорционально медленнее, и оба сустава начнут и остановят свое движение одновременно. 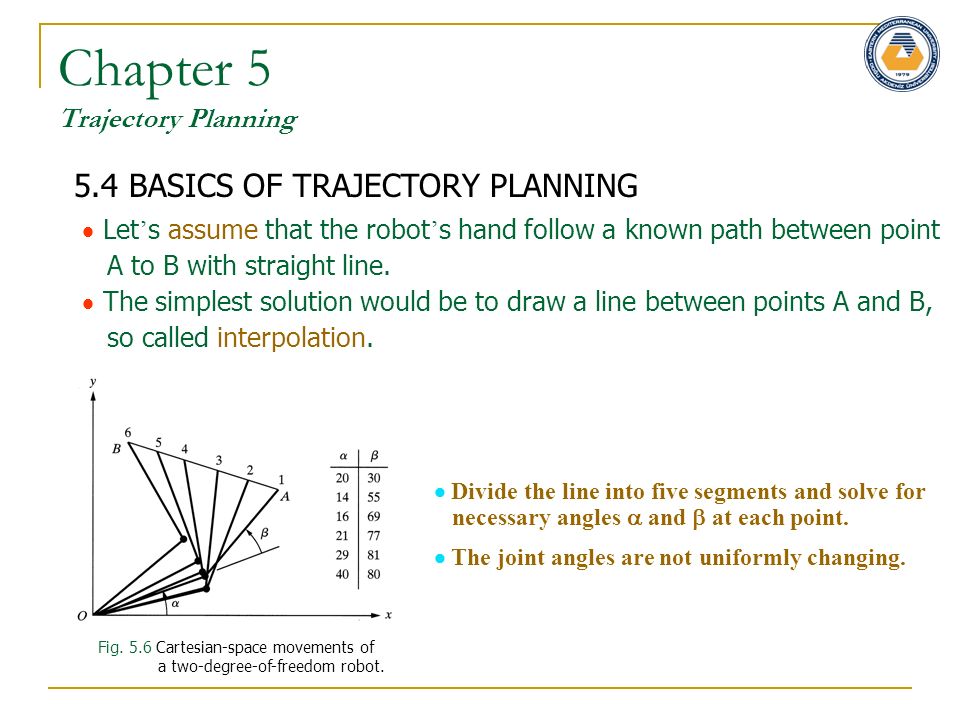
7
Глава 5 Планирование траектории 5.4 ОСНОВЫ ТРАЕКТОРНОГО ПЛАНИРОВАНИЯ Рис. 5.6 Декартово-космические движения робота с двумя степенями свободы. Разделите линию на пять сегментов и найдите необходимые углы и в каждой точке. Углы соединения не изменяются равномерно. Предположим, что рука робота следует по известному пути между точками А и В по прямой. Простейшим решением было бы провести линию между точками A и B, так называемую интерполяцию. 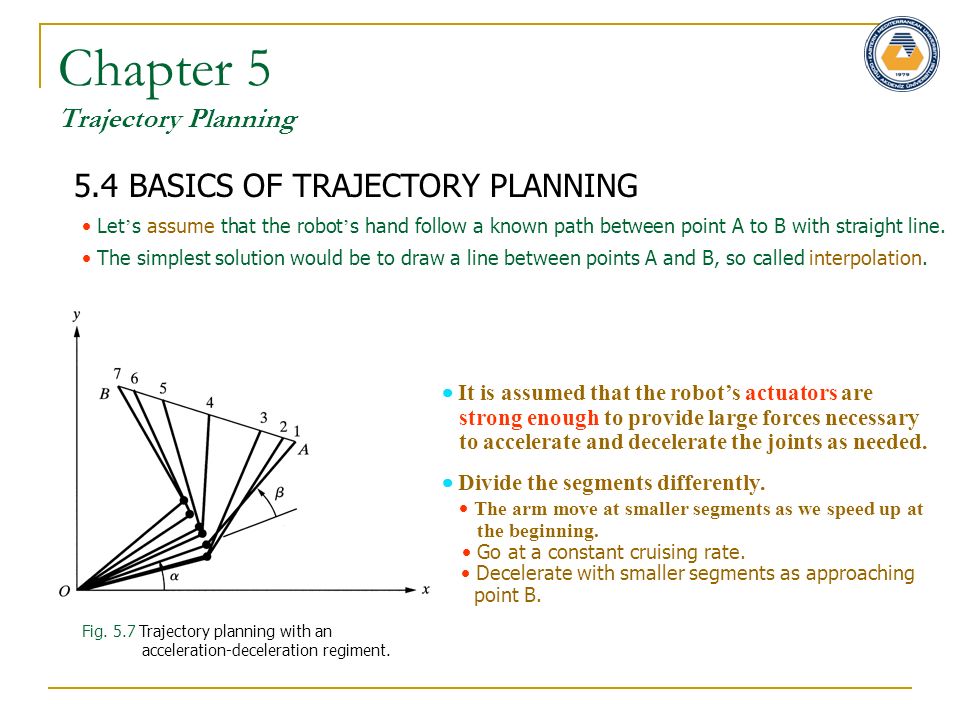
8
Глава 5 Планирование траектории 5.4 ОСНОВЫ ТРАЕКТОРНОГО ПЛАНИРОВАНИЯ Рис. 5.7. Планирование траектории с полком ускорения-замедления. Предполагается, что исполнительные механизмы робота достаточно сильны, чтобы обеспечить большие усилия, необходимые для ускорения и замедления соединений по мере необходимости. Разделите сегменты по-разному. Рука двигается в меньших сегментах, поскольку мы ускоряем в начале. Идите с постоянной скоростью крейсерской. Ускорение с меньшими отрезками по мере приближения к точке B. Предположим, что рука робота следует по известной траектории между точками A и B по прямой линии. Простейшим решением было бы провести линию между точками A и B, так называемую интерполяцию. 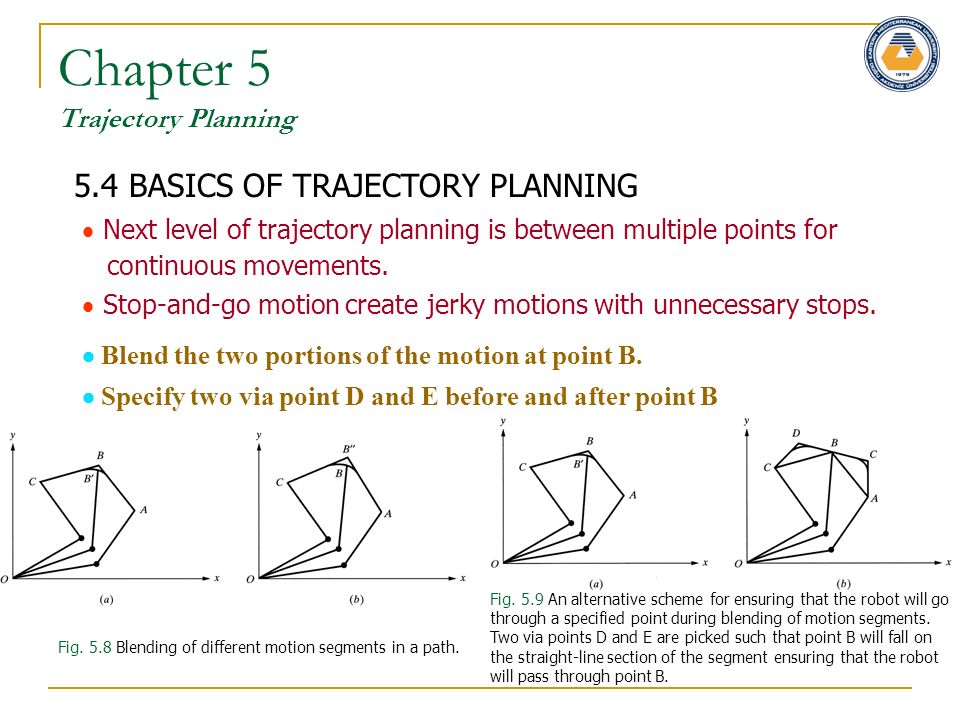
9
Глава 5 Планирование траектории 5.4 ОСНОВЫ ТРАЕКТОРНОГО ПЛАНИРОВАНИЯ Рис. 5.8 Смешивание различных сегментов движения в траектории. Смешайте две части движения в точке B. Следующий уровень планирования траектории находится между несколькими точками для непрерывных движений. Стоп-и-движение создают резкие движения с ненужными остановками.Рис. 5.9. Альтернативная схема, обеспечивающая прохождение робота через заданную точку во время смешивания сегментов движения. Две промежуточные точки D и E выбираются таким образом, чтобы точка B попала на прямолинейный участок сегмента, гарантируя, что робот пройдет через точку B. Укажите две промежуточные точки D и E до и после точки B 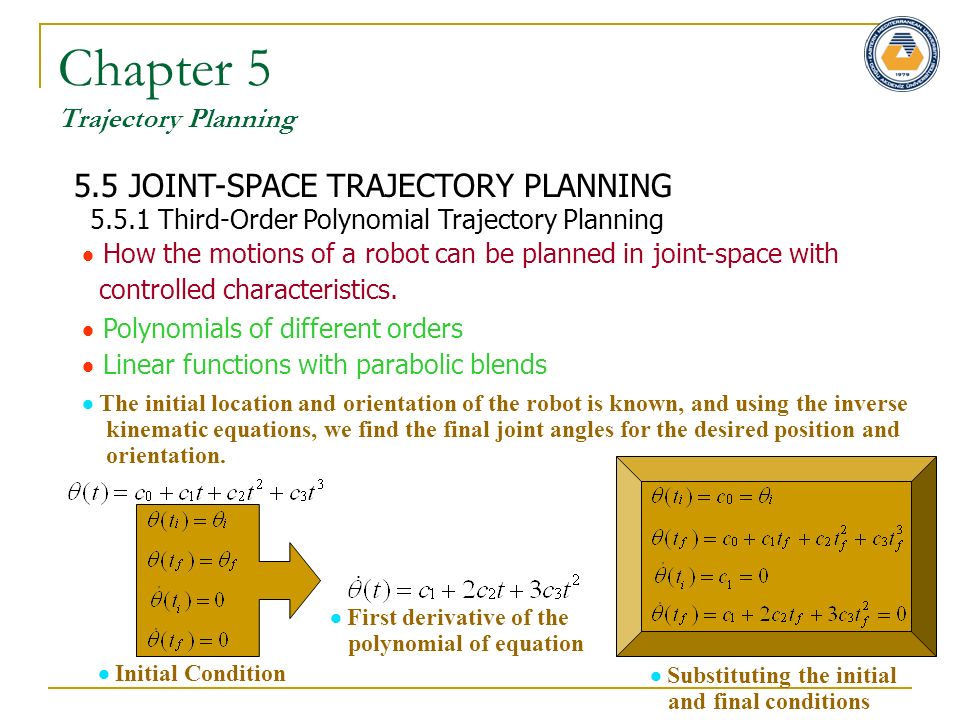
10
Глава 5 Планирование траектории 5.5 ПЛАНИРОВАНИЕ ТРАЕКТОРИИ СОВМЕСТНОГО ПРОСТРАНСТВА Как можно планировать движения робота в совместном пространстве с контролируемыми характеристиками. Полиномы разных порядков Линейные функции с параболическими смесями 5.5.1 Планирование траектории полиномов третьего порядка Начальное местоположение и ориентация робота известны, и с помощью обратных кинематических уравнений мы находим конечные углы соединения для желаемого положения и ориентации. Начальное условие Первая производная многочлена уравнения Подстановка начальных и конечных условий 
11
Пример Желательно, чтобы первый шарнир шестиосевого робота проходил с начального угла 30 o до конечного угла 75 o за 5 секунд.Используя полином третьего порядка, вычислите угол соединения в 1, 2, 3 и 4 секунды. 
12
Глава 5 Планирование траектории 5.5 ПЛАНИРОВАНИЕ ТРАЕКТОРИИ СОВМЕСТНОГО ПРОСТРАНСТВА Укажите начальное и конечное ускорения для сегмента. Чтобы использовать полином пятого порядка для планирования траектории, общее количество граничных условий равно 6. 5.5.2 Планирование полинома пятого порядка Вычисление коэффициентов полинома пятого порядка с положением, скоростью и границей ускорения условия могут быть возможны с помощью следующих уравнений.
Планирование траектории
крутящих моментов Система управления движением Система планирования траектории Робот Положение, скорость, ускорение Планирование траектории • Цель: сгенерировать исходные входные данные для управления движением система, которая гарантирует, что манипулятор выполняет запланированную траекторию
Траектория и траектория • Траектория: местоположение точек в объединенном пространстве или в рабочем пространстве • Траектория: траектория, на которой закон времени определен в терминах скорости и / или ускорения t
Траектория и траектория Ограничения траектории описания траектории (препятствия), налагаемые динамикой робота (плавные) (пределы, немодельные резонансные режимы) Совместные (конечные эффекторные) траектории с точки зрения положения, Скорость и ускорение Алгоритм планирования траектории
Путь а nd Траектория • Спецификация геометрического пути • Экстремальные точки, возможные промежуточные точки, геометрические примитивы, интерполирующие точки • Спецификация закона времени движения • Общее время траектории, максимальная скорость и ускорение, скорость и ускорение в точках интереса
Совместный Space Trajectory Параметры траектории в пространстве операций Параметры траектории в пространстве стыка Алгоритм обратной кинематики Алгоритм планирования траектории Начальное и конечное местоположение конечного эффектора, время в пути и т. Д.Совместные (конечные эффекторные) траектории с точки зрения положения, скорости и ускорения
Объединенная космическая траектория • Требования к алгоритму планирования совместной космической траектории • Сгенерированная траектория должна легко рассчитываться • Положение и скорость (ускорение) должны быть непрерывной функцией времени • Нежелательные эффекты должны быть сведены к минимуму • Движение от точки к точке • Переход от начальной к конечной конфигурации соединения за заданное время tf
Движение от точки к точке q (tf) Окончательное q (t2) «Задержка» q (t1) «Отрыв» q (t0) Начальный рисунок 4-2 от Фу, Гонсалеса и Ли
Движение от точки к точке • Полиномиальная интерполяция • Пример: начальная и конечная положение и скорость будут даны.
Движение от точки к точке
Движение от точки к точке
Движение от точки к точке • Пример: также приводятся начальное и конечное ускорение. • Шесть ограничений (начальное и конечное положение, скорость и ускорение • Заказ не менее пяти
Движение от точки к точке • Трапециевидный профиль скорости • Непосредственная проверка того, нарушают ли скорость и ускорение механические пределы
Движение точка-точка • Площадь, ограниченная профилем скорости с учетом ускорения
Движение точка-точка
Движение точка-точка • При следующих условиях: • начальное и конечное задано положение • начальная и конечная скорость установлены на ноль • указаны максимальная скорость и ускорение • какое минимальное время в пути?
Движение по траектории • Недостатки одного полинома высокого порядка • Подходящее количество полиномов низкого порядка
Эксплуатация Космическая траектория • Не легко предсказать движение конечного эффектора из-за кинемати cs нелинейность • Планирование движения по траектории аналогично пространству суставов • Другой метод, если движение конечного эффектора должно следовать заданной траектории движения, такой как линия, круг и т. д.
Двухзвенный планарный рычаг Параметры
Кулачки • Программирование движения, исторически связанное с механическими кулачками • Постоянная скорость вращения распределительного вала преобразуется в переменное линейное смещение клапана (или другого устройства, присоединенного к толкателю кулачка) • Распределительные валы в автомобильных двигателях (все 4 удара) • Швейная машина (более старый механический стиль)
Фотографии Cams Промышленные автомобильные двигатели http: //www.howstuffworks.com / camshaft1.htm
Профили движения кулачка — DRD • Задержка — Подъем — Задержка • Начальный период без движения («задержка») • «Подъем» до максимального смещения • Окончательный период без движения («Задержка») »)« Смещение »смещения, s« подъем »s = 0, v = 0, a = 0 s = smax, v = 0, a = 0« время ожидания », t
Профили движения кулачка — DRRD • Задержка — Подъем — Возврат — Задержка • начальный период отсутствия движения («задержка») • «подъем» до максимального смещения • Немедленное «возвращение» к началу координат • окончательный период отсутствия движения («задержка») s = smax, v = 0, a0 Смещение, s «подъем» «возврат» s = 0, v = 0, a = 0 с = 0, v = 0, a = 0 «задержка» Время «задержки», t
Профили движения кулачка — RR • Подъем — Возврат • «Подъем» до максимального смещения • Немедленно «возврат» к исходному объекту • Нет «задержки» — повторите то же самое s = smax, v = 0, a0 Смещение, s «подъем» «возврат» s = 0, v = 0, a0 s = 0, v = 0, a0 время, t
Accel.-Vel.-Disp. # 1 Нулевой порядок, A = постоянное ускорение, A Время, t T Первый порядок, V = k1t Скорость, V Время, t T Смещение, S Второй порядок, S = k2t2 Время, t T
эта область равно этому значению эта область равна этому значению Accel.-Vel.-Disp. # 1a Ускорение, A Time, t T Скорость, V Time, t T Смещение, S Time, t T
Accel.-Vel.-Disp. # 1b Подходит для ускорения с ускорением 25 м / с2, A Время, сек 0 0,1 0.2 0,3 V3 V2 Найти числовые значения для скорости V1, V2 и V3 V1, VT S3 Найти числовые значения для смещения S1, S2 и S3 S2, S S1 T
Общая кривая Форма: y = Kxn Площадь под кривой y = Kxn между x = 0 и x = x1 — Обратите внимание, что y1 = Kx1n, поэтому
Accel.-Vel.-Disp. # 2 Подходит для «задержки — подъема» 25 м / с2 Ускорение, A Время, с 0 0,1 0,2 0,3 V3 V2 Найти числовые значения для скорости V1, V2 и V3 V1, VT S3 Найти числовые значения для S1, S2 и S3 S2 Смещение, S S1 T
Accel.-Vel.-Disp. # 3 Подходит для «подъема — подъема» 25 м / с2 Ускорение, A Время, с 0 0,15 0,3 V1 V2 Найти числовые значения для скорости V1 и V2, VT S2 Найти числовые значения для смещения S1 и S2, S S1 T
Accel.-Vel.-Disp. # 4 Подходит для «задержки — подъема» 25 м / с2 Ускорение, A Время, с 0 0,1 0,2 0,3 V3 V2 Найти числовые значения для скорости V1, V2 и V3 V1, VT S3 Найти числовые значения для S1, S2 и S3 S2 Смещение, S S1 T
Подходит для «подъема-возврата» 25 м / с2 0.4 0,5 0,6 Время, с A -25 м / с2 0,1 0,2 0,3 Найти числовые значения для V4 и V5 V3 V2 V4 V5 V1 VT Найти числовые значения для S4, S5 и S6 S6 S5 S4 S3 S2 S S1 T
Аналитические Решение • Решить предыдущую задачу аналитически: Подсказка — решить первые части (для t <0,3 с), найти граничные условия для 2-х частей
Решить численно • Использовать Excel и трапециевидную интеграцию
A Числовой трюк • Используйте этот трюк для повышения точности, когда у вас есть резкие изменения ускорения, «удваивающиеся» при любых резких переходах
Программирование движений # 2 Движения суставов роботов
Типичное движение роботов q (tf) Final q (t2) «Отключение» q (t1) «Отключение» q (t0) Начальный рисунок 4-2 от Фу, Гонсалеса и Ли
Ограничения положения • Начальное ПО сечение, q1 • начальная скорость и ускорение (обычно = 0) • позиция отрыва, q2 • скорость и ускорение должны совпадать здесь • положение посадки, q3 • скорость и ускорение должны совпадать здесь • конечное положение, qf • конечная скорость и ускорение (обычно = 0)
Типичное решение • Траектория «4-3-4» • Полином 4-го порядка от начального к отрыву • Полином 3-го порядка от начального к отрыву • Полином 4-го порядка от набора — до конечной • траектория «3-5-3» • та же, что и выше, но поли 3-го и 5-го порядка • 5-кубическая траектория • кубические сплайны, используемые для 5 сегментов • отрыв к уклону, разделенный на 3 сегмента
«4-3-4» Траектория • 1-й сегмент: • 2-й сегмент: • 3-й сегмент: • 14 неизвестных — нужно 14 уравнений!
Граничные условия # 1- # 3 • 1.Начальная позиция, q0 = q (t0) (установите t0 = 0) • 2. Начальная скорость = w0 (обычно 0) • 3. Начальное ускорение = a0 (обычно 0)
Граничные условия # 4- # 5 • 4. Положение отрыва, q (t1) • 5. Положение отрыва, q (t1)
Граничные условия # 4- # 5 • 4. Положение отрыва, q (t1) • 5. Положение отрыва, q (t1)
Граничные условия # 6- # 7 • 6. Соответствие скорости отрыва с обеих сторон • 7.Ускорение старта соответствует обеим сторонам
Граничные условия № 8- # 9 • 8. Положение приведения в порядок, q (t2) • 9. Положение приведения в исходное положение, q (t2)
Граница Условия # 10 — # 11 • 10. Согласование скорости с обеих сторон. • 11. Согласование ускорения с обеих сторон.
Граничные условия # 12- # 14 • 12. Конечная позиция, q (tf ) • 13. Конечная скорость, vf (обычно 0) • 14. Конечное ускорение, af (обычно 0)
Формат решения • 14 одновременных линейных уравнений с 14 неизвестными: • 11 значений, необходимых для поиска решения:
Формат решения • Решить, используя Matlab (или, возможно, Maple)
После решения Matlab • Как только мы найдем 14 коэффициентов, как мы найдем скорости и ускорения? • Возьмите производную h2 (t), h3 (t), h4 (t), чтобы получить скорость. • Возьмите производную скорости, чтобы получить ускорение.• Оба легко наносятся на график в Matlab или Excel
RoboticsChapter 5 — Планирование траектории и траектории Dr. Amit Goradia
Темы • Введение — 2 часа • Преобразование координат — 6 часов • Прямая кинематика — 6 часов • Обратная кинематика — 6 часов • Скорость кинематики — 2 часа • Планирование траектории — 6 часов • Динамика робота (введение) — 2 часа • Управление силой (введение) — 1 час • Планирование задач — 6 часов
Robot Motion Planning • Планирование пути • Геометрический путь • Проблемы: обход препятствий, кратчайший путь • Планирование траектории, • «интерполировать» или «аппроксимировать» желаемый путь с помощью класса полиномиальных функций • Создать последовательность на основе времени «контрольного набора точки »для управления манипулятором от начальной конфигурации до места назначения.
Мир состоит из… • Препятствий • Уже занятых пространств мира • Другими словами, роботы не могут туда попасть • Свободное пространство • Незанятое пространство в мире • Роботы «могут» уйти здесь • Чтобы определить, куда может пойти робот, нам нужно обсудить, что такое пространство конфигурации
пространство конфигурации • Обозначения: • A: один жесткий объект — (робот) • W: евклидово пространство, в котором движется A; • B1,… Bm: фиксированные жесткие препятствия, распределенные в W • FW — мировая рама (неподвижная рама) • FA — рама робота (движущаяся рама, жестко связанная с роботом) Конфигурация q of A представляет собой спецификацию физического состояния (положение и ориентация ) A w.к.т. фиксированная окружающая среда FW. Пространство конфигурации — это пространство всех возможных конфигураций робота.
Определения • Конфигурация: спецификация всех переменных, которые полностью определяют систему • Пример: Конфигурация робота dof: • Пространство конфигурации (пространство C): Набор всех конфигураций • Свободная конфигурация: конфигурация, которая выполняет не сталкиваться с препятствиями • Свободное пространство (F): набор всех свободных конфигураций • Это подмножество C
C Cfree qslug Cobs qrobot Пространство конфигурации 2D-планировщика Робот Пространство конфигурации A — это пространство (C ) из всех возможных конфигураций А.Точечный робот (свободный полет, без ограничений) Для точечного робота, движущегося в 2-D плоскости, C-space равен
C y Cfree qgoal Z Cobs qstart x Пространство конфигурации робота, движущегося в 3D Для точки Робот, движущийся в 3D, C-spaceis В чем разница между евклидовым и C-пространством?
Пространство конфигурации шарнирного робота 2R манипулятор bbaa 2R Пространство конфигурации топология
Пространство конфигурации 360 qrobot 270 b 180 b 90 a qgoal a 0 45 135 90 180 Две точки в рабочей области робота Torus ( Обтекание по горизонтали и вертикали)
Область конфигурации Если конфигурация робота находится в синей области, он столкнется с препятствием 360 qrobot 270 b 180 b 90 a qslug a 0 45 135 90 180 Препятствие в рабочей области робота a Представление «C-пространство» Каково измерение C-пространства робота-пумы (6R)? Визуализация C-пространства высокой размерности затруднена
Планирование движения Найти путь без столкновений от начальной конфигурации до конфигурации цели с учетом ограничений (геометрических, физических, временных) концепции C-пространства обеспечивают обобщенную структуру изучить задачу планирования движения Отдельная задача для каждого робота?
Робот как точечный объект Расширить препятствие (я) Уменьшить робота не совсем правильно…
Рост препятствий Робот C-препятствия
Суммы Минковского Это расширение одной плоской формы другой называется суммой Минковского ski Прямоугольный робот, который может переводить только P RRPP R = { p + r | p P и r R} (операция расширения) Используется в робототехнике для обеспечения доступности свободных путей.
Дополнительные размеры Каким будет С-препятствие, если прямоугольный робот (красный) может перемещаться и вращаться в плоскости.(Синий прямоугольник является препятствием.) Y Прямоугольный робот, который может переводить и вращать x
C-препятствие в трехмерном Как будет выглядеть пространство конфигурации прямоугольного робота 3DOF (красного цвета) в этом мире? (Препятствие синее.) 3-D 180º y 0º x мы можем остаться в 2d?
Один кусочек C-препятствия Взятие одного кусочка C-препятствия, в котором робот поворачивается на 45 градусов … P RR y 45 градусов P x
2-D проекция yx почему не держать это так просто?
Проблемы с проекцией qinit qgoal слишком консервативен!
Методы планирования движения Задача планирования движения состоит из следующего: Входные данные Вывод • Геометрические описания робота и его окружения (препятствия) • Начальная и конечная конфигурации • Путь от начала до конца (или признание того, что ничего не существует) существует) qrobot qgoal Постановка задачи Вычислить путь без столкновений для жесткого или сочлененного движущегося объекта среди статических препятствий Что делать?
Методы планирования движения (1) Подходы к дорожной карте (2) Разложение ячеек (3) Потенциальные поля (4) Алгоритмы ошибок Цель — уменьшить пространство N-мерной конфигурации до набора одномерных путей для поиска.2) N = количество вершин в C-пространстве. Дорожная карта: графы видимости Графы видимости: в многоугольном (или многогранном) конфигурационном пространстве постройте все отрезки, которые соединяют вершины друг с другом (и которые не пересекают сами препятствия). ). • Формируется путем соединения всех «видимых» вершин, начальной и конечной точек друг с другом. • Чтобы две точки были «видимыми», между ними не должно быть никаких препятствий. • По периметру препятствий существуют пути. Из Cfree определяется граф. Преобразует задачу в поиск в графе.
График видимости в действии • Сначала нарисуйте линии видимости от начала и цели до всех «видимых» вершин и уголков мира. начало цели
График видимости в действии • Во-вторых, нарисуйте линии видимости из каждой вершины каждого препятствия, как прежде. Помните, что линии по краям также являются линиями обзора. начало цели
цель старт График видимости • Повторяйте, пока не закончите. Поскольку карта была в C-пространстве, каждая строка потенциально представляет часть пути от начала до цели.
Недостатки графа видимости Графики видимости не сохраняют свою оптимальность в больших измерениях: кратчайший путь кратчайший путь в графе видимости Кроме того, пути, которые они находят, являются «полусвободными», то есть в контакте с препятствиями. Без зазоров
Дорожная карта: диаграммы Вороного «официальная» диаграмма Вороного (отрезки линий образуют диаграмму Вороного, которая выделяет набор точек) Обобщенный граф Вороного (GVG): расположение точек, равноудаленных от ближайших двух или более границ препятствий , включая границу рабочего пространства.Свойство: максимальное расстояние между точками и препятствиями.
Дорожная карта: диаграммы Вороного • GVG формируется путями, равноудаленными от двух ближайших объектов • максимизируя расстояние между препятствиями. • Это создает очень безопасную дорожную карту, которая максимально избегает препятствий.
Диаграмма Вороного: Метрики • Множество способов измерения расстояния; два: • L1 метрика • (x, y): | x | + | y | = const • Метрика L2 • (x, y): x2 + y2 = const
Диаграмма Вороного (L1) Обратите внимание на отсутствие изогнутых ребер
Диаграмма Вороного (L2) Обратите внимание на изогнутые ребра
Методы планирования движения • Подходы к дорожной карте • График видимости • Диаграмма Вороного • Разложение ячеек • Точное разложение ячеек (трапециевидное) • Приблизительное разложение ячеек (квадродерево) • Потенциальные поля • Гибридные локальные / глобальные
Точность ячеек Трапецеидальная декомпозиция: декомпозиция свободного пространства на трапециевидные и треугольные ячейки Граф связности, представляющий отношение смежности между клетками (алгоритм Sweepline)
Точная декомпозиция клеток Трапецеидальная декомпозиция: Поиск на графике пути (последовательность последовательных ячеек )
Точное разложение клеток Трапецеидальное разложение: Trans сформировать последовательность клеток в свободный путь (например,g., соединяя средние точки пересечения двух последовательных ячеек)
Оптимальность Трапецеидальная декомпозиция: 15 ячеек 9 ячеек Получение минимального количества выпуклых ячеек является NP-полным. Трапецеидальная декомпозиция является точной и полной, но не оптимальной, в мире может быть больше деталей, чем нужно беспокоить о задаче …
Приблизительная декомпозиция соты Декомпозиция квадродерева: рекурсивно подразделяет каждое смешанное препятствие / свободно (под) область на четыре четверти… Quadtree:
Дальнейшее разложение Разложение Quadtree: рекурсивно делит каждое смешанное препятствие / свободную (под) область на четыре четверти … Quadtree:
Даже дальнейшее разложение Ячейка Quadtree Разложение: • Прямоугольное рекурсивно разлагается на меньшие прямоугольники. • При определенном уровне разрешения используются только ячейки, внутренности которых полностью находятся в свободном пространстве. • Поиск в этом графе дает путь без столкновений. Опять же, используйте алгоритм поиска в графе, чтобы найти путь. от начала до цели это полный алгоритм планирования пути? я.находит ли он путь, когда он существует? Quadtree
Вероятностные методы дорожной карты • Что такое PRM (вероятностный метод дорожной карты) • Вероятностная дорожная карта — это дискретное представление непрерывного пространства конфигурации, генерируемого путем случайной выборки свободных конфигураций C-пространства и соединения этих точек в график • Полное планирование пути в многомерных C-пространствах очень сложно • Методы PRM повышают производительность за счет обмена полнотой на вероятностную полноту • Двухфазный подход: фаза обучения, фаза запроса
с ~ s ~ gg Вероятностная дорожная карта Методы • Вероятностные методы для поэтапного построения дорожной карты в свободном пространстве робота. • Управляемый эффективностью. • Роботы с большим количеством степеней свободы (C-пространства с высокой яркостью). • Статические среды.
. Этап обучения • Этап обучения: случайным образом выбрать свободное место и создать список узлов в свободном пространстве.• Соедините всех ближайших соседей, используя быстрый местный планировщик. • Сохранить график, узлы которого являются конфигурациями, а ребра — это пути, рассчитанные локальным планировщиком. • Шаг расширения: Найти «сложные» узлы и развернуть график вокруг них, используя методы случайного обхода.
Этап запроса • Найти путь с самого начала и цели к двум узлам дорожной карты. • Выполните поиск на графике, чтобы найти последовательность ребер, соединяющих эти узлы в дорожной карте. • Объединение последовательных сегментов дает реальный путь для робота.
Методы планирования движения • Подходы к дорожной карте • Разложение ячеек • Точное разложение ячеек (трапециевидное) • Приблизительное разложение ячеек (квадродерево) • Потенциальные поля • Гибридные локальные / глобальные
Метод потенциального поля (рабочее поле ) Принцип) — Местоположение цели создает привлекательный потенциал — притягивает робота к цели — Препятствия создают отталкивающий потенциал — отталкивает робота от препятствий — Отрицательный градиент общего потенциала рассматривается как искусственная сила, прикладываемая к робот — пусть сумма сил управляет роботом С-препятствия
Метод потенциального поля • Вычисление силы притяжения к цели С-препятствия Привлекательный потенциал
Метод потенциального поля • Вычисление отталкивающего отталкивать от препятствий Потенциал отталкивания Создать потенциальный барьер вокруг Область С-препятствий, которую нельзя преодолеть с помощью конфигурации робота. Обычно желательно, чтобы потенциал отталкивания не влиял на движение робота, когда он находится достаточно далеко от С-препятствий.
Метод потенциального поля • Вычислить a сила отталкивания от препятствий • Потенциал отталкивания
Метод потенциального поля • Сумма потенциала Потенциал притяжения Потенциал отталкивания C-препятствие Сумма потенциалов
майнинг траекторий Хоюнг Дженг L Ман Лунг Ю ‡ Кристиан С. Йенсен * † Политехническая школа Лозанны (EPFL) ‡ Гонконгский политехнический университет * Орхусский университет ACMGIS’2011
Введение и обзор Дисковые траектории движения Сравнительные паттерны движения Плотность движения траектории Заключение
Введение • Повышение осведомленности о местонахождении • Утопление данных о траектории, но жажда знаний ,• Анализ траектории. • Появляющаяся и быстро развивающаяся тема в области анализа данных. • Касается группировки подобных траекторий. • Области применения и использования • Оптимизация транспорта • Прогнозирование • Анализ движения животных, социальный анализ • Анализ событий командных видов спорта • Анализ трафика
Процесс обнаружения шаблонов
Классификация шаблонов траекторий • Задачи добычи на траекториях • Кластеризация траектории • Группировка траекторий на основе геометрической близости в пространственном / пространственно-временном пространстве.• Объединение траекторий. • При наличии двух наборов данных траекторий получить все пары одинаковых траекторий. • Пространственные и пространственно-временные шаблоны
Классификация шаблонов траекторий • Гранулярность шаблонов траекторий • Глобальные и частичные модели. • Глобальный: основной единицей обнаружения паттернов является целая траектория. • Частичное: касается суб-траекторий для обнаружения закономерностей некоторой продолжительности. • Индивидуальные и групповые модели. • Индивидуальный: обычные модели личности. • Группа: общие шаблоны различных объектов.• Ограниченные траектории. • Пространственные ограничения: движение в пространственных сетях. • Временные ограничения: периодичность.
Введение и обзор Шаблоны относительных движений Шаблоны траекторий на основе дисков Шаблоны траекторий на основе плотности Заключение Шаблоны относительных движений
Обзор • Ключевые особенности • Определите похожие движения в наборе траекторий движущихся объектов. • REMO (относительное движение): концепция анализа.• Преобразуйте необработанные траектории в атрибуты движения (скорость, азимут движения). • Типы паттернов. • Основные движения: постоянство, совпадение, трендсеттер. • Пространственные движения: след, стадо, лидерство. • Совокупные / раздельные движения: сближение, столкновение, расхождение, распад. [GIScience’02, IJGIS’05, SDH’04, CEUS’06]
Основные модели движения • Концепция • Описание событий движения без учета абсолютных положений. • Определения • Констанция: последовательность равных атрибутов движения для последовательных времен.• Совпадение: встречаемость нескольких объектов с одинаковыми атрибутами движения. • Trendsetter: определенный шаблон движения, который совместно используется набором других объектов в будущем. Например, «постоянство» + «совпадение». constance concurrence trendsetter
Пространственные шаблоны движения • Концепция • Основные шаблоны движения + пространственное ограничение (область) • Определения • Трек: отдельные объекты, каждый перемещается в пределах диапазона, сохраняя одно и то же движение. «Констанция» + пространственное ограничение ,• Flock: набор объектов, которые перемещаются в пределах диапазона, сохраняя при этом одно и то же движение. «Совпадение» + пространственное ограничение. • Лидерство: один лидер, за которым следует набор объектов с одинаковым движением. «Законодатель мод» + пространственное ограничение.
Агрегатные / раздельные шаблоны движения • Концепция • Описание агрегации и разделения движений объектов. • Определения • Сходимость • Набор объектов в течение интервала времени, которые совместно используют азимутальные векторы движения, пересекающиеся в данном пространственном диапазоне.• фиксирует поведение группы объектов, которые сходятся в определенном регионе. • Встреча. • Набор объектов, которые появятся в заданном пространственном диапазоне одновременно через несколько временных точек. • Записывает экстраполированное (будущее) собрание набора объектов в пространственном диапазоне. • Дивергенция • Противоположная концепция «конвергенции». • Движение назад, а не вперед. • Расставание. • Противоположное понятие «встреча». • Например, отходя от места встречи.
Обсуждение • Значение • Концептуальная основа для многих последующих исследований по обнаружению траектории.• Недостатки • Сложно определить абсолютное расстояние между двумя объектами. • В основном имеет дело с азимутами движения, состоящими из определенного числа углов (обычно 8). Поиск подходящего числа углов важен, но нетривиален. • Отсутствие точек данных на траекториях существенно снижает точность и эффективность обнаружения паттернов.
Введение и обзор Шаблоны относительных движений Шаблоны траекторий на основе диска Шаблоны траекторий на основе плотности Заключение Шаблоны траекторий на основе диска
Обзор • Основные функции • Расширьте относительные шаблоны движения.• Вместо атрибутов движения евклидовы расстояния используются для определения шаблона. • Основные относительные шаблоны движения больше не рассматриваются. • Круговые пространственные ограничения используются только. • Интеграция временных ограничений в определениях паттернов. • Типы паттернов • Перспективные паттерны: встреча, конвергенция. • Схемы, управляемые стадом: стадо, встреча, лидерство. [SAC’07, GeoInformatica’08, CG’08, GIS’04, GIS’09]
Перспективные модели • Концепция • Шаблоны на будущих траекториях объектов, при условии, что объекты сохраняют свои текущие скорости и направления.• Определения. • Встреча (m, r): группа, состоящая как минимум из m объектов, которые будут одновременно поступать на диск с радиусом r. • Конвергенция (m, r): группа, состоящая как минимум из m объектов, которые будут проходить через диск с радиусом. т (не обязательно в то же время).
Шаблоны, управляемые флокированием • Концепция • Расширение «Флокирования» в относительных схемах движения с использованием евклидова расстояния. • Определения • Флок (m, k, r): группа, состоящая как минимум из m объектов, которые движутся вместе, по крайней мере, k последовательных моментов времени, оставаясь при этом на диске с радиусом r.• Встреча (m, k, r): группа, состоящая как минимум из m объектов, которые остаются вместе на неподвижном диске с радиусом r в течение не менее k последовательных моментов времени.
Обсуждение • Значение • Большое количество последующих исследований расширяют относительные паттерны движения. • Значительный прогресс как в концепциях, так и в методах обнаружения. • Недостатки • Выбор правильного размера диска r затруднен. • Большое r может захватывать объекты, которые интуитивно не входят в одну группу. • Маленькая буква r может пропустить некоторые объекты, которые интуитивно находятся в одной группе.• Одно значение для r может быть неуместным. • Географический размер группы обычно различается на практике. • Например, проблема с потерями-скоплениями:
Введение и обзор Относительные схемы движения Дискретные траектории Образцы основанные на плотности траектории Образцы Заключение Основанные на плотности траектории
Обзор • Ключевые особенности • Недостатки адресов дисковые шаблоны. • Используйте концепции плотности. • Разрешить захват общих траекторий произвольной формы и протяженности.• Типы паттернов • TRACLUS: траектория кластеризации. • Движущийся кластер: последовательность пространственных кластеров. • Конвой: стадо на основе плотности. • Варианты: динамические / развивающиеся / действующие конго • Рой: расслабленный во времени конвой. • Варианты: закрытый рой, ведомый
e pq p ‘pqqpo Понятия плотности, заданные e и m • Достижимый напрямую плотность • Достигаемый плотность • Соединение плотности m = 3 [KDD’96]
9000 TRACLUS • Концепция • Кластеризация сегментов траектории, связанных по плотности.• Время не считается. • Процедура • Разделить траекторию на под-траектории. • Кластеризация DBSCAN выполняется на под-траекториях. • Представлять кластер репрезентативной (под-) траекторией [SIGMOD’07]
Перемещение кластера • Концепция • Набор объектов, которые перемещаются близко друг к другу в течение некоторого времени. • Определение • Последовательность последовательных кластеров моментальных снимков, которые совместно используют по крайней мере заданное θ общих объектов. [SSTD’05]
Конвой • Концепция • Плотно-связанный «стадо (m, k, r)».• Определение • По заданным e, m и k найдите все группы объектов, чтобы каждая группа состояла из объектов, связанных плотностью w.r.t.e, и в течение как минимум k последовательных моментов времени. [PVLDB’08]
Swarm • Концепция • Конвой с расслабленным временем. • Принятие кратковременных отклонений объектов. • Определение • По заданным значениям e, m и kmin найдите все группы объектов, чтобы каждая группа состояла из объектов, связанных с плотностью w.r.t.e, и в течение как минимум kmintime-точек (не обязательно последовательных времен).[PVLDB’10]
Дискуссия • Значение • Основной поток в текущем исследовании по анализу траекторий. • Резюме
Введение и обзор Шаблоны относительных движений Шаблоны траекторий на основе дисков Шаблоны траекторий на основе плотности Заключение Заключение
Заключение в целом Обзор шаблонов траекторий Схемы относительных движений взгляд на основе траекторий на основе дисков Образцы траекторий
Список литературы [GIScience’02] Лауб, П., Imfeld, S .: Анализ относительного движения в группах отслеживаемых объектов движущихся точек. В: GIScience, стр. 132–144 (2002) [IJGIS’05] Лаубе П., Имфельд С., Вейбель Р. Обнаружение относительных закономерностей движения в группах движущихся точечных объектов. Международный журнал географической информатики 19 (6), 639–668 (2005) [SDH’04] Лауб, П., ван Кревельд, М., Имфельд, С .: Поиск ремодетектирования относительных моделей движения в геопространственных линиях жизни. В кн .: Материалы Международного симпозиума по обработке пространственных данных, с.201–214 (2004) [CEUS’06] Лаубе П., Пурвес Р.С.: Подход к оценке методов обнаружения движущихся объектов в пространственно-временных данных. Компьютеры, окружающая среда и городские системы 30 (3), 347–374 (2006) [GIS’06] Gudmundsson et al., Вычисление скоплений с наибольшей продолжительностью в данных траектории, 2006 [PVLDB’08] Jeung et al., Discovery of Convoys in Базы данных о траекториях, 2008 [PVLDB’10] Ли, З., Дин, Б., Хан, Дж., Кейс, Р .: Рой: добыча расслабленных временных кластеров движущихся объектов. PVLDB 3, 723–734 (2010) [SAC’07] Андерссон, М., Gudmundsson, J., Laube, P., Wolle, T .: Отчетность моделей лидерства среди траекторий. В: SAC, стр. 3–7 (2007) [GeoInformatica’08] Андерссон М., Гудмундссон Дж., Лаубе П., Воль, Т .: Сообщение о лидерах и последователях по траекториям движущихся точечных объектов. GeoInformatica 12 (4), 497–528 (2008) [CG’08] Бенкерт М., Гудмундссон Дж., Хбнер Ф., Воль, Т .: Отчетность о стаде стада. Вычислительная геометрия 41 (1), 111125 (2008) [GIS’04] Gudmundsson J., van Kreveld, M., Speckmann, B .: Эффективное обнаружение моделей движения в пространственно-временных наборах данных.В кн .: Материалы международного симпозиума ACM «Достижения в геоинформационных системах», с. 250–257 (2004) [GIS’09] Виейра М.Р., Бакалов П., Цотрас В.Ю. Онлайн обнаружение скоплений стада в пространстве -временные данные. В: Материалы 17-й Международной конференции ACM SIGSPATIAL по достижениям в геоинформационных системах, стр. 286–295 (2009) [KDD’96] Эстер М., Кригель Х.П., Сандер Дж., Сюй, X .: A алгоритм на основе плотности для обнаружения кластеров в больших пространственных базах данных с шумом.В: Материалы Международной конференции ACM SIGKDD по обнаружению знаний и добыче данных, стр. 226–231 (1996) [SSTD’05] Калнис П., Мамулис Н., Бакирас С. С .: Об обнаружении движущихся кластеров в пространстве -временные данные. В: Материалы Международного симпозиума по пространственным и временным базам данных, с. 364–381 (2005)

