Самостоятельная работа по геометрии (9 класс) по теме «Простейшие задачи в координатах. Уравнение окружности»

Самостоятельная работа ( Г – 9 )

«Простейшие задачи в координатах. Уравнение окружности»

I вариант

1. Найдите длину вектора .

2. Найдите координаты середины отрезка АВ, если А(5; — 3), В(3; — 7).

3. Найдите координаты вектора , если А(2; — 5), В(- 3; 4).

4. Найдите расстояние между точками М(- 5; 1) и N(- 2; — 3).

5. Найдите координаты центра окружности с диаметром CD, если С(4; 7), D(2; — 3).

6. Лежит ли точка А(2; — 1) на окружности, заданной уравнением

(х – 2)² + (у – 3)² = 25 ?

7. Напишите уравнение окружности, если ее центр – точка О(4; 5), а радиус равен 3.

8. * Напишите уравнение окружности с центром в начале координат, если она проходит через точку С(- 2; 3).

9. *Лежит ли точка Р(2; — 6) внутри круга, ограниченного окружностью

(х – 5)² + (у + 3)² = 16 ?

10. *Определите вид треугольника, заданного координатами своих вершин: А(0; 2), В(2; 6), С(6; -1).

II вариант

1. Найдите расстояние между точками А(- 1; 3) и В(2; — 1).

2. Найдите координаты вектора , если С(- 1;6), D(3; — 2).

3. Найдите длину вектора .

4. Найдите координаты середины отрезка АВ, если А(3; — 2), В(- 3; 6).

5. Найдите координаты центра окружности с диаметром РК, если Р(- 5; 2), К(- 3;8).

6. Лежит ли точка А(2; 4) на окружности, заданной уравнением

(х + 5)² + (у – 4)² = 49 ?

7. Напишите уравнение окружности, если ее центр – точка О(2; — 4), а радиус равен 9.

8. *Напишите уравнение окружности с центром в точке Р(- 2; -1), если она проходит через точку Q(1; 3).

9. *Лежит ли точка S(-7; 4) вне круга, ограниченного окружностью

(х + 1)² + (у – 2)² = 36 ?

10. Определите вид треугольника, заданного координатами своих вершин:

М(-8; — 3), N(- 2; 6), К(4; — 3).

infourok.ru

Открытый урок «Простейшие задачи в координатах» 9 класс геометрия

МКОУ «Новопетровская СШ»

Предмет: математика.

Конспект урока геометрии по теме:

«Простейшие задачи в координатах»

Проводился в рамках РМО учителей математики.

Класс: 9

Автор: Маркина Галина Анатольевна,

учитель математики первой категории

2015 год

Обобщающий урок по теме: Простейшие задачи в координатах

1. Цель урока: совершенствование навыков решения задач методом координат, рассмотрение простейших задач в координатах и их применение в процессе решения задач

Задачи:

— обучающие: формирование у учащихся навыков и умений находить координаты середины отрезка, определять длину вектора по его координатам и определять расстояние между точками с заданными координатами;

— развивающие: обеспечить развитие устной и письменной речи учащихся, развитие у учащихся интеллектуальных способностей, самостоятельности, способности к оценочным действиям;

— воспитательные: воспитание у учащихся познавательного интереса к предмету посредством применения новейших информационных технологий обучения.

Ход урока

1. Организационный момент

Здравствуйте, друзья. Садитесь. Посмотрите, сколько у нас сегодня много гостей. Какое у вас настроение? Давайте настроимся на работу. Глубоко вдохните. Выдохните. Вдохните в себя тепло солнечных лучей. Повернитесь друг к другу и улыбнитесь, а теперь улыбнитесь мне, а я улыбнусь вам. Если урок начинается с улыбки, то можно надеяться, что он пройдет удачно. А я желаю вам плодотворной и успешной работы на протяжении всего урока.

2. Проверка домашнего задания

Откройте тетради с домашней работой. Выполните самопроверку, сравнив свое решение с ответами, которые вы видите на экране.

3. Актуализация знаний

Давайте повторим те геометрические понятия, которые вам знакомы и сегодня понадобятся на уроке.

1. Координаты вектора – это коэффициенты разложения вектора по коллинеарным векторам.

2. Каждая координата суммы двух векторов равна сумме соответствующих координат этих векторов.

3. Координата вектора равна разности соответствующих координат.

4. Постановка учебной задачи

Что мы изучали на прошлом уроке? (ответы учащихся)

Всё ли мы узнали, изучили по этой теме? Какие задачи стоят перед нами на сегодняшнем уроке? (Закрепить умение решать задачи по определению координаты середины отрезка и длины вектора).

Как можно сформулировать тему нашего урока?

5. Решение задач:

Тема урока: Простейшие задачи в координатах

Откройте тетради и запишите тему урока. У вас на столе лежат листы самооценки. Поставьте себе оценки за домашнюю работу и устную работу. Посмотрите внимательно, какие цели можно поставить для себя на урок? (продолжить фразу)

Вспомнить формулы ….

Научиться применять …

Время у нас ограничено, впереди нас ждут решения интересных задач.

Цель урока: рассмотреть простейшие задачи в координатах и научиться применять их на практике.

Вы разбились на группы. Посмотрите друг на друга. Вам комфортно в таком составе. Хорошо. Проведем с вами мини исследование. Перед вами листы, на которых сформулировано задание. Какова ваша задача? (выполнив полученные задания сделать вывод о простейших задачах в координатах).

2. Работа в группах 4 минуты.

3. Вывод по работе в группах.

4. Мы с вами знаем, как найти координаты середины вектора, зная координаты его начала и конца (сформулировать, спросить ученика) и узнали, как найти длину вектора (сформулировать, спросить ученика). Что еще мы узнали, соединив эти две задачи вместе. ( длину отрезка, расстояние между двумя точками зная координаты этих точек).

Пусть точка М имеет координаты (х₁; у₁), а точка N имеет координаты (х₂; у₂), длина вектора │MN│= │MN│=

Я вам хочу подарить закладки, с основными формулами сегодняшнего урока.

6. Первичное усвоение материала. Устное решение задач.

Теория без практики – мертва, практика без теории невозможна. Теперь мы готовы решать задачи.

Оцените свою активность при решении задач и поставьте отметку в лист самооценки.

7. Первичная проверка усвоение материала:

Как мы можем проверить усвоен ли материал? (Выполнить самостоятельную)

(самостоятельная работа с самопроверкой в классе).

Но для начала дадим своим глазам отдохнуть.

Зарядка для глаз.

Выполнение теста: возьмите карточки и выполните предложенные задания.

Тест (отводится 7 минут).

— Обменяйтесь работами и выполните взаимопроверку. Поставьте оценку, используя критерии

«5» — без ошибок

«4» — 1 ошибка

«3» — 2 ошибки

Перенесите оценку за тест в лист самооценки.

Поднимите руки:

— Кто получил «5»?

— Кто получил «4»?

8. Включение знаний в систему Работа с учебником № 942,

9.Домашнее задание

1. п. 89, № 940 (а, в),

2. № 947 (а) (любителям математики)

3. Подготовить сообщение о Рене Декарте (кто хочет знать больше).

Попытайтесь ответить на вопрос: Почему я взяла имя данного ученого?

10. Итог урока.

Вот и закончился урок

Нам надо подвести итог

— Каким сегодня был для нас урок (закрепление или открытие)?

— Что закрепили на уроке? ( решение простейших задач в координатах: длина вектора, длина отрезка, координаты середины отрезка)

— Вернемся к листу самооценки. В начале нашего урока вы поставили свою цель, ответьте себе на вопрос: Достиг ли я своей цели? Сделайте соответствующую отметку в листе самооценки.

— Кто достиг своей цели, поднимите руки.

— А теперь поставьте себе оценку за урок ( найдите среднее арифметическое своих оценок). Поставить ребятам оценки и аргументировать их.

— Кто получил «5»?

— Кто получил «4»?

— Рефлексия «Оцени себя на уроке». (спросить двух — трех учеников)

Учащимся дается индивидуальная карточка, в которой нужно подчеркнуть фразы, характеризующие работу ученика на уроке по трем направлениям.

Урок Я на уроке Итог

1. интересно 1. работал 1. понял материал

2. скучно 2. отдыхал 2. узнал больше, чем знал

3.безразлично 3.помогал другим 3. не понял

— Вы сегодня хорошо работали, помогали друг другу и справились со всеми заданиями. Благодарю всех за активную работу.

Говорю вам большое спасибо. Урок окончен. До свидания.

infourok.ru

Самостоятельная работа по геометрии. 9 класс. Тема: Простейшие задачи в координатах

Подробности

Категория: Самостоятельные работы по геометрии. 9 класс

 

САМОСТОЯТЕЛЬНАЯ РАБОТА ПО ГЕОМЕТРИИ

9 КЛАСС

ТЕМА: ПРОСТЕЙШИЕ ЗАДАЧИ В КООРДИНАТАХ

 

ВАРИАНТ 1

  1. Вершины треугольника АВС имеют координаты А (−4; 2), В (2; −8), С (10; 16). Отрезок AD — медиана треугольника АВС, а АЕ — медиана треугольника ACD. Найдите

  Ответ: 

 

  2. На осях координат найдите точки, равноудаленные от концов отрезка АВ, если А (−3; 5) и В (6; 4).

  Ответ: (1; 0) и (0; −9).

 

  3. Докажите, что треугольник АВС равнобедренный, и найдите его площадь, если вершины треугольника имеют координаты А (0; 1), В (1; −4), С (5; 2).

  Ответ: S = 13.

 

ВАРИАНТ 2

  1. Вершины треугольника АВС имеют координаты А (−4; 2), В (2; −8), С (10; 16). Отрезок AD — медиана треугольника АВС, а АЕ — медиана треугольника ABD. Найдите

  Ответ:

 

  2. На осях координат найдите точки, равноудаленные от концов отрезка АВ, если А (4; −3) и В (8; 1).

  Ответ: (5; 0) и (0; 5).

 

  3. Докажите, что треугольник АВС равнобедренный, и найдите его площадь, если вершины треугольника имеют координаты А (−4; 1), В (−2; 4), С (1; 2).

  Ответ: S = 6,5.

 

• < Назад
• Вперёд >

metodbook.ru

Простейшие задачи в координатах. 9 класс. План- конспект и презентация урока.

Тема урока: «Простейшие задачи в координатах».

Цели урока: 1) Научится решать задачи с использованием системы координат:

а) нахождение координат середины отрезка;

б) определение длины вектора;

в) определение расстояния между точками.

2) Подготовится к решению задач с использованием метода координат.

Демонстрация: Презентация с решением простейших задач в координатах.

Оборудование: 1) Компьютер.

2) Мультимедийный проектор.

3) Экран.

4) Мультимедийный проектор.

5) Карточки с дифференцированными заданиями.

Структура урока: 1) Организационный момент.

2) Повторение. Проверка домашнего задания.

3) Изучение нового материала.

а) нахождение координат середины отрезка;

б) определение длины вектора;

в) определение расстояния между точками.

4) Закрепление.

5) Домашнее задание.

Литература: 1) Л.С. Атанасян, Б.Ф. Бутузов, С.Б. Кадомцев др. Учебник геометрии для 7-9 классов средней школы. М.: Просвещение 2014.

2) Б.Г. Зив и др. Задачи по геометрии для 7-11 классов. М.: Просвещение. 2015.

3) Л.С. Киселева и др. Методические рекомендации к курсу геометрии 6-8 классов. М.: Просвещение. 2014.

Ход урока.

1. Организационный момент.

Приветствие учащихся. Определение отсутствующих.

2.Повторение. Проверка выполнения домашнего задания.

1) Что называется вектором?

2) Что называется длиной вектора?

3) Как определяется длина вектора?

4) Какие вектора называются коллинеарными?

5) Как выполняется сложение, вычитание векторов и умножение вектора на число? (Три ученика у доски выполняют практические действия над векторами.)

6) Как определяются координаты вектора.

7) Как определяются координаты вектора по его координатам начала и конца.

8) Сформулируйте теорему Пифагора.

3. Изучение нового материала.

1) Сообщение темы и целей урока. (Изучение нового материала проводится с помощью компьютера. Подготовленная презентация демонстрируется через мультимедийный проектор на экран. Меняя слайды презентации объясняется новая тема.)

2) Для повторения определения координат векторов рассмотрим слайд с различными векторами.

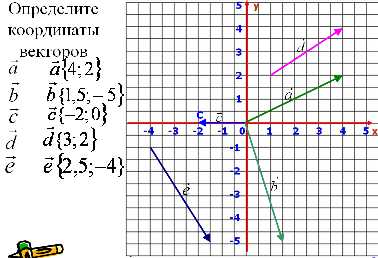
Ученики определяют координаты векторов и через небольшое время сравнивают с ответами.

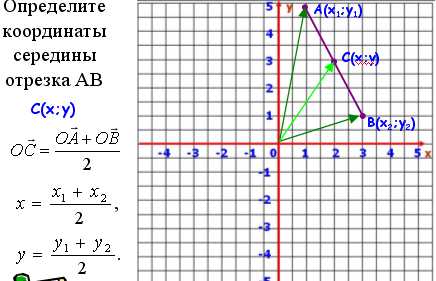
3) Демонстрируется слайд с просьбой определить координаты середины отрезка АВ (с числовыми координатами). Учащиеся легко определяют координаты точки С и пытаются придумать правило для определения координат середины отрезка (как среднее арифметическое координат концов отрезка).

4) Произвести вывод формулы расчета координат середины отрезка (с использованием задачи №1 п. 84).

5) В качестве закрепления демонстрируется слайд с задачами на нахождение координат середины отрезка.

а) Определите координаты точки К — середины отрезка MN, если M(2;-5) и N(4;-1) K(3;-3).

б) Определите координаты точки R — середины отрезка PQ, если P(-3;0) и Q(8;0) R(2,5;0).

6) Далее рассматривается слайд для определения длины векторов (при этом учащиеся должны догадаться использовать теорема Пифагора при определении длины векторов неколлинеарных базисным векторам).

7) Аналогично выводится формула определения длины векторов по их координатам.

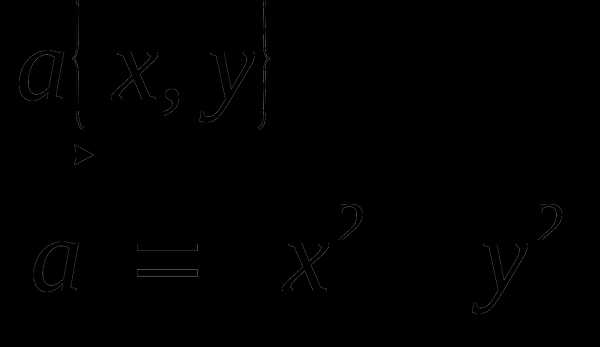
8) В качестве закрепления предлагается решить задачку на определение длин нескольких векторов.

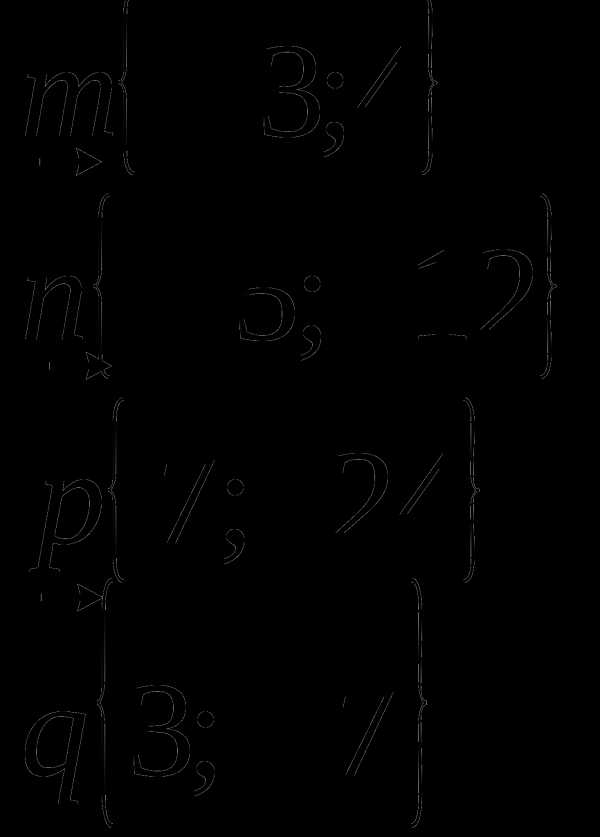
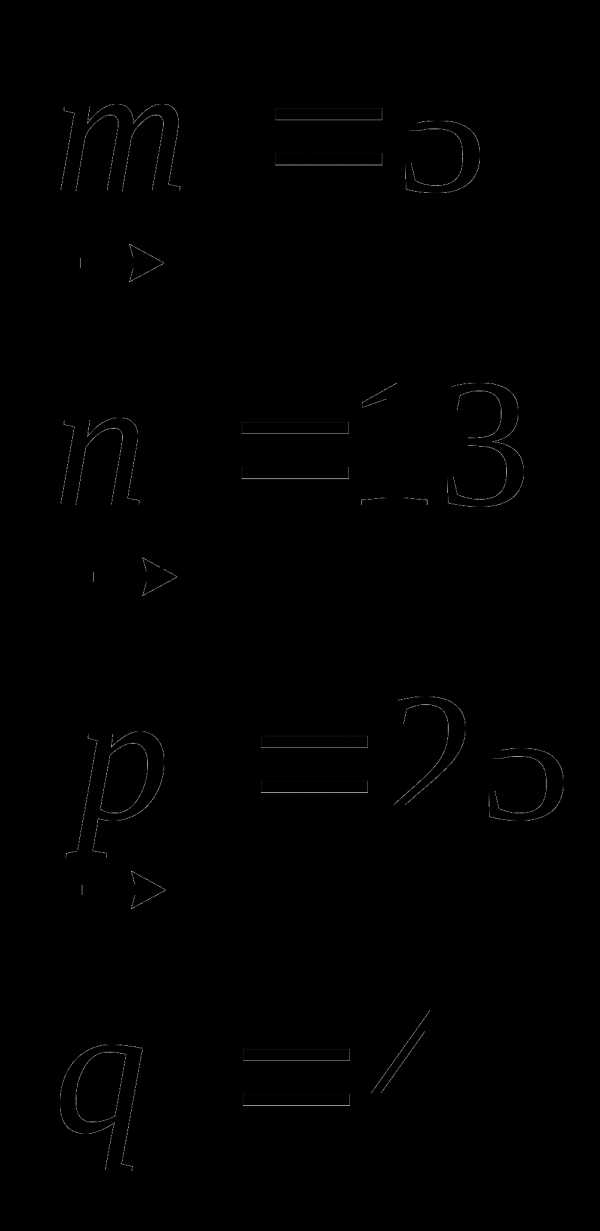
9) Демонстрируется слайд с методом определения длины отрезка по координатам концов отрезка (учащихся следует подвести к превращению отрезка в вектор и сведению к задаче о нахождении длины вектора).

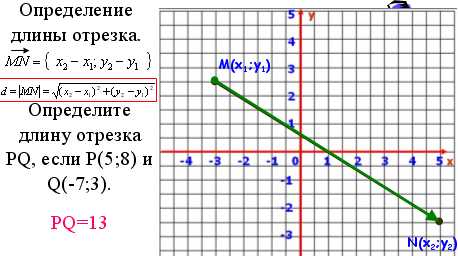
4. Закрепление.

1. Что нового узнали на уроке?

2. Как находятся координаты середины отрезка?

3. Как находится длина вектора по его координатам?

4. Как определить длину отрезка по координатам концов отрезка?

5. Решите задачи: №№ 937, 938 а)д)е), 940 а) б), 942.

5.Домашнее задание

1. Итоги урока.

2. Оценки за урок.

3. Домашнее задание: п89, №№ 936, 938 в)г), 940 в)г).

infourok.ru

Тест по геометрии (9 класс) по теме: Простейшие задачи в координатах

По теме: методические разработки, презентации и конспекты

Урок по теме «Простейшие задачи в координатах»

урок по формированию и контроля знаний, умений и навыков по теме «Простейшие задачи в координатах». Содержит математический диктант в 2 вариантахи практикум по решению задач….

Самостоятельная работа по геометрии для 11 класса по теме: «Простейшие задачи в координатах», по учебнику Атанасяна.

Актуализация знаний по теме: «Простейшие задачи в координатах». Нахождение координат вектора по координатам точек, выяснение коллениарности и компланарности точек….

Урок геометрии в 9 классе по теме «Простейшие задачи в координатах» (Конспект + Презентация)

Урок геометрии в 9 классе по теме «Простейшие задачи в координатах» (Конспект + Презентация)…

Конспект и презентация урока геометрии в 9 классе с использованием ЭОР «Простейшие задачи в координатах»

Конспект и презентация урока геометрии в 9 классе с использованием ЭОР «Простейшие задачи в координатах»….

Урок геометрии в 9 классе. Тема: «Простейшие задачи в координатах». Презентация к уроку.

Методическая разработка включает конспект урока геометрии в 9 классе по теме «Простейшие задачи в координатах» и презентацию к уроку. Предназначена для использования в общеобразовательных классах. УМК…

Координаты вектора. Простейшие задачи в координатах. Тематический зачет по геометрии в 9 классе.

Л.С.Атанасян, В.Ф.Бутузов, С.Б. Кадомцев, Э.Я. Позняк, И.И.Юдина, геометрия 7-9Цель: обобщить знания учащихся по теме: «Метод координат. Простейшие задачи в координатах», установить нет ли пробелов….

9 класс. Самостоятельная работа (С-3). Связь между координатами вектора и координатами его начала и конца. Простейшие задачи в координатах.

9 класс. Самостоятельная работа (С-3). Связь между координатами вектора и координатами его начала и конца. Простейшие задачи в координатах. Дидактические материалы. Б.Г. Зив…

nsportal.ru

Самостоятельная работа по геометрии по теме Простейшие задачи в координатах, 9 класс

Геометрия 9 класс
Самостоятельная работа по теме: «Простейшие задачи в координатах»
I вариант
Найдите координаты вектора AB, если А(-7; 6), В(-1; 2).
Найдите длину вектора AB, если А(-7; 6), В(-1; 2).
Найдите координаты точки К, которая является серединой отрезка MN ,
если М(6; -5), N(3; -9)
Найдите расстояние между точками M и N, т.е. длину отрезка MN, если М(6; -5), N(3; -9)
Найдите медиану CD треугольника АВС, вершины которого имеют координаты: А(-1; 2), В(5; -6), С(6; 4)
Геометрия 9 класс
Самостоятельная работа по теме: «Простейшие задачи в координатах»
II вариант
Найдите координаты вектора MN, если M(4; -5), N(7; -9).
Найдите длину вектора MN, если M(4; -5), N(7; -9).
Найдите координаты точки C, которая является серединой отрезка AB ,
если A(-2; 1), B(-10; -5)
Найдите расстояние между точками A и B, т.е. длину отрезка AB, если A(-2; 1),
B(-10; -5)
Найдите медиану BD треугольника АВС, вершины которого имеют координаты: А(-2; -3), В(-3; 5), С(4; 1)
Геометрия 9 класс
Самостоятельная работа по теме: «Простейшие задачи в координатах»
I вариант
Найдите координаты вектора AB, если А(-7; 6), В(-1; 2).
Найдите длину вектора AB, если А(-7; 6), В(-1; 2).
Найдите координаты точки К, которая является серединой отрезка MN ,
если М(6; -5), N(3; -9)
Найдите расстояние между точками M и N, т.е. длину отрезка MN, если М(6; -5), N(3; -9)
Найдите медиану CD треугольника АВС, вершины которого имеют координаты: А(-1; 2), В(5; -6), С(6; 4)

Геометрия 9 класс
Самостоятельная работа по теме: «Простейшие задачи в координатах»
II вариант
Найдите координаты вектора MN, если M(4; -5), N(7; -9).
Найдите длину вектора MN, если M(4; -5), N(7; -9).
Найдите координаты точки C, которая является серединой отрезка AB ,
если A(-2; 1), B(-10; -5)
Найдите расстояние между точками A и B, т.е. длину отрезка AB, если A(-2; 1),
B(-10; -5)
Найдите медиану BD треугольника АВС, вершины которого имеют координаты: А(-2; -3), В(-3; 5), С(4; 1)
Самостоятельная работа по теме: «Простейшие задачи в координатах»
II вариант
Найдите координаты вектора MN, если M(4; -5), N(7; -9).
Найдите длину вектора MN, если M(4; -5), N(7; -9).
Найдите координаты точки C, которая является серединой отрезка AB ,
если A(-2; 1), B(-10; -5)
Найдите расстояние между точками A и B, т.е. длину отрезка AB, если A(-2; 1),
B(-10; -5)
Найдите медиану BD треугольника АВС, вершины которого имеют координаты: А(-2; -3), В(-3; 5), С(4; 1)
Геометрия 9 класс
Самостоятельная работа по теме: «Простейшие задачи в координатах»
I вариант
Найдите координаты вектора AB, если А(-7; 6), В(-1; 2).
Найдите длину вектора AB, если А(-7; 6), В(-1; 2).
Найдите координаты точки К, которая является серединой отрезка MN ,
если М(6; -5), N(3; -9)
Найдите расстояние между точками M и N, т.е. длину отрезка MN, если М(6; -5), N(3; -9)
Найдите медиану CD треугольника АВС, вершины которого имеют координаты: А(-1; 2), В(5; -6), С(6; 4)

univerfiles.com

Самостоятельная работа по теме Простейшие задачи в координатах (9 класс)

Геометрия 9 класс

Самостоятельная работа по теме:
«Простейшие задачи в координатах»

I вариант

Найдите координаты вектора 13 EMBED Equation.3 1415, если А(-7; 6), В(-1; 2).

Найдите длину вектора 13 EMBED Equation.3 1415, если А(-7; 6), В(-1; 2).

Найдите координаты точки К, которая является серединой отрезка MN , если М(6; -5), N(3; -9)

Найдите расстояние между точками M и N, т.е. длину отрезка MN, если М(6; -5), N(3; -9)

Найдите медиану CD треугольника АВС, вершины которого имеют координаты: А(-1; 2), В(5; -6), С(6; 4)

Геометрия 9 класс

Самостоятельная работа по теме:
«Простейшие задачи в координатах»

II вариант

Найдите координаты вектора 13 EMBED Equation.3 1415, если M(4; -5), N(7; -9).

Найдите длину вектора 13 EMBED Equation.3 1415, если M(4; -5), N(7; -9).

Найдите координаты точки C, которая является серединой отрезка AB , если A(-2; 1), B(-10; -5)

Найдите расстояние между точками A и B, т.е. длину отрезка AB, если A(-2; 1), B(-10; -5)

Найдите медиану BD треугольника АВС, вершины которого имеют координаты: А(-2; -3), В(-3; 5), С(4; 1)

Геометрия 9 класс

Самостоятельная работа по теме:
«Простейшие задачи в координатах»

III вариант

Найдите координаты вектора 13 EMBED Equation.3 1415, если А(8; -5), В(2; 3).

Найдите длину вектора 13 EMBED Equation.3 1415, если А(8; -5), В(2; 3).

Найдите координаты точки К, которая является серединой отрезка MN , если М(1; -5), N(-2; -1)

Найдите расстояние между точками M и N, т.е. длину отрезка MN, если М(1; -5), N(-2; -1)

Найдите медиану AD треугольника АВС, вершины которого имеют координаты: А(2; 4), В(-5; -1), С(3; -5)

Геометрия 9 класс

Самостоятельная работа по теме:
«Простейшие задачи в координатах»

IV вариант

Найдите координаты вектора 13 EMBED Equation.3 1415, если M(-1; -7), N(2; -3).

Найдите длину вектора 13 EMBED Equation.3 1415, если M(-1; -7), N(2; -3).

Найдите координаты точки C, которая является серединой отрезка AB , если A(5; -4), B(-3; 2)

Найдите расстояние между точками A и B, т.е. длину отрезка AB, если A(5; -4), B(-3; 2)

Найдите медиану NP треугольника MNK, вершины которого имеют координаты: M(-4; 3), N(-3; —
·
·
·
·
·
·

weburok.com