Самостоятельная работа по геометрии 9 класс – ГДЗ по геометрии 9 класс самостоятельные и контрольные работы Иченская

Содержание

ГДЗ по геометрии 9 класс самостоятельные и контрольные работы Иченская

ГДЗ > Геометрия > 9 класс > Самостоятельные и контрольные работы по геометрии 9 класс. ФГОС Иченская Просвещение

Изображения обложек учебников приведены на страницах данного сайта исключительно в качестве иллюстративного материала (ст. 1274 п. 1 части четвертой Гражданского кодекса Российской Федерации)

Для планомерной и эффективной подготовки к сдаче итоговой аттестации в 9-м классе (ОГЭ по математике) важно глубоко и полно проработать все темы входящих в экзамен дисциплин. Особенно много трудностей вызывают задания по геометрии. Проводя регулярный самостоятельный контроль своих знаний в течение года, девятиклассники будут более уверены, успешно подготовятся к испытанию.
Хорошее учебное пособие, способное помочь в достижении такого результата — самостоятельные и контрольные работы по геометрии для 9 класса, рекомендуемые многими учителями-предметниками. Автор сборника – Иченская М. А., подошла к его созданию творчески, сбалансировав глубокую проработку сложных тем и отработку до автоматизма заданий, связанных с использованием базовых аксиом и теорем по геометрии.

Материалы позволяют понять, какие именно тематики вызывают наибольшие вопросы, проблемы и проработать их максимально подробно. Для тех, кто использует пособие в целях самостоятельной подготовки, необходим решебник к нему. День за днем отрабатывая решения по нему, девятиклассники поймут логику получения верных ответов. Также они научатся грамотно, правильно записывать их. От того, насколько верной будет запись, в немалой степени зависит итоговая оценка на ОГЭ.

КР-1. Глава X. Метод координат:

КР-2. Глава XI. Соотношения между сторонами и углами треугольника:

КР-3. Глава XII. Длина окружности и площадь круга:

КР-4. Глава XIII. Движения:

КР-5. Итоговая контрольная работа:

С-1. Координаты вектора:

С-2. Простейшие задачи в координатах:

С-3. Уравнения окружности и прямой:

С-4. Синус, косинус, тангенс угла:

С-5. Соотношения между сторонами и углами треугольника:

С-6. Скалярное произведение векторов:

С-7. Правильные многоугольники:

С-8. Длина окружности и площадь круга:

С-9. Понятие движения:

С-10. Параллельный перенос и поворот:

С-11. Решение задач:

С-12. Решение задач:

С-13. Решение задач:

1. Треугольники:

2. Четырехугольники:

3. Окружность. Правильные многоугольники:

www.euroki.org

Самостоятельные и контрольные работы по геометрии 9 класс

Самостоятельная работа по теме «Скалярное произведение векторов»

1 вариант

1. Вычислите скалярное произведение векторов а и b, если а{-5; 2} и b{3; 9}.

2. При каком значении х векторы а и b перпендикулярны, если а {4; -3} и b{-6; х}.

3. Найти угол между векторами а и b, если а {5; 5√3} и b{4; 4√3}.

2 вариант

1. Вычислите скалярное произведение векторов а и b, если а{6; -4} и b{1; 2}.

2. При каком значении х векторы а и b перпендикулярны, если а {-9; -5} и b{2; х}.

3. Найти угол между векторами а и b, если а {2; -2√2} и b{1; -√2}.

Самостоятельная работа по теме «Скалярное произведение векторов»

1 вариант

1. Вычислите скалярное произведение векторов а и b, если а{-5; 2} и b{3; 9}.

2. При каком значении х векторы а и b перпендикулярны, если а {4; -3} и b{-6; х}.

3. Найти угол между векторами а и b, если а {5; 5√3} и b{4; 4√3}.

2 вариант

1. Вычислите скалярное произведение векторов а и b, если а{6; -4} и b{1; 2}.

2. При каком значении х векторы а и b перпендикулярны, если а {-9; -5} и b{2; х}.

3. Найти угол между векторами а и b, если а {2; -2√2} и b{1; -√2}.

Самостоятельная работа по теме «Скалярное произведение векторов»

1 вариант

1. Вычислите скалярное произведение векторов а и b, если а{-5; 2} и b{3; 9}.

2. При каком значении х векторы а и b перпендикулярны, если а {4; -3} и b{-6; х}.

3. Найти угол между векторами а и b, если а {5; 5√3} и b{4; 4√3}.

2 вариант

1. Вычислите скалярное произведение векторов а и b, если а{6; -4} и b{1; 2}.

2. При каком значении х векторы а и b перпендикулярны, если а {-9; -5} и b{2; х}.

3. Найти угол между векторами а и b, если а {2; -2√2} и b{1; -√2}.

infourok.ru

Самостоятельные работы по геометрии 9 класс к учебнику Геометрия 9 (авторы В.Ф.Бутузов. С.Б. Кадомцев)

Самостоятельная работа по теме «Вписанная и описанная окружности»

1 вариант

1.Центр вписанной окружности – это точка пересечения _______________ треугольника.

2.Если все стороны треугольника касаются окружности, то окружность называется ______________, а треугольник называется __________________________.

3.Сформулируйте теорему о пересечении серединных перпендикуляров к сторонам треугольника.

4.Сформулируйте теорему об окружности, описанной около треугольника.

5.Радиус вписанной в равносторонний треугольник окружности равен 2 см, чему равен радиус описанной около этого треугольника окружности?

6.Биссектрисы углов С и В треугольника АВС пересекаются в точке О, угол С равен 110 градусам, угол В равен 40 градусам. Чему равна градусная мера угла САО?

7.Треугольник АВС вписан в окружность, дуга ВС равна 80 градусам. Чему равна градусная мера угла ВАС?

8.Прямоугольный треугольник АВС вписан в окружность, гипотенуза АС равна 36 см. Чему равен радиус описанной около этого треугольника окружности?

9.Треугольник ВОК вписан в окружность, сторона ВО является диаметром окружности. Назовите прямой угол этого треугольника.

10.В равнобедренный треугольник АВС с основанием АС вписана окружность, К, М, Т – точки касания соответственно сторон АВ, ВС и АС. Найдите периметр треугольника АВС, если АТ = 6 см, ВМ = 3 см.

2 вариант

1.Центр описанной окружности – это точка пересечения ____________________треугольника.

2.Если все вершины треугольника лежат на окружности, то окружность называется

___________ , а треугольник называется ___________________________.

3.Сформулируйте теорему о пересечении биссектрис треугольника.

4.Сформулируйте теорему о вписанной в треугольник окружности.

5.Радиус описанной около равностороннего треугольника окружности равен 4 см, чему равен радиус вписанной в этот треугольник окружности ?

6.Биссектрисы углов А и В треугольника АВС пересекаются в точке О, угол А равен 120 градусам, угол В равен 30 градусам. Чему равна градусная мера угла АСО?

7.ТреугольникАВС вписан в окружность, угол В равен 65 градусам. Чему равна градусная мера дуги АС?

8.Прямоугольный треугольник АВС вписан в окружность, гипотенуза ВС равна 14 см. Чему равен диаметр описанной около этого треугольника окружности?

9. Треугольник ТОР вписан в окружность, сторона ОР является диаметром окружности. Назовите прямой угол этого треугольника.

10. В равнобедренный треугольник ТМК с основанием ТК вписана окружность, А, В. С – точки касания соответственно сторон ТМ, МК и КТ. Найдите периметр треугольника ТМК, если ВК = 5 см, АМ = 2 см.

Самостоятельная работа по теме «Многоугольник»

1 вариант

1.Многоугольник-это простая замкнутая ______________________________

2.Если все стороны многоугольника касаются окружности, то окружность называется

_____________________, а многоугольник называется _________________

3.Начертите выпуклый семиугольник.

4.Чему равна сумма углов выпуклого шестиугольника?

5.Сумма углов выпуклого многоугольника равна 900 градусам. Чему равно число его сторон?

6.Сумма двух противоположных сторон описанного четырехугольника равна 18 см. Найдите его периметр.

7.В окружность вписан четырехугольник АВСD, угол А равен 60 градусам, угол В равен 80 градусам. Найти углы С и D.

8.Найдите количество диагоналей восьмиугольника.

9.Найдите углы правильного двенадцатиугольника.

10.Сформулируйте теорему об окружности, описанной около правильного многоугольника.

2 вариант

1.Выпуклый многоугольник называется _____________, если равны все его стороны и углы.

2.Если все вершины многоугольника лежат на окружности, то окружность называется ________________, а многоугольник называется ____________

3.Начертите выпуклый восьмиугольник.

4.Чему равна сумма углов выпуклого семиугольника?

5.Сумма углов выпуклого многоугольника равна 540 градусам. Чему равно число его сторон?

6.Периметр описанного четырехугольника АВСD равен 38 см. Найдите сумму АВ+СD.

7.В окружность вписан четырехугольник АВСD, угол В равен 120 градусам, угол С равен 110 градусам. Найти углы А и D.

8.Найдите количество диагоналей девятиугольника.

9.Найдите углы правильного десятиугольника.

10.Сформулируйте теорему об окружности, вписанной в правильный многоугольник.

Самостоятельная работа по теме «Четырехугольники»

1 вариант

1. Параллелограммом называется четырехугольник, противоположные стороны которого попарно __________________________________________.

2. Если один из углов параллелограмма прямой, то этот параллелограмм — _____________.

3. Сформулируйте особое свойство ромба.

4. Трапецией называется четырехугольник, две стороны которого параллельны, а две другие стороны __________________________.

5.Трапеция называется равнобедренной, если ______________________.

6. Назовите и начертите фигуру, имеющую только две оси симметрии.

7. Один угол параллелограмма на 80 градусов больше другого. Найдите все углы параллелограмма.

8. В ромбе АВСD диагонали АС и ВD пересекаются в точке О. Назовите вид треугольника АВО.

9. Острый угол равнобедренной трапеции равен 30 градусам. Найдите все углы этой трапеции.

10. Одна сторона прямоугольника в 2 раза больше другой. Найдите все стороны прямоугольника, если периметр прямоугольника равен 24 см.

2 вариант

1. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — __________________________.

2. Параллелограмм, все стороны которого равны, называется _____________.

3. Сформулируйте особое свойство прямоугольника.

4. Параллельные стороны трапеции называются ее _______________, а две другие стороны называются ______________________.

5. Трапеция называется прямоугольной, если ___________________________.

6. Назовите и начертите фигуру, имеющую только одну ось симметрии.

7. Один угол параллелограмма на 60 градусов больше другого. Найдите все углы параллелограмма.

8. В ромбе АВСD проведена диагональ АС. Назовите вид треугольника АВС.

9. Острый угол прямоугольной трапеции равен 40 градусам. Найдите все углы этой трапеции.

10. Одна сторона прямоугольника в 3 раза больше другой. Найдите все стороны прямоугольника, если периметр прямоугольника равен 24 см.

Контрольная работа № 3 по теме «Многоугольники»

1 вариант

1.Диагонали прямоугольника АВСD пересекаются в точке О,

угол АВО равен 36 градусам. Найдите угол АОD.

2. Найдите углы равнобедренной трапеции, если один из ее углов на 30 градусов больше другого.

3.Стороны параллелограмма относятся как 1 : 2 , а его периметр равен 30 см. Найдите все стороны параллелограмма.

4.В прямоугольной трапеции АВСD с основаниями ВС и АD угол А равен 90 градусам, а угол D равен 45 градусам. Найдите большее основание АD, если боковая сторона АВ равна 7 см, а меньшее основание ВС равно 5 см.

2 вариант

1.Диагонали прямоугольника МNKP пересекаются в точке О,

угол МОN равен 64 градусам. Найдите угол ОМР.

2.Найдите углы прямоугольной трапеции, если один из углов при одной из боковых сторон на 48 градусов больше другого угла при этой же боковой стороне.

3.Стороны параллелограмма относятся как 3 : 1 , а его периметр равен 40 см. Найдите все стороны параллелограмма.

4. В равнобедренной трапеции АВСD c основаниями ВС и АD угол А равен 60 градусам, боковая сторона АВ равна 4 см, меньшее основание ВС равно 5 см. Найдите большее основание АD.

Контрольная работа № 3 по теме «Многоугольники»

1 вариант

1.Диагонали прямоугольника АВСD пересекаются в точке О,

угол АВО равен 36 градусам. Найдите угол АОD.

2. Найдите углы равнобедренной трапеции, если один из ее углов на 30 градусов больше другого.

3.Стороны параллелограмма относятся как 1 : 2 , а его периметр равен 30 см. Найдите все стороны параллелограмма.

2 вариант

1.Диагонали прямоугольника МNKP пересекаются в точке О,

угол МОN равен 64 градусам. Найдите угол ОМР.

3.Стороны параллелограмма относятся как 3 : 1 , а его периметр равен 40 см. Найдите все стороны параллелограмма.

Самостоятельная работа по теме «Средняя линия треугольника и трапеции»

1 вариант

1.Сформулируйте определение средней линии треугольника.

2.Средняя линия трапеции параллельна ___________ и равна __________.

3.Прямая, проходящая через середину стороны треугольника __________ другой его стороне, делит третью сторону пополам.
4.Найдите среднюю линию треугольника, если она параллельна стороне равной 7 см.

5.Основания трапеции равны 8 см и 10 см.Найдите среднюю линию трапеции

6.Диагонали параллелограмма АВСD пересекаются в точке О, точка М – середина стороны ВС. Найдите ОМ, если АВ = 6см.

7.Сколько средних линий можно провести в трапеции?

8.Одно из оснований трапеции вдвое больше другого, а средняя линия трапеции равна 15 см. Найдите основания трапеции.

2 вариант

1.Сформулируйте определение средней линии трапеции.

2.Средняя линия треугольника _______ одной из его сторон и равна ______.

3.Прямая, проходящая через середину боковой стороны трапеции _________

ее основаниям, проходит через середину другой боковой стороны.

4.Найдите среднюю линию треугольника, если она параллельна стороне равной 9 см.

5.Основания трапеции равны 9 см и 15 см.Найдите среднюю линию трапеции

6.Диагонали параллелограмма АВСD пересекаются в точке О, точка М – середина стороны АD. Найдите ОМ, если АВ = 8 см.

7.Сколько средних линий можно провести в треугольнике?

8.Одно из оснований трапеции втрое больше другого, а средняя линия равна 12 см. Найдите основания трапеции.

Самостоятельная работа по теме «Теорема Фалеса»

1 вариант

1. Сформулируйте теорему о пересечении высот треугольника.

2. Если на одной из сторон угла от его вершины отложить последовательно несколько ___________ отрезков и через их концы провести _____________ прямые, пересекающие другую сторону угла, то они отсекут на второй стороне равные между собой отрезки.

3.Что называют ортоцентром треугольника.

4.Укажите вид треугольника, в котором ортоцентр расположен вне треугольника.

5. На стороне угла с вершиной О отложены равные друг другу отрезки ОА1, А1А2, А2А3, А3А4, ….., А8А9, и через их концы проведены параллельные прямые, пересекающие другую сторону угла в точках В1, В2,……, В9. Найдите В3В7, если ОВ9=27 см.

6.Условие задачи № 5. Найдите В3В6, если В2В7=60 см.

7. Медианы АА1 и ВВ1 треугольника АВС пересекаются в точке О. Найдите АА1, если АО = 12см.

8. Медианы АА1 и ВВ1 треугольника АВС пересекаются в точке О. Найдите АО, если АА1 = 27 см.

2 вариант

1. Сформулировать теорему о пересечении медиан треугольника.

3.Укажите вид треугольника, в котором ортоцентр расположен внутри треугольника.

4.Укажите вид треугольника, в котором ортоцентр расположен в одной из вершин треугольника.

6. Условие задачи № 5. Найдите В2В7, если В1В7=60 см.

7. Медианы АА1 и ВВ1 треугольника АВС пересекаются в точке О. Найдите АО, если АА1 = 36 см.

8. Медианы АА1 и ВВ1 треугольника АВС пересекаются в точке О. Найдите АА1, если АО = 18 см.

Контрольная работа № 4 по теме «Теорема Фалеса»

1 вариант

1. Отрезки МК, КР и МР – средние линии треугольника АВС. Найдите стороны треугольника, если МК= 8 см, КР = 6,5 см, МР = 7 см. (рис. 1)

2. В треугольнике АВС отрезок ЕР параллелен стороне АВ и АЕ = ЕС. Найдите периметр треугольника АВС, если

АЕ = 8см, ВР = 7 см и АВ = 13 см. (рис. 2)

3. Медианы АА1 и ВВ1 треугольника АВС пересекаются в точке О. Найдите ВВ1, если ВО = 18 см.

4. Одно из оснований трапеции втрое больше другого, а средняя линия трапеции равна 14 см. Найдите основания трапеции.

2 вариант

1. Отрезки МК, КР и МР – средние линии треугольника АВС. Найдите МК, КР и МР, если АВ = 15 см, ВС= 12 см,

АС = 8 см. (рис. 1)

2. В треугольнике АВС отрезок ЕР параллелен стороне АВ и АЕ = ЕС. Найдите периметр треугольника АВС, если

АЕ = 9 см, ВР = 6 см и ЕР = 7 см. (рис. 2)

3. Медианы АА1 и ВВ1 треугольника АВС пересекаются в точке О. Найдите ВО, если ВВ1 = 33 см.

4. Одно из оснований трапеции на 6 см больше другого, а средняя линия трапеции равна 13 см. Найдите основания трапеции.

1 вариант

2. В треугольнике АВС отрезок ЕР параллелен стороне АВ и АЕ = ЕС. Найдите периметр треугольника АВС, если

АЕ = 8см, ВР = 7 см и АВ = 13 см. (рис. 2)

3. Медианы АА1 и ВВ1 треугольника АВС пересекаются в точке О. Найдите ВВ1, если ВО = 18 см.

2 вариант

1. Отрезки МК, КР и МР – средние линии треугольника АВС. Найдите МК, КР и МР, если АВ = 15 см, ВС= 12 см,

АС = 8 см. (рис. 1)

2. В треугольнике АВС отрезок ЕР параллелен стороне АВ и АЕ = ЕС. Найдите периметр треугольника АВС, если

АЕ = 9 см, ВР = 6 см и ЕР = 7 см. (рис. 2)

3. Медианы АА1 и ВВ1 треугольника АВС пересекаются в точке О. Найдите ВО, если ВВ1 = 33 см.

Самостоятельная работа по теме «Пропорциональные отрезки. Косинус и синус острого угла»

1 вариант

1. Сформулируйте определение синуса острого угла.

2. Запишите основное тригонометрическое тождество.

3. Если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то косинусы этих углов ________________.

4. Может ли косинус острого угла быть больше 1?

5. Отрезки АВ и СD пропорциональны отрезкам А1В1 и С1D1. Найдите С1D1, если АВ = 36 см, СD = 20 см, А1В1 = 27 см.

6. В треугольнике АВС угол С – прямой, АВ = 13 см, АС= 5 см, ВС= 12 см. Найдите синусы углов А и В.

7. В треугольнике АВС угол С – прямой, АВ = 10 см, АС= 6 см, ВС= 8 см. Найдите косинусы углов А и В.

8. Найдите sinA , если cosA = 0,6.

2 вариант

1. Сформулируйте определение косинуса острого угла.

2. Отрезки АВ и СD пропорциональны отрезкам А1В1 и С1D1, если __________________________________.

3. Если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то синусы этих углов ________________.

4. Может ли синус острого угла быть меньше 1?

5. Отрезки АВ и СD пропорциональны отрезкам А1В1 и С1D1. Найдите СD, если АВ = 48 см, С1D1= 10 см, А1В1 = 16 см.

6. В треугольнике АВС угол С – прямой, АВ = 5 см, АС= 3 см, ВС= 4 см. Найдите косинусы углов А и В.

7. В треугольнике АВС угол С – прямой, АВ = 17 см, АС= 8 см, ВС= 15 см. Найдите синусы углов А и В.

8. Найдите cosA , если sinA= 0,8.

Самостоятельная работа по теме «Среднее геометрическое, среднее арифметическое двух отрезков, теорема Пифагора».

1 вариант

1. Отрезок XY называется средним геометрическим отрезков

АВ и СD, если ___________.

2. Верно ли утверждение «Среднее арифметическое двух неравных отрезков меньше их среднего геометрического».

3. Сформулируйте теорему Пифагора.

4. Запишите длины сторон любого пифагорового треугольника.

5. Найдите длину отрезка АВ, если он является средним геометрическим отрезков СК = 4 см и МЕ = 9 см.

6. В треугольнике АВС угол С прямой. Найдите АВ, если АС = 8м, ВС = 15м.

7. В треугольнике АВС угол С прямой. Найдите АС, если АВ = 10м, ВС = 6м.

8. Найдите углы треугольника, стороны которого равны 1, 1, 2.

2 вариант

1. Высота прямоугольного треугольника, проведенная к гипотенузе, является __________________ отрезков, на которые она разделяет гипотенузу.

2. Верно ли утверждение «Среднее арифметическое двух равных отрезков больше их среднего геометрического».

3. Сформулируйте теорему, обратную теореме Пифагора.

4. Запишите длины сторон египетского треугольника.

5. Найдите длину отрезка АВ, если он является средним геометрическим отрезков СК = 2 см и МЕ = 32 см.

6. В треугольнике АВС угол С прямой. Найдите АВ, если АС = 12м, ВС = 5м.

7. В треугольнике АВС угол С прямой. Найдите АС, если АВ = 17м, ВС = 8м.

8. Найдите углы треугольника, стороны которого равны 1, 3, 2.

Самостоятельная работа по теме

«Теоремы синусов и косинусов»

1 вариант

1.Сформулируйте теорему косинусов.

2.Если треугольник прямоугольный, то теорема косинусов для гипотенузы превращается в теорему ______________.

3.Запишите теорему синусов для треугольника АВС.

4.Запишите теорему косинусов для стороны КМ треугольника КМР.

5.Найдите радиус описанной около треугольника МТЕ окружности, если МТ = 6 см, а угол Е равен 30 градусам.

6.Определите вид треугольника со сторонами 5, 7 и 9.

7.Определите вид треугольника со сторонами 6. 8 и 10.

8.Определите вид треугольника со сторонами 7, 9 и 11.

2 вариант

1.Сформулируйте теорему синусов.

2.Отношение стороны треугольника к синусу противолежащего угла равно ______________ описанной окружности.

3.Запишите теорему синусов для треугольника КМР.

4.Запишите теорему косинусов для стороны ВС треугольника АВС.

5.Найдите диаметр описанной около треугольника ВСК окружности, если ВК = 14 см, а угол С равен 30 градусам.

6.Определите вид треугольника со сторонами 6, 10 и 11.

7.Определите вид треугольника со сторонами 4, 6 и 8.

8.Определите вид треугольника со сторонами 5, 12 и 13.

Контрольная работа № 5 по теме «Решение треугольников»

1 вариант

1. Найдите периметр прямоугольника АВСD, если АВ = 9 см,

ВD = 15 см.

2. Найдите сторону ВС треугольника АВС, если АС = 1 см,

угол А равен 45 градусам, угол В равен 60 градусам.

3. Найдите сторону АВ треугольника АВС, если ВС= 3 см,

АС = 7 см, угол С равен 60 градусам.

4. В треугольнике АВС проведена биссектриса АD. Найдите ВD,

если АВ = 4 см, ВС= 5 см, АС= 6 см.

2 вариант

1. Найдите периметр прямоугольника АВСD, если АВ = 12 см,

ВD = 20 см.

2. Найдите сторону ВС треугольника АВС, если АС = 1 см,

угол А равен 45 градусам, угол В равен 30 градусам.

3. Найдите сторону АВ треугольника АВС, если ВС= 5 см,

АС = 6 см, угол С равен 60 градусам.

4. В треугольнике АВС проведена биссектриса АD. Найдите ВD,

если АВ = 6 см, ВС= 7 см, АС= 8 см.

1 вариант

1. Найдите периметр прямоугольника АВСD, если АВ = 9 см,

ВD = 15 см.

2. Найдите сторону ВС треугольника АВС, если АС = 1 см,

угол А равен 45 градусам, угол В равен 60 градусам.

3. Найдите сторону АВ треугольника АВС, если ВС= 3 см,

АС = 7 см, угол С равен 60 градусам.

4. В треугольнике АВС проведена биссектриса АD. Найдите ВD,

если АВ = 4 см, ВС= 5 см, АС= 6 см.

2 вариант

1. Найдите периметр прямоугольника АВСD, если АВ = 12 см,

ВD = 20 см.

2. Найдите сторону ВС треугольника АВС, если АС = 1 см,

угол А равен 45 градусам, угол В равен 30 градусам.

3. Найдите сторону АВ треугольника АВС, если ВС= 5 см,

АС = 6 см, угол С равен 60 градусам.

4. В треугольнике АВС проведена биссектриса АD. Найдите ВD,

если АВ = 6 см, ВС= 7 см, АС= 8 см.

Самостоятельная работа по теме

«Признаки подобия треугольников»

1 вариант

1.Два треугольника называются подобными, если стороны одного треугольника __________ сторонам другого треугольника.

2.Сформулируйте 1 признак подобия треугольников.

3.Чему равен коэффициент подобия равных треугольников?

4.Будут ли подобны равносторонние треугольники?

5.Каким сторонам треугольника DEF пропорциональны стороны АВ, ВС и СА треугольника АВС, если угол А равен углу F, а

угол В равен углу Е. Ответ запишите в виде АВ:ВС:СА = ________.

6.В треугольниках АВС и КОМ угол А равен углу К. Подобны ли эти треугольники?

7.Треугольники АВС и А1В1С1 подобны и угол А равен углу А1, а угол В равен углу В1. Найдите АВ если А1В1 = 6, ВС = 4, В1С1=8.

8.Стороны треугольника равны 7 см, 9 см и 13 см. Найдите наименьшую сторону подобного ему треугольника, у которого наибольшая сторона равна 39 см.

2 вариант

1.Если два треугольника подобны, то углы одного треугольника соответственно ____________ углам другого.

2.Сформулируйте 2 признак подобия треугольников.

3.Чему равно отношение периметров двух подобных треугольников?

4.Будут ли подобны равные треугольники?

5.Каким сторонам треугольника DEF пропорциональны стороны АВ, ВС и СА треугольника АВС, если угол А равен углу E, а

угол В равен углу F. Ответ запишите в виде АВ:ВС:СА = _______.

6.В треугольниках АРК и МВС угол А равен углу М. Подобны ли эти треугольники?

7.Треугольники АВС и А1В1С1 подобны и угол А равен углу А1, а угол В равен углу В1. Найдите АВ если А1В1 = 4, ВС = 3, В1С1=6.

8.Стороны треугольника равны 8 см, 9 см и 12 см. Найдите наибольшую сторону подобного ему треугольника, у которого наименьшая сторона равна 24.

Итоговая контрольная работа по геометрии за курс 8 класса

1 вариант

1. Отрезки МК, КР и МР – средние линии треугольника АВС. Найдите стороны треугольника, если МК= 8 см, КР = 6,5 см, МР = 7 см.

2. Найдите периметр прямоугольника АВСD, если АВ = 9 см,

ВD = 15 см.

3.Точка О – центр окружности, описанной около треугольника АВС. Найдите угол АВС, если угол АОВ равен 114 градусам, а угол ВОС равен 124 градусам.

4. В прямоугольной трапеции АВСD с основаниями ВС и АD угол А равен 90 градусам, а угол D равен 45 градусам. Найдите большее основание АD, если боковая сторона АВ = 7 см, а меньшее основание ВС = 5 см.

2 вариант

1. Отрезки МК, КР и МР – средние линии треугольника АВС. Найдите МК, КР и МР, если

АВ = 15 см, ВС= 12 см, АС = 8 см.

2. Найдите периметр прямоугольника АВСD, если АВ = 12 см,

ВD = 20 см.

3.Точка О – центр окружности, описанной около

треугольника КТР. Найдите угол КТР, если угол

КОТ равен 105 градусам, а угол ТОР равен 107

градусам.

4. В равнобедренной трапеции АВСD c основаниями ВС и АD угол А равен 60 градусам, боковая сторона АВ = 4 см, меньшее основание ВС = 5 см.

Найдите большее основание АD.

Самостоятельная работа по теме «Площади многоугольника, прямоугольника, треугольника»

1 вариант

1. Сколько квадратных миллиметров в одном квадратном метре?

2. Верно ли утверждение: любые два равносоставленных многоугольника равновелики?

3. Найти площадь ромба, если его диагонали равны 45 и 20.

4. Найти площадь прямоугольного треугольника со сторонами 6, 10 и 8.

5. Коэффициент подобия двух треугольников равен 5. Найти отношение площади большего треугольника к площади меньшего.

6. Найти площадь треугольника, если высота равна 6, а основание в два раза больше.

7. Чему равно отношение площадей треугольников, имеющих равные высоты?

8. Диагонали квадрата АВСD пересекаются в точке О.Площадь треугольника АВО равна 16 см. Найти сторону квадрата.

2 вариант

1. Сколько квадратных дециметров в одном квадратном километре?

2. Верно ли утверждение: любые два равновеликих многоугольника равносоставлены?

3. Найти площадь квадрата, если его диагональ равна 14.

4. Найти площадь прямоугольного треугольника со сторонами 5, 13 и 12.

5. Коэффициент подобия двух треугольников равен 6. Найти отношение площади большего треугольника к площади меньшего.

6. Найти площадь треугольника, если высота равна 14, а основание в два раза меньше.

7. Чему равно отношение площадей треугольников, имеющих равные основания?

8. Диагонали квадрата АВСD пересекаются в точке О.Найти площадь треугольника АВО, если сторона квадрата равна 10 см.

Самостоятельная работа по теме

«Площади параллелограмма и трапеции»

1 вариант

1.Верно ли утверждение: Площадь ромба равна

произведению стороны и высоты, проведенной к этой стороне.

2.Верно ли утверждение: Площадь трапеции АВСD с основаниями АВ и СD и высотой ВН вычисляется по формуле:

S = ВН (АВ + СD): 2.

3. Чему равна площадь треугольника АВС, если площадь параллелограмма АВСD равна 8 кв. см.

4.Сторона параллелограмма равна 21см, а высота, проведенная к ней 15 см. Найдите площадь параллелограмма.

5.Стороны параллелограмма равны 6 и 8 см, а угол между ними равен 30 градусов. Найдите площадь параллелограмма.

6.В прямоугольной трапеции основания равны 6 и 10 см, меньшая боковая сторона 5 см. Найдите площадь трапеции.

7.Площадь трапеции с основаниями 5 и 13 см равна 72 кв.см. Найдите высоту трапеции.

8.В параллелограмме АВСD стороны равны 14 и 8 см, высота, проведенная к большей стороне, равна 4 см. Найдите площадь параллелограмма и вторую высоту.

2 вариант

1.Верно ли утверждение: Площадь параллелограмма равна произведению двух его соседних сторон.

2.Верно ли утверждение: Площадь трапеции АВСD с основаниями ВС и АD и высотой СН вычисляется по формуле:

S = СН (ВС + СD): 2.

3. Чему равна площадь параллелограмма АВСD, если площадь треугольника ВСD равна 8 кв. см.

4.Сторона параллелограмма 17 см, а его площадь 187 кв.см. Найдите высоту, проведенную к данной стороне.

5.Стороны параллелограмма равны 4 и 7 см, а угол между ними

равен 45 градусов. Найдите площадь параллелограмма.

6.В прямоугольной трапеции основания равны 4 и 12 см, меньшая боковая сторона 6 см. Найдите площадь трапеции

7.Площадь трапеции с основаниями 7 и 9 см равна 72 кв.см. Найти высоту трапеции.

8. В параллелограмме АВСD высоты равны 10 и 5 см, площадь параллелограмма равна 60 кв.см. Найдите стороны параллелограмма.

Контрольная работа по теме

«Площадь многоугольника»

1 вариант

1.Сторона треугольника равна 5 см, а высота, проведенная к ней, в два раза больше стороны. Найдите площадь треугольника.

2.Стороны параллелограмма равны 6см и 8 см, а угол между ними равен 30 градусам. Найдите площадь параллелограмма.

3.Вычислите площадь трапеции АВСD с основаниями АD и ВС, если АD = 24 см, ВС=16см, угол А равен 45 градусам, а угол D равен 90 градусам.

4.Стороны треугольника равны 10 см, 13 см и 13 см. Найдите длину высоты, проведенной к меньшей стороне.

2 вариант

1.Сторона треугольника равна 12 см, а высота, проведенная к ней в три раза меньше стороны. Найдите площадь треугольника.

2.Стороны параллелограмма равны 4см и 7 см, а угол между ними равен 150 градусам. Найдите площадь параллелограмма.

3.Вычислите площадь трапеции АВСD с основаниями АD и ВС, если АD = 27 см, ВС=13см, СD = 10 cм, а угол D равен 30 градусам.

4.Стороны треугольника равны 10 см, 10 см и 16 см. Найдите длину высоты, проведенной к большей стороне.

Контрольная работа по теме

«Длина окружности и площадь круга»

1 вариант

1. Длина окружности равна 8 . Вычислите площадь круга, ограниченного данной окружностью.

2. Вычислите длину дуги окружности с радиусом

4 см, если ее градусная мера равна 120 градусам. Чему равна площадь соответствующего данной дуге кругового сектора?

3. Найдите площадь кольца, ограниченного двумя окружностями с общим центром и радиусами 3 5см и 7 2 см

4. В квадрат со стороной 6 см вписана окружность. Найдите длину окружности и площадь круга, ограниченного этой окружностью.

2 вариант

1. Длина окружности равна 10 . Вычислите площадь круга, ограниченного данной окружностью.

2. Вычислите длину дуги окружности с радиусом

10 см, если ее градусная мера равна 150 градусам. Чему равна площадь соответствующего данной дуге кругового сектора?

3. Найдите площадь кольца, ограниченного двумя окружностями с общим центром и радиусами 5 3см и

8 2 см.

4. В квадрат со стороной 8 см вписана окружность. Найдите длину окружности и площадь круга, ограниченного этой окружностью.

Контрольная работа по теме

«Площадь многоугольника»

1 вариант

2.Катеты прямоугольного треугольника равны 6 и 8 см. Найдите гипотенузу и площадь треугольника.

3.Найдите площадь и периметр ромба, если его диагонали равны 8 и 10 см.

4.Вычислите площадь трапеции АВСD с основаниями АD и ВС, если АD = 24 см, ВС=16см, угол А равен 45 градусам, а угол D равен 90 градусам.

2 вариант

2.Один из катетов прямоугольного треугольника равен 12 см, а гипотенуза 13 см. Найдите второй катет и площадь треугольника.

3.Диагонали ромба равны 16 и 12 см. Найдите его площадь и периметр.

4.Вычислите площадь трапеции АВСD с основаниями АD и ВС, если АD = 27 см, ВС=13см, СD = 10 cм, а угол D равен 30 градусам.

infourok.ru

ГДЗ по геометрии 9 класс контрольные и самостоятельные работы Журавлев, Малышева

ГДЗ > Геометрия > 9 класс > Контрольные и самостоятельные работы по геометрии 9 класс Журавлев, Малышева Экзамен

Освоение геометрии, по анализу данных результатов текущих проверочных работ, ВПР и итоговых испытаний, является наиболее сложной задачей в рамках школы. Чтобы успешно подготовиться к ОГЭ, желательно не только регулярно решать много задач по дисциплине, но и использовать решебник, чтобы вникнуть в логику получения верных результатов. Более того, такая работа должна быть систематической, в идеале — ежедневной.
Педагоги-предметники, рекомендуя грамотно работать с ГДЗ, советуют обращать внимание на особенности самого сборника, учебника. Например, контрольные и самостоятельные работы по геометрии 9 класс, составленные группой авторов под руководством Малышевой Л. А. и Журавлева С. Г., разбиты на 4 варианта. Каждый предполагает свой уровень сложности, что учтено и в подаче ответов в разъяснительных материалах.
Имея под рукой такой комплекс, можно планомерно и качественно подготовиться и получить высокий балл на обязательном экзамене по математике, куда включен блок геометрии. Все задания, вызвавшие наибольшие затруднения, следует решить еще раз, во второй половине года, ближе к экзамену. Это, по мнению экспертов, позволит максимально повысить шансы на получение высокой оценки и твердых знаний.

По учебнику Атанасяна:

КР-1. Метод координат:

КР-2. Соотношение между сторонами и углами треугольника:

КР-3. Длина окружности и площадь круга:

КР-4. Движение:

КР-5. Итоговая:

По учебнику Погорелова:

КР-1. Подобие фигур:

КР-2. Решение треугольников:

КР-3. Многоугольники:

КР-4. Площади фигур:

По учебнику Атанасяна:

СР-1. Координаты вектора:

СР-2. Простейшие задачи в координатах:

СР-3. Уравнение окружности:

СР-4. Уравнение прямой:

СР-5. Применение векторов и координат к решению задач:

СР-6. Синус, косинус, тангенс угла:

СР-7. Теорема о площади треугольника. Теорема синусов:

СР-8. Теорема косинусов. Решение треугольников:

СР-9. Скалярное произведение векторов:

СР-10. Решение треугольников. Скалярное произведение:

СР-11. Правильные многоугольники:

СР-12. Длина окружности, площадь круга, площадь кругового сектора:

СР-13. Понятие движения:

СР-14. Параллельный перенос и поворот:

По учебнику Погорелова:

СР-1. Преобразование подобия и его свойства:

СР-2. Признаки подобия треугольников:

СР-3. Подобие прямоугольных треугольников. Свойство биссектрисы:

СР-4. Подобие треугольников:

СР-5. Теорема о вписанных углах и ее следствия:

СР-6. Применение теоремы о вписанных углах и ее следствий в задачах:

СР-7. Теорема косинусов. Соотношение диагоналей и сторон параллелограмма:

СР-8. Теорема синусов и ее следствия:

СР-9. Теоремы косинусов и синусов:

СР-10. Выпуклый многоугольник:

СР-11. Правильные многоугольники:

СР-12. Длина окружности. Радианная мера угла:

СР-13. Площадь прямоугольника, квадрата, параллелограмма:

СР-14. Площадь треугольника:

СР-15. Площадь трапеции, площадь четырехугольника:

СР-16. Окружность и многоугольники:

СР-17. Площади подобных фигур. Площадь круга:

СР-18. Площади фигур:

Самостоятельная работа по геометрии ( 9 класс )

Вариант 2 1. Катеты прямоугольного треугольника равны и 1. Найдите синус наибольшего угла этого треугольника.

Вариант 1

1. В треугольнике ABC угол C равен , АС=24, ВС=7. Найдите sin А.

2. В треугольнике ABC угол C прямой, BC = 6 , sin A = 0,3. Найдите AB.

2. В треугольнике АВС угол С=90°,АС=20,

cos А= . Найдите .

3 В треугольнике ABC угол C равен 90°, AC = 10, tgA = 0,5. Найдите BC.

3. В треугольнике ABC угол C равен 90°, BC = 15, tq А = . Найдите AC.

4. В треугольнике АВС угол С равен 90°, sin А=0,5; Найдите АВ.

В треугольнике ABC угол C равен 90⁰, ВС=4 ,

cos А=, Найдите AC.

Вариант 3

1. Один из острых углов прямоугольного треугольника равен 57°. Найдите его другой острый угол.

2. Найдите гипотенузу прямоугольного треугольника, если его катеты равны соответственно 12 и 5 см.

3.В прямоугольном треугольнике гипотенуза и катет соответственно равны 50м и 30м . Найдите гипотенузу этого треугольника.

4. В треугольнике известно, что АС=6см, ВС=8см , угол равен 90°. Найдите синус, косинус, тангенс и котангенс угла А.

Вариант 4

1. Один из острых углов прямоугольного треугольника равен 19°. Найдите его другой острый угол.

2. Найдите катет прямоугольного треугольника, если его другой катет и гипотенуза соответственно равны 12 дм и 13 дм.

3.В прямоугольном треугольнике катеты равны 7м и 3м соответственно. Найдите гипотенузу этого треугольника.

4. В треугольнике известно, что ВС=8см, АВ=10см, угол равен 90°. Найдите синус, косинус, тангенс и котангенс угла В.

infourok.ru

Самостоятельные работы по геометрии для 9 класса

ДИДАКТИЧЕСКИЕ МАТЕРИАЛЫ ДЛЯ 9 КЛАССА ПО ГЕОМЕТРИИ

ДЛЯ ПОДГОТОВКИ К ГИА

САМОСТОЯТЕЛЬНАЯ РАБОТА

(Тема: Площадь треугольника)

1). В треугольнике одна из сторон равна 12, а опущенная на неё высота равна 5. Найти площадь треугольника.

2). В треугольнике одна из сторон равна 12, а другая 10. Угол между этими сторонами равен .

Найти площадь треугольника.

3). В треугольнике одна из сторон равна 5, а другая . Угол между этими сторонами равен .

Найти площадь треугольника.

4). Периметр равностороннего треугольника равен 30. Найти площадь треугольника,

делённую на .

5). В треугольнике АВС точка О – середина стороны АВ, точка К – середина стороны ВС. Площадь треугольника АВС равна 100. Найти площадь треугольника ОВК.

САМОСТОЯТЕЛЬНАЯ РАБОТА

(Тема: Площадь прямоугольного треугольника)

1). (1 балл) В прямоугольном треугольнике один из катетов равен 10, а угол, лежащий напротив него, равен 45°. Найдите площадь треугольника.

2). (1 балл) В прямоугольном треугольнике один из катетов равен 4, а острый угол, прилежащий к нему, равен 45°. Найдите площадь треугольника.

3). (1 балл) В прямоугольном треугольнике один из катетов равен 10, острый угол, прилежащий к нему, равен 60°, а гипотенуза равна 20. Найдите площадь треугольника, делённую на .

4). (2 балла) Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 28 и 100.

САМОСТОЯТЕЛЬНАЯ РАБОТА

(Тема: Средняя линия трапеции)

1). (1 балл) В равнобедренной трапеции АВСО перпендикуляр, проведённый из вершины С, делит основание на отрезки, больший из которых равен 7 см. Найти среднюю линию трапеции.

2). (2 балла) В равнобедренной трапеции один из углов равен , боковая сторона равна 8 м, а меньшее основание равно 6 см. Найти среднюю линию трапеции.

3). (2 балла) В прямоугольной трапеции больший угол равен , большая боковая сторона 12 см, а меньшее основание равно 8 см. Найти среднюю линию трапеции.

САМОСТОЯТЕЛЬНАЯ РАБОТА

(Тема: Векторы)

1). Найти координаты вектора , если А(7; -12) и В(0; -3).

2). Найти координаты точки В, если А(0; -7 ), а вектор .

3). Найти длину вектора , если его координаты равны .

4). Точка С – середина отрезка АВ. Найти координаты точки С, если А(-2; 5) и В(0; 11).

5). Найти длину отрезка АВ, если А(1; -3) и В(5; 0).

САМОСТОЯТЕЛЬНАЯ РАБОТА № 2

(Тема: Касательная, хорда, секущая, радиус)

Касательные в точках A и B к окружности с центром O пересекаются под углом 72°. Найдите угол ABO. Ответ дайте в градусах.

2. 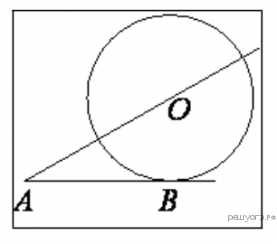К окружности с центром в точке проведены касательная и секущая . Найдите радиус окружности, если , .

3. Отрезок касается окружности радиуса 54 с центром в точке . Окружность пересекает отрезок в точке . Найдите .

4. Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 8.

5.Радиус OB окружности с центром в точке O пересекает хорду AC в точке D и перпендикулярен ей. Найдите длину хорды AC, если BD = 1 см, а радиус окружности равен 5 см.

САМОСТОЯТЕЛЬНАЯ РАБОТА

(Тема: Центральные и вписанные углы)

Найдите ∠KOM, если известно, что градусная мера дуги MN равна 124°, а градусная мера дуги KN равна 180°.

2. Точка О — центр окружности, ∠AOB = 84° (см. рисунок). Найдите величину угла ACB (в градусах).

3.На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA = 38°. Найдите угол NMB. Ответ дайте в градусах.

4. 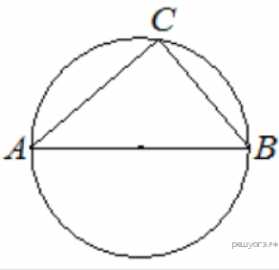Центр окружности, описанной около треугольника , лежит на стороне . Найдите угол , если угол равен 44°. Ответ дайте в градусах.

5. В угол C величиной 72° вписана окружность, которая касается сторон угла в точках A и B, точка O — центр окружности. Найдите угол AOB. Ответ дайте в градусах.

САМОСТОЯТЕЛЬНАЯ РАБОТА

(Тема: Окружность, описанная около многоугольника)

1. В окружность вписан равносторонний восьмиугольник. Найдите величину угла ABC.

2. Боковая сторона равнобедренного треугольника равна 5. Угол при вершине, противолежащий основанию, равен 120°. Найдите диаметр окружности, описанной около этого треугольника.

3. Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB = BC и ∠ABC = 167°. Найдите величину угла BOC. Ответ дайте в градусах.

4. Четырехугольник ABCD вписан в окружность. Угол ABC равен 72°, угол CAD равен 50°. Найдите угол ABD. Ответ дайте в градусах.

5. Найдите площадь квадрата, описанного вокруг окружности радиуса 5.

САМОСТОЯТЕЛЬНАЯ РАБОТА

(Тема: Многоугольники)

1. Сумма трех углов выпуклого четырехугольника равна 300°. Найдите четвертый угол. Ответ дайте в градусах.

2. ABCDEFGH — правильный восьмиугольник. Найдите угол EFG. Ответ дайте в градусах.

3. Два угла вписанного в окружность четырехугольника равны 82° и 58°. Найдите больший из оставшихся углов. Ответ дайте в градусах.

4. Четырёхугольник ABCD вписан в окружность. Угол ABC равен 136°, угол CAD равен 82°. Найдите угол ABD. Ответ дайте в градусах.

5. В выпуклом четырехугольнике ABCD AB = BC, AD = CD, ∠B = 77°, ∠D = 141°. Найдите угол A. Ответ дайте в градусах.

САМОСТОЯТЕЛЬНАЯ РАБОТА

(Тема: Параллелограмм)

1.В параллелограмме ABCD проведена диагональ AC. Угол DAC равен 47°, а угол CAB равен 11°. Найдите больший угол параллелограмма ABCD. Ответ дайте в градусах.

2. Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 25° и 30°. Найдите больший угол параллелограмма.

3. Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 60° и 55°. Найдите меньший угол параллелограмма.

4. В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и ∠ACD = 104°. Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.

5. Найдите величину острого угла параллелограмма , если биссектриса угла образует со стороной угол, равный 31°. Ответ дайте в градусах.

САМОСТОЯТЕЛЬНАЯ РАБОТА

(Тема: Ромб)

1. Высота BH ромба ABCD делит его сторону AD на отрезки AH = 44 и HD = 11. Найдите площадь ромба.

2. Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 19, а одна из диагоналей ромба равна 76. Найдите углы ромба.

В ответе запишите величины различных углов в порядке возрастания через точку с запятой.

3. Сторона ромба равна 34, а острый угол равен 60° . Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?

Перечислите эти длины в ответе через точку с запятой в порядке возрастания.

4. Точка O — центр окружности, на которой лежат точки P, Q и R таким образом, что OPQR — ромб. Найдите углы ORQ и RQP . Ответ дайте в градусах.

5. Площадь ромба равна 27, а периметр равен 36. Найдите высоту ромба.

САМОСТОЯТЕЛЬНАЯ РАБОТА

(Тема: Равнобедренные треугольники)

1.В равнобедренном треугольнике ABC с основанием AC внешний угол при вершине C равен 123°. Найдите величину угла ABC. Ответ дайте в градусах.

2. Сторона равностороннего треугольника равна . Найдите медиану этого треугольника.

3. Боковая сторона равнобедренного треугольника равна 10, а основание равно 12. Найдите площадь этого треугольника.

4. Высота равностороннего треугольника равна . Найдите сторону этого треугольника.

5. В треугольнике известно,

что , . Найдите угол . Ответ дайте в градусах.

САМОСТОЯТЕЛЬНАЯ РАБОТА

(Тема: Треугольники общего вида)

1. У треугольника со сторонами 16 и 2 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 1. Чему равна высота, проведённая ко второй стороне?

2. В треугольнике ABC проведена биссектриса AL, угол ALC равен 112°, угол ABC равен 106°. Найдите угол ACB. Ответ дайте в градусах.

3. В треугольнике ABC проведены медиана BM и высота BH . Известно, что AC = 84 и BC = BM. Найдите AH.

4. В треугольнике ABC BM — медиана и BH – высота. Известно, что AC = 216, HC = 54 и ∠ACB = 40°. Найдите угол AMB. Ответ дайте в градусах.

5. В треугольнике известно, что , — медиана, . Найдите .

САМОСТОЯТЕЛЬНАЯ РАБОТА

(Тема: Углы)

1. Углы, отмеченные на рисунке одной дугой, равны. Найдите угол α. Ответ дайте в градусах.

2. Найдите величину угла DOK, если OK — биссектриса угла AOD, ∠DOB = 108°. Ответ дайте в градусах.

3. На плоскости даны четыре прямые. Известно, что , , . Найдите . Ответ дайте в градусах.

4. Прямые m и n параллельны. Найдите ∠3, если ∠1 = 22°, ∠2 = 72°. Ответ дайте в градусах.

5. Углы, отмеченные на рисунке одной дугой, равны. Найдите угол . Ответ дайте в градусах.

САМОСТОЯТЕЛЬНАЯ РАБОТА

(Тема: Прямоугольный треугольник)

1). В треугольнике угол равен 90°, . Найдите .

2). В треугольнике угол прямой, . Найдите .

3). В треугольнике ABC угол C равен 90°, AC = 20, tgA = 0,5. Найдите BC.

4). В треугольнике угол прямой, . Найдите .

5). В треугольнике ABC угол C равен 90°, AC = 12 , tgA = 1,5. Найдите BC.

САМОСТОЯТЕЛЬНАЯ РАБОТА

(Тема: Площади фигур)

1. Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 12 и 13.

2. Один из острых углов прямоугольного треугольника равен 43°. Найдите его другой острый угол. Ответ дайте в градусах.

3. Два катета прямоугольного треугольника равны 16 и 30. Найдите гипотенузу этого треугольника.

4. В треугольнике известно, что , , угол равен 90°. Найдите радиус описанной окружности этого треугольника.

5. В прямоугольном треугольнике катет и гипотенуза равны 5 и 13 соответственно. Найдите другой катет этого треугольника.

infourok.ru

Самостоятельная работа по геометрии ( 9 класс) по материалам ОГЭ

Вариант 2.

1.В прямоугольном треугольнике один из катетов равен 10, а угол, лежащий напротив него, равен . Найдите площадь треугольника.

2.Четырехугольник вписан в окружность. Угол равен , угол равен . Найдите угол . Ответ дайте в градусах.

3.Периметр ромба равен 40, а один из углов равен . Найдите площадь ромба.

4.В трапеции , , а её площадь равна 12. Найдите площадь треугольника .

5.Прямая, параллельная стороне треугольника , пересекает стороны и в точках и соответственно. Найдите , если , .

6.В выпуклом четырёхугольнике углы и равны. Докажите, что углы и также равны.

Вариант 3.

1.Площадь прямоугольного треугольника равна . Один из острых углов равен . Найдите длину катета, лежащего напротив этого угла.

2.На отрезке выбрана точка так, что и . Построена окружность с центром , проходящая через . Найдите длину касательной, проведённой из точки к этой окружности.

3.Основания трапеции равны 18 и 12, одна из боковых сторон равна , а угол между ней и одним из оснований равен . Найдите площадь трапеции.
4.В треугольнике отмечены середины и сторон и соответственно. Площадь треугольника равна 57. Найдите площадь четырёхугольника .

5.Прямая, параллельная стороне треугольника , пересекает стороны и в точках и соответственно. Найдите , если , , .

6.Докажите, что отрезок, соединяющий середины оснований трапеции, делит её на две равные по площади части.

Вариант 4.

1.Площадь прямоугольного треугольника равна . Один из острых углов . Найдите длину гипотенузы.

2. Длина хорды окружности равна 72, а расстояние от центра окружности до этой хорды равно 27. Найдите диаметр окружности.

3.Основания трапеции равны 18 и 12, одна из боковых сторон равна 6, а синус угла между ней и одним из оснований равен . Найдите площадь трапеции.

4.Катеты прямоугольного треугольника равны 18 и 24. Найдите высоту, проведённую к гипотенузе.

5. Биссектриса угла параллелограмма пересекает сторону в точке . Найдите периметр параллелограмма, если , .

6.Известно, что около четырёхугольника можно описать окружность и что продолжения сторон и четырёхугольника пересекаются в точке . Докажите, что треугольники и подобны

Вариант 5.

1.Периметр равнобедренного треугольника равен 16, а боковая сторона — 5. Найдите площадь треугольника.

2.На окружности по разные стороны от диаметра взяты точки и . Известно, что . Найдите угол . Ответ дайте в градусах.

3.Основания трапеции равны 18 и 12, одна из боковых сторон равна 6, а косинус угла между ней и одним из оснований равен . Найдите площадь трапеции.

4.Площадь параллелограмма равна 6. Точка — середина стороны . Найдите площадь трапеции .

5.Точка является основанием высоты, проведённой из вершины прямого угла треугольника к гипотенузе . Найдите , если , .

6.Точка — середина боковой стороны трапеции . Докажите, что площадь треугольника равна половине площади трапеции.

infourok.ru

Самостоятельная работа по геометрии 9 класс – ГДЗ по геометрии 9 класс самостоятельные и контрольные работы Иченская

ГДЗ по геометрии 9 класс самостоятельные и контрольные работы Иченская

Самостоятельные и контрольные работы по геометрии 9 класс

Самостоятельные работы по геометрии 9 класс к учебнику Геометрия 9 (авторы В.Ф.Бутузов. С.Б. Кадомцев)

ГДЗ по геометрии 9 класс контрольные и самостоятельные работы Журавлев, Малышева

Похожие решебники по геометрии 9 класс

Самостоятельная работа по геометрии ( 9 класс )

Самостоятельные работы по геометрии для 9 класса

Самостоятельная работа по геометрии ( 9 класс) по материалам ОГЭ

Добавить комментарий Отменить ответ