Презентация к уроку геометрии (9 класс) на тему: Векторы

По теме: методические разработки, презентации и конспекты

Конспект урока на тему «Вектор. Модуль вектора. Равенство векторов. Сложение векторов.»

Математика…

презентация к уроку на тему «Вектор. Модуль вектора. Равенство векторов. Сложение векторов.»

презентация к уроку на тему «Вектор. Модуль вектора. Равенство векторов. Сложение векторов.»…

презентация «Векторы.Действия над векторами.Проекция вектора»

В 10 классе при рассмотрении основ кинематики возникает необходимость работы учащимся с векторными величинами. Данная презентация может быть использована для повторения  математических основ поня…

«Координаты вектора. Действия над векторами, заданными координатами. Построение векторов с помощью программы GeoGebra»

Разработка урока геометрии в 9 классе с помощью программы GeoGebra….

презентация по геометрии «Понятие вектора. Длина вектора. Равенство векторов.»

Презентация по геометрии «Понятие вектора. Длина вектора. Равенство векторов.» Изучение нового материала….

Векторы. Модуль вектора. Равенство векторов. Коллинеарные векторы.

Презентация для изучения нового материала….

Интерактивный тест «Векторы. Сумма векторов. Умножение вектора на число»

Данный ресурс представляет собой мультимедийный тест для 10 класса в 2-х вариантах.Ресурс является презентацией с использованием макросов, создан в программе PowerPoint по конструктору тестов Ко…

nsportal.ru

9 кл умножение вектора на число

Рисунки Савченко Е.М. Все рисунки в презентации выполнены с помощью инструментов панели рисования программы Microsoft PowerPoint .

Цель урока:

• Рассмотреть основные свойства умножения вектора на число
• Сформировать навыки решения задач на применение свойств умножения вектора на число

х

3

1

х

х

-4

JO = CK

XD = CK

–

–

СК = JO

4

4

A

B

N

D

C

х

0

NN = XD

M

R

E

S

F

х

ХТ = XD

х не существует

Q

V

U

Y

T

1

х

XT = XT

I

G

X

P

O

— 1

х

TX = XT

K

H

J

L

Z

3

О – точка пересечения медиан треугольника.

3

B

х

ВК = ОК

1

х

–

К

O = В K

3

х

2

ОВ = КО

T

O

A

K

C

4

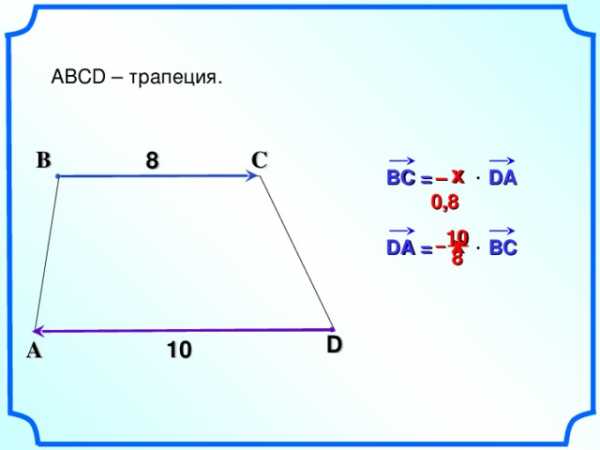
ABCD – трапеция.

С

В

8

х

– 0, 8

BC = DA

10

х

–

DA = BC

8

D

А

10

5

Умножение вектора на число обладает следующими основными свойствами.

a

b

b

l

k

Для любых , и любых чисел , справедливы равенства:

k (l a)

(kl)a =

1

Сочетательный закон

(k+l)a =

ka + la

2

«Геометрия 7-9» Л.С. Атанасян и др.

Первый распределительный закон

ka + kb

k (a + b) =

3

Второй распределительный закон

6

y = m – n

х = m + n,

№ 781 Пусть

n

m

Выразите через и

векторы

2х – 2у

1

2х + у

2

«Геометрия 7-9» Л.С. Атанасян и др.

1

– х – у

3

7

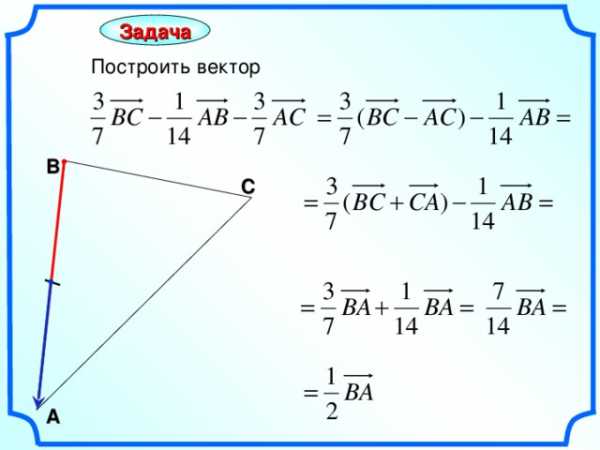
Задача

Построить вектор

В

С

Гаврилова Н.Ф. «Поурочные разработки по геометрии: 9 класс». – М.: ВАКО, 2007. – 320 с. – (В помощь школьному учителю)

А

7

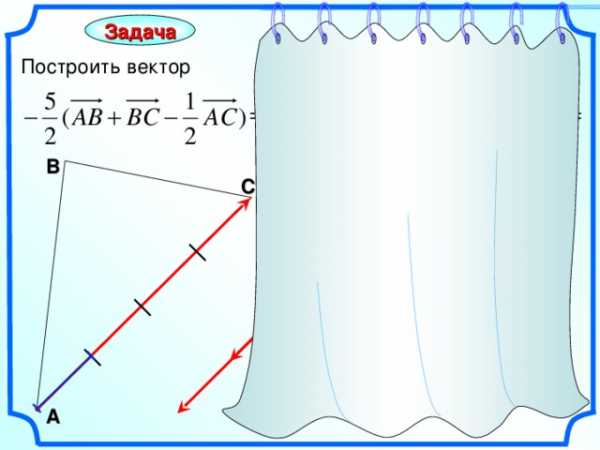
Задача

Построить вектор

В

С

Гаврилова Н.Ф. «Поурочные разработки по геометрии: 9 класс». – М.: ВАКО, 2007. – 320 с. – (В помощь школьному учителю)

А

9

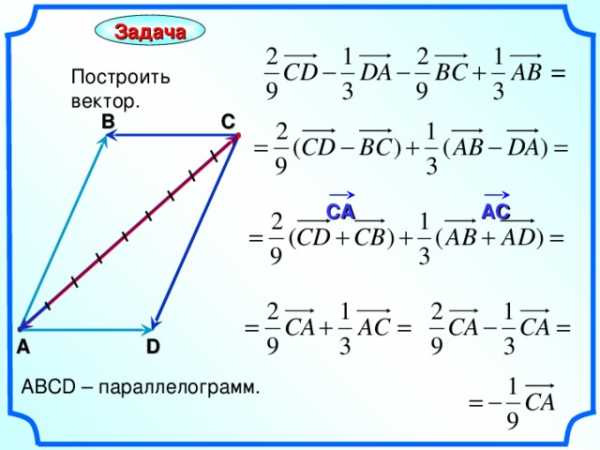
Задача

=

Построить вектор.

В

С

CA

AC

Гаврилова Н.Ф. «Поурочные разработки по геометрии: 9 класс». – М.: ВАКО, 2007. – 320 с. – (В помощь школьному учителю)

D

А

АВС D – параллелограмм.

10

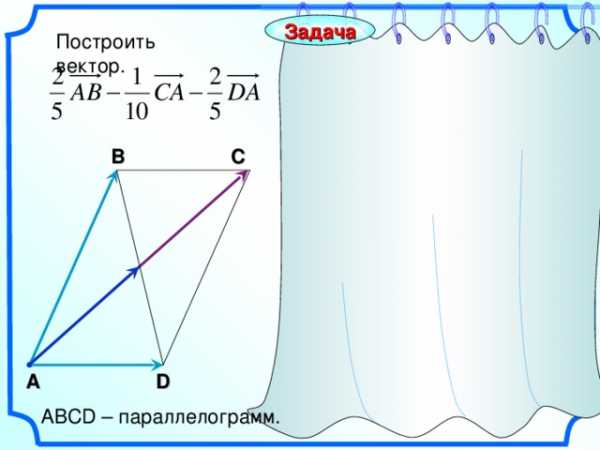
Задача

Построить вектор.

С

В

AC

Гаврилова Н.Ф. «Поурочные разработки по геометрии: 9 класс». – М.: ВАКО, 2007. – 320 с. – (В помощь школьному учителю)

D

А

АВС D – параллелограмм.

11

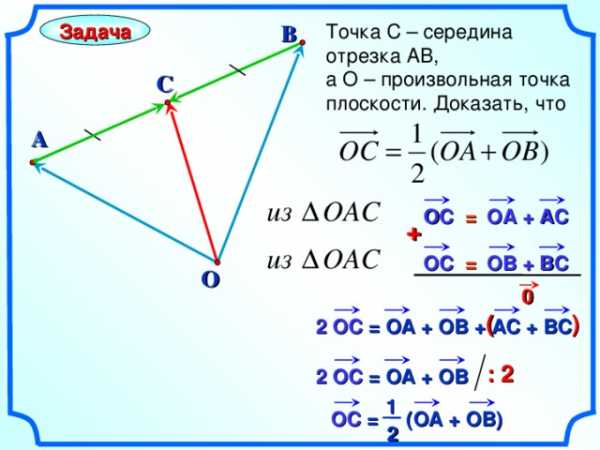
Точка С – середина отрезка АВ,

а О – произвольная точка плоскости. Доказать, что

B

Задача

C

A

O С =

O А + АС

+

O С =

O В + ВС

O

0

«Геометрия 7-9» Л.С. Атанасян и др.

( )

2 O С = ОА + ОВ + АС + ВС

: 2

2 O С = ОА + ОВ

1

O С = (ОА + ОВ)

2

12

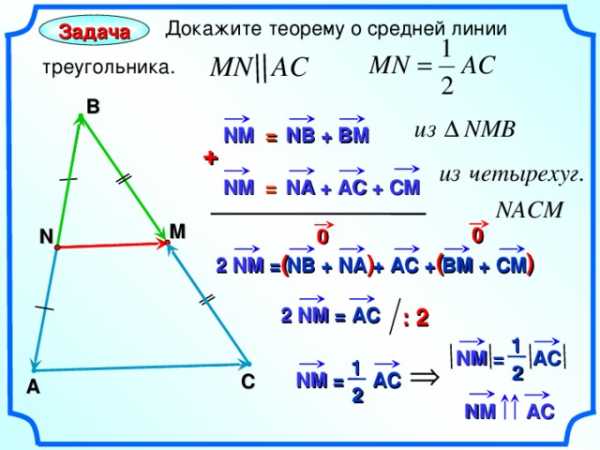
Докажите теорему о средней линии

треугольника.

Задача

В

NB + BM

NM =

+

NA + A С + CM

NM =

M

0

0

N

( )

( )

2 NM = NB + NA + АС + В M + CM

«Геометрия 7-9» Л.С. Атанасян и др.

2 NM = AC

: 2

1

NM = AC

1

2

NM = AC

С

A

2

NM

AC

13

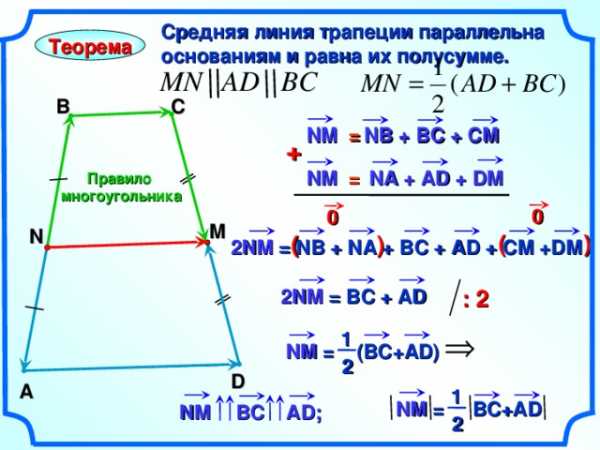
Средняя линия трапеции параллельна

основаниям и равна их полусумме.

Теорема

В

С

NB + B С + СМ

NM =

+

NA + AD + DM

NM =

Правило

многоугольника

0

0

M

N

( )

( )

2 NM = NB + NA + B С + AD + CM +DM

: 2

2 NM = В C + AD

«Геометрия 7-9» Л.С. Атанасян и др.

1

NM = (BC+AD)

2

D

A

1

NM = BC+AD

BC

AD;

NM

2

14

АВС D – ромб. Е ВС, ВЕ : ЕС = 3 : 1,

К – середина DC , АВ = , AD = . Выразите через

векторы и векторы:

Задача

b

a

a

b

В

AE

a

AK

E

А

С

Гаврилова Н.Ф. «Поурочные разработки по геометрии: 9 класс». – М.: ВАКО, 2007. – 320 с. – (В помощь школьному учителю)

KE

b

K

D

15

kopilkaurokov.ru

Урок геометрии по теме «Умножение вектора на число» (9 класс)

МБОУ СОШ №7 г. Гулькевичи Краснодарского края

«Умножение

вектора на число»

Урок геометрии

в 9-ом классе.

Выполнила

учитель математики

Кличева Г. А.

2014г

Тема урока: «Умножение вектора на число»

(9-й класс)

Цель:

1. Ввести понятие умножения вектора на число.

2. Ознакомить учащихся со свойствами умножения вектора на число.

Ход урока

1. Организационный момент.

2. Актуализация знаний учащихся.

1. Проверка домашнего задания №770, №772 (два ученика оформляют решения на доске).

2. Фронтальная работа с классом устно по готовым чертежам.

В С

А D

а) Найти сумму векторов: АВ и ВС; СВ и СD; АС и DА; DC, BD и АВ; АВ и –АD; АС и – DС;

б) Докажите, что векторы -АВ + АD= -СВ + СD; АD – ВD= АС- ВС;

в) .В С

А D

Докажите, что векторы |АВ + ВС|= 2| АО|; ВА – DA = ОD – ОВ; Найдите длину вектора |АО — DО – СD|, если АВ = 5, АD = 12.

3. Изучение нового материала.

1. Задание 1. (Для самостоятельного решения, один ученик решает на обратной стороне доски).

Начертите векторы а и b так, что: а) а и b сонаправлены, |b|= 3|a| ;

б) а и b противоположно направлены, |b|= ½*|a|.

2. Ввести понятие умножения ненулевого вектора на число.

Сформулировать основные свойства умножения вектора на число.

— Произведением ненулевого вектора а на число

k называется такой вектор b, длина которого равна |k|*|a|, причем векторы a и b сонаправлены при k≥0 и притивоположно направлены при k≤0;

— Для любого числа k и любого вектора a векторы a и ka коллинеарны$

— Произведение нулевого вектора на любое число считается нулевой вектор.

k*0 = 0;

Произведение любого вектора на число нуль есть нулевой вектор 0*а = 0.

Задание 2. Назовите вектор, который получится в результате умножения.

B

C

D

N

R

E

S

F

V

T

Y

U

O

P

X

G

A

M

Q

I

H J K L Z

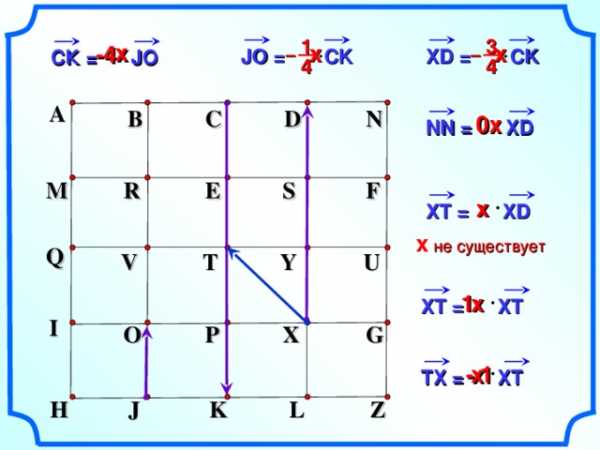
Задание 3. Назовите вектор, который получится в результате умножения.

B

C

D

N

R

E

S

F

V

T

Y

U

O

P

X

G

A

M

Q

I

H J K L Z

СК = *JO; JO = *CK ; XD =*CK ; NN = *XD; ХТ = *XD; XT =*XT; TX = * XT.

— Умножение вектора на число обладает следующими основными свойствами.

Для любых векторов а и b и любых чисел k и l, справедливы равенства:

1. (kl)a = k (l a) Сочетательный закон

2. (k+l)a = ka + la Первый распределительный закон

3. k (a + b) = ka + kb Второй распределительный закон

4. Закрепление изученного материала.

Задание 4. Работа по учебнику

Задача №775, № 776(а,в,е), №781(б,в), №780(а).

V. Домашнее задание :

п. 83, № 776б,г,д), №777.

VI. Итог урока: — сформулируйте правило умножения ненулевого вектора на число, основные свойства умножения вектора на число.

.

infourok.ru

Умножение вектора на число — презентация, доклад, проект

Обратная связь

Если не удалось найти и скачать доклад-презентацию, Вы можете заказать её на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: [email protected]

Мы в социальных сетях

Социальные сети давно стали неотъемлемой частью нашей жизни. Мы узнаем из них новости, общаемся с друзьями, участвуем в интерактивных клубах по интересам

ВКонтакте >

Что такое Myslide.ru?

Myslide.ru — это сайт презентаций, докладов, проектов в формате PowerPoint. Мы помогаем учителям, школьникам, студентам, преподавателям хранить и обмениваться своими учебными материалами с другими пользователями.

---

Для правообладателей >

myslide.ru

Презентация к уроку геометрии в 9 классе по теме: «Векторы.»

Слайд 1

на тему Проект по геометрии ВЕКТОРЫ

Слайд 2

ОПРЕДЕЛЕНИЕ Отрезок, для которого указано, какая из его граничных точек считается началом, а какая – концом, называется направленным отрезком или вектором .

Слайд 3

На рисунках вектор изображается отрезком со стрелкой, показывающей направление вектора. Вектор обозначается двумя заглавными латинскими буквами со стрелкой над ними (например, AB , где A -начало, а B -конец вектора). Любая точка на плоскости так же является вектором. Такой вектор называется нулевым и обозначается двумя одинаковыми буквами. ( MM ) .

Слайд 4

Векторы называются коллинеарными , если они лежат либо на одной прямой, либо на параллельных прямых. Нулевой вектор считается коллинеарным к любому вектору. Так же, если векторы направлены одинаково, то они называются сонаправленными, а если противоположно, то противоположно направленными . Обозначается это так : A B, или A B . Векторы считаются равными , если они сонаправленны и их длины равны.

Слайд 5

1. Если точка A – начало вектора a , то говорят, что вектор а отложен от точки A . Откладывание вектора от точки. Вектор a отложен от точки A 2 . От любо точки М можно отложить вектор, равный данному вектору а , и при том только один. Пример : допустим, что вектор а ненулевой. Проведем через точку М прямую, параллельную вектору а . Проведем отрезок, Равный вектору а. Это и есть искомый вектор.

Слайд 6

Сложение и вычитание векторов Пусть а и b – два вектора. Отложим вектор AB , который = а Затем, от точки B отложим вектор BC , равный b Вектор AC называется суммой векторов а и b . Это правило сложения векторов называется правилом треугольника AB+BC=AC

Слайд 7

Теорема: Для любых векторов а, b и c справедливы равенства: a + b = b + a (переместительный закон). 2. (а + b ) + c = a + ( b + c ) ( сочетательный закон). Доказав свойство 1. мы обосновали Правило параллелограмма .

Слайд 8

Чтобы сложить несколько векторов нужно складывать их поочередно, при этом в любом порядке. Например, как показано на рисунке, первый складывается со вторым, их сумма – с третьим, и т. д. Аналогично можно построить сумму любого количества векторов. Это называется правилом многоугольника

Слайд 9

Разностью векторов а и b называется такой вектор, сумма которого с вектором b равна вектору а . Теорема: для любых векторов а и b справедливо равенство

Слайд 10

Умножение вектора на число Произведением ненулевого вектора а на число k называется такой вектор b , длина которого равна | k | x | a | , причем векторы а и b сонаправлены при k > или = 0 , и противоположно направлены при k

Слайд 11

Проект подготовил Руденко Андрей (9кл.) спасибо за внимание

nsportal.ru

Умножение вектора на число

Здравствуйте!

Устно:

Пусть дан ненулевой вектор . Какой из векторов, изображенных на рисунке, равен вектору:

 

1) + ;

2) + + ?

 

2) + + =

2

 

3

 

Классная работа

Умножение вектора на число

0, то ; если k Векторы и коллинеарны.   «

Произведением ненулевого вектора и числа k , отличного от нуля, называют такой вектор , что:

 

если k

Векторы и коллинеарны.

 

Теорема:

Если векторы и коллинеарны и , то существует такое число k, что

 

Теорема:

Если вектор имеет координаты , то вектор k имеет координаты .

 

Например,

 

3

Свойства умножения:

Для любых чисел k, m и любых векторов справедливы равенства:

 

• — сочетательное свойство;
• — первое распределительное свойство;
• — второе распределительное свойство.

Работаем с учебником:

№ 522, 524, 526, 527, 529

Домашнее задание:

Параграф 15

Разобрать доказательство теорем

№ 523, 525, 528

Спасибо за урок!

videouroki.net

Презентация на тему Умножение вектора на число для 9 класса

Термины вектор имеет основополагающее значение в алгебре и геометрии. Они возникли как результат соответствующих понятий в классической геометрии на плоскости и в пространстве. Соответственно, в качестве основных операций приняты
(а) умножение вектора на число, и
(б) сумма двух векторов.
Результатом этих операций является вектор того же типа.

Слайды презентации

Скачать презентацию Умножение вектора на число

Слайды презентации

Скачать презентацию Умножение вектора на число для 9 класса

Множество элементов, называемых векторами, для которых результатом двух указанных выше операций снова является вектором того же направления, называется линейным или векторным пространством. В этом якобы в силу некоторые дополнительные условия, касающиеся умножения и сложения числа операций (а) и (б) (формальные определения и примеры приведены в упражнениях 2.1-2.3). Для линейного векторного пространства используется и термин линейки.

В категории линейных пространств и падающих предметов, которые обычно не рассматривается в линейной алгебре, например, множество всех числовых функций, определенных на заданном интервале. В этой книге, интересуют в основном из векторов и операций, которые называются. Kraynomerni векторные пространства, которые являются основным предметом курса «Линейная алгебра» (бесконечное пространство, как правило , рассматривается в анализе). Векторы в таких пространствах представлены сложенных конечных множеств целых чисел (компонент вектора), где умножение вектора с числом и сложения двух векторов выполняется поэлементно. Для удобства, элементы векторной графики доступны в виде столбца или строки.

shkolnye-prezentacii.ru