Математика 9 класс экзамены – Тест: Подготовка к экзамену — Математика 9 класс
Решебник к выпускному экзамену по математике 9 класс
- ГДЗ
- 1 Класс
- Математика
- Английский язык
- Русский язык
- Немецкий язык
- Природоведение
- Основы здоровья
- Музыка
- Литература
- Окружающий мир
- Человек и мир
- 2 Класс
- Математика
- Английский язык
- Русский язык
- Немецкий язык
- Белорусский язык
- Украинский язык
- Информатика
- Природоведение
- Основы здоровья
- Музыка
- Литература
- Окружающий мир
- Человек и мир
- Технология
- 3 Класс
- Математика
- Английский язык
- Русский язык
- Немецкий язык
- Белорусский язык
- Украинский язык
- Информатика
- Литература
- Окружающий мир
- Человек и мир
- Испанский язык
- 4 Класс
- Математика
- Английский язык
- Русский язык
- Немецкий язык
- Белорусский язык
- Украинский язык
- Информатика
- Основы здоровья
- Музыка
resheba.me
Разработка заданий по геометрии 9 класс для подготовки к экзамену по математике
Подготовка к экзамену по математике в 9 классе (геометрия)
Хочу предложить следующий вид работы по повторению знаний геометрического материала. Задания на таких карточках детей заинтересовывают, заставляют ликвидировать пробелы, закрепить математические знания.
В целом позволят успешно подготовиться к экзаменам.
Данный вид работы можно предложить после повторения теории по геометрии, перед решением задач, а также после изучения данной темы.
Дети записывают ответы в карточках, что позволяет учителю быстро проверить и оценить знания. Эти карточки можно использовать в 8 классе, а также в 10 и 11 классах.
Задания для подготовки к ОГЭ по геометрии.
1. Соотнеси утверждения с треугольником.
Запиши номера в соответствующий столбик.
1. Все стороны равны
2. Две стороны равны
3. Каждая сторона меньше суммы двух других сторон
4. Каждая сторона не больше двух сторон
5.Все медианы, высоты, биссектрисы совпадают
6. Высота является биссектрисой и медианой
7. Все углы по 60°
8. Два угла равны
9. Все углы разные
10. Все внешние углы равны
11. Один угол может быть равным 90°
12. Один угол может быть больше 90°
Ответы:
1, 3, 7, 102, 3, 8, 11, 12
3, 5, 9, 11, 12
2. Соотнеси утверждения с трапецией.
Запиши номера в соответствующий столбик.
1. Диагонали точкой пересечения делятся пополам
2. Диагонали равны
3. Углы при каждом основании равны
4. Противоположные углы равны
5. Не противоположные углы образуют в сумме 180°
6. Два угла прямые
7. Боковые стороны равны
8. Высота равна боковой стороне
9. Если провести диагонали, то образуются 2 равнобедренных подобных треугольника
10. Площадь равна произведению полусуммы оснований на высоту
11. Площадь равна произведению средней линии на высоту
Ответы:
3, 5, 7, 9, 10, 115, 6, 8, 10, 11
3. Соотнеси утверждения с четырехугольником.
Запиши номера в соответствующий столбик.
1. Диагонали равны
2. Диагонали взаимно перпендикулярны
3. Диагонали являются биссектрисами углов
4. Диагонали точкой пересечения делятся пополам
5. Все стороны равны
6. Противоположные стороны равны
7. Противоположные стороны попарно параллельны
8. Противоположные углы равны
9. Все углы равны
10. Сумма противоположных углов равна 180°
11. Площадь равна квадрату сторон
12. Площадь равна произведению смежных сторон
13. Площадь равна произведению основания на высоту
14. Площадь равна половине произведения диагоналей
Ответы
infourok.ru
Анализ пробных экзаменов по математике в 9 классах
Анализ пробного экзамена
по математике(ОГЭ) в 9 –х классах
по математике
Экзаменационная работа состоит из заданий, из которых20 заданий базового уровня(часть1), 4 задания повышенного уровня(часть2) и2 задания высокого уровня сложности(часть2). Работа состоит из трёх модулей: «Алгебра», «Геометрия», «Реальная математика».
Модуль «Алгебра» содержит11 заданий: в части1 — восемь заданий; в части2 — три задания. Модуль «Геометрия» содержит восемь заданий: в части1 — пять заданий; в части2 — три задания. Модуль «Реальная математика» содержит семь заданий: все задания этого модуля— в части1.:
Целью работы была диагностика уровня знаний учащихся по математике на данном этапе обучения для планирования процесса подготовки к ОГЭ в оставшееся до государственной итоговой аттестации время.
Номер задания
21
22
23
24
25
26
Максимальное количество баллов
2
3
4
2
3
4
Шкала пересчета первичного балла за выполнение
Отметка по пятибалльной шкале
«2»
«3»
«4»
«5»
Суммарный балл за работу в целом
0-7
8-15
16-22
23-38
Анализ пробного экзамена по математике, проведенного в 9-х классах
в октябре.
Пробный экзамен по математике писали учащиеся 9 А и 9 Б классов:
9 А 20 учащихся
9 Б 27 учащихся
Итого 47 учащихся
Обобщенный план варианта КИМ и количество учеников, справившихся с заданиями.
Пробный экзамен (февраль 2015г.)
№ задания
Основные проверяемые требования
Количесво учеников, справившихся с заданием
% выполнения
% невыполнения
Часть 1
Модуль «Алгебра»
1
Уметь выполнять вычисления и преобразования
46
17
83
2
Уметь выполнять вычисления и преобразования
33
30
70
3
Уметь выполнять вычисления и преобразования, уметь выполнять преобразования алгебраических выражений
35
29
71
4
Уметь решать уравнения, неравенства и их системы
37
10
90
5
Уметь строить и читать графики функций
32
33
67
6
Уметь строить и читать графики функций
32
33
67
7
Уметь выполнять преобразования алгебраических выражений.
23
45
55
8
Уметь решать уравнения, неравенства и их системы .
40
18
82
Модуль «Геометрия»
9
Уметь выполнять действия с геометрическими фигурами, координатами и векторами.
25
49
51
10
Уметь выполнять действия с геометрическими фигурами, координатами и векторами.
32
70
30
11
Уметь выполнять действия с геометрическими фигурами, координатами и векторами
26
58
42
12
Уметь выполнять действия с геометрическими фигурами, координатами и векторами
26
58
42
13
Проводить доказательные рассуждения при решении задач, оценивать логическую правильность рассуждений, распознавать ошибочные заключения.
19
79
21
Модуль «Реальная математика»
14
Пользоваться основными единицами длины, массы, времени, скорости, площади, объёма; выражать более крупные единицы через более мелкие и наоборот.
39
28
72
15
Описывать с помощью функций различные реальные зависимости между величинами; интерпретировать графики реальных зависимо-стей
33
13
87
16
Решать несложные практические расчетные задачи; решать задачи, связанные с отношением, пропорциональностью величин, дробями, процентами; пользоваться оценкой и прикидкой при практических расчетах; интерпретировать результаты решения задач с учётом ограничений, связанных с реальными свойствами рассматриваемых объектов
29
36
64
17
Описывать реальные ситуации на языке геометрии, исследовать построенные модели с использованием геометрических понятий и теорем, решать практические задачи, связанные с нахождением геометрических величин
26
42
58
18
Анализировать реальные числовые данные, представленные в таблицах, на диаграммах, графиках
28
33
67
19
Решать практические задачи, требующие систематического перебора вариантов; сравнивать шансы наступления случайных событий, оценивать вероятности случайного события, сопоставлять и исследовать модели реальной ситуацией с использованием аппарата вероятности и статистики
19
59
41
20
Осуществлять практические расчеты по формулам, составлять несложные формулы, выражающие зависимости между величинами
37
30
70
Часть 2
Модуль «Алгебра»
21
Уметь выполнять преобразования алгебраических выражений, решать уравнения, неравенства и их системы, строить и читать графики функций
16
69
31
22
Уметь выполнять преобразования алгебраических выражений, решать уравнения, неравенства и их системы, строить и читать графики функций, строить и исследовать простейшие математические модели
11
72
28
23
Уметь выполнять преобразования алгебраических выражений, решать уравнения, неравенства и их системы, строить и читать графики функций, строить и исследовать простейшие математические модели
14
66
34
Модуль «Геометрия»
24
Уметь выполнять действия с геометрическими фигурами, координатами и векторами
8
84
16
25
Проводить доказательные рассуждения при решении задач, оценивать логическую правильность рассуждений, распознавать ошибочные заключения
0
100
0
26
Уметь выполнять действия с геометрическими фигурами, координатами и векторами
0
100
0
Анализ выполненных работ показал, что качество подготовки выпускников 9-х классов по математике
успеваемость – 76%
средняя оценка 3.4
.
Обобщенный план варианта КИМ и количество учеников, справившихся с заданиями.
Пробный экзамен (декабрь 2015г.)
Пробный экзамен по математике писали учащиеся 9 А и 9 Б классов:
9 А 22 учащихся
9 Б 27 учащихся
Итого 49 учащихся
№ задания
Основные проверяемые требования
Количесво учеников, справившихся с заданием
% выполнения
% невыполнения
Часть 1
Модуль «Алгебра»
1
Уметь выполнять вычисления и преобразования
46
15
85
2
Уметь выполнять вычисления и преобразования
33
28
72
3
Уметь выполнять вычисления и преобразования, уметь выполнять преобразования алгебраических выражений
35
30
70
4
Уметь решать уравнения, неравенства и их системы
37
13
87
5
Уметь строить и читать графики функций
32
38
62
6
Уметь строить и читать графики функций
32
34
66
7
Уметь выполнять преобразования алгебраических выражений.
23
50
50
8
Уметь решать уравнения, неравенства и их системы .
40
28
72
Модуль «Геометрия»
9
Уметь выполнять действия с геометрическими фигурами, координатами и векторами.
25
49
51
10
Уметь выполнять действия с геометрическими фигурами, координатами и векторами.
32
70
30
11
Уметь выполнять действия с геометрическими фигурами, координатами и векторами
26
52
48
12
Уметь выполнять действия с геометрическими фигурами, координатами и векторами
26
58
42
13
Проводить доказательные рассуждения при решении задач, оценивать логическую правильность рассуждений, распознавать ошибочные заключения.
19
79
21
Модуль «Реальная математика»
14
Пользоваться основными единицами длины, массы, времени, скорости, площади, объёма; выражать более крупные единицы через более мелкие и наоборот.
39
28
72
15
Описывать с помощью функций различные реальные зависимости между величинами; интерпретировать графики реальных зависимо-стей
33
13
87
16
Решать несложные практические расчетные задачи; решать задачи, связанные с отношением, пропорциональностью величин, дробями, процентами; пользоваться оценкой и прикидкой при практических расчетах; интерпретировать результаты решения задач с учётом ограничений, связанных с реальными свойствами рассматриваемых объектов
29
36
64
17
Описывать реальные ситуации на языке геометрии, исследовать построенные модели с использованием геометрических понятий и теорем, решать практические задачи, связанные с нахождением геометрических величин
26
42
58
18
Анализировать реальные числовые данные, представленные в таблицах, на диаграммах, графиках
28
33
67
19
Решать практические задачи, требующие систематического перебора вариантов; сравнивать шансы наступления случайных событий, оценивать вероятности случайного события, сопоставлять и исследовать модели реальной ситуацией с использованием аппарата вероятности и статистики
19
59
41
20
Осуществлять практические расчеты по формулам, составлять несложные формулы, выражающие зависимости между величинами
37
30
70
Часть 2
Модуль «Алгебра»
21
Уметь выполнять преобразования алгебраических выражений, решать уравнения, неравенства и их системы, строить и читать графики функций
16
69
31
22
Уметь выполнять преобразования алгебраических выражений, решать уравнения, неравенства и их системы, строить и читать графики функций, строить и исследовать простейшие математические модели
11
82
18
23
Уметь выполнять преобразования алгебраических выражений, решать уравнения, неравенства и их системы, строить и читать графики функций, строить и исследовать простейшие математические модели
14
76
24
Модуль «Геометрия»
24
Уметь выполнять действия с геометрическими фигурами, координатами и векторами
8
90
10
25
Проводить доказательные рассуждения при решении задач, оценивать логическую правильность рассуждений, распознавать ошибочные заключения
0
100
0
26
Уметь выполнять действия с геометрическими фигурами, координатами и векторами
0
100
0
Анализ выполненных работ показал, что качество подготовки выпускников 9-х классов по математике
успеваемость – 77%
средняя оценка 3.6
Результаты выполнения заданий экзаменационной работы отдельно по каждой части.
Часть 1. Выполнили верно задания 1, базовой, части
Количество выпускников
Часть 1, тестовая часть (число учащихся)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
1часть
49
31
33
17
24
31
31
17
17
9
16
17
9
9
24
31
9
24
12
16
17
Часть 1. Выполнили верно задания 1, базовой, части в %
Количество выпускников
Часть 1, тестовая часть (%)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
1часть
49
62,5
87,5
25
50
62,5
62,5
25
25
12,5
37,5
25
12,5
12,5
50
62,5
12,5
50
25
37,5
25
Самый высокий процент выполнения заданий базовой части этой работы в 9 классах — № 1, № 2, № 5, № 6, № 15 ,
№1. Арифметические действия с обыкновенными и десятичными дробями.
№ 2. Работа с координатной прямой.
№ 5. Соответствие между графиками функций и формулами, которые их задают.
№ 6. Прогрессии.
№ 15. Определение данных по графику
Заданием под номером 9, 12, 13, 16 учащиеся справились на очень низком уровне (12,5 %).Самыми распространенными ошибками были: слабое знание теорем и аксиом по геометрии, правильное выполнение чертежа.
Преподавание алгебры в школе осуществляется на основе учебника: Алгебра. 9 класс. В 2 ч. А.Г. Мордкович и др. – М. : Мнемозина, 2012.
Результаты выполнения заданий 2 части экзаменационной работы
К выполнению второй части приступили 38 учащихся (57,5), не приступили 21 учащихся ( 42,5%)
Количество выпускников
Число учащихся, справившихся со
2 частью работы
21
22
23
24
25
26
Вся 2 часть
49
19
26
—
5
—
—
—
Количество выпускников
Число учащихся, справившихся со
2 частью работы (%)
21
22
23
24
25
26
Вся 2 часть
49
39
53
Учащиеся на высоком уровне (36 %)справились с заданием № 21,22
Какие основные ошибки были допущены: невнимательность при чтении задачи
Количество выпускников
Верно выполнили 1 часть (18 заданий)
Верно выполнили 1 часть
(18 заданий) в %
Верно выполнили 2 часть
(5 заданий)
Верно выполнили 2 часть
(5 заданий) в %
в октябре
47
30
64
15
32
в декабре
49
32
65
18
37
Наблюдается положительная динамика усвоения материала и применения знаний при выполнении экзаменациооной работы.
Качество знаний обучающихся 9 класса составило 42,7 %. В критической зоне находятся умения выполнять арифметические вычисления, преобразовывать выражения, содержащие алгебраические дроби. Также были выявлены проблемы с выполнением действий с геометрическими фигурами, чтением графиков функций. Следует отметить, что темы «Арифметическая и геометрическая прогрессия», «Начальные сведения из теории вероятностей» не являются в настоящее время изученными (так как по образовательному стандарту эти темы находятся в зоне ближайшего изучения — во втором полугодии учебного года), следовательно, задания, связанные с данными темами, обучающимися не выполнялись.
Лучшие индивидуальные результаты показали:Кашапова О.,Галимуллин И,Загиров Р.,Михайлова Д.,Кулиахметов Т., Кондратов Д.
Худшие индивидуальные результаты: Сарваров Д.,Гилязов А.,Исламов Р.,Ряхина О.,Зубков В.,Хаматзянова О.. Причина – слабое развитие интеллектуально-познавательной сферы. Определены мероприятия на развитие интеллектуально-познавательной сферы данных обучающихся.
В оставшееся до окончания учебного года время, следует уделить повышенное внимание отработке навыков арифметических вычислений, анализу графиков функций, заданиям геометрического содержания, заданиям, связанным с преобразованием выражений (сокращение дробей, преобразования многочленов).
Выводы и предложения:
Учителю математики С.Н.Гончарук рекомендовать:
повысить персональную ответственность за качество подготовки учащихся 9 классов к сдаче государственной (итоговой) аттестации по математике.
определить индивидуально для каждого учащегося перечень тем, по которым у них есть хоть малейшие продвижения, и работать над их развитием индивидуально, в том числе через компьютерные обучающие программы и онлайн тестирование
в оставшееся до итоговой аттестации время регулярно проводить устную работу на уроках с повторением действий с рациональными числами с целью закрепления вычислительных навыков учащихся;
усилить работу по ликвидации и предупреждению выявленных пробелов: уметь заранее предвидеть трудности учащихся при выполнении типичных заданий, использовать приемы по снятию этих трудностей с целью предотвращения дополнительных ошибок (разъяснение, иллюстрации, рисунки, таблицы, схемы, комментарии к домашним заданиям)
выделить «проблемные» 3-4 темы в каждом конкретном классе и работать над ликвидацией пробелов в знаниях и умениях учащихся по этим темам, после чего можно постепенно подключать другие темы;
организовать в классе разноуровневое повторение по выбранным темам;
со слабыми учащимися в первую очередь закрепить достигнутые успехи, предоставляя им возможность выполнять 15 – 20 минутную самостоятельную работу, в которую включены задания на отрабатываемую тему; определить индивидуально для каждого учащегося перечень тем, по которым у них есть хоть малейшие продвижения, и работать над их развитием
с сильными учащимися, помимо тренировки в решении задач базового уровня сложности (в виде самостоятельных работ), проводить разбор методов решения задач повышенного уровня сложности, проверяя усвоение этих методов на самостоятельных работах и дополнительных занятиях.
усилить практическую направленность обучения, включая соответствующие задания «на проценты», графики реальных зависимостей, текстовые задачи с построением математических моделей реальных ситуаций
обратить внимание на формирование вычислительного навыка у выпускников 9-х классов
организовать работу с использованием бланков ответов с целью совершенствования умений и навыков работать с ними
infourok.ru
Алгебра 9 класс, Часть 1
Present Simple (Indefinite) – настоящее простое (неопределенное) время. Образование и употреблениеPresent Simple относится к наиболее часто встречающимся в предложении временам английского языка и обозначает действие, происходящее регулярно, постоянно, что можно увидеть в следующем примере:
| Jane is a nurse. She works in a hospital. Jane looks after patients. | Джейн – медсестра. Она работает в больнице. Джейн ухаживает за пациентами. |
В приведенном примере охарактеризовано действие, совершаемое Джейн регулярно (например, с понедельника по пятницу). Однако это вовсе не означает, что это же действие Джейн совершает прямо сейчас: возможно, сейчас у нее выходной, и она отдыхает или занимается чем-то, не связанным с профессией.
Далее приведем правила образования Present Simple Tense и примеры предложений в таблицах.
Образование утвердительной формы Present Simple
| to drive | I drive a bus because I am a bus driver. | Я вожу автобус, потому что я – водитель автобуса. |
| to sleep | Koala bears sleep up to 22 hours a day. | Коалы спят до 22 часов в сутки. |
| to go away | They usually go away on holidays. | Они обычно уезжают во время отпуска. |
Однако если подлежащее в предложении выражено формой 3-го лица единственного числа (чему соответствуют местоимения he – он, she – она, it — оно), то глагол получает окончание –(e)s:
| to travel | He usually travels two times a year. | Он обычно отправляется в путешествие два раза в год. |
| to earn | Tom earns a lot of money. | Том зарабатывает много денег. |
| to smoke | Jim smokes 10 cigarettes a day. | Джим курит по 10 сигарет в день. |
Особенности образования формы 3-го лица единственного числа некоторых глаголов
- Если глагол оканчивается на –s, -z, -sh, -ch,-x или – о, то при образовании этой формы добавляется окончание –es:
| to pass | passes | Jim always passes the ball to me. | Джим всегда передает мяч мне. |
| to buzz | buzzes | This bee buzzes very loudly. | Эта пчела жужжит очень громко. |
| to wash | washes | Mary washes the dishes in a restaurant. | Мери моет посуду в ресторане. |
| to teach | teaches | Tom teaches history at school. | Том преподает историю в школе. |
| to fix | fixes | Alex fixes cars at Phil’s Garage. | Алекс ремонтирует машины в «Гараже у Фила». |
| to go | goes | Jessica goes to a disco every Saturday. | Джессика ходит на дискотеку каждую субботу. |
Стоит обратить внимание на то, что буква -e- в окончании в таком случае читается как [I] (кроме глаголов на -о), тогда как при добавлении – s к глаголу с «немой» (нечитаемой) –е в конце, -е остается непроизносимой. Сравните:
to watch – watches [wɔtʃız]
to make – makes [meıks]
- Если глагол оканчивается на – у, то следует обратить внимание на то, какая буква стоит перед– у: гласная означает, что – у сохраняется при добавлении окончания, согласная – значит, — у превратится в –ie:
| o play | plays | Ann often plays with her little nephew. | Энн часто играет со своим маленьким племянником. |
| to study | studies | John studies medicine at university. | Джон изучает медицину в университете. |
Образование отрицательной формы в Present Simple
Если требуется употребить глагол с частицей not, то есть составить отрицательное предложение, потребуется вспомогательный глагол do для большинства случаев и его форма does для 3-го лица единственного числа. Непосредственно к вспомогательному глаголу добавляется частица not, что на практике дает довольно часто следующие сокращения:
do not = don’t
does not = doesn’t
Вспомогательный глагол в одной из указанных выше отрицательных форм ставится непосредственно перед смысловым глаголом, который обязательно стоит в исходной форме, то есть окончание –(e)s в 3-м лице единственного числа не добавляется. Это связано с тем, что окончание –(e)s в таком случае уже присутствует у вспомогательного глагола в форме doesn’t. Например:
| We don’t like coffee. | Мы не любим кофе. |
| He doesn’t play basketball at school. | Он не играет в баскетбол в школе. |
| They don’t have breakfast in the morning. | Они не завтракают по утрам. |
| Sarah doesn’t walk her dog in the afternoon. | Сара не выгуливает свою собаку во второй половине дня. |
Образование вопросительных форм в Present Simple
Формой, на которой базируется составление любого типа вопроса (а всего их 5), является форма общего вопроса, то есть вопроса, требующего ответа «Да» или «Нет». Она образуется путем постановки на первое место в предложении все того же вспомогательного глагола Do или его формы Does для 3-го лица единственного числа, за которым последуют подлежащее и смысловой глагол в исходной форме соответственно:
Do/Does + S + V1…?
где S – подлежащее, а V1 – смысловой глагол в исходной форме.
| Do you like winter sports? | Ты любишь зимние виды спорта? |
| Does he help you with your homework? | Он помогает тебе с твоей домашней работой? |
Ответом на подобные вопросы часто служат слова Yes/Да и No/Нет. Однако ответ только при помощи одного из этих слов будет недостаточным в английском языке. Традиционно краткий ответ на общий вопрос строится по следующим схемам:
а) для утвердительного ответа: Yes, SP + do/does., где SP – подлежащее в форме личного местоимения, например:
| –Do you travel a lot? – Yes, I do. | – Ты много путешествуешь? – Да. |
| – Does Mary work in a hotel? – Yes, she does. | – Мери работает в гостинице? – Да. |
| – Do your friends speak English? – No, they don’t. | – Твои друзья говорят по-английски? – Нет. |
| – Does James drive a school bus? – No, he doesn’t. | – Джеймс водит школьный автобус? – Нет. |
Специальный вопрос или вопрос с вопросительным словом запрашивает конкретную информацию и строится по схеме:
Wh + do/does + S + V1…?
где Wh – вопросительное слово, S – подлежащее, а V1 – смысловой глагол в исходной форме, например:
| When do you leave for school in the morning? | Когда ты уходишь в школу утром? |
| How long does the baby sleep in the afternoon? | Как долго младенец спит после обеда? |
| Who do you stay with when you are in London? | У кого ты остаешься, когда бываешь в Лондоне? |
Однако следует отметить, что эта схема не подходит для вопросов, начинающихся со слова Who в значении «Кто?» и (реже) What в значении «Что?» (в именительном падеже), так как подобные вопросы не относятся к группе специальных. Это вопросы к подлежащему, которые требуют образования по следующей схеме:
Who/What + V(e)s …?
Глагол в таких вопросах чаще всего принимает форму 3-го лица единственного числа (V(e)s), например:
| Who lives in this house? | Кто живет в этом доме? |
| What happens if you add acid to water? | Что происходит, если добавить кислоту в воду? |
Альтернативный вопрос, предполагающий некий выбор из двух или более объектов или действий, строится точно по аналогии с общим вопросом, но требует наличия в предложении союза or/или, например:
| Do you prefer tea or coffee for breakfast? | Ты предпочитаешь чай или кофе на завтрак? |
| Does Tom help or bother you? | Том помогает или мешает тебе? |
Разделительный вопрос, или так называемый «вопрос-ярлычок», представляет собой небольшое добавление к утвердительному или отрицательному предложению и ставит под сомнение сказанное в нем. Переводится на русский язык такой вопрос всегда одинаково – «не так ли? / не правда ли?», а вот образуется по-разному в зависимости от структуры исходного предложения, например:
| You speak Japanese, don’t you? | Ты говоришь по-японски, не правда ли? |
| Tom doesn’t smoke, does he? | Том не курит, не так ли? |
Разделительный вопрос строится по следующим схемам:
а) для утвердительного базового предложения: don’t/doesn’t +SP?
b) для отрицательного базового предложения: do/does +SP?
Приведенные правила образования утвердительных (Affirmative), вопросительных (Interrogative) и отрицательных (Negative) форм позволяют понять как образуется Present Simple, а легко запомнить их можно по следующей таблице (на примере глагола go):
| Affirmative | Negative | Interrogative |
| I go | I don’t go | Do I go ? |
| You go | You don’t go | Do you go ? |
| He goes | He doesn’t go | Does he goes ? |
| She goes | She doesn’t go | Does she goes ? |
| It goes | It doesn’t go | Does it goes ? |
| We go | We don’t go | Do we go ? |
| You go | You don’t go | Do you go ? |
| They go | They don’t go | Do they go ? |
Таблица образования утвердительных, отрицательных и вопросительных предложений в Present Simple Tense
Особые случаи образования форм Present Simple
Отдельные глаголы, среди которых, главным образом, вспомогательные и модальные, образуют соответствующие формы настоящего простого времени не по приведенным выше правилам:
- Глагол to be – «быть» имеет следующие формы: I am, he/she/it is, you/we/they are. Вопросительные и отрицательные формы образуются без вспомогательного глагола do/does.
- Глагол to have – «иметь» в 3-м лице ед. числа имеет форму has.
- Глагол can – «мочь, уметь» во всех лицах имеет одинаковую форму can. Отрицание имеет вид can’t/cannot, а вопрос строится без do/does.
- Глагол must – «быть должным» также обладает одинаковой формой во всех лицах – must. Отрицание имеет форму mustn’t, а вопрос образуется без участия do/does.
| действие, происходящее регулярно | I usually get up at 7 o’clock. | Я обычно встаю в 7 часов. |
| действие, происходящее постоянно | We live in a small village near Dublin. | Мы живем в маленькой деревне рядом с Дублином. |
| общеизвестные факты | Water freezes at 0ºC. | Вода замерзает при 0ºC. |
| действия, которые произойдут в будущем согласно плану или расписанию | Our train arrives at 8:30 p.m. | Наш поезд прибудет в 8:30 вечера. |
| последовательность действий, выполняющая роль своего рода перспективного планирования | I graduate from the university, take a year off, travel a lot, find an interesting job and only then think of getting married. | Я выпускаюсь из университета, беру год отдыха, много путешествую, нахожу интересную работу и только потом задумываюсь о замужестве. |
| действия, произошедшие в прошлом, в заголовках для эмоционального «приближения» события | Terrorists organize riots in Paris. | Террористы организовали беспорядки в Париже. |
Таким образом, настоящее простое время находит широкое применение в речи и является одним из базовых элементов, на которых строится последующее изучение английского языка.
onlinetestpad.com
Тест по математике для учеников 9 класса. Онлайн — тест по математике (9 класс). Онлайн
Предлагаемый тест предназначен для девятиклассников и позволяет проверить базовые знания учащихся по алгебре и геометрии. Для успешного решения теста не требуется знаний, выходящих за рамки школьной программы по математике для 9 класса.
Вам будет предложено 20 вопросов различной сложности. Каждый правильный ответ приносит 1 балл. Максимальная оценка за выполнение теста равна 20.
Постарайтесь затратить на решение предложенного варианта не более 120 минут. Не используйте в процессе работы микрокалькулятор, учебники, справочную литературу.
Ответом к заданию в большинстве случаев является целое число или конечная десятичная дробь. Не пишите в ответе размерности величин, не забывайте переводить обыкновенные дроби в десятичные! В качестве разделителя разрядов используйте запятую, а не точку!
Если ваш результат превысит 16 баллов, можете быть уверены: вы заслуживаете оценки «отлично». Если вы наберете 12-16 баллов, это можно считать хорошим итогом.
А вот в случае, если ваша оценка будет ниже 7 баллов, ситуация плачевная! Вы плохо знакомы со школьным курсом математики, причем речь идет не только о программе 9 класса, но и о существенных пробелах за 5-8 классы. И неважно, что в школе вы имеете оценку «хорошо» по алгебре и геометрии. К сожалению, часто школьные оценки бывают необъективны. Пора начинать работать! Не забывайте, что в конце этого учебного года вам предстоит сдавать ОГЭ по математике!
Успехов!
01. Вычислите без использования микрокалькулятора: (1,87 + 0,13):(5,241 — 5,239).
02. Каждый год количество автомобилей в городе Х увеличивается на 5%. Сейчас в городе Х 4000000 автомобилей. Сколько машин будет в городе через 3 года?
03. Решите уравнение (x+3)2 = (x-2)2. Если уравнение имеет несколько корней, в ответе укажите меньший из них.
04. 1 Сентября Маша решила один пример, 2 Сентября — три примера, 3 Сентября — 5 и т. д. Если данная закономерность сохранится, сколько примеров придется решить Маше 25 Сентября (того же года)?
05. Установите соответствие между формулой, задающей функцию, и описанием графика данной функции.
| А) y = -3x2 + 17x — 38 | 1) парабола, вершина которой находится в точке N(2;5) |
| Б) y = x2 — 10x + 25 | 2) парабола, ветви которой направлены вниз |
| В) y = x2 — 4x + 9 | 3) гипербола |
| Г) y = 8/(x-3) + 160 | 4) парабола, касающаяся оси Ох |
06. Решите неравенство: (x — 3)(x2 — 49) > 0. В ответе укажите количество целых решений данного неравенства, лежащих в интервале (1;10).
07. Периметр прямоугольного участка земли равен 100 м, а его площадь — 600 м2. Найдите длину и ширину данного участка, В ответе укажите разность между длиной и шириной (в м).
08. Вычислите значение выражения при a = 1,798 и b = 0,2:
b2−a22⋅(2aa+b+3a−ba−b)+2,5a2 {b^2-a^2} over {2} `cdot` ( {2a} over {a+b} `+ `{3a-b} over {a-b})`+`2,5a^2
09. Решите уравнение x2 + 4x + 4 = 1/(x+2) (рекомендуем использовать графический способ). Если уравнение имеет несколько корней, в ответе укажите наибольший из них.
10. Маленькая гусеница съедает лист салата за 12 дней, большая — за 6 дней. За сколько дней будет съеден лист салата, если гусеницы будут есть его вместе?
11. Вычислите без использования калькулятора:
1236(317)2⋅(2)140{12^{36}} over {(3^{17})^{2}cdot (sqrt{2})^{140} }
12. Отметьте верные утверждения (ответов может быть несколько).
- Диагональ квадрата со стороной 5 выражается рациональным числом.
- При умножении рационального числа на иррациональное не может получиться целый результат.
- Между двумя неравными числами можно поместить бесконечное количество рациональных чисел.
- Квадратный корень из натурального числа может быть лишь целым или иррациональным числом.
- При умножении рационального числа на иррациональное не может получиться целый результат.
13. Два игральных кубика подброшены одновременно. Какова вероятность того, что суммарное количество очков, выпавшее на двух кубиках, не превысит 3?
14. Найдите те значения р, при которых уравнение | 3x2 -12x +10 | — p = 0 имеет ровно 3 корня. Если таких значений будет несколько, в ответе укажите наибольшее из них.
15. Вычислите площадь ромба, если сумма длин его диагоналей равна 15 и одна из них в 2 раза больше другой.
16. Найдите длину вектора АВ, если известны координаты точек А и В: A(124;761), B(127;765).
17. Стороны параллелограмма равны 6 см и 8 см, а угол между ними составляет 120о. Найдите меньшую диагональ параллелограмма. Ответ округлите до сотых.
18. Длина окружности равна 20 π. Найдите высоту правильного треугольника, вписанного в эту окружность.
19. Отметьте верные утверждения (ответов может быть несколько).
20. Сплав №1 содержит 30% золота по массе, сплав №2 — 70% золота. Сплавы соединили в отношении 2:3 (по массе) и получили 7.6 кг нового сплава №3. Сколько кг чистого золота следует добавить к образцу №3, чтобы получить сплав, содержащий 62% золота?
Возможно, вас заинтересуют следующие онлайн-тесты по математике:
www.repetitor2000.ru
Решебник (ГДЗ) по математике за 9 класс
Решебники, ГДЗ
- 1 Класс
- Математика
- Русский язык
- Английский язык
- Информатика
- Немецкий язык
- Литература
- Человек и мир
- Природоведение
- Основы здоровья
- Музыка
- Окружающий мир
- 2 Класс
- Математика
- Русский язык
- Белорусский язык
- Английский язык
- Информатика
- Украинский язык
- Немецкий язык
- Литература
- Человек и мир
- Природоведение
- Основы здоровья
- Музыка
- Окружающий мир
- Технология
- 3 Класс
- Математика
- Русский язык
- Белорусский язык
- Английский язык
- Информатика
- Украинский язык
- Немецкий язык
- Литература
- Человек и мир
- Музыка
- Окружающий мир
- Испанский язык
- 4 Класс
- Математика
- Русский язык
- Белорусский язык
- Английский язык
- Информатика
- Украинский язык
- Немецкий язык
- Литература
megaresheba.ru
Анализ пробного экзамена по математике в 9 классе
Анализ пробного экзамена
по математике(ОГЭ) в 9 классе
МКОУ Поваренская СОШ
Дата проведения – 16.02.2015
Число учащихся участвующих в ОГЭ – 12
Число выполнявших работу – 11
Процент выполнения – 36
Экзаменационная работа состоит из заданий, из которых20 заданий базового уровня(часть1), 4 задания повышенного уровня(часть2) и2 задания высокого уровня сложности(часть2). Работа состоит из трёх модулей: «Алгебра», «Геометрия», «Реальная математика».
Модуль «Алгебра» содержит11 заданий: в части1 — восемь заданий; в части2 — три задания. Модуль«Геометрия» содержит восемь заданий: в части1 — пять заданий; в части2 — три задания. Модуль«Реальная математика» содержит семь заданий: все задания этого модуля— в части1.:
Целью работы была диагностика уровня знаний учащихся по математике на данном этапе обучения для планирования процесса подготовки к ОГЭ в оставшееся до государственной итоговой аттестации время.
Анализ пробного экзамена по математике, проведенного в 9 классе МКОУ
Подробные результаты представлены в таблицах.
Таблица набранных баллов.
ФИ
№ задания
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Итого
баллов
1
1
1
1
1
1
1
1
1
8
2
1
1
1
1
4
3
1
1
1
1
1
1
1
8
4
1
1
5
1
1
6
1
1
1
1
1
1
1
1
8
7
1
1
1
1
1
1
6
8
1
1
1
3
9
1
1
2
10
1
1
1
1
1
1
1
1
8
11
1
1
1
1
1
1
1
1
8
0
5
4
1
6
2
0
5
2
5
0
1
3
6
4
3
0
4
0
5
Обобщенный план варианта КИМ и количество учеников, справившихся с заданиями.
№ задания
Основные проверяемые требования
Количесво учеников, справившихся с заданием
% выполнения
% невыполнения
Часть 1
Модуль «Алгебра»
1
Уметь выполнять вычисления и преобразования
0
0
100
2
Уметь выполнять вычисления и преобразования
5
45
55
3
Уметь выполнять вычисления и преобразования, уметь выполнять преобразования алгебраических выражений
4
36
64
4
Уметь решать уравнения, неравенства и их системы
1
9
91
5
Уметь строить и читать графики функций
6
55
45
6
Уметь строить и читать графики функций
1
9
91
7
Уметь выполнять преобразования алгебраических выражений.
0
0
100
8
Уметь решать уравнения, неравенства и их системы .
5
45
55
Модуль «Геометрия»
9
Уметь выполнять действия с геометрическими фигурами, координатами и векторами.
2
18
82
10
Уметь выполнять действия с геометрическими фигурами, координатами и векторами.
5
45
55
11
Уметь выполнять действия с геометрическими фигурами, координатами и векторами
0
0
100
12
Уметь выполнять действия с геометрическими фигурами, координатами и векторами
1
9
91
13
Проводить доказательные рассуждения при решении задач, оценивать логическую правильность рассуждений, распознавать ошибочные заключения.
6
55
45
Модуль «Реальная математика»
14
Пользоваться основными единицами длины, массы, времени, скорости, площади, объёма; выражать более крупные единицы через более мелкие и наоборот.
6
55
45
15
Описывать с помощью функций различные реальные зависимости между величинами; интерпретировать графики реальных зависимо-стей
4
36
64
16
Решать несложные практические расчетные задачи; решать задачи, связанные с отношением, пропорциональностью величин, дробями, процентами; пользоваться оценкой и прикидкой при практических расчетах; интерпретировать результаты решения задач с учётом ограничений, связанных с реальными свойствами рассматриваемых объектов
3
27
73
17
Описывать реальные ситуации на языке геометрии, исследовать построенные модели с использованием геометрических понятий и теорем, решать практические задачи, связанные с нахождением геометрических величин
0
0
100
18
Анализировать реальные числовые данные, представленные в таблицах, на диаграммах, графиках
3
27
73
19
Решать практические задачи, требующие систематического перебора вариантов; сравнивать шансы наступления случайных событий, оценивать вероятности случайного события, сопоставлять и исследовать модели реальной ситуацией с использованием аппарата вероятности и статистики
0
0
100
20
Осуществлять практические расчеты по формулам, составлять несложные формулы, выражающие зависимости между величинами
5
45
55
Часть 2
Модуль «Алгебра»
21
Уметь выполнять преобразования алгебраических выражений, решать уравнения, неравенства и их системы, строить и читать графики функций
0
0
100
22
Уметь выполнять преобразования алгебраических выражений, решать уравнения, неравенства и их системы, строить и читать графики функций, строить и исследовать простейшие математические модели
0
0
100
23
Уметь выполнять преобразования алгебраических выражений, решать уравнения, неравенства и их системы, строить и читать графики функций, строить и исследовать простейшие математические модели
0
0
100
Модуль «Геометрия»
24
Уметь выполнять действия с геометрическими фигурами, координатами и векторами
0
0
100
25
Проводить доказательные рассуждения при решении задач, оценивать логическую правильность рассуждений, распознавать ошибочные заключения
0
0
100
26
Уметь выполнять действия с геометрическими фигурами, координатами и векторами
0
0
100
Анализ выполненных работ показал, что качество подготовки выпускников 9 класса по математике составило 0%%), абсолютная успеваемость – 45%. Средний балл -2,5.
Проанализировав полученные данные мы их представили в виде диаграммы:
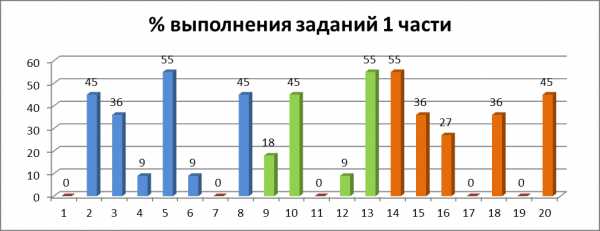
Критический уровень знаний выпускники показали при решении заданий №№ 1, 7, 11, 17, 20 – 0% выполнения.
Средний уровень знаний выпускники показали при решении заданий №№ 5, 13, 14.
В части 2 отсутствуют развернутые решения, поэтому в части 2 ребята баллы не набрали.
Выводы и предложения:
Учителю математики О.А. Домоводовой рекомендовать:
повысить персональную ответственность за качество подготовки учащихся 9 классов к сдаче государственной (итоговой) аттестации по математике.
-определить индивидуально для каждого учащегося перечень тем, по которым у них есть хоть малейшие продвижения, и работать над их развитием индивидуально, в том числе через компьютерные обучающие программы и онлайн тестирование
в оставшееся до итоговой аттестации время регулярно проводить устную работу на уроках с повторением действий с рациональными числами с целью закрепления вычислительных навыков учащихся;
усилить работу по ликвидации и предупреждению выявленных пробелов: уметь заранее предвидеть трудности учащихся при выполнении типичных заданий, использовать приемы по снятию этих трудностей с целью предотвращения дополнительных ошибок (разъяснение, иллюстрации, рисунки, таблицы, схемы, комментарии к домашним заданиям)
выделить «проблемные» 3-4 темы в каждом конкретном классе и работать над ликвидацией пробелов в знаниях и умениях учащихся по этим темам, после чего можно постепенно подключать другие темы;
организовать в классе разноуровневое повторение по выбранным темам;
со слабыми учащимися в первую очередь закрепить достигнутые успехи, предоставляя им возможность выполнять 15 – 20 минутную самостоятельную работу, в которую включены задания на отрабатываемую тему; определить индивидуально для каждого учащегося перечень тем, по которым у них есть хоть малейшие продвижения, и работать над их развитием
с сильными учащимися, помимо тренировки в решении задач базового уровня сложности (в виде самостоятельных работ), проводить разбор методов решения задач повышенного уровня сложности, проверяя усвоение этих методов на самостоятельных работах и дополнительных занятиях.
усилить практическую направленность обучения, включая соответствующие задания «на проценты», графики реальных зависимостей, текстовые задачи с построением математических моделей реальных ситуаций
обратить внимание на формирование вычислительного навыка у выпускников 9-х классов
организовать работу с использованием бланков ответов с целью совершенствования умений и навыков работать с ними
Заместитель директора по УВР Е.Г. Тропина
infourok.ru

