Информатика система счисления 9 класс: Урок информатики в 9-м классе. Тема: «Системы счисления»

Урок информатики в 9-м классе. Тема: «Системы счисления»

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

Тип урока: Урок изучения новой темы.

Дидактическая цель: создать условия для актуализации и закрепления учебной информации

Цель урока:

Образовательная:

знакомство с понятием «система счисления»;
умение различать виды систем счисления и применять их на практическом занятии;
умение правильно записывать числа в системах счисления;
формирование способности для применения правил перевода чисел из одной системы счисления в другие.

Развивающая:

развивать логическое мышление, умение обобщать, конкретизировать;
формирование внимания, умения наблюдать и закреплять знания;

Воспитательная:

воспитывать самостоятельность, уважительное отношение друг к друг;
воспитание информационной культуры учащихся.

Методы обучения: наглядный, информационно-развивающий, опрос.

Формы организации познавательной деятельности: индивидуальная.

Средства обучения: учебник Семакина “Информатика и ИКТ. 9 класс. ” учебник для 9 класса общеобразовательных учреждений, рабочие тетради, авторучки, проектор, компьютер, компьютерная презентация по теме урока.

План урока:

Организационный момент.
Изучение нового материала.
Физкультминутка.
Формирование умений, навыков.
Домашнее задание

Ход урока

1. Организационный момент.

Приветствие, проверка присутствующих. Мы сегодня начинаем изучение новой темы. Данная тема очень важна. Хотелось бы отметить умение решать задачи на систему счисления дает возможность набрать более высокие баллы, что очень важно при сдаче ЕГЭ и поступлении в ВУЗЫ. Открываем тетрадки, записываем сегодняшнее число и тему: СИСТЕМЫ СЧИСЛЕНИЯ.

План темы

Историческая справка
Определение системы счисления
Виды системы счисления
Правила перевода чисел из одной системы счисления в другую

2. Объяснение нового материала (по плану, приложение 3)

2.1. Историческая справка

Люди научились считать еще в незапамятные времена. Сначала они просто различали один предмет перед ними или нет. Если предмет был не один, то говорили «много». Постепенно появилось слово для обозначения двух предметов. Счет парами очень удобен.

Наиболее древней и простой «счетной машиной» издавна являются пальцы рук и ног. И даже в наше время еще пользуются этим «счетным прибором», который всегда при нас. На пальцах можно решать примеры не только в пределах десяти. В древние времена люди ходили босиком. Поэтому они могли пользоваться для счета пальцами как рук, так и ног.

Записывали числа поначалу совсем просто: делали зарубки на куске дерева или кости. На этой кости тридцать тысяч лет назад сделаны нарезки, они показывают, что уже тогда наши предки умели не только считать, но и записывать результаты счета!

Когда понадобилось записывать большие числа, то для пятерок и десяток стали придумывать новые знаки. Вот как египтяне записывали число 3 246:

Запомнить большие числа трудно, поэтому к «счетной машине» рук и ног добавляли механические приспособления. Веревочные счеты с узелками применялись и в России, и во многих странах Европы. Остатками этого способа является практикуемое еще до сих пор завязывание узелков на носовых платках «на память». Так, одни пользовались для запоминания чисел камешками, зернами, веревкой с узелками, другие — палочками с зарубками. Это были первые счетные приборы, которые в конце концов привели к образованию различных систем счисления

2.2. Система счисления — это совокупность правил и приемов записи чисел с помощью набора цифровых знаков.

позиционные, когда значение каждой цифры числа определяется ее позицией в записи числа;
непозиционные, когда значение цифры в числе не зависит от ее места в записи числа.

Непозиционные СС. Единичная система счисления. Находки археологов на стоянках первобытных людей свидетельствуют о том, что первоначально количество предметов отображали равным количеством каких-либо значков (бирок): зарубок, черточек, точек. Позже значки стали группировать по три или по пять. Такая система записи чисел называется единичной (унарной), так как любое число в ней образуется путем повторения одного знака, символизирующего единицу. Отголоски единичной системы счисления встречаются и сегодня (счетные палочки для обучения счету; полоски, нашитые на рукаве, означают на каком курсе учится курсант военного училища). Неудобства такой системы записи чисел и ограниченность ее применения очевидны: чем большее число надо записать, тем длиннее строка из палочек.

Римская система счисления является непозиционной системой. В ней для записи чисел используются буквы латинского алфавита. При записи чисел в римской системе счисления значением числа является алгебраическая сумма цифр, в него входящих. При этом цифры в записи числа следуют, как правило, в порядке убывания их значений, и не разрешается записывать рядом более трех одинаковых цифр. В том случае, когда за цифрой с большим значением следует цифра с меньшим, ее вклад в значение числа в целом является отрицательным. Типичные примеры, иллюстрирующие общие правила записи чисел в римской система счисления, приведены в таблице.

Таблица 1. Запись чисел в римской системе счисления

1	2	3	4	5	6	7	8	9	10	50	100	500	1000
I	II	III	IV	V	VI	VII	VIII	IX	X	L	C	D	M

Недостатком римской системы является отсутствие формальных правил записи чисел и, соответственно, арифметических действий с многозначными числами. По причине неудобства и большой сложности в настоящее время римская система счисления используется там, где это действительно удобно: в литературе (нумерация глав), в оформлении документов (серия паспорта, ценных бумаг и др.), в декоративных целях на циферблате часов и в ряде других случаев.

Мы с вами более подробно рассмотрим позиционные системы счисления.

В позиционной системе счисления основными понятиями являются понятие алфавита и основания системы счисления.

Алфавитом системы счисления называется совокупность всех цифр.

Количество цифр, необходимых для записи числа в системе, называют основанием системы счисления. Основание системы записывается в справа числа в нижнем индексе: 78₁₀, 1100010₁₂, AF12₁₆ и т. д.

Количество цифр, составляющих алфавит, называется его мощностью.

В позиционных системах счисления один и тот же числовой знак (цифра) в записи числа имеет различные значения в зависимости от того места(разряда), где он расположен.

Разряд — номер позиции в числе. Нумеруются справа налево, начиная с нуля.

Пример. Число6184₁₀ запишется в форме многочлена следующим образом:

6184₁₀ = 6*10 ³ +1*10 ² +8*10 ¹ +4*10 ⁰

2.3. Виды систем счисления.

В компьютерах принято использовать 4 основные системы счисления – двоичную, восьмеричную, десятичную и шестнадцатеричную. Именно их подробно рассмотрим.

Десятичная система счисления – в настоящее время наиболее известная и используемая. Древнее изображение десятичных цифр не случайно: каждая цифра обозначает число по количеству углов в ней. Например, 0 — углов нет, 1 — один угол, 2 — два угла и т.д. Написание десятичных цифр претерпело существенные изменения. Форма, которой мы пользуемся, установилась в XVI веке.

Десятичная система впервые появилась в Индии примерно в VI веке новой эры. Индийская нумерация использовала девять числовых символов и нуль для обозначения пустой позиции

Десятичная система использует десять цифр – 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9, а также символы “+” и “–” для обозначения знака числа и запятую или точку для разделения целой и дробной частей числа.

Если взять правило, по которым строятся числа в десятичной системе счисления, заменив основание 10 на натуральное число N, можно построить позиционную систему счисления с основанием N.

В вычислительных машинах используется двоичная система счисления, её основание — число 2. Для записи чисел в этой системе используют только две цифры — 0 и 1. Двоичная система счисления была придумана математиками и философами задолго до появления компьютеров, еще в ХVII — ХIХ веках. Двоичная система удобна для компьютера, но неудобна для человека: числа получаются длинными и их трудно записывать и запоминать. Конечно, можно перевести число в десятичную систему и записывать в таком виде, а потом, когда понадобится перевести обратно, но все эти переводы трудоёмки. Поэтому применяются системы счисления, родственные двоичной — восьмеричная и шестнадцатеричная. Для записи чисел в этих системах требуется соответственно 8 и 16 цифр. В 16-теричной первые 10 цифр общие, а дальше используют заглавные латинские буквы. Шестнадцатеричная цифра A соответствует десятеричному числу 10, шестнадцатеричная B – десятичному числу 11 и т. д. Использование этих систем объясняется тем, что переход к записи числа в любой из этих систем от его двоичной записи очень прост. Ниже приведена таблица соответствия чисел, записанных в разных системах.

Учащиеся заполняют таблицу в тетрадях (приложение 1, таблица 1).

2.4. Правила перевода чисел из одной системы счисления в другую

Перевод чисел из одной системы счисления в другую составляет важную часть машинной арифметики. Рассмотрим основные правила перевода.

1. При переводе числа из двоичной (восьмеричной, шестнадцатеричной) системы в десятичную надо это число представить в виде суммы степеней основания его системы счисления.

Числа 10100110₂ , 703₈ , 23FA1₁₆ перевести в десятичную систему счисления.

10100110₂=1*2⁷+0*2⁶+1*2⁵+0*2⁴+0*2³+1*2²+1*2¹+0*2⁰=128+32+4+2=166₁₀

703₈=7*8²+0*8¹+3*8⁰=448+3=447₁₀

23FA1₁₆=2*16⁴+3*16³+15*16²+10*16¹+1*16⁰=131072+12288+3840+160+1=147361

2. Правило перевода из десятичной системы счисления в систему с основанием q:

1. Последовательно выполнять деление исходного числа и получаемых частных на q до тех пор, пока не получим частное, меньшее делителя.

2. Полученные при таком делении остатки – цифры числа в системе счисления q – записать в обратном порядке (снизу вверх).

Пример. Перевести числа из десятичной системы счисления

3. Чтобы перевести число из двоичной системы в восьмеричную (шестнадцатеричную), его нужно разбить на триады (тетрады), начиная с младшего разряда (справа налево), в случае необходимости дополнив старшую триаду (тетраду) нулями, и каждую триаду (тетраду) заменить соответствующей восьмеричной (шестнадцатеричной) цифрой (табл.).

Число 10010110111₂ перевести в восьмеричную и в шестнадцатеричную системы счисления.

4. Для перевода восьмеричного (шестнадцатеричного) числа в двоичное необходимо каждую цифру заменить эквивалентной ей двоичной триадой (тетрадой).

Числа 726₈ и 74С₁₆ перевести в двоичную систему счисления.

726₈= 111 010 110₂

74С₁₆ = 0111 0100 1100₂ (при записи числа первый 0 не пишется)

5. При переходе из восьмеричной системы счисления в шестнадцатеричную и обратно, необходим промежуточный перевод чисел в двоичную систему.

Число FAE₁₆ перевести в восьмеричную систему счисления.

FAE₁₆=111110101110₂

111 110 101 110₂=7656₈

Число 635₈ перевести в шестнадцатеричную систему счисления.

635₈ =110011101₂

1 1001 1101₂=19D₁₆

3. Физкультминутка (см. презентация 2)

4. Формирование умений и навыков

Работа с вопросником. Отвечают устно на вопросы, используя свой конспект.

5. Домашнее задание (приложение 4)

Учить конспект, прочитать §16 по учебнику.
Написать дату своего дня рождения в римской системе счисления.

Подведение итогов урока.

План-конспект урока по информатике и икт (9 класс): Урок информатики в 9 классе «Системы счисления и правила перевода чисел из одной системы счисления в другую»

Филимоненкова Лорхен Викторовна

учитель информатики МОУ СОШ д.

Болотнянская средняя школа

Открытый урок по информатике в 8 классе

Тема : Системы счисления

Цели :

повторить и закрепить знания по теме,
закрепить навыки применения компьютера в учебной деятельности,
развить познавательные интересы, интеллектуальные способности, возможности самооценки, расширить кругозор,
сформировать у каждого ученика положительное отношение к предмету, воспитать ответственное отношение к учёбе, чувство взаимопомощи.

Тип урока : семинар.

Подготовительный этап:

Обсуждение с учениками темы семинарского занятия и его планирование.
Подбор учениками информации для выступлений и подготовка её на компьютере.
Разработка тестовых и индивидуальных заданий для учащихся.

Материалы и оборудование: плакаты, раздаточный материал (тесты), компьютер.

План урока:

Совместно с учениками обсудить цели урока.
Рассказ ученика об истории чисел «От пальцев до калькулятора».
Обзор учениками материала по теме «Системы счисления»: классификация, основные определения, представление чисел в различных системах счисления.
Работа на местах: № 8 (стр.42 – учебник).
Игровой момент «Весёлая пятиминутка».
Демонстрация учениками алгоритмов перевода целых чисел из одной системы счисления в другую.
Демонстрация учениками правил выполнения арифметических операций в позиционных системах счислениях (на примере двоичной системы счисления).
Тестовые задания «Двоичная арифметика». Проверка за компьютером в ППО «Калькулятор».
Подведение итогов урока.
Оценки за урок.
Домашнее задание.

Уч. 1 : «От пальцев до калькулятора»

В древние времена, когда люди начали считать, появилась потребность в записи чисел. Первоначально количество предметов отображали равным количеством каких-нибудь значков : насечек, чёрточек, точек.

Изучение археологами «записок» времён палеолита на кости, камне, дереве показало, что люди стремились группировать отметки по 2, 3, 5, 7, 10 штук. Такая группировка облегчала счёт. Люди учились считать не только единицами, но и парами, тройками, пятёрками, десятками и пр. Поскольку первым вычислительным инструментом у человека были пальцы, поэтому счёт чаще всего вели группами по 5 или по 10 предметов.

В дальнейшем своё название получил десяток десятков (сотня), десяток сотен (тысяча) и т.д. Такие узловые числа для удобства записи стали обозначать особыми значками – цифрами. Некоторые народы древности (римляне, славяне) использовали также буквы для обозначения цифр.

До наших дней дошли многие средства обработки информации, т.е. счётные инструменты, которые стимулировали развитие земледелия, торговли, мореплавания, астрономии и многих других областей практической и научной деятельности людей. Нетрудно догадаться, что первым счётным средством для человека были его пальцы. Туземцы Новой Гвинеи по описаниям русского путешественника Н.Н.Миклухо-Маклая считают, загибая пальцы одной руки, произнося при этом «бе, бе, бе…». Досчитав до пяти, они говорят «ибон-бе» (рука). Затем они загибают пальцы другой руки, снова повторяют «бе, бе, бе…», пока не дойдут до «ибон али» (две руки). Затем они идут дальше, приговаривая «бе, бе, бе…», пока не дойдут до «самба-бе» и «самба-али» (одна нога, две ноги). Если нужно считать дальше, папуасы пользуются пальцами рук и ног кого-нибудь другого.

В V веке до н.э. в Греции и Египте получил распространение абак ,что в переводе с греческого означает счётная доска. Вычисления на абаке производились перемещением камешков по желобам на мраморной доске. Китайский вариант абака – суан-пан. Потомком абака можно назвать и русские счёты.

В начале XVII века шотландский математик Джон Непер ввёл понятие логарифма. Затем в течение двух веков развивались вычислительные инструменты, основанные на использовании этой математической функции. В результате появилась логарифмическая линейка.

В 1645 году французский математик Блез Паскаль создал первую счётную машину, которая позволяла выполнять сложение многозначных чисел.

Немецкий учёный Лейбниц, а немного позже русские изобретатели П.Л.Чебышев и В.Т.Однер , создали механический арифмометр, на котором можно было выполнять все четыре арифметические операции. Арифмометр был предшественником современного калькулятора – маленького электронно-вычислительного устройства.

Но мечтой изобретателей вычислительной техники было создание считающего автомата, который бы без вмешательства человека производил расчёты по заранее составленной программе. Автором первого проекта вычислительного автомата был профессор Кембриджского университета Чарльз Бэббидж. Аналитическая машина Бэббиджа – это уже универсальное средство, объединяющее в себе обработку, хранение информации и обмен исходными данными и результатами с человеком.

Уч.2:

Система счисления — это способ изображения чисел и соответствующие ему правила действия над числами.

Системы счисления

Позиционные: Непозиционные:

Вавилонская Римская

60- ая Славянская

12- ая

2- ая

8- ая

10- ая

16- ая

Уч.3: Непозиционные системы

счисления

В таких системах счисления от положения знака в записи числа не зависит величина, которую он обозначает.

Например, в римских числах цифры записываются слева направо в порядке убывания. В таком случае их значения складываются. Если слева записана меньшая цифра, а справа большая, то их значения вычитаются.

I V X L C D M

1 5 10 50 100 500 1000

Представление числа в непозиционной римской системе счисления

MCMXCVII = 1000 + (-100 + 1000) + (-10 + 100) +

+ 5 + 1+ 1 = 1997

Уч.4 : Позиционные системы счисления

Впервые идея позиционной системы счисления возникла в древнем Вавилоне. В позиционных системах счисления величина, обозначаемая цифрой в записи числа, зависит от её позиции. Количество используемых цифр называется основанием позиционной системы счисления.

Система счисления	Основание	Алфавит цифр
Десятичная	10	0,1,2,3,4,5,6,7,8,9
Двоичная	2	0,1
Восьмеричная	8	0,1,2,3,4,5,6,7
Шестнадцатеричная	16	0,1,2,3,4,5,6,7,8,9, А(10), В(11), С(12), D(13), E(14), F(15)

Представление числа в позиционной десятичной системе счисления

32478 = 3*10000 + 2*1000 + 4*100 + 7*10 + 8 =

4 3 2 1 0

= 3*10 + 2*10 + 4*10 + 7*10 +8*10 ,

Отсюда видно, что всякое десятичное число можно представить как сумму произведений составляющих его цифр на соответствующие степени десятки.

Работа на местах: задание №8 (стр.42 – учебник)

Записать последовательность десяти чисел натурального ряда, начиная с нуля, для позиционных систем с основаниями 2, 3, 4, 5, 6.

Ответ:

	N=10	1	2	3	4	5	6	7	8	9
Роман	N=2	1	10	11	100	101	110	111	1000	1001
Максим	N=3	1	2	10	11	12	20	21	22	100
Ольга	N=4	1	2	3	10	11	12	13	20	21
Анжела	N=5	1	2	3	4	10	11	12	13	14
Татьяна	N=6	1	2	3	4	5	10	11	12	13

Игровой момент «Весёлая пятиминутка»:

Вам нужно решить следующую задачу:

«В бумагах одного чудака математика найдена была его автобиография. Она начиналась следующими удивительными словами: «Я окончил курс университета 44 лет от роду. Спустя год, 100-летним молодым человеком, я женился на 34-летней девушке. Незначительная разница в возрасте — всего 11 лет — способствовала тому, что мы жили общими интересами и мечтами. Спустя немного лет у меня была уже и маленькая семья из 10 детей» .

Чем объяснить странные противоречия в числах этого отрывка? Восстановите их истинный смысл.

Ответ: недесятичная система счисления — вот единственная причина кажущейся противоречивости приведенных чисел. Основание этой системы определяется фразой: «спустя год (после 44 лет), 100-летним молодым человеком…». Если от прибавления одной единицы число 44 преображается в 100, то, значит, цифра 4 — наибольшая в этой системе (как 9 — в десятичной), а, следовательно, основанием системы является 5. Т. е. все числа в автобиографии записаны в пятеричной системе счисления.

44 -> 24, 100 ->25, 34 — >19, 11 ->6, 10 ->5

Я хочу задать вам ещё несколько «несерьёзных» вопросов:

1. Когда 2х2=100? (В двоичной системе)

2. Когда 2х2=11? (В троичной системе)

3. Когда 2х3=11? (В пятеричной системе)

4. Когда 3х3=13? (В шестеричной системе)

5. В какой системе счисления число 222 является самым большим из

всех трёхзначных чисел ? (В троичной системе счисления)

6. Следующие двоичные числа расположите в порядке возрастания: 1001, 111, 010, 100. 1101, 10001.

Ответ: 010, 100, 111, 1001, 1101, 10001.

Уч.5: Алгоритм перевода целых десятичных чисел в двоичную систему счисления и, наоборот.

Перевод целого десятичного числа в другую систему счисления, в том числе двоичную, производится путём деления с остатком на основание системы (например, двойку). Полученный остаток – это младший разряд искомого числа, а полученное частное снова делится с остатком, который равен второй справа цифре и т.д. Так продолжается до тех пор, пока частное не станет меньше делителя (основания системы). Это частное – старшая цифра искомого числа.

Десятичное число (целое частное)	Делитель (основание системы)	Остаток
19	2	1
9	2	1
4	2	0
2	2	0
1	2	1

19 (10) = 10011 (2)

Чтобы перевести двоичное целое число в десятичную систему, его нужно представить в виде суммы произведений составляющих его цифр на соответствующие степени основания системы , т.е. десятки.

5 4 3 2 1 0

101101 (2) = 1*2 + 0*2 + 1*2 + 1*2 + 0*2 + 1* 2 =

= 32 + 8 + 4 + 1 = 45 (10)

Уч.6: Алгоритм перевода чисел из восьмеричной системы счисления в двоичную и, наоборот.

Для перевода целого двоичного числа в восьмеричное его нужно разбить на группы по три цифры (триады), справа налево, а затем преобразовать каждую группу в восьмеричную цифру. Если в последней, левой, группе окажется меньше трёх цифр, то необходимо её дополнить слева нулями.

Восьмеричная с.с.	Двоичная с.с.
0	000
1	001
2	010
3	011
4	100
5	101
6	110
7	111

101 001 (2) = 51 (8)

16 (8) = 001 110 (2) = 1110 (2)

Уч.7: Алгоритм перевода чисел из шестнадцатеричной системы счисления в двоичную и, наоборот.

Для перевода целого двоичного числа в шестнадцатеричное его нужно разбить на группы по четыре цифры (тетрады), начиная справа, и, если в последней левой группе окажется меньше четырёх цифр, дополнить её слева нулями. Затем надо преобразовать каждую группу в шестнадцатеричную цифру, воспользовавшись для этого предварительно составленной таблицей.

Шестнадцатеричная с.с	Двоичная с.с.
0	0000
1	0001
2	0010
3	0011
4	0100
5	0101
6	0110
7	0111
8	1000
9	1001
A	1010
B	1011
C	1100
D	1101
E	1110
F	1111

101001 (2) = 0010 1001 (2) = 29 (16)

5В3 = 0101 1011 0011 (2) = 10110110011 (2)

Уч.8 : Двоичная арифметика.

0 + 0 = 0 0 * 0 = 0

0 + 1 = 1 0 * 1 = 0

1 + 0 = 1 1 * 0 = 0

1 + 1 = 10 1 * 1 = 1

0 – 0 = 0

1 – 0 = 1

1 – 1 = 0

0 – 1 = 11

Тесты «Двоичная арифметика»

1.Сложите двоичные числа 111 и 100:

а) 1011; б) 1000; в) 1010 ; г) 1110

2. Найдите разность между двумя двоичными числами 111 и 10 :

а) 100; б) 110 ; в) 101; г) 11

3.Найдите произведение двух двоичных чисел 11 и 11:

а) 1000; б) 1001; в) 1011; г) 1010

4. Найдите частное двух двоичных чисел:

110111 и 1011 :

а) 10; б)11; в)100; г)101

Ключ к тестам:

1-а, 2- в, 3- б, 4- г.

Проверка за компьютером результатов арифметических вычислений в ППО «Калькулятор».

Подведение итогов.

Оценки за урок.

Задание на дом : глава 1, № 10 (стр. 42, учебник)

Список литературы:

1.И. Семакин и др. Информатика. Базовый курс. 7-9 кл., Москва, Юнимедиастайл, 2002.

2.Н.Угринович. Информатика и информационные технологии. 10-11 кл., Москва, Лаборатория Базовых Знаний, 2002.

Содержание

Системы счисления, ИКТ, 9 класс

Теоретический материал

для выполнения заданий ОГЭ (задание №13)

по теме «Системы счисления»

Первое необходимое умение для выполнения: Перевод из любой СС (далее и здесь СС-система счисления) в десятичную СС:

Каждую цифру разряда числа данного в любой СС пронумеровать справа налево числами от 0 и т д до последней значимой цифры разряда.
Составить числовое выражение в виде суммы (сложения) нескольких произведений (умножение), количество произведений зависит от количества цифр разрядов исходного числа.
Каждое произведение — это один множитель сама цифра разряда, а второй множитель — это основание (число) исходной СС возведенной в степень соответствующей цифре проставленной над цифрой, которая выступает в роли первого множителя.
Вычислить полученное числовое выражение, в первую очередь возвести каждое число в степени, посчитать каждое произведение, вычислить сумму полученных произведений.

Пример:

Число 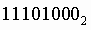перевести в десятичную систему счисления.

1й шаг:

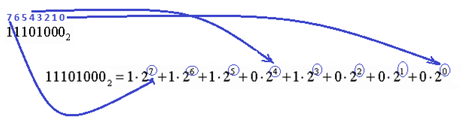
2-3 шаг:

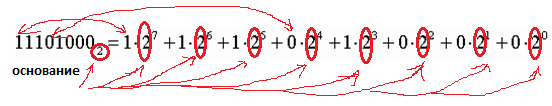
4 шаг =232₁₀

Второе необходимое умение для выполнения: Перевод из десятичной СС в любую СС:

Десятичное данное число необходимо поделить уголком на основание (число) той СС в которую необходимо перевести. Делить снова на основание необходимо, если неполное частное (частное) больше основания СС той СС в которую переводим. Делим до тех пор, пока неполное частное (частное) не станет меньше основания СС в которую переводим.
Чтобы получить ответ надо записать ряд чисел, начиная с последнего получившегося неполного частного (частное), далее записываем по порядку остатки от деления, причем второй цифрой ответа будет остаток последнего деления, третьей цифрой остаток от предпоследнего деления и т.д.

Пример:

Число 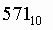перевести в восьмеричную систему счисления.

Поскольку необходимо перевести в восьмеричную, то делим на 8.

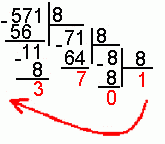
Ответ: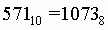

Третье необходимое умение для выполнения: Перевод из двоичной СС в восьмеричную СС:

Данное число в двоичной системе счисления разбить на «тройки» триады начиная справа двигаясь влево. Последний разряд или два разряда оставшиеся без «тройки» дополнить справа необходимым количеством нулей.
Заменить каждую «тройку» соответствующим числом из таблицы:
соответствующее ей число
Триада «тройка»
соответствующее ей число
000
0
100
4
001
1
101
5
010
2
110
6
011
3
111
7
В таком же порядке, записав полученные числа, получим ответ в восьмеричной СС.

Пример:

Число 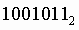перевести в восьмеричную систему счисления.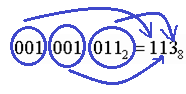

Четвертое необходимое умение для выполнения: Перевод из восьмеричной СС в двоичную СС:

В данном числе в восьмеричной СС каждую цифру разряда заменить тройками «Триадами»
соответствующая цифре триада
Цифра (разряд) исходного числа
соответствующая цифре триада
0
000
4
100
1
001
5
101
2
010
6
110
3
011
7
111
Записав полученные тройки в том же порядке что и были даны соответствующие им цифры в исходном, получим ответ в двоичной СС.

Пример:

Число 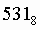перевести в двоичную систему счисления.

Пятое необходимое умение для выполнения: Перевод из двоичной СС в шестнадцатеричную СС:

Данное число в двоичной системе счисления разбить на «четверки» тетрады начиная справа двигаясь влево. Последний разряд или два или три разряда оставшиеся без «четверки» дополнить справа необходимым количеством нулей.
Заменить каждую «четверку» соответствующим числом из таблицы:
соответствующее ей число
Тетрада «четверка»
соответствующее ей число
0000
0
1000
8
0001
1
1001
9
0010
2
1010
A
0011
3
1011
B
0100
4
1100
C
0101
5
1101
D
0110
6
1110
E
0111
7
1111
F
В таком же порядке, записав полученные числа, получим ответ в шестнадцатеричной СС.

Пример:

Число 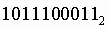перевести в шестнадцатеричную систему счисления.

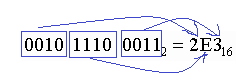
Шестое необходимое умение для выполнения: Перевод из шестнадцатеричной СС в двоичную СС:

В данном числе шестнадцатеричной СС каждую цифру разряда заменить четверками «Тетрадами»
соответствующая цифре триада
Цифра (разряд) исходного числа
соответствующая цифре триада
0
0000
8
1000
1
0001
9
1001
2
0010
A
1010
3
0011
B
1011
4
0100
C
1100
5
0101
D
1101
6
0110
E
1110
7
0111
F
1111
Записав полученные «четверки» в том же порядке что и были даны соответствующие им цифры в исходном, получим ответ в двоичной СС.

Пример:

Число 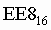перевести в двоичную систему счисления.

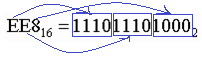
Седьмое необходимое умение для выполнения: Перевод из шестнадцатеричной СС в восьмеричную СС:

В данное число по алгоритму из умения № 6 переводим в двоичную
Полученное двоичное число используя умение № 3 получаем число в восьмеричной системе счисления

Восьмое необходимое умение для выполнения: Перевод из восьмеричной СС в шестнадцатеричную СС:

В данное число по алгоритму из умения № 6 переводим в двоичную
Полученное двоичное число используя умение № 3 получаем число в восьмеричной системе счисления

ЗАДАЧИ из базы заданий:

(в данном материале были взяты задания с сайта https://inf-oge.sdamgia.ru/)

1. Переведите двоичное число 1101101 в десятичную систему счисления.

2. Переведите число 135 из десятичной системы счисления в двоичную систему счисления. Сколько единиц содержит полученное число? В ответе укажите одно число — количество единиц.

3. Переведите двоичное число 1100110 в десятичную систему счисления.

4. Переведите число 111 из десятичной системы счисления в двоичную систему счисления. Сколько единиц содержит полученное число? В ответе укажите одно число — количество единиц.

5. Переведите число FE из шестнадцатеричной системы счисления в двоичную систему счисления.

6. Переведите число 73 из восьмеричной системы счисления в двоичную систему счисления.

7. Переведите число 10111 из двоичной системы счисления в десятичную систему счисления.

8. Переведите число 150 из восьмеричной системы счисления в десятичную систему счисления.

9. Переведите число А2 из шестнадцатеричной системы счисления в десятичную систему счисления.

10. Переведите число 10101001 из двоичной системы счисления в десятичную систему счисления. В ответе напишите полученное число.

11. Переведите число 156 из десятичной системы счисления в двоичную систему счисления. Сколько единиц содержит полученное число? В ответе укажите одно число — количество единиц.

12. Переведите число 126 из десятичной системы счисления в двоичную систему счисления. В ответе укажите двоичное число. Основание системы счисления указывать не нужно.

13. Некоторое число в двоичной системе счисления записывается как 1010110. Запишите это число в десятичной системе счисления.

14. Переведите число 147 из десятичной системы счисления в двоичную систему счисления. Сколько нулей содержит полученное число? В ответе укажите одно число — количество значащих нулей.

15. Переведите число 259 из десятичной системы счисления в двоичную систему счисления. Сколько единиц содержит полученное число? В ответе укажите одно число — количество единиц.

16. Переведите число 11011101 из двоичной системы счисления в восьмеричную. В ответе укажите количество получившихся разрядов (значимых).

17. Переведите число 4315₈ в двоичную систему счисления. В ответе укажите количество единиц в получившемся числе.

18. Переведите число 100001110 из двоичной системы счисления в шестнадцатеричную. В ответе укажите само число в шестнадцатеричной СС, основание указывать не надо.

Дополнительные задачи:

В системе счисления с некоторым основанием десятичное число 49 записывается в виде 100. Укажите это основание.

Решение: Необходимо составить уравнение (в котором за x будет основание неизвестной СС), и заглянуть в первое умение, а значит, число 100 в неизвестной СС представить в виде суммы, над нулем справа первым будет нуль, над вторым нулем будет 1, и над единицей 2, а значит получается: 1x²+0x¹+0x⁰=49

Получаем, после преобразований x²=49, два корня x=7 или x=-7 – посторонний корень. Значит число было записано в семеричной СС. Ответ: 7

Решить самостоятельно:

1. В системе счисления с некоторым основанием десятичное число 24 записывается в виде 30. Укажите это основание.

2. Десятичное число 63 в некоторой системе счисления записывается как 120. Определите основание системы счисления.

3. Десятичное число 57 в некоторой системе счисления записывается как 212. Определите основание системы счисления.

4. Десятичное число 59 в некоторой системе счисления записывается как 214. Определите основание системы счисления.

5. Десятичное число 81 в некоторой системе счисления записывается как 144. Определите основание системы счисления.

6. Десятичное число 59 в некоторой системе счисления записывается как 214. Определите основание системы счисления.

В каких системах счисления перевод числа 37₁₀ оканчивается на 7? В ответе указать все возможные, если их несколько указать через запятую.

Решение: представим число 37 в виде суммы чисел, одно из слагаемых будет равно 7, т.е. 37=30+7. Теперь найдем кратные второму слагаемому 30:3,5,6,10,15,30. А теперь либо все из перечисленных чисел могут быть основаниями удовлетворяющих условию задачи, либо даем пояснение почему нет. 3,5,6 не могут – так как мы заведомо знаем что оканчивается 7, а значит в этой СС есть цифра 7, а в СС 3,5,6 этой цифры нет. Далее 10 это исходная СС. Значит ответ: 15,30.

Решить самостоятельно:

1. Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 39 оканчивается на 3.

2. Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 40 оканчивается на 4.

3. Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 32 оканчивается на 4.

4. Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 29 оканчивается на 5.

3. Решите уравнение 121_x + 1₁₀ = 101₇. Ответ запишите в троичной СС, основание СС в ответ записывать не надо.

Решение: необходимо число с неизвестной системой СС, представить в виде суммы произведений (смотреть умение 1), так же поступить с числом в семеричной СС. Получаем:

1·x²+2·x¹+1·x⁰ + 1=1·7²+0·7¹+1·7⁰. Упрощаем выражение и получаем: x²+2x+1+1=49+0+1. Получаем квадратное уравнение: x²+2x-48=0. Решив которое любым удобным способом получаем корни: 6 или -8. Но -8 посторонний корень, поскольку x это основание СС. Искомая СС это шестеричная. Но по условию задачи основание искомой СС необходимо перевести в троичную СС. Для этого воспользуемся умением вторым, поделим 6 на 3. Получим 20₃. Значит ответ: 20.

Решить самостоятельно:

1. Решите уравнение: 121_x + 1₁₀ = 101₈ Ответ запишите в троичной системе (основание системы счисления в ответе писать не нужно).

2. Решите уравнение 100 ₇ + x = 200₅. Ответ запишите в шестнадцатеричной системе (основание системы счисления в ответе писать не нужно).

3. Решите уравнение 60 ₈ + x = 100₇. Ответ запишите в шестеричной системе (основание системы счисления в ответе писать не нужно).

4. Решите уравнение: 42₆ + x = 42₇ Ответ запишите в десятичной системе счисления.

5. Решите уравнение: 100₅ + x = 200₄. Ответ запишите в семеричной системе (основание системы счисления в ответе писать не нужно).

6. Решите уравнение: 60₈ + x = 200₅. Ответ запишите в шестеричной системе (основание системы счисления в ответе писать не нужно).

7. Решите уравнение: 100₇ + x = 210₅. Ответ запишите в шестеричной системе (основание системы счисления в ответе писать не нужно).

8. Решите уравнение: 60₈ + x = 60₉. Ответ запишите в шестеричной системе (основание системы счисления в ответе писать не нужно).

9. Решите уравнение 34₅ + x=34₇. Ответ запишите в восьмеричной системе счисления. Основание системы в ответе писать не нужно.

10. Решите уравнение 54₆+x = 54₇. Ответ запишите в восьмеричной системе счисления. Основание системы в ответе писать не нужно.

11. Решите уравнение: 211_x + 3₁₀ = 135₆ Ответ запишите в троичной системе (основание системы счисления в ответе писать не нужно).

12. Решите уравнение: 57_x + 7₁₀ = 202₆ Ответ запишите в четверичной системе (основание системы счисления в ответе писать не нужно).

13. Решите уравнение: 234_x + 5₁₀ = 223₅ Ответ запишите в пятеричной системе (основание системы счисления в ответе писать не нужно).

14. Решите уравнение: 133_x + 6₁₀ = 142₇ Ответ запишите в четверичной системе (основание системы счисления в ответе писать не нужно).

15. Решите уравнение: 116_x + 11₁₀ = 108₉ Ответ запишите в троичной системе (основание системы счисления в ответе писать не нужно).

Ответы:

№

Отв

№

Отв

109

104

102

162

169

11111110

111011

1111110

10Е

Ответы к дополнительным задачам:

Задача 1

№

Отв

№

Отв

Ответы к дополнительным задачам:

Задача 2

№

Отв

4,6,9,12,18,36

7,14,28

6,9,12,18,36

6,8,12,24

Ответы к дополнительным задачам:

Задача 3

№

Отв

№

Отв

Презентация к уроку по информатике и икт (9 класс) на тему: Презентация по теме «Системы счисления. Арифметические операции в позиционных системах счисления» для 9, 10 кл.

Слайд 1

Системы счисления учитель информатики МБОУ «СОШ № 128» И.А. Мерс

Слайд 2

Содержание : Двоичное кодирование в ПК Что такое система счисления? Непозиционные системы счисления Позиционные системы счисления Перевод в 10-тичную СС Перевод из 10-тичной СС Перевод из 2-ной в 8-ную и обратно Перевод из 2-ной в 16-ную и обратно Опрос Арифметические операции в позиционных СС Сложение и вычитание в 2-ой СС Умножение в 2-ой СС Сложение и вычитание в 8-ой СС Решение примеров

Слайд 3

Двоичное кодирование в компьютере Вся информация, которую обрабатывает компьютер должна быть представлена двоичным кодом с помощью двух цифр: 0 и 1 . Эти два символа принято называть двоичными цифрами или битами , или двоичным кодом . С точки зрения технической реализации использование двоичной системы счисления для кодирования информации оказалось намного более простым, чем применение других способов. Недостаток двоичного кодирования – длинные коды. Но в технике легче иметь дело с большим количеством простых элементов, чем с небольшим числом сложных. 0 – отсутствие электрического сигнала; 1 – наличие электрического сигнала .

Слайд 4

С помощью двух цифр 0 и 1 можно закодировать любое сообщение. Это явилось причиной того, что в компьютере обязательно должно быть организованно два важных процесса: кодирование и декодирование. Кодирование – преобразование входной информации в форму, воспринимаемую компьютером, т.е. двоичный код. Декодирование – преобразование данных из двоичного кода в форму, понятную человеку. Способы кодирования и декодирования информации в компьютере, в первую очередь, зависит от вида информации, а именно, что должно кодироваться: числа, текст, графические изображения или звук. меню

Слайд 5

Система счисления Почему мы используем цифры от 0 до 9? А как можно считать еще? Оказывается, существует множество вариантов! И это зависит от такого понятия, как система счисления . Система счисления (СС) — способ записи чисел с помощью набора специальных знаков, называемых цифрами. меню

Слайд 6

Виды систем счисления СИСТЕМЫ СЧИСЛЕНИЯ ПОЗИЦИОННЫЕ НЕПОЗИЦИОННЫЕ В непозиционных системах счисления величина , которую обозначает цифра, не зависит от положения в числе. XXI В позиционных системах счисления величина , обозначаемая цифрой в записи числа, зависит от её положения в числе ( позиции ). 211

Слайд 7

Непозиционные системы счисления Ярким примером фактически непозиционной системы счисления является римская , в которой в качестве цифр используются латинские буквы: I обозначает 1, V — 5, X — 10, L — 50, C — 100, D — 500, M -1000. Натуральные числа записываются при помощи повторения этих цифр. Например, II = 1 + 1 = 2, здесь символ I обозначает 1 независимо от места в числе. Для правильной записи больших чисел римскими цифрами необходимо сначала записать число тысяч, затем сотен, затем десятков и, наконец, единиц. Пример: число 1789 . Одна тысяча M , семь сотен DCC , восемьдесят LXXX , девять IX . Запишем их вместе: MDCCLXXXIX . MDCCLXXXIX=1000+(500+100+100)+(50+10+10+10)+(10-1)=1789 Для изображения чисел в непозиционной системе счисления нельзя ограничится конечным набором цифр. Кроме того, выполнение арифметических действий в них крайне неудобно. меню

Слайд 8

Первые позиционные системы счисления Самой первой такой системой, когда счетным «прибором» служили пальцы рук, была пятеричная . Следующей возникла двенадцатеричная система счисления. Возникла она в древнем Шумере. Возможно, что она возникала у них из подсчёта фаланг на руке большим пальцем. На ее широкое использование в прошлом указывает сохранившиеся в ряде стран способы отсчета времени, денег и соотношения между некоторыми единицами измерения. Год состоит из 12 месяцев, а половина суток состоит из 12 часов. Элементом двенадцатеричной системы в современности может служить счёт дюжинами. Английский фунт состоит из 12 шиллингов.

Слайд 9

Следующая позиционная система счисления была придумана еще в Древнем Вавилоне, причем вавилонская нумерация была шестидесятеричная , т.е. в ней использовалось шестьдесят цифр! В более позднее время использовалась арабами, а также древними и средневековыми астрономами. Шестидесятеричная система счисления, как считают исследователи, являет собой синтез уже вышеупомянутых пятеричной и двенадцатеричной систем. В настоящее время наиболее распространены десятичная , двоичная , восьмеричная и шестнадцатеричная системы счисления.

Слайд 10

Десятичная система счисления Десятичная система счисления — позиционная система счисления по основанию 10. Предполагается, что основание 10 связано с количеством пальцев на руках у человека. Наиболее распространённая система счисления в мире. Для записи чисел используются символы 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , называемые арабскими цифрами.

Слайд 11

Двоичная система счисления Двоичная система счисления — позиционная система счисления с основанием 2. Используются цифры 0 и 1. Двоичная система используется в цифровых устройствах, поскольку является наиболее простой и удовлетворяет требованиям: Чем меньше значений существует в системе, тем проще изготовить отдельные элементы. Чем меньше количество состояний у элемента, тем выше помехоустойчивость и тем быстрее он может работать. Простота создания таблиц сложения и умножения — основных действий над числами

Слайд 12

Алфавит двоичной, восьмеричной, десятичной и шестнадцатеричной систем счисления Система счисления Основание Алфавит цифр Двоичная 2 0, 1 Восьмеричная 8 0, 1, 2, 3, 4, 5, 6, 7 Десятичная 10 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 Шестнадцатеричная 16 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F Количество используемых цифр называется основанием системы счисления .

Слайд 13

Соответствие десятичной, двоичной, восьмеричной и шестнадцатеричной систем счисления p=10 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 p=2 0 1 10 11 100 101 110 111 1000 1001 1010 1011 1100 1101 1110 1111 10000 p=8 0 1 2 3 4 5 6 7 10 11 12 13 14 15 16 17 20 p=16 0 1 2 3 4 5 6 7 8 9 A B C D E F 10 При одновременной работе с несколькими системами счисления для их различения основание системы обычно указывается в виде нижнего индекса, который записывается в десятичной системе: 321 10 — это число 321 в десятичной системе счисления; 101000001 2 — то же число, но в двоичной системе. Двоичное число 101000001 2 можно расписать в виде: 101000001 2 = 1*2 8 + 0*2 7 + 1*2 6 + 0*2 5 + 0*2 4 +0*2 3 + 0*2 2 + 0*2 1 + 1*2 0 .

Слайд 14

Перевод чисел из любой позиционной системы счисления в десятичную Чтобы перевести целое число из позиционной системы счисления с основанием p в десятичную , нужно справа налево, начиная с 0, расставить разряды, потом каждую цифру умножить на основание системы счисления из которой переводим в степени этого разряда. Например, переведем число 11001 2 в десятичную систему счисления. Для этого представим это число в виде степеней двойки и произведем вычисления в десятичной системе счисления. 11001 2 = 1*2 4 + 1*2 3 + 0*2 2 + 0*2 1 + 1*2 0 = 1*16 +1*8 + 0*4 + 0*2 + 1*1 = 16 + 8 + 0 + 0 + 1 = 25 10 Рассмотрим еще один пример. Переведем число 12,34 8 в десятичную систему счисления. 12,34 8 = 1*8 1 + 2*8 0 + 3*8 -1 + 4*8 -2 = 1*8 + 2*1 + 3*1/8 +4*1/64 = 10 + 0,375 + 0,0625 = 10,4375 10 0 1 2 3 4 0 1 -1 -2 меню

Слайд 15

Перевод целых десятичных чисел в 2, 8, 16-ую системы счисления

Слайд 16

Перевод чисел из десятичной системы счисления в любую другую Перевод из десятичной системы счисления в систему счисления с основанием p осуществляется последовательным делением десятичного числа и его десятичных частных на p , а затем выписыванием последнего частного и остатков в обратном порядке. Переведем десятичное число 20 10 в двоичную систем счисления (основание системы счисления p=2). В итоге получили 20 10 = 10100 2 .

Слайд 17

Перевести десятичное число 26 в двоичную, троичную, шестнадцатеричную системы 26 10 →Х 2 26 0 13 1 6 0 3 1 1 1 26 10 =11010 2 26 10 →Х 3 26 2 8 2 2 2 26 10 =222 3 26 10 →Х 16 26 10 1 1 26 10 =1А 16 ПЕРЕВОД ЦЕЛОГО ДЕСЯТИЧНОГО ЧИСЛА МЕТОДОМ ПОЭТАПНОГО ДЕЛЕНИЯ

Слайд 18

Перевести десятичную дробь 0,375 0 375 * 2 0 750 2 1 500 2 1 000 0,375 10 =0,011 2 0 375 * 3 1 125 3 0 375 3 1 125 0,375 10 =0,101 3 0 375 16 2 250 3 75 6 000 0,375 10 =0,6 16

Слайд 19

Переведи в 2-ую СС 26,375 10 →Х 2 26 10 =11010 2 0,375 10 =0,011 2 26,375 10 =11010,011 2

Слайд 20

Прочитайте стихотворение. Переведите встречающиеся в нем числительные из двоичной системы счисления в десятичную. Необыкновенная девчонка (А. Н. Стариков) Ей было тысяча сто лет, Она в 101-ый класс ходила, В портфеле по сто книг носила – Все это правда, а не бред. Когда, пыля десятком ног, Она шагала по дороге, За ней всегда бежал щенок С одним хвостом, зато стоногий. Она ловила каждый звук Своими десятью ушами, И десять загорелых рук Портфель и поводок держали. И десять темно-синих глаз Рассматривали мир привычно,… Но станет все совсем обычным, Когда поймете наш рассказ.

Слайд 21

Задания: Запишите число в римской системе счисления: 2013= Запишите в развернутом виде числа: 1234 10 = 345 8 = 11010 2 = Переведите числа в десятичную систему счисления: 274 8 = BE 16 = 110,101 2 = Как будет записываться число 24 10 в двоичной системе счисления? 123 10 в восьмеричной? меню

Слайд 22

Перевод 2  8 СС Очень просто! Направо и налево от точки откладываем триады — группы по три цифры, после чего записываем их в соответствующем 8-ном виде. Неполные триады дополняются нулями. Пример: 1011010,01101 2 = 001 011 010,011 010 2 = 132,32 8 Обратно — с точностью до наоборот: 257,31 8 = 010 101 111, 011 001 2 = 10101111,011001 2

Слайд 23

Системы счисления, используемые в ЭВМ (с основанием 2 n ) Перевести число 1100101001101010111 2 в восьмеричную систему счисления 001 100 101 001 101 010 111 1 4 5 1 5 2 7 Получаем 1451527 8 меню

Слайд 24

Перевод 2  16 СС Очень просто! Направо и налево от точки откладываем тетрады — группы по четыре цифры, после чего записываем их в соответствующем 16-ном виде. Неполные тетрады дополняются нулями. Пример: 1011010110,011001 2 = 0010 11 01 0110,011 010 2 = 132,32 8 Обратно — с точностью до наоборот: 257,31 8 = 010 101 111, 011 001 2 = 10101111,011001 2

Слайд 25

Перевести число 1100101001101010111 2 в шестнадцатеричную систему счисления 0110 0101 0011 0101 0111 6 5 3 5 7 Получаем 65357 16

Слайд 26

Перевести число из восьмеричной системы счисления в шестнадцатеричную 1451527 8 Х 16 меню

Слайд 27

Согласны ли Вы с утверждениями….? № Согласны ли вы с утверждением Да Нет 1 Система счисления – это знаковая система, в которой числа записываются по определенным правилам с помощью символов некоторого алфавита, называемых цифрами. 2 Все системы счисления делятся на три большие группы: позиционные, непозиционные и полупозиционные. 3 В позиционных системах счисления количественное значение цифры зависит от ее позиции в числе. 4 Основанием двоичной системы счисления является число 4 5 Число А21С FD4 записано в шестнадцатеричной системе счисления. 6 Число 156 7 записано с ошибкой. 7 Число 10, записанное в десятичной системе счисления, в двоичной системе счисления записывается как 1011 8 Число 10, записанное в десятичной системе счисления, меньше числа 10, записанного в восьмеричной системе счисления. 9 Число 3005,23 4 записано с ошибкой. 10 Число 6 398 записано в восьмеричной системе счисления.

Слайд 28

№ Согласны ли вы с утверждением Да Нет 1 Система счисления – это знаковая система, в которой числа записываются по определенным правилам с помощью символов некоторого алфавита, называемых цифрами. 2 Все системы счисления делятся на три большие группы: позиционные, непозиционные и полупозиционные. 3 В позиционных системах счисления количественное значение цифры зависит от ее позиции в числе. 4 Основанием двоичной системы счисления является число 4 5 Число А21С FD4 записано в шестнадцатеричной системе счисления. 6 Число 156 7 записано с ошибкой. 7 Число 10, записанное в десятичной системе счисления, в двоичной системе счисления записывается как 1011 8 Число 10, записанное в десятичной системе счисления, меньше числа 10, записанного в восьмеричной системе счисления. 9 Число 3005,23 4 записано с ошибкой. 10 Число 6 398 записано в восьмеричной системе счисления. + + + + + + + + + + Проверь себя меню

Слайд 29

«Арифметические операции в позиционных системах счисления»

Слайд 30

Все позиционные системы счисления «одинаковы», а именно, во всех них выполняются арифметические операции по одним и тем же правилам: справедливы одни и те же законы арифметики: — коммутативный ( п ереместительный): m + n = n + m m · n = n · m ассоциативный (сочетательный): ( m + n ) + k = m + ( n + k ) = m + n + k ( m · n ) · k = m · ( n · k ) = m · n · k дистрибутивный (распределительный): ( m + n ) · k = m · k + n · k справедливы правила сложения, вычитания и умножения столбиком ; правила выполнения арифметических операций опираются на таблицы сложения и умножения. меню

Слайд 31

Сложение в двоичной системе счисления: 0+0=0 0+1=1 1+0=1 1+1= 1 0 2 1 + 1 + 1 = 1 1 2 перенос 1 0 1 1 0 2 1 1 1 0 1 1 2 1 1 0 0 0 1 1 0 2 1 1 1 1 Сложение в 10-ой СС 99 1 100

Слайд 32

Примеры: 101101 2 + 11111 2 111011 2 + 11011 2 111011 2 + 10011 2

Слайд 33

Вычитание в двоичной системе счисления: 0-0=0 1-1=0 1-0=1 1 0 2 -1=1 заем 1 0 0 0 1 0 1 2 1 1 0 1 1 2 0 2 1   0 10 2 1 0 0 1 1 10 2 0 1 0 Вычитание в 10-ой СС 100 1 99

Слайд 34

Примеры: 101101 2 – 11111 2 11011 2 – 1101 2 101010 2 – 10011 2 меню

Слайд 35

Умножение в двоичной системе счисления : * 0 1 0 0 0 1 0 1

Слайд 36

101101 2 * 101 2 + 101101 000000 101101 11100001 2 11011 2 * 1101 2 101011111 2 меню

Слайд 37

Арифметические операции в 8-ричной СС сложение 1 5 6 8 + 6 6 2 8 1 1 6 + 2 = 8 = 1* 8 + 0 5 + 6 + 1 = 1 2 = 1* 8 + 4 1 + 6 + 1 = 8 = 1* 8 + 0 1 Перенос 1 в след. разряд Перенос 1 в след. разряд 1 0 8 0 4 Перенос 1 в след. разряд

Слайд 38

Пример 3 5 3 8 + 7 3 6 8 1 3 5 3 8 + 7 7 7 8

Слайд 39

Арифметические операции в 8-ричной СС вычитание 2 1 5 6 8 — 6 6 2 8 1 6 -2 = 4 5 — 6 + 1*8 = 7 0 — 6 + 1 *8 = 2 заем 4 8 2 7 заем

Слайд 40

Примеры 4 1 5 3 8 – 6 6 7 8 1 1 6 1 8 – 7 3 2 8 меню

Слайд 41

Решение примеров

Слайд 42

Задание №1 1. Переведите числа данные в десятичной СС в двоичную , а затем в шестнадцатеричную СС: а) 143,25 б) 3 12,5 2. Переведите данное число в десятичную СС: а) 10110101,1 б) 100100110,10101

Слайд 43

ОТВЕТ на задание №1 1. 143,25 10 10001111,01 2 8 F ,4 16 3 12,5 10 10 0 1 11 000,1 2 13 8,8 16 2. 10110101,1 2 181,5 10 100 1 00110,1011 2 2 94 ,065625 10

Слайд 44

Задание №2 Переведите в восьмеричную и шестнадцатеричную СС: 110010,101 2 1011010011,01 2 1101111011,01 2 101000010,0111 2

Слайд 45

110010,101 2 =62,5 8 =32,А 16 1011010011,01 2 =1323,2 8 = 2D3,4 16 1101111011,01 2 =1573,2 8 = 37B,4 16 101000010,0111 2 =502,34 8 = 142,7 16 ОТВЕТ на задание № 2

Слайд 46

Задание №3 1. Сложите данные числа: 11 00 11 00 1,0011 2 + 111 0 111 0 1,0101 2 2. Выполните вычитание: 1101100110,01 2 – 110000010,1011 2 3.Выполните умножение: 1001111 2 х 1000100 2

Слайд 47

Ответ на задание №3 1. 11 0 0 11 00 1,0010 2 2. 1 101 100 110 ,0100 2 + 111 0 11 1 0 1,0101 2 — 110 000 010 ,1011 2 1 101 110 110 ,0111 2 0 1 11 100 011, 1 001 2 3. 1 001 111 2 х 1 000 100 2 1 010 011 111 1 00 2

Слайд 48

Задание №4 1. Переведите число данное в десятичной CC в двоичную , а затем в шестнадцатеричную CC : а) 670 10 б) 162 10 2. Переведите данное число в десятичную CC : а) 1111100111 2 б) 1001011 2

Слайд 49

ОТВЕТ на задание №4 1. 670 10 1010011110 2 29Е 16 162 10 10100010 2 А2 16 2. 1111100111 2 999 10 1001011 2 7 5 10

Слайд 50

Восстановить неизвестные цифры, обозначенные *, определив вначале в какой системе счисления изображены числа. А) 5 * 5 5 Б) 1 5 2 6 * 2 2 7 * 4 2 * 1 5 * 4 6 5 4 Решение А) 5 * 5 5 * 2 2 7 * 1 5 * 4 1) 5+7=12=1  8+4 р=8 2) 5+2+1=8=1  8+0 * =0 3) * +2+1=5 * =2 4) 5+ * =1 5+ * =1  8+1 * =4 5) *=1 Б) 1 5 2 6 * 4 2 6 5 4 1) 6-2=4 2) 2+р-4=5 р=7 3) 4 +7-*=6 *= 5 0 2 4 1 5

Урок информатики «Системы счисления» (9 класс)

Тема урока: Системы счисления

Цель урока: закрепление, обобщение и систематизация знаний учащихся по теме «Системы счисления» — правил перевода и выполнения арифметических операций в различных системах счисления, в том числе с использованием нестандартных заданий.

Задачи урока:

Тип урока: урок обобщения и систематизации знаний.

Формы и методы обучения: словесный, наглядный, практический — индивидуальная работа.

Место проведения урока: кабинет информатики.

Оснащение урока: интерактивная доска, алфавит русского языка.

План урока

Орг. момент – 1 мин.
Вводное слово – 2 мин.
Систематизация теоретических знаний – 30 мин.
Заключение – 5 мин.
Задание на дом – 2 мин.

Ход урока

1. Беседа с дежурным.

Здравствуйте.

Кто сегодня дежурный?

Кто из учащихся отсутствует на уроке?

Дежурный отвечает.

2.Вводное слово.

Сегодня у нас заключительный урок по теме «Системы счисления». Мы повторим, обобщим и приведем в систему изученный материал по данный теме. Ваша задача показать теоретические знания основных понятий, правил перевода чисел и выполнения арифметических действий в различных системах счисления. План работы на уроке следующий:

Графический диктант.
Кроссворд «Системы счисления. Основные понятия».
Заполнение таблицы.
Решение неравенств.
Числовые последовательности.
Загадка поэта.
Русская поговорка.
Рождение цветка.
Числовой лабиринт.

Учащиеся слушают.

3. Систематизация теоретических знаний. Учащиеся выполняют задания на проверку теоретического материала по теме урока. Все задания данного этапа урока выполняются каждым учащимся индивидуально.

Задание 1. Графический диктант.

Если утверждение верно, ученик ставит знак _ , если неверно – знак /\ .

Система счисления – это способ представления чисел и соответствующие ему правила действий над числами.
Информация, хранящаяся в компьютере, представлена в троичной системе счисления.
В двоичной системе счисления 11 + 1 = 12.
Существует множество позиционных систем счисления, и они отличаются друг от друга алфавитами.
В 16-ричной системе счисления символ F используется для обозначения числа 15.
Римская система счисления – это позиционная система счисления.
В двоичной системе счисления: один + один = один ноль ноль.

(Результат выполнения задания: _ /\ /\ _ _ /\_ )

Задание 2. Кроссворд «Системы счисления. Основные понятия».

(Учитель вызывает учащихся по желанию и он пишет на доске правильный ответ).

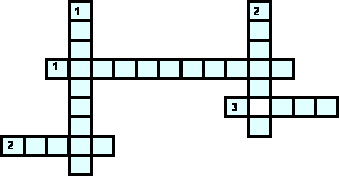
По горизонтали:

Название системы счисления, в которой вклад каждой цифры в величину числа зависит от ее положения в последовательности цифр, изображающей число.
Последовательность чисел, каждое из которых задает значение цифры «по месту» или «вес» каждого разряда.
Символы, при помощи которых записывается число.

По вертикали:

Знаменатель геометрической прогрессии, члены которой образуют базис позиционной системы счисления.
Совокупность различных цифр, используемых а позиционной системе счисления для записи чисел.

(Ответы на кроссворд. По горизонтали: 1. Позиционная. 2. Базис. 3. Цифры. По вертикали: 1. Основание. 2. Алфавит.)

Задание 3. Заполнение таблицы. (Выполняют устно)

(Правильно заполненная таблица имеет вид:

Задание 4. Решение неравенств.

Поставьте вместо знака ? знак <, > или =.

28510 ? 11D16 (Ответ: 28510 = 28510 )

1111112 ? 11118 (Ответ: 6310 < 58510 )

6С16 ? 1010012 (Ответ: 10810 > 4110 )

5516 ? 1258 (Ответ: 8510 = 8510 )

Задание 5. Числовые последовательности.

Расположите числа, записанные в различных системах счисления, в порядке возрастания:

35₁₀, 36₈, 3А₁₆, 100101₂, 130₄ (Ответ: 130₄ , 36₈, 35₁₀,

100101₂, 3А₁₆)

111001₂, 64₈, 9Е₁₆, 25₁₀, 210₃ (Ответ: 210₃, 25₁₀, 64₈,

111001₂, 9Е₁₆)

72₈, 156₁₀, 101001₂, 8В₁₆, 232₅ (Ответ: 101001₂, 72₈, 232₅,

8В₁₆, 156₁₀)

Задание 6. Загадка поэта.

Прочитайте шуточное стихотворение А. Н. Старикова «Необыкновенная девочка» и попробуйте разгадать загадку поэта. Для этого выпишите упомянутые в стихотворении числа и переведите их в десятичную систему счисления.

Ей было тысяча сто лет,

Она в сто первый класс ходила,

В портфеле по сто книг носила.

Все это правда, а не бред.

Она ловила каждый звук

Своими десятью ушами,

И десять загорелых рук

Портфель и поводок держали.

Когда, пыля десятком ног,

Она шагала по дороге,

За ней всегда бежал щенок

С одним хвостом, зато стоногий.

И десять темно-синих глаз

Рассматривали мир привычно …

Но станет все совсем обычным,

Когда поймете наш рассказ.

Задание 7. Русская поговорка.

Здесь зашифрована известная русская поговорка. Прочитайте ее, двигаясь с помощью двоичных цифр в определенной последовательности.

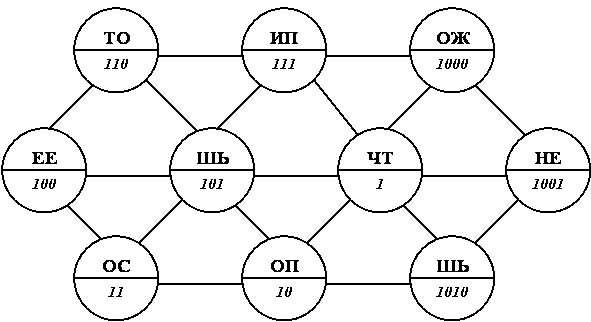
(Ответ: ЧТО ПОСЕЕШЬ, ТО И ПОЖНЕШЬ)

Задание 8. Рождение цветка.

Понаблюдаем за рождением цветка: сначала появился один листочек, затем второй … и вот распустился бутон. Постепенно подрастая, цветок показывает нам некоторое двоичное число. Если вы до конца проследите за ростом цветка, то узнаете, сколько дней ему понадобилось, чтобы вырасти.

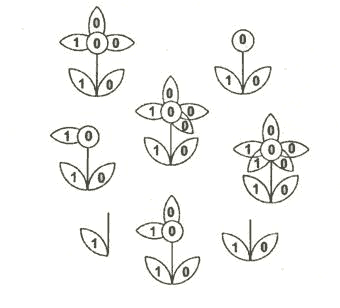
(Ответ: 10010001₂=145 дней)

Задание 9. Числовой лабиринт.

Переведите числа, записанные в различных системах счисления, в десятичную систему счисления; затем полученные после вычисления числа замените буквами русского алфавита, которые имеют соответствующие порядковые номера; запишите полученное слово.

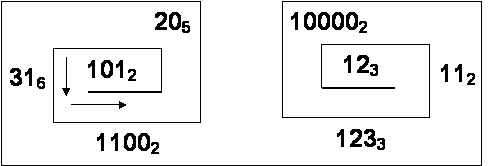
(Ответ: ДИСКОВОД)

Выполняют задание в тетрадях.

Потом обмениваются тетрадями и проверяют ответы друг у друга.

Учащиеся зарисовывают кроссворд себе в тетрадь и выполняют задание.

Учащиеся высказывают свои мнения и проверяют.

Выполняют в тетради и проверяют с учителем.

Выполняют задание в тетради. Проверяют: один ученик у доски предоставляет правильный ответ.

Ребята переводят числа в десятичную систему счисления и читают стихотворение:

Ей было 12 лет,

Она в 5 класс ходила,

В портфеле по четыре книги носила.

Все это правда, а не бред.

Она ловила каждый звук

Своими двумя ушами,

И две загорелые руки

Портфель и поводок держали.

Когда, пыля двумя ногами,

Она шагала по дороге,

За ней всегда бежал щенок

С одним хвостом, зато четырехногий.

И двое темно-синих глаз

Рассматривали мир привычно …

Но станет все совсем обычным,

Когда поймете наш рассказ.

Выполняют задание у доски. (расставляя в правильную последовательность круги)

Выполняет один ученик у доски.

Выполняют в тетрадях. Сверяют ответы с доски.

6. Заключение.

Рефлексия:

— Какое задание было самым интересным?

— Какое задание, по вашему мнению, было самым сложным?

— С какими трудностями вы столкнулись, выполняя задания?

— Какие задания вы считаете самыми интересными и какие задания можете предложить по данной теме?

Вы сегодня работали хорошо, справились с поставленной перед вами задачей, а также показали хорошие знания по теме «Системы счисления». За работу на уроке вы получаете следующие оценки (объявляются оценки каждого ученика за работу на уроке).

Спасибо всем за хорошую работу. Молодцы!

Высказывают свои мнения.

7. Задание на дом.

Придумайте свои задания-ребусы представленные в различных системах счисления.

Системы счисления 9 класс

Описание презентации по отдельным слайдам:

1 слайд

Описание слайда:

Подготовил: учитель информатики Смирнова М.В. СИСТЕМЫ СЧИСЛЕНИЯ МАТЕМАТИЧЕСКИЕ ОСНОВЫ ИНФОРМАТИКИ

2 слайд

Описание слайда:

Система счисления — это знаковая система, в которой приняты определённые правила записи чисел. Цифры — знаки, при помощи которых записываются числа,. Алфавит системы счисления — совокупность цифр. Общие сведения Древнеславянская система счисления Вавилонская система счисления Египетская система счисления

3 слайд

Описание слайда:

Узловые числа обозначаются цифрами. Узловые и алгоритмические числа Алгоритмические числа получаются в результате каких-либо операций из узловых чисел.  100 +  10 + =

4 слайд

Описание слайда:

Простейшая и самая древняя система — так называемая унарная система счисления. В ней для записи любых чисел используется всего один символ — палочка, узелок, зарубка, камушек. Унарная система счисления Примеры узлов «кипу»

5 слайд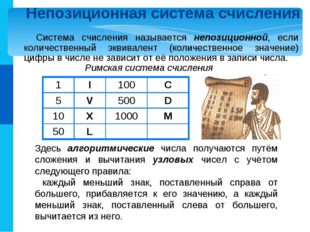

Описание слайда:

Римская система счисления Непозиционная система счисления Система счисления называется непозиционной, если количественный эквивалент (количественное значение) цифры в числе не зависит от её положения в записи числа. Здесь алгоритмические числа получаются путём сложения и вычитания узловых чисел с учётом следующего правила: каждый меньший знак, поставленный справа от большего, прибавляется к его значению, а каждый меньший знак, поставленный слева от большего, вычитается из него. 1 I 100 C 5 V 500 D 10 X 1000 M 50 L

6 слайд

Описание слайда:

Система счисления называется позиционной, если количественный эквивалент цифры в числе зависит от её положения в записи числа. Основание позиционной системы счисления равно количеству цифр, составляющих её алфавит. Алфавит десятичной системы составляют цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Позиционная система счисления

7 слайд

Описание слайда:

Цифры 1234567890 сложились в Индии около 400 г. н. э. Арабы стали пользоваться подобной нумерацией около 800 г. н. э. Примерно в 1200 г. н. э. эту нумерацию начали применять в Европе. Десятичная система счисления

8 слайд

Описание слайда:

Двоичная система счисления Двоичной системой счисления называется позиционная система счисления с основанием 2. Двоичный алфавит: 0 и 1. Для целых двоичных чисел можно записать: an–1an–2…a1a0 = an–12n–1 + an–22n–2 +…+ a020 Например: 100112 =124+023+022+121+120 = 24 +21 + 20 =1910 Правило перевода двоичных чисел в десятичную систему счисления: Вычислить сумму степеней двойки, соответствующих единицам в свёрнутой форме записи двоичного числа

9 слайд

Описание слайда:

Правило перевода целых десятичных чисел в двоичную систему счисления an–12n–1+an–22n–2+… a121 +a0 = an–12n–2 +…+ a1 (остаток a0) 2 an–12n–1+an–22n–2+… a1 = an–12n–3+…+ a2 (остаток a1) 2 . . . an–12n–1+an–22n–2+… a2 = an–12n–4 +…+ a3 (остаток a2) 2 На n-м шаге получим набор цифр: a0a1a2…an–1

10 слайд

Описание слайда:

«Компьютерные» системы счисления Двоичная система используется в компьютерной технике, так как: двоичные числа представляются в компьютере с помощью простых технических элементов с двумя устойчивыми состояниями; представление информации посредством только двух состояний надёжно и помехоустойчиво; двоичная арифметика наиболее проста; существует математический аппарат, обеспечивающий логические преобразования двоичных данных. Двоичный код удобен для компьютера. Человеку неудобно пользоваться длинными и однородными кодами. Специалисты заменяют двоичные коды на величины в восьмеричной или шестнадцатеричной системах счисления.

Курс профессиональной переподготовки

Учитель информатики

Курс профессиональной переподготовки

Учитель математики и информатики

Курс повышения квалификации

Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:

Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВнеурочная деятельностьВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое

Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс

Выберите учебник: Все учебники

Выберите тему: Все темы

также Вы можете выбрать тип материала:

Общая информация

Номер материала: ДБ-136745

Оставьте свой комментарий

Открытый урок по теме Системы счисления 9 класс

Конспект «открытого» урока информатики в 9 классе

Тема: «Обобщающий урок по теме «Системы счисления»

Подготовила: учитель информатики МБУ СОШ № 74,

Рыбалкина Оксана Семеновна

Дата урока:

Класс: 9 А

Присутствуют: заместитель директора по УВР С.И. Резвова, учителя МБУ СОШ № 74

Дидактическая цель урока: создать условия для повторения и осмоления системы знаний по теме «Системы счисления»

Задачи урока:

I. Формирование предметной компетенции:

Познавательные — повторить понятия «система счисления», определение «позиционные и непозиционные СС»; повторить правила перевода чисел из одной СС в другую и наоборот.

Практические — учить детей работать с инженерным калькулятором

II. Формирование метапредметных компетенций:

Регулятивные компетенции — определять отличие схемы от рисунка — развивать внимание, логическое мышление, умение сопоставлять и делать вывод, творческие умения;

Коммуникативные компетенции — работать в коллективе, слушать и слышать учителя, адекватно реагировать на ошибки, принимать решения.

III. Воспитательные задачи:

Вызвать интерес к изучению информатики как науке, изучающей хранение, передачу и обработку информации.

Тип урока: Обобщение и систематизация знаний и способов действий

Методы обучения: проблемное обучение, проектный метод, здоровьесберегающая технология, ИКТ-технология

Формы работы: фронтальная, индивидуальная, групповая

Дидактический материал: карточки с заданиями, текст стихотворения

Оборудование: раздаточный материал, АРМ учителя, проектор, ноутбуки, телефоны

Перечень используемых ЭОР

№

Название ресурса

Тип, вид ресурса

Форма предъявления информации (иллюстрация, презентация, видеофрагменты, тест, модель и т.д.)

Гиперссылка на ресурс, обеспечивающий доступ к ЭОР

Понятие о системах счисления

информационный

видеофрагмент

http://www.fcior.edu.ru/card/1610/ponyatie-o-sistemah-schisleniya.html

Системы счисления (N 170369)

Информационный, анимация

Интерактивный мультфильм

http://school-collection.edu.ru/catalog/res/15925a41-8dd5-48c5-9187-31628f22b89a/?

ХОД УРОКА:

Организационный момент

Учитель: Приветствует учащихся, проверяет готовность рабочего места школьников к учебному занятию

— Здравствуйте, ребята. Сегодня нам понадобятся рабочие тетради, ручки, ноутбуки и сотовые телефоны.

Учащиеся: Приветствуют учителя, проверяют наличие дидактических материалов для работы на занятии, слушают учителя

Актуализация знаний

Учитель:

— Урок мы начнем с небольшого стихотворения (Приложение 1, Рисунок 1):

Читает стихотворение:

СКОЛЬКО ЛЕТ ДЕВОЧКЕ

(А. Стариков)

Ей было тысяча сто лет,

Она в сто первый класс ходила,

В портфеле по сто книг носила —

Все это правда, а не бред.

Когда, пыля десятком ног,

Она шагала по дороге,

За ней всегда бежал щенок

С одним хвостом, зато стоногий.

Она ловила каждый звук

Своими десятью ушами,

И десять загорелых рук

Портфель и поводок держали.

И десять темно-синих глаз

Рассматривали мир привычно,

Но станет все совсем обычным,

Когда поймете наш рассказ

Учитель: задает вопросы по стихотворению, актуализирует внимание учащихся

— Скажите, пожалуйста, что в этом стихотворении необычного?

-Что необходимо сделать, чтобы стихотворение стало понятным?

Учащиеся: слушают учителя, отвечают на вопросы

— Перевести числа из двоичной системы счисления в десятичную.

Учитель:

— Давайте вспомним определение системы счисления.

— Назовите основные системы счисления?

Ученик: Двоичная, десятичная, восьмеричная, шестнадцатеричная (Рисунок 3).

Учитель:

— Чтобы стихотворение стало понятным, переведем числа из двоичной системы счисления в десятичную

(Рисунок 1). Читаем первую строчку: Ей было тысяча сто лет. Как мы переведем число из двоичной СС в

десятичную. Вспомним правила перевода вместе. Вы работаете в тетрадях, а я у доски.

(Учитель на доске переводит первое число из двоичной системы счисления в десятичную).

— Итак, девочке было 12 лет (Рисунок 4).

А теперь каждый из вас самостоятельно переведет все остальные числа в десятичную систему счисления (у вас есть ровно 3 минуты).

(ученики работают в тетрадях)

Учитель:

Итак, проверяем:

— В какой класс ходила девочка?

Ученик: в 5 класс (Рисунок 5)

Учитель:

— Сколько книг она носила?

Ученик: 4 книги (Рисунок 6)

Учитель:

— Сколько было ног, рук, ушей и глаз у девочки?

Ученик: конечно по 2 (Рисунок 7).

Учитель: Показывает интерактивный мультфильм (ЭОР № 2), предлагает выписать в тетрадь пример перевода чисел из десятичной системы счисления в другую.

III. Постановка цели и задач урока. Мотивация учебной деятельности учащихся.

Учитель: Сообщает тему урока, предлагает сформулировать учебную задачу

— Мы с вами вспомнили правила перевода из двоичной СС и десятичную.

— А как перевести числа из 8 и 16 сс в десятичную? Точно также.

— Итак, вы уже, наверное догадались чем мы сегодня на уроке будем заниматься.

Учащиеся: Слушают учителя, формулируют учебную задачу урока

— На уроке мы будем повторять тему «системы счисления»

Учитель: Разъясняет условия и последовательность работы школьников

— Сегодня мы проведем урок – обобщение и систематизация знаний по теме «системы счисления». Мы повторим привила перевода из одной СС в другую и наоборот, научимся переводить числа с помощью инженерного калькулятора.

Итак, открываем тетради и записываем дату и тему урока «Системы счисления».

III. Закрепление, систематизация и контроль знаний и способов действий.

Учитель: актуализирует внимание учащихся на экран, задает вопросы (ЭОР № 1)

— Посмотрите на экран и скажите, в какой системе счисления могут быть записаны числа?

2007, 10101, 343434, F12A ?

— Вы знаете, что все СС делятся на 2 большие группы. Какие?

— К какой группе систем счисления относятся эти числа?

Учащиеся: слушают, отвечают на вопросы о непозиционных систем счисления, позиционной системы счисления, формулы перевода чисел из любой системы счисления в десятичную.

— Позиционные и непозиционные. К позиционной.

Учитель: актуализирует внимание учащихся на экран, задает вопросы (Презентация)

— Что вы можешь сказать о числах 333 и ХХХ ?

— Чему в десятичной системе счисления равны следующие числа, записанные римскими цифрами:

а) XI; б) LX; в) MXD?

— По каким правилам вы перевели числа из римской СС в десятичную.

— А эти числа к какой системе счисления относятся?

Учащиеся: К непозиционной.

Учитель: организует самостоятельную работу перевода числа в десятичную СС

— Переведите самостояельно римское число в десятичную СС

M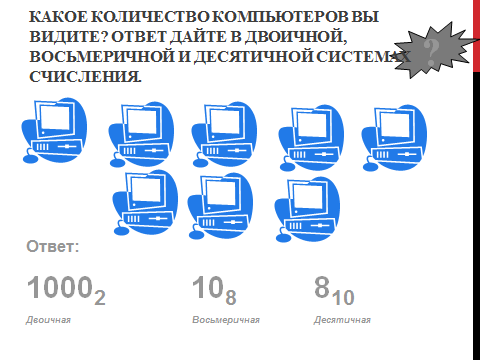CMXLVI (1946)

Учащиеся: работают самостоятельно, выполняют задания в рабочей тетради

Учитель:

— Это число вам о чем-нибудь говорит? Это год появления первого компьютера в США (Эниак)

-Итак, мы с вами вспомнили, что системы счисления делятся на позиционные и непозиционные СС и вспомнили правила перевода римских чисел.

— Какое количество компьютеров вы видите? Ответ дайте в двоичной, восьмеричной и десятичной системах счисления.

— Вспомним правила перевода чисел из 10-ичной СС в любую другую. Разберем вместе с вами первый пример, я у доски, а вы в тетрадях. У вас есть одна минута.

Учащиеся: работают самостоятельно, выполняют задания в рабочей тетради

Учитель: организует фронтальную работу проверки задания

— Итак, что у вас получилось?

— Хорошо, мы повторили перевод чисел из 10-ой СС в любую другую СС. Молодцы

Физкультминутка

Учитель организует небольшой перерыв, просит учащихся выполнить упражнения для глаз (Презентация)

Учитель: организует работу в парах.

— Сейчас мы еще раз убедились, на сколько это трудоемкий процесс с использованием только математических навыков. Для перевода чисел из одной системы счисления в другую и проведения вычислений в различных системах счисления можно использовать приложения, которые обычно называются научными или инженерными калькуляторами. Какое стандартное приложение входит в состав операционной системы Windows? (Калькулятор)

Воспользуемся этим приложением для вычислений. Используя инженерный калькулятор выполним задания по карточкам

Задания для парной работы

Учащиеся: выполняют работу в парах, организуют взаимопроверку, взаимооценку

1) Переведите числа из одной системы счисления в другую:

12816 — Х2 Ответ:1001010002

6418— Х16 Ответ:1A116

2) Какое из чисел 1100112, 1118, 1В16 является наибольшим, наименьшим?

Ответ: 1В16 < 1100112 < 1118.

— Чтобы проверить правильность выполнения заданий обменяйтесь с соседями карточками и проверьте друг у друга ответы. И поставьте оценки за работу.

IV. Контроль усвоения, обсуждение допущенных ошибок и их коррекция.

Учитель: контроль усвоения знаний и умений через работу по карточкам.

Работа с карточками (Приложение 3)

— У вас у каждого на столе лежат карточки с зашифрованными словами. Но каждая буква представлена в какой-то СС. Вам нужно перевести каждую цифру.

Учащиеся: выполняют задания в тетради, отвечают устно

Учитель: корректирует деятельность учащихся, разбирает допущенные ошибки

V. Подведение итогов. Рефлексия.

Учитель: организует беседу по вопросам

— Какие цели, задачи стояли перед нами в начале урока?

— Смогли ли вы их достичь?

— Какой материал был трудным, непонятным?

— А что воспринималось легко?

— Попробуйте дать оценку уроку

Учащиеся: отвечают на вопросы, анализирую свою деятельность на уроке

Учитель: оценивает работу учащихся, выставляет оценки за урок

— Вы сегодня хорошо поработали на уроке. Особенно активными были…

VI. Информация о домашнем задании

Учитель: формулирует домашнее задание

— Выполните творческое задание (Приложение 4) – раскрасьте рисунок, определив его цвета, с помощью перевода чисел в десятичную систему счисления.

Учащиеся: записывают домашнее задание.

Заместитель директора по УВР С.И. Резвова

Приложение № 1

Приложение № 2

1) Переведите числа из одной системы счисления в другую:

12816 — Х2 Ответ: 1001010002

6418— Х16 Ответ: 1A116

2) Какое из чисел 1100112, 1118, 1В16 является наибольшим, наименьшим?

Ответ: 1В16 < 1100112 < 1118.

Приложение № 3

КАРТОЧКА № 1

Используя таблицу кодировки букв и правила перевода чисел 2®10, расшифруйте приведенное слово: 1101₂ 0100₂ 1010₂ 1011₂

Буква

10-тичный код

Ответ: _____________

КАРТОЧКА № 2

Используя таблицу кодировки букв и правила перевода чисел 2®10, расшифруйте приведенное слово: 1011₂ 1100₂ 0100₂ 1000₂ 1110₂

Буква

10-тичный код

Ответ: ___________

КАРТОЧКА № 3

Используя таблицу кодировки букв и правила перевода чисел 2®10, расшифруйте приведенное слово: 1100₂ 0100₂ 0101₂ 1011₂

Буква

10-тичный код

Ответ: ____________

КАРТОЧКА № 4

Используя таблицу кодировки букв и правила перевода чисел 2®10, расшифруйте приведенное слово: 0010₂ 1011₂ 1000₂ 1110₂ 0010₂ 1011₂

Буква

10-тичный код

Ответ: ______________

КАРТОЧКА № 5

Используя таблицу кодировки букв и правила перевода чисел 2®10, расшифруйте приведенное слово: 0011₂ 0110₂ 1011₂ 1101₂

Буква

10-тичный код

Ответ: ______________

Приложение № 4

Творческое домашнее задание

Возьмите цветные карандаши (6 цветов) с номерами в десятичной системе счисления. Задание: раскрасить рисунок соответствующим цветом.

100 – ЗЕЛЕНЫЙ

101 – ГОЛУБОЙ

110 — КРАСНЫЙ

111 – ЖЕЛТЫЙ

1000 – КОРИЧНЕВЫЙ

1001 – ЧЕРНЫЙ

Примечания на 9-е и 10-е дополнения десятичного вычитания | 11 класс> Информатика> Система счисления и их преобразование

В компьютерной системе вычитание не выполняется непосредственно как арифметическое вычитание. Это выполнено техникой, названной дополнением. Это процесс многократного добавления.

Где «r» — основа системы счисления.

В двоичной системе счисления существует два типа дополнения: 1-дополнение и 2-дополнение.

Аналогично, десятичная система счисления имеет дополнение 9 и 10.

1-е дополнение двоичного числа получается вычитанием каждого бита на 1. Мы можем получить 1-е дополнение, просто заменив 1 на 0 и 0 на 1.

Вычитание двоичных чисел с использованием 1-го дополнения

Здесь приведены следующие шаги:

Создайте оба числа с одинаковым количеством битов.
Определите 1-е дополнение числа к вычитаемому (вычитаемое).
Добавьте 1-е дополнение к данному числу, из которого мы вычитаем (minuend).
Если в результате после добавления есть какой-либо дополнительный бит (перенос), удалите и добавьте его к результату иначе (т. Е. Если не существует никакого переноса).
отрицательный знак, чтобы получить окончательный результат.

Пример: вычесть 1110000 из 1100000

Дополнение двоичного числа 2-х получается путем добавления двоичного числа 1 к дополнению числа 1-го числа.

Вычитание с использованием 2-х дополнений:

Здесь приведены следующие шаги:

Создайте оба числа с одинаковым количеством битов.
Определите 2-е дополнение к числу, которое нужно вычесть (вычесть).
Добавьте 2-е дополнение к данному числу, из которого мы вычитаем (minuend).
Если нет выхода, определите 2-е дополнение результата и префикс отрицательным знаком, чтобы получить окончательный результат.

Пример: Вычтите 1110000 из 1100000

Дополнение 9 и 10 дополнений

Дополнение десятичного числа 9 можно получить, вычитая каждую цифру числа из 9.

Например, 9-е дополнение к 3 равно 6 (9-3 = 6), а 234 — 765 (999-234 = 765).

Десятичное дополнение десятичного числа можно получить, добавив 1 к младшей значащей цифре 9-го дополнения этого числа. Например, 10-кратное дополнение к 3 равно 7 (9-3 = 6 + 1 = 7), а 123 — 877.

Вычитание десятичного числа с использованием 9-кратного дополнения

Ниже приведены шаги, приведенные ниже:

Сделайте оба числа, имеющие одинаковое количество цифр.
Определите 9-е дополнение числа, из которого мы вычли (вычитаем).
Добавьте 9-е дополнение к данному числу, из которого мы вычитаем (minuend).
Если в результате после добавления есть какая-либо дополнительная цифра (перенос), удалите ее и добавьте к дополнению результата и добавьте к отрицательному знаку префикс, чтобы получить окончательный результат.

Например Отнимите (123) ₁₀ Из (345) ₁₀
9-е дополнение 123 = (999 -123) = 876
Добавление 9-го дополнения с 345, т.е.e 345 + 876 = 1221

В результате наиболее значимая цифра 1 является переносом. Таким образом, добавьте этот перенос к оставшимся цифрам 221
, т. Е. 221 + 1 = 222
. Следовательно, (222) ₁₀ является необходимым результатом после вычитания (123) ₁₀ из (345) _10.

Вычитание с использованием 10-е дополнение:

Ниже приведены шаги, приведенные ниже:

Сделайте оба числа одинаковыми цифрами.
Определите 10-е дополнение числа к вычитаемому (вычитаемое).
Добавьте 10-е дополнение к данному числу, из которого мы вычитаем (minuend).
Если в результате после добавления есть какая-либо дополнительная цифра (перенос), удалите ее из результата, а оставшиеся цифры образуют окончательный результат.
Если кэрри не существует, определите 10-кратное дополнение результата и префикс отрицательным знаком, чтобы получить окончательный результат.

Пример: вычесть (123) ₁₀ из (345) ₁₀

10-дневное дополнение 123 = (999 — 123) = 876 + 1 = 877
Добавление 10-кратного дополнения с 345, я.е. 345 + 877 = 1222
В этом результате наиболее значимой цифрой 1 является перенос. Для удаления результата удалите его.
Следовательно, (222) ₁₀ является требуемым результатом.

Двоичная математика

1. Двоичное добавление

Правило двоичного сложения0 + 0 = 01 + 0 = 10 + 1 = 11 + 1 = 10 (0 с переносом 1) Пример: двоичное сложение101101 +10111 1000100 сумма
2. Двоичное вычитание
Правило для двоичного вычитания 1-1 = 01-0 = 10-1 = 1 (с заимствованием 1) 0-0 = 0 Пример: Бинарное сложение101101 minuend -10111 вычитаемое 1010 разница
3.Двоичное умножение
Правило двоичного умножения1 * 1 = 11 * 0 = 00 * 1 = 00 * 0 = 0 Пример: двоичное умножение 1011 умножение * 1011 множитель10111011 * 0000 +1011 * 1111001 product
4. Двоичное деление
Правило для двоичного деления1 / 1 = 11/0 = не определено0 / 1 = 00/0 = не определено Пример: Binary DivisionDivide 101011 от 110110) 101011 ( 111 частное -110 1001 -110 111 -110 1 остаток
Некоторые основные термины, относящиеся к системе счисления
MSB (старший бит)
Самый левый бит номер называется MSB.
Пример:
1010 = MBS
LSB (младший значащий бит)
Самый правый бит числа называется LSB.
Пример:
1010 = LSB
BIT: одиночное двоичное число 0 или 1
Nibble: комбинация из 4 двоичных битов, например, 1001
байт: комбинация 8 двоичных битов, например, 1001 0111
(Shrestha, Manandhar и Roshan)
Библиография
Shrestha, Prachanda Ram, et al. Computer Essentials . Катманду: Публикация Асмиты, 2014.
Гурунг, Джудха Бахадур и др., Информатика-XI, Бхундипуран Пракашан, Ктм
,Объяснено
баллов GCSE — что такое система маркировки 1-9 и как она работает?

студентов GCSE теперь оцениваются числами вместо букв после того, как старая система была перестроена в 2017 году.

Вот все, что вам нужно знать об изменениях, которые заменяют старую систему U-A * на 1-9 баллов.

Новые сорта начали вводиться в эксплуатацию в 2017 году. Кредит: Alamy.

Что означают новые оценки GCSE?

Новые GCSE были разработаны, чтобы быть более жесткими, что отражается в том, как они оцениваются.

Девятка представляет наилучшую возможную производительность и будет более редкой и более впечатляющей, чем текущая оценка A *.

Между тем, восьмерка находится где-то между A * и A, а семерки стоят столько же, сколько и A.

Аналогично, шестерка — это то же самое, что и высокая оценка B, тогда как пятерка находится где-то между B и C, а четверка соответствует текущей отметке C.

Тройка чуть хуже, чем у текущего D, а двойка немного хуже, чем у E.

Один, наихудший возможный балл, ниже F, в то время как U будет присуждаться за документы, которые невозможно оценить.

Новые оценки GCSE были использованы для результатов 2018 и 2017 годовКредит: Alamy

Какие дальнейшие изменения вносятся в GCSE в этом году?

В 2017 году мы увидели первую партию новых GCSE, присужденных студентам, осваивающим новую систему.

В прошлом студенты получали букву от A *, лучшую возможную оценку, до U за бумагу, которая не достигла какой-либо оценки.

Новые GCSE оцениваются номерами 1-9 вместо традиционных буквенных результатов.

Изменение было разработано, чтобы быть постепенным, с математикой, английским языком и английской литературой первыми предметами, которые перейдут на новый формат оценки в 2017 году.

В 2018 году еще 20 предметов были оценены с помощью новой числовой системы, а не букв, еще 15 предметов были добавлены в 2019 году, и ожидается, что большинство других будут придерживаться новой системы к 2020 году.

Новая система была разработана, чтобы соответствовать более сложным экзаменационным работам GCSEКредит: Alamy

Когда появится новая система для разных предметов?

Лето 2017

английский язык
Английская литература
Математика

Лето 2018

Искусство и дизайн
Биология
Химия
Обучение гражданству
Комбинированная наука (двойная награда)
Информатика
Танец
Драма
Приготовление пищи и питание
География
История
Современные иностранные языки (французский, немецкий, испанский)
Музыка
Физика
Физическое воспитание
Религиоведение

Лето 2019

Древняя история
Астрономия
Бизнес
Классическая цивилизация
Дизайн и технология
Экономика
Электроника
Инжиниринг
Фильм исследования
Геология
Медиа исследования
Современные иностранные языки (арабский, бенгальский, китайский, итальянский, японский, современный греческий, современный иврит, панджабский, польский, русский, урду)
Психология
Социология
Статистика

Лето 2020

Древние языки (библейский иврит)
Современные иностранные языки (гуджарати, персидский, португальский, турецкий)

«UNFAIR»

Бедные подростки могут получить более низкие оценки GCSE и A-level по экзаменационной системе этого года.

ИСПЫТАННЫЕ ПРОЦЕДУРЫ

Учащиеся могут получить GCSE по-французски БЕЗ способности говорить на языке

ДЕЙСТВИЯ КЛАССА Fury as ученики средней школы возвращаются только для «часовых встреч».

CLASS ACT

Тысячи детей, обучающихся на GCSE и A-level, смогут вернуться в школу

УРОВЕНЬ ГРАДА

Планы дать ученикам прогнозируемые результаты экзаменов с сомнением из-за опасений расизма

ШКОЛЬНЫЙ ВЫХОД

ВСЕ школы закрыты до лета до пятницы и экзамены отменены из-за коронавируса

Почему оценки GCSE меняются?

Правительство встряхивает GCSE, чтобы сделать их более жесткими — в надежде, что работодатели отнесутся к ним более серьезно.

Часть этого изменения включает использование новой системы оценок, чтобы сигнализировать о том, что были проведены реформы к экзаменам, и чтобы было легче различать результаты.

Переход на пронумерованные оценки также лучше согласуется с результатами европейских экзаменов, при этом немцы — и большинство других британских конкурентов — используют числовые оценки экзаменов.

Министр образования Ник Гибб дает смешное смешное объяснение новым оценкам GCSE

Мы платим за ваши истории! У вас есть история для новостной команды Sun Online? Напишите нам на советы @ the-sun.co.uk или звоните 0207 782 4368. Мы платим за видео тоже. Нажмите здесь, чтобы загрузить свой.

Примечания по системе счисления: введение и типы | 11 класс> Компьютерные науки> Система счисления и их преобразование

На каждом этапе жизни мы определенно находим использование чисел. Если вам нужно что-то купить, вам придется заплатить определенную сумму денег, за которую вам придется их пересчитать. Аналогично, продавец также будет считать товары, которые вам дают, и то же самое для ваших изменений. Следовательно, систему счисления можно просто определить как способ представления чисел.

Например, система счисления может использоваться для представления количества игроков в определенной игре, например, 11 игроков в футбольной команде, или количества зрителей на концерте, например, 25000 посетителей и т. Д.Таким образом, система счисления также может рассматриваться как набор значений, который используется для представления различных величин.

Десятичная система счисления является наиболее часто используемой системой счисления в нашей повседневной жизни. Эта обычно используемая система счисления также известна как система счисления с основанием 10, потому что она использует только 10 символов, то есть от 0 до 9. Она также известна как система счисления с отрицательным числом, потому что при любом числовом значении эти цифры системы могут легко представлять их.Десятичная система специально используется в интерфейсе компьютера. Вес и положение цифры определяют значение, представленное ею.

В этой системе каждое число состоит из цифр, которые расположены в разных позициях. Позиции 1 ^-й и 2 ^-й цифр в направлении правой части десятичной точки составляют ^-1 и ^-2. Аналогично, позиции 1 ^-й и 2 ^-й цифр в направлении левой части десятичной точки равны 0 и 1 соответственно.

Значение числа определяется путем сложения результатов умножения цифр с весом их положения. Этот метод называется методом расширения. При этом методе крайняя правая цифра номера называется наименьшей значащей цифрой (LSD), поскольку она имеет наименьший вес. Аналогично, крайняя левая цифра номера называется самой значимой цифрой (MSD), так как она имеет наибольший вес.

Примеры:

(a) Вес и позиции каждой цифры числа 796 следующие:

9 9002

позиции	2	1	0
Вес	10 ²	10 ¹	10 ⁰
номинальная стоимость	7		6

В приведенной выше таблице указано, что:
Значение цифры 7 = 7×10 ² = 700
Значение цифры 9 = 9×10 ¹ = 90
Значение цифры 6 = 6×10 ⁰ = 6
Фактическое число может быть сформировано путем сложения значений, полученных цифрами, следующим образом:
700 + 90 + 6 = 796
Здесь, th Цифра 7 в числе 796 является самой значимой цифрой, а 6 — самой младшей цифрой.

(b) Веса и позиции каждой цифры числа 125,64 являются следующими:

-2

Положения	2	1	0	-1	-2
Вес	10 ²	10 ¹	10 ⁰	10 ^-1
Номинальная стоимость	1	2	5	6	4

В приведенной выше таблице указано, что: 9000 значение цифры 1 = 1×10 ² = 100
Значение цифры 2 = 2×10 ¹ = 20
Значение цифры 5 = 5×10 ⁰ = 5
Значение цифры 6 = 6×10 ^-1 = 0.6
Значение цифры 4 = 4×10 ^-2 = 0,4
. Фактическое число может быть сформировано путем сложения значений, полученных цифрами, следующим образом:
100 + 20 + 5 + 0,6 + 0,4 = 125,64

2) Двоичные Система счисления:

Система двоичных чисел

относится к системе счисления, в которой используются только два символа: 0 и 1, то есть 0, почему она называется системой счисления с основанием 2. Он также известен как двоичная цифра (BIT). Эта система счисления особенно используется при внутренней обработке компьютерной системы. Когда мы считаем от 0 в двоичном коде, символы намного чаще заканчиваются, так как эта система использует только 0, а 1 и 2 не существуют.Поэтому мы используем 10 в этой системе, потому что 10 равно 2 в десятичном виде. Комбинация двоичных чисел может использоваться для представления различных величин, таких как 1001. В двоичной системе позиционное значение каждой цифры в два раза превышает номинальное или местное значение цифры ее правой стороны. Вес каждой позиции — это степень 2.

В зависимости от позиции и веса, начальные значения цифр следующие:

0 9953

Пример: конвертировать 101.11

Позиции	3	2	1	0
Вес	2 ³	2 ²	2 ¹	2 ⁰ 9953

9000

2 ^-1

Вакансии

-1

-2

Номинальная стоимость

Вес

2 ³

2¹

9 9003

0
9 9002
9009
0

2 ^-2

В приведенной выше таблице указано, что:
101.101 = 1×2² + 0x2¹ + 1×2 ⁰ + 1×2 ^-1 + 1×2 ^-2
= 1×4 + 0 + 1×1 + 1/2 + 1/4
= 4 + 0 + 1 + 0,5 + 0,25
= 5.75

3) Восьмеричная система счисления:

Восьмеричная система счисления является базовой 8-й системой. Подобно десятичной системе счисления, эта система также используется во внутренней обработке компьютерной системы. Это система, состоящая из восьми цифр, то есть {0, 1, 2, 3, 4, 5, 6, 7}, которая используется для краткого представления длинных двоичных чисел. В этой системе каждая позиция цифры представляет степень 8.Число 708 не будет действительным в этой системе, так как 8 не является действительной цифрой.

В соответствии с положением и весом значение цифр будет следующим:

Пример: преобразовать 128 в десятичное число.

Позиции

весов

0

8³

8²

8¹

8 ⁰

128 = 1×8¹ + 2×8 ⁰
= 1×8 + 2×1
= 8 +

= 8 +

= 8 + 2

= 8 +

= 9 + 2

= 8 +

4) Шестнадцатеричная система счисления:

Шестнадцатеричная система счисления — это система счисления, которая представляет длинные двоичные числа в методе ярлыков.Это базовая 16 система, состоящая из 16 цифр, то есть {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F}, где алфавиты представляют десятичные числа от 10 до 15. Эта система также используется в компьютерной системе, главным образом в управлении памятью. Как следует из названия, позиция каждой цифры представляет степень 16 в этой системе.

В соответствии с положением и весом местное значение цифр выглядит следующим образом:

Пример: преобразование 2A16 в десятичное число.

Позиции

весов

0
16³

16²

16¹

16 ⁰

2A16 = 2×16¹ + Ax16 ⁰
= 2×16 + 10×1
= 32 + 9
= 32 +
= 32 + 10
= 32 + 9
= 32 + 9
= 32 + 9000 Karn & Pudasaini, 2015)

Библиография

Karn, M.K. & Pudasaini, D. (2015). Информатика I. Анамнагар, Катманду: Публикация Будды.