Урок «Основное свойство дроби» (8 класс)

Тема: Основное свойство дроби. Сокращение дробей

Цели урока:

• Формирование знаний и умений по теме «Основное свойство дроби»:
  а) объяснение и первичное закрепление материала;
  б) отработка умений и навыков.

• Повторение знания способов разложения на множители, формул сокращённого умножения.

• Отработка навыков самоконтроля с целью освоения знаниями для выполнения различного вида заданий работы с выражениями.

• Развитие вычислительных навыков.

• Воспитание воли и настойчивости для достижения конечных результатов при решении комбинаторных задач.

Тип урока: Объяснение и первичное закрепление нового материала.

Оборудование: Карточки с практическими заданиями, памятки для учащихся.

Методы работы: фронтальный опрос, практический, индуктивный, проблемно-поисковый метод самостоятельной работы

ХОД УРОКА.

1. Объявление темы и целей урока.

2. Разминка.

а) – Среди данных дробей найдите рациональные. Запишите их в тетради.

– Какая дробь называется рациональной?

 

– Когда рациональная дробь равна нулю?

Разбор

на примере

последней дроби

– Когда рациональная дробь не имеет смысла? Почему?

– Как найти допустимые значения дроби?

Задания с кодовой записью ответов.

Задания по вариантам

Ответы

Код

Первый

Второй

№ 1.

Найдите значение переменной, при которой дробь равна нулю.

 

№ 1.

Найдите значение переменной, при которой дробь равна нулю.

 

0

1

3

2

–3

3

вcе числа,
кроме 0

4

вcе числа,
кроме –3

5

вcе числа,
кроме 3

6

№ 2.

Найдите значение переменной, при которой дробь не имеет смысла.

 

№ 2.

Найдите значение переменной, при которой дробь не имеет смысла.

 

0

7

3

8

–3

9

вcе числа,
кроме 0

0

вcе числа,
кроме –3

1

вcе числа,
кроме 3

2

№ 3.

Найдите допустимые значения переменной для дроби:

 

№ 3.

Найдите допустимые значения переменной для дроби:

 

0

3

3

4

–3

5

вcе числа,
кроме 0

6

вcе числа,
кроме –3

7

вcе числа,
кроме 3

8

Проверка правильности найденных ответов. Самопроверка.

(коды ответов, а ученики сверяют их со своими. 1 вариант: 376. 2 вариант: 188.)

б) – Сегодня на уроке нам потребуется умение раскладывать многочлены на множители. Как это можно сделать? (Применить способ вынесения общего множителя за скобки, способ группировки, знания формул сокращённого умножения.)

• Чтобы вспомнить способ разложения на множители с помощью формул сокращённого умножения, проверьте правильность формул, записанных на доске, и запишите в тетради код правильных ответов.
  1) a² + b² – 2ab = (a – b)²
  2) m² + 2mn – n² = (m – n)²
  3) 2pt – p

  ² – t² = (p – t)²
  4) 2cd + c² + d² = (c + d)²
  5) b² + c² = (b + c)(b – c)
  6) x² – y² = (x – y)(x + y)

3. Изучение новой темы.

а) Подготовительная работа.

Среди данных дробей есть равные. Конечно же, дроби не торопятся сообщить нам о своём “родстве”. Мы должны сами его обнаружить.

³/₆, ¹/₂, ²/₄, ¹/₃, ⁴/₈, ²/₅, ¹/₄, ³/₉.

– Как вы определили, что дроби равны? Каким правилом пользовались?

– Так в чём заключается основное свойство дроби?

б) Новая тема.

А теперь попробуем применить это свойство для алгебраических дробей.
Запишите дроби, равные данной:

со знаменателем 9b, с числителем 2а².

В тетрадях и на доске – запись:

Дополните равенства:

Проверка. 1-й числитель = 6, 2-й числитель = 3b, 1-й знаменатель = ab, 2-й знаменатель = 4by³, 3-й знаменатель = b(a + b) или ab + b².

в) Сокращение дробей.

– Проведём этот этап урока в игровой форме. Послушайте притчу про “Забывчивого парикмахера”.

Парикмахер по растерянности постриг волосы только с половины вашей головы. Если Вы, сокращая дроби, забудете разложить на множители её числитель и знаменатель, то Вы будете очень похожи на этого горе-мастера.

г) Задания с кодовой записью ответов.

Задания по вариантам.

Сократите дроби:

Ответы

Код

Первый

Второй

№ 1.

 

a² / ⁽а² – 3а)

№ 1.

 

х² / ⁽х + ху)

1 /(– 3а)

0

х² /(х + у)

1

х /(1 + ху)

2

а /(а – 3)

3

а /(а² – 3)

4

х /(1 + у)

5

№ 2.

 

(х² – у²⁾ / ⁽х² + ху)

№ 2.

 

(2a – 2b) / (a² – b²⁾

(– у²) / (ху)

6

2 / (a – b)

7

2 / (– 1 )

8

(x – y ) /(x)

9

(– y ) / x

0

2 / (a + b)

1

№ 3

 

39x⁷ /^13x3

№ 3.

 

17x⁵ /^34x6

2х

2

3х

3

1  / 2х

4

1  / 17х

5

26 / х⁴

6

3х⁴

7

1  / 3х⁴

8

26х⁴

9

Проверка кодов. 1 вариант: 397; 2 вариант: 514.

4. Исследовательская работа.

– Как получена вторая дробь из первой?

(Умножением и числителя, и знаменателя на –1.)

Последнюю дробь можно переписать, поставив один из минусов перед дробью:

5. Работа у доски по заданиям учебника:

№ 27, № 29 (1-3), № 30 (1,2).

6. Самостоятельная работа.

№32 (1,2), 33(1)

7. Задание на дом.

Учебник § 2, №28(1-2), 31(1-5)

8. Оценки за урок. Итог урока.

infourok.ru

Технологическая карта к уроку по алгебре 8 класс «Сокращение дробей»

ООО Учебный центр «ПРОФЕССИОНАЛ»

План-конспект урока

по математике

в 8 классе муниципального бюджетного общеобразовательного учреждения

«Средняя школа № 2 им. Е. В. Камышева»

на тему «Сокращение дробей»

Разработал:Филова Елена Викторовна

ФИО

слушатель курсов профессиональной переподготовки «Математика: теория и методика преподавания в образовательной организации»

Проверил: ________________________

ФИО руководителя практики

Г.Гагарин , 2016

Урок по алгебре 8 класса. По УМК Ю.Н. Макарычев и др. Дата 13.09

Дата проведения

Тип урока

Виды деятельности (элементы содержания, контроль)

Планируемые результаты

предметные

Метапредметные УУД: коммуникативные, регулятивные, познавательные; личностные

6

Сокращение дробей

13.09

Урок общеметодической направленности

Формирование у учащихся навыков деятельностях способностей и способностей к структурированию и систематизации изучаемого предметного содержания: работа с опорным конспектами, опрос по теоретическому материалу, проектирование способов выполнения, комментирование выставленных оценок

Познакомится с принципами тождественных преобразований дробей. Научится тождественно сокращать рациональные дроби; формулировать основное свойство рациональных дробей и применять его для преобразований

К: вступать в диалог, участвовать в коллективном обсуждении проблем

Р: вносить коррективы и дополнения в составленные планы

П: выбирать смысловые единицы текста и устанавливать отношения между ними

Л: формирование навыков самодиагностики и самокоррекции деятельности, способности к волевому усилию в преодолении препятствий

Технологии: здоровьесбережения, проблемного обучения, развития исследовательских навыков, дифференцированного подхода в обучении, поэтапного формирования умственных действий

Решаемые проблемы: основное свойство рациональной дроби. Тождества. Тождественные преобразования дробей. Сокращение рациональных дробей

Основная дидактическая цель урока: формировать умение применять основное свойство дроби при сокращении дробей.

Развивать: логическое и критическое мышление

Воспитывать: аккуратность, уважения мнения товарищей, трудолюбие

Оборудование: доска, мел

Учитель приветствует учащихся, проверяет их готовность к уроку.

 Учащиеся готовы к началу работы

 Л: самоопределение.

Р: целеполагание.

II. Устная работа.

– Сократите дробь:

а) ; б) ; в) ; г) ;

д) ; е) ; ж) ; з)

Решают, выполняют работу

 Умение быстрого счета, и анализировать, сопоставлять

П: самостоятельное выделение проблемы, решение проблемы, построение логической цепи рассуждение.

Р: контроль и коррекция

III. Объяснение нового материала

З а д а н и я и в о п р о с ы учащимся:

1. Какие существуют способы разложения многочлена на множители?

2. В чём состоит каждый из этих способов?

3. Разложите на множители многочлен:

а) х²у – 2х; д) х² + 6х + 9;

б) 3a²b – 9ab²; е) а² – 10а + 25;

в) т² – 4п; ж) ax + bx + ay + by.

г) а³ – а; з) ab – b + 3a – 3.

После проведения этой работы следует разобрать пример 3 (с.9) из учебника и сделать в ы в о д: чтобы сократить рациональную дробь, нужно сначала разложить на множители её числитель и знаменатель.

Для успешной работы учащихся на уроке им необходимо не только использовать основное свойство дроби, но и применять ряд других знаний и умений, полученных и сформированных ранее.

Учащиеся должны помнить формулы сокращенного умножения и основные приёмы разложения многочлена на множители. Поэтому начать необходимо с актуализации знаний и умений.

IV. Формирование умений и навыков

1. № 30 (а, в, д), № 32 (в).

2.№ 34(в,г).

3. № 35 (а, в).

Р е ш е н и е

а) .

в) .

Д о п о л н и т е л ь н о можно выполнить № 36 (а).

Р е ш е н и е

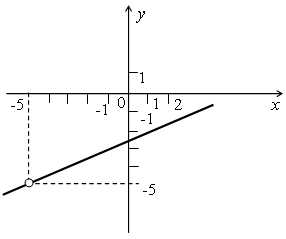
Областью определения этой функции является множество всех чисел, кроме х = –5. Сократим дробь, задающую функцию:

.

Графиком функции является прямая, а графиком функции – та же прямая, но с «выколотой» точкой (–5; –5).

Слушают, анализируют, решают

Решать примеры и задачи , вспоминать правила

 К: инициативное сотрудничество.

П: самостоятельное выделение проблемы, решение проблемы, построение логической цепи рассуждение, доказательства

Р: контроль, коррекция

V. Домашнее задание

§2. №32 (б), 35 (б,г), 40 (а,в,д), 50(а,в, д)

Записывают домашнее задание

VI. Итоги урока

VII. Рефлексия

– В чём состоит основное свойство дроби?

– Когда применяется основное свойство дроби?

– Что нужно сделать, чтобы сократить рациональную дробь?

– Какие существуют способы разложения многочлена на множители?

— оцените себя на сколько Вы поняли тему урока.

 

Отвечают на вопросы

Каждый оценивает свою работу.

 К: умение с достаточной полнотой и точностью выражать свои мысли

П: рефлексия

infourok.ru

Урок 8. Основное свойство алгебраической дроби | Поурочные планы по алгебре 8 класс

Урок 8. Основное свойство алгебраической дроби

25.02.2012 6112 1372

---

Урок 8.

Основное свойство алгебраической дроби.

Цели урока: закрепить умения применять основное свойство дроби; проверить умение сокращать дроби и приводить их к общему знаменателю.

Ход урока.

I. Организационный момент.

II. Проверка домашнего задания.

У доски три учащихся решают задания из № 53(б), 57(а), 58(г). В это время, остальные учащиеся устно проговаривают цепочки решений по рабочим тетрадям № 53 (а, в, г), 57(б, в, г), 58 (а, б, в) до тех пор, пока решают у доски учащиеся, поэтому лучше проверять действия в разброс и выборочно. Затем рассмотреть решенные задания у доски.

III. Решение задач.

Работа у доски: выходят по два ученика решать задания из № 63, 64, 65, решив свой пример, обмениваются примерами, чтобы проверить решение своего соседа.

Для дополнительного вопроса можно использовать задания из № 60.

Для проверки усвоения нового материала провести самостоятельную работу в четырёх вариантах:

I. вариант	№ 66 (а), № 67 (г)
II. вариант	№ 66 (б), № 67 (в)
III. вариант	№ 66 (в), № 67 (б)
IV. вариант	№ 66 (г), № 67 (а)

Подведение итогов.

Домашнее задание: № 68, 69; на дополнительную оценку № 71.

Полный текст материала смотрите в скачиваемом файле.
На странице приведен только фрагмент материала.

tak-to-ent.net

План-конспект урока по алгебре в 8 классе по теме «Сокращение дробей»

У р о к 4
Сокращение дробей

Цели: формировать умение применять основное свойство дроби при сокращении дробей.

Ход урока

I. Организационный момент.

II. Устная работа.

– Сократите дробь:

а) ; б) ; в) ; г) ;

д) ; е) ; ж) ; з) .

III. Объяснение нового материала.

Для успешной работы учащихся на уроке им необходимо не только использовать основное свойство дроби, но и применять ряд других знаний и умений, полученных и сформированных ранее.

Учащиеся должны помнить формулы сокращенного умножения и основные приёмы разложения многочлена на множители. Поэтому начать необходимо с актуализации знаний и умений.

З а д а н и я и в о п р о с ы учащимся:

1. Какие существуют способы разложения многочлена на множители?

2. В чём состоит каждый из этих способов?

3. Разложите на множители многочлен:

а) х²у – 2х; д) х² + 6х + 9;

б) 3a²b – 9ab²; е) а² – 10а + 25;

в) т² – 4п; ж) ax + bx + ay + by.

г) а³ – а; з) ab – b + 3a – 3.

После проведения этой работы следует разобрать пример 3 из учебника и сделать в ы в о д: чтобы сократить рациональную дробь, нужно сначала разложить на множители её числитель и знаменатель.

IV. Формирование умений и навыков.

1. № 29, № 30 (а, в, д), № 32 (а, в).

2. № 31, № 34.

3. № 35 (а, в).

Р е ш е н и е

а) .

в) .

Д о п о л н и т е л ь н о можно выполнить № 36 (а).

Р е ш е н и е

Областью определения этой функции является множество всех чисел, кроме х = –5. Сократим дробь, задающую функцию:

.

Графиком функции является прямая, а графиком функции – та же прямая, но с «выколотой» точкой (–5; –5).

V. Итоги урока.

В о п р о с ы у ч а щ и м с я:

– В чём состоит основное свойство дроби?

– Когда применяется основное свойство дроби?

– Что нужно сделать, чтобы сократить рациональную дробь?

– Какие существуют способы разложения многочлена на множители?

Домашнее задание: № 30 (б, г, е), № 32 (б), № 35 (б, г)

infourok.ru

Конспект урока по Алгебре Основное свойство дроби. Сокращение дробей 8 класс

Глава: «Рациональные дроби».
8 класс.
Тема урока: «Основное свойство дроби. Сокращение дробей».
Цели урока:
Обучающие:
ввести понятия: основного свойства дроби и «тождества»;
научить учащихся применять основное свойство дроби при сокращении дробей;
показать применение основного свойства дроби при сокращении дробей;
показать использование основного свойства дроби для приведения дроби к указанному знаменателю;
совершенствовать вычислительные навыки.
Развивающие:
развивать математическую речь, способствовать формированию логического мышления учащихся.
Воспитательные:
воспитывать творческую активность, культуру общения, интерес к предмету.
Тип урока: изучение нового материала.
Оборудование урока:
компьютер, проектор, экран;
компьютерная презентация;
индивидуальные и практические задания.
Используемые ресурсы
Ю.Н.Макарычев, Н.Г. Миндюк и др. Алгебра 8 класс: учебник для общеобразователь-ных учреждений. М.Просвещение 2010 г.
ЭОР — «Алгебра», 8 класс, Макарычев Ю.Н., HYPERLINK «http://school-collection.edu.ru/catalog/rubr/253f44a5-bb2a-4221-ae16-5b990bb69526/112601/?interface=pupil&class=50&subject=17″МиндюкHYPERLINK «http://school-collection.edu.ru/catalog/rubr/253f44a5-bb2a-4221-ae16-5b990bb69526/112601/?interface=pupil&class=50&subject=17» Н.Г. и др. Единая коллекция ЦОР
Ход урока.
Организация начала урока
Актуализация опорных знаний
Повторить основное свойство обыкновенных дробей, правило сокращения дробей: презентация слайд 2 и 3.
3. Изучение нового материала.
Используя презентацию слайд 4 и 5 ввести понятие алгебраических дробей, допустимых значений слайд 6 и 7.
Ввести понятия: основного свойства дроби и « тождества», используя коллекцию Введение понятий: основного свойства дроби и «тождества» (Теория, пункты 1,2) или презентацию слайды 8 и 9 (на слайде 9 показано примеры применения свойства к алгебраическим дробям).
4. Закрепление изученного материала.
а) Отработка понятия основного свойства дроби (Практика, пункт 3) или презентация слайд 10 и 11.
Сократить дробь и найди соответствующий ответ, задание на сопоставление ответов.
б) Выполнение HYPERLINK «http://school-collection.edu.ru/catalog/rubr/253f44a5-bb2a-4221-ae16-5b990bb69526/112601/?interface=pupil&class=50&subject=17″заданий на сокращение дробей (Практика, пункт 4)
Сократить дробь.
в) Применение основного свойства дроби при уHYPERLINK «http://school-collection.edu.ru/catalog/rubr/253f44a5-bb2a-4221-ae16-5b990bb69526/112601/?interface=pupil&class=50&subject=17″прощение выражений (Практика, пункт 5)
5. Контроль. Обучающая самостоятельная работа
Использование основного свойства дроби для приведения дроби к указанному знаменателю. Обучающая самостоятельная работа (Контроль, пункт 6)
Сокращение дробей, применяя формулы сокращённого умножения. (для более сильных учащихся). Сокращение дробей (Контроль, пункт 7)
6. Итог урока.
Сформулируйте основное свойство дроби?
Приведите примеры алгебраических дробей?

univerfiles.com

Основное свойство дроби. Сокращение дробей

Вы уже знакомы с основным свойством дроби. Давайте вспомним его:

Если числитель и знаменатель дроби умножить или разделить на одно и то же число, отличное от нуля, то значение дроби не изменится.

Иначе говоря, при любых a, b и c верны равенства

Хотелось бы сразу уточнить, что деление числителя и знаменателя на одно и то же число называется сокращением дроби.

Равенство,  справедливо и не только при натуральных, но и при любых значениях переменных a, b и c при которых знаменатель не равен нулю.

Рациональные дроби  тоже можно преобразовывать таким же образом.

Рациональная дробь – это дробь, числитель и знаменатель которой многочлены.

Основное свойство рациональной дроби сводится к тому, что:

Если числитель и знаменатель рациональной дроби умножить на один и тот же ненулевой многочлен, то получится равная ей дробь.

Если числитель и знаменатель рациональной дроби разделить на один и тот же ненулевой многочлен, то получится равная ей дробь.

Например

 

Это равенство верно при всех допустимых значениях переменной. Такие равенства называют тождествами.

Определение:

Тождеством называется равенство, верное при всех допустимых значениях входящих в него переменных.

Два выражения, принимающие равные значения при всех допустимых значениях переменных, называются тождественно равными.

Замену одного такого выражения другим называют тождественным преобразованием выражения.

Равенство

Основное свойство рациональной дроби позволяет сокращать дроби и приводить дробь к новому знаменателю.

Чтобы сократить рациональную дробь, нужно предварительно разложить на множители числитель и знаменатель дроби, а затем разделить их на общие множители.

Задание

Сократить дробь.

Решение:

Задание

Привести дробь к указанному знаменателю.

Решение:

Итоги:

Если числитель и знаменатель рациональной дроби умножить на один и тот же ненулевой многочлен, то получится равная ей дробь.

Если числитель и знаменатель рациональной дроби разделить на один и тот же ненулевой многочлен, то получится равная ей дробь.

Основное свойство рациональной дроби позволяет сокращать дроби и приводить дробь к новому знаменателю.

videouroki.net

Конспект урока по Алгебре «Основное свойство дроби. Сокращение дробей» 8 класс

Глава: «Рациональные дроби».

8 класс.

Тема урока: «Основное свойство дроби. Сокращение дробей».

Цели урока:

Обучающие:

• ввести понятия: основного свойства дроби и «тождества»;

• научить учащихся применять основное свойство дроби при сокращении дробей;

• показать применение основного свойства дроби при сокращении дробей;

• показать использование основного свойства дроби для приведения дроби к указанному знаменателю;

• совершенствовать вычислительные навыки.

Развивающие:

Воспитательные:

• воспитывать творческую активность, культуру общения, интерес к предмету.

Тип урока: изучение нового материала.

Оборудование урока:

• компьютер, проектор, экран;

• компьютерная презентация;

• индивидуальные и практические задания.

Используемые ресурсы

Ход урока.

Повторить основное свойство обыкновенных дробей, правило сокращения дробей: презентация слайд 2 и 3.

3. Изучение нового материала.

• Используя презентацию слайд 4 и 5 ввести понятие алгебраических дробей, допустимых значений слайд 6 и 7.

• Ввести понятия: основного свойства дроби и « тождества», используя коллекцию Введение понятий: основного свойства дроби и «тождества» (Теория, пункты 1,2) или презентацию слайды 8 и 9 (на слайде 9 показано примеры применения свойства к алгебраическим дробям).

4. Закрепление изученного материала.

а) Отработка понятия основного свойства дроби (Практика, пункт 3) или презентация слайд 10 и 11.

б) Выполнение HYPERLINK «http://school-collection.edu.ru/catalog/rubr/253f44a5-bb2a-4221-ae16-5b990bb69526/112601/?interface=pupil&class=50&subject=17»заданий на сокращение дробей (Практика, пункт 4)

в) Применение основного свойства дроби при уHYPERLINK «http://school-collection.edu.ru/catalog/rubr/253f44a5-bb2a-4221-ae16-5b990bb69526/112601/?interface=pupil&class=50&subject=17»прощение выражений (Практика, пункт 5)

5. Контроль. Обучающая самостоятельная работа

• Использование основного свойства дроби для приведения дроби к указанному знаменателю. Обучающая самостоятельная работа (Контроль, пункт 6)

• Сокращение дробей, применяя формулы сокращённого умножения. (для более сильных учащихся). Сокращение дробей (Контроль, пункт 7)

6. Итог урока.

• Сформулируйте основное свойство дроби?

• Приведите примеры алгебраических дробей?

• Что называется тождеством?

• Какие тождественные преобразования можно выполнять, используя основное свойство дроби?

7. Домашнее задание.

doc4web.ru