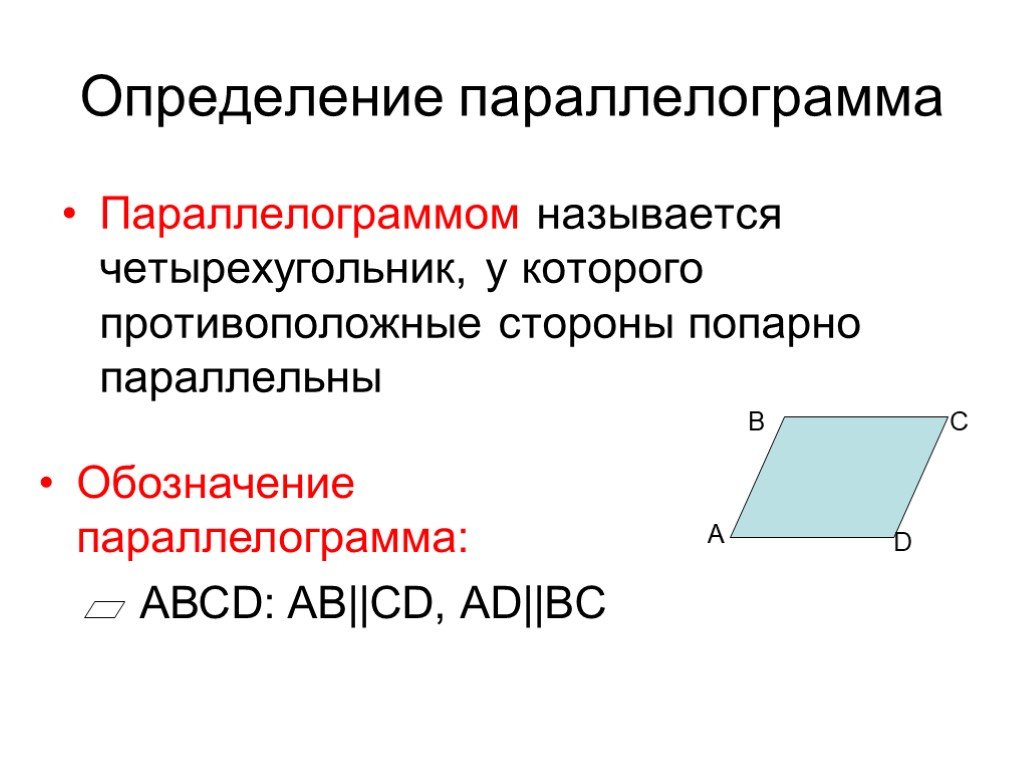
Урок по геометрии параллелограмм 8 класс: Параллелограмм — урок. Геометрия, 8 класс.
Урок геометрии «Четырехугольники. Параллелограмм». 8-й класс
Цели:
- Повторить определение треугольника.
- Сформулировать и выделить виды четырехугольников,
- Сформулировать и выделить виды параллелограмма.
- Сформулировать и доказать свойства параллелограмма.
Задачи развивающие:
- Развитие умения устанавливать закономерности.
- Развивать умения анализировать полученные результаты, делать выводы и ставить новые вопросы;
- Развивать умения составлять алгоритм действий и действовать по алгоритму;
- Развивать умение использовать сформулированные правила при решении задач;
Задачи воспитательные:
- повышение познавательного интереса;
- расширение математического кругозора;
- развитие навыка конструктивного группового взаимодействия (умение выслушать и понять другого, налаживать сотрудничество), независимо от многообразия проявлений их индивидуальности;
- развитие навыка принятия коллективного решения;
- воспитание чувства ответственности, развивать
умения выступать перед аудиторией.

Тип урока: изучение нового материала.
Метод: проблемно-исследовательский.
Форма: комбинированная
Ход урока
1. Вводная беседа.
В 7 классе вы начали изучение школьного предмета геометрии. О свойствах каких геометрических фигур шла речь в прошлом году? (отрезок, прямая, луч, угол, окружность, треугольник).
- Построите в тетради треугольник АВС. Дайте определение треугольника.
- Назовите элементы треугольника (вершины, стороны, углы).
- Какие виды треугольников вы знаете? (по виду углов: прямоугольный, остроугольный, тупоугольный; по количеству равных сторон: равнобедренный, равносторонний, разносторонний)
- Еще раз сформулируйте определение треугольника.
2. Изучение нового материала.
2.1 Определение четырехугольника.
А, если взять не три, а четыре точки на плоскости и попарно соединить отрезками, какая фигура получится?
Выполните построение. У всех ли получился
четырехугольник? Анализируя ответы, добавляем в
определение четырехугольника необходимые
уточнения (1. Никакие три точки из четырех не
должны лежать на одной прямой; 2. Точки соединяем
отрезками последовательно.)
У всех ли получился
четырехугольник? Анализируя ответы, добавляем в
определение четырехугольника необходимые
уточнения (1. Никакие три точки из четырех не
должны лежать на одной прямой; 2. Точки соединяем
отрезками последовательно.)
Вывод: сформулируйте определение четырехугольника.
2.2 Определение выпуклого четырехугольника.
Так же как и треугольники, четырехугольники могут быть разных видов. Попробуем выделить некоторые из них.
Задание № 1. Разделить многоугольники на две группы.
Приложение 1.
По результатам выполнения в беседе формулируем определение выпуклого и невыпуклого четырехугольника.
СЛАЙД № 2, 3.
Вывод:
- Определение выпуклого четырехугольника.
- Определение параллелограмма.
- Определяем виды выпуклых многоугольников.
Задание № 2. Разделить многоугольники на три группы.
Приложение 2.
- По результатам выполнения в беседе формулируем
определение трапеции и параллелограмма.

- Определяем виды параллелограммов: (по равенству сторон, по равенству углов). Формулируем определение прямоугольника, ромба, квадрата.
- Обращаем внимание на то, что каждый раз определения формулируем через близлежащее понятие.
СЛАЙД № 4.
Сформулируйте тему нашей беседы. (“Четырехугольники”).
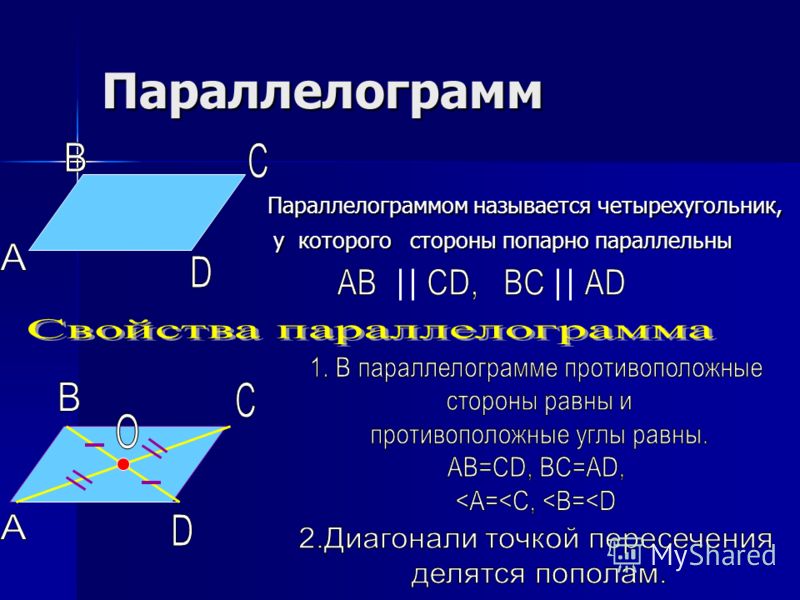
Свойства параллелограмма.
Теперь мы подробнее поговорим о параллелограмме.
СЛАЙДЫ № 5 – 10.
Постройте произвольный параллелограмм АВСD (не ромб, не прямоугольник, не квадрат)
Внимательно рассмотрите его и попробуете найти все его свойства. Проверяем полученные результаты:
СЛАЙДЫ №№ 11 — 12.
Вывод: сформулируйте свойства параллелограмма.
3. Применение изученного материала для решения задач.
3.1 Применение свойств параллелограмма и его определения для решения задач.
Задача 1. Угол ВАD параллелограмма ABCD
равен 50о.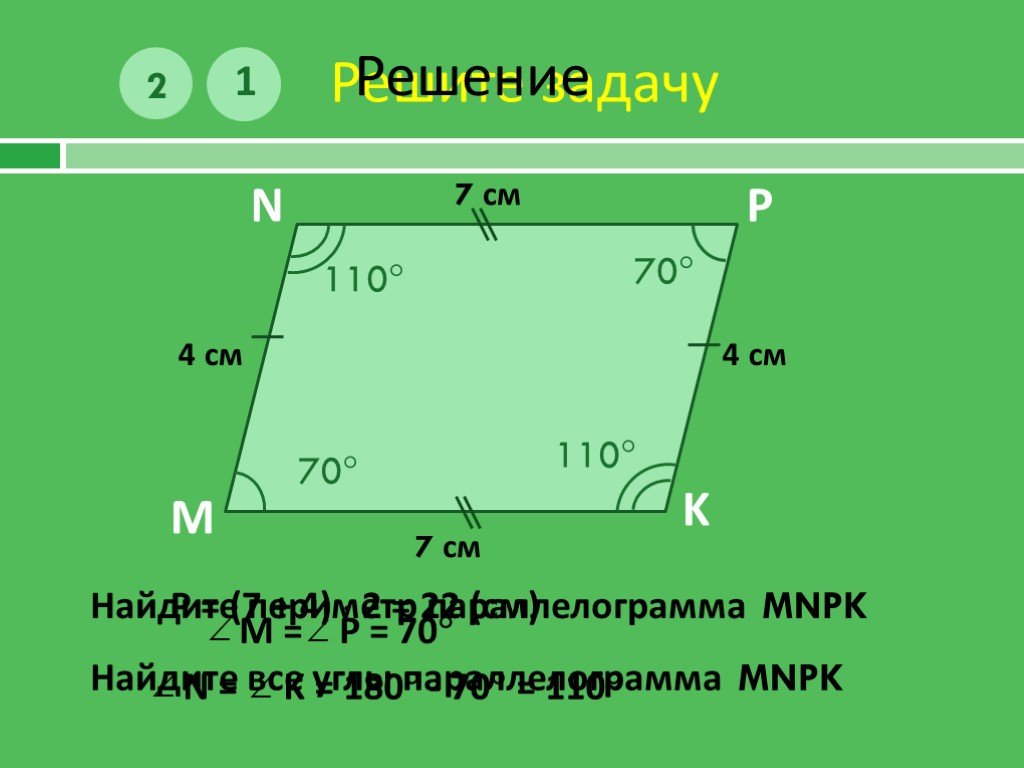 Найдите остальные углы
параллелограмма.
Найдите остальные углы
параллелограмма.
СЛАЙД № 13.
Задача 2. Угол KLM параллелограмма KLMN равен 122о. Найдите остальные углы параллелограмма.
СЛАЙД № 14.
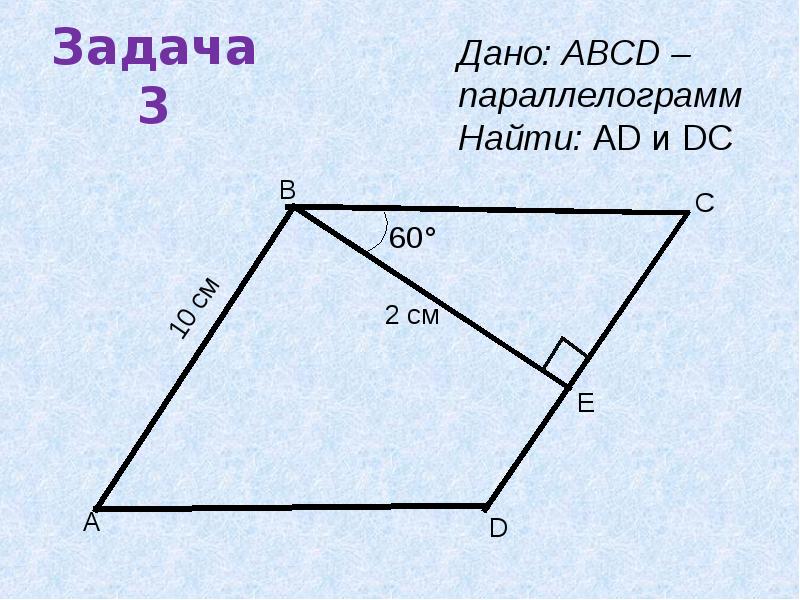
Задача 3. Периметр параллелограмма
равен 90 см и острый угол содержит 60
СЛАЙД № 15.
3.2. Решение задач на развитие интуиции
Необходимо обратить внимание на то, что если утверждение верно, то его необходимо доказать (этим устанавливаем его верность).
Если нет, то необходимо привести один пример, когда утверждение не выполняется.
СЛАЙДЫ № 28-32
Задача 4. А верите ли вы,… что, если, совместить одну пару равных сторон двух равных треугольников, то получится параллелограмм? (неверно)
СЛАЙД № 16.
Задача 5. А верите ли вы,… что если
отрезки АС и BD пересекутся в своей середине т. О,
то четырехугольник ABCD окажется
параллелограммом. (верно, приводим
доказательство)
О,
то четырехугольник ABCD окажется
параллелограммом. (верно, приводим
доказательство)
СЛАЙДЫ № 17 – 19.
Задача 6. А верите ли вы,… что если соединить последовательно отрезками концы двух хорд окружности, то получится параллелограмм? (неверно)
СЛАЙД 20.
Задача 7. А верите ли вы,… что, если, соединить отрезками середины сторон выпуклого четырехугольника, то получится параллелограмм? (верно, доказательство приведем позже)
СЛАЙД № 21.
Задача 8. А верите ли вы,… что, если, в треугольнике MDN соединить отрезками середины его сторон точки A,B,C – середины сторон МD, MN и ND соответственно, то полученный четырехугольник ABCD — параллелограмм? (верно, доказательство приведем позже)
СЛАЙД № 22.
Задача 9. А верите ли вы,…что, если, последовательно соединить отрезками центры двух пересекающихся окружностей и точки их пересечения, то получится параллелограмм? (неверно)
СЛАЙД № 23.
4. Подведение итогов.
- Повторили определение и виды треугольников.
- Сформулировали определения четырехугольника и его видов.
- Сформулировали определения параллелограмма и его видов.
- Сформулировали и доказали свойства параллелограмма.
- Применили свойства параллелограмма к решению задач.
5. Домашнее задание:
Уметь формулировать определения четырехугольника, выпуклого четырехугольника, невыпуклого четырехугольника, трапеции, параллелограмма, ромба, прямоугольника, квадрата. Знать элементы этих фигур.
Знать свойства параллелограмма. Уметь доказывать свойства 1-7 (приложение 3).
Литература.
- Геометрия. 7- 9 классы: учебник для общеобразовательных организаций/ Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др., М.: Просвещение, 2012/
- Геометрия. 7- 9 классы: учебник для
общеобразовательных организаций/ А.В.
 Погорелов,
М.: Просвещение, 2014/
Погорелов,
М.: Просвещение, 2014/
ФИО (полностью) | Гашокина Эмма Темиржановна | ||||
Место работы | МКОУ «СОШ №5», г.Нальчик | ||||
Должность | Учитель математики | ||||
Предмет | геометрия | ||||
Класс | 8 | ||||
Тема и номер урока в теме | Параллелограмм. | ||||
Базовый учебник | Геометрия: Учеб. для 7–9 кл. сред. шк./ Л.С. Атанасян, В. Ф. Бутузов и др. – 3–е изд. – М.: Просвещение, 2006. – 335 с. | Этап урока | Название используемых ЭОР (с указанием порядкового номера из Таблицы 2) | Деятельность учителя (с указанием действий с ЭОР, например, демонстрация) | Деятельность ученика | Время (в мин. |
1 | 2 | 3 | 5 | 6 | 7 |
1 | Организационный момент | Сообщить тему урока, сформулировать цели урока. – На сегодняшнем уроке мы познакомимся с геометрической фигурой — параллелограмм». Вы научитесь применять свойства параллелограмма при решении задач. | Приветствуют учителя Записывают дату и тему урока | 1 | |
2 | Проверка домашнего задания | Проверить решение домашней задачи №370. | Учащиеся сверяют свои ответы и решение с доской. | 3 | |
3 | Актуализация опорных знаний | На данном этапе урока учитель ставит проблему, тем самым показывает практическую значимость данной проблемы, мотивируя учащихся к ее изучению. Чему равна сумма внутренних углов выпуклого п -угольника. | Учащиеся отвечают -Сумма внутренних углов выпуклого n- угольника равна 1800*(n-2). | 4 | |
4 | Ознакомление с новым материалом | 1 2 | Ввести понятие параллелограмма и записать на доске. АВСD- параллелограмм. АВCD, BCAD. Отработка определения параллелограмма в процессе решения устных задач по заготовленным чертежам. Обсуждение свойств параллелограмма в тетрадях и на доске:
| Учащиеся записывают в тетрадях понятие, рисунок. A B D C Учащиеся записывают в тетрадях свойства параллелограмма: 1. 2. DO=OB, AO=OC 3.0, | 15 |
5. | Физминутка. | Читает учитель: Что такое физкультура? Тренировка и игра. Что такое физкультура? Физ и куль и ту и ра! Руки вверх, руки вниз – это физ. Крутим шею, словно руль – это куль. Ловко прыгай в высоту – это ту. Бегай пол часа с утра – это Ра. Занимаясь этим делом, Станешь сильным, ловким, смелым. Плюс – хорошая фигура. Вот что значит физкультура! На четыре — руки шире, Пять – руками помахать. Шесть – за парту тихо сесть. | Класс повторяет за учителем. | 2 | |
5 | Закрепление нового материала | 3 | – Далее будем решать задачи на применение свойств параллелограмма. http://fcior.edu.ru/card/11821/parallelogramm-ego-vidy-priznaki-svoystva-p1.html По окончанию учитель проверяет выполнение работ. После чего делает разбор заданий, которые вызвали затруднения. | Двое уч-ся выходят к доске, остальные работают в тетрадях. Более подготовленные уч-ся решают задачи на опережение и показывают учителю. | 10 |
6 | Подведение итогов урока | Оценить выборочно работу учащихся в течение урока.
| 3 | ||
6 | Домашнее задание | 3 | Учитель комментирует задание, записанное на доске – Выучить формулировку определения параллелограмма, свойства параллелограмма. П. 42, вопросы 6-8, №371а), 372в), 376в,г). | Записывают домашнее задание в дневник | 2 | Название ресурса | Тип, вид ресурса | Форма предъявления информации (иллюстрация, презентация, видеофрагменты, тест, модель и т.д.) | Гиперссылка на ресурс, обеспечивающий доступ к ЭОР |
1 | Определение параллелограмма. | Динамический И | Видеофрагменты с аудио рядом(1) | http://files.school-collection.edu.ru/dlrstore/7ae1d34d-0a01-01b2-01e3-a0ec7f75a9ab/%5BG79_05-02-042%5D_%5BML_003%5D.swf | |
2 | Динамический И | Видеофрагменты с аудио рядом(2,3,4) | http://files. | ||
3 | Статический П | http://fcior.edu.ru/card/11821/parallelogramm-ego-vidy-priznaki-svoystva-p1.html |
Свойства четырехугольников — прямоугольника, квадрата, параллелограмма, ромба, трапеции
7 минут чтения
В евклидовой геометрии четырехугольник — это четырехсторонняя двумерная фигура, сумма внутренних углов которой равна 360°. Слово «четырехугольник» происходит от двух латинских слов «quadri» и «latus», что означает «четыре» и «сторона» соответственно. Поэтому определение свойств четырехугольников важно при попытке отличить их от других многоугольников. Итак, каковы свойства четырехугольников? Четырехугольники обладают двумя свойствами:
- Четырехугольник должен быть замкнутой формы с 4 сторонами
- Сумма всех внутренних углов четырехугольника до 360°
В этой статье вы получите представление о 5 типах четырехугольников (Прямоугольник, Квадрат, Параллелограмм , ромб и трапеция) и узнать о свойствах четырехугольников.
Вот пять типов четырехугольников, обсуждаемых в этой статье:
- Прямоугольник
- Квадрат
- Параллелограмм
- Rhombus
- Trapezium
Вот видео, объясняющее свойства четырехугольника:
Это то, что вы прочитаете в статье:
[Hide]
. На приведенной ниже схеме изображен четырехугольник ABCD и сумма его внутренних углов. Сумма всех внутренних углов равна 360°. Таким образом, ∠A + ∠B + ∠C + ∠D = 360°
| Свойства четырехугольников | Rectangle | Square | Parallelogram | Rhombus | Trapezium | |||||||
| All Sides are equal | No | Yes | No | Yes | No | |||||||
| Противоположные стороны равны | Да | Да | Да | Да | Нет | |||||||
| Противоположные стороны параллельны | Yes | Yes | Yes | Yes | Yes | |||||||
| All angles are equal | Yes | Yes | No | No | No | |||||||
| Opposite angles are equal | Yes | Да | Да | Да | № | |||||||
| Сумма двух соседних углов — 180 | Да | Да | Да | Да | Но. | Да | Да | Но. | Да | Да | Но | Да0067 |
| Bisect each other | Yes | Yes | Yes | Yes | No | |||||||
| Bisect perpendicularly | No | Yes | No | Yes | No |
Let’s discuss each из этих 5 четырехугольников в деталях:
Вот вопросы, которые научат вас, как применять свойства всех 5 четырехугольников, которые вы узнаете в этой статье.
Прямоугольник
Прямоугольник – это четырехугольник с четырьмя прямыми углами. Таким образом, все углы прямоугольника равны (360°/4 = 90°). Более того, противоположные стороны прямоугольника параллельны и равны, а диагонали делят друг друга пополам.
Вот три свойства прямоугольника:
- Все углы прямоугольника равны 90°
- Противоположные стороны прямоугольника равны и параллельны
- Диагонали прямоугольника делят друг друга пополам
Формула прямоугольника – площадь и периметр прямоугольника
Если длина прямоугольника равна L, а ширина равна B, то
- Площадь прямоугольника = длина × ширина или L × B
- Периметр прямоугольника = 2 × (L + B)
Эти правила вопросы помогут вам укрепить свойства прямоугольников
Планируете ли вы поступать в лучшие бизнес-школы? Позвольте нам помочь вам пройти первый этап процесса, то есть сдать GMAT.
Возьмите бесплатную пробную версию GMAT, чтобы узнать свой базовый балл, и начните подготовку к GMAT с нашей бесплатной пробной версии. Мы являемся самой популярной онлайн-компанией по подготовке к GMAT с более чем 2200 отзывами на GMATClub по состоянию на 4 октября 2021 года.
Знаете ли вы, что участники e-GMAT набрали больше 700 баллов, чем когда-либо прежде в истории GMAT Club? Посмотрите это видео, чтобы понять, как e-GMAT достиг этого рекордного результата, инвестируя и внедряя инновации с единственной целью — создать платформу, которая позволяет учащимся достигать и показывать свои лучшие результаты.
Квадрат
Квадрат – это четырехугольник с четырьмя равными сторонами и углами. Это также правильный четырехугольник, поскольку обе его стороны и углы равны. Как и у прямоугольника, у квадрата четыре угла по 90° каждый. Его также можно рассматривать как прямоугольник, две соседние стороны которого равны.
Как и у прямоугольника, у квадрата четыре угла по 90° каждый. Его также можно рассматривать как прямоугольник, две соседние стороны которого равны.
Вот три свойства квадрата:
- Все углы квадрата равны 90°
- Все стороны квадрата равны и параллельны друг другу
- Диагонали делят друг друга перпендикулярно
Формула квадрата – площадь и периметр квадрата
Если сторона квадрата равна а, то
- Площадь квадрата = а × а = а²
- Периметр квадрата = 2 × (а + а) = 4а
Эти практические вопросы помогут вам закрепить свойства квадратов. Начните свой путь к получению Q50-51 на GMAT с помощью онлайн-курса подготовки e-GMAT на основе искусственного интеллекта. Наш xPERT не только выбирает наиболее оптимизированный путь обучения, но и отслеживает ваши улучшения, гарантируя, что вы быстро и надежно достигнете целевого показателя Quant. Посмотрите это видео, чтобы узнать больше:
youtube.com/embed/Hx5TgTucO8U?rel=0″ title=»YouTube video player» frameborder=»0″ allow=»accelerometer rel=0; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>Параллелограмм
Параллелограмм, как следует из названия, представляет собой простой четырехугольник, противоположные стороны которого параллельны. Таким образом, он имеет две пары параллельных сторон. Кроме того, в параллелограмме противоположные углы равны, а их диагонали делят друг друга пополам.
Вот четыре свойства параллелограмма:
- Противоположные углы равны
- Противоположные стороны равны и параллельны
- Диагонали делят друг друга пополам
- Сумма любых двух смежных углов равна 180°
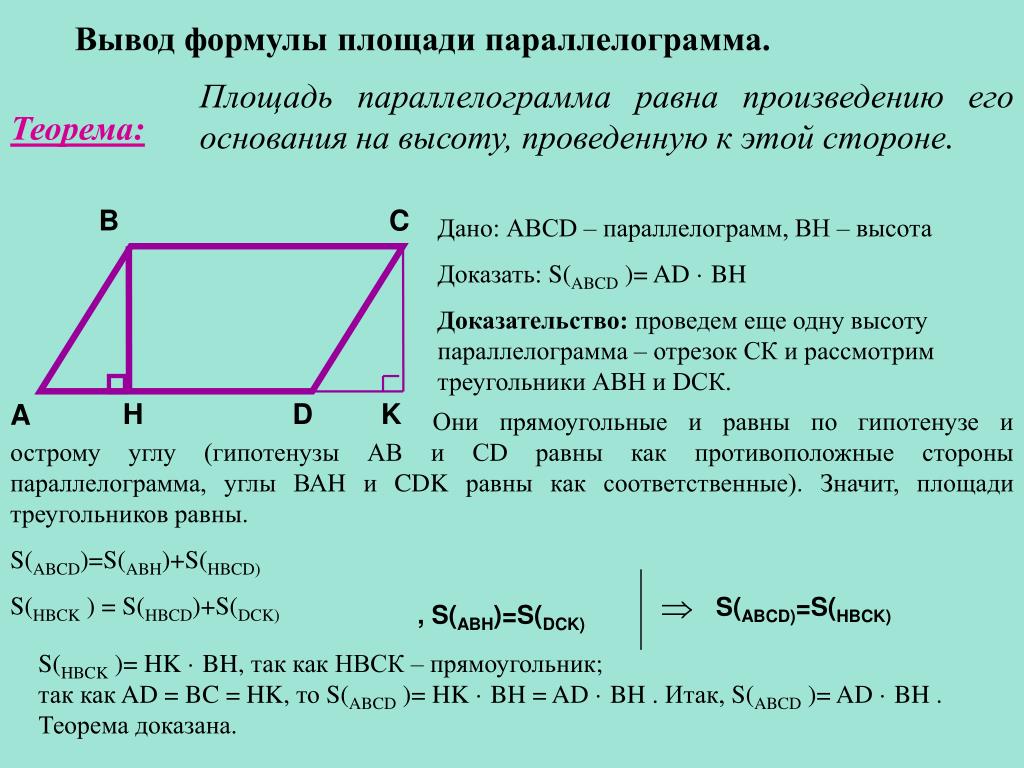
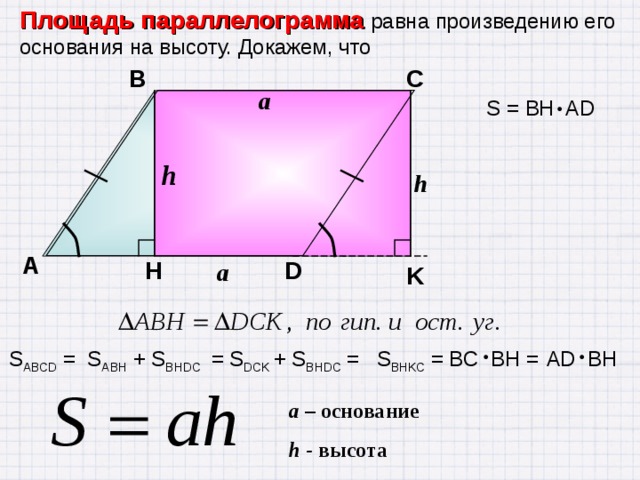
Формулы параллелограмма – площадь и периметр параллелограмма
Если длина параллелограмма равна «l», ширина равна «b», а высота равна «h», то:
- Периметр параллелограмма = 2 × (l + б)
- Площадь параллелограмма = l × h
Эти практические вопросы помогут вам закрепить свойства параллелограмма параллельно друг другу.
Однако углы не равны 9.0°. Ромб с прямыми углами станет квадратом. Другое название ромба — «ромб», так как он похож на ромбовидную масть в игральных картах.
Вот четыре свойства ромба:
- Противоположные углы равны
- Все стороны равны и противоположные стороны параллельны друг другу
- Диагонали делят друг друга перпендикулярно
- Сумма любых двух смежных углов равна 180 °
Формулы ромба – площадь и периметр ромба
Если сторона ромба равна а, то периметр ромба = 4а
Если длина двух диагоналей ромба равна d 1 и d 2 , то площадь ромба = ½ × d 1 × d 2
Эти практические вопросы помогут вам закрепить свойства ромба
Трапеция
Трапеция (называемая в США трапецией) — это четырехугольник, у которого только одна пара параллельных сторон. Параллельные стороны называются «основаниями», а две другие стороны называются «ногами» или боковыми сторонами.
Трапецией называется четырехугольник, у которого выполняется одно свойство:
- Только одна пара противоположных сторон параллельна друг другу
Формулы трапеции – площадь и периметр трапеции
Если высота трапеции равна ‘ h’ (как показано на диаграмме выше), тогда:
- Периметр трапеции = сумма длин всех сторон = AB + BC + CD + DA
- Площадь трапеции = ½ × (сумма длин параллельных сторон) × h = ½ × (AB + CD) × h
Эти практические вопросы помогут вам закрепить свойства трапеции. и периметр различных типов четырехугольников:
Формулы четырехугольника Прямоугольник Square Parallelogram Rhombus Trapezium Area l × b a² l × h ½ × d1 × d2 ½ × (сумма параллельных сторон) × высота Периметр 2 × (L + B) 4A 2 × (L + B) 4A SOM SOM SIPE0067 Дополнительная литература:
- Формулы окружности – площадь и периметр
- Свойства чисел – четные и нечетные | Прайм | HCF & LCM
- Свойства треугольников – Определение | Типы | Классификация
- Линии и углы.
Свойства и их применение
Чтобы успешно сдать GMAT, требуется четко определенный учебный план. Сэкономьте 60+ часов на подготовке к GMAT, выполнив следующие три шага:
Четырехсторонний практический вопрос
Давайте попрактикуемся в применении свойств четырехугольников, ответив на следующие примеры вопросов:
GMAT: Практический вопрос четырехугольников 1
Адам хочет построить забор вокруг своего прямоугольного сада длиной 10 метров и шириной 15 метров. Сколько метров забора он должен купить, чтобы огородить весь сад?
- 20 метров
- 25 метров
- 30 метров
- 40 метров
- 50 метров
Решение
Шаг 1: Дано
- У Адама прямоугольный сад.
- Имеет длину 10 метров и ширину 15 метров.
- Он хочет построить вокруг него забор.
Шаг 2: Найти
- Длина, необходимая для возведения забора вокруг всего сада.
Этап 3: Подход и разработка
Забор можно построить только вокруг внешних сторон сада.
- Итак, общая длина необходимого забора = сумма длин всех сторон сада.
- Поскольку сад прямоугольный, сумма длин всех сторон есть не что иное, как периметр сада.
- Периметр = 2 × (10 + 15) = 50 метров
Отсюда необходимая длина забора 50 метров.
Таким образом, вариант Е является правильным ответом.
GMAT Quadrilaterials Practice Question 2
Стив хочет покрасить одну прямоугольную стену своей комнаты. Стоимость покраски стен составляет 1,5 доллара за квадратный метр. Если длина стены 25 метров, а ширина 18 метров, то какова общая стоимость покраски стены?
- $ 300
- $ 350
- $ 450
- $ 600
- $ 675
Решение
Шаг 1: дано
- Стев хочет покрасить одну стену в его комнате.
- Длина стены 25 метров, ширина 18 метров.
- Стоимость покраски стены $1,5 за квадратный метр.
Шаг 2: Найти
- Общая стоимость покраски стены.
Этап 3: Подход и разработка
- Стена окрашена по всей площади.
- Итак, если мы найдем общую площадь стены в квадратных метрах и умножим ее на стоимость покраски 1 квадратного метра стены, то мы получим общую стоимость.
- Площадь стены = длина × ширина = 25 метров × 18 метров = 450 квадратных метров
- Общая стоимость покраски стены = 450 × 1,5 долл. США = 675 долл. США
Следовательно, правильный ответ — вариант E.
Мы надеемся, что к настоящему моменту вы узнали о различных типах четырехугольников, их свойствах и формулах, а также о том, как применять эти понятия для решения вопросов о четырехугольниках. Применение четырехугольников важно для решения вопросов по геометрии на GMAT.
Если вы планируете сдавать GMAT, мы можем помочь вам с высококачественными учебными материалами, к которым вы можете получить бесплатный доступ, зарегистрировавшись здесь.
Вот еще несколько статей по математике:
- Повышение точности математических вопросов о полигонах
- Вопросы по геометрии – самые распространенные ошибки | GMAT Quant Prep
Посмотрите этот вебинар без геометрии GMAT, на котором мы обсуждаем, как решать 700-уровневые вопросы достаточности данных и проблемные вопросы в четырехугольниках GMAT:
вы получаете доступ к качественному онлайн-контенту для подготовки. Мы являемся самой популярной компанией по подготовке к GMAT на gmatclub с более чем 2200 отзывами по состоянию на 4 октября 2021 года.

Пишите нам по адресу [email protected] в случае возникновения вопросов.
Часто задаваемые вопросы
Какие существуют типы четырехугольников?
Существует 5 типов четырехугольников – прямоугольник, квадрат, параллелограмм, трапеция или трапеция и ромб.
Где я могу найти несколько практических вопросов по четырехугольникам?
В этой статье вы можете найти несколько практических вопросов по четырехугольникам.
Чему равна сумма внутренних углов четырехугольника?
Сумма внутренних углов четырехугольника равна 360°.
Свойства параллелограмма — теоремы, доказательства, примеры
Свойства параллелограмма помогают нам легко и быстро идентифицировать параллелограмм из заданного набора фигур.
Прежде чем мы узнаем о свойствах, давайте сначала узнаем о параллелограммах. Это четырехсторонняя замкнутая фигура с равными и параллельными противоположными сторонами и равными противоположными углами. Давайте узнаем больше о свойствах параллелограмма подробно в этой статье.
1. Каковы свойства параллелограмма? 2. Свойства диагоналей параллелограмма 3. Теоремы о свойствах параллелограмма 4. Часто задаваемые вопросы о свойствах параллелограмма Каковы свойства параллелограмма?
Параллелограмм — это тип четырехугольника, в котором противоположные стороны параллельны и равны. В параллелограмме при вершинах четыре угла. Понимание свойств параллелограмма помогает легко связать его углы и стороны. Кроме того, свойства полезны для вычислений в задачах, касающихся сторон и углов параллелограмма.
Четыре важных свойства углов и сторон параллелограмма таковы:
- Противоположные стороны параллелограмма равны и параллельны друг другу.
- Противолежащие углы равны, т. е. ∠A = ∠C и ∠B = ∠D.
- Все углы параллелограмма в сумме дают 360°, то есть ∠A + ∠B + ∠C + ∠D = 360°.
- Последовательные углы параллелограмма являются дополнительными, т.е.
∠А + ∠В = 180°
∠В + ∠С = 180°
∠С + ∠D = 180°
∠D + ∠А = 180°Все вышеперечисленные свойства справедливы для всех типов параллелограммов, но теперь давайте также узнаем об индивидуальных свойствах некоторых специальных параллелограммов. Три разных параллелограмма — квадрат, прямоугольник и ромб, которые отличаются друг от друга из-за своих свойств, но все они подпадают под категорию параллелограммов.
Свойства квадрата:
- Все четыре стороны квадрата равны.
- Все четыре угла равны и по 90 градусов каждый.
- Диагонали квадрата делят его углы пополам.
- Обе диагонали имеют одинаковую длину.
- Противоположные стороны равны и параллельны друг другу.
Свойства прямоугольника:
- Противоположные стороны прямоугольника равны и параллельны.
- Все четыре угла равны и равны 90 градусов каждый.
- Обе диагонали имеют одинаковую длину.
Свойства ромба:
- Все стороны равны по длине.
- Диагонали делят друг друга пополам под углом 90 градусов.
- Сумма любых двух смежных внутренних углов равна 180 градусов.
- Противоположные стороны равны и параллельны друг другу.
Теперь давайте расширим наши знания, изучив свойства диагоналей параллелограммов в следующем разделе.
Свойства диагоналей параллелограмма
Сначала вспомним значение диагонали. Диагонали – это отрезки, соединяющие противоположные вершины.
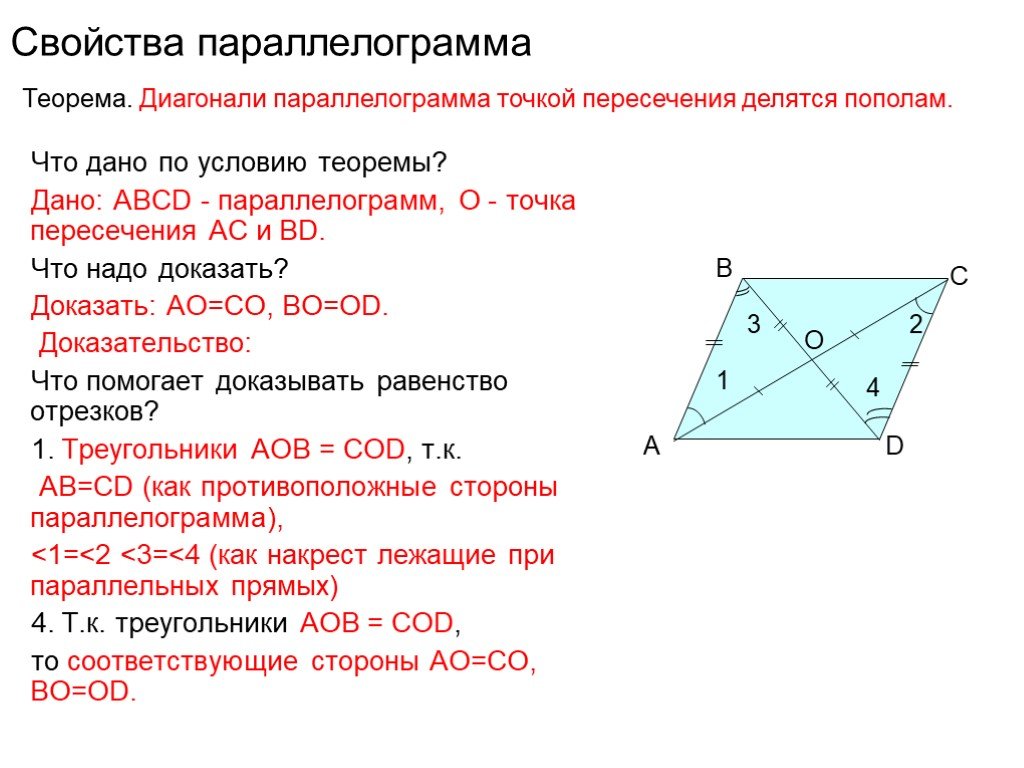
В параллелограмме ABCD (см. рисунок выше) диагонали AC и BD. Предположим, что O — точка пересечения диагоналей AC и BD. Свойства диагоналей параллелограмма следующие:
- Диагонали параллелограмма делят друг друга пополам, т. е. OB = OD и OA = OC.
- Каждая диагональ делит параллелограмм на два конгруэнтных треугольника, т. е. ΔCDA ≅ ΔABC и ΔBAD ≅ ΔDCB.
- Закон параллелограмма: Сумма квадратов сторон равна сумме квадратов диагоналей, т. е. AB 2 + BC 2 + CD 2 + DA 2 = AC 2 + БД 2 .
Теоремы о свойствах параллелограмма
Теоремы о свойствах параллелограмма помогают определить правила решения задач на параллелограммы. Свойства, относящиеся к сторонам и углам параллелограмма, легко понять и применить для решения различных задач. Кроме того, эти теоремы также поддерживают понимание концепций других четырехугольников. Ниже приведены четыре важные теоремы, относящиеся к свойствам параллелограмма:
- Противоположные стороны параллелограмма равны
- Противоположные углы параллелограмма равны
- Диагонали параллелограмма делят друг друга пополам
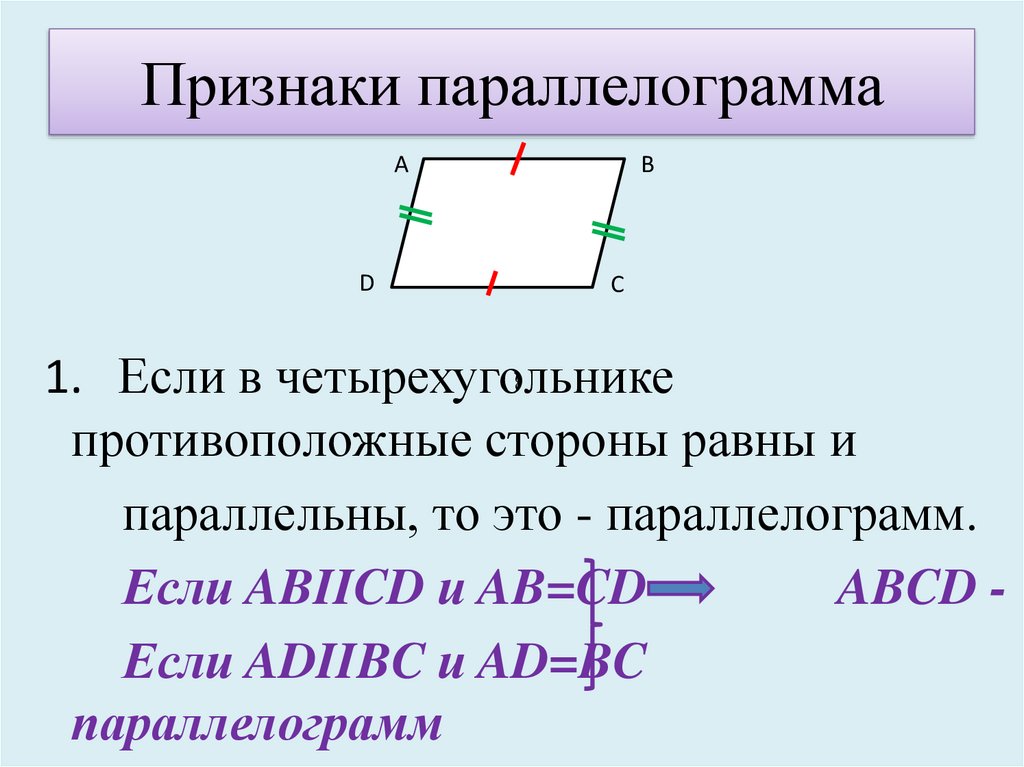
- Если в четырехугольнике одна пара противоположных сторон равна и параллельна, то это параллелограмм
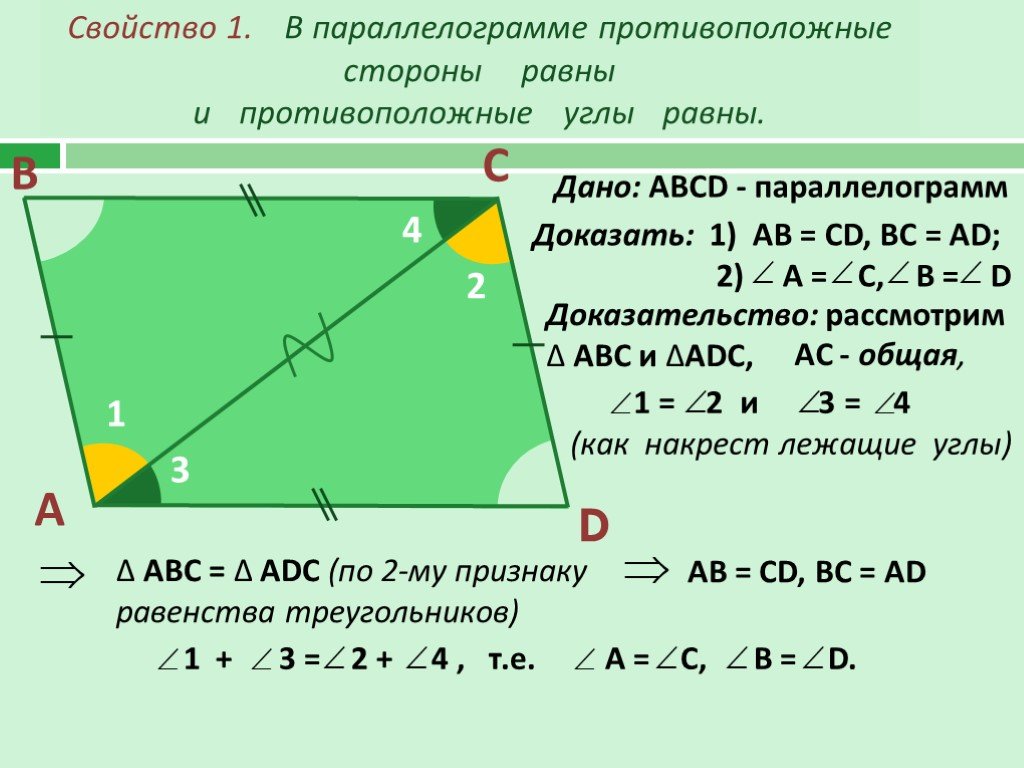
Теорема 1: В параллелограмме противоположные стороны равны.

Доказательство:
Дано: ABCD — параллелограмм.
Доказать: Противоположные стороны равны, AB = CD и BC = AD.
В параллелограмме ABCD сравните треугольники ABC и CDA. В этих треугольниках:
- AC = CA (общая сторона)
- ∠BAC = ∠DCA (альтернативные внутренние углы)
- ∠BCA = ∠DAC (альтернативные внутренние углы)
Следовательно, по критерию ASA оба треугольника конгруэнтны и соответствующие стороны равны. Следовательно, мы имеем AB = CD и BC = AD.
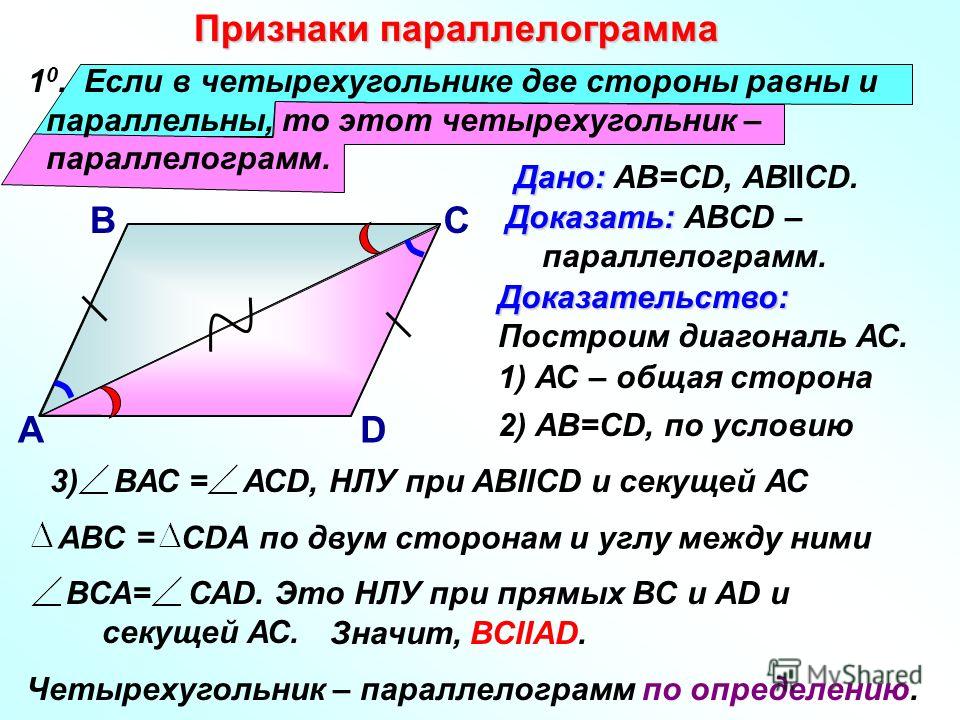
Обратное к теореме 1: если в четырехугольнике противоположные стороны равны, то это параллелограмм.
Доказательство:
Дано: В четырехугольнике ABCD противоположные стороны равны, AB = CD и BC = AD.
Доказать: ABCD — параллелограмм.
В четырехугольнике ABCD дано, что AB = CD и AD = BC.
Теперь сравните два треугольника ABC и CDA. Здесь мы имеем
- AC = AC (общие стороны)
- AB = CD (поскольку внутренние углы равны)
- г. н.э. = до н.э. (дано).
Таким образом, по критерию SSS оба треугольника равны и соответствующие углы равны. Отсюда можно сделать вывод, что ∠BAC = ∠DCA, а ∠BCA = ∠DAC.
Поэтому AB || CD, Британская Колумбия || AD, ABCD — параллелограмм.
Теорема 2. В параллелограмме противоположные углы равны.
Доказательство:
Дано: ABCD — параллелограмм, а ∠A, ∠B, ∠C, ∠D — четыре угла.
Доказать: ∠A = ∠C и ∠B = ∠D
Предположим, что ABCD — параллелограмм. Теперь сравните треугольники ABC и CDA. Здесь у нас есть,
- AC = CA (общая сторона)
- ∠1 = ∠4 (чередующиеся внутренние углы)
- ∠2 = ∠3 (чередующиеся внутренние углы)
Таким образом, согласно ASA, два треугольника конгруэнтны, а это означает, что ∠B = ∠D.
Точно так же мы можем показать, что ∠A = ∠C. Это доказывает, что противоположные углы в любом параллелограмме равны.
Обратное к теореме 2: Если в четырехугольнике противоположные углы равны, то это параллелограмм.
Доказательство:
Дано: ∠A = ∠C и ∠B = ∠D в четырехугольнике ABCD.
Доказать: ABCD — параллелограмм.
Предположим, что ∠A = ∠C и ∠B = ∠D в приведенном выше параллелограмме ABCD. Нам нужно доказать, что ABCD — параллелограмм. Имеем:
∠A + ∠B + ∠C + ∠D = 360º
2(∠A + ∠B) =360º
∠А + ∠В = 180º.
Это должно означать, что AD || ДО Н.Э. Аналогично можно показать, что AB || CD. Следовательно, АД || до н.э. и АВ || CD. Следовательно, ABCD — параллелограмм.
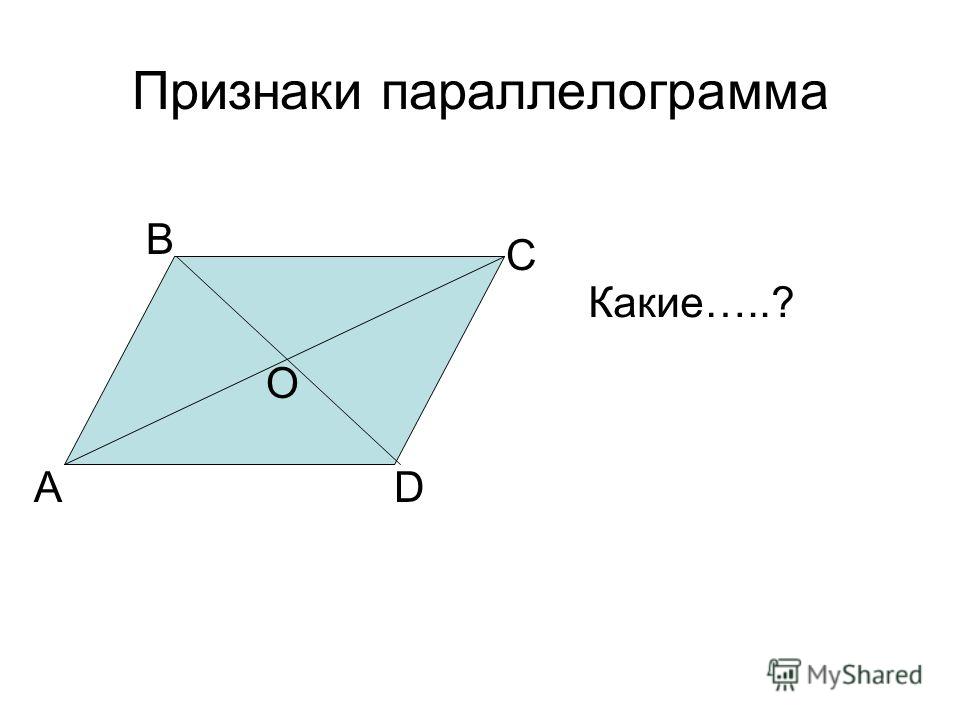
Теорема 3. Диагонали параллелограмма делят друг друга пополам.
Доказательство:
Дано: PQTR — параллелограмм.
PT и QR — диагонали параллелограмма.
Доказать: Диагонали PT и RQ делят друг друга пополам, т. е. PE = ET и ER = EQ.
Сначала предположим, что PQTR — параллелограмм. Сравните треугольники TER и треугольник PEQ. Имеем,
- PQ = RT (противоположные стороны параллелограмма PQTR)
- ∠QRT = ∠PQR (альтернативные внутренние углы)
- ∠PTR = ∠QPT (альтернативные внутренние углы).
По критерию ASA два треугольника конгруэнтны, что означает по CPCTC, PE = ET и RE = EQ. Таким образом, две диагонали PT и RQ делят друг друга пополам, а PE = ET и ER = EQ.
Обратное к теореме 3: Если диагонали в четырехугольнике делят друг друга пополам, то это параллелограмм. В четырехугольнике PQTR, если PE=ET и ER=EQ, то это параллелограмм.
Дано: Диагонали PT и QR делят друг друга пополам.
Доказать: PQRT — параллелограмм.
Доказательство: Предположим, что диагонали PT и QR делят друг друга пополам.
Еще раз сравните треугольник RET и треугольник PEQ. У нас есть:
- RE = Эквалайзер
- ET = PE (диагонали делят друг друга пополам)
- ∠RET =∠PEQ (вертикально противоположные углы).
Следовательно, по критерию SAS два треугольника конгруэнтны. Это означает, что ∠QRT = ∠PQR и ∠PRT = ∠QPT. Следовательно, PQ || РТ и РТ || КТ. Таким образом, PQRT является параллелограммом.
Теорема 4: Если одна пара противоположных сторон равна и параллельна в четырехугольнике, то это параллелограмм.
Доказательство:
Дано: Дано, что AB = CD и AB || CD.
Доказать: ABCD — параллелограмм.
Сравним треугольник AEB и треугольник CED. Имеем,
- AB = CD (дано)
- ∠1 = ∠3 (чередующиеся внутренние углы)
- ∠2 = ∠4 (чередующиеся внутренние углы)
Таким образом, по критерию ASA два треугольника конгруэнтны.
Отсюда можно сделать вывод, что по CPCTC AE = EC, а BE = ED. Следовательно, диагонали AC и BD делят друг друга пополам, а это в дальнейшем означает, что ABCD — параллелограмм.
Важные примечания:
Четырехугольник является параллелограммом, если:
- противоположные стороны четырехугольника равны и параллельны.
- противоположные углы четырехугольника равны.
- диагонали делят друг друга пополам.
- одна пара противоположных сторон равна и параллельна.
Вы знаете?
- Почему воздушный змей не является параллелограммом?
- Является ли равнобедренная трапеция параллелограммом?
Также проверьте:
- Формула параллелограмма
- Площадь параллелограмма
- Свойства прямоугольника
- Разница между прямоугольником и параллелограммом
Часто задаваемые вопросы о свойствах параллелограмма
Каковы 7 свойств параллелограмма?
Семь свойств параллелограмма таковы:
- Противоположные стороны равны.
- Противоположные углы параллелограмма равны.
- Последовательные углы являются дополнительными.
- Если один угол параллелограмма прямой, то все углы прямые.
- Диагонали параллелограмма делят друг друга пополам.
- Каждая диагональ параллелограмма делит его пополам на два равных треугольника.
- Если одна пара противоположных сторон четырехугольника равна и параллельна, то четырехугольник является параллелограммом.
Каковы свойства параллелограмма относительно диагоналей?
Диагонали параллелограмма обладают двумя важными свойствами. Диагональ параллелограмма делит параллелограмм на два равных треугольника. А диагонали параллелограмма делят друг друга пополам.
Диагонали параллелограмма равны?
Диагонали параллелограмма НЕ равны. Противоположные стороны и противоположные углы параллелограмма равны. Диагонали квадрата и прямоугольника равны, что является особым видом параллелограмма.
Каковы четыре важных свойства параллелограмма?
Параллелограмм – это четырехугольник, у которого противоположные стороны равны и параллельны.
Противоположные углы параллелограмма также равны. Короче говоря, параллелограмм можно рассматривать как скрученный прямоугольник. Это скорее прямоугольник, но углы при вершинах не обязательно должны быть прямыми. Четыре важных свойства параллелограмма таковы:
- Противоположные стороны равны
- Противоположные углы равны
- Смежные углы дополнительные
- Диагонали параллелограмма делят друг друга пополам
Можно ли прямоугольник назвать параллелограммом?
Противоположные стороны прямоугольника равны и параллельны. Таким образом, прямоугольник удовлетворяет всем свойствам параллелограмма, поэтому его можно назвать параллелограммом.
Каковы уникальные свойства параллелограммов?
Уникальные свойства параллелограмма, отличающие его от других четырехугольников, приведены ниже:
- Противоположные стороны каждого параллелограмма равны и параллельны.
- Противоположные углы всегда равны.
- Сумма смежных углов всегда равна 180°.




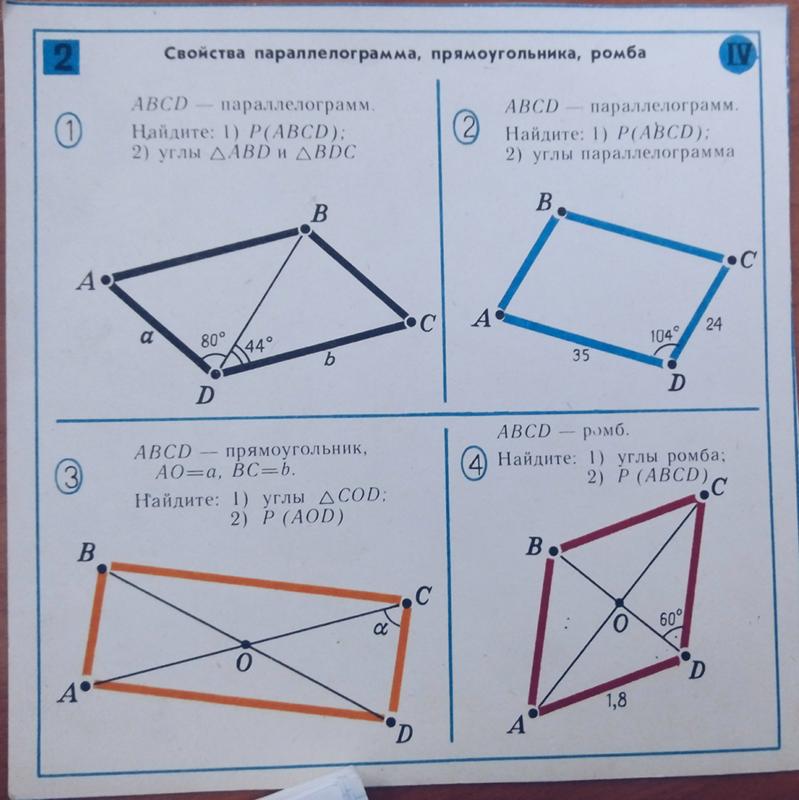 Погорелов,
М.: Просвещение, 2014/
Погорелов,
М.: Просвещение, 2014/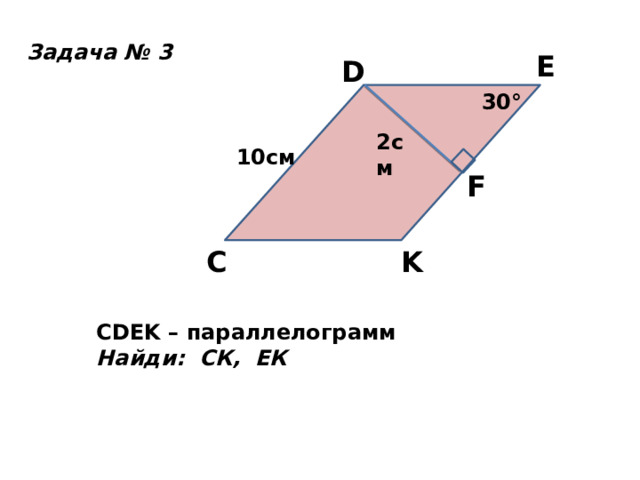 Свойства параллелограмма.
Свойства параллелограмма.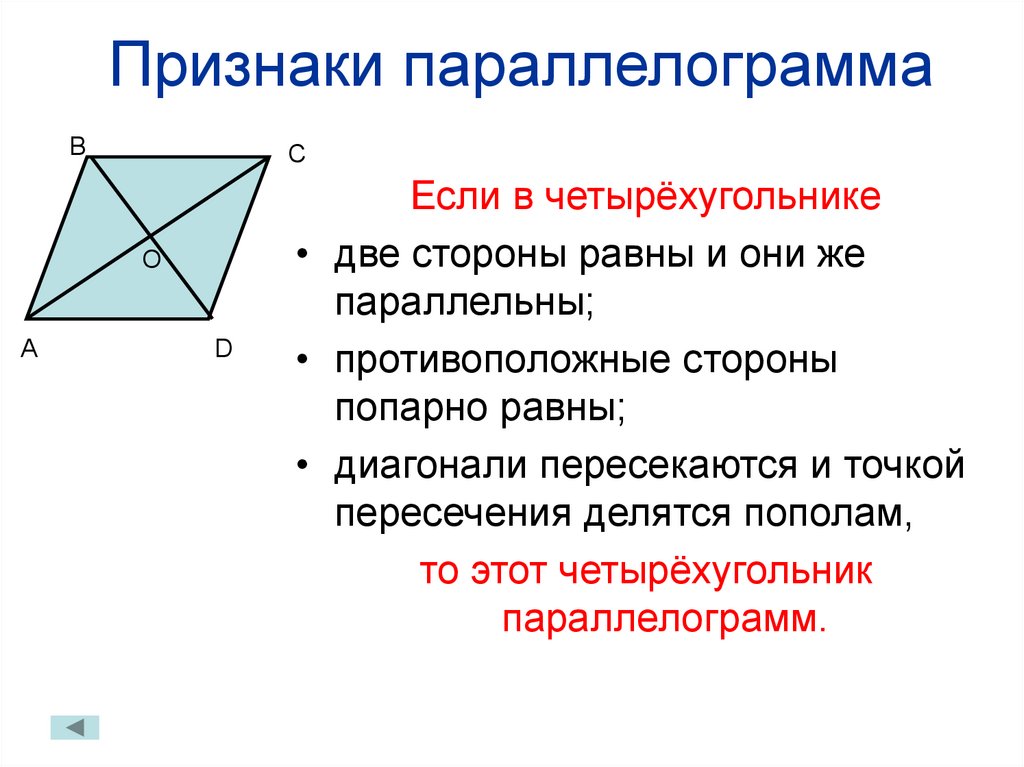 )
) Решение задачи готовит у доски ученик.(Ответ:300, 600, 1200, 1500.)
Решение задачи готовит у доски ученик.(Ответ:300, 600, 1200, 1500.) Термин «параллелограмм» греческого происхождения и, согласно Проклу, был введен Евклидом. Понятие параллелограмма и некоторые его свойства были известны еще пифагорейцам.
Термин «параллелограмм» греческого происхождения и, согласно Проклу, был введен Евклидом. Понятие параллелограмма и некоторые его свойства были известны еще пифагорейцам.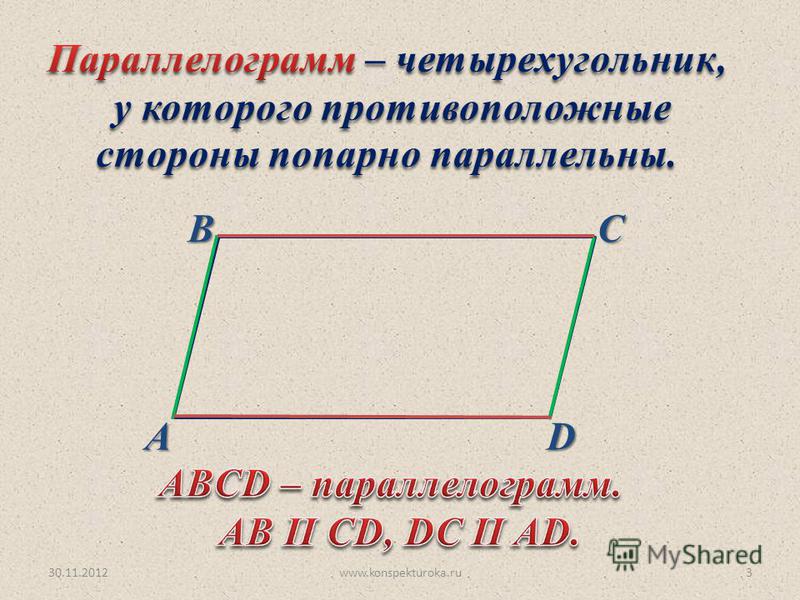 АВ=DC, AD=BC,
АВ=DC, AD=BC,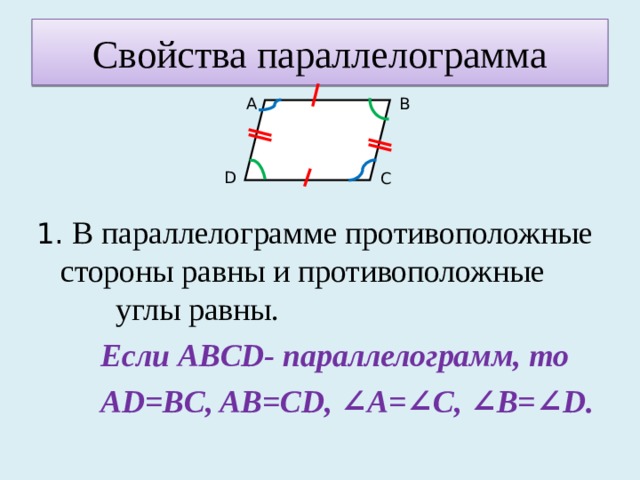
 Собрать на проверку тетради учащихся, Для завершения урока предложить учащимся ответить на вопросы:
Собрать на проверку тетради учащихся, Для завершения урока предложить учащимся ответить на вопросы: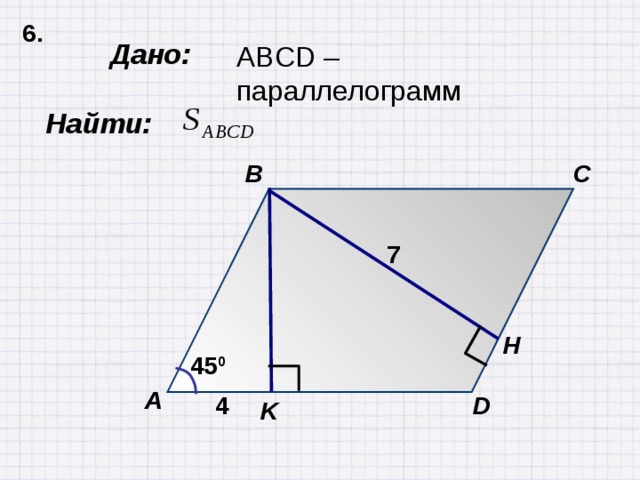 Свойства параллелограмма
Свойства параллелограмма school-collection.edu.ru/dlrstore/7ae1d34d-0a01-01b2-01e3-a0ec7f75a9ab/%5BG79_05-02-042%5D_%5BML_003%5D.swf
school-collection.edu.ru/dlrstore/7ae1d34d-0a01-01b2-01e3-a0ec7f75a9ab/%5BG79_05-02-042%5D_%5BML_003%5D.swf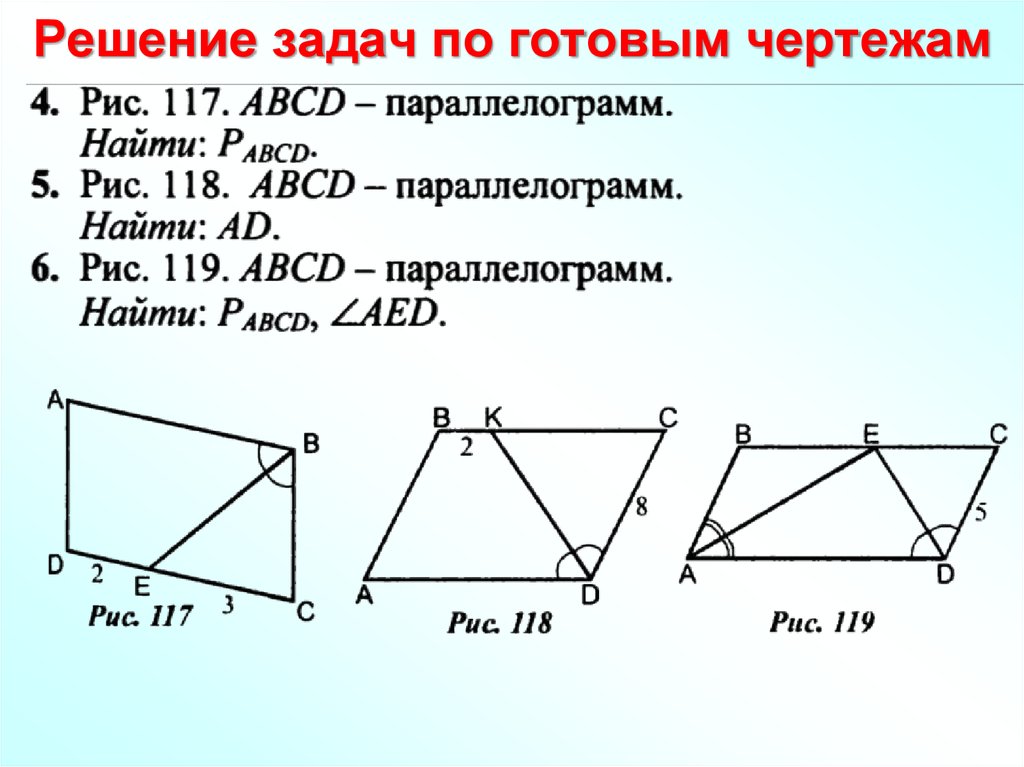 Возьмите бесплатную пробную версию GMAT, чтобы узнать свой базовый балл, и начните подготовку к GMAT с нашей бесплатной пробной версии. Мы являемся самой популярной онлайн-компанией по подготовке к GMAT с более чем 2200 отзывами на GMATClub по состоянию на 4 октября 2021 года.
Возьмите бесплатную пробную версию GMAT, чтобы узнать свой базовый балл, и начните подготовку к GMAT с нашей бесплатной пробной версии. Мы являемся самой популярной онлайн-компанией по подготовке к GMAT с более чем 2200 отзывами на GMATClub по состоянию на 4 октября 2021 года. Однако углы не равны 9.0°. Ромб с прямыми углами станет квадратом. Другое название ромба — «ромб», так как он похож на ромбовидную масть в игральных картах.
Однако углы не равны 9.0°. Ромб с прямыми углами станет квадратом. Другое название ромба — «ромб», так как он похож на ромбовидную масть в игральных картах.
 Свойства и их применение
Свойства и их применение
 Если вы планируете сдавать GMAT, мы можем помочь вам с высококачественными учебными материалами, к которым вы можете получить бесплатный доступ, зарегистрировавшись здесь.
Если вы планируете сдавать GMAT, мы можем помочь вам с высококачественными учебными материалами, к которым вы можете получить бесплатный доступ, зарегистрировавшись здесь.
 Прежде чем мы узнаем о свойствах, давайте сначала узнаем о параллелограммах. Это четырехсторонняя замкнутая фигура с равными и параллельными противоположными сторонами и равными противоположными углами. Давайте узнаем больше о свойствах параллелограмма подробно в этой статье.
Прежде чем мы узнаем о свойствах, давайте сначала узнаем о параллелограммах. Это четырехсторонняя замкнутая фигура с равными и параллельными противоположными сторонами и равными противоположными углами. Давайте узнаем больше о свойствах параллелограмма подробно в этой статье.
 В параллелограмме ABCD (см. рисунок выше) диагонали AC и BD. Предположим, что O — точка пересечения диагоналей AC и BD. Свойства диагоналей параллелограмма следующие:
В параллелограмме ABCD (см. рисунок выше) диагонали AC и BD. Предположим, что O — точка пересечения диагоналей AC и BD. Свойства диагоналей параллелограмма следующие: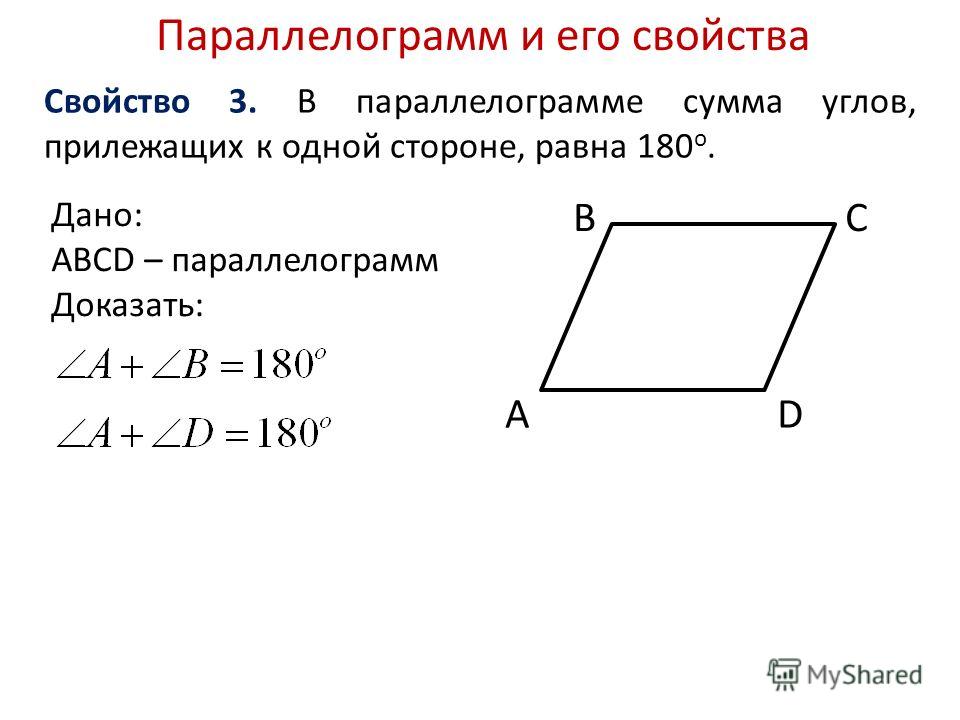
 Теперь сравните два треугольника ABC и CDA. Здесь мы имеем
Теперь сравните два треугольника ABC и CDA. Здесь мы имеем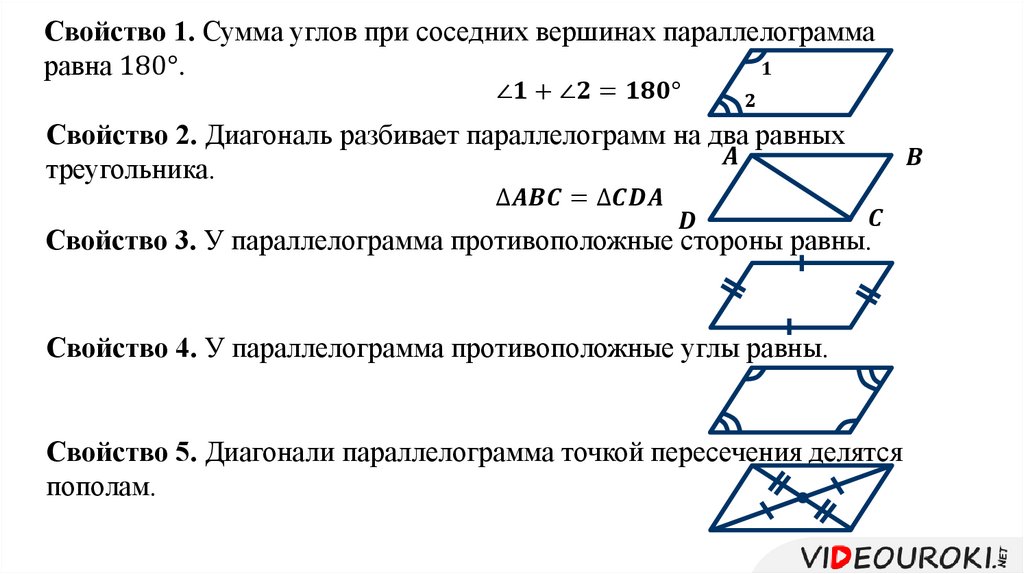 Точно так же мы можем показать, что ∠A = ∠C. Это доказывает, что противоположные углы в любом параллелограмме равны.
Точно так же мы можем показать, что ∠A = ∠C. Это доказывает, что противоположные углы в любом параллелограмме равны.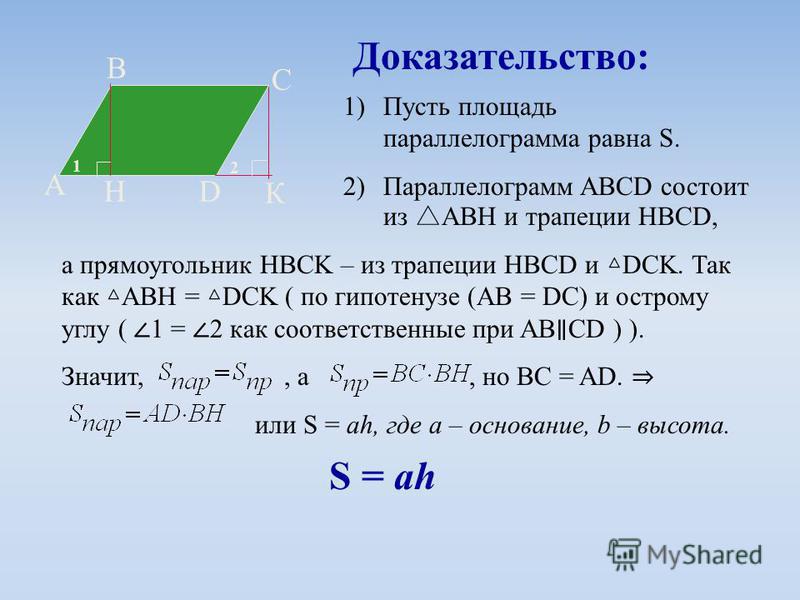 PT и QR — диагонали параллелограмма.
PT и QR — диагонали параллелограмма.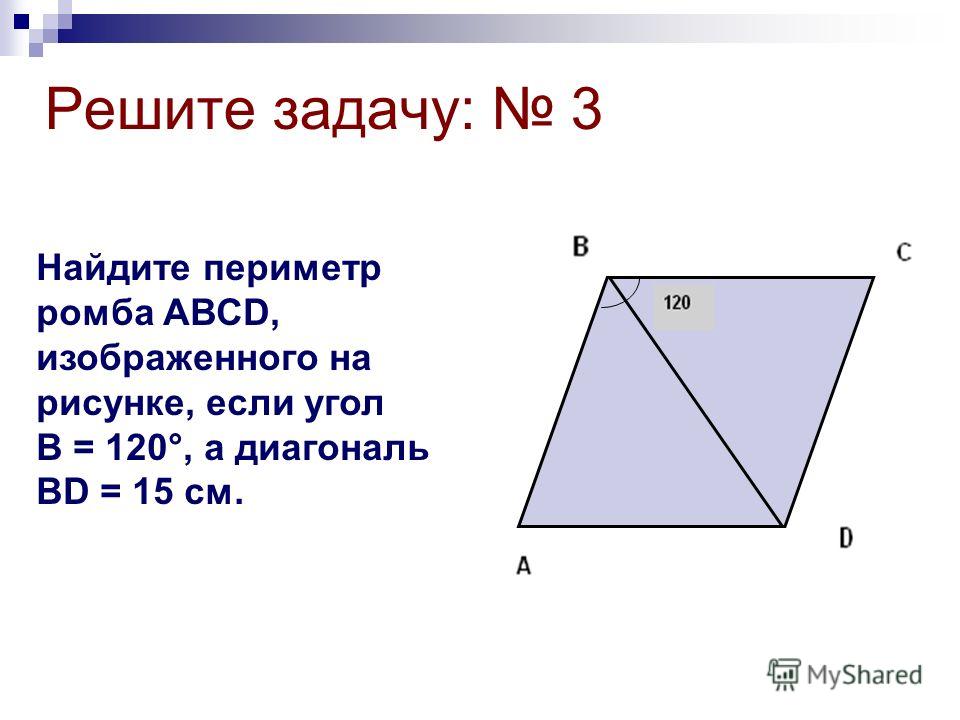 Еще раз сравните треугольник RET и треугольник PEQ. У нас есть:
Еще раз сравните треугольник RET и треугольник PEQ. У нас есть: Отсюда можно сделать вывод, что по CPCTC AE = EC, а BE = ED. Следовательно, диагонали AC и BD делят друг друга пополам, а это в дальнейшем означает, что ABCD — параллелограмм.
Отсюда можно сделать вывод, что по CPCTC AE = EC, а BE = ED. Следовательно, диагонали AC и BD делят друг друга пополам, а это в дальнейшем означает, что ABCD — параллелограмм.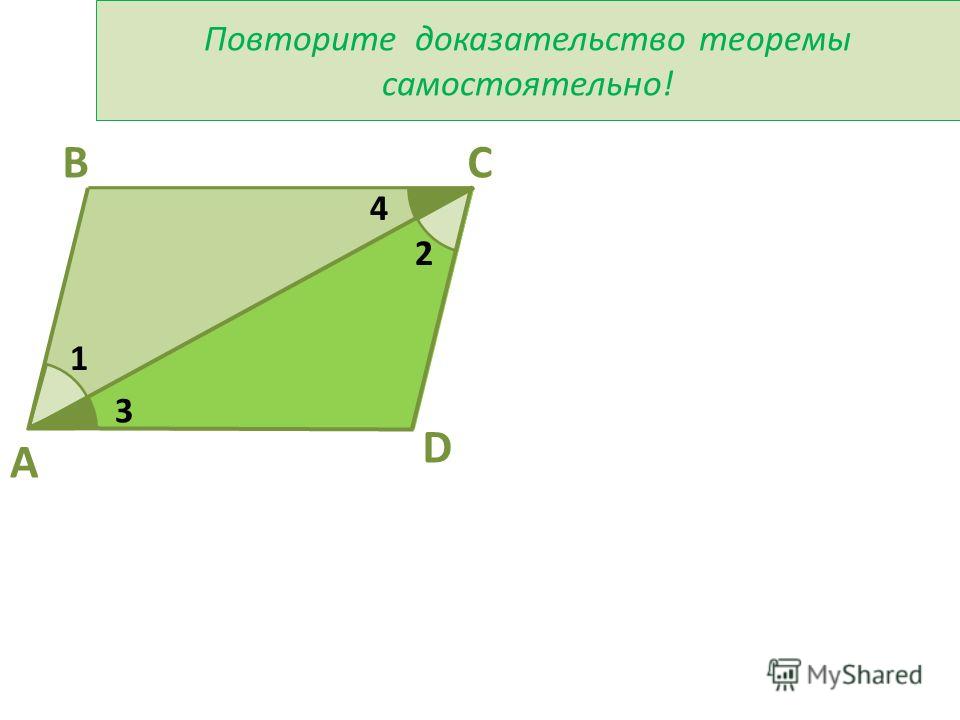
 Противоположные углы параллелограмма также равны. Короче говоря, параллелограмм можно рассматривать как скрученный прямоугольник. Это скорее прямоугольник, но углы при вершинах не обязательно должны быть прямыми. Четыре важных свойства параллелограмма таковы:
Противоположные углы параллелограмма также равны. Короче говоря, параллелограмм можно рассматривать как скрученный прямоугольник. Это скорее прямоугольник, но углы при вершинах не обязательно должны быть прямыми. Четыре важных свойства параллелограмма таковы: