Теорема фалеса презентация 8 класс погорелов: Презентация » теорема Фалеса» 8 класс

Содержание

Теорема Фалеса | Презентация к уроку по геометрии (8 класс) по теме:

Слайд 1

Теорема Фалеса Т еорема. Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне (рис. а) . Теорему Фалеса можно применять для деления отрезка на n равных частей (рис. б) .

Слайд 2

Отношением двух отрезков AB и CD называется число, показывающее сколько раз отрезок CD и его части укладываются в отрезке АВ . Теорема о пропорциональных отрезках Говорят, что отрезки АВ , CD пропорциональны отрезкам A 1 B 1 , C 1 D 1 , если равны их отношения

Слайд 3

http://files.school-collection.edu.ru/dlrstore/7383a6b1-0dac-11dc-8314-0800200c9a66/index.htm

Слайд 4

Теорема. (обобщенная теорема Фалеса) Параллельные прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки.

Слайд 5

Пример 1 Стороны угла с вершиной O пересечены двумя параллельными прямыми в точках A , B и C , D соответственно. Найдите OA , если OB = 15 см и OC : OD = 2 : 5. Ответ: 6 см.

Слайд 6

Пример 2 Докажите, что биссектриса угла треугольника делит противоположную сторону на части, пропорциональные прилежащим сторонам. Решение: Пусть CD биссектриса треугольника ABC . Докажем, что AD : DB = AC : BC . Проведем прямую BE , параллельную CD . В треугольнике BEC угол B равен углу E . Следовательно, BC = EC . По следствию из теоремы о пропорциональных отрезках, AD : DB = AC : CE = AC : BC .

Слайд 7

Упражнение 1 Определите, пропорциональны ли пары отрезков а , b и c , d , если: а) a = 0,8 см, b = 0,3 см, с = 2,4 см, d = 0,9 см; б) а = 50 мм, b = 6 см, с = 10 см, d = 18,5 см. Ответ: а) Да; б) нет.

Слайд 8

Упражнение 2 Среди отрезков a , b , c , d , e выберите пары пропорциональных отрезков, если а = 2 см, b = 17,5 см, с = 16 см, d = 35 см, е = 4 см. Ответ: a , e и b , d .

Слайд 9

Упражнение 3 Даны три отрезка: а , b , и с . Какова должна быть длина четвертого отрезка d , чтобы из них можно было образовать две пары пропорциональных отрезков, если а = 6 см, b = 3 c м, с = 4 см, и отрезок d больше каждого из этих отрезков. Ответ: 8 см.

Слайд 10

Упражнение 6 На одной из сторон угла расположены два отрезка 3 см и 4 см. Через их концы проведены параллельные прямые, образующие на другой стороне также два отрезка. Больший из отрезков равен 6 см. Чему равен другой отрезок? Ответ: 4,5 см.

Слайд 11

Упражнение 7 Стороны угла с вершиной O пересечены двумя параллельными прямыми в точках A , B и C , D соответственно. Найдите: а) CD , если OA = 8 см, AB = 4 см, OD = 6 см; б) OC и OD , если OA : OB = 3 : 5 и OD – OC = 8 см; в) OA и OB , если OC : CD = 2 : 3 и OA + OB = 14 см. Ответ: а) 2 см; б) 12 см и 20 см; в) 4 см и 10 см .

Слайд 12

Упражнение 8 Проекции двух сторон остроугольного треугольника АВС на прямую АС имеют длины 6 см и 4 см. Какую длину имеют проекции медиан этого треугольника на ту же прямую? Ответ: 1 см, 7 см и 8 см. А В С М D К

Слайд 13

Упражнение 9 Каждая из сторон треугольника разделена на три равных отрезка и точки деления соединены отрезками. Найдите периметр образовавшейся при этом фигуры, если периметр исходного треугольника равен p . Ответ: p .

Слайд 14

Упражнение 11 Ответ: c м. На сторонах АВ и АС треугольника АВС взяты соответственно точки D и Е , причем AD = АВ , АЕ = АС . Чему равен отрезок DE , если отрезок ВС равен 5 см?

Слайд 15

Упражнение 12 В треугольнике АВС сторона ВС разделена на четыре равные части и через полученные точки деления проведены прямые, параллельные стороне АВ , равной 18 см. Найдите отрезки этих прямых, заключенные внутри треугольника. Ответ: 4,5 см, 9 см, 13,5 см.

Слайд 16

Упражнение 13 Основания трапеции равны 14 см и 20 см. Одна из боковых сторон разделена на три равные части и через точки деления проведены прямые, параллельные основаниям трапеции. Найдите отрезки этих прямых, заключенные внутри трапеции. Ответ: 16 см и 18 см.

Презентация. Теорема Фалеса. 8 класс.

ТЕОРЕМА

ФАЛЕСА

8 класс

МБОУ «Большаковская СОШ» Яковлева Ирина Владимировна

Фалес Милетский VI век до н. э.

Фалес первым сформулировал и доказал несколько геометрических теорем, среди которых:

1) вертикальные углы равны;

2) имеет место равенство треугольников по одной стороне и двум прилегающим к ней углам;

3) углы при основании равнобедренного треугольника равны;

Фалес научился определять расстояние от берега до корабля. В основе этого способа лежит теорема, названная впоследствии теоремой Фалеса:

Е сли параллельные прямые, пересекающие стороны угла, отсекают равные отрезки на одной его стороне, то они отсекают равные отрезки и на другой его стороне.

Легенда рассказывает о том, что Фалес, будучи в Египте, поразил фараона Амасиса тем, что сумел точно установить высоту пирамиды, дождавшись момента, когда длина тени палки становится равной её высоте, и тогда измерил длину тени пирамиды.

Теорема Фалеса

Теорема. Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне (рис. а).

В режиме слайдов ответы появляются после кликанья мышкой

Теорему Фалеса можно применять для деления отрезка на n равных частей (рис. б).

Теорема о пропорциональных отрезках

Отношением двух отрезков AB и CD называется число, показывающее сколько раз отрезок CD и его части укладываются в отрезке АВ .

Говорят, что отрезки АВ , CD пропорциональны отрезкам A 1 B 1 , C 1 D 1 , если равны их отношения

Теорема. (О пропорциональных отрезках.) Параллельные прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки.

В режиме слайдов ответы появляются после кликанья мышкой

Свойство биссектрисы треугольника

Б иссектриса угла треугольника делит противоположную сторону на части, пропорциональные прилежащим сторонам, т.е. если CD – биссектриса треугольника ABC , то AD : DB = AC : BC .

В режиме слайдов ответы появляются после кликанья мышкой

Доказательство: Проведем прямую BE , параллельную CD . В треугольнике BEC угол B равен углу E . Следовательно, BC = EC . По теореме о пропорциональных отрезках, AD : DB = AC : CE = AC : BC .

Обратное свойство

Е сли луч, проведенный из вершины угла треугольника, делит противоположную сторону на части, пропорциональные сторонам треугольника, прилежащим к лучу, то этот луч является биссектрисой угла треугольника.

Доказательство: Пусть для луча CD выполняется равенство AD : DB = AC : BC . Проведем прямую BE , параллельную CD . По теореме о пропорциональных отрезках, AD : DB = AC : CE . Сравнивая эти два равенства, получаем равенство BC = CE , из которого следует равенство углов CBE и BEC . Но угол CBE равен углу BCD , а угол BEC равен углу ACD . Значит, CD – биссектриса треугольника ABC .

В режиме слайдов ответы появляются после кликанья мышкой

№ 1

Стороны угла с вершиной

O пересечены двумя параллельными прямыми в точках A , C и B , D соответственно. Найдите OC , если OB = BD = 5 и OA = 6.

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: 12.

№ 2

Стороны угла с вершиной O пересечены двумя параллельными прямыми в точках A , C и B , D соответственно. Найдите OD , если OA = 6, AC = 12 и OB = 5.

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: 15.

№ 3

Стороны угла с вершиной O пересечены двумя параллельными прямыми в точках A , C и B , D соответственно. Найдите OA , если OC = 24 и OB : OD = 2 : 3.

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: 16.

№ 4

Стороны угла с вершиной O пересечены двумя параллельными прямыми в точках A , B и C , D соответственно. Найдите OA , если OB = 15 см и OC : OD = 2 : 5 .

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: 6 см.

№ 5

Определите, пропорциональны ли пары отрезков а , b и c , d , если:

а) a = 0,8 см, b = 0,3 см, с = 2,4 см, d = 0,9 см;

б) а = 50 мм, b = 6 см, с = 10 см, d = 18,5 см.

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: а) Да;

б) нет.

№ 6

Среди отрезков a , b , c , d , e выберите пары пропорциональных отрезков, если а

= 2 см, b = 17,5 см, с = 16 см, d = 35 см, е = 4 см.

Ответ: a , e и b , d .

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: 8 см.

№ 7

Даны три отрезка: а , b , и с . Какова должна быть длина четвертого отрезка d , чтобы из них можно было образовать две пары пропорциональных отрезков, если а = 6 см, b = 3 cм, с = 4 см, и отрезок d больше каждого из этих отрезков.

В режиме слайдов ответы появляются после кликанья мышкой

№ 8

На одной из сторон угла расположены два отрезка 3 см и 4 см. Через их концы проведены параллельные прямые, образующие на другой стороне также два отрезка. Больший из отрезков равен 6 см. Чему равен другой отрезок?

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: 4,5 см.

№ 9

Стороны угла с вершиной O пересечены двумя параллельными прямыми в точках A 1 , A 2 и B 1 , B 2 соответственно. Найдите: а) B 1 B 2 , если OA 1 = 8 см, A 1 A 2 = 4 см, OB 2 = 6 см; б) OB 1 и OB 2 , если OA 1 : OA 2 = 3 : 5 и OB 2 – OB 1 = 8 см; в) OA 1 и OA 2 , если OB 1 : B 1 B 2 = 2 : 3 и OA 1 + OA 2 = 14 см.

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: а) 2 см;

б) 12 см и 20 см;

в) 4 см и 10 см .

№ 10

В треугольнике АВС сторона ВС разделена на четыре равные части и через полученные точки деления проведены прямые, параллельные стороне

АВ , равной 18 см. Найдите отрезки этих прямых, заключенные внутри треугольника.

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: 4,5 см, 9 см, 13,5 см.

№ 11

Основания трапеции равны 14 см и 20 см. Одна из боковых сторон разделена на три равные части и через точки деления проведены прямые, параллельные основаниям трапеции. Найдите отрезки этих прямых, заключенные внутри трапеции.

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: 16 см и 18 см.

№ 12

На медиане CC 1 треугольника ABC взята точка M , CM : MC 1 = 3:1. Через нее проведена прямая, параллельная стороне BC , пересекающая сторону

AB в точке N . Найдите отношение AN : NB .

В режиме слайдов ответы появляются после кликанья мышкой

Решение. C 1 N : NB = 1:3, AC 1 = C 1 B , следовательно, AN : NB = 5:3.

№ 13

В треугольнике ABC проведены медианы AA 1 и CC 1 , которые пересекаются в точке M . Найдите отношение CM : MC 1 .

В режиме слайдов ответы появляются после кликанья мышкой

Решение. Проведем отрезок C 1 D , параллельный отрезку AA 1 . Он является средней линией треугольника AA 1 B , следовательно, A 1 D = DB . В треугольнике CC 1 D CA 1 : A 1 D = 1:0,5. Значит, CM : MC 1 = 2:1.

№ 14

На продолжении стороны AC треугольника ABC взята точка K , AC = CK . Через нее и середину L стороны AB проведена прямая, пересекающая сторону BC в точке N . Найдите отношение BN : NC .

В режиме слайдов ответы появляются после кликанья мышкой

Решение. Проведем отрезок BK .

В треугольнике ABK отрезки BC и KL являются медианами. В силу предыдущей задачи, BN : NC = 2:1.

№ 15

На продолжении стороны AC треугольника ABC взята точка D , AC = CD . Через нее и середину E стороны BC проведена прямая, пересекающая сторону AB в точке F . Найдите отношение AF : FB .

В режиме слайдов ответы появляются после кликанья мышкой

Решение. Проведем среднюю линию CG треугольника ADF .

Треугольнике BEF и CEG равны по 2-му признаку. Следовательно, AF = 2 CG = 2 FB , значит, AF : FB = 2:1.

№ 16

В треугольнике ABC проведена медиана СС 1 и отрезок AA 1 , пересекающий CC 1 в точке M , для которого CA 1 : A 1 B = 3:1. Найдите отношение CM : MC 1 .

В режиме слайдов ответы появляются после кликанья мышкой

Решение. Проведем отрезок C 1 D , параллельный отрезку AA 1 .

Он является средней линией треугольника AA 1 B , следовательно, A 1 D = DB . В треугольнике CC 1 D CA 1 : A 1 D = 3:0,5. Значит, CM : MC 1 = 6:1.

№ 17

В треугольнике ABC проведена медиана СС 1 и отрезок AA 1 , пересекающий CC 1 в точке M , для которого CA 1 : A 1 B = 3:1.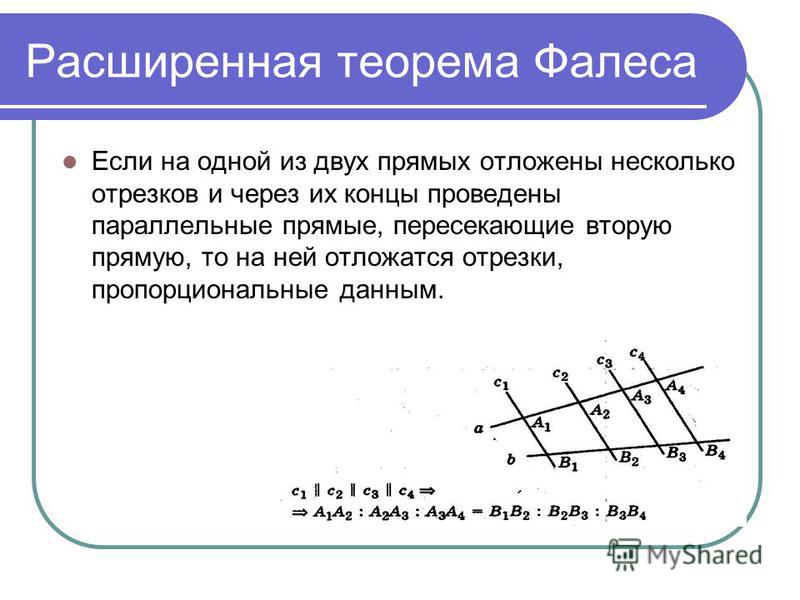 Найдите отношение AM : MA 1 .

В режиме слайдов ответы появляются после кликанья мышкой

Решение. Проведем отрезок A 1 D , параллельный отрезку CC 1 .

Имеем, C 1 D : DB = 3:1. Следовательно, AC 1 : C 1 D = 4:3. Значит, AM : MA 1 = 4:3.

№ 18

В треугольнике ABC проведена медиана СС 1 и отрезок AA 1 , пересекающий CC 1 в точке M , для которого CA 1 : A 1 B = 1:2. Найдите отношение CM : MC 1 .

В режиме слайдов ответы появляются после кликанья мышкой

Решение. Проведем отрезок C 1 D , параллельный отрезку AA 1 .

Он является средней линией треугольника AA 1 B , следовательно, A 1 D = DB . В треугольнике CC 1 D CA 1 : A 1 D = 1:1. Значит, CM : MC 1 = 1:1.

№ 19

В треугольнике ABC проведена медиана СС 1 и отрезок AA 1 , пересекающий CC 1 в точке M , для которого CA 1 : A 1 B = 1:2. Найдите отношение AM : MA 1 .

В режиме слайдов ответы появляются после кликанья мышкой

Решение. Проведем отрезок A 1 D , параллельный отрезку CC 1 .

Имеем, С 1 D : DB = 1:2. Следовательно, AC 1 : C 1 D = 3:1. Значит, AM : MA 1 = 3:1.

№ 20

В треугольнике ABC проведена отрезки AA 1 и отрезок CC 1 , пересекающиеся в точке M , для которых AC 1 : C 1 B = 1:2, CA 1 : A 1 B = 2:1. Найдите отношение CM : MC 1 .

В режиме слайдов ответы появляются после кликанья мышкой

Решение. Проведем отрезок C 1 D , параллельный отрезку AA 1 . Тогда A 1 D : DB = AC 1 : C 1 B = 1:2 . В треугольнике CC 1 D CA 1 : A 1 D = 2 : 1/3. Значит, CM : MC 1 = 6:1.

№ 21

В треугольнике ABC проведена медиана СС 1 и отрезок AA 1 , пересекающий CC 1 в точке M , для которого CA 1 : A 1 B = 2:1. Найдите отношение AM : MA 1 .

В режиме слайдов ответы появляются после кликанья мышкой

Решение. Проведем отрезок A 1 D , параллельный отрезку CC 1 . Тогда C 1 D : DB = 2:1, AC 1 = C 1 B . Следовательно, AC 1 : C 1 D = 3:2. Значит, AM : MA 1 = 3:2.

№ 22

В параллелограмме ABCD точка E – середина стороны CD . Отрезок AE пересекает диагональ BD в точке F . Найдите отношение DF : FB .

В режиме слайдов ответы появляются после кликанья мышкой

Решение. Проведем отрезок CG , параллельный отрезку AE . Обозначим H его точку пересечения с диагональю BD .

В треугольнике CDH EF – средняя линия. Следовательно, DF = FH . В треугольнике ABF GH – средняя линия. Следовательно, BH = HG . Значит, DF : FB = 1 : 2.

№ 23

В параллелограмме ABCD точка E – середина стороны CD . Отрезок AE пересекает диагональ BD в точке F . Найдите отношение AF : FE .

В режиме слайдов ответы появляются после кликанья мышкой

Решение. Проведем отрезок CG , параллельный отрезку AE . Обозначим H его точку пересечения с диагональю BD .

В треугольнике CDH EF – средняя линия. Следовательно, AF = CH = 2 FE . Значит, AF : FE = 2 : 1.

№ 24

В параллелограмме ABCD точки E и F – середины сторон соответственно CD и AD . Отрезки AE и BF пересекаются в точке G . Найдите отношение AG : GE .

Решение. Проведем отрезки CK и DL , Соединяющие вершины параллелограмма с серединами сторон соответственно AB и BC . Обозначим M их точку пересечения, H – точку пересечения отрезков AE и DL .

В режиме слайдов ответы появляются после кликанья мышкой

В треугольнике ADH FG – средняя линия. Следовательно, AG = GH . В треугольнике CDM EH – средняя линия. Следовательно, EH = CM /2 = AG /2. Значит, AG : GE = 2 : 3.

Использованы ресурсы:

геометрия — почему основная теорема о пропорциональности всегда верна?

спросил 6 лет, 8 месяцев назад

Изменено 3 года, 9 месяцев назад

Просмотрено 1к раз

$\begingroup$

Выписка:

Линия, проведенная параллельно одной стороне треугольника, делит две другие стороны в том же отношении.

Теперь есть несколько способов доказать это, а также доказать обратное. Следовательно, мы можем убедить себя, что это действительно так. Но почему? Что такого в природе, что делает это «истинным»?

Если представить два объекта, равномерно движущихся из точки $A$ по линиям $AB$ и $AC$ с разными скоростями, то $x$ и $y$. Вы берете несколько перехватов времени $t_1, t_2, t_3 и т. д. $. Скажем так, точки, которые они делают, помечены так же, как $A_{xt_1}, A_{xt_2} и т. д.$ и $B_{yt_1}, B_{yt_2} и т. д. $… Вы всегда замечали, что $$ A_{xt_1}B_{yt_1} \параллельно A_{xt_2}B_{yt_2} \параллельно A_{xt_3}B_{yt_3} …$$ Я зашел в тупик с этим вопросом: почему так?!

геометрия

$\endgroup$

$\begingroup$

Во многих языках это известно как Теорема Фалеса. Английская Википедия называет это Теоремой Перехвата.

Позвольте мне сначала сказать, что я не согласен с комментариями, что это доказывается с использованием подобных треугольников. Вместо этого для доказательства фактов о подобных треугольниках обычно используется теорема Фалеса.

На странице английской Википедии приведено доказательство теоремы с использованием площади. Но поскольку площадь представляет собой сложное понятие, возможно, предпочтительнее привести доказательство, в котором площадь не используется.

Теорема обычно доказывается в следующие шаги:

Пусть несколько параллельных прямых пересекают две прямые $l_1$ и $l_2$, секущие к ним. Если параллельные прямые отмечают равные отрезки на $l_1$, то они также отмечают равные отрезки на $l_2$. Доказательство этого шага использует факты о параллелограммах и критерии конгруэнтности треугольников.
Даны три параллельные прямые, пересекающие две прямые $l_1$ и $l_2$, предположим, что они отмечают на $l_1$ отрезки, находящиеся в некотором рациональном соотношении. Тогда отрезки, отмеченные на $l_2$, находятся в таком же отношении. Это доказывается вставкой дополнительных параллельных линий так, чтобы все линии были на равном расстоянии друг от друга.
Пункт 2 распространен на иррациональные отношения. Делается это абсурдно: предположим, что отношения на $l_1$ и $l_2$ различны. Тогда должно быть какое-то рациональное отношение, которое больше одного и меньше другого. (Любые два различных действительных числа имеют между собой некоторое рациональное число. Геометрически это соответствует использованию аксиомы Архимеда.) Затем вы используете пункт 2, чтобы получить противоречие.

К сожалению, я не знаю книги на английском языке, где проводится это доказательство. Но доказательство можно найти в Geometría elemental Погорелова (испанский перевод с русского). Кажется вероятным, что доказательство может быть также дано в книге Киселева по геометрии, которая недавно была переведена на английский язык, но я не знаю наверняка.

$\endgroup$

$\begingroup$

Основная идея в том, что два треугольника подобны, потому что их соответствующие углы подобные.

Отсюда (который, конечно, суть доказательства) соответствующие стороны пропорциональны.

Иногда полагая, что теорема верна просто сводится к пониманию доказательства.

$\endgroup$

$\begingroup$

После долгих размышлений это можно доказать с помощью других истин. Например, для закона синусов, т. е.

$$\frac{a}{\sin{A}} = \frac{b}{\sin{B}}= \frac{c}{\sin{C}} $$

Это легко доказать. Нужно понимать, что синус также является отношением. (Плюс, если вы понимаете, как формируется это отношение. Вы можете легко понять это из доказательства).

Но суть этого закона в том, что

$$\frac{\text{длина стороны}}{\text{отношение (длины высоты) от другой вершины к (длине соответствующей соседней стороны )}} = \text{constant}$$

Член в знаменателе зависит от направления стягиваемого угла. Другими словами, отношение длины стороны к синусу противоположных углов всегда имеет постоянную величину.

Параллельные линии просто дают еще один способ выразить соотношение синусов. Следовательно, подключив это к результату закона синусоиды, мы получим желаемое соотношение.

Вот почему… или я так думаю.

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

Основная теорема о пропорциональности | Теорема Фалеса | Утверждение и доказательство

Основная теорема пропорциональности была предложена известным греческим математиком Фалесом, поэтому ее также называют теоремой Фалеса . По мнению известного математика, для любых двух равноугольных треугольников отношение любых двух соответствующих сторон данных треугольников всегда одинаково. На основе этой концепции была предложена основная теорема пропорциональности (BPT). Он дает отношение между сторонами любых двух равноугольных треугольников.

Понятие теоремы Фалеса было введено в подобных треугольниках. Если данные два треугольника подобны друг другу, то

Соответствующие углы обоих треугольников равны
Соответствующие стороны обоих треугольников пропорциональны друг другу

Таким образом, эта теорема также помогает нам лучше понять концепцию подобных треугольников. Теперь давайте попробуем понять основную теорему пропорциональности.

1.	Формулировка основной теоремы пропорциональности
2.	Доказательство основной теоремы о пропорциональности
3.	Обращение к основной теореме пропорциональности
4.	Часто задаваемые вопросы

Доказательство основной теоремы о пропорциональности

Теперь попробуем доказать основное утверждение теоремы о пропорциональности (BPT).

Утверждение: Линия, проведенная параллельно одной стороне треугольника и пересекающая две другие стороны, делит две другие стороны в равных пропорциях.

Дано: Рассмотрим треугольник ΔABC, как показано на данном рисунке. В этом треугольнике мы проводим линию DE, параллельную стороне BC треугольника ΔABC и пересекающую стороны AB и AC в точках D и E соответственно.

Конструкция: На приведенной выше диаграмме создайте воображаемые линии, где вы можете соединить C с D и B с E. Нарисуйте перпендикуляр DP перпендикулярно AE и EQ перпендикулярно AD.

Доказательство:

Рассмотрим треугольники ADE и BDE. Оба эти треугольника находятся на одном основании AB и имеют одинаковую высоту EQ.

(Площадь ADE)/(Площадь BDE) = (1/2 × AD × EQ)/(1/2 × BD × EQ)

(Площадь ADE)/(Площадь BDE) = AD/BD

Теперь рассмотрим треугольники CDE и ADE. Оба эти треугольника лежат на одном основании AC и имеют одинаковую высоту DP.

(Площадь ADE)/(Площадь CDE) = (1/2 × AE × DP)/(1/2 × CE × DP)

(Площадь ADE)/(Площадь CDE) = AE/CE

Оба треугольника BDE и CDE находятся между одним и тем же набором параллельных прямых.

Площадь треугольника BDE = Площадь треугольника CDE

Применяя это, мы имеем (Площадь треугольника ADE)/(Площадь треугольника BDE) = (Площадь треугольника ADE)/(Площадь треугольника CDE)

AD/BD = AE/CE

Следствие:

Приведенное выше доказательство также помогает доказать другую важную теорему, называемую теоремой о средней точке. Теорема о средней точке утверждает, что отрезок, проведенный параллельно одной стороне треугольника, и половина этой стороны делит две другие стороны посередине.

Вывод:

Таким образом, мы доказываем основную теорему о пропорциональности. Следовательно, прямая DE, проведенная параллельно стороне BC треугольника ABC, делит две другие стороны AB, AC в равной пропорции. Кроме того, обратная теорема BPT о средней точке также остается верной. В нем говорится, что линия, проведенная через середину стороны треугольника и параллельная другой стороне, делит пополам третью сторону треугольника.

Обратная основная теорема пропорциональности

В соответствии с обратной теоремой о пропорциональности: «Если отрезок нарисован так, чтобы разделить две стороны треугольника в равных пропорциях, то он параллелен третьей стороне».

Дано:

ABC — треугольник, и прямая DE пересекает стороны AB и AC в равных пропорциях. AD/BD = AE/CE

Доказательство:

Предположим, что DE не параллелен BC. Поэтому проведем еще одну прямую DF, параллельную ВС. Применяя основную теорему пропорциональности, мы имеем: AD/BD = AF/CF. Но уже дано, что: AD/BD = AE/CE. Соблюдая равенство левых частей двух приведенных выше утверждений, мы заключаем следующее утверждение: AE/CE = AF/CF. Добавьте 1 с обеих сторон этого утверждения.

(AE/CE) + 1= (AF/CF) + 1

(AE + CE)/CE = (AF + CF)/CF

AC/CE = AC/CF

∴ CE = CF

Для приведенного выше утверждения точки E и F являются одними и теми же точками, и они совпадают. Следовательно, прямая DE параллельна BC, что доказывает обратное утверждение основной теоремы о пропорциональности.

Важные примечания

Основная теорема пропорциональности. Линия, проведенная параллельно одной стороне треугольника и пересекающая две другие стороны, делит две другие стороны в равной пропорции.
Обратное из основной теоремы о пропорциональности. Линия, проведенная для разрезания двух сторон треугольника в равных пропорциях, параллельна третьей стороне.
Теорема о средней точке. Линия, проведенная параллельно одной стороне треугольника и половине этой стороны, делит две другие стороны в своей середине.

Контрольные вопросы

Диагонали четырехугольника PQRS пересекаются в точке O, так что PO/QO = RO/SO. Докажите, что PQRS — трапеция.

Часто задаваемые вопросы по основной теореме пропорциональности

Что такое Теорема Фалеса?

Теорема Фалеса, которую также называют основной теоремой пропорциональности, утверждает, что линия, проведенная параллельно одной стороне треугольника и пересекающая две другие стороны, делит эти две стороны в равной пропорции.

Каковы применения основной теоремы пропорциональности?

Основная теорема о пропорциональности помогает найти длины, на которые две стороны треугольника делятся линией , проведенной параллельно третьей стороне. Кроме того, у него есть приложения, чтобы найти взаимосвязь между двумя равноугольными треугольниками.

Что такое История Теоремы Фалеса?

Теорема Фалеса была предложена Фалесом, греческим математиком и философом около 625 г. до н.э. Сейчас ее называют основной теоремой пропорциональности, и она помогает найти соотношение между сторонами двух равноугольных треугольников.

Что такое формула основной теоремы пропорциональности?

Базовая формула теоремы пропорциональности для треугольника ABC с точкой D на AB, точкой E на AC и DE // BC выглядит следующим образом,

AD/DB = AE/EC

Что вы подразумеваете под основной теоремой пропорциональности?

Основная теорема о пропорциональности гласит, что если прямая проведена параллельно одной стороне треугольника и пересекает две другие стороны, то две другие стороны она делит в равной пропорции.

Как доказать основную теорему о пропорциональности, вырезая бумагу?

Чтобы показать основную теорему о пропорциональности, вырежьте из цветной бумаги треугольник и обозначьте его вершины как ABC.