Точность и погрешность измерений 7 класс физика – Точность и погрешность измерений — урок. Физика, 7 класс.
Точность и погрешность измерений — урок. Физика, 7 класс.
Измерить какую-нибудь величину — это значит сравнить её с однородной величиной, принятой за единицу.
Всякое измерение может быть выполнено с большей или меньшей точностью.В качестве примера рассмотрим измерение длины бруска линейкой с сантиметровыми делениями.
Вначале определим цену деления линейки. Она будет равна \(1\) см. Если левый конец бруска совместить с нулевым штрихом, то правый будет находиться между \(9\) и \(10\) штрихами, но ближе к \(10\). Какое же из этих двух значений следует принять за длину бруска? Очевидно, то, которое ближе к истинному значению, т.е. \(10\) см. Считая, что длина бруска \(10\) см, мы допустим неточность, так как брусок чуть короче \(10\) см.
В физике допускаемую при измерении неточность называют погрешностью измерений.
Погрешность измерения не может быть больше цены деления измерительного прибора. В нашем случае погрешность измерения бруска не превышает \(1\) см. Если такая точность измерений нас не устраивает, то можно произвести измерения с большей точностью. Но тогда придётся взять масштабную линейку с миллиметровыми делениями, т.е. с ценой деления \(1\) мм. В этом случае длина бруска окажется равной \(9,8\) см.
Для более точных измерений можно воспользоваться штангенциркулем с ценой деления \(0,1\) мм или \(0,05\) мм.
Из этого примера видно, что точность измерений зависит от цены деления шкалы прибора.
Чем меньше цена деления, тем больше точность измерения.
Точность измерения зависит от правильного применения измерительного прибора, расположения глаз при отсчёте по прибору.Вследствие несовершенства измерительных приборов и несовершенства в развитии наших органов чувств, при любом измерении получаются лишь приближённые значения, несколько бóльшие или меньшие истинного значения измеряемой величины.
Во время выполнения лабораторных работ или просто измерений следует считать, что:
Погрешность измерений равна половине цены деления шкалы измерительного прибора.
При записи величин (с учётом погрешности) следует пользоваться формулой: A=a±Δa,
где \(A\) — измеряемая величина, \(a\) — результат измерений, Δa — погрешность измерений (Δ — греческая буква «дельта»).
Источники:
Пёрышкин А.В. Физика. 7 кл. – 14-е изд., стереотип. – М.: Дрофа, 2010.
www.yaklass.ru
Физические величины. Точность и погрешность измерений
Физические величины. Точность и погрешность измерений
Измерять – значит, познавать
Данная тема посвящена физическим величина и их измерениям. В физике часто приходится измерять те или иные величины. Измерить можно высоту дома или длину улицы.
Можно измерить объём воды в колбе или массу воды в стакане.
Но что означают эти измерения? Измерить какую-либо величину – значит сравнить её с однородной величиной, принятой за единицу. Из приведённых выше примеров, можно заметить, что, например, единицей объёма является литр, а единицей массы является грамм. Для удобства была введена международная система единиц, которая называется СИ.
В этой системе длина измеряется в метрах, масса в килограммах, объём — в кубических метрах, время – в секундах и так далее.
Известно что, иногда применяются единицы измерения, которые в десятки, сотни, тысячи и так далее раз больше принятых единиц измерения. Такие единицы измерения называются кратными.
Каждая приставка соответствует тому или иному множителю. Например, «Дека» означает в 10 раз больше, «гекто» — в сто раз больше, «кило» - в тысячу раз больше, «мега» — в миллион раз больше и так далее. Необходимо отметить, что в физике принято записывать такие множители в виде степени числа 10. Например, вместо миллиона записывается 10 6. Также, могут быть использованы единицы, которые в десятки, сотни, тысячи и так далее раз меньше принятых единиц измерения. Такие единицы измерения называются дольными.
Каждая приставка соответствует тому или иному множителю. Например, «Деци» означает в 10 раз меньше, «санти» — в сто раз меньше, «милли» — в тысячу раз меньше, «микро» — в миллион раз меньше и так далее. Эти приставки также записываются в виде степени числа 10. Например, вместо записи числа 0,000001 записывается 10–6.
У каждого ученика имеется линейка, длина которой измеряется в сантиметрах, то есть в единицах, которые в сто раз меньше метра. Поэтому, если длина линейки составляет 15 сантиметров, мы можем сказать, что её длина 0,15 метра.
Линейка – это прибор для измерения длины. Конечно, линейка относится к самым простым измерительным приборам. Существуют значительно более сложные приборы: например, термометр, который применяется для измерения температуры, гигрометр, который используется для измерения влажности или амперметр, который используется для измерения силы электрического тока.
Важно знать, как пользоваться измерительными приборами и насколько могут быть точны те или иные измерения. У каждого ученика есть линейка и карандаш. Можно попытаться измерить длину карандаша. В первую очередь нужно определить, какова цена деления измерительного прибора. Для этого необходимо найти два ближайших штриха шкалы, возле которых указаны значения величины (например, 1 см и 2 см). Далее нужно сосчитать число делений, заключенных между цифрами 1 и 2. При подсчёте получается, что количество этих делений равно 10. Таким образом, между отметками 1 см и 2 см заключено десять делений. Вычитаем из большего числа меньшее и делим на количество делений между ними. В результате вычислений получаем, что цена деления линейки составляет 0,1 см или 1 мм. Данный пример объясняет, как определить цену деления любого измерительного прибора.
Как видно из рисунка, длина карандаша чуть меньше десяти сантиметров. Если бы на этой линейке не было миллиметровых делений, то можно было сказать, что длина карандаша равна десяти сантиметрам. Но это было бы не совсем точное измерение. Такую неточность называют погрешностью измерения. В представленном случае, на линейке есть миллиметровые деления, поэтому можно измерить длину карандаша с более высокой точностью – 9,8 см. Это говорит о том, что чем меньше цена деления, тем больше точность измерения. Ну а большая точность измерения означает меньшую погрешность. Однако абсолютно точных измерений не существует. Если дать один и тот же карандаш каждому ученику из класса и попросить измерить длину карандаша, не у всех получится одинаковый результат. Тем не менее,
Погрешность измерений принято считать равной половине цены деления измерительного прибора. То есть, в рассмотренном случае, погрешность измерений составляет 0,5 мм. Поэтому, после того, как измерили карандаш и записали, что его длина равна 9,8 см, следует записать погрешность.
Знак «±» означает, что указанная длина может быть на полмиллиметра больше или на полмиллиметра меньше. Таким образом, истинное значение длины карандаша находится в промежутке от 9,75 см до 9,85 см.
В общем случае запись измеряемых величин с учетом погрешности имеет следующий вид:
где А – измеряемая величина;а – результат измерения;
Da – погрешность измерений.
Необходимо отметить, что при сложении или вычитании величин с погрешностью, погрешность результата равна сумме погрешностей каждой величины. В этом легко убедиться на примере. На рисунке показаны два отрезка AB и CD, длины которых измерены с определенной погрешностью.
Рассчитаем сумму длин этих отрезков. Из рисунка видно, что отрезок AB равен 1 м ± 1 см. Истинная длина этого отрезка находится в промежутке 99 см ≤ АВ ≤ 101 см. Отрезок CD равен 12 см ± 0,5 см. Истинная длина этого отрезка находится в промежутке от 11,5 см ≤ CD ≤ 12,5 см. Поэтому, сумма длин этих отрезков будет иметь еще большую погрешность. Прежде чем производить вычисления, необходимо перевести обе длины в одинаковые единицы измерения.
Важно отметить, что этот же промежуток мы бы получили, если бы сложили наименьшие и наибольшие длины отрезков AB и CD. Следовательно, при сложении или вычитании величин, измеренных с погрешностями, погрешность результата равна сумме погрешностей каждой из величин.
Упражнения.
Упражнение 1. Заполните таблицу, указав, что из перечисленных слов является физическим телом, единицей измерения, физической величиной или физическим явлением: ветер, Луна, килограмм, дерево, длина, скорость, испарение.
Решение:
Упражнение 2. Родители измерили рост братьев Димы и Васи с помощью рулетки, цена деления которой 1 см. Подсчитайте, насколько см Дима выше, чем Вася.
Решение:
Упражнение 3. Найдите суммарную массу животных с погрешностью.
Решение:
Основные выводы:
– Для описания физических тел или физических явлений вводится физическая величина, которую можно измерить с помощью измерительных приборов или вычислить по формуле.
– Измерение величины – это сравнение её с однородной величиной, принятой за единицу.
– Кратные приставки – это приставки означающие увеличение в десятки, сотни, тысячи и так далее раз.
– Дольные приставки – это приставки, означающие уменьшение в десятки, сотни, тысячи и так далее раз.
– Погрешность измерений – неточность допускаемая при измерении. За погрешность измерений данного прибора принимают половину цены деления этого прибора.
– При сложении или вычитании величин с погрешностями, погрешность результата вычислений равна сумме погрешностей каждой величины.
videouroki.net
Урок по физике 7 класс «Точность измерений и вычислений»
(W) Изучение новой темы
Учитель: Точность измерения зависит от чувствительности прибора и навыка человека, выполняющего измерения.
В физике допускаемую при измерении неточность называют погрешностью измерений. Погрешность измерений не может быть больше цены деления измерительного прибора.
Чем меньше цена деления, тем больше точность измерения.
Точность измерений зависит также от правильного применения измерительного прибора, расположения глаза при отсчёте по прибору. Вследствие несовершенства измерительных приборов и несовершенства в развитии наших органов чувств при любом измерении получаются лишь приближённые значения, несколько большие или меньшие истинного значения измеряемой величины. Во время выполнения лабораторных работ или просто измерений следует считать, что:
Погрешность измерений равна половине цены деления шкалы измерительного прибора.
Абсолютно точных измерений не существует!
Например: измерим длину карандаша и запишем ее длину с учетом приборной погрешности.
Запись величин, с учетом погрешности описывается общей формулой 
L = l +
L –измеряемая величина
l — результат измерения
– погрешность измерения
Погрешность измерения — отклонение измеренного значения величины от её истинного (действительного) значения. Погрешность измерения является характеристикой точности измерения.
Абсолютная погрешность ∆х —является оценкой абсолютной ошибки измерения. Определяется по формуле: Δх = .
Определение цены деления шкалы:
Найти два ближайших штриха шкалы, возле которых написаны значения величин.
Вычесть из большего значения меньшее.
Полученное число разделить на число делений (промежутков), находящихся между ними.
(G) Выполните задание в парах
Определите цену деления линеек

Учитель: В физике и астрономии часто приходится иметь дело с очень большими и слишком малыми числами.
Например, расстояние от Земли до Солнца 150 000 000км, скорость света 300 000 000 м/с, размер молекулы водорода 0.000 000 023см. С такими числами неудобно выполнять математические расчеты. Поэтому мы будем записывать очень большие и малые числа, используя запись в виде произведения двух множителей, один из которых – число а, 1 ≤ а < 10, второй множитель – число 10 с показателем степени
Число считается записанным в стандартном виде, если оно записано в виде , где , п – называют порядком числа. Порядок числа показывает насколько велико число или мало. Большой положительный порядок показывает, что число очень велико, большой по модулю отрицательный порядок показывает, что число очень мало.
1500000000 =1,5•109 км
300000000 = 3•108 м/с
0.000000023 = 2.3•10-8 см
То, что показатель степени числа 10 является натуральным числом, облегчает выполнение упражнения умножения и деления при расчетах.
(Учащиеся в тетрадь записывают математические преобразования)
10m•10n = 10m+n
10m:10n = 10m-n
(10m)n = 10m•n
100 = 1
Лабораторная работа № 1
Цель работы: определение цены деления шкалы приборов, предназначенных для измерения времени и длины.
Приборы и материалы: ученическая линейка, измерительная лента, секундомер или часы со секундной стрелкой.
Задание 1. Определеить цены деления школы измерительных приборов (линейка, рулетка, секундомер или часы)
Ход работы:
1.Выполняю лабораторную работу согласно описанию учебника на ст 29
Результаты измерений и вычислений внесите в таблицу.
Критерии оценивания для лабораторной работы:
Дескриптор
infourok.ru
«Точность и погрешность измерения при проведении лабораторных работ». 7-й класс
Разделы: Физика
Российская школа переживает качественно новый этап своего развития. Современное образование требует интенсификации учебно-воспитательного процесса. Интенсификация обучения сегодня может успешно осуществляться за счёт применения ИКТ как средства и способа обучения, которые расширяют спектр методов и форм проведения занятий с учащимися.
Государственная Итоговая Аттестация требует от девятиклассника практических знаний и умений при проведении практических и лабораторных работ, умения оценить точность и погрешность измерений.
Теоретический подход к этому уже заложен авторами учебников по физике, но практическая часть остаётся на совести учителя. Понятия косвенных измерений, относительной погрешности, способ правильного подбора приборов, правила нахождения погрешностей для приближённых значений физических величин появляется для девятиклассника как-то вдруг, мимоходом. Но опыт показывает, что учащиеся испытывают растерянность при проведении лабораторных работ на этапе расчётов погрешности измеренной величины.
Исходя из своего опыта, я неоднократно убеждалась, что формировать знания и умения в определении погрешности измерения лучше начинать с 7 класса. Изучение понятий абсолютной и относительной погрешностей у учащихся 7 класса не представляет большой трудности и хорошо закрепляется расчётами при проведении фронтальных измерений и выполнении лабораторных работ.
Я создала несколько презентаций к урокам в 7 классе, которые, я думаю, могут помочь учащимся достаточно чётко разобраться в этом вопросе и получить умения и навыки в определении точности и погрешности измерений. Доступность и простота были моими первыми критериями.
Презентация № 1 “Погрешности измерений и их вычисление” сопровождает весь урок по теме “Точность и погрешность измерений”. В ней присутствуют все этапы урока, предполагаются фронтальные опыты по проведению измерений, учащиеся знакомятся с алгоритмом проведения измерения и делают вывод о зависимости точности измерения от цены деления прибора, проверенный практическими фронтальными измерениями. Учащиеся знакомятся с первым критерием качества измерений.
Презентация № 2 “Лабораторная работа №4 “Измерение объёма тела” я использую при проведении одноимённой лабораторной работы. Использую её в качестве введения, а затем по ходу проведения практических измерений прошу учащихся при вычислении погрешности сверять их с примерами на слайдах презентации. Презентация №2, на мой взгляд, помогает учащимся понять, как правильно обращаться с мензуркой, проводить замеры, осознать логику последовательности действий, применить одно из правил нахождения погрешностей для приближённых значений физических величин и ощутить удовлетворение от правильно сделанного вывода.
Презентация № 3 “Лабораторная работа №5 “Определение плотности твёрдого тела” я использую после проведения лабораторной работы №5 по учебнику А.В Пёрышкина, учащиеся её выполняют по описанию учебника без расчётов погрешности. Но на следующем уроке я возвращаюсь к этой лабораторной работе, выдаю тетради для лабораторных работ без приборов. С помощью презентации №3 учащиеся рассчитывают погрешности, используя уже свои показания, сделанными ими на прошлом уроке. Презентация №3 даёт мне возможность закрепить прошлые навыки и ознакомить учащихся с новыми знаниями такими как “косвенные измерения”, даёт представление о сложности вычисления погрешности при косвенных измерениях, впервые указывает на совпадение разрядов приближённых чисел и чисел погрешности при записи физической величины с учётом погрешности.
Презентация № 4 “Относительная погрешность измерения” используется для знакомства с относительной погрешностью перед проведением лабораторной работы №6 “Градуирование пружины и измерение сил динамометром”. Учитывая уровень развития класса в целом, можно воспользоваться презентацией, как на отдельном уроке, так и для введения перед проведением лабораторной работы №6 в классе с высоким уровнем подготовки. В ней представлена формула относительной погрешности и два примера. Перед уроком учащимся уже выданы сантиметровые ленты. Очень быстро проводятся фронтально два измерения длины парты и собственной ручки учащегося, вычисляются относительные погрешности.
Презентация № 5 “Лабораторная работа №6 “Градуирование пружины и измерение сил динамометром”. В ней даны правила правильной работы с динамометром, прошлые знания применяются в совершенно новых условиях, проводится оценка и сравнение точности шкал, знакомство с ещё одним из способов (для учащихся вторым) оценки точности измерений путём сравнения относительных погрешностей и делается вывод о возможности достижения всё большей точности измерения.
Презентация № 6 “Критерии качества измерения” знакомит учащихся со следующим способом оценки качества измерения, а также правильным подбором приборов для проведения измерения. После проведения лабораторной работы № 9 “Выяснение условия равновесия рычага”, на следующем уроке, например, уроке решения задач можно поставить вопрос “От чего зависит качество измерения?”. Напомнить о первом критерии качества измерения, рассмотренном на уроке “Точность и погрешность измерений” при помощи презентации № 1. Следующим слайдом напомнить о втором, для учащихся, критерии качества измерения, рассмотренным во время выполнения лабораторной работы по градуированию шкалы динамометра с помощью презентации № 5, а затем рассмотреть третий критерий на примере недавно выполненной лабораторной работе № 9 с расчётами и выводом. Последний слайд презентации № 6 обобщает все три критерия качества измерения.
После уроков лабораторных работ в качестве домашнего задания можно предложить провести ряд измерений домашних предметов и рассчитать погрешности измерений.
Знания о точности и погрешности измерений, а также практические навыки выполнения расчётов, на мой взгляд, соответствует уровню развития учащегося 7 класса и помогают уже в 8 классе ученику более легко воспринимать новые способы и методы вычисления погрешностей.
Литература:
- Фетисов, В.А. Оценка точности измерений в курсе физики средней школы. -2-е изд., — Москва.: Просвещение, 1991. — 36с .
- 2. Пёрышкин А.В. учебник Физика 7 . -13-е изд., - Москва.: Дрофа, 2011. -159 с.
- images измерение сантиметровой лентой Поиск@Mail.Ru.
Приложение:
15.02.2013
Поделиться страницей:xn--i1abbnckbmcl9fb.xn--p1ai
Измерение физических величин. Точность и погрешность измерений. 7 класс
Измерение физических величин. Точность и погрешность измерений. 7 класс
При изучений физических явлений проводят различные измерения.
Физики измеряют физические величины.
Например:
При изучении падение тела, надо измерить высоту, с которой падает тело, массу тела, его скорость и время падения.
Чтобы узнать, например, зависит ли объем воды или другой жидкости от ее температуры и как зависит, нужно, нагревая воду, измерять и объем, и температуру.
Объем и температура, время и длина, площадь, скорость, масса, сила — это физические величины.
1. Что значит измерить?
Измерить какую-либо физическую величину — это значит сравнить ее с однородной величиной, принятой за единицу этой величины.
Например:
Измерить длину стола — значит сравнить ее с другой длиной, которая принята за единицу длины, например с метром.
В результате измерения величины получаем ее числовое значение, выраженное в принятых единицах.
2. Какие бывают единицы имерения?
Для каждой физической величины приняты свои единицы измерения.
Очень удобно пользоваться одинаковыми единицами физических величин во всех странах мира.
Поэтому с 1963 г. применяется Международная система единиц — СИ (система интернациональная).
единица длины — 1 метр (1м),
единица времени — 1 секунда (1с),
единица массы — 1 килограмм (1 кг).
Кроме того, используются кратные единицы (кратные основной единице), которые в 10, 100, 1000 и т. д. раз больше.
Эти единицы получили наименования с приставками, взятыми из греческого языка.
«Дека» — 10, «гекто» — 100, «кило» — 1000 и др.
Используются и дольные единицы, которые в 10, 100, 1000 и т. д. раз меньше принятых единиц величин.
В них применяют приставки, также взятые из латинского языка. «Деци» — 0,1, «санти» — 0,01, «милли» — 0,001 и др.
Некоторые приставки к названиям единиц:
г — гекто (100 или 102)
к — кило (1000 или 103)
М — мега (1 000 000 или 106)
д — деци (0,1 или 10-1)
с — санти (0,01 или 10-2)
м — милли (0,001 или 10-3)
Например:
Длина столовой ложки 20 см.
Ее длина в метрах (м):
20 см = 0,20 м или 2 • 10-1 м.
3. Что такое измерителный прибор?
Для измерения физических величин нужны измерителные приборы.
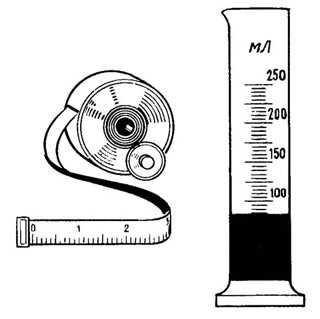
Есть измерителные приборы для простых измерений. Например, измерительная линейка, рулетка, мензурка, применяемая для измерения объема жидкости.
Есть сложные измерительные приборы: секундомеры, термометры и другие.
По мере развития физики и техники приборы усложнялись и появились, например, приборы, при помощи которых изучают строение вещества.
У измерительных приборов есть измерительная шкала, на которой штрихами нанесены деления и написаны значения величин.

Между двумя большими штрихами могут быть дополнительно нанесены несколько делений, не обозначенных числами.
Значение измеряемой величины между ближайшими штрихами называется ценой деления прибора.
Например, у обычной школьной линейки расстояние между двумя ближайшими штрихами составляет 1 мм, это цена деления линейки.
4. Как определить цену деления измерительной шкалы прибора?
Прежде чем использовать измерительный прибор, надо определить цену деления этого прибора.
Надо установить, какому значению величины соответствует каждое самое малое деление.
Для того чтобы определить цену деления, необходимо:
— найти два ближайших штриха шкалы, возле которых написаны значения величины;
— вычесть из большего значения меньшее и полученное число разделить на число делений, находящихся между ними.
5. Примеры определения цены деления
а) Определение цены деления секундомера.
Используем любые два штриха, около которых нанесены значения измеряемой величины (времени), например штрихи с обозначениями 5 и 10 с.
Расстояние между этими штрихами разделено на 10 делений. Значит, цена каждого деления равна:
Секундомер показывает 22 с.
б) Определение цены деления термометра.
Возьмем, например, ближайшие друг к другу штрихи с обозначениями 10 °С и 20 °С. Расстояния между ними разделены на 10 делений. Следовательно,
цена каждого деления будет равна: 20 °С — 10 °С = 10 °С, далее 10 °С : 10 = 1 °С.
Термометр показывает 24 °С.
6.
Что такое точность и погрешность измерений?
Любое измерение может быть выполнено с большей или меньшей точностью.
В физике допускаемую при измерении неточность называют погрешностью измерения.
Погрешность измерения не может быть больше цены деления измерительного прибора.
Из этого примера видно, что точность измерений зависит от цены деления шкалы прибора.
Чем меньше цена деления, тем больше точность измерения.
При измерении принято считать, что: погрешность измерений равна половине цены деления шкалы измерительного прибора.
При записи величин, с учетом погрешности, пользуются формулой:
где А — измеряемая величина,
а — результат измерений,
дельта а — погрешность измерений (треуголник — греч. буква «дельта»).
Например:
Если длина книги 20 см, а цена деления линейки 1 мм, то погрешность измерения будет равна 0,5 мм, или 0,05 см.
Следовательно, длину книги можно записать так:
L = (20 ±0,05) см,
где L — длина книги.
Истинное значение длины книги находится в интервале от 19,95 см до 20,05 см.
Главное:
Измерить какую-либо величину — это значит сравнить ее с однородной величиной, принятой за единицу этой величины.
Основные единицы системы СИ: метр, килограмм, секунда.
Для того чтобы определить цену деления, необходимо:
— найти два ближайших штриха шкалы, возле которых написаны значения величины;
— вычесть из большего значения меньшее и полученное число разделить на число делений, находящихся между ними.
Следующая страница — смотреть
Назад в «Оглавление» — смотреть
class-fizika.ru
Конспект урока «Физические величины. Измерение физических величин. Точность и погрешность измерений.» 7 класс
Учитель: Внимательно посмотрите на тему урока. Давайте попробуем поставить для себя цель и задачи на урок. Для этого помогите мне закончить предложения:
Ученик: Мы должны понять, что называют физической величиной.
Ученик: Мы должны понять, что такое погрешность измерений, где используют погрешность измерений.
Ученик: Мы должны научиться измерять физические величины.
Ученик: Мы должны научиться использовать погрешность измерений при решении задач.
научиться измерять физические величины
Учитель: Верно, сегодня вы научитесь измерять физические величины. Итак, приступим. На предыдущих уроках мы знакомились с приборами, которые будем использовать и в дальнейшем. Сегодня нам эти знания пригодятся. У вас на столе находится оборудование. Подумайте и ответьте, какие величины можно измерять с помощью этих приборов?
Ученик: Весы – массу. Цилиндр – объем. Линейка – длину.
4. Создание ситуации затруднения.
Учитель: Скажите, вы поймете меня, если я скажу: «Длина тела равна 15» или «Масса тела равна 5».
(в беседе прийти к выводу, что необходимо указать единицу измерения физической величины):
«Длина тела равна 15 м».
«Масса тела равна 5 кг».
Учитель: Как определить ширину тетради? (см и мм)
Учитель: Определим температуру воздуха в классе (
5. Первичное усвоение знаний
Учитель: Физической величиной называют количественную характеристику физического тела или явления.
В нашем случае количественной характеристикой является – ширина (20 см)
Физическая величина – это то, что можно измерить, например, длина, высота и т.д. Измерить какую-нибудь величину – это значит сравнить ее с однородной величиной, принятой за единицу
Существует Международная система единиц – СИ (система интернациональная), согласно этой системы мы измеряем каждую величину в определенных единицах измерения (м, с, кг и т.д.)
Международная система единиц- СИ.
Длина- метр (1 м).
Время- секунда (1 с).
Масса- килограмм (1 кг).
Задание классу: дополните предложения (что измеряет прибор):
линейка для измерения……..,часы……….., градусник медицинский…….., мензурка……..
Ответы учеников.
Учитель: Конечно, вы знаете и другие, второстепенные единицы измерения. Например, время можно измерять в минутах, часах. Но важно учесть, что все наши последующие расчеты мы будем стараться вести именно в системе СИ.
Часто применяются единицы, которые в 10, 100, 1000, 1000000 и т. д. раз больше принятых единиц (так называемые кратные единицы). Если используют единицы, которые в 10, 100, 1000, 1000000 и т. д. раз меньше принятых единиц (так называемые дольные единицы).
Учебник стр. 9 таблица 3 1. Приставки к названиям единиц.
Например: дека (дк) – 10, гекто (г) – 100, кило (к) – 1000, мега (М) – 1000000, деци (д) – 0,1, санти (с) – 0,01, мили (м) – 0,001.
Пример: длина стола равна 95 см. Необходимо выразить длину в метрах (м)?
95 см = 95 * 0,01 = 0,95 м
Учитель: Для измерения физических величин применяют измерительные приборы. Самыми простыми измерительными приборами являются рулетка, мензурка (измерительный цилиндр). Более сложными являются термометр, секундомер.
Измерительные приборы имеют шкалу. Это значит, что на приборе нанесены штриховые деления, а рядом написаны значения величин, соответствующие делениям. Расстояния между двумя штрихами, возле которых написаны значения физической величины, могут быть дополнительно разделены ещё на несколько делений. Эти деления не обозначены числами.
Учитель: Прежде чем приступить к любым измерениям, нужно определить, чему равно одно деление на шкале прибора, т.е. узнать цену деления.
Чтобы определить цену деления, нужно найти два ближайших штриха шкалы, около которых написаны числовые значения. Затем из большего значения вычесть меньшее и полученное число разделить на число делений, находящихся между ними.


На экране изображение шкалы линейки.
Учитель: Для того чтобы определить цену деления, необходимо:
1) найти два ближайших штриха шкалы, возле которых написаны значения величины.
Возьмем 3 см и 4 см.
(На линейке указаны единицы измерения величины. Это сантиметры).
2) вычесть из большего значения меньшее и полученный результат разделить на число делений, находящихся между ними.
Между 3 и 4 десять делений: 4 см —3 см = 1 см;
1 см: 10 делений = 0,1 см/деление.
Каждое маленькое деление равно 0,1 см или 1 мм.

Учитель: Погрешность измерений (равна половине цены деления шкалы)
Формула для учета погрешности: А = а∆𝒂
𝑨 – измеряемая величина
𝒂 – результат измерений
∆𝒂 — погрешность измерений
— Как вы думаете, зачем нужно знать погрешность измерения?
Учитель: Какой же прибор точнее, цена деления которого меньше или больше?
Работа в парах:
Учитель: Вам необходимо для линейки определить верхний и нижний предел измерений, цену деления, погрешность. Данной линейкой определить длину деревянного бруска. Первый ряд работает с линейкой №1, второй — № 2, а третий № 3 Результаты своих вычислений и измерений представьте в виде таблицы. (Маршрутный лист)
Ученики заносят данные таблицу.
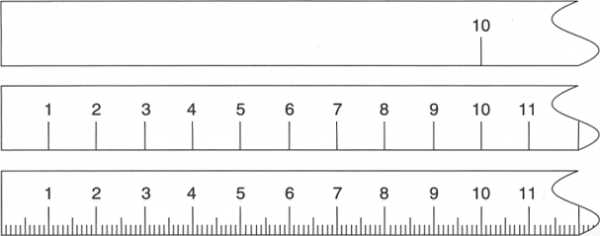
Результат
А = а
Линейка 1
Линейка 2
Линейка 3
infourok.ru
Самостоятельная работа по физике Точность и погрешность измерений 7 класс
Самостоятельная работа по физике Точность и погрешность измерений для учащихся 7 класса с ответами. Самостоятельная работа состоит из 2 вариантов в каждом по 3 задания.
1 вариант
1. Какой множитель означают приставки мега-, санти-, деци-?
2. Запишите в стандартном виде: 100; 6400000; 0,00032.
3. Определите показание прибора с учётом погрешности.
2 вариант
1. Какой множитель означают приставки кило-, мили-, гекто-?
2. Запишите в стандартном виде: 700000; 0,000081; 0,000000015.
3. Определите показание прибора с учётом погрешности.
Ответы на самостоятельную работу по физике Точность и погрешность измерений
1 вариант
1-106; 10-2; 10-1
2-102; 6,4 · 106; 3,2 · 10-4
3-10 ± 0,5
2 вариант
1-103; 10-3; 102
2-7 · 105; 8,1 · 10-5; 1,5 · 10-8
3-5 ± 0,25
testschool.ru

