Смежные и вертикальные углы. Видеоурок. Геометрия 7 Класс

На данном уроке мы рассмотрим и уясним для себя понятие смежные углы. Рассмотрим теорему, которая их касается. Введем понятие «вертикальные углы». Рассмотрим опорные факты, касающиеся этих углов. Далее сформулируем и докажем два следствия об угле между биссектрисами вертикальных углов. В конце занятия рассмотрим несколько задач, посвященных этой теме.

Начнем наш урок с понятия «смежные углы». На рисунке 1 изображен развернутый угол ∠АОС и луч ОВ, который делит данный угол на 2 угла.

                                

Рис. 1. Угол ∠АОС

Рассмотрим углы ∠АОВ и ∠ВОС. Вполне очевидно, что они имеют общую сторону ВО, а стороны АО и ОС являются противолежащими. Лучи ОА и ОС дополняют друг друга, а значит, они лежат на одной прямой. Углы ∠АОВ и ∠ВОС являются смежными.

Определение: Если два угла имеют общую сторону, а две другие стороны являются дополняющими лучами, то данные углы называются смежными.

Теорема 1: Сумма смежных углов – 180^о.

                              

Рис. 2. Чертеж к теореме 1

∠МОL + ∠LON = 180^o. Данное утверждение является верным, так как луч OL делит развернутый угол ∠MON на два смежных угла. То есть мы не знаем градусных мер ни одного из смежных углов, а знаем лишь их сумму – 180^о.

Рассмотрим пересечение двух прямых. На рисунке изображено пересечение двух прямых  в точке О.

    

Рис. 3. Вертикальные углы ∠ВОА и ∠СОD

Определение: Если стороны одного угла являются продолжением второго угла, то такие углы называются вертикальными. Именно поэтому на рисунке изображено две пары вертикальных углов: ∠АОВ и ∠СОD, а также ∠AOD и ∠ВОС.

Теорема 2: Вертикальные углы равны.

Используем рисунок 3. Рассмотрим развернутый угол ∠АОС. ∠АОВ = ∠АОС – ∠ВОС = 180^о – β. Рассмотрим развернутый угол ∠ВОD. ∠CОD = ∠BОD – ∠BОС = 180^о – β.

Из этих соображений мы делаем вывод, что ∠АОВ = ∠СОD = α. Аналогично, ∠AOD = ∠ВОС = β.

Следствие 1: Угол между биссектрисами смежных углов равен 90^о.

                             

Рис. 4. Чертеж к следствию 1

Поскольку ОL – биссектриса угла ∠ВОА, то угол ∠LOB =  , аналогично ∠ВОК =  . ∠LOK = ∠LOB + ∠BOK =  +    =  . Сумма углов α + β равна 180^о, поскольку данные углы – смежные.

Следствие 2: Угол между биссектрисами вертикальных углов равен 180^о.

                  

Рис. 5. Чертеж к следствию 2

KO – биссектриса ∠AOB, LO – биссектриса ∠COD. Очевидно, что ∠KOL = ∠KOB + ∠BOC + ∠COL =  ^o. Сумма углов α + β равна 180^о, так как данные углы – смежные.

Рассмотрим некоторые задачи:

Пример 1:

Найдите угол, смежный с ∠АOС, если ∠АOС = 111^о.

Решение:

Выполним чертеж к задаче:

                             

Рис. 6. Чертеж к примеру 1

Решение

Поскольку ∠АОС = β и ∠СOD = α смежные углы, то α + β = 180^о. То есть 111^о + β = 180^о.

Значит, β = 69^о.

Этот тип задач эксплуатирует теорему о сумме смежных углов.

Пример 2:

Один из смежных углов прямой, каким (острым, тупым или прямым) является другой угол?

Решение:

Если один из углов прямой, а сумма двух углов 180

о, то и другой угол тоже прямой. Эта задача проверяет знания о сумме смежных углов.

Пример 3:

Верно ли, что если смежные углы равны, то они прямые?

Решение:

Составим уравнение: α + β = 180^о, но поскольку α = β, то β + β = 180^о, значит, β = 90^о.

Ответ: Да, утверждение верно.

Пример 4:

Даны два равных угла. Верно ли, что и смежные им углы тоже будут равны?

Решение:

                                                   

Рис. 7. Чертеж к примеру 4

Если два угла равны α, то соответствующие им смежные углы будут 180^о – α. То есть они будут равны между собой.

Ответ: Утверждение верно.

 

Список рекомендованной литературы

1. Александров  А.Д., Вернер А.Л., Рыжик В.И. и др. Геометрия 7. – М.: Просвещение.
2. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия 7. 5-е изд. – М.: Просвещение.
3. \Бутузов В.Ф., Кадомцев С.Б., Прасолова В.В. Геометрия 7 / В.Ф. Бутузова, С.Б. Кадомцев, В.В. Прасолова, под редакцией В.А. Садовничего. – М.: Просвещение, 2010.

 

Рекомендованные ссылки на интернет-ресурсы

1. Измерение отрезков (Источник).
2. Обобщающий урок по геометрии в 7-м классе (Источник).
3. Прямая линия, отрезок (Источник).

 

Рекомендованное домашнее задание

1. № 13, 14. Бутузов В.Ф., Кадомцев С.Б., Прасолова В.В. Геометрия 7 / В.Ф. Бутузова, С.Б. Кадомцев, В.В. Прасолова, под редакцией В.А. Садовничего. – М.: Просвещение, 2010.
2. Найдите два смежных угла, если один из них в 4 раза больше другого.
3. Дан угол. Постройте для него смежный и вертикальный углы. Сколько таких углов можно построить?
4. * В каком случае получается больше пар вертикальных углов: при пересечении трех прямых в одной точке или в трех точках?

interneturok.ru

Луч и угол — урок. Геометрия, 7 класс.

Точка, которая лежит на прямой, разделяет прямую на две части, каждая из которых называется лучом, исходящим из этой точки, а саму точку называют началом каждого из лучей.

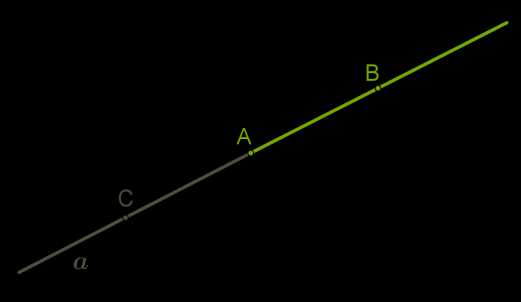
Точка \(A\) разделяет прямую \(a\) на два луча. Так как в задании важно понять, который из лучей рассматривать,

поставим на прямой ещё две точки \(B\) и \(C\) и назовём лучи:

луч \(AB\) и луч \(AC\).

 

Обрати внимание!

Первой точкой всегда называют начальную точку луча.

На этом рисунке любая из точек может быть начальной точкой некоторого луча, который нарисован. Из каждой точки исходят два луча в противоположных направлениях и так же, как прямая, продолжаются бесконечно.

 

Обрати внимание!

Луч \(BC\) — тот же луч \(BA\), но луч \(BC\) oтличается от луча \(AC\). Эти лучи имеют некоторую общую часть.

Угол — геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки. Эти лучи называют сторонами  угла, а их общее начало  — вершиной угла.

 

 

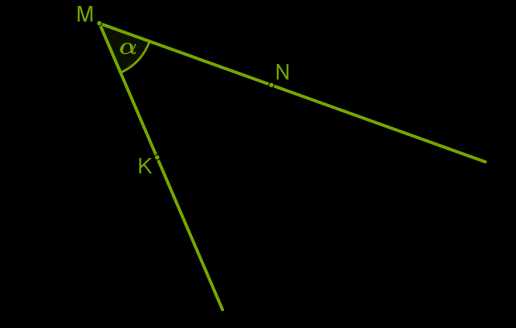
Угол обозначают большими латинскими буквами ∡KMN или малыми греческими буквами, например, α.

 

Обрати внимание!

Угол ∡KMN можно назвать также ∡NMK, но буква вершины всегда пишется посередине.

Иногда угол можно обозначить только одной большой латинской буквой вершины,

цифрой или названиями лучей — малыми латинскими буквами, например, ∡M, ∡1 или ∡mn.

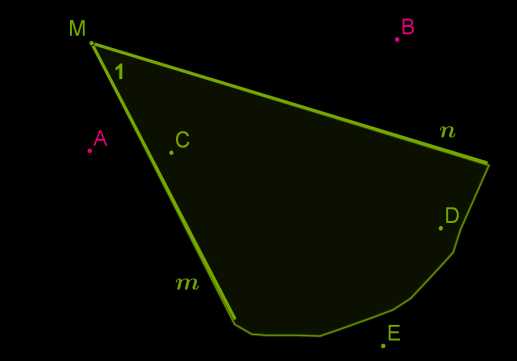
Лучи \(n\) и \(m\) с общим началом в точке \(M\) делят плоскость на две части — внутренняя область угла и внешняя область угла.

Углом можно называть также лучи с общим началом вместе с внутренней областью. Тогда точки \(A\) и \(B\) не принадлежат углу ∡M, а точки \(C\), \(D\) и \(E\) принадлежат углу ∡M.

Если нарисовать два луча, исходящих из одной точки, то внутренняя область образует один угол, а внешняя область образует другой угол.

 

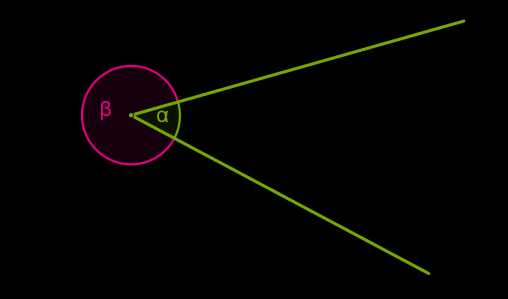
Если обе стороны угла лежат на одной прямой, угол называют развёрнутым.

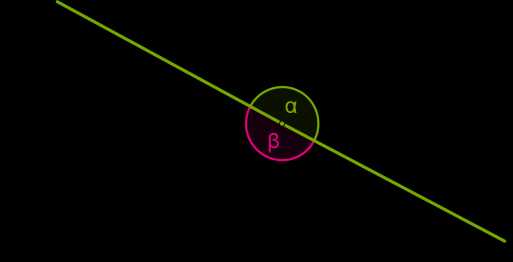У развёрнутого угла любую из двух частей, на которые он разделяет плоскость, можно считать внутренней областью.

 

Если во внутренней области угла провести луч с началом в вершине данного угла, то этот луч делит данный угол на два угла.

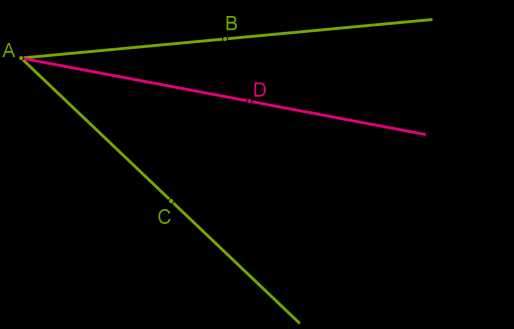
В таком случае очень важно следить за названиями углов, так как мы имеем данный угол и две его части. Например, не совсем понятно, какой угол мы подразумеваем, если пишем ∡A. Лучше использовать три большие буквы, тогда названия углов будут понятны: ∡CAB, ∡CAD, ∡DAB.

www.yaklass.ru

Измерение углов. Видеоурок. Геометрия 7 Класс

Из материала предыдущих уроков мы знаем, что угол – это два луча, выходящие из этой точки. На рисунке 1 изображен угол∠АОВ или , названный в честь лучей, которые из этой точки выходят.

                                                         

Рис. 1. Угол  АОВ

Любой неразвернутый угол имеет внешнюю и внутреннюю области. К примеру, точка М принадлежит внутренней области ∠АОВ.

На предыдущих уроках мы выяснили, что равными фигурами называются те, которые можно совместить наложением. Мы уже умеем сравнивать отрезки. В данный момент мы будем учиться сравнивать углы.

Мы рассмотрели, что в случае, когда один угол является частью другого угла,  данные углы не равны. На рисунке 2 указано это соотношение.

                                                          

Рис. 2. Измерение углов

Однако насколько угол ∠СОА больше угла ∠ВОС? В этом случае нам необходимо ввести эталонный угол и единицы измерения. Рассмотрим рисунок 3.

 

                           

Рис. 3. Угол ∠АОВ – развернутый

В геометрии приняли развернутый угол за 180^о градусов. Это значит, если поделить развернутый угол на 180 частей, то градусная мера одной части будет равна 1^о. Таким образом, больший угол имеет большую градусную меру. Также можно вывести правило суммы градусных мер. К примеру, нам необходимо вычислить градусную меру угла ∠АОВ, а меры углов ∠ВОС и ∠СОА нам известны (см. рис. 2). В таком случае, ∠АОВ = ∠ВОС + ∠СОА. Градусную меру угла можно вычислить, к примеру, транспортиром. На рисунке 4 указаны углы, градусные меры которых равны 150

о и  45^о.

         

Рис. 4. Углы с указанными градусными мерами

Немаловажно уяснить, что углы могут измеряться в минутах и секундах. В одном градусе 60 минут: 1^о = 60^‘. В одной минуте шестьдесят секунд 1′ = 60^«.

В зависимости от величины градусной меры, различают острые, тупые и прямые углы.

   

Рис. 5. Острый, прямой и тупой углы

Прямой ∠АОВ = 90о

Острый 0 < ∠АОВ < 90o

Тупой 90o < ∠АОВ < 180o

Если градусная мера угла равна 90 градусов, то данный угол – прямой. В случае, если мера угла меньше 90⁰, угол острый, а если больше – тупой.

Рассмотрим несколько задач, чтобы закрепить пройденный материал.

Пример 1:

На рисунке изображен угол ∠АОВ, который делится точкой Е на два угла. Найдите градусную меру данного угла, если ∠АОЕ = 44^о, ∠ВОЕ = 77^о.

Рассмотрите случай, когда ∠АОЕ = 12^о37^/, ∠ВОЕ = 108^о25^/

Решение:

Выполним пояснительный рисунок к задаче:

                                                            

Рис. 6. Рисунок к примеру 1

По правилу суммы градусных мер углов, ∠АОВ = ∠ВОЕ + ∠ЕОА. Соответственно, подставим данные в условии значения и выполним подсчет.

1. ∠АОВ = ∠ВОЕ + ∠ЕОА = 44^о + 77^о = 121^о.

2. ∠АОВ =∠ВОЕ + ∠ЕОА = 12^о37^/ + 108^о25^/ = 121^о02^/.

Ответ: 121^о, 121^о02^/.

Пример 2:

На рисунке изображен угол ∠АОВ. Градусная мера данного угла составляет 78^о. Луч ОС делит данный угол на 2 угла. Найдите градусную меру угла ∠ВОС, если угол ∠СОА на 18^о меньше угла ∠ВОС.                         

                                             

Рис. 7. Рисунок к примеру 2

Решение:

Пусть градусная мера угла ∠ВОС равна х^о, тогда мера угла ∠СОА равна (х-18)^о. Поскольку их сумма будет равна 78^о (по условию), составим и решим уравнение:

Х + (х – 18) = 78

2х – 18 = 78

2х = 96

х = 48

Ответ: ∠ВОС = 48^о.

Пример 3:

Луч ОВ делит угол ∠АОС, градусная мера которого составляет 108^о, на 2 части. Найдите градусную меру угла ∠ВОА, если угол ∠ВОА в три раза больше угла ∠ВОС.

                                                              

Рис. 8. Рисунок к примеру 3

Решение:

Решаем эту задачу подобно предыдущей. Пусть градусная мера угла ∠ВОС равна х^о, тогда мера угла ∠ВОА равна (3х)^о. Поскольку их сумма будет равна 108^о (по условию), составим и решим уравнение:

Х + 3х = 108

4х = 108         

х = 27

Соответственно, мера угла ∠ВОА равна (3х)^о, то есть 81^о.

Ответ: 81^о.

Пример 4:

На рисунке изображен развернутый угол ∠АОD. Углы ∠ВОА и ∠СОD равны. Укажите, есть ли на рисунке еще равные углы?

Решение:

Выполним рисунок к задаче.

                                                                         

Рис. 9. Рисунок к примеру 4

Рассмотрим углы ∠АОС и ∠ВОD. Они состоят из равных между собой частей ∠ВОА и ∠СОD, а также общей части ∠ВОС. Выполним следующую запись:

Поскольку ∠ВОС – общий, а ∠АОB = ∠CОD (по условию), то ∠АОС = ∠ВОD.

Ответ: ∠АОС = ∠ВОD.

 

Список рекомендованной литературы

1. Александров  А.Д., Вернер А.Л., Рыжик В.И. и др. Геометрия 7. – М.: Просвещение.
2. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия 7. 5-е изд. – М.: Просвещение.
3. Бутузов В.Ф., Кадомцев С.Б., Прасолова В.В. Геометрия 7 / В.Ф. Бутузов, С.Б. Кадомцев, В.В. Прасолова, под ред. Садовничего В.А. – М.: Просвещение, 2010.

 

Рекомендованные ссылки на интернет-ресурсы

1. Измерение отрезков (Источник).
2. Обобщающий урок по геометрии в 7-м классе (Источник).
3. Прямая линия, отрезок (Источник).

 

Рекомендованное домашнее задание

1. № 11. Бутузов В.Ф., Кадомцев С.Б., Прасолова В.В. Геометрия 7 / В.Ф. Бутузов, С.Б. Кадомцев, В.В. Прасолова, под ред. Садовничего В.А. – М.: Просвещение, 2010.

2. Укажите, чему равна мера угла ∠А, если ∠С = 18^о, а ∠В = 33^о. Сумма всех углов равна 180⁰.

3. Укажите, чему равна градусная мера угла ∠ВОА, если ∠АОС = 108^о, а ∠ВОС в 2 раза больше угла ∠ВОА.

 

4. *Найдите градусную меру угла ∠КОЕ, если ∠СОК = 99^о.

interneturok.ru

Смежные углы / Начальные геометрические сведения / Справочник по геометрии 7-9 класс

1. Главная
2. Справочники
3. Справочник по геометрии 7-9 класс
4. Начальные геометрические сведения
5. Смежные углы

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Точки, прямые, отрезки

Провешивание прямой на местности

Луч

Угол

Равенство геометрических фигур

Сравнение отрезков

Сравнение углов

Длина отрезка

Единицы измерения длины, расстояний

Градусная мера угла

Измерение углов на местности

Вертикальные углы

Перпендикулярные прямые

Построение прямых углов на местности

Начальные геометрические сведения

Правило встречается в следующих упражнениях:

7 класс

Задание 59, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 64, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 175, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 234, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 253, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 263, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 299, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 661, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 715, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 822, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

---

© 2019 — budu5.com, Буду отличником!

budu5.com

Урок геометрии «Смежные и вертикальные углы» (7 класс)

Урок геометрии в 7 классе.

Тема: Смежные и вертикальные углы

Цель урока: Закрепить умения и навыки учащихся по данной теме при решении задач.

Задачи:

I. Организовать деятельность учащихся по изучению и закреплению правил действий над углами (сравнение, сложение и вычитание углов), понятия вертикальных углов и их свойств, понятия биссектрисы.

II. Создать условия для развития у учащихся логического мышления, практических и исследовательских навыков, аналитического мышления, умения грамотно использовать информационные технологии.

III. Способствовать развитию интеллекта и общей математической культуры.

Оборудование: интерактивная доска, мультимедийные средства обучения – диск «Электронный учебник» математика 7 класс, презентация из слайдов, карточки с кроссвордами, индивидуальные разноуровневые задания размноженные в виде рабочей тетради,тесты, индивидуальные оценочные листы(приложение 2), ручка, карандаш, тетрадь, линейка.

Тип урока: обобщающий урок

Используемая технология: технология дифференцированного обучения математике, с применением ИКТ.

«Надо учить не содержанию науки, а деятельности по ее освоению».

В.Г. Белинский.

План урока:

I. Организационный момент – 1 слайд (1 мин)

Девиз урока– 2слайд (1мин)

II. Разминка.

1.Опрос по теории –3слайд (3 мин)

III. Работа по готовым чертежам .– 4-7 слайды (5 мин)

IV. Этап урока: «Кроссворд»(слайд 8-9)

V. Решение задач (10мин)

VI. Физминутка . (слайд 10)

VII. Графический диктант. (слайд 11-12)

VIII. Тестовые задания.

IX. Подведение итогов (2 мин) (слайд 13)

1. Дом. задание – 14 слайд, написать сочинение на тему углы в геометрии и в жизни

2. Рефлексия – 15 слайд

Ход урока

I.Организационный момент – приветствие: проверка готовности к уроку,

-Ребята, сегодня у нас обобщающий урок по теме «Смежные и вертикальные углы». (слайд1)

Мы должны закрепить умения и навыки по данной теме.

У каждого из вас на парте лежат оценочные листы, в течении урока вы должны вписывать туда свои баллы и в конце урока подвести итог.(правила заполнения оценочного листа)

Девиз сегодня на уроке у нас такой:

«Оқусыз білім жоқ ,

Білімсіз күнін жоқ»

«Нет жизни без знания,

Нет знаний без учения»(слайд 2)

Сегодня на уроке мы должны повторить: виды углов, их определения и свойства; показать умение применения этих свойств при решении задач.

Откройте тетради запишите число, классная работа.

II. Разминка.

Начать этап урока со слов немецкого ученого Гольцмана:

«Нет ничего более практичного, чем хорошая теория.»

Итак, Опрос по теории (слайд 3), с самооценкой.

За правильный ответ -1 балл

1. Какая фигура называется углом?

2. Какие углы называют смежными?

3. Какие углы называют вертикальными?

4. Какой луч называется биссектрисой угла?

5. Какие углы называются равными?

6. Чем отличаются смежные и вертикальные углы?(количеством сторон, свойствами, взаиморасположением сторон)

7. При пересечении двух прямых образуются …(пары смежных и пары вертикальных углов)8. Если два угла равны, то…

9. Два угла с общей вершиной равны. Обязательно ли эти углы вертикальные?

10. Обязательно ли два угла с общей стороной смежные?

Подсчитайте количество баллов и внесите в оценочный лист.

III. Работа по готовым чертежам (с комментированием) В этом задании учащиеся оценивают себя также, как на предыдущем этапе урока.(слайд 4-7)

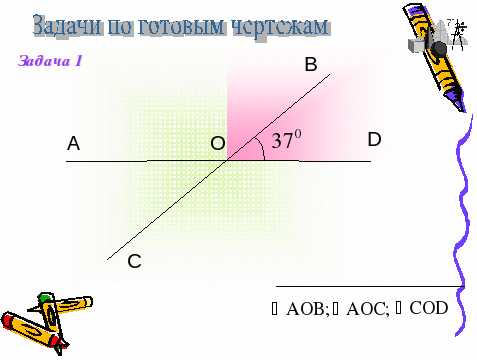
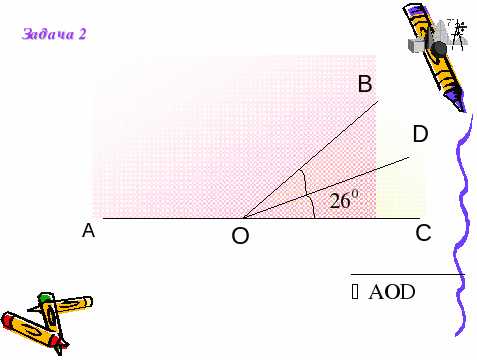
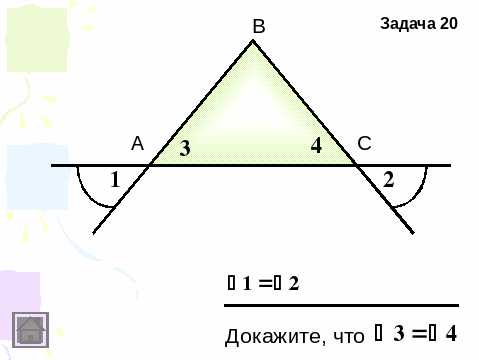
4. «Кроссворд»

Следующий этап урока: «Кроссворд» (слайд 8-9)

У вас на парте лежат листы с кроссвордами, вы сейчас должны, быстро, отвечая на вопросы, вписать правильные ответы в кроссворд (подпишите листы)

1)Как называется угол, градусная мера которого равна 90⁰?

2)1/60 часть градуса?

3)Угол, который меньше прямого угла?

4)Два угла, если при наложении друг на друга их вершины и соответствующие стороны совпадут называются?

5)Что мы делаем с помощью транспортира?

6)Луч, исходящий из вершины угла и делящий угол пополам?

7)Прямоугольник с равными сторонами?

8)Утверждение, истинность, которого не требует доказательства?

— А теперь взаимопроверка (обменялись тетрадями), получили слово пирамида.

Какие ассоциации у вас возникли со словом пирамида? (ответы детей)

— Правильно, родиной пирамид является Египет. Египетские пирамиды – величайшие архитектурные памятники Древнего Египта, среди которых одно из «семи чудес света» — Пирамида Хеопса и почётный кандидат «новых семи чудес света» — Пирамиды Гизы. Пирамиды представляют собой огромные каменные сооружения пирамидальной формы, использовавшиеся в качестве гробниц для фараонов Древнего Египта. Слово « пирамида» — греческое. По мнению одних исследователей, большая куча пшеницы и стала прообразом пирамиды. По мнению других ученых, это слово произошло от названия поминального пирога пирамидальной формы. Всего в Египте было обнаружено 118 гробниц. (слайд 10)

— Одним из древнегреческих учёных является Евклид, он систематизировал весь накопленный материал по геометрии и изложил в своём замечательном труде «Начала». Роль Евклида в истории геометрии так значительна, что геометрию, основы которой он изложил в «Началах», стали называть «Евклидовой геометрией». (слайд 11)

4. Ф

   изминутка для глаз. (слайд 13 с музыкальным

сопровождением)

VI. Решение задач

Решение разноуровневых задач по карточкам

(1 ученик у доски объясняет ход решения задачи, остальные работают в тетрадях). Задания разноуровневые – на «5»,«4» и «3». (Работы собрать на проверку).

Работа у доски:

1) 1.Сумма трёх углов, образовавшихся при пересечении двух прямых, равна 236⁰. Найдите эти углы.

Уровень А

1. Найдите угол смежный с углом АВС, если :

а) АВС=110°; б) АВС = 90°; в) АВС =15°

смежный угол смежный угол смежный угол

равен: равен: равен:

2. Верны или нет следующие утверждения (в случае «нет» напишите рядом верный ответ)

3. Один из смежных углов на 70⁰ больше другого. Найдите величину

каждого угла.

С Дано:АОС и ВОС — смежные

ВОС —АОС =70⁰

А О В Найти:АОС и ВОС.

Уровень В

1. Один из смежных углов в 5 раз больше другого. Найдите эти углы. С

Дано:АОС и ВОС — смежные

С ВОС =5АОС

Найти:АОС и ВОС.

А О В

2. При пересечении двух прямых образовались такие углы, что сумма двух вертикальных из них равна 68°. Определите каждый из четырех углов.

1 2

Дано: 1 и 3, 2 и 4 – вертикальные 4 3

1 + 3 =

Найти:1 , 2, 3 , 4.

3. Сумма трёх углов, образовавшихся при пересечении двух прямых, равна 314⁰. Найдите эти углы.

Уровень С

1.Сумма трёх углов, образовавшихся при пересечении двух прямых, равна 236⁰. Найдите эти углы.

1 2

4 3

2.При пересечении двух прямых образуются четыре угла. Сумма двух углов равна 80⁰ .Найдите величину каждого из этих углов?

3.Даны смежные углы, один в 1,5 раза больше другого. Найдите эти углы. Найдите угол, образованный биссектрисами смежных углов

VII. Графический диктант.

Если верно — ∆

Если не верно —

1. Верно ли , что 2 ⁰ =120 мин

2. Теорема- это утверждение истинность, которого не требует доказательства

3. Углы измеряются в градусах

4. Каждый угол имеет определённую длину, большую нуля

5. Угол смежный прямому – острый

6. Вертикальные углы всегда равны

7. Биссектриса это луч, исходящий из вершины угла

8. Угол, смежный тупому – острый

Если у вас получился вот такой ряд, то вы хорошо усвоили материал.

Поставьте себе в оценочный лист количество баллов.

VIII. Тестовые задания. (открыть электронный учебник)

У каждого из вас на парте тесты с 10 заданиями, за 5 минут вы должны отметить на листах правильные ответы.

Проверка: (эл.учебник математика 7 класс)

Учащиеся поднимают сигнальные карточки с ответами (А- красный, Б- синий, В- зелёный)

Ответы: А,А,Б,Б,А,В,А,А,Б,А.

Поставьте себе в оценочный лист количество баллов.

IX. Подведение итогов (2 мин) (слайд 13)

1. Выставление оценок

2. Дом. задание – (14 слайд), написать сочинение на тему : «Углы в

геометрии и в жизни»

3.Рефлексия – 15 слайд

infourok.ru

Презентация к уроку по геометрии (7 класс) на тему: Луч и угол, урок геометрии 7 класс

Технологическая карта урока		2
Учитель:		Лада Еделева
Предмет:		Математика
Класс:		7
Автор УМК:		Л.С.Атанасян и др.
Тема урока:		Луч и угол
Задачи:
Образовательные:		Организовать работу по формированию представления о луче и угле.
Воспитательные:		Воспитывать культуру умственного труда и культуру общения.
Развивающие:		Развивать внимание, наблюдательность, мышление, интерес к предмету, математическую речь;
Планируемые результаты:
Личностные:		имеют целостное мировоззрение, соответствующее современному уровню развития науки и общественной практики
Предметные:		Владеют базовым понятийным аппаратом по основным разделам содержания; имеют представление об основных изучаемых понятиях как важнейших геометрических моделях, позволяющих описывать и изучать реальные математические процессы и явления
Метапредметные:		владеют первоначальными сведениями об идеях и о методах математики как универсального языка науки и техники, о средствах моделирования явлений и процессов; умеют самостоятельно планировать альтернативные пути достижения целей.
Межпредметные связи:		Черчение; Технология
Формы деятельности:		фронтальная; индивидуальная
Формы обучения:		смешанная
Ресурсы:
Основные:		ПК учителя; электронное приложение к учебнику ; учебник; медиапроектор; презентация по теме
Дополнительные:		видеоурок по теме
Тип урока:		III. Урок применения предметных знаний, умений, навыков
Цель:		Формирование применения предметных знаний, умений, навыков в условиях решения учебных задач повышенной сложности; Создать условия для актуализации знаний учащихся о том, что такое луч и угол, введения на наглядном уровне понятий внутренней и внешней областей неразвернутого угла, ознакомления с различными обозначениями лучей и углов
Этап урока	Деятельность учителя		Деятельность учащихся
			Личностные УУД	Познавательные УУД	Коммуникативные УУД	Регулятивные УУД
Организационный этап	Нацелить обучающихся на урок				мотивация учения, формирование основ гражданской идентичности личности
Проверка домашнего задания, воспроизведение и коррекция опорных знаний учащихся. Актуализация знаний	С помощью презентации проверяется дом.задание ( слайды 1-3)		адекватно воспринимают оценку учителя и одноклассников объясняют самому себе свои отдельные ближайшие цели саморазвития	проводить анализ способов решения задач.	Формулируют собственное мнение и позицию, задают вопросы, слушают собеседника	Выделяют и осознают то, что уже усвоено и что еще подлежит усвоению
Постановка цели и задачи урока. Мотивация учебной деятельности учащихся.	Сообщает тему урока. Предлагает обучающимся сформулировать цели урока. Мотивирует на изучение темы при помощи вопросов о применении луча и угла в дальнейшем для изучения геометрии. (слайд 4)		объясняют самому себе свои отдельные ближайшие цели саморазвития	формулирование познавательной цели	уметь с помощью вопросов добывать недостающую информацию.	Выделяют и осознают то, что уже усвоено и что еще подлежит усвоению
Первичное закрепление новых знаний в знакомой ситуации(типовые)	Вводит понятие луча и угла на основе ранее изученного материала (слайды 5-11)		проявляют широкий интерес к новому учебному материалу, способам решения новых учебных задач	Обрабатывают информацию и передают ее устным, графическим, письменным и символьным способами	уметь с помощью вопросов добывать недостающую информацию. высказывают свою точку зрения и пытаются её обосновать	Критически оценивают полученный ответ, осуществляют самоконтроль, проверяя ответ на соответствие условию
Первичное закрепление новых знаний в измененной ситуации (конструктивные)	1. Предлагает самостоятельно выполнить №8 с дальнейшей проверкой (слайд 12) 2. Вводит понятие внутренней и внешней области угла+ устно задания по закреплению данных понятий( слайды 13-14) 3. № 9, 10, 11 решение вместе+один удоски		проявляют познавательный интерес к изучению математики		уметь с помощью вопросов добывать недостающую информацию. высказывают свою точку зрения и пытаются её обосновать	работают по составленному плану
Творческое применение и добывание знаний в новой ситуации (проблемные задания)	задания 15-16 — устно( слайд 15)		проявляют познавательный интерес к изучению математики	передают содержание в сжатом , выборочном или развёрнутом виде	высказывают свою точку зрения и пытаются её обосновать Формулируют собственное мнение и позицию, задают вопросы, слушают собеседника	работают по составленному плану Выделяют и осознают то, что уже усвоено и что еще подлежит усвоению
Информация о домашнем задании, инструктаж по его выполнению	п.3, 4,+ электронное приложение № 6, 12, 13		объясняют самому себе свои отдельные ближайшие цели саморазвития	проводить анализ способов решения задач.	задавать вопросы, необходимые для организации собственной деятельности	составляют план выполнения задач, решения проблем творческого и поискового характера
Рефлексия (подведение итогов занятия)	Что такое луч? Какие лучи называются дополнительными? Какая геометрическая фигура называется углом? Из каких элементов он состоит?		анализируют соответствие результатов требованиям конкретной учебной задаи	Обрабатывают информацию и передают ее устным способом	умение критично относиться к своему мнению	Выделяют и осознают то, что уже усвоено и что еще подлежит усвоению

nsportal.ru