7 класс алгебра решение систем уравнений – 7 класс. Алгебра. Системы двух уравнений с двумя переменными. — Способы решения систем уравнений с двумя неизвестными.

Содержание

7 класс. Алгебра. Системы двух уравнений с двумя переменными. — Способы решения систем уравнений с двумя неизвестными.

Комментарии преподавателя

Метод подстановки.

Существует несколько методов решения систем. Один из них метод подстановки. Рассмотрим пример.

Пример 1:

Суть метода подстановки заключается в том, что в одном из уравнений нужно выразить одну переменную через вторую и подставить полученное выражение во второе уравнение.

В данном случае удобно выразить х во втором уравнении:

Подставим полученное выражение в первое уравнение:

Преобразуем первое уравнение:

Подставим полученное значение во второе уравнение:

, ,

Получаем следующее решение системы:

Пример 2:

В данном случае некоторая сложность заключается в том, что исходную систему нужно преобразовать, чтобы была возможность удобно и без ошибок применить метод подстановки. Для этого умножим оба уравнения на шесть:

Выразим у из первого уравнения:

Подставим полученное выражение во второе уравнение и выполним преобразования:

, ,

Подставим полученное значение в первое уравнение:

Получаем единственное решение системы, пара чисел:

Вывод:

на данном уроке мы ознакомились с понятием системы двух линейных уравнений с двумя неизвестными и одним из методов ее решения – способом подстановки. Мы решили примеры для понимания и закрепления данной техники.

Источник конспекта: http://interneturok.ru/ru/school/algebra/7-klass/glava-3-sistema-dvuh-lineynyh-uravneniy-s-dvumya-peremennymi/osnovnye-ponyatiya-metod-podstanovki?konspekt&chapter_id=10

Метод сложения.

Рассмотрим еще один способ решения систем двух линейных уравнений с двумя неизвестными – способ алгебраического сложения. Мы решим несколько различных примеров для закрепления техники.

Метод алгебраического сложения, как и метод подстановки, заключается в том, что изначально из двух уравнений с двумя переменными нужно

www.kursoteka.ru

Тренажёр по алгебре (7 класс) на тему: Алгоритм решения систем уравнений методом подстановки и сложения .Алгебра 7 класс.

	Образец решения системы уравнений методом подстановки	АЛГОРИТМ (последовательность шагов при работе)
1.	3х + у = 7 -5х + 2у =3	Выразить из первого уравнения у через х, т.е.перенести 3х в другую часть с противоположным знаком ( т.к. у записан в уравнении без числа(коэффициента)). Получится у = 7 – 3х
2.	у = 7 – 3х	Выделить в рамочку выраженную переменную у. Написать её в той же строчке в системе уравнений.
3.	у = 7 – 3х — 5х + 2(7 – 3х) = 3	Подставить во второе уравнение вместо у выражение (7 – 3х), взяв его в скобки !
4.	х = у =	Приготовить знак системы уравнений и место для будущих ответов х у
5.	-5х + 2·(7 – 3х) = 3 -5х + 14 -6х = 3	«Выйти из системы» и решить отдельно только уравнение с одной переменной х : 1) раскрыть скобки, умножив число перед скобкой на всё что в скобках;
6.	-5х + 14 -6х = 3 -5х — 6х = 3 — 14	2)Перенести число 14 в правую часть уравнения с противоположным знаком, т.е. сделать «сортировку» — буквы к буквам, числа к числам.
7.	— 11х= -11	3)Посчитать значение в левой и правой части уравнения
8.	х = -11:(-11) х = 1	4)Вычислить х как неизвестный множитель, вспомнив простой пример 2 · 3 = 6
9.	х = 1 у =	Заполнить место в системе уравнений для х
10.	у = 7 – 3х = 7 — 3·1 = 7-3 = 4	Найти значение второй переменной у
11.	х = 1 у = 4	Заполнить место в системе уравнений для у
12.	Ответ: (1;4)	Записать ответ в виде координат точки (х;у)

Решить систему уравнений методом подстановки

выбирая удобную переменную для её выражения, когда она записана без числа.

№1. у – 2х = 1 №4. 2х + у = 12

6х – у = 7 7х – 2у = 31

№2. х + у =6 №5. 4х – у = 11

3х – 5у = 2 6х – 2у = 13

№3. 7х – 3у = 13 №6. 8у – х = 4

х – 2у = 5 2х – 21у = 2

Карточка составлена учителем математики Головлянициной Лидией Вадимовной

nsportal.ru

Система линейных уравнений. Алгебра 7 класс.

АЛГЕБРА 7 КЛАСС

Решение систем линейных уравнений



Алгебра стоит на четырёх китах

Число

Уравнение

Тождество

Функция

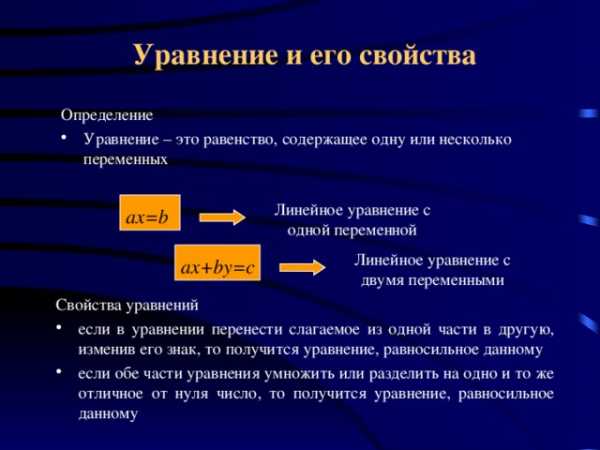
Уравнение и его свойства

Определение

Уравнение – это равенство, содержащее одну или несколько переменных

Линейное уравнение с

одной переменной

ax=b

Линейное уравнение с

двумя переменными

ax+by=c

Свойства уравнений

если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение, равносильное данному
если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному

Система уравнений и её решение

Определения

Системой уравнений называется некоторое количество уравнений, объединенных фигурной скобкой. Фигурная скобка означает, что все уравнения должны выполняться одновременно
Каждая пара значений переменных, которая одновременно является решением всех уравнений системы, называется решением системы
Решением системы уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение системы в верное равенство

Решить систему уравнений — это значит найти все её решения или установить, что их нет

Выразим у через х

Решим

уравнение

Подставим

х=1

Подставим

Из какого-либо уравнения выразить одну переменную через другую
Подставить полученное выражение для переменной в другое уравнение и решить его
Сделать подстановку найденного значения переменной и вычислить значение второй переменной
Записать ответ: х =…; у =… .

Уравняем

модули

коэффи-

циентов

перед у

Решим

уравнение

| |·(-3)

Сложим уравне-

ния почленно

Решим

уравнение

Подставим

Уравнять модули коэффициентов при какой-нибудь переменной
Сложить почленно уравнения системы
Составить новую систему: одно уравнение новое, другое — одно из старых
Решить новое уравнение и найти значение одной переменной
Подставить значение найденной переменной в старое уравнение и найти значение другой переменной
Записать ответ: х=…; у=… .

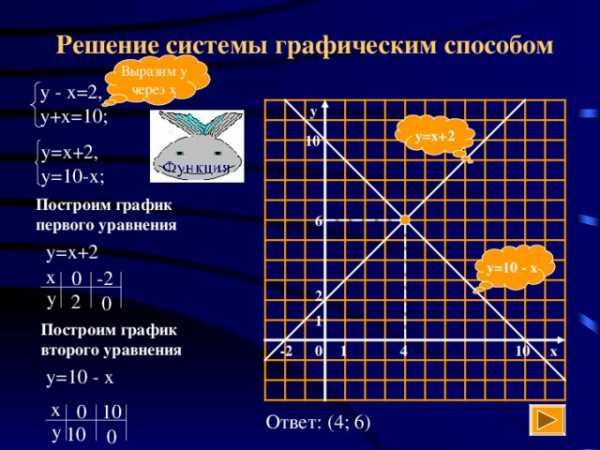
Решение системы графическим способом

Выразим у

через х

y=x+2

Построим график

первого уравнения

y=10 — x

Построим график

второго уравнения

-2

Выразить у через х в каждом уравнении
Построить в одной системе координат график каждого уравнения
Определить координаты точки пересечения
Записать ответ: х=…; у=… , или (х; у)

multiurok.ru

Как решать систему уравнений за 7 класс 🚩 как решать систему уравнений методом подстановки 🚩 Школы

Понять сущность этого способа проще всего на примере решения одной из типичных систем, включающей в себя два уравнения и требующей нахождения значений двух неизвестных. Так, в этом качестве может выступить следующая система, состоящая из уравнений x + 2y = 6 и x — 3y = -18. Для того чтобы решить ее методом подстановки, требуется в любом из уравнений выразить один член через другой. Например, это можно сделать, используя первое уравнение: x = 6 — 2y.

Затем необходимо подставить полученное выражение во второе уравнение вместо x. Результатом такой подстановки станет равенство вида 6 — 2y — 3y = -18. Произведя простые арифметические вычисления, это уравнение легко привести к стандартному виду 5y = 24, откуда y = 4,8. После этого полученное значение следует подставить в выражение, использованное для подстановки. Отсюда x = 6 — 2*4,8 = -3,6.

Затем целесообразно осуществить проверку полученных результатов, подставив их в оба уравнения первоначальной системы. Это даст следующие равенства: -3,6 + 2*4,8 = 6 и -3,6 — 3*4,8 = -18. Оба этих равенства являются верными, благодаря чему можно сделать вывод о том, что система решена правильно.

Второй способ решения подобных систем уравнений носит название способа сложения, который можно проиллюстрировать на основании того же примера. Для его использования следует все члены одного из уравнений умножить на определенный коэффициент, в результате чего один из них станет противоположным другому. Выбор такого коэффициента осуществляется методом подбора, причем одну и ту же систему можно правильно решить, используя разные коэффициенты.

В данном случае целесообразно произвести умножение второго уравнения на коэффициент -1. Таким образом, первое уравнение сохранит свой первоначальный вид x + 2y = 6, а второе приобретет вид -x + 3y = 18. Затем необходимо сложить полученные уравнения: x + 2y — x + 3y = 6 + 18.

Произведя простые вычисления, можно получить уравнение вида 5y = 24, которое аналогично уравнению, ставшему результатом решения системы способом подстановки. Соответственно, корни такого уравнения также окажутся теми же величинами: x = -3,6, y = 4,8. Это наглядно демонстрирует, что оба способа являются одинаково применимыми для решения систем подобного рода, и оба дают одинаковые правильные результаты.

Выбор того или иного способа может зависеть от личных предпочтений ученика или от конкретного выражения, в котором проще выразить один член через другой или подобрать коэффициент, который сделает члены двух уравнений противоположными.

Очень часто при решении задач по алгебре для 7 класса сложность представляют примеры с многочленами. При упрощении примеров или приведении их к заданному виду следует знать основные правила преобразования многочленов. Также ученику потребуются основы работы со скобками. Любой пример можно упростить, сократив выражение на общий делитель, выведя общую часть за скобки или выполнив приведение к общему знаменателю. При любом преобразовании многочлена очень важно учитывать знак каждого его слагаемого.

Инструкция

Запишите заданный пример на листке. Если он представляет собой многочлен, выделите в нем общую часть. Для этого найдите все слагаемые с одинаковым основанием. Одинаковое основание имеют члены с одной буквенной частью, а также с одной степенью. Такие слагаемые называют подобными. Сложите подобные члены. При этом учитывайте знаки, стоящие перед ними. Если перед одним из них стоит знак «-», вместо сложения выполните вычитание членов и с учетом знака же запишите результат. Если знак «-» имеют оба члена, следовательно выполняется их сложение и результат записывается также со знаком «-».

При наличии дробных значений в коэффициентах многочлена, приведите для упрощения примера дроби к общему знаменателю. Для этого умножьте все коэффициенты выражения на одно и то же число так, чтобы при сокращении дробей осталась лишь целая часть. В самом простом случае общий знаменатель является произведением всех знаменателей в дробных коэффициентах. После умножения всех членов, проведите упрощение подобных слагаемых.

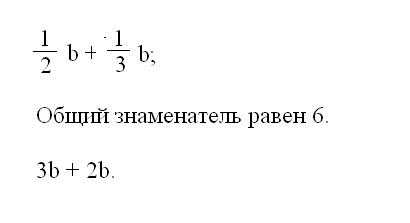
После приведения к общему знаменателю и сложению подобных членов вынесите общие части выражения за скобки. Для этого определите группу членов, где имеется одинаковая часть выражения. Поделите коэффициенты группы на общую часть и запишите ее впереди скобок. В скобках оставьте не весь многочлен, а именно данную группу членов с оставшимися от деления коэффициентами.

Не потеряйте знак при выносе за скобки. Если вы хотите общую часть вынести со знаком «-», то для каждого члена в скобках замените знак на противоположный. Остальные члены, не участвующие в выносе за скобки, запишите до или после скобок с сохранением их знака.

Если за скобки выносится общая часть со степенью, для группы в скобках производится вычитание показателя выносимой степени. При раскрытии скобок степени подобных членов складываются, а коэффициенты умножаются.

Выражение можно сократить на целое число, если на него делятся все коэффициенты многочлена. Проверьте, нет или в заданном примере общего делителя. Для этого найдите для всех коэффициентов число, на которое нацело поделится каждый из них. Выполните деление всех коэффициентов многочлена.

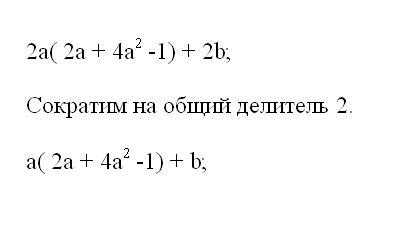
Если для решения примера задано значение буквенной переменной, подставьте ее в преобразованное выражение. Посчитайте результат и запишите. Пример решен.

Алгебру не очень любят в школе. Кому захочется сидеть и решать квадратные уравнения, строить графики, находить интегралы и раскладывать многочлены, если за окном весна, подруга написала важную смс, а поступать вы собираетесь в гуманитарный институт на журналиста? Так как же одолеть эту тяжкую науку?

Инструкция

Если вы обнаружили некоторые пробелы в знаниях, соберите все имеющиеся учебники математики и начинайте их перелистывать в поисках тех тем, которые остались непонятными. Внимательно читайте эти темы и самостоятельно решайте примеры, чтобы понять принцип вычислений. Приобретите справочник по математике, если учебников слишком много и у вас мало времени. Справочники хороши тем, что содержат много информации при сравнительно небольшом объеме. Читайте нужные вам темы, а затем отправляйтесь к задачникам и закрепляйте полученные знания на практике.

Договоритесь о занятиях с репетитором, если самостоятельные занятия для вас – тяжкий и бесполезный труд. Каждый репетитор по сути – тот же учитель, только внимательный именно к вам. Поэтому никогда не стесняйтесь задавать вопросы, уточнять, а главное, не бойтесь ошибаться. Репетитор – ваш проводник в мир алгебры, у него есть собственный план изучения, а также множество разнообразных материалов для самостоятельной и дополнительной работы. Поэтому на начальной ступени изучения или повторения курса алгебры всегда есть смысл найти кого-то, кто разбирается в нем гораздо лучше.

Пишите шпаргалки с формулами и определениями. Речь не о том, чтобы использовать их на экзамене. Развесьте эти маленькие бумажки у себя в квартире, можно в ванной и на кухне, и, разумеется, в уборной (лидер по эффективности повторения изученного материала). Глядя на все эти формулы каждый день, вы сделаете их частью своего сознания и однажды не заметите, как они начнут всплывать у вас в памяти сами собой.

Система уравнений представляет собой совокупность математических записей, каждая из которых содержит некоторое количество переменных. Существует несколько способов их решения.

Вам понадобится

-линейка и карандаш;
-калькулятор.

Инструкция

Решить систему уравнений — означает найти множество всех ее решений, или доказать, что она их не имеет. Её принято записывать с помощью фигурной скобки. Для решения системы уравнений с двумя переменными обычно используют следующие методы: графический способ, способ подстановки и способ сложения. Остановимся подробнее на первом из вышеперечисленных вариантов. Рассмотрим последовательность решения системы, которая состоит из линейных уравнений имеющих вид: a1x + b1y = c1 и a2x + b2y = c2. Где x и y – неизвестные переменные, а b,c – свободные члены. При применении данного способа каждое решение системы представляет собой координаты точек прямых, соответствующих каждому уравнению. Для начала в каждом случае выразите одну переменную через другую. Затем задайте переменной х несколько любых значений. Достаточно два. Подставьте в уравнение и найдите y. Постройте систему координат, отметьте на ней полученные точки и проведите через них прямую. Аналогичные расчеты необходимо провести и для других частей системы.

Точка или точки пересечения построенных графиков и будут являться решением данной совокупности уравнений.

Система имеет единственное решение, если построенные прямые пересекаются и имеют одну общую точку. Она несовместна, если графики параллельны друг другу. И имеет бесконечно много решений, когда прямые сливаются друг с другом.

Данный способ считается очень наглядным. Главным недостатком является то, что вычисленные неизвестные имеют приближенные значения. Более точный результат дают так называемые алгебраические методы.

Любое решение системы уравнений стоит проверить. Для этого подставьте вместо переменных полученные значения. Так же можно найти его решение несколькими методами. Если решение системы верное, то все ответы должны получиться одинаковыми.

Уравнение – это запись математического равенства с одним или несколькими аргументами. Решение уравнения заключается в поиске неизвестных значений аргументов – корней, при которых заданное равенство истинно. Уравнения бывают алгебраические, неалгебраические, линейные, квадратные, кубические и др. Для их решения необходимо освоить тождественные преобразования, переносы, подстановки и другие операции, позволяющие упрощать выражение, сохраняя заданное равенство.

Инструкция

Линейное уравнение в общем случае имеет вид: ах + b = 0, причем неизвестная величина х здесь может быть только в первой степени, также она не должна находится в знаменателе дроби. Однако при постановке задачи часто уравнение предстает, например, в таком виде: х+2/4 + х = 3 – 2*х. В этом случае перед вычислением аргумента необходимо привести уравнение к общему виду. Для этого выполняется ряд преобразований.

Перенесите вторую (правую) часть уравнения по другую сторону равенства. При этом каждое слагаемое поменяет свой знак: х+2/4 + х — 3 + 2*х = 0. Проведите сложение аргументов и чисел, упростив выражение: 4*х – 5/2 = 0. Таким образом, получена общая форма записи линейного уравнения, отсюда легко найти х: 4*х = 5/2, х = 5/8. Помимо описанных операций, при решении уравнений следует использовать 1 и 2 тождественные преобразования. Их суть заключается в том, что обе части уравнения можно сложить с одним и тем же или умножить на одно и то же число или выражение. Полученное уравнение будет выглядеть иначе, но его корни останутся неизменными. Решение квадратных уравнений вида ах² + bх +с = 0 сводится к определению коэффициентов а, b, с и их подстановки в известные формулы. Здесь так же, как правило, для получения записи общего вида необходимо предварительно выполнять преобразования и упрощения выражений. Так, в уравнении вида -х² = (6х + 8)/2 раскройте скобки, перенося правую часть за знак равенства. Получится следующая запись: -х² — 3х + 4 = 0. Умножьте обе части равенства на -1 и запишите результат: х² + 3х — 4 = 0.

Вычислите дискриминант квадратного уравнения по формуле D = b² – 4*a*c = 3² – 4*1*(-4) = 25. При положительном дискриминанте уравнение имеет два корня, формулы нахождения которых таковы: х1 = -b + √(D)/2*а; х2 = -b — √(D)/2*а. Подставьте значения и вычислите: х1 = (-3+5)/2 = 1 и х2 = (-3-5)/2 = -4. Если бы полученный дискриминант был равен нулю, уравнение имело бы лишь один корень, что следует из приведенных формул, а при D

При нахождении корней кубических уравнений используют метод Виета-Кардано. Более сложные уравнения 4 степени вычисляются с помощью замены, в результате которой понижается степень аргументов, и уравнения решаются в несколько этапов, как квадратные.

www.kakprosto.ru

«Решение систем линейных уравнений с двумя переменными» ( алгебра- 7 класс)

Просмотр содержимого документа
«»Решение систем линейных уравнений с двумя переменными» ( алгебра- 7 класс)»

Решение

систем линейных уравнений

с двумя переменными

Алгебра – 7 класс

Системами уравнений называют записи, представляющие собой расположенные друг под другом уравнения, объединенные слева фигурной скобкой, которые обозначают множество всех решений уравнений, одновременно являющихся решениями каждого уравнения системы.

Решением системы уравнений с двумя переменными называется пара значений этих переменных, обращающая каждое уравнение системы в верное числовое равенство, другими словами, являющаяся решением каждого уравнения системы

Формируемые результаты

Предметные : обобщить и систематизировать знания о системах двух линейных уравнений с двумя переменными.

Личностные : формировать умение соотносить полученный результат с поставленной целью.

Метапредметные : формировать умение сравнивать, анализировать, обобщать по разным показателям, моделировать выбор способов деятельности, группировать.

Графическое решение систем

линейных уравнений с двумя переменными

Если угловые коэффициенты прямых различны, то они пересекаются в одной точке, следовательно , система имеет единственное решение .
Если угловые коэффициенты прямых одинаковы, а точки пересечения с осью Оу различны, то прямые параллельны, следовательно, система не имеет решения.
Если уравнения прямых одинаковы, то их графики совпадают, следовательно, система имеет бесконечно много решений .

Решение систем линейных уравнений способом подстановки

4х + у = 2,

х– у = 3.

1-й шаг. Выразить из какого – нибудь уравнения системы одну переменную через другую.

2-й шаг. Подставить в другое уравнение системы вместо этой переменной полученное выражение.

х = 3 + у

4(3 + у) + у = 2,

3-й шаг .

х = 3 + у

4-й шаг.

4(3 + у) + у = 2,

Решить полученное уравнение с одной переменной.

12 + 4у + у = 2,

Найти соответствующее значение второй переменной.

х = 3 + у,

5-й шаг. Записать ответ

х = 3 + ( -2) ,

5у = — 12 + 2,

Ответ : ( 1 ; — 2)

5у = — 10,

х = 1.

у = — 2.

Решение систем линейных уравнений способом подстановки

3х + 2у = — 1,

5х + 4 у = — 3.

1-й шаг Умножить почленно уравнения системы на

такие множители, чтобы коэффициенты при

— 6х – 4у = 2,

2-й шаг . Сложить почленно левые и правые части

5 х + 4у = -3.

уравнений системы.

— х = — 1,

одной из переменных стали противоположными.

3-й шаг .

4-й шаг.

— х = — 1,

Решить получившееся уравнение с одной

Найти соответствующее значение второй

если х = 1 , то 3х + 2у = — 1,

х = — 1 : (-1),

5-й шаг. Записать ответ

переменной.

· 1 + 2у = — 1,

х = 1

переменной.

Ответ : ( 1 ; — 2)

2у = — 4,

у = — 2.

Самостоятельная

работа

Задание № 1

Умножьте одно из уравнений системы на такое число, чтобы с помощью сложения можно было исключить одну из переменных.

а) б)

в)

х – у = 7,

5х + 3у = 2 ;

х + 3у = 1,

— 4х + 2у = 5 ;

2х + 3у = — 2,

5х – 6у = 4.

Задание № 1

а) б)

в)

х – у = 7,

5х + 3у = 2 ;

х + 3у = 1,

— 4х + 2у = 5 ;

2х + 3у = — 2,

5х – 6у = 4.

Задание № 2

Решите систему уравнений способом подстановки и сделайте проверку :

а)

б)

х + 2у = -1,

х — у = — 2 ;

5 х – 3у = 14,

2х + у = 10 .

Задание № 3

Решите способом сложения систему уравнений :

а)

б)

х + у = 4,

3х — у = 20 ;

4 х – 5у = 1,

2х — 3у = 2 ;

multiurok.ru

Решение систем линейных уравнений методом сложения. Номер №200

Вариант 1:

Контрольная работа №1. Тема. Линейное уравнение с одной переменной:

1; 2; 3; 4; 5;

Контрольная работа №2. Тема. Степень с натуральным показателем. Одночлены. Многочлены. Сложение и вычитание многочленов:

1; 2; 3; 4; 5; 6; 7; 8; 9;

Контрольная работа №3. Тема. Умножение одночлена на многочлен. Умножение многочлена на многочлен. Разложение многочленов на множители:

1; 2; 3; 4; 5; 6; 7; 8;

Контрольная работа №4. Тема. Формулы сокращенного умножения:

1; 2; 3; 4; 5; 6; 7;

Контрольная работа №5. Тема. Сумма и разность кубов двух выражений. Применение различных способов разложения многочлена на множители:

1; 2; 3; 4; 5; 6;

Контрольная работа №6. Тема. Функции:

1; 2; 3; 4; 5;

Контрольная работа №7. Тема. Системы линейных уравнений с двумя переменными:

1; 2; 3; 4; 5; 6;

Контрольная работа №8. Тема. Обобщение и систематизация знаний учащихся:

1; 2; 3; 4; 5; 6;

Вариант 2:

Контрольная работа №1. Тема. Линейное уравнение с одной переменной:

1; 2; 3; 4; 5;

1; 2; 3; 4; 5; 6; 7; 8; 9;

1; 2; 3; 4; 5; 6; 7; 8;

Контрольная работа №4. Тема. Формулы сокращенного умножения:

1; 2; 3; 4; 5; 6; 7;

1; 2; 3; 4; 5; 6;

Контрольная работа №6. Тема. Функции:

1; 2; 3; 4; 5;

Контрольная работа №7. Тема. Системы линейных уравнений с двумя переменными:

1; 2; 3; 4; 5; 6;

Контрольная работа №8. Тема. Обобщение и систематизация знаний учащихся:

1; 2; 3; 4; 5; 6;

gdzplus.me

Основные понятия — урок. Алгебра, 7 класс.

1. решить систему уравнений:

x+2y−5=0,2x+4y+3=0.

Графиком уравнения x+2y−5=0 является прямая.

Найдём две пары значений переменных \(x\) и \(y\), удовлетворяющих этому уравнению.

\(x\)	\(5\)	\(0\)
\(y\)	\(0\)	\(2,5\)

Построим на координатной плоскости \(xОy\) прямую l1, проходящую через эти две точки.

Графиком уравнения 2x+4y+3=0 также является прямая.

Найдём две пары значений переменных \(x\) и \(y\), удовлетворяющих этому уравнению.

\(x\)	\(-1,5\)	\(2,5\)
\(y\)	\(0\)	\(-2\)

Построим на координатной плоскости \(xОy\) прямую l2, проходящую через эти две точки.

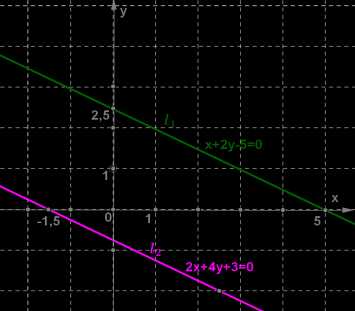
Прямые l1 и l2 параллельны, значит, система не имеет решений, так как нет точек, удовлетворяющих одновременно и одному, и другому уравнению, т. е. принадлежащих одновременно и одной, и другой из построенных прямых.

Ответ: система не имеет решений.

2. Решить систему уравнений:

2x−y−5=0,2x+y−7=0.

Построим графики уравнений системы, преобразуя каждое уравнение к виду линейной функции. Получим из первого уравнения \(y=2x-5\) и из второго уравнения \(y=-2x+7\).

Графиком уравнения \(y=2x-5\) является прямая.

Найдём две пары значений переменных \(x\) и \(y\), удовлетворяющих этому уравнению.

\(x\)	\(0\)	\(3\)
\(y\)	\(-5\)	\(1\)

Построим на координатной плоскости \(xОy\) прямую l1, проходящую через эти две точки.

Графиком уравнения \(y=-2x+7\) также является прямая.

Найдём две пары значений переменных \(x\) и \(y\), удовлетворяющих этому уравнению.

\(x\)	\(0\)	\(1\)
\(y\)	\(7\)	\(5\)

Построим на координатной плоскости \(xОy\) прямую l2, проходящую через эти две точки.

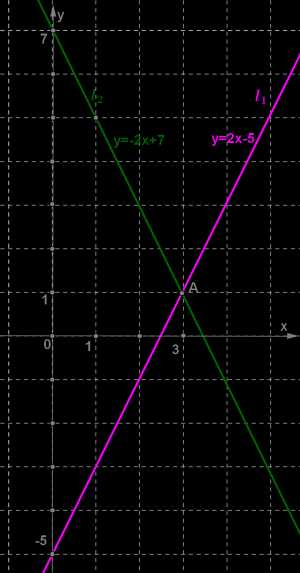
Прямые l1 и l2 пересекаются в точке \(A\), координаты которой — единственное решение заданной системы.

Ответ: \((3;1)\).