Основное свойство дроби 6 класс конспект: Конспект урока математики в 6 классе «Основное свойство дроби»
Конспект урока математики в 6 классе «Основное свойство дроби»
План-конспект урока
по математике
в 6 классе
на тему «Основные свойства дроби»
Разработала: Комиссарова Н.В.
с. Октябрьское, 2017
Тема урока: «Основное свойство дроби»
Дата проведения:.
Тип урока: урок открытия новых знаний
Технология урока.
Цели урока: познакомить с основным свойством дроби и научить применять его в преобразовании дробей; способствовать формированию самооценки учащихся; формирование навыков взаимодействия друг с другом при работе в парах и группах.
Задачи:
Планируемые образовательные результаты.
Предметные: применяют основное свойство дроби
Личностные: умение вести диалог на основе равноправных отношений и взаимного уважения и принятия;
Регулятивные: планировать пути достижения целей; адекватно самостоятельно оценивать правильность выполнения действия и вносить необходимые коррективы в исполнение как в конце действия;
Коммуникативные: устанавливать и сравнивать разные точки зрения, прежде чем принимать решения и делать выбор; осуществлять контроль, коррекцию, оценку действий партнёра, уметь убеждать; работать в группе — устанавливать рабочие отношения;
Познавательные: создавать и преобразовывать модели и схемы для решения задач; давать определение понятиям.
Основные термины, понятия: дробь, правильная дробь, неправильная дробь, числитель, знаменатель.
Оборудование (компьютер, проектор, раздаточный материал, учебник).
План урока:
Организационный момент.
Устный счет
Сообщение темы урока.
Актуализация знаний
Усвоение новых знаний
Первичное закрепление знаний
Физминутка
Самостоятельная работа с самопроверкой по эталону
Рефлексия деятельности.
Информация о домашнем задании
Ход урока
Организационный момент. (1-2 мин.)Деятельность обучающихся
Примечания
— Здравствуйте ребята!
Посмотрите, все ль в порядке:
книжки, ручки и тетрадки?
— У вас у каждого на столах по три карточки, покажите ту, которая соответствует вашему настроению в данный момент.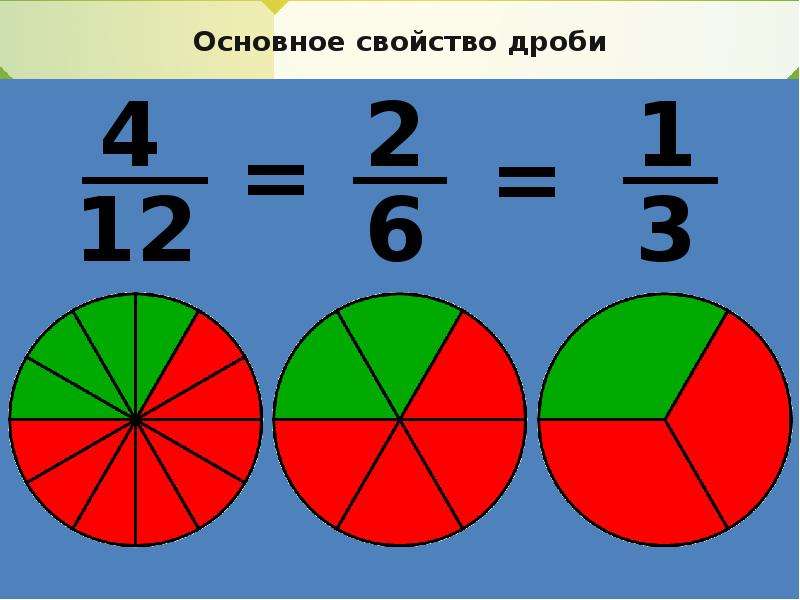
— Да, готовы мы к уроку,
подготовили все к сроку.
Показывают одну из карточек.
Прием проверки настроения «Мордашки»
Устный счет (5 мин.)
— Прочитайте числа: (слайд 1). Назовите числитель и знаменатель каждой дроби.
— Что показывает знаменатель дроби?
— Что показывает числитель дроби?
— На какие группы можно разделить данные числа? (слайд 2)
Читают числа, называют числитель и знаменатель каждой дроби.
— На сколько равных частей разделили целое.
— Сколько таких равных частей взяли.
— Дробные – обыкновенные и десятичные дроби; натуральные числа; число нуль)
Используется презентация
Обучающиеся отвечают по цепочке.
Сообщение темы урока. (3 мин.)
— Как вы думаете, какова тема нашего урока?
— Правильно.(слайд 3) Мы познакомимся сегодня с основным свойством дроби и научимся его применять.
— А вы знаете как называли дроби в первых учебниках математики? Почему?
— Запишите в тетради тему урока «Основное свойство дроби»
— Дроби
— Ломаные числа. Так они показывают часть целого.
Записывают.
Если ученики не знают ответа, то ответ дает учитель.
Актуализация знаний (7 мин.)
— Возьмите циркули и нарисуйте круг. Разделите его на 4 равные части, 3 из них закрасьте. (слайд 4)
— Какая часть круга закрашена? Запишите дробь.
— Теперь каждую четверть круга разделим еще на 4 равные части.
— Какая часть круга закрашена?
Рисуют круг, делят на 4 части, закрашивают 3 из них.
— Три четвертых круга.
Делят каждую четверть круга на 4 части.
— Двенадцать шестнадцатых.
Учитель выполняет построения у доски (или сильный ученик)
Усвоение новых знаний (5 мин.
 )
)
— Мы получили две дроби для записи одной и той же части целого. Что можно сказать об этих дробях?
— Как были получены эти дроби?
— Мы подошли с вами к основному свойству дроби: Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь. (слайд 5)
— Две равные дроби являются различными записями одного и того же числа.
— Дроби равны.
Записывают:
= =
Записывают свойство в тетрадь.
Первичное закрепление новых знаний. (8-10 мин.)
— Приведите примеры равных дробей
— Посмотрите на слайд и назовите равные дроби.(слайд 6) Докажите, что они равны.
— Знали ли вы раньше, что 1/4 и 15/60 часа – это одно и то же время? Какое свойство помогает вам это понять?
—Какое натуральное число нужно записать вместо буквы, чтобы было верным равенство (слайд 7):
Приводят примеры.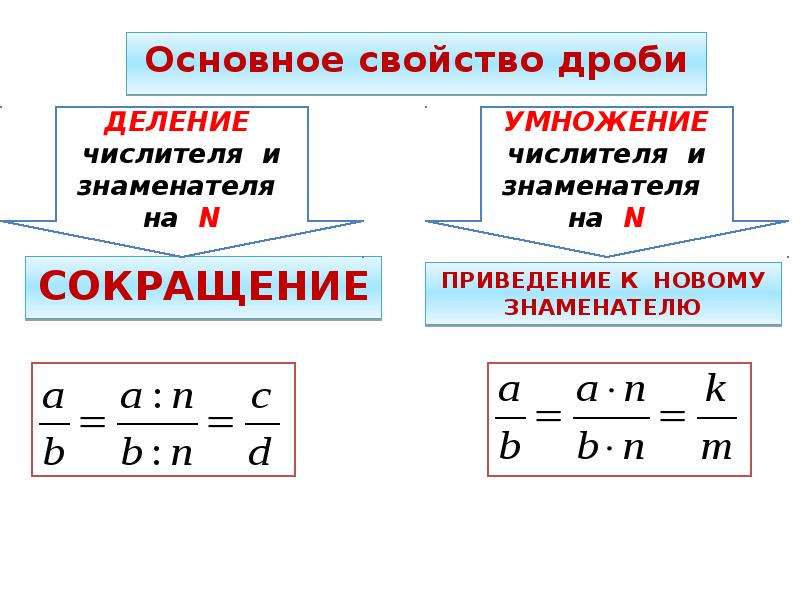 Записывают в тетрадь.
Записывают в тетрадь.
— Основное свойство дроби
= = ; = = ; = = ;
= =
= = ; = = ;
= = ;
= =
=
32:4=8, тогда 24:8=3
х=3
=
10:5=2, тогда 12:2=6, у=6
Работа по учебнику.Стр.35, №212.
Работа по учебнику.Стр.36, №216, №217
Обучающиеся работают у доски по очереди, применяют основное свойство дроби, поясняют свои действия.
Учитель консультирует обучающихся при затруднении.
Обучающиеся работают у доски по очереди, применяют основное свойство дроби, поясняют свои действия.
VII.Физкультминутка (2 мин.)
Раз – подняться, потянуться,
Два – согнуться, разогнуться.
Три – в ладоши три хлопка,
Головою тори кивка.
На четыре — руки шире,
Пять – руками помахать,
Шесть – за парту тихо сесть.
Дежурный проводит зарядку под музыку
VIII. Самостоятельная работа с самопроверкой по эталону (4-6 мин.)
Самостоятельная работа с самопроверкой по эталону (4-6 мин.)
— Восстановите запись (слайд 8):
— Выполните самопроверку (слайд 9)
— Оцените свою работу по критериям:
8 верных ответов – «5»
6-7 верных ответов – «4»
4-5 верных ответов – «3»
менее 4 верных ответов – «2»
а) б) в) г)
д) = е) = ж) з) =
Проводят самопроверку по эталону со слайда.
Оценивают свои работы.
Время на выполнение 5 минут.
IX. Рефлексия деятельности. (4 мин.)
Удалось ли нам решить поставленные перед нами задачи?
Что понравилось на уроке?
Что не понравилось?
Над чем нужно еще работать?
У вас у каждого на столах по три карточки, покажите ту, которая соответствует вашему настроению в данный момент.
 Что повлияло на смену настроения во время урока?
Что повлияло на смену настроения во время урока?
Высказывают мнения, пожелания.
Поднимают карточки, объясняют причины (на уроке все получалось или не получалось, понял материал урока, не понял, интересно было на уроке или неинтересно …)
Прием проверки настроения «Мордашки»
X.Информация о домашнем задании (2-3 мин.)
Учитель комментирует домашнее задание.(слайд 8)
-Урок окончен, спасибо всем за работу!
Записывают задание в дневники.
— До свидания!
П.8 с.34-35 выучить основное свойство дроби ,№237,238, 241 (а) *.
Прочитать текст под рубрикой «Говори правильно» на стр.35.
Список использованной литературы:
Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. Математика, 6 класс. Учебник для общеобразовательных учреждений. – М.: Мнемозина, 2015 г.
В.Н. Рудницкая.
 Тесты по математике к учебнику Н.Я. Виленкина и др. «Математика. 6 класс» М.: «Экзамен», 2013 г.
Тесты по математике к учебнику Н.Я. Виленкина и др. «Математика. 6 класс» М.: «Экзамен», 2013 г.
Этапы урока | Содержание урока. Деятельность учителя | Деятельность обучающихся | Формирование УУД | 1.Организация начала урока | Добрый день, ребята! Каково ваше настроение? Давайте поприветствуем гостей и одноклассников улыбкой и сохраним хорошее настроение в течение всего урока. | Оценивание готовности к уроку, психологический настрой на работу. | Личностные: эмоционально-положительное восприятие учения, уважение друг к другу Коммуникативные: планирование учебной деятельности Регулятивные: саморегуляция | 2. | Ребята, нужны ли в жизни человеку математические знания? А математика может обойтись без дробей? Почему? Что обозначает слово «дробь? В русском языке слово «дробь» появилось в 8 веке, оно происходит от глагола «дробить» — разбивать, ломать на части. В первых учебниках математики (в 17 веке) дроби так и назывались – «ломанные числа». Современную систему записи дробей с числителем и знаменателем создали в Индии. Только там писали знаменатель сверху, а числитель снизу и не писали дробной черты. На Руси дроби называли долями, позднее «ломаными числами». Перед вами названия некоторых дробей: 1/2 — половина, полтина; 1/3- треть; 1/6 – полтреть; 1/4 — четь; 1/8 – полчеть: 1/5 – пятина; 1/10 – десятина. Дробная черта появилась в записи дробей лишь около 300 лет назад. Названия «числитель и знаменатель» ввел в употребление греческий математик Максим Пеануд. | Ответы на вопросы. Высказывание своего мнения. Восприятие и осмысление | Личностные: умение слушать собеседника, обсуждать вопросы Познавательные: поиск и выделение необходимой информации, осознание и произвольное построение речевого высказывания в устной форме Коммуникативные: планирование учебного сотрудничества в устной форме, анализ объектов | Целеполагание | Ребята, мы с вами вспомним как сейчас пишут и читают дроби, числа. Прочитайте числа .(на экране) Ответьте на вопросы: Назовите обыкновенные дроби. Назовите правильные и неправильные дроби. Дайте им определение. Что показывает числитель(знаменатель дроби)? Нет ли среди дробей равных? Почему вы решили, что они равные? Сравните записи этих чисел. Откройте тетради, запишите число, классная работа. Запишите в тетрадь равные дроби. Попробуйте дать определение равных дробей. Перед вами лежат карточки с практическими заданиями. Закрасьте: 1 вариант : 1/3 круга 3/4 квадрата 2/3 полоски 2 вариант : 2/6 круга 9/12 квадрата 10/15 полоски Сравните закрашенные фигуры и сделайте выводы (работа в группах) Запишите результаты своей работы в тетрадях(один человек —на доске) . Какие же дроби получили? Давайте сформулируем определение равных дробей. Итак, дроби равны. Но мы не можем всегда заштриховывать, сравнивать дроби наложением. Проблемный вопрос. Как же одну дробь получить из другой? (дети отвечают). Это свойство очень важное в математике, поэтому его называют «основным». Вы, ребята, сделали открытие!!! Подскажите мне, пожалуйста, какая же тема нашего урока? Какие цели и задачи нам необходимо решить на уроке? Ответьте устно на вопрос. Вам «встречалась» дробь 120/600 ? Как же вы написали ответ в домашней работе? Как вы догадались? Кто вам помог? ФИЗМИНУТКА Найдите равные дроби , «нажав» на них компьютерной мышкой . (Вызываю Морозову Полину). Задаю вопросы классу: Правильно ответила Полина? (поднимают вверх руки, показывают « класс»). Я знаю, что у нее сегодня День рождения(Руки вверх—хлопки). Пожелаем ей много счастья!(руки в стороны). Пусть она всегда получает «5»!(Рисуют двумя руками «5»). Желаем ей крепкого здоровья!(Встают) | Отвечают на вопросы учителя. Работают в группах. Делают вывод:1/3=2/6,3/4=9/12, 2/3=10/15. Дают определение равных дробей. Делают вывод: как из одной дроби получить другую. Получают основное свойство дроби. Формулируют тему урока, определяют цели и задачи. Дети, выполняя задание, объясняют, как получена дробь. Работают устно. Выполняют вслед за учителем | Личностные: умение работать в паре, нравственно-этическая ориентация Коммуникативные: планирование учебного сотрудничества, анализ объектов, обсуждение проблемного вопроса Познавательные: поиск и выделение необходимой информации, осознание и произвольное построение речевого высказывания в устной и письменной форме, самостоятельное создание способов решения проблем, анализ объектов, обсуждение проблемных вопросов Регулятивные: целеполагание | Первичное закрепление новых знаний | 1. Знали ли вы раньше, что 1/4 и 15/60 часа – это одно и то же время? Какое свойство помогает вам это понять? 2.Решение задачи: Мама дала Пете 3/9 , а Оле 9/16 плитки шоколада. Не возникнет ли у детей спор? 3.Найди ошибку в заданиях: 8/10=4/5; 24/32=3/4; 10/20=1/2; 7/21=1/7 | Закрепляют по учебнику новый материал. Применяют основное свойство дроби при решении заданий. Делают вывод, что дети не поссорятся, так как дроби равны. Дать возможность детям выразить свое мнение. | Личностные: осознание ответственности за общее дело Познавательные: выполнение действий по алгоритму, построение логической цепи рассуждений, анализ, обобщение, подведение под понятие Коммуникативные: выражение своих мыслей, использование речевых средств для решения коммуникационных задач, достижение договорённости и согласование общего решения | Самостоятельная работа по эталону | Найти равные дроби. Выполнить задание самостоятельно по вариантам (верхняя строка—-1вариант, 2 строка——2 вариант) с последующей взаимопроверкой. Оценивание результатов работы. | Выполняют самостоятельно с последующей взаимопроверкой. | Познавательные: анализ, синтез, аналогия, подведение под понятие, выполнение действий по алгоритму, умение работать самостоятельно Регулятивные: контроль, коррекция, самооценка,взаимопроверка | Включение новых знаний в систему знаний | Попробуйте выполнить задание
| Вспоминают правило сложения дробей с одинаковыми знаменателями, применяют основное свойство дроби к выполнению задания2. | Личностные: самоопределение, смыслообразование Познавательные: анализ, синтез, обобщение, аналогия, самостоятельное выделение и формулирование познавательной цели, поиск и выделение необходимой информации, проблема выбора эффективного способа решения, планирование, выдвижение гипотез и их обоснование, создание способа решения проблемы Регулятивные: волевая саморегуляция в ситуации затруднения Коммуникативные: выражение своих мыслей, аргументирование своего мнения, учёт разных мнений, планирование учебного сотрудничества со сверстниками, достижение общего решения. | Подведение итогов. Домашнее задание Рефлексия. | Учитель комментирует домашнее задание. П.8,№216,237,221. Прочитать текст под рубрикой «Говори правильно» на стр.35. Учитель предлагает вспомнить, чем занимались на уроке, как установили основное свойство дроби? Удалось ли нам решить поставленные перед нами задачи? Что понравилось на уроке? Что не понравилось? Над чем нужно еще работать? Человек подобен дроби, числитель есть то, что он есть, а знаменатель то, что он о себе думает. Чем больше знаменатель, тем меньше дробь. Л. Н. Толстой Как вы понимаете эти слова? Оценим свою работу. Покажи свое настроение по результатам работы на уроке. Усвоили материал.Были трудности. Плохо усвоили .. . Всем спасибо за урок)) | Записывают в дневники Дети принимают участие в обсуждении. К оцениванию привлекаются учащиеся. | Познавательные: рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности, адекватное понимание причин успеха или неуспеха Коммуникативные: аргументация своего мнения, планирование учебного сотрудничества |
Конспект урока по математике 6 класса Мерзляк по теме Основное свойство дроби | План-конспект урока по математике (6 класс):
Математика 6 класс
Конспект урока по теме «Дроби. Основное свойство дроби»
Цели урока:
1. Образовательные: ввести основное свойство дроби; сформировать умение применять данное свойство на практике; ввести новое действие сокращение дробей.
2. Воспитательные: воспитание аккуратности, дисциплины, настойчивости, ответственного отношения к учебе.
3. Развивающие: развитие памяти, речи, любознательности, познавательного интереса;
формирование представлений о математическом языке, развитие коммуникативных умений и навыков.
Об уроке.
Данный урок является первым по теме «Основное свойство дроби». Цель устного счёта – подготовить учащихся к продуктивной работе на протяжении всего урока, взяты задания на восстановление опорных знаний и умений. На уроке вводится понятие основного свойства дроби, умения — это свойство использовать при выполнении конкретных заданий. Также вводится новое действие с дробями- сокращение дробей. В ходе урока проводится работа по поддержанию и совершенствованию ранее сформированных знаний и умений, в частности, вычислительных навыков. Предлагаются задачи, способствующие развитию учащихся, требующие сообразительности, внимания, анализа и обобщения имеющихся знаний.
Структура урока:
Постановка цели урока.
Устный счёт.
Объяснение нового материала.
Закрепление, отработка нового материала.
Самостоятельная работа.
Итог урока. Домашнее задание.
Ход урока
1. Постановка цели урока.
Добрый день, ребята! Как ваше настроение? Давайте поприветствуем друг друга улыбкой и сохраним хорошее настроение в течение всего урока.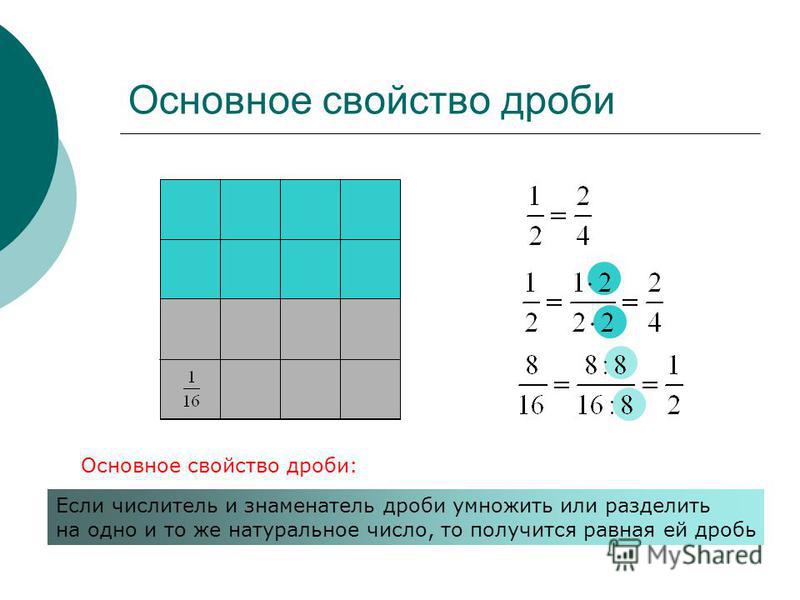
Ребята, нужны ли в жизни человеку математические знания?
А математика может обойтись без дробей?
Почему? Что обозначает слово «дробь?
В русском языке слово «дробь» появилось в 8 веке, оно происходит
от глагола «дробить» — разбивать, ломать на части. В первых учебниках математики (в 17 веке) дроби так и назывались – «ломанные числа».
Современную систему записи дробей с числителем и знаменателем создали в Индии. Только там писали знаменатель сверху, а числитель снизу и не писали дробной черты. На
Руси дроби называли долями, позднее «ломаными числами». Перед вами названия некоторых дробей:
1/2 — половина, полтина;
1/3- треть;
1/6 – полтреть;
1/4 — четь; 1/8 – полчеть:
1/5 – пятина;
1/10 – десятина.
Дробная черта появилась в записи дробей лишь около 300 лет назад. Названия «числитель и знаменатель» ввел в употребление греческий математик Максим Пеануд. Долгое время дроби считались самым трудным разделом математики. У немцев даже сложилась поговорка «попасть в дроби», что означает попасть в трудное положение.
У немцев даже сложилась поговорка «попасть в дроби», что означает попасть в трудное положение.
— Хорошо. Итак мы знаем, что дроби можно получить двумя способами. Знаем, что обыкновенная дробь обозначает. (Что-то целое разделили на н частей и взяли таких частей м.)
— Чем же мы сегодня на уроке будем заниматься? Как вы думаете?
2. Устный счёт
С помощью моделей обыкновенных дробей покажите дроби и объясните, что обозначает числитель и знаменатель каждой дроби.
5/12
3/8
5/6
3. Объяснение нового материала.
А сейчас используя модели дробей проиллюстрируйте дроби:
6/8
9/12
3/4
— Что вы можете заметит, какие дроби получились по величине? (Равные.)
— Можно ли между этими дробями поставить знак равенства? (Да.)
6/8 = 9/12 = 3/4
— Как из дроби 3/4 можно получить дробь 6/8? (3 * 2/4 * 2)
— Как из дроби 3/4 можно получить дробь 9/12? (3 * 3/4 * 3)
— Какое действие надо было выполнить чтобы получить дроби равные данным? (Для получения дроби равной данной надо числитель и знаменатель умножить на одно и тоже число. )
)
— Как из дроби 6/8 получить дробь 9/12? (6 : 2/8 : 2 = 3 * 3/4 * 3 = 9/12)
Т.е. для получения равных дробей можно числитель и знаменатель делить на одно и тоже число.
Вывод: при умножении и делении числителя и знаменателя дроби на одно и тоже число (кроме нуля) ее величина не изменится.
Это свойство очень важное и его называют основным свойством дроби.
Тема нашего урока так и называется «Дроби. Основное свойство дробей».
Открываем тетради, записываем дату, классная работа и тему урока. Открыли учебник на стр. 8 и прочитали данное свойство. Отметили важные слова в этой формулировке. (Числитель, знаменатель и равные.)
Задание: замените дроби 3/12, 15/25, 8/16, 9/15 – равными им дробями с меньшим знаменателем. (Дети выполняют в тетрадях.)
Какое действие вы для этого использовали? (Делили числитель и знаменатель на одно и тоже число.)
Это действие мы будем называть – сокращением дробей.
4. Закрепление нового материала.
Какое действие необходимо выполнить? Проговариваем, на какое число необходимо разделить числитель и знаменатель.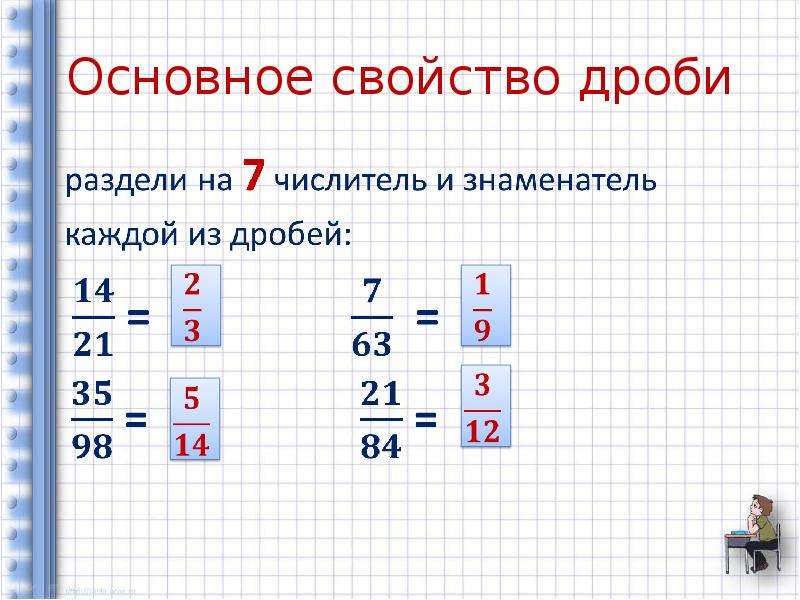
4/10 = 2/5
2/6 = 1/3
9/15 = 3/5
12/16 = 3/4
Следующее задание. Объясните, почему дроби выбранные вами равны дроби 3/7?
6/14
9/21
12/28
Задание «Угадай слово».
Необходимо сократить дроби и каждому правильному ответу найти соответствующую букву. Задание считается выполненным, если слово записано в тетради.
Итак, какое слово у вас получилось. «Молодец».
5. Самостоятельная работа.
Сейчас вы выполните самостоятельную работу на листочках. После выполнения мы работами обмениваемся с соседями по парте и проверяем. Критерии оценивания такие же как всегда:
Без ошибок-5.
Одна ошибка-4.
Две ошибки-3.
Для проверки правильные ответы написаны заранее на обратной стороне доски.
Сдаем листочки с поставленным оценками, я проверю ваши результаты и свои.
2 варианта.
Мы многое успели сегодня на уроке сделать и уже достаточно устали поэтому небольшая игра: дроби написанные на листочках необходимо разложить по двум мешочкам. У каждого мешочка есть своя метка, т.е. в мешок можно положить дроби равные данным.
У каждого мешочка есть своя метка, т.е. в мешок можно положить дроби равные данным.
2/4 2/3 8/12 12/24 3/6 4/6 12/18 9/18 5/10 48/72
Молодцы, к доске можно выбегать бегом. Итак все дроби разложили по своим мешочкам, очень хорошо.
6. Итог урока. Домашнее задание.
— Что нового вы сегодня на уроке узнали? Сформулируйте основное свойство дроби. Молодцы! Сегодня на уроке мы совершенствовали свои знания и умения, применяя полученные знания.
— Откроем дневники и запишем домашнее задание:
Выучить основное свойство дроби и выполнить (стр. 8 — 9), № 6, 7, 8
Самостоятельная работа с взаимопроверкой (10 минут)
Самостоятельная работа «Дроби. Основное свойство дробей» Вариант №1 | Самостоятельная работа «Дроби. Основное свойство дробей» Вариант №2 |
|
|
|
|
4/9, 5/6, 7/2 к знаменателю 18 |
7/8, 5/16, 21/40 к знаменателю 80 |
|
|
5*.
| 5*. Какое натуральное число надо вписать вместо буквы, чтобы было верным равенство:
|
Для мешочка
2/4 | 2/3 | 8/12 | 12/24 | 3/6 |
4/6 | 12/18 | 9/18 | 5/10 | 48/72 |
¾ — м | 1/10 – д | ¼ — е |
1/5 – о | ½ — о | 2/7 — ц |
4/5 – л |
Конспект урока математики в 6 классе «Основное свойство дроби», ФГОС
Урок 1
Основное свойство дроби
Цели: актуализировать знания учащихся по данной теме; повторить, как применяется основное свойство дроби при сокращении дробей и приведении дробей к общему знаменателю.
Ход урока
I. Организационный момент.
II. Устная работа.
1. Вычислите:
а) 2 · 16; е) 105 : 3;
б) 37 + 18; ж) 158 + 19;
в) 160 : 20; з) 110 – 49;
г) 51 – 35; и) 4444 : 11;
д) 30 · 24; к) 7 · 140.
2. Выясните, на какие из чисел 2, 3, 5, 6, 9, 10 делятся данные числа:
а) 2754;
б) 8510;
в) 12345;
г) 9803;
д) 2467122.
3. Найдите НОК и НОД чисел:
а) 24 и 8;
б) 7 и 10;
в) 18 и 45;
г) 12 и 60;
д) 6 и 10.
III. Актуализация знаний.
Актуализация знаний.
1. Из истории вопроса.
В соответствии с пунктом учебника рассмотреть вопрос о появлении дробей, о том, как раньше записывали дроби и как их называли.
2. Правильные и неправильные дроби.
На доске записан ряд дробей:
Задание: разбить данные дроби на две группы по общему признаку.
В первую группу войдут дроби: – правильные дроби.
Во вторую группу войдут дроби: – неправильные дроби.
Повторить с учащимися, какие дроби называются правильными, какие – неправильными. Вспомнить, как выделяется целая часть из неправильной дроби, и представить дроби, вошедшие во вторую группу, в виде смешанных чисел.
3. Основное свойство дроби.
Задача. В пакете имеется 1 кг конфет.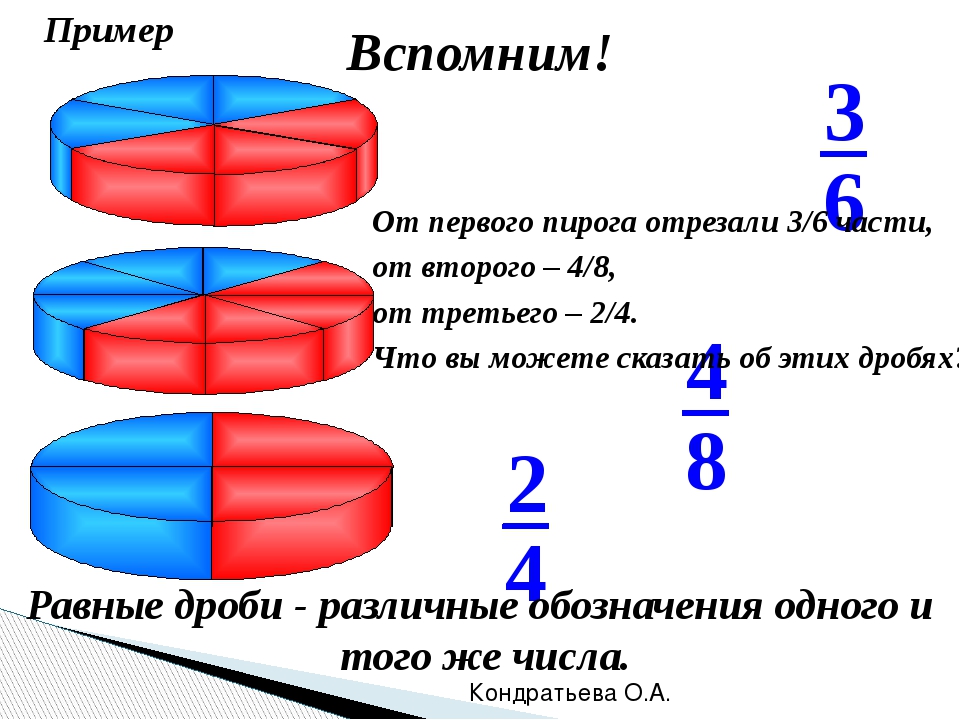 Вам предлагают взять из пакета или 2/3 кг, или 6/9 кг, или 14/21 кг. Что вы выберете?
Вам предлагают взять из пакета или 2/3 кг, или 6/9 кг, или 14/21 кг. Что вы выберете?
Выяснить, что во всех трех случаях получается одно и то же количество конфет. По&
Основное свойство дроби
На этом уроке мы начинаем работать с дробями. Для того чтобы вспомнить, что такое обыкновенная дробь, решим задачу.
Вася разделил шоколадную плитку на 24 кусочка и съел 5 из них. Какая часть шоколадки съедена?
Чтобы записать ответ к этой задаче, в математике используют «двухэтажную» запись числа, то есть дробь.
Определение
Число под чертой дроби называют знаменатель
Число над чертой дроби называют числитель. Он показывает, сколько равных частей взяли.
В нашем случае плитку разделили на 24 части и взяли 5.
Значит, ответ к задаче можно записать обыкновенной
дробью .
Сегодня мы разберём основное свойство дроби.
Пример
В кафе Коля и Маша заказали каждому пиццу. Коля попроси разрезать её на 4 части, а Маша – на 8 частей. Коля съел 2 кусочка, а Маша – 4. Кто из ребят съел больше?
Напомним, половина на математическом языке имеет своё обозначение
Таким образом, если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Это свойство обыкновенной дроби имеет специальное название. Оно называется основным свойством дроби.
Запомните, число 0 – не натуральное, на него нельзя умножать, и тем более делить, числитель и знаменатель.
Например
Это значит, что можно заменить данную дробь другой дробью, равной данной, но с другим числителем и знаменателем.
Значит, дроби можно приводить только к тем
знаменателям, которые кратны исходным.
Дроби, как и натуральные числа, можно изображать точками на координатном луче.
Этот пример ещё раз подтверждает основное свойство дроби.
Задание
Докажем с помощью основного свойства дроби равенство:
Кроме того, основное свойство дроби помогает решать уравнения.
Итоги
С помощью основного свойства дроби можно заменить данную дробь другой дробью, равной данной, но с другим числителем и знаменателем.
Дроби можно приводить только к тем знаменателям, которые кратны исходным.
I. Организационный момент. Здравствуйте, товарищи кадеты! Сегодня на уроке у нас присутствуют гости, поприветствуем их. | Приветствие учителя. Приветствие гостей. | СЛАЙД 1 Число и тема урока на доске | II. Актуализация опорных знаний. 1. Фронтальная работа. Ребята, давайте вспомним правила отыскание части от целого и целого по его части. Чтобы найти часть от целого, надо число, соответствующее целому, разделить на знаменатель и результат умножить на числитель дроби, которая выражает эту часть. Чтобы найти целое по его части, надо число, соответствующее этой части, разделить на числитель и результат умножить на знаменатель дроби, которая выражает эту часть. 2. Устный счет. Найдите: Найдите число, если: | Формулируют правила Устно выполняют вычисления, поднимают руку и говорят ответ | Правила высвечиваются на СЛАЙДЕ 2 СЛАЙД 3 По мере ответов детей появляются ответы на слайде | III. Молодцы, хорошо справились с заданием. А сейчас открываем тетради, записываем число и тему урока: «Основное свойство дроби». Это очень важная тема в курсе математики и алгебры, все преобразования с дробями связаны с этой темой. Рассмотрите данный рисунок на слайде и запишите, какая часть фигуры закрашена зелёным цветом. Постарайтесь найти разные способы. Сравните свои результаты. А сейчас откройте учебник на странице 99, №344. Длина отрезка МN -12 см. Начертите отрезки, длины которых составляют Решение: Используя результаты своей работы, сравните дроби: Дробь можно получить из дроби умножением ее числителя и знаменателя на 2: Дробь 8/12 можно получить из дроби 16/24 делением ее числителя и знаменателя на 2. Обратите внимание на слайд, здесь сформулировано основное свойство дроби: При умножении или деление числителя и знаменателя дроби на одно и то же число (кроме нуля) её величина не изменяется | Записывают число и тему урока Самостоятельное выполнение Сравнение результатов с результатами на слайде Один ученик у доски, остальные в тетрадях. Сравнивают дроби, называя равные, делают выводы Записывают в тетрадь Записывают в тетрадь Читают и записывают формулу в тетрадь | СЛАЙД 4 СЛАЙД 5 СЛАЙД 6 СЛАЙД 7 СЛАЙД 7 СЛАЙД 8 СЛАЙД 9 СЛАЙД 10 | IV. Первичная проверка понимания изученного. Итак, отдохнули, пора приступать к следующему заданию. №346. При выполнении данного задания используем основное свойство дроби. Какое свойство дроби для этого можно использовать? Находим число, на которое можно разделить и числитель, и знаменатель, выполняем деление и записываем результат Деление числителя и знаменателя на одно и то же число называют сокращением дроби | Дети формулируют По цепочке выходят к доске и выполняют вычисления Остальные работают в тетрадях | СЛАЙД 12 Проверка на слайде Формулировка понятия | VI. Домашнее задание: § 21. Выучить правила, № 352, №354 | Записывают в дневник д/з | СЛАЙД 14 | VII. Подведение итогов. 1. Сформулируйте основное свойство дроби. При умножении или деление числителя и знаменателя дроби на одно и то же число (кроме нуля) её величина не изменяется. 2. Сократите дроби: | Формулируют свойство дроби | СЛАЙД 15 |
Конспект урока по математике 6 класс на тему: «Основное свойство дроби»
ОСНОВНОЕ СВОЙСТВО ДРОБИ
Цели: ввести определение основного свойства дроби;
научить применять его при выполнении упражнений и задач;
развивать логическое мышление.
Ход урока
I. Организационный момент.
II. Актуализация знаний и построение проблемы. (На доске записаны дроби)
(На доске записаны дроби)
Выполните действия: ; ;
-Нужно указать какие из этих дробей мы можем сложить или вычесть? (Те, что имеют одинаковый знаменатель?).
-Ребята, как вы думаете, можно ли складывать и вычитать дроби с разными знаменателями? Почему?
Обратимся к исторической справке, которая приведена на странице 116 учебника.
Переходим к новому разделу: «Сложение и вычитание дробей с разными знаменателями», который начинается с первой темы: «Основное свойство дроби».
III. Формирование нового знания.
Начертите два квадрата со стороной 5 см и разделите их на 4 равных квадрата. Закрасьте треть данных квадратов. Запишите под первым квадратом дробь, которая будет соответствовать данному чертежу. (рис.1). На втором чертеже разделите каждый квадрат еще на 5 равных частей и запишите дробь под 2 квадратом, которая будет соответствовать данному чертежу (рис.2)
(1)
Рис. 1 Рис.2
1 Рис.2
-Что произошло с числителем и знаменателем первой дроби? (Увеличились в 5 раз).
-Что можно сказать про данные дроби? (Они равны).
Таким образом, запись (1) действительна. Из чего можно сделать вывод: «Если числитель и знаменатель дроби умножить на одно и то же число, то получится равная ей дробь» (Вывод формулируют сами учащиеся).
-Данное равенство (1) будет выполняться только слева направо? (В обратном порядке тоже).
Значит, основное свойство дроби формулируется: «Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь».
IV. Введение нового знания.
- Прочитать по учебнику раздел «Говорите правильно» стр.35. Выбрав для себя удобный способ, прочитать правильно предложенные равенства:
= ; ;
Приведите свои примеры равенств.
- В парах обсуждают, почему равны дроби из №211. Если готовы к ответу совместно поднимают руки. Таким же образом №212 (в,г).
- Работа у доски и в тетрадях:
А) №214 (С помощью цветных мелков на доске, цветными карандашами в тетрадях).
Б) №216-№218, №220
В)Самостоятельно №221. Затем взаимопроверка с обменом тетрадями.
; m=10 ; ;
Мы показали и объяснили равенство дробей при помощи геометрических фигур, часов. Где еще можно показать равенство дробей? (На координатном луче).
Г) №215
4. Чей ряд быстрее применит основное свойство дроби. (Задание на карточке).
1парта 2 парта 3 парта 4 парта 5 парта
V. Итог урока.
— Можно ли сказать, что равные дроби являются различными записями одного и того же числа? Почему?
VI. Домашнее задание: п. 8; решить № 240(а; в), № 239, № 238.
Просмотр содержимого документа
«Конспект урока по математике 6 класс на тему: «Основное свойство дроби» »
ОСНОВНОЕ СВОЙСТВО ДРОБИ
Цели: ввести определение основного свойства дроби;
научить применять его при выполнении упражнений и задач;
развивать логическое мышление.
Ход урока
I. Организационный момент.
II. Актуализация знаний и построение проблемы. (На доске записаны дроби)
Выполните действия: ; ;
-Нужно указать какие из этих дробей мы можем сложить или вычесть? (Те, что имеют одинаковый знаменатель?).
-Ребята, как вы думаете, можно ли складывать и вычитать дроби с разными знаменателями? Почему?
Обратимся к исторической справке, которая приведена на странице 116 учебника.
Переходим к новому разделу: «Сложение и вычитание дробей с разными знаменателями», который начинается с первой темы: «Основное свойство дроби».
III. Формирование нового знания.
Начертите два квадрата со стороной 5 см и разделите их на 4 равных квадрата. Закрасьте треть данных квадратов. Запишите под первым квадратом дробь, которая будет соответствовать данному чертежу. (рис.1). На втором чертеже разделите каждый квадрат еще на 5 равных частей и запишите дробь под 2 квадратом, которая будет соответствовать данному чертежу (рис.2)
(1)
Рис.1 Рис.2
-Что произошло с числителем и знаменателем первой дроби? (Увеличились в 5 раз).
-Что можно сказать про данные дроби? (Они равны).
Таким образом, запись (1) действительна. Из чего можно сделать вывод: «Если числитель и знаменатель дроби умножить на одно и то же число, то получится равная ей дробь» (Вывод формулируют сами учащиеся).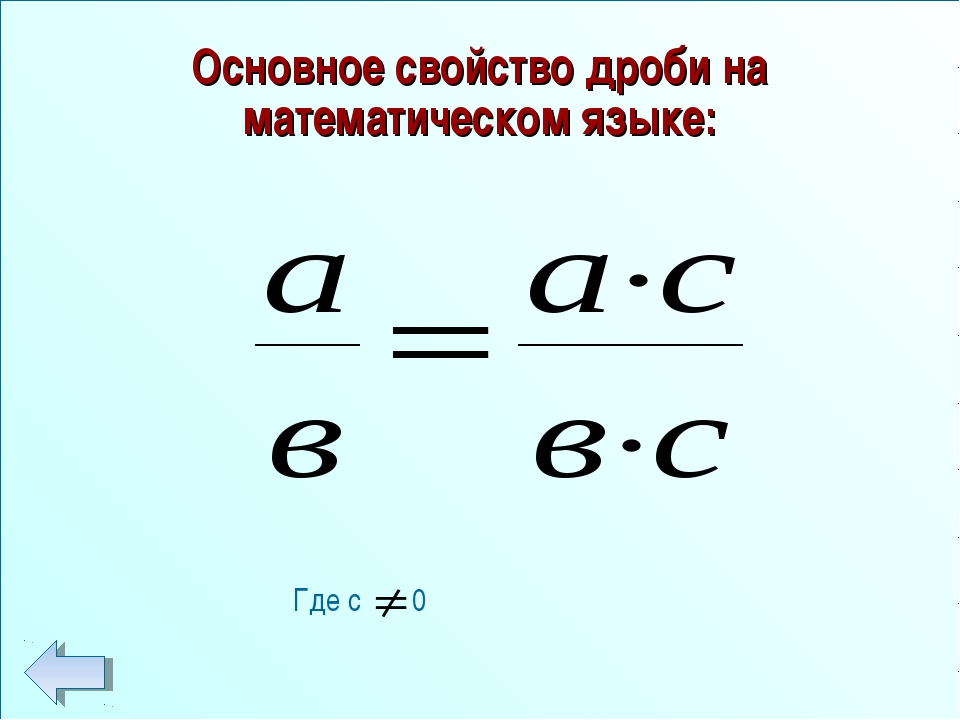
-Данное равенство (1) будет выполняться только слева направо? (В обратном порядке тоже).
Значит, основное свойство дроби формулируется: «Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь».
IV. Введение нового знания.
Прочитать по учебнику раздел «Говорите правильно» стр.35. Выбрав для себя удобный способ, прочитать правильно предложенные равенства:
= ; ;
Приведите свои примеры равенств.
В парах обсуждают, почему равны дроби из №211. Если готовы к ответу совместно поднимают руки. Таким же образом №212 (в,г).
Работа у доски и в тетрадях:
А) №214 (С помощью цветных мелков на доске, цветными карандашами в тетрадях).
Б) №216-№218, №220
В)Самостоятельно №221. Затем взаимопроверка с обменом тетрадями.
; m=10 ; ;
Мы показали и объяснили равенство дробей при помощи геометрических фигур, часов. Где еще можно показать равенство дробей? (На координатном луче).
Где еще можно показать равенство дробей? (На координатном луче).
Г) №215
4. Чей ряд быстрее применит основное свойство дроби. (Задание на карточке).
1парта 2 парта 3 парта 4 парта 5 парта
V. Итог урока.
— Можно ли сказать, что равные дроби являются различными записями одного и того же числа? Почему?
VI. Домашнее задание: п. 8; решить № 240(а; в), № 239, № 238.
Математика, 6 класс, дроби и десятичные дроби, два метода деления дробей на дроби
Многие студенты находят трудным для понимания метод «умножения на обратное». Это нормально, если студенты не могут этого объяснить.
Для решения задач учащиеся могут использовать методы, аналогичные тем, что использовались в Уроке 4, в том числе:
- Нарисуйте модель дивиденда, измените дроби и модель, чтобы показать общий знаменатель, и обведите группы, представленные делителем.

- Перепишите дроби так, чтобы у них был общий знаменатель, и найдите частное новых числителей. Студенты должны уметь объяснить, почему этот метод работает.
- Перепишите задачу, умножив ее на обратную.
- Причина о количестве групп единичных дробей в дивиденде.
У ученика проблемы с запуском.
- Вернитесь к методам из Урока 4. Можете ли вы использовать метод, аналогичный одному из тех, для решения этой проблемы?
- Что означает задача 23 ÷ 35? Что вы пытаетесь найти?
- Помогло бы вам задуматься о том, что означает проблема, если бы дроби имели общий знаменатель?
Студент затрудняется рассуждать о методе общего знаменателя.
- Вы переписали 23 ÷ 35 как 1015 ÷ 915. Что означает переписанная проблема? Что вы пытаетесь найти?
- Вы пытаетесь найти количество групп из 9 пятнадцатых в 10 пятнадцатых.
Студент находит неправильное решение.
- Как проверить правильность своего ответа?
- Подумайте о размерах чисел в задачах. Ваш ответ кажется разумным?
Математическая практика 1: разбираться в проблемах и настойчиво их решать.
Учащиеся должны найти способ разобраться в делении дроби на дробь и найти способ представить и решить данные задачи.
Математическая практика 4: Модель с математикой.
Открытие представляет учащимся реальную задачу, которую они должны смоделировать с помощью математического выражения или уравнения.
- 119
- Чек: 119 × 35 = 109 × 35 = 3045 = 23
Время работы
- Решите задачу 23 ÷ 35 любым методом.
- Проверьте свой ответ.
Можете ли вы использовать умножение, чтобы найти ответ?
Что такое дробь? — Определение и типы — Видео и стенограмма урока
Правильные и неправильные дроби
Во-первых, у нас есть то, что мы называем «правильными» и «неправильными» дробями.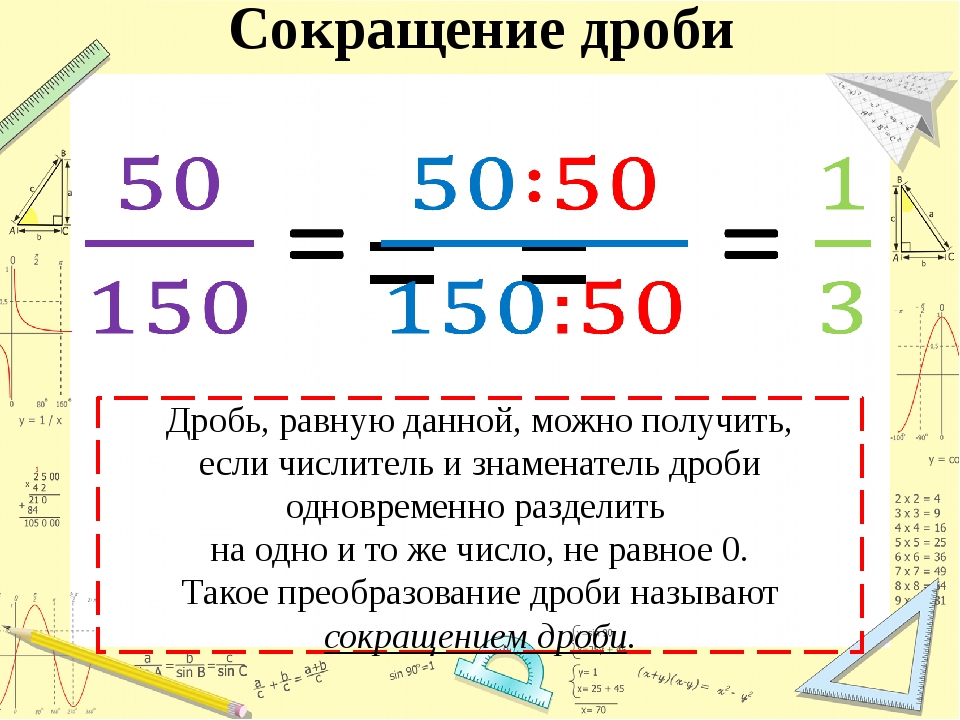 Правильные дроби — это те дроби, у которых числитель меньше знаменателя. Неправильная дробь — это дробь, числитель которой больше знаменателя.Например, дробь 7/8 — правильная дробь, а 8/7 — неправильная дробь.
Правильные дроби — это те дроби, у которых числитель меньше знаменателя. Неправильная дробь — это дробь, числитель которой больше знаменателя.Например, дробь 7/8 — правильная дробь, а 8/7 — неправильная дробь.
Думайте об этом, как о попытке отрезать кусочки всего от одного пирога. С правильной дробью вы можете взять все кусочки только из одного пирога, но с неправильной дробью вам понадобится более одного пирога, чтобы получить необходимое количество ломтиков. Дробь 7/8 говорит вам взять 7 кусочков из пирога с 8 кусочками. Вы можете взять все кусочки только из одного пирога. Но дробь 8/7 говорит, что вам нужно 8 ломтиков от пирога, у которого всего 7 ломтиков.Если в вашем пироге всего 7 ломтиков, вы можете взять только 7 ломтиков из одного пирога. Чтобы получить 8-й ломтик, вам понадобится второй пирог, который также нарезан на 7 частей, из которых вы можете взять один кусок, чтобы сделать 8-й ломтик.
Можно сказать, что неправильные дроби — это жадные дроби, потому что вам нужно более одного целого пирога, чтобы их удовлетворить. Правильные фракции можно получить, сняв кусочки всего с одного пирога.
Правильные фракции можно получить, сняв кусочки всего с одного пирога.
Дроби вроде и отличия
Далее у нас есть дроби вроде и отличия. Как и дроби — это дроби с одинаковым знаменателем. В отличие от дроби — это те дроби, которые отличаются. Например, дроби 3/4 и 2/4 похожи на дроби, потому что у них один и тот же знаменатель — 4. Просто сложите числители и получите ответ более 4, чтобы получить сумму.
Математически 2/4 упрощается до 1/2, потому что мы можем разделить верхнее и нижнее числа на 2. Когда мы можем разделить числитель и знаменатель на одно и то же число, мы должны сделать это, чтобы упростить дробь.Например, дробь 6/9 может быть упрощена до 2/3, поскольку мы можем разделить 6 на 3 и 9 на 3. 6, разделенное на 3, равно 2, а 9, разделенное на 3, равно 3, поэтому 6/9 упрощается до 2/3.
Эквивалентные дроби, напротив, имеют такое же число. 1/2 и 2/4 одинаковы, потому что если вы разделите верхнюю и нижнюю часть 2/4 на 2, вы получите 1/2! В отличие от дробей, это совершенно разные дроби. Например, 2/4 и 6/9 не похожи на дроби, потому что даже если вы их упрощаете, вы получаете разные дроби: 2/4 упрощается до 1/2, а 6/9 упрощается до 2/3.1/2 и 2/3 определенно разные дроби!
Например, 2/4 и 6/9 не похожи на дроби, потому что даже если вы их упрощаете, вы получаете разные дроби: 2/4 упрощается до 1/2, а 6/9 упрощается до 2/3.1/2 и 2/3 определенно разные дроби!
Смешанные числа
Теперь, наконец, у нас есть смешанные числа , также называемые смешанными дробями . Это ваши неправильные дроби, записанные вместе с целым числом и правильной дробью. Например, наша дробь 8/7 из предыдущего может быть записана как 1 1/7, чтобы показать, что нам нужен целый пирог, а затем 1 кусок второго пирога, чтобы заполнить наши 8 ломтиков пирога, который разрезан на 7 частей.
Мы можем записать смешанные числа, как мы только что сделали с целым числом перед дробью, использующей наклонную косую черту, или мы можем написать наше целое число перед дробью, где числа расположены друг над другом.В этом случае все наше число будет центрировано горизонтальной косой чертой. И вот мы закончили наш урок.
Резюме урока
Итак, давайте рассмотрим, что мы узнали. Мы узнали, что дробь говорит нам, сколько частей целого у нас есть. Они записываются с помощью верхнего числа, числителя , и нижнего числа, знаменателя , разделенных косой чертой. Косая черта может быть косой чертой или горизонтальной косой чертой с числителем над знаменателем с косой чертой между ними.
Мы узнали, что дробь говорит нам, сколько частей целого у нас есть. Они записываются с помощью верхнего числа, числителя , и нижнего числа, знаменателя , разделенных косой чертой. Косая черта может быть косой чертой или горизонтальной косой чертой с числителем над знаменателем с косой чертой между ними.
A правильная дробь — это дробь, числитель которой меньше знаменателя. Неправильная дробь — это дробь, числитель которой больше знаменателя. Как и дроби — это дроби с одинаковым знаменателем. В отличие от дроби — это разные дроби.
Если вы можете разделить числитель и знаменатель дроби на одно и то же число, то вы можете упростить эту дробь до ее более простой формы, выполнив деления.Смешанное число — неправильная дробь, состоящая из целого числа и правильной дроби.
Результаты обучения
По завершении этого урока вы сможете:
- Определить дроби и определить части дроби
- Различение правильных и неправильных дробей
- Объясните, почему вам следует упростить дроби и определить одинаковые и непохожие дроби
- Опишите, как написать смешанное число
Математика / Цели обучения математике для третьего класса
Задачи обучения математике для третьего класса
Числа и операции Подсчет наборов чисел, представление чисел, сравнение и порядковые номера, значение разряда
- Представление чисел до 10 000 в различных эквивалентных формах.

- Сосчитайте до 10,000.
- Считайте сотнями и тысячами.
- Сравните и закажите целые числа до 10 000.
- Используйте модели разрядов для чтения, записи и представления чисел до 10 000.
- Перегруппировка модели при сложении и вычитании с разметкой.
- Сложите и вычтите целые числа до 10 000.
- Решите задачи сложения и вычитания с большими числами с помощью столбчатой модели.
- Умножение и деление на 6, 7, 8 и 9.
- Представьте умножение и деление по-разному.
- Умножение единиц, десятков и сотен с перегруппировкой и без нее.
- Используйте свойства сложения и умножения для умножения.
- Разделите 10 и 1 с перегруппировкой и без, без остатка.
- Используйте линейчатые модели для представления ситуаций умножения и деления.
- Решайте одно- и двухэтапные задачи умножения и деления.

- Используйте математические стратегии для сложения, вычитания, умножения и деления.
- Сложите и вычтите деньги.
- Решение реальных задач, связанных с сложением и вычитанием денег.
- Используйте знак доллара и десятичную точку в денежных суммах.
- Разберитесь в значениях и использовании дробей, включая дробную часть множества.
- Помните, что размер дробной части зависит от размера целого.
- Сравните дроби с помощью моделей, числовых линий.
- Определите эквивалентные дроби с помощью моделей, умножения, деления и числовых линий.
- Складывать и вычитать как дроби.
Алгебраическое мышление
Шаблоны и свойства
- Создавайте и анализируйте шаблоны умножения и деления.

- Поймите, что умножение и деление связаны.
- Смоделируйте, определите и объясните свойства умножения.
- Определение четных и нечетных чисел.
- Опишите числовые отношения в контексте.
- Запишите числовые предложения умножения и деления.
- Напишите и решите числовые предложения для одно- и двухэтапных реальных задач.
- Определите недостающие части (количества или символы) в числовых предложениях.
- Понять равенство и неравенство.
Геометрия и измерения
Время и температура
- Считайте время на цифровых часах.
- Укажите время с точностью до минуты.
- Преобразование часов в минуты
- Сложение и вычитание единиц времени.
- Определите истекшее время.
- Считайте термометр Фаренгейта.

- Выберите подходящий инструмент и единицу измерения температуры.
- Используйте ссылки для оценки температуры.
- Определите перпендикулярные и параллельные линии.
- Определите прямые углы и сравните углы с прямыми углами.
- Описывайте, анализируйте, сравнивайте и классифицируйте двумерные формы по их сторонам и углам.
- Классифицируйте и сортируйте многоугольники и четырехугольники по атрибутам и свойствам.
- Исследуйте составление и разложение двухмерных фигур.
- Используйте атрибуты и свойства для решения проблем.
- Выберите соответствующие единицы и инструменты для оценки и измерения длины.
- Для измерения длины используйте мерные стержни, 12-дюймовые линейки и мерки.
- Измерьте длину с точностью до полдюйма и дюйма.
- Используйте ссылки для оценки расстояния.

- Измерьте периметр плоских фигур.
- Выберите подходящий инструмент и стратегию для измерения периметра.
- Найдите и сравните площади плоских фигур в различных квадратных единицах.
- Создайте разные плоские фигуры с одинаковой площадью.
- Сравните площадь и периметр плоских фигур.
- Найдите площадь прямоугольников и составных фигур.
- Оцените и измерьте емкость в литрах и миллилитрах.
- Преобразование метрических единиц мощности.
- Выберите подходящие инструменты и единицы измерения для оценки и измерения объема в кубических единицах.
- Свяжите единицы обычной вместимости друг с другом.
- Раскладывайте твердые фигуры, чтобы найти площадь поверхности.
- Выберите соответствующие единицы и инструменты для оценки и измерения веса.
- Используйте точки отсчета для измерения веса.

- Оцените и найдите массу предметов.
- Преобразование единиц массы.
- Определите симметричные фигуры и одну линию симметрии.
- Решите проблемы, связанные с конгруэнтностью.
- Определите пары фигур, которые показывают переворот, скольжение и поворот.
- Продемонстрируйте, что фигуры и их изображения переворачивания, сдвига и поворота совпадают.
Анализ данных
Сбор, классификация, организация, представление, интерпретация и анализ данных
- Собирайте и систематизируйте данные в виде гистограмм и линейных графиков.
- Расшифровка изображений и гистограмм с шкалами.
- Используйте частотные таблицы, гистограммы, графические изображения и линейные графики для решения реальных проблем.
Математика Мамонт 6 класс Полная программа
Math Mammoth Grade 6 Class Complete Curriculum — это полная математическая программа для 6-го класса, в которой вы найдете все необходимое для обучения математике в 6-м классе. Он доступен как в версии для скачивания, так и в виде печатных копий.
Он доступен как в версии для скачивания, так и в виде печатных копий.
189 страниц
170 страниц уроков
178 страниц
153 страниц уроков
Содержание и образцы 6-A
Содержимое и образцы 6-B
Образец ключа ответа
Руководство пользователя, класс 6
Выравнивание / содержание CCS
FAQ
Цены и заказ
Вы можете приобрести Math Mammoth Grade 6 для загрузки, на компакт-диске или в виде уже распечатанных книг.
Цифровая версия
6 класс: $ 39,50 (скачать)
(два рабочих текста, ключи ответов, тесты, совокупные обзоры, средство создания рабочих листов, Soft-Pak)
Только часть 6-A:
19,75 $ (загрузить)
(Все для первой половины 6 класса по математике; включает Софт-Пак)
Только часть 6-B:
19,75 $ (загрузить)
(Все для второй половины 6 класса по математике; включает Софт-Пак)
Вы будете покупать загружаемые материалы у моего авторизованного реселлера Comecero, LLC.
CD
Полная оценка 6: 44,50 долл. США
(два рабочих текста, ключи ответов, тесты, совокупные обзоры, средство создания рабочих листов, Soft-Pak)
Печатные копии
Ресурсный центр Rainbow продает тексты с идеальным переплетом либо с полноцветными, либо с внутренними страницами в оттенках серого:
Математика Мамонт 6 класс (ч / б)
Математика Мамонт 6 класс (цвет)
Lulu продает книги для студентов, а также книги для тестов и обзоров со спиральным переплетом (катушкой).
Рабочий текст 6-A $ 17,45 (цвет)
Рабочий текст 6-B $ 16,95 (цвет)
Тесты и совокупные обзоры $ 9,95 (цвет)
Ключи ответов $ 12,95 (идеальный переплет)
Другой вариант — приобрести только рабочих текстов учащихся в виде печатных книг и получить цифровую версию вспомогательных материалов : ключи ответов, тесты, совокупные обзоры, средство создания рабочих листов и программное обеспечение Soft-Pak.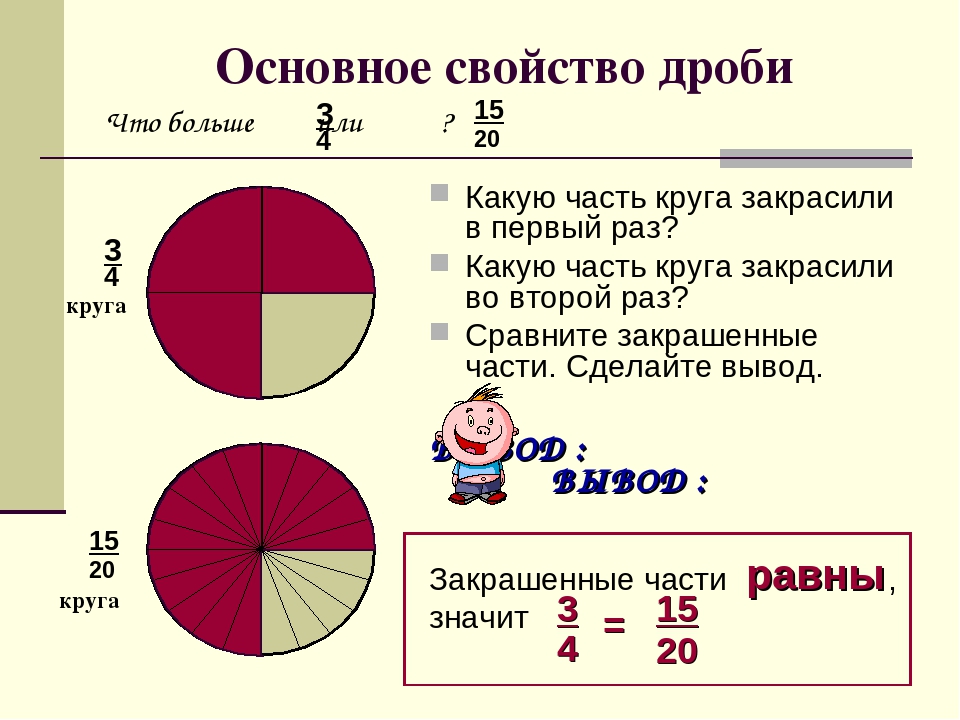 Используйте эту ссылку, чтобы добавить вспомогательные материалы в корзину (8,95 долларов США).
Используйте эту ссылку, чтобы добавить вспомогательные материалы в корзину (8,95 долларов США).
План урока
Вы можете приобрести план уроков по математике Mammoth Grade 6, чтобы использовать его в онлайн-планировщике Homeschool Planet . Учить больше.
В основе учебной программы два студенческих рабочих текста (A и B), каждый из которых охватывает примерно полгода работы по математике. Эти рабочие тексты содержат все инструкции и упражнения из одной книги, что упрощает подготовку к уроку. Рабочие тексты написаны непосредственно ученику, и, таким образом, они позволяют многим ученикам учиться самостоятельно и учиться прямо из книг.
Вы также получите отдельные ключи ответов, тесты по главам, дополнительные совокупные обзоры (я рекомендую вам использовать хотя бы некоторые из них) и универсальное средство для создания рабочих листов (требуется доступ в Интернет) для тех случаев, когда вашему ребенку нужно немного больше практики .
Характеристики
- Math Mammoth фокусируется на концептуальном понимании . В нем объясняется «ПОЧЕМУ», так что ваши дети могут понимать математику, а не просто узнавать «КАК» это делать.
- Концепции часто объясняются с помощью визуальных моделей , за которыми следуют упражнения с использованием этих моделей.Эти визуальные модели могут заменить многие дети манипулятивными средствами; однако при желании очень легко добавить к урокам соответствующие манипуляторы.
- Учебная программа ориентирована на овладение . Это означает, что он довольно долго концентрируется на теме, вникая в ее различные аспекты. Это способствует концептуальному пониманию, в отличие от спиральных учебных программ, которые часто имеют тенденцию слишком много прыгать от темы к теме.
- Требуется очень небольшая подготовка учителей .
- Учебная программа не имеет отдельного руководства для учителя и не написана по сценарию. Во введении к каждой главе есть некоторые примечания для учителя относительно материала главы. Все инструкции написаны непосредственно для ученика в рабочем тексте, а также существуют сопроводительные видеоролики, где вы можете увидеть, как Мария сама преподает материал.
- После введения каждой главы вы найдете список интернет-ссылок и ресурсов (игры, викторины, анимации и т. Д.), Которые можно использовать для развлечения, иллюстраций и дальнейшей практики.
Дополнительные возможности цифровой версии (скачать / CD)
Файлы PDF включены для аннотации. Это означает, что при желании ваш ученик может заполнить их на компьютере, используя пишущую машинку и инструменты рисования в Acrobat Reader версии 9 или выше, или на планшетном устройстве, используя любое приложение PDF с возможностью аннотации. (Узнать больше.)
БОНУС! Если вы приобретете загружаемую версию или версию на компакт-диске, вы также получите полностью программу Soft-Pak. БЕСПЛАТНО .6 программ Soft-Pak (4 математических, 1 языковая, 1 составитель списков) предлагают как экранные, так и печатные задания в формате с низким содержанием графики и высоким содержанием. Подробнее читайте и смотрите скриншоты.
Обзор тем
Основными направлениями обучения в Math Mammoth Grade 6 Grade являются:
- обзор основных операций с целыми числами
- тем для начинающих по алгебре: выражения, уравнения и неравенства
- обзор всей десятичной арифметики
- Введение в коэффициенты и проценты
- разложение на простые множители, GCF и LCM
- обзор дробной арифметики с 5 класса, плюс акцент на деление дробей
- понятие целых чисел, координатная сетка, сложение и вычитание целых чисел
- геометрия: обзор четырехугольников и задачи рисования; площадь треугольников и многоугольников; объем прямоугольных призм с дробными длинами ребер; площадь Статистика
- : концепция распределения, меры центра, меры вариации, коробчатые диаграммы, диаграммы стеблей и листьев, гистограммы
См. Также оглавление 6-A и 6-B (в файлах примеров), которое позволит вам увидеть затронутые темы более подробно.
Дополнения
План урока
Мы предлагаем план урока по математике Mammoth Grade 6 для онлайн-планировщика Homeschool Planet . Он доступен в двух версиях: обычный и план PLUS, который также включает файл плана в формате PDF. Учить больше.
Рабочая тетрадь по обзору навыков
Рабочая тетрадь по обзору навыков мамонта по математике, 6 класс предоставляет дополнительную практику по темам учебной программы по математике мамонта для 6 класса. Я рекомендую вам покупать его только в том случае, если вы уверены, что вашему ученику действительно нужна дополнительная практика.Учить больше.
Введение
В шестом классе ученики знакомятся с истоками алгебры, изучая алгебраические выражения, одну переменную уравнения и неравенства, целые числа и отношения. Мы также проверяем и углубляем понимание учащимися рационального числа: дробные и десятичные дроби изучаются углубленно, а проценты — это новая тема для 6-го класса. В геометрии, студенты учатся вычислять площадь различных многоугольников, а также вычислять объем и площадь поверхности различные твердые тела.Последней важной областью изучения является статистика, где студенты учатся резюмировать и описывать распределения с использованием как меры центра, так и изменчивости.
Год начинается с обзора четырех операций с целыми числами (включая длинное деление), место значение и округление. Студенты также знакомятся с экспонентами и решают некоторые задачи.
Глава 2 начинает изучение вопросов алгебры, сначала углубляясь в выражение и уравнения.Студенты практикуют письмо выражений различными способами, и используют свойства операций и идею поддержания равенства обе стороны уравнения для решения простых одношаговых уравнений. Мы также кратко изучаем неравенства и используем два переменные.
Глава 3 имеет дело с десятичными знаками. Это длинная глава, поскольку мы, , рассматриваем всю десятичную арифметику , просто используя больше десятичные цифры, чем в 5 классе. В этой главе учащиеся также переводят единицы измерения.
Коэффициенты — новая тема (глава 4).Студенты уже знакомы с поиском дробных частей из более ранних классов, и теперь пришло время продвинуть эти знания в изучение соотношений, которые естественным образом возникают в результате деления количество на множество равных частей. Мы изучаем такие темы, как ставки, удельные расценки, эквивалентные соотношения и решение проблем. с использованием стержневых моделей.
Процент (глава 5) — важная тема для полного понимания из-за ее многочисленных приложений в реальной жизни. Цель этой главы — развить базовое понимание процента , увидеть проценты как десятичные дроби и научиться рассчитывать скидки.
В главе 6 мы сначала рассматриваем разложение на простые множители, а затем изучаем наибольший общий множитель и наименьшее общее кратное.
Глава 7 сначала представляет собой подробный обзор операций с дробями из 5-го класса (сложение, вычитание и умножение). Тема этой главы — дробное деление . Студенты также решают некоторые проблемы с фракции.
В главе 8 студенты знакомятся с целыми числами . Они рисуют точки во всех четырех квадрантах координатной плоскости и научитесь складывать и вычитать отрицательные числа.Умножение и деление целых чисел изучается в 7 классе.
В геометрии (глава 9) основное внимание уделяется области полигонов . Это изучается в логической последовательности: во-первых, площадь прямоугольных треугольников, затем площадь параллелограммов, затем площадь треугольников и, наконец, площадь многоугольников. Мы также рассматриваем некоторые темы из более ранних классов (четырехугольники, периметр, базовый рисунок). Другие важные темы в В этой главе производится расчет площади поверхности некоторых твердых тел с использованием сеток и объема прямоугольных призм с дробные длины кромок.
Наконец, в главе 10 студенты изучают статистику. Основная идея заключается в статистическом распределении . Студенты учатся о мерах центра и мерах изменчивости. Они учатся создавать точечные диаграммы, гистограммы, коробчатые диаграммы и стебле-листовые участки. Все эти уроки необходимы для обобщения и анализа распределений.
Отзывы / Свидетельства о программе 6 класса
Взгляд на Math Mammoth — обзор MM6 от Хайме Гравитта на My Homeschool Story blog
Дорогая Мария,Ты обалденный.Большое спасибо за ваш прекрасный учебный план. Я использую учебники для 6-го и 7-го классов для своей дочери из 7-го класса, которая в этом году учится на дому. Мне нравится, что ваша учебная программа соответствует государственным стандартам, поэтому, когда моя дочь вернется в школу, она не отстанет. Моя дочь превратилась из ученика, который не любил математику, в того, кто занимается математикой с утра! Еще раз спасибо!!
Адриан Оркатт-Фрейзер
Октябрь 2015
Что такое единичная дробь? Разъяснение для основных родителей
В этом посте мы объясним, что такое дробная единица, что они означают, и предоставим вам несколько вопросов, которые вы можете использовать для проверки навыков вашего ребенка с KS2, когда дело касается дробей.
Этот блог является частью нашей серии блогов, предназначенных для родителей, поддерживающих домашнее обучение и ищущих ресурсы для домашнего обучения во время эпидемии Covid-19.
Что такое единичная дробь?Единичная дробь — это любая дробь, числителем которой является 1 (верхнее число) и целое число в знаменателе (нижнее число).
Примеры дробных единиц включают:
Присоединяйтесь к Третьему Центру изучения математики в космосе
Чтобы просмотреть всю нашу коллекцию бесплатных и платных ресурсов по математике для учителей и родителей, зарегистрируйтесь, чтобы присоединиться к Центру математики третьего космоса.Это быстро, просто и бесплатно! (Используйте Google Chrome для доступа к Maths Hub)
Когда мой ребенок узнает о дробных единицах?Хотя терминология «доли единицы» еще не введена, ученики года 1 должны:
- распознать, найти и назвать половину как одну из двух равных частей объекта, формы или количества;
- распознает, находит и называет четверть как одну из четырех равных частей объекта, формы или количества.
В классе 2 ученики используют дроби как «дроби» как дискретные (целые числа) и непрерывные (любое числовое значение, например.грамм. 3.6) количества, решая задачи с использованием форм, предметов и количеств.
Они соединяют доли единиц с:
- равным разделением и группировкой;
- в числа, когда их можно вычислить;
- и для измерений, определения долей длины, количества, наборов предметов или форм.
Они также соответствуют 3 / 4 как первому примеру неединичной дроби.
3 класс ученики должны:
- распознавать, находить и записывать дроби дискретного набора предметов: единичные дроби и неединичные дроби с малыми знаменателями;
- распознает и использует дроби как числа: единичные дроби и неединичные дроби с маленькими знаменателями;
- сравнить и упорядочить единичные дроби и дроби с одинаковыми знаменателями;
- начинает понимать единичные и неединичные дроби как числа на числовой прямой и выводить отношения между ними, такие как размер и эквивалентность;
- понимают связь между дробями единиц как операторами (дробями) и делением на целые числа;
- продолжает распознавать дроби в контексте частей целого, чисел, измерений, формы и единичных дробей как деление количества.
Доли единиц затем не упоминаются в учебной программе до года 6 , где ученики используют свое понимание взаимосвязи между дробями единиц и делением, чтобы работать в обратном порядке, умножая количество, которое представляет собой дробь единицы, чтобы найти целое количество (для Например, если длина 1 / 4 равна 36 см, то вся длина равна 36 × 4 = 144 см).
Хотите знать, как объяснить детям другие ключевые слова по математике? Просмотрите наш словарь по основам математики или попробуйте другие термины, относящиеся к дробям единиц:
Практические вопросы дроби единиц для младших школьников
1) Запишите эти числа по порядку, начиная с наименьшего: 1 / 2 , 1 / 4 , 1 / 8 , 1 / 5
2) Обведите самую большую единичную дробь: 1 / 6 , 1 / 4 , 1 / 3 , 1 / 5
3) Оттенок 1 / 5 этой формы (вы можете воссоздать это на листе бумаги):
4) Вычислите 1 / 7 из 21.
Наша программа онлайн-обучения математике предоставляет каждому ребенку индивидуального профессионального репетитора по математике
CMP3 6 класс — Connected Mathematics Project
6-1 Prime Time
Понятия и объяснения | Примеры выполненных домашних заданий | Математический фон
В Prime Time учащиеся будут изучать важные свойства целых чисел. Многие из этих свойств связаны с умножением и делением. Исследования помогут студентам понять взаимосвязь между факторами, мультипликаторами, делителями и продуктами.Студенты также узнают, как свойство распределения связывает умножение и сложение. Исследования этого раздела помогут студентам понять следующие идеи.
- Классифицирует числа как простые или составные
- Определите, какие ситуации требуют общих факторов, общих кратных, наименьшего общего кратного или наибольшего общего множителя
- Разработать стратегии для поиска факторов и кратных, наименьших общих кратных и наибольших общих факторов
- Признать и использовать тот факт, что каждое целое число может быть записано точно одним способом как произведение простых чисел
- Используйте экспоненциальную запись для записи повторяющихся множителей
- Связать разложение двух чисел на простые множители с наименьшим общим кратным и наибольшим общим делителем двух чисел
- Признать, что свойство распределения связывает мультипликативную и аддитивную структуры целых чисел
- Используйте свойства операций с числами, включая соглашение о распределении и порядке операций, для записи эквивалентных числовых выражений.
- Используйте множители и множители для решения проблем, объясните некоторые числовые факты повседневной жизни
Когда ваш ребенок сталкивается с новой проблемой, рекомендуется задать эти вопросы.В этом модуле вы можете задавать такие вопросы, как:
- Поможет ли мне решить проблему разбиение числа на множители?
- Какие общие множители и общие множители есть у чисел?
- Что множители и кратные числа говорят мне о ситуации?
- Когда может быть полезно записать число в факторизованной форме или в виде суммы?
6-2 Сравнение бит и частей
Понятия и объяснения | Примеры выполненных домашних заданий | Математический фон
В курсе «Сравнение битов и частей» ваш ребенок разовьет навыки использования дробей, десятичных знаков, соотношений и процентов для измерения и сравнения величин.
Расследования этого подразделения помогут вам понять, как:
- Используйте язык соотношений и обозначения для сравнения количеств
- Различать дроби как числа и соотношения как сравнения
- Используйте различные стратегии масштабирования и разделения, чтобы рассуждать пропорционально
- Думайте о дробях и десятичных дробях как о расположении и расстоянии в числовой строке
- Гибкое переключение между дробными, десятичными и процентными представлениями
- Найдите абсолютные значения и противоположности и используйте их для описания реальных величин
- Используйте дробные, десятичные и процентные ориентиры для оценки чисел
- Используйте контекст, модели, рисунки или оценки, чтобы рассуждать о ситуациях
- Используйте эквивалент дробей и соотношений для решения задач
- Используйте прейскуранты и расценки для решения проблем
По мере того, как ваш ребенок работает над задачами этого модуля, задавайте себе вопросы о ситуациях, в которых используются дроби, десятичные дроби, отношения и проценты.
- Какие модели или диаграммы могут быть полезны для понимания ситуации и взаимосвязей между количествами?
- Это ситуация для сравнения? Если да, могу ли я использовать соотношение или вычитание?
- Какие стратегии я могу использовать, чтобы найти эквивалентные формы этих дробей, десятичных знаков, отношений или процентов?
- Какие стратегии я могу использовать для сравнения или упорядочения набора дробей, десятичных знаков и процентов?
- Какие стратегии я могу использовать, чтобы рассуждать о числах больше или меньше 0?
- Как я могу использовать расценки или прейскурант для сравнения?
6-3 Давайте будем рациональными
Понятия и объяснения | Примеры выполненных домашних заданий | Математический фон
В курсе Let’s Be Rational ваш ученик разовьет понимание четырех основных арифметических операций с дробями, включая смешанные числа.Они также описывают стратегии использования этих операций при решении задач, связанных с дробями.
Ваш ребенок научится:
- Используйте тесты и другие стратегии для обоснованной оценки результатов операций с дробями, включая смешанные числа
- Разработка способов моделирования сумм, разностей, произведений и частных, включая использование площадей, дробных полос и числовых линий
- Ищите правила для обобщения закономерностей в операциях с дробями
- Используйте свои знания о дробях, эквивалентности дробей и свойствах чисел для разработки алгоритмов сложения, вычитания, умножения и деления дробей
- Определить, когда сложение, вычитание, умножение или деление является подходящей операцией для решения проблемы
- Запишите семейства фактов, чтобы показать обратную связь между сложением и вычитанием, а также между умножением и делением.
- Решать задачи с помощью операций над дробями, включая смешанные числа
- Находите значения переменных, используя операции с дробями, включая смешанные числа
Когда ваш ребенок сталкивается с новой проблемой, рекомендуется задать ему такие вопросы, как:
- Какие модели или диаграммы могут быть полезны для понимания проблемной ситуации и взаимосвязей между величинами?
- Какие модели или диаграммы могут помочь вам решить, какая операция будет полезна для решения проблемы?
- Какова разумная оценка ответа?
6-4 Покрытие и окружение
Понятия и объяснения | Примеры выполненных домашних заданий | Математический фон
В Покрытие и окружение ваш ученик будет исследовать области и периметры фигур.Особое внимание уделяется четырехугольникам и треугольникам. Ваш ребенок также будет исследовать площадь поверхности и объем прямоугольных призм. Им помогут расследования этого подразделения
- Проанализируйте, что значит измерить площадь и периметр
- Связать периметр с окружающей фигурой и площадь с охватом фигуры
- Разработайте стратегии, процедуры и формулы, выраженные словами или символами, для поиска площадей и периметров прямоугольников, параллелограммов и треугольников
- Изучить взаимосвязи между периметром и площадью, в том числе то, что одно может изменяться, а другое остается неизменным
- Проанализируйте, как площадь треугольника и площадь параллелограмма связаны с площадью прямоугольника
- Используйте сети, сделанные из прямоугольников и треугольников, чтобы найти площадь поверхности призм
- Найдите объем прямоугольных призм с дробными длинами сторон
- Используйте периметр, площадь, площадь поверхности и объем для решения проблем.
Когда ваш ребенок сталкивается с новой проблемой, рекомендуется задать такие вопросы, как:
- Какие атрибуты формы важно измерить?
- Требуется точный ответ?
- Как определить, задействована ли площадь или периметр фигуры?
- Что я ищу, когда нахожу район? Когда я найду периметр?
- Какие отношения, касающиеся площади, периметра или того и другого, помогут решить проблему?
- Как определить площадь поверхности призмы по сетке или трехмерному изображению призмы?
- В чем разница между площадью двумерной фигуры и площадью поверхности призмы?
6-5 десятичных операций
Понятия и объяснения | Примеры выполненных домашних заданий | Математический фон
В Decimal Ops ваш ученик научится понимать и использовать четыре операции (+, -, x, ÷,) над десятичными числами.Ваш ребенок также улучшит ваше понимание и навыки работы с процентами.
Ваш ученик научится:
- Сложение, вычитание, умножение и деление десятичных знаков
- Оценить результаты десятичных операций
- Знайте, когда использовать каждую операцию в ситуации с десятичными знаками
- Связать операции над десятичными числами с задачами, связанными с удельными ставками
- Используйте проценты для решения задач
Когда ваш ребенок сталкивается с новой проблемой, рекомендуется задать такие вопросы, как:
- Какие операции над десятичными знаками или процентами помогут в решении этой проблемы?
- Какие алгоритмы помогут с расчетами?
- Примерно сколько будет сумма, разница, произведение или частное?
- Что десятичные дроби и / или проценты в задаче говорят мне о ситуации?
6-6 переменных и шаблонов
Понятия и объяснения | Примеры выполненных домашних заданий | Математический фон
В переменных и паттернах ваш ребенок изучит некоторые основные идеи алгебры и узнает, как использовать эти идеи для решения задач и принятия решений.
Исследования этого раздела помогут вашему ученику научиться:
- Распознавать ситуации, в которых переменные связаны предсказуемым образом
- Описывать закономерности изменений словами, таблицами данных, графиками и уравнениями
- Используйте таблицы данных, графики, уравнения и неравенства для решения проблем
По мере того, как ваш ребенок работает над задачами этого модуля, задавайте ему вопросы о проблемных ситуациях, которые связаны с соответствующими количественными переменными:
- Какие переменные в проблеме?
- Какие переменные зависят от других или изменяются по отношению к ним?
- Как можно использовать таблицу, график, уравнение или неравенство для представления и анализа взаимосвязи между переменными?
6-7 Данные о нас
Понятия и объяснения | Примеры выполненных домашних заданий | Математический фон
В разделе «Данные о нас» вы узнаете о различных способах сбора, организации, отображения и анализа данных.В этом модуле ваш ученик научится:
- Используйте процесс исследования данных, задавая вопросы, собирая и анализируя данные, а также интерпретируя данные, чтобы ответить на вопросы
- Упорядочивайте и представляйте данные с помощью таблиц, точечных графиков, линейных графиков, гистограмм, гистограмм и диаграмм типа «квадрат и усы»
- Опишите общую форму распределения и определите, является ли оно симметричным относительно центрального значения
- Вычислить среднее, медианное значение и режим распределения данных и использовать эти меры, чтобы указать, что типично для распределения
- Опишите изменчивость распределения путем выявления кластеров и пробелов, а также путем вычисления диапазона, межквартильного размаха (IQR) и среднего абсолютного отклонения (MAD)
- Определить, какие статистические меры центра и распространения следует использовать для описания конкретного распределения данных
- Различать категориальные данные и числовые данные и определять, какие графики и статистические данные могут использоваться для представления каждого типа данных
- Сравните два или более распределения данных, в том числе используя меры центра и разброса для сравнения
Когда вы сталкиваетесь с новой проблемой, неплохо задать себе вопросы.В этом модуле вы можете задавать такие вопросы, как:
- Какой вопрос исследуется для сбора этих данных?
- Как мне организовать данные?
- Какие статистические показатели помогут описать распределение данных?
- Что эти статистические показатели скажут мне о распределении данных?
- Как я могу использовать графики и статистику, чтобы сообщить ответ на мой исходный вопрос?
Учебная программа 6-го класса
Ниже приведены необходимые навыки со ссылками на ресурсы, которые помогут в освоении этого навыка.Мы также поощряем множество упражнений и работу с книгами. Curriculum Home
Важно: это только руководство.
Обратитесь в местный орган управления образованием, чтобы узнать их требования.
6 класс | Вычитание
☐ Поймите, что подразумевается под дополнением десятков, дополнением до одной сотни и т. Д. Целого числа; и воспользуйтесь методом вычитания путем сложения.
6 класс | Умножение
☐ Определите и определите нулевое свойство умножения
6 класс | Числа
☐ Чтение и запись целых чисел в триллионы
☐ Определите абсолютное значение и определите абсолютное значение рациональных чисел (включая положительные и отрицательные)
☐ Найдите рациональные числа на числовой прямой (включая положительные и отрицательные)
☐ Порядковые рациональные числа (включая положительные и отрицательные)
☐ Определение и определение коммутативных и ассоциативных свойств сложения и умножения
☐ Вычислять числовые выражения, используя порядок операций (может включать в себя показатели степени два и три)
☐ Определить и определить свойство распределения умножения над сложением
☐ Определение и идентификация идентичности и обратных свойств сложения и умножения
6 класс | Десятичные знаки
☐ Представляют дроби как завершающие или повторяющиеся десятичные знаки
☐ Используйте различные стратегии для сложения, вычитания, умножения и деления десятичных дробей до миллионных долей
6 класс | Дроби
☐ Сложить и вычесть дроби с разными знаменателями
☐ Умножайте и делите дроби с разными знаменателями.
☐ Умножение и деление смешанных дробей с разными знаменателями
☐ Определите мультипликативное обратное (обратное) число
☐ Найдите несколько представлений рациональных чисел (дроби, десятичные дроби и проценты от 0 до 100)
6 класс | Проценты
☐ Чтение, запись и определение процентов от целого (от 0% до 100%)
☐ Решение проблем с процентами, связанными с процентами, ставкой и базой
6 класс | Соотношения
☐ Решение простых пропорций в контексте
☐ Проверить пропорциональность, используя произведение средних, равное произведению крайних значений
☐ Понять концепцию соотношения
☐ Эквивалентные коэффициенты в виде доли
☐ Отличить разницу между ставкой и соотношением
☐ Решите пропорции, используя эквивалентные дроби
6 класс | Измерение
☐ Измерение емкости и вычисление объема прямоугольной призмы
☐ Определите метрические единицы объема (миллилитры, литры)
☐ Укажите эквивалентные метрические единицы вместимости (миллилитры в литры и литры в миллилитры; или наоборот)
☐ Определите инструменты и методы, необходимые для измерения с надлежащим уровнем точности: емкость (метрические единицы)
☐ Определите личные рекомендации для емкости (метрические единицы)
☐ Понять преобразование измерений
☐ Преобразование из градусов Цельсия в градусы Фаренгейта и наоборот
☐ Определите стандартные единицы вместимости США (жидкие унции, чашки, пинты, кварты и галлоны)
☐ Определите эквивалентные стандартные единицы вместимости США (жидкие унции в чашки, чашки в пинты, пинты в кварты и кварты в галлоны; или наоборот)
☐ Определите инструменты и методы, необходимые для измерения с надлежащим уровнем точности: пропускная способность (стандартные единицы США)
☐ Определите личные рекомендации по мощности (стандартные единицы США)
6 класс | Время
☐ Високосные годы
☐ Понимание AD и BC
☐ Знайте, что такое двадцать четыре часа в часах, и как переводить между двадцатичетырехчасовым временем и временем AM / PM.
6 класс | Геометрия (плоскость)
☐ Рассчитайте длину соответствующих сторон подобных треугольников (или других простых аналогичных форм), используя принцип пропорциональности
☐ Вычислить площадь основных многоугольников, нарисованных на координатной плоскости (прямоугольники и фигуры, состоящие из прямоугольников, имеющих стороны с целой длиной)
☐ Определите площади треугольников и четырехугольников (квадратов, прямоугольников, параллелограммов, ромбов и трапеций) и разработайте формулы
☐ Используйте различные стратегии, чтобы найти площадь правильных и неправильных многоугольников
☐ Определить радиус, диаметр, хорды и центральные углы окружности
☐ Понимать взаимосвязь между диаметром и радиусом окружности
☐ Определите площадь и длину окружности круга по соответствующей формуле
☐ Вычислить площадь сектора круга, учитывая размер центрального угла и радиус круга
☐ Понимать взаимосвязь между длиной окружности и диаметром окружности
☐ Определите площадь эллипса по соответствующей формуле
6 класс | Геометрия (сплошная)
☐ Определите объем прямоугольных призм (кубоидов) путем подсчета кубиков и разработайте формулу
6 класс | Алгебра
☐ Используйте подстановку для вычисления алгебраических выражений (может включать в себя показатели степени один, два и три)
☐ Решите и объясните двухэтапные уравнения с целыми числами с помощью обратных операций
☐ Вычислить формулы для заданных входных значений (окружность, площадь, объем, расстояние, температура, процент и т. Д.)
6 класс | Экспоненты
☐ Представляют многократное умножение в экспоненциальной форме
☐ Представьте экспоненциальную форму как повторное умножение
☐ Вычислять выражения с показателями степени, где степень является показателем единицы, двух или трех
6 класс | Координаты
☐ Определите и нанесите точки во всех четырех квадрантах
6 класс | Линейные уравнения
☐ Перевести двухэтапные словесные выражения в алгебраические
☐ Перевести двухступенчатые словесные предложения в алгебраические уравнения
6 класс | Данные
☐ Разработайте концепцию выборки при сборе данных от совокупности и определите лучший метод сбора данных для конкретного вопроса
☐ Записать данные в таблицу частот
☐ Построение диаграмм Венна для сортировки данных
☐ Определите и выровняйте наиболее подходящий график для отображения заданного набора данных (пиктограмма, гистограмма, линейная диаграмма, гистограмма или круговая диаграмма)
☐ Определение среднего значения, режима и медианы для заданного набора данных
☐ Определить диапазон для заданного набора данных
☐ Чтение и интерпретация графиков
☐ Обоснование прогнозов, сделанных на основе данных
☐ Запишите и интерпретируйте данные, используя график стебля и листа.
☐ Рассчитайте относительные частоты по таблице частот.
☐ Чтение и интерпретация частотных таблиц
6 класс | Оценка
☐ Оценка объема, площади и окружности
☐ Обосновать обоснованность сметы
☐ Оценить процент количества (от 0% до 100%)
☐ Обоснуйте обоснованность ответов с помощью оценки (с округлением)
6 класс | Вероятность
☐ Определить вероятность зависимых событий
☐ Определите количество возможных исходов для сложного события, используя фундаментальный принцип подсчета, и используйте его для определения вероятностей событий, когда исходы имеют равную вероятность
☐ Перечислить возможные исходы сложных событий
.

 )
) Что повлияло на смену настроения во время урока?
Что повлияло на смену настроения во время урока? Тесты по математике к учебнику Н.Я. Виленкина и др. «Математика. 6 класс» М.: «Экзамен», 2013 г.
Тесты по математике к учебнику Н.Я. Виленкина и др. «Математика. 6 класс» М.: «Экзамен», 2013 г. Актуализация знаний
Актуализация знаний Долгое время дроби считались самым трудным разделом математики. У немцев даже сложилась поговорка «попасть в дроби», что означает попасть в трудное положение.
Долгое время дроби считались самым трудным разделом математики. У немцев даже сложилась поговорка «попасть в дроби», что означает попасть в трудное положение.

 Работа по учебнику.Стр.34,№212.(проектор)
Работа по учебнику.Стр.34,№212.(проектор)

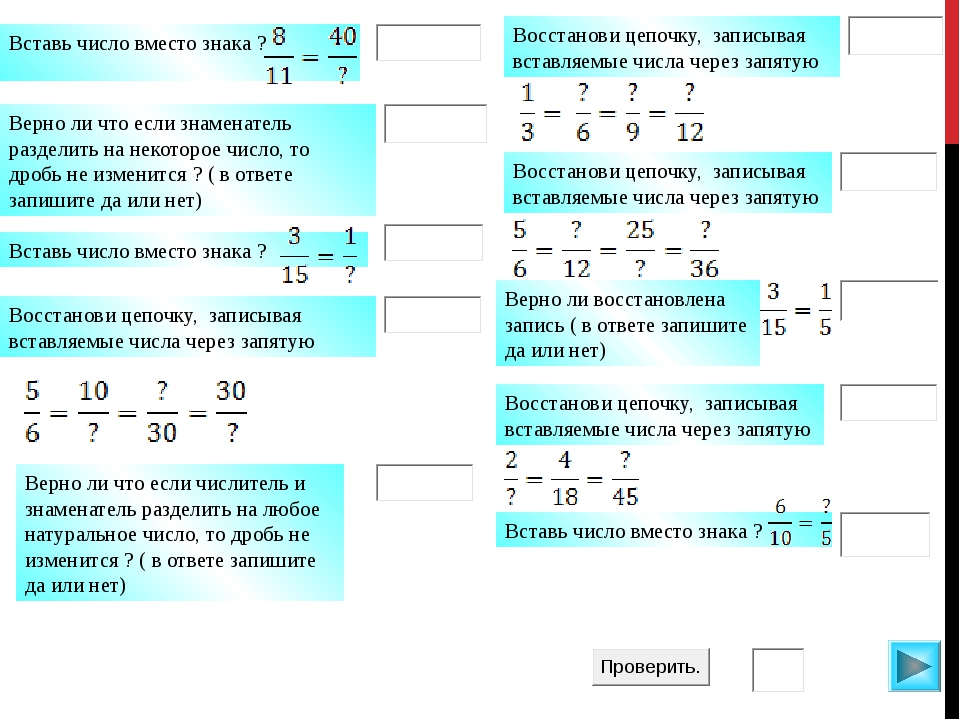

 Какое натуральное число надо вписать вместо буквы, чтобы было верным равенство:
Какое натуральное число надо вписать вместо буквы, чтобы было верным равенство: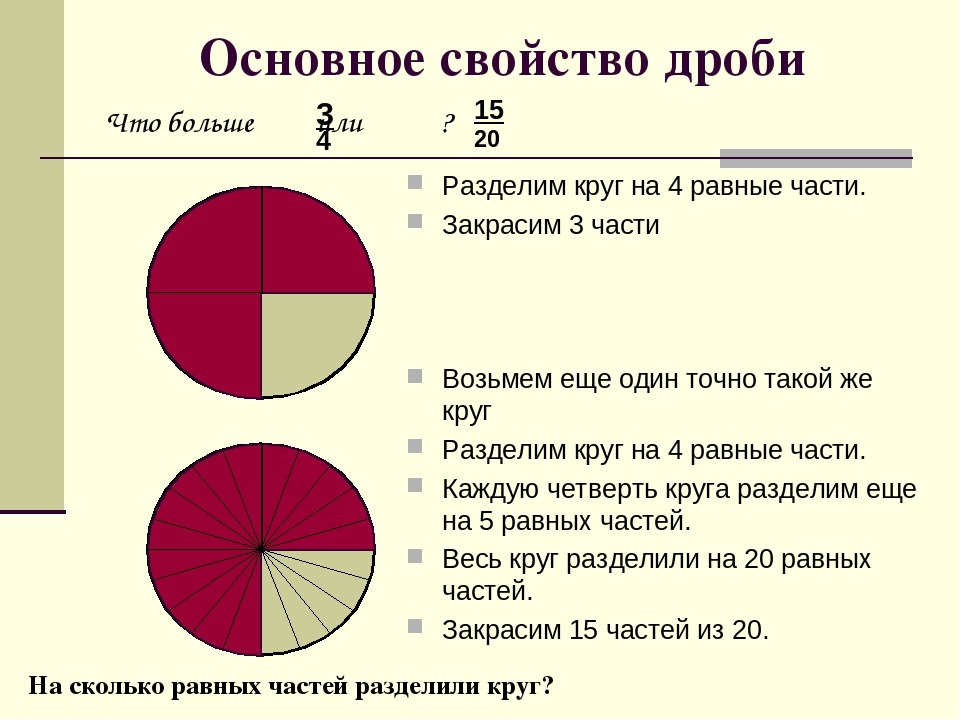
 Изучение новых знаний и способов действий.
Изучение новых знаний и способов действий.
 Информация о домашнем задании.
Информация о домашнем задании.





