Уравнения контрольная работа 5 класс – Контрольная работа по теме «Уравнения» (5 класс)
Контрольная работа по теме «Уравнения» (5 класс)
Вариант 1
1. Решите уравнения:
а) 87 – х = 39
б) z + 24 = 43
в) (38 + у) – 18 = 31
г) 604 + (356 – у) = 887
2. Решите задачу с помощью уравнения.
В вагоне метро ехало 62 пассажира. На остановке из вагона вышло несколько пассажиров, после чего в вагоне осталось 47 человек. Сколько пассажиров выщло из вагона на остановке?
3. Найдите значение выражения:
(223 – m) + (145 – n), при m =167 и n = 93.
4. Упростите выражение:
а) 328 + n +482
б) 378 – (к + 258).
5. На отрезке АВ отмечена точка М. Найдите длину отрезка АВ, если отрезок АМ = 35см, а отрезок МВ короче отрезка АМ на m см. Упростите получившееся выражение и найдите его значение при m = 24.
Вариант 3
1. Решите уравнения:
а) 87 – х = 39
б) z + 24 = 43
в) (38 + у) – 18 = 31
г) 604 + (356 – у) = 887
2. Решите задачу с помощью уравнения.
В вагоне метро ехало 62 пассажира. На остановке из вагона вышло несколько пассажиров, после чего в вагоне осталось 47 человек. Сколько пассажиров выщло из вагона на остановке?
3. Найдите значение выражения:
(223 – m) + (145 – n), при m=167 и n = 93.
4. Упростите выражение:
а) 328 + n +482
б) 378 – (к + 258).
5. На отрезке АСотмечена точка М. Найдите длину отрезка АС, если отрезок АМ = 35 см, а отрезок МС короче отрезка АМ на m см. Упростите получившееся выражение и найдите его значение при m = 24.
Вариант 2
1. Решите уравнения:
а) у – 27 = 45
б) z + 35 = 64
в) 63 –(25+ х)= 26
г) (х — 653) + 308 = 417
2. Решите задачу с помощью уравнения.
Андрей поймал в озере 51 рыбку. Несколько рыбок он подарил другу, после чего у него осталось 37 рыбок. Сколько рыбок Андрей подарил другу?
3. Найдите значение выражения:
(m– 148) — (97+n), при m= 318 и n = 45.
4. Упростите выражение:
а) 527 + n + 293
б) 456 – (к + 146).
5. На отрезке CD отмечена точка N. Найдите длину отрезка CD, если отрезок CN = 45 см, а отрезок ND короче отрезка CN на n см. Упростите получившееся выражение и найдите его значение при n = 36.
Вариант 4
1. Решите уравнения:
а) у – 27 = 45
б) z + 35 = 64
в) 63 – (25 + х) = 26
г) (х — 653) + 308 = 417
2. Решите задачу с помощью уравнения.
Андрей поймал в озере 51 рыбку. Несколько рыбок он подарил другу, после чего у него осталось 37 рыбок. Сколько рыбок Андрей подарил другу?
3. Найдите значение выражения:
(m – 148) — (97 + n), при m = 318 и n = 45.
4. Упростите выражение:
а) 527 + n + 293
б) 456 – (к + 146).
5. На отрезке ВD отмечена точка N. Найдите длину отрезка ВD, если отрезок ВN = 45 см, а отрезок ND короче отрезка ВN на n см. Упростите получившееся выражение и найдите его значение при n = 36.
Вариант 5
1. Решите уравнения:
а) 87 – х = 39
б) z + 24 = 43
в) (38 + у) – 18 = 31
г) 604 + (356 – у) = 887
2. Решите задачу с помощью уравнения.
В вагоне метро ехало 62 пассажира. На остановке из вагона вышло несколько пассажиров, после чего в вагоне осталось 47 человек. Сколько пассажиров выщло из вагона на остановке?
3. Найдите значение выражения:
(223 – m) + (145 – n), при m=167 и n = 93.
4. Упростите выражение:
а) 328 + n +482
б) 378 – (к + 258).
5. На отрезке СВ отмечена точка М. Найдите длину отрезка СВ, если отрезок СМ = 35 см, а отрезок МВ короче отрезка СМ на m см. Упростите получившееся выражение и найдите его значение при m = 24.
Вариант 7
1. Решите уравнения:
а) 87 – х = 39
б) z + 24 = 43
в) (38 + у) – 18 = 31
г) 604 + (356 – у) = 887
2. Решите задачу с помощью уравнения.
В вагоне метро ехало 62 пассажира. На остановке из вагона вышло несколько пассажиров, после чего в вагоне осталось 47 человек. Сколько пассажиров вышло из вагона на остановке?
3. Найдите значение выражения:
(223 – m) + (145 – n), при m=167 и n = 93.
4. Упростите выражение:
а) 328 + n +482
б) 378 – (к + 258).
5. На отрезке АВ отмечена точка Т. Найдите длину отрезка АВ, если отрезок АТ = 35 см, а отрезок ТВ короче отрезка АТ на m см. Упростите получившееся выражение и найдите его значение при m = 24.
Вариант 6
1. Решите уравнения:
а) у – 27 = 45
б) z + 35 = 64
в) 63 – (25 + х) = 26
г) (х — 653) + 308 = 417
2. Решите задачу с помощью уравнения.
Андрей поймал в озере 51 рыбку. Несколько рыбок он подарил другу, после чего у него осталось 37 рыбок. Сколько рыбок Андрей подарил другу?
3. Найдите значение выражения:
(m – 148) — (97 + n), при m = 318 и n = 45.
4. Упростите выражение:
а) 527 + n + 293
5. На отрезке CК отмечена точка N. Найдите длину отрезка CК, если отрезок CN = 45 см, а отрезок NК короче отрезка CN на n см. Упростите получившееся выражение и найдите его значение при n = 36.
Вариант 8
1. Решите уравнения:
а) у – 27 = 45
б) z + 35 = 64
в) 63 – (25 + х) = 26
г) (х — 653) + 308 = 417
2. Решите задачу с помощью уравнения.
Андрей поймал в озере 51 рыбку. Несколько рыбок он подарил другу, после чего у него осталось 37 рыбок. Сколько рыбок Андрей подарил другу?
3. Найдите значение выражения:
(m – 148) — (97 + n), при m = 318 и n = 45.
4. Упростите выражение:
а) 527 + n + 293
б) 456 – (к + 146).
5. На отрезке CD отмечена точка Р. Найдите длину отрезка CD, если отрезок CР = 45 см, а отрезок РD короче отрезка CР на n см. Упростите получившееся выражение и найдите его значение при n = 36.
www.metod-kopilka.ru
Контрольная работа по теме «Решение уравнений». 5 класс
Вариант №
Решить уравнения:
А) 13х + 4х = 408;
Б) 14х + 2х – х + 14 = 299;
В) 36 : х – 2 = 4;
Г)14 ( 3х – 15 ) = 252
Составить и решить уравнение:
Частное разности чисел У и 68 и числа 13 равно 10.
Решить задачу с помощью уравнения:
Дубов в парке было в 3 раза больше, чем берез, а кленов – в 4 раза больше чем берез. Сколько деревьев каждого вида росло в парке, если всего их было 736?
Выполнить действия:
19691 – 19691 : ( 824 – 727 )
Вычислить:
(67 – Х ) + ( 279 — У) при Х = 23, У = 134
Вариант №
Решить уравнения:
А) х + 18х = 3857;
Б) 16х + х – 8х + 52 = 2815;
В) 84 – 56 : х = 70;
Г) 6 ( 2х – 43 ) = 402
Составить и решить уравнение:
Утроенная разность чисел Х и 94 равна 99
Решить задачу с помощью уравнения:
В первом баке молока в 4 раза меньше, чем во втором, а в третьем на 27 литров больше, чем в первом. Сколько литров молока в третьем баке, если всего в трех баках 105 литров?
Выполнить действия:
19536 – 19536 : (237 — 189)
Вычислить:
(267 – Х ) + ( 279 — У) при Х = 213, У = 184
Вариант №
Решить уравнения:
А) 47х – 15х = 2144;
Б) 7х + 5х + х – 29 = 374;
В) х : 4 – 13 = 87;
Г) 8 ( 112 – 5х ) = 816
Составить и решить уравнение:
Разность чисел 64 и У в 3 раза меньше числа 108.
Решить задачу с помощью уравнения:
Между тремя школами разделили 509 кг бананов, причем в одну школу отправили в 7 раз больше бананов, чем во вторую, а в третью — на 158 кг больше, чем во вторую. Сколько бананов отправили в каждую школу?
Выполнить действия:
– 3264 : ( 92-44 )
Вычислить:
(670 – Х ) + ( 2759 — У) при Х = 203, У = 194
Вариант №
Решить уравнения:
А) 14х + 5х = 608;
Б) 19х – х – 14 = 256;
В) 48 : х + 3 = 4;
Г) 15 ( 2х + 11) = 285
Составить и решить уравнение:
Частное суммы чисел Х и 57 и числа 53 равно 2.
Решить задачу с помощью уравнения:
В одном мешке в 3 раза меньше крупы, чем во втором , а в третьем – на 9 кг меньше, чем в первом мешке. Сколько крупы в третьем мешке, если в трех мешках вместе – 339 кг?
Выполнить действия:
20301 – 20301 : ( 296 – 229 )
Вычислить:
(671 – Х ) + ( 2791 — У) при Х = 253, У = 139
Вариант №
Решить уравнения:
А) 53х – 26х = 1863;
Б) 6у + у + 10у + 17 = 323;
В) х : 8 + 24 = 42;
Г) 7 ( 123 – 4х ) = 749
Составить и решить уравнение:
Сумма утроенного числа Х и числа 187 равна 754.
Решить задачу с помощью уравнения:
На заводе в трех цехах работает 626 рабочих. В первом цехе работает в 2 раза больше людей, чем во втором, а в третьем – на 142 человека больше, чем во втором цехе. Сколько работников работает в каждом цехе?
Выполнить действия:
– 315 : ( 162 – 3 47 )
Вычислить:
(1167 – Х ) + ( 2579 — У) при Х = 273, У = 1354
Вариант №
Решить уравнения:
А) а + 23а = 1032;
Б) 19х – 12х – 47 = 1388;
В) х : 9 – 142 = 164;
Г) 23 ( х – 12 ) = 552
Составить и решить уравнение:
Сумма удвоенного числа Х и 99 равна 123.
Решить задачу с помощью уравнения:
Проволоку длиной 456 м разрезали на три части, причем первая часть в 4 раза длиннее, чем третья, а вторая часть – на 114 м длиннее, чем третья. Найти длину каждой части проволоки.
Выполнить действия:
– 4704 : ( 46 + 38 )
Вычислить:
(2607 – Х ) + ( 4279 — У) при Х = 203, У = 1034
multiurok.ru
Контрольная работа по математике «Решение уравнений» 5 класс
Контрольная работа № 3 «Решение уравнений»
ВАРИАНТ 1
1. Решите уравнение:
а) 21 + х = 56; б) у – 89 = 90.
2. Найдите значение выражения:
а) а + т, если а = 20, т = 70;
б) 260 + b – 160, если b = 93.
3. Вычислите, выбирая удобный порядок действий:
а) 6485 + 1977 + 1515; б) 863 – (163 + 387).
4. Решите с помощью уравнения задачу: «В автобусе было 78 пассажиров. На остановке несколько человек вышло и осталось 59 пассажиров. Сколько человек вышло?»
5. На отрезке MN = 19 см отметили точку К такую, что МК = 15 см, и точку F такую, что FN = 13 см. Найдите длину отрезка KF.
——————————————————————————————————————-
ВАРИАНТ 2
1. Решите уравнение:
а) х + 32 = 68; б) 76 – у = 24.
2. Найдите значение выражения:
а) с – п, если с = 80, п = 30;
б) 340 + k – 240, если k = 87.
3. Вычислите, выбирая удобный порядок действий:
а) 7231 + 1437 + 563; б) (964 + 479) – 264.
4. Решите с помощью уравнения задачу: «В санатории было 97 отдыхающих. Несколько человек уехало на экскурсию и осталось 78 отдыхающих. Сколько человек уехало?»
5. На отрезке DE = 25 см отметили точку L такую, что DL = 19 см, и точку P такую, что PE = 17 см. Найдите длину отрезка LP
——————————————————————————————————————-
ВАРИАНТ 3
1. Решите уравнения:
а) 42 + х = 74; б) у – 53 = 48.
2. Найдите значение выражения:
а) b + d, если b = 40, d = 50;
б) 450 + t – 350, если t = 84.
3. Вычислите, выбирая удобный порядок действий:
а) 3817 + 2599 + 1183; б) 759 – (259 + 413).
4. Решите с помощью уравнения задачу: «По озеру плавало 34 лебедя. После того, как несколько лебедей улетело, на озере осталось 16 лебедей. Сколько лебедей улетело?»
5. На отрезке ВК = 31 см отметили точку D такую, что BD = 20 см, и точку Е такую, что КЕ = 15 см. Найдите длину отрезка DE.
———————————————————————————————————————
ВАРИАНТ 4
1. Решите уравнения:
а) х + 15 = 81; б) 65 – у = 37.
2. Найдите значение выражения:
а) k – l, если k = 90, l = 20;
б) 530 + c – 430, если c = 91.
3. Вычислите, выбирая удобный порядок действий:
а) 5384 + 3687 + 1616; б) (851 + 293) – 351.
4. Решите с помощью уравнения задачу: «В корзине лежало 76 яблок. После того, как несколько яблок съели, в корзине осталось 59 яблок. Сколько яблок было съедено?»
5. На отрезке XY = 28 см отметили точку R такую, что XR = 14 см, и точку P такую, что YP = 19 см. Найдите длину отрезка RP.
doc4web.ru
Контрольные работы по математике 5 класс Виленкин
Контрольная работа № 1
«Натуральные числа и шкалы»
Контрольная работа № 1
«Натуральные числа и шкалы»
ВАРИАНТ 11. Сравните числа и запишите ответ с помощью
знака < или >:
а) 2 657 209 и 2 654 879; б) 96 785 и 354 211.
2. Начертите прямую MN и луч CD так, чтобы прямая и луч не пересекались.
3. Запишите цифрами число: триста пятнадцать миллионов восемь тысяч шестьсот.
4. а) Запишите координаты точек А, F, K, О, отмеченных на координатном луче:
б) Начертите координатный луч, единичный отрезок которого равен длине одной клетки тетради. Отметьте на этом луче точки В (8), D (11), Р (1), R (16).
5. Запишите четырехзначное число, которое больше 9987 и оканчивается цифрой 6.
ВАРИАНТ 21. Сравните числа и запишите ответ с помощью
знака < или >:
а) 3 859 407 и 3 859 601; б) 216 312 и 85 796.
2. Начертите луч RP и отрезок BE так, чтобы луч не пересекал отрезок.
3. Запишите цифрами число: шестьсот двадцать три миллиона шестьдесят тысяч двести.
4. а) Запишите координаты точек C, M, O, S, отмеченных на координатном луче:
б) Начертите координатный луч, единичный отрезок которого равен длине одной клетки тетради. Отметьте на этом луче точки A (6), B (12), D (1), F (17).
5. Запишите пятизначное число, которое меньше 10 016 и оканчивается цифрой 7.
Контрольная работа № 1
«Натуральные числа и шкалы»
Контрольная работа № 1
«Натуральные числа и шкалы»
ВАРИАНТ 31. Сравните числа и запишите ответ с помощью
знака > или <:
а) 5 389 780 и 5 386 904; б) 103 636 и 94 577.
2. Начертите прямую AD и отрезок МК так, чтобы прямая
не пересекала отрезок.
3. Запишите цифрами число: пятьсот восемнадцать миллионов тридцать пять тысяч семьсот.
4. а) Запишите координаты точек А, С, K, О, отмеченных на координатном луче:
б) Начертите координатный луч, единичный отрезок которого равен длине одной клетки тетради. Отметьте на этом луче точки А (3), Е (13), М (7), Р (10).
5. Запишите шестизначное число, которое меньше 100 017
и оканчивается цифрой 8.
1. Сравните числа и запишите ответ с помощью
знака > или <:
а) 4 751 384 и 4 761 495; б) 72 465 и 205 671.
2. Начертите лучи OP и MN так, чтобы они
не пересекались.
3. Запишите цифрами число: четыреста пять миллионов девять тысяч двадцать.
4. а) Запишите координаты точек B, C, N, О, отмеченных на координатном луче:
б) Начертите координатный луч, единичный отрезок которого равен длине одной клетки тетради. Отметьте на этом луче точки B (4), D (1), S (15), T (14).
5. Запишите пятизначное число, которое больше 99 987 и оканчивается цифрой 5.
www.metod-kopilka.ru
Контрольная работа по математике 5 класс «Числовые и буквенные выражения.Уравнения»
М – 5 Контрольная работа по теме:
«Числовые и буквенные выражения. Уравнения»
1 вариант 2 вариант
№1. Выполните действия:
1899-3?(427+173) 490 + (592 – 32)?5
№2. Решите уравнения:
а) 87 – х =39 а) у — 27 =45
б) у + 24 = 43 б) 37 + х = 64
в) (38 + у) – 18 =31 в) 63 – (25 + х) =26
г) 604 + (356 – у)=887 г) (х – 653) + 308=417
№3. Вычислите, выбирая удобный порядок действий:
а) 7231 +1437 + 563 а) 6485 + 1977 +1515
б) 863 –(163 + 387) б) (964 + 479) – 264
№4. Упростите выражение:
а) 328 + х +482 а) с + 527 + 293
б) 378 – (с +258) б) 456 – (146 + у)
№5. Решите задачу с помощью уравнения:
В вагоне метро ехало 62 Дима поймал в озере 51
пассажира. На остановке из вагона рыбку. Несколько рыбок
вышло несколько пассажиров, он подарил другу, после
после чего в вагоне осталось чего у него осталось 37
47 человек. Сколько пассажиров рыбок. Сколько рыбок
вышло из вагона на остановке? Дима подарил другу?
№6. Найдите значение выражения, предварительно упростив его:
(462 + а) – 262, если а=578. (875 + у) – 375, если у = 293.
Просмотр содержимого документа
«Контрольная работа по математике 5 класс «Числовые и буквенные выражения.Уравнения»»
М – 5 Контрольная работа по теме:
«Числовые и буквенные выражения. Уравнения»
1 вариант 2 вариант
№1. Выполните действия:
1899-3ˑ(427+173) 490 + (592 – 32)ː5
№2. Решите уравнения:
а) 87 – х =39 а) у — 27 =45
б) у + 24 = 43 б) 37 + х = 64
в) (38 + у) – 18 =31 в) 63 – (25 + х) =26
г) 604 + (356 – у)=887 г) (х – 653) + 308=417
№3. Вычислите, выбирая удобный порядок действий:
а) 7231 +1437 + 563 а) 6485 + 1977 +1515
б) 863 –(163 + 387) б) (964 + 479) – 264
№4. Упростите выражение:
а) 328 + х +482 а) с + 527 + 293
б) 378 – (с +258) б) 456 – (146 + у)
№5. Решите задачу с помощью уравнения:
В вагоне метро ехало 62 Дима поймал в озере 51
пассажира. На остановке из вагона рыбку. Несколько рыбок
вышло несколько пассажиров, он подарил другу, после
после чего в вагоне осталось чего у него осталось 37
47 человек. Сколько пассажиров рыбок. Сколько рыбок
вышло из вагона на остановке? Дима подарил другу?
№6. Найдите значение выражения, предварительно упростив его:
(462 + а) – 262, если а=578. (875 + у) – 375, если у = 293.
kopilkaurokov.ru
Контрольные работы по математике, 5 класс
Контрольная работа № 2
Вариант 1
Выполните действие:
а) 249 638 + 83 554; б) 665 247 — 8296.
а) Какое число на 28 763 больше числа 9338?
б) На сколько число 59 345 больше числа 53 568?
в) На сколько число 59 345 меньше числа 69 965?
В одном ящике 62 кг яблок, что на 18 кг больше, чем во втором. Сколько килограммов яблок во втором ящике?
В треугольнике MFK сторона FK равна 62 см, сторона КМ на 1 дм больше стороны FK, а сторона MF — на 16 см меньше стороны FK. Найдите периметр треугольника MFK и выразите его в дециметрах.
Вдоль аллеи (по прямой) высадили 15 кустов. Расстояние между любыми двумя соседними кустами одинаковое. Найдите это расстояние, если между крайними кустами 210 дм.
____________________________________________________________
Контрольная работа № 2 Вариант 2Выполните действие:
а) 692 545 + 39 647; б) 776 348 — 9397.
а) Какое число на 37 874 больше числа 8137?
б) На сколько число-38 954 больше числа 22 359?
в) На сколько число 38 954 меньше числа 48 234?
В синей коробке 56 игрушек, что на 16 игрушек меньше, чем в красной коробке. Сколько игрушек в красной коробке?
В треугольнике BNP сторона NP равна 73 см, сторона ВР на 1 дм меньше стороны NP, а сторона BN — на 11 см больше стороны NP. Найдите периметр треугольника BNP и выразите его в дециметрах.
Вдоль шоссе (по прямой) высадили 20 деревьев. Расстояние между любыми двумя соседними деревьями одинаковое. Найдите это расстояние, если между крайними деревьями 380м.
Контрольная работа № 3
Вариант 1
Решите уравнения:
а) 21 + х = 56 в) (263 + х) – 97 = 538
б) у – 89 = 90 г) 63 – (25 + х) = 26
Упростите выражение и найдите его значение:
а) 128 + (а + 472), если а = 147 б) 260 + (в – 160), если в = 93
Вычислите, выбирая удобный порядок действий:
а) 6485 + (1977 + 1515) в) (2593 + 1389) — 1593
б) 863 – (163 + 387) г) 3697 – (2697 + 998)
Решите задачу с помощью уравнения. В автобусе было 78 пассажиров. После того как на остановке из него несколько человек вышли, в автобусе осталось 59 пассажиров. Сколько человек вышли из автобуса на остановке?
_______________________________________________________________________________
Контрольная работа № 3
Вариант 2
Решите уравнения:
а) 32 + х = 68 в) (432 + х) – 89 = 724
б) 76 – у = 24 г) 73 – (13 + у) = 21
Упростите выражение и найдите его значение:
а) (453 + а) + 247, если а = 209 б) (123 + в) – 93, если в = 730
Вычислите, выбирая удобный порядок действий:
а) (7231 + 1437) + 563 в) (4597 + 3899) – 2899
б) (964 + 479) – 264 г) 9543 – (3989 + 1543)
Решите задачу с помощью уравнения. В санатории было 97 отдыхающих. После того как несколько человек уехали на экскурсию, в санатории осталось 78 отдыхающих. Сколько отдыхающих уехали на экскурсию?
Контрольная работа № 4
Вариант 1
Найдите значение выражения:
а) 58 · 196 б) 4600 · 1760 в) 405 · 208 г) 17835 : 145 д) 36490 : 178
Решите уравнения:
а) х · 14 = 112 б) 133 : у = 19 в) х : 15 = 90
Вычислите, выбирая удобный порядок действий:
а) 25 · 197 · 4 б) 8 · 567 · 125 в) 50 · 23 · 40
Решите задачу с помощью уравнения.
Коля задумал число, умножил его на 3 и от произведения отнял 7. В результате он получил 50. Какое число задумал Коля?
Угадайте корень уравнения 2 · х – 20 = х + 5 и выполните проверку.
________________________________________________________________________________
Контрольная работа № 4
Вариант 2
Найдите значение выражения:
а) 67 · 189 б) 5300 · 1680 в) 306 · 805 г) 15255 : 135 д) 38130 : 186
Решите уравнения:
а) х · 13 = 182 б) 187 : у = 17 в) х : 14 = 98
Вычислите, выбирая удобный порядок действий:
а) 4 · 289 · 25 б) 8 · 971 · 125 в) 50 · 97 · 20
Решите задачу с помощью уравнения.
Света задумала число, умножил его на 4 и к произведению прибавила 8. В результате она получила 60. Какое число задумала Света?
Угадайте корень уравнения 2 · у – 25 = у + 10 и выполните проверку.
Контрольная работа № 5
Вариант 1
Найдите значение выражения:
а) 684 · 397 – 584 · 397 б) 39 · 58 – 9720 : 27 + 33 в) 23 + 32
Решите уравнения:
а) 7у – 39 = 717 б) х + 3х = 76
Упростите выражение:
а) 24а + 13а + 16а б) 25 · т · 16
В книге напечатаны две сказки. Первая занимает в четыре раза больше страниц, чем вторая, а обе сказки занимают 30 страниц. Сколько страниц занимает каждая сказка?
Угадайте корень уравнения х2 = х : х.
_______________________________________________________________________________
Контрольная работа № 5
Вариант 2
Найдите значение выражения:
а) 798 · 349 — 798 · 249 б) 57 · 38 — 8640 : 24 + 66 в) 33 + 52
Решите уравнения:
а) 8х + 14 = 870 б) 5у – у = 68
Упростите выражение:
а) 37у + 13у + 22у б) 50 · п · 12
В двух корзинах 98 яблок. В первой корзине в шесть раз яблок больше, чем во второй. Сколько яблок в каждой корзине?
Угадайте корень уравнения у3 = у · у.
Контрольная работа № 7
Вариант 1
Выполните действия:
а) 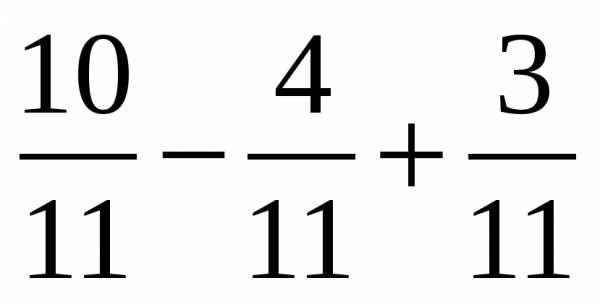 б)
б) 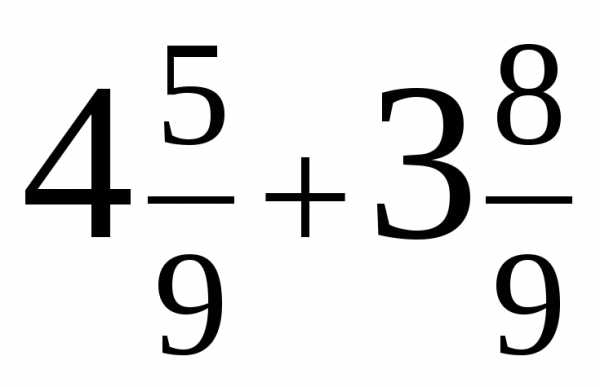 в)
в) 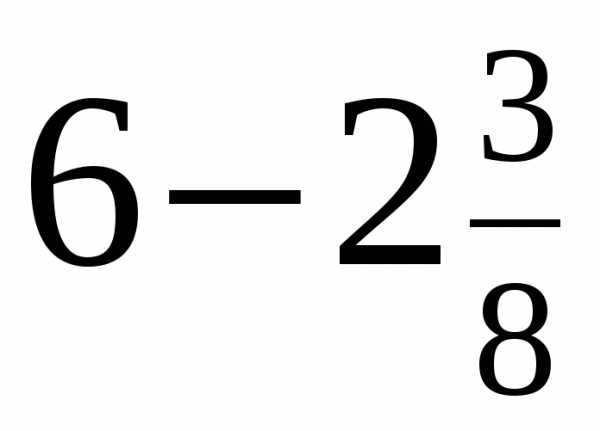 г)
г) 
Турист шел с постоянной скоростью и за 3 ч прошел 14 км. С какой скоростью он шел?
В гараже 45 автомобилей. Из них
 — легковые. Сколько легковых автомобилей в гараже?
— легковые. Сколько легковых автомобилей в гараже?
Решите уравнение:
а) 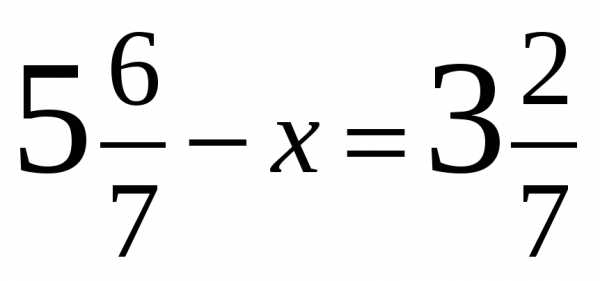 б)
б) 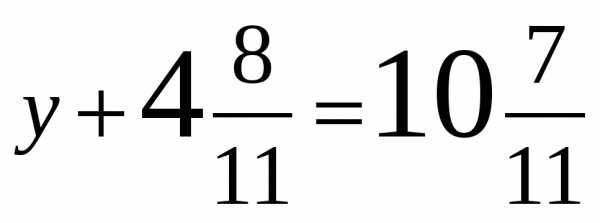
Найти значение выражения:
6*. Какое число надо разделить на 8, чтобы частное равнялось 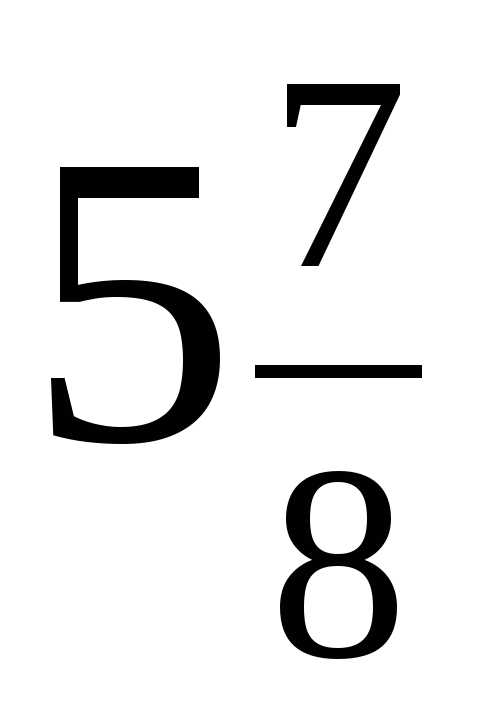 ?
?
___________________________________________________________________________________
Контрольная работа № 7
Вариант 2
Выполните действия:
а)  б)
б)  в)
в) 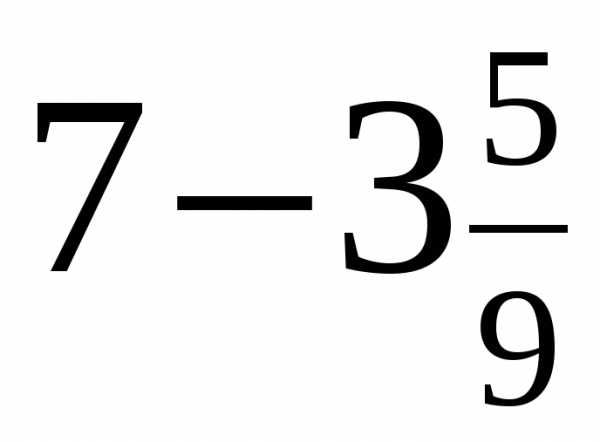 г)
г) 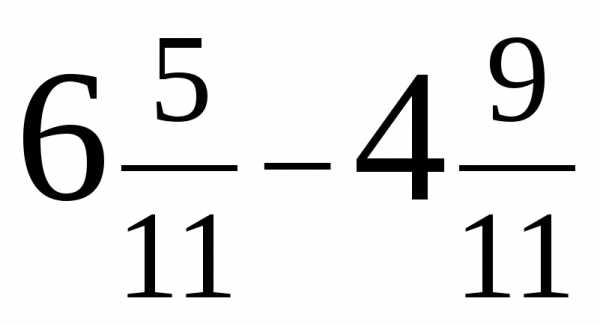
Автомобиль, двигаясь с постоянной скоростью, прошел 14 км за 9 мин. Какова скорость автомобиля?
В классе 24 ученика. Из них
 занимаются в спортивных секциях. Сколько учеников класса занимаются спортом?
занимаются в спортивных секциях. Сколько учеников класса занимаются спортом?
Решите уравнение:
а) 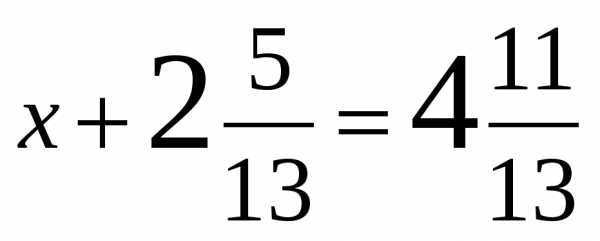 б)
б) 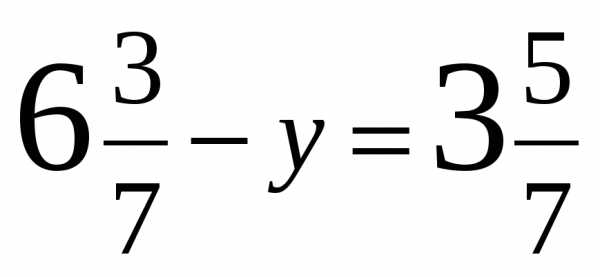
Найти значение выражения:
6*. Какое число надо разделить на 6, чтобы частное равнялось  ?
?
Контрольная работа № 8
Вариант 1
Сравните числа:
а) 7,195 и 12,1 б) 8,276 и 8,3 в) 0,76 и 0,7598
Выразите в километрах:
а) 2 км 156 м б) 8 км 70 м в) 585 м г) 3 м
Выполните действия:
а) 43,58 – 18,693 + 20,3 б) (2,08 + 3,69) – 1,08
Решите уравнения:
а) 45 – х = 38,783 б) (х + 1,7) – 6,02 = 10,4
Собственная скорость лодки равна 8,7 км/ч, а скорость течения реки – 2,9 км/ч. Найдите скорость лодки по течению реки и против течения реки.
Округлите каждое число до единиц, до десятых и до сотых:
а) 584,356 б) 935,0846 в) 0,8355
___________________________________________________________________________________
Контрольная работа № 8
Вариант 2
Сравните числа:
а) 8,2 и 6,984 б) 7,6 и 7,596 в) 0,6387 и 64
Выразите в тоннах:
а) 5 т 235 кг б) 1 т 90 кг в) 624 кг г) 8 кг
Выполните действия:
а) 62,49 – 29,584 + 30,4 б) (5,09 + 8,37) – 4,09
Решите уравнения:
а) х + 27,621 = 38 б) (8,3 – х) – 0,02 = 3,4
Собственная скорость байдарки равна 8,9 км/ч, а скорость течения реки – 3,2 км/ч. Найдите скорость байдарки по течению реки и против течения реки.
Округлите каждое число до единиц, до десятых и до сотых:
а) 573,856 б) 846,0739 в) 0,325
Контрольная работа № 9
Вариант 1
Выполните действия:
а) 4,35 · 18 б) 6,25 · 108 в) 53,3 : 26 г) 19,19 : 19 д) 6 : 24
Решите уравнения:
а) 7у + 2,6 = 27,8 б) (39,38 – х) : 9 = 4,02
Найдите значение выражения (90 – 16,2 : 9) · 5 + 0,08
За какое время лодка проплывет по течению реки расстояние 16,2 км, если собственная скорость лодки равна 3,2 км/ч, а скорость течения реки 1,8 км/ч?
Тракторист за два дня вспахал поле площадью 12,6 га. В первый день он вспахал
 поля. Сколько гектаров он вспахал во второй день?
поля. Сколько гектаров он вспахал во второй день?
_______________________________________________________________________________
Контрольная работа № 9
Вариант 2
Выполните действия:
а) 3,85 · 24 б) 4,75 · 116 в) 35,7 : 34 г) 28,28 : 14 д) 7 : 28
Решите уравнения:
а) 8х – 4,9 = 52,7 б) (х + 14,22) : 6 = 3,07
Найдите значение выражения (40 – 23,2 : 8) · 3 + 0,07
За какое время лодка проплывет против течения реки расстояние 18,3 км, если собственная скорость лодки равна 4,5 км/ч, а скорость течения реки 1,5 км/ч?
За два дня собрали 11,7 ц свеклы. В первый день собрали
 всей свеклы. Сколько центнеров свеклы собрали во второй день?
всей свеклы. Сколько центнеров свеклы собрали во второй день?
Контрольная работа № 10
Вариант 1
Выполните действия:
а) 0,872 · 6,3 б) 1,6 · 7,625 в) 0,045 · 0,1
г) 30,42 : 7,8 д) 0,702 : 0,065 е) 0,026 : 0,01
Найдите среднее арифметическое чисел 32,4; 41; 27,95; 46,9; 55,75.
Найдите значение выражения 296,2 – 2,7 · 6,6 + 6 : 0,15
Поезд 3 ч шел со скоростью 63,2 км/ч и 4 ч со скоростью 76,5 км/ч. Найдите среднюю скорость поезда на всем пути.
Решите уравнения:
а) 8х + 5,7 = 24,1 б) (9,2 – х) : 6 = 0,9
________________________________________________________________________________
Контрольная работа № 10
Вариант 2
Выполните действия:
а) 0,964 · 7,4 б) 2,4 · 7,375 в) 0,72 · 0,01
г) 25,23 : 8,7 д) 0,0918 : 0,0085 е) 0,39 : 0,1
Найдите среднее арифметическое чисел 63; 40,63; 70,4; 67,97.
Найдите значение выражения 398,6 – 3,8 · 7,7 + 3 : 0,06
Легковой автомобиль 2 ч шел со скоростью 55,4 км/ч и ещё 4 ч со скоростью 63,5 км/ч. Найдите среднюю скорость автомобиля на всем пути.
Решите уравнения:
а) 9х + 3,9 = 31,8 б) (х + 4,5) : 7 = 1,2
multiurok.ru
Контрольные работы по математике 5 класс
Контрольные работы из дидактических материалов и пособий для учителя. Программа обеспечивается УМК А.Г. Мерзляка, в состав которого входит:
1. Математика: 5 класс: учебник для учащихся общеобразовательных учреждений / А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. — М.: Вентана-Граф, 2015
2. Математика: 5 класс: дидактические материалы: сборник задач и контрольных работ / А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. — М.: Вентана-Граф, 2015.
3. Математика: 5 класс: рабочая тетрадь №1, №2 / А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. — М.: Вентана-Граф, 2015.
Просмотр содержимого документа
«Контрольные работы по математике 5 класс»
Контрольные работы по математике 5 класс
УМК Мерзляк А.Г., Полонский В.Б., Якир М.С.
Контрольная работа № 1
Натуральные числа
Вариант 1
Запишите цифрами число:
шестьдесят пять миллиардов сто двадцать три миллиона девятьсот сорок одна тысяча восемьсот тридцать семь;
восемьсот два миллиона пятьдесят четыре тысячи одиннадцать:
тридцать три миллиарда девять миллионов один.
Сравните числа: 1) 5 678 и 5 489; 2) 14 092 и 14 605.
Начертите координатный луч и отметьте на нём точки, соответствующие числам 2, 5, 7, 9.
Начертите отрезок FK, длина которого равна 5 см 6 мм, отметьте на нём точку C. Запишите все отрезки, образовавшиеся на рисунке, и измерьте их длины.
Точка К принадлежит отрезку МЕ, МК = 19 см, отрезок КЕ на 17 см больше отрезка МК. Найдите длину отрезка МЕ.
Запишите цифру, которую можно поставить вместо звёздочки, чтобы образовалось верное неравенство (рассмотрите все возможные случаи):
3 78* 3 784; 2) 5 8*5 5 872.
На отрезке CD длиной 40 см отметили точки P и Q так, что CP = 28 см, QD =26 см. Чему равна длина отрезка PQ?
Сравните: 1) 3 км и 2 974 м; 2) 912 кг и 8 ц.
Вариант 2
Запишите цифрами число:
семьдесят шесть миллиардов двести сорок два миллиона семьсот восемьдесят три тысячи сто девяносто пять;
четыреста три миллиона тридцать восемь тысяч сорок девять;
сорок восемь миллиардов семь миллионов два.
Сравните числа: 1) 6 894 и 6 983; 2) 12 471 и 12 324.
Начертите координатный луч и отметьте на нём точки, соответствующие числам 3, 4, 6, 8.
Начертите отрезок АВ, длина которого равна 4 см 8 мм, отметьте на нём точку D. Запишите все отрезки, образовавшиеся на рисунке, и измерьте их длины.
Точка T принадлежит отрезку МN, МT = 19 см, отрезок TN на 18 см меньше отрезка МT. Найдите длину отрезка МN.
Запишите цифру, которую можно поставить вместо звёздочки, чтобы образовалось верное неравенство (рассмотрите все возможные случаи):
2 *14 2 316; 2) 4 78* 4 785.
На отрезке SK длиной 30 см отметили точки A и B так, что SA = 14 см, BK =19 см. Чему равна длина отрезка AB?
Сравните: 1) 3 986 г и 4 кг; 2) 586 см и 6 м.
Вариант 3
Запишите цифрами число:
сорок семь миллиардов двести девяносто три миллиона восемьсот пятьдесят шесть тысяч сто двадцать четыре;
триста семь миллионов семьдесят восемь тысяч двадцать три;
восемьдесят пять миллиардов шесть миллионов пять.
Сравните числа: 1) 7 356 и 7 421; 2) 17 534 и 17 435.
Начертите координатный луч и отметьте на нём точки, соответствующие числам 2, 4, 6, 9.
Начертите отрезок MN, длина которого равна 6 см 4 мм, отметьте на нём точку A. Запишите все отрезки, образовавшиеся на рисунке, и измерьте их длины.
Точка E принадлежит отрезку CK, CE = 15 см, отрезок EK на 24 см больше отрезка CE. Найдите длину отрезка CK.
Запишите цифру, которую можно поставить вместо звёздочки, чтобы образовалось верное неравенство (рассмотрите все возможные случаи):
3 344 3 34*; 2) 2 724 * 619.
На отрезке AC длиной 60 см отметили точки E и F так, что AE = 32 см, FC =34 см. Чему равна длина отрезка EF?
Сравните: 1) 6 т и 5 934кг; 2) 4 м и 512 см.
Вариант 4
Запишите цифрами число:
восемьдесят шесть миллиардов пятьсот сорок один миллион триста семьдесят две тысячи триста сорок два;
шестьсот пять миллионов восемьдесят три тысячи десять;
сорок четыре миллиарда девять миллионов три.
Сравните числа: 1) 9 561 и 9 516; 2) 18 249 и 18 394.
Начертите координатный луч и отметьте на нём точки, соответствующие числам 2, 5, 8, 10.
Начертите отрезок АВ, длина которого равна 7 см 8 мм, отметьте на нём точку D. Запишите все отрезки, образовавшиеся на рисунке, и измерьте их длины.
Точка A принадлежит отрезку BM, BA = 25 см, отрезок AM на 9 см меньше отрезка BA. Найдите длину отрезка BM.
Запишите цифру, которую можно поставить вместо звёздочки, чтобы образовалось верное неравенство (рассмотрите все возможные случаи):
5 64* 5 646; 2) 1 4*2 1 431.
На отрезке OP длиной 50 см отметили точки M и N так, что OM = 24 см, NP =38 см. Чему равна длина отрезка M N?
Сравните: 1) 8 км и 7 962 м; 2) 60 см и 602 мм.
Контрольная работа № 2
Сложение и вычитание натуральных чисел. Числовые и буквенные выражения. Формулы.
Вариант 1
Вычислите: 1) 15 327+ 496 383; 2) 38 020 405 – 9 497 653.
На одной стоянке было 143 автомобиля, что на 17 автомобилей больше, чем на второй. Сколько автомобилей было на обеих стоянках?
Выполните сложение, выбирая удобный порядок вычислений:
(325 + 791) + 675; 2) 428 + 856 + 572 + 244.
Проверьте, верно ли неравенство:
1 674 – (736 + 328) 2 000 – (1 835 – 459).
Найдите значение 𝑎 по формуле 𝑎 = 4𝑏 – 16 при 𝑏 = 8.
Упростите выражение 126 + 𝒙 + 474 и найдите его значение при 𝒙 = 278.
Вычислите:
4 м 73 см + 3 м 47 см; 2) 12 ч 16 мин – 7 ч 32 мин.
Найдите значение выражения, выбирая удобный порядок вычислений:
(713 + 529) – 413; 2) 624 – (137 + 224).
Вариант 2
Вычислите: 1) 17 824+ 128 356; 2) 42 060 503 – 7 456 182.
На одной улице 152 дома, что на 18 домов меньше, чем на другой. Сколько всего домов на обеих улицах?
Выполните сложение, выбирая удобный порядок вычислений:
(624 + 571) + 376; 2) 212 + 497 + 788 + 803.
Проверьте, верно ли неравенство:
1 826 – (923 + 249) 3 000 – (2 542 – 207).
Найдите значение 𝑝 по формуле 𝑝= 40 – 7𝑞 при 𝑞 = 4.
Упростите выражение 235 + y + 465 и найдите его значение при y = 153.
Вычислите:
6 м 23 см + 5 м 87 см; 2) 14 ч 17 мин – 5 ч 23 мин.
Найдите значение выражения, выбирая удобный порядок вычислений:
(837 + 641) – 537; 2) 923 – (215 + 623).
Вариант 3
Вычислите: 1) 26 832 + 573 468; 2) 54 073 507 – 6 829 412.
В одном классе 37 учащихся, что на 9 человек больше, чем во втором. Сколько всего учащихся в обоих классах?
Выполните сложение, выбирая удобный порядок вычислений:
(736 + 821) + 264; 2) 573 + 381 + 919 + 627.
Проверьте, верно ли неравенство:
2 491 – (543 + 1 689) 1 000 – (931 – 186).
Найдите значение 𝑦 по формуле 𝑦 = 3𝑥 + 18 при 𝑥 = 5.
Упростите выражение 433 + 𝑎 + 267 и найдите его значение при 𝑎 = 249.
Вычислите:
7 м 23 см + 4 м 81 см; 2) 6 ч 38 мин – 4 ч 43 мин.
Найдите значение выражения, выбирая удобный порядок вычислений:
(674 + 245) – 374; 2) 586 – (217 + 186).
Вариант 4
Вычислите: 1) 19 829 + 123 471; 2) 61 030 504 – 8 695 371.
На одной книжной полке стоят 23 книги, что на 5 книг меньше, чем на другой. Сколько всего книг стоит на обеих полках?
Выполните сложение, выбирая удобный порядок вычислений:
(349 + 856) + 651; 2) 166 + 452 + 834 + 748.
Проверьте, верно ли неравенство:
1 583 – (742 + 554) 1 000 – (883 – 72).
Найдите значение 𝑥 по формуле 𝑥 = 16 + 8𝑧 при 𝑧 = 7.
Упростите выражение 561 + 𝑏 + 139 и найдите его значение при 𝑏 = 165.
Вычислите:
9 м 41 см + 4 м 72 см; 2) 18 ч 18 мин – 5 ч 24 мин.
Найдите значение выражения, выбирая удобный порядок вычислений:
(563 + 721) – 363; 2) 982 – (316 + 582).
Контрольная работа № 3
Уравнение. Угол. Многоугольники.
Вариант 1
Постройте угол МКА, величина которого равна 74. Проведите произвольно луч КС между сторонами угла МКА. Запишите образовавшиеся углы и измерьте их величины.
Решите уравнение: 1) 𝑥 +37 = 81 2) 150 – 𝑥 = 98.
Одна из сторон треугольника равна 24 см, вторая – в 4 раза короче первой, а третья – на 16 см длиннее второй. Вычислите периметр треугольника.
Решите уравнение: 1) (34 + 𝑥) – 83 = 42 2) 45 – (𝑥 – 16) = 28.
Из вершины развёрнутого угла АВС (см рис.) проведены два луча ВD и ВЕ так, что ∠АВЕ = 154, ∠DВС = 128. Вычислите градусную меру угла DВЕ.
Какое число надо подставить вместо 𝑎, чтобы корнем уравнения
52 – (𝑎 – 𝑥) = 24 было число 40?
Вариант 2
Постройте угол ABC, величина которого равна 168. Проведите произвольно луч BM между сторонами угла ABC. Запишите образовавшиеся углы и измерьте их величины.
Решите уравнение: 1) 21 + 𝑥 = 58 2) 𝑥 – 135 = 76.
Одна из сторон треугольника равна 32 см, вторая – в 2 раза короче первой, а третья – на 6 см короче первой. Вычислите периметр треугольника.
Решите уравнение: 1) (96 – 𝑥) – 15 = 64 2) 31 – (𝑥 + 11) = 18.
Из вершины прямого угла MNK (см рис.) проведены два луча ND и NE так, что ∠MND = 73, ∠KNF = 48. Вычислите градусную меру угла DNF.
Какое число надо подставить вместо 𝑎, чтобы корнем уравнения
64 – (𝑎 – 𝑥) = 17 было число 16?
Вариант 3
Постройте угол FDK, величина которого равна 56. Проведите произвольно луч DT между сторонами угла FDK. Запишите образовавшиеся углы и измерьте их величины.
Решите уравнение: 1) 𝑥 + 42 = 94 2) 284 – 𝑥 = 121.
Одна из сторон треугольника равна 12 см, вторая – в 3 раза длиннее первой, а третья – на 8 см короче второй. Вычислите периметр треугольника.
Решите уравнение: 1) (41 + 𝑥) – 12 = 83 2) 62 – (𝑥 – 17) = 31.
Из вершины развёрнутого угла FAN (см рис.) проведены два луча AK и AP так, что ∠NAP = 110, ∠FAK = 132. Вычислите градусную меру угла PAK.
Какое число надо подставить вместо 𝑎, чтобы корнем уравнения
(69 – 𝑎) – 𝑥 = 23 было число 12?
Вариант 4
Постройте угол NMC, величина которого равна 58. Проведите произвольно луч MB между сторонами угла NMC. Запишите образовавшиеся углы и измерьте их величины.
Решите уравнение: 1) 𝑥 + 53 = 97 2) 142 – 𝑥 = 76.
Одна из сторон треугольника равна 30 см, вторая – в 5 раза короче первой, а третья – на 22 см длиннее второй. Вычислите периметр треугольника.
Решите уравнение: 1) (58 + 𝑥) – 23 = 96 2) 54 – (𝑥 – 19) = 35.
Из вершины прямого угла DMK (см рис.) проведены два луча MB и MC так, что ∠DMB = 51, ∠KMC = 65. Вычислите градусную меру угла BMC.
Какое число надо подставить вместо 𝑎, чтобы корнем уравнения
(𝑎 – 𝑥) – 14 = 56 было число 5?

Контрольная работа № 4
Умножение и деление натуральных чисел. Свойства умножения.
Вариант 1
Вычислите:
36 ∙ 2 418; 3) 1 456 : 28;
175 ∙ 204; 4) 177 000 : 120.
Найдите значение выражения: (326 ∙ 48 – 9 587) : 29.
Решите уравнение:
𝑥 ∙ 14 = 364; 2) 324 : 𝑥 = 9; 3) 19𝑥 — 12𝑥 = 126.
Найдите значение выражения наиболее удобным способом:
25 ∙ 79 ∙ 4; 2) 43 ∙ 89 + 89 ∙ 57.
Купили 7 кг конфет и 9 кг печенья, заплатив за всю покупку 1 200 р. Сколько стоит 1 кг печенья, если 1 кг конфет стоит 120 р?
С одной станции одновременно в одном направлении отправились два поезда. Один из поездов двигался со скоростью 56 км/ч, а второй – 64 км/ч. Какое расстояние будет между поездами через 6 ч после начала движения?
Сколькими нулями оканчивается произведение всех натуральных чисел от 19 до 35 включительно?
Вариант 2
Вычислите:
24 ∙ 1 246; 3) 1 856 : 32;
235 ∙ 108; 4) 175 700 : 140.
Найдите значение выражения: (625 ∙ 25 – 8 114) : 37.
Решите уравнение:
𝑥 ∙ 28 = 336; 2) 312 : 𝑥 = 8; 3) 16𝑥 — 11𝑥 = 225.
Найдите значение выражения наиболее удобным способом:
2 ∙ 83 ∙ 50; 2) 54 ∙ 73 + 73 ∙ 46.
Для проведения ремонта электрической проводки купили 16 одинаковых мотков алюминиевого и 11 одинаковых мотков медного провода. Общая длина купленного провода составляла 650 м. Сколько метров алюминиевого провода было в мотке, если медного провода в одном мотке было 30 м?
Из одного города одновременно в одном направлении выехали два автомобиля. Один из них двигался со скоростью 74 км/ч, а второй – 68 км/ч. Какое расстояние будет между автомобилями через 4 ч после начала движения?
Сколькими нулями оканчивается произведение всех натуральных чисел от 23 до 42 включительно?
Вариант 3
Вычислите:
32 ∙ 1 368; 3) 1 664 : 26;
145 ∙ 306; 4) 216 800 : 160.
Найдите значение выражения: (546 ∙ 31 – 8 154) : 43.
Решите уравнение:
𝑥 ∙ 22 = 396; 2) 318 : 𝑥 = 6; 3) 19𝑥 — 7𝑥 = 144.
Найдите значение выражения наиболее удобным способом:
5 ∙ 97 ∙ 20; 2) 68 ∙ 78 — 78 ∙ 58.
В автомобиль погрузили 5 одинаковых мешков сахара и 3 одинаковых мешка муки. Оказалось, что общая масса груза равна 370 кг. Какова масса одного мешка муки, если масса одного мешка сахара равна 50 кг?
Из одного села одновременно в одном направлении отправились пешеход и велосипедист. Пешеход двигался со скоростью 3 км/ч, а велосипедист – 12 км/ч. Какое расстояние будет между ними через 3 ч после начала движения?
Сколькими нулями оканчивается произведение всех натуральных чисел от 34 до 53 включительно?
Вариант 4
Вычислите:
28 ∙ 2 346; 3) 1 768 : 34;
185 ∙ 302; 4) 220 500 : 180.
Найдите значение выражения: (224 ∙ 46 – 3 232) : 34.
Решите уравнение:
𝑥 ∙ 16 = 384; 2) 371 : 𝑥 = 7; 3) 22𝑥 — 14𝑥 = 112.
Найдите значение выражения наиболее удобным способом:
2 ∙ 87 ∙ 50; 2) 167 ∙ 92 — 92 ∙ 67.
В школьную столовую завезли 8 одинаковых ящиков яблок и 6 одинаковых ящиков апельсинов. Сколько килограммов апельсинов было в одном ящике, если всего было 114 кг яблок и апельсинов, а яблок в каждом ящике было 9 кг?
От одной пристани одновременно в одном направлении отплыли лодка и катер. Лодка плыла со скоростью 14 км/ч, а катер – 21 км/ч. Какое расстояние будет между ними через 5 ч после начала движения?
Сколькими нулями оканчивается произведение всех натуральных чисел от 41 до 64 включительно?
Контрольная работа № 5
Деление с остатком. Площадь прямоугольника. Прямоугольный параллелепипед и его объем. Комбинаторные задачи.
Вариант 1
Выполните деление с остатком: 478 : 15.
Найдите площадь прямоугольника, одна сторона которого равна 14 см, а вторая сторона в 3 раза больше первой.
Вычислите объем и площадь поверхности куба с ребром 3 см.
Длина прямоугольного параллелепипеда равна 18 см, ширина – в 2 раза меньше длины, а высота – на 11 см больше ширины. Вычислите объем параллелепипеда.
Чему равно делимое, если делитель равен 11, неполное частное – 7, а остаток – 6?
Поле прямоугольной формы имеет площадь 6 га. Ширина поля 150 м. Вычислите периметр поля.
Запишите все трёхзначные числа, для записи которых используются только цифры 5, 6 и 0 (цифры не могут повторяться).
Сумма длин всех рёбер прямоугольного параллелепипеда равна 116 см, а два его измерения – 12 см и 11 см. Найдите третье измерение параллелепипеда.
Вариант 2
Выполните деление с остатком: 376 : 18.
Найдите площадь прямоугольника, одна сторона которого равна 21 см, а вторая сторона в 3 раза меньше первой.
Вычислите объем и площадь поверхности куба с ребром 4 дм.
Ширина прямоугольного параллелепипеда равна 6 см, длина – в 5 раз больше ширины, а высота – на 5 см меньше длины. Вычислите объем параллелепипеда.
Чему равно делимое, если делитель равен 17, неполное частное – 5, а остаток – 12?
Поле прямоугольной формы имеет площадь 3 га, его длина – 200 м. Вычислите периметр поля.
Запишите все трёхзначные числа, для записи которых используются только цифры 0, 9 и 4 (цифры не могут повторяться).
Сумма длин всех рёбер прямоугольного параллелепипеда равна 80 см, а два его измерения – 10 см и 4 см. Найдите третье измерение параллелепипеда.
Вариант 3
Выполните деление с остатком: 516 : 19.
Найдите площадь прямоугольника, одна сторона которого равна 17 см, а вторая сторона в 2 раза больше первой.
Вычислите объем и площадь поверхности куба с ребром 5 дм.
Высота прямоугольного параллелепипеда равна 20 см, длина – на 4 см больше высоты, а ширина – в 2 раза меньше длины. Вычислите объем параллелепипеда.
Чему равно делимое, если делитель равен 14, неполное частное – 8, а остаток – 9?
Поле прямоугольной формы имеет площадь 7 га, его длина – 350 м. Вычислите периметр поля.
Запишите все трёхзначные числа, для записи которых используются только цифры 1, 2 и 0 (цифры не могут повторяться).
Сумма длин всех рёбер прямоугольного параллелепипеда равна 100 дм, а два его измерения – 8 дм и 13 дм. Найдите третье измерение параллелепипеда.
Вариант 4
Выполните деление с остатком: 610 : 17.
Найдите площадь прямоугольника, одна сторона которого равна 45 см, а вторая сторона в 5 раз меньше первой.
Вычислите объем и площадь поверхности куба с ребром 2 см.
Длина прямоугольного параллелепипеда равна 20 см, высота – в 4 раза меньше длины, а ширина – на 7 см больше высоты. Вычислите объем параллелепипеда.
Чему равно делимое, если делитель равен 15, неполное частное – 6, а остаток – 14?
Поле прямоугольной формы имеет площадь 4 га, его ширина – 50 м. Вычислите периметр поля.
Запишите все трёхзначные числа, для записи которых используются только цифры 7, 0 и 8 (цифры не могут повторяться).
Сумма длин всех рёбер прямоугольного параллелепипеда равна 72 см, а два его измерения – 6 см и 8 см. Найдите третье измерение параллелепипеда.
Контрольная работа № 6
Обыкновенные дроби
Вариант 1
Сравните числа:
и ; 2) и 1; 3) и 1.
Выполните действия:
+ ; 3) ;
+ 5 ; 4) .
В саду растёт 72 дерева, из них составляют яблони. Сколько яблонь растёт в саду?
Кирилл прочёл 56 страниц, что составило книги. Сколько страниц было в книге?
Преобразуйте в смешанное число дробь:
; 2) .
Найдите все натуральные значения 𝑥, при которых верно неравенство .
Каково наибольшее натуральное значение n, при котором верно неравенство n ?
Найдите все натуральные значения 𝑎, при которых одновременно выполняются условия: дробь правильная, а дробь неправильная.
Вариант 2
Сравните числа:
и ; 2) и 1; 3) и 1.
Выполните действия:
+ ; 3) ;
+ 1 ; 4) .
В гараже стоят 63 машины, из них составляют легковые. Сколько легковых машин стоит в гараже?
В классе 12 учеников изучают французский язык, что составляет всех учеников класса. Сколько учеников в классе?
Преобразуйте в смешанное число дробь:
; 2) .
Найдите все натуральные значения 𝑥, при которых верно неравенство .
Каково наименьшее натуральное значение n, при котором верно неравенство n ?
Найдите все натуральные значения 𝑎, при которых одновременно выполняются условия: дробь правильная, а дробь неправильная.
Вариант 3
Сравните числа:
и ; 2) и 1; 3) и 1.
Выполните действия:
+ ; 3) ;
+ 7 ; 4) .
В классе 36 учеников, из них занимаются спортом. Сколько учеников занимаются спортом?
Ваня собрал 16 вёдер картофеля, что составляет всего урожая. Сколько вёдер картофеля составляет урожай?
Преобразуйте в смешанное число дробь:
; 2) .
Найдите все натуральные значения 𝑥, при которых верно неравенство .
Каково наибольшее натуральное значение n, при котором верно неравенство n ?
Найдите все натуральные значения 𝑎, при которых обе дроби и одновременно будут неправильными.
Вариант 4
Сравните числа:
и ; 2) и 1; 3) и 1.
Выполните действия:
+ ; 3) ;
+ 2 ; 4) .
В пятых классах 64 ученика, из них составляют отличники. Сколько отличников в пятых классах?
Мама приготовила вареники с творогом, а Коля съел 9 штук, что составляет всех вареников. Сколько вареников приготовила мама?
Преобразуйте в смешанное число дробь:
; 2) .
Найдите все натуральные значения 𝑥, при которых верно неравенство 2 .
Каково наименьшее натуральное значение n, при котором верно неравенство n ?
Найдите все натуральные значения 𝑎, при которых одновременно выполняются условия: дробь будет неправильная, а дробь правильная.
Контрольная работа № 7
Понятие о десятичной дроби. Сравнение, округление, сложение и вычитание десятичных дробей.
Вариант 1
Сравните: 1) 14,396 и 14,4; 2) 0,657 и 0, 6565.
Округлите: 1) 16,76 до десятых; 2) 0,4864 до тысячных.
Выполните действия: 1) 3,87 + 32,496; 2) 23,7 – 16,48; 3) 20 – 12,345.
Скорость катера по течению реки равна 24,2 км/ч, а собственная скорость катера – 22,8 км/ч. Найдите скорость катера против течения реки.
Вычислите, записав данные величины в килограммах:
3,4 кг + 839 г; 2) 2 кг 30 г – 1956 г.
Одна сторона треугольника равна 5,6 см, что на 1,4 см больше второй стороны и на 0,7 см меньше третьей. Найдите периметр треугольника.
Напишите три числа, каждое из которых больше 5,74 и меньше 5,76.
Найдите значение выражения, выбирая удобный порядок вычислений:
(8,63 + 3,298) – 5,63; 2) 0,927 – (0,327 + 0,429).
Вариант 2
Сравните: 1) 17,497 и 17,5; 2) 0,346 и 0, 3458.
Округлите: 1) 12,88 до десятых; 2) 0,3823 до сотых.
Выполните действия: 1) 5,62 + 43,299; 2) 25,6 – 14,52; 3) 30 – 14,265.
Скорость катера против течения реки равна 18,6 км/ч, а собственная скорость
катера – 19,8 км/ч. Найдите скорость катера по течению реки.
Вычислите, записав данные величины в метрах:
8,3 м + 784 см; 2) 5 м 4 см – 385 см.
Одна сторона треугольника равна 4,5 см, что на 3,3 см меньше второй стороны и на 0,6 см больше третьей. Найдите периметр треугольника.
Напишите три числа, каждое из которых больше 3,82 и меньше 3,84.
Найдите значение выражения, выбирая удобный порядок вычислений:
(5,94 + 2,383) – 3,94; 2) 0,852 – (0,452 + 0,214).
Вариант 3
Сравните: 1) 12,598 и 12,6; 2) 0,257 и 0, 2569.
Округлите: 1) 17,56 до десятых; 2) 0,5864 до тысячных.
Выполните действия: 1) 4,36 + 27,647; 2) 32,4 – 17,23; 3) 50 – 22,475.
Скорость катера по течению реки равна 19,6 км/ч, а собственная скорость катера – 18,3 км/ч. Найдите скорость катера против течения реки.
Вычислите, записав данные величины в центнерах:
6,7 ц + 584 кг; 2) 6 ц 2 кг – 487 кг.
Одна сторона треугольника равна 3,7 см, что на 0,9 см больше второй стороны и на 1,2 см меньше третьей. Найдите периметр треугольника.
Напишите три числа, каждое из которых больше 7,87 и меньше 7,89.
Найдите значение выражения, выбирая удобный порядок вычислений:
(6,73 + 4,594) – 2,73; 2) 0,791 – (0,291 + 0,196).
Вариант 4
Сравните: 1) 16,692 и 16,7; 2) 0,745 и 0, 7438.
Округлите: 1) 24,87 до десятых; 2) 0,8653 до тысячных.
Выполните действия: 1) 6,72 + 54,436; 2) 27,6 – 15,72; 3) 40 – 11,825.
Скорость катера против течения реки равна 17,8 км/ч, а собственная скорость
катера – 19,4 км/ч. Найдите скорость катера по течению реки.
Вычислите, записав данные величины в метрах:
2,8 м + 524 см; 2) 4 м 6 см – 257 см.
Одна сторона треугольника равна 5,1 см, что на 2,1 см меньше второй стороны и на 0,7 см больше третьей. Найдите периметр треугольника.
Напишите три числа, каждое из которых больше 1,34 и меньше 1,36.
Найдите значение выражения, выбирая удобный порядок вычислений:
(7,86 + 4,183) – 2,86; 2) 0,614 – (0,314 + 0,207).
Контрольная работа № 8
Умножение и деление десятичных дробей
Вариант 1
Вычислите:
0,024 ∙ 4,5; 3) 2,86 : 100; 5) 0,48 : 0,8;
29,41 ∙ 1 000; 4) 4 : 16; 6) 9,1 : 0,07.
Найдите значение выражения: (4 – 2,6) ∙ 4,3 + 1,08 : 1,2.
Решите уравнение: 2,4 (𝑥 + 0,98) = 4,08.
Моторная лодка плыла 1,4 ч по течению реки и 2,2 ч против течения. Какой путь преодолела лодка за всё время движения, если скорость течения равна 1,7 км/ч, а собственная скорость лодки – 19,8 км/ч?
Если в некоторой десятичной дроби перенести запятую вправо через одну цифру, то она увеличится на 14,31. Найдите эту дробь.
Вариант 2
Вычислите:
0,036 ∙ 3,5; 3) 3,68 : 100; 5) 0,56 : 0,7;
37,53 ∙ 1 000; 4) 5 : 25; 6) 5,2 : 0,04.
Найдите значение выражения: (5 – 2,8) ∙ 2,4 + 1,12 : 1,6.
Решите уравнение: 0,084 : (6,2 – 𝑥) = 1,2.
Катер плыл 1,6 ч против течения реки и 2,4 ч по течению. На сколько больше проплыл катер, двигаясь по течению реки, чем против течения, если скорость течения реки равна 2,1 км/ч, а собственная скорость катера – 28,2 км/ч?
Если в некоторой десятичной дроби перенести запятую влево через одну цифру, то она уменьшится на 23,76. Найдите эту дробь.
Вариант 3
Вычислите:
0,064 ∙ 6,5; 3) 4,37 : 100; 5) 0,63 : 0,9;
46,52 ∙ 1 000; 4) 6 : 15; 6) 7,2 : 0,03.
Найдите значение выражения: (6 – 3,4) ∙ 1,7 + 1,44 : 1,6.
Решите уравнение: 1,6 (𝑥 + 0,78) = 4,64.
Теплоход плыл 1,8 ч против течения реки и 2,6 ч по течению. Какой путь преодолел теплоход за всё время движения, если скорость течения равна 2,5 км/ч, а собственная скорость теплохода – 35,5 км/ч?
Если в некоторой десятичной дроби перенести запятую вправо через одну цифру, то она увеличится на 15,93. Найдите эту дробь.
Вариант 4
Вычислите:
0,096 ∙ 5,5; 3) 7,89 : 100; 5) 0,76 : 0,4;
78,53 ∙ 100; 4) 6 : 24; 6) 8,4 : 0,06.
Найдите значение выражения: (7 – 3,6) ∙ 2,8 + 1,32 : 2,2.
Решите уравнение: 0,144 : (3,4 – 𝑥) = 2,4.
Моторная лодка плыла 3,6 ч против течения реки и 1,8 ч по течению. На сколько километров больше проплыла лодка, двигаясь против течения , чем по течению, если скорость течения реки равна 1,2 км/ч, а собственная скорость лодки – 22,4 км/ч?
Если в некоторой десятичной дроби перенести запятую влево через одну цифру, то она уменьшится на 29,52. Найдите эту дробь.
Контрольная работа № 9
Среднее арифметическое. Проценты.
Вариант 1
Найдите среднее арифметическое чисел: 32,6; 38,5; 34; 35,3.
Площадь поля равна 300 га. Рожью засеяли 18 % поля. Сколько гектаров поля засеяли рожью?
Петя купил книгу за 90 р., что составляет 30 % всех денег, которые у него были. Сколько денег было у Пети?
Лодка плыла 2 ч со скоростью 12,3 км/ч и 4 ч со скоростью 13,2 км/ч. Найдите среднюю скорость лодки на всём пути.
Турист прошёл за три дня 48 км. В первый день он прошёл 35 % всего маршрута. Путь пройденный в первый день, составляет 80 % расстояния , пройденного во второй день. Сколько километров прошёл турист в третий день?
В первый день Петя прочитал 40 % всей книги, во второй – 60 % остального, а в третий — оставшиеся 144 страницы. Сколько всего страниц в книге?
Вариант 2
Найдите среднее арифметическое чисел: 26,3; 20,2; 24,7; 18.
В школе 800 учащихся. Сколько пятиклассников в этой школе, если известно, что их количество составляет 12 % количества всех учащихся?
Насос перекачал в бассейн 42 воды, что составляет 60 % объёма бассейна. Найдите объём бассейна.
Автомобиль ехал 3 ч со скоростью 62,6 км/ч и 2 ч со скоростью 65 км/ч. Найдите среднюю скорость автомобиля на всём пути.
Токарь за три дня изготовил 80 деталей. В первый день он выполнил 30 % всей работы. Известно, что количество деталей, изготовленных в первый день, составляет 60 % количества деталей , изготовленных во второй день. Сколько деталей изготовил токарь в третий день?
В первый день тракторная бригада вспахала 30 % площади всего поля, во второй – 75% остального, а в третий — оставшиеся 14 га. Найдите площадь поля.
Вариант 3
Найдите среднее арифметическое чисел: 26,4; 42,6; 31,8; 15.
В магазин завезли 600 кг овощей. Картофель составляет 24% всех завезённых овощей. Сколько килограммов картофеля завезли в магазин?
За первый день турист прошёл расстояние 18 км, что составляет 40 % всего пути, который он должен преодолеть. Найдите длину пути, который должен пройти турист.
Катер плыл 1,5 ч со скоростью 34 км/ч и 2,5 ч со скоростью 30 км/ч. Найдите среднюю скорость катера на всём пути.
За три дня оператор набрал на компьютере 60 страниц. В первый день было выполнено 35 % всей работы. Объём работы, выполненной в первый день, составляет 70 % работы, выполненной во второй день. Сколько страниц было набрано в третий день?
За первый час было продано 84 % всего мороженого, за второй – 78 % остального, а за третий – оставшиеся 44 порции. Сколько порций мороженого было продано за три часа?
Вариант 4
Найдите среднее арифметическое чисел: 43,6; 21,8; 32,4; 11.
Площадь парка равна 40 га. Площадь озера составляет 15 % площади парка. Найдите площадь озера.
За первый час движения автомобиль преодолел расстояние 72 км, что составляет 24 % длины всего пути, который ему надо проехать. Найдите общий путь, который преодолел автомобиль.
Черепаха ползла 2 ч со скоростью 15,3 м/ч и 3 ч со скоростью 12, 4 м/ч. Найдите среднюю скорость черепахи на всём пути.
Три насоса наполнили водой бассейн объёмом 320 . Первый насос заполнил бассейн на 30 %, что составляет 80 % объёма воды, которую перекачал второй насос. Найдите объём воды, которую перекачал третий насос.
В первый день турист прошёл 20% всего пути, во второй – 60 % остального, а в третий – оставшиеся 24 км. Найдите длину пути, который прошёл турист за три дня.
Контрольная работа № 10
Обобщение и систематизация знаний учащихся
за курс математики 5 класса
Вариант 1
Найдите значение выражения: (4,1 – 0,66 : 1,2) ∙ 0,6.
Миша шёл из одного села в другое 0,7 ч по полю и 0,9 ч через лес, пройдя всего 5,31 км.
multiurok.ru


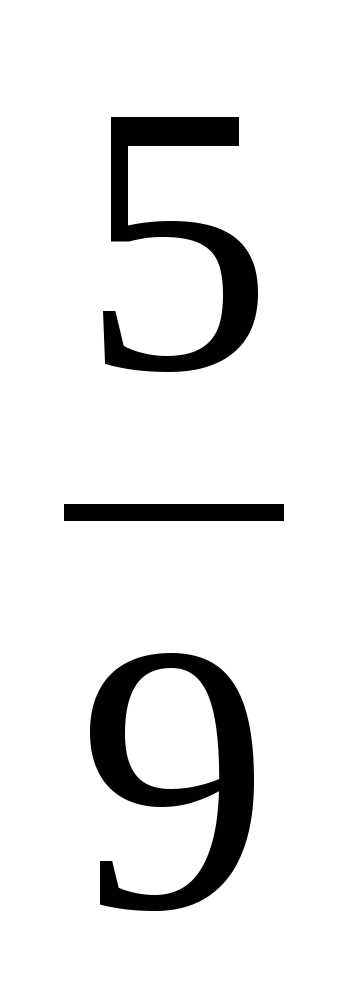 — легковые. Сколько легковых автомобилей в гараже?
— легковые. Сколько легковых автомобилей в гараже? занимаются в спортивных секциях. Сколько учеников класса занимаются спортом?
занимаются в спортивных секциях. Сколько учеников класса занимаются спортом?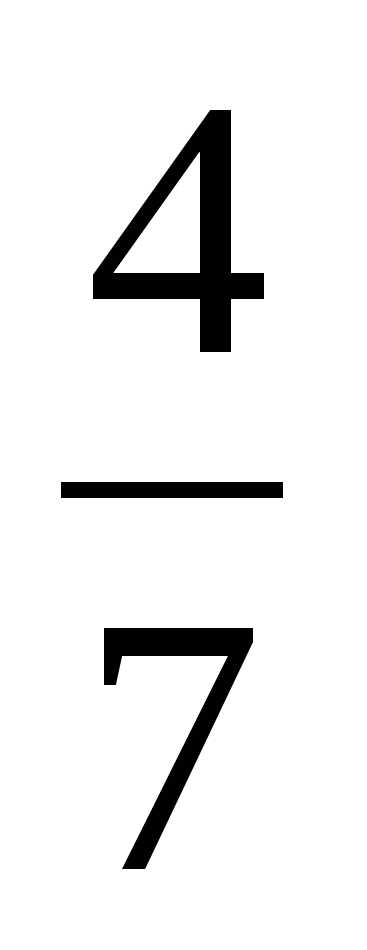 поля. Сколько гектаров он вспахал во второй день?
поля. Сколько гектаров он вспахал во второй день?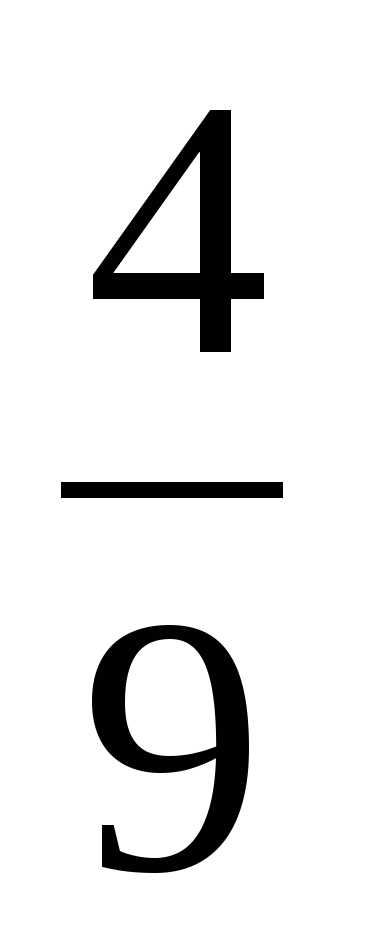 всей свеклы. Сколько центнеров свеклы собрали во второй день?
всей свеклы. Сколько центнеров свеклы собрали во второй день?