Задания к олимпиаде по математике 4 класс с ответами: Олимпиадные задания по математике (4 класс) по теме: Олимпиада по математике с ответами. 4 класс

Олимпиадные задания по математике (4 класс) по теме: Олимпиада по математике с ответами. 4 класс

Содержание

По теме: методические разработки, презентации и конспекты

Олимпиада по математике для 3 класса с ответами

Задачи, примеры, соотношенгия мер длины, массы заданы в нестандартной форме, что позволяет ребёнку использовать знания и умения в новой учебной ситуации….

Текст классного тура олимпиады по математике в 1 классе с ответами.

Задания для классного тура олимпиады по математике в 1 классе….

районная олимпиада по математике с ответами 4 класс

Олимпиада по математике для выпускников начальных классов с ответами и разбаловкой. Данная работа может быть проведена для учащихся по любому УМК. Задания в олимпиаде разнообразные, из разных разделов…

Олимпиада по математике с ответами. 4 класс

Олимпмада по математике с ответами…

Олимпиада по математике в первом классе. Первый этап.(В классе)

Часто дети в первом классе очень хорошо решают логические задачи, но чтобы понять, кто из детей впоследствии станет учстником олимпиад, я провожу мини-олимпиады в классе. Запущенный «пробный шар» прин…

Олимпиада по математике с ответами 4 класс

Олимпиада по математике с ответами 4 класс….

Муниципальный тур олимпиады по математике для 4 класса с ответами.

Задания для муниципального тура олимпиады по математике для учащихся 4 класса.Олимпиада включает 8 заданий с ответами….

Олимпиадные задания по математике для 4 класса с ответами

Олимпиадные задания по математике

4 класс (с ответами)

У доктора Пилюлькина есть лекарство в нескольких сосудах, масса которых 3г, 6г, 9г, 12г, 15, 18, 21г. Других сосудов у доктора нет. Помоги Пилюлькину раздать всё лекарство четверым больным поровну.

Если каждое следующее число на 1 больше предыдущего, то такие числа называют последовательными. Сумма четырёх последовательных чисел равна 318. Найди эти числа.

У Знайки имеются медные монеты в 1, 2, 3 и 5 копеек, которые весят соответственно 1г, 2г, 3г, 5г. Малышу известно, что среди четырёх медных (по одной каждого достоинства) имеется бракованная, меньшего веса. Как при помощи двух взвешиваний на чашечных весах без гирь Знайке определить бракованную монету?

Незнайка решил смастерить будку для своей собаки. У него есть два вида листов фанеры: размером 12х6 дм и размером 9х8 дм. Каждый лист нужно разрезать на 6 прямоугольников размером 4х3 дм. Какого вида листы выгоднее использовать Незнайке, чтобы общая протяжённость линий разреза была как можно меньше?

Пончик и Гусля весят столько, сколько 5 учебников. Гусля весит столько, сколько 4 кошки. Две кошки и Гусля весят столько, сколько 3 учебника. Сколько кошек уравновесят Пончика?

Торопыжка начертил три прямые линии. На каждой из них отметил три точки. Всего Торопыжка отметил 6 точек. Покажи, как он это сделал.

Ответы

1. Решение:

21 г — первому больному

18 + 3 = 21 г — второму больному

15 + 6 = 21 г — третьему больному

12 + 9 = 21 г — четвертому больному

Критерии оценивания:

правильный ответ с объяснением – 3 балла;
правильный ответ без объяснения – 1 балл;
задание не начато или выполнено неправильно – 0 баллов.

2. Решение:

Первый способ.

а + 1 — второе число

а + 2 — третье число

а + 3 — четвертое число

а + а + 1 + а + 2 + а + 3 = 318

4  а + 6 = 318

4  а = 318 – 6

4  а = 312

а = 312 : 4

а = 78 (первое число)

78 + 1 = 79 (второе число)

78 + 2 = 80 (третье число)

78 + 3 = 81 (четвертое число)

Второй способ.

318 : 4 = 79 (ост. 2) Значит 318 = 79 + 79 + 80 + 80 = (79 – 1) + 79 + 80 + (80 + 1) =

78 + 79 + 80 + 81

Критерии оценивания:

правильный ответ с решением – 5 баллов;
правильный ответ без объяснения – 2 балла;
задание не начато или выполнено неправильно – 0 баллов.

3. Решение:

На одну чашу весов поместим монеты 1 к. и 2 к., а на другую – 3 к. При равновесии чашек бракованная монета — 5 к. При нарушении равновесия монета находится в той чаше, которая выше. Пусть в верхней чаше монета 3 к. Тогда она – бракованная. Пусть в верхней чаше монеты 1к. или 2 к. Сделаем второе взвешивание: на одну чашу весов положим монеты 2 к. и 3 к., а на другую 5 к. Если весы в равновесии, то бракованная монета — 1 к. Если же вверх пойдёт чаша, на которой 2 к. и 3 к., то бракованная монета — 1к.

Возможен ещё один способ: сначала на одну чашу поместить монеты 2 к. и 3 к., а на другую – монету 5 к.

Критерии оценивания:

правильный ответ с объяснением – 4 балла;
правильный ответ без объяснения – 2 балла;
задание не начато или выполнено неправильно – 0 баллов.

4. Решение:

Для листов с размерами 12х6 длина всех разрезов равна 12 + 6 х 2 = 24 (дм).

Для листов с размерами 9х8 дм длина всех разрезов равна 9 + 8 х 2 = 25 (дм).

Критерии оценивания:

правильный ответ с объяснением – 4 балла;
правильный ответ без объяснения – 1 балл;
задание не начато или выполнено неправильно – 0 баллов.

5. Решение:

Обозначим Пончика – П, Гуслю – Г, учебник – У, кошку – К. Тогда согласно условия получим:

П + Г = 5У,

Г = 4К,

2К + Г = 3 У.

Тогда 2К + 4К = 3У или 2К = У.

П + 4К = 5У.

Так как У = 2К, то П + 4К = 10К и П = 6К.

Ответ: 6 кошек уравновесят Пончика.

Критерии оценивания:

правильный ответ с объяснением – 5 баллов;
правильный ответ без объяснения – 2 балла;
задание не начато или выполнено неправильно – 0 баллов.

6. Решение:

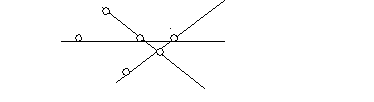
Критерии оценивания:

правильный ответ – 3 балла;
задание не начато или выполнено неправильно – 0 баллов.

Олимпиадные задания по математике (4 класс) по теме: олимпиада по математике для 4 класса

Олимпиада по математике для 4 класса

1. Разминка:

а) В двух залах 50 стульев. Когда из одного зала вынесли 10 стульев, то в залах осталось стульев поровну. Сколько стульев было в каждом зале первоначально?

б) Найти сумму 1+2+3+4+…+98+99+100.

в) Что больше половина половины 20 или четверть четверти 80?

г) К трёхзначному числу слева приписали цифру 1. На сколько увеличилось число?

д) Масса ящика с лимонами 25 кг. После продажи половины всех лимонов, ящик поставили на весы. Весы показали 15 кг. Найдите массу пустого ящика.

е) 3 курицы за 3 дня снесли 3 яйца. Сколько яиц снесут 6 куриц за 6 дней? 9 куриц за 9 дней?

ж) Длина забора 20 метров. Сколько в заборе столбов, если столб от столба стоит на расстоянии двух метров?

2. Нескольким обезьянам раздали 50 бананов так, чтобы каждая получила хотя бы по 1 банану и ни у каких двух обезьян не было поровну бананов. Какое наибольшее количество обезьян могли получить бананы?

3. Запиши ответ цифрами и словами:

а) назови 2 числа, у которых количество цифр равно количеству букв, составляющих название каждого из этих чисел.

б) назови 2 числа, у которых количество букв, составляющих название каждого из этих чисел равно самому числу.

4. Прямоугольный лист бумаги со сторонами 8 см 4 см разрезали на 4 равных части, а затем из них составили квадрат. Как это сделали? Выполни рисунок.

5. В банку попал 1 микроб, и через 10 минут банка была наполнена микробами, причём известно, что количество микробов ежеминутно удваивалось. За сколько минут банка была наполнена микробами наполовину? Запиши ответ и свои рассуждения.

6. Два велосипедиста едут навстречу друг другу, расстояние между ними 240 км. В начальный момент движения взлетает муха и принимается летать вперёд и назад между велосипедистами, пока те не встретятся. Велосипедисты всё это ехали со скоростью 40 км/ч, а муха летала со скоростью 60 км/ч. Какое расстояние пролетела муха?

7. Представь, что ты с другом путешествуешь на суперпоезде. Вы едете в соседних вагонах. Друг едет в 17 вагоне с начала поезда, а ты в 134 с конца. Сколько вагонов в поезде? Запиши ответ и свои рассуждения.

8. Старые часы отстают на 20 секунд в час. Сколько времени они покажут через сутки после того, как стрелки установили на 12 часов? Запиши решение по действиям и свои рассуждения.

9. Маленький коала съедает листья с одного эвкалиптового дерева за 10 часов, а каждый из его родителей ест вдвое быстрее. За сколько времени это семейство объест все листья с одного эвкалиптового дерева? Запиши решение по действиям с пояснениями и ответ.

Ответы:

1. Разминка:

а) В 1 зале – 30 стульев, во 2 зале – 20 стульев.

б) 5050

в) равно

г) на 1000

д) 5 кг

е) 1 курица за 3 дня снесёт 1 яйцо, значит за 6 дней она снесёт 2 яйца, за 9 дней – 3 яйца, тогда 6 куриц за 6 дней снесут 12 яиц, а 9 куриц – 27 яиц.

ж) если 1 считается, то 11 столбов, если не считается, то 10 столбов.

2. 9 обезьян

3. а) 100 – сто, 1000000 – миллион; б) три, одиннадцать

5. 1 мин. – 2, 2 мин. – 4, 3 мин. – 8, 4 мин. – 16, 5 мин. – 32, 6 мин. – 64, 7 мин. – 128, 8 мин. – 256, 9 мин. – 512, 10 мин. – 1024.

1024: 2=512 – 9 мин.

6. 40х2=80 (км\ч) – скорость сближения

240:80=3 (ч.) – были в пути

60х3=180(км)

7. 251 вагон

8. 1) 24х20=480(сек) – отстали

2) 480:60=8(мин) – отстали

3) 24х60=1440(мин) – в сутках.

4) 1440 – 8= 1432 (мин) = 11ч 52 мин – стали показывать.

9. Допустим, что на дереве 1000 листьев.

1) 1000:10=100(л.) – съедает за 1 час маленький коала.

2) 100х2=200(л.) – съедает за 1 час 1 родитель.

3) 200х2+100=500(л.) – съедает за 1 час вся семья.

4) 1000:500=2(ч.) – за это время семейство объест все листья с 1 дерева.

Олимпиадные задания по математике (4 класс) на тему: материалы для подготовки к олимпиаде по математике для 4 класса №1

Олимпиадные задания по математике

1. Не меняя расположения цифр, поставьте между ними знак сложения таким образом, чтобы получилась сумма равная 100. Если понадобится, две любые стоящие рядом цифры считайте двузначным числом. Выполните задание двумя разными способами.

2. Напишите цифрами число, состоящее из 22 миллионов 22 тысяч 22 сотен и 22 единиц.

3. Какие четыре цифры надо вычеркнуть из числа 4921508, чтобы получившееся трёхзначное число было как можно меньше?

4. У царя Гороха 7 сыновей, у каждого его сына по 7 сыновей, а у каждого внука царя Гороха по две дочери. Сколько правнучек у царя Гороха?

5. Шестеро тянут репку: дедка вдвое сильнее бабки, бабка вдвое сильнее внучки, внучка вдвое сильнее Жучки, Жучка вдвое сильнее кошки, кошка вдвое сильнее мышки. Сколько нужно позвать мышек, чтобы они сами вытянули репку?

6. От пристани одновременно в одном направлении отчалили пароход и катер со скоростями соответственно 24 км/ч и 15 км/ч. Через 4 часа пароход сел на мель. Снявшись через некоторое время с мели, он догнал катер через час. Сколько времени простоял пароход на мели?

7. Три команды набрали на олимпиаде 285 баллов. Если бы команда школы №24 набрала на 8 баллов меньше, а команда школы №44 на 12 баллов меньше, команда школы №77 на 7 баллов меньше, то все они набрали бы поровну баллов. Сколько баллов набрали команды школ №24 и №77 вместе?

8. Если сторону квадрата, периметр которого 36 см, уменьшить в 3 раза, то получится ширина прямоугольника, периметр которого 22 см. Найдите длину этого прямоугольника и вычислите площадь.

9. Рысь съедает 600 кг мяса за 6 часов, а тигр в 2 раза быстрее. За какое время они съедят это мясо вместе?

10. 5 землекопов за 5 часов выкапывают 5 метров канавы. Сколько землекопов смогут за 100 часов выкопать 100 метров канавы?

Ответы на олимпиадные задания

1 + 2 + 34 + 56 + 7 = 100

1 + 23 + 4 + 5 + 67 = 100

2. Напишите цифрами число, состоящее из 22 миллионов 22 тысяч 22 сотен и 22 единиц.

22 024 222

1 балл

вычеркнуть цифры 4,9,2,5.

число: 108

1) 7*7=49 (внуков)

2) 49*2= 98(правнучек)

3 балла

Сила кошки = силе 2 мышек

Сила Жучки = силе 4 мышек (2*2)

Сила внучки = силе 8 мышек (4*2)

Сила бабки = силе 16 мышек (8*2)

Сила дедки = силе 32 мышек (16*2)

1+2+4+8+16+32= 63 мышки

4 балла

1) 4+1=5(ч) – был в движении пароход

2) 24∙5=120(км) – расстояние, пройденное пароходом (катер прошёл столько же)

3) 120: 15=8(ч) – был в пути катер

4) 8-5 =3(ч) – время, которое пароход простоял на мели

Ответ: 3 часа пароход стоял на мели.

5 баллов

1) 8+7+12=27 (б)

2) 285-27=258(б)

3) 258:3=86(б)

4) 86+7=93(б)

5) 86+8=94(б)

6) 93+94=187(б)

Ответ: 187 баллов набрали команды школы №77 и №24 вместе.

5 баллов

1) 36:4=9(см) – сторона квадрата

2) 9:3=3 (см) – ширина прямоугольника

3) 3*2=6 (см) – 2 ширины

4) (22-6):2= 8 (см) – длина прямоугольника

5) 8*3=24 (см)

Ответ: 24 квадратных сантиметров площадь прямоугольника.

5 баллов

9. Рысь съедает 600 кг мяса за 6 часов, а тигр в 2 раза быстрее. За какое время они съедят это мясо вместе?

1) 600:6=100(кг) – за 1 час съедает рысь

2) 100*2=200(кг) – за 1 час съедает тигр

3) 100+200=300(кг) – вместе за 1 час

4) 600:300=2 (ч)

Ответ: за 2 часа рысь и тигр съедят это мясо.

4 балла

Если за пять часов пять землекопов выкапывают 5 м канавы, то за 100 ч за время, в 20 раз большее) те же пять землекопов выкопают канаву в 20 раз длиннее, то есть 100 м канавы.

Ответ: 5 землекопов.

4 балла

Олимпиада по математике (4 класс)

Олимпиада по математике – 4 класс

Шифр

Сумма

баллов

2019/2020 уч. год

Кол-во

баллов

1.Бабушка разделила пирог на четвертинки. Потом каждый из получившихся кусочков — ещё на три части.
Один кусочек бабушка оставила себе. Каждый из внуков получил по кусочку, а дедушка съел сразу два. В итоге пирога не осталось.

Сколько внуков у бабушки?

Ответ: __________________

2. Пеппи учится вязать длинные чулки. В первый месяц на изготовление одного чулка у неё уходило 9 часов. В каждый последующий месяц за это же время ей удаётся связать в три раза больше чулок, чем в предыдущий месяц.

Составь закономерность, показывающую изменение времени, затрачиваемого на изготовление пары чулок, и укажи, сколько часов потратит на это Пеппи в третий месяц.

Запиши закономерность: __________________________________

3. Половину суток злодей Игрек тратит на сон. Половину оставшегося времени – на злодеяния. Половину вновь оставшегося времени – на хулиганство. 2 часа 58 минут – на проказы. Всё оставшееся время он все-таки делает что-нибудь полезное и доброе. Сколько времени в сутки Игрек тратит на добрые дела?

Ответ: __________________

4. Страницы книги пронумерованы числами 1, 2, 3, 4, 5 и т. д. Цифра 5 оказалась использована ровно 16 раз. Какое наибольшее число страниц могло быть в этой книге?

Ответ: __________________

5. В парке 15 животных: коровы, кошки и кенгуру. Известно, что ровно 10 из них – не коровы и ровно 8 из них – не кошки. Сколько кенгуру в парке?

Ответ: __________________

6.Проказник Рома захотел узнать, что лежит в сейфе у Алисы. На сейфе — кодовый замок (0,1,2,3). Чтобы открыть сейф, надо набрать комбинацию из двух цифр. Только одна комбинация правильная. За какое время (в секундах) Рома наверняка откроет сейф, если цифры в коде не повторяются? На набор одной комбинации уходит три секунды.

Ответ: __________________

7. Найди произведение чисел, которые расположены одновременно в прямоугольнике и в круге, но не в треугольнике.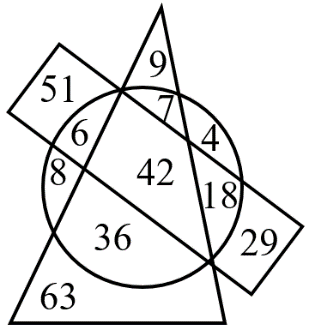

Ответ: ________________

8.Найди периметр прямоугольника, который сложен из разрезанного пополам квадрата площадью 100 см².

Ответ: ________________

9.Масса 1 пакета пшеничной муки и 1 пакета ржаной муки вместе равна 5 кг. В школьную столовую привезли 4 таких пакета ржаной муки и 3 пакета пшеничной муки. Общая масса всей этой муки – 17 кг. Чему равна масса 1 пакета пшеничной муки?

Ответ: __________________

10.У бабушки были мотки синей и белой пряжи. Белой пряжи было на 12 мотков больше, чем синей. После того, как бабушка связала свитер из 7 белых и 7 синих мотков пряжи, белых осталось в 4 раза больше, чем синих. Сколько всего мотков шерсти было у бабушки первоначально?

Ответ: ___________________

Ответы для олимпиады по математике – 4 класс

2019/2020 уч. год

Сколько внуков у бабушки? 4*3=12; 12-1-2=9

Закономерность: 9ч, 3ч, 1ч – 1 чулок; 18 ч, 6ч, 2ч – пара чулок

Ответ: 24:2:2:2-2ч58мин = 2 мин

4. Страницы книги пронумерованы числами 1, 2, 3, 4, 5 и т. д. Цифра 5 оказалась использована ровно 16 раз. Какое наибольшее число страниц могло быть в этой книге? (5,15,25,35,45,50,51,52,53,54,55,56,57,58,59 до 65 страницы)

Ответ: 64 страницы

5. В парке 15 животных: коровы, кошки и кенгуру. Известно, что ровно 10 из них – не коровы и ровно 8 из них – не кошки. Сколько кенгуру в парке? 3

(10+8=18; 18-15=3)

(10, 11,12,13, 20,21,22,23, 30,31,32,33)

Ответ: 108 (18*6)

8.Найди периметр прямоугольника, который сложен из разрезанного пополам квадрата площадью 100 см².

Ответ: 50 см (10*2*2+5*2=50)

(5*3=15 17-15=2 5-2=3)

Ответ: 34 (11 синих и 23 белых)

Олимпиада по математике для 4 класса с ответами.

ОТВЕТЫ

Олимпиада по математике – 2015 год

4____ класс

Ф.И. ученика (цы) ____________________________________________

1. Выбери такое выражение, для нахождения значения которого тебе придется выполнить все четыре арифметических действия. Реши его и узнай год рождения М.В.Ломоносова.

а) (2713х65+2713х35)-2713х100=_______________________________________

б) 864375 — 42054:42054 -321х67=______________________________________

в) (1921-1671)х6+1899:9=______________________________________________

Решение: (1921 – 1671) х 6 + 1899:9 = 1711

2. Самая известная из мозаичных картин М.Ломоносова — «Полтавская баталия». Ее длина 12 аршин, высота 11 аршин. Найдите площадь картины, если 1аршин=71см .

Решение: Длина= 71х12=852см; Ширина= 71х11=781; S=852х781=665412 кв.см

3. Реши задачу. 12 января 1755 года был издан указ об открытии Московского университета, который возглавил М.В.Ломоносов. Занятия начались 26 апреля того же года. Спустя сколько дней после указа начались занятия?(год был не високосный)

Решение: В январе 31 день; 31-12=19 дней; в феврале 28 дней; в марте 31 день; в апреле 26 дней по условию задачи. 19+28+31+26=104 дня.

Решите задачу. Три брата поймали 29 карасей. Когда один брат отложил для ухи 6 рыб, другой 2 карася, а третий брат 3 рыбки. То у каждого осталось равное количество рыб. Сколько карасей поймал каждый из них?

Решение:6+2+3=11рыб на уху

29-11=18 рыб осталось

18:3=6рыб у каждого осталось

6+6=12 6+2=8 6+3=9 12+8+9=29 рыб всего поймали

Ответ:12,8,9 рыб

Реши задачу. Гном разложил свои сокровища в 3 сундука разного цвета, стоящие у стены: в один – драгоценные камни, в другой – золотые монеты, в третий – магические книги. Он помнит, что красный сундук находится правее, чем камни, и что книги – правее красного сундука. В каком сундуке лежат книги, если зелёный сундук стоит левее синего

Ответ: По условию, сундук с камнями стоит левее красного, а сундук с книгами правее красного. Значит, красный сундук стоит посередине и в нём лежат золотые монеты. Так как зелёный и синий сундуки – крайние и зелёный стоит левее синего, то зелёный – крайний слева, а синий – крайний справа. Вспоминая, что камни левее, а книги правее красного сундука, приходим к выводу, что камни лежат в зелёном, а книги – в синем сундуке.

6. Запишите самое большое и самое маленькое число, состоящее из цифр 8, 3,0,5,1 так, чтобы каждая цифра повторялось только один раз._____________________________

Ответ: 85.310 10.358

7. Реши задачу. Из куска проволоки согнули квадрат, площадь которого 36 см². Затем проволоку разогнули и согнули из неё треугольник с равными сторонами. Какова длина стороны треугольника

Ответ:36=6*6(см) — длина стороны квадрата 6*4=24(см) –длина проволоки

24:3=8 (см) – длина стороны треугольника

8. Реши задачу. Цветки картофеля бывают открыты с 6 утра до 2.00 часов дня, цветы льна – от 6.00 до 16.00, а цветки календулы – с 9.00 до 3 часов дня. В какие часы все цветы одновременно открыты? Ответ: с 9.00 до 14.00

9. Начертите на клетчатой бумаге квадрат со стороной 6 см. Разрежьте его на 2 части по ломаной так, чтобы из двух полученных частей можно было составить прямоугольник. Вырезанные детали сдайте вместе с работой. Найдите площадь и периметр прямоугольника.

Ответ: ___________________________________________________

10. Между цифрами поставьте знаки действий и скобки так, чтобы получился 0.

5 4 3 2 1 = 0 Ответ: (5+4): 3- 2- 1 = 0

11. Укажи, сколько четырёхугольников на рисунке.

Ответ: 10

12. Витя ждал гостей на день рождения. Вокруг стола поставили несколько табуретов и несколько стульев. У каждого табурета было по 3 ножки, а у каждого стула – по 4. Ребята заняли все стулья и табуреты, и оказалось, что всех ножек – у стульев, табуретов и ребят – 49. Сколько всего ребят было за столом?

Ответ: Пусть х было стульев, у – табуретов, с – детей, Х + У = С

Х х 3 + У х 4 + С х 2 = 49

Т.К. Х = С – У, получим уравнение

(С – У) х 3 + У х 4 = 49 – 2х С

У = 49 – 5хС

Ножки стульев + ноги детей = 6 ног

Ножки табуретов + ноги детей = 5 ног

Стульев Х, табуретов У.

6хХ + 5хУ = 49 Подбор слагаемых, чтобы первое делилось на 6, второе делилось на 5. 24 + 25 = 49

6 х 4 + 5 х 5 = 49 Значит стульев было 4, табуретов – 5,

Ребят было 4 + 5 = 9.

Проверка: 4 х 4 + 5 х 3 + 9 х 2 = 49 верно

2б.

1б.

2б.

1б.

3б.

1б.

3б.

Итого: 20 баллов

За 1 место – 20 баллов

За 2 место — 19 б.

За 3 место — 17-18 б.

Олимпиада по математике – 2013 год

4____ класс

Ф.И. ученика (цы) ____________________________________________

а) (2713*65+2713*35)-2713*100=_______________________________________

б) 864375 — 42054:42054 -321*67=______________________________________

в) (1921-1671)*6+1899:9=______________________________________________

Решите задачу. Три брата поймали 29 карасей. Когда один брат отложил для ухи 6 рыб, другой 2 карасей, а третий брат 3 рыбки. То у каждого осталось равное количество рыб. Сколько карасей поймал каждый из них?______________________________________________________________

____________________________________________________________________

________________________________________________________________

Реши задачу. Гном разложил свои сокровища в 3 сундука разного цвета, стоящие у стены: в один – драгоценные камни, в другой – золотые монеты, в третий – магические книги. Он помнит, что красный сундук находится правее, чем камни, и что книги – правее красного сундука. В каком сундуке лежат книги, если зелёный сундук стоит левее синего? (ответ нарисуйте и подпишите).

—

_________________________________________________________________________

9. Начертите на клетчатой бумаге квадрат со стороной 6 см. Разрежьте его на 2 части по ломаной так, чтобы из двух полученных частей можно было составить прямоугольник. Вырезанные детали сдайте вместе с работой. Найдите площадь и периметр прямоугольника.

10. Между цифрами поставьте знаки действий и скобки так, чтобы получился 0.

5 4 3 2 1 = 0 _______________________________________________________

11. Укажите, сколько четырёхугольников на рисунке.

_____________________________________

12. Решите задачу. Витя ждал гостей на день рождения. Вокруг стола поставили несколько табуретов и несколько стульев. У каждого табурета было по 3 ножки, а у каждого стула – по 4. Ребята заняли все стулья и табуреты, и оказалось, что всех ножек – у стульев, табуретов и ребят – 49. Сколько всего ребят было за столом?

______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

ЗАКОНЧИВ РАБОТУ, ПРОВЕРЬ ЕЁ!

БЛАГОДАРИМ ЗА УЧАСТИЕ В ОЛИМПИАДЕ!

Олимпиада по математике для 4 класса

Районная олимпиада по математике, 4 класс 2018год

Время проведения: 60 минут

Код участника___________

Задание 1. Запишите шесть чётных чисел подряд так, чтобы самое маленькое число было вдвое меньше самого большого.

Ответ:_____________________________________

Задание 2. Ледники занимают седьмую часть суши, а горы- четверть. Что занимает большую площадь?

Ответ: _______________

Задание 3. Нужно распилить 5 брёвен на 6 частей каждое. Сколько времени на это потребуется, если на один распил уходит 4 минуты?

Ответ: _______________________

Задание 4. Длина стороны квадрата 1 дециметр. Этот квадрат разрезали на квадратики со стороной 1 сантиметр, из которых выложили полосу. Какой длины получилась полоса?

Ответ: ________________

Задание 5. Галя записала числа по порядку от одного до девяносто девяти. Сколько раз Галя написала цифру шесть?

Ответ: ________________

Задание 6. Сколько груш и сколько яблок купила мама, если всего груш и яблок 25 штук, при этом груши составляют пятую часть всех фруктов?

Ответ: груш — __________, яблок — _________

Задание 7. В первом ящике 55 килограммов апельсинов. Когда из него продали 23 килограмма, в нём осталось на 29 килограммов апельсинов меньше, чем во втором и третьем ящиках вместе. Сколько килограммов апельсинов в третьем ящике, если во втором ящике 25 килограммов апельсинов?

Решение: _________________________________________________________

__________________________________________________________________

Ответ: ________________

Задание 8. Ребята повели лошадей на водопой. Сколько было ребят и сколько лошадей, если при подсчёте оказалось 26 голов и 82 ноги?

Ответ: ребят — ___________, лошадей — _______

Задание 9.

Муравьишка ехал на гусенице 24 минуты, а потом пересел на жука и проехал в 4 раза больший путь. Сколько минут он ехал на жуке, если жук передвигается в 8 раз быстрее гусеницы?

Решение: ______________________________

Ответ: ________________

Задание 10. У коллекционера 4000 марок. Половина всех марок — о млекопитающих, четверть — о птицах, половина остатка — о рыбах, а остальные — о рептилиях. Сколько марок с рептилиями к коллекционера?

Ответ: ________________

Задание 11. Ваня начертил квадрат, провел в нем два отрезка. У него получилось 8 треугольников. Как он сумел это сделать?

Ответ:

Задание 12. Две бригады посадили двести двадцать яблонь. Первая бригада сажала в день сорок яблонь, вторая — пятьдесят яблонь. Вторая бригада начала работу на один день позже, чем первая. Сколько яблонь посадила первая бригада?

Ответ: ________________

Задание 13. Из куска проволоки согнули квадрат, площадь которого 36 кв.см. Затем проволоку разогнули и сложили треугольник с равными сторонами. Какова длина стороны треугольника?

Ответ: ___________

Решение: _________________________

__________________________________

Задание 14. Петя бегает в два раза быстрее Коли и в три раза быстрее Маши. На беговой дорожке стадиона Петя, Коля и Маша стартовали одновременно. Петя добежал до финиша на 12 секунд раньше Коли. На сколько секунд Петя прибежал раньше Маши? Запиши рассуждение и ответ.

Ответ: _______________________________________________________________

Задание 15. Есть 5 мисок. В них 100 орехов. В первой и второй мисках суммарно 52 ореха. Во второй и третьей мисках — 43 ореха. В третьей и четвёртой — 34, в четвертой и пятой – 30 орехов. Сколько в каждой миске орехов?

Ответ: _______________________________________________________________

Желаем успехов!

Районная олимпиада по математике, 4 класс (ключ)

Ключи

Задание 1. (2 балла)

Ответ: 10, 12, 14, 16, 18, 20

Задание 2. (2 балла)

Ответ: Горы

Задание 3. (2 балла)

Ответ: 1ч 40 мин.

Задание 4. (2 балла)

Ответ: 1 метр

Задание 5. (2 балла)

Ответ: 20 раз

Задание 6. (2 балла)

Ответ: 5 груш, 20 яблок

Задание 7. (3 балла)

Ответ: 36 кг апельсинов

Решение: 1) 55 — 23 = 32 (кг) осталось в первом ящике

2) 32 +29 = 61(кг) во втором и третьем ящиках

3) 61 — 25 = 36 (кг)

Задание 8. (3 балла)

Ответ: 11 ребят и 15 лошадей.

Задание 9. (3 балла)

Ответ: 12 минут.

(24 · 4) : 8= 12(мин) или (24 : 8) · 4=12(мин)

Задание 10. (4 балла)

Ответ: 500 марок

Задание 11. (4 балла) Ответ:

Задание 12. (4 балла)

Ответ: 120 яблонь

Задание 13. (5 баллов)

Ответ: 8 см

Решение:

36 = 6 ∙ 6 6 см- длина стороны квадрата

6 ∙4 = 24 см — периметр квадрата (длина проволоки)

24: 3 = 8 см — длина стороны треугольника

Задание 14. (5 баллов)

Ответ: На 24 секунды

Раз Коля бегает в два раза медленнее Пети, то на прохождение дистанции он тратит вдвое больше времени. Значит, Коля пробежал дистанцию за 24 секунды, а Петя — за 12 секунд. Тогда Маша пробежала дистанцию за 12 ・ 3 = 36 секунд и отстала от Пети на 36 − 12 = 24

секунды.

Задание 15. (6 баллов)

Решение:

1) 100 – 52 = 48 (ор.) – в 3, 4 и 5-ой мисках.

2) 48 – 34 = 14 (ор.) – в 5-й миске.

3) 30 – 14 = 16 (ор.) – в 4-й миске.

4) 34 – 16 = 18 (ор.) – в 3-й миске.

5) 43 – 18 = 25 (ор.) – во 2-й миске.

6) 52 – 25 = 27 (ор.) – в 1-й миске.

Максимальный балл за все выполненные задания — 52.

90000 Math Olympiad for Elementary School Students 90001 90002 90003 Enroll in this Course 90004 90002 90006 Eligibility: 90007 CTY-level or Advanced CTY-level math score required 90004 90002 90006 Prerequisites: 90007 Successful completion of Grade 3 Mathematics or equivalent; completion of Grade 4 Mathematics preferred 90004 90002 90006 Course Format: 90007 Individually Paced 90004 90002 90006 Course Length: 90007 Typically 3 months 90004 90002 90006 Course Code: 90007 OL1 90004 90025 Course Description 90026 90002 Description 90004 90002 This Math Olympiad course is designed to teach the major strategies of problem solving, to foster mathematical creativity, and to stimulate enthusiasm and love for the types of problems that students encounter in competitive mathematics.90004 90002 This course includes notes, practice problems, assessments, and videos for each topic covered to allow students to learn and review both the material and problem-solving skills. Videos are provided by Art of Problem Solving. As students progress through the course, they will complete free response questions and timed practice exams to help them build experience using strategies that will be useful for real competitions. 90004 90002 Each student is assigned to a CTY instructor to support them and give feedback during their course.Students can contact their instructor via email with any questions or concerns at any time. Live one-on-one online sessions can also be scheduled to prepare for the graded assessments, which include homework, quizzes, and a cumulative final exam. In addition, there are weekly group strategy sessions run by an instructor, where students will learn together. 90004 90002 The weekly strategy session will be held online every Tuesday evening from 7 — 7:50 p.m. ET. Attendance is optional and all sessions are recorded so students can watch them at a later time.Instructions and details are posted on the course website for enrolled students. 90004 90037 Topics include: 90038 90039 90040 Drawing a Picture or Diagram 90041 90040 Using Deduction 90041 90040 Simplification 90041 90040 Finding a Pattern 90041 90040 Making an Organized List 90041 90040 Making a Table 90041 90040 Using Number Operations 90041 90040 Working Backwards 90041 90040 Basic Geometry 90041 90040 Estimation and Elimination 90041 90060 90002 For a detailed list of topics, click the List of Topics tab.90004 90002 90064 90004 90025 Materials Needed 90026 90002 There are no required materials for this course. 90004 90025 List of Topics 90026 90002 This course is designed to teach the major strategies of problem solving, to foster mathematical creativity, and to stimulate enthusiasm and love for the types of problems that students encounter in competitive mathematics. Students explore math topics and strategies in depth, and practice non-routine contest problems. The web-based virtual classroom provides interactive experiences for students.Students and instructors meet in the virtual classroom for problem solving, clarification of concepts, and group sessions. 90004 90037 The following problem solving strategies will be covered in this course: 90038 90076 Topic 1: Drawing a Picture or Diagram 90077 90002 Both theoretical and applied problems will be used to show how a sketch helps to make sense of and model a problem. 90004 90076 Topic 2: Using Deduction 90077 90002 Students will apply principles of logic to solve classic riddles, such as those involving colored hats and identity of the truth-teller, in addition to non-routine math problems.90004 90076 Topic 3: Simplification 90077 90002 Students will learn techniques for decreasing the number and complexity of calculations for simplifying problems involving whole number operations, complex fractions, factorials, and exponents. 90004 90076 Topic 4: Finding a Pattern 90077 90002 Students will investigate patterns involving time, additive number sequences, and repeated multiplication. 90004 90076 Topic 5: Making a List 90077 90002 This topic expands on strategies for making lists for counting and arrangements, along with divisibility and remainders, laying a solid foundation for later work with more formal concepts in modular arithmetic, number theory and combinatorics.90004 90076 Topic 6: Making a Table 90077 90002 Students use tables to compare unknown quantities in an organized way to test possible solutions, which serves as a basis for more algebraic methods in subsequent coursework. 90004 90076 Topic 7: Using Number Operations 90077 90002 Students will broaden their understanding of number operations and factors as they apply methods to solve for unknown digits and complete magic squares. 90004 90076 Topic 8: Working Backwards 90077 90002 This topic exposes students to various situations for which beginning at a given result and working backwards is the best strategy.90004 90076 Topic 9: Basic Geometry 90077 90002 Students develop their ability to change visual perspective as they consider various approaches to non-routine area and perimeter problems. 90004 90076 Topic 10: Estimation and Elimination 90077 90002 Strong estimation skills are often required in making sense of problems and checking reasonableness of solutions. In this topic, students apply their number sense to make estimates as they narrow the number of possible solutions to problems involving exponents, divisibility, and remainders.90004 90025 Technical Requirements 90026 90002 This course requires a properly maintained computer with high-speed internet access and an up-to-date web browser (such as Chrome or Firefox). The student must be able to communicate with the instructor via email. Visit the Technical Requirements and Support page for more details. 90004 90002 90006 Zoom online virtual classroom 90007 90123 This course uses an online virtual classroom for discussions with the instructor. The classroom works on standard computers with the Zoom desktop client and also tablets or handhelds that support the Zoom Mobile app.Students who are unable to attend live sessions will need a computer with the Zoom desktop client installed to watch recorded meetings. The Zoom desktop client and Zoom Mobile App are both available for free download. 90004.