Задача на скорость время расстояние 4 класс: Подборка задач на путь, скорость и расстояние для 4 класса. | Тренажёр по математике (4 класс) по теме:
Подборка задач на путь, скорость и расстояние для 4 класса. | Тренажёр по математике (4 класс) по теме:
Задачи на путь, скорость и расстояние для 4 класса по программе «Школа России».
№1
Караван верблюдов шёл в первый день 8 ч со скоростью 9 км/ч, во второй день – 6 ч со скоростью 8 км/ч, а в третий день – 9 ч со скоростью 7 км/ч. Какое расстояние прошёл караван за 3 дня?
№2
Вертолёт пролетает 840 км за 3 ч, а автомобиль проходит это же расстояние за 7 ч. У кого из них скорость больше и на сколько?
№3
Поезд проходит 320 км за 5 ч. Какое расстояние он пройдёт за 8 ч, двигаясь с этой же скоростью?
№4
Туристы решили пройти за день 30 км. Они уже прошли 3 ч со скоростью 6 км/ч. Какое расстояние им осталось пройти?
За сколько времени они пройдут это расстояние, двигаясь с прежней скоростью?
№5
Ира прошла 15 км за 3 ч, а Петя – 16 км за 4ч. У кого из ребят скорость больше и на сколько?
№6
Автомобиль за 6 ч проехал 480 км. Какое расстояние мог бы проехать автомобиль за это же время, если бы увеличил скорость на 12 км/ч?
Какое расстояние мог бы проехать автомобиль за это же время, если бы увеличил скорость на 12 км/ч?
№7
Первый лыжник за 3 ч пробежал 51 км, а второй лыжник пробежал за это же время на 6 км больше. На сколько километров в час скорость второго лыжника больше скорости первого?
№8
Расстояние от посёлка Солнечное до Тучково 18 км, а от Тучково до Маросейкино – в 4 раз больше. За сколько времени пройдёт автобус расстояние от Солнечного до Маросейкино, если скорость его движения 45 км/ч?
№9
Стоянка геологов находится на расстоянии 250 км от города. Чтобы добраться до стоянки, геологи сначала ехали из города 3 ч на машине со скоростью 72 км/ч, затем 2 ч ехали на лошадях со скоростью 9 км/ч, а после этого 4 ч шли пешком. С какой скоростью они шли пешком?
№10
Орёл за 9 с пролетел 270 м, а сокол за это время пролетел 189 м. На сколько метров в секунду скорость сокола меньше скорости орла?
№11
Катер идёт от одной пристани к другой со скоростью 30 км/ч, а возвращается обратно со скоростью на 10 км/ч большей. За сколько времени катер пройдёт весь путь туда и обратно, если расстояние между пристанями 240 км/ч.
За сколько времени катер пройдёт весь путь туда и обратно, если расстояние между пристанями 240 км/ч.
№12
Волк гонится за Зайцем. Сначала Заяц бежал 2 ч со скоростью 24 км/ч, затем он 3ч ехал на велосипеде, а после этого 5 ч ехал на поезде со скоростью 48 км/ч. Всего Заяц пробежал и проехал 357 км. С какой скоростью он ехал на велосипеде?
Используемая литература
Л.Г. Петерсон. «Математика 3 класс».
Задачи на скорость, время и расстояние: примеры и решение
Скорость — это расстояние, пройденное за единицу времени: за 1 секунду, за 1 минуту, за 1 час и так далее.
Разные объекты имеют разную скорость. Например, средняя скорость пешехода составляет 5 километров в час, скорость велосипедиста — 12 км в час, а автомобиля — 80 км в час. При записи скорости, предлог в заменяют наклонной чертой — км/ч (например, 15 км/ч).
Если весь путь проходится с одинаковой скоростью, то такое движение называется равномерным. Далее будут рассмотрены задачи только на равномерное движение.
Далее будут рассмотрены задачи только на равномерное движение.
Нахождение скорости
Чтобы найти скорость по данному пути (расстоянию) и времени, надо путь разделить на время.
скорость = расстояние : время
Задача 1. Поезд проехал 320 км за 4 часа. Чему равна скорость поезда?
Решение: Чтобы найти скорость поезда, надо расстояние, которое прошёл поезд (320 км), разделить на время поезда в пути (4 ч):
320 : 4 = 80 (км).
Ответ: Скорость поезда равна 80 км/ч.
Задача 2. Турист за 3 часа прошёл 12 км, а велосипедист за 2 часа проехал 24 км. Во сколько раз турист движется медленнее велосипедиста?
Решение: Чтобы узнать во сколько раз скорость туриста меньше, чем у велосипедиста, надо узнать их скорость, разделив пройденные расстояния на затраченное время:
12 : 3 = 4 (км/ч) — скорость туриста,
24 : 2 = 12 (км/ч) — скорость велосипедиста.
Теперь осталось узнать на сколько медленнее движется турист, для этого надо большее число разделить на меньшее:
12 : 4 = 3.
Ответ: Турист движется в 3 раза медленнее, чем велосипедист.Нахождение времени
Чтобы найти время по данному расстоянию и скорости, надо расстояние разделить на скорость.
время = расстояние : скорость
Задача. Лодка преодолела путь в 100 км со скоростью 20 км/ч. Сколько времени плыла лодка?
Решение:
100 : 20 = 5 (ч).
Ответ: Лодка плыла 5 часов.
Нахождение расстояния
Чтобы найти расстояние по данным скорости и времени, надо скорость умножить на время.
расстояние = скорость · время
Задача. Грузовик ехал 12 часов со скоростью 70 км/ч. Какое расстояние проехал грузовик за это время?
Какое расстояние проехал грузовик за это время?
Решение:
70 · 12 = 840 (км).
Ответ: Грузовик за 12 часов проехал 840 км.
Математика 4 класс Богданович. Решебник. ГДЗ. Скорость, время, расстояние.
Сложение и вычитание многозначных чисел.
Категория: —>> Математика 4 класс Богданович
Задание: —>> 381 — 400 401 — 418
наверхЗадание 381.
Рассмотри решение задачи и прочитай объяснение.
Задача. За 2ч автобус проехал 120 км, проезжая за каждый час одинаковое расстояние. Сколько километров автобус проезжал за 1 ч?
Решение: 120 : 2 = 60 (км). Ответ: за 1 ч автобус проезжал 60 км.
Объяснение. Если за каждый час автобус проезжает 60 км, то говорят, что он движется со скоростью 60. км в час.
Это записывают так: 60 км/ч.
Чтобы найти скорость, надо расстояние поделить на время.
Задание 382.
По данным таблицы вычисли скорость движения велосипедиста, пассажирского самолёта, ласточки.
Решение:
- Скорость велосипедиста: 28 км : 2 ч = 14 км/ч.
- Скорость ласточки: 180 км : 2 ч = 90 км/ч.
- Скорость самолета: 1500 км : 3 ч = 500 км/ч.
Задание 383.
Велосипедист был в пути 6 ч, а мотоциклист 2 ч. Велосипедист проехал 72 км, а мотоциклист 100 км. На сколько скорость мотоциклиста больше скорости велосипедиста?
- 1) Какова скорость велосипедиста?
- 2) Какова скорость мотоциклиста?
- 3) На сколько скорость мотоциклиста больше скорости велосипедиста?
Решение:
- 1) 72 : 6 = 12 (км/ч) скорость велосипедиста;
- 2) 100 : 2 = 50 (км) скорость мотоциклиста;
- 3) 50 — 12 = 38 (км/ч).
- Ответ: скорость мотоциклиста на 38 км/ч больше, чем скорость велосипедиста.
Задание 384.
Расстояние 400 м мальчик пробежал туда и обратно за 4 мин. С какой скоростью бежал мальчик?
Решение:

- Ответ: скорость мальчика 100 м/мин.
Задание 385.
Расстояние между условными пунктами K и M на орбите искусственного спутника Земли составляет 320 км. Четвёртую часть этого расстояния спутник пролетел за 10 с. С какой скоростью он летел?
Решение:
- 1) 320 : 4 = 80 (км) четвертая часть расстояния;
- 2) 80 : 10 = 8 (км/с).
- Ответ: скорсть спутника 8 км/с.
Задание 386.
Решение:
| 8000 + 7000 = 15000 | 90000 + 7000 = 97000 | 1500 − 300 = 1200 | 1210 − 300 = 910 |
| 600 + 7000 = 7600 | 23000 + 7000 = 30000 | 2000 − 300 = 1700 | 5200 − 300 = 4900 |
| 60 + 7000 = 7060 | 45000 + 7000 = 52000 | 900 − 300 = 600 | 11000 − 300 = 10700 |
- 2)
- 20 грн 08 к − 59 к = 2008 к − 59 к = 949 к = 9 грн 49 к .

- 12 грн 70 к − 8 грн 07 к = 4 грн 63 к .
3) 3 грн 60 к : 3 = 360 : 3 = 120 к = 1грн 20 к .
Задание 387.
Расстояние между двумя пристанями 320 км. Половину этого расстояния моторная лодка прошла за 4 ч. С какой скоростью шла лодка?
Решение:
- 1) 320 : 2 = 160 (км) половина расстояния;
- 2) 160 : 4 = 40 (км/ч).
- Отвтет: скорость лодки 40 км/ч.
Задание 388.
Расстояние 20 км всадник проехал туда и обратно за 4 ч. С какой скоростью ехал всадник?
Решение:
- 1) 20 + 20 = 40 (км) расстояние туда и обратно;
- 2) 40 : 4 = 10 (км/ч).
- Ответ: скорость всадника 10 км/ч.
Задание 389.
Прочитай задачу и рассмотри её решение.
- Задача. Лыжник был в пути 3 ч, двигаясь со скоростью 12 км/ч. Какое расстояние прошёл лыжник?
- Решение: 12 — 3 = 36 (км).
- Ответ: за 3 ч лыжник прошёл 36 км.

Задание 390.
Пассажирский катер шёл 4 ч, а буксирный 7 ч. Какой из них прошёл большее расстояние и на сколько километров, если скорость пассажирского катера 24 км/ч, а буксирного 14 км/ч?
Решение:
- 1) 24 * 4 = 96 (км) прошел пассажирский катер;
- 2) 14 * 7 = 98 (км) прошел буксирный катер;
- 3) 98 — 96 = 2 (км).
- Ответ: буксирный катер прошел на 2 км больше.
Задание 391.
По данным таблицы найди расстояния.
Решение:
- Пешеход: 5км/ч * 4ч = 20 км .
- Такси: 70 км/ч * 2 ч = 140 км .
- Электропоезд: 120 км/ч * 3 ч = 360 км .
Задание 392.
В течение дня туристы шли пешком 2 ч, на автобусе ехали 3 ч. Пешком они двигались со скоростью 4 км/ч, на автобусе ехали со скоростью 45 км/ч. Какой путь преодолели туристы за день?Решение:
- 1) 2 * 4 = 8 (км) преодолели туристы пешком;
- 2) 3 * 45 = 135 (км) преодолели турсты на автобусе;
- 3) 8 + 135 = 143 (км).

- Ответ: за день туристы преодолели 143 км.
Задание 393.
Решение:
- 54408 + 351875 + 973 = 406283 + 973 = 407256
- 10 ц 3 кг − 4 ц 12 кг = 5 ц 91 кг
- 48350 − 9405 + 598 = 38945 + 598 = 39543
- 8365 − (2120 + 1080) = 8365 − 3200 = 5165
Задание 394.
На птичьем дворе было 16 цыплят, а утят — в 4 раза больше.
- По условию задачи можно поставить такие вопросы:
- 1) Сколько утят было на птичьем дворе?
- 2) Сколько было цыплят и утят вместе?
- 3) На сколько больше было утят, чем цыплят? Выполни устно вычисления и запиши ответы.
Решение:
- 1) 16 * 4 = 64 Утят — 64;
- 2) 16 + 64 = 80 — цыплят и утят.
- 3) 64 — 16 = 48 — Утят на 48 больше, чем цыплят.
Задание 395.
В течение двух дней велосипедист был в дороге 12 ч и за это время проехал 180 км. Сколько километров проедет мотоциклист за 20 ч, если его скорость на 36 км/ч больше скорости велосипедиста?
Решение:
- 1) 180 : 12 = 15 (км/ч) скорость велосипедиста;
- 2) 15 + 36 = 51 (км/ч) скрость мотоциклиста;
- 3) 51 * 20 = 1020 (км).

- Ответ: мотоциклист проедет 1020 км.
Задание 396.
Решение:
- 1) 10 ц 08 кг − 4 ц 12 кг = 5 ц 96 кг
- 2) 12 км 750 м + 4 км 75 м = 16 км 825 м
- 3) 47650 − 875 − 6588 = 46775 − 6588 = 40187
- 4) 3358 − (12 + 778) = 3358 − 790 = 2568
Задание 397.
Автомобиль ехал 2 ч со скоростью 66 км/ч. После этого ему осталось проехать расстояние в 3 раза большее, чем он уже проехал. Какое расстояние должен был проехать автомобиль?
Решение:
- 1) 2 * 66 = 132 (км) проехал автомобиль;
- 2) 132 * 3 = 396 (км) осталось проехать автомобилю;
- 3) 396 + 132 = 528 (км).
- Ответ: автомобиль должен был проехать 528 км.
Задание 398.
Прочитай задачу и рассмотри ее решение.
- Задача. Пассажир проехал на автобусе 180 км. Скорость автобуса 60 км/ч. Сколько времени ехал пассажир на автобусе?
- Решение: 180 : 60 = 3 (ч).

- Ответ: пассажир ехал на автобусе 3 ч.
Чтобы найти время, надо расстояние поделить на скорость.
Задание399.
По данным таблицы найди время движения.
Решение:
- Лыжник: 26 км : 13 км/ч = 2 ч.
- Поезд: 240 км : 60 км/ч = 4 ч.
- Легковой автомобиль: 240 км : 80 км/ч = 3 ч.
Задание 400.
По асфальтированной дороге автомобиль проехал расстояние 210 км со скоростью 70 км/ч, а по грунтовой — 90 км со скоростью 45 км/ч. За какое время автомобиль проехал всё расстояние?
Решение:
- 1) 210 : 70 = 3 (ч) ехал автомобиль по асфальтированной дорогое4;
- 2) 90 : 45 = 2 (ч) ехал автомобиль по грунтовой дороге;
- 3) 3 + 2 = 5 (ч).
- Ответ: автомобиль проехал все расстояние за 5 ч.
Задание: —>> 381 — 400 401 — 418
Задачи на движение
Продолжаем изучать элементарные задачи по математике. Данный урок посвящен задачам на движение.
Данный урок посвящен задачам на движение.
Задача на нахождение расстояния/скорости/времени
Задача 1. Автомобиль двигается со скоростью 80 км/ч. Сколько километров он проедет за 3 часа?
Решение
Если за один час автомобиль проезжает 80 километров, то за 3 часа он проедет в три раза больше. Чтобы найти расстояние, нужно скорость автомобиля (80км/ч) умножить на время движения (3ч)
80 × 3 = 240 км
Ответ: за 3 часа автомобиль проедет 240 километров.
Задача 2. На автомобиле за 3 часа проехали 180 км с одной и той же скоростью. Чему равна скорость автомобиля?
Решение
Скорость — это расстояние, пройденное телом за единицу времени. Под единицей подразумевается 1 час, 1 минута или 1 секунда.
Если за 3 часа автомобиль проехал 180 километров с одной и той же скоростью, то разделив 180 км на 3 часа мы определим расстояние, которое проезжал автомобиль за один час. А это есть скорость движения. Чтобы определить скорость, нужно пройденное расстояние разделить на время движения:
А это есть скорость движения. Чтобы определить скорость, нужно пройденное расстояние разделить на время движения:
180 : 3 = 60 км/ч
Ответ: скорость автомобиля составляет 60 км/ч
Задача 3. За 2 часа автомобиль проехал 96 км, а велосипедист за 6 часов проехал 72 км. Во сколько раз автомобиль двигался быстрее велосипедиста?
Решение
Определим скорость движения автомобиля. Для этого разделим пройденное им расстояние (96км) на время его движения (2ч)
96 : 2 = 48 км/ч
Определим скорость движения велосипедиста. Для этого разделим пройденное им расстояние (72км) на время его движения (6ч)
72 : 6 = 12 км/ч
Узнаем во сколько раз автомобиль двигался быстрее велосипедиста. Для этого найдем отношение 48 к 12
Ответ: автомобиль двигался быстрее велосипедиста в 4 раза.
Задача 4. Вертолет преодолел расстояние в 600 км со скоростью 120 км/ч. Сколько времени он был в полете?
Сколько времени он был в полете?
Решение
Если за 1 час вертолет преодолевал 120 километров, то узнав сколько таких 120 километров в 600 километрах, мы определим сколько времени он был в полете. Чтобы найти время, нужно пройденное расстояние разделить на скорость движения
600 : 120 = 5 часов
Ответ: вертолет был в пути 5 часов.
Задача 5. Вертолет летел 6 часов со скоростью 160 км/ч. Какое расстояние он преодолел за это время?
Решение
Если за 1 час вертолет преодолевал 160 км, то за 6 часов, он преодолел в шесть раз больше. Чтобы определить расстояние, нужно скорость движения умножить на время
160 × 6 = 960 км
Ответ: за 6 часов вертолет преодолел 960 км.
Задача 6. Расстояние от Перми до Казани, равное 723 км, автомобиль проехал за 13 часов. Первые 9 часов он ехал со скоростью 55 км/ч. Определить скорость автомобиля в оставшееся время.
Решение
Определим сколько километров автомобиль проехал за первые 9 часов. Для этого умножим скорость с которой он ехал первые девять часов (55км/ч) на 9
55 × 9 = 495 км
Определим сколько осталось проехать. Для этого вычтем из общего расстояния (723км) расстояние, пройденное за первые 9 часов движения
723 − 495 = 228 км
Эти 228 километров автомобиль проехал за оставшиеся 4 часа. Чтобы определить скорость автомобиля в оставшееся время, нужно 228 километров разделить на 4 часа:
228 : 4 = 57 км/ч
Ответ: скорость автомобиля в оставшееся время составляла 57 км/ч
Скорость сближения
Скорость сближения — это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.
Например, если из двух пунктов навстречу друг другу отправятся два пешехода, причем скорость первого будет 100 м/м, а второго — 105 м/м, то скорость сближения будет составлять 100 + 105, то есть 205 м/м. Это значит, что каждую минуту расстояние между пешеходами будет уменьшáться на 205 метров
Это значит, что каждую минуту расстояние между пешеходами будет уменьшáться на 205 метров
Чтобы найти скорость сближения, нужно сложить скорости объектов.
Предположим, что пешеходы встретились через три минуты после начала движения. Зная, что они встретились через три минуты, мы можем узнать расстояние между двумя пунктами.
Каждую минуту пешеходы преодолевали расстояние равное двухсот пяти метрам. Через 3 минуты они встретились. Значит умножив скорость сближения на время движения, можно определить расстояние между двумя пунктами:
205 × 3 = 615 метров
Можно и по другому определить расстояние между пунктами. Для этого следует найти расстояние, которое прошел каждый пешеход до встречи.
Так, первый пешеход шел со скоростью 100 метров в минуту. Встреча состоялась через три минуты, значит за 3 минуты он прошел 100 × 3 метров
100 × 3 = 300 метров
А второй пешеход шел со скоростью 105 метров в минуту. За три минуты он прошел 105 × 3 метров
105 × 3 = 315 метров
Теперь можно сложить полученные результаты и таким образом определить расстояние между двумя пунктами:
300 м + 315 м = 615 м
Задача 1. Из двух населенных пунктов навстречу друг другу выехали одновременно два велосипедиста. Скорость первого велосипедиста 10 км/ч, а скорость второго — 12 км/ч. Через 2 часа они встретились. Определите расстояние между населенными пунктами
Из двух населенных пунктов навстречу друг другу выехали одновременно два велосипедиста. Скорость первого велосипедиста 10 км/ч, а скорость второго — 12 км/ч. Через 2 часа они встретились. Определите расстояние между населенными пунктами
Решение
Найдем скорость сближения велосипедистов
10 км/ч + 12 км/ч = 22 км/ч
Определим расстояние между населенными пунктами. Для этого скорость сближения умножим на время движения
22 × 2 = 44 км
Решим эту задачу вторым способом. Для этого найдем расстояния, пройденные велосипедистами и сложим полученные результаты.
Найдем расстояние, пройденное первым велосипедистом:
10 × 2 = 20 км
Найдем расстояние, пройденное вторым велосипедистом:
12 × 2 = 24 км
Сложим полученные расстояния:
20 км + 24 км = 44 км
Ответ: расстояние между населенными пунктами составляет 44 км.
Задача 2. Из двух населенных пунктов, расстояние между которыми 60 км, навстречу друг другу выехали одновременно два велосипедиста. Скорость первого велосипедиста 14 км/ч, а скорость второго — 16 км/ч. Через сколько часов они встретились?
Скорость первого велосипедиста 14 км/ч, а скорость второго — 16 км/ч. Через сколько часов они встретились?
Решение
Найдем скорость сближения велосипедистов:
14 км/ч + 16 км/ч = 30 км/ч
За один час расстояние между велосипедистами уменьшается на 30 километров. Чтобы определить через сколько часов они встретятся, нужно расстояние между населенными пунктами разделить на скорость сближения:
60 : 30 = 2 часа
Значит велосипедисты встретились через два часа
Ответ: велосипедисты встретились через 2 часа.
Задача 3. Из двух населенных пунктов, расстояние между которыми 56 км, навстречу друг другу выехали одновременно два велосипедиста. Через два часа они встретились. Первый велосипедист ехал со скоростью 12 км/ч. Определить скорость второго велосипедиста.
Решение
Определим расстояние пройденное первым велосипедистом. Как и второй велосипедист в пути он провел 2 часа. Умножив скорость первого велосипедиста на 2 часа, мы сможем узнать сколько километров он прошел до встречи
Умножив скорость первого велосипедиста на 2 часа, мы сможем узнать сколько километров он прошел до встречи
12 × 2 = 24 км
За два часа первый велосипедист прошел 24 км. За один час он прошел 24:2, то есть 12 км. Изобразим это графически
Вычтем из общего расстояния (56 км) расстояние, пройденное первым велосипедистом (24 км). Так мы определим сколько километров прошел второй велосипедист:
56 км − 24 км = 32 км
Второй велосипедист, как и первый провел в пути 2 часа. Если мы разделим пройденное им расстояние на 2 часа, то узнаем с какой скоростью он двигался:
32 : 2 = 16 км/ч
Значит скорость второго велосипедиста составляет 16 км/ч.
Ответ: скорость второго велосипедиста составляет 16 км/ч.
Скорость удаления
Скорость удаления — это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.
Например, если два пешехода отправятся из одного и того же пункта в противоположных направлениях, причем скорость первого будет 4 км/ч, а скорость второго 6 км/ч, то скорость удаления будет составлять 4+6, то есть 10 км/ч.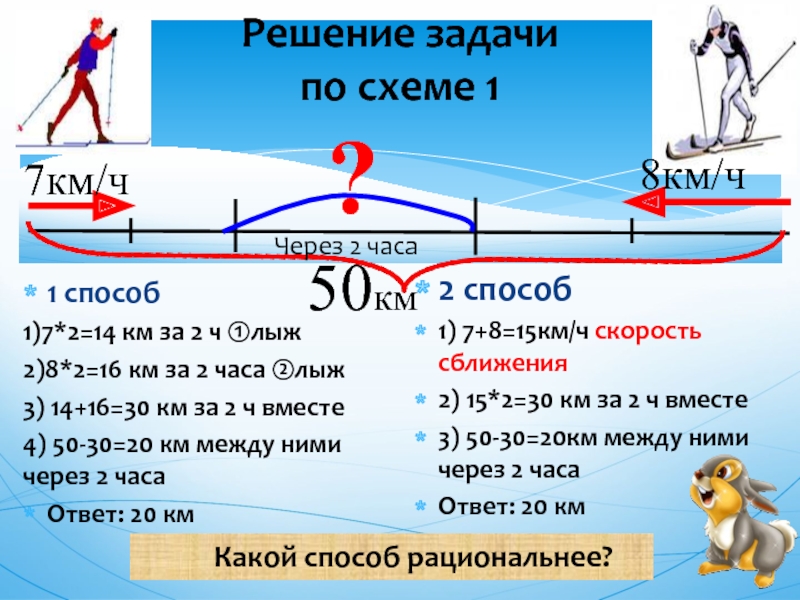 Каждый час расстояние между двумя пешеходами будет увеличиться на 10 километров.
Каждый час расстояние между двумя пешеходами будет увеличиться на 10 километров.
Чтобы найти скорость удаления, нужно сложить скорости объектов.
Так, за первый час расстояние между пешеходами будет составлять 10 километров. На следующем рисунке можно увидеть, как это происходит
Видно, что первый пешеход прошел свои 4 километра за первый час. Второй пешеход также прошел свои 6 километров за первый час. Итого за первый час расстояние между ними стало 4+6, то есть 10 километров.
Через два часа расстояние между пешеходами будет составлять 10×2, то есть 20 километров. На следующем рисунке можно увидеть, как это происходит:
Задача 1. От одной станции отправились одновременно в противоположных направлениях товарный поезд и пассажирский экспресс. Скорость товарного поезда составляла 40 км/ч, скорость экспресса 180 км/ч. Какое расстояние будет между этими поездами через 2 часа?
Решение
Определим скорость удаления поездов. Для этого сложим их скорости:
Для этого сложим их скорости:
40 + 180 = 220 км/ч
Получили скорость удаления поездов равную 220 км/ч. Данная скорость показывает, что за час расстояние между поездами будет увеличиваться на 220 километров. Чтобы узнать какое расстояние будет между поездами через два часа, нужно 220 умножить на 2
220 × 2 = 440 км
Ответ: через 2 часа расстояние будет между поездами будет 440 километров.
Задача 2. Из пункта одновременно в противоположных направлениях отправились велосипедист и мотоциклист. Скорость велосипедиста 16 км/ч, а скорость мотоциклиста — 40 км/ч. Какое расстояние будет между велосипедистом и мотоциклистом через 2 часа?
Решение
Определим скорость удаления велосипедиста и мотоциклиста. Для этого сложим их скорости:
16 км/ч + 40 км/ч = 56 км/ч
Определим расстояние, которое будет между велосипедистом и мотоциклистом через 2 часа. Для этого скорость удаления (56км/ч) умножим на 2 часа
56 × 2 = 112 км
Ответ: через 2 часа расстояние между велосипедистом и мотоциклистом будет 112 км.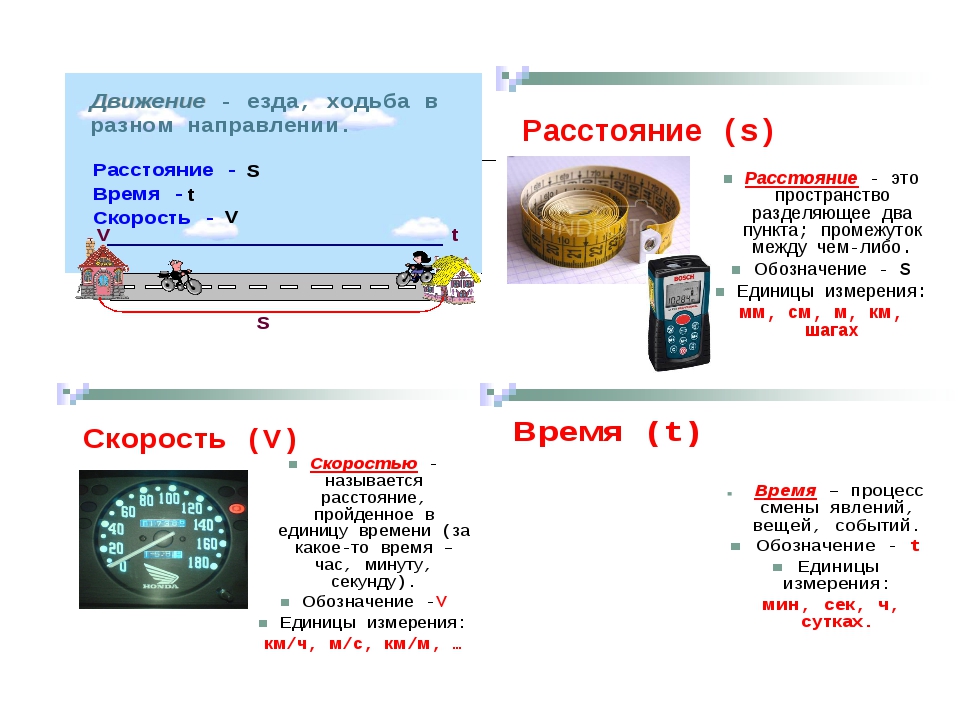
Задача 3. Из пункта одновременно в противоположных направлениях отправились велосипедист и мотоциклист. Скорость велосипедиста 10 км/ч, а скорость мотоциклиста — 30 км/ч. Через сколько часов расстояние между ними будет 80 км?
Решение
Определим скорость удаления велосипедиста и мотоциклиста. Для этого сложим их скорости:
10 км/ч + 30 км/ч = 40 км/ч
За один час расстояние между велосипедистом и мотоциклистом увеличивается на 40 километров. Чтобы узнать через сколько часов расстояние между ними будет 80 км, нужно определить сколько раз 80 км содержит по 40 км
80 : 40 = 2
Ответ: через 2 часа после начала движения, между велосипедистом и мотоциклистом будет 80 километров.
Задача 4. Из пункта одновременно в противоположных направлениях отправились велосипедист и мотоциклист. Через 2 часа расстояние между ними было 90 км. Скорость велосипедиста составляла 15 км/ч. Определить скорость мотоциклиста
Определить скорость мотоциклиста
Решение
Определим расстояние, пройденное велосипедистом за 2 часа. Для этого умножим его скорость (15 км/ч) на 2 часа
15 × 2 = 30 км
На рисунке видно, что велосипедист прошел по 15 километров в каждом часе. Итого за два часа он прошел 30 километров.
Вычтем из общего расстояния (90 км) расстояние, пройденное велосипедистом (30 км). Так мы определим сколько километров прошел мотоциклист:
90 км − 30 км = 60 км
Мотоциклист за два часа прошел 60 километров. Если мы разделим пройденное им расстояние на 2 часа, то узнаем с какой скоростью он двигался:
60 : 2 = 30 км/ч
Значит скорость мотоциклиста составляла 30 км/ч.
Ответ: скорость мотоциклиста составляла 30 км/ч.
Задача на движение объектов в одном направлении
В предыдущей теме мы рассматривали задачи в которых объекты (люди, машины, лодки) двигались либо навстречу другу другу либо в противоположных направлениях. При этом мы находили различные расстояния, которые изменялись между объектами в течении определенного времени. Эти расстояния были либо скоростями сближения либо скоростями удаления.
При этом мы находили различные расстояния, которые изменялись между объектами в течении определенного времени. Эти расстояния были либо скоростями сближения либо скоростями удаления.
В первом случае мы находили скорость сближения — в ситуации, когда два объекта двигались навстречу друг другу. За единицу времени расстояние между объектами уменьшалось на определенное расстояние
Во втором случае мы находили скорость удаления — в ситуации, когда два объекта двигались в противоположных направлениях. За единицу времени расстояние между объектами увеличивалось на определенное расстояние
Но объекты также могут двигаться в одном направлении, причем с различной скоростью. Например, из одного пункта одновременно могут выехать велосипедист и мотоциклист, причем скорость велосипедиста может составлять 20 километров в час, а скорость мотоциклиста — 40 километров в час
На рисунке видно, что мотоциклист впереди велосипедиста на двадцать километров. Связано это с тем, что в час он преодолевает на 20 километров больше, чем велосипедист. Поэтому каждый час расстояние между велосипедистом и мотоциклистом будет увеличиваться на двадцать километров.
Связано это с тем, что в час он преодолевает на 20 километров больше, чем велосипедист. Поэтому каждый час расстояние между велосипедистом и мотоциклистом будет увеличиваться на двадцать километров.
В данном случае 20 км/ч являются скоростью удаления мотоциклиста от велосипедиста.
Через два часа расстояние, пройденное велосипедистом будет составлять 40 км. Мотоциклист же проедет 80 км, отдалившись от велосипедиста еще на двадцать километров — итого расстояние между ними составит 40 километров
Чтобы найти скорость удаления при движении в одном направлении, нужно из большей скорости вычесть меньшую скорость.
В приведенном выше примере, скорость удаления составляет 20 км/ч. Её можно найти путем вычитания скорости велосипедиста из скорости мотоциклиста. Скорость велосипедиста составляла 20 км/ч, а скорость мотоциклиста — 40 км/ч. Скорость мотоциклиста больше, поэтому из 40 вычитаем 20
40 км/ч − 20 км/ч = 20 км/ч
Задача 1.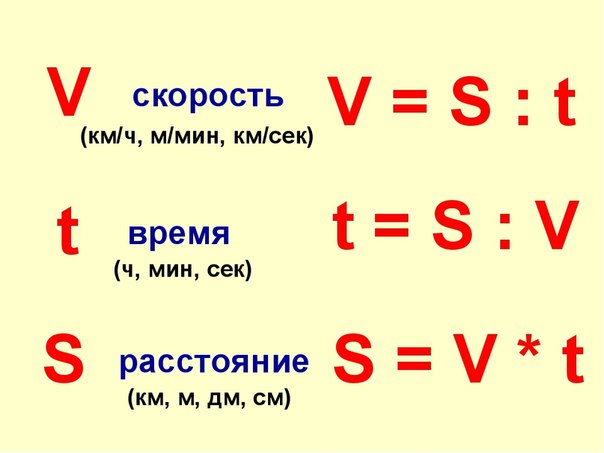 Из города в одном и том же направлении выехали легковой автомобиль и автобус. Скорость автомобиля 120 км/ч, а скорость автобуса 80 км/ч. Какое расстояние будет между ними через 1 час? 2 часа?
Из города в одном и том же направлении выехали легковой автомобиль и автобус. Скорость автомобиля 120 км/ч, а скорость автобуса 80 км/ч. Какое расстояние будет между ними через 1 час? 2 часа?
Решение
Найдем скорость удаления. Для этого из большей скорости вычтем меньшую
120 км/ч − 80 км/ч = 40 км/ч
Каждый час легковой автомобиль отдаляется от автобуса на 40 километров. За один час расстояние между автомобилем и автобусом будет 40 км. За 2 часа в два раза больше:
40 × 2 = 80 км
Ответ: через один час расстояние между автомобилем и автобусом будет 40 км, через два часа — 80 км.
Рассмотрим ситуацию в которой объекты начали свое движение из разных пунктов, но в одном направлении.
Пусть имеется дом, школа и аттракцион. От дома до школы 700 метров
Два пешехода отправились в аттракцион в одно и то же время. Причем первый пешеход отправился в аттракцион от дома со скоростью 100 метров в минуту, а второй пешеход отправился в аттракцион от школы со скоростью 80 метров в минуту. Какое расстояние будет между пешеходами через 2 минуты? Через сколько минут после начала движения первый пешеход догонит второго?
Ответим на первый вопрос задачи — какое расстояние будет между пешеходами через 2 минуты?
Определим расстояние, пройденное первым пешеходом за 2 минуты. Он двигался со скоростью 100 метров в минуту. За две минуты он пройдет в два раза больше, то есть 200 метров
100 × 2 = 200 метров
Определим расстояние, пройденное вторым пешеходом за 2 минуты. Он двигался со скоростью 80 метров в минуту. За две минуты он пройдет в два раза больше, то есть 160 метров
80 × 2 = 160 метров
Теперь нужно найти расстояние между пешеходами
Чтобы найти расстояние между пешеходами, можно к расстоянию от дома до школы (700м) прибавить расстояние, пройденное вторым пешеходом (160м) и из полученного результата вычесть расстояние, пройденное первым пешеходом (200м)
700 м + 160 м = 860 м
860 м − 200 м = 660 м
Либо из расстояния от дома до школы (700м) вычесть расстояние, пройденное первым пешеходом (200м), и к полученному результату прибавить расстояние, пройденное вторым пешеходом (160м)
700 м − 200 м = 500 м
500 м + 160 м = 660 м
Таким образом, через две минуты расстояние между пешеходами будет составлять 660 метров
Попробуем ответить на следующий вопрос задачи: через сколько минут после начала движения первый пешеход догонит второго?
Давайте посмотрим какой была ситуация в самом начале пути — когда пешеходы еще не начали своё движение
Как видно на рисунке, расстояние между пешеходами в начале пути составляло 700 метров. Но уже через минуту после начала движения расстояние между ними будет составлять 680 метров, поскольку первый пешеход двигается на 20 метров быстрее второго:
100 м × 1 = 100 м
80 м × 1 = 80 м
700 м + 80 м − 100 м = 780 м − 100 м = 680 м
Через две минуты после начала движения, расстояние уменьшится еще на 20 метров и будет составлять 660 метров. Это был наш ответ на первый вопрос задачи:
100 м × 2 = 200 м
80 м × 2 = 160 м
700 м + 160 м − 200м = 860 м − 200 м = 660 м
Через три минуты расстояние уменьшится еще на 20 метров и будет уже составлять 640 метров:
100 м × 3 = 300 м
80 м × 3 = 240 м
700 м + 240 м − 300м = 940 м − 300 м = 640 м
Мы видим, что с каждой минутой первый пешеход будет приближáться ко второму на 20 метров, и в конце концов догонит его. Можно сказать, что скорость равная двадцати метрам в минуту является скоростью сближения пешеходов. Правила нахождения скорости сближения и удаления при движении в одном направлении идентичны.
Чтобы найти скорость сближения при движении в одном направлении, нужно из большей скорости вычесть меньшую.
А раз изначальные 700 метров с каждой минутой уменьшаются на одинаковые 20 метров, то мы можем узнать сколько раз 700 метров содержат по 20 метров, тем самым определяя через сколько минут первый пешеход догонит второго
700 : 20 = 35
Значит через 35 минут после начала движения первый пешеход догонит второго. Для интереса узнаем сколько метров прошел к этому времени каждый пешеход. Первый двигался со скоростью 100 метров в минуту. За 35 минут он прошел в 35 раз больше
100 × 35 = 3500 м
Второй шел со скоростью 80 метров в минуту. За 35 минут он прошел в 35 раз больше
80 × 35 = 2800 м
Первый прошел 3500 метров, а второй 2800 метров. Первый прошел на 700 метров больше, поскольку он шел от дома. Если вычесть эти 700 метров из 3500, то мы получим 2800 м
Рассмотрим ситуацию в которой объекты движутся в одном направлении, но один из объектов начал своё движение раньше другого.
Пусть имеется дом и школа. Первый пешеход отправился в школу со скоростью 80 метров в минуту. Через 5 минут вслед за ним в школу отправился второй пешеход со скоростью 100 метров в минуту. Через сколько минут второй пешеход догонит первого?
Второй пешеход начал свое движение через 5 минут. К этому времени первый пешеход уже отдалился от него на какое-то расстояние. Найдём это расстояние. Для этого умножим его скорость (80 м/м) на 5 минут
80 × 5 = 400 метров
Первый пешеход отдалился от второго на 400 метров. Поэтому в момент, когда второй пешеход начнет свое движение, между ними будут эти самые 400 метров.
Но второй пешеход двигается со скоростью 100 метров в минуту. То есть двигается на 20 метров быстрее первого пешехода, а значит с каждой минутой расстояние между ними будет уменьшáться на 20 метров. Наша задача узнать через сколько минут это произойдет.
Например, уже через минуту расстояние между пешеходами будет составлять 380 метров. Первый пешеход к своим 400 метрам пройдет еще 80 метров, а второй пройдет 100 метров
Принцип здесь такой-же, как и в предыдущей задаче. Расстояние между пешеходами в момент движения второго пешехода необходимо разделить на скорость сближения пешеходов. Скорость сближения в данном случае равна двадцати метрам. Поэтому, чтобы определить через сколько минут второй пешеход догонит первого, нужно 400 метров разделить на 20
400 : 20 = 20
Значит через 20 минут второй пешеход догонит первого.
Задача 2. Из двух сел, расстояние между которыми 40 км, одновременно в одном направлении выехали автобус и велосипедист. Скорость велосипедиста 15 км/ч, а скорость автобуса 35 км/ч. Через сколько часов автобус догонит велосипедиста?
Решение
Найдем скорость сближения
35 км/ч − 15 км/ч = 20 км/ч
Определим через часов автобус догонит велосипедиста
40 : 20 = 2
Ответ: автобус догонит велосипедиста через 2 часа.
Задача на движение по реке
Суда двигаются по реке с различной скоростью. При этом они могут двигаться, как по течению реки, так и против течения. В зависимости от того, как они двигаются (по или против течения), скорость будет меняться.
Предположим, что скорость реки составляет 3 км/ч. Если спустить лодку на реку, то река унесет лодку со скоростью 3 км/ч.
Если спустить лодку на стоячую воду, в которой отсутствует течение, то и лодка будет стоять. Скорость движения лодки в этом случае будет равна нулю.
Если лодка плывет по стоячей воде, в которой отсутствует течение, то говорят, что лодка плывет с собственной скоростью.
Например, если моторная лодка плывет по стоячей воде со скоростью 40 км/ч, то говорят что собственная скорость моторной лодки составляет 40 км/ч.
Как определить скорость судна?
Если судно плывет по течению реки, то к собственной скорости судна нужно прибавить скорость течения реки.
Например, если моторная лодка плывет со скоростью 30 км/ч по течению реки, и скорость течения реки составляет 2 км/ч, то к собственной скорости моторной лодки (30 км/ч) необходимо прибавить скорость течения реки (2 км/ч)
30 км/ч + 2 км/ч = 32 км/ч
Течение реки можно сказать помогает моторной лодке дополнительной скоростью равной двум километрам в час.
Если судно плывет против течения реки, то из собственной скорости судна нужно вычесть скорость течения реки.
Например, если моторная лодка плывет со скоростью 30 км/ч против течения реки, и скорость течения реки составляет 2 км/ч, то из собственной скорости моторной лодки (30 км/ч) необходимо вычесть скорость течения реки (2 км/ч)
30 км/ч − 2 км/ч = 28 км/ч
Течение реки в этом случае препятствует моторной лодке свободно двигаться вперед, снижая её скорость на два километра в час.
Задача 1. Скорость катера 40 км/ч, а скорость течения реки 3 км/ч. С какой скоростью катер будет двигаться по течению реки? Против течения реки?
Ответ:
Если катер будет двигаться по течения реки, то скорость его движения составит 40 + 3, то есть 43 км/ч.
Если катер будет двигаться против течения реки, то скорость его движения составит 40 − 3, то есть 37 км/ч.
Задача 2. Скорость теплохода в стоячей воде — 23 км/ч. Скорость течения реки — 3 км/ч. Какой путь пройдет теплоход за 3 часа по течению реки? Против течения?
Решение
Собственная скорость теплохода составляет 23 км/ч. Если теплоход будет двигаться по течению реки, то скорость его движения составит 23 + 3, то есть 26 км/ч. За три часа он пройдет в три раза больше
26 × 3 = 78 км
Если теплоход будет двигаться против течения реки, то скорость его движения составит 23 − 3, то есть 20 км/ч. За три часа он пройдет в три раза больше
20 × 3 = 60 км
Задача 3. Расстояние от пункта А до пункта B лодка преодолела за 3 часа 20 минут, а расстояние от пункта B до А — за 2 часа 50 минут. В каком направлении течет река: от А к В или от В к А, если известно, что скорость яхты не менялась?
Решение
Скорость яхты не менялась. Узнаем на какой путь она затратила больше времени: на путь от А до В или на путь от В до А. Тот путь, который затратил больше времени будет тем путем, течение реки которого шло против яхты
3 часа 20 минут больше, чем 2 часа 50 минут. Это значит, что течение реки снизило скорость яхты и это отразилось на времени пути. 3 часа 20 минут это время, затраченное на путь от от А до В. Значит река течет от пункта B к пункту А
Задача 4. За какое время при движении против течения реки
теплоход пройдет 204 км, если его собственная скорость
15 км/ч, а скорость течения в 5 раз меньше собственной
скорости теплохода?
Решение
Требуется найти время за которое теплоход пройдет 204 километра против течения реки. Собственная скорость теплохода составляет 15 км/ч. Двигается он против течения реки, поэтому нужно определить его скорость при таком движении.
Чтобы определить скорость против течения реки, нужно из собственной скорости теплохода (15 км/ч) вычесть скорость движения реки. В условии сказано, что скорость течения реки в 5 раз меньше собственной скорости теплохода, поэтому сначала определим скорость течения реки. Для этого уменьшим 15 км/ч в пять раз
15 : 5 = 3 км/ч
Скорость течения реки составляет 3 км/ч. Вычтем эту скорость из скорости движения теплохода
15 км/ч − 3 км/ч = 12 км/ч
Теперь определим время за которое теплоход пройдет 204 км при скорости 12 км/ч. В час теплоход проходит 12 километров. Чтобы узнать за сколько часов он пройдет 204 километра, нужно определить сколько раз 204 километра содержит по 12 километров
204 : 12 = 17 ч
Ответ: теплоход пройдет 204 километра за 17 часов
Задача 5. Двигаясь по течению реки, за 6 часов лодка
прошла 102 км. Определите собственную скорость лодки,
если скорость течения – 4 км/ч.
Решение
Узнаем с какой скоростью лодка двигалась по реке. Для этого пройденное расстояние (102км) разделим на время движения (6ч)
102 : 6 = 17 км/ч
Определим собственную скорость лодки. Для этого из скорости по которой она двигалась по реке (17 км/ч) вычтем скорость течения реки (4 км/ч)
17 − 4 = 13 км/ч
Задача 6. Двигаясь против течения реки, за 5 часов лодка
прошла 110 км. Определите собственную скорость лодки,
если скорость течения – 4 км/ч.
Решение
Узнаем с какой скоростью лодка двигалась по реке. Для этого пройденное расстояние (110км) разделим на время движения (5ч)
110 : 5 = 22 км/ч
Определим собственную скорость лодки. В условии сказано, что она двигалась против течения реки. Скорость течения реки составляла 4 км/ч. Это значит, что собственная скорость лодки была уменьшена на 4. Наша задача прибавить эти 4 км/ч и узнать собственную скорость лодки
22 + 4 = 26 км/ч
Ответ: собственная скорость лодки составляет 26 км/ч
Задача 7. За какое время при движении против течения реки лодка
пройдет 56 км, если скорость течения – 2 км/ч, а её
собственная скорость на 8 км/ч больше скорости течения?
Решение
Найдем собственную скорость лодки. В условии сказано, что она на 8 км/ч больше скорости течения. Поэтому для определения собственной скорости лодки, к скорости течения (2 км/ч) прибавим еще 8 км/ч
2 км/ч + 8 км/ч = 10 км/ч
Лодка движется против течения реки, поэтому из собственной скорости лодки (10 км/ч) вычтем скорость движения реки (2 км/ч)
10 км/ч − 2 км/ч = 8 км/ч
Узнаем за какое время лодка пройдет 56 км. Для этого расстояние (56км) разделим на скорость движения лодки:
56 : 8 = 7 ч
Ответ: при движении против течения реки лодка пройдет 56 км за 7 часов
Задачи для самостоятельного решения
Задача 1. Сколько времени потребуется пешеходу, чтобы пройти 20 км, если скорость его равна 5 км/ч?
Решение
За один час пешеход проходит 5 километров. Чтобы определить за какое время он пройдет 20 км, нужно узнать сколько раз 20 километров содержат по 5 км. Либо воспользоваться правилом нахождения времени: разделить пройденное расстояние на скорость движения
20 : 5 = 4 часа
Задача 2. Из пункта А в пункт В велосипедист ехал 5 часов со скоростью 16 км/ч, а обратно он ехал по тому же пути со скоростью 10 км/ч. Сколько времени потратил велосипедист на обратный путь?
Решение
Определим расстояние от пункта А до пункта В. Для этого умножим скорость с которой ехал велосипедист из пункта А в пункт В (16км/ч) на время движения (5ч)
16 × 5 = 80 км
Определим сколько времени велосипедист затратил на обратный путь. Для этого расстояние (80км) разделим на скорость движения (10км/ч)
80 : 10 = 8 ч
Задача 3. Велосипедист ехал 6 ч с некоторой скоростью. После того как он проехал ещё 11 км с той же скоростью, его путь стал равным 83 км. С какой скоростью ехал велосипедист?
Решение
Определим путь, пройденный велосипедистом за 6 часов. Для этого из 83 км вычтем путь, который он прошел после шести часов движения (11км)
83 − 11 = 72 км
Определим с какой скоростью ехал велосипедист первые 6 часов. Для этого разделим 72 км на 6 часов
72 : 6 = 12 км/ч
Поскольку в условии задаче сказано, что остальные 11 км велосипедист проехал с той же скоростью, что и в первые 6 часов движения, то скорость равная 12 км/ч является ответом к задаче.
Ответ: велосипедист ехал со скоростью 12 км/ч.
Задача 4. Двигаясь против течения реки, расстояние в 72 км теплоход проходит за 4ч, а плот такое же расстояние проплывает за 36 ч. За сколько часов теплоход проплывет расстояние 110 км, если будет плыть по течению реки?
Решение
Найдем скорость течения реки. В условии сказано, что плот может проплыть 72 километра за 36 часов. Плот не может двигаться против течения реки. Значит скорость плота с которой он преодолевает эти 72 километра и является скоростью течения реки. Чтобы найти эту скорость, нужно 72 километра разделить на 36 часов
72 : 36 = 2 км/ч
Найдем собственную скорость теплохода. Сначала найдем скорость его движения против течения реки. Для этого разделим 72 километра на 4 часа
72 : 4 = 18 км/ч
Если против течения реки скорость теплохода составляет 18 км/ч, то собственная его скорость равна 18+2, то есть 20 км/ч. А по течению реки его скорость будет составлять 20+2, то есть 22 км/ч
Разделив 110 километров на скорость движения теплохода по течению реки (22 км/ч), можно узнать за сколько часов теплоход проплывет эти 110 километров
110 : 22 = 5 ч
Ответ: по течению реки теплоход проплывет 110 километров за 5 часов.
Задача 5. Из одного пункта одновременно в противоположных направлениях выехали два велосипедиста. Один из них ехал со скоростью 11 км/ч, а второй со скоростью 13 км/ч. Какое расстояние будет между ними через 4 часа?
Решение
Найдем скорость удаления велосипедистов
11 + 13 = 24 км
Узнаем какое расстояние будет между ними через 4 часа
24 × 4 = 96 км
Ответ: через 4 часа расстояние между велосипедистами будет 96 км.
Задача 6. От двух пристаней одновременно навстречу друг другу отошли два теплохода, и через 6 часов они встретились. Какое расстояние до встречи прошел каждый теплоход и какое расстояние между пристанями, если один теплоход шел со скоростью 21 км/ч, а другой — со скоростью 24 км/ч?
Решение
Определим расстояние, пройденное первым теплоходом. Для этого умножим его скорость (21 км/ч) на время движения до встречи (6ч)
21 × 6 = 126 км
Определим расстояние, пройденное вторым теплоходом. Для этого умножим его скорость (24 км/ч) на время движения до встречи (6ч)
24 × 6 = 144 км
Определим расстояние между пристанями. Для этого сложим расстояния, пройденные первым и вторым теплоходами
126 км + 144 км = 270 км
Ответ: первый теплоход прошел 126 км, второй — 144 км. Расстояние между пристанями составляет 270 км.
Задача 7. Одновременно из Москвы и Уфы вышли два поезда. Через 16 часов они встретились. Московский поезд шел со скоростью 51 км/ч. С какой скоростью шел поезд, вышедший из Уфы, если расстояние между Москвой и Уфой 1520 км? Какое расстояние было между поездами через 5 часов после их встречи?
Решение
Определим сколько километров до встречи прошел поезд, вышедший из Москвы. Для этого умножим его скорость (51 км/ч) на 16 часов
51 × 16 = 816 км
Узнаем сколько километров до встречи прошел поезд, вышедший из Уфы. Для этого из расстояния между Москвой и Уфой (1520км) вычтем расстояние, пройденное поездом, вышедшим из Москвы
1520 − 816 = 704 км
Определим скорость с которой шел поезд, вышедший из Уфы. Для этого расстояние, пройденное им до встречи, нужно разделить на 16 часов
704 : 16 = 44 км/ч
Определим расстояние, которое будет между поездами через 5 часов после их встречи. Для этого найдем скорость удаления поездов и умножим эту скорость на 5
51 км/ч + 44 км/ч = 95 км/ч
95 × 5 = 475 км.
Ответ: поезд, вышедший из Уфы, шел со скоростью 44 км/ч. Через 5 часов после их встречи поездов расстояние между ними будет составлять 475 км.
Задача 8. Из одного пункта одновременно в противоположных направлениях отправились два автобуса. Скорость одного автобуса 48 км/ч, другого на 6 км/ч больше. Через сколько часов расстояние между автобусами будет равно 510 км?
Решение
Найдем скорость второго автобуса. Она на 6 км/ч больше скорости первого автобуса
48 км/ч + 6 км/ч = 54 км/ч
Найдем скорость удаления автобусов. Для этого сложим их скорости:
48 км/ч + 54 км/ч = 102 км/ч
За час расстояние между автобусами увеличивается на 102 километра. Чтобы узнать через сколько часов расстояние между ними будет 510 км, нужно узнать сколько раз 510 км содержит по 102 км/ч
510 : 102 = 5 ч
Ответ: 510 км между автобусами будет через 5 часов.
Задача 9. Расстояние от Ростова-на-Дону до Москвы 1230 км. Из Москвы и Ростова навстречу друг другу вышли два поезда. Поезд из Москвы идет со скоростью 63 км/ч, а скорость ростовского поезда составляет скорости московского поезда. На каком расстоянии от Ростова встретятся поезда?Решение
Найдем скорость ростовского поезда. Она составляет скорости московского поезда. Поэтому чтобы определить скорость ростовского поезда, нужно найти от 63 км
63 : 21 × 20 = 3 × 20 = 60 км/ч
Найдем скорость сближения поездов
63 км/ч + 60 км/ч = 123 км/ч
Определим через сколько часов поезда встретятся
1230 : 123 = 10 ч
Узнаем на каком расстоянии от Ростова встретятся поезда. Для этого достаточно найти расстояние, пройденное ростовским поездом до встречи
60 × 10 = 600 км.
Ответ: поезда встретятся на расстоянии 600 км от Ростова.
Задача 10. От двух пристаней, расстояние между которыми 75 км, навстречу друг другу одновременно отошли две моторные лодки. Одна шла со скоростью 16 км/ч, а скорость другой составляла 75% скорости первой лодки. Какое расстояние будет между лодками через 2 ч?
Решение
Найдем скорость второй лодки. Она составляет 75% скорости первой лодки. Поэтому чтобы найти скорость второй лодки, нужно 75% от 16 км
16 × 0,75 = 12 км/ч
Найдем скорость сближения лодок
16 км/ч + 12 км/ч = 28 км/ч
С каждым часом расстояние между лодками будет уменьшáться на 28 км. Через 2 часа оно уменьшится на 28×2, то есть на 56 км. Чтобы узнать какое будет расстояние между лодками в этот момент, нужно из 75 км вычесть 56 км
75 км − 56 км = 19 км
Ответ: через 2 часа между лодками будет 19 км.
Задача 11. Легковая машина, скорость которой 62 км/ч, догоняет грузовую машину, скорость которой 47 км/ч. Через сколько времени и на каком расстоянии от начала движения легковая автомашина догонит грузовую, если первоначальное расстояние между ними было 60 км?
Решение
Найдем скорость сближения
62 км/ч − 47 км/ч = 15 км/ч
Если первоначально расстояние между машинами было 60 километров, то с каждым часом это расстояние будет уменьшáться на 15 км, и в конце концов легковая машина догонит грузовую. Чтобы узнать через сколько часов это произойдет, нужно определить сколько раз 60 км содержит по 15 км
60 : 15 = 4 ч
Узнаем на каком расстоянии от начала движения легковая машина догнала грузовую. Для этого умножим скорость легковой машины (62 км/ч) на время её движения до встречи (4ч)
62 × 4 = 248 км
Ответ: легковая машина догонит грузовую через 4 часа. В момент встречи легковая машина будет на расстоянии 248 км от начала движения.
Задача 12. Из одного пункта в одном направлении одновременно выезжали два мотоциклиста. Скорость одного 35 км/ч, а скорость другого составляла 80% скорости первого мотоциклиста. Какое расстояние будет между ними через 5 часов?
Решение
Найдем скорость второго мотоциклиста. Она составляет 80% скорости первого мотоциклиста. Поэтому чтобы найти скорость второго мотоциклиста, нужно найти 80% от 35 км/ч
35 × 0,80 = 28 км/ч
Первый мотоциклист двигается на 35-28 км/ч быстрее
35 км/ч − 28 км/ч = 7 км/ч
За один час первый мотоциклиста преодолевает на 7 километров больше. С каждым часом она будет приближáться ко второму мотоциклисту на эти 7 километров.
Через 5 часов первый мотоциклист пройдет 35×5, то есть 175 км, а второй мотоциклист пройдет 28×5, то есть 140 км. Определим расстояние, которое между ними. Для этого из 175 км вычтем 140 км
175 − 140 = 35 км
Ответ: через 5 часов расстояние между мотоциклистами будет 35 км.
Задача 13. Мотоциклист, скорость которого 43 км/ч, догоняет велосипедиста, скорость которого 13 км/ч. Через сколько часов мотоциклист догонит велосипедиста, если первоначальное расстояние между ними было 120 км?
Решение
Найдем скорость сближения:
43 км/ч − 13 км/ч = 30 км/ч
Если первоначально расстояние между мотоциклистом и велосипедистом было 120 километров, то с каждым часом это расстояние будет уменьшáться на 30 км, и в конце концов мотоциклист догонит велосипедиста. Чтобы узнать через сколько часов это произойдет, нужно определить сколько раз 120 км содержит по 30 км
120 : 30 = 4 ч
Значит через 4 часа мотоциклист догонит велосипедиста
На рисунке представлено движение мотоциклиста и велосипедиста. Видно, что через 4 часа после начала движения они сровнялись.
Ответ: мотоциклист догонит велосипедиста через 4 часа.
Задача 14. Велосипедист, скорость которого 12 км/ч, догоняет велосипедиста, скорость которого составляет 75 % его скорости. Через 6 часов второй велосипедист догнал велосипедиста, ехавшего первым. Какое расстояние было между велосипедистами первоначально?
Решение
Определим скорость велосипедиста, ехавшего впереди. Для этого найдем 75% от скорости велосипедиста, ехавшего сзади:
12 × 0,75 = 9 км/ч — скорость ехавшего впереди
Узнаем сколько километров проехал каждый велосипедист до того, как второй догнал первого:
12 × 6 = 72 км — проехал ехавший сзади
9 × 6 = 54 км — проехал ехавший впереди
Узнаем какое расстояние было между велосипедистами первоначально. Для этого из расстояния, пройденного вторым велосипедистом (который догонял) вычтем расстояние, пройденное первым велосипедистом (которого догнали)
72 км − 54 км = 18 км
Ответ: между велосипедистами первоначально было 18 км.
Задача 15. Автомобиль и автобус выехали одновременно из одного пункта в одном направлении. Скорость автомобиля 53 км/ч, скорость автобуса 41 км/ч. Через сколько часов после выезда автомобиль будет впереди автобуса на 48 км?
Решение
Найдем скорость удаления автомобиля от автобуса
53 км/ч − 41 км/ч = 12 км/ч
С каждым часом автомобиль будет удаляться от автобуса на 12 километров. На рисунке показано положение машин после первого часа движения
Видно, что автомобиль впереди автобуса на 12 км.
Чтобы узнать через сколько часов автомобиль будет впереди автобуса на 48 километров, нужно определить сколько раз 48 км содержит по 12 км
48 : 12 = 4 ч
Ответ: через 4 часа после выезда автомобиль будет впереди автобуса на 48 километров.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Задачи на движение: скорость, время и расстояние.
Скорость – это физическая величина, показывающая какое расстояние пройдет объект за единицу времени.
Сегодня мы будем решать задачи на:
- движение
- скорость \(v=s/t\)
- время \(t=s/v\)
- расстояние \(s=v*t\)
Расстояние — путь, который нужно преодолеть во время движения.
Время — промежуток действия движения.
Скорость — характеристика движения.
Для решения задач необходимо ввести неизвестную, верно составить и решить уравнение.
Задача 1. Легковая машина прошла расстояние в \(160\) км за два часа. С какой скоростью двигалась машина?
Решение.
\(160/2=80\) км/час
Ответ: \(80.\)
Задача 2. Из города Минск в Смоленск, расстояние между которыми \(346\) км, отправились одновременно велосипедист и автомобилист. Скорость автомобиля \(20\) м/с, а велосипедиста \(20\) км/ч. Какое расстояние будет между ними через \(2\) часа?
Решение.
Мы не можем складывать разные единицы измерения, поэтому надо перевести м/с в км/ч. Как нам перевести км/ч в м/с? В км – 1000 м, в \(1\) ч \(-3600\), в \(1\) км/час\(-1000/3600\) м/c, то есть в \(1\) км/c \(-3600/1000\) м/c. \(20*\frac{3600}{1000}=72\). Итого скорость автомобиля \(72\) км/ч.
Так как автомобилист и велосипедист выехали из одного места и двигаются в одном направлении, расстояние между ними будет нарастать со скоростью:
- 72-20=52(км/ч)
- 52∗2=104 (км) – расстояние между ними через два часа.
Ответ: \(104\) км.
В таких задачах важно понимать:
- если мы умножаем скорость на время, то получаем расстояние;
- если расстояние делим на время, то получаем скорость;
- если расстояние делим на скорость, то получаем время ;
Задача 3. Из А в В тронулись в одно время турист пешком, а второй турист – на велосипеде. В то же время из В в А выдвинулся мотоцикл, который встретился с велосипедистом через 3 часа, а с пешеходом через 4 часов после своего выезда из В. Найти расстояние от А до В, зная, что скорость пешехода 3 км/ч, а велосипедиста 10 км/ч.
10 * 3 = 30 (км) – мотоциклист от А через 3 часа.
3* 4 = 12 (км) – мотоциклист от А через 4 часов.
30 – 12 = 18 (км/ч) – скорость автомобиля.
10 + 18 = 28 (км/ч) – скорость сближения мотоциклиста и велосипедиста.
28 * 3 = 84 (км) – расстояние от А до В.
Ответ: 84 км.
Задача 4. Надувная лодка проплыла \(0,3\) км против течения реки, а затем проплыла еще \(3,9\) км по течению реки, затратив на это \(5\)часов и \(6\) минут. Найдите скорость лодки в стоячей воде, если скорость течения реки \(5\) км/ч.
Решение
Переведем \(5\) часов \(6\) минут в одинаковые единицы измерения, \(6\) мин — это \(\frac{1}{10}\) часа, итого \(5,1\) часа. Введем неизвестную х скорость в стоячей воде, \(x+5-\)скорость по течению, \(x-5-\)против течения реки.
Составляем уравнение:
- \(\frac{3,9}{x+5}+ \frac{0,3}{x-5}=5,1\)
- \(3,9x-19,5+0,3x+1,5=5,1\)
- \(4,2x-18=5,1\)
- \(4,2x=23,1\)
- \(x=5,5 \) км/ч – скорость в стоячей воде.
Ответ: \(5,5\) км/ч.
Запишись на бесплатный пробный урок тут и разберись с тем, что тебе непонятно.
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Урок математики по теме «Скорость. Время. Расстояние». 4-й класс
Цели:
- закрепить знания нахождения скорости, времени, расстояния;
- ввести формулы;
- учиться решать задачи с этими величинами по формулам и без них;
- развивать мышление и память;
- прививать любовь к математике.
Ход урока
1. Организация учащихся.
2. Сообщение темы.
— Сегодня на уроке мы закрепим знания нахождения скорости, времени, расстояния. Будем учиться решать задачи с помощью формул.
— А работать мы будем в форме соревнований трех команд:
- 1 ряд — автомобилисты
- 2 ряд — летчики
- 3 ряд — мотоциклисты
— Баллы будем выставлять на доске
3. Соотнести записи с картинкой.
— Как вы думаете, что написано на доске? (Скорости)
— Соотнесите их с нужной картинкой.
(12 км/ч, 60 км/ч, 5 км/ч, 70 км/ч, 120 км/ч, 800 км/ч, 8 км/с, 50 км/ч,250 км/ч.
Автобус, самолет, ракета, пешеход, поезд, велосипедист , автомобиль, пароход, мотоциклист) Каждая команда выставляет по 3 ученика.
— Как вы понимаете км/сек, км/ч, м/мин.
Решение задач.
а) В тетрадь записываете ответ с наименованием.
Таблица на интерактивной доске.
| Скорость V |
Время t |
Расстояние S |
| 5 м/с | 15 сек. | ? м. |
Муха летела со скоростью 5 м/сек. 15 сек. Какое расстояние она пролетела?
— Что известно?
— Повторите вопрос задачи.
— Как найти расстояние?
— Кто может записать буквами это правило?
— Запишите эту формулу в тетрадь s=v * t.
| Скорость V |
Время t |
Расстояние S |
| ? м/с | 3 сек. | 78 м. |
За 3 сек. Сокол пролетел 78 метров. Какова скорость сокола?
— Что известно?
— Повторите вопрос задачи.
— Как найти скорость?
— Кто может записать буквами это правило?
— Запишите эту формулу в тетрадь v=s:t.
| Скорость V |
Время t |
Расстояние S |
| 10 м./сек | ? сек. | 100 м. |
Грач пролетел 100 метров со скоростью 10 м/сек. Сколько времени он был в пути?
— Что известно?
— Повторите вопрос задачи.
— Как найти время?
— Кто может записать буквами это правило?
— Запишите эту формулу в тетрадь t=s:v.
Баллы. Молодцы!
б) Составление задач.
- 1 ряд — нахождение V
- 2 ряд — нахождение t
- 3 ряд — нахождение S
Баллы. Отлично.
в) Заполнить таблицу.
| Скорость V |
Время t |
Расстояние S |
| 90 км/ч | 6 ч. | ? км. |
| ? км/ч | 30 ч. | 1500 км |
| 70 м/мин. | ? мин. | 840 м |
Решение записываете в тетрадь с наименованием, рядом записываете формулу.
Самостоятельная работа.
Проверка.
90 * 6 = 540 (км)
s=v*t
1500:30=50 (км/ч) v=s:t
840:70=12 (ч) t=s:v
Замечательно!
4. Работа с учебником.
Коллективное решение задачи стр. 60 №4
Две бабы-яги поспорили, что быстроходнее ступа или помело? Одну и ту же дистанцию в 228 км баба-яга в ступе пролетела за 4 ч, а баба яга на помеле за 3 ч. Что больше, скорость ступы или помела?
а) составление таблицы.
| Скорость V |
Время t |
Расстояние S |
|
| ступа | |||
| помело |
б) решение у доски и в тетрадях.
1) 288:4=72 (км/ч) — скорость ступы
2) 288:3=96 (км/ч) — скорость помела
3) 96-72=24 (км/ч) — больше скорость помела, чем скорость ступы.
Ответ запишите самостоятельно.
Баллы.
5. Физминутка.
6. Задача повышенной сложности.
Это очень интересно (на доске написана задача)
— Кто видел счетчик в автомобиле, который ведет отчет километров, которые проехал автомобиль?
— Как он называется (спидометр).
Счетчик автомобиля показал 12921 км. Через 2 час на счетчике опять появилось число, которое читалось одинаково в обоих направлениях. С какой скоростью ехал автомобиль?
Решение.
1) 13031 — 12921=110 (км) — проехал за 2 ч.
2) 110 :2 = 55 (км/ч) — скорость автомобиля.
Ответ.
7. Итоги урока.
— Как найти расстояние, скорость, время (формула).
— Баллы. Итог.
Молодцы! Всем огромное спасибо!
Дополнительная задача.
Туристы ехали в первый день 5 ч. На лодке со скоростью 12 км/ч. Во второй день они были в пути столько же времени, увеличив скорость на 3 км/ч. Сколько километров проехали туристы на лодке во второй день?
Самостоятельно заполнить таблицу и решить задачу.
Простые задачи на движение. 4 класс
{module Адаптивный блок Адсенс в начале статьи}
ПРОСТЫЕ ЗАДАЧИ НА ДВИЖЕНИЕ
4 КЛАСС
Решение простых задач на движение для 4 класса обычно выполняется в одно действие.
Основной формулой для решения задач такого типа является формула зависимости расстояния пройденного объектом от скорости движения данного объекта и времени движения:
S = v · t
где S — расстояние (пройденный путь)
v — скорость объекта (км/ч; м/с)
t — время, в течение которого объект был в движении.
В зависимости от условия задачи, существует несколько способов применения основной формулы для решения задач на движение.
Рассмотрим несколько примеров решения таких задач.
В задаче на движение могут быть известны скорость движения и время движения, а расстояние (пройденный путь) необходимо найти. В данном случае основная формула применяется в своем первоначальном виде.
Пример: Скорость грузового поезда 35 км/час. Поезд был в пути 2 часа. Какое расстояние он прошёл?
Решение: S = v · t = 35 · 2 = 70 (км) — расстояние пройденное поездом.
Ответ: 70.
В задаче на движение могут быть известны расстояние и время, а скорость движения необходимо найти. В данном случае из основной формулы выражается скорость движения.
Пример: Велосипедист проехал 36 км за 2 часа. С какой скоростью он двигался?
Решение: v = S / t = 36 ÷ 2 = 18 (км/час) — скорость движения велосипедиста.
Ответ: 18.
В задаче на движение могут быть известны расстояние и скорость движения, а время в пути необходимо найти. В данном случае из основной формулы нужно выразить время через расстояние и скорость.
Пример: Охотник верхом на лошади проехал 28 км со скоростью 14 км/час. Сколько времени он потратил на дорогу?
Решение: t = S / v = 28 ÷ 14 = 2 (часа) — охотник потратил на дорогу.
Ответ: 2.
Примеры простых задач на движение для 4 класса:
1) Расстояние от города до посёлка 30 км. Сколько времени потребуется пешеходу, чтобы пройти это расстояние со скоростью 6 км/час?
2) Мальчик пробежал 20 м за 10 сек. С какой скоростью бежал мальчик?
3) Крейсер проплыл 80 км со скоростью 40 км/час. Сколько времени он затратил?
4) Муха летела со скоростью 5 м/сек 15 секунд. Какое расстояние она пролетела?
5) Грач пролетел 100 м со скоростью 10 м/сек. Сколько времени он был в пути?
6) За 3 секунды сокол пролетел 78 м. Какова скорость сокола?
7) Орёл летел со скоростью 30 м/с 6 секунд. Сколько метров пролетел орёл?
8) Расстояние в 450 км скорый поезд проехал за 5 часов. С какой скоростью ехал поезд?
9) Лыжник прошёл с одинаковой скоростью 70 км за 5 часов. Какова скорость лыжника?
10) Туристы проехали 5 часов на лодке со скоростью 12 км/час. Какое расстояние они проплыли?
11) Расстояние в 240 км мотоциклист проехал со скоростью 40 км/час. За сколько часов мотоциклист проехал это расстояние?
12) За 2 часа вертолёт пролетел 600 км. С какой скоростью летел вертолёт?
13) За 3 дня верблюд прошёл 240 км. С какой скоростью шёл верблюд?
14) Легковой автомобиль проехал 270 км за 3 часа. С какой скоростью ехал автомобиль?
15) Мотоциклист ехал 4 часа со скоростью 70 км/час. Какое расстояние проехал мотоциклист?
{module Адаптивный блок Адсенс в конце статьи}
Рабочие листы скорости, времени и расстояния
Вы здесь: Главная → Рабочие листы → Скорость, время и расстояниеСоздавайте настраиваемые рабочие листы о постоянной (или средней) скорости, времени и расстоянии для курсов предварительной алгебры и алгебры 1 курсов (6–9 классы). Доступны как PDF, так и html форматы. Вы можете выбрать типы текстовых задач на листе, количество задач, метрические или обычные единицы, способ выражения времени (часы / минуты, дробные или десятичные часы) и объем рабочего пространства для каждой задачи.
Существует СЕМЬ различных типов задач со словами, от простых до сложных, так что вы можете создавать самые разные рабочие листы. Семь типов проблем подробно объясняются в реальном генераторе ниже.
Все рабочие листы включают ключ ответа на 2-й странице файла.
Воспользуйтесь быстрыми ссылками ниже, чтобы создать некоторые распространенные типы рабочих листов.
Простая таблица скорости, времени и расстояния 1: Как далеко можно пройти или сколько времени займет поездка — на полчаса или полчаса
Простая таблица скорости, времени и расстояния 2: Как далеко он может уйти, сколько времени занимает поездка или какова средняя скорость — с использованием целых или получасовых часов
Рабочий лист скорости, времени и расстояния 3: Как далеко он может пройти, сколько времени займет поездка или какова средняя скорость — с использованием четверти часа
Рабочий лист скорости, времени и расстояния 4: Как далеко можно пройти, сколько времени займет поездка или какова средняя скорость — время до 5-минутных интервалов
Рабочий лист 5: скорость, время и расстояние: задачи включают преобразование минут в часы.
Найдите среднюю скорость: время дается до четверти часа.
Найдите среднюю скорость: время дается с точностью до двенадцатой части часа.
Найдите среднюю скорость: задачи связаны с преобразованием единицы времени
Скорость, время и расстояние: более сложные задачи 1
Скорость, время и расстояние: более сложные задачи 2
Алгебра реального мира Эдвард Заккаро
Алгебра часто преподается абстрактно, практически без акцента на том, что такое алгебра и как ее можно использовать для решения реальных задач.Подобно тому, как английский можно переводить на другие языки, текстовые задачи можно «переводить» на математический язык алгебры и легко решать. Алгебра реального мира объясняет этот процесс в удобном для понимания формате с использованием мультфильмов и рисунков. Это упрощает самообучение как для ученика, так и для любого учителя, который никогда не понимал алгебру. Включает главы по алгебре и деньгам, алгебре и геометрии, алгебре и физике, алгебре и рычагам и многому другому. Предназначен для детей 4-9 классов с более высокими математическими способностями и интересами, но может использоваться также учениками старшего возраста и взрослыми.Содержит 22 главы с инструкциями и задачами трех уровней сложности.
=> Узнать больше
Скорость, расстояние и время — средняя алгебра
Глава 8: Рациональные выражения
Задачи о расстоянии, скорости и времени — это стандартное приложение линейных уравнений. При решении этих проблем используйте соотношение : скорость, (скорость или скорость) умножить на , время равно , расстояние .
Например, предположим, что человек должен был проехать 30 км / ч за 4 часа.Чтобы найти общее расстояние, умножьте скорость на время или (30 км / ч) (4 ч) = 120 км.
Задачи, которые здесь предстоит решить, будут состоять на несколько шагов больше, чем описано выше. Итак, чтобы систематизировать информацию о проблеме, используйте таблицу. Пример базовой структуры таблицы ниже:
| Кто или что | Оценить | Время | Расстояние |
|---|---|---|---|
Третий столбец, расстояние, всегда заполняется путем умножения столбцов скорости и времени вместе.Если дано общее расстояние обоих людей или поездок, поместите эту информацию в столбец расстояния. Теперь используйте эту таблицу, чтобы настроить и решить следующие примеры.
Джои и Наташа начинают с одной и той же точки и идут в противоположных направлениях. Джои идет на 2 км / ч быстрее Наташи. Через 3 часа их разделяет 30 километров. Как быстро каждый шагал?
Расстояние, пройденное обоими — 30 км. Следовательно, решаемое уравнение:
Это означает, что Наташа ходит со скоростью 4 км / ч, а Джоуи ходит со скоростью 6 км / ч.
Ник и Хлоя покинули лагерь на каноэ и поплыли вниз по течению со средней скоростью 12 км / ч. Они развернулись и поплыли вверх по течению со средней скоростью 4 км / ч. Общая поездка заняла 1 час. Через сколько времени туристы повернули вниз по течению?
Расстояние, пройденное вниз по течению, равно расстоянию, пройденному ими вверх по течению. Следовательно, решаемое уравнение:
Это означает, что туристы плыли вниз по течению 0,25 часа и потратили 0.Гребля назад 75 ч.
Терри выезжает из дома на велосипеде со скоростью 20 км / ч. Салли уезжает через 6 часов на скутере, чтобы догнать его, едущего со скоростью 80 км / ч. Сколько времени ей понадобится, чтобы его догнать?
Расстояние, пройденное обоими, одинаково. Следовательно, решаемое уравнение:
Это означает, что Терри путешествует 8 часов, а Салли нужно всего 2 часа, чтобы его догнать.
Во время 130-километровой поездки автомобиль двигался со средней скоростью 55 км / ч, а затем снизил скорость до 40 км / ч на оставшуюся часть пути.Поездка заняла 2,5 часа. Как долго машина двигалась со скоростью 40 км / ч?
Расстояние, пройденное обоими — 30 км. Следовательно, решаемое уравнение:
Это означает, что время, потраченное на поездку со скоростью 40 км / ч, составило 0,5 часа.
Задачи расстояния, времени и скорости имеют несколько вариаций, в которых смешиваются неизвестные значения расстояния, скорости и времени. Обычно они включают решение проблемы, в которой суммарное пройденное расстояние равно некоторому расстоянию, или задачи, в которой расстояния, пройденные обеими сторонами, одинаковы.К этим задачам расстояния, скорости и времени мы вернемся позже в этом учебнике, где для их решения потребуются квадратичные решения.
Для вопросов с 1 по 8 найдите уравнения, необходимые для решения проблем. Не решайте.
- A находится в 60 километрах от B. Автомобиль в точке A трогается с места для точки B со скоростью 20 км / ч, в то время как автомобиль в точке B трогается с места для точки A со скоростью 25 км / ч. Сколько времени пройдет до встречи автомобилей?
- Два автомобиля находятся на расстоянии 276 километров друг от друга и начинают движение навстречу друг другу одновременно.Они едут со скоростью, различающейся на 5 км / ч. Если они встречаются через 6 часов, узнайте скорость каждого из них.
- Два поезда, отправляющиеся на одной станции, идут в противоположных направлениях. Они едут со скоростью 25 и 40 км / ч соответственно. Если они начнутся одновременно, как скоро они разделятся на 195 километров?
- Два велосипедных посыльных, Джерри и Сьюзен, едут в противоположных направлениях. Если Джерри едет со скоростью 20 км / ч, с какой скоростью должна ехать Сьюзен, если они разделяют 150 километров за 5 часов?
- Пассажирский и товарный поезд одновременно отправляются навстречу друг другу из двух пунктов, расположенных на расстоянии 300 км.Если скорость пассажирского поезда превышает скорость грузового поезда на 15 км / ч, и они встречаются через 4 часа, какой должна быть скорость каждого?
- Два автомобиля начали движение в противоположных направлениях одновременно из одной и той же точки. Их скорость составляла 25 и 35 км / ч соответственно. Через сколько часов их разделяло 180 километров?
- Человек, имеющий в своем распоряжении десять часов, совершил экскурсию на велосипеде, выехав со скоростью 10 км / ч и вернувшись пешком со скоростью 3 км / ч.Найдите расстояние, которое он проехал.
- Человек идет со скоростью 4 км / ч. Как далеко он может дойти до деревни и вернуться обратно на тележке, которая движется со скоростью 20 км / ч, если ему нужно вернуться домой через 3 часа после того, как он отправился в путь?
Решите вопросы с 9 по 22.
- Мальчик уезжает из дома на автомобиле со скоростью 28 км / ч и ходит обратно со скоростью 4 км / ч. Дорога туда и обратно занимает 2 часа. Как далеко он едет?
- Моторная лодка покидает гавань и движется со средней скоростью 15 км / ч к острову.Средняя скорость на обратном пути составила 10 км / ч. Как далеко находился остров от гавани, если поездка длилась 5 часов?
- Семья ехала на курорт со средней скоростью 30 км / ч, а затем возвращалась по той же дороге со средней скоростью 50 км / ч. Найдите расстояние до курорта, если общее время в пути составило 8 часов.
- В рамках своей летной подготовки пилот-студент должен был вылететь в аэропорт, а затем вернуться. Средняя скорость до аэропорта составляла 90 км / ч, а средняя скорость возврата — 120 км / ч.Найдите расстояние между двумя аэропортами, если общее время полета составило 7 часов.
- Сэм начинает движение со скоростью 4 км / ч от кемпинга на 2 часа впереди Сью, которая движется со скоростью 6 км / ч в том же направлении. Сколько часов потребуется Сью, чтобы догнать Сэма?
- Человек едет 5 км / ч. Проехав 6 часов, другой человек стартует с того же места, что и первый, двигаясь со скоростью 8 км / ч. Когда второй догонит первого?
- Моторная лодка покидает гавань и движется со средней скоростью 8 км / ч к небольшому острову.Два часа спустя круизный лайнер с каютами покидает ту же гавань и движется со средней скоростью 16 км / ч к тому же острову. Через сколько часов после отбытия круизера с каютами он будет рядом с моторной лодкой?
- Бегун на длинные дистанции начал дистанцию со средней скоростью 6 км / ч. Через час второй бегун начал тот же курс со средней скоростью 8 км / ч. Через какое время после старта второго бегуна они догонят первого?
- Двое мужчин едут в противоположных направлениях со скоростью 20 и 30 км / ч одновременно и из одного места.Через сколько часов они будут в 300 км друг от друга?
- Два поезда отправляются одновременно из одного и того же места и движутся в противоположных направлениях. Если скорость одного из них на 6 км / ч больше, чем у другого, и по прошествии 4 часов их разделяет 168 километров, какова скорость каждого из них?
- Два велосипедиста стартуют с одной и той же точки и едут в противоположных направлениях. Один велосипедист едет вдвое быстрее другого. Через три часа их разделяет 72 километра. Найдите рейтинг каждого велосипедиста.
- Два маленьких самолета стартуют из одной точки и летят в противоположных направлениях. Первый самолет летит на 25 км / ч медленнее второго. За два часа самолеты разделяют 430 километров. Найдите скорость каждого самолета.
- Во время 130-километрового пути автомобиль двигался со средней скоростью 55 км / ч, а затем снизил скорость до 40 км / ч на оставшуюся часть пути. Поездка заняла 2,5 часа. Как долго машина двигалась со скоростью 40 км / ч?
- Бегая со средней скоростью 8 м / с, спринтер бежал до конца трассы, а затем возвращался к исходной точке со средней скоростью 3 м / с.Спринтеру потребовалось 55 секунд, чтобы пробежать до конца трассы и вернуться обратно. Найдите длину дорожки.
Ключ ответа 8,8
Speed - Обучающие подходы | IOPSpark
Силы и движение
Классная деятельность для 11-14
Что такое действие для
Обсуждение самого быстрого и самого короткого времени.
Цель упражнения — помочь ученикам понять, что скорость можно ранжировать, сравнивая время, при условии, что пройденное расстояние одинаково.В этом случае ученики должны понимать, что наименьшее время означает наибольшую среднюю скорость.
Что приготовить
- простая гоночная трасса — карниз или расстояние между двумя метрами
- шарики (или мячи для настольного тенниса или полистирола) и соломинки
- счетчик правил и секундомеров
- выберите материалы, чтобы учащиеся не планировали нереально короткие мероприятия
Что происходит во время этого действия
Ученики как можно быстрее раздувают мрамор на гоночной трассе.Ученики соревнуются в группах по четыре человека. Один ученик должен выдувать шарик, в то время как другие записывают время, затраченное на прохождение дистанции 200 сантиметров. Победитель из каждой группы выходит в финальные этапы конкурса.
Указание по безопасности: Будьте осторожны с учениками со значительной астмой или затрудненным дыханием.
Изготовление и использование измерений
В этом упражнении не предполагается, что участники соревнуются друг с другом одновременно. Ученики видят необходимость согласовывать надежные измерения, чтобы найти победителя.Побеждает шарик с наибольшей средней скоростью. Конечно, вам не нужно знать скорость. Побеждает кратчайшее время. В нашем контексте важно расширить задачу до расчета средней скорости мрамора. Поэтому каждой группе необходимо будет вести учет своих результатов. В зависимости от возраста и способностей учеников вы можете предоставить структурированную таблицу результатов или предложить ученикам составить свои собственные.
Некоторым ученикам будет сложно использовать уравнение скорости. Им может не хватать уверенности в математике.Возможно, вы захотите попробовать подход, основанный на простых пропорциях.
Например:
Учитель: Мрамор прошел 200 сантиметров за 5 секунд — на сколько сантиметров он пролетел бы за 10 секунд? Сколько сантиметров за 1 секунду?
Как только ученики узнают, что скорость — это расстояние, пройденное за 1 секунду
, решение задач пропорционально часто может стать более простым.
Учитель: Если я пройду 60 метров за 10 секунд, сколько я пройду за 1 секунду?
Майк: 60 метров разделенные на 10 секунд, значит, вы преодолеете 6 метров за 1 секунду.
Учитель: Какая у меня скорость?
Jaz: 6 метров каждую секунду, что составляет 6 метров в секунду.
Для задач этого типа ученики не используют уравнение скорости напрямую, они вычисляют скорость пропорционально, зная ее единицы.
Частью решения является также выполнение множества примеров с использованием уравнения — сначала на доске, когда весь класс предлагает следующий шаг, затем в небольших группах, работающих над проблемами, и, наконец, на индивидуальном уровне.Некоторым ученикам сложно вспомнить уравнение для расчета скорости. Написав уравнение крупным шрифтом и повесив его на стене, вы устраните это препятствие. На этом этапе нет необходимости заниматься перестройкой уравнения для расчета расстояний. Это будет позже.
Скорость, расстояние и время — средняя алгебра
Задачи о расстоянии, скорости и времени — это стандартное приложение линейных уравнений.При решении этих проблем используйте соотношение : скорость, (скорость или скорость) умножить на , время равно , расстояние .
Например, предположим, что человек должен был проехать 30 км / ч за 4 часа. Чтобы найти общее расстояние, умножьте скорость на время или (30 км / ч) (4 ч) = 120 км.
Задачи, которые здесь предстоит решить, будут состоять на несколько шагов больше, чем описано выше. Итак, чтобы систематизировать информацию о проблеме, используйте таблицу. Пример базовой структуры таблицы ниже:
| Кто или что | Оценить | Время | Расстояние |
|---|---|---|---|
Третий столбец, расстояние, всегда заполняется путем умножения столбцов скорости и времени вместе.Если дано общее расстояние обоих людей или поездок, поместите эту информацию в столбец расстояния. Теперь используйте эту таблицу, чтобы настроить и решить следующие примеры.
Джои и Наташа начинают с одной и той же точки и идут в противоположных направлениях. Джои идет на 2 км / ч быстрее Наташи. Через 3 часа их разделяет 30 километров. Как быстро каждый шагал?
Расстояние, пройденное обоими — 30 км. Следовательно, решаемое уравнение:
Это означает, что Наташа ходит со скоростью 4 км / ч, а Джоуи ходит со скоростью 6 км / ч.
Ник и Хлоя покинули лагерь на каноэ и поплыли вниз по течению со средней скоростью 12 км / ч. Они развернулись и поплыли вверх по течению со средней скоростью 4 км / ч. Общая поездка заняла 1 час. Через сколько времени туристы повернули вниз по течению?
Расстояние, пройденное вниз по течению, равно расстоянию, пройденному ими вверх по течению. Следовательно, решаемое уравнение:
Это означает, что туристы плыли вниз по течению 0,25 часа и потратили 0.Гребля назад 75 ч.
Терри выезжает из дома на велосипеде со скоростью 20 км / ч. Салли уезжает через 6 часов на скутере, чтобы догнать его, едущего со скоростью 80 км / ч. Сколько времени ей понадобится, чтобы его догнать?
Расстояние, пройденное обоими, одинаково. Следовательно, решаемое уравнение:
Это означает, что Терри путешествует 8 часов, а Салли нужно всего 2 часа, чтобы его догнать.
Во время 130-километровой поездки автомобиль двигался со средней скоростью 55 км / ч, а затем снизил скорость до 40 км / ч на оставшуюся часть пути.Поездка заняла 2,5 часа. Как долго машина двигалась со скоростью 40 км / ч?
Расстояние, пройденное обоими — 30 км. Следовательно, решаемое уравнение:
Это означает, что время, потраченное на поездку со скоростью 40 км / ч, составило 0,5 часа.
Задачи расстояния, времени и скорости имеют несколько вариаций, в которых смешиваются неизвестные значения расстояния, скорости и времени. Обычно они включают решение проблемы, в которой суммарное пройденное расстояние равно некоторому расстоянию, или задачи, в которой расстояния, пройденные обеими сторонами, одинаковы.К этим задачам расстояния, скорости и времени мы вернемся позже в этом учебнике, где для их решения потребуются квадратичные решения.
Для вопросов с 1 по 8 найдите уравнения, необходимые для решения проблем. Не решайте.
- A находится в 60 километрах от B. Автомобиль в точке A трогается с места для точки B со скоростью 20 км / ч, в то время как автомобиль в точке B трогается с места для точки A со скоростью 25 км / ч. Сколько времени пройдет до встречи автомобилей?
- Два автомобиля находятся на расстоянии 276 километров друг от друга и начинают движение навстречу друг другу одновременно.Они едут со скоростью, различающейся на 5 км / ч. Если они встречаются через 6 часов, узнайте скорость каждого из них.
- Два поезда, отправляющиеся на одной станции, идут в противоположных направлениях. Они едут со скоростью 25 и 40 км / ч соответственно. Если они начнутся одновременно, как скоро они разделятся на 195 километров?
- Два велосипедных посыльных, Джерри и Сьюзен, едут в противоположных направлениях. Если Джерри едет со скоростью 20 км / ч, с какой скоростью должна ехать Сьюзен, если они разделяют 150 километров за 5 часов?
- Пассажирский и товарный поезд одновременно отправляются навстречу друг другу из двух пунктов, расположенных на расстоянии 300 км.Если скорость пассажирского поезда превышает скорость грузового поезда на 15 км / ч, и они встречаются через 4 часа, какой должна быть скорость каждого?
- Два автомобиля начали движение в противоположных направлениях одновременно из одной и той же точки. Их скорость составляла 25 и 35 км / ч соответственно. Через сколько часов их разделяло 180 километров?
- Человек, имеющий в своем распоряжении десять часов, совершил экскурсию на велосипеде, выехав со скоростью 10 км / ч и вернувшись пешком со скоростью 3 км / ч.Найдите расстояние, которое он проехал.
- Человек идет со скоростью 4 км / ч. Как далеко он может дойти до деревни и вернуться обратно на тележке, которая движется со скоростью 20 км / ч, если ему нужно вернуться домой через 3 часа после того, как он отправился в путь?
Решите вопросы с 9 по 22.
- Мальчик уезжает из дома на автомобиле со скоростью 28 км / ч и ходит обратно со скоростью 4 км / ч. Дорога туда и обратно занимает 2 часа. Как далеко он едет?
- Моторная лодка покидает гавань и движется со средней скоростью 15 км / ч к острову.Средняя скорость на обратном пути составила 10 км / ч. Как далеко находился остров от гавани, если поездка длилась 5 часов?
- Семья ехала на курорт со средней скоростью 30 км / ч, а затем возвращалась по той же дороге со средней скоростью 50 км / ч. Найдите расстояние до курорта, если общее время в пути составило 8 часов.
- В рамках своей летной подготовки пилот-студент должен был вылететь в аэропорт, а затем вернуться. Средняя скорость до аэропорта составляла 90 км / ч, а средняя скорость возврата — 120 км / ч.Найдите расстояние между двумя аэропортами, если общее время полета составило 7 часов.
- Сэм начинает движение со скоростью 4 км / ч от кемпинга на 2 часа впереди Сью, которая движется со скоростью 6 км / ч в том же направлении. Сколько часов потребуется Сью, чтобы догнать Сэма?
- Человек едет 5 км / ч. Проехав 6 часов, другой человек стартует с того же места, что и первый, двигаясь со скоростью 8 км / ч. Когда второй догонит первого?
- Моторная лодка покидает гавань и движется со средней скоростью 8 км / ч к небольшому острову.Два часа спустя круизный лайнер с каютами покидает ту же гавань и движется со средней скоростью 16 км / ч к тому же острову. Через сколько часов после отбытия круизера с каютами он будет рядом с моторной лодкой?
- Бегун на длинные дистанции начал дистанцию со средней скоростью 6 км / ч. Через час второй бегун начал тот же курс со средней скоростью 8 км / ч. Через какое время после старта второго бегуна они догонят первого?
- Двое мужчин едут в противоположных направлениях со скоростью 20 и 30 км / ч одновременно и из одного места.Через сколько часов они будут в 300 км друг от друга?
- Два поезда отправляются одновременно из одного и того же места и движутся в противоположных направлениях. Если скорость одного из них на 6 км / ч больше, чем у другого, и по прошествии 4 часов их разделяет 168 километров, какова скорость каждого из них?
- Два велосипедиста стартуют с одной и той же точки и едут в противоположных направлениях. Один велосипедист едет вдвое быстрее другого. Через три часа их разделяет 72 километра. Найдите рейтинг каждого велосипедиста.
- Два маленьких самолета стартуют из одной точки и летят в противоположных направлениях. Первый самолет летит на 25 км / ч медленнее второго. За два часа самолеты разделяют 430 километров. Найдите скорость каждого самолета.
- Во время 130-километрового пути автомобиль двигался со средней скоростью 55 км / ч, а затем снизил скорость до 40 км / ч на оставшуюся часть пути. Поездка заняла 2,5 часа. Как долго машина двигалась со скоростью 40 км / ч?
- Бегая со средней скоростью 8 м / с, спринтер бежал до конца трассы, а затем возвращался к исходной точке со средней скоростью 3 м / с.Спринтеру потребовалось 55 секунд, чтобы пробежать до конца трассы и вернуться обратно. Найдите длину дорожки.
Ключ ответа 8,8
Как решить проблемы скорости, расстояния и времени
Ссылаясь на изображение выше, вы можете видеть, что покрытие значения, которое вы пытаетесь найти, дает вам вычисление, которое вам необходимо выполнить:
- Чтобы рассчитать скорость , пройдите через S, оставив D над T; Итак, вы знаете, что вам нужно разделить расстояние на время (s = d / t)
- Чтобы рассчитать расстояние , пройдите D, оставив S рядом с T; чтобы вы знали, что вам нужно умножить скорость на время (d = s x t)
- Чтобы рассчитать время , накройте T, оставив D над S; чтобы вы знали, что вам нужно разделить расстояние на скорость (t = d / s)
Скорость вычисления
Поскольку скорость измеряется с использованием разных единиц измерения расстояния и времени (например, миль в час или километров в секунду), она известна как составная мера .
Чтобы определить среднюю скорость, нужно разделить пройденное расстояние на затраченное время .
В некоторых случаях это может быть несложный расчет. Например, чтобы найти среднюю скорость автомобиля, который проехал 120 миль за 2 часа, просто разделите 120 на 2, получив ответ 60 миль в час.
Однако большинство вопросов о скорости, дистанции и времени будут более сложными, и вам может потребоваться преобразовать единицы времени и / или расстояния. Рассмотрим пример ниже:
Рабочий пример:
Рассчитайте среднюю скорость в милях в час бегуна, который преодолевает 20 миль за 3 часа 40 минут.Дайте окончательный ответ с двумя десятичными знаками.
Метод:
Вопрос касается часов и минут, поэтому, во-первых, вам нужно найти единую единицу времени для работы. Преобразование только 3 часов 40 минут в минуты дает в сумме 220. Это делается следующим образом:
3 х 60 = 180
180 + 40 = 220
Используя формулу s = d / t , получаем 20/220 = 0,0909
Помните, вы работали в считанные минуты, а вопрос требует миль в час .0,0909 — это миля бегуна в минуту. Чтобы найти их мили в час, просто умножьте это на 60.
0,0909 х 60 = 5,454
В вопросе требуется окончательный ответ с двумя десятичными знаками, поэтому округлите его до 5,45.
Ответ: Средняя скорость бегуна 5,45 миль / ч .
При расчете скорости всегда убедитесь, что вы работаете с правильными единицами измерения расстояния и времени .
Примерные вопросы расчета скорости
Вопрос 1.:
В своем юношеском теннисном матче на кубок Джек подает туз. Мяч приземляется на 71 фут от места подачи, и это занимает 0,5 секунды. Какова скорость подачи Джека в милях в час? Ответьте с точностью до двух знаков после запятой.
Обратите внимание, что здесь вам нужно будет преобразовать футы в мили, чтобы ответить на вопрос.
Ответ: 96,82 миль / ч .
Вопрос 2:
Две машины совершают одно и то же путешествие из точки А в точку Б.Автомобиль №1 прибывает в точку B за 1 час 10 минут, а автомобиль №2 — за 1 час 20 минут. На сколько миль в час быстрее проехал Car One?
Для этого вопроса вам нужно будет рассчитать скорость обеих машин, чтобы определить разницу.
Ответ: 7,5 миль / ч .
Расчет расстояния
Чтобы рассчитать расстояние, умножьте скорость на время. Это довольно просто, но, опять же, вам может потребоваться преобразовать единицы времени.
Вот пример с разбивкой на него:
Рабочий пример:
Если Джанет идет от своего дома к вокзалу со средней скоростью 5 километров в час, и ей нужно 20 минут, чтобы добраться туда, как далеко от вокзала она живет? Ответьте с точностью до двух знаков после запятой.
Метод:
Из представленной здесь информации вы знаете, с какой скоростью Джанет ходит в час, но чтобы ответить на вопрос, вам нужно знать ее скорость ходьбы в минуту. Чтобы рассчитать это, вы можете просто разделить 5 на 60, так как в часе 60 минут:
5/60 = 0,083
Теперь вы знаете, что Джанет ходит со средней скоростью 0,083 километра в минуту, вы можете использовать формулу d = s x t :
0.083 х 20 = 1,66
Ответ: Джанет живет в , 1,66 км, от вокзала.
Примерные вопросы по расчету расстояния
Вопрос 1:
Сара принимает участие в метании копья в день спорта. В своем лучшем броске копье летит со средней скоростью 12 метров в минуту и находится в воздухе 6 секунд. Какое расстояние в метрах было лучшим броском Сары? Ответьте с точностью до двух знаков после запятой.
Здесь вам нужно будет рассчитать скорость в секунду, чтобы определить расстояние.
Ответ: 1,70 метра — Убедитесь, что вы указали столько десятичных знаков, сколько требует вопрос.
Вопрос 2 .:
Тим совершает благотворительную велопробег за два дня. В первый день он ездит на велосипеде со средней скоростью 10 миль в час в течение 5 часов. На второй день он ездит на велосипеде в течение 6 часов со средней скоростью 12 миль в час. Как далеко в целом была поездка на велосипеде?
Это требует, чтобы вы рассчитали расстояние, пройденное за оба дня.
Ответ: 122 миль
Время расчета
Чтобы рассчитать время, нужно разделить расстояние на скорость. Опять же, обратите особое внимание на любые другие вычисления, которые вам нужно выполнить, чтобы правильно ответить на вопрос. Это может быть преобразование единиц расстояния, например изменение миль / ч в км / ч, или преобразование времени, как в примере ниже:
Рабочий пример:
Высокоскоростной поезд едет прямо из пункта A в пункт B со средней скоростью 200 миль в час.Расстояние между точкой А и точкой Б составляет 545 миль. Сколько времени нужно поезду, чтобы преодолеть это расстояние? Ответьте в часах, минутах и секундах .
Метод:
Сначала примените формулу t = d / s :
545/200 = 2,725
2,725 указывается в часах только потому, что средняя скорость была выражена в милях в час. Преобразуйте 2,725 в часы, минуты и секунды, умножив частичные часы 0,725 на 60, чтобы получить их эквивалент в минутах :
.0.725 х 60 = 43,5
Это все равно не дает целого числа, поэтому необходимо также рассчитать секунды. Умножьте доли минут 0,5 на 60, чтобы получить их эквивалент в секундах :
.0,5 х 60 = 30
Ответ: Поезд преодолел расстояние за 2 часа 43 минуты 30 секунд .
Пример вопросов для расчета времени
Вопрос 1 .:
Коммерческий рейс доставляет пассажиров на расстояние 3 470 миль от Лондона до Нью-Йорка.Если самолет движется со средней скоростью 560 миль в час, сколько времени займет полет? Дайте ответ в считанные минуты с точностью до целой минуты.
Этот вопрос потребует от вас пересчета единиц времени.
Ответ: 372 минуты .
Вопрос 2 .:
Джемма пробегает дистанцию 10 км со средней скоростью 11,2 км / ч. Сколько времени ей потребовалось, чтобы завершить гонку? Ответьте в часах, минутах и секундах .
Опять же, чтобы ответить на этот вопрос, вам нужно будет преобразовать результат вашего расчета времени в часы, минуты и секунды.
Ответ: 0 часов, 53 минуты и 34 секунды — опять же, убедитесь, что вы указали точные единицы измерения, указанные в вопросе.
Как подготовиться к тестам на скорость, дистанцию и время
Хорошие результаты в тесте на скорость и дистанцию - все это связано с хорошей подготовкой.
Вот несколько главных советов для достижения успеха:
- Практикуйтесь в мысленной арифметике, включая таблицы умножения. — Это поможет вам с первого взгляда определить числовые отношения, что значительно упростит и ускорит выполнение расчетов.В частности, очень полезна таблица умножения на 6 умножений, поскольку она относится ко времени (60 минут в час, 60 секунд в минуте).
- Запомните ключевые формулы — В вопросах скорости, расстояния и времени вам всегда будут известны две переменные, поэтому все, что вам нужно сделать, это запомнить правильную формулу, которую нужно применить, чтобы найти третью. Прежде чем приступить к тесту, нарисуйте формулу треугольника, чтобы иметь четкую точку отсчета.
- Разберитесь с преобразованиями — Как и в некоторых из наших примеров вопросов, тесты скорости, расстояния и времени часто требуют от вас преобразования единиц.В некоторых случаях вам может быть предложено измерение скорости в одной единице и запрос расстояния в другой, или наоборот, поэтому вам нужно быть уверенным в преобразованиях. Вы также должны освежить в памяти преобразование времени.
- Сосредоточьтесь на том, чтобы работать точно, но быстро. — Вполне вероятно, что ваш тест будет рассчитан по времени, и вас будут оценивать как по точности ваших ответов, так и по скорости, с которой вы их выполнили. Практика здесь является ключевым моментом. Чем больше вы прорабатываете типовые вопросы, тем быстрее вы сможете определить и выполнить необходимые вычисления.
- Обращайте пристальное внимание на детали — Внимательно прочтите каждый вопрос, пока не будете уверены в том, что от вас просят. Баллы можно легко сбросить, пропустив ключевую часть вопроса, например, отвечая в течение нескольких часов, когда вас просят дать ответ в течение нескольких минут. Еще раз проверьте единицы измерения расстояния. Возможно, вы правильно подсчитали, но если в вашем ответе указано «км / ч», когда должно быть указано «миль / ч», это неверно.
- Избегайте человеческой ошибки — Выполняете ли вы вычисления ручкой и бумагой или с помощью калькулятора, всегда обращайтесь к цифрам, указанным в официальном вопросе теста.Если вы записали заметки, возможно, вы пропустили цифру или запутались в числах. Эти ошибки легко сделать под давлением, поэтому убедитесь, что вы работаете с цифрами, которые точно соответствуют тем, что указаны в вопросе.
- Используйте свой собственный калькулятор — Если в вашем тесте на скорость и время разрешены калькуляторы, убедитесь, что вы используете тот, с которым вы знакомы. Помните, что вы, скорее всего, будете работать в условиях ограниченного времени, и знакомство с вашим оборудованием может сэкономить вам драгоценные секунды.
Конечно, лучший совет о том, как подготовиться к тестам на скорость, дистанцию и время, — это практика. В Интернете доступно множество ресурсов с образцами вопросов и ответами, над которыми нужно работать.
В качестве немного более широкого руководства в этой статье подробно рассматриваются дроби, в том числе способы их преобразования в проценты и обратно, что является полезным навыком для преобразования единиц.
Или здесь есть бесплатные вопросы по числовым вычислениям, чтобы попрактиковаться в сложении, умножении, делении и вычитании.
Кроме того, эта электронная книга содержит 440 практических вопросов, хотя и не только о скорости, дистанции, времени.
Чем больше вы будете их использовать и заниматься математикой в целом, тем более компетентным вы станете.
Задачи и решения по математическим словам
Проблема 1 Днем продавец продал в два раза больше груш, чем утром.
Если он продал в тот день 360 килограммов груш, сколько?
килограммов он продал утром, а сколько днем?
Нажмите, чтобы увидеть решение
Решение:
Пусть $ x $ будет килограммами, которые он
продал утром.Затем днем он продал по 2 доллара за килограммы. Итак
итого $ x + 2x = 3x $. Это должно быть равно 360.
$ 3x = 360 $
$ x = \ frac {360} {3}
$ x = 120 $
Таким образом, продавец продал утром 120 кг и 2 \ cdot 120 = 240 $ кг днем.
Задача 2 Мэри, Питер и Люси собирали каштаны. Мэри собрала в два раза больше каштанов, чем Питер. Люси выбрала
На 2 кг больше Питера. Вместе они собрали 26 кг каштанов. Сколько килограммов набрал каждый из них?
Нажмите, чтобы увидеть решение
Решение:
Пусть $ x $ будет выбранной Питером суммой.Затем Мэри и Люси выбрали $ 2x $ и $ x + 2 $ соответственно.
Итак,
$ x + 2x + x + 2 = 26 $
$ 4x = 24 $
$ x = 6
$ Таким образом, Питер, Мэри и Люси выбрали 6, 12 и 8 кг соответственно.
Задача 3
София закончила $ \ frac {2} {3} $ книги. Она подсчитала, что закончила на 90 страниц больше, чем еще не прочитала. Как долго ее книга?
Нажмите, чтобы увидеть решение
Решение:
Пусть $ x $ будет общим количеством страниц в книге, тогда она закончила $ \ frac {2} {3} \ cdot x $ страниц.
Тогда у нее осталось $ x- \ frac {2} {3} \ cdot x = \ frac {1} {3} \ cdot x $ страниц.
$ \ frac {2} {3} \ cdot x- \ frac {1} {3} \ cdot x = 90 $
$ \ frac {1} {3} \ cdot x = 90 $
$ x = 270 $
Итак, в книге 270 страниц.
Задача 4
Сельскохозяйственное поле можно обработать 6 тракторами за 4 дня. Когда 6 тракторов работают вместе, каждый из них пашет.
120 га в сутки. Если два трактора были перенесены на другое поле,
тогда оставшиеся 4 трактора могут вспахать то же поле за 5 дней.Сколько гектаров в день будет обрабатывать один трактор?
Нажмите, чтобы увидеть решение
Решение:
Если каждый из тракторов за 6 долларов пашет 120 долларов гектаров в день, и они завершат работу за 4 доллара.
дней, то все поле будет: 120 $ \ cdot 6 \ cdot 4 = 720 \ cdot 4 = 2880 $ га. Давайте
предположим, что каждый из четырех тракторов обрабатывал $ x $ гектаров в день. Таким образом, за 5 дней вспахано
$ 5 \ cdot 4 \ cdot x = 20 \ cdot x $ га, что равняется площади всего поля, 2880 га.
Итак, получаем $ 20x = 2880 $
$ x = \ frac {2880} {20} = 144 $. Таким образом, каждый из четырех тракторов будет обрабатывать 144 гектара в день.
Задача 5
Студент выбрал число, умножил его на 2, затем вычел 138 из результата и получил 102. Какое число он выбрал?
Нажмите, чтобы увидеть решение
Решение:
Пусть $ x $ будет выбранным им числом, тогда
$ 2 \ cdot x — 138 = 102 $
$ 2x = 240 $
$ x = 120 $
Задача 6
Я выбрал число и разделил его на 5.Затем я вычел из результата 154 и получил 6. Какое число я выбрал?
Нажмите, чтобы увидеть решение
Решение:
Пусть $ x $ будет выбранным мной числом, тогда
$ \ frac {x} {5} -154 = 6 $
$ \ frac {x} {5} = 160 $
$ x = 800 $
Задача 7
Расстояние между двумя городами 380 км. В этот же момент легковой автомобиль и грузовик начинают движение навстречу друг другу из
разные города. Они встречаются через 4 часа. Если автомобиль движется на 5 км / ч быстрее грузовика, какова их скорость?
Нажмите, чтобы увидеть решение
Основная идея, используемая в задачах такого типа, заключается в том, что расстояние равно скорости, умноженной на время $ S = V \ cdot t $.
| В (км / ч) | т (час) | S (км) | |
| Автомобиль | х + 5 | 4 | 4 (х +5) |
| Грузовик | Х | 4 | 4x |
$ 4x + 4x = 380 — 20 $
$ 8x = 360 $
$ x = \ frac {360} {8} $
$ x = 45 $
Таким образом, скорость грузовика составляет 45 долларов за км / час, а скорость автомобиля — 50 долларов за км / час.
Задача 8
Одна сторона прямоугольника на 3 см короче другой стороны. Если увеличить длину каждой стороны на 1 см, то площадь прямоугольника
увеличится на 18 см 2 . Найдите длины всех сторон.
Нажмите, чтобы увидеть решение
Решение:
Пусть $ x $ будет длиной большей стороны $ x \ gt 3 $, тогда длина другой стороны будет $ x-3 $ см. Тогда площадь S 1 = x (x — 3) см 2 .
После увеличения длины сторон они станут $ (x +1) $ и $ (x — 3 + 1) = (x — 2) $ см в длину.2 + x — 2x — 2
долларов США 2x = 20
долларов США x = 10 долларов США.
Итак, стороны прямоугольника равны $ 10 $ см и $ (10 — 3) = 7 $ см в длину.
Задача 9
В первый год две коровы дали 8100 литров молока. Второй год их производство увеличилось.
на 15% и 10% соответственно, а общее количество молока увеличилось до
9100 литров в год. Сколько литров молока давалось от каждой коровы за год?
Нажмите, чтобы увидеть решение
Решение:
Пусть x будет количеством молока первой коровы
произведен в течение первого года.Затем вторая корова в тот год произвела (8100 — x) литров молока. На второй год каждая корова произвела
столько же молока, сколько в первый год плюс прибавка на 15 \% $ или 10 \% $.
Итак, $ 8100 + \ frac {15} {100} \ cdot x + \ frac {10} {100} \ cdot (8100 — x) = 9100 $
Следовательно, $ 8100 + \ frac {3} {20} x + \ frac {1} {10} (8100 — x) = 9100 $
$ \ frac {1} {20} x = 190 $
$ x = 3800 $
Следовательно,
коровы дали 3800 и 4300 литров молока в первый год и 4370 долларов и 4730 долларов за литр молока во второй год, соответственно.
Проблема 10
расстояние между станциями A и B — 148 км. Экспресс отправился со станции A в сторону станции B со скоростью 80 км / ч. В то же
В это время товарный поезд покинул станцию B в сторону станции A со скоростью 36 км / час. Они встретились на станции C в 12 часов, и к тому времени
экспресс остановился на промежуточной станции на 10 мин, а грузовой поезд остановился на 5 мин. Находим:
а) Расстояние между станциями C и B.
б) Время, когда товарный поезд покинул станцию B.
Нажмите, чтобы увидеть решение
Решение
a) Пусть x будет расстоянием между
станции B и C. Тогда расстояние от станции C до станции A составляет $ (148 — x) $ км. К моменту встречи на станции C экспресс
ехал $ \ frac {148-x} {80} + \ frac {10} {60} $ часов, а грузовой поезд ехал $ \ frac {x} {36} + \ frac {5} {60} $ часов . Поезда ушли одновременно, так что:
$ \ frac {148 — x} {80} + \ frac {1} {6} = \ frac {x} {36} + \ frac {1} {12} $. Общий знаменатель чисел 6, 12, 36, 80 равен 720.Тогда
$ 9 (148 — x) +120 = 20x + 60 $
$ 1332 — 9x + 120 = 20x + 60 $
$ 29x = 1392 $
$ x = 48 $.
Следовательно, расстояние между станциями B и C составляет 48 км.
б) К моменту встречи на станции С фрахт
поезд ехал $ \ frac {48} {36} + \ frac {5} {60} $ часов, то есть 1 доллар в час и 25 долларов в минуту.
Следовательно, он покинул станцию B на отметке $ 12 — (1 + \ frac {25} {60}) = 10 + \ frac {35} {60} $ часов, то есть в 10:35 утра.
Задача 11
Сьюзен едет из города А в город Б.После двух часов езды она
заметила, что она преодолела 80 км и подсчитала, что если она продолжит
двигаясь с той же скоростью, она опаздывала на 15 минут. Так
она увеличила скорость на 10 км / ч и прибыла в город B на 36 минут раньше
чем она планировала.
Найдите расстояние между городами A и B.
Нажмите, чтобы увидеть решение
Решение:
Пусть $ x $ будет расстоянием между A и B. Поскольку Сьюзен преодолела 80 км за 2 часа, ее скорость составила $ V = \ frac {80} {2} = 40 $ км / час.
Если бы она продолжила движение с той же скоростью, она бы опоздала на 15 $ минут, т.е. запланированное время в пути составляет $ \ frac {x} {40} — \ frac {15} {60} $ hr.
Остальное расстояние $ (x — 80) $ км. $ V = 40 + 10 = 50 $ км / час.
Итак, она преодолела расстояние между A и B за $ 2 + \ frac {x — 80} {50} $ hr, и это оказалось на 36 минут меньше, чем планировалось.
Таким образом, запланированное время было $ 2 + \ frac {x -80} {50} + \ frac {36} {60} $.
Когда мы выравниваем выражения для запланированного времени, мы получаем уравнение:
$ \ frac {x} {40} — \ frac {15} {60} = 2 + \ frac {x -80} {50} + \ frac {36} {60} $
$ \ frac {x — 10} {40} = \ frac {100 + x — 80 + 30} {50} $
$ \ frac {x — 10} {4} = \ frac {x +50} {5} $
$ 5x — 50 = 4x + 200 $
$ x = 250 $
Итак, расстояние между городами A и B составляет 250 км.
Задача 12
Чтобы доставить заказ вовремя, компания должна производить 25 деталей в день. После изготовления 25 частей в день по 3
дней компания начала производить на 5 деталей больше в день, а к последнему дню работы было произведено на 100 деталей больше, чем планировалось.
Узнайте, сколько деталей изготовила компания и сколько дней это заняло.
Нажмите, чтобы увидеть решение
Решение:
Пусть $ x $ будет количеством дней, в течение которых компания проработала. Тогда 25x — это
количество деталей, которые они планировали сделать.При новом уровне добычи они
сделано:
$ 3 \ cdot 25 + (x — 3) \ cdot 30 = 75 + 30 (x — 3) $
Следовательно: 25 $ x = 75 + 30 (x -3) — 100 $
$ 25x = 75 + 30x -90 — 100 $
$ 190 -75 = 30x -25 $
$ 115 = 5x $
$ x = 23 $
Итак, компания проработала 23 дня, и они заработали 23 $ \ cdot 25 + 100 = 675 $ штук.
Задача 13
В седьмом классе 24 ученика. Решили посадить на заднем дворе школы березы и розы. Пока каждая девочка посадила по 3
роз, каждые три мальчика посадили по 1 берёзе.К концу дня они посадили растения за 24 доллара. Сколько берез и роз было посажено?
Нажмите, чтобы увидеть решение
Решение:
Пусть $ x $ будет количеством роз. Тогда количество берез — 24 $ — x $, а количество мальчиков — $ 3 \ times (24-x) $. Если каждая девочка посадила 3
роз, в классе $ \ frac {x} {3} $ девочек.
Мы знаем, что в классе 24 ученика. Следовательно, $ \ frac {x} {3} + 3 (24 — x) = 24 $
$ x + 9 (24 — x) = 3 \ cdot 24 $
$ x +216 — 9x = 72 $
$ 216 — 72 = 8x $
$ \ frac {144} {8} = x $
$ x = 18 $
Итак, ученики посадили 18 роз и 24 — x = 24 — 18 = 6 берез.
Задача 14
Автомобиль выехал из города A в сторону города B, двигаясь со скоростью V = 32 км / час. После 3 часов в пути водитель остановился на 15 минут в городе C.
на закрытой дороге ему пришлось изменить маршрут, увеличив поездку на 28 км. Он увеличил скорость до V = 40 км / час, но все равно опоздал на 30 минут. Находка:
а) Расстояние, которое преодолела машина.
b) Время, которое потребовалось, чтобы добраться от C до B.
Щелкните, чтобы увидеть решение
Из постановки задачи мы не знаем, была ли 15-минутная остановка в городе C запланирована или она была запланирована. непредвиденный.Итак, мы должны рассмотреть оба случая.
A
Остановка планировалась. Рассмотрим только поездку из C в B, и пусть $ x $ будет количеством часов, в течение которых водитель
потратил на эту поездку.
Тогда расстояние от C до B равно $ S = 40 \ cdot x $
км. Если бы водитель мог использовать первоначальный маршрут, ему потребовалось бы $ x — \ frac {30} {60} = x — \ frac {1} {2} $ часов, чтобы проехать от C до B. Расстояние от C до B.
согласно первоначальному маршруту $ (x — \ frac {1} {2}) \ cdot 32 $ км, и это
расстояние на $ 28 $ км короче, чем $ 40 \ cdot x $ км.Тогда у нас есть уравнение
$ (x — 1/2) \ cdot 32 + 28 = 40x $
$ 32x -16 +28 = 40x $
$ -8x = -12 $
$ 8x = 12 $.
$ x = \ frac {12} {8} $
$ x = 1 \ frac {4} {8} = 1 \ frac {1} {2} = 1 \ frac {30} {60} = 1 час. 30 минут.
Итак, автомобиль преодолел расстояние от C до B за 1 час 30 минут.
Расстояние от A до B составляет $ 3 \ cdot 32 + \ frac {12} {8} \ cdot 40 = 96 + 60 = 156 $ км.
B
Предположим, ему потребовалось $ x $ часов
чтобы добраться из C в B. Тогда расстояние $ S = 40 \ cdot x $ км.
Водитель не планировал остановку на C. Допустим, он остановился, потому что ему пришлось изменить маршрут.
Потребовалось $ x — \ frac {30} {60} + \ frac {15} {60} = x — \ frac {15} {60} = x — \ frac {1} {4} $ h, чтобы проехать от С к Б.
расстояние от C до B составляет $ 32 (x — \ frac {1} {4}) $ км, что на $ 28 $ км короче, чем $ 40 \ cdot x $, т.е.
$ 32 (x — \ frac {1} {4}) + 28 = 40x $
$ 32x — 8 +28 = 40x $
$ 20 = 8x $
$ x = \ frac {20} {8} = \ frac {5} {2} = 2 \ text {hr} 30 \ text {min}. $
Пройденное расстояние равно $ 40 \ times 2.5 = 100 км $.
Задача 15
Если фермер хочет вспахивать поле фермы вовремя, он должен вспахивать 120 гектаров в день. По техническим причинам он пахал всего 85 гектаров в день, следовательно, ему пришлось пахать на 2 дня больше, чем планировалось, и он
осталось еще 40 га. Какова площадь фермерского поля и сколько дней фермер изначально планировал работать?
Нажмите, чтобы увидеть решение
Решение:
Пусть $ x $ будет количеством дней в первоначальном плане.Следовательно, все поле составляет $ 120 \ cdot x $ га. Фермеру приходилось работать x + 2 доллара в день, и он
вспахали 85 долларов (x + 2) гектаров, оставив 40 гектаров невыпаханными. Тогда у нас есть уравнение:
$ 120x = 85 (x + 2) + 40 $
$ 35x = 210 $
$ x = 6 $.
Итак, фермер планировал завершить работы за 6 дней, а площадь фермерского поля составляет 120 $ \ cdot 6 = 720 $ гектаров.
Задача 16
Столяр обычно делает определенное количество
запчасти за 24 дня. Но он смог увеличить свою производительность на 5 деталей в день, и поэтому он
не только закончил работу всего за 22 дня, но и сделал 80 дополнительных деталей.Сколько частей
плотник обычно делает в день, а сколько штук он делает за 24 дня?
Нажмите, чтобы увидеть решение
Решение:
Пусть $ x $ будет количеством деталей, которые плотник обычно изготавливает ежедневно. За 24 дня он заработал $ 24 \ cdot x $ штук. Его новая суточная производительность составляет x + 5 долларов за штуку и в
$ 22 $ дней он сделал $ 22 \ cdot (x + 5) $ деталей. Это на 80 больше, чем $ 24 \ cdot x $. Следовательно
уравнение:
$ 24 \ cdot x + 80 = 22 (x +5) $
$ 30 = 2x $
$ x = 15 $
Обычно он делает 15 деталей в день, а за 24 дня он зарабатывает 15 $ \ cdot 24 = 360 $ частей.
Задача 17
Байкер преодолел половину расстояния между двумя городами за 2 часа 30 минут.
После этого он увеличил скорость на 2 км / час. Вторую половину дистанции он преодолел за 2 часа 20 минут. Найдите расстояние между двумя городами
и начальная скорость байкера.
Нажмите, чтобы увидеть решение
Решение:
Пусть x км / ч будет начальной скоростью
байкером, то его скорость во второй части поездки составляет x + 2 км / час.
Половина расстояния между двумя городами равна $ 2 \ frac {30} {60} \ cdot x $ км и $ 2 \ frac {20} {60} \ cdot (x + 2) $ км.Из уравнения: $ 2 \ frac {30} {60} \ cdot x = 2 \ frac {20} {60} \ cdot (x + 2) $
получаем $ x = 28 $ км / час.
Начальная скорость байкера — 28 км / ч.
Половина расстояния между двумя городами составляет
$ 2 ч 30 мин \ раз 28 = 2,5 \ раз 28 = 70 $.
Итак, расстояние 2 $ \ умноженное на 70 = 140 $ км.
Задача 18
Поезд преодолел половину расстояния между станциями A и B со скоростью 48 км / час, но затем ему пришлось остановиться на 15 мин. Составить
из-за задержки он увеличил свою скорость на $ \ frac {5} {3} $ м / сек и прибыл на станцию B вовремя.Найдите расстояние между двумя станциями и скорость поезда после остановки.
Нажмите, чтобы увидеть решение
Решение:
Сначала определим скорость поезда после остановки. Скорость
было увеличено на $ \ frac {5} {3} $ м / сек $ = \ frac {5 \ cdot 60 \ cdot 60} {\ frac {3} {1000}} $ км / час = $ 6 $ км / час. Следовательно
новая скорость 48 $ + 6 = 54 $ км / час. Если на покрытие первого
половины расстояния, то на преодоление расстояния требуется $ x — \ frac {15} {60} = x — 0,25 $ ч.
вторая часть.
Итак, уравнение: $ 48 \ cdot x = 54 \ cdot (x — 0,25) $
$ 48 \ cdot x = 54 \ cdot x — 54 \ cdot 0,25 $
$ 48 \ cdot x — 54 \ cdot x = — 13,5 $
$ -6x = — 13,5 $
$ x = 2,25 $ ч.
Все расстояние
$ 2 \ умножить на 48 \ умножить 2,25 = 216 $ км.
Задача 19
Элизабет может выполнить определенную работу за 15 дней, а Тони — только 75%.
эта работа в одно и то же время. Тони работал один в течение нескольких дней, а затем к нему присоединилась Элизабет, так что они закончили остаток работы.
работа за 6 дней, работаем вместе.
Сколько дней проработал каждый из них и какой процент работы каждый из них выполнил?
Нажмите, чтобы увидеть решение
Решение:
Сначала мы найдем ежедневную производительность каждого рабочего. Если мы рассмотрим
вся работа как единица (1), Элизабет выполняет $ \ frac {1} {15} $ работы в день, а Тони выполняет 75 \% $ из $ \ frac {1} {15} $, т.е.
$ \ frac { 75} {100} \ cdot \ frac {1} {15} = \ frac {1} {20} $. Предположим, что Тони работал один
за $ x $ дней. Затем он в одиночку выполнил $ \ frac {x} {20} $ всей работы.За работой
вместе в течение 6 дней двое рабочих закончили $ 6 \ cdot (\ frac {1} {15} + \ frac {1} {20}) = 6 \ cdot \ frac {7} {60} = \ frac {7} { 10} $ работы.
Сумма $ \ frac {x} {20} $ и $ \ frac {7} {10} $ дает нам всю работу, то есть $ 1 $. Получаем уравнение:
$ \ frac {x} {20} + \ frac {7} {10} = 1 $
$ \ frac {x} {20} = \ frac {3} {10} $
$ х = 6 $. Тони проработал 6 + 6 = 12 дней
и Элизабет работала за 6 долларов в день. Часть работы сделана
это $ 12 \ cdot \ frac {1} {20} = \ frac {60} {100} = 60 \% $ для Тони и $ 6 \ cdot \ frac {1} {15} = \ frac {40} {100} = 40 \% $ для Элизабет.
Задача 20
Фермер планировал вспахать поле, выполнив 120
га в сутки. После двух дней работы он увеличил свою дневную производительность на 25% и закончил работу на два дня раньше срока.
а) Какова площадь поля?
б) За сколько дней фермер выполнил свою работу?
c) Через сколько дней фермер планировал завершить работу?
Нажмите, чтобы увидеть решение
Решение:
Прежде всего мы найдем новую суточную производительность
фермер в гектарах в сутки: 25% от 120 гектаров
$ \ frac {25} {100} \ cdot 120 = 30 $ га, поэтому 120 $ + 30 = 150 $ га
новая ежедневная производительность.Пусть x будет запланированным количеством
дней, отведенных на работу. Тогда хозяйство будет 120 \ cdot x $ га. На
с другой стороны, мы получим ту же площадь, если добавим 120 $ \ cdot 2 $ гектаров к
150 $ (х -4) $ га. Тогда мы получим уравнение:
$ 120x = 120 \ cdot 2 + 150 (x -4) $
$ x = 12 $
Итак, изначально предполагалось, что работа займет 12 дней, но на самом деле поле было вспахано за 12-2 дней. = 10 дней.
Площадь поля 120 $ \ cdot 12 = 1440 $ га.
Задача 21
Чтобы покосить травяное поле, бригада косилок планировала обрабатывать 15 гектаров в день.Через 4 рабочих дня они увеличили дневную производительность на
$ 33 \ times \ frac {1} {3} \% $ и закончил работу на 1 день раньше запланированного срока.
A) Какова площадь травяного поля?
Б) Сколько дней понадобилось, чтобы косить все поле?
C) Сколько дней изначально было запланировано для этой работы?
Подсказка : Посмотрите на проблему 20 и решите ее сами.
Ответ: А) 120 га; Б) 7 дней; В) 8 дней.
Задача 22
Поезд идет от станции A до станции B.Если поезд отправляется со станции А
со скоростью 75 км / час, прибывает на станцию B на 48 минут раньше запланированного. Если бы он двигался со скоростью 50 км / час, то к запланированному времени прибытия бы
осталось еще 40 км до станции B. Найти:
A) Расстояние между двумя станциями;
B) Время, необходимое поезду, чтобы добраться из пункта А в пункт Б по расписанию;
C) Скорость поезда по расписанию.
Нажмите, чтобы увидеть решение
Решение:
Пусть $ x $ будет запланированным временем поездки из пункта А в пункт Б.Тогда расстояние
между A и B можно найти двумя способами. С одной стороны, это расстояние составляет $ 75 (x — \ frac {48} {60}) $ км. С другой стороны, это 50 $ + 40 $ км. Таким образом, мы получаем уравнение:
$ 75 (x — \ frac {48} {60}) = 50x + 40 $
$ x = 4 $ час — это запланированное время в пути. В
расстояние между двумя станциями составляет 50 $ \ cdot 4 + 40 = 240 $ км. Тогда скорость, которую поезд должен поддерживать, чтобы идти по расписанию, составляет $ \ frac {240} {4} = 60 $ км / час.
Задача 23
Расстояние между городами A и B составляет 300 км.Один поезд отправляется из города А, а другой — из города.
город B, оба уезжают в один и тот же момент времени и направляются друг к другу. Мы знаем, что один из них на 10 км / час быстрее другого. Находить
скорости обоих поездов, если через 2 часа после отправления расстояние между ними составляет 40 км.
Нажмите, чтобы увидеть решение
Решение:
Пусть скорость более медленного поезда будет $ x $ км / час. Тогда скорость
более быстрый поезд стоит (x + 10) $ км / час. За 2 часа они преодолевают 2x $ км и 2 (x +10) $ км соответственно.Поэтому, если они еще не встретились, весь
расстояние от A до B составляет $ 2x + 2 (x +10) +40 = 4x + 60 $ км. Однако если
они уже встретились и продолжили движение, расстояние будет $ 2x + 2 (x + 10) — 40 = 4x — 20 $ км.
Таким образом, мы получаем следующие уравнения:
$ 4x + 60 = 300 $
$ 4x = 240 $
$ x = 60 $ или
$ 4x — 20 = 300 $
$ 4x = 320 $
$ x = 80 $
Отсюда скорость более медленного поезда составляет 60 долларов США км / час или 80 долларов США км / час, а скорость поезда
более быстрый поезд стоит 70 долларов за км / час или 90 долларов за км / час.
Задача 24
Автобус едет из города А в город Б.Если скорость автобуса составляет 50 км / час, он прибудет в город B на 42 минуты позже запланированного срока. Если автобус увеличивается
его скорость составляет $ \ frac {50} {9} $ м / сек, он прибудет в город B на 30 минут раньше запланированного срока. Находим:
A) Расстояние между двумя городами;
B) Планируемое время прибытия автобуса в B;
C) Скорость автобуса по расписанию.
Нажмите, чтобы увидеть решение
Решение:
Сначала определим скорость автобуса после ее увеличения. Скорость
увеличено на $ \ frac {50} {9} $ м / сек $ = \ frac {50 \ cdot60 \ cdot60} {\ frac {9} {1000}} $ км / час $ = 20 $ км / час.Следовательно, новая скорость составляет $ V = 50 + 20 = 70 $ км / час. Если $ x $ — количество часов по расписанию, то со скоростью 50
км / ч автобус едет из пункта A в пункт B за $ (x + \ frac {42} {60}) $ час. Когда скорость автобуса составляет $ V = 70 $ км / час, время в пути составляет $ x — \ frac {30} {60} $ час. потом
$ 50 (x + \ frac {42} {60}) = 70 (x- \ frac {30} {60}) $
$ 5 (x + \ frac {7} {10}) = 7 (x- \ frac { 1} {2}) $
$ \ frac {7} {2} + \ frac {7} {2} = 7x -5x $
$ 2x = 7 $
$ x = \ frac {7} {2} $ час.
Итак, автобус должен проделать путь за 3 доллара за час 30 долларов за минуту.
Расстояние между двумя городами составляет $ 70 (\ frac {7} {2} — \ frac {1} {2}) = 70 \ cdot 3 = 210 $ км, а запланированная скорость составляет $ \ frac {210} {\ гидроразрыв {7} {2}} = 60 $ км / час.
GMAT Rates практика вопросы | Образец времени, рабочего времени, вопросы
Вы можете получить от двух до четырех вопросов в разделе «Курсы» — скорость, расстояние, время, расы, «Время работы» и «Цистерны для труб» в секции количественного анализа GMAT — в обоих вариантах, а именно о решении проблем и достаточности данных. Испытанные концепции включают вычисление расстояния, скорости, времени, относительной скорости, средней скорости, скорости лодок в потоках, скорости самолетов с попутным ветром, вычислений времени, затрачиваемого на заполнение бака, времени, затрачиваемого на выполнение задачи, отношения, в котором один или несколько рабочие распределяют заработную плату при разной ставке труда.
Примеры практических вопросов GMAT по скорости, расстоянию, времени, рабочему времени и трубам цистерны приведены ниже. Попробуйте ответить на эти вопросы и убедитесь, что вы получили правильный ответ. Если вы еще не ознакомились с пояснительным ответом или видеообъяснениями (где бы они ни были), чтобы узнать, как ответить на вопрос.
Поезд, движущийся со скоростью 72 км / ч, пересекает платформу за 30 секунд, а человек, стоящий на платформе, за 18 секунд.Какая длина платформы в метрах?
- 240 метров
- 360 метров
- 420 метров
- 600 метров
- Невозможно определить
Поезд, движущийся со скоростью 100 км / ч, обгоняет мотоцикл, движущийся со скоростью 64 км / ч, за 40 секунд.Какая длина поезда в метрах?
- 1777 метров
- 1822 метра
- 400 метров
- 1111 метров
- Ни один из этих
Джим путешествует первые 3 часа своего путешествия со скоростью 60 миль в час, а оставшиеся 5 часов — со скоростью 24 мили в час.Какова средняя скорость движения Джима в милях в час?
- 42 миль / ч
- 36 миль / ч
- 37,5 миль / ч
- 42,5 миль / ч
- 48 миль / ч
A бежит на 25% быстрее, чем B, и может позволить B с отрывом в 7 метров закончить гонку ничьей.Какова длина забега?
- 10 метров
- 25 метров
- 45 метров
- 15 метров
- 35 метров
Джейн преодолела расстояние в 340 миль между городом A и городом B, в общей сложности за 5 часов.Если часть расстояния была пройдена со скоростью 60 миль в час, а баланс — со скоростью 80 миль в час, сколько часов она проехала со скоростью 60 миль в час?
- 2 часа 30 минут
- 3 часа
- 2 часа
- 1 час 45 минут
- Ни один из этих
Стив ехал первые 2 часа своего путешествия со скоростью 40 миль в час и последние 3 часа своего путешествия со скоростью 80 миль в час.Какова его средняя скорость передвижения за все путешествие?
- 60 миль / ч
- 56,67 миль / ч
- 53,33 миль / ч
- 64 миль / ч
- 66,67 миль / ч
Работая вместе, Хосе и Джейн могут выполнить поставленную задачу за 20 дней.Однако, если Хосе работал один и выполнил половину задачи, а затем Джейн берет на себя и завершает вторую половину, задача будет выполнена за 45 дней. Сколько времени потребуется Хосе, чтобы выполнить задание, если бы он работал один? Предположим, что Джейн более эффективна, чем Хосе.
- 25 дней
- 30 дней
- 60 дней
- 65 дней
- 36 дней
A может завершить проект за 20 дней, а B может завершить тот же проект за 30 дней.Если A и B начнут работать над проектом вместе, а A завершит работу за 10 дней до завершения проекта, за сколько дней проект будет завершен?
- 18 дней
- 27 дней
- 26.67 дней
- 16 дней
- 12 дней
Раму, который вдвое менее эффективен, чем Криш, потребуется 24 дня, чтобы выполнить задание, если он работал в одиночку.Если Рам и Криш работали вместе, сколько времени им потребуется, чтобы выполнить задание?
- 16 дней
- 12 дней
- 8 дней
- 6 дней
- 18 дней
Попробуйте эти вопросы в качестве бесплатного онлайн-теста по времени
Получите удобную аналитику | Сравнение с другими участниками GMAT | Определите щели в вашей броне