Задачи для 3 класса 1 четверть по математике школа россии: Контрольная работа по математике 3 класс 1 четверть
Проверочная работа «Решение задач»
1 вариант
У Саши в корзине 12 подберёзовиков, а белых грибов в 4 раза меньше. Сколько белых грибов в корзине?
__________________________________________________________________
__________________________________________________________________
В вазе 12 яблок, а груш на 4 меньше. Сколько груш в вазе?
__________________________________________________________________
__________________________________________________________________
В танцевальной группе 5 мальчиков, а девочек в 2 раза больше. Сколько девочек в танцевальной группе?
__________________________________________________________________
__________________________________________________________________
В классе 9 мальчиков, а девочек на 3 больше, чем мальчиков. Сколько девочек в классе?
__________________________________________________________________
__________________________________________________________________
В Сашиной коллекции 12 машинок, а у Вовы в коллекции 6 машинок. Во сколько раз больше машинок у Саши, чем у Вовы?
__________________________________________________________________
___________________________________________________________________
На клумбе расцвели 15 роз и 5 гвоздик. Во сколько раз меньше расцвело гвоздик, чем роз?
__________________________________________________________________
__________________________________________________________________
Лена решила 2 задачи, а примеров в 7 раз больше. Сколько всего заданий решила Лена?
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
На берёзе осталось 10 листиков, а на клёне 16 листочков. На сколько больше осталось листиков клёна, чем листиков берёзы?
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
Проверочная работа «Решение задач»
2 вариант
У Вали в корзине 16 подосиновиков, а лисичек в 4 раза меньше. Сколько лисичек в корзине?
__________________________________________________________________
__________________________________________________________________
Коля собрал 16 яблок, а груш на 4 меньше. Сколько груш в вазе?
__________________________________________________________________
Лёгкой атлетикой занимаются 6 девочек, а мальчиков в 2 раза больше. Сколько мальчиков занимаются лёгкой атлетикой?
__________________________________________________________________
__________________________________________________________________
В классе 6 девочек, а мальчиков на 4 больше, чем девочек. Сколько мальчиков в классе?
__________________________________________________________________
__________________________________________________________________
У Лены 12 кукол, а у Вали 6 кукол. Во сколько раз больше кукол у Лены, чем у Вали?
__________________________________________________________________
___________________________________________________________________
В саду 12 яблонь и 6 груш. Во сколько раз меньше в саду груш, чем яблонь?
__________________________________________________________________
__________________________________________________________________
Игорь собрал 2 модели танков, а моделей самолётов в 3 раза больше. Сколько всего моделей танков и самолётов собрал Игорь?
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
С одной грядки собрали 16 кг лука, а с другой – 6 кг. На сколько больше кг лука собрали с первой грядки, чем со второй??
___________________________________________________________________
___________________________________________________________________
___________________________________________________________________
Варианты контрольных работ 3 кл. 1 четв.
1 вариант.
1. Девочки собрали 9 кг лекарственных трав, а мальчики в 5 раз больше. Сколько лекарственных трав собрали дети?
2. Вычислить:
47 + 3 ∙ 6
24 : (72 – 66)
24 : 3
7 ∙ 5
81: 9
8 ∙ 4
3. Сравни:
9 ∙ 2 … 2 ∙ 8
7 ∙ 3 … 6 ∙ 9
24 : 3 … 12 : 3
42 : 6 … 27 : 9
4. Найти периметр площадь прямоугольника, длина которого 4 см, а ширина 7 см.
5*. На тарелке лежат сливы. Марина взяла половину всех слив, а Алеша – остальные 4 сливы. Сколько слив было на тарелке?
2 вариант.
1. На клумбах около школы ребята вырастили 7 красных роз, а желтых в 3 раза больше. Сколько роз вырастили ребята?
2. Вычислить:
56 + 3 ∙ 6
8 : (53 – 45)
42 : 6
7 ∙ 6
72 : 9
7 ∙ 4
3. Сравни:
7 ∙ 2 … 5 ∙ 3
8 ∙ 3 … 4 ∙ 7
27 : 3 … 12 : 6
32 : 8 … 21 : 7
4. Найти периметр площадь прямоугольника, длина которого 3 см, а ширина 8 см.
5*. Масса арбуза и еще половины такого же арбуза равна 9 кг. Найдите массу целого арбуза.
1 вариант
1. В клетке было 7 белых кроликов, а серых – в три раза больше. Сколько серых кроликов в клетке?
2. На пошив одного платья расходуют 4 м шёлка. Сколько метров шёлка пойдет на 9 таких же платьев?
3. Вставь пропущенные числа, чтобы получились верные равенства.
∙ = 32 ∙ = 36
∙ = 20 ∙ = 63
∙ = 24 ∙ = 54
4. Сравнить:
7 ∙ 5 – 7 … 6 ∙ 4 + 4 6 ∙ 8 + 6 … 5 ∙ 8 + 8
7 ∙ 8 + 7 … 7 ∙ 9 – 7 8 ∙ 2 + 12 … 10 ∙ 3
5. Запиши выражения и найди их значения:
а) произведение чисел 9 и9
б) 8 увеличить в 5 раз
в) 51 уменьшить на 7
г) уменьшаемое 17, вычитаемое 9
д) на сколько 72 меньше 91?
2 вариант
1. У Пети 7 значков, а у Коли – в 4 раза больше. Сколько значков у Коли?
2. В одной банке 3 кг варенья. Сколько кг варенья в девяти таких же банках?
3. Вставь пропущенные числа, чтобы получились верные равенства.
∙ = 72 ∙ = 16
∙ = 30 ∙ = 49
∙ = 56 ∙ = 81
4. Сравнить:
6 ∙ 9 – 6 … 5 ∙ 8 + 5 5 ∙ 7 + 7 … 5 ∙ 8 – 5
8 ∙ 4 + 4 … 5 ∙ 8 – 8 8 ∙ 3 + 3 … 3 ∙ 7 + 7
5. Запиши выражения и найди их значения:
а) произведение чисел 7 и 4
б) 6 увеличить в 9 раз
в) 63 уменьшить на 8
г) уменьшаемое 15, вычитаемое 8
д) на сколько 54 меньше 63?
Вариант I
- Решите задачу:
Бабушка купила 6 рулонов ткани. В каждой из них по 8 метров. Сколько всего ткани купила бабушка?
2. Решите задачу: У мамы 3 детей. Она принесла из магазина 18 конфет и поровну разделила их между детьми. Сколько конфет получил каждый ребёнок?
- Решите уравнения:
x + 45 = 89 86 — y = 38
4. Найти значение выражений:
7 * 3 =
4 * 8 =
18 : 6 =
8 : 4 =
5 * 8 =
12 : 6 =
27 : 9 =
21 : 7 =
5. Найдите значение, представленных выражений:
1) 72 — ( 34 + 20 ) : 3 =
2) 48 + ( 30 — 18 ) * 4 =
Вариант II
- Решите задачу:
В детском саду всего 8 комнат. В каждой комнате по 5 столов. Сколько всего столов в детском саду?
2. Решите задачу: Бабушка принесла из магазина 15 печений и разделила их между 3 внуками поровну? Сколько печений досталось каждому?
3. Решите уравнения:
x + 42 = 96 81 — y = 33
- Найти значение выражений:
9 * 3 =
6 * 7 =
18 : 3 =
4 * 8 =
21 : 3 =
25 : 5 =
12 : 4 =
28 : 2 =
5. Найдите значения, представленных выражений:
1) 82 — ( 12 + 49 ) : 3 =
2) 18 + ( 40 — 28 ) * 3 =
Контрольная работа за 1 четверть «Школа России»
3 класс
1 вариант
Решите задачу:
В куске было 64 м ткани. Из этой ткани сшили 9 пальто, расходуя по 3 м на каждое. Сколько метров ткани осталось в куске?
Решите примеры по действиям:
(15:3) • 9 — 15= 60: (4+6)•3=
- Решите примеры, записывая их столбиком:
38+14= 56+17= 89-16= 74-16=
Решить уравнение х•2=18
Сравните величины:
3см * 13 мм 4мин * 1ч 2дм 3см * 32 см
Решите геометрическую задачу:
Начертите прямоугольник со сторонами 4 см и 2 см и найдите его периметр.
7*. Петя перемножил 2 однозначных числа и получил 49. Запиши эти числа.
Контрольная работа за 1 четверть «Школа России»
3 класс
2 вариант
Решите задачу:
Для изготовления открыток ребята приготовили 50 листов бумаги. Они сделали 7 открыток, расходуя на каждую по 4 листа бумаги. Сколько листов бумаги у ребят осталось?
Решите примеры по действиям:
(24:3) • 2 + 14= 50: (4+6)•8=
Решите примеры, записывая их столбиком:
57+16= 45+26= 68-19= 83-35=
Решить уравнение 25 : х=5
Сравните величины:
4см * 14 мм 3мин * 1ч 5дм 2см * 52 см
Решите геометрическую задачу:
Начертите прямоугольник со сторонами 6 см и 2 см и найдите его периметр.
7*. Ира перемножила 2 однозначных числа и получила 36. Запиши эти числа.
1.Обведите номер числа, которое читается так:
восемьсот семь.
1) 870; 4) 807;
2) 708; 5) 780.
3) 87;
2.Обведите номер числа, при увеличении которого на 1 получается 400.
1) 499; 2) 399; 3) 401; 4) 390.
3.Обведите номер правильного ответа.
Если к числу 56 справа приписать 0, то оно увеличится…
1) в 100 раз; 3) в 10 раз;
2) в 5 раз; 4) в 404 раза.
4. Обведите номер числа, которое представлено в виде суммы разрядных слагаемых.
1)470=400+50+20; 2)541=500+41;
3)754=300+400+50+4; 4)369=300+60+9.
5.Вычислите и обведите номер правильного ответа.
490+320
1) 810; 2)710; 3)530; 4)170.
6.Вычислите и обведите номер правильного ответа.
540-350
1)290; 2)190; 3)890; 4)210.
7. Обведите номер верной записи, не вычисляя.
1)400-280400-281
3)400-280=400-281 4) Сравнить, не вычисляя, нельзя.
8.Обведите номера числовых выражений, значение которых равно 28.
1) 72:3 4) 80-51 7) 4●7
2) 56:2 5) 21+8 8) 84:3
3) 14●2 6) 72-44 9) 32-4
9. Обведите номера числовых выражений, значение которых 3.
1) 72:36 3) 54:18 5) 91:13
2) 81:27 4) 66:22 6) 42:14
10.Обведите номер правильного ответа.
Мама купила 15 килограммов клубники. 1/5 часть всей клубники съели, а из остальной сварили варенье. Сколько килограммов клубники пошло на приготовление варенья?
1)3 кг 2)18 кг 3)12 кг 4)10 кг
11.Решите задачу и обведите номер правильного ответа.
Из 72 метров ткани можно сшить 24 костюма. Сколько таких костюмов можно сшить из 21 метра ткани?
- 3к.; 2) 7к.; 3) 63к; 4) 14к.
12.Обведите номер правильного ответа.
В классной библиотеке 100 книг. 16 книг взяли почитать ученики, а остальные книги расставили на 3 полки поровну. Сколько книг на каждой полке?
1) 84кн.; 2) 81кн.; 3) 28кн.; 4) 56кн.
13.Выберите и обведите номера вариантов правильного решения задачи.
В оранжерее посадили 4 ряда тюльпанов, по 12 цветов в каждом ряду и столько же рядов гвоздик, по 15 цветов в каждом ряду. Сколько всего цветов посадили в оранжерее?
1) (12+15)●4 2) 12●4+15●4
3) (4+12)●15 4) 12●4+12●15
14.Запишите решение задачи по действиям с пояснением и ответ.
Мальчик читал книгу 4 дня по 6 страниц в день и 5 дней по 8 страниц в день. Сколько страниц прочитал мальчик за это время? _______________________________________
_______________________________________________
Вариант 1
1. Выполни вычисления:
| 2 * 6 | 16 : 8 | 3 * 7 | 18 : 2 | 5 * 2 |
| 3 * 5 | 14 : 2 | 8 * 3 | 27 : 3 | 3 * 3 |
Решение: 2 * 6 = 12 16 : 8 = 2 3 * 7 = 21 18 : 2 = 9 5 * 2 = 10 3 * 5 = 15 14 : 2 = 7 8 * 3 = 24 27 : 3 = 9 3 * 3 = 9
2. Сравни выражения и поставь знак >, < или = :
| 7 * 3 + 7 () 7 * 5 | 3 * 5 — 5 () 3 * 4 |
Решение: 7 * 3 + 7 < 7 * 5 3 * 5 — 5 < 3 * 4
3. Реши задачу.
За каждым столиком обедает 4 человека. Сколько человек обедает за тремя такими столиками?
Решение:
- Выражение: 3 * 4 = 12
- Ответ: 12
4. Реши задачу.
Нина разложила 16 елочных шаров в коробки, по 8 шаров в каждую. Сколько коробок заняли эти шары?
Решение:
- Выражение: 16 : 8 = 2
- Ответ: 2
5. Реши задачу
Начерти отрезок длиной 8 см. Обозначь его буквами А и В. Поставь на этом отрезке точку С так, чтобы она разделила его на 2 равных отрезка. Запиши длину отрезка АС. Запиши, сколько отрезков стало на чертеже.
Решение:
- 8 : 2 = 4 длина отрезка AC
- На черетеже стало 2 отрезка.
6. Реши задачу
Отрезки АВ и CD имеют равную длину и пересекаются в точке К, которая делит их на 4 отрезка длиной 4 см, 5 см, 6 см и 7 см. Найди длину отрезка АВ.
Решение:
- 5 + 6 = 4 + 7
- Длина отрезка AB = 11 см.
Вариант 2
1. Выполни вычисления:
| 7 * 2 | 18 : 9 | 3 * 8 | 21 : 7 | 4 * 2 |
| 2 * 8 | 12 : 6 | 4 * 3 | 24 : 3 | 3 * 6 |
Решение: 7 * 2 = 14 18 : 9 = 2 3 * 8 = 24 21 : 7 = 3 4 * 2 = 8 2 * 8 = 16 12 : 6 = 2 4 * 3 = 12 24 : 3 = 8 3 * 6 = 18
2. Сравни выражения и поставь знак >, < или = :
| 8 * 4 — 8 () 8 * 3 | 3 * 6 + 6 () 3 * 5 |
Решение: 8 * 4 — 8 = 8 * 3 3 * 6 + 6 > 3 * 5
3. Реши задачу
На каждой из трех тарелок лежит по 6 пирожков. Сколько пирожков на этих трех тарелках?
Решение:
- Выражение: 6 * 3 = 18
- Ответ: 18
4. Реши задачу
Боря разложил 12 фломастеров поровну в 4 коробки. Сколько фломастеров в одной коробке?
Решение:
- Выражение: 12 : 4 = 3
- Ответ: 3
5. Реши задачу
Начерти отрезок длиной 10 см. Обозначь его буквами М и К. Поставь на этом отрезке точку О так, чтобы она разделила его на 2 равных отрезка. Запиши длину отрезка ОК. Запиши, сколько отрезков стало на чертеже.
Решение:
- Выражение: 10 : 2 = 5
- Ответ: Длина отрезка OK = 5 см. Отрезков на чертеже стало 2.
6. Реши задачу
Отрезки МК и AD имеют равную длину и пересекаются в точке О, которая делит их на 4 отрезка длиной 5 см, 6 см, 7 см и 8 см. Найди длину отрезка AD.
Решение:
- 6 + 7 = 5 + 8
- Длина отрезка AD = 13 см.
Вариант 3
1. Выполни вычисления:
| 9 * 2 | 12 : 3 | 3 * 5 | 18 : 3 | 3 * 2 |
| 2 * 7 | 10 : 2 | 9 * 3 | 9 : 3 | 3 * 8 |
Решение: 9 * 2 = 18 12 : 3 = 4 3 * 5 = 15 18 : 3 = 6 3 * 2 = 6 2 * 7 = 14 10 : 2 = 5 9 * 3 = 27 9 : 3 = 3 3 * 8 = 24
2. Сравни выражения и поставь знак >, < или = :
| 6 * 5 — 6 () 6 * 4 | 7 * 2 + 7 () 7 * 4 |
Решение: 6 * 5 — 6 = 6 * 4 7 * 2 + 7 < 7 * 4
3. Реши задачу
Для одного окна сшили 2 занавески. Сколько занавесок сшили для 5 таких окон?
Решение:
- Выражение: 5 * 2 = 10
- Ответ: 10
4. Реши задачу
В 2 пакета разложили 16 яблок, поровну в каждый пакет. Сколько яблок в одном пакете?
Решение:
- Выражение: 16 : 2 = 8
- Ответ: 8
5. Реши задачу
Начерти отрезок длиной 12 см. Обозначь его буквами А и С. Поставь на этом отрезке точку В так, чтобы она разделила его на 2 равных отрезка. Запиши длину отрезка АВ. Запиши, сколько отрезков стало на чертеже.
Решение:
- Выражение: 12 : 2 = 6
- Ответ: Длина отрезка АВ = 6 см. Отрезков на чертеже стало 2.
6. Реши задачу
Отрезки АО и МК имеют равную длину и пересекаются в точке В, которая делит их на 4 отрезка длиной 6 см, 7 см, 8 см и 9 см. Найди длину отрезка МК.
Решение:
- 8 + 7 = 9 + 6
- Длина отрезка AD = 15 см.
Вариант 4
1 Выполни вычисления:
| 9 * 3 | 18 : 2 | 2 * 8 | 15 : 5 | 8 * 2 |
| 3 * 7 | 12 : 4 | 6 * 3 | 12 : 2 | 2 * 4 |
9 * 3 = 27 18 : 2 = 9 2 * 8 = 16 15 : 5 = 3 8 * 2 = 16 3 * 7 = 21 12 : 4 = 3 6 * 3 = 18 12 : 2 = 6 2 * 4 = 8
2. Сравни выражения и поставь знак >, < или = :
| 8 * 3 + 3 () 8 * 4 | 4 * 9 — 4 () 4 * 7 |
Решение: 8 * 3 + 3 > 8 * 4 4 * 9 — 4 > 4 * 7
3. Реши задачу
На каждой из двух полок стоит по 8 чашек. Сколько чашек на этих двух полках?
Решение:
- Выражение: 8 * 2 = 16
- Ответ: 16
4. Реши задачу
На 3 кофточки пришили 12 пуговиц, поровну на каждую кофточку. Сколько пуговиц пришили на одну кофточку?
Решение:
- Выражение: 12 : 3 = 4
- Ответ: 4
5. Реши задачу
Начерти отрезок длиной 6 см. Обозначь его буквами М и Т. Поставь на этом отрезке точку К так, чтобы она разделила его на 2 равных отрезка. Запиши длину отрезка МК. Запиши, сколько отрезков стало на чертеже.
Решение:
- Выражение: 6 : 2 = 3
- Ответ: Длина отрезка МК = 3 см. Отрезков на чертеже стало 2.
6. Реши задачу
Отрезки МС и BD имеют равную длину и пересекаются в точке А, которая делит их на 4 отрезка длиной 7 см, 8 см, 9 см и 10 см. Найди длину отрезка МС.
Решение:
- 10 + 7 = 9 + 8
- Длина отрезка МС = 17 см.
На странице использованы материалы из книги С. И. Волковой «Математика. Контрольные работы. 1-4 классы» 2008г.
Задачи по математике 3 класс.
| Страница | 1, | 2, | 3 |
Задача 1.
Для приготовления обеда повару понадобилось 24 кг картошки, свеклы в 3 раза меньше, а лука в 2 раза меньше чем свеклы. Сколько килограмм лука потратил повар?
Решение:
- 1) 24 : 3 = 8
- 2) 8 : 2 = 4
- Выражение: 24 : 8 : 2 = 4
- Ответ: 4 кг.
Задача 2
Оля вырезала из бумаги 5 квадратов, 7 треугольников, а кругов в 2 раза больше чем треугольников. Сколько всего Оля вырезала фигур?
Решение:
- 1) 7 * 2 = 14
- 2) 5 + 7 + 14 = 26
- Ответ: 26 фигур.
Задача 3
Первое число 12, второе в 3 раза меньше, а третье в 4 раза больше чем второе. Вычисли сумму этих трех чисел.
Решение:
- 1) 12 : 3 = 4 (второе число)
- 2) 4 * 4 = 16 (третье число)
- 3) 12 + 4 = 16 (сумма первого и второго чисел)
- 4) 16 + 16 = 32 (сумма трех чисел)
- Выражение: 12 : 3 * 4 + 4 + 12 = 32
- Ответ: 32
Задача 4
В школьную столовую привезли 6 кг, лимонов, яблок на 24 кг больше чем лимонов, а груш на 12 кг меньше чем яблок. Сколько килограмм груш привезли в школьную столовую?
Решение:
- 1) 6 + 24 = 30 (в столовую привезли яблок)
- 2) 30 — 12 = 18 (привезли груш)
- Выражение: (6 + 24) — 12 = 18
- Ответ: 18 кг груш привезли в столовую.
Задача 5
Для приготовления обеда повару понадобилось 24 кг картошки, свеклы в 3 раза меньше, а лука в 2 раза меньше чем свеклы. Сколько килограмм лука потратил повар?
Решение:
- 1) 24 : 3 = 8 (понадобилось свеклы)
- 2) 8 : 2 = 4 (понадобилось лука)
- Выражение: 24 : 3 : 2 = 4
- Ответ: 4 кг лука понадобилось повару.
Задача 6
Для приготовления крахмала требуется 6 кг картошки. Сколько крахмала получится из 36 кг картофеля?
Решение:
- 1) 36 : 6 = 6
- Ответ: 6 кг крахмала.
Задача 7
В поход пошли 24 мальчика, а девочек в 3 раза меньше, чем мальчиков. Сколько всего детей пошло в поход?
Решение:
- 1) 24 : 3 = 8 (девочек пошло в поход)
- 2) 24 + 8 = 32
- Выражение: 24 : 3 + 8 = 32
- Ответ: 32.
Задача 8
Ящик с виноградом и три одинаковых ящика с яблоками весят 45 кг. Сколько весит один ящик с яблоками, если ящик с виноградом весит 15 кг.
Решение:
- 1) 45 — 15 = 30 (весят 3 ящика с яблоками)
- 2) 30 : 3 = 10 (весит один ящик с яблоками)
- Выражение: (45 — 10) : 3 = 10
- Ответ: 10 кг.
Задача 9
На детской площадке катались дети на двух и трехколесных велосипедах. Сколько и каких велосипедов было на площадке, если всего было 21 колесо и 8 велосипедов?
Решение:
- 1) 8 * 2 = 16 (было бы колес, если бы все велосипеды были двухколесными)
- 2) 21 — 16 = 5
- 2) 8 — 5 = 3
- Ответ: на площадке было 5 трехколесных велосипедов и 3 двухколесных.
Задача 10
В парке выкорчевали 6 орешников, а вместо них посадили 18 орешников. Во сколько раз больше посадили орешников, чем выкорчевали?
Решение:
- 1) 18 : 6 = 3
- Ответ: в 3 раза больше орешников посадили.
Задача 11
Отцу 36 лет, а сыну 9. Во сколько раз отец старше сына и на сколько лет сын моложе отца?
Решение:
- 1) 36 : 9 = 4
- 2) 36 — 9 = 27
- Ответ: в 4 раза сын моложе отца; на 27 лет отец старше сына.
Задача 12
Автобус за 8 часов работы расходует 48 литров топлива. Сколько литров топлива израсходует автобус за 6 часов работы?
Решение:
- 1) 48 : 8 = 6 (литров топлива автобус расходует за 1 час)
- 2) 6 * 6 = 36 (литров автобус расходует за 6 часов)
- Выражение: 48 : 8 * 6 = 36
- Ответ: 36 литров.
Задача 13
В столовую привезли абрикосы. Из них на компот взяли 3 килограмма, а на варенье в 3 раза больше. Сколько всего абрикос привезли в столовую?
Решение:
- 1) 3 * 3 = 9 (взяли абрикос на варенье)
- 2) 3 + 9 = 12 (всего в столовую привезли абрикос)
- Выражение: 3 * 3 + 3 = 9
- Ответ: 9 кг абрикос.
| Страница | 1, | 2, | 3 |
Школьная и занимательная математика
Текстовые, арифметические, геометрические, комбинаторные задачи, доли и дроби — в обычной школьной математике всё это довольно скучно. Возможно ли вообще научить школьника легко, а главное с интересом решать любые математические и нестандартные задачи?
Признаемся, это совсем не просто. Но если выбрать правильный формат занятий, выстроить обучение от простого к сложному, комбинировать типовые и занимательные, олимпиадные задания, — это возможно!
У нас есть всё, что вы искали
Попробуйте полный курс ЛогикЛайк!Создаем атмосферу, которая помогает третьеклассникам:
- увлеченно впитывать новые математические знания;
- с интересом применять и развивать обретенные навыки;
- повысить успеваемость и интерес к математике и обучению.
Популярные категории заданий
Подборки из обучающего курса ЛогикЛайк Увлекательный и эффективный для детей формат — онлайн занятия математикой и логикой на сайте ЛогикЛайк.Тест PCHS по алгебре
 МАТЕМАТИКА Студенты должны пройти все курсы по математике с оценкой C или выше, чтобы перейти на следующий уровень математики. Только классы, пройденные с оценкой C или выше, будут учитываться при удовлетворении требований поступления в колледж.Если
МАТЕМАТИКА Студенты должны пройти все курсы по математике с оценкой C или выше, чтобы перейти на следующий уровень математики. Только классы, пройденные с оценкой C или выше, будут учитываться при удовлетворении требований поступления в колледж.Если
МАТЕМАТИКА МАТЕМАТИКА
 МАТЕМАТИКА МАТЕМАТИКА 1 443 Этот курс подчеркивает развитие арифметических навыков и подчеркивает концепции, а также вычисления.Мастерство развивается с каждой из основных операций.
МАТЕМАТИКА МАТЕМАТИКА 1 443 Этот курс подчеркивает развитие арифметических навыков и подчеркивает концепции, а также вычисления.Мастерство развивается с каждой из основных операций.
Последовательность математических курсов
 Последовательность курсов по этике С чего начать? Ассоциированные степени и непередаваемые курсы (курс математики ниже предалгебры см. В разделе «Навыки обучения» каталога) MATH M09 PRE-ALGEBRA 3 UNITS
Последовательность курсов по этике С чего начать? Ассоциированные степени и непередаваемые курсы (курс математики ниже предалгебры см. В разделе «Навыки обучения» каталога) MATH M09 PRE-ALGEBRA 3 UNITS
Каталог Cabrillo College 2015-2016
 МАТЕМАТИКА Отдел естественных и прикладных наук Ванда Гарнер, Отдел декана Отдела, аудитория 701 Дженнифер Касс, заведующая отделом, (831) 479-6363 Советник Aptos: (831) 479-6274 для назначения Watsonville
МАТЕМАТИКА Отдел естественных и прикладных наук Ванда Гарнер, Отдел декана Отдела, аудитория 701 Дженнифер Касс, заведующая отделом, (831) 479-6363 Советник Aptos: (831) 479-6274 для назначения Watsonville
Массаж Терапия Математика
 Массаж Терапия Математика MT-2701Комплексивные соматические исследования для массажистов 01 семестр Кредитные викторины и пробный экзамен предоставляются для подготовки к экзамену на получение лицензии государственного медицинского совета штата Огайо.Комплексный
Массаж Терапия Математика MT-2701Комплексивные соматические исследования для массажистов 01 семестр Кредитные викторины и пробный экзамен предоставляются для подготовки к экзамену на получение лицензии государственного медицинского совета штата Огайо.Комплексный
РАЗМЕЩЕНИЕ МАТЕМАТИКИ
 МАТЕМАТИЧЕСКОЕ РАЗМЕЩЕНИЕ Должен ли я сдавать экзамен по математике? Студенты не обязаны сдавать вступительный экзамен. Ваше место по математике определяется вашим подкатегорией по математике на ACT или SAT
МАТЕМАТИЧЕСКОЕ РАЗМЕЩЕНИЕ Должен ли я сдавать экзамен по математике? Студенты не обязаны сдавать вступительный экзамен. Ваше место по математике определяется вашим подкатегорией по математике на ACT или SAT
Жизненный опыт
 Базовые знания Precalculus GEOMETRY Успешное завершение курса с оценкой B или выше. Твердое понимание: Теоремы конгруэнции прямоугольных треугольников Базовая тригонометрия Базовое понимание
Базовые знания Precalculus GEOMETRY Успешное завершение курса с оценкой B или выше. Твердое понимание: Теоремы конгруэнции прямоугольных треугольников Базовая тригонометрия Базовое понимание
МАТЕМАТИКА И СТАТИСТИКА
 Область: Математика Декан: Нэнси Рейтц, Временный Телефон: (916) 484-8215 Консультирование: (916) 484-8572 Математика Степень А.S. степень по математике обеспечивает основу математики для студентов в подготовке
Область: Математика Декан: Нэнси Рейтц, Временный Телефон: (916) 484-8215 Консультирование: (916) 484-8572 Математика Степень А.S. степень по математике обеспечивает основу математики для студентов в подготовке
МАТОВСКАЯ РЕКОМЕНДАЦИЯ
 Руководство по математике Рекомендации по математике основаны на результатах вашего трудоустройства, программе получения степени и карьерных интересах. Оценка места: МАТ 001 или МАТ 00 Вы должны пройти необходимую математику
Руководство по математике Рекомендации по математике основаны на результатах вашего трудоустройства, программе получения степени и карьерных интересах. Оценка места: МАТ 001 или МАТ 00 Вы должны пройти необходимую математику
КОЛЛЕДЖ АЛГЕБРА ОБУЧАЮЩАЯ ОБЩИНА
 КОЛЛЕДЖ АЛГЕБРА ОБУЧАЮЩАЯСЯ ОБЩИНА Общественный колледж Талса, Вест Кампус Ведущий Лори Мейберри, Б.СМС. Доцент кафедры математики и физики [email protected] Национальная конференция NACEP
КОЛЛЕДЖ АЛГЕБРА ОБУЧАЮЩАЯСЯ ОБЩИНА Общественный колледж Талса, Вест Кампус Ведущий Лори Мейберри, Б.СМС. Доцент кафедры математики и физики [email protected] Национальная конференция NACEP
Большие идеи в математике
 Большие идеи в математике, которые важны для всего изучения математики. (По материалам NCTM Curriculum Focal Points, 2006) Большие математические идеи организованы с использованием стандартов математики PA
Большие идеи в математике, которые важны для всего изучения математики. (По материалам NCTM Curriculum Focal Points, 2006) Большие математические идеи организованы с использованием стандартов математики PA
Precalculus Ориентация и FAQ
 Precalculus Orientation и FAQ MATH 1011 (Precalculus) — это четырехчасовой 3-кредитный курс, который готовит студента к исчислению.Охватываемые темы включают линейные, квадратичные, полиномиальные, рациональные, экспоненциальные,
Precalculus Orientation и FAQ MATH 1011 (Precalculus) — это четырехчасовой 3-кредитный курс, который готовит студента к исчислению.Охватываемые темы включают линейные, квадратичные, полиномиальные, рациональные, экспоненциальные,
Академические стандарты по математике
 Академические стандарты для классов Pre K High School, Пенсильвания Департамент образования ВВЕДЕНИЕ Основные стандарты Пенсильвании в классах PreK 5 закладывают прочную основу в целых числах, кроме того,
Академические стандарты для классов Pre K High School, Пенсильвания Департамент образования ВВЕДЕНИЕ Основные стандарты Пенсильвании в классах PreK 5 закладывают прочную основу в целых числах, кроме того,
Алгебра I Кредит Восстановление
 Алгебра I Восстановление кредита ОПИСАНИЕ КУРСА: Цель этого курса — дать студенту возможность овладеть навыками работы с математическими выражениями, уравнениями, графиками и другими темами и их оценки,
Алгебра I Восстановление кредита ОПИСАНИЕ КУРСА: Цель этого курса — дать студенту возможность овладеть навыками работы с математическими выражениями, уравнениями, графиками и другими темами и их оценки,
Чего ожидать от компаса
 Что ожидать от компаса Что такое компас? COMPASS — это набор компьютерных адаптивных тестов, созданных программой American College Test (ACT).Поскольку тесты COMPASS являются «адаптивными к компьютеру»,
Что ожидать от компаса Что такое компас? COMPASS — это набор компьютерных адаптивных тестов, созданных программой American College Test (ACT).Поскольку тесты COMPASS являются «адаптивными к компьютеру»,
Математика 1280/1300, Предварительное исчисление
 Math 1280/1300, Pre-Calculus Преподаватель: Офис: Часы работы: Телефон: E-mail: MyMathLab Код курса: Текст и материалы: ISBN: 1269594060 Автор: Blitzer Название: Precalculus, Books a la Carte Edition Package
Math 1280/1300, Pre-Calculus Преподаватель: Офис: Часы работы: Телефон: E-mail: MyMathLab Код курса: Текст и материалы: ISBN: 1269594060 Автор: Blitzer Название: Precalculus, Books a la Carte Edition Package
Perrysburg High School
 Руководство по выбору курса CCareer для старшей школы Perrysburg 2015 2016 Планирование на будущее…. СОДЕРЖАНИЕ Четырехлетний план … 1 Выпускные требования … 2 Диплом с отличием Критерии … 3 Общие
Руководство по выбору курса CCareer для старшей школы Perrysburg 2015 2016 Планирование на будущее…. СОДЕРЖАНИЕ Четырехлетний план … 1 Выпускные требования … 2 Диплом с отличием Критерии … 3 Общие
Краткий обзор математики за апрель
 Аудитория: школьные лидеры, региональные команды Краткий обзор математики за апрель Инструмент «Математика с первого взгляда» был разработан для поддержки школьных лидеров и региональных команд, которые ищут свидетельства соответствия общему
Аудитория: школьные лидеры, региональные команды Краткий обзор математики за апрель Инструмент «Математика с первого взгляда» был разработан для поддержки школьных лидеров и региональных команд, которые ищут свидетельства соответствия общему
Математика 143 — Колледж алгебры (онлайн)
 Математика 143 — Алгебра в колледже (онлайн) 3 кредита Срок: инструктор: весна 2010 г. Кен Флойд (208) 732-6583 Место нахождения офиса: Часы работы: Шилдс 206E 1-2 вечера, M — F E-mail: kfloyd @ csi.10:00 утра — полдень субботы
Математика 143 — Алгебра в колледже (онлайн) 3 кредита Срок: инструктор: весна 2010 г. Кен Флойд (208) 732-6583 Место нахождения офиса: Часы работы: Шилдс 206E 1-2 вечера, M — F E-mail: kfloyd @ csi.10:00 утра — полдень субботы
Колледж Кредит Плюс Двойная запись
 Plus Dual Enrollment Plus Dual Enrollment — это программа, которая дает учащимся старших классов возможность быть зачисленными на работу в средней школе и в колледже одновременно. Студенты, которые имеют академическую квалификацию
Plus Dual Enrollment Plus Dual Enrollment — это программа, которая дает учащимся старших классов возможность быть зачисленными на работу в средней школе и в колледже одновременно. Студенты, которые имеют академическую квалификацию
Математика 131 колледж алгебры осень 2015
 Math 131 College Algebra Fall 2015 Имя преподавателя: Место нахождения офиса: Часы работы: Офис Телефон: E-mail: Описание курса Этот курс содержит минимальный обзор алгебраических навыков, за которым следует исследование
Math 131 College Algebra Fall 2015 Имя преподавателя: Место нахождения офиса: Часы работы: Офис Телефон: E-mail: Описание курса Этот курс содержит минимальный обзор алгебраических навыков, за которым следует исследование
Требуется согласование
 Необходимо приложить необходимое одобрение ГОСУДАРСТВЕННОГО ОБЩЕСТВЕННОГО КОЛЛЕДЖА СИТУАЦИИ Математика КУРС МАТЕМАТИКА МАТЕМАТИКА 148 НАИМЕНОВАНИЕ Промежуточная алгебра I ЭТОТ КУРС КЛАССИФИЦИРУЕТСЯ КАК: ДЕЙСТВУЮЩАЯ УСТАНОВКА ЦЕНЫ
Необходимо приложить необходимое одобрение ГОСУДАРСТВЕННОГО ОБЩЕСТВЕННОГО КОЛЛЕДЖА СИТУАЦИИ Математика КУРС МАТЕМАТИКА МАТЕМАТИКА 148 НАИМЕНОВАНИЕ Промежуточная алгебра I ЭТОТ КУРС КЛАССИФИЦИРУЕТСЯ КАК: ДЕЙСТВУЮЩАЯ УСТАНОВКА ЦЕНЫ
Высшее образование по математике
 Высшая школа Математика Высшее образование. Типы задач оценки размещения 1.Целые числа, дроби и десятичные дроби 1.1 Операции с целыми числами Сложение с переносом Вычитание с заимствованием Умножение
Высшая школа Математика Высшее образование. Типы задач оценки размещения 1.Целые числа, дроби и десятичные дроби 1.1 Операции с целыми числами Сложение с переносом Вычитание с заимствованием Умножение
Бирмингемские Городские Школы
 Занятие 1 Правила и положения в классе Правила и процедуры Учебный план курса / учебный план LTF Занятие: Интервальная запись (Precal) 2 Предварительная оценка 3 и 4 1.2 Функции и их свойства 5 Занятие LTF:
Занятие 1 Правила и положения в классе Правила и процедуры Учебный план курса / учебный план LTF Занятие: Интервальная запись (Precal) 2 Предварительная оценка 3 и 4 1.2 Функции и их свойства 5 Занятие LTF:
Транскрипция
1 Что такое школьная математика? Лиссабон, Португалия, 30 января 2010 г. Х. Ву * Я благодарен Александре Алвес-Родригес за ее большой вклад в формирование этого документа.

2 Немецкий дирижер Герберт фон Караян однажды сказал, что нет вульгарной музыки, только вульгарное исполнение.Я вспоминаю это высказывание Караяна, потому что математики любят говорить, что школьная математика тривиальна. Поэтому позвольте мне перефразировать Караяна, заявив, что нет тривиальной математики, есть только тривиальное математическое изложение. Я расскажу о своем случае, обсудив несколько основных тем из школьной математики с американской точки зрения, и позвольте вам решить, тривиальны они или нет.

3 Давайте начнем с простого длинного деления 587 на 3.Вы знаете алгоритм: Два вопроса: (1) Что это значит? (2) Почему это правильно? Ответ на (1) состоит в том, что если 587 делится на 3, то частное равно 195, а остаток равен 2. Ответ на (2) займет нас в следующие несколько минут.

4 Мы не можем ответить (2) без четкого понимания ответа на (1). Обычное выражение = 195 R 2 не несет никакой информации и также не имеет смысла, поскольку: левая сторона не является числом, а правая сторона также не является числом.Так что же значит сказать, что левая сторона равна правой стороне? Правильный смысл (1): у нас есть деление с остатком, 587 = (195 3) + 2, где 2 <3. Теперь мы должны доказать, что приведенный выше алгоритм приводит к этому уравнению.

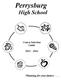
5 Мы анализируем алгоритм длинного деления для каждой цифры частного 195: 5 = (1 3) Тогда: 28 = (9 3)
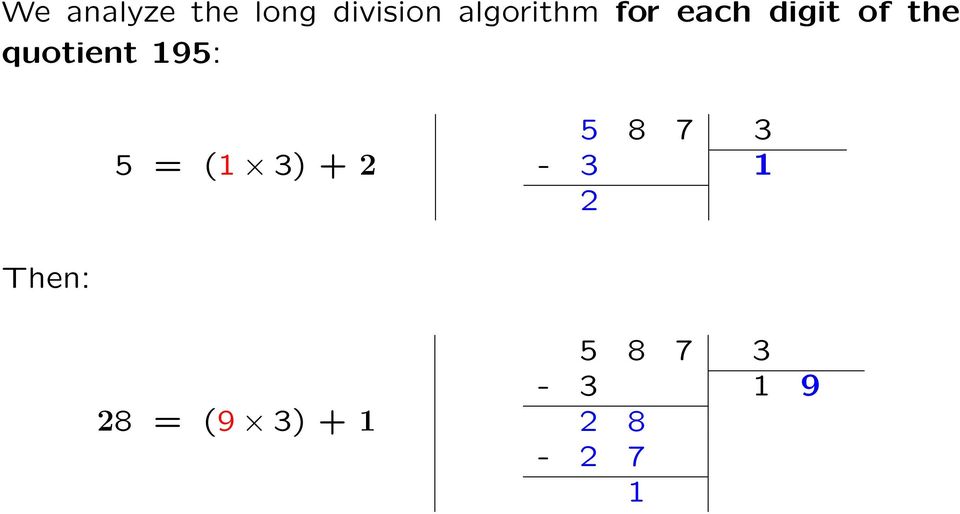
6 И наконец: 17 = (5 3) Таким образом, алгоритм длинного деления представляет собой компактную сводку трех делений с остатком: 5 = (1 3) = (9 3) = (5 3) + 2

7 Вот доказательство того, что 587 = (195 3) + 2: Используя 5 = (1 3) + 2, мы имеем: 587 = (5 100) + (8 10) + 7 = (((1 3) + 2) 100) + (8 10) + 7 = ((1 100) 3) + (28 10) + 7 Используя 28 = (9 3) + 1, получим: 587 = ((1 100) 3) + ( ((9 3) + 1) 10) + 7 = ((1 100) 3) + ((9 10) 3) + 17 Наконец, используя 17 = (5 3) + 2, имеем: 587 = ((1 100) 3) + ((9 10) 3) + (5 3) + 2 = ((1 100) + (9 10) + 5) = (195 3) + 2

8 Это доказательство имеет силу раскрытия фундаментальной идеи, лежащей в основе всех алгоритмов целых чисел: каждый шаг алгоритма включает только одну цифру, когда одна цифра интерпретируется соответствующим образом.Все идет нормально. К сожалению, это сложная математика. Учителя, конечно, должны это знать, но даже пятиклассникам это будет слишком сложно. Чтобы сделать это доказательство пригодным для использования в школьной математике, мы должны максимально упростить его, не жертвуя при этом математической достоверностью объяснения или центральной идеей, что это одна цифра за раз. Следующее является одним из возможных компромиссов.

9 Мы хотим, чтобы целые числа q и r были такими, чтобы 587 = (q 3) + r, где r <3. Число q не может иметь 4 цифры (потому что правая сторона будет превышать левую), поэтому это самое большее 3 цифры число.Его цифра сотен не может быть 2 (опять же, потому что правая сторона будет превышать левую сторону), поэтому его цифра сотен равна 1. Итак, q = T, где T - это двузначное число. Таким образом, что 587 = (100 + T) 3 + r = (T 3) + r = (T 3) + r

10 Теперь 287 = (T 3) + r. Десятичная цифра T может быть равна 9 без какого-либо противоречия (если мы хотим, чтобы r <3, то нам нужно, чтобы T было как можно большим, пока T 3 не превышает 287).Таким образом, T = 90 + S, где S - однозначное число, и, следовательно, 287 = (90 + S) 3 + r = (S 3) + r = (S 3) + r
 .
.11 Наконец, мы имеем 17 = (S 3) + r. Ясно, что мы должны позволить S = 5 и r = 2: 17 = (5 3) Напомним: 587 = (q 3) + r, и мы определили, что цифра сотен, цифра десятков и цифра единиц q равны 1 , 9, 5 соответственно и r = 2. Таким образом, 587 = (195 3) + r

12 Все, что мы до сих пор делали о долгом делении, является частью того, что мы называем школьной математикой.Мы отмечаем, что: (а) Эти соображения не относятся к университетской учебной программе по математике. Они слишком элементарны. (б) Математика не тривиальна. (c) Часть этого обсуждения о снижении уровня математики до уровня пятиклассников выходит за рамки математики как таковой. (d) Обсуждение в (c) не может иметь место без полного понимания математики, лежащей в основе алгоритма длинного деления.

13 Явление, показанное в (a) (d), не является особенным для длинного деления, но разделяется большинством тем школьной математики: (i) преобразование дроби m n из m в n.до десятичной дроби длинным делением (ii) Понятие дроби и всего, что связано с дробями, включая отношение и процент. (iii) Понятие постоянной скорости или постоянной скорости. (iv) Аксиомы и евклидова геометрия.

14 (v) Понятия конгруэнтности и сходства. (vi) Понятие длины и площади, особенно вычисление окружности и площади круга.(vii) Понятие отрицательного числа и всего, что связано с отрицательными числами. (viii) Нахождение максимума или минимума квадратичной функции. (ix) Понятие многочлена и алгебра многочленов.

15 Позвольте мне привести еще одну иллюстрацию явления, показанного в (a) (d), с использованием отрицательных чисел. В Америке наиболее часто задаваемый вопрос в школьной математике: почему отрицательное отрицательное равно положительному? Математики считают это очевидным.Они доказывают нечто более общее: для любых чисел x, y, (x) (y) = xy. Доказательство. Сначала докажем, что (x) z = (xz) для любых x и z. Заметим, что если число A удовлетворяет xy + a = 0, то A = (xy). Но по закону распределения xy + {(x) y} = (x + (x)) y = 0 y = 0, поэтому (x) y = (xy). Пусть теперь z = (y), тогда имеем (x) (y) = (x (y)), который по коммутативному закону равен ((y) x) = ((yx)) = yx = xy. Итак (х) (у) = ху.

16 Университетские математики обычно не понимают, насколько сложен этот простой аргумент.Он не подходит для потребления школьниками. Основное сопротивление принятию отрицательного отрицательного = положительного является психологическим. Если мы сможем объяснить это явление целыми числами (а не дробями), большая часть битвы уже выиграна. Мы дадим относительно простое объяснение того, почему (2) (3) = 2 3. Ключевой шаг заключается в доказательстве (1) (1) = 1

17 Если мы хотим показать, что число равно 1, самый желательный способ — это вычислить его, e.например, если A = 1, потому что A = (12 13) (6 25) 5, A = = 1, но иногда такое прямое вычисление недоступно. Тогда мы должны согласиться на косвенный метод проверки. (Подумайте о том, чтобы окунуть ph-полоску в раствор, чтобы проверить ее на кислотность.) Чтобы проверить, равно ли число A 1, мы спрашиваем: верно ли, что A + (1) = 0? Если так, то мы сделали.

18 Теперь пусть A = (1) (1).Имеем A + (1) = (1) (1) + (1) = (1) (1) + 1 (1) По закону распределения (1) (1) + 1 (1) = ((1 ) + 1) (1) = 0 (1) = 0 Итак, A + (1) = 0, и мы заключаем, что A = 1, т. Е. (1) (1) = 1
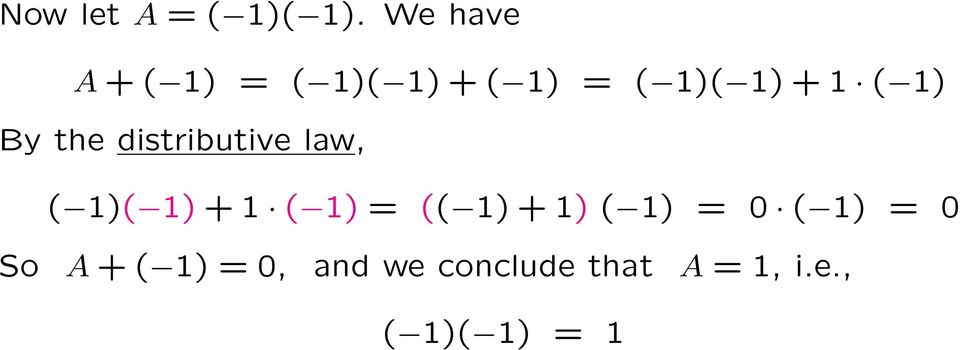
19 Теперь мы можем доказать (2) (3) = 2 3. Сначала покажем (1) (3) = 3. Имеем (1) (3) = (1) ((1) + (1) + ( 1)) который по закону распределения равен (1) (1) + (1) (1) + (1) (1) = = 3 Таким образом (1) (3) = 3.Тогда (2) (3) = ((1) + (1)) (3) = (1) (3) + (1) (3). По тому, что мы только что доказали, последний равен = 2 3. Таким образом, (2) (3) = 2 3. Доказательство (m) (n) = mn для целых чисел m, n аналогично.

20 До сих пор я давал вам кусочки того, что представляет собой школьная математика. Позвольте мне сделать еще один шаг и дать вам более полное представление. Мы знаем, по крайней мере, что это не так: школьная математика — это не университетская математика.Однако, есть еще кое-что. Мы видели, что для того, чтобы сделать математическую тему полезной для школьников, нам нужно сделать дополнительный шаг, чтобы гарантировать, что математическая сущность не будет потеряна. Этот шаг включает в себя больше, чем математические знания; это предполагает знание школьного класса.

21 Мы говорим о том, что школьная математика является продуктом математической инженерии.Что это значит? Инжиниринг: дисциплина адаптации абстрактных научных принципов к процессам и продуктам, которые безопасно реализуют человеческую цель или функцию. Математическая инженерия. Дисциплина превращения абстрактной математики в форму, которую можно правильно преподавать и изучать в классе K 12. Математическая инженерия также известна как математическое образование K 12.
22 Химическое машиностроение: химия из плексигласа в аквариумах, газ, который вы закачиваете в машину, шампунь, лизол… Электротехника: компьютеры с электромагнетизмом, электропитание, iPod, освещение в этом зале, двигатели, … Математическая инженерия: абстрактная математика, школа математики
23 Признание того, что школьная математика является инженерным продуктом, проясняет текущие дебаты по математике образование. Нет никаких противоречий в утверждении, что инженерия не должна пытаться производить что-то, что отвечает человеческим желаниям, но противоречит научным принципам, e.г. вечные двигатели, машины, которые извлекают кислород из воды без использования энергии. Также нет никаких противоречий в утверждении, что инженерия не должна тратить время на создание чего-либо, что не имеет отношения к человеческим потребностям, независимо от того, насколько научно обоснованно.
24 И все же школьная математика когда-то была математически обоснованной, но она явно не относилась к школьной классной комнате: Новая математика 1960-х годов. Введение теории множеств в начальную школу.Чрезмерный акцент на точность (например, различие между числом три и цифрой 3, которая представляет число три). Акцент на абстракции (например, модульная арифметика, числа в произвольных базисах, символическая логика) за счет базовых навыков (вычисления в базе 10).
25 В настоящее время в школьной математике предпринимается слишком много попыток упростить изучение математики, игнорируя основные математические принципы. Рассмотрим предмет дробей в школьной математике.Исследователи в области образования и авторы учебников, похоже, считают, что никакой инженерный процесс не может привести математику дробей в школьный класс. Поэтому их решение состоит в том, чтобы учить дроби не как математике, а как языку, который, возможно, можно выучить с помощью осмоса, слушания историй, использования аналогий и метафор и участия в практических занятиях. В результате страх перед фракциями виден всем.
26 Вот некоторые проблемы, с которыми учат дроби в Америке.Нет определения. Там нет определения фракции (кроме как кусок пиццы). У фракций операторов есть несколько представлений, которые не имеют смысла, потому что, если мы не знаем, что это такое, что там представлять? Также нет определения какой-либо из арифметических операций над дробями: что означает умножение двух кусков пиццы? Нет рассуждений. Аналогии и метафоры заменяют рассуждения. Зачем использовать наименьший общий знаменатель для добавления дробей? Почему бы не добавить дроби так же, как мы умножаем дроби: добавляем числители и знаменатели? Зачем вычислять деление по инвертированию и умножению?
27 Нет согласованности.Это, пожалуй, самая серьезная из трех проблем. Дроби учат как разные числа от целых чисел. Нам говорят, что дети должны принять новые правила для дробей, которые часто противоречат устоявшимся представлениям о целых числах. Более верно: десятичные числа преподаются как отличные числа от дробей. Также нет логической связи между различными понятиями и навыками в рамках предмета дробей. Как ученики могут справиться с такими раздробленными знаниями?
28 Математическая инженерия, когда она грамотно сделана, дает представление о дробях, которое полностью соответствует основным математическим принципам и подходит для учащихся 5-7 классов.Эти инженерные усилия требуют знания школьного класса, а также глубоких математических знаний.
29 Физики и химики давно признали, что практическое применение их теоретических знаний важно и должно рассматриваться как отдельная дисциплина. Школы техники родились. Однако ни математики, ни педагоги, кажется, не признают школьную математику как технический продукт. Каждая группа в конечном итоге производит математику, не относящуюся к школьному классу, или материалы, используемые в классе, но с математической ошибкой.Нам нужна хорошая школьная математика. Нам нужна хорошая математическая инженерия.
30 Более подробное обсуждение математического образования как математической инженерии см. В wu / icmtalk.pdf
.
