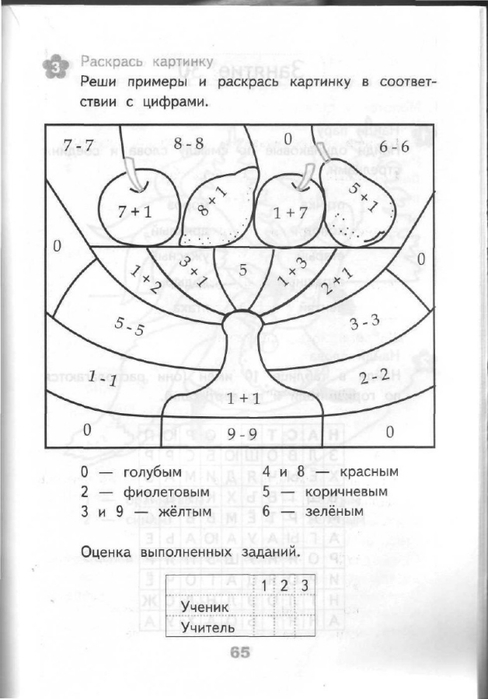
Задания на логику по математике 2 класс: Логические задачи для 2 класса
Логические задачи для 2 класса | Материал по математике (2 класс) на тему:
1. Витя, Саша и Андрей смастерили из бумаги кораблик, змея и аиста. Какую игрушку сделал каждый мальчик, если Витя не сделал кораблика и змея, а Саша не делал кораблик?
_______________________________________________________________________________________
2. Знайка, Кнопочка и Тюбик живут в домах №14, 17, 19. В каком доме живет каждый человек, если Знайка не живет в доме 19 и 17, а Кнопочка не живет в доме 19 ?
______________________________________________________________________________________
3. Володя, Дима и Петя устроили соревнование. Один из мальчиков решил 12 примеров, второй – 13, а третий – 14. Сколько примеров решил каждый мальчик, если Петя решил примеров меньше, чем Дима, а Дима меньше чем Володя ?
________________________________________________________________________________________
4. Сумма двух чисел равна семи, а их разность равна трём.
Найти эти числа.
________________________________________________________________________________________
5. У Алины несколько кукол. Папа подарил ей не день рождения столько же кукол, сколько у неё было. Теперь у Алины 12 кукол. Сколько кукол подарил ей папа? _____________________________________
6. Отца одного гражданина зовут Николай Петрович, а сына – Алексей Владимирович. Как зовут гражданина?
________________________________________________________________________________________
7. Тетрадь дешевле ручки, но дороже карандаша. Что дешевле? ______________________________
8. Ваня живет выше Пети, но ниже Сени, а Коля живет ниже Пети. На каком этаже четырёхэтажного дома живёт каждый из них?
_________________________________________________________________________________________
9. Даша и Маша получили в школе пятёрки: одна – по математике, другая – по чтению. По какому предмету получила пятёрку Даша, если Маша получила эту оценку не по математике ?
________________________________________________________________________________________
10.
Два друга – Федя и Костя – получили в школе двойку и тройку. Федины родители обычно ругают сына за тройки, а привыкшие к тройкам Костины родители ругают его только за двойки. Кому попадет на этот раз, если известно, что Федя не получил тройку ?
_________________________________________________________________________________________
11. В школьном буфете Наташа, Яна и Алёна покупали пирожные – бисквитное с вареньем, бисквитное с кремом и трубочку с кремом. Кто что купил, если каждая девочка съела по одному пирожному, Яна и Алёна любят пирожные с кремом, а Наташа и Алёна купили себе по бисквитному пирожному? ___________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
12.
У трёх подружек – Вики, Ани и Лены – очень красивые куртки – синяя и красная с капюшонами и синяя без капюшона. У кого какая куртка, если Аня и Лена ходят с капюшонами, а у Ани и Вики куртки синего цвета? _____________________________________________________________________________ _________________________________________________________________________________________
13. Вите, Пете и Андрею подарили по видеокассете: одну – с комедией, другую с веселыми мультфильмами, а третью с фантастическим фильмом. Кто что получил в подарок, если известно, что Петя и Витя не любят смотреть мультфильмы, а Андрей и Петя в процессе просмотра хохотали до упаду? __________________________________________________________________________________________________________________________________________________________________________________
14. Три девочки – Таня, Катя и Марина – занимаются в трёх различных кружках – вышивки, танцев и хорового пения. Катя не знакома с девочкой занимающейся танцами.
Таня часто ходит в гости к девочке, занимающейся вышивкой. Подружка Кати — Марина, хочет в следующем году добавить к своим увлечениям занятия пением. Кто из девочек чем занимается?
________________________________________________________________________________________
15. Миша, Коля и Настя решили помочь маме собрать урожай – смородину, крыжовник и вишню. Каждый из них собирал что – то одно. Кто что собирал, если известно, что больше всего было собрано смородины, Миша не собирал крыжовник, а Миша и Коля вдвоём набрали ягод меньше чем Настя ?
__________________________________________________________________________________________________________________________________________________________________________________
Фамилия Имя ____________________________________________________________________________
Задачи на логику 2 класс по математике с ответами
Логические задачи на предположения для 2 класса — с ответами и решением
Логические задачи на метод извлечения
Задачи на логику с использованием методов предположения и метода извлечения с ответами и подробным решением
Логические задачи для юного сыщика — увлекательная книга с заданиями для второклассников и детей постарше
Задачи и задания на логику и математику
]]>Логические задачи на предположения для 2 класса — с ответами и решением
Задача № 1.
Сергей, Игорь, Мишка и Юра играли во дворе в футбол и разбили окно.
— Кто разбил стекло? — спросила тетя Дарья.
— Оконное стекло разбил Юра или Мишка, — ответил Сергей.
— Я оконное стекло не разбивал, — отнекивался Юра.
— Это сделал Мишка, — сказал Игорь.
— Нет, Игорь, ты ошибся, — возразил Мишка.
Кто из ребят разбил оконное стекло, если трое футболистов всегда говорят только правду, а четвертый может и обмануть? Проверь свое внимание и наблюдательность.
Решение и ответ
1) Предположим, что Сергей обманул. Высказывания со соединителем » или » ложно, когда все его части ложны. Поэтому из этого следует, что ни Юра, ни Мишка не разбивали, тогда высказывания Игоря, который, как и все остальные, должен был говорить правду, противоречит тому, что Мишка не разбивал. Поэтому предположение неправильное.
2) Предположим, что обманул Юра, поэтому следует, что он разбил стекло. Учитывая, что высказывания других детей правдивы, а значит и
Игоря.
Мы приходим к тому, что Мишка тоже разбил, что противоречит условию задачи, так как оконное стекло разбил только один из парней.
3) предположим, что Игорь сказал неправду, то есть, Мишка не разбивал оконное стекло. Тогда вторая часть суждения Сергея ошибочна.
Учтя, что оно правильное и имеет союз «или», делаем вывод, что другая его составляющая должна быть истинной. То есть, оконное стекло разбил Юра, и это противоречит правильному суждению Юрки, который утверждает, что он ее не разбивал. Поэтому предположение неправильное.
4) предположим, что неправду сказал Мишка, а значит Игорь не ошибся «Это сделал Мишка». При этом условии суждения и Сергея и
Юрка тоже прав.
Ответ: Мишка разбил оконное стекло.
Задание № 2
Трое друзей — Николай, Олег и Петр во дворе играли в футбол, и один из них случайно разбил мячом оконное стекло. Когда жители квартиры, в которой разбили стекло, спросили, кто это сделал, Николай признался:»это я разбил оконное стекло». Олег сказал:»это не Петр».
Позже выяснилось, что одно из этих утверждений правильное, а одно – ложное. Кто из этих мальчиков разбил оконное стекло?
Решение и ответ:
1) Предположим, что признание Николая правильное, то есть, он разбил стекло. Тогда Олег по условию задачи сказал неправду. Это
означает что оконное стекло разбил Петр, а это противоречит тому, что только один из парней разбил стекло.
2) допустим, Олег сказал правду — оконное стекло не разбил Петр, тогда выражение Николая не является правдой и Николай стекла не разбивал.
Итак, стекло разбил Олег.
Задача № 3
Журналист приехал на аэродром, чтобы пообщаться с пилотом, штурманом и бортинженером одного самолета, фамилии которых — Дубов, Гришко и Солдатенко. Пока журналист разыскивал экипаж, ему пришлось услышать от людей, что:
- Дубов – не пилот;
- Солдатенко – не бортинженер;
- Дубов – бортинженер;
- Солдатенко – не пилот.
Во время беседы с экипажем журналист выяснил, что из четырех суждений соответствует действительности только одно.
каждый член экипажа?
Ответ и решение
1) Предположим, что правильным является суждение первое: «Дубов не пилот», тогда другие суждения неправильные и следует что Солдатенко
бортинженер и Солдатенко пилот. Итак мы пришли к противоречию, ибо каждый член экипажа имеет только одну специальность. Поэтому наше
предположение неверно.
2) Предположим, что правильным является следующее суждение: «Солдатенко не бортинженер», тогда остальные три суждения ошибочны. Это означает, что Дубов – пилот и Солдатенко – пилот. Снова пришли к противоречия.
3) предположим, что правильным является суждение » Дубов бортинженер», тогда аналогично ко второму случаю получаем, что Дубов и Солдатенко являются пилотами.
4) предположим, что является правильным суждение » Солдатенко не пилот», а все остальные неправильные.
Отсюда получаем что: «Дубов – пилот», «Солдатенко – бортинженер», «Гришко – штурман.»
Задача №4
Трех друзей — одноклассников зовут Володя, Слава и Никита.
Кто-то из них потерял дневник. Их другу Вадиму сказали:
- Дневник потерял не Володя.
- Дневник потерял Слава.
Но выяснилось, что одно из этих сообщений правильное, а другое – ложное. Кто же из друзей потерял дневник?
Решение и ответ
В этой задаче надо предполагать возможность, что каждый парень мог потерять свой дневник.
Предположим, что сообщение «дневник потерял не Володя» правильное. Тогда другое суждение ложно, то есть Слава дневника не потерял. Это значит, что его потерял Никита.
Ответ: дневник потерял Никита.
Задача № 5
Во время сбора металлолома Дмитрий, Борис и Богдан нашли большую и тяжелую деталь. Дети начали обсуждать вес детали и из какого она металла.
— Какая там медь, — возразил Борис. — Это самое обычное железо, а весит оно, видимо, килограммов 100.
— Да, это точно не медь, — вмешался в разговор Богдан, — а весит деталь, я полагаю, килограммов 50.
На школьном дворе все сразу выяснилось. Учительница, которая принимала металлолом, сказала:
— Не огорчайтесь, каждый из вас прав только вполовину.
Определи, из какого металла находка и каков ее вес.
Решение и ответ
Для удобства основные суждения можно записать следующим образом:
- Дмитрий: эта штука из чистой меди и весит 30 кг.
- Борис: это железо и весит 100 кг.
- Богдан: это медь и весит 50 кг.
1) Предположим, что в суждении Дмитрия первая часть неправильная, а вторая — правильная. Это означает, что деталь не из чистой
задача наполовину правильная. А это значит, что деталь изготовлена из железа. В этом случае обе части суждения Богдана ложны, а
его ответ, как и других детей, должен быть наполовину правильный. Поэтому наше предположение неверно.
2) Предположим, что в суждении Дмитрия первая часть правильная, а вторая – нет, то есть, деталь из чистой меди и вес ее не 30 кг.
Тогда в суждении Бориса первая часть будет ложной, а значит вторая — истинной.
Из этого следует, что, вес найденного предмета 100 кг. Тогда в утверждении Богдана первая часть будет истинной, а вторая ложной, что соответствует условию задачи.
Ответ: деталь из меди и весит 100 кг.
Задание № 6
Одиннадцатиклассник и Николай, Василий и Сергей –призеры городской математической олимпиады, руководили математическим кружком второклассников. На одном из занятий они предложили детям логическую задачу, которую составил один из них. Второклассникам задача понравилась, и они спросили, кто составил задачу. Ребята ответили так:
Василий : «Сергей задачу не составлял. Задачу составил Николай».
Николай : «Я задачу не составлял. Задачу составил Сергей».
Еще и добавили, что один из них дважды сказал правду, второй- дважды неправду, а третий сказал правду только наполовину. Они предложили малышам самостоятельно определить, кто из них составил задачу.
Определи это и ты.
Ответы и решение
1). Предположим, что Сергей дважды правду сказал. Это означает, что ни Сергей, ни Василий задачу не составляли. Тогда в ответе Василия
2) Допустим, Сергей дважды сказал неправду, то это значит, что задачу составили оба парня: Сергей и Василий, что снова противоречит
условию задачи.
3)Предположим, что Сергей правду сказал только наполовину:
а) пусть, первая часть суждения Сергея правильная, тогда вторая — ложная: это значит, что Василий составлял задачу. Исходя из предположения получаем, что и вторая часть суждения Василия правильная , потому что, первая правильная то и вторая должна быть правильная, то есть, задачу составил Николай. Пришедший в противоречие Николай сочинял задачу и Василий.
б) предположим, что первая часть суждения Сергея – неправильная, то есть, задачу составил Сергей. Тогда, вторая является правильной,
неправильная (дважды неправду сказал). То есть Николай не составлял задачи.
В суждении Николай первая часть тогда будет правильная, то и вторая должно быть правильной (дважды правду сказал). То есть, Сергей составил задачу. В этом случае противоречия не встретили.
Итак, задачи составил Сергей.
Логические задачи на метод извлечения
Задание № 1
Татьяна и Тамара имеют фамилии Иваненко и Сидоренко. Какая фамилия у каждой девочки, если Татьяна живет на одной улице с Сидоренко?
Решение и ответ:
Если Таня живет на одной улице с Сидоренко, то фамилия Сидоренко не Танина, а значит Тамарина, а Татьяна имеет другую из данных двух фамилий: Иваненко.
Задание № 2
Трое друзей: Алексей, Борис и Виктор учатся в одном классе.
Решение и ответ:
Решая задачу, будем заполнять таблицу:
| троллейбус | трамвай | автобус | |
| Алексей | |||
| Борис | |||
| Виктор |
Пользуясь суждением условия задачи «Алексей проводил своего друга до остановки автобуса», делаем вывод, что Алексей автобусом
не ездит, потому что каждый из них ездит разным видом транспорта. Ставим в колонке таблицы «автобус» напротив Алексея прочерк. Если с
троллейбуса третий друг обратился к Борису, это значит, что Алексей шел с Борисом и ни один из них ездит троллейбусом.
Ставим в колонке
«Троллейбус» нашей таблицы прочерки напротив Алексея и Бориса и делаем вывод, что троллейбусом ездит Виктор. Ставим «+» в
колонке «Троллейбус» напротив Виктора, а в других колонках напротив него прочерки.
| троллейбус | трамвай | автобус | |
| Алексей | — | — | |
| Борис | — | ||
| Виктор | + | — | — |
Рассмотрев внимательно таблицу, видим, что Алексей не ездит троллейбусом и автобусом. Так что он ездит трамваем . Отметим это знаком»+». Тогда напротив Бориса в колонке «трамвай» ставим прочерк.
| троллейбус | трамвай | автобус | |
| Алексей | — | + | — |
| Борис | — | — | |
| Виктор | + | — | — |
В таблице отметим, что Борис не ездит ни троллейбусом, ни трамваем.
Это значит, что Борис ездит автобусом.
| троллейбус | трамвай | автобус | |
| Алексей | — | + | — |
| Борис | — | — | + |
| Виктор | + | — | — |
Итак, Алексей ездит трамваем, Борис-автобусом, Виктор – троллейбусом.
Задание № 3
Внимательно прочитай текст и дай точный ответ на вопрос. Кондратенко, Давыдов и Сидоренко живут на одной улице. Один из них работает маляром, второй — плотником, третий — водопроводчиком. Однажды маляр обратился к плотнику, чтобы тот починил дверь в его квартире, но ему сказали, что он помогает Сидоренко ремонтировать пол. Определи профессию каждого, если известно, что водопроводчик никогда не видел Давыдова.
Ответ и решение
Решая задачу, заполним таблицу
| маляр | плотник | водопроводчик | |
| Кондратенко | |||
| Давыдов | |||
| Сидоренко |
Из того, что маляр обратился к плотнику за помощью и плотник сказал, что помогает Сидоренко ремонтировать пол, следует, что Сидоренко
не является маляром и не является плотником.
В таблице напротив Сидоренко в колонках прочерки и делаем вывод, что Сидоренко водопроводчик и это отмечаем знаком «+» в таблице, а напротив Кондратенко и Давыдова в колонке «водопроводчик» ставим прочерки.
| маляр | плотник | водопроводчик | |
| Кондратенко | — | ||
| Давыдов | — | ||
| Сидоренко | — | — | + |
Из того, что водопроводчик никогда не видел Давыдова, означает, что Давыдов не плотник, потому что плотник водопроводчика знает, потому что ему
ремонтирует пол. Итак, ставим в колонке «плотник» напротив Давыдова прочерк.
| маляр | плотник | водопроводчик | |
| Кондратенко | — | ||
| Давыдов | — | — | |
| Сидоренко | — | — | + |
Разглядев таблицу, делаем выводы, что Давыдов не плотник и не водопроводчик, следовательно он маляр и ставим » + » в соответствующей клеточке.
| маляр | плотник | водопроводчик | |
| Кондратенко | — | — | |
| Давыдов | + | — | — |
| Сидоренко | — | — | + |
Если плотником не является Давыдов и Сидоренко то им является Кондратенко. Завершаем заполнение таблицы. Итак, Кондратенко-плотник, Давыдов – маляр, Сидоренко – водопроводчик.
| маляр | плотник | водопроводчик | |
| Кондратенко | — | + | — |
| Давыдов | + | — | — |
| Сидоренко | — | — | + |
Логические задачи на предположение и метод извлечения для 2 класса
Задание № 1
Николай, Саша и Алексей ловили рыбу. Каждый из них поймал разное количество рыб.
Саша и коля поймали вместе 6 рыбин, а Алексей и Николай — 4 рыбины. Сколько Рыбин поймал каждый мальчик?
Задание на предположение.
1. Предположим, что Алексей поймал 1 рыбину, а Николай тогда поймал три (4 – 1 = 3), потому что вместе они поймали 4 рыбины. Из того, что
Саша и коля поймали вместе 6 рыб, следует, что Саша поймал тоже 3 рыбины, а это противоречит тому, что они поймали разное количество
Рыбин. Так что предположение ложное.
2. Предположим, что Алексей поймал 3 рыбины, тогда Николай — 1 рыбу (4 — 3 = 1) . Если Саша с Николаем поймали 6 Рыбин, то Саша поймал 6 – 1 = 5 рыбин.
Задание № 2
Ученики Володя, Саша и Мишка после исполнения контрольной работы сказали:
Володя : «Я написал контрольную на двенадцать баллов».
Саша : «Я написал на десять баллов».
Мишка : «Я написал не на двенадцать».
После проверки выяснилось, что один из мальчиков получил 12 баллов, второй – 11, третий – 10. Какую оценку получил каждый, если известно, что двое из них правильно назвали свою оценку, а один ошибся?
Ответ и решение
Задача на предположение.
Исходим из того, что по условию задачи, один из мальчиков ошибся.
1) Предположим, что ошибся Володя, то есть, он контрольную написал не на 12 баллов. Если Саша написал на 10 баллов контрольную, а Мишка, как и Володя, не на 12 баллов, то мы получили, что ни один из учеников не выполнили контрольную работу на 12 баллов, что противоречит условию задачи.
2) Предположим, что ошибся Саша. Это значит, что Саша написал контрольную не на десять баллов. Если Володя и Мишка сказали правду, то Володя написал контрольную на 12 баллов, из того, что Саша не на 10 баллов написал, следует, что он получил 11 баллов. Тогда Мишка написал контрольную на 10 баллов.
Ответ: Володя – на 12 баллов, Саша – на 11 баллов, Мишка – на 10 баллов.
Задание № 3
В велогонках участвовали пятеро школьников. После завершение соревнований пятеро болельщиков заявили:
— Николай занял первое место, а Иван – четвертое.
— Сергей занял второе место, а Иван – четвертое.
—Сергей занял второе место, а Николай – третье.
— Анатолий занял первое место, а надежда – второе.
— Надежда заняла третье место, а Анатолий – пятое.
Зная, что в заявлениях каждого болельщика одна часть правильная, а вторая – ложная, найди правильное распределение мест.
Эта задача на предположение.
1) Предположим, что первая часть первого утверждения правильная, а вторая ошибочная, то есть Николай занял первое место, а Иван не четвертое. Тогда во втором утверждении вторая часть тоже ложна (ибо она такая же как и вторая часть в первом утверждении). Поэтому первая часть этого суждения должна быть правильной, то есть Сергей занял второе место.
В следующем утверждении первая часть такая же, как и первая в втором утверждении, значит она правильная, тогда вторая часть то есть Николай третьего места не занял. В четвертом суждении: «Анатолий занял первое место, а Надежда-второе», — ни одна из частей не может быть правильной, потому что по предположению первое место занял Николай, а из второго суждения мы сделали вывод, что второе место занял Сергей.
Итак, мы пришли к противоречию, поэтому предположение неправильное.
2) Предположим, что в первом утверждении первая часть ложная, а вторая правильная. Это значит, что Николай не занял первого места, а Иван занял четвертое. Во втором утверждении вторая часть такая как и вторая в первом. Значит она правильная, поэтому первая его часть ложная. Это значит, что Сергей не занял второго места. В третьем утверждении первая часть такая, как и первая во втором, поэтому она ошибочна, значит вторая его часть истинна, то есть Николай занял третье место.
Если Николай занял третье место, то первая часть пятого утверждение: «Надежда заняла третье место, а Анатолий-пятое» — ложная, а значит вторая его часть правильная. То есть Анатолий занял пятое место. Поэтому первая часть четвертого суждения: «Анатолий занял первое место» а Надежда — второе — ложная, а это значит, что вторая егочасть правильная. Итак, Надежда заняла второе место. Осталось не занятым первое место. Поэтому его занял Сергей.
Ответ: первое место – Сергей, второе место – Надежда, третье место – Николай, четвертое место – Иван, пятое место – Анатолий.
Задание № 4
Татьяна, Ирина и Иван живут в одном доме. Каждый из них занимается музыкой: пением, игрой на фортепиано или на скрипке.
Известно, что:
- Ирина живет на том же этаже, что и певец.
- Пианист с Иваном учатся в разных классах.
- Татьяна и певец учатся в одном классе.
Чем занимается каждый из них?
Решение и ответ
Задача на метод извлечения, поэтому удобно решать, заполняя таблицу:
| пение | игра на фортепиано | игра на скрипке | |
| Татьяна | |||
| Ирина | |||
| Иван |
С первого утверждения: «Ирина живет на том же этаже, что и певец » — следует, что Ирина пениями не занимается.
Ставим в колонке
«пение» напротив Ирины прочерк. Из утверждения: «пианист с Иваном учатся в разных классах» – следует, что Иван не является пианистом. Ставим в
таблицы напротив Ивана в колонке «Игра на фортепиано» прочерк. Из следующего утверждения: «Татьяна и певец учатся в одном классе» –
следует, что Татьяна не занимается пением и ставим в таблице напротив нее в колонке «пение» – прочерк.
| пение | игра на фортепиано | игра на скрипке | |
| Татьяна | — | ||
| Ирина | — | ||
| Иван | — |
Осталась в этой колонке одна пустая ячейка напротив Ивана. Это значит, что Иван занимается пением. Ставим знак » + » в этой клеточке, а в другой напротив Ивана — прочерк
| пение | игра на фортепиано | игра на скрипке | |
| Татьяна | — | ||
| Ирина | — | ||
| Иван | + | — |
Возвращаемся снова ко второму и третьему утверждению и делаем вывод, что если Татьяна и певец Иван учатся в одном классе, а пианист с Иваном в разных классах, то Татьяна не является пианистом и ставим прочерк напротив Татьяны в колонке «игра на фортепиано».
| пение | игра на фортепиано | игра на скрипке | |
| Татьяна | — | — | |
| Ирина | — | ||
| Иван | + | — | — |
Тогда в этой колонке осталась пустая клеточка напротив Ирины, то есть она является пианистом и ставим знак » + » в этой ячейке и прочерк напротив Ирины в колонке «Игра на скрипке». Теперь в последней колонке осталась одна пустая клеточка напротив Татьяны. Итак, она играет на скрипке.
| пение | игра на фортепиано | игра на скрипке | |
| Татьяна | — | — | + |
| Ирина | — | + | — |
| Иван | + | — | — |
Ответ: Татьяна – на скрипке, Ирина играет на фортепиано, Иван занимается пением.
Логические задачи для юного сыщика
Эта увлекательная книга поможет ребенку почувствовать себя настоящим детективом и помощь следователю в раскрытии преступлений.
Всего в книге 25 увлекательных задач, которые 2 — классник может решать дома, вместе с родителями. К каждой задаче есть ответ.
Скачать книгу с логическими задачами]]>
Задачи на логику и математику для 2 класса
Математические логические головоломки: Расширение для 2-го класса
Математические логические головоломки для 2-го класса включают в себя 16 головоломок на мышление более высокого порядка, разработанных, чтобы бросить вызов и заинтересовать ваших отличников и быстрых финишеров. Ваши учащиеся будут использовать критическое мышление и навыки решения проблем, создавая при этом четкое понимание основных математических концепций и навыков.
Эти головоломки доступны в формате PDF для печати и в безбумажной версии, созданной с помощью Google Slides™ для виртуального обучения.
Каждое задание напрямую связано с Едиными базовыми стандартами штата по математике.
———————————————— —————————————————
МАТЕМАТИЧЕСКИЕ ПОНЯТИЯ И НАВЫКИ АДРЕС:
• Многозначное сложение и вычитание с перегруппировкой и без нее
• Размещение значения (чтение, запись и сравнение чисел до разряда сотен)
• Свойства сложения (коммутативный, ассоциативный , тождество)
• Пропустить счет в пределах 1000 (2 с, 5 с, 10 с, 100 с)
• Прямоугольные массивы
• Время до ближайших 5 минут
• Деньги (включая долларовые купюры, четверти, десять центов, пятаки и пенни) 9000 3
• Графические изображения
• Дроби как модели площадей (1/4, 1/3, ½, 2/3, ¾)
• Геометрия (идентификация двумерных фигур)
———- ————————————————— ————————————-
ЭТОТ МАТЕРИАЛ ВКЛЮЧАЕТ:
• 16 математических логических головоломок, не требующих подготовки к печати
• Подробный ключ к ответам
• Советы для учителей по выполнению
• Согласование деятельности с CCSS
• Титульный лист для студенческого пакета
— ————————————————— ————————————————————
МАТЕМАТИЧЕСКАЯ ЛОГИКА ЗАГАДКИ ПОДХОДЯТ ДЛЯ:
• Математические центры и станции
• Основные задания
• Доски выбора
• Совместное обучение
• Независимое обогащение или расширение
• Контракты на обучение
• Станции BUILD
——————— ————————————————— —————————
Этот ресурс предназначен для учащихся 2-х классов с высокими способностями.
Вы можете найти логические задачки для 1, 3, 4 и 5 классов ниже:
- Математические логические задачки для 1 класса.
- Математические логические задачки для 3 класса.
- Математические логические задачки для 4 класса.
- Математические логические задачки для 5 класса.
————————————————————- ————————————————— —
Если вам и вашим учащимся нравятся эти занятия, вам также могут понравиться следующие дифференцированные дополнительные занятия:
• Головоломки с цифрами (2-3)
• Головоломки с номерами на доске – 2 класс
• Головоломки с номерами на доске – 3 класс
• Пища для ума! Печатные задания для творческого мышления
• Squiggle Stories: творческое письмо для K-3
————————— ————————————————— ———————
Пожалуйста, свяжитесь со мной, если у вас есть вопросы или отзывы; Я хотел бы услышать от вас!
Кристи
© Кристи Хоу.
Материалы предназначены для личного использования только в одном классе. Для использования в нескольких классах приобретите дополнительные лицензии.
Увлекательные математические занятия и идеи для планов уроков для каждого уровня
Добро пожаловать в центр математических занятий HMH, где вы можете найти увлекательные математические уроки и задания для каждого уровня. Изучите приведенные ниже мероприятия или посетите нашу страницу с полными обучающими ресурсами, чтобы найти еще больше идей для вашего класса и школы.
Наша коллекция математических ресурсов предлагает гораздо больше, чем рабочие листы, чтобы заинтересовать учащихся и отточить их навыки. Он также включает игры, видео, идеи для занятий и практические уроки. Взглянем!
Уроки математики в детском саду
Загрузите эти математические задания для детского сада, чтобы научить своих учеников сложению, числам и счету.
Фасонный стержень
Помогите своим детям в детском саду понять числа и сходство и различие объектов с помощью этих бесплатных загружаемых заданий.
Фасонный стержень
Загрузите эти задания для дошкольников, чтобы научить младших школьников сложению с использованием визуальных представлений.
Фасонный стержень
Посмотреть полный список математических занятий в детском саду.
Уроки математики и занятия для 1–2 классов
Помогите своим детям в 1 классе понять числа через контекст животных.
Фасонный стержень
Расскажите учащимся о различных типах многоугольников в математике, которые можно описать как плоские замкнутые фигуры с тремя или более сторонами.
Фасонный стержень
Использование историй для обучения детей математике — это увлекательный способ изучения математической лексики.
Фасонный стержень
Посмотреть полный список математических заданий для 1–2 классов.
Уроки математики и занятия для 3–5 классов
Помогите учащимся понять информационный текст посредством активного чтения.
Фасонный стержень
Многим ученикам сложно перейти от умножения к делению! Узнайте о делимом, делителе и частном, а также пошаговое объяснение стандартного алгоритма деления.
Ричард Бланкман
Фасонный РедакторС помощью этого задания помогите детям 5-го класса укрепить свои навыки использования операций с целыми числами и отточить навыки измерения.
Фасонный стержень
Посмотреть полный список математических заданий для 3–5 классов.
Уроки математики и занятия для 6–8 классов
Загрузите уроки финансовой грамотности для 6–8 классов, чтобы научить учащихся таким темам, как заработная плата, оклады и карьера.
Фасонный стержень
Линейное уравнение с двумя переменными описывает отношение, в котором значение одной из переменных зависит от значения другой переменной.
Фасонный стержень
Загрузите эти бесплатные математические задания для учащихся, чтобы научить их рассчитывать вовлеченность как реальных, так и вымышленных пользователей Instagram.
Элли Змиески
Младший архитектор по обучению, математика
Посмотреть полный список математических заданий для 6–8 классов.
Уроки математики и занятия для 9–12 классов
Помогите учащимся приобрести навыки в области геометрической вероятности, описания данных, отображения данных и матриц.
Фасонный стержень
Изучите основные идеи о том, что такое булева алгебра, а также немного истории и примеров, а также бесплатное задание для старшеклассников, чтобы попрактиковаться в вычислении логических логических выражений.
Фернандо Х. Кастильо
Скачать уроки математики для старшеклассников, посвященные вероятности, взаимоисключающим и перекрывающимся событиям, а также распознаванию независимых и зависимых событий.
Фасонный стержень
Посмотреть полный список математических заданий для 9–12 классов.
***
Ознакомьтесь с нашими бесплатными учебными ресурсами для всех классов и всех предметов.
Мероприятия и уроки Математика 1-2 классы 3-5 классы PreK-K 6-8 классы 9 класс-12
Похожие материалыДженнифер Корухо
Фасон Редактор