Правила по математике для 2 класса: Основные правила по математике во 2 классе

Материал по математике (2 класс) по теме: Правила по математике 2 класс

	Вопрос	Правило	Пример
1	Компоненты сложения:	Слагаемое + слагаемое = сумма	2 + 3 = 5
2	Как найти неизвестное слагаемое?	Чтобы найти неизвестное слагаемое надо из суммы вычесть известное слагаемое	? + 3 = 5 5 – 3 = 2
3	Компоненты вычитания	Уменьшаемое – вычитаемое = разность	7 – 4 = 3
4	Как найти уменьшаемое?	Чтобы найти уменьшаемое надо к разности прибавить вычитаемое.	? – 4 = 3 4 + 3 = 7
5	Как найти неизвестное вычитаемое?	Чтобы найти вычитаемое надо из уменьшаемого вычесть разность	7 — ? = 3 7 – 3 = 4
6	Как узнать, на сколько одно число больше или меньше другого?	Чтобы узнать, на сколько одно число больше или меньше другого надо из большего вычесть меньшее.	На сколько 8 больше 5? 8 – 5 = 3
7	Как уменьшить число?	Уменьшить — действие вычитание	Уменьши 9 на 3 9 – 3 = 6
8	Как увеличить число?	Увеличить – действие сложение	Увеличь 2 на 6 2 + 6 = 8
9	Однозначные числа	Числа, которые записывают одной цифрой называют однозначными (содержат только разряд единиц)	2, 3, 6. 8
10	Двузначные числа	Числа, которые записывают двумя цифрами называют двузначными. (содержат разряд десятков и разряд единиц)	24 = 2 десятка 4 единицы 38 = 3 десятка 8 единиц 50 = 5 десятков 0 единиц
11	Какие числа называют круглыми?	У круглых двузначных чисел в разряде единиц записывают 0	10, 20, 30, 40, 50, 60, 70, 80, 90
12	Как к двузначному числу прибавить двузначное число?	Чтобы сложить двузначные числа надо к десяткам прибавить десятки, к единицам — единицы	23 + 35 = 58 2 дес + 3 дес = 5 дес 3 ед + 5 ед = 8 ед 5 дес 8 ед = 58
13	Как из двузначного числа вычесть двузначное число?	Чтобы вычесть из двузначного числа двузначное число надо из десятков вычесть десятки, из единиц — единицы	32 — 21 = 11 3 дес — 2 дес = 1 дес 2 ед — 1 ед = 1 ед 1 дес 1 ед = 11

Методическая разработка по математике (2 класс) на тему: Правила. 2 класс

Вопрос	Правило	Пример
Компоненты сложения:	Слагаемое + слагаемое = сумма	2 + 3 = 5
Как найти неизвестное слагаемое?	Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое	? + 3 = 5 5 — 3 = 2
Переместительное свойство сложения	От перестановки слагаемых сумма не меняется.	a + b= b + a
Сочетательное свойство сложение	Чтобы к сумме двух чисел прибавить третье число, можно к первому числу прибавить сумму второго и третьего числа.	(a + b) + c = a + (b + c)
Вычитание суммы из числа	Чтобы вычесть суммы из числа, можно сначала вычесть одно слагаемое, а потом другое.	а – (b + c) = (a – c) — b
Вычитание числа из суммы	Чтобы вычесть число из суммы, можно вычесть его из одного слагаемого и прибавить второе слагаемое.	(a + b) – c = f + (b – c)
Компоненты вычитания	Уменьшаемое – вычитаемое = разность	7 – 4 = 3
Как найти уменьшаемое?	Чтобы найти уменьшаемое, надо к разности прибавить вычитаемое.	? – 4 = 3 4 + 3 = 7
Как найти неизвестное вычитаемое?	Чтобы найти вычитаемое, надо из уменьшаемого вычесть разность.	7 — ? = 3 7 – 3 = 4
Как узнать, на сколько одно число больше или меньше другого?	Чтобы узнать, на сколько одно число больше или меньше другого, надо из большего вычесть меньшее.	На сколько 8 больше 5? 8 – 5 = 3
Однозначные числа	Числа, которые записывают одной цифрой называют однозначными (содержат только разряд единиц)	2, 3, 6. 8
Двузначные числа	Числа, которые записывают двумя цифрами называют двузначными. (содержат разряд десятков и разряд единиц)	24 = 2 десятка 4 единицы 38 = 3 десятка 8 единиц 50 = 5 десятков 0 единиц
Трёхзначные числа	Числа, которые записывают тремя цифрами называют трехзначными. (содержат разряд сотен, разряд десятков и разряд единиц)	723 = 7 сотен 2 десятка 3 единицы 100 = 1 сотня о десятков о единиц
Какие числа называют круглыми?	У круглых двузначных и трехзначных чисел в разряде единиц записывают 0	10, 20, 30, 40, 50, 600
Как к двузначному числу прибавить двузначное число?	Чтобы сложить двузначные числа надо к десяткам прибавить десятки, к единицам — единицы	23 + 35 = 58 2 дес + 3 дес = 5 дес 3 ед + 5 ед = 8 ед 5 дес 8 ед = 58
Как из двузначного числа вычесть двузначное число?	Чтобы вычесть из двузначного числа двузначное число надо из десятков вычесть десятки, из единиц — единицы	32 — 21 = 11 3 дес — 2 дес = 1 дес 2 ед — 1 ед = 1 ед 1 дес 1 ед = 11
Как к трехзначному числу прибавить трехзначное число?	Чтобы сложить трехзначные числа надо к сотням прибавить сотни, к десяткам прибавить десятки, к единицам — единицы	123 + 135 = 258 1 сот + 1 сот = 2 сот 2 дес + 3 дес = 5 дес 3 ед + 5 ед = 8 ед 2 сот 5 дес 8 ед = 158
Как из трехзначного числа вычесть трехзначное число?	Чтобы вычесть из трехзначного числа трехзначное число, надо из сотен вычесть сотни, из десятков вычесть десятки, из единиц — единицы	132 — 121 = 11 1 сот- 1 сот = 0 сот 3 дес — 2 дес = 1 дес 2 ед — 1 ед = 1 ед 1 дес 1 ед = 11
Как найти часть?	Чтобы найти часть, надо из целого вычесть известную часть.	76 – 12 = 64
Как найти целое?	Чтобы найти целое, надо части сложить.	12 + 64 = 76
Что называют разностью?	Разностью называют то, на сколько одно число больше или меньше другого.	12
Как найти разность?	Чтобы найти разность, надо из большего числа вычесть меньшее.	12 23 – 12 = 11
Что называют умножением?	Умножение – это сложение одинаковых слагаемых.	5 + 5 + 5 + 5…
Как называются компоненты умножения?	Множитель ∙ множитель = произведение	а ∙ b = с
Переместительное свойство умножения	От перестановки множителей произведение не изменяется.	а ∙ b = b ∙ а
Взаимосвязь компонентов умножения	При увеличении множителей произведение увеличивается. При уменьшении множителей произведение уменьшается.	2 ∙ 3 = 6 3 ∙ 4 = 12 1 ∙ 2 = 2
Что называют делением?	Деление – это действие, обратное умножению.	а ∙ b = с с : а = б с : б = а
Название компонентов деления	Делимое : делитель = частное	с : а = б
Особые случаи умножения	При умножении любого числа на 0 получится 0. При умножении любого числа на 1 получится то же самое число.	2 ∙ 0 = 0 2 ∙ 1 = 2
Особые случаи деления	При делении числа на себя получается 1. При делении числа на 1 получается то же самое число. При делении нуля на любое число, получится 0. Делить на 0 нельзя!	2 : 2 = 1 2 : 1 = 2 0 : а = 0
Четные числа	Числа, которые делятся на 2, называют четными.	2, 4, 6, 8, 10…
Нечетные числа	Числа, которые не делятся на 2, называют нечетными.	1, 3, 5, 7, 9, 11…
Как найти неизвестный множитель?	Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.	а ∙ ? = с с : а = б ? ∙ b = с с : б = а
Увеличение и уменьшение на несколько единиц	Увеличить число на а единиц значит прибавить а единиц. Уменьшить число на а единиц – вычесть а единиц.	с + а с — а
Увеличение и уменьшение в несколько раз	Увеличить число в а раз значит умножить его на а. Уменьшить число в а раз – разделить его на а.	с ∙ а с : а
Порядок действий	1. В выражении со скобками первым выполняется действие в скобках. 2. В выражении со скобками вторым выполняется деление или умножение. 3. Последним выполняется действие сложение или вычитание. Все действия выполняются слева направо!	4 2 1 5 3 с – d · (b – а) + m : n
Кратное	Кратное чисел а и б– это число с, которое делится на а и б.	12 : 2 12 : 6 12 – кратное чисел 2 и 6.
Делитель	Делитель – это число (а или б), на которое делится с.	12 : 2 12 : 6 2 и 6 делители числа 12.
Уравнение	Уравнение – это равенство с неизвестным компонентом.	23 + х = 41
Что значит решить уравнение?	Решить уравнение – значит найти значение неизвестного компонента (корня).	х = ?
Прямоугольник	Четырехугольник, у которого все углы прямые, называют прямоугольником.
Квадрат	Квадрат – это прямоугольник, у которого все стороны равны.
Длина прямоугольника	Противоположные стороны у прямоугольника равны. Большая сторона называется длиной.
Ширина прямоугольника	Меньшая сторона прямоугольника называется шириной.
Мерка	Мерка – это единица измерения величин.	м, см, кг, г, л, ч….
Величина	Величина – это такое свойство предметов, которое можно измерить и результаты измерений выразить числом.	длина, масса, ёмкость, время, площадь
Периметр	Периметр прямоугольника – это сумма длин всех его сторон.	P = a + a + b + b
Площадь	Площадь – это часть плоскости, которую занимает геометрическая фигура.
Площадь прямоугольника	Площадь прямоугольника равняется произведению его длины и ширины.	S = a ∙ b
Как найти сторону прямоугольника?	Чтобы найти длину одной стороны прямоугольника, надо площадь разделить на длину известной стороны.	а = S : b b = S : а
Виды углов	Острый (меньше прямого угла), прямой, тупой(больше прямого угла).

Учебно-методический материал по математике (2 класс) на тему: Основные правила по математике 2 класс

	Вопрос	Правило	Пример
1	Компоненты сложения (как называются числа при сложении):	Слагаемое + слагаемое = сумма	2 + 3 = 5
2	Как найти неизвестное слагаемое?	Чтобы найти неизвестное слагаемое надо из суммы вычесть известное слагаемое	? + 3 = 5 5 – 3 = 2
3	Компоненты вычитания (как называются числа при вычитании):	Уменьшаемое – вычитаемое = разность	7 – 4 = 3
4	Как найти уменьшаемое?	Чтобы найти уменьшаемое надо к разности прибавить вычитаемое.	? – 4 = 3 4 + 3 = 7
5	Как найти неизвестное вычитаемое?	Чтобы найти вычитаемое надо из уменьшаемого вычесть разность	7 — ? = 3 7 – 3 = 4
6	Как узнать, на сколько одно число больше или меньше другого?	Чтобы узнать, на сколько одно число больше или меньше другого надо из большего вычесть меньшее.	На сколько 8 больше 5? 8 – 5 = 3
7	Как уменьшить число?	Уменьшить — действие вычитание	Уменьши 9 на 3 9 – 3 = 6
8	Как увеличить число?	Увеличить – действие сложение	Увеличь 2 на 6 2 + 6 = 8
9	Однозначные числа	Числа, которые записывают одной цифрой, называют однозначными (содержат только разряд единиц).	2, 3, 6. 8
10	Двузначные числа	Числа, которые записывают двумя цифрами, называют двузначными. (содержат разряд десятков и разряд единиц)	24 = 2 десятка 4 единицы 50 = 5 десятков 0 единиц
11	Какие числа называют круглыми?	У круглых двузначных чисел в разряде единиц записывают 0	10, 20, 30, 40, 50, 60, 70, 80, 90
12	Как к двузначному числу прибавить двузначное число?	Чтобы сложить двузначные числа надо к десяткам прибавить десятки, к единицам — единицы	23 + 35 = 58 2 дес + 3 дес = 5 дес 3 ед + 5 ед = 8 ед 5 дес 8 ед = 58
13	Как из двузначного числа вычесть двузначное число?	Чтобы вычесть из двузначного числа двузначное число надо из десятков вычесть десятки, из единиц — единицы	32 — 21 = 11 3 дес — 2 дес = 1 дес 2 ед — 1 ед = 1 ед 1 дес 1 ед = 11

Материал по математике (2 класс) на тему: Памятка по математике 2-4 класс

Выбор действия:

Название компонентов действий:

сумма

1 слагаемое + 2 слагаемое = Сумма

разность

Уменьшаемое – вычитаемое = разность

произведение

1 множитель · 2 множитель= Произведение

частное

Делимое : делитель = частное

на 3 больше

Формулы:

на 3 меньше

Площадь прямоугольника

S = a · b

в 3 раза больше

Длина прямоугольника

a = S : b

в 3 раза меньше

Ширина прямоугольника

b = S : a

На сколько > или ?

Периметр прямоугольника

P=a+a+b+b

P=a· 2+b ·2

P =(a+b) ·2

Во сколько раз > или ?

Приведение к единице

ВСЕГО

Периметр квадрата

Р = а · 4

ПО…

Или · или :

Длина прямоугольника по известному периметру и ширине

a=(Р-b-b):2

Правила нахождения неизвестных компонентов

Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое х + 5 = 6

Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность 9 – х = 4

Чтобы найти неизвестное уменьшаемое, надо к вычитаемому прибавить разность х – 7 = 5

Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель х · 3 = 12

Чтобы найти неизвестное делимое, надо делитель умножить на частное х : 3 = 2

Чтобы найти неизвестный делитель, надо делимое разделить на частное 8 : х = 2

Выбор действия:

Название компонентов действий:

сумма

1 слагаемое + 2 слагаемое = Сумма

разность

Уменьшаемое – вычитаемое = разность

произведение

1 множитель · 2 множитель= Произведение

частное

Делимое : делитель = частное

на 3 больше

Формулы:

на 3 меньше

Площадь прямоугольника

S = a · b

в 3 раза больше

Длина прямоугольника

a = S : b

в 3 раза меньше

Ширина прямоугольника

b = S : a

На сколько > или ?

Периметр прямоугольника

P=a+a+b+b

P=a· 2+b ·2

P =(a+b) ·2

Во сколько раз > или ?

Приведение к единице

ВСЕГО

Периметр квадрата

Р = а · 4

ПО…

Или · или :

Длина прямоугольника по известному периметру и ширине

a=(Р-b-b):2

Правила нахождения неизвестных компонентов

Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое х + 5 = 6

Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность 9 – х = 4

Чтобы найти неизвестное уменьшаемое, надо к вычитаемому прибавить разность х – 7 = 5

Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель х · 3 = 12

Чтобы найти неизвестное делимое, надо делитель умножить на частное х : 3 = 2

Чтобы найти неизвестный делитель, надо делимое разделить на частное 8 : х = 2

Единицы измерения длины

Единицы измерения площади:

1 см = 10 мм

1 дм = 10 см

1 м = 10 дм

1 м = 10 дм = 100 см

1 км = 1.000 м

1 м2 = 10 дм · 10 дм = 100 дм2

1 м 2 = 100 см ·100 см = 10.000 см2

1 дм2 = 10 см ·10 см = 100 см2

1 дм2 = 100мм · 100мм= 10.000мм2

Единицы измерения массы

Единицы измерения времени

1 кг = 1.000 г

1 тонна = 1.000 кг

1 центнер = 100 кг

1 час = 60 минут

1 минута = 60 секунд

1 сутки = 24 часа

Части слова:
1. Окончание – это изменяемая часть слова	◻
2. Корень-это общая часть родственных слов	∩
3. Приставка — стоит перед корнем и служит для образования новых родственных слов	¬
4. Суффикс — стоит после корня и служит для образования новых родственных слов	˄

Содержание

Сборник «Правил по математике» 2 класс

ПРАВИЛА ПО МАТЕМАТИКЕ 2 класс

Вопрос

Правило

Пример

Компоненты сложения:

Слагаемое + слагаемое = сумма

2 + 3 = 5

Как найти неизвестное слагаемое?

Чтобы найти неизвестное слагаемое надо

из суммы вычесть известное слагаемое

? + 3 = 5

5 – 3 = 2

Компоненты

вычитания

Уменьшаемое – вычитаемое = разность

7 – 4 = 3

Как найти уменьшаемое?

Чтобы найти уменьшаемое надо

к разности прибавить вычитаемое.

? – 4 = 3

4 + 3 = 7

Как найти неизвестное вычитаемое?

Чтобы найти вычитаемое надо

из уменьшаемого вычесть разность

7 — ? = 3

7 – 3 = 4

Как узнать, на сколько одно число больше или меньше другого?

Чтобы узнать, на сколько одно число больше или меньше другого надо из большего вычесть меньшее.

На сколько 8 больше 5?

8 – 5 = 3

Как уменьшить число?

Уменьшить — действие вычитание

Уменьши 9 на 3

9 – 3 = 6

Как увеличить число?

Увеличить – действие сложение

Увеличь 2 на 6

2 + 6 = 8

Однозначные числа

Числа, которые записывают одной цифрой называют однозначными (содержат только разряд единиц)

2, 3, 6. 8

Двузначные числа

Числа, которые записывают двумя цифрами

называют двузначными.

(содержат разряд десятков и разряд единиц)

24 = 2 десятка 4 единицы

38 = 3 десятка 8 единиц

50 = 5 десятков 0 единиц

Какие числа называют круглыми?

У круглых двузначных чисел в разряде единиц

записывают 0

10, 20, 30, 40, 50, 60, 70, 80, 90

Как к двузначному числу прибавить двузначное число?

Чтобы сложить двузначные числа надо

к десяткам прибавить десятки, к единицам — единицы

23 + 35 = 58

2 дес + 3 дес = 5 дес

3 ед + 5 ед = 8 ед

5 дес 8 ед = 58

Как из двузначного числа вычесть двузначное число?

Чтобы вычесть из двузначного числа двузначное число надо

из десятков вычесть десятки, из единиц — единицы

32 — 21 = 11

3 дес — 2 дес = 1 дес

2 ед — 1 ед = 1 ед

1 дес 1 ед = 11

Основные правила по математике во 2 классе

ПРАВИЛА ПО МАТЕМАТИКЕ 2 класс

Вопрос
Правило
Пример

Компоненты сложения:
Слагаемое + слагаемое = сумма

2 + 3 = 5

Как найти неизвестное слагаемое?
Чтобы найти неизвестное слагаемое, надо
из суммы вычесть известное слагаемое

? + 3 = 5
5 — 3 = 2

Переместительное свойство сложения
От перестановки слагаемых сумма не меняется.
a + b= b + a

Сочетательное свойство сложение
Чтобы к сумме двух чисел прибавить третье число, можно к первому числу прибавить сумму второго и третьего числа.
(a + b) + c = a + (b + c)

Вычитание суммы из числа
Чтобы вычесть суммы из числа, можно сначала вычесть одно слагаемое, а потом другое.
а – (b + c) = (a – c) — b

Вычитание числа из суммы
Чтобы вычесть число из суммы, можно вычесть его из одного слагаемого и прибавить второе слагаемое.
(a + b) – c = f + (b – c)

Компоненты
вычитания
Уменьшаемое – вычитаемое = разность
7 – 4 = 3

Как найти уменьшаемое?
Чтобы найти уменьшаемое, надо
к разности прибавить вычитаемое.
? – 4 = 3
4 + 3 = 7

Как найти неизвестное вычитаемое?
Чтобы найти вычитаемое, надо
из уменьшаемого вычесть разность.
7 — ? = 3
7 – 3 = 4

Как узнать, на сколько одно число больше или меньше другого?

Чтобы узнать, на сколько одно число больше или меньше другого, надо из большего вычесть меньшее.

На сколько 8 больше 5?
8 – 5 = 3

Однозначные числа
Числа, которые записывают одной цифрой называют однозначными (содержат только разряд единиц)
2, 3, 6. 8

Двузначные числа
Числа, которые записывают двумя цифрами
называют двузначными.
(содержат разряд десятков и разряд единиц)
24 = 2 десятка 4 единицы
38 = 3 десятка 8 единиц
50 = 5 десятков 0 единиц

Трёхзначные числа
Числа, которые записывают тремя цифрами
называют трехзначными.
(содержат разряд сотен, разряд десятков и разряд единиц)
723 = 7 сотен 2 десятка 3 единицы
100 = 1 сотня о десятков о единиц

Какие числа называют круглыми?
У круглых двузначных и трехзначных чисел в разряде единиц записывают 0
10, 20, 30, 40, 50, 600

Как к двузначному числу прибавить двузначное число?
Чтобы сложить двузначные числа надо
к десяткам прибавить десятки, к единицам — единицы
23 + 35 = 58
2 дес + 3 дес = 5 дес
3 ед + 5 ед = 8 ед
5 дес 8 ед = 58

Как из двузначного числа вычесть двузначное число?
Чтобы вычесть из двузначного числа двузначное число надо
из десятков вычесть десятки, из единиц — единицы
32 — 21 = 11
3 дес — 2 дес = 1 дес
2 ед — 1 ед = 1 ед
1 дес 1 ед = 11

Как к трехзначному числу прибавить трехзначное число?
Чтобы сложить трехзначные числа надо
к сотням прибавить сотни, к десяткам прибавить десятки, к единицам — единицы
123 + 135 = 258
1 сот + 1 сот = 2 сот
2 дес + 3 дес = 5 дес
3 ед + 5 ед = 8 ед
2 сот 5 дес 8 ед = 158

Как из трехзначного числа вычесть трехзначное число?
Чтобы вычесть из трехзначного числа трехзначное число, надо
из сотен вычесть сотни, из десятков вычесть десятки, из единиц — единицы
132 — 121 = 11
1 сот- 1 сот = 0 сот
3 дес — 2 дес = 1 дес
2 ед — 1 ед = 1 ед
1 дес 1 ед = 11

Как найти часть?
Чтобы найти часть, надо из целого вычесть известную часть.
76 – 12 = 64

Как найти целое?
Чтобы найти целое, надо части сложить.
12 + 64 = 76

Что называют разностью?
Разностью называют то, на сколько одн

Учебно-методический материал по математике (2 класс) на тему: Математика. 2 класс. Правила. Часть 1.

По теме: методические разработки, презентации и конспекты

Урок математики. 1 класс (2 часть). Тема: Части фигур» УМК «Школа 2100»

На данном уроке учащиеся практически знакомятся с понятиями «Часть», «Целое». На основе этих понятий учатся составлять выражения на раскрытие конкретных арифметических действий….

Игровое занятие по правилам дорожного движения для ГПД 1 класса «Правила дорожного движения — часть Таблицы Уважения»

Занятие по ПДД проходит в игровой форме. Герои инсценировки Светофор и Автоинспектор вместе с ребятами учат Торопыжку правилам дорожного движения (сигналы светофора, дорожные знаки)….

Математика. 2 класс. Правила. Часть 2.

Правила для повторения материала за 2 класс по математике. Программа «Школа 2100″….

Математика. 2 класс. Правила. Часть 3.

Правила для повторения материала за 2 класс по математике. Программа «Школа 2100″….

Урок математики по теме «Единицы объёма: кубический сантиметр, кубический дециметр, литр «Гармония» автор учебника Н.Б. Истомина «Математика» 4 класс (2 часть)

Урок математики по теме «Единицы объёма. Куб». УМК «Гармония» автор учебника Н.Б.Истомина «Математика» 4 класс (2 часть)…

Обобщение правил написания мягкого знака на конце существительных после шипящих (УМК «Перспектива», 4 класс 2 часть)

Цель: создать условия для систематизации и обобщения знаний и умений по написанию мягкого знака на конце слов после шипящих….

Правило. Части речи. Русский язык.

Правила по русскому языку: части речи ( сущ, прил, гл.)…

для печати второй класс (класс 2) тесты по математике, рабочие листы и мероприятия

Распечатать наш второй класс (класс 2) математика рабочие листы и действия, или администрируйте их как онлайн-тесты. Наши рабочие листы используют разнообразные высококачественные изображения, и некоторые из них соответствуют общим базовым стандартам.

Рабочие листы с маркировкой доступны только подписчикам Help Teaching Pro. Станьте подписчиком, чтобы получить доступ к сотням рабочих листов, соответствующих стандартам.

Дополнение

Арифметические и Числовые Понятия

Подсчет

элементарная математика

Геометрия и измерения

Графики

Деньги

Место Стоимость

Shapes

Статистика и вероятность

Вычитание

Время

Проблемы со словами

© Уведомление об авторских правах: Все листы содержат защищенные авторским правом работы и предназначены для использования отдельными учителями, репетиторами и родителями.Рабочие листы и / или вопросы не могут быть воспроизведены или распространены любым способом за пределами HelpTeaching.com, независимо от предполагаемого использования, без явное разрешение.

,
Таблицы испытаний на делимость | Правила делимости от 2 до 12
Самый быстрый способ точного деления любого числа — использовать простые приемы, называемые правилами делимости. Овладейте искусством деления длинных чисел в один миг с помощью этого набора печатных рабочих листов по тестам делимости для детей от 3-го до 6-го класса. Он содержит таблицу правил делимости для делителей 2-12 и адекватные упражнения для применения этих правил, включающие одиночные и множественные делители. Проверьте навыки с рабочими листами ревизии.Начните с наших бесплатных листов!

Диаграмма правил делимости — от 2 до 12
Приучите детей к этой удобной таблице, чтобы ознакомить их с правилами делимости для делителей в диапазоне от 2 до 12. Запомните эти правила на практике и делите числа, как профи.

Правило делимости на 2
Выясните, делится ли каждое заданное число на 2. Обратите внимание на число, если место его единиц имеет четное число, 0, 2, 4, 6 или 8, затем пометьте его как «делимое» и, если число нечетное, напишите «не делится».

Правило делимости на 3
Специально касаясь применения правила делимости для 3, каждый лист здесь содержит 20 дивидендов. Сложите цифры каждого числа и разделите сумму на 3. Если сумма делится на 3, то число делится на 3.

Правило делимости на 4
Проверьте, делятся ли числа на 4, путем деления последних 2 цифр числа на 4. Пометьте число как «делимое» или «не делимое» на основе остатка, в этой подборке рабочих таблиц теста делимости pdf для класса 4 и 5 класс.

Правило делимости на 5
Число делится на 5? Изучите место в единицах, если число оканчивается на 0 или 5, оно делится на 5, если оно имеет любое другое число, то 5 не является множителем данного числа.

Правило делимости на 6
Попросите детей проанализировать, является ли число в месте в единицах четным и сумма цифр делится на 3, чтобы определить числа, делимые на 6, и соответствующим образом обозначить их.

Правило делимости на 7
Поддержите навыки тестирования чисел на делимость на 7. Удвойте последнюю цифру и вычтите ее из остальной части числа, если разница равна 7, то число делится на 7.

Правило делимости на 8
Получите оптимальную практику с этим набором печатных рабочих листов на тесте делимости 8. Соблюдайте последние три цифры, если они делятся на 8, то доказано, что 8 является фактором числа.

Правило делимости на 9
Определите, какое из чисел делится на 9. Сложите все цифры числа и разделите сумму на 9. Если она делится равномерно, не оставляя остатка, то число делится на 9.

Правило делимости на 10
Этот кластер PDF-таблиц 3-го и 4-го классов содержит простейшие правила делимости. Найдите числа, оканчивающиеся на ноль, и сделайте вывод, что числа делятся на 10.

Правило делимости на 11
Быстрый способ проверить число, делимое на 11, — это сложение чисел в четных и нечетных местах и вычитание двух сумм. Если разность кратна 11, то делимость на 11 доказана.

Правило делимости на 12
Простой способ определить, является ли данное число делимым на 12, состоит в том, чтобы проверить, делится ли число на взаимно простые числа 3 и 4. Примените правила и напишите, какое из чисел делится на 12.

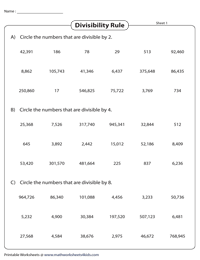
Тесты делимости на 2, 4 и 8
Повторите правила делимости 2, 4 и 8. Обведите все числа, кратные 2 в части A, 4 в части B и 8 в части C. Наилучшим образом оценивает полученные знания.

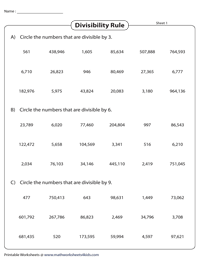
Тесты делимости на 3, 6 и 9
Вспомните правила делимости 3, 6 и 9, чтобы заполнить эти печатные листы. Часть А требует идентификации чисел, кратных 3, Часть В настаивает на выборе чисел, кратных 6, а Часть С — 9.

Тест делимости | Смешанный Обзор | Да / Нет
Проверьте, делятся ли числа на три указанных делителя. Примените соответствующие правила делимости и ответьте «Да» или «Нет», чтобы выполнить это упражнение для детей 5 и 6 классов. Подтвердите понятие делимости в процессе.

Тесты на делимость от 2 до 10 | Смешанный Обзор | Стол
Проверьте, делятся ли числа, указанные в крайнем левом столбце таблицы, на делители 2-10, присутствующие в первом ряду.Примените правила делимости, чтобы быстро прийти к ответу и установить правильные флажки.
,
2-й класс математические игры, интерактивные онлайн-занятия для детей, чтобы практиковать
Добавление чисел игра

Игра чисел для 2-го класса — Игра змей и лестниц
Сложные словесные игры

Дополнительное словесное задание для 2-го класса — Игра змей и лестниц
Сравнение и заказ игры

Игра сравнения и заказа для 2-го класса — Игра змей и лестница
Игра
четных и нечетных чисел

Игра четных и нечетных чисел для 2-го класса — Игра змей и лестниц
Игра
Умножение

Игра умножения для 2-го класса — Игра змей и лестница
Умножение с кратным десяти игры

Умножение на игру, кратную десяти, для 2-го класса — Лестницы и змеи
Пропустить считая двойки, десятки, десятки, игра

Пропустить счет игры по две десятки для 2-го класса — Игра змей и лестница
Вычитание чисел игра

Вычитание чисел для 2-го класса — Змеи и лестница
Игра
вычитание слов проблемы

Слово вычитания, проба
.
экспонентов: основные правила | Purplemath
Purplemath
Экспоненты — это сокращение для повторного умножения одного и того же. Например, сокращение для умножения трех копий числа 5 показано справа от знака «равно» в (5) (5) (5) = 5 ³. «Показатель степени», равный 3 в этом примере, означает, сколько раз умножается значение.То, что умножается, будучи 5 в этом примере, называется «основанием».
Этот процесс использования показателей называется «возведением в степень», где показатель — это «сила». Выражение «5 ³» произносится как «пять, возведенных в третью степень» или «пять в третье».
MathHelp.ком

Существуют две специально названные силы: «второй степени» обычно произносится как «квадрат», а «третьей степени» обычно произносится как «куб». Таким образом, «5 ³» обычно произносится как «пять кубов».
Когда мы имеем дело с числами, мы обычно просто упрощаем; мы предпочли бы иметь дело с «27», чем с «3 ³». Но с переменными нам нужны показатели, потому что мы бы скорее имели дело с « x ⁶», чем с « x‍x‍x‍x‍x‍x ».
Экспоненты
имеют несколько правил, которые мы можем использовать для упрощения выражений.
Чтобы упростить это, я могу думать о том, что означают эти показатели.«К третьему» означает «умножение трех копий», а «к четвертому» означает «умножение четырех копий». Используя этот факт, я могу «расширить» два фактора и затем вернуться к упрощенной форме. Во-первых, я расширяюсь:
( x ³) ( x ⁴) = ( x‍x‍x ) ( x‍x‍x‍x )
Теперь я могу убрать скобки и сложить все факторы:
( x‍x‍x ) ( x‍x‍x‍x ) = x‍x‍x‍x‍x‍x‍x
Это семь копий переменной.«Умножение семи копий» означает «до седьмой степени», поэтому это можно переформулировать как:
x‍x‍x‍x‍x‍x‍x = x ⁷
Собрав все вместе, выполните следующие действия:
( x ³) ( x ⁴) = ( x‍x‍x ) ( x‍x‍x‍x )
= x‍x‍x‍x‍x‍x‍x
= x ⁷
Тогда упрощенная форма ( x ³) ( x ⁴) составляет:
Обратите внимание, что x ⁷ также равно x ^{(3 + 4)}.Это демонстрирует первое основное правило экспоненты:
Каждый раз, когда вы умножаете два термина на одну и ту же базу, вы можете добавлять экспоненты:
( x ^м) ( x ⁿ) = x ^{(m + n)}
Однако, мы НЕ можем упростить ( x ⁴) ( y ³), потому что основания разные: ( x ⁴) ( y ³) = x‍x‍x‍xyyy = ( х ⁴) ( х ³).Ничто не объединяет.
Упростить ( a ⁵ b ³) ( a b ⁷).
Теперь, когда я знаю правило (а именно, что я могу добавить полномочия на одну и ту же базу), я могу начать с перемещения баз, чтобы получить все те же базы рядом друг с другом:
( a ⁵ b ³) ( a b ⁷) = ( a ⁵) ( a ) ( b ³) ( b ⁷)
Теперь я хочу добавить силы на , и на .Тем не менее, второй , кажется, не имеет силы. Что мне добавить на этот срок?
Все, что не имеет силы, в техническом смысле «возносится к власти 1». Все, что касается степени 1, — это просто само по себе, поскольку оно «умножает одну копию» самого себя. Таким образом, приведенное выше выражение можно переписать так:
( a ⁵) ( a ) ( b ³) ( b ⁷) = ( a ⁵) ( a ¹) ( b) ³) ( b ⁷)
Теперь я могу объединить:
( a ⁵) ( a ¹) ( b ³) ( b ⁷) = a ^{5 + 1} b ^{3 + 7} = a ⁶ b ¹⁰
Сложив все это, моя ручная работа будет выглядеть так:
( a ⁵ b ³) ( a b ⁷) = ( a ⁵ a ¹) ( b ³ b) ⁷) =
В следующем примере есть две силы, одна из которых в некотором смысле находится внутри другой.
Чтобы сделать упрощение, я могу начать с размышлений о значениях показателей. «Четвертый» на внешней стороне означает, что я умножаю четыре копии любой базы в скобках. В этом случае основание четвертой степени составляет x ². Умножение четырех копий этой базы дает мне:
Каждый фактор в вышеупомянутом расширении — это «умножение двух копий» переменной.Это расширяется как:
( x ²) ( x ²) ( x ²) ( x ²) = ( x 900 x) ( x 9009) ( x ) ( x ) ( x 900 x)
Сняв скобки, я получаю:
( x 900 x) ( x ) ( x ) ( x ) = xxxxxxxxxxxxx
Это строка из восьми копий переменной.«Умножение восьми копий» означает «до восьмой степени», то есть
x‍x‍x‍x‍x‍x‍x‍x = x ⁸
Собираем все вместе:
( x ²) ⁴ = ( x ²) ( x ²) ( x ²) ( x ²)
= ( x 900 x) ( x ) ( x ) ( x )
= x‍x‍x‍x‍x‍x‍x‍x
= x ⁸
Обратите внимание, что ( x ²) ⁴ = x ⁸ и что 2 × 4 = 8.Это демонстрирует второе правило экспоненты:
Когда у вас есть выражение степени, возведенное в степень, вы можете упростить, умножив внешнюю силу на внутреннюю мощность:
Если у вас есть продукт в скобках, а в скобках — питание, то питание включается для каждого элемента внутри. Например:
( xy ²) ³ = ( xy ²) ( xy ²) ( xy ²)
= ( x‍x‍x ) ( y ² y ² y ²)
= ( x‍x‍x ) ( ггггг )
= x ³ y ⁶
= ( x ) ³ ( y ²) ³
Другой пример будет:
Предупреждение. Это правило НЕ работает, если в скобках указана сумма или разница.Экспоненты, в отличие от умножения, НЕ «распределяют» по сложению.
Например, учитывая (3 + 4) ², НЕ поддавайтесь искушению сказать: « Эй, это равно 3 ² + 4 ² = 9 + 16 = 25 », потому что это неправильно. На самом деле, (3 + 4) ² = (7) ² = 49, а не 25.
В случае сомнений выпишите выражение в соответствии с определением силы. Например, учитывая ( x — 2) ², не пытайтесь делать это в своей голове.Вместо этого запишите это; «Квадрат» означает «умножение двух копий», поэтому:
( x — 2) ² = ( x — 2) ( x — 2)
= x ( x — 2) — 2 ( x — 2)
= xx — 2 x — 2 x + 4
= x ² — 4 x + 4.
Ошибка ошибочной попытки «распределить» показатель степени чаще всего совершается, когда студент пытается сделать все, что у него в голове, вместо того, чтобы показывать свою работу.Делайте вещи аккуратно, и вы не будете так склонны совершать эту ошибку.
Теперь, когда я знаю правило о полномочиях на полномочия, я могу провести 4 по каждому из факторов внутри. (Мне нужно помнить, что с c , внутри скобок, это «в степень 1».)
( a ²) ⁴ ( b ³) ⁴ ( c ¹) ⁴
= ( a ^{2 × 4}) ( b ^{3 × 4}) ( c ^{1 × 4})
= a ⁸ b ¹² c ⁴
Партнерская

Есть еще одно правило, которое может или не может быть охвачено в вашем классе на этом этапе:
Все, что для нулевой степени — это просто «1» (если «все» не равно нулю).
Это правило объяснено на следующей странице. На практике, однако, это правило означает, что некоторые упражнения могут быть намного проще, чем они могут показаться на первый взгляд:
Упростить [(3 x ⁴ y ⁷ z ¹²) ⁵ (–5 x ⁹ y ³ z ⁴) 9000 2 ] ⁰
Кого это волнует в квадратных скобках? Я уверен, что нет, потому что нулевая мощность на внешней стороне означает, что значение всего этого всего 1.Ха!
[(3 x ⁴ y ⁷ z ¹²) ⁵ (–5 x ⁹ y ³ z ⁴) ²] ⁰ = 1
Кстати, как только ваш класс преодолеет «нулевую мощность», вы должны ожидать упражнения, подобного приведенному выше в следующем тесте.Это распространенный вопрос, предназначенный для того, чтобы вы тратили большую часть своего ограниченного времени, но он работает, только если вы не обращаете внимания.
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в упрощении выражений с экспонентами. Попробуйте введенное упражнение или введите собственное упражнение. Затем нажмите кнопку, чтобы сравнить свой ответ с Mathway. (Или пропустите виджет и продолжите урок, или просмотрите множество проработанных примеров здесь.)
Нажмите здесь, чтобы перейти на сайт Mathway, если вы хотите проверить их программное обеспечение или получить дополнительную информацию.
URL: https://www.purplemath.com/modules/exponent.htm
,