Степенная функция с натуральным показателем ее свойства и график 10 класс – Степенная функция, её свойства и график.
План-конспект урока по алгебре (10 класс) на тему: урок по теме:»Степенная функция,её свойства и график.»
По теме: методические разработки, презентации и конспекты
Обобщающий урок по теме «Тригонометрические функции, их свойства и графики».Используемые технологии: дифференцированного обучения, критического мышления, коммуникативного общения, развивающее обучение. …
Интегрированный урок по алгебре и началам анализа и информатике по теме «Показательная функция, ее свойства и график. Создание моделей графиков функций в среде программирования Visual Basic» (11 класс «А»)Применение интеграции в учебном процессе как способа развития аналитических и творческих способностей….
Интегрированный урок алгебры и русского языка по теме «Степенные функции, их свойства и графики».Задачи урока: 1. Научить оперировать имеющимся потенциалом знаний по теме «Степенные функции» в конкретной ситуации. 2. Учить практически применять функциональные стили речи на уроках математики. …
Методическая разработка урока по теме: «Показательная функция, ее свойства и графикПредставлен ход урока, презентация,, лист контроля учета учащихся, конспкт, графики в Excel…
Методическая разработка урока по теме «Показательная функция, её свойства и график»Материал содержит подробный конспект урока в 10 классе по теме «показательная функция, её свойства и график» и презентацию по этой теме. …
Разработка урока по теме «Показательная функция, ее свойства и график»Материал для урока по математике в системе НПО — СПО для 1 курса. Создан план-конспект урока + презентация….
Методическая разработка урока в 10 классе по теме «Степенная функция, ее свойства и график»Методическая разработка урока повторения, обобщения и систематизации знаний по теме «Степенная функция, ее свойства и график» в свете новых стандартов. Представлено полное описание хода уро…
nsportal.ru
3.3.4 Степенная функция с натуральным показателем, её график
Видеоурок: Степенная функция и ее свойства и графикЛекция: Степенная функция с натуральным показателем, её график
Мы постоянно имеем дело с функциями, в которых аргумент имеет некоторую степень:
у = х1, у = х2, у = х3, у = х-1 и т.д.
Графики степенных функций
Итак, сейчас мы рассмотрим несколько возможных случаев степенной функции.
1) у = х2n.
Это означает, что сейчас мы будем рассматривать функции, в которых показатель степени является четным числом.
Характеристика функции:
1. В качестве области значения принимаются все действительные числа.
2. Функция может принимать все положительные значения и число нуль.
3. Функция является четной, поскольку не зависит от знака аргумента, а зависит только от его модуля.
4. Для положительного аргумента функция возрастает, а для отрицательного — убывает.
Графики данных функций напоминают параболу. Например, ниже представлен график функции у = х4.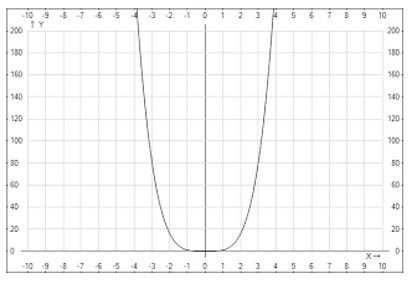
2) Функция имеет нечетный показатель степени: у = х2n+1.
1. Область определения функции — все множество действительных чисел.
2. Область значения функции — может принимать вид любого действительного числа.
3. Данная функция нечетная.
4. Монотонно возрастает на всем промежутке рассмотрения функции.
5. График всех степенных функций с нечетным показателем степени идентичен функции у = х3.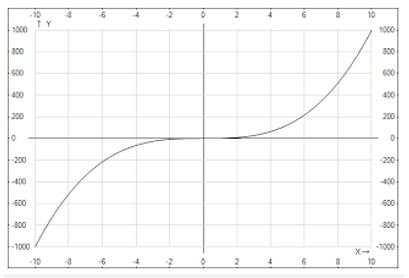
3) Функция имеет четный отрицательный натуральный показатель: у = х-2n.
Все мы знаем, что отрицательный показатель степени позволяет опустить степень в знаменатель и менять знак показателя степени, то есть получится вид у = 1/х2n.
1. Аргумент данной функции может принимать любые значения, кроме нуля, поскольку переменная стоит в знаменателе.
2. Так как показатель степени — четное число, то функция не может принимать отрицательные значения. А раз аргумент не может быть равен нулю, то следует исключить и значение функции, равное нулю. Это значит, что функция может принимать только положительные значения.
3. Данная функция является четной.
4. При отрицательном аргументе функция монотонно возрастает, а при положительном — убывает.
Вид графика функции у = х-2: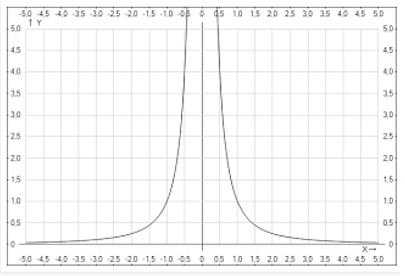
4) Функция с отрицательным нечетным показателем степени у = х-(2n+1).
1. Данная функция существует при всех значениях аргумента, кроме числа нуль.
2. Функция принимает все действительные значения, кроме числа нуль.
3. Данная функция является нечетной.
4. На двух рассматриваемых промежутках убывает.
Рассмотрим пример графика функции с отрицательным нечетным показателем степени на примере у = х-3.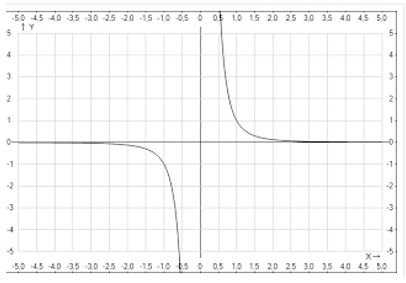
cknow.ru
Степенная функция
Для удобства рассмотрения степенной функции будем рассматривать 4 отдельных случая: степенная функция с натуральным показателем, степенная функция с целым показателем, степенная функция с рациональным показателем и степенная функция с иррациональным показателем.
Степенная функция с натуральным показателем
Для начала введем понятие степени с натуральным показателем.
Определение 1
Степенью действительного числа $a$ с натуральным показателем $n$ называется число, равное произведению $n$ множителей, каждый из которых равняется числу $a$.
Рисунок 1.
$a$ — основание степени.
$n$ — показатель степени.
Рассмотрим теперь степенную функцию с натуральным показателем, её свойства и график.
Определение 2
$f\left(x\right)=x^n$ ($n\in N)$ называется степенной функцией с натуральным показателем.
Для дальнейшего удобства рассмотрим отдельно степенную функцию с четным показателем $f\left(x\right)=x^{2n}$ и степенную функцию с нечетным показателем $f\left(x\right)=x^{2n-1}$ ($n\in N)$.
Свойства степенной функции с натуральным четным показателем
Область определения — все действительные числа.
$f\left(-x\right)={(-x)}^{2n}=x^{2n}=f(x)$ — функция четна.
$f(x)$ — непрерывна на всей области определения.
Область значения — $[0,+\infty )$.
$f'(x)=\left(x^{2n}\right)’=2n\cdot x^{2n-1}$
\[2n\cdot x^{2n-1}=0\] \[x=0\]Функция убывает, при $x\in (-\infty ,0)$ и возрастает, при $x\in (0,+\infty )$.
$f(x)\ge 0$ на всей области определения
$f{»}\left(x\right)={\left(2n\cdot x^{2n-1}\right)}’=2n(2n-1)\cdot x^{2(n-1)}\ge 0$
Функция выпукла на всей области определения.
Поведение на концах области определения:
\[{\mathop{lim}_{x\to -\infty } x^{2n}\ }=+\infty \] \[{\mathop{lim}_{x\to +\infty } x^{2n}\ }=+\infty \]График (рис. 2).
Рисунок 2. График функции $f\left(x\right)=x^{2n}$
Свойства степенной функции с натуральным нечетным показателем
Область определения — все действительные числа.
$f\left(-x\right)={(-x)}^{2n-1}={-x}^{2n}=-f(x)$ — функция нечетна.
$f(x)$ — непрерывна на всей области определения.
Область значения — все действительные числа.
$f’\left(x\right)=\left(x^{2n-1}\right)’=(2n-1)\cdot x^{2(n-1)}\ge 0$
Функция возрастает на всей области определения.
$f\left(x\right)0$, при $x\in (0,+\infty )$.
$f{»\left(x\right)}={\left(\left(2n-1\right)\cdot x^{2\left(n-1\right)}\right)}’=2\left(2n-1\right)(n-1)\cdot x^{2n-3}$
\[2\left(2n-1\right)\left(n-1\right)\cdot x^{2n-3}=0\] \[x=0\]Функция вогнута, при $x\in (-\infty ,0)$ и выпукла, при $x\in (0,+\infty )$.
График (рис. 3).
Рисунок 3. График функции $f\left(x\right)=x^{2n-1}$
Степенная функция с целым показателем
Для начала введем понятие степени с целым показателем.
Определение 3
Степень действительного числа $a$ c целым показателем $n$ определяется формулой:
Рисунок 4.
Рассмотрим теперь степенную функцию с целым показателем, её свойства и график.
Определение 4
$f\left(x\right)=x^n$ ($n\in Z)$ называется степенной функцией с целым показателем.
Если степень больше нуля, то мы приходим к случаю степенной функции с натуральным показателем. Его мы уже рассмотрели выше. При $n=0$ мы получим линейную функцию $y=1$. Её рассмотрение оставим читателю. Осталось рассмотреть свойства степенной функции с отрицательным целым показателем
Свойства степенной функции с отрицательным целым показателем
Область определения — $\left(-\infty ,0\right)(0,+\infty )$.
Если показатель четный, то функция четна, если нечетный, то функция нечетна.
$f(x)$ — непрерывна на всей области определения.
Область значения:
Если показатель четный, то $(0,+\infty )$, если нечетный, то $\left(-\infty ,0\right)(0,+\infty )$.
При нечетном показателе функция убывает, при $x\in \left(-\infty ,0\right)(0,+\infty )$. При четном показателе функция убывает при $x\in (0,+\infty )$. и возрастает, при $x\in \left(-\infty ,0\right)$.
$f(x)\ge 0$ на всей области определения
График (рис. 4).
Степенная функция с рациональным и иррациональным показателем
Определение 5
Степень действительного числа $a$ c рациональным показателем $n$ определяется формулой:
\[a^r=\sqrt[n]{a^m}\]Определение 6
$f\left(x\right)=x^r$ ($r\in Q)$ называется степенной функцией с рациональным показателем.
Определение 7
Степень положительного числа $a$ c иррациональным показателем $\alpha $ называется выражение вида $a^{\alpha }$, значение которого равно пределу последовательности $a^{{\alpha }_0},\ a^{{\alpha }_1},\ a^{{\alpha }_2},\dots $, где ${\alpha }_0,\ {\alpha }_1,{\alpha }_2$ последовательные десятичные приближения иррационального числа $\alpha $.
Определение 8
$f\left(x\right)=x^r$ ($r\in J)$ называется степенной функцией с иррациональным показателем.
Приведем графики степенных функций с рациональным и иррациональным показателем (рис. 5). Рассмотреть, аналогично, свойства этих функции оставим читателю.
Рисунок 6. График функции $f\left(x\right)=x^r$
spravochnick.ru
| 1. |
Формула степенной функции
Сложность: лёгкое |
1 |
| 2. |
График степенной функции (чётный/отрицательный показатель степени)
Сложность: лёгкое |
1 |
| 3. |
Вычисление значеня функции по значению аргумента (целое число)
Сложность: лёгкое |
2 |
| 4. |
Формула функции
Сложность: лёгкое |
2 |
| 5. |
График степенной функции (нечётный/положительный показатель степени)
Сложность: лёгкое |
1 |
| 6. |
Вычисление значения функции по значению аргумента (обыкновенная дробь)
Сложность: лёгкое |
2 |
| 7. |
Построение графика функции корня n-й степени
Сложность: лёгкое |
2 |
| 8. |
График функции корня n-й степени (нечётная степень)
Сложность: лёгкое |
2 |
| 9. |
График функции корня n-й степени (чётная степень)
Сложность: лёгкое |
2 |
| 10. |
Область определения, значений степенной функции
Сложность: среднее | 2 |
| 11. |
Показатель степенной функции
Сложность: среднее |
2 |
| 12. |
График функции вида y=k/x+a
Сложность: среднее |
3 |
| 13. |
График функции вида y=k/(x+a)
Сложность: среднее |
3 |
| 14. |
График функции вида y=1/(x+a)+b
Сложность: среднее |
3 |
| 15. |
Чётность степенной функции (отрицательный показатель степени)
Сложность: среднее |
3 |
| 16. |
Монотонность степенной функции (отрицательный показатель степени)
|
3 |
| 17. |
Наименьшее и наибольшее значения функции (показатель степени больше единицы)
Сложность: среднее |
4 |
| 18. |
Монотонность степенной функции (положительный показатель степени)
Сложность: среднее |
3 |
| 19. |
Чётность степенной функции (положительный показатель степени)
Сложность: среднее |
3 |
| 20. |
Наименьшее и наиболшее значения функции (показатель степени меньше единицы)
Сложность: среднее |
4 |
| 21. |
График функции корня n-й степени вида y=f(x+m)+k
Сложность: среднее |
3 |
| 22. |
График функции, область определения и область значений функции
Сложность: среднее |
4 |
| 23. |
Точки пересечения графиков (чётная степень)
Сложность: среднее |
4 |
| 24. |
Точки пересечения графиков (нечётная степень)
Сложность: среднее |
4 |
| 25. |
Решение уравнения графически (чётная степень)
Сложность: среднее |
5 |
| 26. |
Построение графика степенной функции (положительный показатель степени меньший единицы)
Сложность: сложное |
3 |
| 27. |
Построение графика степенной функции (положительный показатель степени больший единицы)
Сложность: сложное |
3 |
www.yaklass.ru
[Билет 32] Степень с целым показателем. Степенная функция с натуральным и целым показателями, свойства и графики.
Вы знакомы с функциями y=x, y=x2, y=x3, y=1/x и т. д. Все эти функции являются частными случаями степенной функции, т. е. функции y=xp, где p — заданное действительное число.Свойства и график степенной функции существенно зависит от свойств степени с действительным показателем, и в частности от того, при каких значениях x и p имеет смысл степень xp. Перейдем к подобному рассмотрению различных случаев в зависимости от
показателя степени p.
- Показатель p=2n -четное натуральное число.
свойствами:
- область определения — все действительные числа, т. е. множество R;
- множество значений — неотрицательные числа, т. е. y больше или равно 0;
- функция y=x2n четная, так как x2n=(-x)2n
- функция является убывающей на промежутке x<0 и возрастающей на промежуткеx>0.
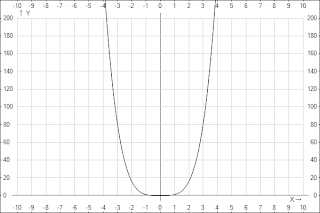
2. Показатель p=2n-1— нечетное натуральное число
В этом случае степенная функция y=x2n-1 , где натуральное число, обладает следующими свойствами:
- область определения — множество R;
- множество значений — множество R;
- функция y=x2n-1 нечетная, так как (-x)2n-1=x2n-1;
- функция является возрастающей на всей действительной оси.
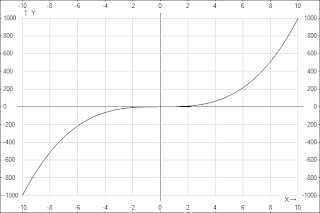
3.Показатель p=-2n, где n — натуральное число.
В этом случае степенная функция y=x-2n=1/x2n обладает следующими свойствами:
- область определения — множество R, кроме x=0;
- множество значений — положительные числа y>0;
- функция y=1/x2n четная, так как 1/(-x)2n=1/x2n;
- функция является возрастающей на промежутке x<0 и убывающей на промежутке x>0.
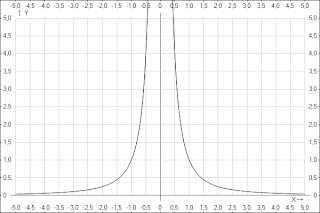
4.Показатель p=-(2n-1), где n — натуральное число.
В этом случае степенная функция y=x-(2n-1) обладает следующими свойствами:
- область определения — множество R, кроме x=0;
- множество значений — множество R, кроме y=0;
- функция y=x-(2n-1) нечетная, так как (-x)-(2n-1) =-x-(2n-1);
- функция является убывающей на промежутках x<0 и x>0.
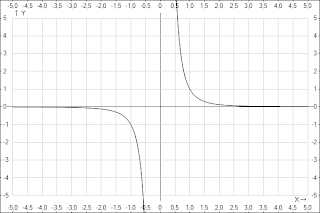
fizmatinf.blogspot.com
Степенная функция её свойства и график
Текст этой презентации
Слайд 1
Степенная функция
Её свойства и график
_____ _______ ______ ________ _____
Слайд 2
у = х2
у = х3
Парабола
Кубическая парабола
Гипербола
у = х
Прямая
Частные случаи степенной функции
Слайд 3
Функция вида у = хр, где р – действительное число называется степенной функцией
Свойства и график степенной функции зависят от свойств степени с действительным показателем, и в частности от того, при каких значениях х и р имеет смысл степень
Слайд 4
Показатель р = 2n – четное натуральное число
1
0
х
у
у = х2, у = х4 , у = х6, у = х8, …
у = х2
Функция у=х2n четная, т.к. (–х)2n = х2n
Слайд 5
y
x
-1 0 1
у = х2
у = х6
Слайд 6
Показатель р = 2n-1 – нечетное натуральное число
1
х
у
у = х3, у = х5, у = х7, у = х9, …
у = х3
Функция у=х2n-1 нечетная, т.к. (–х)2n-1 = – х2n-1
0
Слайд 7
y
x
-1 0 1
у = х3
у = х7
Слайд 8
Показатель р = – 2n, где n – натуральное число
1
0
х
у
у = х-2, у = х-4 , у = х-6, у = х-8, …
Функция у=х2n четная, т.к. (–х)-2n = х-2n
Слайд 9
y
x
-1 0 1
у = х-2
у = х-6
Слайд 10
Показатель р = – (2n-1), где n – натуральное число
1
0
х
у
у = х-3, у = х-5 , у = х-7, у = х-9, …
Функция у=х-(2n-1) нечетная, т.к. (–х)–(2n-1) = –х–(2n-1)
Слайд 11
y
x
-1 0 1
у = х-1
у = х-5
Слайд 12
0
Показатель р – положительное действительное нецелое число
1
х
у
у = х1,3, у = х0,7, у = х2,12, …
Слайд 13
y
x
-1 0 1
у = х0,5
Слайд 14
y
x
-1 0 1
Слайд 15
0
Показатель р – отрицательное действительное нецелое число
1
х
у
у = х-1,3, у = х-0,7, у = х-2,12, …
Слайд 16
y
x
-1 0 1
Слайд 17
Пользуясь рисунком, найти промежутки, на которых график функции лежит выше (ниже) графика функции у = х.
0
1
х
у
у=х
Слайд 18
Пользуясь рисунком, найти промежутки, на которых график функции лежит выше (ниже) графика функции у = х.
у
0
1
х
у=х
Слайд 19
Пользуясь рисунком, найти промежутки, на которых график функции лежит выше (ниже) графика функции у = х.
Слайд 20
y
x
-1 0 1
у = (х + 2)-6
Слайд 21
y
x
-1 0 1
у = х– 6 – 4
Слайд 22
y
x
-1 0 1
у = (х+1)– 4 + 2
Слайд 23
y
x
-1 0 1
у = (х-3)– 3+1
Слайд 24
y
x
-1 0 1
у = (х+3)–2,5 +2
topslide.ru
степенная функция ее свойства и график

Степенная функция её свойства и график
Алгебра 10 класс
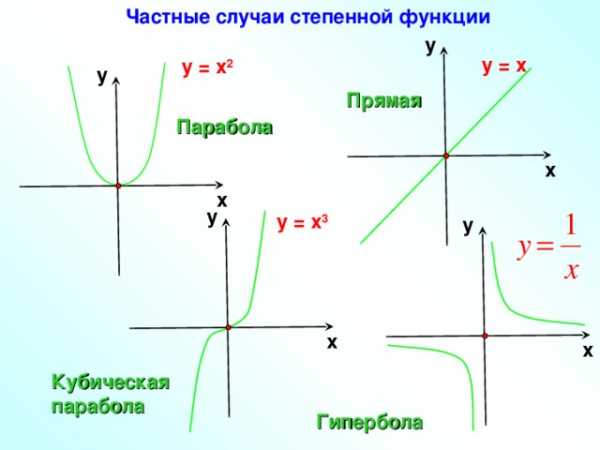
Частные случаи степенной функции
- Частные случаи степенной функции
- Частные случаи степенной функции
- Частные случаи степенной функции
- Частные случаи степенной функции
у
у = х
у = х 2
у
Прямая
Парабола
х
х
у
у = х 3
у
х
х
Кубическая
парабола
Гипербола

Функция вида у = х р , где р – действительное число называется степенной функцией
Свойства и график степенной функции зависят от свойств степени с действительным показателем, и в частности от того, при каких значениях х и р имеет смысл степень
- Свойства и график степенной функции зависят от свойств степени с действительным показателем, и в частности от того, при каких значениях х и р имеет смысл степень
- Свойства и график степенной функции зависят от свойств степени с действительным показателем, и в частности от того, при каких значениях х и р имеет смысл степень
- Свойства и график степенной функции зависят от свойств степени с действительным показателем, и в частности от того, при каких значениях х и р имеет смысл степень
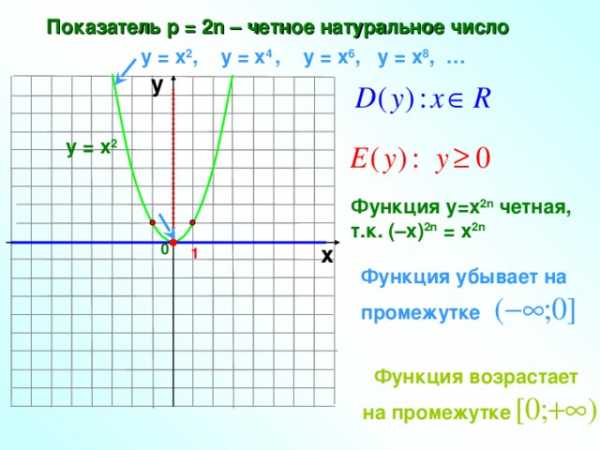
Показатель р = 2n – четное натуральное число
у = х 2 , у = х 4 , у = х 6 , у = х 8 , …
у
у = х 2
Функция у=х 2n четная,
т.к. (–х) 2n = х 2n
х
0
1
Функция убывает на
промежутке
Функция возрастает
на промежутке
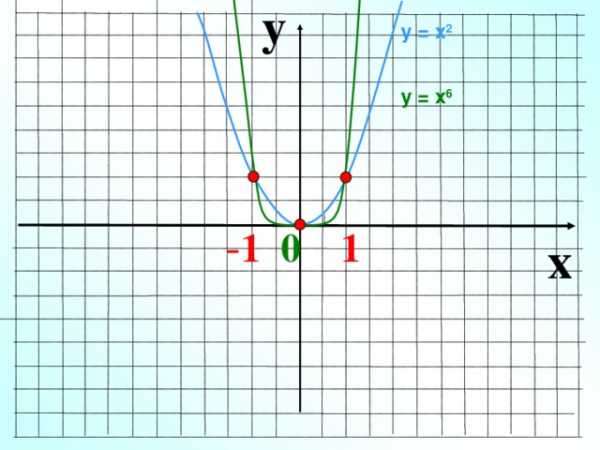
y
у = х 2
у = х 6
— 1 0 1
x
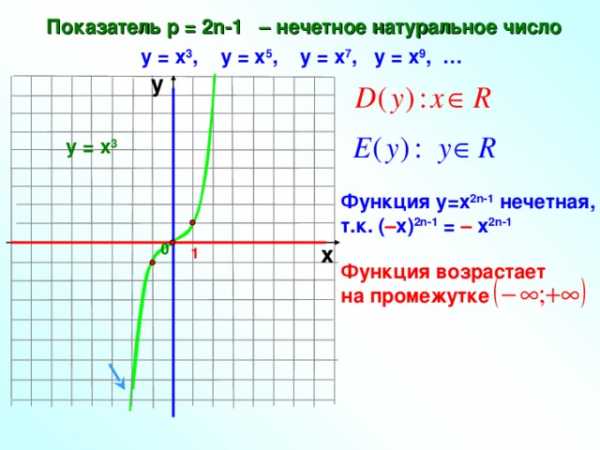
Показатель р = 2n-1 – нечетное натуральное число
у = х 3 , у = х 5 , у = х 7 , у = х 9 , …
у
у = х 3
Функция у=х 2n-1 нечетная,
т.к. ( – х) 2n-1 = – х 2n-1
0
х
1
Функция возрастает на промежутке
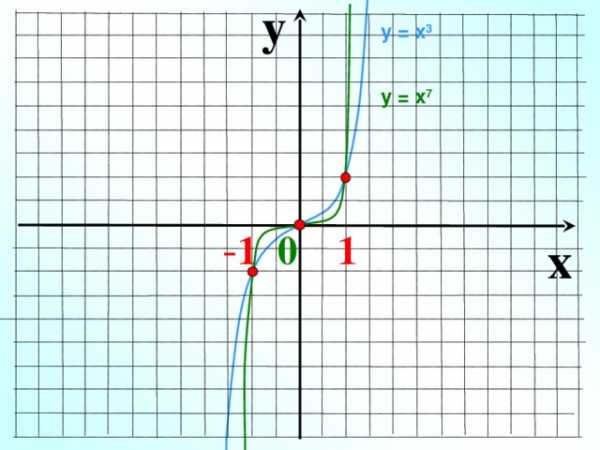
y
у = х 3
у = х 7
— 1 0 1
x
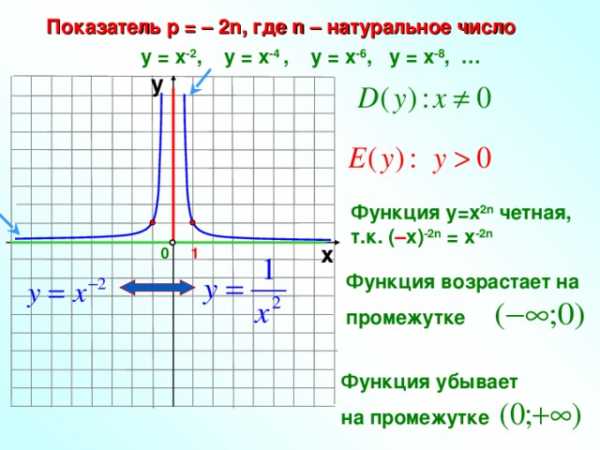
Показатель р = – 2n, где n – натуральное число
у = х -2 , у = х -4 , у = х -6 , у = х -8 , …
у
Функция у=х 2n четная,
т.к. ( – х) -2n = х -2n
х
0
1
Функция возрастает на
промежутке
Функция убывает
на промежутке
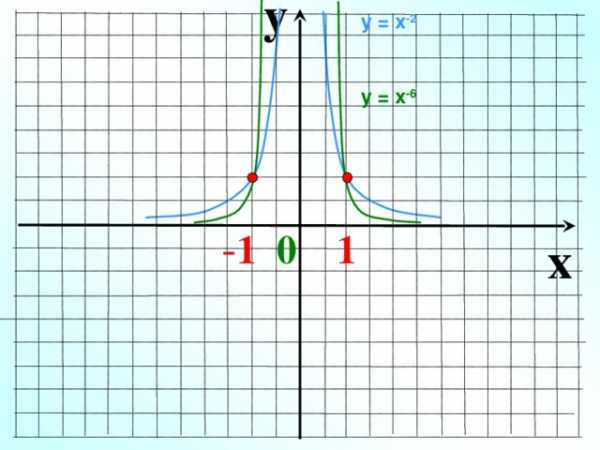
y
у = х -2
у = х -6
— 1 0 1
x
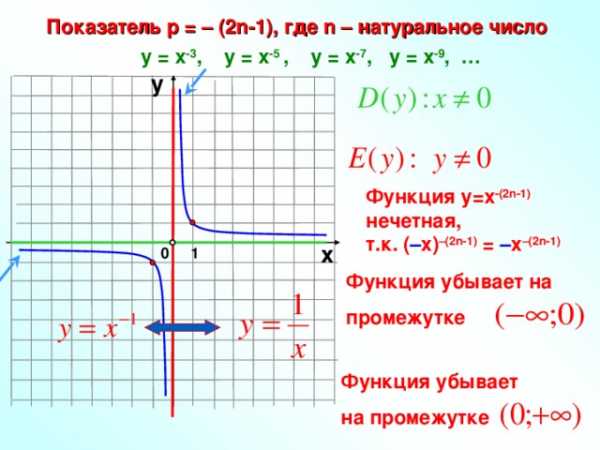
Показатель р = – (2n-1), где n – натуральное число
у = х -3 , у = х -5 , у = х -7 , у = х -9 , …
у
Функция у=х -(2n-1) нечетная,
т.к. ( – х) –(2n-1) = – х –(2n-1)
х
0
1
Функция убывает на
промежутке
Функция убывает
на промежутке
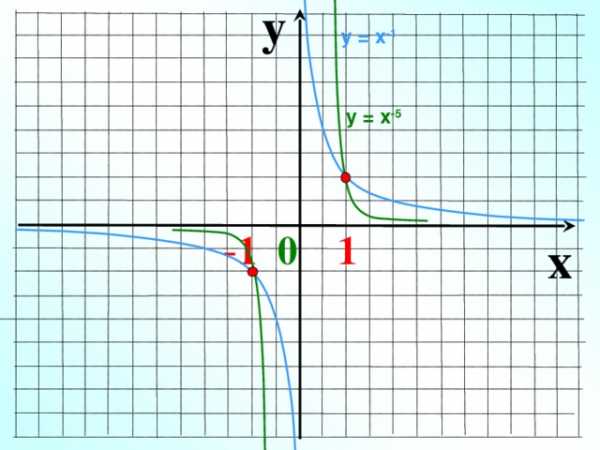
y
у = х -1
у = х -5
— 1 0 1
x
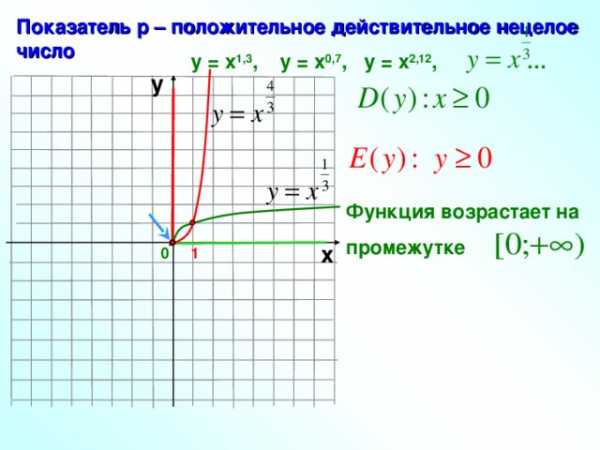
Показатель р – положительное действительное нецелое число
у = х 1,3 , у = х 0,7 , у = х 2,12 , …
у
Функция возрастает на
промежутке
х
0
1
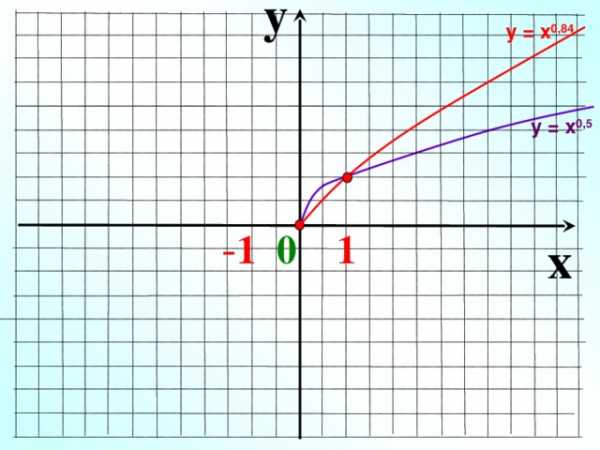
y
у = х 0,84
у = х 0,5
— 1 0 1
x
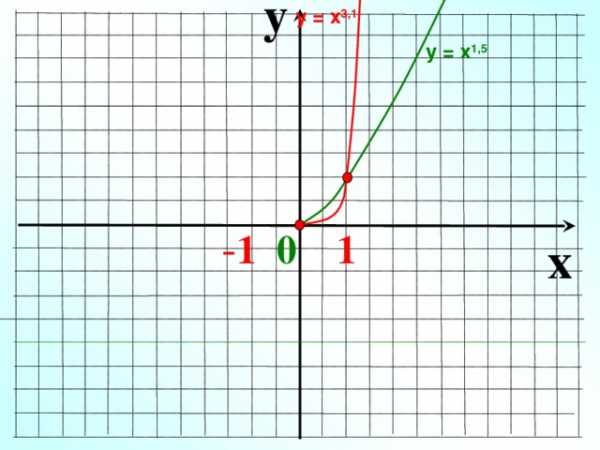
y
у = х 3,1
у = х 1,5
— 1 0 1
x
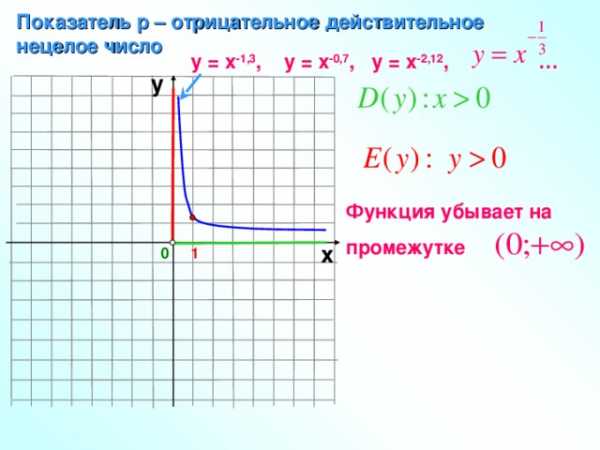
Показатель р – отрицательное действительное
нецелое число
у = х -1,3 , у = х -0,7 , у = х -2,12 , …
у
Функция убывает на
промежутке
х
1
0
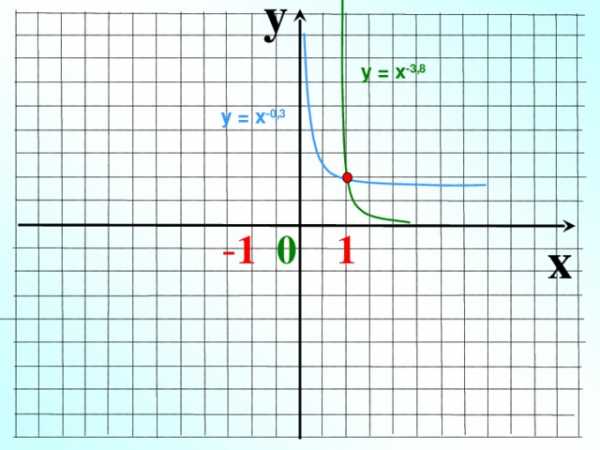
y
у = х -3,8
у = х -0,3
— 1 0 1
x
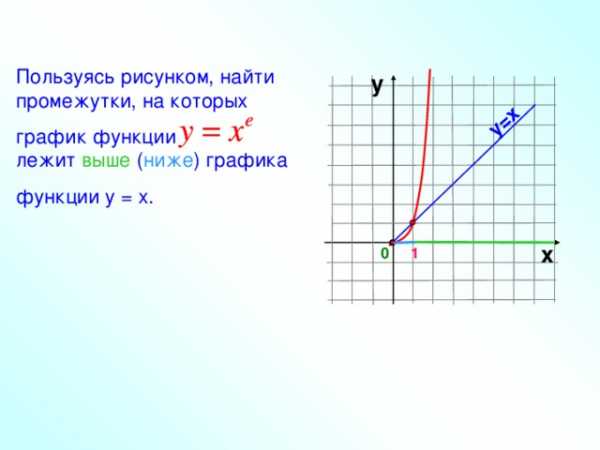
у=х
Пользуясь рисунком, найти промежутки, на которых
график функции лежит выше ( ниже ) графика
функции у = х.
у
х
0
1
16
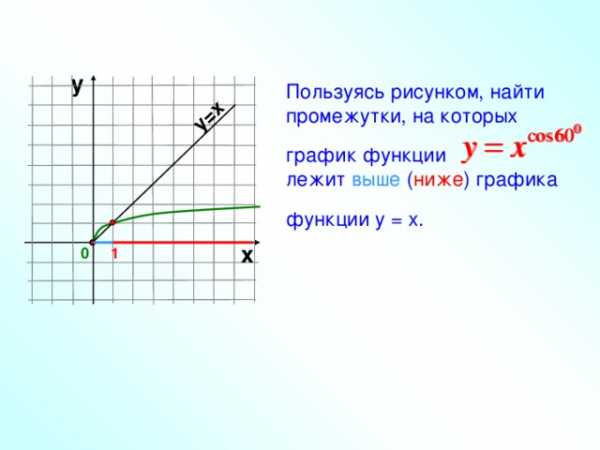
у=х
у
Пользуясь рисунком, найти промежутки, на которых
график функции лежит выше ( ниже ) графика
функции у = х.
х
1
0
16
у=х
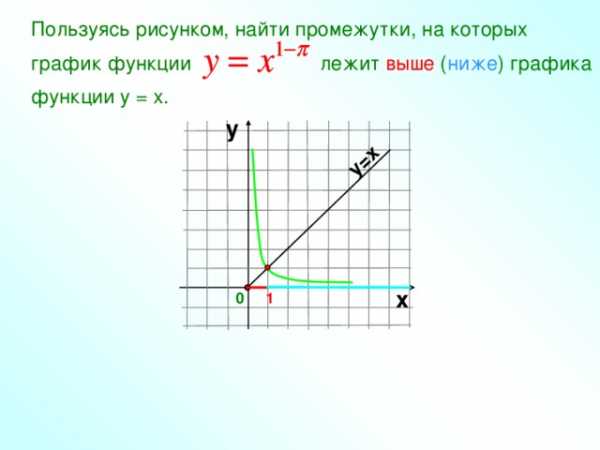
Пользуясь рисунком, найти промежутки, на которых
график функции лежит выше ( ниже ) графика
функции у = х.
у
х
1
0
y
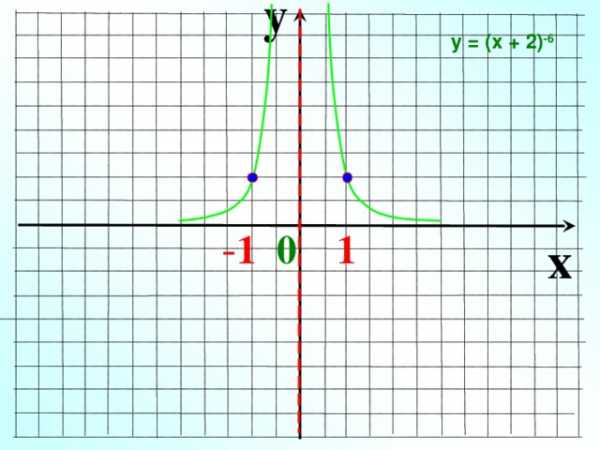
у = (х + 2) -6
— 1 0 1
x
y
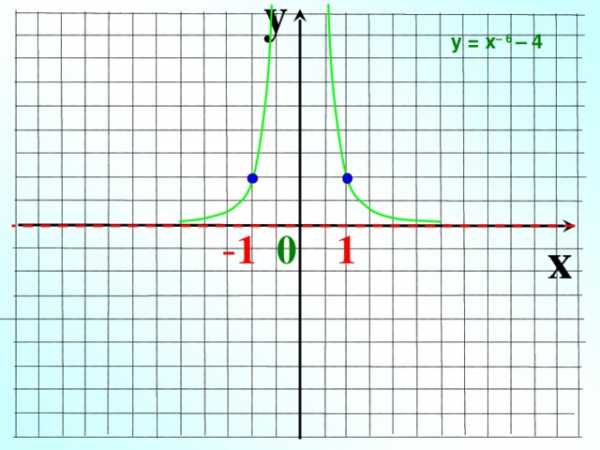
у = х – 6 – 4
— 1 0 1
x
y
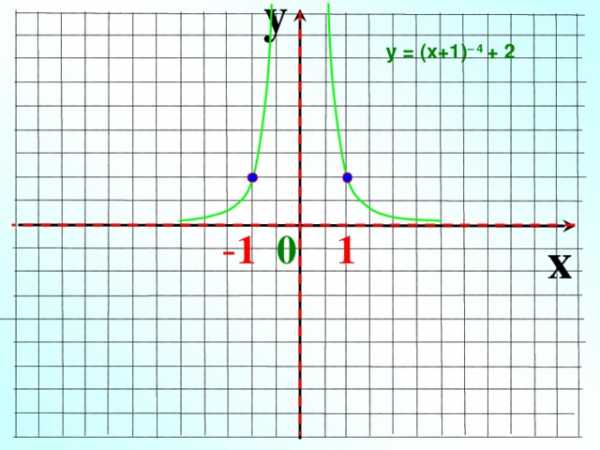
у = (х+1) – 4 + 2
— 1 0 1
x
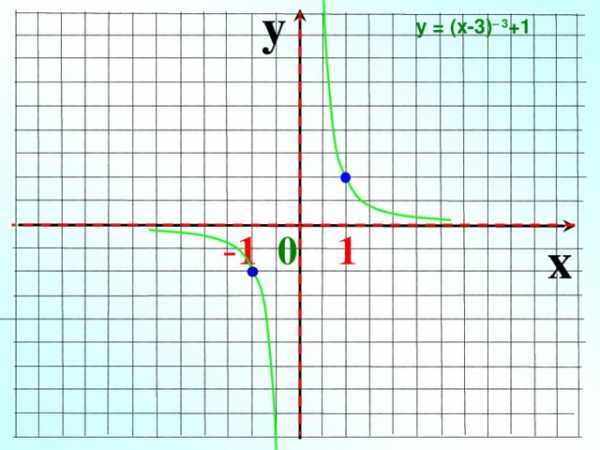
y
у = (х-3) – 3 +1
— 1 0 1
x
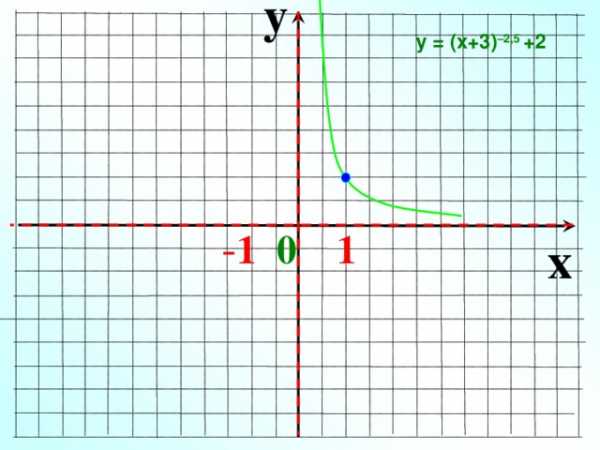
y
у = (х+3) –2,5 +2
— 1 0 1
x
multiurok.ru

