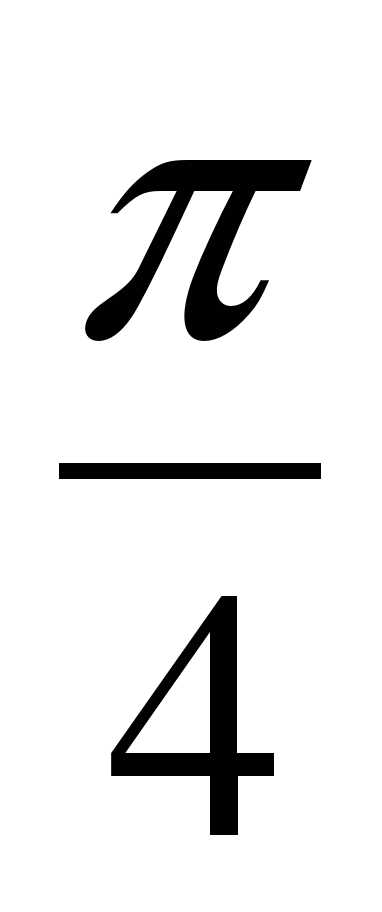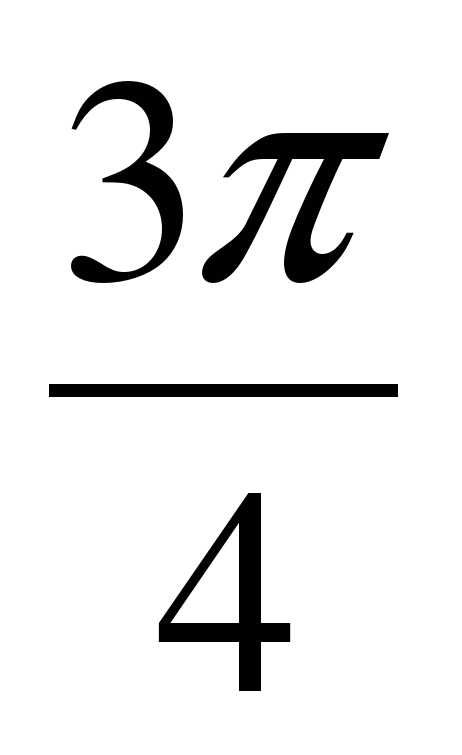Радианная мера угла 10 класс урок – конспект о радианной мере угла 10 класс
конспект о радианной мере угла 10 класс
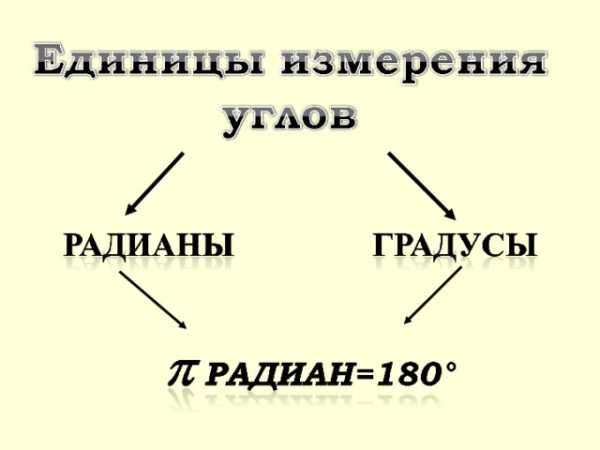
Градусная и радианная мера угла. Тригонометрический круг
Градусная и радианная мера угла. Тригонометрический круг
Если угол содержит α° и одновременно измеряется x радиан, то , где K° — постоянный коэффициент. Подставляя, например, и , получаем . Наоборот, , где .
Пример 1. Выразим в радианной мере величины углов в 90°, 45°, 60° и 27°.
Решение. Из формулы (2) следует: .
Пример 2. Выразим в градусной мере величины углов в радиан.
Решение. Из формулы (2) следует: .
Поворот точки вокруг начала координат
Рассмотрим на координатной плоскости окружность радиуса 1 с центром в начале координат. Ее называют единичной окружностью. Введем понятие поворота точки единичной окружности во круг начала координат на угол α радиан, где α – любое действительное число.
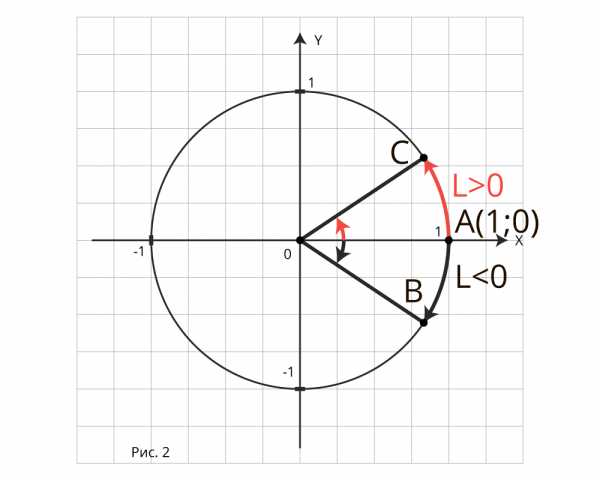
1. 1. Пусть α>0. Предположим, что точка, двигаясь поединичной окружности от точки Р против часовой стрелки, прошла путь длиной α (рис. 1). Конечную точку пути обозначим М.
В этом случае будем говорить, что точка М получена из точки Р поворотом вокруг начала координат на угол α радиан.
2. 2. Пусть α<0. В этом случае поворот на угол α радиан означает, что движение совершалось по часовой стрелке и точка прошла путь длинной (рис. 2).
Поворот на 0 рад означает, что точка остается на месте.
Примеры.
1) При повороте точки Р(1;0) на угол (рис. 3) получается точка М с координатами (0;1).
2) При повороте точки Р(1;0) на угол (рис. 3) получается точка N(0;-1).
3) При повороте точки Р(1;0) на угол (рис. 4) получается точка К(0;-1).
4) При повороте точки Р(1;0) на угол (рис. 4) получается точка Д(-1;0).
Рис. 1
Рис. 2Рис. 3
Рис. 4
Приведем таблицу поворотов на некоторые углы, выраженные в радианной и градусной мерах (рис. 5).
Отметим, что при повороте точки Р(1;0) на 2, т.е. на 360°, точка возвращается на первоначальное положение (см. таблицу). При повороте точки на -2, т.е. на -360°, она также возвращается в первоначальное положение.
Рассмотрим примеры поворотов точки на угол, больший 2, и на угол, меньший -2. Так, при повороте на угол точка совершает два полных оборота против часовой стрелки и проходит еще путь (рис. 6). При повороте на угол точка совершает два полных оборота по часовой стрелке и проходит еще путь в том же направлении (рис. 7).
Рис. 6
Рис. 5
Рис. 7
Свойства тригонометрических функций
Знаки тригонометрических функций
Свойство четности и нечетности
Свойство периодичности
Градусы и радианы
Значения tg и ctg угла α
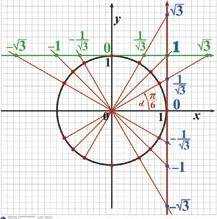
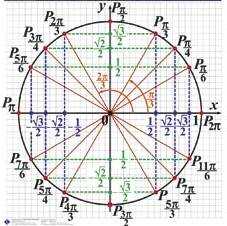
Значения sin и cos угла α
– это угол поворота, при котором конец начального радиуса описывает дугу, длина которой равна радиусу.
1 рад=(180/n)0=570
n0= (nп)/1800
n рад= (n 1800)/п
infourok.ru
Урок 29. радианная мера угла — Алгебра и начала математического анализа — 10 класс
Алгебра и начала математического анализа, 10 классУрок №29. Радианная мера угла
Перечень вопросов, рассматриваемых в теме:
1) Понятие тригонометрической окружности;
2) Поворот точки вокруг начала координат;
3) Длина дуги окружности и площадь кругового сектора.
Глоссарий по теме
Окружность – это замкнутая линия, все точки которой равноудалены от центра.
Радиус окружности – отрезок, соединяющий её центр с любой лежащей на окружности точкой.
Круг – часть плоскости, ограниченная окружностью.
Дуга окружности – кривая линия, лежащая на окружности и ограниченная двумя точками.
Круговой сектор – часть круга, ограниченная двумя радиусами.
Угол в 1 радиан – центральный угол, опирающийся на дугу, равную по длине радиусу окружности.
Основная литература:
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл.– М.: Просвещение, 2014.
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Учебно-методический комплект: Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл.– М.: Просвещение, 2014.
Теоретический материал для самостоятельного изучения
На уроках геометрии мы с вами изучали окружность, её элементы, свойства. Повторим понятие окружности. Это замкнутая линия, все точки которой равноудалены от центра.
Радиусом окружности называется отрезок, соединяющий её центр с любой лежащей на окружности точкой.
На окружности можно выделить дугу. А если рассмотреть круг — часть плоскости, ограниченной окружностью — то можно выделить круговой сектор.
«Окружность бесконечно большого круга и прямая линия – одно и то же» Г. Галилей
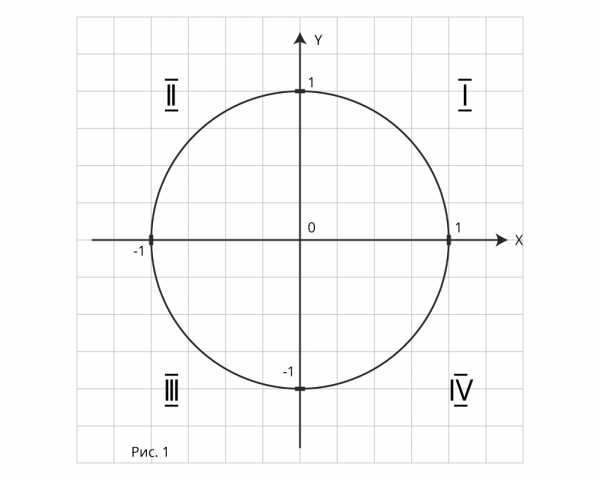
Действительно, и окружность и прямая – бесконечны. Рассмотрим окружность радиуса, равному 1 единичному отрезку, в прямоугольной системе координат хОу с центром в начале координат. Такую окружность называют единичной или тригонометрической. (рис.1)
Длина этой окружности (в предыдущей задаче велотрека), как мы помним из уроков геометрии, . А учитывая, что R=1, , осями координат она поделена на четыре дуги, которые находятся соответственно в I, II, III и IV координатных четвертях.
Вычислите длину каждой дуги.
Ответ. длина каждой дуги равна части окружности или
Длина полуокружности равна А так как образовался развернутый угол, то 180.
Рассмотрим дугу, равную по длине радиусу единичной окружности. Полученный центральный угол РОМ равен длине дуги МР=R.
 рис.3
рис.3
Определение. Углом в 1 радиан называется центральный угол, опирающийся на дугу, равную по длине радиусу окружности.
Обозначается 1рад.
;
α рад=(180/π α)° (1)
Длину дуги l окружности радиуса R (рис.4)

можно вычислять по формуле(3)
А площадь S кругового сектора радиуса R и дугой рад (рис.5)
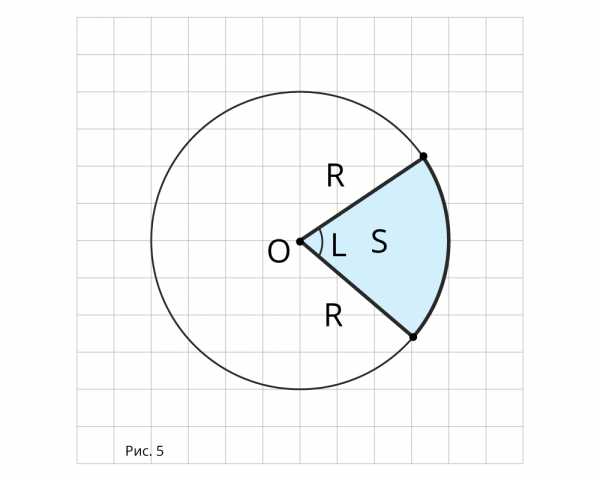
находят по формуле: , где (4)
Вернёмся к единичной окружности в координатной плоскости.
Каждая точка этой окружности будет иметь координаты х и у такие, что выполняются неравенства -1≤ х ≤ 1; -1≤ у ≤ 1.
Введём понятие поворота точки. (рис.2)
- Пусть Тогда точка А(1;0) будет двигаться по единичной окружности против часовой стрелки. Она пройдёт путь α рад от точки А(1;0) до точки В. Говорят, точка В получена из точки А поворотом на угол
- Пусть точка А(1;0) будет двигаться по единичной окружности по часовой стрелки . Она пройдёт путь α рад от точки А(1;0)до точки С. Говорят, точка С получена из точки А поворотом на угол — α.
При повороте на 0 рад точка остаётся на месте.
Давайте рассмотрим такой пример:
при повороте точки М(1;0) на угол получается точка N (0;1). В эту же точку можно попасть из точки М(1;0) при повороте на
угол (рис.6)

(рис.6)
Примеры и разбор решения заданий тренировочного модуля
Пример 1.
Найти градусную меру угла, равного рад.
Решение: Используя формулу (1),
находим .
Так как , то рад, тогда (2)
Ответ: .
Пример 2. Найти радианную меру угла, равного 60.
Решение:
Вычисляем по формуле (2): рад
рад
При обозначении мер угла, наименование «рад» опускают.
Ответ: рад, рад.
Пример 3. Найти длину дуги окружности радиуса 6 см, если её радианная мера .
Решение: Используя формулу (3),
получим:
Ответ: .
Пример 4. Найти площадь сектора, если радиус окружности 10 м, а радианная мера центрального угла .
Решение:
По формуле (4) вычисляем
Ответ: 45 м2
Пример 5. Найти координаты точки М, полученной из точки N(1;0) поворотом на угол, равный .
Решение: Абсцисса точки М равна отрезку ОК, ордината отрезку ОТ=МК. Так как то
прямоугольный равнобедренный треугольник ОМК имеет равные катеты и гипотенузу ОМ=R=1. По теореме Пифагора можно найти длины катетов. Они равны Учитывая, что точка М находится в I координатной четверти, её координаты положительны.
На окружности можно найти координаты любой точки.
Ответ:
resh.edu.ru
Конспект урока по алгебре для 10 класса на тему «Радианная мера углов»
Учитель: Аблякимова Зиядье Мубеиновна
УРОК №
Дата:
Класс:10
Предмет: алгебра
Тема урока: «Радианная мера углов»
Цель урока:
Обучающие: ввести понятие радианной меры углов и дуг; научиться переводить углы из градусной меры в радианную и наоборот.
Развивающие: формировать умение анализировать и делать выводы, вычислительные, расчетные навыки.
Воспитательные: развивать коммуникативные умения, формировать положительную мотивацию к учению, развивать умение говорить и слушать других..
Тип урока: комбинированный.
Ход урока
I. Организационный этап.
II. Актуализация опорных знаний и умений учащихся.
1. Записать формулу длины окружности, вычислить длину окружности при R=3 см.
2. Записать формулу длины дуги в n
III. Изучение нового материала.
При измерении углов в градусах за единицу угла берут угол, который равен 1/180 части развернутого угла и называется угловым градусом. Но в физике, механике, астрономии, математике используется другая мера углов – радианная.
1. Введем радианную меру измерения углов, для этого рассмотрим центральные углы и дуги, соответствующие им.
Пусть – центральный угол, которому соответствуют две дуги ANB и A1N1B1, при чем ОА =, OA1 = 1 (рис.1).
Рис.1
Запишем длины дуг: l= =; l1= =
Найдем отношение длины дуги к радиусу в каждом случае: = ; =
Имеем = . Мы показали, что для данного центрального угла отношение длины дуги, на которую он опирается, к длине соответствующего радиуса – величина постоянная, не зависящая от размеров радиуса. Обозначим = a.
Число a = называется радианной мерой угла ( – длина дуги, соответствующей центральному углу ). За единицу такого угла берут угол, для которого = , тогда a =1. Итак, это угол, мера которого один радиан.
Определение. Угол один радиан – такой центральный угол, длина дуги которого равна длине радиуса.
Замечание. В математической литературе слово «радиан» не пишется. Например если угол АОВ = 2, то это значит, что угол АОВ равен двум радианам.
2. Любой угол, заданный в градусной мере, можно перевести в радианную меру и наоборот.
1) Радианная мера окружности = 2 радиан, то есть = 2 радиан; = радиан.
2) Радианная мера дуги равна .
Если градусная мера угла , то его радианную меру можно найти по формуле: a = , и наоборот = .
IV. Закрепление новых знаний и умений учащихся.
Задание классу
1. Заполнить таблицу, пользуясь полученными формулами.
a
Решение
I способ. = . Найти радианную меру этого угла.
a = ==
II способ. Составим пропорцию ; – a, тогда
a = =
2. Вычислить градусную меру угла 1 радиан; 2 радиана и изобразить эти углы на окружности (1 радиан = 570, 2 радиана = 1140).
V. Домашнее задание: п. 7.2, №7.16, 7.17 (1й столбик).
VI.Итог урока
Учитель отвечает на вопросы учащихся.
infourok.ru
Радианная мера угла
Прежде, чем приступить к рассмотрению новой темы, давайте вспомним, что градусом называют величину центрального угла, которому соответствует часть окружности. Градусная мера угла – это положительное число, которое показывает, сколько раз градус и его части укладываются в измеряемом угле.
А углы можно измерять только в градусах? Сегодня на уроке мы рассмотрим ещё одну единицу измерения углов.
Давайте изобразим окружность с центром в точке и радиусом . Затем проведём вертикальную прямую, которая касается окружности в точке . Эту прямую мы будем считать числовой осью с началом отсчёта в точке . Положительным направлением на прямой будем считать направление вверх. За единичный отрезок на числовой оси возьмём радиус окружности.
Отметим на прямой несколько точек: и , и , и , и , и .
Теперь представим нашу прямую в виде нерастяжимой нити, которая закреплена на окружности в точке . Будем наматывать нить на окружность. При этом точки на числовой прямой с координатами , , , перейдут соответственно в точки окружности , , , . При этом длина дуги равна , длина дуги равна , длина дуги равна , длина дуги равна .
Получается, что каждой точке прямой ставится в соответствие некоторая точка окружности.
Так, точке прямой с координатой ставится в соответствие точка . А значит, угол можем считать единичным? Да, и его мерой мы будем измерять другие углы. Например, угол следует считать равным , а угол равным .
А где используют такой способ измерения углов? Такой способ измерения углов широко используется в математике и физике. Говорят, что углы измеряются в радианной мере.
Единичный угол называют углом в один радиан. Записывают так: рад.
И напомним, что длина дуги равна радиусу нашей окружности.
Сейчас давайте рассмотрим окружность радиуса . И отметим на ней дугу , равную длине радиуса окружности, и угол .
И такой угол называется углом в один радиан? Верно.
Запомните! Центральный угол, опирающийся на дугу, длина которой равна радиусу окружности, называется углом в один радиан.
Интересно, а скольким градусам равен угол в один радиан? Давайте найдём градусную меру угла в один радиан. Мы знаем из курса геометрии, что дуге длиной , то есть полуокружности, соответствует центральный угол, равный . Следовательно, дуге окружности длиной соответствует угол в раз меньший.
Выше мы назвали такой угол углом в один радиан, а значит, можем записать, что рад . , тогда рад .
Если угол содержит рад, то рад . Эту формулу называют формулой перехода от радианной меры к градусной.
Давайте с вами найдём градусную меру угла, равного рад. Для этого воспользуемся формулой перехода от радианной меры к градусной. Подставим вместо : . Сократим на и на . И в результате получим .
Можно ли, наоборот, перейти от градусной меры к радианной? Конечно, можно, но такой переход будет чуть сложнее. Так как угол в равен рад, то рад. Тогда рад. Такую формулу называют формулой перехода от градусной меры к радианной.
Найдём радианную меру угла, равного . Воспользуемся формулой перехода от градусной меры к радианной. Подставим вместо : . Сократим и на . И в результате получим .
Обратите внимание, что при обозначении меры угла в радианах слово «радиан» обычно не пишут: . При этом обозначение градуса в записи меры угла пропускать нельзя.
В следующей таблице представлены углы в градусной и радианной мере, с которыми мы будем встречаться чаще всего.
Отметим, что радианная мера углов позволяет значительно упростить многие формулы в математике, физике, механике. В частности, радианная мера угла удобна для вычисления длины дуги окружности. Так, выше мы выяснили, что угол в рад стягивает дугу, длина которой равна радиусу , а значит, угол в рад стягивает дугу длиной: . Если , то эта формула принимает совсем простой вид: , то есть длина дуги равна величине центрального угла, стягиваемого этой дугой.
Сейчас, прежде чем приступить к выполнению заданий, мы докажем, что площадь кругового сектора радиуса , образованного углом в рад, равна , где .
Докажем это. Известно, что площадь круга вычисляется по формуле: . Площадь полукруга, то есть кругового сектора в рад: . Тогда площадь сектора в рад в раз меньше, то есть . Следовательно, площадь сектора в рад равна .
Ну а сейчас давайте выполним несколько заданий.
Первое задание. Найдите градусную меру угла, выраженную в радианах: а) ; б) ; в) ; г) ; д) .
Решение.
Второе задание. Найдите радианную меру угла, выраженного в градусах: а) ; б) ; в) ; г) .
Решение.
Следующее задание. Чему равен радиус окружности, если дуге длиной см соответствует центральный угол в рад?
Решение.
И ещё одно задание. Дуге кругового сектора соответствует угол, равный рад. Чему равна площадь сектора, если радиус круга равен см?
Решение.
Ну а сейчас немного истории.
Впервые радиан как единица измерения был использован английским математиком Роджером Котсом в 1713 году. Он считал, что радиан является наиболее естественной единицей измерения углов. Термин «радиан» впервые появился в печати в 1873 году в экзаменационных билетах Университета Квинса в Белфасте, составленных британским инженером и физиком Джеймсом Томсоном.
В 1960 году XI Генеральной конференцией по мерам и весам радиан был принят в качестве единицы измерения плоских углов в Международной системе единиц (СИ).
videouroki.net
Радианная мера угла (разработка урока)
Урок-модуль по алгебре. Тема: «Радианная мера угла»Цели урока:
Образовательные:
обеспечить усвоение определения угла в один радиан,
обеспечить запоминание формул перехода от градусной меры угла к радианной и от радианной к градусной,
сформировать умение пользоваться радианным измерением углов на уровне выполнения упражнений по образцу, в измененной и новой ситуации.
Развивающие:
развивать внимание, ясность и точность мысли, умение рассуждать,
развивать умение работать со справочной литературой, учебником и технологической картой урока,
развивать интуицию и логическое мышление, умение выделять существенные признаки математического понятия, сравнивать и обобщать, самостоятельно выполняя задания
развивать элементы алгоритмической культуры, умение планировать и контролировать свою деятельность, работать в заданном времени,
развивать умение оценивать свои знания и возможности, способность преодолевать трудности.
Воспитательные:
воспитывать ценностное отношение к предмету, интерес к его изучению и понимание значимости предмета, через иллюстрацию прикладного характера математики,
воспитывать аккуратность, добросовестное отношение к работе, уважительное отношение к товарищам, умение работать самостоятельно, в парах и коллективе,
формировать систему нравственного отношения к себе, одноклассникам, школе и обществу
Тип урока: усвоение новых знаний
Технология урока: модульное обучение. Урок сопровождается презентацией.
Учебный модуль 1. Организационный момент
На парте у каждого ученика лежат технологические карты (см Приложение). Учитель в начале урока объясняет ученикам, как работать с технологическими картами.
Цель: Подготовить к успешному выполнению заданий на уроке.
Дорогие ребята!
Сегодня вам самим предстоит изучить тему «Радианная мера угла». Работай самостоятельно, в случае затруднений, обратись к товарищу или учителю. Выполняй задания вдумчиво и внимательно.
Учебный модуль 2. Актуализация опорных знаний учащихся
Цель: Повторить определения синуса, косинуса, тангенса и котангенса угла. Подготовить к восприятию нового материала.
Задание для Математического диктанта:
(два ученика пишут на откидных досках, остальные в тетради)
Как называется отношение
 ?
?Как называется отношение
 ?
?Чему равен tgα?
Чему равен sin45º?
Чему равен cos90 º?
Чему равен tg180 º?
Существует ли угол, для которого sinα=0,6?
Существует ли угол, для которого cosβ=-1,5?
Чему равен cos60 º?
Чему равен sin60º?
Задание для работы с технологическим картами:
(решение этого задания поможет вам правильно выполнить № 116, 1 вариант. Сборник задач А.Г. Мерзляк и др.А.Г из домашнего задания)
№1 Запиши в тетради формулы
а) формула длины окружности, вычислите при R = 2 см; (l=2πr)
б) длина дуги в nº. Найти длину дуги при n=60º (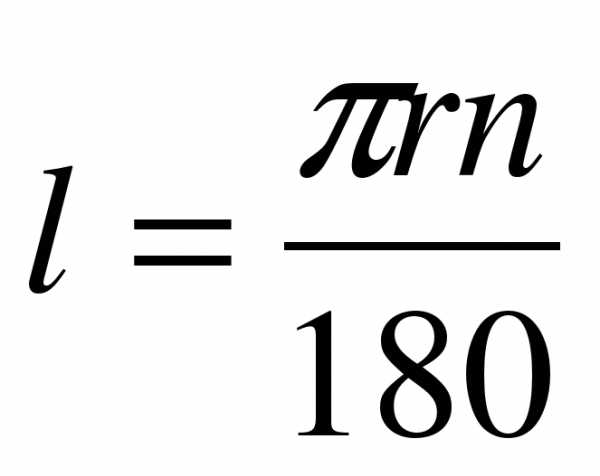 )
)
№ 2 Заполни таблицу в тетради:
(решение этого задания поможет вам правильно выполнить № 3, стр. 238 из домашнего задания)
| 89 | -68 | 91 | 189 | -175 | 245 |
Координатная четверть |
|
|
|
|
|
|
№ 3:
«Выключи свет в окнах», т.е. закрась простым карандашом те клетки, где значения выражения в строке 2 равно выражению, записанному в строке 1.
1 вариант 2 вариант
1 | Sin 90 | Sin 450 | Cos 270 |
| Sin 0 | Cos 0 | tg 0 |
2 | tg 45 | 2Cos 60 | Cos 360 | Cos 90 | Sin 180 | Cos 270 |
Учебный модуль 3. Формулировка темы, цели и задач урока. Мотивация учебной деятельности учащихся
Цель: Познакомиться с определением угла в 1 радиан и формулами, устанавливающими связь между радианным и градусным измерением углов.
При градусном измерении углов за единицу измерения принимается угол, равный 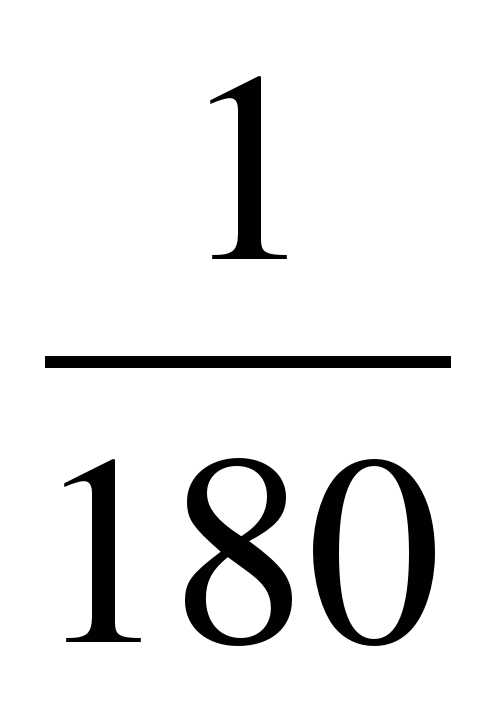 части развернутого угла. Его называют градусом. Углы измеряются в градусах, минутах, секундах.
части развернутого угла. Его называют градусом. Углы измеряются в градусах, минутах, секундах.
Однако в физике, технике, астрономии встречается и другая единица измерения углов, имеющая определенные преимущества. Сегодня мы с ней познакомимся.
Работа с учебником
Задание:
Прочитай внимательно текст учебника (Нелин Е.П. Алгебра. Академический уровень, 10класс, Радел 3, п.16, стр. 235-236.)
Сделай чертеж (см. стр. 236, рис.102). Запиши в тетрадь определение угла в 1 радиан.
Запиши формулы перевода градусной меры угла в радианную и радианной в градусную.
1º=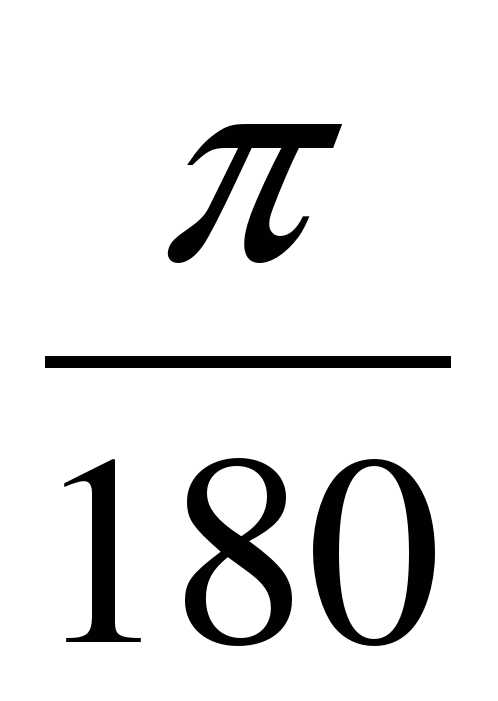 радиан, 1 радиан =
радиан, 1 радиан =  ≈57º
≈57º
Учебный модуль 4. Формирование умений и отработка навыков
Цель: Проверить степень запоминания определения и формул перехода от одной меры угла к другой.
Письменные упражнения (решение этого задания поможет вам правильно выполнить № 4, стр 238 из домашнего задания)
после выполнения осуществляется проверка на экране
1. Найдите градусную меру угла, радианная мера которого равна:
а) 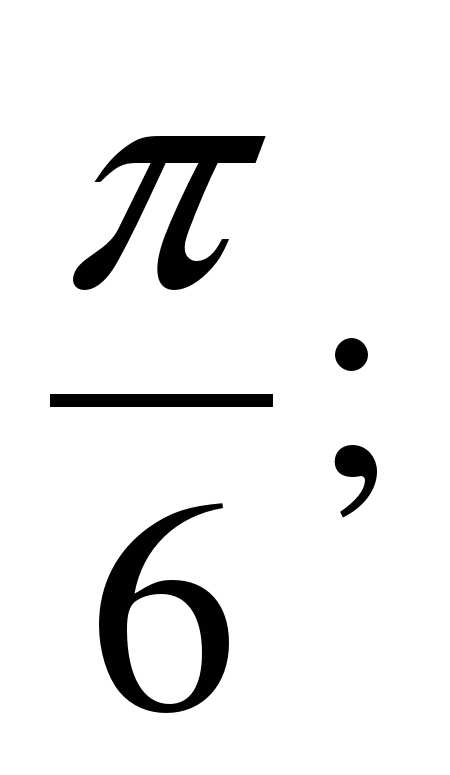 б)
б)  в)
в) 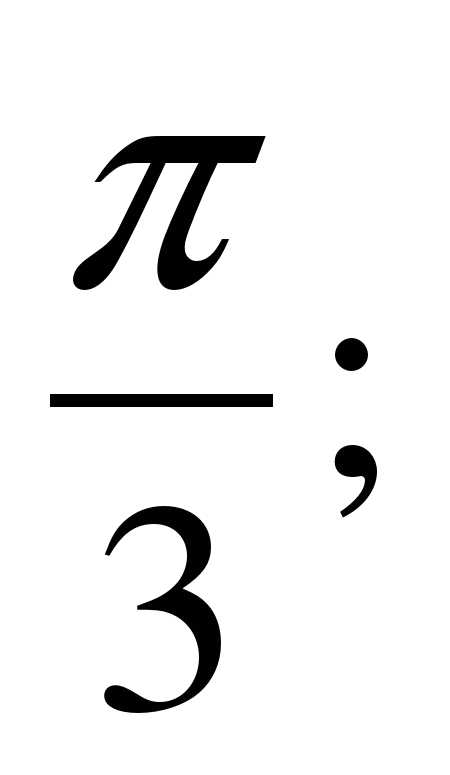 г)
г) 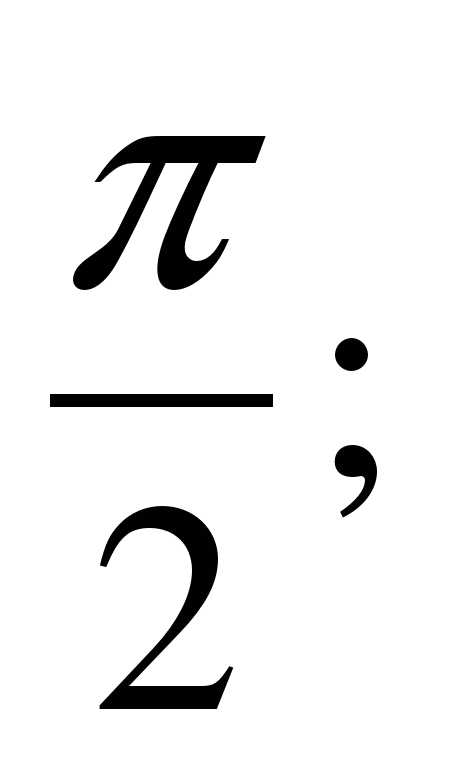 д)
д) 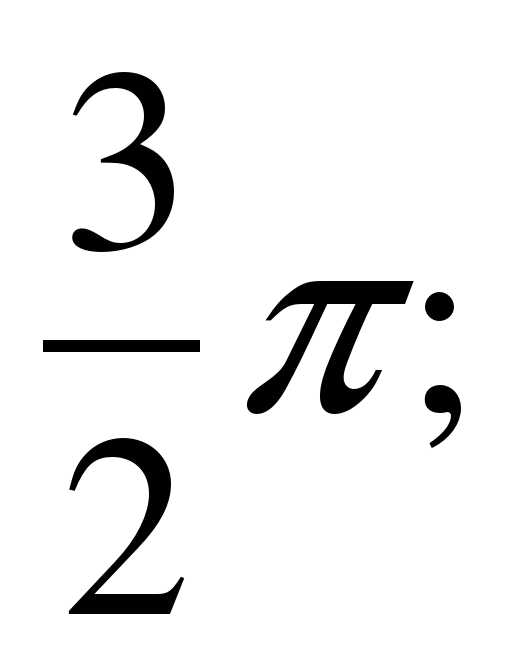 е)
е) 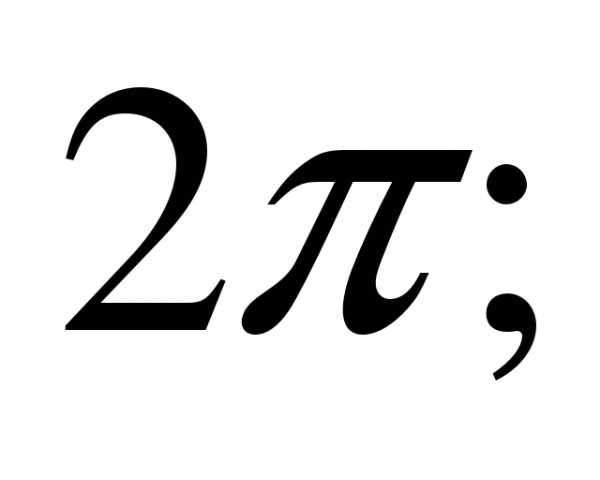 ж)
ж) 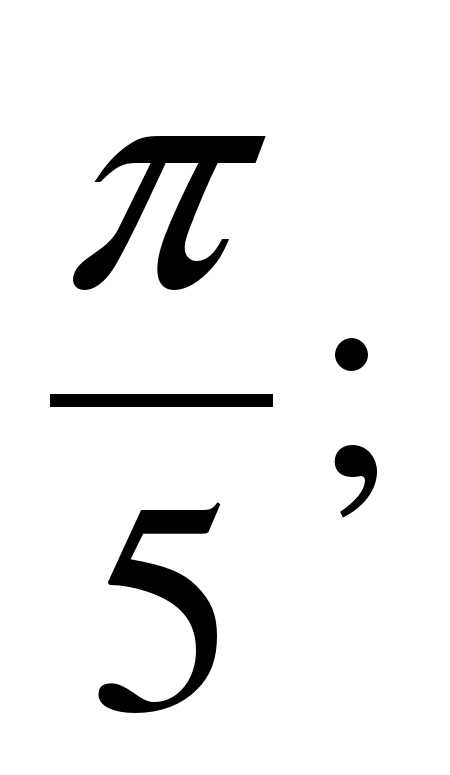 з)
з) 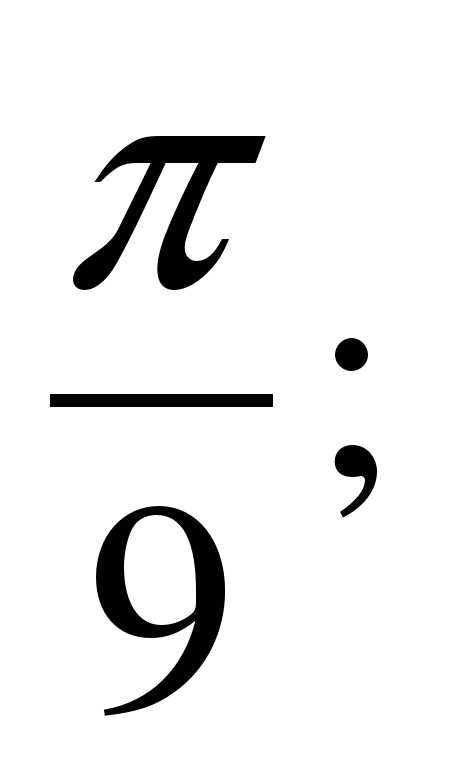 и) 10; к) 0,5
и) 10; к) 0,5
2. Найдите радианную меру углу, равного:
а) 120º; б) 150º; в) 36º; г) 300º; д) -225º.
3. Углом какой четверти является угол α, если:
а) 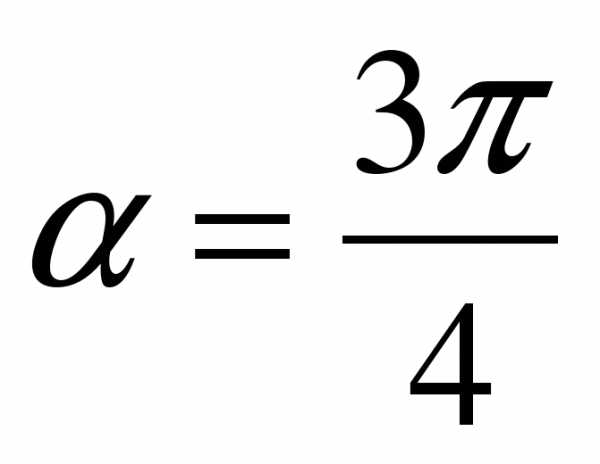 ; б)
; б) 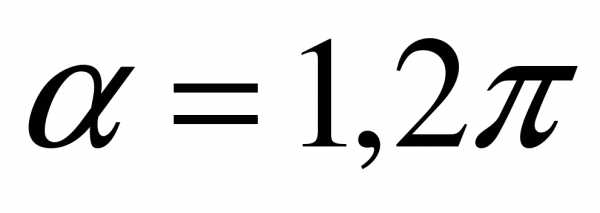 ?
?
Учебный модуль 5. Закрепление новых знаний. Творческая работа.
Цель: Уметь ставить в соответствие величину угла в градусном и радианном измерении. Уметь применять полученные знания в различных ситуациях. Уметь оценивать свои знания и возможности.
Задание для работы с технологическими картами:
Задание:
Выбери задание, соответствующее твоему уровню знаний и интересам:
Упражнения с комментариями по очереди:
Выразите в радианной мере величину угла:
а) -150º; б) 240º; в) 100º.
2. Выразите в градусной мере величину угла:
а)  ; б)
; б) 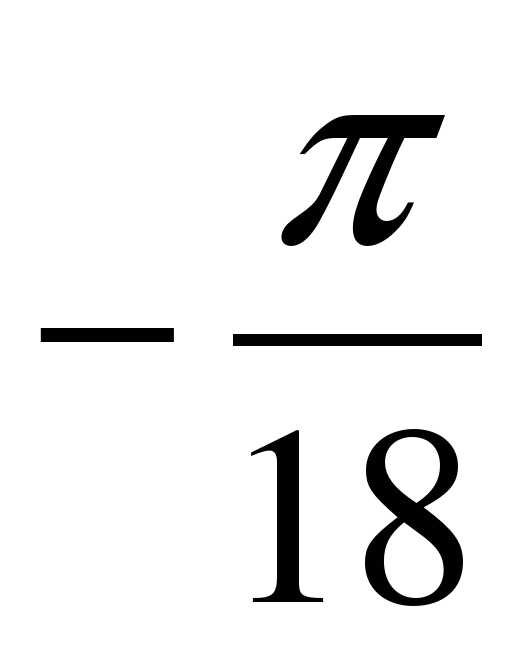 ; в)
; в) 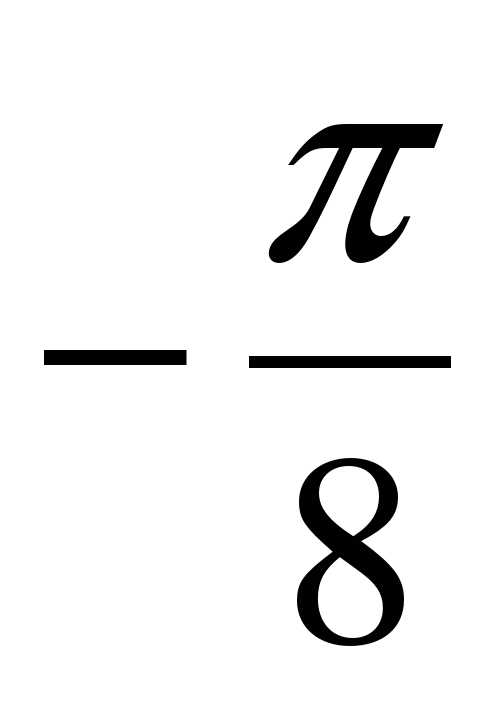 ; г) 3
; г) 3
Упражнения с проверкой в парах: после выполнения ученики меняются выполненными заданиями и проверяют друг друга, исправляют ошибки.
Заполни таблицу:
αº | 60º | 90º | 120º | 150º | 180º | 360º | ||||
а |
|
|
|
|
Упражнения с самопроверкой на экране
Вычислите:
а) 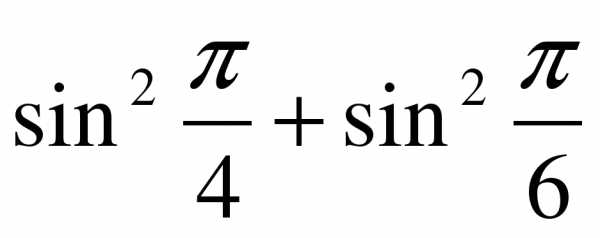 ; б)
; б)
Учебный модуль 6. Подведение итогов урока
Цель: Оценить результаты своей работы.
Задание:
Вернись к началу урока.
Посмотри, достиг ли ты цели.
Поставь все баллы в таблицу у себя на рабочем листе (баллы указаны в технологической карте)
Подсчитай сумму баллов.
Оценка:
5 — 20-21 балл
4 — 17-19 баллов
3 — 12-18 баллов
Рефлексия:
Цель: подвести итоги урока, обсудить, что узнали, как работали – т.е. каждый оценивает свой вклад в достижение поставленных в начале урока целей, свою активность, эффективность работы класса, увлекательность и полезность выбранных форм работы.
Ребята по кругу высказываются одним предложением, выбирая начало фразы из рефлексивного экрана на экране:
сегодня я узнал…
было интересно…
было трудно…
я выполнял задания…
я понял, что…
теперь я могу…
я почувствовал, что…
я приобрел…
я научился…
у меня получилось …
я смог…
я попробую…
меня удивило…
урок дал мне для жизни…
мне захотелось…
Учебный модуль 7. Информация о домашнем задании.
Инструктаж по его выполнению.
Домашнее задание:
Цель: закрепление знаний, умений, навыков и самоконтроль.
Стр 238, №3, 4
Дополнительно, повышенный уровень № 116, 1 вариант. Сборник задач А.Г. Мерзляк и др.
Повторение: стр. 229 №5(1,3).
Технологическая карта (раздается каждому ученику).
Тема: Радианная мера угла.
Учебная цель:
Знать определение угла в один радиан и формулы, устанавливающие связь между радианным и градусным измерением углов.
Уметь пользоваться радианным измерением углов при выполнении упражнений.
Учебный модуль | Учебный элемент | Время | Содержание учебного материала | ||||||||||||||||||||||
Учебный модуль 1. Организация начала занятия. | Учебный элемент 1 | 3 мин. | Цель: Подготовить к успешному выполнению заданий на уроке. Задание: Проверь наличие учебника, тетради, письменных принадлежностей. Работай самостоятельно, в случае затруднений обратись к товарищу или учителю. Выполняй задания вдумчиво и внимательно. Удачи тебе! | ||||||||||||||||||||||
Учебный модуль 2. Актуализация опорных знаний учащихся | Учебный элемент 2 | 3 мин. | Цель: Повторить определения синуса, косинуса, тангенса и котангенса угла. Задание: Контроль: Проверь работу товарища и оцени. Ответы на доске. Оценка:
| ||||||||||||||||||||||
| Учебный элемент 3 | 3 мин. | Цель: Повторить в какой координатной четверти расположен образ луча Ох при повороте около начала координат при различных значениях Задание: Заполни таблицу в тетради:
Контроль: проверь себя по эталону. Оценка:
| ||||||||||||||||||||||
| Учебный элемент 4 | 3 мин. | Цель: Проверить знание значений синуса, косинуса, тангенса и котангенса основных углов. Задание 3: «Выключи свет в окнах», т.е. закрась простым карандашом те клетки, где значения выражения в строке 2 равно выражению, записанному в строке 1. 1 вариант 2 вариант
Контроль: Проверь себя по эталону. Оценка:
| ||||||||||||||||||||||
Учебный модуль 3. Формулировка темы, цели и задач урока. Мотивация учебной деятельности учащихся | Учебный элемент 5 | 8 мин. | Цель: Познакомиться с определением угла в 1 радиан и формулами, устанавливающими связь между радианным и градусным измерением углов, выработать навык перевода градусную меру в радианную и наоборот. Задание: Прочитай внимательно текст учебника Радел 3, п.16, стр. 235-236. Сделай чертеж (см. стр. 236, рис.102). Запиши в тетрадь определение угла в 1 радиан. Запиши формулы перевода градусной меры угла в радианную и радианной в градусную. 1º= | ||||||||||||||||||||||
Учебный модуль 4. Формирование умений и отработка навыков | Учебный элемент 6 | 4 мин. | Цель: Проверить степень запоминания определения и формул перехода от одной меры угла к другой. Письменные упражнения: 1. Найдите градусную меру угла, радианная мера которого равна: а) 2. Найдите радианную меру углу, равного: а) 120º; б) 150º; в) 36º; г) 300º; д) -225º. 3. Углом какой четверти является угол α, если:
| ||||||||||||||||||||||
Учебный модуль 5. Закрепление новых знаний. Творческая работа. | Учебный элемент 7 | 8 мин. | Цель: Уметь ставить в соответствие величину угла в градусном и радианном измерении. Уметь применять полученные знания в различных ситуациях. Уметь оценивать свои знания и возможности. Задание: Выбери задание, соответствующее твоему уровню знаний и интересам: Упражнения с комментариями по очереди:
а) -150º; б) 240º; в) 100º. 2. Выразите в градусной мере величину угла: а) Упражнения с проверкой в парах: после выполнения ученики меняются выполненными заданиями и проверяют друг друга, исправляют ошибки. Заполни таблицу:
Упражнения с самопроверкой на экране Вычислите: а) Контроль: Оценка: 5 — допускается 1 ошибка; 3 — 4-5 ошибок; 4 — 2-3 ошибки; 2 — более 5 ошибок | ||||||||||||||||||||||
Учебный модуль 6. Подведение итогов урока | Учебный элемент 8 | 7 мин. | Цель: Оценить результаты своей работы. Задание: Вернись к началу урока. Посмотри, достиг ли ты цели. Поставь все баллы в таблицу у себя на рабочем листе.
Подсчитай сумму баллов. Оценка: | ||||||||||||||||||||||
Учебный модуль 7. Информация о домашнем задании. | Учебный элемент 9 | 2 мин. | Цель: меть применять знания, полученные на уроке в разных ситуациях. Домашнее задание: Стр 238, №3, 4 Дополнительно, повышенный уровень № 116, 1 вариант. Сборник задач А.Г. Мерзляк и др.А.Г Повторение: стр. 229 №5(1,3) |
videouroki.net
Радианная мера угла — Алгебра


х
а

a
h
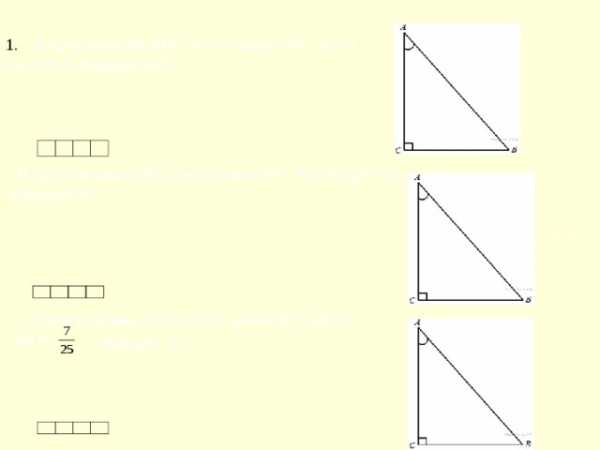
- В треугольнике ABC угол С равен 90°, АС=4,
cosA =0,5. Найдите АВ.
8
2. В треугольнике АВС угол С равен 90°, АС=8, tgA =0,5.
Найдите ВС.
4
3 . В треугольнике АВС угол С равен 90°, АВ=5,
sinA =
Найдите АС .
4
,
8


Цель урока : Рассмотреть связь между радианной и градусной мерами угла и
закрепить умения выполнять переход от радианной меры угла к градусной мере и наоборот .
Задачи:
1 ) учебные :
- дать понятие о радианном измерении углов,
- изучить связь между градусной и радианной мерами измерения углов,
- познакомиться с формулами перевода градусной меры в радианную меру и наоборот,
- получить представление о вычисление длины дуги с использование значений углов в радианах,
- научиться применять формулы, изученные на уроке для решения задач и упражнений.
2) развивающие и воспитательные:
- получение учащимися представлений о появлении тригонометрии как науки, о её практическом применении,
- развитие навыков абстрактного мышления,
- развитие представлений о разностороннем подходе к решению задач.

=1

R =1
R =1
l=R
1рад.

R =1
R =1
l= R

°


Домашнее задание:
§24 (подробно рассмотреть задачу 4 на стр. 167)
№ 536, №537, №541

Ответьте на вопросы:
1. Что означает «тригонометрия»?
2 . Разделом какой науки являлась наука тригонометрия в начале развития?
3. Какие единицы измерения углов Вы знаете?
4. Чему равно радиан?
5. Как перевести из градусной меры в радианную и обратно?
6. Было ли интересно на уроке?
multiurok.ru
План-конспект урока по алгебре (10 класс) на тему: «Радианное измерение углов и дуг. Вращательное движение»
ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ПРОФЕССИОНАЛЬНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
МОСКОВСКОЙ ОБЛАСТИ
«Ногинский колледж»
Открытый урок
по учебной дисциплине «Математика: алгебра и начала математического анализа; геометрия»
по теме:
«Радианное измерение углов и дуг. Вращательное движение»
Разработан преподавателем
Селиной Е.М
Согласовано с методистом
Прокофьевой О.А.
Рассмотрено на заседании
Педагогического совета
№______ от___________ 2017 г.
2017 год
У Т В Е Р Ж ДА Ю
Зам.директора по УМР
Г БПОУ МО
«Ногинский колледж»
_____________А.В. Артёмова
«______» ______________2017 г.
Преподавателю учебных дисциплин «Математика: алгебра и начала математического анализа; геометрия» и «Физика» Селиной Е.М. провести в группе 1 ПК ( 1 курс, по профессии : «19.01.17 «Повар, кондитер») 04 апреля 2017 г. открытый урок по математике по теме:
«Радианное измерение углов и дуг. Вращательное движение»
Председатель предметной цикловой комиссии
Общеобразовательные дисциплины и дисциплины цикла ОГСЭ».
___________ Е.М. Селина
Ногинск, 2017 год
Радианное измерение углов и дуг.
Тип занятия: Занятие-лекция с решением задач практического содержания.
Оборудование: компьютер, проектор, раздаточный материал.
Методы обучения:
1. просмотр презентации;
2. самоконтроль и самоанализ обучающихся;
3. опрос.
Приемы:
1. аналитическая беседа;
2. наблюдение.
Формы:
1. коллективная;
2. индивидуальная.
Технологии:
1. сотрудничества;
2. проблемно-деятельностная;
3. ИКТ-технология.
Принципы:
1. доступности;
2. наглядности;
3. системного подхода к изучению материала.
Цели занятия:
– образовательные:
- изучить формулы перехода от градусной меры угла к радианной и от радианной к градусной,
- сформировать умение пользоваться радианным измерением углов на уровне выполнения упражнений по образцу, в измененной и новой ситуации.
– развивающие:
- развивать внимание, умение рассуждать,
- развивать логическое мышление, умение выделять существенные признаки математического понятия, сравнивать и обобщать
– воспитательные:
- воспитывать ценностное отношение к предмету, интерес к его изучению и понимание значимости предмета, через иллюстрацию прикладного характера математики,
- воспитывать аккуратность, добросовестное отношение к работе, уважительное отношение к товарищам, умение работать самостоятельно, в парах
и коллективе, - формировать систему нравственного отношения к одногрупникам.
Компетенции по ФГОС:
- применять математические методы для решения профессиональных и прикладных задач;
- использовать приемы и методы математического анализа в различных профессиональных ситуациях;
- анализировать результаты измерения величин с допустимой погрешностью, представлять их графически.
Содержание учебной деятельности
Организационный момент
Преподаватель приветствует группу и проверяет ее готовность к занятию.
Обучающиеся приветствуют преподавателя. Староста группы сообщает о явке студентов на занятие.
Постановка дидактической цели
Добрый день! Расскажу Вам одну легенду.
Однажды мастер Золотого века искусства создал скульптуру. Пропорциональное соотношение в построении статуи было идеально. Чтобы его творение увидело больше людей, мастер построил высокий пьедестал. Однако после поднятия статуи на фундамент, статуя смотрелась уродливой. Скульптором не было учтено, что в перспективе к горизонту уменьшаются многие детали и при взгляде снизу вверх уже не создается впечатления ее идеальности. Мастер потерпел фиаско.
Обучающиеся слушают рассказ преподавателя.
Мотивация предстоящей деятельности
Давайте подумаем, в каких областях нашей профессиональной деятельности нам потребуются знания измерения углов? (сначала ответы аудитории)
— как вы заметили из легенды, знания об измерении углом нам потребуются не только в математике, но и в искусстве. Почему люди не смогли увидеть всю красоту скульптуры? Зная примерное расстояние от статуи до точки зрения, а именно от верха статуи до глаз человека и высоту статуи, можно рассчитать синус угла падения взгляда с помощью таблицы, тем самым найдем точку зрения. Ситуация меняется, так как статую поднимают на высоту, поэтому расстояние от верхушки статуи до глаз человека увеличивается, следовательно и синус угла падения увеличивается. А этого скульптор не учел!
Многие задаются вопросами: зачем нужна тригонометрия? Как она используется в нашем мире? С чем может быть связана тригонометрия? И вот ответы на эти вопросы. Тригонометрия или тригонометрические функции используются в астрономии (особенно для расчётов положения небесных объектов), в морской и воздушной навигации, в электронике, в теории вероятности, в статистике, в биологии, в медицинской визуализации, например, компьютерной томографии, в архитектуре, в разработке игр и многих других областях.
Обучающиеся дополняют преподавателя и рассказывают о том, как тригонометрия используется в жизни, где может применяться тригонометрическая функция, рассказывают о небесных объектах и планетах которые они знают.
Приводят примеры применения тригонометрии в строительстве, в морской и воздушной навигации, в электронике, в теории вероятности, в статистике, в биологии, в медицине, в архитектуре, в разработке игр, телефонных приложений и других областях.
— знания об углах нам понадобятся и в пожарной службе. При пожаре необходимо быстро и точно рассчитать угол на который нужно поднять пожарную лестницу к зданию и при этом попасть на нужный этаж.
— в авиации очень важно правильно рассчитать угол, под которым поднимается самолет, чтобы не задеть верхушки деревьев и ближайших построек.
— даже в биологии движение рыб в воде происходит по закону синуса или косинуса, если зафиксировать точку на хвосте, а потом рассмотреть траекторию движения. При плавании тело рыбы принимает форму кривой, которая напоминает график функции y = tgx
Немного из истории…
1. Древние вавилоняне и египтяне изучали тригонометрию как часть астро-номии; разделили окружность на 360°
2. Древние индийцы: ввели названия «синус», «косинус», составили таблицы синусов, косинусов
3. IX-XVвв – Средний и Ближний восток: составляли таблицы котангенса, тангенса, косеканса; ввели понятие единичной окружности
4. Насир ад-Дин Мухаммад ат-Туси (1201-1274) выделил раздел тригонометрии из астрономии
5. Лев Герсонид (1288-1344) – открыл теорему синусов
6. XVII-XIXвв: применение тригономет-рии в механике, физике, технике, как часть математического анализа (Виетт, Бернулли) – тригонометрические символы, графики – синусоиды
7. Л.Эйлер: придал тригонометрии современный вид
Давайте начнем с заданий – разминки. Ответьте на вопросы:
- Чему равен угол квадрата? (900)
- На какой угол поворачивается солдат по команде «кругом»? (1800)
- Чему равен угол между минутной и часовой стрелками на часах, когда они показывают 2ч? (600)
Все ответы вы дали в градусах. Но это не единственная единица измерения углов.
Кто-нибудь знает в чем еще измеряются углы? (в радианах)
Обучающиеся слушают рассказ преподавателя. Предлагают свои варианты ответов.
Изучение нового материала
Записывают тему занятия «Радианное измерение углов и дуг. Вращательное движение». Обучающиеся записывают новый материал в тетрадь.
Градусная мера. Здесь единицей измерения является градус (обозначение °) – это поворот луча на 1 / 360 часть одного полного оборота. Таким образом, полный оборот луча равен 360°.
1/60 часть градуса называется минутой (обозначают 1′).
1/60 часть минуты называется секундой (обозначают 1»).
Радианная мера.
Радианная мера измерения угла есть отношение длины дуги, проведенной произвольным радиусом и заключённой между сторонами этого угла, к радиусу дуги.
Градусная мера угла в 1 радиан равна: Так как дуга длиной πR (полуокружность), стягивает центральный угол в 180°, то дуга длиной R, стягивает угол в π раз меньший, т.е.
Так как π = 3,14, то 1 рад = 57,3°
Если угол содержит α радиан, то его градусная мера равна
И наоборот
Наиболее активные студенты участвуют при решении примеров на поиск радианной и градусной меры угла.
Пример 1.
Найти радианную меру угла равного 1) 30°, 2)135°
Решение:
1) 30° = 30·π / 180 = π/6
2) 135° = 135·π/180 = 3π/4
Пример 2.
Найти градусную меру угла выраженного в радианах 1) π/3 , 2) 4·π/5
Решение:
1) π/3 = 180°/3 = 60°
2) 4π/5 = 4·180°/5 = 144°
Закрепление изученного материала
№1: Переведите в радианную меру углы:
1) 45° 4) 100° 7) 215°
2) 15° 5) 200° 8) 150°
3) 72° 6) 360° 9) 330°
№2: Переведите в градусную меру углы:
1) 3) 5)
2) 4) 6)
Самостоятельная работа
I вариант | II вариант |
1. Переведите в радианную меру углы: | |
1) 60° | 1) 320° |
2) 145° | 2) 105° |
3) 240° | 3) 40° |
2. Переведите в градусную меру углы: | |
1) | 1) |
2) | 2) |
Ответы
I вариант | II вариант |
1. Переведите в радианную меру углы: | |
1) | 1) |
2) | 2) |
3) | 3) |
2. Переведите в градусную меру углы: | |
1) 72° | 1) 405° |
2) 480° | 2) 150° |
Практическая работа
Сейчас я предлагаю Вам выполнить упражнение по созданию рисунка с 3D эффектом.
Первый шаг.
Нам понадобится жесткая бумага. Сгибаем лист ровно по середине. Рисуем в обе стороны прямые линии под одинаковым углом. Линии должны зеркально отражать друг друга. Примерно 35-40 градусов
Второй шаг.
Рисуем ступеньки лестницы с двух сторон, параллельно сгибу листа.
Третий шаг.
Берем линейку и соединяем прямой линией вершины лестницы. Это будет тень. Берем мягкий карандаш и делаем тень. Давить на карандаш не стоит, тень не должна быть слишком темной.
Последний шаг.
Поднимаем одну часть бумаги вверх и разворачиваем бумагу под углом к зрителю. Важно подобрать такой угол, чтобы лестница казалась прямой. Из-за тени будет казаться, что это объемный рисунок.
Обучающиеся выполняют пошагово практическую работу
Подведение итогов
Преподаватель делает выводы по пройденному материалу.
Дает домашнее задание и рекомендует литературу для более глубокого изучения.
Обучающиеся записывают домашнее задание и литературу для самостоятельного изучения нового учебного материала.
В заключение просит ответить на вопросы:
1) Что означает «тригонометрия»?
2) Разделом какой науки являлась тригонометрия в начале развития?
3)Какие единицы измерения углов Вы знаете?
4) Чему равно π радиан?
5) Как перевести из градусной меры в радианную и обратно?
6) Было ли интересно на уроке?
Обучающиеся отвечают на вопросы.
Самостоятельная работа
I вариант 1. Переведите в радианную меру углы: 1) 60° 2) 145° 3) 240° 2. Переведите в градусную меру углы: 1) 2) |
Самостоятельная работа
II вариант 1. Переведите в радианную меру углы: 1) 320° 2) 105° 3) 40° 2. Переведите в градусную меру углы: 1) 2) |
Самостоятельная работа
I вариант 1. Переведите в радианную меру углы: 1) 60° 2) 145° 3) 240° 2. Переведите в градусную меру углы: 1) 2) |
Самостоятельная работа
II вариант 1. Переведите в радианную меру углы: 1) 320° 2) 105° 3) 40° 2. Переведите в градусную меру углы: 1) 2) |
Самостоятельная работа
I вариант 1. Переведите в радианную меру углы: 1) 60° 2) 145° 3) 240° 2. Переведите в градусную меру углы: 1) 2) |
Самостоятельная работа
II вариант 1. Переведите в радианную меру углы: 1) 320° 2) 105° 3) 40° 2. Переведите в градусную меру углы: 1) 2) |
nsportal.ru


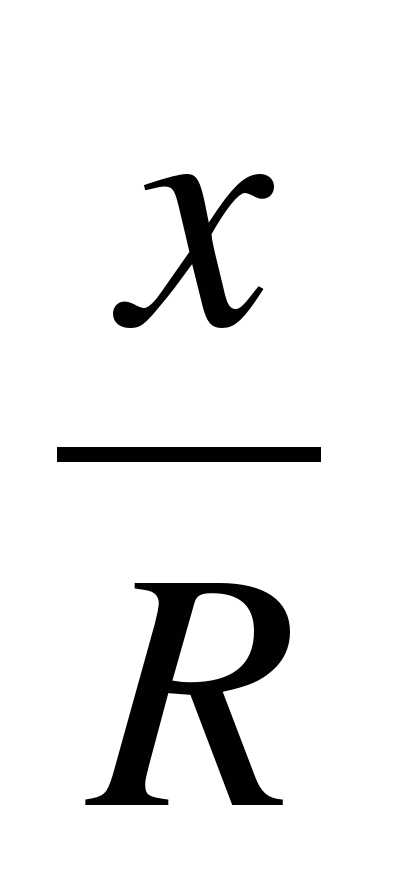 ?
?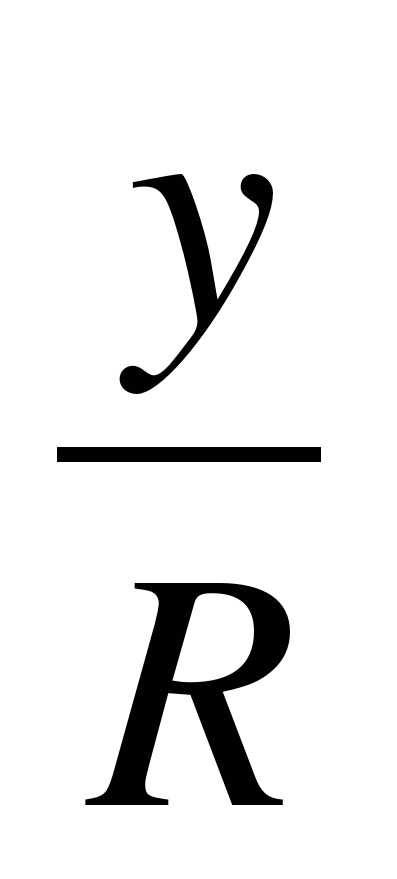 ?
?