Рациональные и действительные числа 10 класс: Рациональные числа — урок. Алгебра, 10 класс.
Действительные числа
Вы уже знакомы с конечными, бесконечными периодическими десятичными дробями, которые являются рациональными числами.
Но в математике существуют и непериодические бесконечные десятичные дроби, которые не являются рациональными числами.
Например, вот такое число: … . Это число является иррациональным.
Итак, иррациональным числом называется бесконечная десятичная непериодическая дробь.
Кстати, иррациональные числа, как и рациональные, могут быть как положительными, так и отрицательными. К примеру, следующие числа:
Первое число положительное иррациональное число, второе – отрицательное иррациональное число.
Числа
, , , ,, являются иррациональными
числами, так как эти числа можно представить в виде 
С понятием иррациональных чисел мы с вами разобрались. Теперь давайте перейдём к действиям с ними. И ответим на такой вопрос: какие же числа получают в результате выполнения арифметических действий с иррациональными числами?
При сложении, вычитании, умножении и делении иррациональных чисел результат может оказаться как рациональным, так и иррациональным числом.
Множество иррациональных чисел принято обозначать заглавной латинской буквой .
Рациональные и иррациональные числа вместе образуют множество действительных чисел.
Множество действительных чисел принято обозначать заглавной латинской буквой . Запись означает, что является действительным числом.
Действительным
числом называется бесконечная десятичная дробь, то есть … или …, где – целое
неотрицательное число, а каждая из букв , , и так далее – это
одна из десяти цифр: , , , , , , , , , .
Например, в записи числа …
, , , , , …
В записи действительного числа …
, , , ,, …
В записи действительного числа …
, , , ,…
В записи действительного числа …
, , , , при .
Действительные числа могут быть как положительными, так и отрицательными, а могут и равняться нулю.
Если все цифры записи бесконечной десятичной дроби равны нулю, то и дробь равна нулю. А если бесконечная десятичная дробь не равна нулю и перед ней стоит знак «+» либо вообще не стоит знака, то это положительное действительное число. А если стоит знак «–», то это отрицательное действительное число.
Все
основные действия и правила над рациональными числами, которые вы
знаете, сохраняются и для действительных чисел. Например,
переместительный, сочетательный и распределительный законы, правила сравнения,
правила раскрытия скобок и так далее.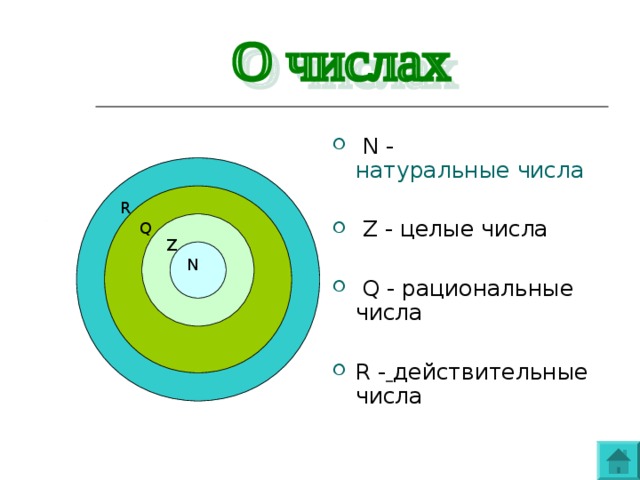
Только арифметические операции над действительными числами, как правило, заменяют операциями над их приближениями.
Например, давайте вычислим
…
…
Если вычислять сумму этих корней с точностью до единицы, то
.
Если вычислять эту же сумму, но с точностью до одной десятой, то
.
А вот если вычислять сумму наших корней с точностью до одной сотой, то
.Обратите внимание:; ; и так далее являются последовательными десятичными приближениями значения . Причём первые два числа с избытком, последнее с недостатком. Заметим, что при вычислении и корня из сами числа и корень мы заменяли на их приближения, то есть рациональными числами, а затем выполняли сложение чисел по известным правилам.
Так же, как и для рациональных чисел, модуль действительного числа обозначается и определяется так:
Например,
…
…
И
ещё нам с вами осталось дать геометрическое истолкование действительных чисел.
Итак, геометрически действительные числа изображаются точками числовой прямой. Множество действительных чисел «заполняет» всю числовую прямую. Причём каждому действительному числу соответствует единственная точка на числовой прямой
Точку, изображающую действительное число , также обозначают буквой .
Отметим, что если действительное число меньше действительного числа , то на числовой прямой точка будет лежать левее точки .
А теперь давайте приступим к практической части нашего урока.
Задание 1. Сравните числа , и .
Решение.
…
…
…
Видим: у данных чисел совпадают целые части и цифры десятых.
Значит ,.
Теперь сравним и .
Видим:
у этих чисел совпадают первые четыре цифры после запятой, а вот пятая цифра
после запятой у значения.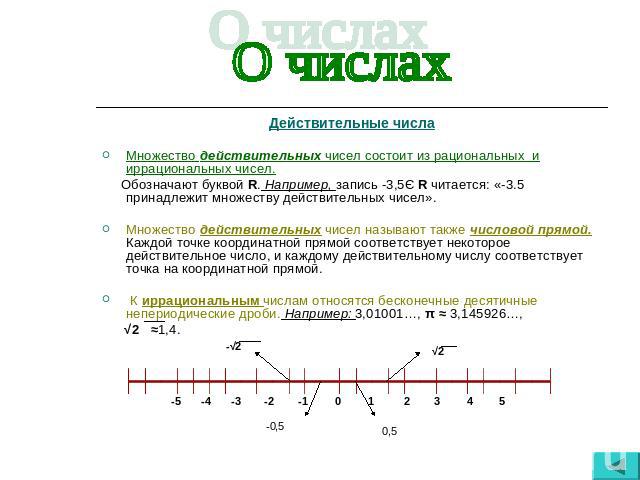
Следовательно
Отсюда получаем,
Задание 2
. Выясните, каким числом (рациональным или иррациональным) является числовое значение выражения .Решение. Раскроем скобки в нашем выражении, применяя формулу квадрата суммы. Воспользуемся следствием из определения квадратного корня.
.
Затем применим свойство корня из произведения. Приведём подобные.
Получим .
Данное число является иррациональным, так как содержит иррациональное число .
Понятие действительного числа | Консультация по алгебре (10 класс) на тему:
- Понятие действительного числа
Первыми числами с которыми вы познакомились в школе, — это натуральные числа: 1, 2, 3, 4, 5, 6…..
Затем вы изучали целые числа. Множество целых чисел состоит из натуральных чисел, целых отрицательных чисел и числа «нуль»: ….-3, -2, -1, 0, 1, 2, 3….
И наконец, вы узнали, что такое рациональные числа.
Число называют рациональным, если его можно записать в виде дроби, где p – целое число, а q – натуральное. Каждое рациональное число может быть разложено в бесконечную десятичную периодическую дробь (для нахождения этого разложения можно разделить уголком числитель дроби p на ее знаменатель q ). Таким образом, рациональные числа имеют два представления (две формы записи) – одно в виде дроби, а другое в виде бесконечной десятичной периодической дроби.
Наряду с бесконечными десятичными периодическими дробями существуют и бесконечные десятичные непериодические дроби, которые называют иррациональными числами. Рациональные и иррациональные числа составляют множество всех действительных чисел. Таким образом, действительное число-это число, которое можно записать в виде бесконечной десятичной дроби. Если число рациональное, то дробь периодическая; если число иррациональное, то дробь непериодическая.
Формально конечную десятичную дробь можно записать в виде бесконечной десятичной периодической дроби двумя способами, например:
2,4=2,4000…=2,4(0)
2,4=2,3999…=2,3(9)
- Множества чисел.
Напомним обозначения некоторых множеств чисел, которые вам часто придется рассматривать:
N — множество всех натуральных чисел
Z — множество всех целых чисел
Q — множество всех рациональных чисел
R — множество всех действительных чисел
R- множество всех положительных действительных чисел
[а;в] — отрезок – множество всех действительных чисел х, удовлетворяющих двойному неравенству а ≤ х ≤ в . Точки а и в называются концами отрезка и принадлежат этому отрезку.
(а;в) – интервал — множество всех действительных чисел х, удовлетворяющих двойному неравенству а
[а;в) – полуинтервал — множество всех действительных чисел х, удовлетворяющих двойному неравенству а ≤ х
(а;в] — полуинтервал — множество всех действительных чисел х, удовлетворяющих двойному неравенству а
Множество не содержащее ни одного элемента, называют пустым множеством. Его обозначают знакомØ.
Тот факт, число принадлежит или не принадлежит множеству чисел, записывают с помощью определенных знаков:- принадлежит, — не принадлежит.
Объединением множеств А и В называют множество, состоящее из всех элементов, принадлежащих хотя бы одному из этих множеств. Обозначают А U В.
Пересечением множеств А и В называют множество, состоящее из всех элементов, каждый из которых принадлежит и множеству А, и множеству В. Обозначается А В.
Если любой элемент множества А является элементом множества В, то А называют подмножеством множества В. Пишут АВ и говорят «А – подмножество В».
- Свойства действительных чисел
Действительные числа обладают следующими свойствами:
- Свойства сложения и вычитания
- а + в = в + а (переместительное свойство сложения)
- (а + в) + с = а + ( в + с) (сочетательное свойство сложения)
- а + 0 = а
- а + (-а) = 0
- Свойства умножения и деления
- а*в = в*а (переместительное свойство умножения)
- (а*в)*с = а*(в*с) (сочетательное свойство умножения)
- а*1 = а
- а * 0 = 0
- –а = (-1)*а
- а* = 1 (а0)
- а*=(в0)
- (а + в)*с = а*с + в*с (распределительное свойство)
Глава 1 (8 ноября).
pmd%PDF-1.3 % 93 0 объект >>>]/ON[137 0 R]/Порядок[]/RBGroups[]>>/OCGs[137 0 R]>>/Страницы 85 0 R/Тип/Каталог>> эндообъект 94 0 объект >/Шрифт>>>/Поля 81 0 R>> эндообъект 90 0 объект >поток приложение/pdf
%_ KN»v }X]þυ=[r}?6e, 9e*˽JВещественные числа 10 класса Решения NCERT и примечания CBSE
Программа по математике для 10 класса направлена на то, чтобы познакомить учащихся с основными и фундаментальными понятиями этой дисциплины для дальнейшего развития в следующих классах. Среди наиболее интересных из этих концепций — действительные числа, которые составляют основу нескольких императивных математических тем. На предыдущих занятиях вы должны были изучить несколько типов чисел, таких как натуральные, целые, рациональные, иррациональные и целые числа. Но знаете ли вы, что все эти типы чисел относятся к реальным числам? Удивительно! Верно? Поскольку мы здесь, чтобы провести вас по этой теме, мы продолжим излагать некоторые остроумные факты, подобные этим. Итак, следите за обновлениями и давайте начнем обсуждение действительных чисел класса 10.
Математические формулы для класса 10
Этот блог включает в себя:
- Что такое реальные числа?
- Натуральные номера
- Целые числа
- Целы
- Рациональные номера
- Иррациональные номера
- ПРЕДУПРЕЖДЕНИЕ РЕАЛЬНОГО Число
- ЭКЛИДНА Практические вопросы по работе с реальными числами
- MCQ по математике для 10 класса: вещественные числа с ответами PDF
Что такое действительные числа?
Все числа, включая положительные, отрицательные и нулевые, относятся к широкой категории действительных чисел .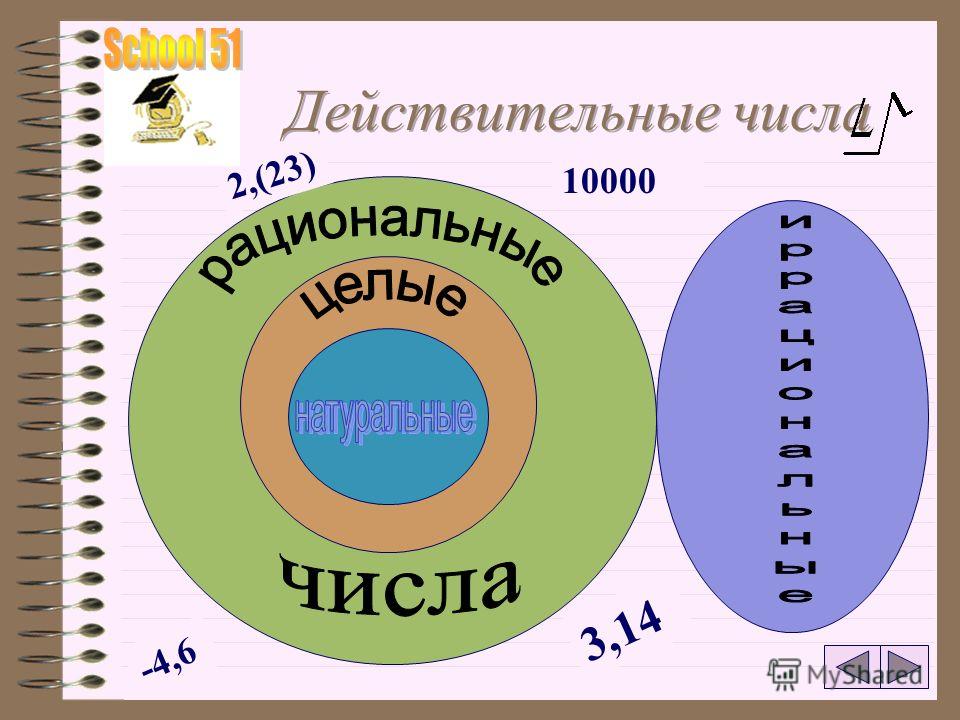
В общих чертах действительные числа представляют собой все те числа, которые не являются мнимыми числами. Таким образом, действительное число сочетает в себе свойства рациональных и иррациональных чисел. Например: 4, 43, -34, -5, 3/4, 5/9, π(3,14) и т. д.
Прежде чем перейти к понятия действительных чисел, давайте быстро вспомним основные типы чисел, которые вы должны были изучить ранее.
Натуральные числа
Натуральные числа представляют собой все положительные числа в природе от 1 до бесконечности. Набор натуральных чисел представлен как «N» и не включает десятичные дроби, дроби или любые отрицательные числа. N = 1, 2, 3, 4, 5, 6, …
Целые числа
Целые числа представляют все положительные числа, включая ноль, и обозначаются буквой «W». W = 0, 1, 2, 3, 4, 5, 6, …
Целые числа
Целые числа включают все положительные и отрицательные числа с нулем, не представляющие десятичной или дробной части. Например, 2, 3, 51, 0, -1, -5, а 2,45, √2 и 10 ¾ не являются целыми числами.
Они представлены как «Я». I = …., -2, -1, 0, 1, 2, …
Краткие математические приемы
Умственная математика: советы и рекомендации
Рациональные числа
Рациональные числа — это числа, которые могут быть представлены в виде дробей и десятичных знаков в виде a/b двух целых чисел с числитель и «b» в качестве отличного от нуля знаменателя. Например, , 2/3, 4/5, 1/2, 10 ¾ и т. д. Они обозначаются буквой «R». R = ½ , ¾ , 5,24, 0,5432 и т. д.
Иррациональные числа
Иррациональные числа представляют собой все числа, которые не являются рациональными числами или не могут быть выражены в отношении каких-либо целых чисел. Например, , √2, √3, √5, √7 и π — иррациональные числа.
Commerce with Maths Stream
Представление действительных чисел
Все типы или формы действительных чисел согласно главе о действительных числах (целые числа, дроби и десятичные дроби) могут быть точно размещены в числовой строке.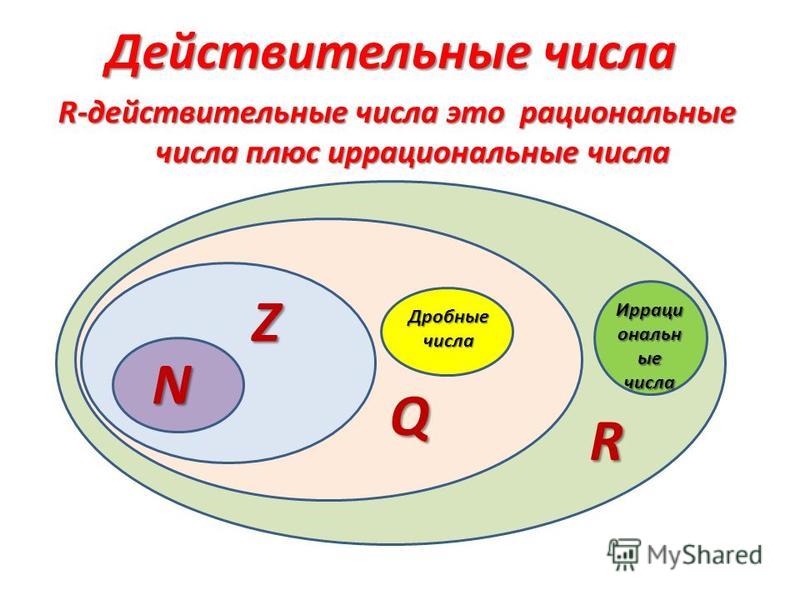
Например, действительное число 4 как 4,0, -3 как -3,0, дроби в форме 2/5 как 0,40, 1/2 как 0,50 и так далее.
Пройди этот математический тест, если считаешь себя гением!
Ведическая математика
Лемма Евклида о делении (алгоритм)
Алгоритм леммы Евклида о делении следует концептуальной формуле [делимое = (делитель x частное) + остаток] . Согласно этой теореме, если есть два положительных целых числа, скажем, p и q, то существуют параллельные целые числа r и s, которые удовлетворяют утверждению как p = qr + s (где s представляет число, равное больше 0 и меньше чем q).
Мы можем легко найти HCF, используя алгоритм Евклида. Давайте рассмотрим простой пример, чтобы получить HCF двух целых чисел 455 и 42 соответственно.
Тогда по лемме Евклида имеем:
455 = 42 × 10 + 35
Аналогично, если мы воспользуемся методом дивидендов (делитель 42, остаток 35), а затем по лемме Евклида,
42 = 35 × 1 + 7
Теперь, двигаясь дальше, делитель становится равным 35, а остаток равен 7, и, используя лемму Евклида, находим:
35 = 7 x 5 + 0
Поскольку остаток становится равным нулю, мы можем остановить процесс, чтобы завершить HCF двух целых чисел 455 и 42 как 7.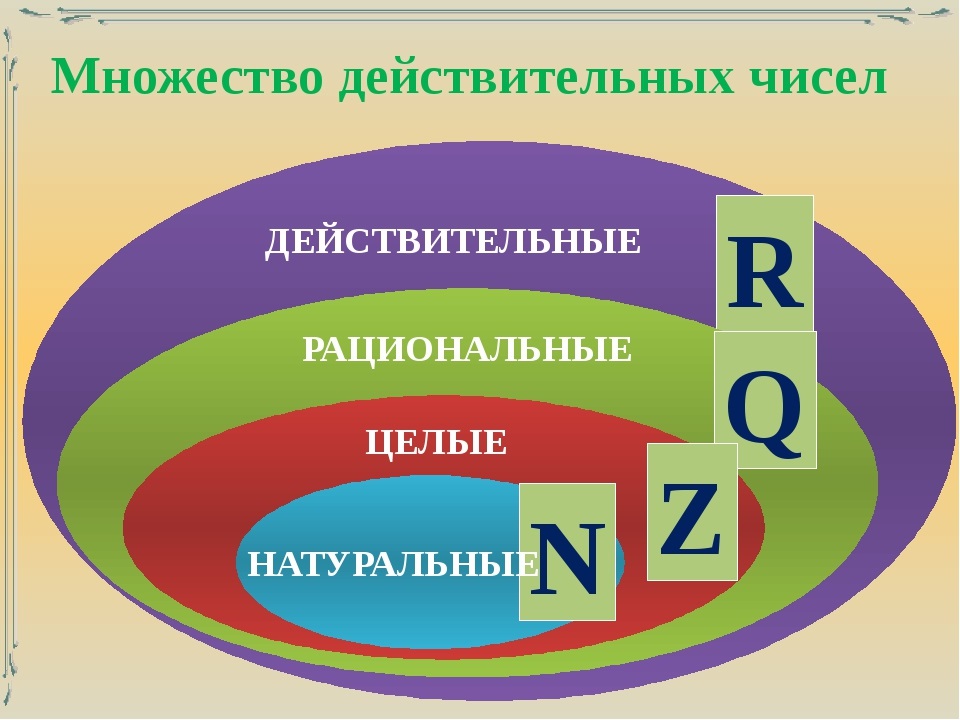
Таким образом, используя алгоритм Евклида, упомянутый в классе 10 «Вещественные числа», вы можете простым способом вычислить HCF двух чисел.
LCM и HCF Для конкурсных экзаменов
Класс 10 ICSE Maths
Десятичное расширение
Изучая главу 10 класса о действительных числах, вы также узнаете о двух способах расширения десятичного рационального числа . Завершающим десятичным расширением являются те, когда десятичное число заканчивается конечными числами. Например, ½ как 0,50 в десятичных дробях и наоборот.
0,375 = 375/1000 = 3 х 5 3 / 2 3 х 5 3 = ⅜
Неконечные десятичные расширения соответствуют тем, когда десятичные дроби не являются конечными. Они могут быть как повторяющимися (рациональные числа), так и неповторяющимися (иррациональные числа).
Например:
7/12 = 0,583333… = 0,583
9/11 = 0,8181… = 0,81 (повторение)
SO, DECMAL EXPANES.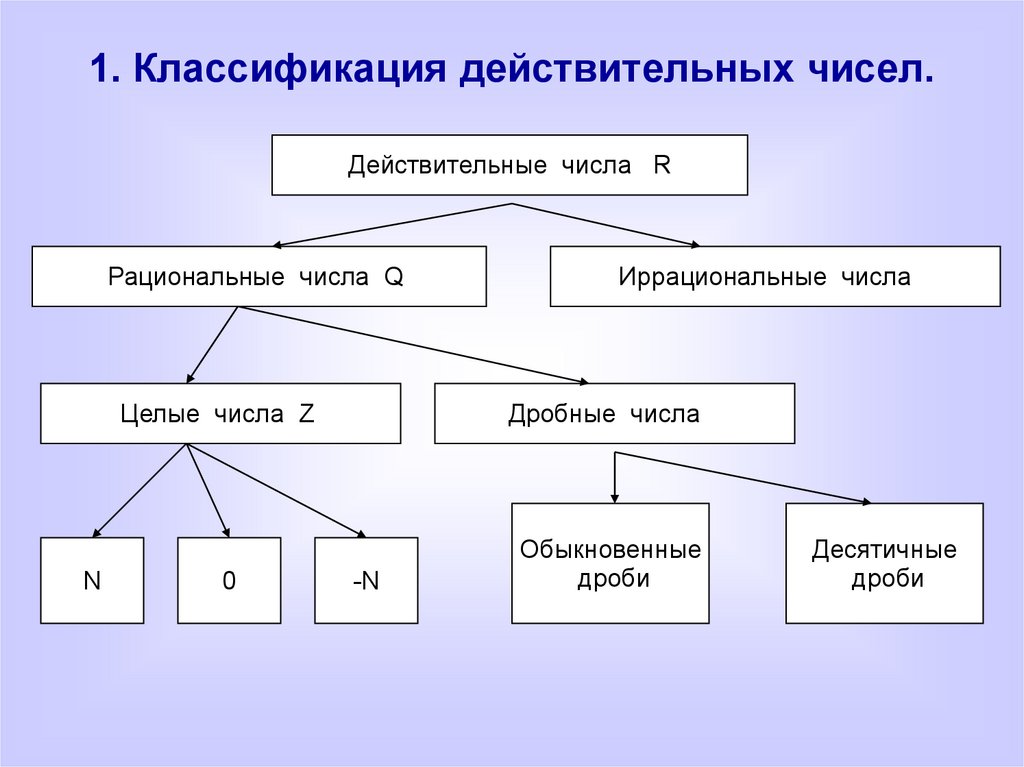
либо прекращающиеся, либо не прекращающиеся.
Математика для конкурсных экзаменов
Основная теорема арифметики
Теорема утверждает, что любое составное число можно представить в виде множителей или произведений простых чисел. Следовательно, независимо от порядка, простая факторизация натурального числа всегда будет уникальной сама по себе. Например, 3 × 5 × 7 x 11 берется так же, как 5 × 7 x 11 x 3, или в любом порядке, в котором они записаны. 10 класс математика действительные числа.
- Десятичное представление рационального числа 43/ 2 4 5 3 закончится после скольких знаков после запятой?
- Найдите наибольшее число, на которое делятся 398, 436 и 542, а в остатках соответственно 7, 11 и 15.
- Express 98 как произведение простых чисел.
- HCF и LCM из двух чисел равны 9 и 459 соответственно. Если одно из чисел равно 27, найдите другое число.
- Найдите HCF и LCM чисел 13 и 17 методом простой факторизации.
