Конспект урока+презентация по информатике на тему Представление чисел в компьютере (10 класс)

ФИО: Воронова Екатерина Николаевна

Место работы: МАОУ «Лицей №1″г. Стерлитамак

Должность: учитель информатики

Тема: Представление чисел в компьютере. Формат с фиксированной и плавающей запятой. Прямой, обратный и дополнительный код.

Класс: 10

Цели урока:

Образовательная:

• формирование знаний учащихся о формах представления числовой информации в компьютере;

• формирование практических навыков по представлению чисел в различных кодах;

Развивающая: развитие алгоритмического мышления, памяти, внимательности;

Воспитательная: воспитывать научное мировоззрение, информационную культуру, расширять кругозор учащихся.

Методы обучения: — объяснительно — иллюстративный;

— практическая работа.

Тип урока: комбинированный.

План урока:

1. Организационный момент – 2 мин.

2. Проверка и актуализация знаний – 8 мин.

3. Объяснение нового материала – 10 мин.

4. Практическая работа – 20 мин.

5. Домашняя работа – 2 мин.

6. Подведение итогов урока, выставление оценок – 2 – 3 мин.

Оборудование: Мультимедийный проектор, презентация.

Ход урока

1. Организационный момент (2 мин)

Здравствуйте, ребята, присаживайтесь. Откройте тетради, запишите число и тему урока.

2. Проверка и актуализация знаний (8 мин)

Перед тем как приступить к изучению новой темы, повторим основные понятия, изученные на прошедших уроках. Давайте вспомним все, что мы знаем о системах счисления.

Вопросы:

1. Что называют системой счисления?

Ответ: Системой счисления называется совокупность символов (цифр) и правил их использования для представления чисел

2. Какие виды систем счисления вы знаете?

Ответ: Позиционные и непозиционные системы счисления

3. Приведите примеры непозиционной системы счисления

Ответ: Римская система, в которой в качестве цифр используются некоторые буквы: I(1), V(5), X(10), L(50), C(100), D(500), M(1000).

4. Как можно записать число в позиционной системе счисления?

Ответ: Любое число в позиционной системе счисления с произвольным основанием можно записать в виде многочлена

, где s — основание системы, а степень соответствует разряду цифры в числе .

Например:

5. Какие примеры вы можете привести позиционной системы счисления?

Ответ: 101010₂— двоичная (основание 2, используются две цифры – 0,1)

345₁₀ – десятичная ( основание 10, используются десять цифр – 0…9)

746₈ – восьмеричная (основание 8, используются 8 цифр – 0…7)

Человек использует десятичную систему счисления, а компьютер – двоичную систему счисления. Поэтому возникает необходимость перевода чисел из десятичной системы в двоичную и наоборот.

6. Как можно перевести любое число в десятичную систему счисления?

Ответ: Нужно воспользоваться многочленом

7. Как можно перевести из десятичной системы счисления в любую систему счисления с произвольным основанием?

8. Ответ: Из 10 2

   13₁₀=1101₂

   Из 10 3

   13₁₀=111₂

   Какие действия мы можем выполнять в двоичной системе счисления?

Ответ: Сложение, вычитание, умножение и деление.

9. Как перевести число, записанное в двоичной системе счисления в шестнадцатеричную?

Ответ: Для того чтобы перевести в восьмеричную систему счисления двоичное число, его нужно разбить на группы по 3 цифры справа на лево (если количество цифр не кратно 3 , то впереди нужно дописать нужное количество нулей) и заменить каждую группу соответствующей восьмеричной цифрой.

1111101 001 ₂= 011 111 101 001₂= 3754₈

10. Как перевести число из шестнадцатеричной системы счисления в двоичную?

Ответ: Для записи шестнадцатеричных цифр используют первые буквы алфавита. Перевод из

16 2 и обратно аналогичен переводу в двоичной системе счисления.

AOF₁₆= 1010 0000 1111₂ и обратно 1111101001₂= 0011 1110 1001₂ = 3Е9₁₆

3. Объяснение нового материала (10 мин)

Вся информация, обрабатываемая компьютерами, хранится в них в двоичном виде. Каким же образом осуществляется это хранение?

Информация, вводимая в компьютер и возникающая в ходе его работы, хранится в его памяти. Память компьютера можно представить как длинную страницу, состоящую из отдельных строк. Каждая такая строка называется ячейкой памяти.

Ячейка – это часть памяти компьютера, вмещающая в себя информацию, доступную для обработки отдельной командой процессора. Содержимое ячейки памяти называется машинным словом.

Ячейка памяти состоит из некоторого числа однородных элементов. Каждый элемент способен находиться в одном из двух состояний и служит для изображения одного из разрядов числа. Именно поэтому каждый элемент ячейки называют

разрядом. Нумерацию разрядов в ячейке принято вести справа налево, самый правый разряд имеет порядковый номер 0. Это младший разряд ячейки памяти, старший разряд имеет порядковый номер (n-1) в n-разрядной ячейке памяти.

Содержимым любого разряда может быть либо 0, либо 1.

Содержимое ячейки памяти называется машинным словом. Ячейка памяти разделяется на разряды, в каждом из которых хранится разряд числа.

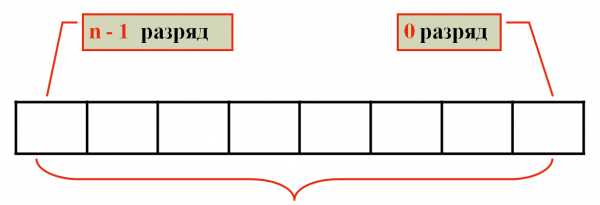
ячейка из n разрядов

Например, самые современные персональные компьютеры являются 64-разрядным, то есть машинное слово и соответственно, ячейка памяти, состоит из 64 разрядов или битов.

Бит

— минимальная единица измерения информации. Каждый бит может принимать значение 0 или 1. Битом также называют разряд ячейки памяти ЭВМ.

Стандартный размер наименьшей ячейки памяти равен восьми битам, то есть восьми двоичным разрядам. Совокупность из 8 битов является основной единицей представления данных – байт.

Байт (от английского byte – слог) – часть машинного слова, состоящая из 8 бит, обрабатываемая в ЭВМ как одно целое. На экране – ячейка памяти, состоящая из 8 разрядов – это байт. Младший разряд имеет порядковый номер 0, старший разряд – порядковый номер 7.

8 бит = 1 байт

Для представления чисел в памяти компьютера используются два формата: формат с фиксированной точкой и формат с плавающей точкой. В формате с фиксированной точкой представляются только целые числа, в формате с плавающей точкой – вещественные числа (целые и дробные).

В подавляющем большинстве задач, решаемых с помощью ЭВМ, многие действия сводятся к операциям над целыми числами. Сюда относятся задачи экономического характера, при решении которых данными служат количества акций, сотрудников, деталей, транспортных средств и т.д. Целые числа используются для обозначения даты и времени, и для нумерации различных объектов: элементов массивов, записей в базах данных, машинных адресов и т.д.

Целые числа могут представляться в компьютере со знаком или без знака.

Целые числа без знака обычно занимают в памяти один или два байта и принимают в однобайтовом формате значения от 00000000₂ до 11111111₂ , а в двухбайтовом формате — от 00000000 00000000₂ до 11111111 11111111₂.

Целые числа со знаком обычно занимают в памяти компьютера один, два или четыре байта, при этом самый левый (старший) разряд содержит информацию о знаке числа. Знак «плюс» кодируется нулем, а «минус» — единицей.

В компьютерной технике применяются три формы записи (кодирования) целых чисел со знаком: прямой код, обратный код, дополнительный код.

Прямой код – это представление числа в двоичной системе счисления, при этом первый разряд отводится под знак числа. Если число положительное, то в первом разряде находится 0, если число отрицательное, в первом разряде указывается единица.

Таким образом, используя прямой код, в 16 – ти разрядной ячейке можно записать 16 – ти разрядное число в двоичной системе счисления. Например:

Положительное десятичное число 24 представляется, как

0

0

0

0

0

0

0

0

0

0

0

1

1

0

0

0

15

14

13

12

11

10

9

8

7

6

5

4

3

2

1

0

Знак числа «+»

Отрицательное десятичное число − 24 представляется, как

1

1

1

1

1

1

1

1

1

1

1

0

0

1

1

1

15

14

13

12

11

10

9

8

7

6

5

4

3

2

1

0

Знак числа «−»

На самом деле прямой код используется почти исключительно для положительных чисел.

Обратный код для положительного числа в двоичной системе счисления совпадает с прямым кодом. Для отрицательного числа все цифры числа заменяются на противоположные (1 на 0, 0 на 1), а в знаковый разряд заносится единица.

Для отрицательных чисел используется так называемый дополнительный код. Это связано с удобством выполнения операций над числами вычислительной техникой.

Дополнительный код используют в основном для представления в компьютере отрицательных чисел. Такой код делает арифметические операции более удобными для выполнения их вычислительной техникой.

В дополнительном коде, также как и прямом, первый разряд отводится для представления знака числа. Прямой и дополнительный код для положительных чисел совпадает. Поскольку прямой код используется почти исключительно для представления положительных чисел, а дополнительный – для отрицательных, то почти всегда, если в первом разряде 1, то мы имеем дело с дополнительным кодом. (Ноль обозначает положительное число, а единица – отрицательное).

Алгоритм получения дополнительного кода для отрицательного числа:

1. Найти прямой код числа (перевести число в двоичную систему счисления число без знака)

2. Получить обратный код. Поменять каждый ноль на единицу, а единицу на ноль (инвертировать число)

3. К обратному коду прибавить 1

Пример: Найдем дополнительный код десятичного числа – 47.

1. Найдем двоичную запись числа 47 (прямой код).

0

0

0

0

0

0

0

0

0

0

1

0

1

1

1

1

15

14

13

12

11

10

9

8

7

6

5

4

3

2

1

0

2. Инвертируем это число (обратный код).

1

1

1

1

1

1

1

1

1

1

0

1

0

0

0

0

15

14

13

12

11

10

9

8

7

6

5

4

3

2

1

0

3. Прибавим 1 к обратному коду и получим запись этого числа в оперативной памяти.

1

1

1

1

1

1

1

1

1

1

0

1

0

0

0

1

15

14

13

12

11

10

9

8

7

6

5

4

3

2

1

0

Почему же используется дополнительный код для представления отрицательного числа?

Так проще выполнять математические операции. Например, у нас два числа, представленных в прямом коде. Одно число положительное, другое – отрицательное и эти числа нужно сложить. Однако просто сложить их нельзя. Сначала компьютер должен определить, что это за числа. Выяснив, что одно число отрицательное, ему следует заменить операцию сложения операцией вычитания. Потом, машина должна определить, какое число больше по модулю, чтобы выяснить знак результата и определиться с тем, что из чего вычитать. В итоге, получается сложный алгоритм. Куда проще складывать числа, если отрицательные преобразованы в дополнительный код.

4. Практическая работа (20 мин)

Задание 1. Записать внутреннее представление следующих десятичных чисел, используя 8 -разрядную ячейку:

64₁₀

8 разрядное представление:

0

1

0

0

0

0

0

0

— 120₁₀

8 разрядное представление:

Прямой код

0

1

1

1

1

0

0

0

Обратный код

1

0

0

0

0

1

1

1

Дополнительный код

1

0

0

0

1

0

0

0

Задание 2. Как запишутся в оперативной памяти компьютера следующие десятичные числа в 16-ти разрядной сетке

57₁₀

16 разрядное представление:

0

0

0

0

0

0

0

0

0

0

1

1

1

0

0

1

200₁₀

16 разрядное представление:

0

0

0

0

0

0

0

0

1

1

0

0

1

0

0

0

— 117₁₀

16-разрядное представление:

Прямой код

0

0

0

0

0

0

0

0

0

1

1

1

0

1

0

1

Обратный код

1

1

1

1

1

1

1

1

1

0

0

0

1

0

1

0

Дополнительный код

1

1

1

1

1

1

1

1

1

0

0

0

1

0

1

1

— 200₁₀

16-разрядное представление:

Прямой код

0

0

0

0

0

0

0

0

1

1

0

0

1

0

0

0

Обратный код

1

1

1

1

1

1

1

1

0

0

1

1

0

1

1

1

Дополнительный код

1

1

1

1

1

1

1

1

0

0

1

1

1

0

0

0

5. Домашняя работа (2 мин)

Задание 1. Получить внутреннее представление целого числа 123₁₀ в 8-разрядной ячейке памяти компьютера.

0

1

1

1

1

0

1

1

Задание 2. Получить внутреннее представление целого числа — 123₁₀ в 8-разрядной ячейке памяти компьютера.

Прямой код

0

1

1

1

1

0

1

1

Обратный код

1

0

0

0

0

1

0

0

Дополнительный код

1

0

0

0

0

1

0

1

Задание 3. Получить внутреннее представление целого числа — 17₁₀ в 16 – ти разрядной ячейке памяти компьютера.

Прямой код

0

0

0

0

0

0

0

0

0

0

0

1

0

0

0

1

Обратный код

1

1

1

1

1

1

1

1

1

1

1

0

1

1

1

0

Дополнительный код

1

1

1

1

1

1

1

1

1

1

1

0

1

1

1

1

6. Подведение итогов урока, выставление оценок (2 – 3 мин)

7. Использованная литература:

1. Информатика и ИКТ. Задачник-практикум: в 2 т. / Л.А. Залогова [и др.]; под ред. И.Г. Семакина, Е.К. Хеннера. – 3 изд. – М.: БИНОМ. Лаборатория знаний, 2011.

2. Семакин И.Г., Залогова Л.А, Русаков С.В., Шестакова Л.В. Информатика и ИКТ: учебник для 9 класса. – М.: БИНОМ. Лаборатория знаний, 2011.

3. Семакин И.Г., Шеина Т.Ю. Преподавание базового курса информатики в средней школе: методическое пособие. М.: БИНОМ. Лаборатория знаний, 2007.

4. Семакин И.Г., Вараксин Г.С. Структурированный конспект базового курса. – М.: Лаборатория Базовых Знаний, 2001.

infourok.ru

Конспект урока информатики в 10 классе «Системы счисления»

МАОУ СШ №2

МЕТОДИЧЕСКАЯ РАЗРАБОТКА УРОКА

Тема: Системы счисления. Работа с системами счисления

10 класс

Выполнил: Небукина С.О.

2015 г.

План урока

По дисциплине: Информатика и ИКТ

Тема: Системы счисления. Работа с системами счисления.

Цели урока: Познакомить учащихся с понятием система счисления, развитием систем счисления от буквенных до позиционных.

Задачи урока:

— обучающие 

• познакомить учащихся с историей возникновения и развития систем счисления, дать классификацию систем счисления.

• ввести новые понятия по теме урока,

• дать представление о позиционной и непозиционной системах счисления, указать на основные преимущества и недостатки этих систем счисления.

-развивающие  

• развивать познавательный интерес учащихся,

• развивать умения анализировать, сравнивать, выделять главное, приводить примеры, 

• развитие внимания, восприятия, познавательного интереса у учащихся, умения обобщать и сравнивать;

• формирование ключевых компетенций, а также активизация творческой деятельности учащихся.

-воспитательные

• научить воспринимать компьютер как инструмент информационной деятельности человека,

• воспитывать самостоятельность, аккуратность, трудолюбие,

• научить отстаивать свою точку зрения

Тип урока:  Урок формирования новых знаний.

Форма занятия учащихся: Фронтальная, индивидуальная, самостоятельная.

Необходимое техническое оборудование:

• Компьютер,

• проектор,

• доска

Ход  урока

Этапы урока

1. Организационный момент урока

Учитель приветствует учащихся, объявляет тему, цель и задачи урока.

2. Актуализация знаний учащихся

Введение

Пифагорийцы говорили: “Всё есть число”. Вы согласны с этим утверждением?

Почему люди разных стран говорят на разных языках, а считают одинаково? Это связано с торговыми расчётами. Еще в древности при покупке и продаже разных товаров люди пришли к выводу, что считать и записывать количество товаров удобней одинаково, так как это значительно облегчает вычисления, поэтому, сегодня мы должны узнать, а как же люди считали в древности?

3. Изучение нового материала

История возникновения системы счисления

Люди научились считать еще в незапамятные времена. Сначала они просто различали один предмет перед ними или нет. Если предмет был не один, то говорили «много». Постепенно появилось слово для обозначения двух предметов. Счет парами очень удобен.

Наиболее древней и простой «счетной машиной» издавна являются пальцы рук и ног. И даже в наше время еще пользуются этим «счетным прибором», который всегда при нас. На пальцах можно решать примеры не только в пределах десяти. В древние времена люди ходили босиком. Поэтому они могли пользоваться для счета пальцами как рук, так и ног.

Записывали числа поначалу совсем просто: делали зарубки на куске дерева или кости. На этой кости тридцать тысяч лет назад сделаны нарезки, они показывают, что уже тогда наши предки умели не только считать, но и записывать результаты счета!

Когда понадобилось записывать большие числа, то для пятерок и десяток стали придумывать новые знаки. Вот как египтяне записывали число 324: 

Запомнить большие числа трудно, поэтому к «счетной машине» рук и ног добавляли механические приспособления. Веревочные счеты с узелками применялись и в России, и во многих странах Европы. Это были первые счетные приборы, которые, в конце концов, привели к образованию различных систем счисления.

Итак, числа записываются с использованием особых знаковых систем, которые называются системами счисления.

Давайте запишем определение систем счисления.

Система счисления – это знаковая система, в которой числа записываются по определенным правилам с помощью символов некоторого алфавита, называемых цифрами.

Все системы счисления делятся на две большие группы: позиционные и непозиционные системы счисления. (Зарисовать в тетрадь схему)

В позиционных СС количественное значение цифры зависит от ее положения в числе. (Записать в тетрадь)

Рассмотрим вначале позиционные СС, например десятичную СС (арабская СС). Число 579. Цифра 5 обозначает пять сотен, 7 – семь десятков, 9 – девять единиц.

Если поменять местами цифры, например, 5 и 7, то цифра 5 – станет обозначать пять десятков, 7 – семь сотен. (Записать пример в тетрадь)

– Как вы думаете, а в непозиционных?

– Одним из примеров непозиционных СС является римская СС (римские числа). Давайте подробнее рассмотрим, по какому принципу образуются числа в римской СС.

В римской СС числа получаются путем прибавления или вычитания. Например, число IX (9) получается путем вычитания единицы из десяти. Теперь переставим единицу слева направо, получили число XI (11) путем прибавления единицы к десяти. Таким образом, дописывая цифру справа от числа, прибавляем её, дописывая цифру слева от числа, отнимаем её. При этом количественное значение цифры от её положения в числе не изменяется. (Записать в тетрадь с слайда пример)

Запишем примеры позиционных и непозиционных СС.

Обратите внимание, что в позиционных СС основание системы равно количеству цифр (знаков в её алфавите) определяет во сколько раз различаются значения одинаковых цифр, стоящих в соседних позициях.

Двоичная система счисления

Знаменитый немецкий ученый Г.В. Лейбниц предложил еще в XVII веке уникальную и простую систему счисления. «Вычисление с помощью двоек…, сведение чисел к простейшим началам (0 и 1)».Сегодня такой способ представления информации, с помощью языка содержащего два символа 0 и 1, широко используется в технических устройствах.

Вся информация в компьютере представлена в виде двоичного кода. Компьютер переводит информацию (числовую, текстовую, графическую, звуковую, видео) в последовательность нулей и единиц. Давайте посмотрим, как можно перевести числа из привычной нам десятичной СС в двоичную СС.

Для начала рассмотрим перевод целых чисел из десятичной СС в двоичную.

Алгоритм перевода из десятичной СС в двоичную СС:

1. Последовательно выполнять деление исходного целого десятичного числа и получаемых целых частных на основание системы (на 2) до тех пор, пока не получится частное, меньшее делителя, то есть меньшее 2.

2. Записать полученные остатки в обратной последовательности.

6

2

3

0

12

—

6

2

26

13

2

27

—

1

1

—

2

—

2

1

1

Теперь рассмотрим обратную задачу – перевод чисел из двоичной СС в десятичную.

Алгоритм перевода из двоичной СС в десятичную СС:

1. Двоичное число записать в развернутой форме.

Давайте вернемся в курс математики и вспомним, как записывается число в развернутой форме.

Запишем число 579 в десятичной СС в развернутой форме.

Мы уже с вами выяснили, что в этом числе цифра 5 означает 5 сотен, 7 – семь десятков, 9 – девять единиц. Число 579 записано в привычной для нас свернутой форме. Мы настолько привыкли к такой форме записи, что уже не замечаем, как в уме умножаем цифры числа на различные степени числа 10.

В развернутой форме записи числа такое умножение записывается в явной форме.

Аналогично, и для двоичной СС. В двоичной СС основание равно 2, а алфавит состоит из двух цифр (0 и 1). Следовательно, числа в двоичной системе в развернутой форме записываются в виде суммы степеней основания 2 с коэффициентами, в качестве которых выступают цифры 0 или 1.

При переводе удобно пользоваться таблицей степеней двойки:

Таблица 1. Степени числа 2

n (степень)

0

1

2

3

4

5

6

7

8

9

10

1

2

4

8

16

32

64

128

256

512

1024

пример:

Итак, вернемся к нашему примеру (через гиперссылку «назад») запишем число 11101001 в развернутой форме.

=

0

1

2

3

4

5

6

7

= 1* 2⁷+1*2⁶+1*2⁵+0*2⁴+1*2³+0*2²+0*2¹+1*2⁰=

= 1*128+1*64+1*32+0*16+1*8+0*4+0*2+1*1=

= 128+64+32+8+1=233

1. Произвести вычисления.

Арифметические операции

Также существует еще и восьмеричная СС. Основанием которой является 8.

Восьмеричная система счисления — позиционная целочисленная система счисления с основанием 8. Для представления чисел в ней используются цифры от 0 до 7.

Восьмеричная система чаще всего используется в областях, связанных с цифровыми устройствами.

В настоящее время восьмеричная система применяется при выставлении прав доступа к файлам и прав исполнения для участников в Linux-системах

Алгоритм перевода из восьмеричной СС в десятичную.

Таблица 2. Степени числа 8

n (степень)

0

1

2

3

4

5

6

1

8

64

512

4096

32768

262144

Пример: Число 75013₈ перевести в десятичную систему счисления.

Алгоритм перевода из десятичной СС в восьмеричную СС

Для перевода десятичного числа в восьмеричную систему его необходимо последовательно делить на 8 до тех пор, пока не останется остаток, меньший или равный 7. Число в восьмеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.

Пример: Число 571₁₀ перевести в восьмеричную систему счисления.

 

Шестнадцатеричная система счисления (шестнадцатеричные числа) — позиционная система счисления по целочисленному основанию 16.

Обычно в качестве шестнадцатеричных цифр используются десятичные цифры от 0 до 9 и латинские буквы от A до F для обозначения цифр от 10₁₀ до 15₁₀, то есть (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F).

Широко используется в низкоуровневом программировании и компьютерной документации, поскольку в современных компьютерах минимальной единицей памяти является 8-битный байт, значения которого удобно записывать двумя шестнадцатеричными цифрами. Такое использование началось с системы IBM/360, где вся документация использовала шестнадцатеричную систему, в то время как в документации других компьютерных систем того времени (даже с 8-битными символами, как, например, PDP-11 или БЭСМ-6) использовали восьмеричную систему.

В стандарте Юникода номер символа принято записывать в шестнадцатеричном виде, используя не менее 4 цифр (при необходимости — с ведущими нулями).

Шестнадцатеричный цвет — запись трёх компонентов цвета (R, G и B) в шестнадцатеричном виде.

Алгоритм перевода из шестнадцатеричной СС в десятичную

Для перевода шестнадцатеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 16, и вычислить по правилам десятичной арифметики:

При переводе удобно пользоваться таблицей степеней числа 16:

Таблица 3. Степени числа 16

n (степень)

0

1

2

3

4

5

6

1

16

256

4096

65536

1048576

16777216

Пример: Число FDA1₁₆  перевести в десятичную систему счисления.

Алгоритм перевода из десятичной СС в шестнадцатеричную СС

Для перевода десятичного числа в шестнадцатеричную систему его необходимо последовательно делить на 16 до тех пор, пока не останется остаток, меньший или равный 15. Число в шестнадцатеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.

Пример: Число 7467₁₀ перевести в шестнадцатеричную систему счисления.

4. Закрепление нового материала

– Теперь вы умеете переводить числа десятичной СС в двоичную СС и обратно. Давайте решим два примера на закрепление ваших знаний.

Примеры для самостоятельного решения и закрепления изученного материала.

Задание № 1. Определить в какой системе счисления ведется рассказ:

«Необыкновенная девочка»
Ей было тысяча сто лет,
Она в сто первый класс ходила,
В портфеле по сто книг носила – 
Все это правда, а не бред.
Когда, пыля десятком ног,
Она шагала по дороге,
За ней всегда бежал щенок
С одним хвостом, зато стоногий.
Она ловила каждый звук
Своими десятью ушами,
И десять загорелых рук
Портфель и поводок держали.
И десять темно-синих глаз
Рассматривали мир привычно…
Но станет все сейчас обычным, 
Когда поймете мой рассказ

(А.Н.Стариков)

Решение:

Выпишем упомянутые в стихотворении числа: 1, 10, 100, 101,1100. Все встречаемые цифры – 0 или 1. Если предположить, что зашифровано разложение по степеням двойки, то получим:

«Ей было тысяча сто лет» – 1100 = 1 ^. 2³ + 1 ^. 2² = 8 + 4 = 12 лет
«Она в сто первый класс ходила» – 101 = 1 ^. 2² + 1 = 4 + 1 = 5 класс
«…пыля десятком ног» – 10 = 21 = 2 ноги
«С одним хвостом, зато стоногий» – 1 = 2⁰ = 1, 100 = 2² = 4 ноги 
и т.д. разобранное число 10.

Ответ: двоичная с.с.

Задание № 2

Даны два числа: A=9D₁₆ и B=237₈. Какое из приведенных ниже чисел С в двоичной системе соответствует неравенству: A

1) 10011010₂

2) 10011110₂

3) 10011111₂

4) 11011110₂

Задание № 3

Значение выражения 11₁₆ + 11₈ : 11₂ в двоичной системе счисления равно

1) 10100₂

2) 110111₂

3) 10101₂

4) 101101₂

Задание № 4

Двоичное число 110110 соответствует шестнадцатеричному числу 

1) 36

2) 66

3) 54

4) D2

Задание № 4

Русская поговорка.

Здесь зашифрована известная русская поговорка. Прочитайте ее, двигаясь с помощью двоичных цифр в определенной последовательности.

(Ответ: ЧТО ПОСЕЕШЬ, ТО И ПОЖНЕШЬ)

5. Подведение итогов урока.

– Сегодня на уроке мы с вами провели большую работу и узнали много нового. Что для вас было новым? Что вы узнали?

Узнали, что числа записываются с использованием особых знаковых систем, которые называются системами счисления.

Все системы счисления делятся на две большие группы. Какие? (Позиционные и непозиционные).

Научились переводить числа из десятичной СС в двоичную и обратно.

6. Домашняя работа

– Заполнить таблицу до конца

–Проверка присутствия учащихся

– Урок окончен. До свидания.

Список литературы

1. Андреева Е.В., Фалина И.Н. Системы счисления и компьютерная арифметика. – М.: ЛБЗ, 200. – 248 с.

2.Белоусова Л.И. Сборник задач по курсу информатики под ред. Л.И. Белоусовой. – М.: Издательство «Экзамен», 2006. – 253 с.

3.Горячев А.В., Шафрин Ю.А. Практикум по информационным технологиям. – М.: ЛБЗ, 1999. – 272 с.

4.Лапчик М.П. и др. Методика преподавания информатики. – М.: Академия, 2001. – 624 с.

5.Софронова Н.В. Теория и методика обучения информатике. – М.: Высшая школа, 2004. – 223 с.

6.Шелепаева А.Х. Поурочные разработки по информатике: 8-9 классы. – М.: ВАКО, 2006. – 272 с.

infourok.ru

Конспект урока информатика 10 кл (Представление чисел в компьютере)

Дата 22.09.2018

Тема: Представление чисел в компьютере.

Класс: 10

Цели урока:

Образовательная:

• формирование знаний учащихся о формах представления числовой информации в компьютере;

• формирование практических навыков по представлению чисел в различных кодах;

Развивающая: развитие алгоритмического мышления, памяти, внимательности;

Воспитательная: воспитывать научное мировоззрение, информационную культуру, расширять кругозор учащихся.

Методы обучения: — объяснительно — иллюстративный;

Тип урока: комбинированный.

План урока:

1. Организационный момент

2. Проверка и актуализация знаний

3. Объяснение нового материала

4. Домашняя работа

5. Подведение итогов урока, выставление оценок

Оборудование: Мультимедийный проектор, презентация.

Ход урока

1. Организационный момент

Приветствие. Запись в тетради число и тема урока.

2. Проверка и актуализация знаний

Перед тем как приступить к изучению новой темы, повторим основные понятия, изученные на прошедших уроках. Давайте вспомним все, что мы знаем о системах счисления.

Вопросы:

1. Что называют системой счисления?

2. Какие виды систем счисления вы знаете?

3. Приведите примеры непозиционной системы счисления

4. Как можно записать число в позиционной системе счисления?

5. Какие примеры вы можете привести позиционной системы счисления?

6. Как можно перевести любое число в десятичную систему счисления?

Ответ: Нужно воспользоваться многочленом

7. Как можно перевести из десятичной системы счисления в любую систему счисления с произвольным основанием?

8. Ответ: Из 10 2

   13₁₀=1101₂

   Из 10 3

   13₁₀=111₂

   Какие действия мы можем выполнять в двоичной системе счисления?

3. Объяснение нового материала

Вся информация, обрабатываемая компьютерами, хранится в них в двоичном виде. Каким же образом осуществляется это хранение?

Информация, вводимая в компьютер и возникающая в ходе его работы, хранится в его памяти. Память компьютера можно представить как длинную страницу, состоящую из отдельных строк. Каждая такая строка называется ячейкой памяти.

Ячейка – это часть памяти компьютера, вмещающая в себя информацию, доступную для обработки отдельной командой процессора. Содержимое ячейки памяти называется машинным словом.

Ячейка памяти состоит из некоторого числа однородных элементов. Каждый элемент способен находиться в одном из двух состояний и служит для изображения одного из разрядов числа. Именно поэтому каждый элемент ячейки называют разрядом. Нумерацию разрядов в ячейке принято вести справа налево, самый правый разряд имеет порядковый номер 0. Это младший разряд ячейки памяти, старший разряд имеет порядковый номер (n-1) в n-разрядной ячейке памяти.

Содержимым любого разряда может быть либо 0, либо 1.

Содержимое ячейки памяти называется машинным словом. Ячейка памяти разделяется на разряды, в каждом из которых хранится разряд числа.

ячейка из n разрядов

Например, самые современные персональные компьютеры являются 64-разрядным, то есть машинное слово и соответственно, ячейка памяти, состоит из 64 разрядов или битов.

Бит — минимальная единица измерения информации. Каждый бит может принимать значение 0 или 1. Битом также называют разряд ячейки памяти ЭВМ.

Стандартный размер наименьшей ячейки памяти равен восьми битам, то есть восьми двоичным разрядам. Совокупность из 8 битов является основной единицей представления данных – байт.

Байт (от английского byte – слог) – часть машинного слова, состоящая из 8 бит, обрабатываемая в ЭВМ как одно целое. На экране – ячейка памяти, состоящая из 8 разрядов – это байт. Младший разряд имеет порядковый номер 0, старший разряд – порядковый номер 7.

8 бит = 1 байт

Для представления чисел в памяти компьютера используются два формата: формат с фиксированной точкой и формат с плавающей точкой. В формате с фиксированной точкой представляются только целые числа, в формате с плавающей точкой – вещественные числа (целые и дробные).

В подавляющем большинстве задач, решаемых с помощью ЭВМ, многие действия сводятся к операциям над целыми числами. Сюда относятся задачи экономического характера, при решении которых данными служат количества акций, сотрудников, деталей, транспортных средств и т.д. Целые числа используются для обозначения даты и времени, и для нумерации различных объектов: элементов массивов, записей в базах данных, машинных адресов и т.д.

Целые числа могут представляться в компьютере со знаком или без знака.

Целые числа без знака обычно занимают в памяти один или два байта и принимают в однобайтовом формате значения от 00000000₂ до 11111111₂ , а в двухбайтовом формате — от 00000000 00000000₂ до 11111111 11111111₂.

Целые числа со знаком обычно занимают в памяти компьютера один, два или четыре байта, при этом самый левый (старший) разряд содержит информацию о знаке числа. Знак «плюс» кодируется нулем, а «минус» — единицей.

В компьютерной технике применяются три формы записи (кодирования) целых чисел со знаком: прямой код, обратный код, дополнительный код.

Прямой код – это представление числа в двоичной системе счисления, при этом первый разряд отводится под знак числа. Если число положительное, то в первом разряде находится 0, если число отрицательное, в первом разряде указывается единица.

Таким образом, используя прямой код, в 16 – ти разрядной ячейке можно записать 16 – ти разрядное число в двоичной системе счисления. Например:

Положительное десятичное число 24 представляется, как

Знак числа «+»

Отрицательное десятичное число − 24 представляется, как

Знак числа «−»

На самом деле прямой код используется почти исключительно для положительных чисел.

Обратный код для положительного числа в двоичной системе счисления совпадает с прямым кодом. Для отрицательного числа все цифры числа заменяются на противоположные (1 на 0, 0 на 1), а в знаковый разряд заносится единица.

Для отрицательных чисел используется так называемый дополнительный код. Это связано с удобством выполнения операций над числами вычислительной техникой.

Дополнительный код используют в основном для представления в компьютере отрицательных чисел. Такой код делает арифметические операции более удобными для выполнения их вычислительной техникой.

В дополнительном коде, также как и прямом, первый разряд отводится для представления знака числа. Прямой и дополнительный код для положительных чисел совпадает. Поскольку прямой код используется почти исключительно для представления положительных чисел, а дополнительный – для отрицательных, то почти всегда, если в первом разряде 1, то мы имеем дело с дополнительным кодом. (Ноль обозначает положительное число, а единица – отрицательное).

Алгоритм получения дополнительного кода для отрицательного числа:

1. Найти прямой код числа (перевести число в двоичную систему счисления число без знака)

2. Получить обратный код. Поменять каждый ноль на единицу, а единицу на ноль (инвертировать число)

3. К обратному коду прибавить 1

Пример: Найдем дополнительный код десятичного числа – 47.

1. Найдем двоичную запись числа 47 (прямой код).

2. Инвертируем это число (обратный код). 3. Прибавим 1 к обратному коду и получим запись этого числа в оперативной памяти.

Почему же используется дополнительный код для представления отрицательного числа?

Так проще выполнять математические операции. Например, у нас два числа, представленных в прямом коде. Одно число положительное, другое – отрицательное и эти числа нужно сложить. Однако просто сложить их нельзя. Сначала компьютер должен определить, что это за числа. Выяснив, что одно число отрицательное, ему следует заменить операцию сложения операцией вычитания. Потом, машина должна определить, какое число больше по модулю, чтобы выяснить знак результата и определиться с тем, что из чего вычитать. В итоге, получается сложный алгоритм. Куда проще складывать числа, если отрицательные преобразованы в дополнительный код.

Закрепление нового материала

Задание 1. Записать внутреннее представление следующих десятичных чисел, используя 8 -разрядную ячейку:

64₁₀

8 разрядное представление:

— 120₁₀

8 разрядное представление:

Задание 2. Как запишутся в оперативной памяти компьютера следующие десятичные числа в 16-ти разрядной сетке

57₁₀

16 разрядное представление:

200₁₀

16 разрядное представление:

— 117₁₀

16-разрядное представление:

— 200₁₀

16-разрядное представление:

4. Домашняя работа

Задание 1. Получить внутреннее представление целого числа 123₁₀ в 8-разрядной ячейке памяти компьютера.

Задание 2. Получить внутреннее представление целого числа — 123₁₀ в 8-разрядной ячейке памяти компьютера.

Задание 3. Получить внутреннее представление целого числа — 17₁₀ в 16 – ти разрядной ячейке памяти компьютера.

5. Подведение итогов урока, выставление оценок

infourok.ru

Сценарий урока по информатике «Представление чисел в компьютер», 10-й класс

Разделы: Информатика

---

Цели:

• образовательные учащиеся знакомятся с алгоритмом представления чисел в компьютере
• развивающие применяют знания, полученных на уроках информатики, математики для оценки знаний полученных на других уроках
• воспитательные учащиеся осознают важность данной темы в изучении математических основ информатики

Оборудование:

• компьютерная программа “Power Point”
• план-конспект урока с пропусками
• карточки самооценки

Ход урока

I. Мотивационо-ориентировочный этап

1. Вхождение в контакт

— Здравствуйте, садитесь.

2. Контроль настроения

— Сегодня замечательный день. Я рада вас видеть. Надеюсь, что мы с вами плодотворно поработаем сегодня на уроке. Перед вами лист самооценки. в течении урока заполняйте его.

3. Постановка учебной задачи

— Скажите какую работу мы выполняли на предыдущих уроках?

1. переводили числа из одной системы счисления в другую;
2. складывали, вычитали, умножали и делили числа в двоичной системе счисления.

Задание №1 Две группы, кто быстрее выполнит задание. На доске фиксировать только ответы. Проверить по слайду 1 (приложение 1).

Выполнить действия в двоичной системе счисления, ответ записать в десятичной системе счисления:

156-96:2+14*2=

156₁₀=10011100₂

96₁₀=1100000₂

2₁₀=10₂

14₁₀=1110₂

1100000:10=110000

1110*10=11100

10011100-110000=1101100

1101100+11100=10001000

Слайд 2 (приложение 1)

250 – (54+42:7)*10=

250₁₀=11111010₂

54₁₀=110110₂

42₁₀=101010₂

7₁₀=111₂

10₁₀=1010₂

101010: 111=110

110110+110=111100

111100*1010=1001011000

11111010-1001011000=?

Первый пример решается как обычно, при выполнении второго возникнут проблемы.

— Что случилось? Почему вы не делаете пример дальше?

Мы не умеем вычитать из меньшего числа большее.

— Тогда скажите чем же мы будем заниматься на сегодняшнем уроке? Поставьте учебную задачу?

Научимся вычитать в двоичной системе из меньшего числа большее.

— Мы научимся записывать целые отрицательные числа в машинных кодах, т.е. в компьютерном представлении. (Слайд 3 приложение 1)

— Записываем в план – конспект урока тему (приложение 2).

Операционно-исполнительный этап

— Для того чтобы, выполнить последнее действие мы с вами вспомним каким действие можно заменить вычитание?

11111010+(-1001011000)= Слайд 4 (приложение 1)

— Для каждого числа в компьютере отводится определенное количество ячеек памяти. В данном случае 16. Как можно записать первое слагаемое, чтобы значение его не изменилось, а в записи было 16 цифр?

Дописать впереди 8 нулей Слайд 5 (приложение 1)

0000000011111010

— Аналогично мы поступим и с модулем второго слагаемого

0000001001011000

-Теперь я вам предлагаю заменить нули на единицы. а единицы на нули.

1111110110100111

Прибавьте к полученному числу 1

1111110110101000

— А теперь сложите первое слагаемое и полученное число Слайд 6 (приложение 1)

0000000011111010

+

1111110110101000

_______________

1111111010100010

— Получили ответ, а как же нам проверить верно ли мы посчитали? Если выполнять действия в десятичной системе счисления то мы должны получить число – 350.

— Предлагаю вам еще один кропотливый трудоемкий процесс. Попробуйте выполнить действия что мы проводили с отрицательным числом в обратном порядке, если все сделано верно мы в итоге должны получить число 350.

— Первое, из числа 1111111010100010 – 1=1111111010100001

— Второе, поменяем нули на единицы, а единицы на нули.

0000000101011110₂=101011110₂=2⁸+2⁶+2⁴+2³+2²+2¹=350₁₀

— Мы с вами рассмотрели не что иное как алгоритм представления отрицательных чисел в компьютере: слайд7 (приложение 1)

1. Записать в двоичной системе счисления модуль данного отрицательного числа.
2. Дописать впереди нули, заполнив всю разрядную сетку.
3. Заменить нули на единицы, а единицы на нули (инвертировать)
4. К полученному числу прибавить 1.

— У кого есть вопросы? Кому, что не понятно?

ответы на вопросы

III. Рефлексивно-оценочный этап

— Кто сидит на первом варианте запишите на листочках в двух экземплярах двузначное отрицательное число. Один переведите сами, а второй предложите соседу.

— Проверьте правильность выполнения задания.

— По слайду давайте повторим алгоритм представления числа в машинных кодах. Заполнить пропуски. Пропущенные слова, записываете в тетрадь.

— Сами проверьте себя.

— Поставьте себе оценку за урок.

— Все ли собой довольны?

— Вспомните какую задачу мы ставили перед собой. Справились ли мы с ней?

Домашнее задание составьте 3 примера на вычитание из меньшего числа большего и выполните их.

Приложение 3

2.04.2008

Поделиться страницей:

xn--i1abbnckbmcl9fb.xn--p1ai

Урок по информатике в 10 классе Представление чисел в компьютере.docx

Ячейка – это часть памяти компьютера, вмещающая в себя информацию, доступную для
обработки отдельной командой процессора. Содержимое ячейки памяти называется
машинным словом.
Ячейка памяти состоит из некоторого числа однородных элементов. Каждый элемент
способен находиться в одном из двух состояний и служит для изображения одного из разрядов
числа. Именно поэтому каждый элемент ячейки называют разрядом.
разрядов в ячейке принято вести справа налево, самый правый разряд имеет порядковый номер 0.
Это младший разряд ячейки памяти, старший разряд имеет порядковый номер (n­1) в n­разрядной
ячейке памяти.
Нумерацию
Содержимым любого разряда может быть либо 0, либо 1.
Содержимое ячейки памяти называется машинным словом. Ячейка памяти разделяется на
разряды, в каждом из которых хранится разряд числа.
ячейка из n разрядов
Например, самые современные персональные компьютеры являются 64­разрядным, то есть
машинное слово и соответственно, ячейка памяти, состоит из 64 разрядов или битов.
Бит — минимальная единица измерения информации. Каждый бит может принимать
значение 0 или 1. Битом также называют разряд ячейки памяти ЭВМ.
Стандартный размер наименьшей ячейки памяти равен восьми битам, то есть восьми
двоичным разрядам. Совокупность из 8 битов является основной единицей представления данных –
байт.
Байт (от английского byte – слог) – часть машинного слова, состоящая из 8 бит,
обрабатываемая в ЭВМ как одно целое. На экране – ячейка памяти, состоящая из 8 разрядов – это
байт. Младший разряд имеет порядковый номер 0, старший разряд – порядковый номер 7.
8 бит = 1 байт
Для представления чисел в памяти компьютера используются два формата: формат с
фиксированной точкой и формат с плавающей точкой. В формате с фиксированной точкой
представляются только целые числа, в формате с плавающей точкой – вещественные числа (целые и
дробные).
В подавляющем большинстве задач, решаемых с помощью ЭВМ, многие действия сводятся к
операциям над целыми числами. Сюда относятся задачи экономического характера, при решении
которых данными служат количества акций, сотрудников, деталей, транспортных средств и т.д.
Целые числа используются для обозначения даты и времени, и для нумерации различных объектов:
элементов массивов, записей в базах данных, машинных адресов и т.д.
Целые числа могут представляться в компьютере со знаком или без знака.
Целые числа без знака обычно занимают в памяти один или два байта и принимают в
однобайтовом формате значения от 000000002 до 111111112 , а в двухбайтовом формате ­ от
00000000 000000002 до 11111111 111111112.

znanio.ru

Конспект урока по информатике для 10 класса по теме «Системы счисления»

План-конспект урока

Системы счисления(10 класс)

Цель урока: закрепление, обобщение и систематизация знаний учащихся по теме «Системы счисления» — правил перевода и выполнения арифметических операций в различных системах счисления с использованием ЭОР.

Задачи урока:   

Тип урока: урок обобщения и систематизации знаний с использованием ЭОР и самостоятельной деятельностью учащихся на компьютерах.

Формы и методы обучения: словесный, наглядный, практический — индивидуальная работа на компьютере.

Оборудование:

• ПК,

• Презентация «Системы счисления»,

• проектор,

• интерактивная приставка,

• ЭОР «Перевод чисел из десятичной в двоичную систему счисления, и обратно, выполнение арифметических операций в двоичной системе счисления»,

• Тренировочный тест по теме «Системы счисления»» на каждый ПК (в Calc),

• ОМС плеер.

I. Организационный момент

Приветствие. Проверка готовности к уроку.

II. Постановка темы, целей урока

Сегодня у нас заключительный урок по теме «Арифметические операции в разных системах счисления».  Мы повторим, обобщим и приведем в систему изученный материал по данный теме. Ваша задача знание правил перевода чисел и выполнения арифметических действий в различных системах счисления.

III. Актуализация знаний учащихся

В начале урока давайте настроимся на работу с помощью графического диктанта.

Если утверждение верно, ученик ставит знак _ , если неверно – знак /\ .

1. Система счисления – это способ представления чисел и соответствующие ему правила действий над числами.

2. Информация, хранящаяся в компьютере, представлена в троичной системе счисления.

3. В двоичной системе счисления 11 + 1 = 12.

4. В позиционных системах счисления количественный эквивалент цифры зависит от её местоположения в записи числа.

5. В 16-ричной системе счисления символ F используется для обозначения числа 15.

6. Римская система счисления – это позиционная система счисления.

7. В двоичной системе счисления: 1 + 1 = 0.

Учащиеся меняются тетрадями и осуществляют взаимопроверку. Ответы на доске.

(Результат выполнения задания:   _ /\ /\ _ _ /\_ )

Разбор заданий, в которых были допущены ошибки.

IV. Повторение изученного материала

N₁₀=7764,1=

N₅=2430,43=

3*10² + 4*10¹ + 8*10⁰ + 1*10^-1 + 2*10^-2=

Гиперссылка на ресурс, обеспечивающий доступ к ЭОР :

http://files.school-collection.edu.ru/dlrstore/fc77f535-0c00-4871-b67c-fa2ecf567d46/9_115.swf (тренировка)

Задания:

1. Какое двоичное число соответствует десятичному числу A: A =117. (Ответ: 1110101)

2. Какое десятичное число соответствует двоичному числу A: А=110001. (Ответ: 49)

3. Выполните сложение в двоичной системе счисления. А=11011+1110. (Ответ: 101001)

4. Выполните умножение в двоичной системе счисления. А=1101·1110. (Ответ: 10110110)

5. Укажите количество двоичных чисел в диапазоне от А до B.

А= 10₂, B=101₂. (Ответ: 4)

V. Диагностика процесса усвоения учебного материала по теме: «Системы счисления»

Проверим ваши знания с помощью теста. У Вас есть возможность проверить себя, как Вы усвоили тему «Перевод чисел из одной системы счисления в другую».

Для этого пересаживаемся за компьютеры и открываем в своей папке документ Тест «Система счисления»

(Тест разработан в OpenOffice.Calc c автоматической системой проверки правильности выбора ответа и выставлением оценки учащемуся)

Краткий инструктаж по выполнению задания.

Теперь, когда Вы прошли самоконтроль, можете оценить свою готовность к контрольной работе.

9, 10 правильных ответов – «5»,

7, 8 правильных ответов – «4»,

5, 6 правильных ответов – «3»

VI. Домашнее задание:

Обратите внимание, на домашнее задание. Задания разноуровневые: состоят из трех частей: Обязательная часть на «3» , с одной * — на «4» , и с двумя ** — на «5». Каждый может выбрать задание для себя.

Домашняя работа

1. Перевести целые десятичные числа 9₁₀, 17₁₀, 243₁₀ в двоичную, восьмеричную и шестнадцатеричную системы счисления.

2*. Перевести десятичные дроби 0,2₁₀, 0,35₁₀ в двоичную, восьмеричную и шестнадцатеричную системы счисления с точностью до трех знаков после запятой.

3**. Перевести десятичные числа 3,5₁₀ , 47,85₁₀ в двоичную, восьмеричную и шестнадцатеричную системы счисления с точностью до трех знаков после запятой.

VII. Формулирование выводов урока. Итоги урока.

Структура и ход урока

№	Этап урока	Использованные средства	Деятельность учителя	Деятельность ученика	Время
1.	Организационный момент		Создание рабочего настроя, проверка готовности к уроку.		1 мин.
2.	Постановка темы, целей урока	Презентация «Системы счисления» Слайд 1-2	Формулирование темы и постановка целей и задач урока.	Записывают тему урока.	2 мин
3.	Актуализация знаний	Слайд 3-4	Проводит опрос учащихся в виде графического диктанта. Показывает ответы диктанта, поясняет задания, в которых были допущены ошибки.	Ученики выполняют задания в тетрадях, после меняются тетрадями и осуществляют взаимопроверку.	5мин.
4.	Повторение изученного материала	Слайд 5-7 ЭОР «Перевод чисел из десятичной в двоичную систему счисления, и обратно, выполнение арифметических операций в двоичной системе счисления»*	Следит за ходом выполнения задания, анализирует решения учащихся, оценивает их деятельность.	Ученики, вызываемые учителем, выходят к доске и решают задания различного типа, с использованием ЭОР и интерактивной приставки. Решения записывают в тетрадях.	20 мин.
5.	Диагностика процесса усвоения учебного материала	Слайд 8-9	Формулирование практического задания	Знакомятся с правилами выполнения задания и критериями оценивания.	15 мин.
6.		Тест, созданный в OpenOfficeCalc на компьютерах учащихся	Следит за ходом выполнения задания, оценивает их деятельность.	Учащиеся за компьютерами выполняют задания, если есть вопросы, задают учителю.
7.	Задание на дом	Слайд 10, раздаточный материал	Поясняет выполнение разноуровневых заданий	Слушают учителя, записывают в дневник (индив.задание)	2 мин.
8.	Формулирование выводов урока	Слайд 11	Формулирует выводы и итоги урока. Выставляет оценки.
*http://files.school-collection.edu.ru/dlrstore/fc77f535-0c00-4871-b67c-fa2ecf567d46/9_115.swf

kopilkaurokov.ru

План — конспект урока по информатике на тему Представление чисел в памяти компьютера (10 класс)

План – конспект по информатике и ИКТ
Урок: 6
Класс: 10 а, 10 б
Дата проведения: 1.10.2016.
Тема. Представление чисел в памяти компьютера
Цель :
Обучающая – сформировать представление у учащихся о форме представления чисел в памяти компьютера.
Воспитывающая – формирование коммуникативных качеств развивающейся личности.
воспитать внимательность, стремление довести дело до намеченного результата; установить взаимные контакты и обмен опытом между обучающимися и учителем. Развивающая — развить логическое мышление; стимулировать к познавательной активности обучающихся.
Тип урока: усвоение новых знаний.
Ход урока
1. Организационный момент
Приветствие, проверка присутствующих, объявление темы и цели урока. Учащиеся записывают тему урока в тетрадях .
2. Сообщение темы и постановка цели урока
Тема нашего сегодняшнего урока: «Представление чисел в памяти компьютера». Сегодня вы узнаете, в каком виде представляется и хранится числовая информация в памяти компьютера. Любая информация в памяти компьютера представляется с помощью нулей и единиц, то есть с помощью двоичной системы счисления. Первоначально компьютеры могли работать только с числами. Теперь это и числа, и тексты, и изображение, и звук.
3. Изучение нового материала
 В двоичной системе счисления для записи чисел используются только две цифры: 0 и 1. Основание двоичной системы равно 2.    Двоичное число представляет собой цепочку нулей и единиц. Например, запись 1102 соответствует десятичному числу 6, так как старшая единица в значение числа вносит 22, а вторая единица вносит 21.    Следует запомнить первые 9 чисел двоичной системы, их запись будет часто употребляться при изложении дальнейшего материала.

       Приведем двоичную запись некоторых степеней числа десять. 
   Из приведенного примера видно, что самым существенным недостатком двоичной системы является быстрый рост числа цифр в двоичном представлении. Используя развернутую форму записи, любое число в двоичной системе счисления можно представить в виде суммы степеней двойки. 
   Все позиционные системы счисления «одинаковы», а именно во всех них арифметические операции выполняются по одним и тем же правилам; справедливы одни и те же законы арифметики: коммутативный, ассоциативный, дистрибутивный; справедливы правила сложения, вычитания, умножения и деления столбиком, знакомые нам по действиям в десятичной системе счисления; правила выполнения арифметических операций опираются на таблицы сложения и умножения Р-ичных цифр. Рабо

univerfiles.com