Определение производной | Презентация к уроку алгебры (10 класс) по теме:

Слайд 1

ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ 1. Задачи, приводящие к понятию производной Составила учитель математики МОУ «Гимназия им. Горького А.М.»: Фабер Г.Н.

Слайд 2

=x 0 + ∆ x Приращение функции и приращение аргумента y=f(x) x 0 f(x)=f(x 0 + ∆x) f(x 0 ) ∆ x ∆ f приращение аргумента : x y ∆ х = х — х 0 (1) Приращение функции : ∆ f = f(x 0 +∆x)-f(x 0 ) (2) ∆ f = f(x)-f(x 0 ) (3) x В окрестности точки х 0 возьмём точку х Пусть х 0 — фиксированная точка, f( х 0 ) — значение функци в точке х 0 Расстояние между точками х и х 0 обозначим ∆х.Оно называется приращением аргумента и равно разности между х и х 0 : Первоначальное значение аргумента получило приращение ∆х, и новое значение х равно х 0 +∆х Функция f( х ) тоже примет новое значение: f(x 0 +∆x) Т.е., значение функции изменилось на величину f(x)-f(x 0 ) = f(x 0 +∆x)-f(x 0 ) , КОТОРАЯ НАЗЫВАЕТСЯ ПРИРАЩЕНИЕМ ФУНКЦИИ И ОБОЗНАЧАЕТСЯ ∆ f Дана функция f(x)

Слайд 3

Задача 1 (о скорости движения). По прямой, на которой заданы начало отсчета, единица измерения (метр) и направление, движется некоторое тело (материальная точка). Закон движения задан формулой s=s ( t ), где t — время (в секундах), s ( t ) — положение тела на прямой (координата движущейся материальной точки) в момент времени t по отношению к началу отсчета (в метрах). Найти скорость движения тела в момент времени t (в м/с).

Слайд 4

Предположим, что в момент времени t тело находилось в точке М пройдя путь от начала движения ОМ = s { t ). Дадим аргументу t приращение ∆ t и рассмотрим момент времени t+∆t Координата материальной точки стала другой, тело в этот момент будет находиться в точке P : OP=s(t+∆t) Значит, за ∆t секунд тело переместилось из точки М в точку Р, т.е. прошло путь МР. Имеем: MP=OP-OM=s(t+∆t)-s(t)=∆s Полученную разность мы назвали в § 26 приращением функции Путь ∆s тело прошло за ∆t секунд. Нетрудно найти среднюю скорость движения тела за промежуток времени [ t;t +∆t] : = А что такое скорость v ( t ) в момент времени t (ее называют иногда мгновенной скоростью)? Можно сказать так: это средняя скорость движения за промежуток времени [ t;t +∆t] при условии , что ∆t выбирается все меньше и меньше; точнее: иными словами, при условии, что ∆t→ 0.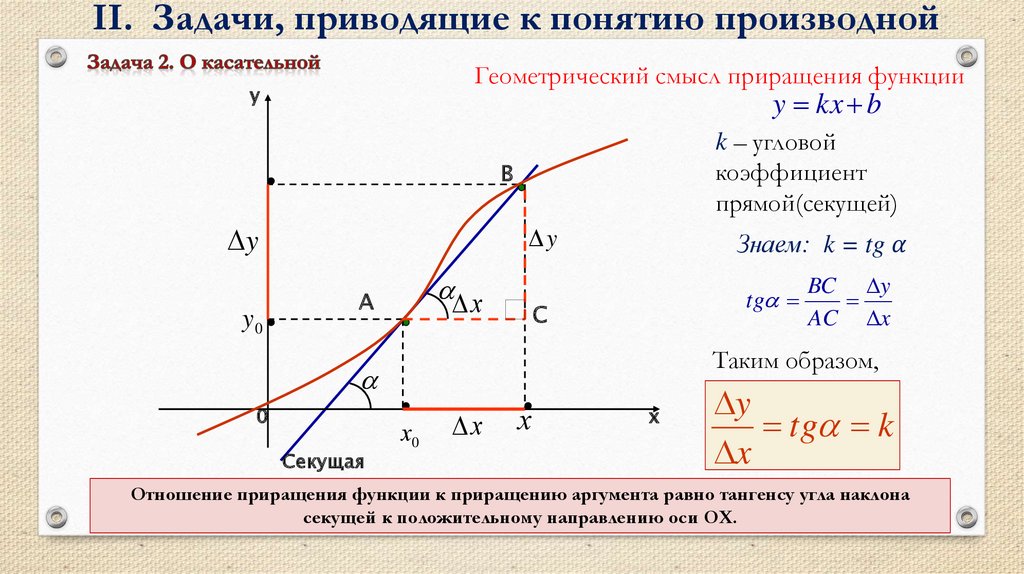 Это значит , что Подводя итог решению задачи 1, получаем:

Слайд 5

Задача 2 Поднимем камешек и затем из состояния покоя отпустим его. Движение свободно падающего тела явно неравномерное. Скорость v постепенно возрастает. Но как именно выглядит зависимость v(t) ?

Слайд 6

Фиксируем момент t , в который мы хотим знать значение скорости v(t) . Пусть h – небольшой промежуток времени, прошедший от момента t . За это время падающее тело пройдёт путь, равный s( t+h )-s(t) . Если промежуток времени h очень мал, то приближённо s( t+h )-s(t) ≈v(t)∙h , или , причём последнее приближённое равенство тем точнее, чем меньше h . Значит величину v(t) скорости в момент t можно рассматривать как предел , к которому стремится отношение, выражающее среднюю скорость на интервале времени от момента t до момента t+h . Сказанное записывают в виде

Слайд 7

Прямая, проходящая через точку М 0 (х 0; f( х 0 ) ), с отрезком которой почти сливается график функции f (х),называют касательной к графику в точке х 0 x 0 f(x 0 ) M 0 X y Тема: Задача, приводимая к понятию “ производная ” 0

Слайд 8

Задача: Определить положение касательной (tg φ ) х у 0 М 0 х 0 f(x 0 ) М х f(x) =x 0 + ∆x ∆ x ∆ f =f(x 0 +∆x)  φ Секущая , поворачиваясь вокруг точки М0, приближается к положению касательной Предельным положением секущей МоМ, когда М неограниченно приближается к Мо, является касательная Пусть дан график функции f( х ) и касательная, проходящая через точку М 0 ,которая образует с положительным направлением оси ОХ угол φ Отметим точку М, координаты которой рассмотрим как приращение координат точки М 0 Через точки М и М 0 проведём секущую, которая образует с осью ОХ угол  Будем перемещать точку М вдоль графика, приближая её к точке М 0. Соответственно будет меняться положение секущей ММ 0 При этом координата х точки М будет стремиться к х 0 К чему будет стремиться приращение аргумента? А к какому углу будет стремиться угол  ?

Слайд 9

Задача о касательной к графику функции y = f(x) x y x 0 М 0 (х 0 ,у 0 ) α А β В x М(х ,у) С ∆х =х-х 0 ∆ f(x) = f(x) — f(x 0 )

Слайд 10

Задача о мгновенной величине тока Обозначим через q = q(t) количество электричества, протекающее через поперечное сечение проводника за время t . Пусть Δ t – некоторый промежуток времени, Δ q = q(t+ Δ t) – q(t) – количество электричества, протекающее через указанное сечение за промежуток времени от момента t до момента t + Δ t . Тогда отношение называют средней силой тока. Мгновенной силой тока в момент времени t называется предел отношения приращения количества электричества Δ q ко времени Δ t , при условии, что Δ t → 0 .

Слайд 11

Выводы Различные задачи привели в процессе решения к одной и той же математической модели – пределу отношения приращения функции к приращению аргумента при условии, что приращение аргумента стремится к нулю. Значит, эту математическую модель надо специально изучить, т.е.: Присвоить ей новый термин. Ввести для неё обозначение. Исследовать свойства новой модели. Определить возможности применения нового понятия — производная

Слайд 12

Задача о скорости химической реакции Средняя скорость растворения соли в воде за промежуток времени [t 0 ; t 1 ] ( масса соли, растворившейся в воде изменяется по закону х = f(t)) определяется по формуле . Скорость растворения в данный момент времени

Слайд 13

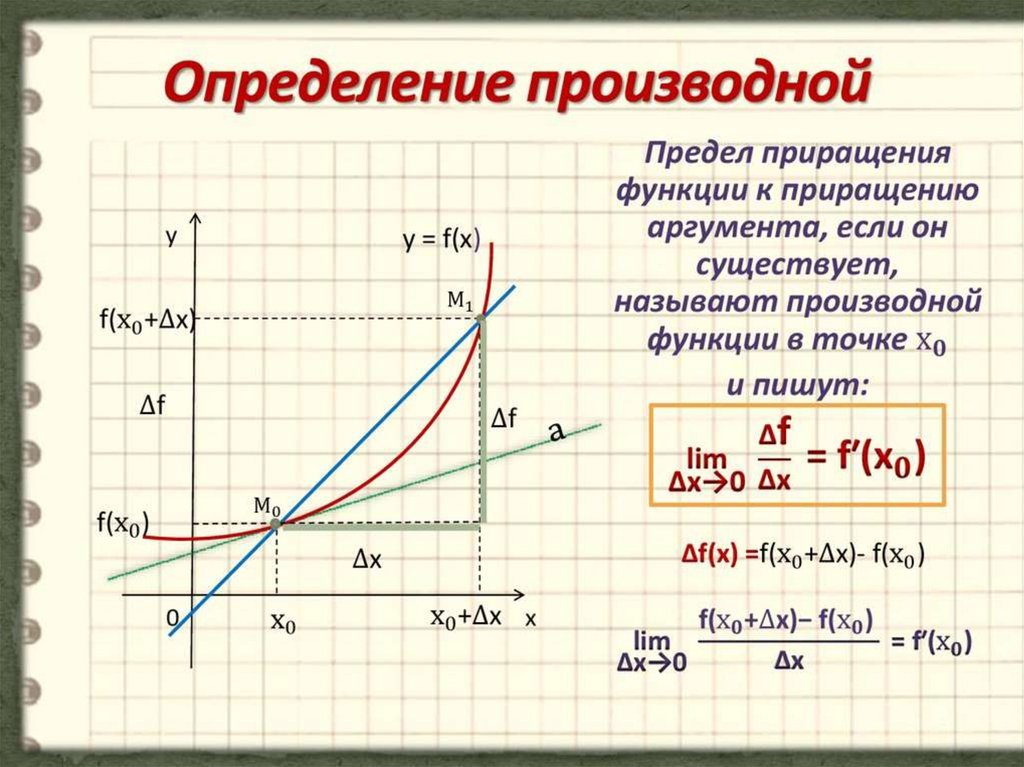
Определение производной Производной функции f в точке х 0 называется предел отношения приращения функции к приращению аргумента при последнем стремящимся к нулю:

Слайд 14

Возвращаясь к рассмотренным задачам, важно подчеркнуть следующее: а) мгновенная скорость неравномерного движения есть производная от пути по времени; б) угловой коэффициент касательной к графику функции в точке ( x 0 ; f(x)) есть производная функции f(x) в точке х = х 0 ; в) мгновенная сила тока I ( t) в момент t есть производная от количества электричества q(t) по времени; Г) скорость химической реакции в данный момент времени t есть производная от количества вещества у( t) , участвующего в реакции, по времени t .

Слайд 15

А л г о р и т м 1) ∆x = x – x 0 2) ∆f = f(x+x 0 ) – f(x 0 ) 3) 4)

Слайд 16

А это значит: Аппарат производной можно использовать при решении геометрических задач, задач из естественных и гуманитарных наук, экономических задач оптимизационного характера. И, конечно, не обойтись без производной при исследовании функции и построении графиков, решении уравнений и неравенств «…нет ни одной области в математике, которая когда-либо не окажется применимой к явлениям действительного мира…» Н.И. Лобачевский

Слайд 17

Основные формулы Средняя скорость = Мгновенная скорость или Скорость изменения функции Значение производной в точке =

Производная, введение и определение в 10 классе по алгебре

Дата публикации: 09 апреля 2017.

Что будем изучать:
1. Введение в понятие производной.
2. Чуть-чуть истории.
3. Определение производной.
4. Производная на графике функции. Геометрический смысл производной.
5. Алгоритм нахождения производной функции.
6. Дифференцирование функции.
7. Примеры.

Введение в понятие производной

Существует множество задач совершенно разных по смыслу, но при этом есть математические модели, которые позволяют рассчитывать решения наших задач совершенно одинаковым способом. Например, если рассмотреть такие задачи как:

а) Есть некоторый счет в банке, который постоянно изменяется один раз в несколько дней, сумма постоянно растет, требуется найти с какой скоростью растет счет.
б) Завод выпускает конфеты, есть некоторый постоянный прирост выпуска конфет, найти насколько быстро увеличивается прирост конфет.

в) Скорость движения автомобиля в некоторый момент времени t, если известно положение автомобиля, и он движется по прямой линии.
г) Нам дан график функции и в некоторой точке к нему проведена касательная, требуется найти тангенс угла наклона к касательной.
Формулировка наших задач совершенно разная, и, кажется, что они решаются совершенно разными способами, но математики придумали как можно решить все эти задачи совершенно одинаковым способом. Было введено понятие производной.

Чуть-чуть истории

Термин производная ввел великий математик – Лагранж, перевод на русский язык получается из французского слова derivee, он же и ввел современные обозначения производной которые мы рассмотрим позже.
Рассматривали понятие производной в своих работах Лейбниц и Ньютон, применение нашему термину они находили в геометрии и механики соответственно.
Чуть позже мы с вами узнаем, что производная определяется через предел, но существует небольшой парадокс в истории математики. Математики научились считать производную раньше, чем ввели понятие предела и собственно поняли, что же такое производная.

Определение производной

Пусть функция y=f(x) определена на некотором интервале, содержащим внутри себя некоторую точку x0. Приращение аргумента Δx – не выходит из нашего интервала. Найдем приращение Δy и составим отношение Δy/Δx, если существует предел этого отношения при Δx стремящимся к нулю, то указанный предел называют производной функции y=f(x) в точке x0 и обозначают f’(x0).

Попробуем объяснить, что такое производная не математическим языком:
На математическом языке: производная — предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю.

На обычном языке: производная – скорость изменения функции в точке x0.
Давайте посмотрим на графики трех функций:

Ребята, как вы думаете, какая из кривых растет быстрее?
Ответ, кажется, очевиден всем 1 кривая растет быстрее остальных. Мы смотрим, насколько круто идет вверх график функции. Другими словами — насколько быстро меняется ордината при изменении х. Одна и та же функция в разных точках может иметь разное значение производной — то есть может меняться быстрее или медленнее.

Производная на графике функции. Геометрический смысл производной

Теперь давайте посмотрим, как же найти производную с помощью графиков функции:

Посмотрим на наш график функции: Проведём в точке c абсциссой x0 касательную к графику функции. Касательная и график нашей функции соприкасаются в точке А. Нам надо оценить, насколько круто вверх идет график функции. Удобная величина для этого — тангенс угла наклона касательной.

Определение. Производная функции в точке x0 равна тангенсу угла наклона касательной, проведённой к графику функции в этой точке.

f’ (x0)=tg(α)

Угол наклона касательной выбирается как угол между касательной и положительным направлением оси абсцисс.
И так производная нашей функции равна:

И так производная в точке x0 равна тангенсу угла наклона касательной, это геометрический смысл производной.

Алгоритм нахождения производной функции

Алгоритм нахождения производной функции y=f(x).
а) Зафиксировать значение x, найти f(x).
б) Найти приращение аргумента x+ Δx, и значение приращения функции f(x+ Δx).
в) Найти приращение функции Δy= f(x+ Δx)-f(x).
г) Составить соотношение: Δy/Δx
д) Вычислить

— это и есть производная нашей функции.

Дифференцирование функции

Если функции y=f(x)имеет производную в точке x, то ее называют дифференцируемой в точке x. Процесс нахождения производной называют дифференцированием функции y=f(x).
Вернемся к вопросу непрерывности функции. Если функция дифференцируема в некоторой точке, тогда к графику функции в этой точке можно провести касательную, функция не может иметь разрыв в этой точки, тогда просто напросто нельзя провести касательную.
И так запишем выше сказанное как определение:
Определение. Если функция дифференцируема в точке x, то она непрерывна в этой точке.
Однако, если функция непрерывна в точке, то это не значит, что она дифференцируема в этой точке. Например, функция y=|x| в точке x=0 непрерывна, но касательную провести нельзя, а значит и производной не существует.

Примеры производной

Найти производную функции: y=3x
Решение:
Будем пользоваться алгоритмом поиска производной.
1) Для фиксированного значения x, значение функции y=3x
2) В точке x+ Δx, y=f(x+ Δx)=3(x+ Δx)=3x+3 Δx

3) Найдем приращение функции: Δy= f(x+ Δx)-f(x)= 3x+3 Δx-3x=3Δx

4) Составим соотношение:

5)Найдем предел:

Ответ: f’ (x)=3

Найти производную функции y=5x²

Решение:
Будем пользоваться алгоритмом поиска производной.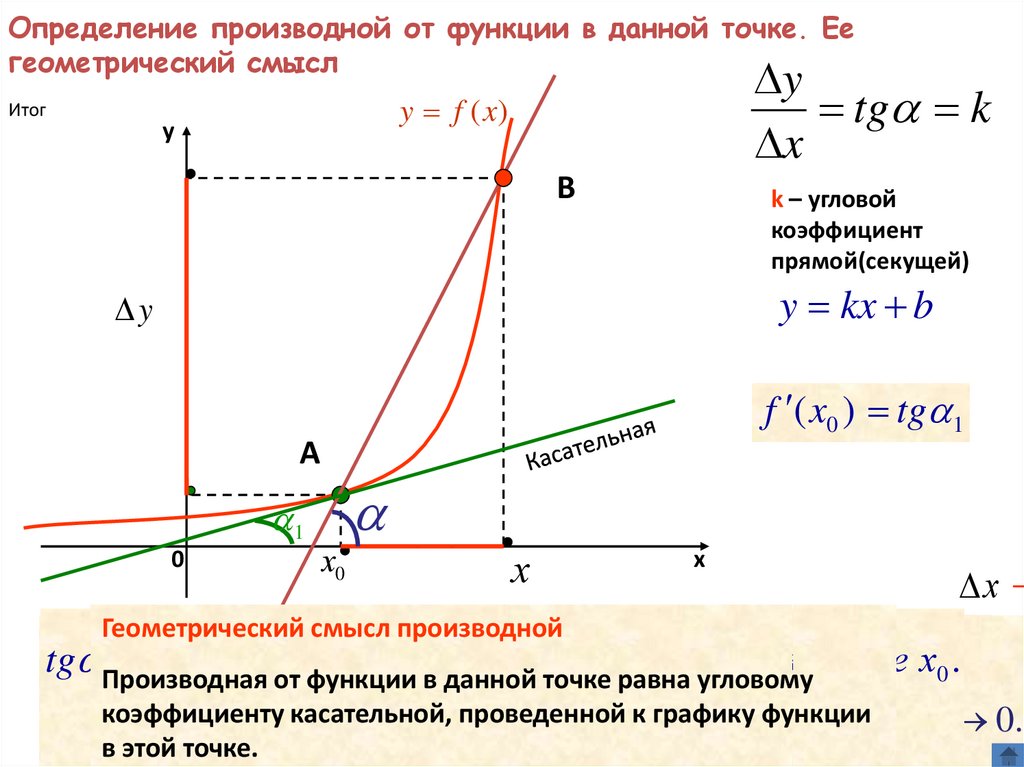 3$.

Исчисление I. Определение производной

Онлайн-заметки Пола
Главная / Исчисление I / Производные / Определение производной

Показать мобильное уведомление Показать все примечания Скрыть все примечания

Мобильное уведомление

Похоже, вы используете устройство с «узкой» шириной экрана ( т. е.

вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

Раздел 3.1: Определение производной

В первом разделе главы «Пределы» мы видели, что вычисление наклона касательной, мгновенной скорости изменения функции и мгновенной скорости объекта в точке \(х = а\) требует от нас для вычисления следующего предела.

\[\ mathop {\lim }\limits_{x \to a} \frac{{f\left( x \right) — f\left( a \right)}}{{x — a}}\]

Мы также видели, что, немного изменив обозначения, этот предел можно также записать как

\[\begin{equation}\mathop {\lim}\limits_{h \to 0} \frac{{f\left({a + h} \right) — f\left(a\right)}}{h } \label{eq:eq1}\end{уравнение}\]

Это такой важный предел, и он возникает во многих местах, что мы даем ему имя. Мы называем это производным от . Вот официальное определение производной.

Определение производной

Производная от \(f\left( x \right)\) по отношению к x является функцией \(f’\left( x \right)\) и определяется как \[\begin{equation}f’\left( x \right) = \mathop {\lim }\limits_{h \to 0} \frac{{f\left({x + h} \right) — f\ слева( x \справа)}}{h} \label{eq:eq2}\end{equation}\]

Обратите внимание, что мы заменили все и в \(\eqref{eq:eq1}\) на x , чтобы признать тот факт, что производная также является функцией.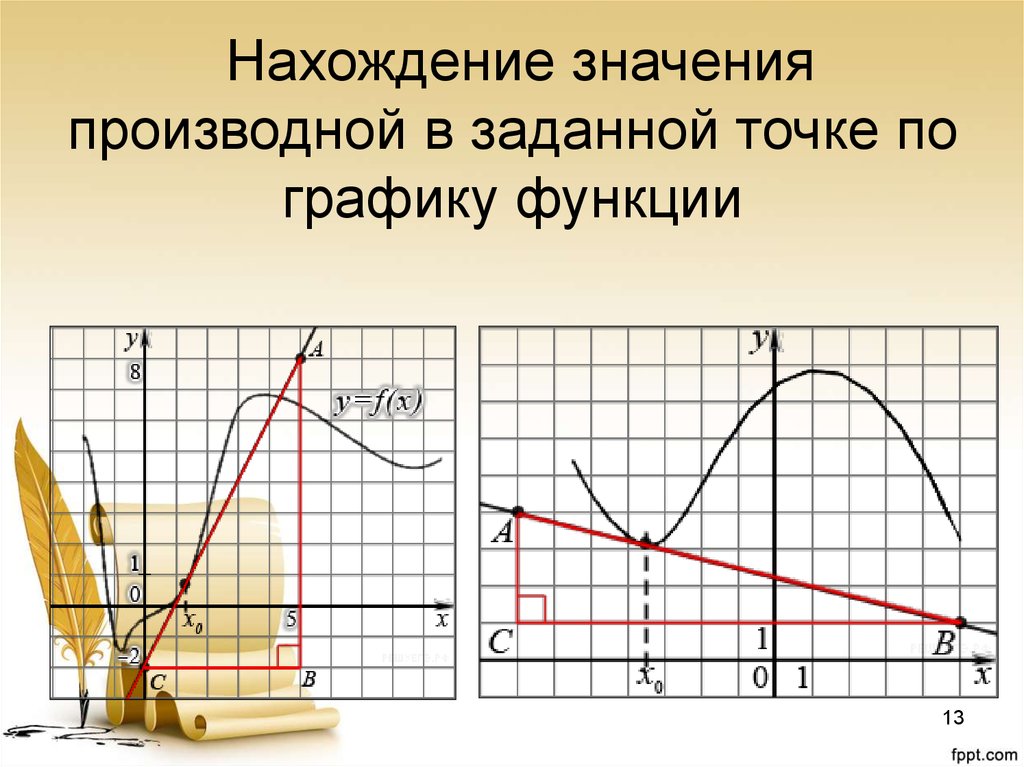

2} — 16ч}}{ч}\конец{выравнивание*}\]

Обратите внимание, что каждое слагаемое в числителе, в котором не было ч , сокращаются, и теперь мы можем вынести ч из числителя, что сократит ч в знаменателе. После этого мы можем вычислить предел.

\[\begin{align*}f’\left( x \right) & = \mathop {\lim }\limits_{h \to 0} \frac{{h\left({4x + 2h — 16} \right )}}}{ч}\\ & = \mathop {\lim}\limits_{h \to 0} 4x + 2h — 16\\ & = 4x — 16\end{align*}\]

Итак, производная

\[f’\влево( х \вправо) = 4x — 16\]

Пример 2 Найдите производную следующей функции, используя определение производной. \[g\left( t \right) = \frac{t}{{t + 1}}\]

Показать решение

Это будет немного сложнее, если говорить об алгебре.

Однако за пределами этого он будет работать точно так же, как и в предыдущих примерах. Во-первых, мы вставляем функцию в определение производной,

\[\begin{align*}g’\left( t \right) & = \mathop {\lim }\limits_{h \to 0} \frac{{g\left({t + h} \right) — g \ left( t \ right)}} {h} \\ & = \ mathop {\ lim } \ limit_ {h \ to 0} \ frac {1} {h} \ left ( {\ frac {{t + h }}{{t + h + 1}} — \frac{t}{{t + 1}}} \right)\end{align*}\]

Обратите внимание, что мы изменили все буквы в определении, чтобы они соответствовали заданной функции. Также обратите внимание, что мы написали дробь гораздо более компактно, чтобы помочь нам в работе.

Как и в случае с первой проблемой, мы не можем просто подставить \(h = 0\). Итак, нам нужно будет немного упростить ситуацию. В этом случае нам нужно будет объединить два члена в числителе в одно рациональное выражение следующим образом.

\[\ begin{align*}g’\left( t \right) & = \mathop {\lim }\limits_{h \to 0} \frac{1}{h}\left({\frac{{\ влево( {t + h} \right)\left( {t + 1} \right) — t\left( {t + h + 1} \right)}}{{\left( {t + h + 1} \right)\left( {t + 1} \right)}}} \right)\\ & = \mathop {\lim }\limits_{h \to 0} \frac{1}{h}\left( { \frac{{{t^2} + t + th + h — \left( {{t^2} + th + t} \right)}}{{\left( {t + h + 1} \right) \left( {t + 1} \right)}}} \right)\\ & = \ mathop {\lim }\limits_{h \to 0} \frac{1}{h}\left({\frac{ h}{{\left( {t + h + 1} \right)\left( {t + 1} \right)}}} \right)\end{align*}\]

Прежде чем закончить, давайте отметим пару вещей. Во-первых, мы не умножали знаменатель. Умножение знаменателя слишком усложнит ситуацию, поэтому давайте не будем усложнять. Далее, как и в первом примере, после упрощения у нас в числителе остались только члены с ч в них, и поэтому теперь мы можем отменить ч на выходе.

Итак, при отмене ч мы можем оценить предел и получить производную. 92}}}\]

Пример 3 Найдите производную следующей функции, используя определение производной. \[R\влево( z \вправо) = \sqrt {5z — 8} \]

Показать решение

Сначала подключите определение производной, как мы сделали это в двух предыдущих примерах.

\[\begin{align*}R’\left( z \right) & = \mathop {\lim }\limits_{h \to 0} \frac{{R\left({z + h} \right) — R \ влево ( z \ вправо)}} {h} \\ & = \ mathop {\ lim } \ limit_ {h \ to 0} \ frac {{\ sqrt {5 \ left ({z + h} \ right) — 8} — \sqrt {5z — 8} }}{h}\end{align*}\]

В этой задаче нам нужно рационализировать числитель. Вы ведь помните рационализацию из класса алгебры, верно? На уроке алгебры вы, вероятно, рационализировали только знаменатель, но вы также можете рационализировать числители. Помните, что при рационализации числителя (в данном случае) мы умножаем и числитель, и знаменатель на числитель, за исключением того, что мы меняем знак между двумя членами. Вот рационализаторская работа для этой задачи,

\[\ begin{align*}R’\left( z \right) & = \ mathop {\lim }\limits_{h \to 0} \frac{{\left({\sqrt {5\left({z + h} \right) — 8} — \sqrt {5z — 8} } \right)}}{h}\frac{{\left( {\sqrt {5\left( {z + h} \right) — 8} + \sqrt {5z — 8} } \right)}}{{\left( {\sqrt {5\left({z + h} \right) — 8} + \sqrt {5z — 8}} \ справа)}}\\ & = \mathop {\lim }\limits_{h \to 0} \frac{{5z + 5h — 8 — \left( {5z — 8} \right)}}{{h\left ( {\ sqrt {5 \ left ( {z + h} \ right) — 8} + \ sqrt {5z — 8} } \ right)}} \\ & = \ mathop {\ lim } \ limits_ {h \ to 0} \frac{{5h}}{{h\left( {\sqrt {5\left({z + h} \right) — 8} + \ sqrt {5z — 8}} \справа)}}\конец{выравнивание*}\]

Опять же, после упрощения в числителе осталось только ч . Итак, отменяем ч и оцениваем лимит.

\[\ begin{align*}R’\left( z \right) & = \mathop {\lim }\limits_{h \to 0} \frac{5}{{\sqrt {5\left({z + h} \right) — 8} + \sqrt {5z — 8} }}\\ & = \frac{5}{{\sqrt {5z — 8} + \sqrt {5z — 8} }}\\ & = \frac{5}{{2\sqrt {5z — 8} }}\end{align*}\]

Итак, мы получаем производную от

\[R’\left( z \right) = \frac{5}{{2\sqrt {5z — 8} }}\]

Давайте рассмотрим еще один пример. Этот будет немного другим, но в нем есть смысл, который нужно сделать.

Пример 4. Определить \(f’\left( 0 \right)\) для \(f\left( x \right) = \left| x \right|\).

Показать решение

Поскольку эта задача требует производной в определенной точке, мы продолжим и используем ее в нашей работе. Это сделает нашу жизнь проще, и это всегда хорошо.

Итак, вставьте определение и упростите.

\[\begin{align*}f’\left( 0 \right) & = \mathop {\lim }\limits_{h \to 0} \frac{{f\left({0 + h} \right) — f\left( 0 \right)}}{h}\\ & = \mathop {\lim}\limits_{h \to 0} \frac{{\left| {0 + ч} \право| — \влево| 0 \right|}}{h}\\ & = \mathop {\lim }\limits_{h \to 0} \frac{{\left| h \right|}}{h}\end{align*}\]

Подобную ситуацию мы уже видели, когда рассматривали пределы бесконечности. Так как в этом разделе мы не можем просто отменить 9+ }} 1\\ & = 1\end{align*}\]

Два односторонних предела различны, поэтому

\[\ mathop {\lim}\limits_{h \to 0} \frac{{\left| ч \справа|}}{ч}\]

не существует. Однако это предел, который дает нам производную, которая нам нужна.

Если предела не существует, то и производная не существует.

В этом примере мы, наконец, увидели функцию, для которой производная не существует в точке. Это факт жизни, о котором мы должны знать. Производные не всегда будут существовать. Обратите также внимание, что это ничего не говорит о том, существует ли производная где-либо еще. На самом деле производная функции абсолютного значения существует в каждой точке, кроме той, которую мы только что рассмотрели, \(x = 0\).

Предыдущее обсуждение приводит к следующему определению.

Определение

Функция \(f\left( x \right)\) называется дифференцируемой в \(x = a\), если \(f’\left( a \right)\) существует и \( f\left( x \right)\) называется дифференцируемой на интервале, если производная существует для каждой точки этого интервала.

Следующая теорема показывает нам очень хорошую связь между непрерывными и дифференцируемыми функциями.

Теорема

Если \(f\left( x \right)\) дифференцируема в \(x = a\), то \(f\left( x \right)\) непрерывна в \(x = a\).

Доказательство этой теоремы см. в разделе «Доказательство различных производных формул» в главе «Дополнительно».

Обратите внимание, что эта теорема не работает в обратном порядке. Рассмотрим \(f\left( x \right) = \left| x \right|\) и взглянем на

\[\ mathop {\lim}\limits_{x \to 0} f\left(x\right) = \mathop {\lim}\limits_{x \to 0} \left| х \ справа | = 0 = f\влево( 0 \вправо)\]

Итак, \(f\left( x \right) = \left| x \right|\) непрерывно в точке \(x = 0\), но мы только что показали выше в примере 4, что \(f\left (x \right) = \left| x \right|\) не дифференцируема в точке \(x = 0\).

Альтернативное обозначение

Далее нам нужно обсудить некоторые альтернативные обозначения производной. Типичное обозначение производной — это «штриховое» обозначение. Однако есть еще одно обозначение, которое иногда используется, поэтому давайте рассмотрим его.

Для функции \(y = f\left( x \right)\) все следующие эквиваленты эквивалентны и представляют собой производную от \(f\left( x \right)\) по х .

\[f’\left( x \right) = y’ = \frac{{df}}{{dx}} = \frac{{dy}}{{dx}} = \frac{d}{{dx} }\left( {f\left( x \right)} \right) = \frac{d}{{dx}}\left( y \right)\]

Поскольку иногда нам также необходимо вычислять производные, нам также нужна запись для вычисления производных при использовании дробной записи.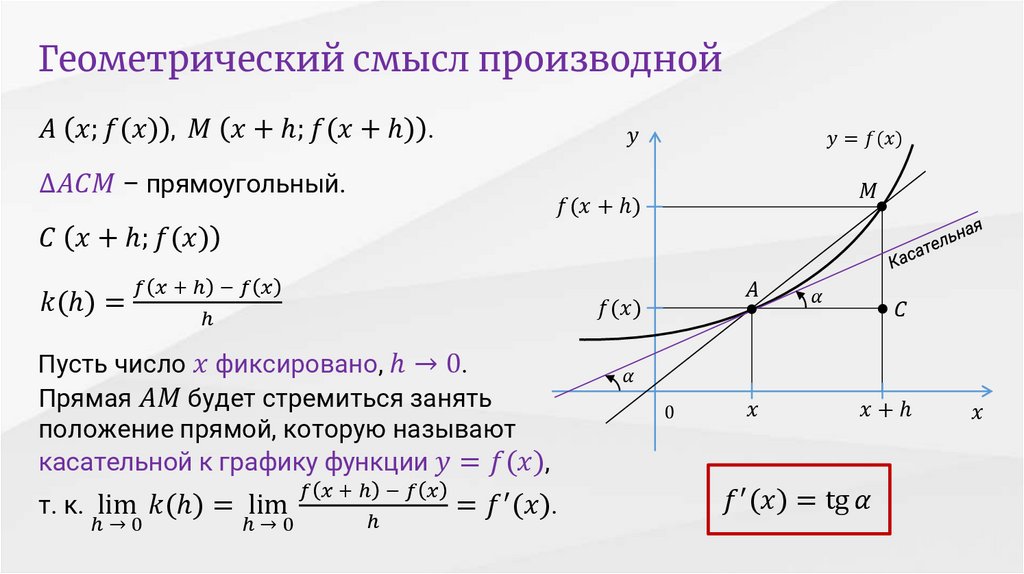 Итак, если мы хотим оценить производную при \(x = a\), все следующие условия эквивалентны.

\[f’\влево( а \вправо) = {\влево. {y’} \right|_{x = a}} = {\left. {\ frac {{df}}{{dx}}} \right|_{x = a}} = {\left. {\ frac {{dy}} {{dx}}} \right|_{x = a}}\]

Также обратите внимание, что иногда мы опускаем часть \(\left( x \right)\) в функции, чтобы несколько упростить запись. В этих случаях следующие условия эквивалентны.

\[f’\влево( х \вправо) = f’\]

В качестве последнего примечания в этом разделе мы признаем, что вычисление большинства производных непосредственно из определения — довольно сложный (и иногда болезненный) процесс, полный возможностей совершать ошибки. Через пару разделов мы начнем разрабатывать формулы и/или свойства, которые помогут нам получить производную многих распространенных функций, чтобы нам не приходилось слишком часто прибегать к определению производной.

Однако это не означает, что не важно знать определение производной! Это важное определение, которое мы всегда должны знать и помнить. Это просто то, с чем мы не собираемся так много работать.

Введение в деривативы

Все дело в уклоне!

Наклон = Изменение Y Изменение X

 

Мы можем найти средний наклон между двумя точками.
Но как найти наклон в точке ? Нечем мерить!
А вот с производными мы используем небольшую разницу… … затем уменьшите до нуля .

Найдем производную!

Чтобы найти производную функции y = f(x), мы используем формулу наклона:

Уклон = Изменение Y Изменение X = Δy Δx

И (из диаграммы) мы видим, что:

от от

х отличается от		х	до	х+Δх
у отличается от		ф(х)	до	ф(х+Δх)

Теперь выполните следующие действия:

• Заполните эту формулу наклона: Δy Δx = f(x+Δx) − f(x) Δx
• Упростим как можно лучше
• Затем заставьте Δx уменьшиться до нуля.

Вот так:

Пример: функция

f(x) = x ²

Мы знаем f(x) = x ² , и мы можем вычислить f(x+Δx) 9010

4 9020 Начните с:

	f(x+Δx) = (x+Δx) 2
Расширение (x + Δx) 2 :		f(x+Δx) = x 2 + 2x Δx + (Δx) 2

 

Формула наклона: f(x+Δx) − f(x) Δx

Вставьте f(x+Δx) и f(x) : x ² + 2x Δx + (Δx) ² − x ² Δx

Упростить (x ² и −x ² отменить): 2x Δx + (Δx) ² Δx

Упрощайте больше (разделите через Δx): = 2x + Δx

Затем, как Δx головы в направлении 0 Мы получаем: = 2x

Результат: производное x ²

. 2x

Другими словами, наклон в точке x равен 2x

 

Пишем dx вместо «Δx направляется к 0» .

И «производное от» обычно пишется d dx like this:

d dx x ² = 2x
«The derivative of x ² equals 2x »
or simply «d dx of x ² равно 2x »

Так что же означает

d dx x ² = 2x ?

Это означает, что для функции x ² наклон или «скорость изменения» в любой точке равен 2x .

Итак, когда x=2 , наклон равен 2x = 4 , как показано здесь:

Или, когда x=5 , наклон равен 2x = 10 и так далее.

Примечание: f'(x) также может использоваться для «производной от»:

f'(x) = 2x
«Производная f(x) равна 2x»
или просто «f-тире x равно 2x»

 

Попробуем другой пример.

Пример: Что такое

d дх х ³ ?

Мы знаем f(x) = x ³ и можем вычислить f(x+Δx) :

Начните с:		f(x+Δx) = (x+Δx) 3
Расширение (x + Δx) 3 :		f(x+Δx) = x 3 + 3x 2 Δx + 3x (Δx) 2 + (Δx) 3

 

Формула наклона: f(x+Δx) − f(x) Δx

Вставьте f(x+Δx) и f(x) : x ³ + 3x ² Δx + 3x (Δx) ² + (Δx) ³ − x ³ Δx

Упростить (x ³ и −x ³ отменить): 3x ² Δx + 3x (Δx) ² + (Δx) ³ Δx

Simplify more (divide through by Δx): 3x ² + 3x Δx + (Δx) ²

Then, as Δx heads towards 0 we get:3x ²

Result: производная от x ³ равна 3x ²

Поиграйте с ним, используя Производный Плоттер.

 

Производные других функций

Мы можем использовать тот же метод для вычисления производных других функций (таких как синус, косинус, логарифмы и т.д.).

Но на практике обычный способ поиска производных состоит в использовании:

Производные правила

 

Пример: какова производная sin(x) ?

В производных правилах это указано как cos(x)

Готово.

Но пользоваться правилами может быть непросто!

Пример: какова производная от cos(x)sin(x) ?

Мы получим неправильный ответ, если попытаемся умножить производную от cos(x) на производную от sin(x) … !

Вместо этого мы используем «Правило продукта», как описано на странице «Производные правила».

И на самом деле получается cos ² (x) − sin ² (x)

Итак, это ваш следующий шаг: научиться пользоваться правилами.

 

Обозначение

«Сжать до нуля» на самом деле записывается в виде предела следующим образом:

f’(x) = lim Δx→0 f(x+Δx) − f(x) Δx

«Производная от f равно
предел, когда Δx стремится к нулю f(x+Δx) — f(x) по Δx»

 

Или иногда производная записывается так (объясняется производными как dy/dx):

dy dx = f(x+dx) − f(x) dx

 

Процесс нахождения производной называется «дифференцированием».