Контрольная работа по алгебре 10 класс модуль действительного числа – Контрольная работа по теме «Действительные числа» в форме ЭГЕ, алгебра, 10-й класс
Контрольная работа по теме «Действительные числа» в форме ЭГЕ, алгебра, 10-й класс
- Изекеева Алина Михайловна, учитель математики
Разделы: Математика
ВАРИАНТ 1
ЧАСТЬ А
А1. Вычислите ;
1. 49. 2. . 3. 4. – 49.
А2. Вычислите ;
1. 2. 2. 3. 4.
А3. Упростите выражение ;
1. 2. 3. 4.
А4. Решите уравнение ;
1. x = 2. 2. 3. 4. x = — 2.
А5. Запишите бесконечную периодическую дробь 0,( 43 ) в виде обыкновенной дроби
1. 2. 3. 4.
ЧАСТЬ В
В1. Сократите дробь ;
В2. Сравните числа ;
В3. Вычислить ;
ЧАСТЬ С
С1. Упростите выражение , если – 1 < x < 2 ;
С2. Упростите выражение .
ВАРИАНТ 2
ЧАСТЬ А
А1. Вычислите ;
1. 2. 36. 3. — 4. – 36.
А2. Вычислите ;
1. 5. 2. 3. 4.
А3. Упростите выражение ;
1. 2. 3. 4.
А4. Решите уравнение ;
1. x = 10. 2. x = 9. 3. x = 6. 4. x = 3.
А5. Запишите бесконечную периодическую дробь 0,3( 6 )в виде обыкновенной дроби
1. 2. 3. 4.
ЧАСТЬ В
В1. Сократите дробь ;
В2. Сравните числа ;
В3. Вычислить ;
ЧАСТЬ С
С1. Упростите выражение , если — 3 < x < — 1.
С2. Упростите выражение .
ВАРИАНТ 3
ЧАСТЬ АА1. Вычислите
1. 25; 2. 3. 4.
А2. Вычислите .
1. 2. 3. 3. 4.
А3. Упростите выражение
1. ; 2. 3. 4.
А4. Решите уравнение ;
1. x = 10. 2. 3. ; 4. 5.
А5. Запишите бесконечную периодическую дробь 0,( 34 ) в виде обыкновенной дроби
1. 2. 3. 4.
ЧАСТЬ В
В1. Сократите дробь ;
В2. Сравните числа
В3. Вычислить
ЧАСТЬ С
С1. Упростите выражение
С2. Упростите выражение
ВАРИАНТ 4
ЧАСТЬ А
А1. Вычислите
1. 2. 7. 3. 4. 49.
А2. Вычислите
1. 2. 3. 3. 4.
1. 2. 3. 4.
А4. Решите уравнение
1. — 2. 3. 4.
А5. Запишите бесконечную периодическую дробь 0,( 248 )в виде обыкновенной дроби
1. 2. 3. 4.
ЧАСТЬ В
В1. Сократите дробь
В2. Сравните числа
В3. Вычислить
ЧАСТЬ С
С1. Упростите выражение
С2. Упростите выражение
Ответы к контрольной работе.
| ВАРИАНТ 1 | ВАРИАНТ 2 | ВАРИАНТ 3 | ВАРИАНТ 4 | ||||
| ЧАСТЬ А | ЧАСТЬ А | ЧАСТЬ А | ЧАСТЬ А | ||||
| А1 | 1 | А1 | 1 | А1 | 2 | А1 | 1 |
| А2 | 2 | А2 | 1 | А2 | 1 | А2 | 2 |
| А3 | 4 | 3 | А3 | 1 | А3 | 2 | |
| А4 | 2 | А4 | 1 | А4 | 3 | А4 | 2 |
| А5 | 2 | А5 | 2 | А5 | 4 | А5 | 3 |
| ЧАСТЬ В | ЧАСТЬ В | ЧАСТЬ В | ЧАСТЬ В | ||||
| 1. | 1. | 1. | 1. | ||||
| 2. знак больше | 2. знак меньше | 2. знак меньше | 2. знак больше | ||||
| 3. 8 | 3. 3 | 3. 2 | 3. 4 | ||||
| ЧАСТЬ С | ЧАСТЬ С | ЧАСТЬ С | ЧАСТЬ С | ||||
| 1. 9 | 1. а | 1. 1 | |||||
| 2. | 2. – 2 | 2. – 3 | 2. 2 | ||||
27.03.2008
urok.1sept.ru
Контрольная работа №3 для 10 классов по математике 2008 год
Карпова И. В., ДВГГУ
В статье на конкретных примерах рассматриваются некоторые методы решения уравнений и неравенств, содержащих переменную под знаком абсолютной величины, в том числе решение уравнений и неравенств с параметрами.
1. Определение и свойства модуля действительного числа
Напомним определение модуля действительного числа:
Определение 1. Модулем действительного числа а называется число , равное самому числу а, если оно неотрицательное и противоположному для а числу, если оно отрицательно.
Таким образом, по определению имеем:
Перечислим основные свойства модуля числа, которые в дальнейшем будем учитывать при решении уравнений и неравенств:
1) ; 5) , ;
2) ; 6)
3) ; 7) ;
4) ; 8) .
Замечание 1. Известно, что любое действительное число а можно интерпретировать, как точку на числовой оси. В связи с этим геометрически – это расстояние от начала координат до точки а. При этом величина задает расстояние между точками а и b на числовой оси.
2. Методы решения уравнений, содержащих переменную под знаком модуля
При решении уравнений, содержащих переменную под знаком модуля, могут быть использованы следующие методы:
— раскрытие модуля по определению;
— возведение обеих частей уравнения в квадрат;
— разбиение области решения уравнения на промежутки знакопостоянства выражений, стоящих под знаком модуля.
Каждый из этих методов рассмотрим на конкретном примере и сделаем необходимые обобщения.
Пример 1. Решить уравнение .
Решение. 1-й способ. Воспользовавшись определением модуля получим совокупность двух систем: 1) или 2) . Решим каждую из этих систем: 1) ; 2) х = 0.
Ответ: х1 = 0; .
2-й способ. Так как обе части уравнения неотрицательны, то возведя их в квадрат, получим уравнение равносильное данному: , учитывая свойство 3, будем иметь: х1 = 0; .
Пример 2. Решить уравнение
Решение. 1-й способ. Уединим выражение, содержащее знак абсолютной величины . Воспользовавшись определением модуля получим совокупность двух систем: 1) ; 2) . Решив полученные системы найдем корни первоначального уравнения: ; .
2-й способ. Возведем обе части уравнения в квадрат, потребовав при этом, чтобы . Получим систему: . Решая полученную систему, получим те же корни. Ответ: ; .
Замечание 2. Уравнение вида может быть решено двумя методами:
— по определению модуля оно равносильно совокупности двух уравнений:
— возведением обеих частей уравнений в квадрат. Учитывая свойство 3, получится уравнение , равносильное данному.
Замечание 3. Уравнение вида может быть решено двумя методами:
— по определению модуля оно равносильно совокупности двух систем:
1) ; 2)
— возведением обеих частей уравнений в квадрат. Учитывая, что правая часть уравнения должна быть неотрицательной, получится система:
Пример 3. Решить уравнение
Решение. Обе части уравнения неотрицательны, поэтому, возведя их в квадрат и учитывая свойство модуля 3, получим уравнение равносильное данному:
Раскрыв скобки и приведя подобные члены, получим квадратное уравнение: , решив которое найдем корни первоначального уравнения: ; .
Замечание 4. Уравнения вида удобно решать методом возведения обеих частей в квадрат, если f(x) и g(x) – многочлены первой степени.
Пример 4. Решить уравнение
Решение. 1) Найдем значения переменной, обращающие выражения, стоящие под знаком абсолютной величины в нуль: ; ; .
2) Нанесем полученные значения на числовую прямую и на каждом из полученных интервалов определим знак каждого выражения, стоящего под знаком абсолютной величины:
х : – – – +
х + 1: – – + +
х + 2: – + + +
3) Пользуясь определением модуля и используя п. 2 раскроем на каждом из интервалов все знаки модулей:
при имеем: ;
при имеем: ;
при имеем: ;
при имеем: .
4) Решим каждое из полученных уравнений: при : х = –2 это значение в интервал не входит; при : х = –2 полученное значение входит в обозначенный интервал; при : ни при каких значениях х уравнение решений не имеет; при : х = –2 в данный интервал это значение не входит.
5) Таким образом, уравнение имеет единственный корень х = –2, так как это значение входит в один из интервалов. Ответ: х = –2.
Замечание 5. Алгоритм, с помощью которого было решено уравнение, можно обобщить для решения любого уравнения, содержащего несколько модулей:
1) Найти значения переменной, обращающие выражения стоящие под знаком абсолютной величины в нуль;
2) Все найденные значения нанести на числовую прямую и на каждом из полученных интервалов определить знак каждого выражения, стоящего под знаком абсолютной величины;
3) Учитывая получившиеся знаки, воспользоваться определением модуля и раскрыть на каждом из интервалов все знаки модулей;
4) Решить каждое из полученных уравнений и из их решений выбрать те, которые принадлежат соответствующему интервалу, они и будут являться решениями первоначального уравнения.
Пример 5. Решить уравнение .
Решение. Заметим, что слагаемые в знаменателе неотрицательны, следовательно сумма равна нулю в том и только в том случае, когда оба слагаемых одновременно равны нулю. Ни при каких значениях переменной этого произойти не может, т. е. знаменатель дроби при любом значении х отличен от нуля.
Для решения воспользуемся сформулированным алгоритмом.
1) ; .
2) + – + +
– – – +
3) При имеем: ;
При имеем ; ;
При имеем: ;
При имеем: .
4) Выбирая из полученных решений те, которые принадлежат соответствующим промежуткам, получим: ; ; .
Ответ: ; ; .
3. Методы решения неравенств, содержащих переменную под знаком модуля
Для того чтобы решить неравенство, содержащее неизвестную под знаком абсолютной величины, можно разбить область допустимых значений неравенства на интервалы, в которых выражения, стоящие под знаком модуля сохраняют знак. На каждом таком интервале решить неравенство (раскрыв предварительно знак абсолютной величины). Объединение полученных решений и будет являться решением первоначального неравенства
Пример 6. Решить неравенство .
Решение. Под знаком модуля стоит квадратный трехчлен, найдем промежутки его знакопостоянства: при и значения трехчлена неотрицательно; при значения трехчлена отрицательны. Учитывая это решим неравенство на каждом из полученных интервалов:
при имеем ,
откуда получаем ;
при имеем
и , откуда получаем ;
при , откуда получаем х = 4.
Объединив найденные на каждом интервале решения, получим решение первоначального неравенства: и х = 4. Ответ: [1; 3], 4.
Пример 7. Решить неравенство .
Решение. По определению модуля имеем совокупность двух систем:
Решая системы, получим: или . Окончательно получаем ответ.
Ответ: .
Замечание 6. В общем случае неравенство вида в соответствии с определением модуля имеет решение только в случае, когда . Неравенство вида при выполняется во всей области определения функции .
Пример 8. Решить неравенство .
Решение. 1-й способ. Воспользовавшись определением модуля, получим совокупность двух систем:
Решая эти системы получим: и . Окончательно получаем
2-й способ. Введем новую переменную , получим неравенство не содержащее знаков модуля: . Решая полученное неравенство методом интервалов, получим: . Перейдем к переменной х: , откуда . Ответ:
Замечание 7. Если неравенство содержит несколько одинаковых выражений под знаками модуля (как это было в примере 8), то его удобно решать методом замены переменной.
4. Уравнения и неравенства с параметрами
Пример 9. При всех а решить уравнение и определить, при каких а оно имеет ровно два решения.
Решение. Сначала воспользуемся алгоритмом, изложенным в замечании 5.
1) Найдем значения переменной, обращающие выражения, стоящие под знаком абсолютной величины в нуль: ; .
2) Нанесем найденные значения на числовую прямую и на каждом из полученных интервалов определим знак каждого выражения, стоящего под знаком абсолютной величины:
х – 2: – – +
х + 3: – + +
3) Пользуясь определением модуля и используя п. 2 раскроем на каждом из интервалов все знаки модулей.
При уравнение будет иметь вид: , откуда имеем:
…………………………………….(1)
Исследуем решения этого уравнения в зависимости от параметра а.
Если а = –1, то (1) примет вид тождества 0 = 0, и решением уравнения (1) будут все . …………………………………………………………………………………….(2)
Если же , то из (1) х = –3, но это значение не входит в исследуемый интервал.
При уравнение будет иметь вид: , откуда имеем:
……………………………………..(3)
Если а = 1, то (3) примет вид тождества 0 = 0, и решением уравнения (3) будут все . …………………………………………………………………………….(4)
Если , то из (1) х = –3…………………………………………………………(5)
При уравнение будет иметь вид:
Если а = –1, то полученное уравнение решений не имеет. ……………………………(6)
Если , то . Выясним при каких значениях а полученное значение х будет входить в исследуемый интервал:
при , …………………………………………(7)
При остальных значениях а на этом интервале уравнение решений не имеет.
Сделаем выводы по проведенному исследованию. Уравнение будет иметь различные решения при: ; ; ; а = 1; . Из (5) следует, что при корень уравнения х = –3; из (2) и (5) следует, что при решениями уравнения будут и х = –3; из (5) и (7) следует, что при решениями уравнения будут х = –3 и , именно на этом интервале уравнение имеет ровно два решения; из (4) и (7) следует, что при а = 1 уравнение имеет решения и = 2; из (5) следует, что при решением уравнения будет х = –3.
Ответ: при х = –3; при ; при х = –3, ; при а = 1 ; при х = –3.
Пример 10. При всех значениях а решить неравенство
Решение. 1. В соответствии с замечанием 6 неравенство при решений не имеет.
2. Пусть . Определим промежутки знакопостоянства выражения, стоящего под знаком модуля: ; ; .
3. Решим неравенство на каждом из полученных интервалов.
Если , то , следовательно, имеем или
…………………………………….(1)
Дискриминант квадратного трехчлена, стоящего в левой части неравенства (1) равен , причем так как , . Поэтому квадратный трехчлен, стоящий в левой части неравенства (1) имеет два действительных корня. Решая неравенство (1) относительно переменной х, получим:
…………………………(2)
Заметим, что при каждом положительном а верны неравенства
; ………………………(3)
Окончательно на этом интервале, получаем, что для любого положительного а решением неравенства будут числа из интервала: .
Если , то , следовательно имеет место неравенство
…………………………………….(4)
Дискриминант квадратного трехчлена, стоящего в левой части неравенства (4) равен . Тогда неравенство (4) при имеет место при любом действительном х.
Если квадратный трехчлен, стоящий в левой части неравенства (4) имеет два действительных корня, поэтому, решая неравенство (4) относительно переменной х, получим: и . Заметим, при этом, что при справедливы неравенства:
………………………….(5)
Тогда на этом интервале окончательно получаем: при решением неравенства является отрезок ; при решение неравенство состоит их двух промежутков: и .
Если , то , следовательно, имеем или
…………………………………….(1)
Решая это неравенство на этом интервале, получаем: .
Сделаем выводы по проведенному исследованию: из п.1 следует, что при неравенство решений не имеет; учитывая неравенства (2), (3), (5) при решением неравенства являются интервалы: и ; учитывая (2) при неравенство имеет решение: .
Ответ: при неравенство решений не имеет; приимеет решения:
; ; при имеет решение: .
Представленные ниже задачи являются контрольным заданием для учащихся 10 классов. Решения необходимо оформить в отдельной тетради и выслать по адресу 680000, г. Хабаровск, ул. Дзержинского, 48, ХКЦТТ, ХКЗФМШ. Для зачета нужно набрать не менее 20 баллов (каждая правильно решенная задача оценивается в 3 балла)
М10.3.1. М10.3.2.
М10.3.3. М10.3.4.
М10.3.5. При всех а решить уравнение
М10.3.6. М10.3.7.
М10.3.8. М10.3.9.
М10.3.10. При всех а решить неравенство .
pandia.ru
Контрольные работы по алгебре, 10 класс.
Контрольная работа №1 по теме:
«Действительные числа»
Вариант №1. Обязательная часть
Бесконечно убывающая геометрическая прогрессия. Формула суммы.
Вычислите:

в)

б)

г)
Упростите выражения:

б)

в)

Разложите на множители: a – 4.
Сократите дробь:

Дополнительная часть
Сравните числа a и b, если:
Упростите выражение:
Вариант №2. Обязательная часть
Арифметический корень натуральной степени. Свойства.
Вычислите:
в)

б)

г)

Упростите выражения:

б)
в)

Разложите на множители:

Сократите дробь:

Дополнительная часть
Сравните числа a и b, если:
Упростите выражение:
Контрольная работа №2 по теме:
«Степенная функция»
Вариант №1.
1. Найти область определения функции  .
.
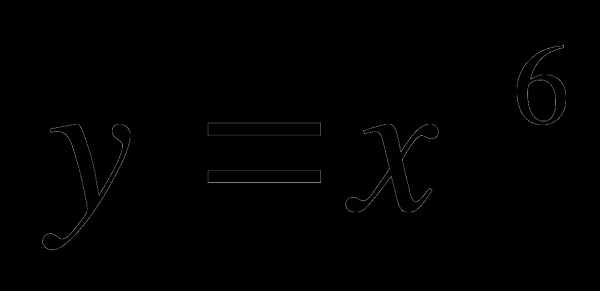
2. Изобразить эскиз графика функции 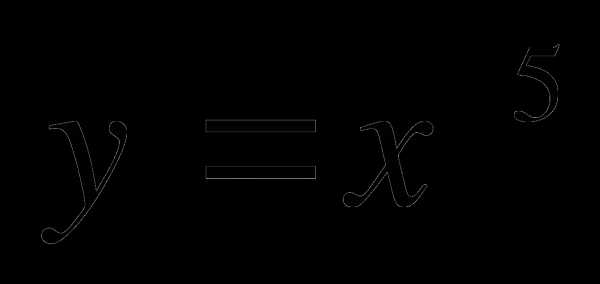 .
.
Указать область определения и множество значений функции.
Выяснить, на каких промежутках функция убывает.
Сравнить числа
 и
и  .
.
Решить уравнение:

2)
3)
Решить неравенство: .
Найти функцию, обратную к ; указать её область определения и множество значений. На одном рисунке построить графики данной функции и функции, обратной к данной.
Вариант №2
Найти область определения функции
 .
.Изобразить эскиз графика функции
 .
.
Указать область определения и множество значений функции.
Выяснить, на каких промежутках функция возрастает.
Сравнить числа
 и
и  .
.
Решить уравнение:
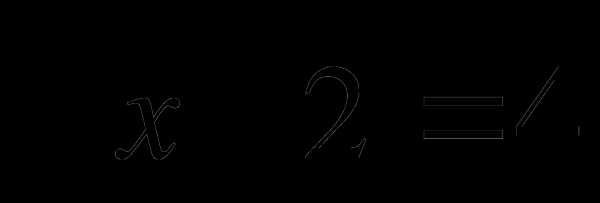 ;
;2);
3);
Решить неравенство: .
Найти функцию, обратную к ; указать её область определения и множество значений. На одном рисунке построить графики данной функции и функции, обратной к данной.
Контрольная работа №3 по теме:
«Показательная функция»
Вариант №1
Решить уравнение:
 ; 2).
; 2).Решить неравенство
 .
.Решить систему уравнений

Решить неравенство:
1)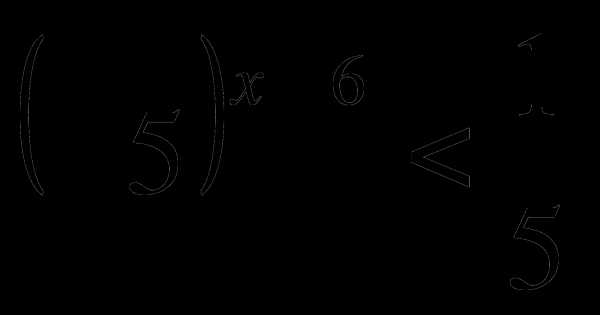 ; 2)
; 2)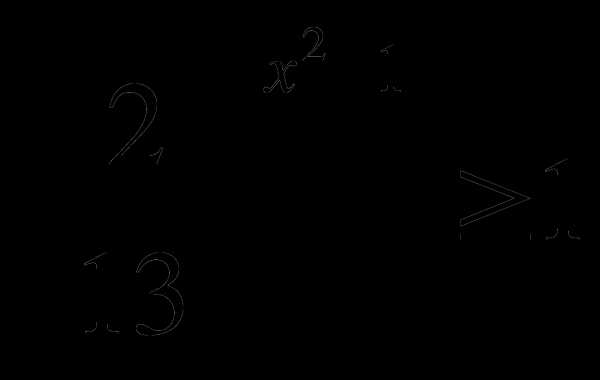 .
.
Решить уравнение .
Решите уравнение: .
В ответе укажите корень уравнения или сумму корней, если их несколько.
Контрольная работа №3 по теме:
«Показательная функция»
Вариант №2
1. Решить уравнение:
; 2).2. Решить неравенство  .
.
3. Решить систему уравнений 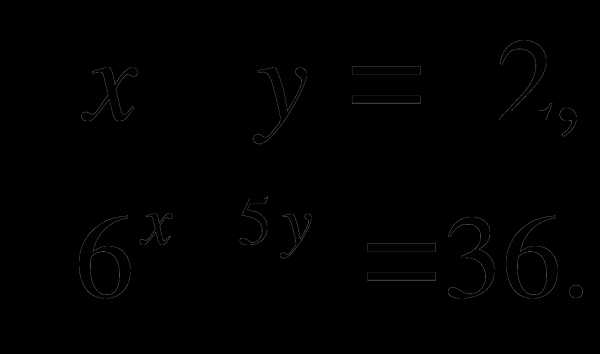
_ 4. Решить неравенство:
1)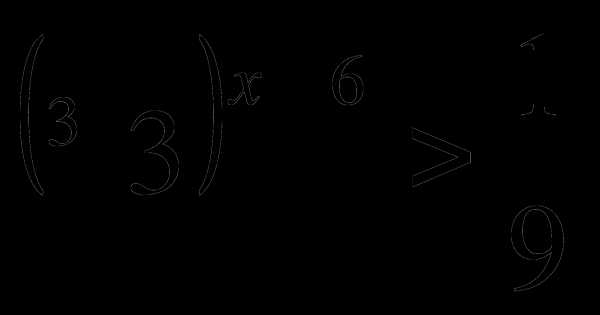 ; 2)
; 2)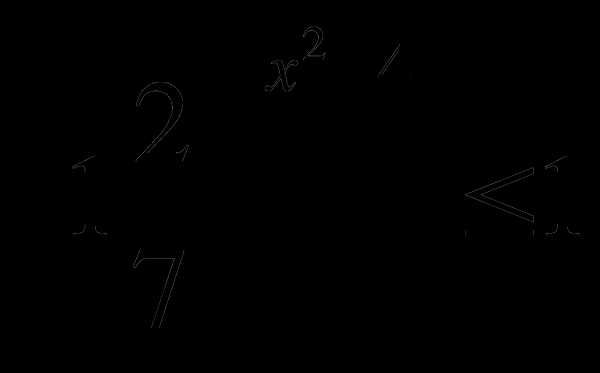 .
.
5. Решить уравнение .
6. Решите уравнение: .
В ответе укажите корень уравнения или сумму корней, если их несколько.
Контрольная работа №4 по теме:
«Логарифмическая функция»
Вариант №1
1. Вычислите:.
2. При каких значениях х имеет смысл выражение:
а);
б)
3. Решите уравнение:
4. Упростите: a0,a1.
5. Дано:. Найти: 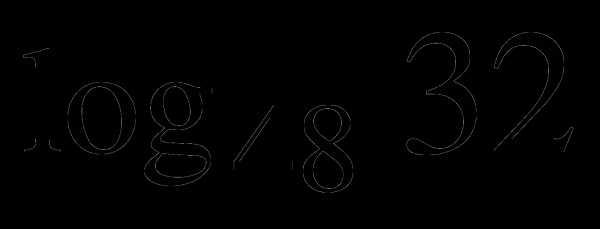 .
.
Контрольная работа №4 по теме:
«Логарифмическая функция»
Вариант №2
1. Вычислите: .
2. При каких значениях x имеет смысл выражение:
а) б)
3. Решите уравнение:
4. Упростите: a0,a1.
5. Дано: Найти: 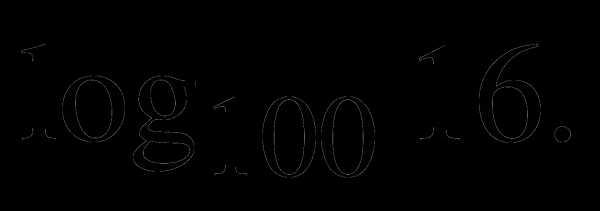
Контрольная работа №5 по теме:
«Тригонометрические формулы»
Вариант №1
1. Решите уравнение:
.
2. Упростите выражение:
а);
б);
в).
3. Пусть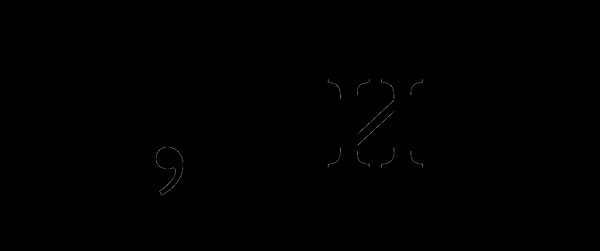 углы треугольника. Докажите тождество:
углы треугольника. Докажите тождество:
.
Контрольная работа №5 по теме:
«Тригонометрические формулы»
Вариант №2
1. Решите уравнение:
.
2. Упростите выражение:
а);
б);
в).
3. Пусть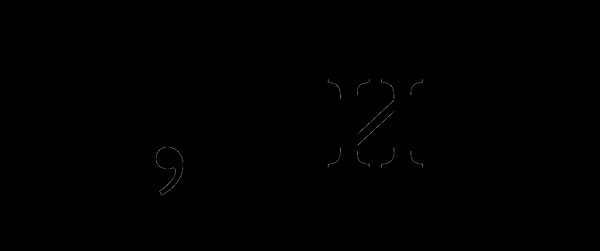 углы треугольника. Докажите тождество:
углы треугольника. Докажите тождество:
.
Контрольная работа №6 по теме:
«Тригонометрические уравнения»
Вариант №1
1. Решите уравнение: sin x —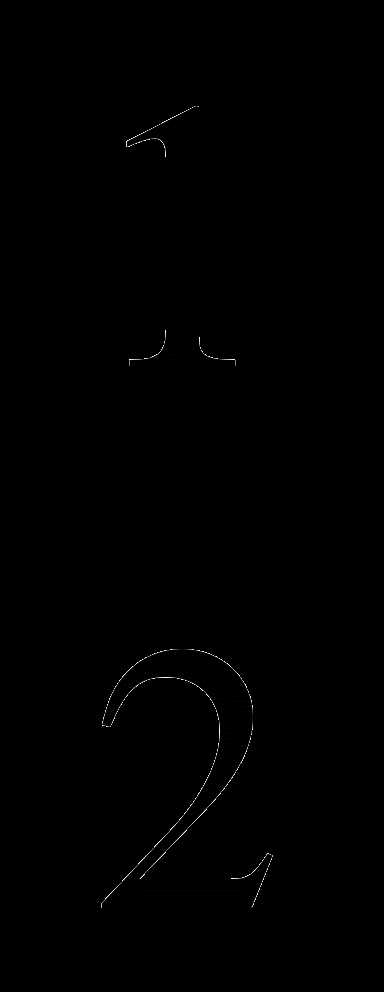 =0
=0
2. Решите уравнение: cos 2x=1
3. Укажите уравнение, которому соответствует решение: :
1) tg x = 1; 2) cos x = 0; 3) sin x = -1; 4) ctg x = .
.
4. На каком из рисунков показано решение неравенства: cos x < ?
?
1) 2) 3) 4)
5. Решите неравенство: tg x ≥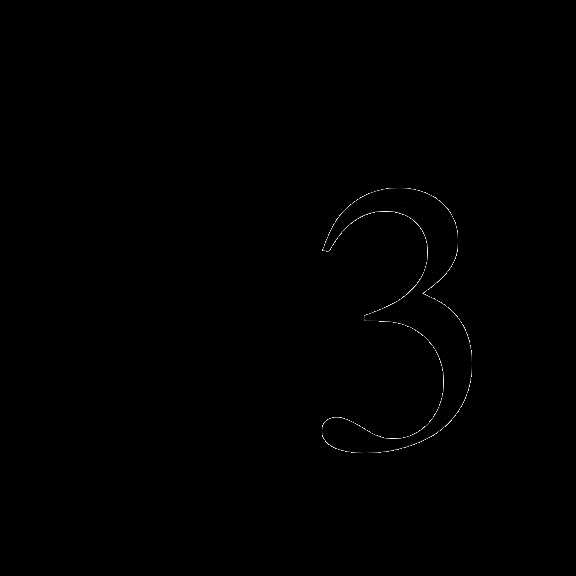 :
:
6. Решите уравнение: 6sin2 x + sin x – 1 = 0
7. Решите уравнение: 2sin2 x —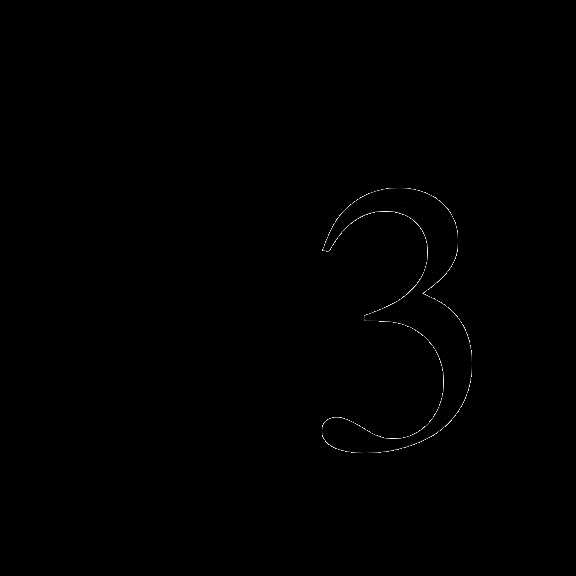 sin 2x =0
sin 2x =0
Контрольная работа №6 по теме:
«Тригонометрические уравнения»
Вариант №2
1. Решите уравнение: sin x + =0
=0
2. Решите уравнение: ctg (x+ )=
)=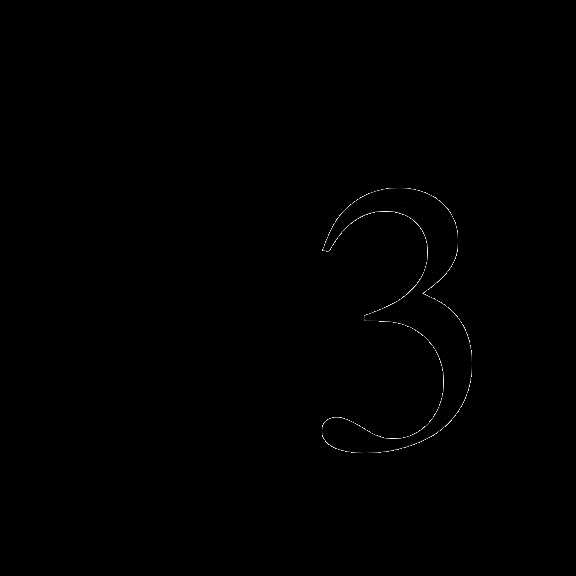
3. Укажите уравнение, которому соответствует решение:  :
:
1) ctg x = -1; 2) cos x = 0; 3) cos x = -1; 4) tg x = 1.
4. На каком из рисунков показано решение неравенства: sin x ≥ ?
?
1) 2) 3) 4) 4)
5. Решите неравенство: ctg x ≥
6. Решите уравнение: cos2 x — 4sin x + 3 = 0
7. Решите уравнение:  sin2 x -3sin x cos x =0
sin2 x -3sin x cos x =0
infourok.ru
План-конспект урока по алгебре (10 класс) на тему: Контрольная работа по теме «Действительные числа» в форме ЭГЕ, алгебра и начала анализа, 10-й класс.
Контрольная работа по теме «Действительные числа» в форме ЭГЕ,
алгебра и начала анализа, 10-й класс.
Нуждина Е.Н.
ВАРИАНТ 1
ЧАСТЬ А
А1. Вычислите ;
1. 49 2. 3. 4. – 49.
А2. Вычислите ;
1. 2. 2. 3. 4.
А3. Упростите выражение ;
1. 2. 3. 4.
А4. Решите уравнение ;
1. x = 2. 2. 3. 4. x = — 2.
А5. Запишите бесконечную периодическую дробь 0,( 43 ) в виде обыкновенной дроби
1. 2. 3. 4.
ЧАСТЬ В
В1. Сократите дробь ;
В2. Сравните числа ;
В3. Вычислить ;
ЧАСТЬ С
С1. Упростите выражение , если – 1
ВАРИАНТ 2
ЧАСТЬ А
А1. Вычислите ;
1. 2. 36. 3. — 4. – 36.
А2. Вычислите ;
1. 5. 2. 3. 4.
А3. Упростите выражение ;
1. 2. 3. 4.
А4. Решите уравнение ;
1. x = 10. 2. x = 9. 3. x = 6. 4. x = 3.
А5. Запишите бесконечную периодическую дробь 0,3( 6 )в виде обыкновенной дроби
1. 2. 3. 4.
ЧАСТЬ В
В1. Сократите дробь ;
В2. Сравните числа ;
В3. Вычислить ;
ЧАСТЬ С
С1. Упростите выражение , если — 3
ВАРИАНТ 3
ЧАСТЬ А
А1. Вычислите
1. 25; 2. 3. 4.
А2. Вычислите .
1. 2. 3. 3. 4.
А3. Упростите выражение
1. ; 2. 3. 4.
А4. Решите уравнение ;
1. x = 10. 2. 3. ; 4. 5.
А5. Запишите бесконечную периодическую дробь 0,( 34 ) в виде обыкновенной дроби
1. 2. 3. 4.
ЧАСТЬ В
В1. Сократите дробь ;
В2. Сравните числа
В3. Вычислить
ЧАСТЬ С
С1. Упростите выражение
ВАРИАНТ 4
ЧАСТЬ А
А1. Вычислите
1. 2. 7. 3. 4. 49.
А2. Вычислите
1. 2. 3. 3. 4.
А3. Упростите выражение .
1. 2. 3. 4.
А4. Решите уравнение
1. — 2. 3. 4.
А5. Запишите бесконечную периодическую дробь 0,( 248 )в виде обыкновенной дроби
1. 2. 3. 4.
ЧАСТЬ В
В1. Сократите дробь
В2. Сравните числа
В3. Вычислить
ЧАСТЬ С
С1. Упростите выражение
Ответы к контрольной работе.
ВАРИАНТ 1 | ВАРИАНТ 2 | ВАРИАНТ 3 | ВАРИАНТ 4 | ||||
ЧАСТЬ А | ЧАСТЬ А | ЧАСТЬ А | ЧАСТЬ А | ||||
А1 | 1 | А1 | 1 | А1 | 2 | А1 | 1 |
А2 | 2 | А2 | 1 | А2 | 1 | А2 | 2 |
А3 | 4 | А3 | 3 | А3 | 1 | А3 | 2 |
А4 | 2 | А4 | 1 | А4 | 3 | А4 | 2 |
А5 | 2 | А5 | 2 | А5 | 4 | А5 | 3 |
ЧАСТЬ В | ЧАСТЬ В | ЧАСТЬ В | ЧАСТЬ В | ||||
1. | 1. | 1. | 1. | ||||
2. знак больше | 2. знак меньше | 2. знак меньше | 2. знак больше | ||||
3. 8 | 3. 3 | 3. 2 | 3. 4 | ||||
ЧАСТЬ С | ЧАСТЬ С | ЧАСТЬ С | ЧАСТЬ С | ||||
1. 9 | 1. –3х — 5 | 1. а | 1. 1 | ||||
nsportal.ru
Контрольная работа по алгебре по теме «Действительные числа» (10 класс)
Контрольная работа по теме «Действительные числа», 10 класс
ВАРИАНТ 1
ЧАСТЬ А
А1. Вычислите ;
1. 49. 2. . 3. 4. – 49.
А2. Вычислите ;
1. 2. 2. 3. 4.
А3. Упростите выражение ;
1. 2. 3. 4.
А4. Решите уравнение ;
1. x = 2. 2. 3. 4. x = — 2.
А5. Запишите бесконечную периодическую дробь 0,( 43 ) в виде обыкновенной дроби
1. 2. 3. 4.
ЧАСТЬ В
В1. Сократите дробь ;
В2. Сравните числа ;
В3. Вычислить ;
ЧАСТЬ С
С1. Упростите выражение , если – 1 < x < 2 ;
С2. Упростите выражение .
Контрольная работа по теме «Действительные числа», 10 класс
ВАРИАНТ 2
ЧАСТЬ А
А1. Вычислите ;
1. 2. 36. 3. — 4. – 36.
А2. Вычислите ;
1. 5. 2. 3. 4.
А3. Упростите выражение ;
1. 2. 3. 4.
А4. Решите уравнение ;
1. x = 10. 2. x = 9. 3. x = 6. 4. x = 3.
А5. Запишите бесконечную периодическую дробь 0,3( 6 )в виде обыкновенной дроби
1. 2. 3. 4.
ЧАСТЬ В
В1. Сократите дробь ;
В2. Сравните числа ;
В3. Вычислить ;
ЧАСТЬ С
С1. Упростите выражение , если — 3 < x < — 1.
С2. Упростите выражение .
infourok.ru
Контрольная работа №1 по теме Действительные числа, 10 класс
Тема: «Контрольная работа по теме «Действительные числа». Цель: контроль знаний, умений и навыков учащихся по изученной теме.Ход урока. 1.Организационный момент. 2.Сообщение темы и целей урока. 3.Выполнение к/р по вариантам.
Вариант 1
1. Вычислите: 13 EMBED Equation.DSMT4 1415; 13 EMBED Equation.DSMT4 1415
2. Упростите выражение: 13 EMBED Equation.DSMT4 1415
3. Решите уравнение : 13 EMBED Equation.DSMT4 1415
___________________________________________________________________________
4. Запишите бесконечную периодическую дробь 0,(43) в виде обыкновенной дроби.
5. Сократите дробь: 13 EMBED Equation.DSMT4 1415
6. Сравните числа: 13 EMBED Equation.DSMT4 1415 13 EMBED Equation.DSMT4 1415и 1; 13 EMBED Equation.DSMT4 1415
7*. Упростите выражение: 13 EMBED Equation.DSMT4 1415
Вариант 2
1. Вычислите: 13 EMBED Equation.DSMT4 1415 13 EMBED Equation.DSMT4 1415
2. Упростите выражение: 13 EMBED Equation.DSMT4 1415
3. Решите уравнение: 13 EMBED Equation.DSMT4 1415
__________________________________________________________________________
4. Запишите бесконечную периодическую дробь 0,3(6) в виде обыкновенной дроби.
5. Сократите дробь: 13 EMBED Equation.DSMT4 1415
6. Сравните числа: 13 EMBED Equation.DSMT4 1415 13 EMBED Equation.DSMT4 1415и 1; 13 EMBED Equation.DSMT4 1415
7*. Упростите выражение : 13 EMBED Equation.DSMT4 1415
4.Подведение итогов урока.
Root EntryEquation NativeEquation NativeEquation NativeEquation Native3Equation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation NativeEquation Native
Приложенные файлы
schoolfiles.net
Контрольная работа №1 по теме Действительные числа, 10 класс
Тема: «Контрольная работа по теме «Действительные числа». Цель: контроль знаний, умений и навыков учащихся по изученной теме.
Ход урока. 1.Организационный момент. 2.Сообщение темы и целей урока. 3.Выполнение к/р по вариантам.
Вариант 1
1. Вычислите: 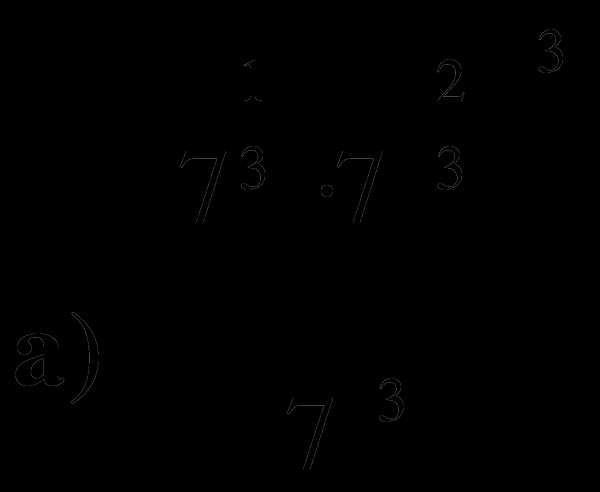 ;
; 
2. Упростите выражение: 
3. Решите уравнение :
___________________________________________________________________________
4. Запишите бесконечную периодическую дробь 0,(43) в виде обыкновенной дроби.
5. Сократите дробь: 
6. Сравните числа: 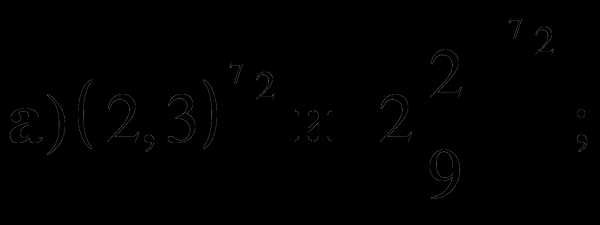
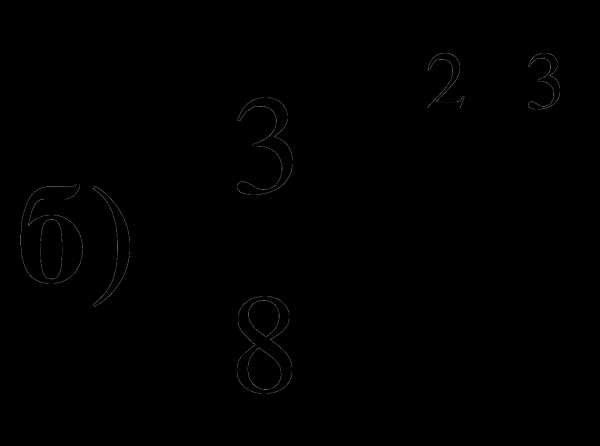 и 1;
и 1;
7*. Упростите выражение:
Вариант 2
1. Вычислите: 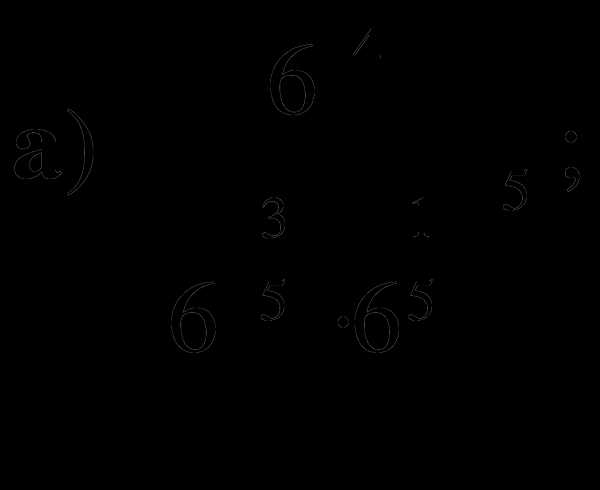
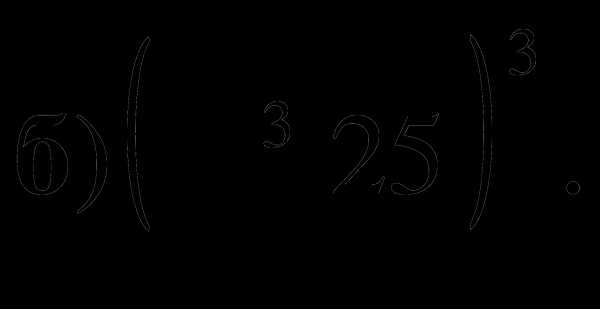
2. Упростите выражение: 
3. Решите уравнение: 
__________________________________________________________________________
4. Запишите бесконечную периодическую дробь 0,3(6) в виде обыкновенной дроби.
5. Сократите дробь: 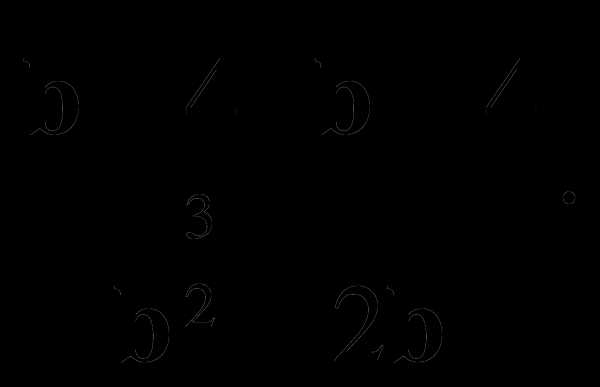
6. Сравните числа: 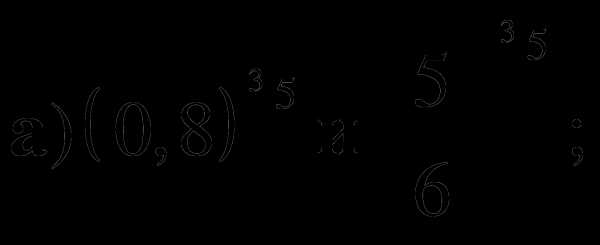
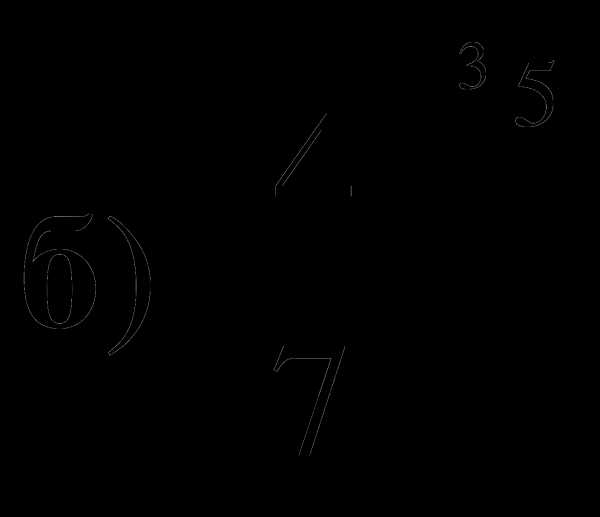 и 1;
и 1;
7*. Упростите выражение :
4.Подведение итогов урока.
infourok.ru


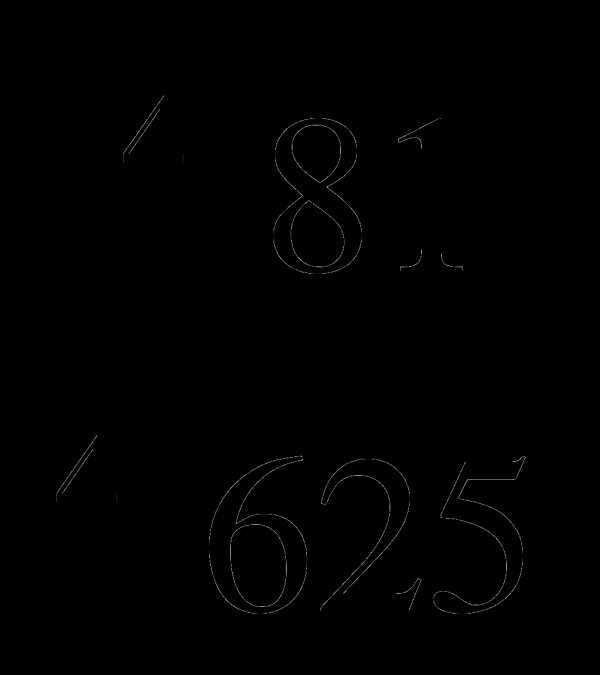


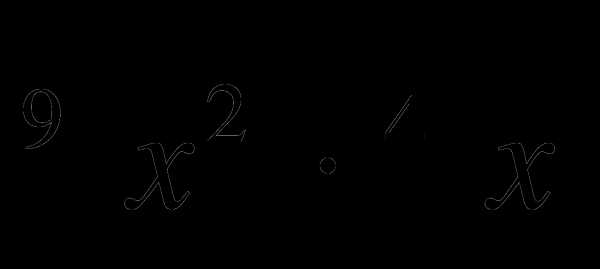
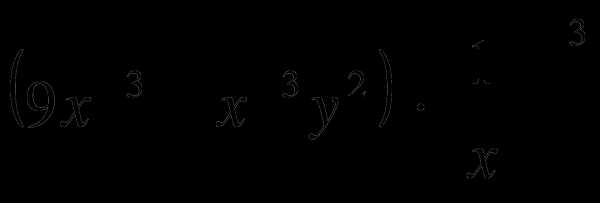
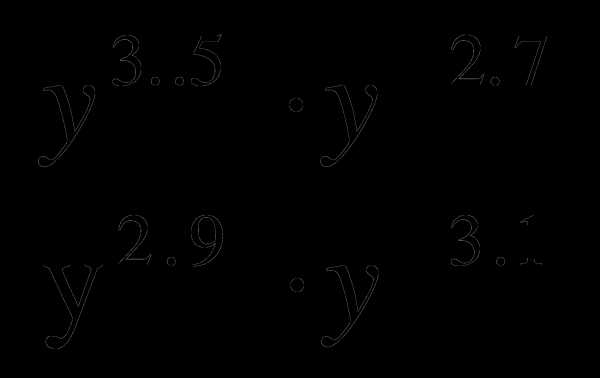
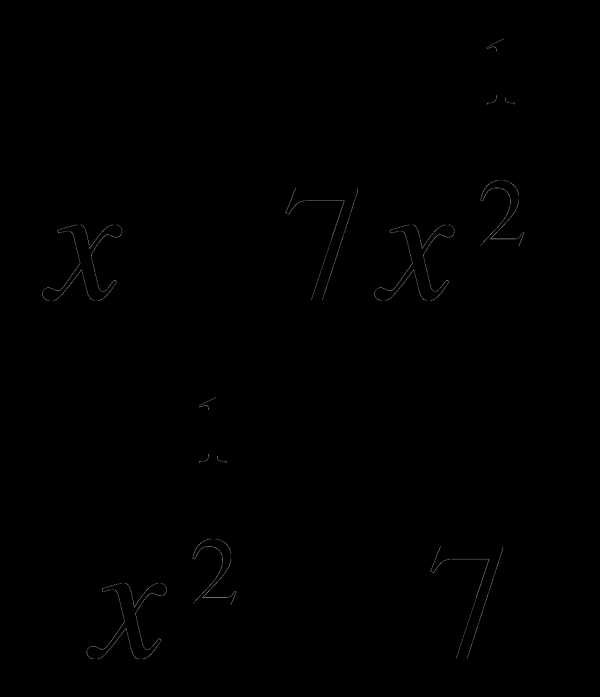

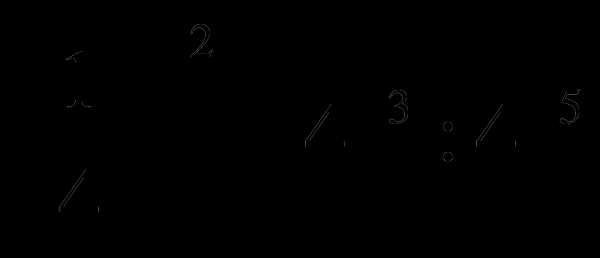
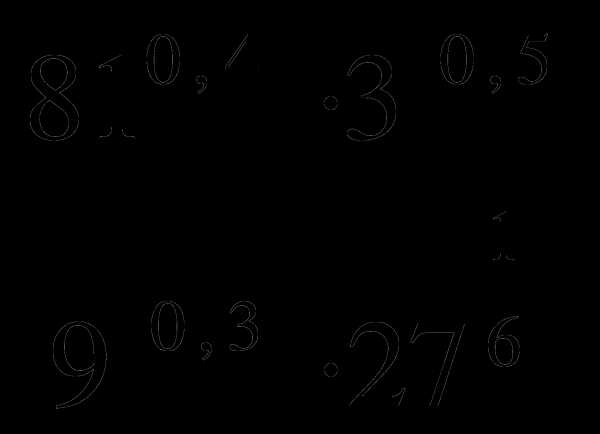
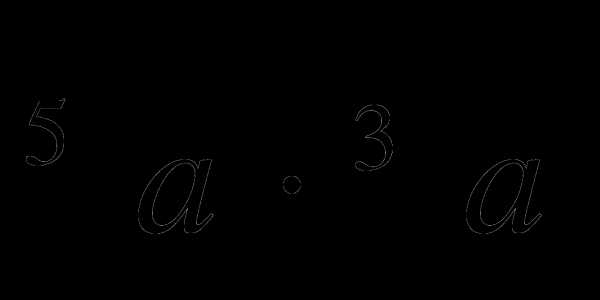
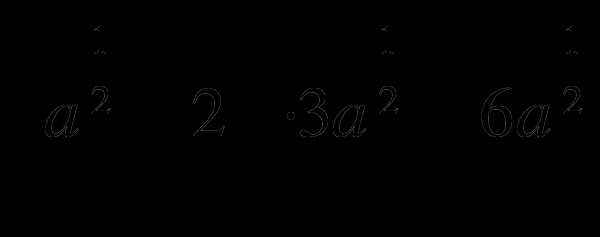
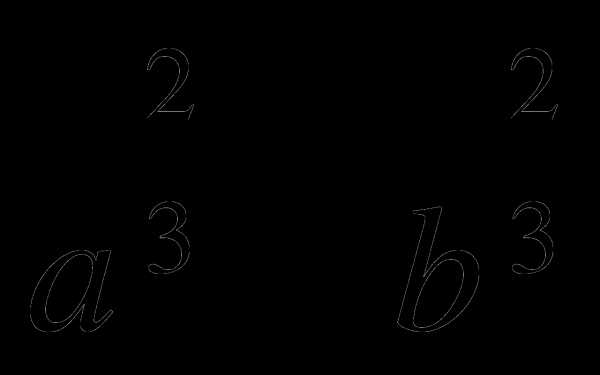
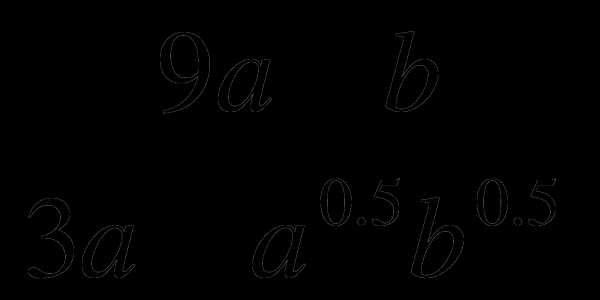
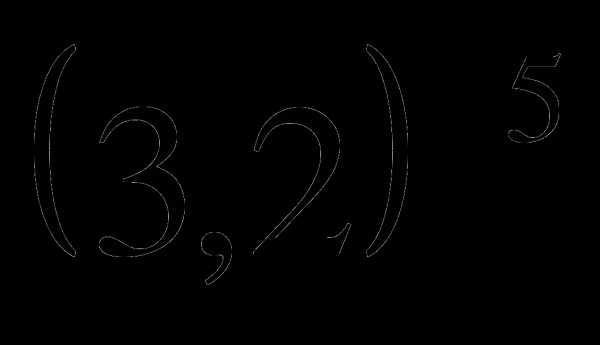 и
и 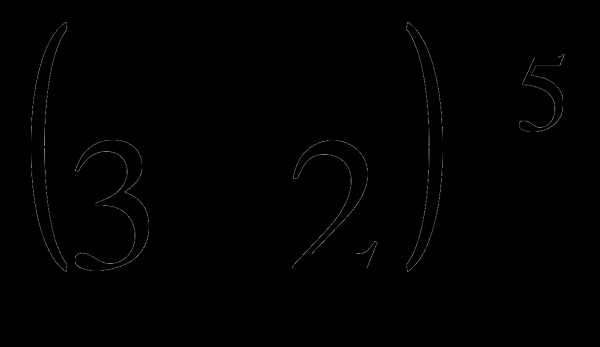 .
.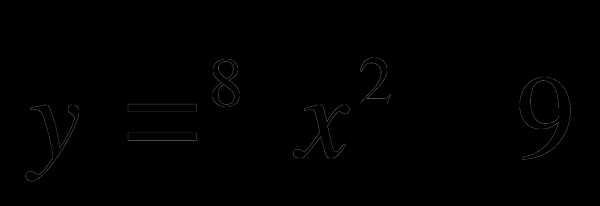 .
. .
. и
и  .
. ; 2).
; 2). .
.