Как оформить задачу по математике 1 класс: Решение и оформление простых задач в 1 классе
Урок 21. задача. структура задачи — Математика — 1 класс
Математика, 1 класс
Урок 21. Задача. Структура задачи.
Перечень вопросов, рассматриваемых на уроке:
- Решение текстовых задач арифметическим способом.
- Структура задачи: условие, вопрос, решение, ответ.
- Решение задач в одно действие на увеличение (уменьшение) числа на несколько единиц.
- Задачи, содержащие отношения «больше (меньше) на..», «больше (меньше) в…».
- Дополнение условий задач недостающими данными или вопросом.
Глоссарий по теме
Компоненты задачи – условие, вопрос, решение, ответ.
Задачи на сложение и вычитание.
Взаимосвязь между условием и вопросом задачи.
Элементы задачи:
1. Условие (что известно в задаче).
2. Вопрос (что нужно узнать).
3. Решение (действие, нахождение неизвестного).
4. Ответ задачи (ответ на вопрос задачи).
Ключевые слова
Текстовая задача; условие задачи; вопрос задачи; решение задачи.
Основная и дополнительная литература по теме урока:
1. Моро М. И., Волкова С. И., Степанова С. В. Математика. Учебник. 1 кл. В 2 ч. Ч. 1.– М.: Просвещение, 2017.– с. 88 – 89.
2. Моро М. И., Волкова С. И. Математика рабочая тетрадь. 1 кл. 1 ч.– М.: Просвещение, — с. 33 – 34.
На уроке мы узнаем, как построена задача и как называются структурные элементы задачи. Научимся решать задачи, записывать решение задачи и ответ. Сможем выделять задачи из предложенных текстов.
Основное содержание урока
Рассмотрите картинку.
Составьте задачу.
Послушайте два рассказа и сравните их:
1. В магазине мама купила 3 перца и 4 морковки. Сколько всего овощей купила мама?
2. В магазине мама купила 3 перца и 4 морковки. В овощах очень много витаминов, они очень полезные.
Какой из этих текстов мы будем изучать на уроке математики, а какой на уроке окружающего мира?
Первый текст на уроке математики, так как в нём есть вопрос, для ответа на который нужно выполнить вычисления, а второй на уроке окружающего мира.
Как называется текст с вопросом, для ответа на который нужны математические вычисления?
Такой текст называется «Задача».
Сегодня на уроке мы узнаем, какой текст называется задачей и из каких частей она состоит.
Тема нашего урока: «Задача. Структура задачи».
Посмотрите ещё раз на текст знакомой нам задачи и ответьте на вопрос.
Что в ней известно?
В магазине мама купила 3 перца и 4 морковки. Сколько всего овощей купила мама?
Что мама купила 3 перца и 4 морковки.
Это называется — условие задачи, другими словами, это то, что в задаче известно.
Что в задаче нужно узнать?
Сколько всего овощей купила мама.
Это вопрос задачи. Это о чём спрашивают в задаче, то, что нужно узнать.
Что нужно сделать, чтобы сосчитать, сколько мама купила овощей?
Нужно к трём прибавить четыре, получится семь овощей.
Это решение задачи.
Ещё раз прочитайте вопрос задачи и ответьте на него.
Мама купила семь овощей.
Это ответ задачи.
На уроке мы поймём, как построена задача – в ней есть условие и вопрос.
Будем учиться решать задачи, записывать решение задачи и ответ.
Составьте условие задачи по рисунку.
В корзинке четыре луковицы, ещё две луковицы лежат рядом.
Задайте вопрос.
Сколько всего луковиц?
Как решить такую задачу? Сложением или вычитанием?
Четыре да ещё две, задача решается сложением.
Запишем решение. К четырём прибавить два получится шесть.
Осталось записать ответ задачи. Ответим на вопрос задачи: всего шесть луковиц.
Ещё раз посмотрите внимательно на этот же рисунок:
Составьте другую задачу, которая будет решаться вычитанием:
В корзине было четыре луковицы, из неё взяли две луковицы.
Задайте вопрос.
Сколько луковиц осталось в корзине?
Как записать решение?
Из четырёх вычесть два, получится две луковицы.
Осталось записать ответ задачи.
Разбор тренировочных заданий.
Рассмотрите рисунок, дополните условие и решите задачу.
Ответ:
На огороде с одного куста сорвали 2 кабачка, а с другого куста 6 кабачков. Сколько кабачков собрали с двух кустов?
2 + 6 = 8 (к.)
Ответ: 8 кабачков.
Выберите только те тексты, которые являются математическими задачами.
Ответ:
Верные равенства обозначьте синим цветом, а неверные красным.
Ответ:
Прочитайте задачу и установите соответствия между её компонентами.
Ответ:
Попробуйте заменить овощи соответствующей цифрой.
Подсказка: у каждой цифры своя маска. На одинаковых цифрах — одинаковые маски.
Ответ:
Ответь на вопросы с помощью таблицы.
Ответ:
Покажите разным цветом, как можно получить число 6.
Ответ:
примеры и способы решения математических задач для родителей
На протяжении всего обучения школьникам приходится решать задачи — в начальной школе по математике, а затем по алгебре, геометрии, физике и химии. И хотя условия задач в разных науках отличаются, способы решения основаны на одних и тех же логических принципах. Понимание того, как устроена простая задача по математике, поможет ребёнку разработать алгоритмы для решения задач из других областей науки. Поэтому учить ребёнка решать задачи необходимо уже с первого класса.
И хотя условия задач в разных науках отличаются, способы решения основаны на одних и тех же логических принципах. Понимание того, как устроена простая задача по математике, поможет ребёнку разработать алгоритмы для решения задач из других областей науки. Поэтому учить ребёнка решать задачи необходимо уже с первого класса.
Нередки случаи, когда точные науки вызывают у детей сопротивление. Видя это, учителя и родители записывают таких детей в «гуманитарии», из-за чего они только укрепляются во мнении, что точные науки — это не для них. Преподаватель математики Анна Эккерман уверена, что проблемы с математикой часто имеют исключительно психологический характер:
Детям вбивают в голову, что математика — это сложно. К длинным нудным параграфам в учебнике сложно подступиться. Учитель ставит на ребёнке клеймо «троечника» или «двоечника». Если не внушать детям, что они глупые и у них ничего не получится, у них получится ровно всё.
Чтобы ребёнку было интересно учить математику, он должен понимать, как эти знания пригодятся ему, даже если он не собирается становиться программистом или инженером.
Математика ежедневно помогает нам считать деньги, без умения вычислять периметр и площадь невозможно сделать ремонт, а навык составления пропорций незаменим в кулинарии — используйте это. Превращайте ежедневные бытовые вопросы в математические задачи для ребёнка: пусть польза математики станет для него очевидна.
Конечно, найти в быту применение иррациональным числам или квадратным уравнениям не так просто. И если польза этих знаний вызывает у подростка вопросы, объясните ему, что с их помощью мы тренируем память, развиваем логическое мышление и остроту ума — навыки, в равной степени необходимые как «технарям», так и «гуманитариям».
<<Форма демодоступа>>
Как правильно научить ребёнка решать задачи
Если ребёнок только начинает осваивать навык решения задач, приучите его придерживаться определённого алгоритма.
1. Внимательно читаем условия
Лучше вслух и несколько раз. После того как ребёнок прочитал задачу, задайте ему вопросы по тексту и убедитесь, что ему понятно, что вычислять нужно количество грибов, а не огурцов. Старайтесь не нервничать, если ребёнок упустил что-то из вида. Дайте ему разобраться самостоятельно. Если в условиях упоминаются неизвестные ребёнку реалии — объясните, о чём идёт речь.
Старайтесь не нервничать, если ребёнок упустил что-то из вида. Дайте ему разобраться самостоятельно. Если в условиях упоминаются неизвестные ребёнку реалии — объясните, о чём идёт речь.
Особую сложность представляют задачи с косвенным вопросом, например:
«Один динозавр съел 16 деревьев, это на 3 меньше, чем съел второй динозавр. Сколько деревьев съел второй динозавр?». Невнимательно прочитав условия, ребёнок посчитает 16−3, и получит неправильный ответ, ведь эта задача на самом деле требует не вычитания, а сложения.
2. Делаем описание задачи
В решении некоторых задач поможет представление данных в виде схемы, графика или рисунка. Чем ярче сложится образ, тем проще будет его осмыслить. Наглядная запись позволит ребёнку не только быстро разобраться в условиях задачи, но и поможет увидеть связь между ними. Часто план решения возникает уже на этом этапе.
Ребёнок должен чётко понимать значения словесных формул и знать, какие математические действия им соответствуют.
3. Выбор способа решения
Наглядно записанное условие должно подтолкнуть ребёнка к нахождению решения. Если этого не произошло, попробуйте задать наводящие вопросы, проиллюстрировать задачу при помощи окружающих предметов или разыграть сценку. Если один из способов объяснения не сработал — придумайте другой. Многократное повторение одного и того же вопроса неэффективно.
Все, даже самые сложные, математические задачи сводятся к принципу «из двух известных получаем неизвестное». Но для нахождения этой пары чисел часто требуется выполнить несколько действий, то есть разложить задачу на несколько более простых.
Ребёнок должен знать способы получения неизвестных данных из двух известных:
- слагаемое = сумма − слагаемое
- вычитаемое = уменьшаемое − разность
- уменьшаемое = вычитаемое + разность
- множитель = произведение ÷ множитель
- делитель = делимое ÷ частное
- делимое = делитель × частное
После того как план действий найден, подробно запишите решение. Оно должно отражать всю последовательность действий — так ребёнок сможет запомнить принцип и пользоваться им в дальнейшем.
Оно должно отражать всю последовательность действий — так ребёнок сможет запомнить принцип и пользоваться им в дальнейшем.
4. Формулировка ответа
Ответ должен быть полным и точным. Это не просто формальность: обдумывая ответ, ребёнок привыкает серьёзно относиться к результатам своего труда. А главное — из описания должна быть понятна логика решения.
Задание из базового курса алгебры домашней онлайн-школы «Фоксфорда», 7 класс
Одна из самых распространённых ошибок — представление в ответе не тех данных, о которых спрашивалось изначально. Если такая проблема возникает, нужно вернуться к первому пункту.
5. Закрепление результата
Не стоит думать, что выполнив задание один раз, ребёнок сразу научится решать задачи. Полученный результат нужно зафиксировать. Для этого подумайте над решённой задачей ещё немного: предложите ребёнку поискать другой способ решения или спросите, как изменится ответ при изменении того или иного параметра в условии.
Важно, чтобы у ребёнка сложился чёткий алгоритм рассуждений и действий в каждом из вариантов.
В нашей онлайн-школе, помимо уроков, ученики могут закреплять свои знания на консультациях в формате открытых часов, где учителя разбирают темы, вызвавшие затруднения, показывают необычные задачи и различные способы их решения.
<<Форма курс 5-11>>
Что поможет ребёнку решать задачи
В заключение расскажем о том, как сделать процесс решения задач проще и интереснее:
- Для того чтобы решать задачи, необходимо уметь считать. Следует выучить с ребёнком таблицу умножения, освоить примеры с дробями и простые уравнения.
- Чтобы решение задач не превратилось для ребёнка в рутину, проявите фантазию. Меняйте текст задания в соответствии с интересами ребёнка. Например, решать задачи на движение будет куда интереснее, если заменить банальные поезда трансформерами, летящими навстречу друг другу в эпической схватке.
- Дети с развитой логикой учатся решать задачи быстрее. Советуем разбавлять чисто математические задания логическими.
 Задачи «с подвохом» избавят ребёнка от шаблонного мышления, а задания с большим количеством лишних данных научат выделять главное из большого количества условий.
Задачи «с подвохом» избавят ребёнка от шаблонного мышления, а задания с большим количеством лишних данных научат выделять главное из большого количества условий.
<<Блок перелинковки>>
После того как ребёнок решит достаточно задач одного типа, предложите ему самому придумать задачу. Это позволит ему не только закрепить материал, но и проявить творческие способности.
Математика 1 класс занимательные задания и примеры
Содержание:
- Знакомство с числами от 1 до 10
- Подготовка к изучению чисел
- Пространственные представления
- Временные представления
- Сравнение количества
- Фигуры
- Длина
- Числа от 1 до 10
- Сложение, вычитание до 10
- Масса
- Симметрия
- Числа от 11 до 20
- Сложение, вычитание до 20
- Последовательности фигур
Знакомство с числами от 1 до 10
Числа от 1 до 10
После того, как ребенок освоил счет до 10, мы знакомим его с четными и нечетными числами. В этом задании ребенок дополнит ряд четными / нечетными числами.
В этом задании ребенок дополнит ряд четными / нечетными числами.
Подготовка к изучению чисел
Счет от 1 до 10
Наша цель — закрепить представления ребенка о цифрах от 1 до 10. Если он будет выполнять подобные здания вместе с Вами, результат будет намного лучше!
Пространственные представления
Слева, справа
Мы предлагаем ребенку потренировать понятия «право» и «лево» с помощью игры. Присоединяйтесь к нему и Вы – это будет настоящее пиратское приключение!
Слева, справа: продолжение
С помощью данного упражнения Ваш ребенок в интересной форме продолжит отрабатывать понятия «право» и «лево», а также повторит известные ему фигуры.
Расположение предметов
Мы подготовили для Вас и Вашего ребенка набор карточек с изображениями лисы. Вырежьте их, попросите ребенка описывать картинки, называя, где находится лиса.
Временные представления
Сначала, потом, после
В этом упражнении ребенок углубляет свои временные представления, совершенствует навыки мышления, а также учится определять последовательность действий.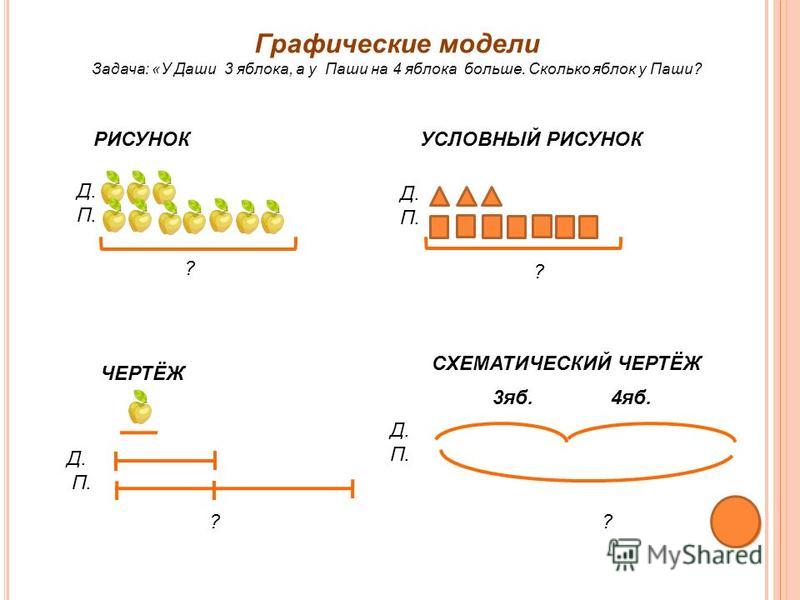
Сравнение количества
Больше и меньше
Мы предлагаем упражнение, в котором перед ребенком стоит задача посчитать объекты, затем сравнить их количество.
Больше, меньше, столько же
Работаем над развитием навыков критического мышления и математических навыков. Повторяем числа от 1 до 10 посредством сравнения количества предметов.
Считаем: что больше?
В этом задании ребенку предлагается сравнить количество конфет в банках и закрасить их. Потом можно попробовать выполнить это задание на время.
Фигуры
Фигуры
Ребенок знакомится с простыми плоскими фигурами, раскрашивает и считает их. Пусть изучение фигур будет веселым!
Учимся узнавать фигуры
С помощью данного упражнения ребенок будет учиться узнавать основные фигуры в различных предметах. Проделайте то же самое в повседневной жизни!
Многоугольник
Дети знакомятся с понятием «многоугольник», учатся различать фигуры, сортировать их и узнавать.
Стороны многоугольника
Дети знакомятся с понятием «многоугольник», учатся различать фигуры, сортировать их и узнавать.
Свойства фигур
Ребенок заполняет таблицу о фигурах: количество сторон, вершин, прямых и изогнутых линий. Цель — расширить представления о фигурах и понятии «симметрия».
Вырезаем фигуры
В этом упражнении ребенку предлагается под Вашим руководством вырезать фигуры и наклеить их рядом с подходящими описаниями.
Длина
Что длиннее?
Ребенок знакомится с понятием длины и учится сравнивать предметы по их длине, используя сравнительные прилагательные.
Сантиметр
В этом упражнении ребенок научится измерять предметы с помощью линейки и фиксировать результат.
Числа от 1 до 10
Число и цифра 5
Ребенок уже имеет представление о счете до 10 и цифрах. Данное упражнение в занимательной форме позволит ребенку закрепить представления о цифре 5.
Числа от 1 до 10
После того, как ребенок освоил счет до 10, мы знакомим его с четными и нечетными числами. В этом задании ребенок дополнит ряд четными / нечетными числами.
Числа от 1 до 10 буквами
Написание чисел буквами может вызвать затруднение у первоклассников. Для того, чтобы снять возможные трудности, рекомендуем выполнить это упражнение.
Для того, чтобы снять возможные трудности, рекомендуем выполнить это упражнение.
Порядковый счет от 1 до 10
Ребенок изучает порядковые числительные от 1 до 10. Чем чаще он считает предметы, тем быстрее будут формироваться его математические навыки.
Какой по порядку?
Мы предлагаем Вам упражнение, которое поможет Вашему ребенку попрактиковать числа от 1 до 10, а также будет способствовать развитию математических навыков.
Сложение, вычитание до 10
Сложение, вычитание вида +/- 1
Ребенок называет, пишет числа от 1 до 10 и математические символы (+, — и =). Ребенок учится совершать действия сложения и вычитания с числом 1.
Сложение, вычитание вида +/- 2
Ребенок называет, пишет числа от 1 до 10 и математические символы (+, — и =). Ребенок учится совершать действия сложения и вычитания с числом 2.
Задачи на сложение с картинками
Цель данного упражнения — представить сложение с помощью картинок и объектов, чтобы лучше понять смысл этого действия.
Задачи на вычитание с картинками
Цель данного упражнения — представить вычитание с помощью картинок и объектов, чтобы лучше понять смысл этого действия.
Сложение, вычитание вида +/- 3
Ребенок называет, пишет числа от 1 до 10 и математические символы (+, — и =). Ребенок учится совершать действия сложения и вычитания с числом 3.
Сложение, вычитание вида +/- 4
Данное упражнения в интересной форме даст Вашему ребенку возможность попрактиковаться в решении простых математических задач.
Сложение, вычитание вида +/- 5
В данном упражнении ребенок практикует действия сложения и вычитания с числом 5, а также повторяет изученные приемы арифметических действий.
Сложение чисел 5, 6, 7, 8, 9
Ребенок называет, пишет числа от 1 до 10 и математические символы (+, — и =). Ребенок учится совершать действия сложения и вычитания с числами 5, 6, 7, 8, 9.
Сложение чисел до 10
Ребенок повторяет изученные приемы сложения чисел в пределах 10, сравнивает их, выбирает наиболее удобный и практикуется в решении задач изученных видов.
Сложение чисел с картинками
Ребенок решает задачи и примеры различного вида. В этом упражнении он закрепит навыки сложения и вычитания с помощью решения задач с картинками.
Сумма одинаковых слагаемых
В этом упражнении мы предлагаем ребенку попрактиковаться в сложении и решить примеры на сложение с одинаковыми слагаемыми необычного вида.
Одинаковые слагаемые
В этом упражнении мы предлагаем ребенку попрактиковаться в сложении и решить примеры на сложение с одинаковыми слагаемыми необычного вида.
Масса
Цель — познакомить ребенка с новой величиной — массой и единицей ее измерения — килограммом; развивать умение решать задачи и примеры изученных видов.
Симметрия
Ребенок знакомится с понятием симметрии, учится создавать симметричные фигуры по образцу, сравнивать результат.
Числа от 11 до 20
Числа до 20
Ребенок знакомится с образованием чисел 2-го десятка, их названиями и порядком следования при счете. Он учится сравнивать их и решать задачи изученных видов.
Чтение чисел от 10 до 20
Ребенок учится образовывать, читать и записывать числа второго десятка, сравнивать числа в пределах 20, опираясь на порядок их следования при счете.
Сложение, вычитание до 20
Сложение, вычитание до 20
Наша цель — научить выполнять действия сложения и вычитания чисел до 20, использовать математическую терминологию при составлении и чтении равенств.
Сложение с числами 2 и 3
Ребенок научится моделировать прием выполнения действия сложения с числами 2 и 3, использовать математическую терминологию при составлении и чтении равенств.
Сложение с числом 4
Ребенок научится моделировать приемы выполнения действия сложения с числом 4, использовать математическую терминологию при составлении и чтении равенств.
Сложение с числом 5
Ребенок научится моделировать приемы выполнения действия сложения с числом 5, использовать математическую терминологию при составлении и чтении равенств.
Сложение с числом 6
Ребенок научится моделировать приемы выполнения действия сложения с числом 6, использовать математическую терминологию при составлении и чтении равенств.
Сложение с числом 7
Ребенок научится моделировать приемы выполнения действия сложения с числом 7, использовать математическую терминологию при составлении и чтении равенств.
Задачи на сложение до 20
Наша цель — закрепить знание таблицы сложения, приемов вычитания, нумерации и состава чисел. Ребенок учится решать текстовые задачи.
Сложение до 20: обобщение
Ребенок работает самостоятельно, применяя свои знания на практике. Он учится определять, что нужно для выполнения задания, анализировать и делать выводы.
Вычитание из чисел до 20
Ребенок научится моделировать приемы выполнения действия вычитания вида 17-?, 18 — ?, использовать математическую терминологию при чтении равенств.
Последовательности фигур
Последовательности фигур
В этом задании ребенку предстоит закончить узоры, опираясь на закономерности в последовательности фигур. Выполнив задание, ребенок может создать свои узоры!
ГДЗ по математике 1 класс учебник Моро, Волкова 2 часть
- Тип: ГДЗ, Решебник.

- Автор: Моро М. И., Волкова С. И., Степанова С. В.
- Год: 2020.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
Решебник — страница 24Готовое домашнее задание
Номер 8.
В магазин привезли 5 ящиков с морковью, а со свеклой на 2 ящика меньше. Сколько ящиков со свеклой привезли в магазин?
Ответ:
Номер 9.
Составь по чертежу одну задачу, в условии которой есть слово больше, а другую – в вопросе которой есть слово меньше. Реши эти задачи.
Ответ:
Задача 1:
Митя нарисовал 2 отрезка. Красный длиной 5 см, а синий на 1 см больше, чем красный. Какой длины синий отрезок?
1) 5 + 1 = 6 (см) — длина синего отрезка.
Ответ: 6 сантиметров.
1) 6 — 5 = 1 (см) — на столько красынй отрезок меньше синего.
 Ответ: 1 сантиметр.
Ответ: 1 сантиметр.
Номер 10.
В первый день в магазине продали 3 велосипеда, а во второй – на 2 больше. Сколько велосипедов продали во второй день? Сколько всего велосипедов продали за эти 2 дня?
Ответ:
Номер 11.
В банку входит 5 стаканов молока, а в нее налили 3 стакана. Сколько еще стаканов молока можно налить в эту банку?
Ответ: Всего входит – 5 с. Налили – 3 с. Осталось места – ? с. 5 − 3 = 2 (с.) – еще можно налить в банку. Ответ: 2 стакана.
Номер 12.
В вагоне метро сидели 5 женщин и 4 мужчины. На станции 1 человек вышел. Сколько человек осталось в вагоне?
Леша решил эту задачу так:
1) 5 + 4 = 9
2) 9 − 1 = 8
Ответ: 8 человек.
Толя решил эту задачу так:
1) 4 − 1 = 3
2) 5 + 3 = 8
Ответ: 8 человек.
Оба решили задачу правильно. Объясни, что узнавал каждым действием Леша и что – Толя. Найди еще одно решение этой задачи.
Найди еще одно решение этой задачи.
Ответ:
Лёша узнал:
1) 5 + 4 = 9 (ч.) – всего в вагоне человек было.
2) 9 − 1 = 8 (ч.) – осталось, когда 1 вышел.
Решение: 1) 5 − 1 = 4 (ж.) – осталось 4 женщины, когда одна вышла. 2) 4 + 4 = 8 (ч.) – стало всего в вагоне женщин и мужчин.
Задание на полях страницы
Ответ:
Рейтинг
👇 Выберите другую страницу 👇
1 часть
| Учебник Моро | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 | 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 | 121 | 122 | 123 | 124 | 125 | 126 | 127 |
|---|
2 часть
| 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 | 101 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 |
|---|
Ваше сообщение отправлено!
+
ГДЗ по математике 1 класс Моро
3. 9/5 — (16 голосов)
9/5 — (16 голосов)
Мамы и папы понимают, что в 1 классе малыш должен с первых уроков по-максимому усваивать весь материал. Из-за этого приходится держать под контролем весь учебный процесс. Однако, познакомившись с программой учебника за 1 класс под редакцией Моро М.И., Волкова С.И., Степанова С.В., взрослые и сами чувствуют себя неуверенно.
Действительно, программа с первых уроков настраивает на серьезное отношение к себе. Решение проблемы просматривается при использовании специального решебника, или как его еще зачастую называю — ГДЗ по математике, в котором все задания заранее решены специалистом в своей области. Для поиска требуемого задания или упражнения по математике для первого класса необходимо выбрать соответствующую часть: первую или вторую, найти искомый номер страницы из учебника, перейти по ссылке на страницу с решением и найти искомый ответ на номер своего примера или задачи.
ГДЗ по математике — часть 1
Страница:
Страница-4-часть-1Страница-5-часть-1Страница-6-часть-1Страница-7-часть-1Страница-8-часть-1Страница 9 часть 1Страница 10 часть 1Странциа 11 часть 1Страница 12 часть 1Страница 13 часть 1Страница 14 часть 1Страница 15 часть 1Страница 16 часть 1Страница 17 часть 1Страница 18 часть 1Страница 19 часть 1Страница 20 часть 1Страница 22 часть 1Страница 23 часть 1Страница 24 часть 1Страница 25 часть 1Страница 26 часть 1Страница 27 часть 1Страница 29 часть 1Страница 30 часть 1Страница 31 часть 1Страница 32 часть 1Страница 33 часть 1Страница 34 часть 1Страница 35 часть 1Страница 36 часть 1Страница 37 часть 1Страница 38 часть 1Страница 39 часть 1Страница 40 часть 1Страница 41 часть 1Страница 42 часть 1Страница 43 часть 1Страница 44 часть 1Страница 45 часть 1Страница 46 часть 1Страница 47 часть 1Страница 48 часть 1Страница 49 часть 1Страница 50 часть 1Страница 51 часть 1Страница 52 часть 1Страница 53 часть 1Страница 54 часть 1Страница 55 часть 1Страница 56 часть 1Страница 57 часть 1Страница 58 часть 1Страница 59 часть 1Страница 60 часть 1Страница 61 часть 1Страница 62 часть 1Страница 63 часть 1Страница 66 часть 1Страница 67 часть 1Страница 68 часть 1Страница 69 часть 1Страница 70 часть 1Страница 71 часть 1Страница 72 часть 1Страница 73 часть 1Страница 74 часть 1Страница 75 часть 1Страница 76 часть 1Страница 77 часть 1Страница 78 часть 1Страница 80 часть 1Страница 81 часть 1Страница 82 часть 1Страница 83 часть 1Страница 84 часть 1Страница 85 часть 1Страница 86 часть 1Страница 87 часть 1Страница 88 часть 1Страница 89 часть 1Страница 90 часть 1Страница 91 часть 1Страница 92 часть 1Страница 93 часть 1Страница 95 часть 1Страница 96 часть 1Страница 97 часть 1Страница 98 часть 1Страница 99 часть 1Страница 100 часть 1Страница 101 часть 1Страница 102 часть 1Страница 103 часть 1Страница 104 часть 1Страница 105 часть 1Страница 106 часть 1Страница 107 часть 1Страница 108 часть 1Страница 109 часть 1Страница 110 часть 1Страница 111 часть 1Страница 112 часть 1Страница 113 часть 1Страница 114 часть 1Страница 115 часть 1Страница 116 часть 1Страница 117 часть 1Страница 118 часть 1Страница 119 часть 1Страница 121 часть 1Страница 122 часть 1Страница 123 часть 1Страница 124 часть 1Страница 125 часть 1Страница 126 часть 1Страница 127 часть 1Решебник по математике — часть 2
Страница:
Страница 4 часть 2Страница 5 часть 2Страница 6 часть 2Страница 7 часть 2Страница 8 часть 2Страница 9 часть 2Страница 10 часть 2Страница 11 часть 2Страница 12 часть 2Страница 13 часть 2Страница 14 часть 2Страница 15 часть 2Страница 16 часть 2Страница 17 часть 2Страница 18 часть 2Страница 19 часть 2Страница 20 часть 2Страница 21 часть 2Страница 23 часть 2Страница 24 часть 2Страница 25 часть 2Страница 26 часть 2Страница 27 часть 2Страница 28 часть 2Страница 29 часть 2Страница 30 часть 2Страница 31 часть 2Страница 32 часть 2Страница 33 часть 2Страница 34 часть 2Страница 35 часть 2Страница 36 часть 2Страница 37 часть 2Страница 38 часть 2Страница 39 часть 2Страница 40 часть 2Страница 41 часть 2Страница 42 часть 2Страница 44 часть 2Страница 46 часть 2Страница 47 часть 2Страница 48 часть 2Страница 49 часть 2Страница 50 часть 2Страница 51 часть 2Страница 52 часть 2Страница 53 часть 2Страница 54 часть 2Страница 55 часть 2Страница 56 часть 2Страница 57 часть 2Страница 58 часть 2Страница 59 часть 2Страница 60 часть 2Страница 61 часть 2Страница 62 часть 2Страница 63 часть 2Страница 64 часть 2Страница 65 часть 2Страница 66 часть 2Страница 67 часть 2Страница 68 часть 2Страница 69 часть 2Страница 70 часть 2Страница 71 часть 2Страница 72 часть 2Страница 73 часть 2Страница 74 часть 2Страница 76 часть 2Страница 77 часть 2Страница 78 часть 2Страница 79 часть 2Страница 80 часть 2Страница 81 часть 2Страница 82 часть 2Страница 83 часть 2Страница 84 часть 2Страница 85 часть 2Страница 86 часть 2Страница 87 часть 2Страница 88 часть 2Страница 89 часть 2Страница 90 часть 2Страница 91 часть 2Страница 92 часть 2Страница 93 часть 2Страница 94 часть 2Страница 95 часть 2Страница 96 часть 2Страница 97 часть 2Страница 100 часть 2Страница 101 часть 2Страница 102 часть 2Страница 103 часть 2Страница 104 часть 2Страница 105 часть 2Страница 106 часть 2Страница 107 часть 2Страница 108 часть 2Страница 109 часть 2Страница 110 часть 2Страница 111 часть 2Решение логических задач — как решать задачи на логику
Логика – это основа рационального мышления и фундамент для развития интеллекта ребенка. Решение различных логических задач дает возможность детям научиться анализировать ситуацию, находить взаимосвязи, отличать главное и второстепенное, формировать стратегию, применять в нужном месте свои знания и навыки.
Решение различных логических задач дает возможность детям научиться анализировать ситуацию, находить взаимосвязи, отличать главное и второстепенное, формировать стратегию, применять в нужном месте свои знания и навыки.
Эти умения пригодятся не только в учебе, но и в реальной жизни. Рассуждая логически, ребенок может грамотно выразить свое мнение, подойти к решению той или иной задачи более осознанно, дать обоснование всевозможным явлениям, быстро сориентироваться в ситуации.
Поэтому решение логических задач должно быть неотъемлемой частью детского развития и образования. А для того, чтобы щелкать их как орешки, нужно понимать, какими приемами и методами пользоваться при решении.
Самое главное в решении логических задач
Понимание разных методов позволяет находить оптимальный вариант решения, что особенно важно в условиях ограниченного времени.
Все задачи на развитие логики можно разделить на группы:
- Математические ребусы;
- Задачи на истинность утверждений;
- Задачи на перемещение, взвешивание или переливание;
- Задачи, которые решаются с конца;
- Работа с множествами;
- Задачи на сопоставление «Кто есть кто?»
Выбор способа решения зависит от того, к какой группе относится задание.
Известные техники решения логических задач
- Табличный метод (таблицы соответствий, истинности, совмещенные, кубические):
таблицы создают наглядность, прозрачность рассуждений, помогают сделать верные выводы. - Применение законов из алгебры логики: вводятся обозначения для простых высказываний и преобразовываются в некую формулу.
- Метод рассуждений: подходит для решения простых задач с небольшим количеством объектов. Последовательное рассуждение над каждым условием задачи приводит к правильному выводу.
- Черчение блок-схем: способ, подходящий для решения задач на переливание, взвешивание.
 Рисуется схема, на которой отмечают последовательность действий и результат, полученный при их выполнении.
Рисуется схема, на которой отмечают последовательность действий и результат, полученный при их выполнении. - Графический метод: подходит для решения задач на объединение или пересечение множеств. Самый популярный графический метод называется «Круги Эйлера». Нарисованная геометрическая схема наглядно показывает отношение между множествами.
- Метод «математический бильярд»: используется для решения задач на переливание жидкостей. Вычерчивается траектория движения бильярдного шара, который отталкивается от бортов стола в форме параллелограмма.
Рассмотрим подробно самые распространенные способы, которые могут использовать в решении логических задач ученики начальных классов:
Табличный метод
Условия задачи и результаты записываем в специальную таблицу. На пересечении строк и столбцов ставим «+», если утверждения не противоречат друг другу и «-», если они расходятся.
Задача:
У Сони, Маши, Антона, Кости и Юры есть домашние животные. У каждого из ребят живет или собака, или кошка, или попугай. Вот только девочки собак не держат, а у мальчиков нет попугаев. У Сони и Маши разные питомцы, а вот у Маши с Антоном – одинаковые. У Сони нет кошки. У Кости с Юрой живут одинаковые животные, а у Антона с Костей – разные. Какие животные живут у каждого?
У каждого из ребят живет или собака, или кошка, или попугай. Вот только девочки собак не держат, а у мальчиков нет попугаев. У Сони и Маши разные питомцы, а вот у Маши с Антоном – одинаковые. У Сони нет кошки. У Кости с Юрой живут одинаковые животные, а у Антона с Костей – разные. Какие животные живут у каждого?
Решение:
Чертим таблицу, где названия столбцов – имена ребят, а названия строк – животные. Ставим в каждой ячейке знаки «+» или «-», опираясь на условия задачи:
1. Девочки собак не держат (ставим «-» на пересечении этих ячеек).
2. У мальчиков нет попугаев (в этих ячейках тоже ставим «-»).
3. У Сони нет кошки (ставим «-»).
4. Значит, у Сони есть попугай (ставим «+»).
5. У Сони и Маши разные питомцы. Получается, у Маши нет попугая (ставим «-»), зато есть кошка (ставим «+»).
6. У Маши с Антоном одинаковые животные. Значит, у Антона тоже живет кошка (ставим «+») и нет собаки (ставим «-»).
7. У Антона с Костей разные питомцы, выходит, что у Кости нет кошки (ставим «-»), зато есть собака (ставим «+»).
8. У Кости с Юрой одинаковые животные, значит у Юры тоже собака (ставим «+»), а не кошка (ставим «-»).
Так мы узнали, какие питомцы живут у каждого из ребят (ячейки со знаком «+»).
Ответ: У Сони попугай, у Маши и Антона кошки, у Кости и Юры собаки.
Круги Эйлера
Чтобы было легче разобраться в условиях задачи и найти решение, чертим круги, каждый из которых – отдельное множество.
Задача:
Всему классу задали на лето читать книжки. В списке литературы были такие произведения, как «Робинзон Крузо» Даниэля Дефо и «Белый клык» Джека Лондона. Известно, что 15 человек из класса прочитали «Робинзон Крузо», а остальные 11 – «Белый клык». Но среди них были 6 ребят, которые прочитали обе книги. Сколько человек прочитало только «Белый клык»?
Решение:
Чертим два круга, каждый из которых – множество детей, прочитавших определенную книгу, а пересечение кругов – дети, прочитавшие обе книги.
1. 15 – 6 = 9 – дети, которые прочитали только «Робинзон Крузо».
15 – 6 = 9 – дети, которые прочитали только «Робинзон Крузо».
2. 11 – 6 = 5 – дети, которые читали лишь «Белый клык».
Ответ: 5 человек.
Метод рассуждений
Поочередно рассматриваем каждое из условий задачи и делаем логические выводы.
Задача:
На столе стоят вазы: голубая, зеленая, розовая и оранжевая. Третьей в ряду стоит та ваза, название цвета которой содержит больше всего букв. А зеленая стоит между оранжевой и розовой. Какая ваза стоит последней?
Решение:
1. Больше всего букв в слове «оранжевая», значит она третья по счету.
2. Если зеленая ваза стоит между оранжевой и розовой, значит, она будет второй в ряду, так как если ее поставить четвертой, то не останется места для розовой.
3. Соответственно, розовая будет стоять первой.
4. Остается голубая, она будет четвертой, то есть последней.
Ответ: голубая ваза.
Метод рассуждений «с конца»
Начинаем раскручивать клубок с конца, а затем сопоставляем результат с условиями задачи.
Задача:
Маме, папе и сыну вместе 125 лет. Когда родился сын, маме был 21 год. А папа старше мамы на 2 года. Сколько лет сейчас каждому из них?
Решение:
1. 21+2= 23 — было папе ( значит вместе родителям было 44 года)
2. (125 — 44) : 3 = 27 — возраст сына
3. 27 + 21 = 48 — возраст мамы
4. 48 + 2 = 50 — возраст папы
Ответ: 27, 48 и 50 лет.
Мы рассмотрели самые популярные и доступные методы, с помощью которых можно легко справиться с заданием. Главное – подобрать подходящий способ решения, который быстро приведет к правильному результату.
Для этого необходимо регулярно практиковаться и развивать свои способности. Отточить навыки решения подобных логических задач и многих других вы можете с помощью образовательной онлайн-платформы «Умназия».
Попробуйте решить вместе с ребенком задачу из раздела «логика» и переходите к регулярным занятиям на тренажере
Поробуйте решить задачу Умназии прямо сейчас!
Попробовать
Математика
Умназисты соревновались в поедании пирожков.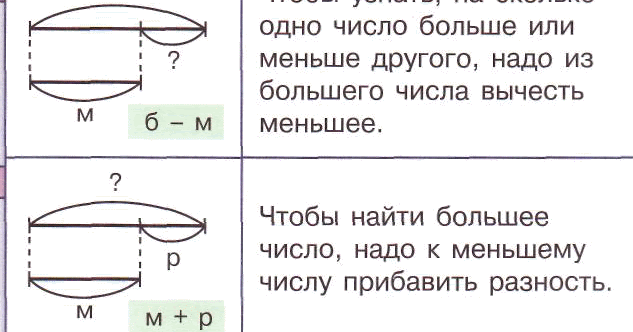 Соревнование длилось ровно 45 минут. За это время все соревнующиеся в сумме съели 179 пирожков.
Соревнование длилось ровно 45 минут. За это время все соревнующиеся в сумме съели 179 пирожков.
Посмотри на информацию о соревнующихся на рисунке. Можешь ли ты сказать, кто из умназистов занял почётное третье место?
Выбери ответ:
Третье место заняла Ума Коала.
Третье место занял Мышлен.
Третье место занял Грамотигр.
Третье место занял Ква-Квариус.
Третье место заняла Сообразебра.
ответить
Логика решения:
Мы знаем, что Мышлен ел по 1 пирожку в минуту, значит за 45 минут соревнования он съел 45 пирожков (1 х 45 = 45).
Если Мышлен съел на 10 пирожков больше, чем Сообразебра, то Сообразебра съела 35 пирожков (45 – 10 = 35).
Если Ума-Коала съела на 5 пирожков меньше, чем Сообразебра, то Ума-Коала съела 30 пирожков (35 – 5 = 30).
Чтобы выяснить, сколько съели Грамотигр и Ква-Квариус, сложим все пирожки, которые съели Мышлен, Ума-Коала и Сообразебра. Получается 45 + 35 + 30 = 110 пирожков.
От общего количества съеденных пирожков вычтем съеденное тремя умназистами: 179 – 110 = 69. Значит, Ква-Квариус и Грамотигр вместе съели 69 пирожков.
Значит, Ква-Квариус и Грамотигр вместе съели 69 пирожков.
Из условия мы знаем, что Грамотигр съел пирожков в 2 раза больше, чем Ква-Квариус.
Допустим, Ква-Квариус съел 23 пирожка, тогда Грамотигр съел в два раза больше, то есть 23 х 2 = 46 пирожков.
Теперь снова сложим их пирожки, чтобы проверить себя: 23 + 46 = 69. Сходится.
Значит, Грамотигр (46 пирожков) занял первое место, Мышлен (45 пирожков) – второе, а Сообразебра (35 пирожков) – третье.
Если вам понравилось, было весело интересно и полезно, то ждем вас на нашей онлайн платформе!
Умназия сегодня — это:
1. Онлайн тренажер развития навыков мышления — логики, внимания, эрудиции.
2. Программа «Культурный код» по развитию кругозора. Для самых любознательных и тех, кого кажется уже ничем не удивить!
3. Курсы развития памяти. Хотите чтобы Ваш ребенок без труда учил стихи, запоминал иностранные слова и всегда помнил про день рождения бабушки? На курсах покажем и расскажем как же этого достичь.
4. Пять ступеней финансовой грамотности. Увлекательная история героя, которая полностью зависит от действий ребенка и не имеет определенного результата. Сможет ли он пройти все финансовые ловушки и освоить пятую ступень?
Ждем вас, будет весело и интересно!
Математика и логика для детей 7-13 лет
Развиваем логическое мышление через решение сюжетных математических задач в интерактивном игровом формате
узнать подробнее
Читайте также:
- 15 сложных загадок на логику
- Загадки на логику с подвохом
- Логические загадки для детей
- Смешные логические загадки
- Загадки Эйнштейна на логику
Ознакомьтесь с этими 50 задачами дня по математике для первоклассников
Начните свой ежедневный урок математики со словесной задачи дня по математике — это отличный способ подготовить почву для обучения. Все мы знаем, что юным ученикам трудно понять текстовые задачи, даже если часть задачи, связанная с математическими операциями, является базовой.
Включайте эти математические задачи для первого класса один раз в день в начале вашего математического блока, чтобы развить уверенность, навыки критического мышления и обучающееся сообщество. Учащиеся привыкнут читать медленно, чтобы понять смысл, а также выделять ключевую информацию. Предложите учащимся записывать уравнения и рисовать картинки, чтобы объяснить свое мышление, так как это помогает им увидеть свет, когда они застряли!
Рассматриваемые темы включают сложение, вычитание, умножение и сравнение. Все, что вам нужно сделать, это опубликовать одну из этих математических задач для первого класса на доске или экране проектора. Тогда пусть дети взять его оттуда!
Хотите весь этот набор текстовых задач в одном простом документе? Получите бесплатный пакет PowerPoint, отправив сообщение электронной почты здесь.
1. У меня было 6 карандашей, и мой учитель дал мне еще 4. Сколько карандашей у меня сейчас?
2. Собака Джины получила 3 угощения в воскресенье и 0 угощений в понедельник. Сколько всего угощений получил щенок Джины?
Сколько всего угощений получил щенок Джины?
3. Джоэл пошел в зоопарк со своей семьей. В первый же час он увидел медведя, 2 тигров и 3 львов. Сколько животных увидел Джоэл в свой первый час в зоопарке?
4. Джексон рассортировал свои машинки по цвету. У него 6 синих машин, 5 зеленых машин и 4 черных машины. Сколько всего машин у Джексона?
5. У Бена 2 зеленых и 4 желтых шарика. Сколько всего шариков у него?
6. В семье Кларков трое детей. Тине 3 года, Джошуа 4 года, а Саманте 7 лет. Если сложить все их возрасты, какова сумма детей Кларков?
7. Если вы пойдете купаться и с вами придут 6 ваших друзей, сколько всего друзей будет плавать?
8. У мамы Рэйчел были цветы в вазе. 3 цветка завяли, и мама Рэйчел вынула их из вазы. Теперь в вазе 5 цветов. Сколько цветов было в вазе изначально?
9. У кошки Хейден родились котята. 3 котенка были серыми, 2 котенка пятнистыми и 7 котят черными. Сколько котят было у кошки Хейден?
Сколько котят было у кошки Хейден?
10. Педро принес с игровой площадки 3 красных и 6 желтых листьев. Сколько всего листьев у него?
11. Габриэлла прочитала 3 книги в понедельник, 6 книг во вторник и 4 книги в среду. Сколько всего книг прочитала Габриэлла?
12. Если у вас 3 кошки, 2 морские свинки и кролик. Сколько милых маленьких носиков у них всего?
13. Если утром на земле лежит 3 дюйма снега, а к обеду выпадает еще 3 дюйма снега. Сколько дюймов снега выпало в тот день?
14. У моей кошки 4 лапы и у собаки моего брата 4 лапы. Сколько всего лап?
15. У меня было 10 копеек, но я потерял 2 из них. Сколько копеек у меня сейчас?
16. За лето Сантьяго прочитал 7 книг. Райан прочитал 5 книг. На сколько больше книг Сантьяго прочитал, чем Райан?
17. Андрей наклеил 10 наклеек на свой блокнот. Когда он пришел в школу, он заметил, что некоторые наклейки отвалились. Сейчас у Андрея на блокноте всего 6 наклеек. Сколько наклеек упало с блокнота Андрея?
Сейчас у Андрея на блокноте всего 6 наклеек. Сколько наклеек упало с блокнота Андрея?
18. Николь любит помогать маме собирать помидоры в саду. Она насчитала в саду 9 помидоров. 6 помидоров были красными, а остальные зелеными. Николь и ее мама собрали все красные помидоры. Сколько зеленых помидоров Николь и ее мама оставили в саду?
19. У нас с сестрой есть 20 пенни. Если у моей сестры 10 пенни, сколько пенни будет у меня?
20. В зоопарке было 8 тигров. 3 тигра переехали в другой зоопарк. Сколько тигров осталось?
21. Эстер прочитала 3 стихотворения. Магенна прочитал еще несколько стихов. Всего они прочитали 7 стихотворений. Сколько стихов прочитал Магена?
22. Отец Хейли купил 8 чизбургеров. Хейли съела 1 из них. Сколько чизбургеров осталось у отца Хейли?
23. Если вы сварите 7 яиц в воде, и количество яиц, которые всплывут, на одно больше, чем количество, которое утонет, сколько яиц всплывет?
24. Рашид любит есть мармеладки. Его любимые мармеладки — желтые. В его сумке было 12 мармеладок. Рашид убрал все желтые мармеладки и съел их, оставив в своей сумке 6 мармеладок. Сколько желтых драже съел Рашид?
Рашид любит есть мармеладки. Его любимые мармеладки — желтые. В его сумке было 12 мармеладок. Рашид убрал все желтые мармеладки и съел их, оставив в своей сумке 6 мармеладок. Сколько желтых драже съел Рашид?
25. У учителя физкультуры было 5 баскетбольных мячей. На следующей неделе учитель физкультуры получил несколько новых баскетбольных мячей. Сейчас у учителя физкультуры 9баскетбольные мячи. Сколько новых баскетбольных мячей получил учитель физкультуры?
26. У Джамала 6 игрушечных самолетов, а у его брата 4 игрушечных самолета. На сколько игрушечных самолетов у Джамала больше, чем у его брата?
27. У Антонио есть шарики. Его брат Алекс дает ему еще 5. Теперь у Антонио 8 шариков. Сколько шариков было у Антонио в начале?
28. Если у вас есть упаковка из 8 мелков, и вы даете своему другу 3 из них для использования во время рисования. Сколько карандашей сейчас у тебя в упаковке?
29. У Эмили есть 4 розовых ластика и несколько белых ластиков. Всего у нее 7 ластиков. Сколько белых ластиков у Эмили?
Всего у нее 7 ластиков. Сколько белых ластиков у Эмили?
30. Энджел подает пиццу на свой день рождения. В пицце 12 кусочков. Ангел и ее гости съедают 8 кусочков пиццы. Сколько кусочков пиццы осталось?
31. Если у вас на полу 9 игрушек, а у вашего младшего брата 6 игрушек на полу. Сколько у тебя еще игрушек на полу?
32. В классе 8 окон. На некоторых окнах есть украшения, на 2 из них нет направлений. Сколько окон украшено украшениями?
33. В субботу вы принесли домой рыбу из зоомагазина. Если 15 из ваших 18 рыб имеют полосы. Сколько ваших рыб без полосок?
34. На вершину забора прилетело 8 птиц. Некоторые птицы улетели, а 6 птиц остались. Сколько птиц улетело?
35. На полке Ноя было 6 книг. Оливия взяла несколько книг. Сейчас на полке 2 книги. Сколько книг взяла Оливия?
36. У Итана несколько папок в рюкзаке и 4 папки на столе. Всего у него 8 папок. Сколько папок в его рюкзаке?
37. У Лиама 8 футболок. На 5 из них изображены супергерои, а остальные сплошные цвета. Сколько футболок Лиама однотонных?
У Лиама 8 футболок. На 5 из них изображены супергерои, а остальные сплошные цвета. Сколько футболок Лиама однотонных?
38. Мэри собирала пазл из 20 частей. Закончив, она обнаружила, что там всего 18 штук. Сколько штук пропало?
39. У Николаса 7 кузенов. Некоторые из его двоюродных братьев — девочки, а трое его двоюродных братьев — мальчики. Сколько двоюродных сестер у Николая?
40. Снег шел 6 часов в понедельник и 4 часа во вторник. Сколько еще часов шел снег в понедельник?
41. Мама Чарли испекла на десерт 12 шоколадных печений. Чарли съел 2 печенья, а его мама и 1 печенье. Сколько шоколадных печений осталось?
42. У Мелани 16 фиолетовых ручек. У Данте 10 синих ручек. У Мелани на ____ больше ручек, чем у Данте.
43. У Софии в банке 75 пенни. Сколько еще пенни ей понадобится, чтобы в ее банке было 100 пенни?
44. На столе стояло 9 чашек газировки. Некоторые чашки были опрокинуты, а 6 еще стояли. Сколько чашек газировки было опрокинуто?
Сколько чашек газировки было опрокинуто?
45. У Грифона 20 настольных игр. Некоторые из них были под его кроватью, а 15 — в шкафу. Сколько настольных игр было под кроватью Гриффина?
46. Антонио заметил 3 оленей, сидящих на вершине холма, но все, что он мог видеть, это их глаза. Сколько глаз видел Антонио во всех?
47. Десмонд увидел 5 кроликов. Он пересчитал все их уши. Сколько кроличьих ушей насчитал Десмонд?
48. Кэти пересчитала все пальцы на ногах, а затем она пересчитала все пальцы на ногах своей мамы. Сколько всего пальцев Кэти насчитала?
49. Что весит больше? Рыжая лисица весом 15 фунтов или дикая индейка весом 24 фунта?
50. Кто больше весит: 150-килограммовый белохвостый олень или 110-килограммовый кенгуру?
Нравятся эти задачи по математике для первого класса? Посетите наш центр первого класса, чтобы получить еще больше ресурсов.
Получите версию этих текстовых задач в формате PPT.
Как учить задачи на сложение и вычитание
Мои ученики мучились с тем, как решать задачи на сложение и вычитание , казалось, целую вечность. Они могли подчеркнуть вопрос и найти числа. В большинстве случаев мои ученики просто складывали два числа вместе, не понимая смысла задачи.
Тьфу.
Можете рассказать?
Я большой сторонник НЕ изучения списков ключевых слов. Это просто не работает последовательно во всех проблемах. Это короткий путь, ведущий к сбоям в математическом мышлении. Я более подробно рассказываю о том, почему это не работает, в статье «Проблема с использованием ключевых слов для решения текстовых задач».
Подробнее о ресурсе для решения задач на сложение и вычитание, который я использую в своем классе, можно прочитать в этом блоге.
Ниже приведены пять стратегий решения математических задач, которые можно использовать при обучении словесным задачам с использованием любого ресурса.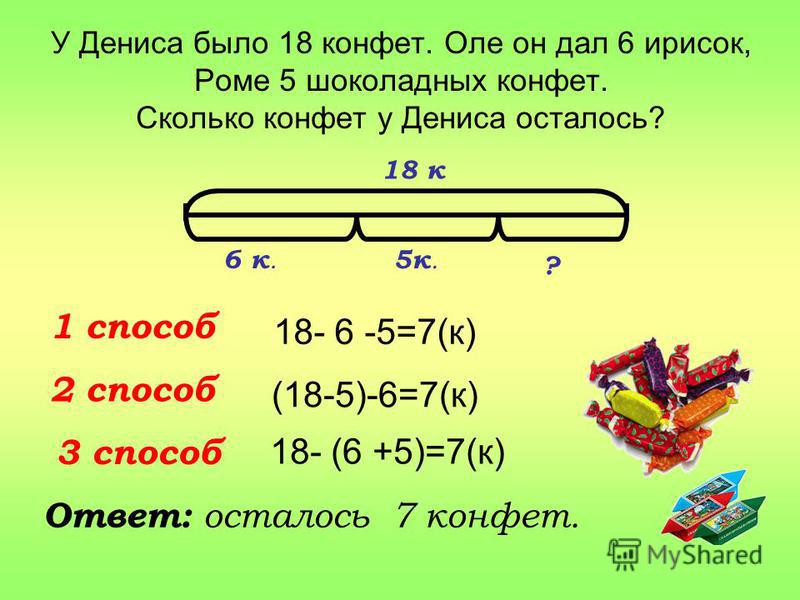
Итак, как мне учить текстовые задачи? Это довольно сложно, но так весело, как только вы войдете в него.
Основные компоненты обучения словесным задачам на сложение и вычитание включают:
- Обучение соотношению чисел s – Как учитель, знайте тип задачи и помогайте учащимся решать действия в задаче
- Различайте Числа – Дайте учащимся правильные числа, чтобы они могли прочитать задачу, не увязая в вычислениях
- Используйте академический словарь – и будьте последовательны в том, что вы используете.
- Хватит искать «Ответ» — дело не в ответе; речь идет о процессе
- Различие между моделями и стратегиями – одна связана с отношениями между числами, а другая связана с тем, как учащиеся «решают» или вычисляют задачу.
Обучаю соотношению чисел в задачах со словами
Я обучаю задачам со словами, удаляя числа. Звучит странно, верно? Удаление отвлекающих факторов помогает учащимся сосредоточиться на проблемной ситуации и понять действие или взаимосвязь чисел. Это также удерживает учащихся от решения задачи до того, как мы поговорим о взаимосвязи чисел.
Это также удерживает учащихся от решения задачи до того, как мы поговорим о взаимосвязи чисел.
Когда я преподаю текстовые задачи, я даю ученикам задачи с пробелами и без чисел. Сначала поговорим о действии в задаче. Мы определяем, добавляется ли что-то к чему-то другому или отнимается от чего-то другого. Это становится нашим уравнением. Мы определяем, что нам нужно решить, и составляем уравнение с пробелами и квадратом для неизвестного числа.
___ + ___ = неизвестно
Хотите бесплатный образец текстовых задач, которые я использую в своем классе? Щелкните ссылку или изображение ниже. БЕСПЛАТНЫЙ образец текстовых задач по типу задачи
Различие чисел в задачах Word
Только после того, как мы обсудили задачу, я даю ученикам числа. Я различаю числа в зависимости от потребностей учащихся. В начале года мы все делаем одни и те же числа, чтобы я мог убедиться, что ученики понимают процесс.
После того, как учащиеся ознакомятся с процессом, я начинаю давать разным учащимся разные числа в зависимости от их уровня математического мышления. Я также меняю числа в течение года с однозначных на двузначные числа. Прелесть пустых мест в том, что я могу вставить в задачу любые числа, которые захочу, чтобы попрактиковаться в стратегиях, над которыми мы работали в классе.
Я также меняю числа в течение года с однозначных на двузначные числа. Прелесть пустых мест в том, что я могу вставить в задачу любые числа, которые захочу, чтобы попрактиковаться в стратегиях, над которыми мы работали в классе.
В какой-то момент мы создаем список слов, но не список ключевых слов. Мы создаем список действий или глаголов и определяем, соединяют ли эти действия что-то или разделяют. Сколько вы можете придумать? Вот несколько идей:
Присоединяйтесь: положил, получил, взял, купил, сделал
Раздельно: съел, потерял, положил, уронил, использовал
Не бойтесь использовать академическую лексику
Я учу своих учеников определять начало проблемы, изменить в задаче и результат в задаче. Я учу их искать неизвестных . Это все слова, которые мы используем при решении задач, и мы изучаем структуру словесной задачи через словарный запас и взаимосвязь чисел.
На самом деле, использование одного и того же словаря для разных типов задач помогает учащимся увидеть взаимосвязь чисел на более глубоком уровне.
Возьмите эти примеры, можете ли вы определить начало , изменение и результат в каждой задаче?
Подсказка: посмотрите на код, используемый для типа задачи в правом нижнем углу.
Для задач сравнения мы используем термины больше , меньше , больше и меньше . Попробуйте решить эти задачи и посмотрите, сможете ли вы определить компоненты словесных задач.
Перестаньте искать «ответ»
Это заблуждение труднее всего разрушить. Студенты не решают словесную задачу, чтобы найти «ответ». Хотя ответ помогает мне, учителю, понять, понял ли ученик взаимосвязь чисел, я хочу, чтобы ученики могли объяснить свой процесс и понять глубину текстовых задач.
Итак, это первоклассники и второклассники. Я знаю.
Мои ученики все еще могут объяснить после обучения, что они начинают ed с одного числа. Проблема результат ед в другом другом номере. Затем учащиеся узнают, что они ищут замену на между этими двумя числами.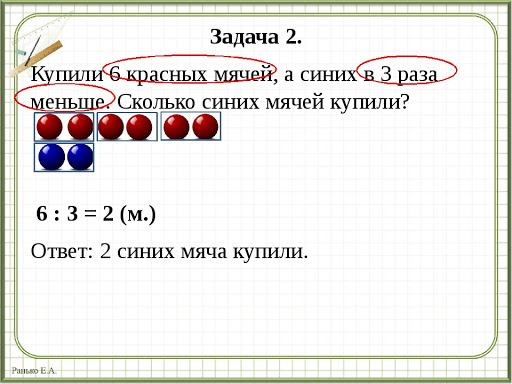
Все дело в отношениях.
Различие между моделями и стратегиями
Пару лет назад я наткнулся на эту статью о необходимости помочь учащимся разработать адекватные модели, чтобы понять взаимосвязь чисел в задаче.
У меня в голове взорвалась лампочка. Мне нужно было провести различие между моделями, которые студенты используют для понимания связи чисел в задаче, и стратегиями решения вычислений в задаче. Эти две вещи работают в тандеме, но очень разные.
Модели — это визуальные способы представления проблем. Стратегии — это способы, которыми учащийся решает задачу, складывая и разбирая числа.
Самое главное в моделях — отойти от них. Я знаю, это звучит странно.
Вы так долго обучаете студентов пользоваться моделями, а потом не хотите, чтобы они использовали модели. Ну, на самом деле, вы хотите, чтобы студенты двигались к эффективности.
Младшие школьники будут разыгрывать задачи, рисовать задачи с изображениями и рисовать задачи с кругами или линиями. Направьте учащихся к эффективности. По мере того, как числа становятся больше, модель должна представлять отношение чисел
Направьте учащихся к эффективности. По мере того, как числа становятся больше, модель должна представлять отношение чисел
Это яркий пример перехода от модели с перевернутой буквой v к модели с стержнями.
Ученик переходит от рисования кругов к использованию перевернутой буквы v.
Учащиеся должны полностью использовать одну модель, прежде чем переходить на другую. Они могут даже использовать два одновременно, пока выясняют сходство между моделями.
Студенты также должны иметь возможность создавать свои собственные модели. Вы увидите, как иногда я давал ученикам копии модели, которые они могли вклеить в свои тетради, а иногда ученики рисовали свою собственную модель. Они должны нести ответственность за выбор того, что лучше всего подходит для них. Начните обучение с конкретных моделей, а затем позвольте учащимся выбрать одну из них для использования. Всегда подталкивайте учащихся к более эффективным моделям.
То же самое касается стратегий для вычислений. Сначала обучайте стратегиям с помощью математических фактов, а затем применяйте их к текстовым задачам, чтобы учащиеся понимали стратегии и могли быстро выбрать одну из них для использования. При обучении сосредоточьтесь на одной или двух стратегиях. Как только учащиеся овладеют некоторыми стратегиями, попросите их выбрать стратегии, которые работают для решения различных задач.
Сначала обучайте стратегиям с помощью математических фактов, а затем применяйте их к текстовым задачам, чтобы учащиеся понимали стратегии и могли быстро выбрать одну из них для использования. При обучении сосредоточьтесь на одной или двух стратегиях. Как только учащиеся овладеют некоторыми стратегиями, попросите их выбрать стратегии, которые работают для решения различных задач.
Будьте целеустремленны в числах, которые вы выбираете для своих словесных задач. Разные наборы чисел подходят для разных стратегий и разных моделей. Используйте числовые наборы, которые учащиеся уже использовали в вычислениях. Если вы научились делать 10, используйте числа, которые составляют 10. Если вы работаете над сложением без перегруппировки, используйте эти наборы чисел. Чем больше связей вы сможете установить между вычислениями и решением задачи, тем лучше.
Приведенные выше примеры в основном предназначены для задач объединения и разделения. Неудивительно, что у наших студентов такие трудности с задачами на сравнение, поскольку мы не учим их в той же степени, что и задачи на соединение и разделение.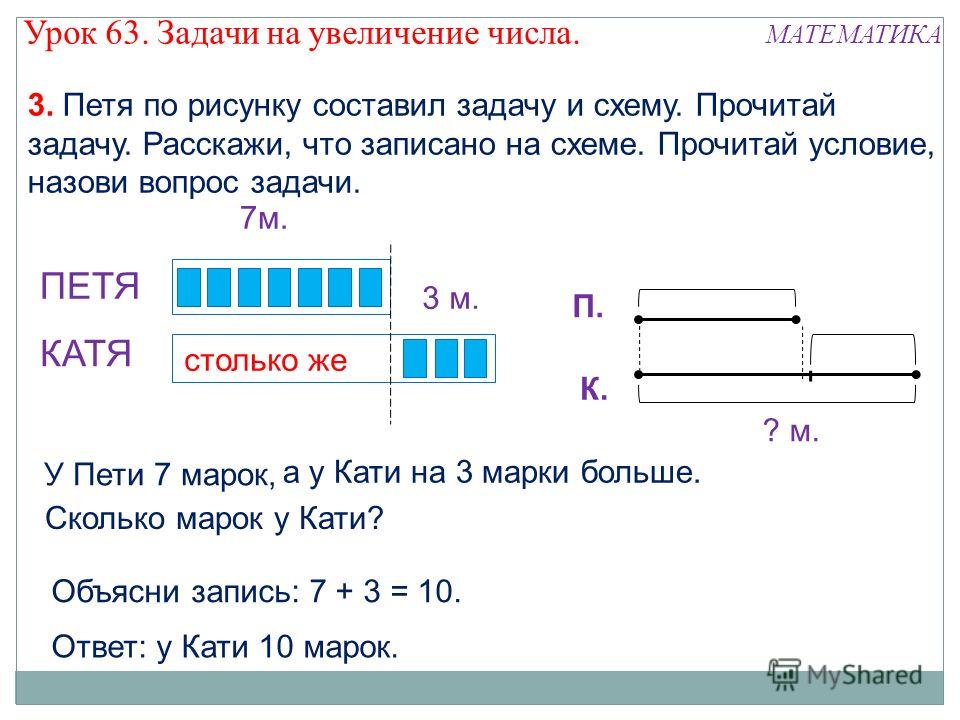 Нашим ученикам нужно еще больше практиковаться в подобных задачах, потому что отношения между числами более абстрактны. Однако я собираюсь оставить это для другого поста в блоге.
Нашим ученикам нужно еще больше практиковаться в подобных задачах, потому что отношения между числами более абстрактны. Однако я собираюсь оставить это для другого поста в блоге.
Хотите БЕСПЛАТНЫЙ образец ресурса, который я использую для обучения задачам на сложение и вычитание по типу задач 9?0219 ? Нажмите на эту ссылку или изображение ниже.
Полный ресурс также доступен в моем магазине для покупки и на сайте Teachers Pay Teachers.
Дополнительные идеи для обучения задачам со словами
Математика для первоклассников — обучение и практика математики для первоклассников
[«`#», «Моя учетная запись»]Учащиеся заглядывают внутрь сложения и вычитания, применяя понимание разрядного значения к 2 -цифровые операции.
Дошкольный классДетский сад1 класс 2 класс 3 класс 4 класс 5
Pre-kindergartenKindergartenКласс 1Класс 2Класс 3Класс 4Класс 5
МОДУЛЬ 1.
 Суммы и разности до 10
Суммы и разности до 10Тема A: Вложенные числа и разложения
Учащиеся изучают сложение до 5, используя конкретные объекты, абстрактные объекты и уравнения. Они изучают значение и правильное использование знаков + и =, а также термины «сложение» и «сумма».
Подсчитайте два слагаемых и определите сумму
Учащиеся определяют, сколько человек в каждой из двух групп, а затем сколько всего в сумме до 5. Они завершают утверждение «X и X дают X», перетаскивая сумму на место
Определить общее количество предметов и два его слагаемых
Учащиеся определяют общее количество предметов двух цветов, а затем определяют количество предметов каждого цвета. Они завершают утверждение «X и X составляют X», перетаскивая сумму на место
Использование знаков + и = в уравнении
Учащиеся знакомятся со знаками + и = и используют их для составления простых уравнений
Определять слагаемые и сумма в уравнении
Учащиеся знакомятся с терминами «сложение» и «сумма». Они определяют слагаемые и сумму в уравнениях
Они определяют слагаемые и сумму в уравнениях
Составление уравнения сложения по картинке
Учащиеся находят сумму уравнения сложения по показанным объектам. Затем они составляют уравнение на основе показанных объектов
Представление объектов в виде кубиков
Учащиеся перетаскивают цветные кубики, чтобы сопоставить объекты. Затем они определяют набор цветных кубиков, соответствующих заданным объектам
Составляют уравнения сложения на основе кубиков и решают уравнения с кубиками и без них
Учащиеся составляют уравнение сложения на основе цветных кубиков и решают его сумму. Они используют уравнения, чтобы показать, что существует более одного способа представления суммы. Затем учащиеся решают уравнения сложения без показанных кубов
Решение уравнений сложения
По заданному выражению сложения учащиеся определяют сумму. Затем они решают уравнения на сложение
Тема B: Счет от встроенных чисел
Учащиеся изучают сложение до 10, используя конкретные объекты, абстрактные объекты, уравнения и числовые связи. Они решают проблемы с отсутствующими слагаемыми и начинают представлять и решать задачи со словами.
Они решают проблемы с отсутствующими слагаемыми и начинают представлять и решать задачи со словами.
Прибавление 0 к числу
Учащиеся прибавляют ноль к однозначному числу. Они решают уравнения, в которых ноль — первое слагаемое, а когда — второе слагаемое
Используйте знак + в уравнении и найдите сумму
Учащиеся складывают однозначные числа, представленные цветными кубиками. Они выбирают знак +, чтобы завершить уравнение и определить сумму
Смоделировать и решить уравнение сложения
Учащиеся используют цветные кубики для представления слагаемых в уравнении, а затем определяют сумму
Запишите уравнение сложения на основе модели, чтобы показать более одного способа получить заданную сумму
Учащиеся пишут уравнение сложения, чтобы соответствовать заданной модели кубиков. Они повторяют этот навык с другим уравнением с той же суммой и замечают, что существует более одного способа показать эту сумму
Показать более одного способа получить заданную сумму
Учащиеся пишут уравнение сложения, чтобы соответствовать заданной модели кубиков. Затем они создают другую модель куба с той же суммой и записывают уравнение, замечая, что существует несколько способов показать эту сумму
Затем они создают другую модель куба с той же суммой и записывают уравнение, замечая, что существует несколько способов показать эту сумму
Решить уравнение сложения (всего до 7)
Учащиеся определяют сумму для уравнений сложения с двумя слагаемыми и в сумме дает 7
Определите части уравнения сложения
Учитывая уравнение сложения, учащиеся определяют первое слагаемое, второе слагаемое, знак плюс и сумму
Запишите уравнение сложения на основе модели и создайте модель, показывающую несколько способов получения заданной суммы.
Учащиеся записывают уравнение сложения, соответствующее заданной модели кубиков. Затем они создают еще одну модель куба с той же суммой и записывают уравнение, замечая, что существует несколько способов показать эту сумму
Решить уравнения сложения до 10 с моделью или без нее
Учащиеся выбирают, просматривать куб или нет модель, чтобы решить уравнения сложения до 10, а затем решить
Решите уравнение сложения (суммы до 10)
Учащиеся определяют сумму уравнений сложения с двумя слагаемыми и суммируют до 10
Моделирование и решение задачи на сложение с объектами
Учащиеся пишут и решают уравнение сложения на основе цветных объекты. Затем они используют объекты, как указано, для моделирования сценария сложения, записывают его в виде уравнения и решают за весь период
Затем они используют объекты, как указано, для моделирования сценария сложения, записывают его в виде уравнения и решают за весь период
Моделируют и решают задачу на сложение с помощью кубов
уравнение и решить для суммы
Написать и решить уравнение сложения на основе задачи со словами
Учащиеся составляют уравнение на основе сценария сложения и решить его
Определить отсутствующее слагаемое на основе модели кубов
Ученики определяют отсутствующее второе слагаемое в уравнении на основе цветных кубиков. Во-первых, подсказки направляют их к части модели, чтобы найти ответ. Затем учащиеся решают без подсказки
Определяют недостающее слагаемое на основе модели кубов
Учащиеся определяют недостающее второе слагаемое в уравнении на основе модели кубов. Во-первых, подсказки направляют их к части модели, чтобы найти ответ. Затем учащиеся решают без подсказки
Определяют недостающее слагаемое в уравнении (Часть 1)
Учащиеся определяют отсутствующее второе слагаемое в уравнении
Определяют отсутствующее слагаемое в уравнении (Часть 2)
Учащиеся определяют отсутствующее второе слагаемое в уравнении, выбирая, решать ли немедленно или моделировать с помощью кубов.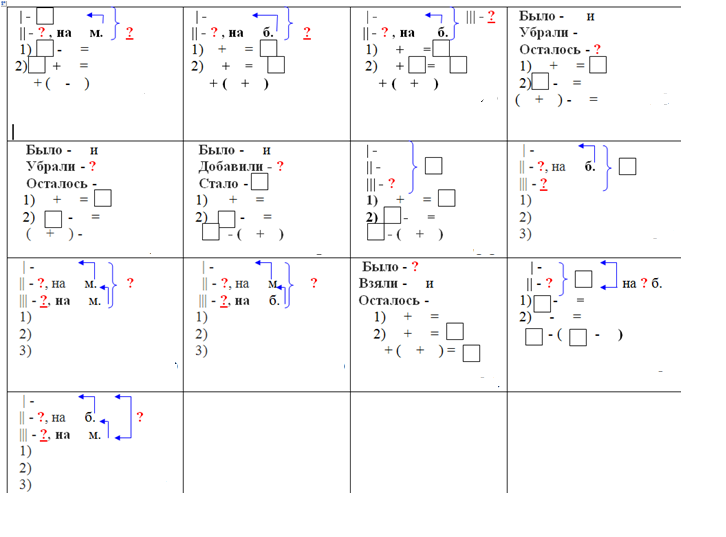 Затем они определяют недостающее первое или второе слагаемое в уравнении 9.0003
Затем они определяют недостающее первое или второе слагаемое в уравнении 9.0003
Определение отсутствующего слагаемого в уравнении
Учащиеся тренируются в решении отсутствующего второго слагаемого в уравнении сложения
Выберите два слагаемых, чтобы получить заданную сумму или модель с кубиками. Они определяют, какое из двух уравнений верно. Затем учащиеся выбирают два слагаемых, чтобы получить заданную сумму.0003
Определите сложения с суммой 10
Учащиеся определяют, какое из двух слагаемых с суммой до 10 является правильным. Они определяют пары слагаемых, сумма которых равна 10
Определяют числовую связь
Учащиеся определяют общее количество объектов, а затем два его слагаемых в зависимости от цвета. Они перетаскивают эти значения в числовую связь. Затем учащиеся находят числовую связь среди трех изображений.
Постройте числовую связь на основе модели кубиков
Учащиеся составляют числовую связь на основе модели цветных кубиков, а затем записывают ее в виде уравнения сложения. Затем учащиеся сначала пишут уравнение на основе модели кубов и строят числовую связь 9.0003
Затем учащиеся сначала пишут уравнение на основе модели кубов и строят числовую связь 9.0003
Постройте числовую связь на основе модели кубиков и заполните ее уравнение сложения.
На основе модели цветных кубиков учащиеся заполняют отсутствующее слагаемое в числовой связи и связанное с ней уравнение сложения. Затем они завершают всю числовую связь на основе модели кубов
Постройте модель, числовую связь и уравнение
Учащиеся создают двухцветную модель кругов. Они строят числовую связь на основе модели и определяют недостающее слагаемое или сумму в соответствующем уравнении 9.0003
Завершите связку чисел
Учащиеся определяют недостающее слагаемое в связке чисел. Затем они определяют два сложения, которые завершают числовую связь с заданной суммой.
Заполните числовую связь, чтобы показать более одного способа достижения заданной суммы.
Ученики определяют два сложения, которые образуют числовую связь с заданной суммой. Затем они определяют два разных слагаемых, чтобы завершить числовую связь с той же суммой
Определить недостающее слагаемое в числовой связи
Учащиеся находят отсутствующее сложение в связке чисел для нескольких связей чисел с одинаковой суммой
Тема C: Развитие беглости сложения в пределах 10
Учащиеся укрепляют свое понимание сложения в пределах 10 и лежащих в его основе концепций по мере разработки более эффективных стратегий решить проблемы. Они используют сценарии сложения с объектами, шаблонами блоков с основанием 10, числовой прямой и уравнениями, чтобы усилить отношения между семействами фактов. Они опираются на имеющиеся знания о составе чисел 6-10 по мере перехода от конкретного к абстрактному.
Они используют сценарии сложения с объектами, шаблонами блоков с основанием 10, числовой прямой и уравнениями, чтобы усилить отношения между семействами фактов. Они опираются на имеющиеся знания о составе чисел 6-10 по мере перехода от конкретного к абстрактному.
Определите отсутствующее слагаемое в уравнениях с суммой и их оборотными фактами
Вычислите отсутствующее слагаемое в уравнениях, сумма которых не превышает 10, с помощью визуальной поддержки. Также вычислите отсутствующее слагаемое в уравнениях, которые в сумме дают максимальное значение 10, используя оборотные факты, или переключите слагаемые, которые в сумме дают максимальное значение 10
Запишите модель блоков с основанием 10 как уравнение сложения
Используйте блоки с основанием 10 и /или оборотные факты, чтобы завершить уравнение сложения. Эти уравнения будут в сумме давать 10 каждый раз, когда
Определите отсутствующее слагаемое в уравнениях, представляющих собой оборотные факты с суммами 4, 5, 6 и 7.
 mssing addends
mssing addendsНахождение отсутствующего слагаемого в уравнении
Нахождение отсутствующего слагаемого в уравнении. Учащиеся будут использовать интерактивную игру, которая поможет им решить отсутствующие слагаемые
Определите отсутствующее слагаемое в уравнениях, спаренных как оборотные факты с суммами 6, 7, 8 и 9
Определите отсутствующее слагаемое в уравнениях, сумма которых равна 6, 7, 8 или 9. Учащиеся также будут использовать оборотные факты для определения пропущенных слагаемых
Выберите правильную сумму для выражения сложения
Выберите один из двух вариантов ответа для каждое числовое выражение, которое им дано. Каждое числовое выражение в сумме дает один из двух ответов
Найдите недостающее слагаемое в уравнениях, объединенных в пары как оборотные факты с суммами 9 и 10
Найдите недостающее слагаемое в уравнениях, сумма которых равна 9или 10. Учащиеся также будут использовать оборотные факты для выявления пропущенных дополнений
Тема D: Стратегии декомпозиции для вычитания
Учащиеся укрепляют свое понимание вычитания в пределах 10 и лежащих в его основе концепций по мере того, как они создают более эффективные стратегии решения задач. Они исследуют взаимосвязь между сложением и вычитанием и все чаще работают с 0 как с вычитаемым и разностью. Они используют сценарии вычитания с объектами, шаблонами блоков с основанием 10, числовой прямой и уравнениями, чтобы усилить отношения между семействами фактов. Они опираются на имеющиеся знания о составе чисел 6-10 по мере перехода от конкретного к абстрактному.
Они исследуют взаимосвязь между сложением и вычитанием и все чаще работают с 0 как с вычитаемым и разностью. Они используют сценарии вычитания с объектами, шаблонами блоков с основанием 10, числовой прямой и уравнениями, чтобы усилить отношения между семействами фактов. Они опираются на имеющиеся знания о составе чисел 6-10 по мере перехода от конкретного к абстрактному.
Запишите сценарий на основе объектов в виде уравнения вычитания с разницей 0 (Часть 1)
Запишите уравнения вычитания, используя два числа. Они напишут эти уравнения вычитания, чтобы они соответствовали картинке, которую им дали
Запишите сценарий числовой строки как уравнение вычитания -0
Узнайте, что вычитание 0 из числа дает вам число, которое вы начали с использования числовой строки. Студенты должны будут идентифицировать как числа, которые вычитаются, так и разницу, основанную на сценарии числовой строки 9.0003
Запишите сценарий числовой прямой как уравнение вычитания с разностью 0
Узнайте, что вычитание числа из самого себя дает разность 0 с помощью числовой строки. Они определят разницу после того, как им будет предложено поработать с числовой строкой
Они определят разницу после того, как им будет предложено поработать с числовой строкой
Определить пропущенные числа в уравнениях вычитания с разницей 0
Решить отсутствующие элементы в уравнениях вычитания, которые приводят к разнице 0. Определить одно из чисел что приводит к разнице в 0 или самой разнице в 0 в зависимости от примера
Вычитание путем перемещения объекта назад по числовой прямой и решение связанного уравнения, которое показывает вычитание из 3, 4 или 5
Вычитание чисел из 3, 4 или 5 с помощью числовой строки. Иногда учащимся будет предложено заполнить один недостающий элемент в уравнении вычитания после взаимодействия со сценариями числовой прямой
Записать сценарий числовой строки как уравнение, которое показывает вычитание из 3, 4 или 5
4 или 5 с помощью числовой строки. Учащимся будет предложено заполнить все элементы уравнения вычитания, включая уменьшаемое, символ операции, вычитаемое и разность 9.0003Запишите сценарий, основанный на объектах, как уравнение вычитания с разностью 0 (Часть 2)
Используйте сценарий, иллюстрированный картинками, для завершения уравнений вычитания.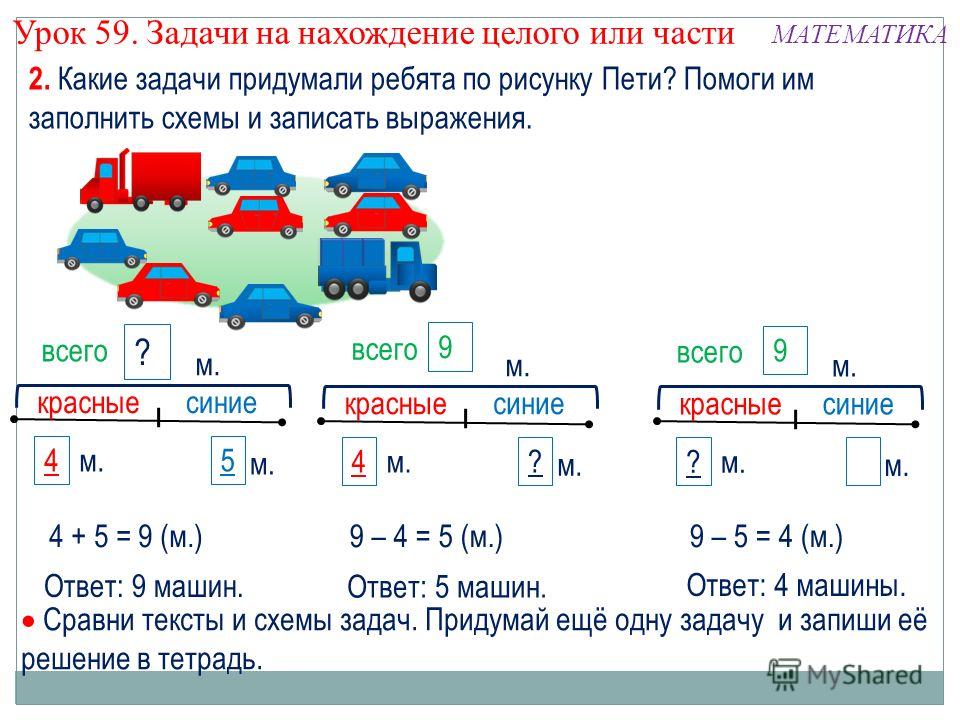 Учащиеся введут уменьшаемое, вычитаемое и разность для каждого уравнения вычитания
Учащиеся введут уменьшаемое, вычитаемое и разность для каждого уравнения вычитания
Используйте блоки с основанием 10 для представления сценариев вычитания с объектами в пределах 5 и определите шаблоны блоков с основанием 10, которые представляют сценарии вычитания с объектами в пределах 5
Выберите число кубов с основанием 10, которые соответствуют количеству удаленных объектов в сценарии, проиллюстрированном рисунками. Оставшаяся разница должна совпадать с количеством оставшихся изображений более
Решите уравнения на основе модели блоков с основанием 10, чтобы вычесть 1 или все, кроме 1
Щелкните количество кубов с основанием 10, которое нужно отнять от суммы, чтобы получить разницу в заданном вам уравнении вычитания. После этого учащиеся будут вводить разность в уравнении вычитания
Записать модель блоков с основанием 10 в виде двух связанных уравнений, которые показывают вычитание из 6
Заполнить слагаемые и суммы в уравнениях, которые дают в сумме 6, учитывая сценарий, проиллюстрированный основанием 10 кубов. Затем учащиеся завершат два уравнения на вычитание, используя 6 и сложения из первого уравнения 9.0003
Затем учащиеся завершат два уравнения на вычитание, используя 6 и сложения из первого уравнения 9.0003
Запишите модель блоков с основанием 10 в виде двух связанных уравнений, которые показывают вычитание из 7 или 8
Вставьте сложения и суммы в уравнения, которые дают в сумме 7 или 8, используя сценарий, иллюстрируемый кубами с основанием 10. Затем учащиеся выполнят два уравнения на вычитание, используя числа 7 или 8 и слагаемые из первого уравнения.
Вычитание путем перемещения объекта назад по числовой прямой и решение связанного уравнения, которое показывает вычитание в пределах 7
Вычитание чисел из 7 с помощью числовой строки . Затем учащимся будет предложено заполнить разницу уравнений вычитания
Запишите модель кубиков с основанием 10 в виде двух связанных уравнений, которые показывают вычитание из 9 или 10
Вставьте сложения и суммы в уравнения, которые дают в сумме 9 или 10. учитывая сценарий, иллюстрируемый кубами с основанием 10. Затем учащиеся завершат два уравнения на вычитание, используя 9 или 10 и слагаемые из первого уравнения.
Затем учащиеся завершат два уравнения на вычитание, используя 9 или 10 и слагаемые из первого уравнения.
Определите пропущенные числа в уравнениях на вычитание из 9
Используя кубы с основанием 10, вставьте пропущенное слагаемое и просуммируйте для уравнений сложения, которые в сумме дают 9. Кроме того, используйте кубы с основанием 10, чтобы заполнить пропущенное вычитаемое и разницу в уравнениях вычитания, которые начинаются с уменьшаемого числа 9
Тема E: Переместительное свойство сложения и знак равенства
Учащиеся узнают о переместительном свойстве сложения, сравнивая сложение выражения с теми же слагаемыми, но в другом порядке. Кроме того, учащиеся тренируются составлять выражения, равные друг другу, вставляя пропущенное слагаемое. Наконец, учащиеся знакомятся со знаком равенства как способом показать, что два выражения равны или одинаковы.
Решите простые уравнения на сложение и убедитесь, что изменение порядка слагаемых не меняет сумму.

С помощью наглядных материалов учащиеся считают и складывают предметы. Затем объекты меняются местами, чтобы показать, что сумма одинакова. Затем учащиеся решают задачи на сложение, используя только числа, и замечают, что изменение порядка слагаемых не меняет сумму. Затем учащиеся сопоставляют выражения с одинаковой суммой, хотя порядок слагаемых меняется
Составляйте равные выражения и решайте уравнения с одинаковыми слагаемыми в другом порядке.
Учащиеся тренируются заполнять пробелы в выражении, чтобы сделать его равным другому выражению. Затем учащиеся практикуются в решении уравнений сложения, которые имеют одинаковые слагаемые и суммы.
Определяют и составляют равные и неравные выражения сложения
Учащиеся решают уравнения с одинаковой суммой, но разными слагаемыми. Затем учащиеся решают уравнения, чтобы увидеть, равны они или нет. Учащиеся практикуют алгебраическое мышление, заполняя пропущенное сложение, в результате чего два выражения будут равны 9. 0003
0003
Использование знака равенства для отображения и создания выражений равенства (Часть 1)
Учащиеся учатся использовать знак равенства для отображения выражений равенства. Затем учащиеся тренируются заполнять одно отсутствующее слагаемое, чтобы сделать уравнение верным, с прямыми инструкциями. являются ли числовые предложения истинными и ложными
Учащиеся практикуются в определении истинных и ложных числовых предложений. Некоторые примеры требуют добавления, а другие нет
Тема F: Развитие навыков вычитания в пределах 10
Учащиеся закрепляют отношения между сложением и вычитанием и отношения между семействами фактов. Они используют знакомые предметы, кубики с основанием 10, числовую прямую и уравнения, чтобы исследовать состав чисел 3-10. Они строят скорость и точность со всеми +/- фактами в пределах 10.
Определите модель числового ряда, которая представляет сценарий вычитания, заданный словами
Посмотрите на три возможных сценария числового ряда, данные вам. Затем выберите тот, который представляет уравнение вычитания, записанное словами
Затем выберите тот, который представляет уравнение вычитания, записанное словами
Найдите недостающие числа в уравнениях вычитания из 4, 5 и 6
Используя сценарии, проиллюстрированные кубами с основанием 10, заполните недостающие элементы уравнений вычитания. Каждое из уравнений вычитания будет начинаться с 4, 5 или 6
Определите недостающие числа в уравнениях вычитания из 6 и 7
Используя сценарии, проиллюстрированные кубами с основанием 10, заполните недостающие элементы уравнений вычитания. Каждое из уравнений вычитания будет начинаться либо с 6, либо с 7
Выберите соответствие выражения вычитания и разности
Используя сценарии, иллюстрированные рисунками, сопоставьте выражения вычитания с соответствующими разностями. Упражнение заканчивается, когда вы переходите от одного игрового поля к другому
Определите недостающие числа в уравнениях вычитания из 7 и 8
Используя сценарии, иллюстрированные кубиками с основанием 10, заполните недостающие элементы уравнений вычитания. Каждое из уравнений вычитания будет начинаться либо с 7, либо с 8
Каждое из уравнений вычитания будет начинаться либо с 7, либо с 8
Найдите недостающие числа в уравнениях вычитания из 8 и 9
Используя сценарии, проиллюстрированные кубами с основанием 10, заполните недостающие элементы уравнений вычитания. Каждое из уравнений вычитания начинается либо с 8, либо с 9
Определите недостающий элемент в уравнении вычитания
Определите, какие элементы отсутствуют в уравнениях вычитания. По мере того, как вы заполняете недостающие элементы уравнений вычитания, головоломка будет медленно решаться
Найдите недостающие числа в уравнениях вычитания из 9 и 10
Используя сценарии, проиллюстрированные кубами с основанием 10, заполните недостающие элементы уравнений вычитания. Каждое из уравнений вычитания начинается с 9 или 10
МОДУЛЬ 2. Знакомство с размещением значений путем сложения и вычитания в пределах 20
Тема A: Подсчет или прибавление десяти для решения неизвестных результатов и общих неизвестных задач
Учащиеся закрепляют свои понимание «десятки» и «единицы» при сортировке, подсчете, сложении и вычитании. Они используют объекты, блоки с основанием 10, числовую прямую и десятичную рамку. Они практикуют различные стратегии, чтобы добавить через 10 и улучшить беглость с +/- фактами в пределах 20.
Они используют объекты, блоки с основанием 10, числовую прямую и десятичную рамку. Они практикуют различные стратегии, чтобы добавить через 10 и улучшить беглость с +/- фактами в пределах 20.
Закрепить знания о числах 11-20, добавив одну цифру к числу десять
Учащиеся выберут правильное сложение, чтобы заполнить таблицу, а затем отработают навыки сложения, введя правильную сумму
Откройте для себя сложения, чтобы получить десять
Откройте для себя сложения с суммой десять. Найдите пропущенное слагаемое в сумме десять и заполните таблицу чисел
Определите пропущенное сложение
Учащиеся продемонстрируют свое мастерство, найдя пропущенное сложение, чтобы завершить уравнение
Практикуйтесь с десятью кадрами
Щелкните и перетащите капли, чтобы завершить десять кадров. Добавьте оставшиеся капли к десяти рамкам, чтобы определить сумму
Используйте десять рамок, чтобы изучить уравнения и определить сумму
Используя десять рамок, учащиеся считают объекты, чтобы определить слагаемые.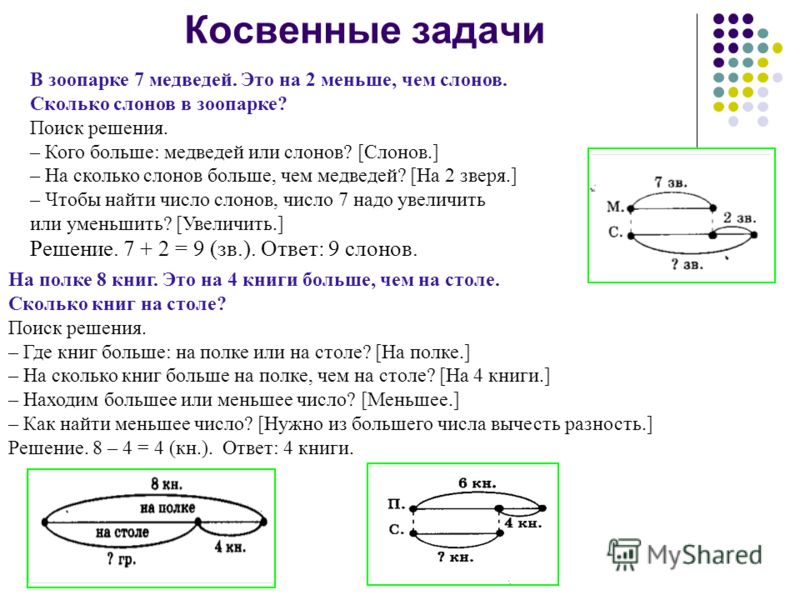 Затем учащиеся заполняют десять рамок и используют наглядные материалы для решения уравнения
Затем учащиеся заполняют десять рамок и используют наглядные материалы для решения уравнения
Используйте блоки с основанием десять, чтобы сделать десять, затем найдите сумму
Нажмите и перетащите блоки с основанием десять, чтобы сначала составить стержень из десяти. Затем учащиеся будут считать свободные блоки и добавлять их к стержню, чтобы определить сумму
Используйте блоки с основанием десять, чтобы определить сумму
Определите количество блоков, необходимых для сборки стержня. Используйте блок с основанием десяти, чтобы определить сумму заданного уравнения
Введение в уравнения с тремя слагаемыми
Используйте блоки разного цвета, чтобы найти слагаемые, равные десяти. Затем добавьте оставшееся слагаемое к десяти, чтобы найти сумму. Введите ответ на уравнение
Разложить слагаемые, чтобы получилось десять, затем сложить, чтобы найти сумму
Разложите одно сложение, чтобы добавить правильное количество блоков в другую группу, чтобы получилось десять.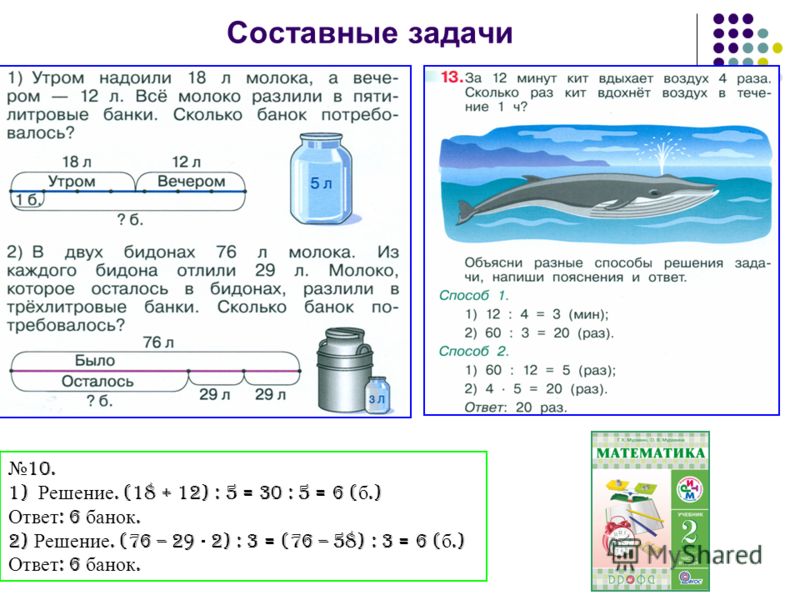 Добавьте десять к оставшимся блокам, чтобы решить уравнение
Добавьте десять к оставшимся блокам, чтобы решить уравнение
Продолжение практики разложения слагаемых для решения уравнения
Разложите одно слагаемое, чтобы получить десять. Добавьте десять к оставшимся блокам, чтобы решить уравнение. Введите сумму в уравнение
Продемонстрируйте знание пропущенного сложения, чтобы получить десять
Введите пропущенное сложение, чтобы завершить уравнение с суммой десяти
Решение с использованием числовой связи
Решайте уравнения, разлагая и находя десять без использования визуальных манипуляций. Введение в использование числовых связей для решения уравнения
Использование числовых связей для решения уравнений сложения
Используя числовые связи, определите, как нужно разделить слагаемое, чтобы получилось десять. Добавьте остаток от деления к десятке, чтобы найти сумму
Продолжение практики использования числовых связей для решения уравнений сложения
Использование числовых связей для нахождения суммы уравнения сложения
Продемонстрировать навыки или попрактиковаться с помощью
Учащимся предоставляется возможность решать уравнения с помощью или без помощи
Решить уравнения сложения с суммами 11-16 для объединения объектов
Решить уравнение сложения для объединения двух объектов в один
Решите уравнения сложения с суммами 11-16
Решите уравнение сложения для создания боевого костюма
Решите уравнения сложения с перегруппировкой
Решите уравнение на сложение, чтобы выиграть математическую битву.
Тема B: Подсчитайте или вычтите из десяти, чтобы решить неизвестный результат и общее количество неизвестных задач
Учащиеся изучают стратегии сложения и вычитания по десяти. Они используют знакомые модели блоков с основанием 10, числовую прямую и десять кадров, чтобы проиллюстрировать смысл операций.
Завершите серию связанных уравнений для вычитания 10 на основе модели блоков с основанием 10
Используя модель куба с основанием 10, вы начнете со значения больше 10. Затем вы будете вычитать 1, 2, 3 , и 4 от этого начального числа
Решите уравнения вычитания через 10, используя числовую прямую
Используя числовую прямую и начав с числа больше 10, вы закончите уравнения вычитания. Скорее всего, вы получите разницу менее 10 каждый раз.
Смоделируйте и решите уравнения вычитания для 10, используя объекты в десятичной системе координат
Имея коробку или контейнер из 10 объектов с дополнительными объектами вне коробки или контейнера, вы закончит уравнения вычитания.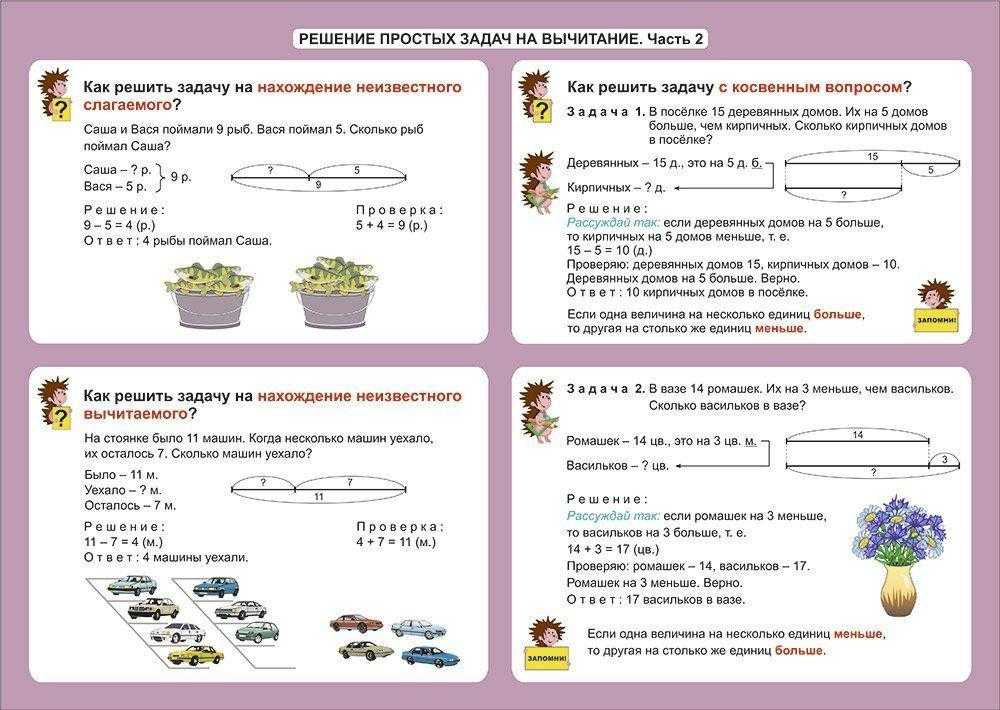 Вы начнете с общего количества объектов больше 10 каждый раз
Вы начнете с общего количества объектов больше 10 каждый раз
Смоделируйте и решите уравнения вычитания по 10, используя блоки с основанием 10 (Часть 1)
Используя модель куба с основанием 10, закончите уравнения вычитания. Начните с более чем 10 кубов каждый раз, когда эта область сортируется в столбце десятков и единиц. Затем удалите числовые кубы, эквивалентные числу, которое вы вычитаете из большего числа.
Смоделируйте и решите уравнения вычитания для 10, используя блоки с основанием 10 (Часть 2)
Используя модель куба с основанием 10, завершите уравнения вычитания. Начните с более чем 10 кубов каждый раз, когда эта область сортируется в столбце десятков и единиц. Затем удалите числовые кубики, эквивалентные числу, которое вы вычитаете из большего числа 9.0003
Решите уравнения вычитания в пределах 20
Используйте модель с основанием 10. Начальное количество кубиков будет эквивалентно уменьшаемому. Десять кубиков будут размещены в столбце десятков, остальные кубики в столбце единиц.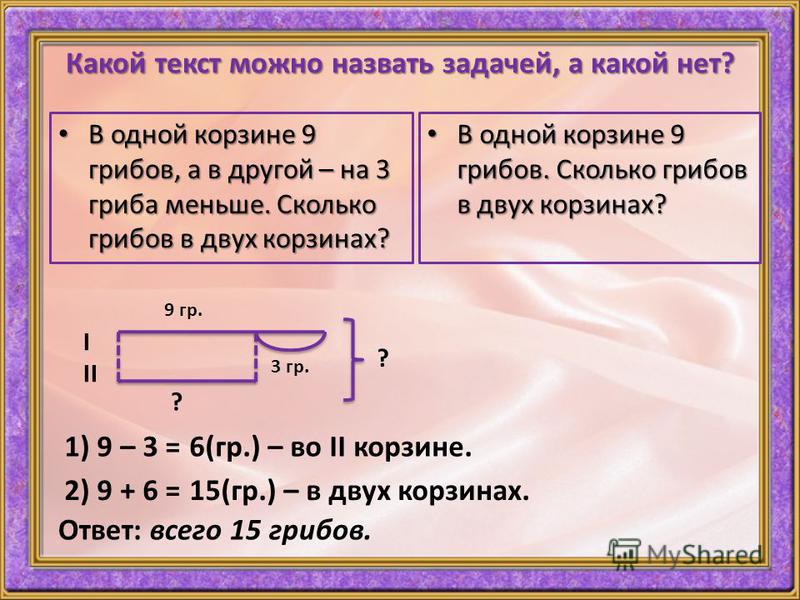 Определите, сколько еще кубиков вам нужно удалить из столбца десятков до e
Определите, сколько еще кубиков вам нужно удалить из столбца десятков до e
Решите уравнения вычитания через 10
Без использования каких-либо наглядных пособий вы будете решать уравнения вычитания. Каждый раз, когда уравнение начинается с числа больше 10
Решите уравнения вычитания 2-значного минус 1-значное из 10
Используя интерактивные иллюстрации, учащиеся будут решать уравнения вычитания. Все эти уравнения вычитания будут двузначными числами минус однозначные числа
Тема C: Разнообразные задачи с разложением подростковых чисел на 1 десяток и несколько единиц
Учащиеся изучают разрядное значение, складывая и вычитая 10. Они используют множественные представления ( объекты, десятикадр, числовая линия, блоки с основанием 10 и уравнения), чтобы перейти от конкретного к абстрактному. Учащиеся развивают беглость с +/- фактами внутри, укрепляя основную концепцию обмена и используя стратегию «отдыха» на 10. Они также решают +/- задачи, в которых все единицы или все десятки складываются или вычитаются.
Решите уравнения на вычитание, содержащие число 10
Используя модель куба с основанием 10, учащиеся будут решать уравнения на сложение и вычитание. Перед завершением каждого уравнения кубы будут добавляться и вычитаться на экране
Завершать уравнения, которые добавляют или вычитают все десятки или все единицы с моделью блоков с основанием 10 и без нее
С использованием и без использования кубов с основанием 10, вы будете выполнить уравнения сложения и вычитания. Когда используются числовые кубы с основанием 10, они будут либо добавлены, либо вычтены из общей суммы перед завершением уравнений вычитания 9.0003
Добавляйте единицы к числам во второй десятке, используя блоки с основанием 10
Используя кубики с основанием 10, которые расположены в столбцах десятков и единиц, чтобы отразить первое слагаемое, вы будете добавлять числовые кубы к столбцу единиц, равному второму слагаемому . После сложения числовых кубов вы определяете окончательную сумму
Вычитание из чисел 11-20 с использованием блоков с основанием 10 кубов из столбца единиц, равных вычитаемому.
 После того, как вы уберете числовые кубики, вы определите окончательную разницу
После того, как вы уберете числовые кубики, вы определите окончательную разницуРешите +/- уравнения, в которых используются числа второго десятка и однозначное число (Часть 1)
В этом упражнении вы вычислите разницу уравнений вычитания. Каждое уравнение включает вычитание однозначных чисел из двузначных чисел
Определение недостающего слагаемого для получения суммы 20 с моделью блоков с основанием 10 и без нее
Используя модель куба с основанием 10, вы определяете, сколько кубов нужно добавить равно 20 числовых кубов. Затем вы завершите соответствующее уравнение сложения
Решите уравнения +/-, в которых используются числа из второго десятка и однозначное число (Часть 2)
В этом упражнении вы будете решать уравнения на сложение и вычитание с двузначным числом меньше 20 и однозначным числом. После правильного ответа на каждое уравнение будет отображаться анимированная иллюстрация.
МОДУЛЬ 3. Упорядочивание и сравнение измерений длины в виде чисел
Тема A: Косвенное сравнение в измерении длины
Учащиеся используют знакомые, реальные объекты, чтобы сформировать чувство сравнения длины. Они определяют самый длинный, самый короткий, длинный и короткий среди объектов, даже если они не выровнены.
Они определяют самый длинный, самый короткий, длинный и короткий среди объектов, даже если они не выровнены.
Определите, какой из двух объектов длиннее или короче, и выровняйте объекты, чтобы сравнить их длину.
Сравните длины двух объектов, нажав на более длинный или более короткий из двух вариантов, как указано. Узнайте, как выравнивать объекты, чтобы иметь возможность более точно оценивать длину
Определите утверждение, которое правильно сравнивает длину двух объектов
Выберите правильное утверждение, которое сравнивает длины двух объектов. Даны три варианта оператора
Определить самый короткий или самый длинный объект в невыровненном наборе из трех объектов
Выберите самый длинный или самый короткий объект, как указано, из трех вариантов. Объекты не выровнены
Упорядочить набор выровненных объектов по длине
Перетащите 3 или 4 объекта, чтобы упорядочить их по длине или высоте
Подсчет расстояний в блоках на карте и сравнение
Подсчет расстояний по сетке карты . Введите значение расстояния. Затем сравните два расстояния и укажите, какое из них длиннее или короче другого
Введите значение расстояния. Затем сравните два расстояния и укажите, какое из них длиннее или короче другого
Подсчитайте расстояния в блоках на карте и создайте путь, который длиннее или короче заданных путей
Практика подсчета расстояний по сетке карты. Затем создайте путь короче или длиннее заданного пути
Тема B: Нестандартные единицы длины
Учащиеся используют скрепки в качестве нестандартной единицы длины для измерения объектов. Они узнают, что единицы измерения должны измерять расстояние от конечной точки до конечной точки без пробелов или перекрытий.
Счет для измерения длины объектов
Узнайте, как измерять длину объектов, используя нестандартные единицы измерения. Скрепки используются для измерения письменных принадлежностей. Введите количество скрепок, равное длине предмета
Измерение длины объектов от одной конечной точки до другой без зазоров и перекрытий
Узнайте, как измерять длину объектов от одной конечной точки до другой, используя нестандартные единицы измерения. Скрепки используются для измерения без зазоров или перекрытия. Введите количество скрепок, равное длине объекта
Скрепки используются для измерения без зазоров или перекрытия. Введите количество скрепок, равное длине объекта
Определите, какой из двух объектов измерен правильно
Выберите правильный способ измерения длины по двум картинкам. Скрепки используются как нестандартный блок. Затем введите значение измерения
Правильное измерение длины объектов с помощью укладочных единиц
Измерение длины объектов с помощью скрепок в качестве нестандартной единицы. Единицы измерения должны быть правильно размещены между конечными точками
Тема C: Интерпретация данных
Учащиеся считают реальные объекты и используют подсчетные отметки или гистограммы для их представления. Они интерпретируют данные, представленные в таблицах и графиках, и используют их, чтобы найти общее количество, на сколько больше и на сколько меньше.
Делайте отметки для подсчета до 5 объектов
Узнайте, как использовать учетные отметки для отслеживания наблюдений. Введите значение, представленное контрольными отметками
Определите общее количество контрольных точек (Часть 1)
Потренируйтесь в интерпретации значения, представленного контрольными отметками. Введите число, показанное на подсчетах
Введите число, показанное на подсчетах
Определите общее количество отметок (Часть 2)
Интерпретируйте значение отметок как часть гоночной игры. Ввод правильного значения продвигает персонажа вперед в гонке.0391
Составьте таблицу учета животных, изображенных на картинке. Интерпретация значений контрольных отметок на диаграмме и нахождение суммы двух значений
Интерпретация данных в таблице с помощью контрольных отметок (уровень 2)
Определите значение контрольных отметок на диаграмме, а затем определите, какой элемент появился больше или меньше всего . Затем найдите сумму трех значений на диаграмме
Интерпретация данных в гистограмме с 1 категорией
Узнайте, как создать и прочитать гистограмму для одной категории
Создайте гистограмму с двумя категориями и используйте ее для интерпретации данных.
Создайте гистограмму с двумя категориями. Определите, какая категория содержит больше или меньше. Найдите разницу между двумя категориями
Интерпретация данных на гистограмме с 3 категориями (Часть 1)
Интерпретация значений трех гистограмм. Сравните значения и найдите сумму всех трех категорий
Сравните значения и найдите сумму всех трех категорий
Интерпретация данных на гистограмме с 3 категориями (Часть 2)
Попрактикуйтесь в интерпретации данных, представленных на гистограмме с 3 категориями. Определите, какая полоса показывает определенное число и сумму двух категорий
МОДУЛЬ 4. Размещение значения, сравнения, сложения и вычитания до 40
Тема A: Десятки и единицы
Учащиеся дополнительно изучают понятие о том, что двузначное число состоит из круглого числа (десятки) плюс единицы. Они определяют итоги, разлагают числа, складывают и вычитают. Учащиеся используют знакомые объекты, блоки с основанием 10, десятичные кадры, уравнения и названия чисел вместе с карточками разрядов. Обратите внимание, что используемые «монеты» предназначены для закрепления концепции десятков, пятерок и единиц, а не для распознавания монет.
Прибавьте десятки к 40 на основе модели блоков с основанием 10.
Имея стержни из 10 кубиков с основанием 10, вы посчитаете количество кубиков десятками. В рамках этого задания вы сначала определите количество десятков, а затем укажите, сколько кубиков в сумме, максимум из 40 кубиков. 10 кубиков, вы будете считать количество кубиков десятками. Во время части этого задания вы сначала определите количество десятков, а затем укажете, сколько всего кубиков, максимум 9.0 кубов
В рамках этого задания вы сначала определите количество десятков, а затем укажите, сколько кубиков в сумме, максимум из 40 кубиков. 10 кубиков, вы будете считать количество кубиков десятками. Во время части этого задания вы сначала определите количество десятков, а затем укажете, сколько всего кубиков, максимум 9.0 кубов
Определить общее количество объектов путем подсчета объектов с заполнением десяти рамок или без них
В этом упражнении вы определите общее количество объектов, показанных путем заполнения десяти рамок. Под десятикадром я подразумеваю коробку, вмещающую не более 10 предметов.
Определить двузначные круглые числа
Это задание связано с математической идеей круглых чисел или чисел, оканчивающихся на ноль. Учитывая группу чисел, вы определите, какие числа будут считаться круглыми
Определить сумму до 40 путем подсчета десятков и единиц с использованием кубиков с основанием 10.
Кубики с основанием 10, рассортированные по палочкам по 10, и оставшиеся кубики, рассортированные по разрозненным одиночным кубикам, подсчитайте количество кубиков. Запишите количество десятков, затем количество единиц и укажите общее количество кубиков. Максимальная сумма будет 40
Запишите количество десятков, затем количество единиц и укажите общее количество кубиков. Максимальная сумма будет 40
Определить общее количество до 40 путем подсчета десятков и единиц, используя объекты в десятирамках
Объекты рассортированы по 10 коробкам, а оставшиеся объекты рассортированы по разбросанным одиночным объектам, подсчитайте количество кубиков. Укажите количество десятков, затем количество единиц и укажите общее количество объектов. Максимальная сумма будет 40
Определить суммы путем подсчета десятков и единиц, используя разбросанные и неодинаковые предметы в десятикадровом
Предметы, рассортированные по 10 коробкам, и оставшиеся предметы, рассортированные по разбросанным одиночным предметам, подсчитайте количество кубиков. Укажите количество десятков, затем количество единиц и укажите общее количество предметов.
Определите общее количество «монет», используя цифры 10, 5 и 1 значения (10 центов, 5 центов, 1 цент). Затем вы посчитаете количество денег, которое у вас есть в каждой задаче 9.
 0003
0003Представлять числа до 40, используя палочки и кубики с основанием 10.
Вам дадут несколько стержней из кубиков с основанием 10 и несколько одиночных кубиков с основанием 10. Затем вам будет предложено выбрать определенное количество кубов из большего количества, с которым вы начинаете. Максимальное значение, которое вам нужно будет отсчитать, будет 40
Определите названия чисел до 40 в числовой строке
В этом упражнении вам будет предоставлена числовая строка с существующими числами. Затем вам нужно будет назвать числа, которые следуют за теми, которые уже находятся в строке чисел. Максимальное значение наибольшего числа, которое вам потенциально придется назвать, равно 40 9.0003
Определите недостающее число до 40 в числовой строке и определите его письменное название
Вам будет предоставлена числовая строка с существующими числами. Вам нужно будет заполнить пробелы в числовой строке отсутствующим числом. Затем вам нужно будет назвать эти числа. Максимальное значение наибольшего числа, которое вам нужно назвать, равно 40
Максимальное значение наибольшего числа, которое вам нужно назвать, равно 40
Разложите двузначные числа до 40 на десятки и единицы с моделью блоков с основанием 10 и без нее
Вам будут даны различные двузначные числа. Вам будет предложено разложить каждое число на десятки и единицы, или вам будет предложено начать разложение и определить число, которое соответствует каждому разложению
Разложите двузначные числа до 40 в круглое двузначное число плюс единицы
В этом упражнении вам будут даны монеты разного номинала (10 центов, 5 центов, 1 цент). Затем вы подсчитаете количество денег, которое у вас есть в каждой задаче
Решите уравнения, которые добавляют или вычитают 1 или 10 с использованием и без моделирования с использованием блоков с основанием 10 (Часть 1)
Вы будете добавлять 1 к различным двузначным числам меньше чем 40 в этой деятельности. Вы будете использовать числовые блоки с основанием 10 для моделирования каждого уравнения сложения
Решите уравнения, которые добавляют или вычитают 1 или 10 с использованием и без моделирования с использованием блоков с основанием 10 (Часть 2)
В этом упражнении вы будете добавлять 10 к различным двузначным числам меньше 40. Вы будете использовать блоки с основанием 10 для моделирования каждого уравнения сложения
Вы будете использовать блоки с основанием 10 для моделирования каждого уравнения сложения
Решите уравнения, которые добавляют или вычитают 1 или 10 с использованием и без моделирования с использованием блоков с основанием 10 (Часть 3)
Вы будете вычитать 1 из различных двузначных чисел меньше 40 в этой деятельности. Вы будете использовать числовые блоки с основанием 10 для моделирования каждого уравнения вычитания
Решите уравнения, которые добавляют или вычитают 1 или 10 с использованием и без моделирования с использованием блоков с основанием 10 (Часть 4)
В этом упражнении вы будете вычитать 10 из различных двузначных чисел меньше 40. Вы будете использовать блоки с основанием 10 для моделирования каждого уравнения вычитания
Решать уравнения, которые добавляют или вычитают 1 или 10 с использованием и без моделирования с использованием блоков с основанием 10 (Часть 5)
Вы будете прибавлять 10, прибавлять 1 к, вычитать 1 и вычтите 10 из различных двузначных чисел в этом упражнении.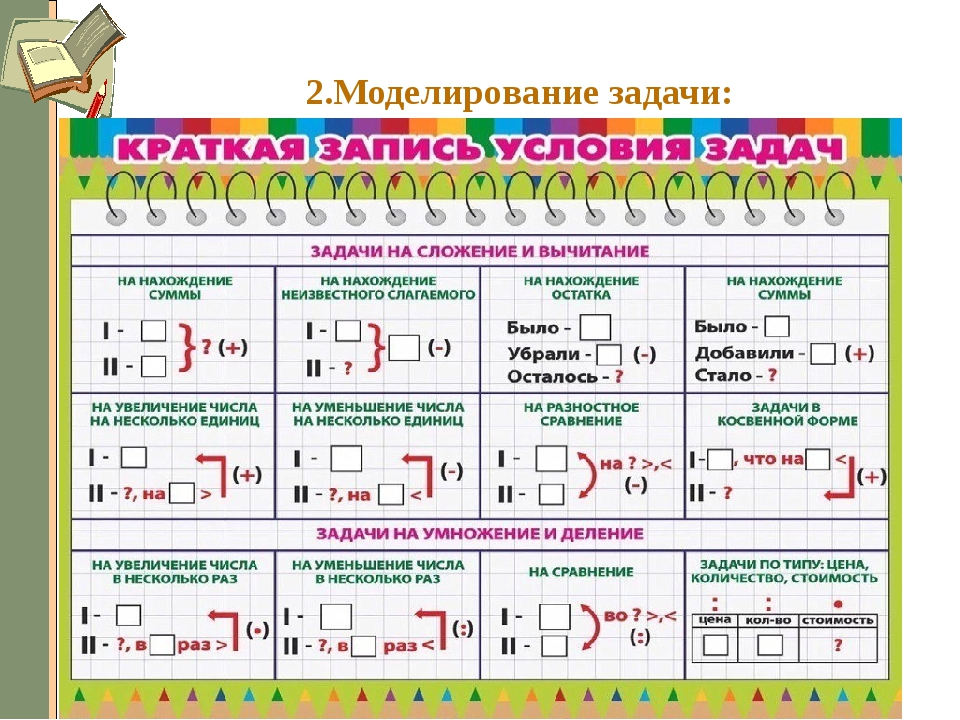 Вы не сможете использовать числовые блоки с основанием 10 для моделирования каждого уравнения
Вы не сможете использовать числовые блоки с основанием 10 для моделирования каждого уравнения
Тема B: Сравнение пар двузначных чисел
Учащиеся сравнивают и упорядочивают числа, укрепляя свое понимание разрядности и последовательности. Они используют знакомые блоки с основанием 10, числовую прямую и начинают использовать знаки неравенства.
Выровняйте разбросанный набор пронумерованных непоследовательных объектов в порядке возрастания
Вам будет предоставлена разрозненная группа объектов с номерами на них. Затем вам будет предложено расположить эти объекты в линию в порядке 9.0003
Сравните два набора разбросанных объектов, используя > или
< с визуальным пособием.Вам будут предоставлены две отдельные группы объектов для сравнения. Вы выберете, какая группа имеет большее количество объектов с помощью наглядного пособия
Выровняйте разрозненный набор пронумерованных, непоследовательных объектов в порядке убывания
Вам будет предоставлена разрозненная группа объектов с номерами на них. Затем вам будет предложено расположить эти объекты в ряд в порядке убывания
Затем вам будет предложено расположить эти объекты в ряд в порядке убывания
Определить пропущенные круглые числа в числовой строке, пронумерованной десятками
Вам будет дана числовая строка, пронумерованная десятками. Затем вам нужно будет заполнить пробелы круглыми числами
Сравните два двузначных числа, используя символы >,
< или = с моделью блоков с основанием 10 и без нееВам будут даны два двузначных числа. Затем вы будете использовать знаки неравенства и равенства, чтобы указать, какое число больше, используя числовые блоки с основанием 10 в качестве наглядного пособия.
Поместите двузначные числа в числовую строку
Имея числовую строку, вы будете размещать числа на ней в реальном времени. Каждое число будет двузначным числом
Сравните двузначные числа с использованием знаков
<, = или > с моделью числовой прямой и без нееВ этом упражнении вы будете сравнивать пары двузначных чисел. Сначала вы поместите каждое число в числовую строку, прежде чем определить, какое число больше
Сравните двузначные числа, используя
<, = или > В этом упражнении вы будете сравнивать пары двузначных чисел. Вы будете использовать знаки неравенства и равенства в каждом примере для сравнения чисел
Вы будете использовать знаки неравенства и равенства в каждом примере для сравнения чисел
Тема C: Сложение и вычитание десятков
Учащиеся работают с круглыми числами, чтобы закрепить понимание разряда на 10 больше и на 10 меньше. Они используют уравнения и числовую прямую для решения задач на сложение и шаблонов счета.
Решите уравнения сложения, которые добавляют круглые числа к 40
В этом упражнении вы будете складывать пары круглых чисел. Максимальное значение каждой суммы будет 40
Посчитайте назад на 10 по числовой прямой (Часть 1)
Для этого действия будет предоставлена числовая строка. Вам будет дан номер, отмеченный на линии, чтобы начать. Затем, следуя пометкам на числовой строке, вы будете считать в обратном порядке на десятки, чтобы заполнить пропущенное число для каждой задачи.
Считайте в обратном порядке на 10 в числовой строке (Часть 2) . Вам будет дан номер, отмеченный на линии, чтобы начать. Затем, следуя пометкам в строке чисел, вы будете считать в обратном порядке на десятки, чтобы заполнить 2 пропущенных числа для каждой задачи
Тема D: Добавление десятков или единиц к двузначному числу
Учащиеся полагаются на растущее понимание обмена на модель и решают задачи на сложение двузначных чисел с обменом, используя знакомые модели и новые стратегии.
Решите уравнения, которые добавляют или вычитают 1 или 10 с использованием и без моделирования с использованием блоков с основанием 10
В этом упражнении вы будете добавлять однозначные числа к различным двузначным числам меньше 40. Вы будете использовать числовые блоки с основанием 10 для моделирования каждого уравнения сложения
Смоделируйте и решите уравнения сложения, которые добавляют однозначное число к двузначному, используя числовую прямую.
В этом упражнении вы будете складывать однозначные числа с двузначными числами. Вам будет разрешено использовать числовую прямую, чтобы помочь с этими уравнениями сложения
Решите уравнения, которые добавляют однозначное число к двузначному числу (Часть 1)
Вы будете добавлять однозначные числа к двузначным числам в эта деятельность. Однако вам не разрешается использовать числовую прямую или любые другие наглядные пособия, чтобы помочь с этими уравнениями сложения
Выберите соответствующее выражение сложения и сумму
В этом упражнении вы будете добавлять однозначные числа к двузначным числам. Вы будете использовать игровую доску, чтобы решать свои проблемы. Как только вы дойдете до другой стороны игрового поля, вы выиграете.
Вы будете использовать игровую доску, чтобы решать свои проблемы. Как только вы дойдете до другой стороны игрового поля, вы выиграете.
Определите недостающее слагаемое, чтобы добавить его к числу следующего раунда с моделью блоков с основанием 10 и без нее
В этом упражнении вы будете решать, какое число добавьте к данному двузначному числу, чтобы перейти к следующему круглому номеру. Вы будете делать это с помощью и без помощи базовой 10-кубической модели 9.0003
Определите отсутствующее слагаемое, чтобы добавить его к следующему круглому числу, и решите уравнение (Часть 1)
В этом упражнении вы будете решать, какое число добавить к заданному двузначному числу, чтобы перейти к следующему круглому числу после размещение двузначного числа на числовой прямой. Вы будете делать это с помощью числовой строки
Определите недостающее слагаемое, чтобы добавить к следующему округленному числу, и решите уравнение (Часть 2)
В этом упражнении вы будете решать, какое число добавить к задано двузначное число, чтобы перейти к следующему раунду. Вы будете делать это без использования каких-либо наглядных пособий
Вы будете делать это без использования каких-либо наглядных пособий
Определите недостающее слагаемое, чтобы добавить его к следующему круглому числу, и решите уравнение (часть 3)
С помощью числовой строки вы определите, что нужно добавить к заданному двузначному числу, чтобы получить следующее круглое число. Вам также нужно будет выяснить, какая первая цифра этого круглого числа
Моделируйте и решайте двузначные уравнения сложения с обменом, используя блоки с основанием 10
Используя модель куба с основанием 10, вы будете решать уравнения сложения. Вы решите, сколько второго слагаемого потребуется, чтобы получить первое слагаемое для следующего круглого числа. Затем вы добавите оставшуюся сумму, чтобы получить окончательную сумму
Решите уравнения сложения через 10, используя числовую прямую
Используя числовую прямую, вы будете решать уравнения сложения. Вы решите, сколько второго слагаемого потребуется, чтобы получить первое слагаемое для следующего круглого числа. Затем вы сложите оставшиеся блоки, чтобы получить окончательную сумму
Затем вы сложите оставшиеся блоки, чтобы получить окончательную сумму
Решите уравнения сложения через 10, разделив слагаемое, чтобы получить десять
Без использования каких-либо наглядных пособий, вы будете решать уравнения сложения. Вы решите, сколько вторых слагаемых потребуется, чтобы получить первое сложение для следующего круглого числа. Затем вы добавите оставшиеся блоки, чтобы получить окончательную сумму
Решите уравнения для сложения однозначного числа с двузначным (Часть 2)
В этом упражнении вы будете складывать однозначные числа с двузначными числами. Вы будете использовать интерактивную иллюстрацию, чтобы мотивировать вас, когда вы будете решать эти уравнения сложения. Максимальное значение суммы будет 40
Тема E: Добавление десятков и единиц к двузначному числу
Учащиеся синтезируют свои знания из предыдущей темы, чтобы складывать десятки и единицы к двузначному числу. Они поддерживаются знакомой моделью блоков с основанием 10 и пошаговым руководством.
Смоделируйте и решите уравнения сложения двузначных чисел в пределах 40, используя кубики с основанием 10.
В этом упражнении вы будете использовать кубы с основанием 10. Вы будете складывать пары двузначных чисел вместе. Максимальное значение этих сумм будет 40
Решите двузначные уравнения сложения в пределах 40 с использованием и без моделирования с использованием блоков с основанием 10
Для этого задания не будет наглядных пособий. Вы будете складывать пары двузначных чисел вместе. Максимальное значение этих сумм будет 40
Решите уравнения сложения двузначных чисел с заменой путем сложения десятков и единиц по отдельности.
В этом упражнении вы будете складывать пары двузначных чисел. Вы сделаете это, разделив десятки и единицы в числах и сложив их отдельно. Максимальное значение этих сумм будет 40
Решите уравнения сложения двузначных чисел
В этом упражнении вы будете складывать пары двузначных чисел. Вы сделаете это без каких-либо наглядных пособий. Максимальное значение этих сумм будет 40
Максимальное значение этих сумм будет 40
Смоделируйте и решите уравнения сложения 2-значных чисел с перестановкой блоков с основанием 10 (Часть 1)
В этом упражнении вы будете использовать модель куба чисел с основанием 10 для сложения пар двузначных чисел. Вы будете разделять числа на десятки и единицы, используя числовые кубы в качестве наглядного пособия. чисел с использованием кубов с основанием 10. Первое сложение будет разделено на десятки и единицы перед началом каждой задачи. Рассортируйте второе слагаемое по десяткам и единицам перед добавлением пары двузначных чисел
Решите уравнения сложения двузначных чисел с заменой путем сложения десятков и единиц по отдельности.
В этом упражнении вы будете складывать пары двузначных чисел. Вы сделаете это, разделив десятки и единицы в числах и сложив их отдельно. Максимальное значение этих сумм будет 40
Решите уравнения, которые складывают двузначные числа через 10
В этом упражнении вы будете складывать пары двузначных чисел. Вы сделаете это без каких-либо наглядных пособий. Максимальное значение этих сумм, возможно, будет больше 40
Вы сделаете это без каких-либо наглядных пособий. Максимальное значение этих сумм, возможно, будет больше 40
МОДУЛЬ 5. Идентификация, составление и разделение фигур
Тема A: Свойства фигур
Учащиеся изучают основные свойства фигур: линии, замкнутые фигуры, стороны и углы. Они учатся определять треугольники, прямоугольники, квадраты, трапеции и шестиугольники.
Определение линий
Научитесь различать линии. Выберите линии в различных ориентациях из группы, содержащей линии и кривые
Определение изогнутых линий
Научитесь определять кривые. Выберите кривые в различных ориентациях и формах из группы, содержащей линии и кривые
Определение закрытых фигур
Определение открытых и закрытых фигур. Выберите все незамкнутые или закрытые фигуры из набора, содержащего и то, и другое
Определите фигуры с заданным количеством сторон
Выберите все фигуры с заданным количеством сторон из набора, содержащего множество закрытых фигур
Подсчитайте количество сторон и углов фигур
Назовите признаки треугольника, прямоугольника и шестиугольника. Выберите открытую или замкнутую форму и укажите, сколько у нее сторон и углов.
Выберите открытую или замкнутую форму и укажите, сколько у нее сторон и углов.
Определение шестиугольников
Изучите характеристики шестиугольника. Затем выберите те фигуры, которые являются шестиугольниками
Определите треугольники, прямоугольники, квадраты и шестиугольники
Сортируйте треугольники, прямоугольники, квадраты и шестиугольники, нажав на существо, которое ест каждый из этих типов фигур
Определите трапецию
Научитесь определять трапецию. Выберите трапецию из двух четырехугольников, затем укажите атрибуты трапеции
Нарисуйте заданные фигуры
Потренируйтесь рисовать различные фигуры, как указано на доске для колышков
Определите заданные фигуры
Выберите имя многоугольника из двух вариантов
Определите формы повседневных предметов
Дано изображение реального мира объект, выберите правильное название многоугольника из 4 вариантов
Тема Б: Половинки и четверти прямоугольников и кругов
Учащиеся учатся определять и считать равные части в разделенной фигуре. Они узнают названия половин и четвертей и используют эти названия для идентификации фигур, разделенных на части.
Они узнают названия половин и четвертей и используют эти названия для идентификации фигур, разделенных на части.
Определить фигуру, которая разделена на половинки (Уровень 1)
Решить, какая из двух одинаковых или разных фигур разделена на две равные части, называемые половинками
Определить фигуру, которая разделена на половинки (Уровень 2)
Решить какая из двух одинаковых или разных фигур разделена пополам
Определить количество равных частей в разделенной фигуре
Дана фигура, разделенная на равные части, определить общее количество равных частей до 4
Определить фигуру, разделенную на четверти
Решить, какая из двух одинаковых или разных фигур разделена на четыре равные части, называемые четвертями ход и идентификация времени. Они изучают части часов и различные типы обозначения времени: X:XX, X часов, X-тридцать и половина первого X.
Определять части часов и время с точностью до часа на часах
Имея цифровые или аналоговые часы, учащиеся определяют время с точностью до часа, а также часовую и минутную стрелки
Определяют ежедневное и ежечасное течение времени
Понимают, что день длится с полуночи до полуночи, и как выглядит это время на аналоговых часах. Определение времени с точностью до часа по аналоговым часам
Определение времени с точностью до часа по аналоговым часам
Определение времени с точностью до часа на цифровых и аналоговых часах
Определение времени с точностью до часа на цифровых или аналоговых часах. Выберите одни из трех цифровых часов, которые соответствуют времени на аналоговых часах
Определение времени с точностью до часа на аналоговых часах
Выберите одни из трех аналоговых часов, которые показывают заданное время с точностью до часа. Переместите часовую стрелку часов, чтобы показать заданное время.
Определите количество минут на аналоговых часах
Определите, сколько минут прошло на аналоговых часах. Понимать, что в часе 60 минут, а в получасе 30 минут
Определять время с точностью до получаса на аналоговых часах и использовать соответствующий язык (Часть 1)
Учащиеся изучают концепцию получаса на аналоговых часах. Они также изучают язык половины X. Затем учащиеся учатся определять время с точностью до получаса на аналоговых часах
Определять время с точностью до получаса на аналоговых часах и использовать соответствующий язык (Часть 2)
Учащиеся учатся говорить X тридцать в качестве альтернативы половине X.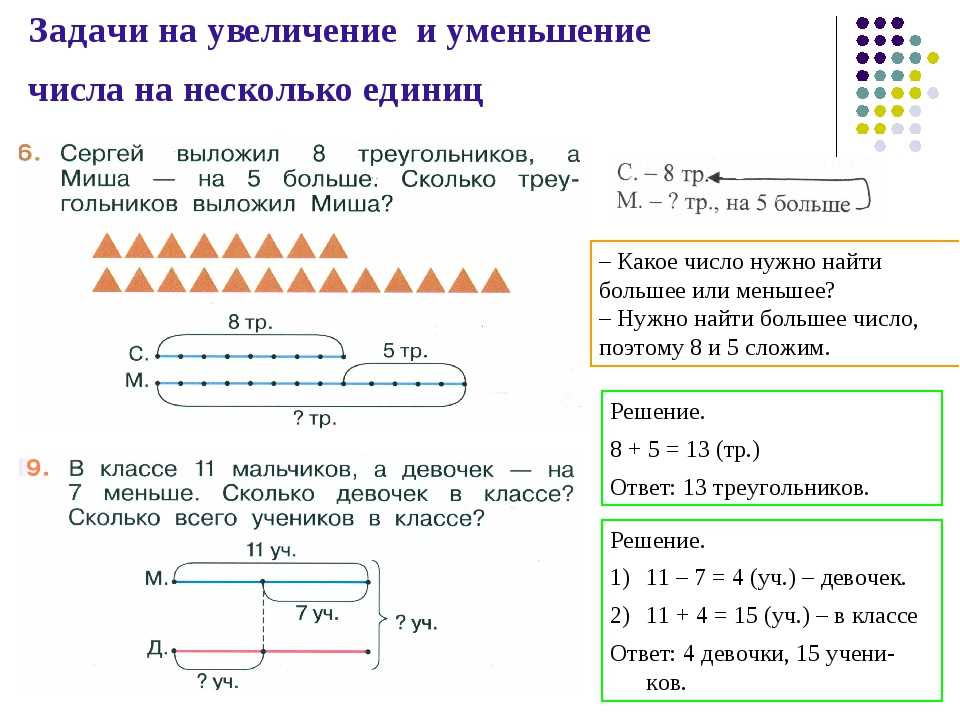 Затем учащиеся тренируются определять время с точностью до получаса на аналоговых часах и выбирать правильное цифровое время
Затем учащиеся тренируются определять время с точностью до получаса на аналоговых часах и выбирать правильное цифровое время
Определять время с точностью до получаса на цифровых и аналоговых часах
Определить время с точностью до получаса на аналоговых и цифровых часах, используя X-тридцать и половину десятого. Показывать время с точностью до часа или получаса на аналоговых часах
Определить время на часах
Определить время до час или полчаса на аналоговых или цифровых часах, набрав или выбрав время. Используйте обозначение X-тридцать, половина первого X, X часов или X:XX
МОДУЛЬ 6. Поместите значение, сравнение, сложение и вычитание до 100
Тема A: Числа до 120
Учащиеся используют знакомые представления (объекты, десятичные кадры, десятичные блоки, числовую прямую, карточки с разрядными значениями, названия чисел и уравнения), чтобы расширить свое понимание разрядных значений на более высокие числа в пределах 100. Они начинают строить свою мысленную модель сто диаграммы, понимая взаимосвязь между числами в столбцах и строках. Они укрепляют понимание того, что двузначные числа состоят из круглого числа (или десятков) плюс единицы.
Они укрепляют понимание того, что двузначные числа состоят из круглого числа (или десятков) плюс единицы.
Определить отсутствующее круглое число до 100 в числовой строке и определить его письменное название
В этом упражнении вы будете использовать числовую прямую. Вы будете называть числа десятками, начиная с нуля и заканчивая 100
Расположите круглые числа, как цифрами, так и прописью, на вертикальной числовой линии
В этом упражнении вы будете размещать круглые числа от нуля до 100 на числе линия. Цифры будут написаны на дирижаблях, которые вы «приземлили» на числовой линии
Определите двузначные суммы на основе блоков с основанием 10 и карточек с номиналом
Для этого задания будут использоваться кубики с основанием 10. Вам будет предоставлено определенное количество 10 кубиков с числами и определенное количество кубиков с отдельными числами, чтобы определить общее количество кубиков с числами 9.0003
Определить 2-значное количество объектов в блоках из десяти кадров или десятичных блоков
Вам будут даны группы из 10 объектов, расположенных в 10-кадрах, а также отдельные объекты за пределами 10-кадров. Затем вы будете использовать 10-фреймы и отдельные объекты для подсчета общего количества объектов. эта деятельность. Вы закончите заполнение как можно большего числа 10-кадров и добавите оставшиеся объекты в объекты, расположенные в 10-кадрах
Затем вы будете использовать 10-фреймы и отдельные объекты для подсчета общего количества объектов. эта деятельность. Вы закончите заполнение как можно большего числа 10-кадров и добавите оставшиеся объекты в объекты, расположенные в 10-кадрах
Представление заданного двузначного числа с помощью блоков с основанием 10
Для этого задания будут использоваться кубы с основанием 10. Вы будете использовать 10-кубические стержни и отдельные кубики с числами, чтобы представить сумму, указанную в каждой задаче
Определить двузначные круглые числа
В этом упражнении вы будете выбирать круглые числа, меньшие или равные 100. Вам будет дана группа чисел, и вам нужно будет выбрать круглые числа из каждой группы
Разложить двузначные числа на круглое число плюс единицы
Для начала этой деятельности вам будет предоставлена серия двузначных чисел до 100. Вы разобьёте каждое число на круглое число и однозначное число
Определите двузначное количество блоков с основанием 10, подсчитав десятки и единицы
Для этого упражнения будет использоваться модель куба числа с основанием 10. Вам будет предоставлено определенное количество 10-кубовых палочек и отдельных числовых кубиков. Затем вы определите, сколько всего кубиков
Вам будет предоставлено определенное количество 10-кубовых палочек и отдельных числовых кубиков. Затем вы определите, сколько всего кубиков
Определить общее количество, считая десятки и единицы, используя разбросанные и неодинаковые предметы в десятикадровых кадрах
Для этого задания будут использоваться группы похожих и непохожих объектов, расположенных внутри и вне 10-кадров. Затем вы подсчитаете общее количество объектов в целом.
Разложите двузначные числа на десятки и единицы с моделью блоков с основанием 10 и без нее
Для этого задания будут использоваться кубы с основанием 10. С помощью этой модели числового куба разложите двузначные числа. Каждое число будет либо представлено числовыми кубами в начале, либо вам придется представлять каждое число числовыми кубами перед 9-м числом.0003
Решите +/- 1 и +/- 10 уравнений с моделью блоков с основанием 10 и без нее
В этом упражнении вы будете прибавлять 10, прибавлять 1, вычитать 1 и вычитать 10 из различных двузначных чисел. . Вы не сможете использовать числовые блоки с основанием 10 для моделирования каждого уравнения. Максимальное значение каждой конечной суммы будет 99
. Вы не сможете использовать числовые блоки с основанием 10 для моделирования каждого уравнения. Максимальное значение каждой конечной суммы будет 99
Считайте вперед и назад в пределах десяти по числовой строке
Числовая строка будет использоваться, чтобы помочь Вам со счетом в прямом и обратном порядке. По мере того, как вы будете считать вперед и назад, вы будете заполнять данные пробелы в числовой строке, предоставленной
Выровняйте разрозненный набор пронумерованных непоследовательных объектов в порядке возрастания
Получив наглядное пособие, вы будете располагать числа в порядке возрастания. Числа в этом упражнении будут меньше 100
Выровняйте разрозненный набор пронумерованных непоследовательных объектов в порядке убывания
С помощью наглядного пособия вы будете располагать числа в порядке убывания. Числа в этом упражнении будут меньше 100
Сравните двузначные суммы с набором из 10, 5 и 1 монет
Имея определенную сумму денег в монетах в 1 цент, 5 центов и 10 центов и группу предметов с различной ценой, вы определите, какой предмет вы можете купить на указанную сумму денег
Определить пропущенные числа на диаграмме сотен
В начале этого задания вам будет предоставлена в основном заполненная таблица чисел в порядке от 1 до 100. Затем вы заполните пропуски недостающими числами
Затем вы заполните пропуски недостающими числами
Определите на 10 меньше, на 10 больше, на 1 меньше и на 1 больше на сотенной диаграмме с ограниченной нумерацией
В начале этого задания вам будет предоставлена слегка заполненная таблица чисел в порядке от 1 до 100. Затем вы заполните пропуски недостающими числами
Добавление круглых чисел с использованием блоков и полос
Для этого упражнения будет использоваться модель кубов с основанием 10. Вы будете добавлять пары двузначных чисел. Максимальное значение каждой суммы будет меньше 100.
Сложение и вычитание круглых чисел
Для этого задания будет использоваться модель кубов с основанием 10. В этом упражнении вы будете добавлять круглые числа. Максимальное значение каждой суммы будет 90
Решите уравнения для сложения двузначных чисел через 10
Сложение пар двузначных чисел будет в центре внимания этого упражнения. Некоторые проблемы связаны с использованием фактов оборота. Если вы ответите на вопрос неправильно, вы будете использовать числовые кубы с основанием 10, чтобы помочь правильно ответить на вопрос проблемы с вычитанием. Вы будете складывать и вычитать круглые числа из некруглых двузначных чисел
Если вы ответите на вопрос неправильно, вы будете использовать числовые кубы с основанием 10, чтобы помочь правильно ответить на вопрос проблемы с вычитанием. Вы будете складывать и вычитать круглые числа из некруглых двузначных чисел
Определите пропущенные числа в столбцах на сотенной диаграмме с ограниченной нумерацией
Сотовая диаграмма будет предоставлена вам в начале этого задания. Вам нужно будет заполнить столбцы этой таблицы, отсчитывая по десяткам в каждом столбце
Определите еще 1 и еще 10 на сотенной диаграмме с ограниченной нумерацией
В этом упражнении вам будет предоставлена сотенная диаграмма. Вы будете добавлять единицу или десять к каждому числу, указанному в таблице, чтобы перейти от одной стороны диаграммы к другой 9.0003
Завершите и решите уравнения, которые добавляют или вычитают круглое число, используя сотенную таблицу.
В этом упражнении вам будет дана сотенная таблица. Вы будете использовать эту таблицу, чтобы помочь с добавлением круглых чисел к некруглым числам
Определить пропущенные числа в таблице сотен и разложить их на десятки и единицы
Для этого упражнения вам будет предоставлена таблица сотен. Вы определите, какое число должно быть введено в пустое место на сотенной диаграмме. Затем вы разложите это же число на десятки и единицы
Вы определите, какое число должно быть введено в пустое место на сотенной диаграмме. Затем вы разложите это же число на десятки и единицы
Считайте вперед от 100 и выше 100 в числовой строке
Вам будет предоставлена числовая строка с большинством заполненных значений. Вам нужно будет заполнить пробелы, продвигаясь вперед по числовой строке, используя числа, указанные на числовая строка уже. Вы будете вводить значения, которые время от времени превышают 100
Посчитайте в обратном порядке от 100 и выше 100 в числовой строке
Вам будет предоставлена числовая строка с большинством заполненных значений. Вам нужно будет заполнить пробелы, перемещая назад по числовой строке, используя числа, уже представленные в числовой строке. Вы будете предоставлять значения, которые превышают 100 раз в 9 раз.0003
Определите отсутствующее трехзначное число в числовой строке и его письменное название.
Для этого действия будет предоставлена числовая строка с уже помеченными большинством значений. Для каждого вопроса вы будете заполнять одно пропущенное значение. Затем вы будете называть число словами
Для каждого вопроса вы будете заполнять одно пропущенное значение. Затем вы будете называть число словами
Определить общее количество объектов в десяти кадрах за пределами 100
Вам будут предоставлены объекты, предварительно рассортированные по 10 кадрам, и некоторые объекты, которые отложены в сторону сами по себе . Вам нужно будет определить, сколько объектов находится в коробках и сколько в стороне, чтобы определить общее количество объектов
Подсчитайте палочки с основанием 10 сверх 100
Кубики с основанием 10, сгруппированные в палочки длиной 10 кубов, будут доступны в начале этого задания. Затем вам нужно будет определить, сколько всего кубиков. Каждый раз ответом будет круглое число.
Определяйте суммы, превышающие 100, используя плоскость с основанием 10, стержни и кубики
Кубики с основанием 10, сгруппированные в 10 кубиков, стержни вместе с отдельными кубиками будут даны вам в начале эта деятельность. Используйте оба этих наглядных пособия, чтобы подсчитать общее количество кубиков. Некоторые ответы на вопросы будут более 100
Некоторые ответы на вопросы будут более 100
Тема B: Прибавление к 100 с использованием разрядных значений
Учащиеся используют знакомые блоки с основанием 10, числовой ряд и уравнения для работы с круглыми числами. Для решения задач они полагаются на счет, позиционное значение и навыки сложения/вычитания. Учащиеся используют знакомые манипуляторы для решения задач на сложение двузначных чисел с обменом и без обмена. Они также решают задачи на вычитание двузначных чисел без обмена.
Решайте уравнения, прибавляя или вычитая 10 из круглого числа 9 или из него0391
В этом упражнении вы будете прибавлять и вычитать 10 из круглых чисел. Вы будете использовать кубы с основанием 10, чтобы помочь с некоторыми задачами, но некоторые из задач не позволяют использовать эти кубики
Сложение и вычитание круглых чисел с моделью блоков с основанием 10 и без нее
Сложение и вычитание круглых чисел будет в центре внимания этого занятия. Вы будете использовать числовые кубики с основанием 10, чтобы помочь с некоторыми задачами, но некоторые задачи не позволяют использовать эти кубики
Запишите и решите уравнения, которые добавляют круглое число к двузначному числу на основе модели блоков с основанием 10.

Целью этого упражнения будет добавление круглого числа к другим двузначным числам. Вы смоделируете эти уравнения сложения, используя кубы с основанием 10
Запишите и решите уравнения, которые вычитают круглое число из двузначного числа на основе модели блоков с основанием 10
Вычитание круглого числа из других двузначных чисел будет основной акцент в этом упражнении. Вы смоделируете эти уравнения сложения, используя числовые кубы с основанием 10 9.0003
Моделируйте и решайте уравнения, которые добавляют круглое число к двузначному числу, используя блоки с основанием 10. Вы будете добавлять круглые числа к другим двузначным числам.
Моделирование и решение уравнений, которые складывают два двузначных числа с использованием блоков с основанием 10.
Моделирование и решение уравнений сложения будет основной целью этого занятия. Вы будете складывать пары двузначных чисел вместе
Моделирование и решение уравнений сложения двух двузначных чисел с использованием блоков с основанием 10.

Моделирование и решение уравнений сложения. Сложите пары двузначных чисел вместе. Одно из двух чисел будет смоделировано для вас с помощью кубов с основанием 10. Определите, сколько кубиков вам нужно для представления второго числа, прежде чем складывать пару чисел.
Смоделируйте и решите уравнения для сложения двух двузначных чисел с использованием блоков с основанием 10.
Смоделируйте и решите уравнения сложения. Сложите пары двузначных чисел вместе. Одно из двух чисел будет смоделировано для вас с помощью кубов с основанием 10. Определите, сколько кубиков вам нужно для представления второго числа, прежде чем складывать пару чисел
Сложите 10 с помощью десятикадра (в пределах 100)
Для начала этого действия вам будет предоставлено определенное количество объектов. Какое-то их количество будет помещено в 10-кадровые коробки, а какое-то нет. Вам необходимо определить, сколько всего объектов
Смоделируйте и решите уравнения сложения двузначных чисел с обменом и без, используя блоки с основанием 10.

Кубы числа с основанием 10 будут использоваться для сложения пар двузначных чисел в этом упражнении. Вы будете сортировать кубы по столбцам десятков и единиц, прежде чем в конечном итоге сложить пару чисел вместе
Моделируйте и решайте уравнения сложения двузначных чисел с обменом и без, используя блоки с основанием 10.
Моделируйте и решайте уравнения сложения. Сложите пары двузначных чисел вместе. Одно из двух чисел будет смоделировано для вас с помощью кубов с основанием 10. Определите, сколько кубиков вам нужно для представления второго числа, прежде чем складывать пару чисел
Решить уравнения сложения двузначных чисел с обменом и без обмена путем сложения десятков и единиц по отдельности
Сложение пар из двух двузначных чисел — цель этого упражнения. . Однако числа будут разделены на десятки и единицы, чтобы вы могли добавить их отдельно, прежде чем вычислить окончательную сумму
Тема C: Монеты и их номиналы
Учащиеся изучают орел и решку монеты пенни, никеля, десятицентовой монеты и четвертака. Они узнают ценность каждой монеты, как считать их коллекцию и как считать смешанную коллекцию монет. Учащиеся сопоставляют изображение монеты, имя и номинал.
Они узнают ценность каждой монеты, как считать их коллекцию и как считать смешанную коллекцию монет. Учащиеся сопоставляют изображение монеты, имя и номинал.
Определите монету и ее стоимость
Изучите внешний вид обеих сторон монеты. Поймите его стоимость как один цент и рассчитайте общую стоимость до 6 пенни
Определите десятицентовую монету и ее стоимость
Исследуйте внешний вид монеты с обеих сторон. Поймите ее стоимость как десять центов и рассчитайте общую стоимость до 6 десятицентовиков
Сопоставьте пенни или десятицентовую монету с ее названием, внешним видом и стоимостью
Выберите название монеты, изображение и достоинство, которые все представляют десятицентовую монету или пенни
Определить общую стоимость набора десятицентовиков и пенни
При заданном наборе десятицентовиков и пенни введите общую стоимость
Обмен одной десятицентовой монеты на десять пенни
Считайте и обменивайте пенни на десять центов. Используйте пенни и десятицентовики, чтобы показать в общей сложности 12 центов двумя разными способами.
Используйте пенни и десятицентовики, чтобы показать в общей сложности 12 центов двумя разными способами.
Определить пятицентовую монету и ее стоимость
Изучить внешний вид обеих сторон пятицентовой монеты. Поймите ее стоимость как пять центов и рассчитайте общую стоимость до 6 пятицентовых монет
Сопоставьте пенни, пятицентовик или десять центов с их названием, внешним видом и стоимостью (Часть 1)
Определите, соответствует ли название монеты показанному изображению. Сопоставьте пенни, десять центов и пятицентовиков с их названием и номиналом 9.0003
Сопоставьте пенни, никель или десятицентовик с их названием, внешним видом и номиналом (Часть 2)
Определите, соответствует ли показанная монета заданному названию. Сопоставьте пенни, десятицентовики и пятицентовые монеты с их названием и номиналом
Определите пенни, пятицентовые монеты или десятицентовые монеты по цвету или размеру
Определите пенни, пятицентовые монеты и десятицентовые монеты из коллекции монет, даже если детали монет размыты
Обмен пенни, пятицентовика и десятицентовика
Подсчет и обмен пенни, пятицентовика и десятицентовика. Подсчитайте сумму коллекции пятаков и пенни
Подсчитайте сумму коллекции пятаков и пенни
Показать заданную сумму, используя пятаки и пенни
Получив общее значение, выберите пятаки и пенни, чтобы получить сумму
Определите четвертак и его стоимость
Исследуйте внешний вид обеих сторон четверти. Поймите его стоимость как двадцать пять центов. Сортировка пенни, пятицентовика, десятицентовика и четвертака по стоимости
120 задачек по математике для учащихся 1-8 классов
Вы сидите за своим столом, готовый составить математическую викторину, тест или задание. Вопросы перетекают в документ, пока вы не нажмете раздел для текстовых задач.
Всплеск творчества не помешал бы. Но не приходит.
Независимо от того, являетесь ли вы учителем 3-го или 8-го класса, готовящим учеников к старшей школе, перевод математических понятий в примеры из реального мира, безусловно, может быть проблемой.
Этот ресурс — источник вашего творчества. Содержит примеры и шаблоны математических задач для 1-8 классов.
Всего 120 примеров.
Список примеров дополнен советами по созданию увлекательных и сложных математических задач.
120 Проблемы с математическим словом, категория навыка Дополнительные проблемыЛучше всего для: 1 -й класс, 2 -й класс
1. Добавление до 100219. 1 из ее бросков попал в обруч. 2 ее броска не попали в кольцо. Сколько всего было выстрелов?
2. Добавление к 20: У Адрианны есть 10 жевательных резинок, которыми она может поделиться со своими друзьями. На всех ее друзей не хватило жвачки, поэтому она пошла в магазин, чтобы купить еще 3 штуки жвачки. Сколько жевательной резинки сейчас у Адрианны?
3. Добавление к 100: У Адрианны есть 10 жевательных резинок, которыми она может поделиться со своими друзьями. Жвачки не хватило на всех ее друзей, поэтому она пошла в магазин и купила 70 штук клубничной жвачки и 10 штук жевательной резинки. Сколько жевательной резинки сейчас у Адрианны?
Сколько жевательной резинки сейчас у Адрианны?
4. Добавление Чуть более 100: В ресторане 175 обычных стульев и 20 детских стульев. Сколько всего стульев в ресторане?
5. Прибавление к 1000: Сколько печенья вы продали, если продали 320 шоколадных и 270 ванильных печений?
6. Прибавление до 10 000 и более: В магазине товаров для хобби обычно продается 10 576 коллекционных карточек в месяц. В июне магазин товаров для хобби продал на 15 498 коллекционных карточек больше, чем обычно. В целом, сколько коллекционных карточек продал магазин товаров для хобби в июне?
7. Добавление 3 чисел: У Билли дома было 2 книги. Он пошел в библиотеку, чтобы взять еще 2 книги. Затем он купил 1 книгу. Сколько книг сейчас у Билли?
8. Добавление 3 чисел до 100 и более: Эшли купила большой пакет конфет. В пакете было 102 синих леденца, 100 красных леденцов и 94 зеленых леденца. Сколько всего конфет было?
Сколько всего конфет было?
Подходит для: 1-й класс, второй класс
9. Вычитание до 10: Всего в пиццерии было 3 пиццы. Клиент купил 1 пиццу. Сколько пицц осталось?
10. Вычитание до 20: Ваша подруга сказала, что у нее 11 наклеек. Когда ты помог ей убрать стол, у нее было всего 10 наклеек. Сколько наклеек не хватает?
11. Вычитание до 100: У Адрианны есть 100 жевательных резинок, которыми она может поделиться со своими друзьями. Когда она пошла в парк, она поделилась 10 кусочками клубничной жвачки. Когда она вышла из парка, Адрианна поделилась еще 10 кусочками жевательной резинки. Сколько жевательной резинки сейчас у Адрианны?
Решайте математические задачи с помощью Prodigy Math
Присоединяйтесь к миллионам учителей, использующих Prodigy, чтобы сделать обучение увлекательным и разнообразным, отвечая на внутриигровые вопросы, включая математические задачи с 1 по 8 класс!
Посмотрите, как работает Prodigy Math!
12. Вычитание Чуть больше 100: Ваша команда набрала 123 очка. В первом тайме было набрано 67 очков. Сколько голов было забито во втором тайме?
Вычитание Чуть больше 100: Ваша команда набрала 123 очка. В первом тайме было набрано 67 очков. Сколько голов было забито во втором тайме?
13. Вычитание до 1000: У Натана большая муравьиная ферма. Он решил продать некоторых из своих муравьев. Он начал с 965 муравьев. Он продал 213 штук. Сколько у него сейчас муравьев?
14. Вычитание до 10 000 и более: В магазине товаров для хобби обычно продается 10 576 коллекционных карточек в месяц. В июле магазин товаров для хобби продал в общей сложности 20 777 коллекционных карточек. На сколько коллекционных карточек магазин товаров для хобби продал в июле по сравнению с обычным месяцем?
15. Вычитание 3 чисел: У Шарлин была упаковка из 35 карандашей. Она отдала 6 своей подруге Терезе. Она дала 3 своей подруге Мэнди. Сколько карандашей осталось у Шарлин?
16. Вычитание 3 чисел до 100 и выше: Эшли купила большой пакет конфет, чтобы поделиться с друзьями. Всего было 296 конфет. Она дала Мариссе 105 конфет. Она также подарила Кайле 86 конфет. Сколько конфет осталось?
Всего было 296 конфет. Она дала Мариссе 105 конфет. Она также подарила Кайле 86 конфет. Сколько конфет осталось?
Подходит для: 2-й класс, 3-й класс
17. Умножение однозначных целых чисел: Адрианне нужно разрезать сковороду с пирожными на кусочки. Она нарезает 6 ровных столбиков и 3 ровных ряда на сковороду. Сколько у нее брауни?
18. Умножение двузначных целых чисел: Кинотеатр имеет 25 рядов сидений по 20 мест в каждом ряду. Сколько мест всего?
19. Умножение целых чисел, оканчивающихся на 0: Компания по производству одежды производит 4 разных вида толстовок. Каждый год компания производит 60 000 толстовки каждого вида. Сколько толстовок производит компания каждый год?
20. Умножение 3 целых чисел: Каменщик укладывает кирпичи в 2 ряда по 10 кирпичей в каждом ряду. Сверху каждого ряда уложена стопка из 6 кирпичей. Сколько всего кирпичей?
Сколько всего кирпичей?
21. Умножение 4 целых чисел: Кейли зарабатывает 5 долларов в час, доставляя газеты. Она доставляет газеты 3 раза в неделю по 4 часа. Сколько денег заработает Кейли после доставки газет в течение 8 недель?
Проблемы со словами на делениеПодходит для: 3-й класс, 4-й класс, 5-й класс
22. Деление однозначных целых чисел: Если у вас есть 4 конфеты, разделенные поровну на 2 пакета, сколько конфет в каждом пакете?
23. Деление двузначных целых чисел: Если у вас есть 80 билетов на ярмарку и каждая поездка стоит 5 билетов, сколько поездок вы можете совершить?
24. Деление чисел, оканчивающихся на 0: У школы есть 20 000 долларов на покупку нового компьютерного оборудования. Если каждая единица оборудования стоит 50 долларов, сколько всего единиц оборудования может купить школа?
25. Деление 3 целых чисел: Мелисса покупает 2 упаковки теннисных мячей за 12 долларов. Всего вместе 6 теннисных мячей. Сколько стоит 1 упаковка теннисных мячей? Сколько стоит 1 теннисный мяч?
Всего вместе 6 теннисных мячей. Сколько стоит 1 упаковка теннисных мячей? Сколько стоит 1 теннисный мяч?
26. Устный перевод Остатки: Итальянский ресторан получает партию из 86 котлет из телятины. Если для приготовления блюда требуется 3 котлеты, то сколько котлет останется в ресторане после приготовления максимально возможного количества блюд?
Словесные задачи со смешанными операциямиПодходит для: 3-й класс, 4-й класс, 5-й класс
27. Смешивание сложения и вычитания: В библиотеке 235 книг. В понедельник выносят 123 книги. Во вторник привезли 56 книг. Сколько книг сейчас?
28. Смешивание умножения и деления: Есть группа из 10 человек, которые заказывают пиццу. Если каждый человек получит по 2 ломтика, а в каждой пицце по 4 ломтика, сколько пицц он должен заказать?
29. Смешивание умножения, сложения и вычитания: У Ланы есть 2 мешочка, по 2 шарика в каждом. У Маркуса есть 2 мешка по 3 шарика в каждом. Сколько еще шариков у Маркуса?
У Маркуса есть 2 мешка по 3 шарика в каждом. Сколько еще шариков у Маркуса?
30. Смешивание, сложение и вычитание: У Ланы есть 3 мешка с одинаковым количеством шариков, всего 12 шариков. У Маркуса есть 3 мешка с одинаковым количеством шариков, всего 18 шариков. Сколько еще шариков у Маркуса в каждом мешке?
Упорядочивание и задачи со смыслом чиселПодходит для: 2-й класс, 3-й класс
31. Счет для предварительного просмотра Умножение: В вашем классе есть 2 классные доски. Если на каждую доску нужно 2 куска мела, сколько всего вам понадобится?
32. Подсчет до предварительного просмотра: В вашем классе есть 3 классные доски. На каждой доске по 2 мелка. Это означает, что всего имеется 6 кусочков мела. Если убрать с каждой доски по 1 кусочку мела, сколько всего их будет?
33. Составление чисел: Какое число 6 десятков и 10 единиц?
34. Угадывание чисел: У меня 7 в разряде десятков. У меня четное число в разряде единиц. У меня меньше 74. Какой у меня номер?
Угадывание чисел: У меня 7 в разряде десятков. У меня четное число в разряде единиц. У меня меньше 74. Какой у меня номер?
35. Нахождение Ордена: В хоккейном матче Митчелл набрал больше очков, чем Уильям, но меньше очков, чем Остон. Кто набрал больше всего очков? Кто набрал меньше всего очков?
Задачи на дробиПодходит для: 3-й класс, 4-й класс, 5-й класс, 6-й класс
36. Нахождение частей группы: Джулия посетила 10 домов на своей улице на Хэллоуин. 5 домов подарили ей плитку шоколада. Какая часть домов на улице Юли подарила ей плитку шоколада?
37. Нахождение дробей единиц измерения: Хизер рисует портрет своей лучшей подруги Лизы. Для удобства она делит портрет на 6 равных частей. Какая дробь представляет каждую часть портрета?
38. Сложение дробей с одинаковыми знаменателями: Ной каждый день проходит ⅓ километра до школы. Он также проходит ⅓ километра, чтобы вернуться домой после школы. Сколько всего километров он прошел?
Он также проходит ⅓ километра, чтобы вернуться домой после школы. Сколько всего километров он прошел?
39. Вычитание дробей с одинаковыми знаменателями: На прошлой неделе Уитни подсчитала, сколько коробок сока она ела на школьные обеды. У нее было ⅗ случая. На этой неделе дело сократилось до ⅕. Сколько из ящика выпила Уитни?
40. Сложение целых чисел и дробей с одинаковыми знаменателями: В обеденное время кафе-мороженое подавало 6 ¼ шариков шоколадного мороженого, 5 ¾ шариков ванильного и 2 ¾ шарика клубничного. Сколько шариков мороженого подали в кафе?
41. Вычитание целых чисел и дробей с одинаковыми знаменателями: На вечеринку Хайме приготовила 5 ⅓ бутылок колы для своих друзей. Она выпила ⅓ бутылки сама. Ее друзья выпили 3 ⅓. Сколько бутылок колы осталось у Хайме?
42. Сложение дробей с разными знаменателями: 902:19 Кевин выполнил ½ школьного задания. В тот вечер, когда он был дома, он выполнил ⅚ другого задания. Сколько заданий выполнил Кевин?
Сколько заданий выполнил Кевин?
43. Вычитание дробей с разными знаменателями: Упаковывая школьные обеды для своих детей, Пэтти использовала ⅞ упаковки ветчины. Она также использовала ½ упаковки индейки. Насколько больше ветчины, чем индейки, съела Пэтти?
44. Умножение дробей: Во время урока физкультуры в среду ученики пробежали ¼ километра. В четверг они пробежали на ½ меньше километров, чем в среду. Сколько километров пробежали студенты в четверг? Запишите ответ в виде дроби.
45. Разделение на дроби: Производитель одежды использует ⅕ бутылки цветного красителя для изготовления одной пары брюк. Вчера производитель использовал ⅘ бутылки. Сколько пар брюк сделал производитель?
46. Умножение дробей на целые числа: На этой неделе Марк выпил ⅚ пакета молока. Фрэнк выпил в 7 раз больше молока, чем Марк. Сколько пакетов молока выпил Фрэнк? Запишите ответ в виде дроби, целого или смешанного числа.
Подходит для: 4-й класс, 5-й класс
47. Добавление десятичных знаков: У вас есть 2,6 грамма йогурта в вашей миске, и вы добавляете еще одну ложку 1,3 грамма. Сколько йогурта у вас всего?
48. Вычитание десятичных дробей: У Джеммы было 25,75 грамма глазури, чтобы сделать торт. Она решила использовать только 15,5 граммов глазури. Сколько глазури осталось у Джеммы?
49. Умножение десятичных дробей на целые числа: 902:19 Каждый день Маршалл проходит в общей сложности 0,9 км в школу и обратно. Через 4 дня сколько километров он пройдет?
50. Деление десятичных дробей на целые числа: Чтобы сделать Пизанскую башню из спагетти, миссис Робинсон купила 2,5 кг спагетти. Всего ее ученики смогли построить 10 падающих башен. Сколько килограмм спагетти нужно, чтобы сделать 1 падающую башню?
51. Сложение и вычитание десятичных дробей: У Рокко в холодильнике 1,5 литра апельсиновой газировки и 2,25 литра виноградной газировки. У Антонио есть 1,15 литра апельсиновой газировки и 0,62 литра виноградной газировки. Насколько больше газировки у Рокко, чем у Анджело?
У Антонио есть 1,15 литра апельсиновой газировки и 0,62 литра виноградной газировки. Насколько больше газировки у Рокко, чем у Анджело?
52. Смешивание умножения и деления десятичных дробей: 4 дня в неделю Лаура занимается боевыми искусствами по 1,5 часа. Учитывая, что неделя состоит из 7 дней, каково ее среднее время тренировок в день каждую неделю?
Сравнение и упорядочивание текстовых задачПодходит для: Детский сад, 1-й класс, 2-й класс
У кого больше?
54. Сравнение двузначных целых чисел: У вас 50 конфет, а у вашего друга 75 конфет. У кого больше?
55. Сравнение различных переменных: На детской площадке 5 баскетбольных мячей. На площадке 7 футбольных мячей. Есть еще баскетбольные или футбольные мячи?
56. Последовательность однозначных целых чисел: У Эрика 0 наклеек. Каждый день он получает еще 1 наклейку. Сколько дней до того, как он получит 3 стикера?
Сколько дней до того, как он получит 3 стикера?
57. Счет с пропуском по нечетным числам: 902:19 Натали начала с 5. Она считала пятерками. Могла ли она назвать цифру 20?
58. Счет с пропуском по четным числам: Наташа начала с 0. Она считала с пропуском восьмерками. Могла ли она назвать число 36?
59. Последовательность двузначных чисел: Каждый месяц Джереми добавляет одинаковое количество карточек в свою коллекцию бейсбольных карточек. В январе у него было 36. 48 в феврале. 60 марта. Сколько бейсбольных карточек будет у Джереми в апреле?
Проблемы со словами на времяПодходит для: 1-й класс, 2-й класс
66. Преобразование часов в минуты: Джереми помогал своей маме в течение 1 часа. Сколько минут он помогал ей?
69. Добавление времени: Если вы просыпаетесь в 7:00 и вам требуется 1 час 30 минут, чтобы собраться и дойти до школы, в какое время вы доберетесь до школы?
70. Время вычитания: Если поезд отправляется в 14:00. и прибывает в 16:00, сколько времени пассажиры находились в поезде?
Время вычитания: Если поезд отправляется в 14:00. и прибывает в 16:00, сколько времени пассажиры находились в поезде?
71. Поиск времени начала и окончания: Ребекка вышла из магазина своего отца, чтобы пойти домой без двадцати семь вечера. Через сорок минут она была дома. Во сколько она пришла домой?
Задачи на деньгиПодходит для: 1-й класс, 2-й класс, 3-й класс, 4-й класс, 5-й класс
60. Добавление денег: Томас и Мэтью копят деньги, чтобы вместе купить видеоигру . Томас сэкономил 30 долларов. Мэтью сэкономил 35 долларов. Сколько денег они накопили вместе в общей сложности?
61. Вычитание денег: Томас накопил 80 долларов. Он использует свои деньги, чтобы купить видеоигру. Видеоигра стоит 67 долларов. Сколько денег у него осталось?
62. Умножение денег: Тим получает 5 долларов за доставку газеты. Сколько денег останется у него после доставки бумаги 3 раза?
63. Делим деньги: Роберт потратил $184,59 на покупку 3 хоккейных клюшек. Если каждая хоккейная клюшка стоила одинаково, сколько стоила 1?
Делим деньги: Роберт потратил $184,59 на покупку 3 хоккейных клюшек. Если каждая хоккейная клюшка стоила одинаково, сколько стоила 1?
64. Сложение денег с десятичными знаками: Вы пошли в магазин и купили жвачку за 1,25 доллара и присоску за 0,50 доллара. Сколько у вас было всего?
65. Вычитание денег с десятичной дробью: Вы пришли в магазин с 5,50 долларами. Вы купили жевательную резинку за 1,25 доллара, плитку шоколада за 1,15 доллара и присоску за 0,50 доллара. Сколько денег у вас осталось?
67. Применение пропорциональных отношений к деньгам: Джейкоб хочет пригласить 20 друзей на свой день рождения, что будет стоить его родителям 250 долларов. Если вместо этого он решит пригласить 15 друзей, сколько денег это будет стоить его родителям? Предположим, что зависимость прямо пропорциональна.
68. Применение процентов к деньгам: Ретта положила 100 долларов на банковский счет, который приносит 20% годовых. Сколько процентов будет накоплено за 1 год? И если она не будет снимать деньги, сколько денег будет на счету через 1 год?
Сколько процентов будет накоплено за 1 год? И если она не будет снимать деньги, сколько денег будет на счету через 1 год?
Подходит для: 1-й класс, 2-й класс, 3-й класс, 4-й класс
72. Сравнение измерений: сантиметров — линейка Cassandra2. Апрельская линейка имеет длину 30 сантиметров. На сколько сантиметров длиннее линейка апреля?
73. Контекстуальные измерения: Представьте себе школьный автобус. Какая единица измерения лучше всего описывает длину автобуса? Сантиметры, метры или километры?
74. Добавление измерений: Папа Миши хочет попытаться сэкономить деньги на бензине, поэтому он следит за тем, сколько он использует. В прошлом году папа Миши израсходовал 100 литров бензина. В этом году ее папа израсходовал 90 литров бензина. Сколько всего газа он израсходовал за два года?
75. Вычитание измерений: Отец Миши хочет попытаться сэкономить на бензине, поэтому он следит за тем, сколько он использует. За последние два года папа Миши израсходовал 200 литров бензина. В этом году он израсходовал 100 литров газа. Сколько газа он использовал в прошлом году?
За последние два года папа Миши израсходовал 200 литров бензина. В этом году он израсходовал 100 литров газа. Сколько газа он использовал в прошлом году?
76. Умножение объема и массы: Кира хочет, чтобы у нее были крепкие кости, поэтому она выпивает 2 литра молока каждую неделю. Через 3 недели сколько литров молока выпьет Кира?
77. Разделение объема и массы: Лилиан занимается садоводством, поэтому она купила 1 кг земли. Она хочет равномерно распределить почву между своими двумя растениями. Сколько получит каждое растение?
78. Преобразование массы: Ингер идет в продуктовый магазин и покупает 3 тыквы весом 500 грамм каждая. Сколько килограммов тыквы купила Ингер?
79. Преобразование Объем: Шад имеет прилавок с лимонадом и продает 20 чашек лимонада. В каждой чашке было 500 миллилитров. Сколько всего литров Шад продал?
80. Преобразование Длина: Стейси и Милда сравнивают свой рост. Стейси ростом 1,5 метра. Милда на 10 сантиметров выше Стейси. Какой рост у Мильды в сантиметрах?
Стейси ростом 1,5 метра. Милда на 10 сантиметров выше Стейси. Какой рост у Мильды в сантиметрах?
81. Понимание расстояния и направления: Автобус отправляется из школы, чтобы отвезти учащихся на экскурсию. Автобус проезжает 10 км на юг, 10 км на запад, еще 5 км на юг и 15 км на север. Чтобы вернуться в школу, в каком направлении должен ехать автобус? Сколько километров он должен пройти в этом направлении?
Соотношения и процентные задачиПодходит для: 4 класс, 5 класс, 6 класс
82. В поисках пропавшего номера: Соотношение трофеев Дженни и трофеев Мередит составляет 7:4. У Дженни 28 трофеев. Сколько их у Мередит?
83. Поиск недостающих номеров: Соотношение трофеев Дженни и трофеев Мередит составляет 7:4. Разница между числами 12. Что это за числа?
84. Сравнение соотношений: В школьном младшем оркестре 10 саксофонистов и 20 трубачей. В старшем оркестре школы 18 саксофонистов и 29трубачи. В какой группе больше трубачей и саксофонистов?
В старшем оркестре школы 18 саксофонистов и 29трубачи. В какой группе больше трубачей и саксофонистов?
85. Определение процентов: Мэри опросила учеников своей школы, чтобы узнать, какие у них любимые виды спорта. Из 1200 студентов 455 назвали хоккей своим любимым видом спорта. Какой процент студентов назвал хоккей своим любимым видом спорта?
86. Определение процента изменения: Десять лет назад население Оквилля составляло 67 624 человека. Теперь он на 190% больше. Какова численность населения Оквилля в настоящее время?
87. Определение процентов числа: На стойке проката коньков 60% из 120 коньков предназначены для мальчиков. Если остальные коньки для девочек, то сколько их?
88. Вычисление средних значений: В течение 4 недель Уильям работал волонтером в качестве помощника на уроках плавания. В первую неделю он работал волонтером 8 часов. Он добровольно работал 12 часов на второй неделе и еще 12 часов на третьей неделе. На четвертой неделе он вызвался на 9 часов. Сколько часов в среднем он работал волонтером в неделю?
На четвертой неделе он вызвался на 9 часов. Сколько часов в среднем он работал волонтером в неделю?
Подходит для: 4-й класс, 5-й класс, 6-й класс, 7-й класс
шоу, поэтому он осматривает всех мальчиков. Будет ли выборка репрезентативной или необъективной?
90. Понимание осязаемой вероятности: На гранях кубика с правильным числом указаны числа 1, 2, 3, 4, 5 и 6. Вы бросаете кубик 12 раз. Сколько раз вы должны выбросить 1?
91. Изучение дополнительных событий: Числа от 1 до 50 в шляпе. Если вероятность выпадения четного числа равна 25/50, какова вероятность НЕ выпадения четного числа? Выразите эту вероятность дробью.
92. Исследование Экспериментальная Вероятность: Магазин пиццы недавно продал 15 пицц. 5 из этих пицц были пепперони. Если ответить дробью, какова экспериментальная вероятность того, что следующей пиццей будет пепперони?
93. Знакомство с отношениями данных: Маурита и Феличе проходят по 4 теста. Вот результаты 4 тестов Мауриты: 4, 4, 4, 4. Вот результаты 3 из 4 тестов Феличе: 3, 3, 3. Если среднее значение Мауриты по 4 тестам на 1 балл выше, чем у Феличе, то оценка 4-го теста Феличе?
Знакомство с отношениями данных: Маурита и Феличе проходят по 4 теста. Вот результаты 4 тестов Мауриты: 4, 4, 4, 4. Вот результаты 3 из 4 тестов Феличе: 3, 3, 3. Если среднее значение Мауриты по 4 тестам на 1 балл выше, чем у Феличе, то оценка 4-го теста Феличе?
94. Введение пропорциональных отношений: Магазин А продает 7 фунтов бананов за 7 долларов. Магазин B продает 3 фунта бананов за 6 долларов. В каком магазине выгоднее?
95. Написание уравнений для пропорциональных отношений: Лайонел любит футбол, но не может заставить себя тренироваться. Таким образом, он стимулирует себя с помощью видеоигр. Существует пропорциональная зависимость между количеством упражнений, которые выполняет Лайонел в разрешении x , и тем, сколько часов он играет в видеоигры в разрешении и . Когда Лайонел выполняет 10 упражнений, он играет в видеоигры 30 минут. Напишите уравнение связи между x и и .
Геометрические текстовые задачиПодходит для: 4-й класс, 5-й класс, 6-й класс, 7-й класс, 8-й класс
96. Знакомство с периметром: В театре стоят 4 стула. Есть 5 рядов. Используя строки в качестве единицы измерения, что такое периметр?
Знакомство с периметром: В театре стоят 4 стула. Есть 5 рядов. Используя строки в качестве единицы измерения, что такое периметр?
97. Знакомство с площадью: В театре стоят 4 стула в ряд. Есть 5 рядов. Сколько всего стульев?
98. Вводный том: Аарон хочет знать, сколько конфет может поместиться в его контейнере. Контейнер имеет высоту 20 см, длину 10 см и ширину 10 см. Каков объем контейнера?
99. Понимание двухмерных фигур: Кевин рисует фигуру с 4 равными сторонами. Какую фигуру он нарисовал?
100. Нахождение периметра двумерных фигур: Митчелл записал вопросы домашнего задания на квадратном листе бумаги. Каждая сторона бумаги равна 8 сантиметрам. Что такое периметр?
101. Определение площади двумерных фигур: Одна торговая карточка имеет длину 9 сантиметров и ширину 6 сантиметров. Какова его площадь?
102. Понимание трехмерных фигур: Марта рисует фигуру с 6 квадратными гранями. Какую фигуру она нарисовала?
Какую фигуру она нарисовала?
103. Определение площади поверхности трехмерных фигур: Какова площадь поверхности куба, имеющего ширину 2 см, высоту 2 см и длину 2 см?
104. Определение объема 3D-фигур: Контейнер для конфет Аарона имеет высоту 20 сантиметров, длину 10 сантиметров и ширину 10 сантиметров. Контейнер Брюса имеет высоту 25 сантиметров, длину 9 сантиметров и ширину 9 сантиметров. Найдите объем каждой емкости. В зависимости от объема, чей контейнер может вместить больше конфет?
105. Определение прямоугольных треугольников: Треугольник имеет следующие длины сторон: 3 см, 4 см и 5 см. Является ли этот треугольник прямоугольным?
106. Определение равносторонних треугольников: Треугольник имеет следующие длины сторон: 4 см, 4 см и 4 см. Что это за треугольник?
107. Идентификация равнобедренных треугольников: Треугольник имеет следующие длины сторон: 4 см, 5 см и 5 см. Что это за треугольник?
Что это за треугольник?
108. Идентификация разносторонних треугольников: Треугольник имеет следующие длины сторон: 4 см, 5 см и 6 см. Что это за треугольник?
109. Нахождение периметра треугольников: Луиджи построил палатку в форме равностороннего треугольника. Периметр 21 метр. Какова длина каждой из сторон палатки?
110. Определение площади треугольников: Какова площадь треугольника с основанием в 2 единицы и высотой в 3 единицы?
111. Применение теоремы Пифагора: Прямоугольный треугольник имеет одну сторону, не являющуюся гипотенузой, длиной 3 дюйма и мерой гипотенузы 5 дюймов. Какова длина другой стороны, не лежащей в гипотенузе?
112. Нахождение диаметра круга: Жасмин купила новый круглый рюкзак. Его площадь составляет 370 квадратных сантиметров. Какой диаметр круглого рюкзака?
113. Нахождение площади круга: Круглый щит Капитана Америки имеет диаметр 76,2 сантиметра. Какова площадь его щита?
Какова площадь его щита?
114. Определение радиуса окружности: Скайлар живет на ферме, где его отец держит круглый кукурузный лабиринт. Кукурузный лабиринт имеет диаметр 2 километра. Каков радиус лабиринта?
Переменные задачи со словамиПодходит для: 6-й класс, 7-й класс, 8-й класс
115. Определение независимых и зависимых переменных: Виктория печет кексы для своего класса. Количество кексов, которые она делает, зависит от того, сколько у нее одноклассников. Для этого уравнения m — это количество кексов, а c — это количество одноклассников. Какая переменная независимая, а какая зависимая?
116. Написание переменных выражений для сложения: В прошлом футбольном сезоне Триш забила g голов. Алекса забила на 4 гола больше, чем Триш. Напишите выражение, показывающее, сколько голов забила Алекса.
117. Написание переменных выражений для вычитания: Элизабет ест здоровый, сбалансированный завтрак b раз в неделю. Мэдисон иногда пропускает завтрак. Всего Мэдисон съедает на 3 завтрака в неделю меньше, чем Элизабет. Напишите выражение, показывающее, сколько раз в неделю Мэдисон завтракает.
118. Запись переменных выражений для умножения: В прошлом хоккейном сезоне Джек забил г голов. Патрик забил вдвое больше голов, чем Джек. Напишите выражение, показывающее, сколько голов забил Патрик.
119. Написание переменных выражений для деления: У Аманды есть c плиток шоколада. Она хочет распределить плитки шоколада поровну между тремя друзьями. Напишите выражение, показывающее, сколько плиток шоколада получит 1 из ее друзей.
120. Решение уравнений с двумя переменными: Это уравнение показывает, как сумма, которую Лукас зарабатывает на своей внешкольной работе, зависит от того, сколько часов он работает: e = 12 часов . Переменная ч показывает, сколько часов он работает. Переменная e показывает, сколько денег он зарабатывает. Сколько денег заработает Лукас, проработав 6 часов?
Переменная ч показывает, сколько часов он работает. Переменная e показывает, сколько денег он зарабатывает. Сколько денег заработает Лукас, проработав 6 часов?
Вооружившись 120 примерами, чтобы зародить идеи, создание собственных математических задач может увлечь учащихся и обеспечить соответствие урокам. Делать:
- Ссылка на интересы учащихся: Составляя текстовые задачи с интересами учащихся, вы, скорее всего, привлечете внимание. Например, если большая часть вашего класса любит американский футбол, задача измерения может включать дальность броска известного квотербека.
- Сделайте вопросы актуальными: Написание текстовой задачи, отражающей текущие события или проблемы, может привлечь учащихся, давая им четкий и реальный способ применить свои знания.

- Включите имена учащихся: Назвать персонажей вопроса именами учащихся — это простой способ сделать тему более понятной, помогая им решить проблему.
- Будьте откровенны: Повторение ключевых слов формулирует вопрос, помогая учащимся сосредоточиться на основной проблеме.
Нельзя:
- Проверка понимания прочитанного: Красиво подобранные слова и длинные предложения могут скрыть ключевые элементы вопроса. Вместо этого используйте лаконичные фразы и словарный запас для своего класса.
- Сосредоточьтесь на схожих интересах: Слишком много вопросов, связанных с родственными интересами, такими как футбол и баскетбол, могут оттолкнуть или отвлечь некоторых учащихся.
- Отвлекающий маневр: Включение ненужной информации вводит еще один элемент решения задач, который подавляет многих учащихся начальной школы.
Ключ к дифференцированному обучению, текстовые задачи, которые учащиеся могут связать и контекстуализировать, вызовут больший интерес, чем общие и абстрактные задачи.
Вы, вероятно, получите максимальную отдачу от этого ресурса к , используя задачи в качестве шаблонов, слегка изменив их, применив приведенные выше советы. При этом они будут более актуальными и интересными для ваших учащихся.
Тем не менее, имея под рукой 120 задачек по математике, соответствующих учебной программе, вы должны решать задачи по развитию навыков и наводящие на размышления оценки.
Результат?
Лучшее понимание того, как ваши учащиеся обрабатывают контент и демонстрируют понимание, информируя ваш постоянный подход к обучению.
Попробуйте Prodigy сегодня!Общая базовая учебная программа по математике для 1 класса
Общая основная программа по математике для 1 класса | ||||||||||||||||||||||||
Государственные школы Audubon Вовлечение учащихся ~ Воспитание Достижение ~ Развитие глобальных навыков 21 века Написано: Ким Феликс, Патриция Мартел, Бет Канзанзе Название курса: Математика в первом классе Название 2 и ALGEBRAIIC.
Государственные школы Audubon Вовлечение учащихся ~ Воспитание Достижение ~ Развитие глобальных навыков 21-го века Автор: Ким Феликс, Патрисия Мартел, Бет Кансанезе Course Title: First Grade Math Unit Name: Numbers and Operations in Base Ten Grade Level: 1
Государственные школы Audubon Вовлечение учащихся ~ Воспитание Достижение ~ Развитие глобальных навыков 21 века Написано: Ким Феликс, Патриция Мартел, Бет Канзанзе Название курса: Math Math . Заявления о содержании Измерение
длины, косвенно и путем итерации (повторения) единиц длины. Говорить и записывать время с помощью цифровых и
аналоговые часы. Представление и интерпретация данных. Общие базовые стандарты: 1.МД,
1-4 Общие основные вопросы Как
можно ли измерить длину косвенно? Как
могу ли я сказать, который час? Что
значит повторять? Что
это данные? Всеобъемлющее прочное понимание Я могу измерить длину двух объектов с помощью
третий объект. Я могу использовать аналоговые и цифровые часы. Итерация
в математике означает многократное использование математической процедуры. Данные
представляет собой фактическую информацию, которая организована, чтобы помочь мне проанализировать или сделать
решения. Основные вопросы модуля Как
я могу повторить, чтобы измерить? Как
Могу ли я заказать три объекта по длине? Что
самый распространенный способ узнать время? Как
могу ли я систематизировать данные? Подразделение прочного понимания Я могу повторять измерения с помощью
короче объект. Длина объекта измеряется
меньшими единицами того же размера. Время чаще всего указывается в часах
или полчаса. Данные могут быть организованы в
категории. Эти категории можно использовать для
отвечать на вопросы или решать проблемы. Обоснование блока Измерение
и анализ данных являются основой понимания геометрических фигур,
состав и решение задач. Большая часть прикладной математики связана с измерениями. Обзор устройства студентов
научится измерять длину косвенно и путем повторения единиц длины. Они
также познакомятся с определением времени, а также элементарными данными
анализ. |
Вовлечение учащихся ~ Воспитание Достижение ~ Культивирование глобальных навыков 21 -го века
Написано: Ким Феликс, Патриция Мартель, Бет Канзанез
Название. : 1
Заявления о содержании Рассуждение с определением, составлением форм и их атрибутов. | Общие базовые стандарты: 1.Г, 1-3 |
Общие основные вопросы Почему нужно ли мне знать, как различать атрибуты фигур? Что составная форма? Как Могу ли я разложить форму? | Всеобъемлющее прочное понимание Атрибуты фигур
помогите мне понять объекты и составить новые формы. Композиты образованы путем соединения фигур. Форма может быть раскладывается путем разбиения. |
Основные вопросы модуля Что разница между определяющими и неопределяющими атрибутами? Банка Я составляю составные фигуры из других составных фигур? Как можно ли разделить круг или прямоугольник?
| Подразделение прочного понимания Определяющий атрибут включает форму и стороны. Неопределяющий атрибут включает размер, цвет или ориентация. Составные формы могут быть сформированы из другие сложные формы. Круги и прямоугольники могут быть разделены пополам, четвертям и четвертям, что создает меньшие доли целый. |
Обоснование блока Понимание
атрибуты форм обеспечивают основу для распознавания, анализа и
рисование более сложных фигур.
| Обзор устройства студентов будет определять и составлять составные фигуры. Они смогут идентифицировать атрибуты этих форм и разбить круги и прямоугольники. |
Математические навыки для 1-го класса, Чему будет учиться ваш ребенок, Komodo Math
- Математические советы
- Образование
- 1-й
Ваш ребенок идет в первый класс! После года в детском саду ваш первоклассник будет готов к удивительному росту. Для многих детей первый класс — это год, когда они расцветают как читатели и математики. Будьте готовы поддержать математический рост вашего ребенка, изучая математические навыки первого класса.
В первом классе вы можете ожидать, что ваш ребенок узнает:
1.
 Факты сложения и вычитания до 20
Факты сложения и вычитания до 20 Теперь, когда ваш ребенок освоил идею сложения и вычитания, он готов практиковать математические факты. Это означает, что вы будете быстрее решать задачи на сложение и вычитание до 20.
Помогите своему ребенку развить беглость речи, задавая простые задачи на сложение и вычитание. Мы обнаружили, что использование угощений может помочь детям заинтересоваться! Если вашему первокласснику нужна поддержка, поощряйте использование физических предметов или пальцев в качестве инструментов для решения проблем.
2. Сложение и вычитание как обратные операции
Ваш ребенок, вероятно, понимает понятие сложения как «складывания», а вычитания как «разъединения». В первом классе детям предлагается увидеть связи между сложением и вычитанием. Ваш ребенок узнает, что сложение и вычитание являются обратными операциями или что одно противоположно другому, и создаст «семейство фактов» связанных задач на сложение и вычитание.
При работе со сложением и вычитанием попросите ребенка увидеть связи. Например, если у вашего ребенка четыре куклы и три машины, спросите, сколько всего игрушек. Затем спросите, сколько игрушек будет, если убрать четырех кукол.
3. Считай и пиши в пределах 120
Возможно, ваш ребенок научился считать до 20. Но в первом классе дети научатся считать до 120! Это не все. Ожидается, что дети будут не только считать, но и записывать числа. Это отличная практика для понимания многозначных чисел.
Дома: поощряйте ребенка писать числа, когда это возможно. Расскажите о том, как двузначные числа состоят из десятков и единиц, а трехзначные числа состоят из сотен, десятков и единиц. Простое совместное изучение многозначных чисел может стать отличной возможностью для обучения.
4. Сложение в пределах 100
Теперь, когда ваш ребенок понимает числа после 100, а также основные факты сложения и вычитания, пришло время попрактиковаться в сложении в пределах 100. Дети будут практиковаться в сложении однозначных чисел с двузначными. числа, используя такие стратегии, как подсчет и числовые диаграммы. Дети могут практиковаться в сложении больших чисел с помощью таблицы от 1 до 100.
Дети будут практиковаться в сложении однозначных чисел с двузначными. числа, используя такие стратегии, как подсчет и числовые диаграммы. Дети могут практиковаться в сложении больших чисел с помощью таблицы от 1 до 100.
Первоклассники также готовы практиковаться в сложении и вычитании десятков из двузначных чисел.
Дома: помогите ребенку увидеть закономерности при сложении и вычитании десятков. Например, после решения такой задачи, как 59 — 10 = 49, укажите ребенку, что в 49 на 10 меньше, чем в 59. Это еще один отличный способ узнать о разрядности.
5. Измеряйте предметы
В первом классе дети учатся измерять с помощью линеек и более необычных вещей, таких как канцелярские скрепки. После снятия мерок дети сравнивают и упорядочивают предметы по длине.
Дома: дети любят измерять предметы в доме, поэтому держите под рукой пару линеек. Обратите внимание на то, как ваш ребенок пользуется линейкой и снимает мерки. Иногда дети не совсем измеряют от начала до конца, поэтому им может понадобиться небольшая помощь…
Обратите внимание на то, как ваш ребенок пользуется линейкой и снимает мерки. Иногда дети не совсем измеряют от начала до конца, поэтому им может понадобиться небольшая помощь…
6. Рассчитайте время до часа и получаса
Одно из самых сложных понятий, которым учат первоклассников, – это определение времени. . Использование аналоговых часов сбивает с толку, особенно когда дети больше привыкли видеть цифровые часы. В первом классе ваш ребенок узнает о большой и маленькой стрелках часов и будет практиковаться в определении времени с точностью до часа и получаса.
Дома: приобретите аналоговые часы для дома (либо настоящие, либо сделанные специально для обучения). Поговорите с ребенком о времени и о том, как двигаются стрелки часов. Не забудьте просто сосредоточиться на том, чтобы сказать время до часа и получаса, чтобы начать!
7. Понимание основных дробей
Первоклассники также знакомятся с дробями как равными долями. Они научатся делиться на равные группы и выучат основные дроби, такие как ½, ⅓ и ¼. Первоклассники обычно хорошо понимают, что такое справедливость, поэтому научиться делать равные доли должно быть для них относительно легкой задачей!
Они научатся делиться на равные группы и выучат основные дроби, такие как ½, ⅓ и ¼. Первоклассники обычно хорошо понимают, что такое справедливость, поэтому научиться делать равные доли должно быть для них относительно легкой задачей!
Дома: помогите ребенку разделить пиццу, пироги и бутерброды на равные части. При этом говорите о частях целого, которое вы создали.
Первоклассники готовы глубоко погрузиться в математические понятия. Найдите время, чтобы поговорить с ребенком об обучении в классе и приготовьтесь повеселиться!
Нашли это полезным? Ознакомьтесь с нашими руководствами по математике для классов от детского сада до 5-го класса
Написанное Лили Джонс, Лили любит учиться всему. Она работала воспитателем в детском саду и начальных классах, педагогическим тренером, разработчиком учебных программ и тренером для учителей. Она любит смотреть на мир с любопытством и вдохновлять людей всех возрастов любить учиться. Она живет в Калифорнии с мужем, двумя детьми и маленькой собачкой.
О Komodo — Komodo — это увлекательный и эффективный способ улучшить математические навыки K-5. Разработанный для детей от 5 до 11 лет для использования дома, Komodo использует небольшой и частый подход к изучению математики (15 минут, три-пять раз в неделю), который вписывается в занятую семейную рутину. Komodo помогает пользователям развить беглость и уверенность в математике — , не заставляя их долго сидеть у экрана .
Узнайте больше о Komodo и о том, как он ежегодно помогает тысячам детей лучше успевать по математике — вы даже можете попробовать Komodo бесплатно.
Снова в школу — 5 советов, которые помогут вам вернуться к рутине
Вот несколько шагов, которые вы можете предпринять, чтобы вывести детей из режима полных каникул, чтобы первая неделя в школе не выбила вас из колеи.
Мышление — путь к мастерству
Люди с мышлением роста считают, что у них всегда есть потенциал учиться и совершенствоваться.


 Задачи «с подвохом» избавят ребёнка от шаблонного мышления, а задания с большим количеством лишних данных научат выделять главное из большого количества условий.
Задачи «с подвохом» избавят ребёнка от шаблонного мышления, а задания с большим количеством лишних данных научат выделять главное из большого количества условий. 
 Рисуется схема, на которой отмечают последовательность действий и результат, полученный при их выполнении.
Рисуется схема, на которой отмечают последовательность действий и результат, полученный при их выполнении.