Сравнение долей – Сравнение долей. 3 и 4 класс
Правила «Сравнение долей с одинаковыми и разными знаменателями».
Также как и натуральные числа обыкновенные дроби можно сравнивать.
Рассмотрим две неравные дроби на числовой оси. Меньшая дробь будет располагаться левее, а большая — правее.
Равные дроби соответствует одной и той же точке на числовой оси.
На рисунке хорошо видно, что 1/5 < 6/10. Но необязательно пользоваться числовой осью, чтобы сравнивать дроби.
Сравнение дробей с одинаковыми знаменателями
Запомните!
Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше.
Пример. Сравним 1/5 и 4/5.
В обеих дробях одинаковый знаменатель равный 5.
В первой дроби числитель равен 1 и он меньше числителя второй дроби, который равен 4.
Поэтому первая дробь (1/5) меньше второй (4/5).
Сравнение дробей с одинаковыми числителями
Запомните!
Из двух дробей с одинаковыми числителями больше та, у которой знаменатель меньше.
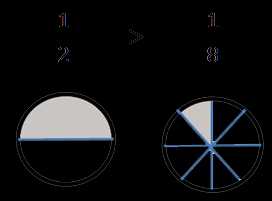
Пример. Сравним 1/2 и 1/8. Ответ:
Правило выше легче понять, если представить, что у вас в руках куски торта. В первом случае торт разделили на 2 части (знаменатель дроби равен 2), и у вас в руках половина торта, а во втором — торт поделили на 8 частей, и у вас в руках маленькая часть торта.
Сравнение дробей с разными знаменателями
Запомните!
Чтобы сравнить дроби с разными знаменателями, нужно привести дроби к общему знаменателю.
После приведения дробей к общему знаменателю, дроби сравниваются по правилу сравнения дробей с одинаковыми знаменателями.
Пример. Сравним 2/7 и 1/14.
Запомните!
Любая неправильная дробь больше любой правильной.
Это объясняется тем, что неправильная дробь всегда больше или равна 1, а правильная дробь всегда меньше 1.
Источник: http://math-prosto.ru
infourok.ru
Урок математики по теме «Сравнение долей»
Разделы: Начальная школа
Цели урока:
- Сформировать способность к сравнению долей.
- Тренировать навыки решения примеров на деление и умножение многозначных чисел.
- Развивать такие операции мышления как анализ, обобщение, сравнение, классификация.
- Воспитывать у учащихся интерес к математике, чувство товарищества, математически грамотную речь.
Планируемые достижения учащихся на уроке (чему учащийся должен научиться, что усвоить):
- научиться сравнивать доли;
- закрепить изученные приемы деления и умножения многозначных чисел.
Оборудование:
- Л.Г. Петерсон, математика, 4-й класс. Учебник-тетрадь в 3-х ч., издательство “Ювента”, 2002.
- лист белой бумаги (квадрат размером 16х16),
- ножницы,
- два цветных карандаша (синий и красный).
- лист бумаги с числовым отрезком.
Ход урока
1. Самоопределение к деятельности (1–2 мин.)
- Над какой темой мы работаем? (Доли).
- Как вы считаете, вы все уже знаете про доли? (Нет).
- Правильно, ребята! Мы еще не все знаем про доли. Сегодня на уроке мы с вами сделаем еще одно открытие про доли, а какое вы об этом узнаете позже.
- Прочитайте высказывание Нивена: «Математику нельзя изучать, глядя, как это делает сосед».
- Как вы его понимаете? (Чтобы понять новый материал, нужно самому активно работать на уроке, а не смотреть, как это делает твой сосед).
- Да, ребята, нельзя изучать математику, не включаясь в работу, а наблюдать со стороны как это делает твой сосед.Тогда за работу!
2. Актуализация знаний и фиксация индивидуального затруднения в деятельности (5–6 мин.)
а) Актуализация мыслительных операций.
– На доске записаны выражения:
| 36 : 2 | 36 : 4 | |
| 738 : 123 | 738 : 6 | |
| 288 : 12 | 288 : 24 |
- Что общего в этих выражения? (все выражения на деление, делимое в выражения одинаковые)
- Чем они отличаются? (разные делимые)
– Не вычисляя, сравните выражения.
- 36 : 2 > 36 : 4
- 738 : 123 < 738 : 6
- 288 : 12 > 288 : 24
– Каким правилом вы пользовались? (При одинаковых делимых, чем больше делитель, тем частное меньше) .
б) Тренировка в записи, чтении и изображении долей на числовом отрезке.
- – Что называют долями? (Равные части целой мерки).
- – Прочитайте доли? (Запись на доске 1/25, 1/6, 1/10, 1/3, 1/18).
- – Как по-другому можно назвать полрубля, полночь? (Половина или )
- – У вас на столах листочки с числовым лучом. Отметьте на нем .
- – Как по-другому можно назвать четверть литра, четверть часа? (Четвертая часть или ).
- – Отметьте на луче .
в) Индивидуальное задание:
– Молодцы! Вы хорошо разобрались, что такое доли, умеете их читать и изображать на числовом отрезке. А теперь я предлагаю вам решить самостоятельно следующую задачу.
Дыня весит 7 кг. Что тяжелее этой дыни или ? (ПРОБЛЕМА!!!)
- – Итак, что тяжелее? < , > )
- – Мнения разделились. Кто же из вас прав?
3. Выявление причины затруднения и постановка цели деятельности (1–2 мин).
- – Какое задание вы выполняли?
- – Почему это задание вызвало затруднение? (Мы не умеем сравнивать доли).
- – Значит, какую цель мы должны достичь на уроке? (Научиться сравнивать доли).
- – Кто назовет тему урока? (Сравнение долей).
4. Построение проекта выхода из затруднения (8–10 мин).
5. Физминутка ( 2–3 мин).
6. Первичное закрепление во внешней речи (4– 5 мин). – Мы с вами сделали открытие, а теперь цель нашей работы? (Потренироваться).
- № 4(а). Расположи в порядке возрастания числа. Ответ: 1/15, 1/12, 1/10, 1/7, 1/5, 1/3.
- № 4(б). Расположи в порядке убывания числа: Ответ: 1/2, 1/3, 1/4, 1/8, 1/9, 1/16,1/25.
7. Самостоятельная работа с самопроверкой по эталону(4–5 мин.)
- – Мы с вами потренировались, а теперь цель нашей дальней шей работы? (Проверить свои знания).
- – А как мы их будем проверять? (Выполним самостоятельную работу).
(Учащиеся выполняют самостоятельную работу по вариантам, по окончании работы сравнивают свою работу по эталону).
| 1 вариант. | 2 вариант | |
Сравни |
||
| 1/6 и 1/18 (>), 1/100 и 1/25 (<), | 1/19 и 1/3 (<), 1/37 и 1/60(>), | |
| и 1/20 (>), | и 1/10 (>), | |
| 1/а и 1/с, где а > с (<) | 1/б и 1/ д, где б>д (<) | |
- – Выполнили работу? Что будем делать дальше? (Проверять работу). Для чего нужно проверять свою работу? ( Чтобы убедиться правильно мы ее выполнили или допустили ошибки).
- – Проверьте себя по эталону для самопроверки и зафиксируйте результат проверки при помощи знаков “+” или “?”
- – Кто допустил ошибки при выполнении задания? (…). В чем причина?
- – Что нам поможет исправить ошибки? (Эталон)
- – Исправьте их. Поднимите руки, у кого все верно.
- – Вы молодцы! Поставьте себе “+”.
8. Включение в систему знаний и повторение( 4–5 мин).
– Мы с вами хорошо потрудились над новым материалом, и я предлагаю вам вспомнить материал прошлых уроков и выполнить на повторение № 14 на с.69. У доски работает ….
Вычисли:
- 186438 : 46 = 4053
- 8090 * 2005 = 16 000 000
9. Рефлексия учебной деятельности.
- – Какую цель мы ставили вначале урока? (Научить сравнивать доли).
- – Достигли мы ее? (Да).
- – Какое правило мы получили? (Чем меньше долей, тем больше каждая доля).
- – Что вам помогло при выполнении с.р.? (Эталон).
- – Кому на уроке было трудно? Вы преодолели свою трудность?
- – Попробуйте оценить свою работу? Работу класса?
- – Покажите жестом, понравился ли вам урок.
- – Спасибо.
15.01.2009
Поделиться страницей:urok.1sept.ru
План-конспект урока по математике (3 класс) на тему: Доли. Сравнение долей
1. Постановка проблемы, введение нового понятия.
— А как что-то разделить на доли?
— Что такое доля?
На доске:
Беру яблоко и говорю:
— С апельсином легко, он с дольками, а что делать с яблоком?
— Я взрослая, отрежу себе побольше, а вы маленькие, вам можно поменьше.
-Правильно я поступила?
-Получились доли?
-Почему?
-А как правильно разрезать?
-Какой вывод можно сделать?
На доске:
— Как второе яблоко правильно разрезать на доли?
— Держу в руках две половинки и спрашиваю:
— На сколько равных долей разрезано яблоко?
— А если я возьму одну из двух долей?
— Как назовем одну долю?
— Ещё разрежу пополам. На сколько частей теперь разрезано яблоко?
— Какая доля получилась?
— Как это записать? Сначала была вторая, теперь четвертая…
Как же нам различать доли при записи.
На доске дети видят следующую запись: 1/4
— Что эта запись обозначает?
— Когда мы «делим» в математике числа, то используем знак (:)
— Но в математике есть ещё один знак деления, он называется «дробная черта «—» и соответственно числа, записанные с этим знаком, называются дробными.
— Как вы думаете, что «обозначает число под чертой?
— А число над чертой?
— В записи нижняя цифра обозначает, на сколько равных частей (долей) разделили целое, а верхняя — сколько таких частей взяли
На доске карточки:
«на сколько частей разделили», «сколько долей взяли»
Интересно знать:
— Современная система записи дробей была создана в Индии, только там не писали дробной черты. А записывать дробь в точности так, как сейчас, стали арабы. Общеупотребительной эта запись дробей стала лишь в XVI веке.
— А при чтении дроби сначала произносится верхняя цифра в виде количественного числительного женского рода — одна, а затем нижняя цифра как порядковое числительное — вторая, третья, четвёртая и т.д.
На доске: «Одна какая»
2. Практическая работа с полосками бумаги. Образование и название долей.
-А теперь вы разделите одну полоску на две доли.
— Как сделаем?
— Сколько таких долей во всей полоске?
— Какие они между собой?
— Заштрихуйте часть.
— Как назовем долю?
— Кто сможет написать название второй части?
— Что обозначает эта запись?
— Разделите вторую полоску бумаги на четыре доли.
— Как это сделать?
— Какие доли между собой?
— Заштрихуйте одну четвертую долю.
— Напишите на этой части её обозначение.
— Что обозначает эта запись?
— Сколько долей получится, если вы разделите полоску пополам трижды?
— Какие доли между собой?
— Как назвать одну долю?
— Как записать её название математически?
— Что обозначает эта запись?
— Заштрихуйте долю и запишите её название.
— Доля — это часть.
— Разрезать.
— Нет.
— Нет.
— Части не равные.
— Части должны быть равные.
— Доля — это равная часть.
— Сначала разрезать пополам
— На две доли.
— Одна доля из двух.
— Вторая.
На четыре.
Четвертая
(Дети сначала предлагают свои варианты записи)
(Мнения детей.)
(Мнения детей.)
(Мнения детей.)
— Перегнем полоску пополам.
— Две
— Равные
— Одна вторая
— 1/2
— Целое разделили на 2 равные части (доли) и взяли одну такую часть
— Сложить пополам, а затем еще раз пополам.
— Равные
— 1/4
Целое разделили на 3 равные части (доли) и взяли одну такую часть
Ответы детей.
Проверка практическим способом.
— Равные.
— Одна третья
— 1/3
Целое разделили на 3 равных частей (долей) и взяли одну такую часть.)
nsportal.ru
Образование и сравнение долей. Видеоурок. Математика 3 Класс
В жизни людям часто приходится делить целое на равные части, доли. На этом уроке вы сможете получить представление о том, как происходит такое образование долей и их названий, научитесь производить их запись, чтение и сравнение
Самая известная доля – это половина. В жизни приставка «пол» встречается очень часто: полкилограмма, полкусочка, полчаса. Доли появляются, когда нужно целое разделить на равные части, допустим, полбуханки хлеба или полчаса.
Доля – это каждая из равных частей единицы. Название доли зависит от того, на сколько частей разделили целое. Разделили на две части – половина (Рис. 1).
Рис. 1. Половина – целое, разделенное на две части
Если разделили на три – это треть (Рис. 2).
Рис. 2. Треть – целое, разделенное на три части
Разделили на четыре части – четверть (Рис. 3).
Рис. 3. Четверть – целое, разделенное на четыре части
Любую долю можно записать как деление двух натуральных чисел. Рассмотрим рисунок 4. Если целое разделили на две доли (синий рисунок), то тогда одну долю можно записать так: . Черта означает знак деления. Если разделили на три части (красный рисунок), то одну долю можно записать так: . Если целое разделили на четыре части (желтые рисунок), то тогда одну долю можно записать так: .
Рис. 4. Различные доли
Уже в древности люди пользовались долями. Для записи, например, в Китае использовали точку, чтобы обозначить долю (Рис. 5).
Рис. 5. Запись долей в Древнем Китае
А в Древнем Египте доли записывали, как показано на рисунке 6.
Рис. 6. Запись долей в Древнем Египте
Потренируемся записывать доли. Для того чтобы записывать доли, нужно выполнять действия по алгоритму.
· Сначала надо посчитать, на сколько равных долей разделено целое, и записать это число под чертой.
· Затем посчитать, сколько долей закрашено, и это число записать над чертой.
Рис. 7. Иллюстрация к заданию 1
Посчитаем, на сколько частей разделен прямоугольник (рис. 7). Он разделен на пять частей, значит, число 5 запишем под чертой: . А закрашена всего одна часть, значит, над чертой запишем единицу: . Доля читается «одна пятая».
Рис. 8. Иллюстрация к заданию 2
Данный прямоугольник разделен на девять частей (рис. 8), поэтому записываем под чертой количество равных частей: . Закрашена одна доля, значит, пишем сверху единицу: . Читается «одна девятая».
Рис. 9. Иллюстрация к заданию 3
Прямоугольник разделен на десять частей (рис. 9). Записываем внизу десять: . Закрашена одна доля, пишем над чертой единицу: . Читается «одна десятая».
Доли на Руси называли «ломаными числами». В старинных инструкциях можно найти такое название долей:
(одна вторая) – половина полтины.
(одна третья) – треть.
(одна четвертая) – четь.
(одна пятая) – пятина.
(одна седьмая) – седьмина.
(одна десятая) – десятина.
В одном классе часть учеников занимается в музыкальной школе, учеников занимаются в спортивной школе, а учеников занимаются в художественной школе. Где занимается больше детей?
Решение
Обратим внимание на число, которое записано под чертой. Оно во всех трех долях одинаковое, потому будем сравнивать только те числа, которые стоят сверху, а там стоят числа 1, 2 и 4. Изобразим на рисунке (Рис. 10).
Рис. 10. Иллюстрация к решению задачи 4
По рисунку видно, что четыре доли – это больше, чем две или одна. Поэтому делаем вывод: (больше, чем и ).
Пример
Рассмотрим три доли: , и . Если над чертой количество долей одинаковое, то будем сравнивать число, которое записано под чертой: 2 доли, 3 доли или 4 доли.
Рассмотрим рисунок 11. Записанные справа доли соответствуют отрезкам слева.
Рис. 11. Иллюстрация к примеру
Отрезок, соответствующий доле больше отрезка, соответствующего доле , а отрезок, соответствующий доле больше отрезка, соответствующего доле . Значит: . Делаем вывод: если наверху количество долей одинаковое, то чем меньше внизу число, тем доля больше.
Тренируемся записывать, читать и сравнивать доли.
На рисунке 12 круг разделен на шесть равных долей.
Рис. 12. Круг, разделенный на 6 долей
В первом круге взята одна доля, потому записываем , читаем «одна шестая». Во втором круге взято четыре доли, записываем , читаем «четыре шестых».
Вспоминаем правило: если под чертой числа одинаковые, то сравниваем числа над чертой. Четыре больше, чем один, ставим знак : , читается так: «одна шестая меньше, чем четыре шестых».
Рассмотрим рисунок 13. Первый круг разделен на три части, возьмем одну часть, запишем: (одна треть). Второй круг разделен на четыре части, возьмем также одну часть и запишем (одна четвертая). Выясним, какая доля больше.
Рис. 13. Иллюстрация к заданию 6
Рассуждаем: если над чертой числа одинаковые, то сравниваем числа под чертой. Четыре больше, чем три (), а значит, долей больше и каждая доля меньше. Делаем вывод: .
Список литературы
- Моро М.И., Волкова С.И. Для тех, кто любит математику. 3 класс. – 64 с.: ил. – Обл.
- Моро М.И., Волкова С.И. Математика. Рабочая тетрадь. 3 класс. В 2 частях. Ч.1. – 80 с.: ил. – Обл. Ч.2. – 80 с.: ил. – Обл.
- Петерсон Л.Г. Математика. 3 класс. Учебник в 3 ч. – М.: 2012. – 112 с. + 96 с. +80 с.
Домашнее задание
- Запиши цифрами: одна пятая, десятина, треть, три девятых, четверть, семь одиннадцатых, три восьмых, половина.
- Какова доля незакрашенной (белой) части прямоугольника? А какова доля закрашенной?
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал Slideshare.net (Источник).
- Интернет-портал Slideshare.net (Источник).
- Интернет-портал Youtube.com (Источник).
- Интернет-портал School-assistant.ru (Источник).
interneturok.ru
| 1. | Сравни доли и вставь пропущенное слово | 1 вид — рецептивный | лёгкое | 4 Б. | По рисунку предлагается сравнить дроби и сделать вывод, вставить пропущенное слово. |
| 2. | Порядок записи долей | 1 вид — рецептивный | лёгкое | 1 Б. | Определяется порядок записи долей. |
| 3. | Расставь доли в нужном порядке | 1 вид — рецептивный | лёгкое | 1 Б. | Требуется данные в условии доли расставить в порядке возрастания или убывания. |
| 4. | Что больше? | 2 вид — интерпретация | среднее | 2 Б. | Требуется сравнить значения долей от разных чисел c одинаковыми единицами измерения. |
| 5. | Прочитай зашифрованное слово | 2 вид — интерпретация | среднее | 2 Б. | Используя рисунок, сравнивают доли и составляют слово, соответствующее буквам на данных рисунках. |
| 6. | Чья доля больше? | 2 вид — интерпретация | среднее | 2 Б. | Анализируя условие задачи и предложенный рисунок, делаем вывод, у какой из девочек закрашена большая доля. |
| 7. | Строительство дороги | 3 вид — анализ | сложное | 3 Б. | Предлагается решить текстовую задачу, используя в ходе решения как нахождение доли от числа, так и сравнение долей. Также требуется ответить на вопрос «на сколько больше». |
| 8. | Сравни выражения с разными единицами измерения | 3 вид — анализ | сложное | 3 Б. | Требуется сравнить значения долей от чисел с разными единицами измерения. |
| 9. | Сравни объёмы | 3 вид — анализ | сложное | 3 Б. | В ходе решения текстовой задачи сравниваются доли от данного в условии объёма, и определяется, во сколько раз один из объёмов меньше или больше другого. |
www.yaklass.ru
Доля. Сравнение долей.
Математика Дата «___»_______ ____ г Класс 3- «Б» (1 четверть) Урок 37 Тема урока: Доля. Сравнение долей. Тип урока: Урок первичного предъявления новых знаний. Цель урока: Первичное знакомство с понятием «Доля», учить называть, записывать, сравнивать доли. Ход урока Этап урока Содержание и деятельность учителя Деятельность учащихся 1.Организационный момент Настроить учащихся на продуктивную работу, обратить внимание на готовность рабочего места. 2.Подго-товка уч-ся к активной деятельно-сти на ос-новном этапе урока 1) Актуализация опорных знаний. Устный счет. — Постарайтесь выполнить задания правильно и узнаете, какой сюрприз я вам подготовила. _ Запишите только ответы в строчку, через запятую. * Число 25 разделить на 25. * На сколько число 26 больше, чем 9? *Во сколько раз число 48 больше 8? *Число 7 увеличьте на 6. *Число 7 увеличьте в 4 раза. * Число 25 уменьшите на 6. *Найдите площадь прямоугольника, если его стороны 2 и 5 см.. *Число 5 увеличьте в 3 раза. — Найдите в алфавите буквы, соответствующие полученным чис-лам, запишите снизу. Какое слово получилось? 2) Формулирование темы и целей урока. -Странно. Почему апельсин? Зачем он на уроке математике? Этот вкусный фрукт поможет вам определить тему сегодняшнего урока. — Посмотрите м/ф! -Почему рассердился волк? -В чем его ошибка? -Что получил каждый из животных мультфильма? — Где в жизни вы встречали это слово? Дети приводят свои примеры. (Долька мандарина, лимонная доль-ка и т.д.) — В математике такие части от целого называются доли. (карточка на доске) Формулирование цели и темы урока -Так какая тема нашего урока? — Какую цель перед собой поставим? (одновременно на доске выставить карточки «Узнать», «Учиться», «образовывать и называть», «сравнивать») — Учиться образовывать и называть …? — Учиться сравнивать …. 1 — А 17 — П 6 — Е 13 — Л 28 — Ь 19 – С 10 — И 15 — Н Апельсин Просмотр уч-ся м/ф «Апельсин» -Ему не доста-лось апельсина. -Он не умеет дружить. -Дольку апель-сина -Доли. -Узнать что та-кое доля. ДОЛИ 3.Изучение новых зна-ний и спо-собов дей-ствий 1) Постановка проблемы, введение нового понятия. -А как это разделить на доли? Что такое доля? На доске: Беру яблоко и говорю: -С апельсином легко, он с дольками, а что делать с яблоком? -Я взрослая, отрежу себе побольше, а вы маленькие, вам можно поменьше. -Правильно я поступила? -Получились доли? -Почему? -А как правильно разрезать? -Какой вывод можно сделать? На доске: -Как второе яблоко правильно разрезать на доли? Держу в руках две половинки и спрашиваю: -На сколько равных долей разрезано яблоко? -А если я возьму одну из двух долей? — Как назовем долю? — Ещё разреу пополам. На сколько частей теперь разрезано яблоко? Какая доля получилась — Как это записать? Сначала была вторая, теперь четвертая… Надо же различать доли при записи. На доске дети видят следующую запись: ¼ — Что эта запись обозначает? — Когда мы «делим» в математике натуральные числа, то использу-ем знак (:) . — Но в математике есть ещё один знак деления, он называется «дробная черта — и соответственно числа, записанные с этим зна-ком, называются дробными. — Как вы думаете, что обозначает число под чертой? — А число над чертой? — В записи нижняя цифра обозначает, на сколько равных частей (долей) разделили целое, а верхняя – сколько таких частей взяли На доске карточки: «на сколько частей разделили», « сколько долей взяли» — Современная система записи дробей была создана в Индии, только там не писали дробной черты. А записывать дробь в точно-сти так, как сейчас, стали арабы. Общеупотребительной эта запись дробей стала лишь в XVI веке. — А при чтении дроби сначала произносится верхняя цифра в виде количественного числительного женского рода – одна, а затем нижняя цифра как порядковое числительное – вторая, третья, чет-вёртая и т.д. На доске: «Одна какая» 2) Практическая работа с полосками бумаги. Образование и назва-ние долей. -А теперь вы разделите одну полоску на две доли. — Как сделаем? — Сколько таких долей во всей полоске? — Какие они между собой? — Заштрихуйте часть. — Как назовем долю? — Кто сможет написать название второй части? — Что обозначает эта запись? — Разделите вторую полоску бумаги на четыре доли. — Как это сделать? — Какие доли между собой? — Заштрихуйте одну четвертую долю. — Напишите на этой части её обозначение. — Что обозначает эта запись? — Сколько долей получится, если вы разделите полоску пополам трижды? — Какие доли между собой? — Как назвать одну долю? — Как записать её название математически? — Что обозначает эта запись? — Заштрихуйте долю и запишите её название. -Доля-это часть. -Разрезать. -Нет. -Нет. Части не равные. -Части должны быть равные. -Доля-это рав-ная часть. -Сначала разре-зать пополам -На две доли. Одна доля из двух. Вторая. На четыре. Четвертая (Дети сначала предлагают свои варианты записи.) (Мнения детей.) (Мнения детей.) (Мнения детей.) Перегнем по-лоску пополам. Две Равные Одна вторая ½ Целое раздели-ли на 2 равные части (доли) и взяли одну та-кую часть Сложить попо-лам, а затем еще раз пополам. Равные ¼ Целое раздели-ли на 4 равные части (доли) и взяли одну та-кую часть Ответы детей. Проверка прак-тическим спо-собом. Равные. Одна восьмая ⅛ Целое раздели-ли на 8 равных частей (долей) и взяли одну та-кую часть.) 4. Первич-ная провер-ка понима-ния изу-ченного 1) Упражнения в образовании и записи долей. Фронтальная работа по слайдам. Слайды 2 – 15 — На сколько долей разделена фигура? — Какие они между собой? — Сколько долей? — Как назвать одну долю? — Запишите. — Как по другому назвать ½, 1/3, ¼. 2) Поиск названия долей в пословицах — Найдите названия долей спрятавшиеся в пословицах. * Один блин и тот пополам. * Один улей – улей, а пять – пасека. * Семеро одного не ждут. Равные Запись в тетра-дях и самопро-верка по слайду. ½ 1/5 1/8 5. Приме-нение зна-ний и спо-собов дей-ствий 1) Создание проблемной ситуации для сравнения долей. — Миша и Даша пригласили гостей. Весь класс! Даша 12 девочек, Миша 16 мальчиков. Одного торта будет достаточно для всех? Ис-пекли два одинаковых торта. Мальчикам – один, девочкам – дру-гой. Выставить две модели тортов. — На сколько одинаковых долей разрезали торт девочкам? — Как назвать эту долю? — Что обозначает число под чертой? — Что обозначает число над чертой? — На сколько равных долей разрезали торт мальчикам? — Как назвать эту долю? — Что обозначает число под чертой? — Что обозначает число над чертой? — Чьи куски будут больше? — А как это выяснить, мне жалко резать такие красивые макеты? 2) практическая работа в сравнении долей полосок. — Давайте посмотрим на полоски, доли на которых мы демонстри-ровали в начале урока. — Вы три раза складывали одинаковые полоски на разное количе-ство долей. Давайте посмотрим, какие доли получались у вас. Положите доли рядом для сравнения. — Расположите доли в порядке возрастания. — Какая доля самая маленькая? Самая большая? — Почему? Вывод о сравнении долей. 3) первичное закрепление умения сравнивать доли. Работа по слайдам 17 — 20 и запись неравенств в тетрадях. — Двум мышкам повезло найти головку сыра. Какая доля досталась каждой? — А если мышек будет 4? — А на восемь мышек? — Сравните получившиеся доли. — Объясните, почему вы так решили. — Три девочки делили плитку шоколада поровну. Какая доля до-сталась каждой? — А если подружек будет 6? — Сравните доли. — Объясните, почему вы так решили. 4) Решение проблемы с делением тортов с опорой на полученное правило сравнения долей. — Давайте вернемся к сравнению долей торта мальчиков и девочек. Чья доля больше? — Почему? Докажите! Перевернуть макеты, убедиться в правильности решения. — Так может не звать никого, а съесть торт вдвоем? 5) Работа в парах. — Найдите самую большую долю и соедините доли в порядке убы-вания. Проверка получившихся цепочек. Соедините первую и последнюю доли. Какая фигура получилась? -Какое правило применяли для выполнения задания? Резерв. Продолжение парной работы. — Составьте цепочку долей, двигаясь по стрелке и записывая доли в порядке возрастания. Количество точек можете выбрать сами. — На 12. 1/12 Записать на доске. На сколько рав-ных частей раз-делили. Ск. долей взяли. На 16. 1/16 Записать на доске. На сколько рав-ных частей раз-делили. Ск. долей взяли. Варианты отве-тов детей. Запись на доске и в тетрадях ½ ¼ ⅛ ⅛ < ¼ < ½ Чем больше число, на кото-рое делили це-лое, тем меньше полученная до-ля Запись дробей и неравенств в тетрадях 1/2 1/4 1/8 1/2 > 1/4 > 1/8 Чем больше число, на кото-рое делили це-лое, тем меньше полученная до-ля 1/3 1/6 1/3 > 1/6 Чем больше число, на кото-рое делили це-лое, тем меньше полученная до-ля Девочек. 1/12 > 1/16 Повторение правила Лучше меньше, но с друзьями. Звезда. Чем больше число, на кото-рое делили це-лое, тем меньше полученная до-ля 6. Подведе-ние итогов. 7. Рефлек-сия 1) Домашнее задание: с. 34 -35, № 2, 3, 7 2)- Вернемся теме и целям нашего урока. Все цели выполнены? — Что такое доля? — Какое главное условие должно быть выполнено при делении на доли? — Что обозначают числа в записи дробей? — Как сравнить доли? Урок целей достиг. — Где вы можете использовать полученные новые знания? Вернемся к м/ф «Апельсин». — На сколько долей волку надо разделить апельсин, чтобы никого не обидеть? Слайд 22 — Какие это будут части? Самооценка успешности Равные части. — В записи ниж-няя цифра обо-значает, на сколько равных частей (долей) разделили це-лое, а верхняя – сколько таких частей взяли. Чем больше число, на кото-рое делили це-лое, тем меньше полученная до-ля При угощении, делении поров-ну. Равные части.
ПЕРЕД СКАЧИВАНИЕМподелитесь материалом:
znanio.ru
Урок математике по теме: «Сравнение долей»
Конспект урока математики по учебнику Л.Г. Петерсон «Сравнение долей».
Цели урока:
Сформировать способность к сравнению долей.
Тренировать навыки решения примеров на деление и умножение многозначных чисел.
Развивать такие операции мышления как анализ, обобщение, сравнение, классификация.
Воспитывать у учащихся интерес к математике, чувство товарищества, математически грамотную речь.
Планируемые достижения учащихся на уроке (чему учащийся должен научиться, что усвоить):
научиться сравнивать доли;
закрепить изученные приемы деления и умножения многозначных чисел.
Оборудование:
Л.Г. Петерсон, математика, 4-й класс. Учебник-тетрадь в 3-х ч., издательство “Ювента”, 2016 г.
лист белой бумаги (квадрат размером 16х16),
ножницы,
два цветных карандаша (зеленый и красный).
лист бумаги с числовым отрезком.
Ход урока
I. Организационный момент.
Прозвенел звонок веселый
Вы начать урок готовы?
Будем слушать, рассуждать,
И друг другу помогать.
II. Актуализация знаний. Постановка проблемы.
1Актуализация знаний и фиксация индивидуального затруднения в деятельностимин.)
а) Актуализация мыслительных операций.
– На доске записаны выражения:
24 : 6
854 : 122
854 : 7
180 : 12
180 : 15
Что общего в этих выражения? (все выражения на деление, делимое в выражения одинаковые)
Чем они отличаются? (разные делимые)
– Не вычисляя, сравните выражения.
24 : 4 > 24 : 6
854 : 122 < 854 : 7
180: 12 > 180: 15
– Каким правилом вы пользовались? (При одинаковых делимых, чем больше делитель, тем частное меньше) .
б) Тренировка в записи, чтении и изображении долей на числовом отрезке.
– Что называют долями? (Равные части целой мерки).
– Прочитайте доли? (Запись на доске 1/15, 1/4, 1/12, 1/5, 1/17).
– Как по-другому можно назвать полрубля, полдень? (Половина или )
– У вас на столах листочки с числовым лучом. Отметьте на нем .
– Как по-другому можно назвать четверть литра, четверть часа? (Четвертая часть или ).
– Отметьте на луче .
в) Индивидуальное задание:
– Молодцы! Вы хорошо разобрались, что такое доли, умеете их читать и изображать на числовом отрезке. А теперь я предлагаю вам решить самостоятельно следующую задачу.
Арбуз весит 7 кг. Что тяжелее этого арбуза или ? (ПРОБЛЕМА!!!)(Обсуждение в группах. Заслушиваются ответы каждой группы).
– Итак, что тяжелее? < , > )
– Мнения разделились. Кто же из вас прав?
3. Выявление причины затруднения и постановка цели деятельности.
– Какое задание вы выполняли? (Сравнивали и ).
– Почему это задание вызвало затруднение? (Мы не умеем сравнивать доли).
– Значит, какую цель мы должны поставить на уроке? (Научиться сравнивать доли).
– Кто назовет тему урока? (Сравнение долей).
4. Построение проекта выхода из затруднения .
– У вас на столах лист бумаги и ножницы. Как вы думаете для чего? (Для работы).
– Правильно. Представьте, что это наш арбуз. Как нам найти ? (Согнуть лист пополам).
– А ? (Еще раз согнуть лист пополам).
– Закрасьте часть зеленым цветом, а — красным цветом и вырежьте их.
– Каким способом будете их сравнивать? (Наложением).
– К какому выводу пришли?( > ).
– Какое правило можно вывести для сравнения долей? (Чем больше долей, тем меньше каждая доля. Чем меньше долей, тем больше каждая доля).
– Сравним наше правило с правилом учебника на с.68. Оно у нас совпало? (Да).
– А сейчас я предлагаю вам поработать в группах и составить из заготовок эталон к нашему правилу. (1/м > 1/б).
– Вернемся к нашей задаче. Так кто же из детей прав? (Тот у кого > ).
– А теперь посмотрите на наш числовой отрезок. Скажите, а он мог нам как — либо помочь? (Да. Чем левее число на отрезке, тем оно меньше, чем правее, тем больше)
5. Физминутка ( Гимнастика для глаз)
6. Первичное закрепление изученного.
-Мы с вами сделали открытие, а теперь какая цель нашей работы? (Потренироваться сравнивать доли).
– Выполним с комментированием № 2 на с.68
– №3 с.68- на доске, № 4(а)- в тетрадях все вместе, № 4(б)- в парах.
№ 4(а). Расположи в порядке возрастания числа. Ответ: 1/15, 1/12, 1/10, 1/7, 1/5, 1/3.
№ 4(б). Расположи в порядке убывания числа: Ответ: 1/2, 1/3, 1/4, 1/8, 1/9, 1/16,1/25.
7. Самостоятельная работа с самопроверкой по эталону– Мы с вами потренировались сравнивать доли, а теперь цель нашей дальнейшей работы? (Проверить свои знания).
(Учащиеся выполняют самостоятельную работу по вариантам, по окончании работы сравнивают свою работу по эталону).
1/7 и 1/19 (>), 1/100 и 1/23 (<),
1/15 и 1/3 (<), 1/39 и 1/60(>),
и 1/20 (>),
и 1/10 (>),
1/а и 1/с, где а > с (<)
1/б и 1/ д, где б>д (<)
– Выполнили работу? Что будем делать дальше? (Проверять работу). Для чего нужно проверять свою работу? ( Чтобы убедиться правильно мы ее выполнили или допустили ошибки).
– Проверьте себя по эталону для самопроверки и зафиксируйте результат проверки при помощи знаков “+” или “?”
– Кто допустил ошибки при выполнении задания? (…). В чем причина?
– Что нам поможет исправить ошибки? (Эталон)
– Исправьте их. Поднимите руки, у кого все верно.
– Вы молодцы! Поставьте себе “+”.
8. Включение в систему знаний и повторение изученного.
– Мы с вами хорошо потрудились над новым материалом, и я предлагаю вам вспомнить материал прошлых уроков и выполнить на повторение № 14 на с.69.
Вычислите:
9. Рефлексия учебной деятельности.
– Какую цель мы поставили вначале урока? (Научиться сравнивать доли).
– Достигли мы ее? (Да).
– Какое правило мы получили? (Чем меньше долей, тем больше каждая доля).
– Что вам помогло при выполнении с.р.? (Эталон).
– Кому на уроке было трудно? Вы преодолели свою трудность?
– Попробуйте оценить свою работу? Работу класса?
— Мне бы хотелось узнать, с каким настроением вы уходите с урока. У вас на партах лежат разноцветные круги. Прикрепите их под табличками.
Я работал на уроке с желанием.Мне было интересно.
Я хорошо понял тему урока.
Я работал на уроке с желанием, но чувствовал себя не очень уверенно.
Я не до конца понял тему урока.
Я работал на уроке без желания, боялся отвечать и выполнять работу.
Я не понял тему урока.
— Спасибо за урок.
infourok.ru

